POPOLAZIONE E CAMPIONI
|
|
|
- Demetrio Maggi
- 5 anni fa
- Visualizzazioni
Transcript
1 p. 1/2 POPOLAZIONE E CAMPIONI POPOLAZIONE insieme di tutti quegli elementi che hanno almeno una caratteristica comune (persone, oggetti,misure, osservazioni). Consideriamo il caso di caratteristiche associate a grandezze misurabili.
2 p. 1/2 POPOLAZIONE E CAMPIONI POPOLAZIONE insieme di tutti quegli elementi che hanno almeno una caratteristica comune (persone, oggetti,misure, osservazioni). Consideriamo il caso di caratteristiche associate a grandezze misurabili. CAMPIONE sottoinsieme finito di elementi estratti a caso dalla popolazione.
3 p. 1/2 POPOLAZIONE E CAMPIONI POPOLAZIONE insieme di tutti quegli elementi che hanno almeno una caratteristica comune (persone, oggetti,misure, osservazioni). Consideriamo il caso di caratteristiche associate a grandezze misurabili. CAMPIONE sottoinsieme finito di elementi estratti a caso dalla popolazione. VARIABILE CASUALE X: funzione che associa in modo univoco ad ogni elemento del campione un numero reale.
4 POPOLAZIONE E CAMPIONI p. 2/2
5 p. 3/2 VARIABILI CASUALI variabile casuale o aleatoria: grandezza che può assumere nel corso di una prova un valore sconosciuto a priori. Legata al verificarsi di un evento casuale.
6 p. 3/2 VARIABILI CASUALI variabile casuale o aleatoria: grandezza che può assumere nel corso di una prova un valore sconosciuto a priori. Legata al verificarsi di un evento casuale. Funzione X che associa ad ogni elemento dello spazio dei risultati (popolazione) S = {E 1, E 2, } uno e un solo numero reale: X(E i ) = x i
7 p. 3/2 VARIABILI CASUALI variabile casuale o aleatoria: grandezza che può assumere nel corso di una prova un valore sconosciuto a priori. Legata al verificarsi di un evento casuale. Funzione X che associa ad ogni elemento dello spazio dei risultati (popolazione) S = {E 1, E 2, } uno e un solo numero reale: X(E i ) = x i variabile casuale discreta: assume valori entro un insieme finito o numerabile (corrispondenza univoca con i numeri naturali)
8 VARIABILI CASUALI variabile casuale o aleatoria: grandezza che può assumere nel corso di una prova un valore sconosciuto a priori. Legata al verificarsi di un evento casuale. Funzione X che associa ad ogni elemento dello spazio dei risultati (popolazione) S = {E 1, E 2, } uno e un solo numero reale: X(E i ) = x i variabile casuale discreta: assume valori entro un insieme finito o numerabile (corrispondenza univoca con i numeri naturali) variabile casuale continua: assume valori entro un insieme non numerabile (corrispondenza univoca con i numeri reali). p. 3/2
9 p. 4/2 VARIABILI CASUALI MISURE Un insieme finito di operazioni di misura può essere pensato come un campione, cioè un particolare sottoinsieme formato da elementi estratti a caso dall insieme di tutte le infinite possibili operazioni di misura (popolazione) che potrebbero essere effettuate sulla stessa grandezza fisica, eseguite col medesimo strumento e sfruttando le medesime procedure.
10 p. 4/2 VARIABILI CASUALI MISURE Un insieme finito di operazioni di misura può essere pensato come un campione, cioè un particolare sottoinsieme formato da elementi estratti a caso dall insieme di tutte le infinite possibili operazioni di misura (popolazione) che potrebbero essere effettuate sulla stessa grandezza fisica, eseguite col medesimo strumento e sfruttando le medesime procedure. Il risultato numerico di una misura affetta da errori casuali è una variabile casuale.
11 p. 5/2 VARIABILI CASUALI DISCRETE Hp: Ogni evento E i abbia una probabilità p i di verificarsi
12 p. 5/2 VARIABILI CASUALI DISCRETE Hp: Ogni evento E i abbia una probabilità p i di verificarsi Gli elementi di S = {E 1,E 2, } sono incompatibili e definiscano l intero spazio dei risultati i=1 p i = 1 (probabilità totale).
13 p. 5/2 VARIABILI CASUALI DISCRETE Hp: Ogni evento E i abbia una probabilità p i di verificarsi Gli elementi di S = {E 1,E 2, } sono incompatibili e definiscano l intero spazio dei risultati i=1 p i = 1 (probabilità totale). Analogia con il caso di una serie di N misure ripetute. Infatti, i risultati possono essere raggruppati in M classi di frequenza relativa f i = n i /N tali che M i=1 f i = 1 e M i=1 n i = N.
14 p. 5/2 VARIABILI CASUALI DISCRETE Hp: Ogni evento E i abbia una probabilità p i di verificarsi Gli elementi di S = {E 1,E 2, } sono incompatibili e definiscano l intero spazio dei risultati i=1 p i = 1 (probabilità totale). Analogia con il caso di una serie di N misure ripetute. Infatti, i risultati possono essere raggruppati in M classi di frequenza relativa f i = n i /N tali che M i=1 f i = 1 e M i=1 n i = N. Dal teorema di Bernoulli sappiamo che se N allora f p, per cui ritroviamo la relazione precedente.
15 VARIABILI CASUALI DISCRETE Hp: Ogni evento E i abbia una probabilità p i di verificarsi Gli elementi di S = {E 1,E 2, } sono incompatibili e definiscano l intero spazio dei risultati i=1 p i = 1 (probabilità totale). Analogia con il caso di una serie di N misure ripetute. Infatti, i risultati possono essere raggruppati in M classi di frequenza relativa f i = n i /N tali che M i=1 f i = 1 e M i=1 n i = N. Dal teorema di Bernoulli sappiamo che se N allora f p, per cui ritroviamo la relazione precedente. Un campione di misure ripetute in identiche condizioni della stessa grandezza corrisponde ad eventi incompatibili. Se N è molto grande, vale la condizione di normalizzazione delle frequenze relative. p. 5/2
16 p. 6/2 DISTRIBUZIONI DI PROBABILITÀ Distribuzione di probabilità P(X) di una variabile casuale X: relazione che stabilisce una corrispondenza univoca tra i valori di tale variabile e la loro probabilità.
17 p. 6/2 DISTRIBUZIONI DI PROBABILITÀ Distribuzione di probabilità P(X) di una variabile casuale X: relazione che stabilisce una corrispondenza univoca tra i valori di tale variabile e la loro probabilità.
18 p. 7/2 DISTRIBUZIONI DI PROBABILITÀ Prova o esperimento: lancio di un dado
19 p. 7/2 DISTRIBUZIONI DI PROBABILITÀ Prova o esperimento: lancio di un dado Variabile casuale: numero uscito X = {1, 2, 3, 4, 5, 6}
20 p. 7/2 DISTRIBUZIONI DI PROBABILITÀ Prova o esperimento: lancio di un dado Variabile casuale: numero uscito X = {1, 2, 3, 4, 5, 6} Distribuzione di probabilità: P(X) = {1/6, 1/6, 1/6, 1/6, 1/6, 1/6}
21 p. 8/2 DISTRIBUZIONI DI PROBABILITÀ Prova o esperimento: lancio di 2 dadi
22 p. 8/2 DISTRIBUZIONI DI PROBABILITÀ Prova o esperimento: lancio di 2 dadi Variabile casuale: somma dei punteggi X = 2, 3, 4, 12 undici elementi X i = i + 1; i = 1, 2, 3,...11
23 p. 8/2 DISTRIBUZIONI DI PROBABILITÀ Prova o esperimento: lancio di 2 dadi Variabile casuale: somma dei punteggi X = 2, 3, 4, 12 undici elementi X i = i + 1; i = 1, 2, 3,...11 Il numero di possibili coppie è 6 2. Dobbiamo considerare le combinazioni che corrispondono alla stessa somma dei punteggi, e.g. 4 = = = 3 + 1, 3 eventi incompatibili (probabilità totale).
24 p. 8/2 DISTRIBUZIONI DI PROBABILITÀ Prova o esperimento: lancio di 2 dadi Variabile casuale: somma dei punteggi X = 2, 3, 4, 12 undici elementi X i = i + 1; i = 1, 2, 3,...11 Il numero di possibili coppie è 6 2. Dobbiamo considerare le combinazioni che corrispondono alla stessa somma dei punteggi, e.g. 4 = = = 3 + 1, 3 eventi incompatibili (probabilità totale). Si noti che nel lancio di due dadi, l uscita di due numeri corrisponde a 2 eventi compatibili indipendenti (probabilità composta).
25 p. 8/2 DISTRIBUZIONI DI PROBABILITÀ Prova o esperimento: lancio di 2 dadi Variabile casuale: somma dei punteggi X = 2, 3, 4, 12 undici elementi X i = i + 1; i = 1, 2, 3,...11 Il numero di possibili coppie è 6 2. Dobbiamo considerare le combinazioni che corrispondono alla stessa somma dei punteggi, e.g. 4 = = = 3 + 1, 3 eventi incompatibili (probabilità totale). Si noti che nel lancio di due dadi, l uscita di due numeri corrisponde a 2 eventi compatibili indipendenti (probabilità composta). Quindi P(4) = P(1, 3) + P(2, 2) + P(3, 1) = 1/6 1/6 + 1/6 1/6 + 1/6 1/6 = 3/36
26 p. 9/2 DISTRIBUZIONI DI PROBABILITÀ La distribuzione di probabilità risultante è:
27 DISTRIBUZIONI DI PROBABILITÀ p. 10/2
28 DISTRIBUZIONI DI PROBABILITÀ p. 11/2
29 p. 12/2 UNZIONE DI DISTRIBUZIONE CUMULATIVA La funzione di distribuzione cumulativa associa ad ogni valore x della variabile casuale X la somma delle probabilità che la stessa assuma valori x. F(x) = P(X, x) = x i x p(x i )
30 p. 12/2 UNZIONE DI DISTRIBUZIONE CUMULATIVA La funzione di distribuzione cumulativa associa ad ogni valore x della variabile casuale X la somma delle probabilità che la stessa assuma valori x. F(x) = P(X, x) = x i x p(x i ) Nel caso del lancio di un dado si avra
31 p. 12/2 UNZIONE DI DISTRIBUZIONE CUMULATIVA La funzione di distribuzione cumulativa associa ad ogni valore x della variabile casuale X la somma delle probabilità che la stessa assuma valori x. F(x) = P(X, x) = x i x p(x i ) Nel caso del lancio di un dado si avra Nel caso di variabili discrete è rappresentata da una funzione a gradini, non decrescente, che raggiunge il massimo a 1.
32 p. 13/2 VALORE DI ASPETTAZIONE Il valore di aspettazione o speranza matematica di una variabile casuale discreta X è E(x) = i p ix i
33 p. 13/2 VALORE DI ASPETTAZIONE Il valore di aspettazione o speranza matematica di una variabile casuale discreta X è E(x) = i p ix i Terminologia inglese: expected value
34 p. 13/2 VALORE DI ASPETTAZIONE Il valore di aspettazione o speranza matematica di una variabile casuale discreta X è E(x) = i p ix i Terminologia inglese: expected value Il valore medio della variabile X su un campione finito di dimensione N, suddiviso in M gruppi è x = M i=1 f ix i Sappiamo che f i p i per N + (Th. di Bernoulli).
35 p. 13/2 VALORE DI ASPETTAZIONE Il valore di aspettazione o speranza matematica di una variabile casuale discreta X è E(x) = i p ix i Terminologia inglese: expected value Il valore medio della variabile X su un campione finito di dimensione N, suddiviso in M gruppi è x = M i=1 f ix i Sappiamo che f i p i per N + (Th. di Bernoulli). x E(x) per N : importante, abbiamo collegato la media aritmetica osservata alla distribuzione teorica!!!
36 p. 13/2 VALORE DI ASPETTAZIONE Il valore di aspettazione o speranza matematica di una variabile casuale discreta X è E(x) = i p ix i Terminologia inglese: expected value Il valore medio della variabile X su un campione finito di dimensione N, suddiviso in M gruppi è x = M i=1 f ix i Sappiamo che f i p i per N + (Th. di Bernoulli). x E(x) per N : importante, abbiamo collegato la media aritmetica osservata alla distribuzione teorica!!! E(x) può non esistere, la serie non converge; E(x) può non appartenere al dominio di X.
37 p. 14/2 LORE DI ASPETTAZIONE (caso discre Lancio del dado (uscita di una faccia) E(x) = 1/ / /6 6 = 21 6 = 3.5
38 p. 14/2 LORE DI ASPETTAZIONE (caso discre Lancio del dado (uscita di una faccia) E(x) = 1/ / /6 6 = 21 6 = 3.5 Lancio di 2 dadi (somma dei punteggi) E(x) = = 7
39 p. 15/2 INFORMAZIONI Prossime lezioni Giorno Ora Dove 17/02 14:30 P50 19/02 14:30 LABORATORIO (Via Loredan) 24/02 14:30 P50? da definirsi 26/02 14:30 Aula informatica (6 gruppi) 03/03 14:30 P50 05/03 14:30 Aula informatica (6 gruppi)
40 p. 15/2 INFORMAZIONI Prossime lezioni Giorno Ora Dove 17/02 14:30 P50 19/02 14:30 LABORATORIO (Via Loredan) 24/02 14:30 P50? da definirsi 26/02 14:30 Aula informatica (6 gruppi) 03/03 14:30 P50 05/03 14:30 Aula informatica (6 gruppi) Decidere la spartizione tra i 2 due turni per l aula inform.
41 p. 16/2 VALORE DI ASPETTAZIONE Il valore di aspettazione o speranza matematica di una variabile casuale discreta X è E(x) = i p ix i
42 p. 16/2 VALORE DI ASPETTAZIONE Il valore di aspettazione o speranza matematica di una variabile casuale discreta X è E(x) = i p ix i Terminologia inglese: expected value
43 p. 16/2 VALORE DI ASPETTAZIONE Il valore di aspettazione o speranza matematica di una variabile casuale discreta X è E(x) = i p ix i Terminologia inglese: expected value Il valore medio della variabile X su un campione finito di dimensione N, suddiviso in M gruppi è x = M i=1 f ix i Sappiamo che f i p i per N + (Th. di Bernoulli).
44 p. 16/2 VALORE DI ASPETTAZIONE Il valore di aspettazione o speranza matematica di una variabile casuale discreta X è E(x) = i p ix i Terminologia inglese: expected value Il valore medio della variabile X su un campione finito di dimensione N, suddiviso in M gruppi è x = M i=1 f ix i Sappiamo che f i p i per N + (Th. di Bernoulli). x E(x) per N : importante, abbiamo collegato la media aritmetica osservata alla distribuzione teorica!!!
45 p. 16/2 VALORE DI ASPETTAZIONE Il valore di aspettazione o speranza matematica di una variabile casuale discreta X è E(x) = i p ix i Terminologia inglese: expected value Il valore medio della variabile X su un campione finito di dimensione N, suddiviso in M gruppi è x = M i=1 f ix i Sappiamo che f i p i per N + (Th. di Bernoulli). x E(x) per N : importante, abbiamo collegato la media aritmetica osservata alla distribuzione teorica!!! E(x) può non esistere, la serie non converge; E(x) può non appartenere al dominio di X.
46 p. 17/2 VARIANZA DI UNA DISTRIBUZIONE DISCRETA Errore di una variabile casuale: x E(x)
47 p. 17/2 VARIANZA DI UNA DISTRIBUZIONE DISCRETA Errore di una variabile casuale: x E(x) Varianza: definita come il valore di aspettazione della variabile casuale [x E(x)] 2 V ar(x) = σ 2 x= E { [x E(x)] 2} = i p i[x i E(x)] 2
48 p. 17/2 VARIANZA DI UNA DISTRIBUZIONE DISCRETA Errore di una variabile casuale: x E(x) Varianza: definita come il valore di aspettazione della variabile casuale [x E(x)] 2 V ar(x) = σ 2 x= E { [x E(x)] 2} = i p i[x i E(x)] 2 Si dimostra che: σ 2 x = E(x 2 ) [E(x)] 2
49 p. 17/2 VARIANZA DI UNA DISTRIBUZIONE DISCRETA Errore di una variabile casuale: x E(x) Varianza: definita come il valore di aspettazione della variabile casuale [x E(x)] 2 V ar(x) = σ 2 x= E { [x E(x)] 2} = i p i[x i E(x)] 2 Si dimostra che: σ 2 x = E(x 2 ) [E(x)] 2 Deviazione standard o errore quadratico medio σ x : radice quadrata della varianza.
50 p. 18/2 OMBINAZIONI LINEARI: VALORE DI ASPETTAZION Sia f = ax + by + cz, con a, b, c coefficienti costanti
51 p. 18/2 OMBINAZIONI LINEARI: VALORE DI ASPETTAZION Sia f = ax + by + cz, con a, b, c coefficienti costanti Siano E(x), E(y), E(z), i valori di aspettazione
52 p. 18/2 OMBINAZIONI LINEARI: VALORE DI ASPETTAZION Sia f = ax + by + cz, con a, b, c coefficienti costanti Siano E(x), E(y), E(z), i valori di aspettazione Si dimostra che:
53 p. 18/2 OMBINAZIONI LINEARI: VALORE DI ASPETTAZION Sia f = ax + by + cz, con a, b, c coefficienti costanti Siano E(x), E(y), E(z), i valori di aspettazione Si dimostra che: E(f) = ae(x) + be(y) + ce(z)
54 p. 18/2 OMBINAZIONI LINEARI: VALORE DI ASPETTAZION Sia f = ax + by + cz, con a, b, c coefficienti costanti Siano E(x), E(y), E(z), i valori di aspettazione Si dimostra che: E(f) = ae(x) + be(y) + ce(z) La media aritmetica può essere vista come combinazione lineare delle N misure, con coefficienti tutti uguali a 1/N.
55 p. 18/2 OMBINAZIONI LINEARI: VALORE DI ASPETTAZION Sia f = ax + by + cz, con a, b, c coefficienti costanti Siano E(x), E(y), E(z), i valori di aspettazione Si dimostra che: E(f) = ae(x) + be(y) + ce(z) La media aritmetica può essere vista come combinazione lineare delle N misure, con coefficienti tutti uguali a 1/N. Applicando il teorema si ottiene E( x) = E(x)
56 p. 18/2 OMBINAZIONI LINEARI: VALORE DI ASPETTAZION Sia f = ax + by + cz, con a, b, c coefficienti costanti Siano E(x), E(y), E(z), i valori di aspettazione Si dimostra che: E(f) = ae(x) + be(y) + ce(z) La media aritmetica può essere vista come combinazione lineare delle N misure, con coefficienti tutti uguali a 1/N. Applicando il teorema si ottiene E( x) = E(x) Il valore di aspettazione della popolazione delle medie aritmetiche dei campioni di dimensione finita N coincide con il valore di aspettazione della popolazione stessa.
57 p. 19/2 COMBINAZIONI LINEARI: VARIANZA Hp: le variabili x,y, z siano statisticamente indipendenti, cioè corrispondenti ad eventi compatibili indipendenti.
58 p. 19/2 COMBINAZIONI LINEARI: VARIANZA Hp: le variabili x,y, z siano statisticamente indipendenti, cioè corrispondenti ad eventi compatibili indipendenti. Si dimostra che: σ f 2 = a 2 σ x 2 + b 2 σ y 2 + c 2 σ z 2 +
59 p. 19/2 COMBINAZIONI LINEARI: VARIANZA Hp: le variabili x,y, z siano statisticamente indipendenti, cioè corrispondenti ad eventi compatibili indipendenti. Si dimostra che: σ f 2 = a 2 σ x 2 + b 2 σ y 2 + c 2 σ z 2 + Una combinazione lineare, a coefficienti costanti, di due variabili casuali statisticamente indipendenti ha varianza uguale alla combinazione lineare delle rispettive varianze, con coefficienti pari ai quadrati dei coefficienti rispettivi.
60 p. 19/2 COMBINAZIONI LINEARI: VARIANZA Hp: le variabili x,y, z siano statisticamente indipendenti, cioè corrispondenti ad eventi compatibili indipendenti. Si dimostra che: σ f 2 = a 2 σ x 2 + b 2 σ y 2 + c 2 σ z 2 + Una combinazione lineare, a coefficienti costanti, di due variabili casuali statisticamente indipendenti ha varianza uguale alla combinazione lineare delle rispettive varianze, con coefficienti pari ai quadrati dei coefficienti rispettivi. Ritrovere questo risultato nell ambito della propagazione degli errori nelle misure effettuate con metodi indiretti.
61 p. 19/2 COMBINAZIONI LINEARI: VARIANZA Hp: le variabili x,y, z siano statisticamente indipendenti, cioè corrispondenti ad eventi compatibili indipendenti. Si dimostra che: σ f 2 = a 2 σ x 2 + b 2 σ y 2 + c 2 σ z 2 + Una combinazione lineare, a coefficienti costanti, di due variabili casuali statisticamente indipendenti ha varianza uguale alla combinazione lineare delle rispettive varianze, con coefficienti pari ai quadrati dei coefficienti rispettivi. Ritrovere questo risultato nell ambito della propagazione degli errori nelle misure effettuate con metodi indiretti. Due variabili casuali che differiscano per una quantità costante hanno la stessa varianza. t = x + cost. σ 2 t = σ 2 x (...gli errori sistematici non alterano la precisione dei dati...)
62 p. 20/2 L ERRORE QUADRATICO MEDIO DELLA MEDIA Variabile casuale: media aritmetica x = 1 N N i=1 x i: combinazione lineare delle N misure con coefficienti uguali a 1/N
63 p. 20/2 L ERRORE QUADRATICO MEDIO DELLA MEDIA Variabile casuale: media aritmetica x = 1 N N i=1 x i: combinazione lineare delle N misure con coefficienti uguali a 1/N Varianza σ x 2 = 1 N 2 N i=1 σ xi 2 = 1 N 2 Nσ x 2 σ x 2 = σ x 2 N
64 p. 20/2 L ERRORE QUADRATICO MEDIO DELLA MEDIA Variabile casuale: media aritmetica x = 1 N N i=1 x i: combinazione lineare delle N misure con coefficienti uguali a 1/N Varianza σ x 2 = 1 N 2 N i=1 σ xi 2 = 1 N 2 Nσ x 2 σ x 2 = σ x 2 IMPLICAZIONI: L errore quadratico medio della media di un campione N
65 p. 20/2 L ERRORE QUADRATICO MEDIO DELLA MEDIA Variabile casuale: media aritmetica x = 1 N N i=1 x i: combinazione lineare delle N misure con coefficienti uguali a 1/N Varianza σ x 2 = 1 N 2 N i=1 σ xi 2 = 1 N 2 Nσ x 2 σ x 2 = σ x 2 IMPLICAZIONI: L errore quadratico medio della media di un campione è minore dell analogo errore delle singole misure. N
66 p. 20/2 L ERRORE QUADRATICO MEDIO DELLA MEDIA Variabile casuale: media aritmetica x = 1 N N i=1 x i: combinazione lineare delle N misure con coefficienti uguali a 1/N Varianza σ x 2 = 1 N 2 N i=1 σ xi 2 = 1 N 2 Nσ x 2 σ x 2 = σ x 2 IMPLICAZIONI: L errore quadratico medio della media di un campione è minore dell analogo errore delle singole misure. tende a zero al crescere del numero di misure effettuato. N
67 p. 21/2 DISTRIBUZIONE UNIFORME DISCRETA La funzione di distribuzione di probabilità assume lo stesso valore per tutti i valori della variabile casuale: p(x) = p per ogni x = 1, n
68 p. 21/2 DISTRIBUZIONE UNIFORME DISCRETA La funzione di distribuzione di probabilità assume lo stesso valore per tutti i valori della variabile casuale: p(x) = p per ogni x = 1, n Dalla condizione di normalizzazione: p i = 1/n
69 p. 21/2 DISTRIBUZIONE UNIFORME DISCRETA La funzione di distribuzione di probabilità assume lo stesso valore per tutti i valori della variabile casuale: p(x) = p per ogni x = 1, n Dalla condizione di normalizzazione: p i = 1/n Valore si aspettazione E(x) = 1 1/n+2 1/n n 1/n = 1/n = 1 n (Si è usata la relazione nx i = i=1 n(n + 1) 2 n i = 1 n i=1 n(n + 1) 2 = n dalla teoria delle progressioni aritmetiche )
70 p. 21/2 DISTRIBUZIONE UNIFORME DISCRETA La funzione di distribuzione di probabilità assume lo stesso valore per tutti i valori della variabile casuale: p(x) = p per ogni x = 1, n Dalla condizione di normalizzazione: p i = 1/n Valore si aspettazione E(x) = 1 1/n+2 1/n n 1/n = 1/n = 1 n (Si è usata la relazione nx i = i=1 n(n + 1) Varianza: n ( n σ 2 i=1 = i2 i=1 i ) 2 = n n ( n + 1 2n + 1 n + 1 ) = n n i = 1 n i=1 n(n + 1) 2 = n dalla teoria delle progressioni aritmetiche ) (n + 1)(2n + 1) 6 (Si è usata la relazione P n i=1 i2 = n(n+1)(2n+1) 6 ) 4n + 2 3n 3 6 (n + 1)2 4 = = n2 1 12
71 p. 21/2 DISTRIBUZIONE UNIFORME DISCRETA La funzione di distribuzione di probabilità assume lo stesso valore per tutti i valori della variabile casuale: p(x) = p per ogni x = 1, n Dalla condizione di normalizzazione: p i = 1/n Valore si aspettazione E(x) = 1 1/n+2 1/n n 1/n = 1/n = 1 n (Si è usata la relazione nx i = i=1 n(n + 1) Varianza: n ( n σ 2 i=1 = i2 i=1 i ) 2 = n n ( n + 1 2n + 1 n + 1 ) = n n i = 1 n i=1 n(n + 1) 2 = n dalla teoria delle progressioni aritmetiche ) (n + 1)(2n + 1) 6 (Si è usata la relazione P n i=1 i2 = n(n+1)(2n+1) 6 ) 4n + 2 3n 3 6 (n + 1)2 4 = = n Il valore di aspettazione e la varianza del punteggio associato al lancio di un dado sono : E(x) = = 3.5 e σ 2 =
72 p. 22/2 ESERCIZI Data una serie di n misure {m i }, come cambiano media aritmetica e scarto quadratico medio se ogni misura è moltiplicata per 2: y i = 2 x i? è incrementata di 2: y i = 2 + x i?
73 p. 23/2 ESERCIZI Considera la seguente distribuzione di frequenza. Qual è la frequenza mancante nella posizione occupata dall asterisco? Classi Freq. ass. Freq. cumulata in % fino a % * 64.00% % % % più di % A)25 B)15 C)16 D)3
74 p. 24/2 ESERCIZI Data la seguente distribuzione di probabilità: x P(x) Quale delle seguenti affermazioni è vera? A)P(X > 3) = 0.51 B)P(X 3) = 0.65 C)P(2 X 5) = 0.33 D)P(X < 6) = 1
Capitolo 5. Variabili casuali discrete
 Capitolo 5 Variabili casuali discrete Come già anticipato nel paragrafo 3, nella teoria della probabilità, una variabile casuale (o variabile aleatoria o variabile stocastica o random variable) può essere
Capitolo 5 Variabili casuali discrete Come già anticipato nel paragrafo 3, nella teoria della probabilità, una variabile casuale (o variabile aleatoria o variabile stocastica o random variable) può essere
Variabili aleatorie. Variabili aleatorie e variabili statistiche
 Variabili aleatorie Variabili aleatorie e variabili statistiche Nelle prime lezioni, abbiamo visto il concetto di variabile statistica : Un oggetto o evento del mondo reale veniva associato a una certa
Variabili aleatorie Variabili aleatorie e variabili statistiche Nelle prime lezioni, abbiamo visto il concetto di variabile statistica : Un oggetto o evento del mondo reale veniva associato a una certa
LA DISTRIBUZIONE NORMALE o DI GAUSS
 p. 1/2 LA DISTRIBUZIONE NORMALE o DI GAUSS Osservando gli istogrammi delle misure e degli scarti, nel caso di osservazioni ripetute in identiche condizioni Gli istogrammi sono campanulari e simmetrici,
p. 1/2 LA DISTRIBUZIONE NORMALE o DI GAUSS Osservando gli istogrammi delle misure e degli scarti, nel caso di osservazioni ripetute in identiche condizioni Gli istogrammi sono campanulari e simmetrici,
Le variabili casuali o aleatorie
 Le variabili casuali o aleatorie Intuitivamente un numero casuale o aleatorio è un numero sul cui valore non siamo certi per carenza di informazioni - ad esempio la durata di un macchinario, il valore
Le variabili casuali o aleatorie Intuitivamente un numero casuale o aleatorio è un numero sul cui valore non siamo certi per carenza di informazioni - ad esempio la durata di un macchinario, il valore
Teorema del limite centrale TCL Questo importante teorema della statistica inferenziale si applica a qualsiasi variabile aleatoria che sia combinazion
 Teorema del limite centrale TCL Questo importante teorema della statistica inferenziale si applica a qualsiasi variabile aleatoria che sia combinazione lineare di N variabili aleatorie le cui funzioni
Teorema del limite centrale TCL Questo importante teorema della statistica inferenziale si applica a qualsiasi variabile aleatoria che sia combinazione lineare di N variabili aleatorie le cui funzioni
Principi di Statistica a.a
 Principi di Statistica a.a. 2014-2015 Dr. Luca Secondi 1. Introduzione al corso 1.01Variabili casuali Distribuzioni di probabilità 1 Corso di laurea in Biotecnologie Matematica e PRINCIPI DI STATISTICA
Principi di Statistica a.a. 2014-2015 Dr. Luca Secondi 1. Introduzione al corso 1.01Variabili casuali Distribuzioni di probabilità 1 Corso di laurea in Biotecnologie Matematica e PRINCIPI DI STATISTICA
Teorema del limite centrale TCL
 Teorema del limite centrale TCL Questo importante teorema della statistica inferenziale si applica a qualsiasi variabile aleatoria che sia combinazione lineare di N variabili aleatorie le cui funzioni
Teorema del limite centrale TCL Questo importante teorema della statistica inferenziale si applica a qualsiasi variabile aleatoria che sia combinazione lineare di N variabili aleatorie le cui funzioni
STIME STATISTICHE. Consideriamo il caso della misura di una grandezza fisica che sia affetta da errori casuali. p. 2/2
 p. 1/1 INFORMAZIONI Prossime lezioni Giorno Ora Dove 10/02 14:30 P50 11/02 14:30 Laboratorio (via Loredan) 17/02 14:30 P50 23/02 14:30 P50 25/02 14:30 Aula informatica (6-7 gruppi) 02/03 14:30 P50 04/03
p. 1/1 INFORMAZIONI Prossime lezioni Giorno Ora Dove 10/02 14:30 P50 11/02 14:30 Laboratorio (via Loredan) 17/02 14:30 P50 23/02 14:30 P50 25/02 14:30 Aula informatica (6-7 gruppi) 02/03 14:30 P50 04/03
Elaborazione statistica di dati
 Elaborazione statistica di dati 1 CONCETTI DI BASE DI STATISTICA ELEMENTARE 2 Taratura strumenti di misura IPOTESI: grandezza da misurare identica da misura a misura Per la presenza di errori casuali,
Elaborazione statistica di dati 1 CONCETTI DI BASE DI STATISTICA ELEMENTARE 2 Taratura strumenti di misura IPOTESI: grandezza da misurare identica da misura a misura Per la presenza di errori casuali,
VARIABILI CASUALI CONTINUE
 p. 1/1 VARIABILI CASUALI CONTINUE Una variabile casuale continua può assumere tutti gli infiniti valori appartenenti ad un intervallo di numeri reali. p. 1/1 VARIABILI CASUALI CONTINUE Una variabile casuale
p. 1/1 VARIABILI CASUALI CONTINUE Una variabile casuale continua può assumere tutti gli infiniti valori appartenenti ad un intervallo di numeri reali. p. 1/1 VARIABILI CASUALI CONTINUE Una variabile casuale
p. 1/2 STIME STATISTICHE Consideriamo il caso della misura di una grandezza fisica che sia affetta da errori casuali.
 p. 1/2 STIME STATISTICHE Consideriamo il caso della misura di una grandezza fisica che sia affetta da errori casuali. p. 1/2 STIME STATISTICHE Consideriamo il caso della misura di una grandezza fisica
p. 1/2 STIME STATISTICHE Consideriamo il caso della misura di una grandezza fisica che sia affetta da errori casuali. p. 1/2 STIME STATISTICHE Consideriamo il caso della misura di una grandezza fisica
Tecniche di sondaggio
 SMID a.a. 2005/2006 Corso di Statistica per la Ricerca Sperimentale Tecniche di sondaggio 24/1/2006 Nomenclatura Indicheremo con P una popolazione, con N la sua numerosità, con k la sua etichetta e con
SMID a.a. 2005/2006 Corso di Statistica per la Ricerca Sperimentale Tecniche di sondaggio 24/1/2006 Nomenclatura Indicheremo con P una popolazione, con N la sua numerosità, con k la sua etichetta e con
RICHIAMI DI CALCOLO DELLE PROBABILITÀ
 UNIVERSITA DEL SALENTO INGEGNERIA CIVILE RICHIAMI DI CALCOLO DELLE PROBABILITÀ ing. Marianovella LEONE INTRODUZIONE Per misurare la sicurezza di una struttura, ovvero la sua affidabilità, esistono due
UNIVERSITA DEL SALENTO INGEGNERIA CIVILE RICHIAMI DI CALCOLO DELLE PROBABILITÀ ing. Marianovella LEONE INTRODUZIONE Per misurare la sicurezza di una struttura, ovvero la sua affidabilità, esistono due
Modelli probabilistici variabili casuali
 Modelli probabilistici variabili casuali Le variabili casuali costituiscono il legame tra il calcolo della probabilità e gli strumenti di statistica descrittiva visti fino ad ora. Idea: pensiamo al ripetersi
Modelli probabilistici variabili casuali Le variabili casuali costituiscono il legame tra il calcolo della probabilità e gli strumenti di statistica descrittiva visti fino ad ora. Idea: pensiamo al ripetersi
DISTRIBUZIONI DI PROBABILITA (parte 1) 1 / 19
 DISTRIBUZIONI DI PROBABILITA (parte 1) 1 / 19 Variabili casuali (o aleatorie) 2 / 19 Disponendo di metodi corretti per raccogliere i dati e costruire i campioni data una popolazione, i valori numerici
DISTRIBUZIONI DI PROBABILITA (parte 1) 1 / 19 Variabili casuali (o aleatorie) 2 / 19 Disponendo di metodi corretti per raccogliere i dati e costruire i campioni data una popolazione, i valori numerici
APPUNTI DI STATISTICA INFERENZIALE. Avalle Fulvia, maggio 2014, ITSOS MARIE CURIE CLASSI 4A BIO e 4B BIO
 APPUNTI DI STATISTICA INFERENZIALE Avalle Fulvia, maggio 2014, ITSOS MARIE CURIE CLASSI 4A BIO e 4B BIO PREREQUISITI VARIABILE ALEATORIA (QUANTITATIVA): è una funzione che associa un numero reale ad ogni
APPUNTI DI STATISTICA INFERENZIALE Avalle Fulvia, maggio 2014, ITSOS MARIE CURIE CLASSI 4A BIO e 4B BIO PREREQUISITI VARIABILE ALEATORIA (QUANTITATIVA): è una funzione che associa un numero reale ad ogni
Variabili casuali. - di Massimo Cristallo -
 Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 16 e 27 maggio 2013 - di Massimo Cristallo - Variabili casuali
Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 16 e 27 maggio 2013 - di Massimo Cristallo - Variabili casuali
2. Introduzione alla probabilità
 . Introduzione alla probabilità Carla Seatzu, 8 Marzo 008 Definizioni preliminari: Prova: è un esperimento il cui esito è aleatorio Spazio degli eventi elementari: è l insieme Ω di tutti i possibili esiti
. Introduzione alla probabilità Carla Seatzu, 8 Marzo 008 Definizioni preliminari: Prova: è un esperimento il cui esito è aleatorio Spazio degli eventi elementari: è l insieme Ω di tutti i possibili esiti
Elaborazione statistica di dati
 Elaborazione statistica di dati CONCETTI DI BASE DI STATISTICA ELEMENTARE Taratura strumenti di misura IPOTESI: grandezza da misurare identica da misura a misura Collaudo sistemi di produzione IPOTESI:
Elaborazione statistica di dati CONCETTI DI BASE DI STATISTICA ELEMENTARE Taratura strumenti di misura IPOTESI: grandezza da misurare identica da misura a misura Collaudo sistemi di produzione IPOTESI:
Statistica ARGOMENTI. Calcolo combinatorio
 Statistica ARGOMENTI Calcolo combinatorio Probabilità Disposizioni semplici Disposizioni con ripetizione Permutazioni semplici Permutazioni con ripetizioni Combinazioni semplici Assiomi di probabilità
Statistica ARGOMENTI Calcolo combinatorio Probabilità Disposizioni semplici Disposizioni con ripetizione Permutazioni semplici Permutazioni con ripetizioni Combinazioni semplici Assiomi di probabilità
Modelli matematici di fenomeni aleatori Variabilità e casualità
 Modelli matematici di fenomeni aleatori Variabilità e casualità La casualità è alla base della scelta degli individui che compongono un campione ai fini di un indagine statistica. La casualità è alla base
Modelli matematici di fenomeni aleatori Variabilità e casualità La casualità è alla base della scelta degli individui che compongono un campione ai fini di un indagine statistica. La casualità è alla base
Corsi di Laurea in Scienze Biologiche Prova scritta di Informatica e Statistica Generale (A). 05/07/2006
 Corsi di Laurea in Scienze Biologiche Prova scritta di Informatica e Statistica Generale (A). 0/07/006 COGNOME NOME MATRICOLA.) Sia {x, x,..., x n } IR una popolazione statistica numerica relativa ad una
Corsi di Laurea in Scienze Biologiche Prova scritta di Informatica e Statistica Generale (A). 0/07/006 COGNOME NOME MATRICOLA.) Sia {x, x,..., x n } IR una popolazione statistica numerica relativa ad una
1 4 Esempio 2. Si determini la distribuzione di probabilità della variabile casuale X = punteggio ottenuto lanciando un dado. Si ha immediatamente:
 CAPITOLO TERZO VARIABILI CASUALI. Le variabili casuali e la loro distribuzione di probabilità In molte situazioni, dato uno spazio di probabilità S, si è interessati non tanto agli eventi elementari (o
CAPITOLO TERZO VARIABILI CASUALI. Le variabili casuali e la loro distribuzione di probabilità In molte situazioni, dato uno spazio di probabilità S, si è interessati non tanto agli eventi elementari (o
Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Teoria della probabilità A.A
 Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Teoria della probabilità A.A. 2004-05 Alberto Perotti DELEN-DAUIN Esperimento casuale Esperimento suscettibile di più
Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Teoria della probabilità A.A. 2004-05 Alberto Perotti DELEN-DAUIN Esperimento casuale Esperimento suscettibile di più
Statistica. Lezione : 17. Variabili casuali
 Corsi di Laurea: a.a. 2018-19 Diritto per le Imprese e le istituzioni Scienze Internazionali dello Sviluppo e della Cooperazione Statistica Variabili casuali Lezione : 17 Docente: Alessandra Durio 1 Contenuti
Corsi di Laurea: a.a. 2018-19 Diritto per le Imprese e le istituzioni Scienze Internazionali dello Sviluppo e della Cooperazione Statistica Variabili casuali Lezione : 17 Docente: Alessandra Durio 1 Contenuti
Sperimentazioni di Fisica I mod. A Statistica - Lezione 3
 Sperimentazioni di Fisica I mod. A Statistica - Lezione 3 A Garfagnini, M Mazzocco, C Sada Dipartimento di Fisica G. Galilei, Università di Padova AA 2014/2015 Elementi di Teoria della Probabilità L ineliminabile
Sperimentazioni di Fisica I mod. A Statistica - Lezione 3 A Garfagnini, M Mazzocco, C Sada Dipartimento di Fisica G. Galilei, Università di Padova AA 2014/2015 Elementi di Teoria della Probabilità L ineliminabile
Variabili aleatorie discrete. Giovanni M. Marchetti Statistica Capitolo 5 Corso di Laurea in Economia
 Variabili aleatorie discrete Giovanni M. Marchetti Statistica Capitolo 5 Corso di Laurea in Economia 2015-16 1 / 45 Variabili aleatorie Una variabile aleatoria è simile a una variabile statistica Una variabile
Variabili aleatorie discrete Giovanni M. Marchetti Statistica Capitolo 5 Corso di Laurea in Economia 2015-16 1 / 45 Variabili aleatorie Una variabile aleatoria è simile a una variabile statistica Una variabile
PROBABILITÀ SCHEDA N. 5 SOMMA E DIFFERENZA DI DUE VARIABILI ALEATORIE DISCRETE
 Matematica e statistica: dai dati ai modelli alle scelte www.dima.unige/pls_statistica Responsabili scientifici M.P. Rogantin e E. Sasso (Dipartimento di Matematica Università di Genova) PROBABILITÀ SCHEDA
Matematica e statistica: dai dati ai modelli alle scelte www.dima.unige/pls_statistica Responsabili scientifici M.P. Rogantin e E. Sasso (Dipartimento di Matematica Università di Genova) PROBABILITÀ SCHEDA
Statistica descrittiva I. La frequenza
 Statistica descrittiva I. La frequenza Supponiamo di ripetere n volte un esperimento che può dare esito 0 o 1, il numero di uni su n ripetizioni è detto frequenza di 1: f 1,n = #{esperimenti con esito
Statistica descrittiva I. La frequenza Supponiamo di ripetere n volte un esperimento che può dare esito 0 o 1, il numero di uni su n ripetizioni è detto frequenza di 1: f 1,n = #{esperimenti con esito
Matematica e Statistica per Scienze Ambientali
 per Scienze Ambientali Variabili aleatorie - Appunti 1 1 Dipartimento di Matematica Sapienza, Università di Roma Roma, Gennaio 2013 Variabili aleatorie Un numero aleatorio è un esempio di variabile aleatoria.
per Scienze Ambientali Variabili aleatorie - Appunti 1 1 Dipartimento di Matematica Sapienza, Università di Roma Roma, Gennaio 2013 Variabili aleatorie Un numero aleatorio è un esempio di variabile aleatoria.
Variabile casuale E 6 E 5 E 4. R S x1 E 2
 Variabile casuale Una Variabile Casuale X è una regola (funzione reale) che associa ad E (evento elementare di S) uno ed un solo numero reale. Notazione: X: variabile casuale : realizzazione di una variabile
Variabile casuale Una Variabile Casuale X è una regola (funzione reale) che associa ad E (evento elementare di S) uno ed un solo numero reale. Notazione: X: variabile casuale : realizzazione di una variabile
Capitolo 10. La media pesata Calcolo della media pesata
 Capitolo 0 La media pesata Supponiamo che una stessa grandezza sia stata misurata da osservatori differenti (es. velocità della luce) in laboratori con strumenti e metodi di misura differenti: Laboratorio
Capitolo 0 La media pesata Supponiamo che una stessa grandezza sia stata misurata da osservatori differenti (es. velocità della luce) in laboratori con strumenti e metodi di misura differenti: Laboratorio
Modelli di probabilità
 Modelli di probabilità Corso di STATISTICA Ordinario di, Università di Napoli Federico II Professore supplente, Università della Basilicata a.a. 0/0 Obiettivo dell unità didattica Definire i concetti di
Modelli di probabilità Corso di STATISTICA Ordinario di, Università di Napoli Federico II Professore supplente, Università della Basilicata a.a. 0/0 Obiettivo dell unità didattica Definire i concetti di
Ulteriori Conoscenze di Informatica e Statistica
 Ulteriori Conoscenze di Informatica e Statistica Carlo Meneghini Dip. di fisica via della Vasca Navale 84, st. 83 (I piano) tel.: 06 55 17 72 17 meneghini@fis.uniroma3.it Indici di forma Descrivono le
Ulteriori Conoscenze di Informatica e Statistica Carlo Meneghini Dip. di fisica via della Vasca Navale 84, st. 83 (I piano) tel.: 06 55 17 72 17 meneghini@fis.uniroma3.it Indici di forma Descrivono le
TECNICHE DI SIMULAZIONE
 TECNICHE DI SIMULAZIONE MODELLI STATISTICI, RICHIAMI Francesca Mazzia Dipartimento di Matematica Università di Bari a.a. 2004/2005 TECNICHE DI SIMULAZIONE p. 1 Modelli statistici nella simulazione Nel
TECNICHE DI SIMULAZIONE MODELLI STATISTICI, RICHIAMI Francesca Mazzia Dipartimento di Matematica Università di Bari a.a. 2004/2005 TECNICHE DI SIMULAZIONE p. 1 Modelli statistici nella simulazione Nel
Sperimentazioni di Fisica I mod. A Statistica - Lezione 2
 Sperimentazioni di Fisica I mod. A Statistica - Lezione 2 A. Garfagnini M. Mazzocco C. Sada Dipartimento di Fisica G. Galilei, Università di Padova AA 2014/2015 Elementi di Statistica Lezione 2: 1. Istogrammi
Sperimentazioni di Fisica I mod. A Statistica - Lezione 2 A. Garfagnini M. Mazzocco C. Sada Dipartimento di Fisica G. Galilei, Università di Padova AA 2014/2015 Elementi di Statistica Lezione 2: 1. Istogrammi
Variabili aleatorie. Variabili aleatorie
 Variabili aleatorie Distribuzione binomiale Si supponga che uno studente affronti un esame composto da domande chiuse. Una sola delle 5 alternative di risposta proposta per ciascuna domanda è vera Supponiamo
Variabili aleatorie Distribuzione binomiale Si supponga che uno studente affronti un esame composto da domande chiuse. Una sola delle 5 alternative di risposta proposta per ciascuna domanda è vera Supponiamo
1 Eventi. Operazioni tra eventi. Insiemi ed eventi. Insieme dei casi elementari. Definizione di probabilità.
 Quella che segue e la versione compatta delle slides usate a lezioni. NON sono appunti. Come testo di riferimento si può leggere Elementi di calcolo delle probabilità e statistica Rita Giuliano. Ed ETS
Quella che segue e la versione compatta delle slides usate a lezioni. NON sono appunti. Come testo di riferimento si può leggere Elementi di calcolo delle probabilità e statistica Rita Giuliano. Ed ETS
Esercizi di Probabilità e Statistica
 Esercizi di Probabilità e Statistica Samuel Rota Bulò 6 giugno 26 Statistica Esercizio Sia {X n } n una famiglia di v.a. di media µ e varianza σ 2. Verificare che X = n n X i σ 2 = n (X i µ) 2 S 2 = n
Esercizi di Probabilità e Statistica Samuel Rota Bulò 6 giugno 26 Statistica Esercizio Sia {X n } n una famiglia di v.a. di media µ e varianza σ 2. Verificare che X = n n X i σ 2 = n (X i µ) 2 S 2 = n
Esercitazioni di Statistica
 Esercitazioni di Statistica Stima Puntuale Prof. Livia De Giovanni statistica@dis.uniroma.it Esercizio In ciascuno dei casi seguenti determinare quale tra i due stimatori S e T per il parametro θ è distorto
Esercitazioni di Statistica Stima Puntuale Prof. Livia De Giovanni statistica@dis.uniroma.it Esercizio In ciascuno dei casi seguenti determinare quale tra i due stimatori S e T per il parametro θ è distorto
Probabilità e Statistica Esercizi
 Corso di PIANIFICAZIONE DEI TRASPORTI 1 ing. Antonio Comi Marzo 2006 Probabilità e Statistica Esercizi 1 Variabile aleatoria X(E): funzione che associa ad un evento E dello spazio delle prove un numero
Corso di PIANIFICAZIONE DEI TRASPORTI 1 ing. Antonio Comi Marzo 2006 Probabilità e Statistica Esercizi 1 Variabile aleatoria X(E): funzione che associa ad un evento E dello spazio delle prove un numero
UNIVERSITA DEGLI STUDI DI BRESCIA-FACOLTA DI MEDICINA E CHIRURGIA CORSO DI LAUREA IN INFERMIERISTICA SEDE DI DESENZANO dg STATISTICA MEDICA.
 Lezione 4 DISTRIBUZIONE DI FREQUENZA 1 DISTRIBUZIONE DI PROBABILITA Una variabile i cui differenti valori seguono una distribuzione di probabilità si chiama variabile aleatoria. Es:il numero di figli maschi
Lezione 4 DISTRIBUZIONE DI FREQUENZA 1 DISTRIBUZIONE DI PROBABILITA Una variabile i cui differenti valori seguono una distribuzione di probabilità si chiama variabile aleatoria. Es:il numero di figli maschi
! X (92) X n. P ( X n X ) =0 (94)
 Convergenza in robabilità Definizione 2 Data una successione X 1,X 2,...,X n,... di numeri aleatori e un numero aleatorio X diremo che X n tende in probabilità a X escriveremo X n! X (92) se fissati comunque
Convergenza in robabilità Definizione 2 Data una successione X 1,X 2,...,X n,... di numeri aleatori e un numero aleatorio X diremo che X n tende in probabilità a X escriveremo X n! X (92) se fissati comunque
Probabilita' mediante l'analisi combinatoria D n,k =Disposizioni di n oggetti a k a k (o di classe k)
 Probabilita' mediante l'analisi combinatoria D n,k =Disposizioni di n oggetti a k a k (o di classe k) Nel calcolo del numero di modalita' con cui si presenta un evento e' utile talvolta utilizzare le definizioni
Probabilita' mediante l'analisi combinatoria D n,k =Disposizioni di n oggetti a k a k (o di classe k) Nel calcolo del numero di modalita' con cui si presenta un evento e' utile talvolta utilizzare le definizioni
assuma valori in un determinato intervallo è data dall integrale della sua densità ( = )=
 VARIABILI ALEATORIE CONTINUE Esistono parecchi fenomeni reali per la cui descrizione le variabili aleatorie discrete non sono adatte. Per esempio è necessaria una variabile aleatoria continua ovvero una
VARIABILI ALEATORIE CONTINUE Esistono parecchi fenomeni reali per la cui descrizione le variabili aleatorie discrete non sono adatte. Per esempio è necessaria una variabile aleatoria continua ovvero una
Statistica inferenziale, Varese, 18 novembre 2009 Prima parte - Modalità B
 Statistica inferenziale, Varese, 18 novembre 2009 Prima parte - Modalità B Cognome Nome: Part time: Numero di matricola: Diurno: ISTRUZIONI: Il punteggio relativo alla prima parte dell esame viene calcolato
Statistica inferenziale, Varese, 18 novembre 2009 Prima parte - Modalità B Cognome Nome: Part time: Numero di matricola: Diurno: ISTRUZIONI: Il punteggio relativo alla prima parte dell esame viene calcolato
Alcune v.a. discrete notevoli
 Alcune v.a. discrete notevoli Variabile aleatoria Bernoulliana Il risultato X di un esperimento aleatorio può essere classificato nel modo che segue: successo oppure insuccesso. Indichiamo: Successo =
Alcune v.a. discrete notevoli Variabile aleatoria Bernoulliana Il risultato X di un esperimento aleatorio può essere classificato nel modo che segue: successo oppure insuccesso. Indichiamo: Successo =
MODELLI STATISTICI, RICHIAMI
 MODELLI STATISTICI, RICHIAMI Corso di Tecniche di Simulazione, a.a. 2005/2006 Francesca Mazzia Dipartimento di Matematica Università di Bari 11 Aprile 2006 Francesca Mazzia (Univ. Bari) MODELLI STATISTICI,
MODELLI STATISTICI, RICHIAMI Corso di Tecniche di Simulazione, a.a. 2005/2006 Francesca Mazzia Dipartimento di Matematica Università di Bari 11 Aprile 2006 Francesca Mazzia (Univ. Bari) MODELLI STATISTICI,
Calcolo delle Probabilità e Statistica Matematica previsioni 2003/04
 Calcolo delle Probabilità e Statistica Matematica previsioni 2003/04 LU 1/3 Esempi di vita reale : calcolo delle probabilità, statistica descrittiva e statistica inferenziale. Lancio dado/moneta: definizione
Calcolo delle Probabilità e Statistica Matematica previsioni 2003/04 LU 1/3 Esempi di vita reale : calcolo delle probabilità, statistica descrittiva e statistica inferenziale. Lancio dado/moneta: definizione
Elementi di Teoria della Probabilità
 Elementi di Teoria della Probabilità Alcune definizioni iniziali: Fenomeno casuale: fenomeno ripetibile (almeno in teoria) infinite volte che può manifestarsi in diverse modalità, imprevedibili singolarmente,
Elementi di Teoria della Probabilità Alcune definizioni iniziali: Fenomeno casuale: fenomeno ripetibile (almeno in teoria) infinite volte che può manifestarsi in diverse modalità, imprevedibili singolarmente,
UNIVERSITA DEGLI STUDI DI BRESCIA-FACOLTA DI MEDICINA E CHIRURGIA CORSO DI LAUREA IN INFERMIERISTICA SEDE DI DESENZANO dg STATISTICA MEDICA.
 Lezione 4 DISTRIBUZIONE DI FREQUENZA 1 DISTRIBUZIONE DI PROBABILITA Una variabile i cui differenti valori seguono una distribuzione di probabilità si chiama variabile aleatoria. Es:il numero di figli maschi
Lezione 4 DISTRIBUZIONE DI FREQUENZA 1 DISTRIBUZIONE DI PROBABILITA Una variabile i cui differenti valori seguono una distribuzione di probabilità si chiama variabile aleatoria. Es:il numero di figli maschi
Ulteriori Conoscenze di Informatica e Statistica
 ndici di forma Ulteriori Conoscenze di nformatica e Statistica Descrivono le asimmetrie della distribuzione Carlo Meneghini Dip. di fisica via della Vasca Navale 84, st. 83 ( piano) tel.: 06 55 17 72 17
ndici di forma Ulteriori Conoscenze di nformatica e Statistica Descrivono le asimmetrie della distribuzione Carlo Meneghini Dip. di fisica via della Vasca Navale 84, st. 83 ( piano) tel.: 06 55 17 72 17
I modelli probabilistici
 e I modelli probabilistici Finora abbiamo visto che esistono modelli probabilistici che possiamo utilizzare per prevedere gli esiti di esperimenti aleatori. Naturalmente la previsione è di tipo probabilistico:
e I modelli probabilistici Finora abbiamo visto che esistono modelli probabilistici che possiamo utilizzare per prevedere gli esiti di esperimenti aleatori. Naturalmente la previsione è di tipo probabilistico:
Indice. Prefazione. 4 Sintesi della distribuzione di un carattere La variabilità Introduzione La variabilità di una distribuzione 75
 00PrPag:I-XIV_prefazione_IAS 8-05-2008 17:56 Pagina V Prefazione XI 1 La rilevazione dei fenomeni statistici 1 1.1 Introduzione 1 1.2 Caratteri, unità statistiche e collettivo 1 1.3 Classificazione dei
00PrPag:I-XIV_prefazione_IAS 8-05-2008 17:56 Pagina V Prefazione XI 1 La rilevazione dei fenomeni statistici 1 1.1 Introduzione 1 1.2 Caratteri, unità statistiche e collettivo 1 1.3 Classificazione dei
Variabili casuali multidimensionali
 Capitolo 1 Variabili casuali multidimensionali Definizione 1.1 Le variabili casuali multidimensionali sono k-ple ordinate di variabili casuali unidimensionali definite sullo stesso spazio di probabilità.
Capitolo 1 Variabili casuali multidimensionali Definizione 1.1 Le variabili casuali multidimensionali sono k-ple ordinate di variabili casuali unidimensionali definite sullo stesso spazio di probabilità.
Propagazione delle varianze, conosciuta come propagazione degli errori.
 Propagazione delle varianze, conosciuta come propagazione degli errori. Siano x 1, x 2, x n n variabili casuali e poniamo,, ) = y ( ) Supponiamo inoltre nota la matrice delle covarianze delle x e vogliamo
Propagazione delle varianze, conosciuta come propagazione degli errori. Siano x 1, x 2, x n n variabili casuali e poniamo,, ) = y ( ) Supponiamo inoltre nota la matrice delle covarianze delle x e vogliamo
MATEMATICA FINANZIARIA RISCHI: RAPPRESENTAZIONE E GESTIONE (CENNI)
 Matematica Finanziaria, a.a. 2011/2012 p. 1/315 UNIVERSITA DEGLI STUDI DI PARMA FACOLTA DI ECONOMIA MATEMATICA FINANZIARIA RISCHI: RAPPRESENTAZIONE E GESTIONE (CENNI) ANNAMARIA OLIVIERI a.a. 2011/2012
Matematica Finanziaria, a.a. 2011/2012 p. 1/315 UNIVERSITA DEGLI STUDI DI PARMA FACOLTA DI ECONOMIA MATEMATICA FINANZIARIA RISCHI: RAPPRESENTAZIONE E GESTIONE (CENNI) ANNAMARIA OLIVIERI a.a. 2011/2012
Statistica. Capitolo 5. Variabili Aleatorie Discrete e Distribuzioni di Probabilità. Chap 5-1
 Statistica Capitolo 5 Variabili Aleatorie Discrete e Distribuzioni di Probabilità Statistics for Business and Economics, 6e 007 Pearson Education, Inc. Chap 5-1 Obiettivi del Capitolo Dopo aver completato
Statistica Capitolo 5 Variabili Aleatorie Discrete e Distribuzioni di Probabilità Statistics for Business and Economics, 6e 007 Pearson Education, Inc. Chap 5-1 Obiettivi del Capitolo Dopo aver completato
Calcolo delle Probabilità 2
 Prova d esame di Calcolo delle Probabilità 2 Maggio 2006 Sia X una variabile aleatoria distribuita secondo la densità seguente ke x 1 x < 0 f X (x) = 1/2 0 x 1. 1. Determinare il valore del parametro reale
Prova d esame di Calcolo delle Probabilità 2 Maggio 2006 Sia X una variabile aleatoria distribuita secondo la densità seguente ke x 1 x < 0 f X (x) = 1/2 0 x 1. 1. Determinare il valore del parametro reale
Indirizzo Giuridico Economico Aziendale
 LE VARIABILI CASUALI In molti fenomeni aleatori il risultato di un esperimento è una grandezza che assume valori in modo casuale. Pensa ad esempio al numero di auto che si presentano ad un casello autostradale
LE VARIABILI CASUALI In molti fenomeni aleatori il risultato di un esperimento è una grandezza che assume valori in modo casuale. Pensa ad esempio al numero di auto che si presentano ad un casello autostradale
Corso C Geomatica. Teoria degli errori. Massimiliano Cannata
 Corso C111.01 - Geomatica Teoria degli errori Rappresentazione di una misura di precisione ( x ± σ x ) u x = misura σ x = incertezza della misura u = unità di misura Il problema degli errori in topografia
Corso C111.01 - Geomatica Teoria degli errori Rappresentazione di una misura di precisione ( x ± σ x ) u x = misura σ x = incertezza della misura u = unità di misura Il problema degli errori in topografia
Teoria della probabilità Variabili casuali
 Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Teoria della probabilità Variabili casuali A.A. 2008-09 Alberto Perotti DELEN-DAUIN Variabile casuale Una variabile
Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Teoria della probabilità Variabili casuali A.A. 2008-09 Alberto Perotti DELEN-DAUIN Variabile casuale Una variabile
Note sulla probabilità
 Note sulla probabilità Maurizio Loreti Dipartimento di Fisica Università degli Studi di Padova Anno Accademico 2002 03 1 La distribuzione del χ 2 0.6 0.5 N=1 N=2 N=3 N=5 N=10 0.4 0.3 0.2 0.1 0 0 5 10 15
Note sulla probabilità Maurizio Loreti Dipartimento di Fisica Università degli Studi di Padova Anno Accademico 2002 03 1 La distribuzione del χ 2 0.6 0.5 N=1 N=2 N=3 N=5 N=10 0.4 0.3 0.2 0.1 0 0 5 10 15
Definizione della variabile c 2 Distribuzione della variabile c 2
 Definizione della variabile c Distribuzione della variabile c In queste definizioni ho N variabili indipendenti, nessun vincolo e quindi N coincide con i gradi di libertà In un sistema fisico dove il numero
Definizione della variabile c Distribuzione della variabile c In queste definizioni ho N variabili indipendenti, nessun vincolo e quindi N coincide con i gradi di libertà In un sistema fisico dove il numero
La media e la mediana sono indicatori di centralità, che indicano un centro dei dati.
 La media e la mediana sono indicatori di centralità, che indicano un centro dei dati. Un indicatore che sintetizza in un unico numero tutti i dati, nascondendo quindi la molteplicità dei dati. Per esempio,
La media e la mediana sono indicatori di centralità, che indicano un centro dei dati. Un indicatore che sintetizza in un unico numero tutti i dati, nascondendo quindi la molteplicità dei dati. Per esempio,
Distribuzioni di probabilità nel continuo
 Distribuzioni di probabilità nel continuo Prof.ssa Fabbri Francesca Classe 5C Variabili casuali continue Introduzione: Una Variabile Casuale o Aleatoria è una grandezza che, nel corso di un esperimento
Distribuzioni di probabilità nel continuo Prof.ssa Fabbri Francesca Classe 5C Variabili casuali continue Introduzione: Una Variabile Casuale o Aleatoria è una grandezza che, nel corso di un esperimento
STATISTICA APPLICATA Prof.ssa Julia Mortera. INTRODUZIONE al STATISTICA
 STATISTICA APPLICATA Prof.ssa Julia Mortera INTRODUZIONE al CAMPIONAMENTO e all INFERENZA STATISTICA Inferenza Statistica Nell inferenza statistica si usano le statistiche campionarie per fare previsioni
STATISTICA APPLICATA Prof.ssa Julia Mortera INTRODUZIONE al CAMPIONAMENTO e all INFERENZA STATISTICA Inferenza Statistica Nell inferenza statistica si usano le statistiche campionarie per fare previsioni
P ( X n X > ɛ) = 0. ovvero (se come distanza consideriamo quella euclidea)
 10.4 Convergenze 166 10.4.3. Convergenza in Probabilità. Definizione 10.2. Data una successione X 1, X 2,...,,... di vettori aleatori e un vettore aleatorio X aventi tutti la stessa dimensione k diremo
10.4 Convergenze 166 10.4.3. Convergenza in Probabilità. Definizione 10.2. Data una successione X 1, X 2,...,,... di vettori aleatori e un vettore aleatorio X aventi tutti la stessa dimensione k diremo
Campionamento. Una grandezza fisica e' distribuita secondo una certa PDF
 Campionamento Una grandezza fisica e' distribuita secondo una certa PDF La pdf e' caratterizzata da determinati parametri Non abbiamo una conoscenza diretta della pdf Possiamo determinare una distribuzione
Campionamento Una grandezza fisica e' distribuita secondo una certa PDF La pdf e' caratterizzata da determinati parametri Non abbiamo una conoscenza diretta della pdf Possiamo determinare una distribuzione
Metodi di Monte Carlo: un'applicazione
 Metodi di Monte Carlo: un'applicazione Metodi di Monte Carlo: definizione Brevi richiami sui concetti base utilizzati Variabile casuale Valore di aspettazione Varianza Densità di probabilità Funzione cumulativa
Metodi di Monte Carlo: un'applicazione Metodi di Monte Carlo: definizione Brevi richiami sui concetti base utilizzati Variabile casuale Valore di aspettazione Varianza Densità di probabilità Funzione cumulativa
Capitolo 5 Variabili aleatorie discrete notevoli Insegnamento: Statistica Applicata Corso di Laurea in "Scienze e Tecnologie Alimentari"
 Levine, Krehbiel, Berenson Statistica Capitolo 5 Variabili aleatorie discrete notevoli Insegnamento: Statistica Applicata Corso di Laurea in "Scienze e Tecnologie Alimentari" Unità Integrata Organizzativa
Levine, Krehbiel, Berenson Statistica Capitolo 5 Variabili aleatorie discrete notevoli Insegnamento: Statistica Applicata Corso di Laurea in "Scienze e Tecnologie Alimentari" Unità Integrata Organizzativa
LE DISTRIBUZIONI CAMPIONARIE
 LE DISTRIBUZIONI CAMPIONARIE Argomenti Principi e metodi dell inferenza statistica Metodi di campionamento Campioni casuali Le distribuzioni campionarie notevoli: La distribuzione della media campionaria
LE DISTRIBUZIONI CAMPIONARIE Argomenti Principi e metodi dell inferenza statistica Metodi di campionamento Campioni casuali Le distribuzioni campionarie notevoli: La distribuzione della media campionaria
Statistica Corso di laurea in Biotecnologie I esonero - 19 aprile 2010
 Statistica Corso di laurea in Biotecnologie I esonero - 9 aprile 00 Esercizio Determinare, a P X ; b PX < /; c il terzo quartile della distribuzione, nei casi ix N, ; iix variabile aleatoria continua con
Statistica Corso di laurea in Biotecnologie I esonero - 9 aprile 00 Esercizio Determinare, a P X ; b PX < /; c il terzo quartile della distribuzione, nei casi ix N, ; iix variabile aleatoria continua con
Lezione 12. Statistica. Alfonso Iodice D Enza Università degli studi di Cassino. Lezione 12. A. Iodice.
 discrete uniforme Bernoulli Poisson Statistica Alfonso Iodice D Enza iodicede@unicas.it Università degli studi di Cassino () Statistica 1 / 56 Outline discrete uniforme Bernoulli Poisson 1 2 discrete 3
discrete uniforme Bernoulli Poisson Statistica Alfonso Iodice D Enza iodicede@unicas.it Università degli studi di Cassino () Statistica 1 / 56 Outline discrete uniforme Bernoulli Poisson 1 2 discrete 3
Statistica. Lezione 4
 Università degli Studi del Piemonte Orientale Corso di Laurea in Infermieristica Corso integrato in Scienze della Prevenzione e dei Servizi sanitari Statistica Lezione 4 a.a 2011-2012 Dott.ssa Daniela
Università degli Studi del Piemonte Orientale Corso di Laurea in Infermieristica Corso integrato in Scienze della Prevenzione e dei Servizi sanitari Statistica Lezione 4 a.a 2011-2012 Dott.ssa Daniela
Materiale didattico per il corso di Statistica I Quinta esercitazione SOLUZIONI
 Materiale didattico per il corso di Statistica I Quinta esercitazione SOLUZIONI Claudia Furlan Anno Accademico 006-007 Ringrazio Carlo Gaetan, Nicola Sartori e Aldo Solari per il materiale, aggiunte e
Materiale didattico per il corso di Statistica I Quinta esercitazione SOLUZIONI Claudia Furlan Anno Accademico 006-007 Ringrazio Carlo Gaetan, Nicola Sartori e Aldo Solari per il materiale, aggiunte e
Il valore atteso di una v.a. (discreta)
 di una v.a. (discreta) Introduciamo un nuovo concetto. DEFINIZIONE DI VALORE ATTESO DI UNA V.A. DISCRETA Sia X : Ω R una v.a. discreta avente come immagine in R l insieme V. di X è il numero reale E(X)
di una v.a. (discreta) Introduciamo un nuovo concetto. DEFINIZIONE DI VALORE ATTESO DI UNA V.A. DISCRETA Sia X : Ω R una v.a. discreta avente come immagine in R l insieme V. di X è il numero reale E(X)
LE VARIABILI CASUALI A 1, A 2.,..., A k., p 2.,..., p k. generati da una specifica prova sono necessari ed incompatibili:
 LE VARIABILI CASUALI Introduzione Data prova, ad essa risultano associati i k eventi A, A,..., A k con le relative probabilità p, p,..., p k. I k eventi A i generati da una specifica prova sono necessari
LE VARIABILI CASUALI Introduzione Data prova, ad essa risultano associati i k eventi A, A,..., A k con le relative probabilità p, p,..., p k. I k eventi A i generati da una specifica prova sono necessari
VARIABILI CASUALI. Fino ad ora abbiamo definito:
 VARIABILI CASUALI Fino ad ora abbiamo definito: Lo SPAZIO CAMPIONARIO Ω : Come totalità dei possibili risultati di un esperimento Gli EVENTI : Come sottoinsiemi dello spazio campionario La FUNZIONE DI
VARIABILI CASUALI Fino ad ora abbiamo definito: Lo SPAZIO CAMPIONARIO Ω : Come totalità dei possibili risultati di un esperimento Gli EVENTI : Come sottoinsiemi dello spazio campionario La FUNZIONE DI
University of Messina, Italy
 ERRORI CASUALI ELL AALISI CHIMICA Errori casuali Gli errori casuali si incontrano tutte le volte che un sistema di misura viene usato al massimo della sua sensibilità. In queste circostanze i risultati
ERRORI CASUALI ELL AALISI CHIMICA Errori casuali Gli errori casuali si incontrano tutte le volte che un sistema di misura viene usato al massimo della sua sensibilità. In queste circostanze i risultati
Es.: una moneta viene lanciata 3 volte. X = n. di T nei primi 2 lanci Y = n. di T negli ultimi 2 lanci
 Es.: una moneta viene lanciata 3 volte. X = n. di T nei primi 2 lanci Y = n. di T negli ultimi 2 lanci X\Y 0 1 2 0 1/8 1/8 0 1/4 1 1/8 1/4 1/8 1/2 2 0 1/8 1/8 1/4 1/4 1/2 1/4 1 X e Y non sono indip. Se
Es.: una moneta viene lanciata 3 volte. X = n. di T nei primi 2 lanci Y = n. di T negli ultimi 2 lanci X\Y 0 1 2 0 1/8 1/8 0 1/4 1 1/8 1/4 1/8 1/2 2 0 1/8 1/8 1/4 1/4 1/2 1/4 1 X e Y non sono indip. Se
Le variabili casuali discrete
 Piano Lauree Scientifiche in Statistica AA 27/8 Azione C: Formazione Insegnanti Le variabili casuali discrete Giovanni De Luca giovanni.deluca@uniparthenope.it Sommario o Definizione e caratteristiche
Piano Lauree Scientifiche in Statistica AA 27/8 Azione C: Formazione Insegnanti Le variabili casuali discrete Giovanni De Luca giovanni.deluca@uniparthenope.it Sommario o Definizione e caratteristiche
Distribuzioni di probabilità
 Distribuzioni di probabilità Si sono diverse distribuzioni di probabilità: quelle di cui parleremo sono la distribuzione binomiale, quella di Poisson, quella uniforme, quella normale, quella del χ² e la
Distribuzioni di probabilità Si sono diverse distribuzioni di probabilità: quelle di cui parleremo sono la distribuzione binomiale, quella di Poisson, quella uniforme, quella normale, quella del χ² e la
Significato probabilistico di σ: su 100 misure, 68.3 hanno probabilità di cadere nell intervallo x σ, x +σ, 95.5 nell intervallo
 Significato probabilistico di σ: su 1 misure, 68.3 hanno probabilità di cadere nell intervallo x σ, x +σ, 95.5 nell intervallo x σ, x + σ e 99.7 nell intervallo x 3 σ, x + 3 Se si considerano campioni
Significato probabilistico di σ: su 1 misure, 68.3 hanno probabilità di cadere nell intervallo x σ, x +σ, 95.5 nell intervallo x σ, x + σ e 99.7 nell intervallo x 3 σ, x + 3 Se si considerano campioni
Probabilità classica. Distribuzioni e leggi di probabilità. Probabilità frequentista. Probabilità soggettiva
 Probabilità classica Distribuzioni e leggi di probabilità La probabilità di un evento casuale è il rapporto tra il numero dei casi favorevoli ed il numero dei casi possibili, purchè siano tutti equiprobabili.
Probabilità classica Distribuzioni e leggi di probabilità La probabilità di un evento casuale è il rapporto tra il numero dei casi favorevoli ed il numero dei casi possibili, purchè siano tutti equiprobabili.
La statistica descrittiva
 La statistica Davanti a un insieme di dati, li considera e 1 presenta i dati in forma sintetica, grafica e/o tabulare; 2 caratterizza alcuni aspetti in modo sintetico: indici di posizione (es. valore medio),
La statistica Davanti a un insieme di dati, li considera e 1 presenta i dati in forma sintetica, grafica e/o tabulare; 2 caratterizza alcuni aspetti in modo sintetico: indici di posizione (es. valore medio),
ES.2.2. Consideriamo un esperimento statistico definito da un insieme Ω di risultati possibili. Una partizione finita di Ω è una sequenza di K eventi
 ES22 1 Variabili aleatorie discrete Consideriamo un esperimento statistico definito da un insieme Ω di risultati possibili Una partizione finita di Ω è una sequenza di K eventi A 1, A 2 A k A K necessari
ES22 1 Variabili aleatorie discrete Consideriamo un esperimento statistico definito da un insieme Ω di risultati possibili Una partizione finita di Ω è una sequenza di K eventi A 1, A 2 A k A K necessari
CP110 Probabilità: Esame 4 luglio Testo e soluzione
 Dipartimento di Matematica, Roma Tre Pietro Caputo 2011-12, II semestre 4 luglio, 2012 CP110 Probabilità: Esame 4 luglio 2012 Testo e soluzione 1. (6 pts) Una scatola contiene 10 palline numerate da 1
Dipartimento di Matematica, Roma Tre Pietro Caputo 2011-12, II semestre 4 luglio, 2012 CP110 Probabilità: Esame 4 luglio 2012 Testo e soluzione 1. (6 pts) Una scatola contiene 10 palline numerate da 1
Esercizio 1. Durante un inchiesta su 500 studenti frequentanti i corsi di Algebra (A), Fisica (F) e Statistica è stato rilevato che:
 Esercizio 1 Durante un inchiesta su 500 studenti frequentanti i corsi di Algebra (A), Fisica (F) e Statistica è stato rilevato che: A 329 F 186 S 295 AS 217 AF 83 FS 63 AFS 53 Determinare la partizione
Esercizio 1 Durante un inchiesta su 500 studenti frequentanti i corsi di Algebra (A), Fisica (F) e Statistica è stato rilevato che: A 329 F 186 S 295 AS 217 AF 83 FS 63 AFS 53 Determinare la partizione
Problema Posto s = n 2 a) calcolare la somma s per n=30 b) determinare il più piccolo intero n tale che s>30000
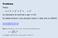 Problema Posto s = 1 2 + 2 2 + 3 2 + + n 2 a) calcolare la somma s per n=30 b) determinare il più piccolo intero n tale che s>30000 Somma quadrati (for next).xlsm Somma quadrati (do loop).xlsm Nota La
Problema Posto s = 1 2 + 2 2 + 3 2 + + n 2 a) calcolare la somma s per n=30 b) determinare il più piccolo intero n tale che s>30000 Somma quadrati (for next).xlsm Somma quadrati (do loop).xlsm Nota La
Dispensa di Statistica
 Dispensa di Statistica 1 parziale 2012/2013 Diagrammi... 2 Indici di posizione... 4 Media... 4 Moda... 5 Mediana... 5 Indici di dispersione... 7 Varianza... 7 Scarto Quadratico Medio (SQM)... 7 La disuguaglianza
Dispensa di Statistica 1 parziale 2012/2013 Diagrammi... 2 Indici di posizione... 4 Media... 4 Moda... 5 Mediana... 5 Indici di dispersione... 7 Varianza... 7 Scarto Quadratico Medio (SQM)... 7 La disuguaglianza
Analisi degli Errori di Misura. 08/04/2009 G.Sirri
 Analisi degli Errori di Misura 08/04/2009 G.Sirri 1 Misure di grandezze fisiche La misura di una grandezza fisica è descrivibile tramite tre elementi: valore più probabile; incertezza (o errore ) ossia
Analisi degli Errori di Misura 08/04/2009 G.Sirri 1 Misure di grandezze fisiche La misura di una grandezza fisica è descrivibile tramite tre elementi: valore più probabile; incertezza (o errore ) ossia
STATISTICA: esercizi svolti sulle VARIABILI CASUALI
 STATISTICA: esercizi svolti sulle VARIABILI CASUALI VARIABILI CASUALI 2 VARIABILI CASUALI. Variabili casuali generiche. Si supponga che un dado truccato, formato da sei facce contrassegnate dai numeri
STATISTICA: esercizi svolti sulle VARIABILI CASUALI VARIABILI CASUALI 2 VARIABILI CASUALI. Variabili casuali generiche. Si supponga che un dado truccato, formato da sei facce contrassegnate dai numeri
PROBABILITÀ SCHEDA N. 5 SOMMA E DIFFERENZA DI DUE VARIABILI ALEATORIE DISCRETE
 PROBABILITÀ SCHEDA N. 5 SOMMA E DIFFERENZA DI DUE VARIABILI ALEATORIE DISCRETE 1. Distribuzione congiunta Ci sono situazioni in cui un esperimento casuale non si può modellare con una sola variabile casuale,
PROBABILITÀ SCHEDA N. 5 SOMMA E DIFFERENZA DI DUE VARIABILI ALEATORIE DISCRETE 1. Distribuzione congiunta Ci sono situazioni in cui un esperimento casuale non si può modellare con una sola variabile casuale,
Computazione per l interazione naturale: fondamenti probabilistici (1)
 Computazione per l interazione naturale: fondamenti probabilistici (1) Corso di Interazione uomo-macchina II Prof. Giuseppe Boccignone Dipartimento di Scienze dell Informazione Università di Milano boccignone@dsi.unimi.it
Computazione per l interazione naturale: fondamenti probabilistici (1) Corso di Interazione uomo-macchina II Prof. Giuseppe Boccignone Dipartimento di Scienze dell Informazione Università di Milano boccignone@dsi.unimi.it
RICHIAMI DI STATISTISTICA E CALCOLO DELLE PROBABILITA
 RICHIAMI DI STATISTISTICA E CALCOLO DELLE PROBABILITA La Statistica è la disciplina che studia gli eventi non deterministici (o incerti) riguardo ai quali non si ha una completa conoscenza. Tali eventi
RICHIAMI DI STATISTISTICA E CALCOLO DELLE PROBABILITA La Statistica è la disciplina che studia gli eventi non deterministici (o incerti) riguardo ai quali non si ha una completa conoscenza. Tali eventi
LEZIONE 2.5. corso di statistica. Francesco Lagona Università Roma Tre. LEZIONE 2.5 p. 1/12
 LEZIONE 2.5 p. 1/12 LEZIONE 2.5 corso di statistica Francesco Lagona Università Roma Tre LEZIONE 2.5 p. 2/12 distribuzione doppia di due variabili aleatorie consideriamo la distribuzione doppia di due
LEZIONE 2.5 p. 1/12 LEZIONE 2.5 corso di statistica Francesco Lagona Università Roma Tre LEZIONE 2.5 p. 2/12 distribuzione doppia di due variabili aleatorie consideriamo la distribuzione doppia di due
PROBABILITÀ ELEMENTARE
 Prefazione alla seconda edizione XI Capitolo 1 PROBABILITÀ ELEMENTARE 1 Esperimenti casuali 1 Spazi dei campioni 1 Eventi 2 Il concetto di probabilità 3 Gli assiomi della probabilità 3 Alcuni importanti
Prefazione alla seconda edizione XI Capitolo 1 PROBABILITÀ ELEMENTARE 1 Esperimenti casuali 1 Spazi dei campioni 1 Eventi 2 Il concetto di probabilità 3 Gli assiomi della probabilità 3 Alcuni importanti
Prefazione Ringraziamenti dell'editore Il sito web dedicato al libro Test online: la piattaforma McGraw-Hill Education Guida alla lettura
 INDICE GENERALE Prefazione Ringraziamenti dell'editore Il sito web dedicato al libro Test online: la piattaforma McGraw-Hill Education Guida alla lettura XI XIV XV XVII XVIII 1 LA RILEVAZIONE DEI FENOMENI
INDICE GENERALE Prefazione Ringraziamenti dell'editore Il sito web dedicato al libro Test online: la piattaforma McGraw-Hill Education Guida alla lettura XI XIV XV XVII XVIII 1 LA RILEVAZIONE DEI FENOMENI
