Outline. 1 v.c. continue. 2 v.c. Normale. 3 v.c. Esponenziale. Lezione 13. A. Iodice. v.c. continue. v.c. Normale. v.c.
|
|
|
- Adamo Randazzo
- 5 anni fa
- Visualizzazioni
Transcript
1 Statistica Alfonso Iodice D Enza iodicede@unicas.it Università degli studi di Cassino () Statistica 1 / 48
2 Outline () Statistica 2 / 48
3 Variabili casuali continue Una variabile casuale X è continua se, per ogni valore x 0 è nota la probabilità che tale assuma valori in un intervallo (x 0, x 0 + dx). In particolare P (x 0 < X x 0 + dx) = f(x 0 )dx Perchè sia ben specificata la continua deve soddisfare i postulati di Kolmogorov, ovvero deve risultare che f(x) 0, e che + f(x)dx = 1 () Statistica 3 / 48
4 Variabili casuali continue La probabilità associata ad un intervallo di valori di una continua X è data dall area al di sotto della funzione di densità di probabilità, ovvero corrisponde all integrale della funzione di densità nell intervallo considerato () Statistica 4 / 48
5 Variabili casuali continue Se la variabile casuale continua, la probabilità che X assuma esattamente il valore x 0 nulla. Risulta infatti P (x 0 < X x 0 ) x0 x 0 f(x)dx = 0 Per calcolare la probabilità che la X assuma valori nell intervallo (x 1, x 2 ) P (x 1 < X x 2 ) x2 x 1 f(x)dx () Statistica 5 / 48
6 Funzione di ripartizione per La funzione di ripartizione F (x 0 ) di una continua calcolata nel punto x 0 data da F (x 0 ) = P (X x 0 ) = x0 f(x)dx Caratteristiche di F (x) La funzione di ripartizione non decrescente e tale che 0 F (x) 1 () Statistica 6 / 48
7 Variabili casuali continue generiche Una partita di football dura 60 minuti ed è suddivisa in 4 quarti da 15 minuti. Le sostituzioni dei giocatori sono illimitati. Si supponga che i minuti in cui un certo giocatore è impiegato seguano la seguente funzione di densità di probabilità Qual è la probabilità che il giocatore giochi terzo quarto in poi? Qual è la probabilità che il giocatore giochi i 20 minuti centrali della partita? Qual è la probabilità che il giocatore giochi i primi 40 minuti della partita? () Statistica 7 / 48
8 Variabili casuali continue generiche Qual è la probabilità che il giocatore giochi dal terzo quarto in poi? La probabilità cercata è P (X 30) P (X 30) = P (30 X 45) + P (45 X 60) = 15 ( ) + 15 (0.0167) = = 0.6 () Statistica 8 / 48
9 Variabili casuali continue generiche Qual è la probabilità che il giocatore giochi i 20 minuti centrali della partita? La probabilità cercata è P (20 X 40) P (20 X 40) = P (20 X 30) + P (30 X 40) = 10 (0.0167) + 10 ( ) = = 0.4 () Statistica 9 / 48
10 Variabili casuali continue generiche Qual è la probabilità che il giocatore giochi i primi 40 minuti della partita? La probabilità cercata è P (X 40) P (X 40) = P (0 X 15) + P (15 X 30) + P (30 X 40) = 15 (0.01) + 15 (0.0167) + 10 ( ) = = () Statistica 10 / 48
11 Variabili casuali continue generiche Alle 2 del pomeriggio uno studente comincia a studiare. Alle 6 del pomeriggio uscirà di casa, ma fino ad allora studierà. Tenendo conto delle varie ed eventuali distrazioni, prevede che l intensità del suo studio sarà caratterizzato dalla seguente funzione di densità di probabilità: Qual è l altezza della curva dopo 2 ore di studio? Qual è la probabilità che il tempo di studio superiore a 3 ore? Qual è la probabilità che il tempo di studio sia compreso tra 1 e 3 ore? () Statistica 11 / 48
12 Variabili casuali continue generiche Qual è l altezza della curva dopo 2 ore di studio? Per trovare l altezza in corrispondenza della seconda ora di studio basta tener conto di due cose: la formula per il calcolo dell area del triangolo A = b h ; l area del triangolo è A = 1. 2 A = b h 2 = 1 = 4 h 2 da cui h = A 2 b = 2/4 = 0.5 () Statistica 12 / 48
13 Variabili casuali continue generiche Qual è la probabilità che il tempo di studio superiore a 3 ore? L area del rettangolo dato da C + A è data dal prodotto tra la base b = 1 e l altezza h = 0.5 ottenuta in precedenza. Essendo Area(C + A) = = 0.5, essa coincide con Area(C + B) = 0.5 in quanto corrisponde alla metà dell area del triangolo (densità totale, uguale ad 1 per definizione). Ne consegue che i triangoli rettangoli A e B sono uguali (hanno uguale area, uguale base (b = 1) ). Inoltre la somma dei due cateti dei triangoli (in blu e verde) deve essere pari a 0.5: ciascuno di essi è dunque pari a Quindi Area(A) = Area(B) = = 0.125, da cui P (X > 3) = () Statistica 13 / 48
14 Variabili casuali continue generiche Qual è la probabilità che il tempo di studio sia compreso tra 1 e 3 ore? Sulla base dei risultati ottenuti in precedenza, e data la simmetria della funzione di densità considerata, P (X < 1) = P (X > 3). La probabilità cercata è dunque. P (1 < X < 3) = 1 [P (X < 1) + P (X > 3)] = 1 [ ] = 0.75 () Statistica 14 / 48
15 Variabile casuale Normale Una continua X una o Gaussiana, di parametri µ e σ 2, se definita la funzione di densità f(x 0 ) = 1 1 (x µ) 2 2πσ 2 e 2 σ 2 con < x < +, X N(µ, σ 2 ) E possibile definire il valore atteso e la varianza della Normale che corrispondono ai parametri della distribuzione, dal momento che E(X) = µ e V ar(x) = σ 2 () Statistica 15 / 48
16 La, µ = 10, σ = 5 () Statistica 16 / 48
17 La, µ σ < X < µ σ () Statistica 17 / 48
18 La, µ 2σ < X < µ 2σ () Statistica 18 / 48
19 La, µ 3σ < X < µ 3σ () Statistica 19 / 48
20 La, variazione al variare dei parametri () Statistica 20 / 48
21 La, variazione al variare dei parametri () Statistica 21 / 48
22 Variabile casuale Standardizzata Data la continua X distribuita come N(µ, σ 2 ), la standardizzazione di X, ovvero Z = X µ σ rappresenta la Normale Standardizzata Z si distribuisce come N(0, 1), con funzione di densità f(z) = 1 2π e z2 2 ; < z < + () Statistica 22 / 48
23 La standardizzata () Statistica 23 / 48
24 La In seguito ad uno studio interno di un istituto bancario è stato rilevato che i tempi di attesa per le operazioni di sportello si distribuiscono secondo una Normale con media pari a 20 e varianza pari a 9. Qual è la probabilità che il tempo di attesa... superi i 25 minuti; sia inferiore ai 16 minuti; sia compreso tra 18 e 21 minuti. () Statistica 24 / 48
25 La superi i 25 minuti; () Statistica 25 / 48
26 La superi i 25 minuti; la prima operazione da fare è standardizzare il problema z = = A questo punto è possibile utilizzare le tavole della distribuzione normale stardizzata per trovare la probabilità di interesse. () Statistica 26 / 48
27 La superi i 25 minuti; la prima operazione da fare è standardizzare il problema z = = A questo punto è possibile utilizzare le tavole della distribuzione normale stardizzata per trovare la probabilità di interesse. () Statistica 26 / 48
28 La superi i 25 minuti; la prima operazione da fare è standardizzare il problema z = = A questo punto è possibile utilizzare le tavole della distribuzione normale stardizzata per trovare la probabilità di interesse. () Statistica 26 / 48
29 La superi i 25 minuti; la prima operazione da fare è standardizzare il problema z = = A questo punto è possibile utilizzare le tavole della distribuzione normale stardizzata per trovare la probabilità di interesse. P (Z 1.66) = 1 P (Z 1.66) = = () Statistica 26 / 48
30 La sia inferiore a 16 minuti; () Statistica 27 / 48
31 La sia inferiore a 16 minuti; la prima operazione da fare è standardizzare il problema z = = A questo punto è possibile utilizzare le tavole della distribuzione normale stardizzata per trovare la probabilità di interesse. () Statistica 28 / 48
32 La sia inferiore a 16 minuti; la prima operazione da fare è standardizzare il problema z = = A questo punto è possibile utilizzare le tavole della distribuzione normale stardizzata per trovare la probabilità di interesse. () Statistica 28 / 48
33 La sia inferiore a 16 minuti; la prima operazione da fare è standardizzare il problema z = = A questo punto è possibile utilizzare le tavole della distribuzione normale stardizzata per trovare la probabilità di interesse. P (Z 1.33) = P (Z 1.33) = () Statistica 28 / 48
34 La sia compreso tra 18 e 21 minuti; () Statistica 29 / 48
35 La sia compreso tra 18 e 21 minuti; la prima operazione da fare è standardizzare il problema z 1 = = 0.66 e z 1 = = A questo punto è possibile utilizzare le tavole della distribuzione normale stardizzata per trovare la probabilità di interesse. () Statistica 30 / 48
36 La sia compreso tra 18 e 21 minuti; la prima operazione da fare è standardizzare il problema z 1 = = 0.66 e z 1 = = A questo punto è possibile utilizzare le tavole della distribuzione normale stardizzata per trovare la probabilità di interesse. () Statistica 30 / 48
37 La sia compreso tra 18 e 21 minuti; la prima operazione da fare è standardizzare il problema z 1 = = 0.66 e z 1 = = A questo punto è possibile utilizzare le tavole della distribuzione normale stardizzata per trovare la probabilità di interesse. () Statistica 30 / 48
38 La sia compreso tra 18 e 21 minuti; la prima operazione da fare è standardizzare il problema z 1 = = 0.66 e z 1 = = A questo punto è possibile utilizzare le tavole della distribuzione normale stardizzata per trovare la probabilità di interesse. P ( 0.66 Z 0.33) = P (Z 0.33) P (Z 0.66) = P (Z 0.33) [1 P (Z 0.66)] = (1.745) = 0.37 () Statistica 30 / 48
39 La Si consideri una variabile casuale X distribuita secondo una Normale con µ = 8 e σ = 3. indicare i quartili della distribuzione; indicare il 95 o percentile; () Statistica 31 / 48
40 La Primo quartile () Statistica 32 / 48
41 La Secondo quartile=mediana=media () Statistica 33 / 48
42 La Terzo quartile () Statistica 34 / 48
43 La indicare i quartili della distribuzione Con l aiuto delle tavole è necessario trovare i valori corrispondenti a Z 0.25 Z 0.5 Z 0.75 Essendo una distribuzione Normale, la mediana coincide con la media quindi Z 0.5 = 0.Utilizzando le tavole della distribuzione normale stardizzata per trovare i valori di Z restanti, Quindi... per la simmetria della curva Normale risulta essere inoltre Z 0.25 = Per trovare i valori corrispondenti della variabile casuale X si utilizza la formula inversa di standardizzazione () Statistica 35 / 48
44 La indicare i quartili della distribuzione Con l aiuto delle tavole è necessario trovare i valori corrispondenti a Z 0.25 Z 0.5 Z 0.75 Essendo una distribuzione Normale, la mediana coincide con la media quindi Z 0.5 = 0.Utilizzando le tavole della distribuzione normale stardizzata per trovare i valori di Z restanti, () Statistica 35 / 48
45 La Quindi... indicare i quartili della distribuzione Con l aiuto delle tavole è necessario trovare i valori corrispondenti a Z 0.25 Z 0.5 Z 0.75 Essendo una distribuzione Normale, la mediana coincide con la media quindi Z 0.5 = 0.Utilizzando le tavole della distribuzione normale stardizzata per trovare i valori di Z restanti, P (Z Z 0.75 ) = 0.75 da cui Z 0.75 = = per la simmetria della curva Normale risulta essere inoltre Z 0.25 = Per trovare i valori corrispondenti della variabile casuale X si utilizza la formula inversa di standardizzazione X 0.5 = 8 X 0.25 = Z 0.25 σ + µ = = X 0.75 = Z 0.75 σ + µ = = () Statistica 35 / 48
46 La indicare il 95 o percentile () Statistica 36 / 48
47 La indicare il 95 o percentile Con l aiuto delle tavole è necessario trovare il valore corrispondente a 0.95 Ricorrendo alle tavole... () Statistica 37 / 48
48 La Quindi... indicare il 95 o percentile Con l aiuto delle tavole è necessario trovare il valore corrispondente a 0.95 Z 0.95 = = Per ottenere il valore della variabile X X 0.95 = Z 0.95 σ + µ = = () Statistica 37 / 48
49 Approssimazione della Binomiale alla Normale Sia X una variabile casuale distribuita secondo una Binomiale di parametri n = 25 e p = 0.6. E possibile approssimare X con una continua Y N(µ, σ 2 ) dove µ = n p = = 15 σ 2 = n p (1 p) = = 6 σ = 6 = 2.45 Si supponga di essere interessati a P (X 13). calcolo Normale Per utilizzare l approssimazione normale è necessario standardizzare il problema calcolo Binomiale Z = X µ Utilizzando il calcolo Binomiale si ha σ = = 0.82 dunque, 2.45 P (X 13) P (Y 13) = P (Z 0.82) = ( ) 25 P (X 13) = 0.6 x x = x=0 x Effettuando una correzione di continuità pari a 0.5 = X µ Z = σ = = P (X 13) P (Y 13.5) = P (Z 0.61) = Evidentemente rappresenta un approssimazione migliore di rispetto a () Statistica 38 / 48
50 Approssimazione della Binomiale alla Normale Probabilità calcolate con p.m.f. Binomiale e con al c.d.f. Normale: l area in blue rappresenta la probabilità che si perderebbe approssimando senza correzione della continuità: in particolare l area vale =0.061 () Statistica 39 / 48
51 Approssimazione della Binomiale alla Normale Si consideri l esperimento consistente nel lancio di una moneta 120 volte. Trovare la probabilità che esca testa tra il 40% e il 60% dei lanci; più dei 5 del totale dei lanci. 8 () Statistica 40 / 48
52 Approssimazione della Binomiale alla Normale tra il 40% e il 60% dei lanci; () Statistica 41 / 48
53 Approssimazione della Binomiale alla Normale tra il 40% e il 60% dei lanci; È possibile determinare tale probabilità in due modi diversi. Il primo modo consiste nell utilizzare l approssimazione della binomiale alla normale. La numero di teste in 120 lanci si distribuisce come una binomiale di parametri (n = 120, p = 1 2 ). Il numero di successi corrispondenti al 40% del totale di 120 prove è 48, mentre il 60% corrisponde a 72. correzione della continuità La numero di teste è discreta,anche se approssimata da una continua. Si è interessati alla probabilità che essa assuma valori compresi nell interallo [47.5, 72.5] al fine di includere nel calcolo gli estremi 48 e 72. I parametri della normale cui si approssima la binomiale sono µ = np = = 60 e σ = np(1 p) = = Standardizzando i valori z 1 = = 2.28 e z 2 = = 2.28 Dalla simmetria della normale, segue che P ( 2.28 <= X <= 2.28) = 2 P (0 <= X <= 2.28) = = () Statistica 42 / 48
54 Approssimazione della Binomiale alla Normale Il secondo metodo consiste nel ricorrere alla distribuzione delle proporzioni p(1 p) campionarie, la cui media è data da µ p = p e σ p = N. Rispetto ai dati del problema µ p = p = 0.5 e σ p = = Standardizzando il problema rispetto ai parametri della distribuzione campionaria z 1 = = 2.19 e z = = 2.19 La probabilità corrispondente è P ( 2.19 <= X <= 2.19) = 2 P (0 <= X <= 2.19) = = correzione di continuità Il risultato non coincide con quanto ottenuto utilizzando l approssimazione della binomiale alla normale perchè la proporzione è una variabile discreta. Per tenere conto di questo bisogna sottrarre (1/2N) = 1/(2 120) = a 0.4 ed aggiungere la stessa quantità a 0.6. Pertanto gli estremi dell intervallo di valori standardizzati è z 1 = = 2.28 e z 2 = Che porta alla coincidenza tra i risultati nei due metodi = 2.28 () Statistica 43 / 48
55 Approssimazione della Binomiale alla Normale più di dei 5 8 del totale dei lanci. () Statistica 44 / 48
56 Approssimazione della Binomiale alla Normale più di dei 5 del totale dei lanci. 8 La proporzione corrispondente a 5 = Standardizzando il problema 8 tenendo conto del fatto che la proporzione è una variabile discreta si ottiene z = = 2.65 La probabilità corrispondente è P (z >= 2.65) = 1 P (z < 2.65)= =0.004 () Statistica 45 / 48
57 Variabile Casuale La Variabile Casuale (Negativa) modellizza il tempo di attesa prima del verificarsi di un determinato evento. In particolare sia X il tempo di attesa f(x) = λe λx se x 0; f(x) = 0 altrimenti. in cui il parametro della distribuzione λ rappresenta il reciproco del tempo medio del verificarsi dell evento considerato. La funzione di ripartizione è F (X) = 1 e λx E(X) = 1 λ V ar(x) = 1 λ 2 Proprietà di assenza di memoria P (X > t + s X > t) = P (X > s) s, t 0 In sostanza l andamento esponenziale presuppone che se una lampadina ha funzionato per un certo tempo t, la probabilità che essa funzioni per un ulteriore tempo s non dipende dal tempo precedente di funzionamento. () Statistica 46 / 48
58 Variabile Casuale (Negativa) Il responsabile dell illuminazione di un palazzo ha a disposizione 3 lampadine di riserva. Ciascuna delle lampadine utilizzate dura in media 200 ore e il responsabile deve aspettare 24 ore perchè gli vengano consegnate nuove lampadine di riserva. In altre parole, se si fulminano pi di tre lampadine entro le 24 ore, il responsabile non sarà in grado di sostituirle. Qual è la probabilità che il responsabile non sia in grado di sostituire le eventuali lampadine fulminate. Svolgimento. Si consideri di ragionare in termini di centinaia di ore. Il tempo medio è dunque pari a 2 (in centinaia di ore). Il parametro della distribuzione esponenziale è dunque λ = 1 2 = 0.5. Il problema sorge se 3 lampadine si fulminano entro le 24h (ovvero 0.24 in centinaia di ore). () Statistica 47 / 48
59 Variabile Casuale (Negativa) La probabilità che il tempo di rottura di una singola lampadina nelle 24h P (X 0.24) si calcola facendo ricorso alla funzione di ripartizione esponenziale F (0.24) = P (X 0.24) = 1 e λ x = 1 e = = Poichè la rottura di ciascuna lampadina è indipendente da quella delle altre, la probabilità della simultanea rottura di 3 lampadine è uguale al prodotto delle singole probabilità. P (X X X ) = = P (X ) P (X ) P (X ) = = = () Statistica 48 / 48
Statistica. Alfonso Iodice D Enza
 Statistica Alfonso Iodice D Enza iodicede@unina.it Università degli studi di Cassino () Statistica 1 / 17 Outline 1 () Statistica 2 / 17 Outline 1 2 () Statistica 2 / 17 Outline 1 2 3 () Statistica 2 /
Statistica Alfonso Iodice D Enza iodicede@unina.it Università degli studi di Cassino () Statistica 1 / 17 Outline 1 () Statistica 2 / 17 Outline 1 2 () Statistica 2 / 17 Outline 1 2 3 () Statistica 2 /
Statistica. Alfonso Iodice D Enza
 Statistica Alfonso Iodice D Enza iodicede@unina.it Università degli studi di Cassino () Statistica 1 / 27 Outline 1 () Statistica 2 / 27 Outline 1 2 () Statistica 2 / 27 Outline 1 2 3 () Statistica 2 /
Statistica Alfonso Iodice D Enza iodicede@unina.it Università degli studi di Cassino () Statistica 1 / 27 Outline 1 () Statistica 2 / 27 Outline 1 2 () Statistica 2 / 27 Outline 1 2 3 () Statistica 2 /
Esercitazione 5 del corso di Statistica 2 Prof. Domenico Vistocco
 Esercitazione del corso di Statistica Prof. Domenico Vistocco Alfonso Iodice D Enza May 30, 007 1 Esercizio Si consideri una popolazione caratterizzata dai numeri, 3, 6, 8, 11. Si considerino tutti i possibili
Esercitazione del corso di Statistica Prof. Domenico Vistocco Alfonso Iodice D Enza May 30, 007 1 Esercizio Si consideri una popolazione caratterizzata dai numeri, 3, 6, 8, 11. Si considerino tutti i possibili
Lezione 12. Statistica. Alfonso Iodice D Enza Università degli studi di Cassino. Lezione 12. A. Iodice.
 discrete uniforme Bernoulli Poisson Statistica Alfonso Iodice D Enza iodicede@unicas.it Università degli studi di Cassino () Statistica 1 / 56 Outline discrete uniforme Bernoulli Poisson 1 2 discrete 3
discrete uniforme Bernoulli Poisson Statistica Alfonso Iodice D Enza iodicede@unicas.it Università degli studi di Cassino () Statistica 1 / 56 Outline discrete uniforme Bernoulli Poisson 1 2 discrete 3
Esercitazione 4 del corso di Statistica 2 Prof. Domenico Vistocco
 Esercitazione 4 del corso di Statistica 2 Prof. Domenico Vistocco Alfonso Iodice D Enza May 23, 2007 1 Esercizio Si consideri un mazzo di carte francesi di 2 carte e si supponga di stare giocando a poker.
Esercitazione 4 del corso di Statistica 2 Prof. Domenico Vistocco Alfonso Iodice D Enza May 23, 2007 1 Esercizio Si consideri un mazzo di carte francesi di 2 carte e si supponga di stare giocando a poker.
DISTRIBUZIONI DI PROBABILITA (parte 2) 1 / 27
 DISTRIBUZIONI DI PROBABILITA (parte 2) 1 / 27 Funzione di ripartizione per variabili casuali discrete 2 / 27 Data una variabile casuale discreta possiamo calcolare, analogamente al caso continuo, la probabilità
DISTRIBUZIONI DI PROBABILITA (parte 2) 1 / 27 Funzione di ripartizione per variabili casuali discrete 2 / 27 Data una variabile casuale discreta possiamo calcolare, analogamente al caso continuo, la probabilità
Distribuzioni di probabilità nel continuo
 Distribuzioni di probabilità nel continuo Prof.ssa Fabbri Francesca Classe 5C Variabili casuali continue Introduzione: Una Variabile Casuale o Aleatoria è una grandezza che, nel corso di un esperimento
Distribuzioni di probabilità nel continuo Prof.ssa Fabbri Francesca Classe 5C Variabili casuali continue Introduzione: Una Variabile Casuale o Aleatoria è una grandezza che, nel corso di un esperimento
Esercitazione del 04/06/2015 Probabilità e Statistica Foglio 14
 Esercitazione del 0/06/05 Probabilità e Statistica Foglio David Barbato Esercizio. Ci sono 0 monetine di cui 5 con due teste, con due croci e regolari una moneta regolare ha una faccia testa e una faccia
Esercitazione del 0/06/05 Probabilità e Statistica Foglio David Barbato Esercizio. Ci sono 0 monetine di cui 5 con due teste, con due croci e regolari una moneta regolare ha una faccia testa e una faccia
ESERCITAZIONE 21 : VARIABILI ALEATORIE CONTINUE
 ESERCITAZIONE 21 : VARIABILI ALEATORIE CONTINUE e-mail: tommei@dm.unipi.it web: www.dm.unipi.it/ tommei Ricevimento: su appuntamento Dipartimento di Matematica, piano terra, studio 114 7 Maggio 2013 Esercizio
ESERCITAZIONE 21 : VARIABILI ALEATORIE CONTINUE e-mail: tommei@dm.unipi.it web: www.dm.unipi.it/ tommei Ricevimento: su appuntamento Dipartimento di Matematica, piano terra, studio 114 7 Maggio 2013 Esercizio
Due variabili aleatorie X ed Y si dicono indipendenti se comunque dati due numeri reali a e b si ha. P {X = a, Y = b} = P {X = a}p {Y = b}
 Due variabili aleatorie X ed Y si dicono indipendenti se comunque dati due numeri reali a e b si ha P {X = a, Y = b} = P {X = a}p {Y = b} Una variabile aleatoria χ che assume i soli valori 1, 2,..., n
Due variabili aleatorie X ed Y si dicono indipendenti se comunque dati due numeri reali a e b si ha P {X = a, Y = b} = P {X = a}p {Y = b} Una variabile aleatoria χ che assume i soli valori 1, 2,..., n
Variabili casuali. - di Massimo Cristallo -
 Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 16 e 27 maggio 2013 - di Massimo Cristallo - Variabili casuali
Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 16 e 27 maggio 2013 - di Massimo Cristallo - Variabili casuali
Alcune v.a. discrete notevoli
 Alcune v.a. discrete notevoli Variabile aleatoria Bernoulliana Il risultato X di un esperimento aleatorio può essere classificato nel modo che segue: successo oppure insuccesso. Indichiamo: Successo =
Alcune v.a. discrete notevoli Variabile aleatoria Bernoulliana Il risultato X di un esperimento aleatorio può essere classificato nel modo che segue: successo oppure insuccesso. Indichiamo: Successo =
Statistica Applicata all edilizia: alcune distribuzioni di probabilità
 Statistica Applicata all edilizia: Alcune distribuzioni di probabilità E-mail: orietta.nicolis@unibg.it 23 marzo 2010 Indice Distribuzioni di probabilità discrete 1 Distribuzioni di probabilità discrete
Statistica Applicata all edilizia: Alcune distribuzioni di probabilità E-mail: orietta.nicolis@unibg.it 23 marzo 2010 Indice Distribuzioni di probabilità discrete 1 Distribuzioni di probabilità discrete
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2006/07
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 006/07 Esercizio 1 Prova scritta del 16/1/006 In un ufficio postale lavorano due impiegati che svolgono lo stesso compito in maniera indipendente, sbrigando
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 006/07 Esercizio 1 Prova scritta del 16/1/006 In un ufficio postale lavorano due impiegati che svolgono lo stesso compito in maniera indipendente, sbrigando
MATEMATICA E STATISTICA CORSO A III COMPITINO 20 Marzo 2009
 MATEMATICA E STATISTICA CORSO A III COMPITINO Marzo 9 SOLUZIONI. () Sia X una variabile aleatoria binomiale con valor medio uguale a 5/; la varianza di X può valere? Giustificare la risposta. Il valor
MATEMATICA E STATISTICA CORSO A III COMPITINO Marzo 9 SOLUZIONI. () Sia X una variabile aleatoria binomiale con valor medio uguale a 5/; la varianza di X può valere? Giustificare la risposta. Il valor
Esercitazione: La distribuzione NORMALE
 Esercitazione: La distribuzione NORMALE Uno dei più importanti esempi di distribuzione di probabilità continua è dato dalla distribuzione Normale (curva normale o distribuzione Gaussiana); è una delle
Esercitazione: La distribuzione NORMALE Uno dei più importanti esempi di distribuzione di probabilità continua è dato dalla distribuzione Normale (curva normale o distribuzione Gaussiana); è una delle
PROBABILITA. Distribuzione di probabilità
 DISTRIBUZIONI di PROBABILITA Distribuzione di probabilità Si definisce distribuzione di probabilità il valore delle probabilità associate a tutti gli eventi possibili connessi ad un certo numero di prove
DISTRIBUZIONI di PROBABILITA Distribuzione di probabilità Si definisce distribuzione di probabilità il valore delle probabilità associate a tutti gli eventi possibili connessi ad un certo numero di prove
Statistica. Lezione : 18, 19. Variabili casuali
 Corsi di Laurea: a.a. 2017-18 Diritto per le Imprese e le istituzioni Scienze dell Amministrazione e Consulenza del Lavoro sienze Internazionali dello Sviluppo e della Cooperazione Statistica Variabili
Corsi di Laurea: a.a. 2017-18 Diritto per le Imprese e le istituzioni Scienze dell Amministrazione e Consulenza del Lavoro sienze Internazionali dello Sviluppo e della Cooperazione Statistica Variabili
Università degli studi della Tuscia. Principi di Statistica dr. Luca Secondi A.A. 2014/2015. Esercitazione di riepilogo Variabili casuali
 Università degli studi della Tuscia Principi di Statistica dr. Luca Secondi A.A. 014/015 Esercitazione di riepilogo Variabili casuali ESERCIZIO 1 Il peso delle compresse di un determinato medicinale si
Università degli studi della Tuscia Principi di Statistica dr. Luca Secondi A.A. 014/015 Esercitazione di riepilogo Variabili casuali ESERCIZIO 1 Il peso delle compresse di un determinato medicinale si
CAPITOLO QUINTO DISTRIBUZIONE NORMALE
 CAPITOLO QUINTO DISTRIBUZIONE NORMALE 1. Probabilità nel continuo Fino ad ora abbiamo considerato casi in cui l insieme degli eventi elementari è finito. Vediamo, mediante due semplici esempi, come si
CAPITOLO QUINTO DISTRIBUZIONE NORMALE 1. Probabilità nel continuo Fino ad ora abbiamo considerato casi in cui l insieme degli eventi elementari è finito. Vediamo, mediante due semplici esempi, come si
UNIVERSITA DEGLI STUDI DI BRESCIA-FACOLTA DI MEDICINA E CHIRURGIA CORSO DI LAUREA IN INFERMIERISTICA SEDE DI DESENZANO dg STATISTICA MEDICA.
 Lezione 4 DISTRIBUZIONE DI FREQUENZA 1 DISTRIBUZIONE DI PROBABILITA Una variabile i cui differenti valori seguono una distribuzione di probabilità si chiama variabile aleatoria. Es:il numero di figli maschi
Lezione 4 DISTRIBUZIONE DI FREQUENZA 1 DISTRIBUZIONE DI PROBABILITA Una variabile i cui differenti valori seguono una distribuzione di probabilità si chiama variabile aleatoria. Es:il numero di figli maschi
Statistica. Esercitazione 10. Alfonso Iodice D Enza iodicede@unicas.it. Università degli studi di Cassino. Statistica. A. Iodice. V.C.
 uniforme Bernoulli binomiale di Esercitazione 10 Alfonso Iodice D Enza iodicede@unicas.it Università degli studi di Cassino () 1 / 55 Outline uniforme Bernoulli binomiale di 1 uniforme 2 Bernoulli 3 4
uniforme Bernoulli binomiale di Esercitazione 10 Alfonso Iodice D Enza iodicede@unicas.it Università degli studi di Cassino () 1 / 55 Outline uniforme Bernoulli binomiale di 1 uniforme 2 Bernoulli 3 4
LEZIONE 2.6. corso di statistica. Francesco Lagona Università Roma Tre. LEZIONE 2.6 p. 1/15
 LEZIONE 2.6 p. 1/15 LEZIONE 2.6 corso di statistica Francesco Lagona Università Roma Tre LEZIONE 2.6 p. 2/15 variabili aleatorie continue consideriamo la distribuzione del fatturato mensile in una popolazione
LEZIONE 2.6 p. 1/15 LEZIONE 2.6 corso di statistica Francesco Lagona Università Roma Tre LEZIONE 2.6 p. 2/15 variabili aleatorie continue consideriamo la distribuzione del fatturato mensile in una popolazione
DISTRIBUZIONI DI PROBABILITA (parte 1) 1 / 19
 DISTRIBUZIONI DI PROBABILITA (parte 1) 1 / 19 Variabili casuali (o aleatorie) 2 / 19 Disponendo di metodi corretti per raccogliere i dati e costruire i campioni data una popolazione, i valori numerici
DISTRIBUZIONI DI PROBABILITA (parte 1) 1 / 19 Variabili casuali (o aleatorie) 2 / 19 Disponendo di metodi corretti per raccogliere i dati e costruire i campioni data una popolazione, i valori numerici
La funzione di distribuzione Gaussiana normale
 La funzione di distribuzione Gaussiana normale Nicola Morganti 25 aprile 2004 Indice Proprietà fondamentali 2 Standard Normal Density Function 3 3 Esempio applicativo 5 Proprietà fondamentali L utilizzo
La funzione di distribuzione Gaussiana normale Nicola Morganti 25 aprile 2004 Indice Proprietà fondamentali 2 Standard Normal Density Function 3 3 Esempio applicativo 5 Proprietà fondamentali L utilizzo
Corso di Laurea: Diritto per le Imprese e le istituzioni a.a Statistica. Probabilità. Lezioni : 11, 12. Docente: Alessandra Durio
 Corso di Laurea: Diritto per le Imprese e le istituzioni a.a. 2016-17 Statistica Probabilità Lezioni : 11, 12 Docente: Alessandra Durio 1 Contenuti 1. Variabili casuali notevoli DISCRETE (uniforme, di
Corso di Laurea: Diritto per le Imprese e le istituzioni a.a. 2016-17 Statistica Probabilità Lezioni : 11, 12 Docente: Alessandra Durio 1 Contenuti 1. Variabili casuali notevoli DISCRETE (uniforme, di
La funzione di ripartizione caratterizza la v.a. Ad ogni funzione di ripartizione corrisponde una ed una sola distribuzione.
 Funzione di ripartizione X v.a. a valori in IR F X (x) = P (X x), x IR Indice X omesso quando chiaro Proprietà funzione di ripartizione F (i) F X (x) ; x (ii) è non decrescente Sia a < b P (a < X b) =
Funzione di ripartizione X v.a. a valori in IR F X (x) = P (X x), x IR Indice X omesso quando chiaro Proprietà funzione di ripartizione F (i) F X (x) ; x (ii) è non decrescente Sia a < b P (a < X b) =
SCHEDA DIDATTICA N 7
 FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA CIVILE CORSO DI IDROLOGIA PROF. PASQUALE VERSACE SCHEDA DIDATTICA N 7 LA DISTRIBUZIONE NORMALE A.A. 01-13 La distribuzione NORMALE Uno dei più importanti
FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA CIVILE CORSO DI IDROLOGIA PROF. PASQUALE VERSACE SCHEDA DIDATTICA N 7 LA DISTRIBUZIONE NORMALE A.A. 01-13 La distribuzione NORMALE Uno dei più importanti
Distribuzione esponenziale. f(x) = 0 x < 0
 Distribuzione esponenziale Funzione densità f(x) = λe λx x 0 0 x < 0 Funzione parametrica (λ) 72 Funzione di densità della distribuzione esponenziale 1 0.9 0.8 0.7 λ=1 0.6 f(x) 0.5 0.4 0.3 λ=1/2 0.2 0.1
Distribuzione esponenziale Funzione densità f(x) = λe λx x 0 0 x < 0 Funzione parametrica (λ) 72 Funzione di densità della distribuzione esponenziale 1 0.9 0.8 0.7 λ=1 0.6 f(x) 0.5 0.4 0.3 λ=1/2 0.2 0.1
CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 2
 CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 2 Dott.ssa Antonella Costanzo a.costanzo@unicas.it Esercizio 1. La variabile Uniforme Continua Data una scheda telefonica da 5 euro di cui non si sa se sia
CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 2 Dott.ssa Antonella Costanzo a.costanzo@unicas.it Esercizio 1. La variabile Uniforme Continua Data una scheda telefonica da 5 euro di cui non si sa se sia
1! 4! = 5. Quindi la probabilità di ottenere 1 successo su 5 lanci sarà 5 2 = 5! 2! 3! = 10
 Note sulla Distribuzione Binomiale La distribuzione binomiale è relativa ad una variabile aleatoria discreta, che descrive i possibili risultati di un esperimento composto da n prove. In particolare, definisce
Note sulla Distribuzione Binomiale La distribuzione binomiale è relativa ad una variabile aleatoria discreta, che descrive i possibili risultati di un esperimento composto da n prove. In particolare, definisce
STATISTICA A D (72 ore)
 STATISTICA A D (72 ore) Marco Riani mriani@unipr.it http://www.riani.it Tipologia di v.a. v.a. discreta numero finito di valori (infinità numerabile) x 1 x 2,, x k con probabilità p 1 p 2, p k Esempio:
STATISTICA A D (72 ore) Marco Riani mriani@unipr.it http://www.riani.it Tipologia di v.a. v.a. discreta numero finito di valori (infinità numerabile) x 1 x 2,, x k con probabilità p 1 p 2, p k Esempio:
ESERCITAZIONE N. 5 corso di statistica
 ESERCITAZIONE N. 5corso di statistica p. 1/27 ESERCITAZIONE N. 5 corso di statistica Marco Picone Università Roma Tre ESERCITAZIONE N. 5corso di statistica p. 2/27 Introduzione Variabili aleatorie discrete
ESERCITAZIONE N. 5corso di statistica p. 1/27 ESERCITAZIONE N. 5 corso di statistica Marco Picone Università Roma Tre ESERCITAZIONE N. 5corso di statistica p. 2/27 Introduzione Variabili aleatorie discrete
Statistica Inferenziale
 Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Riepilogo lezione 4 Abbiamo visto: Distribuzioni discrete Modelli probabilistici nel discreto Distribuzione uniforme
Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Riepilogo lezione 4 Abbiamo visto: Distribuzioni discrete Modelli probabilistici nel discreto Distribuzione uniforme
Probabilità classica. Distribuzioni e leggi di probabilità. Probabilità frequentista. Probabilità soggettiva
 Probabilità classica Distribuzioni e leggi di probabilità La probabilità di un evento casuale è il rapporto tra il numero dei casi favorevoli ed il numero dei casi possibili, purchè siano tutti equiprobabili.
Probabilità classica Distribuzioni e leggi di probabilità La probabilità di un evento casuale è il rapporto tra il numero dei casi favorevoli ed il numero dei casi possibili, purchè siano tutti equiprobabili.
Calcolo delle Probabilità e Statistica Matematica Fisciano, 10/1/2012
 Fisciano, 10/1/2012 Esercizio 1 Un esperimento consiste nel generare a caso un vettore di interi (x 1, x 2, x 3, x 4 ), dove x i {1, 2, 3, 4, 5, 6} i. (i) Si individui lo spazio campionario, determinandone
Fisciano, 10/1/2012 Esercizio 1 Un esperimento consiste nel generare a caso un vettore di interi (x 1, x 2, x 3, x 4 ), dove x i {1, 2, 3, 4, 5, 6} i. (i) Si individui lo spazio campionario, determinandone
esperimento casuale: è un esperimento condotto sotto l effetto del caso; evento elementare: ciascuno dei possibili esiti di un esperimento casuale;
 Capitolo 15 Suggerimenti agli esercizi a cura di Elena Siletti Esercizio 15.1: Suggerimento Si ricordi che: esperimento casuale: è un esperimento condotto sotto l effetto del caso; evento elementare: ciascuno
Capitolo 15 Suggerimenti agli esercizi a cura di Elena Siletti Esercizio 15.1: Suggerimento Si ricordi che: esperimento casuale: è un esperimento condotto sotto l effetto del caso; evento elementare: ciascuno
5 - Esercizi: Probabilità e Distribuzioni di Probabilità (Uniforme, Gaussiana)
 5 - Esercizi: Probabilità e Distribuzioni di Probabilità (Uniforme, Gaussiana) Esercizio 1: Una variabile casuale e caratterizzata da una distribuzione uniforme tra 0 e 10. Calcolare - a) la probabilità
5 - Esercizi: Probabilità e Distribuzioni di Probabilità (Uniforme, Gaussiana) Esercizio 1: Una variabile casuale e caratterizzata da una distribuzione uniforme tra 0 e 10. Calcolare - a) la probabilità
tabelle grafici misure di
 Statistica Descrittiva descrivere e riassumere un insieme di dati in maniera ordinata tabelle grafici misure di posizione dispersione associazione Misure di posizione Forniscono indicazioni sull ordine
Statistica Descrittiva descrivere e riassumere un insieme di dati in maniera ordinata tabelle grafici misure di posizione dispersione associazione Misure di posizione Forniscono indicazioni sull ordine
DISTRIBUZIONE NORMALE (1)
 DISTRIBUZIONE NORMALE (1) Nella popolazione generale molte variabili presentano una distribuzione a forma di campana, bene caratterizzata da un punto di vista matematico, chiamata distribuzione normale
DISTRIBUZIONE NORMALE (1) Nella popolazione generale molte variabili presentano una distribuzione a forma di campana, bene caratterizzata da un punto di vista matematico, chiamata distribuzione normale
UNIVERSITA DEGLI STUDI DI BRESCIA-FACOLTA DI MEDICINA E CHIRURGIA CORSO DI LAUREA IN INFERMIERISTICA SEDE DI DESENZANO dg STATISTICA MEDICA.
 Lezione 4 DISTRIBUZIONE DI FREQUENZA 1 DISTRIBUZIONE DI PROBABILITA Una variabile i cui differenti valori seguono una distribuzione di probabilità si chiama variabile aleatoria. Es:il numero di figli maschi
Lezione 4 DISTRIBUZIONE DI FREQUENZA 1 DISTRIBUZIONE DI PROBABILITA Una variabile i cui differenti valori seguono una distribuzione di probabilità si chiama variabile aleatoria. Es:il numero di figli maschi
Lezione 13 Corso di Statistica. Domenico Cucina
 Lezione 13 Corso di Statistica Domenico Cucina Università Roma Tre D. Cucina (domenico.cucina@uniroma3.it) 1 / 20 obiettivi della lezione comprendere il concetto di variabile aleatoria continua familiarizzare
Lezione 13 Corso di Statistica Domenico Cucina Università Roma Tre D. Cucina (domenico.cucina@uniroma3.it) 1 / 20 obiettivi della lezione comprendere il concetto di variabile aleatoria continua familiarizzare
Esercitazione del 21/02/2012 Istituzioni di Calcolo delle Probabilità
 Esercitazione del /0/0 Istituzioni di Calcolo delle Probabilità David Barbato Funzione di ripartizione Sia F X una funzione da in. consideriamo le seguenti condizioni: F X è non decrescente lim ( ) x F
Esercitazione del /0/0 Istituzioni di Calcolo delle Probabilità David Barbato Funzione di ripartizione Sia F X una funzione da in. consideriamo le seguenti condizioni: F X è non decrescente lim ( ) x F
Soluzione Esercizio 1 (pag 1):
 8 - Test di Ipotesi Esercizio 1: Dopo anni di esperienza e noto che la distribuzione della concentrazione di rame nel sangue umano e ben descritta da una distribuzione gaussiana di parametri μ=3.2 10-5
8 - Test di Ipotesi Esercizio 1: Dopo anni di esperienza e noto che la distribuzione della concentrazione di rame nel sangue umano e ben descritta da una distribuzione gaussiana di parametri μ=3.2 10-5
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica ST410 - Statistica 1 - A.A. 2014/2015 II Esonero - 15 Gennaio 2015
 UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica ST410 - Statistica 1 - A.A. 014/015 II Esonero - 15 Gennaio 015 1 3 4 5 6 Tot. Avvertenza: Svolgere ogni esercizio nello spazio assegnato,
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica ST410 - Statistica 1 - A.A. 014/015 II Esonero - 15 Gennaio 015 1 3 4 5 6 Tot. Avvertenza: Svolgere ogni esercizio nello spazio assegnato,
Corso di Istituzioni di Matematiche con Elementi di Statistica. anno accademico 2015/2016 corso A-L (G. Gaeta & N. Bressan)
 Corso di Istituzioni di Matematiche con Elementi di Statistica anno accademico 215/216 corso A-L (G. Gaeta & N. Bressan) Esercizi Foglio 9 (Funzioni aleatorie; distribuzioni di probabilita ) Esercizio
Corso di Istituzioni di Matematiche con Elementi di Statistica anno accademico 215/216 corso A-L (G. Gaeta & N. Bressan) Esercizi Foglio 9 (Funzioni aleatorie; distribuzioni di probabilita ) Esercizio
Esercitazione del 16/04/2019 Istituzioni di Calcolo delle Probabilità
 Esercitazione del 6/04/09 Istituzioni di Calcolo delle Probabilità David Barbato Nozioni di riepilogo con esercizi Distribuzione di una funzione di una variabile aleatoria discreta. Sia X una variabile
Esercitazione del 6/04/09 Istituzioni di Calcolo delle Probabilità David Barbato Nozioni di riepilogo con esercizi Distribuzione di una funzione di una variabile aleatoria discreta. Sia X una variabile
Approfondimento 3.3. Approssimazione della distribuzione binomiale alla normale
 Approfondimento 3.3 Approssimazione della distribuzione binomiale alla normale Come aveva notato de Moivre, se il numero di prove è sufficientemente ampio e la probabilità del successo π sufficientemente
Approfondimento 3.3 Approssimazione della distribuzione binomiale alla normale Come aveva notato de Moivre, se il numero di prove è sufficientemente ampio e la probabilità del successo π sufficientemente
Esercitazione del 28/10/2011 Calcolo delle probabilità
 Esercitazione del 28/0/20 Calcolo delle probabilità Distribuzione di una funzione di una variabile aleatoria discreta. Sia X una variabile aletoria discreta, sia f una funzione da in, se Y := f(x) allora
Esercitazione del 28/0/20 Calcolo delle probabilità Distribuzione di una funzione di una variabile aleatoria discreta. Sia X una variabile aletoria discreta, sia f una funzione da in, se Y := f(x) allora
Esercitazione n. 3 - Corso di STATISTICA - Università della Basilicata - a.a. 2011/12 Prof. Roberta Siciliano
 Esercitazione n. 3 - Corso di STATISTICA - Università della Basilicata - a.a. 2011/12 Prof. Roberta Siciliano Esercizio 1 Una moneta viene lanciata 6 volte. Calcolare a) La probabilità che escano esattamente
Esercitazione n. 3 - Corso di STATISTICA - Università della Basilicata - a.a. 2011/12 Prof. Roberta Siciliano Esercizio 1 Una moneta viene lanciata 6 volte. Calcolare a) La probabilità che escano esattamente
STATISTICA (2) ESERCITAZIONE 2. Dott.ssa Antonella Costanzo
 STATISTICA (2) ESERCITAZIONE 2 5.02.2014 Dott.ssa Antonella Costanzo Esercizio 1. La v.c. Normale: uso delle tavole E noto che un certo tipo di dati si distribuiscono secondo una gaussiana di media 10
STATISTICA (2) ESERCITAZIONE 2 5.02.2014 Dott.ssa Antonella Costanzo Esercizio 1. La v.c. Normale: uso delle tavole E noto che un certo tipo di dati si distribuiscono secondo una gaussiana di media 10
CP110 Probabilità: Esame 13 settembre Testo e soluzione
 Dipartimento di Matematica, Roma Tre Pietro Caputo 2011-12, II semestre 13 settembre, 2012 CP110 Probabilità: Esame 13 settembre 2012 Testo e soluzione 1. (6 pts) Una scatola contiene 10 palline, 8 bianche
Dipartimento di Matematica, Roma Tre Pietro Caputo 2011-12, II semestre 13 settembre, 2012 CP110 Probabilità: Esame 13 settembre 2012 Testo e soluzione 1. (6 pts) Una scatola contiene 10 palline, 8 bianche
Esercitazioni di Statistica Matematica A Lezione 7. Variabili aleatorie continue
 Esercitazioni di Statistica Matematica A Lezione 7 Variabili aleatorie continue.) Determinare la costante k R tale per cui le seguenti funzioni siano funzioni di densità. Determinare poi la media e la
Esercitazioni di Statistica Matematica A Lezione 7 Variabili aleatorie continue.) Determinare la costante k R tale per cui le seguenti funzioni siano funzioni di densità. Determinare poi la media e la
Il campionamento e l inferenza. Il campionamento e l inferenza
 Il campionamento e l inferenza Popolazione Campione Dai dati osservati mediante scelta campionaria si giunge ad affermazioni che riguardano la popolazione da cui essi sono stati prescelti Il campionamento
Il campionamento e l inferenza Popolazione Campione Dai dati osservati mediante scelta campionaria si giunge ad affermazioni che riguardano la popolazione da cui essi sono stati prescelti Il campionamento
Variabili aleatorie. Variabili aleatorie
 Variabili aleatorie Distribuzione binomiale Si supponga che uno studente affronti un esame composto da domande chiuse. Una sola delle 5 alternative di risposta proposta per ciascuna domanda è vera Supponiamo
Variabili aleatorie Distribuzione binomiale Si supponga che uno studente affronti un esame composto da domande chiuse. Una sola delle 5 alternative di risposta proposta per ciascuna domanda è vera Supponiamo
Calcolo delle Probabilità e Statistica, Ingegneria Civile e A&T e Informatica I prova finale a.a. 2016/17
 Calcolo delle Probabilità e Statistica, Ingegneria Civile e A&T e Informatica I prova finale aa 6/ Punteggi: : 3 + 6; : + + + ; 3: + Una scatola contiene monete; 8 di queste sono equilibrate, mentre le
Calcolo delle Probabilità e Statistica, Ingegneria Civile e A&T e Informatica I prova finale aa 6/ Punteggi: : 3 + 6; : + + + ; 3: + Una scatola contiene monete; 8 di queste sono equilibrate, mentre le
Introduzione al modello Uniforme
 Introduzione al modello Uniforme Esempio: conversione Analogico/Digitale Errore di quantizzazione Ampiezza Continua Discreta x () t x ( t ) q Tempo Discreto Continuo Segnale Analogico ( ) x t k t t Segnale
Introduzione al modello Uniforme Esempio: conversione Analogico/Digitale Errore di quantizzazione Ampiezza Continua Discreta x () t x ( t ) q Tempo Discreto Continuo Segnale Analogico ( ) x t k t t Segnale
Dipartimento di Sociologia e Ricerca Sociale. Corso di Laurea in Sociologia. Insegnamento di Statistica (a.a ) dott.ssa Gaia Bertarelli
 Dipartimento di Sociologia e Ricerca Sociale Corso di Laurea in Sociologia Insegnamento di Statistica (a.a. 2018-2019) dott.ssa Gaia Bertarelli Esercitazione n. 7 1. Utilizzando le tavole della distribuzione
Dipartimento di Sociologia e Ricerca Sociale Corso di Laurea in Sociologia Insegnamento di Statistica (a.a. 2018-2019) dott.ssa Gaia Bertarelli Esercitazione n. 7 1. Utilizzando le tavole della distribuzione
Esercitazione del 28/02/2012 Istituzioni di Calcolo delle Probabilità
 Esercitazione del 8/0/01 Istituzioni di Calcolo delle Probabilità David Barbato barbato@math.unipd.it Esercizio 1. Sia X una v.a. aleatoria assolutamente continua con densità f X data da { 0 x < 0 f X
Esercitazione del 8/0/01 Istituzioni di Calcolo delle Probabilità David Barbato barbato@math.unipd.it Esercizio 1. Sia X una v.a. aleatoria assolutamente continua con densità f X data da { 0 x < 0 f X
SOLUZIONI DEL 2 0 TEST DI PREPARAZIONE ALLA 1 a PROVA INTERMEDIA
 SOLUZIONI DEL 0 TEST DI PREPARAZIONE ALLA 1 a PROVA INTERMEDIA Esercizio 0.1 Una moneta non truccata viene lanciata 10 volte. Calcolare la probabilità che non esca mai testa. Quale risulta la probabilità
SOLUZIONI DEL 0 TEST DI PREPARAZIONE ALLA 1 a PROVA INTERMEDIA Esercizio 0.1 Una moneta non truccata viene lanciata 10 volte. Calcolare la probabilità che non esca mai testa. Quale risulta la probabilità
PROBABILITÀ SCHEDA N. 3 VARIABILI ALEATORIE BINOMIALE E NORMALE. 1. La variabile aleatoria di Bernoulli e la variabile aleatoria binomiale
 PROBABILITÀ SCHEDA N. 3 VARIABILI ALEATORIE BINOMIALE E NORMALE In questa scheda vedremo due famiglie di variabili aleatorie (una discreta e una continua), che ci serviranno per descrivere uno dei risultati
PROBABILITÀ SCHEDA N. 3 VARIABILI ALEATORIE BINOMIALE E NORMALE In questa scheda vedremo due famiglie di variabili aleatorie (una discreta e una continua), che ci serviranno per descrivere uno dei risultati
STATISTICA (2) ESERCITAZIONE 1. Dott.ssa Antonella Costanzo
 STATISTICA (2) ESERCITAZIONE 1 29.01.2014 Dott.ssa Antonella Costanzo Esercizio 1. Modelli discreti di probabilità: le v.c. binomiale e geometrica (come caso particolare della v.c. binomiale negativa)
STATISTICA (2) ESERCITAZIONE 1 29.01.2014 Dott.ssa Antonella Costanzo Esercizio 1. Modelli discreti di probabilità: le v.c. binomiale e geometrica (come caso particolare della v.c. binomiale negativa)
COMPITO DI SCIENZE NATURALI 23 gennaio Modulo di probabilità e statistica SOLUZIONI
 COMPITO DI SCIENZE NATURALI 23 gennaio 22 Modulo di probabilità e statistica SOLUZIONI. In Svizzera, al primo gennaio di ogni anno, tutti i cittadini vengono sottoposti a vaccinazione contro l influenza
COMPITO DI SCIENZE NATURALI 23 gennaio 22 Modulo di probabilità e statistica SOLUZIONI. In Svizzera, al primo gennaio di ogni anno, tutti i cittadini vengono sottoposti a vaccinazione contro l influenza
Modelli probabilistici variabili casuali
 Modelli probabilistici variabili casuali Le variabili casuali costituiscono il legame tra il calcolo della probabilità e gli strumenti di statistica descrittiva visti fino ad ora. Idea: pensiamo al ripetersi
Modelli probabilistici variabili casuali Le variabili casuali costituiscono il legame tra il calcolo della probabilità e gli strumenti di statistica descrittiva visti fino ad ora. Idea: pensiamo al ripetersi
X ~ N (20, 16) Soluzione
 ESERCIZIO 3.1 Il tempo di reazione ad un esperimento psicologico effettuato su un gruppo di individui si distribuisce normalmente con media µ = 20 secondi e scarto quadratico medio σ = 4 secondi: X ~ N
ESERCIZIO 3.1 Il tempo di reazione ad un esperimento psicologico effettuato su un gruppo di individui si distribuisce normalmente con media µ = 20 secondi e scarto quadratico medio σ = 4 secondi: X ~ N
Materiale didattico per il corso di Statistica I Quarta esercitazione SOLUZIONI
 Materiale didattico per il corso di Statistica I Quarta esercitazione SOLUZIONI Claudia Furlan 1 Anno Accademico 2006-2007 1 Ringrazio Carlo Gaetan, Nicola Sartori e Aldo Solari per il materiale, aggiunte
Materiale didattico per il corso di Statistica I Quarta esercitazione SOLUZIONI Claudia Furlan 1 Anno Accademico 2006-2007 1 Ringrazio Carlo Gaetan, Nicola Sartori e Aldo Solari per il materiale, aggiunte
Distribuzione di Probabilità
 Distribuzione di Probabilità Sia X variabile con valori discreti X 1, X 2,..., X N aventi probabilità p 1, p 2,..., p N ( i p i = 1) (X variabile discreta aleatoria, o stocastica, o casuale, random) Funzione
Distribuzione di Probabilità Sia X variabile con valori discreti X 1, X 2,..., X N aventi probabilità p 1, p 2,..., p N ( i p i = 1) (X variabile discreta aleatoria, o stocastica, o casuale, random) Funzione
Lezione n. 1 (a cura di Irene Tibidò)
 Lezione n. 1 (a cura di Irene Tibidò) Richiami di statistica Variabile aleatoria (casuale) Dato uno spazio campionario Ω che contiene tutti i possibili esiti di un esperimento casuale, la variabile aleatoria
Lezione n. 1 (a cura di Irene Tibidò) Richiami di statistica Variabile aleatoria (casuale) Dato uno spazio campionario Ω che contiene tutti i possibili esiti di un esperimento casuale, la variabile aleatoria
Probabilità 1, laurea triennale in Matematica Prova scritta sessione invernale a.a. 2008/09 del 26/01/2010
 Probabilità 1, laurea triennale in Matematica Prova scritta sessione invernale a.a. 2008/09 del 26/01/2010 1. Nello scaffale di un negozio vi sono 20 CD-Rom di software, di cui 2 di grafica e gli altri
Probabilità 1, laurea triennale in Matematica Prova scritta sessione invernale a.a. 2008/09 del 26/01/2010 1. Nello scaffale di un negozio vi sono 20 CD-Rom di software, di cui 2 di grafica e gli altri
Statistica Corso Base (Serale) Dott.ssa Cristina Mollica
 Statistica Corso Base (Serale) Dott.ssa Cristina Mollica cristina.mollica@uniroma1.it Variabili casuali Esercizio 1. Determinare la distribuzione di probabilità e la funzione di ripartizione della variabile
Statistica Corso Base (Serale) Dott.ssa Cristina Mollica cristina.mollica@uniroma1.it Variabili casuali Esercizio 1. Determinare la distribuzione di probabilità e la funzione di ripartizione della variabile
assuma valori in un determinato intervallo è data dall integrale della sua densità ( = )=
 VARIABILI ALEATORIE CONTINUE Esistono parecchi fenomeni reali per la cui descrizione le variabili aleatorie discrete non sono adatte. Per esempio è necessaria una variabile aleatoria continua ovvero una
VARIABILI ALEATORIE CONTINUE Esistono parecchi fenomeni reali per la cui descrizione le variabili aleatorie discrete non sono adatte. Per esempio è necessaria una variabile aleatoria continua ovvero una
Corso di Laurea Triennale in Matematica Calcolo delle Probabilità I (docenti G. Nappo, F. Spizzichino)
 Corso di Laurea Triennale in Matematica Calcolo delle Probabilità I (docenti G. Nappo, F. Spizzichino Prova di mercoledì 22 Settembre 24 (tempo a disposizione: 2 ore e 4 minuti. consegna compiti e inizio
Corso di Laurea Triennale in Matematica Calcolo delle Probabilità I (docenti G. Nappo, F. Spizzichino Prova di mercoledì 22 Settembre 24 (tempo a disposizione: 2 ore e 4 minuti. consegna compiti e inizio
Scanned by CamScanner
 Scanned by CamScanner Scanned by CamScanner Scanned by CamScanner Scanned by CamScanner Scanned by CamScanner Scanned by CamScanner Scanned by CamScanner Università di Cassino Corso di Statistica Esercitazione
Scanned by CamScanner Scanned by CamScanner Scanned by CamScanner Scanned by CamScanner Scanned by CamScanner Scanned by CamScanner Scanned by CamScanner Università di Cassino Corso di Statistica Esercitazione
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica ST410 - Statistica 1 - A.A. 2013/2014. I Esonero - 29 Ottobre Tot.
 UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica ST410 - Statistica 1 - A.A. 2013/2014 I Esonero - 29 Ottobre 2013 1 2 3 4 5 6 7 8 Tot. Avvertenza: Svolgere ogni esercizio nello spazio assegnato,
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica ST410 - Statistica 1 - A.A. 2013/2014 I Esonero - 29 Ottobre 2013 1 2 3 4 5 6 7 8 Tot. Avvertenza: Svolgere ogni esercizio nello spazio assegnato,
RICHIAMI DI CALCOLO DELLE PROBABILITÀ
 UNIVERSITA DEL SALENTO INGEGNERIA CIVILE RICHIAMI DI CALCOLO DELLE PROBABILITÀ ing. Marianovella LEONE INTRODUZIONE Per misurare la sicurezza di una struttura, ovvero la sua affidabilità, esistono due
UNIVERSITA DEL SALENTO INGEGNERIA CIVILE RICHIAMI DI CALCOLO DELLE PROBABILITÀ ing. Marianovella LEONE INTRODUZIONE Per misurare la sicurezza di una struttura, ovvero la sua affidabilità, esistono due
ES.2.3. è pari ad 1. Una variabile aleatoria X che assume valori su tutta la retta si dice distribuita
 ES.2.3 1 Distribuzione normale La funzione N(x; µ, σ 2 = 1 e 1 2( x µ σ 2 2πσ 2 si chiama densità di probabilità normale (o semplicemente curva normale con parametri µ e σ 2. La funzione è simmetrica rispetto
ES.2.3 1 Distribuzione normale La funzione N(x; µ, σ 2 = 1 e 1 2( x µ σ 2 2πσ 2 si chiama densità di probabilità normale (o semplicemente curva normale con parametri µ e σ 2. La funzione è simmetrica rispetto
Statistica. Alfonso Iodice D Enza
 Statistica Alfonso Iodice D Enza iodicede@unicas.it Università degli studi di Cassino () Statistica 1 / 33 Outline 1 2 3 4 5 6 () Statistica 2 / 33 Misura del legame Nel caso di variabili quantitative
Statistica Alfonso Iodice D Enza iodicede@unicas.it Università degli studi di Cassino () Statistica 1 / 33 Outline 1 2 3 4 5 6 () Statistica 2 / 33 Misura del legame Nel caso di variabili quantitative
UNIVERSITÀ di ROMA TOR VERGATA
 UNIVERSITÀ di ROMA TOR VERGATA Corso di Laurea Magistrale in Scienze della Nutrizione Umana Corso di Statistica Medica, anno 205- P.Baldi Lista di esercizi 5, 8 febbraio 20. Esercizio Si fanno 25 estrazioni
UNIVERSITÀ di ROMA TOR VERGATA Corso di Laurea Magistrale in Scienze della Nutrizione Umana Corso di Statistica Medica, anno 205- P.Baldi Lista di esercizi 5, 8 febbraio 20. Esercizio Si fanno 25 estrazioni
Probabilità Esercitazione n. 6 del 24/05/2016
 Corso di Laurea in Matematica Applicata Probabilità Esercitazione n. 6 del 24/05/2016 Docente: Bruno Gobbi V.C. NORMALE, ESPONENZIALE NEGATIVA E UNIFORME CONTINUA 1) La pressione del sangue segue una distribuzione
Corso di Laurea in Matematica Applicata Probabilità Esercitazione n. 6 del 24/05/2016 Docente: Bruno Gobbi V.C. NORMALE, ESPONENZIALE NEGATIVA E UNIFORME CONTINUA 1) La pressione del sangue segue una distribuzione
DISTRIBUZIONI DI PROBABILITA
 DISTRIBUZIONI DI PROBABILITA La distribuzione di probabilità e un modello matematico, uno schema di riferimento, che ha caratteristiche note e che può essere utilizzato per rispondere a delle domande derivate
DISTRIBUZIONI DI PROBABILITA La distribuzione di probabilità e un modello matematico, uno schema di riferimento, che ha caratteristiche note e che può essere utilizzato per rispondere a delle domande derivate
Matematica Applicata L-A Definizioni e teoremi
 Definizioni e teoremi Settembre - Dicembre 2008 Definizioni e teoremi di statistica tratte dalle lezioni del corso di Matematica Applicata L- A alla facoltà di Ingegneria Elettronica e delle Telecomunicazioni
Definizioni e teoremi Settembre - Dicembre 2008 Definizioni e teoremi di statistica tratte dalle lezioni del corso di Matematica Applicata L- A alla facoltà di Ingegneria Elettronica e delle Telecomunicazioni
Distribuzioni di probabilità discrete. Prof.ssa Fabbri Francesca Classe 5C
 Distribuzioni di probabilità discrete Prof.ssa Fabbri Francesca Classe 5C Esempio Consideriamo un urna con 6 palline Verdi e 4 palline Gialle; estraiamo senza reimmissione 3 palline e valutiamo l evento:
Distribuzioni di probabilità discrete Prof.ssa Fabbri Francesca Classe 5C Esempio Consideriamo un urna con 6 palline Verdi e 4 palline Gialle; estraiamo senza reimmissione 3 palline e valutiamo l evento:
Scrivere su ogni foglio NOME e COGNOME. Le risposte devono essere giustificate sui fogli protocollo e riportate nel foglio RISPOSTE.
 Corso di Laurea Triennale in Matematica Corso di Calcolo delle Probabilità A. A. /5 prova scritta (//5(docenti G. Nappo, F. Spizzichino La prova scritta consiste nello svolgimento dei punti non facoltativi
Corso di Laurea Triennale in Matematica Corso di Calcolo delle Probabilità A. A. /5 prova scritta (//5(docenti G. Nappo, F. Spizzichino La prova scritta consiste nello svolgimento dei punti non facoltativi
Es.: una moneta viene lanciata 3 volte. X = n. di T nei primi 2 lanci Y = n. di T negli ultimi 2 lanci
 Es.: una moneta viene lanciata 3 volte. X = n. di T nei primi 2 lanci Y = n. di T negli ultimi 2 lanci X\Y 0 1 2 0 1/8 1/8 0 1/4 1 1/8 1/4 1/8 1/2 2 0 1/8 1/8 1/4 1/4 1/2 1/4 1 X e Y non sono indip. Se
Es.: una moneta viene lanciata 3 volte. X = n. di T nei primi 2 lanci Y = n. di T negli ultimi 2 lanci X\Y 0 1 2 0 1/8 1/8 0 1/4 1 1/8 1/4 1/8 1/2 2 0 1/8 1/8 1/4 1/4 1/2 1/4 1 X e Y non sono indip. Se
STATISTICA: esercizi svolti sulle VARIABILI CASUALI
 STATISTICA: esercizi svolti sulle VARIABILI CASUALI VARIABILI CASUALI 2 VARIABILI CASUALI. Variabili casuali generiche. Si supponga che un dado truccato, formato da sei facce contrassegnate dai numeri
STATISTICA: esercizi svolti sulle VARIABILI CASUALI VARIABILI CASUALI 2 VARIABILI CASUALI. Variabili casuali generiche. Si supponga che un dado truccato, formato da sei facce contrassegnate dai numeri
Laboratorio di Calcolo Paola Gallo
 Studio di una funzione Dopo aver calcolato limiti, massimi, minimi e flessi siamo in grado di stabilire noi quali estremi di variabilità e che passo dare alle mie x per poter visualizzare bene nel grafico
Studio di una funzione Dopo aver calcolato limiti, massimi, minimi e flessi siamo in grado di stabilire noi quali estremi di variabilità e che passo dare alle mie x per poter visualizzare bene nel grafico
7 - Distribuzione Poissoniana
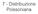 7 - Distribuzione Poissoniana Probabilita' (poissoniana) o densita' di probabilita' (gaussiana) 0.7 Poisson, λ=0.5 Gaussiana, µ=λ=0.5, σ= 0.6 0.5 0.4 0.3 0.2 0.1 0 0.5 0 0.5 1 1.5 2 2.5 3 3.5 4 n = numero
7 - Distribuzione Poissoniana Probabilita' (poissoniana) o densita' di probabilita' (gaussiana) 0.7 Poisson, λ=0.5 Gaussiana, µ=λ=0.5, σ= 0.6 0.5 0.4 0.3 0.2 0.1 0 0.5 0 0.5 1 1.5 2 2.5 3 3.5 4 n = numero
LA DISTRIBUZIONE NORMALE (Vittorio Colagrande)
 LA DISTRIBUZIONE NORMALE (Vittorio Colagrande) Allo scopo di interpolare un istogramma di un carattere statistico X con una funzione continua (di densità), si può far ricorso nell analisi statistica alla
LA DISTRIBUZIONE NORMALE (Vittorio Colagrande) Allo scopo di interpolare un istogramma di un carattere statistico X con una funzione continua (di densità), si può far ricorso nell analisi statistica alla
Facoltà di Ingegneria Calcolo delle Probabilità e Statistica Ingegneria Civile e A&T e Informatica
 Facoltà di Ingegneria Calcolo delle Probabilità e Statistica Ingegneria Civile e A&T e Informatica Prima prova scritta A.A. 8-9 Durata della prova h Punteggi: ) + + ; ) + + + ; ) +. Totale. Esercizio Sia
Facoltà di Ingegneria Calcolo delle Probabilità e Statistica Ingegneria Civile e A&T e Informatica Prima prova scritta A.A. 8-9 Durata della prova h Punteggi: ) + + ; ) + + + ; ) +. Totale. Esercizio Sia
Distribuzione Normale. Dott. Claudio Verona
 Distribuzione Normale Dott. Claudio Verona Rappresentazione di valori ottenuti da misure ripetute Il primo problema che si riscontra nelle misure ripetute più volte è trovare un metodo conveniente per
Distribuzione Normale Dott. Claudio Verona Rappresentazione di valori ottenuti da misure ripetute Il primo problema che si riscontra nelle misure ripetute più volte è trovare un metodo conveniente per
Probabilità e Statistica per l Informatica Esercitazione 4
 Probabilità e Statistica per l Informatica Esercitazione 4 Esercizio : [Ispirato all Esercizio, compito del 7/9/ del IV appello di Statistica e Calcolo delle probabilità, professori Barchielli, Ladelli,
Probabilità e Statistica per l Informatica Esercitazione 4 Esercizio : [Ispirato all Esercizio, compito del 7/9/ del IV appello di Statistica e Calcolo delle probabilità, professori Barchielli, Ladelli,
Modulo di Statistica e Tecnologia (Dott. Giorgio Poletti
 Laurea in Scienze dell Educazione Insegnamento di Pedagogia Sperimentale (Prof. Paolo Frignani) Modulo di Statistica e Tecnologia (Dott. Giorgio Poletti giorgio.poletti@unife.it) (discrete) variabile casuale
Laurea in Scienze dell Educazione Insegnamento di Pedagogia Sperimentale (Prof. Paolo Frignani) Modulo di Statistica e Tecnologia (Dott. Giorgio Poletti giorgio.poletti@unife.it) (discrete) variabile casuale
Esercitazione del 04/06/2015 Probabilità e Statistica Foglio 13
 Esercitazione del 04/06/2015 Probabilità e Statistica Foglio 13 David Barbato Approssimazioni normali. Theorem 1 (Teorema del limite centrale). Siano X 1,..., X n variabili aleatorie indipendenti ed identicamente
Esercitazione del 04/06/2015 Probabilità e Statistica Foglio 13 David Barbato Approssimazioni normali. Theorem 1 (Teorema del limite centrale). Siano X 1,..., X n variabili aleatorie indipendenti ed identicamente
Funzioni di probabilità per variabili casuali discrete e continue
 Funzioni di probabilità per variabili casuali discrete e continue Prof.ssa Antonella Bitetto Facoltà di Economia Aziendale, Dipartimento di Management Università degli Studi di Torino PER USO DIDATTICO
Funzioni di probabilità per variabili casuali discrete e continue Prof.ssa Antonella Bitetto Facoltà di Economia Aziendale, Dipartimento di Management Università degli Studi di Torino PER USO DIDATTICO
V.C. RETTANGOLARE o UNIFORME
 V.C. RETTANGOLARE o UNIFORME La v.c. continua RETTANGOLARE o UNIFORME descrive il modello probabilistico dell equiprobabilità. [ a b] X, con densità di probabilità associata: P( x) 1 b a con P(x) costante.
V.C. RETTANGOLARE o UNIFORME La v.c. continua RETTANGOLARE o UNIFORME descrive il modello probabilistico dell equiprobabilità. [ a b] X, con densità di probabilità associata: P( x) 1 b a con P(x) costante.
Variabile casuale E 6 E 5 E 4. R S x1 E 2
 Variabile casuale Una Variabile Casuale X è una regola (funzione reale) che associa ad E (evento elementare di S) uno ed un solo numero reale. Notazione: X: variabile casuale : realizzazione di una variabile
Variabile casuale Una Variabile Casuale X è una regola (funzione reale) che associa ad E (evento elementare di S) uno ed un solo numero reale. Notazione: X: variabile casuale : realizzazione di una variabile
Esercizi di Probabilità e Statistica
 Esercizi di Probabilità e Statistica Samuel Rota Bulò 2 aprile 200 Funzioni di v.a., Media e Varianza Esercizio Calcolare la media delle distribuzioni binomiale, e quella di Poisson. Di quest ultima calcolare
Esercizi di Probabilità e Statistica Samuel Rota Bulò 2 aprile 200 Funzioni di v.a., Media e Varianza Esercizio Calcolare la media delle distribuzioni binomiale, e quella di Poisson. Di quest ultima calcolare
