18.1 Applicazioni lineari tra spazi di dimensione finita. i=1. i=1. 1,...,x 00 n), allora[v 0 + v 00 ] B =(x x 00. i=1. i=1
|
|
|
- Ernesto Morini
- 4 anni fa
- Visualizzazioni
Transcript
1 Lezione 8 8. Applicazioni lineari tra spazi di dimensione finita Siano V e W spazi vettoriali su K = R, C ed f : V! W un applicazione K lineare. Supponiamo che V sia finitamente generato: allora sappiamo che Im(f) èasuavolta finitamente generato per il punto (iii) della Proposizione 7.3. Per questo motivo, qualora il dominio di un applicazione lineare sia finitamente generato, a patto di cambiare opportunamente il codominio si può supporre che anch esso sia finitamente generato. Il seguente risultato afferma che, per descrivere un applicazione lineare definita su uno spazio vettoriale finitamente generato, è sufficiente avere un numero finito di informazioni. Proposizione 8.. Siano V e W spazi vettoriali finitamente generati su K = R, C. Sia B =(v,...,v n ) una base di V. Dati w,...,w n 2 W esiste un unica applicazione K lineare f : V! W tale che f(v i )=w i per i =,...,n. Dimostrazione. Supponiamo che una tale f esista. Essendo f lineare se v 2 V e [v] B =(x,...,x n ) si deve avere X n nx nx f(v) =f x i v i = x i f(v i )= x i w i, (8..) da cui segue immediatamente l unicità Verifichiamo che la formula (8..) definisce un applicazione K lineare f soddisfacente la tesi. Chiaramente [v i ] B = e i 2 K n, dunque f(v i ) = w i, i =,...,n. Se poi 2 K si ha [ v] B =( x,..., x n ),dunque nx X n f( v) = ( x i )w i = x i w i = f(v). Se v,v 2 V e [v ] B =(x,...,x n), [v ] B =(x,...,x n), allora[v + v ] B =(x + x,...,x n + x n) erisulta nx nx nx f(v + v )= (x i + x i )w i = x iw i + x i w i = f(v )+f(v ). Concludiamo che f è un applicazione K lineare. Dalla Proposizione 8. deduciamo che se due applicazioni lineari coincidono sugli elementi di una base del dominio, esse coincidono ovunque, come spiegato nel seguente risultato. 85
2 O / 86 Corollario 8.2. Siano V e W spazi vettoriali finitamente generati su K = R, C e sia B =(v,...,v n ) una base di V.Allora: (i) se f,g: V! W sono K lineari e tali che f(v i )=g(v i ) per i =,...,n,allora f = g; (ii) se h: V! W è K lineare e tale che h(v i )= W h = V,W. per i =,...,n,allora Diamo ora alcuni esempi di applicazione della Proposizione e del Corollario di cui sopra. Esempio 8.3. In R 3 siano dati v =(,, ), v 2 =(,, ), v 3 =(2,, ). Fissiamo poi w =(, ), w 2 =(, ), w 3 =(, 2) in R 2. Si verifichi che B =(v,v 2,v 3 ) èunabasedir 3 : segue dalla Proposizione 8. che esiste un unica applicazione lineare f : R 3! R 2 tale che f(v i )=w i, i =, 2, 3. Poiché (x, y, z) =yv +( x +3y 2z) v 2 +(x 2y + z) v 3, segue che f(x, y, z) =f(yv +( x +3y 2z)v 2 +(x 2y + z)v 3 ) = yw +( x +3y 2z)w 2 +(x 2y + z)w 3 =(x 2y +2z,2x 3y +2z). Esempio 8.4. In R 3 siano dati v =(,, ), v 2 =(,, ), v 3 =(2,, ), v 4 =(4,, ). Fissiamo poi w =(, ), w 2 =(, ), w 3 =(, 2), w 4 =(, 3) in R 2. È chiaro che v,v 2,v 3,v 4 non possono formare una base di R 3,quindinon possiamo applicare direttamente la Proposizione 8.. Tuttavia, dall esempio precedente, sappiamo che esiste un unica applicazione lineare f : R 3! R 2 tale che f(v i )=w i per i =, 2, 3: sidevestabiliresevaleanche f(v 4 )=w 4.Atalescopo,outilizziamolaformulagiàottenutaperf, oppureosserviamo che v 4 = v + v 2 + v 3 :dunqueaffinchéf(v 4 )=w 4 si deve avere la relazione w 4 = f(v 4 )=f(v + v 2 + v 3 )=f(v )+f(v 2 )+f(v 3 )=w + w 2 + w 3, che è di immediata verifica. Cosa si può affermare se si sostituisce w 4 con w 4 =(, )? Prendiamo adesso in considerazione il caso degli isomorfismi, sempre tra spazi vettoriali di dimensione finita. Proposizione 8.5. Siano V e W spazi vettoriali finitamente generati su un campo K = R, C. AlloraV = W se e solo se dim K (V )=dim K (W ). Dimostrazione. Siano f : V! W un isomorfismo e B =(v,...,v n ) e D =(w,...,w m ) basi di V e W rispettivamente. Consideriamo il seguente diagramma V f / W (8..2) [ ] B K n g K m [ ] D
3 / O 87 dove la mappa g èdatadallacomposizione g =[ ] D f [ ] B : Kn! K m. Essendo composizione di applicazioni lineari biettive, g èlineareebiettiva,quindièunisomorfismo. Poiché g = µ A per una qualche A 2 K m,n,comemostratonell Esempio7.4,deduciamochen = m dall Esempio Viceversa, supponiamo che dim K (V )=dim K (W ) esianob =(v,...,v n ) e D =(w,...,w n ) basi di V e W rispettivamente. Possiamo considerare il diagramma (8..2) nel caso particolare in cui n = m e g = id K n èl applicazioneidentità;invertendoilsensodellefrecceverticalitroviamo V [ ] B f W [ ] D K n id K n / K n Allora V = W,poichél applicazione f =[ ] D id K n [ ] B : V! W, essendo composizione di isomorfismi, è essa stessa un isomorfismo. Esempio 8.6. Riprendiamo in considerazione i sottospazi TS n (K) (matrici triangolari superiori) e Sim n (K) (matrici simmetriche) di K n,n, K = R, C. Nell Esempio 6.2 abbiamo calcolato che dim K (TS n (K)) = n(n +)/2. Sia A 2 K n,n ;alloraa + t A 2 Sim n (K) ed è definita l applicazione f : TS n (K)! Sim n (K) A 7! A + t A. Più in dettaglio, se A =(a i,j ) 6i,j6n,alloraf(A) =B =(b i,j ) 6i,j6n 2 Sim n (K) dove 8 >< a i,j se i<j, b i,j = 2a i,i se i = j, (8..3) >: se i>j. Chiaramente f è K lineare: in fatti se 2 K e A, A,A 2 TS n (K) risulta a j,i f( A) = A + t ( A) = A + t A = (A + t A)= f(a), f(a + A )=A + A + t (A + A )=A + A + t A + t A = A + t A + A + t A = f(a )+f(a ). Dimostriamo che f èunisomorfismo.datab =(b i,j ) 6i,j6n 2 Sim n (K), risulta B = f(a) con A =(a i,j ) 6i,j6n 2 TS n (K) definita da 8 >< b i,j se i<j, a i,j = b i,i /2 se i = j, >: se i>j,
4 O O / 88 quindi f èsuriettiva. Inoltre f èiniettiva,cioèker(f) ={ n,n }:sea =(a i,j ) 6i,j6n 2 TS n (K) ètale che f(a) = n,n,dallarelazione(8..3)seguechea i,j ==2a i,i,ovveroa = n,n. La Proposizione 8.5 garantisce dunque che come anticipato nell Esempio 6.3 dim K (Sim n (K)) = dim K (TS n (K)) = n(n+) 2, Similmente si consideri l insieme delle matrici antisimmetriche di K n,n Alt n (K) ={ A 2 K n,n t A = A }. Si verifichi che Alt n (K) èunsottospaziovettorialedik n,n echel applicazione g : STS n (K) A 7! A! Alt n (K) t A èunisomorfismo:inparticolare dim K (Alt n (K)) = dim K (STS n (K)) = n(n ) Matrice di un applicazione lineare Siano V e W spazi vettoriali finitamente generati su un campo K = R, C esiano B =(v,...,v n ) e D =(w,...,w m ) basi di V e W rispettivamente. Come abbiamo visto nella dimostrazione della Proposizione 8.5, invece di studiare direttamente una certa applicazione K lineare f : V! W,puòrisultarepiùagevolecomporla con opportuni isomorfismi con spazi vettoriali semplici come K n e K m estudiare al suo posto l applicazione K lineare composta K n! K m utilizzando quanto visto negli Esempi 7.4 e Nella dimostrazione della Proposizione 8.5 abbiamo visto che a un applicazione K lineare f : V! W possiamo associare il diagramma (8..2), cioè V [ ] B K n f g / W K m [ ] D dove, per definizione, g èl applicazionek lineare g =[ ] B f [ ] D. Dall Esempio 7.4 segue l esistenza di una matrice A 2 K m,n tale che l applicazione g del diagramma sia della forma µ A,lamoltiplicazioneperA: [ ] B V f / W [ ] D K n µ A / K m (8.2.)
5 La matrice A dipende sia dall applicazione f che dalle basi B e D. Sinoti che le colonne di A sono µ A (E j, )=([ ] D f [ ] B )(E j,): poiché [ ] B (E j,) =v j, segue che le colonne di A non sono altro che ([ ] D f)(v j )=[f(v j )] D :cioèlaj esima colonna di A èformatadallecomponentirispettoallabasefissatanelcodominiodi f (disposte in colonna!) del j esimo vettore della base fissata nel dominio di f. Definizione 8.7 (Matrice di un applicazione lineare). Siano V e W spazi vettoriali finitamente generati su un campo K = R, C esianob =(v,...,v n ) e D =(w,...,w m ) basi di V e W rispettivamente. Se f : V! W èun applicazionek lineare, definiamo matrice di f rispetto alle basi B e D la matrice MD B (f) avente per colonne le componenti delle immagini dei vettori di B rispetto a D. 89 B Nel caso in cui V = K n e W = K m,lamatricedif non è altro che la matrice di f rispetto alle basi canoniche nel senso della definizione data sopra. In particolare quindi M C C (µ A)=A. Esempio 8.8. Sia W uno spazio vettoriale di dimensione 2 su R, dotato di una base D =(w,w 2 ),esiconsideril applicazione f : R 3! W (x, y, z) 7! xw +(2y + z)w 2. Detta C =(e,e 2,e 3 ) la base canonica di R 3,lamatriceMD C (f) èunamatrice2 3 le cui colonne sono [f(e i )] D.Sihache f(e )=w, f(e 2 )=2w 2, f(e 3 )=w 2, quindi le coordinate di tali vettori sono [f(e )] D =(, ) =, [f(e 2 )] D =(, 2) =, [f(e 2 3 )] D =(, ) = elamatricecercataè M C D(f) =. 2 Esempio 8.9. Si consideri l applicazione Se 2 R e p (x),p 2 (x) 2 R[x],siha f : R[x]! R[x] 2 p(x) 7! xp(x). f( p(x)) = x( p(x)) = (xp(x)) = f(p(x)), f(p (x)+p 2 (x)) = x(p (x)+p 2 (x)) = xp (x)+xp 2 (x) =f(p (x)) + f(p 2 (x)), quindi f è R lineare.
6 O! > 9 M B D Consideriamo le basi B =(,x) in R[x] e D =(,x,x 2 ) in R[x] 2 edeterminiamo (f). Risulta [f()] D =[x] D =(,, ) A, [f(x)] D =[x 2 ] D =(,, ) A, quindi MD(f) B A. Si noti che [f(a + bx)] D = M B D (f)[a + bx] B. Osservazione 8.. Alla luce della definizione di matrice associata ad un applicazione lineare, la Proposizione 7.3 può essere interpretata dicendo che dati V e W spazi vettoriali su K = R, C e f : V! W un applicazione K lineare, l immagine Im(f) èilsottospaziodiw generato dai vettori le cui componenti sono le colonne della matrice M B D (f), doveb =(v,...,v n ) e D =(w,...,w m ) sono basi di V e W rispettivamente. Osservazione 8.. Una conseguenza diretta della definizione e dell Osservazione 7. è che la matrice associata ad un applicazione lineare si comporta bene rispetto alla composizione di applicazioni: siano infatti U, V, W spazi vettoriali finitamente generati su K = R, C di dimensioni p, n,m rispettivamente, dotati di basi A, B, D rispettivamente. Siano g : U! V, f : V! W due applicazioni K lineari con matrici associate MB A(g) e M D B (f). Alloralamatriceassociataallacomposizione f g : U! W rispetto alle basi A di U e D di W è M A D (f g) =M B D(f)M A B (g), come si può dedurre anche dal seguente diagramma commutativo U [ ] A K p g / µ M A(g) B f g / VO [ ] B [ ] B f K n / µ M B (f) D / W [ ] D K m. µ M A D (f g) Un altra conseguenza immediata è che se f : V! W èinvertibile,allora M D B (f )=(M B D(f)).
7 9 Tenendo conto che dal diagramma (8.2.) segue che g = ([ ] D f [ ] B ), otteniamo la seguente serie di affermazioni equivalenti: X 2 Ker(g) K n, g(x) = K m, ([ ] D f [ ] B )(X) = K m, [f(v)] D =([ ] D f)(v) = K m, dove v =[ ] B (X),, f(v) =([ ] D [ ] D f)(v) =[ ] D ( K m)= W, v 2 Ker(f) V. In particolare, restringendo [ ] B a Ker(g), otteniamounisomorfismofraker(g) e Ker(f). Similmente,restringendo[ ] B a Im(f) otteniamo un isomorfismo fra Im(f) e Im(g). Posto A = MD B(f), risultag = µ A e, quindi, dalla Proposizione 6.4 segue dim K (Im(f)) = dim K (Im(µ A )) = rk(a), dim K (Ker(f)) = dim K (Ker(µ A )) = n rk(a). In particolare abbiamo immediatamente il seguente risultato, spesso chiamato Teorema della dimensione: esso non è altro che il Teorema di Rouché Capelli, o Proposizione 5.2 Proposizione 8.2 (Teorema della dimensione). Siano V e W spazi vettoriali finitamente generati su K = R, C. Sef : V! W èun applicazionek lineare si ha dim K (V )=dim K (Ker(f)) + dim K (Im(f)). Corollario 8.3. Siano V e W spazi vettoriali finitamente generati su K = R, C esiaf : V! W un applicazione K lineare. (i) Se f èiniettiva,alloradim K (V ) 6 dim K (W ); (ii) se f èsuriettiva,alloradim K (V ) > dim K (W ). Quanto visto sopra ci permette di studiare un applicazione lineare tra spazi vettoriali di dimensione finita in modo più facile, studiandola cioè tramite la sua matrice rispetto a basi fissate (che possiamo scegliere comode ). Esempio 8.4. Il lettore verifichi che l applicazione f : R[x] 2! R 2,2 a + b a+ c a + bx + cx 2 7! b c b c èlineare. Fissiamo le basi B = (,x,x 2 ) e D = (E,,E,2,E 2,,E 2,2 ) in R[x] 2 e R 2,2 rispettivamente. Poiché [f()] D = apple D =(,,, ), [f(x)] D = apple D =(,,, ),
8 92 [f(x 2 )] D = apple segue che la matrice di A rispetto alle basi B e D è A = B A. Possiamo calcolare D =(,,, ), dim(ker(f)) = dim(ker(µ A )) = 3 rk(a) =, dim(im(f)) = dim(im(µ A )) = rk(a) =2, da cui deduciamo che f non è né iniettiva né suriettiva. Se vogliamo studiare Ker(f) ed Im(f) più in dettaglio, possiamo studiare Ker(µ A ) e Im(µ A ).RisolvendoilsistemaAX = 4, otteniamo quindi Ker(µ A )={ (a, a, a) a 2 R }, Ker(f) ={ p(x) 2 R[x] 2 [p(x)] B 2 Ker(µ A ) } = { a ax ax 2 a 2 R } = L x x 2. In particolare dim R (Ker(f)) =, comegiàvistosopra. Una conseguenza immediata è che 2,2 = f( x x 2 )=f() f(x) f(x 2 ) ovvero f(x 2 )=f() f(x), quindi Im(f) =L f(),f(x),f(x 2 ) = L f(),f(x). Poiché f(x) 62 L(f()), seguechedim R (Im(f)) = 2, comegiàvistosopra. Esempio 8.5. Nell Esempio 7.2 abbiamo verificato che, se ~v 2 V 3 (O) èun vettore fissato, risulta Im( ~v )={ ~w 2 V 3 (O) 9~v 2 V 3 (O) tale che ~w = ~v ~v } ~v? = { ~w 2 V 3 (O) h~w, ~v i =} Se ~v = ~, alloraim( ~v )=L(~); se,invece,~v 6= ~, ancora l Esempio 7.2 ci permette di affermare che dim R (Ker( ~v )) =, dunque la Proposizione 8.2 implica dim R (Im( ~v )) = 2. D altraparte~v? èunsottospaziodiv 3 (O) (il lettore lo verifichi per esercizio) non contenente ~v : poiché dim R (V 3 (O)) = 3 segue che dim R (~v? ) 6 2. Essendo Im( ~v ) ~v? segue allora che deve valere l uguaglianza, come anticipato. Si noti che, fissato un sistema di riferimento ~ı~ı ~ k,risulta~v = a~ı + b~ı + c ~ k. La matrice di ~v rispetto alla stessa base B =(~ı, ~ı, ~ k) fissata nel dominio e codominio è c b A c a A. b a
9 Esempio 8.6. Si considerino v =(, 2, ), v 2 =(,, ), v 3 =(,, 2) in R 3 e A =, A 2 2 =, A 3 = 3 93 in R 2,2.Poichérisulta 2 2 A =rk@ A =3, 2 segue che v,v 2,v 3 sono linearmente indipendenti, quindi per la Proposizione 6.7 si ha che B =(v,v 2,v 3 ) èunabasedir 3. Per la Proposizione 8. esiste un unica applicazione lineare f : R 3! R 2,2 tale che f(v i )=A i, i =, 2, 3. Vogliamo studiare tale applicazione: a tale scopo scriviamone la matrice rispetto a basi opportunamente scelte nel dominio e nel codominio. Nel dominio abbiamo varie scelte possibili, ad esempio la base canonica C. Per semplificare al massimo la forma della matrice e, di conseguenza, i calcoli, la scelta migliore è, però, quella di prendere la base B =(v,v 2,v 3 ). Anche nel codominio possiamo fare molte scelte lecite: potremmo ad esempio prendere la base E =(E,,E,2,E 2,,E 2,2 ),mapersemplificarealmassimoiconti una scelta migliore è D =(A,A 2,E,2,E 2, ) (verificare, per esercizio, che D èbase di R 2,2 ). Si ha f(v )=A =A +A 2 +E,2 +E 2, ) [f(v )] D =(,,, ), f(v 2 )=A 2 =A +A 2 +E,2 +E 2, ) [f(v 2 )] D =(,,, ), f(v 3 )=A 3 =A +A 2 +E,2 +E 2, ) [f(v 3 )] D =(,,, ), quindi M = MD(f) B = B A. Èfacilevederedallamatricecheglielementie,e 2 della base canonica di R 4 formano una base di Im(µ M ) R 4.QuindiA =[ ] D (e ), A 2 =[ ] D (e 2), formano una base (A,A 2 ) di Im(f). Inoltre Ker(µ M ) ègeneratodalsingolovettoree =(,, ): dalmomentoche (, 2, ) = v + v 2 v 3 =[ ] (e), seguecheker(f) ègeneratodalvettore(, 2, ). B Per esercizio si calcoli ME C(f): siverifichichem E C(f) 6= M D B (f) echeprocedendo come fatto sopra con la matrice ME C(f) in luogo di M D B (f) si riottengono gli stessi risultati.
10 Endomorfismi Proposizione 8.7. Siano V e W spazi vettoriali finitamente generati su K = R, C con dim K (V )=dim K (W ). Siaf : V! W un applicazione lineare. Le seguenti affermazioni sono equivalenti: f èiniettiva, f èsuriettiva, f èunisomorfismo. Dimostrazione. Per definizione, se f è un isomorfismo è sia iniettiva che suriettiva. Supponiamo f sia iniettiva, quindi che dim K (Ker(f)) = : per la Proposizione 8.2 e per l ipotesi segue allora che dim K (W )=dim K (V )=dim K (Im(f)), quindiperlaproposizione6.9 Im(f) =W,cioèf èanchesuriettiva,equindièunisomorfismo. Se f èsuriettiva,alloradim K (V )=dim K (W )=dim K (Im(f)), quindidim K (Ker(f)) = per la Proposizione 8.2, cioè f èancheiniettiva,quindièunisomorfismo. Vediamo ora un esempio che illustra l utilità della precedente proposizione. Esempio 8.8. Si consideri l applicazione f : C 3! C[x] 2 (a, b, c) 7! a +(a + b)x +(a + b + c)x 2. Si ha che (a, b, c) 2 Ker(f) se e solo se a +(a + b)x +(a + b + c)x 2 =se e solo se a = a + b = a + b + c =,cioèseesolose(a, b, c) =(,, ): quindif èiniettiva. Grazie alla Proposizione 8.7 possiamo concludere che f è un isomorfismo senza doverne studiare la suriettività. Ad un analogo risultato si poteva arrivare osservando che la matrice di f rispetto alla base canonica di C 3 ed alla base (,x,x 2 ) di C[x] 2 è A A, che è invertibile. Consideriamo adesso un applicazione lineare da uno spazio vettoriale in se stesso. Definizione 8.9 (Endomorfismi). Sia V uno spazio vettoriale su K = R, C. Un endomorfismo di V èun applicazionelinearef : V! V. Chiaramente la Proposizione 8.7 si applica, in particolare, agli endomorfismi di spazi vettoriali finitamente generati. Tuttavia essa non è valida se si lavora con uno spazio non finitamente generato: esistono endomorfismi suriettivi ma non iniettivi, oviceversainiettivimanonsuriettivi,comemostranoiseguentiesempi.
11 Esempio 8.2. Sia I =]a, b[ R un intervallo aperto non vuoto. Nell Esempio 7.8 abbiamo osservato che l applicazione D : C (I)!C (I) èlineare,quindièun endomorfismo. Tale applicazione non è iniettiva, ma è suriettiva per un ben noto risultato di analisi. Esempio 8.2. Sia K = R, C esiconsideril applicazione f : K[x]! K[x] p(x) 7! xp(x). 95 Si verifichi che f è lineare (e quindi un endomorfismo). Chiaramente f èiniettiva, ma non è suriettiva, perché i polinomi costanti non sono in Im(f). Un caso particolarmente importante di endomorfismo è l identità in uno spazio vettoriale finitamente generato V su K = R, C. Definizione 8.22 (Matrice del cambiamento di base). Siano V uno spazio vettoriale su K = R, C e B =(v,...,v n ) e D =(w,...,w n ) due basi di V. La matrice M B D (id V ) avente per colonne le componenti dei vettori di B rispetto a D èdettamatrice del cambiamento di base da B a D. Osserviamo subito che per ogni vettore v 2 V vale la relazione [v] D = M B D(id V )[v] B. Un modo per ricordarsi la definizione è vedere la relazione sopra come una specie di cancellazione in croce: [v] D = M B D(id V )[v] B. Si noti anche che vale la relazione M B D(id V )=(M D B (id V )). Esempio Si consideri lo spazio vettoriale V = R 3,siaC =(e,e 2,e 3 ) la sua base canonica e siano B =(v,v 2,v 3 ) e D =(w,w 2,w 3 ) altre due basi, dove 2 v A, v 2 A, v 3 2A w A, w 2 2A, w 3 A. 3 Il lettore verifichi che si tratta in effetti di vettori indipendenti. Le matrici di cambiamento di base più semplici da scrivere sono quelle di passaggio dalle basi B e D aquellacanonica,semplicementeperchéabbiamogiàle componenti dei loro vettori rispetto a C. Sihache 2 MC B (id V )=@ 2 A, MC D (id V )=@ 2 A. 3
12 96 Per calcolare le matrici di cambiamento di base dalla canonica C alle nuove basi B e D dobbiamo invece fare un po più fatica. Cominciamo da MB C(id V ): possiamo direttamente la definizione e calcolare le componenti [e i ] B esplicitamente, oppure possiamo usare l Osservazione 8. e ricordarci che MB(id C V )=(MC B (id V )) 2 A. Il lettore verifichi il calcolo dell inversa e trovi la matrice M C D (id V ). Passiamo adesso a calcolare la matrice di cambiamento di base M D B (id V ): di nuovo, grazie alll Osservazione 8. si ha che MB D (id V )=MB(id C V )M D (id C V ) A A Lasciamo al lettore la verifica che MD(id B V )=MD(id C V )M B (id C V ) =(MC D (id V )) MC B (id V )=@ 3/2 /2 /2 /2 /2 5/2 A. 2 3 B Testi diversi utilizzano notazioni e nomi diversi per la matrice di cambiamento di base, ad esempio A B!D, [T ] BD emoltealtre. Segnaliamoallettorechepurtroppo alcuni testi usano anche la notazione MB D per intendere la matrice di cambio di base da D a B, ovveroesattamentel inversadellanostra.
LEZIONE 21 [ ] D [ ] 1. k n. k m. k n,1 k m,1
![LEZIONE 21 [ ] D [ ] 1. k n. k m. k n,1 k m,1 LEZIONE 21 [ ] D [ ] 1. k n. k m. k n,1 k m,1](/thumbs/92/110228368.jpg) LEZIONE 21 21.1. Matrice di un applicazione lineare. Siano V e W spazi vettoriali su k = R, C finitamente generati e siano = (v 1,..., v n ) e = (w 1,..., w m ) basi di V e W rispettivamente. Come abbiamo
LEZIONE 21 21.1. Matrice di un applicazione lineare. Siano V e W spazi vettoriali su k = R, C finitamente generati e siano = (v 1,..., v n ) e = (w 1,..., w m ) basi di V e W rispettivamente. Come abbiamo
LEZIONE 17. B : kn k m.
 LEZIONE 17 17.1. Isomorfismi tra spazi vettoriali finitamente generati. Applichiamo quanto visto nella lezione precedente ad isomorfismi fra spazi vettoriali di dimensione finita. Proposizione 17.1.1.
LEZIONE 17 17.1. Isomorfismi tra spazi vettoriali finitamente generati. Applichiamo quanto visto nella lezione precedente ad isomorfismi fra spazi vettoriali di dimensione finita. Proposizione 17.1.1.
APPLICAZIONI LINEARI
 APPLICAZIONI LINEARI Fra le applicazioni definite tra spazi vettoriali sono particolarmente significative quelle che conservano le operazioni, dette applicazioni lineari. Definizione Siano V, W due k-s.v.
APPLICAZIONI LINEARI Fra le applicazioni definite tra spazi vettoriali sono particolarmente significative quelle che conservano le operazioni, dette applicazioni lineari. Definizione Siano V, W due k-s.v.
LEZIONE 12. Y = f(x) = f( x j,1 f(e j ) = x j,1 A j = AX = µ A (X),
 LEZIONE 1 1.1. Matrice di un applicazione lineare. Verifichiamo ora che ogni applicazione lineare f: R n R m è della forma µ A per un unica A R m,n. Definizione 1.1.1. Per ogni j 1,..., n indichiamo con
LEZIONE 1 1.1. Matrice di un applicazione lineare. Verifichiamo ora che ogni applicazione lineare f: R n R m è della forma µ A per un unica A R m,n. Definizione 1.1.1. Per ogni j 1,..., n indichiamo con
CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI A.A. 2018/2019 PROF. VALENTINA BEORCHIA
 CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Matrici associate a un applicazione lineare 1 2 Cambiamenti di base 4 3 Diagonalizzazione 6 1 MATRICI ASSOCIATE
CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Matrici associate a un applicazione lineare 1 2 Cambiamenti di base 4 3 Diagonalizzazione 6 1 MATRICI ASSOCIATE
Algebra lineare e geometria AA Appunti sul cambio di base in uno spazio vettoriale
 Algebra lineare e geometria AA. 8-9 Appunti sul cambio di base in uno spazio vettoriale Matrice di un applicazione lineare Siano V e W due spazi vettoriali su un campo K {R, C}, entrambi finitamente generati,
Algebra lineare e geometria AA. 8-9 Appunti sul cambio di base in uno spazio vettoriale Matrice di un applicazione lineare Siano V e W due spazi vettoriali su un campo K {R, C}, entrambi finitamente generati,
Soluzione degli esercizi di algebra lineare (del 26 ottobre 2018)
 Soluzione degli esercizi di algebra lineare (del 26 ottobre 28) Esercizio. Siano V un K-spazio vettoriale con base B = (v,..., v n ) e W un K-spazio vettoriale con base C = (w,..., w m ), e sia f : V W
Soluzione degli esercizi di algebra lineare (del 26 ottobre 28) Esercizio. Siano V un K-spazio vettoriale con base B = (v,..., v n ) e W un K-spazio vettoriale con base C = (w,..., w m ), e sia f : V W
APPLICAZIONI LINEARI
 APPLICAZIONI LINEARI Esercizi Esercizio Date le seguenti applicazioni lineari f : R 2 R 3 definita da fx y = x 2y x + y x + y; 2 g : R 3 R 2 definita da gx y z = x + y x y; 3 h : Rx] 2 R 2 definita da
APPLICAZIONI LINEARI Esercizi Esercizio Date le seguenti applicazioni lineari f : R 2 R 3 definita da fx y = x 2y x + y x + y; 2 g : R 3 R 2 definita da gx y z = x + y x y; 3 h : Rx] 2 R 2 definita da
ENDOMORFISMI. ove B := (v 1,v 2,v 3 ). (1) Determinare gli autovalori di f e le relative molteplicità algebriche e geometriche.
 ENDOMORFISMI Esercizi Esercizio 1 Siano v 1 := T (1, 1, 1, 0), v 2 := T (0, 1, 2, 1), v 3 := T (0, 0, 1, 1) Consideriamo V := L(v 1,v 2,v 3 ) R 4 e sia f End R (V ) associato alla matrice A := MB B (f)
ENDOMORFISMI Esercizi Esercizio 1 Siano v 1 := T (1, 1, 1, 0), v 2 := T (0, 1, 2, 1), v 3 := T (0, 0, 1, 1) Consideriamo V := L(v 1,v 2,v 3 ) R 4 e sia f End R (V ) associato alla matrice A := MB B (f)
Algebra Lineare. a.a Gruppo A-H. Prof. P. Piazza Soluzioni del compito pomeridiano del 6/12/2004
 Algebra Lineare. a.a. 004-05. Gruppo A-H. Prof. P. Piazza Soluzioni del compito pomeridiano del 6/1/004 Esercizio 1. Siano V e W due spazi vettoriali e sia F : V W un isomorfismo (quindi F è lineare e
Algebra Lineare. a.a. 004-05. Gruppo A-H. Prof. P. Piazza Soluzioni del compito pomeridiano del 6/1/004 Esercizio 1. Siano V e W due spazi vettoriali e sia F : V W un isomorfismo (quindi F è lineare e
GEOMETRIA 1 terza parte
 GEOMETRIA 1 terza parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 32 index Applicazioni lineari 1 Applicazioni lineari 2 Nucleo e
GEOMETRIA 1 terza parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 32 index Applicazioni lineari 1 Applicazioni lineari 2 Nucleo e
Algebra lineare e geometria AA Appunti sul cambio di base in uno spazio vettoriale
 Algebra lineare e geometria AA. -7 Appunti sul cambio di base in uno spazio vettoriale Matrice di un applicazione lineare Siano V e W due spazi vettoriali su un campo K {R, C}, entrambi finitamente generati,
Algebra lineare e geometria AA. -7 Appunti sul cambio di base in uno spazio vettoriale Matrice di un applicazione lineare Siano V e W due spazi vettoriali su un campo K {R, C}, entrambi finitamente generati,
Geometria e Topologia I 18 maggio
 Geometria e Topologia I 18 maggio 2005 64 17 Mappe affini (17.1) Definizione. Siano X e Y due spazi affini sullo stesso campo K. Una funzione f : X Y si dice affine (anche, mappa affine o trasformazione
Geometria e Topologia I 18 maggio 2005 64 17 Mappe affini (17.1) Definizione. Siano X e Y due spazi affini sullo stesso campo K. Una funzione f : X Y si dice affine (anche, mappa affine o trasformazione
LEZIONE 16. Proposizione 16.1.2. Siano V e W spazi vettoriali su k = R, C. Se f: V W
 LEZIONE 16 16.1. Applicazioni lineari iniettive e suriettive. Ricordo le seguenti due definizioni valide per applicazioni di qualsiasi tipo ϕ: X Y fra due insiemi. L applicazione ϕ si dice iniettiva se
LEZIONE 16 16.1. Applicazioni lineari iniettive e suriettive. Ricordo le seguenti due definizioni valide per applicazioni di qualsiasi tipo ϕ: X Y fra due insiemi. L applicazione ϕ si dice iniettiva se
Foglio di esercizi numero 2 Corso di Fondamenti di Algebra Lineare e Geometria Ingegneria Aerospaziale e Meccanica
 Foglio di esercizi numero 2 Corso di Fondamenti di Algebra Lineare e Geometria Ingegneria Aerospaziale e Meccanica Esercizio 1. Sia f l endomorfismo di R 4 definito nel modo seguente: f(x, y, z, w) = (w,
Foglio di esercizi numero 2 Corso di Fondamenti di Algebra Lineare e Geometria Ingegneria Aerospaziale e Meccanica Esercizio 1. Sia f l endomorfismo di R 4 definito nel modo seguente: f(x, y, z, w) = (w,
CORSO DI MATEMATICA II Prof. Paolo Papi ESERCIZI. 1). Stabilire quali dei seguenti sottoinsiemi di V sono sottospazi vettoriali. (a) V = R 3.
 CORSO DI MATEMATICA II Prof Paolo Papi ESERCIZI ) Stabilire quali dei seguenti sottoinsiemi di V sono sottospazi vettoriali (a) V = R 3 () W = {(x,,x 3 ) x,x 3 R} (2) W 2 = {(x,,x 3 ) x,x 3 R} (3) W 3
CORSO DI MATEMATICA II Prof Paolo Papi ESERCIZI ) Stabilire quali dei seguenti sottoinsiemi di V sono sottospazi vettoriali (a) V = R 3 () W = {(x,,x 3 ) x,x 3 R} (2) W 2 = {(x,,x 3 ) x,x 3 R} (3) W 3
0.1 Coordinate in uno spazio vettoriale
 0.. COORDINATE IN UNO SPAZIO VETTORIALE 0. Coordinate in uno spazio vettoriale Sia V uno spazio vettoriale di dimensione finita n costruito sul campo K. D ora in poi, ogni volta che sia fissata una base
0.. COORDINATE IN UNO SPAZIO VETTORIALE 0. Coordinate in uno spazio vettoriale Sia V uno spazio vettoriale di dimensione finita n costruito sul campo K. D ora in poi, ogni volta che sia fissata una base
SPAZI VETTORIALI CON PRODOTTO SCALARE A =
 SPAZI VETTORIALI CON PRODOTTO SCALARE Esercizi Esercizio. Nello spazio euclideo standard (R 2,, ) sia data la matrice 2 3 A = 3 2 () Determinare una base rispetto alla quale A sia la matrice di un endomorfismo
SPAZI VETTORIALI CON PRODOTTO SCALARE Esercizi Esercizio. Nello spazio euclideo standard (R 2,, ) sia data la matrice 2 3 A = 3 2 () Determinare una base rispetto alla quale A sia la matrice di un endomorfismo
Esempio. L immagine di f è l insieme dei vettori w = (w 1, w 2 ) R 2 che hanno w 1 = w 2. Quindi:
 Nucleo, immagine e loro proprietà [Abate, 5.2] Data una applicazione lineare f : V W, chiamiamo nucleo di f l insieme N(f) := { v V : f(v) = 0 W } Se S V è un sottoinsieme del dominio, indichiamo con f(s)
Nucleo, immagine e loro proprietà [Abate, 5.2] Data una applicazione lineare f : V W, chiamiamo nucleo di f l insieme N(f) := { v V : f(v) = 0 W } Se S V è un sottoinsieme del dominio, indichiamo con f(s)
APPLICAZIONI LINEARI O OMOMORFISMI
 42 APPLICAZIONI LINEARI O OMOMORFISMI Definizione 9 Dati due spazi vettoriali U e V sullo stesso campo K, una applicazione f : U V è detta lineare o omomorfismo se soddisfa le seguenti due condizioni:
42 APPLICAZIONI LINEARI O OMOMORFISMI Definizione 9 Dati due spazi vettoriali U e V sullo stesso campo K, una applicazione f : U V è detta lineare o omomorfismo se soddisfa le seguenti due condizioni:
Soluzioni primi compitini - Geometria 1
 Soluzioni primi compitini - Geometria Caterina Vernieri Ottobre 7 Le soluzioni proposte non sono state riviste dai professori Soluzioni Primi Compitini - G I compitino 7//3 Esercizio Al variare di α R
Soluzioni primi compitini - Geometria Caterina Vernieri Ottobre 7 Le soluzioni proposte non sono state riviste dai professori Soluzioni Primi Compitini - G I compitino 7//3 Esercizio Al variare di α R
Algebra lineare e geometria AA Esercitazione del 14/6/2018
 Algebra lineare e geometria AA. 2017-2018 Esercitazione del 14/6/2018 1) Siano A, B due matrici n n tali che 0 < rk(a) < rk(b) = n. (a) AB è invertibile. (b) rk(ab) = nrk(b). (c) det(ab) = det(a). (d)
Algebra lineare e geometria AA. 2017-2018 Esercitazione del 14/6/2018 1) Siano A, B due matrici n n tali che 0 < rk(a) < rk(b) = n. (a) AB è invertibile. (b) rk(ab) = nrk(b). (c) det(ab) = det(a). (d)
Esercizi Applicazioni Lineari
 Esercizi Applicazioni Lineari (1) Sia f : R 4 R 2 l applicazione lineare definita dalla legge f(x, y, z, t) = (x + y + z, y + z + t). (a) Determinare il nucleo di f, l immagine di f, una loro base e le
Esercizi Applicazioni Lineari (1) Sia f : R 4 R 2 l applicazione lineare definita dalla legge f(x, y, z, t) = (x + y + z, y + z + t). (a) Determinare il nucleo di f, l immagine di f, una loro base e le
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof. F.Podestà, a.a
 APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
Geometria I 2009-mag
 Geometria I 2009-mag-06 124 17 Mappe affini Cfr: Nacinovich, Cap V, 3 [3]. (17.1) Definizione. Siano X e Y due spazi affini sullo stesso campo K. Una funzione f : X Y si dice affine (anche, mappa affine
Geometria I 2009-mag-06 124 17 Mappe affini Cfr: Nacinovich, Cap V, 3 [3]. (17.1) Definizione. Siano X e Y due spazi affini sullo stesso campo K. Una funzione f : X Y si dice affine (anche, mappa affine
16.1 Dimensione di uno spazio vettoriale
 Lezione 6 6 Dimensione di uno spazio vettoriale Abbiamo visto nella lezione precedente come l esistenza di una base in uno spazio vettoriale V su un campo K permetta di sostituire a V,chepuòessere complicato
Lezione 6 6 Dimensione di uno spazio vettoriale Abbiamo visto nella lezione precedente come l esistenza di una base in uno spazio vettoriale V su un campo K permetta di sostituire a V,chepuòessere complicato
Corso di Laurea in Fisica. Geometria. a.a Canale 3 Prof. P. Piazza Magiche notazioni
 Corso di Laurea in Fisica. Geometria. a.a. 23-4. Canale 3 Prof. P. Piazza Magiche notazioni Siano V e W due spazi vettoriali e sia T : V W un applicazione lineare. Fissiamo una base B per V ed una base
Corso di Laurea in Fisica. Geometria. a.a. 23-4. Canale 3 Prof. P. Piazza Magiche notazioni Siano V e W due spazi vettoriali e sia T : V W un applicazione lineare. Fissiamo una base B per V ed una base
Applicazioni Lineari. Nota Bene: Questo materiale non deve essere considerato come sostituto delle lezioni.
 Politecnico di Torino. Applicazioni Lineari. Nota Bene: Questo materiale non deve essere considerato come sostituto delle lezioni. Argomenti: Basi e coordinate. Applicazioni lineari. Matrici come applicazioni
Politecnico di Torino. Applicazioni Lineari. Nota Bene: Questo materiale non deve essere considerato come sostituto delle lezioni. Argomenti: Basi e coordinate. Applicazioni lineari. Matrici come applicazioni
LEZIONE 15. Esempio L applicazione f: R 3 R 2. è lineare. Infatti si ha che se α R, (x, y, z) R 3 risulta
 LEZIONE 15 15.1. Applicazioni lineari ed esempi. Definizione 15.1.1. Siano V e W spazi vettoriali su k = R, C. Un applicazione f: V W si dice k lineare se: (AL1) per ogni v 1, v 2 V si ha f(v 1 + v 2 )
LEZIONE 15 15.1. Applicazioni lineari ed esempi. Definizione 15.1.1. Siano V e W spazi vettoriali su k = R, C. Un applicazione f: V W si dice k lineare se: (AL1) per ogni v 1, v 2 V si ha f(v 1 + v 2 )
ENDOMORFISMI. NOTE DI ALGEBRA LINEARE
 ENDOMORFISMI. NOTE DI ALGEBRA LINEARE 2010-11 MARCO MANETTI: 15 GENNAIO 2011 1. Endomorfismi e sottospazi invarianti Definizione 1.1. Sia V uno spazio vettoriale su K. Un endomorfismo di V è una qualsiasi
ENDOMORFISMI. NOTE DI ALGEBRA LINEARE 2010-11 MARCO MANETTI: 15 GENNAIO 2011 1. Endomorfismi e sottospazi invarianti Definizione 1.1. Sia V uno spazio vettoriale su K. Un endomorfismo di V è una qualsiasi
CORSO DI MATEMATICA DISCRETA I (ALGEBRA) Prof. Paolo Papi ESERCIZI
 CORSO DI MATEMATICA DISCRETA I (ALGEBRA) Prof. Paolo Papi ESERCIZI ). Siano A, B, C insiemi. Provare che (A B) C = A (B C) A (B C) =(A B) (A C) C(A B) =C(A) C(B). 2). Definiamo la differenza simmetrica
CORSO DI MATEMATICA DISCRETA I (ALGEBRA) Prof. Paolo Papi ESERCIZI ). Siano A, B, C insiemi. Provare che (A B) C = A (B C) A (B C) =(A B) (A C) C(A B) =C(A) C(B). 2). Definiamo la differenza simmetrica
Tutorato di GE110. Universitá degli Studi Roma Tre - Corso di Laurea in Matematica
 Universitá degli Studi Roma Tre - Corso di Laurea in Matematica Tutorato di GE110 A.A. 2014-2015 - Docente: Prof. Angelo Felice Lopez Tutori: Federico Campanini e Giulia Salustri Soluzioni Tutorato 12
Universitá degli Studi Roma Tre - Corso di Laurea in Matematica Tutorato di GE110 A.A. 2014-2015 - Docente: Prof. Angelo Felice Lopez Tutori: Federico Campanini e Giulia Salustri Soluzioni Tutorato 12
Elementi di Algebra Lineare Applicazioni lineari
 Elementi di Algebra Lineare Applicazioni lineari Cristina Turrini UNIMI - 2015/2016 Cristina Turrini (UNIMI - 2015/2016) Elementi di Algebra Lineare 1 / 18 index Applicazioni lineari 1 Applicazioni lineari
Elementi di Algebra Lineare Applicazioni lineari Cristina Turrini UNIMI - 2015/2016 Cristina Turrini (UNIMI - 2015/2016) Elementi di Algebra Lineare 1 / 18 index Applicazioni lineari 1 Applicazioni lineari
Intersezione e somma di sottospazi vettoriali
 Capitolo 6 Intersezione e somma di sottospazi vettoriali 6.1 Introduzione Ricordiamo le definizioni di intersezione e somma di due sottospazi vettoriali. Anche in questo caso rimandiamo al testo di geometria
Capitolo 6 Intersezione e somma di sottospazi vettoriali 6.1 Introduzione Ricordiamo le definizioni di intersezione e somma di due sottospazi vettoriali. Anche in questo caso rimandiamo al testo di geometria
DIAGONALIZZAZIONE. M(f) =
 DIAGONALIZZAZIONE Esercizi Esercizio 1. Sia f End(R 3 ) associato alla matrice M(f) = 0 1 2 0. 2 (1) Determinare gli autovalori di f e le relative molteplicità. (2) Determinare gli autospazi di f e trovare,
DIAGONALIZZAZIONE Esercizi Esercizio 1. Sia f End(R 3 ) associato alla matrice M(f) = 0 1 2 0. 2 (1) Determinare gli autovalori di f e le relative molteplicità. (2) Determinare gli autospazi di f e trovare,
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni. 5. Rango
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 5 Rango Definizione 1 Sia A M m,n (K) una matrice m n a coefficienti nel campo K Il rango
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 5 Rango Definizione 1 Sia A M m,n (K) una matrice m n a coefficienti nel campo K Il rango
Intersezione e somma di sottospazi vettoriali
 Capitolo 7 Intersezione e somma di sottospazi vettoriali 7.1 Introduzione Ricordiamo le definizioni di intersezione e somma di due sottospazi vettoriali. Anche in questo caso rimandiamo al testo di geometria
Capitolo 7 Intersezione e somma di sottospazi vettoriali 7.1 Introduzione Ricordiamo le definizioni di intersezione e somma di due sottospazi vettoriali. Anche in questo caso rimandiamo al testo di geometria
Per capire meglio il concetto di combinazione lineare prendiamo in considerazione alcuni esempi.
 Lezione 14 14.1 Combinazioni lineari Definizione 14.1. Sia V uno spazio vettoriale su un campo K = R, C esiano v 1,...,v n 2 V vettori fissati. Un vettore v 2 V si dice combinazione lineare di v 1,...,v
Lezione 14 14.1 Combinazioni lineari Definizione 14.1. Sia V uno spazio vettoriale su un campo K = R, C esiano v 1,...,v n 2 V vettori fissati. Un vettore v 2 V si dice combinazione lineare di v 1,...,v
Lezione Il metodo degli scarti
 Lezione 15 15.1 Il metodo degli scarti Sia dato uno spazio vettoriale V su un campo K = R, C esianov 1,...,v n 2 V vettori fissati. Quanto visto nella lezione precedente ci suggerisce il seguente algoritmo
Lezione 15 15.1 Il metodo degli scarti Sia dato uno spazio vettoriale V su un campo K = R, C esianov 1,...,v n 2 V vettori fissati. Quanto visto nella lezione precedente ci suggerisce il seguente algoritmo
Nozioni e notazioni: concetti primitivi di insieme, elemento ed appartenenza.
 Geometria I lezione del 30 settembre 2013 Presentazione del corso. Nozioni e notazioni: concetti primitivi di insieme, elemento ed appartenenza. Insiemi numerici: i numeri naturali, gli interi, i numeri
Geometria I lezione del 30 settembre 2013 Presentazione del corso. Nozioni e notazioni: concetti primitivi di insieme, elemento ed appartenenza. Insiemi numerici: i numeri naturali, gli interi, i numeri
NOTE DI ALGEBRA LINEARE v = a 1 v a n v n, w = b 1 v b n v n
 NOTE DI ALGEBRA LINEARE 2- MM 9 NOVEMBRE 2 Combinazioni lineari e generatori Sia K un campo e V uno spazio vettoriale su K Siano v,, v n vettori in V Definizione Un vettore v V si dice combinazione lineare
NOTE DI ALGEBRA LINEARE 2- MM 9 NOVEMBRE 2 Combinazioni lineari e generatori Sia K un campo e V uno spazio vettoriale su K Siano v,, v n vettori in V Definizione Un vettore v V si dice combinazione lineare
Esercizi Di Geometria 1 (BAER) Canale 1
 Esercizi Di Geometria 1 (BAER) Canale 1 SETTIMANA 9 (23 29 Novembre 2015) da consegnare Mercoledi 2 Dicembre. Esercizio 1. Sia E = (V,, ) uno spazio metrico finito dimensionale. sottospazio vettoriale
Esercizi Di Geometria 1 (BAER) Canale 1 SETTIMANA 9 (23 29 Novembre 2015) da consegnare Mercoledi 2 Dicembre. Esercizio 1. Sia E = (V,, ) uno spazio metrico finito dimensionale. sottospazio vettoriale
Esercizi per il corso di Algebra e Geometria L.
 Esercizi per il corso di Algebra e Geometria L AA 2006/2007 1 Foglio 1 In tutti gli esercizi che seguiranno lo spazio ambiente sarà il piano cartesiano a valori nel campo dei numeri reali, dove supporremo
Esercizi per il corso di Algebra e Geometria L AA 2006/2007 1 Foglio 1 In tutti gli esercizi che seguiranno lo spazio ambiente sarà il piano cartesiano a valori nel campo dei numeri reali, dove supporremo
CORSI DI LAUREA IN MATEMATICA E FISICA
 CORSI DI LAUREA IN MATEMATICA E FISICA FOGLIO DI ESERCIZI # 6 GEOMETRIA 1 Esercizio 6.1 (Esercizio 5.1). Scrivere un vettore w R 3 linearmente dipendente dal vettore v ( 1, 9, 0). Per esempio il vettore
CORSI DI LAUREA IN MATEMATICA E FISICA FOGLIO DI ESERCIZI # 6 GEOMETRIA 1 Esercizio 6.1 (Esercizio 5.1). Scrivere un vettore w R 3 linearmente dipendente dal vettore v ( 1, 9, 0). Per esempio il vettore
Corso di Geometria - CdL triennale in Ingegneria a.a
 Corso di Geometria - CdL triennale in Ingegneria a.a. 8-9 C. Liverani, J. Garofali Tutorato del 3/5/9 Cambiamenti di base Per fissare le notazioni ricordiamo che date due basi B = {v,..., v n } e B = {v,...,
Corso di Geometria - CdL triennale in Ingegneria a.a. 8-9 C. Liverani, J. Garofali Tutorato del 3/5/9 Cambiamenti di base Per fissare le notazioni ricordiamo che date due basi B = {v,..., v n } e B = {v,...,
GE110 - Geometria 1. Prova in Itinere 2 27 Maggio 2010
 GE110 - Geometria 1 Prova in Itinere 2 27 Maggio 2010 COGNOME e NOME : Problema 1: Problema 2: Problema 3: 1 2 Problema 1. Nello spazio affine reale A 5 R si fissi il riferimento affine canonico, e siano
GE110 - Geometria 1 Prova in Itinere 2 27 Maggio 2010 COGNOME e NOME : Problema 1: Problema 2: Problema 3: 1 2 Problema 1. Nello spazio affine reale A 5 R si fissi il riferimento affine canonico, e siano
Esercizi su applicazioni lineari. Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V,W,U spazi vettoriali su K.
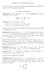 Esercizi su applicazioni lineari Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V,W,U spazi vettoriali su K. 1. Cose da ricordare Definizione 1.1. Una funzione f : V W si
Esercizi su applicazioni lineari Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V,W,U spazi vettoriali su K. 1. Cose da ricordare Definizione 1.1. Una funzione f : V W si
Esempi. In R 2, le coppia (2, 5) è combinazione lineare dei vettori (0, 1) e (1, 1). Infatti:
 Combinazioni lineari [Abate, 4.2] Sia V uno spazio vettoriale e v 1, v 2,..., v n dei vettori di V. Diremo che un vettore w V è combinazione lineare dei vettori v 1,..., v n se esistono a 1, a 2,..., a
Combinazioni lineari [Abate, 4.2] Sia V uno spazio vettoriale e v 1, v 2,..., v n dei vettori di V. Diremo che un vettore w V è combinazione lineare dei vettori v 1,..., v n se esistono a 1, a 2,..., a
p(ϕ) = a 0 Id + a 1 ϕ + + a n ϕ n,
 1. Autospazi e autospazi generalizzati Sia ϕ: V V un endomorfismo. Allora l assegnazione x ϕ induce un morfismo di anelli ρ: K[x] End K (V ). Più esplicitamente, al polinomio p dato da viene associato
1. Autospazi e autospazi generalizzati Sia ϕ: V V un endomorfismo. Allora l assegnazione x ϕ induce un morfismo di anelli ρ: K[x] End K (V ). Più esplicitamente, al polinomio p dato da viene associato
LEZIONE 12. v = α 1 v α n v n =
 LEZIONE 12 12.1. Combinazioni lineari. Definizione 12.1.1. Sia V uno spazio vettoriale su k = R, C e v 1,..., v n V vettori fissati. Un vettore v V si dice combinazione lineare di v 1,..., v n se esistono
LEZIONE 12 12.1. Combinazioni lineari. Definizione 12.1.1. Sia V uno spazio vettoriale su k = R, C e v 1,..., v n V vettori fissati. Un vettore v V si dice combinazione lineare di v 1,..., v n se esistono
Prova scritta di Geometria 1 Docente: Giovanni Cerulli Irelli 20 Gennaio 2017
 Prova scritta di Geometria Docente: Giovanni Cerulli Irelli Gennaio 7 Esercizio. Si considerino i seguenti tre punti dello spazio euclideo: P :=, Q :=, R :=.. Dimostrare che P, Q ed R non sono collineari.
Prova scritta di Geometria Docente: Giovanni Cerulli Irelli Gennaio 7 Esercizio. Si considerino i seguenti tre punti dello spazio euclideo: P :=, Q :=, R :=.. Dimostrare che P, Q ed R non sono collineari.
Geometria I. Esercizi svolti.
 Geometria I. Esercizi svolti. Alcuni esercizi svolti dal mio libro Appunti di Geometria I (Pitagora Editore). Es..5, p. 64. Siano F, H due sotto spazi vettoriali del k-spazio vettoriale E. Se H F, allora
Geometria I. Esercizi svolti. Alcuni esercizi svolti dal mio libro Appunti di Geometria I (Pitagora Editore). Es..5, p. 64. Siano F, H due sotto spazi vettoriali del k-spazio vettoriale E. Se H F, allora
1.1 Matrici a coefficienti in R. Vi sono alcuni casi particolari che vale la pena evidenziare:
 Lezione Matrici a coefficienti in R Definizione Siano m, n Z numeri interi positivi Una matrice m n acoefficientiinrèuninsiemedimn numeri reali disposti su m righe ed n colonne circondata da parentesi
Lezione Matrici a coefficienti in R Definizione Siano m, n Z numeri interi positivi Una matrice m n acoefficientiinrèuninsiemedimn numeri reali disposti su m righe ed n colonne circondata da parentesi
CORSO DI ALGEBRA (M-Z) Prof. A. Venezia
 CORSO DI ALGEBRA (M-Z) Prof. A. Venezia 2018-19 Complementi ed Esercizi APPLICAZIONI LINEARI Siano V e V spazi vettoriali sul campo K. Una applicazione L: V V si dice lineare se: 1 AL. L(v+w) = L(v) +
CORSO DI ALGEBRA (M-Z) Prof. A. Venezia 2018-19 Complementi ed Esercizi APPLICAZIONI LINEARI Siano V e V spazi vettoriali sul campo K. Una applicazione L: V V si dice lineare se: 1 AL. L(v+w) = L(v) +
A. Languasco - Esercizi Matematica B - 2. Spazi Vettoriali e Trasformazioni lineari 1
 A. Languasco - Esercizi Matematica B - 2. Spazi Vettoriali e Trasformazioni lineari 1 A: Spazi vettoriali e sottospazi Corso di Matematica B - Ingegneria Informatica Testi di Esercizi A1. Provare che l
A. Languasco - Esercizi Matematica B - 2. Spazi Vettoriali e Trasformazioni lineari 1 A: Spazi vettoriali e sottospazi Corso di Matematica B - Ingegneria Informatica Testi di Esercizi A1. Provare che l
Esercizi 1 Spazi vettoriali. { (x, y, z) R 3 (x, y, z) (2, 2, 2) } ;
 Esercizi 1 Spazi vettoriali Esercizio. Si dica quali dei seguenti sottoinsiemi di R 3 sono sottospazi vettoriali su R: { (x y z R 3 x y z Z } ; { (x y z R 3 x y z Q } ; { (x y z R 3 (x y z (2 2 2 } ; {
Esercizi 1 Spazi vettoriali Esercizio. Si dica quali dei seguenti sottoinsiemi di R 3 sono sottospazi vettoriali su R: { (x y z R 3 x y z Z } ; { (x y z R 3 x y z Q } ; { (x y z R 3 (x y z (2 2 2 } ; {
LEZIONE 8. k e w = wx ı + w y j + w z. k di R 3 definiamo prodotto scalare di v e w il numero
 LEZINE 8 8.1. Prodotto scalare. Dati i vettori geometrici v = v x ı + v y j + v z k e w = wx ı + j + k di R 3 definiamo prodotto scalare di v e w il numero v, w = ( v x v y v z ) w x = v x + v y + v z.
LEZINE 8 8.1. Prodotto scalare. Dati i vettori geometrici v = v x ı + v y j + v z k e w = wx ı + j + k di R 3 definiamo prodotto scalare di v e w il numero v, w = ( v x v y v z ) w x = v x + v y + v z.
LEZIONE Equazioni matriciali. Negli Esempi e si sono studiati più sistemi diversi AX 1 = B 1, AX 2 = R m,n, B = (b i,h ) 1 i m
 LEZIONE 4 41 Equazioni matriciali Negli Esempi 336 e 337 si sono studiati più sistemi diversi AX 1 = B 1, AX 2 = B 2,, AX p = B p aventi la stessa matrice incompleta A Tale tipo di problema si presenta
LEZIONE 4 41 Equazioni matriciali Negli Esempi 336 e 337 si sono studiati più sistemi diversi AX 1 = B 1, AX 2 = B 2,, AX p = B p aventi la stessa matrice incompleta A Tale tipo di problema si presenta
Parte 7. Autovettori e autovalori
 Parte 7. Autovettori e autovalori A. Savo Appunti del Corso di Geometria 23-4 Indice delle sezioni Endomorfismi, 2 Cambiamento di base, 3 3 Matrici simili, 6 4 Endomorfismi diagonalizzabili, 7 5 Autovettori
Parte 7. Autovettori e autovalori A. Savo Appunti del Corso di Geometria 23-4 Indice delle sezioni Endomorfismi, 2 Cambiamento di base, 3 3 Matrici simili, 6 4 Endomorfismi diagonalizzabili, 7 5 Autovettori
ESERCIZI DI ALGEBRA LINEARE. Vincenzo Di Gennaro
 ESERCIZI DI ALGEBRA LINEARE Vincenzo Di Gennaro Sono raccolti, in ordine cronologico, gli esercizi di Algebra Lineare proposti nelle prove scritte per i vari corsi di Geometria che ho tenuto presso la
ESERCIZI DI ALGEBRA LINEARE Vincenzo Di Gennaro Sono raccolti, in ordine cronologico, gli esercizi di Algebra Lineare proposti nelle prove scritte per i vari corsi di Geometria che ho tenuto presso la
Esercizi di Geometria 1 - Foglio 3bis
 Esercizi di Geometria - Foglio 3bis Alessandro Rubin (alex.rubin@outlook.com) Si ringrazia Ricardo Tzantzoglou per il codice L A TEX condiviso dicembre 7 Esercizio. Sia f : V W un applicazione e G = {(v,
Esercizi di Geometria - Foglio 3bis Alessandro Rubin (alex.rubin@outlook.com) Si ringrazia Ricardo Tzantzoglou per il codice L A TEX condiviso dicembre 7 Esercizio. Sia f : V W un applicazione e G = {(v,
Elementi di Algebra Lineare Applicazioni lineari
 Elementi di Algebra Lineare Applicazioni lineari Cristina Turrini UNIMI - 2016/2017 Cristina Turrini (UNIMI - 2016/2017) Elementi di Algebra Lineare 1 / 50 index Applicazioni lineari 1 Applicazioni lineari
Elementi di Algebra Lineare Applicazioni lineari Cristina Turrini UNIMI - 2016/2017 Cristina Turrini (UNIMI - 2016/2017) Elementi di Algebra Lineare 1 / 50 index Applicazioni lineari 1 Applicazioni lineari
Autovalori e autovettori
 Autovalori e autovettori Definizione 1 (per endomorfismi). Sia V uno spazio vettoriale su di un campo K e f : V V un suo endomorfismo. Si dice autovettore per f ogni vettore x 0 tale che f(x) = λx, per
Autovalori e autovettori Definizione 1 (per endomorfismi). Sia V uno spazio vettoriale su di un campo K e f : V V un suo endomorfismo. Si dice autovettore per f ogni vettore x 0 tale che f(x) = λx, per
Corsi di laurea in Matematica e Matematica per le Applicazioni Esame scritto di Algebra Lineare del 7/2/2002
 Esame scritto di Algebra Lineare del 7/2/2002 Esercizio 1 Sia h R e sia f : R[x] 3 R 3 l applicazione lineare tale che f(1) = (1, 1, h) f(1 + x) = (h + 2, 0, h) f(x 2 ) = (0, 0, 1) f(1 + x + x 3 ) = (h
Esame scritto di Algebra Lineare del 7/2/2002 Esercizio 1 Sia h R e sia f : R[x] 3 R 3 l applicazione lineare tale che f(1) = (1, 1, h) f(1 + x) = (h + 2, 0, h) f(x 2 ) = (0, 0, 1) f(1 + x + x 3 ) = (h
Sottospazi vettoriali
 Capitolo 6 Sottospazi vettoriali 6.1 Introduzione Riprendiamo un argomento già studiato ampiamente nel corso di Geometria, i sottospazi vettoriali di uno spazio vettoriale. Ci limiteremo a darne la definizione,
Capitolo 6 Sottospazi vettoriali 6.1 Introduzione Riprendiamo un argomento già studiato ampiamente nel corso di Geometria, i sottospazi vettoriali di uno spazio vettoriale. Ci limiteremo a darne la definizione,
LEZIONE 9. Figura 9.1.1
 LEZIONE 9 9.1. Equazioni cartesiane di piani. Abbiamo visto come rappresentare parametricamente un piano. Un altro interessante metodo di rappresentazione di un piano nello spazio è tramite la sua equazione
LEZIONE 9 9.1. Equazioni cartesiane di piani. Abbiamo visto come rappresentare parametricamente un piano. Un altro interessante metodo di rappresentazione di un piano nello spazio è tramite la sua equazione
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI
 CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
LEZIONE 13. v =α 1 v α i 1 v i 1 + α i v i = =α 1 v α i 1 v i 1 + α i (λ 1 v λ i 1 v i 1 ) =
 LEZIONE 13 13.1. Il metodo degli scarti. Sia dato uno spazio vettoriale V su k = R, C e siano v 1,..., v n V. Quanto visto nella lezione precedente ci suggerisce il seguente algoritmo per stabilire se
LEZIONE 13 13.1. Il metodo degli scarti. Sia dato uno spazio vettoriale V su k = R, C e siano v 1,..., v n V. Quanto visto nella lezione precedente ci suggerisce il seguente algoritmo per stabilire se
Compito di MD 4 Giugno 2014
 Compito di MD 4 Giugno 2014 IMPORTANTE: Non si possono consultare libri e appunti. Non si possono usare calcolatrici, computer o altri dispositivi elettronici. Non saranno valutate risposte prive di motivazioni,
Compito di MD 4 Giugno 2014 IMPORTANTE: Non si possono consultare libri e appunti. Non si possono usare calcolatrici, computer o altri dispositivi elettronici. Non saranno valutate risposte prive di motivazioni,
Lezione 5: Applicazioni Lineari. 1 Definizione di applicazione lineare
 Lezione 5: Applicazioni Lineari Le applicazioni lineari sono funzioni tra spazi vettoriali che ne rispettano la struttura, cioe che conservano le operazioni di somma tra vettori e moltiplicazione di un
Lezione 5: Applicazioni Lineari Le applicazioni lineari sono funzioni tra spazi vettoriali che ne rispettano la struttura, cioe che conservano le operazioni di somma tra vettori e moltiplicazione di un
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Lezioni di Algebra Lineare V. Autovalori e autovettori
 Lezioni di Algebra Lineare V. Autovalori e autovettori Versione novembre 2008 Contenuto 1. Cambiamenti di base 2. Applicazioni lineari, matrici e cambiamenti di base 3. Autovalori e autovettori 2 1. Cambiamenti
Lezioni di Algebra Lineare V. Autovalori e autovettori Versione novembre 2008 Contenuto 1. Cambiamenti di base 2. Applicazioni lineari, matrici e cambiamenti di base 3. Autovalori e autovettori 2 1. Cambiamenti
Le risposte vanno giustificate con chiarezza. 1) Nello spazio vettoriale V delle matrici 2 2 a coefficienti reali, considera le matrici A 1 = , A 4 =
 Università degli Studi di Roma Tor Vergata. Corso di Laurea in Matematica Esame di Geometria 1 con Elementi di Storia Prof. F. Tovena 30 gennaio 2015 Le risposte vanno giustificate con chiarezza. 1 Nello
Università degli Studi di Roma Tor Vergata. Corso di Laurea in Matematica Esame di Geometria 1 con Elementi di Storia Prof. F. Tovena 30 gennaio 2015 Le risposte vanno giustificate con chiarezza. 1 Nello
ALGEBRA LINEARE E GEOMETRIA: ESERCIZI 5. Indice. 2. Esercizi 5
 ALGEBRA LINEARE E GEOMETRIA: ESERCIZI 5 Indice 1. Principali definizioni 1 2. Esercizi 5 Operazioni con le matrici 1. Principali definizioni Ricordiamo le principali definizioni legate alle matrici a coefficienti
ALGEBRA LINEARE E GEOMETRIA: ESERCIZI 5 Indice 1. Principali definizioni 1 2. Esercizi 5 Operazioni con le matrici 1. Principali definizioni Ricordiamo le principali definizioni legate alle matrici a coefficienti
Lezione Risoluzione di sistemi
 Lezione Risoluzione di sistemi Sia AX = B un sistema di equazioni lineari, con la sua matrice completa associate (A B) Per la Proposizione sappiamo di poter trasformare con operazioni elementari di riga
Lezione Risoluzione di sistemi Sia AX = B un sistema di equazioni lineari, con la sua matrice completa associate (A B) Per la Proposizione sappiamo di poter trasformare con operazioni elementari di riga
Rango di una matrice e teorema di Rouché-Capelli
 Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
i) la somma e il prodotto godano delle proprietà associativa, commutativa e distributiva;
 1 Spazi vettoriali 11 Definizioni ed assiomi Definizione 11 Un campo è un insieme K dotato di una operazione somma K K K, (x, y) x + y e di una operazione prodotto K K K, (x, y) xy tali che i) la somma
1 Spazi vettoriali 11 Definizioni ed assiomi Definizione 11 Un campo è un insieme K dotato di una operazione somma K K K, (x, y) x + y e di una operazione prodotto K K K, (x, y) xy tali che i) la somma
Anno Accademico 2017/2018
 Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2017/2018 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2017/2018 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
h, i: V V! R (v 1,v 2 ) 7! hv 1,v 2 i ! R v 7! hv, v 0 i èlineare. Perlacommutativitàdelprodottoscalaresegueanchelalinearità dell applicazione
 Lezione. Prodotti scalari Definizione. (Prodotto scalare). Sia V uno spazio vettoriale su R. Un prodotto scalare su V è un applicazione tale che valgono i seguenti assiomi: h, i: V V! R (v,v ) 7! hv,v
Lezione. Prodotti scalari Definizione. (Prodotto scalare). Sia V uno spazio vettoriale su R. Un prodotto scalare su V è un applicazione tale che valgono i seguenti assiomi: h, i: V V! R (v,v ) 7! hv,v
Matrici simili, invarianti e decomposizione di matrici 1 / 14
 Matrici simili, invarianti e decomposizione di matrici 1 / 14 Applicazioni lineari 2 / 14 Se X = t [x 1,...,x n ] sono le coordinate di un generico vettore rispetto alla base canonica, possiamo assumere
Matrici simili, invarianti e decomposizione di matrici 1 / 14 Applicazioni lineari 2 / 14 Se X = t [x 1,...,x n ] sono le coordinate di un generico vettore rispetto alla base canonica, possiamo assumere
Anno Accademico 2016/2017
 Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2016/2017 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2016/2017 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Sapienza Università di Roma Corso di laurea in Ingegneria Energetica Geometria A.A ESERCIZI DA CONSEGNARE prof.
 Sapienza Università di Roma Corso di laurea in Ingegneria Energetica Geometria A.A. 2015-2016 ESERCIZI DA CONSEGNARE prof. Cigliola Consegna per Martedì 6 Ottobre Esercizio 1. Una matrice quadrata A si
Sapienza Università di Roma Corso di laurea in Ingegneria Energetica Geometria A.A. 2015-2016 ESERCIZI DA CONSEGNARE prof. Cigliola Consegna per Martedì 6 Ottobre Esercizio 1. Una matrice quadrata A si
Omomorfismi e matrici
 Capitolo 12 Omomorfismi e matrici 121 Introduzione Nel corso di Geometria è stato visto come associare una matrice ad un omomorfismo tra spazi vettoriali Rimandiamo al testo del corso per esempi e esercizi
Capitolo 12 Omomorfismi e matrici 121 Introduzione Nel corso di Geometria è stato visto come associare una matrice ad un omomorfismo tra spazi vettoriali Rimandiamo al testo del corso per esempi e esercizi
INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 19 GIUGNO 2012
 INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 19 GIUGNO 2012 MATTEO LONGO Esercizio 1. Al variare del parametro a R, si consideri l applicazione lineare L a : R R definita dalle
INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 19 GIUGNO 2012 MATTEO LONGO Esercizio 1. Al variare del parametro a R, si consideri l applicazione lineare L a : R R definita dalle
Matematica discreta 1 [145016]
![Matematica discreta 1 [145016] Matematica discreta 1 [145016]](/thumbs/94/119285443.jpg) Facoltà di Scienze Matematiche, Fisiche e Naturali anno accademico 2008/09 Registro dell'attività didattica Matematica discreta 1 [145016] Attività didattica: Attività didattica [codice] Corso di studio
Facoltà di Scienze Matematiche, Fisiche e Naturali anno accademico 2008/09 Registro dell'attività didattica Matematica discreta 1 [145016] Attività didattica: Attività didattica [codice] Corso di studio
ESERCIZI DI ALGEBRA LINEARE. Vincenzo Di Gennaro
 ESERCIZI DI ALGEBRA LINEARE Vincenzo Di Gennaro Sono raccolti, in ordine cronologico, gli esercizi di Algebra Lineare proposti nelle prove scritte per i vari corsi di Geometria 1 che ho tenuto presso la
ESERCIZI DI ALGEBRA LINEARE Vincenzo Di Gennaro Sono raccolti, in ordine cronologico, gli esercizi di Algebra Lineare proposti nelle prove scritte per i vari corsi di Geometria 1 che ho tenuto presso la
Capitolo IX DIAGONALIZZAZIONE DI MATRICI SIMMETRICHE
 Capitolo IX DIAGONALIZZAZIONE DI MATRICI SIMMETRICHE 1. Matrici ortogonali Ricordiamo che, nel Cap. VII, abbiamo studiato le matrici di cambio di base in un R spazio vettoriale. In tale occasione, abbiamo
Capitolo IX DIAGONALIZZAZIONE DI MATRICI SIMMETRICHE 1. Matrici ortogonali Ricordiamo che, nel Cap. VII, abbiamo studiato le matrici di cambio di base in un R spazio vettoriale. In tale occasione, abbiamo
AUTOVALORI, AUTOVETTORI, AUTOSPAZI
 AUTOVALORI, AUTOVETTORI, AUTOSPAZI. Esercizi Esercizio. Sia f : R 3 R 3 l endomorfismo definito da f(x, y, z) = (x+y, y +z, x+z). Calcolare gli autovalori ed una base per ogni autospazio di f. Dire se
AUTOVALORI, AUTOVETTORI, AUTOSPAZI. Esercizi Esercizio. Sia f : R 3 R 3 l endomorfismo definito da f(x, y, z) = (x+y, y +z, x+z). Calcolare gli autovalori ed una base per ogni autospazio di f. Dire se
Corso di Laurea in Fisica. Geometria 1. a.a Gruppo B. Prof. P. Piazza Soluzioni compito a casa del 17/11/06 B =
 Corso di Laurea in Fisica. Geometria. a.a. 26-7. Gruppo B. Prof. P. Piazza Soluzioni compito a casa del 7//6 Soluzione esercizio. Sia B {e, e 2 } e sia B {v, v 2 }. La matrice B del cambiamento di base
Corso di Laurea in Fisica. Geometria. a.a. 26-7. Gruppo B. Prof. P. Piazza Soluzioni compito a casa del 7//6 Soluzione esercizio. Sia B {e, e 2 } e sia B {v, v 2 }. La matrice B del cambiamento di base
ESAME DI GEOMETRIA. 6 febbraio 2002 CORREZIONE QUIZ
 ESAME DI GEOMETRIA 6 febbraio CORREZIONE QUIZ. La parte reale di ( + i) 9 è positiva. QUIZ Si può procedere in due modi. Un primo modo è osservare che ( + i) =i, dunque ( + i) 9 =(+i)(i) 4 = 4 ( + i) :
ESAME DI GEOMETRIA 6 febbraio CORREZIONE QUIZ. La parte reale di ( + i) 9 è positiva. QUIZ Si può procedere in due modi. Un primo modo è osservare che ( + i) =i, dunque ( + i) 9 =(+i)(i) 4 = 4 ( + i) :
Appunti del corso di geometria 1. G. Bande
 Appunti del corso di geometria 1 G. Bande 21 febbraio 2011 2 Indice 1 Spazi vettoriali 5 1.0.1 Esempi di spazi vettoriali.................. 6 1.1 Sottospazi vettoriali......................... 7 1.1.1
Appunti del corso di geometria 1 G. Bande 21 febbraio 2011 2 Indice 1 Spazi vettoriali 5 1.0.1 Esempi di spazi vettoriali.................. 6 1.1 Sottospazi vettoriali......................... 7 1.1.1
Lezione Determinanti
 Lezione 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Lezione 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE110 - Geometria 1 a.a Seconda prova di esonero TESTO E SOLUZIONI
 UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE110 - Geometria 1 a.a. 2014-2015 Seconda prova di esonero TESTO E SOLUZIONI 1. Sia V uno spazio vettoriale di dimensione 4 con base {e 1,
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE110 - Geometria 1 a.a. 2014-2015 Seconda prova di esonero TESTO E SOLUZIONI 1. Sia V uno spazio vettoriale di dimensione 4 con base {e 1,
Complemento ortogonale e proiezioni
 Complemento ortogonale e proiezioni Dicembre 9 Complemento ortogonale di un sottospazio Sie E un sottospazio di R n Definiamo il complemento ortogonale di E come l insieme dei vettori di R n ortogonali
Complemento ortogonale e proiezioni Dicembre 9 Complemento ortogonale di un sottospazio Sie E un sottospazio di R n Definiamo il complemento ortogonale di E come l insieme dei vettori di R n ortogonali
Ingegneria Gestionale - Corso di Analisi II e Algebra anno accademico 2008/2009
 Ingegneria Gestionale - Corso di Analisi II e Algebra anno accademico 28/29 Dire se le seguenti proposizioni sono vere o false: ESERCITAZIONE. Proposizione Vera Falsa f : R R 4 rk(f f : R 4 R rk(f f :
Ingegneria Gestionale - Corso di Analisi II e Algebra anno accademico 28/29 Dire se le seguenti proposizioni sono vere o false: ESERCITAZIONE. Proposizione Vera Falsa f : R R 4 rk(f f : R 4 R rk(f f :
