SPAZI METRICI. Uno spazio metrico X con metrica d si indica con il simbolo (X, d). METRICI 1
|
|
|
- Adriana Sarti
- 8 anni fa
- Visualizzazioni
Transcript
1 SPAZI METRICI Nel piano R 2 o nello spazio R 3 la distanza fra due punti è la lunghezza, o norma euclidea, del vettore differenza di questi due punti. Se p = (x, y, z) è un vettore in coordinate ortonormali, la sua lunghezza è: p = x 2 + y 2 + z 2 Se p 1 = (x 1, y 1, z 1 ) e p 2 = (x 2, y 2, z 2 ), la loro distanza è: d(p 1, p 2 ) = p 2 p 1 = (x 2 x 1 ) 2 + (y 2 y 1 ) 2 + (z 2 z 1 ) 2 Questa distanza si chiama metrica euclidea o pitagorica, per distinguerla da altre metriche. Definizione 1 Uno spazio metrico è un insieme X fornito di una funzione distanza (=metrica) d : X X [0, + [ che verifica le seguenti tre condizioni (per ogni coppia di punti): (D 1 ) d(x, y) 0 e inoltre d(x, y) = 0 x = y. (D 2 ) d(x, y) = d(y, x) (D 3 ) d(x, z) d(x, y) + d(y, z). Uno spazio metrico X con metrica d si indica con il simbolo (X, d). Esercizio. Verificare che: d(x, y) d(y, z) d(x, z) METRICI 1
2 Esempi. R n con la distanza euclidea: d 2 (x, y) = y x = = n (y k x k ) 2, k=1 ove x = (x 1,..., x n ) e y = (y 1,..., y n ). È difficile verificare la disuguaglianza triangolare. R 2 con la metrica del reticolato (o di Manhattan): d 1 (x, y) = x 1 y 1 + x 2 y 2, ove x = (x 1, x 2 ) e y = (y 1, y 2 ). y x2 y2 x (y 1, x 2 ) R 2 con la metrica del sup: x 1 y 1 d (x, y) = max{ x 1 y 1, x 2 y 2 }, ove... Distanza geodetica in S 2, sfera dei versori di R 3. S 2 = {u R 3 : u = u u2 2 + u2 3 = 1} d(u, v) = arccos(u v) Si tratta della lunghezza del minore fra i due archi di cerchio massimo di estremi u e v. METRICI 2
3 R 2 con la distanza delle valli. Se x = (x 1, x 2 ) e y = (y 1, y 2 ): d(x, y) = { y2 x 2 se x 1 = y 1 x 2 + x 1 y 1 + y 2 se x 1 y 1 y 2 y x 2 y 2 x y x 1 x 1 y 1 x 2 x R 2 con la metrica del riccio: { x y se x e y sono proporzionali, d(x, y) = x + y altrimenti. O METRICI 3
4 Metrica discreta su un insieme E. Si fissa una costante α > 0 e si definisce per x y: d(x, y) = un qualsiasi numero α in modo che valga (D 3 ) Ad esempio: d(x, y) = α x y. Siano E un insieme e g : E R una funzione iniettiva. La posizione d g (x, y) = g(x) g(y) definisce una metrica su E. Definizione 2 Se S X e d è una metrica su X, allora d S = d S S è una metrica su S, detta metrica indotta, e (S, d S ) si dice sottospazio metrico di (X, d). Scriveremo sempre (S, d). Esempi. La metrica indotta su Z 2 dalla metrica euclidea di R 2 è discreta, α = 1. La metrica indotta su S 1 = {(x 1, x 2 ) : x x 2 2 = 1} dalla metrica del riccio di R 2 è discreta, α = 2. Definizione 3 Dati uno spazio metrico (X, d), un punto a X e un numero reale r > 0, si definiscono: palla aperta di centro a e raggio r: B(a, r[= {x X : d(a, x) < r} palla chiusa di centro a e raggio r: Se necessario si usa B d in luogo di B. B(a, r] = {x X : d(a, x) r} METRICI 4
5 Esercizio. Disegnare le palle in R 2 con le metriche d 2, d 1 e d. metrica d 1 B(a, r] a r a metrica d B(a, r] Esempio. Sia p 1 un numero reale. La funzione d p (x, y) = ( x 1 y 1 p + x 2 y 2 p ) 1 p definisce una metrica su R 2 (difficile!). Vedere nella dispensa la forma delle palle. Domande. Chi sono le palle (aperte e chiuse) nella metrica discreta? Chi sono le palle nella metrica geodetica della sfera? Quali sono le palle (aperte e chiuse) di raggio π? Come sono fatte le palle nella metrica del riccio? E nella metrica delle valli? a METRICI 5
6 Spazi di funzioni. Sia T un insieme e K indichi il corpo reale o il corpo complesso. Con il simbolo K T indichiamo l insieme delle funzioni da T a K. K T diventa uno spazio vettoriale su K con le operazioni definite puntualmente: (f + g)(t) = f(t) + g(t), (λf)(t) = λ(f(t)) Un sottospazio (vettoriale) interessante è: B(T, K) = l (T, K) insieme delle funzioni limitate da T a K. Su di esso è definita la metrica della convergenza uniforme: d (f, g) = g f = sup{ g(t) f(t) : t T } Verifica della disuguaglianza triangolare: f(t) h(t) f(t) g(t) + g(t) h(t) f g + g h Siccome la disuguaglianza è vera per ogni t T, il termine è maggiorato da ( ). sup t T f(t) h(t) = f h Esercizio. Siano f B(T, R) con la metrica d e r > 0 in R. Allora: B(f, r[ {g B(T, R) : f(t) r < g(t) < f(t) + r t T } B(f, r] Rendersi conto che la seconda inclusione è sempre stretta, mentre la prima è un uguaglianza T è finito. ( ) T METRICI 6
7 Consideriamo lo spazio X = C([a, b], K) delle funzioni continue su [a, b] con valori in K. Si ha X B([a, b], K) per il teorema di Weierstrass. Quindi X può essere munito della metrica d. Esercizio. Siano f e g in C([0, 4], R) così definite: f(x) = x log x se x > 0, f(0)=0, g(x) = x Calcolare d (f, g). Un altra distanza su X = C([a, b], K) è quella della media di ordine 1: d 1 (f, g) = g f 1 = g(t) f(t) dt Un altra è quella della media di ordine 2: d 2 (f, g) = g f 2 = ( [a,b] [a,b] g(t) f(t) 2 dt) 1 2 o in generale della media di ordine p, con p 1 reale: d p (f, g) = g f p = ( g(t) f(t) p dt) p 1 Esercizio. Calcolare d 1 (f, g) e d 2 (f, g), dove f e g sono le funzioni dell esercizio precedente. [a,b] METRICI 7
8 Spazi vettoriali normati Definizione 4 Se X è un K-spazio vettoriale, una norma su X è una funzione : X [0, + [ tale che: (N 1 ) x 0 per ogni x X; x = 0 x = 0. (N 2 ) αx = α x, per ogni α K e ogni x X. (N 3 ) x + y x + y, per ogni x, y X. Un K-spazio vettoriale con una norma assegnata si chiama spazio normato. Uno spazio normato diventa uno spazio metrico assegnando come distanza: d(x, y) = x y La verifica delle proprietà (D i ) si fa usando le (N i ). (D 1 ) e (D 2 ) sono immediate. Verifichiamo la (D 3 ): d(x, z) = x z = (x y)+y z) N 3 x y + y z = d(x, y)+d(y, z) Non ogni metrica su uno spazio vettoriale è indotta da una norma (v. metrica del riccio). Sussiste anzi il seguente fatto: Se la metrica d è indotta da una norma: (1) d è invariante per traslazioni, cioè: d(x + a, y + a) = d(x, y), x, y, a X (2) d è assolutamente omogenea, cioè: d(αx, αy) = α d(x, y), α K, x, y X Viceversa, se una metrica d soddisfa (1) e (2), allora la posizione x = d(x, 0) definisce una norma su X che ha d come distanza associata. METRICI 8
9 Definizione 5 Se (X, ) è uno spazio vettoriale normato, si chiama palla unitaria (chiusa) la palla chiusa di centro il vettore nullo e di raggio 1: B X = B(0, 1] = {x X : x 1} La sfera unitaria è l insieme dei versori: S X = {x X : x = 1} Esercizio. Siano (X, ) uno spazio vettoriale normato, a X e r > 0. Dimostrare che B(a, r] = a + rb X. Le distanze d p, con p 1, e d definite precedentemente su R 2 (oppure su R n o su C n ), sono indotte dalle seguenti norme: ( n )1 p x p = x k p, x K n k=1 x = max{ x k : k = 1,..., n}, x K n La verifica della subadditività per p per p > 1 è difficile. Comunque per p = 2, se n (x y) = x k y k è l usuale prodotto scalare di K n, k=1 allora x 2 = (x x) 2 1 è una norma indotta da un prodotto scalare e quindi soddisfa (N 3 ) (ricordare le disuguaglianze di Schwarz e di Minkowski). Su B(T, K) = l (T, K) la distanza d è indotta dalla norma: f = sup{ f(t) : t T } Sottospazi vettoriali interessanti di B([a, b], K) sono: C([a, b], K), C 1 ([a, b], K) Su di essi si può ancora considerare la norma. Su X = C([a, b], K) la metrica della media di ordine p è indotta dalla norma: f p = ( f p ) p 1 METRICI 9 [a,b]
10 Esercizio. Sia l 1 = l 1 (N, K) l insieme delle successioni a valori in K che formano serie assolutamente convergenti; cioè una successione x : N K sta in l 1 se e solo se: x 1 = + k=0 x k < +. Dimostrare che l 1 è spazio vettoriale e che 1 è una norma su di esso. Definizione 6 Siano (X, d) e (Y, ρ) spazi metrici. Una funzione f : X Y si dice un isometria se conserva le distanze, cioè se: ρ(f(x), f(y)) = d(x, y), x, y X Ogni isometria è iniettiva; l inversa di un isometria (da f(x) X) è un isometria; la composizione di due isometrie è un isometria. Due spazi metrici si dicono isometrici se fra essi esiste un isometria biiettiva. Proposizione 7 Ogni spazio metrico (X, d) è isometrico a un sottospazio metrico di uno spazio vettoriale normato. Dimostrazione. Sia Y = B(X, R) con e sia a X fissato. Per ogni x X sia ϕ x : X R così definito: ϕ x (t) = d(t, x) d(t, a), t X ϕ x Y (cioè è limitata) perché: ϕ x (t) = d(t, x) d(t, a) d(x, a) Inoltre la mappa x ϕ x è un isometria da (X, d) a (Y, d ). Attenzione: per questo, con abuso di notazione, può essere comodo indicare con x y la distanza, anche in uno spazio metrico non normato (in generale x y non esiste in X). METRICI 10
11 Definizione 8 Siano (X, d) e (Y, ρ) spazi metrici. Una funzione f : X Y si dice lipschitziana se esiste una costante l 0 tale che: ρ(f(x), f(y)) l d(x, y), x, y X l è detta costante di Lipschitz. Esercizio. L estremo inferiore delle costanti di Lipschitz per una funzione lipschitziana è ancora una costante di Lipschitz. Essa si chiama la costante di Lipschitz. Su R si considera sempre la metrica t s. Esercizi. Sia I un intervallo di R e f : I R una funzione derivabile. Dimostrare che f è lipschitziana f è limitata. Sia (X, ) uno spazio vettoriale normato. Allora x x è una funzione lipschitziana da X in [0, + [ (segue da x y x y ). Definizione 9 Siano (X, d) uno spazio metrico e A un sottoinsieme non vuoto di X. Si consideri la funzione d(, A) : X [0, + [, detta distanza da A, definita ponendo per ogni x X: Proposizione 10 Si ha: d(x, A) = inf{d(x, y) : y A} d(x, A) d(y, A) d(x, y) Dimostrazione. Basta dimostrare che d(x, A) d(x, y) + d(y, A). Poiché d(x, A) d(x, a) d(x, y) + d(y, a) a A, passando all inf a A a destra, si ottiene quanto voluto. METRICI 11
12 Definizione 11 Il diametro di un sottoinsieme A di uno spazio metrico (X, d) è: diam A = sup{d(x, y) : x, y A}, dove il sup può essere anche + Si pone diam = 0. Un sottoinsieme si dice limitato se ha diametro finito (cioè R). Esercizi. Il diametro di una palla di raggio r > 0 è 2r. Dare un esempio in cui il diametro è strettamente < 2r. Dimostrare che in uno spazio vettoriale normato tale diametro è esattamente 2r. Un sottoinsieme è limitato è contenuto in una palla. Un unione finita di sottoinsiemi limitati è un sottoinsieme limitato. Sia A = [a, b] [c, d] R 2. Trovare il diametro di A in d 2, d 1, d. Sia E = {x R 2 : x = x 2 = r}. Chi è il diametro di E in d? E in d 1? Topologia di uno spazio metrico La topologia serve per dare nozioni di vicinanza e di convergenza. Definizione 12 Siano (X, d) uno spazio metrico e A X. A si dice aperto se è vuoto oppure se è unione di palle aperte. La topologia dello spazio metrico (X, d) è la famiglia τ d, o più semplicemente τ, costituita da tutti i sottoinsiemi aperti. La coppia (X, τ) è detta spazio topologico metrizzabile. Un insieme si dice chiuso se il suo complementare è un insieme aperto. METRICI 12
13 Esercizio. Se p B(a, r[ e s r d(p, a), allora B(p, s[ B(a, r[. Se q B(a, r] e t d(q, a) r, allora B(q, t[ B(a, r] =. Prima conseguenza: ogni palla chiusa è un insieme chiuso. p a a q Seconda conseguenza dell esercizio precedente. Proposizione 13 A è aperto per ogni p A esiste un numero reale δ > 0 tale che B(p, δ[ A. Dimostrazione. Sufficienza: immediata. Necessità. Sia p A con A insieme aperto. Esiste una palla aperta B(a, r[ tale che p B(a, r[ A. Sia s r d(p, a). Per l esercizio precedente si ottiene: B(p, s[ B(a, r[ A Proposizione 14 La topologia τ di uno spazio metrico soddisfa le seguenti proprietà: (A 1 ), X τ; (A 2 ) se A λ τ per ogni λ Λ, allora: A λ τ λ Λ ogni unione arbitraria di aperti è un aperto. (A 3 ) se A 1,..., A m τ, allora: A 1 A m τ ogni intersezione finita di aperti è un aperto. METRICI 13
14 Dimostrazione. (A 1 ) ovvia. (A 2 ) unione di unioni di palle aperte... (A 3 ). Basta dimostrarlo per due insiemi aperti A 1 e A 2 ; useremo la prop. 13. Sia p A 1 A 2. Esistono allora r 1 > 0 e r 2 > 0 tali che: B(p, r 1 [ A 1, B(p, r 2 [ A 2 Supponiamo r 1 r 2. Allora ovviamente B(p, r 1 [ A 1 A 2. Esercizio. Mostrare con un esempio che un intersezione arbitraria di insiemi aperti non è in generale un insieme aperto. Definizione 15 Un sottoinsieme C di X si dice chiuso se il suo complementare X \ C = {x X : x C} è un aperto. Esercizio. I singoletti (insiemi del tipo {x}) sono insiemi chiusi. Dalla dualità di De Morgan si ottengono le seguenti proprietà dei chiusi: (C 1 ) X, sono chiusi; (C 2 ) se C λ è chiuso per ogni λ Λ, allora λ Λ C λ è chiuso; (C 3 ) se C 1,..., C m sono chiusi, allora C 1 C m è chiuso. Esercizio. Mostrare con un esempio che un unione arbitraria di insiemi chiusi non è in generale un insieme chiuso. Definizione 16 Un sottoinsieme U di X si dice intorno di un punto p X se esiste un aperto A tale che: p A U cioè U deve contenere un insieme aperto che contiene p. Meditazione: un insieme è aperto se e solo se è intorno di ogni suo punto METRICI 14
15 La famiglia I p di tutti gli intorni di p si chiama filtro degli intorni di p. Proprietà di I p : (I 1 ) U I p si ha p U; (I 2 ) se U I p e U V X, allora V I p ; (I 3 ) se U, V I p, allora U V I p ; (I 4 ) se U I p allora esiste A U con p A e tale che A I x per ogni x A. Definizione 17 Una famiglia B p di sottoinsiemi di X si dice base per il filtro degli intorni di p se: i) per ogni U B p si ha U I p ; ii) per ogni V I p si ha che esiste U B p tale che U V. Esercizio. Verificare che in uno spazio metrico ciascuna delle seguenti famiglie è base per gli intorni di p: a) {B(p, δ[: δ > 0} b) {B(p, δ] : δ > 0} c) {B(p, 1 n [: n = 1, 2,...} Quando si parla di R n si intende con la topologia usuale o euclidea, cioè quella indotta dalla metrica euclidea x y. Esercizio. In R la famiglia degli intervalli aperti che contengono un punto p costituisce una base per il filtro degli intorni di p. Sia U aperto non vuoto di R. Dimostrare che U contiene sia numeri razionali sia numeri irrazionali. Generalizzare il risultato a R n. METRICI 15
16 Sia A X. Si dice chiusura di A in X, e si indica con A o con cl X (A), il seguente insieme: È il più piccolo chiuso che contiene A. Proprietà: (Cl 1 ) A X si ha A A; A = {C : C A, C chiuso in X} (Cl 2 ) se A, B X allora A B = A B; (Cl 3 ) per ogni A X si ha (A) = A. Esercizio. Dopo aver osservato che in R ogni intervallo aperto non vuoto contiene numeri razionali, dedurre che Q = R. È vero che R \ Q = R? Esercizio. Dimostrare che A B A B, e che l inclusione può essere stretta. Proposizione 18 Siano p X e A X. Allora: p A se e solo se per ogni intorno U di p si ha U A. Importante Siano d la metrica che induce la topologia di X e A X, A. Allora: A = {x X : d(x, A) = 0} Si dice interno di A, indicato con A oppure int X (A): A= {U : U A, U aperto in X} È il massimo sottoinsieme aperto contenuto in A. Se p A, allora p si dice interno ad A. Fatto: X \ A = int(x \ A). Un punto p si dice di frontiera per A se p non è interno né ad A né a X \ A, cioè se ogni intorno di p contiene punti di A e punti di X \ A. Si chiama frontiera di A e si indica con fr X (A) o A l insieme dei punti di frontiera per A. METRICI 16
17 Fatti: fr(a) = A X \ A = fr(x \ A). A = A fr A. p fr A U I p si ha U A e U (X \ A). fr A è un insieme chiuso. Un insieme è chiuso se e solo se contiene la propria frontiera. Definizione 19 Un punto p X si dice punto di accumulazione per un sottoinsieme A di X se ogni intorno U di p contiene punti di A diversi da p. Un punto p A si dice isolato in A se non è di accumulazione per A. Fatti: L insieme dei punti di accumulazione per A si chiama derivato di A e si indica con A. Si ha: A = A A Il punto p è di accumulazione per A se e solo se ogni intorno di p contiene infiniti punti di A. Esercizio. Trovare la chiusura, l interno, la frontiera, il derivato e l insieme dei punti isolati dei seguenti insiemi: A R A = Q ]0, 1[ {2} A R A =], 0[ {1} A R 2 A = Q 2 ([0, 1] [0, 1]) A R A = {m + 1 n : m Z, n 1, n N} A R R A = Q Q con la topologia della metrica del riccio METRICI 17
18 Definizione 20 Un sottoinsieme D X si dice denso in X se una delle seguenti condizioni equivalenti è soddisfatta: 1) D = X. 2) Ogni aperto non vuoto contiene punti di D. Ad esempio, Q e R \ Q sono entrambi densi in R. Esercizio. L intersezione di due aperti densi è aperto e denso. Definizione 21 Sia (x j ) j N una successione di punti di X e sia p X. Si dice che lim x j = p se per ogni intorno U di p esiste j N tale che x j U per ogni j j cioè se la successione (x j ) j N sta definitivamente in ogni intorno di p. Osservazione. In B(X, R) con la norma della convergenza uniforme si consideri una successione (f j ) j N di funzioni. Se lim f j = f B(X, R), allora per ogni x X si ha lim f j (x) = f(x) R. Il viceversa non è vero. 1 f Morale: la convergenza uniforme implica la convergenza puntuale, ma non viceversa. Teorema 22 Sia (X, τ) spazio metrizzabile e siano p X e A X. Allora: p A esiste una successione (x j ) j N con x j A j tale che lim x j = p. p A esiste una successione (x j ) j N con x j A \ {p} j tale che lim x j = p. In questo caso la successione si può prendere iniettiva. 1 4 f 1 METRICI 18
4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale
 4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale Spazi Metrici Ricordiamo che uno spazio metrico è una coppia (X, d) dove X è un insieme e d : X X [0, + [ è una funzione, detta metrica,
4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale Spazi Metrici Ricordiamo che uno spazio metrico è una coppia (X, d) dove X è un insieme e d : X X [0, + [ è una funzione, detta metrica,
Per lo svolgimento del corso risulta particolarmente utile considerare l insieme
 1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
A i è un aperto in E. i=1
 Proposizione 1. A è aperto se e solo se A c è chiuso. Dimostrazione. = : se x o A c, allora x o A = A o e quindi esiste r > 0 tale che B(x o, r) A; allora x o non può essere di accumulazione per A c. Dunque
Proposizione 1. A è aperto se e solo se A c è chiuso. Dimostrazione. = : se x o A c, allora x o A = A o e quindi esiste r > 0 tale che B(x o, r) A; allora x o non può essere di accumulazione per A c. Dunque
Esistenza di funzioni continue non differenziabili in alcun punto
 UNIVERSITÀ DEGLI STUDI DI CAGLIARI FACOLTÀ DI SCIENZE MATEMATICHE, FISICHE E NATURALI CORSO DI LAUREA IN MATEMATICA Esistenza di funzioni continue non differenziabili in alcun punto Relatore Prof. Andrea
UNIVERSITÀ DEGLI STUDI DI CAGLIARI FACOLTÀ DI SCIENZE MATEMATICHE, FISICHE E NATURALI CORSO DI LAUREA IN MATEMATICA Esistenza di funzioni continue non differenziabili in alcun punto Relatore Prof. Andrea
19. Inclusioni tra spazi L p.
 19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8. Cognome:... Nome:... Matricola:...
 Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 2011/2012
 Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
10. Insiemi non misurabili secondo Lebesgue.
 10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
TOPOLOGIA ALBERTO SARACCO
 TOPOLOGIA ALBERTO SARACCO Abstract. Le presenti note saranno il più fedeli possibile a quanto detto a lezione. I testi consigliati sono Jänich [1], Kosniowski [2] e Singer- Thorpe [3]. Un ottimo libro
TOPOLOGIA ALBERTO SARACCO Abstract. Le presenti note saranno il più fedeli possibile a quanto detto a lezione. I testi consigliati sono Jänich [1], Kosniowski [2] e Singer- Thorpe [3]. Un ottimo libro
Parte 6. Applicazioni lineari
 Parte 6 Applicazioni lineari A Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Applicazioni fra insiemi, 2 Applicazioni lineari tra spazi vettoriali, 2 3 Applicazioni lineari da R n a R
Parte 6 Applicazioni lineari A Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Applicazioni fra insiemi, 2 Applicazioni lineari tra spazi vettoriali, 2 3 Applicazioni lineari da R n a R
Insiemi di livello e limiti in più variabili
 Insiemi di livello e iti in più variabili Insiemi di livello Si consideri una funzione f : A R, con A R n. Un modo per poter studiare il comportamento di una funzione in più variabili potrebbe essere quello
Insiemi di livello e iti in più variabili Insiemi di livello Si consideri una funzione f : A R, con A R n. Un modo per poter studiare il comportamento di una funzione in più variabili potrebbe essere quello
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
Ottimizazione vincolata
 Ottimizazione vincolata Ricordiamo alcuni risultati provati nella scheda sulla Teoria di Dini per una funzione F : R N+M R M di classe C 1 con (x 0, y 0 ) F 1 (a), a = (a 1,, a M ), punto in cui vale l
Ottimizazione vincolata Ricordiamo alcuni risultati provati nella scheda sulla Teoria di Dini per una funzione F : R N+M R M di classe C 1 con (x 0, y 0 ) F 1 (a), a = (a 1,, a M ), punto in cui vale l
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI
 CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
1.1. Spazi metrici completi
 SPAZI METRICI: COMPLETEZZA E COMPATTEZZA Note informali dalle lezioni 1.1. Spazi metrici completi La nozione di convergenza di successioni è centrale nello studio degli spazi metrici. In particolare è
SPAZI METRICI: COMPLETEZZA E COMPATTEZZA Note informali dalle lezioni 1.1. Spazi metrici completi La nozione di convergenza di successioni è centrale nello studio degli spazi metrici. In particolare è
f(x) = 1 x. Il dominio di questa funzione è il sottoinsieme proprio di R dato da
 Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
È difficile verificare la disuguaglianza triangolare. x1 y1. x2 y2. R 2 con la metrica del sup: d : X X [0,+ [ distanza (=metrica)
 SPAZI METRICI Nel piano R 2 o nello spazio R 3 la distanza fra due punti è la lunghezza, o norma euclidea, del vettore differenza di questi due punti. Se p = (x,y,z) è un vettore in coordinate ortonormali,
SPAZI METRICI Nel piano R 2 o nello spazio R 3 la distanza fra due punti è la lunghezza, o norma euclidea, del vettore differenza di questi due punti. Se p = (x,y,z) è un vettore in coordinate ortonormali,
EQUAZIONI DIFFERENZIALI. 1. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x 2 log t (d) x = e t x log x (e) y = y2 5y+6
 EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
RICHIAMI SULLE MATRICI. Una matrice di m righe e n colonne è rappresentata come
 RICHIAMI SULLE MATRICI Una matrice di m righe e n colonne è rappresentata come A = a 11 a 12... a 1n a 21 a 22... a 2n............ a m1 a m2... a mn dove m ed n sono le dimensioni di A. La matrice A può
RICHIAMI SULLE MATRICI Una matrice di m righe e n colonne è rappresentata come A = a 11 a 12... a 1n a 21 a 22... a 2n............ a m1 a m2... a mn dove m ed n sono le dimensioni di A. La matrice A può
IL CALCOLO VETTORIALE (SUPPLEMENTO AL LIBRO)
 IL CALCOLO VETTORIALE SUPPLEMENTO AL LIBRO CLAUDIO BONANNO Contents. Campi di vettori e operatori 2. Il lavoro di un campo di vettori 5 2.. Lavoro e campi conservativi 6 2.2. Lavoro e campi irrotazionali:
IL CALCOLO VETTORIALE SUPPLEMENTO AL LIBRO CLAUDIO BONANNO Contents. Campi di vettori e operatori 2. Il lavoro di un campo di vettori 5 2.. Lavoro e campi conservativi 6 2.2. Lavoro e campi irrotazionali:
1 Applicazioni Lineari tra Spazi Vettoriali
 1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
Lezioni di Matematica 1 - I modulo
 Lezioni di Matematica 1 - I modulo Luciano Battaia 16 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezione del 16/10/2008 1 / 13 L introduzione dei numeri reali si può
Lezioni di Matematica 1 - I modulo Luciano Battaia 16 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezione del 16/10/2008 1 / 13 L introduzione dei numeri reali si può
l insieme Y è detto codominio (è l insieme di tutti i valori che la funzione può assumere)
 Che cos è una funzione? Assegnati due insiemi X e Y si ha una funzione elemento di X uno e un solo elemento di Y. f : X Y se esiste una corrispondenza che associa ad ogni Osservazioni: l insieme X è detto
Che cos è una funzione? Assegnati due insiemi X e Y si ha una funzione elemento di X uno e un solo elemento di Y. f : X Y se esiste una corrispondenza che associa ad ogni Osservazioni: l insieme X è detto
Proof. Dimostrazione per assurdo. Consideriamo l insieme complementare di P nell insieme
 G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria).
 Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Forme bilineari e prodotti scalari. Definizione Dato lo spazio vettoriale V (K) sul campo K, una funzione. b :
 Forme bilineari e prodotti scalari Definizione Dato lo spazio vettoriale V (K) sul campo K, una funzione b : { V V K ( v, w) b( v, w), si dice forma bilineare su V se per ogni u, v, w V e per ogni k K:
Forme bilineari e prodotti scalari Definizione Dato lo spazio vettoriale V (K) sul campo K, una funzione b : { V V K ( v, w) b( v, w), si dice forma bilineare su V se per ogni u, v, w V e per ogni k K:
4. Operazioni binarie, gruppi e campi.
 1 4. Operazioni binarie, gruppi e campi. 4.1 Definizione. Diremo - operazione binaria ovunque definita in A B a valori in C ogni funzione f : A B C - operazione binaria ovunque definita in A a valori in
1 4. Operazioni binarie, gruppi e campi. 4.1 Definizione. Diremo - operazione binaria ovunque definita in A B a valori in C ogni funzione f : A B C - operazione binaria ovunque definita in A a valori in
2.1 Definizione di applicazione lineare. Siano V e W due spazi vettoriali su R. Un applicazione
 Capitolo 2 MATRICI Fra tutte le applicazioni su uno spazio vettoriale interessa esaminare quelle che mantengono la struttura di spazio vettoriale e che, per questo, vengono dette lineari La loro importanza
Capitolo 2 MATRICI Fra tutte le applicazioni su uno spazio vettoriale interessa esaminare quelle che mantengono la struttura di spazio vettoriale e che, per questo, vengono dette lineari La loro importanza
I appello - 24 Marzo 2006
 Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
2 FUNZIONI REALI DI VARIABILE REALE
 2 FUNZIONI REALI DI VARIABILE REALE 2.1 CONCETTO DI FUNZIONE Definizione 2.1 Siano A e B due insiemi. Una funzione (o applicazione) f con dominio A a valori in B è una legge che associa ad ogni elemento
2 FUNZIONI REALI DI VARIABILE REALE 2.1 CONCETTO DI FUNZIONE Definizione 2.1 Siano A e B due insiemi. Una funzione (o applicazione) f con dominio A a valori in B è una legge che associa ad ogni elemento
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Dipendenza dai dati iniziali
 Dipendenza dai dati iniziali Dopo aver studiato il problema dell esistenza e unicità delle soluzioni dei problemi di Cauchy, il passo successivo è vedere come le traiettorie di queste ultime dipendono
Dipendenza dai dati iniziali Dopo aver studiato il problema dell esistenza e unicità delle soluzioni dei problemi di Cauchy, il passo successivo è vedere come le traiettorie di queste ultime dipendono
CONCETTO DI LIMITE DI UNA FUNZIONE REALE
 CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
Prova scritta di Geometria 2 Prof. M. Boratynski
 10/9/2008 Es. 1: Si consideri la forma bilineare simmetrica b su R 3 associata, rispetto alla base canonica {e 1, e 2, e 3 } alla matrice 3 2 1 A = 2 3 0. 1 0 1 1) Provare che (R 3, b) è uno spazio vettoriale
10/9/2008 Es. 1: Si consideri la forma bilineare simmetrica b su R 3 associata, rispetto alla base canonica {e 1, e 2, e 3 } alla matrice 3 2 1 A = 2 3 0. 1 0 1 1) Provare che (R 3, b) è uno spazio vettoriale
STRUTTURE ALGEBRICHE
 STRUTTURE ALGEBRICHE Operazioni in un insieme Sia A un insieme non vuoto; una funzione f : A A A si dice operazione binaria (o semplicemente operazione), oppure legge di composizione interna. Per definizione
STRUTTURE ALGEBRICHE Operazioni in un insieme Sia A un insieme non vuoto; una funzione f : A A A si dice operazione binaria (o semplicemente operazione), oppure legge di composizione interna. Per definizione
Convessità e derivabilità
 Convessità e derivabilità Definizione 1 (convessità per funzioni derivabili) Sia f : (a, b) R derivabile su (a, b). Diremo che f è convessa o concava su (a, b) se per ogni 0 (a,b) il grafico di f sta tutto
Convessità e derivabilità Definizione 1 (convessità per funzioni derivabili) Sia f : (a, b) R derivabile su (a, b). Diremo che f è convessa o concava su (a, b) se per ogni 0 (a,b) il grafico di f sta tutto
RETTE, PIANI, SFERE, CIRCONFERENZE
 RETTE, PIANI, SFERE, CIRCONFERENZE 1. Esercizi Esercizio 1. Dati i punti A(1, 0, 1) e B(, 1, 1) trovare (1) la loro distanza; () il punto medio del segmento AB; (3) la retta AB sia in forma parametrica,
RETTE, PIANI, SFERE, CIRCONFERENZE 1. Esercizi Esercizio 1. Dati i punti A(1, 0, 1) e B(, 1, 1) trovare (1) la loro distanza; () il punto medio del segmento AB; (3) la retta AB sia in forma parametrica,
LEZIONE 16. Proposizione 16.1.2. Siano V e W spazi vettoriali su k = R, C. Se f: V W
 LEZIONE 16 16.1. Applicazioni lineari iniettive e suriettive. Ricordo le seguenti due definizioni valide per applicazioni di qualsiasi tipo ϕ: X Y fra due insiemi. L applicazione ϕ si dice iniettiva se
LEZIONE 16 16.1. Applicazioni lineari iniettive e suriettive. Ricordo le seguenti due definizioni valide per applicazioni di qualsiasi tipo ϕ: X Y fra due insiemi. L applicazione ϕ si dice iniettiva se
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI
 FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
LEZIONE 31. B i : R n R. R m,n, x = (x 1,..., x n ). Allora sappiamo che è definita. j=1. a i,j x j.
 LEZIONE 31 31.1. Domini di funzioni di più variabili. Sia ora U R n e consideriamo una funzione f: U R m. Una tale funzione associa a x = (x 1,..., x n ) U un elemento f(x 1,..., x n ) R m : tale elemento
LEZIONE 31 31.1. Domini di funzioni di più variabili. Sia ora U R n e consideriamo una funzione f: U R m. Una tale funzione associa a x = (x 1,..., x n ) U un elemento f(x 1,..., x n ) R m : tale elemento
Parte 2. Determinante e matrice inversa
 Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
Capitolo 1 ANALISI COMPLESSA
 Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
Funzioni in più variabili
 Funzioni in più variabili Corso di Analisi 1 di Andrea Centomo 27 gennaio 2011 Indichiamo con R n, n 1, l insieme delle n-uple ordinate di numeri reali R n4{(x 1, x 2,,x n ), x i R, i =1,,n}. Dato X R
Funzioni in più variabili Corso di Analisi 1 di Andrea Centomo 27 gennaio 2011 Indichiamo con R n, n 1, l insieme delle n-uple ordinate di numeri reali R n4{(x 1, x 2,,x n ), x i R, i =1,,n}. Dato X R
Lezione 1. Gli Insiemi. La nozione di insieme viene spesso utilizzata nella vita di tutti i giorni; si parla dell insieme:
 Lezione 1 Gli Insiemi La nozione di insieme viene spesso utilizzata nella vita di tutti i giorni; si parla dell insieme: degli iscritti ad un corso di laurea delle stelle in cielo dei punti di un piano
Lezione 1 Gli Insiemi La nozione di insieme viene spesso utilizzata nella vita di tutti i giorni; si parla dell insieme: degli iscritti ad un corso di laurea delle stelle in cielo dei punti di un piano
I tre concetti si possono descrivere in modo unitario dicendo che f e iniettiva, suriettiva, biiettiva se e solo se per ogni b B l equazione
 Lezioni del 29 settembre e 1 ottobre. 1. Funzioni iniettive, suriettive, biiettive. Sia f : A B una funzione da un insieme A ad un insieme B. Sia a A e sia b = f (a) B l elemento che f associa ad a, allora
Lezioni del 29 settembre e 1 ottobre. 1. Funzioni iniettive, suriettive, biiettive. Sia f : A B una funzione da un insieme A ad un insieme B. Sia a A e sia b = f (a) B l elemento che f associa ad a, allora
Equazioni differenziali ordinarie
 Equazioni differenziali ordinarie Denis Nardin January 2, 2010 1 Equazioni differenziali In questa sezione considereremo le proprietà delle soluzioni del problema di Cauchy. Da adesso in poi (PC) indicherà
Equazioni differenziali ordinarie Denis Nardin January 2, 2010 1 Equazioni differenziali In questa sezione considereremo le proprietà delle soluzioni del problema di Cauchy. Da adesso in poi (PC) indicherà
1 Serie di Taylor di una funzione
 Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Applicazioni lineari
 Applicazioni lineari Esempi di applicazioni lineari Definizione. Se V e W sono spazi vettoriali, una applicazione lineare è una funzione f: V W tale che, per ogni v, w V e per ogni a, b R si abbia f(av
Applicazioni lineari Esempi di applicazioni lineari Definizione. Se V e W sono spazi vettoriali, una applicazione lineare è una funzione f: V W tale che, per ogni v, w V e per ogni a, b R si abbia f(av
Funzioni con dominio in R n
 0.1 Punti e vettori di R n Politecnico di Torino. Funzioni con dominio in R n Nota Bene: delle lezioni. Questo materiale non deve essere considerato come sostituto Molto spesso risulta che una quantita
0.1 Punti e vettori di R n Politecnico di Torino. Funzioni con dominio in R n Nota Bene: delle lezioni. Questo materiale non deve essere considerato come sostituto Molto spesso risulta che una quantita
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica.
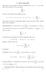 8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
SPAZI TOPOLOGICI. La nozione di spazio topologico è più generale di quella di spazio metrizzabile.
 SPAZI TOPOLOGICI La nozione di spazio topologico è più generale di quella di spazio metrizzabile. Definizione 1 Uno spazio topologico (X, τ) è una coppia costituita da un insieme X e da una famiglia τ
SPAZI TOPOLOGICI La nozione di spazio topologico è più generale di quella di spazio metrizzabile. Definizione 1 Uno spazio topologico (X, τ) è una coppia costituita da un insieme X e da una famiglia τ
5. La teoria astratta della misura.
 5. La teoria astratta della misura. 5.1. σ-algebre. 5.1.1. σ-algebre e loro proprietà. Sia Ω un insieme non vuoto. Indichiamo con P(Ω la famiglia di tutti i sottoinsiemi di Ω. Inoltre, per ogni insieme
5. La teoria astratta della misura. 5.1. σ-algebre. 5.1.1. σ-algebre e loro proprietà. Sia Ω un insieme non vuoto. Indichiamo con P(Ω la famiglia di tutti i sottoinsiemi di Ω. Inoltre, per ogni insieme
Università di Trieste Facoltà d Ingegneria. Esercizi sul calcolo differenziale in IR N. Dott. Franco Obersnel
 Università di Trieste Facoltà d Ingegneria Esercizi sul calcolo differenziale in IR N Dott Franco Obersnel Esercizio 1 Si calcoli la derivata direzionale nell origine lungo la direzione y del versore v
Università di Trieste Facoltà d Ingegneria Esercizi sul calcolo differenziale in IR N Dott Franco Obersnel Esercizio 1 Si calcoli la derivata direzionale nell origine lungo la direzione y del versore v
G. Pareschi ALGEBRE DI BOOLE. 1. Algebre di Boole
 G. Pareschi ALGEBRE DI BOOLE 1. Algebre di Boole Nel file precedente abbiamo incontrato la definizione di algebra di Boole come reticolo: un algebra di Boole e un reticolo limitato, complementato e distributivo.
G. Pareschi ALGEBRE DI BOOLE 1. Algebre di Boole Nel file precedente abbiamo incontrato la definizione di algebra di Boole come reticolo: un algebra di Boole e un reticolo limitato, complementato e distributivo.
Definizione DEFINIZIONE
 Definizione Funzione reale di due variabili reali Indichiamo con R 2 l insieme di tutti i vettori bidimensionali. Dato un sottoinsiemed R 2, una funzione f: D R è una legge che assegna a ogni punto (x,
Definizione Funzione reale di due variabili reali Indichiamo con R 2 l insieme di tutti i vettori bidimensionali. Dato un sottoinsiemed R 2, una funzione f: D R è una legge che assegna a ogni punto (x,
Equazioni alle differenze finite (cenni).
 AL 011. Equazioni alle differenze finite (cenni). Sia a n } n IN una successione di numeri reali. (Qui usiamo la convenzione IN = 0, 1,,...}). Diremo che è una successione ricorsiva o definita per ricorrenza
AL 011. Equazioni alle differenze finite (cenni). Sia a n } n IN una successione di numeri reali. (Qui usiamo la convenzione IN = 0, 1,,...}). Diremo che è una successione ricorsiva o definita per ricorrenza
Sulla monotonia delle funzioni reali di una variabile reale
 Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
Due dimostrazioni alternative nella teoria di Ramsey
 Due dimostrazioni alternative nella teoria di Ramsey 28 Marzo 2007 Introduzione Teoria di Ramsey: sezione della matematica a metà tra la combinatoria e la teoria degli insiemi. La questione tipica è quella
Due dimostrazioni alternative nella teoria di Ramsey 28 Marzo 2007 Introduzione Teoria di Ramsey: sezione della matematica a metà tra la combinatoria e la teoria degli insiemi. La questione tipica è quella
TOPOLOGIE. Capitolo 2. 2.1 Spazi topologici
 Capitolo 2 TOPOLOGIE Ogni spazio che si considera in gran parte della matematica e delle sue applicazioni è uno spazio topologico di qualche tipo: qui introduciamo in generale le nozioni di base della
Capitolo 2 TOPOLOGIE Ogni spazio che si considera in gran parte della matematica e delle sue applicazioni è uno spazio topologico di qualche tipo: qui introduciamo in generale le nozioni di base della
RELAZIONI BINARIE. Proprietà delle relazioni Data una relazione R, definita in un insieme non vuoto U, si hanno le seguenti proprietà :
 RELAZIONI INARIE Dati due insiemi non vuoti, A detto dominio e detto codominio, eventualmente coincidenti, si chiama relazione binaria (o corrispondenza) di A in, e si indica con f : A, (oppure R ) una
RELAZIONI INARIE Dati due insiemi non vuoti, A detto dominio e detto codominio, eventualmente coincidenti, si chiama relazione binaria (o corrispondenza) di A in, e si indica con f : A, (oppure R ) una
Limiti e continuità di funzioni reali di una variabile
 di funzioni reali di una variabile Corso di Analisi Matematica - capitolo VI Facoltà di Economia, UER Maria Caterina Bramati Université Libre de Bruxelles ECARES 22 Novembre 2006 Intuizione di ite di funzione
di funzioni reali di una variabile Corso di Analisi Matematica - capitolo VI Facoltà di Economia, UER Maria Caterina Bramati Université Libre de Bruxelles ECARES 22 Novembre 2006 Intuizione di ite di funzione
SIMULAZIONE TEST ESAME - 1
 SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
INTEGRALI DEFINITI. Tale superficie viene detta trapezoide e la misura della sua area si ottiene utilizzando il calcolo di un integrale definito.
 INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
x 2 + y2 4 = 1 x = cos(t), y = 2 sin(t), t [0, 2π] Al crescere di t l ellisse viene percorsa in senso antiorario.
![x 2 + y2 4 = 1 x = cos(t), y = 2 sin(t), t [0, 2π] Al crescere di t l ellisse viene percorsa in senso antiorario. x 2 + y2 4 = 1 x = cos(t), y = 2 sin(t), t [0, 2π] Al crescere di t l ellisse viene percorsa in senso antiorario.](/thumbs/39/18585741.jpg) Le soluzioni del foglio 2. Esercizio Calcolare il lavoro compiuto dal campo vettoriale F = (y + 3x, 2y x) per far compiere ad una particella un giro dell ellisse 4x 2 + y 2 = 4 in senso orario... Soluzione.
Le soluzioni del foglio 2. Esercizio Calcolare il lavoro compiuto dal campo vettoriale F = (y + 3x, 2y x) per far compiere ad una particella un giro dell ellisse 4x 2 + y 2 = 4 in senso orario... Soluzione.
Esercizi svolti. 1. Si consideri la funzione f(x) = 4 x 2. a) Verificare che la funzione F(x) = x 2 4 x2 + 2 arcsin x è una primitiva di
 Esercizi svolti. Si consideri la funzione f() 4. a) Verificare che la funzione F() 4 + arcsin è una primitiva di f() sull intervallo (, ). b) Verificare che la funzione G() 4 + arcsin π è la primitiva
Esercizi svolti. Si consideri la funzione f() 4. a) Verificare che la funzione F() 4 + arcsin è una primitiva di f() sull intervallo (, ). b) Verificare che la funzione G() 4 + arcsin π è la primitiva
I polinomi 1; x;x 2 ;x 3 sono linearmente indipendenti; infatti. 0= 1 1+ 2 x+ 3 x 2 + 4 x 3 =) 1 = 2 == 4 =0
 ASPETTI TEORICI Spazio vettoriale Un insieme qualunque di inniti elementi V = fv i g si dice uno spazio vettoriale sull'insieme dei numeri reali R se: { E possibile denire un'operazione binaria fra gli
ASPETTI TEORICI Spazio vettoriale Un insieme qualunque di inniti elementi V = fv i g si dice uno spazio vettoriale sull'insieme dei numeri reali R se: { E possibile denire un'operazione binaria fra gli
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria Elettronica
 Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria Elettronica Terzo Appello del corso di Geometria e Algebra II Parte - Docente F. Flamini, Roma, 7/09/2007 SVOLGIMENTO COMPITO III APPELLO
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria Elettronica Terzo Appello del corso di Geometria e Algebra II Parte - Docente F. Flamini, Roma, 7/09/2007 SVOLGIMENTO COMPITO III APPELLO
3 GRAFICI DI FUNZIONI
 3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
x 1 + x 2 3x 4 = 0 x1 + x 2 + x 3 = 0 x 1 + x 2 3x 4 = 0.
 Problema. Sia W il sottospazio dello spazio vettoriale R 4 dato da tutte le soluzioni dell equazione x + x 2 + x = 0. (a. Sia U R 4 il sottospazio dato da tutte le soluzioni dell equazione Si determini
Problema. Sia W il sottospazio dello spazio vettoriale R 4 dato da tutte le soluzioni dell equazione x + x 2 + x = 0. (a. Sia U R 4 il sottospazio dato da tutte le soluzioni dell equazione Si determini
1 Insiemi e terminologia
 1 Insiemi e terminologia Assumeremo come intuitiva la nozione di insieme e ne utilizzeremo il linguaggio come strumento per studiare collezioni di oggetti. Gli Insiemi sono generalmente indicati con le
1 Insiemi e terminologia Assumeremo come intuitiva la nozione di insieme e ne utilizzeremo il linguaggio come strumento per studiare collezioni di oggetti. Gli Insiemi sono generalmente indicati con le
Parte 3. Rango e teorema di Rouché-Capelli
 Parte 3. Rango e teorema di Rouché-Capelli A. Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Rango di una matrice, 2 Teorema degli orlati, 3 3 Calcolo con l algoritmo di Gauss, 6 4 Matrici
Parte 3. Rango e teorema di Rouché-Capelli A. Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Rango di una matrice, 2 Teorema degli orlati, 3 3 Calcolo con l algoritmo di Gauss, 6 4 Matrici
Completezza e compattezza
 1 Completezza e compattezza Spazi metrici completi Data una successione x : N X, j x j, una sua sottosuccessione è la composizione x ν, ove ν : N N è strettamente crescente. Data una successione (x j )
1 Completezza e compattezza Spazi metrici completi Data una successione x : N X, j x j, una sua sottosuccessione è la composizione x ν, ove ν : N N è strettamente crescente. Data una successione (x j )
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
Le funzioni reali di variabile reale
 Prof. Michele Giugliano (Gennaio 2002) Le funzioni reali di variabile reale ) Complementi di teoria degli insiemi. A) Estremi di un insieme numerico X. Dato un insieme X R, si chiama maggiorante di X un
Prof. Michele Giugliano (Gennaio 2002) Le funzioni reali di variabile reale ) Complementi di teoria degli insiemi. A) Estremi di un insieme numerico X. Dato un insieme X R, si chiama maggiorante di X un
Massimi e minimi vincolati
 Massimi e minimi vincolati In problemi di massimo e minimo vincolato viene richiesto di ricercare massimi e minimi di una funzione non definita su tutto R n, ma su un suo sottoinsieme proprio. Esempio:
Massimi e minimi vincolati In problemi di massimo e minimo vincolato viene richiesto di ricercare massimi e minimi di una funzione non definita su tutto R n, ma su un suo sottoinsieme proprio. Esempio:
Iniziamo con un esercizio sul massimo comun divisore: Esercizio 1. Sia d = G.C.D.(a, b), allora:
 Iniziamo con un esercizio sul massimo comun divisore: Esercizio 1. Sia d = G.C.D.(a, b), allora: G.C.D.( a d, b d ) = 1 Sono state introdotte a lezione due definizioni importanti che ricordiamo: Definizione
Iniziamo con un esercizio sul massimo comun divisore: Esercizio 1. Sia d = G.C.D.(a, b), allora: G.C.D.( a d, b d ) = 1 Sono state introdotte a lezione due definizioni importanti che ricordiamo: Definizione
ALCUNE APPLICAZIONI DEL CALCOLO DIFFERENZIALE
 ALCUNE APPLICAZIONI DEL CALCOLO DIFFERENZIALE Sia I un intervallo di R e siano a = inf(i) R { } e b = sup(i) R {+ }; i punti di I diversi dagli estremi a e b, ( e quindi appartenenti all intervallo aperto
ALCUNE APPLICAZIONI DEL CALCOLO DIFFERENZIALE Sia I un intervallo di R e siano a = inf(i) R { } e b = sup(i) R {+ }; i punti di I diversi dagli estremi a e b, ( e quindi appartenenti all intervallo aperto
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Esercizi su lineare indipendenza e generatori
 Esercizi su lineare indipendenza e generatori Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V uno spazio vettoriale su K Cose da ricordare Definizione Dei vettori v,,v
Esercizi su lineare indipendenza e generatori Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V uno spazio vettoriale su K Cose da ricordare Definizione Dei vettori v,,v
1. PRIME PROPRIETÀ 2
 RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
FUNZIONE REALE DI UNA VARIABILE
 FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
Analisi Mat. 1 - Ing. Inform. - Soluzioni del compito del 23-3-06
 Analisi Mat. - Ing. Inform. - Soluzioni del compito del 3-3-6 Sia p il polinomio di quarto grado definito da pz = z 4. Sia S il settore circolare formato dai numeri complessi che hanno modulo minore o
Analisi Mat. - Ing. Inform. - Soluzioni del compito del 3-3-6 Sia p il polinomio di quarto grado definito da pz = z 4. Sia S il settore circolare formato dai numeri complessi che hanno modulo minore o
ALGEBRA I: CARDINALITÀ DI INSIEMI
 ALGEBRA I: CARDINALITÀ DI INSIEMI 1. CONFRONTO DI CARDINALITÀ E chiaro a tutti che esistono insiemi finiti cioè con un numero finito di elementi) ed insiemi infiniti. E anche chiaro che ogni insieme infinito
ALGEBRA I: CARDINALITÀ DI INSIEMI 1. CONFRONTO DI CARDINALITÀ E chiaro a tutti che esistono insiemi finiti cioè con un numero finito di elementi) ed insiemi infiniti. E anche chiaro che ogni insieme infinito
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
ESERCIZI APPLICAZIONI LINEARI
 ESERCIZI APPLICAZIONI LINEARI PAOLO FACCIN 1. Esercizi sulle applicazioni lineari 1.1. Definizioni sulle applicazioni lineari. Siano V, e W spazi vettoriali, con rispettive basi B V := (v 1 v n) e B W
ESERCIZI APPLICAZIONI LINEARI PAOLO FACCIN 1. Esercizi sulle applicazioni lineari 1.1. Definizioni sulle applicazioni lineari. Siano V, e W spazi vettoriali, con rispettive basi B V := (v 1 v n) e B W
( x) ( x) 0. Equazioni irrazionali
 Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
OGNI SPAZIO VETTORIALE HA BASE
 1 Mimmo Arezzo OGNI SPAZIO VETTORIALE HA BASE CONVERSAZIONE CON ALCUNI STUDENTI DI FISICA 19 DICEMBRE 2006 2 1 Preliminari Definizione 1.0.1 Un ordinamento parziale (o una relazione d ordine parziale)
1 Mimmo Arezzo OGNI SPAZIO VETTORIALE HA BASE CONVERSAZIONE CON ALCUNI STUDENTI DI FISICA 19 DICEMBRE 2006 2 1 Preliminari Definizione 1.0.1 Un ordinamento parziale (o una relazione d ordine parziale)
Esponenziali elogaritmi
 Esponenziali elogaritmi Potenze ad esponente reale Ricordiamo che per un qualsiasi numero razionale m n prendere n>0) si pone a m n = n a m (in cui si può sempre a patto che a sia un numero reale positivo.
Esponenziali elogaritmi Potenze ad esponente reale Ricordiamo che per un qualsiasi numero razionale m n prendere n>0) si pone a m n = n a m (in cui si può sempre a patto che a sia un numero reale positivo.
Esercitazione del 16-11-11 Analisi I
 Esercitazione del 6-- Analisi I Dott.ssa Silvia Saoncella silvia.saoncella 3[at]studenti.univr.it a.a. 00-0 Esercizio. Determinare se la funzione f() è continua nel suo dominio sin se 0 f() = 0 se = 0
Esercitazione del 6-- Analisi I Dott.ssa Silvia Saoncella silvia.saoncella 3[at]studenti.univr.it a.a. 00-0 Esercizio. Determinare se la funzione f() è continua nel suo dominio sin se 0 f() = 0 se = 0
VC-dimension: Esempio
 VC-dimension: Esempio Quale è la VC-dimension di. y b = 0 f() = 1 f() = 1 iperpiano 20? VC-dimension: Esempio Quale è la VC-dimension di? banale. Vediamo cosa succede con 2 punti: 21 VC-dimension: Esempio
VC-dimension: Esempio Quale è la VC-dimension di. y b = 0 f() = 1 f() = 1 iperpiano 20? VC-dimension: Esempio Quale è la VC-dimension di? banale. Vediamo cosa succede con 2 punti: 21 VC-dimension: Esempio
Ancora sugli insiemi. Simbologia
 ncora sugli insiemi Un insieme può essere specificato in vari modi; il più semplice è fare un elenco dei suoi elementi. d esempio l insieme delle nostre lauree triennali è { EOOM, EON, EOMM, EOMK EOTU}
ncora sugli insiemi Un insieme può essere specificato in vari modi; il più semplice è fare un elenco dei suoi elementi. d esempio l insieme delle nostre lauree triennali è { EOOM, EON, EOMM, EOMK EOTU}
Moto uniforme sul toro bidimensionale
 4/3/06 Luigi Chierchia Moto uniforme sul toro bidimensionale 1. Il toro bidimensionale Denotiamo con R l insieme dei numeri reali e con Z l insieme dei numeri interi (con segno) {..., 2, 1, 0, 1, 2,...};
4/3/06 Luigi Chierchia Moto uniforme sul toro bidimensionale 1. Il toro bidimensionale Denotiamo con R l insieme dei numeri reali e con Z l insieme dei numeri interi (con segno) {..., 2, 1, 0, 1, 2,...};
Rette e curve, piani e superfici
 Rette e curve piani e superfici ) dicembre 2 Scopo di questo articolo è solo quello di proporre uno schema riepilogativo che metta in luce le caratteristiche essenziali delle equazioni di rette e curve
Rette e curve piani e superfici ) dicembre 2 Scopo di questo articolo è solo quello di proporre uno schema riepilogativo che metta in luce le caratteristiche essenziali delle equazioni di rette e curve
Alcune nozioni preliminari di teoria elementare di insiemi e funzioni
 Alcune nozioni preliminari di teoria elementare di insiemi e funzioni Alberto Pinto Corso di Matematica - NUCT 1 Insiemi 1.1 Generalità Diamo la definizione di insieme secondo Georg Cantor, matematico
Alcune nozioni preliminari di teoria elementare di insiemi e funzioni Alberto Pinto Corso di Matematica - NUCT 1 Insiemi 1.1 Generalità Diamo la definizione di insieme secondo Georg Cantor, matematico
1 Convessità olomorfa
 1 Convessità olomorfa Esercizio 1 Sia f O(C n ) e sia X = {f = 0}; dimostrare che, per ogni K compatto di X, l inviluppo K O(Cn ) è contenuto in X. Esercizio 2 Fissato un reale δ (0, 2π), consideriamo
1 Convessità olomorfa Esercizio 1 Sia f O(C n ) e sia X = {f = 0}; dimostrare che, per ogni K compatto di X, l inviluppo K O(Cn ) è contenuto in X. Esercizio 2 Fissato un reale δ (0, 2π), consideriamo
Algebra Lineare e Geometria
 Algebra Lineare e Geometria Corso di Laurea in Ingegneria Elettronica A.A. 2013-2014 Prova d esame del 16/06/2014. 1) a) Determinare la matrice associata all applicazione lineare T : R 3 R 4 definita da
Algebra Lineare e Geometria Corso di Laurea in Ingegneria Elettronica A.A. 2013-2014 Prova d esame del 16/06/2014. 1) a) Determinare la matrice associata all applicazione lineare T : R 3 R 4 definita da
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
