Derivate delle funzioni di una variabile. Il problema delle tangenti
|
|
|
- Mariano Pace
- 7 anni fa
- Visualizzazioni
Transcript
1 Derivate delle funzioni di una variabile Il concetto di derivata di una funzione di una variabile è uno dei più importanti di tutta la matematica sia per le sue implicazioni di natura puramente teorica, sia per le numerose applicazioni di tipo pratico. La nozione di derivata è alla base del calcolo differenziale ce, insieme con il calcolo integrale, costituisce l'analisi infinitesimale. Il calcolo differenziale fu inventato, nel XVII secolo, da Newton e Leibniz, ce indipendentemente l uno dall altro, introdussero la nozione di derivata e di differenziale. I problemi ce in particolare diedero origine al concetto di derivata e ce per tale motivo rappresentano il punto di partenza per il calcolo differenziale, sono: il problema delle tangenti e il problema della velocità istantanea. Storicamente, la derivata si presenta come la risposta più efficace al problema delle tangenti, cioè al problema di come determinare la retta tangente a una qualsiasi curva in un suo punto. Già i greci si erano occupati della questione: Arcimede, Apollonio e Pappo avevano elaborato metodi ingegnosi per costruire tangenti alle conice e a curve più complesse, come la famosa spirale di Arcimede. Si trattava comunque di metodi particolari, applicabili caso per caso, e ce non possedevano perciò il carattere di procedimento generale, valido per tutte le curve. Nel Seicento ance Fermat e Cartesio, con l introduzione della geometria analitica, diedero un notevole impulso alle ricerce in questo campo. Il problema delle tangenti Per definire la retta tangente ad una curva in un suo punto non è possibile estendere ad essa la definizione adottata dalla geometria elementare nel caso della circonferenza ( Si ciama tangente alla circonferenza in un suo punto P quella particolare retta avente in comune con la circonferenza soltanto il punto P percé la retta tangente ad una qualsiasi curva in un suo punto P a in comune con la curva almeno due punti. Non è possibile utilizzare neance l altra definizione ce si dà in geometria elementare per la tangente e ce afferma: La tangente è la retta ce, passante per P, lascia la curva tutta da una stessa parte rispetto alla retta. Infatti, nel caso di una curva qualsiasi, la tangente può lasciare la curva da parti opposte.
2 E invece più opportuno introdurre il concetto di tangente attraverso un procedimento di tipo dinamico. Ossia: Si ciama tangente ad una curva piana in un suo punto P la posizione ite (se esiste della retta P P ce unisce P con un altro punto P della curva, allorcé il punto P, mouvendosi sulla curva, si avvicina indefinitamente a P. Data questa definizione di tangente si pone il problema di trovare l equazione della retta tangente ad una curva di equazione y in un suo punto P. Procedimento risolutivo del problema delle tangenti Sappiamo ce l equazione della tangente passante per il punto P (, y è: y-y m(- dove m rappresenta il coefficiente angolare della y y retta ed è dato da m. Per determinare il valore di m (tgα consideriamo sulla curva un altro punto Q di coordinate [o, ]. Il coefficiente angolare della secante PQ sarà: m Il coefficiente angolare della tangente (se Q P sarà: m RQ Poicé tgβ tgβ tgα PR Quindi: se la curva y, nel punto di ascissa, ammette una retta tangente, non parallela all asse y, il coefficiente angolare di tale retta è dato dal
3 Tale ite, quando esiste ed è finito, viene detto derivata della funzione calcolata nel punto. Da questo e da altri problemi è nata la definizione di derivata. Definizione Derivate Data la funzione y definita in un intervallo [a, b] si ciama derivata della funzione nel punto ] a, b[ il ite, se esiste ed è finito, del rapporto incrementale al tendere a zero dell'incremento della variabile indipendente. Note Se da si passa ad un altro punto qualunque, dell'intervallo [a, b], si dice ce si è dato alla variabile l'incremento (positivo o negativo. La differenza:, tra i valori ce la funzione assume quando la variabile passa dal valore al valore, si ciama incremento della funzione e può avere valore positivo, negativo o nullo. Il rapporto si ciama rapporto incrementale della funzione relativo al punto e all'incremento ; precisamente, si ciama rapporto incrementale destro o sinistro secondo ce sia: >, oppure: <. La derivata si indica con uno qualunque dei seguenti simboli: [ ] f (, y'(, D, D, (La notazione f '( risale a LAGRANGE, la notazione D a CAUCHY. Pertanto la derivata f (o della funzione è definita dalla relazione: d d, ecc. f''( nell'ipotesi ce il ite esista e sia finito. L'operazione con la quale si calcola la derivata di una funzione è detta la derivazione di questa funzione. Può darsi ce, pur non esistendo il ite per del rapporto incrementale, esista e sia finito tuttavia il ite a sinistra o il ite a destra, od entrambi; questi si ciameranno allora, rispettivamente, derivata sinistra e derivata destra di f ( in Nel seguito quando diremo ce la funzione f ( è derivabile nel punto, intenderemo sempre ce in questo punto esista finita sia la derivata sinistra ce la derivata destra e ce queste siano fra loro eguali..
4 Negli estremi a e b, dell'intervallo [a, b], la derivata coincide rispettivamente con la derivata destra e sinistra. Se la funzione f ( è derivabile in ogni punto interno all'intervallo [a, b] e se ammette derivata destra nel punto a e derivata sinistra nel punto b, la si dice derivabile nell'intervallo ciuso [a, b]. Teorema Se una funzione è derivabile nel punto, allora è necessariamente continua in tale punto. L incremento della funzione può essere così scritto: con Considerando i iti, per, di entrambi i membri, si a: [ f ( f ( ] Poicé per ipotesi f è derivabile f''( e quindi [ f ( f ( ] f '( Ricordando ce una funzione f è continua in quando si verifica ce: f f ovvero quando f f si a ce la f è continua in. Da questo teorema segue ce: ( ( [ ( ( ] Nei punti di discontinuità una funzione non può ammettere derivata. La proprietà inversa del teorema dato non è vera; cioè: se una funzione è continua in un punto non è detto ce sia derivabile in tale punto. Esempi La funzione y 3 è continua in, ma non è ivi derivabile ( il ite del rapporto incrementale per è. 2 La funzione y è continua in, ma non è ivi derivabile ( i iti destro e sinistro del rapporto incrementale, per, non sono uguali. Dunque: la derivabilità è un condizione più restrittiva della continuità. Osservazioni Si parla di derivata, per le funzioni definite su un intervallo, nei punti interni all'intervallo (a, b. La derivata di f in (a, b, quando esiste, è un numero. Se la derivata di f esiste in ogni punto di (a, b, allora possiamo pensare alla funzione di dominio (a, b ce associa ad ogni punto (a, b quel numero ce è la derivata di f in. Tale funzione si dice «funzione derivata». In generale la funzione derivata è una funzione avente come dominio l'insieme dei punti in cui esiste la derivata di f, ed è tale ce il valore da essa assunto in è f '(.
5 Significato geometrico di derivata Considerando il problema delle tangenti, da cui, storicamente, trae origine la derivata, si può affermare ce il rapporto incrementale della funzione si identifica con il coefficiente angolare della secante PQ ce unisce i due punti di ascissa e. Facendo tendere a accade conseguentemente ce: Il punto Q tende al punto P La secante r tende alla retta tangente t Il coefficiente angolare di r tende al coefficiente angolare di t Il rapporto incrementale tende alla derivata della funzione in. Da tutto ciò segue ce: La derivata di una funzione in un suo punto rappresenta il coefficiente angolare della retta tangente in quel punto alla curva di equazione y. Nota La derivabilità di una funzione in un punto implica l esistenza della tangente alla curva nel punto corrispondente. Derivate di alcune funzioni elementari Funzione yc y Derivata y y y n y n n- y ysen y 2 y cos ycos y -sen ylog a ylog ya ye y y log e a y a log a y e log a
6 Teoremi sul calcolo delle derivate Teorema. La derivata di una funzione costante yk, il cui insieme di definizione è R, è zero. y O yk k - k Preso un punto Teorema 2. La derivata della funzione y è y. y y O Preso un punto a: Teorema 3. / / La derivata della funzione y n con n N è la funzione y n n-. Teorema 4. La derivata della funzione y Preso un punto a: / / / - / è la funzione y 2 ( 2 ( ( (
7 Teorema 5. La derivata della funzione ysen è y cos in tutto R Preso un punto si a: sen( sen sen cos cos sen sen sen (cos cos sen (cos sen sen cos cos sen sen cos sen cos cos Si dimostra in modo analogo il seguente teorema: Teorema 6. La derivata della funzione cos è y - sen. Teorema 7. La derivata della funzione ylog a (con a> e a, definita in In particolare, se si pone ae e quindi log e, si a: La derivata della funzione ylog è y. Teorema 8. R, è y La funzione ye è sempre derivabile in R e la sua derivata è la funzione y e. Preso un punto a: e e e e e e ( e e ( e e e In modo analogo si dimostra ce: Teorema 9. La derivata della funzione ya (con a costante positiva e R è y a log a. log a e
8 Il calcolo con le derivate La determinazione della derivata di funzioni aventi una rappresentazione analitica piuttosto complessa, applicando la definizione di derivata è, a volte, molto laboriosa. I seguenti teoremi consentiranno di semplificare la procedura di calcolo della derivata di una generica funzione. Teorema della somma Se e g( sono due funzioni derivabili in un intervallo I allora ance la funzione somma g( è derivabile in I e risulta: [ g( ] y' f'( g' ( y cioè la derivata della somma di funzioni è uguale alla somma delle derivate delle singole funzioni. Se è un punto qualsiasi di I, il rapporto incrementale della funzione somma in è: [ g( ] [ g( ] - g( g( Passando al ite per si a: - g( g( f'( [ g( ] [ g( ] g'( - g( g( In particolare se g( è la funzione costante, cioè se è g(k, si a: y k y' f' In modo analogo si dimostra ce: Teorema della differenza [ ] ( Se e g( sono due funzioni derivabili in un intervallo I allora ance la funzione differenza -g( è derivabile in I e risulta: y [ - g( ] y' f'( g' ( cioè la derivata della differenza tra funzioni è uguale alla differenza delle derivate delle singole funzioni. In generale: La derivata della somma algebrica di più funzioni derivabili è uguale alla somma algebrica delle derivate delle singole funzioni.
9 Teorema del prodotto Se e g( sono due funzioni derivabili in un intervallo I allora ance la funzione prodotto g( è derivabile in I e risulta: y [ g( ] y' f'( g( g'( cioè la derivata del prodotto di due funzioni è uguale al prodotto della derivata della prima funzione per la seconda più il prodotto della derivata della seconda funzione per la prima. Se è un punto qualsiasi di I, il rapporto incrementale della funzione prodotto in è: [ g( ] [ g( ] g( g( g( g( g( g( g( Passando al ite per si a: sottraendo e sommando - g( g( g( g( g( al numeratore si a [ g( ] [ g( ] g( - g( g'( g( f'( g( In particolare se g( è la funzione costante, cioè se è g(k, si a: y k y' k f'( cioè la derivata del prodotto di una costante per una funzione è uguale al prodotto della costante per la derivata della funzione. In generale, si a: La derivata del prodotto di n funzioni è uguale alla somma degli n prodotti della derivata di ciascuna funzione per le rimanenti n- funzioni non derivate. In modo analogo si dimostra ce:
10 Teorema del quoziente Se e g( sono due funzioni derivabili in un intervallo I ed è g(, I, allora ance la funzione quoziente / g( è derivabile in I e risulta: f'( g( g'( y y' 2 g( g( cioè la derivata del quoziente di due funzioni è uguale ad una frazione avente per denominatore il quadrato del divisore e per numeratore il prodotto della derivata del dividendo per il divisore diminuito del prodotto del dividendo per la derivata del divisore. In particolare, se, e quindi f (, si a: y g( y' g'( [ g( ] 2 cioè la derivata della reciproca di una funzione derivabile è uguale ad una frazione avente per denominatore il quadrato della funzione e per numeratore l opposto della della derivata della funzione. In particolare: y y' 2
11 Derivata delle funzioni composte Per determinare la derivata delle funzioni ottenibili attraverso operazioni di composizione di due o più funzioni si ricorre al seguente teorema: Sia g ( una funzione definita in un intervallo I e derivabile in I e sia f ( z una funzione definita in I, tale ce gi ( I, e derivabile nel punto z g(. Allora la funzione composta F( f[ g( ] è derivabile in, e si a: F f z g '( '( '( cioè la derivata di una funzione composta è uguale al prodotto delle derivate delle funzioni componenti. Questo teorema è estendibile ance al caso in cui le funzioni componenti siano più di due. Ad esempio, se è: y f g ( y f( z, z g( u, u ( { } Esempio 2 Derivare la funzione y sen( Le funzioni componenti sono: 2 2 g( e f ( z sen z y' cos( (2 e quindi: y ' f '( z g '( u '( u Applicando la regola di derivazione di una funzione composta, è possibile ricavare altre due regole di derivazione: f ( a Se a>, a e è derivabile, allora ance y a è derivabile e risulta: f ( y' a f '( lna b In particolare, per ae, si a: f ( y' e f '( Derivata delle funzioni inverse Data la funzione y definita e invertibile in un intervallo I, se è derivabile in I, vale il teorema: Sia y una funzione continua e derivabile in un intervallo I e sia g(y la sua inversa, se è derivabile nel punto I, con derivata f (, allora ance g(y è derivabile nel punto y e si a: g'( y f '( cioè la derivata di una funzione inversa è il reciproco della derivata della funzione data.
12 Esempio n La funzione y è l inversa di y n y ny n n ' n n n n n (
13 Derivate di ordine superiore al primo Se la funzione è una funzione derivabile in un intervallo (a, b e la sua derivata f ( è una funzione anc essa derivabile in (a, b, allora si dice derivata seconda (o derivata del secondo ordine la derivata della derivata di. La derivata seconda si indica con uno dei simboli: y, f (, D 2 y, D 2 Esempio: y6 3 y 8 2 y 36 Se la derivata seconda è una funzione ancora derivabile, si dice derivata terza (o del terzo ordine la derivata della seconda. La derivata terza si indica con uno dei simboli: y, f (, D 3 y, D 3 In generale, la derivata n-esima, o di ordine n, di una funzione è la derivata della derivata di ordine (n--esimo. Per indicare la derivata quarta, quinta,... di una funzione si usano i simboli: y IV, y V, y VI,..., y n Per uniformità la derivata f ( viene detta derivata prima. Nota In generale le derivate successive anno una rappresentazione analitica più complessa della funzione. Nel caso delle funzioni polinomiali invece, le derivate successive diventano più semplici e per una funzione polinomiale di grado n, tutte le derivate successive, a partire da quella di ordine n, si annullano. Esempio: y3 2 y 6 y 6 y y IV,... Applicazioni del calcolo delle derivate alla geometria. Equazione della tangente a una curva Data la curva di equazione y, il coefficiente angolare della tangente alla curva in un punto di ascissa è f ( y-y f ( (- 2. Equazione della normale ad una curva Si ciama normale alla curva nel punto P(, y, la retta perpendicolare alla tangente alla curva in P(, y. La sua equazione è: y-y (- f'(
ELEMENTI DI ANALISI MATEMATICA
 Caterina Vespia ELEMENTI DI ANALISI MATEMATICA E-Book di Matematica per il triennio Volume 2 Le derivate U.D. 3 - Derivate delle funzioni di una variabile PREREQUISITI Concetto di limite Teoremi e operazioni
Caterina Vespia ELEMENTI DI ANALISI MATEMATICA E-Book di Matematica per il triennio Volume 2 Le derivate U.D. 3 - Derivate delle funzioni di una variabile PREREQUISITI Concetto di limite Teoremi e operazioni
Derivate delle funzioni di una variabile.
 Derivate delle funzioni di una variabile. Il concetto di derivata di una funzione di una variabile è uno dei più fecondi della matematica ed è quello su cui si basa il calcolo differenziale. I problemi
Derivate delle funzioni di una variabile. Il concetto di derivata di una funzione di una variabile è uno dei più fecondi della matematica ed è quello su cui si basa il calcolo differenziale. I problemi
rapporto tra l'incremento della funzione e l' incremento corrispondente della
 DERIVATA Sia y f() una funzione reale definita in un intorno di. Si consideri un incremento (positivo o negativo) di : h; la funzione passerà allora dal valore f( ) a quello di f( +h), subendo così un
DERIVATA Sia y f() una funzione reale definita in un intorno di. Si consideri un incremento (positivo o negativo) di : h; la funzione passerà allora dal valore f( ) a quello di f( +h), subendo così un
P[x; f(x)] y = f(x) le coordinate del punto P possono essere scritte anche come DERIVATA DI UNA FUNZIONE RAPPORTO INCREMENTALE
![P[x; f(x)] y = f(x) le coordinate del punto P possono essere scritte anche come DERIVATA DI UNA FUNZIONE RAPPORTO INCREMENTALE P[x; f(x)] y = f(x) le coordinate del punto P possono essere scritte anche come DERIVATA DI UNA FUNZIONE RAPPORTO INCREMENTALE](/thumbs/102/154758748.jpg) DERIVATA DI UNA FUNZIONE RAPPORTO INCREMENTALE Consideriamo una funzione reale y=f(x), definita in un intervallo [a, b] di numeri reali che appartiene al dominio D della funzione ( [a, b] è contenuto in
DERIVATA DI UNA FUNZIONE RAPPORTO INCREMENTALE Consideriamo una funzione reale y=f(x), definita in un intervallo [a, b] di numeri reali che appartiene al dominio D della funzione ( [a, b] è contenuto in
PENDENZA (ripasso classe II)
 PENDENZA (ripasso classe II) Vediamo di definire quantitativamente il concetto di pendenza. Già ritroviamo la pendenza indicata in percentuale nei cartelli di pericolo nelle strade di montagna. La definizione
PENDENZA (ripasso classe II) Vediamo di definire quantitativamente il concetto di pendenza. Già ritroviamo la pendenza indicata in percentuale nei cartelli di pericolo nelle strade di montagna. La definizione
4. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE.
 4. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE. Molto spesso rappresenta l evoluzione di un fenomeno al passare del tempo. Se siamo interessati a sapere con che rapidità il fenomeno si evolve
4. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE. Molto spesso rappresenta l evoluzione di un fenomeno al passare del tempo. Se siamo interessati a sapere con che rapidità il fenomeno si evolve
Appunti di Matematica 5 - Derivate - Derivate. Considero una funzione e sia e definita in un intorno completo di.
 Derivate Definizione di derivata di f(x) in x D o f Considero una funzione e sia e definita in un intorno completo di. Consideriamo il rapporto (detto rapporto incrementale ) È evidente che il rapporto
Derivate Definizione di derivata di f(x) in x D o f Considero una funzione e sia e definita in un intorno completo di. Consideriamo il rapporto (detto rapporto incrementale ) È evidente che il rapporto
(1;1) y=2x-1. Fig. G4.1 Retta tangente a y=x 2 nel suo punto (1;1).
 G4 Derivate G4 Significato geometrico di derivata La derivata di una funzione in un suo punto è il coefficiente angolare della sua retta tangente Esempio G4: La funzione = e la sua retta tangente per il
G4 Derivate G4 Significato geometrico di derivata La derivata di una funzione in un suo punto è il coefficiente angolare della sua retta tangente Esempio G4: La funzione = e la sua retta tangente per il
Le Derivate. Appunti delle lezioni di matematica di A. Pisani Liceo Classico Dante Alighieri
 Le Derivate Appunti delle lezioni di matematica di A. Pisani Liceo Classico Dante Alighieri Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato durante
Le Derivate Appunti delle lezioni di matematica di A. Pisani Liceo Classico Dante Alighieri Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato durante
Giovanni Rapisarda. Derivata di una funzione. df dx. Sia. una funzione definita in un intervallo. Fissato un punto
 Derivata di una funzione Sia una funzione definita in un intervallo a, b R. Fissato un punto appartenente allinsieme di definizione della funzione, sia P (, f ( )) il punto di ascissa appartenente al grafico
Derivata di una funzione Sia una funzione definita in un intervallo a, b R. Fissato un punto appartenente allinsieme di definizione della funzione, sia P (, f ( )) il punto di ascissa appartenente al grafico
PreCorso di Matematica - PCM CANALE M-Z settembre 2019
 PreCorso di Matematica - PCM CANALE M-Z settembre 2019 DOCENTE: M. Auteri LE DERIVATE La pendenza di un tratto di strada rettilineo è misurata dal coefficiente angolare della retta LE DERIVATE La pendenza
PreCorso di Matematica - PCM CANALE M-Z settembre 2019 DOCENTE: M. Auteri LE DERIVATE La pendenza di un tratto di strada rettilineo è misurata dal coefficiente angolare della retta LE DERIVATE La pendenza
y x y x A (x 1,y 1 ) = (c, f(c)) B(x 2,y 2 ) = (c+h, f(c+h)) m =
 DERIVATA DI UNA FUNZIONE IN UN PUNTO SIGNIFICATO GEOMETRICO. EQUAZIONE DELLA RETTA TANGENTE AL GRAFICO NEL PUNTO DI TANGENZA. REGOLE DI DERIVAZIONE. CONTINUITA E DERIVABILITA PUNTI DI NON DERIVABILITA
DERIVATA DI UNA FUNZIONE IN UN PUNTO SIGNIFICATO GEOMETRICO. EQUAZIONE DELLA RETTA TANGENTE AL GRAFICO NEL PUNTO DI TANGENZA. REGOLE DI DERIVAZIONE. CONTINUITA E DERIVABILITA PUNTI DI NON DERIVABILITA
Sul concetto di derivata di una funzione con riferimento ad alcune sue applicazioni nel campo matematico e fisico.
 Sul concetto di derivata di una funzione con riferimento ad alcune sue applicazioni nel campo matematico e fisico. Introduzione In matematica la derivata di una funzione è uno dei cardini dellanalisi matematica
Sul concetto di derivata di una funzione con riferimento ad alcune sue applicazioni nel campo matematico e fisico. Introduzione In matematica la derivata di una funzione è uno dei cardini dellanalisi matematica
Equazione della retta tangente al grafico di una funzione
 Equazione della retta tangente al grafico di una funzione Abbiamo già visto che in un sistema di assi cartesiani ortogonali, è possibile determinare l equazione di una retta r non parallela agli assi coordinati,
Equazione della retta tangente al grafico di una funzione Abbiamo già visto che in un sistema di assi cartesiani ortogonali, è possibile determinare l equazione di una retta r non parallela agli assi coordinati,
Anno 5 Regole di derivazione
 Anno 5 Regole di derivazione 1 Introduzione In questa lezione mostreremo quali sono le regole da seguire per effettuare la derivata di una generica funzione. Seguendo queste regole e conoscendo le derivate
Anno 5 Regole di derivazione 1 Introduzione In questa lezione mostreremo quali sono le regole da seguire per effettuare la derivata di una generica funzione. Seguendo queste regole e conoscendo le derivate
Derivata di una funzione
 Derivata di una funzione Prof. E. Modica http://www.galois.it erasmo@galois.it Il problema delle tangenti Quando si effettua lo studio delle coniche viene risolta una serie di esercizi che richiedono la
Derivata di una funzione Prof. E. Modica http://www.galois.it erasmo@galois.it Il problema delle tangenti Quando si effettua lo studio delle coniche viene risolta una serie di esercizi che richiedono la
Conoscenze. L operazione di divisione (la divisione di due polinomi) - La divisibilità fra polinomi (la regola di Ruffini, il teorema. del resto.
 Classe: TERZA (Liceo Artistico) Pagina 1 / 2 della Matematica La scomposizione dei polinomi in fattori primi L operazione di divisione (la divisione di due polinomi) - La divisibilità fra polinomi (la
Classe: TERZA (Liceo Artistico) Pagina 1 / 2 della Matematica La scomposizione dei polinomi in fattori primi L operazione di divisione (la divisione di due polinomi) - La divisibilità fra polinomi (la
Quick calculus Capitolo 1 Il problema della tangente
 Quick calculus Capitolo 1 Il problema della tangente Introduzione Ricavare una retta tangente ad una curva di secondo grado come un circonferenza o una parabola, è un problema che si risolve facilmente.
Quick calculus Capitolo 1 Il problema della tangente Introduzione Ricavare una retta tangente ad una curva di secondo grado come un circonferenza o una parabola, è un problema che si risolve facilmente.
LA DERIVATA DI UNA FUNZIONE. Prof Giovanni Ianne
 LA ERIVATA I UNA FUNZIONE Pro. Giovanni Ianne /22 Come si determina la retta tangente a una curva in un punto P? Per una circonerenza, la tangente è la retta che interseca la curva solo in P. IL PROBLEMA
LA ERIVATA I UNA FUNZIONE Pro. Giovanni Ianne /22 Come si determina la retta tangente a una curva in un punto P? Per una circonerenza, la tangente è la retta che interseca la curva solo in P. IL PROBLEMA
(1;1) y=2x-1. Fig. G5.1 Retta tangente a y=x 2 nel suo punto (1;1).
 G5. Derivate G5. Significato geometrico di derivata La derivata di una funzione in un suo punto è il coefficiente angolare della sua retta tangente. Esempio G5.: La funzione = e la sua retta tangente per
G5. Derivate G5. Significato geometrico di derivata La derivata di una funzione in un suo punto è il coefficiente angolare della sua retta tangente. Esempio G5.: La funzione = e la sua retta tangente per
DERIVATE. Equazione della retta tangente al grafico di f nel suo punto P(x 0 ;y 0 ):
 DERIVATE La derivata di una funzione in un punto c, quando esiste, rappresenta il coefficiente angolare della retta tangente al grafico della funzione nel suo punto di ascissa c: f ( c) = Df ( c) = m tg
DERIVATE La derivata di una funzione in un punto c, quando esiste, rappresenta il coefficiente angolare della retta tangente al grafico della funzione nel suo punto di ascissa c: f ( c) = Df ( c) = m tg
Istituzioni di Matematiche quarta parte
 Istituzioni di Matematiche quarta parte anno acc. 2012/2013 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 22 index Derivate 1 Derivate 2 Teoremi
Istituzioni di Matematiche quarta parte anno acc. 2012/2013 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 22 index Derivate 1 Derivate 2 Teoremi
TEORIA SULLE DERIVATE SECONDA. La condizione di continuità di una funzione è condizione necessaria ma non sufficiente per la sua derivabilità.
 PROF.SSA MAIOLINO D. TEORIA SULLE DERIVATE SECONDA CONTINUITA DELLE FUNZIONI DERIVABILI Se una unzione y( è derivabile in un punto 0, allora è continua in 0. La condizione di continuità di una unzione
PROF.SSA MAIOLINO D. TEORIA SULLE DERIVATE SECONDA CONTINUITA DELLE FUNZIONI DERIVABILI Se una unzione y( è derivabile in un punto 0, allora è continua in 0. La condizione di continuità di una unzione
APPUNTI DI MATEMATICA: I limiti e la continuità Le derivate. Prof. ssa Prenol R.
 APPUNTI DI MATEMATICA: I iti e la continuità Le derivate Prof. ssa Prenol R. INTERVALLI e INTORNI Definizione di intervallo: è un sottoinsieme di numeri reali e può essere - ilitato: graficamente viene
APPUNTI DI MATEMATICA: I iti e la continuità Le derivate Prof. ssa Prenol R. INTERVALLI e INTORNI Definizione di intervallo: è un sottoinsieme di numeri reali e può essere - ilitato: graficamente viene
ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA
 ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA PRIMA PARTE Intervallo limitato di numeri reali Dati due numeri reali a e b, con a
ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA PRIMA PARTE Intervallo limitato di numeri reali Dati due numeri reali a e b, con a
DERIVATE. 1.Definizione di derivata.
 DERIVATE Definizione di derivata Sia y = f( una funzione continua Fissato un punto o appartenente all insieme di definizione della funzione y = f(,sia Po = (; f(o il punto di ascissa o appartenente al
DERIVATE Definizione di derivata Sia y = f( una funzione continua Fissato un punto o appartenente all insieme di definizione della funzione y = f(,sia Po = (; f(o il punto di ascissa o appartenente al
Derivate. Rette per uno e per due punti. Rette per uno e per due punti
 Introduzione Rette per uno e per due punti Rette per uno e per due punti Rette secanti e tangenti Derivata d una funzione in un punto successive Derivabilità a destra e a sinistra Rette per uno e per due
Introduzione Rette per uno e per due punti Rette per uno e per due punti Rette secanti e tangenti Derivata d una funzione in un punto successive Derivabilità a destra e a sinistra Rette per uno e per due
Calcolo differenziale I
 Calcolo differenziale I Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Derivate Analisi Matematica 1 1 / 25 Definizione: rapporto incrementale Sia f : A
Calcolo differenziale I Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Derivate Analisi Matematica 1 1 / 25 Definizione: rapporto incrementale Sia f : A
Le derivate parziali
 Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
SYLLABUS DI MATEMATICA Liceo Linguistico Classe III
 SYLLABUS DI MATEMATICA Liceo Linguistico Classe III LE EQUAZIONI DI SECONDO GRADO Le equazioni di secondo grado e la loro risoluzione. La formula ridotta. Equazioni pure, spurie e monomie. Le relazioni
SYLLABUS DI MATEMATICA Liceo Linguistico Classe III LE EQUAZIONI DI SECONDO GRADO Le equazioni di secondo grado e la loro risoluzione. La formula ridotta. Equazioni pure, spurie e monomie. Le relazioni
Teorema del valor medio e di Rolle
 Prof Chirizzi Marco wwwelettronealtervistaorg wwwprofessoremypodcastcom Teorema del valor medio e di Rolle f una funzione continua nell intervallo chiuso [ b ] Sia ( esso Si dimostra che esiste almeno
Prof Chirizzi Marco wwwelettronealtervistaorg wwwprofessoremypodcastcom Teorema del valor medio e di Rolle f una funzione continua nell intervallo chiuso [ b ] Sia ( esso Si dimostra che esiste almeno
Corso di Analisi Matematica. Calcolo differenziale
 a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Calcolo differenziale Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Calcolo differenziale Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
SIMULAZIONE TERZA PROVA DOMANDE CHIUSE CAMPO DI ESISTENZA. 4 è: x 6x. = è:
 SIMULAZIONE TERZA PROVA DOMANDE CHIUSE CAMPO DI ESISTENZA Il campo di esistenza della funzione f() = 4 + a) ± b) c) d) > - + Il campo di esistenza della funzione f() = + a) b) -, - c) - < - d) > - Campo
SIMULAZIONE TERZA PROVA DOMANDE CHIUSE CAMPO DI ESISTENZA Il campo di esistenza della funzione f() = 4 + a) ± b) c) d) > - + Il campo di esistenza della funzione f() = + a) b) -, - c) - < - d) > - Campo
Quadro riassuntivo di geometria analitica
 Quadro riassuntivo di geometria analitica IL PIANO CARTESIANO (detta ascissa o coordinata x) e y quella dall'asse x (detta ordinata o coordinata y). Le coordinate di un punto P sono: entrambe positive
Quadro riassuntivo di geometria analitica IL PIANO CARTESIANO (detta ascissa o coordinata x) e y quella dall'asse x (detta ordinata o coordinata y). Le coordinate di un punto P sono: entrambe positive
Argomento 6 Derivate
 Argomento 6 Derivate Derivata in un punto Definizione 6. Data una funzione f definita su un intervallo I e 0 incrementale di f in 0 di incremento h = 0 = il rapporto I, si chiama rapporto per = 0 + h =
Argomento 6 Derivate Derivata in un punto Definizione 6. Data una funzione f definita su un intervallo I e 0 incrementale di f in 0 di incremento h = 0 = il rapporto I, si chiama rapporto per = 0 + h =
Derivate e studio di funzioni di una variabile
 Derivate e studio di funzioni di una variabile Paolo Montanari Appunti di Matematica Derivate e studio di funzioni 1 Rapporto incrementale e derivata Sia f(x) una funzione definita in un intervallo X R
Derivate e studio di funzioni di una variabile Paolo Montanari Appunti di Matematica Derivate e studio di funzioni 1 Rapporto incrementale e derivata Sia f(x) una funzione definita in un intervallo X R
1) D0MINIO. Determinare il dominio della funzione f (x) = ln ( x 3 4x 2 3x). Deve essere x 3 4x 2 3x > 0. Ovviamente x 0.
 D0MINIO Determinare il dominio della funzione f ln 4 + Deve essere 4 + > 0 Ovviamente 0 Se > 0, 4 + 4 + quindi 0 < < > Se < 0, 4 + 4 4 e, ricordando che < 0, deve essere 4 < 0 dunque 7 < < 0 Il campo di
D0MINIO Determinare il dominio della funzione f ln 4 + Deve essere 4 + > 0 Ovviamente 0 Se > 0, 4 + 4 + quindi 0 < < > Se < 0, 4 + 4 4 e, ricordando che < 0, deve essere 4 < 0 dunque 7 < < 0 Il campo di
Derivate. 24 settembre 2007
 Derivate 24 settembre 2007 Rapporto incrementale di una funzione Siano f : X R e x 0 X. La funzione g x0 (x) = f(x) f(x 0) x x 0 si chiama rapporto incrementale di f relativo al punto x 0. E[g x0 ] = X
Derivate 24 settembre 2007 Rapporto incrementale di una funzione Siano f : X R e x 0 X. La funzione g x0 (x) = f(x) f(x 0) x x 0 si chiama rapporto incrementale di f relativo al punto x 0. E[g x0 ] = X
RAPPORTO INCREMENTALE E DERIVATA PRIMA. Agg Tutorial di Paola Barberis
 RAPPORTO INCREMENTALE E DERIVATA PRIMA Agg 2017 - Tutorial di Paola Barberis Come misurare la CRESCITA MEDIA di una funzione fra due punti A e B? introduzione A=(1;3) Incremento orizzontale B=(4;5) y=f(x)
RAPPORTO INCREMENTALE E DERIVATA PRIMA Agg 2017 - Tutorial di Paola Barberis Come misurare la CRESCITA MEDIA di una funzione fra due punti A e B? introduzione A=(1;3) Incremento orizzontale B=(4;5) y=f(x)
04 - Numeri Complessi
 Università degli Studi di Palermo Scuola Politecnica Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica 04 - Numeri Complessi Anno Accademico 2015/2016 M. Tumminello,
Università degli Studi di Palermo Scuola Politecnica Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica 04 - Numeri Complessi Anno Accademico 2015/2016 M. Tumminello,
Le Funzioni. Modulo Esponenziali Logaritmiche. Prof.ssa Maddalena Dominijanni
 Le Funzioni Modulo Esponenziali Logaritmiche Definizione di modulo o valore assoluto Se x è un generico numero reale, il suo modulo o valore assoluto è: x = x se x 0 -x se x
Le Funzioni Modulo Esponenziali Logaritmiche Definizione di modulo o valore assoluto Se x è un generico numero reale, il suo modulo o valore assoluto è: x = x se x 0 -x se x
4. Derivata di una funzione
 1 4 Derivata di una funzione La derivata in un punto Per studiare in maniera più dettagliata l'andamento di una funzione, ci serve un modo per descrivere la velocità con cui cambiano i valori della funzione
1 4 Derivata di una funzione La derivata in un punto Per studiare in maniera più dettagliata l'andamento di una funzione, ci serve un modo per descrivere la velocità con cui cambiano i valori della funzione
3. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE.
 3. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE. Molto spesso y = f(x) rappresenta l evoluzione di un fenomeno al passare del tempo x.se siamo interessati a sapere con che rapidità il fenomeno
3. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE. Molto spesso y = f(x) rappresenta l evoluzione di un fenomeno al passare del tempo x.se siamo interessati a sapere con che rapidità il fenomeno
y retta tangente retta secante y = f(x)
 Retta tangente f(x ) 1 y P 1 retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x 1 x quando P tende a P 0 1 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0,
Retta tangente f(x ) 1 y P 1 retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x 1 x quando P tende a P 0 1 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0,
Derivate. Hynek Kovarik. Analisi A. Università di Brescia. Hynek Kovarik (Università di Brescia) Derivate Analisi A 1 / 33
 Derivate Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Derivate Analisi A 1 / 33 Definizione: rapporto incrementale Sia f : domf R R. Dati x 1, x 2 domf con x 1 x
Derivate Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Derivate Analisi A 1 / 33 Definizione: rapporto incrementale Sia f : domf R R. Dati x 1, x 2 domf con x 1 x
Derivazione. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Derivazione Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Derivazione Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Le derivate: introduzione storica
 Le derivate: introduzione storica I due fondamentali capitoli dell analisi matematica sono il calcolo differenziale e il calcolo integrale. Mentre il calcolo integrale trova le sue origini nella matematica
Le derivate: introduzione storica I due fondamentali capitoli dell analisi matematica sono il calcolo differenziale e il calcolo integrale. Mentre il calcolo integrale trova le sue origini nella matematica
La derivata. variabile indipendente x. Definiamo f := f(x) f(x 0 ) l incremento (positivo o negativo) della variabile dipendente.
 La derivata Sia f : domf R R; sia x 0 domf, f sia definita in I r (x 0 ) e sia x I r (x 0 ). ments Definiamo x := x x 0 l incremento (positivo o negativo) della f(x 0 ) + x + x) variabile indipendente
La derivata Sia f : domf R R; sia x 0 domf, f sia definita in I r (x 0 ) e sia x I r (x 0 ). ments Definiamo x := x x 0 l incremento (positivo o negativo) della f(x 0 ) + x + x) variabile indipendente
Istituto d Istruzione Superiore A. Tilgher Ercolano (Na)
 Premessa Istituto d Istruzione Superiore A. Tilgher Ercolano (Na) Questa breve trattazione non vuole costituire una guida completa ed esauriente sull argomento, ma vuole fornire solamente i concetti fondamentali
Premessa Istituto d Istruzione Superiore A. Tilgher Ercolano (Na) Questa breve trattazione non vuole costituire una guida completa ed esauriente sull argomento, ma vuole fornire solamente i concetti fondamentali
UNITÀ DIDATTICA 2 LE FUNZIONI
 UNITÀ DIDATTICA LE FUNZIONI. Le funzioni Definizione. Siano A e B due sottoinsiemi non vuoti di R. Si chiama funzione di A in B una qualsiasi legge che fa corrispondere a ogni elemento A uno ed un solo
UNITÀ DIDATTICA LE FUNZIONI. Le funzioni Definizione. Siano A e B due sottoinsiemi non vuoti di R. Si chiama funzione di A in B una qualsiasi legge che fa corrispondere a ogni elemento A uno ed un solo
Definizione (Derivata come limite del rapporto incrementale) Se esiste finito (cioè, non + o ) il limite del rapporto incrementale
 Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come ite del rapporto incrementale) Se esiste finito (cioè, non + o ) il ite del rapporto incrementale
Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come ite del rapporto incrementale) Se esiste finito (cioè, non + o ) il ite del rapporto incrementale
Variazione di una funzione
 a) Variazione di una funzione Variazione di : Δ= 2-1 Δf Variazione di f: Δf= 2-1 =f( 2 )-f( 1 ) b) 1 Δ 2 In questo caso a una variazione di, Δ, corrisponde una piccola variazione di f, Δf Δf In questo
a) Variazione di una funzione Variazione di : Δ= 2-1 Δf Variazione di f: Δf= 2-1 =f( 2 )-f( 1 ) b) 1 Δ 2 In questo caso a una variazione di, Δ, corrisponde una piccola variazione di f, Δf Δf In questo
FUNZIONI REALI DI UNA VARIABILE REALE
 FUNZIONI REALI DI UNA VARIABILE REALE INTERVALLI Per definire il campo di esistenza (o dominio) di una funzione reale di variabile reale y=f()si devono indicare talvolta insiemi di numeri reali che su
FUNZIONI REALI DI UNA VARIABILE REALE INTERVALLI Per definire il campo di esistenza (o dominio) di una funzione reale di variabile reale y=f()si devono indicare talvolta insiemi di numeri reali che su
I RADICALI QUADRATICI
 I RADICALI QUADRATICI 1. Radici quadrate Definizione di radice quadrata: Si dice radice quadrata di un numero reale positivo o nullo a, e si indica con a, il numero reale positivo o nullo (se esiste) che,
I RADICALI QUADRATICI 1. Radici quadrate Definizione di radice quadrata: Si dice radice quadrata di un numero reale positivo o nullo a, e si indica con a, il numero reale positivo o nullo (se esiste) che,
Retta Tangente. y retta tangente. retta secante y = f(x) f(x )
 Retta Tangente f(x ) y P retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x x quando P tende a P 0 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0, f(x 0 ))
Retta Tangente f(x ) y P retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x x quando P tende a P 0 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0, f(x 0 ))
MATEMATICA LA CIRCONFERENZA GSCATULLO
 MATEMATICA LA CIRCONFERENZA GSCATULLO La Circonferenza La circonferenza e la sua equazione Introduzione e definizione La circonferenza è una conica, ovvero quella figura ottenuta tagliando un cono con
MATEMATICA LA CIRCONFERENZA GSCATULLO La Circonferenza La circonferenza e la sua equazione Introduzione e definizione La circonferenza è una conica, ovvero quella figura ottenuta tagliando un cono con
Richiami sullo studio di funzione
 Richiami sullo studio di funzione Per studiare una funzione y = f() e disegnarne un grafico approssimativo, possiamo procedere in ordine secondo i seguenti passi:. determinare il campo di esistenza (o
Richiami sullo studio di funzione Per studiare una funzione y = f() e disegnarne un grafico approssimativo, possiamo procedere in ordine secondo i seguenti passi:. determinare il campo di esistenza (o
Elementi di matematica - dott. I. GRASSI
 Gli assi cartesiani e la retta. Il concetto di derivata. È ormai d uso comune nei libri, in televisione, nei quotidiani descrivere fenomeni di varia natura per mezzo di rappresentazioni grafiche. Tali
Gli assi cartesiani e la retta. Il concetto di derivata. È ormai d uso comune nei libri, in televisione, nei quotidiani descrivere fenomeni di varia natura per mezzo di rappresentazioni grafiche. Tali
I TEOREMI DEL CALCOLO DIFFERENZIALE
 I TEOREMI DEL CALCOLO DIFFERENZIALE 1. DEFINIZIONI. TEOREMI DEL CALCOLO DIFFERENZIALE.1 TEOREMA DELL ESTREMANTE LOCALE. TEOREMI DI ROLLE, CAUCHY, LAGRANGE.3 TEOREMI CONSEGUENTI AL T. DI LAGRANGE 3. DETERMINAZIONE
I TEOREMI DEL CALCOLO DIFFERENZIALE 1. DEFINIZIONI. TEOREMI DEL CALCOLO DIFFERENZIALE.1 TEOREMA DELL ESTREMANTE LOCALE. TEOREMI DI ROLLE, CAUCHY, LAGRANGE.3 TEOREMI CONSEGUENTI AL T. DI LAGRANGE 3. DETERMINAZIONE
Si tratta di una funzione definita a tratti, il cui intervallo di definizione è suddiviso in 4 intervalli, AO-OB-BC- CD.
 PROBLEMA 1 Sia una funzione continua sull intervallo chiuso [-4, 6]. Il suo grafico, riportato in figura, passa per i punti A(-4;0), O(0,0),B(2;2), C(4;2), D(6;0) e consiste della semicirconferenza di
PROBLEMA 1 Sia una funzione continua sull intervallo chiuso [-4, 6]. Il suo grafico, riportato in figura, passa per i punti A(-4;0), O(0,0),B(2;2), C(4;2), D(6;0) e consiste della semicirconferenza di
LA CIRCONFERENZA E LA SUA EQUAZIONE
 LA CIRCONFERENZA E LA SUA EQUAZIONE LA CIRCONFERENZA COME LUOGO GEOMETRICO DEFINIZIONE Assegnato nel piano un punto C, detto centro, si chiama circonferenza la curva piana luogo geometrico dei punti equidistanti
LA CIRCONFERENZA E LA SUA EQUAZIONE LA CIRCONFERENZA COME LUOGO GEOMETRICO DEFINIZIONE Assegnato nel piano un punto C, detto centro, si chiama circonferenza la curva piana luogo geometrico dei punti equidistanti
Matematica e Statistica per Scienze Ambientali
 per Scienze Ambientali Derivate - Appunti 1 1 Dipartimento di Matematica Sapienza, Università di Roma Roma, Novembre 2013 Retta secante un grafico e rapporto incrementale Sia f una funzione e x 0 un punto
per Scienze Ambientali Derivate - Appunti 1 1 Dipartimento di Matematica Sapienza, Università di Roma Roma, Novembre 2013 Retta secante un grafico e rapporto incrementale Sia f una funzione e x 0 un punto
( ) ( ) DERIVATE. $ ed è finito lim
 DERIVATE La derivata di una unzione in un punto c, quando esiste, rappresenta il coeiciente angolare della retta tangente al graico della unzione nel suo punto di ascissa c: ( c) = D ( c) = m tg = tanα,
DERIVATE La derivata di una unzione in un punto c, quando esiste, rappresenta il coeiciente angolare della retta tangente al graico della unzione nel suo punto di ascissa c: ( c) = D ( c) = m tg = tanα,
Matematica Lezione 18
 Università di Cagliari Corso di Laurea in Farmacia Matematica Lezione 18 Sonia Cannas 4/12/2018 Metodo di bisezione Se f : [a, b] R è continua e tale che f (a) f (b) < 0 sono soddisfatte le ipotesi del
Università di Cagliari Corso di Laurea in Farmacia Matematica Lezione 18 Sonia Cannas 4/12/2018 Metodo di bisezione Se f : [a, b] R è continua e tale che f (a) f (b) < 0 sono soddisfatte le ipotesi del
METODO DI CAVALIERI-SIMPSON (o delle parabole) (per il calcolo approssimato 1 di integrali definiti)
 METODO DI CVLIERI-SIMPSON (o delle parabole) (per il calcolo approssimato di integrali definiti) ssieme ai metodi dei Rettangoli e dei Trapezi costituisce l insieme dei metodi di Integrazione Numerica
METODO DI CVLIERI-SIMPSON (o delle parabole) (per il calcolo approssimato di integrali definiti) ssieme ai metodi dei Rettangoli e dei Trapezi costituisce l insieme dei metodi di Integrazione Numerica
1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: c) x + 1 d)x sin x.
 Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
LICEO CLASSICO ANDREA DA PONTEDERA
 ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classe 5A PROGRAMMA DI MATEMATICA svolto fino al 15 aprile (evidenziate in giallo le aggiunte rispetto al file precedente) Intervallo limitato
ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classe 5A PROGRAMMA DI MATEMATICA svolto fino al 15 aprile (evidenziate in giallo le aggiunte rispetto al file precedente) Intervallo limitato
C I R C O N F E R E N Z A...
 C I R C O N F E R E N Z A... ESERCITAZIONI SVOLTE 3 Equazione della circonferenza di noto centro C e raggio r... 3 Equazione della circonferenza di centro C passante per un punto A... 3 Equazione della
C I R C O N F E R E N Z A... ESERCITAZIONI SVOLTE 3 Equazione della circonferenza di noto centro C e raggio r... 3 Equazione della circonferenza di centro C passante per un punto A... 3 Equazione della
26 - Funzioni di più Variabili Limiti e Derivate
 Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 26 - Funzioni di più Variabili Limiti e Derivate Anno Accademico 2013/2014 M.
Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 26 - Funzioni di più Variabili Limiti e Derivate Anno Accademico 2013/2014 M.
CALCOLO DEL RAGGIO DI CURVATURA DI UNA CURVA REGOLARE DI E Q UAZI O NE y = f (x ), ivi derivabile almeno due volte, e che la derivata seconda
 ALOLO DEL RAGGIO DI URVATURA DI UNA URVA REGOLARE DI E Q UAZI O NE Supponiamo che b sia una unzione deinita in, ivi derivabile almeno due volte, e che in la derivata seconda sia diversa da zero, e indichiamo
ALOLO DEL RAGGIO DI URVATURA DI UNA URVA REGOLARE DI E Q UAZI O NE Supponiamo che b sia una unzione deinita in, ivi derivabile almeno due volte, e che in la derivata seconda sia diversa da zero, e indichiamo
Tutorato di analisi 1
 Tutorato di analisi 1 Alen Kushova Collegio Volta 1 / 8 Introduzione Derivata Interpretazione geometrica Differenziabilità Regole di calcolo Esercizi 2 / 8 Derivata Sia f : [a, b] R una funzione e sia
Tutorato di analisi 1 Alen Kushova Collegio Volta 1 / 8 Introduzione Derivata Interpretazione geometrica Differenziabilità Regole di calcolo Esercizi 2 / 8 Derivata Sia f : [a, b] R una funzione e sia
Esercitazione 9 - Funzioni
 Esercitazione 9 - Funzioni DEFINIZIONI DI BASE Dati due insiemi X e Y, si dice funzione f : X Y una legge che associa ad ogni elemento X uno ed un solo elemento = f() Y. L insieme X è il dominio della
Esercitazione 9 - Funzioni DEFINIZIONI DI BASE Dati due insiemi X e Y, si dice funzione f : X Y una legge che associa ad ogni elemento X uno ed un solo elemento = f() Y. L insieme X è il dominio della
Argomento 6: Derivate Esercizi. I Parte - Derivate
 6: Derivate Esercizi I Parte - Derivate E. 6.1 Calcolare le derivate delle seguenti funzioni: 1) log 5 3 + cos ) + 3 + 4 + 3 3) 5 tan 4) ( + 3e ) sin 5) arctan( + 1) 6) log 7) 10) + + 3 8) 3 3 1 + 16 11)
6: Derivate Esercizi I Parte - Derivate E. 6.1 Calcolare le derivate delle seguenti funzioni: 1) log 5 3 + cos ) + 3 + 4 + 3 3) 5 tan 4) ( + 3e ) sin 5) arctan( + 1) 6) log 7) 10) + + 3 8) 3 3 1 + 16 11)
Esercitazioni di Matematica Generale A.A. 2016/2017 Pietro Pastore Lezione del 12 Dicembre Calcolo di Derivate
 Esercitazioni di Matematica Generale A.A. 206/207 Pietro Pastore Lezione del 2 Dicembre 206 Calcolo di Derivate Nella seguente tabella elenchiamo le derivate delle funzioni elementari f() f () k 0 n e
Esercitazioni di Matematica Generale A.A. 206/207 Pietro Pastore Lezione del 2 Dicembre 206 Calcolo di Derivate Nella seguente tabella elenchiamo le derivate delle funzioni elementari f() f () k 0 n e
Università degli Studi di Cagliari Dipartimento di Matematica e Informatica Corso di Laurea in Chimica. Matematica 2.
 Università degli Studi di Cagliari Dipartimento di Matematica e Informatica Corso di Laurea in Chimica Matematica 2 9 Maggio 2018 Schema Lezione numero 15 Outiline Regola di derivazione delle funzioni
Università degli Studi di Cagliari Dipartimento di Matematica e Informatica Corso di Laurea in Chimica Matematica 2 9 Maggio 2018 Schema Lezione numero 15 Outiline Regola di derivazione delle funzioni
PROGRAMMA DI MATEMATICA
 PROGRAMMA DI MATEMATICA Classe 1 A /1 B GRAFICA anno scolastico 2015-2016 La teoria degli insiemi Il concetto di insieme, il simbolo di appartenenza, la rappresentazione grafica di Eulero- Venn, la rappresentazione
PROGRAMMA DI MATEMATICA Classe 1 A /1 B GRAFICA anno scolastico 2015-2016 La teoria degli insiemi Il concetto di insieme, il simbolo di appartenenza, la rappresentazione grafica di Eulero- Venn, la rappresentazione
Soluzioni del Foglio 6
 ANALISI Soluzioni del Foglio 6 1 novembre 2009 6.1. Esercizio. Calcolare le derivate delle seguenti funzioni: x + 1 x 2 + 1, ex (sin(x) + cos(x)), e x arcsin(x) 1 x 2, x arctan(x), ln(1 + e x2 ) x + 1
ANALISI Soluzioni del Foglio 6 1 novembre 2009 6.1. Esercizio. Calcolare le derivate delle seguenti funzioni: x + 1 x 2 + 1, ex (sin(x) + cos(x)), e x arcsin(x) 1 x 2, x arctan(x), ln(1 + e x2 ) x + 1
MATEMATICA MATURITA LINGUISTICA. Istituto Paritario A.Ruiz Istituto Paritario A.Ruiz
 MATEMATICA MATURITA LINGUISTICA Istituto Paritario A.Ruiz Istituto Paritario A.Ruiz 1 MATEMATICA MATURITA LINGUISTICA 1. CLASSIFICAZIONE FUNZIONI FUNZIONI ALGEBRICHE (in cui compaiono le quattro operazioni):
MATEMATICA MATURITA LINGUISTICA Istituto Paritario A.Ruiz Istituto Paritario A.Ruiz 1 MATEMATICA MATURITA LINGUISTICA 1. CLASSIFICAZIONE FUNZIONI FUNZIONI ALGEBRICHE (in cui compaiono le quattro operazioni):
Esercizi di Analisi Matematica
 Università degli Studi di Udine Anno Accademico 00/ Facoltà di Scienze Matematiche Fisiche e Naturali Corso di Laurea in Informatica e TWM Esercizi di Analisi Matematica Esercizi sul primo semestre del
Università degli Studi di Udine Anno Accademico 00/ Facoltà di Scienze Matematiche Fisiche e Naturali Corso di Laurea in Informatica e TWM Esercizi di Analisi Matematica Esercizi sul primo semestre del
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 2007 Sessione suppletiva
 ESAME DI STAT DI LIE SIENTIFI RS DI RDINAMENT 7 Sessione suppletiva Il candidato risolva uno dei due problemi e 5 dei quesiti in cui si articola il questionario. PRBLEMA Rispetto a un sistema di assi cartesiani
ESAME DI STAT DI LIE SIENTIFI RS DI RDINAMENT 7 Sessione suppletiva Il candidato risolva uno dei due problemi e 5 dei quesiti in cui si articola il questionario. PRBLEMA Rispetto a un sistema di assi cartesiani
Calcolo Differenziale. Corsi di Laurea in Tecniche di Radiologia ecc... A.A Analisi Matematica - Calcolo Differenziale - p.
 Calcolo Differenziale Corsi di Laurea in Tecniche di Radiologia ecc... A.A. 2010-2011 - Analisi Matematica - Calcolo Differenziale - p. 1/33 Velocità istantanea Percorriamo il tratto di strada tra Udine
Calcolo Differenziale Corsi di Laurea in Tecniche di Radiologia ecc... A.A. 2010-2011 - Analisi Matematica - Calcolo Differenziale - p. 1/33 Velocità istantanea Percorriamo il tratto di strada tra Udine
M174sett.tex. 4a settimana Inizio 22/10/2007. Terzo limite fondamentale (sul libro, p. 113, è chiamato secondo ) lim x 1 x 0 x
 M74sett.te 4a settimana Inizio 22/0/2007 Terzo ite fondamentale (sul libro, p. 3, è chiamato secondo ) e 0 =. La tangente al grafico nel punto (0,0) risulta y = (vedremo poi perché). Ricordare che e è
M74sett.te 4a settimana Inizio 22/0/2007 Terzo ite fondamentale (sul libro, p. 3, è chiamato secondo ) e 0 =. La tangente al grafico nel punto (0,0) risulta y = (vedremo poi perché). Ricordare che e è
Programma di MATEMATICA
 Classe 3B Indirizzo ELETTRONICA ED ELETTROTECNICA 1. MODULO 1: GEOMETRIA ANALITICA La parabola: la parabola come luogo geometrico del piano. Rappresentazione della parabola nel piano cartesiano e ricerca
Classe 3B Indirizzo ELETTRONICA ED ELETTROTECNICA 1. MODULO 1: GEOMETRIA ANALITICA La parabola: la parabola come luogo geometrico del piano. Rappresentazione della parabola nel piano cartesiano e ricerca
Esercitazioni di Analisi Matematica FUNZIONI CUBICHE. Effettuare lo studio completo delle seguenti funzioni di terzo grado intere:
 FUNZIONI CUBICHE Effettuare lo studio completo delle seguenti funzioni di terzo grado intere: 1) y = fx) = x 3 + 2x 2 + x 2) y = fx) = x 3 + x 2 + x + 2 3) y = fx) = x 3 + 2x 2 + x 4 4) y = fx) = x 3 +
FUNZIONI CUBICHE Effettuare lo studio completo delle seguenti funzioni di terzo grado intere: 1) y = fx) = x 3 + 2x 2 + x 2) y = fx) = x 3 + x 2 + x + 2 3) y = fx) = x 3 + 2x 2 + x 4 4) y = fx) = x 3 +
Cosa vuol dire misurare l'area di una figura piana a contorno curvilineo?
 Cosa vuol dire misurare l'area di una figura piana a contorno curvilineo? Idea elementare: 1. fissare un quadratino come unità di misura 2. contare quante volte questo può essere riportato nella figura
Cosa vuol dire misurare l'area di una figura piana a contorno curvilineo? Idea elementare: 1. fissare un quadratino come unità di misura 2. contare quante volte questo può essere riportato nella figura
Corso di Analisi Matematica
 Corso di Laurea in Ingegneria Edile Corso di DERIVATE Lucio Demeio Dipartimento di Ingegneria Industriale e delle Scienze Matematiche Secanti e tangenti Sia f : D R, sia I = [a, b] oppure I = (a, b),
Corso di Laurea in Ingegneria Edile Corso di DERIVATE Lucio Demeio Dipartimento di Ingegneria Industriale e delle Scienze Matematiche Secanti e tangenti Sia f : D R, sia I = [a, b] oppure I = (a, b),
04 - Numeri Complessi
 Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 04 - Numeri Complessi Anno Accademico 2013/2014 M. Tumminello, V. Lacagnina e
Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 04 - Numeri Complessi Anno Accademico 2013/2014 M. Tumminello, V. Lacagnina e
2. SIGNIFICATO FISICO DELLA DERIVATA
 . SIGNIFICATO FISICO DELLA DERIVATA Esempi 1. Un auto viaggia lungo un percorso rettilineo, con velocità costante uguale a 70 km/h. Scrivere la legge oraria s= s(t) e rappresentarla graficamente. 1. Scriviamo
. SIGNIFICATO FISICO DELLA DERIVATA Esempi 1. Un auto viaggia lungo un percorso rettilineo, con velocità costante uguale a 70 km/h. Scrivere la legge oraria s= s(t) e rappresentarla graficamente. 1. Scriviamo
Matematica. Tutorato Attivo: Derivate. Alessio Bianchi. Matematica 20 maggio 2017
 Matematica Tutorato Attivo: Derivate Alessio Bianchi email: alessio.bianchi02@universitadipavia.it Home page: https://bianchiunipv.wordpress.com/ Matematica 20 maggio 2017 Alessio Bianchi Tutorato Attivo:
Matematica Tutorato Attivo: Derivate Alessio Bianchi email: alessio.bianchi02@universitadipavia.it Home page: https://bianchiunipv.wordpress.com/ Matematica 20 maggio 2017 Alessio Bianchi Tutorato Attivo:
Lezione 18 (8 gennaio) Limiti
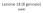 Lezione 18 (8 gennaio) Limiti Ripasso f x = ln 3 x 1 D = (1, + ) ln 3 x 1 + x 1 = ln 3 1 + 1 = ln 3 = ln(+ ) = + 0 + ln 3 x + x 1 = ln 3 + 1 = ln 3 + = ln(0+ ) = 1 Esempi di forme indeterminate x + x3
Lezione 18 (8 gennaio) Limiti Ripasso f x = ln 3 x 1 D = (1, + ) ln 3 x 1 + x 1 = ln 3 1 + 1 = ln 3 = ln(+ ) = + 0 + ln 3 x + x 1 = ln 3 + 1 = ln 3 + = ln(0+ ) = 1 Esempi di forme indeterminate x + x3
Esercitazione n 5. 1 Limiti e continuità di funzioni in più variabili. Esercizio 1: Si verifichi che la funzione f definita per ogni (x, y) R 2 da
 Esercitazione n 5 1 Limiti e continuità di funzioni in più variabili Esercizio 1: Si verifici ce la funzione f definita per ogni (, y) R 2 da { 4 y 4 se (, y) (0, 0) f(, y) = 2 +y 2 0 se (, y) = (0, 0)
Esercitazione n 5 1 Limiti e continuità di funzioni in più variabili Esercizio 1: Si verifici ce la funzione f definita per ogni (, y) R 2 da { 4 y 4 se (, y) (0, 0) f(, y) = 2 +y 2 0 se (, y) = (0, 0)
Stabilire se il punto di coordinate (1,1) appartiene alla circonferenza centrata nell origine e di raggio 1.
 Definizione di circonferenza e cerchio. Equazione della circonferenza centrata in O e di raggio R. Esercizi. La circonferenza e il cerchio Definizioni: dato un punto C nel piano cartesiano e dato un numero
Definizione di circonferenza e cerchio. Equazione della circonferenza centrata in O e di raggio R. Esercizi. La circonferenza e il cerchio Definizioni: dato un punto C nel piano cartesiano e dato un numero
Equazioni Polinomiali II Parabola
 Equazioni Polinomiali II Parabola - 0 Equazioni Polinomiali del secondo grado (Polinomi II) Forma Canonica e considerazioni La forma canonica dell equazione polinomiale di grado secondo è la seguente:
Equazioni Polinomiali II Parabola - 0 Equazioni Polinomiali del secondo grado (Polinomi II) Forma Canonica e considerazioni La forma canonica dell equazione polinomiale di grado secondo è la seguente:
Politecnico di Milano Corso di Analisi e Geometria 1. Federico Lastaria. Curve nello spazio Gennaio Lunghezza d arco
 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria Curve nello spazio Gennaio 013 Indice 1 Lunghezza d arco 1 1.1 Parametrizzazione alla lunghezza d arco..................... 1. Ogni
Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria Curve nello spazio Gennaio 013 Indice 1 Lunghezza d arco 1 1.1 Parametrizzazione alla lunghezza d arco..................... 1. Ogni
Funzione derivabile. La derivata.
 Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come limite del rapporto incrementale) Se esiste finito (cioè, non + o ) il limite del rapporto
Funzione derivabile. La derivata. Dati: f I R funzione; I R intervallo aperto ; x 0 I. Definizione (Derivata come limite del rapporto incrementale) Se esiste finito (cioè, non + o ) il limite del rapporto
LE DERIVATE. La pendenza di un tratto di strada: è misurata dal coefficiente angolare della retta se il tratto è rettilineo.
 La pendenza di un tratto di strada: è misurata dal coeiciente angolare della retta se il tratto è rettilineo. 1 La pendenza di un tratto P,R non rettilineo descritto da y è data dal coeiciente angolare
La pendenza di un tratto di strada: è misurata dal coeiciente angolare della retta se il tratto è rettilineo. 1 La pendenza di un tratto P,R non rettilineo descritto da y è data dal coeiciente angolare
TEOREMI FONDAMENTALI DEL CALCOLO DIFFERENZIALE
 TEOREMI FONDAMENTALI DEL CALCOLO DIFFERENZIALE Teorema di Rolle Se una funzione yf(x) continua nell intervallo chiuso [a, b] e derivabile in (a, b),assume agli estremi a e b dell intervallo valori uguali
TEOREMI FONDAMENTALI DEL CALCOLO DIFFERENZIALE Teorema di Rolle Se una funzione yf(x) continua nell intervallo chiuso [a, b] e derivabile in (a, b),assume agli estremi a e b dell intervallo valori uguali
