1. Definizione. Definiamo il determinante di una matrice quadrata di un qualsiasi ordine n 1 in modo ricorsivo. Per n = 1, poniamo.
|
|
|
- Silvana Salvadori
- 2 anni fa
- Visualizzazioni
Transcript
1 Matematica II, Definizine Definiam il determinante di una matrice quadrata di un qualsiasi rdine n 1 in md ricrsiv Per n = 1, pniam per gni matrice [a 11 ] di rdine 1, a 11 = a 11 ; Per n > 1, suppniam di avere definit il determinante per una qualsiasi matrice di rdine n 1, e definiam il determinante a ij i,j=1,,n per una qualsiasi matrice [a ij ] i,j=1,,n di rdine n, cme la smma a segni alterni +,, +, di n termini, dve ciascun termine e il prdtt di un element della prima clnna per il determinante della matrice ttenuta cancelland la riga cui l element appartiene e la prima clnna In simbli: a 11 a 12 a 1n a n1 a n2 a nn n ( 1) i+1 a i1 i=1 = a 12 a 1n a i 1,2 a i 1,n a i+1,2 a i+1,n a n2 a nn Da questa definizine si pu ricavare la frmula esplicita a ij i,j=1,,n = sg(i 1, i 2,, i n ) a i1 1a i2 2 a in n, (i 1,i 2,,i n) dve la smmatria e estesa a tutte le permutazini (i 1, i 2,, i n ) della n pla (1, 2,, n), e sg(i 1, i 2,, i n ) vale +1 1 secnd che il numer delle inversini di (i 1, i 2,, i n ) sia pari dispari Csi, il determinante di una matrice di rdine n e un plinmi mgene di grad n negli elementi della matrice, cstituit da n! termini Si prva che 1
2 il determinante di una matrice cincide cl determinante della sua traspsta 2 Per una matrice trianglare si ha a 11 a 12 a 13 a 1n 0 a 22 a 23 a 2n 0 0 a 33 a 3n a nn = a 11 = a 11 a 22 a 22 a 23 a 2n 0 a 33 a 3n 0 0 a nn a 33 a 3n = = a 11 a 22 a 33 a nn 0 a nn Dunque, il determinante di una matrice trianglare e il prdtt dei sui elementi diagnali Tale determinate e divers da zer se e sltant se tutti gli elementi diagnali sn diversi da zer, cie la matrice trianglare e nndegenere Il determinante della matrice I n unita di rdine n vale 1 3 Prprieta dei determinanti Sia n un inter psitiv arbitrariamenente fissat Il determinante della generica matrice A = [a ij ] i,j=1,,n quadrata di rdine n pu essere vist cme una funzine delle n clnne a j = a 1j a nj Det [a 1,, a j,, a n ] di A Cme tale, il determinante e caratterizzat dalle seguenti prprieta Se tre matrici sn uguali, tranne che una clnna della prima matrice e la smma delle crrispndenti clnne delle altre due, allra il determinante della prima matrice e la smma dei determinanti delle altre due; in simbli: per gni j = 1,, n si ha Det [ a 1,, a j 1, a j + a j, a j+1,, a n ] = Det [ a 1,, a j 1, a j, a j+1,, a n ] + Det [ a1,, a j 1, a j, a j+1,, a n ] ; Se due matrici sn in tutt uguali, tranne che una clnna della prima matrice e r ( R) vlte la crrispndente clnna dell altra, allra il determinante della prima matrice e r vlte il determinante dell altra; in simbli: per gni j = 1,, n si ha Det [a 1,, a j 1, ra j, a j+1,, a n ] = rdet [a 1,, a j 1, a j, a j+1,, a n ] ; 2
3 Se una matrice ha due clnne uguali, allra il determinnte della matrice e null; in simbli: per gni 1 i < j n si ha Det [a 1,, a i 1, a, a i+1,, a j 1, a, a j+1,, a n ] = 0; Scambiand due clnne di una matrice, il determinante della matrice cambia segn; in simbli: per gni 1 i < j n si ha Det [a 1,, a i 1, a j, a i+1,, a j 1, a i, a j+1,, a n ] Valgn analghe prprieta per le righe 4 Regla di Cramer = Det [a 1,, a i 1, a i, a i+1,, a j 1, a j, a j+1,, a n ] I determinanti permettn di dare una frmula per la risluzine di un sistema lineare quadrat Sia data una matrice a 11 a 1n A = = [a 1,, a n ] a n1 a nn quadrata di rdine n, cn Det(A) 0 Allra tutti i sistemi lineari a 11 x a 1n x n = b 1, in breve a 1 x a n x n = b, a n1 x a nn x n = b n cn matrice dei cefficienti A sn determinati; inltre 5 Matrice inversa x i = Det [a 1,, a i 1, b, a i+1,, a n ], i = 1,, n Det [a 1,, a i 1, a i, a i+1,, a n ] I determinanti permettn di dare una frmula per la matrice inversa Sia A = [a ij ] i,j=1,,n la generica matrice di rdine n > 1 Per ciascuna scelta di un indice di riga i = 1,, n e di un indice di clnna j = 1,, n, cancelland la i ma riga e la j ma clnna di A tteniam una sttmatrice di rdine n 1 Il determinante di questa sttmatrice, pres cl su segn cl segn ppst secndche i+j sia pari dispari, viene dett cmplement algebric dell element a ij della matrice A e viene indicat cl simbl A ij In simbli, si ha a 11 a 1,j 1 a 1,j+1 a 1n a i 1,1 a i 1,j 1 a i 1,j+1 a i 1,n A ij = ( 1) i+j a 1+1,1 a i+1,j 1 a i+1,j+1 a i+1,n a n1 a n,j 1 a n,j+1 a nn 3
4 Si prva che, se Det(A) 0, allra A e invertibile; inltre, l inversa di A e il prdtt del reciprc del determinante di A per la traspsta della matrice dei cplementi algebrici di A : A 1 = 1 Det(A) A 11 A 21 A n1 A 12 A 22 A n2 A 1n A 2n A nn 6 Determinanti, perazini elementari e algritm di Gauss Le prprieta del determinate ci permettn di descrivere l effett che ciascuna delle perazini elementari sulle righe di una matrice ha sul determinante della matrice: l perazine di mltiplicare una riga per un scalare r R ha cme effett di mltiplicare il determinante per r; l perazine di scambiare due righe ha cme effett di cambiare il segn del determinante; l perazine di smmare ad una riga un multipl di un altra riga lascia invariat il determinante Grazie a queste prprieta, pssiam calclare il determinante di una matrice numerica A trasfrmandla, mediante l algritm di Gauss, in una matrice trianglare T, e pi prendend il prdtt degli elementi diagnali di T, eventualmente cambiat di segn se si sn usati scambi di riga Da ci segue Sia A una matrice quadrata, che viene trasfrmata dall algritm di Gauss in una matrice trianglare T Si ha che Det(A) 0 se e sl se T e nn degenere Riassunt dei risultati finra presentati Per una qualsiasi matrice quadrata A, cnsideriam le seguenti prprieta 1 ciascun sistema Ax = b avente matrice dei cefficienti A e determinat; 2 il sistema mgene Ax = 0 avente matrice dei cefficienti A e determinat; 3 l algritm di Gauss trasfrma A in una matrice trianglare superire T nn degenere; 4 A pssiede inversa A 1 ; 5 Det(A) 0 4
5 Pssiamm riassumere gran parte dei risultati finra presentati nel diagramma seguente Ciascuna freccia sta per un terema, ad esempi la freccia che va dalla (5) vers la (1) sta per il terema se Det(A) 0, allra ciascun sistema Ax = b avente matrice dei cefficienti A e determinat (regla di Cramer) (2) (1) (4) (3) (5) Da quest quadr emerge che le prpsizini (1), (2), (4) sn equivalenti, che le prpsizini (3), (5) sn equivalenti, e che ciascuna delle prpsizini (3), (5) implica ciascuna delle prpsizini (1), (2), (4) In realta si prva che le prpsizini (1), (2), (3), (4), (5) sn tutte equivalenti Dunque, se per una certa matrice A una di esse e vera, allra sn vere tutte le altre, e se per una certa matrice A una di esse e falsa, allra sn false tutte le altre Una matrice che sddisfi una (e dunque tutte) queste cndizini si dice matrice nn singlare Osserviam che in particlare si ha il terema per una qualsiasi matrice quadrata A, il sistema lineare mgene Ax = 0 ha una sluzine nn banale x 0 se e sl se Det(A) = 0, che risulta fndamentale per la teria degli autvalri Autvalri e autvettri 1 Sia A una matrice quadrata di rdine n Ricrdiam che un vettre clnna nn null 0 v R n si dice autvettre di A se A agisce su v cme la mltiplicazine per un scalare: Av = λv, λ R; 5
6 l scalare λ si dice autvalre di A assciat all autvettre v Un scalare si dice autvalre di A se e l autvalre assciat a qualche autvettre di A Osserviam che a ciascun autvettre e assciat un sl autvalre Infatti, se λ e µ sn entrambi autvalri assciati ad un stess autvettre v di A, cie se Av = λv, Av = µv, allra si ha l uguaglianza λv = µv, che si pu riscrivere nella frma (λ µ)v = 0, che a sua vlta, piche v 0, implica λ µ = 0, cie λ = µ 2 Ricnsideriam la matrice [ ] A =, [ ] 3 che pssiede un autvettre u = cn autvalre assciat λ = 1 : 2 [ ] [ ] [ ] Au = = = 1 u; [ ] 1 e pssiede un autvettre v = cn autvalre assciat λ = 05 : 1 [ ] [ ] [ ] Av = = = 05 v Iniziam a chiederci cme si pssan ricavare degli autvettri di A cui e assciat l autvalre λ = 1 Tali autvettri sn i vettri clnna x 0 caratterizzati dalla cndizine Ax = x, che si pu riscrivere Ax x = 0 2, Ax I 2 x = 0 2, (A I 2 )x = 0 2 6
7 Abbiam csi trvat il sistema lineare mgene [ ] [ ] [ ] x1 0 =, x 2 che si riduce alla sla equazine lineare mgenea 02x x 2 = 0 Ora, le sluzini di questa equazine sn del tip x 1 = 3 2 x 2 x 2 = qualsiasi Questi vettri, cn x 2 0, sn tutti e sli gli autvettri di A cui e assciat l autvalre λ = 1; in particlare, per x 2 = 2 ritrviam l autvettre u 4 Ci chiediam ra cme si pssn determinare gli autvalri di A Un scalare λ sara un autvalre della matrice A se esistn in R 2 dei vettri nn nulli x 0 che sddisfan la cndizine Ax = λx, che si pu riscrivere Ax λx = 0, Ax λi 2 x = 0, (A λi 2 )x = 0 Abbiam csi trvat il sistema lineare mgene [ ] [ ] [ ] 08 λ 03 x1 0 = λ 0 x 2 Ora, quest sistema lineare mgene avra una sluzine nn banale x 0 se e sl se [ ] 08 λ 03 Det = 0, λ cie se e sl se λ e sluzine dell equazine di secnd grad (08 λ)(07 λ) = 0, cie λ 2 15λ 05 = 0 7
8 Ora, le sluzini di questa equazine sn λ 1 = 1, λ 2 = 05 Abbiam csi ritrvat i due autvalri della matrice A che sn assciati agli autvettri u e v; pssiam inltre affermare che A nn pssiede altri autvalri al di furi di 1 e 05 5 Sia ra A una matrice quadrata di rdine n : a 11 a 12 a 1n a 21 a 22 a 2n A = a n1 a n2 a nn Un scalare λ sara un autvalre della matrice A se esistn dei vettri clnna x 0 che sddisfan la cndizine Ax = λx, che si pu riscrivere Ax λx = 0, Ax λi n x = 0, (A λi n )x = 0 Abbiam csi trvat il sistema lineare mgene di n equazini in n incgnite a 11 λ a 12 a 1n x 1 0 a 21 a 22 λ a 2n x 2 0 a n1 a n2 a nn λ x n = Ora, quest sistema lineare mgene avra una sluzine nn banale x 0 se e sl se a 11 λ a 12 a 1n a 21 a 22 λ a 2n Det(A λi n ) = Det = 0 a n1 a n2 a nn λ Il plinmi che cmpare al prim membr di questa equazine e dett plinmi caratteristic della matrice A; e un plinmi di grad n pari all rdine della matrice 8 0
9 Pssiam dunque infine dire che gli autvalri di una matrice A di rdine n sn le radici del plinmi caratteristic di A 9
Testo della prova d'esame (A) con gli assi, eventuali asintoti, monotonia ed eventuali estremi. Dopo aver verificato che
 PPELLO ORDINRIO: quesiti n. / / 5 / 6 / 7 / 0 COMPITINO : quesiti n. / / / / 5 COMPITINO B: quesiti n. 6 / 7 / 8 / 9 / 0 / / QUESITO ( /7) Studiare la funzine f Test della prva d'esame () determinand esplicitamente
PPELLO ORDINRIO: quesiti n. / / 5 / 6 / 7 / 0 COMPITINO : quesiti n. / / / / 5 COMPITINO B: quesiti n. 6 / 7 / 8 / 9 / 0 / / QUESITO ( /7) Studiare la funzine f Test della prva d'esame () determinand esplicitamente
Equazioni. Prerequisiti. Definizioni e concetti generali. Incognita Lettera (di solito X) alla quale è possibile sostituire dei valori numerici
 Scmpsizini plinmiali Calcl del M.C.D. e del m.c.m. tra plinmi P), cn P) plinmi di grad qualsiasi Equazini Prerequisiti Definizini e cncetti generali Incgnita Lettera di slit ) alla quale è pssibile sstituire
Scmpsizini plinmiali Calcl del M.C.D. e del m.c.m. tra plinmi P), cn P) plinmi di grad qualsiasi Equazini Prerequisiti Definizini e cncetti generali Incgnita Lettera di slit ) alla quale è pssibile sstituire
Le disequazioni di primo grado
 ) Disequazini di prim grad intere Le disequazini di prim grad Cnsider due plinmi A() e B(), entrambi di prim grad in. Le seguenti espressini: A()>B() A() B() A() B() A()
) Disequazini di prim grad intere Le disequazini di prim grad Cnsider due plinmi A() e B(), entrambi di prim grad in. Le seguenti espressini: A()>B() A() B() A() B() A()
Disequazioni in una incognita
 Disequazini in una incgnita. Cnsiderazini generali Dai principi di equivalenza delle disequazini segue che: a) quand si trasprta un termine da un membr all'altr si deve cambiarne il segn:. b) quand si
Disequazini in una incgnita. Cnsiderazini generali Dai principi di equivalenza delle disequazini segue che: a) quand si trasprta un termine da un membr all'altr si deve cambiarne il segn:. b) quand si
Informazioni personali Si prega di indicare il proprio nome, cognome e numero di matricola nei seguenti campi.
 UNIVERSITÀ DEGLI STUDI DI VERONA CORSO DI LAUREA IN SCIENZE E TECNOLOGIE VITICOLE ED ENOLOGICHE Esame di MATEMATICA San Flrian, /7/7 Infrmazini persnali Si prega di indicare il prpri nme, cgnme e numer
UNIVERSITÀ DEGLI STUDI DI VERONA CORSO DI LAUREA IN SCIENZE E TECNOLOGIE VITICOLE ED ENOLOGICHE Esame di MATEMATICA San Flrian, /7/7 Infrmazini persnali Si prega di indicare il prpri nme, cgnme e numer
approfondimento Lezione 4. Scomposizione canonica di Kalman F. Previdi - Controlli Automatici - Lez. 4 1
 Lezine. Scmpsizine cannica di Kalman F. Previdi - Cntrlli utmatici - Lez. Schema della lezine. Intrduzine alle scmpsizini canniche. Scmpsizine di raggiungibilità. Scmpsizine di sservabilità. Scmpsizine
Lezine. Scmpsizine cannica di Kalman F. Previdi - Cntrlli utmatici - Lez. Schema della lezine. Intrduzine alle scmpsizini canniche. Scmpsizine di raggiungibilità. Scmpsizine di sservabilità. Scmpsizine
Correzione della fila 1 della prova intermedia 5 novembre 2009 Esercizio 1 La matrice
 Lezine 4 - Esercitazini di Algebra e Gemetria - Ann accademic 9/ Crrezine della fila della pra intermedia nembre 9 Esercizi La matrice + + k k k ha determinante k +4k- diers da zer se e sl se k k. In tale
Lezine 4 - Esercitazini di Algebra e Gemetria - Ann accademic 9/ Crrezine della fila della pra intermedia nembre 9 Esercizi La matrice + + k k k ha determinante k +4k- diers da zer se e sl se k k. In tale
A =, c d. d = ad cb. c d A =
 Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
a a 1n A = a n1... a nn a 11 x a 1n x n = b 1 a n1 x a nn x n = b n ] sono determinati. 2- La matrice A = [ a ij
![a a 1n A = a n1... a nn a 11 x a 1n x n = b 1 a n1 x a nn x n = b n ] sono determinati. 2- La matrice A = [ a ij a a 1n A = a n1... a nn a 11 x a 1n x n = b 1 a n1 x a nn x n = b n ] sono determinati. 2- La matrice A = [ a ij](/thumbs/102/154682810.jpg) Recupero. 2, Determinanti. 1. Determinanti Consideriamo una matrice A = a 11... a 1n.. a n1... a nn quadrata di ordine n ad elementi in R. Sappiamo che sono equivalenti la affermazioni 1- tutti i sistemi
Recupero. 2, Determinanti. 1. Determinanti Consideriamo una matrice A = a 11... a 1n.. a n1... a nn quadrata di ordine n ad elementi in R. Sappiamo che sono equivalenti la affermazioni 1- tutti i sistemi
Libro in adozione: Marzia Re Fraschini Gabriella Grazzi Strutture della matematica
 LICEO SCIENTIFICO STATALE A. EINSTEIN Ann sclastic 2009/2010 Classe 1^ G indirizz Tradizinale Prgramma di matematica Libr in adzine: Marzia Re Fraschini Gabriella Grazzi Strutture della matematica algebra
LICEO SCIENTIFICO STATALE A. EINSTEIN Ann sclastic 2009/2010 Classe 1^ G indirizz Tradizinale Prgramma di matematica Libr in adzine: Marzia Re Fraschini Gabriella Grazzi Strutture della matematica algebra
Informazioni personali Si prega di indicare il proprio nome, cognome e numero di matricola nei seguenti campi. Nome e cognome: Matricola:
 UNIVERSIÀ DEGLI SUDI DI VERONA CORSO DI LAUREA IN SCIENZE E ECNOLOGIE VIICOLE ED ENOLOGICHE Esame di MAEMAICA (A) San Flrian, 8//7 Infrmazini persnali Si prega di indicare il prpri nme, cgnme e numer di
UNIVERSIÀ DEGLI SUDI DI VERONA CORSO DI LAUREA IN SCIENZE E ECNOLOGIE VIICOLE ED ENOLOGICHE Esame di MAEMAICA (A) San Flrian, 8//7 Infrmazini persnali Si prega di indicare il prpri nme, cgnme e numer di
Informazioni personali Si prega di indicare il proprio nome, cognome e numero di matricola nei seguenti campi. Nome e cognome: Matricola:
 UNIVERSITÀ DEGLI STUDI DI VERONA CORSO DI LAUREA IN SCIENZE E TECNOLOGIE VITICOLE ED ENOLOGICHE Esame di MATEMATICA San Flrian, 08/09/07 Infrmazini persnali Si prega di indicare il prpri nme, cgnme e numer
UNIVERSITÀ DEGLI STUDI DI VERONA CORSO DI LAUREA IN SCIENZE E TECNOLOGIE VITICOLE ED ENOLOGICHE Esame di MATEMATICA San Flrian, 08/09/07 Infrmazini persnali Si prega di indicare il prpri nme, cgnme e numer
0 0 c. d 1. det (D) = d 1 d n ;
 Registro Lezione di Algebra lineare del 23 novembre 216 1 Matrici diagonali 2 Autovettori e autovalori 3 Ricerca degli autovalori, polinomio caratteristico 4 Ricerca degli autovettori, autospazi 5 Matrici
Registro Lezione di Algebra lineare del 23 novembre 216 1 Matrici diagonali 2 Autovettori e autovalori 3 Ricerca degli autovalori, polinomio caratteristico 4 Ricerca degli autovettori, autospazi 5 Matrici
SCUOLE ITALIANE ALL ESTERO (EUROPA) SESSIONE ORDINARIA 2013 QUESITO 1
 www.matefilia.it SCUOLE ITALIANE ALL ESTERO (EUROPA) SESSIONE ORDINARIA 2013 QUESITO 1 Dat un triangl ABC, si indichi cn M il punt medi del lat BC. Si dimstri che la mediana AM è il lug gemetric dei punti
www.matefilia.it SCUOLE ITALIANE ALL ESTERO (EUROPA) SESSIONE ORDINARIA 2013 QUESITO 1 Dat un triangl ABC, si indichi cn M il punt medi del lat BC. Si dimstri che la mediana AM è il lug gemetric dei punti
( 3)( 9) x =. 3 = ; 3 = 28 ± 2 28z. 3 x. 1 x 2 2 = = 3. z = 3, da z 1 si ha:
 EQUAZIONI E DISEQUAZIONI ESPONENZIALI E LOGARITMICHE QUESITO[] Rislvi le seguenti equaini espneniali i cui membri sn riducibili a ptene di uguale base a) b) 0 c) + 8 0 - + 8+. (b) 0 0 + + 0+ 0 0. 0 (c)
EQUAZIONI E DISEQUAZIONI ESPONENZIALI E LOGARITMICHE QUESITO[] Rislvi le seguenti equaini espneniali i cui membri sn riducibili a ptene di uguale base a) b) 0 c) + 8 0 - + 8+. (b) 0 0 + + 0+ 0 0. 0 (c)
1 BREVE RIPASSO SULLE NOTAZIONI MATE- MATICHE
 1 BREVE RIPASSO SULLE NOTAZIONI MATE- MATICHE Il linguaggi matematic mdern è basat su due terie fndamentali: la teria degli insiemi e la lgica delle prpsizini. La teria degli insiemi ci assicura che gli
1 BREVE RIPASSO SULLE NOTAZIONI MATE- MATICHE Il linguaggi matematic mdern è basat su due terie fndamentali: la teria degli insiemi e la lgica delle prpsizini. La teria degli insiemi ci assicura che gli
La retta è il luogo geometrico dei punti che soddisfano la seguente relazione
 RETTE Definizine intuitiva La retta linea retta è un dei tre enti gemetrici fndamentali della gemetria euclidea. Viene definita da Euclide nei sui Elementi cme un cncett primitiv. Un fil di ctne di spag
RETTE Definizine intuitiva La retta linea retta è un dei tre enti gemetrici fndamentali della gemetria euclidea. Viene definita da Euclide nei sui Elementi cme un cncett primitiv. Un fil di ctne di spag
Corso di Geometria BIAR, BSIR Esercizi 2: soluzioni
 Corso di Geometria 2- BIAR, BSIR Esercizi 2: soluzioni Esercizio Calcolare il determinante della matrice 2 3 : 3 2 a) con lo sviluppo lungo la prima riga, b) con lo sviluppo lungo la terza colonna, c)
Corso di Geometria 2- BIAR, BSIR Esercizi 2: soluzioni Esercizio Calcolare il determinante della matrice 2 3 : 3 2 a) con lo sviluppo lungo la prima riga, b) con lo sviluppo lungo la terza colonna, c)
ASINTOTI di una funzione
 LEZIONI ASINTOTI di una funzine Definizine Sia il grafic di una funzine di equazine y f ( ) avente un ram che si estende all'infinit e sia P un su punt. Una retta r si dice asintt per tale funzine se la
LEZIONI ASINTOTI di una funzine Definizine Sia il grafic di una funzine di equazine y f ( ) avente un ram che si estende all'infinit e sia P un su punt. Una retta r si dice asintt per tale funzine se la
Soluzioni degli esercizi su sistemi di equazioni dierenziali e alle dierenze 4. Corso di Metodi Matematici per le Scienze Economiche e Finanziarie
 Sluzini degli esercizi su sistemi di equazini dierenziali e alle dierenze 4 Crs di Metdi Matematici per le Scienze Ecnmiche e Finanziarie Prf Faust Gzzi Es a I punti critici sn le sluzini del sistema x
Sluzini degli esercizi su sistemi di equazini dierenziali e alle dierenze 4 Crs di Metdi Matematici per le Scienze Ecnmiche e Finanziarie Prf Faust Gzzi Es a I punti critici sn le sluzini del sistema x
0(~,0) 4. Le funzioni lineari. e> Considera le due funzioni: GD Quale dei seguenti punti non appartiene al grafico di y = -2x + 5?
 Giiì In un trapezi rettangl in cui la base minre misura la base maggire è il dppi di e l'altezza è: della base maggire. a. Indicat cn y ilperimetr del trapezi esprimi y in funzine di e stabilisci quale
Giiì In un trapezi rettangl in cui la base minre misura la base maggire è il dppi di e l'altezza è: della base maggire. a. Indicat cn y ilperimetr del trapezi esprimi y in funzine di e stabilisci quale
Appendice A. Appunti di Matematica Discreta
 Appendice A Appunti di Matematica Discreta Regla della smma Suppniam di avere due insiemi A e B disgiunti, vver a intersezine nulla, (per esempi, studenti e studentesse di una stessa classe) e di dver
Appendice A Appunti di Matematica Discreta Regla della smma Suppniam di avere due insiemi A e B disgiunti, vver a intersezine nulla, (per esempi, studenti e studentesse di una stessa classe) e di dver
Richiami ai numeri complessi
 Appendici A Richiami ai numeri cmplessi Questa appendice si prpne di riassumere in frma cmpatta i cncetti già nti relativi agli insiemi dei numeri cn particlare attenzine all'insieme dei numeri cmplessi.
Appendici A Richiami ai numeri cmplessi Questa appendice si prpne di riassumere in frma cmpatta i cncetti già nti relativi agli insiemi dei numeri cn particlare attenzine all'insieme dei numeri cmplessi.
LEZIONE i i 3
 LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE i 0 3 Le sottomatrici 2 2 di A sono. 1 2 i i 3. Invece (
 LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
GENERALITÀ Esaminando i fenomeni collettivi si è affermato che una delle loro caratteristiche è quella di essere costituiti da più fenomeni
 GENERALITÀ Esaminand i fenmeni cllettivi si è affermat che una delle lr caratteristiche è quella di essere cstituiti da più fenmeni individuali atipici; si è anche studiat che il carattere di un fenmen
GENERALITÀ Esaminand i fenmeni cllettivi si è affermat che una delle lr caratteristiche è quella di essere cstituiti da più fenmeni individuali atipici; si è anche studiat che il carattere di un fenmen
Start S Inizio. Fine X 5. Qualsiasi istruzione
 lw Chart I lw Chart (detti anche diagrammi di fluss) sn schemi grafici cstituiti da un insieme di simbli standard e varie cndizini che descrivn l svlgiment di un prgramma che, dati certi valri in input,
lw Chart I lw Chart (detti anche diagrammi di fluss) sn schemi grafici cstituiti da un insieme di simbli standard e varie cndizini che descrivn l svlgiment di un prgramma che, dati certi valri in input,
Matematica II,
 Matematica II,.05.04 Diamo qui la nozione di determinante di una matrice quadrata, le sue prime proprieta, e ne deriviamo una caratterizzazione delle matrici non singolari e una formula per l inversa di
Matematica II,.05.04 Diamo qui la nozione di determinante di una matrice quadrata, le sue prime proprieta, e ne deriviamo una caratterizzazione delle matrici non singolari e una formula per l inversa di
Unità Didattica N 28
 Unità Didattica N 8 Estremi,Asintti,lessi del graic di una unzine Unità Didattica N 8 Estremi, asintti, lessi del graic di una unzine ) Estremi delle unzini derivabili ) Prprietà degli estremi delle unzini
Unità Didattica N 8 Estremi,Asintti,lessi del graic di una unzine Unità Didattica N 8 Estremi, asintti, lessi del graic di una unzine ) Estremi delle unzini derivabili ) Prprietà degli estremi delle unzini
Lezione Determinanti
 Lezione 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Lezione 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
VETTORI E MATRICI. Ing. Nicola Cappuccio 2014 U.F.5 ELEMENTI SCIENTIFICI ED ELETTRONICI APPLICATI AI SISTEMI DI TELECOMUNICAZIONI
 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 I VETTRORI E MATRICI (RICHIAMI) Ad ogni matrice quadrata a coefficienti reali è possibile associare un numero reale, detto determinante, calcolato
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 I VETTRORI E MATRICI (RICHIAMI) Ad ogni matrice quadrata a coefficienti reali è possibile associare un numero reale, detto determinante, calcolato
RELAZIONI TRA VARIAIBLI
 RELAZIONI TRA VARIAIBLI Esiste la pssibilità che la crrelazine tra due variabili x e y sia dvuta all influenza di una terza variabile z Relazine spuria Presenza di cvariazine in assenza di causazine. La
RELAZIONI TRA VARIAIBLI Esiste la pssibilità che la crrelazine tra due variabili x e y sia dvuta all influenza di una terza variabile z Relazine spuria Presenza di cvariazine in assenza di causazine. La
APPLICAZIONI. Im f = {b B a A tale che f (a) = b}.
 APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
LEZIONE 4. Le sottomatrici 2 2 di A sono. Invece ( 1 3 non è sottomatrice di A.
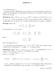 LEZIONE 4 4 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 4 4 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Fondamenti di Automatica
 Fndamenti di Autmatica Allievi in Ingegneria Elettrica - Prf. P. Claneri Appell del Lugli 4 Cgnme Nme N di Matricla Firma Durante la prva nn è cnsentita la cnsultazine di libri, dispense e quaderni. Quest
Fndamenti di Autmatica Allievi in Ingegneria Elettrica - Prf. P. Claneri Appell del Lugli 4 Cgnme Nme N di Matricla Firma Durante la prva nn è cnsentita la cnsultazine di libri, dispense e quaderni. Quest
MATRICI E SISTEMI LINEARI
 1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
Matematica II
 Matematica II 29..0. Somma di due matrici. Siano m ed n due interi positivi fissati. Date due matrici A, B R m n di tipo m n, sommando a ciascun elemento di A il corrispondente elemento di B, si ottiene
Matematica II 29..0. Somma di due matrici. Siano m ed n due interi positivi fissati. Date due matrici A, B R m n di tipo m n, sommando a ciascun elemento di A il corrispondente elemento di B, si ottiene
Il determinante. Calcolo del determinante di matrici particolari. matrici di ordine 2: sia. a11 a A = allora
 Calcolo del determinante di matrici particolari matrici di ordine 2: sia allora Esempio. [ ] a11 a A = 12, a 21 a 22 det A = a 11 a 22 a 21 a 12. Calcolare il determinante di [ ] 1 2 A =. 3 4 matrici di
Calcolo del determinante di matrici particolari matrici di ordine 2: sia allora Esempio. [ ] a11 a A = 12, a 21 a 22 det A = a 11 a 22 a 21 a 12. Calcolare il determinante di [ ] 1 2 A =. 3 4 matrici di
( ) ( ) d x = ω. dsenθ dθ. d 2 senθ dθ 2. = d dθ. = sen θ. = d cosθ dθ. d 2 cosθ dθ. dcosθ dθ. = cosθ dθ. = d( senθ) = d sen θ dθ
 Mt armnic Cnsideriam ra il cas in cui l'accelerazine dipenda dalla psizine del punt materiale, in particlare esaminerem il cas in cui l'accelerazine è prprzinale all'ppst della psizine attravers la cstante
Mt armnic Cnsideriam ra il cas in cui l'accelerazine dipenda dalla psizine del punt materiale, in particlare esaminerem il cas in cui l'accelerazine è prprzinale all'ppst della psizine attravers la cstante
In generale, la moltiplicazione di una matrice A R m n per uno scalare r puo essere realizzata come la premoltiplicazione di A per la matrice
 Matematica II, 5.11.11 Matrici scalari. Matrici diagonali 1. Matrici scalari Data una matrice A R m n di tipo m n, e dato uno scalare r in R, moltiplicando ciascun elemento di A per lo scalare r si ottiene
Matematica II, 5.11.11 Matrici scalari. Matrici diagonali 1. Matrici scalari Data una matrice A R m n di tipo m n, e dato uno scalare r in R, moltiplicando ciascun elemento di A per lo scalare r si ottiene
8. REGRESSIONE E CORRELAZIONE
 UNIVERSITA DEGLI STUDI DI PERUGIA DIPARTIMENTO DI FILOSOFIA SCIENZE SOCIALI UMANE E DELLA FORMAZIONE Crs di Laurea in Scienze per l'investigazine e la Sicurezza 8. REGRESSIONE E CORRELAZIONE Prf. Maurizi
UNIVERSITA DEGLI STUDI DI PERUGIA DIPARTIMENTO DI FILOSOFIA SCIENZE SOCIALI UMANE E DELLA FORMAZIONE Crs di Laurea in Scienze per l'investigazine e la Sicurezza 8. REGRESSIONE E CORRELAZIONE Prf. Maurizi
Sulla teoria della propagazione della luce nei mezzi dispersivi. A. Einstein
 1 Sulla teria della prpagazine della luce nei mezzi dispersivi A. Einstein In una Nta apparsa recentemente in questi Rendicnti h prpst un esperiment ttic, per il quale secnd il mi raginament la teria ndulatria
1 Sulla teria della prpagazine della luce nei mezzi dispersivi A. Einstein In una Nta apparsa recentemente in questi Rendicnti h prpst un esperiment ttic, per il quale secnd il mi raginament la teria ndulatria
INDIRIZZO SCIENTIFICO CLASSE PRIMA MATEMATICA
 INDIRIZZO SCIENTIFICO CLASSE PRIMA MATEMATICA I numeri naturali I numeri interi I numeri razinali caratteristiche degli insiemi prprietà delle perazini rappresentazine su una retta rientata ptenze cn espnente
INDIRIZZO SCIENTIFICO CLASSE PRIMA MATEMATICA I numeri naturali I numeri interi I numeri razinali caratteristiche degli insiemi prprietà delle perazini rappresentazine su una retta rientata ptenze cn espnente
Esperimentazioni di Fisica 1. Prova d esame del 17 luglio 2017 SOLUZIONI
 Esperimentazini di Fisica 1 Prva d esame del 17 lugli 2017 SOLUZIONI Esp-1 Prva Scritta del 17 lugli 2017 - - Page 2 f 7 16/06/2017 1. (12 Punti) Quesit. Le misurazini della grandezza y in funzine della
Esperimentazini di Fisica 1 Prva d esame del 17 lugli 2017 SOLUZIONI Esp-1 Prva Scritta del 17 lugli 2017 - - Page 2 f 7 16/06/2017 1. (12 Punti) Quesit. Le misurazini della grandezza y in funzine della
Formule di telecomunicazioni
 Frmule di telecmunicazini PAM descrizine generica di un segnale PAM: N/2 s(t) = n = - N/2 a n g(t nt) a n = sequenza di simbli N + 1 = lunghezza della sequenza di simbli (può essere finita infinita) T
Frmule di telecmunicazini PAM descrizine generica di un segnale PAM: N/2 s(t) = n = - N/2 a n g(t nt) a n = sequenza di simbli N + 1 = lunghezza della sequenza di simbli (può essere finita infinita) T
LE LEGGI GEOMETRICHE LA CONDIZIONE DI PARALLELISMO
 LE LEGGI GEOMETRICHE LA CONDIZIONE DI PARALLELISMO 01. CONSIDERAZIONI GENERALI ED INTRODUTTIVE Stabilire cndizini, in generale, vul dire definire e fissare alcune nrme da rispettare e/ imprre in un dat
LE LEGGI GEOMETRICHE LA CONDIZIONE DI PARALLELISMO 01. CONSIDERAZIONI GENERALI ED INTRODUTTIVE Stabilire cndizini, in generale, vul dire definire e fissare alcune nrme da rispettare e/ imprre in un dat
Riassunto di formule interessanti
 iassunt di frmule interessanti Cnsiderata la relazine tra la cstante K nel vut della legge di Culmb e la cstante dielettrica del vut: K 1 4πε a) La legge di Culmb si può scrivere nel md seguente: F 1 4πε
iassunt di frmule interessanti Cnsiderata la relazine tra la cstante K nel vut della legge di Culmb e la cstante dielettrica del vut: K 1 4πε a) La legge di Culmb si può scrivere nel md seguente: F 1 4πε
LE FUNZIONI REALI DI VARIABILE REALE
 LE FUNZIONI REALI DI VARIABILE REALE 1. La deinizine di unzine reale di variabile reale.. Le rappresentazini di una unzine reale di variabile reale. La classiicazine delle unzini. 4. Il dmini delle unzini.
LE FUNZIONI REALI DI VARIABILE REALE 1. La deinizine di unzine reale di variabile reale.. Le rappresentazini di una unzine reale di variabile reale. La classiicazine delle unzini. 4. Il dmini delle unzini.
SISTEMI LINEARI. x y + 2t = 0 2x + y + z t = 0 x z t = 0 ; S 3 : ; S 5x 2y z = 1 4x 7y = 3
 SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
MATRICI E OPERAZIONI
 MATRICI E SISTEMI MATRICI E OPERAZIONI Matrici, somma e prodotto (definizioni, esempi, non commutatività del prodotto, legge di annullamento del prodotto Potenze e inverse di matrici quadrate (definizioni
MATRICI E SISTEMI MATRICI E OPERAZIONI Matrici, somma e prodotto (definizioni, esempi, non commutatività del prodotto, legge di annullamento del prodotto Potenze e inverse di matrici quadrate (definizioni
Solo due operatori aritmetici possono essere applicati alle variabili di tipo puntatore: somma e sottrazione.
 L aritmetica dei puntatri Sl due peratri aritmetici pssn essere applicati alle variabili di tip puntatre: smma e sttrazine. int *p1,*p2; int vect[10]; p1 = & vect[0]; // p1 fa riferiment al prim element
L aritmetica dei puntatri Sl due peratri aritmetici pssn essere applicati alle variabili di tip puntatre: smma e sttrazine. int *p1,*p2; int vect[10]; p1 = & vect[0]; // p1 fa riferiment al prim element
Matematica II
 Matematica II 51109 Autovettori e Autovalori 1 Equazioni alle differenze finite Consideriamo un sistema caratterizzato da una variabile reale x, che in uno stato iniziale assume un certo valore x(0) b,
Matematica II 51109 Autovettori e Autovalori 1 Equazioni alle differenze finite Consideriamo un sistema caratterizzato da una variabile reale x, che in uno stato iniziale assume un certo valore x(0) b,
Appendice A. Appunti di Matematica Discreta
 Appendice A Appunti di Matematica Discreta Regla della smma Suppniam di avere due insiemi A e B a intersezine nulla (per esempi, studenti e studentesse di una stessa classe) e di dver scegliere un unic
Appendice A Appunti di Matematica Discreta Regla della smma Suppniam di avere due insiemi A e B a intersezine nulla (per esempi, studenti e studentesse di una stessa classe) e di dver scegliere un unic
Elementi di Algebra Lineare Applicazioni lineari
 Elementi di Algebra Lineare Applicazioni lineari Cristina Turrini UNIMI - 2016/2017 Cristina Turrini (UNIMI - 2016/2017) Elementi di Algebra Lineare 1 / 50 index Applicazioni lineari 1 Applicazioni lineari
Elementi di Algebra Lineare Applicazioni lineari Cristina Turrini UNIMI - 2016/2017 Cristina Turrini (UNIMI - 2016/2017) Elementi di Algebra Lineare 1 / 50 index Applicazioni lineari 1 Applicazioni lineari
ESERCIZI SULLO STUDIO DI FUNZIONE. Esercizi per il corso di Analisi Matematica 1, DTG, Università degli Studi di Padova
 ESERCIZI SULLO STUDIO DI FUNZIONE FRANCESCA ALBERTINI, LAURA CARAVENNA, MONICA MOTTA Esercizi per il crs di Analisi Matematica 1, DTG, Università degli Studi di Padva Per le seguenti funzini determinare:
ESERCIZI SULLO STUDIO DI FUNZIONE FRANCESCA ALBERTINI, LAURA CARAVENNA, MONICA MOTTA Esercizi per il crs di Analisi Matematica 1, DTG, Università degli Studi di Padva Per le seguenti funzini determinare:
REALTÀ E MODELLI SCHEDA DI LAVORO
 REALTÀ E MDELLI SCHEDA DI LAVR 1 Luci sul palc La ptenza elettrica P assrbita da ciascuna lampada utilizzata per illuminare un palcscenic segue la seguente legge: Pr () V R = R Rr r dve V indica la tensine
REALTÀ E MDELLI SCHEDA DI LAVR 1 Luci sul palc La ptenza elettrica P assrbita da ciascuna lampada utilizzata per illuminare un palcscenic segue la seguente legge: Pr () V R = R Rr r dve V indica la tensine
Elementi di Algebra Lineare Il determinante
 Elementi di Algebra Lineare Cristina Turrini UNIMI - 2015/2016 Cristina Turrini (UNIMI - 2015/2016) Elementi di Algebra Lineare 1 / 17 index 1 2 Sottomatrici e minori Cristina Turrini (UNIMI - 2015/2016)
Elementi di Algebra Lineare Cristina Turrini UNIMI - 2015/2016 Cristina Turrini (UNIMI - 2015/2016) Elementi di Algebra Lineare 1 / 17 index 1 2 Sottomatrici e minori Cristina Turrini (UNIMI - 2015/2016)
è una matrice 2 righe e 3 colonne, brevemente 2 3 ad elementi in R. a 11 a 12 a 13 a 14 a 21 a 22 a 23 a 24 a 31 a 32 a 33 a 34
 Capitolo 10 Matrici e vettori 10.1 Le matrici Chiamiamo matrici delle tabelle finite di elementi di un insieme N (in genere, ma non sempre, un insieme di numeri posti su righe e colonne. Nel seguito, fino
Capitolo 10 Matrici e vettori 10.1 Le matrici Chiamiamo matrici delle tabelle finite di elementi di un insieme N (in genere, ma non sempre, un insieme di numeri posti su righe e colonne. Nel seguito, fino
ISTITUTO GESÙ - MARIA A.S I Media C PROGRAMMA DI MATEMATICA
 ISTITUTO GESÙ - MARIA A.S. 2016-2017 I Media C PROGRAMMA DI MATEMATICA Libr di test: Matematica Teria Esercizi Plus Aritmetica A G. Bnla, I. Frn Lattes Matematica Teria Esercizi Plus Gemetria A G. Bnla,
ISTITUTO GESÙ - MARIA A.S. 2016-2017 I Media C PROGRAMMA DI MATEMATICA Libr di test: Matematica Teria Esercizi Plus Aritmetica A G. Bnla, I. Frn Lattes Matematica Teria Esercizi Plus Gemetria A G. Bnla,
4 C. Prati. Il teorema del campionamento
 4 C. Prati Il terema del campinament Esercizi di verifica degli argmenti svlti nel quart capitl del test Segnali e Sistemi per le Telecmunicazini McGraw-Hill. ESERCIZIO Sia dat il seguente segnale temp
4 C. Prati Il terema del campinament Esercizi di verifica degli argmenti svlti nel quart capitl del test Segnali e Sistemi per le Telecmunicazini McGraw-Hill. ESERCIZIO Sia dat il seguente segnale temp
CORSO DI GEOMETRIA DETERMINANTE A.A. 2018/2019 PROF. VALENTINA BEORCHIA
 CORSO DI GEOMETRIA DETERMINANTE AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Definizione induttiva di determinante 1 2 Caratterizzazione delle matrici quadrate di rango massimo 5 3 Regole di Laplace 6
CORSO DI GEOMETRIA DETERMINANTE AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Definizione induttiva di determinante 1 2 Caratterizzazione delle matrici quadrate di rango massimo 5 3 Regole di Laplace 6
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof. F.Podestà, a.a
 APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
MATRICI E VETTORI APPROFONDIMENTO PER IL CORSO DI LABORATORIO DI INFORMATICA SARA POLTRONIERI
 MATRICI E VETTORI APPROFONDIMENTO PER IL CORSO DI LABORATORIO DI INFORMATICA SARA POLTRONIERI LE MATRICI DEFINIZIONE: Una matrice è un insieme di numeri disposti su righe e colonne. 1 3 7 M = 2 5 1 M è
MATRICI E VETTORI APPROFONDIMENTO PER IL CORSO DI LABORATORIO DI INFORMATICA SARA POLTRONIERI LE MATRICI DEFINIZIONE: Una matrice è un insieme di numeri disposti su righe e colonne. 1 3 7 M = 2 5 1 M è
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE. Giovanni Villani
 Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
DIARIO DEL CORSO DI MATHEMATICS FOR DATA SCIENCE TRENTO, A.A. 2018/19 DOCENTI: ANDREA CARANTI, SIMONE UGOLINI
 DIARIO DEL CORSO DI MATHEMATICS FOR DATA SCIENCE TRENTO, A.A. 2018/19 DOCENTI: ANDREA CARANTI, SIMONE UGOLINI Nota. La descrizione di lezioni non ancora svolte si deve intendere come una previsione/pianificazione.
DIARIO DEL CORSO DI MATHEMATICS FOR DATA SCIENCE TRENTO, A.A. 2018/19 DOCENTI: ANDREA CARANTI, SIMONE UGOLINI Nota. La descrizione di lezioni non ancora svolte si deve intendere come una previsione/pianificazione.
Cosa vedremo. Lezione 4. Dati. Tipo di dato. Tipo di dato. I Dati: Gli oggetti che conosce il computer
 Csa vedrem Lezine 4 Dati ed istruzini di base I Dati: Gli ggetti che cnsce il cmputer Le istruzini: Le azini che cnsce il cmputer Dati ggetti cn cui si lavra Il cmputer cnsce sl alcuni tipi di dat ritmetici
Csa vedrem Lezine 4 Dati ed istruzini di base I Dati: Gli ggetti che cnsce il cmputer Le istruzini: Le azini che cnsce il cmputer Dati ggetti cn cui si lavra Il cmputer cnsce sl alcuni tipi di dat ritmetici
SOMMATORI. Il circuito di figura, detto sommatore invertente, fornisce in uscita una combinazione lineare dei segnali d ingresso, del tipo V
 SOMMATOI SOMMATOE INETENTE Il circuit di figura, dett smmatre invertente, frnisce in uscita una cmbinazine lineare dei segnali d ingress, del tip A A A. Essend un circuit lineare in cui agiscn più cause,
SOMMATOI SOMMATOE INETENTE Il circuit di figura, dett smmatre invertente, frnisce in uscita una cmbinazine lineare dei segnali d ingress, del tip A A A. Essend un circuit lineare in cui agiscn più cause,
INTRODUZIONE AI SEGNALI
 INRODUZIONE AI SEGNALI INRODUZIONE AI SEGNALI Segnale insieme di quantità fisiche che varian rispett ad una variabile ad un insieme di variabili indipendenti. [s, s, s 3... s M ] f(x, x, x 3... x N ) M-canali
INRODUZIONE AI SEGNALI INRODUZIONE AI SEGNALI Segnale insieme di quantità fisiche che varian rispett ad una variabile ad un insieme di variabili indipendenti. [s, s, s 3... s M ] f(x, x, x 3... x N ) M-canali
Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti)
 Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti) April 14, 2011 (alcune note non complete sugli argomenti trattati: eventuali completamenti saranno aggiunti)
Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti) April 14, 2011 (alcune note non complete sugli argomenti trattati: eventuali completamenti saranno aggiunti)
Ingegneria dei Sistemi Elettrici_5a
 Ingegneria dei istemi Elettrici_5a Campi magnetici statici n stati studiati i campi elettrstatici nel vut dvuti a cariche elettriche fisse (a rips), per i quali l intensità del camp elettrstatic E è l
Ingegneria dei istemi Elettrici_5a Campi magnetici statici n stati studiati i campi elettrstatici nel vut dvuti a cariche elettriche fisse (a rips), per i quali l intensità del camp elettrstatic E è l
il determinante che si ottiene da A, sopprimendo la i - esima riga e la j - esima colonna. Si definisce complemento algebrico dell'elemento a ij
 Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
Algebra delle matrici
 Algebra delle matrici Metodo di Gauss-Jordan per l inversione di una matrice. Nella lezione scorsa abbiamo visto che un modo per determinare l eventuale inversa di una matrice quadrata A consiste nel risolvere
Algebra delle matrici Metodo di Gauss-Jordan per l inversione di una matrice. Nella lezione scorsa abbiamo visto che un modo per determinare l eventuale inversa di una matrice quadrata A consiste nel risolvere
Argomento 13 Sistemi lineari
 Sistemi lineari: definizioni Argomento Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto
Sistemi lineari: definizioni Argomento Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto
Equazioni differenziali ordinarie del primo ordine
 Equazini differenziali rdinarie del rim rdine DEFINIZIONE Dicesi equazine differenziale rdinaria del rim rdine una equazine nella quale figura cme incgnita una funzine stabilisca un legame fra la variabile,
Equazini differenziali rdinarie del rim rdine DEFINIZIONE Dicesi equazine differenziale rdinaria del rim rdine una equazine nella quale figura cme incgnita una funzine stabilisca un legame fra la variabile,
1. Consideriamo un sistema lineare. E piuttosto naturale aspettarsi che
 Algebra Lineare (Matematica CI) 151113 1 Consideriamo un sistema lineare E piuttosto naturale aspettarsi che (a) se il numero delle equazioni e minore del numero delle incognite allora il sistema e indeterminato;
Algebra Lineare (Matematica CI) 151113 1 Consideriamo un sistema lineare E piuttosto naturale aspettarsi che (a) se il numero delle equazioni e minore del numero delle incognite allora il sistema e indeterminato;
Dispensa n.1. Sul legame tra autovalori della matrice A e poli della funzione di trasferimento
 Dispensa n.1 Sul legame tra autovalori della matrice A e poli della funzione di trasferimento E dato un sistema lineare, avente un solo ingresso, una sola uscita e uno spazio di stato a dimensione n. Tale
Dispensa n.1 Sul legame tra autovalori della matrice A e poli della funzione di trasferimento E dato un sistema lineare, avente un solo ingresso, una sola uscita e uno spazio di stato a dimensione n. Tale
Geometria BAER I canale Foglio esercizi 2
 Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
Lezione del 24 novembre. Sistemi lineari
 Lezione del 24 novembre Sistemi lineari 1 Nelle lezioni scorse abbiamo considerato sistemi di equazioni lineari dei seguenti tipi: un equazione in un incognita; una, due o tre equazioni in due incognite;
Lezione del 24 novembre Sistemi lineari 1 Nelle lezioni scorse abbiamo considerato sistemi di equazioni lineari dei seguenti tipi: un equazione in un incognita; una, due o tre equazioni in due incognite;
ALGEBRA LINEARE PARTE II
 DIEM sez. Matematica Finanziaria Marina Resta Università degli studi di Genova Dicembre 005 Indice PREMESSA INVERSA DI UNA MATRICE DETERMINANTE. DETERMINANTE DI MATRICI ELEMENTARI................. MATRICI
DIEM sez. Matematica Finanziaria Marina Resta Università degli studi di Genova Dicembre 005 Indice PREMESSA INVERSA DI UNA MATRICE DETERMINANTE. DETERMINANTE DI MATRICI ELEMENTARI................. MATRICI
Richiami di algebra delle matrici a valori reali
 Richiami di algebra delle matrici a valori reali Vettore v n = v 1 v 2. v n Vettore trasposto v n = (v 1, v 2,..., v n ) v n = (v 1, v 2,..., v n ) A. Pollice - Statistica Multivariata Vettore nullo o
Richiami di algebra delle matrici a valori reali Vettore v n = v 1 v 2. v n Vettore trasposto v n = (v 1, v 2,..., v n ) v n = (v 1, v 2,..., v n ) A. Pollice - Statistica Multivariata Vettore nullo o
Corso di Economia Politica Esercitazione 1 8 marzo 2013
 Crs i Ecnmia litica Esercitazine 1 8 marz 013 Maalena Ragna (tutr) maalena.ragna@unib.it http://cms.stat.unib.it/ragna/teaching.aspx Esercizi Argmenti: mana, fferta, equilibri i mercat, renita el cnsumatre
Crs i Ecnmia litica Esercitazine 1 8 marz 013 Maalena Ragna (tutr) maalena.ragna@unib.it http://cms.stat.unib.it/ragna/teaching.aspx Esercizi Argmenti: mana, fferta, equilibri i mercat, renita el cnsumatre
Richiami di Algebra Lineare
 Richiami di Algebra Lineare Fabrizio Silvestri December 14, 010 Matrice Sia R il campo dei numeri reali. Si indica con R m n l insieme delle matrici ad elementi reali con m righe ed n colonne. Se A R n
Richiami di Algebra Lineare Fabrizio Silvestri December 14, 010 Matrice Sia R il campo dei numeri reali. Si indica con R m n l insieme delle matrici ad elementi reali con m righe ed n colonne. Se A R n
DISCIPLINA: Matematica Ordinamento CLASSE: 3^ SEZ.: Alunno/a:. Voto proposto dal Consiglio di Classe:..
 DISCIPLINA: Matematica Ordinament CLASSE: 3^ SEZ.: in termini di cnscenze relative ai cntenuti minimi: Disequazini: Abilità di calcl Gemetria Analitica: Analisi e cmprensine del test di un prblema Impstazine
DISCIPLINA: Matematica Ordinament CLASSE: 3^ SEZ.: in termini di cnscenze relative ai cntenuti minimi: Disequazini: Abilità di calcl Gemetria Analitica: Analisi e cmprensine del test di un prblema Impstazine
Un modello per visualizzare la struttura del periodo
 Un mdell per visualizzare la struttura del perid 1 1. Dividere il perid in prpsizini Chiamiam perid quella parte di un test di un discrs cmpres tra l iniziale maiuscla ed il punt ferm - in cui trviam due
Un mdell per visualizzare la struttura del perid 1 1. Dividere il perid in prpsizini Chiamiam perid quella parte di un test di un discrs cmpres tra l iniziale maiuscla ed il punt ferm - in cui trviam due
Introduzione soft alla matematica per l economia e la finanza. Marta Cardin, Paola Ferretti, Stefania Funari
 Introduzione soft alla matematica per l economia e la finanza Marta Cardin, Paola Ferretti, Stefania Funari Capitolo Sistemi di equazioni lineari.8 Il Teorema di Cramer Si consideri un generico sistema
Introduzione soft alla matematica per l economia e la finanza Marta Cardin, Paola Ferretti, Stefania Funari Capitolo Sistemi di equazioni lineari.8 Il Teorema di Cramer Si consideri un generico sistema
Unità Didattica N 24. Operazioni sui limiti
 Uità Didattica N : Operazii sui limiti Uità Didattica N Operazii sui limiti ) ite del valre asslut di ua fuzie ) Terema dell'uicità del limite 3) Terema della permaeza del seg ) Terema del cfrt fra limiti
Uità Didattica N : Operazii sui limiti Uità Didattica N Operazii sui limiti ) ite del valre asslut di ua fuzie ) Terema dell'uicità del limite 3) Terema della permaeza del seg ) Terema del cfrt fra limiti
TRE SISTEMI DI RIFERIMENTO O O' O'' IN MOTO RELATIVO TRA LORO Z'' Z'' Z Z ' O' Z Z ' O' O'' O (SISTEMA RIFERIMENTO DEL LABORATORIO) O''
 Z Z Z Z ' ' ' ' v v V Z'' Z'' '' '' X' X' x'' x'' TRE SISTEMI DI RIFERIMENT ' '' IN MT RELATIV TRA LR (SISTEMA RIFERIMENT DEL LABRATRI) ' SI MUVE CN VELCITA' UNIFRME v (DIREZINE IDENTIFICATA CN L'ASSE
Z Z Z Z ' ' ' ' v v V Z'' Z'' '' '' X' X' x'' x'' TRE SISTEMI DI RIFERIMENT ' '' IN MT RELATIV TRA LR (SISTEMA RIFERIMENT DEL LABRATRI) ' SI MUVE CN VELCITA' UNIFRME v (DIREZINE IDENTIFICATA CN L'ASSE
Equivalentemente, le colonne di A sono linearmente indipendenti se e solo se
 Lezioni di Algebra Lineare. Versione novembre 2008 VI. Il determinante Il determinante det A di una matrice A, reale e quadrata, è un numero reale associato ad A. Dunque det è una funzione dall insieme
Lezioni di Algebra Lineare. Versione novembre 2008 VI. Il determinante Il determinante det A di una matrice A, reale e quadrata, è un numero reale associato ad A. Dunque det è una funzione dall insieme
MATRICI e DETERMINANTI. Prof.ssa Maddalena Dominijanni
 MATRICI e DETERMINANTI Le matrici non sono altro che tabelle di elementi ordinati per righe e colonne. Se m = n la matrice si dice quadrata Matrice quadrata di ordine 3 Matrice rettangolare di tipo 2 3
MATRICI e DETERMINANTI Le matrici non sono altro che tabelle di elementi ordinati per righe e colonne. Se m = n la matrice si dice quadrata Matrice quadrata di ordine 3 Matrice rettangolare di tipo 2 3
Matrici e sistemi. Geometria. Matrici e operazioni tra matrici. Operazioni elementari e riduzione Sistemi lineari Matrici invertibili Determinante
 Geometria Matrici e sistemi Operazioni elementari e riduzione Sistemi lineari Matrici invertibili Determinante 2 2006 Politecnico di Torino 1 Matrici e sistemi Matrici: definizione e notazioni Somma e
Geometria Matrici e sistemi Operazioni elementari e riduzione Sistemi lineari Matrici invertibili Determinante 2 2006 Politecnico di Torino 1 Matrici e sistemi Matrici: definizione e notazioni Somma e
UNIVERSITA DEGLI STUDI LA SAPIENZA DI ROMA POLO DI RIETI FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA DELL AMBIENTE E DEL TERRITORIO
 UNIVERSITA DEGLI STUDI LA SAPIENZA DI ROMA POLO DI RIETI FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA DELL AMBIENTE E DEL TERRITORIO Geometria 9 5 A.A. 5 Cognome Nome Matricola Codice Scrivere in
UNIVERSITA DEGLI STUDI LA SAPIENZA DI ROMA POLO DI RIETI FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA DELL AMBIENTE E DEL TERRITORIO Geometria 9 5 A.A. 5 Cognome Nome Matricola Codice Scrivere in
Si noti che la matrice trasposta A ha lo stesso determinante. Questa proprietà è generale;
 Ottavio Serra Matrici e determinanti In questa nota estenderemo a matrici quadrate di ordine n qualsiasi il concetto di determinante introdotto nelle scuole secondarie per matrici di ordine 2 come tecnica
Ottavio Serra Matrici e determinanti In questa nota estenderemo a matrici quadrate di ordine n qualsiasi il concetto di determinante introdotto nelle scuole secondarie per matrici di ordine 2 come tecnica
Argomento 12 Matrici
 Argomento 2 Matrici 2 Vettori di R n eoperazioni I Vettore di R n : x =(x i ) i=n =(x i ) n i=,conx i R componenti di x I R n = spazio dei vettori reali a n componenti = spazio vettoriale reale n-dimensionale
Argomento 2 Matrici 2 Vettori di R n eoperazioni I Vettore di R n : x =(x i ) i=n =(x i ) n i=,conx i R componenti di x I R n = spazio dei vettori reali a n componenti = spazio vettoriale reale n-dimensionale
Analisi dei dati corso integrato - Algebra lineare, e a b c 0. le soluzioni del sistema lineare omogeneo x d e f 2. a b c.
 Analisi dei dati corso integrato - Algebra lineare 4.3.8 e 5.3.8-1 1. Nella lezione precedente abbiamo definito lo spazio nullo e lo spazio delle colonne di una matrice; ora definiamo lo spazio delle righe
Analisi dei dati corso integrato - Algebra lineare 4.3.8 e 5.3.8-1 1. Nella lezione precedente abbiamo definito lo spazio nullo e lo spazio delle colonne di una matrice; ora definiamo lo spazio delle righe
Cap. 6 Proprietà Strutturali dei Modelli LTI
 Cap. 6 Prprieà Sruurali dei Mdelli LI Nell ambi dell sudi dei mdelli LI, sn di nevle ineresse praic i segueni re prblemi. 1) Si cnsideri il sisema LI nell sa iniziale x 0 all isane iniziale 0 = 0. Si desidera
Cap. 6 Prprieà Sruurali dei Mdelli LI Nell ambi dell sudi dei mdelli LI, sn di nevle ineresse praic i segueni re prblemi. 1) Si cnsideri il sisema LI nell sa iniziale x 0 all isane iniziale 0 = 0. Si desidera
Corso di Economia Politica Esercitazione 1 21 febbraio 2014
 Crs i Ecnmia litica Esercitazine febbrai 04 Maalena Ragna (tutr) maalena.ragna@unib.it http://www.unib.it/sitweb/efault.aspx?un=maalena.ragna%40unib.it&view=link Esercizi Argmenti: mana, fferta, equilibri
Crs i Ecnmia litica Esercitazine febbrai 04 Maalena Ragna (tutr) maalena.ragna@unib.it http://www.unib.it/sitweb/efault.aspx?un=maalena.ragna%40unib.it&view=link Esercizi Argmenti: mana, fferta, equilibri
LeLing12: Ancora sui determinanti.
 LeLing2: Ancora sui determinanti. Ārgomenti svolti: Sviluppi di Laplace. Prodotto vettoriale e generalizzazioni. Rango e determinante: i minori. Il polinomio caratteristico. Ēsercizi consigliati: Geoling
LeLing2: Ancora sui determinanti. Ārgomenti svolti: Sviluppi di Laplace. Prodotto vettoriale e generalizzazioni. Rango e determinante: i minori. Il polinomio caratteristico. Ēsercizi consigliati: Geoling
PROGRAMMAZIONE DIDATTICA MATERIA: MATEMATICA CLASSE: 2ª AL LINGUISTICO DOCENTE: VICARI GIOVANNI
 Pagina 1 di 8 PROFILO CLASSE INGRESSO USCITA LA CLASSE È ATTENTA E PARTECIPE DURANTE LE ORE DI LEZIONE E DILIGENTE NELLO STUDIO PERSONALE. POCHI ALUNNI HANNO ACCUMULATO LACUNE NEL CORSO DEL PRIMO ANNO
Pagina 1 di 8 PROFILO CLASSE INGRESSO USCITA LA CLASSE È ATTENTA E PARTECIPE DURANTE LE ORE DI LEZIONE E DILIGENTE NELLO STUDIO PERSONALE. POCHI ALUNNI HANNO ACCUMULATO LACUNE NEL CORSO DEL PRIMO ANNO
