Logica figurale. 1 Quanti quadrati contengono la stella? A. 1 B. 2 C. 5 D. 6 E Quanti triangoli sono rappresentati nella figura?
|
|
|
- Gianluca Casini
- 7 anni fa
- Visualizzazioni
Transcript
1 Logica figurale 1 Quanti quadrati contengono la stella? A. 1 B. 2 C. 5 D. 6 E. 9 2 Quanti triangoli sono rappresentati nella figura? A. 6 B. 8 C. 9 D. 10 E Quanti sono i quadrati presenti nella seguente figura? A. 24 B. 30 C. 59 D. 36
2 4 Quante figure femminili sono contenute nella figura seguente? A. 8 B. 16 C. 18 D. 12 E. 17
3 5 Cosa è rappresentato nel disegno di E. G. Boring? A. Una giovane e una vecchia donna B. Una giovane donna C. Una giovane donna e un rapace D. Un rapace e una vecchia donna E. Nessuna delle precedenti 6 Osservando il disegno proposto, quale delle seguenti coppie è formata da linee parallele? A. Solo la B B. Entrambe C. Nessuna D. Solo la A
4 7 Dopo aver osservato la figura sapreste dire se contiene linee curve ed indicarle? A. Sono curve le sole due linee orizzontali B. Non contiene linee curve C. Sono curve le linee indicate con le lettere C e D D. Sono curve le linee indicate con le lettere A e B 8 Osservare attentamente la figura ed individuare l affermazione corretta. A. La linea contrassegnata con A è più lunga di quella contrassegnata con B B. La linea contrassegnata con B è più lunga di quella contrassegnata con A C. Le linee contrassegnate con A e B hanno la stessa lunghezza D. La linea contrassegnata con B è esattamente pari ad un terzo della linea contrassegnata con A 9 Quale cerchio contiene il $ più grande? A. Il cerchio 3 B. Il cerchio 1 C. Tutti i $ sono uguali D. Il cerchio 2
5 10 È possibile tracciare, senza alzare la penna dal foglio o ripetere più volte lo stesso tracciato, sei linee rette in maniera da toccare tutti i sedici punti? A. No, è possibile tracciare solo cinque linee rette B. No, per tracciare sei linee rette occorre alzare almeno una volta la penna dal foglio C. Si, è possibile D. No, per tracciare sei linee rette occorre ripetere lo stesso tracciato per almeno due volte 11 Ogni figura geometrica può essere ottenuta attraverso la combinazione di elementi geometrici più piccoli (pezzi). Quali di queste figure sono ottenute con gli stessi pezzi? A. La n. 1 e la n. 2 B. La n. 2 e la n. 4 C. La n. 1 e la n. 4 D. La n. 2 e la n. 3 E. Sono tutte equivalenti
6 12 Nel seguente sistema le ruote dentate sono libere di ruotare attorno a un perno fisso. Se la ruota dentata C gira in senso orario, in quale senso gira la ruota dentata E? A. Il sistema di ingranaggi non può funzionare B. Nessuna delle altre alternative è corretta C. In senso inverso rispetto alla ruota dentata B D. Nello stesso senso della ruota dentata B E. In senso antiorario
7 13 Facendo riferimento al seguente ingranaggio risponda alle domande seguenti. Se la ruota A gira in senso orario: A. la ruota D gira in senso antiorario e la pallina P si muove in direzione 2 B. la ruota E gira in senso orario e la pallina P si muove in direzione 2 C. la ruota B gira in senso antiorario e la pallina P si muove in direzione 2 D. la ruota C gira in senso orario e la pallina P si muove in direzione 1 Se la ruota B gira in senso orario: A. la ruota D gira in senso antiorario e la pallina P si muove in direzione 2 B. la ruota C gira in senso antiorario e la pallina P si muove in direzione 2 C. la ruota E gira in senso orario e la pallina P si muove in direzione 1 D. la ruota A gira in senso antiorario e la pallina P si muove in direzione 1 Se la ruota D gira in senso antiorario: A. la ruota A gira in senso antiorario e la pallina P si muove in direzione 1 B. la ruota E gira in senso orario e la pallina P si muove in direzione 2 C. la ruota C gira in senso orario e la pallina P si muove in direzione 1 D. la ruota B gira in senso antiorario e la pallina P si muove in direzione 2 14 Quanti fra i seguenti 5 disegni possono essere tracciati senza staccare la penna dal foglio e senza passare due volte per lo stesso segmento? A. 5 B. 4 C. 3 D. 2 E. 1
8 15 Quale foratura si ottiene piegando e forando un foglio di carta secondo le modalità indicate nella figura in alto? A. Figura 1 B. Figura 5 C. Figura 3 D. Figura 4 E. Figura 2 16 Quale figura tridimensionale deriva dal ripiegamento del modello contenuto nel riquadro seguente?
9 17 18 Trova la figura che continua la serie.
10 19 Individuare la figura che completa la serie seguente: A. B. C. D. 20 Indica quale figura completa la serie.
11 21 Individua la figura che completa la sequenza. A. B. C. D. E. 22 Trova la figura che continua la serie.
12 23 Completa la serie seguente. A. 1 B. 2 C. 3 D Trova la figura che continua la serie. 25 Indicare la figura che completa la serie:
13 26 Individuare la figura che completa logicamente la proporzione: 27 Trova la figura che continua la serie. 28 Completare la seguente serie: A. B. C. D. E.
14 29 Indicare la figura da scartare. 30 Individua tra le seguenti la figura che non appartiene alla serie. 31 Il disegno indicato con la lettera «A», dopo essere stato ribaltato e ruotato è riproposto A. Nella figura contrassegnata dal numero 2 B. Nella figura contrassegnata dal numero 3 C. Nella figura contrassegnata dal numero 4 D. Nella figura contrassegnata dal numero 1
15 32 33 Completare la seguente serie: A. B. C. D. E.
16 34 35 Si consideri la seguente sequenza: Indicare quale delle 5 figure continua la sequenza indicata. A. Figura 4 B. Figura 2 C. Figura 5 D. Figura 1 E. Figura 3
17 36 Individua la figura che completa la sequenza. A. B. C. D. E. 37 Completare la seguente analogia figurale. A. B. C.
18 38 Individuare la figura mancante. A. B. C. D.
19 39 Individuare, tra le quattro figure proposte ( a, b, c o d ), la figura mancante nel seguente riquadro: A. B. C. D.
20 40 Individua la figura mancante. 41 Scegliere fra le alternative proposte quella che completa la serie.
21 42 Di seguito è presentata una configurazione incompleta. Individuate fra le cinque alternative proposte quella che completa il quadro. A. La figura indicata dalla lettera E B. La figura indicata dalla lettera C C. La figura indicata dalla lettera A D. La figura indicata dalla lettera B E. La figura indicata dalla lettera D 43 Individua la figura che termina correttamente la sequenza.
22 44 Si osservi la seguente serie incompleta di figure: quale delle alternative proposte ( a, b, c o d ) la completa correttamente? A. B. C. D. 45 Eliminare uno dei cinque disegni della serie. 46
23 47 Indicare in quale dei seguenti box contrassegnati da numeri è riproposto il disegno contrassegnato dalla lettera «A» dopo essere stato ribaltato e ruotato. A. Nel box contrassegnato con il numero 2 B. Nel box contrassegnato con il numero 3 C. Nel box contrassegnato con il numero 4 D. Nel box contrassegnato con il numero 1 48 Partendo dalla disposizione proposta, è possibile, togliendo sei graffette, ottenere tre quadrati di diverse dimensioni? A. Si, è possibile costruire tre quadrati di diverse dimensioni adiacenti l uno all altro e con uno spigolo in comune B. No, è possibile formare solo due quadrati di diverse dimensioni intersecati C. Si, è possibile formare tre quadrati, di cui il più grande contenente quello medio e quello medio contenente il più piccolo D. No
24 49 Utilizzando una volta sola i frammenti dall 1 al 9, quante volte è possibile ricostruire il disegno a sinistra? A. 4 volte B. 3 volte C. 2 volte D. Con i frammenti proposti non è possibile ricostruire il disegno a sinistra 50 Dopo aver osservato attentamente i disegni proposti individuare il disegno intruso. A. Il disegno intruso è in C B. Il disegno intruso è in A C. Il disegno intruso è in E D. Il disegno intruso è in B
RLA0001 Individuare il disegno intruso. a) Disegno A. b) Disegno B. c) Disegno C. d) Disegno D. b
 RLA0001 Individuare il disegno intruso. a) Disegno A. b) Disegno B. c) Disegno C. d) Disegno D. b RLA0002 Individuare fra le figure proposte quella che è logico inserire quale quarto termine della proporzione
RLA0001 Individuare il disegno intruso. a) Disegno A. b) Disegno B. c) Disegno C. d) Disegno D. b RLA0002 Individuare fra le figure proposte quella che è logico inserire quale quarto termine della proporzione
a) Con i box 1, 2, 3, 4, 6. b) Con i box 1, 2, 3, 4, 8. c) Con i box 1, 3, 6, 5, 8 d) Con i box 1, 3, 6, 4, 7. c
 RLA0001 Con quali delle seguenti tessere incastrate perfettamente è possibile formare la seguente stringa alfanumerica 4N - 1F - MB - SH 63 a) Con i box 1, 2, 3, 4, 6. b) Con i box 1, 2, 3, 4, 8. c) Con
RLA0001 Con quali delle seguenti tessere incastrate perfettamente è possibile formare la seguente stringa alfanumerica 4N - 1F - MB - SH 63 a) Con i box 1, 2, 3, 4, 6. b) Con i box 1, 2, 3, 4, 8. c) Con
3. Osserva attentamente il centro della corda e la distanza con il centro del cerchio M. Cosa constati?
 Corde 1. Ruota la retta a attorno al punto A e leggi il testo di colore verde. a) La retta, quando è una secante? Quando una tangente? Quando la retta non è né l una né l altra? b) Quante tangenti e quante
Corde 1. Ruota la retta a attorno al punto A e leggi il testo di colore verde. a) La retta, quando è una secante? Quando una tangente? Quando la retta non è né l una né l altra? b) Quante tangenti e quante
a) 2, 5 e 12. b) 9, 6 e 5. c) 7, 6 e 5. d) 4, 5 e 12. d
 RSB0001 Con quali dei seguenti numeri devono essere sostituite, rispettivamente, le lettere X, Y e Z perché la somma dei numeri in ogni serie di tre cerchi uniti dalle linee rette dia come risultato sempre
RSB0001 Con quali dei seguenti numeri devono essere sostituite, rispettivamente, le lettere X, Y e Z perché la somma dei numeri in ogni serie di tre cerchi uniti dalle linee rette dia come risultato sempre
a) Disegno B. b) Disegno D. c) Disegno A. d) Disegno C. b
 RVA0001 Considerando che alcune linee interne dei disegni (A, B, C, D) sono state cancellate, quale disegno è possibile formare con le figure geometriche date? Disegno B. Disegno D. Disegno A. Disegno
RVA0001 Considerando che alcune linee interne dei disegni (A, B, C, D) sono state cancellate, quale disegno è possibile formare con le figure geometriche date? Disegno B. Disegno D. Disegno A. Disegno
Poligoni. Enti geometrici fondamentali. Formati dei fogli. Squadratura del foglio
 Poligoni Enti geometrici fondamentali Gli enti geometrici fondamentali sono le rette e le curve. I segmenti sono frammenti di retta, mentre gli archi sono frammenti di curva. Un angolo esprime l inclinazione
Poligoni Enti geometrici fondamentali Gli enti geometrici fondamentali sono le rette e le curve. I segmenti sono frammenti di retta, mentre gli archi sono frammenti di curva. Un angolo esprime l inclinazione
Test di autovalutazione
 Test di autovalutazione Test 0 10 0 30 0 0 0 70 80 90 100 n Il mio punteggio, in centesimi, è n Rispondi a ogni quesito segnando una sola delle alternative. n onfronta le tue risposte con le soluzioni.
Test di autovalutazione Test 0 10 0 30 0 0 0 70 80 90 100 n Il mio punteggio, in centesimi, è n Rispondi a ogni quesito segnando una sola delle alternative. n onfronta le tue risposte con le soluzioni.
a) È maggiore nel disegno III: corrisponde a 45/72.
 RSB0001 Dati i quadrati I, II e III, la superficie non annerita. a) È maggiore nel disegno III: corrisponde a 45/72. b) É uguale nei disegni I e III: corrisponde ai 46/72. c) È maggiore nel disegno I:
RSB0001 Dati i quadrati I, II e III, la superficie non annerita. a) È maggiore nel disegno III: corrisponde a 45/72. b) É uguale nei disegni I e III: corrisponde ai 46/72. c) È maggiore nel disegno I:
Esercitazioni di. LOGICA e MATEMATICA. per la preparazione della PROVA NAZIONALE INVALSI CLASSE PRIMA
 Esercitazioni di LOGICA e MATEMATICA per la preparazione della PROVA NAZIONALE INVALSI CLASSE PRIMA prof.ssa Lina Migliaccio 1 I test di Bertoldino 1. In una stalla ci sono 15 pecore. Scappano tutte tranne
Esercitazioni di LOGICA e MATEMATICA per la preparazione della PROVA NAZIONALE INVALSI CLASSE PRIMA prof.ssa Lina Migliaccio 1 I test di Bertoldino 1. In una stalla ci sono 15 pecore. Scappano tutte tranne
1 Costruisci una costellazione
 foglio di lavoro Cos è una costellazione? Risponderai alla seguente domanda: Qual è l aspetto di una costellazione, quando la osserviamo da diverse angolazioni? 1 Costruisci una costellazione 1 L insegnante
foglio di lavoro Cos è una costellazione? Risponderai alla seguente domanda: Qual è l aspetto di una costellazione, quando la osserviamo da diverse angolazioni? 1 Costruisci una costellazione 1 L insegnante
Competizione 14 Marzo 2013
 Competizione 14 Marzo 2013 Proposta di soluzione? Usare un solo foglio risposta per ogni esercizio per il quale deve essere riportata una sola soluzione, pena l'annullamento.? Sono richieste spiegazioni
Competizione 14 Marzo 2013 Proposta di soluzione? Usare un solo foglio risposta per ogni esercizio per il quale deve essere riportata una sola soluzione, pena l'annullamento.? Sono richieste spiegazioni
quadrilatero generico parallelogramma rombo rettangolo quadrato
 Pavimentare 1. Quali forme di quadrilateri puoi costruire? Schizza tutte le forme possibili e scrivi il loro nome. 2. Cosa rappresentano i piccoli punti rossi sui lati del quadrilatero? 3. a) Costruisci
Pavimentare 1. Quali forme di quadrilateri puoi costruire? Schizza tutte le forme possibili e scrivi il loro nome. 2. Cosa rappresentano i piccoli punti rossi sui lati del quadrilatero? 3. a) Costruisci
a) Nel primo. b) In entrambi: 36 nel primo e 30 nel secondo.
 RSB0001 Calcolare a quali numeri corrispondono rispettivamente il «?» e il «??» a) 3 e 7. b) 2 e 9. c) 3 e 8. d) 2 e 7. a RSB0002 Ciascuno dei rettangoli proposti é stato suddiviso in 110 quadretti uguali
RSB0001 Calcolare a quali numeri corrispondono rispettivamente il «?» e il «??» a) 3 e 7. b) 2 e 9. c) 3 e 8. d) 2 e 7. a RSB0002 Ciascuno dei rettangoli proposti é stato suddiviso in 110 quadretti uguali
Triangoli rettangoli. Problema
 Triangoli rettangoli 1. a) Sposta il vertice C 1, fino a quando stimi che l angolo nel vertice C 1 sia 90. b) Allo stesso modo sposta i vertici da C 2 fino a C 9 fino a quando stimi che l angolo sia 90.
Triangoli rettangoli 1. a) Sposta il vertice C 1, fino a quando stimi che l angolo nel vertice C 1 sia 90. b) Allo stesso modo sposta i vertici da C 2 fino a C 9 fino a quando stimi che l angolo sia 90.
a) Circa 5 milioni b) Circa 10 milioni c) Circa 45 milioni d) Circa 15 milioni d RSA0001
 RSA0001 a) Circa 5 milioni b) Circa 10 milioni c) Circa 45 milioni d) Circa 15 milioni d Facendo riferimento al grafico, qual è il fatturato previsto in Asia per l Anno 2? RSA0002 A che cosa è uguale 3
RSA0001 a) Circa 5 milioni b) Circa 10 milioni c) Circa 45 milioni d) Circa 15 milioni d Facendo riferimento al grafico, qual è il fatturato previsto in Asia per l Anno 2? RSA0002 A che cosa è uguale 3
PROIEZIONI ORTOGONALI: SEZIONI CONICHE
 www.aliceappunti.altervista.org PROIEZIONI ORTOGONALI: SEZIONI CONICHE 1) PREMESSA: Il cono è una superficie generata da una retta con un estremo fisso e l altro che ruota. La retta prende il nome di GENERATRICE.
www.aliceappunti.altervista.org PROIEZIONI ORTOGONALI: SEZIONI CONICHE 1) PREMESSA: Il cono è una superficie generata da una retta con un estremo fisso e l altro che ruota. La retta prende il nome di GENERATRICE.
Scheda (2) per lo svolgimento delle attività
 Matebilandia 256 dimostrare che i due tipi di moto, deferente/epiciclo e rotolamento di due circonferenze, sono assimilabili; conoscere alcune delle curve famose; prevedere il tipo di curva che scaturirà
Matebilandia 256 dimostrare che i due tipi di moto, deferente/epiciclo e rotolamento di due circonferenze, sono assimilabili; conoscere alcune delle curve famose; prevedere il tipo di curva che scaturirà
TITOLO: LEGGERE I QUADRILATERI
 TITOLO: LEGGERE I QUADRILATERI Competenze di riferimento: Comprendere ed interpretare l informazione: comprendere messaggi verbali e non verbali di vario genere; individuare ed interpretare l informazione,
TITOLO: LEGGERE I QUADRILATERI Competenze di riferimento: Comprendere ed interpretare l informazione: comprendere messaggi verbali e non verbali di vario genere; individuare ed interpretare l informazione,
Scuole Infanzia Primaria Secondaria di primo grado
 Scuole Infanzia Primaria Secondaria di primo grado Privilegiare una DIDATTICA LABORATORIALE intesa come insieme strutturato di attività finalizzato alla costruzione di SIGNIFICATI La didattica laboratoriale
Scuole Infanzia Primaria Secondaria di primo grado Privilegiare una DIDATTICA LABORATORIALE intesa come insieme strutturato di attività finalizzato alla costruzione di SIGNIFICATI La didattica laboratoriale
a) Al nido il Cigno sono iscritti 180 bambini tra 7-12 mesi, 150 bambini tra 3-6 mesi e 160 bambini tra mesi.
 RSB0001 Supponendo che il grafico proposto sia relativo ai bambini iscritti/ospitati da quattro nidi d infanzia, suddivisi per età, indicare quale affermazione è corretta. a) Al nido il Cigno sono iscritti
RSB0001 Supponendo che il grafico proposto sia relativo ai bambini iscritti/ospitati da quattro nidi d infanzia, suddivisi per età, indicare quale affermazione è corretta. a) Al nido il Cigno sono iscritti
Kangourou Italia Gara del 17 marzo 2005 Categoria Junior Per studenti di seconda o terza superiore
 junior_05_d.qxp 21/02/2005 16.13 Pagina 22 Kangourou Italia Gara del 17 marzo 2005 Categoria Per studenti di seconda o terza superiore I quesiti dal N. 1 al N. 10 valgono 3 punti ciascuno 1. A Kangourou
junior_05_d.qxp 21/02/2005 16.13 Pagina 22 Kangourou Italia Gara del 17 marzo 2005 Categoria Per studenti di seconda o terza superiore I quesiti dal N. 1 al N. 10 valgono 3 punti ciascuno 1. A Kangourou
1 Congruenza diretta e inversa
 1 Congruenza diretta e inversa PROPRIETÀ. La congruenza tra due figure piane mantiene inalterata la lunghezza dei segmenti e l ampiezza degli angoli; ciò che cambia è la posizione delle figure nel piano.
1 Congruenza diretta e inversa PROPRIETÀ. La congruenza tra due figure piane mantiene inalterata la lunghezza dei segmenti e l ampiezza degli angoli; ciò che cambia è la posizione delle figure nel piano.
Corso di Laurea in Matematica per l Informatica e la Comunicazione Scientifica
 Corso di Laurea in Matematica per l Informatica e la Comunicazione Scientifica Soluzione del compito di Matematica Discreta 1 del 25 luglio 200 1. Qual è il numero di applicazioni f : A = {1,..., 5} B
Corso di Laurea in Matematica per l Informatica e la Comunicazione Scientifica Soluzione del compito di Matematica Discreta 1 del 25 luglio 200 1. Qual è il numero di applicazioni f : A = {1,..., 5} B
Un poligono può avere tre, quattro, cinque o più lati. Il vertice è il punto d incontro di due lati; i vertici si indicano
 Pagina 1 di 13 I poligoni I poligoni sono figure piane che hanno come contorno una linea spezzata chiusa formatada almeno tre segmenti consecutivi. Un poligono può avere tre, quattro, cinque o più lati.
Pagina 1 di 13 I poligoni I poligoni sono figure piane che hanno come contorno una linea spezzata chiusa formatada almeno tre segmenti consecutivi. Un poligono può avere tre, quattro, cinque o più lati.
DECLINAZIONE COMPETENZE SCUOLA PRIMARIA: MATEMATICA CLASSI 1 a 2 a 3 a
 DECLINAZIONE COMPETENZE SCUOLA PRIMARIA: MATEMATICA CLASSI 1 a 2 a 3 a COMPETENZE 1. Operare con i numeri nel calcolo scritto e mentale CONOSCENZE CONTENUTI A. I numeri da 0 a 20 B. I numeri da 20 a 100
DECLINAZIONE COMPETENZE SCUOLA PRIMARIA: MATEMATICA CLASSI 1 a 2 a 3 a COMPETENZE 1. Operare con i numeri nel calcolo scritto e mentale CONOSCENZE CONTENUTI A. I numeri da 0 a 20 B. I numeri da 20 a 100
A forma di... Osserva e colora seguendo le indicazioni.
 A forma di... Osserva e colora seguendo le indicazioni. Gli oggetti a forma di cilindro di verde. Gli oggetti a forma di parallelepipedo di rosa. Gli oggetti a forma di sfera di azzurro. Il cubo Costruire
A forma di... Osserva e colora seguendo le indicazioni. Gli oggetti a forma di cilindro di verde. Gli oggetti a forma di parallelepipedo di rosa. Gli oggetti a forma di sfera di azzurro. Il cubo Costruire
La prospettiva e i suoi strumenti teorici e tecnici
 Dispense del Corso di Disegno, tenuto da Riccardo Migliari nella Facoltà di Architettura Ludovico Quaroni della Sapienza Università di Roma nell Anno Accademico 2009 2010 La prospettiva e i suoi strumenti
Dispense del Corso di Disegno, tenuto da Riccardo Migliari nella Facoltà di Architettura Ludovico Quaroni della Sapienza Università di Roma nell Anno Accademico 2009 2010 La prospettiva e i suoi strumenti
Disegna la figura di cui vuoi la trasformata e gli oggetti (asse o centro di simmetria, vettore,...) che caratterizzano la trasformazione
 LE TRASFORMAZIONI IN CABRI Per ottenere la figura immagine di una figura data in una trasformazione Disegna la figura di cui vuoi la trasformata e gli oggetti (asse o centro di simmetria, vettore,...)
LE TRASFORMAZIONI IN CABRI Per ottenere la figura immagine di una figura data in una trasformazione Disegna la figura di cui vuoi la trasformata e gli oggetti (asse o centro di simmetria, vettore,...)
Un famoso teorema. Una possibile costruzione del quadrato (stabile) di lato AB:
 Un famoso teorema Un famoso teorema Si deve premettere: 1) Definizione di quadrato (già nota nella scuola media) 2) Prop. I.46: Costruzione del quadrato di lato il segmento dato con riga e compasso. Se
Un famoso teorema Un famoso teorema Si deve premettere: 1) Definizione di quadrato (già nota nella scuola media) 2) Prop. I.46: Costruzione del quadrato di lato il segmento dato con riga e compasso. Se
Uso degli strumenti per il disegno
 1 Uso degli strumenti per il disegno Disegno ornamentale Completa la griglia sottostante tracciando una sola diagonale nei quadrati, con direzione alternata. Successivamente colora la metà di ogni quadrato
1 Uso degli strumenti per il disegno Disegno ornamentale Completa la griglia sottostante tracciando una sola diagonale nei quadrati, con direzione alternata. Successivamente colora la metà di ogni quadrato
Esercitazione in preparazione alla Prova Invalsi di Matematica
 VERSO LA PROVA nazionale scuola secondaria di primo grado Esercitazione in preparazione alla Prova Invalsi di Matematica 1 marzo 013 ISTRUZIONI Questa prova di matematica contiene domande a risposta multipla
VERSO LA PROVA nazionale scuola secondaria di primo grado Esercitazione in preparazione alla Prova Invalsi di Matematica 1 marzo 013 ISTRUZIONI Questa prova di matematica contiene domande a risposta multipla
un rettangolo, due quadrati e un cerchio un cerchio, due triangoli e un quadrato due quadrati, un cerchio, un triangolo
 questa figura è formata da... un rettangolo, due quadrati e un cerchio un cerchio, due triangoli e un quadrato due quadrati, un cerchio, un triangolo osserva la sequenza di numeri 3 6 12 24 in questa sequenza
questa figura è formata da... un rettangolo, due quadrati e un cerchio un cerchio, due triangoli e un quadrato due quadrati, un cerchio, un triangolo osserva la sequenza di numeri 3 6 12 24 in questa sequenza
ISTITUTO COMPRENSIVO DI DONGO curricolo verticale per la scuola primaria Area di apprendimento: MATEMATICA
 IL NUMERO ISTITUTO COMPRENSIVO DI DONGO curricolo verticale per la scuola primaria Area di apprendimento: MATEMATICA - opera con numeri naturali e decimali - utilizza il calcolo scritto e mentale 1 2 ordinare
IL NUMERO ISTITUTO COMPRENSIVO DI DONGO curricolo verticale per la scuola primaria Area di apprendimento: MATEMATICA - opera con numeri naturali e decimali - utilizza il calcolo scritto e mentale 1 2 ordinare
Quale delle seguenti affermazioni è vera? RSA0003 a) 5 b) 3 c) 6 d) 2 a
 RSA0001 a) Figura 3 b) Figura 1 c) Figura 2 d) Figura 4 d RSA0002 Quale, tra le figure proposte, è uguale a quella data ruotata in senso antiorario di 130? a) Il numero dei libri di saggistica venduti
RSA0001 a) Figura 3 b) Figura 1 c) Figura 2 d) Figura 4 d RSA0002 Quale, tra le figure proposte, è uguale a quella data ruotata in senso antiorario di 130? a) Il numero dei libri di saggistica venduti
Giochi con due specchi. (Laboratorio sulla simmetria rotazionale)
 Giochi con due specchi. (Laboratorio sulla simmetria rotazionale) Prima parte. Abbiamo a disposizione alcune coppie di specchi, dei piccoli oggetti (poligoni, matite, palline), alcuni disegni. Tra due
Giochi con due specchi. (Laboratorio sulla simmetria rotazionale) Prima parte. Abbiamo a disposizione alcune coppie di specchi, dei piccoli oggetti (poligoni, matite, palline), alcuni disegni. Tra due
Risposte ai quesiti D E H D
 Perugia, dic. 2009/gen. 2010 Risposte ai quesiti 1. Dati i quadrati CD e C D, come in figura, provare che la perpendicolare uscente da alla retta DD passa per il punto medio del segmento quale che sia
Perugia, dic. 2009/gen. 2010 Risposte ai quesiti 1. Dati i quadrati CD e C D, come in figura, provare che la perpendicolare uscente da alla retta DD passa per il punto medio del segmento quale che sia
Quadro riassuntivo di geometria analitica
 Quadro riassuntivo di geometria analitica IL PIANO CARTESIANO (detta ascissa o coordinata x) e y quella dall'asse x (detta ordinata o coordinata y). Le coordinate di un punto P sono: entrambe positive
Quadro riassuntivo di geometria analitica IL PIANO CARTESIANO (detta ascissa o coordinata x) e y quella dall'asse x (detta ordinata o coordinata y). Le coordinate di un punto P sono: entrambe positive
Anno Accademico 2005-06
 Università degli Studi di Firenze Dipartimento di Meccanica e Tecnologie Industriali CORSO DI: DISEGNO MECCANICO (FI) CORSO DI: DISEGNO TECNICO IND.LE (PO) Anno Accademico 2005-06 Docenti: Modulo 2: RAPPRESENTAZIONE
Università degli Studi di Firenze Dipartimento di Meccanica e Tecnologie Industriali CORSO DI: DISEGNO MECCANICO (FI) CORSO DI: DISEGNO TECNICO IND.LE (PO) Anno Accademico 2005-06 Docenti: Modulo 2: RAPPRESENTAZIONE
LE TRASFORMAZIONI GEOMETRICHE
 pag. 1 LE TRASFORMAZIONI GEOMETRICHE Trasformazione geometrica Movimento rigido Traslazione Simmetria Costruzione di due punti simmetrici rispetto ad una retta Poligoni aventi assi di simmetria Rotazione
pag. 1 LE TRASFORMAZIONI GEOMETRICHE Trasformazione geometrica Movimento rigido Traslazione Simmetria Costruzione di due punti simmetrici rispetto ad una retta Poligoni aventi assi di simmetria Rotazione
Competenza matematica e competenze di base in scienze e tecnologia
 UDA: 1. I numeri razionali Tempi: settembre - novembre L alunno si muove con sicurezza nel calcolo anche con i numeri razionali, ne padroneggia le diverse rappresentazioni e stima la grandezza di un numero
UDA: 1. I numeri razionali Tempi: settembre - novembre L alunno si muove con sicurezza nel calcolo anche con i numeri razionali, ne padroneggia le diverse rappresentazioni e stima la grandezza di un numero
PIANO CARTESIANO. NB: attenzione ai punti con una coordinata nulla: si trovano sugli assi
 PIANO CARTESIANO Il piano cartesiano è individuato da due rette perpendicolari (ortogonali) che si incontrano in un punto O detto origine del piano cartesiano. Si fissa sulla retta orizzontale il verso
PIANO CARTESIANO Il piano cartesiano è individuato da due rette perpendicolari (ortogonali) che si incontrano in un punto O detto origine del piano cartesiano. Si fissa sulla retta orizzontale il verso
CURRICULO VERTICALE COMPETENZE IN AMBITO LOGICO MATEMATICO. SCUOLA secondaria di secondaria di primo grado
 CURRICULO VERTICALE COMPETENZE IN AMBITO LOGICO MATEMATICO SCUOLA secondaria di secondaria di primo grado classe 1^ TRAGUARDI per lo sviluppo L alunno si muove con sicurezza nel calcolo con i numeri Naturali
CURRICULO VERTICALE COMPETENZE IN AMBITO LOGICO MATEMATICO SCUOLA secondaria di secondaria di primo grado classe 1^ TRAGUARDI per lo sviluppo L alunno si muove con sicurezza nel calcolo con i numeri Naturali
L interno di un pezzo cavo puó essere rappresentato con linee tratteggiate. Se la geometria del pezzo é complessa questo metodo non garantisce peró
 SEZIONI L interno di un pezzo cavo puó essere rappresentato con linee tratteggiate. Se la geometria del pezzo é complessa questo metodo non garantisce peró una facile interpretazione del disegno. Si ricorre
SEZIONI L interno di un pezzo cavo puó essere rappresentato con linee tratteggiate. Se la geometria del pezzo é complessa questo metodo non garantisce peró una facile interpretazione del disegno. Si ricorre
RSA0001 Quale numero deve essere inserito nella seguente serie numerica? a) Il numero 4. b) Il numero 2. c) Il numero 9. d) Il numero 7.
 RSA0001 Quale numero deve essere inserito nella seguente serie numerica? a) Il numero 4. b) Il numero 2. c) Il numero 9. d) Il numero 7. d RSA0002 Quale frazione del disegno è quadrettata? a) 1/3. b) 2/3.
RSA0001 Quale numero deve essere inserito nella seguente serie numerica? a) Il numero 4. b) Il numero 2. c) Il numero 9. d) Il numero 7. d RSA0002 Quale frazione del disegno è quadrettata? a) 1/3. b) 2/3.
1 La traslazione. 2 La composizione di traslazioni. 3 La rotazione
 1 La traslazione Per poter applicare una traslazione ad una generica figura geometrica si deve: ± creare il vettore di traslazione AB mediante il comando Vettore tra due punti; ± cliccare con il mouse
1 La traslazione Per poter applicare una traslazione ad una generica figura geometrica si deve: ± creare il vettore di traslazione AB mediante il comando Vettore tra due punti; ± cliccare con il mouse
Progetto Informatica. Primo esempio Gruppo 1. Laura Tarsitano
 Progetto Informatica Primo esempio Gruppo 1 Laura Tarsitano laura.tarsitano@criadcoding.it Come costruire un micromondo Quando si costruisce un micromondo su Snap! bisogna immaginare di costruire uno spettacolo
Progetto Informatica Primo esempio Gruppo 1 Laura Tarsitano laura.tarsitano@criadcoding.it Come costruire un micromondo Quando si costruisce un micromondo su Snap! bisogna immaginare di costruire uno spettacolo
a) Devono trascorrere 63 ore.
 RSA0001 A che cosa è uguale. se: a) 4. b) 11. c) 3. d) 5. c +. +. +. +. = 22. +. = 8 +. = 11 RSA0002 Supponendo che l'orologio A segni le ore del mattino, e che l'orologio B segni le ore del pomeriggio,
RSA0001 A che cosa è uguale. se: a) 4. b) 11. c) 3. d) 5. c +. +. +. +. = 22. +. = 8 +. = 11 RSA0002 Supponendo che l'orologio A segni le ore del mattino, e che l'orologio B segni le ore del pomeriggio,
2. Quesiti dell area scientifica e scientifico-tecnologica
 2. Quesiti dell area scientifica e scientifico-tecnologica Logica 01 Scegliere fra le alternative proposte quella che completa la serie: a b c d e 02 Un auto percorre 20.000 km nel corso di un lungo viaggio.
2. Quesiti dell area scientifica e scientifico-tecnologica Logica 01 Scegliere fra le alternative proposte quella che completa la serie: a b c d e 02 Un auto percorre 20.000 km nel corso di un lungo viaggio.
Un cono circolare retto ha area di base 9π cm 2 e altezza 4 cm. L area della superficie totale del cono è di cm 2
 Le due rette r ed s nello spazio sono sghembe (non si intersecano e non sono parallele) e le loro direzioni formano un angolo di 45. Ruotando s attorno ad r si ottiene a) Un piano Un cilindro completo
Le due rette r ed s nello spazio sono sghembe (non si intersecano e non sono parallele) e le loro direzioni formano un angolo di 45. Ruotando s attorno ad r si ottiene a) Un piano Un cilindro completo
Per studiare lo spostamento prodotto R*T ragioniamo nel modo seguente:
 DECIMA LEZIONE COMPOSIZIONE DI ISOMETRIE Stiamo studiando la composizione delle isometrie elementari: 1. Traslazioni e rotazioni, che sono isometrie dirette; 2. Riflessioni e glisso-riflessioni, che sono
DECIMA LEZIONE COMPOSIZIONE DI ISOMETRIE Stiamo studiando la composizione delle isometrie elementari: 1. Traslazioni e rotazioni, che sono isometrie dirette; 2. Riflessioni e glisso-riflessioni, che sono
Istituto Comprensivo di Pralboino Curricolo Verticale
 MATEMATICA CLASSE SECONDA SECONDARIA INDICATORE NUMERI TRAGUARDI OBIETTIVI di APPRENDIMENTO CONTENUTI L alunno si muove con sicurezza nel calcolo anche con i numeri razionali, ne padroneggia le diverse
MATEMATICA CLASSE SECONDA SECONDARIA INDICATORE NUMERI TRAGUARDI OBIETTIVI di APPRENDIMENTO CONTENUTI L alunno si muove con sicurezza nel calcolo anche con i numeri razionali, ne padroneggia le diverse
ATTIVITA DIDATTICA SVOLTA nell A. S. 2017/18
 ATTIVITA DIDATTICA SVOLTA nell A. S. 2017/18 Indirizzo Materia Costruzioni Ambiente e Territorio Tecnologie e Tecniche della rappresentazione grafica Classe Docente 1 E Conoscenze (sapere) Modulo n 1 Fondamenti
ATTIVITA DIDATTICA SVOLTA nell A. S. 2017/18 Indirizzo Materia Costruzioni Ambiente e Territorio Tecnologie e Tecniche della rappresentazione grafica Classe Docente 1 E Conoscenze (sapere) Modulo n 1 Fondamenti
Categoria Benjamin Per studenti del primo e secondo anno della scuola media inferiore. I quesiti dal N.1 al N. 10 valgono 3 punti ciascuno
 Categoria Benjamin Per studenti del primo e secondo anno della scuola media inferiore I quesiti dal N.1 al N. 10 valgono 3 punti ciascuno 1. Risposta D) (2008 200 8) + 2008 = 1800 + 2008 = 3808. 2. Risposta
Categoria Benjamin Per studenti del primo e secondo anno della scuola media inferiore I quesiti dal N.1 al N. 10 valgono 3 punti ciascuno 1. Risposta D) (2008 200 8) + 2008 = 1800 + 2008 = 3808. 2. Risposta
Soluzioni delle Esercitazioni IV 08-12/10/2018
 Soluzioni delle Esercitazioni IV 08-/0/08 A. Insiemi limitati, estremo superiore/inferiore. In alcuni casi l insieme è dato esplicitamente, in altri occorre prima determinare l insieme. (a) L insieme (,
Soluzioni delle Esercitazioni IV 08-/0/08 A. Insiemi limitati, estremo superiore/inferiore. In alcuni casi l insieme è dato esplicitamente, in altri occorre prima determinare l insieme. (a) L insieme (,
Anno Scolastico PROVA DI MATEMATICA. Di preparazione all esame. Scuola Secondaria di I grado. Classe Terza. Codici. Scuola:... Classe:...
 Ministero dell Istruzione dell Università e della Ricerca Istituto nazionale per la valutazione del sistema educativo di istruzione e di formazione Anno Scolastico 008 009 PROVA DI MATEMATICA Di preparazione
Ministero dell Istruzione dell Università e della Ricerca Istituto nazionale per la valutazione del sistema educativo di istruzione e di formazione Anno Scolastico 008 009 PROVA DI MATEMATICA Di preparazione
Kangourou della Matematica 2006 finale nazionale italiana Mirabilandia, 8 maggio 2006
 LIVELLO ÉCOLIER E1. (5 punti ) Qual è il multiplo di 11 più vicino a 1000? E2. (7 punti ) Le lettere della parola ELA sono tutte distinte fra loro. Fa corrispondere ad ogni lettera di questa parola una
LIVELLO ÉCOLIER E1. (5 punti ) Qual è il multiplo di 11 più vicino a 1000? E2. (7 punti ) Le lettere della parola ELA sono tutte distinte fra loro. Fa corrispondere ad ogni lettera di questa parola una
Cosa puoi dire del quadrilatero ABCD? Come sono i lati, le diagonali, gli angoli?
 Dal parallelogramma al rombo (fase 1 e 2) Fase 1 Disegna due circonferenze concentriche c e c di centro O; disegna su c un punto A e su c un punto B; traccia la retta r passante per i punti A e O, chiama
Dal parallelogramma al rombo (fase 1 e 2) Fase 1 Disegna due circonferenze concentriche c e c di centro O; disegna su c un punto A e su c un punto B; traccia la retta r passante per i punti A e O, chiama
Geogebra. a. La lancetta è ruotata? SI NO. Se sì attorno a quale punto?
 Geogebra L ANGOLO 1. Nel programma Geogebra, fai doppio clic sull icona e scegli Circonferenza dati centro e raggio. 2. Posizionati al centro della finestra di geometria e fai clic. Nella finestra che
Geogebra L ANGOLO 1. Nel programma Geogebra, fai doppio clic sull icona e scegli Circonferenza dati centro e raggio. 2. Posizionati al centro della finestra di geometria e fai clic. Nella finestra che
LA GEOMETRIA DELLA TARTARUGA
 LA GEOMETRIA DELLA TARTARUGA CAPITOLO 4 Tracciare figure Iniziamo con una figura semplice: il QUADRATO. Certamente sai che un quadrato ha tutti i lati uguali e gli angoli uguali. Dopo aver avviato Logo
LA GEOMETRIA DELLA TARTARUGA CAPITOLO 4 Tracciare figure Iniziamo con una figura semplice: il QUADRATO. Certamente sai che un quadrato ha tutti i lati uguali e gli angoli uguali. Dopo aver avviato Logo
Due esempi di simmetria
 Due esempi di simmetria Giugno 2002 1 Le simmetrie del triangolo equilatero 1.1 Il triangolo equilatero è una figura dotata di simmetria. Cosa significa questa affermazione? In cosa consiste la sua simmetria?
Due esempi di simmetria Giugno 2002 1 Le simmetrie del triangolo equilatero 1.1 Il triangolo equilatero è una figura dotata di simmetria. Cosa significa questa affermazione? In cosa consiste la sua simmetria?
Lezione 6 Richiami di Geometria Analitica
 1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
Quadrilateri. Il Parallelogramma
 Il Parallelogramma 2. Fai clic su Ic3 e scegli Retta per due punti : disegna la retta a. 3. Fai clic su Ic2 e scegli Nuovo Punto : fai clic fuori dalla retta a 4. Fai clic su Ic4 e scegli Retta parallela
Il Parallelogramma 2. Fai clic su Ic3 e scegli Retta per due punti : disegna la retta a. 3. Fai clic su Ic2 e scegli Nuovo Punto : fai clic fuori dalla retta a 4. Fai clic su Ic4 e scegli Retta parallela
METODI E TECNOLOGIE PER L INSEGNAMETO DELLA MATEMATICA. LEZIONE n 13
 METODI E TECNOLOGIE PER L INSEGNAMETO DELLA MATEMATICA LEZIONE n 13 Parte terza TRASFORMAZIONI GEOMETRICHE Dalle indicazioni nazionali: Descrivere, denominare e classificare figure geometriche, identificando
METODI E TECNOLOGIE PER L INSEGNAMETO DELLA MATEMATICA LEZIONE n 13 Parte terza TRASFORMAZIONI GEOMETRICHE Dalle indicazioni nazionali: Descrivere, denominare e classificare figure geometriche, identificando
Compiti vacanze IIG a.s Alunno:
 Compiti vacanze IIG a.s. 2015-2016 Alunno: Numeri razionali assoluti 1 Completa, come nell esempio. 2 Sistema ciascuna lettera al posto giusto sulla semiretta numerica. A = 0,2 B = 0,9 C = 1,15 D = 0,6
Compiti vacanze IIG a.s. 2015-2016 Alunno: Numeri razionali assoluti 1 Completa, come nell esempio. 2 Sistema ciascuna lettera al posto giusto sulla semiretta numerica. A = 0,2 B = 0,9 C = 1,15 D = 0,6
Kangourou Italia Gara del 15 marzo 2007 Categoria Student Per studenti di quarta o quinta della secondaria di secondo grado
 Testi_07.qxp 6-04-2007 2:07 Pagina 28 Kangourou Italia Gara del 5 marzo 2007 Categoria Per studenti di quarta o quinta della secondaria di secondo grado I quesiti dal N. al N. 0 valgono 3 punti ciascuno.
Testi_07.qxp 6-04-2007 2:07 Pagina 28 Kangourou Italia Gara del 5 marzo 2007 Categoria Per studenti di quarta o quinta della secondaria di secondo grado I quesiti dal N. al N. 0 valgono 3 punti ciascuno.
Test di autovalutazione
 UNITÀ LE TRSFORMZIONI GEOMETRIHE: OMOTETIE E SIMILITUDINI Test Test di autovalutazione 0 0 0 0 0 0 0 70 80 90 00 n Il mio punteggio, in centesimi, è L omotetia è una trasformazione geometrica che a lascia
UNITÀ LE TRSFORMZIONI GEOMETRIHE: OMOTETIE E SIMILITUDINI Test Test di autovalutazione 0 0 0 0 0 0 0 70 80 90 00 n Il mio punteggio, in centesimi, è L omotetia è una trasformazione geometrica che a lascia
Ci proponiamo di mostrare che fatalmente si ricade in una delle precedenti isometrie.
 UNDICESIMA LEZIONE DECOMPOSIZIONE DI ISOMETRIE Chiudiamo la discussione sulle isometrie facendo vedere come si analizza una generica isometria. Ciò significa in questa lezione consideriamo una qualsiasi
UNDICESIMA LEZIONE DECOMPOSIZIONE DI ISOMETRIE Chiudiamo la discussione sulle isometrie facendo vedere come si analizza una generica isometria. Ciò significa in questa lezione consideriamo una qualsiasi
Illustrazione 1: Telaio. Piantanida Simone 1 G Scopo dell'esperienza: Misura di grandezze vettoriali
 Piantanida Simone 1 G Scopo dell'esperienza: Misura di grandezze vettoriali Materiale utilizzato: Telaio (carrucole,supporto,filo), pesi, goniometro o foglio con goniometro stampato, righello Premessa
Piantanida Simone 1 G Scopo dell'esperienza: Misura di grandezze vettoriali Materiale utilizzato: Telaio (carrucole,supporto,filo), pesi, goniometro o foglio con goniometro stampato, righello Premessa
Figure. Nome e cognome:
 Figure Nome e cognome: Data: 1. Secondo te, di cosa si occupa la geometria? Dopo il confronto nel gruppo Finale 2. Prova a dire cos è: a] Un punto b] Una retta c] Un piano 1 3. Quali relazioni possono
Figure Nome e cognome: Data: 1. Secondo te, di cosa si occupa la geometria? Dopo il confronto nel gruppo Finale 2. Prova a dire cos è: a] Un punto b] Una retta c] Un piano 1 3. Quali relazioni possono
Le simmetrie dei poliedri regolari
 Le simmetrie dei poliedri regolari Le isometrie del piano e dello spazio sono state classificate da due illustri matematici. Per quanto riguarda il piano, il teorema di Chasles, del 8, afferma che nel
Le simmetrie dei poliedri regolari Le isometrie del piano e dello spazio sono state classificate da due illustri matematici. Per quanto riguarda il piano, il teorema di Chasles, del 8, afferma che nel
Un approccio costruttivo alle trasformazioni geometriche del piano
 Un approccio costruttivo alle trasformazioni geometriche del piano Le cosiddette trasformazioni geometriche elementari del piano sono corrispondenze bigettive, del piano su se stesso, caratterizzate dalla
Un approccio costruttivo alle trasformazioni geometriche del piano Le cosiddette trasformazioni geometriche elementari del piano sono corrispondenze bigettive, del piano su se stesso, caratterizzate dalla
Per ruotare la figura fino a disporla parallela al occorre individuarne un qualsiasi segmento orizzontale. Per tale segmento, o per una parallela ad e
 Determinare la forma reale del triangolo rappresentato effettuando il ribaltamento (o la rotazione) del piano a cui appartiene. Nome Cognome Classe Data Per ruotare la figura fino a disporla parallela
Determinare la forma reale del triangolo rappresentato effettuando il ribaltamento (o la rotazione) del piano a cui appartiene. Nome Cognome Classe Data Per ruotare la figura fino a disporla parallela
Anno accademico 2005-06
 Università degli Studi di Firenze Dipartimento di Meccanica e Tecnologie Industriali CORSO DI: DISEGNO MECCANICO (FI) CORSO DI: DISEGNO TECNICO IND.LE (PO) Anno accademico 2005-06 Docenti: Modulo 2: RAPPRESENTAZIONE
Università degli Studi di Firenze Dipartimento di Meccanica e Tecnologie Industriali CORSO DI: DISEGNO MECCANICO (FI) CORSO DI: DISEGNO TECNICO IND.LE (PO) Anno accademico 2005-06 Docenti: Modulo 2: RAPPRESENTAZIONE
Si è potuto constatare che il completamento serie è un test molto utilizzato nelle prove di selezione.
 Si è potuto constatare che il completamento serie è un test molto utilizzato nelle prove di selezione. Con serie si intendono successioni di oggetti, disposti secondo un legame logico nascosto, che bisogna
Si è potuto constatare che il completamento serie è un test molto utilizzato nelle prove di selezione. Con serie si intendono successioni di oggetti, disposti secondo un legame logico nascosto, che bisogna
Istituzioni di Matematiche II Recupero seconda prova intermedia (6 giugno 2003)
 Istituzioni di Matematiche II Recupero seconda prova intermedia (6 giugno 2003) Nome Cognome 1. Considerando gli oggetti in figura, costruire: (a) il poligono ottenuto dal poligono A per riflessione rispetto
Istituzioni di Matematiche II Recupero seconda prova intermedia (6 giugno 2003) Nome Cognome 1. Considerando gli oggetti in figura, costruire: (a) il poligono ottenuto dal poligono A per riflessione rispetto
MATEMATICA TRAGUARDI PER LO SVILUPPO DELLE COMPETENZE AL TERMINE DELLA SCUOLA SECONDARIA DI PRIMO GRADO
 MATEMATICA TRAGUARDI PER LO SVILUPPO DELLE COMPETENZE AL TERMINE DELLA SCUOLA SECONDARIA DI PRIMO GRADO - L alunno si muove con sicurezza nel calcolo anche con i numeri razionali, ne padroneggia le diverse
MATEMATICA TRAGUARDI PER LO SVILUPPO DELLE COMPETENZE AL TERMINE DELLA SCUOLA SECONDARIA DI PRIMO GRADO - L alunno si muove con sicurezza nel calcolo anche con i numeri razionali, ne padroneggia le diverse
Fonte: I testi sono tratti dal sito di Ornella Crétaz ***
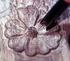 Fonte: I testi sono tratti dal sito di Ornella Crétaz www.intaglionline.it *** In questa parte del corso vengono descritti i procedimenti per tracciare correttamente figure geometriche elementari che possono
Fonte: I testi sono tratti dal sito di Ornella Crétaz www.intaglionline.it *** In questa parte del corso vengono descritti i procedimenti per tracciare correttamente figure geometriche elementari che possono
- Spiega il procedimento seguito, anche in forma scritta, mantenendo il controllo sia sul processo risolutivo, sia sui risultati.
 SCUOLA SECONDARIA TRAGUARDI DI SVILUPPO DELLE COMPETENZE MATEMATICA - L alunno si muove con sicurezza nel calcolo anche con i numeri razionali, ne padroneggia le diverse rappresentazioni e stima la grandezza
SCUOLA SECONDARIA TRAGUARDI DI SVILUPPO DELLE COMPETENZE MATEMATICA - L alunno si muove con sicurezza nel calcolo anche con i numeri razionali, ne padroneggia le diverse rappresentazioni e stima la grandezza
A B C D E F G H I L M N O P Q R S T U V Z
 IL VOCABOLARIO GEOMETRICO A B C D E F G H I L M N O P Q R S T U V Z A A: è il simbolo dell area di una figura geometrica Altezza: è la misura verticale e il segmento che parte da un vertice e cade perpendicolarmente
IL VOCABOLARIO GEOMETRICO A B C D E F G H I L M N O P Q R S T U V Z A A: è il simbolo dell area di una figura geometrica Altezza: è la misura verticale e il segmento che parte da un vertice e cade perpendicolarmente
TRIANGOLI. La somma degli angoli interni di un triangolo è sempre uguale a 180. (180 3) 540 = = 180. ortocentro-incontro altezze
 cateto TRIANGOLI 1. PROPRIETÀ, PUNTI NOTEVOLI DEL TRIANGOLO E SOMMA DEGLI ANGOLI È il più semplice dei poligoni, costituito da tre lati. In un, oltre ai lati ed agli angoli, si distinguono: altezza: perpendicolare
cateto TRIANGOLI 1. PROPRIETÀ, PUNTI NOTEVOLI DEL TRIANGOLO E SOMMA DEGLI ANGOLI È il più semplice dei poligoni, costituito da tre lati. In un, oltre ai lati ed agli angoli, si distinguono: altezza: perpendicolare
GEOMETRIE PARTICOLARI
 orso di disegno tecnico e progettuale M06 () GOMTRI PRTIOLRI sercizio Rufa -.. 2015-2016 - I anno di Graphic esign prof. Lombardo - prof. Salvatori Spirali Spirale a due centri con raccordamenti di semicerchi
orso di disegno tecnico e progettuale M06 () GOMTRI PRTIOLRI sercizio Rufa -.. 2015-2016 - I anno di Graphic esign prof. Lombardo - prof. Salvatori Spirali Spirale a due centri con raccordamenti di semicerchi
Simulazione della Prova Nazionale Invalsi di Matematica
 VERSO LA PROVA nazionale scuola secondaria di primo grado Simulazione della Prova Nazionale Invalsi di Matematica 2 6 aprile 202 ISTRUZIONI Questa prova di matematica contiene 26 domande a risposta multipla
VERSO LA PROVA nazionale scuola secondaria di primo grado Simulazione della Prova Nazionale Invalsi di Matematica 2 6 aprile 202 ISTRUZIONI Questa prova di matematica contiene 26 domande a risposta multipla
Matrici di Raven e Bochum
 Matrici di Raven e Bochum @ Le matrici di Raven e di Bochum sono tabelle 3 3 (ovvero con 3 righe e 3 colonne), o 3 5 (ovvero con 3 righe e 5 colonne), contenenti in ogni cella, tranne in una o due, alcuni
Matrici di Raven e Bochum @ Le matrici di Raven e di Bochum sono tabelle 3 3 (ovvero con 3 righe e 3 colonne), o 3 5 (ovvero con 3 righe e 5 colonne), contenenti in ogni cella, tranne in una o due, alcuni
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria A.A. 2009/10
 UNIVERSITÀ DEGLI STUDI DI PDOV Facoltà di Ingegneria Corso di Disegno Tecnico Industriale per i Corsi di Laurea triennale in Ingegneria Meccanica e in Ingegneria dell Energia Costruzioni geometriche in
UNIVERSITÀ DEGLI STUDI DI PDOV Facoltà di Ingegneria Corso di Disegno Tecnico Industriale per i Corsi di Laurea triennale in Ingegneria Meccanica e in Ingegneria dell Energia Costruzioni geometriche in
C C B B. Fig. C4.1 Isometria.
 4. Isometrie 4.1 Definizione di isometria Date due figure congruenti è possibile passare da una all altra con una trasformazione. Una trasformazione geometrica in un piano è una funzione biunivoca che
4. Isometrie 4.1 Definizione di isometria Date due figure congruenti è possibile passare da una all altra con una trasformazione. Una trasformazione geometrica in un piano è una funzione biunivoca che
Kangourou della Matematica 2007 Categoria Benjamin Per studenti di prima o seconda della scuola secondaria di primo grado
 Kangourou della Matematica 2007 Categoria Benjamin Per studenti di prima o seconda della scuola secondaria di primo grado 1. Risposta D). Fra i fattori del prodotto vi è 0. 2. Risposta C). Si tratta di
Kangourou della Matematica 2007 Categoria Benjamin Per studenti di prima o seconda della scuola secondaria di primo grado 1. Risposta D). Fra i fattori del prodotto vi è 0. 2. Risposta C). Si tratta di
1 L'omotetia. 2 Il teorema del rapporto dei perimetri e delle aree di due triangoli simili
 1 L'omotetia Per definire un'omotetia bisogna disegnare una generica figura nel piano (nel nostro caso utilizzeremo un triangolo), un punto (il centro dell'omotetia) e un numero (il rapporto k dell'omotetia).
1 L'omotetia Per definire un'omotetia bisogna disegnare una generica figura nel piano (nel nostro caso utilizzeremo un triangolo), un punto (il centro dell'omotetia) e un numero (il rapporto k dell'omotetia).
MATEMATICA classe PRIMA
 MATEMATICA classe PRIMA OBIETTIVI DI APPRENDIMENTO MATEMATICA Classe PRIMA SECONDARIA A 1.1.1. Riconoscere,rappresentare e operare correttamente con gli insiemi matematici. A 1.1.2. Scrivere, leggere,
MATEMATICA classe PRIMA OBIETTIVI DI APPRENDIMENTO MATEMATICA Classe PRIMA SECONDARIA A 1.1.1. Riconoscere,rappresentare e operare correttamente con gli insiemi matematici. A 1.1.2. Scrivere, leggere,
Le proiezioni ortogonali
 Le proiezioni ortogonali principi generali proiezione di figure geometriche piane proiezioni di solidi geometrici proiezioni di pezzi meccanici principi generali delle proiezioni proiettare per rappresentare
Le proiezioni ortogonali principi generali proiezione di figure geometriche piane proiezioni di solidi geometrici proiezioni di pezzi meccanici principi generali delle proiezioni proiettare per rappresentare
COMPITI VACANZE ESTIVE 2017 MATEMATICA Scuola Media Montessori Cardano al Campo (VA)
 COMPITI VACANZE ESTIVE 017 MATEMATICA Scuola Media Montessori Cardano al Campo (VA) Nel presente documento sono elencati gli esercizi da svolgere nel corso delle vacanze estive 017 da parte degli studenti
COMPITI VACANZE ESTIVE 017 MATEMATICA Scuola Media Montessori Cardano al Campo (VA) Nel presente documento sono elencati gli esercizi da svolgere nel corso delle vacanze estive 017 da parte degli studenti
VERIFICA DI MATEMATICA 3^C IPSIA 3 aprile 2017 rispondere su un foglio protocollo da riconsegnare entro 10 aprile 2017 NOME E COGNOME.
 VERIFICA DI MATEMATICA 3^C IPSIA 3 aprile 2017 rispondere su un foglio protocollo da riconsegnare entro 10 aprile 2017 NOME E COGNOME 1 Disegnare il triangolo OAB e determinarne il perimetro e l'area.
VERIFICA DI MATEMATICA 3^C IPSIA 3 aprile 2017 rispondere su un foglio protocollo da riconsegnare entro 10 aprile 2017 NOME E COGNOME 1 Disegnare il triangolo OAB e determinarne il perimetro e l'area.
LE SEQUENZE Questi esercizi sono i più comuni e i più frequenti. Sono prove che si basano su un semplice principio costituito dalla ricerca della
 LE SEQUENZE Questi esercizi sono i più comuni e i più frequenti. Sono prove che si basano su un semplice principio costituito dalla ricerca della regola che spiega la progressione di una certa sequenza
LE SEQUENZE Questi esercizi sono i più comuni e i più frequenti. Sono prove che si basano su un semplice principio costituito dalla ricerca della regola che spiega la progressione di una certa sequenza
Analisi prove Invalsi 2016 Matematica classe V
 Analisi prove Invalsi 2016 Matematica classe V ITEM: D1 Numeri L alunno deve passare da un numero espresso in lettere alla sua rappresentazione in cifre decimali: deve sapere leggere e scrivere i numeri
Analisi prove Invalsi 2016 Matematica classe V ITEM: D1 Numeri L alunno deve passare da un numero espresso in lettere alla sua rappresentazione in cifre decimali: deve sapere leggere e scrivere i numeri
GRIGLIA DI CORREZIONE 2012 Matematica Classe V Scuola Primaria
 GRIGLIA DI CORREZIONE 2012 Matematica Classe V Scuola Primaria LEGENDA AMBITI: NU (Numeri), SF (Spazio e figure), DP (Dati e previsioni), RF (Relazioni e funzioni) LEGENDA PROCESSI: 1. Conoscere e padroneggiare
GRIGLIA DI CORREZIONE 2012 Matematica Classe V Scuola Primaria LEGENDA AMBITI: NU (Numeri), SF (Spazio e figure), DP (Dati e previsioni), RF (Relazioni e funzioni) LEGENDA PROCESSI: 1. Conoscere e padroneggiare
1) Con la riga appoggiata al bordo sinistro del foglio e la squadra appoggiata alla riga, traccia lunghe 2 linee di
 9 cm 9 cm ) Con la riga appoggiata al bordo sinistro del foglio e la squadra appoggiata alla riga, traccia lunghe linee di costruzione orizzontali, con la matita H, distanti 9 cm. ) Sulle costruzioni orizzontali,
9 cm 9 cm ) Con la riga appoggiata al bordo sinistro del foglio e la squadra appoggiata alla riga, traccia lunghe linee di costruzione orizzontali, con la matita H, distanti 9 cm. ) Sulle costruzioni orizzontali,
Kangourou della Matematica 2019 Coppa Junior a squadre Semifinale turno A Cervia, 6 maggio Quesiti
 Kangourou della Matematica 2019 Coppa Junior a squadre Semifinale turno A Cervia, 6 maggio 2019 Quesiti 1. Ai minimi termini Riducete ai minimi termini la frazione (1 + 3 + 5 + + 51) / (4 + 6 + 8 + + 54)
Kangourou della Matematica 2019 Coppa Junior a squadre Semifinale turno A Cervia, 6 maggio 2019 Quesiti 1. Ai minimi termini Riducete ai minimi termini la frazione (1 + 3 + 5 + + 51) / (4 + 6 + 8 + + 54)
