Statistica 1 A.A. 2015/2016
|
|
|
- Adelmo Paoli
- 7 anni fa
- Visualizzazioni
Transcript
1 Corso di Laurea in Economia e Finanza Statistica 1 A.A. 2015/2016 (8 CFU, corrispondenti a 48 ore di lezione frontale e 24 ore di esercitazione) Prof. Luigi Augugliaro 1 / 52
2 Adattamento di una distribuzione teorica ad una distribuzione empirica La valutazione della bontà di adattamento di una distribuzione teorica ad una distribuzione empirica avviene attraverso le seguenti fasi: i. in funzione della natura della variabile statistica in esame si sceglie il modello probabilistico più ideneo; ii. valutazione della bontà di adattamento mediante l indice X 2 = k (n i n i ) 2 i=1 ni a) stima dei parametri incogniti del modello probabilistico scelto; b) calcolo delle frequenze teoriche ni ; c) valutazione della bontà di adattamento mediante il confronto dell indice X 2 con il valore critico k 1, dove k è il numero di modalità/classi della distribuzione di frequenza in esame. 2 / 52
3 Momenti empirici I momenti empirici, i quali costituiscono la versione empirica dei momenti teorici, svolgono un ruolo centrale all interno del metodo dei momenti per la stima dei parametri di una funzione di distribuzione di probabilità o di una funzione di densità. I momenti empirici consentono inoltre di definire la versione empirica dell indice teorico di asimmetria β 1 e dell indice di curtosi β 2. 3 / 52
4 Sia (x 1, x 2,..., x n) un campione di numerosità n. Definiamo momento empirico di ordine r e origine m la quantità n i=1 ˆµ m,r = (x i m) r. n La precedente definizione mostra che il momento empirico di origine 0 e ordine 1 è la media artimetica n i=1 ˆµ 0,1 = x i = x n I momementi empirici di ordine r e origine la media aritmetica x vengono definiti momenti empirici centrati di ordine r, formalmente n i=1 ˆµ r = (x i x) r. n L espressione precedente mostra che il momento empirico centrato di ordine 2 è l indice varianza n i=1 ˆµ 2 = (x i x) 2. n 4 / 52
5 Quando si dispone di una distribuzione di frequenza, il momento empirico di ordine r e origine m viene definito nel seguente modo n i=1 ˆµ m,r = (x i m) r n i. n dove n i è la frequenza assoluta associata ad x i. Se si dispone di una distribuzione di frequenza in classi, la formula precedente si modifica utilizzando i valori centrale di ogni classe, ovvero n i=1 ˆµ m,r = (x i c m) r n i n 5 / 52
6 Il problema della bontà di adattamento: esempio 1 Un gruppo di 80 studenti è stato sottoposto ad un test attitudinale per l ammissione ad un corso di studi. Viene riportata la distribuzione di frequenze della variabile Numero di errori commessi: X n i Tot. 80 Individuare il modello teorico più opportuno da adattare alla distribuzione osservata e verificarne la bontà di adattamento. 6 / 52
7 La variabile statistica osservata numero di errori commessi è una variabile quantitativa discreta, quindi la nostra scelta si limita ai modelli studiati per le variabili aleatorie discrete, ovvero la variabile aleatoria binomiale e la variabile aleatoria di Poisson. Osservazioni: i. la variabile in esame può assumere solamente un numero finito di valori, ovvero il numero totale n di domande riportate nel questionario. Notiamo che n non è noto; ii. la distribuzione di frequenza sembra mostrare che la variabile considerata non descrive un evento raro. Sulla base delle osservazioni precedenti si deduce che il modello probabilistico più idoneo è il modello binomiale. 7 / 52
8 Come visto in precedenza, la funzione di distribuzione di probabilità di una variabile aleatoria binomiale ( ) n p(x) = π x (1 π) n x x è indicizzata da due parametri: n = numero di prove; π = probabilità dell evento successo. Poiché n e π non sono noti è necessario utilizzare un metodo opportuno per la stima dei due parametri. Il metodo che utilizzeremo prende il nome di metodo dei momenti. 8 / 52
9 Il metodo dei momenti è uno dei più vecchi metodi di stima puntuale proposti in letteratura e venne introdotto da Karl Pearson alla fine del Il metodo consiste nell uguagliare i momenti teorici con i momenti empirici. risoluzione del sistema così ottenuto fornisce le stime dei parametri incogniti. La Consideriamo quindi il sistema { ˆnˆπ = x ˆnˆπ(1 ˆπ) = σ 2 dove x e σ 2 sono rispettivamente la media aritmetica e la varianza calcolata sui dati. 9 / 52
10 Sostituendo nella seconda equazione ˆnˆπ con x si ricava x(1 ˆπ) = σ 2 quindi 1 ˆπ = σ2 x Noto ˆπ, sostituendo nella prima equazione si ricava quindi ˆπ = 1 σ2 x. ˆn = xˆπ. Poiché ˆn non è un numero intero si utilizza come stima del parametro n sempre l intero successivo. 10 / 52
11 L esempio 1 che segue consente di chiarire perché ˆn deve sempre essere arrotondato all intero successivo. Sia X una variabile aleatoria binomiale di parametri n e π. Dalla tabella X n i x i n i xi 2 xi 2 n i Tot si ricava che x = = 1.85 σ2 = = Applicando le formule precedenti si ricava ˆπ = 1 σ2 x = 0.82 ˆn = xˆπ = 2.26 Poiché la variabile X assume massimo valore 3, si deduce che ˆn non può essere arrotondato al valore 2 dato che ˆn è una stima del numero totale di prove compiute. 1 l autore è in debito con il Prof. Mineo e il Prof. Chiodi per l esempio suggerito. 11 / 52
12 Con riferimento alla variabile numero di errori commessi, dalla seguente tabella x i n i x i n i xi 2 xi 2 n i Tot si ricava che x = 4.84 e σ 2 = Utilizzando le formule precedenti si ricava ˆπ = 1 σ2 x Utilizzando l intero successivo si ricava che ˆn = 19. = 0.26 ˆn = xˆπ = / 52
13 Sulla base dei precedenti risultati, le probabilità teoriche sono fornite dalla seguente funzione di distribuzione di probabilità ( 19 ) ˆp(x i ) = 0.26 x i (1 0.26) (19 x i ) x i Le frequenze teoriche, denotate con ni, sono ottenute moltiplicando le probabilità teoriche, ˆp(x i ), per il totale delle osservazioni, ovvero 80. x n i ˆp(x i ) ni (n i ni ) (n i ni )2 (n i ni )2 /ni Tot, Poiché X 2 = è inferiore a k 1 = 11 1 = 10 si deduce che il modello binomiale descrive bene i dati a nostra disposizione. 13 / 52
14 Il problema della bontà di adattamento: esempio 2 Un gruppo di 76 studenti è stato sottoposto ad un test attitudinale per l ammissione ad un corso di studi. Viene riportata la distribuzione di frequenze della variabile Numero di errori commessi su un totale di 10 domande: x n Tot. 76 Individuare il modello teorico più opportuno da adattare alla distribuzione osservata e verificarne l adattamento. 14 / 52
15 La variabile statistica osservata numero di errori commessi su un totale di 10 domande è una variabile quantitativa discreta, quindi la nostra scelta si limita ai modelli studiati per le variabili aleatorie discrete, ovvero la variabile aleatoria binomiale e la variabile aleatoria di Poisson. Osservazioni: i. la variabile in esame può assumere solamente un numero finito di valori. Notiamo che n è noto; ii. la distribuzione di frequenza mostra che la variabile considerata non sembra descrivere un evento raro. Sulla base delle osservazioni precedenti si deduce che il modello probabilistico più idoneo è il modello binomiale. 15 / 52
16 Come visto in precedenza, la funzione di distribuzione di probabilità di una variabile aleatoria binomiale ( ) n p(x) = π x (1 π) n x x è indicizzata da due parametri: n = numero di prove; π = probabilità dell evento successo. Dalla descrizione dell esperimento si deduce che il parametro n è noto ed uguale a 10. Il parametro π è incognito e verrà stimato con il metodo dei momenti. Uguagliando il valore atteso della variabile aleatoria binomiale alla media aritmetica si ricava che ˆπ = x n. E(X ) = n ˆπ = x 16 / 52
17 La seguente tabella mostra che x = x n x n Tot = 4.89 da cui si ricava che ˆπ = = / 52
18 Sulla base dei precedenti risultati, le probabilità teoriche sono fornite dalla seguente funzione di distribuzione di probabilità ( 10 ) ˆp(x i ) = x i ( ) (10 x i ) x i Le frequenze teoriche, denotate con ni, sono ottenute moltiplicando le probabilità teoriche, ˆp(x i ), per il totale delle osservazioni, ovvero 76. x n i ˆp(x i ) ni (n i ni ) (n i ni )2 (n i ni )2 /ni Tot / 52
19 Sulla base dei risultati precedenti si ricava che X 2 = Poiché X 2 è più grande di k 1 = 11 1 = 10, i risultati sembrano suggerire che non vi sia un buon adattamento. L analisi della tabella utilizzata per il calcolo dell indice X 2 x n i ˆp i ni (n i ni ) (n i ni )2 (n i ni )2 /ni mostra che il cattivo adattamento è dovuto solamente ai valori (n i ni )2 /ni delle prime due righe e delle ultime due righe. 19 / 52
20 Il problema della bontà di adattamento: esempio 3 Negli ultimi anni si è assistito ad un evoluzione delle modalità di accesso wireless ad Internet sia in termini di affidabilità che di prestazioni. All interno di questo nuovo settore tecnologico le femtocelle, piccole stazioni radio domestiche in grado di coprire un ufficio o un appartamento e gestite in remoto dagli operatori di telefonia mobile, consentono di eliminare i problemi di trasmissione che si verificano all interno di luoghi di ridotte dimensioni. Per valutare le prestazioni di una nuova femtocella, un gruppo di ingegneri ha rilevato per 100 giorni il numero di interferenze giornaliere, denotato con X, ottenendo la seguente distribuzione di frequenza X n i Sulla base della descrizione del fenomeno oggetto di studio, il candidato scelga il più adeguato modello probabilistico e ne valuti l adattamento mediante l indice più adeguato. 20 / 52
21 La variabile statistica osservata numero di interferenze giornaliere è una variabile quantitativa discreta, quindi la nostra scelta si limita ai modelli studiati per le variabili aleatorie discrete, ovvero la variabile aleatoria binomiale e la variabile aleatoria di Poisson. Osservazioni: i. la variabile in esame può assumere, almeno da un punto di vista teorico, un numero infinito di valori. ii. la variabile in esame sembra descrivere un evento raro. Sulla base delle osservazioni precedenti si deduce che il modello probabilistico più idoneo è il modello di Poisson. 21 / 52
22 La funzione di distribuzione di probabilità della variabile aleatoria di Poisson dipende da un solo parametro incognito p(x) = λx e λ x! λ = valore atteso della variabile aleatoria X. L applicazione del metodo dei momenti mostra che il parametro λ può essere stimato tramite la media aritmetica, ovvero ˆλ = x = k i=1 x i n i n 22 / 52
23 La tabella mostra che ˆλ = x i n i x i n i Tot k i=1 x i n i n = = / 52
24 Sulla base della stima del parametro λ, le probabilità teoriche sono fornite dalla seguente funzione p(x i ) = 3.06x i e 3.06 x i! Le frequenze teoriche, denotate con n i, sono ottenute moltiplicando le probabilità teoriche, p(x i ), per il totale delle osservazioni, ovvero 100. x i n i p(x i ) ni n i ni (n i ni )2 (n i ni )2 /ni Tot Poiché l indice X 2 è inferiore a k 1 = 9 1 = 8 si può ritenere che il modello teorico di Poisson descrive bene i dati a nostra disposizione. 24 / 52
25 Di seguito è riportata la distribuzione di frequenza del numero di prodotti realizzati giornalmente da una data azienda e definiti difettosi. x n Sulla base della descrizione del fenomeno oggetto di studio, il candidato scelga il più adeguato modello probabilistico e ne valuti l adattamento mediante l indice più adeguato. 25 / 52
26 La variabile statistica osservata numero di prodotti difettosi è una variabile quantitativa discreta, quindi la nostra scelta si limita ai modelli studiati per le variabili aleatorie discrete, ovvero la variabile aleatoria binomiale e la variabile aleatoria di Poisson. Osservazioni: i. la variabile in esame può assumere, almeno da un punto di vista teorico, un numero infinito di valori. ii. la variabile in esame sembra descrivere un evento raro. Sulla base delle osservazioni precedenti si deduce che il modello probabilistico più idoneo è il modello di Poisson. 26 / 52
27 La funzione di distribuzione di probabilità della variabile aleatoria di Poisson dipende da un solo parametro incognito p(x) = λx e λ x! λ = valore atteso della variabile aleatoria X. L applicazione del metodo dei momenti mostra che il parametro λ può essere stimato tramite la media aritmetica, ovvero ˆλ = x = k i=1 x i n i n 27 / 52
28 La tabella mostra che ˆλ = x i n i x i n i Tot k i=1 x i n i n = = / 52
29 Sulla base della stima del parametro λ, le probabilità teoriche sono fornite dalla seguente funzione p(x i ) = 2.96x i e 2.96 x i! Le frequenze teoriche, denotate con n i, sono ottenute moltiplicando le probabilità teoriche, p(x i ), per il totale delle osservazioni, ovvero 100. x i n i p(x i ) ni n i ni (n i ni )2 (n i ni )2 /ni Tot Poiché l indice X 2 è inferiore a k 1 = 9 1 = 8 si può ritenere che il modello teorico di Poisson non descrive bene i dati a nostra disposizione. 29 / 52
30 Il problema della bontà di adattamento: esempio 4 Di seguito è riportata la distribuzione di frequenza in classi ottenuta mediante un campione 100 misure sperimentali rilevate in un punto di un circuito elettrico tramite voltmetro digitale. classi n i Individuare il modello teorico più opportuno da adattare alla distribuzione osservata e verificarne l adattamento. 30 / 52
31 Poiché la variabile statistica osservata è una variabile quantitativa continua, l unico modello teorico di cui possiamo valutare la bontà di adattamento è il modello di Gauss. La funzione di densità dipende dai due parametri incogniti f X (x; µ, σ) = 1 σ (x µ) 2 2π e 2σ 2, µ = valore atteso della variabile aleatoria X σ = deviazione standard della variabile aleatoria X. I parametri µ e σ possono essere stimati attraverso la media aritmetica e la deviazione standard campionaria. 31 / 52
32 Dalla tabella classi n i x c i x c i n i (x c i )2 (x c i )2 n i Tot si ricava k i=1 ˆµ = x = x i cn i = n k i=1 ˆσ = (x i c)2 n i x n 2 = / 52
33 Il calcolo dell indice X 2 = k (n i n i ) 2 i=1 n si fonda sull utilizzo delle frequenze teoriche i ni definite come ni = n P(x i < X < x i+1 ) Utilizzando la relazione P(x i < X < x i+1 ) = P(z i < Z < z i+1 ) = P(Z < z i+1 ) P(Z < z i ) = F (z i+1 ) F (z i ) si ricava che per il calcolo delle frequenze teoriche è necessario calcolare i valori standardizzati z i = x i ˆµ = x i ˆσ ed utilizzare il prontuario delle probabilità integrali della distribuzione normale standardizzata. 33 / 52
34 Dallo studio della seguente tabella si ricava che x i+1 z i+1 F i+1 0 F i+1 F i n i n i (n i n i ) (n i n i ) 2 (n i n i ) 2 /n i Tot X 2 = Poiché l indice X 2 è inferiore al valore k 1 = 6 1 = 5, si deduce che la distribuzione di Gauss descrive bene la distribuzione osservata. 34 / 52
35 I risultati ottenuti in precedenza trovano conferma nella seguente rappresentazione grafica f i Volt 35 / 52
36 Il problema della bontà di adattamento: esempio 5 Per valutare il livello di inquinamento di un dato fiume del territorio italiano, un gruppo di studiosi ha misurato il livello di nitrogeno presente in un punto fissato del fiume. Di seguito viene riportata la distribuzione di frequenza in classi ottenuta attraverso un campione di 112 rilevazioni sperimentali. Classi n i Tot. 112 Individuare il modello teorico più opportuno da adattare alla distribuzione osservata e verificarne l adattamento. 36 / 52
37 Poiché la variabile statistica osservata è una variabile quantitativa continua, l unico modello teorico di cui possiamo valutare la bontà di adattamento è il modello di Gauss f i N 2O Il grafico sembra suggerire che il modello di Gauss non descrive bene i dati a nostra disposizione. Una conferma a tale ipotesi è ottenuta mediante l indice X / 52
38 La funzione di densità dipende dai due parametri incogniti f X (x; µ, σ) = 1 σ (x µ) 2 2π e 2σ 2, µ = valore atteso della variabile aleatoria X σ = deviazione standard della variabile aleatoria X. I parametri µ e σ possono essere stimati attraverso la media aritmetica e la deviazione standard. 38 / 52
39 Dalla tabella si ricava classi n i x c i x c i n i (x c i )2 (x c i )2 n i Tot k i=1 ˆµ = x = x i cn i = n k i=1 ˆσ = (x i c)2 n i x n 2 = / 52
40 Il calcolo dell indice X 2 = k (n i n i ) 2 i=1 n si fonda sull utilizzo delle frequenze teoriche i ni definite come ni = n P(x i < X < x i+1 ) Utilizzando la relazione P(x i < X < x i+1 ) = P(z i < Z < z i+1 ) = P(Z < z i+1 ) P(Z < z i ) = F (z i+1 ) F (z i ) si ricava che per il calcolo delle frequenze teoriche è necessario calcolare i valori standardizzati z i = x i ˆµ = x i ˆσ ed utilizzare il prontuario delle probabilità integrali della distribuzione normale standardizzata. 40 / 52
41 Poiché ni = n[f (z i+1 ) F (z i )], si ricava che il calcolo dell indice X 2 si basa sulla seguente tabella x i+1 z i+1 F i+1 F i+1 F i n i n i (n i n i ) (n i n i )2 (n i n i ) Tot da cui si ricava che X 2 = Poiché l indice X 2 è superiore a k 1 = 8 1 = 7 si deduce che la distribuzione di Gauss non descrive bene la distribuzione osservata. n i 41 / 52
42 I risultati ottenuti in precedenza trovano conferma nella seguente rappresentazione grafica f i N 2O dalla quale si evence che il modello di Gauss non descrive bene i dati a nostra disposizione. 42 / 52
43 Esercizi I test ADAC sono tra le più affidabili e attendibili prove sugli pneumatici. L ultimo test condotto ha avuto come obiettivo il confronto di 3 differenti prodotti, indicati con P 1, P 2 e P 3, con un prodotto di riferimento, indicato con P 0. Il test è stato ripetuto 100 volte per ogni prodotto e nella seguente tabella sono riportati i risultati ottenuti. Il test fornisce un valore reale compreso tra 0 e 100 e i valori crescenti indicano un miglioramento nella performance dei pneumatici. Tabella: Risultati del test ADAC Test Tot. P P P P Sulla base della descrizione del fenomeno in esame scegliere il più opportuno modello probabilistico e verificarne l adattamento alle distribuzioni dei prodotti P 0, P 1, P 2 e P / 52
44 Un azienda di credito ha ripartito un campione di 140 dei propri clienti in due categorie definite solvente e insolvente. La tabella seguente riporta la distribuzione dei finanziamenti concessi dall azienda di credito in funzione delle due categorie considerate Finanziamenti concessi (dati per migliaia di euro) Cliente solvente insolvente Sulla base dei dati riportati in tabella, si scelga il modello probabilistico più adeguato per descrivere la distribuzione di frequenze dei clienti di tipo solvente e se ne valuti la bontà di adattamento mendiante adeguato indice statistico. 44 / 52
45 Per valutare le prestazioni di un nuovo processore per personal computer, il direttore del reparto ricerca e sviluppo ha ripetuto, sullo stesso processore, cento volte lo stesso benchmark prestazionale. Il benchmark utilizzato fornisce un valore continuo e di seguito è riportata la distribuzione di frequenze in classi dei risultati ottenuti. Tabella: Distribuzione di frequenze in classi dei risultati del benchmark considerato Benchmark n i Tot. 100 Il candidato valuti la bontà di adattamento al modello probabilistico ritenuto più adeguato per i dati riportati in tabella. Commentare adeguatamente i risultati ottenuti. 45 / 52
46 Di seguito è riportata la distribuzione di frequenze in classi delle sovvenzioni cambiarie concesse da una data banca ai propri clienti. Tabella: Distribuzione di frequenze in classi delle sovvenzioni cambiarie (dati in migliaia di euro) Sovvenzioni n i < Tot. 76 Il candidato valuti la bontà di adattamento al modello probabilistico ritenuto più adeguato per i dati riportati in tabella. 46 / 52
47 Per valutare la qualità del proprio processo produttivo, l addetto al controllo della qualità di un azienda produttrice di lampadine estrae con reimmisione, dal totale della produzione mensile, trenta campioni di numerosità dieci. Su ogni campione viene rilevato il numero di lampadine difettose. La tabella riporta i dati rilevati. Tabella: Numero di lampadine difettose rilevato su trenta campioni i. Il candidato costruisca e rappresenti graficamente la distribuzione di frequenze della variabile numero di lampadine difettose. ii. Il candidato adatti alla variabile numero di lampadine difettose il modello teorico che ritiene più opportuno e ne valuti l adattamento attraverso un adeguato indice. 47 / 52
48 Si sono rilevati i guasti meccanici riportati da 40 autovetture FIAT e da 60 autovetture OPEL, possedute da un azienda di spedizioni, nei primi km di percorrenza. I dati sono sintetizzati nella seguente tabella che riporta le frequenze assolute: N. Guasti Fiat Opel Si adatti alla variabile osservata, distintamente per i due tipi di autovettura, la variabile casuale che si ritiene più opportuna, e si calcoli, su ciascuna delle due distribuzioni, un indice di bontà di adattamento. Su quale delle due distribuzioni l adattamento si può ritenere migliore? 48 / 52
49 In un impresa di soccorso stradale sono state registrate le richieste giornaliere di intervento, su un arco di 100 giorni, ottenendo la seguente distribuzione di frequenza: interventi n Il candidato adatti alla variabile numero di interventi giornalieri il modello teorico che ritiene più opportuno e ne valuti l adattamento attraverso un adeguato indice. 49 / 52
50 In un campione casuale di 130 circuiti elettronici è stato osservato il numero dei difetti presenti. La distribuzione di frequenza del numero dei difetti è riportata nella seguente tabella: n. di difetti frequenza osservata Il candidato adatti alla variabile numero di difetti il modello teorico che ritiene più opportuno e ne valuti l adattamento attraverso un adeguato indice. 50 / 52
51 La seguente distribuzione descrive il numero di particelle rilasciate durante il decadimento radioattivo del Polonio, in intervalli di 72 secondi: x n Il candidato adatti alla variabile considerata il modello teorico che ritiene più opportuno e ne valuti l adattamento attraverso un adeguato indice. 51 / 52
52 La seguente tabella mostra la distribuzione di frequenze del numero dei parti, rilevato in una clinica, nell arco di un periodo di 100 giorni: n. parti frequenze Il candidato adatti alla variabile considerata il modello teorico che ritiene più opportuno e ne valuti l adattamento attraverso un adeguato indice. 52 / 52
Probabilità classica. Distribuzioni e leggi di probabilità. Probabilità frequentista. Probabilità soggettiva
 Probabilità classica Distribuzioni e leggi di probabilità La probabilità di un evento casuale è il rapporto tra il numero dei casi favorevoli ed il numero dei casi possibili, purchè siano tutti equiprobabili.
Probabilità classica Distribuzioni e leggi di probabilità La probabilità di un evento casuale è il rapporto tra il numero dei casi favorevoli ed il numero dei casi possibili, purchè siano tutti equiprobabili.
Variabili casuali. - di Massimo Cristallo -
 Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 16 e 27 maggio 2013 - di Massimo Cristallo - Variabili casuali
Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 16 e 27 maggio 2013 - di Massimo Cristallo - Variabili casuali
Corso Integrato di Statistica Informatica e Analisi dei Dati Sperimentali. Esercitazione E
 Corso Integrato di Statistica Informatica e Analisi dei Dati Sperimentali A.A 2009-2010 Esercitazione E Scopo dell esercitazione Applicazioni del teorema del limite centrale. Rappresentazione delle incertezze
Corso Integrato di Statistica Informatica e Analisi dei Dati Sperimentali A.A 2009-2010 Esercitazione E Scopo dell esercitazione Applicazioni del teorema del limite centrale. Rappresentazione delle incertezze
Statistica 1 A.A. 2015/2016
 Corso di Laurea in Economia e Finanza Statistica 1 A.A. 2015/2016 (8 CFU, corrispondenti a 48 ore di lezione frontale e 24 ore di esercitazione) Prof. Luigi Augugliaro 1 / 19 Analisi dell associazione
Corso di Laurea in Economia e Finanza Statistica 1 A.A. 2015/2016 (8 CFU, corrispondenti a 48 ore di lezione frontale e 24 ore di esercitazione) Prof. Luigi Augugliaro 1 / 19 Analisi dell associazione
PROBABILITA. Distribuzione di probabilità
 DISTRIBUZIONI di PROBABILITA Distribuzione di probabilità Si definisce distribuzione di probabilità il valore delle probabilità associate a tutti gli eventi possibili connessi ad un certo numero di prove
DISTRIBUZIONI di PROBABILITA Distribuzione di probabilità Si definisce distribuzione di probabilità il valore delle probabilità associate a tutti gli eventi possibili connessi ad un certo numero di prove
ESAME. 9 Gennaio 2017 COMPITO A
 ESAME 9 Gennaio 2017 COMPITO A Cognome Nome Numero di matricola 1) Approssimare tutti i calcoli alla quarta cifra decimale. 2) Ai fini della valutazione si terrà conto solo ed esclusivamente di quanto
ESAME 9 Gennaio 2017 COMPITO A Cognome Nome Numero di matricola 1) Approssimare tutti i calcoli alla quarta cifra decimale. 2) Ai fini della valutazione si terrà conto solo ed esclusivamente di quanto
Statistica 1 A.A. 2015/2016
 Corso di Laurea in Economia e Finanza Statistica 1 A.A. 2015/2016 (8 CFU, corrispondenti a 48 ore di lezione frontale e 24 ore di esercitazione) Prof. Luigi Augugliaro 1 / 35 Il modello di regressione
Corso di Laurea in Economia e Finanza Statistica 1 A.A. 2015/2016 (8 CFU, corrispondenti a 48 ore di lezione frontale e 24 ore di esercitazione) Prof. Luigi Augugliaro 1 / 35 Il modello di regressione
Esercitazioni di Statistica
 Esercitazioni di Statistica Stima Puntuale Prof. Livia De Giovanni statistica@dis.uniroma.it Esercizio In ciascuno dei casi seguenti determinare quale tra i due stimatori S e T per il parametro θ è distorto
Esercitazioni di Statistica Stima Puntuale Prof. Livia De Giovanni statistica@dis.uniroma.it Esercizio In ciascuno dei casi seguenti determinare quale tra i due stimatori S e T per il parametro θ è distorto
ESAME. 9 Gennaio 2017 COMPITO B
 ESAME 9 Gennaio 2017 COMPITO B Cognome Nome Numero di matricola 1) Approssimare tutti i calcoli alla quarta cifra decimale. 2) Ai fini della valutazione si terrà conto solo ed esclusivamente di quanto
ESAME 9 Gennaio 2017 COMPITO B Cognome Nome Numero di matricola 1) Approssimare tutti i calcoli alla quarta cifra decimale. 2) Ai fini della valutazione si terrà conto solo ed esclusivamente di quanto
Capitolo 5 Variabili aleatorie discrete notevoli Insegnamento: Statistica Applicata Corso di Laurea in "Scienze e Tecnologie Alimentari"
 Levine, Krehbiel, Berenson Statistica Capitolo 5 Variabili aleatorie discrete notevoli Insegnamento: Statistica Applicata Corso di Laurea in "Scienze e Tecnologie Alimentari" Unità Integrata Organizzativa
Levine, Krehbiel, Berenson Statistica Capitolo 5 Variabili aleatorie discrete notevoli Insegnamento: Statistica Applicata Corso di Laurea in "Scienze e Tecnologie Alimentari" Unità Integrata Organizzativa
Ulteriori Conoscenze di Informatica e Statistica
 Ulteriori Conoscenze di Informatica e Statistica Carlo Meneghini Dip. di fisica via della Vasca Navale 84, st. 83 (I piano) tel.: 06 55 17 72 17 meneghini@fis.uniroma3.it Indici di forma Descrivono le
Ulteriori Conoscenze di Informatica e Statistica Carlo Meneghini Dip. di fisica via della Vasca Navale 84, st. 83 (I piano) tel.: 06 55 17 72 17 meneghini@fis.uniroma3.it Indici di forma Descrivono le
Esame di Statistica (10 o 12 CFU) CLEF 11 febbraio 2016
 Esame di Statistica 0 o CFU) CLEF febbraio 06 Esercizio Si considerino i seguenti dati, relativi a 00 clienti di una banca a cui è stato concesso un prestito, classificati per età e per esito dell operazione
Esame di Statistica 0 o CFU) CLEF febbraio 06 Esercizio Si considerino i seguenti dati, relativi a 00 clienti di una banca a cui è stato concesso un prestito, classificati per età e per esito dell operazione
Distribuzioni e inferenza statistica
 Distribuzioni e inferenza statistica Distribuzioni di probabilità L analisi statistica spesso studia i fenomeni collettivi confrontandoli con modelli teorici di riferimento. Tra di essi, vedremo: la distribuzione
Distribuzioni e inferenza statistica Distribuzioni di probabilità L analisi statistica spesso studia i fenomeni collettivi confrontandoli con modelli teorici di riferimento. Tra di essi, vedremo: la distribuzione
Statistica 2. Esercitazioni. Dott. Luigi Augugliaro 1. Università di Palermo
 Statistica 2 Esercitazioni Dott. L 1 1 Dipartimento di Scienze Statistiche e Matematiche S. Vianelli, Università di Palermo ricevimento: lunedì ore 15-17 mercoledì ore 15-17 e-mail: luigi.augugliaro@unipa.it
Statistica 2 Esercitazioni Dott. L 1 1 Dipartimento di Scienze Statistiche e Matematiche S. Vianelli, Università di Palermo ricevimento: lunedì ore 15-17 mercoledì ore 15-17 e-mail: luigi.augugliaro@unipa.it
Capitolo 6 La distribuzione normale
 Levine, Krehbiel, Berenson Statistica Casa editrice: Pearson Capitolo 6 La distribuzione normale Insegnamento: Statistica Corso di Laurea Triennale in Economia Dipartimento di Economia e Management, Università
Levine, Krehbiel, Berenson Statistica Casa editrice: Pearson Capitolo 6 La distribuzione normale Insegnamento: Statistica Corso di Laurea Triennale in Economia Dipartimento di Economia e Management, Università
Statistica 1 A.A. 2015/2016
 Corso di Laurea in Economia e Finanza Statistica 1 A.A. 2015/2016 (8 CFU, corrispondenti a 48 ore di lezione frontale e 24 ore di esercitazione) Prof. Luigi Augugliaro 1 / 88 La variabile aleatoria Nello
Corso di Laurea in Economia e Finanza Statistica 1 A.A. 2015/2016 (8 CFU, corrispondenti a 48 ore di lezione frontale e 24 ore di esercitazione) Prof. Luigi Augugliaro 1 / 88 La variabile aleatoria Nello
Statistica 1 A.A. 2015/2016
 Corso di Laurea in Economia e Finanza Statistica 1 A.A. 2015/2016 (8 CFU, corrispondenti a 48 ore di lezione frontale e 24 ore di esercitazione) Prof. Luigi Augugliaro 1 / 88 La variabile aleatoria Nello
Corso di Laurea in Economia e Finanza Statistica 1 A.A. 2015/2016 (8 CFU, corrispondenti a 48 ore di lezione frontale e 24 ore di esercitazione) Prof. Luigi Augugliaro 1 / 88 La variabile aleatoria Nello
STATISTICA AZIENDALE Modulo Controllo di Qualità
 STATISTICA AZIENDALE Modulo Controllo di Qualità A.A. 009/10 - Sottoperiodo PROA DEL 14 MAGGIO 010 Cognome:.. Nome: Matricola:.. AERTENZE: Negli esercizi in cui sono richiesti calcoli riportare tutte la
STATISTICA AZIENDALE Modulo Controllo di Qualità A.A. 009/10 - Sottoperiodo PROA DEL 14 MAGGIO 010 Cognome:.. Nome: Matricola:.. AERTENZE: Negli esercizi in cui sono richiesti calcoli riportare tutte la
TECNICHE DI SIMULAZIONE
 TECNICHE DI SIMULAZIONE Analisi e scelta dei dati di input Francesca Mazzia Dipartimento di Matematica Università di Bari a.a. 2004/2005 TECNICHE DI SIMULAZIONE p. 1 Dati di input Per l esecuzione di una
TECNICHE DI SIMULAZIONE Analisi e scelta dei dati di input Francesca Mazzia Dipartimento di Matematica Università di Bari a.a. 2004/2005 TECNICHE DI SIMULAZIONE p. 1 Dati di input Per l esecuzione di una
Ulteriori Conoscenze di Informatica e Statistica
 ndici di forma Ulteriori Conoscenze di nformatica e Statistica Descrivono le asimmetrie della distribuzione Carlo Meneghini Dip. di fisica via della Vasca Navale 84, st. 83 ( piano) tel.: 06 55 17 72 17
ndici di forma Ulteriori Conoscenze di nformatica e Statistica Descrivono le asimmetrie della distribuzione Carlo Meneghini Dip. di fisica via della Vasca Navale 84, st. 83 ( piano) tel.: 06 55 17 72 17
Capitolo 6. La distribuzione normale
 Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 6 La distribuzione normale Insegnamento: Statistica Corso di Laurea Triennale in Ingegneria Gestionale Facoltà di Ingegneria, Università
Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 6 La distribuzione normale Insegnamento: Statistica Corso di Laurea Triennale in Ingegneria Gestionale Facoltà di Ingegneria, Università
tabelle grafici misure di
 Statistica Descrittiva descrivere e riassumere un insieme di dati in maniera ordinata tabelle grafici misure di posizione dispersione associazione Misure di posizione Forniscono indicazioni sull ordine
Statistica Descrittiva descrivere e riassumere un insieme di dati in maniera ordinata tabelle grafici misure di posizione dispersione associazione Misure di posizione Forniscono indicazioni sull ordine
UNIVERSITÀ DEGLI STUDI DI NAPOLI FEDERICO II DIPARTIMENTO DI INGEGNERIA AEROSPAZIALE D.I.A.S. STATISTICA PER L INNOVAZIONE. a.a.
 UNIVERSITÀ DEGLI STUDI DI NAPOLI FEDERICO II DIPARTIMENTO DI INGEGNERIA AEROSPAZIALE D.I.A.S. STATISTICA PER L INNOVAZIONE a.a. 2007/2008 1,00 0,90 0,80 0,70 0,60 0,50 0,40 0,30 0,20 0,10 0,00 CDF empirica
UNIVERSITÀ DEGLI STUDI DI NAPOLI FEDERICO II DIPARTIMENTO DI INGEGNERIA AEROSPAZIALE D.I.A.S. STATISTICA PER L INNOVAZIONE a.a. 2007/2008 1,00 0,90 0,80 0,70 0,60 0,50 0,40 0,30 0,20 0,10 0,00 CDF empirica
Analisi e scelta dei dati di input
 Analisi e scelta dei dati di input Corso di Tecniche di Simulazione, a.a. 2005/2006 Francesca Mazzia Dipartimento di Matematica Università di Bari 24 Aprile 2006 Francesca Mazzia (Univ. Bari) Analisi e
Analisi e scelta dei dati di input Corso di Tecniche di Simulazione, a.a. 2005/2006 Francesca Mazzia Dipartimento di Matematica Università di Bari 24 Aprile 2006 Francesca Mazzia (Univ. Bari) Analisi e
C.I. di Metodologia clinica
 C.I. di Metodologia clinica Modulo 5. I metodi per la sintesi e la comunicazione delle informazioni sulla salute Quali errori influenzano le stime? L errore casuale I metodi per la produzione delle informazioni
C.I. di Metodologia clinica Modulo 5. I metodi per la sintesi e la comunicazione delle informazioni sulla salute Quali errori influenzano le stime? L errore casuale I metodi per la produzione delle informazioni
Statistica Descrittiva Soluzioni 6. Indici di variabilità, asimmetria e curtosi
 ISTITUZIONI DI STATISTICA A A 2007/2008 Marco Minozzo e Annamaria Guolo Laurea in Economia del Commercio Internazionale Laurea in Economia e Amministrazione delle Imprese Università degli Studi di Verona
ISTITUZIONI DI STATISTICA A A 2007/2008 Marco Minozzo e Annamaria Guolo Laurea in Economia del Commercio Internazionale Laurea in Economia e Amministrazione delle Imprese Università degli Studi di Verona
Intervalli di confidenza
 Probabilità e Statistica Esercitazioni a.a. 2009/2010 C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica Intervalli di confidenza Ines Campa Probabilità e Statistica - Esercitazioni
Probabilità e Statistica Esercitazioni a.a. 2009/2010 C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica Intervalli di confidenza Ines Campa Probabilità e Statistica - Esercitazioni
Esercizio 1 Nella seguente tabella sono riportate le lunghezze in millimetri di 40 foglie di platano:
 4. STATISTICA DESCRITTIVA ESERCIZI Esercizio 1 Nella seguente tabella sono riportate le lunghezze in millimetri di 40 foglie di platano: 138 164 150 132 144 125 149 157 146 158 140 147 136 148 152 144
4. STATISTICA DESCRITTIVA ESERCIZI Esercizio 1 Nella seguente tabella sono riportate le lunghezze in millimetri di 40 foglie di platano: 138 164 150 132 144 125 149 157 146 158 140 147 136 148 152 144
Università degli studi della Tuscia. Principi di Statistica dr. Luca Secondi A.A. 2014/2015. Esercitazione di riepilogo Variabili casuali
 Università degli studi della Tuscia Principi di Statistica dr. Luca Secondi A.A. 014/015 Esercitazione di riepilogo Variabili casuali ESERCIZIO 1 Il peso delle compresse di un determinato medicinale si
Università degli studi della Tuscia Principi di Statistica dr. Luca Secondi A.A. 014/015 Esercitazione di riepilogo Variabili casuali ESERCIZIO 1 Il peso delle compresse di un determinato medicinale si
DISTRIBUZIONE NORMALE (1)
 DISTRIBUZIONE NORMALE (1) Nella popolazione generale molte variabili presentano una distribuzione a forma di campana, bene caratterizzata da un punto di vista matematico, chiamata distribuzione normale
DISTRIBUZIONE NORMALE (1) Nella popolazione generale molte variabili presentano una distribuzione a forma di campana, bene caratterizzata da un punto di vista matematico, chiamata distribuzione normale
Esperimentazioni di Fisica 1. Prova in itinere del 12 giugno 2018
 Esperimentazioni di Fisica 1 Prova in itinere del 1 giugno 018 Esp-1 Prova in Itinere n. - - Page of 6 1/06/018 1. (1 Punti) Quesito L incertezza da associare alle misurazioni eseguite con un certo strumento
Esperimentazioni di Fisica 1 Prova in itinere del 1 giugno 018 Esp-1 Prova in Itinere n. - - Page of 6 1/06/018 1. (1 Punti) Quesito L incertezza da associare alle misurazioni eseguite con un certo strumento
Dipartimento di Sociologia e Ricerca Sociale. Corso di Laurea in Sociologia. Insegnamento di Statistica (a.a ) dott.ssa Gaia Bertarelli
 Dipartimento di Sociologia e Ricerca Sociale Corso di Laurea in Sociologia Insegnamento di Statistica (a.a. 2018-2019) dott.ssa Gaia Bertarelli Esercitazione n. 7 1. Utilizzando le tavole della distribuzione
Dipartimento di Sociologia e Ricerca Sociale Corso di Laurea in Sociologia Insegnamento di Statistica (a.a. 2018-2019) dott.ssa Gaia Bertarelli Esercitazione n. 7 1. Utilizzando le tavole della distribuzione
N.B. Per la risoluzione dei seguenti esercizi, si fa riferimento alle Tabelle riportate alla fine del documento.
 N.B. Per la risoluzione dei seguenti esercizi, si fa riferimento alle Tabelle riportate alla fine del documento. Esercizio 1 Un chimico che lavora per una fabbrica di batterie, sta cercando una batteria
N.B. Per la risoluzione dei seguenti esercizi, si fa riferimento alle Tabelle riportate alla fine del documento. Esercizio 1 Un chimico che lavora per una fabbrica di batterie, sta cercando una batteria
Statistica Inferenziale
 Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Riepilogo lezione 4 Abbiamo visto: Distribuzioni discrete Modelli probabilistici nel discreto Distribuzione uniforme
Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Riepilogo lezione 4 Abbiamo visto: Distribuzioni discrete Modelli probabilistici nel discreto Distribuzione uniforme
DISTRIBUZIONI DI PROBABILITA (parte 3) 1 / 34
 DISTRIBUZIONI DI PROBABILITA (parte 3) 1 / 34 Distribuzione Binomiale 2 / 34 La più importante distribuzione di probabilità per variabili casuali discrete è la distribuzione binomiale. Questa distribuzione
DISTRIBUZIONI DI PROBABILITA (parte 3) 1 / 34 Distribuzione Binomiale 2 / 34 La più importante distribuzione di probabilità per variabili casuali discrete è la distribuzione binomiale. Questa distribuzione
Intervalli di confidenza
 Probabilità e Statistica Esercitazioni a.a. 2006/2007 C.d.L.: Ingegneria per l Ambiente ed il Territorio, Ingegneria Civile, Ingegneria Gestionale, Ingegneria dell Informazione C.d.L.S.: Ingegneria Civile
Probabilità e Statistica Esercitazioni a.a. 2006/2007 C.d.L.: Ingegneria per l Ambiente ed il Territorio, Ingegneria Civile, Ingegneria Gestionale, Ingegneria dell Informazione C.d.L.S.: Ingegneria Civile
Università del Piemonte Orientale. Corso di Laurea Triennale di Infermieristica Pediatrica ed Ostetricia. Corso di Statistica Medica
 Università del Piemonte Orientale Corso di Laurea Triennale di Infermieristica Pediatrica ed Ostetricia Corso di Statistica Medica Le distribuzioni teoriche di probabilità La distribuzione Normale (o di
Università del Piemonte Orientale Corso di Laurea Triennale di Infermieristica Pediatrica ed Ostetricia Corso di Statistica Medica Le distribuzioni teoriche di probabilità La distribuzione Normale (o di
UNIVERSITA DEGLI STUDI DI BRESCIA-FACOLTA DI MEDICINA E CHIRURGIA CORSO DI LAUREA IN INFERMIERISTICA SEDE DI DESENZANO dg STATISTICA MEDICA.
 Lezione 4 DISTRIBUZIONE DI FREQUENZA 1 DISTRIBUZIONE DI PROBABILITA Una variabile i cui differenti valori seguono una distribuzione di probabilità si chiama variabile aleatoria. Es:il numero di figli maschi
Lezione 4 DISTRIBUZIONE DI FREQUENZA 1 DISTRIBUZIONE DI PROBABILITA Una variabile i cui differenti valori seguono una distribuzione di probabilità si chiama variabile aleatoria. Es:il numero di figli maschi
Statistica Inferenziale
 Statistica Inferenziale a) L Intervallo di Confidenza b) La distribuzione t di Student c) La differenza delle medie d) L intervallo di confidenza della differenza Prof Paolo Chiodini Dalla Popolazione
Statistica Inferenziale a) L Intervallo di Confidenza b) La distribuzione t di Student c) La differenza delle medie d) L intervallo di confidenza della differenza Prof Paolo Chiodini Dalla Popolazione
INTRODUZIONE AL DOE come strumento di sviluppo prodotto Francesca Campana Parte 2 Concetti di base
 INTRODUZIONE AL DOE come strumento di sviluppo prodotto Francesca Campana Parte Concetti di base Pagina CONCETTI STATISTICI DI PARTENZA - DESCRITTORI DI UNA VARIABILE RANDOM - GRAFICI UTILI - DISTRIBUZIONI
INTRODUZIONE AL DOE come strumento di sviluppo prodotto Francesca Campana Parte Concetti di base Pagina CONCETTI STATISTICI DI PARTENZA - DESCRITTORI DI UNA VARIABILE RANDOM - GRAFICI UTILI - DISTRIBUZIONI
STATISTICA CORSO BASE. Prova scritta del Tempo: 2 ore Cognome e Nome:... Matricola:...
 STATISTICA CORSO BASE. Prova scritta del 7-2-2013. Tempo: 2 ore Cognome e Nome:.............................. Matricola:.............................. Attenzione: Prima di affrontare la prova si consiglia
STATISTICA CORSO BASE. Prova scritta del 7-2-2013. Tempo: 2 ore Cognome e Nome:.............................. Matricola:.............................. Attenzione: Prima di affrontare la prova si consiglia
Statistica Corso Base (Serale) Dott.ssa Cristina Mollica
 Statistica Corso Base Serale Dott.ssa Cristina Mollica cristina.mollica@uniroma1.it Campionamento Esercizio 1. Da una ricerca si è osservato che il peso del prodotto A varia tra i e i 530 grammi. 1 Ipotizzando
Statistica Corso Base Serale Dott.ssa Cristina Mollica cristina.mollica@uniroma1.it Campionamento Esercizio 1. Da una ricerca si è osservato che il peso del prodotto A varia tra i e i 530 grammi. 1 Ipotizzando
Tipi di variabili. Indici di tendenza centrale e di dispersione
 Tipi di variabili. Indici di tendenza centrale e di dispersione L. Boni Variabile casuale In teoria della probabilità, una variabile casuale (o variabile aleatoria o variabile stocastica o random variable)
Tipi di variabili. Indici di tendenza centrale e di dispersione L. Boni Variabile casuale In teoria della probabilità, una variabile casuale (o variabile aleatoria o variabile stocastica o random variable)
Esercizio 1. Stima intervallare: IC per la media incognita (varianza ignota)
 STATISTICA (2) ESERCITAZIONE 5 26.02.2014 Dott.ssa Antonella Costanzo Esercizio 1. Stima intervallare: IC per la media incognita (varianza ignota) Il responsabile del controllo qualità di un azienda che
STATISTICA (2) ESERCITAZIONE 5 26.02.2014 Dott.ssa Antonella Costanzo Esercizio 1. Stima intervallare: IC per la media incognita (varianza ignota) Il responsabile del controllo qualità di un azienda che
Statistica Inferenziale
 Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Riepilogo lezione 8 Abbiamo visto: Metodi per la determinazione di uno stimatore Metodo di massima verosimiglianza
Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Riepilogo lezione 8 Abbiamo visto: Metodi per la determinazione di uno stimatore Metodo di massima verosimiglianza
Intervalli di confidenza
 Probabilità e Statistica Esercitazioni a.a. 2017/2018 C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica Intervalli di confidenza Marco Pietro Longhi Probabilità e Statistica
Probabilità e Statistica Esercitazioni a.a. 2017/2018 C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica Intervalli di confidenza Marco Pietro Longhi Probabilità e Statistica
1.1 Obiettivi della statistica Struttura del testo 2
 Prefazione XV 1 Introduzione 1.1 Obiettivi della statistica 1 1.2 Struttura del testo 2 2 Distribuzioni di frequenza 2.1 Informazione statistica e rilevazione dei dati 5 2.2 Distribuzioni di frequenza
Prefazione XV 1 Introduzione 1.1 Obiettivi della statistica 1 1.2 Struttura del testo 2 2 Distribuzioni di frequenza 2.1 Informazione statistica e rilevazione dei dati 5 2.2 Distribuzioni di frequenza
Statistica Applicata all edilizia: alcune distribuzioni di probabilità
 Statistica Applicata all edilizia: Alcune distribuzioni di probabilità E-mail: orietta.nicolis@unibg.it 23 marzo 2010 Indice Distribuzioni di probabilità discrete 1 Distribuzioni di probabilità discrete
Statistica Applicata all edilizia: Alcune distribuzioni di probabilità E-mail: orietta.nicolis@unibg.it 23 marzo 2010 Indice Distribuzioni di probabilità discrete 1 Distribuzioni di probabilità discrete
DISTRIBUZIONI DI PROBABILITA (parte 1) 1 / 19
 DISTRIBUZIONI DI PROBABILITA (parte 1) 1 / 19 Variabili casuali (o aleatorie) 2 / 19 Disponendo di metodi corretti per raccogliere i dati e costruire i campioni data una popolazione, i valori numerici
DISTRIBUZIONI DI PROBABILITA (parte 1) 1 / 19 Variabili casuali (o aleatorie) 2 / 19 Disponendo di metodi corretti per raccogliere i dati e costruire i campioni data una popolazione, i valori numerici
UNIVERSITA DEGLI STUDI DI BRESCIA-FACOLTA DI MEDICINA E CHIRURGIA CORSO DI LAUREA IN INFERMIERISTICA SEDE DI DESENZANO dg STATISTICA MEDICA.
 Lezione 4 DISTRIBUZIONE DI FREQUENZA 1 DISTRIBUZIONE DI PROBABILITA Una variabile i cui differenti valori seguono una distribuzione di probabilità si chiama variabile aleatoria. Es:il numero di figli maschi
Lezione 4 DISTRIBUZIONE DI FREQUENZA 1 DISTRIBUZIONE DI PROBABILITA Una variabile i cui differenti valori seguono una distribuzione di probabilità si chiama variabile aleatoria. Es:il numero di figli maschi
Campionamento La statistica media campionaria e la sua distribuzione. Paola Giacomello Dip. Scienze Sociali ed Economiche Uniroma1
 Campionamento La statistica media campionaria e la sua distribuzione 1 Definisco il problema da studiare: es. tempo di percorrenza tra abitazione e università Carattere: tempo ossia v.s. continua Popolazione:
Campionamento La statistica media campionaria e la sua distribuzione 1 Definisco il problema da studiare: es. tempo di percorrenza tra abitazione e università Carattere: tempo ossia v.s. continua Popolazione:
STATISTICA A K (60 ore)
 STATISTICA A K (60 ore) Marco Riani mriani@unipr.it http://www.riani.it Richiami sulla regressione Marco Riani, Univ. di Parma 1 MODELLO DI REGRESSIONE y i = a + bx i + e i dove: i = 1,, n a + bx i rappresenta
STATISTICA A K (60 ore) Marco Riani mriani@unipr.it http://www.riani.it Richiami sulla regressione Marco Riani, Univ. di Parma 1 MODELLO DI REGRESSIONE y i = a + bx i + e i dove: i = 1,, n a + bx i rappresenta
DISTRIBUZIONI DI CAMPIONAMENTO
 DISTRIBUZIONI DI CAMPIONAMENTO 12 DISTRIBUZIONE DI CAMPIONAMENTO DELLA MEDIA Situazione reale Della popolazione di tutti i laureati in odontoiatria negli ultimi 10 anni, in tutte le Università d Italia,
DISTRIBUZIONI DI CAMPIONAMENTO 12 DISTRIBUZIONE DI CAMPIONAMENTO DELLA MEDIA Situazione reale Della popolazione di tutti i laureati in odontoiatria negli ultimi 10 anni, in tutte le Università d Italia,
Programma della parte introduttiva: Lezione 5
 Programma della parte introduttiva: Lezione 5 Cap. 3 Presentazione e confronto tra misure Cap. 4 Propagazione delle incertezze Cap 5 Misure ripetute e stimatori Cap.6 Organizzazione e presentazione dei
Programma della parte introduttiva: Lezione 5 Cap. 3 Presentazione e confronto tra misure Cap. 4 Propagazione delle incertezze Cap 5 Misure ripetute e stimatori Cap.6 Organizzazione e presentazione dei
Occorre trovare la distribuzione di DM
 Esercizio In una prova sul carico di rottura di due tipi di corda si dispone di 2 campioni di ampiezza 26 e 35 rispettivamente. Nel primo campione la media è 185,3Kg, nel secondo campione la media è 175,2Kg.
Esercizio In una prova sul carico di rottura di due tipi di corda si dispone di 2 campioni di ampiezza 26 e 35 rispettivamente. Nel primo campione la media è 185,3Kg, nel secondo campione la media è 175,2Kg.
STATISTICA 1 ESERCITAZIONE 6
 STATISTICA 1 ESERCITAZIONE 6 Dott. Giuseppe Pandolfo 5 Novembre 013 CONCENTRAZIONE Osservando l ammontare di un carattere quantitativo trasferibile su un collettivo statistico può essere interessante sapere
STATISTICA 1 ESERCITAZIONE 6 Dott. Giuseppe Pandolfo 5 Novembre 013 CONCENTRAZIONE Osservando l ammontare di un carattere quantitativo trasferibile su un collettivo statistico può essere interessante sapere
Verifica delle ipotesi
 Statistica inferenziale Stima dei parametri Verifica delle ipotesi Concetti fondamentali POPOLAZIONE o UNIVERSO Insieme degli elementi cui si rivolge il ricercatore per la sua indagine CAMPIONE Un sottoinsieme
Statistica inferenziale Stima dei parametri Verifica delle ipotesi Concetti fondamentali POPOLAZIONE o UNIVERSO Insieme degli elementi cui si rivolge il ricercatore per la sua indagine CAMPIONE Un sottoinsieme
Università del Piemonte Orientale Corso di Laurea in Medicina e Chirurgia. Corso di Statistica Medica. La distribuzione Normale (o di Gauss)
 Università del Piemonte Orientale Corso di Laurea in Medicina e Chirurgia Corso di Statistica Medica La distribuzione Normale (o di Gauss) Corso di laurea in medicina e chirurgia - Corso di Statistica
Università del Piemonte Orientale Corso di Laurea in Medicina e Chirurgia Corso di Statistica Medica La distribuzione Normale (o di Gauss) Corso di laurea in medicina e chirurgia - Corso di Statistica
Statistica 1. Esercitazioni. Dott. Luigi Augugliaro 1. Università di Palermo
 Statistica 1 Esercitazioni Dott. 1 1 Dipartimento di Scienze Statistiche e Matematiche S. Vianelli, Università di Palermo ricevimento: lunedì ore 15-17 mercoledì ore 15-17 e-mail: luigi.augugliaro@unipa.it
Statistica 1 Esercitazioni Dott. 1 1 Dipartimento di Scienze Statistiche e Matematiche S. Vianelli, Università di Palermo ricevimento: lunedì ore 15-17 mercoledì ore 15-17 e-mail: luigi.augugliaro@unipa.it
UNIVERSITÀ DEGLI STUDI DI PERUGIA
 SIGI, Statistica II, esercitazione n. 3 1 UNIVERSITÀ DEGLI STUDI DI PERUGIA FACOLTÀ DI ECONOMIA CORSO DI LAUREA S.I.G.I. STATISTICA II Esercitazione n. 3 Esercizio 1 Una v.c. X si dice v.c. esponenziale
SIGI, Statistica II, esercitazione n. 3 1 UNIVERSITÀ DEGLI STUDI DI PERUGIA FACOLTÀ DI ECONOMIA CORSO DI LAUREA S.I.G.I. STATISTICA II Esercitazione n. 3 Esercizio 1 Una v.c. X si dice v.c. esponenziale
I modelli probabilistici
 e I modelli probabilistici Finora abbiamo visto che esistono modelli probabilistici che possiamo utilizzare per prevedere gli esiti di esperimenti aleatori. Naturalmente la previsione è di tipo probabilistico:
e I modelli probabilistici Finora abbiamo visto che esistono modelli probabilistici che possiamo utilizzare per prevedere gli esiti di esperimenti aleatori. Naturalmente la previsione è di tipo probabilistico:
Gli intervalli di confidenza. Intervallo di confidenza per la media (σ 2 nota) nel caso di popolazione Gaussiana
 Statistica Lez. 1 Gli intervalli di confidenza Intervallo di confidenza per la media (σ nota) nel caso di popolazione Gaussiana Sia X una v.c Gaussiana di media µ e varianza σ. Se X 1, X,..., X n è un
Statistica Lez. 1 Gli intervalli di confidenza Intervallo di confidenza per la media (σ nota) nel caso di popolazione Gaussiana Sia X una v.c Gaussiana di media µ e varianza σ. Se X 1, X,..., X n è un
Stima puntuale di parametri
 Probabilità e Statistica Esercitazioni a.a. 2009/2010 C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica Stima puntuale di parametri Ines Campa Probabilità e Statistica -
Probabilità e Statistica Esercitazioni a.a. 2009/2010 C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica Stima puntuale di parametri Ines Campa Probabilità e Statistica -
INTRODUZIONE AL DOE come strumento di sviluppo prodotto Francesca Campana Parte 2 Concetti di base
 INTRODUZIONE AL DOE come strumento di sviluppo prodotto Francesca Campana Parte Concetti di base Pagina CONCETTI STATISTICI DI PARTENZA statistica descrittiva - DESCRITTORI DI UNA VARIABILE RANDOM - GRAFICI
INTRODUZIONE AL DOE come strumento di sviluppo prodotto Francesca Campana Parte Concetti di base Pagina CONCETTI STATISTICI DI PARTENZA statistica descrittiva - DESCRITTORI DI UNA VARIABILE RANDOM - GRAFICI
Cenni di statistica statistica
 Cenni di statistica La statistica è una disciplina che ha come fine lo studio quantitativo e qualitativo di un particolare fenomeno in condizioni di incertezza o non determinismo, ovvero di non completa
Cenni di statistica La statistica è una disciplina che ha come fine lo studio quantitativo e qualitativo di un particolare fenomeno in condizioni di incertezza o non determinismo, ovvero di non completa
Laboratorio di Probabilità e Statistica
 Laboratorio di Probabilità e Statistica lezione 5 Massimo Guerriero Ettore Benedetti Indice Lezione Prerequisiti dalla lezione scorsa Media e varianza campionaria Legge dei grandi numeri Teorema del limite
Laboratorio di Probabilità e Statistica lezione 5 Massimo Guerriero Ettore Benedetti Indice Lezione Prerequisiti dalla lezione scorsa Media e varianza campionaria Legge dei grandi numeri Teorema del limite
RICHIAMI DI CALCOLO DELLE PROBABILITÀ
 UNIVERSITA DEL SALENTO INGEGNERIA CIVILE RICHIAMI DI CALCOLO DELLE PROBABILITÀ ing. Marianovella LEONE INTRODUZIONE Per misurare la sicurezza di una struttura, ovvero la sua affidabilità, esistono due
UNIVERSITA DEL SALENTO INGEGNERIA CIVILE RICHIAMI DI CALCOLO DELLE PROBABILITÀ ing. Marianovella LEONE INTRODUZIONE Per misurare la sicurezza di una struttura, ovvero la sua affidabilità, esistono due
MODELLI STATISTICI, RICHIAMI
 MODELLI STATISTICI, RICHIAMI Corso di Tecniche di Simulazione, a.a. 2005/2006 Francesca Mazzia Dipartimento di Matematica Università di Bari 11 Aprile 2006 Francesca Mazzia (Univ. Bari) MODELLI STATISTICI,
MODELLI STATISTICI, RICHIAMI Corso di Tecniche di Simulazione, a.a. 2005/2006 Francesca Mazzia Dipartimento di Matematica Università di Bari 11 Aprile 2006 Francesca Mazzia (Univ. Bari) MODELLI STATISTICI,
Probabilità e Statistica
 Probabilità e Statistica Intervalli di confidenza Marco Pietro Longhi C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica a.s. 2018/2019 Marco Pietro Longhi Prob. e Stat. 1
Probabilità e Statistica Intervalli di confidenza Marco Pietro Longhi C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica a.s. 2018/2019 Marco Pietro Longhi Prob. e Stat. 1
Stima puntuale di parametri
 Probabilità e Statistica Esercitazioni a.a. 006/007 C.d.L.: Ingegneria per l Ambiente ed il Territorio, Ingegneria Civile, Ingegneria Gestionale, Ingegneria dell Informazione C.d.L.S.: Ingegneria Civile
Probabilità e Statistica Esercitazioni a.a. 006/007 C.d.L.: Ingegneria per l Ambiente ed il Territorio, Ingegneria Civile, Ingegneria Gestionale, Ingegneria dell Informazione C.d.L.S.: Ingegneria Civile
Sommario. 2 I grafici Il sistema di coordinate cartesiane Gli istogrammi I diagrammi a torta...51
 Sommario 1 I dati...15 1.1 Classificazione delle rilevazioni...17 1.1.1 Esperimenti ripetibili (controllabili)...17 1.1.2 Rilevazioni su fenomeni non ripetibili...18 1.1.3 Censimenti...19 1.1.4 Campioni...19
Sommario 1 I dati...15 1.1 Classificazione delle rilevazioni...17 1.1.1 Esperimenti ripetibili (controllabili)...17 1.1.2 Rilevazioni su fenomeni non ripetibili...18 1.1.3 Censimenti...19 1.1.4 Campioni...19
Laboratorio di Chimica Fisica. Analisi Statistica
 Università degli Studi di Bari Dipartimento di Chimica 9 giugno F.Mavelli- Laboratorio Chimica Fisica - a.a. 3-4 F.Mavelli Laboratorio di Chimica Fisica a.a. 3-4 Analisi Statistica dei Dati Analisi Statistica
Università degli Studi di Bari Dipartimento di Chimica 9 giugno F.Mavelli- Laboratorio Chimica Fisica - a.a. 3-4 F.Mavelli Laboratorio di Chimica Fisica a.a. 3-4 Analisi Statistica dei Dati Analisi Statistica
ESERCIZIO 1. Soluzione. X =numero di passeggeri giornaliero
 ESERCIZIO 1 La somma dei numeri di passeggeri di un autoservizio suburbano rilevati in 7 giorni scelti a caso è pari a 385. Si assuma un modello gaussiano per descrivere il numero giornaliero di passeggeri.
ESERCIZIO 1 La somma dei numeri di passeggeri di un autoservizio suburbano rilevati in 7 giorni scelti a caso è pari a 385. Si assuma un modello gaussiano per descrivere il numero giornaliero di passeggeri.
STATISTICA (2) ESERCITAZIONE Dott.ssa Antonella Costanzo
 STATISTICA (2) ESERCITAZIONE 7 11.03.2014 Dott.ssa Antonella Costanzo Esercizio 1. Test di indipendenza tra mutabili In un indagine vengono rilevate le informazioni su settore produttivo (Y) e genere (X)
STATISTICA (2) ESERCITAZIONE 7 11.03.2014 Dott.ssa Antonella Costanzo Esercizio 1. Test di indipendenza tra mutabili In un indagine vengono rilevate le informazioni su settore produttivo (Y) e genere (X)
Modelli probabilistici variabili casuali
 Modelli probabilistici variabili casuali Le variabili casuali costituiscono il legame tra il calcolo della probabilità e gli strumenti di statistica descrittiva visti fino ad ora. Idea: pensiamo al ripetersi
Modelli probabilistici variabili casuali Le variabili casuali costituiscono il legame tra il calcolo della probabilità e gli strumenti di statistica descrittiva visti fino ad ora. Idea: pensiamo al ripetersi
ISTITUTO TECNICO INDUSTRIALE STATALE FOCACCIA DISCIPLINA : CALCOLO PROGRAMMAZIONE MODULARE ANNO SCOLASTICO 2010/2011 CLASSI : III, IV, V
 ISTITUTO TECNICO INDUSTRIALE STATALE FOCACCIA DISCIPLINA : CALCOLO PROGRAMMAZIONE MODULARE ANNO SCOLASTICO 010/011 CLASSI : III, IV, V Docenti Marino Teresa Scaramella Franca Napoli Raffaele Matarazzo
ISTITUTO TECNICO INDUSTRIALE STATALE FOCACCIA DISCIPLINA : CALCOLO PROGRAMMAZIONE MODULARE ANNO SCOLASTICO 010/011 CLASSI : III, IV, V Docenti Marino Teresa Scaramella Franca Napoli Raffaele Matarazzo
Esercitazioni di Statistica Matematica A Lezione 7. Variabili aleatorie continue
 Esercitazioni di Statistica Matematica A Lezione 7 Variabili aleatorie continue.) Determinare la costante k R tale per cui le seguenti funzioni siano funzioni di densità. Determinare poi la media e la
Esercitazioni di Statistica Matematica A Lezione 7 Variabili aleatorie continue.) Determinare la costante k R tale per cui le seguenti funzioni siano funzioni di densità. Determinare poi la media e la
PROVA SCRITTA DI STATISTICA. cod CLEA-CLAPI-CLEFIN-CLELI cod CLEA-CLAPI-CLEFIN-CLEMIT. 5 Novembre 2003 SOLUZIONI MOD.
 PROVA SCRITTA DI STATISTICA cod. 4038 CLEA-CLAPI-CLEFIN-CLELI cod. 5047 CLEA-CLAPI-CLEFIN-CLEMIT 5 Novembre 003 SOLUZIONI MOD. A In 8 facoltà di un ateneo italiano vengono rilevati i seguenti dati campionari
PROVA SCRITTA DI STATISTICA cod. 4038 CLEA-CLAPI-CLEFIN-CLELI cod. 5047 CLEA-CLAPI-CLEFIN-CLEMIT 5 Novembre 003 SOLUZIONI MOD. A In 8 facoltà di un ateneo italiano vengono rilevati i seguenti dati campionari
Una variabile casuale è una variabile che assume determinati valori in modo casuale (non deterministico).
 VARIABILI CASUALI 1 definizione Una variabile casuale è una variabile che assume determinati valori in modo casuale (non deterministico). Esempi l esito di una estrazione del Lotto; il risultato di una
VARIABILI CASUALI 1 definizione Una variabile casuale è una variabile che assume determinati valori in modo casuale (non deterministico). Esempi l esito di una estrazione del Lotto; il risultato di una
Modelli di probabilità
 Modelli di probabilità Corso di STATISTICA Ordinario di, Università di Napoli Federico II Professore supplente, Università della Basilicata a.a. 0/0 Obiettivo dell unità didattica Definire i concetti di
Modelli di probabilità Corso di STATISTICA Ordinario di, Università di Napoli Federico II Professore supplente, Università della Basilicata a.a. 0/0 Obiettivo dell unità didattica Definire i concetti di
x, y rappresenta la coppia di valori relativa La rappresentazione nel piano cartesiano dei punti ( x, y ),( x, y ),...,( x, y )
 Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 0/03 lezioni di statistica del 5 e 8 aprile 03 - di Massimo Cristallo - A. Le relazioni tra i fenomeni
Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 0/03 lezioni di statistica del 5 e 8 aprile 03 - di Massimo Cristallo - A. Le relazioni tra i fenomeni
PROBABILITÀ ELEMENTARE
 Prefazione alla seconda edizione XI Capitolo 1 PROBABILITÀ ELEMENTARE 1 Esperimenti casuali 1 Spazi dei campioni 1 Eventi 2 Il concetto di probabilità 3 Gli assiomi della probabilità 3 Alcuni importanti
Prefazione alla seconda edizione XI Capitolo 1 PROBABILITÀ ELEMENTARE 1 Esperimenti casuali 1 Spazi dei campioni 1 Eventi 2 Il concetto di probabilità 3 Gli assiomi della probabilità 3 Alcuni importanti
Casa dello Studente. Casa dello Studente
 Esercitazione - 14 aprile 2016 ESERCIZIO 1 Di seguito si riporta il giudizio (punteggio da 0 a 5) espresso da un gruppo di studenti rispetto alle diverse residenze studentesche di un Ateneo: a) Si calcolino
Esercitazione - 14 aprile 2016 ESERCIZIO 1 Di seguito si riporta il giudizio (punteggio da 0 a 5) espresso da un gruppo di studenti rispetto alle diverse residenze studentesche di un Ateneo: a) Si calcolino
Statistica descrittiva in una variabile
 Statistica descrittiva in una variabile Dott. Nicola Pintus A.a. 2018-2019 Cosa è la statistica? La statistica è la scienza che studia con metodi matematici fenomeni collettivi. La statistica descrittiva
Statistica descrittiva in una variabile Dott. Nicola Pintus A.a. 2018-2019 Cosa è la statistica? La statistica è la scienza che studia con metodi matematici fenomeni collettivi. La statistica descrittiva
Campionamento e stima di parametri
 Sia X una variabile aleatoria associata a un dato esperimento. Ripetiamo l esperimento n volte, ottenendo una famiglia di valori sperimentali della v.a. X : X = (X 1, X 2,..., X n ) ogni X i é una v.a.
Sia X una variabile aleatoria associata a un dato esperimento. Ripetiamo l esperimento n volte, ottenendo una famiglia di valori sperimentali della v.a. X : X = (X 1, X 2,..., X n ) ogni X i é una v.a.
Probabilità e Statistica
 Probabilità e Statistica Stima puntuale di parametri Marco Pietro Longhi C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica a.s. 018/019 Marco Pietro Longhi Prob. e Stat.
Probabilità e Statistica Stima puntuale di parametri Marco Pietro Longhi C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica a.s. 018/019 Marco Pietro Longhi Prob. e Stat.
LEZIONI DI STATISTICA MEDICA
 LEZIONI DI STATISTICA MEDICA Lezione n.11 - Principi dell inferenza statistica - Campionamento - Distribuzione campionaria di una media e di una proporzione - Intervallo di confidenza di una media e di
LEZIONI DI STATISTICA MEDICA Lezione n.11 - Principi dell inferenza statistica - Campionamento - Distribuzione campionaria di una media e di una proporzione - Intervallo di confidenza di una media e di
Indice. centrale, dispersione e forma Introduzione alla Statistica Statistica descrittiva per variabili quantitative: tendenza
 XIII Presentazione del volume XV L Editore ringrazia 3 1. Introduzione alla Statistica 5 1.1 Definizione di Statistica 6 1.2 I Rami della Statistica Statistica Descrittiva, 6 Statistica Inferenziale, 6
XIII Presentazione del volume XV L Editore ringrazia 3 1. Introduzione alla Statistica 5 1.1 Definizione di Statistica 6 1.2 I Rami della Statistica Statistica Descrittiva, 6 Statistica Inferenziale, 6
Materiale didattico per il corso di Statistica I Quarta esercitazione SOLUZIONI
 Materiale didattico per il corso di Statistica I Quarta esercitazione SOLUZIONI Claudia Furlan 1 Anno Accademico 2006-2007 1 Ringrazio Carlo Gaetan, Nicola Sartori e Aldo Solari per il materiale, aggiunte
Materiale didattico per il corso di Statistica I Quarta esercitazione SOLUZIONI Claudia Furlan 1 Anno Accademico 2006-2007 1 Ringrazio Carlo Gaetan, Nicola Sartori e Aldo Solari per il materiale, aggiunte
Argomenti della lezione: Campionamento Stima Distribuzione campionaria Campione Popolazione Sottoinsieme degli elementi (o universo) dell '
 Lezione 2 Argomenti della lezione: La statistica inferenziale: concetti di base Campionamento Stima Distribuzione campionaria Popolazione (o universo) Insieme di tutti gli elementi cui si rivolge il ricercatore
Lezione 2 Argomenti della lezione: La statistica inferenziale: concetti di base Campionamento Stima Distribuzione campionaria Popolazione (o universo) Insieme di tutti gli elementi cui si rivolge il ricercatore
Statistica 1- parte II
 Statistica 1- parte II Esercitazione 2 Dott.ssa Antonella Costanzo 18/02/2016 Esercizio 1. IC media incognita, varianza nota Una fabbrica A produce matite colorate. Una prova su 100 matite scelte a caso
Statistica 1- parte II Esercitazione 2 Dott.ssa Antonella Costanzo 18/02/2016 Esercizio 1. IC media incognita, varianza nota Una fabbrica A produce matite colorate. Una prova su 100 matite scelte a caso
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2006/07
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 006/07 Esercizio 1 Prova scritta del 16/1/006 In un ufficio postale lavorano due impiegati che svolgono lo stesso compito in maniera indipendente, sbrigando
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 006/07 Esercizio 1 Prova scritta del 16/1/006 In un ufficio postale lavorano due impiegati che svolgono lo stesso compito in maniera indipendente, sbrigando
Modulo di Statistica e Tecnologia (Dott. Giorgio Poletti
 Laurea in Scienze dell Educazione Insegnamento di Pedagogia Sperimentale (Prof. Paolo Frignani) Modulo di Statistica e Tecnologia (Dott. Giorgio Poletti giorgio.poletti@unife.it) (discrete) variabile casuale
Laurea in Scienze dell Educazione Insegnamento di Pedagogia Sperimentale (Prof. Paolo Frignani) Modulo di Statistica e Tecnologia (Dott. Giorgio Poletti giorgio.poletti@unife.it) (discrete) variabile casuale
LE VARIABILI CASUALI A 1, A 2.,..., A k., p 2.,..., p k. generati da una specifica prova sono necessari ed incompatibili:
 LE VARIABILI CASUALI Introduzione Data prova, ad essa risultano associati i k eventi A, A,..., A k con le relative probabilità p, p,..., p k. I k eventi A i generati da una specifica prova sono necessari
LE VARIABILI CASUALI Introduzione Data prova, ad essa risultano associati i k eventi A, A,..., A k con le relative probabilità p, p,..., p k. I k eventi A i generati da una specifica prova sono necessari
7 - Distribuzione Poissoniana
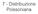 7 - Distribuzione Poissoniana Probabilita' (poissoniana) o densita' di probabilita' (gaussiana) 0.7 Poisson, λ=0.5 Gaussiana, µ=λ=0.5, σ= 0.6 0.5 0.4 0.3 0.2 0.1 0 0.5 0 0.5 1 1.5 2 2.5 3 3.5 4 n = numero
7 - Distribuzione Poissoniana Probabilita' (poissoniana) o densita' di probabilita' (gaussiana) 0.7 Poisson, λ=0.5 Gaussiana, µ=λ=0.5, σ= 0.6 0.5 0.4 0.3 0.2 0.1 0 0.5 0 0.5 1 1.5 2 2.5 3 3.5 4 n = numero
Distribuzione esponenziale. f(x) = 0 x < 0
 Distribuzione esponenziale Funzione densità f(x) = λe λx x 0 0 x < 0 Funzione parametrica (λ) 72 Funzione di densità della distribuzione esponenziale 1 0.9 0.8 0.7 λ=1 0.6 f(x) 0.5 0.4 0.3 λ=1/2 0.2 0.1
Distribuzione esponenziale Funzione densità f(x) = λe λx x 0 0 x < 0 Funzione parametrica (λ) 72 Funzione di densità della distribuzione esponenziale 1 0.9 0.8 0.7 λ=1 0.6 f(x) 0.5 0.4 0.3 λ=1/2 0.2 0.1
STATISTICA (modulo II - Inferenza Statistica) Soluzione Esercitazione I
 Soluzione Esercitazione I Esercizio A. Si indichi con A i l evento la banca i decide di aprire uno sportello per il quale Pr(A i = 0.5 (e dunque Pr(A i = 0.5 per i =, 2, 3. Lo spazio degli eventi dato
Soluzione Esercitazione I Esercizio A. Si indichi con A i l evento la banca i decide di aprire uno sportello per il quale Pr(A i = 0.5 (e dunque Pr(A i = 0.5 per i =, 2, 3. Lo spazio degli eventi dato
