Quando non espressamente detto, intendiamo che: f : R R x 0 R è punto di accumulazione per dom(f).
|
|
|
- Tommasa Novelli
- 7 anni fa
- Visualizzazioni
Transcript
1 Teoremi sui iti Quando non espressamente detto, intendiamo che: f : R R 0 R è punto di accumulazione per dom(f). Teorema di unicità del ite. Supponiamo che f ammetta ite l (finito o infinito) per 0. Allora f non ha altri iti per 0. La dimostrazione è svolta a lezione. Una dimostrazione alternativa è riportata a pag. 92 del libro di testo. c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Teoremi sui iti cap4a.pdf 1
2 Teorema di permanenza del segno. Supponiamo che esista f() = l R. Se l > 0, allora esiste un intorno I( 0 ) del 0 punto 0, tale che f() > 0 per ogni I( 0 )\{ 0 }. y l I( 0 ) 0 La dimostrazione è svolta a lezione. Una dimostrazione alternativa è riportata a pag del libro di testo. c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Teoremi sui iti cap4a.pdf 2
3 Corollario al teorema di permanenza del segno. Supponiamo che esista f() = l R e che esista un intorno I( 0 ) del punto 0, 0 tale che f() 0 per ogni I( 0 )\{ 0 }. Allora l 0. y l I( 0 ) 0 La dimostrazione è svolta a lezione. c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Teoremi sui iti cap4a.pdf 3
4 Limiti delle funzioni elementari Ricordando i grafici delle funzioni elementari abbiamo: c = c c = c (c costante) + = 2 = + 3 = { se n è disp. n = + se n è pari. { 0 se α > 0 = 0 +α + se α < 0 = = = + + n = + + α = { + se α > 0 0 se α < 0 c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Limiti delle funzioni elementari cap4a.pdf 4
5 Limiti delle funzioni elementari 0 +log() = e = 0 sin() = cos() = tan() = log() = e = + sin() = + cos() = + tan() = + c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Limiti delle funzioni elementari cap4a.pdf 5
6 Operazioni con i simboli + e Ricordiamo che R = { } R { } è detta retta reale estesa. Definiamo le operazioni su R. Immaginiamo che gli operandi di queste operazioni siano i risultati del calcolo di certi iti. Somma Prodotto +(+ ) = + +( ) = R (+ )+(+ ) = + ( )+( ) = (+ ) = +, ( ) = R + (+ ) =, ( ) = + R (+ ) (+ ) = +, ( ) ( ) = +, (+ ) ( ) = c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Algebra dei iti cap4a.pdf 6
7 Divisione + = = 0, + = +, + =, 0 R = R + = + R = R\{0} Non sono definite le seguenti operazioni: (+ )+( ), ± (± ) 0, ±, 0 0 0, 0 0, 1 Sono dette forme indeterminate perchè il risultato non è sempre lo stesso. Esse devono essere indagate e risolte caso per caso, con opportune regole. Ad esempio, (+ ) +( ) potrebbe dare come risultato l R, oppure +, oppure, a seconda di cosa rappresentano i vari infiniti. c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Algebra dei iti cap4a.pdf 7
8 Algebra dei iti Teorema. Se f() = l 1 R e g() = l 2 R, allora, 0 0 quando l espressione a secondo membro è definita (non si hanno forme indeterminate), si ha (f()+g()) = f()+ g() = l 1 +l (f() g()) = f() g() = l 1 l (f() g()) = ( f()) ( g()) = l 1 l f() f() 0 g() = 0 g() = l 1 (g() 0, I( 0 )\{ 0 }) l 2 0 Es. + ( 2+ 1 ) 1 = = 2+ 1 = 2+0 = 2 + c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Algebra dei iti cap4a.pdf 8
9 Esempi di forme indeterminate Vediamo se possiamo applicare il teorema dell algebra dei iti. Calcoliamo (supponendo di poter applicare l algebra dei iti) 2 1? + (2 1) + 1 = = + +3 ( +3) + +3 = + + =forma indeterminata + Quindi l algebra dei iti, da sola, NON permette di risolvere il ite Vediamo un secondo ite: 2 +2 ( 2 +2)? = ( ) = 0 =forma indeterminata 0 Anche qui l algebra dei iti, da sola, NON dà alcun aiuto. Vediamo come risolvere queste forme ideterminate c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Algebra dei iti cap4a.pdf 9
10 Forme indeterminate + + (3 2 +1) = + 3 (2) = + +1 forma indeterminata Devo procedere in altro modo: [ ( + (3 2 +1) = )] ( ) ( 3 = ) 3 = + (1 0+0) = + risultato corretto In un polinomio, quando +, prevale sempre il monomio di grado massimo: + (3 2 +1) = + 3 = + + ( ) = + ( 43 ) = c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Algebra dei iti cap4a.pdf 10
11 Forme indeterminate generate da rapporti di polinomi Es Lavoro come prima, sia sul numeratore che sul denominatore = = 2 + = = +2 4 = 2 = = = = = +2 2 = 2 1 = c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Algebra dei iti cap4a.pdf 11
12 Forme indeterminate 0 generate da rapporti di polinomi 0 Es = In questo caso si raccoglie al numeratore ed al denominatore la potenza minima, si semplifica e poi si applica l algebra dei iti = 0 Es = ( +2) (1+ 2 ) = = 2 4 (1 2) = =. ( 4) = (1 2) = = ( 4) 0 2 (1 2) = (1 2) = 4 0 = c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Algebra dei iti cap4a.pdf 12
13 Primo Teorema del confronto. Supponiamo che f ammetta ite l 1 R per 0 e la funzione g ammetta ite l 2 R per 0. Se esiste un intorno I( 0 ) di 0 tale che f() g() per ogni I( 0 )\{ 0 }, allora l 1 l 2. y l 2 l 1 I( 0 ) 0 La dimostrazione è svolta a lezione. Una dimostrazione alternativa è riportata a pag. 94 del libro di testo. c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Teoremi del confronto cap4a.pdf 13
14 Secondo Teorema del confronto. Siano date tre funzioni: f, g e h e supponiamo che esistano e siano uguali i iti f() = h() = l. 0 0 Se esiste un intorno I( 0 ) in cui siano definite le tre funzioni, tranne al più nel punto 0, tale che f() g() h() I( 0 )\{ 0 }, allora si ha 0 g() = l. y h() g() l 0 f() c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Teoremi del confronto cap4a.pdf 14
15 Funzioni itate Sia f : R R, con dominio dom(f) R. Def. Diciamo che f è itata se il suo insieme immagine im(f) è un insieme itato in R. Def. Diciamo che f è itata inferiormente se il suo insieme immagine im(f) è un insieme itato inferiormente in R. Def. Diciamo che f è itata superiormente se il suo insieme immagine im(f) è un insieme itato superiormente in R. Esempi. f() = sin(), g() = cos(), h() = arctan() sono funzioni itate. ( Infatti im(f) = im(g) = [ 1,1], im(h) = π 2, π ) sono tutti insiemi itati 2 f() = sin() g() = cos() h() = arctan() c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Funzioni itate cap4a.pdf 15
16 Esempi di funzioni NON itate. f() = e, è solo itata inferiormente, im(f) = R + g() = log() non è itata, im(g) = R, h() = 2 è solo itata superiormente, im(h) = R {0} f() = e g() = log() h() = 2 c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Funzioni itate cap4a.pdf 16
17 Sia A dom(f) e B = f(a) (l immagine di A attraverso f). Def. Diciamo che f è itata su A se B è un insieme itato in R. y y B B A A 2 f è itata su A 1 = (1,5). B 1 = (0.2,2.8) è un insieme itato. f non è itata su A 2 = (0,2). Si ha 0 f() = + e B 2 = (1.5,+ ) non è un insieme itato. c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Funzioni itate cap4a.pdf 17
18 Funzioni itate (definizione equivalente) Def. Una funzione f è itata in un intorno I( 0 ) del punto 0, se esiste una costante C > 0 tale che f() C, I( 0 ). y y f(i( 0 )) f(i( 0 )) C 0 = 3 0 = 0 I( 0 ) I( 0 ) f è itata nell intorno I(3) ma non è itata nell intorno I(0) c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Funzioni itate cap4a.pdf 18
19 OSSERVAZIONE Dire che f è itata nell intorno I( 0 ) NON vuole dire che esiste 0 f() Esempio. Sia f() = sin(). L insieme immagine di f è imf = [ 1,1] è un insieme itato (ammette sia maggioranti che minoranti), quindi f è itata su tutto il suo dominio, cioè su R. Consideriamo anche la seconda definizione data. Abbiamo 1 f() 1 R, quindi possiamo dire che f() C R con C = 1 (vedi def. a pag. 13). Quindi f è itata in un intorno di 0 = +. Tuttavia + f() Infatti f continua a oscillare e la definizione di ite non è soddisfatta per alcun valore di l. (si vedano pag di cap3a.pdf). c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Funzioni itate cap4a.pdf 19
20 Corollario al II thm del confronto Def. Se 0 g() = 0, si dice che g è infinitesima per 0. Teorema. Sia f una funzione itata in un intorno di 0 e sia g una funzione infinitesima per 0. Allora 0 (f()g()) = 0, ovvero la funzione prodotto fg è infinitesima per 0. Es. + sin(). f() = sin() è itata: sin() 1 e g() = 1 sin() g() = 0. Allora = è tale che c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Teoremi del confronto cap4a.pdf 20
21 sin() Limite fondamentale 0 Dim. 1 P T = 1 Lavoro con 0, osservo che f() = sin() è pari. Se l angolo POA = allora l arco AP è lungo, e A( OPA) = 2. O H A Infatti AP: 2πr = : 2π, AP= r = ; A( OPA) : πr 2 = : 2π, A( OPA) = 2 A( POA) = e PH OA 2 = sin(), A( TOA) = TA OA = tan() A( POA) A( OPA) A( TOA) ovvero sin() 2 2 tan(). 2 c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Primo ite fondamentale cap4a.pdf 21
22 Moltiplicando sin() 2 2 tan() 2 per 2 sin() si ha e invertendo il tutto: 1 sin() 1 cos() cos() sin() 1. Per il secondo teorema del confronto, facendo tendere a 0: cos() = 1, sin() 1 = 1 e quindi = c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Primo ite fondamentale cap4a.pdf 22
23 Riferimenti bibliografici Canuto-Tabacco: Sect , 4.1.2, Esercizi Canuto Tabacco: Es. 1, 2, 3 del Cap. 4. c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Bibliografia cap4a.pdf 23
Quando non espressamente detto, intendiamo che: f : R R x 0 R è punto di accumulazione per dom(f).
 Teoremi sui iti Quando non espressamente detto, intendiamo che: f : R R 0 R è punto di accumulazione per dom(f). Teorema di unicità del ite. Supponiamo che f ammetta ite l (finito o infinito) per 0. Allora
Teoremi sui iti Quando non espressamente detto, intendiamo che: f : R R 0 R è punto di accumulazione per dom(f). Teorema di unicità del ite. Supponiamo che f ammetta ite l (finito o infinito) per 0. Allora
Teoremi sui limiti. Teorema di unicità del limite. Supponiamo che f ammetta limite l R per x x 0. Allora f non ha altri limiti per x x 0.
 Teoremi sui iti Teorema di unicità del ite. Supponiamo che f ammetta ite l R per 0. Allora f non ha altri iti per 0. (Dimostrazione: appunti della lezione o libro pag. 9) Teorema di permanenza del segno.
Teoremi sui iti Teorema di unicità del ite. Supponiamo che f ammetta ite l R per 0. Allora f non ha altri iti per 0. (Dimostrazione: appunti della lezione o libro pag. 9) Teorema di permanenza del segno.
Algebra dei limiti. quando l espressione a secondo membro è definita (non si hanno forme indeterminate), si ha. lim. f (x)
 Algebra dei limiti Teorema. Se lim f () = l R e lim g() = m R, allora, 0 0 quando l espressione a secondo membro è definita (non si hanno forme indeterminate), si ha lim (f () + g()) = lim f () + lim g()
Algebra dei limiti Teorema. Se lim f () = l R e lim g() = m R, allora, 0 0 quando l espressione a secondo membro è definita (non si hanno forme indeterminate), si ha lim (f () + g()) = lim f () + lim g()
La derivata. variabile indipendente x. Definiamo f := f(x) f(x 0 ) l incremento (positivo o negativo) della variabile dipendente.
 La derivata Sia f : domf R R; sia x 0 domf, f sia definita in I r (x 0 ) e sia x I r (x 0 ). ments Definiamo x := x x 0 l incremento (positivo o negativo) della f(x 0 ) + x + x) variabile indipendente
La derivata Sia f : domf R R; sia x 0 domf, f sia definita in I r (x 0 ) e sia x I r (x 0 ). ments Definiamo x := x x 0 l incremento (positivo o negativo) della f(x 0 ) + x + x) variabile indipendente
ANALISI MATEMATICA I per Ingegneria Aerospaziale - A.A Diario delle lezioni. Mercoledì 2 ottobre 2013 (2 ore)
 c Andrea Dall Aglio - Analisi Matematica: Diario delle lezioni - 8 novembre 0 ANALISI MATEMATICA I per Ingegneria Aerospaziale - A.A. 0-04 Diario delle lezioni Questo è un indice degli argomenti trattati
c Andrea Dall Aglio - Analisi Matematica: Diario delle lezioni - 8 novembre 0 ANALISI MATEMATICA I per Ingegneria Aerospaziale - A.A. 0-04 Diario delle lezioni Questo è un indice degli argomenti trattati
CONTINUITA. c Paola Gervasio - Analisi Matematica 1 - A.A. 2018/19 Limiti di funzioni - Funzioni continue cap3b.pdf 1
 CONTINUITA c Paola Gervasio - Analisi Matematica - A.A. 208/9 Limiti di funzioni - Funzioni continue cap3b.pdf Ricordiamo la definizione di limite lim 0 f () = l R: I ε (l), I δ ( 0 ) : dom(f ) I δ ( 0
CONTINUITA c Paola Gervasio - Analisi Matematica - A.A. 208/9 Limiti di funzioni - Funzioni continue cap3b.pdf Ricordiamo la definizione di limite lim 0 f () = l R: I ε (l), I δ ( 0 ) : dom(f ) I δ ( 0
STUDIO di FUNZIONE. c Paola Gervasio - Analisi Matematica 1 - A.A. 2018/19 Studio di funzione cap6b.pdf 1
 STUDIO di FUNZIONE c Paola Gervasio - Analisi Matematica 1 - A.A. 2018/19 Studio di funzione cap6b.pdf 1 Punti di estremo: punto di massimo assoluto Def. Sia 0 dom(f) = D. Si dice che 0 è un punto di massimo
STUDIO di FUNZIONE c Paola Gervasio - Analisi Matematica 1 - A.A. 2018/19 Studio di funzione cap6b.pdf 1 Punti di estremo: punto di massimo assoluto Def. Sia 0 dom(f) = D. Si dice che 0 è un punto di massimo
LIMITI DI FUNZIONI. c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Limiti di funzioni cap3a.pdf 1
 LIMITI DI FUNZIONI c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Limiti di funzioni cap3a.pdf 1 Intorni Def. Siano 0 R e r R +. Chiamiamo intorno di centro 0 e raggio r l intervallo aperto e limitato
LIMITI DI FUNZIONI c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Limiti di funzioni cap3a.pdf 1 Intorni Def. Siano 0 R e r R +. Chiamiamo intorno di centro 0 e raggio r l intervallo aperto e limitato
Limiti e continuità. Teoremi sui limiti. Teorema di unicità del limite Teorema di permanenza del segno Teoremi del confronto Algebra dei limiti
 Limiti e continuità Teorema di unicità del ite Teorema di permanenza del segno Teoremi del confronto Algebra dei iti 2 2006 Politecnico di Torino 1 Se f(x) =` ` è unico Per assurdo, siano ` 6= `0 con f(x)
Limiti e continuità Teorema di unicità del ite Teorema di permanenza del segno Teoremi del confronto Algebra dei iti 2 2006 Politecnico di Torino 1 Se f(x) =` ` è unico Per assurdo, siano ` 6= `0 con f(x)
Limiti di funzioni di una variabile
 Capitolo 6 Limiti di funzioni di una variabile 6.1 Limiti all infinito La definizione di ite data per le successioni si può immediatamente trasportare al caso di una funzione definita in un qualunque insieme
Capitolo 6 Limiti di funzioni di una variabile 6.1 Limiti all infinito La definizione di ite data per le successioni si può immediatamente trasportare al caso di una funzione definita in un qualunque insieme
I POLINOMI DI TAYLOR. c Paola Gervasio - Analisi Matematica 1 - A.A. 17/18 Sviluppi di Taylor cap7.pdf 1
 I POLINOMI DI TAYLOR c Paola Gervasio - Analisi Matematica 1 - A.A. 17/18 Sviluppi di Taylor cap7.pdf 1 Calcolo di forme indeterminate del tipo 0/0 Avevamo già visto (cap4a.pdf, pag. 1) che quando si deve
I POLINOMI DI TAYLOR c Paola Gervasio - Analisi Matematica 1 - A.A. 17/18 Sviluppi di Taylor cap7.pdf 1 Calcolo di forme indeterminate del tipo 0/0 Avevamo già visto (cap4a.pdf, pag. 1) che quando si deve
Forme indeterminate e limiti notevoli
 Forme indeterminate e iti notevoli Limiti e continuità Forme indeterminate e iti notevoli Forme indeterminate Teorema di sostituzione Limiti notevoli Altre forme indeterminate 2 2006 Politecnico di Torino
Forme indeterminate e iti notevoli Limiti e continuità Forme indeterminate e iti notevoli Forme indeterminate Teorema di sostituzione Limiti notevoli Altre forme indeterminate 2 2006 Politecnico di Torino
f(x) lim x c g(x) = lim x c f(x) lim x c g(x)
 Matematica I, 10.10.2012 Limiti di funzioni (II) 1. Limiti e Operazioni Algebriche L operazione di ite di successioni si comporta bene rispetto alle operazioni algebriche di somma (e sottrazione), prodotto
Matematica I, 10.10.2012 Limiti di funzioni (II) 1. Limiti e Operazioni Algebriche L operazione di ite di successioni si comporta bene rispetto alle operazioni algebriche di somma (e sottrazione), prodotto
LIMITI - CONFRONTO LOCALE Test di autovalutazione
 LIMITI - CONFRONTO LOCALE Test di autovalutazione 1. Per 0 le funzioni 1 cos e sin (a) sono infinitesime dello stesso ordine (b) 1 cos è infinitesima di ordine inferiore (c) 1 cos è infinitesima di ordine
LIMITI - CONFRONTO LOCALE Test di autovalutazione 1. Per 0 le funzioni 1 cos e sin (a) sono infinitesime dello stesso ordine (b) 1 cos è infinitesima di ordine inferiore (c) 1 cos è infinitesima di ordine
I POLINOMI DI TAYLOR. c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Sviluppi di Taylor cap7.pdf 1
 I POLINOMI DI TAYLOR c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Sviluppi di Taylor cap7.pdf 1 Il simbolo o piccolo Siano f (x) e g(x) funzioni infinitesime per x x 0 e consideriamo f (x) il lim
I POLINOMI DI TAYLOR c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Sviluppi di Taylor cap7.pdf 1 Il simbolo o piccolo Siano f (x) e g(x) funzioni infinitesime per x x 0 e consideriamo f (x) il lim
ANALISI MATEMATICA I-A. Prova scritta del 1/9/2009 TUTTE LE RISPOSTE DEVONO ESSERE MOTIVATE
 ANALISI MATEMATICA I-A CORSO DI LAUREA IN FISICA Prova scritta del /9/009 TUTTE LE RISPOSTE DEVONO ESSERE MOTIVATE ESERCIZIO. Punti 8 Risolvere la seguente equazione nel campo complesso w 6 w 64 = 64 3
ANALISI MATEMATICA I-A CORSO DI LAUREA IN FISICA Prova scritta del /9/009 TUTTE LE RISPOSTE DEVONO ESSERE MOTIVATE ESERCIZIO. Punti 8 Risolvere la seguente equazione nel campo complesso w 6 w 64 = 64 3
FUNZIONI. y Y. Def. L insieme Y è detto codominio di f. Es. Siano X = R, Y = R e f : x y = 1 x associo il suo inverso). (ad un numero reale
 FUNZIONI Siano X e Y due insiemi. Def. Una funzione f definita in X a valori in Y è una corrispondenza (una legge) che associa ad ogni elemento X al più un elemento in Y. X Y Def. L insieme Y è detto codominio
FUNZIONI Siano X e Y due insiemi. Def. Una funzione f definita in X a valori in Y è una corrispondenza (una legge) che associa ad ogni elemento X al più un elemento in Y. X Y Def. L insieme Y è detto codominio
Infiniti e Infinitesimi
 Infiniti e Infinitesimi Infiniti e Infinitesimi Def. Una funzione f() si dice infinitesima per (o per ), punto di accumulazione per il dominio di f(), se: f ( ) ( oppure f ( ) ) Infiniti e Infinitesimi
Infiniti e Infinitesimi Infiniti e Infinitesimi Def. Una funzione f() si dice infinitesima per (o per ), punto di accumulazione per il dominio di f(), se: f ( ) ( oppure f ( ) ) Infiniti e Infinitesimi
Def. L unico elemento y Y associato ad un elemento x domf si dice immagine. di x attraverso f e si scrive y = f(x) (oppure f : x y = f(x)).
 FUNZIONI Siano X e due insiemi. Def. Una funzione f definita in X a valori in è una corrispondenza (una legge) che associa ad ogni elemento X al piú un elemento in. Def. L insieme è detto codominio di
FUNZIONI Siano X e due insiemi. Def. Una funzione f definita in X a valori in è una corrispondenza (una legge) che associa ad ogni elemento X al piú un elemento in. Def. L insieme è detto codominio di
Studio Qualitativo di Funzione
 Studio Qualitativo di Funzione Reperire un certo numero di informazioni per descrivere a livello qualitativo l andamento del grafico di una funzione f 1. campo di esistenza (cioè, l insieme di definizione)
Studio Qualitativo di Funzione Reperire un certo numero di informazioni per descrivere a livello qualitativo l andamento del grafico di una funzione f 1. campo di esistenza (cioè, l insieme di definizione)
Lezioni di Matematica 1 - I modulo
 Lezioni di Matematica 1 - I modulo Luciano Battaia 20 novembre 2008 L. Battaia - http://www.batmath.it Mat. 1 - I mod. Lez. del 20/11/2008 2 / 14 Definizione. Una funzione f si dice infinitesima in x 0
Lezioni di Matematica 1 - I modulo Luciano Battaia 20 novembre 2008 L. Battaia - http://www.batmath.it Mat. 1 - I mod. Lez. del 20/11/2008 2 / 14 Definizione. Una funzione f si dice infinitesima in x 0
Def. L insieme Y è detto codominio di f. Es. Siano X = R, Y = R e f : x y = 1 x. (ad un numero reale associo. il suo inverso). 2 2/3... e... 0.
 FUNZIONI Siano X e Y due insiemi. Def. Una funzione f definita in X a valori in Y è una corrispondenza (una legge) che associa ad ogni elemento X al piú un elemento in Y. PSfrag replacements X Y Def. L
FUNZIONI Siano X e Y due insiemi. Def. Una funzione f definita in X a valori in Y è una corrispondenza (una legge) che associa ad ogni elemento X al piú un elemento in Y. PSfrag replacements X Y Def. L
Limiti di funzioni e continuità
 Limiti di funzioni e continuità Paolo Montanari Appunti di Matematica Limiti di funzioni e continuità 1 Funzioni limitate La funzione f(x) è limitata superiormente se esiste un numero reale M tale che
Limiti di funzioni e continuità Paolo Montanari Appunti di Matematica Limiti di funzioni e continuità 1 Funzioni limitate La funzione f(x) è limitata superiormente se esiste un numero reale M tale che
Funzioni Continue. se (e solo se) 0
 f : A R R A ' Funzioni Continue La funzione f si dice continua in f ( f ( se (e solo se A Ne seguono tre proprietà affinché f( sia continua in :. Devono esistere finiti il ite destro e sinistro di f( in.
f : A R R A ' Funzioni Continue La funzione f si dice continua in f ( f ( se (e solo se A Ne seguono tre proprietà affinché f( sia continua in :. Devono esistere finiti il ite destro e sinistro di f( in.
Teorema di sostituzione o del limite di funzioni composte
 Teorema di sostituzione o del limite di funzioni composte Questo teorema serve per calcolare il limite di funzioni composte sfruttando limiti fondamentali o altri limiti già noti. TEOREMA. Se esiste lim
Teorema di sostituzione o del limite di funzioni composte Questo teorema serve per calcolare il limite di funzioni composte sfruttando limiti fondamentali o altri limiti già noti. TEOREMA. Se esiste lim
Modulo o "valore assoluto"
 Modulo o "valore assoluto" Dato x R definiamo modulo o valore assoluto di x il numero reale positivo x se x 0 x = x se x < 0 Sfrag replacements Es. 5 è 5. 2.34 è 2.34 Dal punto di vista geometrico x rappresenta
Modulo o "valore assoluto" Dato x R definiamo modulo o valore assoluto di x il numero reale positivo x se x 0 x = x se x < 0 Sfrag replacements Es. 5 è 5. 2.34 è 2.34 Dal punto di vista geometrico x rappresenta
Esercizi svolti. g(x) = sono una l inversa dell altra. Utilizzare la rappresentazione grafica di f e f 1 per risolvere l equazione f(x) = g(x).
 Esercizi svolti. Discutendo graficamente la disequazione > 3 +, verificare che l insieme delle soluzioni è un intervallo e trovarne gli estremi.. Descrivere in forma elementare l insieme { R : + > }. 3.
Esercizi svolti. Discutendo graficamente la disequazione > 3 +, verificare che l insieme delle soluzioni è un intervallo e trovarne gli estremi.. Descrivere in forma elementare l insieme { R : + > }. 3.
STUDIO di FUNZIONE. c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Studio di funzione cap6b.pdf 1
 STUDIO di FUNZIONE c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Studio di funzione cap6b.pdf 1 Punti di estremo: punto di massimo assoluto Def. Sia 0 dom(f) = D. Si dice che 0 è un punto di massimo
STUDIO di FUNZIONE c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Studio di funzione cap6b.pdf 1 Punti di estremo: punto di massimo assoluto Def. Sia 0 dom(f) = D. Si dice che 0 è un punto di massimo
ESERCIZI SUI PUNTI DI DISCONTINUITÀ TRATTI DA TEMI D ESAME
 ESERCIZI SUI PUNTI DI DISCONTINUITÀ TRATTI DA TEMI D ESAME a cura di Michele Scaglia FUNZIONI CONTINUE Sia f : domf R una funzione e sia x 0 domf (esista cioè f(x 0 ) R) Possono verificarsi due casi: il
ESERCIZI SUI PUNTI DI DISCONTINUITÀ TRATTI DA TEMI D ESAME a cura di Michele Scaglia FUNZIONI CONTINUE Sia f : domf R una funzione e sia x 0 domf (esista cioè f(x 0 ) R) Possono verificarsi due casi: il
Abbiamo già visto nel capitolo sulle funzioni che, negli estremi del suo dominio, una funzione può avere degli asintoti.
 Capitolo 7 Limiti di funzioni Abbiamo già visto nel capitolo sulle funzioni che, negli estremi del suo dominio, una funzione può avere degli asintoti. Ricordiamo che un asintoto verticale = a si presenta
Capitolo 7 Limiti di funzioni Abbiamo già visto nel capitolo sulle funzioni che, negli estremi del suo dominio, una funzione può avere degli asintoti. Ricordiamo che un asintoto verticale = a si presenta
Topologia della retta reale. Concetto intuitivo di limite. Definizioni di limite. Teoremi sui limiti. Applicazioni. Angela Donatiello 1
 Topologia della retta reale. Concetto intuitivo di ite. Definizioni di ite. Teoremi sui iti. Applicazioni. Angela Donatiello TOPOLOGIA DELLA RETTA REALE Esiste una corrispondenza biunivoca tra l insieme
Topologia della retta reale. Concetto intuitivo di ite. Definizioni di ite. Teoremi sui iti. Applicazioni. Angela Donatiello TOPOLOGIA DELLA RETTA REALE Esiste una corrispondenza biunivoca tra l insieme
FUNZIONI. y Y. Def. L insieme Y è detto codominio di f. Es. Siano X = R, Y = R e f : x y = 1 x associo il suo inverso). (ad un numero reale
 FUNZIONI Siano X e Y due insiemi. Def. Una funzione f definita in X a valori in Y è una corrispondenza (una legge) che associa ad ogni elemento X al piú un elemento in Y. X Y Def. L insieme Y è detto codominio
FUNZIONI Siano X e Y due insiemi. Def. Una funzione f definita in X a valori in Y è una corrispondenza (una legge) che associa ad ogni elemento X al piú un elemento in Y. X Y Def. L insieme Y è detto codominio
Limiti di funzioni a +
 Limiti di funzioni a + Consideriamo una funzione = f() reale a variabile reale, di dominio D R. Sia f definita in un intorno di +. Def. La funzione f tende al limite l R per tendente a + e si scrive se
Limiti di funzioni a + Consideriamo una funzione = f() reale a variabile reale, di dominio D R. Sia f definita in un intorno di +. Def. La funzione f tende al limite l R per tendente a + e si scrive se
Limiti di funzioni. Hynek Kovarik. Università di Brescia. Analisi Matematica 1
 Limiti di funzioni Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi Matematica 1 1 / 38 Cenni di topologia La nozione di intorno
Limiti di funzioni Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi Matematica 1 1 / 38 Cenni di topologia La nozione di intorno
Istituzioni di Matematiche terza parte
 Istituzioni di Matematiche terza parte anno acc. 2013/2014 Univ. degli Studi di Milano D.Bambusi, C.Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 45 index Il concetto di ite 1 Il
Istituzioni di Matematiche terza parte anno acc. 2013/2014 Univ. degli Studi di Milano D.Bambusi, C.Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 45 index Il concetto di ite 1 Il
Limiti di funzioni. Parte 2 calcolo. prof. Paolo Sarti Liceo Scientifico Statale A. Volta Milano, 10/2016
 Limiti di funzioni Parte calcolo prof. Paolo Sarti Liceo Scientifico Statale A. Volta Milano, /6 L insieme R Il calcolo dei iti delle funzioni reali di variabile reale avviene nell insieme esteso dei numeri
Limiti di funzioni Parte calcolo prof. Paolo Sarti Liceo Scientifico Statale A. Volta Milano, /6 L insieme R Il calcolo dei iti delle funzioni reali di variabile reale avviene nell insieme esteso dei numeri
LEZIONI Dispense a cura del docente Teorema degli Zeri e Teorema di Weierstrass.
 LEZIONI 8-9-0 Contents 8.4. Teorema degli Zeri e Teorema di Weierstrass 95 8.5. Ulteriori nozioni sui iti di funzioni. 0 8.6. Asintoto obliquo. 07 8.7. Funzione Inversa. Continuità della funzione inversa.
LEZIONI 8-9-0 Contents 8.4. Teorema degli Zeri e Teorema di Weierstrass 95 8.5. Ulteriori nozioni sui iti di funzioni. 0 8.6. Asintoto obliquo. 07 8.7. Funzione Inversa. Continuità della funzione inversa.
Studio qualitativo del grafico di una funzione
 Studio qualitativo del grafico di una funzione Obiettivo: ottenere informazioni per descrivere qualitativamente l andamento del grafico di una funzione f campo di esistenza (cioè, l insieme di definizione)
Studio qualitativo del grafico di una funzione Obiettivo: ottenere informazioni per descrivere qualitativamente l andamento del grafico di una funzione f campo di esistenza (cioè, l insieme di definizione)
Analisi matematica I. Confronto locale di funzioni. Simboli di Landau. Infinitesimi ed infiniti Politecnico di Torino 1
 Analisi matematica I Confronto locale di funzioni Infinitesimi ed infiniti 2 2006 Politecnico di Torino 1 Confronto locale di funzioni Definizioni dei simboli di Landau Proprietà dei simboli di Landau
Analisi matematica I Confronto locale di funzioni Infinitesimi ed infiniti 2 2006 Politecnico di Torino 1 Confronto locale di funzioni Definizioni dei simboli di Landau Proprietà dei simboli di Landau
Argomenti svolti. 4. Venerdì 22 ottobre. 2 ora. Un po di logica elementare: proposizioni e loro negazione. Esercizi: 1 Sia. n + 1
 Argomenti svolti.. Lunedì 8 ottobre. ora. Presentazione del corso. Il campo R. Assiomi che riguardano le operazioni e prime loro conseguenze. 2. Martedì 9 ottobre. 2 ore. Annullamento del prodotto. Equazioni.
Argomenti svolti.. Lunedì 8 ottobre. ora. Presentazione del corso. Il campo R. Assiomi che riguardano le operazioni e prime loro conseguenze. 2. Martedì 9 ottobre. 2 ore. Annullamento del prodotto. Equazioni.
Successioni numeriche
 Successioni numeriche Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Successioni Analisi A 1 / 35 Definizione Una successione a valori reali è una funzione f : N R
Successioni numeriche Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Successioni Analisi A 1 / 35 Definizione Una successione a valori reali è una funzione f : N R
Confronto asintotico.
 AMA Ing.Edile - Prof. Colombo 1 Esercitazioni: Francesco Di Plinio - francesco.diplinio@libero.it Le soluzioni (complete) delle esercitazioni 5 e 6 saranno disponibili online a partire da lunedì. Confronto
AMA Ing.Edile - Prof. Colombo 1 Esercitazioni: Francesco Di Plinio - francesco.diplinio@libero.it Le soluzioni (complete) delle esercitazioni 5 e 6 saranno disponibili online a partire da lunedì. Confronto
Limiti di funzioni. Mauro Saita Versione provvisoria. Ottobre 2015
 Limiti di funzioni Mauro Saita e-mail maurosaita@tiscalinet.it Versione provvisoria. Ottobre 2015 Indice 1 Limiti 2 1.1 Definizione di ite................................ 2 1.2 Alcuni teoremi sui iti..............................
Limiti di funzioni Mauro Saita e-mail maurosaita@tiscalinet.it Versione provvisoria. Ottobre 2015 Indice 1 Limiti 2 1.1 Definizione di ite................................ 2 1.2 Alcuni teoremi sui iti..............................
Calcolo infinitesimale
 Calcolo infinitesimale L operazione di limite L operazione di limite ha lo scopo di descrivere il comportamento di una funzione nei pressi di un punto di accumulazione per il suo dominio. Limite finito
Calcolo infinitesimale L operazione di limite L operazione di limite ha lo scopo di descrivere il comportamento di una funzione nei pressi di un punto di accumulazione per il suo dominio. Limite finito
Istituzioni di Matematiche seconda parte
 Istituzioni di Matematiche seconda parte anno acc. 2010/2011 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 26 index 1 2 Continuità Cristina Turrini
Istituzioni di Matematiche seconda parte anno acc. 2010/2011 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 26 index 1 2 Continuità Cristina Turrini
15 LIMITI DI FUNZIONI
 5 LIMITI DI FUNZIONI Estendiamo la nozione di ite a funzioni reali di variabile reale. Definizione (caratterizzazione per successioni) Si ha f(x) = L (x 0, L R) se e solo se per ogni successione a n x
5 LIMITI DI FUNZIONI Estendiamo la nozione di ite a funzioni reali di variabile reale. Definizione (caratterizzazione per successioni) Si ha f(x) = L (x 0, L R) se e solo se per ogni successione a n x
 Limiti di funzioni all infinito (1) lim f(x) = λ R x K>0 : x > K f(x) λ < ε (2) lim f(x) = x M>0 >0 K>0 : x > K f(x) > M (3) lim f(x) = x M>0 >0 K>0 : x > K f(x) < < M Se f(x) è definita in un intorno
Limiti di funzioni all infinito (1) lim f(x) = λ R x K>0 : x > K f(x) λ < ε (2) lim f(x) = x M>0 >0 K>0 : x > K f(x) > M (3) lim f(x) = x M>0 >0 K>0 : x > K f(x) < < M Se f(x) è definita in un intorno
13 LIMITI DI FUNZIONI
 3 LIMITI DI FUNZIONI Estendiamo la nozione di ite a funzioni reali di variabile reale. Definizione caratterizzazione per successioni) Si ha fx) = L x 0, L R) se e solo se per ogni successione a n x 0 con
3 LIMITI DI FUNZIONI Estendiamo la nozione di ite a funzioni reali di variabile reale. Definizione caratterizzazione per successioni) Si ha fx) = L x 0, L R) se e solo se per ogni successione a n x 0 con
Una funzione è continua in un intervallo chiuso e limitato [a,b] se e solo se è continua in ogni punto dell intervallo.
![Una funzione è continua in un intervallo chiuso e limitato [a,b] se e solo se è continua in ogni punto dell intervallo. Una funzione è continua in un intervallo chiuso e limitato [a,b] se e solo se è continua in ogni punto dell intervallo.](/thumbs/100/143663280.jpg) FUNZIONI CONTINUE. PUNTI DI DISCONTINUITA. OPERAZIONI SUI LIMITI. CALCOLO DI LIMITI CHE SI PRESENTANO IN FORMA INDETERMINATA LIMITI NOTEVOLI E APPLICAZIONI Angela Donatiello DEF. di Funzione Continua in
FUNZIONI CONTINUE. PUNTI DI DISCONTINUITA. OPERAZIONI SUI LIMITI. CALCOLO DI LIMITI CHE SI PRESENTANO IN FORMA INDETERMINATA LIMITI NOTEVOLI E APPLICAZIONI Angela Donatiello DEF. di Funzione Continua in
Corso di Analisi Matematica Limiti di funzioni
 Corso di Analisi Matematica Limiti di funzioni Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 39 1 Definizione di ite 2 Il calcolo dei
Corso di Analisi Matematica Limiti di funzioni Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 39 1 Definizione di ite 2 Il calcolo dei
CORSO DI ANALISI MATEMATICA 2 SOLUZIONI ESERCIZI PROPOSTI 11/03/2013
 CORSO DI ANALISI MATEMATICA SOLUZIONI ESERCIZI PROPOSTI /0/0 D.BARTOLUCCI, D.GUIDO ESERCIZIO: Sia 0 R e. Il Polinomio di Taylor I A 0 := {f : U f,0 R : U f,0 è un intorno di 0, f è continua in U f,0 },
CORSO DI ANALISI MATEMATICA SOLUZIONI ESERCIZI PROPOSTI /0/0 D.BARTOLUCCI, D.GUIDO ESERCIZIO: Sia 0 R e. Il Polinomio di Taylor I A 0 := {f : U f,0 R : U f,0 è un intorno di 0, f è continua in U f,0 },
QUINTA LEZIONE (11/11/2009) Argomenti trattati: calcolo di limiti, continuitá di una funzione.
 QUINTA LEZIONE //9) Argomenti trattati: calcolo di iti, continuitá di una funzione. Esercizi svolti. Calcolo di iti Nello svolgere i seguenti iti daremo per assodato la conoscenza di alcuni iti fondamentali:
QUINTA LEZIONE //9) Argomenti trattati: calcolo di iti, continuitá di una funzione. Esercizi svolti. Calcolo di iti Nello svolgere i seguenti iti daremo per assodato la conoscenza di alcuni iti fondamentali:
M174sett.tex. 4a settimana Inizio 22/10/2007. Terzo limite fondamentale (sul libro, p. 113, è chiamato secondo ) lim x 1 x 0 x
 M74sett.te 4a settimana Inizio 22/0/2007 Terzo ite fondamentale (sul libro, p. 3, è chiamato secondo ) e 0 =. La tangente al grafico nel punto (0,0) risulta y = (vedremo poi perché). Ricordare che e è
M74sett.te 4a settimana Inizio 22/0/2007 Terzo ite fondamentale (sul libro, p. 3, è chiamato secondo ) e 0 =. La tangente al grafico nel punto (0,0) risulta y = (vedremo poi perché). Ricordare che e è
MATEMATICA MATEMATICA FINANZIARIA
 MATEMATICA e MATEMATICA FINANZIARIA a.a. 7-8 Corso di laurea in Economia Aziendale Fascicolo n. Limite di funzioni e applicazioni. Limite di una funzione Funzioni continue Calcolo dei iti Asintoti Prof.ssa
MATEMATICA e MATEMATICA FINANZIARIA a.a. 7-8 Corso di laurea in Economia Aziendale Fascicolo n. Limite di funzioni e applicazioni. Limite di una funzione Funzioni continue Calcolo dei iti Asintoti Prof.ssa
x 3 2x 2 + 6x x 4 3x = lim x(6 2x + x 2 ) x( 3 + x 3 ) (6 2x + x 2 ) ( 3 + x 3 ) = lim = 2
 Calcolo di forme indeterminate del tipo 0/0 Quando si deve calcolare il limite di rapporto di funzioni infintesime per x 0, si raccoglie la potenza di x al minimo esponente. Es. lim x 0 x 3 2x 2 + 6x x
Calcolo di forme indeterminate del tipo 0/0 Quando si deve calcolare il limite di rapporto di funzioni infintesime per x 0, si raccoglie la potenza di x al minimo esponente. Es. lim x 0 x 3 2x 2 + 6x x
Limiti di funzioni di due variabili
 Limiti di funzioni di due variabili Definizione 1 Sia f : A R 2 R e x 0 = (x 0, y 0 ) punto di accumulazione di A. Diciamo che se e solo se Diciamo che se e solo se f(x) = f(x, y) = L x x 0 (x,y) (x 0,y
Limiti di funzioni di due variabili Definizione 1 Sia f : A R 2 R e x 0 = (x 0, y 0 ) punto di accumulazione di A. Diciamo che se e solo se Diciamo che se e solo se f(x) = f(x, y) = L x x 0 (x,y) (x 0,y
CORSO DI LAUREA IN FISICA
 CORSO DI LAUREA IN FISICA ANALISI MATEMATICA I BREVI RICHIAMI DELLA TEORIA DEI LIMITI. Confronto di infinitesimi. Sia A sottoinsieme di R, sia 0 punto di accumulazione di A nella topologia di R quindi
CORSO DI LAUREA IN FISICA ANALISI MATEMATICA I BREVI RICHIAMI DELLA TEORIA DEI LIMITI. Confronto di infinitesimi. Sia A sottoinsieme di R, sia 0 punto di accumulazione di A nella topologia di R quindi
IIID Matematica Aprile ) Cosa significa dire che una funzione reale di variabile reale è continua?
 1) Cosa significa dire che una funzione reale di variabile reale è continua? 2) Dire se la funzione f(x) = x x 2 5 è a continua per x = 5 ; b continua per x = 3 ; c continua per x = π 2 ; 3) Cosa si intente
1) Cosa significa dire che una funzione reale di variabile reale è continua? 2) Dire se la funzione f(x) = x x 2 5 è a continua per x = 5 ; b continua per x = 3 ; c continua per x = π 2 ; 3) Cosa si intente
Funzioni continue. Hynek Kovarik. Università di Brescia. Analisi Matematica 1
 Funzioni continue Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 1 / 44 Funzioni continue Definizione Siano f : A
Funzioni continue Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 1 / 44 Funzioni continue Definizione Siano f : A
tele limite è unico. Ciò significa che se non può accadere che una funzione abbia limiti diversi per x. Se per assurdo si avesse che lim f ( x)
 Calcolo dei iti (C. DIMAURO) Per il calcolo dei iti ci serviamo di alcuni teoremi. Tali teoremi visti nel caso in cui, valgono anche quando Teorema dell unicità del ite: se una funzione ammette ite per
Calcolo dei iti (C. DIMAURO) Per il calcolo dei iti ci serviamo di alcuni teoremi. Tali teoremi visti nel caso in cui, valgono anche quando Teorema dell unicità del ite: se una funzione ammette ite per
1 - CONFRONTO LOCALE: I SIMBOLI DI LANDAU
 - CONFRONTO LOCALE: I SIMBOLI DI LANDAU Nello studio del comportamento di una funzione vicino ad un punto x 0, dopo aver visto se la funzione ammette ite (finito, nullo o infinito), per x x 0, può interessare
- CONFRONTO LOCALE: I SIMBOLI DI LANDAU Nello studio del comportamento di una funzione vicino ad un punto x 0, dopo aver visto se la funzione ammette ite (finito, nullo o infinito), per x x 0, può interessare
Teorema degli zeri. Essendo f continua in a e in b, per il teorema della
 Teorema degli zeri Una funzione reale f continua nell intervallo chiuso e itato [a; b] che assuma valori di segno opposto negli estremi di tale intervallo, si annulla in almeno un punto ad esso interno
Teorema degli zeri Una funzione reale f continua nell intervallo chiuso e itato [a; b] che assuma valori di segno opposto negli estremi di tale intervallo, si annulla in almeno un punto ad esso interno
Argomento delle lezioni del corso di Analisi A.A
 Argomento delle lezioni del corso di Analisi A.A.2011-2012 30 gennaio 2012 Lezione 1-2 (5 ottobre 2011) Numeri naturali, interi, razionali. Definizione intuitiva dei reali attraverso la retta. Definizione
Argomento delle lezioni del corso di Analisi A.A.2011-2012 30 gennaio 2012 Lezione 1-2 (5 ottobre 2011) Numeri naturali, interi, razionali. Definizione intuitiva dei reali attraverso la retta. Definizione
Analisi Matematica 1+2
 Università degli Studi di Genova Facoltà di Ingegneria - Polo di Savona via Cadorna 7-700 Savona Tel. +39 09 264555 - Fax +39 09 264558 Ingegneria Gestionale Analisi Matematica +2 A.A 998/99 - Prove parziali
Università degli Studi di Genova Facoltà di Ingegneria - Polo di Savona via Cadorna 7-700 Savona Tel. +39 09 264555 - Fax +39 09 264558 Ingegneria Gestionale Analisi Matematica +2 A.A 998/99 - Prove parziali
UNIVERSITA DEL SALENTO CORSO DI LAUREA IN MATEMATICA Prova scritta di ANALISI MATEMATICA I 19/01/09
 UNIVERSITA DEL SALENTO Prova scritta di ANALISI MATEMATICA I 19/01/09 1 Determinare sup/inf max/min) e insieme dei punti di accumulazione del seguente insieme: E = {x R e x 5e x + 6) arctan x 1 x) < 1}
UNIVERSITA DEL SALENTO Prova scritta di ANALISI MATEMATICA I 19/01/09 1 Determinare sup/inf max/min) e insieme dei punti di accumulazione del seguente insieme: E = {x R e x 5e x + 6) arctan x 1 x) < 1}
Limite Destro Finito
 Limite Destro Finito Quando la variabile assume valori via via più vicini ad a (ma sempre maggiori di a), i corrispondenti valori di f() si avvicinano sempre più al valore L. y scelta di ε y = f () y scelta
Limite Destro Finito Quando la variabile assume valori via via più vicini ad a (ma sempre maggiori di a), i corrispondenti valori di f() si avvicinano sempre più al valore L. y scelta di ε y = f () y scelta
CORSO DI LAUREA IN MATEMATICA
 CORSO DI LAUREA IN MATEMATICA ESERCITAZIONI DI ANALISI MATEMATICA I BREVI RICHIAMI DELLA TEORIA DEI LIMITI. Confronto di infinitesimi. Sia A sottoinsieme di R, sia 0 punto di accumulazione di A nella topologia
CORSO DI LAUREA IN MATEMATICA ESERCITAZIONI DI ANALISI MATEMATICA I BREVI RICHIAMI DELLA TEORIA DEI LIMITI. Confronto di infinitesimi. Sia A sottoinsieme di R, sia 0 punto di accumulazione di A nella topologia
Ricorrendo alle definizioni di limite, si dimostrano importanti risultati. Vedremo: che, se esiste, il limite lim
 Teoremi sui limiti Ricorrendo alle definizioni di limite, si dimostrano importanti risultati. Vedremo: che, se esiste, il limite lim f () può dare informazioni locali (= che valgono nell intorno di c)
Teoremi sui limiti Ricorrendo alle definizioni di limite, si dimostrano importanti risultati. Vedremo: che, se esiste, il limite lim f () può dare informazioni locali (= che valgono nell intorno di c)
APPUNTI DI MATEMATICA: I limiti e la continuità Le derivate. Prof. ssa Prenol R.
 APPUNTI DI MATEMATICA: I iti e la continuità Le derivate Prof. ssa Prenol R. INTERVALLI e INTORNI Definizione di intervallo: è un sottoinsieme di numeri reali e può essere - ilitato: graficamente viene
APPUNTI DI MATEMATICA: I iti e la continuità Le derivate Prof. ssa Prenol R. INTERVALLI e INTORNI Definizione di intervallo: è un sottoinsieme di numeri reali e può essere - ilitato: graficamente viene
Dimostrazione. Indichiamo con α e β (finiti o infiniti) gli estremi dell intervallo I. Poniamo
 C.6 Funzioni continue Pag. 114 Dimostrazione del Corollario 4.25 Corollario 4.25 Sia f continua in un intervallo I. Supponiamo che f ammetta, per x tendente a ciascuno degli estremi dell intervallo, iti
C.6 Funzioni continue Pag. 114 Dimostrazione del Corollario 4.25 Corollario 4.25 Sia f continua in un intervallo I. Supponiamo che f ammetta, per x tendente a ciascuno degli estremi dell intervallo, iti
y = x 3 infinitesimo per x 3 lim = l 0 allora f(x) è dello stesso ordine di g(x), ossia tendono a DEF. Una funzione y = f(x) si dice infinitesimo per
 INFINITI ED INFINITESIMI. ASINTOTI DI UNA FUNZIONE. GRAFICO PROBABILE DI UNA FUNZIONE. TEOREMI SULLE FUNZIONI CONTINUE ESERCIZI SULLA CONTINUITA E SULLA CLASSIFICAZIONE DELLE DISCONTINUITA DI UNA FUNZIONE
INFINITI ED INFINITESIMI. ASINTOTI DI UNA FUNZIONE. GRAFICO PROBABILE DI UNA FUNZIONE. TEOREMI SULLE FUNZIONI CONTINUE ESERCIZI SULLA CONTINUITA E SULLA CLASSIFICAZIONE DELLE DISCONTINUITA DI UNA FUNZIONE
Argomento 6 Derivate
 Argomento 6 Derivate Derivata in un punto Definizione 6. Data una funzione f definita su un intervallo I e 0 incrementale di f in 0 di incremento h = 0 = il rapporto I, si chiama rapporto per = 0 + h =
Argomento 6 Derivate Derivata in un punto Definizione 6. Data una funzione f definita su un intervallo I e 0 incrementale di f in 0 di incremento h = 0 = il rapporto I, si chiama rapporto per = 0 + h =
Istituzioni di Matematiche terza parte
 Istituzioni di Matematiche terza parte anno acc. 2011/2012 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 35 index Il concetto di limite 1 Il
Istituzioni di Matematiche terza parte anno acc. 2011/2012 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 35 index Il concetto di limite 1 Il
Successioni numeriche
 Successioni numeriche Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Successioni Analisi Matematica 1 1 / 48 Definizione Una successione a valori reali è
Successioni numeriche Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Successioni Analisi Matematica 1 1 / 48 Definizione Una successione a valori reali è
Svolgimento degli esercizi del Capitolo 1
 Analisi Matematica a edizione Svolgimento degli esercizi del Capitolo a) Si ha perciò si distinguono due casi: I) se x < 7,siha x 7 se x 7 x 7 7 x se x < 7, x 7 7 x x x 5 x 5, e poiché 5 > 7 la disequazione
Analisi Matematica a edizione Svolgimento degli esercizi del Capitolo a) Si ha perciò si distinguono due casi: I) se x < 7,siha x 7 se x 7 x 7 7 x se x < 7, x 7 7 x x x 5 x 5, e poiché 5 > 7 la disequazione
Continuità di funzioni
 Continuità di funzioni Annalisa Cesaroni, Paola Mannucci e Alvise Sommariva Università degli Studi di Padova Dipartimento di Matematica 2 novembre 2015 Annalisa Cesaroni, Paola Mannucci e Alvise Sommariva
Continuità di funzioni Annalisa Cesaroni, Paola Mannucci e Alvise Sommariva Università degli Studi di Padova Dipartimento di Matematica 2 novembre 2015 Annalisa Cesaroni, Paola Mannucci e Alvise Sommariva
( x) ( ) = lim. x = = lim. lim. lim. lim = = + sin. lim 1 = lim + +
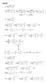 Esercizi 9 6 6 6 9 pongo quindi 5 5 5 Pongo e e Pongo e e [ ln ln ] ln [ ln ln ] ln ln ln cos ln cos ln ln cos,7,69,6 ln ln, 7 ln 5,69 ln ln cos ln ln ln e Calcolare il dominio e gli eventuali atoti verticali
Esercizi 9 6 6 6 9 pongo quindi 5 5 5 Pongo e e Pongo e e [ ln ln ] ln [ ln ln ] ln ln ln cos ln cos ln ln cos,7,69,6 ln ln, 7 ln 5,69 ln ln cos ln ln ln e Calcolare il dominio e gli eventuali atoti verticali
Corso di Laurea in Scienze Biologiche Prova in Itinere di Matematica 20/12/2006
 Corso di Laurea in Scienze Biologiche Prova in Itinere di Matematica 20/2/2006 COGNOME NOME MATRICOLA.) Determinare 2. + 2 Possibile svolgimento. Il ite proposto si presenta nella forma indeterminata [
Corso di Laurea in Scienze Biologiche Prova in Itinere di Matematica 20/2/2006 COGNOME NOME MATRICOLA.) Determinare 2. + 2 Possibile svolgimento. Il ite proposto si presenta nella forma indeterminata [
Funzioni di più variabli: dominio, limiti, continuità
 Funzioni di più variabli: dominio, limiti, continuità Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Funzioni di più variabli Analisi Matematica B 1 /
Funzioni di più variabli: dominio, limiti, continuità Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Funzioni di più variabli Analisi Matematica B 1 /
Funzioni di più variabli: dominio, limiti, continuità
 Funzioni di più variabli: dominio, limiti, continuità Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Funzioni di più variabli Analisi Matematica B 1 /
Funzioni di più variabli: dominio, limiti, continuità Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Funzioni di più variabli Analisi Matematica B 1 /
Analisi Matematica 1 Soluzioni prova scritta n. 1
 Analisi Matematica Soluzioni prova scritta n Corso di laurea in Matematica, aa 008-009 5 giugno 009 Sia a n la successione definita per ricorrenza: a n+ 3 a n a 3 n, a 3 a n+ 3 a n a 3 n, a 3 a n+ 3 a
Analisi Matematica Soluzioni prova scritta n Corso di laurea in Matematica, aa 008-009 5 giugno 009 Sia a n la successione definita per ricorrenza: a n+ 3 a n a 3 n, a 3 a n+ 3 a n a 3 n, a 3 a n+ 3 a
Correzione del secondo compitino di Analisi 1 e 2 A.A. 2014/2015
 Correzione del secondo compitino di Analisi e 2 AA 20/205 Luca Ghidelli, Giovanni Paolini, Leonardo Tolomeo febbraio 206 Esercizio Testo Dire per quali valori del parametro reale α, < α 3, la funzione
Correzione del secondo compitino di Analisi e 2 AA 20/205 Luca Ghidelli, Giovanni Paolini, Leonardo Tolomeo febbraio 206 Esercizio Testo Dire per quali valori del parametro reale α, < α 3, la funzione
ESERCIZI SUI PUNTI DI NON DERIVABILITÀ TRATTI DA TEMI D ESAME
 ESERCIZI SUI PUNTI DI NON DERIVABILITÀ TRATTI DA TEMI D ESAME a cura di Michele Scaglia FUNZIONI DERIVABILI Sia f : domf R una funzione e sia 0 domf di accumulazione per domf Chiamiamo derivata prima di
ESERCIZI SUI PUNTI DI NON DERIVABILITÀ TRATTI DA TEMI D ESAME a cura di Michele Scaglia FUNZIONI DERIVABILI Sia f : domf R una funzione e sia 0 domf di accumulazione per domf Chiamiamo derivata prima di
CALCOLO DEI LIMITI = =
 CALCOLO DEI LIMITI Tenendo conto dei teoremi dei iti e delle proprietà simboliche dell infinito è possibile calcolare il risultato di diversi tipi di ite. Negli esercizi di questo tipo si sostituisce alla
CALCOLO DEI LIMITI Tenendo conto dei teoremi dei iti e delle proprietà simboliche dell infinito è possibile calcolare il risultato di diversi tipi di ite. Negli esercizi di questo tipo si sostituisce alla
15. Funzioni continue: esercizi
 15. Funzioni continue: esercizi Esercizio 15.7. Data la funzione f : R f(r) con legge α se 0 f() = β 2 se > 0, 1. dire se per α = β = 1 la funzione è invertibile e, in caso affermativo, determinare dominio,
15. Funzioni continue: esercizi Esercizio 15.7. Data la funzione f : R f(r) con legge α se 0 f() = β 2 se > 0, 1. dire se per α = β = 1 la funzione è invertibile e, in caso affermativo, determinare dominio,
Nota: A meno che non sia specificato diversamente, si intende che i teoremi, lemmi, proposizioni sotto menzionati siano stati dimostrati a lezione.
 Programma di Analisi Matematica 1 (Canale ICM) svolto per lezioni - A. Languasco - C. Vagnoni 1 Nota: A meno che non sia specificato diversamente, si intende che i teoremi, lemmi, proposizioni sotto menzionati
Programma di Analisi Matematica 1 (Canale ICM) svolto per lezioni - A. Languasco - C. Vagnoni 1 Nota: A meno che non sia specificato diversamente, si intende che i teoremi, lemmi, proposizioni sotto menzionati
Argomento 3 Limiti e calcolo dei limiti I
 Argomento 3 Limiti e calcolo dei iti I Distanza e intorni In tutta la trattazione che segue si parlerà indistintamente di un numero reale o del corrispondente punto sulla retta euclidea (vedi Arg.). Definizione
Argomento 3 Limiti e calcolo dei iti I Distanza e intorni In tutta la trattazione che segue si parlerà indistintamente di un numero reale o del corrispondente punto sulla retta euclidea (vedi Arg.). Definizione
Funzioni continue. quando. se è continua x I.
 Funzioni continue Definizione: f() si dice continua in 0 D f quando (*) 0 f () f ( 0 ) Definizione: f() si dice continua in I D f se è continua I. Avevamo già dato questa definizione parlando del f ().
Funzioni continue Definizione: f() si dice continua in 0 D f quando (*) 0 f () f ( 0 ) Definizione: f() si dice continua in I D f se è continua I. Avevamo già dato questa definizione parlando del f ().
8. Il teorema dei due carabinieri
 8. Il teorema dei due carabinieri Teorema del confronto (o dei due carabinieri) Consideriamo due funzioni f( ), g( ) per le quali risulti, in un punto di accumulazione per i loro domini : f ( ) g( ) Se
8. Il teorema dei due carabinieri Teorema del confronto (o dei due carabinieri) Consideriamo due funzioni f( ), g( ) per le quali risulti, in un punto di accumulazione per i loro domini : f ( ) g( ) Se
Capitolo 7. Studio di funzione
 Capitolo 7 Studio di funzione Consideriamo una funzione f : (a, b) R R. Abbiamo che 0 (a, b) è un punto di minimo relativo se esiste un intorno I( 0 ) (a, b) tale che f() f( 0 ) per ogni I( 0 ). massimo
Capitolo 7 Studio di funzione Consideriamo una funzione f : (a, b) R R. Abbiamo che 0 (a, b) è un punto di minimo relativo se esiste un intorno I( 0 ) (a, b) tale che f() f( 0 ) per ogni I( 0 ). massimo
CAPITOLO VI LIMITI DI FUNZIONI
 CAPITOLO VI LIMITI DI FUNZIONI. CONCETTO DI LIMITE Esula dallo scopo di questo libro la trattazione della teoria sui iti. Tuttavia, pensando di fare cosa gradita allo studente, che deve possedere questa
CAPITOLO VI LIMITI DI FUNZIONI. CONCETTO DI LIMITE Esula dallo scopo di questo libro la trattazione della teoria sui iti. Tuttavia, pensando di fare cosa gradita allo studente, che deve possedere questa
Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 2 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata, Matematica
 DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 2 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 2 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
Simboli di Landau. Equivalenza. Esempi (limiti notevoli).
 Simboli di Landau Conducono ad un algebra snella e significativa per il calcolo di iti Procurano un linguaggio tecnico per confrontare il comportamento di due funzioni nell intorno bucato di c (comportamento
Simboli di Landau Conducono ad un algebra snella e significativa per il calcolo di iti Procurano un linguaggio tecnico per confrontare il comportamento di due funzioni nell intorno bucato di c (comportamento
Infiniti e infinitesimi col simbolo di Laudau
 E Infiniti e infinitesimi col simbolo di Laudau Nel capitolo dedicato ai iti abbiamo osservato che, quando esiste, il ite del rapporto di due successioni entrambe divergenti o entrambe infinitesime può
E Infiniti e infinitesimi col simbolo di Laudau Nel capitolo dedicato ai iti abbiamo osservato che, quando esiste, il ite del rapporto di due successioni entrambe divergenti o entrambe infinitesime può
Grafico delle funzioni elementari
 Grafico delle funzioni elementari Funzione lineare y = m + q m, q R C.E. R Non Limitata Funzione valore assoluto y= C.E. R Limitata inferiormente in = 3 Funzione potenza y = n, n N, pari C.E. R Limitata
Grafico delle funzioni elementari Funzione lineare y = m + q m, q R C.E. R Non Limitata Funzione valore assoluto y= C.E. R Limitata inferiormente in = 3 Funzione potenza y = n, n N, pari C.E. R Limitata
Matematica A Corso di Laurea in Chimica. Prova scritta del Tema A
 Matematica A Corso di Laurea in Chimica Prova scritta del 7..6 Tema A P) Data la funzione f(x) = ex+ x determinarne (a) campo di esistenza; (b) zeri e segno; (c) iti agli estremi del campo di esistenza
Matematica A Corso di Laurea in Chimica Prova scritta del 7..6 Tema A P) Data la funzione f(x) = ex+ x determinarne (a) campo di esistenza; (b) zeri e segno; (c) iti agli estremi del campo di esistenza
Prefazione LUCIANO ROMANO
 3 Prefazione Il testo, rivolto agli studenti universitari che si apprestano ad affrontare l esame di Analisi Matematica, propone un iniziale parte teorica e suggerimenti sulla risoluzione della vasta gamma
3 Prefazione Il testo, rivolto agli studenti universitari che si apprestano ad affrontare l esame di Analisi Matematica, propone un iniziale parte teorica e suggerimenti sulla risoluzione della vasta gamma
3 LIMITI. 3.1 Operazioni in R {± } x R x + (+ ) = + x + ( ) = x + = 0 x. x R = 0. x > 0 x (+ ) = + x ( ) = x < 0 x (+ ) = x ( ) = = x.
 3 LIMITI 3. Operazioni in R {± } R + (+ ) = + + ( ) = R + = 0 = 0 > 0 (+ ) = + ( ) = < 0 (+ ) = ( ) = + > 0 0 + = + 0 = < 0 0 + = 0 = + (+ ) + (+ ) = + ( ) + ( ) = (+ ) (+ ) = + (+ ) ( ) = Non è possibile
3 LIMITI 3. Operazioni in R {± } R + (+ ) = + + ( ) = R + = 0 = 0 > 0 (+ ) = + ( ) = < 0 (+ ) = ( ) = + > 0 0 + = + 0 = < 0 0 + = 0 = + (+ ) + (+ ) = + ( ) + ( ) = (+ ) (+ ) = + (+ ) ( ) = Non è possibile
Soluzioni delle Esercitazioni V 15-19/10/ x 1 = = /x + = 0. 1+e x = 1. lnx 1+1/x = = = +.
 Soluzioni delle Esercitazioni V 5-9/0/208 A. Limiti I iti che seguono si possono calcolare con l algebra dei iti. 2 3 4 5 6 7 8 9 0 +2 3 = +2 3 = 3 2. e = ) e = e. / + = 0 + = 0 + = 0. +e = +0 = = 0. +/
Soluzioni delle Esercitazioni V 5-9/0/208 A. Limiti I iti che seguono si possono calcolare con l algebra dei iti. 2 3 4 5 6 7 8 9 0 +2 3 = +2 3 = 3 2. e = ) e = e. / + = 0 + = 0 + = 0. +e = +0 = = 0. +/
