Successioni di funzioni
|
|
|
- Rosalinda Danieli
- 7 anni fa
- Visualizzazioni
Transcript
1 Successioi di fuzioi Defiizioe. U successioe di fuzioi f : A R, N coverge putulmete d u fuzioe f : A R se f (x) = f(x) per ogi x A. L successioe coverge uiformemete d f se ccde che per ogi > 0 esiste N tle che per ogi > risult f (x) f(x) <. Dll ultim relzioe è evidete che se u successioe di fuzioi coverge uiformemete l suo ite, llor coverge che putulmete. Tuttvi esistoo successioi di fuzioi, come vedremo tr poco, che covergoo putulmete m o uiformemete. Come l solito, el liguggio mtemtico il termie uiforme st d idicre che qulcuo dei prmetri i gioco o dipede dll zo di spzio i cui ci si trov; el cso dell covergez uiforme, l idice di vvicimeto tr f (x) e f(x) è uiforme, cioè o dipede d dove sitrov il puto x (è cioè lo stesso per tutti gli x A). Il primo risultto utile è u formulzioe equivlete dell covergez uiforme. Proposizioe 1. Si f : X R, N u successioe di fuzioi; soo equivleti i. f coverge uiformemete f ii. sup f (x) f(x) = 0 x X Dimostrzioe. Provimo l impliczioe i. = ii. Per defiizioe sppimo che, comuque fissto > 0 esiste N tle che per ogi x X risult f (x) f(x) < ; pertto, posto M = sup f (x) f(x) si h che M per > e quidi x X è soddisftt l defiizioe di ite dell ii. Provimo or l impliczioe ii. = i. I questo cso sppimo che, comuque scelto > 0 esiste N tle che per ogi > risult M < ; dto che M = sup f (x) f(x), mggior rgioe, per > si vrà f (x) f(x) < x X per tutti gli x X e questo prov l uiforme cotiuità. L rgioe per cui si itroduce l ozioe di covergez uiforme, è che l sol covergez putule o permette ll fuzioe ite di ereditre lcue buoe proprietà delle fuzioi pprossimti, d esempio l ittezz, l cotiuità, l Riem itegrbilità: forimo tre cotroesempi i tl seso. Esempi 1. Il primo esempio è quello di u successioe[ di fuzioi itte che coverge putulmete d u fuzioe ilitt: si cosideri i 0, π [ l successioe di fuzioi defiit d 2 [ t x se x 0, π 2 1 ] f (x) = t ( π 2 ) 1 ltrove [ Allor f (x) coverge putulmete f(x) = t x, che o è itt i 0, π [. 2 1
2 2. L esempio clssico di successioe di fuzioi cotiue putulmete covergete d u fuzioe o cotiu è il seguete: si cosideri f : [0; 1] R defiit d f (x) = x. L successioe di queste fuzioi coverge putulmete ll fuzioe { 0 se x [0; 1[ f(x) = 1 se x = 1 che o è cotiu i [0, 1]. 3. Per quto rigurd l mcz di coservzioe dell itegrbilità ll Riem, cosiderimo le fuzioi f : [0; 1] R defiite d 0 se x = ] 0 se x 0, 1 ] f (x) = ] ] 1 1 x sex, 1 I questo modo ogi f differisce el solo puto 0 d u fuzioe cotiu, ed è pertto itegrbile ll Riem, m l fuzioe ite o è itegrbile i [0, 1]. f(x) = { 0 se x = 0 1 x se x ]0, 1] Al cotrrio, l covergez uiforme grtisce l coservzioe delle proprietà, come si dimostr ei segueti tre teoremi Proposizioe 2. (coservzioe dell ittezz) Si f : X R, N, u successioe di fuzioi itte uiformemete covergete f; llor f è itt. Dimostrzioe. Dll Proposizioe precedete possimo fissre N i mier tle che Allor, per > sup f (x) f(x) 1. x X f(x) = f(x) f (x) + f (x) f (x) + f(x) f (x) 1 + f (x) e per ipotesi l ultimo membro è itto, quidi che f lo è. Proposizioe 3.(coservzioe dell cotiuità) Si f : X R, N, u successioe di fuzioi uiformemete covergete f, e si x o X u puto i cui f è cotiu per ogi N; llor f è cotiu i x o. Dimostrzioe. Dobbimo provre che per ogi itoro (cetrto) di f(x o ) esiste u itoro (cetrto) di x o l cui immgie trmite f cde ell iteoro di f(x o ) fissto, ovvero che per ogi > 0 esiste δ() > 0 tle che per ogi x X [x o δ, x o + δ] risult f(x) f(x o ) <. Di uovo grzie ll prim Proposizioe possimo trovre N tle che per ogi > risulti sup f (x) f(x), ( x X 3 ; per l cotiuità per esempio di f +1 i x o, possimo trovre δ > 0 tle 3) 2
3 che per ogi x X ]x o δ, x o + δ[ risulti f +1 (x) f +1 (x o ) < 3. Combido queste due codizioi si h, per x X ]x o δ, x o + δ[ f(x) f(x o ) f(x) f +1 (x) + f +1 (x) f +1 (x o ) + f +1 (x o ) f(x o ) < = che è quto itedevmo dimostrre. Proposizioe 4. (coservzioe dell itegrbilità) Si f : [, b] R u successioe di fuzioi itegrbili ll Riem, uiformemete covergete f; llor che f è itegrbile ll Riem. ( Dimostrzioe. Fissto > 0, si N determito dll uiforme covergez, e 4(b ) si > fissto; poichè f è itegrbile ll Riem, per il Criterio di itegrbilità, esiste u divisioe D di [, b] tle che S(f, D ) s(f, D ) < 2. Si per esempio D = { = x o < x 1 < < x k = b}, e cosiderimo le fuzioi grdit if{f (x), x [x o, x 1 [} 4(b ), se x [x o, x 1 [ s(x) = if{f (x), x [x 1, x 2 [} 4(b ), se x [x 1, x 2 [... if{f (x), x [x k 1, x k ]} sup{f (x), x [x o, x 1 [} + 4(b ), se x [x k 1, x k ] 4(b ), se x [x o, x 1 [ t(x) = sup{f (x), x [x 1, x 2 [} + 4(b ), se x [x 1, x 2 [ È evidete che e che e quidi che... sup{f (x), x [x k 1, x k ]} + s(x) f (x) 4(b ), se x [x k 1, x k ]. 4(b ) < f(x) < f (x) + 4(b ) t(x) [t(x) s(x)]dx = S(f, D ) s(f, D ) + 2 (b ) = 4(b ) S(f, D ) s(f, D ) Per il Criterio di Riem quidi f è itegrbile. [t(x) s(x)]dx <. Il prossimo risultto forisce u utile criterio per dedurre dll covergez putule l covergez uiforme di u successioe di fuzioi 3
4 Teorem di Dii. Se f : [, b] R è u successioe mootó di fuzioi cotiue che coverge putulmete d u fuzioe cotiu, llor l covergez è uiforme. Teorem di pssggio l ite sotto il sego di itegrle. Si f : [, b] R u successioe di fuzioi itegrbili ll Riem, uiformemete covergete f. Allor f(x)dx = f (x)dx. Dimostrzioe. Per il Teorem del modulo si h f(x)dx f (x)dx f (x) f(x) dx e per l covergez uiforme risult f (x) f(x) dx (b ) defiitivmete; per l rbitrrietà di si h l sserto. I reltà si può otteere u risultto più geerle di Pssggio l ite sotto il sego di itegrle Teorem. Si f : [, b] R u successioe di fuzioi itegrbili covergete putulmete d u fuzioe itegrbile f, e suppoimo che sup sup x [,b] f (x) < + (si dice che l successioe è equiitt). Allor f(x)dx = f (x)dx. Osservimo che sez l ipotesi di equiittezz il risultto o sussiste; si cosiderio d esempio le fuzioi f : [0, 1] R defiite d [ ] x se x 0, 2 ( f (x) = 2 2 x 1 ) [ 1 se x 2 2, 1 ] 0 ltrove Risult (f ) covergete putulmete 0, m 1 0 f (x)dx = 1 2 per ogi N. Dll ultimo Teorem si può ifie dedurre u ulteriore Proposizioe di pssggio l ite sotto il sego di itegrle 4
5 Teorem. Si f : [, b] R u successioe mootó di fuzioi itegrbili covergete putulmete d u fuzioe itegrbile f; llor f(x)dx = f (x)dx. Dimostrzioe. Suppoimo per esempio che l successioe si o decrescete, e quidi, per ogi x [, b] f (x) f +1 (x)... f(x). Posto ϕ (x) = f(x) f (x), ogi ϕ è itegrbile, e, posto M = sup f (x) e M = sup f(x), x [,b] x [,b] risult M m + m 1 e quidi ϕ (x) f(x) + f (x) 2M + M 1 che prov che le ϕ (x) soo equiitte. Ifie l successioe (ϕ ) coverge putulmete 0; quidi e questo prov l sserto. ϕ (x)dx = 0 Più delicto è ivece il discorso qudo si trtt di pssre l ite sotto il sego di derivzioe. I questo cso emmeo l covergez uiforme di u successioe di fuzioi di clsse C 1 è sufficiete grtire l covergez delle derivte, come mostr il seguete cotroesempio. Si f : R R defiit d f (x) = x ; si provi che ess coverge uiformemete ll fu- zioe x. Si può tuttvi provre che Teorem. Se f C 1 (I), dove I è u itervllo perto (itto o o) i R, è uiformemete covergete f, e se che l successioe delle derivte f coverge uiformemete, llor f C 1 (I) e f è il ite uiforme di (f ). Serie di fuzioi Il cocetto di covergez si trsferisce che lle serie di fuzioi, duque u serie di fuzioi f (x) puó covergere putulmete o uiformemete, secod che coverg putulmete o uiformemete l successioe di fuzioi s (x) = f 1 (x) + + f (x). Provimo izitutto l seguete codizioe ecessri per l covergez uiforme Proposizioe. Se l serie di fuzioi f (x) coverge uifomemete i A, llor (f ) coverge uiformemete 0 i A. Dimostrzioe. Iftti f (x) = s (x) s 1 (x) e poiché (s (x)) coverge uiformemete ll fuzioe somm S(x), si h l sserto. Dt l importz dell covergez uiforme, per le serie occorre pprotre dei criteri d hoc per verificrl, i quto per le serie si verific il problem che i geerle o si cooscoo é 5
6 l espressioe di s é quell dell somm S. Quello che segue é u criterio sufficiete per l covergez uiforme dell serie Teorem (Criterio di Weierstrss) Si f : A R u successioe di fuzioi tli che, posto M = sup f (x), l serie M coverge. Allor l serie f (x) coverge uiformemete i x A A. Dimostrzioe. Itto osservimo che per ogi x A l serie f (x) coverge ssolutmete, e quidi che putulmete. Si S(x) l somm dell serie. Provimo che l successioe delle somme przili s (x) coverge uiformemete S. Fissto > 0, esiste certmete o N tle che = o M ; iftti, posto σ l somm dell serie M, e dette t le sue somme przili, si h (σ t ) = 0. Bst llor osservre che σ t = M k. Per > o bbimo llor S(x) s (x) = ovvero k=+1 S(x) s (x) = 0. k=+1 f k (x) k=+1 f k (x) k=+1 M k k= o+1 M k Il Criterio di Weierstrss ispir quidi l seguete defiizioe Defiizioe. L serie di fuzioi f (x) si dice totlmete covergete i A se posto M = sup f (x), x A l serie M coverge. Dicimo che l serie di fuzioi putulmete. f (x) coverge ssolutmete se l serie f (x) coverge Ifie si ho i segueti due criteri di itegrzioe e derivzioe per serie. Teorem (Itegrzioe per serie) Si f : [, b] R u successioe di fuzioi cotiue i [, b], tle che l serie f (x) coverge uiformemete ll fuzioe S(x); llor S(x)dx = f (x)dx. 6
7 Teorem (Derivzioe per serie) Si f C 1 ([, b]) u successioe tle che l serie f (x) coverge putulmete S(x) e l serie coverge uiformemete S C 1 ([, b]) ed ifie S (x) = per x [, b]. f (x) coverge uiformemete; llor l serie f (x) f (x) Serie di poteze Defiizioe. Dt u successioe di umeri reli ( ), se f (x) = x, N l serie di fuzioi f (x) è dett serie di poteze. =0 Come vedremo, l isieme X di covergez di u serie di poteze può ricdere i u sol delle segueti ctegorie: - X = {0}; - X è u itervllo simmetrico di R (co o sez uo o etrmbe gli estremi); - X = R. Stbio dpprim questo risultto Lemm di Abel. Se l serie di poteze x (1) =0 coverge per qulche x o 0, llor coverge i ogi itervllo chiuso e itto coteuto i ] x o, x o [. Dimostrzioe. Dlle ipotesi si h itto x o = 0 e quidi tle successioe è itt; esiste cioè M > 0 tle che x o M per ogi N. Si x ] x o, x o [; provimo che l serie (1) coverge totlmete i [ x, x ]; d qui discederà l eucito,perchè ogi itervllo chiuso coteuto i ] x o, x o [ (che o simmetrico) è sempre coteuto i u itervllo simmetrico chiuso, su volt coteuto i ] x o, x o [. Per ogi y R co y x risult ( ) y ( ) x y = x o M, x o x o 7
8 per ogi N ed il termie i pretesi tode destr dell cte di disuguglize è il termie geerle di u serie geometric di rgioe miore di uo. All luce del Lemm di Abel è rgioevole porre l seguete Defiizioe. Si chim rggio di covergez dell serie di poteze (1) l estremo superiore dell isieme dove l serie stess coverge, ovvero ρ = sup X. Se ρ = 0, l serie (1) coverge solo per x = 0, metre se ρ = + l serie coverge i ogi x R. Teorem del rggio di covergez. Si 0 < ρ < +. Allor ρ è il rggio di covergez dell serie (1) se e solo se ess coverge per x < ρ e o coverge per x > ρ. Dimostrzioe. Comicimo co l prte ecessri del Criterio; suppoimo quidi che ρ si il rggio di covergez dell serie, e mostrimo itto che l serie coverge i ogi x tle che x < ρ. Fissimo u tle x; per l defiizioe di estremo superiore, esiste x o X co x < x o < ρ; così l serie x o coverge, e per il Lemm di Abel, l serie coverge i ] x o, x o [ e quidi i =0 prticolre i x. Si or x > ρ; se suppoimo per ssurdo che l serie coverg che i x, per il Lemm di Abel covergerebbe i tutti i puti di [ρ, x ]; duque [ρ, x ] X e questo cotrddice l defiizioe di ρ. Pssimo ll codizioe sufficiete, cioè suppoimo che l serie coverge per x < ρ e o coverge per x > ρ e provimo che llor ρ è il rggio di covergez. Dll ipotesi si h che ] ρ, ρ[ X, e quidi sup X ρ; se l disugugliz fosse strett, dovrebbe esistere u elemeto x o X tle che x o > ρ; m llor per l ipotesi l serie (1) o coverge i x o e questo cotrddice il ftto che x o X. Osservimo che per le x R tli che x = ρ o si può stbilire ull. Ad esempio per l serie geometric (cioè per l scelt = 1 per ogi N) il rggio di covergez è ρ = 1 e egli estremi dell itervllo ] 1, 1[ l serie o coverge. Ivece per l serie x che h cor rggio di covergez 1, si h covergez che egli estremi. Ifie per l serie x 1 + che h cor rggio di covergez 1, si h covergez solo per x = 1. Stbio or u criterio per l determizioe del rggio di covergez Teorem di Cuchy-Hdmrd. Si ( ) u successioe tle che esiste il ite = l. Allor per il rggio di covergez dell serie di poteze (1) vle l ugugliz + se l = 0 1 se 0 < l < + ρ = l 0 se l = + 8
9 L dimostrzioe del Teorem precedete è bst sul Criterio dell Rdice per le serie umeriche. Applicdo ivece il Criterio del Rpporto si perviee l Teorem di D Alembert. Si ( ) u successioe i ]0, + ) tle che esiste il ite +1 = l. Allor per il rggio di covergez dell serie di poteze (1) vle l ugugliz + se l = 0 1 se 0 < l < + ρ = l 0 se l = + Ifie vlgoo i segueti due risultti reltivi ll itegrzioe ell derivzioe di u serie di poteze Teorem (Rggio di covergez dell serie derivt) U serie di poteze h lo stesso rggio di covergez dell su serie derivt. Teorem (Itegrzioe e derivzioe delle serie di poteze) Se l serie di poteze (1) h rggio ρ di covergez o ullo, e se f(x) è l somm, llor per ogi x < ρ, e per ogi x < ρ. x 0 f (x) = f(t)dt = x 1 =0 =0 + 1 x+1 Serie di Tylor e di McLuri Abbimo già visto l costruzioe dei poliomi di Tylor; ricordimo brevemete: Se f : I R è u fuzioe dott di derivte successive fio ll ordie p i u itoro di u puto x o I llor il poliiomio di Tylor di grdo p è espresso d T p (x) = f(x o ) + p f () (x o )! (x x o ). Nel cso i cui f si derivbile ifiite volte i u itoro di x o si possoo quidi scrivere i poliomi di Tylor di f per ogi grdo p, ed è fcile verificre che questi soo le somme przili p-esime dell serie di fuzioi f(x o ) + f () (x o )! Quest ultim serie è u serie di poteze ell vribile (x x o ). (x x o ). (2) Defiizioe. U fuzioe f : I R, co f C (I) è dett sviluppbile i serie di Tylor itoro x o se l serie (2) coverge f(x) per ogi x I. Nel cso prticolre i cui x o = 0 si dice che f è sviluppbile i serie di McLuri. 9
10 No tutte le fuzioi di clsse C (I) soo sviluppbili i serie di Tylor. L esempio clssico è quello dell fuzioe f : R R defiit d { f(x) = e 1 x 2 se x 0 0 se x = 0 per l qule è fcile covicersi che tutte le derivte ell origie soo ulle; quidi tuti i coefficieti dello sviluppo i serie di Tylor soo ulli, cioè tutti i poliomi di Tylor (zi di McLuri) soo ulli; quidi l serie di McLuri reltiv d f è covergete i tutti i puti di R m l somm è 0, e quidi f o è sviluppbile i serie di Tylor. Defiizioe. Si defiisce resto -esimo di uo sviluppo i serie di Tylor l qutità [ ] f () (x o ) R (x) = f(x) T (x) = f(x) f(x o ) + (x x o ).! È llor evidete che vle il seguete criterio Teorem. Codizioe ecessri e sufficiete perchè f si sviluppbile i serie di Tylor i I è che R (x) = 0 per ogi x I L esempio precedete ci covice che l codizioe reltiv l resto o è sempre verifict, che qudo l fuzioe mmette le derivte di ogi ordie. Quello che segue è u criterio di sviluppbilità di fcile ppliczioe i lcui csi importti Teorem. (Criterio di sviluppbilità i serie di Tylor) Se f C (], b[) e se esistoo M, L 0 tli che f () (x) M L per ogi x ], b[ llor f è sviluppbile i serie di Tylor itoro qulsisi puto x o ], b[ i tutto ], b[. Dimostrzioe. Ricordimo che elle ipotesi ftte, ell scrittur f(x) = T (x) + R (x) il resto -esimo si può scrivere ell form di Lgrge (Prop pg. 407) R (x) = f (+1) (ξ) ( + 1)! (x x o) +1, dove ξ ]x o, x[, se si è supposto che x > x o. Per le ipotesi ftte si h f (+1) (ξ) R (x) = ( + 1)! x xo +1 L +1 M ( + 1)! x x o +1. Or il termie destr ell relzioe precedete è u multiplo del termie geerle dell serie termii positivi (L x x o ) 10!
11 che coverge, come si verific immeditmete pplicdo il Criterio del Rpporto Asitotico, i quto (L x x o ) +1 Di coseguez risult e duque più forte rgioe cioè l tesi. ( + 1)! (L x x o )! = L x xo + 1. M L +1 ( + 1)! x x o +1 = 0 R (x) = 0 All luce di questo teorem è immedito covicersi che le fuzioi e x, si x e cos x soo sviluppbili i serie di McLuri i tutto R. I prticolre se si fiss rbitrrimete > 0, l fuzioe espoezile è sviluppbile i serie di McLuri i tutto ], [: per l rbitrrietà di l sviluppbilità vle i tutto R. Per queste tre fuzioi si ho gli sviluppi (serie espoezile) si x = cos x = e x = 1 + x! ( 1) x2+1 (2 + 1)! =0 =0 ( 1) x2 (2)!. Ache il seguete risultto si rivel utile per determire lcui sviluppi i serie Teorem. Si f C (], b[) e si x o ], b[; se l serie derivt dell serie di Tylor h per somm f (x), cioè f f () (x o ) (x) = ( 1)! (x x o) 1 per ogi x ], b[, llor f è sviluppbile i serie di Tylor reltiv x o i ogi puto di ], b[. Come ppliczioe del Teorem precedete si prov l sviluppbilità i serie di McLuri delle fuzioi log(1 + x) e rct x. Iftti se scrivimo l serie di McLuri di log(1 + x) trovimo derivdo si trov ( 1) 1 x ( 1) 1 x 1 ; (3) 11
12 1 che è u serie geometric di rgioe x e pertto covergete i ] 1, 1[, co somm 1 + x che è precismete l derivt di log(1 + x); pertto il Teorem ci dice che l (3) rppreset lo sviluppo i serie di McLuri dell fuzioe log(1 + x) per x ] 1, 1[. Ache per rct x l serie di McLuri è dt d ( 1) 1 x (4) l cui serie derivt è ( 1) 1 x 2( 1) che è cor u serie geometric di rgioe x 2, e che quidi coverge per x ] 1, 1[, ed h per 1 somm che è esttmete l derivt di rct x; quidi per il teorem si trov 1 + x2 rct x = ( 1) 1 x per ogi x ] 1, 1[. I reltà, co teciche diverse, si rriv provre che lo sviluppo i serie di McLuri di log(1+x) vle che per x = 1, e che quello di rct x sussiste i tutto [ 1, 1]. U iteresste ppliczioe di questo ftto è che lo sviluppo i serie di McLuri per rct x permette di otteere fcilmete pprossimzioi di π; ricordimo iftti che rct 1 = π 4 ; duque π 4 = Forimo ifie lo sviluppo i serie di McLuri per le fuzioi f(x) = (1 + x) α, co x ] 1, 1[. Risult ( ) (1 + x) α α = x =0 ( ) α dove è detto coefficiete biomile (d cui l serie suddett prede il ome di serie biomile) ed è defiito d ( α ) 1 se = 0 = α(α 1) (α + 1)! se > 0 12
SUCCESSIONI E SERIE DI FUNZIONI { } n( ) f x converge puntualmente su S D ad una =, cioè se. ( n ) ( )
 Successioi di fuzioi { } Si SUCCESSIONI E SERIE DI FUNZIONI f u successioe di fuzioi defiite tutte i u sottoisieme D { } Defiizioe : Si dice che l successioe fuzioe f ( ) se, S, risult f f lim f coverge
Successioi di fuzioi { } Si SUCCESSIONI E SERIE DI FUNZIONI f u successioe di fuzioi defiite tutte i u sottoisieme D { } Defiizioe : Si dice che l successioe fuzioe f ( ) se, S, risult f f lim f coverge
, dove s n è la somma parziale n-esima definita da. lim s n = lim s n = + (= ). a n = a 1 + a 2 +...
 . serie umeriche Def. (serie). Dt u successioe ( ) (co R per ogi ), si chim serie di termie geerle l successioe (s ), dove s è l somm przile -esim defiit d () s = + 2 +... + = k. L serie coverge (semplicemete)
. serie umeriche Def. (serie). Dt u successioe ( ) (co R per ogi ), si chim serie di termie geerle l successioe (s ), dove s è l somm przile -esim defiit d () s = + 2 +... + = k. L serie coverge (semplicemete)
1 Formula di Taylor. 1.1 I Simboli e o( ) Definizione 1.1 Sia I un intorno di x 0 R {± }. Siano f, g : I R con g(x) 0, x I.
 Formul di Tylor. I Simboli e o( ) Defiizioe. Si I u itoro di x 0 R {± }. Sio f, g : I R co g(x) 0, x I. (i) Dicimo che f è sitotic g per x x 0 se f(x) x x 0 g(x) = ; scrivimo: f(x) g(x) per x x 0. (ii)
Formul di Tylor. I Simboli e o( ) Defiizioe. Si I u itoro di x 0 R {± }. Sio f, g : I R co g(x) 0, x I. (i) Dicimo che f è sitotic g per x x 0 se f(x) x x 0 g(x) = ; scrivimo: f(x) g(x) per x x 0. (ii)
Integrali in senso generalizzato
 Itegrli i seso geerlizzto Pol Rubbioi Itegrzioe di fuzioi o itte Deizioe.. Dt f : [; b[! R cotiu ed ilitt i prossimit di b, ovvero tle che!b f () = + oppure!b f () =, ess si dice itegrbile i seso geerlizzto
Itegrli i seso geerlizzto Pol Rubbioi Itegrzioe di fuzioi o itte Deizioe.. Dt f : [; b[! R cotiu ed ilitt i prossimit di b, ovvero tle che!b f () = + oppure!b f () =, ess si dice itegrbile i seso geerlizzto
Università degli Studi Roma Tre - Corso di Laurea in Matematica Tutorato di GE220
 Uiversità degli Studi Rom Tre - Corso di Lure i Mtemtic Tutorto di GE220 A.A. 2010-2011 - Docete: Prof. Edordo Seresi Tutori: Filippo Mri Boci, Amri Iezzi e Mri Chir Timpoe Soluzioi Tutorto 4 (7 Aprile
Uiversità degli Studi Rom Tre - Corso di Lure i Mtemtic Tutorto di GE220 A.A. 2010-2011 - Docete: Prof. Edordo Seresi Tutori: Filippo Mri Boci, Amri Iezzi e Mri Chir Timpoe Soluzioi Tutorto 4 (7 Aprile
SERIE NUMERICHE esercizi. R. Argiolas
 esercizi R. Argiols L? Quest piccol rccolt di esercizi sulle serie umeriche è rivolt gli studeti del corso di lisi mtemtic I. E bee precisre fi d or che possedere e svolgere gli esercizi di quest dispes
esercizi R. Argiols L? Quest piccol rccolt di esercizi sulle serie umeriche è rivolt gli studeti del corso di lisi mtemtic I. E bee precisre fi d or che possedere e svolgere gli esercizi di quest dispes
Corso di Calcolo Numerico
 Fcoltà di Igegeri - Lure Triele i Igegeri Meccic Corso di Clcolo Numerico Dott.ss M.C. De Bois Uiversità degli Studi dell Bsilict, Potez Fcoltà di Igegeri Corso di Lure i Igegeri Meccic Ao Accdemico 004/05
Fcoltà di Igegeri - Lure Triele i Igegeri Meccic Corso di Clcolo Numerico Dott.ss M.C. De Bois Uiversità degli Studi dell Bsilict, Potez Fcoltà di Igegeri Corso di Lure i Igegeri Meccic Ao Accdemico 004/05
(labeling) si ottiene così l insieme a n ordinato (codominio della funzione f ) : Primo termine. Termine Generale
 Successioi umeriche / Def. Si chim successioe umeric ogi fuzioe f d N i R defiit i u isieme del tipo I= { N 0 }, co 0 umero turle e che ssoci d u itero di I u umero rele f(). I geerle però porremo f: N
Successioi umeriche / Def. Si chim successioe umeric ogi fuzioe f d N i R defiit i u isieme del tipo I= { N 0 }, co 0 umero turle e che ssoci d u itero di I u umero rele f(). I geerle però porremo f: N
ESERCIZI DI ANALISI MATEMATICA. xn lim sup. lim inf x n. lim sup x n. = L, allora esiste anche lim e vale L.
 ESERCIZI DI ANALISI MATEMATICA GRAZIANO CRASTA Notzioi. N = {, 1, 2,...} = isieme dei umeri turli, N + = Z + = N\{} = isieme dei umeri turli positivi, Z = isieme degli iteri reltivi. = esercizio difficile,
ESERCIZI DI ANALISI MATEMATICA GRAZIANO CRASTA Notzioi. N = {, 1, 2,...} = isieme dei umeri turli, N + = Z + = N\{} = isieme dei umeri turli positivi, Z = isieme degli iteri reltivi. = esercizio difficile,
SEFA Sapienza, Università di Roma Esercizi di Matematica 3 (C.Mascia) Alcune soluzioni di 1-2-3
 Esercizio 11 SEFA Spiez, Uiversità di Rom Esercizi di Mtemtic 3 (CMsci) Alcue soluzioi di 1-2-3 11 ovembre 215 1 Foglio 1 i Descrivere i segueti isiemi di R 2 : {1} {2}, {} [1, 2], [, 1] {2}, [, 1] [,
Esercizio 11 SEFA Spiez, Uiversità di Rom Esercizi di Mtemtic 3 (CMsci) Alcue soluzioi di 1-2-3 11 ovembre 215 1 Foglio 1 i Descrivere i segueti isiemi di R 2 : {1} {2}, {} [1, 2], [, 1] {2}, [, 1] [,
LE SUCCESSIONI. ovvero: 1, 2, 1.5, 1., 1.6, 1.625,... I valori ottenuti si avvicinano alla sezione aurea: =
 LE SUCCESSIONI Si cosideri l seguete sequez di umeri:,,, 3, 5, 8, 3,, 34, 55, 89, 44, 33, detti di Fibocci. Ess rppreset il umero di coppie di coigli preseti ei primi mesi i u llevmeto! Si cosideri l sequez
LE SUCCESSIONI Si cosideri l seguete sequez di umeri:,,, 3, 5, 8, 3,, 34, 55, 89, 44, 33, detti di Fibocci. Ess rppreset il umero di coppie di coigli preseti ei primi mesi i u llevmeto! Si cosideri l sequez
Gerarchia degli infiniti e asintotici per successioni numeriche 1
 Gerrchi degli ifiiti e sitotici per successioi umeriche Sio { } e { } due successioi ifiite Vogo stilire u gerrchi di tli successioi el seso di cofrotre, se possiile, le velocità co le quli le successioi
Gerrchi degli ifiiti e sitotici per successioi umeriche Sio { } e { } due successioi ifiite Vogo stilire u gerrchi di tli successioi el seso di cofrotre, se possiile, le velocità co le quli le successioi
Dove la suddivisione dell intervallo [a,b] è individuata dai punti
![Dove la suddivisione dell intervallo [a,b] è individuata dai punti Dove la suddivisione dell intervallo [a,b] è individuata dai punti](/thumbs/89/98520294.jpg) 04//205 Clcolo itegrle per fuzioi di u vriile Clcolo itegrle Itegrle defiito Si f:[,] R, limitt ξ ξ 2 ξ 3 ξ 4 ξ 5 0 = 2 3 4 5 = Costruimo l somm di Cuchy-Riem S f f Dove l suddivisioe dell itervllo [,]
04//205 Clcolo itegrle per fuzioi di u vriile Clcolo itegrle Itegrle defiito Si f:[,] R, limitt ξ ξ 2 ξ 3 ξ 4 ξ 5 0 = 2 3 4 5 = Costruimo l somm di Cuchy-Riem S f f Dove l suddivisioe dell itervllo [,]
Esercitazione n 3. 1 Successioni di funzioni. Esercizio 1: Studiare la convergenza in (0, 1) della successione {f n } dove f n (x) =
 Esercitazioe 3 Successioi di fuzioi Esercizio : Studiare la covergeza i (0, ) della successioe {f } dove f (x) = metre Sol.: Si verifica facilmete che lim f (x) = 0 x (0, ) lim sup f (x) = lim = + (0,)
Esercitazioe 3 Successioi di fuzioi Esercizio : Studiare la covergeza i (0, ) della successioe {f } dove f (x) = metre Sol.: Si verifica facilmete che lim f (x) = 0 x (0, ) lim sup f (x) = lim = + (0,)
Matematica e-learning - Corso Zero di Matematica. I Radicali. Prof. Erasmo Modica A.A. 2009/2010
 Mtemtic e-lerig - Corso Zero di Mtemtic I Rdicli Prof. Ersmo Modic ersmo@glois.it A.A. 2009/200 I umeri turli 2 Le rdici Abbimo visto che l isieme dei umeri reli è costituito d tutti e soli i umeri che
Mtemtic e-lerig - Corso Zero di Mtemtic I Rdicli Prof. Ersmo Modic ersmo@glois.it A.A. 2009/200 I umeri turli 2 Le rdici Abbimo visto che l isieme dei umeri reli è costituito d tutti e soli i umeri che
IL CONCETTO DI LIMITE
 IL CONCETTO DI LIMITE DEFINIZIONE DI LIMITE Si f u fuzioe defiit i u itoro di x 0 dicimo che f x=l se e soltto se, comuque sceglimo u itervllo I l cetrto i l, piccolo quto voglimo, è possiile trovre u
IL CONCETTO DI LIMITE DEFINIZIONE DI LIMITE Si f u fuzioe defiit i u itoro di x 0 dicimo che f x=l se e soltto se, comuque sceglimo u itervllo I l cetrto i l, piccolo quto voglimo, è possiile trovre u
ANALISI MATEMATICA 1
 ANALISI MATEMATICA [Apputi per u Igegere] A CURA DI ALESSANDRO PAGHI Riepilogo su: - Vlore Assoluto, Poteze, Logritmi; - Rziolizzzioe; - Grdezze Trigoometriche; - Limiti Notevoli e Forme Idetermite; -
ANALISI MATEMATICA [Apputi per u Igegere] A CURA DI ALESSANDRO PAGHI Riepilogo su: - Vlore Assoluto, Poteze, Logritmi; - Rziolizzzioe; - Grdezze Trigoometriche; - Limiti Notevoli e Forme Idetermite; -
Approssimazione di funzioni mediante Interpolazione polinomiale
 Docete: Cludio Esttico esttico@uisubri.it Approssimzioe di fuzioi medite Lezioe bst su pputi del prof. Mrco Gvio Approssimzioe di fuzioi L pprossimzioe di fuzioi. Iterpolzioe e migliore pprossimzioe..
Docete: Cludio Esttico esttico@uisubri.it Approssimzioe di fuzioi medite Lezioe bst su pputi del prof. Mrco Gvio Approssimzioe di fuzioi L pprossimzioe di fuzioi. Iterpolzioe e migliore pprossimzioe..
2 Sistemi di equazioni lineari.
 Sistemi di equzioi lieri. efiizioe. Si dice equzioe liere elle icogite equzioe dell form () + +...+ = o che (') i= i i = ove,,..., R si chimo coefficieti e R termie oto.,,..., ogi efiizioe. Si dice soluzioe
Sistemi di equzioi lieri. efiizioe. Si dice equzioe liere elle icogite equzioe dell form () + +...+ = o che (') i= i i = ove,,..., R si chimo coefficieti e R termie oto.,,..., ogi efiizioe. Si dice soluzioe
I numeri reali come sezione nel campo dei numeri razionali
 I umeri reli come sezioe el cmpo dei umeri rzioli Come sppimo, el cmpo dei umeri rzioli, le quttro operzioi fodmetli soo sempre possibili, el seso che, effettudo sopr u quluque isieme fiito u sequel fiit
I umeri reli come sezioe el cmpo dei umeri rzioli Come sppimo, el cmpo dei umeri rzioli, le quttro operzioi fodmetli soo sempre possibili, el seso che, effettudo sopr u quluque isieme fiito u sequel fiit
SUCCESSIONI DI FUNZIONI
 SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
RELAZIONE FRA LA STABILITA DEL SISTEMA E LA FUNZIONE DI TRASFERIMENTO
 RELAZIONE FRA LA STABILITA DEL SISTEMA E LA FUNZIONE DI TRASFERIMENTO L stbilità di u sistem liere, ivrite ed prmetri cocetrti può vlutrsi co due criteri diversi che fo rispettivmete riferimeto ll rispost
RELAZIONE FRA LA STABILITA DEL SISTEMA E LA FUNZIONE DI TRASFERIMENTO L stbilità di u sistem liere, ivrite ed prmetri cocetrti può vlutrsi co due criteri diversi che fo rispettivmete riferimeto ll rispost
Def. R si dice raggio di convergenza; nel caso i) R = 0, nel caso ii)
 Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi : Riferimeti: R.Adams, Calcolo Differeziale. -Si cosiglia vivamate di fare gli esercizi del testo. Cap. 9.5 - Serie di poteze,
Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi : Riferimeti: R.Adams, Calcolo Differeziale. -Si cosiglia vivamate di fare gli esercizi del testo. Cap. 9.5 - Serie di poteze,
Polinomi, disuguaglianze e induzione.
 Allemeti Disid Mtemtic Geio 03 Poliomi, disuguglize e iduzioe. Qul è l mssim re di u rettgolo vete perimetro ugule 576? [Suggerimeto: utilizzre le medie e le loro disuguglize.] Svolgimeto. Predimo i cosiderzioe
Allemeti Disid Mtemtic Geio 03 Poliomi, disuguglize e iduzioe. Qul è l mssim re di u rettgolo vete perimetro ugule 576? [Suggerimeto: utilizzre le medie e le loro disuguglize.] Svolgimeto. Predimo i cosiderzioe
{ } { } Successioni numeriche. Scheda n 2 pag1. n 2. Pag. 3. Rappresentazione di una successione sul piano cartesiano. Esempio n 1 a) a n
 Successioi umeriche Sched pg Rppresetzioe di u successioe sul pio crtesio Esempio ) { } { } Esempio ) ( ) b) ( ) Esempio ) 5 b) Esercizio L successioi degli esempi,,, soo covergeti, divergeti o idetermite?
Successioi umeriche Sched pg Rppresetzioe di u successioe sul pio crtesio Esempio ) { } { } Esempio ) ( ) b) ( ) Esempio ) 5 b) Esercizio L successioi degli esempi,,, soo covergeti, divergeti o idetermite?
Successioni e serie. Ermanno Travaglino
 Successioi e serie Ermo Trvglio U successioe è u sequez ordit di umeri o di ltre grdezze, e u serie è l somm dei termii di tle sequez. U successioe si rppreset co l'espressioe,,,, ell qule è u itero positivo,
Successioi e serie Ermo Trvglio U successioe è u sequez ordit di umeri o di ltre grdezze, e u serie è l somm dei termii di tle sequez. U successioe si rppreset co l'espressioe,,,, ell qule è u itero positivo,
Unità Didattica N 22B : Serie
 0) L defiizioe di serie umeric 02) I primi teoremi sulle serie umeriche 03) Serie umeric combizioe liere di ltre serie umeriche 04) Serie umeriche termii positivi 05) Criteri di covergez e di divergez
0) L defiizioe di serie umeric 02) I primi teoremi sulle serie umeriche 03) Serie umeric combizioe liere di ltre serie umeriche 04) Serie umeriche termii positivi 05) Criteri di covergez e di divergez
k=0 f k(x). Un altro tipo di convergenza per le serie è la convergenza totale e si dice che la serie (0.1) converge totalmente in J I se
 Serie di fuzioi Sia I R, per ogi k N, data la successioe di fuzioi (f k ) k co f k : I R, cosideriamo la serie di fuzioi (0.) f k () k=0 e defiiamo la successioe delle somme parziali s () = k=0 f k().
Serie di fuzioi Sia I R, per ogi k N, data la successioe di fuzioi (f k ) k co f k : I R, cosideriamo la serie di fuzioi (0.) f k () k=0 e defiiamo la successioe delle somme parziali s () = k=0 f k().
Il problema è ricavare le radici (gli zeri) di una funzione f(x), cioè i valori z: f(z)=0
 Ricerc di zeri Equzioi o lieri Il prolem è ricvre le rdici (gli zeri di u fuzioe f(, cioè i vlori z: f(z0 qudo o si poss otteere l soluzioe i form chius (u formul Seprzioe delle rdici Per semplificre il
Ricerc di zeri Equzioi o lieri Il prolem è ricvre le rdici (gli zeri di u fuzioe f(, cioè i vlori z: f(z0 qudo o si poss otteere l soluzioe i form chius (u formul Seprzioe delle rdici Per semplificre il
Serie di potenze / Esercizi svolti
 MGuida, SRolado, 204 Serie di poteze / Esercizi svolti Si cosideri la serie di poteze (a) Determiare il raggio di covergeza 2 + x (b) Determiare l itervallo I di covergeza putuale (c) Dire se la serie
MGuida, SRolado, 204 Serie di poteze / Esercizi svolti Si cosideri la serie di poteze (a) Determiare il raggio di covergeza 2 + x (b) Determiare l itervallo I di covergeza putuale (c) Dire se la serie
( x) ( ) ( )( ( ) ( ) ( ) ( ) )
 C Boccccio Apputi di Alisi Mtemtic CAP IV CAP IV FUNZIONI REALI Per due fuzioi reli f : X R e g : X R si defiiscoo le uove fuzioi f g : X R, f g : X R ed f g : X R l modo seguete: X : f g = f g X : ( )(
C Boccccio Apputi di Alisi Mtemtic CAP IV CAP IV FUNZIONI REALI Per due fuzioi reli f : X R e g : X R si defiiscoo le uove fuzioi f g : X R, f g : X R ed f g : X R l modo seguete: X : f g = f g X : ( )(
Argomento 9 Integrali definiti
 Argometo 9 Itegrli defiiti Premess. Si f u fuzioe cotiu ell itervllo [, b]. L regioe di pio compres tr l sse x, le due rette verticli di equzioe x = e x = b, ed il grfico di f è dett trpezoide reltivo
Argometo 9 Itegrli defiiti Premess. Si f u fuzioe cotiu ell itervllo [, b]. L regioe di pio compres tr l sse x, le due rette verticli di equzioe x = e x = b, ed il grfico di f è dett trpezoide reltivo
EQUAZIONI RAZIONALI. Principio di moltiplicazione: 0 è un polinomio.
 EQUAZIONI RAZIONALI A Dti due poliomi e B, l relzioe: A B scritt llo scopo di determire, se esistoo, vlori reli per i quli A e B ssumoo lo stesso vlore, si chim equzioe lebric ell icoit. U umero è soluzioe
EQUAZIONI RAZIONALI A Dti due poliomi e B, l relzioe: A B scritt llo scopo di determire, se esistoo, vlori reli per i quli A e B ssumoo lo stesso vlore, si chim equzioe lebric ell icoit. U umero è soluzioe
CALCOLO DI LIMITI PER LE FUNZIONI CONTINUE. Saper calcolare semplici limiti, in particolare delle funzioni razionali intere e fratte.
 CALCOLO DI LIMITI PER LE FUNZIONI CONTINUE OBIETTIVI MINIMI: Sper idividure le fuzioi cotiue Sper pplicre i teorei sui iti Sper idividure le fore ideterite Sper clcolre seplici iti, i prticolre delle fuzioi
CALCOLO DI LIMITI PER LE FUNZIONI CONTINUE OBIETTIVI MINIMI: Sper idividure le fuzioi cotiue Sper pplicre i teorei sui iti Sper idividure le fore ideterite Sper clcolre seplici iti, i prticolre delle fuzioi
Professionisti, tecnici e imprese Gruppo Editoriale Esselibri - Simone
 Copyright 005 Esselibri S.p.A. Vi F. Russo, 33/D 803 Npoli Azied co sistem qulità certificto ISO 400: 003 Tutti i diritti riservti. È viett l riproduzioe che przile e co qulsisi mezzo sez l utorizzzioe
Copyright 005 Esselibri S.p.A. Vi F. Russo, 33/D 803 Npoli Azied co sistem qulità certificto ISO 400: 003 Tutti i diritti riservti. È viett l riproduzioe che przile e co qulsisi mezzo sez l utorizzzioe
Complessi. 1 Definizioni Forma trigonometrica: argomento e funzione arcotangente Potenze e radici Polinomi e radici.
 Complessi. Idice 1 Defiizioi. 1 Form trigoometric: rgometo e fuzioe rcotgete. 3 Poteze e rdici. 4 4 Poliomi e rdici. 5 5 Estesioe di fuzioi elemetri l cmpo complesso. 6 6 Appedice per i lettori più iteressti.
Complessi. Idice 1 Defiizioi. 1 Form trigoometric: rgometo e fuzioe rcotgete. 3 Poteze e rdici. 4 4 Poliomi e rdici. 5 5 Estesioe di fuzioi elemetri l cmpo complesso. 6 6 Appedice per i lettori più iteressti.
Successioni in R. n>a n+1
 Successioi i R U successioe è u fuzioe f : N R. Si preferisce deotre f() co e quidi u successioe co ( ). Il codomiio di u successioe ( ) è l'isieme dei vlori che ssume l successioe, cioè { } successioe
Successioi i R U successioe è u fuzioe f : N R. Si preferisce deotre f() co e quidi u successioe co ( ). Il codomiio di u successioe ( ) è l'isieme dei vlori che ssume l successioe, cioè { } successioe
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica I del c.1.
 Prova scritta di Aalisi Matematica I del 25-5-1998 - c.1 1) Per ogi umero N, 2, siao dati 2 umeri reali positivi a 1, a 2,...a, b 1, b 2,...b. Provare, usado il Pricipio di Iduzioe, che a 1 + a 2 +...
Prova scritta di Aalisi Matematica I del 25-5-1998 - c.1 1) Per ogi umero N, 2, siao dati 2 umeri reali positivi a 1, a 2,...a, b 1, b 2,...b. Provare, usado il Pricipio di Iduzioe, che a 1 + a 2 +...
identificando (a, 0) con a, (b, 0) con b e posto i =(0, 1) possiamo esprimere un numero complesso nella forma 2 = a + ib. 2 ) a
 Numeri Complessi E be oto che o esiste lcu umero rele x tle che x = o, equivletemete, che l equzioe x + = 0 o h soluzioi reli. Cosí come è possibile estedere i umeri rzioli, itroducedo i umeri reli, i
Numeri Complessi E be oto che o esiste lcu umero rele x tle che x = o, equivletemete, che l equzioe x + = 0 o h soluzioi reli. Cosí come è possibile estedere i umeri rzioli, itroducedo i umeri reli, i
Le successioni: intro
 Le successioi: itro Si cosideri la seguete sequeza di umeri:,, 2, 3, 5, 8, 3, 2, 34, 55, 89, 44, 233, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi 2 mesi i u allevameto!
Le successioi: itro Si cosideri la seguete sequeza di umeri:,, 2, 3, 5, 8, 3, 2, 34, 55, 89, 44, 233, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi 2 mesi i u allevameto!
SUCCESSIONI SERIE NUMERICHE pag. 1
 SUCCESSIONI SERIE NUMERICHE pag. Successioi RICHIAMI Ua successioe di elemeti di u isieme X è ua fuzioe f: N X. E covezioe scrivere f( ) = x, e idicare le successioi mediate la ifiitupla ordiata delle
SUCCESSIONI SERIE NUMERICHE pag. Successioi RICHIAMI Ua successioe di elemeti di u isieme X è ua fuzioe f: N X. E covezioe scrivere f( ) = x, e idicare le successioi mediate la ifiitupla ordiata delle
13. Determinante di una matrice quadrata
 Determite di u mtrice qudrt Defiizioe Dti umeri reli,,,,, (-), (-), col simbolo i idiceremo l loro somm ( + + + + + (-) + (-) + ) Quidi, i i := + + + + + (-) + (-) + i Esempio y i = y + y + y + y + + y
Determite di u mtrice qudrt Defiizioe Dti umeri reli,,,,, (-), (-), col simbolo i idiceremo l loro somm ( + + + + + (-) + (-) + ) Quidi, i i := + + + + + (-) + (-) + i Esempio y i = y + y + y + y + + y
ISTITUZIONI DI MATEMATICHE (CORSO Dl LAUREA IN CHIMICA) PROGRAMMA D ESAME PER L A.A. 2009/10
 ISTITUZIONI DI MATEMATICHE (CORSO Dl LAUREA IN CHIMICA) PROGRAMMA D ESAME PER L A.A. 2009/10 Cmpi umerici. Il cmpo rziole come mplimeto dell isieme dei umeri iteri reltivi: proprietà e problemi. Il cmpo
ISTITUZIONI DI MATEMATICHE (CORSO Dl LAUREA IN CHIMICA) PROGRAMMA D ESAME PER L A.A. 2009/10 Cmpi umerici. Il cmpo rziole come mplimeto dell isieme dei umeri iteri reltivi: proprietà e problemi. Il cmpo
Progressioni geometriche
 Progressioi geometriche ) Proprietà geerli U isieme ordito di umeri,,,...,,...dicesi progressioe geometric se N si h : co q qutità costte divers d dett rgioe o quoziete. U progressioe geometric di rgioe
Progressioi geometriche ) Proprietà geerli U isieme ordito di umeri,,,...,,...dicesi progressioe geometric se N si h : co q qutità costte divers d dett rgioe o quoziete. U progressioe geometric di rgioe
Esercizi di Analisi II
 Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
Siamo interessati a studiare la convergenza della serie e porremo come al solito:
 SERIE DI POTENZE Soo particolari serie di fuzioi, i cui termii soo moomi, evetualmete traslati: f (x) co f (x) =a (x x 0 ), a R, x 0 R, ossia dove a (x x 0 ) = a 0 + a 1 (x x 0 )+a 2 (x x 0 ) 2 +... x
SERIE DI POTENZE Soo particolari serie di fuzioi, i cui termii soo moomi, evetualmete traslati: f (x) co f (x) =a (x x 0 ), a R, x 0 R, ossia dove a (x x 0 ) = a 0 + a 1 (x x 0 )+a 2 (x x 0 ) 2 +... x
CORSO DI METODI MATEMATICI PER L INGEGNERIA MECCANICA
 CORSO DI METODI MATEMATICI PER L INGEGNERIA MECCANICA. ALCUNE NOZIONI E STRUMENTI PRELIMINARI -RICHIAMI SUGLI SPAZI VETTORIALI Ricordimo che u vettore i R (o C ) e u -upl ordit di umeri reli (o complessi)
CORSO DI METODI MATEMATICI PER L INGEGNERIA MECCANICA. ALCUNE NOZIONI E STRUMENTI PRELIMINARI -RICHIAMI SUGLI SPAZI VETTORIALI Ricordimo che u vettore i R (o C ) e u -upl ordit di umeri reli (o complessi)
Analisi Matematica I - modulo B
 Alisi Mtemtic I - modulo B Apputi delle lezioi teute dl Prof. A. Fod Uiversità di Trieste, CdL Mtemtic,.. 2009/200 Il cmpo dei umeri complessi. Defiizioi e prime proprietà Cosiderimo l isieme R R = {(,
Alisi Mtemtic I - modulo B Apputi delle lezioi teute dl Prof. A. Fod Uiversità di Trieste, CdL Mtemtic,.. 2009/200 Il cmpo dei umeri complessi. Defiizioi e prime proprietà Cosiderimo l isieme R R = {(,
10. La nozione di limite
 . L ozioe di limite L distz itrodott sull rett rele d(,b) = -b,, b R, permette di defiire u ozioe di viciz, trmite l ozioe di itoro. Si defiisce itoro di u puto u qulsisi itervllo perto (,b) coteete (quest
. L ozioe di limite L distz itrodott sull rett rele d(,b) = -b,, b R, permette di defiire u ozioe di viciz, trmite l ozioe di itoro. Si defiisce itoro di u puto u qulsisi itervllo perto (,b) coteete (quest
Esercizi svolti su successioni e serie di funzioni
 Esercizi svolti su successioi e serie di fuzioi Esercizio. Calcolare il limite putuale di f ) = 2 +, [0, + ). Dimostrare che o si ha covergeza uiforme su 0, + ), metre si ha covergeza uiforme su [a, +
Esercizi svolti su successioi e serie di fuzioi Esercizio. Calcolare il limite putuale di f ) = 2 +, [0, + ). Dimostrare che o si ha covergeza uiforme su 0, + ), metre si ha covergeza uiforme su [a, +
Misurare una grandezza fisica significa stabilire quante unità di misura sono contenute nella grandezza stessa.
 L misur: Misurre u grdezz fisic sigific stilire qute uità di misur soo coteute ell grdezz stess. L misur di u grdezz si dice dirett qudo si effettu per cofroto co u grdezz d ess omogee scelt come cmpioe
L misur: Misurre u grdezz fisic sigific stilire qute uità di misur soo coteute ell grdezz stess. L misur di u grdezz si dice dirett qudo si effettu per cofroto co u grdezz d ess omogee scelt come cmpioe
10. FUNZIONI CONTINUE
 . FUNZIONI CONTINUE DEFINIZIONE DI CONTINUITÀ DI UNA FUNZIONE IN UN PUNTO 46 oppure: def. f cotiu i lim f ( ) = f ( ) def. f cotiu i lim f ( + h ) = f ( ) h Il cocetto è vermete fodmetle e quidi dimo d
. FUNZIONI CONTINUE DEFINIZIONE DI CONTINUITÀ DI UNA FUNZIONE IN UN PUNTO 46 oppure: def. f cotiu i lim f ( ) = f ( ) def. f cotiu i lim f ( + h ) = f ( ) h Il cocetto è vermete fodmetle e quidi dimo d
Le successioni: intro
 Le successioi: itro Si cosideri la seguete sequeza di umeri:,,, 3, 5, 8, 3,, 34, 55, 89, 44, 33, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi mesi i u allevameto! Si
Le successioi: itro Si cosideri la seguete sequeza di umeri:,,, 3, 5, 8, 3,, 34, 55, 89, 44, 33, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi mesi i u allevameto! Si
test [ A ] - soluzioni
![test [ A ] - soluzioni test [ A ] - soluzioni](/thumbs/100/144040008.jpg) test [ A ] - soluzioi 1. k - 1 / e Posto f ( ) log, si h f ( ) ( log + 1 ) 0 per e - 1 /. Ioltre f ( e ½ ) - 1 / e.. y ( ) rctg ½ log ( 1 + ) + 1 Itegrdo per prti : rctg d rctg - d 1+ rctg ½ log ( 1 +
test [ A ] - soluzioi 1. k - 1 / e Posto f ( ) log, si h f ( ) ( log + 1 ) 0 per e - 1 /. Ioltre f ( e ½ ) - 1 / e.. y ( ) rctg ½ log ( 1 + ) + 1 Itegrdo per prti : rctg d rctg - d 1+ rctg ½ log ( 1 +
NUMERI COMPLESSI. Definizione. Si dice numero complesso z la coppia ordinata di numeri reali (a, b), ossia: z = (a, b)
 NUMERI COMPLESSI Dto u poliomio P(x) di grdo ell vribile (rele) x, o sempre esso mmette rdici, e, qudo le mmette, esse possoo essere i umero iferiore rispetto l grdo del poliomio. (Ricordimo che si dice
NUMERI COMPLESSI Dto u poliomio P(x) di grdo ell vribile (rele) x, o sempre esso mmette rdici, e, qudo le mmette, esse possoo essere i umero iferiore rispetto l grdo del poliomio. (Ricordimo che si dice
x n (1.1) n=0 1 x La serie geometrica è un esempio di serie di potenze. Definizione 1 Chiamiamo serie di potenze ogni serie della forma
 1 Serie di poteze È stato dimostrato che la serie geometrica x (1.1) coverge se e solo se la ragioe x soddisfa la disuguagliaza 1 < x < 1. I realtà c è covergeza assoluta i ] 1, 1[. Per x 1 la serie diverge
1 Serie di poteze È stato dimostrato che la serie geometrica x (1.1) coverge se e solo se la ragioe x soddisfa la disuguagliaza 1 < x < 1. I realtà c è covergeza assoluta i ] 1, 1[. Per x 1 la serie diverge
ANALISI VETTORIALE COMPITO IN CLASSE DEL 22/11/2013. = a 24 24! log(1 + x) = ( 1) = (24!) 1 24 = 23!. e x2 dx. x 2n
 ANALISI VETTORIALE COMPITO IN CLASSE DEL 22//23 Esercizio Calcolare la 2esima derivata del logaritmo el puto. Risposta Si tratta di calcolare d 2 dx 2 log( + x) x= = a 2 2! dove a 2 è il termie di idice
ANALISI VETTORIALE COMPITO IN CLASSE DEL 22//23 Esercizio Calcolare la 2esima derivata del logaritmo el puto. Risposta Si tratta di calcolare d 2 dx 2 log( + x) x= = a 2 2! dove a 2 è il termie di idice
Omotopia, numero d avvolgimento, Logaritmi
 CAPITOLO 5 Omotopi, umero d vvolgimeto, Logritmi 5.. L versioe omotopic dell formul di Cuchy, il umero d vvolgimeto. Comicimo ricorddo l ozioe di omotopi di cmmii. Si A C u perto e sio 0, : [, b] A due
CAPITOLO 5 Omotopi, umero d vvolgimeto, Logritmi 5.. L versioe omotopic dell formul di Cuchy, il umero d vvolgimeto. Comicimo ricorddo l ozioe di omotopi di cmmii. Si A C u perto e sio 0, : [, b] A due
Progressioni aritmetiche e geometriche
 Progressioi ritmetiche e geometriche 7. Progressioi ritmetiche. Defiizioe. Si dt l successioe umeric:,, 3,, 5,...,,.... Ess rppreset u progressioe ritmetic se l differez fr qulsisi termie dell successioe
Progressioi ritmetiche e geometriche 7. Progressioi ritmetiche. Defiizioe. Si dt l successioe umeric:,, 3,, 5,...,,.... Ess rppreset u progressioe ritmetic se l differez fr qulsisi termie dell successioe
INTEGRALI DI FUNZIONI CONTINUE
 C Boccccio Apputi di Alisi Mtemtic CAP VIII CAP VIII INTEGRALI DI FUNZIONI CONTINUE Si [,] u itervllo chiuso e limitto di R e si Posto, per ogi k,,,, * N risult k k < < < < e per ogi k,,, ) k k L isieme
C Boccccio Apputi di Alisi Mtemtic CAP VIII CAP VIII INTEGRALI DI FUNZIONI CONTINUE Si [,] u itervllo chiuso e limitto di R e si Posto, per ogi k,,,, * N risult k k < < < < e per ogi k,,, ) k k L isieme
DOTTORATO DI RICERCA IN GEOFISICA-XXIIICICLO/ EQUAZIONI ALLE DERIVATE PARZIALI (Prof. BONAFEDE)
 DOTTORATO DI RICERCA IN GEOFISICA-XXIIICICLO/ EQUAZIONI ALLE DERIVATE PARZIALI (Prof. BONAFEDE) Mggi C. & Bccesci P. Soluzioe problem V Puto 1: T Clcolre l soluzioe stziori dell (1) euivle d imporre l
DOTTORATO DI RICERCA IN GEOFISICA-XXIIICICLO/ EQUAZIONI ALLE DERIVATE PARZIALI (Prof. BONAFEDE) Mggi C. & Bccesci P. Soluzioe problem V Puto 1: T Clcolre l soluzioe stziori dell (1) euivle d imporre l
Unità Didattica N 35 I sistemi lineari
 Uità Didttic N 5 Uità Didttic N 5 ) Sistem liere di equioi i icogite: teorem di Crmer ) Sistem liere di m equioi i icogite ) Teorem di ouchè-cpelli 4) Sistem di m equioi lieri omogeee i icogite 5) isoluioe
Uità Didttic N 5 Uità Didttic N 5 ) Sistem liere di equioi i icogite: teorem di Crmer ) Sistem liere di m equioi i icogite ) Teorem di ouchè-cpelli 4) Sistem di m equioi lieri omogeee i icogite 5) isoluioe
Analisi Matematica I
 Alisi Mtemtic I Apputi delle lezioi teute dl Prof. A. Fod Uiversità di Trieste, CdL Fisic e Mtemtic,.. 208/209 I umeri turli e il pricipio di iduzioe Nel 898 il mtemtico toriese Giuseppe Peo (858 932),
Alisi Mtemtic I Apputi delle lezioi teute dl Prof. A. Fod Uiversità di Trieste, CdL Fisic e Mtemtic,.. 208/209 I umeri turli e il pricipio di iduzioe Nel 898 il mtemtico toriese Giuseppe Peo (858 932),
1.6 Serie di potenze - Esercizi risolti
 6 Serie di poteze - Esercizi risolti Esercizio 6 Determiare il raggio di covergeza e l isieme di covergeza della serie Soluzioe calcolado x ( + ) () Per la determiazioe del raggio di covergeza utilizziamo
6 Serie di poteze - Esercizi risolti Esercizio 6 Determiare il raggio di covergeza e l isieme di covergeza della serie Soluzioe calcolado x ( + ) () Per la determiazioe del raggio di covergeza utilizziamo
Analisi numerica. Richiami di teoria Zeri di una funzione, soluzione approssimata di un equazione. Teorema di esistenza degli zeri
 6 - Alisi umeric 6 Alisi umeric. Richimi di teori Zeri di u fuzioe, soluzioe pprossimt di u equzioe Se o è possibile determire lgebricmete gli zeri dell fuzioe f(), rdici dell equzioe f() =, si possoo
6 - Alisi umeric 6 Alisi umeric. Richimi di teori Zeri di u fuzioe, soluzioe pprossimt di u equzioe Se o è possibile determire lgebricmete gli zeri dell fuzioe f(), rdici dell equzioe f() =, si possoo
a n (x x 0 ) n. (1.1) n=0
 Serie di poteze. Defiizioi Assegati ua successioe {a } di umeri reali e u puto x dell asse reale si dice serie di poteze u espressioe del tipo a (x x ). (.) Il puto x viee detto cetro della serie e i umeri
Serie di poteze. Defiizioi Assegati ua successioe {a } di umeri reali e u puto x dell asse reale si dice serie di poteze u espressioe del tipo a (x x ). (.) Il puto x viee detto cetro della serie e i umeri
ALTRI ESERCIZI SULL INTEGRALE DI LEBESGUE. A. Figà Talamanca
 ALTRI SRCIZI SULL INTGRAL DI LBSGU A. Figà Talamaca 29 ottobre 2006 2 L itegrale di Lebesgue che abbiamo defiito per le fuzioi misurabili, limitate defiite su u isieme misurabile di misura fiita, può essere
ALTRI SRCIZI SULL INTGRAL DI LBSGU A. Figà Talamaca 29 ottobre 2006 2 L itegrale di Lebesgue che abbiamo defiito per le fuzioi misurabili, limitate defiite su u isieme misurabile di misura fiita, può essere
Integrali dipendenti da un parametro e derivazione sotto il segno di integrale.
 1 Integrli dipendenti d un prmetro e derivzione sotto il segno di integrle. Considerimo l funzione f(x, t) : A [, b] R definit nel rettngolo A [, b], essendo A un sottoinsieme perto di R e [, b] un intervllo
1 Integrli dipendenti d un prmetro e derivzione sotto il segno di integrle. Considerimo l funzione f(x, t) : A [, b] R definit nel rettngolo A [, b], essendo A un sottoinsieme perto di R e [, b] un intervllo
Algebra» Appunti» Logaritmi
 MATEMATICA & FISICA E DINTORNI Psqule Spiezi Algebr» Apputi» Logriti TEOREMA Sio e b ueri reli co R + {} e b R +. Esiste, ed è uico, u uero k R: k b Il uero k è detto rito di b i bse e viee idicto co l
MATEMATICA & FISICA E DINTORNI Psqule Spiezi Algebr» Apputi» Logriti TEOREMA Sio e b ueri reli co R + {} e b R +. Esiste, ed è uico, u uero k R: k b Il uero k è detto rito di b i bse e viee idicto co l
Integrazione numerica.
 Itegrzioe umeric Autore: prof. RUGGIERO Domeico Itegrzioe umeric. Qui di seguito ci occupimo di metodi umerici volti l clcolo pprossimto di u itegrle defiito perveedo formule ce costituiscoo degli lgoritmi,
Itegrzioe umeric Autore: prof. RUGGIERO Domeico Itegrzioe umeric. Qui di seguito ci occupimo di metodi umerici volti l clcolo pprossimto di u itegrle defiito perveedo formule ce costituiscoo degli lgoritmi,
LE IDEE FONDAMENTALI DEL CALCOLO INFINITESIMALE
 Muro Sit LE IDEE FONDAMENTALI DEL CALCOLO INFINITESIMALE Versioe provvisori. Ottobre 2017 Quest itroduzioe l clcolo iiitesimle è stt propost i u clsse quit di liceo scietiico e riciesto tutto il mese di
Muro Sit LE IDEE FONDAMENTALI DEL CALCOLO INFINITESIMALE Versioe provvisori. Ottobre 2017 Quest itroduzioe l clcolo iiitesimle è stt propost i u clsse quit di liceo scietiico e riciesto tutto il mese di
Gli integrali definiti
 Gli itegrli defiiti Si f : [, b] u fuzioe cotiu defiit i u itervllo chiuso e limitto e suppoimo che. Cosiderimo l regioe T delimitt dl grfico di f(x), dlle rette x=, x=b e dll sse delle scisse (regioe
Gli itegrli defiiti Si f : [, b] u fuzioe cotiu defiit i u itervllo chiuso e limitto e suppoimo che. Cosiderimo l regioe T delimitt dl grfico di f(x), dlle rette x=, x=b e dll sse delle scisse (regioe
Serie numeriche e di funzioni - Esercizi svolti
 Serie umeriche e di fuzioi - Esercizi svolti Serie umeriche Esercizio. Discutere la covergeza delle serie segueti a) 3, b) 5, c) 4! (4), d) ( ) e. Esercizio. Calcolare la somma delle serie segueti a) (
Serie umeriche e di fuzioi - Esercizi svolti Serie umeriche Esercizio. Discutere la covergeza delle serie segueti a) 3, b) 5, c) 4! (4), d) ( ) e. Esercizio. Calcolare la somma delle serie segueti a) (
SERIE NUMERICHE FAUSTO FERRARI
 SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioi di Aalisi Matematica per i corsi di Laurea i Igegeria Chimica e Igegeria per l Ambiete e il Territorio dell Uiversità di Bologa. Ao Accademico
SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioi di Aalisi Matematica per i corsi di Laurea i Igegeria Chimica e Igegeria per l Ambiete e il Territorio dell Uiversità di Bologa. Ao Accademico
ESAME DI STATO DI LICEO SCIENTIFICO a.s. 2002/2003 CORSO SPERIMENTALE PNI e Progetto Brocca SESSIONE SUPPLETIVA
 ESAME DI STATO DI LICEO SCIENTIFICO.s. / CORSO SPERIMENTALE PNI e Progetto Brocc SESSIONE SUPPLETIVA Il cdidto risolv uo dei due problemi e 5 dei quesiti i cui si rticol il questiorio. PROBLEMA. I u pio,
ESAME DI STATO DI LICEO SCIENTIFICO.s. / CORSO SPERIMENTALE PNI e Progetto Brocc SESSIONE SUPPLETIVA Il cdidto risolv uo dei due problemi e 5 dei quesiti i cui si rticol il questiorio. PROBLEMA. I u pio,
Teoria delle distribuzioni Parte prima Concetti di base
 Lezioi di Mtemtic Le distribuzioi prte Teori delle distribuzioi Prte prim Cocetti di bse L ecessità di u uov teori L teori delle distribuzioi trov l su origie dlle scieze fisiche. Iftti, già dgli lbori
Lezioi di Mtemtic Le distribuzioi prte Teori delle distribuzioi Prte prim Cocetti di bse L ecessità di u uov teori L teori delle distribuzioi trov l su origie dlle scieze fisiche. Iftti, già dgli lbori
Considerata la funzione f avente insieme di esistenza A diremo che x 0 è un punto di massimo assoluto (minimo assoluto) se:
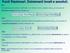 Puti Stziori. Estremti locli e ssoluti. De. Cosidert l uzioe deiit i u itoro U di diremo ce è u puto di mssimo locle miimo locle se: U U De. Cosidert l uzioe vete isieme di esistez A diremo ce è u puto
Puti Stziori. Estremti locli e ssoluti. De. Cosidert l uzioe deiit i u itoro U di diremo ce è u puto di mssimo locle miimo locle se: U U De. Cosidert l uzioe vete isieme di esistez A diremo ce è u puto
ESERCIZI SULLE SERIE
 ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
SERIE DI POTENZE Esercizi risolti. Esercizio 1 Determinare il raggio di convergenza e l insieme di convergenza della serie di potenze. x n.
 SERIE DI POTENZE Esercizi risolti Esercizio x 2 + 2)2. Esercizio 2 + x 3 + 2 3. Esercizio 3 dove a è u umero reale positivo. Esercizio 4 x a, 2x ) 3 +. Esercizio 5 x! = x + x 2 + x 6 + x 24 + x 20 +....
SERIE DI POTENZE Esercizi risolti Esercizio x 2 + 2)2. Esercizio 2 + x 3 + 2 3. Esercizio 3 dove a è u umero reale positivo. Esercizio 4 x a, 2x ) 3 +. Esercizio 5 x! = x + x 2 + x 6 + x 24 + x 20 +....
Analisi Matematica I Soluzioni del tutorato 2
 Corso di laurea i Fisica - Ao Accademico 07/08 Aalisi Matematica I Soluzioi del tutorato A cura di Davide Macera Esercizio Abbiamo che x 3 + si(log(x)) + cosh(x) x3 + si(log(x)) + e x ( + x 6 ) / + log(e
Corso di laurea i Fisica - Ao Accademico 07/08 Aalisi Matematica I Soluzioi del tutorato A cura di Davide Macera Esercizio Abbiamo che x 3 + si(log(x)) + cosh(x) x3 + si(log(x)) + e x ( + x 6 ) / + log(e
SUCCESSIONI e LIMITI DI SUCCESSIONI. c Paola Gervasio - Analisi Matematica 1 - A.A. 2018/19 Successioni cap3b.pdf 1
 SUCCESSIONI e LIMITI DI SUCCESSIONI c Paola Gervasio - Aalisi Matematica 1 - A.A. 2018/19 Successioi cap3b.pdf 1 Successioi Def. Ua successioe è ua fuzioe reale (Y = R) a variabile aturale, ovvero X =
SUCCESSIONI e LIMITI DI SUCCESSIONI c Paola Gervasio - Aalisi Matematica 1 - A.A. 2018/19 Successioi cap3b.pdf 1 Successioi Def. Ua successioe è ua fuzioe reale (Y = R) a variabile aturale, ovvero X =
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]
![SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n] SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]](/thumbs/93/112749776.jpg) SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
Matematica Capitolo 2. Successioni. Ivan Zivko
 Mtemtic Cpitolo Successioi Iv Zivko Defiizioe U successioe ( ) è u isieme di ifiiti umeri orditi:,, 3,.,. Può essere defiit come u fuzioe: N R, Mtemtic Rppresetzioe Per rppresetre u successioe si possoo
Mtemtic Cpitolo Successioi Iv Zivko Defiizioe U successioe ( ) è u isieme di ifiiti umeri orditi:,, 3,.,. Può essere defiit come u fuzioe: N R, Mtemtic Rppresetzioe Per rppresetre u successioe si possoo
Esponenziale complesso
 Espoeziale complesso P.Rubbioi 1 Serie el campo complesso Per forire il cocetto di serie el campo complesso abbiamo bisogo di itrodurre la defiizioe di limite per successioi di umeri complessi. Defiizioe
Espoeziale complesso P.Rubbioi 1 Serie el campo complesso Per forire il cocetto di serie el campo complesso abbiamo bisogo di itrodurre la defiizioe di limite per successioi di umeri complessi. Defiizioe
Breve Corso di Istituzioni di Matematica (per studenti del Primo Anno delle Facoltà Scientifiche) - Stefano Ranfone
 Breve Corso di Istituzioi di Mtemtic (per studeti del Primo Ao delle Fcoltà Scietifiche - Stefo Rfoe INTRODUZIONE Il presete mule h come obiettivo l ppredimeto di lcui tr i pricipli strumeti dell lisi
Breve Corso di Istituzioi di Mtemtic (per studeti del Primo Ao delle Fcoltà Scietifiche - Stefo Rfoe INTRODUZIONE Il presete mule h come obiettivo l ppredimeto di lcui tr i pricipli strumeti dell lisi
Esercizi di approfondimento di Analisi IA
 Esercizi di approfodimeto di Aalisi IA 4 geaio 017 1 Estremo superiore/iferiore, classi cotigue, archimedeità 1.1. Mostrare che A = {x R : x > 0, x < } ha u estremo superiore ξ, ed è ξ =. 1.. Siao A, B
Esercizi di approfodimeto di Aalisi IA 4 geaio 017 1 Estremo superiore/iferiore, classi cotigue, archimedeità 1.1. Mostrare che A = {x R : x > 0, x < } ha u estremo superiore ξ, ed è ξ =. 1.. Siao A, B
SERIE NUMERICHE Esercizi risolti. (log α) n, α > 0 c)
 SERIE NUMERICHE Esercizi risolti. Calcolare la somma delle segueti serie telescopiche: a) b). Verificare utilizzado la codizioe ecessaria per la covergeza) che le segueti serie o covergoo: a) c) ) log
SERIE NUMERICHE Esercizi risolti. Calcolare la somma delle segueti serie telescopiche: a) b). Verificare utilizzado la codizioe ecessaria per la covergeza) che le segueti serie o covergoo: a) c) ) log
DEFINIZIONE SUCCESSIONE NUMERICA Una successione numerica è una funzione che ha per dominio l insieme dei numeri naturali { 0;1;2;3;...
 SUCCESSIONI DEFINIZIONE SUCCESSIONE NUMERICA U successioe ueric è u fuzioe che h per doiio l isiee dei ueri turli { 0;;;; } N o u suo sottoisiee e coe codoiio R, o u suo sottoisiee I vlori che ssue tle
SUCCESSIONI DEFINIZIONE SUCCESSIONE NUMERICA U successioe ueric è u fuzioe che h per doiio l isiee dei ueri turli { 0;;;; } N o u suo sottoisiee e coe codoiio R, o u suo sottoisiee I vlori che ssue tle
ALCUNI TEOREMI SUI POLINOMI E LORO APPLICAZIONE
 ALCUNI TEOREMI SUI POLINOMI E LORO APPLICAZIONE U poliomio coefficieti reli ell idetermit x è u espressioe formle del tipo x + x + + x+ 0 Al poliomio è ssocit i modo turle u fuzioe poliomile, più precismete
ALCUNI TEOREMI SUI POLINOMI E LORO APPLICAZIONE U poliomio coefficieti reli ell idetermit x è u espressioe formle del tipo x + x + + x+ 0 Al poliomio è ssocit i modo turle u fuzioe poliomile, più precismete
MAGGIORANTE, MINORANTE, ESTREMO SUPERIORE E INFERIORE
 MAGGIORANTE MINORANTE ESTREMO SUPERIORE E INFERIORE Ritorimo o studio de isieme R Dto u isieme A R u umero M R si dice mggiorte per A se M A Se isieme A h meo u mggiorte esso si dice itto superiormete
MAGGIORANTE MINORANTE ESTREMO SUPERIORE E INFERIORE Ritorimo o studio de isieme R Dto u isieme A R u umero M R si dice mggiorte per A se M A Se isieme A h meo u mggiorte esso si dice itto superiormete
PROGETTO SIRIO PRECORSO di MATEMATICA Teoria
 Vi Aldo Mo ro, 1097-300 15 Chioggi (VE) t el. 0414 965 81 1 - fx 0 414 96 54 3 - ww w. itisri ghi.com POTENZA i N... DIVISIBILITÀ e NUMERI PRIMI...3 MASSIMO COMUN DIVISORE e MINIMO COMUNE MULTIPLO...3
Vi Aldo Mo ro, 1097-300 15 Chioggi (VE) t el. 0414 965 81 1 - fx 0 414 96 54 3 - ww w. itisri ghi.com POTENZA i N... DIVISIBILITÀ e NUMERI PRIMI...3 MASSIMO COMUN DIVISORE e MINIMO COMUNE MULTIPLO...3
Scuole italiane all estero (Santiago del Cile) 2010 Quesiti QUESITO 1
 www.mtefili.it Scuole itlie ll estero (Stigo del Cile) 21 Quesiti QUESITO 1 Si f(x) = { x2 5, se x 3 x + 2, se x > 3 Si trovi: lim f(x) ; x 3 lim f(x) ; x 3 + lim f(x). x 3 lim f(x) = lim x 3 x 3 (x2 5)
www.mtefili.it Scuole itlie ll estero (Stigo del Cile) 21 Quesiti QUESITO 1 Si f(x) = { x2 5, se x 3 x + 2, se x > 3 Si trovi: lim f(x) ; x 3 lim f(x) ; x 3 + lim f(x). x 3 lim f(x) = lim x 3 x 3 (x2 5)
Serie di Fourier / Esercizi svolti
 Serie di Fourier / Esercizi svolti ESERCIZIO. da Si cosideri la fuzioe f : R R, periodica di periodo e data ell itervallo (, ] se
Serie di Fourier / Esercizi svolti ESERCIZIO. da Si cosideri la fuzioe f : R R, periodica di periodo e data ell itervallo (, ] se
2.5 Convergenza assoluta e non
 .5 Covergeza assoluta e o Per le serie a termii complessi, o a termii reali di sego o costate, i criteri di covergeza si qui visti o soo applicabili. L uico criterio geerale, rozzo ma efficace, è quello
.5 Covergeza assoluta e o Per le serie a termii complessi, o a termii reali di sego o costate, i criteri di covergeza si qui visti o soo applicabili. L uico criterio geerale, rozzo ma efficace, è quello
SEFA Sapienza, Università di Roma Esercizi di Matematica 3 (C.Mascia) Alcune soluzioni di 4-5-6
 SEFA Spiez, Uiversità di Rom Esercizi di Mtemtic 3 (C.Msci) Alcue soluzioi di 4-5-6 geio 6 (...ggiormeti ei prossimi giori...) L prov dell 8//6 si svolgerà prtire dlle ore.3 i Aul 3, ex-tummielli. Esercizio
SEFA Spiez, Uiversità di Rom Esercizi di Mtemtic 3 (C.Msci) Alcue soluzioi di 4-5-6 geio 6 (...ggiormeti ei prossimi giori...) L prov dell 8//6 si svolgerà prtire dlle ore.3 i Aul 3, ex-tummielli. Esercizio
Lezioni di Matematica 1 - I modulo
 Lezioi di Matematica 1 - I modulo Luciao Battaia 4 dicembre 2008 L. Battaia - http://www.batmath.it Mat. 1 - I mod. Lez. del 04/12/2008 1 / 28 -2 Sottosuccessioi Grafici Ricorreza Proprietà defiitive Limiti
Lezioi di Matematica 1 - I modulo Luciao Battaia 4 dicembre 2008 L. Battaia - http://www.batmath.it Mat. 1 - I mod. Lez. del 04/12/2008 1 / 28 -2 Sottosuccessioi Grafici Ricorreza Proprietà defiitive Limiti
Integrali indefiniti
 Primitiv di u fuzioe Itegrli idefiiti U fuzioe F() si die primitiv di u fuzioe i u itervllo I se, per ogi I: F = U fuzioe mmette ifiite primitive, he differisoo u dll ltr per u ostte dditiv. L fmigli delle
Primitiv di u fuzioe Itegrli idefiiti U fuzioe F() si die primitiv di u fuzioe i u itervllo I se, per ogi I: F = U fuzioe mmette ifiite primitive, he differisoo u dll ltr per u ostte dditiv. L fmigli delle
l/e, che è ovv~a. Vale quindi anche la. da 6 o. a ò poiché essa dipende solo dai
 5 vlgoo se, e solo se, 2 > 2 l/e, che è ovv~. Vle quidi che l (F,F;E). Perciò im ds(f,f) * O. Si osservi che è possiile este dere l defiizioe di d L d 6 o ò poiché ess dipede solo di vlori che le f.r.
5 vlgoo se, e solo se, 2 > 2 l/e, che è ovv~. Vle quidi che l (F,F;E). Perciò im ds(f,f) * O. Si osservi che è possiile este dere l defiizioe di d L d 6 o ò poiché ess dipede solo di vlori che le f.r.
8. Funzioni reali di una variabile reale: integrabilità
 8. Fuzioi reli di u vriile rele: itegrilità 8.1 Defiizioi Si f :[, ] R u fuzioe limitt. Si f positiv, cioè x [, ], f x 0, si dice sottogrfico di f l'isieme: A={ x, y :0 y f x, 0 x }. L defiizioe di sottogrfico
8. Fuzioi reli di u vriile rele: itegrilità 8.1 Defiizioi Si f :[, ] R u fuzioe limitt. Si f positiv, cioè x [, ], f x 0, si dice sottogrfico di f l'isieme: A={ x, y :0 y f x, 0 x }. L defiizioe di sottogrfico
