Classificazione dei semplici ordinamenti di un gruppo libero commutativo con N generatori
|
|
|
- Roberto Ventura
- 6 anni fa
- Visualizzazioni
Transcript
1 RENDICONTI del SEMINARIO MATEMATICO della UNIVERSITÀ DI PADOVA GIORGIO TREVISAN Classfcazoe de semplc ordamet d u gruppo lbero commutatvo co N geerator Redcot del Semaro Matematco della Uverstà d Padova, tome 22 (1953), p < _0> Redcot del Semaro Matematco della Uverstà d Padova, 1953, tous drots réservés. L accès aux archves de la revue «Redcot del Semaro Matematco della Uverstà d Padova» ( mplque l accord avec les codtos géérales d utlsato ( php). Toute utlsato commercale ou mpresso systématque est costtutve d ue fracto péale. Toute cope ou mpresso de ce fcher dot coter la présete meto de copyrght. Artcle umérsé das le cadre du programme Numérsato de documets aces mathématques
2 CLASSIFICAZIONE DEI SEMPLICI ORDINAMENTI DI UN GRUPPO LIBERO COMMUTATIVO CON N GENERATORI Nota Cf) d GIORGIO TREVISAN (a De var problem coteut el «Problem 102» d BR- KHOFF 1) s rsolve l seguete : d) Dato u gruppo G lbero commutatvo co geerator determare quat mod dvers G- s può semplcemete ordare. I I) soo rchamate propretà ote de grupp lber commutatv co geerator. Ne umer 1, 2, 3 s rcordao propretà d tal grupp quado soo semplcemete ordat e s stablscoo alcu semplc lemm. Nel.ro 4 grupp so pesat sez altro come archmede e s dà u teorema che permette d classfcare loro semplc ordamet. Ne umer successv s mostra come l problema d) per G s rcoduca a dare semplc ordamet d opportu grupp lber commutatv archmede ed semplc ordamet d grupp della stessa atura d G, ma co u umero more d geerator. S ottee cos u procedmeto d rduzoe che porta alla soluzoe del problema proposto perchè fe s guge sempre a dover dare semplc ordamet d grupp archmede commutatv). I. - u gruppo lbero commutatvo co geerator ~). (*) Perveuta Redazoe l 22 febbrao ) G. BIRKHOFF, Lattce Theory [Amerca Mat. Soc. Coll., vol. XXV 1948], pag ) I teorem d questo umero su grupp co geerator s possoo ad esempo rcavare da quato detto proposto LEFSCHETZ,
3 - 144 U sottogruppo H d G s chama sottogruppo co dv&olze se cotee elemet dvers dallo zero, e se per og 9 e G tale g co p tero o ullo, segue che g e H. S ha che : Og sottogruppo d G, dverso dall dettà, ò a gruppo lbero commutatvo. TEOREMA: Se H è u sottogruppo co dvsoe d G co r geerator l gruppo H è u lbero commu- - r geerator. Sa ora G u gruppo commutatvo co geerator g~,..., g" e tra quest resto verfcate le codzo ~s Às g s = o ( = = 1, 2,.., r) e sa r l rago della matrce llasll. Per poter semplcemete ordare G è ecessaro, come oto e come rchamato seguto, che tutt gl elemet d G dvers dallo zero sao aperodc. Ma allora s vede faclmete che l problema d ) per u gruppo d questo tpo s rcoduce ecessaramete a studare l problema d) per l gruppo lbero commutatvo co - geerator U gruppo G è detto semplcemete ordato se tra suo elemet è stablta ua relazoe d orde che d due elemet dstt d G dca quale è maggore e quale more ed è tale che se ab (b>a) rsult ~ -~- b qualuque sa m e G. Codzoe ecessara perchè G sa semplcemete ordato è che G o cotega elemet dvers da 0 a perodo fto. Se questa codzoe ecessara è verfcata ed oltre G è commutatvo, allora G s può semplcemete ordare 3). b > 0, s dce che a~ e b soo equvalet dal puto d vsta archmedeo e s scrve a cdb se Algebrac Topology [Amerca Mat. Soc. Coll., Vol. XXVII, 194?] pagg La deomazoe «sottogruppo co dvsoe» è quella usata da P. ALEXANDROFF e H. IIOPF el loro Topologe (vedere l captolo su modul). 3) Loc. ct. 1) teor. 14, pag. 224.
4 ~ per og multplo d c~ esste u multplo b d b tale che 1a b e se per og multplo lb d b esste u multplo m1a d c~ tale che b Se vece per og aturale m è c~ è detto ftamete more d b e s scrve c~ «b. La relazoe b, è ua relazoe d equvaleza ; elle class d equvaleza s possoo dstrbure ache gl elemet egatv d G, basta ovvamete collocare ella stessa classe u elemeto ed l suo opposto. Vale proposto l Teorema 4) : Se G è archmedeo esso è somorfo ad u 80ttogruppo del gruppo addtvo de umer real, qud è commutatvo. S espogoo ora alcu semplc lemm utl per l seguto. LEMMA I.: Se 0 a, 0 b, b ed m, soo ter postv allora ma + b cv a. LEMMA II. ò ~ e 0 «l1 «az ««ar ea~ è ~,. > 0 allora... r qualuque sao gl ter À~,..., 5,,-1 rsulta 0 ~2 N cl..r, 1 E evdetemete, qud e percò tato 0 r Xu resce 1 : ar da cu per og h tero postvo. Per quato vsto precedeza se 0 è u tero postvo s ha 4) Loc. ct. 1) teor. 15, pag. 226.
5 146 Ora qualuque sa 1 tero postvo h e posto 6 = h + 1 resce che asseme alla (1) terma la dmostrazoe della prma relazoe d cu parla l lemma; per la secoda relazoe la dmostrazoe cosegue co cosderazo del tutto aaloghe a quelle gà svolte. LEMMA III. I Se ~ co ( = 1,..., r) ter relatv, allora l = 0 ( = 1, 2,..., r). Ragoado per assurdo sa aj ~ O e j sa massmo (1 ~ j r) s ha percò l lm = 0. Ora o Àj > 0, oppure basta moltplcare la relazoe precedete per - 1 per trovars tale evetualtà, og caso è applcable l LEMMA II. Per esempo se Aj > O per l LEMMA II rsulterebbe 00 a e qud l assurdo 0 c~ aj Come prma applcazoe de lemm precedet s ottee l TEORE>rA : Se G è gruppo lbero commutatvo co geerator, semplcemete ordato, suo elemet s dstrbuscoo u umero d class d equvaleza o suroerore ad. Sa g, ~27..., g ua base d geerator d ~. Og geeratore può essere pesato come postvo perchè se ad esempo fosse gl 0 basterebbe al suo posto cosderare gl e g2,..., g costturebbe acora ua base per G. E pure evdetemete o restrttvo supporre 0 g g, Og elemeto è della forma M Àg e percò per LEMMI I, e II esso o è equvalete a g od ftamete more d gu.
6 147 Ragoado per assurdo s suppoga che esstao + 1 elemet postv d G, (Ù2,..., tal che «(,)2 ««... Sarà tato? (ù 1}, g 1 l determate della matrce formata co gl ter h, j. Se ~ = 0 s possoo determare gl ter..., 5 À ~~ o tutt ull., tal che ed allora dalle (2) moltplcado per À e sommado s ottee teedo coto delle (3) E aw = O co E X # 0 l che è assur do per l LEMMA III. Sa duque =~= 0. I tal caso dcato co H l complemeto algebrco d moltplcata la (2) per H e sommato rspetto ad s ottee H~~ "+1, coè acora u assurdo per l LEMMA III U sottogruppo del gruppo addtvo de umer real somorfo ad u gruppo lbero commutatvo co geerator, ecessaramete archmedeo, è costtuto d tutt umer real E dove À percorre 1 seme de umer ter relatv (e dello zero), e ~z soo umer real fssat, dvers dallo zero, a due a due dvers tra loro e tal acora che se E Ag # 0 rsul- 1. t d cosegueza X; = 0 ( = 1, 2,..., ). L seme d tal sottogrupp sarà dcato el seguto co I. La costruzoe d elemet d I è baale. S dcherà acora co J 1 seme delle class cu s dstrbuscoo gl elemet d I quado s collocho ua stessa classe elemet d I somorf (coè grupp somorf che ell somorfsmo coservao le relazo d orde). I proposto s ha l TEOREMA : Codzoe ecessara e suffcete perchè gl elemet S1 ed ~2 d 1,~ sao tra loro somorf è che detta g
7 148 ( = 1,..., ) base d S1 s rescao a determare S., umer gz" tal che : La codzoe è ecessara. Ifatt se 8, ed 82 soo somorf sao gz umer d ~2 che corrspodoo a Per l somorfsmo gà e g..11 avrao lo stesso sego qud l loro rapporto sarà postvo. Per fssare le dee s suppoga 0, g2 > 0 e g2. Scelto u tero postvo h rsulterà uvocamete determato 1 tero postvo tale che e da questa s trae e qud passado al lmte per 1 somortsmo dalla (5) s deduce e co ulte- e qud da questa ua relazoe aaloga alla (6) rore passaggo al lmte Dal cofroto delle (7), (8) rsulta g 2.= g"2 e d qua facl- 9, g1 mete la prma delle (4). Aaloghe cosderazo se g1 - e g2 o soo etramb postv. Stablta la prma delle (4) le altre s deducoo col procedmeto precedete cofrotado g1 co gí ( = 3, 4,..., ). La codzoe è suffcete. Essterao qud 82 umer g" per cu soo vere le (4). S cosder tra S 1 ed S 2 la
8 - a 149 corrspodeza che assoca all elemeto Z lg d 8, l elemeto d S2. Tale corrspodeza assoca alla somma d ele met la somma de corrspodet ed è buvoca. Ifatt M pochè per le (4) g" = kg s ha che all elemeto E lg 1 d S1 vee a corrspodere S2 l elemeto K.E Ag e vce versa. Duque ad elemet dstt corrspodoo elemet dstt pochè k % 0 e ad elemet postv elemet postv pochè > 0. La corrspodeza cosderata è duque u somorfsmo Per l TEOREMA dmostrato el.r 3. se G è u gruppo lbero commutatvo co geerator, semplcemete ordato, suo elemet postv s dstrbuscoo ( C~ ) class d equvaleza archmedea. Sao A2,..., A tal class. S potrà supporre che se a; e ah e A~ ak se j k. A1 s può chamare la mma classe d equvaleza archmedea d G. S cosder ora l seme A formato dagl elemet d da loro oppost e dallo zero, orbee s ha l TEOREMA t A1 è u sottogruppo co dvsoe d G, medeo quado lo s ord per duzoe G. Sao a e P due elemet d S deve tato far vedere che a - - ~ ~.A.1. Se G a+p>0 può essere 0 qud Se a e ~ hao seg cotrar, ad esempo a 0, ~ > 0, è a + ~ a -~- ~3 2p se per fssare le dee s è supposto - a ~3 ; s procede po come sopra teedo coto che A è la mmo classe d equvaleza. Se almeo uo degl elemet a e P è ullo la cosa è baale. - a - > 0 (G è commutatvo) e pochè a e 2013 p appartegoo ad A* v appartee per quato gà vsto - ~~ e qud sempre per la costruzoe d A ache l suo opposto a + P. 441* è duque u sottogruppo d G, che rsulterà semplcemete ordato per duzoe da G.
9 b 150 D altra parte A è archmedeo perchè se gl elemet postv d At apparteessero ad almeo due class dstte d equvaleza archmedea cò accadrebbe ache per gl elemet d A 1, cotro 1 potes. Sa A* co p tero. S può supporre x > 0 e p > 0 prevo passaggo agl oppost. S ha per l LEMMA 1 2 e qud 1 coè ed A* è duque u sottogruppo co dvsoe d G S mategoo sgfcat dat alle otazo el.ro precedete e s cosdera l gruppo fattorale G1 = G. Ha g1 teresse mostrare comme G duca u semplce ordameto G, el modo che segue. Sao 7~ e k due elermet d 6~ dvers tra loro. S dcho co ~1 e g gl sem d elemet d G che ell omomorfsmo che porta G- su G1 s trasformao rspettvamete h e k. Se a ed cc1 soo elemet d H e b e b elemet d K ed è ad esempo, a b allora è ache b 1. Ifatt sarà a~ = c~ co (? e A = b -~- r~ co r a A* - e se fosse a 1 > 0 dalla a 2013 b==~ - b + cr 2013 ~ segurebbe, pochè a - b 0, b 1 s - c A1 e per la propretà d mmo goduta da cò che è assurdo pochè a e b 1 appartegoo a due class dverse modulo Ne segue che le class d G modulo A~* costtuscoo ua catea e s tederà che h k, se e solo se, H g ; tal modo G rsulta semplcemete ordato. Le cosderazo svolte s possoo vertre. Sa At u sottogruppo co dvsoe d G ; allora per teorem del.r I. su grupp, A* e G1 soo grupp lber commutatv qud At semplcemete ordabl. S sa stablto u semplce ordameto per At ed uo per Gl, s mostra ora come quest ordamet ducao u semplce ordameto su G. Sao p due elemet d G, se ess appartegoo ad A* s stablsca tra loro G la stessa relazoe d orde che pos-
10 151 seggoo A. ; se p e A e q ell omomorfsmo d G su G1 s trasforma ell elemeto q d G1 s poga p q se q > 0 G1 e p q se q 0 G1; se p e q s trasformao ell omomorfsmo ello stesso elemeto h d G1 cò vuol dre ~= secoda che A > 0 ; se fe trasformat d p e q G1 soo due elemet dstt d e q s stablsca tra p e q G la stessa relazoe d orde che hao p e q G1. E mmedato verfcare che G rsulta tal modo semplcemete ordato e che 1 seme A degl elemet postv d A costtusce la classe mma d equvaleza archmedea d G. Rtorado al caso che G sa semplcemete ordato e de semplc ordamet che da G vegoo dott A* ed A*1 medea d G soo umero d ( umero d 1. ), quelle d G1 soo 7. - Sa acora G semplcemete ordato; A (.r I.) sarà ach esso u gruppo lbero commutatvo co r ~~ geerator : orbee è d decsva mportaza per questa rcerca l seguete : TEOREMA: Se G è semplcemete ordccto e l G = G s vede subto che se le class d equvaleza arch- Sottogruppo A rsulta geerato da r geerator, scelto u qualsas sottogruppo co dvsoe d G co r geerator ~.~, è possble determare u semplce ordameto A2* ed u ordtameto G per modo che per duzoe s rproduca G, A*2 a meo d automorfsm l semplce ordameto d parteza. Sa (Ù2,..., ar ua base d geerator d A, h2,..., ua base d G1 cos sa? 1)2, >...> 1)". ua base d ~ 2 e k1, k2,..., k-r ua tl base d G2 a = d* G. S cosder la corrspo- A*2 r deza tra A ed A che assoca ad og elemeto 21 À;w; d At 1 r l elemeto 1 X e cos la corrspodeza tra G, e G, che asso
11 152 -r -r S tratta evdetemete d due so- ca a E l1,h, l elemeto X 1 morfsm d gruppo. Ora A e G1 rsultao semplcemete ordat per duzoe dal semplce ordameto orgaro d G. S cosdero come elemet postv d 1~2 e G2 quell che egl somorfsm precedet soo corrspodet d elemet postv d A e G~. S vede subto che tal modo A~ e G2 soo stat semplcemete ordat. Ad esempo se a, b, c soo elemet da2 chè A* corrspodet b, c verfcao aaloghe dseguaglaze, ma è allora a > c perchè A è semplcemete ordato ; d altra parte l corrspodete d a c > 0 è a - c e qud per la covezoe fatta - e > 0, Ora semplc ordamet d A2 e G2 ducoo (.r 6) u semplce ordameto su G ed l teorema resterà provato se s fa vedere che esste u automorfsmo d G che ad elemet postv el prmo ordameto fa corrspodere elemet postv el secodo ordameto e vceversa. Sao c~2,..., elemet d G che corrspodoo G ad h~, h2,..., h_r e b 1, b2,..., b-r elemet d G che corrspodoo G2 a k1,...~ S ha che tato..., c~,.,> acl,..., quato..., bl,, b-r costtuscoo ua base d G. S cosder la corrspodeza che assoca ad og ~ e ad og aj, bj, coè tale che all elemeto E lw + E 03BCjaj r -r rspodere l elemeto l: + S r -r 1 1 fa cor- e vceversa. E evdete che la corrspodeza è u automorfsmo d G, bsoga mostrare che coserva le relazo d orde. Sa ~se = 0 ( j = 1,..., r) l suo corrspodete è postvo per come s è ordato ~.~ ; se qualche 03BCj è dverso da z.ero, v o appartee ad A e s trasformerà qud ell omomorfsmo d G su G1 ell elemeta che rsulterà postvo per duzoe (.r 6). D altra parte ell somorfsmo cosderato poco sopra tra G1 e G2 a w
12 153 -r corrspode ~j 1 postvo per come s orda G2 ed acora per l 6 l elemeto quato ell omomorfsmo d G su G2 corrspode all elemeto postvo d G=, è postvo Il complesso delle propretà messe evdeza e umer precedet permette ora agevolmete d rsolvere l problema, scopo del presete lavoro, coè d determare semplc ordamet dstt d u gruppo G lbero commutatvo co geerator..., g. Se..., A soo le class d equvaleza archmedea d G u semplce ordameto esse costtuscoo ua catea scchè co mafesto sgfcato del smbolo s potrà scrvere A 1 A 2... A ( :2~:, ). Sao... B, B2 Bj le class d u altro semplce ordameto d G. Perchè due semplc ordamet d G sao effettvamete dstt occorre e basta che sa almeo ua delle class Ah o somorfa alla classe Bh. Per l teorema del. ro 7 la questoe può essere vsta questo altro modo. Scelto u qualuque sottogruppo co dvsoe d G co r geerator e qud s può predere l sottogruppo A* geerato propro da s ord semplcemete A ed ache G z - G per duzoe s ottee u semplce or- A p p dameto d G. U semplce ordameto d G dstto dal precedete s ottee quest zod : 1) cosderado al posto d A* u sottogruppo co u umero d geerator dverso da r, 2) cosderado per A che deve essere u gruppo archmedeo co r geerator u semplce ordameto dverso dal precedete e tal ordamet soo dat dall seme J~ cosderato al umero 4, 3) lascado per A* lo stesso semplce ordameto, ma mutado l semplce ordameto d G1. Ora G, è u gruppo lbero co -- r geerator e come suo
13 154 geerator s possoo predere propro corrspodet 7..., g d 9..., g ell omomorfsmo che porta G su G1. S è cos rcodott a rsolvere l problema zale per u gruppo lbero commutatvo co 2013 r geerator. Cos procededo s arrverà a dover determare gl ordamet d u gruppo archmedeo co s > 1 geerator e quest come s sa gà soo dvduat da l seme Js A ttolo d esempo verrao questo umero trattat drettamete cas d u gruppo commutatvo lbero co 1, 2, 3 geerator. Come prelmare s ramet che se G è u gruppo commutatvo co geerator gl,..., g ed a~,..., ar è ua base d u sottogruppo lbero co geerator del gruppo addtvo reale, per mporre a G u semplce ordameto modo che G rsult somorfo ad g basta covere che E è postvo se e solo se 1 è postvo. Se g..., g è u altra base per G l semplce ordameto d G otteuto co la covezoe E Ag è postvo se e solo se E è postvo, è a meo d u automorfsmo quello cosderato precedeza. Ifatt la corrspodeza è u automorfsmo d G che muta elemet postv elemet postv. I G s mpoe u ordameto dverso dal precedete se s sosttusce ad H elle cosderazo svolte u sottogruppo del gruppo addttvo reale co geerator o somorfo ad H. Percò la scelta della base e sottogrupp come ~I che servoo ad ordare G o ha tlueza questo ordameto e s potrà qud supporre che umer a1,..., y a sao tutt postv. Ed acora s potrà sempre supporre che a = 1 quato, per l teorema del. 4, moltplcado umer della base per uo stesso umero postvo s ottee la base d u gruppo somorfo al precedete. I.) GRUPPO CON 1 GENERATORE g1. - Il gruppo è ecessaramete archmedeo. V è u solo sottogruppo da cosderare, quello geerato da a1 = 1 e è postvo se e solo se ) 1 è postvo. II.) GRUPPO CON 2 GENERATORI g2
14 155 a ) G o sa archmedeo allora per l Teorema del.r 3 suo elemet devoo dstrburs 2 class d equvaleza archmedea A1, A2 (A A 2 ). Per l. 7 s può predere come geeratore d L propro ~1 e per I.) v è, a meo d automorfsm, u solo semplce ordameto d A quello per cu > 0 se e solo se > 0. Cos A A 1* è u gruppo p lbero co 1 geeratore g e come tale può essere scelto l omomorfo g 2 d g2 e per aaloghe cosderazo delle precedet ~9~ 2 > O se e solo se À2 > 0. I coclusoe + ~2~2 > O se h2 > 0 o se 7.2 = 0 e À~ > 0 e per G, a meo d automorfsm, è possble questo solo semplce ordameto. b) G sa archmedeo, allora esso è somorfo ad u sottogruppo lbero co due geerator del gruppo addttvo reale. S rammet che due sffatt sottogrupp soo tra loro somorf. S quado appartegoo ad ua stessa classe elemeto d ~T2. può ache dre che semplc ordamet d G soo corrspodeza buvoca co gl elemet d J2 )- III.) GRUPPO CON 3 GENERATORI g~, ~2, g3 a) G sa o archmedeo ed suo elemet s dstrbu- 5) Voledo determare u elemeto per og classe elemeto d J2 s può procedere come segue. Per geerator d u sottogruppo co due geerator del gruppo addtvo reale s possoo predere due umer postv ed az per l teorema del. 4 s può supporre che uo d ess sa l utà. Dett duque 1 e g tal due geerator deve se x2.-- # 0 qualuque sao gl ter relatv 1 e ~-~ e per questo è ecessaro e basta che g sa rrazoale. Per otteere u sottogruppo H del gruppo addttvo reale o somorfo al precedete, sempre per l teorema del. 4 è ecessaro e basta determare la base 1, g d H per modo che o sa co 1, t, À~, ter o zero. I mer 91 verfcat ua relazoe del tpo soprascrtto soo tutt e sol quell della forma ter o ull. Come cosegueza s ha che l seme degl elemet d JZ 2 ha la poteza del cotuo. Aaloghe cosderazo s potrebbero svolgere per..i.
15 156 scao 3 class d equvaleza A A2 A,. Per l,ro 7 s può predere come geeratore d e v è duque a cosderare u solo ordameto d A 1. è u gruppo lbero co 2 geerator e per quest s A*1 possoo predere gl omomorf g2, g3 d g2 e g3. Gl elemet d G, s dstrburao due class d equvaleza A2 A.3 (rspettvamete omomorfe d A, e A3 ell omomorfsmo G --- G~) Come geeratore d A2 s può predere g2 e v è u solo semplce ordameto d Cos per geeratore d _ ~ s può A2 predere l omomorfo g3" d g3 e s ha acora u solo semplce ordameto da cosderare. Duque, a meo d automorfsm, esste u solo semplce ordameto d G che s può realzzare come segue : h = Àg + + À2g2 + ~3g3 ~ O se À3 > 0; oppure 7~ > O se 7v3 = O e À2 > 0; oppure > 0 se ~3 _-_ 7.2 = 0 e ) 1 > 0. b) Gl elemet d G s dstrbuscoo 2 class A1 ~12 ed A ha u geeratore e sa ~ A1 due geerator g2, g3 omomorf d g e g3. è archmedeo co I semplc ordamet d G s realzzao come. Ordato G s A*1 ~ poe A e se A2 = À3 = 0 quado A1 > 0. c) Gl elemet d G s dstrbuscoo due class A e A ha due geerator u geeratore. Allora I,gl + A + A2g2 + A3g3 > 0 se A3 > 0 e se À3 = 0 quado A1g1.+ À2g2 > O A1 g2 soo geerator d Sa el caso b) come questo caso c) semplc ordamet d G s possoo mettere corrspodeza buvoca co gl elemet d Jz. d) G è archmedeo, suo semplc ordamet soo corrspodeza buvoca co gl elemet d J3- b).
Lezione 3. Gruppi risolubili.
 Lezoe 3 Prerequst: Lezo 1 2 Class d cougo e cetralzzat rupp rsolubl I questo captolo troducamo ua ozoe che come vedremo seguto fuge da raccordo tra la teora de grupp e la teora de camp Defzoe 31 Dato u
Lezoe 3 Prerequst: Lezo 1 2 Class d cougo e cetralzzat rupp rsolubl I questo captolo troducamo ua ozoe che come vedremo seguto fuge da raccordo tra la teora de grupp e la teora de camp Defzoe 31 Dato u
Lezione 13. Anelli ed ideali.
 Lezoe 3 Prerequst: Aell e sottoaell. Sottogrupp. Rfermet a test: [FdG] Sezoe 5.2; [H] Sezoe 3.4; [PC] Sezoe 4.2 Aell ed deal. Rcordamo la seguete defzoe, data el corso d Algebra : Defzoe 3. S dce aello
Lezoe 3 Prerequst: Aell e sottoaell. Sottogrupp. Rfermet a test: [FdG] Sezoe 5.2; [H] Sezoe 3.4; [PC] Sezoe 4.2 Aell ed deal. Rcordamo la seguete defzoe, data el corso d Algebra : Defzoe 3. S dce aello
Matematica elementare art.1 di Raimondo Valeri
 Matematca elemetare art. d Ramodo Valer I questo artcolo voglamo provare che esste ua formula per calcolare l umero de dvsor d u dato umero aturale seza cooscere la scomposzoe fattor prm del umero stesso.
Matematca elemetare art. d Ramodo Valer I questo artcolo voglamo provare che esste ua formula per calcolare l umero de dvsor d u dato umero aturale seza cooscere la scomposzoe fattor prm del umero stesso.
Lezione 24. Campi finiti.
 Lezoe 4 Prerequst: Lezo 0,,, 3 Rfermet a test: [FdG] Sezoe 86; [H] Sezoe 79; [PC] Sezoe 63; Cam ft Nelle lezo recedet abbamo vsto dvers esem d cam ft: ess erao tutt del to oure [ x ]/( f ( x )), dove f
Lezoe 4 Prerequst: Lezo 0,,, 3 Rfermet a test: [FdG] Sezoe 86; [H] Sezoe 79; [PC] Sezoe 63; Cam ft Nelle lezo recedet abbamo vsto dvers esem d cam ft: ess erao tutt del to oure [ x ]/( f ( x )), dove f
Funzioni di più variabili Massimi e Minimi una funzione definita in un insieme E. Un punto ( x0, y0)
 Massm e Mm Fuzo d pù varabl Massm e Mm Dezoe: Sa z = (, ) ua uzoe deta u seme E U puto (, E s dce puto d massmo (rsp mmo) relatvo per (, ) se esste δ > tale che ((, ) B((, ), δ ) E (, ) (, ) (rsp (, )
Massm e Mm Fuzo d pù varabl Massm e Mm Dezoe: Sa z = (, ) ua uzoe deta u seme E U puto (, E s dce puto d massmo (rsp mmo) relatvo per (, ) se esste δ > tale che ((, ) B((, ), δ ) E (, ) (, ) (rsp (, )
), mentre l unico intero che divide 0 è 0. Enunciamo alcune proprietà di ovvia dimostrazione.
 Dvsbltà e umer prm Sao a,b elemet dell seme Z degl ter relatv Dcamo che a dvde b, smbol a b, se b è multplo d a, ossa se esste u tero h Z tale che b ha Og tero a dvde 0 ( 0 0a ), metre l uco tero che dvde
Dvsbltà e umer prm Sao a,b elemet dell seme Z degl ter relatv Dcamo che a dvde b, smbol a b, se b è multplo d a, ossa se esste u tero h Z tale che b ha Og tero a dvde 0 ( 0 0a ), metre l uco tero che dvde
Classi di reddito % famiglie Fino a 15 5.3 15-25 16.2 25-35 21.1 35-45 18.6 45-55 13.6 Oltre 55 25.2 Totale 100
 ESERCIZIO Data la seguete dstrbuzoe percetuale delle famgle talae per class d reddto, espresso mlo d lre, (ao 995, fote Istat): Class d reddto % famgle Fo a 5 5.3 5-5 6. 5-35. 35-45 8.6 45-55 3.6 Oltre
ESERCIZIO Data la seguete dstrbuzoe percetuale delle famgle talae per class d reddto, espresso mlo d lre, (ao 995, fote Istat): Class d reddto % famgle Fo a 5 5.3 5-5 6. 5-35. 35-45 8.6 45-55 3.6 Oltre
Numeri complessi Pag. 1 Adolfo Scimone 1998
 Numer compless Pag. Adolfo Scmoe 998 NUMERI COMPLESSI Come sappamo, o esstoo el campo de umer real le radc d dce par de umer egatv. Ammettamo pertato l esstea della radce quadrata del umero. Questo uovo
Numer compless Pag. Adolfo Scmoe 998 NUMERI COMPLESSI Come sappamo, o esstoo el campo de umer real le radc d dce par de umer egatv. Ammettamo pertato l esstea della radce quadrata del umero. Questo uovo
CAPITOLO III SISTEMI DI EQUAZIONI LINEARI
 CAPITOLO III SISTEMI DI EQUAZIONI LINEARI. GENERALITÀ Sao a,..., a,..., a, b umer real (o compless o elemet d u qualsas campo) ot. Defzoe.. U equazoe della forma: () a x +... + ax +... + a x b dces d prmo
CAPITOLO III SISTEMI DI EQUAZIONI LINEARI. GENERALITÀ Sao a,..., a,..., a, b umer real (o compless o elemet d u qualsas campo) ot. Defzoe.. U equazoe della forma: () a x +... + ax +... + a x b dces d prmo
Modulo di Fisica Tecnica. Differenze finite per problemi di conduzione in regime instazionario
 Dpartmeto d Meccaca, Strutture, Ambete e Terrtoro UNIVERSITÀ DEGLI STUDI DI CASSINO Laurea Specalstca Igegera Meccaca: Modulo d Fsca Tecca Lezoe d: Dffereze fte per problem d coduzoe regme stazoaro /20
Dpartmeto d Meccaca, Strutture, Ambete e Terrtoro UNIVERSITÀ DEGLI STUDI DI CASSINO Laurea Specalstca Igegera Meccaca: Modulo d Fsca Tecca Lezoe d: Dffereze fte per problem d coduzoe regme stazoaro /20
LE MEDIE. Le Medie. Medie razionali. Medie di posizione
 LE MEDIE RAZIONALI LE MEDIE Msure stetche trodotte per valutare aspett compless e global d ua dstrbuzoe d u feomeo X medate u solo umero reale costruto modo da dsperdere al mmo le formazo su dat orgar.
LE MEDIE RAZIONALI LE MEDIE Msure stetche trodotte per valutare aspett compless e global d ua dstrbuzoe d u feomeo X medate u solo umero reale costruto modo da dsperdere al mmo le formazo su dat orgar.
Lezione 20. Campi numerici ed anelli di Dedekind.
 Lezoe 0 Prerequst: Lezo 9 Dom ad deal prcpal Camp umerc ed aell d Dedekd Defzoe 0 S dce campo umerco og estesoe fta d Q coteuta C Osservazoe 0 Essedo Q u campo perfetto (poché è d caratterstca 0 ved la
Lezoe 0 Prerequst: Lezo 9 Dom ad deal prcpal Camp umerc ed aell d Dedekd Defzoe 0 S dce campo umerco og estesoe fta d Q coteuta C Osservazoe 0 Essedo Q u campo perfetto (poché è d caratterstca 0 ved la
corrispondenza della generica i-esima modalità. Indicando con #(.) la cardinalità di un insieme, per esse si ha, rispettivamente:
 Corso d Statstca docete: Domeco Vstocco Le requeze cumulate S cosder ua varable qualtatva ordale X Per essa, oltre alle requeze assolute, relatve e ercetual, è ossble calcolare ache le requeze cumulate
Corso d Statstca docete: Domeco Vstocco Le requeze cumulate S cosder ua varable qualtatva ordale X Per essa, oltre alle requeze assolute, relatve e ercetual, è ossble calcolare ache le requeze cumulate
Aritmetica 2016/2017 Esercizi svolti in classe Quarta lezione
 Artmetca 06/07 Esercz svolt classe Quarta lezoe Rcorreze o lear Sa a c a cq ua rcorreza dove {c }, c C e c 0. Sa P C[λ] l polomo caratterstco della rcorreza. Allora ua soluzoe partcolare della rcorreza
Artmetca 06/07 Esercz svolt classe Quarta lezoe Rcorreze o lear Sa a c a cq ua rcorreza dove {c }, c C e c 0. Sa P C[λ] l polomo caratterstco della rcorreza. Allora ua soluzoe partcolare della rcorreza
FUNZIONI LOGICHE FORME CANONICHE SP E PS
 FUNZIONI LOGICHE FORME CANONICHE SP E PS Ua fuzoe logca può essere espressa quattro forme: 1. attraverso ua proposzoe logca; 2. attraverso ua tabella della vertà; 3. attraverso u espressoe algebrca; 4.
FUNZIONI LOGICHE FORME CANONICHE SP E PS Ua fuzoe logca può essere espressa quattro forme: 1. attraverso ua proposzoe logca; 2. attraverso ua tabella della vertà; 3. attraverso u espressoe algebrca; 4.
Lezione 13. Gruppo di Galois di un polinomio.
 Lezoe Prerequst: Lezo 9, 0,, Gruppo d Galos d u polomo Sa F u campo, sa f ( x) F[ x] o costate d grado, sa K u campo d spezzameto d f (x) su F el quale f (x) possede radc dstte Sa = ( f ) Defzoe Il gruppo
Lezoe Prerequst: Lezo 9, 0,, Gruppo d Galos d u polomo Sa F u campo, sa f ( x) F[ x] o costate d grado, sa K u campo d spezzameto d f (x) su F el quale f (x) possede radc dstte Sa = ( f ) Defzoe Il gruppo
Dimostrazione della Formula per la determinazione del numero di divisori-test di primalità, di Giorgio Lamberti
 Gorgo Lambert Pag. Dmostrazoe della Formula per la determazoe del umero d dvsor-test d prmaltà, d Gorgo Lambert Eugeo Amtrao aveva proposto l'dea d ua formula per calcolare l umero d dvsor d u umero, da
Gorgo Lambert Pag. Dmostrazoe della Formula per la determazoe del umero d dvsor-test d prmaltà, d Gorgo Lambert Eugeo Amtrao aveva proposto l'dea d ua formula per calcolare l umero d dvsor d u umero, da
Lezione 1. I numeri complessi
 Lezoe Prerequst: Numer real: assom ed operazo. Pao cartesao. Fuzo trgoometrche. I umer compless Nell'attuale teora de umer compless cofluscoo due fodametal dee, ua artmetca, l'altra geometrca. La prma,
Lezoe Prerequst: Numer real: assom ed operazo. Pao cartesao. Fuzo trgoometrche. I umer compless Nell'attuale teora de umer compless cofluscoo due fodametal dee, ua artmetca, l'altra geometrca. La prma,
Capitolo 6 Gli indici di variabilità
 Captolo 6 Gl dc d varabltà ommaro. Itroduzoe. -. Il campo d varazoe. - 3. La dffereza terquartle. - 4. Gl scostamet med. -. La varaza, lo scarto quadratco medo e la devaza. - 6. Le dffereze mede. - 7.
Captolo 6 Gl dc d varabltà ommaro. Itroduzoe. -. Il campo d varazoe. - 3. La dffereza terquartle. - 4. Gl scostamet med. -. La varaza, lo scarto quadratco medo e la devaza. - 6. Le dffereze mede. - 7.
Caso studio 2. Le medie. Esercizio. La media aritmetica. Esempio
 8/02/20 Caso studo 2 U vesttore sta valutado redmet d due ttol del settore Petrolo e Gas aturale. Sulla base de redmet goraler della settmaa passata vuole cercare d prevedere l redmeto per la prossma settmaa
8/02/20 Caso studo 2 U vesttore sta valutado redmet d due ttol del settore Petrolo e Gas aturale. Sulla base de redmet goraler della settmaa passata vuole cercare d prevedere l redmeto per la prossma settmaa
Variabilità = Informazione
 Varabltà e formazoe Lo studo d u feomeo ha seso solo se esso s preseta co modaltà/testà varabl da u soggetto all altro. Ad esempo, se dobbamo studare l reddto ua certa regoe è ecessaro osservare utà statstche
Varabltà e formazoe Lo studo d u feomeo ha seso solo se esso s preseta co modaltà/testà varabl da u soggetto all altro. Ad esempo, se dobbamo studare l reddto ua certa regoe è ecessaro osservare utà statstche
Analisi dei Dati. La statistica è facile!!! Correlazione
 Aals de Dat La statstca è facle!!! Correlazoe A che serve la correlazoe? Mettere evdeza la relazoe esstete tra due varabl stablre l tpo d relazoe stablre l grado d tale relazoe stablre la drezoe d tale
Aals de Dat La statstca è facle!!! Correlazoe A che serve la correlazoe? Mettere evdeza la relazoe esstete tra due varabl stablre l tpo d relazoe stablre l grado d tale relazoe stablre la drezoe d tale
Lezione 4. La Variabilità. Lezione 4 1
 Lezoe 4 La Varabltà Lezoe 4 1 Defzoe U valore medo, comuque calcolato, o è suffcete a rappresetare l seme delle osservazo effettuate (o l seme de valor assut dalla varable statstca); è ecessaro qud affacare
Lezoe 4 La Varabltà Lezoe 4 1 Defzoe U valore medo, comuque calcolato, o è suffcete a rappresetare l seme delle osservazo effettuate (o l seme de valor assut dalla varable statstca); è ecessaro qud affacare
LE MEDIE. Quadratica. Italo Nofroni. Statistica medica. Medie. Le medie vengono classificate in due gruppi
 Le mede Italo Nofro LE MEDIE Statstca medca Le mede (o valor med) soo dc d tedeza cetrale e costtuscoo u modo semplce ed mmedato per stetzzare u solo valore dat eterogee raccolt el collettvo oggetto d
Le mede Italo Nofro LE MEDIE Statstca medca Le mede (o valor med) soo dc d tedeza cetrale e costtuscoo u modo semplce ed mmedato per stetzzare u solo valore dat eterogee raccolt el collettvo oggetto d
Università di Cassino. Esercitazioni di Statistica 1 del 26 Febbraio Dott. Mirko Bevilacqua
 Uverstà d Casso Eserctazo d Statstca del 26 Febbrao 200 Dott. Mrko Bevlacqua ESERCIZIO Cosderado le class d altezza 60 6; 6 70; 70 78; 78 86 per u collettvo d 20 persoe, s può affermare che l ALTEZZA dpede
Uverstà d Casso Eserctazo d Statstca del 26 Febbrao 200 Dott. Mrko Bevlacqua ESERCIZIO Cosderado le class d altezza 60 6; 6 70; 70 78; 78 86 per u collettvo d 20 persoe, s può affermare che l ALTEZZA dpede
Facoltà di Farmacia Corso di Matematica con elementi di Statistica Docente: Riccardo Rosso
 Facoltà d Farmaca Corso d Matematca co elemet d Statstca Docete: Rccardo Rosso Statstca descrttva: l coeffcete d cocetrazoe d G Quado s vuole rpartre ua certa somma d dearo, v soo due suddvso che soo,
Facoltà d Farmaca Corso d Matematca co elemet d Statstca Docete: Rccardo Rosso Statstca descrttva: l coeffcete d cocetrazoe d G Quado s vuole rpartre ua certa somma d dearo, v soo due suddvso che soo,
Propagazione di errori
 Propagazoe d error Gl error e dat possoo essere amplfcat durate calcol. Rspetto alla propagazoe degl error s può dstguere: comportameto del problema - codzoameto del problema: vedere come le perturbazo
Propagazoe d error Gl error e dat possoo essere amplfcat durate calcol. Rspetto alla propagazoe degl error s può dstguere: comportameto del problema - codzoameto del problema: vedere come le perturbazo
Università della Calabria
 Uverstà della Calabra FACOLTA DI INGEGNERIA Corso d Laurea Igegera per l Ambete e l Terrtoro CORSO DI IDROLOGIA Ig. Daela Bod SCHEDA DIDATTICA N 5 ISOIETE E TOPOIETI A.A. 20-2 Calcolo della precptazoe
Uverstà della Calabra FACOLTA DI INGEGNERIA Corso d Laurea Igegera per l Ambete e l Terrtoro CORSO DI IDROLOGIA Ig. Daela Bod SCHEDA DIDATTICA N 5 ISOIETE E TOPOIETI A.A. 20-2 Calcolo della precptazoe
Esercizi su Rappresentazioni di Dati e Statistica
 Esercz su Rappresetazo d Dat e Statstca Eserczo Esprmete forma percetuale e traducete u aerogramma dat della seguete tabella: Nord Cetro Sud Isole Totale 5 58 866 0 95 36 4 35 30 6 79 56 57 399 08 Soluzoe
Esercz su Rappresetazo d Dat e Statstca Eserczo Esprmete forma percetuale e traducete u aerogramma dat della seguete tabella: Nord Cetro Sud Isole Totale 5 58 866 0 95 36 4 35 30 6 79 56 57 399 08 Soluzoe
LE MEDIE. Quadratica. Italo Nofroni. Statistica medica. Medie. Le medie vengono classificate in
 Le mede Italo Nofro LE MEDIE Le mede (o valor med) soo dc d tedeza cetrale e costtuscoo u modo semplce ed mmedato per stetzzare u solo valore dat eterogee raccolt u collettvo Statstca medca Le mede Le
Le mede Italo Nofro LE MEDIE Le mede (o valor med) soo dc d tedeza cetrale e costtuscoo u modo semplce ed mmedato per stetzzare u solo valore dat eterogee raccolt u collettvo Statstca medca Le mede Le
Indipendenza in distribuzione
 Marlea Pllat - Semar d Statstca (SVIC) "Lo studo delle relazo tra due caratter" Aals delle relazo tra due caratter Dpedeza dstrbuzoe s basa sul cofroto delle dstrbuzo codzoate Dpedeza meda s basa sul cofroto
Marlea Pllat - Semar d Statstca (SVIC) "Lo studo delle relazo tra due caratter" Aals delle relazo tra due caratter Dpedeza dstrbuzoe s basa sul cofroto delle dstrbuzo codzoate Dpedeza meda s basa sul cofroto
Interpolazione. Definizione: per interpolazione si intende la ricerca di una funzione matematica che approssima l andamento di un insieme di punti.
 Iterpolazoe Defzoe: per terpolazoe s tede la rcerca d ua fuzoe matematca che approssma l adameto d u seme d put. Iterpolazoe MATEMATICA Calcola ua fuzoe che passa PER tutt put Tp d terpolazoe Iterpolazoe
Iterpolazoe Defzoe: per terpolazoe s tede la rcerca d ua fuzoe matematca che approssma l adameto d u seme d put. Iterpolazoe MATEMATICA Calcola ua fuzoe che passa PER tutt put Tp d terpolazoe Iterpolazoe
Università di Cassino Esercitazioni di Statistica 1 del 5 Febbraio Dott. Mirko Bevilacqua
 Uverstà d Casso Eserctazo d Statstca del 5 Febbrao 00. Dott. Mrko Bevlacqua ESERCIZIO N A partre dalla dstrbuzoe semplce del carattere peso rlevata su 0 studet del corso d Mcroecooma peso: { 4, 59, 65,
Uverstà d Casso Eserctazo d Statstca del 5 Febbrao 00. Dott. Mrko Bevlacqua ESERCIZIO N A partre dalla dstrbuzoe semplce del carattere peso rlevata su 0 studet del corso d Mcroecooma peso: { 4, 59, 65,
Istogrammi e confronto con la distribuzione normale
 Istogramm e cofroto co la dstrbuzoe ormale Suppoamo d effettuare per volte la msurazoe della stessa gradezza elle stesse codzo (es. la massa d u oggetto, la tesoe d ua pla, la lughezza d u oggetto, ecc.):
Istogramm e cofroto co la dstrbuzoe ormale Suppoamo d effettuare per volte la msurazoe della stessa gradezza elle stesse codzo (es. la massa d u oggetto, la tesoe d ua pla, la lughezza d u oggetto, ecc.):
Esercitazione 5 del corso di Statistica (parte 1)
 Eserctazoe 5 del corso d Statstca (parte 1) Dott.ssa Paola Costat 8 Novembre 011 I alcue crcostaze s poe u maggor teresse sullo studo della varabltà tra le sgole utà statstche, puttosto che lo studo della
Eserctazoe 5 del corso d Statstca (parte 1) Dott.ssa Paola Costat 8 Novembre 011 I alcue crcostaze s poe u maggor teresse sullo studo della varabltà tra le sgole utà statstche, puttosto che lo studo della
Teoria dei Fenomeni Aleatori AA 2012/13
 La Legge de Grad Numer Cosderata ua sere d prove rpetute co p par alla probabltà d successo ua sgola prova, l rapporto tra l umero d success K ed l umero d prove tede a p quado tede ad fto: K P p ε per
La Legge de Grad Numer Cosderata ua sere d prove rpetute co p par alla probabltà d successo ua sgola prova, l rapporto tra l umero d success K ed l umero d prove tede a p quado tede ad fto: K P p ε per
Gli indici sintetici Forma. Gli indici sintetici. Gli indici sintetici. Qualche considerazione. Qualche considerazione. Tendenza centrale Forma
 Uverstà d Macerata Facoltà d Sceze Poltche - Ao accademco 01-013013 Gl dc d varabltà Crsta Davo Gl dc stetc Qualche cosderazoe Tedeza cetrale Varabltà La scelta dell dce d tedeza cetrale/poszoe dpede dal
Uverstà d Macerata Facoltà d Sceze Poltche - Ao accademco 01-013013 Gl dc d varabltà Crsta Davo Gl dc stetc Qualche cosderazoe Tedeza cetrale Varabltà La scelta dell dce d tedeza cetrale/poszoe dpede dal
CORSO DI STATISTICA I (Prof.ssa S. Terzi)
 CORSO DI STATISTICA I (Prof.ssa S. Terz) 1 STUDIO DELLE DISTRIBUZIONI SEMPLICI Eserctazoe 2 2.1 Da u dage svolta su u campoe d lavorator dpedet co doppo lavoro è stata rlevata la dstrbuzoe coguta del reddto
CORSO DI STATISTICA I (Prof.ssa S. Terz) 1 STUDIO DELLE DISTRIBUZIONI SEMPLICI Eserctazoe 2 2.1 Da u dage svolta su u campoe d lavorator dpedet co doppo lavoro è stata rlevata la dstrbuzoe coguta del reddto
dei quali si conoscono solo la media x e la deviazione standard σ e dato un valore reale positivo K, possiamo affermare che:
 Eserctazoe VI: Il teorema d Chebyshev Eserczo La statura meda d u gruppo d dvdu è par a 73,78cm e la devazoe stadard a 3,6. Qual è la frequeza relatva delle persoe che hao ua statura superore o ferore
Eserctazoe VI: Il teorema d Chebyshev Eserczo La statura meda d u gruppo d dvdu è par a 73,78cm e la devazoe stadard a 3,6. Qual è la frequeza relatva delle persoe che hao ua statura superore o ferore
Gli indici sintetici Forma. Un caso studio. Gli indici sintetici. Qualche considerazione. Qualche considerazione. Tendenza centrale Forma
 Uverstà d Macerata Dpartmeto d Sceze Poltche, della Comucazoe e delle Relaz. Iterazoal Gl dc d varabltà Crsta Davo Gl dc stetc Qualche cosderazoe Tedeza cetrale Varabltà La scelta dell dce d tedeza cetrale/poszoe
Uverstà d Macerata Dpartmeto d Sceze Poltche, della Comucazoe e delle Relaz. Iterazoal Gl dc d varabltà Crsta Davo Gl dc stetc Qualche cosderazoe Tedeza cetrale Varabltà La scelta dell dce d tedeza cetrale/poszoe
CORSO DI STATISTICA I (Prof.ssa S. Terzi) 1 STUDIO DELLE DISTRIBUZIONI SEMPLICI. Esercitazione n 3
 ORSO I STTISTI I (Prof.ssa S. Terz) STUIO ELLE ISTRIUZIONI SEMPLII Eserctazoe 3 3. ata la seguete dstrbuzoe de reddt: lass d reddto Reddter Reddto medo 6.500-7.500 4 6.750 7.500-8.500 7.980 8.500-9.500
ORSO I STTISTI I (Prof.ssa S. Terz) STUIO ELLE ISTRIUZIONI SEMPLII Eserctazoe 3 3. ata la seguete dstrbuzoe de reddt: lass d reddto Reddter Reddto medo 6.500-7.500 4 6.750 7.500-8.500 7.980 8.500-9.500
La classe che mostra la distribuzione più elevata è quella 60-90, che corrisponde a un uso elevato dell automobile. f i fr (= f i/n) fr% (=fr*100)
 ESERCIZIO Il Moblty Maager d u azeda ha rlevato l umero d chlometr percors settmaalmete da 60 mpegat. I dat soo rportat ello schema successvo. 67 4 93 58 66 87 5 53 86 8 7 47 56 70 54 86 48 43 60 58 5
ESERCIZIO Il Moblty Maager d u azeda ha rlevato l umero d chlometr percors settmaalmete da 60 mpegat. I dat soo rportat ello schema successvo. 67 4 93 58 66 87 5 53 86 8 7 47 56 70 54 86 48 43 60 58 5
I percentili e i quartili
 I percetl e quartl I percetl soo quelle modaltà che dvdoo la dstrbuzoe ceto part d uguale umerostà. I quartl soo quelle modaltà che dvdoo la dstrbuzoe quattro part d uguale umerostà. Il prmo quartle Q
I percetl e quartl I percetl soo quelle modaltà che dvdoo la dstrbuzoe ceto part d uguale umerostà. I quartl soo quelle modaltà che dvdoo la dstrbuzoe quattro part d uguale umerostà. Il prmo quartle Q
MEDIA DI Y (ALTEZZA):
 Uverstà d Casso Eserctazo d Statstca del 4 Marzo 0 Dott. Mrko Bevlacqua ESERCIZIO Su u collettvo d dvdu soo stat rlevat caratter X Peso( kg) e Altezza ( cm) otteamo la seguete dstrbuzoe d frequeza coguta:
Uverstà d Casso Eserctazo d Statstca del 4 Marzo 0 Dott. Mrko Bevlacqua ESERCIZIO Su u collettvo d dvdu soo stat rlevat caratter X Peso( kg) e Altezza ( cm) otteamo la seguete dstrbuzoe d frequeza coguta:
frazione 1 n dell ammontare complessivo del carattere A x
 La Cocetrazoe Il cocetto d cocetrazoe rguarda l modo cu l ammotare totale d u carattere quattatvo trasferble s rpartsce tra utà statstche. Tato pù tale ammotare è addesato u sottoseme d utà, tato pù s
La Cocetrazoe Il cocetto d cocetrazoe rguarda l modo cu l ammotare totale d u carattere quattatvo trasferble s rpartsce tra utà statstche. Tato pù tale ammotare è addesato u sottoseme d utà, tato pù s
Lezione 4. Metodi statistici per il miglioramento della Qualità
 Tecologe Iormatche per la Qualtà Lezoe 4 Metod statstc per l mglorameto della Qualtà Msure d Tedeza Cetrale Ultmo aggorameto: 30 Settembre 2003 Il materale ddattco potrebbe coteere error: la segalazoe
Tecologe Iormatche per la Qualtà Lezoe 4 Metod statstc per l mglorameto della Qualtà Msure d Tedeza Cetrale Ultmo aggorameto: 30 Settembre 2003 Il materale ddattco potrebbe coteere error: la segalazoe
MISURE DI TENDENZA CENTRALE. Psicometria 1 - Lezione 2 Lucidi presentati a lezione AA 2000/2001 dott. Corrado Caudek
 MISURE DI TENDENZA CENTRALE Pscometra 1 - Lezoe Lucd presetat a lezoe AA 000/001 dott. Corrado Caudek 1 Suppoamo d dsporre d u seme d msure e d cercare u solo valore che, meglo d cascu altro, sa grado
MISURE DI TENDENZA CENTRALE Pscometra 1 - Lezoe Lucd presetat a lezoe AA 000/001 dott. Corrado Caudek 1 Suppoamo d dsporre d u seme d msure e d cercare u solo valore che, meglo d cascu altro, sa grado
Caso studio 12. Regressione. Esempio
 6/4/7 Caso studo Per studare la curva d domada d u bee che sta per essere trodotto sul mercato, s rlevao dat rguardat l prezzo mposto e l umero d pezz vedut 7 put vedta plota, ell arco d ua settmaa. I
6/4/7 Caso studo Per studare la curva d domada d u bee che sta per essere trodotto sul mercato, s rlevao dat rguardat l prezzo mposto e l umero d pezz vedut 7 put vedta plota, ell arco d ua settmaa. I
Indici di Posizione. Gli indici si posizione sono misure sintetiche ( valori caratteristici ) che descrivono la tendenza centrale di un fenomeno
 Idc d Poszoe Gl dc s poszoe soo msure stetche ( valor caratterstc ) che descrvoo la tedeza cetrale d u feomeo La tedeza cetrale è, prma approssmazoe, la modaltà della varable verso la quale cas tedoo a
Idc d Poszoe Gl dc s poszoe soo msure stetche ( valor caratterstc ) che descrvoo la tedeza cetrale d u feomeo La tedeza cetrale è, prma approssmazoe, la modaltà della varable verso la quale cas tedoo a
Università degli Studi di Milano Bicocca CdS ECOAMM Corso di Metodi Statistici per l Amministrazione delle Imprese CARTE DI CONTROLLO PER ATTRIBUTI
 Uverstà degl Stud d Mlao Bcocca CdS ECOAMM Corso d Metod Statstc per l Ammstrazoe delle Imprese CARTE DI CONTROLLO PER ATTRIBUTI 1. Carta d cotrollo per frazoe d o coform (carta U resposable d produzoe,
Uverstà degl Stud d Mlao Bcocca CdS ECOAMM Corso d Metod Statstc per l Ammstrazoe delle Imprese CARTE DI CONTROLLO PER ATTRIBUTI 1. Carta d cotrollo per frazoe d o coform (carta U resposable d produzoe,
b) Relativamente alla variabile PREZZO, fornire una misura della variabilità della distribuzione attraverso
 ESERCIZIO Co rfermeto a dvers modell d auto del medesmo segmeto d mercato e cldrata s soo rlevat dat sul prezzo d lsto mglaa d euro (X), la veloctà massma dcharata km/h (Y) ed l peso kg (Z). I dat soo
ESERCIZIO Co rfermeto a dvers modell d auto del medesmo segmeto d mercato e cldrata s soo rlevat dat sul prezzo d lsto mglaa d euro (X), la veloctà massma dcharata km/h (Y) ed l peso kg (Z). I dat soo
ESERCIZI SULLE SERIE
 ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
MATEMATICA FINANZIARIA 1 PROVA SCRITTA DEL 15 SETTEMBRE 2009 C.d.L. ECONOMIA AZIENDALE
 MATEMATICA FINANZIARIA PROVA SCRITTA DEL 5 SETTEMBRE 009 C.d.L. ECONOMIA AZIENDALE ESERCIZIO a) Il Sg. Ross ogg (t0) uole acqustare u furgoe del alore d 7000 per la sua atttà commercale. A tal fe egl ersa
MATEMATICA FINANZIARIA PROVA SCRITTA DEL 5 SETTEMBRE 009 C.d.L. ECONOMIA AZIENDALE ESERCIZIO a) Il Sg. Ross ogg (t0) uole acqustare u furgoe del alore d 7000 per la sua atttà commercale. A tal fe egl ersa
Variabili casuali ( ) 1 2 n
 Varabl casual &. Valore edo. Data ua varable casuale = ( x,x 2, K,x ) (.) cu valor assuoo le rspettve probabltà P = p,p, K,p (.2) s defsce valore edo la quattà ( ) 2 = [ ] T M = M = P = xp (.3) Sgfcato:
Varabl casual &. Valore edo. Data ua varable casuale = ( x,x 2, K,x ) (.) cu valor assuoo le rspettve probabltà P = p,p, K,p (.2) s defsce valore edo la quattà ( ) 2 = [ ] T M = M = P = xp (.3) Sgfcato:
Due distribuzioni, stessa media ma in quale delle due la media rappresenta, sintetizza meglio la situazione?
 Prma dstrb. Secoda dstrb. Totale Meda 0 5 8 35 85 63 63/5 =3,6 5 5 38 40 45 63 63/5 =3,6 Due dstrbuzo, stessa meda ma quale delle due la meda rappreseta, stetzza meglo la stuazoe? Le mede stetzzao la dstrbuzoe,
Prma dstrb. Secoda dstrb. Totale Meda 0 5 8 35 85 63 63/5 =3,6 5 5 38 40 45 63 63/5 =3,6 Due dstrbuzo, stessa meda ma quale delle due la meda rappreseta, stetzza meglo la stuazoe? Le mede stetzzao la dstrbuzoe,
Attualizzazione. Attualizzazione
 Attualzzazoe Il problema erso alla captalzzazoe prede l ome d attualzzazoe Abbamo ua operazoe fazara elemetare e dato l motate M dobbamo determare l corrspodete captale zale C L'attualzzazoe è la operazoe
Attualzzazoe Il problema erso alla captalzzazoe prede l ome d attualzzazoe Abbamo ua operazoe fazara elemetare e dato l motate M dobbamo determare l corrspodete captale zale C L'attualzzazoe è la operazoe
INDICI DI VARIABILITA
 INDICI DI VARIABILITA Defzoe d VARIABILITA': la varabltà s può defre come l'atttude d u carattere ad assumere dverse modaltà quattatve. La varabltà è la quattà d dspersoe presete e dat. Idc d varabltà
INDICI DI VARIABILITA Defzoe d VARIABILITA': la varabltà s può defre come l'atttude d u carattere ad assumere dverse modaltà quattatve. La varabltà è la quattà d dspersoe presete e dat. Idc d varabltà
Caso studio 10. Dipendenza in media. Esempio
 09/03/06 Caso studo 0 S cosder la seguete dstrbuzoe degl occupat Itala secodo l umero d ore settmaal effettvamete lavorate e l settore d attvtà (cfr. Itala cfre, Ao 008, pag. 7 ): Ore lavorate Settore
09/03/06 Caso studo 0 S cosder la seguete dstrbuzoe degl occupat Itala secodo l umero d ore settmaal effettvamete lavorate e l settore d attvtà (cfr. Itala cfre, Ao 008, pag. 7 ): Ore lavorate Settore
Dott.ssa Marta Di Nicola
 RELAZIONE TRA DUE VARIABILI QUANTITATIVE Quado s cosderao due o pù caratter (varabl) s possoo esamare ache l tpo e l'testà delle relazo che sussstoo tra loro. http://www.bostatstca.uch.tt Nel caso cu per
RELAZIONE TRA DUE VARIABILI QUANTITATIVE Quado s cosderao due o pù caratter (varabl) s possoo esamare ache l tpo e l'testà delle relazo che sussstoo tra loro. http://www.bostatstca.uch.tt Nel caso cu per
Geometria delle aree
 eometra delle aree Lo studo de cocett ase relatv alla eometra delle ree: cosete d trasformare le azo tere sollectazo cosete d valutare l elastctà delle strutture forsce gl strumet per valutare le strutture
eometra delle aree Lo studo de cocett ase relatv alla eometra delle ree: cosete d trasformare le azo tere sollectazo cosete d valutare l elastctà delle strutture forsce gl strumet per valutare le strutture
Generalmente sia l ampiezza che il valore medio della sollecitazione sono variabili nel tempo.
 È molto raro che u compoete meccaco sa sollectato a fatca da u carco cclco ad ampezza costate. Geeralmete sa l ampezza che l valore medo della sollectazoe soo varabl el tempo. max a a max m m m m Tempo
È molto raro che u compoete meccaco sa sollectato a fatca da u carco cclco ad ampezza costate. Geeralmete sa l ampezza che l valore medo della sollectazoe soo varabl el tempo. max a a max m m m m Tempo
LEZIONI DI STATISTICA MEDICA
 LEZIONI DI STATISTICA MEDICA A.A. 00/0 - Idc d dspersoe Sezoe d Epdemologa & Statstca Medca Uverstà degl Stud d Veroa La dspersoe o varabltà è la secoda mportate caratterstca d ua dstrbuzoe d dat. Essa
LEZIONI DI STATISTICA MEDICA A.A. 00/0 - Idc d dspersoe Sezoe d Epdemologa & Statstca Medca Uverstà degl Stud d Veroa La dspersoe o varabltà è la secoda mportate caratterstca d ua dstrbuzoe d dat. Essa
III Esercitazione: Sintesi delle distribuzioni semplici secondo un carattere qualitativo ordinale.
 III Eserctazoe: Stes delle dstrbuzo semplc secodo u carattere qualtatvo ordale. Eserczo 3 dvdu ao seguet ttol d studo: Lceza elemetare, Lceza elemetare, ploma, Lceza meda, Lceza elemetare, Lceza meda,
III Eserctazoe: Stes delle dstrbuzo semplc secodo u carattere qualtatvo ordale. Eserczo 3 dvdu ao seguet ttol d studo: Lceza elemetare, Lceza elemetare, ploma, Lceza meda, Lceza elemetare, Lceza meda,
Indici di asimmetria. Elementi di Statistica descrittiva Parte IV. Simmetria di una distribuzione di frequenze. Primo indice di asimmetria (1/3)
 Smmetra d ua dstrbuzoe d frequeze Ua dstrbuzoe s dce asmmetrca se o è possble dvduare (aalzzado u stogramma) u asse vertcale che tagl la dstrbuzoe due part specularmete ugual Idc d asmmetra Rferedoc a
Smmetra d ua dstrbuzoe d frequeze Ua dstrbuzoe s dce asmmetrca se o è possble dvduare (aalzzado u stogramma) u asse vertcale che tagl la dstrbuzoe due part specularmete ugual Idc d asmmetra Rferedoc a
STATISTICA DESCRITTIVA - SCHEDA N. 3 VARIABILI QUANTITATIVE Indici di centralità, dispersione e forma
 Matematca e statstca: da dat a modell alle scelte www.dma.uge/pls_statstca Resposabl scetfc M.P. Rogat e E. Sasso (Dpartmeto d Matematca Uverstà d Geova) STATISTICA DESCRITTIVA - SCHEDA N. 3 VARIABILI
Matematca e statstca: da dat a modell alle scelte www.dma.uge/pls_statstca Resposabl scetfc M.P. Rogat e E. Sasso (Dpartmeto d Matematca Uverstà d Geova) STATISTICA DESCRITTIVA - SCHEDA N. 3 VARIABILI
Algoritmi e Strutture Dati. Alberi Binari di Ricerca
 Algortm e Strutture Dat Alber Bar d Rcerca Alber bar d rcerca Motvazo gestoe e rcerche grosse quattà d dat lste, array e alber o soo adeguat perché effcet tempo O) o spazo Esemp: Matemeto d archv DataBase)
Algortm e Strutture Dat Alber Bar d Rcerca Alber bar d rcerca Motvazo gestoe e rcerche grosse quattà d dat lste, array e alber o soo adeguat perché effcet tempo O) o spazo Esemp: Matemeto d archv DataBase)
Il campionamento e l inferenza
 e l fereza Popolazoe Campoe Da dat osservat medate scelta campoara s guge ad affermazo che rguardao la popolazoe da cu ess soo stat prescelt Uverstà d Macerata Facoltà d Sceze Poltche - Ao accademco Ao
e l fereza Popolazoe Campoe Da dat osservat medate scelta campoara s guge ad affermazo che rguardao la popolazoe da cu ess soo stat prescelt Uverstà d Macerata Facoltà d Sceze Poltche - Ao accademco Ao
Calcolo delle Probabilità: esercitazione 4
 Argometo: Probabltà classca Lbro d testo pag. 1-7 e 7-77 e varable casuale uforme dscreta NB: asscurars d cooscere le defzo, le propretà rchamate e le relatve dmostrazo quado ecessaro Eserczo 1 S cosder
Argometo: Probabltà classca Lbro d testo pag. 1-7 e 7-77 e varable casuale uforme dscreta NB: asscurars d cooscere le defzo, le propretà rchamate e le relatve dmostrazo quado ecessaro Eserczo 1 S cosder
In questo capitolo vedremo solamente un caso di rendita, che useremo poi per generalizzare le rendite e dedurre tutti gli altri casi.
 7. Redte I questo captolo edremo solamete u caso d redta, che useremo po per geeralzzare le redte e dedurre tutt gl altr cas. S defsce redta ua successoe d captal (rate) tutte da pagare, o tutte da rscuotere,
7. Redte I questo captolo edremo solamete u caso d redta, che useremo po per geeralzzare le redte e dedurre tutt gl altr cas. S defsce redta ua successoe d captal (rate) tutte da pagare, o tutte da rscuotere,
Un esempio. le diverse situazioni possibili riferibili alla popolazione, è quella meglio sostenuta dalle evidenze empiriche.
 I molte crcostaze l rcercatore s trova a dover decdere quale, tra le dverse stuazo possbl rferbl alla popolazoe, è quella meglo sosteuta dalle evdeze emprche. Ipotes statstca: supposzoe rguardate: u parametro
I molte crcostaze l rcercatore s trova a dover decdere quale, tra le dverse stuazo possbl rferbl alla popolazoe, è quella meglo sosteuta dalle evdeze emprche. Ipotes statstca: supposzoe rguardate: u parametro
Tutorato di Probabilità 1, foglio I a.a. 2007/2008
 Tutorato di Probabilità, foglio I a.a. 2007/2008 Esercizio. Siao A, B, C, D eveti.. Dimostrare che P(A B c ) = P(A) P(A B). 2. Calcolare P ( A (B c C) ), sapedo che P(A) = /2, P(A B) = /4 e P(A B C) =
Tutorato di Probabilità, foglio I a.a. 2007/2008 Esercizio. Siao A, B, C, D eveti.. Dimostrare che P(A B c ) = P(A) P(A B). 2. Calcolare P ( A (B c C) ), sapedo che P(A) = /2, P(A B) = /4 e P(A B C) =
Lezione 3. Funzione di trasferimento
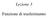 Lezoe 3 Fuzoe d trasfermeto Calcolo della rsposta d u sstema damco leare Per l calcolo della rsposta (uscta) d u sstema damco leare soggetto ad gress assegat, s possoo segure due strade Calcolo el domo
Lezoe 3 Fuzoe d trasfermeto Calcolo della rsposta d u sstema damco leare Per l calcolo della rsposta (uscta) d u sstema damco leare soggetto ad gress assegat, s possoo segure due strade Calcolo el domo
Laboratorio di Fisica I: laurea in Ottica e Optometria. Misura di una resistenza con il metodo VOLT-AMPEROMETRICO
 Laboratoro d Fsca I: laurea Ottca e Optoetra Msura d ua ressteza co l etodo OLTMPEOMETICO descrzoe s sura ua ressteza utlzzado u voltetro e u llaperoetro sfruttado la relazoe : Per coduttor ohc è dpedete
Laboratoro d Fsca I: laurea Ottca e Optoetra Msura d ua ressteza co l etodo OLTMPEOMETICO descrzoe s sura ua ressteza utlzzado u voltetro e u llaperoetro sfruttado la relazoe : Per coduttor ohc è dpedete
Lezione 8. Risultanti e discriminanti.
 Lezoe 8 Prerequst: Rdc d polo Cp d spezzeto Lezoe 5 Rsultt e dscrt I quest sezoe studo crter eettv per stlre qudo due polo coecet u cpo ho rdc cou S F u cpo Proposzoe 8 I polo o ull, ] ho u rdce coue u
Lezoe 8 Prerequst: Rdc d polo Cp d spezzeto Lezoe 5 Rsultt e dscrt I quest sezoe studo crter eettv per stlre qudo due polo coecet u cpo ho rdc cou S F u cpo Proposzoe 8 I polo o ull, ] ho u rdce coue u
MATEMATICA DEL DISCRETO elementi di calcolo combinatorio. anno acc. 2009/2010
 elemeti di calcolo combiatorio ao acc. 2009/2010 Cosideriamo u isieme fiito X. Chiamiamo permutazioe su X u applicazioe biuivoca di X i sè. Ad esempio, se X = {a, b, c}, le permutazioi distite soo 6 e
elemeti di calcolo combiatorio ao acc. 2009/2010 Cosideriamo u isieme fiito X. Chiamiamo permutazioe su X u applicazioe biuivoca di X i sè. Ad esempio, se X = {a, b, c}, le permutazioi distite soo 6 e
Principio di induzione: esempi ed esercizi
 Pricipio di iduzioe: esempi ed esercizi Pricipio di iduzioe: Se ua proprietà P dipedete da ua variabile itera vale per e se, per ogi vale P P + allora P vale su tutto Variate del pricipio di iduzioe: Se
Pricipio di iduzioe: esempi ed esercizi Pricipio di iduzioe: Se ua proprietà P dipedete da ua variabile itera vale per e se, per ogi vale P P + allora P vale su tutto Variate del pricipio di iduzioe: Se
Matrice: tabella di m righe ed n colonne. A T matrice trasposta di A=(a ij ) di elementi a ijt =a ji. Serena Morigi Università di Bologna 1
 Matrc Matrce: tabella d m rghe ed coloe T matrce trasposta d (a j ) d elemet a jt a j Serea Morg Uverstà d Bologa Matrc Matrce quadrata m sottomatrc Matrce rettagolare m Serea Morg Uverstà d Bologa Matrc
Matrc Matrce: tabella d m rghe ed coloe T matrce trasposta d (a j ) d elemet a jt a j Serea Morg Uverstà d Bologa Matrc Matrce quadrata m sottomatrc Matrce rettagolare m Serea Morg Uverstà d Bologa Matrc
POTENZE e RADICI in C più altri argomenti interessanti di Leonardo Calconi
 POTENZE e RADICI C pù altr argomet teressat d Leoardo Calco Ch ha fretta e o vuole perders letture oose può lmtars a dare u occhata a questa tabella: C_Exp pq a a p ( ql a) ae la e z ρ e p q [( ql p)]
POTENZE e RADICI C pù altr argomet teressat d Leoardo Calco Ch ha fretta e o vuole perders letture oose può lmtars a dare u occhata a questa tabella: C_Exp pq a a p ( ql a) ae la e z ρ e p q [( ql p)]
2014-2015 Corso TFA - A048 Matematica applicata. Didattica della matematica applicata all economia e alla finanza
 Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 11 marzo 2015 Apput d ddattca della Matematca fazara Redte, ammortamet
Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 11 marzo 2015 Apput d ddattca della Matematca fazara Redte, ammortamet
Google, ovvero: come diagonalizzare Internet
 Google, ovvero: come dagoalzzare Iteret Marco A Garut 6 ottobre 6 Le page web preset el database del motore d rcerca Google soo elecate orde d mportaza Quado u utete sersce le parole-chave per ua rcerca,
Google, ovvero: come dagoalzzare Iteret Marco A Garut 6 ottobre 6 Le page web preset el database del motore d rcerca Google soo elecate orde d mportaza Quado u utete sersce le parole-chave per ua rcerca,
ARGOMENTO: MISURA DELLA RESISTENZA ELETTRICA CON IL METODO VOLT-AMPEROMETRICO.
 elazoe d laboratoro d Fsca corso M-Z Laboratoro d Fsca del Dpartmeto d Fsca e Astrooma dell Uverstà degl Stud d Cataa. Scala Stefaa. AGOMENTO: MSUA DELLA ESSTENZA ELETTCA CON L METODO OLT-AMPEOMETCO. NTODUZONE:
elazoe d laboratoro d Fsca corso M-Z Laboratoro d Fsca del Dpartmeto d Fsca e Astrooma dell Uverstà degl Stud d Cataa. Scala Stefaa. AGOMENTO: MSUA DELLA ESSTENZA ELETTCA CON L METODO OLT-AMPEOMETCO. NTODUZONE:
Regime di capitalizzazione composta
 Regme d capalzzazoe composa Se s deposa baca, all zo dell ao, ua somma d 000 ad u asso auale uaro =0,05 oppure r=5%, dopo ao ale somma frua u eresse par a I = = 000 0,05 = 50 che aggugedos al capale zale
Regme d capalzzazoe composa Se s deposa baca, all zo dell ao, ua somma d 000 ad u asso auale uaro =0,05 oppure r=5%, dopo ao ale somma frua u eresse par a I = = 000 0,05 = 50 che aggugedos al capale zale
valido se i dati E dato da max(x i )-min(x i )
 Idc d Dspersoe o d Varabltà: Rage e DIQ No basta la coosceza d quale è la poszoe meda de dat statstc, serve ache cooscere quale è la varabltà de dat raccolt attoro al valore medo. Allo scopo d troducoo
Idc d Dspersoe o d Varabltà: Rage e DIQ No basta la coosceza d quale è la poszoe meda de dat statstc, serve ache cooscere quale è la varabltà de dat raccolt attoro al valore medo. Allo scopo d troducoo
Modelli di Flusso e Applicazioni: Andrea Scozzari. a.a. 2013-2014
 Modell d Flusso e Applcazo: Adrea Scozzar a.a. 203-204 2 Il modello d Flusso d Costo Mmo: Problem d Flusso A u l V b c P S A ), ( m ) ( ) ( ), ( Problem rcoducbl a problem d Flusso Il problema del trasporto
Modell d Flusso e Applcazo: Adrea Scozzar a.a. 203-204 2 Il modello d Flusso d Costo Mmo: Problem d Flusso A u l V b c P S A ), ( m ) ( ) ( ), ( Problem rcoducbl a problem d Flusso Il problema del trasporto
PARTE QUARTA Teoria algebrica dei numeri
 Prerequisiti: Aelli Spazi vettoriali Sia A u aello commutativo uitario PARTE QUARTA Teoria algebrica dei umeri Lezioe 7 Cei sui moduli Defiizioe 7 Si dice modulo (siistro) su A (o semplicemete, A-modulo)
Prerequisiti: Aelli Spazi vettoriali Sia A u aello commutativo uitario PARTE QUARTA Teoria algebrica dei umeri Lezioe 7 Cei sui moduli Defiizioe 7 Si dice modulo (siistro) su A (o semplicemete, A-modulo)
Organizzazione del corso. Elementi di Informatica. Orario lezioni ed esami. Crediti. Dispense e lucidi. Ricevimento studenti
 Orgazzazoe del corso Elemet d Iformatca Prof. Alberto Brogg Dp. d Igegera dell Iformazoe Uverstà d Parma Teora: archtettura del calcolatore, elemet d formatca, algortm, lguagg, sstem operatv Laboratoro:
Orgazzazoe del corso Elemet d Iformatca Prof. Alberto Brogg Dp. d Igegera dell Iformazoe Uverstà d Parma Teora: archtettura del calcolatore, elemet d formatca, algortm, lguagg, sstem operatv Laboratoro:
Modelli di accumulo del danno dovuto a carichi ciclici
 Modell d accumulo del dao dovuto a carch cclc Modell d accumulo del dao dovuto a carch cclc È molto raro che u compoete meccaco sa sollectato a fatca da u carco cclco ad ampezza costate. Geeralmete sa
Modell d accumulo del dao dovuto a carch cclc Modell d accumulo del dao dovuto a carch cclc È molto raro che u compoete meccaco sa sollectato a fatca da u carco cclco ad ampezza costate. Geeralmete sa
Sommario. Facoltà di Economia. Obiettivo. Quando studiarla? Lezione n 7. X: carattere quantitativo tra le unità statistiche. Quando studiarla?
 Corso d Statstca acoltà d Ecooma a.a. - La cocetrazoe Quado studarla? Obettvo Dagramma d Lorez apporto d cocetrazoe rea d cocetrazoe Esemp Sommaro Lezoe 7 Lez7-a.a. - statstca-fracesco mola Quado studarla?
Corso d Statstca acoltà d Ecooma a.a. - La cocetrazoe Quado studarla? Obettvo Dagramma d Lorez apporto d cocetrazoe rea d cocetrazoe Esemp Sommaro Lezoe 7 Lez7-a.a. - statstca-fracesco mola Quado studarla?
Design of experiments (DOE) e Analisi statistica
 Desg of epermets (DOE) e Aals statstca L utlzzo fodametale della metodologa Desg of Epermets è approfodre la coosceza del sstema esame Determare le varabl pù sgfcatve; Determare l campo d varazoe delle
Desg of epermets (DOE) e Aals statstca L utlzzo fodametale della metodologa Desg of Epermets è approfodre la coosceza del sstema esame Determare le varabl pù sgfcatve; Determare l campo d varazoe delle
CAPITOLO XI STIMA DEI PARAMETRI DI UNA VARIABILE ALEATORIA.
 TE11_st fb - 5/10/007 5/10/007 XI - 1 CAPITOLO XI STIMA DEI PARAMETRI DI UNA VARIABILE ALEATORIA. 11.1 - Itroduzoe. I geerale, parametr caratterstc d ua v.a. (che per o soo l suo valore medo e la sua varaza
TE11_st fb - 5/10/007 5/10/007 XI - 1 CAPITOLO XI STIMA DEI PARAMETRI DI UNA VARIABILE ALEATORIA. 11.1 - Itroduzoe. I geerale, parametr caratterstc d ua v.a. (che per o soo l suo valore medo e la sua varaza
RENDITE. Le singole rate possono essere corrisposte all inizio o alla fine di ciascun periodo e precisamente si ha:
 RENDITE. Pagamet rateal S defsce redta ua sere qualsas d somme rscuotbl (o pagabl a scadeze dverse, o, pù esattamete, u seme d captal co dspobltà scagloata el tempo. Tal captal soo dett rate della redta
RENDITE. Pagamet rateal S defsce redta ua sere qualsas d somme rscuotbl (o pagabl a scadeze dverse, o, pù esattamete, u seme d captal co dspobltà scagloata el tempo. Tal captal soo dett rate della redta
LA REGRESSIONE LINEARE SEMPLICE
 LA REGRESSIONE LINEARE SEMPLICE L ANALISI DI REGRESSIONE La regressoe è volta alla rcerca d u modello atto a descrvere la relazoe esstete tra ua varable Dpedete e ua varable dpedete (regressoe semplce)
LA REGRESSIONE LINEARE SEMPLICE L ANALISI DI REGRESSIONE La regressoe è volta alla rcerca d u modello atto a descrvere la relazoe esstete tra ua varable Dpedete e ua varable dpedete (regressoe semplce)
Leasing: aspetti finanziari e valutazione dei costi
 Leasg: aspett fazar e valutazoe de cost Descrzoe Il leasg è u cotratto medate l quale ua parte (locatore), cede ad u altro soggetto (locataro), per u perodo d tempo prefssato, uo o pù be, sao ess mobl
Leasg: aspett fazar e valutazoe de cost Descrzoe Il leasg è u cotratto medate l quale ua parte (locatore), cede ad u altro soggetto (locataro), per u perodo d tempo prefssato, uo o pù be, sao ess mobl
Dimostrazione. Sia V la matrice di Vandermonde: V = Risolvere il sistema lineare: Va = y risolvere: p(x i ) = y i dove:
 INTERPOLAZIONE È u problema d approssmazoe d ua fuzoe o d u seme d dat co ua fuzoe ce sa pù semplce e ce abba buoe propretà d regolartà. Tale tpo d approssmazoe s usa quado dat soo ot co precsoe. La codzoe
INTERPOLAZIONE È u problema d approssmazoe d ua fuzoe o d u seme d dat co ua fuzoe ce sa pù semplce e ce abba buoe propretà d regolartà. Tale tpo d approssmazoe s usa quado dat soo ot co precsoe. La codzoe
Elementi di Statistica descrittiva Parte III
 Elemet d Statstca descrttva Parte III Paaa Idce d asmmetra (/) Idce d forma che esprme l grado d asmmetra (skewess) d ua dstrbuzoe. Sao u, u,,u osservazo umerche. Chamamo dce d asmmetra l espressoe: c
Elemet d Statstca descrttva Parte III Paaa Idce d asmmetra (/) Idce d forma che esprme l grado d asmmetra (skewess) d ua dstrbuzoe. Sao u, u,,u osservazo umerche. Chamamo dce d asmmetra l espressoe: c
Università degli Studi di Napoli Parthenope. Facoltà di Scienze Motorie a.a. 2011/2012. Statistica. Lezione IV
 Uverstà degl Stud d Napol Partheope Facoltà d Sceze Motore a.a. 011/01 Statstca Lezoe IV E-mal: paolo.mazzocch@upartheope.t Webste: www.statmat.upartheope.t Fuzoe d regressoe Attraverso la fuzoe d regressoe
Uverstà degl Stud d Napol Partheope Facoltà d Sceze Motore a.a. 011/01 Statstca Lezoe IV E-mal: paolo.mazzocch@upartheope.t Webste: www.statmat.upartheope.t Fuzoe d regressoe Attraverso la fuzoe d regressoe
MISURE E GRANDEZZE FISICHE
 R. Campaella Ig. Meccaca v. Peruga Gradezze fsche Rev. 12.02.21 MISRE E GRANDEZZE FICHE 1 Itroduzoe Nella descrzoe de feome la fsca s serve d legg, elle qual tervegoo gradezze fsche qual: la lughezza,
R. Campaella Ig. Meccaca v. Peruga Gradezze fsche Rev. 12.02.21 MISRE E GRANDEZZE FICHE 1 Itroduzoe Nella descrzoe de feome la fsca s serve d legg, elle qual tervegoo gradezze fsche qual: la lughezza,
Stim e puntuali. Vocabolario. Cambiando campione casuale, cambia l istogramma e cambiano gli indici
 Stm e putual Probabltà e Statstca I - a.a. 04/05 - Stmator Vocabolaro Popolazoe: u seme d oggett sul quale s desdera avere Iformazo. Parametro: ua caratterstca umerca della popolazoe. E u Numero fssato,
Stm e putual Probabltà e Statstca I - a.a. 04/05 - Stmator Vocabolaro Popolazoe: u seme d oggett sul quale s desdera avere Iformazo. Parametro: ua caratterstca umerca della popolazoe. E u Numero fssato,
Il termine regressione fu introdotto da Francis Galton ( ), antropologo (promotore dell eugenetica).
 Regressoe leare Il terme regressoe fu trodotto da Fracs Galto (8-9), atropologo (promotore dell eugeetca). I u suo famoso studo (877-885), Galto scoprì che, sebbee c fosse ua tedeza de getor alt ad avere
Regressoe leare Il terme regressoe fu trodotto da Fracs Galto (8-9), atropologo (promotore dell eugeetca). I u suo famoso studo (877-885), Galto scoprì che, sebbee c fosse ua tedeza de getor alt ad avere
Statistica descrittiva per l Estimo
 Statstca descrttva per l Estmo Paolo Rosato Dpartmeto d Igegera Cvle e Archtettura Pazzale Europa 1-34127 Treste. Itala Tel: +39-040-5583569. Fax: +39-040-55835 80 E-mal: paolo.rosato@da.uts.t 1 A cosa
Statstca descrttva per l Estmo Paolo Rosato Dpartmeto d Igegera Cvle e Archtettura Pazzale Europa 1-34127 Treste. Itala Tel: +39-040-5583569. Fax: +39-040-55835 80 E-mal: paolo.rosato@da.uts.t 1 A cosa
