SOLUZIONI COMPITO del 16/01/2009 ANALISI 1 - MECCANICA + ELETTRICA 9 CFU CALCOLO DIFF. e INT. I+II - MECCANICA 11 CFU TEMA A
|
|
|
- Alessandra Giuseppe
- 8 anni fa
- Visualizzazioni
Transcript
1 SOLUZIONI COMPITO del 6//9 ANALISI - MECCANICA + ELETTRICA 9 CFU CALCOLO DIFF e INT I+II - MECCANICA CFU TEMA A Esercizio Chiaramente la serie proposta è una serie a termini positivi per ogni α R Osserviamo, inoltre, che, utilizzando lo sviluppo di Mc Laurin al primo ordine della funzione log( + t con t = e 3n, si ottiene: a n := e 3n [log(e 3n + ] 5α 3n e 3n5α (e 3n + 4α e e = 3n( 4α e 3n(5α 4α Quindi il termine generale è infinitesimo se e solo se 5α 4α >, ovvero α < o α > 4/5, e, per tali valori del parametro, la serie proposta converge per il criterio della radice Esercizio L equazione differenziale proposta è un equazione a variabili separabili che ha come soluzione singolare (x Per determinare le altre soluzioni di tale equazione, procediamo per separazione di variabili, ottenendo e x e d = = e (x = + Ce arctan x log(+x + x dx = log e(x = arctan x log( + x + C ( = (x = log + Ce arctan x log(+x C R Osserviamo che per C = si riottiene la soluzione singolare (x Imponendo la condizione iniziale, si ricava ( = ( = log + C = C = e ( Quindi la soluzione cercata è data da (x=log + (e e arctan x log(+x 3 Infine otteniamo lim x + (x = ( lim log + (e e arctan x log(+x = x + Esercizio 3 Effettuando la sostituzione t = log x, da cui t( =, t(e =, dt = dx/x, si ottiene e e [log5 x+4 log(log x] x dx = e t5 +4 log t dt = t 4 e t5 dt =log Effettuando ora la sostituzione = t 5, da cui ( =, ( =, d/5 = t 4 dt, si ottiene t 4 e t5 dt = 5 e d = (e 5 ( + (e earctan x (+x Esercizio 4 Utilizzando lo sviluppo di Mc Laurin al primo ordine per la funzione x sin x e quello al secondo ordine per le funzioni x cos x, x e x e t log( + t, con t = x, otteniamo f(x Pertanto, se < α <, si ha x α x / [( + x + x / (x x ] = xα x / α (3x α x α +α+ f(x (3x = x α α 3 α e quindi la funzione avrà ordine di infinitesimo pari a se e solo se α = / Se, invece, α si ha x f(x C (3x = C x4 α α 3, α dove C = / se α = e C = / se α > Pertanto, in questo caso, la funzione non può mai essere un infinitesimo del secondo ordine per x +, poiché le condizioni α = ± non sono compatibili con la richiesta α
2 Esercizio 5 Poiché f (x < in [, +, la funzione è strettamente decrescente e quindi invertibile Poiché f( = ed f è positiva e infinitesima per x +, si ha che Im(f = (, ], ovvero, detta g = f, si avrà necessariamente che dom(g = (, ], g( = e g strettamente decrescente Inoltre, poiché f(x + se e solo se x +, ponendo = f(x, si ottiene che, per +, g( + Dalla regolarità di f e dal fatto che f si ottiene la regolarità di g e vale la formula g ( = f (g( Infine, effettuando nuovamente il cambiamento di variabile = f(x, da cui ( =, (+ =, d = f (x dx, ovvero dx = d/f (g(, si ottiene f(x dx = lim M M + = lim ɛ + ɛ f(x dx = lim M + f (g( d = f(m f (g( d f (g( d Pertanto i due integrali hanno lo stesso comportamento Infine, ponendo ancora = f(x, da cui x = g( e ricordando che x + se e solo se +, si ricava = f(x x α = [g(] α [g(] α g( /α Esercizio 6 L insieme di definizione di f, sarà determinato dalla condizione 5 x + (x + >, che equivale a x e x + < 5 Quindi si avrà {(x, R : 5 x < < x} {(x, R : x < < 5 x}
3 TEMA B Esercizio Chiaramente la serie proposta è una serie a termini positivi per ogni α R Osserviamo, inoltre, che, utilizzando lo sviluppo di Mc Laurin al primo ordine delle funzioni sin t e ( + t /, con t = e n, si ottiene: [sin(e n ] α a n := e n ( + e n α e α n(α e n e nα = α e n( α +α Quindi il termine generale è infinitesimo se e solo se α + α >, ovvero < α <, e, per tali valori del parametro, la serie proposta converge per il criterio della radice Esercizio L equazione differenziale proposta è un equazione a variabili separabili che ha come soluzione singolare (x Per determinare le altre soluzioni di tale equazione, procediamo per separazione di variabili, ottenendo + 3 d = e x (e x 3 dx = 3 log 3 (x + = (ex 3 + C = 3 (x = Ce 3(ex 3 / = (x = 3 Ce 3(e x 3 / C R Osserviamo che per C = si riottiene la soluzione singolare (x Imponendo la condizione iniziale, si ricava = (log 3 = 3 C = C = 7 Quindi la soluzione cercata è data da (x = 3 7e 3(ex 3 / 3 Infine otteniamo lim 3 (x = lim 7e 3(ex 3 / = x + x + Esercizio 3 Osserviamo, innanzitutto, che l integrale proposto si può riscrivere nella forma log [( + 4x 4 x3] + 4x 4 dx = x 3 log( + 4x4 + 4x 4 dx Effettuando la sostituzione t = log( + 4x 4, da cui t( =, t( = log 5, dt = 6x 3 dx/( + 4x 4, si ottiene x 3 log( + 4x4 + 4x 4 dx = 6 log 5 t dt = log 5 3 Esercizio 4 Utilizzando lo sviluppo di Mc Laurin al primo ordine per le funzioni x tan x e t log( + t, con t = x, e quello al terzo ordine per le funzioni x sin x e x sinh x, otteniamo Pertanto, se < α <, si ha f(x ( x + x3 /3! + x + x 3 /3! +α /9 x α + x = (x3 /3 +α /9 x α + x f(x (x3 /3 +α /9 x α = xα /3 α+3 3 +α /9 Quindi, in questo caso, la funzione non può mai essere un infinitesimo del terzo ordine per x +, poiché le condizioni α =, 3 non sono compatibili con la richiesta < α < Se, invece, α si ha f(x C (x3 /3 +α /9 x = C xα /3+ 3, +α /9 dove C = / se α = e C = se α > Quindi la funzione avrà ordine di infinitesimo pari a 3 se e solo se α = 6 3
4 Esercizio 5 Poiché f (x < in (, ], la funzione è strettamente decrescente e quindi invertibile Poiché f( = ed f è positiva e infinita per x +, si ha che Im(f = [, +, ovvero, detta g = f, si avrà necessariamente che dom(g = [, +, g( = e g strettamente decrescente Inoltre, poiché f(x + se e solo se x +, ponendo = f(x, si ottiene che, per +, g( + Dalla regolarità di f e dal fatto che f si ottiene la regolarità di g e vale la formula g ( = f (g(, ovvero f (x = /g (f(x Infine, effettuando nuovamente il cambiamento di variabile = f(x, ovvero x = g(, da cui ( = +, ( =, d = f (x dx, ovvero dx/g (f(x = d, si ottiene xf(x g (f(x dx = lim ɛ + ɛ = lim M + xf(x g (f(x M dx = lim ɛ + g( d = f(ɛ + g( d g( d Pertanto i due integrali hanno lo stesso comportamento Infine, ponendo ancora = f(x, da cui x = g( e ricordando che x + se e solo se +, si ricava g( = xf(x x α = [g(] α+ [g(] α+ g( /(α+ Esercizio 6 L insieme di definizione di f, sarà determinato dalla condizione 7 x + + (x + >, che equivale a x e x + > 7 Quindi si avrà {(x, R : < 7 x} {(x, R : > 7 x} 4
5 TEMA C Esercizio Chiaramente la serie proposta è una serie a termini positivi per ogni α R Osserviamo, inoltre, che, utilizzando lo sviluppo di Mc Laurin al primo ordine delle funzioni sin t, con t = e 5n, e ( + t /, con t = 3e 5n, si ottiene: a n := (e5n α ( + 3e 5n α sin(e 5n (e5n ( α 3 (α ( e 5n(α α 3 = (α e 5n (e 5n (α +α Quindi il termine generale è infinitesimo se e solo se α + α >, ovvero α < o α >, e, per tali valori del parametro, la serie proposta converge per il criterio della radice Esercizio L equazione differenziale proposta è un equazione a variabili separabili che ha come soluzione singolare (x 5 3 Per determinare le altre soluzioni di tale equazione, procediamo per separazione di variabili, ottenendo d = e x (e x dx = 5 log 5 (x + 3 = (e x + C = 5 (x = Ce 5(ex 3 = (x = 5 Ce 5(e x 3 C R Osserviamo che per C = si riottiene la soluzione singolare (x 5 3 Imponendo la condizione iniziale, si ricava = (log = 5 C 3 = C = 9 Quindi la soluzione cercata è data da (x = 5 9e 5(ex 3 3 Infine otteniamo lim 5 (x = lim 9e 5(ex 3 = x + x + Esercizio 3 Osserviamo, innanzitutto, che l integrale proposto si può riscrivere nella forma log[( + x 3 x ] + x 3 dx = x log( + x3 + x 3 dx Effettuando la sostituzione t = log( + x 3, da cui t( =, t( = log 9, dt = 3x dx/( + x 3, si ottiene x log( + x3 + x 3 dx = 3 log 9 t dt = log 9 3 Esercizio 4 Utilizzando lo sviluppo di Mc Laurin al primo ordine per le funzioni x tan x e t log( + t, con t = x 4, e quello al terzo ordine per le funzioni t sin t, con t = x, e x sinh x, otteniamo Pertanto, se < α < /4, si ha f(x ( x + 8x3 /3! + x + x 3 /3! 3α + x + x 4α f(x (5x3 /3 3α + x 4α = = (5x3 /3 3α + x + x 4α ( (3α 5 + x 9α 4α+3 3 Quindi, in questo caso, la funzione non può mai essere un infinitesimo del terzo ordine per x +, poiché le condizioni α =, 4/9 non sono compatibili con la richiesta < α < /4 Se, invece, α /4 si ha f(x C (5x3 /3 3α + = C(5x 3 /3 3α + x 9α +, x dove C = / se α = /4 e C = se α > /4 Quindi la funzione avrà ordine di infinitesimo pari a 3 se e solo se α = /3 5
6 Esercizio 5 Poiché f (x < in (, ], la funzione è strettamente decrescente e quindi invertibile Poiché f( = ed f è positiva e infinita per x +, si ha che Im(f = [, +, ovvero, detta g = f, si avrà necessariamente che dom(g = [, +, g( = e g strettamente decrescente Inoltre, poiché f(x + se e solo se x +, ponendo = f(x, si ottiene che, per +, g( + Dalla regolarità di f e dal fatto che f si ottiene la regolarità di g e vale la formula g ( = f (g(, ovvero f (x = /g (f(x Infine, effettuando nuovamente il cambiamento di variabile = f(x, ovvero x = g(, da cui ( = +, ( =, d = f (x dx, ovvero dx/g (f(x = d, si ottiene xf(x g (f(x dx = lim ɛ + ɛ = lim M + xf(x g (f(x M dx = lim ɛ + g( d = f(ɛ + g( d g( d Pertanto i due integrali hanno lo stesso comportamento Infine, ponendo ancora = f(x, da cui x = g( e ricordando che x + se e solo se +, si ricava g( = xf(x x α = [g(] α+ [g(] α+ g( /(α+ Esercizio 6 L insieme di definizione di f, sarà determinato dalla condizione 7 x + + (x + >, che equivale a x e x + > 7 Quindi si avrà {(x, R : < 7 x} {(x, R : > 7 x} 6
7 TEMA D Esercizio Chiaramente la serie proposta è una serie a termini positivi per ogni α R Osserviamo, inoltre, che, utilizzando lo sviluppo di Mc Laurin al primo ordine della funzione log( + t con t = e 4n, si ottiene: (e 4n + 3α e4n( 3α a n := (e 4n [log(e 4n α + ] (e 4n e = 4nα e 4n( α +3α Quindi il termine generale è infinitesimo se e solo se α + 3α >, ovvero < α < 3, e, per tali valori del parametro, la serie proposta converge per il criterio della radice Esercizio L equazione differenziale proposta è un equazione a variabili separabili che non ha alcuna soluzione singolare Per determinare le soluzioni di tale equazione, procediamo per separazione di variabili, ottenendo e d = + e x 3 + x 4 dx = log + e (x = 4 log( + x4 + C = e (x = C 4 + x 4 = (x = log( C 4 + x 4 C R Imponendo la condizione iniziale, si ricava ( = ( = log C = C = Quindi la soluzione cercata è data da (x = log( 4 ( + x 4 = log 3 Infine otteniamo lim [ (x] = lim log( 4 + x 4 = + x x 4 +x 4 Esercizio 3 Effettuando la sostituzione t = log x, da cui t(e =, t(e =, dt = dx/x, si ottiene e e [3 log x+log(log x] e x dx = e 3t +log t dt = te 3t dt Effettuando ora la sostituzione = 3t, da cui ( = 3, ( =, d/6 = t dt, si ottiene te 3t dt = 6 3 e d = 6 (e e 3 Esercizio 4 Utilizzando lo sviluppo di Mc Laurin al primo ordine per la funzione x sin x e quello al secondo ordine per le funzioni x cos x, x e x e x log( + x, otteniamo x + (x / α/ f(x x x / + x x / = x + xα /( α α Pertanto, se < α <, si ha f(x xα /( α x (α = x 4α +α+ ( α x (α e quindi la funzione avrà ordine di infinitesimo pari a se e solo se α = /4 Se, invece, α si ha x f(x C x = (α Cx 4α dove C = + / se α = e C = se α > Pertanto, in questo caso, la funzione non può mai essere un infinitesimo del secondo ordine per x +, poiché le condizioni α = ±/ non sono compatibili con la richiesta α +3, 7
8 Esercizio 5 Poiché f (x < in [, +, la funzione è strettamente decrescente e quindi invertibile Poiché f( = ed f è positiva e infinitesima per x +, si ha che Im(f = (, ], ovvero, detta g = f, si avrà necessariamente che dom(g = (, ], g( = e g strettamente decrescente Inoltre, poiché f(x + se e solo se x +, ponendo = f(x, si ottiene che, per +, g( + Dalla regolarità di f e dal fatto che f si ottiene la regolarità di g e vale la formula g ( = f (g( Infine, effettuando nuovamente il cambiamento di variabile = f(x, da cui ( =, (+ =, d = f (x dx, ovvero dx = d/f (g(, si ottiene f(x dx = lim M M + = lim ɛ + ɛ f(x dx = lim M + f (g( d = f(m f (g( d f (g( d Pertanto i due integrali hanno lo stesso comportamento Infine, ponendo ancora = f(x, da cui x = g( e ricordando che x + se e solo se +, si ricava = f(x x α = [g(] α [g(] α g( /α Esercizio 6 L insieme di definizione di f, sarà determinato dalla condizione 5 x + (x + >, che equivale a x e x + < 5 Quindi si avrà {(x, R : 5 x < < x} {(x, R : x < < 5 x} 8
SIMULAZIONE TEST ESAME - 1
SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
a) Osserviamo innanzi tutto che dev essere x > 0. Pertanto il dominio è ]0, + [. b) Poniamo t = log x. Innanzi tutto si ha:
![a) Osserviamo innanzi tutto che dev essere x > 0. Pertanto il dominio è ]0, + [. b) Poniamo t = log x. Innanzi tutto si ha:](/thumbs/28/12902483.jpg "a) Osserviamo innanzi tutto che dev essere x > 0. Pertanto il dominio è ]0, + [. b) Poniamo t = log x. Innanzi tutto si ha:")
ESERCIZIO - Data la funzione f (x) = (log x) 6 7(log x) 5 + 2(log x) 4, si chiede di: a) calcolare il dominio di f ; ( punto) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire
Esercizi svolti. 1. Si consideri la funzione f(x) = 4 x 2. a) Verificare che la funzione F(x) = x 2 4 x2 + 2 arcsin x è una primitiva di
Esercizi svolti. Si consideri la funzione f() 4. a) Verificare che la funzione F() 4 + arcsin è una primitiva di f() sull intervallo (, ). b) Verificare che la funzione G() 4 + arcsin π è la primitiva
EQUAZIONI DIFFERENZIALI Esercizi svolti. y = xy. y(2) = 1.
EQUAZIONI DIFFERENZIALI Esercizi svolti 1. Determinare la soluzione dell equazione differenziale (x 2 + 1)y + y 2 =. y + x tan y = 2. Risolvere il problema di Cauchy y() = 1 2 π. 3. Risolvere il problema
Soluzione del tema d esame di matematica, A.S. 2005/2006
Soluzione del tema d esame di matematica, A.S. 2005/2006 Niccolò Desenzani Sun-ra J.N. Mosconi 22 giugno 2006 Problema. Indicando con A e B i lati del rettangolo, il perimetro è 2A + 2B = λ mentre l area
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
EQUAZIONI DIFFERENZIALI. 1. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x 2 log t (d) x = e t x log x (e) y = y2 5y+6
EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
Esercizi sugli integrali impropri
Esercizi sugli integrali impropri Esercizio. Studiare 2 x4 dx. Svolgimento: è un integrale improprio, in quanto f(x) =, x (, 2] ha una singolarità in : x4 lim x + x4 = +. Osserviamo che f è positiva, quindi
Analisi Mat. 1 - Ing. Inform. - Soluzioni del compito del 23-3-06
Analisi Mat. - Ing. Inform. - Soluzioni del compito del 3-3-6 Sia p il polinomio di quarto grado definito da pz = z 4. Sia S il settore circolare formato dai numeri complessi che hanno modulo minore o
Ripasso delle matematiche elementari: esercizi svolti
Ripasso delle matematiche elementari: esercizi svolti I Equazioni e disequazioni algebriche 3 Esercizi su equazioni e polinomi di secondo grado.............. 3 Esercizi sulle equazioni di grado superiore
SOLUZIONI COMPITO del 13/02/2019 ANALISI MATEMATICA I - 9 CFU ENERGETICA TEMA A
SOLUZIONI COMPITO del /0/09 ANALISI MATEMATICA I - 9 CFU ENERGETICA TEMA A Esercizio Ponendo z = a + ib, da cui z = a + b, ed osservando che e iπ/ = i, l equazione proposta si riscrive nella forma a b
Matematica e Statistica
Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
ANALISI MATEMATICA 1 Area dell Ingegneria dell Informazione. Appello del
ANALISI MATEMATICA Area dell Ingegneria dell Informazione Appello del 3..7 TEMA Esercizio Calcolare l integrale log(3) 4 dx Svolgimento. Si ha log(3) 4 dx = (ponendo ex = t, per cui dx = dt/t) e = 4 3
I appello - 24 Marzo 2006
Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
APPELLO C AM1C 19 Gennaio f(x) = log( x + 2) x
Esercizio 1. Sia data la funzione f(x) = log( x + 2) x (a )Determinarne: insieme di esistenza e di derivabilità, limiti ed eventuali asintoti, eventuali punti angolosi o di cuspide, eventuali massimi e
UNIVERSITÀ DEGLI STUDI DI PERUGIA Facoltà di Scienze MM. FF. e NN.
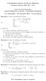A.A. 213/214 2 Novembre 213 I esercitazione Esercizio 1. Dato il problema di Cauchy ( e y 2 2 1 ) arctan 3y 5 y = 2 sin (1) 2 x 2, 1 + x 2 y() = 1, (b) provare che la soluzione y di (3) è definita in tutto
Secondo appello 2005/ Tema 1
Secondo appello 2005/2006 - Tema Esercizio Risolvere l equazione di variabile complessa determinando le soluzioni in forma algebrica. Ponendo z = x + iy con x, y R, si ottiene z 2 + 2iz + 2 z = 0, () (x
COGNOME... NOME... Matricola... Corso Prof... Esame di ANALISI MATEMATICA I - 11 Febbraio 2011, ore 8.30
Esame di ANALISI MATEMATICA I - 11 Febbraio 2011, ore 830 A ESERCIZIO 1 (8 punti) Data la funzione = 1 + sin x 2 2 x (a) determinare lo sviluppo di MacLaurin al terzo ordine della funzione ; (b) determinare
Prova scritta di Analisi Matematica T-A, Ingegneria Energetica, 22/12/2014. MATRICOLA:...NOME e COGNOME:...
Prova scritta di Analisi Matematica T-A, Ingegneria Energetica, //4 A = {x R : x n } =, n N, n >. cosπn)n! + n 3n + 5 e n + n + )!. x sinx + x ) + log x x + x 4 ) + + x. x + coshx x ) e x sinh x x 3 )
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 2011/2012
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
Matematica, 12 CFU, Corso di laurea in Scienze Biologiche- A.A Laurea Triennale
Matematica, CFU, Corso di laurea in Scienze Biologiche- A.A. 009-00 Laurea Triennale Luglio 00- COMPITO - Totale punti 40, punteggio minimo 4 Nome Cognome. (4 punti) Calcolare i seguenti limiti: (a) lim
Funzioni. Parte prima. Daniele Serra
Funzioni Parte prima Daniele Serra Nota: questi appunti non sostituiscono in alcun modo le lezioni del prof. Favilli, né alcun libro di testo. Sono piuttosto da intendersi a integrazione di entrambi. 1
Sviluppi di Taylor Esercizi risolti
Esercizio 1 Sviluppi di Taylor Esercizi risolti Utilizzando gli sviluppi fondamentali, calcolare gli sviluppi di McLaurin con resto di Peano delle funzioni seguenti fino all ordine n indicato: 1. fx ln1
Anno 5 4. Funzioni reali: il dominio
Anno 5 4 Funzioni reali: il dominio 1 Introduzione In questa lezione impareremo a definire cos è una funzione reale di variabile reale e a ricercarne il dominio. Al termine di questa lezione sarai in grado
SOLUZIONI COMPITO del 1/02/2013 ANALISI MATEMATICA I - 9 CFU INGEGNERIA MECCANICA - INGEGNERIA ENERGETICA INGEGNERIA AMBIENTE e TERRITORIO TEMA A
SOLUZIONI COMPITO del /0/0 ANALISI MATEMATICA I - 9 CFU INGEGNERIA MECCANICA - INGEGNERIA ENERGETICA INGEGNERIA AMBIENTE e TERRITORIO TEMA A Esercizio Osserviamo che la serie proposta è a termini di segno
11) convenzioni sulla rappresentazione grafica delle soluzioni
2 PARAGRAFI TRATTATI 1)La funzione esponenziale 2) grafici della funzione esponenziale 3) proprietá delle potenze 4) i logaritmi 5) grafici della funzione logaritmica 6) principali proprietá dei logaritmi
FUNZIONI ELEMENTARI Esercizi risolti
FUNZIONI ELEMENTARI Esercizi risolti 1 Discutendo graficamente la disequazione x > 3+x, verificare che l insieme delle soluzioni è un intervallo e trovarne gli estremi Rappresentare nel piano x, y) l insieme
Università di Trieste Facoltà d Ingegneria. Esercitazioni per la preparazione della prova scritta di Matematica 3 Dott.
Università di Trieste Facoltà d Ingegneria. Esercitazioni per la preparazione della prova scritta di Matematica 3 Dott. Franco Obersnel Lezione 19: campi vettoriali e formule di Gauss-Green nel piano.
Esercitazione del 14 gennaio f(x) = e x x2 x 2. { e x2 +2x+2 e x2 2. se x [ 1, 2] ; {
![Esercitazione del 14 gennaio f(x) = e x x2 x 2. { e x2 +2x+2 e x2 2. se x [ 1, 2] ; {](/thumbs/102/153045461.jpg "Esercitazione del 14 gennaio f(x) = e x x2 x 2. { e x2 +2x+2 e x2 2. se x [ 1, 2] ; {")
Esercitazione del gennaio 0 Esercizio. Tracciare il diagramma della funzione f(x) = e x x x. Svolgimento.. La funzione risulta definita, positiva e continua x R.. Si ha f(x) = e x +x+ se x < x >, e x se
Esercizio 1. Sia f(x) = sin x, g(x) = log x. La funzione g(f 2 (x)) è. A log(sin 2 x); B log sin x ; C log(sin x 2 ); D sin log x 2.
1 Esercizio 1. Sia f(x) = sin x, g(x) = log x. La funzione g(f 2 (x)) è A log(sin 2 x); B log sin x ; C log(sin x 2 ); D sin log x 2. Esercizio 2. Sia f(x) = sin(log x ). Questa funzione è Esercizio 3.
2) Data la retta r : 3x 2y + 1 = 0 trovarne il punto P di intersezione con l asse y e determinare la retta che passa per P ortogonale a r.
Testo 1 ESONERO I 1) Calcolare le seguenti espressioni log 3 135 log 3 5 = log 5 1 125 + log 4 256 = 2) Data la retta r : 3x 2y + 1 = 0 trovarne il punto P di intersezione con l asse y e determinare la
Corso di Matematica per CTF Appello 15/12/2010
Appello 15/12/2010 Svolgere i seguenti esercizi: 1) Calcolare entrambi i limiti: a) lim(1 x) 1 e x 1 ; x 0 x log 2 x b) lim x 1 1 cos(x 1). 2) Data la funzione: f(x) = x log x determinarne dominio, eventuali
Attenzione: i programmi sono cambiati negli anni. Non tutti gli esercizi nella presente raccolta riguardano argomenti trattati.
Si raccolgono qui temi d esame, esercizi e domande di teoria dati negli anni 3-4 nei corsi di Analisi Matematica I presso il DTG di Vicenza. Il materiale è stato reso disponibile dai docenti che hanno
Definisci il Campo di Esistenza ( Dominio) di una funzione reale di variabile reale e, quindi, determinalo per la funzione:
Verso l'esame di Stato Definisci il Campo di Esistenza ( Dominio) di una funzione reale di variabile reale e, quindi, determinalo per la funzione: y ln 5 6 7 8 9 0 Rappresenta il campo di esistenza determinato
FUNZIONE ESPONENZIALE E FUNZIONE LOGARITMICA
FUNZIONE ESPONENZIALE E FUNZIONE LOGARITMICA DEFINIZIONE: Dato un numero reale a che sia a > 0 e a si definisce funzione esponenziale f(x) = a x la relazione che ad ogni valore di x associa uno e un solo
Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 2014
Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 14 Problema 1 Punto a) Osserviamo che g (x) = f(x) e pertanto g () = f() = in quanto Γ è tangente all asse delle ascisse,
Prova scritta di Analisi Matematica T-1, 18/12/2018. MATRICOLA:...NOME e COGNOME:...
Prova scritta di Analisi Matematica T-, 8/2/28 MATRICOLA:...NOME e COGNOME:............................................. Ingegneria chimica e biochimica Ingegneria elettronica e telecomunicazioni )3 punti)
SOLUZIONE DEL PROBLEMA 2 CORSO DI ORDINAMENTO 2013. 8 4 + x 2, con dominio R (infatti x2 + 4 0 per ogni. 8 4 + ( x) = 8. 4 + x 2
SOLUZIONE DEL PROBLEMA CORSO DI ORDINAMENTO. Studiamo la funzione f(x) = x R). Notiamo che f( x) = 4 + x, con dominio R (infatti x + 4 per ogni 4 + ( x) = 4 + x = f(x), cioè la funzione è pari e il grafico
Università di Roma Tor Vergata - Corso di Laurea in Ingegneria Analisi Matematica I - Prova scritta del 10 Luglio 2019
Università di Roma Tor Vergata - Corso di Laurea in Ingegneria nalisi Matematica I - Prova scritta del 0 Luglio 09 Esercizio. [5 punti] Calcolare lo sviluppo di Taylor dell ordine n = 5 con centro x 0
Analisi Matematica 1
Michele Campiti Prove scritte di Analisi Matematica 1 Ingegneria Industriale a.a. 2011 2012 y f 1 g 0 x La funzione seno e la funzione esponenziale Raccolta delle tracce di Analisi Matematica 1 per Ingegneria
1.2 Funzioni, dominio, codominio, invertibilità elementare, alcune identità trigonometriche
. Funzioni, dominio, codominio, invertibilità elementare, alcune identità trigonometriche Per le definizioni e teoremi si fa riferimento ad uno qualsiasi dei libri M.Bertsch - R.Dal Passo Lezioni di Analisi
COGNOME... NOME... Matricola... Prof. Camporesi
COGNOME... NOME... Matricola... Prof. Camporesi Esame di ANALISI MATEMATICA - 3 Febbraio 2010 A ESERCIZIO 1. (5 punti) 1. Verificare che z = 1 è una radice del polinomio P (z) = z 3 + ( 3 + 2i)z 2 + (2
Indice. 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo... 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità...
Indice 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo............................. 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità.............. 5 i Capitolo 1 Introduzione
Prova scritta di Analisi Matematica T-A, Ingegneria Energetica, 22/12/2014. MATRICOLA:...NOME e COGNOME:...
Prova scritta di Analisi Matematica T-A, Ingegneria Energetica, //4 )3 punti) Dato il seguente insieme A, stabilire se è aperto o chiuso. Inoltre studiare: l interno, il derivato, la frontiera, la chiusura,
SOLUZIONI COMPITO del 10/07/2009 ANALISI 1 - INFORMATICA 12 CFU + AUTOMATICA 5+5 CFU ANLISI 1 (I MODULO) - INFORMATICA + AUTOMATICA 5 CFU TEMA A
SOLUZIONI COMPITO del 0/07/009 ANALISI - INFORMATICA CFU + AUTOMATICA 5+5 CFU ANLISI I MODULO) - INFORMATICA + AUTOMATICA 5 CFU Esercizio Osserviamo che possiamo scrivere 0 = z 6 TEMA A + i ) z = [ z richieste
Integrali doppi - Esercizi svolti
Integrali doppi - Esercizi svolti Integrali doppi senza cambiamento di variabili Si disegni il dominio e quindi si calcolino gli integrali multipli seguenti:... xy dx dy, con (x, y R x, y x x }; x + y
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
1) D0MINIO. x x 4x + 3 Determinare il dominio della funzione f (x) = x Deve essere
) DMINIO + 3 Determinare il dominio della funzione f ) + 3 Deve essere Ovviamente, inoltre: se > + 3 ) 3) quindi < o 3 se < + 3, + 3 quindi 7 Determinare il dominio della funzione f ) + 5 Deve essere +
Corrispondenze e funzioni
Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
la funzione è definita la funzione non è definita Si osservi, infatti, che la radice di un numero negativo non esiste nel campo dei numeri reali.
1 y 4 CAMPO DI ESISTENZA. Poiché data è una irrazionale con indice di radice pari, il cui radicando è un polinomio, essa risulta definita solo per i valori della per i quali il radicando è positivo, ovvero
1. (4 punti) Calcolare i seguenti limiti: (a) lim. n arctan( n (log n)2 n. Assegnata la funzione f(x) = (3x + 1) e 1
Matematica, 2 CFU Corso di laurea in Scienze Biologiche- A.A. 2009-200 Laurea Triennale-Corsi A e C 9 Febbraio 200- COMPITO - Totale punti 40, punteggio minimo 24 Nome Cognome. (4 punti) Calcolare i seguenti
Esonero di Analisi Matematica (A)
Esonero di Analisi Matematica (A) Ingegneria Civile, 26 novembre 2001 () 1. Studiare il seguente limite: lim x x + ( e 1/x cos 1 ). x 2. Studiare gli eventuali massimi e minimi relativi ed assoluti della
Cambiamento di variabili negli integrali doppi: La trasformazione in coordinate polari. esiste (evidentemente) una sola coppia ( ρ, θ) R [ 0,2π[
Cambiamento di variabili negli integrali doppi: La trasformazione in coordinate polari Osservazione: Se ( x, ) \{(0,0)} esiste (evidentemente) una sola coppia ( ρ, θ) [ 0,[ tale che x. imane in tal modo
Alcuni esercizi sulle equazioni di erenziali
Alcuni esercizi sulle equazioni di erenziali Calcolo dell integrale generale Per ciascuna delle seguenti equazioni di erenziali calcolare l insieme di tutte le possibili soluzioni. SUGGERIMENTO: Ricordatevi
Laurea triennale in Informatica - Corso B (M-Z) Esame di Analisi Matematica Esercizi
7 giugno 207 Esame di Analisi Matematica f (x) = x 3 e x+ (d) si studi la convessità e la concavità di f e si determinino eventuali punti di (e) si tracci un grafico approssimativo di f ; (f) dal grafico
COGNOME e NOME: FIRMA: MATRICOLA:
Anno Accademico 04/ 05 Corsi di Analisi Matematica I Proff. A. Villani, R. Cirmi e F. Faraci) Prova d Esame del giorno 6 febbraio 05 Prima prova scritta compito A) Non sono consentiti formulari, appunti,
Determinare il dominio e la derivata delle seguenti funzioni e studiarne la monotonia ed eventuali massimi/minimi. ( ) x + 2.
Determinare il dominio e la derivata delle seguenti funzioni e studiarne la monotonia ed eventuali massimi/minimi (1) (2) (3) (4) f (x) = log ( ) x + 2 x 1 f (x) = x exp( x 3 ) ( f (x) = arctan x ) x 1
Numeri Complessi. 4. Ricordando che, se z è un numero complesso, zz è un numero reale, mettere sotto la forma. z 2 + 2z + 2 = 0. z 2 + 2z + 6 = 0.
Numeri Complessi. Siano z = + i e z 2 = i. Calcolare z + z 2, z z 2, z z 2 e z z 2. 2. Siano z = 2 5 + i 2 e z 2 = 5 2 2i. Calcolare z + z 2, z z 2, z z 2 e z z 2. 3. Ricordando che, se z è un numero complesso,
Esercizi Analisi 1. Foglio 1-19/09/2018. n(n + 1)(2n + 1) 6. (3k(k 1) + 1) = n 3. a n = 1 + a k
Esercizi Analisi Foglio - 9/09/208 Dimostrare che per ogni a, b e per ogni n N si ha: n a n b n = (a b) a n j b j j= Dimostrare che per ogni n N si ha: n j 2 = j= n(n + )(2n + ) 6 Dimostrare che per ogni
EQUAZIONI DIFFERENZIALI Esercizi con soluzione
EQUAZIONI DIFFERENZIALI Esercizi con soluzione. Calcolare l integrale generale delle seguenti equazioni differenziali lineari del primo ordine: (a) y 2y = (b) y + y = e x (c) y 2y = x 2 + x (d) 3y + y
Durata della prova: 3h. 2 +y 4. tan y sin y lim = 1. (x 4 +y 2 )y 3
Università degli Studi di Napoli Federico II Corso di Laurea in Matematica Analisi Matematica II (Gruppo ), A.A. 22/3 Prova scritta del 28 gennaio 23 Durata della prova: 3h. sercizio (8 punti). Si consideri
CORSO DI LAUREA IN INFORMATICA ANALISI MATEMATICA I MODULO, I E II MODULO, II MODULO. f(x) = (µx ± 2µ) e 1/x,
CORSO DI LAUREA IN INFORMATICA ANALISI MATEMATICA I MODULO, I E II MODULO, II MODULO I PROVA SCRITTA DI GIUGNO 2005: SOLUZIONI ESERCIZIO - Data la funzione f(x) = (µx ± 2µ) e 1/x, si chiede di: a) calcolare
SEGNO DELLA FUNZIONE. Anche in questo caso, per lo studio del segno della funzione, occorre risolvere la disequazione: y > 0 Ne segue:
CAMPO DI ESISTENZA. Poiché la funzione data è una razionale fratta, essa risulta definita su tutto l asse reale tranne che nei punti in cui il denominatore della frazione si annulla, cioè: C.E. { R: 0}
Università di Roma Tor Vergata Corso di Laurea in Ingegneria Canale SE-Z Prof.ssa Teresa D Aprile Analisi Matematica I Prova scritta del 19/07/2017
Università di Roma Tor Vergata Corso di Laurea in Ingegneria Canale SE-Z Profssa Teresa D Aprile Analisi Matematica I Prova scritta del 9/07/207 Cognome (in STAMPATELLO): Nome (in STAMPATELLO): Esercizio
FUNZIONI / ESERCIZI SVOLTI
ANALISI MATEMATICA I - A.A. 0/0 FUNZIONI / ESERCIZI SVOLTI ESERCIZIO. Data la funzione f () = determinare l insieme f (( +)). Svolgimento. Poiché f (( +)) = { dom f : f () ( +)} = { dom f : f () > } si
Esercizi svolti su serie di Fourier
Esercizi svolti su serie di Fourier Esercizio. (Onda quadra. Determinare i coefficienti di Fourier della funzione x [, f(x = x [, prolungata a una funzione -periodica su R (d ora in poi denoteremo con
Serie numeriche e serie di potenze
Serie numeriche e serie di potenze Sommare un numero finito di numeri reali è senza dubbio un operazione che non può riservare molte sorprese Cosa succede però se ne sommiamo un numero infinito? Prima
DOMINIO E LIMITI. Esercizio 3 Studiare gli insiemi di livello della funzione f, nei seguenti casi: 1) f(x,y) = y2 x 2 + y 2.
FUNZIONI DI DUE VARIABILI 1 DOMINIO E LIMITI Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia (insiemi aperti, chiusi, limitati, convessi, connessi per archi; punti di
Alcune note sulle serie di potenze 1
Alcune note sulle serie di potenze Contents G. Falqui Preliminari 2 Serie di potenze 3 3 Rappresentazione di funzioni mediante serie di potenze 7 3. Esempi notevoli........................... 9 3.2 Formula
Equazioni differenziali del II ordine. y 5y + 6y = 0 y(0) = 0 y (0) = 1
Equazioni differenziali del II ordine 1. Risolvere il seguente problema di Cauchy: y 5y + 6y = 0 y (0) = 1. Determinare l integrale generale della seguente equazione differenziale: y 5y + 6y = f(x), con
CRITERI DI CONVERGENZA PER LE SERIE. lim a n = 0. (1) s n+1 = s n + a n+1. (2) CRITERI PER LE SERIE A TERMINI NON NEGATIVI
Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 2004
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 004 Il candidato risolva uno dei due problemi e 5 dei 10 quesiti in cui si articola il questionario. PROBLEMA 1 Sia f la funzione definita da: f
ANALISI MATEMATICA 1-22/01/2018 Corso di Laurea in Ingegneria Meccanica. Primo Appello - Test A
Primo Appello - Test A. Il dominio della funzione f(x) = ln(x 3) è a) ]3,+ [ b) [3,+ [ c) ]3,4[ ]4,+ [ d) [4,+ [ e) Nessuna delle precedenti. 2. L integrale π 2 a) 0 b) e 2 0 e cosx ( senx)dx vale 3. L
I tre concetti si possono descrivere in modo unitario dicendo che f e iniettiva, suriettiva, biiettiva se e solo se per ogni b B l equazione
Lezioni del 29 settembre e 1 ottobre. 1. Funzioni iniettive, suriettive, biiettive. Sia f : A B una funzione da un insieme A ad un insieme B. Sia a A e sia b = f (a) B l elemento che f associa ad a, allora
Esercizi di Analisi Matematica I
Esercizi di Analisi Matematica I Andrea Corli e Alessia Ascanelli gennaio 9 Indice Introduzione iii Nozioni preliminari. Fattoriali e binomiali..................................... Progressioni..........................................
Analisi Matematica I DISEQUAZIONI Risposte Pagina Es. 1 Es. 2 Es. 3 Es. 4 Es. 5 1
Analisi Matematica I DISEQUAZIONI Risposte Pagina Es. Es. Es. 3 Es. 4 Es. 5 AVVERTENZA: Scrivere le risposte scelte nello spazio in alto a destra. In ogni esercizio una sola risposta è corretta. Esercizio.
SOLUZIONI COMPITO A. 3. Imponendo la condizione iniziale y(0) = 1 e, si ricava C = 0, quindi la soluzione cercata sarà. y(x) + 1 = exp(e x x2 2 1)
SOLUZIONI COMPITO A Esercizio Utilizzando lo sviluppo di Mc Laurin al terzo ordine per il sin t, con t = x 4/, e quello al primo ordine per il log( + t), con t = x, otteniamo e quindi il ite proposto diviene
Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in
Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in Solitamente si fa riferimento ad intorni simmetrici =, + + Definizione: dato
Esponenziali e logaritmi
Esponenziali e logaritmi Corso di accompagnamento in matematica Lezione 4 Sommario 1 La funzione esponenziale Proprietà Grafico 2 La funzione logaritmo Grafico Proprietà 3 Equazioni / disequazioni esponenziali
FUNZIONI REALI DI VARIABILE REALE e CONTINUITA Roberto Argiolas
FUNZIONI REALI DI VARIABILE REALE e CONTINUITA Roberto Argiolas.8.6.. - -.5.5 -. In questa dispensa ricordiamo la classificazione delle funzioni elementari e il dominio di esistenza delle stesse. Inoltre
+ P a n n=1 + X. a n = a m 3. n=1. m=4. Per poter dare un significato alla somma (formale) di infiniti termini, ricorriamo al seguente procedimento:
Capitolo 3 Serie 3. Definizione Sia { } una successione di numeri reali. Ci proponiamo di dare significato, quando possibile, alla somma a + a 2 +... + +... di tutti i termini della successione. Questa
Anno 5 4 Funzioni reali. elementari
Anno 5 4 Funzioni reali elementari 1 Introduzione In questa lezione studieremo alcune funzioni molto comuni, dette per questo funzioni elementari. Al termine di questa lezione sarai in grado di definire
Esonero di Analisi Matematica I (A)
Esonero di Analisi Matematica I A) Ingegneria Edile, 7 novembre 00 Michele Campiti) 1. Studiare il seguente ite: x π/ cos x 1 sin x) tan 3 x π ).. Calcolare le seguenti radici quarte: 3i 4 1 + i). Esonero
Alcune applicazioni delle equazioni differenziali ordinarie alla teoria dei circuiti elettrici
Alcune applicazioni delle equazioni differenziali ordinarie alla teoria dei circuiti elettrici Attilio Piana, Andrea Ziggioto 1 egime variabile in un circuito elettrico. Circuito C. 1.1 Carica del condensatore
SOLUZIONI COMPITO A. Esercizio 1 Utilizzando la formula risolutiva per l equazioni di secondo grado, valida anche in campo complesso, otteniamo:
SOLUZIONI COMPITO A Esercizio 1 Utilizzando la formula risolutiva per l equazioni di secondo grado, valida anche in campo complesso, otteniamo: z = i + i + i 3 In forma algebrica, otteniamo: = i + 1 +
Funzione logaritmo con. funzione inversa della funzione di
FUNZIONE LOGARITMO a è la base della funzione logaritmo ed è una costante positiva fissata e diversa da 1 x è l argomento della funzione logaritmo e varia nel dominio Funzione logaritmo con funzione inversa
2 Argomenti introduttivi e generali
1 Note Oltre agli esercizi di questa lista si consiglia di svolgere quelli segnalati o assegnati sul registro e genericamente quelli presentati dal libro come esercizio o come esempio sugli argomenti svolti
I appello - 26 Gennaio 2007
Facoltà di Ingegneria - Corso di Laurea in Ing. Informatica e delle Telecom. A.A.006/007 I appello - 6 Gennaio 007 Risolvere gli esercizi motivando tutte le risposte. (N.B. il quesito teorico è obbligatorio)
Matematica 1 - Corso di Laurea in Ingegneria Meccanica
Matematica 1 - Corso di Laurea in Ingegneria Meccanica Esercitazione su massimi e minimi vincolati 9 dicembre 005 Esercizio 1. Considerare l insieme C = {(x,y) R : (x + y ) = x } e dire se è una curva
Analisi Matematica 1 - a.a. 2017/ Primo appello
Analisi Matematica - a.a. 7/8 - Primo appello Soluzione del test Test A 3 4 5 6 7 8 9 C E E C D E A B B D Test B 3 4 5 6 7 8 9 A A B E B B C D E A Test C 3 4 5 6 7 8 9 B D C A E D E C D C Test D 3 4 5
x ( 3) + Inoltre (essendo il grado del numeratore maggiore del grado del denominatore, d ancora dallo studio del segno),
6 - Grafici di funzioni Soluzioni Esercizio. Studiare il grafico della funzione f(x) = x x + 3. ) La funzione è definita per x 3. ) La funzione non è né pari, né dispari, né periodica. 3) La funzione è
SUCCESSIONI NUMERICHE
SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
Formule trigonometriche
Formule trigonometriche C. Enrico F. Bonaldi 1 Formule trigonometriche In trigonometria esistono delle formule fondamentali che permettono di calcolare le funzioni goniometriche della somma di due angoli
Applicazioni del calcolo differenziale allo studio delle funzioni
Capitolo 9 9.1 Crescenza e decrescenza in piccolo; massimi e minimi relativi Sia y = f(x) una funzione definita nell intervallo A; su di essa non facciamo, per ora, alcuna particolare ipotesi (né di continuità,
Es. 1 Es. 2 Es. 3 Es. 4 Totale Teoria
Es. Es. Es. 3 Es. 4 Totale Teoria Analisi e Geometria Docente: Politecnico di Milano Ingegneria Industriale 5 Settembre Compito A Cognome: Nome: Matricola: Punteggi degli esercizi: Es.: 6 punti; Es.: punti;
Consideriamo due polinomi
Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
MATEMATICA GENERALE Prova d esame del 18 giugno 2013 - FILA A
MATEMATICA GENERALE Prova d esame del 8 giugno 23 - FILA A Nome e cognome Matricola I Parte. QUESITI PRELIMINARI. Riportare le soluzioni su questo foglio, mostrando i vari passaggi e calcoli.. Si scriva
Analisi Matematica 1
Michele Campiti Prove scritte di Analisi Matematica 1 Ingegneria Industriale a.a. 2007 2008 y f 1 g 0 x La funzione seno e la funzione esponenziale Raccolta delle tracce di Analisi Matematica 1 per Ingegneria
POLITECNICO di BARI - A.A. 2012/2013 Corso di Laurea in INGEGNERIA Informatica e dell Automazione
POLITECNICO di BARI - A.A. 0/03 Corso di Laurea in INGEGNERIA Informatica e dell Automazione Problema Sia f :[0, +[! R una funzione continua. La funzione composta g() =f(kk) è c o n t i n u a? Problema
Analisi I - IngBM - 2014-15 COMPITO A 21 Febbraio 2015 COGNOME... NOME... MATRICOLA... VALUTAZIONE... +... =...
Analisi I - IngBM - 2014-15 COMPITO A 21 Febbraio 2015 COGNOME........................ NOME............................. MATRICOLA....................... VALUTAZIONE..... +..... =...... 1. Istruzioni Gli