Alberi binari ( 7.3)
|
|
|
- Mariana Guidi
- 8 anni fa
- Просмотров:
Транскрипт
1 Alberi binari ( 7.3) + a 3 b Albero Binario ( 7.3) DEFINIZIONE Albero Binario è un albero ordinato in cui ogni nodo ha al più due figli. Un albero binario si dice proprio se ogni nodo ha o zero o figli DEFINIZIONE RICORSIVA Albero Binario (proprio) : o è l'insieme vuoto o è un elemento (nodo radice) con un sottoalbero sinistro e un sottoalbero destro r Sin Des
2 Albero Binario rappresentazione nodo radice 44 7 nodi interni nodi esterni Arithmetic Expression Tree Albero binario che rappresenta una espressione aritmetica nodi interni operatori nodi esterni operandi Esempio: albero binario per l espressione : ( (a - ) + (3 b)) + a 3 b 4
3 Decision Tree Albero binario associato ad un processo decisionale nodi interni: domande con risposta si/no nodi esterni: decisioni Esempio: decidere come fare il pranzo Want a fast meal? Yes How about coffee? No On expense account? Yes No Yes No Starbucks Spike s Al Forno Café Paragon 5 BinaryTree ADT ( 7.3.) L ADT BinaryTree ADT estende l ADT Tree, i.e., eredita tutti i metodi dell ADT Tree, più ne aggiunge di nuovi: Metodi addizionali : position left (p) position right (p) boolean hasleft (p) boolean hasright (p) Ulteriori metodi di modifica (update) possono essere definiti dalle strutture dati che implementano il BinaryTree ADT 6 3
4 BinaryTree Interface ( 7.3.) public interface BinaryTree<E> extends Tree<E> { public Position<E> left (Position<E> v) throws InvalidPositionException, BoundaryViolationException; public Position<E> right (Position<E> v) throws InvalidPositionException, BoundaryViolationException; public boolean hasleft (Position<E> v) throws InvalidPositionException; public boolean hasright (Position<E> v) throws InvalidPositionException; 7 Albero Binario proprietà ( 7.3.3) Teorema: Un albero binario completo con n nodi ha altezza h = log n, infatti : limite inferiore: poichè vi sono i nodi alla profondità i = 0,, h - e almeno un nodo alla profondità h, risulta : n h- + = ( - h ) / (-) = h così, n h, i.e., h log n depth 0 h h keys h 8 4
5 Albero Binario proprietà ( 7.3.3) Limite superiore: poichè vi sono al più h nodi alla profondità h, risulta: n h- + h = h+ - così, n+ h+, i.e., log (n+)- h log (n+)- h log n h = log n depth 0 h h keys h 9 Albero Binario proprietà ( 7.3.3) Notazione n numero nodi n E numero nodi esterni n I numero nodi interni h altezza Proprietà n E = n I + n = n E h n I h (n )/ n E h h log n E h log (n + ) 0 5
6 Albero Binario proprietà ( 7.3.3) Teorema: in albero binario proprio risulta : n E = n I + removeaboveexternal A A B D D c c A A A c D D Albero Binario Algoritmi di attraversamento ( 7.3.6)
7 Albero Binario inorder ( 7.3.6) Algorithm inorder( T, v ) if hasleft (T, v) inorder (left (T, v)) visit(t, v) if hasright (T, v) inorder (right (T, v)) Albero Binario postorder ( 7.3.6) Esempio di postorder: valutazione di una espressione il metodo ricorsivo ritorna il valore di un sotto_albero quando visita un nodo interno applica l operatore ai valori ottenuti visitando i sottoalberi sinistro e destro Algorithm evalexpr(t,v) + if isexternal (T,v) return v.element () else 5 3 x evalexpr(leftchild (T,v)) y evalexpr(rightchild (T,v)) operator stored at v return x y 4 7
8 Albero Binario Attraversamento Successore nell inordine di un dato nodo: il primo nodo dell albero visitato è il nodo g successore di b è h (il nodo più a sinistra nel sottoalbero destro) il successore di i è a (il padre del primo figlio sinistro risalendo) a b c d e f g h i l m 5 Albero Binario Inorder Iterator () Il primo nell inordine : il più a sinistra nel sottoalbero sinistro della radice x () () (3) Schema dell attraversamento : S D se sotto-albero destro non è vuoto, il successivo è il primo nel sotto-albero destro altrimenti, il successivo è il padre del primo figlio sinistro che si incontra risalendo di figlio in padre 6 8
9 Interfaccia Iterator<E> public interface Iterator<E> { boolean hasnext() // Returns true if the iteration has more elements Enext() // Returns the next element in the interation void remove() // Removes from the underlying collection the last element // returned by the iterator (optional operation) 7 Albero Binario Inorder Iterator () public class InorderPositionsIterator<E> implements Iterator<E> { posizione corrente private Position<E> cur; private BinaryTree<E> T; private Position<E> inorderfirst( Position<E> p ) { while ( T.hasLeft(p) ) p = T.left(p); return p; il costruttore il primo nell inordine nel sottoalbero p InorderPositionsIterator( BinaryTree<E> T ) { this.t = T; cur = inorderfirst(t.root()); l albero su cui iterare attuale posizione corrente 8 9
10 Albero Binario Inorder Iterator (3) public boolean hasnext() { return cur!= null; prima ritorna la posizione public E next() { corrente e poi la aggiorna if ( cur == null ) throw new NoSuchElementException(); Position<E> pos = cur; if ( T.isInternal(cur) ) cur = inorderfirst(t.right(cur)); else { while (! T.isRoot(cur) && cur == T.right(T.parent(cur)) ) cur = T.parent(cur); if ( cur == T.root() ) cur = null; else cur = T.parent(cur); return pos; risale sino al primo figlio sinistro risale di figlio in padre il successore è il padre del primo figlio sinistro 9 Albero Binario Inorder Iterator (4) public void remove() throws UnsupportedOperationException { throw new UnsupportedOperationException("remove"); //fine InorderIterator 0 0
11 Utilizzo di Inorder Iterator LinkedBinaryTree<Integer> T = new LinkedBinaryTree<Integer>(); // Un albero binario T // // Un iteratore sull albero binario T Iterator<Position<Integer>> itp; itp = new InorderPositionsIterator<Integer>(T); while ( itp.hasnext() ) { Position<Integer> x = itp.next(); if ( T.isInternal(x) ) System.out.println("--> " + x.element() ); Albero Binario Tour di Eulero ( 7.3.6) 44 Eulero tour sin 7 des 78 sot sin preordine sot inordine des postordine 48 6
12 Tour di Eulero pseudocodice Algorithm eulertour( T, v) //Albero binario action for visiting node v on left if T.hasLeft( T, v ) then eulertour( T, T.left(T, v ) ) action for visiting node v from below if T.hasRight(v) then eulertour( T, T.right(T, v ) ) action for visiting node v on right 3 Albero Binario EuleroTour ( 7.3.6) Algorithm printexpression(t, v) //Albero binario proprio if T.isExternal (v) print( v.element () ) else print( ( ) //PRE printexpression( T, T.left(v) ) print( v.element () ) //OPERATOR printexpression( T, T.right(v) ) print ( ) ) //POST + (( (a )) + (3 b)) 3 b a 4
13 Template Method Pattern ( 7.3.7) Algoritmo generico che può essere specializzato con la ridefinizione (overloading) di alcuni metodi Realizzato mediante una classe astratta Java I metodi di visita possono essere ridefiniti da sottoclassi Il Template method eulertour<e,r> viene ricorsivamente invocato sul figlio sinistro e sul figlio destro un oggetto TourResult con i campi left, right e out tiene traccia dell output delle chiamate ricorsive al metodo EulerTour 5 Template Method Pattern ( 7.3.7) public abstract class EulerTour <E,R> { protected BinaryTree<E> tree; Classe astratta metodo astratto public abstract R execute( BinaryTree<E> T ); protected void init( BinaryTree<E> T ) { tree = T; // metodo concreto 6 3
14 Template Method Pattern ( 7.3.7) protected R eulertour ( Position<E> v ) { TourResult<R> r = new TourResult<R>(); visitleft(v, r ); if ( tree.hasleft(v) ) r.left = eulertour(tree.left(v) ); visitbelow(v,r); if ( tree.hasright(v) ) r.right = eulertour(tree.right(v) ); visitright(v,r); return r.out; Metodo concreto, il motore dell algoritmo, realizzato ricorsivamente 7 Template Method Pattern ( 7.3.7) protected void visitleft ( Position<E> v, TourResult<R> r ) { ; protected void visitright ( Position<E> v, TourResult<R> r ) { ; protected void visitbelow ( Position<E> v, TourResult<R> r ) { ; //class EulerTourTamassia Metodi che debbono essere ridefiniti dalla classe che specializza la classe astratta 8 4
15 Template Method Pattern public class PrintExpressionTour<E,R> extends EulerTour<E,R> { public R execute( BinaryTree<E> T ) { Specializzazione della classe init(t); astratta per la costruzione di System.out.println("Expression: "); eulertour(t.root()); un espressione parentizzata System.out.println(); return null; dell albero protected void visitleft ( Position<E> v ) { if (tree.isinternal(v) ) System.out.print( " ( ); protected void visitright ( Position<E> v ) { if (tree.isinternal(v) ) System.out.print( ") ); protected void visitbelow ( Position<E> v ) { if ( v.element()!= null ) System.out.print(v.element()); //class 9 Template Method Pattern public static void main( String argv[] ) throws Exception { BinaryTree T; // PrintExpressionTour pe = new PrintExpressionTour(); pe.execute(t); //main 30 5
16 Albero Binario Strutture dati per l implementazione di albero binario e ennario 3 Linked Structure for Binary Trees ( 7.3.4) Un nodo è rappresentato da un oggetto contenente : il rif. all Elemento il rif. al nodo Padre il rif. al nodo figlio Sin il rif. al nodo figlio Des B B A D A D C E C E L oggetto Nodo implementa l ADT Position 3 6
17 Array Rappresentation of Binary Trees ( 7.3.5) Parent(i) i/ a Left(i) *i Right(i) *i+ b 3 c 4 d 5 e 6 f 7 g a b c d e f g 33 Rappresentazione albero ennario Un nodo è rappresentato da un oggetto contenente : il rif. all Elemento il rif. al nodo Padre B il rif. alla Sequenza dei nodi figli A D F B A D F C E C E 34 7
18 Rappresentazione albero binario 35 Rappresentazione di un albero (foresta) con un albero binario A A TRASFORMAZIONE B B C D E C E F G F D Il primo figlio diviene il figlio sinistro Il primo fratello destro diviene figlio destro G 36 8
Attraversamento di un albero (binario)
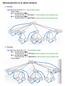 Attraversamento di un albero (binario) 1) Preordine Algorithm binarypreorder( T, v) //caso di albero binario Visita il nodo v; binarypreorder( T, T.leftChild(v)); //Attraversamento ricorsivo sottoalbero
Attraversamento di un albero (binario) 1) Preordine Algorithm binarypreorder( T, v) //caso di albero binario Visita il nodo v; binarypreorder( T, T.leftChild(v)); //Attraversamento ricorsivo sottoalbero
Implementazione ADT: Alberi
 Implementazione ADT: Alberi Livelli di astrazione 2001/2002 1 Esercitazione 5 (E6): alberi (tree) albero struttura dati fondamentale, soprattutto per le operazioni di ricerca tipi di albero con radice
Implementazione ADT: Alberi Livelli di astrazione 2001/2002 1 Esercitazione 5 (E6): alberi (tree) albero struttura dati fondamentale, soprattutto per le operazioni di ricerca tipi di albero con radice
Alberi. Strutture dati: Alberi. Alberi: Alcuni concetti. Alberi: definizione ricorsiva. Alberi: Una prima realizzazione. Alberi: prima Realizzazione
 Alberi Strutture dati: Alberi Strutture gerarchiche di dati Esempi Il file system di un sistema operativo L organigramma di un azienda Alberi generali, alberi n-ari, alberi binari, Ogni nodo ha un unico
Alberi Strutture dati: Alberi Strutture gerarchiche di dati Esempi Il file system di un sistema operativo L organigramma di un azienda Alberi generali, alberi n-ari, alberi binari, Ogni nodo ha un unico
Alberi binari e alberi binari di ricerca
 Alberi binari e alberi binari di ricerca Violetta Lonati Università degli studi di Milano Dipartimento di Scienze dell Informazione Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica
Alberi binari e alberi binari di ricerca Violetta Lonati Università degli studi di Milano Dipartimento di Scienze dell Informazione Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica
Laboratorio 9 ( Java 4 ) Classe astratta per BFS su grafo
 Laboratorio 9 ( Java ) Classe astratta per BFS su grafo Testo esercitazione Scaricare il file EseBFS.zip, scompattarlo ed analizzare le classi in esso contenute con particolare attenzione alla classe astratta
Laboratorio 9 ( Java ) Classe astratta per BFS su grafo Testo esercitazione Scaricare il file EseBFS.zip, scompattarlo ed analizzare le classi in esso contenute con particolare attenzione alla classe astratta
Algoritmi e Strutture Dati
 Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 2006/07 Il concetto di dato Il concetto di tipo di dato Insertion Sort for j 2 to lenght[a]
Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 2006/07 Il concetto di dato Il concetto di tipo di dato Insertion Sort for j 2 to lenght[a]
Alberi ed Alberi Binari
 Alberi ed Alberi Binari Il tipo di dato Albero Un albero è una struttura di data organizzata gerarchicamente. È costituito da un insieme di nodi collegati tra di loro: ogni nodo contiene dell informazione,
Alberi ed Alberi Binari Il tipo di dato Albero Un albero è una struttura di data organizzata gerarchicamente. È costituito da un insieme di nodi collegati tra di loro: ogni nodo contiene dell informazione,
Alberi. Alberi: definizioni. Alberi Binari. Esercizi su alberi binari: metodi ricorsivi. Struttura dati per alberi generici. ASD-L - Luca Tesei
 Alberi Alberi: definizioni Alberi Binari Esercizi su alberi binari: metodi ricorsivi Struttura dati per alberi generici 1 Alberi Gli alberi sono strutture dati naturalmente ricorsive Un albero è un particolare
Alberi Alberi: definizioni Alberi Binari Esercizi su alberi binari: metodi ricorsivi Struttura dati per alberi generici 1 Alberi Gli alberi sono strutture dati naturalmente ricorsive Un albero è un particolare
Dati e Algoritmi I (Pietracaprina) Esercizi su Alberi Binari di Ricerca e (2,4)-Tree
 Dati e Algoritmi I (Pietracaprina) Esercizi su Alberi Binari di Ricerca e (2,4)-Tree Dati e Algoritmi I (Pietracaprina): Esercizi 1 Problema 1 Si definisca Interval Tree un albero binario di ricerca le
Dati e Algoritmi I (Pietracaprina) Esercizi su Alberi Binari di Ricerca e (2,4)-Tree Dati e Algoritmi I (Pietracaprina): Esercizi 1 Problema 1 Si definisca Interval Tree un albero binario di ricerca le
Alberi Binario in Java
 Alberi Binario in Java Realizzare un albero binario di ricerca. L albero binario è di ricerca se esiste una relazione di ordinamento tra i valori dei nodi (valori comparabili). In particolare, dato un
Alberi Binario in Java Realizzare un albero binario di ricerca. L albero binario è di ricerca se esiste una relazione di ordinamento tra i valori dei nodi (valori comparabili). In particolare, dato un
Binary Search Trees (BST) Algoritmi sui BST. Algoritmi - Ricerca. Fondamenti di Informatica T2 Modulo 2. Università di Bologna A.A.
 Università degli Studi di Bologna Facoltà di Ingegneria Fondamenti di Informatica T Modulo Corso di Laurea in Ingegneria Informatica Anno accademico 00/009 Binary Search Trees (BST) Also Known As Alberi
Università degli Studi di Bologna Facoltà di Ingegneria Fondamenti di Informatica T Modulo Corso di Laurea in Ingegneria Informatica Anno accademico 00/009 Binary Search Trees (BST) Also Known As Alberi
Problemi di ordinamento
 Problemi di ordinamento Input: una sequenza di n numeri a 1, a 2,..., a n ; Output: una permutazione a 1, a 2,..., a n di a 1, a 2,..., a n tale che a 1 a 2... a n. Generalmente, la sequenza è rappresentata
Problemi di ordinamento Input: una sequenza di n numeri a 1, a 2,..., a n ; Output: una permutazione a 1, a 2,..., a n di a 1, a 2,..., a n tale che a 1 a 2... a n. Generalmente, la sequenza è rappresentata
Esercitazione 6. Alberi binari di ricerca
 Esercitazione 6 Alberi binari di ricerca Struttura base Rappresentabile attraverso una struttura dati concatenata in cui ogni nodo è un oggetto di tipo struttura Ogni nodo contiene: campo chiave (key)
Esercitazione 6 Alberi binari di ricerca Struttura base Rappresentabile attraverso una struttura dati concatenata in cui ogni nodo è un oggetto di tipo struttura Ogni nodo contiene: campo chiave (key)
Espressioni aritmetiche
 Espressioni aritmetiche Consideriamo espressioni costruite a partire da variabili e costanti intere mediante applicazione delle operazioni di somma, sottrazione, prodotto e divisione (intera). Ad esempio:
Espressioni aritmetiche Consideriamo espressioni costruite a partire da variabili e costanti intere mediante applicazione delle operazioni di somma, sottrazione, prodotto e divisione (intera). Ad esempio:
Lezione 7 Alberi binari: visite e alberi di ricerca
 Lezione 7 Alberi binari: visite e alberi di ricerca Informatica 6 Maggio 2015 Operazioni sugli alberi: visita La visita di un albero esplora tutti i nodi ed esegue una qualche operazione su di essi. Per
Lezione 7 Alberi binari: visite e alberi di ricerca Informatica 6 Maggio 2015 Operazioni sugli alberi: visita La visita di un albero esplora tutti i nodi ed esegue una qualche operazione su di essi. Per
Alberi e alberi binari I Un albero è un caso particolare di grafo
 Alberi e alberi binari Un albero è un caso particolare di grafo È costituito da un insieme di nodi collegati tra di loro mediante archi Gli archi sono orientati (ogni arco esce da un nodo origine ed entra
Alberi e alberi binari Un albero è un caso particolare di grafo È costituito da un insieme di nodi collegati tra di loro mediante archi Gli archi sono orientati (ogni arco esce da un nodo origine ed entra
Esempi in Java di program.ne O-O
 Esempi in Java di program.ne O-O Ereditarietà Polimorfismo statico e dinamico Esercitazione laboratorio Interfaccia Comparable e Comparator 1 Gerarchia di ereditarietà Persona IS_A Docente Studente Tecnico
Esempi in Java di program.ne O-O Ereditarietà Polimorfismo statico e dinamico Esercitazione laboratorio Interfaccia Comparable e Comparator 1 Gerarchia di ereditarietà Persona IS_A Docente Studente Tecnico
Alberi. Gli alberi sono una generalizzazione delle liste che consente di modellare delle strutture gerarchiche come questa: Largo. Fosco.
 Alberi Alberi Gli alberi sono una generalizzazione delle liste che consente di modellare delle strutture gerarchiche come questa: Largo Fosco Dora Drogo Frodo Dudo Daisy Alberi Gli alberi sono una generalizzazione
Alberi Alberi Gli alberi sono una generalizzazione delle liste che consente di modellare delle strutture gerarchiche come questa: Largo Fosco Dora Drogo Frodo Dudo Daisy Alberi Gli alberi sono una generalizzazione
Per semplicità eliminiamo le ripetizioni nell'albero.
 Albero binario di ricerca 20 40 100 95 Un albero binario di ricerca é un albero binario in cui ogni nodo ha un etichetta minore o uguale a quelle dei nodi nel sottoalbero radicato nel figlio destro e maggiore
Albero binario di ricerca 20 40 100 95 Un albero binario di ricerca é un albero binario in cui ogni nodo ha un etichetta minore o uguale a quelle dei nodi nel sottoalbero radicato nel figlio destro e maggiore
Alberi n-ari: specifiche sintattiche e semantiche. Realizzazioni. Visita di alberi n-ari.
 Alberi n-ari: specifiche sintattiche e semantiche. Realizzazioni. Visita di alberi n-ari. Algoritmi e Strutture Dati + Lab A.A. / Informatica Università degli Studi di Bari Aldo Moro Nicola Di Mauro ALBERO
Alberi n-ari: specifiche sintattiche e semantiche. Realizzazioni. Visita di alberi n-ari. Algoritmi e Strutture Dati + Lab A.A. / Informatica Università degli Studi di Bari Aldo Moro Nicola Di Mauro ALBERO
Algoritmi e Strutture Dati. HeapSort
 Algoritmi e Strutture Dati HeapSort Selection Sort: intuizioni L algoritmo Selection-Sort scandisce tutti gli elementi dell array a partire dall ultimo elemento fino all inizio e ad ogni iterazione: Viene
Algoritmi e Strutture Dati HeapSort Selection Sort: intuizioni L algoritmo Selection-Sort scandisce tutti gli elementi dell array a partire dall ultimo elemento fino all inizio e ad ogni iterazione: Viene
lezione 9 min-heap binario Heap e Alberi posizionali generali
 lezione 9 Heap e Alberi posizionali generali min-heap binario Un min-heap è un albero binario quasi completo in cui ogni nodo i diverso dalla radice soddisfa la seguente proprietà: il valore memorizzato
lezione 9 Heap e Alberi posizionali generali min-heap binario Un min-heap è un albero binario quasi completo in cui ogni nodo i diverso dalla radice soddisfa la seguente proprietà: il valore memorizzato
Algoritmi e Strutture Dati. Alberi
 Algoritmi e Strutture Dati Alberi Alberto Montresor Università di Trento 2017/10/19 This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License. Sommario 1 Introduzione
Algoritmi e Strutture Dati Alberi Alberto Montresor Università di Trento 2017/10/19 This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License. Sommario 1 Introduzione
Alberi Binari di Ricerca
 Alberi Binari di Ricerca Algoritmi su gli alberi binari: visite Dato un puntatore alla radice di un albero vogliamo scandire in modo sistematico tutti i nodi di tale albero In una lista abbiamo una unica
Alberi Binari di Ricerca Algoritmi su gli alberi binari: visite Dato un puntatore alla radice di un albero vogliamo scandire in modo sistematico tutti i nodi di tale albero In una lista abbiamo una unica
Alberto Montresor Università di Trento
 !! Algoritmi e Strutture Dati! Capitolo 5 - Alberi!!! Alberto Montresor Università di Trento!! This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike License. To view a copy
!! Algoritmi e Strutture Dati! Capitolo 5 - Alberi!!! Alberto Montresor Università di Trento!! This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike License. To view a copy
Note per la Lezione 4 Ugo Vaccaro
 Progettazione di Algoritmi Anno Accademico 2016 2017 Note per la Lezione 4 Ugo Vaccaro Ripasso di nozioni su Alberi Ricordiamo che gli alberi rappresentano una generalizzazione delle liste, nel senso che
Progettazione di Algoritmi Anno Accademico 2016 2017 Note per la Lezione 4 Ugo Vaccaro Ripasso di nozioni su Alberi Ricordiamo che gli alberi rappresentano una generalizzazione delle liste, nel senso che
ADT Coda con priorità
 Code con priorità ADT Coda con priorità Una coda con priorità è una struttura dati dinamica che permette di gestire una collezione di dati con chiave numerica. Una coda con priorità offre le operazioni
Code con priorità ADT Coda con priorità Una coda con priorità è una struttura dati dinamica che permette di gestire una collezione di dati con chiave numerica. Una coda con priorità offre le operazioni
LE STRUTTURE DATI DINAMICHE: GLI ALBERI. Cosimo Laneve
 LE STRUTTURE DATI DINAMICHE: GLI ALBERI Cosimo Laneve 1 argomenti 1. definizione di alberi e nozioni relative 2. implementazione degli alberi, creazione, visita 3. algoritmo di visita iterativa e sua implementazione
LE STRUTTURE DATI DINAMICHE: GLI ALBERI Cosimo Laneve 1 argomenti 1. definizione di alberi e nozioni relative 2. implementazione degli alberi, creazione, visita 3. algoritmo di visita iterativa e sua implementazione
Algoritmi e Strutture Dati & Laboratorio di Algoritmi e Programmazione
 Algoritmi e Strutture Dati & Laboratorio di Algoritmi e Programmazione Appello dell 8 Febbraio 2005 Esercizio 1 (ASD) 1. Dire quale delle seguenti affermazioni è vera giustificando la risposta. (a) lg
Algoritmi e Strutture Dati & Laboratorio di Algoritmi e Programmazione Appello dell 8 Febbraio 2005 Esercizio 1 (ASD) 1. Dire quale delle seguenti affermazioni è vera giustificando la risposta. (a) lg
Dati e Algoritmi I (Pietracaprina) Esercizi sugli Alberi
 Dati e Algoritmi I (Pietracaprina) Esercizi sugli Alberi Dati e Algoritmi I (Pietracaprina): Esercizi 1 Problema 1 Dimostrare che un albero non vuoto con n nodi interni, dove ogni nodo interno ha almeno
Dati e Algoritmi I (Pietracaprina) Esercizi sugli Alberi Dati e Algoritmi I (Pietracaprina): Esercizi 1 Problema 1 Dimostrare che un albero non vuoto con n nodi interni, dove ogni nodo interno ha almeno
Esercizio 1. E vero che in un AVL il minimo si trova in una foglia o nel penultimo livello? FB = -1. livello 0 FB = -1. livello 1 FB = -1.
 Esercizio 1 E vero che in un AVL il minimo si trova in una foglia o nel penultimo livello? FB = -1 livello 0 FB = -1 FB = -1 livello 1 FB = -1 livello 2 livello 3 L altezza è 3, il minimo si trova nel
Esercizio 1 E vero che in un AVL il minimo si trova in una foglia o nel penultimo livello? FB = -1 livello 0 FB = -1 FB = -1 livello 1 FB = -1 livello 2 livello 3 L altezza è 3, il minimo si trova nel
Dati e Algoritmi 1: A. Pietracaprina. Mappa/Dizionario (I parte)
 Dati e Algoritmi 1: A. Pietracaprina Mappa/Dizionario (I parte) 1 Mappa/Dizionario Definizione generale Collezione di entry che supporta, come metodi principali: ricerca, inserimento, rimozione Vari ADT:
Dati e Algoritmi 1: A. Pietracaprina Mappa/Dizionario (I parte) 1 Mappa/Dizionario Definizione generale Collezione di entry che supporta, come metodi principali: ricerca, inserimento, rimozione Vari ADT:
Albero binario. Alberi binari (introduzione) Terminologia. Alberi di ricerca binaria (BST)
 Albero binario 2 Alberi binari (introduzione) Struttura di dati bidimensionale formata da nodi costituiti ciascuno dai dati da memorizzare e da due link Ver. 2.4 20 - Claudio Fornaro - Corso di programmazione
Albero binario 2 Alberi binari (introduzione) Struttura di dati bidimensionale formata da nodi costituiti ciascuno dai dati da memorizzare e da due link Ver. 2.4 20 - Claudio Fornaro - Corso di programmazione
Algoritmi e Strutture Dati
 Algoritmi e Strutture Dati Capitolo 5 - Alberi Alberto Montresor Università di Trento This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike License. To view a copy of this
Algoritmi e Strutture Dati Capitolo 5 - Alberi Alberto Montresor Università di Trento This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike License. To view a copy of this
Programmazione a oggetti
 Programmazione a oggetti Quanti oggetti, tra di loro parlando, fanno programmi. Pilu Crescenzi [email protected] Università di Firenze Programmazione a oggetti p.1/32 Cosa è un oggetto Una scatola software
Programmazione a oggetti Quanti oggetti, tra di loro parlando, fanno programmi. Pilu Crescenzi [email protected] Università di Firenze Programmazione a oggetti p.1/32 Cosa è un oggetto Una scatola software
Le liste. ADT e strutture dati per la rappresentazione di sequenze. Ugo de' Liguoro - Algoritmi e Sperimentazioni 03/04 - Lez. 5
 Le liste ADT e strutture dati per la rappresentazione di sequenze L ADT delle liste Una lista di valori di tipo A è una sequenza finita: a1, a2, L, an dove ai A, per ogni i valore lunghezza posizione L
Le liste ADT e strutture dati per la rappresentazione di sequenze L ADT delle liste Una lista di valori di tipo A è una sequenza finita: a1, a2, L, an dove ai A, per ogni i valore lunghezza posizione L
Informatica 3. LEZIONE 12: Liste. Modulo 1: ADT lista e implementazione basata su array Modulo 2: Lista concatenata
 Informatica 3 LEZIONE 12: Liste Modulo 1: ADT lista e implementazione basata su array Modulo 2: Lista concatenata Informatica 3 Lezione 12 - Modulo 1 ADT lista e implementazione basata su array Introduzione
Informatica 3 LEZIONE 12: Liste Modulo 1: ADT lista e implementazione basata su array Modulo 2: Lista concatenata Informatica 3 Lezione 12 - Modulo 1 ADT lista e implementazione basata su array Introduzione
Alberi Binari di Ricerca
 Alberi Binari di Ricerca Prof. G. M. Farinella [email protected] www.dmi.unict.it/farinella Riferimenti Bibliografici Cormen T.H., Leiserson C.E., Rivest R.L Introduction to Algorithms, Third Edition,
Alberi Binari di Ricerca Prof. G. M. Farinella [email protected] www.dmi.unict.it/farinella Riferimenti Bibliografici Cormen T.H., Leiserson C.E., Rivest R.L Introduction to Algorithms, Third Edition,
Esercizi su alberi binari
 Esercizi su alberi binari Esercizi svolti: Determinazione nodi contenti verifica completezza verifica quasi completezza lunghezza del cammino interno determinazione ultima foglia in un quasi completo verifica
Esercizi su alberi binari Esercizi svolti: Determinazione nodi contenti verifica completezza verifica quasi completezza lunghezza del cammino interno determinazione ultima foglia in un quasi completo verifica
Capitolo 9. Tipi enumerativi, tipi generici e interfacce. c 2005 Pearson Education Italia Capitolo 9-1 / 73
 Capitolo 9 Tipi enumerativi, tipi generici e interfacce c 2005 Pearson Education Italia Capitolo 9-1 / 73 Sommario: Tipi enumerativi, tipi generici e interfacce 1 Definizione di tipi enumerativi La classe
Capitolo 9 Tipi enumerativi, tipi generici e interfacce c 2005 Pearson Education Italia Capitolo 9-1 / 73 Sommario: Tipi enumerativi, tipi generici e interfacce 1 Definizione di tipi enumerativi La classe
Lezione 12 Tabelle Hash
 Lezione 12 Tabelle Hash Rossano Venturini [email protected] Pagina web del corso http://didawiki.cli.di.unipi.it/doku.php/informatica/all-b/start Esercizio 2 ABR: Visita Scrivere un programma che legga
Lezione 12 Tabelle Hash Rossano Venturini [email protected] Pagina web del corso http://didawiki.cli.di.unipi.it/doku.php/informatica/all-b/start Esercizio 2 ABR: Visita Scrivere un programma che legga
Marco Faella I pattern Template Method e Factory Method
 Marco Faella I pattern Template Method e Factory Method 12 Lezione n. Parole chiave: Java Corso di Laurea: Informatica Insegnamento: Linguaggi di Programmazione II Email Docente: [email protected]
Marco Faella I pattern Template Method e Factory Method 12 Lezione n. Parole chiave: Java Corso di Laurea: Informatica Insegnamento: Linguaggi di Programmazione II Email Docente: [email protected]
La classe java.lang.object
 La classe java.lang.object In Java: Gerarchia di ereditarietà semplice Ogni classe ha una sola super-classe Se non viene definita esplicitamente una super-classe, il compilatore usa la classe predefinita
La classe java.lang.object In Java: Gerarchia di ereditarietà semplice Ogni classe ha una sola super-classe Se non viene definita esplicitamente una super-classe, il compilatore usa la classe predefinita
Polimorfismo parametrico vs polimorfismo per inclusione
 Polimorfismo parametrico vs polimorfismo per inclusione Esercizio Definire il tipo di dato Stack con operazioni Push( element ) Pop() Non forzare una specifica implementazione Non forzare un tipo specifico
Polimorfismo parametrico vs polimorfismo per inclusione Esercizio Definire il tipo di dato Stack con operazioni Push( element ) Pop() Non forzare una specifica implementazione Non forzare un tipo specifico
Implementazione Java di un ADT
 Implementazione Java di un ADT Primo passo definire l'interfaccia (API) dell' ADT (l'api descrive i nomi dei metodi che l'adt supporta e come essi sono dichiarati e usati) Secondo passo scrivere il codice
Implementazione Java di un ADT Primo passo definire l'interfaccia (API) dell' ADT (l'api descrive i nomi dei metodi che l'adt supporta e come essi sono dichiarati e usati) Secondo passo scrivere il codice
Heap Ordinamento e code di priorità. Ugo de' Liguoro - Algoritmi e Sperimentazioni 03/04 - Lez. 9
 Heap Ordinamento e code di priorità Heap: definizione Definizione. Uno Heap (binario) è un albero binario finito i cui vertici sono etichettati da elementi di un insieme linearmente ordinato (chiavi),
Heap Ordinamento e code di priorità Heap: definizione Definizione. Uno Heap (binario) è un albero binario finito i cui vertici sono etichettati da elementi di un insieme linearmente ordinato (chiavi),
Main System Monitor Keyboard
 Composite 57 8. Composite (Gof pag. 163) 8.1. Descrizione Consente la costruzione di gerarchie di oggetti composti. Gli oggetti composti possono essere conformati da oggetti singoli, oppure da altri oggetti
Composite 57 8. Composite (Gof pag. 163) 8.1. Descrizione Consente la costruzione di gerarchie di oggetti composti. Gli oggetti composti possono essere conformati da oggetti singoli, oppure da altri oggetti
Algoritmi e Strutture Dati
 Heap Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 2006/07 Heap Heap binari: definizione Un heap binario è una struttura dati composta
Heap Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 2006/07 Heap Heap binari: definizione Un heap binario è una struttura dati composta
Esercizi Capitolo 6 - Alberi binari di ricerca
 Esercizi Capitolo 6 - Alberi binari di ricerca Alberto Montresor 9 Agosto, 204 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente, è possibile
Esercizi Capitolo 6 - Alberi binari di ricerca Alberto Montresor 9 Agosto, 204 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente, è possibile
Il TDA Tree. Alberi. Esempio. Alberi. Applicazioni. Definizione di albero
 Il T Tree lberi In informatica, un albero è un modello astratto di una struttura dati gerarchica Struttura dati non lineare Si pensi al file system di un sistema operativo Le relazioni in un albero sono
Il T Tree lberi In informatica, un albero è un modello astratto di una struttura dati gerarchica Struttura dati non lineare Si pensi al file system di un sistema operativo Le relazioni in un albero sono
Algoritmi e Strutture Dati. Tipo di dato astratto e Strutture dati elementari
 Algoritmi e Strutture Dati Tipo di dato astratto e Strutture dati elementari 1 Argomenti della lezione Tipi di dato astratto Strutture dati elementari Liste o Implementazione di liste in Java Stack Code
Algoritmi e Strutture Dati Tipo di dato astratto e Strutture dati elementari 1 Argomenti della lezione Tipi di dato astratto Strutture dati elementari Liste o Implementazione di liste in Java Stack Code
