In questa lezione. Alberi binari: [CLRS09] cap. 12 per la visita inorder. visite e esercizi su alberi binari. Prof. E. Fachini - Intr. Alg.
|
|
|
- Ugo Caruso
- 5 anni fa
- Visualizzazioni
Transcript
1 In questa lezione Alberi binari: visite e esercizi su alberi binari [CLRS09] cap. 12 per la visita inorder!1
2 Visita inordine di un albero binario visita inordine(x) se l albero x non è nullo allora visita inordine il sottoalbero sinistro di x visita x visita inordine il sottoalbero destro di x 4 Input: Output: !2
3 Rappresentazione in memoria Dato un albero binario t. alberi binari Nella rappresentazione in memoria assumiamo che ogni nodo di t abbia un campo key, che contiene la chiave del dato un campo left, con un puntatore al figlio sinistro, un campo right, con un puntatore al figlio destro un campo p, con un puntatore al padre!3
4 Rappresentazione in memoria nil 50 p key left right nil rappresentazione 20 nil nil 40 nil 60 nil nil 35 nil nil!4
5 Visita inordine di un albero binario Inordine(x) if x nil then Inordine(left[x]) print key[x] Inordine(right[x]) 4 Inordine(4) Inordine(3) Inordine(1) Inordine(nil) print key(1) Input: 3 5 print key(3) Output: 1 3 7!5
6 Visita inordine Inordine(x) if x nil then Inordine(left[x]) print key[x] Inordine(right[x]) Input: Inordine(4) Inordine(3) Inordine(2) Inordine(7) print key(7) print key(2) print key(4) 7 Output: !6
7 Visita inordine Inordine(x) if x nil then Inordine(left[x]) print key[x] Inordine(right[x]) 4 Inordine(4) Inordine(5) Inordine(8) print key(8) print key(5) Input: Output: !7
8 Complessità visita inordine Sia n il numero dei nodi dell albero binario e m quello del suo sottoalbero sinistro allora la relazione di ricorrenza è T(0) = c T(n) = T(m) + T(n-m-1) + d (c,d >0) Ipotizziamo che T(n) = O(n). Verifichiamo che T(n) kn, per una costante k>0, a partire da un certo n in poi. T(n) = T(m) + T(n-m-1) + d km + k(n-m-1) + d = km + kn - km - k + d = kn - k + d si vuole che kn - k + d kn questo è vero per k d. Guardiamo al caso base T(1) = T(0) + T(0) + d = 2c+d e scegliamo quindi k = 2c+d, per concludere che T(n) = O(n) perché abbiamo trovato una costante k tale che T(n) kn per ogni n n0=0. Inordine(x) if x nil then Inordine(left[x]) print key[x] Inordine(right[x]) Quindi T(n) = O(n)!8
9 Complessità visita inordine Inordine(x) if x nil then Inordine(left[x]) print key[x] Inordine(right[x]) T(n) = Ω(n), perchè tutti i nodi sono visitati. T(n) = Θ(n)!9
10 Altre visite Inordine(x) if x nil then Inordine(x.left) print key(x.right) Inordine(x.right) Postorder(x) if x nil then Postorder(x.left) Postorder(x.right) print key[x] definiamo altre due visite modificando l ordine di visita della radice rispetto ai suoi sottoalberi, Visita postorder : visita il sottoalbero sinistro visita il sottoalbero destro visita la radice Visita preordine : visita la radice visita il sottoalbero sinistro visita il sottoalbero destro Preordine(x) if x nil then print key[x] Preordine(x.left) Preordine(x.right) T(n) = Θ(n)!10
11 Altri conteggi: numero dei nodi nnodi(x) input: x è il puntatore alla radice di un albero binario output: il numero dei nodi dell albero di radice x if x == nil then return 0 n1 = nnodi(x.left) n2 = nnodi(x.right) n = n1 + n2 + 1 return n E una visita postorder in cui la visita di un nodo è effettuata calcolando la somma dei valori ottenuti dalle visite dei due sotto alberi. Il tempo di esecuzione dell algoritmo per il calcolo del numero dei nodi, n, è θ(n).!11
12 Altri conteggi: numero dei nodi nnodi(x) input: x è il puntatore alla radice di un albero binario output: il numero dei nodi dell albero di radice x if x == nil then return 0 return nnodi(x.left) + nnodi(x.right) +1 La versione più snella.!12
13 Altri conteggi: altezza Altezza(x) input: x è il puntatore alla radice di un albero binario output: l altezza dell albero di radice x if x == nil then return -1 h1 = Altezza(x.left) h2 = Altezza(x.right) h = max{h1,h2} +1 return h E una visita postorder in cui la visita di un nodo è effettuata calcolando l altezza in base ai valori ottenuti dalle visite dei due sotto alberi. Il tempo di esecuzione dell algoritmo per il calcolo dell altezza, in un albero con n nodi, è θ(n).!13
14 Altri conteggi: altezza 2 Altezza(x) input: x è il puntatore alla radice di un albero binario output: l altezza dell albero di radice x if x == nil then return -1 return max{altezza(x.left),altezza(x.right)} +1 Versione più sintetica e veloce!!14
15 Esercizio 2 Si costruisca un algoritmo ricorsivo che verifica se un albero binario t, rappresentato con strutture a puntatori, è completo. b a c l albero è completo sse in tutti i nodi i due sottoalberi hanno la stessa altezza d e f g u i j m p q r s h1 h2 se h1=h2 e i due sottoalberi sono completi restituiamo h1+1 altrimenti? prendiamo -2 che non è un altezza.!15
16 Esercizio 2 Si costruisca un algoritmo ricorsivo che verifica se un albero binario t, rappresentato con strutture a puntatori, è completo. VerCompl(T) input: un albero binario T, rappresentato con strutture a puntatori postc: restituisce l altezza dell albero se l albero è completo, -2 altrimenti. if (T==NIL) return -1 h1=vercompl(t.left) h2=vercompl(t.right) if (h1=-2) or ( h2=-2) then return -2 //almeno uno non è completo else if (h1=h2) then return h1+1 else return -2 É una visita in postordine quindi VerCompl ha tempo di esecuzione asintotico in Θ(n), se n è il numero dei nodi dell albero binario!16
17 Esercizio 3 Si costruisca un algoritmo ricorsivo che verifica se un albero binario t, rappresentato con strutture a puntatori, è quasi completo. h= -1 h = 0, i due sottoalberi hanno altezza uguale -1 h = 1, il sinistro ha altezza h1=0 e il destro h2= -1, O.K. h = 1, il sinistro ha altezza h1=0 e il destro h2 = 0, O.K. generalizzando è quasi completo se i due sottoalberi sono completi e hanno altezze h1=h2 oppure h2+1=h1!17
18 Esercizio 3 Si costruisca un algoritmo ricorsivo che verifica se un albero binario t, rappresentato con strutture a puntatori, è quasi completo. h= -1 h= 0, i due sottoalberi hanno altezza uguale -1 h = 1, il sinistro ha altezza h1=-1 e il destro h2= 0, NO in generale se i due sottoalberi sono completi e h2= h1+1 NO!18
19 Esercizio 3 Si costruisca un algoritmo ricorsivo che verifica se un albero binario t, rappresentato con strutture a puntatori, è quasi completo. si generalizza al caso in cui il sinistro è quasi completo e il destro completo e h1= h2+1, O.K. si generalizza al caso in cui il sinistro è completo e il destro quasi completo e h1= h2, O.K.!19
20 Esercizio 3 Riassumendo i casi sì sono: il sinistro è completo e il destro quasi completo e h1= h2 il sinistro è quasi completo e il destro completo e h1= h2+1 i due sottoalberi sono completi e hanno altezze h1=h2, e tutto l albero è completo oppure se h1= h2+1 e l albero è quasi completo!20
21 Esercizio 3 Dobbiamo distinguere tra il caso in cui il sotto albero sinistro è quasi completo da quello in cui è completo i due sottoalberi del sotto albero sinistro sono completi e hanno altezze h1=h2 +1, e il sotto albero destro ha altezza h1 Per distinguere i due casi in cui le altezze devono essere uguali, ma in un caso si ha l albero completo e nell altro no, si usa una variabile booleana che viene restituita con l altezza!21
22 Esercizio 3 Si costruisca un algoritmo ricorsivo che verifica se un albero binario t, rappresentato con strutture a puntatori, è quasi completo. VerQCompl(T) input: il puntatore, T, alla radice di un albero binario output: una coppia (x,h) in cui h è l altezza dell albero e x=q se l albero è quasi completo,mentre x=c se l albero è completo, x=c e h=-2 altrimenti. if (T==NIL) return (c,-1) É una visita in postordine (x,h1)=vercompl(t.left) quindi VerCompl ha tempo di esecuzione (y,h2)=vercompl(t.right) asintotico in Θ(n), nel caso peggiore, se if (h1=-2) or ( h2=-2) then return (c,-2) n è il numero dei nodi dell albero binario elseif (x=c and y=c and h1=h2 then return (c,h1+1) elseif (x=c and y=q and h1=h2) or (x=c and y=c and h1=h2+1)) then return (q,h1+1) elseif (x=q and y=c and h1=h2+1) then return (q,h1+1) else return (c,-2)!22
23 Numero di nodi con una chiave minore di un dato valore Si definisca un algoritmo ricorsivo che, dato in input il puntatore alla radice di un albero binario e un intero k, dà in output il numero di nodi di un albero binario T di chiave minore a k Se k = 12 allora la radice deve essere contata Se k = 9 allora la radice non deve essere contata Si tratta di una visita in post order, come quella per il calcolo del numero dei nodi, solo che la radice non produce sempre un incremento!23
24 Numero di nodi con una chiave minore di un dato valore nminori(t, k) input: un puntatore,t, alla radice di un albero binario e un intero k output: il numero di elementi il cui campo intero è più piccolo di k if (T == NILL) return 0; if (T.key < k) return nminori(t.left,k)+ nminori(t.right,k) +1; else return nminori(t.left,k)+ nminori(t.right,k); Tempo di esecuzione della visita Θ(n) in tutti i casi, se n è il numero dei nodi dell albero binario.!24
25 Cercare una chiave in un albero binario Si definisca un algoritmo ricorsivo che, dato in input un albero binario T e una chiave k, dà in output il puntatore a un nodo di chiave k se presente, NIL altrimenti Se la chiave cercata non è 10 va cercata nei sottoalberi Si tratta di una visita in preorder, infatti si prosegue sui sotto alberi solo se la radice non ha una chiave uguale a quella cercata!25
26 Cercare una chiave in un albero binario Si definisca un algoritmo ricorsivo che, dato in input un albero binario T e una chiave k, dà in output il puntatore a un nodo di chiave k se presente, NIL altrimenti. cerca(t, x) input: un puntatore, T, alla radice di un albero binario e x un intero output:il puntatore al primo nodo dell'albero di chiave x se lo trova, NIL altrimenti if T== NIL return NIL if (T.key == x) return T temp = cerca(t.left,x) if (temp == NIL) return cerca(t.right,x) return temp Tempo di esecuzione della visita Θ(n) nel caso peggiore e Θ(1) nel migliore.!26
27 Nodi su un cammino Si definisca un algoritmo ricorsivo che, dato un albero binario T, le cui chiavi non si ripetono, e due chiavi x e y, dà in output 1 se c'è un cammino padri-figli che porta da un nodo di chiave x a uno di chiave y, 0 altrimenti Per esempio 10 e 8 sono su un cammino padri-figli, mentre 6 e 10 no L idea è cercare x e poi cercare y nel sotto albero radicato in x.!27
28 Nodi su un cammino Si definisca un algoritmo ricorsivo che dà in output 1 se c'è un cammino padri-figli che porta da un nodo di chiave x a uno di chiave y, 0 altrimenti. Cammino(T, x, y) input: un puntatore, T, alla radice di un albero binario e due interi x e y prec: le chiavi in T non si ripetono output:1 se c'è un cammino padri-figli che porta dal nodo di chiave x a quello di chiave y, 0 altrimenti. if (cerca(cerca(t,x),y)) NIL return 1 else return 0 Tempo di esecuzione Θ(n) nel caso peggiore, dove n è il numero dei nodi, per esempio se x non è presente. Se si trova x poi la visita si riduce al sotto albero radicato in x. Θ(1) nel caso migliore, per esempio x è la radice e y uno dei suoi figli.!28
29 Uguaglianza tra due alberi Si definisca un algoritmo ricorsivo che, dati in input i puntatori alle radici di due alberi binari T e U, dà in output 1 se T=U, 0 altrimenti = !29
30 Uguaglianza tra due alberi Si definisca un algoritmo ricorsivo che, dati in input i puntatori alle radici di due alberi binari T e U, dà in output 1 se T=U, 0 altrimenti. Uguali(T, U) input: due puntatori, T e U, alla radice di due albero binari output:1 se T e U sono uguali, 0 altrimenti. if (T == NIL and U == NIL) return 1 se sono entrambi vuoti sono uguali else if (T == NIL and U NIL ) or (T NIL and U == NIL) return 0 if (T.key == U.key) return Uguali(T.left,U.left) and Uguali(T.right,U.right) else return 0 Detto n il numero dei nodi dell albero più piccolo, il tempo di esecuzione è Θ(n) nel caso peggiore, se i due alberi sono uguali, oppure il primo è prefisso del secondo. Θ(1) nel caso migliore, uno è vuoto e l altro no, oppure le chiavi delle radici sono diverse.!30
31 Alberi da visite visita inordine: visita preordine: visita inordine: visita preordine: !31
32 Alberi da visite visita inordine: visita preordine: Nella visita in preordine il primo è la radice Nella visita inordine il sottoalbero sinistro è visitato prima della radice, quindi sono nodi del sottoalbero sinistro e 8 5 del destro. Applicando ricorsivamente il ragionamento ai due sottoalberi, si ottiene che 3 è la radice del sottoalbero sinistro e 5 del destro.!32
33 Alberi da visite visita inordine: visita preordine: sono i nodi del sottoalbero sinistro e 8 5 quelli del destro Dalla visita inordine del sottoalbero sinistro ricaviamo che 1 è l unico nodo nel sottoalbero sinistro di 3 e 7 2 in quello destro Poichè nella visita preordine 2 è visitato prima di 7, 2 è la radice e 7 sta nel sottoalbero sinistro perchè precede 2 nella visita inordine.!33
34 Alberi da visite visita inordine: visita preordine: sono i nodi del sottoalbero sinistro e 8 5 quelli del destro. Poichè nella visita inordine 8 è visitato prima di 5, 8 sta nel sottoalbero sinistro !34
35 Alberi da visite CostrAB(inordine, preordine) Input: due arrays inordine e preordine con le visite inorder e preorder rispettivamente, prec:inordine e preordine sono non vuoti, di elementi distinti output: il puntatore alla radice dell albero binario T, la cui visita inorder è inordine e quella in preorder è preordine in_lo = 0; in_hi = inordine.len - 1; pre_lo= 0; pre_hi=in_hi return CostrAB_aus(inordine, preordine,in_lo,in_hi,pre_lo,pre_hi) Si utilizza una funzione di ricerca in un vettore cerca(inordine,in_lo,in_hi,x) Input: un vettore inordine, due indici in_lo e in_hi che individuano l intervallo di ricerca in inordine e la chiave x da cercare. prec:inordine è non vuoto, di elementi distinti e lo hi postc: restituisce la posizione in in di x!35
36 Alberi da visite CostrAB_aus(inordine, preordine,in_lo,in_hi,pre_lo,pre_hi) Input: due sequenze inordine e preordine con le visite inorder e preorder rispettivamente, in_lo e in_hi sono gli indici che individuano la porzione di inordine su cui si costruisce l albero, mentre pre_lo e pre_hi sono gli indici che individuano la porzione di preordine su cui si costruisce l albero prec:inordine e preordine contengono elementi distinti output: dà in output il puntatore alla radice dell albero binario T, la cui visita inorder è inordine e quella in preorder è preordine if lo > hi then return NIL crea un nodo T, con T.key = preordine[pre_lo] e campi puntatori a NIL if lo = hi then return T j = cerca(inordine,in_lo,in_hi,t.key) j è l indice della radice in inordine, il sottoalbero sinistro contiene i nodi inordine[in_lo j-1] e il destro i nodi inordine[j+1... in_hi]. La porzione di preordine che contiene i nodi del sotto albero sinistro è compresa tra l indice pre_lo+1 e quello ottenuto sommando il numero di elementi nel sotto albero sinistro, j-in_lo, a pre_lo. Invece i nodi nel sotto albero destro in preordine sono quelli a seguire, quindi dall indice pre_lo+1 + (j-in_lo) e pre_hi T.left = CostrAB_aus(inordine, preordine,in_lo,j-1,pre_lo+1,pre_lo + (j - in_lo)) T.right = CostrAB_aus(inordine, preordine,j+1,in_hi,pre_lo + (j - in_lo)+1,pre_hi) return T!36
37 Alberi da visite Relazioni di ricorrenza per CostrAB_aus. T(n) = T(0) + T(n-1) + cn che si semplifica con T(n) = T(n-1) + cn Sappiamo che T(n) = O(n 2 ). Verifichiamo che T(n) kn 2, per una costante k>0, a partire da un certo n in poi. Usiamo l induzione. T(n) = T(n-1) + cn (per l ipotesi induttiva) k(n-1) 2 + cn = k(n n) + cn = kn 2 + k - 2kn + cn Imponendo la disuguaglianza: kn 2 + k - 2kn + cn kn 2 k - 2kn + cn 0 2kn - k cn Questa disuguaglianza è vera per k = c e n 1!37
38 Alberi da visite Relazioni di ricorrenza per CostrAB_aus. T(n) = T(n/2) + T(n/2) + cn/2 che si semplifica con T(n) = 2T(n/2) + cn Sappiamo che T(n) = Θ(n lg n).!38
39 Numero di nodi contenti Si definisca un algoritmo ricorsivo che dà in output il numero di nodi contenti nel'albero di input, se non è vuota e -1 altrimenti. Un nodo e' contento se nell'albero in esso radicato ci sono piu' nodi figli sinistri che destri.!39
40 nodi contenti non è contento è contento ed è l unico contento, dare 1 nessuno è contento, dare 0 se si hanno n1 nodi contenti nel sotto albero sinistro e n2 in quello destro e se il numero dei nodi nel sotto albero sinistro è minore di quello nel sotto albero destro allora dare n1+n2+1, altrimenti n1+n2!40
41 Numero di nodi contenti, pseudocodicce Si definisca un algoritmo ricorsivo che dà in output il numero di nodi contenti nel'albero di input, se non è vuota e -1 altrimenti. Un nodo e' contento se nell'albero in esso radicato ci sono piu' nodi figli sinistri che destri. contenti(t) input: il puntatore alla radice di un albero binario output: il numero dei nodi contenti in T (n,contenti) = contaux(t); return contenti} Il tempo di esecuzione è quello di una visita in postordine, quindi Θ(n), dove n è il numero dei nodi di T. contaux(t) input: il puntatore alla radice di un albero binario e una variabile intera n output: la coppia con il numero dei nodi e il numero dei nodi contenti in T if T è nil return (0,0) if T è una foglia return (1,0) if (T.left nil) then (n1,contenti) = contaux(t.left) if (T.right nil) then (n2,contenti) = contaux(t.right) if (n1 - n2 > 0) then return (n1+n2+1,contenti+1) else return (n1+n2+1,contenti)!41
42 Ultima Foglia Dato un albero binario T, quasi completo (cioè completo fino al penultimo livello, con le foglie al più su due livelli e con le foglie sull ultimo livello tutte a sinistra) implementato con strutture a puntatori, si implementi un algoritmo che ricevuto in input T restituisce in output il puntatore all ultima foglia. L algoritmo deve avere una complessita O((lg n) 2 ), se n è il numero degli elementi in T. Si illustri l idea algoritmica prima di passare alla stesura in pseudocodice, in cui prima di tutto si deve indicare l output atteso delle singole funzioni utilizzate, oltre ad eventuali vincoli sull input. Esempio: nel primo albero la risposta è il link al nodo 1, nel secondo al nodo 2 più a destra
43 Casi base: 16 Analisi problema Come posso individuare il sotto albero che contiene l ultima foglia? Osserviamo che se la lunghezza del cammino più a sinistra nel sotto albero sinistro e destro sono uguali allora l ultima foglia è nel sotto albero destro, altrimenti nel sinistro. Sia CPS la funzione che restituisce il numero di nodi attraversati lungo un cammino che parte dalla radice e scende lungo legami padre-figlio sinistro fino a che il nodo è privo di figlio sinistro.
44 Verso la soluzione se CPS(T.left) = CPS(T.right) dirigo la ricerca nel sottoalbero destro CPS(T.left) = CPS(T.right) CPS(T.left) = CPS(T.right) se CPS(T.left) = CPS(T.right) + 1 dirigo la ricerca nel sottoalbero sinistro CPS(T.left) = CPS(T.right) + 1 CPS(T.left) = CPS(T.right) + 1 Tempo di esecuzione di CSP Θ(h) = Θ(lg n)
45 UltimaFoglia(T) Input: un albero binario T precond: T è quasi completo output: il puntatore all ultima foglia Pseudocodice if (T == NIL o è una foglia) then return T m = CPS(T.left) m = CPS(T.right) if (m == m ) then return UltimaFoglia(T.right) if (m == m + 1) then return UltimaFoglia(T.left) m = m CPS(T) Input: un albero binario T output: il numero di nodi attraversati lungo un cammino che parte dalla radice e scende lungo legami padre-figlio sinistro fino a che il nodo è privo di figlio sinistro. %Se T è Nil dà 0 se T è un solo nodo dà 1 Tempo di esecuzione T(h) = T(h-1) + Θ(h) in tutti i casi. Quindi Θ(h 2 ) e h = lg n. m = m +1
Esercizi su alberi binari
 Esercizi su alberi binari Esercizi svolti: Determinazione nodi contenti verifica completezza verifica quasi completezza lunghezza del cammino interno determinazione ultima foglia in un quasi completo verifica
Esercizi su alberi binari Esercizi svolti: Determinazione nodi contenti verifica completezza verifica quasi completezza lunghezza del cammino interno determinazione ultima foglia in un quasi completo verifica
Esercizi su ABR. Prof. E. Fachini - Intr. Alg.!1
 Esercizi su ABR Confronto proprietà ABR e Max-Heap. Proprietà del cammino radice-foglia individuato da una ricerca. Fusione di due ABR. Il successivo calcolato dalla radice Costruzione di un ABR bilanciato
Esercizi su ABR Confronto proprietà ABR e Max-Heap. Proprietà del cammino radice-foglia individuato da una ricerca. Fusione di due ABR. Il successivo calcolato dalla radice Costruzione di un ABR bilanciato
Esercizi BST - AVL. E. Fachini
 Esercizi BST - AVL. Verifica che un ABR è un AVL 2. verifica bilanciamento in altezza di un ABR 3. Costruzione alberi di Fibonacci 4. Calcolo altezza albero AVL in O(lg n) 5. split di una ABR intorno a
Esercizi BST - AVL. Verifica che un ABR è un AVL 2. verifica bilanciamento in altezza di un ABR 3. Costruzione alberi di Fibonacci 4. Calcolo altezza albero AVL in O(lg n) 5. split di una ABR intorno a
Esercizio 1. E vero che in un AVL il minimo si trova in una foglia o nel penultimo livello? FB = -1. livello 0 FB = -1. livello 1 FB = -1.
 Esercizio 1 E vero che in un AVL il minimo si trova in una foglia o nel penultimo livello? FB = -1 livello 0 FB = -1 FB = -1 livello 1 FB = -1 livello 2 livello 3 L altezza è 3, il minimo si trova nel
Esercizio 1 E vero che in un AVL il minimo si trova in una foglia o nel penultimo livello? FB = -1 livello 0 FB = -1 FB = -1 livello 1 FB = -1 livello 2 livello 3 L altezza è 3, il minimo si trova nel
Introduzione agli algoritmi Prova di esame del 19/9/2016 Prof.sse E. Fachini - R. Petreschi. Parte prima
 Introduzione agli algoritmi Prova di esame del 19/9/2016 Prof.sse E. Fachini - R. Petreschi Parte prima 1) Si dimostri il teorema sulla limitazione inferiore per il tempo asintotico di esecuzione nel caso
Introduzione agli algoritmi Prova di esame del 19/9/2016 Prof.sse E. Fachini - R. Petreschi Parte prima 1) Si dimostri il teorema sulla limitazione inferiore per il tempo asintotico di esecuzione nel caso
In questa lezione Alberi binari di ricerca: la cancellazione
 In questa leione Alberi binari di ricerca: la cancellaione 1 L algoritmo di Hibbard per cancellare (1962) Sia il nodo da cancellare: 1) è una foglia: si rimuove 2) ha un solo figlio x: si rende x figlio
In questa leione Alberi binari di ricerca: la cancellaione 1 L algoritmo di Hibbard per cancellare (1962) Sia il nodo da cancellare: 1) è una foglia: si rimuove 2) ha un solo figlio x: si rende x figlio
Alberi. Se x è il genitore di y, allora y è un figlio di x. Un albero binario è un albero in cui ogni nodo ha al massimo due figli.
 Alberi Un albero è un insieme di oggetti, chiamati nodi, su cui è definita una relazione binaria G(x, y) che leggiamo x è genitore di y tale che: 1. esiste un unico nodo, chiamato radice, che non ha genitori;
Alberi Un albero è un insieme di oggetti, chiamati nodi, su cui è definita una relazione binaria G(x, y) che leggiamo x è genitore di y tale che: 1. esiste un unico nodo, chiamato radice, che non ha genitori;
Alberi ed Alberi Binari
 Alberi ed Alberi Binari Il tipo di dato Albero Un albero è una struttura di data organizzata gerarchicamente. È costituito da un insieme di nodi collegati tra di loro: ogni nodo contiene dell informazione,
Alberi ed Alberi Binari Il tipo di dato Albero Un albero è una struttura di data organizzata gerarchicamente. È costituito da un insieme di nodi collegati tra di loro: ogni nodo contiene dell informazione,
Moltiplicazione veloce di interi
 Moltiplicazione veloce di interi Ogni numero intero w di n cifre può essere scritto come 10 n/2 w s + w d w s indica il numero formato dalle n/2 cifre più significative di w w d denota il numero formato
Moltiplicazione veloce di interi Ogni numero intero w di n cifre può essere scritto come 10 n/2 w s + w d w s indica il numero formato dalle n/2 cifre più significative di w w d denota il numero formato
Alberi Binari di Ricerca
 Alberi Binari di Ricerca Algoritmi su gli alberi binari: visite Dato un puntatore alla radice di un albero vogliamo scandire in modo sistematico tutti i nodi di tale albero In una lista abbiamo una unica
Alberi Binari di Ricerca Algoritmi su gli alberi binari: visite Dato un puntatore alla radice di un albero vogliamo scandire in modo sistematico tutti i nodi di tale albero In una lista abbiamo una unica
alberi completamente sbilanciati
 alberi completamente sbilanciati Il numero dei nodi al livello i è 1, per 0 i altezza L altezza h di un albero completamente sbilanciato con n nodi è h = n-1 1 Un albero completamente bilanciato o pieno
alberi completamente sbilanciati Il numero dei nodi al livello i è 1, per 0 i altezza L altezza h di un albero completamente sbilanciato con n nodi è h = n-1 1 Un albero completamente bilanciato o pieno
Un albero completamente bilanciato o pieno (full) alberi completamente sbilanciati. Un albero binario completo
 alberi completamente sbilanciati Un albero completamente bilanciato o pieno (full) Definizione: Un albero è pieno se tutte le foglie sono sullo stesso livello e ogni nodo non foglia ha due figli. Il numero
alberi completamente sbilanciati Un albero completamente bilanciato o pieno (full) Definizione: Un albero è pieno se tutte le foglie sono sullo stesso livello e ogni nodo non foglia ha due figli. Il numero
Esercizi su ABR. Prof. E. Fachini - Intr. Alg. 1
 Esercizi su ABR Confronto proprietà ABR e Max-Heap. Verifica stato dell albero a seguito di inserimento e cancellazione di uno stesso elemento e viceversa. Proprietà del cammino radice-foglia individuato
Esercizi su ABR Confronto proprietà ABR e Max-Heap. Verifica stato dell albero a seguito di inserimento e cancellazione di uno stesso elemento e viceversa. Proprietà del cammino radice-foglia individuato
Introduzione agli algoritmi Prova di esame del 30/6/2016 Prof.sse E. Fachini - R. Petreschi
 B Introduzione agli algoritmi Prova di esame del 30/6/2016 Prof.sse E. Fachini - R. Petreschi Si consideri l operazione di inserimento in un AVL. Si supponga di trovarsi nel caso in cui una rotazione a
B Introduzione agli algoritmi Prova di esame del 30/6/2016 Prof.sse E. Fachini - R. Petreschi Si consideri l operazione di inserimento in un AVL. Si supponga di trovarsi nel caso in cui una rotazione a
Si imposti la relazione di ricorrenza che ne descrive la complessità e la si risolva utilizzando il metodo della sostituzione.
 parte II - A 2 Si consideri la seguente funzione: analizzami(int n) c = 1 k = n*n while k > 1 do k = k/2 for i = 0 to 3 do if n >1 then analizzami(n/4) Si imposti la relazione di ricorrenza che ne descrive
parte II - A 2 Si consideri la seguente funzione: analizzami(int n) c = 1 k = n*n while k > 1 do k = k/2 for i = 0 to 3 do if n >1 then analizzami(n/4) Si imposti la relazione di ricorrenza che ne descrive
Algoritmi e Strutture di Dati
 Algoritmi e Strutture di Dati Visite di alberi m.patrignani Nota di copyright queste slides sono protette dalle leggi sul copyright il titolo ed il copyright relativi alle slides (inclusi, ma non limitatamente,
Algoritmi e Strutture di Dati Visite di alberi m.patrignani Nota di copyright queste slides sono protette dalle leggi sul copyright il titolo ed il copyright relativi alle slides (inclusi, ma non limitatamente,
23/10/2016. gli alberi. alcune definizioni. un esempio. LABORATORIO DI PROGRAMMAZIONE 2 Corso di laurea in matematica.
 gli alberi Un albero è una struttura dati NON LINEARE organizzata gerarchicamente. LABORATORIO DI PROGRAMMAZIONE 2 Corso di laurea in matematica È costituito da un insieme di nodi collegati tra di loro:
gli alberi Un albero è una struttura dati NON LINEARE organizzata gerarchicamente. LABORATORIO DI PROGRAMMAZIONE 2 Corso di laurea in matematica È costituito da un insieme di nodi collegati tra di loro:
Esercitazione 6. Alberi binari di ricerca
 Esercitazione 6 Alberi binari di ricerca Struttura base Rappresentabile attraverso una struttura dati concatenata in cui ogni nodo è un oggetto di tipo struttura Ogni nodo contiene: campo chiave (key)
Esercitazione 6 Alberi binari di ricerca Struttura base Rappresentabile attraverso una struttura dati concatenata in cui ogni nodo è un oggetto di tipo struttura Ogni nodo contiene: campo chiave (key)
Visite di alberi binari. Laboratorio di Algoritmi e Strutture Dati
 Visite di alberi binari Laboratorio di Algoritmi e Strutture Dati Visita di Alberi Gli alberi possono essere visitati (o attraversati) in diversi modi: Visita in Preordine: prima si visita il nodo e poi
Visite di alberi binari Laboratorio di Algoritmi e Strutture Dati Visita di Alberi Gli alberi possono essere visitati (o attraversati) in diversi modi: Visita in Preordine: prima si visita il nodo e poi
Esercizi di Algoritmi e Strutture Dati
 Esercizi di Algoritmi e Strutture Dati Moreno Marzolla marzolla@cs.unibo.it Ultimo aggiornamento: 3 novembre 2010 1 Trova la somma/1 Scrivere un algoritmo che dati in input un array A[1... n] di n interi
Esercizi di Algoritmi e Strutture Dati Moreno Marzolla marzolla@cs.unibo.it Ultimo aggiornamento: 3 novembre 2010 1 Trova la somma/1 Scrivere un algoritmo che dati in input un array A[1... n] di n interi
In questa lezione. Heap binario heapsort. [CLRS10] cap. 6, par Prof. E. Fachini - Intr. Alg.
![In questa lezione. Heap binario heapsort. [CLRS10] cap. 6, par Prof. E. Fachini - Intr. Alg. In questa lezione. Heap binario heapsort. [CLRS10] cap. 6, par Prof. E. Fachini - Intr. Alg.](/thumbs/92/108221303.jpg) In questa lezione Heap binario heapsort [CLRS10] cap. 6, par. 6.1-6.4!1 Heap binari Un heap binario è una struttura dati consistente di un array visto come un albero binario. A= 5 60 65 30 50 18 40 25
In questa lezione Heap binario heapsort [CLRS10] cap. 6, par. 6.1-6.4!1 Heap binari Un heap binario è una struttura dati consistente di un array visto come un albero binario. A= 5 60 65 30 50 18 40 25
Note per la Lezione 4 Ugo Vaccaro
 Progettazione di Algoritmi Anno Accademico 2016 2017 Note per la Lezione 4 Ugo Vaccaro Ripasso di nozioni su Alberi Ricordiamo che gli alberi rappresentano una generalizzazione delle liste, nel senso che
Progettazione di Algoritmi Anno Accademico 2016 2017 Note per la Lezione 4 Ugo Vaccaro Ripasso di nozioni su Alberi Ricordiamo che gli alberi rappresentano una generalizzazione delle liste, nel senso che
d. Cancellazione del valore 5 e. Inserimento del valore 1
 Esercizio1 Si consideri un albero binario non vuoto in cui a ciascun nodo v è associato un numero reale v.val. Scrivere un algoritmo che, dato in input l'albero T e un numero reale x, restituisce true
Esercizio1 Si consideri un albero binario non vuoto in cui a ciascun nodo v è associato un numero reale v.val. Scrivere un algoritmo che, dato in input l'albero T e un numero reale x, restituisce true
Visite di alberi binari. Laboratorio di Algoritmi e Strutture Dati
 Visite di alberi binari Laboratorio di Algoritmi e Strutture Dati Visita di Alberi Gli alberi possono essere visitati (o attraversati) in diversi modi: Visita in Preordine: prima si visita il nodo e poi
Visite di alberi binari Laboratorio di Algoritmi e Strutture Dati Visita di Alberi Gli alberi possono essere visitati (o attraversati) in diversi modi: Visita in Preordine: prima si visita il nodo e poi
L albero e un tipo astratto di dati usato per rappresentare relazioni gerarchiche.
 Lezioni di C L albero e un tipo astratto di dati usato per rappresentare relazioni gerarchiche. qstruttura del file system qalbero genealogico qorganigramma qalbero di decisione q... s=6*8+((2+42)*(5+12)+987*7*123+15*54)
Lezioni di C L albero e un tipo astratto di dati usato per rappresentare relazioni gerarchiche. qstruttura del file system qalbero genealogico qorganigramma qalbero di decisione q... s=6*8+((2+42)*(5+12)+987*7*123+15*54)
Problemi di ricerca in insiemi ordinati
 Problemi di ricerca in insiemi ordinati Abbiamo visto che, per trovare un elemento in un insieme ordinato, con l algoritmo della ricerca binaria restringiamo l intervallo della ricerca alla metà in ogni
Problemi di ricerca in insiemi ordinati Abbiamo visto che, per trovare un elemento in un insieme ordinato, con l algoritmo della ricerca binaria restringiamo l intervallo della ricerca alla metà in ogni
Alberi binari di ricerca
 Alberi binari di ricerca Ilaria Castelli castelli@dii.unisi.it Università degli Studi di Siena Dipartimento di Ingegneria dell Informazione A.A. 2009/20010 I. Castelli Alberi binari di ricerca, A.A. 2009/20010
Alberi binari di ricerca Ilaria Castelli castelli@dii.unisi.it Università degli Studi di Siena Dipartimento di Ingegneria dell Informazione A.A. 2009/20010 I. Castelli Alberi binari di ricerca, A.A. 2009/20010
Problemi di ordinamento
 Problemi di ordinamento Input: una sequenza di n numeri a 1, a 2,..., a n ; Output: una permutazione a 1, a 2,..., a n di a 1, a 2,..., a n tale che a 1 a 2... a n. Generalmente, la sequenza è rappresentata
Problemi di ordinamento Input: una sequenza di n numeri a 1, a 2,..., a n ; Output: una permutazione a 1, a 2,..., a n di a 1, a 2,..., a n tale che a 1 a 2... a n. Generalmente, la sequenza è rappresentata
Esercizi Capitolo 6 - Alberi binari di ricerca
 Esercizi Capitolo 6 - Alberi binari di ricerca Alberto Montresor 9 Agosto, 204 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente, è possibile
Esercizi Capitolo 6 - Alberi binari di ricerca Alberto Montresor 9 Agosto, 204 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente, è possibile
Per semplicità eliminiamo le ripetizioni nell'albero.
 Albero binario di ricerca 20 40 100 95 Un albero binario di ricerca é un albero binario in cui ogni nodo ha un etichetta minore o uguale a quelle dei nodi nel sottoalbero radicato nel figlio destro e maggiore
Albero binario di ricerca 20 40 100 95 Un albero binario di ricerca é un albero binario in cui ogni nodo ha un etichetta minore o uguale a quelle dei nodi nel sottoalbero radicato nel figlio destro e maggiore
Alberi binari e alberi binari di ricerca
 Università degli studi di Milano Dipartimento di Informatica Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica Alberi Un albero è una collezione non vuota di: nodi con nome e informazioni
Università degli studi di Milano Dipartimento di Informatica Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica Alberi Un albero è una collezione non vuota di: nodi con nome e informazioni
Alberi binari e alberi binari di ricerca
 Alberi binari e alberi binari di ricerca Violetta Lonati Università degli studi di Milano Dipartimento di Scienze dell Informazione Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica
Alberi binari e alberi binari di ricerca Violetta Lonati Università degli studi di Milano Dipartimento di Scienze dell Informazione Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica
Dati e Algoritmi 1: A. Pietracaprina. Alberi Binari
 Dati e Algoritmi 1: A. Pietracaprina Alberi Binari 1 Definizione Un alberto binario T è un albero ordinato in cui Nota ogni nodo interno ha 2 figli ogni nodo non radice è etichettato come figlio sinistro
Dati e Algoritmi 1: A. Pietracaprina Alberi Binari 1 Definizione Un alberto binario T è un albero ordinato in cui Nota ogni nodo interno ha 2 figli ogni nodo non radice è etichettato come figlio sinistro
Divide et impera su alberi
 Divide et impera su alberi Caso base: peru = null o una foglia Decomposizione: riformula il problema per i sottoalberi radicati nei figli di u. Ricombinazione: ottieniilrisultatoconricombina 1 Decomponibile(u):
Divide et impera su alberi Caso base: peru = null o una foglia Decomposizione: riformula il problema per i sottoalberi radicati nei figli di u. Ricombinazione: ottieniilrisultatoconricombina 1 Decomponibile(u):
Alberi binari (radicati e ordinati) della radice Il padre del nodo 5 e del nodo 3
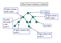 Alberi binari (radicati e ordinati) Il figlio sinistro della radice Il padre del nodo 5 e del nodo 3 4 3 Il figlio sinistro del nodo 2 2 5 1 6 7 8 9 La radice Il figlio destro della radice una foglia Figlio
Alberi binari (radicati e ordinati) Il figlio sinistro della radice Il padre del nodo 5 e del nodo 3 4 3 Il figlio sinistro del nodo 2 2 5 1 6 7 8 9 La radice Il figlio destro della radice una foglia Figlio
Alberi binari e alberi binari di ricerca
 Alberi binari e alberi binari di ricerca Violetta Lonati Università degli studi di Milano Dipartimento di Informatica Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica giovedì 9
Alberi binari e alberi binari di ricerca Violetta Lonati Università degli studi di Milano Dipartimento di Informatica Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica giovedì 9
Strutture dati Alberi binari
 Strutture dati - 2 - Alberi binari Definizione L albero è un insieme di elementi (nodi), sui quali è definita una relazione di discendenza con due proprietà: esiste un solo nodo radice senza predecessori
Strutture dati - 2 - Alberi binari Definizione L albero è un insieme di elementi (nodi), sui quali è definita una relazione di discendenza con due proprietà: esiste un solo nodo radice senza predecessori
Dati e Algoritmi I (Pietracaprina) Esercizi su Alberi Binari di Ricerca e (2,4)-Tree
 Dati e Algoritmi I (Pietracaprina) Esercizi su Alberi Binari di Ricerca e (2,4)-Tree Dati e Algoritmi I (Pietracaprina): Esercizi 1 Problema 1 Si definisca Interval Tree un albero binario di ricerca le
Dati e Algoritmi I (Pietracaprina) Esercizi su Alberi Binari di Ricerca e (2,4)-Tree Dati e Algoritmi I (Pietracaprina): Esercizi 1 Problema 1 Si definisca Interval Tree un albero binario di ricerca le
Algoritmi e Strutture Dati & Laboratorio di Algoritmi e Programmazione
 Algoritmi e Strutture Dati & Laboratorio di Algoritmi e Programmazione Appello del 24 Gennaio 2007 Esercizio 1 (ASD) 1. Sia T (n) = T (n/6) + T (n/3) + Θ(n). Considerare ciascuna delle seguenti affermazioni
Algoritmi e Strutture Dati & Laboratorio di Algoritmi e Programmazione Appello del 24 Gennaio 2007 Esercizio 1 (ASD) 1. Sia T (n) = T (n/6) + T (n/3) + Θ(n). Considerare ciascuna delle seguenti affermazioni
Struttura di dati che può essere usata sia come dizionario, sia come coda con priorità
 Albero binario di ricerca Struttura di dati che può essere usata sia come dizionario, sia come coda con priorità Proprietà: sia x un nodo di un (sotto)albero binario di ricerca Se y è un nodo del sottoalbero
Albero binario di ricerca Struttura di dati che può essere usata sia come dizionario, sia come coda con priorità Proprietà: sia x un nodo di un (sotto)albero binario di ricerca Se y è un nodo del sottoalbero
In questa lezione. Costruire un max-heap. [CLRS01] cap. 6 par Prof. E. Fachini - Intr. Alg.
![In questa lezione. Costruire un max-heap. [CLRS01] cap. 6 par Prof. E. Fachini - Intr. Alg. In questa lezione. Costruire un max-heap. [CLRS01] cap. 6 par Prof. E. Fachini - Intr. Alg.](/thumbs/91/104723414.jpg) In questa lezione Costruire un max-heap [CLRS01] cap. 6 par. 6.3!1 Heapsort: analisi Heapsort(A) Build-Max-Heap(A) for i = A.length downto 2 do scambia A[1] e A[i] A.heap-size = A.heap-size - 1 Max-Heapify
In questa lezione Costruire un max-heap [CLRS01] cap. 6 par. 6.3!1 Heapsort: analisi Heapsort(A) Build-Max-Heap(A) for i = A.length downto 2 do scambia A[1] e A[i] A.heap-size = A.heap-size - 1 Max-Heapify
In questa lezione. Il Mergesort: primo esempio di applicazione della tecnica divide et impera analisi tempo di esecuzione del Mergesort
 In questa lezione Il Mergesort: primo esempio di applicazione della tecnica divide et impera analisi tempo di esecuzione del Mergesort [CLRS] par. 2.3. Prof. E. Fachini - Intr. Alg.!1 Progettazione di
In questa lezione Il Mergesort: primo esempio di applicazione della tecnica divide et impera analisi tempo di esecuzione del Mergesort [CLRS] par. 2.3. Prof. E. Fachini - Intr. Alg.!1 Progettazione di
Alberi. Alberi: definizioni. Alberi Binari. Esercizi su alberi binari: metodi ricorsivi. Struttura dati per alberi generici. ASD-L - Luca Tesei
 Alberi Alberi: definizioni Alberi Binari Esercizi su alberi binari: metodi ricorsivi Struttura dati per alberi generici 1 Alberi Gli alberi sono strutture dati naturalmente ricorsive Un albero è un particolare
Alberi Alberi: definizioni Alberi Binari Esercizi su alberi binari: metodi ricorsivi Struttura dati per alberi generici 1 Alberi Gli alberi sono strutture dati naturalmente ricorsive Un albero è un particolare
algoritmi e strutture di dati
 algoritmi e strutture di dati alberi radicati m.patrignani nota di copyright queste slides sono protette dalle leggi sul copyright il titolo ed il copyright relativi alle slides (inclusi, ma non limitatamente,
algoritmi e strutture di dati alberi radicati m.patrignani nota di copyright queste slides sono protette dalle leggi sul copyright il titolo ed il copyright relativi alle slides (inclusi, ma non limitatamente,
INTRODUZIONE AGLI ALGORITMI 25 Giugno 2018 Prof.ssa Fachini/Prof.ssa Petreschi I PARTE
 INTRODUZIONE AGLI ALGORITMI 25 Giugno 2018 Prof.ssa Fachini/Prof.ssa Petreschi I PARTE 1. Definire il concetto di stabilità di un algoritmo di ordinamento e dire se, e sotto quali ipotesi, i seguenti algoritmi
INTRODUZIONE AGLI ALGORITMI 25 Giugno 2018 Prof.ssa Fachini/Prof.ssa Petreschi I PARTE 1. Definire il concetto di stabilità di un algoritmo di ordinamento e dire se, e sotto quali ipotesi, i seguenti algoritmi
Alberi binari di ricerca
 Alberi binari di ricerca Gli alberi binari di ricerca sono ottime strutture dati per memorizzare coppie di elementi (k, e) chiave elemento di un dizionario. Un albero binario di ricerca T è un albero binario
Alberi binari di ricerca Gli alberi binari di ricerca sono ottime strutture dati per memorizzare coppie di elementi (k, e) chiave elemento di un dizionario. Un albero binario di ricerca T è un albero binario
Esercizi per il corso di Algoritmi, anno accademico 2011/12
 Esercizi per il corso di Algoritmi, anno accademico 2011/12 Esercizi sulla Tecnica Divide et Impera N.B. Tutti gli algoritmi vanno scritti in pseudocodice (non in Java, nè in C++, etc. ). Di tutti gli
Esercizi per il corso di Algoritmi, anno accademico 2011/12 Esercizi sulla Tecnica Divide et Impera N.B. Tutti gli algoritmi vanno scritti in pseudocodice (non in Java, nè in C++, etc. ). Di tutti gli
Gli ordini di visita di un albero binario di 9 nodi sono i seguenti: A, E, B, F, G, C, D, I, H (anticipato)
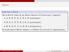 Alberi Indovina l albero Gli ordini di visita di un albero binario di 9 nodi sono i seguenti: A, E, B, F, G, C, D, I, H (anticipato) B, G, C, F, E, H, I, D, A (posticipato) B, E, G, F, C, A, D, H, I (simmetrico).
Alberi Indovina l albero Gli ordini di visita di un albero binario di 9 nodi sono i seguenti: A, E, B, F, G, C, D, I, H (anticipato) B, G, C, F, E, H, I, D, A (posticipato) B, E, G, F, C, A, D, H, I (simmetrico).
Esempi. Albero di interi. Struttura che non è un albero!
 albero si dice "grafo diretto" un insieme di nodi legati "a due a due" da archi direzionati (puntatori) un albero è un grafo diretto in cui ogni nodo può avere un solo arco entrante ed un qualunque numero
albero si dice "grafo diretto" un insieme di nodi legati "a due a due" da archi direzionati (puntatori) un albero è un grafo diretto in cui ogni nodo può avere un solo arco entrante ed un qualunque numero
Esercizi parte 3. La classe ArrayBinTree dovra implementare, tra le altre, l operazione seguente: padre: dato un nodo, restituire l indice del padre.
 Esercizi parte 3 RAPPRESENTAZIONE DI ALBERI BINARI 1. Definire una classe LinkedBinTree che implementa alberi binari in modo collegato, con nodi implementati come oggetti di classe BinNode. La classe dovra
Esercizi parte 3 RAPPRESENTAZIONE DI ALBERI BINARI 1. Definire una classe LinkedBinTree che implementa alberi binari in modo collegato, con nodi implementati come oggetti di classe BinNode. La classe dovra
Alberi. Strutture dati: Alberi. Alberi: Alcuni concetti. Alberi: definizione ricorsiva. Alberi: Una prima realizzazione. Alberi: prima Realizzazione
 Alberi Strutture dati: Alberi Strutture gerarchiche di dati Esempi Il file system di un sistema operativo L organigramma di un azienda Alberi generali, alberi n-ari, alberi binari, Ogni nodo ha un unico
Alberi Strutture dati: Alberi Strutture gerarchiche di dati Esempi Il file system di un sistema operativo L organigramma di un azienda Alberi generali, alberi n-ari, alberi binari, Ogni nodo ha un unico
PROGRAMMAZIONE II canale A-D luglio 2008 TRACCIA DI SOLUZIONE
 PROGRAMMAZIONE II canale A-D 2007-2008 14 luglio 2008 TRACCIA DI SOLUZIONE 1. Si vogliono realizzare mediante puntatori delle liste circolari, cioè delle liste tali che l ultimo elemento della lista punta
PROGRAMMAZIONE II canale A-D 2007-2008 14 luglio 2008 TRACCIA DI SOLUZIONE 1. Si vogliono realizzare mediante puntatori delle liste circolari, cioè delle liste tali che l ultimo elemento della lista punta
ALBERI DI RICERCA BINARI (O ALBERI BINARI DI RICERCA)
 ALBERI DI RICERCA BINARI (O ALBERI BINARI DI RICERCA) Definizione induttiva: un albero vuoto è un albero di ricerca binario un albero non vuoto avente per radice l'elemento (di chiave) x e per sottoalberi
ALBERI DI RICERCA BINARI (O ALBERI BINARI DI RICERCA) Definizione induttiva: un albero vuoto è un albero di ricerca binario un albero non vuoto avente per radice l'elemento (di chiave) x e per sottoalberi
Dati e Algoritmi I (Pietracaprina) Esercizi sugli Alberi
 Dati e Algoritmi I (Pietracaprina) Esercizi sugli Alberi Dati e Algoritmi I (Pietracaprina): Esercizi 1 Problema 1 Dimostrare che un albero non vuoto con n nodi interni, dove ogni nodo interno ha almeno
Dati e Algoritmi I (Pietracaprina) Esercizi sugli Alberi Dati e Algoritmi I (Pietracaprina): Esercizi 1 Problema 1 Dimostrare che un albero non vuoto con n nodi interni, dove ogni nodo interno ha almeno
Albero binario. Alberi binari (introduzione) Terminologia. Alberi di ricerca binaria (BST)
 Albero binario 2 Alberi binari (introduzione) Struttura di dati bidimensionale formata da nodi costituiti ciascuno dai dati da memorizzare e da due link Ver. 2.4 20 - Claudio Fornaro - Corso di programmazione
Albero binario 2 Alberi binari (introduzione) Struttura di dati bidimensionale formata da nodi costituiti ciascuno dai dati da memorizzare e da due link Ver. 2.4 20 - Claudio Fornaro - Corso di programmazione
Organigramma Gerarchia. (Tree) Nessuna persona può avere più di un superiore Ogni persona può essere superiore di altre
 Alberi Struttura dati Albero Organigramma Gerarchia (Tree) Nessuna persona può avere più di un superiore Ogni persona può essere superiore di altre Esempio di un organigramma di un azienda Tree terminology
Alberi Struttura dati Albero Organigramma Gerarchia (Tree) Nessuna persona può avere più di un superiore Ogni persona può essere superiore di altre Esempio di un organigramma di un azienda Tree terminology
Algoritmi e Strutture Dati
 Algoritmi e Strutture Dati Capitolo 5 - Alberi Alberto Montresor Università di Trento This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike License. To view a copy of this
Algoritmi e Strutture Dati Capitolo 5 - Alberi Alberto Montresor Università di Trento This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike License. To view a copy of this
Università degli Studi di Camerino Laurea in Informatica Prima Prova Parziale del corso di Algoritmi e Strutture Dati
 Università degli Studi di Camerino Laurea in Informatica Prima Prova Parziale del corso di Algoritmi e Strutture Dati Docente: Maria Rita Di Berardini 19 dicembre 2007 Nome: Cognome: N.Matricola: Note:
Università degli Studi di Camerino Laurea in Informatica Prima Prova Parziale del corso di Algoritmi e Strutture Dati Docente: Maria Rita Di Berardini 19 dicembre 2007 Nome: Cognome: N.Matricola: Note:
Algoritmi e Strutture di Dati
 Algoritmi e Strutture di Dati Alberi binari di ricerca m.patrignani Nota di copyright queste slides sono protette dalle leggi sul copyright il titolo ed il copyright relativi alle slides (inclusi, ma non
Algoritmi e Strutture di Dati Alberi binari di ricerca m.patrignani Nota di copyright queste slides sono protette dalle leggi sul copyright il titolo ed il copyright relativi alle slides (inclusi, ma non
In questa lezione. Heapsort. ordinamento con complessità, nel caso peggiore, O(nlogn) [CLRS01] cap. 6 da pag. 106 a pag. 114
![In questa lezione. Heapsort. ordinamento con complessità, nel caso peggiore, O(nlogn) [CLRS01] cap. 6 da pag. 106 a pag. 114 In questa lezione. Heapsort. ordinamento con complessità, nel caso peggiore, O(nlogn) [CLRS01] cap. 6 da pag. 106 a pag. 114](/thumbs/65/52995013.jpg) In questa lezione Heapsort ordinamento con complessità, nel caso peggiore, O(nlogn) [CLRS01] cap. 6 da pag. 106 a pag. 11 1 Paternità L heapsort è stato pubblicato da J. W. J. Williams nel 106. Pochi mesi
In questa lezione Heapsort ordinamento con complessità, nel caso peggiore, O(nlogn) [CLRS01] cap. 6 da pag. 106 a pag. 11 1 Paternità L heapsort è stato pubblicato da J. W. J. Williams nel 106. Pochi mesi
Algoritmi e Strutture Dati
 Strutture Elementari Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino 29 ottobre 2008 Strutture Dati Astratte Il concetto di dato Il concetto
Strutture Elementari Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino 29 ottobre 2008 Strutture Dati Astratte Il concetto di dato Il concetto
Algoritmi e Strutture Dati. HeapSort
 Algoritmi e Strutture Dati HeapSort Selection Sort: intuizioni L algoritmo Selection-Sort scandisce tutti gli elementi dell array a partire dall ultimo elemento fino all inizio e ad ogni iterazione: Viene
Algoritmi e Strutture Dati HeapSort Selection Sort: intuizioni L algoritmo Selection-Sort scandisce tutti gli elementi dell array a partire dall ultimo elemento fino all inizio e ad ogni iterazione: Viene
In questa lezione Strutture dati elementari: Pila Coda Loro uso nella costruzione di algoritmi.
 In questa lezione Strutture dati elementari: Pila Coda Loro uso nella costruzione di algoritmi. 1 strutture dati (astratte) Una struttura dati astratti consiste di uno o più insiemi con delle operazioni
In questa lezione Strutture dati elementari: Pila Coda Loro uso nella costruzione di algoritmi. 1 strutture dati (astratte) Una struttura dati astratti consiste di uno o più insiemi con delle operazioni
ALGORITMI E STRUTTURE DATI
 ALGORITMI E STRUTTURE DATI Esercitazioni AndreA Orlandini http://www.dia.uniroma3.it/~orlandin/asd/ e-mail: orlandin@dia.uniroma3.it Orario di ricevimento: Martedì 14.00-16.00 Puntatori e Alberi, ABR StudentiDIA
ALGORITMI E STRUTTURE DATI Esercitazioni AndreA Orlandini http://www.dia.uniroma3.it/~orlandin/asd/ e-mail: orlandin@dia.uniroma3.it Orario di ricevimento: Martedì 14.00-16.00 Puntatori e Alberi, ABR StudentiDIA
Soluzioni della settima esercitazione di Algoritmi 1
 Soluzioni della settima esercitazione di Algoritmi 1 Beniamino Accattoli 19 dicembre 2007 1 Grafi Un grafo è non orientato se descrivendo un arco come una coppia di vertici (i,j) l ordine è ininfluente
Soluzioni della settima esercitazione di Algoritmi 1 Beniamino Accattoli 19 dicembre 2007 1 Grafi Un grafo è non orientato se descrivendo un arco come una coppia di vertici (i,j) l ordine è ininfluente
Algoritmi e Strutture Dati. Alberi
 Algoritmi e Strutture Dati Alberi Alberto Montresor Università di Trento 2017/10/19 This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License. Sommario 1 Introduzione
Algoritmi e Strutture Dati Alberi Alberto Montresor Università di Trento 2017/10/19 This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License. Sommario 1 Introduzione
Algoritmi e Strutture Dati
 Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 2006/07 Il concetto di dato Il concetto di tipo di dato Insertion Sort for j 2 to lenght[a]
Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 2006/07 Il concetto di dato Il concetto di tipo di dato Insertion Sort for j 2 to lenght[a]
Algoritmi e Strutture Dati. HeapSort
 Algoritmi e Strutture Dati HeapSort Selection Sort: intuizioni L algoritmo Selection-Sort scandisce tutti gli elementi dell array a partire dall ultimo elemento fino all inizio e ad ogni iterazione: Viene
Algoritmi e Strutture Dati HeapSort Selection Sort: intuizioni L algoritmo Selection-Sort scandisce tutti gli elementi dell array a partire dall ultimo elemento fino all inizio e ad ogni iterazione: Viene
Alberi. Gli alberi sono una generalizzazione delle liste che consente di modellare delle strutture gerarchiche come questa: Largo. Fosco.
 Alberi Alberi Gli alberi sono una generalizzazione delle liste che consente di modellare delle strutture gerarchiche come questa: Largo Fosco Dora Drogo Frodo Dudo Daisy Alberi Gli alberi sono una generalizzazione
Alberi Alberi Gli alberi sono una generalizzazione delle liste che consente di modellare delle strutture gerarchiche come questa: Largo Fosco Dora Drogo Frodo Dudo Daisy Alberi Gli alberi sono una generalizzazione
Esercizi di Algoritmi e Strutture Dati
 Esercizi di Algoritmi e Strutture Dati Moreno Marzolla marzolla@cs.unibo.it Ultimo aggiornamento: 29 novembre 2010 1 Rotazioni semplici in ABR Si consideri l operazione di rotazione semplice applicata
Esercizi di Algoritmi e Strutture Dati Moreno Marzolla marzolla@cs.unibo.it Ultimo aggiornamento: 29 novembre 2010 1 Rotazioni semplici in ABR Si consideri l operazione di rotazione semplice applicata
Prova di Algoritmi e s.d. (1o anno) 17 Settembre TESTO e RISPOSTE
 Prova di Algoritmi e s.d. (1o anno) 17 Settembre 2002 TESTO e RISPOSTE Esercizio 1 (punti 7 in prima approssimazione) Consideriamo alberi binari con insieme dei nodi NODI = N (l'insieme dei naturali).
Prova di Algoritmi e s.d. (1o anno) 17 Settembre 2002 TESTO e RISPOSTE Esercizio 1 (punti 7 in prima approssimazione) Consideriamo alberi binari con insieme dei nodi NODI = N (l'insieme dei naturali).
Verificare se un albero binario è bilanciato
 Verificare se un albero binario è bilanciato Definizione: Un albero è bilanciato nel Numero dei Nodi, brevemente n- bilanciato, quando, per ogni sottoalbero t radicato in un suo nodo, il numero dei nodi
Verificare se un albero binario è bilanciato Definizione: Un albero è bilanciato nel Numero dei Nodi, brevemente n- bilanciato, quando, per ogni sottoalbero t radicato in un suo nodo, il numero dei nodi
Lezione 12 Tabelle Hash
 Lezione 12 Tabelle Hash Rossano Venturini rossano@di.unipi.it Pagina web del corso http://didawiki.cli.di.unipi.it/doku.php/informatica/all-b/start Esercizio 2 ABR: Visita Scrivere un programma che legga
Lezione 12 Tabelle Hash Rossano Venturini rossano@di.unipi.it Pagina web del corso http://didawiki.cli.di.unipi.it/doku.php/informatica/all-b/start Esercizio 2 ABR: Visita Scrivere un programma che legga
Algoritmi e Strutture Dati
 Maria Rita Di Berardini 2, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino 2 Polo di Scienze Università di Camerino ad Ascoli Piceno Il concetto di dato Il concetto
Maria Rita Di Berardini 2, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino 2 Polo di Scienze Università di Camerino ad Ascoli Piceno Il concetto di dato Il concetto
Esercizi Capitolo 6 - Alberi binari di ricerca
 Esercizi Capitolo 6 - Alberi binari di ricerca Alberto Montresor 23 settembre 200 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente, è possibile
Esercizi Capitolo 6 - Alberi binari di ricerca Alberto Montresor 23 settembre 200 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente, è possibile
Laboratorio di algoritmi e strutture dati
 Laboratorio di algoritmi e strutture dati Docente: Violetta Lonati mercoledì 25 novemb009 L esercitazione di oggi prevede di utilizzare gli alberi binari e in particolare gli alberi binari di ricerca.
Laboratorio di algoritmi e strutture dati Docente: Violetta Lonati mercoledì 25 novemb009 L esercitazione di oggi prevede di utilizzare gli alberi binari e in particolare gli alberi binari di ricerca.
Alberi Binari di Ricerca. Vittorio Maniezzo Università di Bologna
 Alberi Binari di Ricerca 1 Vittorio Maniezzo Università di Bologna Look up table, dati ordinati Collezione di dati nella forma di coppie attributo / valore, in cui i campi chiave sono ordinabili. Caso
Alberi Binari di Ricerca 1 Vittorio Maniezzo Università di Bologna Look up table, dati ordinati Collezione di dati nella forma di coppie attributo / valore, in cui i campi chiave sono ordinabili. Caso
Alberi Binari di Ricerca
 Alberi Binari di Ricerca 1 Vittorio Maniezzo Università di Bologna Look up table, dati ordinati Collezione di dati nella forma di coppie attributo / valore, in cui i campi chiave sono ordinabili. Caso
Alberi Binari di Ricerca 1 Vittorio Maniezzo Università di Bologna Look up table, dati ordinati Collezione di dati nella forma di coppie attributo / valore, in cui i campi chiave sono ordinabili. Caso
Alberto Montresor Università di Trento
 !! Algoritmi e Strutture Dati! Capitolo 5 - Alberi!!! Alberto Montresor Università di Trento!! This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike License. To view a copy
!! Algoritmi e Strutture Dati! Capitolo 5 - Alberi!!! Alberto Montresor Università di Trento!! This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike License. To view a copy
Correzione prima esercitazione: metodo distinct
 Alberi binari lezione 7 Correzione prima esercitazione: metodo distinct // post: ritorna il numero di elementi distinti del multi insieme public int distinct( ) { int d = 0; int i = 0; int j; // INV1:
Alberi binari lezione 7 Correzione prima esercitazione: metodo distinct // post: ritorna il numero di elementi distinti del multi insieme public int distinct( ) { int d = 0; int i = 0; int j; // INV1:
Alberi Binari di Ricerca e Alberi Rosso-Neri
 Alberi Binari di Ricerca e Alberi Rosso-Neri Obiettivi Studiare strutture dati che consentano di effettuare in modo efficiente le operazioni di Minimo e massimo Successore Inserimento e cancellazione Ricerca
Alberi Binari di Ricerca e Alberi Rosso-Neri Obiettivi Studiare strutture dati che consentano di effettuare in modo efficiente le operazioni di Minimo e massimo Successore Inserimento e cancellazione Ricerca
Algoritmi e Strutture Dati Laboratorio 15/12/2008. Daniele Loiacono
 Algoritmi e Strutture Dati Laboratorio 15/12/2008 Problema della compressione Rappresentare i dati in modo efficiente Impiegare il numero minore di bit per la rappresentazione Goal: risparmio spazio su
Algoritmi e Strutture Dati Laboratorio 15/12/2008 Problema della compressione Rappresentare i dati in modo efficiente Impiegare il numero minore di bit per la rappresentazione Goal: risparmio spazio su
Alberi Binari di Ricerca
 Alberi Binari di Ricerca Prof. G. M. Farinella gfarinella@dmi.unict.it www.dmi.unict.it/farinella Riferimenti Bibliografici Cormen T.H., Leiserson C.E., Rivest R.L Introduction to Algorithms, Third Edition,
Alberi Binari di Ricerca Prof. G. M. Farinella gfarinella@dmi.unict.it www.dmi.unict.it/farinella Riferimenti Bibliografici Cormen T.H., Leiserson C.E., Rivest R.L Introduction to Algorithms, Third Edition,
Laboratorio di algoritmi e strutture dati
 Laboratorio di algoritmi e strutture dati Docente: Violetta Lonati mercoledì 15 novemb017 L esercitazione di oggi prevede di utilizzare gli alberi binari e in particolare gli alberi binari di ricerca.
Laboratorio di algoritmi e strutture dati Docente: Violetta Lonati mercoledì 15 novemb017 L esercitazione di oggi prevede di utilizzare gli alberi binari e in particolare gli alberi binari di ricerca.
Alberi binari: definizione e alcune proprietà
 Alberi binari: definizione e alcune proprietà Alberi binari Un albero binario è un albero con radice in cui ogni nodo ha al più due figli. In maniera più formale: Definizione. (Alberi binari) Un albero
Alberi binari: definizione e alcune proprietà Alberi binari Un albero binario è un albero con radice in cui ogni nodo ha al più due figli. In maniera più formale: Definizione. (Alberi binari) Un albero
Algoritmi e strutture dati
 Algoritmi e strutture dati Roberto Cordone A. A. 2015-16 Capitolo 3 Implementazioni dei dizionari ordinati Nota: queste dispense sono un rapido riassunto delle lezioni svolte nel dicembre 2015 e gennaio
Algoritmi e strutture dati Roberto Cordone A. A. 2015-16 Capitolo 3 Implementazioni dei dizionari ordinati Nota: queste dispense sono un rapido riassunto delle lezioni svolte nel dicembre 2015 e gennaio
Alberi. Gli alberi sono una generalizzazione delle liste che consente di modellare delle strutture gerarchiche come questa: Largo. Fosco.
 Alberi Alberi Gli alberi sono una generalizzazione delle liste che consente di modellare delle strutture gerarchiche come questa: Largo Fosco Dora Drogo Dudo Frodo Daisy Alberi Gli alberi sono una generalizzazione
Alberi Alberi Gli alberi sono una generalizzazione delle liste che consente di modellare delle strutture gerarchiche come questa: Largo Fosco Dora Drogo Dudo Frodo Daisy Alberi Gli alberi sono una generalizzazione
Informatica Generale Homework di Recupero 2018
 Informatica Generale Homework di Recupero 08 docente: Ivano Salvo Sapienza Università di Roma email: salvo@di.uniroma.it Istruzioni per l Homework di Recupero Ogni studente deve totalizzare 5 punti per
Informatica Generale Homework di Recupero 08 docente: Ivano Salvo Sapienza Università di Roma email: salvo@di.uniroma.it Istruzioni per l Homework di Recupero Ogni studente deve totalizzare 5 punti per
Introduzione agli Algoritmi Appello esame del 2 luglio 2015 Prof. Emanuela Fachini (canale 1) e Prof. Irene Finocchi (canale 2) Parte 1
 Parte 1 Le risposte non motivate non saranno prese in considerazione. Negli esercizi di progettazione, prima di passare allo pseudocodice descrivete l'idea algoritmica soggiacente. Per tutti gli algoritmi
Parte 1 Le risposte non motivate non saranno prese in considerazione. Negli esercizi di progettazione, prima di passare allo pseudocodice descrivete l'idea algoritmica soggiacente. Per tutti gli algoritmi
Espressioni aritmetiche
 Espressioni aritmetiche Consideriamo espressioni costruite a partire da variabili e costanti intere mediante applicazione delle operazioni di somma, sottrazione, prodotto e divisione (intera). Ad esempio:
Espressioni aritmetiche Consideriamo espressioni costruite a partire da variabili e costanti intere mediante applicazione delle operazioni di somma, sottrazione, prodotto e divisione (intera). Ad esempio:
Algoritmi Greedy. Tecniche Algoritmiche: tecnica greedy (o golosa) Un esempio
 Algoritmi Greedy Tecniche Algoritmiche: tecnica greedy (o golosa) Idea: per trovare una soluzione globalmente ottima, scegli ripetutamente soluzioni ottime localmente Un esempio Input: lista di interi
Algoritmi Greedy Tecniche Algoritmiche: tecnica greedy (o golosa) Idea: per trovare una soluzione globalmente ottima, scegli ripetutamente soluzioni ottime localmente Un esempio Input: lista di interi
Alberi. Alberi: Esempio di utilizzo
 Sono strutture dati del tipo: Alberi SOTTOALBERO n1 RADICE DELL ALBERO () n2 n n4 Profondità o Livello 0 1 n n n n n n 2 NODI FOGLIA (LEAF NODES) 1 Alberi: Esempio di utilizzo Rappresentazione di un file
Sono strutture dati del tipo: Alberi SOTTOALBERO n1 RADICE DELL ALBERO () n2 n n4 Profondità o Livello 0 1 n n n n n n 2 NODI FOGLIA (LEAF NODES) 1 Alberi: Esempio di utilizzo Rappresentazione di un file
LE STRUTTURE DATI DINAMICHE: GLI ALBERI. Cosimo Laneve
 LE STRUTTURE DATI DINAMICHE: GLI ALBERI Cosimo Laneve 1 argomenti 1. definizione di alberi e nozioni relative 2. implementazione degli alberi, creazione, visita 3. algoritmo di visita iterativa e sua implementazione
LE STRUTTURE DATI DINAMICHE: GLI ALBERI Cosimo Laneve 1 argomenti 1. definizione di alberi e nozioni relative 2. implementazione degli alberi, creazione, visita 3. algoritmo di visita iterativa e sua implementazione
Notare come questo schema ricalchi una tipica dimostrazione per induzione. Ció noné casuale in quanto un algoritmo ricorsivo altri non éche una dimost
 Appunti Senza Pretese di Programmazione II: Costruzione di un Albero Bilanciato Alessandro Panconesi DSI, La Sapienza via Salaria 113, 00198, Roma Consideriamo un problema che ci consentirá di vedere un
Appunti Senza Pretese di Programmazione II: Costruzione di un Albero Bilanciato Alessandro Panconesi DSI, La Sapienza via Salaria 113, 00198, Roma Consideriamo un problema che ci consentirá di vedere un
ricerca di un elemento, verifica dell appartenenza di un elemento
 Alberi Binari di Ricerca Gli alberi binari di ricerca (o, alberi di ricerca binaria) sono strutture dati che consentono, su un insieme di elementi con un ordine totale le operazioni di: ricerca di un elemento,
Alberi Binari di Ricerca Gli alberi binari di ricerca (o, alberi di ricerca binaria) sono strutture dati che consentono, su un insieme di elementi con un ordine totale le operazioni di: ricerca di un elemento,
