Sommatori e Moltiplicatori
|
|
|
- Carolina Giusti
- 6 anni fa
- Visualizzazioni
Transcript
1 Sommatori e Moltiplicatori Prof. Alberto Borghese Dipartimento di Scienze dell Informazione [email protected] Università degli Studi di Milano Riferimenti: B.5 sul Patterson, per i moltiplicatori HW, capitolo 9 fino a sul Fummi, Per gli algoritmi di moltiplicazione: capitolo 3 (fino a 3.4) del Patterson. /23 Sommario Sommatori Moltiplicatori 2/23
2 Somma e prodotto logico A B Y Somma => OR A B Y Moltiplicazione => AND A B Y A B Y 3/23 Tabella della verità della somma: (Half) Adder ad bit a b a b somma riporto r HA s s = a b r = ab a b s r La somma è diventata un operazione logica! Cammini critici: Somma = ; Riporto = ; Complessità Somma = porta; Riporto = porta; 4/23 2
3 Tabella della verità della somma completa: a b r in somma riporto Full Adder ad bit s = m + m 2 + m 4 + m 7 r = m 3 + m 5 + m 6 + m 7 s = a b r in + a b r in + a b r in + a b r in = _ = (a b) r in + (ab + ab) r in = = (a b) r in + (a b) r in r in a b _ r out = a b r in + a b r in + a b r in + a b r in = ab + (a b) r in r out FA s 5/23 s = (a b) r in + (a b) r in r out =ab+ (a b) r in Implementazione circuitale r in r in a (a b) (a b) ab r out b!r in!(a b) s r in 7 porte logiche. Cammini critici: s -> 3; r out -> 3 6/23 3
4 r s = out = Semplificazione circuitale ( a b) rin + ( a b) rin = ( a b) ab + ( a b) r in r in a b r in s r in 5 porte logiche. Cammini critici: s > 2; r out -> 3 a r out b 7/23 Implementazione mediante PLA a b r in somma r out SOP: costruisco i mintermini e li sommo. r in a b 8/23 AND OR r out s 4
5 Esercizi Scrivere il circuito che esegue la somma di: in base 2. Riportare tutte le uscite delle porte logiche. Scrivere il circuito che esegue la seguente sottrazione: 5-2 in base 2. Riportare tutte le uscite delle porte logiche. 9/23 Sommario Addizionatori Moltiplicatori /23 5
6 Moltiplicazione binaria Moltiplicando Moltiplicatore x 27 = Prodotto x = /23 La moltiplicazione binaria Possiamo vederla come: Un primo stadio in cui si mette in AND ciascun bit del moltiplicatore con il moltiplicando. Un secondo stadio in cui si effettuano le somme (full adder) dei bit sulle righe contenenti i prodotti parziali. 2/23 6
7 Moltiplicazione binaria Prodotti parziali Riporto Somma parziale Moltiplicando Moltiplicatore x 27 x = = = = -> 297 Prodotto 3/23 Moltiplicazione binaria (su 4 bit) Prodotti parziali (AND) Somma parziale (Sommatori) Prodotto Moltiplicando Moltiplicatore x = * * 2 + * *2 = **2 2 = Il prodotto parziale è = Moltiplicando incolonnato opportunamente 4/23 7
8 La matrice dei prodotti parziali Prodotti parziali In binario i prodotti parziali sono degli AND. 5/23 Il circuito che effettua i prodotti Prodotti parziali 6/23 8
9 La matrice dei prodotti parziali In binario i prodotti parziali sono degli AND. 7/23 Somma delle prime 2 righe dei prodotti parziali Somma dei primi 2 prodotti parziali: Aggiunge il terzo prodotto parziale: HA e FA non sono equivalenti per i diversi cammini critici. 8/23 x = = -> 297 9
10 Somma della terza riga I primi due prodotti parziali sono sommati dalla prima batteria di sommatori. Ogni altro prodotto parziale è sommato da un ulteriore batteria di sommatori. x 27 x = = = = -> 297 9/23 Circuito completo della somma dei prodotti parziali N- batterie di sommatori Problema: overflow: A e B su 32 bit => P su 64 bit. 2/23
11 b3 Valutazione della complessità Complessità: Half Adder: 2 porte Full Adder: 5 porte Stadio AND: 3 A su N bit B su M bit N * M porte AND Stadio OR: N sommatori per riga M- righe Numero porte se N = M = 4 -> 48 riga Altre righe Numero porte = (N-2) * 5 + 2*2 + (M-2) * (N-) * 5 + (M-2)*2 2/23 b2 Valutazione del cammino critico Cammini critici: Half Adder: Somma porta Riporto porta Full Adder: Somma - 2 porte Riporto - 3 porte Gli AND operano in parallelo: ritardo Cammino critico: 2 22/23
12 Diapositiva 2 b3 prova lalfafdafdakmn adf borghese; 4/3/25 Diapositiva 22 b2 prova lalfafdafdakmn adf borghese; 4/3/25
13 Sommario Addizionatori Moltiplicatori 23/23 2
Lezione 7 Sommatori e Moltiplicatori
 Architettura degli Elaboratori e delle Reti Lezione 7 Sommatori e Moltiplicatori Proff. A. Borghese, F. Pedersini Dipartimento di Scienze dell Informazione Università degli Studi di Milano L 7 /36 Sommario
Architettura degli Elaboratori e delle Reti Lezione 7 Sommatori e Moltiplicatori Proff. A. Borghese, F. Pedersini Dipartimento di Scienze dell Informazione Università degli Studi di Milano L 7 /36 Sommario
Lezione 7 ALU: Moltiplicazione e divisione
 Architettura degli Elaboratori e delle Reti Lezione 7 ALU: Moltiplicazione e divisione F. Pedersini Dipartimento di Scienze dell Informazione Università degli Studi di Milano L 7 1/34 Sommario! Sommatori
Architettura degli Elaboratori e delle Reti Lezione 7 ALU: Moltiplicazione e divisione F. Pedersini Dipartimento di Scienze dell Informazione Università degli Studi di Milano L 7 1/34 Sommario! Sommatori
Es. 05. Addizionatori (Half Adder, Full Adder); sommatori a n bit (con e. complemento a due e sottrazione; overflow.
 Es. 05 Addizionatori (Half Adder, Full Adder); sommatori a n bit (con e senza riporto); conversione in complemento a due e sottrazione; overflow. Es. 1 Si scriva la tabella di verità per un addizionatore
Es. 05 Addizionatori (Half Adder, Full Adder); sommatori a n bit (con e senza riporto); conversione in complemento a due e sottrazione; overflow. Es. 1 Si scriva la tabella di verità per un addizionatore
Firmware Multiplier. Sommario
 Firmware Multiplier Prof. lberto Borghese Dipartimento di Informatica [email protected] Università degli Studi di Milano Riferimenti sul Patterson 5a ed.: B.6 & 3.4 /33 Sommario Il moltiplicatore firmware
Firmware Multiplier Prof. lberto Borghese Dipartimento di Informatica [email protected] Università degli Studi di Milano Riferimenti sul Patterson 5a ed.: B.6 & 3.4 /33 Sommario Il moltiplicatore firmware
Aritmetica binaria e circuiti aritmetici
 Aritmetica binaria e circuiti aritmetici Architetture dei Calcolatori (lettere A-I) Addizioni binarie Le addizioni fra numerali si effettuano cifra a cifra (come in decimale) portando il riporto alla cifra
Aritmetica binaria e circuiti aritmetici Architetture dei Calcolatori (lettere A-I) Addizioni binarie Le addizioni fra numerali si effettuano cifra a cifra (come in decimale) portando il riporto alla cifra
Circuiti combinatori
 Laboratorio di Architetture degli Elaboratori I Corso di Laurea in Informatica, A.A. 2017-2018 Università degli Studi di Milano Circuiti combinatori Nicola Basilico Dipartimento di Informatica Via Comelico
Laboratorio di Architetture degli Elaboratori I Corso di Laurea in Informatica, A.A. 2017-2018 Università degli Studi di Milano Circuiti combinatori Nicola Basilico Dipartimento di Informatica Via Comelico
Firmware Division & Floating pointer adder
 Firmware Division & Floating pointer adder Prof. Alberto Borghese Dipartimento di Scienze dell Informazione [email protected] Università degli Studi di Milano Riferimenti sul Patterson: 3.4, 3.5 1/47
Firmware Division & Floating pointer adder Prof. Alberto Borghese Dipartimento di Scienze dell Informazione [email protected] Università degli Studi di Milano Riferimenti sul Patterson: 3.4, 3.5 1/47
Firmware Division. Prof. Alberto Borghese Dipartimento di Informatica Università degli Studi di Milano
 Firmware Division Prof. Alberto Borghese Dipartimento di Informatica [email protected] Università degli Studi di Milano Riferimenti sul Patterson 5a ed.: 3.4, 3.5 1/36 Sommario Divisione intera Circuiti
Firmware Division Prof. Alberto Borghese Dipartimento di Informatica [email protected] Università degli Studi di Milano Riferimenti sul Patterson 5a ed.: 3.4, 3.5 1/36 Sommario Divisione intera Circuiti
Reti Logiche Combinatorie
 Reti Logiche Combinatorie Modulo 4 Università di Cagliari Dipartimento di Ingegneria Elettrica ed Elettronica Laboratorio di Microelettronica e Bioingegneria (EOLAB) Logica combinatoria Un blocco di logica
Reti Logiche Combinatorie Modulo 4 Università di Cagliari Dipartimento di Ingegneria Elettrica ed Elettronica Laboratorio di Microelettronica e Bioingegneria (EOLAB) Logica combinatoria Un blocco di logica
Floating pointer adder & Firmware Division. Sommario
 Floating pointer adder & Firmware Division Prof. Alberto Borghese Dipartimento di Scienze dell Informazione [email protected] Università degli Studi di Milano Riferimenti sul Patterson: 3.4, 3.5 1/43
Floating pointer adder & Firmware Division Prof. Alberto Borghese Dipartimento di Scienze dell Informazione [email protected] Università degli Studi di Milano Riferimenti sul Patterson: 3.4, 3.5 1/43
Firmware Division. Prof. Alberto Borghese Dipartimento di Informatica Università degli Studi di Milano
 Firmware Division Prof. Alberto Borghese Dipartimento di Informatica [email protected] Università degli Studi di Milano Riferimenti sul Patterson 5a ed.: 3.4, 3.5 1/36 Sommario Divisione intera Circuiti
Firmware Division Prof. Alberto Borghese Dipartimento di Informatica [email protected] Università degli Studi di Milano Riferimenti sul Patterson 5a ed.: 3.4, 3.5 1/36 Sommario Divisione intera Circuiti
Dalla tabella alla funzione canonica
 Dalla tabella alla funzione canonica La funzione canonica è la funzione logica associata alla tabella di verità del circuito che si vuole progettare. Essa è costituita da una somma di MinTerm con variabili
Dalla tabella alla funzione canonica La funzione canonica è la funzione logica associata alla tabella di verità del circuito che si vuole progettare. Essa è costituita da una somma di MinTerm con variabili
Lezione 7 Sommatori e Moltiplicatori
 Architettura degli Elaboratori e delle Reti Lezione 7 Sommatori e Moltiplicatori Proff. A. Borghese, F. Pedersini Dipartimento di Scienze dell Informazione Università degli Studi di Milano L 7 1/36 Sommario!
Architettura degli Elaboratori e delle Reti Lezione 7 Sommatori e Moltiplicatori Proff. A. Borghese, F. Pedersini Dipartimento di Scienze dell Informazione Università degli Studi di Milano L 7 1/36 Sommario!
Circuiti Combinatori
 Circuiti Combinatori circuiti combinatori sono circuiti nei quali le uscite dipendono solo dalla combinazione delle variabili logiche presenti nello stesso istante all ingresso Essi realizzano: Operazioni
Circuiti Combinatori circuiti combinatori sono circuiti nei quali le uscite dipendono solo dalla combinazione delle variabili logiche presenti nello stesso istante all ingresso Essi realizzano: Operazioni
Aritmetica dei calcolatori. La rappresentazione dei numeri
 Aritmetica dei calcolatori Rappresentazione dei numeri naturali e relativi Addizione a propagazione di riporto Addizione veloce Addizione con segno Moltiplicazione con segno e algoritmo di Booth Rappresentazione
Aritmetica dei calcolatori Rappresentazione dei numeri naturali e relativi Addizione a propagazione di riporto Addizione veloce Addizione con segno Moltiplicazione con segno e algoritmo di Booth Rappresentazione
Esercitazioni di Reti Logiche. Lezione 4
 Esercitazioni di Reti Logiche Lezione 4 Progettazione dei circuiti logici combinatori Zeynep KIZILTAN [email protected] Argomenti Procedura di analisi dei circuiti combinatori. Procedura di sintesi
Esercitazioni di Reti Logiche Lezione 4 Progettazione dei circuiti logici combinatori Zeynep KIZILTAN [email protected] Argomenti Procedura di analisi dei circuiti combinatori. Procedura di sintesi
Moduli Combinatori. Moduli Combinatori. Corso di Architetture degli Elaboratori
 Moduli Combinatori Moduli Combinatori Corso di Architetture degli Elaboratori Coder Circuito codificatore x x z z k n=2 k x n La linea su cui si ha valore viene codificata in uscita mediante log 2 n bit
Moduli Combinatori Moduli Combinatori Corso di Architetture degli Elaboratori Coder Circuito codificatore x x z z k n=2 k x n La linea su cui si ha valore viene codificata in uscita mediante log 2 n bit
Progetto di Circuiti Aritmetici
 Progetto di Circuiti Aritmetici Maurizio Palesi Maurizio Palesi 1 Introduzione Caratteristiche principali di valutazione Velocità Valutata per il caso peggiore Costo Precisione Es., operazioni in virgola
Progetto di Circuiti Aritmetici Maurizio Palesi Maurizio Palesi 1 Introduzione Caratteristiche principali di valutazione Velocità Valutata per il caso peggiore Costo Precisione Es., operazioni in virgola
Appunti di informatica. Lezione 3 anno accademico Mario Verdicchio
 Appunti di informatica Lezione 3 anno accademico 2015-2016 Mario Verdicchio Numeri binari in memoria In un calcolatore, i numeri binari sono tipicamente memorizzati in sequenze di caselle (note anche come
Appunti di informatica Lezione 3 anno accademico 2015-2016 Mario Verdicchio Numeri binari in memoria In un calcolatore, i numeri binari sono tipicamente memorizzati in sequenze di caselle (note anche come
PSPICE simulazione di circuiti digitali Flip Flop M/S, Moltiplicatore parallelo, Memoria SRAM, sommatore, comparatore
 PSPICE simulazione di circuiti digitali Flip Flop M/S, Moltiplicatore parallelo, Memoria SRAM, sommatore, comparatore Laboratorio di Architettura degli Elaboratori - A.A. 24/25 Il flip flop di tipo Master/Slave
PSPICE simulazione di circuiti digitali Flip Flop M/S, Moltiplicatore parallelo, Memoria SRAM, sommatore, comparatore Laboratorio di Architettura degli Elaboratori - A.A. 24/25 Il flip flop di tipo Master/Slave
Reti Logiche Combinatorie
 Testo di riferimento: [Congiu] - 2.4 (pagg. 37 57) Reti Logiche Combinatorie 00.b Analisi Minimizzazione booleana Sintesi Rete logica combinatoria: definizione 2 Una rete logica combinatoria èuna rete
Testo di riferimento: [Congiu] - 2.4 (pagg. 37 57) Reti Logiche Combinatorie 00.b Analisi Minimizzazione booleana Sintesi Rete logica combinatoria: definizione 2 Una rete logica combinatoria èuna rete
Esercizi svolti Y Z. 1. Date le seguenti funzioni logiche ricavare le corrispondenti reti logiche realizzate con porte elementari AND, OR, NOT.
 Esercizi svolti 1. Date le seguenti funzioni logiche ricavare le corrispondenti reti logiche realizzate con porte elementari ND, OR, NOT. a) F= b) F= F= 2. Date le seguenti funzioni logiche ricavare le
Esercizi svolti 1. Date le seguenti funzioni logiche ricavare le corrispondenti reti logiche realizzate con porte elementari ND, OR, NOT. a) F= b) F= F= 2. Date le seguenti funzioni logiche ricavare le
Esercitazioni di Reti Logiche
 Esercitazioni di Reti Logiche Sintesi di Reti Combinatorie & Complementi sulle Reti Combinatorie Zeynep KIZILTAN Dipartimento di Scienze dell Informazione Universita degli Studi di Bologna Anno Academico
Esercitazioni di Reti Logiche Sintesi di Reti Combinatorie & Complementi sulle Reti Combinatorie Zeynep KIZILTAN Dipartimento di Scienze dell Informazione Universita degli Studi di Bologna Anno Academico
Es. 8 Moltiplicazione e divisione tra numeri interi (Firmware)
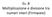 Es. 8 Moltiplicazione e divisione tra numeri interi (Firmware) Circuito della moltiplicazione Moltiplicando (A), 32 bit 32 32 ALU 32 Operazione: P = A x B 32 add P Prodotto (P), 63 32 bit Moltiplicatore
Es. 8 Moltiplicazione e divisione tra numeri interi (Firmware) Circuito della moltiplicazione Moltiplicando (A), 32 bit 32 32 ALU 32 Operazione: P = A x B 32 add P Prodotto (P), 63 32 bit Moltiplicatore
Aritmetica dei Calcolatori 2
 Laboratorio di Architettura 1 aprile 2011 1 Operazioni bit a bit 2 Rappresentazione binaria con segno 3 Esercitazione Operazioni logiche bit a bit AND OR XOR NOT IN OUT A B A AND B 0 0 0 0 1 0 1 0 0 1
Laboratorio di Architettura 1 aprile 2011 1 Operazioni bit a bit 2 Rappresentazione binaria con segno 3 Esercitazione Operazioni logiche bit a bit AND OR XOR NOT IN OUT A B A AND B 0 0 0 0 1 0 1 0 0 1
una rete combinatoria è un circuito logico avente n ingressi (x 1
 Reti combinatorie una rete combinatoria è un circuito logico avente n ingressi (x,,,x n ) ed m uscite (y,y 2,,y m ), ciascuno dei quali assume valori binari (/), e tale che a ciascuna combinazione degli
Reti combinatorie una rete combinatoria è un circuito logico avente n ingressi (x,,,x n ) ed m uscite (y,y 2,,y m ), ciascuno dei quali assume valori binari (/), e tale che a ciascuna combinazione degli
Moltiplicazione e ALU
 Moltiplicazione e ALU Docente teoria: prof. Federico Pedersini (https://homes.di.unimi.it/pedersini/ae-inf.html) Docente laboratorio: Matteo Re (https://homes.di.unimi.it/re/arch1-lab-2017-2018.html) 1
Moltiplicazione e ALU Docente teoria: prof. Federico Pedersini (https://homes.di.unimi.it/pedersini/ae-inf.html) Docente laboratorio: Matteo Re (https://homes.di.unimi.it/re/arch1-lab-2017-2018.html) 1
I circuiti digitali: dalle funzioni logiche ai circuiti
 Architettura dei calcolatori e delle Reti Lezione 4 I circuiti digitali: dalle funzioni logiche ai circuiti Proff. A. Borghese, F. Pedersini Dipartimento di Scienze dell Informazione Università degli Studi
Architettura dei calcolatori e delle Reti Lezione 4 I circuiti digitali: dalle funzioni logiche ai circuiti Proff. A. Borghese, F. Pedersini Dipartimento di Scienze dell Informazione Università degli Studi
Il livello logico digitale
 Il livello logico digitale porte logiche e moduli combinatori Algebra di commutazione Algebra booleana per un insieme di due valori Insieme di elementi A={,} Operazioni NOT (operatore unario) => = e =
Il livello logico digitale porte logiche e moduli combinatori Algebra di commutazione Algebra booleana per un insieme di due valori Insieme di elementi A={,} Operazioni NOT (operatore unario) => = e =
Architettura degli Elaboratori
 circuiti combinatori: ALU slide a cura di Salvatore Orlando, Marta Simeoni, Andrea Torsello 1 ALU ALU (Arithmetic Logic Unit) circuito combinatorio all interno del processore per l esecuzione di istruzioni
circuiti combinatori: ALU slide a cura di Salvatore Orlando, Marta Simeoni, Andrea Torsello 1 ALU ALU (Arithmetic Logic Unit) circuito combinatorio all interno del processore per l esecuzione di istruzioni
senza stato una ed una sola
 Reti Combinatorie Un calcolatore è costituito da circuiti digitali (hardware) che provvedono a realizzare fisicamente il calcolo. Tali circuiti digitali possono essere classificati in due classi dette
Reti Combinatorie Un calcolatore è costituito da circuiti digitali (hardware) che provvedono a realizzare fisicamente il calcolo. Tali circuiti digitali possono essere classificati in due classi dette
I circuiti digitali: dalle funzioni logiche ai circuiti (le SOP)
 I circuiti digitali: dalle funzioni logiche ai circuiti (le SOP) Prof. Alberto Borghese Dipartimento di Informatica [email protected] Università degli Studi di Milano Riferimento al testo: Sezione C.3;
I circuiti digitali: dalle funzioni logiche ai circuiti (le SOP) Prof. Alberto Borghese Dipartimento di Informatica [email protected] Università degli Studi di Milano Riferimento al testo: Sezione C.3;
Addizionatori: metodo Carry-Lookahead. Costruzione di circuiti combinatori. Standard IEEE754
 Addizionatori: metodo Carry-Lookahead Costruzione di circuiti combinatori Standard IEEE754 Addizionatori Il circuito combinatorio che implementa l addizionatore a n bit si basa su 1-bit adder collegati
Addizionatori: metodo Carry-Lookahead Costruzione di circuiti combinatori Standard IEEE754 Addizionatori Il circuito combinatorio che implementa l addizionatore a n bit si basa su 1-bit adder collegati
Esercitazione 02. Circuiti Aritmetici. Gianluca Brilli 09/04/19 ARCHITETTURA DEI CALCOLATORI 1
 Esercitazione 02 Circuiti Aritmetici Gianluca Brilli [email protected] 09/04/19 ARCHITETTURA DEI CALCOLATORI 1 Esercizio 01 Creare un nuovo sottocircuito chiamato "adder_1", e implementarvici
Esercitazione 02 Circuiti Aritmetici Gianluca Brilli [email protected] 09/04/19 ARCHITETTURA DEI CALCOLATORI 1 Esercizio 01 Creare un nuovo sottocircuito chiamato "adder_1", e implementarvici
Reti Combinatorie: sintesi
 Reti Combinatorie: sintesi Sintesi di reti combinatorie Una rete combinatoria realizza una funzione di commutazione Data una tabella di verità è possibile ricavare più espressioni equivalenti che la rappresentano.
Reti Combinatorie: sintesi Sintesi di reti combinatorie Una rete combinatoria realizza una funzione di commutazione Data una tabella di verità è possibile ricavare più espressioni equivalenti che la rappresentano.
Le operazioni. di somma. e sottrazione
 Le operazioni di somma e sottrazione S. Salvatori marzo 2016 (36 di 171) L'unità aritmetico-logica La ALU rappresenta l'elemento principale di una CPU quale dispositivo di elaborazione. ALU AI BUS ESTERNI
Le operazioni di somma e sottrazione S. Salvatori marzo 2016 (36 di 171) L'unità aritmetico-logica La ALU rappresenta l'elemento principale di una CPU quale dispositivo di elaborazione. ALU AI BUS ESTERNI
Codifica e aritmetica binaria
 Codifica e aritmetica binaria Corso ACSO prof. Cristina Silvano, Politecnico di Milano Codifica binaria dell informazione Il calcolatore utilizza un alfabeto binario: usiamo dispositivi elettronici digitali
Codifica e aritmetica binaria Corso ACSO prof. Cristina Silvano, Politecnico di Milano Codifica binaria dell informazione Il calcolatore utilizza un alfabeto binario: usiamo dispositivi elettronici digitali
Calcolatori Elettronici
 Calcolatori Elettronici LIVELLO ORGANIZZAZIONE: SCHEMI DI BASE ALU e REGISTER FILE Massimiliano Giacomin 1 DOVE CI TROVIAMO LIVELLO SIST. OP. Application Binary Interface (ABI) ISA Instruction Set Architecture
Calcolatori Elettronici LIVELLO ORGANIZZAZIONE: SCHEMI DI BASE ALU e REGISTER FILE Massimiliano Giacomin 1 DOVE CI TROVIAMO LIVELLO SIST. OP. Application Binary Interface (ABI) ISA Instruction Set Architecture
