I-Compitino LOGICA 14 giugno 2014
|
|
|
- Alina Rota
- 10 anni fa
- Visualizzazioni
Transcript
1 I-Compitino LOGICA 14 giugno 2014 nome: cognome: - Scrivete in modo CHIARO. Elaborati illegibili non saranno considerati. - NON si considerano le BRUTTE copie. - Ricordatevi di ESPLICITARE l uso della regola dello scambio sia a destra che a sinistra del sequente (se non lo fate perdete punti!). - Ricordatevi di ETICHETTARE LE DERIVAZIONI CON LE REGOLE USATE (se non lo fate perdete punti!) - Specificate le regole derivate che usate e che non sono menzionate nel foglio allegato al compito. Mostrare se i sequenti di seguito sono validi o meno e soddisfacibili o meno in logica classica (nel caso di non validità i punti vanno aumentati della metà arrotondata per difetto nel caso di sequenti con sole proposizioni e per eccesso nel caso di sequenti con formule predicative) 3 punti ( ( B C ) (B C ) ) ( A ) x ( C(x) B(x) ) w C(w) x B(x) w ( z w = z z w z ) 6 punti w ( x y y = x z w z ) w ( C(w) & A(w) D(w) ) w D(w) w ( C(w) A(w) ) C(w) w D(w) & w D(w) Formalizzare in sequente le argomentazioni di seguito. Si provi se il sequente ottenuto è valido e soddisfacibile o meno rispetto alla semantica della logica classica con uguaglianza motivando la risposta (nel caso di non validità i punti vanno aumentati della metà arrotondata per eccesso): 1
2 (7 punti) C è un unica auto da corsa parcheggiata nel viale. La Ferrari rossa è un auto da corsa ed è parcheggiata nel viale. La macchina di Guido è un auto da corsa. Solo se la macchina di Guido è uguale alla Ferrari rossa allora la macchina di Guido è parcheggiata nel viale. P (x)=x è parcheggiata nel viale A(x)=auto da corsa f =Ferrari rossa g=macchina di Guido (3 punti) Soltanto se è estate, c è caldo e afa. Se c è caldo ma non c è afa allora non è estate ma è primavera o autunno. E=è estate A=è autunno P=è primavera C=c è caldo A=c è afa () Le occasioni buone vanno colte al volo. Ogni occasione è buona oppure non è importante. Ogni occasione va colta al volo oppure non è importante. O(y) =y è un occasione B(x)= x è buona I(x)= x è importante V (x)=x va colta al volo (8 punti) In qualche bosco cresce qualche fungo velenoso. Non si dà il caso che in ogni bosco i funghi che vi crescono non siano velenosi. C(x, y)=x cresce in y F (x) =x è un fungo V (x) =x è velenoso B(x)=x è un bosco () Qualcuno applaude. Quelli che non sono contenti non applaudono. A(y) =y applaude 2
3 C(x)=x è contento (10 punti) In ogni bosco cresce qualche fungo velenoso e qualche fungo non velenoso. Non si dà il caso che in qualche bosco crescano soltanto funghi non velenosi. C(x, y)=x cresce in y F (x) =x é un fungo V (x) =x é velenoso B(x)=x è un bosco (6 punti) Non esistono astronauti che abbiamo messo piede su Saturno o su Giove. Nessuno ha messo piede su Saturno. A(x)= x è un astronauta S(x, y)=x ha messo piede su y s=saturno g=giove (7 punti) Pierre sa l Inglese e il Francese. L Inglese è una lingua ed anche il Francese lo è. L Inglese è diverso dal Francese. Non si dà il caso che Pierre sappia un unica lingua. S(y, x) =y sa x L(x)= x è una lingua f= Francese i= Inglese p=pierre Formalizzare i seguenti enunciati e stabilirne la validità e nel caso di non validità se sono soddisfacibili (nel caso di non validità i punti vanno aumentati della metà arrotondata per eccesso): - (12 punti) Non si dà il caso che, se tutti sono esseri divini allora esiste un qualcosa che se è mortale allora tutti gli uomini sono mortali. M(x)= x è mortale D(x)= x è essere divino U(x)= x è un uomo 3
4 - (13 punti) Esiste un tizio di Roma che non è un cuoco di alcun ristorante e che cucina per tutti e soltanto quelli che non si cucinano da soli. C(x, y)= x cucina per y R(x, y)= x è un cuoco del ristorante y T (x)= x un tizio di Roma (30 punti) Sia T tor la teoria ottenuta estendendo LC = con la formalizzazione dei seguenti assiomi: - Non si dà il caso che non vadano sulla torre Eiffel nè Tino, nè Veronica e nè Noemi. - Tino va sulla torre Eiffel solo se piove e ci va anche Eleonora. - Se e solo se non piove Noemi non va sulla torre Eiffel. - Noemi va sulla torre Eiffel solo se non ci va Veronica. - Se Veronica va sulla torre Eiffel allora piove. Si consiglia di usare: P=piove T (x)=x va sulla torre Eiffel t=tino v=veronica n=noemi e=eleonora Dedurre poi in T tor le seguenti affermazioni: - Se non piove allora Noemi non va sulla torre Eiffel e neppure Tino ci va. - Se Veronica va sulla torre Eiffel allora ci va anche Noemi. - Veronica non va sulla torre Eiffel. - Tino o Noemi vanno sulla torre Eiffel. - Se Tino va sulla torre Eiffel allora ci va anche Noemi. - Qualcuno va sulla torre Eiffel. - Piove. - Noemi va sulla torre Eiffel. - Se Tino è diverso da Noemi, e Tino va sulla torre Eiffel, non si dà il caso che soltanto uno vada sulla torre Eiffel. (30 punti) Sia T fig la teoria ottenuta estendendo LC = con la formalizzazione dei seguenti assiomi: - Se uno è figlio di Leo ed è più grande di un altro, pure figlio di Leo, e quest ultimo è più grande di un altro ancora, pure figlio di Leo allora il primo è più grande del terzo. - Nessun figlio di Leo è più grande di se stesso. - Melania, Alvise, Ugo e Filippo sono figli di Leo. 4
5 - Melania è più grande di Alvise. - Nessun figlio di Leo è più grande di Filippo. - Ugo è più grande di Melania. - Presi comunque due figli di Leo, diversi fra loro, o uno è più grande dell altro o quest altro è più grande del primo. Si consiglia di usare: G(x, y)= x è più grande di y F (x, y)=x è figlio di y l=leo u=ugo m=melania a=alvise f=filippo Dedurre poi in T fig le seguenti affermazioni: - Ugo è più grande di Alvise. - Ugo non è più grande di Filippo. - Filippo è più grande di Melania. - Filippo è più grande di tutti i figli di Leo eccetto se stesso. - Melania non è più grande di Ugo Stabilire se la formalizzazioni delle seguenti regole, se non sono già formalizzate, sono valide e lo stesso per le loro inverse (l analisi di una inversa raddoppia i punti). - (10 punti) È estate, z è in vacanza z è contento È estate, tutti sono in vacanza Tutti sono contenti. 1 ove E=È estate V (y)= y è in vacanza C(z)= z è contento - (7 punti) Γ, B Γ A Γ B&A, 2 5
6 - (10 punti) y canta z applaude Qualcuno canta Tutti applaudono 3 ove C(y)= y canta A(z)= z applaude 6
7 Logica classica- LC = ax-id ax- Γ, A, Γ, A, Γ,, Γ Σ, Γ, Θ, Γ, Σ Σ, Γ, Θ, Γ, Σ sc sx ax- Γ,, Γ Σ,, Θ,, Γ Σ,, Θ,, sc dx Γ, A, B Γ, A&B & S Γ A, Γ B, Γ A&B, Γ, A Γ, B Γ, A B S Γ A, B, Γ A B, D Γ A, Γ, A S Γ, A Γ A, D Γ A, Γ, B S Γ, A B Γ, x A(x), A(t) Γ, x A(x) S Γ, A B, Γ A B, D Γ A(w), Γ xa(x), Γ, A(w) Γ, x A(x) S (w V L(Γ, x A(x), )) Γ A(t), x A(x), Γ x A(x), Σ, t = s, Γ(t) (t), Σ, Γ(s), t = s (s), = S = ax Γ t = t, & D D (w V L(Γ, xa(x), )) D si ricorda che t s t = s Regole derivate o valide in LC = -ax sx1 Γ, A, Γ, A, Γ C -ax sx2 Γ, A, Γ, A, Γ C -ax dx1 Γ Σ, A, Σ, A, Σ -ax dx2 Γ Σ, A, Σ, A, Σ Γ, A Γ, A S Γ A, Γ A, D Γ, Γ Σ Γ, Γ, Γ Σ in sx Γ(t) (t) Γ(s), t=s (s) = S v Γ Σ, Σ Γ Σ, Σ, Σ in dx Γ, A(t) Γ, x A(x) Sv Γ A(t), Γ x A(x), Dv rf Γ, t = t, sm Γ, t = u u = t, 7
Algebra e Logica Matematica. Calcolo delle proposizioni Logica del primo ordine
 Università di Bergamo Anno accademico 2006 2007 Ingegneria Informatica Foglio Algebra e Logica Matematica Calcolo delle proposizioni Logica del primo ordine Esercizio.. Costruire le tavole di verità per
Università di Bergamo Anno accademico 2006 2007 Ingegneria Informatica Foglio Algebra e Logica Matematica Calcolo delle proposizioni Logica del primo ordine Esercizio.. Costruire le tavole di verità per
x u v(p(x, fx) q(u, v)), e poi
 0.1. Skolemizzazione. Ogni enunciato F (o insieme di enunciati Γ) è equisoddisfacibile ad un enunciato universale (o insieme di enunciati universali) in un linguaggio estensione del linguaggio di F (di
0.1. Skolemizzazione. Ogni enunciato F (o insieme di enunciati Γ) è equisoddisfacibile ad un enunciato universale (o insieme di enunciati universali) in un linguaggio estensione del linguaggio di F (di
FUNZIONI CONVESSE. + e x 0
 FUNZIONI CONVESSE Sia I un intervallo aperto di R (limitato o illimitato) e sia f(x) una funzione definita in I. Dato x 0 I, la retta r passante per il punto P 0 (x 0, f(x 0 )) di equazione y = f(x 0 )
FUNZIONI CONVESSE Sia I un intervallo aperto di R (limitato o illimitato) e sia f(x) una funzione definita in I. Dato x 0 I, la retta r passante per il punto P 0 (x 0, f(x 0 )) di equazione y = f(x 0 )
15 febbraio 2010 - Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a. 2009-2010 COGNOME... NOME... N. MATRICOLA...
 15 febbraio 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura
15 febbraio 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura
Esercitazione. Proposizioni. April 16, 2015. Esercizi presi dal libro di Rosen (useremo 0 per False e 1 per True). Problema 15, sezione 1.1.
 Esercitazione Proposizioni April 16, 2015 Esercizi presi dal libro di Rosen (useremo 0 per False e 1 per True). Problema 15, sezione 1.1. 1. Consideriamo le proposizioni: - p : Gli orsi grizzly sono stati
Esercitazione Proposizioni April 16, 2015 Esercizi presi dal libro di Rosen (useremo 0 per False e 1 per True). Problema 15, sezione 1.1. 1. Consideriamo le proposizioni: - p : Gli orsi grizzly sono stati
I tre concetti si possono descrivere in modo unitario dicendo che f e iniettiva, suriettiva, biiettiva se e solo se per ogni b B l equazione
 Lezioni del 29 settembre e 1 ottobre. 1. Funzioni iniettive, suriettive, biiettive. Sia f : A B una funzione da un insieme A ad un insieme B. Sia a A e sia b = f (a) B l elemento che f associa ad a, allora
Lezioni del 29 settembre e 1 ottobre. 1. Funzioni iniettive, suriettive, biiettive. Sia f : A B una funzione da un insieme A ad un insieme B. Sia a A e sia b = f (a) B l elemento che f associa ad a, allora
Sapienza, Università di Roma. Ingegneria, Scienze M. F.N., Scienze Statistiche 11 settembre 2009
 Sapienza, Università di Roma Facoltà di Ingegneria, Scienze M. F.N., Scienze Statistiche 11 settembre 009 1. È data una sequenza di n numeri dispari consecutivi. etto M il maggiore della sequenza ed m
Sapienza, Università di Roma Facoltà di Ingegneria, Scienze M. F.N., Scienze Statistiche 11 settembre 009 1. È data una sequenza di n numeri dispari consecutivi. etto M il maggiore della sequenza ed m
Appunti sul corso di Complementi di Matematica - prof. B.Bacchelli. 03 - Equazioni differenziali lineari omogenee a coefficienti costanti.
 Appunti sul corso di Complementi di Matematica - prof. B.Bacchelli 03 - Equazioni differenziali lineari omogenee a coefficienti costanti. Def. Si dice equazione differenziale lineare del secondo ordine
Appunti sul corso di Complementi di Matematica - prof. B.Bacchelli 03 - Equazioni differenziali lineari omogenee a coefficienti costanti. Def. Si dice equazione differenziale lineare del secondo ordine
Sui concetti di definizione, teorema e dimostrazione in didattica della matematica
 Liceo Scientifico Statale P. Paleocapa, Rovigo XX Settimana della Cultura Scientifica e Tecnologica 19 marzo 2010 Sui concetti di definizione, teorema e dimostrazione in didattica della matematica Prof.
Liceo Scientifico Statale P. Paleocapa, Rovigo XX Settimana della Cultura Scientifica e Tecnologica 19 marzo 2010 Sui concetti di definizione, teorema e dimostrazione in didattica della matematica Prof.
EQUAZIONI DIFFERENZIALI. 1. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x 2 log t (d) x = e t x log x (e) y = y2 5y+6
 EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
MATEMATICA E STATISTICA CORSO B PROF. MARCO ABATE. 23 novembre 2006
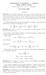 MATEMATICA E STATISTICA CORSO B PROF. MARCO ABATE PRIMO COMPITINO FILA B SOLUZIONI 3 novembre 006. Parte I Esercizio.. Al mercato della frutta i prezzi sono scontati rispetto ai prezzi nei supermercati.
MATEMATICA E STATISTICA CORSO B PROF. MARCO ABATE PRIMO COMPITINO FILA B SOLUZIONI 3 novembre 006. Parte I Esercizio.. Al mercato della frutta i prezzi sono scontati rispetto ai prezzi nei supermercati.
x 2 + y2 4 = 1 x = cos(t), y = 2 sin(t), t [0, 2π] Al crescere di t l ellisse viene percorsa in senso antiorario.
![x 2 + y2 4 = 1 x = cos(t), y = 2 sin(t), t [0, 2π] Al crescere di t l ellisse viene percorsa in senso antiorario. x 2 + y2 4 = 1 x = cos(t), y = 2 sin(t), t [0, 2π] Al crescere di t l ellisse viene percorsa in senso antiorario.](/thumbs/39/18585741.jpg) Le soluzioni del foglio 2. Esercizio Calcolare il lavoro compiuto dal campo vettoriale F = (y + 3x, 2y x) per far compiere ad una particella un giro dell ellisse 4x 2 + y 2 = 4 in senso orario... Soluzione.
Le soluzioni del foglio 2. Esercizio Calcolare il lavoro compiuto dal campo vettoriale F = (y + 3x, 2y x) per far compiere ad una particella un giro dell ellisse 4x 2 + y 2 = 4 in senso orario... Soluzione.
EQUAZIONI DIFFERENZIALI Esercizi svolti. y = xy. y(2) = 1.
 EQUAZIONI DIFFERENZIALI Esercizi svolti 1. Determinare la soluzione dell equazione differenziale (x 2 + 1)y + y 2 =. y + x tan y = 2. Risolvere il problema di Cauchy y() = 1 2 π. 3. Risolvere il problema
EQUAZIONI DIFFERENZIALI Esercizi svolti 1. Determinare la soluzione dell equazione differenziale (x 2 + 1)y + y 2 =. y + x tan y = 2. Risolvere il problema di Cauchy y() = 1 2 π. 3. Risolvere il problema
Corso di Laurea in Scienze e Tecnologie Biomolecolari. NOME COGNOME N. Matr.
 Corso di Laurea in Scienze e Tecnologie Biomolecolari Matematica e Statistica II Prova di esame del 18/7/2013 NOME COGNOME N. Matr. Rispondere ai punti degli esercizi nel modo più completo possibile, cercando
Corso di Laurea in Scienze e Tecnologie Biomolecolari Matematica e Statistica II Prova di esame del 18/7/2013 NOME COGNOME N. Matr. Rispondere ai punti degli esercizi nel modo più completo possibile, cercando
CORSO DI LAUREA IN INGEGNERIA.
 CORSO DI LAUREA IN INGEGNERIA. FOGLIO DI ESERCIZI 4 GEOMETRIA E ALGEBRA LINEARE 2010/11 Esercizio 4.1 (2.2). Determinare l equazione parametrica e Cartesiana della retta dello spazio (a) Passante per i
CORSO DI LAUREA IN INGEGNERIA. FOGLIO DI ESERCIZI 4 GEOMETRIA E ALGEBRA LINEARE 2010/11 Esercizio 4.1 (2.2). Determinare l equazione parametrica e Cartesiana della retta dello spazio (a) Passante per i
CONVESSITÀ NELLA GEOMETRIA DEL TAXI DI MINKOWSKI
 CONVESSITÀ NELLA GEOMETRIA DEL TAXI DI MINKOWSKI ELISABETTA AVIZZANO NICOLETTA CAPOTORTO CHIARA CEROCCHI GIORGIO CICCARELLA IVAN COLAVITA EMANUELE DI CARO SERENA NUNZIATA AMANDA PISELLI ANDREA PIEPOLI
CONVESSITÀ NELLA GEOMETRIA DEL TAXI DI MINKOWSKI ELISABETTA AVIZZANO NICOLETTA CAPOTORTO CHIARA CEROCCHI GIORGIO CICCARELLA IVAN COLAVITA EMANUELE DI CARO SERENA NUNZIATA AMANDA PISELLI ANDREA PIEPOLI
CRITERI DI CONVERGENZA PER LE SERIE. lim a n = 0. (1) s n+1 = s n + a n+1. (2) CRITERI PER LE SERIE A TERMINI NON NEGATIVI
 Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
STATISTICA ESERCITAZIONE 11 Dott. Giuseppe Pandolfo 3 febbraio 2015. Modelli continui di probabilità: la v.c. uniforme continua
 STATISTICA ESERCITAZIONE 11 Dott. Giuseppe Pandolfo febbraio 2015 Modelli continui di probabilità: la v.c. uniforme continua Esercizio 1 Anna ha una gift card da 50 euro. Non si sa se sia mai stata utilizzata
STATISTICA ESERCITAZIONE 11 Dott. Giuseppe Pandolfo febbraio 2015 Modelli continui di probabilità: la v.c. uniforme continua Esercizio 1 Anna ha una gift card da 50 euro. Non si sa se sia mai stata utilizzata
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Corso di Laurea in Scienze e Tecnologie Biomolecolari. NOME COGNOME N. Matr.
 Corso di Laurea in Scienze e Tecnologie Biomolecolari Matematica e Statistica II Prova di esame dell 11/1/2012 NOME COGNOME N. Matr. Rispondere alle domande nel modo più completo possibile, cercando di
Corso di Laurea in Scienze e Tecnologie Biomolecolari Matematica e Statistica II Prova di esame dell 11/1/2012 NOME COGNOME N. Matr. Rispondere alle domande nel modo più completo possibile, cercando di
Sommario. Definizione di informatica. Definizione di un calcolatore come esecutore. Gli algoritmi.
 Algoritmi 1 Sommario Definizione di informatica. Definizione di un calcolatore come esecutore. Gli algoritmi. 2 Informatica Nome Informatica=informazione+automatica. Definizione Scienza che si occupa dell
Algoritmi 1 Sommario Definizione di informatica. Definizione di un calcolatore come esecutore. Gli algoritmi. 2 Informatica Nome Informatica=informazione+automatica. Definizione Scienza che si occupa dell
Politecnico di Milano Facoltà di Ingegneria dell Informazione AGENTI AUTONOMI E SISTEMI MULTIAGENTE Appello COGNOME E NOME
 Politecnico di Milano Facoltà di Ingegneria dell Informazione AGENTI AUTONOMI E SISTEMI MULTIAGENTE Appello COGNOME E NOME 5 luglio 2006 RIGA COLONNA MATRICOLA Il presente plico pinzato, composto di quattro
Politecnico di Milano Facoltà di Ingegneria dell Informazione AGENTI AUTONOMI E SISTEMI MULTIAGENTE Appello COGNOME E NOME 5 luglio 2006 RIGA COLONNA MATRICOLA Il presente plico pinzato, composto di quattro
Indice generale. Modulo 1 Algebra 2
 Indice generale Modulo 1 Algebra 2 Capitolo 1 Scomposizione in fattori. Equazioni di grado superiore al primo 1.1 La scomposizione in fattori 2 1.2 Raccoglimento a fattor comune 3 1.3 Raccoglimenti successivi
Indice generale Modulo 1 Algebra 2 Capitolo 1 Scomposizione in fattori. Equazioni di grado superiore al primo 1.1 La scomposizione in fattori 2 1.2 Raccoglimento a fattor comune 3 1.3 Raccoglimenti successivi
x (x i ) (x 1, x 2, x 3 ) dx 1 + f x 2 dx 2 + f x 3 dx i x i
 NA. Operatore nabla Consideriamo una funzione scalare: f : A R, A R 3 differenziabile, di classe C (2) almeno. Il valore di questa funzione dipende dalle tre variabili: Il suo differenziale si scrive allora:
NA. Operatore nabla Consideriamo una funzione scalare: f : A R, A R 3 differenziabile, di classe C (2) almeno. Il valore di questa funzione dipende dalle tre variabili: Il suo differenziale si scrive allora:
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE
 LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
IRINA E GIOVANNI. La giornata di Irina
 IRINA E GIOVANNI La giornata di Irina La mia sveglia suona sempre alle 7.00 del mattino: mi alzo, vado in bagno e mi lavo, mi vesto, faccio colazione e alle 8.00 esco di casa per andare a scuola. Spesso
IRINA E GIOVANNI La giornata di Irina La mia sveglia suona sempre alle 7.00 del mattino: mi alzo, vado in bagno e mi lavo, mi vesto, faccio colazione e alle 8.00 esco di casa per andare a scuola. Spesso
Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 2014
 Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 14 Problema 1 Punto a) Osserviamo che g (x) = f(x) e pertanto g () = f() = in quanto Γ è tangente all asse delle ascisse,
Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 14 Problema 1 Punto a) Osserviamo che g (x) = f(x) e pertanto g () = f() = in quanto Γ è tangente all asse delle ascisse,
Questionario per casa 6 Febbraio 2012
 1 Il numero 4 2004 + 2 4008 è uguale a a) 4 4012 b) 4 4008 c) 4 2004 d) 2 4009 e) 2 2012 Questionario per casa 6 Febbraio 2012 2 La statura media dei 20 studenti di una certa classe è 163,5 cm. Se ciascuno
1 Il numero 4 2004 + 2 4008 è uguale a a) 4 4012 b) 4 4008 c) 4 2004 d) 2 4009 e) 2 2012 Questionario per casa 6 Febbraio 2012 2 La statura media dei 20 studenti di una certa classe è 163,5 cm. Se ciascuno
Capitolo 7: Teoria generale della calcolabilitá
 Capitolo 7: Teoria generale della calcolabilitá 1 Differenti nozioni di calcolabilitá (che seguono da differenti modelli di calcolo) portano a definire la stessa classe di funzioni. Le tecniche di simulazione
Capitolo 7: Teoria generale della calcolabilitá 1 Differenti nozioni di calcolabilitá (che seguono da differenti modelli di calcolo) portano a definire la stessa classe di funzioni. Le tecniche di simulazione
Regione Liguria Disposizioni e criteri per l esercizio, il controllo, la manutenzione e l ispezione degli impianti termici
 1. Con che periodicità si devono effettuare i controlli di manutenzione sugli impianti termici? L art. 7 del DPR 16/04/2013 n. 74 ha disposto che le operazioni di controllo ed eventuale manutenzione su
1. Con che periodicità si devono effettuare i controlli di manutenzione sugli impianti termici? L art. 7 del DPR 16/04/2013 n. 74 ha disposto che le operazioni di controllo ed eventuale manutenzione su
Elementi di Algebra Relazionale
 Note dalle lezioni di INFORMATICA (per gli allievi della classe quinta - indirizzo MERCURIO) Elementi di Algebra Relazionale prof. Stefano D.L.Campanozzi I.T.C. Giulio Cesare Bari - a.s. 2008-2009 1 Introduzione
Note dalle lezioni di INFORMATICA (per gli allievi della classe quinta - indirizzo MERCURIO) Elementi di Algebra Relazionale prof. Stefano D.L.Campanozzi I.T.C. Giulio Cesare Bari - a.s. 2008-2009 1 Introduzione
ANNO SCOLASTICO 2014-2015
 ATTIVITÀ DI SPERIMENTAZIONE IN CLASSE PREVISTA NELL AMBITO DEL PROGETTO M2014 PROMOSSO DALL ACCADEMIA DEI LINCEI PER LE SCUOLE PRIMARIE E SECONDARIE DI I GRADO ANNO SCOLASTICO 2014-2015 Il Centro matematita,
ATTIVITÀ DI SPERIMENTAZIONE IN CLASSE PREVISTA NELL AMBITO DEL PROGETTO M2014 PROMOSSO DALL ACCADEMIA DEI LINCEI PER LE SCUOLE PRIMARIE E SECONDARIE DI I GRADO ANNO SCOLASTICO 2014-2015 Il Centro matematita,
Calcolo dei Sequenti Predicativo: Note ed Esercizi
 Calcolo dei Sequenti Predicativo: Note ed Esercizi [email protected] 15 novembre 2007 1 Logica predicativa: sintassi La logica proposizionale è piuttosto limitata. La logica predicativa estende quella
Calcolo dei Sequenti Predicativo: Note ed Esercizi [email protected] 15 novembre 2007 1 Logica predicativa: sintassi La logica proposizionale è piuttosto limitata. La logica predicativa estende quella
Parte 2. Determinante e matrice inversa
 Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
COME PARLARE DI DISLESSIA IN CLASSE.
 COME PARLARE DI DISLESSIA IN CLASSE. UNA METAFORA PER SPIEGARE I DSA La psicologa americana ANIA SIWEK ha sviluppato in anni di pratica professionale un modo semplice ed efficace di spiegare i DSA ai bambini,
COME PARLARE DI DISLESSIA IN CLASSE. UNA METAFORA PER SPIEGARE I DSA La psicologa americana ANIA SIWEK ha sviluppato in anni di pratica professionale un modo semplice ed efficace di spiegare i DSA ai bambini,
11. Formalizzazione in linguaggio predicativo
 11. Formalizzazione in linguaggio predicativo Il linguaggio predicativo è ottenuto estendendo il linguaggio proposizionale (quello con,, &,, ) con predicati A(x), B(x, y), C(x, y, z..) dipendenti da un
11. Formalizzazione in linguaggio predicativo Il linguaggio predicativo è ottenuto estendendo il linguaggio proposizionale (quello con,, &,, ) con predicati A(x), B(x, y), C(x, y, z..) dipendenti da un
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI
 FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
INTEGRALI DEFINITI. Tale superficie viene detta trapezoide e la misura della sua area si ottiene utilizzando il calcolo di un integrale definito.
 INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
Predicati e Quantificatori
 Predicati e Quantificatori Limitazioni della logica proposizionale! Logica proposizionale: il mondo è descritto attraverso proposizioni elementari e loro combinazioni logiche! I singoli oggetti cui si
Predicati e Quantificatori Limitazioni della logica proposizionale! Logica proposizionale: il mondo è descritto attraverso proposizioni elementari e loro combinazioni logiche! I singoli oggetti cui si
Esercizi di Calcolo delle Probabilità con Elementi di Statistica Matematica
 Esercizi di Calcolo delle Probabilità con Elementi di Statistica Matematica Lucio Demeio Dipartimento di Scienze Matematiche Università Politecnica delle Marche 1. Esercizio. Siano X ed Y due variabili
Esercizi di Calcolo delle Probabilità con Elementi di Statistica Matematica Lucio Demeio Dipartimento di Scienze Matematiche Università Politecnica delle Marche 1. Esercizio. Siano X ed Y due variabili
Amministrazione classi
 Amministrazione classi Guida breve per il docente che amministra la classe Premessa Le classi vengono creata solo dall amministratore della Scuola. Il docente che è stato inserito nella classe come moderatore
Amministrazione classi Guida breve per il docente che amministra la classe Premessa Le classi vengono creata solo dall amministratore della Scuola. Il docente che è stato inserito nella classe come moderatore
Andrea Pagano, Laura Tedeschini Lalli
 3.5 Il toro 3.5.1 Modelli di toro Modelli di carta Esempio 3.5.1 Toro 1 Il modello di toro finito che ciascuno può costruire è ottenuto incollando a due a due i lati opposti di un foglio rettangolare.
3.5 Il toro 3.5.1 Modelli di toro Modelli di carta Esempio 3.5.1 Toro 1 Il modello di toro finito che ciascuno può costruire è ottenuto incollando a due a due i lati opposti di un foglio rettangolare.
Temi di Esame a.a. 2012-2013. Statistica - CLEF
 Temi di Esame a.a. 2012-2013 Statistica - CLEF I Prova Parziale di Statistica (CLEF) 11 aprile 2013 Esercizio 1 Un computer è collegato a due stampanti, A e B. La stampante A è difettosa ed il 25% dei
Temi di Esame a.a. 2012-2013 Statistica - CLEF I Prova Parziale di Statistica (CLEF) 11 aprile 2013 Esercizio 1 Un computer è collegato a due stampanti, A e B. La stampante A è difettosa ed il 25% dei
Alcune nozioni di base di Logica Matematica
 Alcune nozioni di base di Logica Matematica Ad uso del corsi di Programmazione I e II Nicola Galesi Dipartimento di Informatica Sapienza Universitá Roma November 1, 2007 Questa é una breve raccolta di
Alcune nozioni di base di Logica Matematica Ad uso del corsi di Programmazione I e II Nicola Galesi Dipartimento di Informatica Sapienza Universitá Roma November 1, 2007 Questa é una breve raccolta di
Laboratorio di Alfabetizzazione Informatica - Esame 20 settembre 2013.
 Laboratorio di Alfabetizzazione Informatica - Esame 20 settembre 2013. Questo documento contiene le istruzioni per lo svolgimento dell esame. La durata della prova è 60 minuti e richiede lo svolgimento
Laboratorio di Alfabetizzazione Informatica - Esame 20 settembre 2013. Questo documento contiene le istruzioni per lo svolgimento dell esame. La durata della prova è 60 minuti e richiede lo svolgimento
L espressione torna invece sempre vera (quindi la soluzione originale) se cambiamo contemporaneamente il verso: 1 < 0.
 EQUAZIONI E DISEQUAZIONI Le uguaglianze fra espressioni numeriche si chiamano equazioni. Cercare le soluzioni dell equazione vuol dire cercare quelle combinazioni delle lettere che vi compaiono che la
EQUAZIONI E DISEQUAZIONI Le uguaglianze fra espressioni numeriche si chiamano equazioni. Cercare le soluzioni dell equazione vuol dire cercare quelle combinazioni delle lettere che vi compaiono che la
ESERCIZI APPLICAZIONI LINEARI
 ESERCIZI APPLICAZIONI LINEARI PAOLO FACCIN 1. Esercizi sulle applicazioni lineari 1.1. Definizioni sulle applicazioni lineari. Siano V, e W spazi vettoriali, con rispettive basi B V := (v 1 v n) e B W
ESERCIZI APPLICAZIONI LINEARI PAOLO FACCIN 1. Esercizi sulle applicazioni lineari 1.1. Definizioni sulle applicazioni lineari. Siano V, e W spazi vettoriali, con rispettive basi B V := (v 1 v n) e B W
Analisi Complessa. Prova intermedia del 7 novembre 2002 - Soluzioni. (z 11 1) 11 1 = 0.
 Analisi Complessa Prova intermedia del 7 novembre 2002 - Soluzioni Esercizio. Si consideri l equazione z 0. Quante soluzioni distinte esistono in C? Quante di esse sono contenute all interno del disco
Analisi Complessa Prova intermedia del 7 novembre 2002 - Soluzioni Esercizio. Si consideri l equazione z 0. Quante soluzioni distinte esistono in C? Quante di esse sono contenute all interno del disco
STRINGHE di un ALFABETO. Consideriamo un alfabeto di simboli V V è un insieme finito e non vuoto. Alfabeto della lingua inglese I={a,b,c,..
 STRINGHE di un ALFABETO Consideriamo un alfabeto di simboli V V è un insieme finito e non vuoto Alfabeto binario A={0,1} Alfabeto della lingua inglese I={a,b,c,..z} Stringhe o parole Gli elementi di V
STRINGHE di un ALFABETO Consideriamo un alfabeto di simboli V V è un insieme finito e non vuoto Alfabeto binario A={0,1} Alfabeto della lingua inglese I={a,b,c,..z} Stringhe o parole Gli elementi di V
Limiti e continuità delle funzioni reali a variabile reale
 Limiti e continuità delle funzioni reali a variabile reale Roberto Boggiani Versione 4.0 9 dicembre 2003 1 Esempi che inducono al concetto di ite Per introdurre il concetto di ite consideriamo i seguenti
Limiti e continuità delle funzioni reali a variabile reale Roberto Boggiani Versione 4.0 9 dicembre 2003 1 Esempi che inducono al concetto di ite Per introdurre il concetto di ite consideriamo i seguenti
Amministrazione gruppi (Comunità)
 Amministrazione gruppi (Comunità) Guida breve per il docente che amministra il gruppo Premessa Di regola i gruppi sono creati all interno della Scuola. Nel caso in cui vi fosse la necessità di aprire un
Amministrazione gruppi (Comunità) Guida breve per il docente che amministra il gruppo Premessa Di regola i gruppi sono creati all interno della Scuola. Nel caso in cui vi fosse la necessità di aprire un
NORMALIZZAZIONE DI SCHEMI RELAZIONALI. Prof.ssa Rosalba Giugno
 NORMALIZZAZIONE DI SCHEMI RELAZIONALI Prof.ssa Rosalba Giugno PROBLEMA GENERALE La progettazione concettuale e logica produce uno schema relazionale che rappresenta la realta dei dati nella nostra applicazione.
NORMALIZZAZIONE DI SCHEMI RELAZIONALI Prof.ssa Rosalba Giugno PROBLEMA GENERALE La progettazione concettuale e logica produce uno schema relazionale che rappresenta la realta dei dati nella nostra applicazione.
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
G3. Asintoti e continuità
 G3 Asintoti e continuità Un asintoto è una retta a cui la funzione si avvicina sempre di più senza mai toccarla Non è la definizione formale, ma sicuramente serve per capire il concetto di asintoto Nei
G3 Asintoti e continuità Un asintoto è una retta a cui la funzione si avvicina sempre di più senza mai toccarla Non è la definizione formale, ma sicuramente serve per capire il concetto di asintoto Nei
Lezione 1. Gli Insiemi. La nozione di insieme viene spesso utilizzata nella vita di tutti i giorni; si parla dell insieme:
 Lezione 1 Gli Insiemi La nozione di insieme viene spesso utilizzata nella vita di tutti i giorni; si parla dell insieme: degli iscritti ad un corso di laurea delle stelle in cielo dei punti di un piano
Lezione 1 Gli Insiemi La nozione di insieme viene spesso utilizzata nella vita di tutti i giorni; si parla dell insieme: degli iscritti ad un corso di laurea delle stelle in cielo dei punti di un piano
Kangourou Italia Gara del 22 marzo 2011 Categoria Ecolier Per studenti di quarta o quinta della scuola primaria
 Testi_11Mat.qxp 19-05-2011 21:20 Pagina 5 Kangourou Italia Gara del 22 marzo 2011 Categoria Per studenti di quarta o quinta della scuola primaria I quesiti dal N. 1 al N. 8 valgono 3 punti ciascuno 1.
Testi_11Mat.qxp 19-05-2011 21:20 Pagina 5 Kangourou Italia Gara del 22 marzo 2011 Categoria Per studenti di quarta o quinta della scuola primaria I quesiti dal N. 1 al N. 8 valgono 3 punti ciascuno 1.
Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata, Matematica
 DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
Test d ingresso di Matematica per la secondaria di secondo grado Test d ingresso di matematica per la secondaria di 2 grado
 Test d ingresso di matematica per la secondaria di 2 grado Cognome e nome: Classe Data. Tra i numeri naturali da a 20, quali sono quelli pari e multipli di tre? A.2, 4, 6, 8, 0, 2, 4, 6, 8, 20, 3, 6, 9,
Test d ingresso di matematica per la secondaria di 2 grado Cognome e nome: Classe Data. Tra i numeri naturali da a 20, quali sono quelli pari e multipli di tre? A.2, 4, 6, 8, 0, 2, 4, 6, 8, 20, 3, 6, 9,
Basi di dati 9 febbraio 2010 Compito A
 Basi di dati 9 febbraio 2010 Compito A Domanda 0 (5%) Leggere e rispettare le seguenti regole: Scrivere nome, cognome, matricola (se nota), corso di studio e lettera del compito (ad esempio, A) sui fogli
Basi di dati 9 febbraio 2010 Compito A Domanda 0 (5%) Leggere e rispettare le seguenti regole: Scrivere nome, cognome, matricola (se nota), corso di studio e lettera del compito (ad esempio, A) sui fogli
Amministrazione gruppi (all interno della Scuola)
 Amministrazione gruppi (all interno della Scuola) Guida breve per il docente che amministra il gruppo Premessa Il gruppo viene creato solo dall amministratore della Scuola. Il docente che è stato inserito
Amministrazione gruppi (all interno della Scuola) Guida breve per il docente che amministra il gruppo Premessa Il gruppo viene creato solo dall amministratore della Scuola. Il docente che è stato inserito
CAPITOLO 8 LA VERIFICA D IPOTESI. I FONDAMENTI
 VERO FALSO CAPITOLO 8 LA VERIFICA D IPOTESI. I FONDAMENTI 1. V F Un ipotesi statistica è un assunzione sulle caratteristiche di una o più variabili in una o più popolazioni 2. V F L ipotesi nulla unita
VERO FALSO CAPITOLO 8 LA VERIFICA D IPOTESI. I FONDAMENTI 1. V F Un ipotesi statistica è un assunzione sulle caratteristiche di una o più variabili in una o più popolazioni 2. V F L ipotesi nulla unita
1. Distribuzioni campionarie
 Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
MATEMATICA E STATISTICA CORSO B PROF. MARCO ABATE. 6 giugno 2007
 MATEMATICA E STATISTICA CORSO B PROF. MARCO ABATE SOLUZIONI SECONDO SCRITTO 6 giugno 2007 1. Parte I Esercizio 1.1. Il negozio di scarpe sotto casa tua questa settimana ha diminuito tutti i prezzi del
MATEMATICA E STATISTICA CORSO B PROF. MARCO ABATE SOLUZIONI SECONDO SCRITTO 6 giugno 2007 1. Parte I Esercizio 1.1. Il negozio di scarpe sotto casa tua questa settimana ha diminuito tutti i prezzi del
