Moltiplicazione veloce di interi
|
|
|
- Fabriciano Volpi
- 4 anni fa
- Visualizzazioni
Transcript
1
2 Moltiplicazione veloce di interi Ogni numero intero w di n cifre può essere scritto come 10 n/2 w s + w d w s indica il numero formato dalle n/2 cifre più significative di w w d denota il numero formato dalle n/2 cifre meno significative. Ad esempio può essere scritto come Per moltiplicare due numeri x e y, valel uguaglianza xy =(10 n/2 x s + x d )(10 n/2 y s + y d ) =10 n x s y s +10 n/2 (x s y d + x d y s )+x d y d Decomposizione: se x e y hanno almeno due cifre, dividili come numeri x s, x d, y s e y d aventi ciascuno la metà delle cifre. Ricorsione: calcola ricorsivamente le moltiplicazioni x s y s, x s y d, x d y s e x d y d. Ricombinazione: combina i numeri risultanti usando l uguaglianza riportata sopra.
3 Moltiplicazione veloce di interi l algoritmo esegue quattro moltiplicazioni di due numeri di n/2 cifre (ad un costo di T (n/2)), e tre somme di numeri di n cifre (a un costo O(n)) la moltiplicazione per il valore 10 k può essere realizzata spostando le cifre di k posizioni verso sinistra e riempiendo di 0 la parte destra il costo della decomposizione e della ricombinazione è cn Vale la relazione di ricorrenza T (n) apple c0 se n apple 1 4T (n/2) + cn altrimenti
4 Moltiplicazione veloce di interi T (n) apple c0 se n apple 1 4T (n/2) + cn altrimenti Assumiamo per semplicità n =2 k per un certo k eapplichiamoiterativamente la relazione di ricorrenza: T (n) apple cn +4T (n/2) apple cn +4(cn/2+4T (n/2 2 )) = cn +2cn +4 2 T (n/2 2 ) apple cn +2cn +4 2 (cn/2 2 +4T (n/2 3 )) = cn +2cn +2 2 cn +4 3 T (n/2 3 ) apple apple cn +2cn +2 2 cn i 1 cn +4 i T (n/2 i ) = cn Xi 1 j=0 2 j +4 i T (n/2 i )=cn2 i cn +4 i T (n/2 i ) Ponendo i = k =log 2 n si ha T (n) apple cn 2 cn + n 2 T (1) = O(n 2 ).
5 Moltiplicazione veloce di interi Èpossibileprogettareunalgoritmopiùveloce? Abbiamo visto che xy =10 n x s y s +10 n/2 (x s y d + x d y s )+x d y d. Osserviamo che sommando e sottraendo x s y s + x d y d a x s y d + x d y s si ha x s y d + x d y s = x s y d + x d y s + x s y s + x d y d x s y s x d y d = x s y s + x d y d +(x s y d + x d y s x s y s x d y d ) Poiché x s y d + x d y s x s y s x d y d = (x s x d ) (y s y d )allorapossiamo scrivere x s y d + x d y s = x s y s + x d y d (x s x d ) (y s y d ) quindi il valore x s y d + x d y s può essere calcolato facendo uso di x s y s, x d y d e (x s x d ) (y s y d ) Quindi per computare il prodotto xy sono necessarie tre moltiplicazioni e non più quattro come prima
6 Moltiplicazione veloce di interi Si ha quindi la relazione di ricorrenza T (n) apple c0 se n apple 1 3T (n/2) + cn altrimenti Assumiamo per semplicità n =2 k,peruncertok, eapplichiamoiterativamente la relazione di ricorrenza: T (n) apple cn +3T (n/2) apple cn +3(cn/2+3T (n/2 2 )) = cn +(3/2)cn +3 2 T (n/2 2 ) apple cn +(3/2)cn+3 2 (cn/2 2 +3T (n/2 3 )) = cn +(3/2)cn +(3/2) 2 cn +3 3 T (n/2 3 ) apple apple cn +(3/2)cn +(3/2) 2 cn +...+(3/2) i 1 cn +3 i T (n/2 i ) Xi 1 (3/2) = cn (3/2) j +3 i T (n/2 i i 1 )=cn +3 i T (n/2 i ) 3/2 1 j=0 = 2cn((3/2) i 1) + 3 i T (n/2 i )=2cn(3/2) i 2cn +3 i T (n/2 i ) Continua nella prossima slide
7 Ponendo i = k =log 2 n si ha T (n) apple 2cn(3/2) log 2 n 2cn +3 log 2 n T (1) = 2cn 2 log (3/2) log 2 n 2 = 2cn 2 log n log 2 (3/2) 2 2cn + 2cn + = 2cn n log 2 (3/2) 2cn + n log 2 3 T (1) = 2cn n log cn + n log 2 3 T (1) = 2cn log 2 3 2cn + n log 2 3 T (1) 2 log 2 3 log 2 n T (1) 2 log 2 n log 2 3 T (1) apple 2cn log 2 3 2cn + n log 2 3 c 0 = O(n log 2 3 )=O(n 1,585 )
8 Sottosequenza di somma massima di un array di numeri Dato un array a di n numeri positivi e negativi trovare la sottosequenza di numeri consecutivi la cui somma è massima. N.B. Se l array contiene solo numeri positivi, il massimo si ottiene banalmente prendendo come sequenza quella di tutti i numeri dell array; se l array contiene solo numeri negativi il massimo si ottiene prendendo come sottosequenza quella formata dalla locazione contenente il numero più grande. Isoluzione:Perognicoppiadiindici(i, j) coni apple j dell array computa la somma degli elementi nella sottosequenza degli elementi di indice compreso tra i e j e restituisci la sottosequenza per cui questa somma è max. Costo della I soluzione: O(n 3 )perché Xn 1 i=0 Xn 1 (j i +1) = j=i = = Xn 1 Xn i i=0 k=1 n 1 k = Xn 1 (n i +1)(n i)/2 i=0 X ((n i) 2 /2+(n i)/2) = i=0 nx a 2 /2+ a=1 nx a/2 a=1 nx (a 2 /2+a/2) = 1/2(n(n +1)(2n +1)/6) + 1/2(n(n +1)/2) = (n 3 ). a=1
9 Sottosequenza di somma massima di un array di numeri II soluzione Osserviamo che la somma degli elementi di indice compreso tra i e j può essere ottenuta sommando a[j] allasommadeglielementidi indice compreso tra i e j 1. Di conseguenza, per ogni i, lasommadegli elementi in tutte le sottosequenze che partono da i possono essere computate con un costo totale pari a (n i). Il costo totale è quindi Xn 1 i=0 (n i) = nx nx (i) = ( i) = (n 2 ) i=1 i=1
10 Sottosequenza di somma massima di un array di numeri III soluzione: Divide et Impera Algoritmo A: 1 Se i = j viene restituita la sottosequenza formata da a[i] 2 Se i < j si invoca ricorsivamente A(i, (i + j)/2) e A((i + j)/2+1, j): la sottosequenza cercata o è una di quelle restituite dalle 2 chiamate ricorsive ositrovaacavallodelleduemetàdell array 3 La sottosequenza di somma massima tra quelle che intersecano entrambe le metà dell array si trova nel seguente modo: si scandisce l array a partire dall indice (i + j)/2 andandoaritrosofinoachesi arriva all inizio dell array sommando via via gli elementi scanditi: ad ogni iterazione si confronta la somma ottenuta fino a quel momento con il valore max s 1 delle somme ottenute in precedenza e nel caso aggiorna il max s 1 el indicein corrispondenza del quale è stato ottenuto. si scandisce l array a partire dal indice (i + j)/2 +1andandoinavantifinoache osiraggiungelafinedell arraysommandoglielementiscanditi:adogni iterazione si confronta la somma ottenuta fino a quel momento con il valore max s 2 delle somme ottenute in precedenza e nel caso aggiorna il max s 2 el indicein corrispondenza del quale è stato ottenuto. La sottosequenza di somma massima tra quelle che intersecano le due metà dell array è quella di somma s 1 + s 2. 4 L algoritmo restituisce la sottosequenza massima tra quella restituita dalla prima chiamata ricorsiva, quella restituita dalla seconda chiamata ricorsiva e quella di somma s 1 + s 2
11 Sottosequenza di somma massima di un array di numeri Tempo di esecuzione dell algoritmo Divide et Impera c0 se n =1 T (n) apple 2T n + cn altrimenti 2 Il tempo di esecuzione quindi è O(n log n).
12 Sottosequenza di somma massima di un array di numeri IV soluzione: Chiamiamo s j la sottosequenza di somma massima che tra quelle che terminano in j. Sihas j+1 =max{s j + a[j +1], a[j +1]}. Questo valore si calcola in tempo costante per ogni j. L algoritmocalcolaquesti valori per ogni j eprendeilmassimodeglin valori computati. Il tempo dell algoritmo quindi è O(n).
13 Esempi di relazioni di ricorrenza della forma T (n) apple T (n/ )+n k Ricerca binaria T (n) apple c0 T (n/2) + c se n apple 1oppurek è l e l e m e n t o c e n t r a l e altrimenti Si ha =1, =2,k =0. Siccome = k,siamonelsecondocasoesiha T (n) =O(n k log n)) = O(log n).
14 Esempi di relazioni di ricorrenza della forma T (n) apple T (n/ )+n k Nell ordinamento per fusione, T (n) apple c0 se n apple 1 2T (n/2) + cn altrimenti Quindi, =2, =2ek =1 siamo nel caso = k equindit (n) =O(n k log n) =O(n log n).
15 Esempi di relazioni di ricorrenza della forma T (n) apple T (n/ )+n k Moltiplicazione veloce di interi: primo algoritmo c0 se n apple 1 T (n) apple 4T (n/2) + cn altrimenti Applicazione del risultato provato: si ha che =4, =2ek =1 > k,quindisiapplicailterzocasoesihat (n) =O(n log 2 4 )=O(n 2 ) Moltiplicazione veloce di interi: secondo algoritmo T (n) apple c0 se n apple 1 3T (n/2) + cn altrimenti Applicando il risultato dimostrato, si ha che =3, =2ek =1 > k,quindisiapplicailterzocasoesihat (n) =O(n log 2 3 )=O(n 1,585 )
16 Divide et impera su alberi Caso base: peru = null o una foglia Decomposizione: riformula il problema per i sottoalberi radicati nei figli di u. Ricombinazione: ottieniilrisultatoconricombina 1 Decomponibile(u): 2 if (u == null) { 3 return valore base; 4 } else { 5 i=0; FOR( ciascun figlio f di u ){ 6 risultatifigli[i] = Decomponibile(f); 7 i=i+1 } 8 return Ricombina(risultatiFigli); 9 } La ricombinazione dei risultati della chiamate ricorsive sui figli potrebbe essere e ettuata anche nel for man mano che vengono ottenuti i risultati delle chiamate sui figli.
17 Divide et impera su alberi binari Caso base: peru = null o una foglia Decomposizione: riformula il problema per i sottoalberi radicati nei figli u.sx e u.dx Ricombinazione: ottieniilrisultatoconricombina 1 Decomponibile(u): 2 if (u == null) { 3 return valore base; 4 } else { 5 risultatosx = Decomponibile(u.sx); 6 risultatodx = Decomponibile(u.dx); 7 return Ricombina(risultatoSX, risultatodx); 8 }
18
19 Algoritmi ricorsivi su alberi: dimensione Calcolo della dimensione d = numero di nodi Caso base: albero vuoto ) d =0 Caso induttivo: d =1+dimensionedelsottoalberosinistro+dimensione del sottoalbero destro 1 Dimensione( u ): 2 if (u == null) { 3 return 0; 4 } else { 5 dimensionesx = Dimensione( u.sx ); 6 dimensionedx = Dimensione( u.dx ); 7 return dimensionesx + dimensionedx + 1; 8 } Se si vuole conoscere la dimensione di tutto l albero, si invoca Dimensione con u uguale alla radice
20 Algoritmi ricorsivi su alberi: altezza Calcolo dell altezza h di un nodo: caso base per null ) h = 1 passo induttivo: h =1+massimaaltezzadeifigli 1 Altezza( u ): 2 if (u == null) { 3 return -1; 4 } else { 5 altezzasx = Altezza( u.sx ); 6 altezzadx = Altezza( u.dx ); 7 return max( altezzasx, altezzadx ) + 1; 8 } Per calcolare l altezza dell albero, si invoca Altezza con u uguale alla radice
21 Visita di un albero binario: inorder simmetrica (inorder): 1 Simmetrica( u ): 2 if (u!= null) { 3 Simmetrica( u.sx ); 4 elabora(u); 5 Simmetrica( u.dx ); 6 } O(n) tempopern nodi
22 Visita di un albero binario: preorder anticipata (preorder): 1 Anticipata( u ): 2 if (u!= null) { 3 elabora(u); 4 Antiticipata( u.sx ); 5 Antiticipata( u.dx ); 6 } O(n) tempopern nodi
23 Visita di un albero binario: postorder posticipata (postorder): 1 Posticipata( u ): 2 if (u!= null) { 3 Posticipata( u.sx ); 4 Posticipata( u.dx ); 5 elabora(u); 6 } O(n) tempopern nodi
24 Esempio dell uso delle visite
25 Uso della visita postorder per valutare l espressione aritmetica rapprentata da un albero binario 1 Valuta( u ): 2 if (u==null) { 3 return null; 4 } 5 if (u.sx == null && u.dx==null) { 6 return u.dato; 7 } else { 8 valsinistra=valuta( u.sx ); 9 valdestra= Valuta( u.dx ); 10 ris= Calcola(u.dato,valSinistra,valDestra); 11 return ris; 12 } La funzione Calcola invocata su u.dato, valsinistra e valdestra, applica l operatore memorizzato nel nodo interno u ai valori valsinistra e valdestra. N.B.: la condizione del primo if è soddisfatta (u è n u l l ) s o l o s e inizialmente la funzione Valuta è invocata su null. Se inizialmente Valuta è invocata su un nodo u 6= null allora la condizione del primo if non sarà mai soddisfatta perché quando è invocata su una foglia, la funzione restituisce il contenuto della foglia.
26 Algoritmo per verificare se un albero binario è completamente bilanciato Definizioni: Albero binario completo: ogninodointernohasempreduefiglinonvuoti Albero completamente bilanciato: alberocompletocontuttelefoglie alla stessa profondità Esempio:
27 Algoritmo per verificare se un albero binario è completamente bilanciato Def. ricorsiva di albero completamente bilanciato: Un albero binario vuoto è completamente bilanciato Una albero binario con almeno un nodo è completamente bilanciato se e solo se il sottoalbero destro e il sottoalbero sinistro della radice sono completamente bilanciati e hanno la stessa altezza (per convenzione, un albero vuoto ha altezza -1) N.B. In un albero completamente bilanciato l altezza dell albero corrisponde alla profondità di tutte le foglie Indichiamo con T (u) ilsottoalberodit radicato in u Risolviamo un problema più generale per T (u), calcolandone anche l altezza oltre che a dire se è completamente bilanciato o meno La ricorsione restituisce una coppia (booleano, intero) Tempo di risoluzione: O(n) tempo per n nodi 1 CompletamenteBilanciato( u ): 2 if (u == null) { 3 return <true, -1>; 4 } else { 5 <bilsx,altsx> = CompletamenteBilanciato( u.sx ); 6 <bildx,altdx> = CompletamenteBilanciato( u.dx ); 7 bil = bilsx && bildx && (altsx == altdx); 8 altezza = max(altsx, altdx) + 1; 9 return <bil,altezza>; 10 }
28 Algoritmi ricorsivi su alberi: profondità di un nodo La radice ha profondità 0 I figli della radice hanno profondità pari a 1, e così via Un nodo ha profondità p ha i figli a profondità p +1 Versione iterativa dell algoritmo per calcolare la profondità di un nodo u p = 0; while (u.padre!= null) { p = p + 1; u = u.padre; } Definizione ricorsiva di profondità di un nodo: La radice ha profondità 0 I nodi diversi dalla radice hanno profondità pari alla profondità del padre + 1 Versione ricorsiva dell algoritmo per calcolare la profondità di un nodo u 1 Profondita( u ): 2 if (u.padre==null) { 3 return 0; 4 } 5 return profondita(u.padre)+1;
29 Trasmissione dell informazione tra chiamate ricorsive postorder : l informazione è trasferita dalle foglie alla radice la soluzione del problema per T (u) puòessereottenutadallasoluzioni dei sottoproblemi per T (u.sx) et (u.dx) passaggio dei parametri : informazione passata attraverso i parametri dalla radice alle foglie la soluzione del problema per T (u) puòesserreottenutautilizzando l informazione raccolta dalla radice fino al nodo u Esempio: stampa la profondità di tutti i nodi 1 Profondita( u, p ): 2 if (u!= null) { 3 print profondità di u è pari a p; 4 Profondita( u.sx, p+1 ); 5 Profondita( u.dx, p+1 ); 6 } Il parametro p indica la profondità del nodo u. Sevogliamostamparele profondità di tutti i nodi dobbiamo invocare la funzione con u uguale all indirizzo della radice dell albero e p =0.
30 Algoritmo per trovare i nodi cardine Trasferiamo informazione simultaneamente dalle foglie alla radice e dalla radice verso le foglie combinando i due approcci della slide precedente Nodo u è c a r d i n e s e e s o l o s e profondita(u) =altezza(t (u)) 1 Cardine( u, p ): 2 if (u == null) { 3 return -1; 4 } else { 5 altezzasx = Cardine( u.sx, p+1 ); 6 altezzadx = Cardine( u.dx, p+1 ); 7 altezza = max( altezzasx, altezzadx ) + 1; 8 if (p == altezza) print u.dato; 9 return altezza; 10 }
Divide et impera su alberi
 Divide et impera su alberi Caso base: peru = null o una foglia Decomposizione: riformula il problema per i sottoalberi radicati nei figli di u. Ricombinazione: ottieniilrisultatoconricombina 1 Decomponibile(u):
Divide et impera su alberi Caso base: peru = null o una foglia Decomposizione: riformula il problema per i sottoalberi radicati nei figli di u. Ricombinazione: ottieniilrisultatoconricombina 1 Decomponibile(u):
Selezione per distribuzione
 Selezione per distribuzione Problema: selezione dell elemento con rango r in un array a di n elementi distinti. Si vuole evitare di ordinare a NB: Il problema diventa quello di trovare il minimo quando
Selezione per distribuzione Problema: selezione dell elemento con rango r in un array a di n elementi distinti. Si vuole evitare di ordinare a NB: Il problema diventa quello di trovare il minimo quando
Ricerca con una chiave k Assumiamo l esistenza di un descrittore albero con i campi: albero.radice (=null per l albero vuoto) albero.dimensione (=0 pe
 Ricerca con una chiave k Assumiamo l esistenza di un descrittore albero con i campi: albero.radice (=null per l albero vuoto) albero.dimensione (=0 per l albero vuoto) La funzione Ricerca prende in input
Ricerca con una chiave k Assumiamo l esistenza di un descrittore albero con i campi: albero.radice (=null per l albero vuoto) albero.dimensione (=0 per l albero vuoto) La funzione Ricerca prende in input
Note per la Lezione 4 Ugo Vaccaro
 Progettazione di Algoritmi Anno Accademico 2016 2017 Note per la Lezione 4 Ugo Vaccaro Ripasso di nozioni su Alberi Ricordiamo che gli alberi rappresentano una generalizzazione delle liste, nel senso che
Progettazione di Algoritmi Anno Accademico 2016 2017 Note per la Lezione 4 Ugo Vaccaro Ripasso di nozioni su Alberi Ricordiamo che gli alberi rappresentano una generalizzazione delle liste, nel senso che
d. Cancellazione del valore 5 e. Inserimento del valore 1
 Esercizio1 Si consideri un albero binario non vuoto in cui a ciascun nodo v è associato un numero reale v.val. Scrivere un algoritmo che, dato in input l'albero T e un numero reale x, restituisce true
Esercizio1 Si consideri un albero binario non vuoto in cui a ciascun nodo v è associato un numero reale v.val. Scrivere un algoritmo che, dato in input l'albero T e un numero reale x, restituisce true
In questa lezione. Alberi binari: [CLRS09] cap. 12 per la visita inorder. visite e esercizi su alberi binari. Prof. E. Fachini - Intr. Alg.
![In questa lezione. Alberi binari: [CLRS09] cap. 12 per la visita inorder. visite e esercizi su alberi binari. Prof. E. Fachini - Intr. Alg. In questa lezione. Alberi binari: [CLRS09] cap. 12 per la visita inorder. visite e esercizi su alberi binari. Prof. E. Fachini - Intr. Alg.](/thumbs/93/113927179.jpg) In questa lezione Alberi binari: visite e esercizi su alberi binari [CLRS09] cap. 12 per la visita inorder!1 Visita inordine di un albero binario visita inordine(x) se l albero x non è nullo allora visita
In questa lezione Alberi binari: visite e esercizi su alberi binari [CLRS09] cap. 12 per la visita inorder!1 Visita inordine di un albero binario visita inordine(x) se l albero x non è nullo allora visita
Esercizi su BST. IASD a.a A. De Bonis
 Esercizi su BST Esercizio 1 Scrivere un algoritmo che prendein input un albero binarioe restituisce true se e solo se l alberoe` un albero binariodi ricerca. L algoritmo deve utilizzaresolo una quantita`
Esercizi su BST Esercizio 1 Scrivere un algoritmo che prendein input un albero binarioe restituisce true se e solo se l alberoe` un albero binariodi ricerca. L algoritmo deve utilizzaresolo una quantita`
Algoritmi e Strutture Dati
 Algoritmi e Strutture Dati Modelli di calcolo e metodologie di analisi Domenico Fabio Savo 1 Notazione asintotica f(n) = tempo di esecuzione / occupazione di memoria di un algoritmo su input di dimensione
Algoritmi e Strutture Dati Modelli di calcolo e metodologie di analisi Domenico Fabio Savo 1 Notazione asintotica f(n) = tempo di esecuzione / occupazione di memoria di un algoritmo su input di dimensione
Algoritmi e strutture di dati 2
 Algoritmi e strutture di dati 2 Paola Vocca Lezione 1: Divide et Impera 1 Paradigma del divide et impera Strutturato in tre fasi. Sia Π() istanza di dimensione di un problema computazionale Π (dove è immediato
Algoritmi e strutture di dati 2 Paola Vocca Lezione 1: Divide et Impera 1 Paradigma del divide et impera Strutturato in tre fasi. Sia Π() istanza di dimensione di un problema computazionale Π (dove è immediato
GLI ALBERI BINARI DI RICERCA. Cosimo Laneve
 GLI ALBERI BINARI DI RICERCA Cosimo Laneve argomenti 1. alberi binari di ricerca 2. la ricerca di elementi e la complessità computazionale 3. operazione di cancellazione di elementi 4. esempi/esercizi
GLI ALBERI BINARI DI RICERCA Cosimo Laneve argomenti 1. alberi binari di ricerca 2. la ricerca di elementi e la complessità computazionale 3. operazione di cancellazione di elementi 4. esempi/esercizi
Esercizi di Algoritmi e Strutture Dati
 Esercizi di Algoritmi e Strutture Dati Moreno Marzolla marzolla@cs.unibo.it Ultimo aggiornamento: 3 novembre 2010 1 Trova la somma/1 Scrivere un algoritmo che dati in input un array A[1... n] di n interi
Esercizi di Algoritmi e Strutture Dati Moreno Marzolla marzolla@cs.unibo.it Ultimo aggiornamento: 3 novembre 2010 1 Trova la somma/1 Scrivere un algoritmo che dati in input un array A[1... n] di n interi
Dati e Algoritmi 1: A. Pietracaprina. Alberi Binari
 Dati e Algoritmi 1: A. Pietracaprina Alberi Binari 1 Definizione Un alberto binario T è un albero ordinato in cui Nota ogni nodo interno ha 2 figli ogni nodo non radice è etichettato come figlio sinistro
Dati e Algoritmi 1: A. Pietracaprina Alberi Binari 1 Definizione Un alberto binario T è un albero ordinato in cui Nota ogni nodo interno ha 2 figli ogni nodo non radice è etichettato come figlio sinistro
Il numero dei nodi al livello i è 1, per 0 i altezza L altezza h di un albero completamente sbilanciato con n nodi è h = n-1
 alberi completamente sbilanciati Il numero dei nodi al livello i è 1, per 0 i altezza L altezza h di un albero completamente sbilanciato con n nodi è h = n-1 1 Un albero completamente bilanciato o pieno
alberi completamente sbilanciati Il numero dei nodi al livello i è 1, per 0 i altezza L altezza h di un albero completamente sbilanciato con n nodi è h = n-1 1 Un albero completamente bilanciato o pieno
Esame di Algoritmi e Strutture Dati Corso di Laurea in Ingegneria Informatica Canali A-L, M-Z
 Esame di Algoritmi e Strutture Dati Corso di Laurea in Ingegneria Informatica Canali A-L, M-Z Anno Accademico 2002-2003 9 luglio 2002-03 Domanda 1, punti 6 Si consideri la seguente classe Java, in cui,
Esame di Algoritmi e Strutture Dati Corso di Laurea in Ingegneria Informatica Canali A-L, M-Z Anno Accademico 2002-2003 9 luglio 2002-03 Domanda 1, punti 6 Si consideri la seguente classe Java, in cui,
Algoritmi e Strutture Dati & Laboratorio di Algoritmi e Programmazione
 Algoritmi e Strutture Dati & Laboratorio di Algoritmi e Programmazione Appello del 24 Gennaio 2007 Esercizio 1 (ASD) 1. Sia T (n) = T (n/6) + T (n/3) + Θ(n). Considerare ciascuna delle seguenti affermazioni
Algoritmi e Strutture Dati & Laboratorio di Algoritmi e Programmazione Appello del 24 Gennaio 2007 Esercizio 1 (ASD) 1. Sia T (n) = T (n/6) + T (n/3) + Θ(n). Considerare ciascuna delle seguenti affermazioni
alberi completamente sbilanciati
 alberi completamente sbilanciati Il numero dei nodi al livello i è 1, per 0 i altezza L altezza h di un albero completamente sbilanciato con n nodi è h = n-1 1 Un albero completamente bilanciato o pieno
alberi completamente sbilanciati Il numero dei nodi al livello i è 1, per 0 i altezza L altezza h di un albero completamente sbilanciato con n nodi è h = n-1 1 Un albero completamente bilanciato o pieno
Esercizio 1. E vero che in un AVL il minimo si trova in una foglia o nel penultimo livello? FB = -1. livello 0 FB = -1. livello 1 FB = -1.
 Esercizio 1 E vero che in un AVL il minimo si trova in una foglia o nel penultimo livello? FB = -1 livello 0 FB = -1 FB = -1 livello 1 FB = -1 livello 2 livello 3 L altezza è 3, il minimo si trova nel
Esercizio 1 E vero che in un AVL il minimo si trova in una foglia o nel penultimo livello? FB = -1 livello 0 FB = -1 FB = -1 livello 1 FB = -1 livello 2 livello 3 L altezza è 3, il minimo si trova nel
Un albero completamente bilanciato o pieno (full) alberi completamente sbilanciati. Un albero binario completo
 alberi completamente sbilanciati Un albero completamente bilanciato o pieno (full) Definizione: Un albero è pieno se tutte le foglie sono sullo stesso livello e ogni nodo non foglia ha due figli. Il numero
alberi completamente sbilanciati Un albero completamente bilanciato o pieno (full) Definizione: Un albero è pieno se tutte le foglie sono sullo stesso livello e ogni nodo non foglia ha due figli. Il numero
Esercizi su ABR. Prof. E. Fachini - Intr. Alg.!1
 Esercizi su ABR Confronto proprietà ABR e Max-Heap. Proprietà del cammino radice-foglia individuato da una ricerca. Fusione di due ABR. Il successivo calcolato dalla radice Costruzione di un ABR bilanciato
Esercizi su ABR Confronto proprietà ABR e Max-Heap. Proprietà del cammino radice-foglia individuato da una ricerca. Fusione di due ABR. Il successivo calcolato dalla radice Costruzione di un ABR bilanciato
Esercizi BST - AVL. E. Fachini
 Esercizi BST - AVL. Verifica che un ABR è un AVL 2. verifica bilanciamento in altezza di un ABR 3. Costruzione alberi di Fibonacci 4. Calcolo altezza albero AVL in O(lg n) 5. split di una ABR intorno a
Esercizi BST - AVL. Verifica che un ABR è un AVL 2. verifica bilanciamento in altezza di un ABR 3. Costruzione alberi di Fibonacci 4. Calcolo altezza albero AVL in O(lg n) 5. split di una ABR intorno a
Strutture dati Alberi binari
 Strutture dati - 2 - Alberi binari Definizione L albero è un insieme di elementi (nodi), sui quali è definita una relazione di discendenza con due proprietà: esiste un solo nodo radice senza predecessori
Strutture dati - 2 - Alberi binari Definizione L albero è un insieme di elementi (nodi), sui quali è definita una relazione di discendenza con due proprietà: esiste un solo nodo radice senza predecessori
Alberi binari e alberi binari di ricerca
 Università degli studi di Milano Dipartimento di Informatica Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica Alberi Un albero è una collezione non vuota di: nodi con nome e informazioni
Università degli studi di Milano Dipartimento di Informatica Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica Alberi Un albero è una collezione non vuota di: nodi con nome e informazioni
Alberi Binari di Ricerca
 Alberi Binari di Ricerca Algoritmi su gli alberi binari: visite Dato un puntatore alla radice di un albero vogliamo scandire in modo sistematico tutti i nodi di tale albero In una lista abbiamo una unica
Alberi Binari di Ricerca Algoritmi su gli alberi binari: visite Dato un puntatore alla radice di un albero vogliamo scandire in modo sistematico tutti i nodi di tale albero In una lista abbiamo una unica
Esempi. Albero di interi. Struttura che non è un albero!
 albero si dice "grafo diretto" un insieme di nodi legati "a due a due" da archi direzionati (puntatori) un albero è un grafo diretto in cui ogni nodo può avere un solo arco entrante ed un qualunque numero
albero si dice "grafo diretto" un insieme di nodi legati "a due a due" da archi direzionati (puntatori) un albero è un grafo diretto in cui ogni nodo può avere un solo arco entrante ed un qualunque numero
Alberi ed Alberi Binari di Ricerca
 Alberi ed Alberi Binari di Ricerca Il tipo di dato Albero Un albero è una struttura di data organizzata gerarchicamente. È costituito da un insieme di nodi collegati tra di loro: ogni nodo contiene dell
Alberi ed Alberi Binari di Ricerca Il tipo di dato Albero Un albero è una struttura di data organizzata gerarchicamente. È costituito da un insieme di nodi collegati tra di loro: ogni nodo contiene dell
Nozioni di base (II Parte)
 Nozioni di base (II Parte) 1 Ricorsione [GTG14, Par. 5.1-5.4 and 13.1] Algoritmo Ricorsivo: algoritmo che invoca se stesso (su istanze sempre più piccole) sfruttando la nozione di induzione. La soluzione
Nozioni di base (II Parte) 1 Ricorsione [GTG14, Par. 5.1-5.4 and 13.1] Algoritmo Ricorsivo: algoritmo che invoca se stesso (su istanze sempre più piccole) sfruttando la nozione di induzione. La soluzione
Alberi binari e alberi binari di ricerca
 Alberi binari e alberi binari di ricerca Violetta Lonati Università degli studi di Milano Dipartimento di Informatica Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica giovedì 9
Alberi binari e alberi binari di ricerca Violetta Lonati Università degli studi di Milano Dipartimento di Informatica Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica giovedì 9
Algoritmo di ordinamento sul posto che ha tempo di esecuzione :
 QuickSort Algoritmo di ordinamento sul posto che ha tempo di esecuzione : O(n2 ) nel caso peggiore O(n log n) nel caso medio Nonostante le cattive prestazioni nel caso peggiore, rimane il miglior algoritmo
QuickSort Algoritmo di ordinamento sul posto che ha tempo di esecuzione : O(n2 ) nel caso peggiore O(n log n) nel caso medio Nonostante le cattive prestazioni nel caso peggiore, rimane il miglior algoritmo
Alberi binari e alberi binari di ricerca
 Alberi binari e alberi binari di ricerca Violetta Lonati Università degli studi di Milano Dipartimento di Scienze dell Informazione Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica
Alberi binari e alberi binari di ricerca Violetta Lonati Università degli studi di Milano Dipartimento di Scienze dell Informazione Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica
Alberi ed Alberi Binari
 Alberi ed Alberi Binari Il tipo di dato Albero Un albero è una struttura di data organizzata gerarchicamente. È costituito da un insieme di nodi collegati tra di loro: ogni nodo contiene dell informazione,
Alberi ed Alberi Binari Il tipo di dato Albero Un albero è una struttura di data organizzata gerarchicamente. È costituito da un insieme di nodi collegati tra di loro: ogni nodo contiene dell informazione,
Alberi binari (radicati e ordinati) della radice Il padre del nodo 5 e del nodo 3
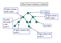 Alberi binari (radicati e ordinati) Il figlio sinistro della radice Il padre del nodo 5 e del nodo 3 4 3 Il figlio sinistro del nodo 2 2 5 1 6 7 8 9 La radice Il figlio destro della radice una foglia Figlio
Alberi binari (radicati e ordinati) Il figlio sinistro della radice Il padre del nodo 5 e del nodo 3 4 3 Il figlio sinistro del nodo 2 2 5 1 6 7 8 9 La radice Il figlio destro della radice una foglia Figlio
Algoritmi e Strutture Dati. HeapSort
 Algoritmi e Strutture Dati HeapSort Selection Sort: intuizioni L algoritmo Selection-Sort scandisce tutti gli elementi dell array a partire dall ultimo elemento fino all inizio e ad ogni iterazione: Viene
Algoritmi e Strutture Dati HeapSort Selection Sort: intuizioni L algoritmo Selection-Sort scandisce tutti gli elementi dell array a partire dall ultimo elemento fino all inizio e ad ogni iterazione: Viene
Introduzione agli algoritmi Prova di esame del 19/9/2016 Prof.sse E. Fachini - R. Petreschi. Parte prima
 Introduzione agli algoritmi Prova di esame del 19/9/2016 Prof.sse E. Fachini - R. Petreschi Parte prima 1) Si dimostri il teorema sulla limitazione inferiore per il tempo asintotico di esecuzione nel caso
Introduzione agli algoritmi Prova di esame del 19/9/2016 Prof.sse E. Fachini - R. Petreschi Parte prima 1) Si dimostri il teorema sulla limitazione inferiore per il tempo asintotico di esecuzione nel caso
ADT Dizionario. Ordered search table. Supponiamo che sia definita una relazione d'ordine totale sulle chiavi del dizionario D:
 Ordered search table Supponiamo che sia definita una relazione d'ordine totale sulle chiavi del dizionario D: possiamo memorizzare le entrate di D in un array list S in ordine non decrescente di chiavi:
Ordered search table Supponiamo che sia definita una relazione d'ordine totale sulle chiavi del dizionario D: possiamo memorizzare le entrate di D in un array list S in ordine non decrescente di chiavi:
Algoritmi e Strutture Dati. HeapSort
 Algoritmi e Strutture Dati HeapSort Selection Sort: intuizioni L algoritmo Selection-Sort scandisce tutti gli elementi dell array a partire dall ultimo elemento fino all inizio e ad ogni iterazione: Viene
Algoritmi e Strutture Dati HeapSort Selection Sort: intuizioni L algoritmo Selection-Sort scandisce tutti gli elementi dell array a partire dall ultimo elemento fino all inizio e ad ogni iterazione: Viene
Algoritmi di ordinamento
 Algoritmi e Strutture Dati Ordinamento Dato un insieme S di n oggetti presi da un dominio totalmente ordinato, ordinare S Algoritmi di ordinamento Esempi: ordinare una lista di nomi alfabeticamente, o
Algoritmi e Strutture Dati Ordinamento Dato un insieme S di n oggetti presi da un dominio totalmente ordinato, ordinare S Algoritmi di ordinamento Esempi: ordinare una lista di nomi alfabeticamente, o
Esercizi su alberi binari
 Esercizi su alberi binari Esercizi svolti: Determinazione nodi contenti verifica completezza verifica quasi completezza lunghezza del cammino interno determinazione ultima foglia in un quasi completo verifica
Esercizi su alberi binari Esercizi svolti: Determinazione nodi contenti verifica completezza verifica quasi completezza lunghezza del cammino interno determinazione ultima foglia in un quasi completo verifica
Lezione 7 Alberi binari: visite e alberi di ricerca
 Lezione 7 Alberi binari: visite e alberi di ricerca Informatica 6 Maggio 2015 Operazioni sugli alberi: visita La visita di un albero esplora tutti i nodi ed esegue una qualche operazione su di essi. Per
Lezione 7 Alberi binari: visite e alberi di ricerca Informatica 6 Maggio 2015 Operazioni sugli alberi: visita La visita di un albero esplora tutti i nodi ed esegue una qualche operazione su di essi. Per
Algoritmi e strutture dati
 Algoritmi e Strutture Dati Capitolo 4 Ordinamento Ordinamento Dato un insieme S di n oggetti presi da un dominio totalmente ordinato, ordinare S Esempi: ordinare alfabeticamente lista di nomi, o insieme
Algoritmi e Strutture Dati Capitolo 4 Ordinamento Ordinamento Dato un insieme S di n oggetti presi da un dominio totalmente ordinato, ordinare S Esempi: ordinare alfabeticamente lista di nomi, o insieme
Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano. Usa la tecnica del divide et impera:
 MergeSort Usa la tecnica del divide et impera: 1 Divide: dividi l array a metà 2 Risolvi i due sottoproblemi ricorsivamente 3 Impera: fondi le due sottosequenze ordinate 1 Esempio di esecuzione 7 2 4 5
MergeSort Usa la tecnica del divide et impera: 1 Divide: dividi l array a metà 2 Risolvi i due sottoproblemi ricorsivamente 3 Impera: fondi le due sottosequenze ordinate 1 Esempio di esecuzione 7 2 4 5
ESERCITAZIONI DI INTRODUZIONE AGLI ALGORITMI (A.A. 08/09)
 ESERCITAZIONI DI INTRODUZIONE AGLI ALGORITMI (A.A. 0/0) DISPENSA N. 6 Esercizi su alberi di ricerca e AVL Notazione: Per un albero T scriviamo T per indicare il numero dei nodi di T e h(t ) per indicare
ESERCITAZIONI DI INTRODUZIONE AGLI ALGORITMI (A.A. 0/0) DISPENSA N. 6 Esercizi su alberi di ricerca e AVL Notazione: Per un albero T scriviamo T per indicare il numero dei nodi di T e h(t ) per indicare
Algoritmo di ordinamento sul posto che ha tempo di esecuzione :
 QuickSort Algoritmo di ordinamento sul posto che ha tempo di esecuzione : - O(n 2 ) nel caso peggiore - O(n log n) nel caso medio Nonostante le cattive prestazioni nel caso peggiore, rimane il miglior
QuickSort Algoritmo di ordinamento sul posto che ha tempo di esecuzione : - O(n 2 ) nel caso peggiore - O(n log n) nel caso medio Nonostante le cattive prestazioni nel caso peggiore, rimane il miglior
Dati e Algoritmi I (Pietracaprina) Esercizi sugli Alberi
 Dati e Algoritmi I (Pietracaprina) Esercizi sugli Alberi Dati e Algoritmi I (Pietracaprina): Esercizi 1 Problema 1 Dimostrare che un albero non vuoto con n nodi interni, dove ogni nodo interno ha almeno
Dati e Algoritmi I (Pietracaprina) Esercizi sugli Alberi Dati e Algoritmi I (Pietracaprina): Esercizi 1 Problema 1 Dimostrare che un albero non vuoto con n nodi interni, dove ogni nodo interno ha almeno
Fondamenti di Programmazione - Prof.ssa Gargano Anno Acc Esercitazioni 2009
 Fondamenti di Programmazione - Prof.ssa Gargano Anno Acc. 2008-09 Esercitazioni 2009 1. Mostrare per induzione che per ogni intero positivo n 0, la seguente affermazione S(n) é vera: S(n): n i=0 2i = 2
Fondamenti di Programmazione - Prof.ssa Gargano Anno Acc. 2008-09 Esercitazioni 2009 1. Mostrare per induzione che per ogni intero positivo n 0, la seguente affermazione S(n) é vera: S(n): n i=0 2i = 2
LABORATORIO DI PROGRAMMAZIONE 2 Corso di laurea in matematica. Algoritmi ricorsivi
 LABORATORIO DI PROGRAMMAZIONE 2 Corso di laurea in matematica Marco Lapegna Dipartimento di Matematica e Applicazioni Universita degli Studi di Napoli Federico II wpage.unina.it/lapegna Partiamo da un
LABORATORIO DI PROGRAMMAZIONE 2 Corso di laurea in matematica Marco Lapegna Dipartimento di Matematica e Applicazioni Universita degli Studi di Napoli Federico II wpage.unina.it/lapegna Partiamo da un
Alberi binari: definizione e alcune proprietà
 Alberi binari: definizione e alcune proprietà Alberi binari Un albero binario è un albero con radice in cui ogni nodo ha al più due figli. In maniera più formale: Definizione. (Alberi binari) Un albero
Alberi binari: definizione e alcune proprietà Alberi binari Un albero binario è un albero con radice in cui ogni nodo ha al più due figli. In maniera più formale: Definizione. (Alberi binari) Un albero
Albero binario. Alberi binari (introduzione) Terminologia. Alberi di ricerca binaria (BST)
 Albero binario 2 Alberi binari (introduzione) Struttura di dati bidimensionale formata da nodi costituiti ciascuno dai dati da memorizzare e da due link Ver. 2.4 20 - Claudio Fornaro - Corso di programmazione
Albero binario 2 Alberi binari (introduzione) Struttura di dati bidimensionale formata da nodi costituiti ciascuno dai dati da memorizzare e da due link Ver. 2.4 20 - Claudio Fornaro - Corso di programmazione
Esercizi parte 3. La classe ArrayBinTree dovra implementare, tra le altre, l operazione seguente: padre: dato un nodo, restituire l indice del padre.
 Esercizi parte 3 RAPPRESENTAZIONE DI ALBERI BINARI 1. Definire una classe LinkedBinTree che implementa alberi binari in modo collegato, con nodi implementati come oggetti di classe BinNode. La classe dovra
Esercizi parte 3 RAPPRESENTAZIONE DI ALBERI BINARI 1. Definire una classe LinkedBinTree che implementa alberi binari in modo collegato, con nodi implementati come oggetti di classe BinNode. La classe dovra
Esercizi Capitolo 6 - Alberi binari di ricerca
 Esercizi Capitolo 6 - Alberi binari di ricerca Alberto Montresor 9 Agosto, 204 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente, è possibile
Esercizi Capitolo 6 - Alberi binari di ricerca Alberto Montresor 9 Agosto, 204 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente, è possibile
come segue: data una collezione C di elementi e una un elemento che verifica la proprietà P
 Problemi di Ricerca Carla Binucci e Walter Didimo Il problema della Ricerca In generale, il Problema della Ricerca è definito come segue: data una collezione C di elementi e una proprietà P, determinare
Problemi di Ricerca Carla Binucci e Walter Didimo Il problema della Ricerca In generale, il Problema della Ricerca è definito come segue: data una collezione C di elementi e una proprietà P, determinare
ALBERI : introduzione SOMMARIO ALBERI ALBERI. ALBERI: introduzione ALBERI BINARI: introduzione VISITE RICORSIVE DI ALBERI
 SOMMARIO ALBERI: introduzione ALBERI BINARI: introduzione VISITE RICORSIVE DI ALBERI Dimensione e Altezza ALBERI BINARI DI RICERCA (BST) Introduzione Ricerca, inserimento e cancellazione Implementazione
SOMMARIO ALBERI: introduzione ALBERI BINARI: introduzione VISITE RICORSIVE DI ALBERI Dimensione e Altezza ALBERI BINARI DI RICERCA (BST) Introduzione Ricerca, inserimento e cancellazione Implementazione
Algoritmi e Strutture Dati
 Algoritmi e Strutture Dati Capitolo 4 Ordinamento Ordinamento Dato un insieme S di n oggetti presi da un dominio totalmente ordinato, ordinare S Esempi: ordinare una lista di nomi alfabeticamente, o un
Algoritmi e Strutture Dati Capitolo 4 Ordinamento Ordinamento Dato un insieme S di n oggetti presi da un dominio totalmente ordinato, ordinare S Esempi: ordinare una lista di nomi alfabeticamente, o un
Esercizi per il corso di Algoritmi, anno accademico 2011/12
 Esercizi per il corso di Algoritmi, anno accademico 2011/12 Esercizi sulla Tecnica Divide et Impera N.B. Tutti gli algoritmi vanno scritti in pseudocodice (non in Java, nè in C++, etc. ). Di tutti gli
Esercizi per il corso di Algoritmi, anno accademico 2011/12 Esercizi sulla Tecnica Divide et Impera N.B. Tutti gli algoritmi vanno scritti in pseudocodice (non in Java, nè in C++, etc. ). Di tutti gli
LE STRUTTURE DATI DINAMICHE: GLI ALBERI. Cosimo Laneve
 LE STRUTTURE DATI DINAMICHE: GLI ALBERI Cosimo Laneve 1 argomenti 1. definizione di alberi e nozioni relative 2. implementazione degli alberi, creazione, visita 3. algoritmo di visita iterativa e sua implementazione
LE STRUTTURE DATI DINAMICHE: GLI ALBERI Cosimo Laneve 1 argomenti 1. definizione di alberi e nozioni relative 2. implementazione degli alberi, creazione, visita 3. algoritmo di visita iterativa e sua implementazione
Un esempio di mutua ricorsione
 Inserimento in un ABR n-bilanciato Un esempio di mutua ricorsione con gli alberi bilanciati in altezza, proprietà più debole, si ottiene maggiore semplicità delle operazioni di ribilanciamento (niente
Inserimento in un ABR n-bilanciato Un esempio di mutua ricorsione con gli alberi bilanciati in altezza, proprietà più debole, si ottiene maggiore semplicità delle operazioni di ribilanciamento (niente
Lezione 12 Tabelle Hash
 Lezione 12 Tabelle Hash Rossano Venturini rossano@di.unipi.it Pagina web del corso http://didawiki.cli.di.unipi.it/doku.php/informatica/all-b/start Esercizio 2 ABR: Visita Scrivere un programma che legga
Lezione 12 Tabelle Hash Rossano Venturini rossano@di.unipi.it Pagina web del corso http://didawiki.cli.di.unipi.it/doku.php/informatica/all-b/start Esercizio 2 ABR: Visita Scrivere un programma che legga
ricerca di un elemento, verifica dell appartenenza di un elemento
 Alberi Binari di Ricerca Gli alberi binari di ricerca (o, alberi di ricerca binaria) sono strutture dati che consentono, su un insieme di elementi con un ordine totale le operazioni di: ricerca di un elemento,
Alberi Binari di Ricerca Gli alberi binari di ricerca (o, alberi di ricerca binaria) sono strutture dati che consentono, su un insieme di elementi con un ordine totale le operazioni di: ricerca di un elemento,
COGNOME E NOME (IN STAMPATELLO) MATRICOLA
 Politecnico di Milano Facoltà di Ingegneria dell Informazione Informatica 3 Proff. Campi, Ghezzi, Matera e Morzenti Appello del 14 Settembre 2006 Recupero II Parte COGNOME E NOME (IN STAMPATELLO) MATRICOLA
Politecnico di Milano Facoltà di Ingegneria dell Informazione Informatica 3 Proff. Campi, Ghezzi, Matera e Morzenti Appello del 14 Settembre 2006 Recupero II Parte COGNOME E NOME (IN STAMPATELLO) MATRICOLA
Pensiero Algoritmico. Lezione 3 23 Novembre Ripasso. Anatomia di un programma. Anatomia di un programma. Ozalp Babaoglu Università di Bologna
 Pensiero Algoritmico Lezione 3 23 Novembre 2016 Ozalp Babaoglu Università di Bologna Ripasso Definizione del problema Astrarre i dettagli, costruire un modello Costruire l algoritmo che risolve il problema
Pensiero Algoritmico Lezione 3 23 Novembre 2016 Ozalp Babaoglu Università di Bologna Ripasso Definizione del problema Astrarre i dettagli, costruire un modello Costruire l algoritmo che risolve il problema
Alberi binari di ricerca
 Alberi binari di ricerca Ilaria Castelli castelli@dii.unisi.it Università degli Studi di Siena Dipartimento di Ingegneria dell Informazione A.A. 2009/20010 I. Castelli Alberi binari di ricerca, A.A. 2009/20010
Alberi binari di ricerca Ilaria Castelli castelli@dii.unisi.it Università degli Studi di Siena Dipartimento di Ingegneria dell Informazione A.A. 2009/20010 I. Castelli Alberi binari di ricerca, A.A. 2009/20010
Università degli Studi di Camerino Laurea in Informatica Prima Prova Parziale del corso di Algoritmi e Strutture Dati
 Università degli Studi di Camerino Laurea in Informatica Prima Prova Parziale del corso di Algoritmi e Strutture Dati Docente: Maria Rita Di Berardini 19 dicembre 2007 Nome: Cognome: N.Matricola: Note:
Università degli Studi di Camerino Laurea in Informatica Prima Prova Parziale del corso di Algoritmi e Strutture Dati Docente: Maria Rita Di Berardini 19 dicembre 2007 Nome: Cognome: N.Matricola: Note:
Problemi di ordinamento
 Problemi di ordinamento Input: una sequenza di n numeri a 1, a 2,..., a n ; Output: una permutazione a 1, a 2,..., a n di a 1, a 2,..., a n tale che a 1 a 2... a n. Generalmente, la sequenza è rappresentata
Problemi di ordinamento Input: una sequenza di n numeri a 1, a 2,..., a n ; Output: una permutazione a 1, a 2,..., a n di a 1, a 2,..., a n tale che a 1 a 2... a n. Generalmente, la sequenza è rappresentata
23/10/2016. gli alberi. alcune definizioni. un esempio. LABORATORIO DI PROGRAMMAZIONE 2 Corso di laurea in matematica.
 gli alberi Un albero è una struttura dati NON LINEARE organizzata gerarchicamente. LABORATORIO DI PROGRAMMAZIONE 2 Corso di laurea in matematica È costituito da un insieme di nodi collegati tra di loro:
gli alberi Un albero è una struttura dati NON LINEARE organizzata gerarchicamente. LABORATORIO DI PROGRAMMAZIONE 2 Corso di laurea in matematica È costituito da un insieme di nodi collegati tra di loro:
Algoritmi e Strutture di Dati
 Algoritmi e Strutture di Dati Visite di alberi m.patrignani Nota di copyright queste slides sono protette dalle leggi sul copyright il titolo ed il copyright relativi alle slides (inclusi, ma non limitatamente,
Algoritmi e Strutture di Dati Visite di alberi m.patrignani Nota di copyright queste slides sono protette dalle leggi sul copyright il titolo ed il copyright relativi alle slides (inclusi, ma non limitatamente,
Alberi. Definizioni principali
 Definizioni principali Un albero è una struttura dati che contiene oggetti organizzati gerarchicamente (a differenza della lista di nodi, dell'array list, i cui elementi sono organizzati linearmente) radice
Definizioni principali Un albero è una struttura dati che contiene oggetti organizzati gerarchicamente (a differenza della lista di nodi, dell'array list, i cui elementi sono organizzati linearmente) radice
Sommario della lezione:
 Sommario della lezione: Metodologie per il progetto di algoritmi: La Tecnica Divide et Impera Esempi di applicazione a: Ricerca del massimo e minimo di una sequenza di numeri Calcolo di potenze di numeri
Sommario della lezione: Metodologie per il progetto di algoritmi: La Tecnica Divide et Impera Esempi di applicazione a: Ricerca del massimo e minimo di una sequenza di numeri Calcolo di potenze di numeri
Esercitazione 6. Alberi binari di ricerca
 Esercitazione 6 Alberi binari di ricerca Struttura base Rappresentabile attraverso una struttura dati concatenata in cui ogni nodo è un oggetto di tipo struttura Ogni nodo contiene: campo chiave (key)
Esercitazione 6 Alberi binari di ricerca Struttura base Rappresentabile attraverso una struttura dati concatenata in cui ogni nodo è un oggetto di tipo struttura Ogni nodo contiene: campo chiave (key)
Corso di Programmazione
 II Accertamento del 27 Marzo 2001 / A Risolvi i seguenti esercizi, riporta le soluzioni in modo chiaro negli appositi riquadri e giustifica sinteticamente le risposte utilizzando i fogli protocollo. Cosa
II Accertamento del 27 Marzo 2001 / A Risolvi i seguenti esercizi, riporta le soluzioni in modo chiaro negli appositi riquadri e giustifica sinteticamente le risposte utilizzando i fogli protocollo. Cosa
Algoritmi di ordinamento
 Capitolo 7 Algoritmi di ordinamento 7.1 Selection sort L algoritmo di ordinamento per selezione opera nel modo seguente: supponiamo che i primi k elementi siano ordinati; l algoritmo sceglie il minimo
Capitolo 7 Algoritmi di ordinamento 7.1 Selection sort L algoritmo di ordinamento per selezione opera nel modo seguente: supponiamo che i primi k elementi siano ordinati; l algoritmo sceglie il minimo
QuickSort Università degli Studi di Milano
 QuickSort Algoritmo di ordinamento sul posto che ha tempo di esecuzione : - O(n 2 ) nel caso peggiore - O(n log n) nel caso medio Nonostante le cattive prestazioni nel caso peggiore, rimane il miglior
QuickSort Algoritmo di ordinamento sul posto che ha tempo di esecuzione : - O(n 2 ) nel caso peggiore - O(n log n) nel caso medio Nonostante le cattive prestazioni nel caso peggiore, rimane il miglior
Algoritmi e Strutture Dati
 Algoritmi Ricorsivi e Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 2006/07 I conigli di Fibonacci Ricerca Binaria L isola dei conigli
Algoritmi Ricorsivi e Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 2006/07 I conigli di Fibonacci Ricerca Binaria L isola dei conigli
Dati e Algoritmi 1: A. Pietracaprina. Alberi
 Dati e Algoritmi 1: A. Pietracaprina Alberi 1 Cos è un albero? root$ Albero Informalmente: collezione di nodi; collegamenti: minimali (che garantiscano la connessione); di tipo padre-figlio struttura gerarchica
Dati e Algoritmi 1: A. Pietracaprina Alberi 1 Cos è un albero? root$ Albero Informalmente: collezione di nodi; collegamenti: minimali (che garantiscano la connessione); di tipo padre-figlio struttura gerarchica
Alberi binari. Alberi Albero binario Heap tree
 Alberi binari Alberi Albero binario eap tree Albero Ogni nodo può avere un numero arbitrario di figli Un nodo senza figli viene detto foglia siste un nodo particolare chiamato radice, tutti gli altri hanno
Alberi binari Alberi Albero binario eap tree Albero Ogni nodo può avere un numero arbitrario di figli Un nodo senza figli viene detto foglia siste un nodo particolare chiamato radice, tutti gli altri hanno
Alberi. Gli alberi sono una generalizzazione delle liste che consente di modellare delle strutture gerarchiche come questa: Largo. Fosco.
 Alberi Alberi Gli alberi sono una generalizzazione delle liste che consente di modellare delle strutture gerarchiche come questa: Largo Fosco Dora Drogo Frodo Dudo Daisy Alberi Gli alberi sono una generalizzazione
Alberi Alberi Gli alberi sono una generalizzazione delle liste che consente di modellare delle strutture gerarchiche come questa: Largo Fosco Dora Drogo Frodo Dudo Daisy Alberi Gli alberi sono una generalizzazione
Alberi. Se x è il genitore di y, allora y è un figlio di x. Un albero binario è un albero in cui ogni nodo ha al massimo due figli.
 Alberi Un albero è un insieme di oggetti, chiamati nodi, su cui è definita una relazione binaria G(x, y) che leggiamo x è genitore di y tale che: 1. esiste un unico nodo, chiamato radice, che non ha genitori;
Alberi Un albero è un insieme di oggetti, chiamati nodi, su cui è definita una relazione binaria G(x, y) che leggiamo x è genitore di y tale che: 1. esiste un unico nodo, chiamato radice, che non ha genitori;
Laboratorio 26 Aprile 2012
 Laboratorio 26 Aprile 2012 Albero binario di ricerca: Ricerca Scrivere un programma che legga da tastiera una sequenza di n interi distinti e li inserisca in un albero binario di ricerca (senza ribilanciamento)
Laboratorio 26 Aprile 2012 Albero binario di ricerca: Ricerca Scrivere un programma che legga da tastiera una sequenza di n interi distinti e li inserisca in un albero binario di ricerca (senza ribilanciamento)
Alberi binari di ricerca
 Alberi binari di ricerca Gli alberi binari di ricerca sono ottime strutture dati per memorizzare coppie di elementi (k, e) chiave elemento di un dizionario. Un albero binario di ricerca T è un albero binario
Alberi binari di ricerca Gli alberi binari di ricerca sono ottime strutture dati per memorizzare coppie di elementi (k, e) chiave elemento di un dizionario. Un albero binario di ricerca T è un albero binario
ESERCITAZIONI DI INTRODUZIONE AGLI ALGORITMI (A.A. 08/09)
 ESERCITAZIONI DI INTRODUZIONE AGLI ALGORITMI (A.A. 08/09) DISPENSA N. 4 1. Ricerca Binaria Ricorsiva L algoritmo Ricerca Binaria risolve il problema della ricerca di una chiave in un vettore. È un esempio
ESERCITAZIONI DI INTRODUZIONE AGLI ALGORITMI (A.A. 08/09) DISPENSA N. 4 1. Ricerca Binaria Ricorsiva L algoritmo Ricerca Binaria risolve il problema della ricerca di una chiave in un vettore. È un esempio
alla categoria di automi a minor potenza riconoscitiva possibile. }, dove k è un parametro.
 Algoritmi e Prin Appello del 2 Settembre 20 Informatica 2 ore e 30 minuti. Chi deve sostenere solo il modulo di Informatica teorica deve svolgere gli Esercizi 1 e 2 in 1 ora e minuti. Chi deve sostenere
Algoritmi e Prin Appello del 2 Settembre 20 Informatica 2 ore e 30 minuti. Chi deve sostenere solo il modulo di Informatica teorica deve svolgere gli Esercizi 1 e 2 in 1 ora e minuti. Chi deve sostenere
L albero e un tipo astratto di dati usato per rappresentare relazioni gerarchiche.
 Lezioni di C L albero e un tipo astratto di dati usato per rappresentare relazioni gerarchiche. qstruttura del file system qalbero genealogico qorganigramma qalbero di decisione q... s=6*8+((2+42)*(5+12)+987*7*123+15*54)
Lezioni di C L albero e un tipo astratto di dati usato per rappresentare relazioni gerarchiche. qstruttura del file system qalbero genealogico qorganigramma qalbero di decisione q... s=6*8+((2+42)*(5+12)+987*7*123+15*54)
Divide et impera (Divide and Conquer) Dividi il problema in sottoproblemi piu` semplici e risolvili ricorsivamente
 Divide et impera (Divide and Conquer) Dividi il problema in sottoproblemi piu` semplici e risolvili ricorsivamente Divide et impera - Schema generale Divide-et-impera (P, n) if n k then risolvi direttamente
Divide et impera (Divide and Conquer) Dividi il problema in sottoproblemi piu` semplici e risolvili ricorsivamente Divide et impera - Schema generale Divide-et-impera (P, n) if n k then risolvi direttamente
Dati e Algoritmi I (Pietracaprina) Esercizi su Alberi Binari di Ricerca e (2,4)-Tree
 Dati e Algoritmi I (Pietracaprina) Esercizi su Alberi Binari di Ricerca e (2,4)-Tree Dati e Algoritmi I (Pietracaprina): Esercizi 1 Problema 1 Scrivere una versione iterativa di TreeSearch con la stessa
Dati e Algoritmi I (Pietracaprina) Esercizi su Alberi Binari di Ricerca e (2,4)-Tree Dati e Algoritmi I (Pietracaprina): Esercizi 1 Problema 1 Scrivere una versione iterativa di TreeSearch con la stessa
Fondamenti teorici e programmazione
 Fondamenti teorici e programmazione FTP(A) - modb Lezione 9 di ricerca binaria F.Bonchi Dip.to Informatica Fondamenti teorici e programmazione (A) - modb a.a. 2018/19 pag. 1 liberi Un albero libero è un
Fondamenti teorici e programmazione FTP(A) - modb Lezione 9 di ricerca binaria F.Bonchi Dip.to Informatica Fondamenti teorici e programmazione (A) - modb a.a. 2018/19 pag. 1 liberi Un albero libero è un
Alberi. Gli alberi sono una generalizzazione delle liste che consente di modellare delle strutture gerarchiche come questa: Largo. Fosco.
 Alberi Alberi Gli alberi sono una generalizzazione delle liste che consente di modellare delle strutture gerarchiche come questa: Largo Fosco Dora Drogo Dudo Frodo Daisy Alberi Gli alberi sono una generalizzazione
Alberi Alberi Gli alberi sono una generalizzazione delle liste che consente di modellare delle strutture gerarchiche come questa: Largo Fosco Dora Drogo Dudo Frodo Daisy Alberi Gli alberi sono una generalizzazione
Alberi e alberi binari I Un albero è un caso particolare di grafo
 Alberi e alberi binari I Un albero è un caso particolare di grafo I I I I È costituito da un insieme di nodi collegati tra di loro mediante archi Gli archi sono orientati (ogni arco esce da un nodo origine
Alberi e alberi binari I Un albero è un caso particolare di grafo I I I I È costituito da un insieme di nodi collegati tra di loro mediante archi Gli archi sono orientati (ogni arco esce da un nodo origine
Alberi e alberi binari I Un albero è un caso particolare di grafo
 Alberi e alberi binari Un albero è un caso particolare di grafo È costituito da un insieme di nodi collegati tra di loro mediante archi Gli archi sono orientati (ogni arco esce da un nodo origine ed entra
Alberi e alberi binari Un albero è un caso particolare di grafo È costituito da un insieme di nodi collegati tra di loro mediante archi Gli archi sono orientati (ogni arco esce da un nodo origine ed entra
Alberi. Strutture dati: Alberi. Alberi: Alcuni concetti. Alberi: definizione ricorsiva. Alberi: Una prima realizzazione. Alberi: prima Realizzazione
 Alberi Strutture dati: Alberi Strutture gerarchiche di dati Esempi Il file system di un sistema operativo L organigramma di un azienda Alberi generali, alberi n-ari, alberi binari, Ogni nodo ha un unico
Alberi Strutture dati: Alberi Strutture gerarchiche di dati Esempi Il file system di un sistema operativo L organigramma di un azienda Alberi generali, alberi n-ari, alberi binari, Ogni nodo ha un unico
Ricerca di Massimo e Minimo di un Array
 Universitá degli Studi di Salerno Corso di Introduzione agli Algoritmi e Strutture Dati Prof. Ugo Vaccaro Anno Acc. 2014/15 p. 1/18 Ricerca di Massimo e Minimo di un Array Problema. Trova l elemento di
Universitá degli Studi di Salerno Corso di Introduzione agli Algoritmi e Strutture Dati Prof. Ugo Vaccaro Anno Acc. 2014/15 p. 1/18 Ricerca di Massimo e Minimo di un Array Problema. Trova l elemento di
In questa lezione: correttezza del mergesort Analisi del mergesort: relazioni di ricorrenza e alberi della ricorsione
 In questa lezione: correttezza del mergesort Analisi del mergesort: relazioni di ricorrenza e alberi della ricorsione Prof E Fachini - Intr Alg 1 MergeSort: correttezza MergeSort (A,p,r) if p < r then
In questa lezione: correttezza del mergesort Analisi del mergesort: relazioni di ricorrenza e alberi della ricorsione Prof E Fachini - Intr Alg 1 MergeSort: correttezza MergeSort (A,p,r) if p < r then
ALGORITMI Docente: Prof. Domenico Cantone
 CORSO SPECILE DI DURT NNULE PER IL CONSEGUIMENTO DELL BILITZIONE LL INSEGNMENTO NELL SCUOL SECONDRI DI I e II GRDO Indirizzo Fisico - Informatico - Matematico a.a. 00/07 - Classe - Informatica LGORITMI
CORSO SPECILE DI DURT NNULE PER IL CONSEGUIMENTO DELL BILITZIONE LL INSEGNMENTO NELL SCUOL SECONDRI DI I e II GRDO Indirizzo Fisico - Informatico - Matematico a.a. 00/07 - Classe - Informatica LGORITMI
Struttura di dati che può essere usata sia come dizionario, sia come coda con priorità
 Albero binario di ricerca Struttura di dati che può essere usata sia come dizionario, sia come coda con priorità Proprietà: sia x un nodo di un (sotto)albero binario di ricerca Se y è un nodo del sottoalbero
Albero binario di ricerca Struttura di dati che può essere usata sia come dizionario, sia come coda con priorità Proprietà: sia x un nodo di un (sotto)albero binario di ricerca Se y è un nodo del sottoalbero
Algoritmi e Strutture Dati
 Algoritmi Ricorsivi e Ricorrenze Maria Rita Di Berardini 2, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino 2 Polo di Scienze Università di Camerino ad Ascoli Piceno
Algoritmi Ricorsivi e Ricorrenze Maria Rita Di Berardini 2, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino 2 Polo di Scienze Università di Camerino ad Ascoli Piceno
In questa lezione Alberi binari di ricerca
 In questa lezione Alberi binari di ricerca!1 Dizionari Un dizionario è una struttura dati costituita da un insieme con le operazioni di inserimento, cancellazione e verifica di appartenenza di un elemento.
In questa lezione Alberi binari di ricerca!1 Dizionari Un dizionario è una struttura dati costituita da un insieme con le operazioni di inserimento, cancellazione e verifica di appartenenza di un elemento.
Algoritmi e Strutture Dati
 Strutture Elementari Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino 29 ottobre 2008 Strutture Dati Astratte Il concetto di dato Il concetto
Strutture Elementari Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino 29 ottobre 2008 Strutture Dati Astratte Il concetto di dato Il concetto
5. DIVIDE AND CONQUER I
 Divide-et-Impera (Divide and conquer) 5. DIVIDE AND CONQUER I Mergesort e Relazioni di ricorrenza Esempi di progettazione D&I Moltiplicazione di interi Contare inversioni Divide-et-Impera. Definizione
Divide-et-Impera (Divide and conquer) 5. DIVIDE AND CONQUER I Mergesort e Relazioni di ricorrenza Esempi di progettazione D&I Moltiplicazione di interi Contare inversioni Divide-et-Impera. Definizione
Esercizi proposti Risolvere i problemi seguenti su espressioni rappresentate come alberi binari, mediante la dichiarazione di tipo
 Esercizi proposti 8 INDICZIONI DI CRTTERE GENERLE: Quando scrivete una funzione che ne utilizza una ausiliaria, chiedetevi sempre se l ausiliaria è necessaria, ricordando che è utile quando: (a) servono
Esercizi proposti 8 INDICZIONI DI CRTTERE GENERLE: Quando scrivete una funzione che ne utilizza una ausiliaria, chiedetevi sempre se l ausiliaria è necessaria, ricordando che è utile quando: (a) servono
Esercitazione 8. Corso di Tecniche di programmazione. Laurea in Ingegneria Informatica
 Dipartimento di Informatica e Sistemistica Antonio Ruberti Sapienza Università di Roma Esercitazione 8 Corso di Tecniche di programmazione Laurea in Ingegneria Informatica (Canale di Ingegneria delle Reti
Dipartimento di Informatica e Sistemistica Antonio Ruberti Sapienza Università di Roma Esercitazione 8 Corso di Tecniche di programmazione Laurea in Ingegneria Informatica (Canale di Ingegneria delle Reti
Analisi algoritmi ricorsivi e relazioni di ricorrenza
 Analisi algoritmi ricorsivi e relazioni di ricorrenza Punto della situazione Finora abbiamo affrontato: il tempo di esecuzione di un algoritmo, l analisi asintotica con le notazioni asintotiche e la tecnica
Analisi algoritmi ricorsivi e relazioni di ricorrenza Punto della situazione Finora abbiamo affrontato: il tempo di esecuzione di un algoritmo, l analisi asintotica con le notazioni asintotiche e la tecnica
Lezione 9 Alberi binari: visite ed esercizi
 Lezione 9 Alberi binari: visite ed esercizi Informatica 4 Maggio 2016 Operazioni sugli alberi: visita La visita di un albero esplora tutti i nodi ed esegue una qualche operazione su di essi. Per esempio,
Lezione 9 Alberi binari: visite ed esercizi Informatica 4 Maggio 2016 Operazioni sugli alberi: visita La visita di un albero esplora tutti i nodi ed esegue una qualche operazione su di essi. Per esempio,
Algoritmi e Strutture Dati
 Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 2006/07 Il concetto di dato Il concetto di tipo di dato Insertion Sort for j 2 to lenght[a]
Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 2006/07 Il concetto di dato Il concetto di tipo di dato Insertion Sort for j 2 to lenght[a]
