Corso di Programmazione
|
|
|
- Violetta Leoni
- 5 anni fa
- Visualizzazioni
Transcript
1 II Accertamento del 27 Marzo 2001 / A Risolvi i seguenti esercizi, riporta le soluzioni in modo chiaro negli appositi riquadri e giustifica sinteticamente le risposte utilizzando i fogli protocollo. Cosa calcola la procedura f? Calcola i risultati della valutazione delle espressioni Scheme: (f 1 2) (f 2 1) (f 3 3) (f 4 5) (f 5 0) e ipotizza il risultato della generica valutazione (f m n). (define f (lambda (x y) ; x, y naturali (g (- x 1) y null) (lambda (x y z) (if (= y 0) z (g x (- y 1) (cons (+ x y) z Descrivi sinteticamente una possibile rappresentazione in Scheme degli insiemi con un numero finito di elementi (qualsiasi). Quindi realizza le seguenti operazioni sugli insiemi. insieme-vuoto? verifica se un dato insieme è vuoto; rimuovi assume come valore l insieme che si ottiene togliendo un elemento dall insieme argomento, se l elemento c è, oppure l insieme stesso; unione realizza l unione insiemistica. ; Operazioni relative all'adt "Insiemi" ; (insieme-vuoto? <insieme>) : insieme -> booleano ; (rimuovi <elemento> <insieme>) : elemento x insieme -> insieme ; (unione <insieme> <insieme>) : insieme x insieme -> insieme ; ecc. Supponi che sia data un opportuna realizzazione degli alberi binari, accessibile attraverso le operazioni introdotte qui di seguito. Utilizzando tali operazioni definisci una procedura in Scheme per verificare se due alberi binari sono speculari (uno è l'immagine riflessa dell altro). ; Operazioni relative all'adt "Alberi binari" ; (vuoto? <albero>) : albero -> booleano ; (sottoalbero-sinistro <albero>) : albero -> albero ; (sottoalbero-destro <albero>) : albero -> albero ; (nodo-radice <albero>) : albero -> nodo 4. Definizione di procedure in Scheme Definisci formalmente una procedura in Scheme per risolvere il seguente problema: dato un numero naturale positivo n, generare tutti e soli i numeri primi minori o uguali a n. Rappresenta la soluzione attraverso una lista ordinata di numeri primi. 5. Dimostrazioni per induzione Considera la procedura f e dimostra per induzione che il valore dell espressione (f L) è dato da: x 2 (define f ; L lista di naturali (lambda (L) (g L 0 ) (lambda (L S) (if (null? L) S (g (cdr L) (+ S (* (car L) (car L ) In particolare: Scrivi formalmente la proprietà che intendi dimostrare per induzione. Scrivi formalmente la proprietà che esprime il caso base. Scrivi formalmente l ipotesi induttiva. Scrivi formalmente la proprietà che si deve dimostrare come passo induttivo. Dimostra formalmente il caso base. Dimostra formalmente il passo induttivo.
2 II Accertamento del 27 Marzo 2001 / B Risolvi i seguenti esercizi, riporta le soluzioni in modo chiaro negli appositi riquadri e giustifica sinteticamente le risposte utilizzando i fogli protocollo. Cosa calcola la procedura f? Calcola i risultati della valutazione delle espressioni Scheme: (f 1 2) (f 2 1) (f 3 3) (f 4 5) (f 5 0) e ipotizza il risultato della generica valutazione (f m n). (define f (lambda (u v) ; u, v naturali (g '() (- (+ u v) 1) v) (lambda (t u v) (if (= v 0) t (g (cons u t) (- u 1) (- v 1 Descrivi sinteticamente una possibile rappresentazione in Scheme degli insiemi con un numero finito di elementi (qualsiasi). Quindi realizza le seguenti operazioni sugli insiemi. insieme-vuoto assume come valore l insieme vuoto; rimuovi calcola l insieme che si ottiene togliendo un elemento dall insieme argomento, se l elemento c è, oppure l insieme stesso; intersezione realizza l intersezione insiemistica. ; Operazioni relative all'adt "Insiemi" ; (insieme-vuoto) : -> insieme ; (rimuovi <elemento> <insieme>) : elemento x insieme -> insieme ; (intersezione <insieme> <insieme>) : insieme x insieme -> insieme ; ecc. Supponi che sia data un opportuna realizzazione degli alberi binari, accessibile attraverso le operazioni introdotte qui di seguito. Utilizzando tali operazioni definisci una procedura in Scheme per verificare se due alberi binari sono identici. ; Operazioni relative all'adt "Alberi binari" ; (vuoto? <albero>) : albero -> booleano ; (sottoalbero-sinistro <albero>) : albero -> albero ; (sottoalbero-destro <albero>) : albero -> albero ; (nodo-radice <albero>) : albero -> nodo 4. Definizione di procedure in Scheme Definisci formalmente una procedura in Scheme per risolvere il seguente problema: dato un numero naturale positivo n, generare tutti e soli i numeri minori o uguali a n che non sono numeri primi. Rappresenta la soluzione attraverso una lista ordinata. 5. Dimostrazioni per induzione Considera la procedura f e dimostra per induzione che il valore dell espressione (f L) è dato da: x (define f (lambda (L) ; L lista di naturali (g 0 L) (lambda (A L) (if (null? L) A (g (+ A (car L (cdr L In particolare: Scrivi formalmente la proprietà che intendi dimostrare per induzione. Scrivi formalmente la proprietà che esprime il caso base. Scrivi formalmente l ipotesi induttiva. Scrivi formalmente la proprietà che si deve dimostrare come passo induttivo. Dimostra formalmente il caso base. Dimostra formalmente il passo induttivo. 2
3 II Accertamento del 27 Marzo 2001 / C Risolvi i seguenti esercizi, riporta le soluzioni in modo chiaro negli appositi riquadri e giustifica sinteticamente le risposte utilizzando i fogli protocollo. Cosa calcola la procedura f? Calcola i risultati della valutazione delle espressioni Scheme: (f 1 2) (f 2 1) (f 3 3) (f 4 5) (f 5 0) e ipotizza il risultato della generica valutazione (f m n). (define f (lambda (x y) ; x, y naturali (g x y null) (lambda (x y z) (if (= y 0) z (g (+ x 1) (- y 1) (cons x z Descrivi sinteticamente una possibile rappresentazione in Scheme degli insiemi con un numero finito di elementi (qualsiasi). Quindi realizza le seguenti operazioni sugli insiemi. insieme-vuoto? verifica se un dato insieme è vuoto; aggiungi assume come valore l insieme che si ottiene aggiungendo un elemento all insieme argomento, se non c è già, oppure l insieme stesso; differrenza assume come valore l insieme degli elementi che appartengono al primo argomento (che è un insieme) ma non al secondo. ; Operazioni relative all'adt "Insiemi" ; (insieme-vuoto? <insieme>) : insieme -> booleano ; (aggiungi <elemento> <insieme>) : elemento x insieme -> insieme ; (differenza <insieme> <insieme>) : insieme x insieme -> insieme ; ecc. Supponi che sia data un opportuna realizzazione degli alberi binari, accessibile attraverso le operazioni introdotte qui di seguito. Utilizzando tali operazioni definisci una procedura in Scheme per calcolare l altezza di un albero binario, cioè il numero di nodi del più lungo cammino dalla radice a una foglia. ; Operazioni relative all'adt "Alberi binari" ; (vuoto? <albero>) : albero -> booleano ; (sottoalbero-sinistro <albero>) : albero -> albero ; (sottoalbero-destro <albero>) : albero -> albero ; (nodo-radice <albero>) : albero -> nodo 4. Definizione di procedure in Scheme Definisci formalmente una procedura in Scheme per risolvere il seguente problema: dato un numero naturale positivo n, calcolare la fattorizzazione di n in fattori primi. Rappresenta la fattorizzazione attraverso una lista ordinata di numeri primi in cui ciascun fattore primo compare esattamente tante volte quanto è il valore del relativo esponente nella fattorizzazione di n. 5. Dimostrazioni per induzione Considera la procedura f e dimostra per induzione che il valore dell espressione (f L) è dato da: (x+1) (define f ; L lista di naturali (lambda (L) (g 1 L ) (lambda (Q L) (if (null? L) Q (g (* (+ (car L) 1) Q) (cdr L In particolare: Scrivi formalmente la proprietà che intendi dimostrare per induzione. Scrivi formalmente la proprietà che esprime il caso base. Scrivi formalmente l ipotesi induttiva. Scrivi formalmente la proprietà che si deve dimostrare come passo induttivo. Dimostra formalmente il caso base. Dimostra formalmente il passo induttivo. 3
4 II Accertamento del 27 Marzo 2001 / D Risolvi i seguenti esercizi, riporta le soluzioni in modo chiaro negli appositi riquadri e giustifica sinteticamente le risposte utilizzando i fogli protocollo. Cosa calcola la procedura f? Calcola i risultati della valutazione delle espressioni Scheme: (f 1 2) (f 2 1) (f 3 3) (f 4 5) (f 5 0) e ipotizza il risultato della generica valutazione (f m n). (define f (lambda (u v) ; u, v naturali (g '() u (- (+ u v) 1 (lambda (t u v) (if (> u v) t (g (cons u t) (+ u 1) v) Descrivi sinteticamente una possibile rappresentazione in Scheme degli insiemi con un numero finito di elementi (qualsiasi). Quindi realizza le seguenti operazioni sugli insiemi. insieme-vuoto assume come valore l insieme vuoto; aggiungi valuta l insieme che si ottiene aggiungendo un elemento all insieme argomento, se non c è già, oppure l insieme stesso; diffsimmetrica (differenza simmetrica) assume come valore l insieme degli elementi che appartengono a uno dei due argomenti (che sono insiemi) ma non ad entrambi. ; Operazioni relative all'adt "Insiemi" ; (insieme-vuoto) : -> insieme ; (aggiungi <elemento> <insieme>) : elemento x insieme -> insieme ; (diff-simmetrica <insieme> <insieme>) : insieme x insieme -> insieme ; ecc. Supponi che sia data un opportuna realizzazione degli alberi binari, accessibile attraverso le operazioni introdotte qui di seguito. Utilizzando tali operazioni definisci una procedura in Scheme per calcolare il numero complessivo di nodi di un albero binario. ; Operazioni relative all'adt "Alberi binari" ; (vuoto? <albero>) : albero -> booleano ; (sottoalbero-sinistro <albero>) : albero -> albero ; (sottoalbero-destro <albero>) : albero -> albero ; (nodo-radice <albero>) : albero -> nodo 4. Definizione di procedure in Scheme Definisci formalmente una procedura in Scheme per risolvere il seguente problema: dato un numero naturale positivo n, calcolare la fattorizzazione di n in fattori primi. Rappresenta la fattorizzazione attraverso una lista di coppie, dove ciascun fattore primo risulta associato al relativo esponente nella fattorizzazione di n. 5. Dimostrazioni per induzione Considera la procedura f e dimostra per induzione che il valore dell espressione (f L) è dato da: x (define f (lambda (L) ; x lista di naturali (g L 1) (lambda (L P) (if (null? L) P (g (cdr L) (* (car L) P In particolare: Scrivi formalmente la proprietà che intendi dimostrare per induzione. Scrivi formalmente la proprietà che esprime il caso base. Scrivi formalmente l ipotesi induttiva. Scrivi formalmente la proprietà che si deve dimostrare come passo induttivo. Dimostra formalmente il caso base. Dimostra formalmente il passo induttivo. 4
5 II Accertamento del 27 Marzo 2001 / A (f 1 2) (1 2) (f 2 1) (2) (f 3 3) (3 4 5) caso generale: (f m n) (m m+1... m+n 1) (f 4 5) ( ) (f 5 0) () Definizione delle procedure: Vedi la realizzazione completa di una struttura dati "Insiemi" presentata dopo queste schede. Gli insiemi sono rappresentati da liste senza ripetizioni. (define speculari? (lambda (albero1 albero2) (cond ((and (vuoto? albero1) (vuoto? albero2 #t) ((or (vuoto? albero1) (vuoto? albero2 #f) (else (and (equal? (nodo-radice albero1) (nodo-radice albero2 (speculari? (sottoalbero-sinistro albero1) (sottoalbero-destro albero2 (speculari? (sottoalbero-destro albero1) (sottoalbero-sinistro albero2 5
6 4. Definizione di procedure in Scheme (define lista-primi (lambda (n) (numeri-primi 2 n) (define numeri-primi (lambda (k n) (cond ((> k n) null) ((primo-da? 2 k) (cons k (numeri-primi (+ k 1) n (else (numeri-primi (+ k 1) n (define primo-da? (lambda (d n) (cond ((= d n) #t) ((> (remainder n d) 0) (primo-da? (+ d 1) n (else #f) 5. Dimostrazioni per induzione Dimostrazioni su foglio allegato. Proprietà da dimostrare per induzione: Proprietà dimostrata nel caso base: Per ogni lista di naturali L e per ogni naturale S (g L S) S + x 2 Per ogni naturale S (g '() S) S (Dimostrazione per induzione sulla lunghezza di L) Ipotesi induttiva: Per ogni lista di naturali L di lunghezza L < n, con n > 0, e per ogni naturale S (g L S) S + x 2 Proprietà dimostrata nel passo induttivo: Per ogni lista di naturali L di lunghezza L = n, e per ogni naturale S (g L S) S + x 2 6
7 II Accertamento del 27 Marzo 2001 / B (f 1 2) (1 2) (f 2 1) (2) (f 3 3) (3 4 5) caso generale: (f m n) (m m+1... m+n 1) (f 4 5) ( ) (f 5 0) () Definizione delle procedure: Vedi la realizzazione completa di una struttura dati "Insiemi" presentata dopo queste schede. Gli insiemi sono rappresentati da liste senza ripetizioni. (define identici? (lambda (albero1 albero2) (cond ((and (vuoto? albero1) (vuoto? albero2 #t) ((or (vuoto? albero1) (vuoto? albero2 #f) (else (and (equal? (nodo-radice albero1) (nodo-radice albero2 (identici? (sottoalbero-sinistro albero1) (sottoalbero-sinistro albero2 (identici? (sottoalbero-destro albero1) (sottoalbero-destro albero2 7
8 4. Definizione di procedure in Scheme (define lista-non-primi (lambda (n) (numeri-non-primi 2 n ) (define numeri-non-primi (lambda (k n) (cond ((> k n) null) ((primo-da? 2 k) (numeri-non-primi (+ k 1) n (else (cons k (numeri-non-primi (+ k 1) n (define primo-da? (lambda (d n) (cond ((= d n) #t) ((> (remainder n d) 0) (primo-da? (+ d 1) n (else #f) 5. Dimostrazioni per induzione Dimostrazioni su foglio allegato. Proprietà da dimostrare per induzione: Proprietà dimostrata nel caso base: Per ogni lista di naturali L e per ogni naturale A (g A L) A + x Per ogni naturale A (g A '( A (Dimostrazione per induzione sulla lunghezza di L) Ipotesi induttiva: Per ogni lista di naturali L di lunghezza L < n, con n > 0, e per ogni naturale A (g A L) A + x Proprietà dimostrata nel passo induttivo: Per ogni lista di naturali L di lunghezza L = n, e per ogni naturale A (g A L) A + x 8
9 II Accertamento del 27 Marzo 2001 / C (f 1 2) (2 1) (f 2 1) (2) (f 3 3) (5 4 3) caso generale: (f m n) (m+n 1 m+n 2... m) (f 4 5) ( ) (f 5 0) () Definizione delle procedure: Vedi la realizzazione completa di una struttura dati "Insiemi" presentata dopo queste schede. Gli insiemi sono rappresentati da liste senza ripetizioni. (define max (lambda (x y) (if (< x y) y x) (define altezza (lambda (albero) (if (vuoto? albero) 0 (+ 1 (max (altezza (sottoalbero-sinistro albero (altezza (sottoalbero-destro albero 9
10 4. Definizione di procedure in Scheme (define fattorizzazione (lambda (n) (fattorizzazione-da 2 n) (define fattorizzazione-da (lambda (k n) (cond ((= n 1) null) ((= (remainder n k) 0) (cons k (fattorizzazione-da k (quotient n k) (else (fattorizzazione-da (+ k 1) n 5. Dimostrazioni per induzione Dimostrazioni su foglio allegato. Proprietà da dimostrare per induzione: Proprietà dimostrata nel caso base: Per ogni lista di naturali L e per ogni naturale Q (g Q L) Q (x+1) Per ogni naturale Q (g Q '( Q (Dimostrazione per induzione sulla lunghezza di L) Ipotesi induttiva: Per ogni lista di naturali L di lunghezza L < n, con n > 0, e per ogni naturale Q (g Q L) Q (x+1) Proprietà dimostrata nel passo induttivo: Per ogni lista di naturali L di lunghezza L = n, e per ogni naturale Q (g Q L) Q (x+1) 10
11 II Accertamento del 27 Marzo 2001 / D (f 1 2) (2 1) (f 2 1) (2) (f 3 3) (5 4 3) caso generale: (f m n) (m+n 1 m+n 2... m) (f 4 5) ( ) (f 5 0) () Definizione delle procedure: Vedi la realizzazione completa di una struttura dati "Insiemi" presentata dopo queste schede. Gli insiemi sono rappresentati da liste senza ripetizioni. (define numero-nodi (lambda (albero) (if (vuoto? albero) 0 (+ 1 (numero-nodi (sottoalbero-sinistro albero (numero-nodi (sottoalbero-destro albero 11
12 4. Definizione di procedure in Scheme (define fattorizzazione (lambda (n) (fattorizzazione-da 2 n ) (define fattorizzazione-da (lambda (k n) (cond ((= n 1) null) ((= (remainder n k) 0) (cons (cons k (esponente k n (fattorizzazione-da (+ k 1) (riduci n k) (else (fattorizzazione-da (+ k 1) n (define esponente (lambda (p n) (if (= (remainder n p) 0) (+ (esponente p (quotient n p 1) 0 (define riduci (lambda (n p) (if (= (remainder n p) 0) (riduci (quotient n p) p) n 5. Dimostrazioni per induzione Dimostrazioni su foglio allegato. Proprietà da dimostrare per induzione: Proprietà dimostrata nel caso base: Per ogni lista di naturali L e per ogni naturale P (g L P) P x Per ogni naturale P (g '() P) P (Dimostrazione per induzione sulla lunghezza di L) Ipotesi induttiva: Per ogni lista di naturali L di lunghezza L < n, con n > 0, e per ogni naturale P (g L P) P x Proprietà dimostrata nel passo induttivo: Per ogni lista di naturali L di lunghezza L = n, e per ogni naturale P (g L P) P x 12
13 ; Realizzazione dell'adt "Insiemi" ; ; (insieme-vuoto) : -> insieme ; (insieme-vuoto? <insieme>) : insieme -> booleano ; (aggiungi <elemento> <insieme>) : elemento x insieme -> insieme ; (rimuovi <elemento> <insieme>) : elemento x insieme -> insieme ; (unione <insieme> <insieme>) : insieme x insieme -> insieme ; (intersezione <insieme> <insieme>) : insieme x insieme -> insieme ; (differenza <insieme> <insieme>) : insieme x insieme -> insieme ; (diff-simmetrica <insieme> <insieme>) : insieme x insieme -> insieme (define insieme-vuoto (lambda () null (define insieme-vuoto? null?) (define appartiene? (lambda (el ins) (cond ((null? ins) #f) ((equal? (car ins) el) #t) (else (appartiene? el (cdr ins (define aggiungi (lambda (el ins) (cond ((null? ins) (cons el null ((equal? (car ins) el) ins) (else (cons (car ins) (aggiungi el (cdr ins) (define rimuovi (lambda (el ins) (cond ((null? ins) null) ((equal? (car ins) el) (cdr ins (else (cons (car ins) (rimuovi el (cdr ins) (define unione (lambda (ins1 ins2) (if (null? ins1) ins2 (unione (cdr ins1) (aggiungi (car ins1) ins2 (define intersezione (lambda (ins1 ins2) (cond ((null? ins1) null) ((appartiene? (car ins1) ins2) (cons (car ins1) (intersezione (cdr ins1) ins2 (else (intersezione (cdr ins1) ins2 (define differenza (lambda (ins1 ins2) (if (null? ins2) ins1 (differenza (rimuovi (car ins2) ins1) (cdr ins2 (define diff-simmetrica (lambda (ins1 ins2) (cond ((null? ins1) ins2) ((appartiene? (car ins1) ins2) (diff-simmetrica (cdr ins1) (rimuovi (car ins1) ins2 (else (cons (car ins1) (diff-simmetrica (cdr ins1) ins2 13
Corso di Programmazione
 II Accertamento del 15 Marzo 2002 / A Risolvi i seguenti esercizi, riporta le soluzioni in modo chiaro negli appositi riquadri e giustifica sinteticamente le risposte utilizzando i fogli protocollo. Cosa
II Accertamento del 15 Marzo 2002 / A Risolvi i seguenti esercizi, riporta le soluzioni in modo chiaro negli appositi riquadri e giustifica sinteticamente le risposte utilizzando i fogli protocollo. Cosa
Corso di Programmazione
 Corso di Programmazione I Accertamento del 21 Dicembre 2000 / A cognome e nome Risolvi i seguenti esercizi, riporta le soluzioni in modo chiaro negli appositi riquadri e giustifica sinteticamente le risposte
Corso di Programmazione I Accertamento del 21 Dicembre 2000 / A cognome e nome Risolvi i seguenti esercizi, riporta le soluzioni in modo chiaro negli appositi riquadri e giustifica sinteticamente le risposte
Corso di Programmazione
 Corso di Programmazione I Accertamento del 3 Dicembre 2002 / A Risolvi i seguenti esercizi, riporta le soluzioni in modo chiaro negli appositi riquadri e giustifica sinteticamente le risposte utilizzando
Corso di Programmazione I Accertamento del 3 Dicembre 2002 / A Risolvi i seguenti esercizi, riporta le soluzioni in modo chiaro negli appositi riquadri e giustifica sinteticamente le risposte utilizzando
Corso di Programmazione
 Corso di Programmazione II Accertamento del 15 Marzo 2005 / A cognome e nome Risolvi i seguenti esercizi, riporta le soluzioni in modo chiaro negli appositi spazi e giustifica sinteticamente le risposte.
Corso di Programmazione II Accertamento del 15 Marzo 2005 / A cognome e nome Risolvi i seguenti esercizi, riporta le soluzioni in modo chiaro negli appositi spazi e giustifica sinteticamente le risposte.
Corso di Programmazione
 II Accertamento del 24 Marzo 2003 / A Risolvi i seguenti esercizi, riporta le soluzioni in modo chiaro negli appositi riquadri e giustifica sinteticamente le risposte, utilizzando se necessario lo spazio
II Accertamento del 24 Marzo 2003 / A Risolvi i seguenti esercizi, riporta le soluzioni in modo chiaro negli appositi riquadri e giustifica sinteticamente le risposte, utilizzando se necessario lo spazio
Corso di Programmazione
 Corso di Programmazione II Accertamento del 27 Marzo 2007 / A cognome e nome Risolvi i seguenti esercizi, riporta le soluzioni in modo chiaro negli appositi spazi e giustifica sinteticamente le risposte.
Corso di Programmazione II Accertamento del 27 Marzo 2007 / A cognome e nome Risolvi i seguenti esercizi, riporta le soluzioni in modo chiaro negli appositi spazi e giustifica sinteticamente le risposte.
Corso di Programmazione
 Corso di Programmazione II Accertamento del 22 Marzo 2006 / A cognome e nome Risolvi i seguenti esercizi, riporta le soluzioni in modo chiaro negli appositi spazi e giustifica sinteticamente le risposte.
Corso di Programmazione II Accertamento del 22 Marzo 2006 / A cognome e nome Risolvi i seguenti esercizi, riporta le soluzioni in modo chiaro negli appositi spazi e giustifica sinteticamente le risposte.
Esempio: rappresentare gli insiemi
 Esempio: rappresentare gli insiemi Problema: rappresentare gli insiemi Vedremo che la scelta della rappresentazione per implementarli non è così ovvia come era stato per i numeri razionali In realtà ci
Esempio: rappresentare gli insiemi Problema: rappresentare gli insiemi Vedremo che la scelta della rappresentazione per implementarli non è così ovvia come era stato per i numeri razionali In realtà ci
Alberi binari: definizione e alcune proprietà
 Alberi binari: definizione e alcune proprietà Alberi binari Un albero binario è un albero con radice in cui ogni nodo ha al più due figli. In maniera più formale: Definizione. (Alberi binari) Un albero
Alberi binari: definizione e alcune proprietà Alberi binari Un albero binario è un albero con radice in cui ogni nodo ha al più due figli. In maniera più formale: Definizione. (Alberi binari) Un albero
Alberi binari (radicati e ordinati) della radice Il padre del nodo 5 e del nodo 3
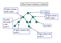 Alberi binari (radicati e ordinati) Il figlio sinistro della radice Il padre del nodo 5 e del nodo 3 4 3 Il figlio sinistro del nodo 2 2 5 1 6 7 8 9 La radice Il figlio destro della radice una foglia Figlio
Alberi binari (radicati e ordinati) Il figlio sinistro della radice Il padre del nodo 5 e del nodo 3 4 3 Il figlio sinistro del nodo 2 2 5 1 6 7 8 9 La radice Il figlio destro della radice una foglia Figlio
Divide et impera su alberi
 Divide et impera su alberi Caso base: peru = null o una foglia Decomposizione: riformula il problema per i sottoalberi radicati nei figli di u. Ricombinazione: ottieniilrisultatoconricombina 1 Decomponibile(u):
Divide et impera su alberi Caso base: peru = null o una foglia Decomposizione: riformula il problema per i sottoalberi radicati nei figli di u. Ricombinazione: ottieniilrisultatoconricombina 1 Decomponibile(u):
Corso di Programmazione
 Corso di Programmazione I Accertamento del 14 Dicembre 2007 / A cognome e nome Risolvi i seguenti esercizi, riporta le soluzioni in modo chiaro negli appositi spazi e giustifica sinteticamente le risposte.
Corso di Programmazione I Accertamento del 14 Dicembre 2007 / A cognome e nome Risolvi i seguenti esercizi, riporta le soluzioni in modo chiaro negli appositi spazi e giustifica sinteticamente le risposte.
Corso di Programmazione
 Corso di Programmazione III Accertamento del 19 Giugno 2002 / A cognome e nome Risolvi i seguenti esercizi e riporta le soluzioni in modo chiaro su questo foglio, giustificando sinteticamente le risposte.
Corso di Programmazione III Accertamento del 19 Giugno 2002 / A cognome e nome Risolvi i seguenti esercizi e riporta le soluzioni in modo chiaro su questo foglio, giustificando sinteticamente le risposte.
Alberi. Alberi: definizioni. Alberi Binari. Esercizi su alberi binari: metodi ricorsivi. Struttura dati per alberi generici. ASD-L - Luca Tesei
 Alberi Alberi: definizioni Alberi Binari Esercizi su alberi binari: metodi ricorsivi Struttura dati per alberi generici 1 Alberi Gli alberi sono strutture dati naturalmente ricorsive Un albero è un particolare
Alberi Alberi: definizioni Alberi Binari Esercizi su alberi binari: metodi ricorsivi Struttura dati per alberi generici 1 Alberi Gli alberi sono strutture dati naturalmente ricorsive Un albero è un particolare
Espressioni aritmetiche
 Espressioni aritmetiche Consideriamo espressioni costruite a partire da variabili e costanti intere mediante applicazione delle operazioni di somma, sottrazione, prodotto e divisione (intera). Ad esempio:
Espressioni aritmetiche Consideriamo espressioni costruite a partire da variabili e costanti intere mediante applicazione delle operazioni di somma, sottrazione, prodotto e divisione (intera). Ad esempio:
Alberi binari e alberi binari di ricerca
 Università degli studi di Milano Dipartimento di Informatica Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica Alberi Un albero è una collezione non vuota di: nodi con nome e informazioni
Università degli studi di Milano Dipartimento di Informatica Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica Alberi Un albero è una collezione non vuota di: nodi con nome e informazioni
PROGRAMMAZIONE II canale A-D luglio 2008 TRACCIA DI SOLUZIONE
 PROGRAMMAZIONE II canale A-D 2007-2008 14 luglio 2008 TRACCIA DI SOLUZIONE 1. Si vogliono realizzare mediante puntatori delle liste circolari, cioè delle liste tali che l ultimo elemento della lista punta
PROGRAMMAZIONE II canale A-D 2007-2008 14 luglio 2008 TRACCIA DI SOLUZIONE 1. Si vogliono realizzare mediante puntatori delle liste circolari, cioè delle liste tali che l ultimo elemento della lista punta
Alberi binari e alberi binari di ricerca
 Alberi binari e alberi binari di ricerca Violetta Lonati Università degli studi di Milano Dipartimento di Informatica Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica giovedì 9
Alberi binari e alberi binari di ricerca Violetta Lonati Università degli studi di Milano Dipartimento di Informatica Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica giovedì 9
Algoritmi e Strutture di Dati
 Algoritmi e Strutture di Dati Alberi radicati m.patrignani Nota di copyright queste slides sono protette dalle leggi sul copyright il titolo ed il copyright relativi alle slides (inclusi, ma non limitatamente,
Algoritmi e Strutture di Dati Alberi radicati m.patrignani Nota di copyright queste slides sono protette dalle leggi sul copyright il titolo ed il copyright relativi alle slides (inclusi, ma non limitatamente,
d. Cancellazione del valore 5 e. Inserimento del valore 1
 Esercizio1 Si consideri un albero binario non vuoto in cui a ciascun nodo v è associato un numero reale v.val. Scrivere un algoritmo che, dato in input l'albero T e un numero reale x, restituisce true
Esercizio1 Si consideri un albero binario non vuoto in cui a ciascun nodo v è associato un numero reale v.val. Scrivere un algoritmo che, dato in input l'albero T e un numero reale x, restituisce true
Dati e Algoritmi I (Pietracaprina) Esercizi sugli Alberi
 Dati e Algoritmi I (Pietracaprina) Esercizi sugli Alberi Dati e Algoritmi I (Pietracaprina): Esercizi 1 Problema 1 Dimostrare che un albero non vuoto con n nodi interni, dove ogni nodo interno ha almeno
Dati e Algoritmi I (Pietracaprina) Esercizi sugli Alberi Dati e Algoritmi I (Pietracaprina): Esercizi 1 Problema 1 Dimostrare che un albero non vuoto con n nodi interni, dove ogni nodo interno ha almeno
Esercizi su alberi binari
 Esercizi su alberi binari Esercizi svolti: Determinazione nodi contenti verifica completezza verifica quasi completezza lunghezza del cammino interno determinazione ultima foglia in un quasi completo verifica
Esercizi su alberi binari Esercizi svolti: Determinazione nodi contenti verifica completezza verifica quasi completezza lunghezza del cammino interno determinazione ultima foglia in un quasi completo verifica
Moltiplicazione veloce di interi
 Moltiplicazione veloce di interi Ogni numero intero w di n cifre può essere scritto come 10 n/2 w s + w d w s indica il numero formato dalle n/2 cifre più significative di w w d denota il numero formato
Moltiplicazione veloce di interi Ogni numero intero w di n cifre può essere scritto come 10 n/2 w s + w d w s indica il numero formato dalle n/2 cifre più significative di w w d denota il numero formato
Alberi ed Alberi Binari
 Alberi ed Alberi Binari Il tipo di dato Albero Un albero è una struttura di data organizzata gerarchicamente. È costituito da un insieme di nodi collegati tra di loro: ogni nodo contiene dell informazione,
Alberi ed Alberi Binari Il tipo di dato Albero Un albero è una struttura di data organizzata gerarchicamente. È costituito da un insieme di nodi collegati tra di loro: ogni nodo contiene dell informazione,
Laboratorio di Python
 , Esercizi su alberi Università di Bologna 16 maggio 2013 Sommario 1 2 Consegna non avvenuta Meno di 10 studenti hanno inviato l esercizio svolto. Definizione ricorsiva alberi binari Un albero binario
, Esercizi su alberi Università di Bologna 16 maggio 2013 Sommario 1 2 Consegna non avvenuta Meno di 10 studenti hanno inviato l esercizio svolto. Definizione ricorsiva alberi binari Un albero binario
Alberi binari e alberi binari di ricerca
 Alberi binari e alberi binari di ricerca Violetta Lonati Università degli studi di Milano Dipartimento di Scienze dell Informazione Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica
Alberi binari e alberi binari di ricerca Violetta Lonati Università degli studi di Milano Dipartimento di Scienze dell Informazione Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica
Linguaggi e Grammatiche Liberi da Contesto
 N.Fanizzi-V.Carofiglio Dipartimento di Informatica Università degli Studi di Bari 22 aprile 2016 1 Linguaggi Liberi da Contesto 2 Grammatiche e Linguaggi Liberi da Contesto G = (X, V, S, P) è una grammatica
N.Fanizzi-V.Carofiglio Dipartimento di Informatica Università degli Studi di Bari 22 aprile 2016 1 Linguaggi Liberi da Contesto 2 Grammatiche e Linguaggi Liberi da Contesto G = (X, V, S, P) è una grammatica
alberi completamente sbilanciati
 alberi completamente sbilanciati Il numero dei nodi al livello i è 1, per 0 i altezza L altezza h di un albero completamente sbilanciato con n nodi è h = n-1 1 Un albero completamente bilanciato o pieno
alberi completamente sbilanciati Il numero dei nodi al livello i è 1, per 0 i altezza L altezza h di un albero completamente sbilanciato con n nodi è h = n-1 1 Un albero completamente bilanciato o pieno
Albero binario. Alberi binari (introduzione) Terminologia. Alberi di ricerca binaria (BST)
 Albero binario 2 Alberi binari (introduzione) Struttura di dati bidimensionale formata da nodi costituiti ciascuno dai dati da memorizzare e da due link Ver. 2.4 20 - Claudio Fornaro - Corso di programmazione
Albero binario 2 Alberi binari (introduzione) Struttura di dati bidimensionale formata da nodi costituiti ciascuno dai dati da memorizzare e da due link Ver. 2.4 20 - Claudio Fornaro - Corso di programmazione
Algoritmi e Strutture Dati. HeapSort
 Algoritmi e Strutture Dati HeapSort Selection Sort: intuizioni L algoritmo Selection-Sort scandisce tutti gli elementi dell array a partire dall ultimo elemento fino all inizio e ad ogni iterazione: Viene
Algoritmi e Strutture Dati HeapSort Selection Sort: intuizioni L algoritmo Selection-Sort scandisce tutti gli elementi dell array a partire dall ultimo elemento fino all inizio e ad ogni iterazione: Viene
Un albero completamente bilanciato o pieno (full) alberi completamente sbilanciati. Un albero binario completo
 alberi completamente sbilanciati Un albero completamente bilanciato o pieno (full) Definizione: Un albero è pieno se tutte le foglie sono sullo stesso livello e ogni nodo non foglia ha due figli. Il numero
alberi completamente sbilanciati Un albero completamente bilanciato o pieno (full) Definizione: Un albero è pieno se tutte le foglie sono sullo stesso livello e ogni nodo non foglia ha due figli. Il numero
Algoritmi e Strutture di Dati
 Algoritmi e Strutture di Dati Visite di alberi m.patrignani Nota di copyright queste slides sono protette dalle leggi sul copyright il titolo ed il copyright relativi alle slides (inclusi, ma non limitatamente,
Algoritmi e Strutture di Dati Visite di alberi m.patrignani Nota di copyright queste slides sono protette dalle leggi sul copyright il titolo ed il copyright relativi alle slides (inclusi, ma non limitatamente,
Per semplicità eliminiamo le ripetizioni nell'albero.
 Albero binario di ricerca 20 40 100 95 Un albero binario di ricerca é un albero binario in cui ogni nodo ha un etichetta minore o uguale a quelle dei nodi nel sottoalbero radicato nel figlio destro e maggiore
Albero binario di ricerca 20 40 100 95 Un albero binario di ricerca é un albero binario in cui ogni nodo ha un etichetta minore o uguale a quelle dei nodi nel sottoalbero radicato nel figlio destro e maggiore
Algoritmi e Strutture Dati. HeapSort
 Algoritmi e Strutture Dati HeapSort Selection Sort: intuizioni L algoritmo Selection-Sort scandisce tutti gli elementi dell array a partire dall ultimo elemento fino all inizio e ad ogni iterazione: Viene
Algoritmi e Strutture Dati HeapSort Selection Sort: intuizioni L algoritmo Selection-Sort scandisce tutti gli elementi dell array a partire dall ultimo elemento fino all inizio e ad ogni iterazione: Viene
Alberi. Strutture dati: Alberi. Alberi: Alcuni concetti. Alberi: definizione ricorsiva. Alberi: Una prima realizzazione. Alberi: prima Realizzazione
 Alberi Strutture dati: Alberi Strutture gerarchiche di dati Esempi Il file system di un sistema operativo L organigramma di un azienda Alberi generali, alberi n-ari, alberi binari, Ogni nodo ha un unico
Alberi Strutture dati: Alberi Strutture gerarchiche di dati Esempi Il file system di un sistema operativo L organigramma di un azienda Alberi generali, alberi n-ari, alberi binari, Ogni nodo ha un unico
Alberi. CORDA Informatica. A. Ferrari. Testi da. Marco Bernardo Edoardo Bontà. Dispense del Corso di. Algoritmi e Strutture Dati
 Alberi CORDA Informatica A. Ferrari Testi da Marco Bernardo Edoardo Bontà Dispense del Corso di Algoritmi e Strutture Dati Albero - definizione Albero Figli, fratelli, nodi, foglie Grado, livello, altezza,
Alberi CORDA Informatica A. Ferrari Testi da Marco Bernardo Edoardo Bontà Dispense del Corso di Algoritmi e Strutture Dati Albero - definizione Albero Figli, fratelli, nodi, foglie Grado, livello, altezza,
Prova di Algoritmi e s.d. (1o anno) 17 Settembre TESTO e RISPOSTE
 Prova di Algoritmi e s.d. (1o anno) 17 Settembre 2002 TESTO e RISPOSTE Esercizio 1 (punti 7 in prima approssimazione) Consideriamo alberi binari con insieme dei nodi NODI = N (l'insieme dei naturali).
Prova di Algoritmi e s.d. (1o anno) 17 Settembre 2002 TESTO e RISPOSTE Esercizio 1 (punti 7 in prima approssimazione) Consideriamo alberi binari con insieme dei nodi NODI = N (l'insieme dei naturali).
Alberi. Gli alberi sono una generalizzazione delle liste che consente di modellare delle strutture gerarchiche come questa: Largo. Fosco.
 Alberi Alberi Gli alberi sono una generalizzazione delle liste che consente di modellare delle strutture gerarchiche come questa: Largo Fosco Dora Drogo Frodo Dudo Daisy Alberi Gli alberi sono una generalizzazione
Alberi Alberi Gli alberi sono una generalizzazione delle liste che consente di modellare delle strutture gerarchiche come questa: Largo Fosco Dora Drogo Frodo Dudo Daisy Alberi Gli alberi sono una generalizzazione
Organigramma Gerarchia. (Tree) Nessuna persona può avere più di un superiore Ogni persona può essere superiore di altre
 Alberi Struttura dati Albero Organigramma Gerarchia (Tree) Nessuna persona può avere più di un superiore Ogni persona può essere superiore di altre Esempio di un organigramma di un azienda Tree terminology
Alberi Struttura dati Albero Organigramma Gerarchia (Tree) Nessuna persona può avere più di un superiore Ogni persona può essere superiore di altre Esempio di un organigramma di un azienda Tree terminology
Lezione 12 Tabelle Hash
 Lezione 12 Tabelle Hash Rossano Venturini rossano@di.unipi.it Pagina web del corso http://didawiki.cli.di.unipi.it/doku.php/informatica/all-b/start Esercizio 2 ABR: Visita Scrivere un programma che legga
Lezione 12 Tabelle Hash Rossano Venturini rossano@di.unipi.it Pagina web del corso http://didawiki.cli.di.unipi.it/doku.php/informatica/all-b/start Esercizio 2 ABR: Visita Scrivere un programma che legga
Alberi n-ari: specifiche sintattiche e semantiche. Realizzazioni. Visita di alberi n-ari.
 Alberi n-ari: specifiche sintattiche e semantiche. Realizzazioni. Visita di alberi n-ari. Algoritmi e Strutture Dati + Lab A.A. / Informatica Università degli Studi di Bari Aldo Moro Nicola Di Mauro ALBERO
Alberi n-ari: specifiche sintattiche e semantiche. Realizzazioni. Visita di alberi n-ari. Algoritmi e Strutture Dati + Lab A.A. / Informatica Università degli Studi di Bari Aldo Moro Nicola Di Mauro ALBERO
Note per la Lezione 4 Ugo Vaccaro
 Progettazione di Algoritmi Anno Accademico 2016 2017 Note per la Lezione 4 Ugo Vaccaro Ripasso di nozioni su Alberi Ricordiamo che gli alberi rappresentano una generalizzazione delle liste, nel senso che
Progettazione di Algoritmi Anno Accademico 2016 2017 Note per la Lezione 4 Ugo Vaccaro Ripasso di nozioni su Alberi Ricordiamo che gli alberi rappresentano una generalizzazione delle liste, nel senso che
Informatica 3. Informatica 3. LEZIONE 14: Alberi binari: introduzione. Lezione 14 - Modulo 1. Definizioni. Introduzione. Definizioni e proprietà
 Informatica 3 Informatica 3 LEZIONE 14: Alberi binari: introduzione Lezione 14 - Modulo 1 Modulo 1: Definizioni e proprietà Modulo 2: Attraversamento degli alberi binari Definizioni e proprietà Politecnico
Informatica 3 Informatica 3 LEZIONE 14: Alberi binari: introduzione Lezione 14 - Modulo 1 Modulo 1: Definizioni e proprietà Modulo 2: Attraversamento degli alberi binari Definizioni e proprietà Politecnico
Alberi e alberi binari I Un albero è un caso particolare di grafo
 Alberi e alberi binari I Un albero è un caso particolare di grafo I I I I È costituito da un insieme di nodi collegati tra di loro mediante archi Gli archi sono orientati (ogni arco esce da un nodo origine
Alberi e alberi binari I Un albero è un caso particolare di grafo I I I I È costituito da un insieme di nodi collegati tra di loro mediante archi Gli archi sono orientati (ogni arco esce da un nodo origine
Nozioni di base (II Parte)
 Nozioni di base (II Parte) 1 Ricorsione [GTG14, Par. 5.1-5.4 and 13.1] Algoritmo Ricorsivo: algoritmo che invoca se stesso (su istanze sempre più piccole) sfruttando la nozione di induzione. La soluzione
Nozioni di base (II Parte) 1 Ricorsione [GTG14, Par. 5.1-5.4 and 13.1] Algoritmo Ricorsivo: algoritmo che invoca se stesso (su istanze sempre più piccole) sfruttando la nozione di induzione. La soluzione
Alberi e alberi binari I Un albero è un caso particolare di grafo
 Alberi e alberi binari Un albero è un caso particolare di grafo È costituito da un insieme di nodi collegati tra di loro mediante archi Gli archi sono orientati (ogni arco esce da un nodo origine ed entra
Alberi e alberi binari Un albero è un caso particolare di grafo È costituito da un insieme di nodi collegati tra di loro mediante archi Gli archi sono orientati (ogni arco esce da un nodo origine ed entra
Fondamenti teorici e programmazione
 Fondamenti teorici e programmazione FTP(A) - modb Lezione 9 di ricerca binaria F.Bonchi Dip.to Informatica Fondamenti teorici e programmazione (A) - modb a.a. 2018/19 pag. 1 liberi Un albero libero è un
Fondamenti teorici e programmazione FTP(A) - modb Lezione 9 di ricerca binaria F.Bonchi Dip.to Informatica Fondamenti teorici e programmazione (A) - modb a.a. 2018/19 pag. 1 liberi Un albero libero è un
Richiami di matematica discreta: grafi e alberi. Paolo Camurati Dip. Automatica e Informatica Politecnico di Torino
 Richiami di matematica discreta: grafi e alberi Paolo Camurati Dip. Automatica e Informatica Politecnico di Torino Grafi Definizione: G = (V,E) V: insieme finito di vertici E: insieme finito di archi,
Richiami di matematica discreta: grafi e alberi Paolo Camurati Dip. Automatica e Informatica Politecnico di Torino Grafi Definizione: G = (V,E) V: insieme finito di vertici E: insieme finito di archi,
Esercizio 1. E vero che in un AVL il minimo si trova in una foglia o nel penultimo livello? FB = -1. livello 0 FB = -1. livello 1 FB = -1.
 Esercizio 1 E vero che in un AVL il minimo si trova in una foglia o nel penultimo livello? FB = -1 livello 0 FB = -1 FB = -1 livello 1 FB = -1 livello 2 livello 3 L altezza è 3, il minimo si trova nel
Esercizio 1 E vero che in un AVL il minimo si trova in una foglia o nel penultimo livello? FB = -1 livello 0 FB = -1 FB = -1 livello 1 FB = -1 livello 2 livello 3 L altezza è 3, il minimo si trova nel
In questa lezione Alberi binari di ricerca: la cancellazione
 In questa leione Alberi binari di ricerca: la cancellaione 1 L algoritmo di Hibbard per cancellare (1962) Sia il nodo da cancellare: 1) è una foglia: si rimuove 2) ha un solo figlio x: si rende x figlio
In questa leione Alberi binari di ricerca: la cancellaione 1 L algoritmo di Hibbard per cancellare (1962) Sia il nodo da cancellare: 1) è una foglia: si rimuove 2) ha un solo figlio x: si rende x figlio
Matematica Lezione 2
 Università di Cagliari Corso di Laurea in Farmacia Matematica Lezione 2 Sonia Cannas 12/10/2018 Avviso Le lezioni di martedì dalle 9:00 alle 11:00 sono spostate in aula DELTA. Insieme complementare Definizione
Università di Cagliari Corso di Laurea in Farmacia Matematica Lezione 2 Sonia Cannas 12/10/2018 Avviso Le lezioni di martedì dalle 9:00 alle 11:00 sono spostate in aula DELTA. Insieme complementare Definizione
RISOLUZIONE IN LOGICA PROPOSIZIONALE. Giovanna D Agostino Dipartimento di Matemaica e Informatica, Università di Udine
 RISOLUZIONE IN LOGICA PROPOSIZIONALE Giovanna D Agostino Dipartimento di Matemaica e Informatica, Università di Udine 1. Risoluzione Definitione 1.1. Un letterale l è una variabile proposizionale (letterale
RISOLUZIONE IN LOGICA PROPOSIZIONALE Giovanna D Agostino Dipartimento di Matemaica e Informatica, Università di Udine 1. Risoluzione Definitione 1.1. Un letterale l è una variabile proposizionale (letterale
Esercitazione 8. Corso di Tecniche di programmazione. Laurea in Ingegneria Informatica
 Dipartimento di Informatica e Sistemistica Antonio Ruberti Sapienza Università di Roma Esercitazione 8 Corso di Tecniche di programmazione Laurea in Ingegneria Informatica (Canale di Ingegneria delle Reti
Dipartimento di Informatica e Sistemistica Antonio Ruberti Sapienza Università di Roma Esercitazione 8 Corso di Tecniche di programmazione Laurea in Ingegneria Informatica (Canale di Ingegneria delle Reti
Un heap binario è un albero binario con le seguenti caratteristiche:
 Heap Un heap binario è un albero binario con le seguenti caratteristiche: È quasi completo: tutti i livelli, tranna al più l ultimo sono completi e le foglie dell ultimo livello sono tutte adossate a sinistra.
Heap Un heap binario è un albero binario con le seguenti caratteristiche: È quasi completo: tutti i livelli, tranna al più l ultimo sono completi e le foglie dell ultimo livello sono tutte adossate a sinistra.
Alberi. Albero binario. Un albero binario è un albero (ordinato) in cui ciascun nodo può avere al massimo due figli (figlio destro e figlio sinistro)
 Albero binario Un albero binario è un albero (ordinato) in cui ciascun nodo può avere al massimo due figli (figlio destro e figlio sinistro) albero binario proprio: ogni nodo interno ha esattamente due
Albero binario Un albero binario è un albero (ordinato) in cui ciascun nodo può avere al massimo due figli (figlio destro e figlio sinistro) albero binario proprio: ogni nodo interno ha esattamente due
Laboratorio di Algoritmi
 Laboratorio di Algoritmi Corso di Laurea in Matematica Roberto Cordone DI - Università degli Studi di Milano Lezioni: Martedì 8.30-10.30 in aula 3 Mercoledì 10.30-13.30 in aula 2 Giovedì 15.30-18.30 in
Laboratorio di Algoritmi Corso di Laurea in Matematica Roberto Cordone DI - Università degli Studi di Milano Lezioni: Martedì 8.30-10.30 in aula 3 Mercoledì 10.30-13.30 in aula 2 Giovedì 15.30-18.30 in
L albero e un tipo astratto di dati usato per rappresentare relazioni gerarchiche.
 Lezioni di C L albero e un tipo astratto di dati usato per rappresentare relazioni gerarchiche. qstruttura del file system qalbero genealogico qorganigramma qalbero di decisione q... s=6*8+((2+42)*(5+12)+987*7*123+15*54)
Lezioni di C L albero e un tipo astratto di dati usato per rappresentare relazioni gerarchiche. qstruttura del file system qalbero genealogico qorganigramma qalbero di decisione q... s=6*8+((2+42)*(5+12)+987*7*123+15*54)
Algoritmi e Strutture Dati. Capitolo 6 Il problema del dizionario
 Algoritmi e Strutture Dati Capitolo 6 Il problema del dizionario Il tipo dato Dizionario Suppongo sempre che mi venga dato un riferimento diretto all elemento da cancellare Applicazioni: gestione archivi
Algoritmi e Strutture Dati Capitolo 6 Il problema del dizionario Il tipo dato Dizionario Suppongo sempre che mi venga dato un riferimento diretto all elemento da cancellare Applicazioni: gestione archivi
Esercizi Capitolo 6 - Alberi binari di ricerca
 Esercizi Capitolo 6 - Alberi binari di ricerca Alberto Montresor 9 Agosto, 204 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente, è possibile
Esercizi Capitolo 6 - Alberi binari di ricerca Alberto Montresor 9 Agosto, 204 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente, è possibile
Algoritmi e Strutture Dati & Laboratorio di Algoritmi e Programmazione
 Algoritmi e Strutture Dati & Laboratorio di Algoritmi e Programmazione Appello del 24 Gennaio 2007 Esercizio 1 (ASD) 1. Sia T (n) = T (n/6) + T (n/3) + Θ(n). Considerare ciascuna delle seguenti affermazioni
Algoritmi e Strutture Dati & Laboratorio di Algoritmi e Programmazione Appello del 24 Gennaio 2007 Esercizio 1 (ASD) 1. Sia T (n) = T (n/6) + T (n/3) + Θ(n). Considerare ciascuna delle seguenti affermazioni
algoritmi e strutture di dati
 algoritmi e strutture di dati alberi radicati m.patrignani nota di copyright queste slides sono protette dalle leggi sul copyright il titolo ed il copyright relativi alle slides (inclusi, ma non limitatamente,
algoritmi e strutture di dati alberi radicati m.patrignani nota di copyright queste slides sono protette dalle leggi sul copyright il titolo ed il copyright relativi alle slides (inclusi, ma non limitatamente,
Gli heap. Sommario. Fulvio CORNO - Matteo SONZA REORDA Dip. Automatica e Informatica Politecnico di Torino
 Gli heap Fulvio CORNO - Matteo SONZA REORDA Dip. Automatica e Informatica Politecnico di Torino 1 a.a. 2001/2002 Sommario Gli heap L algoritmo Heapsort Le code con priorità. 2 a.a. 2001/2002 Matteo SONZA
Gli heap Fulvio CORNO - Matteo SONZA REORDA Dip. Automatica e Informatica Politecnico di Torino 1 a.a. 2001/2002 Sommario Gli heap L algoritmo Heapsort Le code con priorità. 2 a.a. 2001/2002 Matteo SONZA
Linguaggi di Programmazione Corso C. Parte n.3 Linguaggi Liberi da Contesto e Linguaggi Contestuali. Nicola Fanizzi
 Linguaggi di Programmazione Corso C Parte n.3 Linguaggi Liberi da Contesto e Linguaggi Contestuali Nicola Fanizzi (fanizzi@di.uniba.it) Dipartimento di Informatica Università degli Studi di Bari Grammatiche
Linguaggi di Programmazione Corso C Parte n.3 Linguaggi Liberi da Contesto e Linguaggi Contestuali Nicola Fanizzi (fanizzi@di.uniba.it) Dipartimento di Informatica Università degli Studi di Bari Grammatiche
Dati e Algoritmi 1: A. Pietracaprina. Alberi Binari
 Dati e Algoritmi 1: A. Pietracaprina Alberi Binari 1 Definizione Un alberto binario T è un albero ordinato in cui Nota ogni nodo interno ha 2 figli ogni nodo non radice è etichettato come figlio sinistro
Dati e Algoritmi 1: A. Pietracaprina Alberi Binari 1 Definizione Un alberto binario T è un albero ordinato in cui Nota ogni nodo interno ha 2 figli ogni nodo non radice è etichettato come figlio sinistro
1 PRELIMINARI 1.1 NOTAZIONI. denota l insieme vuoto. a A si legge a appartiene a A oppure a è elemento di A.
 1 PRELIMINARI 1.1 NOTAZIONI denota l insieme vuoto. a A si legge a appartiene a A oppure a è elemento di A. B A si legge B è un sottoinsieme di A e significa che ogni elemento di B è anche elemento di
1 PRELIMINARI 1.1 NOTAZIONI denota l insieme vuoto. a A si legge a appartiene a A oppure a è elemento di A. B A si legge B è un sottoinsieme di A e significa che ogni elemento di B è anche elemento di
ALBERI ORIENTATI. Definizione: Albero orientato = rooted tree = grafo orientato con le seguenti proprietà: - ha un nodo fissato, detto radice (r);
 ALBERI ORIENTATI Pagina 1 ALBERI ORIENTATI 15:05 Definizione: Albero orientato = rooted tree = grafo orientato con le seguenti proprietà: - ha un nodo fissato, detto radice (r); - per ogni nodo v, esiste
ALBERI ORIENTATI Pagina 1 ALBERI ORIENTATI 15:05 Definizione: Albero orientato = rooted tree = grafo orientato con le seguenti proprietà: - ha un nodo fissato, detto radice (r); - per ogni nodo v, esiste
Algoritmi e Strutture di Dati
 Algoritmi e Strutture di Dati Code di priorità (Heap e heap_sort) m.patrignani Nota di copyright queste slides sono protette dalle leggi sul copyright il titolo ed il copyright relativi alle slides (inclusi,
Algoritmi e Strutture di Dati Code di priorità (Heap e heap_sort) m.patrignani Nota di copyright queste slides sono protette dalle leggi sul copyright il titolo ed il copyright relativi alle slides (inclusi,
Corso di Linguaggi di Programmazione
 Corso di Linguaggi di Programmazione Lezione 4 Alberto Ceselli alberto.ceselli@unimi.it Dipartimento di Tecnologie dell Informazione Università degli Studi di Milano 5 Marzo 2013 Scheme - L interprete
Corso di Linguaggi di Programmazione Lezione 4 Alberto Ceselli alberto.ceselli@unimi.it Dipartimento di Tecnologie dell Informazione Università degli Studi di Milano 5 Marzo 2013 Scheme - L interprete
Alberi: definizioni e dimostrazioni induttive.
 Alberi: definizioni e dimostrazioni induttive. Gennaio 2005 Iniziamo con l introdurre la nozione di albero. Con N indichiamo l insieme dei numeri naturali (zero escluso) e con N l insieme delle liste finite
Alberi: definizioni e dimostrazioni induttive. Gennaio 2005 Iniziamo con l introdurre la nozione di albero. Con N indichiamo l insieme dei numeri naturali (zero escluso) e con N l insieme delle liste finite
In questa lezione. Alberi binari: [CLRS09] cap. 12 per la visita inorder. visite e esercizi su alberi binari. Prof. E. Fachini - Intr. Alg.
![In questa lezione. Alberi binari: [CLRS09] cap. 12 per la visita inorder. visite e esercizi su alberi binari. Prof. E. Fachini - Intr. Alg. In questa lezione. Alberi binari: [CLRS09] cap. 12 per la visita inorder. visite e esercizi su alberi binari. Prof. E. Fachini - Intr. Alg.](/thumbs/93/113927179.jpg) In questa lezione Alberi binari: visite e esercizi su alberi binari [CLRS09] cap. 12 per la visita inorder!1 Visita inordine di un albero binario visita inordine(x) se l albero x non è nullo allora visita
In questa lezione Alberi binari: visite e esercizi su alberi binari [CLRS09] cap. 12 per la visita inorder!1 Visita inordine di un albero binario visita inordine(x) se l albero x non è nullo allora visita
Heap binomiali. Oltre alle precedenti operazioni fondamentali degli heap riunibili, sugli heap binomiali definiremo anche le due ulteriori operazioni:
 Heap binomiali Gli heap binomiali sono strutture dati su cui si possono eseguire efficientemente le operazioni: Make(H) : crea un heap vuoto. Insert(H, ) : aggiunge il nodo allo heap. Minimum(H) : ritorna
Heap binomiali Gli heap binomiali sono strutture dati su cui si possono eseguire efficientemente le operazioni: Make(H) : crea un heap vuoto. Insert(H, ) : aggiunge il nodo allo heap. Minimum(H) : ritorna
Introduzione agli algoritmi Prova di esame del 19/9/2016 Prof.sse E. Fachini - R. Petreschi. Parte prima
 Introduzione agli algoritmi Prova di esame del 19/9/2016 Prof.sse E. Fachini - R. Petreschi Parte prima 1) Si dimostri il teorema sulla limitazione inferiore per il tempo asintotico di esecuzione nel caso
Introduzione agli algoritmi Prova di esame del 19/9/2016 Prof.sse E. Fachini - R. Petreschi Parte prima 1) Si dimostri il teorema sulla limitazione inferiore per il tempo asintotico di esecuzione nel caso
Alberi. Gli alberi sono una generalizzazione delle liste che consente di modellare delle strutture gerarchiche come questa: Largo. Fosco.
 Alberi Alberi Gli alberi sono una generalizzazione delle liste che consente di modellare delle strutture gerarchiche come questa: Largo Fosco Dora Drogo Dudo Frodo Daisy Alberi Gli alberi sono una generalizzazione
Alberi Alberi Gli alberi sono una generalizzazione delle liste che consente di modellare delle strutture gerarchiche come questa: Largo Fosco Dora Drogo Dudo Frodo Daisy Alberi Gli alberi sono una generalizzazione
Esempi. Albero di interi. Struttura che non è un albero!
 albero si dice "grafo diretto" un insieme di nodi legati "a due a due" da archi direzionati (puntatori) un albero è un grafo diretto in cui ogni nodo può avere un solo arco entrante ed un qualunque numero
albero si dice "grafo diretto" un insieme di nodi legati "a due a due" da archi direzionati (puntatori) un albero è un grafo diretto in cui ogni nodo può avere un solo arco entrante ed un qualunque numero
Lezione 9 Alberi binari: visite ed esercizi
 Lezione 9 Alberi binari: visite ed esercizi Informatica 4 Maggio 2016 Operazioni sugli alberi: visita La visita di un albero esplora tutti i nodi ed esegue una qualche operazione su di essi. Per esempio,
Lezione 9 Alberi binari: visite ed esercizi Informatica 4 Maggio 2016 Operazioni sugli alberi: visita La visita di un albero esplora tutti i nodi ed esegue una qualche operazione su di essi. Per esempio,
Algoritmi e strutture dati
 Algoritmi e Strutture Dati Capitolo 4 Ordinamento Ordinamento Dato un insieme S di n oggetti presi da un dominio totalmente ordinato, ordinare S Esempi: ordinare alfabeticamente lista di nomi, o insieme
Algoritmi e Strutture Dati Capitolo 4 Ordinamento Ordinamento Dato un insieme S di n oggetti presi da un dominio totalmente ordinato, ordinare S Esempi: ordinare alfabeticamente lista di nomi, o insieme
Esercizi Capitolo 10 - Code con priorità e insiemi disgiunti
 Esercizi Capitolo 10 - Code con priorità e insiemi disgiunti Alberto Montresor 19 Agosto, 2014 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente,
Esercizi Capitolo 10 - Code con priorità e insiemi disgiunti Alberto Montresor 19 Agosto, 2014 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente,
Algoritmi e Strutture Dati
 Alberi AVL Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 26/7 Alberi AVL Definizione (bilanciamento in altezza): un albero è bilanciato
Alberi AVL Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 26/7 Alberi AVL Definizione (bilanciamento in altezza): un albero è bilanciato
Ricerca con una chiave k Assumiamo l esistenza di un descrittore albero con i campi: albero.radice (=null per l albero vuoto) albero.dimensione (=0 pe
 Ricerca con una chiave k Assumiamo l esistenza di un descrittore albero con i campi: albero.radice (=null per l albero vuoto) albero.dimensione (=0 per l albero vuoto) La funzione Ricerca prende in input
Ricerca con una chiave k Assumiamo l esistenza di un descrittore albero con i campi: albero.radice (=null per l albero vuoto) albero.dimensione (=0 per l albero vuoto) La funzione Ricerca prende in input
Gli heap. Sommario. Algoritmi e Programmazione Avanzata. Fulvio CORNO - Matteo SONZA REORDA Dip. Automatica e Informatica Politecnico di Torino
 Gli heap Fulvio CORNO - Matteo SONZA REORDA Dip. Automatica e Informatica Politecnico di Torino 1 a.a. 2001/2002 Sommario Gli heap L algoritmo Heapsort Le code con priorità. 2 a.a. 2001/2002 Politecnico
Gli heap Fulvio CORNO - Matteo SONZA REORDA Dip. Automatica e Informatica Politecnico di Torino 1 a.a. 2001/2002 Sommario Gli heap L algoritmo Heapsort Le code con priorità. 2 a.a. 2001/2002 Politecnico
Algoritmi e strutture dati 16 Dicembre 2004 Canali A L e M Z Cognome Nome Matricola
 Algoritmi e strutture dati 16 Dicembre 04 Canali A L e M Z Cognome Nome Matricola Problema 1 (6 punti) Determinare la funzione calcolata dal metodo mistero e la sua complessità computazionale in funzione
Algoritmi e strutture dati 16 Dicembre 04 Canali A L e M Z Cognome Nome Matricola Problema 1 (6 punti) Determinare la funzione calcolata dal metodo mistero e la sua complessità computazionale in funzione
Esercizi Capitolo 10 - Code con priorità e insiemi disgiunti
 Esercizi Capitolo 10 - Code con priorità e insiemi disgiunti Alberto Montresor 27 marzo 2012 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente,
Esercizi Capitolo 10 - Code con priorità e insiemi disgiunti Alberto Montresor 27 marzo 2012 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente,
Esercizi parte 3. La classe ArrayBinTree dovra implementare, tra le altre, l operazione seguente: padre: dato un nodo, restituire l indice del padre.
 Esercizi parte 3 RAPPRESENTAZIONE DI ALBERI BINARI 1. Definire una classe LinkedBinTree che implementa alberi binari in modo collegato, con nodi implementati come oggetti di classe BinNode. La classe dovra
Esercizi parte 3 RAPPRESENTAZIONE DI ALBERI BINARI 1. Definire una classe LinkedBinTree che implementa alberi binari in modo collegato, con nodi implementati come oggetti di classe BinNode. La classe dovra
alla categoria di automi a minor potenza riconoscitiva possibile. }, dove k è un parametro.
 Algoritmi e Prin Appello del 2 Settembre 20 Informatica 2 ore e 30 minuti. Chi deve sostenere solo il modulo di Informatica teorica deve svolgere gli Esercizi 1 e 2 in 1 ora e minuti. Chi deve sostenere
Algoritmi e Prin Appello del 2 Settembre 20 Informatica 2 ore e 30 minuti. Chi deve sostenere solo il modulo di Informatica teorica deve svolgere gli Esercizi 1 e 2 in 1 ora e minuti. Chi deve sostenere
DISTRIBUZIONI DI OGGETTI DISTINTI
 DISTRIBUZIONI Pagina 1 DISTRIBUZIONI DI OGGETTI DISTINTI 12:09 r oggetti distinti, n scatole distinte # distribuzioni di r oggetti distinti in n scatole distinte # stringhe di lunghezza r i cui elementi
DISTRIBUZIONI Pagina 1 DISTRIBUZIONI DI OGGETTI DISTINTI 12:09 r oggetti distinti, n scatole distinte # distribuzioni di r oggetti distinti in n scatole distinte # stringhe di lunghezza r i cui elementi
Introduzione ai grafi. Introduzione ai grafi p. 1/2
 Introduzione ai grafi Introduzione ai grafi p. 1/2 Grafi Un grafo G é costituito da una coppia di insiemi (V,A) dove V é detto insieme dei nodi e A é detto insieme di archi ed é un sottinsieme di tutte
Introduzione ai grafi Introduzione ai grafi p. 1/2 Grafi Un grafo G é costituito da una coppia di insiemi (V,A) dove V é detto insieme dei nodi e A é detto insieme di archi ed é un sottinsieme di tutte
Algoritmi e Strutture Dati. Capitolo 3 Strutture dati elementari
 lgoritmi e Strutture Dati Capitolo 3 Strutture dati elementari Gestione di collezioni di oggetti Tipo di dato: Specifica una collezione di oggetti e delle operazioni di interesse su tale collezione (es.
lgoritmi e Strutture Dati Capitolo 3 Strutture dati elementari Gestione di collezioni di oggetti Tipo di dato: Specifica una collezione di oggetti e delle operazioni di interesse su tale collezione (es.
Il tipo astratto coda con priorità: specifiche sintattiche e semantiche. Realizzazioni.
 Il tipo astratto coda con priorità: specifiche sintattiche e semantiche. Realizzazioni. Algoritmi e Strutture Dati + Lab A.A. 14/15 Informatica Università degli Studi di Bari Aldo Moro Nicola Di Mauro
Il tipo astratto coda con priorità: specifiche sintattiche e semantiche. Realizzazioni. Algoritmi e Strutture Dati + Lab A.A. 14/15 Informatica Università degli Studi di Bari Aldo Moro Nicola Di Mauro
Laboratorio di Informatica. Lezione 8: Liste e alberi
 Laboratorio di rmatica Lezione 8: Liste e alberi Il programma della lezione 7 (parte 1) #include #include typedef struct node char key[20]; int volte; struct node *psnnext; NODE, *PNODE;
Laboratorio di rmatica Lezione 8: Liste e alberi Il programma della lezione 7 (parte 1) #include #include typedef struct node char key[20]; int volte; struct node *psnnext; NODE, *PNODE;
ricerca di un elemento, verifica dell appartenenza di un elemento
 Alberi Binari di Ricerca Gli alberi binari di ricerca (o, alberi di ricerca binaria) sono strutture dati che consentono, su un insieme di elementi con un ordine totale le operazioni di: ricerca di un elemento,
Alberi Binari di Ricerca Gli alberi binari di ricerca (o, alberi di ricerca binaria) sono strutture dati che consentono, su un insieme di elementi con un ordine totale le operazioni di: ricerca di un elemento,
Algoritmi e Strutture Dati
 Algoritmi e Strutture Dati Alberi di ricerca Domenico Fabio Savo 1 Dizionari Gli alberi di ricerca sono usati per realizzare in modo efficiente il tipo di dato Dizionario 2 Alberi binari di ricerca (BST
Algoritmi e Strutture Dati Alberi di ricerca Domenico Fabio Savo 1 Dizionari Gli alberi di ricerca sono usati per realizzare in modo efficiente il tipo di dato Dizionario 2 Alberi binari di ricerca (BST
Algoritmi e Strutture Dati. Capitolo 3 Strutture dati elementari
 Algoritmi e Strutture Dati Capitolo 3 Strutture dati elementari Gestione di collezioni di oggetti Tipo di dato: Specifica una collezione di oggetti e delle operazioni di interesse su tale collezione (es.
Algoritmi e Strutture Dati Capitolo 3 Strutture dati elementari Gestione di collezioni di oggetti Tipo di dato: Specifica una collezione di oggetti e delle operazioni di interesse su tale collezione (es.
Laboratorio di Python
 Alberi, Esercizi su alberi Università di Bologna 15 e 17 maggio 2013 Sommario Correzione esercizi 1 Correzione esercizi 2 Esercizi Correzione esercizi Definire una funzione che preso un dizionario di studenti
Alberi, Esercizi su alberi Università di Bologna 15 e 17 maggio 2013 Sommario Correzione esercizi 1 Correzione esercizi 2 Esercizi Correzione esercizi Definire una funzione che preso un dizionario di studenti
come segue: data una collezione C di elementi e una un elemento che verifica la proprietà P
 Problemi di Ricerca Carla Binucci e Walter Didimo Il problema della Ricerca In generale, il Problema della Ricerca è definito come segue: data una collezione C di elementi e una proprietà P, determinare
Problemi di Ricerca Carla Binucci e Walter Didimo Il problema della Ricerca In generale, il Problema della Ricerca è definito come segue: data una collezione C di elementi e una proprietà P, determinare
Esercizi Capitolo 6 - Alberi binari di ricerca
 Esercizi Capitolo 6 - Alberi binari di ricerca Alberto Montresor 23 settembre 200 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente, è possibile
Esercizi Capitolo 6 - Alberi binari di ricerca Alberto Montresor 23 settembre 200 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente, è possibile
Lezione 7 Alberi binari: visite e alberi di ricerca
 Lezione 7 Alberi binari: visite e alberi di ricerca Informatica 6 Maggio 2015 Operazioni sugli alberi: visita La visita di un albero esplora tutti i nodi ed esegue una qualche operazione su di essi. Per
Lezione 7 Alberi binari: visite e alberi di ricerca Informatica 6 Maggio 2015 Operazioni sugli alberi: visita La visita di un albero esplora tutti i nodi ed esegue una qualche operazione su di essi. Per
Algoritmi e Strutture Dati
 Maria Rita Di Berardini, Emanuela Merelli Scuola di Scienze e Tecnologie Università di Camerino Definizione (bilanciamento in altezza): un albero è bilanciato in altezza se le altezze dei sottoalberi sinistro
Maria Rita Di Berardini, Emanuela Merelli Scuola di Scienze e Tecnologie Università di Camerino Definizione (bilanciamento in altezza): un albero è bilanciato in altezza se le altezze dei sottoalberi sinistro
Esercizio. 2 i=i*2) j=j*2)
 Esercizio 1 Esercizio 2 i=i*2) j=j*2) Soluzione Il frammento è composto da due parti quasi identiche. L unica differenza è il modo in cui crescono i contatori. Nella prima parte la crescita è lineare mentre
Esercizio 1 Esercizio 2 i=i*2) j=j*2) Soluzione Il frammento è composto da due parti quasi identiche. L unica differenza è il modo in cui crescono i contatori. Nella prima parte la crescita è lineare mentre
