Il Mondo della Tartaruga - Programmazione LOGO
|
|
|
- Brigida Manca
- 9 anni fa
- Visualizzazioni
Transcript
1 Un pó di storia Il Logo é un ambiente di apprendimento, non solo uno dei piú potenti linguaggi di programmazione oggi disponibili per personal computer. Il Mondo della Tartaruga - Programmazione LOGO Prof. Domenico Beneventano Università di Modena e Reggio Emilia 6 maggio 2003 Il piú popolare dei prodotti Logo élaturtle, la tartaruga. Originariamente era un piccolo robot azionato da motori che la facevano muovere su spessi fogli di cartone e su cui disegnava con una penna che poteva essere abbassata o alzata dal foglio. Era comandata attraverso una piccola tastiera collegata ad computer, con semplici istruzioni. 1 Presupposti Teorici del LOGO I presupposti teorici del Logo si trovano nella teoria dell apprendimento elaborata da Jean Piaget. Ambiente Egosintonico Questo linguaggio si propone di offrire all allievo un ambiente egosintonico sfruttando alcune idee e creazioni (es il LISP) dell intelligenza artificiale. Ambiente Stimolante al cui interno é possibile imparare attraverso la manipolazione di una serie di materiali e di strumenti, realizzando cosí una serie di esperienze che sfociano nella costruzione di concetti profondi, acquisiti sperimentando. La Tartaruga ai tempi nostri La tartaruga, Turtle, é diventata un oggetto grafico sullo schermo del computer, vive una vita elettronica animata istruita attraverso il linguaggio di programmazione Logo. Costruzione di Algoritmi trasferendo le capacitá di riflessione acquisite sperimentando, si arriva alla costruzione di algoritmi che, proposti dapprima all automa Turtle, vengono successivamente trasferiti nella costruzione di piú astratte strutture informatiche che fanno uso di parole, stringhe e vettori. In accordo con il corpo 2 3
2 Geometria Tradizionale Î Geometria della Tartaruga Geometria Tradizionale Î Geometria della Tartaruga La geometria tradizionale é costruita su astrazioni: Un punto senza dimensioni Una linea che ha una lunghezza ma non ha spessore concetti difficili da afferrare per i bambini. La tartaruga éinvece un oggetto reale che puó essere manipolato, chiamiamolo piú esattamente un oggetto di transizione tra il concreto, il robot, e l astratto, apparendo come un piccolo triangolo sullo schermo che puó essere comandato e istruito ad eseguire compiti diversi, legati soprattutto alla creazione di disegni di vario tipo e colorati. 4 5 Facciamo muovere la tartaruga Geometria Tradizionale Î Geometria della Tartaruga Digita PCS e premi Enter per visualizzare la tartaruga Geometria analitica si fonda su un sistema esterno di riferimento e la posizione del punto é individuata dalle coordinate. Geometria della tartaruga é egosintonica, in accordo con il corpo. La tartaruga si muove come tu ti muovi, pensi al tuo movimento e puoi ordinare alla tartaruga di compierne di simili. La geometria della tartaruga non vuole sostituire la geometria tradizionale, é un punto d ingresso alternativo alle astrazioni geometriche e matematiche. Si presta ugualmente bene ad apprendere alcuni concetti di base sia per i bambini che per gli adulti. La tartaruga si trova nella sua HOME nel centro dello schermo. Per far muovere la tartaruga dobbiamo dare: Comando: Cosa fare. Argomento: Quante volte farlo. Enter: Muoviti. Per far scrivere / non far scrivere la tartaruga dobbiamo dare: GIU :Penna giù. SU :Penna su. 6 7
3 Comandi di Movimento Avanti (AV) Indietro (IN) Destra (DE) Sinistra (SI) In Micromondi, si può scrivere indifferentemente il comando per intero (esempio: Avanti 100) oppure la sua abbreviazione (esempio: AV 100). in maiuscolo (esempio: AVANTI 100) oppure in minuscolo (esempio: avanti 100) Esercitiamoci Proviamo a disegnare due semplici poligoni: IMPORTANTE :Inqueste dispense si usano a volte queste ulteriori abbreviazioni: Avanti (A), Destra (D), Indietro (I) e Sinistra (S) Tali abbreviazioni non sono accettate da Micromondi: quindi in Micromondi occorre sostituirle (ad esempio, A 100 deve essere sostituita con avanti 100 oppure AV 100) N.B. ricordati di premere Enter dopo ogni comando!! 8 Notate delle similitudini nei comandi necessari a disegnare le due figure? 9 Il Comando RIPETI Il comando RIPETI ci aiuta nel disegno di poligoni regolari, vediamone la sintassi: RIPETI Ò Comando1 Arg1 Comando2 Arg2... ComandoN ArgN Poligono Lati Angolo Instruzioni 3 RIPETI 3 AV DE Il comando RIPETI Riesci a vedere una similitudine tra Lati e Angolo, quale relazione esiste tra il numero di lati e l angolo per ogni poligono? Se N = numero di lati, allora Angolo = 360/N! semplice no!! 4 RIPETI 4 AV DE 10 11
4 Variabili Procedure Definire una procedura vuol dire, in parole semplici, assegnare un nome ad una sequenza di istruzioni, per poterle richiamare in un secondo momento digitando il nome della procedura. PER SQUARE RIPETI 4 A 50 D 90 Per richiamare la procedura basta digitare: SQUARE (e dare Enter) Una procedura puó essere richiamata con dei parametri: dei valori da associare ad una variabile presente nella procedura. Una variabile é un area di memoria a cui viene associato un nome e nella quale si puó memorizzare un valore. PER TRIANGOLO :SIZE RIPETI 3 A :SIZE D 120 La prima riga (PER TRIANGOLO :SIZE) dice al computer di associare ad un area di memoria il nome SIZE e di memorizzare in essa il numero che trova accanto a TRIANGOLO nella chiamata della procedura. Il comando AV :SIZE dice alla tartaruga di muoversi in avanti di tanti passi quanto é il valore che si trova nell area di memoria chiamata SIZE Lavorare con piú variabili Ancora sulle procedure Una procedura puó essere richiamata all interno di un altra procedura: PER MODELLO RIPETI 3 TRIANGOLO 100 D 120 In questo esempio la procedura MODELLO richiama la procedura TRIANGOLO passandogli come parametro d ingresso 100. Una procedura puó essere definita con piú di1pa- rametro d ingresso. I parametri devono seguire il nome della procedura ed avere nomi distinti: PER RETTANGOLO :H :W RIPETI 2 A :H D 90 A :W D 90 In questo esempio la procedura RETTANGOLO viene definita con due parametri H (height = altezza) e W (Width = larghezza) e ripete 2 volte il disegno: PER RETTANGOLO :H :W RIPETI 2 A :H D 90 A :W D
5 Divertiamoci!!! Proviamo a disegnare una sedia, come in figura: Divertiamoci!!!! Dopo la sedia ci vuole un tavolo: INIZIO INIZIO Proviamo a definire la procedura sedia: PER SEDIA AVANTI 40 INDIETRO 20 DESTRA 90 AVANTI 16 DESTRA 90 AVANTI 20 Per disegnarlo dobbiamo prima allontanarci dalla sedia: SU SINISTRA 90 AVANTI 24 SINISTRA 90 GIU Divertiamoci!!!! Adesso definiamo la procedura TAVOLO: PER TAVOLO AVANTI 50 DESTRA 90 AVANTI 100 DESTRA 90 AVANTI 50 Adesso abbiamo una sedia ed un tavolo facile no Domanda e Risposta In Micromondi possiamo interagire con la tartaruga, lei fa le domande con il comando: DOMANDA testo della domanda La nostra risposta sará contenuta nella variabile speciale risposta, vediamo un esempio (cliccate Invio dopo ogni comando): DOMANDA ETA? MOSTRA RISPOSTA dopo il comando DOMANDA ETA? appare una finestra, immettendo un valore e cliccando su OK sulla console comandi (quella in basso a destra) apparirá il valore da noi immesso
6 Disegniamo un Poligono Abbiamo giá visto come disegnare un poligono: PER POLIGONO :NLATI :LUNG RIPETI :NLATI AV :LUNG DE 360 / :NLATI Adesso vogliamo fare in modo che sia la tartaruga a chiederci il numero di lati e la lunghezza di ciascun lato del nostro poligono: Disegniamo un Poligono La tartaruga deve quindi formulare due domande: Quanti lati? DOMANDA Quanti lati? Dimensione del lato : DOMANDA Dimensione lato : Disegniamo un Poligono Vediamo di costruire la procedura CHIEDIPO- LIGONO, definiamo l istruzione di inizio e fine procedura: PER CHIEDIPOLIGONO All interno dobbiamo far si che la tartaruga formuli 2 domande; poiché la nostra risposta andrá sempre nella variabile risposta, prima di formulare la seconda dobbiamo memorizzare il suo valore in una variabile da noi definita. Disegniamo un Poligono PER CHIEDIPOLIGONO DOMANDA NUMERO LATI? ASSEGNA "NUMEROLATI RISPOSTA Cosa abbiamo fatto qui?, la tartaruga ci chiede il numero di lati e poi assegna alla variabile di nome NUMEROLATI (notare l uso delle ) il valore di risposta (che essendo una variabile speciale non ha bisogno dei :) 22 23
7 Disegniamo un Poligono Il principio é lo stesso per chiedere la dimensione del lato, per cui scriveremo all interno della procedura CHIEDIPOLIGONO: PER CHIEDIPOLIGONO DOMANDA NUMERO LATI? ASSEGNA "NUMEROLATI RISPOSTA DOMANDA DIMENSIONE LATO : ASSEGNA "DIMENSIONELATO RISPOSTA... Se non avessimo scritto ASSEGNA NUMEROLATI RISPOSTA, dopo la seconda domanda avremmo perso il numero di lati. Disegniamo un Poligono A questo punto abbiamo tutti i dati necessari per chiamare la procedura POLIGONO: PER CHIEDIPOLIGONO DOMANDA NUMERO LATI? ASSEGNA "NUMEROLATI RISPOSTA DOMANDA DIMENSIONE LATO : ASSEGNA "DIMENSIONELATO RISPOSTA POLIGONO :NUMEROLATI :DIMENSIONELATO Differenza fra Nome e Valore di una variabile La tartaruga di Micromondi distingue il nome di una variabile dal valore ad essa associato attraverso l uso delle e del: Nome variabile miavariabile Valore variabile :miavariabile E facile capire quando usare le o i: Usiamo le nell istruzione ASSEGNA (es: ASSEGNA MIAVARIABILE 2) Usiamo i : nelle Espressioni Matematiche :miavariabile - 1 Definizioni di procedure con parametri PER POLIGONO :NLATI :LUNG. Nelle chiamate di procedure con parametri POLIGONO :NLATI :LUNG (vedi esempio in CHIEDIPOLIGONO) Esercitiamoci con i cerchi Un cerchio lo possiamo vedere come un poligono di 360 lati, per cui possiamo definirne la procedura nel seguente modo: PER CERCHIO :RAGGIO RIPETI 360 AV :RAGGIO DE 1 Per far si che la tartaruga disegni tanti cerchi uno dentro l altro, dobbiamo variare il raggio all interno del ripeti Quello che vogliamo fare é partire da un valore iniziale di raggio e cambiarne il valore ad ogni cerchio disegnato
8 dettiamo delle condizioni alla tartaruga Esercitiamoci con i cerchi PER CERCHI :ncerchi ASSEGNA raggio 2 RIPETI :ncerchi cerchio :raggio assegna raggio :raggio -.3 PER CERCHI :ncerchi Definiamo una procedura di nome CERCHI che ha bisogno del valore (quindi :) del parametro ncerchi. ASSEGNA raggio 2 Assegniamo alla variabile di nome raggio il valore di partenza 2. RIPETI :ncerchi Ripetiamo un numero di volte pari al valore di ncerchi (il parametro d ingresso) le istruzioni rachiuse tra parentesi quadre. cerchio :raggio richiamiamo la procedura cerchio passandole il valore della variabile raggio. assegna raggio :raggio Assegniamo alla variabile di nome raggio il valore di raggio meno 0.3 (:raggio -0.3 é un espressione matematica) 28 In LOGO é possibile condizionare il comportamento della tartaruga al verificarsi o meno di una condizione. Una condizione é un espressione di cui é possibile affermare se sia vera o falsa (es: 5 2, 2+1=3) La tartaruga riesce a valutare una condizione con il comando SE SE condizione istruzioni se condizione é vera Ad esempio: PER SETIMUOVI DOMANDA NUMERO PASSI? SE RISPOSTA > 50 AV RISPOSTA Se alla tartaruga diamo un numero di passi maggiore di 50 la condizione RISPOSTA 50 sará verae la vedremo muoversi in avanti di un numero di passi pari al valore da noi dato come risposta, altrimenti rimarrá ferma perché non saprá cosa fare 29 Alternative con il comando SE la tartaruga fa qualcosa solo se la condizione é vera, per dargli un alternativa dobbiamo usare il comando SEALTRIMENTI SEALTRIMENTI condizione istruzioni se condizione é vera istruzioni se condizione é falsa Ad esempio: PER SETIMUOVI2 DOMANDA NUMERO PASSI? SEALTRIMENTI RISPOSTA > 50 AV RISPOSTA IN RISPOSTA La tartaruga valuta la condizione risposta 50, se é vera va in avanti altrimenti va indietro di un numero di passi pari al valore da noi dato come risposta. 30 Esempio avanzato Ipotizziamo di avere tre numeri: num1, num2 e num3 e di volerne individuare il maggiore: Prima di tutto dobbiamo valutare chi tra num1 e num2 éilpiú grande : SEALTRIMENTI :num1 > :num2 nel caso in cui sia num1 il piú grande (condizione vera) dobbiamo confrontarlo con num3 : SEALTRIMENTI :num1 > :num2 SEALTRIMENTI :num1 > :num3 31
9 Esempio avanzato Esempio avanzato Se la condizione é vera mostriamo num1 se é falsa mostriamo num3: SEALTRIMENTI :num1 > :num2 SEALTRIMENTI :num1 > :num3 MOSTRA :num1 MOSTRA :num3 Finora abbiamo esaminato il caso in cui la condizone :num1 :num2 fosse vera, dobbiamo vedere cosa fare se é falsa: SEALTRIMENTI :num1 > :num2 SEALTRIMENTI :num1 > :num3 MOSTRA :num1 MOSTRA :num3 :num1 < :num Esempio avanzato In questo caso dobbiamo valutare num2 con num3 come fatto in precedenza con num1: SEALTRIMENTI :num1 > :num2 SEALTRIMENTI :num1 > :num3 MOSTRA :num1 MOSTRA :num3 SEALTRIMENTI :num2 > :num3 MOSTRA :num2 MOSTRA :num3 Esempio avanzato Quindi la nostra procedura massimo sará: PER MASSIMO :num1 :num2 :num3 SEALTRIMENTI :num1 > :num2 SEALTRIMENTI :num1 > :num3 MOSTRA :num1 MOSTRA :num3 SEALTRIMENTI :num2 > :num3 MOSTRA :num2 MOSTRA :num
10 ESERCIZIO: La casa Costruiamo la nostra casetta: Le mura Le mura sono rappresentabili attraverso un quadrato: PER CASA RIPETI 4 AV 100 DE Il tetto A questo punto la tartaruga é tornata a casa, deve usare una scala per salire sul tetto: AV 100 DE 30 Ora possiamo costruire il nostro tetto, che altro non é che un triangolo: RIPETI 3 AV 100 DE 120 Dopo aver costruito il tetto dobbiamo far scendere la tartaruga dal tetto: Conclusioni sulla casa ricapitolando la nostra casa é definita dalla seguente procedura: PER CASA RIPETI 4 AV 100 DE 90 (le mura) AV 100 DE 30 (la salita sulle scale) RIPETI 3 AV 100 DE 120 (il tetto) SI 30 IN 100 (la discesa dalle scale) SI 30 IN
11 Varianti alla casa Possiamo cercare di definire 2 procedure per la salita e la discesa dal tetto: PER SALITA AV 100 DE 30 PER DISCESA SI 30 IN 100 Il paese La tartaruga nella sua casa si sente sola, utilizziamo allora la procedura CASA per costruire un paese in cui possano venire ad abitare altre tartarughe: PER PAESE RIPETI 4 CASA SU DE 90 AV 200 SI 90 GIU A questo punto la casa é costruita cosí: PER CASA RIPETI 4 AV 100 DE 90 (le mura) SALITA (la salita sulle scale) RIPETI 3 AV 100 DE 120 (il tetto) DISCESA (la discesa dalle scale) Variante al paese Volendo possiamo definire una procedura spazio: PER SPAZIO SU DE 90 AV 200 SI 90 GIU In questo modo la procedura PAESE cambia: La chiesa Proviamo adesso a costruire una chiesa: PER CHIESA PER PAESE RIPETI 4 CASA SPAZIO 42 43
12 La Torre Componenti di una chiesa La chiesa che vogliamo costruire é composta da: 2Torri: La torre é composta da un rettangolo e da un triangolo, il triangolo lo sappiamo giá disegnare non il rettangolo PER RETTANGOLO RIPETI 2 AV 200 DE 90 AV 100 DE 90 Modifichiamo le procedure SALITA e DISCESA per far salire la tartaruga sulla torre: 1 casa: PER SALITA :a AV :a DE 30 PER DISCESA :a SI 30 IN :a La procedura CHIESA La procedura TORRE A questo punto la procedura TORRE é definita come: PER TORRE RETTANGOLO SALITA 200 RIPETI 3 AV 100 DE 90 DISCESA 200 La chiesa puó essere cosí definita: PER CHIESA TORRE DE 90 AV 100 SI 90 CASA DE 90 DE 100 SI 90 TORRE Notate l utilitá delle procedure, conn 5 righe ho costruito una chiesa!!! 46 47
Logo. è il punto in cui si trova la tartaruga al momento dell avvio del programma
 Logo COMANDI LOGO AVANTI INDIETRO DESTRA SINISTRA PULISCHERMO PULISCITESTO NASTARTA A I D S PS PT NT nasconde la tartaruga PULISCI MOSTARTA TANA SULAPENNA PENNAGIU CANCEPENNA PENNAINVERSA MT mostra la
Logo COMANDI LOGO AVANTI INDIETRO DESTRA SINISTRA PULISCHERMO PULISCITESTO NASTARTA A I D S PS PT NT nasconde la tartaruga PULISCI MOSTARTA TANA SULAPENNA PENNAGIU CANCEPENNA PENNAINVERSA MT mostra la
per l Innovazione Didattica
 Pensiero Computazionale e Coding per l Innovazione Didattica Algoritmo e Ripeti Laura Tarsitano PENSIERO COMPUTAZIONALE PER L'INNOVAZIONE DIDATTICA 1 Algoritmo/Sequenza Una lista di passi da seguire per
Pensiero Computazionale e Coding per l Innovazione Didattica Algoritmo e Ripeti Laura Tarsitano PENSIERO COMPUTAZIONALE PER L'INNOVAZIONE DIDATTICA 1 Algoritmo/Sequenza Una lista di passi da seguire per
LA GEOMETRIA DELLA TARTARUGA
 LA GEOMETRIA DELLA TARTARUGA CAPITOLO 4 Tracciare figure Iniziamo con una figura semplice: il QUADRATO. Certamente sai che un quadrato ha tutti i lati uguali e gli angoli uguali. Dopo aver avviato Logo
LA GEOMETRIA DELLA TARTARUGA CAPITOLO 4 Tracciare figure Iniziamo con una figura semplice: il QUADRATO. Certamente sai che un quadrato ha tutti i lati uguali e gli angoli uguali. Dopo aver avviato Logo
Logo. http://www.softronix.com/logo.html (Setup Kit)
 Logo Logo è un linguaggio di programmazione essenzialmente didattico; È orientato alla creazione di grafica vettoriale, ma può essere usato per fare qualsiasi tipo di programma; MSWLogo è una versione
Logo Logo è un linguaggio di programmazione essenzialmente didattico; È orientato alla creazione di grafica vettoriale, ma può essere usato per fare qualsiasi tipo di programma; MSWLogo è una versione
1. IL CERCHIO COLORATO
 1. IL CERCHIO COLORATO Utilizzare l icona per inserire un segmento di data lunghezza Cliccare sul punto (estremo) e scrivere quindi la lunghezza del segmento (10 per esempio) Cliccare col tasto destro
1. IL CERCHIO COLORATO Utilizzare l icona per inserire un segmento di data lunghezza Cliccare sul punto (estremo) e scrivere quindi la lunghezza del segmento (10 per esempio) Cliccare col tasto destro
Introduzione all uso di Geogebra
 Curricolo verticale di Matematica - Progetto SIGMA (dare SIGnificato al fare MAtematica) Laboratorio di geometria a.s 2013/14 Quali poligoni tassellano il piano? Scuola secondaria di primo grado Introduzione
Curricolo verticale di Matematica - Progetto SIGMA (dare SIGnificato al fare MAtematica) Laboratorio di geometria a.s 2013/14 Quali poligoni tassellano il piano? Scuola secondaria di primo grado Introduzione
Progetto Informatica. Primo esempio Gruppo 1. Laura Tarsitano
 Progetto Informatica Primo esempio Gruppo 1 Laura Tarsitano [email protected] Come costruire un micromondo Quando si costruisce un micromondo su Snap! bisogna immaginare di costruire uno spettacolo
Progetto Informatica Primo esempio Gruppo 1 Laura Tarsitano [email protected] Come costruire un micromondo Quando si costruisce un micromondo su Snap! bisogna immaginare di costruire uno spettacolo
GIU RIPETI 4 [AV 100 DE
 CAPITOLO TERZO QUI INCONTRIAMO DELLE PRIMITIVE DAVVERO STRAORDINARIE COME RIPETI, ACASO, ASPETTA, DAICOLORE, DAISPESSORELINEA, DAICOLORETESTO, CON LE QUALI POSSIAMO FARE TANTISSIME COSE QUI SCOPRIRAI CHE
CAPITOLO TERZO QUI INCONTRIAMO DELLE PRIMITIVE DAVVERO STRAORDINARIE COME RIPETI, ACASO, ASPETTA, DAICOLORE, DAISPESSORELINEA, DAICOLORETESTO, CON LE QUALI POSSIAMO FARE TANTISSIME COSE QUI SCOPRIRAI CHE
Foglio elettronico Microsoft Office Excel 2003
 Foglio elettronico Microsoft Office Excel 2003 04/06/2015 Nonni su internet 2015 1 Il foglio elettronico è un programma che possiamo usare per creare tabelle di numeri e calcolare automaticamente somme,
Foglio elettronico Microsoft Office Excel 2003 04/06/2015 Nonni su internet 2015 1 Il foglio elettronico è un programma che possiamo usare per creare tabelle di numeri e calcolare automaticamente somme,
Introduzione. La scheda didattica è stata ideata grazie ad uno spunto del prof. Stefano Penge dell Università La Sapienza di Roma.
 Costruire l'area del quadrato con Scratch Autore: Lorenzo Cesaretti Categoria: Coding Introduzione Vediamo come creare un algoritmo per la costruzione dell'area di un quadrato, chiedendo la lunghezza del
Costruire l'area del quadrato con Scratch Autore: Lorenzo Cesaretti Categoria: Coding Introduzione Vediamo come creare un algoritmo per la costruzione dell'area di un quadrato, chiedendo la lunghezza del
Usa lo sfoglialibro sul computer. Usa il libro attivo sul computer
 Usa lo sfoglialibro sul computer Come sfogliare il libro 2 L indice delle pagine 3 L anteprima delle pagine 4 La funzione di ricerca/1 5 La funzione di ricerca/2 6 La funzione Inserisci nota /1 7 La funzione
Usa lo sfoglialibro sul computer Come sfogliare il libro 2 L indice delle pagine 3 L anteprima delle pagine 4 La funzione di ricerca/1 5 La funzione di ricerca/2 6 La funzione Inserisci nota /1 7 La funzione
francesca fattori speranza bozza gennaio 2018
 DERIVATE APPLICATE ALLO STUDIO DI FUNZIONE. OM Le derivate servono a trovare eventuali massimi e minimi delle funzioni. Ho pensato questo modulo in questo modo: concetto di derivata; calcolo di una derivata
DERIVATE APPLICATE ALLO STUDIO DI FUNZIONE. OM Le derivate servono a trovare eventuali massimi e minimi delle funzioni. Ho pensato questo modulo in questo modo: concetto di derivata; calcolo di una derivata
Sessione 3 LA GEOMETRIA DELLA TARTARUGA: UNA MATEMATICA FATTA PER APPRENDERE
 Sessione 3 LA GEOMETRIA DELLA TARTARUGA: UNA MATEMATICA FATTA PER APPRENDERE La geometria della Tartaruga è uno stile di geometria diverso dagli altri, come lo stile assiomatico d'euclide e lo stile analitico
Sessione 3 LA GEOMETRIA DELLA TARTARUGA: UNA MATEMATICA FATTA PER APPRENDERE La geometria della Tartaruga è uno stile di geometria diverso dagli altri, come lo stile assiomatico d'euclide e lo stile analitico
(ED IMPARARE LE REGOLE DELLE OPERAZIONI)
 COME CALCOLARE IL PERIMETRO DI UN RETTANGOLO (ED IMPARARE LE REGOLE DELLE OPERAZIONI) Mettiamo che io abbia 8 panini, per calcolare la loro somma posso fare panino+panino+panino+panino+panino+panino+panino+panino=
COME CALCOLARE IL PERIMETRO DI UN RETTANGOLO (ED IMPARARE LE REGOLE DELLE OPERAZIONI) Mettiamo che io abbia 8 panini, per calcolare la loro somma posso fare panino+panino+panino+panino+panino+panino+panino+panino=
SCRATCH CECILIA MONTI DIGITAL CO-FONDATRICE E DOCENTE PRESSO MAKER SCHOOL TRADATE
 SCRATCH CECILIA MONTI DIGITAL CHAMPION @MOZZATE [email protected] CO-FONDATRICE E DOCENTE PRESSO MAKER SCHOOL TRADATE CHE COS È SCRATCH? Scratch è un software gratuito basato su un linguaggio
SCRATCH CECILIA MONTI DIGITAL CHAMPION @MOZZATE [email protected] CO-FONDATRICE E DOCENTE PRESSO MAKER SCHOOL TRADATE CHE COS È SCRATCH? Scratch è un software gratuito basato su un linguaggio
Nella finestra successiva dovremo cercare l immagine che vogliamo appiccicare nel file.
 Come realizzare i disegni in Autocad partendo da un immagine L obbiettivo di questo articolo, è quello di poter avere a disposizione le linee di costruzione in qualsiasi scala, senza dover fare decine
Come realizzare i disegni in Autocad partendo da un immagine L obbiettivo di questo articolo, è quello di poter avere a disposizione le linee di costruzione in qualsiasi scala, senza dover fare decine
[PRIMA DI VIDEOSCRIVERE ]
![[PRIMA DI VIDEOSCRIVERE ] [PRIMA DI VIDEOSCRIVERE ]](/thumbs/60/45240873.jpg) Manuale di preparazione alla videoscrittura per bambini e persone che non hanno mai usato una tastiera. by Cinzia [PRIMA DI VIDEOSCRIVERE ] Una piccola guida di preparazione alla scrittura col computer,
Manuale di preparazione alla videoscrittura per bambini e persone che non hanno mai usato una tastiera. by Cinzia [PRIMA DI VIDEOSCRIVERE ] Una piccola guida di preparazione alla scrittura col computer,
Excel di Microsoft o Calc di OpenOffice sono programmi per la gestione dei fogli di calcolo
 FOGLI DI CALCOLO Excel di Microsoft o Calc di OpenOffice sono programmi per la gestione dei fogli di calcolo COMANDI BASE Comandi di APRI, SALVA, SALVA CON NOME, CHIUDI, STAMPA nel menù FILE. Comandi di
FOGLI DI CALCOLO Excel di Microsoft o Calc di OpenOffice sono programmi per la gestione dei fogli di calcolo COMANDI BASE Comandi di APRI, SALVA, SALVA CON NOME, CHIUDI, STAMPA nel menù FILE. Comandi di
Fondamenti di Informatica T-1
 Fondamenti di Informatica T-1 Introduzione al linguaggio Java - Input/Output, Variabili, Tipi Tutor: Allegra De Filippo [email protected] a.a. 2015/2016 Fondamenti di Informatica T-1 Allegra De
Fondamenti di Informatica T-1 Introduzione al linguaggio Java - Input/Output, Variabili, Tipi Tutor: Allegra De Filippo [email protected] a.a. 2015/2016 Fondamenti di Informatica T-1 Allegra De
LEZIONE 2 COORDINATE RELATIVE
 LEZIONE 2 In questa lezione vediamo come muoversi nell area grafica per disegnare qualsiasi oggetto. Come abbiamo visto nella prima lezione Autocad utilizza le coordinate cartesiane come riferimento per
LEZIONE 2 In questa lezione vediamo come muoversi nell area grafica per disegnare qualsiasi oggetto. Come abbiamo visto nella prima lezione Autocad utilizza le coordinate cartesiane come riferimento per
La stampa da CAD tramite il layout BREVE TUTORIAL
 La stampa da CAD tramite il layout BREVE TUTORIAL corso di Analisi della città e degli Insediamenti c.d.l. in Scienze dell Architettura prof. Francesco Alberti 3b 3a Gli elementi dell area di lavoro CAD
La stampa da CAD tramite il layout BREVE TUTORIAL corso di Analisi della città e degli Insediamenti c.d.l. in Scienze dell Architettura prof. Francesco Alberti 3b 3a Gli elementi dell area di lavoro CAD
INTRODUZIONE ALLA PROGRAMMAZIONE
 INTRODUZIONE ALLA PROGRAMMAZIONE Prof. Enrico Terrone A. S: 2008/09 Definizioni Programmare significa risolvere problemi col computer, cioè far risolvere problemi al computer attraverso un insieme di informazioni
INTRODUZIONE ALLA PROGRAMMAZIONE Prof. Enrico Terrone A. S: 2008/09 Definizioni Programmare significa risolvere problemi col computer, cioè far risolvere problemi al computer attraverso un insieme di informazioni
Archimede UNDER 14 Dal ritagliare al dimostrare: i rettangoli isoperimetrici. La seguente proposta didattica mostra
 RUBRICA Dal ritagliare al dimostrare: i rettangoli isoperimetrici di Monica Testera La seguente proposta didattica mostra come, da attività semplici e manipolative quali il ritaglio di figure su cartoncini
RUBRICA Dal ritagliare al dimostrare: i rettangoli isoperimetrici di Monica Testera La seguente proposta didattica mostra come, da attività semplici e manipolative quali il ritaglio di figure su cartoncini
Il disegno vettoriale - scheda di approfondimento
 Il disegno vettoriale - scheda di approfondimento età +11 - autore ADVidea - licenza CC 2.5 testo Tecnica per il [tuo] futuro su DidaSfera.it BBN editrice Ti ricordiamo infatti che l utilizzo di un programma
Il disegno vettoriale - scheda di approfondimento età +11 - autore ADVidea - licenza CC 2.5 testo Tecnica per il [tuo] futuro su DidaSfera.it BBN editrice Ti ricordiamo infatti che l utilizzo di un programma
Presenta: I Poligoni e loro proprietà
 Presenta: I Poligoni e loro proprietà Scuola secondaria di I grado: classe prima Ricordiamo: ü Le figure geometriche fondamentali: rette, semirette, segmenti, angoli. ü Il concetto di lunghezza e di ampiezza
Presenta: I Poligoni e loro proprietà Scuola secondaria di I grado: classe prima Ricordiamo: ü Le figure geometriche fondamentali: rette, semirette, segmenti, angoli. ü Il concetto di lunghezza e di ampiezza
Usare il mouse e la tastiera
 Usare il mouse e la tastiera Questa risorsa didattica è stata realizzata dallo staff di Pane e Internet per lo svolgimento di un corso di formazione rivolto ai migranti, organizzato nel primo semestre
Usare il mouse e la tastiera Questa risorsa didattica è stata realizzata dallo staff di Pane e Internet per lo svolgimento di un corso di formazione rivolto ai migranti, organizzato nel primo semestre
Laboratorio di informatica
 GEOMETRIA ANALITICA CON GEOGEBRA Oltre che per lo studio della geometria euclidea, come abbiamo fatto lo scorso anno, il software Geogebra (geometria + algebra) può essere utilizzato per lo studio della
GEOMETRIA ANALITICA CON GEOGEBRA Oltre che per lo studio della geometria euclidea, come abbiamo fatto lo scorso anno, il software Geogebra (geometria + algebra) può essere utilizzato per lo studio della
VBA è un linguaggio di scripting derivato da Visual Basic, da cui prende il nome. Come ogni linguaggio ha le sue regole.
 Excel VBA VBA Visual Basic for Application VBA è un linguaggio di scripting derivato da Visual Basic, da cui prende il nome. Come ogni linguaggio ha le sue regole. 2 Prima di iniziare. Che cos è una variabile?
Excel VBA VBA Visual Basic for Application VBA è un linguaggio di scripting derivato da Visual Basic, da cui prende il nome. Come ogni linguaggio ha le sue regole. 2 Prima di iniziare. Che cos è una variabile?
Laboratorio di informatica
 Laboratorio di informatica GEOMETRIA DELLO SPAZIO Introduzione a Geogebra 3D La versione 5 di Geogebra prevede anche la possibilità di lavorare in ambiente 3D. Basta aprire Visualizza - Grafici 3D: sullo
Laboratorio di informatica GEOMETRIA DELLO SPAZIO Introduzione a Geogebra 3D La versione 5 di Geogebra prevede anche la possibilità di lavorare in ambiente 3D. Basta aprire Visualizza - Grafici 3D: sullo
NUMERI SCUOLA SECONDARIA I GRADO
 NUMERI Eseguire addizioni, sottrazioni, moltiplicazioni, divisioni e confronti tra i numeri conosciuti (numeri naturali, numeri interi, frazioni e numeri decimali), quando possibile a mente oppure utilizzando
NUMERI Eseguire addizioni, sottrazioni, moltiplicazioni, divisioni e confronti tra i numeri conosciuti (numeri naturali, numeri interi, frazioni e numeri decimali), quando possibile a mente oppure utilizzando
CORSO BASE DI AUTOCAD
 CORSO BASE DI AUTOCAD 27/11/12 ing. P. Rordorf arch. D. Bruni arch. A. Chiesa ing. A. Ballarini 1(13) 1. Vantaggi del CAD CAD sta per Computer-Aided Design cioè PROGETTAZIONE ASSISTITIA DAL COMPUTER Rispetto
CORSO BASE DI AUTOCAD 27/11/12 ing. P. Rordorf arch. D. Bruni arch. A. Chiesa ing. A. Ballarini 1(13) 1. Vantaggi del CAD CAD sta per Computer-Aided Design cioè PROGETTAZIONE ASSISTITIA DAL COMPUTER Rispetto
La geometria con il CABRI
 La geometria con il CABRI Cabrì è un micromondo dove si "materializzano" gli enti astratti della geometria elementare del piano (punti, rette, angoli, figure) sotto forma di disegni, su "fogli virtuali"
La geometria con il CABRI Cabrì è un micromondo dove si "materializzano" gli enti astratti della geometria elementare del piano (punti, rette, angoli, figure) sotto forma di disegni, su "fogli virtuali"
Stabilire se il punto di coordinate (1,1) appartiene alla circonferenza centrata nell origine e di raggio 1.
 Definizione di circonferenza e cerchio. Equazione della circonferenza centrata in O e di raggio R. Esercizi. La circonferenza e il cerchio Definizioni: dato un punto C nel piano cartesiano e dato un numero
Definizione di circonferenza e cerchio. Equazione della circonferenza centrata in O e di raggio R. Esercizi. La circonferenza e il cerchio Definizioni: dato un punto C nel piano cartesiano e dato un numero
Fasi di creazione di un programma
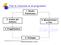 Fasi di creazione di un programma 1. Studio Preliminare 2. Analisi del Sistema 6. Manutenzione e Test 3. Progettazione 5. Implementazione 4. Sviluppo Sviluppo di programmi Per la costruzione di un programma
Fasi di creazione di un programma 1. Studio Preliminare 2. Analisi del Sistema 6. Manutenzione e Test 3. Progettazione 5. Implementazione 4. Sviluppo Sviluppo di programmi Per la costruzione di un programma
LE TRASFORMAZIONI GEOMETRICHE
 LE TRASFORMAZIONI GEOMETRICHE LA SIMMETRIA ASSIALE Definizione: il simmetrico P di un punto P, rispetto alla simmetria assiale di asse r gode delle seguenti proprietà: P e P sono equidistanti da r e il
LE TRASFORMAZIONI GEOMETRICHE LA SIMMETRIA ASSIALE Definizione: il simmetrico P di un punto P, rispetto alla simmetria assiale di asse r gode delle seguenti proprietà: P e P sono equidistanti da r e il
francesca fattori speranza - versione febbraio 2018 { y > 0 4) DETERMINAZIONE DEL TIPO DI FUNZIONE (PARI, DISPARI, PERIODICA)
 STUDIO DI FUNZIONE francesca fattori speranza - versione febbraio 2018 1) DOMINIO O CONDIZIONE DI ESISTENZA 2) INTERSEZIONE CON GLI ASSI y f (x) intersezione asse x : { y 0 y f (x) intersezione asse y
STUDIO DI FUNZIONE francesca fattori speranza - versione febbraio 2018 1) DOMINIO O CONDIZIONE DI ESISTENZA 2) INTERSEZIONE CON GLI ASSI y f (x) intersezione asse x : { y 0 y f (x) intersezione asse y
Geogebra. a. La lancetta è ruotata? SI NO. Se sì attorno a quale punto?
 Geogebra L ANGOLO 1. Nel programma Geogebra, fai doppio clic sull icona e scegli Circonferenza dati centro e raggio. 2. Posizionati al centro della finestra di geometria e fai clic. Nella finestra che
Geogebra L ANGOLO 1. Nel programma Geogebra, fai doppio clic sull icona e scegli Circonferenza dati centro e raggio. 2. Posizionati al centro della finestra di geometria e fai clic. Nella finestra che
L ANGOLO (2) MISURA DELL ANGOLO Per avere la misura di un angolo, che si chiama ampiezza, si deve ricorrere ad uno strumento: il goniometro.
 Geogebra L ANGOLO (2) MISURA DELL ANGOLO Per avere la misura di un angolo, che si chiama ampiezza, si deve ricorrere ad uno strumento: il goniometro. In Geogebra c è un icona che ci permette di misurare
Geogebra L ANGOLO (2) MISURA DELL ANGOLO Per avere la misura di un angolo, che si chiama ampiezza, si deve ricorrere ad uno strumento: il goniometro. In Geogebra c è un icona che ci permette di misurare
Sviluppo di programmi
 Sviluppo di programmi Per la costruzione di un programma conviene: 1. condurre un analisi del problema da risolvere 2. elaborare un algoritmo della soluzione rappresentato in un linguaggio adatto alla
Sviluppo di programmi Per la costruzione di un programma conviene: 1. condurre un analisi del problema da risolvere 2. elaborare un algoritmo della soluzione rappresentato in un linguaggio adatto alla
Modulo 1 Concetti di base della Tecnologia dell Informazione
 Modulo 1 Concetti di base della Tecnologia dell Informazione 1.0.1.1 1.0.1.2 1.0.1.3 Algoritmi Definizione di algoritmo e sua rappresentazione grafica Per algoritmo si intende un procedimento, che permette
Modulo 1 Concetti di base della Tecnologia dell Informazione 1.0.1.1 1.0.1.2 1.0.1.3 Algoritmi Definizione di algoritmo e sua rappresentazione grafica Per algoritmo si intende un procedimento, che permette
Coding con Scratch. Coding unplugged e con il PC nella scuola primaria
 Coding con Scratch Coding unplugged e con il PC nella scuola primaria Per riuscire a completare un compito, un robot ha bisogno di avere una precisa sequenza di istruzioni (PROGRAMMA) da poter eseguire
Coding con Scratch Coding unplugged e con il PC nella scuola primaria Per riuscire a completare un compito, un robot ha bisogno di avere una precisa sequenza di istruzioni (PROGRAMMA) da poter eseguire
Fondamenti di informatica T-1 (A K) Esercitazione 2 Basi del linguaggio Java
 Fondamenti di informatica T-1 (A K) Esercitazione 2 Basi del linguaggio Java AA 2018/2019 Tutor Lorenzo Rosa [email protected] 2 Programma Introduzione al calcolatore e Java Linguaggio Java, basi e
Fondamenti di informatica T-1 (A K) Esercitazione 2 Basi del linguaggio Java AA 2018/2019 Tutor Lorenzo Rosa [email protected] 2 Programma Introduzione al calcolatore e Java Linguaggio Java, basi e
usare le funzioni aritmetiche e logiche di base come. Volgiamo costruire un foglio elettronico in cui registriamo i voti presi
 4.3 Funzioni e formule 4.3.1 Funzioni aritmetiche e logiche 4.3.1.1. usare le funzioni aritmetiche e logiche di base come addizione, sottrazione, moltiplicazione, divisione Volgiamo costruire un foglio
4.3 Funzioni e formule 4.3.1 Funzioni aritmetiche e logiche 4.3.1.1. usare le funzioni aritmetiche e logiche di base come addizione, sottrazione, moltiplicazione, divisione Volgiamo costruire un foglio
GEOGEBRA 4.0. guida introduttiva. Finita l installazione di GeoGebra 4.0 viene creata sul desktop una icona come questa:
 GEOGEBRA 4.0 guida introduttiva Finita l installazione di GeoGebra 4.0 viene creata sul desktop una icona come questa: fai doppio clic e si apre una finestra come la seguente. Sotto la barra dei menu a
GEOGEBRA 4.0 guida introduttiva Finita l installazione di GeoGebra 4.0 viene creata sul desktop una icona come questa: fai doppio clic e si apre una finestra come la seguente. Sotto la barra dei menu a
Processamento delle immagini
 Processamento delle immagini Docente: Domenico Daniele Bloisi Novembre 2017 Esercizio 1 Utilizzare il linguaggio di programmazione Python e la libreria OpenCV per visualizzare sullo schermo il logo ASL
Processamento delle immagini Docente: Domenico Daniele Bloisi Novembre 2017 Esercizio 1 Utilizzare il linguaggio di programmazione Python e la libreria OpenCV per visualizzare sullo schermo il logo ASL
SCUOLA SECONDARIA DI SECONDO GRADO. Contenuti Attività Metodo Strumenti Durata (in ore)
 SCUOLA SECONDARIA DI SECONDO GRADO Obiettivi di apprendimento Contenuti Attività Metodo Strumenti Durata (in ore) Valutazione degli obiettivi di apprendimento Valutazione della competenza Conoscere i poligoni
SCUOLA SECONDARIA DI SECONDO GRADO Obiettivi di apprendimento Contenuti Attività Metodo Strumenti Durata (in ore) Valutazione degli obiettivi di apprendimento Valutazione della competenza Conoscere i poligoni
EXCEL software Excel .xlxs, La cella intestazione della colonna intestazione di righe l indirizzo della cella testo numeri formule
 EXCEL Il software Excel appartiene alla categoria dei fogli elettronici. Ogni foglio è composto da 1.048.576 righe per 16.384 colonne suddivise in celle che è possibile collegare tra loro: in tal modo
EXCEL Il software Excel appartiene alla categoria dei fogli elettronici. Ogni foglio è composto da 1.048.576 righe per 16.384 colonne suddivise in celle che è possibile collegare tra loro: in tal modo
ISTRUZIONI PER INIZIARE
 1 ISTRUZIONI PER INIZIARE Questa è la barra di menu: serve per dare tutte le informazioni sui file che devi creare, salvare, ecc. Questa icona serve per chiudere a bordo pagina il file e poi riaprirlo
1 ISTRUZIONI PER INIZIARE Questa è la barra di menu: serve per dare tutte le informazioni sui file che devi creare, salvare, ecc. Questa icona serve per chiudere a bordo pagina il file e poi riaprirlo
Piastrelliamo i rettangoli
 Per la quinta primaria Piastrelliamo i rettangoli Qui sotto vedete un rettangolo, disegnato sulla carta a quadretti. Potete immaginare che sia una stanza, che vogliamo piastrellare, con delle piastrelle
Per la quinta primaria Piastrelliamo i rettangoli Qui sotto vedete un rettangolo, disegnato sulla carta a quadretti. Potete immaginare che sia una stanza, che vogliamo piastrellare, con delle piastrelle
LEZIONE 1. 10/05/16 1 Dott. Aniello Castiglione. INTRODUZIONE A SCRATCH Laboratorio di Informatica per l Educazione A. A.
 LEZIONE 1 10/05/16 1 Dott. Aniello Castiglione INTRODUZIONE A SCRATCH Laboratorio di Informatica per l Educazione A. A. 2015/2016 INTRODUZIONE Scratch è un nuovo linguaggio di programmazione visuale che
LEZIONE 1 10/05/16 1 Dott. Aniello Castiglione INTRODUZIONE A SCRATCH Laboratorio di Informatica per l Educazione A. A. 2015/2016 INTRODUZIONE Scratch è un nuovo linguaggio di programmazione visuale che
FONDAMENTI DI INFORMATICA
 FONDAMENTI DI INFORMATICA Prof. Alfredo Accattatis Slide (rielaborate) del prof. Emiliano Casalicchio [email protected] Esercizio (1) Dati due vettori V1 e V2 scrivere un algoritmo che permetta
FONDAMENTI DI INFORMATICA Prof. Alfredo Accattatis Slide (rielaborate) del prof. Emiliano Casalicchio [email protected] Esercizio (1) Dati due vettori V1 e V2 scrivere un algoritmo che permetta
Tutorato di Fondamenti di Informatica TUTOR: DAVIDE GHIANI, GIULIA ORRU
 Tutorato di Fondamenti di Informatica PROFESSORE: GIAN LUCA MARCIALIS TUTOR: DAVIDE GHIANI, GIULIA ORRU Organizzazione Informazioni di contatto: [email protected] Davide Ghiani Giulia Orrù
Tutorato di Fondamenti di Informatica PROFESSORE: GIAN LUCA MARCIALIS TUTOR: DAVIDE GHIANI, GIULIA ORRU Organizzazione Informazioni di contatto: [email protected] Davide Ghiani Giulia Orrù
COMANDI DI DISEGNO POLIGONO
 COMANDI DI DISEGNO Poligono Rettangolo Arco Cerchio Ellisse POLIGONO Il comando poligono è semplicissimo viene richiesto il numero dei lati, digitate un valore da 3 a 1024, cliccare un punto per il centro
COMANDI DI DISEGNO Poligono Rettangolo Arco Cerchio Ellisse POLIGONO Il comando poligono è semplicissimo viene richiesto il numero dei lati, digitate un valore da 3 a 1024, cliccare un punto per il centro
La geometria della riga e compasso: Primo incontro
 La geometria della riga e compasso: Primo incontro Progetto Lauree Scientifiche A.S. 2010/2011 Università degli Studi di Firenze 23/11/2010 Quando si devono rappresentare disegni geometrici, è importante
La geometria della riga e compasso: Primo incontro Progetto Lauree Scientifiche A.S. 2010/2011 Università degli Studi di Firenze 23/11/2010 Quando si devono rappresentare disegni geometrici, è importante
I Circuiti combinatori: LOGISIM
 1 ISTITUTO DI ISTRUZIONE SUPERIORE ANGIOY I Circuiti combinatori: LOGISIM Prof. G. Ciaschetti 1. Le porte logiche Un circuito combinatorio (o sistema combinatorio o rete combinatoria) è un circuito elettrico,
1 ISTITUTO DI ISTRUZIONE SUPERIORE ANGIOY I Circuiti combinatori: LOGISIM Prof. G. Ciaschetti 1. Le porte logiche Un circuito combinatorio (o sistema combinatorio o rete combinatoria) è un circuito elettrico,
Progetto Indicazioni Nazionali 2015/2016. I.C. G. Marconi Castelfranco Emilia (Modena)
 Progetto Indicazioni Nazionali 2015/2016 I.C. G. Marconi Castelfranco Emilia (Modena) Perimetro e area in gioco Docente: Antonella Casarini Classe: VB I.C. G. Marconi Artefatti: squadretta/goniometro,
Progetto Indicazioni Nazionali 2015/2016 I.C. G. Marconi Castelfranco Emilia (Modena) Perimetro e area in gioco Docente: Antonella Casarini Classe: VB I.C. G. Marconi Artefatti: squadretta/goniometro,
1 La traslazione. 2 La composizione di traslazioni. 3 La rotazione
 1 La traslazione Per poter applicare una traslazione ad una generica figura geometrica si deve: ± creare il vettore di traslazione AB mediante il comando Vettore tra due punti; ± cliccare con il mouse
1 La traslazione Per poter applicare una traslazione ad una generica figura geometrica si deve: ± creare il vettore di traslazione AB mediante il comando Vettore tra due punti; ± cliccare con il mouse
Esercitazioni di Informatica (CIV)
 Esercitazioni di Informatica (CIV) Introduzione Andrea Romanoni e-mail: [email protected] website: http://home.deib.polimi.it/romanoni/ 21 ottobre 2015 L informatica: questa sconosciuta Perchè
Esercitazioni di Informatica (CIV) Introduzione Andrea Romanoni e-mail: [email protected] website: http://home.deib.polimi.it/romanoni/ 21 ottobre 2015 L informatica: questa sconosciuta Perchè
3 Omotetie del piano. 4 Omotetie del piano. Fondamenti e didattica della matematica B. Geometria delle similitudini. k = 3.
 1 2 Fondamenti e didattica della matematica B 5 marzo 2007 Geometria delle similitudini Marina Bertolini ([email protected]) Dipartimento di Matematica F.Enriques Università degli Studi di
1 2 Fondamenti e didattica della matematica B 5 marzo 2007 Geometria delle similitudini Marina Bertolini ([email protected]) Dipartimento di Matematica F.Enriques Università degli Studi di
Il quadrato di binomio, assieme allaa differenza dei quadrati che vedremo in seguito, è uno dei più importanti prodotti notevoli.
 PRODOTTI NOTEVOLI I prodotti notevoli sono identità matematiche molto utilizzate nella risoluzione di espressioni algebriche letterali in quanto permettono uno svolgimento rapido dei calcoli, inoltre si
PRODOTTI NOTEVOLI I prodotti notevoli sono identità matematiche molto utilizzate nella risoluzione di espressioni algebriche letterali in quanto permettono uno svolgimento rapido dei calcoli, inoltre si
Frequenza risposte. Che io arrivi da solo alla soluzione: 2. Lascio fare a loro: 2
 Allegato 1 Dati raccolti tramite questionari quantitativi e qualitativi Dati raccolti a inizio percorso su un totale di 16 allievi. Domande Quando devi risolvere un problema di matematica preferisci lavorare
Allegato 1 Dati raccolti tramite questionari quantitativi e qualitativi Dati raccolti a inizio percorso su un totale di 16 allievi. Domande Quando devi risolvere un problema di matematica preferisci lavorare
DISPENSA ACCESS (OFFICE 2010 BETA)
 DISPENSA ACCESS (OFFICE 2010 BETA) 2. LE RELAZIONI. Una relazione può essere definita come un legame tra due tabelle basato sul valore di uno o più campi di ciascuna delle due tabelle. Di solito i campi
DISPENSA ACCESS (OFFICE 2010 BETA) 2. LE RELAZIONI. Una relazione può essere definita come un legame tra due tabelle basato sul valore di uno o più campi di ciascuna delle due tabelle. Di solito i campi
Primi passi con Bee-Bot e Cubetto
 Primi passi con Bee-Bot e Cubetto CARATTERISTICHE DI BEE BOT Bee-Boot è un robot giocattolo che aiuta i bambini a muoversi nello spazio Progettato per i bambini di scuola dell'infanzia e dei primi anni
Primi passi con Bee-Bot e Cubetto CARATTERISTICHE DI BEE BOT Bee-Boot è un robot giocattolo che aiuta i bambini a muoversi nello spazio Progettato per i bambini di scuola dell'infanzia e dei primi anni
Coding e robotica. CTS di Reggio Emilia
 Coding e robotica CTS di Reggio Emilia Cos è il Centro di Supporto Territoriale per le nuove tecnologie https://docs.google.com/presentation/d/1fxngmfnzytrx0rogokppferspvh4scmkyd5ch09m2lm/edit?usp=sharing
Coding e robotica CTS di Reggio Emilia Cos è il Centro di Supporto Territoriale per le nuove tecnologie https://docs.google.com/presentation/d/1fxngmfnzytrx0rogokppferspvh4scmkyd5ch09m2lm/edit?usp=sharing
