Algoritmi e Strutture Dati
|
|
|
- Elisa Federici
- 8 anni fa
- Просмотров:
Транскрипт
1 Programmazione dinamica Algoritmi e Strutture Dati Capitolo Programmazione dinamica Alberto Montresor Università di Trento This work is licensed under the Creative Commons AttributionNonCommercialShareAlike License. To view a copy of this license, visit or send a letter to Creative Commons, Howard Street, th Floor, San Francisco, California, 9, USA. Divideetimpera Tecnica ricorsiva Approccio topdown (problemi divisi in sottoproblemi) Vantaggioso solo quando i sottoproblemi sono indipendenti Altrimenti, gli stessi sottoproblemi possono venire risolti più volte Programmazione dinamica Tecnica iterativa Approccio bottomup Vantaggiosa quando ci sono sottoproblemi in comune Esempio semplice: il triangolo di Tartaglia Coefficienti binomiali Triangolo di Tartaglia Coefficienti binomiali C(n, k) = Il numero di modi di scegliere k oggetti da un insieme di n oggetti I coefficienti di un equazione di grado n n = k ( n! k! (n k)! = se k =_ k = n C(n,k ) + C(n,k) altrimenti Versione ricorsiva Deriva direttamente dalla definizione Domanda Complessità? nx (a + b) n = C(n, k)a n k= k b k integer C(integer n, k) if n = k or k =then return else return C(n,k ) + C(n,k)
2 Triangolo di Tartaglia Quando applicare la programmazione dinamica? Versione iterativa Sottostruttura ottima Basata su programmazione dinamica Domanda Complessità? tartaglia(integer n, integer[][]c) for i to n do C[i, ] C[i, i] for i to n do for j to i do C[i, j] C[i,j ] + C[i,j] E' possibile combinare le soluzioni dei sottoproblemi per trovare la soluzione di un problema più grande PS: In tempo polinomiale! Le decisioni prese per risolvere un problema rimangono valide quando esso diviene un sottoproblema di un problema più grande Sottoproblemi ripetuti Un sottoproblema può occorrere più volte Spazio dei sottoproblemi Deve essere polinomiale Programmazione dinamica Catena di moltiplicazione di matrici Caratterizzare la struttura di una soluzione ottima Definire ricorsivamente il valore di una soluzione ottima La soluzione ottima ad un problema contiene le soluzioni ottime ai sottoproblemi Calcolare il valore di una soluzione ottima bottomup (cioè calcolando prima le soluzioni ai casi più semplici) Si usa una tabella per memorizzare le soluzioni dei sottoproblemi Evitare di ripetere il lavoro più volte, utilizzando la tabella Costruire la (una) soluzione ottima. Problema: Data una sequenza di matrici A, A, A,, An, compatibili a al prodotto, vogliamo calcolare il loro prodotto. Cosa vogliamo ottimizzare La moltiplicazione di matrici si basa sulla moltiplicazione scalare come operazione elementare. Vogliamo calcolare il prodotto impiegando il numero minore possibile di moltiplicazioni Attenzione: Il prodotto di matrici non è commutativo......ma è associativo: (A A) A = A (A A) 7 8
3 Catena di moltiplicazione tra matrici matrici: A B C x x x Catena di moltiplicazione tra matrici matrici: A B C D x x x x (A B ) ((A B ) C ) (B C) (A (B C)) # Moltiplicazioni Memoria = = = = ((( A B ) C ) D ) : 87 moltiplicazioni (( A ( B C )) D ) : moltiplicazioni (( A B ) ( C D )) : moltiplicazioni ( A (( B C ) D )) : moltiplicazioni ( A ( B ( C D ))) : moltiplicazioni ((( A B ) C ) D ) : 87 ( A B ) = (( A B ) C ) = (( A B ) C ) D = Applicare la programmazione dinamica Parentesizzazione Le fasi principali: Definizione: Una parentesizzazione Pi,j del prodotto Ai Ai+ Aj consiste Caratterizzare la struttura di una soluzione ottima nella matrice Ai, se i = j; Definire ricorsivamente il valore di una soluzione ottima Calcolare il valore di una soluzione ottima bottomup (dal basso verso l alto) nel prodotto di due parentesizzazioni (Pi,k Pk+,j), altrimenti. (A (A A )) (A (A A )) Costruzione di una soluzione ottima Nei lucidi successivi: Vediamo ora una ad una le quattro fasi del processo di sviluppo applicate al problema della parentesizzazione ottima Esempio: (A (A A )) (A (A A )) k= Ultima moltiplicazione (A (A A )) (A (A A )) A (A A ) A (A A ) A A A A
4 Parentesizzazione ottima Parentesizzazione ottima Parentesizzazione ottima Definiamo una relazione di ricorrenza Determinare il numero di moltiplicazioni scalari necessari per i prodotti tra le matrici in ogni parentesizzazione Scegliere una delle parentesizzazioni che richiedono il numero minimo di moltiplicazioni P(n): numero di parentesizzazioni per n matrici A A A An L'ultima moltiplicazione può occorrere in n posizioni diverse Fissato l'indice k dell'ultima moltiplicazione, abbiamo P(k) parentesizzazioni per A A A Ak Motivazione: P(nk) parentesizzazioni per Ak+ Ak+ An Vale la pena di spendere un po' di tempo per cercare la parentesizzazione migliore, per risparmiare tempo dopo Domanda P n P (n) = k= P (k)p (n k) n> n = Quante sono le parentesizzazioni possibili? n=, n=, n=??? n P(n) 9 8 Parentesizzazione ottima Definizioni Equazione di ricorrenza: Denoteremo nel seguito con: P n P (n) = k= P (k)p (n k) n> n = A A A An il prodotto di n matrici da ottimizzare ci il numero di righe della matrice Ai Soluzione: nesimo numero catalano P (n) =C(n ) = n n = n + n n / ci il numero di colonne della matrice Ai A[i..j] il prodotto Ai Ai+ Aj P[i..j] una parentesizzazione di A[i..j] (non necessariamente ottima) Domanda: Più semplicemente, dimostrare che P(n) = Ω( n ) Conseguenza: la forza bruta (tentare tutte le possibili parentesizzazioni) non funziona
5 Struttura di una parentesizzazione ottima Struttura di una parentesizzazione ottima Sia A[i..j] = Ai Ai+ Aj una sottosequenza del prodotto di matrici Teorema (sottostruttura ottima) Si consideri una parentesizzazione ottima P[i..j] di A[i..j] Esiste una ultima moltiplicazione : in altre parole, esiste un indice k tale che P[i..j] = P[i..k] P[k+..j] Se P[i..j] = P[i..k] P[k+..j] è una parentesizzazione ottima del prodotto A[i..j], allora P[i..k] e P[k+..j] sono parentesizzazioni ottime dei prodotti A[i..k] e A[k+..j], rispettivamente. Domanda: Quali sono le caratteristiche delle due sottoparti P[i..k] e P[k+..j]? ( P[i..k] ) ( P[k+..j] ) P[i..k] P[k+..j]?? Dimostrazione Ragionamento per assurdo Supponiamo esista un parentesizzazione ottima P'[i..k] di A[i..k] con costo inferiore a P[i..k] Allora, P'[i..k] P[k+..j] sarebbe una parentesizzazione di A[i..j] con costo inferiore a P[i..j], assurdo. 7 8 Struttura di una parentesizzazione ottima Definire ricorsivamente il valore di una soluzione ottima In altre parole: Il teorema afferma che esiste una sottostruttura ottima: Ogni soluzione ottima al problema della parentesizzazione contiene al suo interno le soluzioni ottime dei due sottoproblemi Programmazione dinamica: L'esistenza di sottostrutture ottime è una delle caratteristiche da cercare per decidere se la programmazione dinamica è applicabile Definizione: sia M[i,j] il numero minimo di prodotti scalari richiesti per calcolare il prodotto A[i,j] Come calcolare M[i,j]? Caso base: i=j. Allora, M[i,j] = Passo ricorsivo: i < j. Esiste una parentesizzazione ottima P[i..j] = P[i..k] P[k+..j]; sfruttiamo la ricorsione: M[i,j] = M[i,k] + M[k+,j] + ci ck cj Prossima fase: Definire ricorsivamente il costo di una soluzione ricorsiva Prodotti per P[i..k] Prodotti per P[k+..j] Prodotto di una coppia di matrici: u n. righe: prima matrice u n. colonne: ultima matrice 9
6 Definire ricorsivamente il valore di una soluzione ottima Ma qual è il valore di k? Non lo conosciamo ma possiamo provarli tutti! k può assumere valori fra i e j La formula finale: M[i,j] = mini k < j { M[i,k] + M[k+, j] + ci ck cj } Esempio L R L R M[,] = min k < { M[,k] + M[k+,] + c c k c } = M[,] + M[,] + c c c = c c c i \ j Esempio L R L R L R M[,] = min k< { M[,k] + M[k+,] + c c k c } = min { M[,] + M[,] + c c c, M[,] + M[,] + c c c } i \ j Esempio L R L R L R M[,] = min k< { M[,k] + M[k+,] + c c k c } = min { M[,] + M[,] + c c c, M[,] + M[,] + c c c, M[,] + M[,] + c c c } i \ j
7 Esempio Esempio L i \ Rj L i \ Rj M[,] = min k< { M[,k] + M[k+,] + c c k c } = min { M[,] + M[,] + c c c, M[,] + M[,] + c c c, M[,] + M[,] + c c c, M[,] + M[,] + c c c } M[,] = min k< { M[,k] + M[k+,] + c c k c } = min { M[,] + M[,] + c c c, M[,] + M[,] + c c c, M[,] + M[,] + c c c, M[,] + M[,] + c c c, M[,] + M[,] + c c c } Calcolo bottomup del valore della soluzione Soluzione ricorsiva topdown Passiamo ora al terzo passo della programmazione dinamica: calcolare in modo bottomup il valore della soluzione ottima Ma la definizione ricorsiva di M[i,j] suggerisce di utilizzare un approccio ricorsivo topdown per risolvere il problema: Lanciamo il problema sulla sequenza completa [,n] Il meccanismo ricorsivo individua i sottoproblemi da risolvere Proviamo... male non fa ;) Input: un array c[..n] con le dimensioni delle matrici, c[] è il numero di righe della prima matrice c[i] è il numero di colonne della matrice Ai u integer recpar(integer[]c, integer i, integer j) if i = j then return else min + for integer k i to j do integer q recpar(c, i, k)+recpar(c, k +, j)+c[i if q<min then min q return min Domanda: Complessità risultante? ] c[k] c[j] 7 8
8 Critica all'approccio topdown Calcolare la soluzione ottima in modo bottomup Alcune riflessioni E' interessante notare che il numero di possibili problemi è molto inferiore a n La soluzione ricorsiva topdown è Ω( n ) Non è poi migliore dell'approccio basato su forza bruta! Qual è il problema? Il problema principale è che molti problemi vengono risolti più volte Ogni sottoproblema uno per ogni scelta di i e j (con i j n): n + n = (n ) Sottoproblemi con i < j È risolvibile utilizzando le soluzioni dei sottoproblemi che sono state eventualmente già calcolate e memorizzate nell'array Idea chiave della programmazione dinamica: Sottoproblemi con i = j Mai calcolare più di una volta la soluzione ad un sottoproblema 9 Calcolare la soluzione ottima in modo bottomup Algoritmo L algoritmo parentesizzazione() prende in ingresso un array c[..n] con le dimensioni delle matrici c[] è il numero di righe della A c[i] è il numero di righe della matrice Ai+ il numero di colonne della matrice Ai utilizza (e ritorna) due matrici n n ausiliarie: M[i,j] che contiene i costi minimi dei sottoproblemi A[i..j] S[i,j] che contiene il valore di k che minimizza il costo per il sottoproblema parentesizzazione(integer[]c, integer[][]m, integer[][]s, integer n) integer i, j, h, k, t for i to n do h varia sulle diagonali sopra quella principale M[i, i] for h to n do i e j assumono i valori delle for i to n h +do celle nella diagonale h j i + h M[i, j] + for k i to j do t M[i, k]+m[k +,j]+c[i ] c[k] c[j] if t<m[i, j] then M[i, j] t L S[i, j] k Calcola tutti i possibili valori e conserva solo il più piccolo
9 L i \ i Rj i c i 7 L i \ Rj i c i 7 M[ ] S[ ] M[,] = min k { M[,k] + M[k+,] + c c k c } = min { M[,] + M[,] + c c c, M[,] + M[,] + c c c, M[,] + M[,] + c c c } = min { * 8 *, * *, * * } = min { 8,, 8 } = 8 M[,] = min k { M[,k] + M[k+,] + c c k c } = min { M[,] + M[,] + c c c, M[,] + M[,] + c c c, M[,] + M[,] + c c c } = min { * 8 *, * *, * * } = min { 8,, 8 } = 8 Calcolare la soluzione ottima in modo bottomup Costruire una soluzione ottima Considerazioni sull'algoritmo Costo computazionale: O(n ) Nota Lo scopo della terza fase era calcolare in modo bottomup il valore della soluzione ottima Questo valore si trova in M[,n] Possiamo definire un algoritmo che costruisce la soluzione a partire dall'informazione calcolata da parentesizzazione(). La matrice S ci permette di determinare il modo migliore di moltiplicare le matrici. S[i,j]=k contiene infatti il valore k su cui dobbiamo spezzare il prodotto A[i..j] Ci dice cioè che per calcolare A[i..j] dobbiamo prima calcolare A[i..k] e A[k+..j] e poi moltiplicarle tra loro. Per alcuni problemi E' anche necessario mostrare la soluzione trovata Ma questo è un processo facilmente realizzabile tramite un algoritmo ricorsivo Per questo motivo registriamo informazioni sulla soluzione mentre procediamo in maniera bottomup
10 Costruire una soluzione ottima stampapar(integer[][]s, integer i, integer j) if i = j then print A[ ; print i; print ] else print ( stampapar(s, i,s[i, j]) print stampapar(s, S[i, j]+, j) print ) Costruire una soluzione ottima integer[][]multiply(integer[][]s, integer i, integer j) if i = j then return A[i] else integer[][]x multiply(s, i, S[i, j]) integer[][]y multiply(s, S[i, j]+,j) return matrixmultiplication(x, Y ) 7 8 Esempio di esecuzione Numeri di Fibonacci A = A k A k+ = A A A = A k A k+ =A A A = A k A k+ =A.. A A = A k A k+ = A A A = A k A k+ =A A A L i \ Rj S[ ] = ( ( A (A A ) ) ( (A A ) A ) ) Definiti ricorsivamente F() = F() = F(n) = F(n)+F(n) Un po' di storia Leonardo di Pisa, detto Fibonacci Utilizzati per descrivere la crescita di una popolazione di conigli (!) In natura: Pigne, conchiglie, parte centrale dei girasoli, etc. In informatica: Alberi AVL minimi, Heap di Fibonacci, etc. 9
11 Implementazione ricorsiva Implementazione iterativa integer fibonacci(integer n) if n then return else return fibonacci(n ) + fibonacci(n ) Complessità computazionale integer fibonacci(integer n) integer[]f new integer[...max(n, )] F [] F [] for integer i to n do F [i] F [i ] + F [i ] return F [n] Complessità In tempo: O(n) In spazio: O(n) Array di n elementi T (n) = T (n ) + T (n ) + () n> () n = n 7 f [ ] 8 Soluzione T(n) = O( n ) Implementazione iterativa risparmio memoria Zaino integer fibonacci(integer n) integer F,F,F F F F for integer i to n do F F F F F F + F return F n 7 Complessità In tempo: O(n) In spazio: O() variabili Input Un intero positivo C la capacità dello zaino n oggetti, tali che l oggetto iesimo è caratterizzato da: Problema un profitto pi e un volume vi, entrambi interi positivi trovare un sottoinsieme S di {,..., n} di oggetti tale che il volume totale non superi la capacità massima e il profitto totale sia massimo F 8 v(s) = X is v i apple C F 8 F 8 p(s) = X is p i
12 Zaino Zaino Caratterizzazione del problema Tabella per programmazione dinamica P(i, c) è il sottoproblema dato dai primi i oggetti da inserire in uno zaino con capacità c Il problema originale corrisponde a P(n, C) Teorema sottostruttura ottima Sia S(i, c) una soluzione ottima per il problema P(i, c) Possono darsi due casi: Se i S(i, c), allora S(i, c){i} è una soluzione ottima per il sottoproblema P(i, cvi ) Se i S(i, c), allora S(i, c) è una soluzione ottima D[i, c] contiene il profitto massimo ottenibile per il problema P(i,c) 8 >< se c< D[i, c] = se i =_ c = >: max{d[i,c],d[i,c v i ]+p[i]} altrimenti Alcune considerazioni Costo di un algoritmo di programmazione dinamica bottomup: O(nC) Non è detto che tutti i problemi debbano essere risolti per il sottoproblema P(i, c) Dimostrazione per assurdo Memoization Zaino annotato Memoization (annotazione) Tecnica che fonde l'approccio di memorizzazione della programmazione dinamica con l'approccio topdown di divideetimpera Quando un sottoproblema viene risolto per la prima volta, viene memorizzato in una tabella ogni volta che si deve risolvere un sottoproblema, si controlla nella tabella se è già stato risolto precedentemente SI: si usa il risultato della tabella NO: si calcola il risultato e lo si memorizza In tal modo, ogni sottoproblema viene calcolato una sola volta e memorizzato come nella versione bottomup Note sulla soluzione è un valore speciale per indicare che un certo problema non è stato risolto Gli elementi della tabella D sono inizializzati con il valore integer zaino(integer[]p, integer[]v, integer i, integer c, integer[][]d) if c<then return if i =or c =then return if D[i, c] =? then D[i, c] max(zaino(p, v,i, c,d), zaino(p, v,i, c v[i], D)+p[i]) return D[i, c] 7 8
13 Discussione su memoization Memoization in Python Caso pessimo Nel caso pessimo, è comunque O(nC) Quando si verifica? Inizializzazione E necessario inizializzare D costo O(nC) Se il costo dell inizializzazione è asintoticamente inferiore al costo di ricombinare i risultati, si ottiene un guadagno Altrimenti: è possibile utilizzare una tabella hash Complessità pseudopolinomiale La complessità O(nC) è polinomiale nella dimensione dell input? from functools import wraps def memo(func): cache = def wrap(*args): if args not in cache: cache[args] = func(*args) return cache[args] return def fib(n): if n<: return else: return fib(n) + fib(n) 9 Bioinformatica Caratterizzazione del problema DNA Definizione Una stringa di molecole chiamate basi Solo quattro basi: Adenina, Citosina, Guanina, Timina Esempi Due esempi di DNA: AAAATTGA, TAACGATAG Date due sequenze, è lecito chiedersi quanto siano simili Una sequenza T è una sottosequenza di P se T è ottenuta da P rimuovendo uno o più elementi Alternativamente: T è definito come il sottoinsieme degli indici l'insieme di elementi di P che compaiono anche in T Gli elementi rimanenti devono comparire nello stesso ordine, anche se non devono essere necessariamente contigui in P Una è sottostringa dell'altra? Esempio Distanza di editing: costo necessario per trasformare una nell'altra P = AAAATTGA, T = AAATA La più lunga sottosequenza (anche non contigua) comune ad entrambe Nota La sequenza nulla è una sottosequenza di ogni sequenza
14 Caratterizzazione del problema Caratterizzazione del problema Definizione: Problema LCS Date due sequenze P e T, una sequenza Z è una sottosequenza comune di P e T se Z è sottosequenza sia di P che di T Input: due sequenze di simboli, P e T Output: Trovare la più lunga sottosequenza Z comune a P e T Scriviamo Z CS(P, T) Common Subsequence, o CS Esempio P = AAAATTGA Definizione: T = TAACGATA Date due sequenze P e T, una sequenza è una sottosequenza comune massimale di P e T, se Z CS(P, T) e non esiste una sequenza W CS(P, T) tale che W > Z LCS(P,T) =???? Scriviamo Z LCS(P, T) Longest Common Subsequence, o LCS Prima di provare con la programmazione dinamica, proviamo di forza bruta... Risoluzione tramite enumerazione Caratterizzazione della soluzione ottima integer LCSesaustivo(ITEM[]P,ITEM[]T) integer max ITEM[] nil foreach sottosequenza Z di P do if Z è una sottosequenza di T then if Z > max then max Z Z return Data una sequenza P=(p,, pn): denoteremo con P(i) l iesimo prefisso di P, cioè la sottosequenza ( p,, pi ) Esempio: P = ABDCCAABD P() denota la sottosequenza nulla P() = ABD P() = ABDCCA u Domanda: Quante sono le sottosequenze di P?
15 Caratterizzazione della soluzione ottima Dimostrazione Teorema (Sottostruttura ottima) Date le due sequenze P=(p,, pm) e T=(t,, tn), sia Z=(z,,zk ) una LCS di P e T. pm= tn zk = pm = tn e Z(k) LCS( P(m), T(n) ). pm tn e zk pm Z LCS( P(m), T ). pm tn e zk tn Z LCS( P, T(n) ) Dimostrazione Punto Supponiamo per assurdo che zk pm = tn Si consideri W=Zpm. Allora W CS(P,T) e W > Z, assurdo Quindi zk = pm = tn Supponiamo per assurdo che Z(k) LCS( P(m), T(n) ) Allora esiste W LCS( P(m), T(n) ) tale che W > Z(k) Quindi Wpm CS(P,T) e Wpm > Z, assurdo P[,,m] T[,,n] a a P[,,m] T[,,n] Z[,,k] a Z[,,k] 7 8 Dimostrazione Cosa ci dice il teorema? Punto (Punto simmetrico) Se pm = tn, dobbiamo risolvere un sottoproblema Se zk pm, allora Z CS(P(m), T) LCS( P(m), T(n) ) Per assurdo ipotizziamo che Z LCS(P(m), T) allora esiste W LCS(P(m), T) tale che: W > Z La definizione ricorsiva è la seguente: LCS(P,T) = LCS( P(m), T(n) ) pm Allora è anche vero che W LCS(P, T), contraddicendo l'ipotesi Se pm tn, dobbiamo risolvere due sottoproblemi LCS( P(m), T ) LCS( P, T(n) ) P[,,m] T[,,n] Z[,,k]? b a P[,,m] T[,,n] Z[,,k]? b A questo punto, dobbiamo scegliere la LCS più lunga fra le La definizione ricorsiva è la seguente: LCS(P,T) = longest( LCS( P(m), T ), LCS( P, T(n) ) ) 9
16 LCS basato su programmazione dinamica LCS basato su programmazione dinamica Definiamo una tabella per memorizzare la lunghezza della LCS associati ai sottoproblemi: Definiamo una tabella per memorizzare informazioni necessarie ad ottenere la stringa finale D[... m,... n] tabella di (m+) (n+) elementi, dove P = m, T = n B[... m,... n] tabella di (m+) (n+) elementi, dove P = m, T = n D[i,j] lunghezza della LCS di P(i) e T(j) Goal finale: Calcolare D[m,n] lunghezza della LCS di P e T B[i,j] puntatore alla entry della tabella stessa che identifica il sottoproblema ottimo scelto durante il calcolo del valore D[i,j] Valori possibili: Formulazione ricorsiva se i = j = D[i, j] = D[i,j ] + se i> j> p i = t j max{d[i,j],d[i, j ]} se i> j> p i = t j deriva da i,j deriva da i,j deriva da i,j j j TACCBT ATBCBD deriva da i,j deriva da i,j deriva da i,j i A T B C B D T A C ACGGCT CTCTGT deriva da i,j deriva da i,j deriva da i,j i C T C T G T A C G C G B C T T se i = j = D[i, j] = D[i,j ] + se i> j> p i = t j max{d[i,j],d[i, j ]} se i> j> p i = t j se i = j = D[i, j] = D[i,j ] + se i> j> p i = t j max{d[i,j],d[i, j ]} se i> j> p i = t j
17 Calcolo del valore della soluzione ottima integer lcs(integer[][]d, ITEM[]P, ITEM[]T, integer i, integer j) if i =or j =then return if D[i, j] =? then if P [i] =T [j] then D[i, j] lcs(d, P, T, i,j ) + else D[i, j] max(lcs(d,p, T, i, j), lcs(d,p, T, i, j )) return D[i, j] ABDDBE BEBEDE deriva da i,j deriva da i,j deriva da i,j j i B E B E D E A B D D B E se i = j = D[i, j] = D[i,j ] + se i> j> p i = t j max{d[i,j],d[i, j ]} se i> j> p i = t j TACCBT ATBCBD deriva da i,j deriva da i,j deriva da i,j j i A T B C B D T A C C B T Alcune ottimizzazioni La matrice B può essere eliminata: Il valore di D[i,j] dipende solo dai valori D[i,j], D[i,j] e D[i,j]. In tempo costante si può quindi determinare quale di questi tre è stato usato, e perciò quale sia il tipo di freccia Se ci serve solo calcolare la lunghezza della LCS, possiamo ridurre la tabella D[i,j] a due sole righe di lunghezza min{ n, m } Ad ogni istante (cioè per ogni coppia i,j), ci servono i valori D[i,j], D[i,j] e D[i,j] Esercizio se i = j = D[i, j] = D[i,j ] + se i> j> p i = t j max{d[i,j],d[i, j ]} se i> j> p i = t j 7 8
18 Stampa della soluzione ottima LCS e diff integer printlcs(item[]t,item[]p, integer[][]d, integer i, integer j) if i = and j = then if T [i] =P [j] then printlcs(t,p,d,i,j ) print P [i] else if D[i,j] >D[i, j ] then printlcs(t,p,d,i,j) else printlcs(t,p,d,i,j ) Costo computazionale A ogni passo, almeno uno fra i e j viene decrementato: θ(m+n) diff Esamina due file di testo, e ne evidenzia le differenze a livello di riga. Lavorare a livello di riga significa che i confronti fra simboli sono in realtà confronti fra righe, e che n ed m sono il numero di righe dei due file Ottimizzazioni diff è utilizzato soprattutto per codice sorgente; è possibile applicare euristiche sulle righe iniziali e finali per distinguere le righe utilizzo di funzioni hash 9 Questo è il testo originale alcune linee non dovrebbero cambiare mai altre invece vengono rimosse altre vengono aggiunte Figura.: Questo è il testo nuovo alcune linee non dovrebbero cambiare mai altre invece vengono cancellate altre vengono aggiunte come questa Questo è il testo originale + Questo è il testo nuovo alcune linee non dovrebbero cambiare mai altre invece vengono rimosse + cancellate altre vengono aggiunte + come questa Il file original.txt (a sinistra); il file new.txt (al centro); l output di diff original.txt new.txt (a destra). 7 String matching approssimato Esempio Input Input una stringa P = p pm (pattern) questoèunoscempio una stringa T = t tn (testo), con m n unesempio Definizione Domanda Un occorrenza kapprossimata di P in T, con k m, è una copia della stringa P nella stringa T in cui sono ammessi k errori (o differenze) tra caratteri di P e caratteri di T, del seguente tipo: () i corrispondenti caratteri in P e in T sono diversi (sostituzione) () un carattere in P non è incluso in T (inserimento) () un carattere in T non è incluso in P (cancellazione) Qual è il minimo valore k per cui si trova una occorrenza kapprossimata? A partire da dove? Con quali errori? Problema: Trovare un occorrenza kapprossimata di P in T per cui k sia minimo. 7 7
19 Sottostruttura ottima Sottostruttura ottima Definizione Definizione Tabella D[...m,...n], i cui elementi D[i,j] contengono il minimo valore k per cui esiste una occorrenza kapprossimata di P(i) in T(j) Tabella D[...m,...n], i cui elementi D[i,j] contengono il minimo valore k per cui esiste una occorrenza kapprossimata di P(i) in T(j) D[i,j] può essere uguale a D[i,j], se pi = tj avanza su entrambi i caratteri (uguali) D[i,j]+, se pi tj avanza su entrambi i caratteri (sostituzione) D[i,j]+ avanza sul pattern (inserimento) D[i,j]+ avanza sul testo (cancellazione) p i t D[i, j] D[i, j] t j j +/+ + Ricordate che cerchiamo il minimo: se i = D[i, j] = i se j = min{d[i, j ] +,D[i, j] +, D[i, j ] + } altrimenti =, se p i = t j, oppure =, se p i = t j. ormale, ma è chiaro che tale definizione illustra p i D[i, j] D[i, j] Ricostruzione della soluzione finale Algoritmo String matching approssimato Si noti che: D[m,j] = k se e solo se c è un occorrenza kapprossimata di P in T che termina in tj la soluzione del problema è data dal valore di D[m,j] più piccolo, per j n A B A B A P T integer stringmatching(item[]p, ITEM[]T, integer m, integer n) integer[][]d new integer[...m][...n] for integer i to m do D[i, ] i for integer j to n do D[,j] for i to m do for j to n do integer t D[i,j ] + iif(p [i] =T [j],, ) t min(t, D[i,j] + ) t min(t, D[i, j ] + ) D[i, j] t Domanda: complessità? B A B integer min D[m, ] integer pos for j to n do if D[m, j] < min then min D[m, j] pos j return pos 7 7
20 String matching approssimato Insieme indipendente di intervalli pesati Variante dello string matching approssimato: Distanza di editing (Distanza di Levenshtein) Date due stringhe, vogliamo conoscere il numero minimo di operazioni (sostituzione, inserimento, cancellazione) necessarie per trasformare una nell altra (o viceversa, visto che inserimento e cancellazione sono simmetriche) Esempio: distanza fra google e yahoo? Algoritmo? Come (e se) dobbiamo modificare le condizioni iniziali? Come (e se) dobbiamo modificare la definizione ricorsiva? Input Siano dati n intervalli distinti [a, b[,..., [an,bn[ della retta reale, aperti a destra, dove all intervallo i è associato un peso wi, i n. Definizione Due intervalli i e j si dicono disgiunti se: bj ai oppure bi aj Output: ai bi aj Trovare un insieme indipendente di peso massimo, ovvero un sottoinsieme di intervalli tutti disgiunti tra di loro tale che la somma dei pesi degli intervalli nel sottoinsieme sia la più grande possibile bj Esempio: Prenotazione di una sala conferenza in un hotel Preelaborazione Definizione ricorsiva Per poter applicare la programmazione dinamica, è necessario effettuare una preelaborazione Ordiniamo gli intervalli per estremi finali non decrescenti b b bn Per ogni intervallo i, sia pi = j il predecessore di i, dove j < i è il massimo indice tale che [aj, bj [ è disgiunto da [ai, bi [ (se non esiste j, allora pi = ) Definizione ricorsiva del peso di una soluzione ottima D[n] è il problema originario D[i] = max{d[i ],w i + D[p i ]}, i =,...,n. Costo della procedura risultante O(n log n) per l ordinamento Teorema sottostruttura ottima Sia P[i] il sottoproblema dato dai primi i intervalli e sia S[i] una sua soluzione ottima di peso D[i] Se l intervallo iesimo non fa parte di tale soluzione, allora deve valere D[i] = D[i ], dove si assume D[] = ; O(n log n) per il calcolo degli indici pi O(n) per il riempimento della tabella O(n) per la ricostruzione della soluzione Esercizio: altrimenti, deve essere D[i] = wi + D[pi] Scrivere algoritmo per il calcolo degli indici pi 79 8
21 Codice SET maxinterval(integer[]a, integer[]b, integer[]w, integer n) { ordina gli intervalli per estremi di fine crescenti } { calcola p j } integer[]d new integer[...n] D[] for i to n do D[i] max(d[i ],w[i]+d[p i ]) i n SET S Set() while i>do if D[i ] >w[i]+d[p i ] then i i else S.insert(i) i p i return S 8
Programmazione dinamica
 Programmazione dinamica Violetta Lonati Università degli studi di Milano Dipartimento di Informatica Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica Violetta Lonati Programmazione
Programmazione dinamica Violetta Lonati Università degli studi di Milano Dipartimento di Informatica Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica Violetta Lonati Programmazione
Programmazione dinamica
 Programmazione dinamica Ilaria Castelli [email protected] Università degli Studi di Siena Dipartimento di Ingegneria dell Informazione A.A. 29/21 I. Castelli Programmazione dinamica, A.A. 29/21 1/35
Programmazione dinamica Ilaria Castelli [email protected] Università degli Studi di Siena Dipartimento di Ingegneria dell Informazione A.A. 29/21 I. Castelli Programmazione dinamica, A.A. 29/21 1/35
Algoritmi e strutture di dati 2
 Paola Vocca Lezione 4: Programmazione dinamica 1 Caratteristiche Programmazione dinamica: paradigma basato sullo stesso principio utilizzato per il divide et impera o il problema viene decomposto in sotto-problemi
Paola Vocca Lezione 4: Programmazione dinamica 1 Caratteristiche Programmazione dinamica: paradigma basato sullo stesso principio utilizzato per il divide et impera o il problema viene decomposto in sotto-problemi
Il problema dello zaino
 Il problema dello zaino (knapsack problem) Damiano Macedonio [email protected] Copyright 2010 2012 Moreno Marzolla, Università di Bologna (http://www.moreno.marzolla.name/teaching/asd2011b/) This work is licensed
Il problema dello zaino (knapsack problem) Damiano Macedonio [email protected] Copyright 2010 2012 Moreno Marzolla, Università di Bologna (http://www.moreno.marzolla.name/teaching/asd2011b/) This work is licensed
Algoritmi greedy. Gli algoritmi che risolvono problemi di ottimizzazione devono in genere operare una sequenza di scelte per arrivare alla soluzione
 Algoritmi greedy Gli algoritmi che risolvono problemi di ottimizzazione devono in genere operare una sequenza di scelte per arrivare alla soluzione Gli algoritmi greedy sono algoritmi basati sull idea
Algoritmi greedy Gli algoritmi che risolvono problemi di ottimizzazione devono in genere operare una sequenza di scelte per arrivare alla soluzione Gli algoritmi greedy sono algoritmi basati sull idea
Note per la Lezione 6 Ugo Vaccaro
 Progettazione di Algoritmi Anno Accademico 2016 2017 Note per la Lezione 6 Ugo Vaccaro Ancora sulla tecnica Programmazione Dinamica Nella lezione scorsa abbiamo appreso che la tecnica Divide-et-Impera,
Progettazione di Algoritmi Anno Accademico 2016 2017 Note per la Lezione 6 Ugo Vaccaro Ancora sulla tecnica Programmazione Dinamica Nella lezione scorsa abbiamo appreso che la tecnica Divide-et-Impera,
Esercizi di Algoritmi e Strutture Dati
 Esercizi di Algoritmi e Strutture Dati Moreno Marzolla http://www.moreno.marzolla.name/ Ultima Modifica: 7 ottobre 202 Copyright Portions of this work are Copyright 202, Moreno Marzolla. This work is licensed
Esercizi di Algoritmi e Strutture Dati Moreno Marzolla http://www.moreno.marzolla.name/ Ultima Modifica: 7 ottobre 202 Copyright Portions of this work are Copyright 202, Moreno Marzolla. This work is licensed
Tecniche Algoritmiche: divide et impera
 Tecniche Algoritmiche: divide et impera Una breve presentazione F. Damiani - Alg. & Lab. 04/05 Divide et impera (o Divide and conquer) Per regnare occorre tenere divisi i nemici e trarne vantaggio F. Damiani
Tecniche Algoritmiche: divide et impera Una breve presentazione F. Damiani - Alg. & Lab. 04/05 Divide et impera (o Divide and conquer) Per regnare occorre tenere divisi i nemici e trarne vantaggio F. Damiani
Tempo e spazio di calcolo (continua)
 Tempo e spazio di calcolo (continua) I numeri di Fibonacci come case study (applichiamo ad un esempio completo le tecniche illustrate nei lucidi precedenti) Abbiamo introdotto tecniche per la correttezza
Tempo e spazio di calcolo (continua) I numeri di Fibonacci come case study (applichiamo ad un esempio completo le tecniche illustrate nei lucidi precedenti) Abbiamo introdotto tecniche per la correttezza
Algoritmi e Strutture Dati
 Algoritmi Ricorsivi e Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 2006/07 I conigli di Fibonacci Ricerca Binaria L isola dei conigli
Algoritmi Ricorsivi e Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 2006/07 I conigli di Fibonacci Ricerca Binaria L isola dei conigli
Dati e Algoritmi I (Pietracaprina) Esercizi sulle Nozioni di Base
 Dati e Algoritmi I (Pietracaprina) Esercizi sulle Nozioni di Base Dati e Algoritmi I (Pietracaprina): Esercizi 1 Problema 1. Sia T una stringa arbitraria di lunghezza n 1 su un alfabeto Σ. È sempre possibile
Dati e Algoritmi I (Pietracaprina) Esercizi sulle Nozioni di Base Dati e Algoritmi I (Pietracaprina): Esercizi 1 Problema 1. Sia T una stringa arbitraria di lunghezza n 1 su un alfabeto Σ. È sempre possibile
Esercizi Capitolo 10 - Code con priorità e insiemi disgiunti
 Esercizi Capitolo 10 - Code con priorità e insiemi disgiunti Alberto Montresor 19 Agosto, 2014 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente,
Esercizi Capitolo 10 - Code con priorità e insiemi disgiunti Alberto Montresor 19 Agosto, 2014 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente,
Cammini minimi fra tutte le coppie
 Capitolo 12 Cammini minimi fra tutte le coppie Consideriamo il problema dei cammini minimi fra tutte le coppie in un grafo G = (V, E, w) orientato, pesato, dove possono essere presenti archi (ma non cicli)
Capitolo 12 Cammini minimi fra tutte le coppie Consideriamo il problema dei cammini minimi fra tutte le coppie in un grafo G = (V, E, w) orientato, pesato, dove possono essere presenti archi (ma non cicli)
Esercizi vari. Alberto Montresor. 19 Agosto, 2014
 Esercizi vari Alberto Montresor 19 Agosto, 2014 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente, è possibile saltare alle rispettive soluzioni
Esercizi vari Alberto Montresor 19 Agosto, 2014 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente, è possibile saltare alle rispettive soluzioni
Fondamenti di Informatica 6. Algoritmi e pseudocodifica
 Vettori e matrici #1 Fondamenti di Informatica 6. Algoritmi e pseudocodifica Corso di Laurea in Ingegneria Civile A.A. 2010-2011 1 Semestre Prof. Giovanni Pascoschi Le variabili definite come coppie
Vettori e matrici #1 Fondamenti di Informatica 6. Algoritmi e pseudocodifica Corso di Laurea in Ingegneria Civile A.A. 2010-2011 1 Semestre Prof. Giovanni Pascoschi Le variabili definite come coppie
Algoritmi e Strutture di Dati (3 a Ed.) String matching. Alan Bertossi, Alberto Montresor
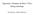 Algoritmi e Strutture di Dati (3 a Ed.) String matching Alan Bertossi, Alberto Montresor STRING MATCHING. Date una stringa P di m caratteri (pattern) e una stringa T di n caratteri, con m n, trovare un
Algoritmi e Strutture di Dati (3 a Ed.) String matching Alan Bertossi, Alberto Montresor STRING MATCHING. Date una stringa P di m caratteri (pattern) e una stringa T di n caratteri, con m n, trovare un
Esercizi Capitolo 10 - Code con priorità e insiemi disgiunti
 Esercizi Capitolo 10 - Code con priorità e insiemi disgiunti Alberto Montresor 27 marzo 2012 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente,
Esercizi Capitolo 10 - Code con priorità e insiemi disgiunti Alberto Montresor 27 marzo 2012 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente,
Problemi, istanze, soluzioni
 lgoritmi e Strutture di Dati II 2 Problemi, istanze, soluzioni Un problema specifica una relazione matematica tra dati di ingresso e dati di uscita. Una istanza di un problema è formata dai dati di un
lgoritmi e Strutture di Dati II 2 Problemi, istanze, soluzioni Un problema specifica una relazione matematica tra dati di ingresso e dati di uscita. Una istanza di un problema è formata dai dati di un
Esercizi Capitolo 6 - Alberi binari di ricerca
 Esercizi Capitolo 6 - Alberi binari di ricerca Alberto Montresor 9 Agosto, 204 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente, è possibile
Esercizi Capitolo 6 - Alberi binari di ricerca Alberto Montresor 9 Agosto, 204 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente, è possibile
Esercizi Capitolo 11 - Strutture di dati e progettazione di algoritmi
 Esercizi Capitolo 11 - Strutture di dati e progettazione di algoritmi Alberto Montresor 19 Agosto, 2014 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore
Esercizi Capitolo 11 - Strutture di dati e progettazione di algoritmi Alberto Montresor 19 Agosto, 2014 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore
Algoritmi e Strutture Dati (Mod. B) Algoritmi Greedy (parte I)
 Algoritmi e Strutture Dati (Mod. B) Algoritmi Greedy (parte I) Algoritmi greedy Gli algoritmi per problemi di ottimizzazione devono in genere operare una sequenza di scelte per arrivare alla soluzione
Algoritmi e Strutture Dati (Mod. B) Algoritmi Greedy (parte I) Algoritmi greedy Gli algoritmi per problemi di ottimizzazione devono in genere operare una sequenza di scelte per arrivare alla soluzione
Parte III: Algoritmo di Branch-and-Bound
 Parte III: Algoritmo di Branch-and-Bound Divide et Impera Sia z * max {c T x : x S} (1) un problema di ottimizzazione combinatoria difficile da risolvere. Domanda: E possibile decomporre il problema (1)
Parte III: Algoritmo di Branch-and-Bound Divide et Impera Sia z * max {c T x : x S} (1) un problema di ottimizzazione combinatoria difficile da risolvere. Domanda: E possibile decomporre il problema (1)
LEZIONE 3. a + b + 2c + e = 1 b + d + g = 0 3b + f + 3g = 2. a b c d e f g
 LEZIONE 3 3.. Matrici fortemente ridotte per righe. Nella precedente lezione abbiamo introdotto la nozione di soluzione di un sistema di equazioni lineari. In questa lezione ci poniamo il problema di descrivere
LEZIONE 3 3.. Matrici fortemente ridotte per righe. Nella precedente lezione abbiamo introdotto la nozione di soluzione di un sistema di equazioni lineari. In questa lezione ci poniamo il problema di descrivere
Esercitazione 10 Algorithmi e Strutture Dati (Informatica) A.A 2015/2016
 Esercitazione 10 Algorithmi e Strutture Dati (Informatica) A.A 2015/2016 Tong Liu May 10, 2016 Elementi fondamentali Un algoritmo non deterministico è un algoritmo che posto di fronte alla necessità di
Esercitazione 10 Algorithmi e Strutture Dati (Informatica) A.A 2015/2016 Tong Liu May 10, 2016 Elementi fondamentali Un algoritmo non deterministico è un algoritmo che posto di fronte alla necessità di
UNIVERSITÀ DEGLI STUDI DI PAVIA FACOLTÀ DI INGEGNERIA. Matlab: esempi ed esercizi
 UNIVERSITÀ DEGLI STUDI DI PAVIA FACOLTÀ DI INGEGNERIA Matlab: esempi ed esercizi Sommario e obiettivi Sommario Esempi di implementazioni Matlab di semplici algoritmi Analisi di codici Matlab Obiettivi
UNIVERSITÀ DEGLI STUDI DI PAVIA FACOLTÀ DI INGEGNERIA Matlab: esempi ed esercizi Sommario e obiettivi Sommario Esempi di implementazioni Matlab di semplici algoritmi Analisi di codici Matlab Obiettivi
Algoritmi e strutture dati. Analisi di algoritmi Funzioni di costo, notazione asintotica
 Algoritmi e strutture dati Analisi di algoritmi Funzioni di costo, notazione asintotica Alberto Montresor Università di Trento 2016/09/11 This work is licensed under a Creative Commons Attribution-ShareAlike
Algoritmi e strutture dati Analisi di algoritmi Funzioni di costo, notazione asintotica Alberto Montresor Università di Trento 2016/09/11 This work is licensed under a Creative Commons Attribution-ShareAlike
2.2 Alberi di supporto di costo ottimo
 . Alberi di supporto di costo ottimo Problemi relativi ad alberi hanno numerose applicazioni: progettazione di reti (comunicazione, teleriscaldamento,...) memorizzazione compatta di sequenze (DNA) diffusione
. Alberi di supporto di costo ottimo Problemi relativi ad alberi hanno numerose applicazioni: progettazione di reti (comunicazione, teleriscaldamento,...) memorizzazione compatta di sequenze (DNA) diffusione
ALGORITMI CORSO DI STUDIO IN INFORMATICA (laurea triennale) UNIVERSITÀ DEGLI STUDI DI CATANIA ANNO ACCADEMICO 2014/15
 ANNO ACCADEMICO 2014/15 1 a prova in itinere 13 gennaio 2015 ESERCIZIO 1 Si risolva l equazione di ricorrenza al variare del parametro reale a>1. T (n) = 27 n a T + n 2 log n a ESERCIZIO 2 Si ordinino
ANNO ACCADEMICO 2014/15 1 a prova in itinere 13 gennaio 2015 ESERCIZIO 1 Si risolva l equazione di ricorrenza al variare del parametro reale a>1. T (n) = 27 n a T + n 2 log n a ESERCIZIO 2 Si ordinino
11.4 Chiusura transitiva
 6 11.4 Chiusura transitiva Il problema che consideriamo in questa sezione riguarda il calcolo della chiusura transitiva di un grafo. Dato un grafo orientato G = hv,ei, si vuole determinare il grafo orientato)
6 11.4 Chiusura transitiva Il problema che consideriamo in questa sezione riguarda il calcolo della chiusura transitiva di un grafo. Dato un grafo orientato G = hv,ei, si vuole determinare il grafo orientato)
PROGRAMMAZIONE DINAMICA
 PROGRAMMAZIONE DINAMICA 6.1 PROGRAMMAZIONE DINAMICA Sebbene elementi del metodo fossero già presenti in tecniche di ottimizzazione note in precedenza, si deve a Bellman lo studio sistematico (iniziato
PROGRAMMAZIONE DINAMICA 6.1 PROGRAMMAZIONE DINAMICA Sebbene elementi del metodo fossero già presenti in tecniche di ottimizzazione note in precedenza, si deve a Bellman lo studio sistematico (iniziato
Algoritmi e Strutture Dati
 Algoritmi e Strutture Dati Capitolo 1 Un introduzione informale agli algoritmi Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Definizione informale di algoritmo Insieme di istruzioni, definite
Algoritmi e Strutture Dati Capitolo 1 Un introduzione informale agli algoritmi Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Definizione informale di algoritmo Insieme di istruzioni, definite
Un esempio di calcolo di complessità: insertion sort
 Un esempio di calcolo di complessità: insertion sort Vediamo su un esempio come si può calcolare la complessità di un algoritmo... L esempio è un metodo semplice per ordinare arrays: insertion sort, o
Un esempio di calcolo di complessità: insertion sort Vediamo su un esempio come si può calcolare la complessità di un algoritmo... L esempio è un metodo semplice per ordinare arrays: insertion sort, o
Ottimizza la somma. Supponete di avere in input un vettore di n interi positivi distinti V [1... n] e un valore W. Scrivere un algoritmo che:
![Ottimizza la somma. Supponete di avere in input un vettore di n interi positivi distinti V [1... n] e un valore W. Scrivere un algoritmo che: Ottimizza la somma. Supponete di avere in input un vettore di n interi positivi distinti V [1... n] e un valore W. Scrivere un algoritmo che:](/thumbs/56/38634171.jpg) Ottimizza la somma Supponete di avere in input un vettore di n interi positivi distinti V [1... n] e un valore W. Scrivere un algoritmo che: 1 restituisca il massimo valore X = n i=1 x[i]v [i] tale che
Ottimizza la somma Supponete di avere in input un vettore di n interi positivi distinti V [1... n] e un valore W. Scrivere un algoritmo che: 1 restituisca il massimo valore X = n i=1 x[i]v [i] tale che
la edit distance tra X e Y è la distanza relativa all allineamento (o agli allineamenti) che minimizza tale distanza.
 Algoritmica 14/15 EDIT DISTANCE Il problema della edit distance (distanza di edizione, in una versione in italiano scarsamente usata) è alla base dei problemi di confronto fra sequenze perché il meccanismo
Algoritmica 14/15 EDIT DISTANCE Il problema della edit distance (distanza di edizione, in una versione in italiano scarsamente usata) è alla base dei problemi di confronto fra sequenze perché il meccanismo
Alberto Montresor Università di Trento
 !! Algoritmi e Strutture Dati! Capitolo 5 - Alberi!!! Alberto Montresor Università di Trento!! This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike License. To view a copy
!! Algoritmi e Strutture Dati! Capitolo 5 - Alberi!!! Alberto Montresor Università di Trento!! This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike License. To view a copy
Algoritmi Greedy. Tecniche Algoritmiche: tecnica greedy (o golosa) Un esempio
 Algoritmi Greedy Tecniche Algoritmiche: tecnica greedy (o golosa) Idea: per trovare una soluzione globalmente ottima, scegli ripetutamente soluzioni ottime localmente Un esempio Input: lista di interi
Algoritmi Greedy Tecniche Algoritmiche: tecnica greedy (o golosa) Idea: per trovare una soluzione globalmente ottima, scegli ripetutamente soluzioni ottime localmente Un esempio Input: lista di interi
Esercizi Capitolo 7 - Hash
 Esercizi Capitolo 7 - Hash Alberto Montresor 19 Agosto, 2014 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente, è possibile saltare alle rispettive
Esercizi Capitolo 7 - Hash Alberto Montresor 19 Agosto, 2014 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente, è possibile saltare alle rispettive
Note per la Lezione 7 Ugo Vaccaro
 Progettazione di Algoritmi Anno Accademico 2016 2017 Note per la Lezione 7 Ugo Vaccaro Sempre sulla tecnica Programmazione Dinamica Ricordiamo che lo sviluppo di algoritmi basati sulla Programmazione Dinamica
Progettazione di Algoritmi Anno Accademico 2016 2017 Note per la Lezione 7 Ugo Vaccaro Sempre sulla tecnica Programmazione Dinamica Ricordiamo che lo sviluppo di algoritmi basati sulla Programmazione Dinamica
Introduzione alla programmazione Esercizi risolti
 Esercizi risolti 1 Esercizio Si determini se il diagramma di flusso rappresentato in Figura 1 è strutturato. A B C D F E Figura 1: Diagramma di flusso strutturato? Soluzione Per determinare se il diagramma
Esercizi risolti 1 Esercizio Si determini se il diagramma di flusso rappresentato in Figura 1 è strutturato. A B C D F E Figura 1: Diagramma di flusso strutturato? Soluzione Per determinare se il diagramma
Algoritmi e Strutture Dati
 Algoritmi e Strutture Dati Informazioni sul corso + Un introduzione informale agli algoritmi Domenico Fabio Savo 1 Domenico Fabio Savo Email: [email protected] Web: http://www.dis.uniroma1.it/~savo
Algoritmi e Strutture Dati Informazioni sul corso + Un introduzione informale agli algoritmi Domenico Fabio Savo 1 Domenico Fabio Savo Email: [email protected] Web: http://www.dis.uniroma1.it/~savo
Algoritmi per operazioni con le matrici
 Algoritmi per operazioni con le matrici 1 Sommario Definizioni Alcune operazioni principali sulle matrici Somma di due matrici Trasposta di una matrice Prodotto di matrici: algoritmo classico Prodotto
Algoritmi per operazioni con le matrici 1 Sommario Definizioni Alcune operazioni principali sulle matrici Somma di due matrici Trasposta di una matrice Prodotto di matrici: algoritmo classico Prodotto
Lezione 6 programmazione in Java
 Lezione 6 programmazione in Java Nicola Drago [email protected] Dipartimento di Informatica Università di Verona Anteprima Le costanti I vettori Cos è un vettore Come si usa I vari tipi di vettori Esempi
Lezione 6 programmazione in Java Nicola Drago [email protected] Dipartimento di Informatica Università di Verona Anteprima Le costanti I vettori Cos è un vettore Come si usa I vari tipi di vettori Esempi
Programmazione dinamica
 Capitolo 6 Programmazione dinamica 6.4 Il problema della distanza di edit tra due stringhe x e y chiede di calcolare il minimo numero di operazioni su singoli caratteri (inserimento, cancellazione e sostituzione)
Capitolo 6 Programmazione dinamica 6.4 Il problema della distanza di edit tra due stringhe x e y chiede di calcolare il minimo numero di operazioni su singoli caratteri (inserimento, cancellazione e sostituzione)
RISOLUZIONE DI SISTEMI LINEARI
 RISOLUZIONE DI SISTEMI LINEARI Algebra lineare numerica 1 La risoluzione di un sistema lineare è il nucleo principale del processo di risoluzione di circa il 70% di tutti i problemi reali Per la risoluzione
RISOLUZIONE DI SISTEMI LINEARI Algebra lineare numerica 1 La risoluzione di un sistema lineare è il nucleo principale del processo di risoluzione di circa il 70% di tutti i problemi reali Per la risoluzione
Sistemi lineari. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ [email protected] Lorenzo Pareschi (Univ. Ferrara)
Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ [email protected] Lorenzo Pareschi (Univ. Ferrara)
Cognome e Nome : Corso e Anno di Immatricolazione: Modalità di Laboratorio (Progetto/Prova) :
 PROGRAMMAZIONE (Corsi B e C) Pre-appello di Gennaio 2004 (A.A. 2003/2004) PROGRAMMAZIONE (B e C) S. Straordinaria - Appello di Gennaio (A.A. 2002/2003) 22 Gennaio 2004 ore 11 Aula II di Facoltà (Durata:
PROGRAMMAZIONE (Corsi B e C) Pre-appello di Gennaio 2004 (A.A. 2003/2004) PROGRAMMAZIONE (B e C) S. Straordinaria - Appello di Gennaio (A.A. 2002/2003) 22 Gennaio 2004 ore 11 Aula II di Facoltà (Durata:
Programmazione dinamica. Progettazione di Algoritmi a.a Matricole congrue a 1 Docente: Annalisa De Bonis
 Programmazione dinamica Progettazione di Algoritmi a.a. 2016-17 Matricole congrue a 1 Docente: Annalisa De Bonis 1 Paradigmi della Progettazione degli Algoritmi Greedy. Costruisci una soluzione in modo
Programmazione dinamica Progettazione di Algoritmi a.a. 2016-17 Matricole congrue a 1 Docente: Annalisa De Bonis 1 Paradigmi della Progettazione degli Algoritmi Greedy. Costruisci una soluzione in modo
Un tipico esempio è la definizione del fattoriale n! di un numero n, la cui definizione è la seguente:
 Pag 29 4) La ricorsione 4.1 Funzioni matematiche ricorsive Partiamo da un concetto ben noto, quello delle funzioni matematiche ricorsive. Una funzione matematica è detta ricorsiva quando la sua definizione
Pag 29 4) La ricorsione 4.1 Funzioni matematiche ricorsive Partiamo da un concetto ben noto, quello delle funzioni matematiche ricorsive. Una funzione matematica è detta ricorsiva quando la sua definizione
Algoritmi e Strutture Dati
 Algoritmi e Strutture Dati Capitolo 5 - Alberi Alberto Montresor Università di Trento This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike License. To view a copy of this
Algoritmi e Strutture Dati Capitolo 5 - Alberi Alberto Montresor Università di Trento This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike License. To view a copy of this
Introduzione al Metodo del Simplesso. 1 Soluzioni di base e problemi in forma standard
 Introduzione al Metodo del Simplesso Giacomo Zambelli 1 Soluzioni di base e problemi in forma standard Consideriamo il seguente problema di programmazione lineare (PL), relativo all esempio di produzione
Introduzione al Metodo del Simplesso Giacomo Zambelli 1 Soluzioni di base e problemi in forma standard Consideriamo il seguente problema di programmazione lineare (PL), relativo all esempio di produzione
Programmazione in Python. Moreno Marzolla
 Programmazione in Python Moreno Marzolla http://www.moreno.marzolla.name/ Copyright 2011, Moreno Marzolla (http://www.moreno.marzolla.name/teaching/labinf2011/) This work is licensed under the Creative
Programmazione in Python Moreno Marzolla http://www.moreno.marzolla.name/ Copyright 2011, Moreno Marzolla (http://www.moreno.marzolla.name/teaching/labinf2011/) This work is licensed under the Creative
2.2 Alberi di supporto di costo ottimo
 . Alberi di supporto di costo ottimo Problemi relativi ad alberi hanno numerose applicazioni: progettazione di reti (comunicazione, teleriscaldamento,...) protocolli reti IP memorizzazione compatta di
. Alberi di supporto di costo ottimo Problemi relativi ad alberi hanno numerose applicazioni: progettazione di reti (comunicazione, teleriscaldamento,...) protocolli reti IP memorizzazione compatta di
Introduzione soft alla matematica per l economia e la finanza. Marta Cardin, Paola Ferretti, Stefania Funari
 Introduzione soft alla matematica per l economia e la finanza Marta Cardin, Paola Ferretti, Stefania Funari Capitolo Sistemi di equazioni lineari.8 Il Teorema di Cramer Si consideri un generico sistema
Introduzione soft alla matematica per l economia e la finanza Marta Cardin, Paola Ferretti, Stefania Funari Capitolo Sistemi di equazioni lineari.8 Il Teorema di Cramer Si consideri un generico sistema
Esercizi per il corso di Algoritmi
 1 Esercizi per il corso di Algoritmi Esercizi sulla Tecnica Programmazione Dinamica 1. Esercizio: Si consideri la seguente variante del problema dello Zaino 0/1. L input é costituito da n oggetti a 1...,a
1 Esercizi per il corso di Algoritmi Esercizi sulla Tecnica Programmazione Dinamica 1. Esercizio: Si consideri la seguente variante del problema dello Zaino 0/1. L input é costituito da n oggetti a 1...,a
Un algoritmo realizza una relazione funzionale tra i valori di input e quelli di output
 Un algoritmo realizza una relazione funzionale tra i valori di input e quelli di output F = { (s, s ) } per ogni s esiste una e una sola coppia (s, s ). Esempio: un algoritmo che calcola il quadrato di
Un algoritmo realizza una relazione funzionale tra i valori di input e quelli di output F = { (s, s ) } per ogni s esiste una e una sola coppia (s, s ). Esempio: un algoritmo che calcola il quadrato di
LE STRUTTURE DATI DINAMICHE: GLI ALBERI. Cosimo Laneve
 LE STRUTTURE DATI DINAMICHE: GLI ALBERI Cosimo Laneve 1 argomenti 1. definizione di alberi e nozioni relative 2. implementazione degli alberi, creazione, visita 3. algoritmo di visita iterativa e sua implementazione
LE STRUTTURE DATI DINAMICHE: GLI ALBERI Cosimo Laneve 1 argomenti 1. definizione di alberi e nozioni relative 2. implementazione degli alberi, creazione, visita 3. algoritmo di visita iterativa e sua implementazione
Laboratorio di Informatica
 Laboratorio di Informatica Seconda lezione a Python Dottore Paolo Parisen Toldin - [email protected] Dottoressa Sara Zuppiroli - [email protected] L'importanza di capire Perché non dobbiamo dichiarare
Laboratorio di Informatica Seconda lezione a Python Dottore Paolo Parisen Toldin - [email protected] Dottoressa Sara Zuppiroli - [email protected] L'importanza di capire Perché non dobbiamo dichiarare
Esempio : i numeri di Fibonacci
 Esempio : i numeri di Fibonacci La successione di Fibonacci F 1, F 2,... F n,... è definita come: F 1 =1 F 2 =1 F n =F n 1 F n 2,n 2 Leonardo Fibonacci (Pisa, 1170 Pisa, 1250) http://it.wikipedia.org/wiki/leonardo_fibonacci
Esempio : i numeri di Fibonacci La successione di Fibonacci F 1, F 2,... F n,... è definita come: F 1 =1 F 2 =1 F n =F n 1 F n 2,n 2 Leonardo Fibonacci (Pisa, 1170 Pisa, 1250) http://it.wikipedia.org/wiki/leonardo_fibonacci
Gestione della produzione e della supply chain Logistica distributiva
 Gestione della produzione e della supply chain Logistica distributiva Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena Convergenza dell algoritmo Se non
Gestione della produzione e della supply chain Logistica distributiva Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena Convergenza dell algoritmo Se non
Motivazione: Come si fa? Matrici simmetriche. Fattorizzazioni di matrici speciali
 Motivazione: Fattorizzazioni di matrici speciali Diminuire la complessità computazionale = evitare operazioni inutili = risparmiare tempo di calcolo Diminuire l occupazione di memoria Come si fa? Si tiene
Motivazione: Fattorizzazioni di matrici speciali Diminuire la complessità computazionale = evitare operazioni inutili = risparmiare tempo di calcolo Diminuire l occupazione di memoria Come si fa? Si tiene
1 Definizione di sistema lineare omogeneo.
 Geometria Lingotto. LeLing1: Sistemi lineari omogenei. Ārgomenti svolti: Definizione di sistema lineare omogeneo. La matrice associata. Concetto di soluzione. Sistemi equivalenti. Operazioni elementari
Geometria Lingotto. LeLing1: Sistemi lineari omogenei. Ārgomenti svolti: Definizione di sistema lineare omogeneo. La matrice associata. Concetto di soluzione. Sistemi equivalenti. Operazioni elementari
Ordinamenti per confronto: albero di decisione
 Ordinamenti per confronto: albero di decisione Albero di decisione = rappresentazione grafica di tutte le possibili sequenze di confronti eseguite da un algoritmo assegnato di ordinamento per confronto
Ordinamenti per confronto: albero di decisione Albero di decisione = rappresentazione grafica di tutte le possibili sequenze di confronti eseguite da un algoritmo assegnato di ordinamento per confronto
MATRICI E SISTEMI LINEARI
 1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
Fondamenti di Informatica
 Fondamenti di Informatica AlgoBuild: Strutture selettive, iterative ed array Prof. Arcangelo Castiglione A.A. 2016/17 AlgoBuild : Strutture iterative e selettive OUTLINE Struttura selettiva Esempi Struttura
Fondamenti di Informatica AlgoBuild: Strutture selettive, iterative ed array Prof. Arcangelo Castiglione A.A. 2016/17 AlgoBuild : Strutture iterative e selettive OUTLINE Struttura selettiva Esempi Struttura
Dati aggregati. Violetta Lonati
 Università degli studi di Milano Dipartimento di Scienze dell Informazione Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica - in breve: Definizione di tipi Array Stringhe Strutture
Università degli studi di Milano Dipartimento di Scienze dell Informazione Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica - in breve: Definizione di tipi Array Stringhe Strutture
Alberi Binari di Ricerca
 Alberi Binari di Ricerca Algoritmi su gli alberi binari: visite Dato un puntatore alla radice di un albero vogliamo scandire in modo sistematico tutti i nodi di tale albero In una lista abbiamo una unica
Alberi Binari di Ricerca Algoritmi su gli alberi binari: visite Dato un puntatore alla radice di un albero vogliamo scandire in modo sistematico tutti i nodi di tale albero In una lista abbiamo una unica
ESERCIZI SULLE MATRICI
 ESERCIZI SULLE MATRICI Consideriamo il sistema lineare a, x + a, x + + a,n x n = b a, x + a, x + + a,n x n = b a m, x + a m, x + + a m,n x n = b m di m equazioni in n incognite che ha a, a,n A = a m, a
ESERCIZI SULLE MATRICI Consideriamo il sistema lineare a, x + a, x + + a,n x n = b a, x + a, x + + a,n x n = b a m, x + a m, x + + a m,n x n = b m di m equazioni in n incognite che ha a, a,n A = a m, a
Appunti sui Codici di Reed Muller. Giovanni Barbarino
 Appunti sui Codici di Reed Muller Giovanni Barbarino Capitolo 1 Codici di Reed-Muller I codici di Reed-Muller sono codici lineari su F q legati alle valutazioni dei polinomi sullo spazio affine. Per semplicità
Appunti sui Codici di Reed Muller Giovanni Barbarino Capitolo 1 Codici di Reed-Muller I codici di Reed-Muller sono codici lineari su F q legati alle valutazioni dei polinomi sullo spazio affine. Per semplicità
A.A CORSO DI ALGEBRA 1. PROFF. P. PIAZZA, E. SPINELLI. SOLUZIONE ESERCIZI FOGLIO 5.
 A.A. 2015-2016. CORSO DI ALGEBRA 1. PROFF. P. PIAZZA, E. SPINELLI. SOLUZIONE ESERCIZI FOGLIO 5. Esercizio 5.1. Determinare le ultime tre cifre di n = 13 1625. (Suggerimento. Sfruttare il Teorema di Eulero-Fermat)
A.A. 2015-2016. CORSO DI ALGEBRA 1. PROFF. P. PIAZZA, E. SPINELLI. SOLUZIONE ESERCIZI FOGLIO 5. Esercizio 5.1. Determinare le ultime tre cifre di n = 13 1625. (Suggerimento. Sfruttare il Teorema di Eulero-Fermat)
LEZIONE 2. ( ) a 1 x 1 + a 2 x a n x n = b, ove a j, b R sono fissati.
 LEZIONE 2 2 Sistemi di equazioni lineari Definizione 2 Un equazione lineare nelle n incognite x, x 2,, x n a coefficienti reali, è un equazione della forma (2 a x + a 2 x 2 + + a n x n = b, ove a j, b
LEZIONE 2 2 Sistemi di equazioni lineari Definizione 2 Un equazione lineare nelle n incognite x, x 2,, x n a coefficienti reali, è un equazione della forma (2 a x + a 2 x 2 + + a n x n = b, ove a j, b
Risoluzione di sistemi lineari sparsi e di grandi dimensioni
 Risoluzione di sistemi lineari sparsi e di grandi dimensioni Un sistema lineare Ax = b con A R n n, b R n, è sparso quando il numero di elementi della matrice A diversi da zero è αn, con n α. Una caratteristica
Risoluzione di sistemi lineari sparsi e di grandi dimensioni Un sistema lineare Ax = b con A R n n, b R n, è sparso quando il numero di elementi della matrice A diversi da zero è αn, con n α. Una caratteristica
Array e Oggetti. Corso di Laurea Ingegneria Informatica Fondamenti di Informatica 1. Dispensa 12. A. Miola Dicembre 2006
 Corso di Laurea Ingegneria Informatica Fondamenti di Informatica 1 Dispensa 12 Array e Oggetti A. Miola Dicembre 2006 http://www.dia.uniroma3.it/~java/fondinf1/ Array e Oggetti 1 Contenuti Array paralleli
Corso di Laurea Ingegneria Informatica Fondamenti di Informatica 1 Dispensa 12 Array e Oggetti A. Miola Dicembre 2006 http://www.dia.uniroma3.it/~java/fondinf1/ Array e Oggetti 1 Contenuti Array paralleli
