Che cosa c è nella lezione. Questa lezione si occupa di teoria dei grafi: la rappresentazione dei grafi. le visite dei grafi
|
|
|
- Concetta Palmisano
- 5 anni fa
- Visualizzazioni
Transcript
1 Algoritmi e Programmazione Aanzata - teoria 1/18 Che cosa c è nella lezione Qesta lezione si occpa di teoria dei grafi: la rappresentazione dei grafi le isite dei grafi gli alberi ricoprenti minimi i cammini minimi. /18
2 Algoritmi e Programmazione Aanzata - teoria 3/18 Rappresentazione Tramite: lista di adiacenza; matrice di adiacenza. /18
3 Lista di adiacenza Dato G = (V, E), lista di adiacenza: ettore A di V elementi; A[i] contiene il pntatore alla lista dei ertici adiacenti a i. /18 : grafo non orientato A /18
4 : grafo orientato /18 : grafo orientato pesato /3 3/ / 3/ /1 1/ / 3 1 8/18
5 Vantaggi/santaggi 1/ Grafi orientati: elementi complessii nelle liste = E Grafi non orientati: elementi complessii nelle liste = E Complessità spaziale S(n) = O(ma( V, E )) = O( V+E ) antaggioso per grafi sparsi. /18 Vantaggi/santaggi / Santaggi: erifica dell esistenza di arco (,) mediante scansione della lista di adiacenza di ; so di memoria per i pesi dei grafi pesati. 1/18
6 Matrice di adiacenza Dato G = (V, E), matrice di adiacenza: matrice A di V V elementi A[i,j] = 1 se (i, j) E se (i, j) E grafi non orientati: A simmetrica. 11/18 : grafo non orientato 1 A /18
7 : grafo orientato 1 A /18 : grafo orientato pesato 1 3 A /18
8 : grafo orientato pesato Complessità spaziale S(n) = Θ( V ) antaggioso per grafi densi No costi aggintiiper i pesi Accesso efficiente alla topologia del grafo. 1/18 Algoritmi e Programmazione Aanzata - teoria 1/18
9 Algoritmi di isita Visita di n grafo G=(V, E): a partire da n ertice dato s, segendo gli archi con na certa strategia, elencare i ertici incontrati. Algoritmi: in ampiezza (breadth-first search, BFS); in profondità (depth-first search, DFS). 1/18 Visita in ampiezza: principi base 1/ Scoperta di n ertice: prima olta che si incontra nella isita. Ampiezza: espande ttta la frontiera tra erticigià scoperti/non ancora scoperti (sa coda Q). Vertici: bianchi: non ancora scoperti; grigi: scoperti, ma non completati; neri: scoperti e completati. 18/18
10 Visita in ampiezza: principi base / Dato ertice : d[] = distanza di da s; π(): padre di nell albero della isita. 1/18 Algoritmo 1/ Inizializzazione d[s]=, π[s] = NIL, colore[s] = grigio altri ertici : d[]=, π[] = NIL, colore[] = bianco Q ={s}. /18
11 Algoritmo / Fintanto che Q non dienta oto: estrai da Q l elemento in testa ertice bianco e adiacente ad - d[] = d[] +1, colore[] = grigio, π[] = - inserisci in Q colore[] = nero. 1/18 Q π r s t w /18
12 Q s π s r s t w 3/18 Q r w π s r w r s t 1 1 w /18
13 Q w π s r w r s t 1 1 w /18 Q t π s r w t r s t 1 1 w /18
14 Q t π s r w t r s t 1 1 w /18 Q π s r w t r s t w 8/18
15 Q π s r w t r s t w /18 Q π s r w t r s t w 3/18
16 Q π s r w r s t 1 3 t 1 3 w 31/18 Complessità Operazioni slla coda 3/18
17 Complessità O( V ) Operazioni slla coda 33/18 Complessità Operazioni slla coda Scansione delle liste di adiacenza 3/18
18 Complessità Operazioni slla coda Scansione delle liste di adiacenza O( E ) 3/18 Complessità Operazioni slla coda Scansione delle liste di adiacenza T(n) = O( V + E ). 3/18
19 Proprietà 1/ Raggingibilità A partire da n ertice s: determina ttti i ertici raggingibili da s 3/18 Proprietà / Cammini minimi: la isita in ampiezza determina la minima distanza tra s e ogni ertice raggingibile da esso. π s Cammino minimo da s a : s, w, t, lnghezza = 3 r w t 38/18
20 Visita in profondità A partire da n ertice s: isita ttti i ertici del grafo (raggingibili da s e non) etichetta ogni ertice con tempo di scoperta/tempo di fine elaborazione d[]/f[] etichetta ogni arco: - grafi orientati: T(ree), B(ackward), F(orward), C(ross) - grafi non orientati: T(ree), B(ackward) genera na foresta di alberi della isita in profondità. 3/18 Principi base Profondità: espande l ltimo ertice scoperto che ha ancora ertici non ancora scoperti adiacenti Scoperta di n ertice: prima olta che si incontra nella isita Vertici: bianchi: non ancora scoperti grigi: scoperti, ma non completati neri: scoperti e completati. /18
21 Strttre dati 1/ Grafo come lista delle adiacenze Tempo discreto time Vettore d dei tempi di scoperta Vettore f dei tempi di fine elaborazione Vettore colore. 1/18 Strttre dati / Vettore π dei predecessori (per costrire gli alberi di isita in profondità) Etichette degli archi T, B, F, C. /18
22 Algoritmo 1/ Inizializzazione π[] = NIL, colore[] = bianco time = ertice bianco, isita ricorsia 3/18 Algoritmo / Visita ricorsia da : colore[] = grigio, d[] = time++ ertice bianco e adiacente a - π[] =, isita ricorsia a partire da colore[] = nero f[] = time++ /18
23 time = π r s t w /18 time = 1 r π 1/ r s t w /18
24 time = r π s r s t 1/ / w /18 time = 3 r π s r s t w 1/ / 3/ w 8/18
25 time = r π s r s t w 1/ / 3/ w /18 time = r π s r s t w 1/ / 3/ w /18
26 time = r π s r s t w 1/ / / 3/ w 1/18 time = r π s r s t w 1/ / / 3/ w /18
27 time = 8 r π s r s t w 1/8 / / 3/ w 3/18 time = r π t s r s t w 1/8 / / / 3/ w /18
28 time = 1 r π t s r s t w 1/8 / / / 3/ 1/ w /18 time = 11 r π t s r s t w 1/8 / / / 3/ 1/11 w /18
29 time = 1 r π t s r s t w 1/8 / /1 / 3/ 1/11 w /18 Complessità Inizializzazione 8/18
30 Complessità Θ( V ) Inizializzazione /18 Complessità Inizializzazione Visita ricorsia da /18
31 Complessità Inizializzazione Visita ricorsia da Θ( E ) 1/18 Complessità Inizializzazione Visita ricorsia da T(n) = Θ( V + E ) /18
32 Classificazione degli archi Grafo orientato: T: archi dell'albero della isita in profondità B: connettono n ertice ad n so antenato nell albero F: connettono n ertice ad n so discendente nell albero C: archi rimanenti. Grafo non orientato: solo archi T e B. 3/18 Estensione della isita Qando si incontra n arco (,) si considera il colore del ertice in qel momento: se colore[]=bianco, (,) è T se colore[]=grigio, (,) è B se colore[]=nero: - se d[]<d[]) (,) è F - se d[]>d[]) (,) è C. /18
33 b a s e c d f g b a T 3/ / B T T F T C s 1/1 T B e 11/1 T / /8 1/13 1/1 C C C c d f g /18 Soente si ridisegna il grafo a partire dagli alberi della isita in profondità. B b T s T a F T d C C f T e C T g B T C c /18
34 Algoritmi e Programmazione Aanzata - teoria /18 Alberi ricoprenti minimi G=(V,E) grafo non orientato, pesato w: E R e connesso Albero ricoprente minimo (non nico) grafo G'=(V, T) doe T E aciclico minimizza w(t)=σ w(,). Aciciclità e copertra di ttti i ertici G è n albero 8/18
35 Approccio greed Approccio greed: a ogni passo, scelta della solzione localmente ottima; non garantisce solzione globalmente ottima. /18 Algoritmo generico A= sottoinsieme di albero ricoprente minimo, inizialmente oto Fintanto che A non è n albero ricoprente minimo, aggingi ad A n arco (,) sicro Inarianza: (,) sicro agginto a n sottoinsieme di n albero ricoprente minimo prodce ancora n sottoinsieme di n albero ricoprente minimo. /18
36 Tagli e archi 1/ G=(V,E) grafo non orientato, pesato, connesso. Taglio = partizione di V in S e V-S V = S V-S e S V-S = (,) E attraersa il taglio S e V-S (o iceersa). 1/18 Tagli e archi / Un taglio rispetta n insieme A di archi se nessn arco di A attraersa il taglio. Un arco si dice leggero se ha peso minimo tra gli archi che attraersano il taglio. /18
37 8 b c d S a 11 i 1 e 8 1 h g f 1 V-S 3/18 (b,c) attraersa il taglio 8 b c d S a 11 i 1 e 8 h g f 1 1 V-S /18
38 il taglio rispetta A A={(a,b), (c,f), (f,g), (g,h)} 8 b c d S a 11 i 1 e 8 h g f 1 1 V-S /18 (c,d) è n arco leggero 8 b c d S a 11 i 1 e 8 h g f 1 1 V-S /18
39 Archi sicri: teorema G=(V,E) grafo non orientato, pesato, connesso. A = sottoinsieme di n qalche albero ricoprente minimo di G; (S,V-S) taglio qalnqe che rispetta A; (,) n arco leggero che attraersa (S,V-S). (,) è sicro per A. /18 Archi sicri: corollario G=(V,E) grafo non orientato, pesato, connesso. A = sottoinsieme di n qalche albero ricoprente minimo di G; C albero nella foresta G A = (V,A); (,) n arco leggero che connette C ad n'altra componente in G A. (,) è sicro per A. 8/18
40 Algoritmo di Krskal Basato s algoritmo generico Corollario per determinare l arco sicro: foresta di alberi, inizialmente ertici singoli; ordinamento degli archi per pesi crescenti; iterazione selezione di n arco sicro: arco di peso minimo che connette alberi generando n albero; terminazione: considerati ttti i ertici. /18 8 b c d a 11 i 1 e 8 h g f 1 1 8/18
41 8 b c d a 11 i 1 e 8 h g f /18 8 b c d a 11 i 1 e 8 h g f 1 1 8/18
42 8 b c d a 11 i 1 e 8 h g f /18 8 b c d a 11 i 1 e 8 h g f 1 1 8/18
43 8 b c d a 11 i 1 e 8 h g f 1 1 8/18 8 b c d a 11 i 1 e 8 h g f 1 1 8/18
44 Complessità Dipende dalle strttre dati tilizzate. Con strttre efficienti T(n) = O( E lg E ). 8/18 Algoritmo di Prim Basato sll algoritmo generico Uso del teorema per determinare l arco sicro: inizialmente A = {r} (r = radice dell albero) iterazione: arco di peso minimo che connette n ertice di A con n ertice di V-A; terminazione: considerati ttti i ertici. 88/18
45 Strttra dati Coda a priorità: contiene ttti i ertici non appartenenti ad A. ke[] = minimo tra i pesi degli archi che collegano a n qalnqe ertice in A. Se non è collegato a nessn ertice in A, allora ke[]=. 8/18 A 8 b c d V-A a 11 i 1 e r 8 1 h g f 1 /18
46 A 8 b c d V-A a 11 i 1 e 8 1 h g f 1 1/18 A 8 b c d V-A a 11 i 1 e 8 1 h g f 1 /18
47 A 8 b c d V-A a 11 i 1 e 8 1 h g f 1 3/18 A 8 b c d V-A a 11 i 1 e 8 1 h g f 1 /18
48 A 8 b c d V-A a 11 i 1 e 8 1 h g f 1 /18 A 8 b c d V-A a 11 i 1 e 8 1 h g f 1 /18
49 A 8 b c d V-A a 11 i 1 e 8 1 h g f 1 /18 A 8 b c d a 11 i 1 e 8 1 h g f 1 8/18
50 Complessità T(n) = O( V lg V + E lg V ) = O( E lg V ) Con strttre dati particolari (heap di Fibonacci) T(n) = O( E + V lg V ). /18 Algoritmi e Programmazione Aanzata - teoria 1/18
51 Cammini minimi G=(V,E) grafo orientato, pesato (w: E R) Definizioni: peso w(p) di n cammino p: w(p) = Σ k i=1 w( i-1, i ) peso δ(,) di n cammino minimo da a : δ(,) = min{w(p): se p } altrimenti Cammino minimo da a : qalsiasi cammino p con w(p) = δ(,) 11/18 Problemi classici Cammini minimi: da sorgente singola: cammino minimo e so peso da s a ogni altro ertice - algoritmo di Dijkstra - algoritmo di Bellman-Ford con destinazione singola tra na coppia di ertici tra ttte le coppie di ertici. 1/18
52 Archi con pesi negatii (,) E per ci w(,) < ma ciclo a peso < : algoritmo di Djikstra: solzione ottima non garantita; algoritmo di Bellman-Ford: solzione ottima garantita. ciclo a peso < : problema non definito, solzione: algoritmo di Djikstra: risltato senza significato; algoritmo di Bellman-Ford: rilea ciclo <. 13/18 3 a - b s c d g -3 3 e f - 8 1/18
53 3 a s c d g b e f /18 Rappresentazione 1/ Vettore dei predecessori: V p[] = parent() se NIL altrimenti Sottografo dei predecessori: G p =(V p,e p ), doe - V p = { V: p[] NIL} {s} - E p = {(p[], ) E : V p - {s}} 1/18
54 Rappresentazione / Albero dei cammini minimi: G = (V, E ) doe V V e E E V : insieme dei ertici raggingibili da s s radice dell albero V l nico cammino semplice da s a in G è n cammino minimo da s a in G Nei grafi non pesati: algoritmo di isita in ampiezza. 1/18 3 s /18
55 s /18 s /18
56 Fondamenti teorici 1/3 Lemma: n sottocammino di n cammino minimo è n cammino minimo. G=(V,E): grafo orientato, pesato w: E R. p=< 1,,, k >: n cammino minimo da 1 a k. i, j 1 i j k, p ij =< i, i+1,, j >: sottocammino di p da i a j. p ij è n cammino minimo da i a j. 111/18 Fondamenti teorici /3 Corollario: G=(V,E): grafo orientato, pesato w: E R. Cammino minimo p da s a decomposto in n sottocammino da s a n arco (,). Allora d(s,)=d(s,)+w(,) 11/18
57 Fondamenti teorici 3/3 Lemma: G=(V,E): grafo orientato, pesato w: E R. (,) E d(s,) d(s,) + w(,) 113/18 Rilassamento d[]: stima (limite speriore) del peso del cammino minimo da s a inizialmente: V d[]=, π[] = NIL; d[s] = Rilassare: (= aggiornare) d[] e π [] erificando se coniene il cammino da s a e l arco (,): if (d[]>d[]+w(,)) { d[] = d[]+w(,); π [] ; } 11/18
58 d[] = d[] = w(,) = d[]>d[] + w(,) Rilassamento d[] = p[] = cammino minimo da s a = cammino minimo da s a + arco (,) 11/18 d[] = d[] = w(,) = d[]<d[] + w(,) Rilassamento Il rilassamento non ha ato effetto 11/18
59 Proprietà 1/3 Lemma: G=(V,E): grafo orientato, pesato w: E R. (,) E Dopo il rilassamento di (,) si ha che: d[] d[] + w(,) 11/18 Proprietà /3 Lemma: G=(V,E): grafo orientato, pesato w: E R. sorgente s V inizializzazione di d e π V d[] δ(s,) per ttti i passi di rilassamento sgli archi qando d[] = δ(s,), allora d[] non cambia più. 118/18
60 Proprietà 3/3 Lemma: G=(V,E): grafo orientato, pesato w: E R. sorgente s V cammino minimo da s a composto da cammino da s a arco (,) inizializzazione di d e π applicazione del rilassamento s (,) se prima del rilassamento d[] = δ(s,) dopo il rilassamento d[] = δ(s,). 11/18 Applicazione Rilassamento: applicato 1 olta ad ogni arco (Dijkstra) o più olte (Bellman-Ford); ordine con ci si rilassano gli archi. 1/18
61 Algoritmo di Dijkstra Ipotesi: archi a peso < Strategia: greed S: insieme dei ertici il ci peso di cammino minimo da s è già stato determinato V-S: coda a priorità Q dei ertici ancora da stimare. Termina per Q oto: estrae da V-S (d[] minimo) inserisce in S rilassa ttti gli archi scenti da. 11/ s 3 1/18
62 s S={} Q={s/, /,/, /, / } 13/18 s S={s} rela (s,), (s,) Q={/, /1,/, / } 1/18
63 s S={s, } rela (,), (,), (,) Q={/, /8,/1,} 1/18 s S={s,, } rela (,s), (,) Q={/8,/13} 1/18
64 s S={s,,, } rela (,), (,) Q={/} 1/18 s S={s,,,, } rela (,) Q={} 18/18
65 Complessità V-S: coda a priorità Q dei ertici ancora da stimare. 1/18 Θ( V ) V-S: coda a priorità Q dei ertici ancora da stimare. Complessità 13/18
66 Complessità V-S: coda a priorità Q dei ertici ancora da stimare. Termina per Q oto estrae da V-S (d[] minimo) 131/18 Complessità V-S: coda a priorità Q dei ertici ancora da stimare. Termina per Q oto estrae da V-S (d[] minimo) O(lg V ) 13/18
67 Complessità V-S: coda a priorità Q dei ertici ancora da stimare. Termina per Q oto estrae da V-S (d[] minimo) inserisce in S rilassa ttti gli archi scenti da 133/18 Complessità V-S: coda a priorità Q dei ertici ancora da stimare. Termina per Q oto estrae da V-S (d[] minimo) inserisce in S rilassa ttti gli archi scenti da O(lg V ) O( E ) 13/18
68 Complessità V-S: coda a priorità Q dei ertici ancora da stimare. Termina per Q oto estrae da V-S (d[] minimo) inserisce in S rilassa ttti gli archi scenti da T(n) = O(( V + E ) lg V ) 13/18 Algoritmo di Bellman-Ford Ipotesi: possono archi a peso < Rilea cicli < Strategia: greed Inizializzazione di d V -1 passi di rilassamento sgli archi V esimo rilassamento: diminisce almeno na stima: ciclo < altrimenti solzione ottima. 13/18
69 z Archi in ordine lessicografico: (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) 13/18 z Passo 1 (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) 138/18
70 13/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo 1 1/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo 1
71 11/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo 1 1/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo 1
72 13/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo 1 1/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo 1
73 1/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo 1 1/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo 1
74 1/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo 1 18/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo 11
75 1/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo 11 1/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo 11
76 11/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo 11 1/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo
77 13/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo 1/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo
78 1/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo 1/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo
79 1/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo 18/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo 3
80 1/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo 3 1/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo 3
81 11/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo 3 1/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo 3
82 13/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo 3 1/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo 3
83 1/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo 3 1/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo 3
84 1/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo 3 18/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo
85 1/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo 1/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo -
86 11/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo - 1/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo -
87 13/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo - 1/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo -
88 1/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo - 1/18 z (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) Passo -
89 z Passo (,) (,) (,) (,) (,) (,) (,) (,z) (z,) (z,) 1/18 Al V -esimo passo di rilassamento non diminisce alcna stima: terminazione con solzione ottima 18/18
90 Complessità Inizializzazione 1/18 Complessità Inizializzazione O( V ) 18/18
91 Complessità Inizializzazione V - 1 passi di rilassamento sgli archi 181/18 Complessità Inizializzazione O( V E ) V - 1 passi di rilassamento sgli archi 18/18
92 Complessità Inizializzazione V - 1 passi di rilassamento sgli archi V - esimo rilassamento 183/18 Complessità Inizializzazione V - 1 passi di rilassamento sgli archi V - esimo rilassamento O( E ) 18/18
93 Complessità Inizializzazione V - 1 passi di rilassamento sgli archi V - esimo rilassamento T(n) = O( V E ) 18/18
Grafo diretto Università degli Studi di Milano
 Grafo diretto Un grafo diretto G è na coppia ordinata (V, E), doe V è l insieme dei ertici {,,,,n} (anche detti nodi). E V V è n insieme di coppie ordinate (,) dette archi diretti 6 V= {,,,4,5,6,7} 7 4
Grafo diretto Un grafo diretto G è na coppia ordinata (V, E), doe V è l insieme dei ertici {,,,,n} (anche detti nodi). E V V è n insieme di coppie ordinate (,) dette archi diretti 6 V= {,,,4,5,6,7} 7 4
Grafi: cammini minimi
 Algoritmi e Programmaione Aanata EIP Grafi: cammini minimi Flio CORNO - Matteo SONZA REORDA Dip. Atomatica e Informatica Politecnico di Torino Sommario Introdione Algoritmo di Dijkstra Algoritmo di Bellman-Ford.
Algoritmi e Programmaione Aanata EIP Grafi: cammini minimi Flio CORNO - Matteo SONZA REORDA Dip. Atomatica e Informatica Politecnico di Torino Sommario Introdione Algoritmo di Dijkstra Algoritmo di Bellman-Ford.
PROBLEMA DEI CAMMINI MINIMI [CORMEN ET AL. CAP. 24] Il costo di cammino minimo da un vertice u ad un vertice v è definito nel seguente modo:
![PROBLEMA DEI CAMMINI MINIMI [CORMEN ET AL. CAP. 24] Il costo di cammino minimo da un vertice u ad un vertice v è definito nel seguente modo: PROBLEMA DEI CAMMINI MINIMI [CORMEN ET AL. CAP. 24] Il costo di cammino minimo da un vertice u ad un vertice v è definito nel seguente modo:](/thumbs/95/123186961.jpg) PROBLEMA DEI CAMMINI MINIMI [CORMEN ET AL. CAP. 24] Sia G = (V,E) un grafo orientato ai cui archi è associato un costo W(u,v). Il costo di un cammino p = (v 1,v 2,...,v k ) è la somma dei costi degli archi
PROBLEMA DEI CAMMINI MINIMI [CORMEN ET AL. CAP. 24] Sia G = (V,E) un grafo orientato ai cui archi è associato un costo W(u,v). Il costo di un cammino p = (v 1,v 2,...,v k ) è la somma dei costi degli archi
Depth-first search. Visita in profondità di un grafo Algoritmo Esempio Complessità dell algoritmo Proprietà Ordinamento topologico
 Depth-first search Visita in profondità di n grafo Algoritmo Esempio Complessità dell algoritmo Proprietà Ordinamento topologico Depth-first search Dato n grafo G=(V,E) e n specifico ertice s chiamato
Depth-first search Visita in profondità di n grafo Algoritmo Esempio Complessità dell algoritmo Proprietà Ordinamento topologico Depth-first search Dato n grafo G=(V,E) e n specifico ertice s chiamato
Università Roma Tre - PAS Classe A048 "Matematica Applicata" - Corso di Informatica a.a. 2013/2014
 Università Roma Tre Dipartimento di Matematica e Fisica Percorso Abilitante Speciale Classe A08 Matematica Applicata Corso di Informatica Algoritmi su Grafi Marco Liverani (liverani@mat.uniroma.it) Sommario
Università Roma Tre Dipartimento di Matematica e Fisica Percorso Abilitante Speciale Classe A08 Matematica Applicata Corso di Informatica Algoritmi su Grafi Marco Liverani (liverani@mat.uniroma.it) Sommario
Algoritmi e Strutture Dati
 Introduzione ai grafi Grafi: Definizione e Algoritmi di visita Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 2007/08 Introduzione ai
Introduzione ai grafi Grafi: Definizione e Algoritmi di visita Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 2007/08 Introduzione ai
Teoria dei grafi: ricerca di percorsi a minimo costo Ing. Valerio Lacagnina
 Metodi diide-et-impera, programmazione dinamica e algoritmi greed La programmazione dinamica, come il metodo diide-et-impera, risole n problema mettendo insieme le solzioni di n certo nmero di sottoproblemi.
Metodi diide-et-impera, programmazione dinamica e algoritmi greed La programmazione dinamica, come il metodo diide-et-impera, risole n problema mettendo insieme le solzioni di n certo nmero di sottoproblemi.
Appunti del corso di Informatica 1 (IN110 Fondamenti) 7 Grafi e alberi: introduzione
 Università di Roma Tre Dipartimento di Matematica e Fisica Corso di Laurea in Matematica Appunti del corso di Informatica (IN0 Fondamenti) Grafi e alberi: introduzione Marco Liverani (liverani@mat.uniroma.it)
Università di Roma Tre Dipartimento di Matematica e Fisica Corso di Laurea in Matematica Appunti del corso di Informatica (IN0 Fondamenti) Grafi e alberi: introduzione Marco Liverani (liverani@mat.uniroma.it)
Algoritmi e strutture dati
 Algoritmi e Strutture Dati Cammini minimi Definizioni Sia G = (V,E) un grafo orientato pesato sugli archi. Il costo di un cammino π = è dato da: Un cammino minimo tra una coppia di
Algoritmi e Strutture Dati Cammini minimi Definizioni Sia G = (V,E) un grafo orientato pesato sugli archi. Il costo di un cammino π = è dato da: Un cammino minimo tra una coppia di
Visita di grafi. Vittorio Maniezzo - Università di Bologna
 Visita di grafi Vittorio Manieo - Uniersità di Bologna Liste di adiacena Lista di adiacenadi n ertice : lista che concatena ttti i ertici adiacenti a Il grafo pò essere rappresentato dalle liste di adiacena
Visita di grafi Vittorio Manieo - Uniersità di Bologna Liste di adiacena Lista di adiacenadi n ertice : lista che concatena ttti i ertici adiacenti a Il grafo pò essere rappresentato dalle liste di adiacena
Grafi (orientati): cammini minimi
 Grafi (orientati): cammini minimi Una breve presentazione Definizioni Sia G=(V,E) un grafo orientato con costi w sugli archi. Il costo di un cammino π= è dato da: Un cammino minimo tra
Grafi (orientati): cammini minimi Una breve presentazione Definizioni Sia G=(V,E) un grafo orientato con costi w sugli archi. Il costo di un cammino π= è dato da: Un cammino minimo tra
Esercitazione 7. Grafi. Rappresentazione e algoritmi di visita
 Esercitazione 7 Grafi Rappresentazione e algoritmi di visita Grafo G = (V,E) non orientato 1 1 G = (V,E) orientato 6 Rappresentazione Grafo G = (V,E) metodi standard per la rappresentazione Liste di adiacenza
Esercitazione 7 Grafi Rappresentazione e algoritmi di visita Grafo G = (V,E) non orientato 1 1 G = (V,E) orientato 6 Rappresentazione Grafo G = (V,E) metodi standard per la rappresentazione Liste di adiacenza
Visite in Grafi BFS e DFS
 Visite in Grafi BFS e DFS Visita di un Grafo Obiettivo: Visitare una sola volta tutti i nodi del grafo. Es.: visitare un porzione del grafo del Web Difficoltà: Presenza di cicli: Marcare i nodi visitati
Visite in Grafi BFS e DFS Visita di un Grafo Obiettivo: Visitare una sola volta tutti i nodi del grafo. Es.: visitare un porzione del grafo del Web Difficoltà: Presenza di cicli: Marcare i nodi visitati
Problema del cammino minimo
 Algoritmi e Strutture di Dati II Problema del cammino minimo Un viaggiatore vuole trovare la via più corta per andare da una città ad un altra. Possiamo rappresentare ogni città con un nodo e ogni collegamento
Algoritmi e Strutture di Dati II Problema del cammino minimo Un viaggiatore vuole trovare la via più corta per andare da una città ad un altra. Possiamo rappresentare ogni città con un nodo e ogni collegamento
K 4 è planare? E K 3,3 e K 5 sono planari? Sì! No! (Teorema di Kuratowski) K 5. Camil Demetrescu, Irene Finocchi, Giuseppe F.
 K 4 è planare? Sì! E K 3,3 e K 5 sono planari? K 5 No! (Teorema di Kuratowski) 1 Un albero è un grafo bipartito? SÌ! Ma un grafo bipartito è sempre un albero?? 2 Algoritmi e Strutture Dati Capitolo 11
K 4 è planare? Sì! E K 3,3 e K 5 sono planari? K 5 No! (Teorema di Kuratowski) 1 Un albero è un grafo bipartito? SÌ! Ma un grafo bipartito è sempre un albero?? 2 Algoritmi e Strutture Dati Capitolo 11
Visite in Grafi BFS e DFS. PDF created with FinePrint pdffactory trial version
 Visite in Grafi BFS e DFS Visita di un Grafo 8Obiettivo: 4Visitare una sola volta tutti i nodi del grafo. 4Es.: visitare un porzione del grafo del Web 8Difficoltà : 4Presenza di cicli: Marcare i nodi visitati
Visite in Grafi BFS e DFS Visita di un Grafo 8Obiettivo: 4Visitare una sola volta tutti i nodi del grafo. 4Es.: visitare un porzione del grafo del Web 8Difficoltà : 4Presenza di cicli: Marcare i nodi visitati
Algoritmi e Strutture dati Mod B. Grafi Percorsi Minimi: algoritmi esatti e algoritmi euristici (A*)
 Algoritmi e Strutture dati Mod B Grafi Percorsi Minimi: algoritmi esatti e algoritmi euristici (A*) Grafi: Percorsi minimi Un percorso minimo in un grafo G= grafo pesato orientato, con funzione di
Algoritmi e Strutture dati Mod B Grafi Percorsi Minimi: algoritmi esatti e algoritmi euristici (A*) Grafi: Percorsi minimi Un percorso minimo in un grafo G= grafo pesato orientato, con funzione di
Cammini Minimi. Algoritmo di Dijkstra. Cammino in un grafo
 Cammini Minimi Algoritmo di Dijkstra Cammino in un grafo Dato un grafo G=(V,E), un Cammino (Percorso) in G è un insieme di vertici v 1, v 2,.., v k tali che (v i, v i+1 ) E v 1 v 2 v 3 v k In un grafo
Cammini Minimi Algoritmo di Dijkstra Cammino in un grafo Dato un grafo G=(V,E), un Cammino (Percorso) in G è un insieme di vertici v 1, v 2,.., v k tali che (v i, v i+1 ) E v 1 v 2 v 3 v k In un grafo
Algoritmi e Strutture di Dati II 2. Visite di grafi
 Algoritmi e Strutture di Dati II 2 Visite di grafi Gli algoritmi di visita di un grafo hanno come obiettivo l esploraione di tutti i nodi e gli archi del grafo. Vi sono due modi principali per esplorare
Algoritmi e Strutture di Dati II 2 Visite di grafi Gli algoritmi di visita di un grafo hanno come obiettivo l esploraione di tutti i nodi e gli archi del grafo. Vi sono due modi principali per esplorare
Cammini Minimi. Algoritmo di Dijkstra
 Cammini Minimi Algoritmo di Dijkstra Cammino in un grafo Dato un grafo G=(V,E), un Cammino (Percorso) in G è un insieme di vertici v 1, v 2,.., v k tali che (v i, v i+1 ) E v 1 v 2 v 3 v k In un grafo
Cammini Minimi Algoritmo di Dijkstra Cammino in un grafo Dato un grafo G=(V,E), un Cammino (Percorso) in G è un insieme di vertici v 1, v 2,.., v k tali che (v i, v i+1 ) E v 1 v 2 v 3 v k In un grafo
Esempi. non. orientato. orientato
 Definizione! Un grafo G = (V,E) è costituito da un insieme di vertici V ed un insieme di archi E ciascuno dei quali connette due vertici in V detti estremi dell arco.! Un grafo è orientato quando vi è
Definizione! Un grafo G = (V,E) è costituito da un insieme di vertici V ed un insieme di archi E ciascuno dei quali connette due vertici in V detti estremi dell arco.! Un grafo è orientato quando vi è
Algoritmi e Strutture Dati
 Algoritmi e Strutture Dati Capitolo 12 Grafi e visite di grafi Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Definizione Un grafo G=(V,E) consiste in: - un insieme V di vertici (o nodi) - un insieme
Algoritmi e Strutture Dati Capitolo 12 Grafi e visite di grafi Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Definizione Un grafo G=(V,E) consiste in: - un insieme V di vertici (o nodi) - un insieme
Algoritmi & Laboratorio
 Acknowledgement Lucidi da F. Damiani, a.a. 2004-2005 C. Demetrescu et al, Algoritmi e strutture dati, McGraw-Hill M. Zacchi, a.a. 2003-2004 I lucidi non sono un sostituto per il libro di testo non contengono
Acknowledgement Lucidi da F. Damiani, a.a. 2004-2005 C. Demetrescu et al, Algoritmi e strutture dati, McGraw-Hill M. Zacchi, a.a. 2003-2004 I lucidi non sono un sostituto per il libro di testo non contengono
Cammini minimi. Definizioni. Distanza fra vertici. Proprietà dei cammini minimi. Algoritmi e Strutture Dati
 Algoritmi e Strutture Dati Definizioni Sia G=(V,E) un grafo orientato con costi w sugli archi. Il costo di un cammino π= è dato da: Cammini minimi Un cammino minimo tra una coppia di
Algoritmi e Strutture Dati Definizioni Sia G=(V,E) un grafo orientato con costi w sugli archi. Il costo di un cammino π= è dato da: Cammini minimi Un cammino minimo tra una coppia di
Algoritmi e Strutture Dati
 Algoritmi Elementari su Grafi Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino Polo di Scienze Università di Camerino ad Ascoli Piceno Visita
Algoritmi Elementari su Grafi Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino Polo di Scienze Università di Camerino ad Ascoli Piceno Visita
Grafi (non orientati e connessi): minimo albero ricoprente
 Grafi (non orientati e connessi): minimo albero ricoprente Una breve presentazione Definizioni Sia G=(V,E) un grafo non orientato e connesso. Un albero ricoprente di G è un sottografo T G tale che: T è
Grafi (non orientati e connessi): minimo albero ricoprente Una breve presentazione Definizioni Sia G=(V,E) un grafo non orientato e connesso. Un albero ricoprente di G è un sottografo T G tale che: T è
Grafi: definizioni e visite
 Grafi: definizioni e visite Grafi (non orientati) Grafo (non orientato): G = (V, E) V = nodi (o vertici) E = archi fra coppie di nodi distinti. Modella relazioni fra coppie di oggetti. Parametri della
Grafi: definizioni e visite Grafi (non orientati) Grafo (non orientato): G = (V, E) V = nodi (o vertici) E = archi fra coppie di nodi distinti. Modella relazioni fra coppie di oggetti. Parametri della
Sommario. Rappresentazione dei grafi. Ordinamento topologico. Visita in ampiezza Visita in profondità
 Visite Grafi Sommario Rappresentazione dei grafi Visita in ampiezza Visita in profondità Ordinamento topologico Visita in ampiezza La visita in ampiezza breadth-first-search (BFS) di un grafo dato un vertice
Visite Grafi Sommario Rappresentazione dei grafi Visita in ampiezza Visita in profondità Ordinamento topologico Visita in ampiezza La visita in ampiezza breadth-first-search (BFS) di un grafo dato un vertice
Appunti lezione Capitolo 13 Programmazione dinamica
 Appunti lezione Capitolo 13 Programmazione dinamica Alberto Montresor 12 Novembre, 2015 1 Domanda: Fattore di crescita dei numeri catalani Vogliamo dimostrare che cresce almeno come 2 n. La nostra ipotesi
Appunti lezione Capitolo 13 Programmazione dinamica Alberto Montresor 12 Novembre, 2015 1 Domanda: Fattore di crescita dei numeri catalani Vogliamo dimostrare che cresce almeno come 2 n. La nostra ipotesi
Grafi pesati Minimo albero ricoprente
 Algoritmi e Strutture Dati Definizioni Grafi pesati Minimo albero ricoprente Sia G=(V,E) un grafo non orientato e connesso. Un albero ricoprente di G è un sottografo T G tale che: T è un albero; T contiene
Algoritmi e Strutture Dati Definizioni Grafi pesati Minimo albero ricoprente Sia G=(V,E) un grafo non orientato e connesso. Un albero ricoprente di G è un sottografo T G tale che: T è un albero; T contiene
Informatica 3. LEZIONE 24: Grafi. Modulo 1: Rappresentazione e implementazione di grafi Modulo 2: Attraversamento di un grafo
 Informatica 3 LEZIONE 24: Grafi Modulo 1: Rappresentazione e implementazione di grafi Modulo 2: Attraversamento di un grafo Informatica 3 Lezione 24 - Modulo 1 Rappresentazione e implementazione di grafi
Informatica 3 LEZIONE 24: Grafi Modulo 1: Rappresentazione e implementazione di grafi Modulo 2: Attraversamento di un grafo Informatica 3 Lezione 24 - Modulo 1 Rappresentazione e implementazione di grafi
Algoritmi & Laboratorio
 lbero ricoprente sia dato un grafo connesso e non orientato un albero ricoprente è un sottografo che contiene tutti nodi è aciclico è connesso cknowledgement Lucidi da. Damiani, a.a. 00-00. Demetrescu
lbero ricoprente sia dato un grafo connesso e non orientato un albero ricoprente è un sottografo che contiene tutti nodi è aciclico è connesso cknowledgement Lucidi da. Damiani, a.a. 00-00. Demetrescu
Grafi. V = {a, b, c, d} E = {(a, b), (a, c), (c, a), (d, d), (b, d)}
 Grafi Grafo orientato (o diretto) = (V,E) V = nodi o vertici - E = archi (edges) V = {a, b, c, d} E = {(a, b), (a, c), (c, a), (d, d), (b, d)} archi uscenti da un nodo x: (x, y) archi incidenti su un nodo
Grafi Grafo orientato (o diretto) = (V,E) V = nodi o vertici - E = archi (edges) V = {a, b, c, d} E = {(a, b), (a, c), (c, a), (d, d), (b, d)} archi uscenti da un nodo x: (x, y) archi incidenti su un nodo
2 OTTIMIZZAZIONE SU GRAFI. E. Amaldi Fondamenti di R.O. Politecnico di Milano 1
 2 OTTIMIZZAZIONE SU GRAFI E. Amaldi Fondamenti di R.O. Politecnico di Milano 1 Molti problemi decisionali possono essere formulati utilizzando il linguaggio della teoria dei grafi. Esempi: - problemi di
2 OTTIMIZZAZIONE SU GRAFI E. Amaldi Fondamenti di R.O. Politecnico di Milano 1 Molti problemi decisionali possono essere formulati utilizzando il linguaggio della teoria dei grafi. Esempi: - problemi di
Il Problema dell Albero Ricoprente Minimo (Shortest Spanning Tree - SST)
 Il Problema dell Albero Ricoprente Minimo (Shortest Spanning Tree - SST) È dato un grafo non orientato G=(V,E). Ad ogni arco e i E, i=1,,m, è associato un costo c i 0 7 14 4 10 9 11 8 12 6 13 5 17 3 2
Il Problema dell Albero Ricoprente Minimo (Shortest Spanning Tree - SST) È dato un grafo non orientato G=(V,E). Ad ogni arco e i E, i=1,,m, è associato un costo c i 0 7 14 4 10 9 11 8 12 6 13 5 17 3 2
Laboratorio di Algoritmi e Strutture Dati
 Laboratorio di Algoritmi e Strutture Dati Aniello Murano http://people.na.infn.it people.na.infn.it/~murano/ Grafi pesati e alberi minimi di copertura Riepilogo delle lezioni precedenti Definizione di
Laboratorio di Algoritmi e Strutture Dati Aniello Murano http://people.na.infn.it people.na.infn.it/~murano/ Grafi pesati e alberi minimi di copertura Riepilogo delle lezioni precedenti Definizione di
uscente entrante adiacente Figure B.2 (a) (b) (c) incident from leaves incident to enters incident on adjacent degree isolated
 Grafi Si dice grafo un insieme di nodi legati "a due a due" da archi direzionati (o no) I grafi sono strutture dati di fondamentale importanza in informatica Vi sono centinaia di problemi computazionali
Grafi Si dice grafo un insieme di nodi legati "a due a due" da archi direzionati (o no) I grafi sono strutture dati di fondamentale importanza in informatica Vi sono centinaia di problemi computazionali
Algoritmi e Strutture Dati (Mod. B) Algoritmi su grafi Ricerca in profondità (Depth-First Search) Parte II
 Algoritmi e Strutture Dati (Mod. B) Algoritmi su grafi Ricerca in profondità (Depth-First Search) Parte II Classificazione digli archi Sia G la foresta DF generata da DFS sul grafo G. Arco d albero: gli
Algoritmi e Strutture Dati (Mod. B) Algoritmi su grafi Ricerca in profondità (Depth-First Search) Parte II Classificazione digli archi Sia G la foresta DF generata da DFS sul grafo G. Arco d albero: gli
Richiami di Teoria dei Grafi. Paolo Detti Dipartimento di Ingegneria dell Informazione Università di Siena
 Richiami di Teoria dei Grafi Paolo Detti Dipartimento di Ingegneria dell Informazione Università di Siena Teoria dei grafi La Teoria dei Grafi costituisce, al pari della Programmazione Matematica, un corpo
Richiami di Teoria dei Grafi Paolo Detti Dipartimento di Ingegneria dell Informazione Università di Siena Teoria dei grafi La Teoria dei Grafi costituisce, al pari della Programmazione Matematica, un corpo
Grafi (non orientati e connessi): minimo albero ricoprente
 .. Grafi (non orientati e connessi): minimo albero ricoprente Una presentazione alternativa (con ulteriori dettagli) Problema: calcolo del minimo albero di copertura (M.S.T.) Dato un grafo pesato non orientato
.. Grafi (non orientati e connessi): minimo albero ricoprente Una presentazione alternativa (con ulteriori dettagli) Problema: calcolo del minimo albero di copertura (M.S.T.) Dato un grafo pesato non orientato
Cammini minimi in grafi:
 Algoritmi e strutture dati Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Cammini minimi in grafi: una trilogia Cammini minimi in grafi: Episodio III: la fine della trilogia Input: nelle puntate
Algoritmi e strutture dati Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Cammini minimi in grafi: una trilogia Cammini minimi in grafi: Episodio III: la fine della trilogia Input: nelle puntate
Algoritmi e strutture dati
 Algoritmi e Strutture Dati Minimo albero ricoprente Sia G = (V, E) un grafo connesso non orientato. Definizioni Un albero ricoprente di G è un sottografo T G tale che: T è un albero; T contiene tutti i
Algoritmi e Strutture Dati Minimo albero ricoprente Sia G = (V, E) un grafo connesso non orientato. Definizioni Un albero ricoprente di G è un sottografo T G tale che: T è un albero; T contiene tutti i
Algoritmi e Strutture dati Mod B. Grafi: Percorsi Minimi (parte I)
 Algoritmi e Strutture dati Mod B Grafi: Percorsi Minimi (parte I) Grafi: Percorsi minimi Un percorso minimo in un grafo G= grafo pesato orientato, con funzione di peso w: E fi che mappa archi in pesi
Algoritmi e Strutture dati Mod B Grafi: Percorsi Minimi (parte I) Grafi: Percorsi minimi Un percorso minimo in un grafo G= grafo pesato orientato, con funzione di peso w: E fi che mappa archi in pesi
Teoria dei Grafi Parte I. Alberto Caprara DEIS - Università di Bologna
 Teoria dei Grafi Parte I Alberto Caprara DEIS - Università di Bologna acaprara@deis.unibo.it Teoria dei Grafi Paradigma di rappresentazione di problemi Grafo G : coppia (V,E) V = insieme di vertici E =
Teoria dei Grafi Parte I Alberto Caprara DEIS - Università di Bologna acaprara@deis.unibo.it Teoria dei Grafi Paradigma di rappresentazione di problemi Grafo G : coppia (V,E) V = insieme di vertici E =
Minimo albero di copertura
 apitolo 0 Minimo albero di copertura efinizione 0.. ato un grafo G = (V, E) non orientato e connesso, un albero di copertura di G è un sottoinsieme T E tale che il sottografo (V, T ) è un albero libero.
apitolo 0 Minimo albero di copertura efinizione 0.. ato un grafo G = (V, E) non orientato e connesso, un albero di copertura di G è un sottoinsieme T E tale che il sottografo (V, T ) è un albero libero.
Teoria dei Grafi Parte I
 Teoria dei Grafi Parte I Daniele Vigo D.E.I.S. - Università di Bologna dvigo@deis.unibo.it Teoria dei Grafi Paradigma di rappresentazione di problemi Grafo G : coppia (V,E) V = insieme di vertici E = insieme
Teoria dei Grafi Parte I Daniele Vigo D.E.I.S. - Università di Bologna dvigo@deis.unibo.it Teoria dei Grafi Paradigma di rappresentazione di problemi Grafo G : coppia (V,E) V = insieme di vertici E = insieme
Introduzione ai grafi
 TFA A048 Anno Accademico 2012-13 Outline Cenni storici sui grafi Nozioni introduttive: cammini, connessione, alberi, cicli Cammini di costo minimo Origini storiche La nascita della teoria dei grafi risale
TFA A048 Anno Accademico 2012-13 Outline Cenni storici sui grafi Nozioni introduttive: cammini, connessione, alberi, cicli Cammini di costo minimo Origini storiche La nascita della teoria dei grafi risale
Laboratorio di Algoritmi e Strutture Dati
 Laboratorio di Algoritmi e Strutture Dati Prof. Aniello Murano Componenti fortemente connesse e Alberi minimi di copertura Corso di Laurea Codice insegnamento Email docente Anno accademico Informatica
Laboratorio di Algoritmi e Strutture Dati Prof. Aniello Murano Componenti fortemente connesse e Alberi minimi di copertura Corso di Laurea Codice insegnamento Email docente Anno accademico Informatica
Grafi: visite. Una breve presentazione. F. Damiani - Alg. & Lab. 04/05 (da C. Demetrescu et al - McGraw-Hill)
 Grafi: visite Una breve presentazione Visite di grafi Scopo e tipi di visita Una visita (o attraversamento) di un grafo G permette di esaminare i nodi e gli archi di G in modo sistematico Problema di base
Grafi: visite Una breve presentazione Visite di grafi Scopo e tipi di visita Una visita (o attraversamento) di un grafo G permette di esaminare i nodi e gli archi di G in modo sistematico Problema di base
Algoritmi e Strutture Dati
 Algoritmi e Strutture Dati Capitolo 3 Cammini minimi: algoritmo di Dijkstra Cammini minimi in grafi: cammini minimi a singola sorgente (senza pesi negativi) Cammini minimi in grafi pesati Sia G=(V,E,w)
Algoritmi e Strutture Dati Capitolo 3 Cammini minimi: algoritmo di Dijkstra Cammini minimi in grafi: cammini minimi a singola sorgente (senza pesi negativi) Cammini minimi in grafi pesati Sia G=(V,E,w)
Algoritmi e Strutture Dati
 Algoritmi e Strutture Dati Capitolo 13 Cammini minimi: Algoritmo di Dijkstra (*) (ACM in grafi diretti e non diretti senza archi di peso negativo) Punto della situazione Algoritmo basato sull ordinamento
Algoritmi e Strutture Dati Capitolo 13 Cammini minimi: Algoritmo di Dijkstra (*) (ACM in grafi diretti e non diretti senza archi di peso negativo) Punto della situazione Algoritmo basato sull ordinamento
Algoritmi di visita di un grafo
 Algoritmi di isita di n grafo Ilaria Castelli castelli@dii.nisi.it Uniersità degli Stdi di Siena Dipartimento di Ingegneria dell Informazione A.A. 2009/2010 I. Castelli Visita di n grafo, A.A. 2009/2010
Algoritmi di isita di n grafo Ilaria Castelli castelli@dii.nisi.it Uniersità degli Stdi di Siena Dipartimento di Ingegneria dell Informazione A.A. 2009/2010 I. Castelli Visita di n grafo, A.A. 2009/2010
Richiami di matematica discreta: grafi e alberi. Paolo Camurati Dip. Automatica e Informatica Politecnico di Torino
 Richiami di matematica discreta: grafi e alberi Paolo Camurati Dip. Automatica e Informatica Politecnico di Torino Grafi Definizione: G = (V,E) V: insieme finito di vertici E: insieme finito di archi,
Richiami di matematica discreta: grafi e alberi Paolo Camurati Dip. Automatica e Informatica Politecnico di Torino Grafi Definizione: G = (V,E) V: insieme finito di vertici E: insieme finito di archi,
Grafi (orientati): cammini minimi
 .. Grafi (orientati): cammini minimi Una presentazione alternativa (con ulteriori dettagli) Un algoritmo greedy per calcolare i cammini minimi da un vertice sorgente in un grafo orientato e pesato, senza
.. Grafi (orientati): cammini minimi Una presentazione alternativa (con ulteriori dettagli) Un algoritmo greedy per calcolare i cammini minimi da un vertice sorgente in un grafo orientato e pesato, senza
B.1 I grafi: notazione e nomenclatura
 Appendice B Grafi e Reti In questa appendice richiamiamo i principali concetti relativi a grafi e reti; descriviamo inoltre alcune classi di strutture dati che possono essere utilizzate per implementare
Appendice B Grafi e Reti In questa appendice richiamiamo i principali concetti relativi a grafi e reti; descriviamo inoltre alcune classi di strutture dati che possono essere utilizzate per implementare
Grafi. Sommario. Definizioni Rappresentazione dei grafi Algoritmi di visita Esempi in C
 Grafi Sommario Definizioni Rappresentazione dei grafi Algoritmi di visita Esempi in C 1 Esempi Relazioni di parentela Alberi genealogici Relazioni tra classi nei linguaggi OO Grafo del Web Assetti societari
Grafi Sommario Definizioni Rappresentazione dei grafi Algoritmi di visita Esempi in C 1 Esempi Relazioni di parentela Alberi genealogici Relazioni tra classi nei linguaggi OO Grafo del Web Assetti societari
LABORATORIO DI ALGORITMI E STRUTTURE DATI A-L. Ingegneria e scienze informatiche Cesena A.A: 2016/2017 Docente: Greta Sasso
 LABORATORIO DI ALGORITMI E STRUTTURE DATI A-L Ingegneria e scienze informatiche Cesena A.A: 2016/2017 Docente: Greta Sasso Grafi Un grafo è una struttura definita come un insieme di nodi (o vertici) che
LABORATORIO DI ALGORITMI E STRUTTURE DATI A-L Ingegneria e scienze informatiche Cesena A.A: 2016/2017 Docente: Greta Sasso Grafi Un grafo è una struttura definita come un insieme di nodi (o vertici) che
Lezioni di Ricerca Operativa
 Lezioni di Ricerca Operativa Estratto per la parte di programmazione lineare e ottimizzazione sui grafi Corso di Metodi di Ottimizzazione per l'ingegneria della Sicurezza Laurea Magistrale in Ingegneria
Lezioni di Ricerca Operativa Estratto per la parte di programmazione lineare e ottimizzazione sui grafi Corso di Metodi di Ottimizzazione per l'ingegneria della Sicurezza Laurea Magistrale in Ingegneria
Grafi non orientati. Grafi (non orientati) Rappresentazione di Grafi: matrice delle adiacenze. Tipiche applicazioni di modelli basati su grafi
 Grafi non orientati Grafi (non orientati) Notazione. G = (V, E) V = nodi (o vertici). E = archi (o lati) tra coppie di nodi. Modella relazioni definite tra coppie di oggetti. aglia di un grafo: numero
Grafi non orientati Grafi (non orientati) Notazione. G = (V, E) V = nodi (o vertici). E = archi (o lati) tra coppie di nodi. Modella relazioni definite tra coppie di oggetti. aglia di un grafo: numero
Grafi: ordinamento topologico
 .. Grafi: ordinamento topologico Che cosa e e come si calcola Che cosa e un ordinamento topologico F. Damiani - Alg. & Lab. 04/05 Una definizione di ordinamento topologico Definizione. Funzione σ: V {1,
.. Grafi: ordinamento topologico Che cosa e e come si calcola Che cosa e un ordinamento topologico F. Damiani - Alg. & Lab. 04/05 Una definizione di ordinamento topologico Definizione. Funzione σ: V {1,
Note per la Lezione 21 Ugo Vaccaro
 Progettazione di Algoritmi Anno Accademico 20 20 Note per la Lezione 2 Ugo Vaccaro In questa lezione introdurremo il concetto di grafo, esamineremo le loro più comuni rappresentazioni ed introdurremo i
Progettazione di Algoritmi Anno Accademico 20 20 Note per la Lezione 2 Ugo Vaccaro In questa lezione introdurremo il concetto di grafo, esamineremo le loro più comuni rappresentazioni ed introdurremo i
Algoritmi e Strutture Dati Grafi. Daniele Loiacono
 lgoritmi e Strutture ati Grafi Riferimenti 2 Questo materiale è tratto dalle trasparenze del corso lgoritmi e Strutture ati del prof. lberto Montresor dell Università di Trento. (http://www.dit.unitn.it/~montreso/asd/index.shtml)
lgoritmi e Strutture ati Grafi Riferimenti 2 Questo materiale è tratto dalle trasparenze del corso lgoritmi e Strutture ati del prof. lberto Montresor dell Università di Trento. (http://www.dit.unitn.it/~montreso/asd/index.shtml)
Cammini minimi con sorgente singola
 Capitolo 11 Cammini minimi con sorgente singola efinizione 11.1. Sia G = (V,, w) un grafo orientato e pesato; dato il cammino p = v 0, v 1,..., v k in G, il valore w(p) = k i=1 w(v i 1, v i ) rappresenta
Capitolo 11 Cammini minimi con sorgente singola efinizione 11.1. Sia G = (V,, w) un grafo orientato e pesato; dato il cammino p = v 0, v 1,..., v k in G, il valore w(p) = k i=1 w(v i 1, v i ) rappresenta
Teoria dei Grafi Elementi di base della Teoria dei Grafi
 L. Pallottino, Sistemi Robotici Distribuiti - Versione del 4 Marzo 2015 42 Teoria dei Grafi Elementi di base della Teoria dei Grafi Definizione 1. Un grafo G = (V, E) è composto da un insieme finito di
L. Pallottino, Sistemi Robotici Distribuiti - Versione del 4 Marzo 2015 42 Teoria dei Grafi Elementi di base della Teoria dei Grafi Definizione 1. Un grafo G = (V, E) è composto da un insieme finito di
Alberi di copertura minimi
 Alberi di copertura minimi 1 Problema Nella progettazione di circuiti elettronici è spesso necessario collegare i morsetti. Per connettere un insieme di n morsetti si può usare un insieme di n-1 fili elettrici.
Alberi di copertura minimi 1 Problema Nella progettazione di circuiti elettronici è spesso necessario collegare i morsetti. Per connettere un insieme di n morsetti si può usare un insieme di n-1 fili elettrici.
Introduzione ai grafi. Introduzione ai grafi p. 1/2
 Introduzione ai grafi Introduzione ai grafi p. 1/2 Grafi Un grafo G é costituito da una coppia di insiemi (V,A) dove V é detto insieme dei nodi e A é detto insieme di archi ed é un sottinsieme di tutte
Introduzione ai grafi Introduzione ai grafi p. 1/2 Grafi Un grafo G é costituito da una coppia di insiemi (V,A) dove V é detto insieme dei nodi e A é detto insieme di archi ed é un sottinsieme di tutte
Terzo allenamento. Olimpiadi Italiane di Informatica - Selezione territoriale
 Terzo allenamento Olimpiadi Italiane di Informatica - Selezione territoriale Luca Chiodini luca@chiodini.org - l.chiodini@campus.unimib.it 22 marzo 2016 Programma 1. Lettura di un problema tratto dalle
Terzo allenamento Olimpiadi Italiane di Informatica - Selezione territoriale Luca Chiodini luca@chiodini.org - l.chiodini@campus.unimib.it 22 marzo 2016 Programma 1. Lettura di un problema tratto dalle
Shortest-Paths Problem - definizioni
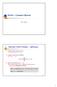 Grafo Cammini Minimi GT 3.6 Shortet-Path Problem - definizioni G (V,E) grafo orientato, peato, con fnzione peo w: E R Lnghezza (peo) di n cammino p = < 0,,..., k > : k w( p) = i= 0 Ditanza tra ertici e
Grafo Cammini Minimi GT 3.6 Shortet-Path Problem - definizioni G (V,E) grafo orientato, peato, con fnzione peo w: E R Lnghezza (peo) di n cammino p = < 0,,..., k > : k w( p) = i= 0 Ditanza tra ertici e
Esercizi Union-Find e su Grafi. Ugo Vaccaro
 Progettazione di Algoritmi Anno Accademico 0 07 Esercizi Union-Find e su Grafi. Ugo Vaccaro. Esercizio: Scrivere pseudocodice per Make-Set, Union, e Find-Set usando la rappresentazione attraverso liste
Progettazione di Algoritmi Anno Accademico 0 07 Esercizi Union-Find e su Grafi. Ugo Vaccaro. Esercizio: Scrivere pseudocodice per Make-Set, Union, e Find-Set usando la rappresentazione attraverso liste
Teoria dei Grafi Concetti fondamentali
 Teoria dei Grafi Concetti fondamentali I grafi sono un mezzo per rappresentare relazioni binarie. Ad esempio: due città connesse da una strada due calcolatori connessi in una rete telematica due persone
Teoria dei Grafi Concetti fondamentali I grafi sono un mezzo per rappresentare relazioni binarie. Ad esempio: due città connesse da una strada due calcolatori connessi in una rete telematica due persone
Dati e Algoritmi 1: A. Pietracaprina. Grafi (II parte)
 Dati e Algoritmi 1: A. Pietracaprina Grafi (II parte) 1 Breath-First Search (algoritmo iterativo) Si assume una rappresentazione tramite liste di adiacenza. L ordine con cui si visitano i vicini di un
Dati e Algoritmi 1: A. Pietracaprina Grafi (II parte) 1 Breath-First Search (algoritmo iterativo) Si assume una rappresentazione tramite liste di adiacenza. L ordine con cui si visitano i vicini di un
Introduzione ai grafi. Introduzione ai grafi p. 1/2
 Introduzione ai grafi Introduzione ai grafi p. 1/2 Grafi Un grafo G è costituito da una coppia di insiemi (V,A) dove V è detto insieme dei nodi e A è detto insieme di archi ed è un sottinsieme di tutte
Introduzione ai grafi Introduzione ai grafi p. 1/2 Grafi Un grafo G è costituito da una coppia di insiemi (V,A) dove V è detto insieme dei nodi e A è detto insieme di archi ed è un sottinsieme di tutte
Quarto allenamento. Olimpiadi Italiane di Informatica - Selezione territoriale
 Quarto allenamento Olimpiadi Italiane di Informatica - Selezione territoriale Luca Chiodini luca@chiodini.org - l.chiodini@campus.unimib.it 30 marzo 2017 Programma 1. Lettura e analisi di un problema 2.
Quarto allenamento Olimpiadi Italiane di Informatica - Selezione territoriale Luca Chiodini luca@chiodini.org - l.chiodini@campus.unimib.it 30 marzo 2017 Programma 1. Lettura e analisi di un problema 2.
Grafi: visita generica
 .. Grafi: visita generica Una presentazione alternativa (con ulteriori dettagli) Algoritmi di visita Scopo: visitare tutti i vertici di un grafo (si osservi che per poter visitare un vertice occorre prima
.. Grafi: visita generica Una presentazione alternativa (con ulteriori dettagli) Algoritmi di visita Scopo: visitare tutti i vertici di un grafo (si osservi che per poter visitare un vertice occorre prima
Laboratorio di Algoritmi e Strutture Dati
 Laboratorio di Algoritmi e Strutture Dati Prof. Aniello Murano Grafi: Implementazione ed operazioni di base Corso di Laurea Codice insegnamento Email docente Anno accademico Laboratorio di Algoritmi e
Laboratorio di Algoritmi e Strutture Dati Prof. Aniello Murano Grafi: Implementazione ed operazioni di base Corso di Laurea Codice insegnamento Email docente Anno accademico Laboratorio di Algoritmi e
Algoritmi e Strutture Dati. Capitolo 12 Minimo albero ricoprente: Algoritmo di Kruskal
 Algoritmi e Strutture Dati Capitolo 12 Minimo albero ricoprente: Algoritmo di Kruskal Progettare una rete stradale Supponiamo di dover progettare una rete stradale in cui il costo di costruzione di un
Algoritmi e Strutture Dati Capitolo 12 Minimo albero ricoprente: Algoritmo di Kruskal Progettare una rete stradale Supponiamo di dover progettare una rete stradale in cui il costo di costruzione di un
COMPLEMENTI DI SHORTEST-PATH. ASD Fabrizio d'amore
 COMPLEMENTI DI SHORTEST-PATH ASD 2016-17 Fabrizio d'amore problemi di shortest-path (SP) grafo di riferimento G=(V,E) semplice/orientato pesato pesi non negativi pesi arbitrari, ma no cicli a peso negativo
COMPLEMENTI DI SHORTEST-PATH ASD 2016-17 Fabrizio d'amore problemi di shortest-path (SP) grafo di riferimento G=(V,E) semplice/orientato pesato pesi non negativi pesi arbitrari, ma no cicli a peso negativo
2.2 Alberi di supporto di costo ottimo
 . Alberi di supporto di costo ottimo Problemi relativi ad alberi hanno numerose applicazioni: progettazione di reti (comunicazione, teleriscaldamento,...) memorizzazione compatta di sequenze (DNA) diffusione
. Alberi di supporto di costo ottimo Problemi relativi ad alberi hanno numerose applicazioni: progettazione di reti (comunicazione, teleriscaldamento,...) memorizzazione compatta di sequenze (DNA) diffusione
2.3 Cammini ottimi. E. Amaldi Fondamenti di R.O. Politecnico di Milano 1
 . Cammini ottimi E. Amaldi Fondamenti di R.O. Politecnico di Milano .. Cammini minimi e algoritmo di Dijkstra Dato un grafo orientato G = (N, A) con una funzione di costo c : A c ij R e due nodi s e t,
. Cammini ottimi E. Amaldi Fondamenti di R.O. Politecnico di Milano .. Cammini minimi e algoritmo di Dijkstra Dato un grafo orientato G = (N, A) con una funzione di costo c : A c ij R e due nodi s e t,
Alberi e arborescenze di costo minimo
 Alberi e arborescenze di costo minimo Complementi di Ricerca Operativa Giovanni Righini Dipartimento di Tecnologie dell Informazione - Università degli Studi di Milano Definizioni - 1 Un grafo G = (V,
Alberi e arborescenze di costo minimo Complementi di Ricerca Operativa Giovanni Righini Dipartimento di Tecnologie dell Informazione - Università degli Studi di Milano Definizioni - 1 Un grafo G = (V,
Quinto appello 27/6/ = 4. B b B = 2 b N = 4
 Quinto appello // RICERCA OPERATIVA (a.a. /) Nome: Cognome: Matricola: ) Si risolva il problema di PL dato applicando l algoritmo del Simplesso Duale, per via algebrica, a partire dalla base B {, }. Per
Quinto appello // RICERCA OPERATIVA (a.a. /) Nome: Cognome: Matricola: ) Si risolva il problema di PL dato applicando l algoritmo del Simplesso Duale, per via algebrica, a partire dalla base B {, }. Per
Cammini minimi. Damiano Macedonio
 Cammini minimi Damiano Macedonio mace@unive.it Copyright 2010 2012, Moreno Marzolla, Università di Bologna, Italy (http://www.moreno.marzolla.name/teaching/asd2011b/) Modifications Copyright c 2015, Damiano
Cammini minimi Damiano Macedonio mace@unive.it Copyright 2010 2012, Moreno Marzolla, Università di Bologna, Italy (http://www.moreno.marzolla.name/teaching/asd2011b/) Modifications Copyright c 2015, Damiano
Algoritmi e Strutture Dati 2/ed Quiz a risposta multipla
 Camil Demetrescu Irene Finocchi Giuseppe F. Italiano Algoritmi e Strutture Dati 2/ed Quiz a risposta multipla Indice 1 Un introduzione informale agli algoritmi 1 2 Modelli di calcolo e metodologie di
Camil Demetrescu Irene Finocchi Giuseppe F. Italiano Algoritmi e Strutture Dati 2/ed Quiz a risposta multipla Indice 1 Un introduzione informale agli algoritmi 1 2 Modelli di calcolo e metodologie di
Dati e Algoritmi I (Pietracaprina) Esercizi svolti sui Grafi
 Dati e Algoritmi I (Pietracaprina) Esercizi svolti sui Grafi Dati e Algoritmi I (Pietracaprina): Esercizi 1 Problema 1 (Esercizio C-14.34 del testo [GTG14]) Sia G = (V, E) un grafo non diretto con n =
Dati e Algoritmi I (Pietracaprina) Esercizi svolti sui Grafi Dati e Algoritmi I (Pietracaprina): Esercizi 1 Problema 1 (Esercizio C-14.34 del testo [GTG14]) Sia G = (V, E) un grafo non diretto con n =
Algoritmi e Strutture Dati. Scelta della struttura dati
 Algoritmi e Strutture Dati Scelta della struttura dati Alberto Montresor Università di Trento 2018/06/11 This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Algoritmi e Strutture Dati Scelta della struttura dati Alberto Montresor Università di Trento 2018/06/11 This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
2.2 Alberi di supporto di costo ottimo
 . Alberi di supporto di costo ottimo Problemi relativi ad alberi hanno numerose applicazioni: progettazione di reti (comunicazione, teleriscaldamento,...) memorizzazione compatta di sequenze (DNA) diffusione
. Alberi di supporto di costo ottimo Problemi relativi ad alberi hanno numerose applicazioni: progettazione di reti (comunicazione, teleriscaldamento,...) memorizzazione compatta di sequenze (DNA) diffusione
RICERCA OPERATIVA (a.a. 2017/18) Nome: Cognome: Matricola:
 Primo appello 9//8 RICERCA OPERATIVA (a.a. 7/8) Nome: Cognome: Matricola: ) Si risolva il seguente problema di PL max x + x x + x x x x x applicando l algoritmo del Simplesso Primale, per via algebrica,
Primo appello 9//8 RICERCA OPERATIVA (a.a. 7/8) Nome: Cognome: Matricola: ) Si risolva il seguente problema di PL max x + x x + x x x x x applicando l algoritmo del Simplesso Primale, per via algebrica,
Algoritmi e Strutture Dati
 Algoritmi e strutture dati Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Algoritmi e Strutture Dati Capitolo 2 Minimo albero ricoprente: Algoritmo di Prim Il problema del calcolo di un Minimum
Algoritmi e strutture dati Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Algoritmi e Strutture Dati Capitolo 2 Minimo albero ricoprente: Algoritmo di Prim Il problema del calcolo di un Minimum
Ordinamenti. Grafo : definizione. Un grafo G = (V,E)è composto da: V: insieme di vertici E V V: insieme di archi (edge) che connettono i vertici
 Ordinamenti 1 Vittorio Maniezzo Università di Bologna Grafo : definizione Un grafo G = (V,E)è composto da: V: insieme di vertici E V V: insieme di archi (edge) che connettono i vertici Un arco a= {u,v}
Ordinamenti 1 Vittorio Maniezzo Università di Bologna Grafo : definizione Un grafo G = (V,E)è composto da: V: insieme di vertici E V V: insieme di archi (edge) che connettono i vertici Un arco a= {u,v}
A UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Studi in Ingegneria Informatica Ricerca Operativa 1 Seconda prova intermedia 13 giugno 2011
 A UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Stdi in Ingegneria Informatica Ricerca Operativa Seconda prova intermedia gigno Nome: Cognome: Matricola: voglio sostenere la prova orale il giorno venerdì //
A UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Stdi in Ingegneria Informatica Ricerca Operativa Seconda prova intermedia gigno Nome: Cognome: Matricola: voglio sostenere la prova orale il giorno venerdì //
Problema: attraversamento di un grafo. Definizione del problema
 Problema: attraversamento di un grafo Visita: attenzione alle soluzioni facili Definizione del problema Prendere ispirazione dalla visita degli alberi Dato un grafo =(V, ) ed un vertice r di V (detto sorgente
Problema: attraversamento di un grafo Visita: attenzione alle soluzioni facili Definizione del problema Prendere ispirazione dalla visita degli alberi Dato un grafo =(V, ) ed un vertice r di V (detto sorgente
Soluzioni della settima esercitazione di Algoritmi 1
 Soluzioni della settima esercitazione di Algoritmi 1 Beniamino Accattoli 19 dicembre 2007 1 Grafi Un grafo è non orientato se descrivendo un arco come una coppia di vertici (i,j) l ordine è ininfluente
Soluzioni della settima esercitazione di Algoritmi 1 Beniamino Accattoli 19 dicembre 2007 1 Grafi Un grafo è non orientato se descrivendo un arco come una coppia di vertici (i,j) l ordine è ininfluente
Algoritmi e Strutture Dati (Mod. B) Algoritmi su grafi Ricerca in profondità (Depth-First Search) Parte III
 Algoritmi e Strutture Dati (Mod. B) Algoritmi su grafi Ricerca in profondità (Depth-First Search) Parte III Applicazioni di DFS Due prolemi: calcolare l ordinamento topologico indotto da un grafo aciclico.
Algoritmi e Strutture Dati (Mod. B) Algoritmi su grafi Ricerca in profondità (Depth-First Search) Parte III Applicazioni di DFS Due prolemi: calcolare l ordinamento topologico indotto da un grafo aciclico.
2.2 Alberi di supporto di costo ottimo
 . Alberi di supporto di costo ottimo Problemi relativi ad alberi hanno numerose applicazioni: progettazione di reti (comunicazione, teleriscaldamento,...) protocolli reti IP memorizzazione compatta di
. Alberi di supporto di costo ottimo Problemi relativi ad alberi hanno numerose applicazioni: progettazione di reti (comunicazione, teleriscaldamento,...) protocolli reti IP memorizzazione compatta di
Lezione del 7/12/04 [2 ore, in AULA C, dalle 11:00 alle 13:00]
![Lezione del 7/12/04 [2 ore, in AULA C, dalle 11:00 alle 13:00] Lezione del 7/12/04 [2 ore, in AULA C, dalle 11:00 alle 13:00]](/thumbs/94/118862333.jpg) Lezione del 7/2/04 [2 ore, in UL, dalle :00 alle 3:00] di: lgoritmi & Laboratorio (Modulo ) "Riassunto" della lezione: Sono stati svolti i seguenti esercizi (alla lavagna).. Dato il grafo in fig.(a): a
Lezione del 7/2/04 [2 ore, in UL, dalle :00 alle 3:00] di: lgoritmi & Laboratorio (Modulo ) "Riassunto" della lezione: Sono stati svolti i seguenti esercizi (alla lavagna).. Dato il grafo in fig.(a): a
