Quick Sort. PARTITION(A,p,r) risistema il sottoarray A[p...r] e riporta l indice q:
|
|
|
- Giustina Murgia
- 5 anni fa
- Visualizzazioni
Transcript
1 Quick Sort - Ordinamento in loco - Tempo di esecuzione nel caso peggiore: Θ(n 2 ) - Tempo di esecuzione nel caso medio: Θ(n lg n) - I fattori costanti nascosti nella notazione Θ sono abbastanza piccoli - Basato sul paradigma divide et impera: Per ordinare un sottoarray A[p...r]: Divide: A[p...r] è ripartito (e risistemato) in due sottoarray non vuoti A[p...q] e A[q r], in modo che ogni elemento del primo sia minore o uguale a ogni elemento del secondo. L indice q viene calcolato dalla procedura di partizionamento. Impera: i due sottoarray A[p...q] e A[q r] sono ordinati, ricorsivamente. Combina: non c è niente da fare: A[p...r] è ordinato. PARTITION(A,p,r) risistema il sottoarray A[p...r] e riporta l indice q: Quick Sort - Algoritmo QUICKSORT(A) QUICK(A,p,r) 1. QUICK(A,1,length[A]) 1. if p<r 2. ;; il sottoarray contiene almeno 2 elementi 3. then q <- PARTITION(A,p,r). QUICK(A,p,q) 5. QUICK(A,q+1,r) III-1
2 Partizionamento dell array (I) Il sottoarray A[p...r] viene risistemato in loco. Il primo elemento del sottoarray, A[p] viene scelto come pivot: alla fine, tutti gli elementi in A[p...q] conterranno elementi minori o uguali a A[p] e tutti gli elementi in A[q r] conterranno elementi maggiori o uguali a A[p] x <- A[p] ;; x e il pivot Le due regioni di sinistra e di destra vengono costruite per stadi: inizialmente sono entrambe vuote, e si usano gli indici i e j per i due estremi i <- p-1 j <- r+1 ;; la regione A[p...i] e vuota ;; la regione A[j...r] e vuota i p r INIZIO CICLO: ripetuto finché i < j. L indice j viene spostato verso sinistra, finché non si trova un elemento minore o uguale al pivot (A[j] x): repeat j <- j-1 until A[j] <= x i j Simmetricamente, l indice i viene spostato a destra, fino a trovare un elemento maggiore o uguale al pivot (A[i] x): j III-2
3 Partizionamento dell array (II) repeat i <- i+1 until A[i] >= x Inizialmente il ciclo termina subito con i = p, perché A[p] x i j Ora si ha A[i] x alla sinistra di A[j] x: i due elementi vengono scambiati i j Poiché ancora i < j, il ciclo riprende: l indice j si sposta a sinistra finché A[j] x e l indice i si sposta a destra finché A[i] x: i j Poiché ancora i < j, si scambiano di posto A[i] e A[j]: Ancora si ha i < j quindi il ciclo ricomincia: i j j i FINE CICLO: Ora i > j, non si effettua nessuno scambio e il ciclo termina. L indice riportato q è j. III-3
4 L algoritmo Partition PARTITION(A,p,r) 1. x <- A[p] 2. i <- p-1 3. j <- r+1. while i < j 5. do repeat j <- j-1 6. until A[j] <= x 7. repeat i <- i+1 8. until A[i] >= x 9. if i < j 10. then scambia A[i] <-> A[j] 11. return j III-
5 Partition - Caso base I Primo caso: array composto da due elementi ordinati. Pivot = 1 i p r 1 3 j while i<j (SI) repeat j<-j-1 until A[j]<=1 repeat i<-i+1 until A[i]>=1 SI FERMA CON j=p SI FERMA SUBITO CON i=p if i<j...(no) p r 1 3 ij while i<j... (NO) ---> FINE PARTIZIONE III-5
6 Partition - Caso base II Secondo caso: array composto da due elementi non ordinati. Pivot = 3 i p r 3 1 while i<j (SI) repeat j<-j-1 SI FERMA SUBITO CON j=r until A[j]<=3 repeat i<-i+1 SI FERMA SUBITO CON i=p until A[i]>=3 if i<j then scambia A[i] <-> A[j] p r 1 3 i j Alla successiva iterazione gli indici i e j si accavallano e viene restituito q = j = 1, come nel caso precedente. j III-6
7 Il tempo di esecuzione di Partition Se n è il numero di elementi del sottoarray A[p...r] T PARTITION (n) Θ(n) Per ogni posizione del sottoarray viene eseguita almeno un assegnazione ad i oppure una a j. Quindi il costo di PARTITION è Ω(n). Oltre all assegnazione, per ogni elemento del sottoarray vengono eseguiti al massimo due test (uno per ciascuno dei due cicli until) ed eventualmente il test e lo scambio dell istruzione if che segue: tutte operazioni a costo costante. Quindi il costo del ciclo while è O(n). L inizializzazione di i, j e l assegnazione a x richiedono tempo costante. Quindi il costo dell algoritmo è anche O(n). Esercizi 1. Che cosa succederebbe nel QUICKSORT se PARTITION(A,p,r) restituisse un valore q uguale a r? 2. Illustrare le operazioni di PARTITION sull array A = 13, 19, 9, 5, 12, 8, 7,, 11, 2, 6, 21 (8.1-1) 3. Quale valore restituisce PARTITION se tutti gli elementi dell array A[p...r] hanno lo stesso valore? (8.1-2). Illustrare le operazioni di PARTITION su un array già ordinato. 5. Illustrare le operazioni di PARTITION su un array ordinato in senso decrescente. III-7
8 Complessità del Quick Sort - Analisi del caso peggiore (I) Partizionamento sbilanciato Esempio 1: gli elementi sono ordinati al contrario p r i Pivot = 7 while i<j repeat j<-j-1 SI FERMA SUBITO CON j=r until A[j]<=7 j repeat i<-i+1 until A[i]>=7 SI FERMA CON i=p if i<j then scambia A[i] <-> A[j] while i<j p r i j III-8
9 repeat j<-j-1 until A[j]<=7 repeat i<-i+1 until A[i]>=7 SI FERMA SUBITO CON j=r-1 SI FERMA CON i=r if i<j... (NO) p r j i La prima partizione produce i sottoarray A[p...j] e A[i... r]. Pivot = 1 while i<j repeat j<-j-1 until A[j]<=1 SI FERMA CON j=p i p r j repeat i<-i+1 until A[i]>=1 SI FERMA SUBITO CON i=p if i<j... (NO) III-9
10 p r ij - La seconda partizione produce i sottoarray A[p... j] e A[i r]. - Anche la terza partizione viene effettuata su un sottoarray ordinato in senso inverso. III-10
11 Complessità del Quick Sort - Analisi del caso peggiore (II) Partizionamento sbilanciato Esempio 2: gli elementi sono già ordinati p r i j Il pivot è 1. while i<j repeat j<-j-1 SI FERMA CON j=p until A[j]<=1 repeat i<-i+1 until A[i]>=1 SI FERMA SUBITO CON i=p if i<j... (NO) Quando l array è già ordinato in senso crescente il pivot viene sempre preso a sinistra. Ogni partizione di una regione di n elementi genera, una regione con un solo elemento e l altra con n 1. Essendo il costo della partizione Θ(n) nel caso peggiore l equazione di ricorrenza diventa: T quick (0) = a T quick (n + 1) = T quick (n) + Θ(n) III-11
12 Con Θ(n) polinomio di primo grado. Applicando il primo teorema per la soluzione delle equazioni di ricorrenza: allora T(0) = a T(n + 1) = T(n) + g(n) T(n) = a + n 1 k=0 g(k) si ha T quick (n) = n Θ(k) = Θ( n k) = Θ(n 2 ) k=1 k=1 Quindi, T quick (n) è Θ(n 2 ) (nel caso peggiore) III-12
13 Complessità del Quick Sort - Analisi del caso migliore Ad ogni partizionamento il pivot definisce due regioni di uguale dimensione (+-1). T quick (0) = c 0 T quick (n) = 2 T quick (n/2) + Θ(n) Se Per il secondo caso del Master Theorem, ponendo: a = 2, b = 2, Θ(n) = c n = p(n k ), k = 1 ed essendo a = b k il tempo d esecuzione risulta T quick (n) = Θ(n lg n) T(n) = per a, b 1 e p(n k ) un polinomio di grado k. Allora: caso 1: T(n) = Θ(n log ba ) se a > b k. caso 2: T(n) = Θ(n k lg n) se a = b k. caso 3: T(n) = Θ(n k ) se a < b k. MASTER THEOREM c 0 se n = 0 a T(n/b) + p(n k ) se n > 0 III-13
14 Complessità del Quick Sort - Caso medio (I) Idea intuitiva: Distribuzione dei nodi nei due sottoarray - Caso generale Il pivot partiziona sempre l array in 1/ e 3/ T(n) quick = Θ(d n) = Θ(n logn) ( 3 ) 3 ( 3 ) = ( 3 ) 2 ( 3 ) 3.. ( 3 ) d = 1 componente III-1
15 Complessità del Quick Sort - Caso medio (II) Sia d il numero di partizioni che vengono effettuate: Per quale valore di d, (3/) d n = 1? O equivalentemente (poiché k = 1 sse log 2 k = 0): Per quale valore di d, log 2 ( (3 log 2 3 d n = 0 ) d n ) log 3 d 2 + log 2 n = 0 d log log 2 n = 0 d ( 0.) + log 2 n = 0 log 2 n = d 0. = 0? 2.5 log 2 n = d (2.5 = 1 0. ) d = 2.5 log 2 n T(n) quick = Θ(d n) = Θ(2.5n logn) = Θ(n logn) III-15
16 Come evitare il caso peggiore Si può modificare l array imponendo una disposizione degli elementi che sia il più casuale possibile; quando si esegue la partition si sceglie a caso un elemento che viene scambiato col primo e che diventa il pivot. pseudorandom-number-generator: int*int --> int Applicato a due interi a e b, restituisce un numero nell intervallo [a,b]. Nel caso del quick sort a e b sono gli indici minimo e massimo del sottoarray che si sta ordinando. Poichè il costo della funzione pseudorandom-number-generator è Θ(1) il costo complessivo del quick sort non cambia. III-16
17 Generatore di numeri pseudo-casuali X 0 valore iniziale X 0 0 a moltiplicatore a 0 c incremento c 0 m modulo m > X 0, m > a, m > c Linear Congruential Method X n+1 = (ax n + c) mod m ( ) TH: La sequenza generata da ( ) ha periodo di lunghezza m sse i) gcd(c, m) = 1 (c e m sono relativamente primi tra loro); ii) b = a 1 è un multiplo di p per ogni p che divide m; iii) b è un multiplo di se m è un multiplo di. III-17
QUICKSORT. Basato sul paradigma divide-et-impera (come MERGE-SORT)
 QUICKSORT Basato sul paradigma divide-et-impera (come MERGE-SORT) Divide: stabilisce un valore di q tale da dividere l array A[p.. r] in due sottoarray non vuoti A[p.. q] e A[q+1.. r], dove ogni elemento
QUICKSORT Basato sul paradigma divide-et-impera (come MERGE-SORT) Divide: stabilisce un valore di q tale da dividere l array A[p.. r] in due sottoarray non vuoti A[p.. q] e A[q+1.. r], dove ogni elemento
Gli algoritmi ricorsivi di ordinamento. Paolo Camurati Dip. Automatica e Informatica Politecnico di Torino
 ordinamento Paolo Camurati Dip. Automatica e Informatica Politecnico di Torino Merge Sort Ricorsivo, divide et impera Stabile Divisione: due sottovettori SX e DX rispetto al centro del vettore. p r A.A.
ordinamento Paolo Camurati Dip. Automatica e Informatica Politecnico di Torino Merge Sort Ricorsivo, divide et impera Stabile Divisione: due sottovettori SX e DX rispetto al centro del vettore. p r A.A.
Esercitazione 2. Quicksort
 Esercitazione 2 Quicksort Caratteristiche Algoritmo di ordinamento mediamente molto efficiente Vantaggio: ordinamento sul posto Basato sul paradigma divide et impera (come merge sort) Elemento chiave:
Esercitazione 2 Quicksort Caratteristiche Algoritmo di ordinamento mediamente molto efficiente Vantaggio: ordinamento sul posto Basato sul paradigma divide et impera (come merge sort) Elemento chiave:
Algoritmo di ordinamento sul posto che ha tempo di esecuzione :
 QuickSort Algoritmo di ordinamento sul posto che ha tempo di esecuzione : - O(n 2 ) nel caso peggiore - O(n log n) nel caso medio Nonostante le cattive prestazioni nel caso peggiore, rimane il miglior
QuickSort Algoritmo di ordinamento sul posto che ha tempo di esecuzione : - O(n 2 ) nel caso peggiore - O(n log n) nel caso medio Nonostante le cattive prestazioni nel caso peggiore, rimane il miglior
Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano. Usa la tecnica del divide et impera:
 MergeSort Usa la tecnica del divide et impera: 1 Divide: dividi l array a metà 2 Risolvi i due sottoproblemi ricorsivamente 3 Impera: fondi le due sottosequenze ordinate 1 Esempio di esecuzione 7 2 4 5
MergeSort Usa la tecnica del divide et impera: 1 Divide: dividi l array a metà 2 Risolvi i due sottoproblemi ricorsivamente 3 Impera: fondi le due sottosequenze ordinate 1 Esempio di esecuzione 7 2 4 5
Albero di Riscorsione
 Albero di Riscorsione Albero di ricorsione Un albero di ricorsione è un modo di visualizzare cosa accade in un algoritmo divide et impera L etichetta della radice rappresenta il costo non ricorsivo della
Albero di Riscorsione Albero di ricorsione Un albero di ricorsione è un modo di visualizzare cosa accade in un algoritmo divide et impera L etichetta della radice rappresenta il costo non ricorsivo della
Algoritmi e Strutture Dati
 Algoritmi di Ordinamento Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino 13 novembre 2008 Il problema dell ordinamento Il problema dell ordinamento
Algoritmi di Ordinamento Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino 13 novembre 2008 Il problema dell ordinamento Il problema dell ordinamento
Algoritmi e Strutture Dati
 Algoritmi di Ordinamento Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino Il problema dell ordinamento Il problema dell ordinamento di un insieme
Algoritmi di Ordinamento Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino Il problema dell ordinamento Il problema dell ordinamento di un insieme
Algoritmi e Strutture di Dati I 1. Algoritmi e Strutture di Dati I Massimo Franceschet francesc
 Algoritmi e Strutture di Dati I 1 Algoritmi e Strutture di Dati I Massimo Franceschet http://www.sci.unich.it/ francesc m.franceschet@unich.it Algoritmi e Strutture di Dati I 2 Problema dell ordinamento
Algoritmi e Strutture di Dati I 1 Algoritmi e Strutture di Dati I Massimo Franceschet http://www.sci.unich.it/ francesc m.franceschet@unich.it Algoritmi e Strutture di Dati I 2 Problema dell ordinamento
Quicksort Moltiplicazione di interi Master Theorem Valutazione del tempo di esecuzione di algoritmi iterativi e ricorsivi
 Quicksort Moltiplicazione di interi Master Theorem Valutazione del tempo di esecuzione di algoritmi iterativi e ricorsivi Algoritmi basati sulla tecnica Divide et Impera In questo corso: Ricerca binaria
Quicksort Moltiplicazione di interi Master Theorem Valutazione del tempo di esecuzione di algoritmi iterativi e ricorsivi Algoritmi basati sulla tecnica Divide et Impera In questo corso: Ricerca binaria
Algoritmi e Strutture Dati
 Algoritmi di Ordinamento Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino Il problema dell ordinamento Il problema dell ordinamento di un insieme
Algoritmi di Ordinamento Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino Il problema dell ordinamento Il problema dell ordinamento di un insieme
Definizioni di base. Algoritmo: procedura computazionale ben definita che prende valori in input e produce valori in output.
 ANALISI DELLA COMPLESSITÀ DEGLI ALGORITMI Definizioni di base Algoritmo: procedura computazionale ben definita che prende valori in input e produce valori in output. Un algoritmo è uno strumento per risolvere
ANALISI DELLA COMPLESSITÀ DEGLI ALGORITMI Definizioni di base Algoritmo: procedura computazionale ben definita che prende valori in input e produce valori in output. Un algoritmo è uno strumento per risolvere
Problemi di ordinamento
 Problemi di ordinamento Input: una sequenza di n numeri a 1, a 2,..., a n ; Output: una permutazione a 1, a 2,..., a n di a 1, a 2,..., a n tale che a 1 a 2... a n. Generalmente, la sequenza è rappresentata
Problemi di ordinamento Input: una sequenza di n numeri a 1, a 2,..., a n ; Output: una permutazione a 1, a 2,..., a n di a 1, a 2,..., a n tale che a 1 a 2... a n. Generalmente, la sequenza è rappresentata
Si può fare di meglio?
 Si può fare di meglio? Gli algoritmi visti fino ad ora hanno costo O(n 2 ) È possibile fare di meglio? Quanto meglio? Algoritmi e Strutture Dati 1 Algoritmi divide et impera Idea generale Divide: Scomporre
Si può fare di meglio? Gli algoritmi visti fino ad ora hanno costo O(n 2 ) È possibile fare di meglio? Quanto meglio? Algoritmi e Strutture Dati 1 Algoritmi divide et impera Idea generale Divide: Scomporre
Due algoritmi di ordinamento. basati sulla tecnica Divide et Impera: Mergesort e Quicksort
 Due algoritmi di ordinamento basati sulla tecnica Divide et Impera: Mergesort e Quicksort (13 ottobre 2009, 2 novembre 2010) Ordinamento INPUT: un insieme di n oggetti a 1, a 2,, a n presi da un dominio
Due algoritmi di ordinamento basati sulla tecnica Divide et Impera: Mergesort e Quicksort (13 ottobre 2009, 2 novembre 2010) Ordinamento INPUT: un insieme di n oggetti a 1, a 2,, a n presi da un dominio
Per regnare occorre tenere divisi i nemici e trarne vantaggio. fai ad ogni passo la scelta più conveniente
 Progetto di algoritmi sequenziali (un solo esecutore ) Divide et Impera Per regnare occorre tenere divisi i nemici e trarne vantaggio Greedy fai ad ogni passo la scelta più conveniente Buoni risultati
Progetto di algoritmi sequenziali (un solo esecutore ) Divide et Impera Per regnare occorre tenere divisi i nemici e trarne vantaggio Greedy fai ad ogni passo la scelta più conveniente Buoni risultati
Algoritmi di Ordinamento
 Algoritmi di Ordinamento 1 Algoritmi di ordinamento Selection Sort Quick Sort Lower bound alla complessità degli algoritmi di ordinamento Statistiche di ordine 2 Selection Sort SelectionSort(dati[]) {
Algoritmi di Ordinamento 1 Algoritmi di ordinamento Selection Sort Quick Sort Lower bound alla complessità degli algoritmi di ordinamento Statistiche di ordine 2 Selection Sort SelectionSort(dati[]) {
Analisi algoritmi ricorsivi e relazioni di ricorrenza
 Analisi algoritmi ricorsivi e relazioni di ricorrenza Punto della situazione Finora abbiamo affrontato: il tempo di esecuzione di un algoritmo, l analisi asintotica con le notazioni asintotiche e la tecnica
Analisi algoritmi ricorsivi e relazioni di ricorrenza Punto della situazione Finora abbiamo affrontato: il tempo di esecuzione di un algoritmo, l analisi asintotica con le notazioni asintotiche e la tecnica
Divide et impera. Vittorio Maniezzo Università di Bologna
 Divide et impera 1 Vittorio Maniezzo Università di Bologna Divide et Impera Divide et impera: Dividi: se l istanza del problema da risolvere è troppo complicata per essere risolta direttamente, dividila
Divide et impera 1 Vittorio Maniezzo Università di Bologna Divide et Impera Divide et impera: Dividi: se l istanza del problema da risolvere è troppo complicata per essere risolta direttamente, dividila
ALGORITMI DI ORDINAMENTO E RICERCA BINARIA. Docente: Giorgio Giacinto AA 2008/2009. problema dell ordinamento in modi diversi
 Università degli Studi di Cagliari Corso di Laurea Specialistica in Ingegneria per l Ambiente ed il Territorio Corso di Laurea Specialistica in Ingegneria Civile - Strutture FONDAMENTI DI INFORMATICA 2
Università degli Studi di Cagliari Corso di Laurea Specialistica in Ingegneria per l Ambiente ed il Territorio Corso di Laurea Specialistica in Ingegneria Civile - Strutture FONDAMENTI DI INFORMATICA 2
Esercizi per il corso di Algoritmi, anno accademico 2011/12
 Esercizi per il corso di Algoritmi, anno accademico 2011/12 Esercizi sulla Tecnica Divide et Impera N.B. Tutti gli algoritmi vanno scritti in pseudocodice (non in Java, nè in C++, etc. ). Di tutti gli
Esercizi per il corso di Algoritmi, anno accademico 2011/12 Esercizi sulla Tecnica Divide et Impera N.B. Tutti gli algoritmi vanno scritti in pseudocodice (non in Java, nè in C++, etc. ). Di tutti gli
QuickSort (1962, The Computer Journal)
 QuickSort (1962, The Computer Journal) Charles Antony Richard Hoare (1934 -) Attualmente senior researcher al Microsoft Research Center di Cambridge Hoare ha vinto nel 1980 il Turing Award, il premio più
QuickSort (1962, The Computer Journal) Charles Antony Richard Hoare (1934 -) Attualmente senior researcher al Microsoft Research Center di Cambridge Hoare ha vinto nel 1980 il Turing Award, il premio più
Sommario. Un algoritmo di ordinamento di complessità lineare: CountingSort. [CLRS10] cap. 8 par.8.2
![Sommario. Un algoritmo di ordinamento di complessità lineare: CountingSort. [CLRS10] cap. 8 par.8.2 Sommario. Un algoritmo di ordinamento di complessità lineare: CountingSort. [CLRS10] cap. 8 par.8.2](/thumbs/95/124053831.jpg) Sommario Un algoritmo di ordinamento di complessità lineare: CountingSort [CLRS10] cap. 8 par.8.2!1 Ordinamento in tempo lineare. Il limite inferiore Ω(n log n) vale per tutti gli algoritmi di ordinamento
Sommario Un algoritmo di ordinamento di complessità lineare: CountingSort [CLRS10] cap. 8 par.8.2!1 Ordinamento in tempo lineare. Il limite inferiore Ω(n log n) vale per tutti gli algoritmi di ordinamento
Algoritmi e Strutture Dati
 Algoritmi e Strutture Dati Capitolo 4 Ordinamento: Quicksort (*) e metodi di ordinamento lineari Punto della situazione Problema dell ordinamento: Lower bound (n log n) Upper bound O(n log n) Algoritmi
Algoritmi e Strutture Dati Capitolo 4 Ordinamento: Quicksort (*) e metodi di ordinamento lineari Punto della situazione Problema dell ordinamento: Lower bound (n log n) Upper bound O(n log n) Algoritmi
QuickSort Università degli Studi di Milano
 QuickSort Algoritmo di ordinamento sul posto che ha tempo di esecuzione : - O(n 2 ) nel caso peggiore - O(n log n) nel caso medio Nonostante le cattive prestazioni nel caso peggiore, rimane il miglior
QuickSort Algoritmo di ordinamento sul posto che ha tempo di esecuzione : - O(n 2 ) nel caso peggiore - O(n log n) nel caso medio Nonostante le cattive prestazioni nel caso peggiore, rimane il miglior
QuickSort (1962, The Computer Journal)
 QuickSort (1962, The Computer Journal) Charles Antony Richard Hoare (1934 -) Attualmente senior researcher al Microsoft Research Center di Cambridge Hoare ha vinto nel 1980 il Turing Award, il premio più
QuickSort (1962, The Computer Journal) Charles Antony Richard Hoare (1934 -) Attualmente senior researcher al Microsoft Research Center di Cambridge Hoare ha vinto nel 1980 il Turing Award, il premio più
nel trasformare una sequenza di elementi
 Ordinamento Carla Binucci e Walter Didimo Il problema dell ordinamento In generale, il Problema dell ordinamento consiste nel trasformare una sequenza di elementi rendendola ordinata rispetto a un certo
Ordinamento Carla Binucci e Walter Didimo Il problema dell ordinamento In generale, il Problema dell ordinamento consiste nel trasformare una sequenza di elementi rendendola ordinata rispetto a un certo
INFORMATICA GENERALE
 CAROSELLI STEFANO INFORMATICA GENERALE TESINA «LA TECNICA DEL DIVIDE-ET-IMPERA E DUE SUE IMPORTANTI APPLICAZIONI: IL QUICK SORT E IL MERGE SORT» La tecnica del DIVIDE-ET-IMPERA è un metodo di risoluzione
CAROSELLI STEFANO INFORMATICA GENERALE TESINA «LA TECNICA DEL DIVIDE-ET-IMPERA E DUE SUE IMPORTANTI APPLICAZIONI: IL QUICK SORT E IL MERGE SORT» La tecnica del DIVIDE-ET-IMPERA è un metodo di risoluzione
Algoritmi e Strutture Dati
 Algoritmi e Strutture Dati Capitolo 4 Ordinamento: Quicksort (*) e metodi di ordinamento lineari Punto della situazione Problema dell ordinamento: Lower bound (n log n) Upper bound O(n log n) Algoritmi
Algoritmi e Strutture Dati Capitolo 4 Ordinamento: Quicksort (*) e metodi di ordinamento lineari Punto della situazione Problema dell ordinamento: Lower bound (n log n) Upper bound O(n log n) Algoritmi
05EIP. Fulvio Corno, Matteo Sonza Reorda Dip. Automatica e Informatica Politecnico di Torino. Definizione di ricorsione e strategie divide et impera
 La ricorsione Fulvio Corno, Matteo Sonza Reorda Dip. Automatica e Informatica Politecnico di Torino Sommario Definizione di ricorsione e strategie divide et impera Semplici algoritmi ricorsivi Merge Sort
La ricorsione Fulvio Corno, Matteo Sonza Reorda Dip. Automatica e Informatica Politecnico di Torino Sommario Definizione di ricorsione e strategie divide et impera Semplici algoritmi ricorsivi Merge Sort
Laboratorio di Programmazione Appunti sulla lezione 5: Algoritmi di ordinamento (cont.) Alessandra Raffaetà
 Laboratorio di Programmazione Appunti sulla lezione : Algoritmi di ordinamento (cont.) Alessandra Raffaetà Università Ca Foscari Venezia Corso di Laurea in Informatica Bubblesort Idea: Due elementi adiacenti
Laboratorio di Programmazione Appunti sulla lezione : Algoritmi di ordinamento (cont.) Alessandra Raffaetà Università Ca Foscari Venezia Corso di Laurea in Informatica Bubblesort Idea: Due elementi adiacenti
Algoritmi e Strutture Dati. Capitolo 4 Ordinamento: Selection e Insertion Sort
 Algoritmi e Strutture Dati Capitolo 4 Ordinamento: Selection e Insertion Sort Ordinamento Dato un insieme S di n elementi presi da un dominio totalmente ordinato, ordinare S in ordine non crescente o non
Algoritmi e Strutture Dati Capitolo 4 Ordinamento: Selection e Insertion Sort Ordinamento Dato un insieme S di n elementi presi da un dominio totalmente ordinato, ordinare S in ordine non crescente o non
ESERCITAZIONI DI INTRODUZIONE AGLI ALGORITMI (A.A. 08/09)
 ESERCITAZIONI DI INTRODUZIONE AGLI ALGORITMI (A.A. 08/09) DISPENSA N. 4 1. Ricerca Binaria Ricorsiva L algoritmo Ricerca Binaria risolve il problema della ricerca di una chiave in un vettore. È un esempio
ESERCITAZIONI DI INTRODUZIONE AGLI ALGORITMI (A.A. 08/09) DISPENSA N. 4 1. Ricerca Binaria Ricorsiva L algoritmo Ricerca Binaria risolve il problema della ricerca di una chiave in un vettore. È un esempio
Esercizi per il corso di Algoritmi
 1 Esercizi per il corso di Algoritmi Esercizi sulle Notazioni Asintotiche 1. Esercizio: In ciascuno dei seguenti casi, indicare se f(n) = O(g(n)), o se f(n) = Ω(g(n)), oppure entrambi (nel cui caso occorre
1 Esercizi per il corso di Algoritmi Esercizi sulle Notazioni Asintotiche 1. Esercizio: In ciascuno dei seguenti casi, indicare se f(n) = O(g(n)), o se f(n) = Ω(g(n)), oppure entrambi (nel cui caso occorre
Problemi di ricerca in insiemi ordinati
 Problemi di ricerca in insiemi ordinati Abbiamo visto che, per trovare un elemento in un insieme ordinato, con l algoritmo della ricerca binaria restringiamo l intervallo della ricerca alla metà in ogni
Problemi di ricerca in insiemi ordinati Abbiamo visto che, per trovare un elemento in un insieme ordinato, con l algoritmo della ricerca binaria restringiamo l intervallo della ricerca alla metà in ogni
Algoritmi e Strutture Dati
 Algoritmi e Strutture Dati Modelli di calcolo e metodologie di analisi Domenico Fabio Savo 1 Notazione asintotica f(n) = tempo di esecuzione / occupazione di memoria di un algoritmo su input di dimensione
Algoritmi e Strutture Dati Modelli di calcolo e metodologie di analisi Domenico Fabio Savo 1 Notazione asintotica f(n) = tempo di esecuzione / occupazione di memoria di un algoritmo su input di dimensione
Fondamenti di Informatica
 Algoritmi di ordinamento Gli ordinamenti interni sono fatti su sequenze in memoria centrale Fondamenti di Informatica 18. Algoritmi di ordinamento in C++ Gli ordinamenti esterni sono fatti su sequenze
Algoritmi di ordinamento Gli ordinamenti interni sono fatti su sequenze in memoria centrale Fondamenti di Informatica 18. Algoritmi di ordinamento in C++ Gli ordinamenti esterni sono fatti su sequenze
Sommario. Algoritmi di ordinamento lineari: CountingSort. BucketSort. RadixSort
 Sommario Algoritmi di ordinamento lineari:! CountingSort! BucketSort! RadixSort 1 Ordinamento in tempo lineare. Il limite inferiore Ω(n log n) vale per tutti gli algoritmi di ordinamento generali, nel
Sommario Algoritmi di ordinamento lineari:! CountingSort! BucketSort! RadixSort 1 Ordinamento in tempo lineare. Il limite inferiore Ω(n log n) vale per tutti gli algoritmi di ordinamento generali, nel
Ordinamento efficiente: quick-sort
 Ordinamento efficiente: quick-sort Si cerca di ridurre la parte disordinata di più di un elemento per volta (a differenza di selection-sort e bubble-sort) L idea è di ordinare parzialmente l array, in
Ordinamento efficiente: quick-sort Si cerca di ridurre la parte disordinata di più di un elemento per volta (a differenza di selection-sort e bubble-sort) L idea è di ordinare parzialmente l array, in
Fondamenti di Informatica. Algoritmi di Ricerca e di Ordinamento
 Fondamenti di Informatica Algoritmi di Ricerca e di Ordinamento 1 Ricerca in una sequenza di elementi Data una sequenza di elementi, occorre verificare se un elemento fa parte della sequenza oppure l elemento
Fondamenti di Informatica Algoritmi di Ricerca e di Ordinamento 1 Ricerca in una sequenza di elementi Data una sequenza di elementi, occorre verificare se un elemento fa parte della sequenza oppure l elemento
Tecniche Algoritmiche: divide et impera
 Tecniche Algoritmiche: divide et impera Una breve presentazione F. Damiani - Alg. & Lab. 04/05 Divide et impera (o Divide and conquer) Per regnare occorre tenere divisi i nemici e trarne vantaggio F. Damiani
Tecniche Algoritmiche: divide et impera Una breve presentazione F. Damiani - Alg. & Lab. 04/05 Divide et impera (o Divide and conquer) Per regnare occorre tenere divisi i nemici e trarne vantaggio F. Damiani
Algoritmi di ordinamento
 Algoritmi di ordinamento Il problema Vogliamo ordinare un array monodimensionale in modo crescente per il caso decrescente valgono le stesse considerazioni Vari algoritmi possibili Diverse caratteristiche
Algoritmi di ordinamento Il problema Vogliamo ordinare un array monodimensionale in modo crescente per il caso decrescente valgono le stesse considerazioni Vari algoritmi possibili Diverse caratteristiche
Algoritmi di Ordinamento Corso di Informatica Laurea in Fisica. prof. ing. Corrado Santoro
 Algoritmi di Ordinamento Corso di Informatica Laurea in Fisica prof. ing. Corrado Santoro ፫ Bubble Sort Se l i-esimo elemento è maggiore dell elemento i+-esimo, essi vengono scambiati. Si termina quando
Algoritmi di Ordinamento Corso di Informatica Laurea in Fisica prof. ing. Corrado Santoro ፫ Bubble Sort Se l i-esimo elemento è maggiore dell elemento i+-esimo, essi vengono scambiati. Si termina quando
Progetto Corda. Alberto Ferrari. Alberto Ferrari Ingegneria dell'informazione, UniPR. 18/12/2017 Progetto Corda
 Progetto Corda Alberto Ferrari Alberto Ferrari Ingegneria dell'informazione, UniPR file:///e:/cordanoweb/lez/array.html#3 1/33 Array (ordinamento) 2/33 file:///e:/cordanoweb/lez/array.html#3 2/33 Sort
Progetto Corda Alberto Ferrari Alberto Ferrari Ingegneria dell'informazione, UniPR file:///e:/cordanoweb/lez/array.html#3 1/33 Array (ordinamento) 2/33 file:///e:/cordanoweb/lez/array.html#3 2/33 Sort
Algoritmi di ordinamento
 Algoritmi di ordinamento! Selection Sort! Quick Sort! Lower bound alla complessità degli algoritmi di ordinamento Ordinamento 1 Selection Sort SelectionSort(dati[]) { for (i=0; idati.length-1; i++) { min
Algoritmi di ordinamento! Selection Sort! Quick Sort! Lower bound alla complessità degli algoritmi di ordinamento Ordinamento 1 Selection Sort SelectionSort(dati[]) { for (i=0; idati.length-1; i++) { min
Algoritmi e strutture dati
 Algoritmi e Strutture Dati Capitolo 4 Ordinamento Ordinamento Dato un insieme S di n oggetti presi da un dominio totalmente ordinato, ordinare S Esempi: ordinare alfabeticamente lista di nomi, o insieme
Algoritmi e Strutture Dati Capitolo 4 Ordinamento Ordinamento Dato un insieme S di n oggetti presi da un dominio totalmente ordinato, ordinare S Esempi: ordinare alfabeticamente lista di nomi, o insieme
Esercizi sulla complessità di frammenti di pseudo-codice
 Esercizi sulla complessità di frammenti di pseudo-codice Esercizio 1 Si determini la complessità temporale del seguente frammento di pseudo-codice in funzione di n. Il ciclo contiene solo istruzioni elementari;
Esercizi sulla complessità di frammenti di pseudo-codice Esercizio 1 Si determini la complessità temporale del seguente frammento di pseudo-codice in funzione di n. Il ciclo contiene solo istruzioni elementari;
Laboratorio di Algoritmi e Strutture Dati Ingegneria e Scienze Informatiche - Cesena A.A
 Ingegneria e Scienze Informatiche - Cesena A.A. 2014-2015 pietro.dilena@unibo.it MergeSort MergeSort MergeSort: esempio MergeSort: pseudocodice Algoritmo di ordinamento ricorsivo basato sulla tecnica Divide
Ingegneria e Scienze Informatiche - Cesena A.A. 2014-2015 pietro.dilena@unibo.it MergeSort MergeSort MergeSort: esempio MergeSort: pseudocodice Algoritmo di ordinamento ricorsivo basato sulla tecnica Divide
Note su quicksort per ASD 2010-11 (DRAFT)
 Note su quicksort per ASD 010-11 (DRAFT) Nicola Rebagliati 7 dicembre 010 1 Quicksort L algoritmo di quicksort è uno degli algoritmi più veloci in pratica per il riordinamento basato su confronti. L idea
Note su quicksort per ASD 010-11 (DRAFT) Nicola Rebagliati 7 dicembre 010 1 Quicksort L algoritmo di quicksort è uno degli algoritmi più veloci in pratica per il riordinamento basato su confronti. L idea
Università degli Studi di Camerino Laurea in Informatica Prima Prova Parziale del corso di Algoritmi e Strutture Dati
 Università degli Studi di Camerino Laurea in Informatica Prima Prova Parziale del corso di Algoritmi e Strutture Dati Docente: Maria Rita Di Berardini 19 dicembre 2007 Nome: Cognome: N.Matricola: Note:
Università degli Studi di Camerino Laurea in Informatica Prima Prova Parziale del corso di Algoritmi e Strutture Dati Docente: Maria Rita Di Berardini 19 dicembre 2007 Nome: Cognome: N.Matricola: Note:
In questa lezione. Il Mergesort: primo esempio di applicazione della tecnica divide et impera analisi tempo di esecuzione del Mergesort
 In questa lezione Il Mergesort: primo esempio di applicazione della tecnica divide et impera analisi tempo di esecuzione del Mergesort [CLRS] par. 2.3. Prof. E. Fachini - Intr. Alg.!1 Progettazione di
In questa lezione Il Mergesort: primo esempio di applicazione della tecnica divide et impera analisi tempo di esecuzione del Mergesort [CLRS] par. 2.3. Prof. E. Fachini - Intr. Alg.!1 Progettazione di
ALGORITMI DI ORDINAMENTO
 ALGORITMI DI ORDINAMENTO Scopo: ordinare una sequenza di elementi in base a una certa relazione d ordine lo scopo finale è ben definito algoritmi equivalenti diversi algoritmi possono avere efficienza
ALGORITMI DI ORDINAMENTO Scopo: ordinare una sequenza di elementi in base a una certa relazione d ordine lo scopo finale è ben definito algoritmi equivalenti diversi algoritmi possono avere efficienza
Algoritmi e Strutture di Dati I 1. Algoritmi e Strutture di Dati I Massimo Franceschet
 Algoritmi e Strutture di Dati I 1 Algoritmi e Strutture di Dati I Massimo Franceschet Algoritmi e Strutture di Dati I 2 Problemi Un problema specifica in termini generali una relazione che intercorrere
Algoritmi e Strutture di Dati I 1 Algoritmi e Strutture di Dati I Massimo Franceschet Algoritmi e Strutture di Dati I 2 Problemi Un problema specifica in termini generali una relazione che intercorrere
Algoritmi di ordinamento
 Algoritmi di ordinamento Il problema Vogliamo ordinare un array monodimensionale in modo crescente per il caso decrescente valgono le stesse considerazioni Vari algoritmi possibili Diverse caratteristiche
Algoritmi di ordinamento Il problema Vogliamo ordinare un array monodimensionale in modo crescente per il caso decrescente valgono le stesse considerazioni Vari algoritmi possibili Diverse caratteristiche
Laboratorio di Algoritmi e Strutture Dati
 Laboratorio di Algoritmi e Strutture Dati Marco Tarini e-mail: marco.tarini@uninsubria.it Argomenti del corso Calcolo del tempo di computazione di un algoritmo: Esercizi di analisi formale: sommatorie,
Laboratorio di Algoritmi e Strutture Dati Marco Tarini e-mail: marco.tarini@uninsubria.it Argomenti del corso Calcolo del tempo di computazione di un algoritmo: Esercizi di analisi formale: sommatorie,
Algoritmi e Strutture Dati. Divide-et-impera
 Algoritmi e Strutture Dati Divide-et-impera Alberto Montresor Università di Trento 2018/12/05 This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License. Sommario 1
Algoritmi e Strutture Dati Divide-et-impera Alberto Montresor Università di Trento 2018/12/05 This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License. Sommario 1
Bubble Sort. Bubble Sort
 Bubble Sort Bubble Sort Se l i-esimo elemento è maggiore dell elemento i+-esimo, essi vengono scambiati. Si termina quando non vi sono più scambi da fare. Nessuno scambio effettuato: Il vettore è ordinato
Bubble Sort Bubble Sort Se l i-esimo elemento è maggiore dell elemento i+-esimo, essi vengono scambiati. Si termina quando non vi sono più scambi da fare. Nessuno scambio effettuato: Il vettore è ordinato
Laboratorio di Algoritmi e Strutture Dati. Aniello Murano. people.na.infn.it/~murano/ Murano Aniello - Lab. di ASD Terza Lezione
 Laboratorio di Algoritmi e Strutture Dati Aniello Murano http://people.na.infn.it people.na.infn.it/~murano/ Heap e Heapsort Algoritmi di ordinamento Insertion Sort Quicksort Heapsort Insertion Sort L
Laboratorio di Algoritmi e Strutture Dati Aniello Murano http://people.na.infn.it people.na.infn.it/~murano/ Heap e Heapsort Algoritmi di ordinamento Insertion Sort Quicksort Heapsort Insertion Sort L
ALGORITMI E STRUTTURE DATI
 ALGORITMI E STRUTTURE DATI Esercitazioni AndreA Orlandini http://www.dia.uniroma3.it/~orlandin/asd/ e-mail: orlandin@dia.uniroma3.it Orario di ricevimento: Martedì 14.00-16.00 Introduzione al C + Array
ALGORITMI E STRUTTURE DATI Esercitazioni AndreA Orlandini http://www.dia.uniroma3.it/~orlandin/asd/ e-mail: orlandin@dia.uniroma3.it Orario di ricevimento: Martedì 14.00-16.00 Introduzione al C + Array
Ordinamento di una lista: bubble-sort
 Ordinamento di una lista: bubble-sort L idea è di far galleggiare il minimo della lista nelle prima posizione Riduco la parte di lista da considerare, escludendo le prime posizioni già ordinate Ordinamento:
Ordinamento di una lista: bubble-sort L idea è di far galleggiare il minimo della lista nelle prima posizione Riduco la parte di lista da considerare, escludendo le prime posizioni già ordinate Ordinamento:
Esercizi di Algoritmi e Strutture Dati
 Esercizi di Algoritmi e Strutture Dati Moreno Marzolla marzolla@cs.unibo.it Ultimo aggiornamento: 3 novembre 2010 1 Trova la somma/1 Scrivere un algoritmo che dati in input un array A[1... n] di n interi
Esercizi di Algoritmi e Strutture Dati Moreno Marzolla marzolla@cs.unibo.it Ultimo aggiornamento: 3 novembre 2010 1 Trova la somma/1 Scrivere un algoritmo che dati in input un array A[1... n] di n interi
Algoritmi di ordinamento: Array e ricorsione
 Laboratorio di Algoritmi e Strutture Dati Aniello Murano http://people.na.infn.it people.na.infn.it/~murano/ 1 Algoritmi di ordinamento: Array e ricorsione 2 1 Insertion Sort Quicksort Heapsort Indice
Laboratorio di Algoritmi e Strutture Dati Aniello Murano http://people.na.infn.it people.na.infn.it/~murano/ 1 Algoritmi di ordinamento: Array e ricorsione 2 1 Insertion Sort Quicksort Heapsort Indice
In questa lezione: correttezza del mergesort Analisi del mergesort: relazioni di ricorrenza e alberi della ricorsione
 In questa lezione: correttezza del mergesort Analisi del mergesort: relazioni di ricorrenza e alberi della ricorsione Prof E Fachini - Intr Alg 1 MergeSort: correttezza MergeSort (A,p,r) if p < r then
In questa lezione: correttezza del mergesort Analisi del mergesort: relazioni di ricorrenza e alberi della ricorsione Prof E Fachini - Intr Alg 1 MergeSort: correttezza MergeSort (A,p,r) if p < r then
Laboratorio di Algoritmi e Strutture Dati II Semestre 2005/2006. Ordinamenti: mergesort e quicksort
 Laboratorio di Algoritmi e Strutture Dati II Semestre 2005/2006 Ordinamenti: mergesort e quicksort Marco Antoniotti Mergesort e Quicksort Due importantissimi algoritmi di ordinamento La conoscenza completa
Laboratorio di Algoritmi e Strutture Dati II Semestre 2005/2006 Ordinamenti: mergesort e quicksort Marco Antoniotti Mergesort e Quicksort Due importantissimi algoritmi di ordinamento La conoscenza completa
Quicksort. Quicksort: idea di base. Riprendiamo il problema dell'ordinamento di n oggetti.
 Riprendiamo il problema dell'ordinamento di n oggetti. Quicksort Per questo problema abbiamo già visto gli algoritmi insertion-sort e mergesort. Il tempo di esecuzione di insertion-sort è (n 2 ). Il tempo
Riprendiamo il problema dell'ordinamento di n oggetti. Quicksort Per questo problema abbiamo già visto gli algoritmi insertion-sort e mergesort. Il tempo di esecuzione di insertion-sort è (n 2 ). Il tempo
ORDINAMENTO PER SELEZIONE ORDINAMENTO PER SELEZIONE ORDINAMENTO VELOCE CONFRONTI
 ORDINAMENTO PER SELEZIONE Per l analisi delle prestazioni di tale algoritmo di ordinamento, si considerano i due cicli for annidati: poiché i confronti avvengono nel ciclo interno si ha che n 2 i= 0 (
ORDINAMENTO PER SELEZIONE Per l analisi delle prestazioni di tale algoritmo di ordinamento, si considerano i due cicli for annidati: poiché i confronti avvengono nel ciclo interno si ha che n 2 i= 0 (
Ordinamenti e crescita della complessità
 Ordinamenti e crescita della complessità Informatica@SEFA 07/08 - Lezione Massimo Lauria Venerdì, 7 Ottobre 07 Nota bibliografica: Il contenuto di questa e di alcune delle prossime
Ordinamenti e crescita della complessità Informatica@SEFA 07/08 - Lezione Massimo Lauria Venerdì, 7 Ottobre 07 Nota bibliografica: Il contenuto di questa e di alcune delle prossime
Lezione 4 Ugo Vaccaro
 Progettazione di Algoritmi Anno Accademico 2017 2018 Lezione 4 Ugo Vaccaro Introduciamo ora la notazione Ω, che ci sarà utile quando vorremo valutare limitazioni inferiori al tempo di esecuzione di algoritmi
Progettazione di Algoritmi Anno Accademico 2017 2018 Lezione 4 Ugo Vaccaro Introduciamo ora la notazione Ω, che ci sarà utile quando vorremo valutare limitazioni inferiori al tempo di esecuzione di algoritmi
COGNOME E NOME (IN STAMPATELLO) MATRICOLA
 Politecnico di Milano Facoltà di Ingegneria dell Informazione Informatica 3 Proff. Campi, Ghezzi, Matera e Morzenti Seconda prova in itinere 4 Luglio 2006 COGNOME E NOME (IN STAMPATELLO) MATRICOLA Risolvere
Politecnico di Milano Facoltà di Ingegneria dell Informazione Informatica 3 Proff. Campi, Ghezzi, Matera e Morzenti Seconda prova in itinere 4 Luglio 2006 COGNOME E NOME (IN STAMPATELLO) MATRICOLA Risolvere
Scopo: ordinare una sequenza di elementi in base a una certa relazione d ordine. Ipotesi: gli elementi siano memorizzati in un array.
 ALGORITMI DI ORDINAMENTO Scopo: ordinare una sequenza di elementi in base a una certa relazione d ordine lo scopo finale è ben definito algoritmi equivalenti diversi i algoritmi i possono avere efficienza
ALGORITMI DI ORDINAMENTO Scopo: ordinare una sequenza di elementi in base a una certa relazione d ordine lo scopo finale è ben definito algoritmi equivalenti diversi i algoritmi i possono avere efficienza
ALGORITMI DI ORDINAMENTO
 ALGORITMI DI ORDINAMENTO Scopo: ordinare una sequenza di elementi in base a una certa relazione d ordine lo scopo finale è ben definito algoritmi equivalenti diversi algoritmi possono avere efficienza
ALGORITMI DI ORDINAMENTO Scopo: ordinare una sequenza di elementi in base a una certa relazione d ordine lo scopo finale è ben definito algoritmi equivalenti diversi algoritmi possono avere efficienza
Tempo e spazio di calcolo
 Tempo e spazio di calcolo Modelli di calcolo e metodologie di analisi F. Damiani - Alg. & Lab. 04/05 (da M. Zacchi - Alg. & Lab. 03/04) In quale modo stimiamo il tempo di calcolo? Possiamo considerare
Tempo e spazio di calcolo Modelli di calcolo e metodologie di analisi F. Damiani - Alg. & Lab. 04/05 (da M. Zacchi - Alg. & Lab. 03/04) In quale modo stimiamo il tempo di calcolo? Possiamo considerare
In questa lezione. Heapsort. ordinamento con complessità, nel caso peggiore, O(nlogn) [CLRS01] cap. 6 da pag. 106 a pag. 114
![In questa lezione. Heapsort. ordinamento con complessità, nel caso peggiore, O(nlogn) [CLRS01] cap. 6 da pag. 106 a pag. 114 In questa lezione. Heapsort. ordinamento con complessità, nel caso peggiore, O(nlogn) [CLRS01] cap. 6 da pag. 106 a pag. 114](/thumbs/65/52995013.jpg) In questa lezione Heapsort ordinamento con complessità, nel caso peggiore, O(nlogn) [CLRS01] cap. 6 da pag. 106 a pag. 11 1 Paternità L heapsort è stato pubblicato da J. W. J. Williams nel 106. Pochi mesi
In questa lezione Heapsort ordinamento con complessità, nel caso peggiore, O(nlogn) [CLRS01] cap. 6 da pag. 106 a pag. 11 1 Paternità L heapsort è stato pubblicato da J. W. J. Williams nel 106. Pochi mesi
Dati e Algoritmi I (Pietracaprina) Esercizi sulle Nozioni di Base
 Dati e Algoritmi I (Pietracaprina) Esercizi sulle Nozioni di Base Dati e Algoritmi I (Pietracaprina): Esercizi 1 Problema 1. Sia T una stringa arbitraria di lunghezza n 1 su un alfabeto Σ. È sempre possibile
Dati e Algoritmi I (Pietracaprina) Esercizi sulle Nozioni di Base Dati e Algoritmi I (Pietracaprina): Esercizi 1 Problema 1. Sia T una stringa arbitraria di lunghezza n 1 su un alfabeto Σ. È sempre possibile
Casi di prova. Il problema dell ordinamento. Casi di prova. Casi di prova. Casi di prova
 Casi di prova Casi di prova Quando si vuole testare un algoritmo si devono costruire vari casi di prova. Invece di eseguire il programma più volte si può costruire un file di dati contenente tutti i casi
Casi di prova Casi di prova Quando si vuole testare un algoritmo si devono costruire vari casi di prova. Invece di eseguire il programma più volte si può costruire un file di dati contenente tutti i casi
Insert sort. Considero il primo elemento a 1. cerco il minimo tra gli elementi 3...N. scambio il minimo trovato con il primo e- lemento
 Insert sort Considero il primo elemento a 1 cerco il minimo tra gli elementi 2...N scambio il minimo trovato con il primo e- lemento considero ora a 2 cerco il minimo tra gli elementi 3...N scambio il
Insert sort Considero il primo elemento a 1 cerco il minimo tra gli elementi 2...N scambio il minimo trovato con il primo e- lemento considero ora a 2 cerco il minimo tra gli elementi 3...N scambio il
Esercizi su ABR. Prof. E. Fachini - Intr. Alg.!1
 Esercizi su ABR Confronto proprietà ABR e Max-Heap. Proprietà del cammino radice-foglia individuato da una ricerca. Fusione di due ABR. Il successivo calcolato dalla radice Costruzione di un ABR bilanciato
Esercizi su ABR Confronto proprietà ABR e Max-Heap. Proprietà del cammino radice-foglia individuato da una ricerca. Fusione di due ABR. Il successivo calcolato dalla radice Costruzione di un ABR bilanciato
CAPITOLO 2. Divide et Impera
 CAPITOLO 2 Divide et Impera In questo capitolo discuteremo alcuni algoritmi progettati mediante la tecnica di progettazione del Divide et Impera. Algoritmi progettati usando questa tecnica consistono di
CAPITOLO 2 Divide et Impera In questo capitolo discuteremo alcuni algoritmi progettati mediante la tecnica di progettazione del Divide et Impera. Algoritmi progettati usando questa tecnica consistono di
COGNOME E NOME (IN STAMPATELLO) MATRICOLA
 Politecnico di Milano Facoltà di Ingegneria dell Informazione Informatica 3 Proff. Campi, Ghezzi, Matera e Morzenti Appello del 14 Settembre 2006 Recupero II Parte COGNOME E NOME (IN STAMPATELLO) MATRICOLA
Politecnico di Milano Facoltà di Ingegneria dell Informazione Informatica 3 Proff. Campi, Ghezzi, Matera e Morzenti Appello del 14 Settembre 2006 Recupero II Parte COGNOME E NOME (IN STAMPATELLO) MATRICOLA
Algoritmi di ordinamento: Array e ricorsione
 Laboratorio di Algoritmi e Strutture Dati Aniello Murano http://people.na.infn.it people.na.infn.it/~murano/ 1 Algoritmi di ordinamento: Array e ricorsione 2 1 Indice Algoritmi di ordinamento: Insertion
Laboratorio di Algoritmi e Strutture Dati Aniello Murano http://people.na.infn.it people.na.infn.it/~murano/ 1 Algoritmi di ordinamento: Array e ricorsione 2 1 Indice Algoritmi di ordinamento: Insertion
Introduzione al Corso di Algoritmi
 Introduzione al Corso di Algoritmi Di cosa parliamo oggi: Una discussione generale su cosa studieremo, perchè lo studeriemo, come lo studieremo,... Un esempio illustrativo di cosa studeriemo Informazione
Introduzione al Corso di Algoritmi Di cosa parliamo oggi: Una discussione generale su cosa studieremo, perchè lo studeriemo, come lo studieremo,... Un esempio illustrativo di cosa studeriemo Informazione
n n 1 n = > Il calcolo del fattoriale La funzione fattoriale, molto usata nel calcolo combinatorio, è così definita
 Il calcolo del fattoriale La funzione fattoriale, molto usata nel calcolo combinatorio, è così definita n! = 1 n( n 1)! se se n n = > 0 0 dove n è un numero intero non negativo Il calcolo del fattoriale
Il calcolo del fattoriale La funzione fattoriale, molto usata nel calcolo combinatorio, è così definita n! = 1 n( n 1)! se se n n = > 0 0 dove n è un numero intero non negativo Il calcolo del fattoriale
Appendice B. Algoritmi e Complessità
 Appendice B Algoritmi e Complessità 1. Introduzione Un algoritmo A è una procedura passo-passo per risolvere un problema P. Un problema P è caratterizzato dall insieme I delle sue istanze. L algoritmo
Appendice B Algoritmi e Complessità 1. Introduzione Un algoritmo A è una procedura passo-passo per risolvere un problema P. Un problema P è caratterizzato dall insieme I delle sue istanze. L algoritmo
Array e Oggetti. Corso di Laurea Ingegneria Informatica Fondamenti di Informatica 1. Dispensa 12. A. Miola Dicembre 2006
 Corso di Laurea Ingegneria Informatica Fondamenti di Informatica 1 Dispensa 12 Array e Oggetti A. Miola Dicembre 2006 http://www.dia.uniroma3.it/~java/fondinf1/ Array e Oggetti 1 Contenuti Array paralleli
Corso di Laurea Ingegneria Informatica Fondamenti di Informatica 1 Dispensa 12 Array e Oggetti A. Miola Dicembre 2006 http://www.dia.uniroma3.it/~java/fondinf1/ Array e Oggetti 1 Contenuti Array paralleli
In questa lezione. Alberi binari: [CLRS09] cap. 12 per la visita inorder. visite e esercizi su alberi binari. Prof. E. Fachini - Intr. Alg.
![In questa lezione. Alberi binari: [CLRS09] cap. 12 per la visita inorder. visite e esercizi su alberi binari. Prof. E. Fachini - Intr. Alg. In questa lezione. Alberi binari: [CLRS09] cap. 12 per la visita inorder. visite e esercizi su alberi binari. Prof. E. Fachini - Intr. Alg.](/thumbs/93/113927179.jpg) In questa lezione Alberi binari: visite e esercizi su alberi binari [CLRS09] cap. 12 per la visita inorder!1 Visita inordine di un albero binario visita inordine(x) se l albero x non è nullo allora visita
In questa lezione Alberi binari: visite e esercizi su alberi binari [CLRS09] cap. 12 per la visita inorder!1 Visita inordine di un albero binario visita inordine(x) se l albero x non è nullo allora visita
Algoritmi e Strutture Dati 1
 Esonero del 31/03/2009 Compito n 1 Dimostrare che non tutte le funzioni f: ℵ 0,1 sono calcolabili. Dire se, giustificando la risposta applicando la definizione delle notazioni asintotiche, a) n log n =
Esonero del 31/03/2009 Compito n 1 Dimostrare che non tutte le funzioni f: ℵ 0,1 sono calcolabili. Dire se, giustificando la risposta applicando la definizione delle notazioni asintotiche, a) n log n =
Dati e Algoritmi I (Pietracaprina) Esercizi sulle Nozioni di Base
 Dati e Algoritmi I (Pietracaprina) Esercizi sulle Nozioni di Base Dati e Algoritmi I (Pietracaprina): Esercizi 1 Problema 1. Sia T una stringa arbitraria di lunghezza n 1 su un alfabeto Σ. È sempre possibile
Dati e Algoritmi I (Pietracaprina) Esercizi sulle Nozioni di Base Dati e Algoritmi I (Pietracaprina): Esercizi 1 Problema 1. Sia T una stringa arbitraria di lunghezza n 1 su un alfabeto Σ. È sempre possibile
Laboratorio di Informatica
 Corso di Laurea in Informatica e Tecnologie per la Produzione del Software (Track B) - A.A. 2017/2018 Laboratorio di Informatica Algoritmi Fondamentali (Parte 2) docente: Cataldo Musto cataldo.musto@uniba.it
Corso di Laurea in Informatica e Tecnologie per la Produzione del Software (Track B) - A.A. 2017/2018 Laboratorio di Informatica Algoritmi Fondamentali (Parte 2) docente: Cataldo Musto cataldo.musto@uniba.it
Programmazione I - corso B a.a prof. Viviana Bono
 Università di Torino Facoltà di Scienze MFN Corso di Studi in Informatica Programmazione I - corso B a.a. 2009-10 prof. Viviana Bono Blocco 15 Algoritmi su array: selection sort, insertion sort, fusione
Università di Torino Facoltà di Scienze MFN Corso di Studi in Informatica Programmazione I - corso B a.a. 2009-10 prof. Viviana Bono Blocco 15 Algoritmi su array: selection sort, insertion sort, fusione
Ricerca. Per ricerca si intende il procedimento di localizzazione di una particolare informazione in un elenco di dati.
 Ricerca Per ricerca si intende il procedimento di localizzazione di una particolare informazione in un elenco di dati. Il problema della ricerca in termini generali : dato un insieme D = {a 1,a 2,...,a
Ricerca Per ricerca si intende il procedimento di localizzazione di una particolare informazione in un elenco di dati. Il problema della ricerca in termini generali : dato un insieme D = {a 1,a 2,...,a
Algoritmi di ordinamento (I parte)
 Algoritmi di ordinamento (I parte) E2: sommario Classificazione degli algoritmi di ordinamento Studio di due implementazioni di algoritmi che utilizzano interfaccia Comparable Algoritmo per inserimento
Algoritmi di ordinamento (I parte) E2: sommario Classificazione degli algoritmi di ordinamento Studio di due implementazioni di algoritmi che utilizzano interfaccia Comparable Algoritmo per inserimento
ALGORITMI DI ORDINAMENTO ALGORITMI DI ORDINAMENTO
 ALGORITMI DI ORDINAMENTO Scopo: ordinare una sequenza di elementi in base a una certa relazione d ordine lo scopo finale è ben definito algoritmi equivalenti diversi algoritmi possono avere efficienza
ALGORITMI DI ORDINAMENTO Scopo: ordinare una sequenza di elementi in base a una certa relazione d ordine lo scopo finale è ben definito algoritmi equivalenti diversi algoritmi possono avere efficienza
Linguaggio C. Problemi di Ricerca e Ordinamento: Algoritmi e Complessità.
 Linguaggio C Problemi di Ricerca e Ordinamento: Algoritmi e Complessità. 1 Complessità degli Algoritmi Si definisce Complessità di un Algoritmo C(A) la funzione dei parametri rilevanti per A che determina
Linguaggio C Problemi di Ricerca e Ordinamento: Algoritmi e Complessità. 1 Complessità degli Algoritmi Si definisce Complessità di un Algoritmo C(A) la funzione dei parametri rilevanti per A che determina
Pseudo codice. Paolo Bison. Fondamenti di Informatica 1 A.A. 2003/04 Università di Padova. Pseudo codice, Paolo Bison, A.A , p.
 Pseudo codice Paolo Bison Fondamenti di Informatica 1 A.A. 2003/04 Università di Padova Pseudo codice, Paolo Bison, A.A. 2003-04, 2003-09-30 p.1/38 Pseudo codice linguaggio testuale mix di linguaggio naturale
Pseudo codice Paolo Bison Fondamenti di Informatica 1 A.A. 2003/04 Università di Padova Pseudo codice, Paolo Bison, A.A. 2003-04, 2003-09-30 p.1/38 Pseudo codice linguaggio testuale mix di linguaggio naturale
COMPLESSITA COMPUTAZIONALE (II PARTE) Tutor: Francesca Piersigilli
 COMPLESSITA COMPUTAZIONALE (II PARTE) Tutor: Francesca Piersigilli Teoria della complessità Pone le basi per stabilire: 1. la complessità di un problema 2. l efficienza di un algoritmo quanta memoria usa?
COMPLESSITA COMPUTAZIONALE (II PARTE) Tutor: Francesca Piersigilli Teoria della complessità Pone le basi per stabilire: 1. la complessità di un problema 2. l efficienza di un algoritmo quanta memoria usa?
ripeto il procedimento a partire da a j cerco il minimo tra j +1 ed N scambio il valore trovato con a j ripeto finché j non è N 1
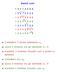 Insert sort Considero il primo elemento a 1 cerco il minimo tra gli elementi 2...N scambio il minimo trovato con il primo e- lemento considero ora a 2 cerco il minimo tra gli elementi 3...N scambio il
Insert sort Considero il primo elemento a 1 cerco il minimo tra gli elementi 2...N scambio il minimo trovato con il primo e- lemento considero ora a 2 cerco il minimo tra gli elementi 3...N scambio il
Algoritmi di Ordinamento
 Algoritmi di Ordinamento Univ. degli Stdi di Cagliari Algoritmi di Ordinamento per Strttre Lineari Una semplice classe di algoritmi e qella degli algoritmi di ordinamento per strttre lineari. La classe
Algoritmi di Ordinamento Univ. degli Stdi di Cagliari Algoritmi di Ordinamento per Strttre Lineari Una semplice classe di algoritmi e qella degli algoritmi di ordinamento per strttre lineari. La classe
Algoritmi e strutture di dati 2
 Algoritmi e strutture di dati 2 Paola Vocca Lezione 1: Divide et Impera 1 Paradigma del divide et impera Strutturato in tre fasi. Sia Π() istanza di dimensione di un problema computazionale Π (dove è immediato
Algoritmi e strutture di dati 2 Paola Vocca Lezione 1: Divide et Impera 1 Paradigma del divide et impera Strutturato in tre fasi. Sia Π() istanza di dimensione di un problema computazionale Π (dove è immediato
