Università degli Studi di Firenze Facoltà di Scienze Matematiche,Fisiche e Naturali
|
|
|
- Gildo Romeo
- 5 anni fa
- Visualizzazioni
Transcript
1 Università degli Studi di Firenze Facoltà di Scienze Matematiche,Fisiche e Naturali Anno Accademico Relazione finale per la Laurea Triennale in Matematica IL CRITERIO DI SYLVESTER SULLE RADICI REALI DEI POLINOMI Relatore: Prof.Giorgio Ottaviani Candidata: Moira Paggini
2 Indice Introduzione 3 1 Definizioni utili Funzioni simmetriche elementari e polinomi simmetrici Somme di potenze e identità di Newton Discriminante e Matrice Bezoutiante. 4 2 CRITERIO DI SYLVESTER Rango e Segnatura della Bezoutiante (Criterio di Sylvester) Corollari e applicazioni 9 3 Esempi 10 Bibliografia 13 2
3 Introduzione Moira Paggini L obiettivo di questa tesi è quello di rispondere alla domanda: come trovare il numero di radici reali di un polinomio a coefficienti reali? Nella prima parte dell elaborato saranno introdotte le funzioni simmetriche elementari e il loro legame con i coefficienti dei polinomi. Dopo di che definireremo le somme di potenze, il discriminante e la Bezoutiante, strumenti utili che ci porteranno al Criterio di Sylvester, cuore della Tesi, il quale ci dice che il numero di radici reali di un polinomio è esattamente uguale alla segnatura della matrice Bezoutiante. Vedremo la sua dimostrazione e alcune osservazioni interessanti riguardanti, in particolare, il numero di radici reali positive e di quelle negative. 1 Definizioni utili La teoria delle funzioni simmetriche è una teoria sviluppata in particolare da Lagrange, Ruffini e Galois, in relazione alla teoria sulle equazioni algebriche in una variabile e alla risoluzione per radicali. Il collegamento principale è dato dalle formule di espressione dei coefficienti di un polinomio, attraverso le sue radici, o per meglio dire, attraverso funzioni simmetriche delle radici. 1.1 Funzioni simmetriche elementari e polinomi simmetrici Definizione 1. Sia K un campo. polinomio simmetrico se Un polinomio f K[x 1,..., x n ] è detto f(x i1,..., x in ) = f(x 1,..., x n ) per ogni possibile permutazione x i1,..., x in delle variabili x 1,..., x n. Definizione 2. Date le variabili x 1,..., x n, noi definiamo le funzioni simmetriche elementari σ 1,..., σ n K[x 1,..., x n ] nel modo seguente: σ 1 = x x n,. σ r = x i1 x i2 x ir, i 1<i 2<...<i r. σ n = x 1 x 2 x n. 3
4 Osservazione 1. Data σ (n) i, la i-esima funzione elementare nelle variabili x 1,..., x n (nota: l apice di σ i indica il numero di variabili e non è una potenza), posso definire anche σ (n) 0 = 1 e σ (n) i = 0 se i < 0 o i > n, e osservo che σ (n) i = σ (n 1) i + x n σ (n 1) i 1 n > 1 i Teorema 1.1 (TEOREMA FONDAMENTALE DEI POLINOMI SIM- METRICI). Ogni polinomio simmetrico in K[x 1,..., x n ] può essere scritto, in modo unico, come un polinomio nelle funzioni simmetriche elementari σ 1,..., σ n, ovvero f simmetrico! g t.c. f(x 1,..., x n ) = g(σ 1,..., σ n ). 1.2 Somme di potenze e identità di Newton Consideriamo ora le seguenti somme di potenze: s k = x k 1 + x k x k n (s 0 = n) Notiamo che s k è simmetrico, vale allora: Teorema 1.2. Se K è un campo di caratteristica 0, allora tutti i polinomi simmetrici in K[x 1,..., x n ] possono essere scritti come un polinomio nelle somme di potenze s 1,..., s n. Osservazione 2. Dalle identità di Newton si evince che ogni funzione simmetrica elementare può essere scritta in termini di somme di potenze e vicersa: σ k = 1 k (σ k 1s 1 σ k 2 s ( 1) k 1 s k ) (σ 1 = s 1 ) 1.3 Discriminante e Matrice Bezoutiante Consideriamo lo spazio C n e lo spazio P n := { x n + a 1 x n a n } dei polinomi monici e consideriamo la funzione : data da Cosí otteniamo un polinomio Π : C n P n Π (x 1,..., x n ) := n (x x i ) i=1 x n σ 1 x n 1 + σ 2 x n ( 1) n σ n = n ( 1) i σ i x n i = 0 che ha radici (x 1,..., x n ), dove i coefficienti σ i sono le funzioni simmetriche elementari delle radici. Tutti i polinomi monici si ottengono in questo modo, per il Teorema Fondamentale dell Algebra. Quindi: i=0 4
5 Proposizione 1.3. Dato un polinomio f(x) = x n + a 1 x n 1 + a 2 x n a n = n a i x n i (a 0 = 1) monico e di radici (x 1,..., x n ), c è una relazione lineare tra i suoi coefficienti (a 1, a 2,..., a n ) e le funzioni simmetriche (σ 1,..., σ n ), più esattamente i=0 a i = ( 1) i σ i Supponiamo di voler studiare una proprietà delle radici in cui serva di valutare alcuni polinomi simmetrici nelle radici, allora possiamo studiarla senza dover calcolare le radici esplicitamente, dal momento che si deve solo sfruttare l espressione formale del polinimo simmetrico e, usando l algoritmo discusso, esprimere il valore di una funzione simmetrica delle radici usando i coefficienti. In altre parole, una funzione simmetrica polinomiale f, a fattori in C n attraverso la funzione Π dà luogo ad una funzione polinomiale calcolabile senza risolvere l equazione f in P n, tale che f=f Π. Un classico esempio è dato proprio dal discriminante. La condizione di avere tutte le radici distinte è chiaramente data da i<j (x j x i ) 0. Il polinomio V (x) = i<j (x j x i ),che in realtà non è simmetrico, rappresenta il determinante della matrice di Vandermonde(n n): 1 x 1 x x n 2 1 x n x 2 x x n 2 2 x n A :=.. 1 x n 1 x 2 n 1... xn 1 n 1 1 x n x 2 n... xn n 1 Proposizione 1.4. V (x) è un polinomio antisimmetrico, cioè, una permutazione delle variabili comporta un cambio di segno nella moltiplicazione in V (x). Osservazione 3. La teoria del segno delle permutazioni può essere dedotta analizzando il determinante di Vandermonde. Infatti, data la trasposizione τ è chiaro che V (x) τ = V (x), ne segue che V (x) β = V (x) o V (x) a seconda se β è un prodotto pari o dispari di trasposizioni. Vediamo immediatamente che V 2 =V V è un polinomio simmetrico, possiamo quindi calcolarlo in termini di funzioni s i (somme di potenze definite sopra) 5
6 come segue: considero la matrice s 0 s 1... s (n 2) s (n 1) s 1 s 2... s (n 1) s n B := A t A =.. s 2(n 2) s (n 2) s 2(n 2) s (2n 3) s (n 1) s (2n 3) s 2(n 1) Definizione 3. La matrice B, con coefficienti B i,j = s i+j 2, é detta Bezoutiante. B è una matrice simmetrica e il determinante è esattamente V 2. Vediamo che esiste un altro modo per esprimere la formula del determinante di B : per il Teorema 1.1 esiste un polinomio D tale che D(σ 1,..., σ n ) = V 2 (x 1,..., x n ). Definizione 4. Il polinomio D è chiamato discriminante di f(x). 2 CRITERIO DI SYLVESTER Vediamo adesso l utilità della matrice Bezoutiante nello studio delle radici reali di un polinomio a coefficienti reali di grado n. 2.1 Rango e Segnatura della Bezoutiante (Criterio di Sylvester) Proposizione 2.1. Il rango della Bezoutiante è uguale al numero di radici distinte. Dimostrazione. Sia f(x) = x n +a 1 x n 1 +a 2 x n a n polinomio monico di grado n a coefficienti in R. Chiamo S l anello quoziente dell anello dei polinomi a coefficienti reali sull ideale (f(x)) generato da f(x) : S = R[x] (f(x)) = { b 1 x n b n b i R, x n = a 1 x n 1 } +... a n esso è formato da tutte le classi di resto modf(x), che sono esattamente tutti i polinomi di grado < n. S è un algebra su R di dimensione n. Facciamo la seguente costruzione: ogni elemento s di S induce una trasformazione lineare L s in S attraverso la moltiplicazione (a sinistra), cioè tale che L s : S S t s t 6
7 Definiamo tr(s) := tr(l s ), cioè la traccia della matrice associata all operatore L s in una base scelta. Successivamente consideriamo la forma bilineare (a, b) := tr(a b), che chiameremo forma traccia di S. Questa è simmetrica e associativa, nel senso che (ab, c) = (a, bc), quindi anche la matrice della forma traccia sarà simmetrica e nella base { 1, x, x 2,..., x n 1} di S assume la forma: tr(1 1) tr(1 x)... tr(1 x n 1 ) tr(1 x) tr(x x) tr(1 x n 1 ) tr(x x n 1 )... tr(x n 1 x n 1 ) tr(l 1 ) tr(l x )... tr(l x n 1) tr(l x ) tr(l x 2) tr(l x n 1) tr(l x n)... tr(l x 2(n 1)) Osserviamo che applicando questa costruzione all algebra R[x] (x n ) la tr(xk ) = tr(l x k) = 0 se k > 0, poiché x è nilpotente. Inoltre tr(1) = n, quindi la matrice della forma traccia è la seguente: tr(1) tr(x)... tr(x n 1 ) n tr(x) tr(x 2 ) = tr(x n 1 ) tr(x n )... tr(x 2(n 1) ) che ha rango 1. In aggiunta la forma traccia ha come nucleo l ideale generato da x, poiché per ogni s in S (x, s) = (x, b 1 x n b n 1 x+b n ) = b 1 (x, x n 1 )+...+b n 1 (x, x)+b n (x, 1) = = b 1 tr(x n ) b n 1 tr(x 2 ) + b n tr(x) = 0 Ora consideriamo la chiusura algebrica di R, cioè C, e applichiamo la costruzione all algebra S C := (f(x)). Fattorizziamo il polinomio nelle sue radici distinte {α 1, α 2,..., α m }, quindi f(x) = m i=1 (x α i) hi dove h i è la molteplicità della radice α i. Quindi la nostra algebra diventa: S C = m (f(x)) = 7 i=1 (x α i ) hi
8 Allora la traccia di un elemento mod f(x) è la somma delle tracce mod(x α i ) hi dell elemento stesso. Cerchiamo di calcolare in mod(x α i ) hi la tr(l t k)per ogni addendo. Per ogni (x α la matrice associata all operatore lineare L i) h i xk, k > 0, nella base { } 1, (x αi ), (x α i ) 2,..., (x α i ) hi, è la matrice triangolare inferiore: αi k αi k αi k αi k da cui segue che tr(l x k) = h i αi k per ogni singolo addendo della somma diretta. Sommando tutti i contributi vediamo che in (f(x)) la tr(l x k) = m i=0 h iαi k, che è proprio la k-esima funzione di Newton delle radici del polinomio f(x). Poiché la matrice associata alla forma traccia, nella base { 1, x, x 2,..., x n 1},è esattamente costituita da queste espressioni, essa coincide con la Bezoutiante delle radici. Facciamo ora un altra osservazione: dal momento che per ogni determinato addendo l ideale generato da (x α i ) è nilpotente, cioè (x α i) h i (x α i ) hi = 0, si ha tr((x α i ) hi ) = 0 e quindi questo ideale è proprio il nucleo della forma traccia. Allora s (x α i) h i : ((x α i ), s) = ((x α i ), b 1 (x α i ) hn b n 1 (x α i ) + b n ) = = b 1 (x α i ), (x α i ) hn 1 ) b n 1 ((x α i ), (x α i )) + b n ((x α i ), 1) = = b 1 tr((x α i ) hn ) b n 1 tr((x α i ) 2 ) + b n tr((x α i )) = 0 Di conseguenza la matrice associata alla forma traccia di ogni addendo ha rango 1, quindi la forma traccia totale, cioè la forma traccia di (f(x)), avrà come rango la somma dei ranghi e quindi proprio m, che era esattamente il numero di radici distinte. Ora consideriamo al posto di un generico f(x), il polinomio con le stesse radici di f ma tutte con molteplicità 1, che chiameremo f rid (x), ottenuto dividendo f(x) per il MCD tra f(x) e la sua derivata f (x). Applichiamo ora la precedente costruzione all algebra S rid = R[x] (f rid (x)). Dividendo le radici distinte in radici reali α 1,..., α k e complesse coniugate β 1, β 1,..., β h, β h, l algebra S rid risulta isomorfa alla somma ortogonale di copie di R e copie di C, e la sua traccia forma è data dalla somma delle tracce forma di ogni copia. Più precisamente ho: R[x] - k copie di R ( date da (x α esse sono isomorfe a R perché α i) i è reale). La matrice associata alla forma traccia ha dimensione (1 1) e quindi è (tr(1)), dove tr(1) = tr(l 1 ) = 1, allora la forma traccia è esattamente 1 e la forma quadratica associata è X 2. Questo significa che le radici reali danno un contributo positivo alla forma quadratica totale, ovvero ogni radice reale conta un + nella segnatura della matrice della forma traccia mod(f(x)). 8
9 - h copie di C,date da R[x] (x β i)(x β i ) R[i] e di conseguenza isomorfe a C. Siano β i = a i + ib i e β i = a i ib i, la matrice associata alla forma traccia ha dimensione (2 2) ed è data da ( ) ( ) ( ) ( ) tr(1) tr(x) L1 L tr(x) tr(x 2 = x 2 βi + β = i 2 2ai ) L x L x 2 β i + β i βi 2 + = β2 2a i i 2(a 2 i b2 i ) I determinanti dei minori principali in questa matrice sono: 2, che è positivo e b 2 i che è negativo. Quindi le radici complesse danno un contributo positivo e uno negativo alla forma quadratica totale relativa alla forma traccia modf(x), ovvero ogni coppia di radici complesse coniugate conta un + e un - nella segnatura della matrice. Poiché la matrice della forma traccia coincide esattamente con la Bezoutiante, esse hanno stessa segnatura. Ho cosí dimostrato il seguente Criterio: Criterio 2.2. (CRITERIO DI SYLVESTER) Il numero di radici reali di un poliniomio f(x) di grado n a coefficienti in R è uguale alla segnatura della sua Bezoutiante. 2.2 Corollari e applicazioni Una matrice A simmetrica e reale è definita positiva, cioè con autovalori tutti positivi, quando la segnatura è (n,0), dove n= rg(a). Abbiamo quindi il seguente corollario: Corollario 2.3. Un polinomio a coefficienti reali ha tutte radici reali se e solo se la matrice Bezoutiante è definita positiva. Vediamo adesso un altra interessante conseguenza di questa dimostrazione che riguarda la positività delle radici reali. Considero la forma quadratica Q(a, a) := tr(xa 2 ). Seguendo lo stesso procedimento della costruzione descritta (f(x)) = m i=1 (x α i) h i sopra, applicata sempre all algebra S C =, voglio calcolarmi la matrice associata a questa nuova forma quadratica, che avrà ancora come componenti le somme k-esime. Intanto osservo che anche per Q il nucleo è dato dall ideale generato da (x α i ), infatti Q((x α i ), s) = tr(x(x α i )(b 1 x n b n 1 x + b n )) = 0 e la matrice associata ad ogni singolo addendo ha ancora rango 1. Però, se ora considero le radici reali α i, la matrice associata alla forma quadratica diventa (tr(x)) = (tr(l x )) = α i Quindi adesso distinguo nella segnatura i contributi che mi danno le radici reali positive da quelle reali negative, più precisamente distinguo i casi in cui l autovalore della matrice è negativo, cioè quando α i < 0, positivo quando α i > 0 o nullo se α i = 0. Per le radici complesse vale lo stesso ragionamento fatto sopra, con l unica differenza che la matrice associata alla forma quadratica in mod(x β i )(x β i ) ora è ( ) tr(x) tr(x 2 ) tr(x 2 ) tr(x 3 = ) ( β i + β i βi 2 + β2 i β 2 i + β2 i β 3 i + β3 i ) 9
10 ma ho sempre un contributo negativo e uno positivo, perché se considero un polinomio di secondo grado a radici complesse f(y) = y 2 + ay + b allora la matrice associata alla forma quadratica diventa: ( ) a a 2 2b a 2 2b a 3 + 3ab che ha determinante b(a 2 4b) < 0, poiché (a 2 4b) < 0 e b = β i β i > 0. La matrice associata a questa nuova forma quadratica è: s 1 s 2... s n 1 s n s 2 s 3... s n s n+1... s 2n 3 s n 1 s n... s 2n 3 s 2(n 1) s n s n+1... s 2(n 1) s 2n 1 la quale ha come segnatura la differenza tra le radici reali positive e quelle negative. Abbiamo adesso a disposizione due criteri per trovare la somma e la differenza tra radici positive e negative, quindi posso trovare esplicitamente il numero di radici positive reali e il numero di quelle negative, tutto questo solo calcolando la segnatura delle due matrici simmetriche definite a partire dai coefficienti di un generico f(x). Un ultima osservazione interessante riguarda le radici reali in un intervallo. Se invece del polinomio f(x) considero il polinomio tralsato f a (x) = f(x+a), la segnatura della matrice definita da Q mi dice il numero di radici reali > a meno il numero di radici reali < a. A questo punto è ovvio che presi in considerazione f a (x) e f b (x), calcolando il numero di radici reali > a e il numero di radici reali > b, la loro differenza mi dà esattamente il numero di radici reali appartententi all intervallo (a, b]. 3 Esempi Prima di vedere qualche esempio è bene sottolineare l importante caratteristica della Bezoutiante di essere una matrice simmetrica a coefficienti reali. Questo comporta che il suo polinomio caratteristico ha tutte radici reali e quindi posso applicare a quest ultimo il Criterio di Cartesio, il quale ci dice che ho tante radici positive(contate con molteplicità) quante sono le variazioni di segno nella successione dei coefficienti non nulli del polinomio. Da qui poi è facile trovare la segnatura. Un altro metodo per trovare la segnatura potrebbe essere quello di valutare i minori principali della Bezoutiante, sempre grazie al fatto che la matrice è simmetrica. Da qui emerge l utilità del Criterio di Sylvester,poiché capire quante radici reali ha un polinomio di qualsiasi grado n, necessita ora solo di calcolare alcune semplici espressioni e qualche determinante. Anche se 10
11 la formula del determinante da valutare si complica all aumentare di n, questo rimane comunque un Criterio molto utile che ci dà delle informazioni sulle radici, considerando il fatto che per polinomi di grado > 5 non esistono delle formule risolutrici per il calcolo delle soluzioni. Vediamo ora qualche esempio di applicazione del Criterio di Sylvester. n=3 Discutiamo le tipologia delle radici x 1, x 2 x 3 del polinomio f(x) = x 3 + a 1 x 2 + a 2 x + a 3 Passo 1) Trasformo i coefficienti nelle funzioni simmetriche. a 1 = σ 1 (= x 1 + x 2 + x 3 ) a 2 = σ 2 (= x 1 x 2 + x 1 x 3 + x 2 x 3 ) a 3 = σ 3 (= x 1 x 2 x 3 ) Passo 2) Trasformo le funzioni simmetriche nelle somme di potenze. s 0 = 3 s 1 = σ 1 s 2 = σ 2 1 2σ 2 s 3 = σ σ 3 3σ 1 σ 2 s 4 = 4σ 1 σ 3 4σ 2 σ σ σ 4 1 Passo 3) Scrivo la Bezoutiante. s 0 s 1 s 2 B = s 1 s 2 s 3 = s 2 s 3 s 4 3 σ 1 σ1 2 2σ 2 σ 1 σ1 2 2σ 2 σ σ 3 3σ 1 σ 2 = σ1 2 2σ 2 σ σ 3 3σ 1 σ 2 4σ 1 σ 3 4σ 2 σ σ2 2 + σ1 4 3 a 1 a 2 1 2a 2 = a 1 a 2 1 2a 2 a 3 1 3a 3 + 3a 1 a 2 a 2 1 2a 2 a 3 1 3a 3 + 3a 1 a 2 4a 1 a 3 4a 2 a a a 4 1 Adesso ho una matrice in funzione solo dei coefficienti di f(x). Quindi, sfruttando esclusivamente questi, posso affermare che: rg(b)= numero di radici distinte sign(b)= numero di radici reali det(b)= discrimintante di B 11
12 Vediamo un esempio numerico : B = f(x) = x 3 + x 1 rango(b) = 3 det(b) = 31 sign(b) = (+, +, ) = (2, 1) 1 radice reale Oss. Nel caso n = 3 la segnatura della Bezoutiante può essere rappresentata solo da uno dei due seguenti tipi : - (3,0), 3 autovalori positivi e 0 negativi det(b) > 0 e ho 3 radici reali. - (2,1), 2 autovalori positivi e 1 negativo det(b) < 0 e ho 1 radice reale I casi (1,2) e (0,3) non possono presentarsi, poiché ogni radice reale contribuisce con un + e una coppia di complesse coniugate con un - e un +. Quindi, in questo caso, basta calcolare il determinante (3 3) per caratterizzare le radici. Studiamo il segno delle radici reali. Calcolo la matrice associata alla forma quadratica Q di f(x), che diventa: s 1 s 2 s 3 s 2 s 3 s 4 = s 3 s 4 s 5 a 1 a 2 1 2a 2 a 3 1 3a 3 + 3a 1 a 2 a 2 1 2a 2 a 3 1 3a 3 + 3a 1 a 2 4a 1 a 3 4a 2 a a a 4 1 = a 3 1 3a 3 + 3a 1 a 2 4a 1 a 3 4a 2 a a a 4 1 5a 3 a 2 1 a a 2 a 3 + 5a 2 a 3 1 5a 1 a Questa ha segnatura (+, +, ) = (2, 1). Un + e il - sono associati alle radici complesse coniugate, l altro contributo è un +, quindi la radice reale è positiva, cioè > 0. Troviamo il numero di radici reali nell intervallo (0, 1]. Dall esempio precedente ho trovato che il polinomio ha una radice reale positiva. Adesso devo calcolare la segnatura della matrice associata a Q per il polinomio traslato f 1 (x) = f(x + 1) = x 3 + 3x 2 + 4x + 1, che è : Questa matrice ha segnatura (, +, ) = (1, 2), ovvero mi dice che il polinomio f 1 (x) ha una radice reale negativa, che equivale a dire che f(x) = f 1 (x 1) ha una radice reale < 1 e nessuna > 1. Dopo di che facendo la differenza tra le radici di f(x) maggiori di 0 e le radici di f(x) maggiori di 1, ottengo le radici di f(x) comprese nell intervallo (0, 1] : posso quindi concludere che ho una radice reale positiva nell intervallo scelto. 12
13 Riferimenti bibliografici [1] G.SANSONE-R.CONTI, Lezioni di Analisi Matematica, volume I,Padova, Cedam, [2] C. PROCESI, Lie groups-an Approach through Invariants and Representations,(Universitext),Springer,2006, [3] D. BURATTA,Tesi triennale,polinomi simmetrici, , reperibile in PolinomiSimmetrici.pdf 13
Applicazioni lineari simmetriche e forme quadratiche reali.
 Applicazioni lineari simmetriche e forme quadratiche reali 1 Applicazioni lineari simmetriche Consideriamo lo spazio IR n col prodotto scalare canonico X Y = t XY = x 1 y 1 + + x n y n Definizione Un applicazione
Applicazioni lineari simmetriche e forme quadratiche reali 1 Applicazioni lineari simmetriche Consideriamo lo spazio IR n col prodotto scalare canonico X Y = t XY = x 1 y 1 + + x n y n Definizione Un applicazione
LEZIONE 15. (15.1.2) p(x) = a 0 x n + a 1 x n a n 1 x + a n = a h x n h.
 LEZIONE 15 15.1. Polinomi a coefficienti complessi e loro e loro radici. In questo paragrafo descriveremo alcune proprietà dei polinomi a coefficienti complessi e delle loro radici. Già nel precedente
LEZIONE 15 15.1. Polinomi a coefficienti complessi e loro e loro radici. In questo paragrafo descriveremo alcune proprietà dei polinomi a coefficienti complessi e delle loro radici. Già nel precedente
A =, c d. d = ad cb. c d A =
 Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
Esercizi 3, 1. Prof. Thomas Parisini. Esercizi 3, 3 Regola:
 Esercizi 3, 1 Esercizi 3, 2 Esercizi Stabilità per sistemi a tempo continuo Analisi degli autovalori Analisi del polinomio caratteristico, criterio di Routh-Hurwitz Stabilità per sistemi a tempo continuo
Esercizi 3, 1 Esercizi 3, 2 Esercizi Stabilità per sistemi a tempo continuo Analisi degli autovalori Analisi del polinomio caratteristico, criterio di Routh-Hurwitz Stabilità per sistemi a tempo continuo
Stabilità per sistemi a tempo continuo
 Esercizi 3, 1 Stabilità per sistemi a tempo continuo Analisi degli autovalori Analisi del polinomio caratteristico, criterio di Routh-Hurwitz Calcolo di Esercizi 3, 2 Esercizi Stabilità per sistemi a tempo
Esercizi 3, 1 Stabilità per sistemi a tempo continuo Analisi degli autovalori Analisi del polinomio caratteristico, criterio di Routh-Hurwitz Calcolo di Esercizi 3, 2 Esercizi Stabilità per sistemi a tempo
Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti)
 Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti) April 14, 2011 (alcune note non complete sugli argomenti trattati: eventuali completamenti saranno aggiunti)
Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti) April 14, 2011 (alcune note non complete sugli argomenti trattati: eventuali completamenti saranno aggiunti)
Unità Didattica N 12 Le equazioni ad una incognita 1. Unità Didattica N 12 Le equazioni ad una incognita
 Unità Didattica N Le equazioni ad una incognita Unità Didattica N Le equazioni ad una incognita ) Equazioni risolubili mediante la decomposizione in fattori ) Equazione biquadratica ) Equazioni irrazionali
Unità Didattica N Le equazioni ad una incognita Unità Didattica N Le equazioni ad una incognita ) Equazioni risolubili mediante la decomposizione in fattori ) Equazione biquadratica ) Equazioni irrazionali
0.1 Spazi Euclidei in generale
 0.1. SPAZI EUCLIDEI IN GENERALE 1 0.1 Spazi Euclidei in generale Sia V uno spazio vettoriale definito su R. Diremo, estendendo una definizione data in precedenza, che V è uno spazio vettoriale euclideo
0.1. SPAZI EUCLIDEI IN GENERALE 1 0.1 Spazi Euclidei in generale Sia V uno spazio vettoriale definito su R. Diremo, estendendo una definizione data in precedenza, che V è uno spazio vettoriale euclideo
Polinomi. Corso di accompagnamento in matematica. Lezione 1
 Polinomi Corso di accompagnamento in matematica Lezione 1 Sommario 1 Insiemi numerici 2 Definizione di polinomio 3 Operazioni tra polinomi 4 Fattorizzazione Corso di accompagnamento Polinomi Lezione 1
Polinomi Corso di accompagnamento in matematica Lezione 1 Sommario 1 Insiemi numerici 2 Definizione di polinomio 3 Operazioni tra polinomi 4 Fattorizzazione Corso di accompagnamento Polinomi Lezione 1
Appunti sui Codici di Reed Muller. Giovanni Barbarino
 Appunti sui Codici di Reed Muller Giovanni Barbarino Capitolo 1 Codici di Reed-Muller I codici di Reed-Muller sono codici lineari su F q legati alle valutazioni dei polinomi sullo spazio affine. Per semplicità
Appunti sui Codici di Reed Muller Giovanni Barbarino Capitolo 1 Codici di Reed-Muller I codici di Reed-Muller sono codici lineari su F q legati alle valutazioni dei polinomi sullo spazio affine. Per semplicità
Determinante, autovalori e autovettori
 Determinante, autovalori e autovettori Lorenzo Pareschi Dipartimento di Matematica, Universitá di Ferrara http://wwwlorenzopareschicom lorenzopareschi@unifeit Lorenzo Pareschi (Univ Ferrara) Determinante,
Determinante, autovalori e autovettori Lorenzo Pareschi Dipartimento di Matematica, Universitá di Ferrara http://wwwlorenzopareschicom lorenzopareschi@unifeit Lorenzo Pareschi (Univ Ferrara) Determinante,
LEZIONE 12. v = α 1 v α n v n =
 LEZIONE 12 12.1. Combinazioni lineari. Definizione 12.1.1. Sia V uno spazio vettoriale su k = R, C e v 1,..., v n V vettori fissati. Un vettore v V si dice combinazione lineare di v 1,..., v n se esistono
LEZIONE 12 12.1. Combinazioni lineari. Definizione 12.1.1. Sia V uno spazio vettoriale su k = R, C e v 1,..., v n V vettori fissati. Un vettore v V si dice combinazione lineare di v 1,..., v n se esistono
INTEGRAZIONE DELLE FUNZIONI RAZIONALI. Figura 0.1. Portafortuna
 INTEGRAZIONE DELLE FUNZIONI RAZIONALI GIOVANNI TORRERO Figura 0.. Portafortuna Consideriamo l equazione. Radici di un polinomio (.) Q(x) 0 Dove Q(x) è un polinomio in x di grado n, vi è un teorema, che
INTEGRAZIONE DELLE FUNZIONI RAZIONALI GIOVANNI TORRERO Figura 0.. Portafortuna Consideriamo l equazione. Radici di un polinomio (.) Q(x) 0 Dove Q(x) è un polinomio in x di grado n, vi è un teorema, che
Appunti di Geometria - 2
 Appunti di Geometria - Samuele Mongodi - s.mongodi@sns.it Cambi di base e applicazioni lineari Richiami Sia V uno spazio vettoriale di dimensione n sul campo K, con base assegnata e,..., e n } (ad esempio
Appunti di Geometria - Samuele Mongodi - s.mongodi@sns.it Cambi di base e applicazioni lineari Richiami Sia V uno spazio vettoriale di dimensione n sul campo K, con base assegnata e,..., e n } (ad esempio
04 - Numeri Complessi
 Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 04 - Numeri Complessi Anno Accademico 2013/2014 M. Tumminello, V. Lacagnina e
Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 04 - Numeri Complessi Anno Accademico 2013/2014 M. Tumminello, V. Lacagnina e
Richiami di algebra delle matrici a valori reali
 Richiami di algebra delle matrici a valori reali Vettore v n = v 1 v 2. v n Vettore trasposto v n = (v 1, v 2,..., v n ) v n = (v 1, v 2,..., v n ) A. Pollice - Statistica Multivariata Vettore nullo o
Richiami di algebra delle matrici a valori reali Vettore v n = v 1 v 2. v n Vettore trasposto v n = (v 1, v 2,..., v n ) v n = (v 1, v 2,..., v n ) A. Pollice - Statistica Multivariata Vettore nullo o
Esame scritto di Geometria I
 Esame scritto di Geometria I Università degli Studi di Trento Corso di laurea in Fisica A.A. 26/27 Appello di febbraio 27 Esercizio Sia f h : R R l applicazione lineare definita da f h (e ) = 2e + (2 h)e
Esame scritto di Geometria I Università degli Studi di Trento Corso di laurea in Fisica A.A. 26/27 Appello di febbraio 27 Esercizio Sia f h : R R l applicazione lineare definita da f h (e ) = 2e + (2 h)e
Proposizione 2 Il polinomio minimo di t corrisponde all annullatore minimale di M V.
 Fogli NON riletti. Grazie per ogni segnalazione di errori. L esempio qui sviluppato vuole mostrare in concreto il significato dei risultati trattati a lezione e qui velocemente riassunti. Si assume che
Fogli NON riletti. Grazie per ogni segnalazione di errori. L esempio qui sviluppato vuole mostrare in concreto il significato dei risultati trattati a lezione e qui velocemente riassunti. Si assume che
EQUAZIONI DI II GRADO
 RICHIAMI SULLE EQUAZIONI DI PRIMO E SECONDO GRADO PROF.SSA ROSSELLA PISCOPO Indice 1 EQUAZIONI DI I GRADO --------------------------------------------------------------------------------------------------
RICHIAMI SULLE EQUAZIONI DI PRIMO E SECONDO GRADO PROF.SSA ROSSELLA PISCOPO Indice 1 EQUAZIONI DI I GRADO --------------------------------------------------------------------------------------------------
Corso di Calcolo Numerico
 Corso di Calcolo Numerico Dott.ssa M.C. De Bonis Università degli Studi della Basilicata, Potenza Facoltà di Ingegneria Corso di Laurea in Ingegneria Meccanica Risoluzione di Equazioni Algebriche Le equazioni
Corso di Calcolo Numerico Dott.ssa M.C. De Bonis Università degli Studi della Basilicata, Potenza Facoltà di Ingegneria Corso di Laurea in Ingegneria Meccanica Risoluzione di Equazioni Algebriche Le equazioni
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014
 FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014 DOCENTE: MATTEO LONGO Rispondere alle domande di Teoria in modo esauriente e completo. Svolgere il maggior numero di esercizi
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014 DOCENTE: MATTEO LONGO Rispondere alle domande di Teoria in modo esauriente e completo. Svolgere il maggior numero di esercizi
Precorso di Matematica
 UNIVERSITÀ DEGLI STUDI ROMA TRE FACOLTA DI ARCHITETTURA Precorso di Matematica Anna Scaramuzza Anno Accademico 2005-2006 4-10 Ottobre 2005 INDICE 1. ALGEBRA................................. 3 1.1 Equazioni
UNIVERSITÀ DEGLI STUDI ROMA TRE FACOLTA DI ARCHITETTURA Precorso di Matematica Anna Scaramuzza Anno Accademico 2005-2006 4-10 Ottobre 2005 INDICE 1. ALGEBRA................................. 3 1.1 Equazioni
e non ci possono chiaramente essere minori di ordine più grande per cui il rango per minori è 2. Rango per pivot: Svolgiamo la riduzione
 18 ottobre 2011 1. Per le matrici seguenti calcolare il rango per minori, il rango per pivot, il rango per righe ed il rango per colonne. Verificare che si ottiene sempre lo stesso numero. Determinare
18 ottobre 2011 1. Per le matrici seguenti calcolare il rango per minori, il rango per pivot, il rango per righe ed il rango per colonne. Verificare che si ottiene sempre lo stesso numero. Determinare
LEZIONE i 0 3 Le sottomatrici 2 2 di A sono. 1 2 i i 3. Invece (
 LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Aritmetica 2009/10 Compitino 1/12/2009. (a) Contare gli elementi nilpotenti di A. (b) Contare gli elementi zero-divisori di A.
 Aritmetica 2009/10 Compitino 1/12/2009 1. Sia A = Z2[x]/(x 5 + x 4 + 1). (a) Contare gli elementi nilpotenti di A. (b) Contare gli elementi zero-divisori di A. Possibile risoluzione: Il polinomio f(x)
Aritmetica 2009/10 Compitino 1/12/2009 1. Sia A = Z2[x]/(x 5 + x 4 + 1). (a) Contare gli elementi nilpotenti di A. (b) Contare gli elementi zero-divisori di A. Possibile risoluzione: Il polinomio f(x)
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria: Elettronica. Corso di Geometria ed Algebra Docente F. Flamini
 Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria: Elettronica Corso di Geometria ed Algebra Docente F. Flamini Capitolo IV - 3: Teorema Spettrale degli operatori autoaggiunti e Teorema
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria: Elettronica Corso di Geometria ed Algebra Docente F. Flamini Capitolo IV - 3: Teorema Spettrale degli operatori autoaggiunti e Teorema
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria Edile ed Edile/Architettura. Geometria Proiettiva Docente F.
 Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria Edile ed Edile/Architettura Geometria Proiettiva Docente F. Flamini CONICHE PROIETTIVE: Classificazione e forme canoniche proiettive Si
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria Edile ed Edile/Architettura Geometria Proiettiva Docente F. Flamini CONICHE PROIETTIVE: Classificazione e forme canoniche proiettive Si
1 Estensioni in C, automorfismi, polinomi.
 Lezioni del 15,18,20,22 aprile, II. Registro dettagliato 1 Estensioni in C, automorfismi, polinomi. 1.1 Estensioni di sottocampi di C. Una coppia di campi, uno contenuto nell altro, si dice estensione
Lezioni del 15,18,20,22 aprile, II. Registro dettagliato 1 Estensioni in C, automorfismi, polinomi. 1.1 Estensioni di sottocampi di C. Una coppia di campi, uno contenuto nell altro, si dice estensione
Gruppi, anelli, campi e polinomi: le prime definizioni.
 Gruppi, anelli, campi e polinomi: le prime definizioni. Ilaria Del Corso 1 GRUPPI Definizione 1.1. Sia G un insieme, G e sia un operazione su G. Si dice che (G, ) è un gruppo se 1. è associativa, ossia
Gruppi, anelli, campi e polinomi: le prime definizioni. Ilaria Del Corso 1 GRUPPI Definizione 1.1. Sia G un insieme, G e sia un operazione su G. Si dice che (G, ) è un gruppo se 1. è associativa, ossia
Richiami di Algebra Lineare
 Richiami di Algebra Lineare Fabrizio Silvestri December 14, 010 Matrice Sia R il campo dei numeri reali. Si indica con R m n l insieme delle matrici ad elementi reali con m righe ed n colonne. Se A R n
Richiami di Algebra Lineare Fabrizio Silvestri December 14, 010 Matrice Sia R il campo dei numeri reali. Si indica con R m n l insieme delle matrici ad elementi reali con m righe ed n colonne. Se A R n
Corso di Matematica per la Chimica
 Dott.ssa Maria Carmela De Bonis a.a. 2013-14 Risoluzione di Equazioni Algebriche Le equazioni algebriche sono equazioni del tipo P(x) = 0 dove P è un polinomio di grado n cioé P(x) = a 1 x n + a 2 x n
Dott.ssa Maria Carmela De Bonis a.a. 2013-14 Risoluzione di Equazioni Algebriche Le equazioni algebriche sono equazioni del tipo P(x) = 0 dove P è un polinomio di grado n cioé P(x) = a 1 x n + a 2 x n
LEZIONE i i 3
 LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Istituzioni di Matematiche, Integrali fratti. corso di laurea in Scienze geologiche. Mauro Costantini
 Istituzioni di Matematiche, Integrali fratti corso di laurea in Scienze geologiche. Mauro Costantini tipo: Il nostro obiettivo è studiare gli integrali (indefiniti e definiti delle funzioni razionali,
Istituzioni di Matematiche, Integrali fratti corso di laurea in Scienze geologiche. Mauro Costantini tipo: Il nostro obiettivo è studiare gli integrali (indefiniti e definiti delle funzioni razionali,
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
y + P(x) y + Q(x) y = 0 y(x) = c 1y 1(x) + c 2 y 2(x).
 Proposizione 4. Se y 1(x) e y (x) sono soluzioni linearmente indipendenti di y + P(x) y + Q(x) y = 0 ogni altra soluzione della stessa equazione si scrive nella forma per una scelta opportuna delle costanti
Proposizione 4. Se y 1(x) e y (x) sono soluzioni linearmente indipendenti di y + P(x) y + Q(x) y = 0 ogni altra soluzione della stessa equazione si scrive nella forma per una scelta opportuna delle costanti
x 1 Fig.1 Il punto P = P =
 Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE
 SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE. Esercizi Esercizio. In R calcolare il modulo dei vettori,, ),,, ) ed il loro angolo. Esercizio. Calcolare una base ortonormale del sottospazio
SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE. Esercizi Esercizio. In R calcolare il modulo dei vettori,, ),,, ) ed il loro angolo. Esercizio. Calcolare una base ortonormale del sottospazio
Numeri complessi. Hynek Kovarik. Analisi A. Università di Brescia. Hynek Kovarik (Università di Brescia) I numeri complessi Analisi A 1 / 37
 Numeri complessi Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) I numeri complessi Analisi A 1 / 37 Introduzione I numeri complessi vengono introdotti perché tutte
Numeri complessi Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) I numeri complessi Analisi A 1 / 37 Introduzione I numeri complessi vengono introdotti perché tutte
LEZIONE 16 A = Verifichiamo se qualcuna fra le entrate a di A è suo autovalore. determinare per quale entrata a di A risulta rk(a ai 2 ) 1.
 LEZIONE 16 16.1. Autovalori, autovettori ed autospazi di matrici. Introduciamo la seguente definizione. Definizione 16.1.1. Siano k = R, C e A k n,n. Un numero λ k si dice autovalore di A su k) se rka
LEZIONE 16 16.1. Autovalori, autovettori ed autospazi di matrici. Introduciamo la seguente definizione. Definizione 16.1.1. Siano k = R, C e A k n,n. Un numero λ k si dice autovalore di A su k) se rka
Un polinomio è un espressione algebrica data dalla somma di più monomi.
 1 I polinomi 1.1 Terminologia sui polinomi Un polinomio è un espressione algebrica data dalla somma di più monomi. I termini di un polinomio sono i monomi che compaiono come addendi nel polinomio. Il termine
1 I polinomi 1.1 Terminologia sui polinomi Un polinomio è un espressione algebrica data dalla somma di più monomi. I termini di un polinomio sono i monomi che compaiono come addendi nel polinomio. Il termine
Massimi e minimi relativi in R n
 Massimi e minimi relativi in R n Si consideri una funzione f : A R, con A R n, e sia x A un punto interno ad A. Definizione: si dice che x è un punto di massimo relativo per f se B(x, r) A tale che f(y)
Massimi e minimi relativi in R n Si consideri una funzione f : A R, con A R n, e sia x A un punto interno ad A. Definizione: si dice che x è un punto di massimo relativo per f se B(x, r) A tale che f(y)
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
TEN Radici quadrate modulo p e modulo p k. Radici quadrate modulo p, con p > 2.
 TEN 2008. Radici quadrate modulo p e modulo p k. Radici quadrate modulo p, con p > 2. Lemma 1. Sia n Z. Sia p > 2 un numero primo. (a) n è un quadrato modulo p se e solo se n p 1 2 1 mod p; (b) Sia n 0
TEN 2008. Radici quadrate modulo p e modulo p k. Radici quadrate modulo p, con p > 2. Lemma 1. Sia n Z. Sia p > 2 un numero primo. (a) n è un quadrato modulo p se e solo se n p 1 2 1 mod p; (b) Sia n 0
04 - Numeri Complessi
 Università degli Studi di Palermo Scuola Politecnica Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica 04 - Numeri Complessi Anno Accademico 2015/2016 M. Tumminello,
Università degli Studi di Palermo Scuola Politecnica Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica 04 - Numeri Complessi Anno Accademico 2015/2016 M. Tumminello,
I numeri complessi. Andrea Corli 31 agosto Motivazione 1. 2 Definizioni 1. 3 Forma trigonometrica di un numero complesso 3
 I numeri complessi Andrea Corli 3 agosto 009 Indice Motivazione Definizioni 3 Forma trigonometrica di un numero complesso 3 4 Radici di un numero complesso 4 5 Equazioni di secondo grado e il teorema fondamentale
I numeri complessi Andrea Corli 3 agosto 009 Indice Motivazione Definizioni 3 Forma trigonometrica di un numero complesso 3 4 Radici di un numero complesso 4 5 Equazioni di secondo grado e il teorema fondamentale
Su alcuni numeri irrazionali
 Su alcuni numeri irrazionali M. Olivieri classe IV E, L.S. E. Majorana Guidonia Scopo di questa breve nota 1 è quello di fornire una dimostrazione elementare dell irrazionalità di alcuni numeri reali.
Su alcuni numeri irrazionali M. Olivieri classe IV E, L.S. E. Majorana Guidonia Scopo di questa breve nota 1 è quello di fornire una dimostrazione elementare dell irrazionalità di alcuni numeri reali.
EQUAZIONI BIQUADRATICHE
 EQUAZIONI PARTICOLARI PROF.SSA ROSSELLA PISCOPO Indice 1 EQUAZIONI BIQUADRATICHE ------------------------------------------------------------------------------------------ 3 2 EQUAZIONI RECIPROCHE -----------------------------------------------------------------------------------------------
EQUAZIONI PARTICOLARI PROF.SSA ROSSELLA PISCOPO Indice 1 EQUAZIONI BIQUADRATICHE ------------------------------------------------------------------------------------------ 3 2 EQUAZIONI RECIPROCHE -----------------------------------------------------------------------------------------------
Localizzazione delle soluzioni di un sistema polinomiale zero-dimensionale in aritmetica esatta
 Localizzazione delle soluzioni di un sistema polinomiale zero-dimensionale in aritmetica esatta Candidato: Leonardo Landi Relatore: Prof. Giorgio Ottaviani 22 Luglio 2014 Ideali zero-dimensionali Ideali
Localizzazione delle soluzioni di un sistema polinomiale zero-dimensionale in aritmetica esatta Candidato: Leonardo Landi Relatore: Prof. Giorgio Ottaviani 22 Luglio 2014 Ideali zero-dimensionali Ideali
Forme bilineari e prodotti scalari
 Forme bilineari e prodotti scalari Il prodotto scalare standard di R n può anche essere scritto come un prodotto riga per colonna u, v R n = u t Iv dove I è la matrice identità. Possiamo generalizzare
Forme bilineari e prodotti scalari Il prodotto scalare standard di R n può anche essere scritto come un prodotto riga per colonna u, v R n = u t Iv dove I è la matrice identità. Possiamo generalizzare
Forme quadratiche in R n e metodo del completamento dei quadrati
 Chapter 1 Forme quadratiche in R n e metodo del completamento dei quadrati Ricordiamo che a determinare il tipo (definita positiva o negativa, semidefinita positiva o negativa, indefinita) di una forma
Chapter 1 Forme quadratiche in R n e metodo del completamento dei quadrati Ricordiamo che a determinare il tipo (definita positiva o negativa, semidefinita positiva o negativa, indefinita) di una forma
1 Addendum su Diagonalizzazione
 Addendum su Diagonalizzazione Vedere le dispense per le definizioni di autovettorre, autovalore e di trasformazione lineare (o matrice) diagonalizzabile. In particolare, si ricorda che una condizione necessaria
Addendum su Diagonalizzazione Vedere le dispense per le definizioni di autovettorre, autovalore e di trasformazione lineare (o matrice) diagonalizzabile. In particolare, si ricorda che una condizione necessaria
Esercizi di Geometria - Foglio 1 Corso di Laurea in Fisica 24 Settembre 2003
 Esercizio 1.1 Esercizi di Geometria - Foglio 1 Corso di Laurea in Fisica 24 Settembre 2003 1. Teoria elementare degli insiemi Descrivere in modo esplicito i seguenti insiemi: (i) L = {x x e una lettera
Esercizio 1.1 Esercizi di Geometria - Foglio 1 Corso di Laurea in Fisica 24 Settembre 2003 1. Teoria elementare degli insiemi Descrivere in modo esplicito i seguenti insiemi: (i) L = {x x e una lettera
SOLUZIONI ESERCIZI DI IGS. b 0 (mod 3) 1 + 2a + b 0 (mod 3)
 SOLUZIONI ESERCIZI DI IGS 1. Il polinomio f(x) è irriducibile su Q per il criterio di Eisenstein (p = 3). 2. Sia f(x) = X 2 +ax +b Z 3 [X]. Poichè f(x) è di secondo grado, è irriducibile se e solo se non
SOLUZIONI ESERCIZI DI IGS 1. Il polinomio f(x) è irriducibile su Q per il criterio di Eisenstein (p = 3). 2. Sia f(x) = X 2 +ax +b Z 3 [X]. Poichè f(x) è di secondo grado, è irriducibile se e solo se non
Corso di Laurea in Matematica - Esame di Geometria 1. Prova scritta del 7 settembre 2015
 Corso di Laurea in Matematica - Esame di Geometria 1 Prova scritta del 7 settembre 215 Cognome Nome Numero di matricola Voto ATTENZIONE. Riportare lo svolgimento completo degli esercizi. corretti, non
Corso di Laurea in Matematica - Esame di Geometria 1 Prova scritta del 7 settembre 215 Cognome Nome Numero di matricola Voto ATTENZIONE. Riportare lo svolgimento completo degli esercizi. corretti, non
CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI A.A. 2018/2019 PROF. VALENTINA BEORCHIA
 CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Matrici associate a un applicazione lineare 1 2 Cambiamenti di base 4 3 Diagonalizzazione 6 1 MATRICI ASSOCIATE
CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Matrici associate a un applicazione lineare 1 2 Cambiamenti di base 4 3 Diagonalizzazione 6 1 MATRICI ASSOCIATE
Geometria A. Università degli Studi di Trento Corso di laurea in Matematica A.A. 2017/ Maggio 2018 Prova Intermedia
 Geometria A Università degli Studi di Trento Corso di laurea in Matematica A.A. 7/8 Maggio 8 Prova Intermedia Il tempo per la prova è di ore. Durante la prova non è permesso l uso di appunti e libri. Esercizio
Geometria A Università degli Studi di Trento Corso di laurea in Matematica A.A. 7/8 Maggio 8 Prova Intermedia Il tempo per la prova è di ore. Durante la prova non è permesso l uso di appunti e libri. Esercizio
Capitolo 8 Forme quadratiche e loro applicazioni Esercizi svolti Tutorato di geometria e algebra lineare. Marco Robutti
 Capitolo 8 Forme quadratiche e loro applicazioni Esercizi svolti Tutorato di geometria e algebra lineare Marco Robutti 5 Ottobre 2017 1 Introduzione Gli esercizi di questo capitolo riguardano i seguenti
Capitolo 8 Forme quadratiche e loro applicazioni Esercizi svolti Tutorato di geometria e algebra lineare Marco Robutti 5 Ottobre 2017 1 Introduzione Gli esercizi di questo capitolo riguardano i seguenti
INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 17 SETTEMBRE 2012
 INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 7 SETTEMBRE 202 Esercizio. Sia V = R[X] 2 lo spazio vettoriale dei polinomi ax 2 + bx + c nella variabile X di grado al più 2 a coefficienti
INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 7 SETTEMBRE 202 Esercizio. Sia V = R[X] 2 lo spazio vettoriale dei polinomi ax 2 + bx + c nella variabile X di grado al più 2 a coefficienti
Polinomio di Taylor del secondo ordine per funzioni di due variabili
 Esercitazioni del 15 aprile 2013 Polinomio di Taylor del secondo ordine per funzioni di due variabili Sia f : A R 2 R una funzione di classe C 2. Fissato un p unto (x 0, y 0 A consideriamo il seguente
Esercitazioni del 15 aprile 2013 Polinomio di Taylor del secondo ordine per funzioni di due variabili Sia f : A R 2 R una funzione di classe C 2. Fissato un p unto (x 0, y 0 A consideriamo il seguente
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof. F.Podestà, a.a
 APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
ALGEBRA I: SOLUZIONI QUINTA ESERCITAZIONE 9 maggio 2011
 ALGEBRA I: SOLUZIONI QUINTA ESERCITAZIONE 9 maggio 2011 Esercizio 1. Usando l algoritmo euclideo delle divisioni successive, calcolare massimo comune divisore e identità di Bézout per le seguenti coppie
ALGEBRA I: SOLUZIONI QUINTA ESERCITAZIONE 9 maggio 2011 Esercizio 1. Usando l algoritmo euclideo delle divisioni successive, calcolare massimo comune divisore e identità di Bézout per le seguenti coppie
AUTOVALORI, AUTOVETTORI, AUTOSPAZI
 AUTOVALORI, AUTOVETTORI, AUTOSPAZI. Esercizi Esercizio. Sia f : R 3 R 3 l endomorfismo definito da f(x, y, z) = (x+y, y +z, x+z). Calcolare gli autovalori ed una base per ogni autospazio di f. Dire se
AUTOVALORI, AUTOVETTORI, AUTOSPAZI. Esercizi Esercizio. Sia f : R 3 R 3 l endomorfismo definito da f(x, y, z) = (x+y, y +z, x+z). Calcolare gli autovalori ed una base per ogni autospazio di f. Dire se
3/10/ Divisibilità e massimo comun divisore
 MCD in N e Polinomi 3/10/2013 1 Divisibilità e massimo comun divisore 1.1 Divisibilità in N In questa sezione introdurremo il concetto di divisibilità e di massimo comun divisore di due numeri naturali
MCD in N e Polinomi 3/10/2013 1 Divisibilità e massimo comun divisore 1.1 Divisibilità in N In questa sezione introdurremo il concetto di divisibilità e di massimo comun divisore di due numeri naturali
ATTENZIONE: : giustificate le vostre argomentazioni! Geometria Canale 3. Lettere J-PE (Prof P. Piazza) Esame scritto del 12/02/2014. Compito A.
 Geometria Canale. Lettere J-PE (Prof P. Piazza) Esame scritto del 12/02/2014. Compito A. Nome e Cognome: Numero di Matricola: Esercizio Punti totali Punteggio 1 7 2 6 6 4 6+1 5 6+2 Totale 1+ ATTENZIONE:
Geometria Canale. Lettere J-PE (Prof P. Piazza) Esame scritto del 12/02/2014. Compito A. Nome e Cognome: Numero di Matricola: Esercizio Punti totali Punteggio 1 7 2 6 6 4 6+1 5 6+2 Totale 1+ ATTENZIONE:
LEZIONE 4. Le sottomatrici 2 2 di A sono. Invece ( 1 3 non è sottomatrice di A.
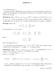 LEZIONE 4 4 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 4 4 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Esercizi del tutoraggio - algebra lineare
 Esercizi del tutoraggio - algebra lineare 13 Novembre 2008 6 Ottobre 2008 Esercizio 1. Siano dati i seguenti punti nel piano. Dire se i vettori geometrici pq e p q sono equipollenti. p = (1, 2) q = (3,
Esercizi del tutoraggio - algebra lineare 13 Novembre 2008 6 Ottobre 2008 Esercizio 1. Siano dati i seguenti punti nel piano. Dire se i vettori geometrici pq e p q sono equipollenti. p = (1, 2) q = (3,
Lezione Diagonalizzazione di matrici
 Lezione 2 2. Diagonalizzazione di matrici Come visto nella precedente lezione, in generale, data una matrice A 2 K n,n con K = R, C,nonèimmediatocheesistasempreunabasecostituitadasuoiautovettori. Definizione
Lezione 2 2. Diagonalizzazione di matrici Come visto nella precedente lezione, in generale, data una matrice A 2 K n,n con K = R, C,nonèimmediatocheesistasempreunabasecostituitadasuoiautovettori. Definizione
Fondamenti di ALGEBRA LINEARE E GEOMETRIA
 Fondamenti di ALGEBRA LINEARE E GEOMETRIA Corso di laurea in Ingegneria Gestionale 2011-2012 Michel Lavrauw Dipartimento di Tecnica e Gestione dei Sistemi Industriali Università di Padova Lezione 7 Capitolo
Fondamenti di ALGEBRA LINEARE E GEOMETRIA Corso di laurea in Ingegneria Gestionale 2011-2012 Michel Lavrauw Dipartimento di Tecnica e Gestione dei Sistemi Industriali Università di Padova Lezione 7 Capitolo
Lezioni di Algebra Lineare V. Autovalori e autovettori
 Lezioni di Algebra Lineare V. Autovalori e autovettori Versione novembre 2008 Contenuto 1. Cambiamenti di base 2. Applicazioni lineari, matrici e cambiamenti di base 3. Autovalori e autovettori 2 1. Cambiamenti
Lezioni di Algebra Lineare V. Autovalori e autovettori Versione novembre 2008 Contenuto 1. Cambiamenti di base 2. Applicazioni lineari, matrici e cambiamenti di base 3. Autovalori e autovettori 2 1. Cambiamenti
Approssimazione di dati e funzioni
 Approssimazione di dati e funzioni Richiamiamo i principali metodi di approssimazione polinomiale di un insieme di dati (x i, y i ), i = 0,..., n. Le ordinate y i possono essere i valori assunti nei nodi
Approssimazione di dati e funzioni Richiamiamo i principali metodi di approssimazione polinomiale di un insieme di dati (x i, y i ), i = 0,..., n. Le ordinate y i possono essere i valori assunti nei nodi
Facoltà di Anno Accademico 2018/19 Registro lezioni del docente PINTUS NICOLA
 Facoltà di Anno Accademico 2018/19 Registro lezioni del docente PINTUS NICOLA Attività didattica GEOMETRIA E ALGEBRA [IN/0079] Partizionamento: Periodo di svolgimento: Docente titolare del corso: PINTUS
Facoltà di Anno Accademico 2018/19 Registro lezioni del docente PINTUS NICOLA Attività didattica GEOMETRIA E ALGEBRA [IN/0079] Partizionamento: Periodo di svolgimento: Docente titolare del corso: PINTUS
Esercizi di Algebra Lineare - Foglio 2
 Esercizi di Algebra Lineare - Foglio ES 1. Sia f : A B una funzione, siano A 1, A A due sottoinsiemi. Dimostrare che f(a 1 A ) = f(a 1 ) f(a ) e che f(a 1 A ) f(a 1 ) f(a ). Inoltre se f è iniettiva, provare
Esercizi di Algebra Lineare - Foglio ES 1. Sia f : A B una funzione, siano A 1, A A due sottoinsiemi. Dimostrare che f(a 1 A ) = f(a 1 ) f(a ) e che f(a 1 A ) f(a 1 ) f(a ). Inoltre se f è iniettiva, provare
1 Polinomio minimo e ampliamenti
 Università degli studi di Roma Tre Corso di Laurea Triennale in Matematica, a.a. 2004/2005 AL2 - Algebra 2, gruppi anelli e campi Soluzioni 10 dicembre 2004 1 Polinomio minimo e ampliamenti 1. Determinare
Università degli studi di Roma Tre Corso di Laurea Triennale in Matematica, a.a. 2004/2005 AL2 - Algebra 2, gruppi anelli e campi Soluzioni 10 dicembre 2004 1 Polinomio minimo e ampliamenti 1. Determinare
M.P. Cavaliere ELEMENTI DI MATEMATICA E LOGICA MATEMATICA DISCRETA STRUTTURE ALGEBRICHE
 M.P. Cavaliere ELEMENTI DI MATEMATICA E LOGICA MATEMATICA DISCRETA STRUTTURE ALGEBRICHE Operazioni in un insieme Sia A un insieme non vuoto; una funzione f : A A A si dice operazione binaria (o semplicemente
M.P. Cavaliere ELEMENTI DI MATEMATICA E LOGICA MATEMATICA DISCRETA STRUTTURE ALGEBRICHE Operazioni in un insieme Sia A un insieme non vuoto; una funzione f : A A A si dice operazione binaria (o semplicemente
Correzione del test d ingresso CLEF-CLEI proposto l 11 settembre 2003
 Correzione del test d ingresso CLEF-CLEI proposto l 11 settembre 2003 Sotto alle domande trovate le risposte corrette e, in testo enfatizzato, alcune considerazioni sulla valutazione del singolo quesito.
Correzione del test d ingresso CLEF-CLEI proposto l 11 settembre 2003 Sotto alle domande trovate le risposte corrette e, in testo enfatizzato, alcune considerazioni sulla valutazione del singolo quesito.
Geometria UNO Il polinomio minimo
 Geometria UNO Il polinomio minimo Corso di Laurea in Matematica Anno Accademico 2013/2014 Alberto Albano 5 marzo 2014 Queste note sono un riassunto delle lezioni di venerdì 8 marzo e martedì 11 marzo.
Geometria UNO Il polinomio minimo Corso di Laurea in Matematica Anno Accademico 2013/2014 Alberto Albano 5 marzo 2014 Queste note sono un riassunto delle lezioni di venerdì 8 marzo e martedì 11 marzo.
Liceo Scientifico Statale S. Cannizzaro Palermo Classe III D EQUAZIONI POLINOMIALI Divisione di polinomi, teorema del resto e teorema di Ruffini
 Divisione di polinomi, teorema del resto e teorema di Ruffini Teorema (della divisione con resto tra due polinomi in una variabile). Dati due polinomi A x e B x, con B x 0, esistono sempre, e sono unici,
Divisione di polinomi, teorema del resto e teorema di Ruffini Teorema (della divisione con resto tra due polinomi in una variabile). Dati due polinomi A x e B x, con B x 0, esistono sempre, e sono unici,
12 gennaio Commenti esame di geometria - Ing. gestionale - a.a
 Questo documento riporta commenti, approfondimenti o metodi di soluzione alternativi per alcuni esercizi dell esame Ovviamente alcuni esercizi potevano essere risolti utilizzando metodi ancora diversi
Questo documento riporta commenti, approfondimenti o metodi di soluzione alternativi per alcuni esercizi dell esame Ovviamente alcuni esercizi potevano essere risolti utilizzando metodi ancora diversi
ALGEBRA C. MALVENUTO
 ALGEBRA CANALE A-L ESAME SECONDA PARTE SECONDO ESONERO 27 GENNAIO 22 C. MALVENUTO Istruzioni. Completare subito la parte inferiore di questa pagina con il proprio nome, cognome e firma. Scrivere solamente
ALGEBRA CANALE A-L ESAME SECONDA PARTE SECONDO ESONERO 27 GENNAIO 22 C. MALVENUTO Istruzioni. Completare subito la parte inferiore di questa pagina con il proprio nome, cognome e firma. Scrivere solamente
Lezione Diagonalizzazione ortogonale per matrici simmetriche
 Lezione 22 22. Diagonalizzazione ortogonale per matrici simmetriche La Proposizione 2. afferma che ogni matrice simmetrica reale è diagonalizzabile su R: ilrisultatoprincipalediquestasezioneèchelamatricechediagonalizzapuò
Lezione 22 22. Diagonalizzazione ortogonale per matrici simmetriche La Proposizione 2. afferma che ogni matrice simmetrica reale è diagonalizzabile su R: ilrisultatoprincipalediquestasezioneèchelamatricechediagonalizzapuò
NOTE DI ALGEBRA LINEARE v = a 1 v a n v n, w = b 1 v b n v n
 NOTE DI ALGEBRA LINEARE 2- MM 9 NOVEMBRE 2 Combinazioni lineari e generatori Sia K un campo e V uno spazio vettoriale su K Siano v,, v n vettori in V Definizione Un vettore v V si dice combinazione lineare
NOTE DI ALGEBRA LINEARE 2- MM 9 NOVEMBRE 2 Combinazioni lineari e generatori Sia K un campo e V uno spazio vettoriale su K Siano v,, v n vettori in V Definizione Un vettore v V si dice combinazione lineare
1 Fattorizzazione di polinomi
 1 Fattorizzazione di polinomi Polinomio: un polinomio di grado n nella variabile x, è dato da p(x) = a n x n + a n 1 x n 1 + + a 1 x + a 0 con a n 0, a 0 è detto termine noto, a k è detto coefficiente
1 Fattorizzazione di polinomi Polinomio: un polinomio di grado n nella variabile x, è dato da p(x) = a n x n + a n 1 x n 1 + + a 1 x + a 0 con a n 0, a 0 è detto termine noto, a k è detto coefficiente
CdL in Ingegneria del Recupero Edilizio ed Ambientale
 CdL in Ingegneria del Recupero Edilizio ed Ambientale Prova scritta di Geometria- 29 Settembre 29 Durata della prova: tre ore. È vietato uscire dall aula prima di aver consegnato definitivamente il compito.
CdL in Ingegneria del Recupero Edilizio ed Ambientale Prova scritta di Geometria- 29 Settembre 29 Durata della prova: tre ore. È vietato uscire dall aula prima di aver consegnato definitivamente il compito.
p(ϕ) = a 0 Id + a 1 ϕ + + a n ϕ n,
 1. Autospazi e autospazi generalizzati Sia ϕ: V V un endomorfismo. Allora l assegnazione x ϕ induce un morfismo di anelli ρ: K[x] End K (V ). Più esplicitamente, al polinomio p dato da viene associato
1. Autospazi e autospazi generalizzati Sia ϕ: V V un endomorfismo. Allora l assegnazione x ϕ induce un morfismo di anelli ρ: K[x] End K (V ). Più esplicitamente, al polinomio p dato da viene associato
Elementi di Algebra e di Matematica Discreta Strutture algebriche: anelli
 Elementi di Algebra e di Matematica Discreta Strutture algebriche: anelli Cristina Turrini UNIMI - 2016/2017 Cristina Turrini (UNIMI - 2016/2017) Elementi di Algebra e di Matematica Discreta 1 / 29 index
Elementi di Algebra e di Matematica Discreta Strutture algebriche: anelli Cristina Turrini UNIMI - 2016/2017 Cristina Turrini (UNIMI - 2016/2017) Elementi di Algebra e di Matematica Discreta 1 / 29 index
c A (a c = b) Le ipotesi che abbiamo ci dicono che esistono h, k A tali che:
 Definizione 1. Dato un insieme A, un operazione su A è una applicazione da A A a valori in A. Definizione 2. Se A è un insieme con una operazione, dati a, b A diciamo che a divide b (e scriviamo a b) se
Definizione 1. Dato un insieme A, un operazione su A è una applicazione da A A a valori in A. Definizione 2. Se A è un insieme con una operazione, dati a, b A diciamo che a divide b (e scriviamo a b) se
0.1 Coordinate in uno spazio vettoriale
 0.. COORDINATE IN UNO SPAZIO VETTORIALE 0. Coordinate in uno spazio vettoriale Sia V uno spazio vettoriale di dimensione finita n costruito sul campo K. D ora in poi, ogni volta che sia fissata una base
0.. COORDINATE IN UNO SPAZIO VETTORIALE 0. Coordinate in uno spazio vettoriale Sia V uno spazio vettoriale di dimensione finita n costruito sul campo K. D ora in poi, ogni volta che sia fissata una base
Per capire meglio il concetto di combinazione lineare prendiamo in considerazione alcuni esempi.
 Lezione 14 14.1 Combinazioni lineari Definizione 14.1. Sia V uno spazio vettoriale su un campo K = R, C esiano v 1,...,v n 2 V vettori fissati. Un vettore v 2 V si dice combinazione lineare di v 1,...,v
Lezione 14 14.1 Combinazioni lineari Definizione 14.1. Sia V uno spazio vettoriale su un campo K = R, C esiano v 1,...,v n 2 V vettori fissati. Un vettore v 2 V si dice combinazione lineare di v 1,...,v
Numeri complessi. Hynek Kovarik. Università di Brescia. Analisi Matematica 1
 Numeri complessi Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) I numeri complessi Analisi Matematica 1 1 / 34 Introduzione L introduzione dei numeri complessi
Numeri complessi Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) I numeri complessi Analisi Matematica 1 1 / 34 Introduzione L introduzione dei numeri complessi
Capitolo 5 Campi finiti
 Capitolo 5 Campi finiti Definizione 5.1. Un campo finito K (cioè composto da un numero finito di elementi) si dice campo di Galois. Il numero dei suoi elementi si dice ordine e si denota con K. Un campo
Capitolo 5 Campi finiti Definizione 5.1. Un campo finito K (cioè composto da un numero finito di elementi) si dice campo di Galois. Il numero dei suoi elementi si dice ordine e si denota con K. Un campo
Corso di Laurea in Fisica. Geometria. a.a Prof. P. Piazza Diagonalizzazione delle forme bilineari simmetriche
 Corso di Laurea in Fisica. Geometria. a.a. 2009-10. Prof. P. Piazza Diagonalizzazione delle forme bilineari simmetriche Sia V uno spazio vettoriale reale. Sia 1. Osservazioni preliminari. : V V R un
Corso di Laurea in Fisica. Geometria. a.a. 2009-10. Prof. P. Piazza Diagonalizzazione delle forme bilineari simmetriche Sia V uno spazio vettoriale reale. Sia 1. Osservazioni preliminari. : V V R un
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI
 CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
Esempio con n = 2. f(x) = x x2 2 x 1x 2
 Forme quadratiche Definizione 40. Una forma quadratica di n variabili è un polinomio omogeneo di grado 2 in n variabili. Si tratta quindi di una funzione f : R n R somma di monomi di grado 2 nelle n variabili.
Forme quadratiche Definizione 40. Una forma quadratica di n variabili è un polinomio omogeneo di grado 2 in n variabili. Si tratta quindi di una funzione f : R n R somma di monomi di grado 2 nelle n variabili.
COMPITO DI ALGEBRA 1 18 giugno 2019
 COMPITO DI ALGEBRA 1 18 giugno 2019 1. (a) Sia G un gruppo di ordine 8 11 19. Dimostrare che G contiene un sottogruppo normale di ordine 11 19. (b) Determinare il mimimo intero n per cui S n contiene un
COMPITO DI ALGEBRA 1 18 giugno 2019 1. (a) Sia G un gruppo di ordine 8 11 19. Dimostrare che G contiene un sottogruppo normale di ordine 11 19. (b) Determinare il mimimo intero n per cui S n contiene un
Giovanna Carnovale. October 18, Divisibilità e massimo comun divisore
 MCD in N e Polinomi Giovanna Carnovale October 18, 2011 1 Divisibilità e massimo comun divisore 1.1 Divisibilità in N In questa sezione introdurremo il concetto di divisibilità e di massimo comun divisore
MCD in N e Polinomi Giovanna Carnovale October 18, 2011 1 Divisibilità e massimo comun divisore 1.1 Divisibilità in N In questa sezione introdurremo il concetto di divisibilità e di massimo comun divisore
Corso di Laurea in Fisica. Geometria 1. a.a Gruppo B. Prof. P. Piazza Soluzioni compito a casa del 17/11/06 B =
 Corso di Laurea in Fisica. Geometria. a.a. 26-7. Gruppo B. Prof. P. Piazza Soluzioni compito a casa del 7//6 Soluzione esercizio. Sia B {e, e 2 } e sia B {v, v 2 }. La matrice B del cambiamento di base
Corso di Laurea in Fisica. Geometria. a.a. 26-7. Gruppo B. Prof. P. Piazza Soluzioni compito a casa del 7//6 Soluzione esercizio. Sia B {e, e 2 } e sia B {v, v 2 }. La matrice B del cambiamento di base
Algebra Lineare ed Elementi di Geometria Corso di Laurea in Matematica Applicata MODULO 1
 Algebra Lineare ed Elementi di Geometria Corso di Laurea in Matematica Applicata MODULO 1 Prof. Lidia Angeleri Anno accademico 2015-2016 1 1 appunti aggiornati in data 14 gennaio 2016 Indice I Gruppi 3
Algebra Lineare ed Elementi di Geometria Corso di Laurea in Matematica Applicata MODULO 1 Prof. Lidia Angeleri Anno accademico 2015-2016 1 1 appunti aggiornati in data 14 gennaio 2016 Indice I Gruppi 3
