Problema del Job Shop
|
|
|
- Brigida Parisi
- 4 anni fa
- Visualizzazioni
Transcript
1 Problema del Job Shop
2 Job Shop n job, m macchine iascun job j è composto da una sequenza di task (t j (),,t j (r j )) ogni task t j (k) deve essere eseguito su una specifica macchina i = m j (k) (richiedendo un tempo p ij ). Tutte le macchine hanno capacità unitaria. Quindi, ad ogni job è associata una sequenza (m j (),,m j (r j )) (con possibili ripetizioni) di macchine, detta instradamento Ogni macchina è dotata di un buffer di ingresso in cui i job possono attendere prima di essere processati Problema: decidere la sequenza di processamento su ciascuna macchina in modo da minimizzare il tempo di completamento di tutti i job (makespan)
3 Esempio job m j () [p m(),j ] [] [] m j () [p m(),j ] [] [] m j () [p m(),j ] [] [] Una soluzione: precede sulla macchina precede sulla macchina 5 7 se precedesse macchina? sulla
4 aso particolare: Flow Shop iascun job j è composto da m task, e tutti i job hanno la stessa sequenza (,,, m) di visita delle macchine J m- m Il buffer di ingresso consente i sorpassi: la sequenza di processamento della macchina i + può essere diversa da quella sulla macchina i. Il numero di soluzioni è pari a (n!) m In assenza di buffer di ingresso (permutation flow shop) il sequenziamento è unico su tutte le macchine e ci sono n! soluzioni
5 Formulazione Grafo disgiuntivo disgiuntiva N = {,..., t } Insieme di tutti i task. Se ogni job visita tutte le macchine esattamente una volta t = nm Sia G = (V, t M ) un grafo orientato costruito come segue. V contiene un vertice per ogni task più due vertici s e z t contiene, per ogni job j, l insieme degli archi associati alla catena dei suoi task più gli archi (s, t j ()) [(t j (r j ), z)] M k=,,m ( k ) in cui k contiene una coppia (disgiuntiva) di archi (t i, t j ) e (t j, t i ) per ogni coppia di task t i, t j da eseguirsi sulla machina k.
6 Lunghezze Esempio degli archi job m j () [p m(),j ] m j () [p m(),j ] m j () [p M(),j ] [] [] [] [] [] [] s 0 0,,,,,, z d ogni arco (t i, t j ) si associa una lunghezza pari alla durata del task t i
7 Esempio Selezione efinizione. Un insieme S k di archi in k che contiene esattamente un elemento per ciascuna coppia disgiuntiva è detto selezione parziale della macchina k. Una selezione S k è aciclica se (il corrispondente grafo parziale) non contiene cicli orientati. Una selezione aciclica S k corrisponde (biunivocamente) ad un sequenziamento delle operazioni sulla macchina k. efinizione. L unione degli insiemi S k, k =,, m è detta selezione completa.
8 Selezioni Esempio complete e cicli L unione di selezioni acicliche può non essere aciclica 0,,, s 0,,, l contrario, nel caso di flow shop, l unione di selezioni acicliche è aciclica Se c è un ciclo la selezione non può corrispondere a schedule ammissibili (provare a costruire uno schedule) z
9 Riformulazione Esempio 0 s 0 Ogni soluzione ammissibile del problema di Job Shop corrisponde biunivocamente ad una selezione completa aciclica Il valore di una soluzione (makespan) è pari alla lunghezza del cammino massimo da s a z,,,,,, z 5 7 Job shop: trovare una selezione completa aciclica che minimizzi la lunghezza del cammino massimo.
10 Variabili decisionali: n j R τ istante di inizio del task j τ n min t i i j j i p τ τ ), ( M k j i p p k j j i i i j τ τ τ τ, ), ( N j j τ 0 Formulazione disgiuntiva
11 Variabili decisionali: x ij = 0 se l arco (i, j) è rimosso, = altrimenti min ( i, j ) P ( i, j ) x x ij x ij + u l ij x ij Formulazione non compatta u, per ogni s z cammino P xij, per ogni ciclo x ji, per ogni coppia disgiuntiva ( i, j) =, ( i, j) ij t {0,}, ( i, j)
12 Esempio: problema dei giornali S G FT E S T E S FT G
13 Soluzione ammissibile S FT G E S T giornale FT Lett. Lett. Lett. Lett. G E S
14 S G FT E 0 0 S 0 T 60 FT 90 G ammino critico E S
15 FT Soluzione non ammissibile S T E S G S E G FT Lett. Lett. Lett. Lett. giornale
16 Soluzione non ammissibile S FT G E S T Osservazione. Se S è aciclica, allora ogni S k è aciclica. Il vice-versa non è vero.
17 Regole di dispatching FFS (First ome First Served): ogni macchina esegue l operazione processabile secondo l ordine di arrivo MWR (Most Work Remaining): fra le operazioni processabili, ogni macchina processa quella con il maggior tempo di processamento residuo (su tutte le macchine rimanenti della sequenza) SPT (Shortest Processing Time): ogni macchina processa l operazione disponibile più breve
18 Esempio: FFS job m j () [p m(),j ] m j () [p m(),j ] m j () [p M(),j ] m j () [p M(),j ] [] [] [] [] [] [5] [6] [] [7] [] t = 0:
19 Esempio: FFS job m j () [p m(),j ] m j () [p m(),j ] m j () [p M(),j ] m j () [p M(),j ] [] [] [] [] [] [5] [6] [] [7] [] t = :
20 Esempio: FFS job m j () [p m(),j ] m j () [p m(),j ] m j () [p M(),j ] m j () [p M(),j ] [] [] [] [] [] [5] [6] [] [7] [] t = : 5 9
21 Esempio: FFS job m j () [p m(),j ] m j () [p m(),j ] m j () [p M(),j ] m j () [p M(),j ] [] [] [] [] [] [5] [6] [] [7] [] t = 5: 5 9
22 Esempio: FFS job m j () [p m(),j ] m j () [p m(),j ] m j () [p M(),j ] m j () [p M(),j ] [] [] [] [] [] [5] [6] [] [7] [] t = 9: 5 9 6
23 Esempio: FFS job m j () [p m(),j ] m j () [p m(),j ] m j () [p M(),j ] m j () [p M(),j ] [] [] [] [] [] [5] [6] [] [7] [] t = : 5 9 6
24 Esempio: FFS job m j () [p m(),j ] m j () [p m(),j ] m j () [p M(),j ] m j () [p M(),j ] [] [] [] [] [] [5] [6] [] [7] [] t = 6:
25 Esempio: FFS job m j () [p m(),j ] m j () [p m(),j ] m j () [p M(),j ] m j () [p M(),j ] [] [] [] [] [] [5] [] [] [7] [] t = :
26 Selezione completa FFS s 0 0,,, 5,,,, z 0 7,,, 7 ammino critico s-(,)-(,)-(,)-(,)-(,)-z di lunghezza 5
27 Ricerca Locale Teorema. Sia S una soluzione ammissibile (selezione completa aciclica) e (i,j) un arco disgiuntivo di un cammino critico del grafo G(S). llora, sostituendo (i,j) con (j,i) si ottiene una nuova selezione completa aciclica (cioè una nuova soluzione ammissibile) Il vicinato di una soluzione S è definito come l insieme delle soluzioni ottenibili scambiando il verso di un arco disgiuntivo appartenente ad un cammino critico. Teorema. Per ogni soluzione S esiste una sequenza finita di mosse che genera una soluzione ottima
28 FFS: soluzione di partenza s 0 0,,, 5,,,, z 0 7,,, 7 ammino critico s-(,)-(,)-(,)-(,)-(,)-z di lunghezza 5 ue possibili mosse: (,)-(,) oppure (,)-(,). La seconda produce una soluzione di costo 7 (provare)
29 mossa : peggiorativa s 0 0,,, 5,,,, z 0 7,,, 7 Scambio arco (,)-(,) di lunghezza con (,)-(,) di lunghezza ammino critico s-(,)-(,)-(,)-(,)-(,)-(,)-z di lunghezza 9
30 mossa s 0 0,,, 7 5,,,, z 0 7,,, 7 Scambio arco (,)-(,) di lunghezza con (,)-(,) di lunghezza 7 ammino critico s-(,)-(,)-(,)-(,)-(,)-z di lunghezza (!!)
31 Soluzione dopo mosse: migliora FFS job m j () [p m(),j ] m j () [p m(),j ] m j () [p M(),j ] m j () [p M(),j ] [] [] [] [] [] [5] [] [] [7] [] t = : 5 9 7
32 Euristica Shifting ottleneck ostruisce una selezione completa aciclica construendo iterativamente selezioni parziali acicliche d ogni passo viene costruita la selezione parziale della macchina più critica (bottleneck) m iterazioni: ad ogni passo, la macchina bottleneck cambia (shifting) Passo generico. Input: M 0 insieme delle macchine già sequenziate. ostruisce il grafo G(M 0 ) fissando l orientamento degli archi associati alle macchine in M 0 ed eliminando gli archi disgiuntivi associati alle macchine in M \ M 0.. alcola la lunghezza max (M 0 ) del cammino critico su G(M 0 ).. Identifica e sequenzia la macchina collo di bottiglia e aggiorna il grafo
33 . eterminazione della macchina collo di bottiglia Ogni iterazione introduce dei nuovi archi nel grafo, quelli della selezione parziale aciclica della macchina collo di bottiglia corrente. Quindi, al procedere dell algoritmo max (M 0 ) aumenta (non diminuisce). Una misura di criticità delle macchine è la seguente: la macchina collo di bottiglia è quella il cui sequenziamento produce il massimo aumento di max (M 0 ) In particolare, per ogni macchina k, si minimizza l aumento massimo del makespan rispetto a max (M 0 ) provocato dal sequenziamento di k
34 . Minimizzazione del massimo ritardo La relazione di precedenza ottenuta fissando le selezioni parziali delle macchine in M 0 implica che, ad ogni task j è associato istante prima del quale j non può iniziare, cioè una release date r j per un certo task j, sia x la lunghezza del percorso critico da S a u in G(M 0 ). llora, con il sequenziamento fissato, j non può iniziare prima di x. s x j z
35 . Minimizzazione del massimo ritardo Per un certo task j, sia y la lunghezza del percorso critico da u a T in G(M 0 ). llora, se si vuole rispettare il makespan corrente max (M 0 ), j non può terminare dopo l istante max (M 0 ) y. s x j y max (M 0 ) z l insieme dei task di una macchina k determina quindi un istanza del problema /r j /L max. efiniamo L max (k) il valore della sua soluzione ottima La macchina k* = argmax (L max (k): k M \ M 0 ) è detta collo di bottiglia
36 . Sequenziamento di k* La macchina collo di bottiglia k* è sequenziata in accordo alla soluzione ottima del problema /r j /L max. M 0 := M 0 {k*}; aggiorna il grafo fissando gli archi di k* ggiorna il valore del cammino critico max (M 0 K*) = max (M 0 ) + L max (k*) (verificare sull esempio)
37 Validità Teorema. Gli archi orientati associati alla soluzione ottima di un problema a macchina singola non creano cicli nel grafo G(M 0 ). onseguenza: la selezione completa ottenuta dalle selezioni acicliche generate nelle singole iterazioni è aciclica.
Problema del Job Shop
 Problema del Job hop Job hop n ob, m macchine iascun ob è composto da una sequenza di task (t (1),,t (r )) ogni task t (k) deve essere eseguito su una specifica macchina i = m (k) (richiedendo un tempo
Problema del Job hop Job hop n ob, m macchine iascun ob è composto da una sequenza di task (t (1),,t (r )) ogni task t (k) deve essere eseguito su una specifica macchina i = m (k) (richiedendo un tempo
Grafo per n/m/g/c max r i =0
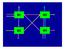 M1 M2 M3 M JOB SHOP SENZA RICIRCOLAZIONE Grafo per n/m/g/c max r i =0 Archi (precedenze) disgiuntivi(macch.) Arco(precedenza) congiuntivo(pezzi) 1,1 2,1 3,1 I 2,2 1,2,2 3,2 F 1,3 2,3,3 Operazione(i,j):
M1 M2 M3 M JOB SHOP SENZA RICIRCOLAZIONE Grafo per n/m/g/c max r i =0 Archi (precedenze) disgiuntivi(macch.) Arco(precedenza) congiuntivo(pezzi) 1,1 2,1 3,1 I 2,2 1,2,2 3,2 F 1,3 2,3,3 Operazione(i,j):
1. Considerazioni generali
 1. Considerazioni generali Modelli di shop scheduling In molti ambienti produttivi l esecuzione di un job richiede l esecuzione non simultanea di un certo numero di operazioni su macchine dedicate. Ogni
1. Considerazioni generali Modelli di shop scheduling In molti ambienti produttivi l esecuzione di un job richiede l esecuzione non simultanea di un certo numero di operazioni su macchine dedicate. Ogni
Parte 3: Gestione dei progetti, Shop scheduling
 Parte : Gestione dei progetti, Shop scheduling Rappresentazione reticolare di un progetto Insieme di attività {,...,n} p i durata (nota e deterministica dell attività i) relazione di precedenza fra attività:
Parte : Gestione dei progetti, Shop scheduling Rappresentazione reticolare di un progetto Insieme di attività {,...,n} p i durata (nota e deterministica dell attività i) relazione di precedenza fra attività:
Organizzazione della produzione
 Scheduling Organizzazione della produzione PRODOTTO che cosa chi ORGANIZZAZIONE PROCESSO come FLUSSO DI PRODUZIONE COORDINAMENTO PIANIFICAZIONE SCHEDULING quando Pianificazione della produzione: schedulazione
Scheduling Organizzazione della produzione PRODOTTO che cosa chi ORGANIZZAZIONE PROCESSO come FLUSSO DI PRODUZIONE COORDINAMENTO PIANIFICAZIONE SCHEDULING quando Pianificazione della produzione: schedulazione
1) Disegnare la rete di progetto con le attività sugli archi, e la rete di progetto con le attività sui nodi.
 Un progetto di ricerca e sviluppo di una società si compone di 12 (principali) attività con precedenze, durate normali b ij (in giorni), costi diretti c ij (in dollari) delle attività alla loro durata
Un progetto di ricerca e sviluppo di una società si compone di 12 (principali) attività con precedenze, durate normali b ij (in giorni), costi diretti c ij (in dollari) delle attività alla loro durata
Organizzazione della produzione
 Scheduling Organizzazione della produzione PRODOTTO che cosa chi ORGANIZZAZIONE PROCESSO come FLUSSO DI PRODUZIONE COORDINAMENTO PIANIFICAZIONE SCHEDULING quando Pianificazione della produzione: schedulazione
Scheduling Organizzazione della produzione PRODOTTO che cosa chi ORGANIZZAZIONE PROCESSO come FLUSSO DI PRODUZIONE COORDINAMENTO PIANIFICAZIONE SCHEDULING quando Pianificazione della produzione: schedulazione
Ricerca per ispezione guidata (Branch and Bound) per min L max con r j 0
 Per esporre il più importante algoritmo per lo scheduling in sistemi ad instradamento differenziato occorre considerare un estensione del min L max Ricerca per ispezione guidata (Branch and Bound) per
Per esporre il più importante algoritmo per lo scheduling in sistemi ad instradamento differenziato occorre considerare un estensione del min L max Ricerca per ispezione guidata (Branch and Bound) per
Makespan con set-up dipendenti dalla sequenza. 1/s jk /C max
 Makespan con set-up dipendenti dalla sequenza 1/s jk /C max 1/s jk /C max Un tempo di riattrezzaggio (set-up) s jk è richiesto fra il processamento di j e quello di k. In questo caso, C max dipende dalla
Makespan con set-up dipendenti dalla sequenza 1/s jk /C max 1/s jk /C max Un tempo di riattrezzaggio (set-up) s jk è richiesto fra il processamento di j e quello di k. In questo caso, C max dipende dalla
Un approccio esatto per il job shop
 Un approccio esatto per il ob shop Riferimenti lezione: rucker, P., Jurisch,. & Sievers,. (994) branch and bound algorithm for the ob scheduling shop problem, Discrete pplied Mathematics, Vol. 49, No.
Un approccio esatto per il ob shop Riferimenti lezione: rucker, P., Jurisch,. & Sievers,. (994) branch and bound algorithm for the ob scheduling shop problem, Discrete pplied Mathematics, Vol. 49, No.
CASE STUDY 2. Fabbricazione dell acciaio. Un problema di pianificazione: Minimizzazione dei costi di carica del forno. Dati. Formulazione del problema
 CASE STUDY 2 Fabbricazione dell acciaio Gestione delle risorse produttive nell industria siderurgica Un problema di pianificazione: Minimizzazione dei costi di carica del forno Magazzini materie prime
CASE STUDY 2 Fabbricazione dell acciaio Gestione delle risorse produttive nell industria siderurgica Un problema di pianificazione: Minimizzazione dei costi di carica del forno Magazzini materie prime
Linea di 4 macchine con buffer
 La soluzione del 2JSP è la generalizzazione di quella data da Aker per 2 lavori J i di m operazioni in serie da eseguire su una linea con buffer intermedi: ciascuno di lunghezza temporale t i sulla macchina
La soluzione del 2JSP è la generalizzazione di quella data da Aker per 2 lavori J i di m operazioni in serie da eseguire su una linea con buffer intermedi: ciascuno di lunghezza temporale t i sulla macchina
Esercitazione: Job shop scheduling con vincoli di processo. 22/12/2010 Ottimizzazione della Logistica
 Esercitazione: ob shop scheduling con vincoli di processo 1 Descrizione del problema di scheduling capacitato Analizziamo una semplice officina meccanica con macchine. l processo tecnologico di un job
Esercitazione: ob shop scheduling con vincoli di processo 1 Descrizione del problema di scheduling capacitato Analizziamo una semplice officina meccanica con macchine. l processo tecnologico di un job
Metodi di Ottimizzazione mod. Modelli per la pianificazione delle attività
 Metodi di Ottimizzazione mod. Modelli per la pianificazione delle attività Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena Metodi di Ottimizzazione mod.
Metodi di Ottimizzazione mod. Modelli per la pianificazione delle attività Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena Metodi di Ottimizzazione mod.
Modelli di Programmazione Lineare. PRTLC - Modelli
 Modelli di Programmazione Lineare PRTLC - Modelli Schema delle esercitazioni Come ricavare la soluzione ottima Modelli Solver Come ricavare una stima dell ottimo Rilassamento continuo - generazione di
Modelli di Programmazione Lineare PRTLC - Modelli Schema delle esercitazioni Come ricavare la soluzione ottima Modelli Solver Come ricavare una stima dell ottimo Rilassamento continuo - generazione di
Tecniche euristiche Ricerca Locale
 Tecniche euristiche Ricerca Locale PRTLC - Ricerca Locale Schema delle esercitazioni Come ricavare la soluzione ottima Modelli Solver commerciali Come ricavare una stima dell ottimo: rilassamenti Rilassamento
Tecniche euristiche Ricerca Locale PRTLC - Ricerca Locale Schema delle esercitazioni Come ricavare la soluzione ottima Modelli Solver commerciali Come ricavare una stima dell ottimo: rilassamenti Rilassamento
1. Considerazioni generali
 1. Considerazioni generali Modelli di shop scheduling In molti ambienti produttivi l esecuzione di un job richiede l esecuzione non simultanea di un certo numero di operazioni su macchine dedicate. Ogni
1. Considerazioni generali Modelli di shop scheduling In molti ambienti produttivi l esecuzione di un job richiede l esecuzione non simultanea di un certo numero di operazioni su macchine dedicate. Ogni
Algoritmo basato su cancellazione di cicli
 Algoritmo basato su cancellazione di cicli Dato un flusso ammissibile iniziale, si costruisce una sequenza di flussi ammissibili di costo decrescente. Ciascun flusso è ottenuto dal precedente flusso ammissibile
Algoritmo basato su cancellazione di cicli Dato un flusso ammissibile iniziale, si costruisce una sequenza di flussi ammissibili di costo decrescente. Ciascun flusso è ottenuto dal precedente flusso ammissibile
Modelli dei Sistemi di Produzione Modelli e Algoritmi della Logistica
 Modelli dei Sistemi di Produzione Modelli e Algoritmi della Logistica 2010-11 Scheduling: Introduzione CARLO MANNINO Sapienza Università di Roma Dipartimento di Informatica e Sistemistica Problemi di scheduling
Modelli dei Sistemi di Produzione Modelli e Algoritmi della Logistica 2010-11 Scheduling: Introduzione CARLO MANNINO Sapienza Università di Roma Dipartimento di Informatica e Sistemistica Problemi di scheduling
3.3 Problemi di PLI facili
 3.3 Problemi di PLI facili Consideriamo un generico problema di PLI espresso in forma standard min{c t x : Ax = b, x Z n +} (1) dove A Z m n con n m, e b Z m. Supponiamo che A sia di rango pieno. Sia P
3.3 Problemi di PLI facili Consideriamo un generico problema di PLI espresso in forma standard min{c t x : Ax = b, x Z n +} (1) dove A Z m n con n m, e b Z m. Supponiamo che A sia di rango pieno. Sia P
Richiami di Teoria dei Grafi. Paolo Detti Dipartimento di Ingegneria dell Informazione Università di Siena
 Richiami di Teoria dei Grafi Paolo Detti Dipartimento di Ingegneria dell Informazione Università di Siena Teoria dei grafi La Teoria dei Grafi costituisce, al pari della Programmazione Matematica, un corpo
Richiami di Teoria dei Grafi Paolo Detti Dipartimento di Ingegneria dell Informazione Università di Siena Teoria dei grafi La Teoria dei Grafi costituisce, al pari della Programmazione Matematica, un corpo
PROBLEMI SU GRAFO (combinatori)
 PROLMI SU GRO (combinatori) In molti problemi il numero di soluzioni ammissibili è finito. Questi problemi sono quasi sempre descritti su grafi. Rete stradale: come andare da a in tempo minimo? Grafo orientato
PROLMI SU GRO (combinatori) In molti problemi il numero di soluzioni ammissibili è finito. Questi problemi sono quasi sempre descritti su grafi. Rete stradale: come andare da a in tempo minimo? Grafo orientato
Programmazione della produzione nei sistemi automatizzati
 Programmazione della produzione nei sistemi automatizzati 1 Programmazione della produzione Pianificazione di lungo periodo: quali prodotti collocare sul mercato (livello strategico) Pianificazione aggregata
Programmazione della produzione nei sistemi automatizzati 1 Programmazione della produzione Pianificazione di lungo periodo: quali prodotti collocare sul mercato (livello strategico) Pianificazione aggregata
Organizzazione della produzione
 Scheduling Organizzazione della produzione PROOTTO che cosa chi ORGNIZZZIONE PROCESSO come FLUSSO I PROUZIONE COORINMENTO PINIFICZIONE SCHEULING quando Pianificazione della produzione: schedulazione di
Scheduling Organizzazione della produzione PROOTTO che cosa chi ORGNIZZZIONE PROCESSO come FLUSSO I PROUZIONE COORINMENTO PINIFICZIONE SCHEULING quando Pianificazione della produzione: schedulazione di
RICERCA OPERATIVA (a.a. 2018/19)
 Secondo appello //9 RICERCA OPERATIVA (a.a. 8/9) Nome: Cognome: Matricola: ) Si consideri il seguente problema di PL: min y + y y y y y = y + y y = y, y, y, y Si verifichi se la soluzione ȳ =,,, sia ottima
Secondo appello //9 RICERCA OPERATIVA (a.a. 8/9) Nome: Cognome: Matricola: ) Si consideri il seguente problema di PL: min y + y y y y y = y + y y = y, y, y, y Si verifichi se la soluzione ȳ =,,, sia ottima
Certificati dei problemi in NP
 Certificati dei problemi in NP La stringa y viene in genere denominata un certificato Un Certificato è una informazione ausiliaria che può essere utilizzata per verificare in tempo polinomiale nella dimensione
Certificati dei problemi in NP La stringa y viene in genere denominata un certificato Un Certificato è una informazione ausiliaria che può essere utilizzata per verificare in tempo polinomiale nella dimensione
Macchine parallele M 1 M 2 M 3 J 1 J 2 LAVORI J 3 J 4
 Macchine parallele M 1 J 1 J 2 LAVORI M 2 J 3 J 4 M 3 Macchine parallele Scheduling su macchine parallele scorrelate R C max Descrizione del problema n lavori devono essere processati da m macchine diverse
Macchine parallele M 1 J 1 J 2 LAVORI M 2 J 3 J 4 M 3 Macchine parallele Scheduling su macchine parallele scorrelate R C max Descrizione del problema n lavori devono essere processati da m macchine diverse
RICERCA OPERATIVA (a.a. 2017/18) Nome: Cognome: Matricola:
 Sesto appello 7/7/8 RICERCA OPERATIVA (a.a. 7/8) Nome: Cognome: Matricola: ) Si risolva il seguente problema di PL applicando l algoritmo del Simplesso Duale, per via algebrica, a partire dalla base B
Sesto appello 7/7/8 RICERCA OPERATIVA (a.a. 7/8) Nome: Cognome: Matricola: ) Si risolva il seguente problema di PL applicando l algoritmo del Simplesso Duale, per via algebrica, a partire dalla base B
Ottimizzazione Combinatoria e Reti (a.a. 2007/08)
 o Appello 6/07/008 Ottimizzazione Combinatoria e Reti (a.a. 007/08) Nome Cognome: Matricola: ) Dopo avere finalmente superato l esame di Ricerca Operativa, Tommaso è pronto per partire in vacanza. Tommaso
o Appello 6/07/008 Ottimizzazione Combinatoria e Reti (a.a. 007/08) Nome Cognome: Matricola: ) Dopo avere finalmente superato l esame di Ricerca Operativa, Tommaso è pronto per partire in vacanza. Tommaso
2.3.5 Pianificazione di progetti
 ..5 Pianificazione di progetti Un progetto è costituito da un insieme di attività i, con i =,..., m, ciascuna di durata d i stima Tra alcune coppie di attività esistono relazioni di precedenza del tipo
..5 Pianificazione di progetti Un progetto è costituito da un insieme di attività i, con i =,..., m, ciascuna di durata d i stima Tra alcune coppie di attività esistono relazioni di precedenza del tipo
Week #9 Assessment. Practice makes perfect... November 23, 2016
 Week #9 Assessment Practice makes perfect... November 23, 2016 Esercizio 1 Un azienda di trasporto deve caricare m camion {1,..., m} in modo da servire giornalmente un dato insieme di clienti. Nei camion
Week #9 Assessment Practice makes perfect... November 23, 2016 Esercizio 1 Un azienda di trasporto deve caricare m camion {1,..., m} in modo da servire giornalmente un dato insieme di clienti. Nei camion
Macchine parallele M 1 M 2 M 3 J 1 J 2 LAVORI J 3 J 4
 Macchine parallele M 1 J 1 J 2 LAVORI M 2 J 3 J 4 M 3 Macchine parallele Scheduling su macchine parallele scorrelate R C max Descrizione del problema n lavori devono essere processati da m macchine diverse
Macchine parallele M 1 J 1 J 2 LAVORI M 2 J 3 J 4 M 3 Macchine parallele Scheduling su macchine parallele scorrelate R C max Descrizione del problema n lavori devono essere processati da m macchine diverse
2.2 Alberi di supporto di costo ottimo
 . Alberi di supporto di costo ottimo Problemi relativi ad alberi hanno numerose applicazioni: progettazione di reti (comunicazione, teleriscaldamento,...) protocolli reti IP memorizzazione compatta di
. Alberi di supporto di costo ottimo Problemi relativi ad alberi hanno numerose applicazioni: progettazione di reti (comunicazione, teleriscaldamento,...) protocolli reti IP memorizzazione compatta di
3 CENNI DI TEORIA DELLA COMPLESSITA COMPUTAZIONALE. E. Amaldi Fondamenti di R.O. Politecnico di Milano 1
 3 CENNI DI TEORIA DELLA COMPLESSITA COMPUTAZIONALE E. Amaldi Fondamenti di R.O. Politecnico di Milano 1 Scopo: Stimare l onere computazionale per risolvere problemi di ottimizzazione e di altra natura
3 CENNI DI TEORIA DELLA COMPLESSITA COMPUTAZIONALE E. Amaldi Fondamenti di R.O. Politecnico di Milano 1 Scopo: Stimare l onere computazionale per risolvere problemi di ottimizzazione e di altra natura
Ottimizzazione nella Gestione dei Progetti - Esercitazione 1: calcolo degli schedule ottimi
 Università degli Studi di Roma La Sapienza Ottimizzazione nella Gestione dei Progetti - Esercitazione : calcolo degli schedule ottimi di FABIO D ANDREAGIOVANNI Dipartimento di Informatica e Sistemistica
Università degli Studi di Roma La Sapienza Ottimizzazione nella Gestione dei Progetti - Esercitazione : calcolo degli schedule ottimi di FABIO D ANDREAGIOVANNI Dipartimento di Informatica e Sistemistica
La Gestione dei Progetti. Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena
 La Gestione dei Progetti Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena Relazioni di precedenze generalizzate Le relazioni di precedenza viste fino ad
La Gestione dei Progetti Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena Relazioni di precedenze generalizzate Le relazioni di precedenza viste fino ad
Le attuali tendenze del mercato
 Minimizzazione del makespan mediante un software di scheduling in un Job Shop ed in un Flexible Flow Shop A partire da una classificazione dell architettura delle linee produttive, viene proposto un caso
Minimizzazione del makespan mediante un software di scheduling in un Job Shop ed in un Flexible Flow Shop A partire da una classificazione dell architettura delle linee produttive, viene proposto un caso
Esame di Ricerca Operativa del 19/07/19. Esercizio 1. (a) Risolvere mediante il metodo del simplesso il seguente problema di programmazione lineare:
 Esame di Ricerca Operativa del /0/ (Cognome) (Nome) (Numero di Matricola) Esercizio. (a) Risolvere mediante il metodo del simplesso il seguente problema di programmazione lineare: max x +x x + x x x x
Esame di Ricerca Operativa del /0/ (Cognome) (Nome) (Numero di Matricola) Esercizio. (a) Risolvere mediante il metodo del simplesso il seguente problema di programmazione lineare: max x +x x + x x x x
Approcci esatti per il job shop
 Approcci esatti per il job shop Riferimenti lezione: Carlier, J. (1982) The one-machine sequencing problem, European Journal of Operational Research, Vol. 11, No. 1, pp. 42-47 Carlier, J. & Pinson, E.
Approcci esatti per il job shop Riferimenti lezione: Carlier, J. (1982) The one-machine sequencing problem, European Journal of Operational Research, Vol. 11, No. 1, pp. 42-47 Carlier, J. & Pinson, E.
2.2 Alberi di supporto di costo ottimo
 . Alberi di supporto di costo ottimo Problemi relativi ad alberi hanno numerose applicazioni: progettazione di reti (comunicazione, teleriscaldamento,...) diffusione di messaggi segreti memorizzazione
. Alberi di supporto di costo ottimo Problemi relativi ad alberi hanno numerose applicazioni: progettazione di reti (comunicazione, teleriscaldamento,...) diffusione di messaggi segreti memorizzazione
Il problema del commesso viaggiatore
 Il problema del commesso viaggiatore Mauro Passacantando Dipartimento di Informatica Largo B. Pontecorvo 3, Pisa mpassacantando@di.unipi.it M. Passacantando TFA 2012/13 - Corso di Ricerca Operativa Università
Il problema del commesso viaggiatore Mauro Passacantando Dipartimento di Informatica Largo B. Pontecorvo 3, Pisa mpassacantando@di.unipi.it M. Passacantando TFA 2012/13 - Corso di Ricerca Operativa Università
Project Scheduling: CPM time analysis
 1. Intoduzione Una volta costruita la rete di progetto AOA (attività sugli archi) G = (N, A) è possibile fare una prima analisi del progetto a partire dalla conoscenza delle durate (tempi di esecuzione)
1. Intoduzione Una volta costruita la rete di progetto AOA (attività sugli archi) G = (N, A) è possibile fare una prima analisi del progetto a partire dalla conoscenza delle durate (tempi di esecuzione)
5 PROGRAMMAZIONE LINEARE INTERA (PLI) E. Amaldi Fondamenti di R.O. Politecnico di Milano 1
 5 PROGRAMMAZIONE LINEARE INTERA (PLI) E. Amaldi Fondamenti di R.O. Politecnico di Milano Programma lineare intero: (PLI) min c T x Ax b x 0 intero Ipotesi: A, b interi La condizione di interezza non è
5 PROGRAMMAZIONE LINEARE INTERA (PLI) E. Amaldi Fondamenti di R.O. Politecnico di Milano Programma lineare intero: (PLI) min c T x Ax b x 0 intero Ipotesi: A, b interi La condizione di interezza non è
Linea monoprodotto con assiemature (modello:pettine): lotto, flusso. Minimo tempo di completamento: pezzo singolo, lotto finito, linea satura
 Linea monoprodotto con assiemature (modello:pettine): lotto, flusso Minimo tempo di completamento: pezzo singolo, lotto finito, linea satura Sistemi di movimentazione PIPELINE In questo tipo di sistemi
Linea monoprodotto con assiemature (modello:pettine): lotto, flusso Minimo tempo di completamento: pezzo singolo, lotto finito, linea satura Sistemi di movimentazione PIPELINE In questo tipo di sistemi
Esame di Ricerca Operativa del 07/06/2019
 Esame di Ricerca Operativa del 0/0/09 (Cognome) (Nome) (Numero di Matricola) Esercizio. (a) Risolvere il seguente problema di programmazione lineare applicando l algoritmo del simplesso duale: min y y
Esame di Ricerca Operativa del 0/0/09 (Cognome) (Nome) (Numero di Matricola) Esercizio. (a) Risolvere il seguente problema di programmazione lineare applicando l algoritmo del simplesso duale: min y y
ASSEGNAMENTO DELLE OPERAZIONI DI TAGLIO NELLA PRODUZIONE DI CAPI DI ABBIGLIAMENTO
 ASSEGNAMENTO DELLE OPERAZIONI DI TAGLIO NELLA PRODUZIONE DI CAPI DI ABBIGLIAMENTO Lo scenario produttivo Una nota azienda produce capi di abbigliamento per l alta moda Ogni capo è costituito da vari pezzi
ASSEGNAMENTO DELLE OPERAZIONI DI TAGLIO NELLA PRODUZIONE DI CAPI DI ABBIGLIAMENTO Lo scenario produttivo Una nota azienda produce capi di abbigliamento per l alta moda Ogni capo è costituito da vari pezzi
Esame di Ricerca Operativa del 20/02/18
 Esame di Ricerca Operativa del //8 (Cognome) (Nome) (Numero di Matricola) Esercizio. (a) Risolvere mediante l algoritmo del simplesso duale il seguente problema di programmazione lineare: min x x +x x
Esame di Ricerca Operativa del //8 (Cognome) (Nome) (Numero di Matricola) Esercizio. (a) Risolvere mediante l algoritmo del simplesso duale il seguente problema di programmazione lineare: min x x +x x
Sistemi Organizzativi
 Sistemi Organizzativi Lezione 12/12/2004 Introduzione al corso e definizioni di base Informazioni generali Pre-requisiti: lassi di complessità Metodi enumerativi: - programmazione dinamica - branch-and-bound
Sistemi Organizzativi Lezione 12/12/2004 Introduzione al corso e definizioni di base Informazioni generali Pre-requisiti: lassi di complessità Metodi enumerativi: - programmazione dinamica - branch-and-bound
5.1 Metodo Branch and Bound
 5. Metodo Branch and Bound Consideriamo un generico problema di ottimizzazione min{ c(x) : x X } Idea: Ricondurre la risoluzione di un problema difficile a quella di sottoproblemi più semplici effettuando
5. Metodo Branch and Bound Consideriamo un generico problema di ottimizzazione min{ c(x) : x X } Idea: Ricondurre la risoluzione di un problema difficile a quella di sottoproblemi più semplici effettuando
2 OTTIMIZZAZIONE SU GRAFI. E. Amaldi Fondamenti di R.O. Politecnico di Milano 1
 2 OTTIMIZZAZIONE SU GRAFI E. Amaldi Fondamenti di R.O. Politecnico di Milano 1 Molti problemi decisionali possono essere formulati utilizzando il linguaggio della teoria dei grafi. Esempi: - problemi di
2 OTTIMIZZAZIONE SU GRAFI E. Amaldi Fondamenti di R.O. Politecnico di Milano 1 Molti problemi decisionali possono essere formulati utilizzando il linguaggio della teoria dei grafi. Esempi: - problemi di
Approcci euristici per il job shop
 Approcci euristici per il job shop Riferimenti lezione: Nowicki, E. & Smutnicki, C. (1996) A fast taboo search algorithm for the job shop problem, Management Science, Vol. 42, No. 6, pp. 797-813 1 Problema
Approcci euristici per il job shop Riferimenti lezione: Nowicki, E. & Smutnicki, C. (1996) A fast taboo search algorithm for the job shop problem, Management Science, Vol. 42, No. 6, pp. 797-813 1 Problema
Introduzione ai grafi
 TFA A048 Anno Accademico 2012-13 Outline Cenni storici sui grafi Nozioni introduttive: cammini, connessione, alberi, cicli Cammini di costo minimo Origini storiche La nascita della teoria dei grafi risale
TFA A048 Anno Accademico 2012-13 Outline Cenni storici sui grafi Nozioni introduttive: cammini, connessione, alberi, cicli Cammini di costo minimo Origini storiche La nascita della teoria dei grafi risale
Parte V: Rilassamento Lagrangiano
 Parte V: Rilassamento Lagrangiano Tecnica Lagrangiana Consideriamo il seguente problema di Programmazione Lineare Intera: P 1 min c T x L I Ax > b Cx > d x > 0, intera in cui A = matrice m x n C = matrice
Parte V: Rilassamento Lagrangiano Tecnica Lagrangiana Consideriamo il seguente problema di Programmazione Lineare Intera: P 1 min c T x L I Ax > b Cx > d x > 0, intera in cui A = matrice m x n C = matrice
Prima prova Intermedia di Ricerca Operativa 2 COMPITO A Esercizio 1 (7 punti): LIFO
 Prima prova Intermedia di Ricerca Operativa 2 COMPITO A 13 novembre 2015 Nome e Cognome Matricola: Esercizio 1 (7 punti): Si consideri il seguente problema di programmazione lineare intera. max 32x 1 +
Prima prova Intermedia di Ricerca Operativa 2 COMPITO A 13 novembre 2015 Nome e Cognome Matricola: Esercizio 1 (7 punti): Si consideri il seguente problema di programmazione lineare intera. max 32x 1 +
RICERCA OPERATIVA (a.a. 2011/12) Nome: Cognome: Matricola:
 5 o Appello 8/0/0 RICERCA OPERATIVA (a.a. 0/) Nome: Cognome: Matricola: ) Si individui un albero dei cammini minimi di radice sul grafo in figura, utilizzando l algoritmo più appropriato dal punto di vista
5 o Appello 8/0/0 RICERCA OPERATIVA (a.a. 0/) Nome: Cognome: Matricola: ) Si individui un albero dei cammini minimi di radice sul grafo in figura, utilizzando l algoritmo più appropriato dal punto di vista
1) Data la seguente istanza di TSP (grafo completo con 5 nodi): c 12 = 52; c 13 = 51; c 14 = 40; c 15 = 53; c 23 = 44;
 1) Data la seguente istanza di TSP (grafo completo con 5 nodi): c 12 = 52; c 13 = 51; c 14 = 40; c 15 = 53; c 23 = 44; c 24 = 15; c 25 = 12; c 34 = 32; c 35 = 55; c 45 = 24 Si calcoli l ottimo duale (formulazione
1) Data la seguente istanza di TSP (grafo completo con 5 nodi): c 12 = 52; c 13 = 51; c 14 = 40; c 15 = 53; c 23 = 44; c 24 = 15; c 25 = 12; c 34 = 32; c 35 = 55; c 45 = 24 Si calcoli l ottimo duale (formulazione
Alberi di copertura. Mauro Passacantando. Dipartimento di Informatica Largo B. Pontecorvo 3, Pisa
 Alberi di copertura Mauro Passacantando Dipartimento di Informatica Largo B. Pontecorvo, Pisa mpassacantando@di.unipi.it M. Passacantando TFA 0/ - Corso di Ricerca Operativa Università di Pisa / 9 Definizioni
Alberi di copertura Mauro Passacantando Dipartimento di Informatica Largo B. Pontecorvo, Pisa mpassacantando@di.unipi.it M. Passacantando TFA 0/ - Corso di Ricerca Operativa Università di Pisa / 9 Definizioni
RICERCA OPERATIVA (a.a. 2016/17) Nome: Cognome: Matricola:
 Secondo appello //0 RICERCA OPERATIVA (a.a. 0/) Nome: Cognome: Matricola: ) Si risolva il seguente problema di PL max x x x x x + x x x per via algebrica, mediante l algoritmo del Simplesso Primale a partire
Secondo appello //0 RICERCA OPERATIVA (a.a. 0/) Nome: Cognome: Matricola: ) Si risolva il seguente problema di PL max x x x x x + x x x per via algebrica, mediante l algoritmo del Simplesso Primale a partire
RICERCA OPERATIVA (a.a. 2008/09) Nome: Cognome: Matricola:
 o Appello /09/009 RICERCA OPERATIVA (a.a. 008/09) Nome: Cognome: Matricola: ) Si applichi l algoritmo di Kruskal per determinare un albero di copertura di costo minimo sul grafo in figura. Per ogni iterazione
o Appello /09/009 RICERCA OPERATIVA (a.a. 008/09) Nome: Cognome: Matricola: ) Si applichi l algoritmo di Kruskal per determinare un albero di copertura di costo minimo sul grafo in figura. Per ogni iterazione
Programmazione della produzione MT MT
 Programmazione della produzione Architettura gerarchica del processo di programmazione M P S livello 1 - livello di fabbrica orizzonte temporale lungo (12-24 mesi) Master Production Schedule n settimane
Programmazione della produzione Architettura gerarchica del processo di programmazione M P S livello 1 - livello di fabbrica orizzonte temporale lungo (12-24 mesi) Master Production Schedule n settimane
Algoritmi euristici. Parte I: metodi classici
 Algoritmi euristici. Parte I: metodi classici Daniele Vigo D.E.I.S. - Università di Bologna dvigo@deis.unibo.it rev. 1.0 - febbraio 2003 Algoritmi Euristici Algoritmi Euristici, Approssimati, Approssimanti
Algoritmi euristici. Parte I: metodi classici Daniele Vigo D.E.I.S. - Università di Bologna dvigo@deis.unibo.it rev. 1.0 - febbraio 2003 Algoritmi Euristici Algoritmi Euristici, Approssimati, Approssimanti
Università Roma Tre - PAS Classe A048 "Matematica Applicata" - Corso di Informatica a.a. 2013/2014
 Università Roma Tre Dipartimento di Matematica e Fisica Percorso Abilitante Speciale Classe A08 Matematica Applicata Corso di Informatica Algoritmi su Grafi Marco Liverani (liverani@mat.uniroma.it) Sommario
Università Roma Tre Dipartimento di Matematica e Fisica Percorso Abilitante Speciale Classe A08 Matematica Applicata Corso di Informatica Algoritmi su Grafi Marco Liverani (liverani@mat.uniroma.it) Sommario
I problemi di scheduling
 I problemi di scheduling ESTRATTO DAL VOLUME Operations Management Modelli e metodi per la logistica II Edizione Autore: Giuseppe Bruno Edizioni Scientifiche Italiane SOMMARIO. I problemi di scheduling
I problemi di scheduling ESTRATTO DAL VOLUME Operations Management Modelli e metodi per la logistica II Edizione Autore: Giuseppe Bruno Edizioni Scientifiche Italiane SOMMARIO. I problemi di scheduling
Esame di Ricerca Operativa del 09/04/2019. (Cognome) (Nome) (Numero di Matricola)
 Esame di Ricerca Operativa del 09/0/09 (Cognome) (Nome) (Numero di Matricola) Esercizio. (a) Risolvere tramite l algoritmo del simplesso il seguente problema di programmazione lineare: max x x x + x x
Esame di Ricerca Operativa del 09/0/09 (Cognome) (Nome) (Numero di Matricola) Esercizio. (a) Risolvere tramite l algoritmo del simplesso il seguente problema di programmazione lineare: max x x x + x x
Grafi (orientati): cammini minimi
 Grafi (orientati): cammini minimi Una breve presentazione Definizioni Sia G=(V,E) un grafo orientato con costi w sugli archi. Il costo di un cammino π= è dato da: Un cammino minimo tra
Grafi (orientati): cammini minimi Una breve presentazione Definizioni Sia G=(V,E) un grafo orientato con costi w sugli archi. Il costo di un cammino π= è dato da: Un cammino minimo tra
Progettazione di Algoritmi
 Corso di laurea in Informatica Prova scritta del: Progettazione di Algoritmi 06/07/2016 Prof. De Prisco Inserire i propri dati nell apposito spazio. Non voltare la finché non sarà dato il via. Dal via
Corso di laurea in Informatica Prova scritta del: Progettazione di Algoritmi 06/07/2016 Prof. De Prisco Inserire i propri dati nell apposito spazio. Non voltare la finché non sarà dato il via. Dal via
2 OTTIMIZZAZIONE SU GRAFI. E. Amaldi Fondamenti di R.O. Politecnico di Milano 1
 2 OTTIMIZZAZIONE SU GRAFI E. Amaldi Fondamenti di R.O. Politecnico di Milano 1 Molti problemi decisionali possono essere formulati utilizzando il linguaggio della teoria dei grafi. Esempi: - problemi di
2 OTTIMIZZAZIONE SU GRAFI E. Amaldi Fondamenti di R.O. Politecnico di Milano 1 Molti problemi decisionali possono essere formulati utilizzando il linguaggio della teoria dei grafi. Esempi: - problemi di
Automazione 12 Febbraio 2018
 Automazione 12 Febbraio 2018 Esercizio 1 Si consideri un sistema di automazione operante a livello di coordinamento per il controllo di un robot pick-and-place (PNP1) così caratterizzato: Task A 1 ) ogni
Automazione 12 Febbraio 2018 Esercizio 1 Si consideri un sistema di automazione operante a livello di coordinamento per il controllo di un robot pick-and-place (PNP1) così caratterizzato: Task A 1 ) ogni
Appunti del corso di Informatica 1 (IN110 Fondamenti) 7 Grafi e alberi: introduzione
 Università di Roma Tre Dipartimento di Matematica e Fisica Corso di Laurea in Matematica Appunti del corso di Informatica (IN0 Fondamenti) Grafi e alberi: introduzione Marco Liverani (liverani@mat.uniroma.it)
Università di Roma Tre Dipartimento di Matematica e Fisica Corso di Laurea in Matematica Appunti del corso di Informatica (IN0 Fondamenti) Grafi e alberi: introduzione Marco Liverani (liverani@mat.uniroma.it)
Gestione della produzione e della supply chain Logistica distributiva
 Gestione della produzione e della supply chain Logistica distributiva Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena Convergenza dell algoritmo Se non
Gestione della produzione e della supply chain Logistica distributiva Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena Convergenza dell algoritmo Se non
Minimo albero di copertura
 apitolo 0 Minimo albero di copertura efinizione 0.. ato un grafo G = (V, E) non orientato e connesso, un albero di copertura di G è un sottoinsieme T E tale che il sottografo (V, T ) è un albero libero.
apitolo 0 Minimo albero di copertura efinizione 0.. ato un grafo G = (V, E) non orientato e connesso, un albero di copertura di G è un sottoinsieme T E tale che il sottografo (V, T ) è un albero libero.
Flusso a Costo Minimo
 Sapienza Università di Roma - Dipartimento di Ingegneria Informatica, Automatica e Gestionale Flusso a Costo Minimo Docente: Renato Bruni bruni@dis.uniroma.it Corso di: Ottimizzazione Combinatoria Dal
Sapienza Università di Roma - Dipartimento di Ingegneria Informatica, Automatica e Gestionale Flusso a Costo Minimo Docente: Renato Bruni bruni@dis.uniroma.it Corso di: Ottimizzazione Combinatoria Dal
Problemi di localizzazione di servizi (Facility Location Problems)
 9. Problemi di Localizzazione di Servizi 1 Problemi di localizzazione di servizi (Facility Location Problems) Dato un insieme di clienti richiedenti una data domanda di merce e dato un insieme di possibili
9. Problemi di Localizzazione di Servizi 1 Problemi di localizzazione di servizi (Facility Location Problems) Dato un insieme di clienti richiedenti una data domanda di merce e dato un insieme di possibili
Problemi di Ottimizzazione
 Problemi di Ottimizzazione Obiettivo: misura della qualità di una soluzione. Vincoli: condizioni che devono essere soddisfatte per ottenere una soluzione ammissibile. Problema di Ottimizzazione: determina
Problemi di Ottimizzazione Obiettivo: misura della qualità di una soluzione. Vincoli: condizioni che devono essere soddisfatte per ottenere una soluzione ammissibile. Problema di Ottimizzazione: determina
Programmazione Lineare Intera: Piani di Taglio
 Programmazione Lineare Intera: Piani di Taglio Andrea Scozzari a.a. 2014-2015 April 22, 2015 Andrea Scozzari (a.a. 2014-2015) Programmazione Lineare Intera: Piani di Taglio April 22, 2015 1 / 23 Programmazione
Programmazione Lineare Intera: Piani di Taglio Andrea Scozzari a.a. 2014-2015 April 22, 2015 Andrea Scozzari (a.a. 2014-2015) Programmazione Lineare Intera: Piani di Taglio April 22, 2015 1 / 23 Programmazione
1. Classificazione delle risorse
 1. Classificazione delle risorse Classificazione delle risorse in base alla disponibilità. - Risorse rinnovabili Sono risorse utilizzate per l esecuzione di una attività per tutta la sua durata, ma sono
1. Classificazione delle risorse Classificazione delle risorse in base alla disponibilità. - Risorse rinnovabili Sono risorse utilizzate per l esecuzione di una attività per tutta la sua durata, ma sono
1 TEORIA DELLE RETI 1. 1 Teoria delle reti. 1.1 Grafi
 1 TEORIA DELLE RETI 1 1 Teoria delle reti 1.1 Grafi Intuitivamente un grafo è un insieme finito di punti (nodi o vertici) ed un insieme di frecce (archi) che uniscono coppie di punti Il verso della freccia
1 TEORIA DELLE RETI 1 1 Teoria delle reti 1.1 Grafi Intuitivamente un grafo è un insieme finito di punti (nodi o vertici) ed un insieme di frecce (archi) che uniscono coppie di punti Il verso della freccia
BOLLETTINO UNIONE MATEMATICA ITALIANA
 BOLLETTINO UNIONE MATEMATICA ITALIANA Sezione A La Matematica nella Società e nella Cultura Marco Pranzo Algoritmi ed applicazioni per problemi di job shop scheduling complessi Bollettino dell Unione Matematica
BOLLETTINO UNIONE MATEMATICA ITALIANA Sezione A La Matematica nella Società e nella Cultura Marco Pranzo Algoritmi ed applicazioni per problemi di job shop scheduling complessi Bollettino dell Unione Matematica
Capitolo 3: Ottimizzazione Discreta. E. Amaldi DEI, Politecnico di Milano
 Capitolo 3: Ottimizzazione Discreta E. Amaldi DEI, Politecnico di Milano 3.1 Modelli di PLI e PLMI Moltissimi problemi decisionali complessi possono essere formulati come problemi di Programmazione Lineare
Capitolo 3: Ottimizzazione Discreta E. Amaldi DEI, Politecnico di Milano 3.1 Modelli di PLI e PLMI Moltissimi problemi decisionali complessi possono essere formulati come problemi di Programmazione Lineare
RICERCA OPERATIVA (a.a. 2015/16) Nome: Cognome: Matricola:
 o Appello 8// RICERCA OPERATIVA (a.a. /) Nome: Cognome: Matricola: ) Si risolva il seguente problema di PL max x x x x x x + x x per via algebrica, mediante l algoritmo del Simplesso Primale a partire
o Appello 8// RICERCA OPERATIVA (a.a. /) Nome: Cognome: Matricola: ) Si risolva il seguente problema di PL max x x x x x x + x x per via algebrica, mediante l algoritmo del Simplesso Primale a partire
Gestione dello Stallo
 Gestione dello Stallo Il problema dello stallo Un insieme di processi bloccati ognuno in possesso di una risorsa ed in attesa di acquisire una risorsa posseduta da un altro processo (nell'insieme). Esempio
Gestione dello Stallo Il problema dello stallo Un insieme di processi bloccati ognuno in possesso di una risorsa ed in attesa di acquisire una risorsa posseduta da un altro processo (nell'insieme). Esempio
Processi di cost management - Programmazione multiperiodale
 Processi di cost management - Programmazione multiperiodale Queste slide (scrte da Carlo Mannino) riguardano il problema di gestione delle attivà di un progetto allorché i costi di esecuzione sono legati
Processi di cost management - Programmazione multiperiodale Queste slide (scrte da Carlo Mannino) riguardano il problema di gestione delle attivà di un progetto allorché i costi di esecuzione sono legati
Quinto appello 27/6/ = 4. B b B = 2 b N = 4
 Quinto appello // RICERCA OPERATIVA (a.a. /) Nome: Cognome: Matricola: ) Si risolva il problema di PL dato applicando l algoritmo del Simplesso Duale, per via algebrica, a partire dalla base B {, }. Per
Quinto appello // RICERCA OPERATIVA (a.a. /) Nome: Cognome: Matricola: ) Si risolva il problema di PL dato applicando l algoritmo del Simplesso Duale, per via algebrica, a partire dalla base B {, }. Per
RICERCA OPERATIVA (a.a. 2015/16) Nome: Cognome: Matricola:
 o Appello // RICERCA OPERATIVA (a.a. /) Nome: Cognome: Matricola: ) Si consideri il seguente problema di PL: max x + x x x x x x + x x Si applichi l algoritmo del Simplesso Duale, per via algebrica, a
o Appello // RICERCA OPERATIVA (a.a. /) Nome: Cognome: Matricola: ) Si consideri il seguente problema di PL: max x + x x x x x x + x x Si applichi l algoritmo del Simplesso Duale, per via algebrica, a
I Appello Ricerca Operativa 2 bis Compito A
 I Appello Ricerca Operativa 2 bis Compito A Cognome e nome:. Esercizio 1. Si consideri il problema del matching di cardinalità massima in un grafo G ed il suo problema di decisione associato: esiste un
I Appello Ricerca Operativa 2 bis Compito A Cognome e nome:. Esercizio 1. Si consideri il problema del matching di cardinalità massima in un grafo G ed il suo problema di decisione associato: esiste un
RICERCA OPERATIVA (a.a. 2016/17) Nome: Cognome: Matricola:
 Sesto appello // RICERCA OPERATIVA (a.a. /) Nome: Cognome: Matricola: ) Si risolva il seguente problema di PL max x x x x x x + x x per via algebrica, mediante l algoritmo del Simplesso Primale a partire
Sesto appello // RICERCA OPERATIVA (a.a. /) Nome: Cognome: Matricola: ) Si risolva il seguente problema di PL max x x x x x x + x x per via algebrica, mediante l algoritmo del Simplesso Primale a partire
PROBLEMA DEI CAMMINI MINIMI [CORMEN ET AL. CAP. 24] Il costo di cammino minimo da un vertice u ad un vertice v è definito nel seguente modo:
![PROBLEMA DEI CAMMINI MINIMI [CORMEN ET AL. CAP. 24] Il costo di cammino minimo da un vertice u ad un vertice v è definito nel seguente modo: PROBLEMA DEI CAMMINI MINIMI [CORMEN ET AL. CAP. 24] Il costo di cammino minimo da un vertice u ad un vertice v è definito nel seguente modo:](/thumbs/95/123186961.jpg) PROBLEMA DEI CAMMINI MINIMI [CORMEN ET AL. CAP. 24] Sia G = (V,E) un grafo orientato ai cui archi è associato un costo W(u,v). Il costo di un cammino p = (v 1,v 2,...,v k ) è la somma dei costi degli archi
PROBLEMA DEI CAMMINI MINIMI [CORMEN ET AL. CAP. 24] Sia G = (V,E) un grafo orientato ai cui archi è associato un costo W(u,v). Il costo di un cammino p = (v 1,v 2,...,v k ) è la somma dei costi degli archi
A-2 a PI. Esercizio 2. Domanda 3
 A-2 a PI Ricerca Operativa 1 Seconda prova intermedia È dato il problema di PL in figura. 1. Facendo uso delle condizioni di ortogonalità, dimostrare o confutare l ottimalità della soluzione x = 1; x =
A-2 a PI Ricerca Operativa 1 Seconda prova intermedia È dato il problema di PL in figura. 1. Facendo uso delle condizioni di ortogonalità, dimostrare o confutare l ottimalità della soluzione x = 1; x =
ALGORITMI DI OTTIMIZZAZIONE M Esercizi Parte I
 ALGORITMI DI OTTIMIZZAZIONE M Esercizi Parte I Esercizio 1 Dati n oggetti ed un contenitore, ad ogni oggetto j (j = 1,, n) sono associati un peso p j ed un costo c j (con p j e c j interi positivi). Si
ALGORITMI DI OTTIMIZZAZIONE M Esercizi Parte I Esercizio 1 Dati n oggetti ed un contenitore, ad ogni oggetto j (j = 1,, n) sono associati un peso p j ed un costo c j (con p j e c j interi positivi). Si
Problema di flusso massimo
 p. 1/5 Problema di flusso massimo Si consideri una rete, ovvero un grafo orientato G = (V,A). Attraverso tale rete si fa viaggiare quello che chiameremo genericamente un flusso di "prodotto". A seconda
p. 1/5 Problema di flusso massimo Si consideri una rete, ovvero un grafo orientato G = (V,A). Attraverso tale rete si fa viaggiare quello che chiameremo genericamente un flusso di "prodotto". A seconda
Algoritmi e strutture dati
 Algoritmi e Strutture Dati Cammini minimi Definizioni Sia G = (V,E) un grafo orientato pesato sugli archi. Il costo di un cammino π = è dato da: Un cammino minimo tra una coppia di
Algoritmi e Strutture Dati Cammini minimi Definizioni Sia G = (V,E) un grafo orientato pesato sugli archi. Il costo di un cammino π = è dato da: Un cammino minimo tra una coppia di
Esercitazione 6 Algorithmi e Strutture Dati (Informatica) A.A 2015/2016
 Esercitazione 6 Algorithmi e Strutture Dati (Informatica) A.A 2015/2016 Tong Liu April 14, 2016 Elementi Fondamentali Rappresentazione n = V numero di vertici (nodi) m = E numero di archi Matrice di adiacenza:
Esercitazione 6 Algorithmi e Strutture Dati (Informatica) A.A 2015/2016 Tong Liu April 14, 2016 Elementi Fondamentali Rappresentazione n = V numero di vertici (nodi) m = E numero di archi Matrice di adiacenza:
Esame di Ricerca Operativa - 18 aprile 2007 Facoltà di Ingegneria - Udine - CORREZIONE -
 Esame di Ricerca Operativa - 18 aprile 007 Facoltà di Ingegneria - Udine - CORREZIONE - Problema 1 (4 punti): Una raffineria miscela 4 tipi di petrolio greggio in diverse proporzioni per ottenere 3 diversi
Esame di Ricerca Operativa - 18 aprile 007 Facoltà di Ingegneria - Udine - CORREZIONE - Problema 1 (4 punti): Una raffineria miscela 4 tipi di petrolio greggio in diverse proporzioni per ottenere 3 diversi
ESERCIZIO 1: Punto 1
 ESERCIZIO : Punto La seguente matrice è una matrice delle distanze di un istanza del problema del Commesso Viaggiatore. - - - - - - - Calcolare.Il valore del rilassamento che si ottiene determinando l
ESERCIZIO : Punto La seguente matrice è una matrice delle distanze di un istanza del problema del Commesso Viaggiatore. - - - - - - - Calcolare.Il valore del rilassamento che si ottiene determinando l
Modelli di processi produttivi. Livello: operativo, decisionale, di controllo
 Modelli di processi produttivi Livello: operativo, decisionale, di controllo Produzione discreta: classificazione storica Dal punto di vista storico i sistemi di produzione discreta sono stati classificati
Modelli di processi produttivi Livello: operativo, decisionale, di controllo Produzione discreta: classificazione storica Dal punto di vista storico i sistemi di produzione discreta sono stati classificati
Algoritmi e Strutture Dati (Mod. B) Algoritmi su grafi Ricerca in profondità (Depth-First Search) Parte II
 Algoritmi e Strutture Dati (Mod. B) Algoritmi su grafi Ricerca in profondità (Depth-First Search) Parte II Classificazione digli archi Sia G la foresta DF generata da DFS sul grafo G. Arco d albero: gli
Algoritmi e Strutture Dati (Mod. B) Algoritmi su grafi Ricerca in profondità (Depth-First Search) Parte II Classificazione digli archi Sia G la foresta DF generata da DFS sul grafo G. Arco d albero: gli
