Problemi algoritmici e Complessità degli algoritmi
|
|
|
- Costanza Marchetti
- 8 anni fa
- Просмотров:
Транскрипт
1 Problemi algoritmici e Complessità degli algoritmi Università degli Studi di Salerno Corso di Laurea in Scienze della comunicazione Informatica generale Docente: Angela Peduto A.A. 2005/2006 Problemi algoritmici! Ma quali sono i tipi di problemi che possono essere risolti tramite un algoritmo ( Problemi algoritmici )?! Un problema algoritmico è caratterizzato dalla conoscenza precisa di due elementi:! L insieme degli input ammissibili! L insieme degli output desiderati in funzione degli input! Un problema algoritmico applicato ad un particolare input è detto istanza del problema 2 1
2 Algoritmi computazionali! Input: prevalentemente numerici! Output: numerici, come risultato di elaborazioni computazionali sugli stessi input o da loro determinate! Esempio num. 1! Input: due numeri interi a e b! Output: il numero intero a*b 2! Esempio num. 2! Input: due numeri interi J e K! Output: La somma di tutti gli interi da J e K! Nota: il numero di somme da effettuare (e quindi la durata dell algoritmo) non è nota a priori (come per il caso precedente), ma la si conosce solo al momento dell esecuzione dell algoritmo 3 Algoritmi decisionali (1)! Input: qualsiasi! Output: Valore SI se una certa proprietà dei dati input è verificata, NO altrimenti! Esempio num. 3! Input: un numero intero positivo, K! Output: SI se K è primo NO altrimenti! Nota: l algoritmo prevede certamente e l esecuzione di calcoli, ma il risultato non è numerico 4 2
3 Algoritmi decisionali (2)! Esempio num. 4 (commesso viaggiatore versione decisionale)! Input: Carta stradale con n città collegate da strade di cui si conosce la lunghezza e un numero intero K! Output: SI se esiste un itinerario di lunghezza massima pari a K che tocca tutte le città. NO altrimenti (cioè non esiste oppure tutti gli itinerari sono più lunghi di K chilometri) 5 Algoritmi di riorganizzazione dei dati! Input: qualsiasi lista di dati omogenei (parole, numeri, date, )! Output: stessa lista con gli elementi riorganizzati in base a determinate priorità! Esempio num. 5 (ordinamento)! Input: una lista di parole! Output: lista in ordine alfabetico! Nota: il problema è di tipo non numerico e presenta un numero di elementi input che è noto solo al momento dell esecuzione dell algoritmo o addirittura solo al suo termine. 6 3
4 Algoritmi di ricerca (1)! Input: due liste di dati omogenei (parole, numeri, date, ). La seconda lista può consistere anche di un solo elemento! Output: Elenco delle strutture comuni alle due liste! Esempio num. 6 (ricerca)! Input: Un testo e una singola parola (detta pattern)! Output: Tutte le occorrenze del pattern! Nota: Il problema è di tipo non numerico e presenta un numero di elementi input che è noto solo al momento dell esecuzione dell algoritmo o addirittura solo al suo termine 7 Algoritmi di ricerca (2)! Esempio num. 7 (String matching)! Input: Un testo e un dizionario! Output: Tutte le occorrenze delle parole del dizionario nel testo! Note: il problema è di tipo non numerico e presenta un numero di elementi input che è noto solo al momento dell esecuzione dell algoritmo o addirittura solo al suo termine. Inoltre devono essere individuate anche parole parzialmente sovrapposte. Spesso si vuole conoscere anche la frequenza delle occorrenze delle singole parole. 8 4
5 Algoritmi di ricerca (2)! Esempio num. 8 (Calcolo del massimo o del minimo)! Input: Una lista di oggetti omogenei (parole, numeri, )! Output: l elemento più grande o quello più piccolo! Nota: Il problema presenta un numero di elementi input che è noto solo al momento dell esecuzione dell algoritmo o addirittura solo al suo termine. Esso può riguardare un insieme di parole, come un insieme di numeri che, per esempio, rappresentano l età di un gruppo di persone di cui si vuole conoscere la più anziana o la più giovane 9 Algoritmi di ottimizzazione (1)! Input: un insieme di elementi omogenei di tipo qualsiasi purché sia loro associata una funzione di costo (o di misura). Il problema può presentare dei vincoli sulle modalità di raggruppamento o di organizzazione dei dati! Output: Riorganizzazione dei dati input in modo da ottimizzare la funzione di costo! Esempio num. 9 (commesso viaggiatore versione ottimizzazione)! Input: carta stradale con n città collegate da strade di cui si conosce la lunghezza e due città fissate, A e B! Output: il tragitto più breve che unisca A e B 10 5
6 Algoritmi di ottimizzazione (2)! Esempio num. 10 (Bin Packing versione monodimensionale)! Input: una lista di oggetti omogenei (pacchetti) a cui è associata una misura, espressa da un numero reale compreso tra 0 e 1 e un insieme di contenitori (Bin) tutti della stessa capacità (pari ad 1).! Output: Raggruppamento dei pacchetti in modo da utilizzare il minor numero di bins.! Nota: Il problema trova moltissime applicazioni! Distribuzione di spot pubblicitari all interno di trasmissioni TV! Taglio di elementi da nastro trasportatore! Ottimizzazione del carico di una flotta di camion! Distribuzione di brani musicali su un insieme di CD! Distribuzione dei processi a un sistema multiprocessoe! Algoritmi di Bin Packing sono attualmente utilizzati per la allocazione della RAM in un sistema multiprogrammato 11 Un problema due algoritmi! Si vuole calcolare la somma dei primi 100 numeri interi positivi, cioè la somma ! Algoritmo diretto (detto di forza bruta) Var x, somma integer; begin somma:=0; x:=0; while x < 100 do begin x:= x+1; somma:=somma+x; end; write(somma); end. 12 6
7 Un problema e due algoritmi (2)! Oppure utiliziamo la formula di Gauss secondo la quale =(100*101)/2 e diamone l algoritmo var somma: integer; begin somma:=(100*101)/2; write(somma); end! Quindi questo è un problema computazionale che ammette più di un algoritmo 13 Un problema e due algoritmi (2)! Generalizzando l algoritmo per la somma dei primi N numeri interi positivi var N, x, somma: integer; begin 1. read(n); 2. Somma:=0; 3. x:=0; 4. while x < N do begin 5. x:=x+1; 6. somma:=somma+x; end; 7. Write(somma); 14 7
8 Un problema e due algoritmi (3)! Formula di Gauss: N=(N*(N+1))/2 Var N, somma: integer; begin 1. Read (N); 2. Somma:=(N*(N+1))/2; 3. Write(somma); End. 15 Quante operazioni sono richieste da ciascun algoritmo?! Il primo algoritmo richiede:! 1 operazione di lettura dell input (istruzione1),! 2 operazioni di inizializzazione (istruzioni 2 e 3),! N confronti (confronto nell istruzione 4, ripetuto N volte),! 2*N somme (istruzioni 5 e 6 ripetute N volte l una)! 1 operazione finale di stampa del risultato (istruzione 7) 16 8
9 Quante operazioni sono richieste da ciascun algoritmo? (2)! Per cui il primo algoritmo! Per N=100 richiede complessivamente =304 operazioni! Per N=200 richiede complessivamente =604 operazioni, cioè quasi il doppio delle operazioni richieste per N=100! Si noti che il numero delle operazioni che esegue il primo algoritmo è di fatto proporzionale al valore N letto in input 17 Quante operazioni sono richieste da ciascun algoritmo? (3)! Il secondo algoritmo richiede:! 1 operazione iniziale di lettura dell input (istruzione 1)! 3 operazioni aritmetiche: una somma, una moltiplicazione e una divisione (istruzione 2)! 1 operazione finale di stampa del risultato (istruzione 3)! Si noti che il numero delle operazioni che esegue il primo algoritmo è di fatto proporzionale al valore N letto in input 18 9
10 Quante operazioni sono richieste da ciascun algoritmo? (3)! Il secondo algoritmo richiede:! 1 operazione iniziale di lettura dell input (istruzione 1)! 3 operazioni aritmetiche: una somma, una moltiplicazione ed una divisione (istruzione 2)! 1 operazione finale di stampa del risultato (istruzione 3)! Si noti che il numero delle operazioni che esegue il secondo algoritmo è indipendente dal valore N letto in input! Anzi esso esegue sempre lo stesso numero di operazioni 19 Confronto tra algoritmi per lo stesso problema! Diremo allora che:! Il primo algoritmo ha un tempo di esecuzione proporzionale al numero di addendi da sommare! Il secondo algoritmo ha un tempo di esecuzione costante! Il primo algoritmo è quindi più costoso in termini di numero di operazioni rispetto al secondo! Inoltre il primo algoritmo è tanto più costoso quanto più è grande il numero N in input! Il secondo algoritmo ha un tempo di esecuzione che è indipendente dal valore di N! quindi la differenza tra i due algoritmi è tanto più a vantaggio del secondo quanto più grande è N 20 10
11 Criteri di valutazione degli algoritmi! Valutazione quantitativa di un algoritmo! Dipendente dalla dimensione dei dati di input! Intuitivamente ci aspettiamo che un algoritmo che elabora dati input sia più lento dello stesso algoritmo quando elabora di dati input! Indipendentemente dalla velocità del singolo computer sul quale l algoritmo verrà implementato! Vogliamo sapere quanto è veloce una soluzione, non quanti millisecondi impiega sul mio computer anche perché questo valore cambia da computer a computer e dipende, sullo stesso computer, da altri fattori contingenti quale ad esempio il carico globale del sistema.! Vogliamo una valutazione parametrica della velocità dell algoritmo, legata solo al numero di operazioni che esso effettua 21 Criteri di valutazione degli algoritmi (2)! La teoria degli algoritmi mette effettivamente a disposizione un insieme di strumenti per poter valutare un algoritmo in base ai seguenti criteri valutativi:! Il tempo di esecuzione espresso in termini del numero di operazioni elementari che esso fa sui dati input, mettendosi nella ipotesi del caso peggiore (Worst Case Analysis)! Lo spazio di memoria occupato come il numero massimo di dati elementari che esso ha bisogno di vedere contemporaneamente durante la computazione, mettendosi nell ipotesi del caso peggiore (Worst Case Analysis) 22 11
12 Criteri di valutazione degli algoritmi (3)! Il numero di operazioni elementari dipende dall algoritmo e non dalla velocità del singolo computer quindi ci si svincola dai valori tecnologici prestazionali del singolo computer! Il tempo effettivo di esecuzione dell algoritmo dipende poi dal tempo che il singolo computer impiega per eseguire tali operazioni elementari 23 Il caso peggiore! La legge di Muphy Se c è una possibilità che qualcosa possa andare male, allora è certo che andrà male! Il caso migliore spesso non è significativo! In situazioni pratiche, dobbiamo garantirci che la computazione termini comunque entro un tempo massimo, e questo è possibile valutarlo solo considerando la situazione più sfortunata (e quindi più lenta) possibile.! (es. per andare ad A a B con e senza traffico ) 24 12
13 Il caso peggiore (2)! Nelle prossime lezioni vedremo il caso si due algoritmi per la ricerca in un o schedario con di schede! Caso migliore entrambi: 1 operazione! Caso peggiore del primo: di operazioni! Caso peggiore: 30 operazioni 25 Criteri qualitativi! Sono requisiti qualitativi di un algoritmo (molto meno importanti di quelli quantitativi )! Adattabilità dell algoritmo a soluzioni diverse! Semplicità! Modularità! Eleganza 26 13
Diagramma a blocchi per la selezione, in un mazzo di chiavi, di quella che apre un lucchetto
 Diagramma a blocchi per la selezione, in un mazzo di chiavi, di quella che apre un lucchetto 14 1. Dato un numero dire se è positivo o negativo 2. e se il numero fosse nullo? 3. Eseguire il prodotto tra
Diagramma a blocchi per la selezione, in un mazzo di chiavi, di quella che apre un lucchetto 14 1. Dato un numero dire se è positivo o negativo 2. e se il numero fosse nullo? 3. Eseguire il prodotto tra
Studio degli algoritmi
 COMPLESSITÀ COMPUTAZIONALE DEGLI ALGORITMI Fondamenti di Informatica a.a.2006/07 Prof. V.L. Plantamura Dott.ssa A. Angelini Studio degli algoritmi Dato un problema P, le problematiche riguardano: Sintesi
COMPLESSITÀ COMPUTAZIONALE DEGLI ALGORITMI Fondamenti di Informatica a.a.2006/07 Prof. V.L. Plantamura Dott.ssa A. Angelini Studio degli algoritmi Dato un problema P, le problematiche riguardano: Sintesi
COMPLESSITÀ COMPUTAZIONALE DEGLI ALGORITMI
 COMPLESSITÀ COMPUTAZIONALE DEGLI ALGORITMI Fondamenti di Informatica a.a.200.2005/06 Prof. V.L. Plantamura Dott.ssa A. Angelini Confronto di algoritmi Uno stesso problema può essere risolto in modi diversi,
COMPLESSITÀ COMPUTAZIONALE DEGLI ALGORITMI Fondamenti di Informatica a.a.200.2005/06 Prof. V.L. Plantamura Dott.ssa A. Angelini Confronto di algoritmi Uno stesso problema può essere risolto in modi diversi,
Come ragiona il computer. Problemi e algoritmi
 Come ragiona il computer Problemi e algoritmi Il problema Abbiamo un problema quando ci poniamo un obiettivo da raggiungere e per raggiungerlo dobbiamo mettere a punto una strategia Per risolvere il problema
Come ragiona il computer Problemi e algoritmi Il problema Abbiamo un problema quando ci poniamo un obiettivo da raggiungere e per raggiungerlo dobbiamo mettere a punto una strategia Per risolvere il problema
Un esempio per iniziare. Il controllo del programma in C. Altri cenni su printf() Esercizi (printf) printf( 8!=%d, fatt);
 Un esempio per iniziare Il controllo del programma in C DD Cap.3 pp.91-130 /* calcolo di 8!*/ #include #define C 8 int main() int i=1; int fatt=1; while (i
Un esempio per iniziare Il controllo del programma in C DD Cap.3 pp.91-130 /* calcolo di 8!*/ #include #define C 8 int main() int i=1; int fatt=1; while (i
Un esempio di calcolo di complessità: insertion sort
 Un esempio di calcolo di complessità: insertion sort Vediamo su un esempio come si può calcolare la complessità di un algoritmo... L esempio è un metodo semplice per ordinare arrays: insertion sort, o
Un esempio di calcolo di complessità: insertion sort Vediamo su un esempio come si può calcolare la complessità di un algoritmo... L esempio è un metodo semplice per ordinare arrays: insertion sort, o
Fortran in pillole : prima parte
 Fortran in pillole : prima parte Annamaria Mazzia Dipartimento di Metodi e Modelli Matematici per le Scienze Applicate Corso di Metodi Numerici per l Ingegneria Introduzione al Fortran Un libro consigliato
Fortran in pillole : prima parte Annamaria Mazzia Dipartimento di Metodi e Modelli Matematici per le Scienze Applicate Corso di Metodi Numerici per l Ingegneria Introduzione al Fortran Un libro consigliato
Algoritmi di ricerca. Per ricerca si intende qui il procedimento di localizzare una particolare informazione in un elenco di dati.
 E. Calabrese: Fondamenti di Informatica Algoritmi-1 Algoritmi di ricerca Per ricerca si intende qui il procedimento di localizzare una particolare informazione in un elenco di dati. Per esempio: - cercare
E. Calabrese: Fondamenti di Informatica Algoritmi-1 Algoritmi di ricerca Per ricerca si intende qui il procedimento di localizzare una particolare informazione in un elenco di dati. Per esempio: - cercare
LABORATORIO DI INFORMATICA
 LABORATORIO DI INFORMATICA Corso di laurea in Scienze della Formazione Primaria a.a.2014/2015 A cura del Prof. Sergio Miranda 2 LEZIONE N.6 Algoritmi GLI ALGORITMI (1/5) Un algoritmo è una sequenza di
LABORATORIO DI INFORMATICA Corso di laurea in Scienze della Formazione Primaria a.a.2014/2015 A cura del Prof. Sergio Miranda 2 LEZIONE N.6 Algoritmi GLI ALGORITMI (1/5) Un algoritmo è una sequenza di
Elaborazione dell informazione
 Elaborazione dell informazione Primo esempio Ricominciamo dai numeri (45 + 25) è definita rigorosamente Un primo calcolatore (a) Figura 1.1 Configurazione del pallottoliere (a) prima e (b) dopo l esecuzione
Elaborazione dell informazione Primo esempio Ricominciamo dai numeri (45 + 25) è definita rigorosamente Un primo calcolatore (a) Figura 1.1 Configurazione del pallottoliere (a) prima e (b) dopo l esecuzione
Definizione FONDAMENTI DI INFORMATICA. Esempio di algoritmo: determinare il maggiore di due numeri interi x, y. Proprietà degli algoritmi
 Università degli Studi di Cagliari Corsi di Laurea in Ingegneria Chimica e Ingegneria Meccanica FONDAMENTI DI INFORMATICA http://www.diee.unica.it/~marcialis/fi A.A. 201/2017 Docente: Gian Luca Marcialis
Università degli Studi di Cagliari Corsi di Laurea in Ingegneria Chimica e Ingegneria Meccanica FONDAMENTI DI INFORMATICA http://www.diee.unica.it/~marcialis/fi A.A. 201/2017 Docente: Gian Luca Marcialis
Il concetto di calcolatore e di algoritmo
 Il concetto di calcolatore e di algoritmo Elementi di Informatica e Programmazione Percorso di Preparazione agli Studi di Ingegneria Università degli Studi di Brescia Docente: Massimiliano Giacomin Informatica
Il concetto di calcolatore e di algoritmo Elementi di Informatica e Programmazione Percorso di Preparazione agli Studi di Ingegneria Università degli Studi di Brescia Docente: Massimiliano Giacomin Informatica
In molte applicazioni sorge il problema di sapere in quanti modi possibili si può presentare un certo fenomeno.
 Definizione Oggetto del calcolo combinatorio è quello di determinare il numero dei modi mediante i quali possono essere associati, secondo prefissate regole, gli elementi di uno stesso insieme o di più
Definizione Oggetto del calcolo combinatorio è quello di determinare il numero dei modi mediante i quali possono essere associati, secondo prefissate regole, gli elementi di uno stesso insieme o di più
MODELLI QUANTITATIVI. f x r = c
 MODELLI QUANTITATIVI Qualunque sia il modello di estrazione di regolarità o di conoscenze dai dati empirici, esiste sempre una base statistica da cui occorre partire. Un fenomeno linguistico specifico
MODELLI QUANTITATIVI Qualunque sia il modello di estrazione di regolarità o di conoscenze dai dati empirici, esiste sempre una base statistica da cui occorre partire. Un fenomeno linguistico specifico
PROGRAMMAZIONE STRUTTURATA
 PROGRAMMAZIONE STRUTTURATA Programmazione strutturata 2 La programmazione strutturata nasce come proposta per regolamentare e standardizzare le metodologie di programmazione (Dijkstra, 1965) Obiettivo:
PROGRAMMAZIONE STRUTTURATA Programmazione strutturata 2 La programmazione strutturata nasce come proposta per regolamentare e standardizzare le metodologie di programmazione (Dijkstra, 1965) Obiettivo:
Massimo Benerecetti Tabelle Hash
 Massimo Benerecetti Tabelle Hash # Lezione n. Parole chiave: Corso di Laurea: Informatica Insegnamento: Algoritmi e Strutture Dati I Email Docente: [email protected] A.A. 2009-2010 Rappresentazione di insiemi
Massimo Benerecetti Tabelle Hash # Lezione n. Parole chiave: Corso di Laurea: Informatica Insegnamento: Algoritmi e Strutture Dati I Email Docente: [email protected] A.A. 2009-2010 Rappresentazione di insiemi
Problemi, algoritmi, calcolatore
 Problemi, algoritmi, calcolatore Informatica e Programmazione Ingegneria Meccanica e dei Materiali Università degli Studi di Brescia Prof. Massimiliano Giacomin Problemi, algoritmi, calcolatori Introduzione
Problemi, algoritmi, calcolatore Informatica e Programmazione Ingegneria Meccanica e dei Materiali Università degli Studi di Brescia Prof. Massimiliano Giacomin Problemi, algoritmi, calcolatori Introduzione
Fondamenti di Informatica
 Fondamenti di Informatica AlgoBuild: Strutture selettive, iterative ed array Prof. Arcangelo Castiglione A.A. 2016/17 AlgoBuild : Strutture iterative e selettive OUTLINE Struttura selettiva Esempi Struttura
Fondamenti di Informatica AlgoBuild: Strutture selettive, iterative ed array Prof. Arcangelo Castiglione A.A. 2016/17 AlgoBuild : Strutture iterative e selettive OUTLINE Struttura selettiva Esempi Struttura
Informatica ALGORITMI E LINGUAGGI DI PROGRAMMAZIONE. Francesco Tura. F. Tura
 Informatica ALGORITMI E LINGUAGGI DI PROGRAMMAZIONE Francesco Tura [email protected] 1 Lo strumento dell informatico: ELABORATORE ELETTRONICO [= calcolatore = computer] Macchina multifunzionale Macchina
Informatica ALGORITMI E LINGUAGGI DI PROGRAMMAZIONE Francesco Tura [email protected] 1 Lo strumento dell informatico: ELABORATORE ELETTRONICO [= calcolatore = computer] Macchina multifunzionale Macchina
6 - Blocchi e cicli. Programmazione e analisi di dati Modulo A: Programmazione in Java. Paolo Milazzo
 6 - Blocchi e cicli Programmazione e analisi di dati Modulo A: Programmazione in Java Paolo Milazzo Dipartimento di Informatica, Università di Pisa http://pages.di.unipi.it/milazzo milazzo di.unipi.it
6 - Blocchi e cicli Programmazione e analisi di dati Modulo A: Programmazione in Java Paolo Milazzo Dipartimento di Informatica, Università di Pisa http://pages.di.unipi.it/milazzo milazzo di.unipi.it
Laboratorio di Architettura lezione 5. Massimo Marchiori W3C/MIT/UNIVE
 Laboratorio di Architettura lezione 5 Massimo Marchiori W3C/MIT/UNIVE Da Alto a Basso livello: compilazione Come si passa da un linguaggio di alto livello a uno di basso livello? Cioe a dire, come lavora
Laboratorio di Architettura lezione 5 Massimo Marchiori W3C/MIT/UNIVE Da Alto a Basso livello: compilazione Come si passa da un linguaggio di alto livello a uno di basso livello? Cioe a dire, come lavora
Array in Fortran 90. Ing. Luca De Santis. Anno accademico 2006/2007. DIS - Dipartimento di informatica e sistemistica
 Array in Fortran 90 Ing. Luca De Santis DIS - Dipartimento di informatica e sistemistica Anno accademico 2006/2007 Fortran 90: array DIS - Dipartimento di informatica e sistemistica 1 / 25 Cosa vedremo
Array in Fortran 90 Ing. Luca De Santis DIS - Dipartimento di informatica e sistemistica Anno accademico 2006/2007 Fortran 90: array DIS - Dipartimento di informatica e sistemistica 1 / 25 Cosa vedremo
Algoritmi, Strutture Dati e Programmi. UD 2.b: Programmazione in Pascal
 Algoritmi, Strutture Dati e Programmi : Programmazione in Pascal Prof. Alberto Postiglione AA 2007-2008 Università degli Studi di Salerno Il Linguaggio di Programmazione Pascal Esistono molti linguaggi
Algoritmi, Strutture Dati e Programmi : Programmazione in Pascal Prof. Alberto Postiglione AA 2007-2008 Università degli Studi di Salerno Il Linguaggio di Programmazione Pascal Esistono molti linguaggi
TEORIE E TECNICHE PER LA COMUNICAZIONE DIGITALE
 TEORIE E TECNICHE PER LA COMUNICAZIONE DIGITALE Riccardo Dondi Dipartimento di Scienze dei linguaggi, della comunicazione e degli studi culturali Università degli Studi di Bergamo Informazione sul corso
TEORIE E TECNICHE PER LA COMUNICAZIONE DIGITALE Riccardo Dondi Dipartimento di Scienze dei linguaggi, della comunicazione e degli studi culturali Università degli Studi di Bergamo Informazione sul corso
Appunti di informatica. Lezione 3 anno accademico Mario Verdicchio
 Appunti di informatica Lezione 3 anno accademico 2015-2016 Mario Verdicchio Numeri binari in memoria In un calcolatore, i numeri binari sono tipicamente memorizzati in sequenze di caselle (note anche come
Appunti di informatica Lezione 3 anno accademico 2015-2016 Mario Verdicchio Numeri binari in memoria In un calcolatore, i numeri binari sono tipicamente memorizzati in sequenze di caselle (note anche come
Programma del corso. Introduzione Rappresentazione delle Informazioni Calcolo proposizionale Architettura del calcolatore Reti di calcolatori
 Programma del corso Introduzione Rappresentazione delle Informazioni Calcolo proposizionale Architettura del calcolatore Reti di calcolatori Cos è un Calcolatore? Un computer (calcolatore) è una macchina
Programma del corso Introduzione Rappresentazione delle Informazioni Calcolo proposizionale Architettura del calcolatore Reti di calcolatori Cos è un Calcolatore? Un computer (calcolatore) è una macchina
Algoritmo: procedimento non ambiguo che in un numero finito di passi risolve un problema (o una classe di problemi)
 LABORATORIO DI PROGRAMMAZIONE Corso di laurea in matematica 2 LA MACCHINA DI VON NEUMANN Marco Lapegna Dipartimento di Matematica e Applicazioni Universita degli Studi di Napoli Federico II wpage.unina.it/lapegna
LABORATORIO DI PROGRAMMAZIONE Corso di laurea in matematica 2 LA MACCHINA DI VON NEUMANN Marco Lapegna Dipartimento di Matematica e Applicazioni Universita degli Studi di Napoli Federico II wpage.unina.it/lapegna
Costanti e Variabili
 Parte 3 Costanti e Variabili Identificatori Un identificatore è un nome che viene associato a diverse entità (costanti, tipi, variabili, funzioni, ecc.) e serve ad identificare la particolare entità Gli
Parte 3 Costanti e Variabili Identificatori Un identificatore è un nome che viene associato a diverse entità (costanti, tipi, variabili, funzioni, ecc.) e serve ad identificare la particolare entità Gli
Informatica Teorica. Macchine a registri
 Informatica Teorica Macchine a registri 1 Macchine a registri RAM (Random Access Machine) astrazione ragionevole di un calcolatore nastro di ingresso nastro di uscita unità centrale in grado di eseguire
Informatica Teorica Macchine a registri 1 Macchine a registri RAM (Random Access Machine) astrazione ragionevole di un calcolatore nastro di ingresso nastro di uscita unità centrale in grado di eseguire
6) Descrivere con un diagramma a blocchi un algoritmo che legga da input due numeri ne calcoli il prodotto in termini di somme ripetute.
 I due esercizi seguenti su un esempio semplice (trovare il massimo tra due o tra tre numeri) introducono la descrizione di algoritmi con diagrammi a blocchi, le strutture di controllo sequenza e condizione,
I due esercizi seguenti su un esempio semplice (trovare il massimo tra due o tra tre numeri) introducono la descrizione di algoritmi con diagrammi a blocchi, le strutture di controllo sequenza e condizione,
Sistemi lineari. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ [email protected] Lorenzo Pareschi (Univ. Ferrara)
Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ [email protected] Lorenzo Pareschi (Univ. Ferrara)
I costrutti forniti dal linguaggio si dividono in corrispondenti classi di istruzioni
 Classi di istruzioni In maniera simile a quanto fatto per i dati, un linguaggio mette a disposizione dei costrutti per realizzare la parte esecutiva dell algoritmo. Questa consiste di: Leggi i valori di
Classi di istruzioni In maniera simile a quanto fatto per i dati, un linguaggio mette a disposizione dei costrutti per realizzare la parte esecutiva dell algoritmo. Questa consiste di: Leggi i valori di
Lezione 4. Sommario. L artimetica binaria: I numeri relativi e frazionari. I numeri relativi I numeri frazionari
 Lezione 4 L artimetica binaria: I numeri relativi e frazionari Sommario I numeri relativi I numeri frazionari I numeri in virgola fissa I numeri in virgola mobile 1 Cosa sono inumeri relativi? I numeri
Lezione 4 L artimetica binaria: I numeri relativi e frazionari Sommario I numeri relativi I numeri frazionari I numeri in virgola fissa I numeri in virgola mobile 1 Cosa sono inumeri relativi? I numeri
Problemi, istanze, soluzioni
 lgoritmi e Strutture di Dati II 2 Problemi, istanze, soluzioni Un problema specifica una relazione matematica tra dati di ingresso e dati di uscita. Una istanza di un problema è formata dai dati di un
lgoritmi e Strutture di Dati II 2 Problemi, istanze, soluzioni Un problema specifica una relazione matematica tra dati di ingresso e dati di uscita. Una istanza di un problema è formata dai dati di un
in termini informali: un algoritmo è una sequenza ordinata di operazioni che risolve un problema specifico
 Click to edit Algoritmo Master title style algoritmo: un insieme ordinato di operazioni non ambigue ed effettivamente computabili che, quando eseguito, produce un risultato e si arresta in un tempo finito
Click to edit Algoritmo Master title style algoritmo: un insieme ordinato di operazioni non ambigue ed effettivamente computabili che, quando eseguito, produce un risultato e si arresta in un tempo finito
Cognome e Nome : Corso e Anno di Immatricolazione: Modalità di Laboratorio (Progetto/Prova) :
 PROGRAMMAZIONE (Corsi B e C) Pre-appello di Gennaio 2004 (A.A. 2003/2004) PROGRAMMAZIONE (B e C) S. Straordinaria - Appello di Gennaio (A.A. 2002/2003) 22 Gennaio 2004 ore 11 Aula II di Facoltà (Durata:
PROGRAMMAZIONE (Corsi B e C) Pre-appello di Gennaio 2004 (A.A. 2003/2004) PROGRAMMAZIONE (B e C) S. Straordinaria - Appello di Gennaio (A.A. 2002/2003) 22 Gennaio 2004 ore 11 Aula II di Facoltà (Durata:
<Nome Tabella>.<attributo>
 Informatica Generale (AA 07/08) Corso di laurea in Scienze della Comunicazione Facoltà di Lettere e Filosofia Università degli Studi di Salerno : SQL (2) Tabelle mult., variabili, aggreg, group Prof. Alberto
Informatica Generale (AA 07/08) Corso di laurea in Scienze della Comunicazione Facoltà di Lettere e Filosofia Università degli Studi di Salerno : SQL (2) Tabelle mult., variabili, aggreg, group Prof. Alberto
LEZIONE 11 IMPARIAMO A PROGRAMMARE: I DATI E LE VARIABILI Laboratorio di Informatica per l Educazione A. A. 2014/2015
 1 LEZIONE 11 IMPARIAMO A PROGRAMMARE: I DATI E LE VARIABILI A. A. 2014/2015 PRIMI PASSI La più semplice sequenza di istruzioni che possiamo scrivere è quella costituita da un solo comando. come si fa a
1 LEZIONE 11 IMPARIAMO A PROGRAMMARE: I DATI E LE VARIABILI A. A. 2014/2015 PRIMI PASSI La più semplice sequenza di istruzioni che possiamo scrivere è quella costituita da un solo comando. come si fa a
Complementi ed Esercizi di Informatica Teorica II
 Complementi ed Esercizi di Informatica Teorica II Vincenzo Bonifaci 21 maggio 2008 4 Problemi di ottimizzazione: il Bin Packing Il problema bin packing è il seguente: dato un insieme di n oggetti di dimensioni
Complementi ed Esercizi di Informatica Teorica II Vincenzo Bonifaci 21 maggio 2008 4 Problemi di ottimizzazione: il Bin Packing Il problema bin packing è il seguente: dato un insieme di n oggetti di dimensioni
Fondamenti di Informatica. Definizione di Algoritmo. Algoritmo Euclideo. Prof.V.L.Plantamura Informatica e Comunicazione Digitale a.a.
 Fondamenti di Informatica Prof.V.L.Plantamura Informatica e Comunicazione Digitale a.a. 006-007 Definizione di Algoritmo Def.: Per Algoritmo si intende un elenco di istruzioni che specificano una serie
Fondamenti di Informatica Prof.V.L.Plantamura Informatica e Comunicazione Digitale a.a. 006-007 Definizione di Algoritmo Def.: Per Algoritmo si intende un elenco di istruzioni che specificano una serie
Lezione 6 programmazione in Java
 Lezione 6 programmazione in Java Nicola Drago [email protected] Dipartimento di Informatica Università di Verona Anteprima Le costanti I vettori Cos è un vettore Come si usa I vari tipi di vettori Esempi
Lezione 6 programmazione in Java Nicola Drago [email protected] Dipartimento di Informatica Università di Verona Anteprima Le costanti I vettori Cos è un vettore Come si usa I vari tipi di vettori Esempi
Problema: dati i voti di tutti gli studenti di una classe determinare il voto medio della classe.
 Problema: dati i voti di tutti gli studenti di una classe determinare il voto medio della classe. 1) Comprendere il problema 2) Stabilire quali sono le azioni da eseguire per risolverlo 3) Stabilire la
Problema: dati i voti di tutti gli studenti di una classe determinare il voto medio della classe. 1) Comprendere il problema 2) Stabilire quali sono le azioni da eseguire per risolverlo 3) Stabilire la
e Algoritmi Marco Piastra Intelligenza Artificiale I Soddisfacibilità
 Intelligenza Artificiale I Soddisfacibilità e Algoritmi Marco Piastra Intelligenza Artificiale I - A.A. 2010- Soddisfacibilità e Semantic Tableau [1] Problemi e decidibilità (automatica) Problema Un problema
Intelligenza Artificiale I Soddisfacibilità e Algoritmi Marco Piastra Intelligenza Artificiale I - A.A. 2010- Soddisfacibilità e Semantic Tableau [1] Problemi e decidibilità (automatica) Problema Un problema
Fondamenti di Informatica - 1. Prof. B.Buttarazzi A.A. 2011/2012
 Fondamenti di Informatica - 1 Prof. B.Buttarazzi A.A. 2011/2012 Sommario I sistemi di numerazione Il sistema binario Altri sistemi di numerazione Algoritmi di conversione Esercizi 07/03/2012 2 Sistemi
Fondamenti di Informatica - 1 Prof. B.Buttarazzi A.A. 2011/2012 Sommario I sistemi di numerazione Il sistema binario Altri sistemi di numerazione Algoritmi di conversione Esercizi 07/03/2012 2 Sistemi
Algoritmi e loro proprietà. Che cos è un algoritmo? Un esempio di algoritmo
 1 Cos è l informatica? L informatica è la scienza della rappresentazione e dell elaborazione dell informazione Algoritmi e loro proprietà Proprietà formali degli Algoritmi Efficienza rispetto al tempo
1 Cos è l informatica? L informatica è la scienza della rappresentazione e dell elaborazione dell informazione Algoritmi e loro proprietà Proprietà formali degli Algoritmi Efficienza rispetto al tempo
Addizionatori: metodo Carry-Lookahead. Costruzione di circuiti combinatori. Standard IEEE754
 Addizionatori: metodo Carry-Lookahead Costruzione di circuiti combinatori Standard IEEE754 Addizionatori Il circuito combinatorio che implementa l addizionatore a n bit si basa su 1-bit adder collegati
Addizionatori: metodo Carry-Lookahead Costruzione di circuiti combinatori Standard IEEE754 Addizionatori Il circuito combinatorio che implementa l addizionatore a n bit si basa su 1-bit adder collegati
Informatica. Come si risolve un problema?
 Informatica Elaborazione automatica dell informazione Esempio di elaborazione: rubrica, elenco telefonico. Ogni problema di elaborazione dell informazione è caratterizzato da: un insieme di dati di partenza
Informatica Elaborazione automatica dell informazione Esempio di elaborazione: rubrica, elenco telefonico. Ogni problema di elaborazione dell informazione è caratterizzato da: un insieme di dati di partenza
LA PROGRAMMAZIONE MATEMATICA (p.m.)
 LA PROGRAMMAZIONE MATEMATICA (p.m.) Un problema di programmazione matematica è un problema di ottimizzazione riconducibile alla seguente espressione generale: ricercare i valori delle variabili x 1, x
LA PROGRAMMAZIONE MATEMATICA (p.m.) Un problema di programmazione matematica è un problema di ottimizzazione riconducibile alla seguente espressione generale: ricercare i valori delle variabili x 1, x
Cosa si intende con stato
 Il concetto di stato Cosa si intende con stato I una particolare configurazione delle informazioni di una macchina, che in qualche modo memorizza le condizioni in cui si trova, e che cambia nel tempo passando
Il concetto di stato Cosa si intende con stato I una particolare configurazione delle informazioni di una macchina, che in qualche modo memorizza le condizioni in cui si trova, e che cambia nel tempo passando
Errori frequenti Cicli iterativi Array. Cicli e array. Laboratorio di Programmazione I. Corso di Laurea in Informatica A.A.
 Cicli e array Laboratorio di Programmazione I Corso di Laurea in Informatica A.A. 2016/2017 Calendario delle lezioni Lez. 1 Lez. 2 Lez. 3 Lez. 4 Lez. 5 Lez. 6 Lez. 7 Lez. 8 - Introduzione all ambiente
Cicli e array Laboratorio di Programmazione I Corso di Laurea in Informatica A.A. 2016/2017 Calendario delle lezioni Lez. 1 Lez. 2 Lez. 3 Lez. 4 Lez. 5 Lez. 6 Lez. 7 Lez. 8 - Introduzione all ambiente
VBA è un linguaggio di scripting derivato da Visual Basic, da cui prende il nome. Come ogni linguaggio ha le sue regole.
 Excel VBA VBA Visual Basic for Application VBA è un linguaggio di scripting derivato da Visual Basic, da cui prende il nome. Come ogni linguaggio ha le sue regole. 2 Prima di iniziare. Che cos è una variabile?
Excel VBA VBA Visual Basic for Application VBA è un linguaggio di scripting derivato da Visual Basic, da cui prende il nome. Come ogni linguaggio ha le sue regole. 2 Prima di iniziare. Che cos è una variabile?
Introduzione agli Algoritmi 4. Problemi. Dal Problema alla Soluzione
 Sommario Problemi e soluzioni Definizione informale di algoritmo e esempi Proprietà degli algoritmi Input/Output, Variabili Algoritmi senza input o output 1 2 Problema Definizione (dal De Mauro Paravia):
Sommario Problemi e soluzioni Definizione informale di algoritmo e esempi Proprietà degli algoritmi Input/Output, Variabili Algoritmi senza input o output 1 2 Problema Definizione (dal De Mauro Paravia):
Fattorizzazione di interi e crittografia
 Fattorizzazione di interi e crittografia Anna Barbieri Università degli Studi di Udine Corso di Laurea in Matematica (Fattorizzazione e crittografia) 14 Maggio 2012 1 / 46 Il teorema fondamentale dell
Fattorizzazione di interi e crittografia Anna Barbieri Università degli Studi di Udine Corso di Laurea in Matematica (Fattorizzazione e crittografia) 14 Maggio 2012 1 / 46 Il teorema fondamentale dell
Le parole dell informatica: algoritmo e decidibilità
 Le parole dell informatica: algoritmo e decidibilità Angelo Montanari Dipartimento di Matematica e Informatica Università degli Studi di Udine Ciclo di seminari su un Vocabolario Filosofico dell Informatica
Le parole dell informatica: algoritmo e decidibilità Angelo Montanari Dipartimento di Matematica e Informatica Università degli Studi di Udine Ciclo di seminari su un Vocabolario Filosofico dell Informatica
Rappresentazione degli algoritmi
 Rappresentazione degli algoritmi Universitá di Ferrara Ultima Modifica: 21 ottobre 2014 1 1 Diagramma di flusso Utilizzare il diagramma di flusso per rappresentare gli algoritmi che risolvono i seguenti
Rappresentazione degli algoritmi Universitá di Ferrara Ultima Modifica: 21 ottobre 2014 1 1 Diagramma di flusso Utilizzare il diagramma di flusso per rappresentare gli algoritmi che risolvono i seguenti
Università degli Studi di Verona. Algoritmie Diagrammidiflusso. Gennaio Sergio Marin Vargas. Dipartimento di Biotecnologie
 Università degli Studi di Verona Dipartimento di Biotecnologie Laurea in Biotecnologie Corso di Informatica2014/2015 Algoritmie Diagrammidiflusso Gennaio 2015 - Sergio Marin Vargas Problemi e soluzioni
Università degli Studi di Verona Dipartimento di Biotecnologie Laurea in Biotecnologie Corso di Informatica2014/2015 Algoritmie Diagrammidiflusso Gennaio 2015 - Sergio Marin Vargas Problemi e soluzioni
Capitolo 8: Teoria della complessitá
 Capitolo 8: Teoria della complessitá 1 La Teoria della calcolabilitá considera aspetti qualitativi della soluzione di problemi. Distingue il calcolabile dal non calcolabile. La Teoria della complessitá
Capitolo 8: Teoria della complessitá 1 La Teoria della calcolabilitá considera aspetti qualitativi della soluzione di problemi. Distingue il calcolabile dal non calcolabile. La Teoria della complessitá
Dall algoritmo al programma
 Dall algoritmo al programma Il concetto di algoritmo Un algoritmo è una sequenza di passi necessari per risolvere un problema o eseguire una computazione In alcuni casi, lo stesso problema/computazione
Dall algoritmo al programma Il concetto di algoritmo Un algoritmo è una sequenza di passi necessari per risolvere un problema o eseguire una computazione In alcuni casi, lo stesso problema/computazione
Un tipico esempio è la definizione del fattoriale n! di un numero n, la cui definizione è la seguente:
 Pag 29 4) La ricorsione 4.1 Funzioni matematiche ricorsive Partiamo da un concetto ben noto, quello delle funzioni matematiche ricorsive. Una funzione matematica è detta ricorsiva quando la sua definizione
Pag 29 4) La ricorsione 4.1 Funzioni matematiche ricorsive Partiamo da un concetto ben noto, quello delle funzioni matematiche ricorsive. Una funzione matematica è detta ricorsiva quando la sua definizione
Macchine di Turing: somma di due numeri
 Informatica Teorica 2/2 M.Di Ianni Macchine di Turing: somma di due numeri Vogliamo definire una macchina di Turing che, presi in input due numeri n e m espressi in notazione binaria, calcola il valore
Informatica Teorica 2/2 M.Di Ianni Macchine di Turing: somma di due numeri Vogliamo definire una macchina di Turing che, presi in input due numeri n e m espressi in notazione binaria, calcola il valore
Algoritmi e Strutture di Dati (3 a Ed.) String matching. Alan Bertossi, Alberto Montresor
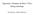 Algoritmi e Strutture di Dati (3 a Ed.) String matching Alan Bertossi, Alberto Montresor STRING MATCHING. Date una stringa P di m caratteri (pattern) e una stringa T di n caratteri, con m n, trovare un
Algoritmi e Strutture di Dati (3 a Ed.) String matching Alan Bertossi, Alberto Montresor STRING MATCHING. Date una stringa P di m caratteri (pattern) e una stringa T di n caratteri, con m n, trovare un
PROBLEMI ALGORITMI E PROGRAMMAZIONE
 PROBLEMI ALGORITMI E PROGRAMMAZIONE SCIENZE E TECNOLOGIE APPLICATE CLASSE SECONDA D PROGRAMMARE = SPECIFICARE UN PROCEDIMENTO CAPACE DI FAR SVOLGERE AD UNA MACCHINA UNA SERIE ORDINATA DI OPERAZIONI AL
PROBLEMI ALGORITMI E PROGRAMMAZIONE SCIENZE E TECNOLOGIE APPLICATE CLASSE SECONDA D PROGRAMMARE = SPECIFICARE UN PROCEDIMENTO CAPACE DI FAR SVOLGERE AD UNA MACCHINA UNA SERIE ORDINATA DI OPERAZIONI AL
Fondamenti di Informatica 6. Algoritmi e pseudocodifica
 Vettori e matrici #1 Fondamenti di Informatica 6. Algoritmi e pseudocodifica Corso di Laurea in Ingegneria Civile A.A. 2010-2011 1 Semestre Prof. Giovanni Pascoschi Le variabili definite come coppie
Vettori e matrici #1 Fondamenti di Informatica 6. Algoritmi e pseudocodifica Corso di Laurea in Ingegneria Civile A.A. 2010-2011 1 Semestre Prof. Giovanni Pascoschi Le variabili definite come coppie
Teoria della Calcolabilità!
 Teoria della Calcolabilità! Si occupa delle questioni fondamentali circa la potenza e le limitazioni dei sistemi di calcolo.! L'origine risale alla prima metà del ventesimo secolo, quando i logici matematici
Teoria della Calcolabilità! Si occupa delle questioni fondamentali circa la potenza e le limitazioni dei sistemi di calcolo.! L'origine risale alla prima metà del ventesimo secolo, quando i logici matematici
Elementi di Complessità Computazionale
 Elementi di Complessità Computazionale Ultima modifica 23.06.2004 Il problema Esiste una misura oggettiva per valutare l'efficienza di un algoritmo? In che relazione sono gli input di un algoritmo con
Elementi di Complessità Computazionale Ultima modifica 23.06.2004 Il problema Esiste una misura oggettiva per valutare l'efficienza di un algoritmo? In che relazione sono gli input di un algoritmo con
Lezione 3. I numeri relativi
 Lezione 3 L artimetcia binaria: i numeri relativi i numeri frazionari I numeri relativi Si possono rappresentare i numeri negativi in due modi con modulo e segno in complemento a 2 1 Modulo e segno Si
Lezione 3 L artimetcia binaria: i numeri relativi i numeri frazionari I numeri relativi Si possono rappresentare i numeri negativi in due modi con modulo e segno in complemento a 2 1 Modulo e segno Si
Corso di Informatica Generale (C. L. Economia e Commercio) Ing. Valerio Lacagnina Rappresentazione dei numeri relativi
 Codice BCD Prima di passare alla rappresentazione dei numeri relativi in binario vediamo un tipo di codifica che ha una certa rilevanza in alcune applicazioni: il codice BCD (Binary Coded Decimal). È un
Codice BCD Prima di passare alla rappresentazione dei numeri relativi in binario vediamo un tipo di codifica che ha una certa rilevanza in alcune applicazioni: il codice BCD (Binary Coded Decimal). È un
Tecniche di Ordinamento dei Vettori
 Tecniche di Ordinamento dei Vettori Corso di Laurea Ingegneria Corso B A.A. 2010-2011 1 Contenuto 1) Generalità 2) Metodi a Minimo Ingombro di Memoria 2.1) Ordinamento per selezione ( Selection Sort )
Tecniche di Ordinamento dei Vettori Corso di Laurea Ingegneria Corso B A.A. 2010-2011 1 Contenuto 1) Generalità 2) Metodi a Minimo Ingombro di Memoria 2.1) Ordinamento per selezione ( Selection Sort )
STRUTTURA E LOGICA DI FUNZIONAMENTO DEL COMPUTER
 1 STRUTTURA E LOGICA DI FUNZIONAMENTO DEL COMPUTER Un computer e una macchina che riceve in ingresso delle informazioni, le elabora secondo un determinato procedimento e produce dei risultati che vengono
1 STRUTTURA E LOGICA DI FUNZIONAMENTO DEL COMPUTER Un computer e una macchina che riceve in ingresso delle informazioni, le elabora secondo un determinato procedimento e produce dei risultati che vengono
Esercitazione 1 Conversione di base
 Esercitazione 1 Conversione di base A.A. 2017-18 Esercizio 1 (M) Scrivere un programma che esegua la conversione di un numero reale qualunque da base 10 a base β {2,..., 16}, utilizzando gli M-function
Esercitazione 1 Conversione di base A.A. 2017-18 Esercizio 1 (M) Scrivere un programma che esegua la conversione di un numero reale qualunque da base 10 a base β {2,..., 16}, utilizzando gli M-function
Il Concetto Intuitivo di Calcolatore. Esercizio. I Problemi e la loro Soluzione. (esempio)
 Il Concetto Intuitivo di Calcolatore Elementi di Informatica e Programmazione Ingegneria Gestionale Università degli Studi di Brescia Docente: Prof. Alfonso Gerevini Variabile di uscita Classe di domande
Il Concetto Intuitivo di Calcolatore Elementi di Informatica e Programmazione Ingegneria Gestionale Università degli Studi di Brescia Docente: Prof. Alfonso Gerevini Variabile di uscita Classe di domande
Foglio Elettronico Lezione 1
 - Introduzione - Celle e riferimenti - Formule - Approfondimenti - Funzioni logiche Sommario Introduzione - Foglio elettronico o foglio di calcolo - Cos'è? Strumento per raccogliere dati organizzati in
- Introduzione - Celle e riferimenti - Formule - Approfondimenti - Funzioni logiche Sommario Introduzione - Foglio elettronico o foglio di calcolo - Cos'è? Strumento per raccogliere dati organizzati in
Unità A2. Progettazione concettuale. Obiettivi. Astrazione. Astrazione per aggregazione
 Obiettivi Unità A2 Progettazione concettuale Imparare ad astrarre i dati per definire entità. Saper distinguere tra astrazione per classificazione, per aggregazione e per generalizzazione. Saper distinguere
Obiettivi Unità A2 Progettazione concettuale Imparare ad astrarre i dati per definire entità. Saper distinguere tra astrazione per classificazione, per aggregazione e per generalizzazione. Saper distinguere
Linguaggi di programmazione - Principi e paradigmi 2/ed Maurizio Gabbrielli, Simone Martini Copyright The McGraw-Hill Companies srl
 Approfondimento 2.1 Non è questo il testo dove trattare esaurientemente queste tecniche semantiche. Ci accontenteremo di dare un semplice esempio delle tecniche basate sui sistemi di transizione per dare
Approfondimento 2.1 Non è questo il testo dove trattare esaurientemente queste tecniche semantiche. Ci accontenteremo di dare un semplice esempio delle tecniche basate sui sistemi di transizione per dare
Note per la Lezione 4 Ugo Vaccaro
 Progettazione di Algoritmi Anno Accademico 2016 2017 Note per la Lezione 4 Ugo Vaccaro Ripasso di nozioni su Alberi Ricordiamo che gli alberi rappresentano una generalizzazione delle liste, nel senso che
Progettazione di Algoritmi Anno Accademico 2016 2017 Note per la Lezione 4 Ugo Vaccaro Ripasso di nozioni su Alberi Ricordiamo che gli alberi rappresentano una generalizzazione delle liste, nel senso che
Formalismi per la descrizione di algoritmi
 Formalismi per la descrizione di algoritmi Per descrivere in passi di un algoritmo bisogna essere precisi e non ambigui Il linguaggio naturale degli esseri umani si presta a interpret non univoche Si usano
Formalismi per la descrizione di algoritmi Per descrivere in passi di un algoritmo bisogna essere precisi e non ambigui Il linguaggio naturale degli esseri umani si presta a interpret non univoche Si usano
