LA MEDIA CAMPIONARIA 14-1
|
|
|
- Giuseppina Rosso
- 5 anni fa
- Visualizzazioni
Transcript
1 LA MEDIA CAMPIONARIA Prendiamo un urna e inseriamo 10 palline numerate da 0 a 9 (questa è la nostra popolazione ). La media dei 10 valori è 4.5 (questa è la media vera µ). La varianza dei 10 valori è 8.25 (questa è la varianza vera σ 2 ). Estraiamo (con rimessa) un certo numero n di palline dall urna (un campione casuale semplice) e calcoliamo la media degli n valori estratti. Chiamiamo questo valore media campionaria (o, meglio, una realizzazione della media campionaria). Vediamo cosa succede ripetendo questo esperimento più volte, facendo anche variare n (la dimensione del campione). 14-1
2 Parametri e statistiche Parametro: valore che descrive la popolazione. Di solito è incognito in quanto non è possibile esaminare l intera popolazione. Statistica: è un numero calcolato direttamente sulla base dei dati campionari a nostra disposizione. Di solito viene usato per la stima di parametri di cui non si conosce il valore. 14-2
3 > pop <- c(0:9); pr <- rep(1/10,10) > nrep <- 20; tmp <- rep(na,nrep) > > for (i in 1:20) tmp[i] <- mean(sample(pop, 2, replace = TRUE, prob = pr)); print(tmp) [1] > for (i in 1:20) tmp[i] <- mean(sample(pop, 5, replace = TRUE, prob = pr)); print(tmp) [1] > for (i in 1:20) tmp[i] <- mean(sample(pop, 10, replace = TRUE, prob = pr)); print(tmp) [1]
4 > for (i in 1:20) tmp[i] <- mean(sample(pop, 100 replace = TRUE, prob = pr)); print(tmp) [1] > for (i in 1:20) tmp[i] <- mean(sample(pop, 1000, replace = TRUE, prob = pr)); print(tmp) [1] > for (i in 1:20) tmp[i] <- mean(sample(pop, 10000, replace = TRUE, prob = pr)); print(tmp) [1]
5 LA MEDIA CAMPIONARIA Quando consideriamo il valore medio di una variabile calcolata su campione (casuale semplice), osserviamo che il risultato numerico che otteniamo dipende dal campione. Vale a dire che, a seconda del campione, la media che calcoliamo varia. Quindi la media calcolata su di un campione (media campionaria) è una variabile casuale. Essendo una variabile casuale, avrà una distribuzione di probabilità, una media e una varianza. 14-5
6 Distribuzioni campionarie La distribuzione campionaria di una statistica è la distribuzione dei valori che la statistica assume in tutti i possibili campioni con la stessa numerosità, estratti dalla stessa popolazione. 14-6
7 LA MEDIA CAMPIONARIA Al crescere della dimensione del campione (n) alcuni risultati diventano meno frequenti (quelli più estremi ), mentre altri (quelli più centrali ) diventano più frequenti. In particolare i valori osservati sembrano addensarsi intorno alla media vera, cioè a 4.5 (nel nostro esempio). 14-7
8 LA MEDIA CAMPIONARIA Ripetiamo ora lo stesso esperimento (estrazione di un campione casuale semplice di n palline) non poche volte, ma numerosissime volte (N). Annotiamo ogni volta la media delle n osservazioni (la media campionaria). Alla fine delle N ripetizioni ( repliche ) calcoliamo la media delle N medie campionarie e la varianza delle N medie campionarie. Ripartiamo da capo modificando n (la dimensione del campione). 14-8
9 pop <- c(0:9) xm <- sim(n= 1,pop,nrep=10000) xm <- sim(n= 2,pop,nrep=10000) xm <- sim(n= 4,pop,nrep=10000) xm <- sim(n= 8,pop,nrep=10000) xm <- sim(n= 16,pop,nrep=10000) xm <- sim(n= 32,pop,nrep=10000) xm <- sim(n= 64,pop,nrep=10000) xm <- sim(n=128,pop,nrep=10000) 14-9
10 14-10
11 LA MEDIA CAMPIONARIA Ripetendo lo stesso esperimento numerosissime volte (N), facendo variare di volta in volta la dimensione del campione (n), la media delle N medie (medie campionarie) rimane sostanzialmente stabile (cioè non dipende da n). La media di tutte le possibili medie campionarie è sempre uguale alla media vera (cioè alla media della popolazione da cui è stato estratto il campione). Diciamo che la media campionaria è uno stimatore non distorto (unbiased) della media vera µ
12 14-12
13 14-13
14 LA MEDIA CAMPIONARIA Ripetendo lo stesso esperimento numerosissime volte (N), facendo variare di volta in volta la dimensione del campione (n), la varianza delle N medie campionarie si riduce al crescere di n. Sembra proprio che esista una legge (una funzione) che lega la varianza della media campionaria alla dimensione del campione. Moltiplichiamo fra loro varianza (delle medie campionarie) e dimensione del campione corrispondente e vediamo il risultato su un grafico
15 14-15
16 LA MEDIA CAMPIONARIA Il prodotto fra varianza e dimensione del campione è approssimativamente costante. Nell esempio questa costante è 8.25 (la varianza dei dati originali). In effetti la varianza di tutte le possibili medie campionarie calcolate su campioni di dimensione n è inversamente proporzionale alla dimensione del campione. Nel nostro esempio abbiamo: ( ) Var X n = n 14-16
17 LA MEDIA CAMPIONARIA La funzione che lega fra loro la varianza della media campionaria e la dimensione del campione è l iperbole (equilatera). Quando la dimensione del campione raddoppia, la varianza della media campionaria si dimezza. Per dimezzare la deviazione standard della media campionaria (l errore standard) occorre però quadruplicare la dimensione del campione Verifichiamo graficamente la relazione Var ( X ) = n 14-17
18 14-18
19 14-19
20 LA MEDIA CAMPIONARIA Quanto illustrato prima con un esempio ha validità molto più generale (non dipende dall esempio scelto). Indichiamo con X una qualsiasi variabile casuale (lo stesso vale per qualsiasi insieme di dati empirici). Indichiamo con µ la media di X. Indichiamo con σ 2 la varianza di X. Consideriamo ora la media (media campionaria) di un campione casuale semplice di n osservazioni estratto da X. Indicheremo questa variabile casuale con Xn 14-20
21 LA MEDIA CAMPIONARIA Allora, la media (il valore atteso) della media campionaria è (sempre) µ (non dipende da n)
22 LA MEDIA CAMPIONARIA Allora, la media (il valore atteso) della media campionaria è (sempre) µ (non dipende da n). 2 La varianza della media campionaria è σ n 14-22
23 Una giustificazione teorica per le due regole precedenti Una media è essenzialmente una somma di quantità simili divisa per una costante (il numero degli addendi della somma). Dal punto di vista teorico, ciò che si somma sono variabili casuali (di cui il ricercatore osserva delle realizzazioni). È possibile dimostrare che la media (il valore atteso) della somma di due variabili casuali è sempre la somma delle due medie. È pure possibile dimostrare che la varianza della somma di due variabili casuali è la somma delle due varianze, se le due variabili casuali sono fra loro indipendenti
24 Una giustificazione teorica per le due regole precedenti Le due regole precedenti si generalizzano al caso della somma di un numero qualsiasi di variabili casuali: la media (il valore atteso) della somma di n variabili casuali è sempre la somma delle n medie; la varianza della somma di n variabili casualièlasommadellenvarianze,selen variabili casuali sono fra loro indipendenti
25 Una giustificazione teorica per le due regole precedenti Siano X 1, X 2,, X n, n variabili casuali indipendenti e identicamente distribuite, ciascunaconmedia µevarianza σ 2. SiaS n lasommadellenvariabili.allora: Var E ( S ) = µ + µ µ = nµ n ( S ) = σ 2 + σ σ 2 = nσ 2 n 14-25
26 Una giustificazione teorica per le due regole precedenti La media campionaria (di n variabili casuali indipendenti e identicamente distribuite) è la somma delle n variabili casuali divisa per n. Quindi: E S n 1 n ( ) n X = E = E( S ) = nµ = µ n n 1 n Var 1 n ( ) n X = Var = Var( S ) n S n 2 n = 1 n 2 2 nσ = σ n
27 LA MEDIA CAMPIONARIA Allora, la media (il valore atteso) della media campionaria è (sempre) µ (non dipende da n). La varianza della media campionaria è La deviazione standard (l errore standard) della media campionaria è σ n 2 σ n 14-27
28 LA MEDIA CAMPIONARIA Allora, la media (il valore atteso) della media campionaria è (sempre) µ (non dipende da n). La varianza della media campionaria è La deviazione standard (l'errore standard) della media campionaria è σ n E la forma della distribuzione della media campionaria quale sarà? Dipende 2 σ n 14-28
29 xm <- simnorm(n=1,mu=60,sigma=12,nrep=10000) 14-29
30 xm <- simunifc(n=1,nrep=10000) 14-30
31 xm <- simunifc(n=2,nrep=10000) 14-31
32 xm <- simunifc(n=10,nrep=10000) 14-32
33 xm <- simexp(n=1,nrep=10000) 14-33
34 xm <- simexp(n=50,nrep=10000) 14-34
35 xm <- simexp(n=100,nrep=10000) 14-35
36 LA MEDIA CAMPIONARIA Allora, la media (il valore atteso) della media campionaria è (sempre) µ (non dipende da n). La varianza della media campionaria è La deviazione standard (l'errore standard) della media campionaria è σ n Al crescere della dimensione del campione, la distribuzione della media campionaria tende alla distribuzione normale. Questo vale anche se consideriamo delle distribuzioni empiriche. 2 σ n 14-36
37 istogramma(laureati$voto30) 14-37
38 istogramma(laureati$votofinale) 14-38
39 La deviazione standard della media campionaria è chiamata, specie nella letteratura anglosassone, errore standard della media campionaria. Rispetto alla deviazione standard della variabile che si sta analizzando, l errore standard (della m.c.) ha un significato diverso. Infatti, mentre la deviazione standard della variabile che si sta analizzando è quella che è, la grandezza dell errore standard è, almeno in parte, sotto il controllo del ricercatore. Infatti, se facciamo crescere n, l errore standard diminuirà fino a diventare quasi zero
40 Se l errore standard fosse esattamente zero, vorrebbe dire che la nostra stima della media coinciderebbe con la media vera. In altre parole, la nostra stima avrebbe una precisione assoluta (infinita). Qualsiasi stimatore ha un errore standard che è da interpretare come una misura inversa della precisione della stima. È proprio l aumento di precisione con cui stimiamo la media vera che costringe la media campionaria fra le due barriere tracciate nel grafico che illustra la legge dei grandi numeri
41 LA LEGGE DEI GRANDI NUMERI 14-41
Distribuzioni campionarie
 1 Inferenza Statistica Descrittiva Distribuzioni campionarie Statistica Inferenziale: affronta problemi di decisione in condizioni di incertezza basandosi sia su informazioni a priori sia sui dati campionari
1 Inferenza Statistica Descrittiva Distribuzioni campionarie Statistica Inferenziale: affronta problemi di decisione in condizioni di incertezza basandosi sia su informazioni a priori sia sui dati campionari
Tecniche di sondaggio
 SMID a.a. 2005/2006 Corso di Statistica per la Ricerca Sperimentale Tecniche di sondaggio 24/1/2006 Nomenclatura Indicheremo con P una popolazione, con N la sua numerosità, con k la sua etichetta e con
SMID a.a. 2005/2006 Corso di Statistica per la Ricerca Sperimentale Tecniche di sondaggio 24/1/2006 Nomenclatura Indicheremo con P una popolazione, con N la sua numerosità, con k la sua etichetta e con
APPUNTI DI STATISTICA INFERENZIALE. Avalle Fulvia, maggio 2014, ITSOS MARIE CURIE CLASSI 4A BIO e 4B BIO
 APPUNTI DI STATISTICA INFERENZIALE Avalle Fulvia, maggio 2014, ITSOS MARIE CURIE CLASSI 4A BIO e 4B BIO PREREQUISITI VARIABILE ALEATORIA (QUANTITATIVA): è una funzione che associa un numero reale ad ogni
APPUNTI DI STATISTICA INFERENZIALE Avalle Fulvia, maggio 2014, ITSOS MARIE CURIE CLASSI 4A BIO e 4B BIO PREREQUISITI VARIABILE ALEATORIA (QUANTITATIVA): è una funzione che associa un numero reale ad ogni
DISTRIBUZIONI DI PROBABILITA (parte 3) 1 / 34
 DISTRIBUZIONI DI PROBABILITA (parte 3) 1 / 34 Distribuzione Binomiale 2 / 34 La più importante distribuzione di probabilità per variabili casuali discrete è la distribuzione binomiale. Questa distribuzione
DISTRIBUZIONI DI PROBABILITA (parte 3) 1 / 34 Distribuzione Binomiale 2 / 34 La più importante distribuzione di probabilità per variabili casuali discrete è la distribuzione binomiale. Questa distribuzione
Dato che i risultati ottenuti tramite campioni casuali ed esperimenti comparativi sono legati al caso, non possiamo essere certi che le nostre
 Campione Dato che i risultati ottenuti tramite campioni casuali ed esperimenti comparativi sono legati al caso, non possiamo essere certi che le nostre conclusioni siano corrette. Quello che possiamo fare
Campione Dato che i risultati ottenuti tramite campioni casuali ed esperimenti comparativi sono legati al caso, non possiamo essere certi che le nostre conclusioni siano corrette. Quello che possiamo fare
Il campionamento e l inferenza. Il campionamento e l inferenza
 Il campionamento e l inferenza Popolazione Campione Dai dati osservati mediante scelta campionaria si giunge ad affermazioni che riguardano la popolazione da cui essi sono stati prescelti Il campionamento
Il campionamento e l inferenza Popolazione Campione Dai dati osservati mediante scelta campionaria si giunge ad affermazioni che riguardano la popolazione da cui essi sono stati prescelti Il campionamento
I modelli probabilistici
 e I modelli probabilistici Finora abbiamo visto che esistono modelli probabilistici che possiamo utilizzare per prevedere gli esiti di esperimenti aleatori. Naturalmente la previsione è di tipo probabilistico:
e I modelli probabilistici Finora abbiamo visto che esistono modelli probabilistici che possiamo utilizzare per prevedere gli esiti di esperimenti aleatori. Naturalmente la previsione è di tipo probabilistico:
Distribuzione Normale
 Distribuzione Normale istogramma delle frequenze di un insieme di misure di una grandezza che può variare con continuità popolazione molto numerosa, costituita da una quantità praticamente illimitata di
Distribuzione Normale istogramma delle frequenze di un insieme di misure di una grandezza che può variare con continuità popolazione molto numerosa, costituita da una quantità praticamente illimitata di
Statistica Inferenziale
 Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Riepilogo lezione 6 Abbiamo visto: Definizione di popolazione, di campione e di spazio campionario Distribuzione
Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Riepilogo lezione 6 Abbiamo visto: Definizione di popolazione, di campione e di spazio campionario Distribuzione
Distribuzione Normale
 Distribuzione Normale istogramma delle frequenze di un insieme di misure relative a una grandezza che può variare con continuità popolazione molto numerosa, costituita da una quantità praticamente illimitata
Distribuzione Normale istogramma delle frequenze di un insieme di misure relative a una grandezza che può variare con continuità popolazione molto numerosa, costituita da una quantità praticamente illimitata
Statistica Inferenziale
 Statistica Inferenziale a) L Intervallo di Confidenza b) La distribuzione t di Student c) La differenza delle medie d) L intervallo di confidenza della differenza Prof Paolo Chiodini Dalla Popolazione
Statistica Inferenziale a) L Intervallo di Confidenza b) La distribuzione t di Student c) La differenza delle medie d) L intervallo di confidenza della differenza Prof Paolo Chiodini Dalla Popolazione
STATISTICA INDUTTIVA: STIMA DI PARAMETRI STIMA PUNTUALE
 S.S.I.S TOSCANA F.I.M. -II anno STATISTICA INDUTTIVA: STIMA DI PARAMETRI STIMA PUNTUALE PROBLEMA 1 Vogliamo valutare la percentuale p di donne fumatrici tra le donne in età fertile. Procediamo all estrazione
S.S.I.S TOSCANA F.I.M. -II anno STATISTICA INDUTTIVA: STIMA DI PARAMETRI STIMA PUNTUALE PROBLEMA 1 Vogliamo valutare la percentuale p di donne fumatrici tra le donne in età fertile. Procediamo all estrazione
Esercitazione 4 Distribuzioni campionarie e introduzione ai metodi Monte Carlo
 Esercitazione 4 Distribuzioni campionarie e introduzione ai metodi Monte Carlo 1. Gli studi di simulazione possono permetterci di apprezzare alcune delle proprietà di distribuzioni campionarie ricavate
Esercitazione 4 Distribuzioni campionarie e introduzione ai metodi Monte Carlo 1. Gli studi di simulazione possono permetterci di apprezzare alcune delle proprietà di distribuzioni campionarie ricavate
Distribuzione normale
 Distribuzione normale istogramma delle frequenze di un insieme di misure relative a una grandezza che varia con continuità popolazione molto numerosa, costituita da una quantità praticamente illimitata
Distribuzione normale istogramma delle frequenze di un insieme di misure relative a una grandezza che varia con continuità popolazione molto numerosa, costituita da una quantità praticamente illimitata
Argomenti della lezione: Campionamento Stima Distribuzione campionaria Campione Popolazione Sottoinsieme degli elementi (o universo) dell '
 Lezione 2 Argomenti della lezione: La statistica inferenziale: concetti di base Campionamento Stima Distribuzione campionaria Popolazione (o universo) Insieme di tutti gli elementi cui si rivolge il ricercatore
Lezione 2 Argomenti della lezione: La statistica inferenziale: concetti di base Campionamento Stima Distribuzione campionaria Popolazione (o universo) Insieme di tutti gli elementi cui si rivolge il ricercatore
1. Quali sono i possibili campioni di numerosità 2 senza reimmissione? X 1 e X 2 sono indipendenti?
 Esercizio 1 Consideriamo una popolazione X, dove X = {3,5,7}. 1. Quali sono i possibili campioni di numerosità 2 senza reimmissione? X 1 e X 2 sono indipendenti? 2. Quali sono i possibili campioni di numerosità
Esercizio 1 Consideriamo una popolazione X, dove X = {3,5,7}. 1. Quali sono i possibili campioni di numerosità 2 senza reimmissione? X 1 e X 2 sono indipendenti? 2. Quali sono i possibili campioni di numerosità
Modelli descrittivi, statistica e simulazione
 Modelli descrittivi, statistica e simulazione Master per Smart Logistics specialist Roberto Cordone (roberto.cordone@unimi.it) Statistica inferenziale Cernusco S.N., giovedì 25 febbraio 2016 (9.00/13.00)
Modelli descrittivi, statistica e simulazione Master per Smart Logistics specialist Roberto Cordone (roberto.cordone@unimi.it) Statistica inferenziale Cernusco S.N., giovedì 25 febbraio 2016 (9.00/13.00)
lezione 4 AA Paolo Brunori
 AA 2016-2017 Paolo Brunori dove eravamo arrivati - abbiamo individuato la regressione lineare semplice (OLS) come modo immediato per sintetizzare una relazione fra una variabile dipendente (Y) e una indipendente
AA 2016-2017 Paolo Brunori dove eravamo arrivati - abbiamo individuato la regressione lineare semplice (OLS) come modo immediato per sintetizzare una relazione fra una variabile dipendente (Y) e una indipendente
Gli intervalli di confidenza. Intervallo di confidenza per la media (σ 2 nota) nel caso di popolazione Gaussiana
 Statistica Lez. 1 Gli intervalli di confidenza Intervallo di confidenza per la media (σ nota) nel caso di popolazione Gaussiana Sia X una v.c Gaussiana di media µ e varianza σ. Se X 1, X,..., X n è un
Statistica Lez. 1 Gli intervalli di confidenza Intervallo di confidenza per la media (σ nota) nel caso di popolazione Gaussiana Sia X una v.c Gaussiana di media µ e varianza σ. Se X 1, X,..., X n è un
Programma della parte introduttiva: Lezione 5
 Programma della parte introduttiva: Lezione 5 Cap. 3 Presentazione e confronto tra misure Cap. 4 Propagazione delle incertezze Cap 5 Misure ripetute e stimatori Cap.6 Organizzazione e presentazione dei
Programma della parte introduttiva: Lezione 5 Cap. 3 Presentazione e confronto tra misure Cap. 4 Propagazione delle incertezze Cap 5 Misure ripetute e stimatori Cap.6 Organizzazione e presentazione dei
05. Errore campionario e numerosità campionaria
 Statistica per le ricerche di mercato A.A. 01/13 05. Errore campionario e numerosità campionaria Gli schemi di campionamento condividono lo stesso principio di fondo: rappresentare il più fedelmente possibile,
Statistica per le ricerche di mercato A.A. 01/13 05. Errore campionario e numerosità campionaria Gli schemi di campionamento condividono lo stesso principio di fondo: rappresentare il più fedelmente possibile,
L indagine campionaria Lezione 3
 Anno accademico 2007/08 L indagine campionaria Lezione 3 Docente: prof. Maurizio Pisati Variabile casuale Una variabile casuale è una quantità discreta o continua il cui valore è determinato dal risultato
Anno accademico 2007/08 L indagine campionaria Lezione 3 Docente: prof. Maurizio Pisati Variabile casuale Una variabile casuale è una quantità discreta o continua il cui valore è determinato dal risultato
Esercitazioni di Statistica
 Esercitazioni di Statistica Stima Puntuale Prof. Livia De Giovanni statistica@dis.uniroma.it Esercizio In ciascuno dei casi seguenti determinare quale tra i due stimatori S e T per il parametro θ è distorto
Esercitazioni di Statistica Stima Puntuale Prof. Livia De Giovanni statistica@dis.uniroma.it Esercizio In ciascuno dei casi seguenti determinare quale tra i due stimatori S e T per il parametro θ è distorto
LE DISTRIBUZIONI CAMPIONARIE
 LE DISTRIBUZIONI CAMPIONARIE Argomenti Principi e metodi dell inferenza statistica Metodi di campionamento Campioni casuali Le distribuzioni campionarie notevoli: La distribuzione della media campionaria
LE DISTRIBUZIONI CAMPIONARIE Argomenti Principi e metodi dell inferenza statistica Metodi di campionamento Campioni casuali Le distribuzioni campionarie notevoli: La distribuzione della media campionaria
La media campionaria. MEDIA CAMPIONARIA Date n v.a. X 1,..., X n indipendenti e identicamente distribuite (in breve i.i.d.), la v.a.
 La media MEDIA CAMPIONARIA Date n v.a. X 1,..., X n indipendenti e identicamente distribuite (in breve i.i.d.), la v.a. X n = 1 n è detta media. n X i, i=1 In altre parole, se le X 1,...,X n sono il risultato
La media MEDIA CAMPIONARIA Date n v.a. X 1,..., X n indipendenti e identicamente distribuite (in breve i.i.d.), la v.a. X n = 1 n è detta media. n X i, i=1 In altre parole, se le X 1,...,X n sono il risultato
Costruzione di macchine. Modulo di: Progettazione probabilistica e affidabilità. Marco Beghini. Lezione 7: Basi di statistica
 Costruzione di macchine Modulo di: Progettazione probabilistica e affidabilità Marco Beghini Lezione 7: Basi di statistica Campione e Popolazione Estrazione da una popolazione (virtualmente infinita) di
Costruzione di macchine Modulo di: Progettazione probabilistica e affidabilità Marco Beghini Lezione 7: Basi di statistica Campione e Popolazione Estrazione da una popolazione (virtualmente infinita) di
Distribuzione Normale
 Distribuzione Normale istogramma delle frequenze di un insieme di misure di una grandezza che può variare con continuità popolazione molto numerosa, costituita da una quantità praticamente illimitata di
Distribuzione Normale istogramma delle frequenze di un insieme di misure di una grandezza che può variare con continuità popolazione molto numerosa, costituita da una quantità praticamente illimitata di
Verifica delle ipotesi
 Statistica inferenziale Stima dei parametri Verifica delle ipotesi Concetti fondamentali POPOLAZIONE o UNIVERSO Insieme degli elementi cui si rivolge il ricercatore per la sua indagine CAMPIONE Un sottoinsieme
Statistica inferenziale Stima dei parametri Verifica delle ipotesi Concetti fondamentali POPOLAZIONE o UNIVERSO Insieme degli elementi cui si rivolge il ricercatore per la sua indagine CAMPIONE Un sottoinsieme
Probabilità classica. Distribuzioni e leggi di probabilità. Probabilità frequentista. Probabilità soggettiva
 Probabilità classica Distribuzioni e leggi di probabilità La probabilità di un evento casuale è il rapporto tra il numero dei casi favorevoli ed il numero dei casi possibili, purchè siano tutti equiprobabili.
Probabilità classica Distribuzioni e leggi di probabilità La probabilità di un evento casuale è il rapporto tra il numero dei casi favorevoli ed il numero dei casi possibili, purchè siano tutti equiprobabili.
Esercizi di Probabilità e Statistica
 Esercizi di Probabilità e Statistica Samuel Rota Bulò 6 giugno 26 Statistica Esercizio Sia {X n } n una famiglia di v.a. di media µ e varianza σ 2. Verificare che X = n n X i σ 2 = n (X i µ) 2 S 2 = n
Esercizi di Probabilità e Statistica Samuel Rota Bulò 6 giugno 26 Statistica Esercizio Sia {X n } n una famiglia di v.a. di media µ e varianza σ 2. Verificare che X = n n X i σ 2 = n (X i µ) 2 S 2 = n
Teorema del Limite Centrale
 Teorema del Limite Centrale Problema. Determinare come la media campionaria x e la deviazione standard campionaria s misurano la media µ e la deviazione standard σ della popolazione. È data una popolazione
Teorema del Limite Centrale Problema. Determinare come la media campionaria x e la deviazione standard campionaria s misurano la media µ e la deviazione standard σ della popolazione. È data una popolazione
Inferenza su una popolazione
 Inferenza su una popolazione La distribuzione di x(m) ha media pari a μ, quindi x(m) è uno stimatore non distorto della media della popolazione μ. Per fare inferenza sulla media dobbiamo avere un CCS,
Inferenza su una popolazione La distribuzione di x(m) ha media pari a μ, quindi x(m) è uno stimatore non distorto della media della popolazione μ. Per fare inferenza sulla media dobbiamo avere un CCS,
La distribuzione t. Federico Plazzi. 7 Novembre 2015
 La distribuzione t Federico Plazzi 7 Novembre 2015 Popolazione e campioni Popolazione e campioni Definizioni ed assunzioni di partenza Campione: l insieme di individui che abbiamo potuto osservare. Popolazione
La distribuzione t Federico Plazzi 7 Novembre 2015 Popolazione e campioni Popolazione e campioni Definizioni ed assunzioni di partenza Campione: l insieme di individui che abbiamo potuto osservare. Popolazione
Introduzione all'inferenza Lezione 4
 Last updated April 16, 2016 Introduzione all'inferenza Lezione 4 G. Bacaro Statistica CdL in Scienze e Tecnologie per l'ambiente e la Natura I anno, II semestre Introduzione all inferenza Popolazione Campione
Last updated April 16, 2016 Introduzione all'inferenza Lezione 4 G. Bacaro Statistica CdL in Scienze e Tecnologie per l'ambiente e la Natura I anno, II semestre Introduzione all inferenza Popolazione Campione
Laboratorio di Didattica di elaborazione dati 5 STIMA PUNTUALE DEI PARAMETRI. x i. SE = n.
 5 STIMA PUNTUALE DEI PARAMETRI [Adattato dal libro Excel per la statistica di Enzo Belluco] Sia θ un parametro incognito della distribuzione di un carattere in una determinata popolazione. Il problema
5 STIMA PUNTUALE DEI PARAMETRI [Adattato dal libro Excel per la statistica di Enzo Belluco] Sia θ un parametro incognito della distribuzione di un carattere in una determinata popolazione. Il problema
Cap. 7 Distribuzioni campionarie
 Cap. 7 Distribuzioni campionarie 1 Popolazione e Campione Una popolazione è l insieme di tutte le unità oggetto di studio Tutti i potenziali votanti nelle prossime elezioni Tutti i pezzi prodotti oggi
Cap. 7 Distribuzioni campionarie 1 Popolazione e Campione Una popolazione è l insieme di tutte le unità oggetto di studio Tutti i potenziali votanti nelle prossime elezioni Tutti i pezzi prodotti oggi
STATISTICA APPLICATA Prof.ssa Julia Mortera. INTRODUZIONE al STATISTICA
 STATISTICA APPLICATA Prof.ssa Julia Mortera INTRODUZIONE al CAMPIONAMENTO e all INFERENZA STATISTICA Inferenza Statistica Nell inferenza statistica si usano le statistiche campionarie per fare previsioni
STATISTICA APPLICATA Prof.ssa Julia Mortera INTRODUZIONE al CAMPIONAMENTO e all INFERENZA STATISTICA Inferenza Statistica Nell inferenza statistica si usano le statistiche campionarie per fare previsioni
STATISTICA INFERENZIALE
 STATISTICA INFERENZIALE Introduzione L insieme di tutte le unità statistiche che compongono il fenomeno collettivo considerato costituisce l universo statistico o, semplicemente, universo. L insieme costituito
STATISTICA INFERENZIALE Introduzione L insieme di tutte le unità statistiche che compongono il fenomeno collettivo considerato costituisce l universo statistico o, semplicemente, universo. L insieme costituito
Statistica Applicata all edilizia: Stime e stimatori
 Statistica Applicata all edilizia E-mail: orietta.nicolis@unibg.it 15 marzo 2011 Statistica Applicata all edilizia: Indice 1 2 Statistica Applicata all edilizia: Uno dei problemi principali della statistica
Statistica Applicata all edilizia E-mail: orietta.nicolis@unibg.it 15 marzo 2011 Statistica Applicata all edilizia: Indice 1 2 Statistica Applicata all edilizia: Uno dei problemi principali della statistica
Statistica inferenziale
 Statistica inferenziale Problema Nello studio delle distribuzioni teoriche di probabilità si suppone di conoscere i principali parametri della popolazione che esaminiamo (ad esempio la media, varianza).
Statistica inferenziale Problema Nello studio delle distribuzioni teoriche di probabilità si suppone di conoscere i principali parametri della popolazione che esaminiamo (ad esempio la media, varianza).
Teorema del limite centrale TCL Questo importante teorema della statistica inferenziale si applica a qualsiasi variabile aleatoria che sia combinazion
 Teorema del limite centrale TCL Questo importante teorema della statistica inferenziale si applica a qualsiasi variabile aleatoria che sia combinazione lineare di N variabili aleatorie le cui funzioni
Teorema del limite centrale TCL Questo importante teorema della statistica inferenziale si applica a qualsiasi variabile aleatoria che sia combinazione lineare di N variabili aleatorie le cui funzioni
Contenuto del capitolo
 Capitolo 8 Stima 1 Contenuto del capitolo Proprietà degli stimatori Correttezza: E(Stimatore) = parametro da stimare Efficienza Consistenza Intervalli di confidenza Per la media - per una proporzione Come
Capitolo 8 Stima 1 Contenuto del capitolo Proprietà degli stimatori Correttezza: E(Stimatore) = parametro da stimare Efficienza Consistenza Intervalli di confidenza Per la media - per una proporzione Come
Matematica con elementi di Informatica
 Statistica descrittiva ed inferenziale Matematica con elementi di Informatica Tiziano Vargiolu Dipartimento di Matematica vargiolu@math.unipd.it Corso di Laurea Magistrale in Chimica e Tecnologie Farmaceutiche
Statistica descrittiva ed inferenziale Matematica con elementi di Informatica Tiziano Vargiolu Dipartimento di Matematica vargiolu@math.unipd.it Corso di Laurea Magistrale in Chimica e Tecnologie Farmaceutiche
Statistica Metodologica
 Statistica Metodologica Esercizi di Probabilita e Inferenza Silvia Figini e-mail: silvia.figini@unipv.it Problema 1 Sia X una variabile aleatoria Bernoulliana con parametro p = 0.7. 1. Determinare la media
Statistica Metodologica Esercizi di Probabilita e Inferenza Silvia Figini e-mail: silvia.figini@unipv.it Problema 1 Sia X una variabile aleatoria Bernoulliana con parametro p = 0.7. 1. Determinare la media
Esercizi di statistica
 Esercizi di statistica Test a scelta multipla (la risposta corretta è la prima) [1] Il seguente campione è stato estratto da una popolazione distribuita normalmente: -.4, 5.5,, -.5, 1.1, 7.4, -1.8, -..
Esercizi di statistica Test a scelta multipla (la risposta corretta è la prima) [1] Il seguente campione è stato estratto da una popolazione distribuita normalmente: -.4, 5.5,, -.5, 1.1, 7.4, -1.8, -..
Il confronto fra medie
 L. Boni Obiettivo Verificare l'ipotesi che regimi alimentari differenti non producano mediamente lo stesso effetto sulla gittata cardiaca Ipotesi nulla IPOTESI NULLA La dieta non dovrebbe modificare in
L. Boni Obiettivo Verificare l'ipotesi che regimi alimentari differenti non producano mediamente lo stesso effetto sulla gittata cardiaca Ipotesi nulla IPOTESI NULLA La dieta non dovrebbe modificare in
CONFRONTO TRA LA MEDIE DI DUE CAMPIONI INDIPENDENTI
 CONFRONTO TRA LA MEDIE DI DUE CAMPIONI INDIPENDENTI ipotesi sul confronto tra le medie di due campioni indipendenti Obiettivo: decidere, attraverso il confronto tra le medie dei due campioni indipendenti,
CONFRONTO TRA LA MEDIE DI DUE CAMPIONI INDIPENDENTI ipotesi sul confronto tra le medie di due campioni indipendenti Obiettivo: decidere, attraverso il confronto tra le medie dei due campioni indipendenti,
si tratta del test del chi-quadro di adattamento e di quello di indipendenza. 1 l ipotesi che la popolazione segua una legge fissata;
 di : dado : normale Finora abbiamo visto test d ipotesi per testare ipotesi differenti, ma tutte concernenti il valore atteso di una o due popolazioni. In questo capitolo vediamo come testare 1 l ipotesi
di : dado : normale Finora abbiamo visto test d ipotesi per testare ipotesi differenti, ma tutte concernenti il valore atteso di una o due popolazioni. In questo capitolo vediamo come testare 1 l ipotesi
Ulteriori Conoscenze di Informatica e Statistica. Popolazione. Campione. I risultati di un esperimento sono variabili aleatorie.
 Ulteriori Conoscenze di Informatica e Statistica Carlo Meneghini Dip. di fisica via della Vasca Navale 84, st. 83 (I piano) tel.: 06 55 17 72 17 meneghini@fis.uniroma3.it I risultati di un esperimento
Ulteriori Conoscenze di Informatica e Statistica Carlo Meneghini Dip. di fisica via della Vasca Navale 84, st. 83 (I piano) tel.: 06 55 17 72 17 meneghini@fis.uniroma3.it I risultati di un esperimento
Statistica. Lezione 4
 Università degli Studi del Piemonte Orientale Corso di Laurea in Infermieristica Corso integrato in Scienze della Prevenzione e dei Servizi sanitari Statistica Lezione 4 a.a 2011-2012 Dott.ssa Daniela
Università degli Studi del Piemonte Orientale Corso di Laurea in Infermieristica Corso integrato in Scienze della Prevenzione e dei Servizi sanitari Statistica Lezione 4 a.a 2011-2012 Dott.ssa Daniela
P ( X n X > ɛ) = 0. ovvero (se come distanza consideriamo quella euclidea)
 10.4 Convergenze 166 10.4.3. Convergenza in Probabilità. Definizione 10.2. Data una successione X 1, X 2,...,,... di vettori aleatori e un vettore aleatorio X aventi tutti la stessa dimensione k diremo
10.4 Convergenze 166 10.4.3. Convergenza in Probabilità. Definizione 10.2. Data una successione X 1, X 2,...,,... di vettori aleatori e un vettore aleatorio X aventi tutti la stessa dimensione k diremo
Brevi cenni all intervallo di confidenza
 Brevi cenni all intervallo di confidenza INFERENZA STATISTICA L INFERENZA STATISTICA è un insieme di metodi con cui si cerca di «raggiungere una conclusione» sulla popolazione, sulla base delle informazioni
Brevi cenni all intervallo di confidenza INFERENZA STATISTICA L INFERENZA STATISTICA è un insieme di metodi con cui si cerca di «raggiungere una conclusione» sulla popolazione, sulla base delle informazioni
Distribuzioni e inferenza statistica
 Distribuzioni e inferenza statistica Distribuzioni di probabilità L analisi statistica spesso studia i fenomeni collettivi confrontandoli con modelli teorici di riferimento. Tra di essi, vedremo: la distribuzione
Distribuzioni e inferenza statistica Distribuzioni di probabilità L analisi statistica spesso studia i fenomeni collettivi confrontandoli con modelli teorici di riferimento. Tra di essi, vedremo: la distribuzione
ESERCIZIO 1. Soluzione. X =numero di passeggeri giornaliero
 ESERCIZIO 1 La somma dei numeri di passeggeri di un autoservizio suburbano rilevati in 7 giorni scelti a caso è pari a 385. Si assuma un modello gaussiano per descrivere il numero giornaliero di passeggeri.
ESERCIZIO 1 La somma dei numeri di passeggeri di un autoservizio suburbano rilevati in 7 giorni scelti a caso è pari a 385. Si assuma un modello gaussiano per descrivere il numero giornaliero di passeggeri.
Esercitazione 3 - Statistica II - Economia Aziendale Davide Passaretti 23/5/2017
 Esercitazione 3 - Statistica II - Economia Aziendale Davide Passaretti 3/5/017 Contents 1 Intervalli di confidenza 1 Intervalli su un campione 1.1 Intervallo di confidenza per la media................................
Esercitazione 3 - Statistica II - Economia Aziendale Davide Passaretti 3/5/017 Contents 1 Intervalli di confidenza 1 Intervalli su un campione 1.1 Intervallo di confidenza per la media................................
Il processo inferenziale consente di generalizzare, con un certo grado di sicurezza, i risultati ottenuti osservando uno o più campioni
 La statistica inferenziale Il processo inferenziale consente di generalizzare, con un certo grado di sicurezza, i risultati ottenuti osservando uno o più campioni E necessario però anche aggiungere con
La statistica inferenziale Il processo inferenziale consente di generalizzare, con un certo grado di sicurezza, i risultati ottenuti osservando uno o più campioni E necessario però anche aggiungere con
Statistica Inferenziale Soluzioni 3. Verifica di ipotesi
 ISTITUZIONI DI STATISTICA A. A. 007/008 Marco Minozzo e Annamaria Guolo Laurea in Economia del Commercio Internazionale Laurea in Economia e Amministrazione delle Imprese Università degli Studi di Verona
ISTITUZIONI DI STATISTICA A. A. 007/008 Marco Minozzo e Annamaria Guolo Laurea in Economia del Commercio Internazionale Laurea in Economia e Amministrazione delle Imprese Università degli Studi di Verona
Corso di Laurea in Ingegneria Informatica e Automatica (M-Z) Università di Roma La Sapienza
 Corso di Laurea in Ingegneria Informatica e Automatica (M-Z) Università di Roma La Sapienza CALCOLO DELLE PROBABILITÀ E STATISTICA ESAME DEL 16/06/2016 NOME: COGNOME: MATRICOLA: Esercizio 1 Cinque lettere
Corso di Laurea in Ingegneria Informatica e Automatica (M-Z) Università di Roma La Sapienza CALCOLO DELLE PROBABILITÀ E STATISTICA ESAME DEL 16/06/2016 NOME: COGNOME: MATRICOLA: Esercizio 1 Cinque lettere
Variabili aleatorie. Variabili aleatorie
 Variabili aleatorie Distribuzione binomiale Si supponga che uno studente affronti un esame composto da domande chiuse. Una sola delle 5 alternative di risposta proposta per ciascuna domanda è vera Supponiamo
Variabili aleatorie Distribuzione binomiale Si supponga che uno studente affronti un esame composto da domande chiuse. Una sola delle 5 alternative di risposta proposta per ciascuna domanda è vera Supponiamo
ES.2.2. Consideriamo un esperimento statistico definito da un insieme Ω di risultati possibili. Una partizione finita di Ω è una sequenza di K eventi
 ES22 1 Variabili aleatorie discrete Consideriamo un esperimento statistico definito da un insieme Ω di risultati possibili Una partizione finita di Ω è una sequenza di K eventi A 1, A 2 A k A K necessari
ES22 1 Variabili aleatorie discrete Consideriamo un esperimento statistico definito da un insieme Ω di risultati possibili Una partizione finita di Ω è una sequenza di K eventi A 1, A 2 A k A K necessari
STATISTICA A K (60 ore)
 STATISTICA A K (60 ore) Marco Riani mriani@unipr.it http://www.riani.it STIMA PUNTUALE (p. 55) Il parametro è stimato con un unico valore Esempio: stima della share di un programma TV = % di spettatori
STATISTICA A K (60 ore) Marco Riani mriani@unipr.it http://www.riani.it STIMA PUNTUALE (p. 55) Il parametro è stimato con un unico valore Esempio: stima della share di un programma TV = % di spettatori
UNIVERSITÀ di ROMA TOR VERGATA
 UNIVERSITÀ di ROMA TOR VERGATA Corso di Laurea Magistrale in Scienze della Nutrizione Umana Corso di Statistica Medica, anno 2015-16 P.Baldi Lista di esercizi 4, 11 febbraio 2016. Esercizio 1 Una v.a.
UNIVERSITÀ di ROMA TOR VERGATA Corso di Laurea Magistrale in Scienze della Nutrizione Umana Corso di Statistica Medica, anno 2015-16 P.Baldi Lista di esercizi 4, 11 febbraio 2016. Esercizio 1 Una v.a.
Prova d esame di Istituzioni di Calcolo delle Probabilità Laurea Triennale in Scienze Statistica. 09/09/2013
 Prova d esame di Istituzioni di Calcolo delle Probabilità Laurea Triennale in Scienze Statistica. 09/09/2013 COGNOME e NOME... N. MATRICOLA... Esercizio 1. (V. 12 punti.) Supponiamo di avere due urne che
Prova d esame di Istituzioni di Calcolo delle Probabilità Laurea Triennale in Scienze Statistica. 09/09/2013 COGNOME e NOME... N. MATRICOLA... Esercizio 1. (V. 12 punti.) Supponiamo di avere due urne che
Campionamento e stima di parametri
 Sia X una variabile aleatoria associata a un dato esperimento. Ripetiamo l esperimento n volte, ottenendo una famiglia di valori sperimentali della v.a. X : X = (X 1, X 2,..., X n ) ogni X i é una v.a.
Sia X una variabile aleatoria associata a un dato esperimento. Ripetiamo l esperimento n volte, ottenendo una famiglia di valori sperimentali della v.a. X : X = (X 1, X 2,..., X n ) ogni X i é una v.a.
LEZIONI DI STATISTICA MEDICA
 LEZIONI DI STATISTICA MEDICA Lezione n.11 - Principi dell inferenza statistica - Campionamento - Distribuzione campionaria di una media e di una proporzione - Intervallo di confidenza di una media e di
LEZIONI DI STATISTICA MEDICA Lezione n.11 - Principi dell inferenza statistica - Campionamento - Distribuzione campionaria di una media e di una proporzione - Intervallo di confidenza di una media e di
Università di Pavia Econometria. Richiami di Statistica. Eduardo Rossi
 Università di Pavia Econometria Richiami di Statistica Eduardo Rossi Università di Pavia Campione casuale Siano (Y 1, Y 2,..., Y N ) variabili casuali tali che le y i siano realizzazioni mutuamente indipendenti
Università di Pavia Econometria Richiami di Statistica Eduardo Rossi Università di Pavia Campione casuale Siano (Y 1, Y 2,..., Y N ) variabili casuali tali che le y i siano realizzazioni mutuamente indipendenti
STIMA DELLA VARIANZA CAMPIONARIA
 STIMA DELLA VARIANZA CAMPIONARIA Abbiamo visto che una stima puntuale corretta per il valore atteso µ delle variabili aleatorie X i è x n = (x 1 +.. + x n )/n. Una stima puntuale della varianza σ 2 delle
STIMA DELLA VARIANZA CAMPIONARIA Abbiamo visto che una stima puntuale corretta per il valore atteso µ delle variabili aleatorie X i è x n = (x 1 +.. + x n )/n. Una stima puntuale della varianza σ 2 delle
Parametri statistici
 SMID a.a. 2004/2005 Corso di Metodi Statistici in Biomedicina Parametri statistici 24/1/2005 Deviazione standard della media La variabilità di una distribuzione può quindi essere espressa da un indice
SMID a.a. 2004/2005 Corso di Metodi Statistici in Biomedicina Parametri statistici 24/1/2005 Deviazione standard della media La variabilità di una distribuzione può quindi essere espressa da un indice
STATISTICA A D (72 ore)
 STATISTICA A D (72 ore) Marco Riani mriani@unipr.it http://www.riani.it Esercizio In un urna vi sono N/2 palline bianche e N/2 palline nere. Si supponga di estrarre un campione con ripetizione di dimensione
STATISTICA A D (72 ore) Marco Riani mriani@unipr.it http://www.riani.it Esercizio In un urna vi sono N/2 palline bianche e N/2 palline nere. Si supponga di estrarre un campione con ripetizione di dimensione
Analisi di Regressione Multipla
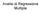 Analisi di Regressione Multipla Stima OLS della relazione Test Score/STR : TestScore! = 698.9.8 STR, R =.05, SER = 18.6 (10.4) (0.5) E una stima credibile dell effetto causale sul rendimento nei test di
Analisi di Regressione Multipla Stima OLS della relazione Test Score/STR : TestScore! = 698.9.8 STR, R =.05, SER = 18.6 (10.4) (0.5) E una stima credibile dell effetto causale sul rendimento nei test di
La statistica è la scienza che permette di conoscere il mondo intorno a noi attraverso i dati.
 RICHIAMI DI STATISTICA La statistica è la scienza che permette di conoscere il mondo intorno a noi attraverso i dati. Quale è la media della distribuzione del reddito dei neolaureati? Per rispondere dovremmo
RICHIAMI DI STATISTICA La statistica è la scienza che permette di conoscere il mondo intorno a noi attraverso i dati. Quale è la media della distribuzione del reddito dei neolaureati? Per rispondere dovremmo
Università del Piemonte Orientale. Corso di Laurea Triennale di Infermieristica Pediatrica ed Ostetricia. Corso di Statistica Medica
 Università del Piemonte Orientale Corso di Laurea Triennale di Infermieristica Pediatrica ed Ostetricia Corso di Statistica Medica Campionamento e distribuzione campionaria della media CdL Infermieristica
Università del Piemonte Orientale Corso di Laurea Triennale di Infermieristica Pediatrica ed Ostetricia Corso di Statistica Medica Campionamento e distribuzione campionaria della media CdL Infermieristica
Metodologia Sta,s,ca Applicata in Ambito Biomedico e Clinico TERZA PARTE. Mauro Gambaccini Anno accademico 2018/19
 Metodologia Sta,s,ca Applicata in Ambito Biomedico e Clinico TERZA PARTE Mauro Gambaccini -------------------- Anno accademico /9 DISTRIBUZIONI CAMPIONARIE Prendiamo palline uguali numerate da a 9 3 9
Metodologia Sta,s,ca Applicata in Ambito Biomedico e Clinico TERZA PARTE Mauro Gambaccini -------------------- Anno accademico /9 DISTRIBUZIONI CAMPIONARIE Prendiamo palline uguali numerate da a 9 3 9
Tutorato di Complementi di Analisi Matematica e Statistica 30 maggio 2016
 Tutorato di Complementi di Analisi Matematica e Statistica 30 maggio 2016 Esercizi possibili di probabilità e statistica Notazioni: U(a, b) è la distribuzione di probabilità uniforma nell intervallo (a,
Tutorato di Complementi di Analisi Matematica e Statistica 30 maggio 2016 Esercizi possibili di probabilità e statistica Notazioni: U(a, b) è la distribuzione di probabilità uniforma nell intervallo (a,
Ulteriori Conoscenze di Informatica e Statistica
 Ulteriori Conoscenze di Informatica e Statistica Carlo Meneghini Dip. di fisica via della Vasca Navale 84, st. 83 (I piano) tel.: 06 55 17 72 17 meneghini@fis.uniroma3.it Indici di forma Descrivono le
Ulteriori Conoscenze di Informatica e Statistica Carlo Meneghini Dip. di fisica via della Vasca Navale 84, st. 83 (I piano) tel.: 06 55 17 72 17 meneghini@fis.uniroma3.it Indici di forma Descrivono le
RICHIAMI DI CALCOLO DELLE PROBABILITÀ
 UNIVERSITA DEL SALENTO INGEGNERIA CIVILE RICHIAMI DI CALCOLO DELLE PROBABILITÀ ing. Marianovella LEONE INTRODUZIONE Per misurare la sicurezza di una struttura, ovvero la sua affidabilità, esistono due
UNIVERSITA DEL SALENTO INGEGNERIA CIVILE RICHIAMI DI CALCOLO DELLE PROBABILITÀ ing. Marianovella LEONE INTRODUZIONE Per misurare la sicurezza di una struttura, ovvero la sua affidabilità, esistono due
ESAME. 9 Gennaio 2017 COMPITO B
 ESAME 9 Gennaio 2017 COMPITO B Cognome Nome Numero di matricola 1) Approssimare tutti i calcoli alla quarta cifra decimale. 2) Ai fini della valutazione si terrà conto solo ed esclusivamente di quanto
ESAME 9 Gennaio 2017 COMPITO B Cognome Nome Numero di matricola 1) Approssimare tutti i calcoli alla quarta cifra decimale. 2) Ai fini della valutazione si terrà conto solo ed esclusivamente di quanto
Statistica inferenziale, Varese, 18 novembre 2009 Prima parte - Modalità D
 Statistica inferenziale, Varese, 18 novembre 2009 Prima parte - Modalità D Cognome Nome: Part time: Numero di matricola: Diurno: ISTRUZIONI: Il punteggio relativo alla prima parte dell esame viene calcolato
Statistica inferenziale, Varese, 18 novembre 2009 Prima parte - Modalità D Cognome Nome: Part time: Numero di matricola: Diurno: ISTRUZIONI: Il punteggio relativo alla prima parte dell esame viene calcolato
ESAME. 9 Gennaio 2017 COMPITO A
 ESAME 9 Gennaio 2017 COMPITO A Cognome Nome Numero di matricola 1) Approssimare tutti i calcoli alla quarta cifra decimale. 2) Ai fini della valutazione si terrà conto solo ed esclusivamente di quanto
ESAME 9 Gennaio 2017 COMPITO A Cognome Nome Numero di matricola 1) Approssimare tutti i calcoli alla quarta cifra decimale. 2) Ai fini della valutazione si terrà conto solo ed esclusivamente di quanto
University of Messina, Italy
 ERRORI CASUALI ELL AALISI CHIMICA Errori casuali Gli errori casuali si incontrano tutte le volte che un sistema di misura viene usato al massimo della sua sensibilità. In queste circostanze i risultati
ERRORI CASUALI ELL AALISI CHIMICA Errori casuali Gli errori casuali si incontrano tutte le volte che un sistema di misura viene usato al massimo della sua sensibilità. In queste circostanze i risultati
Statistica inferenziale, Varese, 18 novembre 2009 Prima parte - Modalità B
 Statistica inferenziale, Varese, 18 novembre 2009 Prima parte - Modalità B Cognome Nome: Part time: Numero di matricola: Diurno: ISTRUZIONI: Il punteggio relativo alla prima parte dell esame viene calcolato
Statistica inferenziale, Varese, 18 novembre 2009 Prima parte - Modalità B Cognome Nome: Part time: Numero di matricola: Diurno: ISTRUZIONI: Il punteggio relativo alla prima parte dell esame viene calcolato
ESERCIZIO 1 Si considerino n v.c. Xi (i = 1,, n) tra loro indipendenti e somiglianti con media 10 e varianza 4. Si determini:
 ESERCIZIO 1 Si considerino n v.c. Xi (i = 1,, n) tra loro indipendenti e somiglianti con media 10 e varianza 4. Si determini: VALORE ATTESO Variabile casuale SOMMA delle n variabili Variabile casuale MEDIA
ESERCIZIO 1 Si considerino n v.c. Xi (i = 1,, n) tra loro indipendenti e somiglianti con media 10 e varianza 4. Si determini: VALORE ATTESO Variabile casuale SOMMA delle n variabili Variabile casuale MEDIA
La funzione di distribuzione Gaussiana normale
 La funzione di distribuzione Gaussiana normale Nicola Morganti 25 aprile 2004 Indice Proprietà fondamentali 2 Standard Normal Density Function 3 3 Esempio applicativo 5 Proprietà fondamentali L utilizzo
La funzione di distribuzione Gaussiana normale Nicola Morganti 25 aprile 2004 Indice Proprietà fondamentali 2 Standard Normal Density Function 3 3 Esempio applicativo 5 Proprietà fondamentali L utilizzo
Intervallo di confidenza.
 Intervallo di confidenza annarita.vestri@uniroma1.it campione inferenza popolazione Media Riportare sempre anche la deviazione standard Stima puntuale di Media, dev.standard, numerosità Qualche semplice
Intervallo di confidenza annarita.vestri@uniroma1.it campione inferenza popolazione Media Riportare sempre anche la deviazione standard Stima puntuale di Media, dev.standard, numerosità Qualche semplice
CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 5
 CORSO DI STATISTICA (parte 2) - ESERCITAZIONE Dott.ssa Antonella Costanzo a.costanzo@unicas.it Esercizio 1. Approssimazione normale della Poisson (TLC) In un determinato tratto di strada il numero di incidenti
CORSO DI STATISTICA (parte 2) - ESERCITAZIONE Dott.ssa Antonella Costanzo a.costanzo@unicas.it Esercizio 1. Approssimazione normale della Poisson (TLC) In un determinato tratto di strada il numero di incidenti
7. STATISTICA DESCRITTIVA
 7. STATISTICA DESCRITTIVA Quando si effettua un indagine statistica si ha a che fare con un numeroso insieme di oggetti, detto popolazione del quale si intende esaminare una o più caratteristiche (matricole
7. STATISTICA DESCRITTIVA Quando si effettua un indagine statistica si ha a che fare con un numeroso insieme di oggetti, detto popolazione del quale si intende esaminare una o più caratteristiche (matricole
Confronto tra due popolazioni Lezione 6
 Last updated May 9, 06 Confronto tra due popolazioni Lezione 6 G. Bacaro Statistica CdL in Scienze e Tecnologie per l'ambiente e la Natura I anno, II semestre Concetti visti nell ultima lezione Le media
Last updated May 9, 06 Confronto tra due popolazioni Lezione 6 G. Bacaro Statistica CdL in Scienze e Tecnologie per l'ambiente e la Natura I anno, II semestre Concetti visti nell ultima lezione Le media
distribuzione della popolazione campionata distribuzione di quantità che dipendono dal campione (distribuzioni campionarie)
 Obiettivi lezione 4 CAPIRE: distribuzione della popolazione campionata distribuzione di quantità che dipendono dal campione (distribuzioni campionarie) CONOSCERE: Le distribuzioni della media campionaria,
Obiettivi lezione 4 CAPIRE: distribuzione della popolazione campionata distribuzione di quantità che dipendono dal campione (distribuzioni campionarie) CONOSCERE: Le distribuzioni della media campionaria,
DISTRIBUZIONI DI CAMPIONAMENTO
 DISTRIBUZIONI DI CAMPIONAMENTO 12 DISTRIBUZIONE DI CAMPIONAMENTO DELLA MEDIA Situazione reale Della popolazione di tutti i laureati in odontoiatria negli ultimi 10 anni, in tutte le Università d Italia,
DISTRIBUZIONI DI CAMPIONAMENTO 12 DISTRIBUZIONE DI CAMPIONAMENTO DELLA MEDIA Situazione reale Della popolazione di tutti i laureati in odontoiatria negli ultimi 10 anni, in tutte le Università d Italia,
Campionamento e distribuzioni campionarie
 Campionamento e distribuzioni campionarie Prof. Giuseppe Verlato Sezione di Epidemiologia e Statistica Medica, Università di Verona Inferenza statistica = processo che, partendo dalle informazioni contenute
Campionamento e distribuzioni campionarie Prof. Giuseppe Verlato Sezione di Epidemiologia e Statistica Medica, Università di Verona Inferenza statistica = processo che, partendo dalle informazioni contenute
Università del Piemonte Orientale. Corsi di laurea triennale di area tecnica. Corso di Statistica Medica. Intervalli di confidenza
 Università del Piemonte Orientale Corsi di laurea triennale di area tecnica Corso di Statistica Medica Intervalli di confidenza Corsi di laurea triennale di area tecnica - Corso di Statistica Medica -
Università del Piemonte Orientale Corsi di laurea triennale di area tecnica Corso di Statistica Medica Intervalli di confidenza Corsi di laurea triennale di area tecnica - Corso di Statistica Medica -
Facoltà di ECONOMIA Corso di Statistica a.a. 2005/2006 Esame del 27/09/2006 Calcolo delle Probabilità e Inferenza
 Esame del 27/09/2006 Calcolo delle Probabilità e Inferenza 1. Si consideri un urna contenente 10 palline numerate di forma uguale ma di diverso colore (R=rosso, V=verde, N=nero). Numero 1 2 3 4 5 6 7 8
Esame del 27/09/2006 Calcolo delle Probabilità e Inferenza 1. Si consideri un urna contenente 10 palline numerate di forma uguale ma di diverso colore (R=rosso, V=verde, N=nero). Numero 1 2 3 4 5 6 7 8
Questo calcolo richiede che si conoscano media e deviazione standard della popolazione.
 Università del Piemonte Orientale Corso di laurea in biotecnologie Corso di Statistica Medica La distribuzione t - student 1 Abbiamo visto nelle lezioni precedenti come il calcolo del valore Z, riferito
Università del Piemonte Orientale Corso di laurea in biotecnologie Corso di Statistica Medica La distribuzione t - student 1 Abbiamo visto nelle lezioni precedenti come il calcolo del valore Z, riferito
Campione: Esercitazioni di Statistica Corsi di Laurea Infermiesristica Pediatrica e Ostetricia - I anno 1
 Campione: - raccolta finita di elementi estratti da una popolazione - scopo dell estrazione è quello di ottenere informazioni sulla popolazione - il campione deve essere rappresentativo della popolazione
Campione: - raccolta finita di elementi estratti da una popolazione - scopo dell estrazione è quello di ottenere informazioni sulla popolazione - il campione deve essere rappresentativo della popolazione
distribuzioni campionarie
 distribuzioni campionarie cosa sono sampling distribution la distribuzione teorica di una statistica campionaria, supponendo di estrarre ripetuti campioni p.e., la distribuzione di tutte le medie di campioni
distribuzioni campionarie cosa sono sampling distribution la distribuzione teorica di una statistica campionaria, supponendo di estrarre ripetuti campioni p.e., la distribuzione di tutte le medie di campioni
Distribuzioni campionarie. Antonello Maruotti
 Distribuzioni campionarie Antonello Maruotti Outline 1 Introduzione 2 Concetti base Si riprendano le considerazioni fatte nella parte di statistica descrittiva. Si vuole studiare una popolazione con riferimento
Distribuzioni campionarie Antonello Maruotti Outline 1 Introduzione 2 Concetti base Si riprendano le considerazioni fatte nella parte di statistica descrittiva. Si vuole studiare una popolazione con riferimento
POPOLAZIONE E CAMPIONI
 p. 1/2 POPOLAZIONE E CAMPIONI POPOLAZIONE insieme di tutti quegli elementi che hanno almeno una caratteristica comune (persone, oggetti,misure, osservazioni). Consideriamo il caso di caratteristiche associate
p. 1/2 POPOLAZIONE E CAMPIONI POPOLAZIONE insieme di tutti quegli elementi che hanno almeno una caratteristica comune (persone, oggetti,misure, osservazioni). Consideriamo il caso di caratteristiche associate
Università del Piemonte Orientale. Corso di laurea in medicina e chirurgia. Corso di Statistica Medica. La distribuzione t - student
 Università del Piemonte Orientale Corso di laurea in medicina e chirurgia Corso di Statistica Medica La distribuzione t - student 1 Abbiamo visto nelle lezioni precedenti come il calcolo del valore Z,
Università del Piemonte Orientale Corso di laurea in medicina e chirurgia Corso di Statistica Medica La distribuzione t - student 1 Abbiamo visto nelle lezioni precedenti come il calcolo del valore Z,
