Computazione per l interazione naturale: clustering e riduzione di dimensionalità
|
|
|
- Ottavia Marchi
- 5 anni fa
- Visualizzazioni
Transcript
1 Computazione per l interazione naturale: clustering e riduzione di dimensionalità Corso di Interazione uomo-macchina II Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it Apprendimento non supervisionato //Il clustering
2 Il problema del clustering Trovare strutture coerenti nei dati Esempio: Old Faithful dataset Una singola Gaussiana è insufficiente Supponiamo di avere 2 clusters (agglomerati) Vogliamo assegnare ciascun punto ad uno dei due cluster Unmetodo di clustering semplice: k-means K-means clustering //Esempio
3 K-means clustering //Esempio K-means clustering //Esempio
4 K-means clustering //Esempio K-means clustering //Esempio
5 K-means clustering //Esempio K-means clustering //Esempio
6 K-means clustering //Esempio K-means clustering //Esempio
7 K-means clustering //Algoritmo: ipotesi Dati (non etichettati) in uno spazio di features di dimensione D: Ipotizziamo K possibili clusters (è il nostro modello) Supponiamo che esista per ciascun punto n una variabile binaria che vale 1 se il punto n appartiene al cluster k Questo tipo di variabile è detta indicatore (indicator variable), ed è in generale una variabile latente (non la conosciamo) K-means clustering //Algoritmo: misura di qualità del cluster Ci serve una misura di coerenza interna o compattezza per i punti di un cluster: distanza totale di tutti i punti dal baricentro del cluster Numero di punti allocati nel cluster k: Qualità complessiva del clustering: il criterio da ottimizzare
8 K-means clustering //Algoritmo: ottimizzazione Due insiemi di parametri:, 1. Fissato derivo rispetto a : il criterio si annulla quando il punto è assegnato alla media più vicina 2. Fissato derivo rispetto a Itero fino a convergenza K-means clustering //Algoritmo function [M,z,e] = kmeans(x,k,max_its) %KMEANS Semplice implementazione del k-means clustering % Input: % Data matrix X (N x D) % Numero di cluster K % Massimo numero di iterazioni Max_Its % Output: % Matrice M (K x D) - le K medie % Vettore z (N x 1): z(n)=k indica il Cluster 1.. K a cui ciascun punto x_n e' stato assegnato [N,D]=size(X); %N - num punti, D dimensione dati I=randperm(N); %permutazione random degli interi 1:N - usata %per settare in modo random le K medie iniziali M=X(I(1:K),:); %M matrice K x D dei mean values - selezionate in modo random Mo = M; for t=1:max_its %Crea la distance matrix N x K: indica la distanza di ciascun punto X_n dai K centri for k=1:k Dist(:,k) = sum((x - repmat(m(k,:),n,1)).^2,2); end %Minima distanza di K da ciascun punto. [i,z]=min(dist,[],2); %Abbiamo gli assegnamenti ai clusters: ricalcoliamo i centri dei %cluster for k=1:k if size(find(z==k))>0 M(k,:) = mean(x(find(z==k),:)); end end %Calcoliamo Z matrice N x K: indictor matrix - di elementi z_nk Z = zeros(n,k); for n=1:n Z(n,z(n)) = 1; end %Calcola il valore corrente del criterio di errore minimizzato da K-means e = sum(sum(z.*dist)./n); fprintf('%d Error = %f\n', t, e); Mo = M; end
9 K-means clustering //Segmentazione dell immagine come clustering K regioni/cluster, ad esempio di colore: ogni punto (pixel) è un vettore [R G B] Esempio: K=4 Se si usa per codificare/comprimere: vector quantization K-means clustering //Segmentazione dell immagine come clustering
10 Cluster non Gaussiani Proviamo a generare una distribuzione di punti campionando da due Gaussiane 2D (due processi diversi) aventi i seguenti parametri La distribuzione risultante è non Gaussiana e non puo essere fittata con un unica Gaussiana (si può ma l errore è elevato Cluster non Gaussiani Proviamo a generare una distribuzione di punti campionando da due Gaussiane (due processi diversi) aventi i seguenti parametri
11 Misture di Gaussiane Possiamo rappresentare la distribuzione ottenuta come la mistura di due Gaussiane (mixture of Gaussians) probabilità che x sia generato da probabilità che x sia generato da Misture di Gaussiane //caso generale Possiamo rappresentare una distribuzione non Gaussiana come mistura di M Gaussiane
12 Misture di Gaussiane //stima dei parametri (ML) Supponiamo di avere i dati Assumiamo un modello MoG Vogliamo stimare Misture di Gaussiane //stima dei parametri (ML) Supponiamo di avere i dati Assumiamo un modello MoG Vogliamo stimare Supponiamo di avere la matrice Z degli indicatori: il punto n è stato generato da Gaussiana m il punto n non è stato generato da Gaussiana m
13 Misture di Gaussiane //stima dei parametri (ML) Supponiamo di avere la matrice Z degli indicatori: La stima ML dei parametri è la stima dei parametri di ciascuna Gaussiana m contando solo i punti che gli indicatori assegnano a quella Gaussiana il punto n è stato generato da Gaussiana m il punto n non è stato generato da Gaussiana m Per conto la frazione di punti nel cluster m Misture di Gaussiane //stima dei parametri (ML) Problema: NON ABBIAMO la matrice Z degli indicatori il punto n è stato generato da Gaussiana m il punto n non è stato generato da Gaussiana m sono variabili latenti o nascoste (hidden) Per una stima ML, ci serve la La verosimiglianza dei dati Se avessimo i parametri
14 Misture di Gaussiane //stima dei parametri (ML) Se avessimo i parametri = h variabili hidden Misture di Gaussiane //stima dei parametri (ML) Passando alla log-verosimiglianza Difficile da massimizzare in forma analitica per la presenza di Possiamo però determinare un lower bound più semplice e massimizzare il lower bound
15 Uno strumento per approssimare Disuguaglianza di Jensen: per una funzione convessa di x Uno strumento per approssimare Per una funzione concava, si inverte la disuguaglianza Esempio: funzione logaritmica
16 Misture di Gaussiane //stima dei parametri (ML) Passando alla log-verosimiglianza (Jensen) Lower Bound Misture di Gaussiane //stima dei parametri (ML) Risultato se massimizzo il lower bound massimizzo la likelihood Lower Bound Sotto l ipotesi i.i.d Probabilità che per tutti gli n Probabilità che
17 Misture di Gaussiane //stima dei parametri (ML): algoritmo EM Fino a convergenza: E(xpectation) step: fissati i parametri, otteniamo gli indicatori M(aximization) step: fissati gli indicatori, otteniamo i parametri Misture di Gaussiane //stima dei parametri (ML): algoritmo EM Expectation Derivando:
18 Misture di Gaussiane //stima dei parametri (ML): algoritmo EM Maximization: nel caso Gaussiano Derivando: Misture di Gaussiane //Algoritmo Expectation-Maximization Fino a convergenza: E(xpectation) step: fissati i parametri, otteniamo gli indicatori M(aximization) step: fissati gli indicatori, otteniamo i parametri
19 Misture di Gaussiane //Algoritmo EM: log-likelihood durante iterazioni intuitivamente: quando L non cresce più di tanto, posso terminare le iterazioni Misture di Gaussiane //Algoritmo Expectation-Maximization (da PMTK3) iter = 1; done = false; loglikhist = zeros(maxiter + 1, 1); while ~done [ess, ll] = estep(model, data); loglikhist(iter) = ll; model = mstep(model, ess); done = (iter > maxiter) ( (iter > 1) &&... convergencetest(loglikhist(iter), loglikhist(iter-1), convtol, true)); iter = iter + 1; end loglikhist = loglikhist(1:iter-1);
20 Misture di Gaussiane //Algoritmo Expectation-Maximization Misture di Gaussiane //Algoritmo Expectation-Maximization
21 Misture di Gaussiane //Algoritmo Expectation-Maximization Misture di Gaussiane //Algoritmo Expectation-Maximization
22 Misture di Gaussiane //Algoritmo Expectation-Maximization Misture di Gaussiane //Algoritmo Expectation-Maximization
23 Misture di Gaussiane //Algoritmo Expectation-Maximization massimizzazzione della log-likelihood durante le iterazioni di EM Variazione della max log-likelihood al variare del numero di componenti M Misture di Gaussiane //Algoritmo Expectation-Maximization Predizione: dopo aver appreso i parametri e la matrice Z, se volessi classificare un nuovo dato è sufficiente usare il passo di Expectation che corrisponde a Bayes e classificare in base alla regola map arg max m
24 EM e k-means Il modo di funzionare ci ricorda quello del k-means Infatti il k-means è un caso particolare (degenere) di EM, che si ottiene considerando Gaussiane isotrope/sferiche (con matrice di covarianza fissata = matrice identità) In questo caso devo stimare solo le medie. Passo E Passo M EM e k-means
25 Mistura di Gaussiane //punto di vista generativo Mistura di Gaussiane //punto di vista generativo 2. Campiono il dato x 1. Campiono la componente
26 Mistura di Gaussiane //punto di vista generativo Bayesiano Mistura di Gaussiane //punto di vista generativo Bayesiano Se intraprendiamo un inferenza Bayesiana sulla congiunta, otteniamo una forma non integrabile analiticamente Adottiamo un approssimazione variazionale basata sulla disuguaglianza di Jensen: Variational Bayes Se nelle formule di VB assumiamo che siano delta di Dirac (ML), otteniamo le equazioni di EM come caso particolare Variational Bayes EM k-means
27 Modelli per la riduzione di dimensionlità Riduzione di dimensionalità Qual è la dimensionalità intrinseca a questi due data set?
28 Analisi per componenti principali Principal Component Analysis (PCA) Trovare un piccolo numero (dimensione) di direzioni che spiega le correlazioni nei dati di input: lo spazio latente Si possono rappresentare i dati proiettandoli su tali direzioni I dati sono continui, il mapping tra lo spazio latente e lo spazio dei dati osservati è lineare Utile per: Analisi per componenti principali //Descrizione intuitiva N vettori di dati di dimensionalità D:, Spazio di proiezione (latente) di dimensionalità k<<d Si cercano le direzioni ortogonali di massima varianza La struttura dei vettori è rappresentata nella matrice di covarianza empirica Le direzioni cercate sono gli autovettori di C
29 Esempio Analisi per componenti principali //Descrizione intuitiva Si selezionano gli autovettori di C Si proiettano i vettori di input nel sottospazio: Si puo ricostruire x usando K autovettori
30 Analisi per componenti principali //Descrizione intuitiva Analisi per componenti principali //Descrizione intuitiva Calcolo della base Proiezione e ricostruzione
31 Analisi per componenti principali //Esempi Dati input D= Autovettori (K=48) Analisi per componenti principali //Esempi K=10 K=100
32 Analisi per componenti principali //Esempi Analisi per componenti principali //Esempi
33 PCA (1) //Direzione di massima varianza Consideriamo il mapping dallo spazio latente x a y Trovare w in maniera da massimizzare var(y) sotto il vincolo Si può dimostrare che w* è autovettore di C PCA (2) //Minimizzazione dell errore di ricostruzione Consideriamo il mapping dallo spazio latente x a y Vogliamo minimizzare l errore quadratico di ricostruzione Risolvendo per alfa e sostituendo Con il vincolo
34 Modelli a variabili latenti //PCA probabilistica (PPCA) Si utilizza un modello generativo
Computazione per l interazione naturale: modelli a variabili latenti (clustering e riduzione di dimensionalità)
 Computazione per l interazione naturale: modelli a variabili latenti (clustering e riduzione di dimensionalità) Corso di Interazione Naturale Prof. Giuseppe Boccignone Dipartimento di Informatica Università
Computazione per l interazione naturale: modelli a variabili latenti (clustering e riduzione di dimensionalità) Corso di Interazione Naturale Prof. Giuseppe Boccignone Dipartimento di Informatica Università
Riduzione di dimensionalità
 Riduzione di dimensionalità SCUOLA DI SPECIALIZZAZIONE IN FISICA MEDICA Corso di Sistemi di Elaborazione dell Informazione Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it
Riduzione di dimensionalità SCUOLA DI SPECIALIZZAZIONE IN FISICA MEDICA Corso di Sistemi di Elaborazione dell Informazione Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it
Computazione per l interazione naturale: Regressione probabilistica
 Computazione per l interazione naturale: Regressione probabilistica Corso di Interazione Naturale Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it boccignone.di.unimi.it/in_2016.html
Computazione per l interazione naturale: Regressione probabilistica Corso di Interazione Naturale Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it boccignone.di.unimi.it/in_2016.html
Computazione per l interazione naturale: Regressione probabilistica
 Computazione per l interazione naturale: Regressione probabilistica Corso di Interazione Naturale Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it boccignone.di.unimi.it/in_2017.html
Computazione per l interazione naturale: Regressione probabilistica Corso di Interazione Naturale Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it boccignone.di.unimi.it/in_2017.html
Computazione per l interazione naturale: Regressione probabilistica
 Computazione per l interazione naturale: Regressione probabilistica Corso di Interazione Naturale Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it boccignone.di.unimi.it/in_2018.html
Computazione per l interazione naturale: Regressione probabilistica Corso di Interazione Naturale Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it boccignone.di.unimi.it/in_2018.html
Computazione per l interazione naturale: processi gaussiani
 Computazione per l interazione naturale: processi gaussiani Corso di Interazione uomo-macchina II Prof. Giuseppe Boccignone Dipartimento di Scienze dell Informazione Università di Milano boccignone@dsi.unimi.it
Computazione per l interazione naturale: processi gaussiani Corso di Interazione uomo-macchina II Prof. Giuseppe Boccignone Dipartimento di Scienze dell Informazione Università di Milano boccignone@dsi.unimi.it
Modelli Probabilistici per la Computazione Affettiva: Learning/Inferenza parametri
 Modelli Probabilistici per la Computazione Affettiva: Learning/Inferenza parametri Corso di Modelli di Computazione Affettiva Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano
Modelli Probabilistici per la Computazione Affettiva: Learning/Inferenza parametri Corso di Modelli di Computazione Affettiva Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano
Computazione per l interazione naturale: Modelli dinamici
 Computazione per l interazione naturale: Modelli dinamici Corso di Interazione uomo-macchina II Prof. Giuseppe Boccignone Dipartimento di Scienze dell Informazione Università di Milano boccignone@dsi.unimi.it
Computazione per l interazione naturale: Modelli dinamici Corso di Interazione uomo-macchina II Prof. Giuseppe Boccignone Dipartimento di Scienze dell Informazione Università di Milano boccignone@dsi.unimi.it
Computazione per l interazione naturale: classificazione probabilistica
 Computazione per l interazione naturale: classificazione probabilistica Corso di Interazione uomo-macchina II Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it
Computazione per l interazione naturale: classificazione probabilistica Corso di Interazione uomo-macchina II Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it
Computazione per l interazione naturale: classificazione probabilistica
 Computazione per l interazione naturale: classificazione probabilistica Corso di Interazione Naturale Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it boccignone.di.unimi.it/in_2016.html
Computazione per l interazione naturale: classificazione probabilistica Corso di Interazione Naturale Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it boccignone.di.unimi.it/in_2016.html
Computazione per l interazione naturale: fondamenti probabilistici (2)
 Computazione per l interazione naturale: fondamenti probabilistici (2) Corso di Interazione uomo-macchina II Prof. Giuseppe Boccignone Dipartimento di Scienze dell Informazione Università di Milano boccignone@di.unimi.it
Computazione per l interazione naturale: fondamenti probabilistici (2) Corso di Interazione uomo-macchina II Prof. Giuseppe Boccignone Dipartimento di Scienze dell Informazione Università di Milano boccignone@di.unimi.it
Computazione per l interazione naturale: Regressione lineare
 Computazione per l interazione naturale: Corso di Interazione uomo-macchina II Prof. Giuseppe Boccignone Dipartimento di Scienze dell Informazione Università di Milano boccignone@dsi.unimi.it http://homes.dsi.unimi.it/~boccignone/l
Computazione per l interazione naturale: Corso di Interazione uomo-macchina II Prof. Giuseppe Boccignone Dipartimento di Scienze dell Informazione Università di Milano boccignone@dsi.unimi.it http://homes.dsi.unimi.it/~boccignone/l
Computazione per l interazione naturale: macchine che apprendono
 Computazione per l interazione naturale: macchine che apprendono Corso di Interazione uomo-macchina II Prof. Giuseppe Boccignone Dipartimento di Scienze dell Informazione Università di Milano boccignone@dsi.unimi.it
Computazione per l interazione naturale: macchine che apprendono Corso di Interazione uomo-macchina II Prof. Giuseppe Boccignone Dipartimento di Scienze dell Informazione Università di Milano boccignone@dsi.unimi.it
Regressione. Apprendimento supervisionato //Regressione. Corso di Sistemi di Elaborazione dell Informazione
 Regressione SCUOLA DI SPECIALIZZAZIONE IN FISICA MEDICA Corso di Sistemi di Elaborazione dell Informazione Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it
Regressione SCUOLA DI SPECIALIZZAZIONE IN FISICA MEDICA Corso di Sistemi di Elaborazione dell Informazione Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it
Computazione per l interazione naturale: Regressione lineare (MSE)
 Computazione per l interazione naturale: Regressione lineare (MSE) Corso di Interazione Naturale Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it boccignone.di.unimi.it/in_2015.html
Computazione per l interazione naturale: Regressione lineare (MSE) Corso di Interazione Naturale Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it boccignone.di.unimi.it/in_2015.html
Cenni di apprendimento in Reti Bayesiane
 Sistemi Intelligenti 216 Cenni di apprendimento in Reti Bayesiane Esistono diverse varianti di compiti di apprendimento La struttura della rete può essere nota o sconosciuta Esempi di apprendimento possono
Sistemi Intelligenti 216 Cenni di apprendimento in Reti Bayesiane Esistono diverse varianti di compiti di apprendimento La struttura della rete può essere nota o sconosciuta Esempi di apprendimento possono
Computazione per l interazione naturale: regressione logistica Bayesiana
 Computazione per l interazione naturale: regressione logistica Bayesiana Corso di Interazione uomo-macchina II Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it
Computazione per l interazione naturale: regressione logistica Bayesiana Corso di Interazione uomo-macchina II Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it
Computazione per l interazione naturale: fondamenti probabilistici (2)
 Computazione per l interazione naturale: fondamenti probabilistici (2) Corso di Interazione uomo-macchina II Prof. Giuseppe Boccignone Dipartimento di Scienze dell Informazione Università di Milano boccignone@dsi.unimi.it
Computazione per l interazione naturale: fondamenti probabilistici (2) Corso di Interazione uomo-macchina II Prof. Giuseppe Boccignone Dipartimento di Scienze dell Informazione Università di Milano boccignone@dsi.unimi.it
Computazione per l interazione naturale: Regressione lineare Bayesiana
 Computazione per l interazione naturale: Bayesiana Corso di Interazione uomo-macchina II Prof. Giuseppe Boccignone Dipartimento di Scienze dell Informazione Università di Milano boccignone@di.unimi.it
Computazione per l interazione naturale: Bayesiana Corso di Interazione uomo-macchina II Prof. Giuseppe Boccignone Dipartimento di Scienze dell Informazione Università di Milano boccignone@di.unimi.it
Computazione per l interazione naturale: macchine che apprendono
 Comput per l inter naturale: macchine che apprendono Corso di Inter uomo-macchina II Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it http://boccignone.di.unimi.it/ium2_2014.html
Comput per l inter naturale: macchine che apprendono Corso di Inter uomo-macchina II Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it http://boccignone.di.unimi.it/ium2_2014.html
Computazione per l interazione naturale: macchine che apprendono
 Computazione per l interazione naturale: macchine che apprendono Corso di Interazione uomo-macchina II Prof. Giuseppe Boccignone Dipartimento di Scienze dell Informazione Università di Milano boccignone@dsi.unimi.it
Computazione per l interazione naturale: macchine che apprendono Corso di Interazione uomo-macchina II Prof. Giuseppe Boccignone Dipartimento di Scienze dell Informazione Università di Milano boccignone@dsi.unimi.it
Apprendimento Automatico
 Apprendimento Automatico Metodi Bayesiani - Naive Bayes Fabio Aiolli 13 Dicembre 2017 Fabio Aiolli Apprendimento Automatico 13 Dicembre 2017 1 / 18 Classificatore Naive Bayes Una delle tecniche più semplici
Apprendimento Automatico Metodi Bayesiani - Naive Bayes Fabio Aiolli 13 Dicembre 2017 Fabio Aiolli Apprendimento Automatico 13 Dicembre 2017 1 / 18 Classificatore Naive Bayes Una delle tecniche più semplici
Gaussian processes (GP)
 Gaussian processes (GP) Corso di Modelli di Computazione Affettiva Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it Giuseppe.Boccignone@unimi.it http://boccignone.di.unimi.it/compaff017.html
Gaussian processes (GP) Corso di Modelli di Computazione Affettiva Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it Giuseppe.Boccignone@unimi.it http://boccignone.di.unimi.it/compaff017.html
Computazione per l interazione naturale: Richiami di ottimizzazione (3) (e primi esempi di Machine Learning)
 Computazione per l interazione naturale: Richiami di ottimizzazione (3) (e primi esempi di Machine Learning) Corso di Interazione Naturale Prof. Giuseppe Boccignone Dipartimento di Informatica Università
Computazione per l interazione naturale: Richiami di ottimizzazione (3) (e primi esempi di Machine Learning) Corso di Interazione Naturale Prof. Giuseppe Boccignone Dipartimento di Informatica Università
Computazione per l interazione naturale: classificazione supervisionata
 Computazione per l interazione naturale: classificazione supervisionata Corso di Interazione uomo-macchina II Prof. Giuseppe Boccignone Dipartimento di Scienze dell Informazione Università di Milano boccignone@dsi.unimi.it
Computazione per l interazione naturale: classificazione supervisionata Corso di Interazione uomo-macchina II Prof. Giuseppe Boccignone Dipartimento di Scienze dell Informazione Università di Milano boccignone@dsi.unimi.it
Learning finite Mixture- Models. Giuseppe Manco
 Learning finite Mixture- Models Giuseppe Manco Clustering La problematica del clustering è relativa al learning non supervisionato Abbiamo un dataset con istanze la cui etichetta è sconosciuta Obiettivo
Learning finite Mixture- Models Giuseppe Manco Clustering La problematica del clustering è relativa al learning non supervisionato Abbiamo un dataset con istanze la cui etichetta è sconosciuta Obiettivo
Regressione Lineare. Corso di Intelligenza Artificiale, a.a Prof. Francesco Trovò
 Regressione Lineare Corso di Intelligenza Artificiale, a.a. 2017-2018 Prof. Francesco Trovò 23/04/2018 Regressione Lineare Supervised Learning Supervised Learning: recap È il sottocampo del ML più vasto
Regressione Lineare Corso di Intelligenza Artificiale, a.a. 2017-2018 Prof. Francesco Trovò 23/04/2018 Regressione Lineare Supervised Learning Supervised Learning: recap È il sottocampo del ML più vasto
Algoritmi di minimizzazione EM Mixture models
 Algoritmi di minimizzazione E ixture models I. Frosio AIS Lab. frosio@dsi.unimi.it /58 Overview Stima di due rette (riassunto) inimizzazione: metodi di ordine zero (simplesso, ) inimizzazione: metodi di
Algoritmi di minimizzazione E ixture models I. Frosio AIS Lab. frosio@dsi.unimi.it /58 Overview Stima di due rette (riassunto) inimizzazione: metodi di ordine zero (simplesso, ) inimizzazione: metodi di
Stima dei parametri. I parametri di una pdf sono costanti che caratterizzano la sua forma. r.v. parameter. Assumiamo di avere un campione di valori
 Stima dei parametri I parametri di una pdf sono costanti che caratterizzano la sua forma r.v. parameter Assumiamo di avere un campione di valori Vogliamo una funzione dei dati che permette di stimare i
Stima dei parametri I parametri di una pdf sono costanti che caratterizzano la sua forma r.v. parameter Assumiamo di avere un campione di valori Vogliamo una funzione dei dati che permette di stimare i
Apprendimento Automatico
 Apprendimento Automatico Metodi Bayesiani Fabio Aiolli 11 Dicembre 2017 Fabio Aiolli Apprendimento Automatico 11 Dicembre 2017 1 / 19 Metodi Bayesiani I metodi Bayesiani forniscono tecniche computazionali
Apprendimento Automatico Metodi Bayesiani Fabio Aiolli 11 Dicembre 2017 Fabio Aiolli Apprendimento Automatico 11 Dicembre 2017 1 / 19 Metodi Bayesiani I metodi Bayesiani forniscono tecniche computazionali
Minimi quadrati e massima verosimiglianza
 Minimi quadrati e massima verosimiglianza 1 Introduzione Nella scorsa lezione abbiamo assunto che la forma delle probilità sottostanti al problema fosse nota e abbiamo usato gli esempi per stimare i parametri
Minimi quadrati e massima verosimiglianza 1 Introduzione Nella scorsa lezione abbiamo assunto che la forma delle probilità sottostanti al problema fosse nota e abbiamo usato gli esempi per stimare i parametri
Sistemi che apprendono: Introduzione
 Sistemi che apprendono: Introduzione SCUOLA DI SPECIALIZZAZIONE IN FISICA MEDICA Corso di Sistemi di Elaborazione dell Informazione Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano
Sistemi che apprendono: Introduzione SCUOLA DI SPECIALIZZAZIONE IN FISICA MEDICA Corso di Sistemi di Elaborazione dell Informazione Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano
Stima dei Parametri. Corso di Apprendimento Automatico Laurea Magistrale in Informatica Nicola Fanizzi
 Laurea Magistrale in Informatica Nicola Fanizzi Dipartimento di Informatica Università degli Studi di Bari 20 gennaio 2009 Sommario Introduzione Stima dei parametri di massima verosimiglianza Stima dei
Laurea Magistrale in Informatica Nicola Fanizzi Dipartimento di Informatica Università degli Studi di Bari 20 gennaio 2009 Sommario Introduzione Stima dei parametri di massima verosimiglianza Stima dei
Rischio statistico e sua analisi
 F94 Metodi statistici per l apprendimento Rischio statistico e sua analisi Docente: Nicolò Cesa-Bianchi versione 7 aprile 018 Per analizzare un algoritmo di apprendimento dobbiamo costruire un modello
F94 Metodi statistici per l apprendimento Rischio statistico e sua analisi Docente: Nicolò Cesa-Bianchi versione 7 aprile 018 Per analizzare un algoritmo di apprendimento dobbiamo costruire un modello
Riconoscimento e recupero dell informazione per bioinformatica
 Riconoscimento e recupero dell informazione per bioinformatica Clustering: metodologie Manuele Bicego Corso di Laurea in Bioinformatica Dipartimento di Informatica - Università di Verona Sommario Tassonomia
Riconoscimento e recupero dell informazione per bioinformatica Clustering: metodologie Manuele Bicego Corso di Laurea in Bioinformatica Dipartimento di Informatica - Università di Verona Sommario Tassonomia
Modelli Probabilistici per la Computazione Affettiva: Inferenza approssimata con Monte Carlo
 Modelli Probabilistici per la Computazione Affettiva: Inferenza approssimata con Monte Carlo Corso di Modelli di Computazione Affettiva Prof. Giuseppe Boccignone Dipartimento di Informatica Università
Modelli Probabilistici per la Computazione Affettiva: Inferenza approssimata con Monte Carlo Corso di Modelli di Computazione Affettiva Prof. Giuseppe Boccignone Dipartimento di Informatica Università
A.A /49 frosio\
 Expectation Maximization I. Frosio A.A. 009-00 /49 http:\\homes.dsi.unimi.it\ frosio\ Overview Stima di due rette (riassunto) Minimizzazione: metodi di ordine zero (simplesso, ) Minimizzazione: i i i metodi
Expectation Maximization I. Frosio A.A. 009-00 /49 http:\\homes.dsi.unimi.it\ frosio\ Overview Stima di due rette (riassunto) Minimizzazione: metodi di ordine zero (simplesso, ) Minimizzazione: i i i metodi
Regressione Lineare e Regressione Logistica
 Regressione Lineare e Regressione Logistica Stefano Gualandi Università di Pavia, Dipartimento di Matematica email: twitter: blog: stefano.gualandi@unipv.it @famo2spaghi http://stegua.github.com 1 Introduzione
Regressione Lineare e Regressione Logistica Stefano Gualandi Università di Pavia, Dipartimento di Matematica email: twitter: blog: stefano.gualandi@unipv.it @famo2spaghi http://stegua.github.com 1 Introduzione
Clustering. Leggere il Capitolo 15 di Riguzzi et al. Sistemi Informativi
 Clustering Leggere il Capitolo 15 di Riguzzi et al. Sistemi Informativi Clustering Raggruppare le istanze di un dominio in gruppi tali che gli oggetti nello stesso gruppo mostrino un alto grado di similarità
Clustering Leggere il Capitolo 15 di Riguzzi et al. Sistemi Informativi Clustering Raggruppare le istanze di un dominio in gruppi tali che gli oggetti nello stesso gruppo mostrino un alto grado di similarità
Clustering. Leggere il Capitolo 15 di Riguzzi et al. Sistemi Informativi
 Clustering Leggere il Capitolo 15 di Riguzzi et al. Sistemi Informativi Clustering Raggruppare le istanze di un dominio in gruppi tali che gli oggetti nello stesso gruppo mostrino un alto grado di similarità
Clustering Leggere il Capitolo 15 di Riguzzi et al. Sistemi Informativi Clustering Raggruppare le istanze di un dominio in gruppi tali che gli oggetti nello stesso gruppo mostrino un alto grado di similarità
Apprendimento Bayesiano
 Apprendimento Automatico 232 Apprendimento Bayesiano [Capitolo 6, Mitchell] Teorema di Bayes Ipotesi MAP e ML algoritmi di apprendimento MAP Principio MDL (Minimum description length) Classificatore Ottimo
Apprendimento Automatico 232 Apprendimento Bayesiano [Capitolo 6, Mitchell] Teorema di Bayes Ipotesi MAP e ML algoritmi di apprendimento MAP Principio MDL (Minimum description length) Classificatore Ottimo
Computazione per l interazione naturale: fondamenti probabilistici
 Computazione per l interazione naturale: fondamenti probabilistici Corso di Interazione Naturale Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it boccignone.di.unimi.it/in_2017.html
Computazione per l interazione naturale: fondamenti probabilistici Corso di Interazione Naturale Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it boccignone.di.unimi.it/in_2017.html
Expectation Maximization
 Expectation Maximization I. Frosio A.A. 010-011 1/54 http:\\homes.dsi.unimi.it\frosio\ Overview Stima di due rette (riassunto) Minimizzazione: metodi di ordine zero (simplesso, ) Minimizzazione: metodi
Expectation Maximization I. Frosio A.A. 010-011 1/54 http:\\homes.dsi.unimi.it\frosio\ Overview Stima di due rette (riassunto) Minimizzazione: metodi di ordine zero (simplesso, ) Minimizzazione: metodi
IL CRITERIO DELLA MASSIMA VEROSIMIGLIANZA
 Metodi per l Analisi dei Dati Sperimentali AA009/010 IL CRITERIO DELLA MASSIMA VEROSIMIGLIANZA Sommario Massima Verosimiglianza Introduzione La Massima Verosimiglianza Esempio 1: una sola misura sperimentale
Metodi per l Analisi dei Dati Sperimentali AA009/010 IL CRITERIO DELLA MASSIMA VEROSIMIGLIANZA Sommario Massima Verosimiglianza Introduzione La Massima Verosimiglianza Esempio 1: una sola misura sperimentale
Stima dei parametri. La v.c. multipla (X 1, X 2,.., X n ) ha probabilità (o densità): Le f( ) sono uguali per tutte le v.c.
 Stima dei parametri Sia il carattere X rappresentato da una variabile casuale (v.c.) che si distribuisce secondo la funzione di probabilità f(x). Per investigare su tale carattere si estrae un campione
Stima dei parametri Sia il carattere X rappresentato da una variabile casuale (v.c.) che si distribuisce secondo la funzione di probabilità f(x). Per investigare su tale carattere si estrae un campione
Statistica Applicata all edilizia: Stime e stimatori
 Statistica Applicata all edilizia E-mail: orietta.nicolis@unibg.it 15 marzo 2011 Statistica Applicata all edilizia: Indice 1 2 Statistica Applicata all edilizia: Uno dei problemi principali della statistica
Statistica Applicata all edilizia E-mail: orietta.nicolis@unibg.it 15 marzo 2011 Statistica Applicata all edilizia: Indice 1 2 Statistica Applicata all edilizia: Uno dei problemi principali della statistica
Tecniche di riconoscimento statistico
 On AIR s.r.l. Tecniche di riconoscimento statistico Applicazioni alla lettura automatica di testi (OCR) Parte 2 Teoria della decisione Ennio Ottaviani On AIR srl ennio.ottaviani@onairweb.com http://www.onairweb.com/corsopr
On AIR s.r.l. Tecniche di riconoscimento statistico Applicazioni alla lettura automatica di testi (OCR) Parte 2 Teoria della decisione Ennio Ottaviani On AIR srl ennio.ottaviani@onairweb.com http://www.onairweb.com/corsopr
La likelihood. , x 2. } sia prodotto a partire dal particolare valore di a: ; a... f x N. La probabilità che l'i ma misura sia compresa tra x i
 La likelihood E' dato un set di misure {x 1, x 2, x 3,...x N } (ciascuna delle quali puo' essere multidimensionale) Supponiamo che la pdf (f) dipenda da un parametro a (anch'esso eventualmente multidimensionale)
La likelihood E' dato un set di misure {x 1, x 2, x 3,...x N } (ciascuna delle quali puo' essere multidimensionale) Supponiamo che la pdf (f) dipenda da un parametro a (anch'esso eventualmente multidimensionale)
Kernel Methods. Corso di Intelligenza Artificiale, a.a Prof. Francesco Trovò
 Kernel Methods Corso di Intelligenza Artificiale, a.a. 2017-2018 Prof. Francesco Trovò 14/05/2018 Kernel Methods Definizione di Kernel Costruzione di Kernel Support Vector Machines Problema primale e duale
Kernel Methods Corso di Intelligenza Artificiale, a.a. 2017-2018 Prof. Francesco Trovò 14/05/2018 Kernel Methods Definizione di Kernel Costruzione di Kernel Support Vector Machines Problema primale e duale
Computazione per l interazione naturale: fondamenti probabilistici
 Computazione per l interazione naturale: fondamenti probabilistici Corso di Interazione Naturale Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it boccignone.di.unimi.it/in_2016.html
Computazione per l interazione naturale: fondamenti probabilistici Corso di Interazione Naturale Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it boccignone.di.unimi.it/in_2016.html
Sistemi di Elaborazione dell Informazione 170. Caso Non Separabile
 Sistemi di Elaborazione dell Informazione 170 Caso Non Separabile La soluzione vista in precedenza per esempi non-linearmente separabili non garantisce usualmente buone prestazioni perchè un iperpiano
Sistemi di Elaborazione dell Informazione 170 Caso Non Separabile La soluzione vista in precedenza per esempi non-linearmente separabili non garantisce usualmente buone prestazioni perchè un iperpiano
Statistica 2 parte ARGOMENTI
 Statistica 2 parte ARGOMENTI Vettori gaussiani Matrice di covarianza e sua positività Marginali di un vettore normale Trasformazioni affini di vettori normali Indipendenza delle componenti scorrelate di
Statistica 2 parte ARGOMENTI Vettori gaussiani Matrice di covarianza e sua positività Marginali di un vettore normale Trasformazioni affini di vettori normali Indipendenza delle componenti scorrelate di
Algoritmi di classificazione supervisionati
 Corso di Bioinformatica Algoritmi di classificazione supervisionati Giorgio Valentini DI Università degli Studi di Milano 1 Metodi di apprendimento supervisionato per problemi di biologia computazionale
Corso di Bioinformatica Algoritmi di classificazione supervisionati Giorgio Valentini DI Università degli Studi di Milano 1 Metodi di apprendimento supervisionato per problemi di biologia computazionale
Teoria e Tecniche del Riconoscimento Clustering
 Facoltà di Scienze MM. FF. NN. Università di Verona A.A. 2010-11 Teoria e Tecniche del Riconoscimento Clustering Sommario Tassonomia degli algoritmi di clustering Algoritmi partizionali: clustering sequenziale
Facoltà di Scienze MM. FF. NN. Università di Verona A.A. 2010-11 Teoria e Tecniche del Riconoscimento Clustering Sommario Tassonomia degli algoritmi di clustering Algoritmi partizionali: clustering sequenziale
Unsupervised Learning
 Unsupervised Learning Corso di Intelligenza Artificiale, a.a. 2017-2018 Prof. Francesco Trovò 21/05/2018 Unsupervised Learning Unsupervised learning Clustering Dimensionality reduction Data visualization
Unsupervised Learning Corso di Intelligenza Artificiale, a.a. 2017-2018 Prof. Francesco Trovò 21/05/2018 Unsupervised Learning Unsupervised learning Clustering Dimensionality reduction Data visualization
Statistica multivariata 27/09/2016. D.Rodi, 2016
 Statistica multivariata 27/09/2016 Metodi Statistici Statistica Descrittiva Studio di uno o più fenomeni osservati sull INTERA popolazione di interesse (rilevazione esaustiva) Descrizione delle caratteristiche
Statistica multivariata 27/09/2016 Metodi Statistici Statistica Descrittiva Studio di uno o più fenomeni osservati sull INTERA popolazione di interesse (rilevazione esaustiva) Descrizione delle caratteristiche
Università di Siena. Corso di STATISTICA. Parte seconda: Teoria della stima. Andrea Garulli, Antonello Giannitrapani, Simone Paoletti
 Università di Siena Corso di STATISTICA Parte seconda: Teoria della stima Andrea Garulli, Antonello Giannitrapani, Simone Paoletti Master E 2 C Centro per lo Studio dei Sistemi Complessi Università di
Università di Siena Corso di STATISTICA Parte seconda: Teoria della stima Andrea Garulli, Antonello Giannitrapani, Simone Paoletti Master E 2 C Centro per lo Studio dei Sistemi Complessi Università di
Esercitazione su Filtraggio Adattativo (17 Giugno 2008)
 Esercitazione su Filtraggio Adattativo 17 Giugno 008) D. Donno Esercizio 1: Stima adattativa in rumore colorato Una sequenza disturbante x n è ottenuta filtrando un processo bianco u n con un filtro FIR
Esercitazione su Filtraggio Adattativo 17 Giugno 008) D. Donno Esercizio 1: Stima adattativa in rumore colorato Una sequenza disturbante x n è ottenuta filtrando un processo bianco u n con un filtro FIR
Riconoscimento e recupero dell informazione per bioinformatica. Clustering: validazione. Manuele Bicego
 Riconoscimento e recupero dell informazione per bioinformatica Clustering: validazione Manuele Bicego Corso di Laurea in Bioinformatica Dipartimento di Informatica - Università di Verona Sommario Definizione
Riconoscimento e recupero dell informazione per bioinformatica Clustering: validazione Manuele Bicego Corso di Laurea in Bioinformatica Dipartimento di Informatica - Università di Verona Sommario Definizione
Prima prova in Itinere Ist. Mat. 1, Prima parte, Tema ALFA COGNOME: NOME: MATR.:
 Prima prova in Itinere Ist. Mat. 1, Prima parte, Tema ALFA 1) L applicazione lineare f : R 3 R 2 data da f(x, y, z) = (3x + 2y + z, kx + 2y + kz) è suriettiva A: sempre; B: mai; C: per k 1 D: per k 2;
Prima prova in Itinere Ist. Mat. 1, Prima parte, Tema ALFA 1) L applicazione lineare f : R 3 R 2 data da f(x, y, z) = (3x + 2y + z, kx + 2y + kz) è suriettiva A: sempre; B: mai; C: per k 1 D: per k 2;
Università di Siena. Teoria della Stima. Lucidi del corso di. Identificazione e Analisi dei Dati A.A
 Università di Siena Teoria della Stima Lucidi del corso di A.A. 2002-2003 Università di Siena 1 Indice Approcci al problema della stima Stima parametrica Stima bayesiana Proprietà degli stimatori Stime
Università di Siena Teoria della Stima Lucidi del corso di A.A. 2002-2003 Università di Siena 1 Indice Approcci al problema della stima Stima parametrica Stima bayesiana Proprietà degli stimatori Stime
Geometria A. Università degli Studi di Trento Corso di laurea in Matematica A.A. 2017/ Maggio 2018 Prova Intermedia
 Geometria A Università degli Studi di Trento Corso di laurea in Matematica A.A. 7/8 Maggio 8 Prova Intermedia Il tempo per la prova è di ore. Durante la prova non è permesso l uso di appunti e libri. Esercizio
Geometria A Università degli Studi di Trento Corso di laurea in Matematica A.A. 7/8 Maggio 8 Prova Intermedia Il tempo per la prova è di ore. Durante la prova non è permesso l uso di appunti e libri. Esercizio
Uso dell algoritmo di Quantizzazione Vettoriale per la determinazione del numero di nodi dello strato hidden in una rete neurale multilivello
 Tesina di Intelligenza Artificiale Uso dell algoritmo di Quantizzazione Vettoriale per la determinazione del numero di nodi dello strato hidden in una rete neurale multilivello Roberto Fortino S228682
Tesina di Intelligenza Artificiale Uso dell algoritmo di Quantizzazione Vettoriale per la determinazione del numero di nodi dello strato hidden in una rete neurale multilivello Roberto Fortino S228682
Clustering. Introduzione Definizioni Criteri Algoritmi. Clustering Gerarchico
 Introduzione Definizioni Criteri Algoritmi Gerarchico Centroid-based K-means Fuzzy K-means Expectation Maximization (Gaussian Mixture) 1 Definizioni Con il termine (in italiano «raggruppamento») si denota
Introduzione Definizioni Criteri Algoritmi Gerarchico Centroid-based K-means Fuzzy K-means Expectation Maximization (Gaussian Mixture) 1 Definizioni Con il termine (in italiano «raggruppamento») si denota
1 PROCESSI STOCASTICI... 11
 1 PROCESSI STOCASTICI... 11 Introduzione... 11 Rappresentazione dei dati biomedici... 11 Aleatorietà delle misure temporali... 14 Medie definite sul processo aleatorio... 16 Valore atteso... 16 Esercitazione
1 PROCESSI STOCASTICI... 11 Introduzione... 11 Rappresentazione dei dati biomedici... 11 Aleatorietà delle misure temporali... 14 Medie definite sul processo aleatorio... 16 Valore atteso... 16 Esercitazione
Stima dell intervallo per un parametro
 Stima dell intervallo per un parametro In aggiunta alla stima puntuale di un parametro dobbiamo dare l intervallo che rappresenta l incertezza statistica. Questo intervallo deve: comunicare in modo obbiettivo
Stima dell intervallo per un parametro In aggiunta alla stima puntuale di un parametro dobbiamo dare l intervallo che rappresenta l incertezza statistica. Questo intervallo deve: comunicare in modo obbiettivo
Sistemi Intelligenti Relazione tra ottimizzazione e statistica - IV Alberto Borghese
 Sistemi Intelligenti Relazione tra ottimizzazione e statistica - IV Alberto Borghese Università degli Studi di Milano Laboratory of Applied Intelligent Systems (AIS-Lab) Dipartimento di Informatica borghese@di.unimi.it
Sistemi Intelligenti Relazione tra ottimizzazione e statistica - IV Alberto Borghese Università degli Studi di Milano Laboratory of Applied Intelligent Systems (AIS-Lab) Dipartimento di Informatica borghese@di.unimi.it
Metodi di Ottimizzazione
 Metodi di Ottimizzazione Stefano Gualandi Università di Pavia, Dipartimento di Matematica email: twitter: blog: stefano.gualandi@unipv.it @famospaghi, @famoconti http://stegua.github.com Metodi di Ottimizzazione
Metodi di Ottimizzazione Stefano Gualandi Università di Pavia, Dipartimento di Matematica email: twitter: blog: stefano.gualandi@unipv.it @famospaghi, @famoconti http://stegua.github.com Metodi di Ottimizzazione
Clustering. Capitolo Introduzione. 1.2 K-Means
 Capitolo 1 Clustering 1.1 Introduzione 1.2 K-Means Il metodo K-Means [?] é anche conosciuto col nome di C-means clustering, applicato in diversi contesti, tra i quali la compressione delle immagini e di
Capitolo 1 Clustering 1.1 Introduzione 1.2 K-Means Il metodo K-Means [?] é anche conosciuto col nome di C-means clustering, applicato in diversi contesti, tra i quali la compressione delle immagini e di
Riconoscimento e recupero dell informazione per bioinformatica
 Riconoscimento e recupero dell informazione per bioinformatica Clustering: validazione Manuele Bicego Corso di Laurea in Bioinformatica Dipartimento di Informatica - Università di Verona Sommario Definizione
Riconoscimento e recupero dell informazione per bioinformatica Clustering: validazione Manuele Bicego Corso di Laurea in Bioinformatica Dipartimento di Informatica - Università di Verona Sommario Definizione
METODI DI CLASSIFICAZIONE. Federico Marini
 METODI DI CLASSIFICAZIONE Federico Marini Introduzione Nella parte introduttiva dell analisi multivariata abbiamo descritto la possibilità di riconoscere l origine di alcuni campioni come uno dei campi
METODI DI CLASSIFICAZIONE Federico Marini Introduzione Nella parte introduttiva dell analisi multivariata abbiamo descritto la possibilità di riconoscere l origine di alcuni campioni come uno dei campi
Sequenze (Sistemi) di Variabili Aleatorie Se consideriamo un numero di variabili aleatorie, generalmente dipendenti si parla equivalentemente di:
 Teoria dei Fenomeni Aleatori AA 01/13 Sequenze (Sistemi) di Variabili Aleatorie Se consideriamo un numero di variabili aleatorie, generalmente dipendenti si parla equivalentemente di: N-pla o Sequenza
Teoria dei Fenomeni Aleatori AA 01/13 Sequenze (Sistemi) di Variabili Aleatorie Se consideriamo un numero di variabili aleatorie, generalmente dipendenti si parla equivalentemente di: N-pla o Sequenza
Probablità, Statistica e Processi Stocastici
 Probablità, Statistica e Processi Stocastici Franco Flandoli, Università di Pisa Matrice di covarianza Dato un vettore aleatorio (anche non gaussiano) X = (X 1,..., X n ), chiamiamo sua media il vettore
Probablità, Statistica e Processi Stocastici Franco Flandoli, Università di Pisa Matrice di covarianza Dato un vettore aleatorio (anche non gaussiano) X = (X 1,..., X n ), chiamiamo sua media il vettore
9.3 Il metodo dei minimi quadrati in formalismo matriciale
 9.3. IL METODO DEI MINIMI QUADRATI IN FORMALISMO MATRICIALE 121 9.3 Il metodo dei minimi quadrati in formalismo matriciale Per applicare il MMQ a funzioni polinomiali, ovvero a dipendenze di una grandezza
9.3. IL METODO DEI MINIMI QUADRATI IN FORMALISMO MATRICIALE 121 9.3 Il metodo dei minimi quadrati in formalismo matriciale Per applicare il MMQ a funzioni polinomiali, ovvero a dipendenze di una grandezza
LEZIONE ICO
 LEZIONE ICO 9-10-2009 Argomento. Rassegna dei metodi numerici utilizzabili per la soluzione di problemi di ottimizzazione statica. Metodi del gradiente e di Newton e loro derivati. Metodi di penalita e
LEZIONE ICO 9-10-2009 Argomento. Rassegna dei metodi numerici utilizzabili per la soluzione di problemi di ottimizzazione statica. Metodi del gradiente e di Newton e loro derivati. Metodi di penalita e
Elementi di statistica per l econometria
 Indice Prefazione i 1 Teoria della probabilità 1 1.1 Definizioni di base............................. 2 1.2 Probabilità................................. 7 1.2.1 Teoria classica...........................
Indice Prefazione i 1 Teoria della probabilità 1 1.1 Definizioni di base............................. 2 1.2 Probabilità................................. 7 1.2.1 Teoria classica...........................
Computazione per l interazione naturale: fondamenti probabilistici (1)
 Computazione per l interazione naturale: fondamenti probabilistici (1) Corso di Interazione uomo-macchina II Prof. Giuseppe Boccignone Dipartimento di Scienze dell Informazione Università di Milano boccignone@dsi.unimi.it
Computazione per l interazione naturale: fondamenti probabilistici (1) Corso di Interazione uomo-macchina II Prof. Giuseppe Boccignone Dipartimento di Scienze dell Informazione Università di Milano boccignone@dsi.unimi.it
Riconoscimento e recupero dell informazione per bioinformatica
 Riconoscimento e recupero dell informazione per bioinformatica Clustering: metodologie Manuele Bicego Corso di Laurea in Bioinformatica Dipartimento di Informatica - Università di Verona Sommario Tassonomia
Riconoscimento e recupero dell informazione per bioinformatica Clustering: metodologie Manuele Bicego Corso di Laurea in Bioinformatica Dipartimento di Informatica - Università di Verona Sommario Tassonomia
lezione n. 6 (a cura di Gaia Montanucci) Verosimiglianza: L = = =. Parte dipendente da β 0 e β 1
 lezione n. 6 (a cura di Gaia Montanucci) METODO MASSIMA VEROSIMIGLIANZA PER STIMARE β 0 E β 1 Distribuzione sui termini di errore ε i ε i ~ N (0, σ 2 ) ne consegue : ogni y i ha ancora distribuzione normale,
lezione n. 6 (a cura di Gaia Montanucci) METODO MASSIMA VEROSIMIGLIANZA PER STIMARE β 0 E β 1 Distribuzione sui termini di errore ε i ε i ~ N (0, σ 2 ) ne consegue : ogni y i ha ancora distribuzione normale,
Esercitazione del 29 aprile 2014
 Esercitazione del 9 aprile 014 Esercizio 10.13 pg. 94 Complemento: Calcolare la probabilità che un negozio apra tra le sette e venti e le nove e quaranta del mattino. Soluzione: Siccome non è nota la distribuzione
Esercitazione del 9 aprile 014 Esercizio 10.13 pg. 94 Complemento: Calcolare la probabilità che un negozio apra tra le sette e venti e le nove e quaranta del mattino. Soluzione: Siccome non è nota la distribuzione
Campionamento. Una grandezza fisica e' distribuita secondo una certa PDF
 Campionamento Una grandezza fisica e' distribuita secondo una certa PDF La pdf e' caratterizzata da determinati parametri Non abbiamo una conoscenza diretta della pdf Possiamo determinare una distribuzione
Campionamento Una grandezza fisica e' distribuita secondo una certa PDF La pdf e' caratterizzata da determinati parametri Non abbiamo una conoscenza diretta della pdf Possiamo determinare una distribuzione
La Decisione Statistica Campione aleatorio: risultato dell osservazione di un fenomeno soggetto a fluttuazioni casuali.
 La Decisione Statistica Campione aleatorio: risultato dell osservazione di un fenomeno soggetto a fluttuazioni casuali. Analisi del campione: - descrizione sintetica (statistica descrittiva) - deduzione
La Decisione Statistica Campione aleatorio: risultato dell osservazione di un fenomeno soggetto a fluttuazioni casuali. Analisi del campione: - descrizione sintetica (statistica descrittiva) - deduzione
Il problema lineare dei minimi quadrati
 Il problema lineare dei minimi quadrati APPLICAZIONE: Il polinomio di migliore approssimazione nel senso dei minimi quadrati Felice Iavernaro Dipartimento di Matematica Università di Bari 15 Gennaio 2009
Il problema lineare dei minimi quadrati APPLICAZIONE: Il polinomio di migliore approssimazione nel senso dei minimi quadrati Felice Iavernaro Dipartimento di Matematica Università di Bari 15 Gennaio 2009
Metodi computazionali per i Minimi Quadrati
 Metodi computazionali per i Minimi Quadrati Come introdotto in precedenza si considera la matrice. A causa di mal condizionamenti ed errori di inversione, si possono avere casi in cui il e quindi S sarebbe
Metodi computazionali per i Minimi Quadrati Come introdotto in precedenza si considera la matrice. A causa di mal condizionamenti ed errori di inversione, si possono avere casi in cui il e quindi S sarebbe
STATISTICA. Regressione-3 L inferenza per il modello lineare semplice
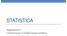 STATISTICA Regressione-3 L inferenza per il modello lineare semplice Regressione lineare: GRAFICO DI DISPERSIONE & & analisi residui A. Valutazione preliminare se una retta possa essere una buona approssimazione
STATISTICA Regressione-3 L inferenza per il modello lineare semplice Regressione lineare: GRAFICO DI DISPERSIONE & & analisi residui A. Valutazione preliminare se una retta possa essere una buona approssimazione
Computazione per l interazione naturale: Richiami di ottimizzazione (3) (e primi esempi di Machine Learning)
 Computazione per l interazione naturale: Richiami di ottimizzazione (3) (e primi esempi di Machine Learning) Corso di Interazione Naturale Prof. Giuseppe Boccignone Dipartimento di Informatica Università
Computazione per l interazione naturale: Richiami di ottimizzazione (3) (e primi esempi di Machine Learning) Corso di Interazione Naturale Prof. Giuseppe Boccignone Dipartimento di Informatica Università
0 altimenti 1 soggetto trova lavoroentro 6 mesi}
 Lezione n. 16 (a cura di Peluso Filomena Francesca) Oltre alle normali variabili risposta che presentano una continuità almeno all'interno di un certo intervallo di valori, esistono variabili risposta
Lezione n. 16 (a cura di Peluso Filomena Francesca) Oltre alle normali variabili risposta che presentano una continuità almeno all'interno di un certo intervallo di valori, esistono variabili risposta
Esame di Calcolo Numerico per Informatica A.A. 2010/11 Proff. S. De Marchi e M. R. Russo 19 settembre 2011
 Esame di Calcolo Numerico per Informatica A.A. 2010/11 Proff. S. De Marchi e M. R. Russo 19 settembre 2011 L esame consiste di 4 domande aperte e 10 esercizi a risposta multipla. Per gli esercizi ci sono
Esame di Calcolo Numerico per Informatica A.A. 2010/11 Proff. S. De Marchi e M. R. Russo 19 settembre 2011 L esame consiste di 4 domande aperte e 10 esercizi a risposta multipla. Per gli esercizi ci sono
IDENTIFICAZIONE DEI MODELLI E ANALISI DEI DATI 1 (Prof. S. Bittanti) Ingegneria Informatica 5 CFU. Appello 23 Luglio 2014 Cognome Nome Matricola
 IDENTIFICAZIONE DEI MODELLI E ANALISI DEI DATI 1 (Prof. S. Bittanti) Ingegneria Informatica 5 CFU. Appello 23 Luglio 201 Cognome Nome Matricola............ Verificare che il fascicolo sia costituito da
IDENTIFICAZIONE DEI MODELLI E ANALISI DEI DATI 1 (Prof. S. Bittanti) Ingegneria Informatica 5 CFU. Appello 23 Luglio 201 Cognome Nome Matricola............ Verificare che il fascicolo sia costituito da
Apprendimento statistico (Statistical Learning)
 Apprendimento statistico (Statistical Learning) Il problema dell apprendimento Inquadriamo da un punto di vista statistico il problema dell apprendimento di un classificatore Un training set S={(x,y ),,(x
Apprendimento statistico (Statistical Learning) Il problema dell apprendimento Inquadriamo da un punto di vista statistico il problema dell apprendimento di un classificatore Un training set S={(x,y ),,(x
Regressione. Lineare Simple linear regression Multiple linear regression Regression vs Geometrical fitting
 Lineare Simple linear regression Multiple linear regression Regression vs Geometrical fitting Non lineare Variabile indipendente non lineare Ottimizzazione numerica (metodi iterativi) 1 Definizioni Nei
Lineare Simple linear regression Multiple linear regression Regression vs Geometrical fitting Non lineare Variabile indipendente non lineare Ottimizzazione numerica (metodi iterativi) 1 Definizioni Nei
Apprendimento statistico (Statistical Learning)
 Apprendimento statistico (Statistical Learning) Il problema dell apprendimento Inquadriamo da un punto di vista statistico il problema dell apprendimento di un classificatore Un training set S={(x,y ),,(x
Apprendimento statistico (Statistical Learning) Il problema dell apprendimento Inquadriamo da un punto di vista statistico il problema dell apprendimento di un classificatore Un training set S={(x,y ),,(x
Presentazione dell edizione italiana
 1 Indice generale Presentazione dell edizione italiana Prefazione xi xiii Capitolo 1 Una introduzione alla statistica 1 1.1 Raccolta dei dati e statistica descrittiva... 1 1.2 Inferenza statistica e modelli
1 Indice generale Presentazione dell edizione italiana Prefazione xi xiii Capitolo 1 Una introduzione alla statistica 1 1.1 Raccolta dei dati e statistica descrittiva... 1 1.2 Inferenza statistica e modelli
Metodi supervisionati di classificazione
 Metodi supervisionati di classificazione Giorgio Valentini e-mail: valentini@dsi.unimi.it DSI - Dipartimento di Scienze dell'informazione Classificazione bio-molecolare di tessuti e geni Diagnosi a livello
Metodi supervisionati di classificazione Giorgio Valentini e-mail: valentini@dsi.unimi.it DSI - Dipartimento di Scienze dell'informazione Classificazione bio-molecolare di tessuti e geni Diagnosi a livello
Laboratorio di Calcolo Numerico
 Laboratorio di Calcolo Numerico M.R. Russo Università degli Studi di Padova Dipartimento di Matematica Pura ed Applicata A.A. 2009/2010 Equazioni non lineari Data una funzione consideriamo il problema
Laboratorio di Calcolo Numerico M.R. Russo Università degli Studi di Padova Dipartimento di Matematica Pura ed Applicata A.A. 2009/2010 Equazioni non lineari Data una funzione consideriamo il problema
Introduzione al MATLAB c Parte 2
 Introduzione al MATLAB c Parte 2 Lucia Gastaldi Dipartimento di Matematica, http://dm.ing.unibs.it/gastaldi/ 24 settembre 2007 Outline 1 M-file di tipo Script e Function Script Function 2 Elementi di programmazione
Introduzione al MATLAB c Parte 2 Lucia Gastaldi Dipartimento di Matematica, http://dm.ing.unibs.it/gastaldi/ 24 settembre 2007 Outline 1 M-file di tipo Script e Function Script Function 2 Elementi di programmazione
