Algoritmi di approssimazione
|
|
|
- Daniela Molteni
- 5 anni fa
- Visualizzazioni
Transcript
1 Algoritmi di approssimazione Corso di Laurea Magistrale in Matematica A.A. 2014/2015
2 Algoritmi di approssimazione: elementi di complessità Sommario Informazioni generali Richiami di algoritmica Un primo esempio di problema difficile Un nucleo di problemi difficili La questione fondamentale Riduzioni fra problemi NP-completezza
3 Algoritmi di approssimazione: elementi di complessità Sommario Informazioni generali Richiami di algoritmica Un primo esempio di problema difficile Un nucleo di problemi difficili La questione fondamentale Riduzioni fra problemi NP-completezza
4 Informazioni generali sul corso Docenti: Mauro Leoncini, Manuela Montangero Sito web del gruppo di algoritmi: Materiale didattico, avvisi, esami,...: dal sito del gruppo seguire il link alla didattica Ricevimento: dal sito del gruppo seguire i link alle pagine dei docenti Modalità d esame: solo orale CFU assegnati: 6
5 Argomenti trattati Problemi computazionalmente difficili Elementi di Teoria della NP-completezza Algoritmi di approssimazione per problemi NP-hard Algoritmi basati su programmazione lineare intera Algoritmi euristici
6 Algoritmi di approssimazione: elementi di complessità Sommario Informazioni generali Richiami di algoritmica Un primo esempio di problema difficile Un nucleo di problemi difficili La questione fondamentale Riduzioni fra problemi NP-completezza
7 Nozioni base di algoritmica Problemi e istanze il problema dell ordinamento un ben preciso insieme di chiavi da ordinare (istanza) Tipi di problemi decisionali: sono quelli che ammettono risposta SI/NO, o VERO/FALSO (ad esempio: il numero p è primo?) di ricerca: sono quelli che chiedono di trovare una, o eventualmente l unica, soluzione (ad esempio, ordinare un insieme di chiavi, trovare un cammino fra due vertici assegnati di un grafo, ecc.) di ottimizzazione: chiedono di trovare la migliore soluzione possibile in base ad dato criterio di costo/guadagno (ad esempio, trovare il cammino di lunghezza minima che congiunge due vertici di un grafo orientato pesato)
8 Nozioni base di algoritmica (2) Dimensione di un istanza: numero di bit (in alcuni casi possiamo usare anche le word) sufficiente a rappresentare l istanza in modo compatto Esempio: un numero intero n è rappresentato in modo compatto mediante notazione binaria; la dimensione è dunque log n Esempio: un grafo G = (V, E) tale che V = {1, 2,..., n} ed E = m è rappresentabile in modo compatto mediante n + 2m numeri in notazione binaria Se π è un istanza del problema Π, la sua dimensione verrà indicata con π
9 Nozioni base di algoritmica (3) Misuriamo il costo computazionale di un dato algoritmo - contando il numero di operazioni elementari (a livello di bit o di word) - in funzione della dimensione delle istanze di input - considerando, per ogni data dimensione, il costo massimo (analisi worst-case) Considerare le operazioni a livello di bit può essere necessario nel caso di problemi che coinvolgono (anche) numeri Importanza di codificare i problemi in modo compatto
10 Nozioni base di algoritmica (4) La complessità computazionale di un problema à la quantità minima di risorse (spazio o tempo) sufficienti per risolverlo, ovvero il costo dell algoritmo di minimo costo che risolve il problema Anche la complessità può quindi essere analizzata nel worst-case, sia a livello di bit che di word Molti autori usano anche la locuzione complessità di un algoritmo, che noi invece eviteremo
11 Algoritmi di approssimazione: elementi di complessità Sommario Informazioni generali Richiami di algoritmica Un primo esempio di problema difficile Un nucleo di problemi difficili La questione fondamentale Riduzioni fra problemi NP-completezza
12 Stabilire se un numero è primo Usiamo il crivello di Eratostene L input è il numero n Tentativamente, marca i numeri 2, 3, 4,..., n come primi Poni i 2 Finché i n - trova il primo numero j i marcato come primo smarca i numeri 2j, 3j,..., n/j j Poni i j + 1 Stampa i numeri ancora marcati Esempio: n = 18 ( 18 = 4)
13 Stabilire se un numero è primo Usiamo il crivello di Eratostene L input è il numero n Tentativamente, marca i numeri 2, 3, 4,..., n come primi Poni i 2 Finché i n - trova il primo numero j i marcato come primo smarca i numeri 2j, 3j,..., n/j j Poni i j + 1 Stampa i numeri ancora marcati Esempio: n = 18 ( 18 = 4)
14 Stabilire se un numero è primo Usiamo il crivello di Eratostene L input è il numero n Tentativamente, marca i numeri 2, 3, 4,..., n come primi Poni i 2 Finché i n - trova il primo numero j i marcato come primo smarca i numeri 2j, 3j,..., n/j j Poni i j + 1 Stampa i numeri ancora marcati Esempio: n = 18 ( 18 = 4)
15 Il crivello di Eratostene Il costo dell algoritmo è O(n) Tuttavia, la dimensione dell input non è n, bensì log n Ne consegue (correttamente) che il crivello di Eratostene è un algoritmo (di costo) esponenziale Considerare n come dimensione dell input equivale a scrivere l input in unario, quindi in modo non compatto Qual è la complessità del problema della primalità?
16 Algoritmi di approssimazione: elementi di complessità Sommario Informazioni generali Richiami di algoritmica Un primo esempio di problema difficile Un nucleo di problemi difficili La questione fondamentale Riduzioni fra problemi NP-completezza
17 Proposizioni logiche in forma normale congiuntiva Dato un insieme di proposizioni logiche elementari (p.e.) I = {x 1, x 2,..., x n }, un letterale L su I è una p.e. oppure la negazione di una p.e. In altri termini L {x i, x i } per un qualche i {1, 2,..., n}. Una formula booleana in Forma Normale Congiuntiva (FNC) su I è del tipo F = C 1 C 2... C m dove ogni elemento C i della congiunzione, detto clausola, ha la seguente forma: C i = L i1 L i2... L iki, k i 1 i = 1,..., m, e a sua volta L ij è un letterale su I.
18 Definiamo alcuni problemi modello Satisfiability (o, più semplicemente, SAT): data una formula proposizionale F in FNC, dire se esiste un assegnamento di verità alle proposizioni elementari che rende vera F Esempio: F = (a b) ( b c) (ā c) è soddisfattibile assegnando ad a il valore T (vero) e a b e c il valore F (falso). k-sat: come SAT, ma con il vincolo che ogni clausola contenga esattamente k letterali.
19 Definiamo alcuni problemi modello (2) INDEPENDENT SET (IS): dato un grafo G = (V, E) e un intero k non maggiore di V, dire se esiste un sottoinsieme V di V, di dimensione almeno k, tale che in G non ci sono archi che uniscono vertici di V. Esempio: nel grafo seguente i vertici B, C e G formano un insieme indipendente di dimensione 3
20 Definiamo alcuni problemi modello (3) Vertex Cover (VC): dato un grafo G = (V, E) e un intero k non maggiore di V, dire se esiste un sottoinsieme V di V, di dimensione almeno k, tale che ogni arco di G ha almeno un estremo in V. Esempio: nel grafo seguente i vertici A, D, E ed F formano una copertura di dimensione 4
21 Definiamo alcuni problemi modello (4) Set Cover (SC): data una collezione {B 1, B 2,..., B m } di sottoinsiemi di uno stesso insieme S ed un intero k m, dire se ci sono k sottoinsiemi la cui unione coincide con S. Esempio: sia S = {1, 2, 3, 4, 5, 6}, B1 = {1, 4}, B2 = {2, 4, 6}, B3 = {1, 5}, B4 = {3, 5, 6}; è facile vedere che 3 sottoinsiemi sono necessari e che S = B1 B 2 B4 = B2 B3 B4
22 Definiamo alcuni problemi modello (5) Travelling Salesman Problem (TSP): dato l insieme di tutte le N = n(n 1) distanze fra n città e un valore t, dire se esiste un cammino chiuso di lunghezza non maggiore di t che tocca tutte le città una e una sola volta Hamiltonian Graph (HG): dato un grafo con n vertici, dire se è Hamiltoniano, cioè se contiene un ciclo semplice di lunghezza n (cioè che passa una e una sola volta da ogni nodo).
23 Algoritmi di approssimazione: elementi di complessità Sommario Informazioni generali Richiami di algoritmica Un primo esempio di problema difficile Un nucleo di problemi difficili La questione fondamentale Riduzioni fra problemi NP-completezza
24 Stabilire la difficoltà dei problemi Sulla base delle conoscenze attuali, per ciascuno dei problemi introdotti vale quanto segue non si dispone di alcun algoritmo efficiente di risoluzione, mediante il quale si possa stabilire che il problema è computazionalmente facile non si dispone di nessuna dimostrazione teorica che consenta di classificare il problema come difficile Ma che cosa vuol dire, per un problema, essere (computazionalmente) facile/difficile?
25 Una scala di difficoltà Cominciamo col fissare una scala di difficoltà Definiamo alcune importanti famiglie di funzioni polinomi: sono del tipo n k, con k > 0 costante superpolinomi: sono del tipo n logk n, con k > 0 costante esponenziali: sono del tipo b nk, con b > 1 e k > 0 costanti Due problemi le cui complessità sono funzioni nella stessa famiglia hanno (essenzialmente) la stessa difficoltà Diversamente, esponenziale è più difficile di superpolinomiale che è più difficile di polinomiale
26 Una scala di difficoltà (2) Ricordiamo che l analisi di complessità prende in considerazione il comportamento asintotico di un algoritmo Ad esempio, consideriamo due algoritmi (per uno stesso problema) che impiegano tempo T 1 (n) = n 100 e T 2 (n) = n/2 Sebbene per un ampio insieme di valori risulti T 1 (n) > T 2 (n), esiste tuttavia un valore n 0 tale che, per ogni n > n 0, si ha T 1 (n) < T 2 (n) n 0 si trova risolvendo l equazione n 100 = n/2 la cui soluzione è un valore compreso fra 2231 e 2232 (e dunque n 0 = 2231)
27 Classi di problemi I problemi vengono classificati utilizzando le ampie classi di funzioni introdotte. Alcune classi importanti P = {Π : k e un algoritmo A che risolve ogni istanza π Π in tempo O( π k )} EXPTIME = {Π : k e un algoritmo A che risolve ogni istanza π Π in tempo O(2 π k )} PSPACE = {Π : k e un algoritmo A che risolve ogni istanza π Π usandoo( π k ) bit di memoria}
28 Classi di problemi (2) Il nucleo della teoria che svilupperemo considererà solo problemi decisionali Le classi P, PSPACE e EXPTIME sono definite in termini di problemi decisionali Si può dimostrare che vale ed inoltre P EXPTIME P PSPACE EXPTIME
29 Tesi di Church-Turing È lecita una domanda: le definizione che abbiamo dato di classi di complessità (e prima ancora di costo di un algoritmo) è una buona definizione? Non è possibile che il costo dipenda in maniera sostanziale dall esecutore, cioè dal modello di calcolo utilizzato? Non c è forse un enorme differenza fra un supercomputer moderno e un PC di 30 anni orsono? La tesi di Church-Turing afferma che, se M 1 ed M 2 sono due ragionevoli modelli di calcolo universali, allora ogni computazione di M 1 può essere simulata da una computazione di M 2 con uno slowdown polinomiale, e viceversa.
30 Di nuovo la domanda fondamentale Quand è che un problema Π è facile? In algoritmica si utilizza il seguente criterio Se il bit-cost di ogni possibile algoritmo per Π è esponenziale, allora Π è certamente difficile Se invece esiste un algoritmo di bit-cost polinomiale, allora il problema Π è facile Non sembra un criterio tanto sensato. Se il polinomio in questione fosse del tipo, poniamo, n 100?
31 Una (parte della) spiegazione I problemi combinatoriali che stiamo esaminando ammettono un numero esponenziale di possibili soluzioni. Ad esempio, nel caso di SAT, se la formula contiene n proposizioni elementari, i possibili assegnamenti di verità sono 2 n Un altro esempio. Nel caso del TSP ci sono (n 1)! possibili permutazioni che corrispondono ad altrettanti ordini di attraversamento delle città (avendo fissato partenza e arrivo dalla città 1). Il costo esponenziale sembra allora emergere quando non esiste una strategia sostanzialmente migliore dell esame esaustivo di tutte le possibili soluzioni approccio brute-force
32 Una (parte della) spiegazione (2) Per i problemi in questione, un algoritmo polinomiale non potrà comunque esaminare tutte le possibili soluzioni, perché queste sono in numero esponenziale, e dunque sono troppe In altri termini, un algoritmo polinomiale non può essere di tipo a forza bruta; esso sfrutta in un qualche modo intelligente il fatto che il problema ammette una soluzione più efficiente della semplice enumerazione di tutte le possibilità Possiamo concludere che un algoritmo di costo n 100, per quanto inefficiente, indica comunque che il problema che esso risolve ammette una strategia diversa dalla forza bruta
33 Una (parte della) spiegazione (3) La precedente osservazione teorica è supportata da considerazioni pratiche, cioè il criterio polinomiale/esponenziale funziona davvero Infatti, se un problema ammette un algoritmo polinomiale, cioè può essere risolto in modo sostanzialmente diverso dalla forza bruta, allora esso ammette quasi sempre un algoritmo con polinomio di grado basso Quasi sempre di detto algoritmo esistono implementazioni concrete efficienti
34 Ricapitolando Se prendiamo per buona la spiegazione data, possiamo concludere che - i problemi nella classe P sono facili - i problemi nell insieme differenza EXPTIME\P sono difficili Sfortunatamente, tutti i problemi che abbiamo elencato, come pure molti altri di grande interesse applicativo, non sono a tutt oggi classificabili ne come facili ne come difficili Ad esempio, per SAT non disponiamo di un algoritmo polinomiale è un problema difficile? Non abbiamo però neppure una dimostrazione che ogni possibile algoritmo richieda tempo esponenziale è un problema facile? Per gli altri problemi definiti la situazione è la stessa
35 Algoritmi di approssimazione: elementi di complessità Sommario Informazioni generali Richiami di algoritmica Un primo esempio di problema difficile Un nucleo di problemi difficili La questione fondamentale Riduzioni fra problemi NP-completezza
36 Un obiettivo più modesto Esplorare lo spazio dei problemi computazionalmente difficili... dando evidenza della difficoltà di alcuni problemi... caratterizzando almeno una ampia classe di essi da un punto di vista matematico il problema A è almeno tanto difficile quanto B il problema A è il più difficile nell ambito di una determinata classe C
37 Uno strumento fondamentale: le riduzioni Diremo che un problema A è riducible a B in tempo polinomiale (o che A è polinomialmente riducibile a B), e scriveremo A P B, se esiste un algoritmo per A con le seguenti proprietà A può invocare l esecuzione di un sottoprogramma (oracolo) in grado di risolvere B il costo attribuito a B è costante il costo complessivo di A (incluse le chiamate a B) è polinomiale Esempio: calcolo del mediano di un insieme di numeri. Il problema è polinomialmente riducibile all ordinamento: si chiama il sottoprogramma per l ordinamento e si prende l elemento centrale della sequenza ordinata.
38 Schema generale di una riduzione
39 Significato delle riduzioni Se A P B allora B è almeno tanto difficile quanto A Infatti se esiste un algoritmo polinomiale per B (da sostituire concretamente all oracolo), cioè se B è facile, allora il costo di A incluse le chiamate di B è anch esso polinomiale, e dunque anche A è facile La simbologia A P B vuole proprio esprimere questo fatto Tutto ciò dipende semplicemente dalle proprietà di chiusura dei polinomi
40 Significato delle riduzioni (2) Supponiamo ancora che A P B Se possiamo dimostrare che la complessità di A è esponenziale (o superpolinomiale) allora non può esistere un algoritmo polinomiale per B, perché abbiamo appena visto che, se esistesse, allora anche A sarebbe risolvibile in tempo poliniamo contraddizione e A P B e B P A allora A e B hanno la stessa difficoltà (scriveremo A P B)
41 Generalità dei problemi decisionali Consideriamo il problema Independent Set La versione di ottimizzazione di questo problema chiede di trovare il massimo insieme indipendente nel grafo di input La verisone decisionale chiede di sapere se, nel grafo di input, esiste uninsieme indipendente di cardinalità assegnata k. Chiaramente la versione di ottimizzazione non è più facile di quella decisionale Infatti, supponiamo di voler sapere se un certo grafo G ha un insieme indipendente di cardinalità almeno k Se risolviamo il problema di ottimizzazione, troviamo l insieme (o un insieme) indipendente di cardinalità massima, che suppomiamo essere k A questo punto, la risposta al problema decisionale è affermativa se e solo se k k
42 Una (auto)riduzione per Independent Set Supponiamo di disporre di un sottoprogramma D per risolvere la versione decisionale di IS Dato G con n vertici, determiniamo dapprima la dimensione massima k di un insieme indipendente di G usando un processo di ricerca binaria Invochiamo D(G, n/2) Se la risposta è affermativa proviamo con D(G, (3/4)n), altrimenti con D(G, n/4)... Si procede quindi alla individuazione di k vertici che formano un IS, nel modo seguente
43 Una (auto)riduzione per Independent Set (2) Si considera un vertice v e lo si elimina dal grafo Si verifica (con una chiamata a D) se la dimensione del massimo IS si riduce In caso affermativo, v è necessariamente parte dell IS di dimensione massima, e dunque si procede cercando, nel sottografo di G ottenuto eliminando v e i vertici ad esso adiacenti, un independent set di dimensione k 1 Altrimenti si procede eliminando un altro vertice nel grafo originale Il numero totale di chiamate a D è al più n + log n
44 Prime riduzioni per problemi decisionali Stabiliremo i seguenti risultati, che illustrano l uso delle riduzioni IS e VC hanno la stessa difficoltà SC è almeno tanto difficile quanto VC IS è almeno tanto difficile quanto 3-SAT
45 Difficoltà relativa di IS e VC Un semplice risultato: dato un grafo G = (V, E), un sottoinsieme S di V è un independent set se e solo se V \S è un vertex cover se (x, y) è un arco di G, allora al più solo uno fra i vertici x e y può stare in S, e quindi almeno uno fra x e y sta in V \S, ne consegue che l arco (x, y) è coperto e dunque V \S è un vertex cover anche il viceversa è immediato Questo implica che un grafo G ha un independent set di dimensione almeno k se e solo se G ha un vertex cover di dimensione non maggiore di n k (n = V ) Vale quindi banalmente IS P VC
46 SC è almeno tanto difficile quanto VC (VC P SC) Dato un problema di vertex covering su un grafo G = (V, E), poniamo S = E e B i = {archi incidenti nel nodo i} cioè ogni sottoinsieme è in corrispondenza biunivoca con un vertice Se esiste una collezione di k sottoinsiemi che copre S, allora i vertici corrispondenti formano un vertex cover
47 IS è almeno tanto difficile quanto 3-SAT (3-SAT P IS) Data una formula booleana in FNC con k clausole, ognuna formata esattamente da 3 letterali, costruiamo un grafo composto da k triangoli opportunamente collegati Esempio: alla formula F = (a b c) ( a b c) ( a b c) corrisponde il seguente grafo
48 3-SAT P IS (2) Algoritmicamente, la riduzione è un po più complessa di quelle viste in precedenza Ad esempio, per risolvere IS usando la black box per VC è sufficiente cambiare l input: da k ad n k, dove n è il numero di vertici del grafo di input e k è la dimensione minima richiesta per il più grande insieme indipendente Solo poco più complessa è la riduzione da VC a SC Nel caso in questione, data la formula, il programma deve costruire il grafo corrispondente prima di invocare la black-box per IS
49 Struttura comune delle riduzioni Tutte le riduzioni viste finora (con l unica eccezione dell autoriduzione per IS) sono comunque costituite da una sola chiamata alla black-box A P B Si noti che la definizione di riduzione consentirebbe un numero polinomiale di chiamate alla black box
50 Il punto sulle riduzioni Riduzioni viste finora: 3-SAT P IS P VC P SC e VC P IS Inoltre, poiché la riducibilità è una relazione transitiva (discende dalla proprietà di chiusura dei polinomi rispetto alla composizione), vale ad esempio: 3-SAT P SC Abbiamo ora uno strumento per (tentare di) stabilire la difficoltà relativa di alcuni problemi Non siamo però ancora in grado di caratterizzare classi di problemi (apparentemente) difficili
51 Algoritmi di approssimazione: elementi di complessità Sommario Informazioni generali Richiami di algoritmica Un primo esempio di problema difficile Un nucleo di problemi difficili La questione fondamentale Riduzioni fra problemi NP-completezza
52 Ricerca e verifica di soluzioni Sembra esserci una chiara differenza, sperimentabile in molti contesti, fra lo sforzo necessario a trovare una soluzione di un problema e verificare che una certa soluzione proposta è effettivamente una soluzione Qualche esempio: in matematica, calcolare un integrale e verificare che una funzione è primitiva di un altra funzione nell algoritmica, scrivere un programma di ordinamento e un programma che verifica se una sequenza è ordinata negli scacchi, trovare le mosse che portano ad un matto e verificare che una sequenza porta effettivamente allo scacco matto
53 Ricerca e verifica di soluzioni (2) Per i problemi computazionali introdotti SAT: è facile verificare (in tempo proporzionale alla lunghezza della formula F ) se un assegnamento di verità agli n letterali di F produce il valore true TSP: è facile verificare (in tempo proporzionale al numero di città) se la lunghezza di un ciclo proposto è minore della soglia richiesta IS: è facile verificare (in tempo proporzionale al numero di archi) se un insieme di vertici è indipendente...
54 Alcune definizioni Dato un problema decisionale A, diremo che gli input legali per A in corrispondenza dei quali la risposta è yes costituisce l insieme delle istanze positive per A (yes-instances) Un programma C è detto certificatore efficiente per A se soddisfa le seguenti condizioni (1) C accetta due parametri in input, I ed S, dove si intende che I rappresenti un istanza di A (2) C impiega tempo polinomiale in I + S (3) Per ogni istanza positiva I di A, esiste una stringa S (detta certificato), la cui lunghezza è al più I k (dove k è una costante che dipende solo da A e da C), tale che C(I, S) = yes
55 La classe NP NP è la classe dei problemi che posseggono un certificatore efficiente, cioè un algoritmo polinomiale di verifica delle soluzioni SAT è in NP: per ogni istanza positiva il certificato è costituito dagli n valori logici dati alle variabili VC è in NP: per ogni istanza positiva il certificato è costituito da una lista di k vertici TSP è in NP: per ogni istanza positiva il certificato è costituito dall ordine di visita delle città...
56 La classe NP (2) Un risultato immediato: P NP: infatti, per ogni problema è risolvibile in tempo polinomiale il certificato è la stringa vuota Stabilire se P = NP o se P NP è uno dei principali problemi aperti in Informatica e uno dei sette Millennium Prize Problems del Clay Mathematics Institute ( NP è in realtà l acronimo di Nondeterministic Polinomial (Time)
57 L interrogativo fondamentale Circa quattro decenni di tentativi di risolvere l enigma non hanno prodotto la soluzione Per dimostrare che P NP sarebbe ovviamente sufficiente dimostrare che un problema in NP (poniamo, 3-SAT ) richiede tempo esponenziale (non polinomiale) Naturalmente, se dimostrassimo che 3-SAT richiede tempo esponenziale avremmo anche dimostrato che ci sono anche altri problemi difficili, ad esempio IS, VC e SC Il viceversa, cioè che se (poniamo) 3-SAT fosse risolvibile in tempo polinomiale allora P = NP, non sembra implicitamente valere da ciò che abbiamo detto finora
58 L interrogativo fondamentale (2) Dalle riduzioni che abbiamo visto sappiamo che SC è almeno tanto difficile quanto IS, VC e 3-SAT Il fatto che SC sia il più difficile dei quattro problemi significa che una sua eventuale facilità implicherebbe la facilità degli altri Ci domandiamo allora: esiste un problema nella classe NP che possiamo dimostrare essere il più difficile della classe Se un tale problema esistesse, potremmo concentrare su quel problema gli eventuali sforzi per dimostrare che P = NP In realtà di tali problemi ne esistono tanti, e vengono detti problemi NP-completi
59 Problemi NP-completi I problemi più difficili per una data classe vengono detti problemi completi per quella classe Un problema A è completo per la classe NP (o, più semplicemente, NP-completo) se e solo se A NP se B NP allora B P A Un problema completo racchiude tutta la difficoltà della classe Trovare un problema completo (a patto che esista) sembra sensibilmente più difficile che stabilire la difficoltà relativa di due problemi specifici
60 Il risultato fondamentale Esistono problemi NP-completi (risultato dovuto indipendentemente a due studiosi, uno americano e uno russo) In particolare SAT è NP-completo (teorema di Cook) La dimostrazione (a posteriori...) non è neppure troppo complessa, ma necessita di molte nozioni preliminari la omettiamo
61 Altri problemi NP-completi Per dimostrare che un problema A NP è NP-completo è ora (cioè dopo il Teorema di Cook) sufficiente trovare un problema B, già noto essere NP-completo, e provare che B P A Ad esempio, alla luce delle riduzioni già viste, se provassimo che SAT P 3-SAT dimostreremmo in un sol colpo che 3-SAT, IS, VC e SC sono problemi NP-completi È questo il modo mediante il quale la collezione di problemi NP-completi cresce Oggi sono noti migliaia di problemi NP-completi, in aree quali logica, informatica, ricerca operativa, economia, ecc.
3 CENNI DI TEORIA DELLA COMPLESSITA COMPUTAZIONALE. E. Amaldi Fondamenti di R.O. Politecnico di Milano 1
 3 CENNI DI TEORIA DELLA COMPLESSITA COMPUTAZIONALE E. Amaldi Fondamenti di R.O. Politecnico di Milano 1 Scopo: Stimare l onere computazionale per risolvere problemi di ottimizzazione e di altra natura
3 CENNI DI TEORIA DELLA COMPLESSITA COMPUTAZIONALE E. Amaldi Fondamenti di R.O. Politecnico di Milano 1 Scopo: Stimare l onere computazionale per risolvere problemi di ottimizzazione e di altra natura
Automi e Linguaggi Formali
 Automi e Linguaggi Formali Problemi intrattabili, classi P e NP A.A. 2014-2015 Alessandro Sperduti sperduti@math.unipd.it Problemi intrattabili Ci occuperemo solo di problemi decidibili, cioè ricorsivi.
Automi e Linguaggi Formali Problemi intrattabili, classi P e NP A.A. 2014-2015 Alessandro Sperduti sperduti@math.unipd.it Problemi intrattabili Ci occuperemo solo di problemi decidibili, cioè ricorsivi.
Complessità computazionale
 Complementi di Algoritmi e Strutture Dati Complessità computazionale Docente: Nicolò Cesa-Bianchi versione 6 marzo 2019 Attenzione: Questo è un riassunto di alcune lezioni messo a disposizione dal docente.
Complementi di Algoritmi e Strutture Dati Complessità computazionale Docente: Nicolò Cesa-Bianchi versione 6 marzo 2019 Attenzione: Questo è un riassunto di alcune lezioni messo a disposizione dal docente.
NP completezza. Problemi astratti
 NP completezza Vittorio Maniezzo - Università di Bologna Problemi astratti Un problema è un entità astratta (es. il TSP). Una istanzadel problema è un suo caso particolare in cui vengono specificati tutti
NP completezza Vittorio Maniezzo - Università di Bologna Problemi astratti Un problema è un entità astratta (es. il TSP). Una istanzadel problema è un suo caso particolare in cui vengono specificati tutti
NP completezza. Vittorio Maniezzo - Università di Bologna
 NP completezza Vittorio Maniezzo - Università di Bologna Problemi astratti Un problema è un entità astratta (es. il TSP). Una istanzadel problema è un suo caso particolare in cui vengono specificati tutti
NP completezza Vittorio Maniezzo - Università di Bologna Problemi astratti Un problema è un entità astratta (es. il TSP). Una istanzadel problema è un suo caso particolare in cui vengono specificati tutti
Complessità e Approssimazione
 1 Complessità e Approssimazione Corso di Laurea in Scienze dell'informazione Corso di Laurea Specialistica in Matematica Docente: Mauro Leoncini 2 Aspetti organizzativi Sito web: http://algo.ing.unimo.it/people/mauro
1 Complessità e Approssimazione Corso di Laurea in Scienze dell'informazione Corso di Laurea Specialistica in Matematica Docente: Mauro Leoncini 2 Aspetti organizzativi Sito web: http://algo.ing.unimo.it/people/mauro
Teoria della Complessità Computazionale
 Teoria della Complessità Computazionale Laura Galli Dipartimento di Informatica Largo B. Pontecorvo 3, 56127 Pisa laura.galli@unipi.it http://www.di.unipi.it/~galli 21 Ottobre 2014 Ricerca Operativa 2
Teoria della Complessità Computazionale Laura Galli Dipartimento di Informatica Largo B. Pontecorvo 3, 56127 Pisa laura.galli@unipi.it http://www.di.unipi.it/~galli 21 Ottobre 2014 Ricerca Operativa 2
Algoritmo per A. !(x) Istanza di B
 Riduzioni polinomiali Una funzione f: T*!T* è detta computabile in tempo polinomiale se esiste una macchina di Turing limitata polinomialmente che la computi. Siano L 1 e L 2 " T* due linguaggi. Una funzione
Riduzioni polinomiali Una funzione f: T*!T* è detta computabile in tempo polinomiale se esiste una macchina di Turing limitata polinomialmente che la computi. Siano L 1 e L 2 " T* due linguaggi. Una funzione
Complessità Strutturale e NP-Completezza
 Complessità Strutturale e NP-Completezza Una breve introduzione Francesco De Rose Alberto Giorgi Università degli Studi di Brescia Facoltà di Ingegneria Corso di Laurea Specialistica in Ingegneria Informatica
Complessità Strutturale e NP-Completezza Una breve introduzione Francesco De Rose Alberto Giorgi Università degli Studi di Brescia Facoltà di Ingegneria Corso di Laurea Specialistica in Ingegneria Informatica
Problemi intrattabili
 Tempo polinomiale ed esponenziale Una Tm M ha complessita in tempo T(n) se, dato un input w di lunghezza n, M si ferma dopo al massimo T (n) passi. Problemi intrattabili Ci occuperemo solo di problemi
Tempo polinomiale ed esponenziale Una Tm M ha complessita in tempo T(n) se, dato un input w di lunghezza n, M si ferma dopo al massimo T (n) passi. Problemi intrattabili Ci occuperemo solo di problemi
Problemi intrattabili, classi P e NP. Problemi intrattabili, classi P e NP
 roblemi intrattabili Ci occuperemo solo di problemi decidibili, cioe ricorsivi. Tra loro, alcuni sono detti trattabili, se si puo provare che sono risolvibili in tempo polinomiale in modo deterministico.
roblemi intrattabili Ci occuperemo solo di problemi decidibili, cioe ricorsivi. Tra loro, alcuni sono detti trattabili, se si puo provare che sono risolvibili in tempo polinomiale in modo deterministico.
Teoria della Complessità Concetti fondamentali
 Teoria della Complessità Concetti fondamentali L oggetto della teoria della complessità è stabilire se un problema sia facile o difficile La difficoltà di un problema è una caratteristica generale e non
Teoria della Complessità Concetti fondamentali L oggetto della teoria della complessità è stabilire se un problema sia facile o difficile La difficoltà di un problema è una caratteristica generale e non
Problemi decisionali. Esempi
 Problemi decisionali La teoria della complessità computazionale è definita principalmente in termini di problemi di decisione Essendo la risposta binaria, non ci si deve preoccupare del tempo richiesto
Problemi decisionali La teoria della complessità computazionale è definita principalmente in termini di problemi di decisione Essendo la risposta binaria, non ci si deve preoccupare del tempo richiesto
Teoria della Complessità Computazionale
 Teoria della Complessità Computazionale Daniele Vigo D.E.I.S. - Università di Bologna dvigo@deis.unibo.it Rev. 1.3, 11/00 rev. 1.3 - Novembre 2000 Teoria della Complessità Studia la difficoltà dei problemi
Teoria della Complessità Computazionale Daniele Vigo D.E.I.S. - Università di Bologna dvigo@deis.unibo.it Rev. 1.3, 11/00 rev. 1.3 - Novembre 2000 Teoria della Complessità Studia la difficoltà dei problemi
Note sulle classi di complessità P, NP e NPC per ASD (DRAFT)
 Note sulle classi di complessità P, NP e NPC per ASD 2010-11 (DRAFT) Nicola Rebagliati 20 dicembre 2010 1 La complessità degli algoritmi Obiettivo principale della teoria della complessità: ottenere una
Note sulle classi di complessità P, NP e NPC per ASD 2010-11 (DRAFT) Nicola Rebagliati 20 dicembre 2010 1 La complessità degli algoritmi Obiettivo principale della teoria della complessità: ottenere una
Certificati dei problemi in NP
 Certificati dei problemi in NP La stringa y viene in genere denominata un certificato Un Certificato è una informazione ausiliaria che può essere utilizzata per verificare in tempo polinomiale nella dimensione
Certificati dei problemi in NP La stringa y viene in genere denominata un certificato Un Certificato è una informazione ausiliaria che può essere utilizzata per verificare in tempo polinomiale nella dimensione
Partizioni intere. =! i# P. Es: Dato {38, 17, 52, 61, 21, 88, 25} possiamo rispondere positivamente al quesito poiché
 Partizioni intere PARTIZIONAMENTO: Dato un insieme di n interi non negativi rappresentati in binario, trovare un sottoinsieme P! {1,2,..., n } tale che! i"p a i =! i# P a i Es: Dato {38, 17, 52, 61, 21,
Partizioni intere PARTIZIONAMENTO: Dato un insieme di n interi non negativi rappresentati in binario, trovare un sottoinsieme P! {1,2,..., n } tale che! i"p a i =! i# P a i Es: Dato {38, 17, 52, 61, 21,
Teoria della complessità
 Teoria della complessità Materiale consigliato: testo del corso capitolo 34 Introduzione agli algoritmi e strutture dati T.H. Cormen, C.E. Leiserson, R.L. Rivest, C. Stein McGraw Hill, 2005 Denise Salvi
Teoria della complessità Materiale consigliato: testo del corso capitolo 34 Introduzione agli algoritmi e strutture dati T.H. Cormen, C.E. Leiserson, R.L. Rivest, C. Stein McGraw Hill, 2005 Denise Salvi
Complessità Computazionale
 Complessità Computazionale La teoria della Computabilità cattura la nozione di algoritmo nel senso che per ogni problema sia esso decisionale o di calcolo di funzione stabilisce dei criteri per determinare
Complessità Computazionale La teoria della Computabilità cattura la nozione di algoritmo nel senso che per ogni problema sia esso decisionale o di calcolo di funzione stabilisce dei criteri per determinare
Teoria della NP-completezza
 Teoria della NP-completezza Ivan Lanese Dipartimento di Informatica Scienza e Ingegneria Università di Bologna Ivan.lanese@gmail.com http://www.cs.unibo.it/~lanese/ NP-completezza 2 Complessità di problemi
Teoria della NP-completezza Ivan Lanese Dipartimento di Informatica Scienza e Ingegneria Università di Bologna Ivan.lanese@gmail.com http://www.cs.unibo.it/~lanese/ NP-completezza 2 Complessità di problemi
Aniello Murano Classe dei problemi NP. Nella lezione precedente abbiamo visto alcuni problemi che ammettono soluzione polinomiale
 Aniello Murano Classe dei problemi NP 13 Lezione n. Parole chiave: Classe NP Corso di Laurea: Informatica Codice: Email Docente: murano@ na.infn.it A.A. 2008-2009 Introduzione alla lezione Nella lezione
Aniello Murano Classe dei problemi NP 13 Lezione n. Parole chiave: Classe NP Corso di Laurea: Informatica Codice: Email Docente: murano@ na.infn.it A.A. 2008-2009 Introduzione alla lezione Nella lezione
Aniello Murano NP- Completezza (prima parte)
 Aniello Murano NP- Completea (prima parte) 14 Leione n. Parole chiave: Npcompletea Corso di Laurea: Informatica Codice: Email Docente: murano@ na.infn.it A.A. 2008-2009 Introduione I problemi NP-completi
Aniello Murano NP- Completea (prima parte) 14 Leione n. Parole chiave: Npcompletea Corso di Laurea: Informatica Codice: Email Docente: murano@ na.infn.it A.A. 2008-2009 Introduione I problemi NP-completi
Sommario. Problemi di decisione, di ricerca e di ottimizzazione: come sono legate le complessità delle diverse versioni dei problemi?
 Sommario Problemi di decisione, di ricerca e di ottimizzazione: come sono legate le complessità delle diverse versioni dei problemi? Decisione vs ricerca Se disponiamo di un efficiente algoritmo per risolvere
Sommario Problemi di decisione, di ricerca e di ottimizzazione: come sono legate le complessità delle diverse versioni dei problemi? Decisione vs ricerca Se disponiamo di un efficiente algoritmo per risolvere
Teoria della NP-completezza. Damiano Macedonio
 Teoria della NP-completezza Damiano Macedonio mace@unive.it Copyright 2010, Moreno Marzolla, Università di Bologna, Italy (http://www.moreno.marzolla.name/teaching/asd2009/) This work is licensed under
Teoria della NP-completezza Damiano Macedonio mace@unive.it Copyright 2010, Moreno Marzolla, Università di Bologna, Italy (http://www.moreno.marzolla.name/teaching/asd2009/) This work is licensed under
Problemi, istanze, soluzioni
 lgoritmi e Strutture di Dati II 2 Problemi, istanze, soluzioni Un problema specifica una relazione matematica tra dati di ingresso e dati di uscita. Una istanza di un problema è formata dai dati di un
lgoritmi e Strutture di Dati II 2 Problemi, istanze, soluzioni Un problema specifica una relazione matematica tra dati di ingresso e dati di uscita. Una istanza di un problema è formata dai dati di un
Teoria della Complessità Computazionale Parte II: Classi di Complessità
 Teoria della Complessità Computazionale arte II: Classi di Complessità Daniele Vigo D.E.I.S. - Università di Bologna dvigo@deis.unibo.it rev. 3.0 - Ottobre 2003 Classi di complessità: ed N classe dei problemi
Teoria della Complessità Computazionale arte II: Classi di Complessità Daniele Vigo D.E.I.S. - Università di Bologna dvigo@deis.unibo.it rev. 3.0 - Ottobre 2003 Classi di complessità: ed N classe dei problemi
Sommario. Caratterizzazione alternativa di NP: il verificatore polinomiale esempi di problemi in NP
 Sommario Caratterizzazione alternativa di NP: il verificatore polinomiale esempi di problemi in NP I conjecture that there is no good algorithm for the traveling salesman problem. My reasons are the same
Sommario Caratterizzazione alternativa di NP: il verificatore polinomiale esempi di problemi in NP I conjecture that there is no good algorithm for the traveling salesman problem. My reasons are the same
3-SAT CLIQUE VERTEX-COVER INDEPENDENT-SET 3-COLORING
 Sommario Esempi di problemi NP-completi: 3-S CLIQUE VEREX-COVER INDEPENDEN-SE 3-COLORING HamCycle SP 3S Consideriamo formule booleane in forma normale congiuntiva (CN) con esattamente 3 letterali per clausola
Sommario Esempi di problemi NP-completi: 3-S CLIQUE VEREX-COVER INDEPENDEN-SE 3-COLORING HamCycle SP 3S Consideriamo formule booleane in forma normale congiuntiva (CN) con esattamente 3 letterali per clausola
Problemi difficili e ricerca esaustiva intelligente
 Problemi difficili e ricerca esaustiva intelligente Progettazione di Algoritmi a.a. 2016-17 Matricole congrue a 1 Docente: Annalisa De Bonis Gli argomenti di questa lezione sono tratti da Dasgupta, Papadimitriou,
Problemi difficili e ricerca esaustiva intelligente Progettazione di Algoritmi a.a. 2016-17 Matricole congrue a 1 Docente: Annalisa De Bonis Gli argomenti di questa lezione sono tratti da Dasgupta, Papadimitriou,
Sommario. Problemi di decisione, di ricerca e di ottimizzazione: come sono legate le complessità delle diverse versioni dei problemi?
 Sommario Problemi di decisione, di ricerca e di ottimizzazione: come sono legate le complessità delle diverse versioni dei problemi? Decisione vs ricerca! Se disponiamo di un efficiente algoritmo per risolvere
Sommario Problemi di decisione, di ricerca e di ottimizzazione: come sono legate le complessità delle diverse versioni dei problemi? Decisione vs ricerca! Se disponiamo di un efficiente algoritmo per risolvere
Riduzioni che preservano l approssimazione e completezza nelle classi di approssimabilità.
 RISULTATI DI NON APPROSSIMABILITA Tecnica di base: gap. Riduzioni che preservano l approssimazione e completezza nelle classi di approssimabilità. Risultati negativi basati su prove verificabili in modo
RISULTATI DI NON APPROSSIMABILITA Tecnica di base: gap. Riduzioni che preservano l approssimazione e completezza nelle classi di approssimabilità. Risultati negativi basati su prove verificabili in modo
Teoria della Calcolabilità!
 Teoria della Calcolabilità Si occupa delle questioni fondamentali circa la potenza e le limitazioni dei sistemi di calcolo. L'origine risale alla prima metà del ventesimo secolo, quando i logici matematici
Teoria della Calcolabilità Si occupa delle questioni fondamentali circa la potenza e le limitazioni dei sistemi di calcolo. L'origine risale alla prima metà del ventesimo secolo, quando i logici matematici
Sommario. Esempi di problemi NP-completi: 3-COLORING TSP. HamCycle
 Sommario Esempi di problemi NP-completi: 3-COLORING HamCycle SP 3-Coloring è NP-hard Una colorazione di un grafo G=(V,E) è una funzione f : V {1,...,n} tale che {u,v} E f(u) f(v). Una 3- colorazione usa
Sommario Esempi di problemi NP-completi: 3-COLORING HamCycle SP 3-Coloring è NP-hard Una colorazione di un grafo G=(V,E) è una funzione f : V {1,...,n} tale che {u,v} E f(u) f(v). Una 3- colorazione usa
Algoritmi e complessità
 Appendice A Algoritmi e complessità In questa appendice vogliamo brevemente richiamare alcuni concetti fondamentali della teoria della complessità computazionale, utili per meglio comprendere la diversa
Appendice A Algoritmi e complessità In questa appendice vogliamo brevemente richiamare alcuni concetti fondamentali della teoria della complessità computazionale, utili per meglio comprendere la diversa
e Algoritmi Marco Piastra Intelligenza Artificiale I Soddisfacibilità
 Intelligenza Artificiale I Soddisfacibilità e Algoritmi Marco Piastra Intelligenza Artificiale I - A.A. 2010- Soddisfacibilità e Semantic Tableau [1] Problemi e decidibilità (automatica) Problema Un problema
Intelligenza Artificiale I Soddisfacibilità e Algoritmi Marco Piastra Intelligenza Artificiale I - A.A. 2010- Soddisfacibilità e Semantic Tableau [1] Problemi e decidibilità (automatica) Problema Un problema
Soddisfacibilità e Semantic Tableau [1]
![Soddisfacibilità e Semantic Tableau [1] Soddisfacibilità e Semantic Tableau [1]](/thumbs/75/72399010.jpg) Intelligenza Artificiale I Soddisfacibilità e Semantic Tableau Marco Piastra Soddisfacibilità e Semantic Tableau [1] Problemi e decidibilità (automatica) Problema In forma rigorosa, un problema è una relazione
Intelligenza Artificiale I Soddisfacibilità e Semantic Tableau Marco Piastra Soddisfacibilità e Semantic Tableau [1] Problemi e decidibilità (automatica) Problema In forma rigorosa, un problema è una relazione
Introduzione Problemi e codifiche Classe P e linguaggi Da NP a NP-C Il mondo NP-C Conclusioni. NP-Completezza
 NP-Completezza e la complessità strutturale degli algoritmi Simone Frassanito Dipartimento di Elettronica per l Automazione Università degli Studi di Brescia Cosa non è l NP-Completezza Si potrebbe pensare
NP-Completezza e la complessità strutturale degli algoritmi Simone Frassanito Dipartimento di Elettronica per l Automazione Università degli Studi di Brescia Cosa non è l NP-Completezza Si potrebbe pensare
Capitolo 8: Teoria della complessitá
 Capitolo 8: Teoria della complessitá 1 La Teoria della calcolabilitá considera aspetti qualitativi della soluzione di problemi. Distingue il calcolabile dal non calcolabile. La Teoria della complessitá
Capitolo 8: Teoria della complessitá 1 La Teoria della calcolabilitá considera aspetti qualitativi della soluzione di problemi. Distingue il calcolabile dal non calcolabile. La Teoria della complessitá
Sommario. Caratterizzazione alternativa di NP: il verificatore polinomiale la classe conp e le relazioni tra P, NP,coNP e EXPTIME
 Sommario Caratterizzazione alternativa di NP: il verificatore polinomiale la classe conp e le relazioni tra P, NP,coNP e EXPTIME HAMPATH - 1 HAMPATH = { G è un grafo diretto con un cammino hamiltoniano
Sommario Caratterizzazione alternativa di NP: il verificatore polinomiale la classe conp e le relazioni tra P, NP,coNP e EXPTIME HAMPATH - 1 HAMPATH = { G è un grafo diretto con un cammino hamiltoniano
Lucchetto con combinazione (3 numeri tra 0 e 39)
 Complessita computazionale ed il problema P / NP Fondamenti di Informatica 2011/12 Lucchetto con combinazione (3 numeri tra 0 e 39) Perche e sicuro? (escludendo che lo si rompa) Combinazione di 3 numberi
Complessita computazionale ed il problema P / NP Fondamenti di Informatica 2011/12 Lucchetto con combinazione (3 numeri tra 0 e 39) Perche e sicuro? (escludendo che lo si rompa) Combinazione di 3 numberi
Algoritmi Euristici. Corso di Laurea in Informatica e Corso di Laurea in Matematica. Roberto Cordone DI - Università degli Studi di Milano
 Algoritmi Euristici Corso di Laurea in Informatica e Corso di Laurea in Matematica Roberto Cordone DI - Università degli Studi di Milano Lezioni: Martedì 14.30-16.30 in Aula Omega Venerdì 14.30-16.30 in
Algoritmi Euristici Corso di Laurea in Informatica e Corso di Laurea in Matematica Roberto Cordone DI - Università degli Studi di Milano Lezioni: Martedì 14.30-16.30 in Aula Omega Venerdì 14.30-16.30 in
Ancora su 2-SAT. può essere pensata come una coppia di implicazioni!! " 1
 Ancora su 2-SAT Qualsiasi clausola a 1! a 2 può essere pensata come una coppia di implicazioni!! " 1 " a 2 e " 2 " a 1 Il caso di letterale singolo a viene considerato come "" a Partendo da una istanza
Ancora su 2-SAT Qualsiasi clausola a 1! a 2 può essere pensata come una coppia di implicazioni!! " 1 " a 2 e " 2 " a 1 Il caso di letterale singolo a viene considerato come "" a Partendo da una istanza
RISOLUZIONE IN LOGICA PROPOSIZIONALE. Giovanna D Agostino Dipartimento di Matemaica e Informatica, Università di Udine
 RISOLUZIONE IN LOGICA PROPOSIZIONALE Giovanna D Agostino Dipartimento di Matemaica e Informatica, Università di Udine 1. Risoluzione Definitione 1.1. Un letterale l è una variabile proposizionale (letterale
RISOLUZIONE IN LOGICA PROPOSIZIONALE Giovanna D Agostino Dipartimento di Matemaica e Informatica, Università di Udine 1. Risoluzione Definitione 1.1. Un letterale l è una variabile proposizionale (letterale
Matroidi, algoritmi greedy e teorema di Rado
 Matroidi, algoritmi greedy e teorema di Rado per il corso di Laboratorio di Algoritmi e Ricerca Operativa Dott. Alberto Leporati / Prof.ssa Enza Messina Dipartimento di Informatica, Sistemistica e Comunicazione
Matroidi, algoritmi greedy e teorema di Rado per il corso di Laboratorio di Algoritmi e Ricerca Operativa Dott. Alberto Leporati / Prof.ssa Enza Messina Dipartimento di Informatica, Sistemistica e Comunicazione
3 CENNI DI TEORIA DELLA COMPLESSITA COMPUTAZIONALE. E. Amaldi Fondamenti di R.O. Politecnico di Milano 1
 3 CENNI DI TEORIA DELLA COMPLESSITA COMPUTAZIONALE E. Amaldi Fondamenti di R.O. Politecnico di Milano 1 Scopo: Stimare l onere computazionale per risolvere problemi di ottimizzazione e di altra natura
3 CENNI DI TEORIA DELLA COMPLESSITA COMPUTAZIONALE E. Amaldi Fondamenti di R.O. Politecnico di Milano 1 Scopo: Stimare l onere computazionale per risolvere problemi di ottimizzazione e di altra natura
Il problema del commesso viaggiatore (TSP) la somma delle distanze tra le città. essere espresso dalla domanda:
 Classe NP: il TSP Il problema del commesso viaggiatore (TSP)! È definito in termini di un insieme di n città c 1,..., c n e di una matrice delle distanze: D = ( d(i,j) ) d(i,j) = distanza(c i, c j )! Un
Classe NP: il TSP Il problema del commesso viaggiatore (TSP)! È definito in termini di un insieme di n città c 1,..., c n e di una matrice delle distanze: D = ( d(i,j) ) d(i,j) = distanza(c i, c j )! Un
In prima approssimazione definiamo trattabili i problemi che possono essere risolti in tempo polinomiale con MT. Motivazioni:
 6.5 Trattabilita' computazionale. In prima approssimazione definiamo trattabili i problemi che possono essere risolti in tempo polinomiale con MT. Motivazioni: - la forte differenza nell'andamento asintotico
6.5 Trattabilita' computazionale. In prima approssimazione definiamo trattabili i problemi che possono essere risolti in tempo polinomiale con MT. Motivazioni: - la forte differenza nell'andamento asintotico
In prima approssimazione definiamo trattabili i problemi che possono essere risolti in tempo polinomiale con MT. Motivazioni:
 6.5 Trattabilita' computazionale. In prima approssimazione definiamo trattabili i problemi che possono essere risolti in tempo polinomiale con MT. Motivazioni: - la forte differenza nell'andamento asintotico
6.5 Trattabilita' computazionale. In prima approssimazione definiamo trattabili i problemi che possono essere risolti in tempo polinomiale con MT. Motivazioni: - la forte differenza nell'andamento asintotico
Elementi di Complessità Computazionale
 Elementi di Complessità Computazionale Ultima modifica 23.06.2004 Il problema Esiste una misura oggettiva per valutare l'efficienza di un algoritmo? In che relazione sono gli input di un algoritmo con
Elementi di Complessità Computazionale Ultima modifica 23.06.2004 Il problema Esiste una misura oggettiva per valutare l'efficienza di un algoritmo? In che relazione sono gli input di un algoritmo con
Algoritmi e Strutture Dati II: Parte B Anno Accademico Lezione 1
 Algoritmi e Strutture Dati II: Parte B Anno Accademico 004-005 Docente: Ugo Vaccaro Lezione 1 Dalla Teoria della NP-Completezza abbiamo appreso che esiste una classe di problemi (NPhard) per cui non è
Algoritmi e Strutture Dati II: Parte B Anno Accademico 004-005 Docente: Ugo Vaccaro Lezione 1 Dalla Teoria della NP-Completezza abbiamo appreso che esiste una classe di problemi (NPhard) per cui non è
Introduzione ai grafi
 TFA A048 Anno Accademico 2012-13 Outline Cenni storici sui grafi Nozioni introduttive: cammini, connessione, alberi, cicli Cammini di costo minimo Origini storiche La nascita della teoria dei grafi risale
TFA A048 Anno Accademico 2012-13 Outline Cenni storici sui grafi Nozioni introduttive: cammini, connessione, alberi, cicli Cammini di costo minimo Origini storiche La nascita della teoria dei grafi risale
Progetto e analisi di algoritmi
 Progetto e analisi di algoritmi Roberto Cordone DTI - Università degli Studi di Milano Polo Didattico e di Ricerca di Crema Tel. 0373 / 898089 E-mail: cordone@dti.unimi.it Ricevimento: su appuntamento
Progetto e analisi di algoritmi Roberto Cordone DTI - Università degli Studi di Milano Polo Didattico e di Ricerca di Crema Tel. 0373 / 898089 E-mail: cordone@dti.unimi.it Ricevimento: su appuntamento
Complementi di Analisi Matematica Ia. Carlo Bardaro
 Complementi di Analisi Matematica Ia Carlo Bardaro Capitolo 1 Elementi di topologia della retta reale 1.1 Intorni, punti di accumulazione e insiemi chiusi Sia x 0 IR un fissato punto di IR. Chiameremo
Complementi di Analisi Matematica Ia Carlo Bardaro Capitolo 1 Elementi di topologia della retta reale 1.1 Intorni, punti di accumulazione e insiemi chiusi Sia x 0 IR un fissato punto di IR. Chiameremo
PSPACE completezza. Un linguaggio A è PSPACE completo se. 1. A è in PSPACE, cioè esiste una TM T che accetta A con complessità di spazio polinomiale.
 Sommario Il problema della verità per formule booleane pienamente quantificate è PSPACE - completo PSPACE come la classe dei giochi. Il gioco geografico generalizzato è PSPACE - completo 1 PSPACE completezza
Sommario Il problema della verità per formule booleane pienamente quantificate è PSPACE - completo PSPACE come la classe dei giochi. Il gioco geografico generalizzato è PSPACE - completo 1 PSPACE completezza
Esercitazioni per il corso di Logica Matematica
 Esercitazioni per il corso di Logica Matematica Luca Motto Ros 02 marzo 2005 Nota importante. Queste pagine contengono appunti personali dell esercitatore e sono messe a disposizione nel caso possano risultare
Esercitazioni per il corso di Logica Matematica Luca Motto Ros 02 marzo 2005 Nota importante. Queste pagine contengono appunti personali dell esercitatore e sono messe a disposizione nel caso possano risultare
LOGICA MATEMATICA PER INFORMATICA (A.A. 12/13)
 LOGICA MATEMATICA PER INFORMATICA (A.A. 12/13) DISPENSA N. 4 Sommario. Dimostriamo il Teorema di Completezza per il Calcolo dei Predicati del I ordine. 1. Teorema di Completezza Dimostriamo il Teorema
LOGICA MATEMATICA PER INFORMATICA (A.A. 12/13) DISPENSA N. 4 Sommario. Dimostriamo il Teorema di Completezza per il Calcolo dei Predicati del I ordine. 1. Teorema di Completezza Dimostriamo il Teorema
Lucchetto con combinazione (3 numeri tra 0 e 39)
 Complessita computazionale ed il problema P / NP Fondamenti di Informatica 2010/11 Lucchetto con combinazione (3 numeri tra 0 e 39) Perche e sicuro? (escludendo che lo si rompa) Ans: Combinazione di 3
Complessita computazionale ed il problema P / NP Fondamenti di Informatica 2010/11 Lucchetto con combinazione (3 numeri tra 0 e 39) Perche e sicuro? (escludendo che lo si rompa) Ans: Combinazione di 3
1 IL LINGUAGGIO MATEMATICO
 1 IL LINGUAGGIO MATEMATICO Il linguaggio matematico moderno è basato su due concetti fondamentali: la teoria degli insiemi e la logica delle proposizioni. La teoria degli insiemi ci assicura che gli oggetti
1 IL LINGUAGGIO MATEMATICO Il linguaggio matematico moderno è basato su due concetti fondamentali: la teoria degli insiemi e la logica delle proposizioni. La teoria degli insiemi ci assicura che gli oggetti
Possibile applicazione
 p. 1/4 Assegnamento Siano dati due insiemi A e B entrambi di cardinalità n. Ad ogni coppia (a i,b j ) A B è associato un valore d ij 0 che misura la "incompatibilità" tra a i e b j, anche interpretabile
p. 1/4 Assegnamento Siano dati due insiemi A e B entrambi di cardinalità n. Ad ogni coppia (a i,b j ) A B è associato un valore d ij 0 che misura la "incompatibilità" tra a i e b j, anche interpretabile
Capitolo 9: Trattabilitá e intrattabilitá dei problemi
 Capitolo 9: Trattabilitá e intrattabilitá dei problemi 1 La classe P : é considerata tradizionalmente come una caratterizzazione formale dei problemi trattabili. n = 2 n = 5 n = 10 n = 100 n = 1000 n 2
Capitolo 9: Trattabilitá e intrattabilitá dei problemi 1 La classe P : é considerata tradizionalmente come una caratterizzazione formale dei problemi trattabili. n = 2 n = 5 n = 10 n = 100 n = 1000 n 2
PROBLEMA DEI CAMMINI MINIMI [CORMEN ET AL. CAP. 24] Il costo di cammino minimo da un vertice u ad un vertice v è definito nel seguente modo:
![PROBLEMA DEI CAMMINI MINIMI [CORMEN ET AL. CAP. 24] Il costo di cammino minimo da un vertice u ad un vertice v è definito nel seguente modo: PROBLEMA DEI CAMMINI MINIMI [CORMEN ET AL. CAP. 24] Il costo di cammino minimo da un vertice u ad un vertice v è definito nel seguente modo:](/thumbs/95/123186961.jpg) PROBLEMA DEI CAMMINI MINIMI [CORMEN ET AL. CAP. 24] Sia G = (V,E) un grafo orientato ai cui archi è associato un costo W(u,v). Il costo di un cammino p = (v 1,v 2,...,v k ) è la somma dei costi degli archi
PROBLEMA DEI CAMMINI MINIMI [CORMEN ET AL. CAP. 24] Sia G = (V,E) un grafo orientato ai cui archi è associato un costo W(u,v). Il costo di un cammino p = (v 1,v 2,...,v k ) è la somma dei costi degli archi
ELEMENTI DI LOGICA MATEMATICA LEZIONE VII
 ELEMENTI DI LOGICA MATEMATICA LEZIONE VII MAURO DI NASSO In questa lezione introdurremo i numeri naturali, che sono forse gli oggetti matematici più importanti della matematica. Poiché stiamo lavorando
ELEMENTI DI LOGICA MATEMATICA LEZIONE VII MAURO DI NASSO In questa lezione introdurremo i numeri naturali, che sono forse gli oggetti matematici più importanti della matematica. Poiché stiamo lavorando
Algoritmi e Strutture Dati II: Parte B Anno Accademico Lezione 4
 Algoritmi e Strutture Dati II: Parte B Anno Accademico 2004-2005 Docente: Ugo Vaccaro Lezione 4 In questa lezione deriveremo un algoritmo di approssimazione per il seguente problema. Approfitteremo dell
Algoritmi e Strutture Dati II: Parte B Anno Accademico 2004-2005 Docente: Ugo Vaccaro Lezione 4 In questa lezione deriveremo un algoritmo di approssimazione per il seguente problema. Approfitteremo dell
Sviluppo di programmi
 Sviluppo di programmi Per la costruzione di un programma conviene: 1. condurre un analisi del problema da risolvere 2. elaborare un algoritmo della soluzione rappresentato in un linguaggio adatto alla
Sviluppo di programmi Per la costruzione di un programma conviene: 1. condurre un analisi del problema da risolvere 2. elaborare un algoritmo della soluzione rappresentato in un linguaggio adatto alla
1) Data la seguente istanza di TSP (grafo completo con 5 nodi): c 12 = 52; c 13 = 51; c 14 = 40; c 15 = 53; c 23 = 44;
 1) Data la seguente istanza di TSP (grafo completo con 5 nodi): c 12 = 52; c 13 = 51; c 14 = 40; c 15 = 53; c 23 = 44; c 24 = 15; c 25 = 12; c 34 = 32; c 35 = 55; c 45 = 24 Si calcoli l ottimo duale (formulazione
1) Data la seguente istanza di TSP (grafo completo con 5 nodi): c 12 = 52; c 13 = 51; c 14 = 40; c 15 = 53; c 23 = 44; c 24 = 15; c 25 = 12; c 34 = 32; c 35 = 55; c 45 = 24 Si calcoli l ottimo duale (formulazione
Algoritmi e Strutture Dati II: Parte B Anno Accademico Lezione 5
 Algoritmi e Strutture Dati II: Parte B Anno Accademico 2004-2005 Docente: Ugo Vaccaro Lezione 5 In questa lezione inizieremo a studiare gli algoritmi di approssimazione per problemi di ottimizzazione NP-hard
Algoritmi e Strutture Dati II: Parte B Anno Accademico 2004-2005 Docente: Ugo Vaccaro Lezione 5 In questa lezione inizieremo a studiare gli algoritmi di approssimazione per problemi di ottimizzazione NP-hard
a cura di Luca Cabibbo e Walter Didimo
 a cura di Luca Cabibbo e Walter Didimo Esercizi di Informatica teorica - Luca Cabibbo e Walter Didimo 1 tipologie di problemi e notazioni sulla complessità classi di complessità appartenenza di problemi
a cura di Luca Cabibbo e Walter Didimo Esercizi di Informatica teorica - Luca Cabibbo e Walter Didimo 1 tipologie di problemi e notazioni sulla complessità classi di complessità appartenenza di problemi
Primi elementi di combinatoria Federico Lastaria, Analisi e Geometria 1
 Politecnico di Milano. Scuola di Ingegneria Industriale e dell Informazione Analisi e Geometria 1 Federico Lastaria Primi elementi di combinatoria 11 Ottobre 2016 Indice 1 Elementi di combinatoria 2 1.1
Politecnico di Milano. Scuola di Ingegneria Industriale e dell Informazione Analisi e Geometria 1 Federico Lastaria Primi elementi di combinatoria 11 Ottobre 2016 Indice 1 Elementi di combinatoria 2 1.1
Lista di esercizi 11 maggio 2016
 Lista di esercizi 11 maggio 2016 1. Determinare il numero di sequenze binarie di lunghezza n che contengano almeno una coppia di 0 consecutivi. Soluzione. Potrebbe essere utile un programma di calcolo
Lista di esercizi 11 maggio 2016 1. Determinare il numero di sequenze binarie di lunghezza n che contengano almeno una coppia di 0 consecutivi. Soluzione. Potrebbe essere utile un programma di calcolo
Teoria della Calcolabilità!
 Teoria della Calcolabilità! Si occupa delle questioni fondamentali circa la potenza e le limitazioni dei sistemi di calcolo.! L'origine risale alla prima metà del ventesimo secolo, quando i logici matematici
Teoria della Calcolabilità! Si occupa delle questioni fondamentali circa la potenza e le limitazioni dei sistemi di calcolo.! L'origine risale alla prima metà del ventesimo secolo, quando i logici matematici
LA TEORIA DELLA COMPLESSITÀ COMPUTAZIONALE
 LA TEORIA DELLA COMPLESSITÀ COMPUTAZIONALE INTRODUZIONE OBIETTIVO: classificare gli algoritmi a seconda delle risorse utilizzate - risorse necessarie (lower bound) - risorse sufficienti (upper bound) Aspetti
LA TEORIA DELLA COMPLESSITÀ COMPUTAZIONALE INTRODUZIONE OBIETTIVO: classificare gli algoritmi a seconda delle risorse utilizzate - risorse necessarie (lower bound) - risorse sufficienti (upper bound) Aspetti
Problemi, algoritmi, calcolatore
 Problemi, algoritmi, calcolatore Informatica e Programmazione Ingegneria Meccanica e dei Materiali Università degli Studi di Brescia Prof. Massimiliano Giacomin Problemi, algoritmi, calcolatori Introduzione
Problemi, algoritmi, calcolatore Informatica e Programmazione Ingegneria Meccanica e dei Materiali Università degli Studi di Brescia Prof. Massimiliano Giacomin Problemi, algoritmi, calcolatori Introduzione
Algoritmi esatti. La teoria ci dice che per problemi difficili (come il
 p. 1/4 Algoritmi esatti La teoria ci dice che per problemi difficili (come il KNAPSACK o, ancora di più, il TSP ) i tempi di risoluzione delle istanze, calcolati tramite analisi worst-case, tendono a crescere
p. 1/4 Algoritmi esatti La teoria ci dice che per problemi difficili (come il KNAPSACK o, ancora di più, il TSP ) i tempi di risoluzione delle istanze, calcolati tramite analisi worst-case, tendono a crescere
UD 4.b: Trattabilità e Intrattabilità INTRODUZIONE
 Algoritmi, Strutture Dati e Programmi : Trattabilità e Intrattabilità INTRODUZIONE Prof. Alberto Postiglione Dispense, cap. 4.2.1 AA 2007-2008 Problemi Intrattabili Problemi Intrattabili Esistono problemi
Algoritmi, Strutture Dati e Programmi : Trattabilità e Intrattabilità INTRODUZIONE Prof. Alberto Postiglione Dispense, cap. 4.2.1 AA 2007-2008 Problemi Intrattabili Problemi Intrattabili Esistono problemi
Algoritmi, Strutture Dati e Programmi. UD 4.b: Trattabilità e Intrattabilità
 Algoritmi, Strutture Dati e Programmi : Trattabilità e Intrattabilità Prof. Alberto Postiglione AA 2007-2008 INTRODUZIONE Dispense, cap. 4.2.1 1 Problemi Intrattabili Esistono problemi che, pur avendo
Algoritmi, Strutture Dati e Programmi : Trattabilità e Intrattabilità Prof. Alberto Postiglione AA 2007-2008 INTRODUZIONE Dispense, cap. 4.2.1 1 Problemi Intrattabili Esistono problemi che, pur avendo
Lezione 4. Problemi trattabili e soluzioni sempre più efficienti. Gianluca Rossi
 Lezione 4 Problemi trattabili e soluzioni sempre più efficienti Gianluca Rossi Trattabile o intrattabile? Consideriamo ora il problema, ben noto a tutti gli studenti a partire dalla scuola media, di calcolare
Lezione 4 Problemi trattabili e soluzioni sempre più efficienti Gianluca Rossi Trattabile o intrattabile? Consideriamo ora il problema, ben noto a tutti gli studenti a partire dalla scuola media, di calcolare
0.1 Spazi Euclidei in generale
 0.1. SPAZI EUCLIDEI IN GENERALE 1 0.1 Spazi Euclidei in generale Sia V uno spazio vettoriale definito su R. Diremo, estendendo una definizione data in precedenza, che V è uno spazio vettoriale euclideo
0.1. SPAZI EUCLIDEI IN GENERALE 1 0.1 Spazi Euclidei in generale Sia V uno spazio vettoriale definito su R. Diremo, estendendo una definizione data in precedenza, che V è uno spazio vettoriale euclideo
PARTE II ALGORITMI APPROSSIMATI PER PROBLEMI DI OTTIMIZZAZIONE NP-HARD
 PARTE II ALGORITMI APPROSSIMATI PER PROBLEMI DI OTTIMIZZAZIONE NP-HARD 1 Complessità di problemi di ottimizzazione Algoritmi approssimati e schemi di approssimazione Tecniche algoritmiche Classi di approssimabilità
PARTE II ALGORITMI APPROSSIMATI PER PROBLEMI DI OTTIMIZZAZIONE NP-HARD 1 Complessità di problemi di ottimizzazione Algoritmi approssimati e schemi di approssimazione Tecniche algoritmiche Classi di approssimabilità
Diario delle Lezioni del Corso di Algoritmimodulo
 Diario delle Lezioni del Corso di Algoritmimodulo Complessità A.A. 2010-2011 Dott.ssa Margherita Zorzi 1 Materiale didattico Libro di testo C.H. Papadimitrious, Computational Complexity, ed Addison-Wesley
Diario delle Lezioni del Corso di Algoritmimodulo Complessità A.A. 2010-2011 Dott.ssa Margherita Zorzi 1 Materiale didattico Libro di testo C.H. Papadimitrious, Computational Complexity, ed Addison-Wesley
Problemi algoritmici e Complessità degli algoritmi
 Problemi algoritmici e Complessità degli algoritmi Università degli Studi di Salerno Corso di Laurea in Scienze della comunicazione Informatica generale Docente: Angela Peduto A.A. 2005/2006 Problemi algoritmici!
Problemi algoritmici e Complessità degli algoritmi Università degli Studi di Salerno Corso di Laurea in Scienze della comunicazione Informatica generale Docente: Angela Peduto A.A. 2005/2006 Problemi algoritmici!
Dentro P e oltre NP?
 Dentro P e oltre NP? Tra P e EXPTIME? EXPTIME PSPACE conp NP P Si sa solo che P EXPTIME PSPACE completezza Un linguaggio A è PSPACE completo se 1.A è in PSPACE, cioè esiste una TM T che accetta A con complessità
Dentro P e oltre NP? Tra P e EXPTIME? EXPTIME PSPACE conp NP P Si sa solo che P EXPTIME PSPACE completezza Un linguaggio A è PSPACE completo se 1.A è in PSPACE, cioè esiste una TM T che accetta A con complessità
Laboratorio di Programmazione Laurea in Ingegneria Civile e Ambientale
 Dipartimento di Ingegneria dell Informazione Università degli Studi di Parma Il problema di fondo Laboratorio di Programmazione Laurea in Ingegneria Civile e Ambientale Algoritmi e Programmazione Stefano
Dipartimento di Ingegneria dell Informazione Università degli Studi di Parma Il problema di fondo Laboratorio di Programmazione Laurea in Ingegneria Civile e Ambientale Algoritmi e Programmazione Stefano
METODI DELLA RICERCA OPERATIVA
 Università degli Studi di Cagliari FACOLTA' DI INGEGNERIA CORSO DI METODI DELLA RICERCA OPERATIVA Dott.ing. Massimo Di Francesco (mdifrance@unica.it) i i Dott.ing. Maria Ilaria Lunesu (ilaria.lunesu@unica.it)
Università degli Studi di Cagliari FACOLTA' DI INGEGNERIA CORSO DI METODI DELLA RICERCA OPERATIVA Dott.ing. Massimo Di Francesco (mdifrance@unica.it) i i Dott.ing. Maria Ilaria Lunesu (ilaria.lunesu@unica.it)
min det det Allora è unimodulare se e solo se det 1, 1, 0 per ogni sottomatrice quadrata di di qualsiasi dimensione.
 Se è unimodulare e è intero allora il poliedro 0 ha vertici interi. Sia un vertice di Per definizione esiste allora una base di tale che, 0 Poiché è non singolare ( invertibile det 0) si ha che det 1 è
Se è unimodulare e è intero allora il poliedro 0 ha vertici interi. Sia un vertice di Per definizione esiste allora una base di tale che, 0 Poiché è non singolare ( invertibile det 0) si ha che det 1 è
Note sull algoritmo di Gauss
 Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
Teoria dell Informazione II Anno Accademico Lezione 6-7
 Teoria dell Informazione II Anno Accademico 2017 2018 Lezione 6-7 Ugo Vaccaro ( ) 1 2 n Data una variabile casuale X = che assume valori i, con probabilità p p 1 p 2 p i, per i = 1,...,n, n vogliamo studiare
Teoria dell Informazione II Anno Accademico 2017 2018 Lezione 6-7 Ugo Vaccaro ( ) 1 2 n Data una variabile casuale X = che assume valori i, con probabilità p p 1 p 2 p i, per i = 1,...,n, n vogliamo studiare
Fasi di creazione di un programma
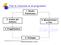 Fasi di creazione di un programma 1. Studio Preliminare 2. Analisi del Sistema 6. Manutenzione e Test 3. Progettazione 5. Implementazione 4. Sviluppo Sviluppo di programmi Per la costruzione di un programma
Fasi di creazione di un programma 1. Studio Preliminare 2. Analisi del Sistema 6. Manutenzione e Test 3. Progettazione 5. Implementazione 4. Sviluppo Sviluppo di programmi Per la costruzione di un programma
Algoritmi e Strutture di Dati
 Algoritmi e Strutture di Dati Complessità dei problemi m.patrignani Nota di copyright queste slides so protette dalle leggi sul copyright il titolo ed il copyright relativi alle slides (inclusi, ma n limitatamente,
Algoritmi e Strutture di Dati Complessità dei problemi m.patrignani Nota di copyright queste slides so protette dalle leggi sul copyright il titolo ed il copyright relativi alle slides (inclusi, ma n limitatamente,
Ragionamento Automatico Richiami di tableaux proposizionali
 Richiami di logica e deduzione proposizionale Ragionamento Automatico Richiami di tableaux proposizionali (L. Carlucci Aiello & F. Pirri: SLL, Cap. 5) La logica proposizionale I tableau proposizionali
Richiami di logica e deduzione proposizionale Ragionamento Automatico Richiami di tableaux proposizionali (L. Carlucci Aiello & F. Pirri: SLL, Cap. 5) La logica proposizionale I tableau proposizionali
Intelligenza Artificiale. Logica proposizionale: calcolo automatico
 Intelligenza Artificiale Logica proposizionale: calcolo automatico Marco Piastra Logica formale (Parte 3) - Parte 3 Calcolo automatico Forme normali ed a clausole Risoluzione e refutazione Forward chaining
Intelligenza Artificiale Logica proposizionale: calcolo automatico Marco Piastra Logica formale (Parte 3) - Parte 3 Calcolo automatico Forme normali ed a clausole Risoluzione e refutazione Forward chaining
Il concetto di calcolatore e di algoritmo
 Il concetto di calcolatore e di algoritmo Elementi di Informatica e Programmazione Percorso di Preparazione agli Studi di Ingegneria Università degli Studi di Brescia Docente: Massimiliano Giacomin Informatica
Il concetto di calcolatore e di algoritmo Elementi di Informatica e Programmazione Percorso di Preparazione agli Studi di Ingegneria Università degli Studi di Brescia Docente: Massimiliano Giacomin Informatica
Corso di Informatica Generale (C. L. Economia e Commercio) Ing. Valerio Lacagnina Rappresentazione dei numeri relativi
 Codice BCD Prima di passare alla rappresentazione dei numeri relativi in binario vediamo un tipo di codifica che ha una certa rilevanza in alcune applicazioni: il codice BCD (Binary Coded Decimal). È un
Codice BCD Prima di passare alla rappresentazione dei numeri relativi in binario vediamo un tipo di codifica che ha una certa rilevanza in alcune applicazioni: il codice BCD (Binary Coded Decimal). È un
Algoritmo. Calcolabilità
 Algoritmo In altri termini, l algoritmo può essere definito come la descrizione di un procedimento che ha le seguenti proprietà: deve essere esplicita e non ambigua per l interlocutore cui è destinata
Algoritmo In altri termini, l algoritmo può essere definito come la descrizione di un procedimento che ha le seguenti proprietà: deve essere esplicita e non ambigua per l interlocutore cui è destinata
