Ottimizzazione Combinatoria Proprietà dei Grafi. Ottimizzazione Combinatoria
|
|
|
- Damiano Leonardi
- 5 anni fa
- Visualizzazioni
Transcript
1 Ottimizzazione Combinatoria Ottimizzazione Combinatoria Proprietà dei Grafi ANTONIO SASSANO Università di Roma La Sapienza Dipartimento di Informatica e Sistemistica Corso di Laurea in Ingegneria Gestionale Roma, 6 Maggio2003 1
2 Grafi TEORIA DEI GRAFI: Studia le proprietà metriche e topologiche delle relazioni binarie Oggetti Nodi Relazioni tra coppie Archi Grafo con: N ={,...,v n } Insieme dei Nodi di G A ={e 1,...,e m } Insieme degli Archi di G e 1 e 5 e 7 e 9 e 8 v e 4 2 e 2 e 3 IPOTESI: Grafo semplice Non esistono archi paralleli o loop archi paralleli loop Quindi: al più un arco per ogni coppia (ordinata) di nodi: Coppia ordinata: Coppia non-ordinata: e h v i v k Arco orientato (v i,v k ) v i v k e h v i e h v k Arco non-orientato v i v k v k v i e h 2
3 Grafi: Archi orientati e non-orientati e h v i v k Arco orientato (v i,v k ) e h v i e h v k Arco non-orientato (v i,v k ) e h e 1 e 5 e 7 e 9 e 2 v e 4 2 e 3 Per ogni arco orientato (v i,v k ) e h diremo: e 8 v i coda di e h v i precede v k e h esce da v i ESEMPIO v k testa di e h v k segue v i e h entra in v k e 1 coda di e 1 Per ogni arco orientato o non orientato diremo: v adiacente a v i k e h incidente su v k e v i v e v i k estremi di e h testa di e 1 precede segue e 2 esce da e 3 entra in adiacente a e 3 incidente su 3
4 Grafi orientati e non-orientati Grafo orientato Ogni arco di A è orientato Grafo orientato Grafo non-orientato Ogni arco di A è non-orientato Grafo non-orientato Grafo misto Ogni arco di A può essere orientato o non-orientato Grafo misto 4
5 Stelle e Intorni STELLA DI v IN G δ G (v) = {e : e =uv } A Insieme degli archi di G incidenti su v δ G (v) = d G (v); GRADO di v e 1 e v3 5 e 3 e 7 e 2 e 4 δ G ( ) = {e 5,, e 7 } d G ( ) = 3 INTORNO DI v IN G N G (v) = {u : vu A } N Insieme dei nodi adiacenti a v in G e v3 5 e 1 e 7 e 2 e 4 e 3 N G ( ) = {,, } 5
6 Stelle in Grafi Orientati STELLA USCENTE DA v IN G + δ G (v) = {e : v coda di e } A Insieme degli archi di G uscenti da v + + δ G (v) = d G (v); GRADO USCENTE e 1 e 5 e 7 + δ G ( ) = {, e 9 } + d G ( ) = 2 v e 4 2 e 2 e 3 e 9 e 8 STELLA ENTRANTE IN v IN G - δ G (v) = {e : v testa di e } A Insieme degli archi di G entranti in v - - δ G (v) = d G (v); GRADO ENTRANTE - e 1 e 2 e 5 e 7 δ G ( ) = {e 3, e 7, e 9 } - d G ( ) = 3 e 4 e 3 e 9 e 8 6
7 Intorni in Grafi Orientati INTORNO+ DI v IN G + N G (v) = {u : vu A } N Teste di archi di G con coda in v e 1 e 5 e 7 e 9 e 8 v e 4 2 e 2 e 3 N + G ( ) = {, } INTORNO- DI v IN G - N G (v) = {u : uv A } N Code di archi di G con testa in v e 9 e 1 e 2 v e 3 5 v e 4 2 e 7 e 3 e 8 N - G ( ) = {,, } 7
8 Tagli e 1 e 2 TAGLIO IN DEFINITO DA S N δ G (S) = {uv : u S e v N-S } A Insieme degli archi di G con un estremo in S e l altro in N-S S e 5 v e 4 2 e 7 e 3 e9 e 8 S= {,,, } δ G (S) = {e 2,e 7,e 8,e 9 } DATI S,T N con S T= : definiamo δ G (S,T) = δ G (S) δ G (T) Insieme degli archi di G con un estremo in S e l altro in T e 1 e 2 e 5 v e 4 2 e 7 T e 3 e 9 e 8 S S = {, } T = {, } δ G (S,T) = {e 3, e 4, e 5 } 8
9 Tagli in Grafi Orientati e 1 e 2 TAGLIO USCENTE DA S N IN G + δ G (S) = {uv : u S e v N-S } A Insieme degli archi di G con coda in S e testa in N-S e 5 e 8 e 7 v e 4 2 e 3 e 9 S= {,,, } + δ G (S) = {e 2, e 7, e 9 } TAGLIO ENTRANTE IN S N IN G - δ G (S) = {uv : u N-S e v S } A Insieme degli archi di G con coda in N-S e testa in S e 1 e 2 e 5 e 8 e 7 e 4 e 3 e 9 S= {, } - δ G (S) = {e 1, e 5, e 4 } 9
10 Sottografi v v3 4 H(N,A ) SOTTOGRAFO DI N N A {uv A: {u,v} N } H(N,A ) SOTTOGRAFO RICOPRENTE DI N =N A {uv A: {u,v} N } Sottografo H(N,A ) v v3 4 Sottografo ricoprente H(N,A ) H(N,A ) SOTTOGRAFO INDOTTO DI N N A = {uv A: {u,v} N } G[{,,, }] N DETERMINA H H=G[N ] Sottografo indotto 10
11 Strutture Speciali: Walk W WALK IN SEQUENZA ALTERNANTE DI NODI e ARCHI W=(V i1, (V i1,v i2 ), V i2, (V i2,v i3 ),, (V ip-1,v ip ), V ip ) v v3 4 V i1 V i2 V i3 V i4 V ip-1 V ip INSIEME DEI NODI DI W: V(W) = {V i1, V i2,.., V ip } INSIEME DEGLI ARCHI DI W: A(W) = {(V i1,v i2 ), (V i2,v i3 ),, (V ip-1,v ip )} V i1 e V ip si dicono NODI ESTREMI DEL WALK {V i2,.., V ip-1 } si dicono NODI INTERNI DEL WALK Archi e nodi possono essere ripetuti Se V i1 V ip (nodi estremi coincidenti) il WALK si dice CHIUSO altrimenti di dice APERTO 11
12 Strutture Speciali: Trail, Cammini e Cicli TRAIL WALK in senza archi ripetuti CAMMINO TRAIL in senza nodi interni ripetuti v v v CICLO CAMMINO CHIUSO (nodi estremi coincidenti) 12
13 Grafi Orientati: Cammini e Cicli Orientati CAMMINO ORIENTATO CAMMINO P=(V i1, (V i1,v i2 ), V i2, (V i2,v i3 ),, (V ip-1,v ip ), V ip ) con: V ik coda di ( V ik,v ik+1 ) per ogni k=1,,p-1 V i1 V i2 V i3 V i4 CICLO ORIENTATO CAMMINO ORIENTATO CHIUSO V i1 V i2 V i3 V i4 13
14 Connessione u CONNESSO A v Esiste un cammino con estremi u e v Connesso a : Relazione di Equivalenza R transitiva: urv vrt urt riflessiva: uru simmetrica: urv vru u Nodi e Coppie di nodi partizionabili in Classi di Equivalenza u u v v t ESEMPI connesso a connesso a connesso a RICORDO non connesso a Data una relazione di equivalenza R N N e detto R(u)={v N: vru } C N è una CLASSE DI EQUIVALENZA C R(u) u C N si partiziona in classi di equivalenza: N=C 1... C C t h C k R Relazione di Equivalenza (urv C h : u,v C h ) = k h 14
15 Componenti Connesse u CONNESSO A v Esiste un cammino con estremi u e v R Connesso a : Relazione di Equivalenza Nodi partizionabili in classi di equivalenza:{c 1,...,C t } C 1 NO C h N =C 1 C 2... C t C h C k = 1 < h < k < t = c(g) Coppie di nodi connesse se e solo se appartengono alla stessa classe di equivalenza. {u,v} C h u connesso a v u C h v C k k h u non connesso a v G[C h ] COMPONENTE CONNESSA DI Sottografo indotto da una classe di equivalenza c(g) = 1 Grafo CONNESSO c(g) > 1 Grafo NON-CONNESSO C 2 G[C 1 ] G[C 2 ] 15
16 Cammini orientati e Connessione urv Esiste un CAMMINO ORIENTATO da u a v R Non è una Relazione di Equivalenza transitiva: urv vrt urt riflessiva: uru non simmetrica: u u u v v t Cosa fare? Rendiamo simmetrica la relazione richiedendo la contemporanea esistenza di un cammino orientato da u a v e di uno da v ad u DEFINIAMO Nuova relazione di equivalenza R F : ur F v vru urv ur F v u FORTEMENTE CONNESSO a v u v 16
17 Connessione Forte ur F v u FORTEMENTE CONNESSO a v Esiste un CAMMINO ORIENTATO da u a v e un CAMMINO ORIENTATO da v a u R F è una Relazione di Equivalenza transitiva: ur F v vr F t ur F t riflessiva: u R F u simmetrica: u u v u v t Nodi partizionabili in classi di equivalenza di R F :{C 1,...,C t } G[C 1 ] G[C 2 ] G[C h ] COMPONENTE FORTEMENTE CONNESSA DI Sottografo indotto da una classe di equivalenza di R F 17
18 Grafi Aciclici e Alberi GRAFO ACICLICO (FORESTA) Grafo senza cicli v 8 v 7 GRAFO ACICLICO CONNESSO ALBERO GRAFO ACICLICO ORIENTATO (DAG) Grafo senza cicli orientati v 7 v 8 18
19 Insiemi Stabili e matching Insieme STABILE Insieme di nodi a coppie non adiacenti nodi indipendenti v 8 v 7 Matching Insieme di archi a coppie non adiacenti archi indipendenti v 8 v 7 19
20 Grafi Bipartiti Grafo Bipartito Insieme dei nodi partizionato in due insiemi stabili v 8 v 7 Grafo Bipartito Non contiene cicli con un numero dispari di nodi Provate a dimostrarlo 20
21 Autovalutazione Teoria dei Grafi 2.1 Vero o Falso? Rimuovendo un taglio da un grafo connesso si ottiene un grafo con due componenti connesse. Il motivo? 2.2 Quanti archi può possedere, al massimo, un grafo con 5 nodi. 2.3 COMPLETARE LA DEFINIZIONE SEGUENTE: Albero Ricoprente di : è un sottografo di Dimostrare che un DAG contiene un nodo con stella uscente vuota. 2.5 Dimostrare che aggiungendo un arco di A ad un albero ricoprente di, si genera un sottografo di contenente un ciclo. 2.6 Dimostrare che in un grafo la somma dei gradi dei nodi è pari al doppio del numero degli archi u N d ( u) = Dimostrare che una Componente Fortemente connessa G di un grafo orientato G contiene un Ciclo Orientato Ricoprente di G. A 21
Introduzione alla Teoria dei Grafi
 Sapienza Uniersità di Roma - Dipartimento di Ingegneria Informatica, Automatica e Gestionale Introduzione alla Teoria dei Grafi Docente: Renato Bruni bruni@dis.uniroma1.it Corso di: Ottimizzazione Combinatoria
Sapienza Uniersità di Roma - Dipartimento di Ingegneria Informatica, Automatica e Gestionale Introduzione alla Teoria dei Grafi Docente: Renato Bruni bruni@dis.uniroma1.it Corso di: Ottimizzazione Combinatoria
Introduzione ai grafi. Introduzione ai grafi p. 1/2
 Introduzione ai grafi Introduzione ai grafi p. 1/2 Grafi Un grafo G é costituito da una coppia di insiemi (V,A) dove V é detto insieme dei nodi e A é detto insieme di archi ed é un sottinsieme di tutte
Introduzione ai grafi Introduzione ai grafi p. 1/2 Grafi Un grafo G é costituito da una coppia di insiemi (V,A) dove V é detto insieme dei nodi e A é detto insieme di archi ed é un sottinsieme di tutte
Ricerca Operativa. Claudio Arbib Universitàdi L Aquila. Esercizi di ottimizzazione combinatoria
 Claudio Arbib Universitàdi L Aquila Ricerca Operativa Esercizi di ottimizzazione combinatoria 00-006 Grafi 9 Esercizio. Un grafo simmetrico G = (V, E) si dice cubico se tutti i suoi vertici hanno grado
Claudio Arbib Universitàdi L Aquila Ricerca Operativa Esercizi di ottimizzazione combinatoria 00-006 Grafi 9 Esercizio. Un grafo simmetrico G = (V, E) si dice cubico se tutti i suoi vertici hanno grado
Introduzione ai grafi. Introduzione ai grafi p. 1/2
 Introduzione ai grafi Introduzione ai grafi p. 1/2 Grafi Un grafo G è costituito da una coppia di insiemi (V,A) dove V è detto insieme dei nodi e A è detto insieme di archi ed è un sottinsieme di tutte
Introduzione ai grafi Introduzione ai grafi p. 1/2 Grafi Un grafo G è costituito da una coppia di insiemi (V,A) dove V è detto insieme dei nodi e A è detto insieme di archi ed è un sottinsieme di tutte
Appunti del corso di Informatica 1 (IN110 Fondamenti) 7 Grafi e alberi: introduzione
 Università di Roma Tre Dipartimento di Matematica e Fisica Corso di Laurea in Matematica Appunti del corso di Informatica (IN0 Fondamenti) Grafi e alberi: introduzione Marco Liverani (liverani@mat.uniroma.it)
Università di Roma Tre Dipartimento di Matematica e Fisica Corso di Laurea in Matematica Appunti del corso di Informatica (IN0 Fondamenti) Grafi e alberi: introduzione Marco Liverani (liverani@mat.uniroma.it)
Lezioni di Ricerca Operativa
 Lezioni di Ricerca Operativa Estratto per la parte di programmazione lineare e ottimizzazione sui grafi Corso di Metodi di Ottimizzazione per l'ingegneria della Sicurezza Laurea Magistrale in Ingegneria
Lezioni di Ricerca Operativa Estratto per la parte di programmazione lineare e ottimizzazione sui grafi Corso di Metodi di Ottimizzazione per l'ingegneria della Sicurezza Laurea Magistrale in Ingegneria
Grafi diretti. Un grafo diretto (o grafo orientato) G è una coppia (V,E) dove. V è u n i n s i e m e d i nodi (o vertici);
 Algoritmi e Strutture di Dati II 2 Grafi diretti Un grafo diretto (o grafo orientato) G è una coppia (V,E) dove V è u n i n s i e m e d i nodi (o vertici); E µ V V è u n i n s i e m e d i archi. Denotiamo
Algoritmi e Strutture di Dati II 2 Grafi diretti Un grafo diretto (o grafo orientato) G è una coppia (V,E) dove V è u n i n s i e m e d i nodi (o vertici); E µ V V è u n i n s i e m e d i archi. Denotiamo
Esempi. non. orientato. orientato
 Definizione! Un grafo G = (V,E) è costituito da un insieme di vertici V ed un insieme di archi E ciascuno dei quali connette due vertici in V detti estremi dell arco.! Un grafo è orientato quando vi è
Definizione! Un grafo G = (V,E) è costituito da un insieme di vertici V ed un insieme di archi E ciascuno dei quali connette due vertici in V detti estremi dell arco.! Un grafo è orientato quando vi è
B.1 I grafi: notazione e nomenclatura
 Appendice B Grafi e Reti In questa appendice richiamiamo i principali concetti relativi a grafi e reti; descriviamo inoltre alcune classi di strutture dati che possono essere utilizzate per implementare
Appendice B Grafi e Reti In questa appendice richiamiamo i principali concetti relativi a grafi e reti; descriviamo inoltre alcune classi di strutture dati che possono essere utilizzate per implementare
Richiami di Teoria dei Grafi. Paolo Detti Dipartimento di Ingegneria dell Informazione Università di Siena
 Richiami di Teoria dei Grafi Paolo Detti Dipartimento di Ingegneria dell Informazione Università di Siena Teoria dei grafi La Teoria dei Grafi costituisce, al pari della Programmazione Matematica, un corpo
Richiami di Teoria dei Grafi Paolo Detti Dipartimento di Ingegneria dell Informazione Università di Siena Teoria dei grafi La Teoria dei Grafi costituisce, al pari della Programmazione Matematica, un corpo
Teoria dei Grafi Concetti fondamentali
 Teoria dei Grafi Concetti fondamentali I grafi sono un mezzo per rappresentare relazioni binarie. Ad esempio: due città connesse da una strada due calcolatori connessi in una rete telematica due persone
Teoria dei Grafi Concetti fondamentali I grafi sono un mezzo per rappresentare relazioni binarie. Ad esempio: due città connesse da una strada due calcolatori connessi in una rete telematica due persone
2 OTTIMIZZAZIONE SU GRAFI. E. Amaldi Fondamenti di R.O. Politecnico di Milano 1
 2 OTTIMIZZAZIONE SU GRAFI E. Amaldi Fondamenti di R.O. Politecnico di Milano 1 Molti problemi decisionali possono essere formulati utilizzando il linguaggio della teoria dei grafi. Esempi: - problemi di
2 OTTIMIZZAZIONE SU GRAFI E. Amaldi Fondamenti di R.O. Politecnico di Milano 1 Molti problemi decisionali possono essere formulati utilizzando il linguaggio della teoria dei grafi. Esempi: - problemi di
Università Roma Tre - PAS Classe A048 "Matematica Applicata" - Corso di Informatica a.a. 2013/2014
 Università Roma Tre Dipartimento di Matematica e Fisica Percorso Abilitante Speciale Classe A08 Matematica Applicata Corso di Informatica Algoritmi su Grafi Marco Liverani (liverani@mat.uniroma.it) Sommario
Università Roma Tre Dipartimento di Matematica e Fisica Percorso Abilitante Speciale Classe A08 Matematica Applicata Corso di Informatica Algoritmi su Grafi Marco Liverani (liverani@mat.uniroma.it) Sommario
Richiami di matematica discreta: grafi e alberi. Paolo Camurati Dip. Automatica e Informatica Politecnico di Torino
 Richiami di matematica discreta: grafi e alberi Paolo Camurati Dip. Automatica e Informatica Politecnico di Torino Grafi Definizione: G = (V,E) V: insieme finito di vertici E: insieme finito di archi,
Richiami di matematica discreta: grafi e alberi Paolo Camurati Dip. Automatica e Informatica Politecnico di Torino Grafi Definizione: G = (V,E) V: insieme finito di vertici E: insieme finito di archi,
Teoria dei Grafi Elementi di base della Teoria dei Grafi
 L. Pallottino, Sistemi Robotici Distribuiti - Versione del 4 Marzo 2015 42 Teoria dei Grafi Elementi di base della Teoria dei Grafi Definizione 1. Un grafo G = (V, E) è composto da un insieme finito di
L. Pallottino, Sistemi Robotici Distribuiti - Versione del 4 Marzo 2015 42 Teoria dei Grafi Elementi di base della Teoria dei Grafi Definizione 1. Un grafo G = (V, E) è composto da un insieme finito di
GRAFI. Cosa sono Grafi non orientati Grafi orientati Grafi pesati Alberi Automi!
 G R A F I 1 GRAFI Cosa sono Grafi non orientati Grafi orientati Grafi pesati Alberi Automi! 2 cip: cip: Pallogrammi Pallogrammi GRAFI: cosa sono I grafi sono una struttura matematica fondamentale: servono
G R A F I 1 GRAFI Cosa sono Grafi non orientati Grafi orientati Grafi pesati Alberi Automi! 2 cip: cip: Pallogrammi Pallogrammi GRAFI: cosa sono I grafi sono una struttura matematica fondamentale: servono
INFORMATICA AA Università degli Studi di Ferrara Facoltà di Scienze MM FF NN Corso di Laurea in «Scienze e Tecnologie per i Beni Culturali»
 Università degli Studi di Ferrara Facoltà di Scienze MM FF NN Corso di Laurea in «Scienze e Tecnologie per i Beni Culturali» AA 2010-2011 INFORMATICA Prof. Giorgio Poletti giorgio.poletti@unife.it Grafi
Università degli Studi di Ferrara Facoltà di Scienze MM FF NN Corso di Laurea in «Scienze e Tecnologie per i Beni Culturali» AA 2010-2011 INFORMATICA Prof. Giorgio Poletti giorgio.poletti@unife.it Grafi
Grafi (non orientati e connessi): minimo albero ricoprente
 Grafi (non orientati e connessi): minimo albero ricoprente Una breve presentazione Definizioni Sia G=(V,E) un grafo non orientato e connesso. Un albero ricoprente di G è un sottografo T G tale che: T è
Grafi (non orientati e connessi): minimo albero ricoprente Una breve presentazione Definizioni Sia G=(V,E) un grafo non orientato e connesso. Un albero ricoprente di G è un sottografo T G tale che: T è
Nozioni base di teoria dei grafi
 Capitolo 2 Nozioni base di teoria dei grafi 2.1 Prime definizioni La teoria dei grafi stdia le proprietà metriche e topologiche delle relazioni binarie. L oggetto della teoria è il cosddetto grafo, oero
Capitolo 2 Nozioni base di teoria dei grafi 2.1 Prime definizioni La teoria dei grafi stdia le proprietà metriche e topologiche delle relazioni binarie. L oggetto della teoria è il cosddetto grafo, oero
min det det Allora è unimodulare se e solo se det 1, 1, 0 per ogni sottomatrice quadrata di di qualsiasi dimensione.
 Se è unimodulare e è intero allora il poliedro 0 ha vertici interi. Sia un vertice di Per definizione esiste allora una base di tale che, 0 Poiché è non singolare ( invertibile det 0) si ha che det 1 è
Se è unimodulare e è intero allora il poliedro 0 ha vertici interi. Sia un vertice di Per definizione esiste allora una base di tale che, 0 Poiché è non singolare ( invertibile det 0) si ha che det 1 è
Fondamenti di informatica
 Fondamenti di informatica 30 novembre 2017 This book is the result of a collaborative effort of a community of people like you, who believe that knowledge only grows if shared. We are waiting for you!
Fondamenti di informatica 30 novembre 2017 This book is the result of a collaborative effort of a community of people like you, who believe that knowledge only grows if shared. We are waiting for you!
UNIVERSITÀ DEGLI STUDI ROMA TRE Collegio Didattico in Ingegneria Informatica corso di Ricerca operativa 2. Esercizi sul problema dell assegnamento
 UNIVERSITÀ DEGLI STUDI ROMA TRE Collegio Didattico in Ingegneria Informatica corso di Ricerca operativa Esercizi sul problema dell assegnamento Richiami di Teoria Ricordiamo che, dato un grafo G=(N,A),
UNIVERSITÀ DEGLI STUDI ROMA TRE Collegio Didattico in Ingegneria Informatica corso di Ricerca operativa Esercizi sul problema dell assegnamento Richiami di Teoria Ricordiamo che, dato un grafo G=(N,A),
Algoritmi e strutture dati
 Algoritmi e Strutture Dati Minimo albero ricoprente Sia G = (V, E) un grafo connesso non orientato. Definizioni Un albero ricoprente di G è un sottografo T G tale che: T è un albero; T contiene tutti i
Algoritmi e Strutture Dati Minimo albero ricoprente Sia G = (V, E) un grafo connesso non orientato. Definizioni Un albero ricoprente di G è un sottografo T G tale che: T è un albero; T contiene tutti i
GRAFI. fig.1 - GRAFI (1) Si avvisa il lettore che certe definizioni che verranno date differiscono da quelle presenti in letteratura.
 GRAFI 1. Definizioni, terminologia, esempi e applicazioni (1) Un grafo orientato (o diretto o di-grafo) G è una coppia (V,E) dove V è un insieme non vuoto ed E una relazione binaria su V, E V V, ossia
GRAFI 1. Definizioni, terminologia, esempi e applicazioni (1) Un grafo orientato (o diretto o di-grafo) G è una coppia (V,E) dove V è un insieme non vuoto ed E una relazione binaria su V, E V V, ossia
Algoritmi e Strutture Dati
 Algoritmi e Strutture Dati Minimo albero ricoprente Fabio Patrizi 1 Albero ricoprente Sia G=(V,E) un grafo non orientato e connesso. Un albero ricoprente di G è un sottografo T G tale che: T è un albero;
Algoritmi e Strutture Dati Minimo albero ricoprente Fabio Patrizi 1 Albero ricoprente Sia G=(V,E) un grafo non orientato e connesso. Un albero ricoprente di G è un sottografo T G tale che: T è un albero;
La teoria dei grafi permette di esprimere in modo sistematico le LKT e LKC con i metodi della
 Grafi La teoria dei grafi permette di esprimere in modo sistematico le LKT e LKC con i metodi della topologia combinatoria. Definizione intuitiva di grafo: Un Grafo è un insieme di nodi (rappresentabili
Grafi La teoria dei grafi permette di esprimere in modo sistematico le LKT e LKC con i metodi della topologia combinatoria. Definizione intuitiva di grafo: Un Grafo è un insieme di nodi (rappresentabili
AMPL Problemi su Reti
 Dipartimento di Matematica Università di Padova Corso di Laurea Informatica Outline Problemi su Reti Cammino Minimo Molti problemi di ottimizzazione combinatoria possono essere modellati ricorrendo ai
Dipartimento di Matematica Università di Padova Corso di Laurea Informatica Outline Problemi su Reti Cammino Minimo Molti problemi di ottimizzazione combinatoria possono essere modellati ricorrendo ai
GE460 - Teoria dei grafi. Soluzioni esame del 28 Gennaio 2013
 GE460 - Teoria dei grafi Soluzioni esame del 28 Gennaio 2013 Problema 1. (1.a) Sia G un grafo connesso p-regolare e G G un suo sottografo. Vero o falso: Se G è p-regolare allora G = G. Soluzione Vero.
GE460 - Teoria dei grafi Soluzioni esame del 28 Gennaio 2013 Problema 1. (1.a) Sia G un grafo connesso p-regolare e G G un suo sottografo. Vero o falso: Se G è p-regolare allora G = G. Soluzione Vero.
Gestione della produzione e della supply chain Logistica distributiva. Paolo Detti Dipartimento di Ingegneria dell Informazione Università di Siena
 Gestione della produzione e della supply chain Logistica distributiva Paolo Detti Dipartimento di Ingegneria dell Informazione Università di Siena Un algoritmo per il flusso a costo minimo: il simplesso
Gestione della produzione e della supply chain Logistica distributiva Paolo Detti Dipartimento di Ingegneria dell Informazione Università di Siena Un algoritmo per il flusso a costo minimo: il simplesso
Alberi e arborescenze di costo minimo
 Alberi e arborescenze di costo minimo Complementi di Ricerca Operativa Giovanni Righini Dipartimento di Tecnologie dell Informazione - Università degli Studi di Milano Definizioni - 1 Un grafo G = (V,
Alberi e arborescenze di costo minimo Complementi di Ricerca Operativa Giovanni Righini Dipartimento di Tecnologie dell Informazione - Università degli Studi di Milano Definizioni - 1 Un grafo G = (V,
Ricerca Operativa. Facoltà di Ingegneria dell Informazione, Informatica e Statistica. (Cenni sui Grafi) Giovanni Fasano.
 Facoltà di Ingegneria dell Informazione, Informatica e Statistica Appunti dalle lezioni di Ricerca Operativa (Cenni sui Grafi) sede di Latina Giovanni Fasano fasano@unive.it http://venus.unive.it/ fasano
Facoltà di Ingegneria dell Informazione, Informatica e Statistica Appunti dalle lezioni di Ricerca Operativa (Cenni sui Grafi) sede di Latina Giovanni Fasano fasano@unive.it http://venus.unive.it/ fasano
Algoritmi e Strutture Dati
 Algoritmi e Strutture Dati Minimo albero ricoprente Domenico Fabio Savo 1 Albero ricoprente Sia G=(V,E) un grafo non orientato e connesso. Un albero ricoprente di G è un sottografo T G tale che: T è un
Algoritmi e Strutture Dati Minimo albero ricoprente Domenico Fabio Savo 1 Albero ricoprente Sia G=(V,E) un grafo non orientato e connesso. Un albero ricoprente di G è un sottografo T G tale che: T è un
Introduzione ai grafi
 TFA A048 Anno Accademico 2012-13 Outline Cenni storici sui grafi Nozioni introduttive: cammini, connessione, alberi, cicli Cammini di costo minimo Origini storiche La nascita della teoria dei grafi risale
TFA A048 Anno Accademico 2012-13 Outline Cenni storici sui grafi Nozioni introduttive: cammini, connessione, alberi, cicli Cammini di costo minimo Origini storiche La nascita della teoria dei grafi risale
Topologia dei circuiti
 Università degli Studi di Pavia Facoltà di Ingegneria Corso di Corso di Teoria dei Circuiti Teoria dei circuiti Topologia dei circuiti Studio della struttura di un circuito dal punto di vista delle connessioni
Università degli Studi di Pavia Facoltà di Ingegneria Corso di Corso di Teoria dei Circuiti Teoria dei circuiti Topologia dei circuiti Studio della struttura di un circuito dal punto di vista delle connessioni
Algoritmi & Laboratorio
 Acknowledgement Lucidi da F. Damiani, a.a. 2004-2005 C. Demetrescu et al, Algoritmi e strutture dati, McGraw-Hill M. Zacchi, a.a. 2003-2004 I lucidi non sono un sostituto per il libro di testo non contengono
Acknowledgement Lucidi da F. Damiani, a.a. 2004-2005 C. Demetrescu et al, Algoritmi e strutture dati, McGraw-Hill M. Zacchi, a.a. 2003-2004 I lucidi non sono un sostituto per il libro di testo non contengono
Proprietà e strutture dei grafi
 Capitolo 3 Proprietà e strutture dei grafi 3.1 Strutture dati per la rappresentazione di grafi La performance di un algoritmo su grafo dipende non solo dall algoritmo stesso, così come è stato descritto
Capitolo 3 Proprietà e strutture dei grafi 3.1 Strutture dati per la rappresentazione di grafi La performance di un algoritmo su grafo dipende non solo dall algoritmo stesso, così come è stato descritto
Algoritmi e Strutture Dati (Mod. B) Algoritmi su grafi Ricerca in profondità (Depth-First Search) Parte II
 Algoritmi e Strutture Dati (Mod. B) Algoritmi su grafi Ricerca in profondità (Depth-First Search) Parte II Classificazione digli archi Sia G la foresta DF generata da DFS sul grafo G. Arco d albero: gli
Algoritmi e Strutture Dati (Mod. B) Algoritmi su grafi Ricerca in profondità (Depth-First Search) Parte II Classificazione digli archi Sia G la foresta DF generata da DFS sul grafo G. Arco d albero: gli
Gestione della produzione e della supply chain Logistica distributiva
 Gestione della produzione e della supply chain Logistica distributiva Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena Convergenza dell algoritmo Se non
Gestione della produzione e della supply chain Logistica distributiva Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena Convergenza dell algoritmo Se non
Circuiti euleriani. F. Pugliese April 22, 2011
 Circuiti euleriani F. Pugliese April, 0 Abstract Diamo una dimostrazione costruttiva dell esistenza di circuiti euleriani nei grafi connessi con vertici tutti di grado pari. Innanzitutto, ricordiamo la
Circuiti euleriani F. Pugliese April, 0 Abstract Diamo una dimostrazione costruttiva dell esistenza di circuiti euleriani nei grafi connessi con vertici tutti di grado pari. Innanzitutto, ricordiamo la
Algoritmi & Laboratorio
 lbero ricoprente sia dato un grafo connesso e non orientato un albero ricoprente è un sottografo che contiene tutti nodi è aciclico è connesso cknowledgement Lucidi da. Damiani, a.a. 00-00. Demetrescu
lbero ricoprente sia dato un grafo connesso e non orientato un albero ricoprente è un sottografo che contiene tutti nodi è aciclico è connesso cknowledgement Lucidi da. Damiani, a.a. 00-00. Demetrescu
K 4 è planare? E K 3,3 e K 5 sono planari? Sì! No! (Teorema di Kuratowski) K 5. Camil Demetrescu, Irene Finocchi, Giuseppe F.
 K 4 è planare? Sì! E K 3,3 e K 5 sono planari? K 5 No! (Teorema di Kuratowski) 1 Un albero è un grafo bipartito? SÌ! Ma un grafo bipartito è sempre un albero?? 2 Algoritmi e Strutture Dati Capitolo 11
K 4 è planare? Sì! E K 3,3 e K 5 sono planari? K 5 No! (Teorema di Kuratowski) 1 Un albero è un grafo bipartito? SÌ! Ma un grafo bipartito è sempre un albero?? 2 Algoritmi e Strutture Dati Capitolo 11
Corso di elettrotecnica Materiale didattico: i grafi
 Corso di elettrotecnica Materiale didattico: i grafi A. Laudani 12 ottobre 2005 I grafi costituiscono uno strumento matematico che permette di descrivere e schematizzare una grande varietà di problemi
Corso di elettrotecnica Materiale didattico: i grafi A. Laudani 12 ottobre 2005 I grafi costituiscono uno strumento matematico che permette di descrivere e schematizzare una grande varietà di problemi
Laboratorio di Algoritmi
 Laboratorio di Algoritmi Corso di Laurea in Matematica Roberto Cordone DI - Università degli Studi di Milano Lezioni: Martedì 8.30-10.30 in aula 3 Mercoledì 10.30-12.30 in Aula 2 Giovedì 8.30-10.30 in
Laboratorio di Algoritmi Corso di Laurea in Matematica Roberto Cordone DI - Università degli Studi di Milano Lezioni: Martedì 8.30-10.30 in aula 3 Mercoledì 10.30-12.30 in Aula 2 Giovedì 8.30-10.30 in
Teoria dei Grafi Parte I. Alberto Caprara DEIS - Università di Bologna
 Teoria dei Grafi Parte I Alberto Caprara DEIS - Università di Bologna acaprara@deis.unibo.it Teoria dei Grafi Paradigma di rappresentazione di problemi Grafo G : coppia (V,E) V = insieme di vertici E =
Teoria dei Grafi Parte I Alberto Caprara DEIS - Università di Bologna acaprara@deis.unibo.it Teoria dei Grafi Paradigma di rappresentazione di problemi Grafo G : coppia (V,E) V = insieme di vertici E =
Ottimizzazione Combinatoria 2 Presentazione
 Ottimizzazione Combinatoria Presentazione ANTONIO SASSANO Università di Roma La Sapienza Dipartimento di Informatica, Automatica e Gestionale «Antonio Ruberti» Roma, Febbraio Prerequisiti (cosa sapete)
Ottimizzazione Combinatoria Presentazione ANTONIO SASSANO Università di Roma La Sapienza Dipartimento di Informatica, Automatica e Gestionale «Antonio Ruberti» Roma, Febbraio Prerequisiti (cosa sapete)
Matrici unimodulari e totalmente unimodulari
 Matrici unimodulari e totalmente unimodulari Sia una matrice intera di dimensione con, si dice unimodulare se presa una qualsiasi sottomatrice di ordine massimo (di dimensione ) vale det = 1, +1, 0. Una
Matrici unimodulari e totalmente unimodulari Sia una matrice intera di dimensione con, si dice unimodulare se presa una qualsiasi sottomatrice di ordine massimo (di dimensione ) vale det = 1, +1, 0. Una
Ottimizzazione Discreta Esercizi V: Soluzioni
 Ottimizzazione Discreta Esercizi V: Soluzioni Grafi e cammini minimi A.A. 214/215 Esercizio 1 (a) Nella terminologia della teoria dei grafi, si chiede di dimostrare che ogni grafo non orientato G = (V,E),
Ottimizzazione Discreta Esercizi V: Soluzioni Grafi e cammini minimi A.A. 214/215 Esercizio 1 (a) Nella terminologia della teoria dei grafi, si chiede di dimostrare che ogni grafo non orientato G = (V,E),
Matematica D (in teledidattica) Docenti: Alberto Tonolo, e nelle sedi locali Susi Osti, Katia Rossi, Stefano Antoniazzi.
 Matematica D (in teledidattica) Docenti: Alberto Tonolo, e nelle sedi locali Susi Osti, Katia Rossi, Stefano Antoniazzi. Testi di riferimento: Ross: A First Course in Probability, Prentice Hall, euro 49,95
Matematica D (in teledidattica) Docenti: Alberto Tonolo, e nelle sedi locali Susi Osti, Katia Rossi, Stefano Antoniazzi. Testi di riferimento: Ross: A First Course in Probability, Prentice Hall, euro 49,95
Laboratorio di Algoritmi
 Laboratorio di Algoritmi Corso di Laurea in Matematica Roberto Cordone DI - Università degli Studi di Milano Lezioni: Martedì 8.30-10.30 in aula 3 Mercoledì 10.30-12.30 in Aula 2 Giovedì 8.30-10.30 in
Laboratorio di Algoritmi Corso di Laurea in Matematica Roberto Cordone DI - Università degli Studi di Milano Lezioni: Martedì 8.30-10.30 in aula 3 Mercoledì 10.30-12.30 in Aula 2 Giovedì 8.30-10.30 in
ALCUNE NOTE SUI GRAFI Tiziana Calamoneri
 ALCUNE NOTE SUI GRAFI Tiziana Calamoneri Un grafo G=(V,E) è costituito da una coppia di insiemi, l insieme finito V di nodi, o vertici, e l insieme finito E di coppie non ordinate di nodi, dette archi,
ALCUNE NOTE SUI GRAFI Tiziana Calamoneri Un grafo G=(V,E) è costituito da una coppia di insiemi, l insieme finito V di nodi, o vertici, e l insieme finito E di coppie non ordinate di nodi, dette archi,
Algoritmi e Strutture Dati Grafi. Daniele Loiacono
 lgoritmi e Strutture ati Grafi Riferimenti 2 Questo materiale è tratto dalle trasparenze del corso lgoritmi e Strutture ati del prof. lberto Montresor dell Università di Trento. (http://www.dit.unitn.it/~montreso/asd/index.shtml)
lgoritmi e Strutture ati Grafi Riferimenti 2 Questo materiale è tratto dalle trasparenze del corso lgoritmi e Strutture ati del prof. lberto Montresor dell Università di Trento. (http://www.dit.unitn.it/~montreso/asd/index.shtml)
ALBERI ORIENTATI. Definizione: Albero orientato = rooted tree = grafo orientato con le seguenti proprietà: - ha un nodo fissato, detto radice (r);
 ALBERI ORIENTATI Pagina 1 ALBERI ORIENTATI 15:05 Definizione: Albero orientato = rooted tree = grafo orientato con le seguenti proprietà: - ha un nodo fissato, detto radice (r); - per ogni nodo v, esiste
ALBERI ORIENTATI Pagina 1 ALBERI ORIENTATI 15:05 Definizione: Albero orientato = rooted tree = grafo orientato con le seguenti proprietà: - ha un nodo fissato, detto radice (r); - per ogni nodo v, esiste
Teoria dei Grafi Parte I
 Teoria dei Grafi Parte I Daniele Vigo D.E.I.S. - Università di Bologna dvigo@deis.unibo.it Teoria dei Grafi Paradigma di rappresentazione di problemi Grafo G : coppia (V,E) V = insieme di vertici E = insieme
Teoria dei Grafi Parte I Daniele Vigo D.E.I.S. - Università di Bologna dvigo@deis.unibo.it Teoria dei Grafi Paradigma di rappresentazione di problemi Grafo G : coppia (V,E) V = insieme di vertici E = insieme
Soluzioni della settima esercitazione di Algoritmi 1
 Soluzioni della settima esercitazione di Algoritmi 1 Beniamino Accattoli 19 dicembre 2007 1 Grafi Un grafo è non orientato se descrivendo un arco come una coppia di vertici (i,j) l ordine è ininfluente
Soluzioni della settima esercitazione di Algoritmi 1 Beniamino Accattoli 19 dicembre 2007 1 Grafi Un grafo è non orientato se descrivendo un arco come una coppia di vertici (i,j) l ordine è ininfluente
Introduzione ai Grafi: Implementazione e operazioni di base
 Laboratorio di Algoritmi e Strutture Dati Aniello Murano http://people.na.infn.it people.na.infn.it/~murano/ 1 Introduzione ai Grafi: Implementazione e operazioni di base 2 1 Informazione Generali (1)
Laboratorio di Algoritmi e Strutture Dati Aniello Murano http://people.na.infn.it people.na.infn.it/~murano/ 1 Introduzione ai Grafi: Implementazione e operazioni di base 2 1 Informazione Generali (1)
Grafi: definizioni e visite
 Grafi: definizioni e visite Grafi (non orientati) Grafo (non orientato): G = (V, E) V = nodi (o vertici) E = archi fra coppie di nodi distinti. Modella relazioni fra coppie di oggetti. Parametri della
Grafi: definizioni e visite Grafi (non orientati) Grafo (non orientato): G = (V, E) V = nodi (o vertici) E = archi fra coppie di nodi distinti. Modella relazioni fra coppie di oggetti. Parametri della
Gestione della produzione e della supply chain Logistica distributiva
 Gestione della produzione e della supply chain Logistica distributiva Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena Struttura delle reti logistiche
Gestione della produzione e della supply chain Logistica distributiva Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena Struttura delle reti logistiche
Dai ponti di Königsberg al postino cinese
 Dai ponti di Königsberg al postino cinese Mauro Passacantando Dipartimento di Informatica Largo B. Pontecorvo, Pisa mpassacantando@di.unipi.it M. Passacantando TFA 2012/1 - Corso di Ricerca Operativa Università
Dai ponti di Königsberg al postino cinese Mauro Passacantando Dipartimento di Informatica Largo B. Pontecorvo, Pisa mpassacantando@di.unipi.it M. Passacantando TFA 2012/1 - Corso di Ricerca Operativa Università
Ottimizzazione su grafi: massimo flusso (parte 1) Ottimizzazione su grafi:massimo flusso (parte 1) p. 1/33
 Ottimizzazione su grafi: massimo flusso (parte 1) Ottimizzazione su grafi:massimo flusso (parte 1) p. 1/33 Ottimizzazione su grafi:massimo flusso (parte 1) p. 2/33 Reti di flusso Una rete di flusso è una
Ottimizzazione su grafi: massimo flusso (parte 1) Ottimizzazione su grafi:massimo flusso (parte 1) p. 1/33 Ottimizzazione su grafi:massimo flusso (parte 1) p. 2/33 Reti di flusso Una rete di flusso è una
2.2 Alberi di supporto di costo ottimo
 . Alberi di supporto di costo ottimo Problemi relativi ad alberi hanno numerose applicazioni: progettazione di reti (comunicazione, teleriscaldamento,...) protocolli reti IP memorizzazione compatta di
. Alberi di supporto di costo ottimo Problemi relativi ad alberi hanno numerose applicazioni: progettazione di reti (comunicazione, teleriscaldamento,...) protocolli reti IP memorizzazione compatta di
Minimo albero di copertura
 apitolo 0 Minimo albero di copertura efinizione 0.. ato un grafo G = (V, E) non orientato e connesso, un albero di copertura di G è un sottoinsieme T E tale che il sottografo (V, T ) è un albero libero.
apitolo 0 Minimo albero di copertura efinizione 0.. ato un grafo G = (V, E) non orientato e connesso, un albero di copertura di G è un sottoinsieme T E tale che il sottografo (V, T ) è un albero libero.
Algoritmi e Strutture Dati
 Introduzione ai grafi Grafi: Definizione e Algoritmi di visita Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 2007/08 Introduzione ai
Introduzione ai grafi Grafi: Definizione e Algoritmi di visita Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino A.A. 2007/08 Introduzione ai
Algoritmi Euristici. Corso di Laurea in Informatica e Corso di Laurea in Matematica. Roberto Cordone DI - Università degli Studi di Milano
 Algoritmi Euristici Corso di Laurea in Informatica e Corso di Laurea in Matematica Roberto Cordone DI - Università degli Studi di Milano Lezioni: Martedì 14.30-16.30 in Aula Omega Venerdì 14.30-16.30 in
Algoritmi Euristici Corso di Laurea in Informatica e Corso di Laurea in Matematica Roberto Cordone DI - Università degli Studi di Milano Lezioni: Martedì 14.30-16.30 in Aula Omega Venerdì 14.30-16.30 in
Le applicazioni degli algoritmi di visita dei grafi. Gianpiero Cabodi e Paolo Camurati Dip. Automatica e Informatica Politecnico di Torino
 Le applicazioni degli algoritmi di visita dei grafi Gianpiero Cabodi e Paolo Camurati Dip. Automatica e Informatica Politecnico di Torino di visita dei grafi 2 Rilevazione di cicli Un grafo è aciclico
Le applicazioni degli algoritmi di visita dei grafi Gianpiero Cabodi e Paolo Camurati Dip. Automatica e Informatica Politecnico di Torino di visita dei grafi 2 Rilevazione di cicli Un grafo è aciclico
«Sciente e Tecnologie dei Beni Culturali»
 5 Informatica CdS in «Sciente e Tecnologie dei Beni Culturali» AA 2014-2015 Mini-sito dell insegnamento: http://www.unife.it/scienze/beni.culturali/insegnamenti/informatica Prof. Giorgio Poletti giorgio.poletti@unife.it
5 Informatica CdS in «Sciente e Tecnologie dei Beni Culturali» AA 2014-2015 Mini-sito dell insegnamento: http://www.unife.it/scienze/beni.culturali/insegnamenti/informatica Prof. Giorgio Poletti giorgio.poletti@unife.it
Grafi pesati Minimo albero ricoprente
 Algoritmi e Strutture Dati Definizioni Grafi pesati Minimo albero ricoprente Sia G=(V,E) un grafo non orientato e connesso. Un albero ricoprente di G è un sottografo T G tale che: T è un albero; T contiene
Algoritmi e Strutture Dati Definizioni Grafi pesati Minimo albero ricoprente Sia G=(V,E) un grafo non orientato e connesso. Un albero ricoprente di G è un sottografo T G tale che: T è un albero; T contiene
Laboratorio di Algoritmi e Strutture Dati
 Laboratorio di Algoritmi e Strutture Dati Prof. Aniello Murano Grafi: Implementazione ed operazioni di base Corso di Laurea Codice insegnamento Email docente Anno accademico Laboratorio di Algoritmi e
Laboratorio di Algoritmi e Strutture Dati Prof. Aniello Murano Grafi: Implementazione ed operazioni di base Corso di Laurea Codice insegnamento Email docente Anno accademico Laboratorio di Algoritmi e
Algoritmi e Strutture Dati. Capitolo 12 Minimo albero ricoprente: Algoritmo di Kruskal
 Algoritmi e Strutture Dati Capitolo 12 Minimo albero ricoprente: Algoritmo di Kruskal Progettare una rete stradale Supponiamo di dover progettare una rete stradale in cui il costo di costruzione di un
Algoritmi e Strutture Dati Capitolo 12 Minimo albero ricoprente: Algoritmo di Kruskal Progettare una rete stradale Supponiamo di dover progettare una rete stradale in cui il costo di costruzione di un
Euristiche per il Problema del Commesso Viaggiatore
 Sapienza Università di Roma - Dipartimento di Ingegneria Informatica, Automatica e Gestionale Euristiche per il Problema del Commesso Viaggiatore Renato Bruni bruni@dis.uniroma.it Il materiale presentato
Sapienza Università di Roma - Dipartimento di Ingegneria Informatica, Automatica e Gestionale Euristiche per il Problema del Commesso Viaggiatore Renato Bruni bruni@dis.uniroma.it Il materiale presentato
2.3.3 Cammini ottimi nei grafi senza circuiti
 .. Cammini ottimi nei grafi senza circuiti Sia un grafo G = (N, A) orientato senza circuiti e una funzione di costo che assegna un valore c ij R ad ogni arco (i, j) A circuito Proprietà I nodi di un grafo
.. Cammini ottimi nei grafi senza circuiti Sia un grafo G = (N, A) orientato senza circuiti e una funzione di costo che assegna un valore c ij R ad ogni arco (i, j) A circuito Proprietà I nodi di un grafo
Progettazione di Algoritmi - lezione 1
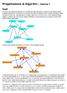 Progettazione di Algoritmi - lezione 1 Grafi Un grafo è una collezione di elementi con una relazione binaria tra di essi. Le situazioni che possono essere modellate dai grafi sono innumerevoli e provengono
Progettazione di Algoritmi - lezione 1 Grafi Un grafo è una collezione di elementi con una relazione binaria tra di essi. Le situazioni che possono essere modellate dai grafi sono innumerevoli e provengono
Algoritmi e Strutture Dati
 Algoritmi e Strutture Dati Capitolo 12 Grafi e visite di grafi Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Definizione Un grafo G=(V,E) consiste in: - un insieme V di vertici (o nodi) - un insieme
Algoritmi e Strutture Dati Capitolo 12 Grafi e visite di grafi Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Definizione Un grafo G=(V,E) consiste in: - un insieme V di vertici (o nodi) - un insieme
Appunti lezione Capitolo 13 Programmazione dinamica
 Appunti lezione Capitolo 13 Programmazione dinamica Alberto Montresor 12 Novembre, 2015 1 Domanda: Fattore di crescita dei numeri catalani Vogliamo dimostrare che cresce almeno come 2 n. La nostra ipotesi
Appunti lezione Capitolo 13 Programmazione dinamica Alberto Montresor 12 Novembre, 2015 1 Domanda: Fattore di crescita dei numeri catalani Vogliamo dimostrare che cresce almeno come 2 n. La nostra ipotesi
Metodi e Modelli per l Ottimizzazione Combinatoria Problema dell assegnamento e matrici totalmente unimodulari
 Metodi e Modelli per l Ottimizzazione Combinatoria Problema dell assegnamento e matrici totalmente unimodulari L. De Giovanni G. Zambelli 1 Problema dell assegnamento Sia dato un grafo non orientato bipartito
Metodi e Modelli per l Ottimizzazione Combinatoria Problema dell assegnamento e matrici totalmente unimodulari L. De Giovanni G. Zambelli 1 Problema dell assegnamento Sia dato un grafo non orientato bipartito
Reti Complesse Biologiche
 Reti Complesse Biologiche Corso di Modelli di Sistemi Biologici II Università di Roma Sapienza Anno Accademico 2008/2009 Fabrizio De Vico Fallani, PhD Dipartimento di Fisiologia Umana e Farmacologia fabrizio.devicofallani@uniroma1.it
Reti Complesse Biologiche Corso di Modelli di Sistemi Biologici II Università di Roma Sapienza Anno Accademico 2008/2009 Fabrizio De Vico Fallani, PhD Dipartimento di Fisiologia Umana e Farmacologia fabrizio.devicofallani@uniroma1.it
uscente entrante adiacente Figure B.2 (a) (b) (c) incident from leaves incident to enters incident on adjacent degree isolated
 Grafi Si dice grafo un insieme di nodi legati "a due a due" da archi direzionati (o no) I grafi sono strutture dati di fondamentale importanza in informatica Vi sono centinaia di problemi computazionali
Grafi Si dice grafo un insieme di nodi legati "a due a due" da archi direzionati (o no) I grafi sono strutture dati di fondamentale importanza in informatica Vi sono centinaia di problemi computazionali
Grafi (non orientati e connessi): minimo albero ricoprente
 .. Grafi (non orientati e connessi): minimo albero ricoprente Una presentazione alternativa (con ulteriori dettagli) Problema: calcolo del minimo albero di copertura (M.S.T.) Dato un grafo pesato non orientato
.. Grafi (non orientati e connessi): minimo albero ricoprente Una presentazione alternativa (con ulteriori dettagli) Problema: calcolo del minimo albero di copertura (M.S.T.) Dato un grafo pesato non orientato
2.2 Alberi di supporto di costo ottimo
 . Alberi di supporto di costo ottimo Problemi relativi ad alberi hanno numerose applicazioni: progettazione di reti (comunicazione, teleriscaldamento,...) memorizzazione compatta di sequenze (DNA) diffusione
. Alberi di supporto di costo ottimo Problemi relativi ad alberi hanno numerose applicazioni: progettazione di reti (comunicazione, teleriscaldamento,...) memorizzazione compatta di sequenze (DNA) diffusione
Progettazione di Algoritmi
 Corso di laurea in Informatica Prova scritta del: Progettazione di Algoritmi 0/06/06 Prof. De Prisco Inserire i propri dati nell apposito spazio. Non voltare la finché non sarà dato il via. Dal via avrai
Corso di laurea in Informatica Prova scritta del: Progettazione di Algoritmi 0/06/06 Prof. De Prisco Inserire i propri dati nell apposito spazio. Non voltare la finché non sarà dato il via. Dal via avrai
Ottimizzazione nella Gestione dei Progetti - Esercitazione 1: calcolo degli schedule ottimi
 Università degli Studi di Roma La Sapienza Ottimizzazione nella Gestione dei Progetti - Esercitazione : calcolo degli schedule ottimi di FABIO D ANDREAGIOVANNI Dipartimento di Informatica e Sistemistica
Università degli Studi di Roma La Sapienza Ottimizzazione nella Gestione dei Progetti - Esercitazione : calcolo degli schedule ottimi di FABIO D ANDREAGIOVANNI Dipartimento di Informatica e Sistemistica
Algoritmi e Strutture Dati. Capitolo 11 Grafi e visite di grafi
 Algoritmi e Strutture Dati Capitolo 11 Grafi e visite di grafi grafi, teoria dei grafi, problemi su grafi Origini storiche Nel 1736, il matematico Eulero, affrontò l annoso problema dei 7 ponti di Königsberg
Algoritmi e Strutture Dati Capitolo 11 Grafi e visite di grafi grafi, teoria dei grafi, problemi su grafi Origini storiche Nel 1736, il matematico Eulero, affrontò l annoso problema dei 7 ponti di Königsberg
PROBLEMI SU GRAFO (combinatori)
 PROLMI SU GRO (combinatori) In molti problemi il numero di soluzioni ammissibili è finito. Questi problemi sono quasi sempre descritti su grafi. Rete stradale: come andare da a in tempo minimo? Grafo orientato
PROLMI SU GRO (combinatori) In molti problemi il numero di soluzioni ammissibili è finito. Questi problemi sono quasi sempre descritti su grafi. Rete stradale: come andare da a in tempo minimo? Grafo orientato
Flusso a Costo Minimo
 Sapienza Università di Roma - Dipartimento di Ingegneria Informatica, Automatica e Gestionale Flusso a Costo Minimo Docente: Renato Bruni bruni@dis.uniroma.it Corso di: Ottimizzazione Combinatoria Dal
Sapienza Università di Roma - Dipartimento di Ingegneria Informatica, Automatica e Gestionale Flusso a Costo Minimo Docente: Renato Bruni bruni@dis.uniroma.it Corso di: Ottimizzazione Combinatoria Dal
Ottimizzazione Combinatoria
 Ottimizzazione Combinatoria Esercitazione AMPL A.A. 2-22 Esercitazione a cura di Silvia Canale contatto e-mail: canale@dis.uniroma.it Università i di Roma La Sapienza Dipartimento di Informatica e Sistemistica
Ottimizzazione Combinatoria Esercitazione AMPL A.A. 2-22 Esercitazione a cura di Silvia Canale contatto e-mail: canale@dis.uniroma.it Università i di Roma La Sapienza Dipartimento di Informatica e Sistemistica
Grafi (orientati): cammini minimi
 Grafi (orientati): cammini minimi Una breve presentazione Definizioni Sia G=(V,E) un grafo orientato con costi w sugli archi. Il costo di un cammino π= è dato da: Un cammino minimo tra
Grafi (orientati): cammini minimi Una breve presentazione Definizioni Sia G=(V,E) un grafo orientato con costi w sugli archi. Il costo di un cammino π= è dato da: Un cammino minimo tra
Dati e Algoritmi 1: A. Pietracaprina. Grafi (II parte)
 Dati e Algoritmi 1: A. Pietracaprina Grafi (II parte) 1 Breath-First Search (algoritmo iterativo) Si assume una rappresentazione tramite liste di adiacenza. L ordine con cui si visitano i vicini di un
Dati e Algoritmi 1: A. Pietracaprina Grafi (II parte) 1 Breath-First Search (algoritmo iterativo) Si assume una rappresentazione tramite liste di adiacenza. L ordine con cui si visitano i vicini di un
2.2 Alberi di supporto di costo ottimo
 . Alberi di supporto di costo ottimo Problemi relativi ad alberi hanno numerose applicazioni: progettazione di reti (comunicazione, teleriscaldamento,...) memorizzazione compatta di sequenze (DNA) diffusione
. Alberi di supporto di costo ottimo Problemi relativi ad alberi hanno numerose applicazioni: progettazione di reti (comunicazione, teleriscaldamento,...) memorizzazione compatta di sequenze (DNA) diffusione
2.2 Alberi di supporto di costo ottimo
 . Alberi di supporto di costo ottimo Problemi relativi ad alberi hanno numerose applicazioni: progettazione di reti (comunicazione, teleriscaldamento,...) diffusione di messaggi segreti memorizzazione
. Alberi di supporto di costo ottimo Problemi relativi ad alberi hanno numerose applicazioni: progettazione di reti (comunicazione, teleriscaldamento,...) diffusione di messaggi segreti memorizzazione
Grafi non orientati. Grafi (non orientati) Rappresentazione di Grafi: matrice delle adiacenze. Tipiche applicazioni di modelli basati su grafi
 Grafi non orientati Grafi (non orientati) Notazione. G = (V, E) V = nodi (o vertici). E = archi (o lati) tra coppie di nodi. Modella relazioni definite tra coppie di oggetti. aglia di un grafo: numero
Grafi non orientati Grafi (non orientati) Notazione. G = (V, E) V = nodi (o vertici). E = archi (o lati) tra coppie di nodi. Modella relazioni definite tra coppie di oggetti. aglia di un grafo: numero
ESERCIZIO 1: Punto 1
 ESERCIZIO : Punto La seguente matrice è una matrice delle distanze di un istanza del problema del Commesso Viaggiatore. - - - - - - - Calcolare.Il valore del rilassamento che si ottiene determinando l
ESERCIZIO : Punto La seguente matrice è una matrice delle distanze di un istanza del problema del Commesso Viaggiatore. - - - - - - - Calcolare.Il valore del rilassamento che si ottiene determinando l
Grafi e reti di flusso
 Grafi e reti di flusso Molti problemi di ottimizzazione sono caratterizzati da una struttura di grafo: in molti casi questa struttura emerge in modo naturale, in altri nasce dal particolare modo in cui
Grafi e reti di flusso Molti problemi di ottimizzazione sono caratterizzati da una struttura di grafo: in molti casi questa struttura emerge in modo naturale, in altri nasce dal particolare modo in cui
Cammini minimi in grafi:
 Algoritmi e strutture dati Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Cammini minimi in grafi: una trilogia Cammini minimi in grafi: Episodio III: la fine della trilogia Input: nelle puntate
Algoritmi e strutture dati Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Cammini minimi in grafi: una trilogia Cammini minimi in grafi: Episodio III: la fine della trilogia Input: nelle puntate
Algoritmi e strutture dati
 Algoritmi e Strutture Dati Cammini minimi Definizioni Sia G = (V,E) un grafo orientato pesato sugli archi. Il costo di un cammino π = è dato da: Un cammino minimo tra una coppia di
Algoritmi e Strutture Dati Cammini minimi Definizioni Sia G = (V,E) un grafo orientato pesato sugli archi. Il costo di un cammino π = è dato da: Un cammino minimo tra una coppia di
Grafi Stessa distanza
 Grafi Stessa distanza In un grafo orientato G, dati due nodi s e v, si dice che: v è raggiungibile da s se esiste un cammino da s a v; la distanza di v da s è la lunghezza del più breve cammino da s a
Grafi Stessa distanza In un grafo orientato G, dati due nodi s e v, si dice che: v è raggiungibile da s se esiste un cammino da s a v; la distanza di v da s è la lunghezza del più breve cammino da s a
