Cov (X, Y ) = E [XY ] µ X µ Y
|
|
|
- Annunziata De Angelis
- 4 anni fa
- Visualizzazioni
Transcript
1 1 Lezione Covarianza e coeffi ciente di correlazione Definition 1 Date due v.a. X, Y, si chiama covarianza tra X ed Y il numero Cov (X, Y ) = E [(X µ X ) (Y µ Y )] dove µ X e µ Y sono le medie di X ed Y. La definizione ha senso se µ X e µ Y sono finiti ed il valor medio complessivo è finito, cosa che accade ad esempio se si suppone che sia E [ X 2] < e E [ Y 2] <. La definizione è quindi analoga, algebricamente, a quella di varianza, e risulta infatti V ar [X] = Cov (X, X) e Cov (X, Y ) = E [XY ] µ X µ Y come per la varianza. Però il numero Cov (X, Y ) può avere segno qualsiasi. Ad esempio, se µ X = 0 e prendiamo Y = X, vale Cov (X, Y ) = E [ X 2]. Anche la covarianza soffre dei problemi di scala noti per la varianza. Qui, non potendo prendere la radice quadrata (Cov (X, Y ) non è sempre positiva), si normalizza in quest altro modo, dividendo per le deviazioni standard. Definition 2 Chiamiamo coeffi ciente di correlazione tra X ed Y il numero definito da ρ (X, Y ) = Scriveremo anche ρ XY al posto di ρ (X, Y ). Cov (X, Y ) σ X σ Y. Si noti che, per la disuguaglianza di Hölder, [ Cov (X, Y ) E (X µ X ) 2] E [(Y µ Y ) 2] e quindi ρ (X, Y ) 1. Questo dimostra la prima delle seguenti proprietà, che tutte insieme chiariscono l aspetto di universalità, o invarianza per cambio di unità di misura (invarianza di scala), di ρ, a differenza della covarianza. Proposition 3 Vale Vale inoltre per ogni a, b R, e per ogni a, b > 0. 1 ρ (X, Y ) 1. Cov (ax, by ) = abcov (X, Y ) ρ (ax, by ) = ρ (X, Y ) 1
2 Proof. Abbiamo già visto come mai 1 ρ (X, Y ) 1. Dimostriamo la seconda proprietà. Vale Vale poi Cov (ax, by ) = E [(ax µ ax ) (by µ by )] = E [(ax aµ X ) (by bµ Y )] ρ (ax, by ) = = abe [(X µ X ) (Y µ Y )] = abcov (X, Y ). Cov (ax, by ) V ar [ax] V ar [by ] = abcov (X, Y ) a 2 b 2 V ar [X] V ar [Y ] = ab ab ρ (X, Y ) e quindi la formula desiderata, se a, b > 0. Nello stesso modo si dimostra la seguente proprietà, che in un certo senso è la linearità della convarianza nei suoi argomenti. Si noti che le costanti additive spariscono, come per la varianza. Proposition 4 Cov (ax + by + c, Z) = acov (X, Z) + bcov (Y, Z) Cov (X, αy + βz + γ) = αcov (X, Y ) + βcov (X, Z). Proof. Basta dimostrare la prima in quanto la covarianza è simmetrica. Vale Cov (ax + by + c, Z) = E [( ax + by + c µ ax+by +c ) (Z µz ) ] = E [(a (X µ X ) + b (Y µ Y )) (Z µ Z )] = acov (X, Z) + bcov (Y, Z). Ricordiamo che se X ed Y sono v.a. indipendenti, allora E [XY ] = µ X µ Y viceversa non è vero in generale). Ne discende subito il seguente risultato. (mentre il Theorem 5 Se X ed Y sono v.a. indipendenti, allora Cov (X, Y ) = 0, ρ (X, Y ) = 0. Viceversa, se Cov (X, Y ) = 0, non è detto che X ed Y siano indipendenti. Se però (X, Y ) è gaussiano (definizione che daremo nel seguito) e Cov (X, Y ) = 0, allora X e Y sono indipendenti. Anche questo fatto contribuisce alla tendenza pratica a ritenere che la condizione Cov (X, Y ) = 0 sia un notevole sintomo di indipendenza. Definition 6 Diciamo che X e Y sono scorrelate se hanno correlazione nulla, ρ (X, Y ) = 0, o equivalentemente se Cov (X, Y ) = 0. 2
3 Quindi l indipendenza implica la scorrelazione. A livello numerico su dati sperimentali, se la correlazione è molto vicino a zero, questo è un buon indicatore di indipendenza, o più precisamente di scorrelazione (invece, dipendendo il numero Cov (X, Y ) dalla scala scelta, la sua vicinanza a zero è meno assoluta, quindi può trarre in inganno). Precisiamo cosa intendiamo con correlazione di dati sperimentali. Stiamo pensando di avere n coppie di valori sperimentali (x 1, y 1 ),..., (x n, y n ), o più espressivamente una tabella X Y 1 x 1 y n x n y n in cui le colonne corrispondono alle variabili e le righe agli individui (unità sperimentali, unità osservate). Di questi dati sperimentali possiamo calcolare la varianza empirica ed il coeffi ciente di correlazione empirico definiti da Ĉov = 1 n (x i x) (y i y), ρ = n (x i x) (y i y) n (x i x) 2. n (y i y) 2 Questi indicatori sono buone stime di quelli teorici, ad esempio per via della legge dei grandi numeri. Fatte queste premesse, la vicinanza a zero di ρ si interpreta come sintomo di indipendenza o comunque bassa dipendenza, la vicinanza ad 1 come elevato legame positivo, a 1 come elevato legame negativo. Esaminiamo questi fatti per mezzo del software R. Innanzi tutto generiamo due campioni di cardinalità 100, con distribuzione gaussiana standard, mostriamo le coppie (x i, y i ) nel piano cartesiano e calcoliamo la correlazione empirica: X=rnorm(100); Y=rnorm(100) cor(x,y) [1] plot(x,y) Questa è una situazione a correlazione sostanzialmente nulla. Costruiamo invece un campione Z simile a X ma un po perturbato in modo aleatorio: Z=X+0.1*rnorm(100) 3
4 cor(x,z) [1] plot(x,z) Questa è una situazione ad elevatissima correlazione positiva. Proviamo poi W=-X+0.5*rnorm(100) cor(x,w) [1] plot(x,w) Quest ultima è una situazione a moderata/elevata correlazione negativa. Si noti che il coeffi ciente di correlazione non è esattamente uguale al coeffi ciente angolare, come si potrebbe pensare dai nomi. Si veda sotto il legame. Il segno di Ĉov corrisponde all inclinazione positiva o negativa della nuvola di punti, come abbiamo visto negli esempi numerici. Gli esempi però sono solo alcuni dei possibili esempi, quindi può essere utile un ragionamento di carattere generale. La formula Ĉov = 1 n n (x i x) (y i y) permette di effettuarlo, anche se in modo un po vago. Il punto (x, y) sta, diciamo, al centro della nuvola, comunque essa sia orientata. Analizziamo il caso in cui sia Ĉov > 0. Questo significa che nella somma n predominano addendi positivi. Per semplicità di ragionamento, supponiamo che siano tutti positivi. Se (x i x) (y i y) > 0, significa che i fattori (x i x) e (y i y) hanno lo stesso segno. Se sono positivi, significa che il punto (x i, y i ) sta a nord-est di (x, y); se sono negativi, significa che sta a sud-ovest. In ogni caso, i punti (x i, y i ) si trovano, rispetto a (x, y), come nel secondo disegno visto sopra. Per semplicità abbiamo ipotizzato che tutti i termini (x i x) (y i y) fossero positivi: in genere non è così, ce ne saranno anche di negativi, ma predominano quelli positivi, quindi predomina la struttura grafica del tipo detto sopra, anche se alcuni punti si troveranno a nord-ovest o sud-est di (x, y). Il ragionamento nel caso Ĉov < 0 è identico. 4
5 Remark 7 Il nome covarianza, inteso come covariazione, corrisponde a quanto appena descritto: si calcolano le variazioni congiunte dei dati x i e y i rispetto ai valori medi x ed y. Menzioniamo infine il fatto che il numero ρ (X, Y ) è una misura del legame lineare tra X ed Y. Questo verrà chiarito sotto con lo studio della regressione lineare. 1.2 Regressione lineare semplice Ipotizziamo che tre v.a. X, Y ed ε siano legate dalla relazione lineare Y = ax + b + ε dove a e b sono numeri reali. Interpretiamo questa scrittura pensando che X ed Y siano legate da una relazione lineare (graficamente una retta di equazione y = ax + b, per cui a si dirà coeffi ciente angolare e b intercetta), perturbata però da un errore casuale ε. La v.a. X verrà detta input, o predittore, o fattore, la Y output, o quantità da predire. Supporremo sempre che ε sia standardizzato: E [ε] = 0. L ventuale media di ε è inglobata in b. Supporremo inoltre che ε ed X siano indipendenti o almeno incorrelate: Cov (X, ε) = 0. Chiameremo modello lineare (semplice) la relazione precedente. Diremo anche modello di regressione lineare (semplice), e chiameremo retta di regressione la retta y = ax + b. Ci poniamo due scopi: 1. trovare formule che permettano di calcolare approssimativamente a, b e la deviazione standard σ ε dell errore ε a partire da dati sperimentali, quando si ipotizza il modello lineare ma non si conoscono i coeffi cienti; 2. interpretare rigorosamente il concetto di coeffi ciente di correlazione nell ambito del modello lineare. Raggiungeremo entrambi gli scopi calcolando valori medi, varianze e covarianze tra le diverse grandezze in gioco. Proposition 8 Se tre v.a. X, Y ed ε sono legate dalla relazione lineare Y = ax + b + ε, X ed ε sono scorrelate e µ ε = 0, e se σ X > 0, allora i coeffi cienti a e b sono univocamente determinati: Cov (Y, X) a = σ 2 X b = µ Y aµ X. 5
6 Inoltre σ 2 ε = σ 2 Y a 2 σ 2 X. Proof. Vale, per linearità e per la proprietà E [ε] = 0, E [Y ] = ae [X] + b. Vale inotre, per le regole sulla varianza (qui usiano la scorrelazione tra X ed ε), Infine, per analoghe ragioni vale da cui V ar [Y ] = a 2 V ar [X] + V ar [ε]. Cov (Y, X) = Cov (ax + b + ε, X) = acov (X, X) + Cov (ε, X) Cov (Y, X) = av ar [X]. Da queste relazioni si ricavano le tre formule. Supponiamo di avere n dati sperimentali, che in questo contesto significa avere n coppie (x 1, y 1 ),..., (x n, y n ) (n individui sono stati esaminati e per ciascuno sono stati trovati i valori di due grandezze X ed Y ). Possiamo calcolare i numeri x = 1 x i, y = 1 n n 1 (x i x) 2 1, n n 1 n (x i x) (y i y) y i (y i y) 2 e considerarli come approssiamzioni (stime) rispettivamente di E [X], E [Y ] V ar [X], V ar [Y ] Cov (X, Y ). Tramite queste approssimazioni possiamo stimare a, b e σ. Indichiamo con â e b le stime empiriche di a, b così trovate. 6
7 Remark 9 (retta di regressione) La retta di equazione y = âx + b è detta retta di regressione associata alla tabella di dati da cui sono stati calcolati â e b. Chiameremo quindi â coeffi ciente angolare e b intercetta, rella regressione lineare. A volte si usa lo stesso linguaggio per i parametri teorici a e b del modello teorico Y = ax + b + ε. Molti software permettono di tracciare la retta di regressione in sovrapposizione al plot dei dati sperimentali, per apprezzare la pendenza Interpretazione di ρ XY La Proposizione 8 stabilice una relazione tra coeffi ciente di correlazione al coeffi ciente angolare a della retta di regressione: Corollary 10 ρ XY = σ X σ Y a. Proof. Dalla Proposizione 8 e dalla definizione di coeffi ciente di correlazione, abbiamo a = Cov (Y, X) σ 2 X = Cov (Y, X) σ X σ Y σ Y σ X = ρ XY σ Y σ X σ quindi a = ρ Y XY σ X. Innanzi tutto questo chiarisce che a non è il coeffi ciente di correlazione, come invece per una sorta di gioco di parole si è spesso portati a credere. Del resto, ρ XY può variare solo tra -1 e 1, mentre la pendenza di una retta può essere maggiore di quella delle bisettrici. Vale però la regola: a > 0 se e solo se ρ XY > 0 (ed analogamente per valori negativi). Quindi ρ XY > 0 è indice di legame lineare diretto, cioè con coeffi ciente angolare positivo, mentre ρ XY < 0 è indice di legame lineare inverso (nel senso: una variabile cresce se l altra cala), cioè con coeffi ciente angolare negativo. Almeno il segno di ρ XY è facilmente interpretabile. Supponiamo di standardizzare sia X sia Y. In realtà non importa che sottraiamo la media, ma è essenziale che dividiamo per la deviazione standard, in modo da ricondurci ad avere σ X = 1 e σ Y = 1. In questo caso ρ XY = a Questo può offrire un interpretazione più stretta. L interpretazione più precisa viene invece dallo studio dell errore. Abbiamo visto sopra che σ 2 ε = σ 2 Y a 2 σ 2 X. 7
8 Sostituendo a = ρ XY σ Y σ X si trova σ 2 ε = σ 2 Y ( 1 ρ 2 XY ). Questo dice che la varianza dell errore, cioè la grandezza che misura quanto preciso sia il legame lineare tra X ed Y, è tanto maggiore quanto più vicino a zero è ρ XY : valori vicini a zero di ρ XY implicano un cattivo legame lineare (errore elevato). Viceversa, valori di ρ XY vicini a ±1 (non importa il segno!), implicano σ ε piccolo e quindi un legame lineare stretto: ρ XY 0 corrisponde a σ ε elevato ( σ Y ) ρ XY ±1 corrisponde a σ ε 0. Quindi, salvo che si esegua una standardizzazione di entrambe le variabili, ρ XY non è legato tanto all inclinazione della retta di regressione quanto piuttosto alla precisione con cui essa descrive il legame tra le variabili. Nel ragionamento precedente bisogna osservare che la grandezza o piccolezza di σ ε è relativa anche alla grandezza o piccolezza di σ Y. Questa è solo una questione di unità di misura delle quantità aleatorie che stiamo esaminando. Il discorso diventa indipendente dall unità di misura e dall ordine di grandezza dei valori tipici di Y se introduciamo la varianza standardizzata dell errore: Per essa vale σ 2 ε σ 2 Y σ 2 ε σ 2 Y. = 1 ρ 2 XY portando ad un ragionamento più universale circa il legame tra entità dell errore e valore di ρ 2 XY. Infine, introduciamo alcuni nuovi nomi. Essi si ispirano all idea che con un modello lineare stiamo cercando di dare una spiegazione della variabilità della grandezza Y. Abbiamo una grandezza Y, essa varia in modo imprevedibile, aleatorio, e noi vorremmo capire se queste variazioni sono almeno in parte spiegabili tramite un legame lineare con un predittore X: quando osserviamo ad es. valori di Y pià grandi della media, questo non è dovuto semplicemente al caso, ma al fatto che il predittore ha assunto valori ad es. più grandi del solito (se a > 0). Tutto però è pur sempre corrotto dall errore, per cui la spiegazione della variabilità di Y offerta dalla retta di regressione non è mai una spiegazione completa. In quest ottica, Y ha una sua varianza, una sua variabilità. L espressione ax + b riesce a spiegarne una parte, l altra resta non spiegata. La parte non spiegata di Y è la differenza tra Y e la parte spiegata, cioè ax + b. Quindi la parte non spiegata di Y è proprio l errore ε (non c è niente di nuovo, è solo una questione di linguaggio). Con questo nuovo linguaggio: 8
9 Definition 11 Chiamiamo varianza spiegata la percentuale della varianza che è stata spiegata da ax + b e varianza non spiegata la percentuale complementare. Siccome la parte di Y non spiegata è ε, in termini matematici la varianza non spiegata è σ 2 ε σ 2 Y mentre la varianza spiegata è 1 σ2 ε σ 2. Y Ma questa è pari a ρ 2 XY! Siamo arrivati al seguente risultato: Proposition 12 Il coeffi ciente di correlazione al quadrato, ρ 2 XY, è la varianza spiegata 1 σ2 ε dalla relazione lineare. σ 2 Y Più ρ 2 XY è alto (vicino a 1) più la relazione lineare riesce a spiegare la variabilità di Y. 1.3 Domande Lezione 1 1. Definizione teorica di covarianza, di coeffi ciente di correlazione e loro formule empiriche (stessa cosa naturalmente per la varianza e la deviazione standard) 2. Invarianza di scala (o meno) di covarianza e correlazione: enunciato e dimostrazione 3. Legami tra indipendenza e condizioni sulla covarianza (risp. correlazione) 4. Vicinanza a zero di ρ rispetto a vicinanza a zero di Ĉov 5. Com è fatta una tabella di dati sperimentali relativi ad una coppia di variabili (X, Y ) 6. Interpretazione grafica del segno di Ĉov, sulla base della formula empirica 7. Significato della vicinanza di ρ a zero o a ±1, in termini di legame lineare tra le variabili 8. Definizione di varianza spiegata nella regressione 9. Legami matematici tra varianza spiegata, coeffi ciente di correlazione e coeffi ciente angolare nella regressione lineare semplice 10. Quando coeffi ciente di correlazione e coeffi ciente angolare coincidono 11. Scrivere i comandi per generare un insieme di 30 numeri casuali con ρ > 0. 9
10 2 Lezione Matrice di covarianza Definition 13 La matrice di covarianza Q (risp. di correlazione ρ) di un vettore X = (X 1,..., X n ) è la matrice n n definita da Q ij = Cov (X i, X j ) (risp. ρ ij = ρ (X i, X j )), per i, j = 1,..., n. Example 14 Nella Lezione 1 abbiamo esaminato il legame tra due variabili aleatorie X ed Y. Possiamo costruire la matrice di covarianza del vettore (X, Y ), data semplicemente da ( La matrice di correlazione è Q = ( ρ = σ 2 X Cov (X, Y ) Cov (X, Y ) σ 2 Y 1 ρ (X, Y ) ρ (X, Y ) 1 Le seguenti proprietà vengono descritte per Q ma valgono anche per ρ. Proposition 15 La matrice di covarianza Q di un vettore aleatorio X = (X 1,..., X n ) è simmetrica Q ij = Q ji ). ). e definita non-negativa per ogni x R n. x T Qx 0 Proof. La simmetria di Q discende dalla simmetria dell operazione di covarianza: Q ij = Cov (X i, X j ) = Cov (X j, X i ) = Q ji. Per la proprietà di definita non-negatività, preso x = (x 1,..., x n ) R n, vale x T Qx = Q ij x i x j = i,j=1 = Cov x i X i, Cov (X i, X j ) x i x j = i,j=1 Cov (x i X i, x j X j ) i,j=1 x j X j = V ar [W ] 0 j=1 dove W = n x ix i. Abbiamo usato la linearità della covarianza in entrambi gli argomenti. 10
11 Il teorema spettrale afferma che ogni matrice simmetrica Q può essere diagonalizzata, nel senso che esiste una base ortonormale e 1,..., e n di R n in cui Q assume la forma λ Q e = λ n Inoltre, i numeri λ i sulla diagonale sono gli autovalori di Q ed i vettori e i sono i corrispondenti autovettori: Qe i = λ i e i. Dal punto di vista algebrico, quanto detto significa che esiste una matrice ortogonale U (cioè tale che UU T = I = U T U, dove I è la matrice identica) ed una matrice diagonale Q e tali che Q = UQ e U T. Inoltre, U ha come colonne una base ortonormale di autovettori e i corrispondenti ai λ i : U = (e 1,..., e n ). Exercise 16 Verificare che, se U = (e 1,..., e n ), Q e è come sopra e Q = UQ e U T, allora Qe 1 = λ 1 e 1 (lo stesso vale per gli altri autovettori). Soluzione. Detto u 1 il vettore ( ) T, vale Qe1 = UQ e U T e 1 = UQ e u 1, in quanto nei prodotti riga per colonna di U T e 1 si devono fare i prodotti scalari degli e i con e 1, tutti zero tranne il primo. Quindi Qe 1 = UQ e u 1 = λ 1 Uu 1 = λ 1 e 1. Siccome una matrice di covarianza Q è anche definita non-negativa, vale Exercise 17 Verificarlo. λ i 0, i = 1,..., n. Soluzione. λ i = λ i e T i e i = e T i Qe i 0. Abbiamo usato il fatto che e T i e i = 1, discendente da U T U = I ed il fatto che λ i e i = Qe i, più la non-negatività di Q. Usando entrambi questi fatti si può definire la radice quadrata di Q. La dimostrazione della proposizione fornisce anche la sua costruzione, che richiede la conoscenza di autovettori e autovalori di Q. Proposition 18 Esiste una matrice simmetrica definita non-negativa Q, detta radice quadrata di Q, avente la proprietà ( Q ) 2 = Q. Proof. In primo luogo possiamo definire facilmente la radice quadrata di Q e, ponendo λ1 0 0 Qe = λn 11
12 Si vede subito che questa è simmetrica ed il suo quadrato è Q e. Tramite questa matrice, tornando indietro, possiamo definire Q := U Qe U T. Si verifica facilmente che la matrice Q è simmetrica ed il suo quadrato è uguale a Q. Infatti Abbiamo ( Q ) T = U ( Qe ) T U T = U Q e U T = Q e ( Q ) 2 = U Qe U T U Q e U T = U Q e Qe U T = UQ e U T = Q in quanto U T U = Id Commenti di algebra lineare Le seguenti note, esterne al corso di statistica, possono essere utili per rammentare il significato preciso e l interpetazione geometrica di alcune espressioni ed alcuni fatti ricordati sopra. Remark 19 Ricordiamo alcuni fatti di algebra lineare. R n è uno spazio vettoriale con prodotto scalare.,., cioè un insieme di elementi (vettori) con certe operazioni (somma di vettori, moltiplicazione per numeri reali, prodotto scalare tra vettori) e certe proprietà. Possiamo chiamare oggetti intrinseci gli oggetti definiti in questi termini, al contrario di quelli definiti tramite coordinate rispetto ad una base. Un vettore x R n è un oggetto intrinseco; quando lo scriviamo nella forma (x 1,..., x n ) rispetto ad una base, questa scrittura non è intrinseca, dipende dalla base. Data una base ortonormale u 1,..., u n, le componenti di un vettore x R n in tale base sono i numeri x, u j, j = 1,..., n. Un applicazione lineare L in R n è un oggetto intrinseco: è una funzione L : R n R n tale che L (αv + βw) = αlv+βlw per ogni v, w R n ed ogni α, β R. Data la base u 1,..., u n, L può essere rappresentata tramite la matrice di componenti Lu i, u j ; questa matrice non è intrinseca. Scriveremo a volte y T x al posto di x, y (o y, x ). Remark 20 Dopo questi commenti di carattere generale, riconosciamo che una matrice rappresenta un applicazione lineare relativamente ad una base specificata. Quindi, data la base canonica di R n, che indicheremo con u 1,..., u n, data la matrice Q, è definita una ben precisa applicazione lineare L : R n R n ; e viceversa, data L e data una qualsiasi base e 1,..., e n di R n, L si scrive in questa base tramite una matrice. Il teorema spettale afferma che se Q era simmetrica, allora esiste una base ortonormale e 1,..., e n in cui la rappresentazione matriciale Q e di L è diagonale. 12
13 Remark 21 Ricordiamo alcuni altri fatti di algebra lineare. Partiamo da una base ortonormale u 1,..., u n, che chiameremo canonica o base originaria. Sia e 1,..., e n un altra base ortonormale. Il vettore u 1, nella base canonica, ha componenti u 1 = e così via per gli altri vettori. Ogni vettore e j ha certe componenti nella base canonica. Indichiamo con U la matrice la cui prima colonna ha le componenti di e 1, la seconda quelle di e 2 e così via. Potremmo scrivere U = (e 1,..., e n ). Vale anche U ij = e T j u i. Quindi U = e 1 e così via, cioè U rappresenta l applicazione lineare che trasforma la base canonica in e 1,..., e n Uu i = e i, i = 1,..., n. Essa è una trasformazione ortogonale: U 1 = U T. Infatti, U 1 trasforma e 1,..., e n nella base canonica (invertendo quanto appena detto su U), e U T fa lo stesso: e T 1 e 1 1 U T e 1 = e T 2 e 1... = 0... e T n e 1 0 e così via. Ricordiamo che le trasformazioni ortogonali sono isometrie, come le rotazioni o le riflessioni. Remark 22 Torniamo alla matrice di covarianza Q ed alla matrice Q e data dal teorema spettrale: sappiamo che Q e è diagonale e rappresenta la stessa trasformazione lineare L, nella nuova base e 1,..., e n. Supponiamo di non sapere altro che questo, cioè che rappresentano la stessa trasformazione lineare L e che Q e ha la forma Q e = λ λ n 13.
14 Da questo deduciamo alcuni fatti: i) Q e = UQU T ii) gli elementi sulla diagonale λ j sono autovalori di L, con autovettori e j iii) λ j 0, j = 1,..., n. Per dimostrare (i), ricordiamo che abbiamo appena visto che (Q e ) ij = e T j Le i e Q ij = u T j Lu i. Inoltre, U ij = e T j u i, quindi e j = n k=1 U kju k, e di conseguenza (Q e ) ij = e T j Le i = U ki U k ju T k Lu k = U ki Q ij U k j = ( UQU T ) ij. k,k =1 k,k =1 Per dimostrare (ii), scriviamo il vettore Le 1 nella base e 1,..., e n : e i è il vettore l applicazione L è rappresentata da Q e, quindi Le 1 è uguale a 1 λ 1 1 Q e 0... = 0... = λ che è λ 1 e 1 nella base e 1,..., e n. Abbiamo verificato che Le 1 = λ 1 e 1, cioè che λ 1 è un autovalore e che e 1 è il corrispondente autovettore. La dimostrazione per λ 2, ecc. è la stessa. Per dimostrare (iii), basta osservare che, nella base e 1,..., e n, Ma e T j Q e e j = λ j. e T j Q e e j = e T j UQU T e j = v T Qv 0 dove v = U T e j, avendo usato la proprietà che Q è definita non-negativa. Quindi λ j Matrici di covarianza empirica e correlazione emprica Supponiamo di avere una tabella di dati del tipo X 1... X p 1 x 1,1... x 1,p 2 x 2,1... x 2,p n x n,1... x n,p ,
15 dove le colonne rappresentano diverse variabili (ad esempio X 1 = PIL,..., X p 1 = spese per istruzione, X p = spese per sanità), le righe rappresentano diversi individui (ad esempio le nazioni europee) ed i valori numerici sono noti, sono stati misurati. Dal punto di vista teorico, abbiamo visto il concetto di matrice di covarianza Q delle v.a. (X 1,..., X p ). Dal punto di vista empirico, possiamo calcolare la matrice di covarianza empirica Q associata alla precedente tabella. La componente Q ij si ottiene calcolando la covarianza empirica tra le colonne i e j: Q ij = 1 n (x k,i x i ) (x k,j x j ) k=1 dove x i = 1 n n k=1 x k,i. Analogamente si può definire la matrice di correlazione empirica ρ di componenti n k=1 ρ ij = (x k,i x i ) (x k,j x j ) n k=1 (x k,i x i ) 2. n k=1 (x k,j x j ) 2 Il significato applicativo di queste matrici è la conseguenza del significato di covarianza e correlazione tra stringhe di dati; nel caso della correlazione, il numero ρ ij misura il legame lineare tra le colonne i e j, con le interpretazioni del segno descritte al paragrafo corrispondente. I legami così catturati sono però a due a due, non globali tra tutte le variabili nel loro complesso. Per ogni coppia di variabili X i e X j, abbiamo il corrispondente coeffi ciente ρ ij. Con software R, data una matrice A, basta calcolare cor(a) e viene restituita la tabella delle correlazioni (la matrice di correlazione). Chiedendo plot(a) si ottiene una figura piuttosto ricca che indica i plot a due a due delle diverse variabili, da cui si può intuire l eventuale legame lineare ed il suo segno. Confrontando la tabella cor(a) col grafico plot(a), si ottiene un primo insieme di informazioni sui legami tra le variabili oggetto di studio. Esemplifichiamo con la seguente tabella, il cui significato verrà descritto altrove: 15
16 PLIC SC SA.SC TD TMI Piem Vaos Lomb TrAA Vene FrVG Ligu EmRo Tosc Umbr Marc Lazi Abru Moli Camp Pugl Basi Cala Sici Sard (per inciso, si può provare a caricarla in R con un semplice copia-incolla tramite il comando A<-read.table("clipboard",dec=,,header=T,row.names=1) che funziona così: si copia da questo file la tabella, si scrive il comando su R e si dà l invio) cor(a) plot(a) PLIC SC SA.SC TD TMI PLIC SC SA.SC TD TMI
17 2.3 Trasformazione lineare (affi ne) dei momenti La soluzione dei seguenti esercizi è basata sulla linearità del valore atteso (e quindi della covarianza, rispetto a ciascuno dei suoi argomenti) Exercise 23 Sia X = (X 1,..., X n ) un vettore casuale, A una matrice n d, cioè A : R n R d, b R d, ed Y = (Y 1,..., Y d ) un vettore casuale definito da Y = AX + b. Sia µ X = ( µ X 1,..., ) µx n il vettore dei valori medi di X, ovvero µ X ( i = E [X i ] e sia µ Y = µ Y 1,..., µ Y ) d il vettore dei valori medi di Y. Allora µ Y = Aµ X + b. Soluzione. L identità Y = AX + b, per componenti significa Y i = A ij X j + b i. Pertanto, per la linearità del valor medio, E [Y i ] = E A ij X j + b i = A ij E [X j ] + b i j=1 j=1 j=1 che è la versione per componenti dell identità da dimostrare. Exercise 24 Sotto le stesse ipotesi, se Q X e Q Y sono le matrici di covarianza di X ed Y, allora Q Y = AQ X A T. 17
18 Soluzione. Sempre usando l identità per componenti scritta sopra, Q Y ij = Cov (Y i, Y j ) = Cov A ii X i + b i, A jj X j + b j = = A ii Cov X i, i =1 i =1 A ii j =1 i =1 A jj X j + b j j =1 A jj Cov ( ) X i, X j = j =1 i =1 j =1 A ii Q X i j A jj avendo usato la linearità della covarianza nelle due componenti. Ricordiamo che, date due matrici A e B, vale (AB) ij = k A ikb kj. Allora i =1 j =1 A ii Q X i j A jj = ( AQ X ) A ij jj. Per interpretare anche quest ultimo come prodotto tra matrici bisogna trasporre A: L esercizio è risolto. = 2.4 Domande Lezione 2 j =1 ( AQ X ) A T ij j j = ( AQ X A T ) ij. j =1 1. Definire matrice di covarianza e correlazione, teorica ed empirica 2. Dimostrazione della simmetria 3. Enunciato e dimostrazione della definita non-negatività 4. Se le variabili X 1,..., X p sono standardizzate, che differenza c è tra la la matrice di covarianza e quella di correlazione? 5. Diagonalizzazione della matrice di covarianza (cosa si può dire su autovalori e autovettori per una matrice di covarianza) 6. Cosa produce il plot di una tabella 7. Enunciare e dimostrare la formula di trasformazione della covarianza sotto trasformazioni affi ni. 18
19 3 Lezione Regressione lineare multipla Supponiamo di avere una tabella di numeri del tipo X 1... X p Y 1 x 1,1... x 1,p y 1 2 x 2,1... x 2,p y n x n,1... x n,p y n dove le colonne rappresentano diverse variabili (ad esempio X 1 = reddito,..., X p = numero anni istruzione, Y = spese per mostre e musei), le righe rappresentano diverse unità sperimentali o individui (persone, città ecc.). Si noti che, a differenza della tabella su cui abbiamo calcolato la matrice di correlazione empirica, qui c è una colonna privilegiata, quella della variabile Y. Ci chiediamo se le variabili Y ed X 1,..., X p siano legate da una relazione funzionale, a meno di errore, della forma: Y = f (X 1,..., X p, ε). Remark 25 (causa-effetto) In quasi tutte le applicazioni concrete di questi modelli si vorrebbe, con essi, quantificare o catturare una relazione causa-effetto: le variabili X i corrispondono alle cause, Y all effetto. Si vorrebbe capire se le variabili X 1,..., X p influiscano su Y ; se Y dipenda da X 1,..., X p. Un maggior reddito induce a maggiori spese per mostre e musei? Ed un maggior grado di istruzione (misurato ad esempio come numero di anni si studio)? Purtroppo bisogna convincersi che la teoria che stiamo sviluppando permette solo di stabilire se ci sia un legame tra queste grandezze, se Y ed X 1,..., X p siano legate da una relazione funzionale (come abbiamo detto sopra). Una cosa è un legame, un altra è una relazione causa-effetto. Il numero di mezzi pubblici di trasporto ed il numero di insegnanti di una nazione occidentale sono legati, correlati positivamente (entrambi sono più elevati nelle nazioni più grandi), ma non hanno alcuna relazione causa-eff etto l uno con l altro. Essi hanno una concausa: la dimensione della nazione. Questo è un fatto abbastanza generale. La presenza di una concausa provoca spesso dei legami, delle correlazioni, ma spesso le grandezze influenzate dalla comune causa non hanno relazione cuasale le une con le altre, non si influenzano a vicenda. Remark 26 Nonostante le precedenti precisazioni, è così intutivo usare un linguaggio del tipo Y dipende da X 1,..., X p che lo faremo anche noi in modo informale. Va sempre ricordato che non può essere preso alla lettera. In alcuni casi corrisponderà alla realtà, in altri no e gli strumenti matematici che sviluppiamo non sono in grado di dirimere questo aspetto interpretativo. 19
20 Le variabili (grandezze) X 1,..., X p verranno dette input, fattori, predittori, mentre la grandezza Y è l output. Remark 27 (fattori e predittori) Il termine fattori (che allude a cause ) è legato ai remark precedenti; non va quindi inteso in senso letterario. E invece interessante capire il perché del termine predittori. Supponiamo di aver stabilito che certe grandezze Y e X 1,..., X p sono legate da una relazione funzionale di quelle che stiamo studiando. Non importa se questa relazione stia eff ettivamente descrivendo una relazione causa-eff etto oppure se, dal punto di vita interpretativo, sia del tutto aritificiosa (come potrebbe essere una relazione tra numero di mezzi pubblici ed il numero di insegnanti). Tale relazione può essere utilizzata per eseguire predizioni: calcolata in nuovi valori delle X 1,..., X p (non già speriementati) essa produce dei corrispondenti valori di Y. Permette di predire il valore di Y in corrispondenza di input mai sperimentati. Se ad esempio Y sono volumi di vendita di un prodotto e le X i sono grandezze socio-economiche del territorio, una volta costruito il modello sulla base di dati speriementati in una regione, possiamo esportare il modello in regioni meno note prevedendo le vendite, sulla base dei dati socio-economici di quella nuova regione. Nel seguito ci limiteremo allo studio di relazioni funzionali di tipo lineare (affi ne) ovvero della forma: Y = a 1 X a p X p + b + ε (b è detta intercetta e gli a i, così come b, sono i parametri del modello). In realtà, la relazione appena scritta è astratta, riguarda le variabili aleatorie (è un po come una legge fisica tipo F = ma). Noi invece siamo partiti da una tabella di dati, e quindi possiamo formulare il problema in modo più concreto, più attinente ai dati. A partire dai dati specifici, esaminiamo una relazione lineare tra essi della forma y i = a 1 x i, a p x i,p + b + ε i i = 1,..., n (1) dove abbiamo introdotto i numeri ε i, detti residui, definiti dalla relazione stessa, cioè da ε i = y i (a 1 x i, a p x i,p + b). Così facendo, non stiamo ipotizzando una relazione lineare tra le variabili: l identità (1) vale sempre, con la definizione data dei residui. Il problema è: quanto sono grandi i residui, affi nché valga la (1)? I residui sono una misura dell errore insito nella relazione lineare. Remark 28 I residui, così definiti, sono funzione dei parametri del modello. Più tardi, i parametri verranno fissati in modo ottimale e chiameremo residui i corrispondenti residui (con questa precisazione intendiamo dire che i residui, a seconda del momento in cui se ne parla, solo funzione dei parametri, oppure sono numeri univocamente individuati da una condizione di ottimalità; in questo momento, sono funzioni dei parametri). 20
21 Possiamo poi calcolare lo scarto quadratico medio dei residui, ancora funzione dei parametri a 1,..., a p, b, SQM (a 1,..., a p, b) = 1 n ε 2 i = 1 n (y i (a 1 x i, a p x i,p + b)) 2. La grandezza SQM (a 1,..., a p, b) misura la bontà del modello lineare Y = a 1 X a p X p + b + ε: se piccola, il modello è buono. La strategia, che illustreremo in detaglio nel paragrafo 3.2.2, sarà di cercare i parametri a 1,..., a p, b che rendono minima la grandezza SQM (a 1,..., a p, b). Tali parametri forniscono il migliore tra i modelli lineari. Indichiamo con â 1,..., â p, b i parametri ottimali, che troveremo nel paragrafo Chiamiamo Y = â 1 X â p X p + b + ε il modello di regressione lineare multipla (regressione lineare semplice nel caso n = 1) associato alla tabella di dati precedente. La varianza dell errore, o dei residui, è ora σ 2 ε = SQM ( ) â 1,..., â p, b = 1 n dove i residui (ora numeri univocamente determinati dai dati) sono dati da ( ε i = y i â 1 x 1,i â p x p,i + b ). La varianza spiegata, o indice R 2, è definita da R 2 = 1 σ2 ε σ 2 Y dove σ 2 Y è la varianza dei dati y 1,..., y n. L idea è che i dati y 1,..., y n hanno una loro variabilità, descritta da σ 2 Y, in situazione di completa ignoranza; ma quando abbiamo a disposizione un modello, esso spiega i dati y 1,..., y n in una certa misura, cioè a meno degli errori ε 1,..., ε n. Quindi la variabilità di questi errori è la variabilità inspiegata, residua. Da qui il nome di (percentuale di) varianza spiegata per il numero 1 σ2 ε. σ 2 Y 3.2 Calcolo dei coeffi cienti Il calcolo dei coeffi cienti si può svolgere in vari modi diversi. Iniziamo con quello più teorico, concettualmente non molto soddisfacente, ma molto veloce e chiaro. ε 2 i 21
22 3.2.1 Calcolo a partire da un modello teorico Consideriamo, come abbiamo fatto nel caso della regressione semplice (p = 1), il modello Y = a 1 X a p X p + b + ε dove le X i, la Y ed ε sono v.a. aleatorie (non dati sperimentali o residui numerici). Proposition 29 Supponiamo che le v.a. X 1,..., X p, Y ed ε siano legate dalla relazione precedente, ε sia scorrelato con ciascuna X i ed abbia media nulla, e la matrice di covarianza Q del vettore (X 1,..., X p ) sia invertibile. Indichiamo con c il vettore di coordinate c j = Cov (Y, X j ) e con a 0 il vettore dei parametri (a 1,..., a p ). Allora i parametri a 1,..., a p, b sono univocamente determinati dalle relazioni: a 0 = Q 1 c b = E [Y ] (a 1 E [X 1 ] a p E [X p ]). Proof. Calcoliamo la covarianza tra Y ed X j : Cov (Y, X j ) = Cov (a 1 X a p X p + b + ε, X j ) = a 1 Cov (X 1, X j ) a p Cov (X p, X j ) + Cov (ε, X j ). Usando la matrice Q = (Cov (X i, X j )) possiamo riscrivere questa indentità come c j = p Q ij a i + Cov (ε, X j ). Avendo ipotizzato che ε sia scorrelato da ciascuna X j, troviamo c j = p Q ji a i (avendo usato che Q è simmetrica) ovvero Qa 0 = c. Quindi a 0 = Q 1 c. Poi, per calcolare b, basta calcolare il valor medio a destra e sinistra dell equazione che definisce il modello: E [Y ] = a 1 E [X 1 ] a p E [X p ] + b. Allora vale b = E [Y ] (a 1 E [X 1 ] a p E [X p ]). 22
23 Questo risultato fornisce anche un modo per calcolare i parametri a partire da una matrice di dati. Si calcola la matrice di covarianza empirica Q della matrice di dati riguardante le variabili X i, si calcola il vettore ĉ delle covarianze empirche tra le variabili X j ed Y, e si calcolano i valori â 0 = Q 1 ĉ. In modo simile si calcola il valore empirico b a partire dai dati Metodo dei minimi quadrati Questo metodo ha il pregio di partire dai dati, piuttosto che dal modello teorico, quindi la sua giustificazione è più chiara. Ha inoltre il pregio di essere un metodo universale per la ricerca di parametri ottimali (nel senso che con opportune modifiche lo si applica ai più svariati contesti, ad esempio allo studio delle serie storiche che vedremo in un altra lezione). Richiede però calcoli un po meno immediati per arrivare alle formule finali. Come già illustrato in una sezione precedente, il metodo consiste nella ricerca dei valori â 1,..., â p, b che rendono minimo lo scarto quadratico medio SQM (a 1,..., a p, b) = 1 n ε 2 i = 1 n (y i (a 1 x i, a p x i,p + b)) 2. Per trovare i parametri ottimali si può procedere in due modi. il più naturale ma più laborioso consiste nello studio delle condizioni necessarie di ottimalità, che rimandiamo al paragrafo Vediamo qui invece un metodo compatto di tipo più geometrico. Riscriviamo l equazione (1) in forma vettoriale. Introduciamo la matrice degli input x 1,1... x 1,p 1 X = x n,1... x n,p 1 (la colonna di uni serve fittiziamente per manipolare l intercetta in modo unificato agli altri parametri), ed i vettori dei parametri, degli output e dei residui: a =, y =, ε = a 1... a p b ottenendo la riscrittura vettoriale di (1): y 1... y n y = Xa + ε L errore quadratico medio (come funzione dei parametri a 1,..., a p, b) si può scrivere SQM (a) = 1 ε 2 i = 1 n n ε 2 = 1 n y Xa ε 1... ε n
24 Vogliamo minimizzarlo. In questa forma il problema ha un interessante interpretazione geometrica. Nello spazio R n abbiamo un punto dato, y, ed il sottospazio Im X, l immagine di R p+1 attraverso X: Im X = { z : z = Xa, a R p+1}. Cercare il punto â R p+1 che minimizza y Xa significa cercare il punto ẑ Im X che minimizza y z, dovendo poi come passo finale trovare â R p+1 tale che Xâ = ẑ. Operativamente, quindi, si devono risolvere due problemi: una minimizzazione min y z z Im X e, detto ẑ il punto di minimo, la risoluzione dell equazione (risolubile perché ẑ Im X) Xa = ẑ. Abbiamo sempre detto il punto... ma l unicità degli oggetti che stiamo cercando va anch essa dimostrata. Lemma 30 Dati un punto y R n ed un sottospazio V R n, esiste uno ed un solo punto ẑ V tale che y ẑ y z per ogni z V. Il vettore y ẑ è perpendicolare a V. Proof. Sia d la dimensione di V, d n. Possiamo costruire una base ortonormale e 1,..., e n di R n tale che e 1,..., e d sia una base di V. I vettori e d+1,..., e n sono ortogonali a V. Il punto y si rappresenta univocamente come y = α 1 e α n e n = α 1 e α d e d + α d+1 e d α n e n = ẑ + w dove ẑ = α 1 e α d e d V, w = y ẑ = α d+1 e d α n e n è perpendicolare a V. Con un po di calcoli che omettiamo si verifica che ẑ è il punto dato; l interpretazione grafica è evidente. Lemma 31 Supponiamo che valga ker X = {0}. Allora, dato ẑ Im X, esiste uno ed un solo punto â R p+1 tale che Xâ = ẑ. Proof. L esistenza è insita nell ipotesi ẑ Im X. L unicità discende dall ipotesi ker X = {0}: se â, ã fossero due soluzioni, allora X (â ã) = 0, quindi â ã ker X, ovvero â ã = 0. Lemma 32 Se ker X = {0}, allora det ( X T X ) 0. 24
25 Proof. Se ker X = {0} allora, per ogni vettore v 0 vale Xv 0, quindi Xv 2 0, quindi X T Xv, v 0. Ma allora X T Xv 0 (altrimenti, se fosse X T Xv = 0, allora sarebbe anche X T Xv, v = 0). Abbiamo dimostrato che v 0 implica X T Xv 0 quindi ker ( X T X ) = {0}. Ma X T X è una matrice quadrata, quindi è non singolare, ovvero det ( X T X ) 0. Theorem 33 Supponiamo che valga ker X = {0}. Allora, esiste uno ed un solo vettore â che minimizza la funzione f (a) = y Xa 2. Esso è dato da â = ( X T X ) 1 X T y. Se inoltre p + 1 = n allora il minimo è nullo e vale â = X 1 y. Proof. Dato y R n, siano ẑ Im X e â R p+1 tali che ẑ minimizza y z, â risolve Xâ = ẑ. Preso a â, posto z = Xa, vale z ẑ e z Im X, quindi ovvero y ẑ < y z y Xâ < y Xa. Abbiamo dimostrato che f (â) < f (a) per ogni a â, quindi â è punto di minimo ed è l unico. Siccome soddisfa Xâ = ẑ, allora (moltiplicando a sinistra ambo i membri per X T ) soddisfa anche X T Xâ = X T ẑ. Per ipotesi e per uno dei lemmi, X T X è invertibile, quindi â = ( X T X ) 1 XT ẑ. Ma X T (ẑ y), a = ẑ y, Xa = 0 per ogni a, perché ẑ y è perpendicolare a Im X. Quindi X T (ẑ y) = 0, cioè X T ẑ = X T y. Abbiamo dimostrato che â = ( X T X ) 1 X T y. Infine, se vale anche la condizione p + 1 = n (quindi det X 0 perché ker X = {0}), le matrici X ed X T sono invertibili, quindi La dimostrazione è completa. â = ( X T X ) 1 X T y = X 1 ( X T ) 1 X T y = X 1 y. Remark 34 L errore relativo ai parametri ottimali ε = y Xâ è ortogonale a Im X (è la proprietà di y ẑ = y Xâ = ε descritta nella dimostrazione). Questo è il riflesso empirico delle proprietà Cov (X i, ε) = 0, i = 1,..., p, e E [ε] = 0 alla 25
26 base del metodo del paragrafo Vediamo in dettaglio. L ortogonalità di ε rispetto a Im X si può esprimere con la condizione X T ε = 0 (come nella dimostrazione appena svolta, vale ε, Xa = X T ε, a per ogni a, da cui si vede l equivalenza tra ortogonalità ad Im X e condizione X T ε = 0). La matrice X T è data da x 1,1... x n,1 X T = x 1,p... x n,p per cui, ad esempio, l ultima componente del vettore X T ε è ( XT ε ) p+1 = ε ε n. Quindi ( X T ε ) p+1 = 0 equivale a ε ε n n = 0, che è la versione empirica di E [ε] = 0. Analogamente si vede che ( X T ε ) = 0 è la versione empirica di Cov (X i i, ε) = 0, per i = 1,..., p. Remark 35 In particolare, abbiamo verificato che ε ε n n = 0. Pertanto la varianza empirica σ 2 ε che compare, ad esempio, nella definizione di R 2 è data da SQM, cioè 1 n n ε2 i, senza bisogno di sottrarre la media empirica, essendo nulla Condizioni di ottimalità Posto f (a 1,..., a p, b) = SQM (a 1,..., a p, b) = 1 (y i (a 1 x i, a p x i,p + b)) n le condizioni necessarie di ottimalità sono f ( ) â 1,..., â p, b = 0, j = 1,..., p a j f b ( ) â 1,..., â p, b = 0 (con un ragionamento sulla convessità di SQM si può mostrare che sono anche suffi cienti, sotto l ipotesi ker X = {0}). Se si ha dimestichezza col calcolo vettoriale si arriva subito al risultato finale. Infatti, con le notazioni vettoriali del paragrafo precedente, f (a) = 1 y Xa 2 n 26
27 da cui, per ogni direzione h R p+1, f (a), h = 2 y Xa, Xh n = 2 X T (y Xa), h n ovvero f (a) = 2 n XT (y Xa). Le condizioni di ottimalità diventano quindi ovvero X T (y Xâ) = 0 X T Xâ = X T y come nel paragrafo precedente. Bisognerebbe poi giustificare che il minimo è unico. Per eventuale maggior chiarezza, svolgiamo i conti, però parecchio laboriosi, senza notazione vettoriale. Vale f a j = 2 n (y i (a 1 x i, a p x i,p + b)) x i,j = 2 n y, x j + 2 n a 1 x,1, x,j n a p x,p, x,j + 2bx j f b = 2 n (y i (a 1 x 1,i a p x p,i + b)) = 2y + 2a 1 x a p x p + 2b dove y è la media degli y 1,..., y n e, per ciascun j = 1,..., p, x j è la media degli x 1,j,..., x n,j ; ed inoltre abbiamo posto y, x,j = y i x i,j, x,k, x,j = x i,k x i,j. Quindi deve valere a 1 x,1, x,j a p x,p, x,j + nbx j = y, x,j, a 1 x a p x p + b = y i = 1,..., p Questo è un sistema di p + 1 equazioni lineari in p + 1 incognite. Si può a questo punto introdurre la matrice A quadrata a p + 1 righe e colonne ed il vettore w A = x,1, x,1... x,p, x,1 x,1, x,1, x,p... x,p, x,p x,p, 1 x,1, 1... x,p, , w = y, x,1... y, x,p y, 1
28 dove 1 indica il vettore con tutti 1, ed y è il vettore delle y i. Allora il calcolo del vettore â 1 â =... â p b si può vedere come la risoluzione di dove Aâ = w. Infine, possiamo riconoscere che la matrice A si ottiene col prodotto X = A = X T X x 1,1... x 1,p x n,1... x n,p 1 è la matrice già introdotta nella sezione precedente. Inoltre, Quindi il problema Av = w ha la forma w = X T y. X T Xâ = X T y. La sua soluzione è quella trovata nella sezione precedente. 3.3 Domande Lezione 3 1. Com è fatta una tabella di dati in un problema di regressione multipla 2. La regressione stabilisce un legame causa-effetto? Può essere usata per fare previsioni? 3. Scrivere un modello di regressione lineare multipla, sia nella versione teorica di legame tra variabili aleatorie, sia in quella più pratica di legame tra dati sperimentali a meno di errore 4. Definizione di residui e formulazione del metodo dei minimi quadrati 5. Formule per i coeffi cienti della regressione multipla (enunciato e dimostrazione del Teorema 33; possibilmente anche un altro approccio) 6. Descrivere graficamente (geometricamente) il procedimendo di ricerca dei parametri ottimali adottato dal Teorema I residui, dipendono dai parametri oppure no? 28
29 3.4 Lezione Osservazioni sulla regressione lineare multipla Overfitting Quando p + 1 = n e det X 0, i residui relativi ai parametri â sono nulli (il minimo di SQM è zero). Da ciò si deduce anche che la varianza spiegata R 2 è 1. Sembrerebbe quindi che un tale modello sia il migliore possibile. Invece per le usuali applicazioni non è così. Il suo potere previsivo può essere scarsissimo, così come la sua capacità di aver capito il problema, i dati. Infatti, un tale modello si adatta perfettamente ai dati sperimentali seguendo al millimetro i suoi accidenti casuali, senza filtrarli, senza riconoscere che alcune variazioni sono rumore, non struttura da catturare. Si può capire bene questo pensando al caso di due variabili X, Y, di cui si conoscano solo due dati sperimentali (1, y 1 ), (2, y 2 ), tali che y 1 e y 2 sono numeri casuali N (0, 1). Il modello corretto sarebbe Y = ε (cioè a = b = 0), mentre se obblighiamo il software a cercare un modello del tipo Y = ax + b + ε (p = 1, p + 1 = 2), esso fitterà perfettamente i due dati trovando la retta che passa per i due punti (1, y 1 ), (2, y 2 ): residui nulli, ma modello dato da una retta senza senso, completamente sbagliata rispetto a Y = ε, ed oltretutto fortemente dipendente dai valori casuali y 1 e y 2. Quando p è troppo grande rispetto al numeri di dati a disposizione, si parla di overfitting Variabilità statistica dei parametri ottimali Per capire l enunciato (o lo spirito) del seguente teorema bisogna immaginare la seguente situazione sperimentale (in realtà questa immaginazione poteva essere descritta sin dall inizio del capitolo, come la base logica del nostro problema di stima dei parametri). Svolgiamo degli esperimenti che coinvolgono le grandezze X 1,..., X p ed Y. Le grandezze X 1,..., X p sono sotto il nostro preciso controllo: possiamo fissarne i valori x i,j (ovvero la matrice X), quando effettuiamo gli esperimenti. Invece non possiamo fissare i valori della grandezza Y, ma li possiamo osservare e registrare. Supponiamo infine che le grandezze siano legate dalla relazione Y = a 1 X a p X p + b + ε, secondo ben precisi valori a 1,..., a p, b che però non conosciamo; e dove ε è un disturbo casuale di media nulla e deviazione standard σ ε. Effettuiamo n esperimenti, ottenendo dei valori y 1,..., y n, che registriamo. Questi valori sono dati dalla formula y i = a 1 x i, a p x i,p + b + ε i dove ε 1,..., ε n sono le realizzazioni casuali dell errore ε accadute in tali esperimenti; ma ricordiamo che noi non conosciamo i parametri di questa formula. Si noti che l unico aspetto causale, imprevedibile, in ciascun esperimento è proprio il valore che assume ε. 29
30 A questo punto, partendo dai dati noti x i,j più i dati misurati y i, calcoliamo il vettore dei parametri ottimali â, secondo il metodo dei minimi quadrati descritto sopra. Il valore ottenuto per â non coincide col valore esatto a = ( a 1,..., a p, b ) (sconosciuto). Ne è una stima. Per inciso, questa filosofia (di avere un modello con parametri esatti ma incogniti ed un procedimento di stima approssimata di tali parametri) è quella generale di tutti i problemi di stima dei parametri, come la stima della media e della varianza di una grandezza aleatoria gaussiana partendo da un campione sperimentale. La mancata coincidenza di â con a, o se si preferisce la variabilità del risultato â, dipendono dalla casualità di ε. La domanda è: che proprietà statistiche ha â? E uno stimatore corretto (non distorto), cioè tale che E [â] = a? La variabilità di â (cioè V ar [â]) è grande? Qui, coi simboli E [â] e V ar [â], si sta pensando a medie rispetto alla casualità di ε: siccome ε è aleatorio, anche gli output y misurati sono aleatori, quindi anche la stima ottimale â è aletoria. Non comportando maggiori diffi coltà, impostiamo la casualità dell errore in modo persino un po più generale: supponiamo che gli errori, casuali, degli n esperimenti, cioè le v.a. ε 1,..., ε n, abbiano matrice di covarianza Q ε. E poi più che suffi ciente pensare al caso base in cui essi sono indipendenti ed ugualmente distribuiti, caso in cui Q ε è diagonale, multiplo dell identità: Q ε = σ 2 εi. Theorem 36 Lo stimatore â è non distorto: E [â] = a e la matrice di covarianza di â è [ (X Qâ = T X ) ] [ 1 X T Q ε X ( X T X ) ] 1. In particolare, se Q ε = σ 2 εid, cioè se gli errori ε i sono indipendenti tra loro e tutti di varianza σ 2 ε, allora Qâ = σ 2 ( ε X T X ) 1. Proof. Con notazioni vettoriali, abbiamo y = Xa + ε dove X ed a sono dati mentre ε è un vettore aleatorio, centrato di covarianza Q ε. Siccome â = ( X T X ) 1 X T y, vale â = ( X T X ) 1 X T Xa + ( X T X ) 1 X T ε = a + ( X T X ) 1 X T ε. Conosciamo le regole di trasformazione di media e covarianza per trasformazioni lineari: E [â] = a e Qâ = [ (X T X ) 1 X T ] Q ε [ (X T X ) 1 X T ] T = [ (X T X ) 1 X T ] Q ε [ X ( X T X ) 1 ]. 30
Dispense di Statistica II
 Dispense di Statistica II Franco Flandoli 2013-14 2 Indice 1 Correlazione e regressione 5 1.1 Covarianza e coeffi ciente di correlazione.................. 5 1.1.1 Regressione lineare semplice....................
Dispense di Statistica II Franco Flandoli 2013-14 2 Indice 1 Correlazione e regressione 5 1.1 Covarianza e coeffi ciente di correlazione.................. 5 1.1.1 Regressione lineare semplice....................
Statistica II Laurea magistrale in Ing. Gestionale a.a. 2012/13 Registro delle lezioni
 Statistica II Laurea magistrale in Ing. Gestionale a.a. 2012/13 Registro delle lezioni Lezione 1 (24/9). Introduzione al corso, composto principalmente dalla sezione sui vettori gaussiani (Cap. 1), dallo
Statistica II Laurea magistrale in Ing. Gestionale a.a. 2012/13 Registro delle lezioni Lezione 1 (24/9). Introduzione al corso, composto principalmente dalla sezione sui vettori gaussiani (Cap. 1), dallo
Scheda n. 13: modelli lineari
 Scheda n. 13: modelli lineari December 4, 2008 1 Combinazioni affini di variabili aleatorie La teoria che stiamo per esporre vuole descrivere relazioni matematiche tra variabili aleatorie: in tali relazioni
Scheda n. 13: modelli lineari December 4, 2008 1 Combinazioni affini di variabili aleatorie La teoria che stiamo per esporre vuole descrivere relazioni matematiche tra variabili aleatorie: in tali relazioni
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof. F.Podestà, a.a
 APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
0.1 Coordinate in uno spazio vettoriale
 0.. COORDINATE IN UNO SPAZIO VETTORIALE 0. Coordinate in uno spazio vettoriale Sia V uno spazio vettoriale di dimensione finita n costruito sul campo K. D ora in poi, ogni volta che sia fissata una base
0.. COORDINATE IN UNO SPAZIO VETTORIALE 0. Coordinate in uno spazio vettoriale Sia V uno spazio vettoriale di dimensione finita n costruito sul campo K. D ora in poi, ogni volta che sia fissata una base
Scheda n. 7: primi elementi sui legami tra più variabili
 Scheda n. 7: primi elementi sui legami tra più variabili October 27, 2008 Matrice di covarianza e di correlazione Supponiamo di esaminare n variabili X,..., X n, ad esempio X = reddito medio, X 2 = tasso
Scheda n. 7: primi elementi sui legami tra più variabili October 27, 2008 Matrice di covarianza e di correlazione Supponiamo di esaminare n variabili X,..., X n, ad esempio X = reddito medio, X 2 = tasso
Old Faithful, Yellowstone Park. Statistica e biometria. D. Bertacchi. Dati congiunti. Tabella. Scatterplot. Covarianza. Correlazione.
 Coppie o vettori di dati Spesso i dati osservati sono di tipo vettoriale. Ad esempio studiamo 222 osservazioni relative alle eruzioni del geyser Old Faithful. Old Faithful, Yellowstone Park. Old Faithful
Coppie o vettori di dati Spesso i dati osservati sono di tipo vettoriale. Ad esempio studiamo 222 osservazioni relative alle eruzioni del geyser Old Faithful. Old Faithful, Yellowstone Park. Old Faithful
Fattorizzazione QR e matrici di Householder
 Fattorizzazione QR e matrici di Householder ottobre 009 In questa nota considereremo un tipo di fattorizzazione che esiste sempre nel caso di matrici quadrate non singolari ad entrate reali. Definizione
Fattorizzazione QR e matrici di Householder ottobre 009 In questa nota considereremo un tipo di fattorizzazione che esiste sempre nel caso di matrici quadrate non singolari ad entrate reali. Definizione
Probablità, Statistica e Processi Stocastici
 Probablità, Statistica e Processi Stocastici Franco Flandoli, Università di Pisa Matrice di covarianza Dato un vettore aleatorio (anche non gaussiano) X = (X 1,..., X n ), chiamiamo sua media il vettore
Probablità, Statistica e Processi Stocastici Franco Flandoli, Università di Pisa Matrice di covarianza Dato un vettore aleatorio (anche non gaussiano) X = (X 1,..., X n ), chiamiamo sua media il vettore
Lezione 6 Richiami di Geometria Analitica
 1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
Probablità, Statistica e Processi Stocastici
 Probablità, Statistica e Processi Stocastici Franco Flandoli, Università di Pisa Programma del corso vettori gaussiani, PCA ed fpca altri metodi di analisi e previsione di serie storiche catene di Markov
Probablità, Statistica e Processi Stocastici Franco Flandoli, Università di Pisa Programma del corso vettori gaussiani, PCA ed fpca altri metodi di analisi e previsione di serie storiche catene di Markov
LEZIONE 3. a + b + 2c + e = 1 b + d + g = 0 3b + f + 3g = 2. a b c d e f g
 LEZIONE 3 3.. Matrici fortemente ridotte per righe. Nella precedente lezione abbiamo introdotto la nozione di soluzione di un sistema di equazioni lineari. In questa lezione ci poniamo il problema di descrivere
LEZIONE 3 3.. Matrici fortemente ridotte per righe. Nella precedente lezione abbiamo introdotto la nozione di soluzione di un sistema di equazioni lineari. In questa lezione ci poniamo il problema di descrivere
CORSO DI GEOMETRIA DETERMINANTE A.A. 2018/2019 PROF. VALENTINA BEORCHIA
 CORSO DI GEOMETRIA DETERMINANTE AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Definizione induttiva di determinante 1 2 Caratterizzazione delle matrici quadrate di rango massimo 5 3 Regole di Laplace 6
CORSO DI GEOMETRIA DETERMINANTE AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Definizione induttiva di determinante 1 2 Caratterizzazione delle matrici quadrate di rango massimo 5 3 Regole di Laplace 6
0.1 Condizione sufficiente di diagonalizzabilità
 0.1. CONDIZIONE SUFFICIENTE DI DIAGONALIZZABILITÀ 1 0.1 Condizione sufficiente di diagonalizzabilità È naturale porsi il problema di sapere se ogni matrice sia o meno diagonalizzabile. Abbiamo due potenziali
0.1. CONDIZIONE SUFFICIENTE DI DIAGONALIZZABILITÀ 1 0.1 Condizione sufficiente di diagonalizzabilità È naturale porsi il problema di sapere se ogni matrice sia o meno diagonalizzabile. Abbiamo due potenziali
LEZIONE 2. ( ) a 1 x 1 + a 2 x a n x n = b, ove a j, b R sono fissati.
 LEZIONE 2 2 Sistemi di equazioni lineari Definizione 2 Un equazione lineare nelle n incognite x, x 2,, x n a coefficienti reali, è un equazione della forma (2 a x + a 2 x 2 + + a n x n = b, ove a j, b
LEZIONE 2 2 Sistemi di equazioni lineari Definizione 2 Un equazione lineare nelle n incognite x, x 2,, x n a coefficienti reali, è un equazione della forma (2 a x + a 2 x 2 + + a n x n = b, ove a j, b
LEZIONE i i 3
 LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Parte 12b. Riduzione a forma canonica
 Parte 2b. Riduzione a forma canonica A. Savo Appunti del Corso di Geometria 202-3 Indice delle sezioni. Coniche, 2. Esempio di riduzione, 4 3. Teoremi fondamentali, 6 4. Come determinare l equazione canonica,
Parte 2b. Riduzione a forma canonica A. Savo Appunti del Corso di Geometria 202-3 Indice delle sezioni. Coniche, 2. Esempio di riduzione, 4 3. Teoremi fondamentali, 6 4. Come determinare l equazione canonica,
Applicazioni lineari simmetriche e forme quadratiche reali.
 Applicazioni lineari simmetriche e forme quadratiche reali 1 Applicazioni lineari simmetriche Consideriamo lo spazio IR n col prodotto scalare canonico X Y = t XY = x 1 y 1 + + x n y n Definizione Un applicazione
Applicazioni lineari simmetriche e forme quadratiche reali 1 Applicazioni lineari simmetriche Consideriamo lo spazio IR n col prodotto scalare canonico X Y = t XY = x 1 y 1 + + x n y n Definizione Un applicazione
Spazi vettoriali euclidei.
 Spazi vettoriali euclidei Prodotto scalare, lunghezza e ortogonalità in R n Consideriamo lo spazio vettoriale R n = { =,,, n R}, n con la somma fra vettori e il prodotto di un vettore per uno scalare definiti
Spazi vettoriali euclidei Prodotto scalare, lunghezza e ortogonalità in R n Consideriamo lo spazio vettoriale R n = { =,,, n R}, n con la somma fra vettori e il prodotto di un vettore per uno scalare definiti
Il metodo dei minimi quadrati
 Il metodo dei minimi quadrati 1 Posizione del problema Introduciamo la problematica con un semplice esempio pratico. Supponiamo di avere a disposizione una certa quantità x di oggetti tutti uguali tra
Il metodo dei minimi quadrati 1 Posizione del problema Introduciamo la problematica con un semplice esempio pratico. Supponiamo di avere a disposizione una certa quantità x di oggetti tutti uguali tra
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria: Elettronica. Corso di Geometria ed Algebra Docente F. Flamini
 Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria: Elettronica Corso di Geometria ed Algebra Docente F. Flamini Capitolo IV - 3: Teorema Spettrale degli operatori autoaggiunti e Teorema
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria: Elettronica Corso di Geometria ed Algebra Docente F. Flamini Capitolo IV - 3: Teorema Spettrale degli operatori autoaggiunti e Teorema
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI
 CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
LEZIONE i 0 3 Le sottomatrici 2 2 di A sono. 1 2 i i 3. Invece (
 LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Scheda n.3: densità gaussiana e Beta
 Scheda n.3: densità gaussiana e Beta October 10, 2008 1 Definizioni generali Chiamiamo densità di probabilità (pdf ) ogni funzione integrabile f (x) definita per x R tale che i) f (x) 0 per ogni x R ii)
Scheda n.3: densità gaussiana e Beta October 10, 2008 1 Definizioni generali Chiamiamo densità di probabilità (pdf ) ogni funzione integrabile f (x) definita per x R tale che i) f (x) 0 per ogni x R ii)
Rango di una matrice e teorema di Rouché-Capelli
 Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
9.3 Il metodo dei minimi quadrati in formalismo matriciale
 9.3. IL METODO DEI MINIMI QUADRATI IN FORMALISMO MATRICIALE 121 9.3 Il metodo dei minimi quadrati in formalismo matriciale Per applicare il MMQ a funzioni polinomiali, ovvero a dipendenze di una grandezza
9.3. IL METODO DEI MINIMI QUADRATI IN FORMALISMO MATRICIALE 121 9.3 Il metodo dei minimi quadrati in formalismo matriciale Per applicare il MMQ a funzioni polinomiali, ovvero a dipendenze di una grandezza
Capitolo IV SPAZI VETTORIALI EUCLIDEI
 Capitolo IV SPAZI VETTORIALI EUCLIDEI È ben noto che in VO 3 si possono considerare strutture più ricche di quella di spazio vettoriale; si pensi in particolare all operazioni di prodotto scalare di vettori.
Capitolo IV SPAZI VETTORIALI EUCLIDEI È ben noto che in VO 3 si possono considerare strutture più ricche di quella di spazio vettoriale; si pensi in particolare all operazioni di prodotto scalare di vettori.
p(ϕ) = a 0 Id + a 1 ϕ + + a n ϕ n,
 1. Autospazi e autospazi generalizzati Sia ϕ: V V un endomorfismo. Allora l assegnazione x ϕ induce un morfismo di anelli ρ: K[x] End K (V ). Più esplicitamente, al polinomio p dato da viene associato
1. Autospazi e autospazi generalizzati Sia ϕ: V V un endomorfismo. Allora l assegnazione x ϕ induce un morfismo di anelli ρ: K[x] End K (V ). Più esplicitamente, al polinomio p dato da viene associato
Esercizi Di Geometria 1 (BAER) Canale 1
 Esercizi Di Geometria 1 (BAER) Canale 1 SETTIMANA 9 (23 29 Novembre 2015) da consegnare Mercoledi 2 Dicembre. Esercizio 1. Sia E = (V,, ) uno spazio metrico finito dimensionale. sottospazio vettoriale
Esercizi Di Geometria 1 (BAER) Canale 1 SETTIMANA 9 (23 29 Novembre 2015) da consegnare Mercoledi 2 Dicembre. Esercizio 1. Sia E = (V,, ) uno spazio metrico finito dimensionale. sottospazio vettoriale
REGRESSIONE E CORRELAZIONE
 REGRESSIONE E CORRELAZIONE Nella Statistica, per studio della connessione si intende la ricerca di eventuali relazioni, di dipendenza ed interdipendenza, intercorrenti tra due variabili statistiche 1.
REGRESSIONE E CORRELAZIONE Nella Statistica, per studio della connessione si intende la ricerca di eventuali relazioni, di dipendenza ed interdipendenza, intercorrenti tra due variabili statistiche 1.
LAUREA IN INGEGNERIA CIVILE ED AMBIENTE-TERRITORIO Corso di Matematica 2 Padova TEMA n.1
 LAUREA IN INGEGNERIA CIVILE ED AMBIENTE-TERRITORIO Corso di Matematica Padova -8-8 TEMA n.1 PARTE 1. Quesiti preliminari Stabilire se le seguenti affermazioni sono vere o false giustificando brevemente
LAUREA IN INGEGNERIA CIVILE ED AMBIENTE-TERRITORIO Corso di Matematica Padova -8-8 TEMA n.1 PARTE 1. Quesiti preliminari Stabilire se le seguenti affermazioni sono vere o false giustificando brevemente
Note per il corso di Geometria Corso di laurea in Ing. Edile/Architettura. 4 Sistemi lineari. Metodo di eliminazione di Gauss Jordan
 Note per il corso di Geometria 2006-07 Corso di laurea in Ing. Edile/Architettura Sistemi lineari. Metodo di eliminazione di Gauss Jordan.1 Operazioni elementari Abbiamo visto che un sistema di m equazioni
Note per il corso di Geometria 2006-07 Corso di laurea in Ing. Edile/Architettura Sistemi lineari. Metodo di eliminazione di Gauss Jordan.1 Operazioni elementari Abbiamo visto che un sistema di m equazioni
CORSO DI STATISTICA (parte 1) - ESERCITAZIONE 6
 CORSO DI STATISTICA (parte 1) - ESERCITAZIONE 6 Dott.ssa Antonella Costanzo a.costanzo@unicas.it Esercizio 1. Associazione, correlazione e dipendenza tra caratteri In un collettivo di 11 famiglie è stata
CORSO DI STATISTICA (parte 1) - ESERCITAZIONE 6 Dott.ssa Antonella Costanzo a.costanzo@unicas.it Esercizio 1. Associazione, correlazione e dipendenza tra caratteri In un collettivo di 11 famiglie è stata
Volumi in spazi euclidei 12 dicembre 2014
 Volumi in spazi euclidei 12 dicembre 2014 1 Definizioni In uno spazio euclideo reale V di dimensione n siano dati k n vettori linearmente indipendenti e sia Π := Π(v 1 v 2... v k ) il parallelepipedo generato
Volumi in spazi euclidei 12 dicembre 2014 1 Definizioni In uno spazio euclideo reale V di dimensione n siano dati k n vettori linearmente indipendenti e sia Π := Π(v 1 v 2... v k ) il parallelepipedo generato
Nel modello omoschedastico la varianza dell errore non dipende da i ed è quindi pari a σ 0.
 Regressione [] el modello di regressione lineare si assume una relazione di tipo lineare tra il valore medio della variabile dipendente Y e quello della variabile indipendente X per cui Il modello si scrive
Regressione [] el modello di regressione lineare si assume una relazione di tipo lineare tra il valore medio della variabile dipendente Y e quello della variabile indipendente X per cui Il modello si scrive
12 gennaio Commenti esame di geometria - Ing. gestionale - a.a
 Questo documento riporta commenti, approfondimenti o metodi di soluzione alternativi per alcuni esercizi dell esame Ovviamente alcuni esercizi potevano essere risolti utilizzando metodi ancora diversi
Questo documento riporta commenti, approfondimenti o metodi di soluzione alternativi per alcuni esercizi dell esame Ovviamente alcuni esercizi potevano essere risolti utilizzando metodi ancora diversi
Algebra delle matrici
 Algebra delle matrici Metodo di Gauss-Jordan per l inversione di una matrice. Nella lezione scorsa abbiamo visto che un modo per determinare l eventuale inversa di una matrice quadrata A consiste nel risolvere
Algebra delle matrici Metodo di Gauss-Jordan per l inversione di una matrice. Nella lezione scorsa abbiamo visto che un modo per determinare l eventuale inversa di una matrice quadrata A consiste nel risolvere
Corso di Matematica Discreta. Anno accademico Appunti sulla diagonalizzazione.
 Corso di Matematica Discreta. Anno accademico 2008-2009 Appunti sulla diagonalizzazione. Autovalori e autovettori di un endomorfismo lineare. Sia T : V V una applicazione lineare da uno spazio vettoriale
Corso di Matematica Discreta. Anno accademico 2008-2009 Appunti sulla diagonalizzazione. Autovalori e autovettori di un endomorfismo lineare. Sia T : V V una applicazione lineare da uno spazio vettoriale
Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti)
 Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti) April 14, 2011 (alcune note non complete sugli argomenti trattati: eventuali completamenti saranno aggiunti)
Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti) April 14, 2011 (alcune note non complete sugli argomenti trattati: eventuali completamenti saranno aggiunti)
25 - Funzioni di più Variabili Introduzione
 Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 25 - Funzioni di più Variabili Introduzione Anno Accademico 2013/2014 M. Tumminello
Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 25 - Funzioni di più Variabili Introduzione Anno Accademico 2013/2014 M. Tumminello
Isometrie e cambiamenti di riferimento
 Isometrie e cambiamenti di riferimento Isometrie Le isometrie sono trasformazioni del piano o dello spazio che conservano angoli e distanze. Esempi sono le rotazioni del piano, le riflessioni in una retta
Isometrie e cambiamenti di riferimento Isometrie Le isometrie sono trasformazioni del piano o dello spazio che conservano angoli e distanze. Esempi sono le rotazioni del piano, le riflessioni in una retta
Statistica II Laurea magistrale in Ing. Gestionale a.a. 2012/13 Esempi di domande brevi. 1. Definizione di quantile gaussiano standard
 Statistica II Laurea magistrale in Ing. Gestionale a.a. 2012/13 Esempi di domande brevi 1. Definizione di quantile gaussiano standard 2. Cosa calcola il comando pnorm (risp. qnorm, dnorm, rnorm) 3. Come
Statistica II Laurea magistrale in Ing. Gestionale a.a. 2012/13 Esempi di domande brevi 1. Definizione di quantile gaussiano standard 2. Cosa calcola il comando pnorm (risp. qnorm, dnorm, rnorm) 3. Come
Punti di massimo o di minimo per funzioni di n variabili reali
 Punti di massimo o di minimo per funzioni di n variabili reali Dati f : A R n R ed X 0 A, X 0 si dice : punto di minimo assoluto se X A, f ( x ) f ( X 0 ) punto di massimo assoluto se X A, f ( x ) f (
Punti di massimo o di minimo per funzioni di n variabili reali Dati f : A R n R ed X 0 A, X 0 si dice : punto di minimo assoluto se X A, f ( x ) f ( X 0 ) punto di massimo assoluto se X A, f ( x ) f (
Corso in Statistica Medica
 Corso in Statistica Medica Introduzione alle tecniche statistiche di elaborazione dati Regressione e correlazione Dott. Angelo Menna Università degli Studi di Chieti G. d Annunziod Annunzio Anno Accademico
Corso in Statistica Medica Introduzione alle tecniche statistiche di elaborazione dati Regressione e correlazione Dott. Angelo Menna Università degli Studi di Chieti G. d Annunziod Annunzio Anno Accademico
A =, c d. d = ad cb. c d A =
 Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
Il Teorema Spettrale. 0.1 Applicazioni lineari simmetriche ed hermitiane
 0.1. APPLICAZIONI LINEARI SIMMETRICHE ED HERMITIANE 1 Il Teorema Spettrale In questa nota vogliamo esaminare la dimostrazione del Teorema Spettrale e studiare le sue conseguenze per quanto riguarda i prodotti
0.1. APPLICAZIONI LINEARI SIMMETRICHE ED HERMITIANE 1 Il Teorema Spettrale In questa nota vogliamo esaminare la dimostrazione del Teorema Spettrale e studiare le sue conseguenze per quanto riguarda i prodotti
Dispensa di Statistica
 Dispensa di Statistica 1 parziale 2012/2013 Diagrammi... 2 Indici di posizione... 4 Media... 4 Moda... 5 Mediana... 5 Indici di dispersione... 7 Varianza... 7 Scarto Quadratico Medio (SQM)... 7 La disuguaglianza
Dispensa di Statistica 1 parziale 2012/2013 Diagrammi... 2 Indici di posizione... 4 Media... 4 Moda... 5 Mediana... 5 Indici di dispersione... 7 Varianza... 7 Scarto Quadratico Medio (SQM)... 7 La disuguaglianza
Algebra lineare e geometria AA Appunti sul cambio di base in uno spazio vettoriale
 Algebra lineare e geometria AA. -7 Appunti sul cambio di base in uno spazio vettoriale Matrice di un applicazione lineare Siano V e W due spazi vettoriali su un campo K {R, C}, entrambi finitamente generati,
Algebra lineare e geometria AA. -7 Appunti sul cambio di base in uno spazio vettoriale Matrice di un applicazione lineare Siano V e W due spazi vettoriali su un campo K {R, C}, entrambi finitamente generati,
LEZIONE 12. v = α 1 v α n v n =
 LEZIONE 12 12.1. Combinazioni lineari. Definizione 12.1.1. Sia V uno spazio vettoriale su k = R, C e v 1,..., v n V vettori fissati. Un vettore v V si dice combinazione lineare di v 1,..., v n se esistono
LEZIONE 12 12.1. Combinazioni lineari. Definizione 12.1.1. Sia V uno spazio vettoriale su k = R, C e v 1,..., v n V vettori fissati. Un vettore v V si dice combinazione lineare di v 1,..., v n se esistono
1. Complemento ortogonale di un vettore non nullo Abbiamo visto che nel piano
 Geometria e Algebra (II), 11.12.12 1. Complemento ortogonale di un vettore non nullo Abbiamo visto che nel piano P O i vettori ortogonali ad un dato vettore non nullo descrivono una retta per O, e nello
Geometria e Algebra (II), 11.12.12 1. Complemento ortogonale di un vettore non nullo Abbiamo visto che nel piano P O i vettori ortogonali ad un dato vettore non nullo descrivono una retta per O, e nello
Analisi Matematica 2
 Analisi Matematica Appunti delle lezioni tenute dal Prof. A. Fonda Università di Trieste CdL Matematica a.a. 07/08 La derivata direzionale In questa sezione E sarà un sottoinsieme aperto di R N x 0 un
Analisi Matematica Appunti delle lezioni tenute dal Prof. A. Fonda Università di Trieste CdL Matematica a.a. 07/08 La derivata direzionale In questa sezione E sarà un sottoinsieme aperto di R N x 0 un
Lezione 5: Applicazioni Lineari. 1 Definizione di applicazione lineare
 Lezione 5: Applicazioni Lineari Le applicazioni lineari sono funzioni tra spazi vettoriali che ne rispettano la struttura, cioe che conservano le operazioni di somma tra vettori e moltiplicazione di un
Lezione 5: Applicazioni Lineari Le applicazioni lineari sono funzioni tra spazi vettoriali che ne rispettano la struttura, cioe che conservano le operazioni di somma tra vettori e moltiplicazione di un
Algebra lineare e geometria AA Appunti sul cambio di base in uno spazio vettoriale
 Algebra lineare e geometria AA. 8-9 Appunti sul cambio di base in uno spazio vettoriale Matrice di un applicazione lineare Siano V e W due spazi vettoriali su un campo K {R, C}, entrambi finitamente generati,
Algebra lineare e geometria AA. 8-9 Appunti sul cambio di base in uno spazio vettoriale Matrice di un applicazione lineare Siano V e W due spazi vettoriali su un campo K {R, C}, entrambi finitamente generati,
Appunti su Indipendenza Lineare di Vettori
 Appunti su Indipendenza Lineare di Vettori Claudia Fassino a.a. Queste dispense, relative a una parte del corso di Matematica Computazionale (Laurea in Informatica), rappresentano solo un aiuto per lo
Appunti su Indipendenza Lineare di Vettori Claudia Fassino a.a. Queste dispense, relative a una parte del corso di Matematica Computazionale (Laurea in Informatica), rappresentano solo un aiuto per lo
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
1 Addendum su Diagonalizzazione
 Addendum su Diagonalizzazione Vedere le dispense per le definizioni di autovettorre, autovalore e di trasformazione lineare (o matrice) diagonalizzabile. In particolare, si ricorda che una condizione necessaria
Addendum su Diagonalizzazione Vedere le dispense per le definizioni di autovettorre, autovalore e di trasformazione lineare (o matrice) diagonalizzabile. In particolare, si ricorda che una condizione necessaria
(V) (FX) L unione di due basi di uno spazio vettoriale è ancora una base dello spazio vettoriale.
 8 gennaio 2009 - PROVA D ESAME - Geometria e Algebra T NOME: MATRICOLA: a=, b=, c= Sostituire ai parametri a, b, c rispettivamente la terzultima, penultima e ultima cifra del proprio numero di matricola
8 gennaio 2009 - PROVA D ESAME - Geometria e Algebra T NOME: MATRICOLA: a=, b=, c= Sostituire ai parametri a, b, c rispettivamente la terzultima, penultima e ultima cifra del proprio numero di matricola
- ciascun autovalore di T ha molteplicità geometrica uguale alla moltplicitaà algebrica.
 Lezioni del 14.05 e 17.05 In queste lezioni si sono svolti i seguenti argomenti. Ripresa del teorema generale che fornisce condizioni che implicano la diagonalizzabilità, indebolimento delle ipotesi, e
Lezioni del 14.05 e 17.05 In queste lezioni si sono svolti i seguenti argomenti. Ripresa del teorema generale che fornisce condizioni che implicano la diagonalizzabilità, indebolimento delle ipotesi, e
Capitolo 8 Forme quadratiche e loro applicazioni Esercizi svolti Tutorato di geometria e algebra lineare. Marco Robutti
 Capitolo 8 Forme quadratiche e loro applicazioni Esercizi svolti Tutorato di geometria e algebra lineare Marco Robutti 5 Ottobre 2017 1 Introduzione Gli esercizi di questo capitolo riguardano i seguenti
Capitolo 8 Forme quadratiche e loro applicazioni Esercizi svolti Tutorato di geometria e algebra lineare Marco Robutti 5 Ottobre 2017 1 Introduzione Gli esercizi di questo capitolo riguardano i seguenti
4 Autovettori e autovalori
 4 Autovettori e autovalori 41 Cambiamenti di base Sia V uno spazio vettoriale tale che dim V n Si è visto in sezione 12 che uno spazio vettoriale ammette basi distinte, ma tutte con la medesima cardinalità
4 Autovettori e autovalori 41 Cambiamenti di base Sia V uno spazio vettoriale tale che dim V n Si è visto in sezione 12 che uno spazio vettoriale ammette basi distinte, ma tutte con la medesima cardinalità
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni. 3. Sistemi di equazioni lineari
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Esercizi svolti. delle matrici
 Esercizi svolti. astratti. Si dica se l insieme delle coppie reali (x, y) soddisfacenti alla relazione x + y è un sottospazio vettoriale di R La risposta è sì, perchè l unica coppia reale che soddisfa
Esercizi svolti. astratti. Si dica se l insieme delle coppie reali (x, y) soddisfacenti alla relazione x + y è un sottospazio vettoriale di R La risposta è sì, perchè l unica coppia reale che soddisfa
Geometria per Fisica e Astrofisica
 Geometria per Fisica e Astrofisica Soluzione esercizi - Foglio 3 Esercizio. Risolvere i seguenti sistemi lineari al variare dei parametri reali α β e k < < (a) x + y z = αx + αy + βz = x + y z = β. (b)
Geometria per Fisica e Astrofisica Soluzione esercizi - Foglio 3 Esercizio. Risolvere i seguenti sistemi lineari al variare dei parametri reali α β e k < < (a) x + y z = αx + αy + βz = x + y z = β. (b)
Prodotti scalari e matrici
 Prodotti scalari e matrici 1 Forme bilineari e matrici In questa sezione vogliamo studiare la corrispondenza biunivoca che esiste tra l insieme delle forme bilineari su di un certo spazio vettoriale V
Prodotti scalari e matrici 1 Forme bilineari e matrici In questa sezione vogliamo studiare la corrispondenza biunivoca che esiste tra l insieme delle forme bilineari su di un certo spazio vettoriale V
Equivalentemente, le colonne di A sono linearmente indipendenti se e solo se
 Lezioni di Algebra Lineare. Versione novembre 2008 VI. Il determinante Il determinante det A di una matrice A, reale e quadrata, è un numero reale associato ad A. Dunque det è una funzione dall insieme
Lezioni di Algebra Lineare. Versione novembre 2008 VI. Il determinante Il determinante det A di una matrice A, reale e quadrata, è un numero reale associato ad A. Dunque det è una funzione dall insieme
LEZIONE 4. Le sottomatrici 2 2 di A sono. Invece ( 1 3 non è sottomatrice di A.
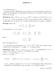 LEZIONE 4 4 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 4 4 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Similitudine (ortogonale) e congruenza (ortogonale) di matrici.
 Lezione del 4 giugno. Il riferimento principale di questa lezione e costituito da parti di: 2 Forme bilineari, quadratiche e matrici simmetriche associate, 3 Congruenza di matrici simmetriche, 5 Forme
Lezione del 4 giugno. Il riferimento principale di questa lezione e costituito da parti di: 2 Forme bilineari, quadratiche e matrici simmetriche associate, 3 Congruenza di matrici simmetriche, 5 Forme
Risoluzione di sistemi lineari sparsi e di grandi dimensioni
 Risoluzione di sistemi lineari sparsi e di grandi dimensioni Un sistema lineare Ax = b con A R n n, b R n, è sparso quando il numero di elementi della matrice A diversi da zero è αn, con n α. Una caratteristica
Risoluzione di sistemi lineari sparsi e di grandi dimensioni Un sistema lineare Ax = b con A R n n, b R n, è sparso quando il numero di elementi della matrice A diversi da zero è αn, con n α. Una caratteristica
Lezioni di Algebra Lineare V. Autovalori e autovettori
 Lezioni di Algebra Lineare V. Autovalori e autovettori Versione novembre 2008 Contenuto 1. Cambiamenti di base 2. Applicazioni lineari, matrici e cambiamenti di base 3. Autovalori e autovettori 2 1. Cambiamenti
Lezioni di Algebra Lineare V. Autovalori e autovettori Versione novembre 2008 Contenuto 1. Cambiamenti di base 2. Applicazioni lineari, matrici e cambiamenti di base 3. Autovalori e autovettori 2 1. Cambiamenti
Word ha il vantaggio che possiamo salvare un po' di risultati, anche grafici
 INTRODUZIONE. TABELLE, CORRELAZIONE E PLOT Usare un foglio txt (o word o simile) di appoggio Word ha il vantaggio che possiamo salvare un po' di risultati, anche grafici Copiare su R il comando A
INTRODUZIONE. TABELLE, CORRELAZIONE E PLOT Usare un foglio txt (o word o simile) di appoggio Word ha il vantaggio che possiamo salvare un po' di risultati, anche grafici Copiare su R il comando A
1 Il polinomio minimo.
 Abstract Il polinomio minimo, così come il polinomio caratterisico, è un importante invariante per le matrici quadrate. La forma canonica di Jordan è un approssimazione della diagonalizzazione, e viene
Abstract Il polinomio minimo, così come il polinomio caratterisico, è un importante invariante per le matrici quadrate. La forma canonica di Jordan è un approssimazione della diagonalizzazione, e viene
Esercitazioni del Marzo di Geometria A
 Esercitazioni del -5 Marzo di Geometria A Università degli Studi di Trento Corso di laurea in Matematica AA 07/08 Matteo Bonini matteobonini@unitnit Esercizio Si consideri la matrice 0 A 0 0 0 0 (i Scrivere
Esercitazioni del -5 Marzo di Geometria A Università degli Studi di Trento Corso di laurea in Matematica AA 07/08 Matteo Bonini matteobonini@unitnit Esercizio Si consideri la matrice 0 A 0 0 0 0 (i Scrivere
ed un operazione di moltiplicazione per scalari reali u u 2u
 Geometria e Algebra (II), 0... Consideriamo il piano della geometria euclidea, intuitivamente inteso, e sia un punto fissato in esso. Sull insieme P dei vettori del piano applicati nel punto sono definite
Geometria e Algebra (II), 0... Consideriamo il piano della geometria euclidea, intuitivamente inteso, e sia un punto fissato in esso. Sull insieme P dei vettori del piano applicati nel punto sono definite
MATRICI E SISTEMI LINEARI
 MATRICI E SISTEMI LINEARI - PARTE I - Felice Iavernaro Dipartimento di Matematica Università di Bari 27 Febbraio 2006 Felice Iavernaro (Univ. Bari) Matrici e Sistemi lineari 27/02/2006 1 / 1 Definizione
MATRICI E SISTEMI LINEARI - PARTE I - Felice Iavernaro Dipartimento di Matematica Università di Bari 27 Febbraio 2006 Felice Iavernaro (Univ. Bari) Matrici e Sistemi lineari 27/02/2006 1 / 1 Definizione
Minimi quadrati ordinari Interpretazione geometrica. Eduardo Rossi
 Minimi quadrati ordinari Interpretazione geometrica Eduardo Rossi Il MRLM Il modello di regressione lineare multipla è usato per studiare le relazioni tra la variabile dipendente e diverse variabili indipendenti
Minimi quadrati ordinari Interpretazione geometrica Eduardo Rossi Il MRLM Il modello di regressione lineare multipla è usato per studiare le relazioni tra la variabile dipendente e diverse variabili indipendenti
Autovalori, Autovettori, Diagonalizzazione.
 Autovalori Autovettori Diagonalizzazione Autovalori e Autovettori Definizione Sia V uno spazio vettoriale sul campo K = R o C e sia T : V V un endomorfismo Un vettore non nullo v V \ {O} si dice autovettore
Autovalori Autovettori Diagonalizzazione Autovalori e Autovettori Definizione Sia V uno spazio vettoriale sul campo K = R o C e sia T : V V un endomorfismo Un vettore non nullo v V \ {O} si dice autovettore
MATRICI ORTOGONALI. MATRICI SIMMETRICHE E FORME QUADRATICHE
 DIAGONALIZZAZIONE 1 MATRICI ORTOGONALI. MATRICI SIMMETRICHE E FORME QUADRATICHE Matrici ortogonali e loro proprietà. Autovalori ed autospazi di matrici simmetriche reali. Diagonalizzazione mediante matrici
DIAGONALIZZAZIONE 1 MATRICI ORTOGONALI. MATRICI SIMMETRICHE E FORME QUADRATICHE Matrici ortogonali e loro proprietà. Autovalori ed autospazi di matrici simmetriche reali. Diagonalizzazione mediante matrici
NOTE DI ALGEBRA LINEARE v = a 1 v a n v n, w = b 1 v b n v n
 NOTE DI ALGEBRA LINEARE 2- MM 9 NOVEMBRE 2 Combinazioni lineari e generatori Sia K un campo e V uno spazio vettoriale su K Siano v,, v n vettori in V Definizione Un vettore v V si dice combinazione lineare
NOTE DI ALGEBRA LINEARE 2- MM 9 NOVEMBRE 2 Combinazioni lineari e generatori Sia K un campo e V uno spazio vettoriale su K Siano v,, v n vettori in V Definizione Un vettore v V si dice combinazione lineare
Note sull algoritmo di Gauss
 Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
x1 + 2x 2 + 3x 3 = 0 nelle tre incognite x 1, x 2, x 3. Possiamo risolvere l equazione ricavando l incognita x 1 x 1 = 2x 2 3x 3 2r 1 3r 2 x 2 x 3
 Matematica II -..9 Spazio delle soluzioni di un sistema lineare omogeneo.. Consideriamo l equazione lineare omogenea nelle tre incognite x, x, x 3. x + x + 3x 3 = Possiamo risolvere l equazione ricavando
Matematica II -..9 Spazio delle soluzioni di un sistema lineare omogeneo.. Consideriamo l equazione lineare omogenea nelle tre incognite x, x, x 3. x + x + 3x 3 = Possiamo risolvere l equazione ricavando
Si noti che la matrice trasposta A ha lo stesso determinante. Questa proprietà è generale;
 Ottavio Serra Matrici e determinanti In questa nota estenderemo a matrici quadrate di ordine n qualsiasi il concetto di determinante introdotto nelle scuole secondarie per matrici di ordine 2 come tecnica
Ottavio Serra Matrici e determinanti In questa nota estenderemo a matrici quadrate di ordine n qualsiasi il concetto di determinante introdotto nelle scuole secondarie per matrici di ordine 2 come tecnica
Esercitazione del
 Esercizi sulla regressione lineare. Esercitazione del 21.05.2013 Esercizio dal tema d esame del 13.06.2011. Si consideri il seguente campione di n = 9 osservazioni relative ai caratteri ed Y: 7 17 8 36
Esercizi sulla regressione lineare. Esercitazione del 21.05.2013 Esercizio dal tema d esame del 13.06.2011. Si consideri il seguente campione di n = 9 osservazioni relative ai caratteri ed Y: 7 17 8 36
Sviluppi e derivate delle funzioni elementari
 Sviluppi e derivate delle funzioni elementari In queste pagine dimostriamo gli sviluppi del prim ordine e le formule di derivazioni delle principali funzioni elementari. Utilizzeremo le uguaglianze lim
Sviluppi e derivate delle funzioni elementari In queste pagine dimostriamo gli sviluppi del prim ordine e le formule di derivazioni delle principali funzioni elementari. Utilizzeremo le uguaglianze lim
Spazi Vettoriali ed Applicazioni Lineari
 Spazi Vettoriali ed Applicazioni Lineari 1. Sottospazi Definizione. Sia V uno spazio vettoriale sul corpo C. Un sottoinsieme non vuoto W di V è un sottospazio vettoriale di V se è chiuso rispetto alla
Spazi Vettoriali ed Applicazioni Lineari 1. Sottospazi Definizione. Sia V uno spazio vettoriale sul corpo C. Un sottoinsieme non vuoto W di V è un sottospazio vettoriale di V se è chiuso rispetto alla
Esercizi vari sulle schede di statistica
 Esercizi vari sulle schede di statistica December 4, 2008 1 Introduzione Nelle prove scritte ci sarà un esercizio relativo alla parte di statistica e la sua implementazione con R. Tale parte dello scritto
Esercizi vari sulle schede di statistica December 4, 2008 1 Introduzione Nelle prove scritte ci sarà un esercizio relativo alla parte di statistica e la sua implementazione con R. Tale parte dello scritto
Probablità, Statistica e Processi Stocastici
 Probablità, Statistica e Processi Stocastici Franco Flandoli, Università di Pisa Riepilogo su PCA (affi ancare scheda R) Si parte da n variabili aleatorie X 1,..., X n. In pratica, si parte da una tabella
Probablità, Statistica e Processi Stocastici Franco Flandoli, Università di Pisa Riepilogo su PCA (affi ancare scheda R) Si parte da n variabili aleatorie X 1,..., X n. In pratica, si parte da una tabella
Corso di Laurea in Fisica. Geometria. a.a Prof. P. Piazza Diagonalizzazione delle forme bilineari simmetriche
 Corso di Laurea in Fisica. Geometria. a.a. 2009-10. Prof. P. Piazza Diagonalizzazione delle forme bilineari simmetriche Sia V uno spazio vettoriale reale. Sia 1. Osservazioni preliminari. : V V R un
Corso di Laurea in Fisica. Geometria. a.a. 2009-10. Prof. P. Piazza Diagonalizzazione delle forme bilineari simmetriche Sia V uno spazio vettoriale reale. Sia 1. Osservazioni preliminari. : V V R un
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette
 Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Contenuti Nel Piano
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Contenuti Nel Piano
{Geometria per [Fisica e (Fisica e Astrofisica)]}
![{Geometria per [Fisica e (Fisica e Astrofisica)]} {Geometria per [Fisica e (Fisica e Astrofisica)]}](/thumbs/103/157763717.jpg) {Geometria per [Fisica e (Fisica e Astrofisica)]} Foglio 9 - Soluzioni Esercizio (facoltativo) Un quadrato magico reale di ordine n è una matrice di M n n (R) tale che sommando gli elementi di ogni sua
{Geometria per [Fisica e (Fisica e Astrofisica)]} Foglio 9 - Soluzioni Esercizio (facoltativo) Un quadrato magico reale di ordine n è una matrice di M n n (R) tale che sommando gli elementi di ogni sua
Richiami di Algebra Lineare
 Richiami di Algebra Lineare Fabrizio Silvestri December 14, 010 Matrice Sia R il campo dei numeri reali. Si indica con R m n l insieme delle matrici ad elementi reali con m righe ed n colonne. Se A R n
Richiami di Algebra Lineare Fabrizio Silvestri December 14, 010 Matrice Sia R il campo dei numeri reali. Si indica con R m n l insieme delle matrici ad elementi reali con m righe ed n colonne. Se A R n
Capitolo 3 Matrici. Marco Robutti. Facoltà di ingegneria Università degli studi di Pavia. Anno accademico
 Capitolo 3 Matrici Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Anno accademico 2017-2018 Tutorato di geometria e algebra lineare Definizione (Matrice) Una matrice A M R (k, n) è
Capitolo 3 Matrici Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Anno accademico 2017-2018 Tutorato di geometria e algebra lineare Definizione (Matrice) Una matrice A M R (k, n) è
AUTOVALORI, AUTOVETTORI, AUTOSPAZI
 AUTOVALORI, AUTOVETTORI, AUTOSPAZI. Esercizi Esercizio. Sia f : R 3 R 3 l endomorfismo definito da f(x, y, z) = (x+y, y +z, x+z). Calcolare gli autovalori ed una base per ogni autospazio di f. Dire se
AUTOVALORI, AUTOVETTORI, AUTOSPAZI. Esercizi Esercizio. Sia f : R 3 R 3 l endomorfismo definito da f(x, y, z) = (x+y, y +z, x+z). Calcolare gli autovalori ed una base per ogni autospazio di f. Dire se
Contenuti aggiuntivi su matrici e determinanti, Dimostrazioni del Capitolo 3
 Contenuti aggiuntivi su matrici e determinanti, Dimostrazioni del Capitolo 3 Dimostrazione 310 Sia W = L(C A ) K Osserviamo che S è una base di W Infatti S è indipendente, inoltre ogni vettore di W dipende
Contenuti aggiuntivi su matrici e determinanti, Dimostrazioni del Capitolo 3 Dimostrazione 310 Sia W = L(C A ) K Osserviamo che S è una base di W Infatti S è indipendente, inoltre ogni vettore di W dipende
Soluzioni della prova scritta di Geometria 1 del 27 giugno 2019 (versione I)
 Soluzioni della prova scritta di Geometria 1 del 7 giugno 019 (versione I) Esercizio 1. Sia R 4 lo spazio quadridimensionale standard munito del prodotto scalare standard con coordinate canoniche (x 1,
Soluzioni della prova scritta di Geometria 1 del 7 giugno 019 (versione I) Esercizio 1. Sia R 4 lo spazio quadridimensionale standard munito del prodotto scalare standard con coordinate canoniche (x 1,
Sequenze (Sistemi) di Variabili Aleatorie Se consideriamo un numero di variabili aleatorie, generalmente dipendenti si parla equivalentemente di:
 Teoria dei Fenomeni Aleatori AA 01/13 Sequenze (Sistemi) di Variabili Aleatorie Se consideriamo un numero di variabili aleatorie, generalmente dipendenti si parla equivalentemente di: N-pla o Sequenza
Teoria dei Fenomeni Aleatori AA 01/13 Sequenze (Sistemi) di Variabili Aleatorie Se consideriamo un numero di variabili aleatorie, generalmente dipendenti si parla equivalentemente di: N-pla o Sequenza
Diagonalizzazione di matrici: autovalori, autovettori e costruzione della matrice diagonalizzante 1 / 13
 Diagonalizzazione di matrici: autovalori, autovettori e costruzione della matrice diagonalizzante 1 / 13 Matrici diagonali 2 / 13 Ricordiamo che una matrice quadrata si dice matrice diagonale se a ij =
Diagonalizzazione di matrici: autovalori, autovettori e costruzione della matrice diagonalizzante 1 / 13 Matrici diagonali 2 / 13 Ricordiamo che una matrice quadrata si dice matrice diagonale se a ij =
Introduzione all algebra delle matrici. Appunti a cura di Lara Ercoli
 Introduzione all algebra delle matrici ppunti a cura di Lara Ercoli Indice Definizioni 3. Matrici particolari............................ 4 2 Operazioni con le matrici 8 2. Somma di matrici.............................
Introduzione all algebra delle matrici ppunti a cura di Lara Ercoli Indice Definizioni 3. Matrici particolari............................ 4 2 Operazioni con le matrici 8 2. Somma di matrici.............................
