Proprietà Elettroniche del Silicio
|
|
|
- Ottaviana Palma
- 9 anni fa
- Просмотров:
Транскрипт
1 Proprietà Elettroniche del Silicio Il Silicio (Si) è un materiale semiconduttore. Il silicio puro ha una resistività elettrica relativamente elevata a temperature ambiente (RT). In un semiconduttore vi sono 2 tipi di portatori di carica: Elettroni (di conduzione) carichi negativamente; Lacune cariche positivamente. La concentrazione (#/cm 3 )dielettronidiconduzioneedilacunepuò essere modificata in vari modi: aggiungendo specifici atomi impurezza (droganti) applicando un campo elettrico cambiando la temperatura irraggiando con particelle energetiche (p. es. fotoni)
2 Proprietà strutturali I solidi possono classificarsi in tre forme: amorfi(atomi disposti irregolarmente, es. vetro) policristalli (piccole regione ordinate dette grani, es. poly-si come elettrodo di gate nei MOSFET) cristalli (ordine a lungo raggio con disposizione regolare degli atomi, es. c-si, diamante)
3 Atomo di Silicio Cristallo di Silicio struttura del diamante I dispositivi a semiconduttore ad elevate prestazioni richiedono un materiale pressochè privo di difetti.
4 Notazione cristallografica Indici di Miller h: inverso dell intercetta sull asse x k: inverso dell intercetta sull asse y Notazione ( h k l ) { h k l } [ h k l ] < h k l > Interpretazione piano cristallino piani equivalenti direzioni cristalline direzioni equivalenti l: inverso dell intercetta sull asse z Si esprimono i valori delle intercette in multipli della costante reticolare; h k ed l sono gli interi più piccoli che stanno nel medesimo rapporto.
5 Piani cristallografici Cella unitaria costante reticolare Si =5.431 Å ρ = N at /V = 8/(5.431 Å) 3 = = atomi/cm 3 vista in direzione <111> vista in direzione <100> vista in direzione <110>
6 r Livelli di energia 3p 2 3s 2 2p 6 2s 2 B a r r i e r a d i p o t e n z i a l e 3p 2 3s 2 2p 6 2s 2 B a r r i e r a d i p o t e n z i a l e 3p 2 3s 2 2p 6 2s 2 1s 2 1s 2 1s 2 Si a>>r Si Si Atomo isolato (idrogeno H) E E 5 4 E 3 E 2 3p 2 3s 2 2p 6 E n ( H) mq 13.6 = = 8ε hn n (Modello di Bohr) ev E 1 2s 2 1s 2 Si
7 Formazione delle bande di energia N atomi disposti regolarmente Si Si Si Si Si 1s 2
8 Formazione delle bande di energia
9 Calcolo formale: Equazione di Schröedinger L equazione di Schröedinger è una relazione matematica che descrive il comportamento ondulatorio di una particella (elettrone) 2 d Ψ 2m( E V) Ψ= dx E è l energia totale, V l energia potenziale, m la massa della particella Ψ è la funzione d onda dell elettrone ΨΨ*dx è la probabilità di trovare l eletrone nell intervallo spaziale dx. 0
10 Equazione di Schröedinger per trovare la relazione esistente tra l energia ed il momento degli elettroni in un semiconduttore occorre risolvere l eq. di Schröedinger (EqSc) elettrone libero (nessuna interazione con ioni reticolo V=0 in EqSc) ikx ( ϖ t) 2π Ψ ( xt, ) = Ae conk= e p= λ ( p momento dell ' elettrone) h p k p = k E = = = m m m λ * de 2 e 2 de = m = m = massa efficace dp m dp relazione parabolica tra energia e momento h λ pesante leggera
11 Tipiche strutture a bande di energia a 0 K
12 Gap di energia per il Silicio cristallino a temperatura ambiente (RT) l ampiezza dela banda proibita per il Si è 1.12 ev E ( T) = T 4 2 in generale g T con con T in gradi Kelvin ed E g in ev
13 Silicio in equilibrio termico: Concentrazione di portatori intrinseci Per predire, quantitativamente, il numero di elettroni (e lacune) liberi in un semiconduttore, occorre conoscere: 1. La densità di stati permessi nella banda di energia 2. La probabilità che questi stati siano occupati
14 Densità degli stati Nello spazio rettangolare k la densità di punti è 4 π 3 k+ dk k 4πk dk ( ) Dividendo per il volume della cella unitaria e tenendo conto del principio di esclusione di Pauli 2 2 4π k dk k 2 = dk = n( k) dk numero di elettroni 3 2 8π π k = k 2 ( = ) 2 2 essendo E m si ottiene ipotizzando m cost ( ) 1 3 ( ) ( ) n E de = 2m E de 2 3 2π
15 Densità degli stati g c (E)dE è la densità degli stati nella banda di conduzione compresa tra E e E+dE analogamente g v (E)dE è la densità di stati nella banda di valenza tra E e E+dE dalla meccanica quantistica 1 gc E m 2 3 n E Ec 2π 1 gv E m 2 3 p Ev E 2π ( ) = ( 2 ) ( ) ( ) = ( 2 ) ( ) m n, m p = massa efficace di elettroni e lacune E c, E v = limite di banda di conduzione e valenza
16 Probabilità di occupazione: distribuzione di Fermi-Dirac La probabilità che una stato di energia sia occupato da un elettrone è descritta dalla distribuzione di Fermi-Dirac f E ( ) = ( ) essendo E f il livello di energia per cui f D (E f ) = 0.5 (probabilità di occupazione pari al 50%) per E >> E f f D (E f ) tende alla statistica di Maxwell- Boltzmann 1 1 D E E kt + ( E Ef ) kt f ( E) e = f ( E) D e f M
17 Probabilità di occupazione: distribuzione di Fermi-Dirac ( f ) f ( E) = e M E E kt questa approssimazione è valida per semiconduttori nondegeneri. Quando un semiconduttore è degenere, cioè quando gli atomi droganti introdotti sono in concentrazione così elevata da interagire tra di loro, va usata f D.
18 Concentrazione portatori Calcoliamo la concentrazione di portatori liberi: =
19 Concentrazione elettroni In definitiva la concentrazione di elettroni liberi in banda di conduzione è data da: E ( ) ( ) ( ) ( ) sup n gc E fd E de gc E fm E de Ec 0 N = = 32 2π mkt n ( c f ) ( c f ) = 2 e N 2 = C e C 32 2π mkt n = = 2 E E kt E E kt densità efficace degli stati in banda di conduzione 19 3 = cm per Si a 25 C
20 Concentrazione lacune Analogamente la concentrazione di lacune libere in banda di valenza è data da: E v ( ) ( ) v p g ( ) ( ) v E f E D E de gv E fm E de inf N = = 32 2π mkt p ( f v) ( f v) = 2 e N 2 = V e V 32 2π mkt p = = E E E kt E E kt densità efficace degli stati in banda di valenza = cm per Si a C
21 Concentrazione intrinseca di portatori Il tasso di eccitazione di elettroni in banda di conduzione (e cioè il tasso di generazione di una coppia e-h) è funzione della temperatura: G = f T ( ) Il tasso di ricombinazione e-h è funzione della temperatura e della concentrazione di e ed h : in equilibrio (condizioni stazionarie) 1 R = npf T ( ) G = R ( vale sempre) 2
22 Legge dell azione di massa in equilibrio (condizioni stazionarie) ( ) 1 G= R np= = n ( ) i pi f2 T i i ( C f ) ( f v) 2 E E kt E E kt i = = C V ( ) EC EV kt = = C C V V i C V E g E g kt 2kT f T n = p = concentrazione intrinseca di elettroni (lacune) n np N e N e n = = N N e N N e N N e
23 Legge dell azione di massa n i è funzione di T ed E g. Sostituendo l espressione di E g ni = T e ( ΔEg ) kT 10 essendo Δ Eg = ni T per il Si E = 1.21 ev a T = 0 K g 10 3 ni cm per Si a T = 25 C n i è il parametro che determina le condizioni operative di un materiale semiconduttore (per drogare efficacemente un materiale il numero di portatori di carica aggiuntivi deve essere >> n i )
24 Livello di Fermi intrinseco dovendo essere n i = n = p sulla base delle relazioni ( E ) 2 c Ei kt π mkt n n= NC e con NC = 2 ( E ) 2 i Ev kt π mkt n p = NV e con NV = 2 E i E + E 3 mp E + E = + ktln 2 4 mn 2 c v c v E i rappresenta il valore assunto dal livello di Fermi E f in un semiconduttore intrinseco (cioè non drogato)
25 Silicio intrinseco (non-drogato) una lacuna (hole = mancanza di carica negativa) è assimilibile ad una carica positiva mobile! n i =10 10 cm -3 art
26 Drogaggio di tipo n Sostituendo un atomo di silicio con un atomo di elementi della V colonna del sistema periodico si crea un elettrone di conduzione. Donori: P, As, Sb rappresentazione 2D P elettrone extra Donore I droganti sono aggiunti per controllare le proprietà elettroniche del materiale. A temperatura ambiente (RT) tutti i donori sono ionizzati e cresce la conducibilità elettrica. Concentrazioni tipiche vanno da cm -3 a10 20 cm -3.
27 Drogaggio di tipo p Sostituendo un atomo di silicio con un atomi di un elemento della III colonna del sistema periodico si crea una lacuna. Accettori: B, In, Al, Ga rappresentazione 2D B +4 lacuna extra Accettore I droganti sono aggiunti per controllare le proprietà elettroniche del materiale. A temperatura ambiente (RT) tutti gli accettori sono ionizzati e cresce la conducibilità elettrica. Concentrazioni tipiche vanno da cm -3 a10 20 cm -3.
28 Drogaggio: livello di Fermi estrinseco N d+ = densità di donori ionizzati (densità di livelli E d non occupati da elettroni, finiti in banda di conduzione) N a- = densità di accettori ionizzati (densità di livelli E a occupati da elettroni che creano lacune in banda di valenza) E c E d drogaggio di tipo n (donori) E c drogaggio di tipo p (accettori) E v E a E v
29 Livello di Fermi estrinseco dalla condizione di neutralità della carica n + N = p + N essendo + a d + N Nd = Nd fd E = e Na = Na fd E = 1+ e 1+ e se E E E ( ovvero anche a T elevate) d a ( 1 ( )) ( ) ( ) f d ( a f ) a f d E E kt E E kt N N e N N quindi n + N = p + N ed essendo np = n + 2 d d a a a d i n= ( N N ) + 4n + ( N N ) ( N 2 N ) per ( N N ) n per il silicio di tipo n d a i d a d a d a i N
30 Livello di Fermi estrinseco poichè deve comunque sempre essere valida la relazione ( Ec E f ) kt ( Ec Ei) kt ( Ei E f ) kt ( Ei E f ) kt n= N e = N e e = n e da cui f C C i E = E + kt i ln n n i 1 analogamente p = Na Nd + ni + Na N d Na Nd 2 ( Ef Ei) kt p p = nie e, quindi E f = Ei kt ln per il silicio di tipo p n 2 2 ( ) 4 ( ) ( ) i
Introduzione. Cosa sono i dispositivi a semiconduttore?
 Introduzione Cosa sono i dispositivi a semiconduttore? con poche eccezioni, qualunque cosa che abbia una risposta corrente-tensione non-lineare è un dispositivo a semiconduttore i semiconduttori possono
Introduzione Cosa sono i dispositivi a semiconduttore? con poche eccezioni, qualunque cosa che abbia una risposta corrente-tensione non-lineare è un dispositivo a semiconduttore i semiconduttori possono
T08: Dispositivi elettronici (3.3.1)
 T08: Dispositivi elettronici (3.3.1) Sommario Richiami sui semiconduttori conduttori, isolanti e semiconduttori bande di energia droganti nei semiconduttori corrente di deriva e diffusione Funzionamento
T08: Dispositivi elettronici (3.3.1) Sommario Richiami sui semiconduttori conduttori, isolanti e semiconduttori bande di energia droganti nei semiconduttori corrente di deriva e diffusione Funzionamento
Dispositivi elettronici
 Dispositivi elettronici Sommario Richiami sui semiconduttori conduttori, isolanti e semiconduttori bande di energia droganti nei semiconduttori corrente di deriva e diffusione Funzionamento della giunzione
Dispositivi elettronici Sommario Richiami sui semiconduttori conduttori, isolanti e semiconduttori bande di energia droganti nei semiconduttori corrente di deriva e diffusione Funzionamento della giunzione
Figura 2.1: Semiconduttori.
 Capitolo 2 Semiconduttori 2.1 Semiconduttori Con il termine semiconduttori si indicano alcuni elementi delle colonne III, IV e V della tavola periodica, caratterizzati da una resistività elettrica ρ intermedia
Capitolo 2 Semiconduttori 2.1 Semiconduttori Con il termine semiconduttori si indicano alcuni elementi delle colonne III, IV e V della tavola periodica, caratterizzati da una resistività elettrica ρ intermedia
Testo di riferimento: Millman-Grabel MICROELECTRONICS McGraw Hill Cap. 1: 1,2,3,4 Cap. 2: 1,2,3,4,6,7,8,(9,10). Cap. 3: 1,2,4,5,6,8,9,10.
 Esperimentazioni di Fisica 3 AA 20122013 Semiconduttori Conduzione nei semiconduttori Semiconduttori intrinseci ed estrinseci (drogati) La giunzione pn Il diodo a semiconduttore Semplici circuiti con diodi
Esperimentazioni di Fisica 3 AA 20122013 Semiconduttori Conduzione nei semiconduttori Semiconduttori intrinseci ed estrinseci (drogati) La giunzione pn Il diodo a semiconduttore Semplici circuiti con diodi
4πε. h m. Eq. di Schrödinger per un atomo di idrogeno:
 Eq. di Schrödinger per un atomo di idrogeno: h m e 1 ψ 4πε r 0 ( r) = Eψ ( r) Questa equazione è esattamente risolubile ed il risultato sono degli orbitali di energia definita E n = m e 1 α 1 1 e mc n
Eq. di Schrödinger per un atomo di idrogeno: h m e 1 ψ 4πε r 0 ( r) = Eψ ( r) Questa equazione è esattamente risolubile ed il risultato sono degli orbitali di energia definita E n = m e 1 α 1 1 e mc n
Materiali dell elettronica allo stato solido
 Materiali dell elettronica allo stato solido I materiali elettronici si suddividono in 3 categorie: Isolanti Resistenza () > 10 5 -cm Semiconduttori 10-3 < < 10 5 -cm Conduttori < 10-3 -cm I semiconduttori
Materiali dell elettronica allo stato solido I materiali elettronici si suddividono in 3 categorie: Isolanti Resistenza () > 10 5 -cm Semiconduttori 10-3 < < 10 5 -cm Conduttori < 10-3 -cm I semiconduttori
conduttori isolanti semiconduttori In un metallo la banda più esterna che contiene elettroni è detta banda di valenza
 Un solido sarà conduttore solo se la banda è parzialmente occupata. Se invece la banda è completamente occupata si possono avere due casi: se la banda successiva è molto alta in energia il solido è un
Un solido sarà conduttore solo se la banda è parzialmente occupata. Se invece la banda è completamente occupata si possono avere due casi: se la banda successiva è molto alta in energia il solido è un
Sommario. Come funziona il Diodo? Giunzione PN a circuito aperto Giunzione PN: polarizzazione diretta Giunzione PN: polarizzazione inversa
 l Diodo Sommario Cos è il Diodo? Concetti di base sulla fisica dei Semiconduttori Silicio ntrinseco Corrente di Deriva e Corrente di Diffusione Silicio Drogato P o N Giunzione PN Come funziona il Diodo?
l Diodo Sommario Cos è il Diodo? Concetti di base sulla fisica dei Semiconduttori Silicio ntrinseco Corrente di Deriva e Corrente di Diffusione Silicio Drogato P o N Giunzione PN Come funziona il Diodo?
Figura 3.1: Semiconduttori.
 Capitolo 3 Semiconduttori Con il termine semiconduttori si indicano alcuni elementi delle colonne III, IV e V della tavola periodica, caratterizzati da una resistività elettrica ρ intermedia tra quella
Capitolo 3 Semiconduttori Con il termine semiconduttori si indicano alcuni elementi delle colonne III, IV e V della tavola periodica, caratterizzati da una resistività elettrica ρ intermedia tra quella
Materiale Energy Gap
 Semiconduttori Materiale diamante silicio germanio Energy Gap 5,3 ev 1,1 ev 0,7 ev 21 Semiconduttori Quando un elettrone, portatore di carica negativa, è promosso da banda di valenza a banda di conduzione,
Semiconduttori Materiale diamante silicio germanio Energy Gap 5,3 ev 1,1 ev 0,7 ev 21 Semiconduttori Quando un elettrone, portatore di carica negativa, è promosso da banda di valenza a banda di conduzione,
Corso di Elettronica Industriale (CdL in Ingegneria Meccatronica, sede di Mantova) Semiconduttori intrinseci e drogati
 Corso di Elettronica Industriale (CdL in Ingegneria Meccatronica, sede di Mantova) Isolanti, conduttori e semiconduttori In un solido si può avere conduzione di carica elettrica (quindi passaggio di corrente)
Corso di Elettronica Industriale (CdL in Ingegneria Meccatronica, sede di Mantova) Isolanti, conduttori e semiconduttori In un solido si può avere conduzione di carica elettrica (quindi passaggio di corrente)
LEGAME METALLICO PROPRIETA METALLICHE NON METALLI SEMIMETALLI METALLI
 LEGAME METALLICO LEGAME METALLICO NON METALLI PROPRIETA METALLICHE Elevata conducibilità elettrica ( 1/ T) Bassa energia di ionizzazione Elevata duttilità e malleabilità Non trasparenza Lucentezza Strutture
LEGAME METALLICO LEGAME METALLICO NON METALLI PROPRIETA METALLICHE Elevata conducibilità elettrica ( 1/ T) Bassa energia di ionizzazione Elevata duttilità e malleabilità Non trasparenza Lucentezza Strutture
Semiconduttori intrinseci
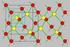 Semiconduttori intrinseci Rappresentazione bidimensionale di un cristallo di silicio a 0 K Rappresentazione bidimensionale di un cristallo di silicio a temperatura ambiente (300 K) In equilibrio termodinamico,
Semiconduttori intrinseci Rappresentazione bidimensionale di un cristallo di silicio a 0 K Rappresentazione bidimensionale di un cristallo di silicio a temperatura ambiente (300 K) In equilibrio termodinamico,
I PORTATORI e la CORRENTE nei DISPOSITIVI SEMICONDUTTORI. Fondamenti di Elettronica
 I PORTATORI e la CORRENTE nei DISPOSITIVI SEMICONDUTTORI 1 Come si può variare la concentrazione di n e/o di p? NON aggiungendo elettroni dall esterno perché il cristallo si caricherebbe ed assumerebbe
I PORTATORI e la CORRENTE nei DISPOSITIVI SEMICONDUTTORI 1 Come si può variare la concentrazione di n e/o di p? NON aggiungendo elettroni dall esterno perché il cristallo si caricherebbe ed assumerebbe
l evoluzione dell elettronica
 1904 tubo a vuoto 1968 circuito integrato l evoluzione dell elettronica 1980 integrati VLSI 1947 transistor oggi integrati ULSI 1971 microprocessore diodi transistor tecnologie costruttive grafici, tabelle,
1904 tubo a vuoto 1968 circuito integrato l evoluzione dell elettronica 1980 integrati VLSI 1947 transistor oggi integrati ULSI 1971 microprocessore diodi transistor tecnologie costruttive grafici, tabelle,
I Materiali. Isolanti, Conduttori, Semiconduttori. giovedì 26 febbraio Corso di Elettronica 1
 I Materiali Isolanti, Conduttori, Semiconduttori Corso di Elettronica 1 Di cosa si parlerà Classificazione dei materiali Drogaggio Giunzione PN Polarizzazione diretta Polarizzazione inversa Corso di Elettronica
I Materiali Isolanti, Conduttori, Semiconduttori Corso di Elettronica 1 Di cosa si parlerà Classificazione dei materiali Drogaggio Giunzione PN Polarizzazione diretta Polarizzazione inversa Corso di Elettronica
il diodo a giunzione transistori ad effetto di campo (FETs) il transistore bipolare (BJT)
 Contenuti del corso Parte I: Introduzione e concetti fondamentali richiami di teoria dei circuiti la simulazione circuitale con SPICE elementi di Elettronica dello stato solido Parte II: Dispositivi Elettronici
Contenuti del corso Parte I: Introduzione e concetti fondamentali richiami di teoria dei circuiti la simulazione circuitale con SPICE elementi di Elettronica dello stato solido Parte II: Dispositivi Elettronici
Trasporto in Semiconduttori e Metalli - Esercizi con soluzioni
 Trasporto in Semiconduttori e Metalli - Esercizi con soluzioni Fisica della Materia Condensata Dipartimento di Matematica e Fisica Università degli Studi Roma Tre A.A. 2016/2017 Trasporto in Semiconduttori
Trasporto in Semiconduttori e Metalli - Esercizi con soluzioni Fisica della Materia Condensata Dipartimento di Matematica e Fisica Università degli Studi Roma Tre A.A. 2016/2017 Trasporto in Semiconduttori
Introduzione al corso di Fisica dei Semiconduttori
 Introduzione al corso di Fisica dei Semiconduttori Mara Bruzzi 8 settembre 016 1 a lezione : dualismo onda-corpuscolo a.l ipotesi di Planck e il corpo nero b.effetto Fotoelettrico c. Primi modelli atomici
Introduzione al corso di Fisica dei Semiconduttori Mara Bruzzi 8 settembre 016 1 a lezione : dualismo onda-corpuscolo a.l ipotesi di Planck e il corpo nero b.effetto Fotoelettrico c. Primi modelli atomici
Legame metallico. Metalli
 LEGAME METALLICO Un metallo può essere descritto come un reticolo di ioni positivi (nucleo più elettroni di core) immersi in una nube di elettroni di valenza mobili (delocalizzati) attorno ai cationi.
LEGAME METALLICO Un metallo può essere descritto come un reticolo di ioni positivi (nucleo più elettroni di core) immersi in una nube di elettroni di valenza mobili (delocalizzati) attorno ai cationi.
(2) cubico a facce centrate (3) esagonale compatto
 IL LEGAME METALLICO La maggior parte dei metalli cristallizza in strutture a massimo impacchettamento, ovvero in solidi in cui si può considerare che gli ioni metallici che occupano le posizioni reticolari,
IL LEGAME METALLICO La maggior parte dei metalli cristallizza in strutture a massimo impacchettamento, ovvero in solidi in cui si può considerare che gli ioni metallici che occupano le posizioni reticolari,
POLITECNICO DI MILANO
 POLITECNICO DI MILANO www.polimi.it ELETTRONICA per ingegneria BIOMEDICA prof. Alberto TOSI Sommario Semiconduttori Conduttori: legge di Ohm Semiconduttori: reticolo, elettroni e lacune, deriva e diffusione
POLITECNICO DI MILANO www.polimi.it ELETTRONICA per ingegneria BIOMEDICA prof. Alberto TOSI Sommario Semiconduttori Conduttori: legge di Ohm Semiconduttori: reticolo, elettroni e lacune, deriva e diffusione
Regione di svuotamento: effetti polarizzazione
 Regione di svuotamento: effetti polarizzazione L applicazione di una tensione modifica il potenziale interno. Assumendo che tutta la tensione risulti applicata alla regione di svuotamento basta sostituire
Regione di svuotamento: effetti polarizzazione L applicazione di una tensione modifica il potenziale interno. Assumendo che tutta la tensione risulti applicata alla regione di svuotamento basta sostituire
I SEMICONDUTTORI. I loro atomi costituiscono uno schema cristallino, noto come centrate nel quale gli atomi sono tenuti a posto dai legami covalenti.
 I SEMICONDUTTORI I semiconduttori hanno un comportamento intermedio fra quello dei conduttori e quello degli isolanti. Presentano una conduttività intermedia fra quella dei conduttori e degli isolanti
I SEMICONDUTTORI I semiconduttori hanno un comportamento intermedio fra quello dei conduttori e quello degli isolanti. Presentano una conduttività intermedia fra quella dei conduttori e degli isolanti
Legame metallico. Non metalli. Semimetalli. Metalli
 Legame metallico Non metalli Metalli Semimetalli Proprietà metalliche elevata conducibilità elettrica (1/T) e termica bassa energia di ionizzazione elevata duttilità e malleabilità non trasparenza lucentezza
Legame metallico Non metalli Metalli Semimetalli Proprietà metalliche elevata conducibilità elettrica (1/T) e termica bassa energia di ionizzazione elevata duttilità e malleabilità non trasparenza lucentezza
Trasporto dei portatori
 Trasporto dei portatori all equilibrio termico gli elettroni in banda di conduzione (le lacune in banda di valenza) si muovono per agitazione termica 3 energia termica = (k costante di Boltzmann) 2 kt
Trasporto dei portatori all equilibrio termico gli elettroni in banda di conduzione (le lacune in banda di valenza) si muovono per agitazione termica 3 energia termica = (k costante di Boltzmann) 2 kt
DIFETTI PUNTUALI INTRINSECI
 DIFETTI PUNTUALI INTRINSECI Calcolo della concentrazione di difetti di equilibrio con la termodinamica statistica: La creazione di un difetto richiede energia ( H f ) ma comporta un grande aumento degli
DIFETTI PUNTUALI INTRINSECI Calcolo della concentrazione di difetti di equilibrio con la termodinamica statistica: La creazione di un difetto richiede energia ( H f ) ma comporta un grande aumento degli
Ricavo della formula
 Dispositivi e Circuiti Elettronici Ricavo della formula E F i E F = k B T ln N A n i Si consideri la relazione di Shockey: ( ) EFi E F p = n i exp k B T Si osservi anche che per x = il semiconduttore è
Dispositivi e Circuiti Elettronici Ricavo della formula E F i E F = k B T ln N A n i Si consideri la relazione di Shockey: ( ) EFi E F p = n i exp k B T Si osservi anche che per x = il semiconduttore è
bande di energia in un conduttore La banda di energia più alta è parzialmente vuota! livello di Fermi Overlap di bande di energia in un conduttore
 g(e) va a zero sia al bordo inferiore che a quello superiore della banda bande di energia in un conduttore La banda di energia più alta è parzialmente vuota! livello di Fermi Overlap di bande di energia
g(e) va a zero sia al bordo inferiore che a quello superiore della banda bande di energia in un conduttore La banda di energia più alta è parzialmente vuota! livello di Fermi Overlap di bande di energia
L effetto Fotovoltaico
 L effetto Fotovoltaico Carla sanna [email protected] [email protected] Carla sanna Cagliari 19 settembre 2008 Sala Anfiteatro, via Roma 253 1 Un po di storia. Becquerel nel 1839
L effetto Fotovoltaico Carla sanna [email protected] [email protected] Carla sanna Cagliari 19 settembre 2008 Sala Anfiteatro, via Roma 253 1 Un po di storia. Becquerel nel 1839
Elettronica II La giunzione p-n: calcolo della relazione tensione-corrente p. 2
 Elettronica II La giunzione p-n: calcolo della relazione tensione-corrente Valentino Liberali Dipartimento di Tecnologie dell Informazione Università di Milano, 26013 Crema e-mail: [email protected]
Elettronica II La giunzione p-n: calcolo della relazione tensione-corrente Valentino Liberali Dipartimento di Tecnologie dell Informazione Università di Milano, 26013 Crema e-mail: [email protected]
I metalli e i semiconduttori, le proprietà elettriche. Le applicazioni.
 I metalli e i semiconduttori, le proprietà elettriche. Le applicazioni. PLS 2016/17 Prof. Daniela Cavalcoli Dip di Fisica e Astronomia Università di Bologna [email protected] outline I solidi
I metalli e i semiconduttori, le proprietà elettriche. Le applicazioni. PLS 2016/17 Prof. Daniela Cavalcoli Dip di Fisica e Astronomia Università di Bologna [email protected] outline I solidi
IL LEGAME METALLICO 1
 IL LEGAME METALLICO 1 Non metalli Metalli Metalloidi Proprietà dei metalli Elevata conducibilità elettrica; Elevata conducibilità termica; Effetto fotoelettrico; Elevata duttilità e malleabilità; Lucentezza;
IL LEGAME METALLICO 1 Non metalli Metalli Metalloidi Proprietà dei metalli Elevata conducibilità elettrica; Elevata conducibilità termica; Effetto fotoelettrico; Elevata duttilità e malleabilità; Lucentezza;
DISPOSITIVI ELETTRONICI
 DIPARTIMENTO DI INGEGNERIA ELETTRICA ELETTRONICA E INFORMATICA Corso di laurea magistrale in Ingegneria elettronica Anno accademico 205/206 - anno DISPOSITIVI ELETTRONICI ING-INF/0-9 CFU - semestre Docente
DIPARTIMENTO DI INGEGNERIA ELETTRICA ELETTRONICA E INFORMATICA Corso di laurea magistrale in Ingegneria elettronica Anno accademico 205/206 - anno DISPOSITIVI ELETTRONICI ING-INF/0-9 CFU - semestre Docente
 Laboratorio di Elettronica Dispositivi elettronici e circuiti Proprieta' e fenomenologia dei semiconduttori. Dispositivi a semiconduttore: * diodo a giunzione * transistor bjt * transistor jfet e mosfet
Laboratorio di Elettronica Dispositivi elettronici e circuiti Proprieta' e fenomenologia dei semiconduttori. Dispositivi a semiconduttore: * diodo a giunzione * transistor bjt * transistor jfet e mosfet
CONDUCIBILITÀ IONICA
 CONDUCIBILITÀ IONICA Movimento di ioni nel reticolo cristallino ionico: trasporto di carica (conduzione ionica). Vacanze del reticolo. Assenza di campo elettrico movimento casuale delle vacanze: non c
CONDUCIBILITÀ IONICA Movimento di ioni nel reticolo cristallino ionico: trasporto di carica (conduzione ionica). Vacanze del reticolo. Assenza di campo elettrico movimento casuale delle vacanze: non c
Comune ordine di riempimento degli orbitali di un atomo
 Comune ordine di riempimento degli orbitali di un atomo Le energie relative sono diverse per differenti elementi ma si possono notare le seguenti caratteristiche: (1) La maggior differenza di energia si
Comune ordine di riempimento degli orbitali di un atomo Le energie relative sono diverse per differenti elementi ma si possono notare le seguenti caratteristiche: (1) La maggior differenza di energia si
Dispositivi e Tecnologie Elettroniche. Il sistema MOS
 Dispositivi e Tecnologie Elettroniche Il sistema MOS l ossido è SiO 2 l ossido è molto sottile ( 40 Å) il metallo è sostituito con silicio policristallino drograto n + (poly) Dispositivi e Tecnologie Elettroniche
Dispositivi e Tecnologie Elettroniche Il sistema MOS l ossido è SiO 2 l ossido è molto sottile ( 40 Å) il metallo è sostituito con silicio policristallino drograto n + (poly) Dispositivi e Tecnologie Elettroniche
11 aprile Annalisa Tirella.
 Scienze dei Materiali A.A. 2010/2011 11 aprile 2011 Annalisa Tirella [email protected] Metalli I metalli sono elementi chimici che possono essere utilizzati sia puri che in forma di leghe
Scienze dei Materiali A.A. 2010/2011 11 aprile 2011 Annalisa Tirella [email protected] Metalli I metalli sono elementi chimici che possono essere utilizzati sia puri che in forma di leghe
Il Legame Ionico. Quando la differenza di elettronegatività fra atomi A e B è molto grande le coppie AB possono essere considerate A + B -
 Il Legame Ionico Quando la differenza di elettronegatività fra atomi A e B è molto grande le coppie AB possono essere considerate A + B - A + B - Le coppie di ioni si attraggono elettrostaticamente Il
Il Legame Ionico Quando la differenza di elettronegatività fra atomi A e B è molto grande le coppie AB possono essere considerate A + B - A + B - Le coppie di ioni si attraggono elettrostaticamente Il
Fisica dello Stato Solido
 Corso di Fisica dello Stato Solido A.A. 2001/2002 Prof. Andrea Di Cicco INFM, Dipartimento di Fisica, via Madonna delle Carceri 62032 Camerino (MC), Italy http://www.unicam.it, http://gnxas.unicam.it LaTeX
Corso di Fisica dello Stato Solido A.A. 2001/2002 Prof. Andrea Di Cicco INFM, Dipartimento di Fisica, via Madonna delle Carceri 62032 Camerino (MC), Italy http://www.unicam.it, http://gnxas.unicam.it LaTeX
La conduzione nei semiconduttori Politecnico di Torino 1
 La conduzione nei semiconduttori 2006 Politecnico di Torino 1 La conduzione nei semiconduttori Concentrazioni di carica libera all equilibrio Correnti nei semiconduttori Modello matematico 3 2006 Politecnico
La conduzione nei semiconduttori 2006 Politecnico di Torino 1 La conduzione nei semiconduttori Concentrazioni di carica libera all equilibrio Correnti nei semiconduttori Modello matematico 3 2006 Politecnico
