Corso di Linguaggi di Programmazione
|
|
|
- Battista Rossetti
- 8 anni fa
- Просмотров:
Транскрипт
1 Corso di Linguaggi di Programmazione Lezione 2 Alberto Ceselli [email protected] Dipartimento di Tecnologie dell Informazione Università degli Studi di Milano 09 Marzo 2010 Controlli automatici di correttezza dei programmi Il punto di vista imperativo Calcolabilità e funzioni
2 Controlli automatici di correttezza dei programmi Obiettivo chiave dei LdP: fornire costrutti che riducano la probabilità di lasciare bug nei programmi... ovvero: il programma implementa effettivamente l algoritmo per cui è progettato. Perchè non costruire verificatori automatici della correttezza dei programmi, e poi utilizzare il linguaggio che preferiamo? Ci sono risultati teorici che dimostrano che non è possibile costruire verificatori perfetti. Verificatore della terminazione di programmi C supponiamo di avere un programma term (alla lavagna...) in ogni caso, term si comporta diversamente dalle specifiche. infatti, term non può essere realizzato!.
3 Programma per il controllo dell utilizzo degli indici negli array (alla lavagna) Riassumendo E impossibile verificare in modo consistente e completo qualsiasi proprietà di un programma che dipenda dall esito della computazione Si possono condurre controlli consistenti, ma incompleti (es. errori in compilazione) Si possono condurre controlli completi, ma inconsistenti (es. warning) es. si possono individuare alcuni segmenti di codice non raggiungibile (ma mai garantire di individuare tutto e solo il codice irraggiungibile in qualsiasi programma) es. si può controllare il matching dei tipi nel passaggio di parametri a procedura, ma la chiamata potrebbe non avvenire si possono condurre controlli a run-time (ma l errore è già avvenuto)
4 Linguaggi di programmazione general purpose Abbiamo dimostrato che non esiste nessun programma C che in ambiente UNIX verifichi la terminazione di un programma (system, exit...) Domanda: dato un linguaggio di programmazione ed un problema calcolabile posso sempre scrivere un programma in quel linguaggio che risolva il problema? Linguaggi di programmazione con questa caratteristica vengono definiti general purpose es. C, C++, Java, LISP, ML, Prolog... ma NON SQL Per caratterizzare i linguaggi general purpose abbiamo bisogno di formalità e generalità. Modelli di calcolo astratti Come dimostrare qualcosa che valga indipendentemente dal linguaggio utilizzato?... con modelli di calcolo astratti es. macchina RAM, macchina di Turing
5 La macchina di Turing La macchina di Turing oggetto matematico, definito in modo completo, formale e molto compatto rudimentale, ma potente almeno quanto gli attuali computer (nastro infinito) i programmi delle MdT non hanno dettagli inutili: il loro comportamento non è ambiguo il comportamento del processore è definito matematicamente, come i programmi
6 La macchina di Turing La macchina di Turing
7 La macchina di Turing Overview: la MdT è una n-upla (S, Σ, I, P, s 0, e +, e ) S è l insieme di possibili stati in cui si può trovare una macchina Σ è l alfabeto di lavoro della macchina I Σ è l alfabeto di input della macchina s 0 è lo stato iniziale della macchina e + è lo stato finale successo della macchina e è lo stato finale fallimento della macchina P è il programma della macchina
8 Programmi per MdT Un programma P per una MdT è un insieme finito di tuple (s, σ, m i, σ, m w, s) s è lo stato in cui si deve trovare la MdT, σ il carattere sul nastro di input m i la direzione in cui spostare la testina del nastro di input, m w la direzione in cui spostare la testina del nastro di lavoro (m i, m w M = {l, r, h}) σ il carattere da scrivere sul nastro di lavoro, s lo stato al termine dell istruzione in altri termini: P : S I M Σ M S Come dimostrare la Turing-equivalenza? dato un linguaggio di programmazione realizzare un simulatore di MdT in quel linguaggio progettare una MdT interprete per quel linguaggio anche con traduzioni intermedie... semplice, dato che i compilatori producono linguaggio macchina una MdT può calcolare tutto quello che sappiamo calcolare (e solo quello). def. linguaggio general purpose: è un linguaggio Turing equivalente N.B. diverso dall equivalenza polinomiale (legata alla complessità dei problemi)
9 Questioni di cardinalità Th: qualsiasi sequenza di naturali può essere codificata con un singolo naturale. Dim: codifico per diagonali (alla lavagna) possiamo anche costruire una formula ( ) x + y + 1 x, y = + y 2 che è una bijezione (invertibile)... ed il gioco può essere ripetuto (per qualsiasi sequenza finita di naturali) il processo di assegnare un naturale (numero di Gödel) ad ogni elemento di un insieme numerabile è detto Gödelizzazione. Questioni di cardinalità Le MdT sono tante quanti i naturali (alla lavagna) I problemi sono più dei naturali (alla lavagna)... non posso avere corrispondenza 1 a 1 tra funzioni e MdT! Th. esiste una MdT universale u, che avendo sul nastro di input la descrizione di una qualsiasi MdT k (codificabile con un naturale) e l input per quella MdT (i) emula il comportamento di k su input i.
10 Funzioni ricorsive Quali sono le funzioni calcolabili? def. funzione f : X Y : una qualsiasi relazione che mette in corrispondenza ad ogni elemento x X uno ed un solo elemento y Y def. funzione parziale g : X Y : è una relazione che può essere non definita per qualche x X (in questo caso g(x) = ) possiamo immaginare che corrisponda a loop infinito in un programma (N.B. g() non è totale, quindi NON è una funzione!) per convenzione g( ) =. def. funzione parziale ricorsiva (FPR)... Funzioni parziali ricorsive La classe delle funzioni parziali ricorsive (FPR) è la più piccola classe di funzioni parziali da N n in N tale per cui 1. la funzione costante 0, successore s() e le proiezioni i-esime appartengono a FPR (descrizione tralasciata) π (n) i 2. applicando sostituzioni e minimalizzazione a FPR si ottengono FPR (descrizione tralasciata) 3. date due FPR g : N n 1 N e h : N n+1 N, la funzione parziale f () ottenuta tramite ricorsione primitiva f (0, x 2... x n ) = g(x 2... x n ) f (y + 1, x 2,... x n ) = h(f (y, x 2... x n ), x 2,..., x n, y) appartiene a FPR.
11 FPR ed indecidibilità algoritmica Risultato principale: si pu dimostrare che le FPR coincidono con le funzioni parziali calcolabili da MdT Ad ogni FPR posso assegnare un indice (quello della MdT che realizza il calcolo corrispondente): ϕ k () (ruolo dei filename) Esiste una MdT universale u, quindi esiste una FPR universale ϕ u () (ruolo di system ) FPR ed indecidibilità algoritmica Th. la funzione parziale inversione { 0 se ϕ u (x, x) = f (x) = altrimenti non è FPR (dim. alla lavagna) Th. la funzione d arresto { 0 se ϕ u (x, y) = h(x, y) = 1 altrimenti non è FPR (dim. alla lavagna)... non perdo nè guadagno nulla rinunciando al concetto di stato della MdT, o restringendomi all utilizzo della ricorsione!
12 La tesi di Church Infatti: tesi di Church Le funzioni calcolabili algoritmicamente sono le funzioni ricorsive. Le funzioni semi-calcolabili algoritmicamente sono le funzioni parziali ricorsive. N.B. La semi-calcolabilità è principalmente utile come concetto di carattere intuitivo. Riassumendo Riassumendo, alcuni dei principali compiti dei LdP sono: fornire strumenti per programmare senza errori (o per accorgersi di aver commesso errori già in fase di compilazione) fornire strutture adeguate a facilitare le fasi di testing... perchè non è possibile realizzare verificatori automatici universali e perfetti di correttezza dei programmi.
13 Riassumendo Abbiamo infatti mostrato come alcuni problemi quali la terminazione dei programmi siano indecidibili (indipendentemente dal paradigma di programmazione o dalle risorse di calcolo dedicate) costruendo particolari controesempi in C descrivendo le Macchine di Turing e caratterizzando in modo formale i linguaggi Turing equivalenti dimostrando che le funzioni, e quindi i problemi sono più delle Macchine di Turing caratterizzando le funzioni parziali e la classe delle funzioni parziali ricorsive, e mettendo in corrispondenza le funzioni parziali ricorsive con le Macchine di Turing dimostrando, ad esempio, che la funzione terminazione non è ricorsiva Riferimenti: Disponibili in rete: P. Bonatti (1999) Cenni informali di calcolabilità S. Vigna (2006) Dispense per il corso di informatica teorica
Le parole dell informatica: algoritmo e decidibilità
 Le parole dell informatica: algoritmo e decidibilità Angelo Montanari Dipartimento di Matematica e Informatica Università degli Studi di Udine Ciclo di seminari su un Vocabolario Filosofico dell Informatica
Le parole dell informatica: algoritmo e decidibilità Angelo Montanari Dipartimento di Matematica e Informatica Università degli Studi di Udine Ciclo di seminari su un Vocabolario Filosofico dell Informatica
Teoria della Calcolabilità!
 Teoria della Calcolabilità!! Si occupa delle questioni fondamentali circa la potenza e le limitazioni dei sistemi di calcolo.!! L'origine risale alla prima metà del ventesimo secolo, quando i logici matematici
Teoria della Calcolabilità!! Si occupa delle questioni fondamentali circa la potenza e le limitazioni dei sistemi di calcolo.!! L'origine risale alla prima metà del ventesimo secolo, quando i logici matematici
Alcune Tracce dei Precedenti Esami del Dottorato di Siena in Logica Matematica ed Informatica Teorica
 Alcune Tracce dei Precedenti Esami del Dottorato di Siena in Logica Matematica ed Informatica Teorica Raccolti e curati da Luca Spada Indice 1 Temi 1 1.1 Logica Matematica.......................... 1 1.2
Alcune Tracce dei Precedenti Esami del Dottorato di Siena in Logica Matematica ed Informatica Teorica Raccolti e curati da Luca Spada Indice 1 Temi 1 1.1 Logica Matematica.......................... 1 1.2
Principio di composizione delle MT
 Principio di composizione delle MT La definizioni date fanno riferimento a situazioni in cui la macchina sia capace di risolvere problemi singoli. E possibile far sì che macchine progettate per problemi
Principio di composizione delle MT La definizioni date fanno riferimento a situazioni in cui la macchina sia capace di risolvere problemi singoli. E possibile far sì che macchine progettate per problemi
La tesi di Church-Turing
 ITLCC 2006/11/12 21:06 page 79 #3 Capitolo 5 La tesi di Church-Turing SOMMARIO Sebbene il concetto di algoritmo abbia avuto una lunga storia nel campo della matematica, il concetto formale di algoritmo
ITLCC 2006/11/12 21:06 page 79 #3 Capitolo 5 La tesi di Church-Turing SOMMARIO Sebbene il concetto di algoritmo abbia avuto una lunga storia nel campo della matematica, il concetto formale di algoritmo
Problemi, algoritmi, calcolatore
 Problemi, algoritmi, calcolatore Informatica e Programmazione Ingegneria Meccanica e dei Materiali Università degli Studi di Brescia Prof. Massimiliano Giacomin Problemi, algoritmi, calcolatori Introduzione
Problemi, algoritmi, calcolatore Informatica e Programmazione Ingegneria Meccanica e dei Materiali Università degli Studi di Brescia Prof. Massimiliano Giacomin Problemi, algoritmi, calcolatori Introduzione
Appunti del corso di Informatica 1 (IN110 Fondamenti) 3 Modelli di calcolo
 Università Roma Tre Dipartimento di Matematica e Fisica Corso di Laurea in Matematica Appunti del corso di Informatica 1 (IN110 Fondamenti) 3 Modelli di calcolo Marco Liverani ([email protected])
Università Roma Tre Dipartimento di Matematica e Fisica Corso di Laurea in Matematica Appunti del corso di Informatica 1 (IN110 Fondamenti) 3 Modelli di calcolo Marco Liverani ([email protected])
Struttura del calcolatore
 Mondo esterno Dati di ingresso Calcolatore Dati di uscita Mondo esterno Il calcolatore elabora dei dati di ingresso per ottenere dati in uscita In linea di principio, ma non solo, il compito svolto da
Mondo esterno Dati di ingresso Calcolatore Dati di uscita Mondo esterno Il calcolatore elabora dei dati di ingresso per ottenere dati in uscita In linea di principio, ma non solo, il compito svolto da
Sistemi di Elaborazione delle Informazioni
 SCUOLA DI MEDICINA E CHIRURGIA Università degli Studi di Napoli Federico II Corso di Sistemi di Elaborazione delle Informazioni Dott. Francesco Rossi a.a. 2016/2017 1 I linguaggi di programmazione e gli
SCUOLA DI MEDICINA E CHIRURGIA Università degli Studi di Napoli Federico II Corso di Sistemi di Elaborazione delle Informazioni Dott. Francesco Rossi a.a. 2016/2017 1 I linguaggi di programmazione e gli
Il concetto di calcolatore e di algoritmo
 Il concetto di calcolatore e di algoritmo Elementi di Informatica e Programmazione Percorso di Preparazione agli Studi di Ingegneria Università degli Studi di Brescia Docente: Massimiliano Giacomin Informatica
Il concetto di calcolatore e di algoritmo Elementi di Informatica e Programmazione Percorso di Preparazione agli Studi di Ingegneria Università degli Studi di Brescia Docente: Massimiliano Giacomin Informatica
Il linguaggio di programmazione Python
 Università Roma Tre Dipartimento di Matematica e Fisica Percorso Abilitante Speciale Classe A048 Matematica Applicata Corso di Informatica Il linguaggio di programmazione Python Marco Liverani ([email protected])
Università Roma Tre Dipartimento di Matematica e Fisica Percorso Abilitante Speciale Classe A048 Matematica Applicata Corso di Informatica Il linguaggio di programmazione Python Marco Liverani ([email protected])
ELABORAZIONE DELLE INFORMAZIONI (ALGORITMI E LINGUAGGI DI PROGRAMMAZIONE)
 1 LEZIONE 9 ELABORAZIONE DELLE INFORMAZIONI (ALGORITMI E LINGUAGGI DI PROGRAMMAZIONE) Laboratorio di Informatica per l Educazione A. A. 2014/2015 IN SINTESI (ELABORAZIONE) Con i COMPUTER, le macchine diventano
1 LEZIONE 9 ELABORAZIONE DELLE INFORMAZIONI (ALGORITMI E LINGUAGGI DI PROGRAMMAZIONE) Laboratorio di Informatica per l Educazione A. A. 2014/2015 IN SINTESI (ELABORAZIONE) Con i COMPUTER, le macchine diventano
Algoritmi e Linguaggi
 Algoritmi e Linguaggi Programmi e linguaggi Un calcolatore è solo un esecutore rapidissimo di istruzioni Un programma è un insieme di istruzioni codificate in un opportuno linguaggio 2 / 21 Linguaggi e
Algoritmi e Linguaggi Programmi e linguaggi Un calcolatore è solo un esecutore rapidissimo di istruzioni Un programma è un insieme di istruzioni codificate in un opportuno linguaggio 2 / 21 Linguaggi e
Il calcolatore universale, origini e nuovi paradigmi
 Il calcolatore universale, origini e nuovi paradigmi Lucia Pomello Università degli studi di Milano Bicocca Dipartimento di Informatica, Sistemistica e Comunicazione 24 febbraio 2017 L evoluzione dell
Il calcolatore universale, origini e nuovi paradigmi Lucia Pomello Università degli studi di Milano Bicocca Dipartimento di Informatica, Sistemistica e Comunicazione 24 febbraio 2017 L evoluzione dell
Teoria della Calcolabilità!
 Teoria della Calcolabilità! Si occupa delle questioni fondamentali circa la potenza e le limitazioni dei sistemi di calcolo.! L'origine risale alla prima metà del ventesimo secolo, quando i logici matematici
Teoria della Calcolabilità! Si occupa delle questioni fondamentali circa la potenza e le limitazioni dei sistemi di calcolo.! L'origine risale alla prima metà del ventesimo secolo, quando i logici matematici
Linguaggi e Ambienti di Programmazione
 Linguaggi e Ambienti di Programmazione Principi e tecniche diffuse che si incontrano spesso nelle applicazioni dell informatica. Compilatori Editor di struttura: riceve in input una sequenza di comandi
Linguaggi e Ambienti di Programmazione Principi e tecniche diffuse che si incontrano spesso nelle applicazioni dell informatica. Compilatori Editor di struttura: riceve in input una sequenza di comandi
Il Software programmabili programma algoritmo
 Il Software La proprietà fondamentale dei calcolatori e` quella di essere programmabili cioè in grado di svolgere compiti diversi a seconda delle istruzioni fornite dall utente mediante un programma, ossia
Il Software La proprietà fondamentale dei calcolatori e` quella di essere programmabili cioè in grado di svolgere compiti diversi a seconda delle istruzioni fornite dall utente mediante un programma, ossia
Teoria della computazione
 Teoria della computazione Dipartimento di Elettronica e Informazione Politecnico di Milano 18 aprile 2017 Cosa possiamo calcolare? Quali problemi siamo in grado di risolvere? Con un certo tipo di formalismo
Teoria della computazione Dipartimento di Elettronica e Informazione Politecnico di Milano 18 aprile 2017 Cosa possiamo calcolare? Quali problemi siamo in grado di risolvere? Con un certo tipo di formalismo
LINGUAGGI DI ALTO LIVELLO. Si basano su una macchina virtuale le cui mosse non sono quelle della macchina hardware
 LINGUAGGI DI ALTO LIVELLO Si basano su una macchina virtuale le cui mosse non sono quelle della macchina hardware 1 LINGUAGGI DI ALTO LIVELLO Barriera di astrazione Fortran Cobol Basic Pascal Python C
LINGUAGGI DI ALTO LIVELLO Si basano su una macchina virtuale le cui mosse non sono quelle della macchina hardware 1 LINGUAGGI DI ALTO LIVELLO Barriera di astrazione Fortran Cobol Basic Pascal Python C
Teoria dell Informazione
 Corso di Laurea Magistrale in Scienze dell Informazione Editoriale, Pubblica e Sociale Teoria dell Informazione Cosa è l informazione L informazione è qualcosa che si possiede e si può dare ad un altro
Corso di Laurea Magistrale in Scienze dell Informazione Editoriale, Pubblica e Sociale Teoria dell Informazione Cosa è l informazione L informazione è qualcosa che si possiede e si può dare ad un altro
Aniello Murano Problemi non decidibili e riducibilità
 Aniello Murano Problemi non decidibili e riducibilità 8 Lezione n. Parole chiave: Riduzione Corso di Laurea: Informatica Codice: Email Docente: murano@ na.infn.it A.A. 2008-2009 Overview Nelle lezioni
Aniello Murano Problemi non decidibili e riducibilità 8 Lezione n. Parole chiave: Riduzione Corso di Laurea: Informatica Codice: Email Docente: murano@ na.infn.it A.A. 2008-2009 Overview Nelle lezioni
Informatica teorica Lez. n 7 Macchine di Turing. Macchine di Turing. Prof. Giorgio Ausiello Università di Roma La Sapienza
 Macchine di Turing Argomenti della lezione Definizione della macchina di Turing Riconoscimento e accettazione di linguaggi Macchine a più nastri La macchina di Turing èun è automa che può leggere e scrivere
Macchine di Turing Argomenti della lezione Definizione della macchina di Turing Riconoscimento e accettazione di linguaggi Macchine a più nastri La macchina di Turing èun è automa che può leggere e scrivere
Informatica Teorica. Appunti della lezione su tesi di Church-Turing e problemi indecidibili
 Informatica Teorica Appunti della lezione su tesi di Church-Turing e problemi indecidibili Tesi di Church- Turing Nel 1936, Church propone di assimilare il conce:o informale di computabilità con il conce:o
Informatica Teorica Appunti della lezione su tesi di Church-Turing e problemi indecidibili Tesi di Church- Turing Nel 1936, Church propone di assimilare il conce:o informale di computabilità con il conce:o
Cosa è l Informatica?
 Cosa è l Informatica? Scienza degli elaboratori elettronici (Computer Science) Scienza dell informazione Scienza della rappresentazione, memorizzazione, elaborazione e trasmissione dell informazione Elaboratore
Cosa è l Informatica? Scienza degli elaboratori elettronici (Computer Science) Scienza dell informazione Scienza della rappresentazione, memorizzazione, elaborazione e trasmissione dell informazione Elaboratore
Macchine di TURING. Alan Mathison Turing ( )
 Macchine di TURING Alan Mathison Turing (1912 1954) Macchine di TURING Alan Mathison Turing (1912 1954) matematico, logico e crittanalista britannico, considerato uno dei padri dell informatica e uno dei
Macchine di TURING Alan Mathison Turing (1912 1954) Macchine di TURING Alan Mathison Turing (1912 1954) matematico, logico e crittanalista britannico, considerato uno dei padri dell informatica e uno dei
Appunti di informatica. Lezione 7 anno accademico Mario Verdicchio
 Appunti di informatica Lezione 7 anno accademico 2016-2017 Mario Verdicchio L algoritmo di Euclide per l MCD Dati due numeri A e B, per trovare il loro MCD procedere nel seguente modo: 1. dividere il maggiore
Appunti di informatica Lezione 7 anno accademico 2016-2017 Mario Verdicchio L algoritmo di Euclide per l MCD Dati due numeri A e B, per trovare il loro MCD procedere nel seguente modo: 1. dividere il maggiore
Informatica 3. LEZIONE 1: Introduzione. Modulo 1: Introduzione al corso Modulo 2: Introduzione ai linguaggi di programmazione
 Informatica 3 LEZIONE 1: Introduzione Modulo 1: Introduzione al corso Modulo 2: Introduzione ai linguaggi di Informatica 3 Lezione 1- Modulo 1 Introduzione al corso Introduzione Corso di Informatica 3
Informatica 3 LEZIONE 1: Introduzione Modulo 1: Introduzione al corso Modulo 2: Introduzione ai linguaggi di Informatica 3 Lezione 1- Modulo 1 Introduzione al corso Introduzione Corso di Informatica 3
FONDAMENTI DI INFORMATICA
 Fondamenti di Informatica FONDAMENTI DI INFORMATICA Domenico Talia [email protected] A.A. 2002-2003 Facoltà di Ingegneria UNICAL Fondamenti di Informatica - D. Talia - UNICAL 1 Fondamenti di Informatica
Fondamenti di Informatica FONDAMENTI DI INFORMATICA Domenico Talia [email protected] A.A. 2002-2003 Facoltà di Ingegneria UNICAL Fondamenti di Informatica - D. Talia - UNICAL 1 Fondamenti di Informatica
Fondamenti Teorici e Programmazione Modulo A: Elementi di Programmazione Corso di Laurea in Informatica Umanistica a.a. 2013/2014
 Fondamenti Teorici e Programmazione Modulo A: Elementi di Programmazione Corso di Laurea in Informatica Umanistica a.a. 2013/2014 E.Occhiuto Dipartimento di Informatica email: [email protected] E. Occhiuto
Fondamenti Teorici e Programmazione Modulo A: Elementi di Programmazione Corso di Laurea in Informatica Umanistica a.a. 2013/2014 E.Occhiuto Dipartimento di Informatica email: [email protected] E. Occhiuto
Studio degli algoritmi
 COMPLESSITÀ COMPUTAZIONALE DEGLI ALGORITMI Fondamenti di Informatica a.a.2006/07 Prof. V.L. Plantamura Dott.ssa A. Angelini Studio degli algoritmi Dato un problema P, le problematiche riguardano: Sintesi
COMPLESSITÀ COMPUTAZIONALE DEGLI ALGORITMI Fondamenti di Informatica a.a.2006/07 Prof. V.L. Plantamura Dott.ssa A. Angelini Studio degli algoritmi Dato un problema P, le problematiche riguardano: Sintesi
Elementi di programmazione
 Fondamenti di Informatica per la Sicurezza a.a. 2003/04 Elementi di programmazione Stefano Ferrari Università degli Studi di Milano Dipartimento di Tecnologie dell Informazione Stefano Ferrari Università
Fondamenti di Informatica per la Sicurezza a.a. 2003/04 Elementi di programmazione Stefano Ferrari Università degli Studi di Milano Dipartimento di Tecnologie dell Informazione Stefano Ferrari Università
Equivalenza di Espressioni Algebriche
 Equivalenza di Espressioni Algebriche Basi di dati e sistemi informativi 1 Equivalenza di Espressioni Algebriche Angelo Montanari Dipartimento di Matematica e Informatica Università di Udine Equivalenza
Equivalenza di Espressioni Algebriche Basi di dati e sistemi informativi 1 Equivalenza di Espressioni Algebriche Angelo Montanari Dipartimento di Matematica e Informatica Università di Udine Equivalenza
Le Macchine di Turing
 Le Macchine di Turing Come è fatta una MdT? Una MdT è definita da: un nastro una testina uno stato interno un programma uno stato iniziale Il nastro Il nastro è infinito suddiviso in celle In una cella
Le Macchine di Turing Come è fatta una MdT? Una MdT è definita da: un nastro una testina uno stato interno un programma uno stato iniziale Il nastro Il nastro è infinito suddiviso in celle In una cella
Modelli e complessità di calcolo
 Modelli e complessità di calcolo Prof. Giorgio Ausiello Orario delle lezioni: Martedi, Mercoledi, Giovedi ore 8.30 10.00 Orario di ricevimento: Lunedi ore 17.00 19.00 Via Ariosto 25 II piano - Ufficio
Modelli e complessità di calcolo Prof. Giorgio Ausiello Orario delle lezioni: Martedi, Mercoledi, Giovedi ore 8.30 10.00 Orario di ricevimento: Lunedi ore 17.00 19.00 Via Ariosto 25 II piano - Ufficio
Introduzione. Fondamenti di Informatica 1. Dispensa 1 Gennaio Contenuti. Alfonso Miola. K Corso di Fondamenti di Informatica 1
 Alfonso Miola Dispensa 1 Gennaio 2001 1 Contenuti K Corso di K Programma del corso K Materiale didattico K Organizzazione didattica K Attività di laboratorio K Prove di valutazione ed esami 2 Corso di
Alfonso Miola Dispensa 1 Gennaio 2001 1 Contenuti K Corso di K Programma del corso K Materiale didattico K Organizzazione didattica K Attività di laboratorio K Prove di valutazione ed esami 2 Corso di
Informatica Teorica. Sezione Cremona + Como. Appello del 20 Luglio 2004
 Informatica Teorica Sezione Cremona + Como Appello del 20 Luglio 2004 Coloro che recuperano la I prova risolvano gli esercizi e 2 tra quelli indicati qui sotto entro un ora. Coloro che recuperano la II
Informatica Teorica Sezione Cremona + Como Appello del 20 Luglio 2004 Coloro che recuperano la I prova risolvano gli esercizi e 2 tra quelli indicati qui sotto entro un ora. Coloro che recuperano la II
Algoritmi e Strutture Dati
 Introduzione al Corso Maria Rita Di Berardini (Camerino), Emanuela Merelli (Ascoli) 1 1 Scuola di Scienze e Tecnologie - Sezione di Informatica Università di Camerino Parte I Il concetto di Algoritmo Il
Introduzione al Corso Maria Rita Di Berardini (Camerino), Emanuela Merelli (Ascoli) 1 1 Scuola di Scienze e Tecnologie - Sezione di Informatica Università di Camerino Parte I Il concetto di Algoritmo Il
Corso di Laurea Ingegneria Informatica
 Corso di Laurea Ingegneria Informatica Presentazione del corso di Fondamenti di Informatica 2 A. Miola Febbraio 2008 http://www.dia.uniroma3.it/~java/fondinf2/ Presentazione Corso 1 Contenuti Corso di
Corso di Laurea Ingegneria Informatica Presentazione del corso di Fondamenti di Informatica 2 A. Miola Febbraio 2008 http://www.dia.uniroma3.it/~java/fondinf2/ Presentazione Corso 1 Contenuti Corso di
Argomenti diagonali. Gianluigi Bellin
 Argomenti diagonali Gianluigi Bellin November 30, 2010 La cardinalità degli insiemi. Consideriamo la relazione di equivalenza tra insiemi ottenuta ponendo A B se e solo se esiste una biiezione f : A B.
Argomenti diagonali Gianluigi Bellin November 30, 2010 La cardinalità degli insiemi. Consideriamo la relazione di equivalenza tra insiemi ottenuta ponendo A B se e solo se esiste una biiezione f : A B.
Programmazione C Massimo Callisto De Donato
 Università degli studi di Camerino Scuola di scienze e tecnologia - Sezione Informatica Programmazione C Massimo Callisto De Donato [email protected] www.cs.unicam.it/massimo.callisto LEZIONE
Università degli studi di Camerino Scuola di scienze e tecnologia - Sezione Informatica Programmazione C Massimo Callisto De Donato [email protected] www.cs.unicam.it/massimo.callisto LEZIONE
FONDAMENTI DI INFORMATICA
 Fondamenti di Informatica FONDAMENTI DI INFORMATICA Domenico Talia [email protected] A.A. 2002-2003 Facoltà di Ingegneria UNICAL Fondamenti di Informatica - D. Talia - UNICAL 1 Fondamenti di Informatica
Fondamenti di Informatica FONDAMENTI DI INFORMATICA Domenico Talia [email protected] A.A. 2002-2003 Facoltà di Ingegneria UNICAL Fondamenti di Informatica - D. Talia - UNICAL 1 Fondamenti di Informatica
LINGUAGGI DI ALTO LIVELLO
 LINGUAGGI DI ALTO LIVELLO Si basano su una macchina virtuale le cui mosse non sono quelle della macchina hardware Linguaggi di alto livello Barriera di astrazione C Fortran Modula-2 Cobol Algol Basic Ada
LINGUAGGI DI ALTO LIVELLO Si basano su una macchina virtuale le cui mosse non sono quelle della macchina hardware Linguaggi di alto livello Barriera di astrazione C Fortran Modula-2 Cobol Algol Basic Ada
Cosa è un programma. Informatica di Base -- R.Gaeta 18
 Cosa è un programma Il programma è la scatola nera che risolve il problema computazionale; Il programma è una sequenza di istruzioni che devono essere eseguite; Il programma è la traduzione per il computer
Cosa è un programma Il programma è la scatola nera che risolve il problema computazionale; Il programma è una sequenza di istruzioni che devono essere eseguite; Il programma è la traduzione per il computer
Cos è un algoritmo. Si dice algoritmo la descrizione di un metodo di soluzione di un problema che sia
 Programmazione Un programma descrive al computer, in estremo dettaglio, la sequenza di passi necessari a svolgere un particolare compito L attività di progettare e realizzare un programma è detta programmazione
Programmazione Un programma descrive al computer, in estremo dettaglio, la sequenza di passi necessari a svolgere un particolare compito L attività di progettare e realizzare un programma è detta programmazione
Programma del corso. Elementi di Programmazione. Introduzione agli algoritmi. Rappresentazione delle Informazioni. Architettura del calcolatore
 Programma del corso Introduzione agli algoritmi Rappresentazione delle Informazioni Architettura del calcolatore Reti di Calcolatori Elementi di Programmazione Algoritmi e programmi Algoritmo Sequenza
Programma del corso Introduzione agli algoritmi Rappresentazione delle Informazioni Architettura del calcolatore Reti di Calcolatori Elementi di Programmazione Algoritmi e programmi Algoritmo Sequenza
CAPITOLO 1 CENNI STORICI
 CAPITOLO 1 CENNI STORICI 1. Gli abachi: calcolare con sassi e palline..... 1 2. I bastoncini di Nepero...... 7 3. Un antico calcolatore analogico: riga+compasso...... 10 4. Oltre le quattro operazioni:
CAPITOLO 1 CENNI STORICI 1. Gli abachi: calcolare con sassi e palline..... 1 2. I bastoncini di Nepero...... 7 3. Un antico calcolatore analogico: riga+compasso...... 10 4. Oltre le quattro operazioni:
Università degli Studi di Verona. Algoritmie Diagrammidiflusso. Gennaio Sergio Marin Vargas. Dipartimento di Biotecnologie
 Università degli Studi di Verona Dipartimento di Biotecnologie Laurea in Biotecnologie Corso di Informatica2014/2015 Algoritmie Diagrammidiflusso Gennaio 2015 - Sergio Marin Vargas Problemi e soluzioni
Università degli Studi di Verona Dipartimento di Biotecnologie Laurea in Biotecnologie Corso di Informatica2014/2015 Algoritmie Diagrammidiflusso Gennaio 2015 - Sergio Marin Vargas Problemi e soluzioni
Corso di Fondamenti di Informatica Linguaggi di Programmazione
 Corso di Fondamenti di Informatica Linguaggi di Programmazione Anno Accademico Francesco Tortorella Linguaggi di programmazione Un calcolatore basato sul modello di von Neumann permette l esecuzione di
Corso di Fondamenti di Informatica Linguaggi di Programmazione Anno Accademico Francesco Tortorella Linguaggi di programmazione Un calcolatore basato sul modello di von Neumann permette l esecuzione di
Fondamenti di Informatica. Definizione di Algoritmo. Algoritmo Euclideo. Prof.V.L.Plantamura Informatica e Comunicazione Digitale a.a.
 Fondamenti di Informatica Prof.V.L.Plantamura Informatica e Comunicazione Digitale a.a. 006-007 Definizione di Algoritmo Def.: Per Algoritmo si intende un elenco di istruzioni che specificano una serie
Fondamenti di Informatica Prof.V.L.Plantamura Informatica e Comunicazione Digitale a.a. 006-007 Definizione di Algoritmo Def.: Per Algoritmo si intende un elenco di istruzioni che specificano una serie
Linguaggi Regolari e Linguaggi Liberi
 Linguaggi Regolari e Linguaggi Liberi Potenza espressiva degli automi Potenza espressiva delle grammatiche 9/11/2004 Programmazione - Luca Tesei 1 Linguaggi Regolari Tutti i linguaggi che possono essere
Linguaggi Regolari e Linguaggi Liberi Potenza espressiva degli automi Potenza espressiva delle grammatiche 9/11/2004 Programmazione - Luca Tesei 1 Linguaggi Regolari Tutti i linguaggi che possono essere
Programmazione di INFORMATICA e Laboratorio
 ISIUO ECNICO SAALE settore ECNOLOGICO ad indirizzo: Elettronica ed Elettrotecnica - Informatica e elecomunicazioni Meccanica, Meccatronica ed Energia "VIORIO EMANUELE III" Via Duca della Verdura, 48-90143
ISIUO ECNICO SAALE settore ECNOLOGICO ad indirizzo: Elettronica ed Elettrotecnica - Informatica e elecomunicazioni Meccanica, Meccatronica ed Energia "VIORIO EMANUELE III" Via Duca della Verdura, 48-90143
ELEMENTI DI PROGRAMMAZIONE a.a. 2012/13 MACCHINE, ALGORITMI, PROGRAMMI
 ELEMENTI DI PROGRAMMAZIONE a.a. 22/3 MACCHINE, ALGORITMI, PROGRAMMI Andrea Prevete, UNINA2 23 UNA GERARCHIA DI MACCHINE macchine combinatorie macchine sequenziali (automi a stati finiti)... macchine di
ELEMENTI DI PROGRAMMAZIONE a.a. 22/3 MACCHINE, ALGORITMI, PROGRAMMI Andrea Prevete, UNINA2 23 UNA GERARCHIA DI MACCHINE macchine combinatorie macchine sequenziali (automi a stati finiti)... macchine di
Introduzione alla programmazione
 Introduzione alla programmazione Risolvere un problema Per risolvere un problema si procede innanzitutto all individuazione Delle informazioni, dei dati noti Dei risultati desiderati Il secondo passo consiste
Introduzione alla programmazione Risolvere un problema Per risolvere un problema si procede innanzitutto all individuazione Delle informazioni, dei dati noti Dei risultati desiderati Il secondo passo consiste
Appunti di informatica. Lezione 5 anno accademico Mario Verdicchio
 Appunti di informatica Lezione 5 anno accademico 2015-2016 Mario Verdicchio L algoritmo di Euclide per l MCD Dati due numeri A e B, per trovare il loro MCD procedere nel seguente modo: 1. dividere il maggiore
Appunti di informatica Lezione 5 anno accademico 2015-2016 Mario Verdicchio L algoritmo di Euclide per l MCD Dati due numeri A e B, per trovare il loro MCD procedere nel seguente modo: 1. dividere il maggiore
C++ Barriera di astrazione. Barriera di astrazione. Basic. Basic. Lisp. Lisp. Pascal. Prolog. Pascal. Prolog. Cobol. Fortran IMPERATIVI FUNZIONALI
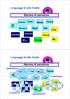 Linguaggi di alto livello Barriera di astrazione C Fortran Cobol Modula-2 Basic Pascal Algol Ada Lisp Smalltalk Simula67 Scheme C++ Prolog ML AN - 1995 Linguaggi di alto livello IMPERATIVI C Fortran Modula-2
Linguaggi di alto livello Barriera di astrazione C Fortran Cobol Modula-2 Basic Pascal Algol Ada Lisp Smalltalk Simula67 Scheme C++ Prolog ML AN - 1995 Linguaggi di alto livello IMPERATIVI C Fortran Modula-2
Appunti su Indipendenza Lineare di Vettori
 Appunti su Indipendenza Lineare di Vettori Claudia Fassino a.a. Queste dispense, relative a una parte del corso di Matematica Computazionale (Laurea in Informatica), rappresentano solo un aiuto per lo
Appunti su Indipendenza Lineare di Vettori Claudia Fassino a.a. Queste dispense, relative a una parte del corso di Matematica Computazionale (Laurea in Informatica), rappresentano solo un aiuto per lo
ALGORITMI: PROPRIETÀ FONDAMENTALI
 ALGORITMI: PROPRIETÀ FONDAMENTALI Non si può risolvere un problema senza prima fissare un insieme di azioni, i di mosse elementari possibili per l'esecutore. Bisogna conoscerne le caratteristiche, le mosse
ALGORITMI: PROPRIETÀ FONDAMENTALI Non si può risolvere un problema senza prima fissare un insieme di azioni, i di mosse elementari possibili per l'esecutore. Bisogna conoscerne le caratteristiche, le mosse
Capitolo 8: Teoria della complessitá
 Capitolo 8: Teoria della complessitá 1 La Teoria della calcolabilitá considera aspetti qualitativi della soluzione di problemi. Distingue il calcolabile dal non calcolabile. La Teoria della complessitá
Capitolo 8: Teoria della complessitá 1 La Teoria della calcolabilitá considera aspetti qualitativi della soluzione di problemi. Distingue il calcolabile dal non calcolabile. La Teoria della complessitá
COMPLESSITÀ COMPUTAZIONALE DEGLI ALGORITMI
 COMPLESSITÀ COMPUTAZIONALE DEGLI ALGORITMI Fondamenti di Informatica a.a.200.2005/06 Prof. V.L. Plantamura Dott.ssa A. Angelini Confronto di algoritmi Uno stesso problema può essere risolto in modi diversi,
COMPLESSITÀ COMPUTAZIONALE DEGLI ALGORITMI Fondamenti di Informatica a.a.200.2005/06 Prof. V.L. Plantamura Dott.ssa A. Angelini Confronto di algoritmi Uno stesso problema può essere risolto in modi diversi,
Informatica 3. LEZIONE 10: Introduzione agli algoritmi e alle strutture dati
 Informatica 3 LEZIONE 10: Introduzione agli algoritmi e alle strutture dati Modulo 1: Perchè studiare algoritmi e strutture dati Modulo 2: Definizioni di base Informatica 3 Lezione 10 - Modulo 1 Perchè
Informatica 3 LEZIONE 10: Introduzione agli algoritmi e alle strutture dati Modulo 1: Perchè studiare algoritmi e strutture dati Modulo 2: Definizioni di base Informatica 3 Lezione 10 - Modulo 1 Perchè
TEORIE E TECNICHE PER LA COMUNICAZIONE DIGITALE
 TEORIE E TECNICHE PER LA COMUNICAZIONE DIGITALE Riccardo Dondi Dipartimento di Scienze dei linguaggi, della comunicazione e degli studi culturali Università degli Studi di Bergamo Informazione sul corso
TEORIE E TECNICHE PER LA COMUNICAZIONE DIGITALE Riccardo Dondi Dipartimento di Scienze dei linguaggi, della comunicazione e degli studi culturali Università degli Studi di Bergamo Informazione sul corso
Matematica e Statistica per Scienze Ambientali
 per Scienze Ambientali Insiemi e Combinatoria - Appunti 1 1 Dipartimento di Matematica Sapienza, Università di Roma Roma, 23 - Ottobre 2012 Il concetto di insieme Non tratterò la teoria assiomatica degli
per Scienze Ambientali Insiemi e Combinatoria - Appunti 1 1 Dipartimento di Matematica Sapienza, Università di Roma Roma, 23 - Ottobre 2012 Il concetto di insieme Non tratterò la teoria assiomatica degli
Linguaggi di alto livello, compilatori e interpreti
 Linguaggi di alto livello, compilatori e interpreti Percorso di Preparazione agli Studi di Ingegneria Università degli Studi di Brescia Docente: Massimiliano Giacomin Il punto della situazione STATO DATI
Linguaggi di alto livello, compilatori e interpreti Percorso di Preparazione agli Studi di Ingegneria Università degli Studi di Brescia Docente: Massimiliano Giacomin Il punto della situazione STATO DATI
Macchine di Turing. Francesco Paoli. Istituzioni di logica, Francesco Paoli (Istituzioni di logica, ) Macchine di Turing 1 / 29
 Macchine di Turing Francesco Paoli Istituzioni di logica, 2016-17 Francesco Paoli (Istituzioni di logica, 2016-17) Macchine di Turing 1 / 29 Alan M. Turing (1912-1954) Francesco Paoli (Istituzioni di logica,
Macchine di Turing Francesco Paoli Istituzioni di logica, 2016-17 Francesco Paoli (Istituzioni di logica, 2016-17) Macchine di Turing 1 / 29 Alan M. Turing (1912-1954) Francesco Paoli (Istituzioni di logica,
Programmazione dinamica
 Programmazione dinamica Violetta Lonati Università degli studi di Milano Dipartimento di Informatica Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica Violetta Lonati Programmazione
Programmazione dinamica Violetta Lonati Università degli studi di Milano Dipartimento di Informatica Laboratorio di algoritmi e strutture dati Corso di laurea in Informatica Violetta Lonati Programmazione
