Scelta della funzione di legame in un modello lineare generalizzato attraverso delle simulazioni. Fabrizio Bettella
|
|
|
- Brigida Viola
- 5 anni fa
- Visualizzazioni
Transcript
1 Scelta della funzione di legame in un modello lineare generalizzato attraverso delle simulazioni Fabrizio Bettella anno accademico 2006/2007
2 2
3 Indice 1 Introduzione 5 2 I modelli lineari generalizzati Un interessante classe di distribuzione Una nuova classe di modelli Stima dei parametri Criteri di selezione del modello 11 4 Studio di simulazione Caso con due regressori positivi Caso con β 2 minore di Caso con tre regressori Caso con quattro regressori Un esempio con dati reali 27 Bibliografia 31 3
4 4 INDICE
5 Capitolo 1 Introduzione In Statistica, è frequentemente di interesse modellare una varibile risposta in funzione di alcune variabili esplicative. Inoltre, è utile disporre di opportuni test statistici per valutare se le variabili esplicative sono significative, ossia se la loro inclusione nel modello è rilevante. Nel linguaggio statistico questa analisi dei dati viene chiamata analisi di regressione. Il nostro interesse in questa tesi sarà rivolto ai modelli lineari generalizzati. I modelli lineari generalizzati rappresentano un estensione dei modelli lineari. Alcuni aspetti salienti saranno riassunti nel Capitolo 2. Spesso, diversi modelli lineari generalizzati possono essere considerati ragionevoli per descrivere un assegnato insieme di dati. Ad esempio, si possono considerare diversi insiemi di variabili esplicative, oppure, per un fissato insieme di esplicative, diverse funzioni di legame. Sono allora utili i metodi di selezione del modello. Il più noto tra questi è il criterio di informazione di Akaike (AIC) introdoto da Akaike (1973) e brevemente richiamato nel Capitolo 3. L obiettivo di questa relazione è valutare tramite uno studio di simulazione le probabilità di selezione corretta dell AIC qualora si desideri selezionare tra due modelli lineari generalizzati per risposte Poisson, caratterizzati da due 5
6 6 CAPITOLO 1. INTRODUZIONE diverse funzioni di legame, con un fissato insieme di variabili esplicative. In particolare, si è interessati a valutare il comportamento dell AIC all aumentare del numero di variabili esplicative per una fissata numerosità campionaria. I risultati della simulazione sono presentati nel Capitolo 4, mentre nel Capitolo 5 viene presentato un esempio con dati reali.
7 Capitolo 2 I modelli lineari generalizzati Un esempio in cui i modelli lineari generalizzati vengono applicati è quello delle visite mediche in funzione dell età. E naturale attendersi che il numero delle visite aumenti con l età in modo non lineare, quindi un modello lineare risulterebbe inadatto. I modelli lineari si basano sull ipotesi di normalità dei dati, ma questo spesso non è plausibile per vari motivi. Ad esempio può succedere che la variabilità della variabile risposta cresca in maniera monotona con il suo valore medio oppure potremmo essere interessati a stimare la probabilità che una certa dose di veleno abbia effetto sulle delle cavie. In tutte queste situazioni non è ipotizzabile la distribuzione normale, e questo lo si può capire considerando la distribuzione della variabile risposta. 2.1 Un interessante classe di distribuzione Le principali variabili casuali che fanno parte dei modelli lineari generalizzati sono: la binomiale, la poisson, la gamma e la normale. Esse costituiscono un sottoinsieme della famiglia di 7
8 8 CAPITOLO 2. I MODELLI LINEARI GENERALIZZATI dispersione esponenziale perché la loro funzione di densità può essere scritta come ( ) ω f (y;θ;ψ) = exp ψ {yθ b(θ)} + c(y;ψ) (2.1) dove θ,ψ sono dei parametri scalari ignoti, ω è una costante nota, e b(.) e c(.) sono funzioni note la cui scelta individua una particolare distribuzione di probabilità. Quando questo risulta vero possiamo scrivere per una varibile continua Y che ( Y DE b(θ), ψ ). ω Per ogni particolare scelta di ψ, detto parametro di dispersione, la f (y; θ) costituisce una famiglia esponenziale di parametro θ. Se ψ e θ variano simultaneamente allora la f (y;θ) non è una famiglia esponenziale. A parte questa precisazione, nel nostro caso consideriamo ψ come fissato. Per una famiglia esponenziale media e varianza sono date rispettivamente E (y) = b (θ). V ar (y) = b (θ) ψ ω 2.2 Una nuova classe di modelli Nei modelli lineari si suppone che le osservazioni y i siano la realizzazione di una variabile casuale Y N ( µ i ;σ 2) e che il predittore lineare η i coincida con x T i β dove xt i è la i-esima riga di X per i = 1,...,n. Inoltre la relazione tra valore medio µ i e il predittore lineare η i è l identità. Schematizzando avremo Y N ( µ i ;σ 2) µ i = η i η i = x T i β. I modelli lineari generalizzati rappresentano un estensione dei modelli lineari per due motivi
9 2.3. STIMA DEI PARAMETRI 9 1. come distribuzione possibile per Y i non considerano solo la ) normale, ma qualunque altra distribuzione DE (b(θ i ); ψ ωi tale che b (θ i ) = µ i 2. ipotizzano varie forme di legame fra il valore medio e il predittore lineare, cioè avremo che g(µ i ) = η i dove g(.) è una funzione monotona derivabile detta funzione di legame. In altre parole diremo che i modelli lineari generalizzati sono ) caratterizzati dai seguenti elementi Y i DE (b(θ i ); ψ con b (θ ωi i ) = µ i struttura stocastica, g(µ i ) = η i funzione legame, η i = x T i β predittore lineare. 2.3 Stima dei parametri Date le osservazioni campionarie y 1,...,y n vogliamo fare inferenza sul parametro β. Il nostro interesse è rivolto a β perchè determina la relazione tra le variabili esplicative e µ, mentre ψ è un parametro di disturbo quando è presente. Indichiamo con p la dimensione di β e con X = (x ij ) la matrice n p con i-esima riga x T i sarà. Essendo le osservazioni indipendenti, la log-verosimiglianza l(β) = n ( ωi (y i θ i b(θ i )) i=1 ψ ) + c i (y i ;ψ) n = l i (β). i=1 Per facilitare il calcolo delle equazioni di verosimiglianza usiamo l i β j = l i θ i θ i µ i µ i η i η i β j (2.2) i cui termini possono essere riscritti nel seguente modo l i = y i b (θ i ) θ i ψ/ω i = y i µ i ψ/ω i, (2.3) µ i = b (θ i ) = ω ivar(y i ), θ i ψ (2.4) η i = x ij. β j (2.5)
10 10 CAPITOLO 2. I MODELLI LINEARI GENERALIZZATI Quindi abbiamo l i = y i µ i ψ/ω i µ i x ij β j ψ/ω i var(y i ) η i A questo punto le equazioni di verosimiglianza per β hanno la seguente forma n i=1 (y i µ i )x ij var(y i ) µ i η i = 0 (j = 1,...,p). (2.6)
11 Capitolo 3 Criteri di selezione del modello Nella letteratura statistica esistono vari metodi o criteri per scegliere un modello tra quelli plausibili. Il piu noto è senza dubbio l AIC, Akaike Information Criterion, ma ve ne sono altri come ad esempio il BIC, Bayesian Information Criterion. Il criterio di Akaike viene calcolato nel seguente modo ( )) 2log L (ˆθ;y + 2p mentre quello Bayesiano è dato da ( )) p log (n) 2log L (ˆθ;y. In entrambi i casi il modello scelto sarà quello che minimizza il criterio. Con il metodo di Akaike si tende a selezionare un modello leggermente sovraparametrizzato per n sufficientemente elevato, mentre con quello Bayesiano per n non elevato si tende a selezionarne uno leggermente sottoparametrizzato. Come detto in precedenza, faremo riferimento all AIC. L obbiettivo è di scegliere un modello intermedio tra tutti quelli correttamente specificati, che bilanci bontà di adattamento ai dati e parsimonia della modellazione. Un modello con molti parametri è piu 11
12 12 CAPITOLO 3. CRITERI DI SELEZIONE DEL MODELLO flessibile e permette una migliore rappresentazione dei dati. Tutto questo è vero fino ad un certo punto, perchè se il modello è troppo ampio può succedere che le stime dei parametri tendano a divenire instabili, cioè gli errori quadratici medi stimati tendono a gonfiarsi. Per generalizzare, i modelli parametrici che si prendono in considerazione sono annidati, cioè avremo Θ 1 Θ 2... Θ k R k dove Θ i per i = 1,...,k rappresenta lo spazio parametrico per un generico modello. Indicando con θ (1),...,θ (k) i parametri { } dei vari modelli, il passaggio da Θ k = θ (k) = (θ 1,...,θ k ) a Θ k 1 avviene attraverso l ipotesi θ k = 0. Aggiungendo ulteriori annullamenti alle componenti otteniamo i corrispondenti modelli di complessità inferiore. I criteri per la selezione di un modello si basano sulle verosimiglianze profilo penalizzate per il numero di parametri presenti. Questa penalizzazione per la dimensione parametrica, nei principali metodi viene basata su considerazioni di informazione predittiva del modello, cioè sulla perdita attesa di efficacia predittiva. I criteri di Akaike e quello Bayesiano derivano proprio da queste considerazioni.
13 Capitolo 4 Studio di simulazione In questo capitolo mostreremo i risulati di alcune simulazioni fatte con R, cioè replicheremo varie numerosità da una disribuzione di Poisson prima con vera media exp (β 1 x ik β k x ik ) e poi con vera media (β 1 x ik β k x ik ) 2. In entrambe le situazioni, verrà confrontato l AIC ottenuto con legame canonico e quello ottenuto con legame radice quadrata. Le numerosità campionarie scelte per questo nostro esperimento sono n = 5,10,20,50 e le replicazioni per ogni campione sono Queste simulazioni prevedono vari casi: valori delle esplicative compresi fra 0 e 1 e valori maggiori di 1; due regressori, compresa l intercetta, entrambi positivi, due regressori, compresa l intercetta, con β 2 minore di 0; tre regressori includendo l intercetta; quattro regressori includendo l intercetta; Nei casi con due parametri, β 1 e β 2, faremo un grafico delle medie per dare un idea del loro andamento. Ovviamente, i casi analizzati avranno le due medie con lo stesso andamento. 13
14 14 CAPITOLO 4. STUDIO DI SIMULAZIONE mu x Figura 4.1: Grafico medie 4.1 Caso con due regressori positivi Nel seguente esempio le due medie in questione sono exp (1 + x i2 ) e (1 + x i2 ) 2. Un grafico per le medie è dato dalla Figura 4.1. Osservandolo si nota che la Poisson con media esponenziale cresce piu rapidamente rispetto all altra. Per valori di x maggiori di 1 avremo le tabelle dalla 4.1 fino alla 4.4, mentre per valori di x minori di 1 le tabelle dalla 4.5 fino alla 4.8.
15 4.1. CASO CON DUE REGRESSORI POSITIVI 15 Link=log Link=sqrt Tabella 4.1: Tabella con n=5 Link=log Link=sqrt Tabella 4.2: Tabella con n=10 Link=log Link=sqrt Tabella 4.3: Tabella con n=20
16 16 CAPITOLO 4. STUDIO DI SIMULAZIONE Link=log 1 0 Link=sqrt 0 1 Tabella 4.4: Tabella con n=50 Link=log Link=sqrt Tabella 4.5: Tabella con n=5 Link=log Link=sqrt Tabella 4.6: Tabella con n=10
17 4.1. CASO CON DUE REGRESSORI POSITIVI 17 Link=log Link=sqrt Tabella 4.7: Tabella con n=20 Link=log Link=sqrt Tabella 4.8: Tabella con n=50
18 18 CAPITOLO 4. STUDIO DI SIMULAZIONE mu x Figura 4.2: Grafico medie 4.2 Caso con β 2 minore di 0 Per questo caso, abbiamo scelto le medie exp (3 0.25x i2 ) e (3 0.25x i2 ) 2. Una rappresentazione grafica è data dalla Figura 4.2. Dalla figura vediamo che la Poisson con media esponenziale decresce un po piu rapidamente rispetto all altra. Le tabelle dalla 4.9 fino alla 4.12 si riferiscono a valori delle esplicative maggiori di 1 mentre dalla 4.13 alla 4.16 per valori minori di 1.
19 4.2. CASO CON β 2 MINORE DI 0 19 Link=log Link=sqrt Tabella 4.9: Tabella con n=5 Link=log Link=sqrt Tabella 4.10: Tabella con n=10 Link=log Link=sqrt Tabella 4.11: Tabella con n=20
20 20 CAPITOLO 4. STUDIO DI SIMULAZIONE Link=log Link=sqrt Tabella 4.12: Tabella con n=50 Link=log Link=sqrt Tabella 4.13: Tabella con n=5 Link=log Link=sqrt Tabella 4.14: Tabella con n=10 Link=log Link=sqrt Tabella 4.15: Tabella con n=20 Link=log Link=sqrt Tabella 4.16: Tabella con n=50
21 4.3. CASO CON TRE REGRESSORI Caso con tre regressori Le funzioni delle medie in questione sono exp ( x i x i3 ) e ( x i x i3 ) 2. In questo esempio non faremo un grafico perchè non sarebbe di grande utilità. Per valori delle esplicative maggiori di 1 abbiamo le tabelle dalla 4.17 alla 4.20, mentre per valori minori di1 avremo quelle dalla 4.21 alla Link=log Link=sqrt Tabella 4.17: Tabella con n=5 Link=log Link=sqrt Tabella 4.18: Tabella con n=10 Link=log Link=sqrt Tabella 4.19: Tabella con n=20
22 22 CAPITOLO 4. STUDIO DI SIMULAZIONE Link=log Link=sqrt Tabella 4.20: Tabella con n=50 Link=log Link=sqrt Tabella 4.21: Tabella con n=5 Link=log Link=sqrt Tabella 4.22: Tabella con n=10 Link=log Link=sqrt Tabella 4.23: Tabella con n=20 Link=log Link=sqrt Tabella 4.24: Tabella con n=50
23 4.4. CASO CON QUATTRO REGRESSORI Caso con quattro regressori Le medie in questione sono date da exp ( x i2 0.15x i x i4 ) e ( x i2 0.15x i i4 ) 2. Con valori delle esplicative maggiori di 1 avremo tabelle dalla 4.25 alla 4.28, mentre con valori minori di 1 le tabelle dalla 4.29 alla [h] Link=log Link=sqrt Tabella 4.25: Tabella con n=5 Link=log Link=sqrt Tabella 4.26: Tabella con n=10 Link=log Link=sqrt Tabella 4.27: Tabella con n=20
24 24 CAPITOLO 4. STUDIO DI SIMULAZIONE Link=log Link=sqrt Tabella 4.28: Tabella con n=50 Link=log Link=sqrt Tabella 4.29: Tabella con n=5 Link=log Link=sqrt Tabella 4.30: Tabella con n=10 Link=log Link=sqrt Tabella 4.31: Tabella con n=20 Link=log Link=sqrt Tabella 4.32: Tabella con n=50
25 4.4. CASO CON QUATTRO REGRESSORI 25 Dalle simulazioni effettuate emerge quanto segue: nel caso con due regressori, entrambi positivi e per valori di x maggiori di 1, all aumentare della numerosità campionaria aumenta anche in maniera significativa la probabilità di selezione del modello generatore; nel caso di due regressori con β 2 minore di 0 la probabilità di selezione del modello generatore varia attorno al 50 per cento, sia per valori di x maggiori di 1 che per valori compresi fra 0 e 1; con tre regressori, entrambi positivi, la probabilità di selezione del modello generatore diminuisce un po rispetto al caso precedente, anche se siamo sempre sul 50 per cento, sia per valori delle x maggiori di 1 che per valori compresi fra 0 e 1; nel caso di quattro regressori, con il solo β 3 minore di 0, si registra una ulteriore diminuzione, anche se non elevata, della probabilità di selezione del modello generatore sia per valori delle x maggiori di 1 che per valori compresi fra 0 e 1. In definitiva dai risultati ottenuti vediamo che il criterio dell AIC, all aumentare del numero delle varibili esplicative, potrebbe non essere attendibile.
26 26 CAPITOLO 4. STUDIO DI SIMULAZIONE
27 Capitolo 5 Un esempio con dati reali L insieme dei dati che useremo contiene variabili che sono state rilevate per studiare se la quantità di silicio presente nei polmoni dipende dalle variabili esplicative rilevate. Con questi dati ci proponiamo di confermare quanto visto precedentemente con le simulazioni e quindi non faremo affermazioni riguardo le variabili in questione. L insieme dei dati è il seguente: group Age Gender Smoke n.positive n.spot 1 exposed 60 M yes exposed 49 M yes control 66 F no control 43 M yes control 67 M yes control 72 M no control 57 M no control 65 M no control 66 F no control 70 M yes
28 28 CAPITOLO 5. UN ESEMPIO CON DATI REALI 11 control 69 F yes control 48 M no control 76 F yes control 72 F no control 70 F yes control 54 M yes control 47 F yes control 50 M no control 52 F no control 66 M no control 71 F yes control 68 M no control 69 M no control 49 F yes control 77 F no control 66 F no control 62 M yes normal 76 F no normal 65 M yes normal 74 M no normal 50 F no normal 82 F no normal 70 M no normal 16 F no normal 61 M yes normal 82 F no normal 66 M no normal 61 M no normal 48 F no normal 68 M no normal 75 M no 0 0
29 29 42 normal 68 M yes normal 80 M no normal 47 M yes normal 67 M no normal 38 F yes normal 55 F no 0 0 Il numero di pazienti è n = 47 e le variabili esplicative rilevate su di essi sono: group :fattore a tre livelli dove exposed rappresenta i decessi per tumore al polmone ed esposizione nel lavoro al silicio,control i decessi per tumore al polmone per cause ignote e normal i decessi per cause ignote; age : l età dei pazienti; gender : fattore che indica il genere dei soggetti; smoke : fattore che ci dice se il soggetto era fumatore oppure no; n.positive : rappresenta il numero di zone del polmone contenenti tracce di silicio; n.spot : indica la quantità di silicio trovata nelle zone del polmone ritenute positive. Si desidera valutare la variabile risposta n.spot (di conteggio), quindi un modello adeguato puo essere una regressione poissoniana. Si adotteranno sia la funzione legame canonica sia quella radice quadrata. La sintassi da usare in R nel primo caso è fit1<-glm(n.spot~group+age+gender+smoke+n.positive,poisson(log)) mentre nel secondo avremo fit2<-glm(n.spot~group+age+gender+smoke+n.positive,poisson(sqrt)).
30 30 CAPITOLO 5. UN ESEMPIO CON DATI REALI I valori nei rispettivi casi dell AIC sono e Sapendo che un piu basso valore dell AIC corrisponde a una maggiore verosimiglianza, in questo caso risulterebbe migliore il legame sqrt. Guardando le simulazioni fatte in precedenza però, notiamo che all aumentare dei regressori la probabilità di selezione fra legame canonico e legame radice quadrata tende a diminuire, e questo si verifica anche considerando valori delle esplicative sia maggiori che minori di 1. Un incremento della numerosità campionaria nei vari esempi non porta a cambiamenti significativi, eccetto nel primo caso per valori di x maggiori di 1. Da ciò si deduce che il criterio appena citato poterbbe essere non adatto per valutare quale legame da utilizzare sia migliore, anche se è nettamente inferiore a
31 Bibliografia [1] Azzalini,A.(2004). Inferenza Statistica. Una presentazione basata sul concetto di verosimiglianza Springer-Verlag, Milano. [2] Pace, L. e Salvan, A. (2001). Introduzione alla Statistica II - Inferenza,verosimiglianza, modelli. Cedam. 31
Modelli lineari generalizzati
 Modelli lineari generalizzati Estensione del modello lineare generale Servono allo studio della dipendenza in media di una variabile risposta da una o più variabili antecedenti Vengono attenuate alcune
Modelli lineari generalizzati Estensione del modello lineare generale Servono allo studio della dipendenza in media di una variabile risposta da una o più variabili antecedenti Vengono attenuate alcune
I modelli probabilistici
 e I modelli probabilistici Finora abbiamo visto che esistono modelli probabilistici che possiamo utilizzare per prevedere gli esiti di esperimenti aleatori. Naturalmente la previsione è di tipo probabilistico:
e I modelli probabilistici Finora abbiamo visto che esistono modelli probabilistici che possiamo utilizzare per prevedere gli esiti di esperimenti aleatori. Naturalmente la previsione è di tipo probabilistico:
Quiz di verifica Classificazione
 Quiz di verifica Classificazione Strumenti Quantitativi per la gestione Le domande 1 4 si riferiscono al seguente problema: Supponiamo di raccogliere dati per un gruppo di studenti della classe di SQG
Quiz di verifica Classificazione Strumenti Quantitativi per la gestione Le domande 1 4 si riferiscono al seguente problema: Supponiamo di raccogliere dati per un gruppo di studenti della classe di SQG
Il modello di regressione lineare multipla. Il modello di regressione lineare multipla
 Introduzione E la generalizzazione del modello di regressione lineare semplice: per spiegare il fenomeno d interesse Y vengono introdotte p, con p > 1, variabili esplicative. Tale generalizzazione diventa
Introduzione E la generalizzazione del modello di regressione lineare semplice: per spiegare il fenomeno d interesse Y vengono introdotte p, con p > 1, variabili esplicative. Tale generalizzazione diventa
Regressione & Correlazione
 Regressione & Correlazione Monia Ranalli Ranalli M. Dipendenza Settimana # 4 1 / 20 Sommario Regressione Modello di regressione lineare senplice Stima dei parametri Adattamento del modello ai dati Correlazione
Regressione & Correlazione Monia Ranalli Ranalli M. Dipendenza Settimana # 4 1 / 20 Sommario Regressione Modello di regressione lineare senplice Stima dei parametri Adattamento del modello ai dati Correlazione
STATISTICA A K (60 ore)
 STATISTICA A K (60 ore) Marco Riani mriani@unipr.it http://www.riani.it Richiami sulla regressione Marco Riani, Univ. di Parma 1 MODELLO DI REGRESSIONE y i = a + bx i + e i dove: i = 1,, n a + bx i rappresenta
STATISTICA A K (60 ore) Marco Riani mriani@unipr.it http://www.riani.it Richiami sulla regressione Marco Riani, Univ. di Parma 1 MODELLO DI REGRESSIONE y i = a + bx i + e i dove: i = 1,, n a + bx i rappresenta
La Decisione Statistica Campione aleatorio: risultato dell osservazione di un fenomeno soggetto a fluttuazioni casuali.
 La Decisione Statistica Campione aleatorio: risultato dell osservazione di un fenomeno soggetto a fluttuazioni casuali. Analisi del campione: - descrizione sintetica (statistica descrittiva) - deduzione
La Decisione Statistica Campione aleatorio: risultato dell osservazione di un fenomeno soggetto a fluttuazioni casuali. Analisi del campione: - descrizione sintetica (statistica descrittiva) - deduzione
Statistica economica
 Statistica economica a.a. 013/14 Dr. Luca Secondi 10.a. Output tipico di un modello di regressione lineare multipla 1 Le analisi basate sul modello di regressione prevedono la stima dei coefficienti associati
Statistica economica a.a. 013/14 Dr. Luca Secondi 10.a. Output tipico di un modello di regressione lineare multipla 1 Le analisi basate sul modello di regressione prevedono la stima dei coefficienti associati
Richiami di inferenza statistica Strumenti quantitativi per la gestione
 Richiami di inferenza statistica Strumenti quantitativi per la gestione Emanuele Taufer Inferenza statistica Parametri e statistiche Esempi Tecniche di inferenza Stima Precisione delle stime Intervalli
Richiami di inferenza statistica Strumenti quantitativi per la gestione Emanuele Taufer Inferenza statistica Parametri e statistiche Esempi Tecniche di inferenza Stima Precisione delle stime Intervalli
Università di Pavia Econometria. Richiami di Statistica. Eduardo Rossi
 Università di Pavia Econometria Richiami di Statistica Eduardo Rossi Università di Pavia Campione casuale Siano (Y 1, Y 2,..., Y N ) variabili casuali tali che le y i siano realizzazioni mutuamente indipendenti
Università di Pavia Econometria Richiami di Statistica Eduardo Rossi Università di Pavia Campione casuale Siano (Y 1, Y 2,..., Y N ) variabili casuali tali che le y i siano realizzazioni mutuamente indipendenti
Richiami di inferenza statistica. Strumenti quantitativi per la gestione. Emanuele Taufer
 Richiami di inferenza statistica Strumenti quantitativi per la gestione Emanuele Taufer Inferenza statistica Inferenza statistica: insieme di tecniche che si utilizzano per ottenere informazioni su una
Richiami di inferenza statistica Strumenti quantitativi per la gestione Emanuele Taufer Inferenza statistica Inferenza statistica: insieme di tecniche che si utilizzano per ottenere informazioni su una
Statistica multivariata Donata Rodi 17/10/2016
 Statistica multivariata Donata Rodi 17/10/2016 Quale analisi? Variabile Dipendente Categoriale Continua Variabile Indipendente Categoriale Chi Quadro ANOVA Continua Regressione Logistica Regressione Lineare
Statistica multivariata Donata Rodi 17/10/2016 Quale analisi? Variabile Dipendente Categoriale Continua Variabile Indipendente Categoriale Chi Quadro ANOVA Continua Regressione Logistica Regressione Lineare
Capitolo 12 La regressione lineare semplice
 Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 12 La regressione lineare semplice Insegnamento: Statistica Corso di Laurea Triennale in Ingegneria Gestionale Facoltà di Ingegneria, Università
Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 12 La regressione lineare semplice Insegnamento: Statistica Corso di Laurea Triennale in Ingegneria Gestionale Facoltà di Ingegneria, Università
Statistica Metodologica Avanzato Test 1: Concetti base di inferenza
 Test 1: Concetti base di inferenza 1. Se uno stimatore T n è non distorto per il parametro θ, allora A T n è anche consistente B lim Var[T n] = 0 n C E[T n ] = θ, per ogni θ 2. Se T n è uno stimatore con
Test 1: Concetti base di inferenza 1. Se uno stimatore T n è non distorto per il parametro θ, allora A T n è anche consistente B lim Var[T n] = 0 n C E[T n ] = θ, per ogni θ 2. Se T n è uno stimatore con
Modelli probabilistici variabili casuali
 Modelli probabilistici variabili casuali Le variabili casuali costituiscono il legame tra il calcolo della probabilità e gli strumenti di statistica descrittiva visti fino ad ora. Idea: pensiamo al ripetersi
Modelli probabilistici variabili casuali Le variabili casuali costituiscono il legame tra il calcolo della probabilità e gli strumenti di statistica descrittiva visti fino ad ora. Idea: pensiamo al ripetersi
Presentazione dell edizione italiana
 1 Indice generale Presentazione dell edizione italiana Prefazione xi xiii Capitolo 1 Una introduzione alla statistica 1 1.1 Raccolta dei dati e statistica descrittiva... 1 1.2 Inferenza statistica e modelli
1 Indice generale Presentazione dell edizione italiana Prefazione xi xiii Capitolo 1 Una introduzione alla statistica 1 1.1 Raccolta dei dati e statistica descrittiva... 1 1.2 Inferenza statistica e modelli
R - Esercitazione 6. Andrea Fasulo Venerdì 22 Dicembre Università Roma Tre
 R - Esercitazione 6 Andrea Fasulo fasulo.andrea@yahoo.it Università Roma Tre Venerdì 22 Dicembre 2017 Il modello di regressione lineare semplice (I) Esempi tratti da: Stock, Watson Introduzione all econometria
R - Esercitazione 6 Andrea Fasulo fasulo.andrea@yahoo.it Università Roma Tre Venerdì 22 Dicembre 2017 Il modello di regressione lineare semplice (I) Esempi tratti da: Stock, Watson Introduzione all econometria
STATISTICA 1, metodi matematici e statistici Introduzione al linguaggio R Esercitazione 7:
 esercitazione 7 p. 1/13 STATISTICA 1, metodi matematici e statistici Introduzione al linguaggio R Esercitazione 7: 20-05-2004 Luca Monno Università degli studi di Pavia luca.monno@unipv.it http://www.lucamonno.it
esercitazione 7 p. 1/13 STATISTICA 1, metodi matematici e statistici Introduzione al linguaggio R Esercitazione 7: 20-05-2004 Luca Monno Università degli studi di Pavia luca.monno@unipv.it http://www.lucamonno.it
Regressione Lineare Semplice e Correlazione
 Regressione Lineare Semplice e Correlazione 1 Introduzione La Regressione è una tecnica di analisi della relazione tra due variabili quantitative Questa tecnica è utilizzata per calcolare il valore (y)
Regressione Lineare Semplice e Correlazione 1 Introduzione La Regressione è una tecnica di analisi della relazione tra due variabili quantitative Questa tecnica è utilizzata per calcolare il valore (y)
Statistica Applicata all edilizia: il modello di regressione
 Statistica Applicata all edilizia: il modello di regressione E-mail: orietta.nicolis@unibg.it 27 aprile 2009 Indice Il modello di Regressione Lineare 1 Il modello di Regressione Lineare Analisi di regressione
Statistica Applicata all edilizia: il modello di regressione E-mail: orietta.nicolis@unibg.it 27 aprile 2009 Indice Il modello di Regressione Lineare 1 Il modello di Regressione Lineare Analisi di regressione
LE DISTRIBUZIONI CAMPIONARIE
 LE DISTRIBUZIONI CAMPIONARIE Argomenti Principi e metodi dell inferenza statistica Metodi di campionamento Campioni casuali Le distribuzioni campionarie notevoli: La distribuzione della media campionaria
LE DISTRIBUZIONI CAMPIONARIE Argomenti Principi e metodi dell inferenza statistica Metodi di campionamento Campioni casuali Le distribuzioni campionarie notevoli: La distribuzione della media campionaria
Modelli a effetti misti
 Probabilità e Statistica per l analisi di dati sperimentali Modelli a effetti misti Sviluppo e gestione di Data Center per il calcolo scientifico ad alte prestazioni Master Progetto PRISMA, UniBA/INFN
Probabilità e Statistica per l analisi di dati sperimentali Modelli a effetti misti Sviluppo e gestione di Data Center per il calcolo scientifico ad alte prestazioni Master Progetto PRISMA, UniBA/INFN
Il processo inferenziale consente di generalizzare, con un certo grado di sicurezza, i risultati ottenuti osservando uno o più campioni
 La statistica inferenziale Il processo inferenziale consente di generalizzare, con un certo grado di sicurezza, i risultati ottenuti osservando uno o più campioni E necessario però anche aggiungere con
La statistica inferenziale Il processo inferenziale consente di generalizzare, con un certo grado di sicurezza, i risultati ottenuti osservando uno o più campioni E necessario però anche aggiungere con
Contenuti: Capitolo 14 del libro di testo
 Test d Ipotesi / TIPICI PROBLEMI DI VERIFICA DI IPOTESI SONO Test per la media Test per una proporzione Test per la varianza Test per due campioni indipendenti Test di indipendenza Contenuti Capitolo 4
Test d Ipotesi / TIPICI PROBLEMI DI VERIFICA DI IPOTESI SONO Test per la media Test per una proporzione Test per la varianza Test per due campioni indipendenti Test di indipendenza Contenuti Capitolo 4
Stima dei parametri. La v.c. multipla (X 1, X 2,.., X n ) ha probabilità (o densità): Le f( ) sono uguali per tutte le v.c.
 Stima dei parametri Sia il carattere X rappresentato da una variabile casuale (v.c.) che si distribuisce secondo la funzione di probabilità f(x). Per investigare su tale carattere si estrae un campione
Stima dei parametri Sia il carattere X rappresentato da una variabile casuale (v.c.) che si distribuisce secondo la funzione di probabilità f(x). Per investigare su tale carattere si estrae un campione
Esempio (Azzalini, pp. 6-15)
 Inferenza statistica procedimento per indurre le caratteristiche non note di un aggregato a partire dalle informazioni disponibili su una parte di esso. Obiettivo del corso presentare la teoria ed i metodi
Inferenza statistica procedimento per indurre le caratteristiche non note di un aggregato a partire dalle informazioni disponibili su una parte di esso. Obiettivo del corso presentare la teoria ed i metodi
CORSO DI STATISTICA (parte 1) - ESERCITAZIONE 6
 CORSO DI STATISTICA (parte 1) - ESERCITAZIONE 6 Dott.ssa Antonella Costanzo a.costanzo@unicas.it Esercizio 1. Associazione, correlazione e dipendenza tra caratteri In un collettivo di 11 famiglie è stata
CORSO DI STATISTICA (parte 1) - ESERCITAZIONE 6 Dott.ssa Antonella Costanzo a.costanzo@unicas.it Esercizio 1. Associazione, correlazione e dipendenza tra caratteri In un collettivo di 11 famiglie è stata
Statistica Applicata all edilizia: Stime e stimatori
 Statistica Applicata all edilizia E-mail: orietta.nicolis@unibg.it 15 marzo 2011 Statistica Applicata all edilizia: Indice 1 2 Statistica Applicata all edilizia: Uno dei problemi principali della statistica
Statistica Applicata all edilizia E-mail: orietta.nicolis@unibg.it 15 marzo 2011 Statistica Applicata all edilizia: Indice 1 2 Statistica Applicata all edilizia: Uno dei problemi principali della statistica
IL CRITERIO DELLA MASSIMA VEROSIMIGLIANZA
 Metodi per l Analisi dei Dati Sperimentali AA009/010 IL CRITERIO DELLA MASSIMA VEROSIMIGLIANZA Sommario Massima Verosimiglianza Introduzione La Massima Verosimiglianza Esempio 1: una sola misura sperimentale
Metodi per l Analisi dei Dati Sperimentali AA009/010 IL CRITERIO DELLA MASSIMA VEROSIMIGLIANZA Sommario Massima Verosimiglianza Introduzione La Massima Verosimiglianza Esempio 1: una sola misura sperimentale
Minimi quadrati ordinari Interpretazione geometrica. Eduardo Rossi
 Minimi quadrati ordinari Interpretazione geometrica Eduardo Rossi Il MRLM Il modello di regressione lineare multipla è usato per studiare le relazioni tra la variabile dipendente e diverse variabili indipendenti
Minimi quadrati ordinari Interpretazione geometrica Eduardo Rossi Il MRLM Il modello di regressione lineare multipla è usato per studiare le relazioni tra la variabile dipendente e diverse variabili indipendenti
lezione n. 6 (a cura di Gaia Montanucci) Verosimiglianza: L = = =. Parte dipendente da β 0 e β 1
 lezione n. 6 (a cura di Gaia Montanucci) METODO MASSIMA VEROSIMIGLIANZA PER STIMARE β 0 E β 1 Distribuzione sui termini di errore ε i ε i ~ N (0, σ 2 ) ne consegue : ogni y i ha ancora distribuzione normale,
lezione n. 6 (a cura di Gaia Montanucci) METODO MASSIMA VEROSIMIGLIANZA PER STIMARE β 0 E β 1 Distribuzione sui termini di errore ε i ε i ~ N (0, σ 2 ) ne consegue : ogni y i ha ancora distribuzione normale,
0 altimenti 1 soggetto trova lavoroentro 6 mesi}
 Lezione n. 16 (a cura di Peluso Filomena Francesca) Oltre alle normali variabili risposta che presentano una continuità almeno all'interno di un certo intervallo di valori, esistono variabili risposta
Lezione n. 16 (a cura di Peluso Filomena Francesca) Oltre alle normali variabili risposta che presentano una continuità almeno all'interno di un certo intervallo di valori, esistono variabili risposta
STATISTICA (2) ESERCITAZIONE Dott.ssa Antonella Costanzo
 STATISTICA (2) ESERCITAZIONE 7 11.03.2014 Dott.ssa Antonella Costanzo Esercizio 1. Test di indipendenza tra mutabili In un indagine vengono rilevate le informazioni su settore produttivo (Y) e genere (X)
STATISTICA (2) ESERCITAZIONE 7 11.03.2014 Dott.ssa Antonella Costanzo Esercizio 1. Test di indipendenza tra mutabili In un indagine vengono rilevate le informazioni su settore produttivo (Y) e genere (X)
assuma valori in un determinato intervallo è data dall integrale della sua densità ( = )=
 VARIABILI ALEATORIE CONTINUE Esistono parecchi fenomeni reali per la cui descrizione le variabili aleatorie discrete non sono adatte. Per esempio è necessaria una variabile aleatoria continua ovvero una
VARIABILI ALEATORIE CONTINUE Esistono parecchi fenomeni reali per la cui descrizione le variabili aleatorie discrete non sono adatte. Per esempio è necessaria una variabile aleatoria continua ovvero una
per togliere l influenza di un fattore es.: quoziente di mortalità = morti / popolazione
 Rapporti statistici di composizione la parte rispetto al tutto percentuali di derivazione per togliere l influenza di un fattore es.: quoziente di mortalità = morti / popolazione di frequenza (tassi) rapporti
Rapporti statistici di composizione la parte rispetto al tutto percentuali di derivazione per togliere l influenza di un fattore es.: quoziente di mortalità = morti / popolazione di frequenza (tassi) rapporti
Metodi statistici per la ricerca sociale Capitolo 15. Regressione logistica: modellare variabili risposta categoriali
 Metodi statistici per la ricerca sociale Capitolo 15. Regressione logistica: modellare variabili risposta categoriali Alessandra Mattei Dipartimento di Statistica, Informatica, Applicazioni (DiSIA) Università
Metodi statistici per la ricerca sociale Capitolo 15. Regressione logistica: modellare variabili risposta categoriali Alessandra Mattei Dipartimento di Statistica, Informatica, Applicazioni (DiSIA) Università
Statistica 2. Esercitazioni. Dott. Luigi Augugliaro 1. Università di Palermo
 Statistica 2 Esercitazioni Dott. L 1 1 Dipartimento di Scienze Statistiche e Matematiche S. Vianelli, Università di Palermo ricevimento: lunedì ore 15-17 mercoledì ore 15-17 e-mail: luigi.augugliaro@unipa.it
Statistica 2 Esercitazioni Dott. L 1 1 Dipartimento di Scienze Statistiche e Matematiche S. Vianelli, Università di Palermo ricevimento: lunedì ore 15-17 mercoledì ore 15-17 e-mail: luigi.augugliaro@unipa.it
La media e la mediana sono indicatori di centralità, che indicano un centro dei dati.
 La media e la mediana sono indicatori di centralità, che indicano un centro dei dati. Un indicatore che sintetizza in un unico numero tutti i dati, nascondendo quindi la molteplicità dei dati. Per esempio,
La media e la mediana sono indicatori di centralità, che indicano un centro dei dati. Un indicatore che sintetizza in un unico numero tutti i dati, nascondendo quindi la molteplicità dei dati. Per esempio,
lezione 4 AA Paolo Brunori
 AA 2016-2017 Paolo Brunori dove eravamo arrivati - abbiamo individuato la regressione lineare semplice (OLS) come modo immediato per sintetizzare una relazione fra una variabile dipendente (Y) e una indipendente
AA 2016-2017 Paolo Brunori dove eravamo arrivati - abbiamo individuato la regressione lineare semplice (OLS) come modo immediato per sintetizzare una relazione fra una variabile dipendente (Y) e una indipendente
PROBABILITÀ ELEMENTARE
 Prefazione alla seconda edizione XI Capitolo 1 PROBABILITÀ ELEMENTARE 1 Esperimenti casuali 1 Spazi dei campioni 1 Eventi 2 Il concetto di probabilità 3 Gli assiomi della probabilità 3 Alcuni importanti
Prefazione alla seconda edizione XI Capitolo 1 PROBABILITÀ ELEMENTARE 1 Esperimenti casuali 1 Spazi dei campioni 1 Eventi 2 Il concetto di probabilità 3 Gli assiomi della probabilità 3 Alcuni importanti
Capitolo 5 Variabili aleatorie discrete notevoli Insegnamento: Statistica Applicata Corso di Laurea in "Scienze e Tecnologie Alimentari"
 Levine, Krehbiel, Berenson Statistica Capitolo 5 Variabili aleatorie discrete notevoli Insegnamento: Statistica Applicata Corso di Laurea in "Scienze e Tecnologie Alimentari" Unità Integrata Organizzativa
Levine, Krehbiel, Berenson Statistica Capitolo 5 Variabili aleatorie discrete notevoli Insegnamento: Statistica Applicata Corso di Laurea in "Scienze e Tecnologie Alimentari" Unità Integrata Organizzativa
Verifica delle ipotesi
 Statistica inferenziale Stima dei parametri Verifica delle ipotesi Concetti fondamentali POPOLAZIONE o UNIVERSO Insieme degli elementi cui si rivolge il ricercatore per la sua indagine CAMPIONE Un sottoinsieme
Statistica inferenziale Stima dei parametri Verifica delle ipotesi Concetti fondamentali POPOLAZIONE o UNIVERSO Insieme degli elementi cui si rivolge il ricercatore per la sua indagine CAMPIONE Un sottoinsieme
Distribuzioni e inferenza statistica
 Distribuzioni e inferenza statistica Distribuzioni di probabilità L analisi statistica spesso studia i fenomeni collettivi confrontandoli con modelli teorici di riferimento. Tra di essi, vedremo: la distribuzione
Distribuzioni e inferenza statistica Distribuzioni di probabilità L analisi statistica spesso studia i fenomeni collettivi confrontandoli con modelli teorici di riferimento. Tra di essi, vedremo: la distribuzione
La verifica delle ipotesi
 La verifica delle ipotesi Se abbiamo un idea di quale possa essere il valore di un parametro incognito possiamo sottoporlo ad una verifica, che sulla base di un risultato campionario, ci permetta di decidere
La verifica delle ipotesi Se abbiamo un idea di quale possa essere il valore di un parametro incognito possiamo sottoporlo ad una verifica, che sulla base di un risultato campionario, ci permetta di decidere
Analisi di Regressione Multipla
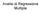 Analisi di Regressione Multipla Stima OLS della relazione Test Score/STR : TestScore! = 698.9.8 STR, R =.05, SER = 18.6 (10.4) (0.5) E una stima credibile dell effetto causale sul rendimento nei test di
Analisi di Regressione Multipla Stima OLS della relazione Test Score/STR : TestScore! = 698.9.8 STR, R =.05, SER = 18.6 (10.4) (0.5) E una stima credibile dell effetto causale sul rendimento nei test di
Tecniche statistiche di analisi del cambiamento
 Tecniche statistiche di analisi del cambiamento 09-Anova per misure ripetute (v. 1.3, 21 novembre 2018) Germano Rossi 1 germano.rossi@unimib.it 1 Dipartimento di Psicologia, Università di Milano-Bicocca
Tecniche statistiche di analisi del cambiamento 09-Anova per misure ripetute (v. 1.3, 21 novembre 2018) Germano Rossi 1 germano.rossi@unimib.it 1 Dipartimento di Psicologia, Università di Milano-Bicocca
s a Inferenza: singolo parametro Sistema di ipotesi: : β j = β j0 H 1 β j0 statistica test t confronto con valore t o p-value
 Inferenza: singolo parametro Sistema di ipotesi: H 0 : β j = β j0 H 1 : β j β j0 statistica test t b j - b s a jj j0 > t a, 2 ( n-k) confronto con valore t o p-value Se β j0 = 0 X j non ha nessuna influenza
Inferenza: singolo parametro Sistema di ipotesi: H 0 : β j = β j0 H 1 : β j β j0 statistica test t b j - b s a jj j0 > t a, 2 ( n-k) confronto con valore t o p-value Se β j0 = 0 X j non ha nessuna influenza
Test delle Ipotesi Parte I
 Test delle Ipotesi Parte I Test delle Ipotesi sulla media Introduzione Definizioni basilari Teoria per il caso di varianza nota Rischi nel test delle ipotesi Teoria per il caso di varianza non nota Test
Test delle Ipotesi Parte I Test delle Ipotesi sulla media Introduzione Definizioni basilari Teoria per il caso di varianza nota Rischi nel test delle ipotesi Teoria per il caso di varianza non nota Test
Selezione del modello Strumenti quantitativi per la gestione
 Selezione del modello Strumenti quantitativi per la gestione Emanuele Taufer Migliorare il modello di regressione lineare (RL) Metodi Selezione Best subset Selezione stepwise Stepwise forward Stepwise
Selezione del modello Strumenti quantitativi per la gestione Emanuele Taufer Migliorare il modello di regressione lineare (RL) Metodi Selezione Best subset Selezione stepwise Stepwise forward Stepwise
CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 5
 CORSO DI STATISTICA (parte 2) - ESERCITAZIONE Dott.ssa Antonella Costanzo a.costanzo@unicas.it Esercizio 1. Approssimazione normale della Poisson (TLC) In un determinato tratto di strada il numero di incidenti
CORSO DI STATISTICA (parte 2) - ESERCITAZIONE Dott.ssa Antonella Costanzo a.costanzo@unicas.it Esercizio 1. Approssimazione normale della Poisson (TLC) In un determinato tratto di strada il numero di incidenti
Costruzione di macchine. Modulo di: Progettazione probabilistica e affidabilità. Marco Beghini. Lezione 7: Basi di statistica
 Costruzione di macchine Modulo di: Progettazione probabilistica e affidabilità Marco Beghini Lezione 7: Basi di statistica Campione e Popolazione Estrazione da una popolazione (virtualmente infinita) di
Costruzione di macchine Modulo di: Progettazione probabilistica e affidabilità Marco Beghini Lezione 7: Basi di statistica Campione e Popolazione Estrazione da una popolazione (virtualmente infinita) di
Tecniche di sondaggio
 SMID a.a. 2005/2006 Corso di Statistica per la Ricerca Sperimentale Tecniche di sondaggio 24/1/2006 Nomenclatura Indicheremo con P una popolazione, con N la sua numerosità, con k la sua etichetta e con
SMID a.a. 2005/2006 Corso di Statistica per la Ricerca Sperimentale Tecniche di sondaggio 24/1/2006 Nomenclatura Indicheremo con P una popolazione, con N la sua numerosità, con k la sua etichetta e con
Elementi di Probabilità e Statistica - 052AA - A.A
 Elementi di Probabilità e Statistica - 05AA - A.A. 014-015 Prima prova di verifica intermedia - 9 aprile 015 Problema 1. Dati due eventi A, B, su uno spazio probabilizzato (Ω, F, P), diciamo che A è in
Elementi di Probabilità e Statistica - 05AA - A.A. 014-015 Prima prova di verifica intermedia - 9 aprile 015 Problema 1. Dati due eventi A, B, su uno spazio probabilizzato (Ω, F, P), diciamo che A è in
1.1 Obiettivi della statistica Struttura del testo 2
 Prefazione XV 1 Introduzione 1.1 Obiettivi della statistica 1 1.2 Struttura del testo 2 2 Distribuzioni di frequenza 2.1 Informazione statistica e rilevazione dei dati 5 2.2 Distribuzioni di frequenza
Prefazione XV 1 Introduzione 1.1 Obiettivi della statistica 1 1.2 Struttura del testo 2 2 Distribuzioni di frequenza 2.1 Informazione statistica e rilevazione dei dati 5 2.2 Distribuzioni di frequenza
Statistica ARGOMENTI. Calcolo combinatorio
 Statistica ARGOMENTI Calcolo combinatorio Probabilità Disposizioni semplici Disposizioni con ripetizione Permutazioni semplici Permutazioni con ripetizioni Combinazioni semplici Assiomi di probabilità
Statistica ARGOMENTI Calcolo combinatorio Probabilità Disposizioni semplici Disposizioni con ripetizione Permutazioni semplici Permutazioni con ripetizioni Combinazioni semplici Assiomi di probabilità
Indice. centrale, dispersione e forma Introduzione alla Statistica Statistica descrittiva per variabili quantitative: tendenza
 XIII Presentazione del volume XV L Editore ringrazia 3 1. Introduzione alla Statistica 5 1.1 Definizione di Statistica 6 1.2 I Rami della Statistica Statistica Descrittiva, 6 Statistica Inferenziale, 6
XIII Presentazione del volume XV L Editore ringrazia 3 1. Introduzione alla Statistica 5 1.1 Definizione di Statistica 6 1.2 I Rami della Statistica Statistica Descrittiva, 6 Statistica Inferenziale, 6
Il modello di regressione (VEDI CAP 12 VOLUME IEZZI, 2009)
 Il modello di regressione (VEDI CAP 12 VOLUME IEZZI, 2009) Quesito: Posso stimare il numero di ore passate a studiare statistica sul voto conseguito all esame? Potrei calcolare il coefficiente di correlazione.
Il modello di regressione (VEDI CAP 12 VOLUME IEZZI, 2009) Quesito: Posso stimare il numero di ore passate a studiare statistica sul voto conseguito all esame? Potrei calcolare il coefficiente di correlazione.
Gli errori nella verifica delle ipotesi
 Gli errori nella verifica delle ipotesi Nella statistica inferenziale si cerca di dire qualcosa di valido in generale, per la popolazione o le popolazioni, attraverso l analisi di uno o più campioni E
Gli errori nella verifica delle ipotesi Nella statistica inferenziale si cerca di dire qualcosa di valido in generale, per la popolazione o le popolazioni, attraverso l analisi di uno o più campioni E
Indice. Prefazione. 4 Sintesi della distribuzione di un carattere La variabilità Introduzione La variabilità di una distribuzione 75
 00PrPag:I-XIV_prefazione_IAS 8-05-2008 17:56 Pagina V Prefazione XI 1 La rilevazione dei fenomeni statistici 1 1.1 Introduzione 1 1.2 Caratteri, unità statistiche e collettivo 1 1.3 Classificazione dei
00PrPag:I-XIV_prefazione_IAS 8-05-2008 17:56 Pagina V Prefazione XI 1 La rilevazione dei fenomeni statistici 1 1.1 Introduzione 1 1.2 Caratteri, unità statistiche e collettivo 1 1.3 Classificazione dei
Probabilità classica. Distribuzioni e leggi di probabilità. Probabilità frequentista. Probabilità soggettiva
 Probabilità classica Distribuzioni e leggi di probabilità La probabilità di un evento casuale è il rapporto tra il numero dei casi favorevoli ed il numero dei casi possibili, purchè siano tutti equiprobabili.
Probabilità classica Distribuzioni e leggi di probabilità La probabilità di un evento casuale è il rapporto tra il numero dei casi favorevoli ed il numero dei casi possibili, purchè siano tutti equiprobabili.
Statistica Applicata all edilizia Lezione: approccio stocastico all analisi delle serie storiche
 Lezione: approccio stocastico all analisi delle serie storiche E-mail: orietta.nicolis@unibg.it 3 maggio 2011 Programma 1 Approccio stocastico all analisi delle serie storiche Programma Approccio stocastico
Lezione: approccio stocastico all analisi delle serie storiche E-mail: orietta.nicolis@unibg.it 3 maggio 2011 Programma 1 Approccio stocastico all analisi delle serie storiche Programma Approccio stocastico
Analisi della Regressione Lineare
 Analisi della Regressione Lineare Master in Tecnologie Bioinformatiche 29/09/06 Adriano Decarli 1 29/09/06 Adriano Decarli 2 29/09/06 Adriano Decarli 3 29/09/06 Adriano Decarli 4 29/09/06 Adriano Decarli
Analisi della Regressione Lineare Master in Tecnologie Bioinformatiche 29/09/06 Adriano Decarli 1 29/09/06 Adriano Decarli 2 29/09/06 Adriano Decarli 3 29/09/06 Adriano Decarli 4 29/09/06 Adriano Decarli
Elementi di statistica per l econometria
 Indice Prefazione i 1 Teoria della probabilità 1 1.1 Definizioni di base............................. 2 1.2 Probabilità................................. 7 1.2.1 Teoria classica...........................
Indice Prefazione i 1 Teoria della probabilità 1 1.1 Definizioni di base............................. 2 1.2 Probabilità................................. 7 1.2.1 Teoria classica...........................
lezione 10 AA Paolo Brunori
 AA 2016-2017 Paolo Brunori Redditi svedesi - il dataset contiene i dati di reddito di 838 individui - il dataset contiene le variabili: sex = sesso age = età edu = anni di istruzione y_gross = reddito
AA 2016-2017 Paolo Brunori Redditi svedesi - il dataset contiene i dati di reddito di 838 individui - il dataset contiene le variabili: sex = sesso age = età edu = anni di istruzione y_gross = reddito
La media e la mediana sono indicatori di centralità, che indicano un centro dei dati.
 La media e la mediana sono indicatori di centralità, che indicano un centro dei dati. Un indicatore che sintetizza in un unico numero tutti i dati, nascondendo quindi la molteplicità dei dati. Per esempio,
La media e la mediana sono indicatori di centralità, che indicano un centro dei dati. Un indicatore che sintetizza in un unico numero tutti i dati, nascondendo quindi la molteplicità dei dati. Per esempio,
Confronto fra gruppi: il metodo ANOVA. Nicola Tedesco (Statistica Sociale) Confronto fra gruppi: il metodo ANOVA 1 / 23
 Confronto fra gruppi: il metodo ANOVA Nicola Tedesco (Statistica Sociale) Confronto fra gruppi: il metodo ANOVA 1 / 23 1 Nella popolazione, per ciascun gruppo la distribuzione della variabile risposta
Confronto fra gruppi: il metodo ANOVA Nicola Tedesco (Statistica Sociale) Confronto fra gruppi: il metodo ANOVA 1 / 23 1 Nella popolazione, per ciascun gruppo la distribuzione della variabile risposta
Modelli lineari generalizzati
 Capitolo 5 Modelli lineari generalizzati I modelli lineari generalizzati costituiscono un estensione del modello lineare generale e servono anch essi allo studio della dipendenza in media di una variabile
Capitolo 5 Modelli lineari generalizzati I modelli lineari generalizzati costituiscono un estensione del modello lineare generale e servono anch essi allo studio della dipendenza in media di una variabile
Minimi quadrati vincolati e test F
 Minimi quadrati vincolati e test F Impostazione del problema Spesso, i modelli econometrici che stimiamo hanno dei parametri che sono passibili di interpretazione diretta nella teoria economica. Consideriamo
Minimi quadrati vincolati e test F Impostazione del problema Spesso, i modelli econometrici che stimiamo hanno dei parametri che sono passibili di interpretazione diretta nella teoria economica. Consideriamo
Metodi statistici per le ricerche di mercato
 Metodi statistici per le ricerche di mercato Prof.ssa Isabella Mingo A.A. 2016-2017 Facoltà di Scienze Politiche, Sociologia, Comunicazione Corso di laurea Magistrale in «Organizzazione e marketing per
Metodi statistici per le ricerche di mercato Prof.ssa Isabella Mingo A.A. 2016-2017 Facoltà di Scienze Politiche, Sociologia, Comunicazione Corso di laurea Magistrale in «Organizzazione e marketing per
Psicometria con Laboratorio di SPSS 2
 Psicometria con Laboratorio di SPSS 2 Regressione lineare semplice (vers. 1.2, 20 marzo 2018) Germano Rossi 1 germano.rossi@unimib.it 1 Dipartimento di Psicologia, Università di Milano-Bicocca 2017-18
Psicometria con Laboratorio di SPSS 2 Regressione lineare semplice (vers. 1.2, 20 marzo 2018) Germano Rossi 1 germano.rossi@unimib.it 1 Dipartimento di Psicologia, Università di Milano-Bicocca 2017-18
Capitolo 8. Intervalli di confidenza. Statistica. Levine, Krehbiel, Berenson. Casa editrice: Pearson. Insegnamento: Statistica
 Levine, Krehbiel, Berenson Statistica Casa editrice: Pearson Capitolo 8 Intervalli di confidenza Insegnamento: Statistica Corso di Laurea Triennale in Economia Dipartimento di Economia e Management, Università
Levine, Krehbiel, Berenson Statistica Casa editrice: Pearson Capitolo 8 Intervalli di confidenza Insegnamento: Statistica Corso di Laurea Triennale in Economia Dipartimento di Economia e Management, Università
STATISTICA. Regressione-3 L inferenza per il modello lineare semplice
 STATISTICA Regressione-3 L inferenza per il modello lineare semplice Regressione lineare: GRAFICO DI DISPERSIONE & & analisi residui A. Valutazione preliminare se una retta possa essere una buona approssimazione
STATISTICA Regressione-3 L inferenza per il modello lineare semplice Regressione lineare: GRAFICO DI DISPERSIONE & & analisi residui A. Valutazione preliminare se una retta possa essere una buona approssimazione
La curva di regressione è il luogo dei punti aventi come ordinate le medie condizionate
 Correlazione e regressione Correlazione: le due variabili casuali sono considerate in modo per così dire simmetrico. Regressione: una delle due variabili dipende dall'altra, che per così dire la precede
Correlazione e regressione Correlazione: le due variabili casuali sono considerate in modo per così dire simmetrico. Regressione: una delle due variabili dipende dall'altra, che per così dire la precede
Old Faithful, Yellowstone Park. Statistica e biometria. D. Bertacchi. Dati congiunti. Tabella. Scatterplot. Covarianza. Correlazione.
 Coppie o vettori di dati Spesso i dati osservati sono di tipo vettoriale. Ad esempio studiamo 222 osservazioni relative alle eruzioni del geyser Old Faithful. Old Faithful, Yellowstone Park. Old Faithful
Coppie o vettori di dati Spesso i dati osservati sono di tipo vettoriale. Ad esempio studiamo 222 osservazioni relative alle eruzioni del geyser Old Faithful. Old Faithful, Yellowstone Park. Old Faithful
Matematica con elementi di Informatica
 Statistica descrittiva ed inferenziale Matematica con elementi di Informatica Tiziano Vargiolu Dipartimento di Matematica vargiolu@math.unipd.it Corso di Laurea Magistrale in Chimica e Tecnologie Farmaceutiche
Statistica descrittiva ed inferenziale Matematica con elementi di Informatica Tiziano Vargiolu Dipartimento di Matematica vargiolu@math.unipd.it Corso di Laurea Magistrale in Chimica e Tecnologie Farmaceutiche
Il modello lineare misto
 Il modello lineare misto (capitolo 9) A M D Marcello Gallucci Univerisità Milano-Bicocca Lezione: 15 GLM Modello Lineare Generale vantaggi Consente di stimare le relazioni fra due o più variabili Si applica
Il modello lineare misto (capitolo 9) A M D Marcello Gallucci Univerisità Milano-Bicocca Lezione: 15 GLM Modello Lineare Generale vantaggi Consente di stimare le relazioni fra due o più variabili Si applica
Regressione Mario Guarracino Laboratorio di Sistemi Informativi Aziendali a.a. 2006/2007
 Regressione Esempio Un azienda manifatturiera vuole analizzare il legame che intercorre tra il costo mensile Y di produzione e il corrispondente volume produttivo X per uno dei propri stabilimenti. Volume
Regressione Esempio Un azienda manifatturiera vuole analizzare il legame che intercorre tra il costo mensile Y di produzione e il corrispondente volume produttivo X per uno dei propri stabilimenti. Volume
Parte I Identificazione di modelli dinamici. 6: Teoria della stima e caratteristiche degli stimatori. Parte I 6, 1
 Parte I 6, 1 Parte I Identificazione di modelli dinamici 6: Teoria della stima e caratteristiche degli stimatori Generalita` Parte I 6, 2 In generale abbiamo: dove sono i dati osservati e` la quantita`
Parte I 6, 1 Parte I Identificazione di modelli dinamici 6: Teoria della stima e caratteristiche degli stimatori Generalita` Parte I 6, 2 In generale abbiamo: dove sono i dati osservati e` la quantita`
Metodi Quantitativi per Economia, Finanza e Management. Lezione n 8 Regressione lineare multipla: le ipotesi del modello, la stima del modello
 Metodi Quantitativi per Economia, Finanza e Management Lezione n 8 Regressione lineare multipla: le ipotesi del modello, la stima del modello 1. Introduzione ai modelli di regressione 2. Obiettivi 3. Le
Metodi Quantitativi per Economia, Finanza e Management Lezione n 8 Regressione lineare multipla: le ipotesi del modello, la stima del modello 1. Introduzione ai modelli di regressione 2. Obiettivi 3. Le
Richiami di probabilità e statistica
 Richiami di probabilità e statistica Una variabile casuale (o aleatoria) X codifica gli eventi con entità numeriche x ed è caratterizzata dalla funzione di distribuzione di probabilità P(x) : P(x)=Pr ob[x
Richiami di probabilità e statistica Una variabile casuale (o aleatoria) X codifica gli eventi con entità numeriche x ed è caratterizzata dalla funzione di distribuzione di probabilità P(x) : P(x)=Pr ob[x
Intervallo di confidenza
 Intervallo di confidenza Prof. Giuseppe Verlato, Prof. Roberto de Marco Sezione di Epidemiologia e Statistica Medica, Università di Verona campione inferenza popolazione Media Riportare sempre anche Stima
Intervallo di confidenza Prof. Giuseppe Verlato, Prof. Roberto de Marco Sezione di Epidemiologia e Statistica Medica, Università di Verona campione inferenza popolazione Media Riportare sempre anche Stima
Intervallo di confidenza
 Intervallo di confidenza Prof. Giuseppe Verlato, Prof. Roberto de Marco Sezione di Epidemiologia e Statistica Medica, Università di Verona campione inferenza popolazione Media Riportare sempre anche Stima
Intervallo di confidenza Prof. Giuseppe Verlato, Prof. Roberto de Marco Sezione di Epidemiologia e Statistica Medica, Università di Verona campione inferenza popolazione Media Riportare sempre anche Stima
Distribuzioni campionarie
 1 Inferenza Statistica Descrittiva Distribuzioni campionarie Statistica Inferenziale: affronta problemi di decisione in condizioni di incertezza basandosi sia su informazioni a priori sia sui dati campionari
1 Inferenza Statistica Descrittiva Distribuzioni campionarie Statistica Inferenziale: affronta problemi di decisione in condizioni di incertezza basandosi sia su informazioni a priori sia sui dati campionari
Università di Pavia Econometria. Minimi quadrati ordinari Interpretazione geometrica. Eduardo Rossi
 Università di Pavia Econometria Minimi quadrati ordinari Interpretazione geometrica Eduardo Rossi Università di Pavia Introduzione L econometria si interessa all analisi dei dati economici. I dati economici
Università di Pavia Econometria Minimi quadrati ordinari Interpretazione geometrica Eduardo Rossi Università di Pavia Introduzione L econometria si interessa all analisi dei dati economici. I dati economici
Corso in Statistica Medica
 Corso in Statistica Medica Introduzione alle tecniche statistiche di elaborazione dati Intervalli di confidenza Dott. Angelo Menna Università degli Studi di Chieti G. d Annunziod Annunzio Anno Accademico
Corso in Statistica Medica Introduzione alle tecniche statistiche di elaborazione dati Intervalli di confidenza Dott. Angelo Menna Università degli Studi di Chieti G. d Annunziod Annunzio Anno Accademico
Computazione per l interazione naturale: Regressione probabilistica
 Computazione per l interazione naturale: Regressione probabilistica Corso di Interazione Naturale Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it boccignone.di.unimi.it/in_2016.html
Computazione per l interazione naturale: Regressione probabilistica Corso di Interazione Naturale Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it boccignone.di.unimi.it/in_2016.html
Statistica descrittiva in due variabili
 Statistica descrittiva in due variabili Dott Nicola Pintus AA 2018-2019 Indichiamo con U la popolazione statistica e con u i le unità statistiche Ad ogni unità statistica associamo i caratteri osservati
Statistica descrittiva in due variabili Dott Nicola Pintus AA 2018-2019 Indichiamo con U la popolazione statistica e con u i le unità statistiche Ad ogni unità statistica associamo i caratteri osservati
Computazione per l interazione naturale: Regressione probabilistica
 Computazione per l interazione naturale: Regressione probabilistica Corso di Interazione Naturale Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it boccignone.di.unimi.it/in_2017.html
Computazione per l interazione naturale: Regressione probabilistica Corso di Interazione Naturale Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it boccignone.di.unimi.it/in_2017.html
Modelli Lineari Generalizzati: un applicazione. Fedi Flavia
 Modelli Lineari Generalizzati: un applicazione Fedi Flavia 6 luglio 2006 Capitolo 1 Introduzione L obbiettivo di questo studio è quello di utilizzare la classe dei modelli lineari generalizzati (GLM) per
Modelli Lineari Generalizzati: un applicazione Fedi Flavia 6 luglio 2006 Capitolo 1 Introduzione L obbiettivo di questo studio è quello di utilizzare la classe dei modelli lineari generalizzati (GLM) per
P ( X n X > ɛ) = 0. ovvero (se come distanza consideriamo quella euclidea)
 10.4 Convergenze 166 10.4.3. Convergenza in Probabilità. Definizione 10.2. Data una successione X 1, X 2,...,,... di vettori aleatori e un vettore aleatorio X aventi tutti la stessa dimensione k diremo
10.4 Convergenze 166 10.4.3. Convergenza in Probabilità. Definizione 10.2. Data una successione X 1, X 2,...,,... di vettori aleatori e un vettore aleatorio X aventi tutti la stessa dimensione k diremo
Metodologia Sperimentale Agronomica / Metodi Statistici per la Ricerca Ambientale
 DIPARTIMENTO DI SCIENZE AGRARIE E AMBIENTALI PRODUZIONE, TERRITORIO, AGROENERGIA Marco Acutis marco.acutis@unimi.it www.acutis.it a.a. 2018-2019 CdS Scienze della Produzione e Protezione delle Piante (g59)
DIPARTIMENTO DI SCIENZE AGRARIE E AMBIENTALI PRODUZIONE, TERRITORIO, AGROENERGIA Marco Acutis marco.acutis@unimi.it www.acutis.it a.a. 2018-2019 CdS Scienze della Produzione e Protezione delle Piante (g59)
MODELLO DI REGRESSIONE LINEARE. le ipotesi del modello di regressione classico, stima con i metodi dei minimi quadrati e di massima verosimiglianza,
 MODELLO DI REGRESSIONE LINEARE le ipotesi del modello di regressione classico, stima con i metodi dei minimi quadrati e di massima verosimiglianza, teorema di Gauss-Markov, verifica di ipotesi e test di
MODELLO DI REGRESSIONE LINEARE le ipotesi del modello di regressione classico, stima con i metodi dei minimi quadrati e di massima verosimiglianza, teorema di Gauss-Markov, verifica di ipotesi e test di
Ulteriori Conoscenze di Informatica e Statistica. Popolazione. Campione. I risultati di un esperimento sono variabili aleatorie.
 Ulteriori Conoscenze di Informatica e Statistica Carlo Meneghini Dip. di fisica via della Vasca Navale 84, st. 83 (I piano) tel.: 06 55 17 72 17 meneghini@fis.uniroma3.it I risultati di un esperimento
Ulteriori Conoscenze di Informatica e Statistica Carlo Meneghini Dip. di fisica via della Vasca Navale 84, st. 83 (I piano) tel.: 06 55 17 72 17 meneghini@fis.uniroma3.it I risultati di un esperimento
Parametri statistici
 SMID a.a. 2004/2005 Corso di Metodi Statistici in Biomedicina Parametri statistici 24/1/2005 Deviazione standard della media La variabilità di una distribuzione può quindi essere espressa da un indice
SMID a.a. 2004/2005 Corso di Metodi Statistici in Biomedicina Parametri statistici 24/1/2005 Deviazione standard della media La variabilità di una distribuzione può quindi essere espressa da un indice
Test per l omogeneità delle varianze
 Test per l omogeneità delle varianze Le carte di controllo hanno lo scopo di verificare se i campioni estratti provengono da un processo produttivo caratterizzato da un unico valore dello s.q.m. σ. Una
Test per l omogeneità delle varianze Le carte di controllo hanno lo scopo di verificare se i campioni estratti provengono da un processo produttivo caratterizzato da un unico valore dello s.q.m. σ. Una
