Stima puntuale. Stimare: attribuire un valore plausibile ad una grandezza. (parametro) non misurabile esattamente.
|
|
|
- Adelaide Parodi
- 4 anni fa
- Visualizzazioni
Transcript
1 Stima puntuale Stimare: attribuire un valore plausibile ad una grandezza (parametro) non misurabile esattamente. Stimatore del parametro θ: ogni statistica T = t(x 1, X 2,..., X n ) utilizzata per stimare θ. NOTA BENE: è una grandezza aleatoria perchè è una funzione del campione che pure è aleatorio Stima: la singola determinazione dello stimatore, t(x 1, x 2,..., x n ). cioè il valore che lo stimatore del parametro assume una volta che esso è valutato sul campione che ho effettivamente estratto
2 Esempio: supponiamo di voler stimare la media di una popolazione. A tal fine estraiamo un campione casuale di ampiezza 5 ed otteniamo i seguenti valori: x 1 = 2, x 2 = 1, x 3 = 0, x 4 = 4, x 5 = 3.5 Come stimatore della media della popolazione (parametro di interesse) decidiamo di usare la media del campione, (il campione è casuale quindi mi aspetto che sia rappresentativo della popolazione da cui l ho estratto). Abbiamo quindi che lo stimatore è T 5 = t(x 1, X 2,..., X 5 ) = X la stima è il valore che lo stimatore assume con riferimento al campione estratto: t(x 1, x 2,..., x 5 ) = = 1.7 quindi la nostra stima è ˆµ = 1.7
3 Criteri di valutazione degli stimatori Errore quadratico medio dello stimatore T = t(x 1, X 2,..., X n ) di θ: MSE θ (T ) = E θ [(T θ) 2 ]. NOTA BENE il MSE (o EQM) è una funzione del parametro θ Confronto tra stimatori sulla base dell errore quadratico medio In generale non esiste uno stimatore con errore quadratico medio uniformemente minimo cioè più piccolo (rispetto agli altri stimatori) per tutti i valori del parametro θ.
4 Stimatori non distorti Lo stimatore T = t(x 1, X 2,..., X n ) di θ si dice non distorto se E θ (T ) = θ, θ. Distorsione (BIAS): B θ (T ) = E θ (T ) θ. può essere positiva (in media sovrastimo il parametro) o negativa (in media sottostimo) Decomposizione dell errore quadratico medio: (da sapere la dimostrazione) MSE θ (T ) = Var θ (T ) + [B θ (T )] 2. Se T è uno stimatore non distorto, MSE θ (T ) = Var θ (T ).
5 Esempio Descriviamo il numero di visitatori settimanale di un negozio di arredamento con un numero aleatorio X. Il numero medio di visite è µ = E(X) e un indice della variabilità delle visite può essere la varianza σ 2 = V (X). Supponiamo di sapere che σ 2 = Si consideri la media campionaria come stimatore del numero medio µ di visite settimanali Lo stimatore è non distorto perchè sappiamo che la media della media campionaria è pari alla media della popolazione E( X) = µ Quanto vale l errore quadratico medio dello stimatore per un campione di ampiezza n = 30? Poichè lo stimatore è non distorto l errore quadratico medio è pari alla varianza dello stimatore (la distorsione è nulla) quindi MSE µ ( X) = Var µ ( X) = σ2 n = = 1.62
6 Notiamo che poichè al denominatore dell errore quadratico medio (EQM) compare l ampiezza del campione, una maggiore ampiezza campionaria darà un errore quadratico medio minore. Inoltre l EQM (o MSE) dipende dalla varianza della popolazione (che compare al numeratore): intuitivamente, se σ 2 è elevato, ossia se il numero di visite varia molto di settimana in settimana, sarà più difficile stimare il numero medio di visite! Infatti, a parità di n, se σ 2 è elevato l errore quadratico medio sarà maggiore
7 Stimatori consistenti La consistenza è una proprietà asintotica di uno stimatore cioè descrive come lo stimatore si comporta all aumentare dell ampiezza del campione. In generale mi aspetto che se l ampiezza del campione aumenta (n ) lo stimatore migliori Concentrazione: uno stimatore T = t(x 1, X 2,..., X n ) di θ è tanto più concentrato attorno a θ quanto maggiore è la probabilità P θ ( T θ < ε), θ per una costante fissata ε > 0 e piccola a piacere Consistenza: uno stimatore T n = t n (X 1, X 2,..., X n ) di θ è consistente in probabilità (o in senso debole) se per ogni ε > 0 si ha lim P θ( T n θ < ε) = 1, n θ.
8 Consistenza in media quadratica: uno stimatore T n di θ è consistente in media quadratica se lim E [ θ (Tn θ) 2] = 0, θ. n (o in senso forte) Quindi uno stimatore è consistente in senso forte se l errore quadratico medio tende a zero all aumentare dell ampiezza del campione estratto Teorema: La consistenza in senso forte implica la consistenza in senso debole Esempio: la media campionaria è uno stimatore, per la media della popolazione, consistente in senso forte (e quindi anche in senso debole) perchè l errore quadratico medio tende a zero al crescere dell ampiezza del campione: lim MSE µ( X) = lim n n σ 2 n = 0
9 Esempio: anche la varianza campionaria (T) è uno stimatore consistente in senso forte per la varianza della popolazione (θ = σ 2 ) in quanto abbiamo che E(S 2 ) = σ 2 cioè lo stimatore è non distorto, quindi l errore quadratico medio coincide con la varianza dello stimatore: Var(S 2 ) = σ4 n β n n 1 e questa quantità tende a zero al tendere di n all infinito Esempio: Voglio stimare la media di una popolazione e come stimatore uso T = 10 cioè la stima è sempre 10 indipendentemente dal campione estratto. Questo stimatore non è consistente nè in senso forte nè in senso debole perchè la stima di fatto non dipende dal campione estratto. Il suo MSE sarà nullo solo quando θ = 10.
10 Uno stimatore T n di θ è asintoticamente non distorto se lim B θ(t n ) = 0, n θ. Se uno stimatore è non distorto a maggior ragione è asintoticamente non distorto Teorema Condizione necessaria e suff. per la consistenza in media quadratica è che uno stimatore sia asintoticamente non distorto e che la varianza tenda a zero al crescere dell ampiezza del campione: lim B θ(t n ) = 0, n θ e lim V (T n) = 0 n Dimostrazione segue dalla scomposizione dell errore quadratico medio come somma di varianza e distorsione al quadrato
11 Stimatori efficienti Dati due stimatori T 1 e T 2 di θ, T 1 è più efficiente di T 2 se MSE θ (T 1 ) MSE θ (T 2 ), θ e la disuguaglianza vale in senso stretto per almeno un valore di θ. La scelta fra due stimatori dello stesso parametro può essere fatta sulla base del rapporto eff θ (T 1, T 2 ) = MSE θ(t 2 ) MSE θ (T 1 ) T 1 si dice più efficiente di T 2 se eff θ (T 1, T 2 ) 1 con la disuguaglianza in senso stretto per almeno un valore di θ Se T 1 e T 2 sono non distorti eff θ (T 1, T 2 ) = Var θ(t 2 ) Var θ (T 1 )
12 ESEMPIO: State stimando un parametro θ. Avete a disposizione due stimatori, T 1 e T 2. Sapete che E(T 1 ) = θ 3 e E(T 2 ) = θ. Sapete inoltre che lo scarto quadratico medio di T 1 è pari a 2 mentre lo scarto quadratico medio di T 2 è pari a 7. Quale stimatore scegliereste? Lo stimatore T 1 è distorto per θ, mentre T 2 è non distorto. Questo non significa che T 2 sia più efficiente! Il confronto fra due stimatori si basa sull errore quadratico medio: preferisco lo stimatore con MSE più piccolo Poiche l errore quadratico medio dipende dalla distorsione ma anche dalla varianza dello stimatore, uno stimatore distorto ma con varianza piccola può essere preferibile ad uno stimatore non distorto ma con varianza elevata. E quello che succede in questo caso.
13 L errore quadratico medio di T 1 è MSE θ (T 1 ) = V θ (T 1 )+(E(T 1 ) θ) 2 = 4+(θ 3 θ) 2 = 4+9 = 13, mentre quello di T 2 è MSE θ (T 2 ) = V θ (T 2 ) = 49. Poichè MSE θ (T 1 ) < MSE θ (T 2 ) per ogni θ, T 1 è più efficiente di T 2. Abbiamo inoltre che eff θ (T 1, T 2 ) = MSE θ(t 2 ) MSE θ (T 1 ) = = 3.7 > 1 quindi ancora si vede che T 1 è più efficiente di T 2 e di conseguenza preferirò usare T 1 nonostante sia distorto
14 ESEMPIO: Per valutare la spesa media mensile µ delle famiglie italiane, si rileva la spesa mensile su un campione casuale di 5 famiglie (solo 5 per semplicità nell esercizio..). Sia (X 1,..., X 5 ) il campione, e consideriamo due possibili stimatori per µ, e X = 5 i=1 X i 5 T = 0.1X X X X X 5. Quale dei due stimatori è più efficiente? Calcoliamo l errore quadratico medio per i due stimatori. MSE( X) = σ2 5 = 0.2 σ2, dove σ 2 indica la varianza della popolazione.
15 Per il secondo stimatore, poichè E(T ) = 0.1E(X 1 ) + 0.2E(X 2 ) E(X 3 ) + 0.2E(X 4 ) + 0.1E(X 5 ) = µ( ) = µ, si ha MSE(T ) = V (T ) = V (X 1 ) V (X 2 ) V (X 3 ) V (X 4 ) V (X 5 ) = 0.26σ 2. Poichè EQM( X) = 0.2σ 2 < 0.26σ 2 = EQM(T ), la media campionaria X è più efficiente di T. (In effetti, potreste dimostrare che la media campionaria è più efficiente di ogni altra combinazione lineare convessa di X 1,..., X n ).
16 T 1n è asintoticamente più efficiente di e T 2n se eff θ (T 1n, T 2n ) = lim n MSE θ (T 2n ) MSE θ (T 1n ) 1, e la disuguaglianza vale in senso stretto per almeno un valore di θ. θ
17 Metodi per la determinazione di uno stimatore Metodo analogico stima per es. la media della popolazione con la media del campione o la proporzione nella popolazione con la proporzione nel campione). Per la varianza della popolazione lo stimatore analogico è ˆσ 2 = 1 n i (X i X) 2 che è distorto, per questo abbiamo introdotto lo stimatore S 2 = 1 n 1 che invece è non distorto i (X i X) 2 Metodo della massima verosimiglianza Metodo dei momenti Metodo dei minimi quadrati si usa per stimare i parametri della retta di regressione Metodo Bayesiano: tiene conto dell opinione iniziale oltre che dei dati campionari
18 ESEMPIO: Sia X 1 = 0, X 2 = 0, X 3 = 0 un campione casuale estratto da una popolazione Bernoulliana con probabilità di successo incognita p. Quale è la stima più verosimile di p? ˆp = 0 Se invece il campione fosse stato X 1 = 1, X 2 = 1, X 3 = 1 la stima più verosimile di p sarebbe: ˆp = 1 Se invece il campione fosse stato X 1 = 1, X 2 = 0, X 3 = 1 quale è la stima più verosimile di p? STIMA DI MASSIMA VEROSIMIGLIANZA
19 Metodo della massima verosimiglianza Funzione di verosimiglianza: sia (x 1, x 2,..., x n ) un campione osservato proveniente da una popolazione descritta dal modello f(x; θ). La funzione di verosimiglianza è la probabilità (densità) di (x 1, x 2,..., x n ) interpretata come funzione del parametro θ, L(θ) = f(x 1,..., x n ; θ) = = f(x 1 ; θ)f(x 2 ; θ) f(x n ; θ) = n f(x i; θ) i=1 nel caso di un campione casuale (quindi con osservazioni iid) La funzione di verosimiglianza consente di ordinare i diversi valori di θ secondo il grado di verosimiglianza che ricevono dai dati campionari. La stima di massima verosimiglianza consiste nel proporre come stima di θ (se esiste) il valore più verosimile, ossia il valore di θ Θ che rende massima la funzione di verosimiglianza L(θ; x 1,..., x n ).
20 Stima di massima verosimiglianza: il valore di θ, ˆθ = t(x 1, x 2,..., x n ), che massimizza la funzione di verosimiglianza, L(ˆθ) = max θ Θ L(θ). Stimatore di massima verosimiglianza: t(x 1, X 2,..., X n ) Generalmente risulta conveniente massimizzare l(θ) = log[l(θ)] risolvendo l equazione dl(θ) dθ = 0 e controllando che in corrispondenza del valore trovato di θ la derivata seconda di l(θ) sia negativa.
21 Esempio Bernoulliana cont.: per il campione casuale (iid) X 1 = 1, X 2 = 1, X 3 = 1 estratto da una popolazione Bernoulliana la funzione di verosimiglianza è L(X 1 = 1, X 2 = 1, X 3 = 1, p) = = P (X 1 = 1)P (X 2 = 1)P (X 3 = 1) = (p)(p)(p) = p 3 0 p 1 quale valore di p massimizza questa funzione? Poichè la funzione di verosimiglianza è una funzione sempre crescente: x^ il massimo di ha per ˆp = 1. x
22 Notate che se cercate di fare la derivata della funzione di verosimiglianza ed uguagliarla a zero dl(p) dp = 3p 2 = 0 ottengo un risultato diverso e sbagliato perchè il massimo si ha sulla frontiera! Se il campione estratto fosse stato X 1 = 0, X 2 = 0, X 3 = 0 la funzione di verosimiglainza sarebbe: L(X 1 = 0, X 2 = 0, X 3 = 0, p) = = P (X 1 = 0)P (X 2 = 0)P (X 3 = 0) = (1 p) 3 0 p 1 che è una funzione sempre decrescente (1 x)^ x e quindi il massimo della funzione si ha per ˆp = 0
23 Se infine il campione estratto fosse stato X 1 = 1, X 2 = 0, X 3 = 1 la funzione di verosimiglianza sarebbe: L(X 1 = 1, X 2 = 0, X 3 = 1, p) = = P (X 1 = 1)P (X 2 = 0)P (X 3 = 1) = p 2 (1 p) 0 p 1 il cui grafico è x^2 * (1 x) x il massimo non è sulla frontiera e lo si può trovare facendo la derivata prima e seconda della funzione di log-verosimiglianza: l(p) = logl(p) = 2log(p) + log(1 p) dl(p) dp = 2/p 1/(1 p) = 0 2(1 p) p p(1 p) = 0 2 2p p = 0
24 Notiamo che prendere il logaritmo di una funzione non sposta il punto di massimo (che è quello che a noi interessa), come si vede dal grafico in cui è riportato il logaritmo della funzione di verosimiglianza di prima log(x^2 * (1 x)) x
25 In generale per un campione X 1,, X n casuale estratto da una popolazione Bernoulliana, la funzione di verosimiglianza è L(X 1, X n, p) = p X i (1 p) n X i l(p) = log(p)( X i ) + log(1 p)(n X i ) dl(p) dp = 1 p ( X i ) 1 1 p (n X i ) = 0 e risolvendo per p otteniamo ˆp = i X i n la derivata seconda risulta sempre negativa quindi si può concludere che questo valore è effettivamente un massimo ed è quindi lo stimatore di massima verosimiglianza
26 Proprietà dello stimatore di massima verosimiglianza Proprietà di invarianza: se ˆθ è lo stimatore di massima verosimiglianza di θ, allora g(ˆθ) è lo stimatore di massima verosimiglianza di g(θ). Sotto certe condizioni di regolarità, lo stimatore di massima verosimiglianza è: consistente; asintoticamente efficiente; e non distorto ha distribuzione limite normale, Lo stimatore di Max Vero non è necessariamente unico
27 ESEMPIO: Vogliamo studiare il tempo di attesa prima che un macchinario si rompa (a) Proponete un modello statistico, fra quelli studiati, per descrivere il tempo d attesa (b) Scrivete la funzione di verosimiglianza in corrispondenza ad un campione casuale (x 1,..., x n ). (c) Immaginate ora che (x 1,..., x n ) = (20, 10, 5, 6, 4, 15). Calcolate la stima di massima verosimiglianza del tempo medio di attesa. RISPOSTA (a) Possiamo ipotizzare che il tempo d attesa X abbia distribuzione esponenziale negativa, f(x; λ) = λe λ x x > 0 0 altrove Il tempo medio d attesa è E(X) = 1/λ e la varianza V (X) = 1/λ 2.
28 (b) La funzione di verosimiglianza in corrispondenza di un generico campione x = (x 1,..., x n ) è L(λ; x) = n i=1 f(x i; λ) = n i=1 λe λ x i = λ n e λ n i=1 x i (c) Massimizziamo la log-verosimiglianza l(λ; x) = log L(λ; x) = n log λ λ n i=1 x i. d dλ l(λ, x) = n λ n x i 0 i=1 per λ n/ n i=1 x i. Dunque ˆλ = 1/ x = 1/10. Per la proprietà di invarianza, la stima del valore atteso è ˆ E(X) = 1/ˆλ = x = 10. Stimiamo ora la deviazione standard e la probabilità di aspettare fra 5 e 8 ore ˆP (5 X 8) = 8 5 1/10e x/10 dx
29 ESEMPIO In un processo di controllo di qualità, siamo interessati al numero mensile di guasti di un certo macchinario. (a) Quale fra le distribuzioni di probabilità che avete studiato potreste proporre come modello statistico per descrivere il numero mensile di guasti? Spiegate cosa rappresenta il parametro del modello proposto. (b) Supponete ora che in un campione casuale di 5 mesi si siano osservati (3, 2, 4, 5, 1) guasti. Scrivete la funzione di verosimiglianza. (c) Determinate infine la stima di massima verosimiglianza della probabilità di non avere nessun guasto. RISPOSTA (a) Possiamo proporre un modello di Poisson: X P ois(λ), ovvero f(x; λ) = e λ λ x x! x = 0, 1, 2,... 0 altrove Il parametro λ rappresenta il numero medio di guasti in un mese, λ = E(X) e anche la varianza λ = V (X).
30 (b) La funzione di verosimiglianza è L(λ; x 1,..., x 5 ) = 5 e λ λ x i = i=1 x i! 1 = x 1! x 5! e 5λ λ 5 i=1 x i 1 = 3!2!4!5! e 5λ λ 15. (c) La probabilità di non avere guasti nel mese è data da p = P (X = 0, λ) = p(0; λ) = e λ. Possiamo determinare la stima di massima verosimiglianza ˆλ di λ e poi utilizzare la proprietà di invarianza degli stimatori di massima verosimiglianza in base alla quale la stima di massima verosimiglianza di p è ˆp = ˆ (e λ ) = e ˆλ. Facendo i calcoli, si trova che il massimo di L(λ; x 1,..., x 5 ) si ha per ˆλ = 5 i=1 x i 5 = 3, da cui ˆp = e 3 = 0.05
31 NOTA BENE: Lo stimatore di massima verosimiglianza non è necessariamente non distorto ma è asintoticamente non distorto Se devo stimare 2 (o più parametri) come nel caso di popolazione normale (µ e σ) faccio la derivata della funzione di verosimiglianza rispetto a ciascuno dei parametri ed uguaglio a zero. Ricavo così un sistema con 2 equazioni a 2 incognite (i 2 parametri) per popolazioni normali lo stimatore di massima verosimiglianza della media è la media campionaria (non distorto) mentre lo stimatore di massima verosimiglianza per la varianza è ˆσ 2 = 1 n n i=1 (X i X) 2 che risulta distorto ma asintoticamente non distorto
32 Metodo dei momenti Nel caso in cui θ sia un parametro vettoriale di dimensione k, il metodo dei momenti consiste nel risolvere rispetto a θ il sistema di equazioni m r = µ r (θ), r = 1,..., k, dove µ r (θ) = E(X r ) è il momento di ordine r della popolazione m r = 1 n n i X r i è il corrispondente momento campionario
33 Esempio Ho un campione estratto da una popolazione Normale con media µ e varianza σ 2 (entrambi incogniti). Voglio trovare con il metodo dei momenti gli stimatori dei due parametri: µ e σ 2. Risolvo allora il seguente sistema con due equazioni e due incognite: cioè E(X) = 1 n i X i E(X 2 ) = 1 n i X 2 i µ = 1 n i X i µ 2 + σ 2 = 1 n i Xi 2 risolvendo il sistema si trova che gli stimatori ottenuti con il metodo dei momenti sono ˆµ = X e ˆσ 2 = 1 n n i=1 (X i X) 2 cioè la media e la varianza del campione rispettivamente
34 Notiamo che lo stimatore ottenuto con il metodo dei momenti per la varianza è distorto (in generale il metodo dei momenti non garantisce che gli stimatori ottenuti siano non distorti! così come non lo garantisce il metodo della massima verosimiglianza) infatti la distorsione è pari a E(ˆσ 2 ) = n 1 n σ2 B θ (ˆσ 2 ) = n 1 n σ2 σ 2 = σ2 n quindi la distorsione è sempre negativa cioè, in media, sottostimo il parametro di interesse Abbiamo invece già visto che uno stimatore non distorto della varianza della popolazione è S 2 = 1 n 1 n i=1 (X i X) 2
35 Per un carattere X con distribuzione di Poisson di parametro λ lo stimatore per λ ottenuto con il metodo dei momenti ˆλ MM si ottiene nel modo seguente: E(X) = 1 n i X 1 ovvero, ricordando che, per questa distribuzione, E(X) = λ, λ = X quindi ˆλ MM = X Notiamo che in questo caso k = 1, dove k è il numero di parametri da stimare, quindi per ottenere lo stimatore dei momenti basta una sola equazione (perchè ho una solo incognita, che è appunto λ) Notiamo che in questo caso lo stimatore di massima verosimiglianza per λ coincide con lo stimatore ottenuto con il metodo dei momenti
36 Per un carattere X con distribuzione di Esponenziale di parametro λ lo stimatore per λ ottenuto con il metodo dei momenti ˆλ MM si ottiene nel modo seguente: E(X) = 1 n i X 1 ovvero quindi 1 λ = X ˆλ MM = 1 X Notiamo che, anche in questo caso k = 1, dove k è il numero di parametri da stimare, quindi per ottenere lo stimatore dei momenti basta una sola equazione (perchè ho una solo incognita, che è appunto λ) Notiamo che, anche in questo caso, lo stimatore di massima verosimiglianza per λ coincide con lo stimatore ottenuto con il metodo dei momenti
37 Per un carattere X con distribuzione di Bernoulliana di parametro p lo stimatore per p ottenuto con il metodo dei momenti ˆλ MM si ricava nel modo seguente: E(X) = 1 n i X 1 ovvero p = X quindi ˆp MM = X Anche in questo caso k = 1 e, anche in questo caso, lo stimatore di massima verosimiglianza per p coincide con lo stimatore ottenuto con il metodo dei momenti
38 Per un carattere X con distribuzione di Binomiale di parametri (n, p) gli stimatori ottenuti con il metodo dei momenti si trovano risolvendo un sistema di due equazioni: E(X) = 1 n i X i E(X 2 ) = 1 n i X 2 i ovvero np = 1 n i X i np(1 p) + (np) 2 = 1 n i Xi 2 Notiamo che, in questo caso, k = 2, dove k è il numero di parametri da stimare, quindi per ottenere lo stimatore dei momenti servono due equazioni (perchè ho due incognite, n e p) Lascio a voi la soluzione del sistema rispetto ad n 4 p.
Statistica Inferenziale
 Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Riepilogo lezione 6 Abbiamo visto: Definizione di popolazione, di campione e di spazio campionario Distribuzione
Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Riepilogo lezione 6 Abbiamo visto: Definizione di popolazione, di campione e di spazio campionario Distribuzione
Esercitazioni di Statistica
 Esercitazioni di Statistica Stima Puntuale Prof. Livia De Giovanni statistica@dis.uniroma.it Esercizio In ciascuno dei casi seguenti determinare quale tra i due stimatori S e T per il parametro θ è distorto
Esercitazioni di Statistica Stima Puntuale Prof. Livia De Giovanni statistica@dis.uniroma.it Esercizio In ciascuno dei casi seguenti determinare quale tra i due stimatori S e T per il parametro θ è distorto
Statistica Inferenziale
 Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Riepilogo lezione 8 Abbiamo visto: Metodi per la determinazione di uno stimatore Metodo di massima verosimiglianza
Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Riepilogo lezione 8 Abbiamo visto: Metodi per la determinazione di uno stimatore Metodo di massima verosimiglianza
Statistica 2. Esercitazioni. Dott. Luigi Augugliaro 1. Università di Palermo
 Statistica 2 Esercitazioni Dott. L 1 1 Dipartimento di Scienze Statistiche e Matematiche S. Vianelli, Università di Palermo ricevimento: lunedì ore 15-17 mercoledì ore 15-17 e-mail: luigi.augugliaro@unipa.it
Statistica 2 Esercitazioni Dott. L 1 1 Dipartimento di Scienze Statistiche e Matematiche S. Vianelli, Università di Palermo ricevimento: lunedì ore 15-17 mercoledì ore 15-17 e-mail: luigi.augugliaro@unipa.it
Statistica Applicata all edilizia: Stime e stimatori
 Statistica Applicata all edilizia E-mail: orietta.nicolis@unibg.it 15 marzo 2011 Statistica Applicata all edilizia: Indice 1 2 Statistica Applicata all edilizia: Uno dei problemi principali della statistica
Statistica Applicata all edilizia E-mail: orietta.nicolis@unibg.it 15 marzo 2011 Statistica Applicata all edilizia: Indice 1 2 Statistica Applicata all edilizia: Uno dei problemi principali della statistica
Stima puntuale di parametri
 Probabilità e Statistica Esercitazioni a.a. 2009/2010 C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica Stima puntuale di parametri Ines Campa Probabilità e Statistica -
Probabilità e Statistica Esercitazioni a.a. 2009/2010 C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica Stima puntuale di parametri Ines Campa Probabilità e Statistica -
Stima puntuale di parametri
 Probabilità e Statistica Esercitazioni a.a. 006/007 C.d.L.: Ingegneria per l Ambiente ed il Territorio, Ingegneria Civile, Ingegneria Gestionale, Ingegneria dell Informazione C.d.L.S.: Ingegneria Civile
Probabilità e Statistica Esercitazioni a.a. 006/007 C.d.L.: Ingegneria per l Ambiente ed il Territorio, Ingegneria Civile, Ingegneria Gestionale, Ingegneria dell Informazione C.d.L.S.: Ingegneria Civile
Stima Puntuale e per Intervallo. Stimatore e stima. Pietro Coretto Università degli Studi di Salerno
 Stima Puntuale e per Intervallo Pietro Coretto pcoretto@unisa.it Università degli Studi di Salerno Corso di Statistica (01700010) CDL in Economia e Management Curriculum in Management e Informatica a.a.
Stima Puntuale e per Intervallo Pietro Coretto pcoretto@unisa.it Università degli Studi di Salerno Corso di Statistica (01700010) CDL in Economia e Management Curriculum in Management e Informatica a.a.
Probabilità e Statistica
 Probabilità e Statistica Stima puntuale di parametri Marco Pietro Longhi C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica a.s. 018/019 Marco Pietro Longhi Prob. e Stat.
Probabilità e Statistica Stima puntuale di parametri Marco Pietro Longhi C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica a.s. 018/019 Marco Pietro Longhi Prob. e Stat.
STATISTICA APPLICATA Prof.ssa Julia Mortera. INTRODUZIONE al STATISTICA
 STATISTICA APPLICATA Prof.ssa Julia Mortera INTRODUZIONE al CAMPIONAMENTO e all INFERENZA STATISTICA Inferenza Statistica Nell inferenza statistica si usano le statistiche campionarie per fare previsioni
STATISTICA APPLICATA Prof.ssa Julia Mortera INTRODUZIONE al CAMPIONAMENTO e all INFERENZA STATISTICA Inferenza Statistica Nell inferenza statistica si usano le statistiche campionarie per fare previsioni
STATISTICA INDUTTIVA: STIMA DI PARAMETRI STIMA PUNTUALE
 S.S.I.S TOSCANA F.I.M. -II anno STATISTICA INDUTTIVA: STIMA DI PARAMETRI STIMA PUNTUALE PROBLEMA 1 Vogliamo valutare la percentuale p di donne fumatrici tra le donne in età fertile. Procediamo all estrazione
S.S.I.S TOSCANA F.I.M. -II anno STATISTICA INDUTTIVA: STIMA DI PARAMETRI STIMA PUNTUALE PROBLEMA 1 Vogliamo valutare la percentuale p di donne fumatrici tra le donne in età fertile. Procediamo all estrazione
Statistica Metodologica Avanzato Test 1: Concetti base di inferenza
 Test 1: Concetti base di inferenza 1. Se uno stimatore T n è non distorto per il parametro θ, allora A T n è anche consistente B lim Var[T n] = 0 n C E[T n ] = θ, per ogni θ 2. Se T n è uno stimatore con
Test 1: Concetti base di inferenza 1. Se uno stimatore T n è non distorto per il parametro θ, allora A T n è anche consistente B lim Var[T n] = 0 n C E[T n ] = θ, per ogni θ 2. Se T n è uno stimatore con
Esercitazione del 29 aprile 2014
 Esercitazione del 9 aprile 014 Esercizio 10.13 pg. 94 Complemento: Calcolare la probabilità che un negozio apra tra le sette e venti e le nove e quaranta del mattino. Soluzione: Siccome non è nota la distribuzione
Esercitazione del 9 aprile 014 Esercizio 10.13 pg. 94 Complemento: Calcolare la probabilità che un negozio apra tra le sette e venti e le nove e quaranta del mattino. Soluzione: Siccome non è nota la distribuzione
Introduzione all inferenza statistica, III lezione
 Introduzione all inferenza statistica, III lezione Carla Rampichini Dipartimento di Statistica Giuseppe Parenti - Firenze - Italia carla@ds.unifi.it - www.ds.unifi.it/rampi/ Dottorato in METODOLOGIA DELLE
Introduzione all inferenza statistica, III lezione Carla Rampichini Dipartimento di Statistica Giuseppe Parenti - Firenze - Italia carla@ds.unifi.it - www.ds.unifi.it/rampi/ Dottorato in METODOLOGIA DELLE
Contenuto del capitolo
 Capitolo 8 Stima 1 Contenuto del capitolo Proprietà degli stimatori Correttezza: E(Stimatore) = parametro da stimare Efficienza Consistenza Intervalli di confidenza Per la media - per una proporzione Come
Capitolo 8 Stima 1 Contenuto del capitolo Proprietà degli stimatori Correttezza: E(Stimatore) = parametro da stimare Efficienza Consistenza Intervalli di confidenza Per la media - per una proporzione Come
I modelli probabilistici
 e I modelli probabilistici Finora abbiamo visto che esistono modelli probabilistici che possiamo utilizzare per prevedere gli esiti di esperimenti aleatori. Naturalmente la previsione è di tipo probabilistico:
e I modelli probabilistici Finora abbiamo visto che esistono modelli probabilistici che possiamo utilizzare per prevedere gli esiti di esperimenti aleatori. Naturalmente la previsione è di tipo probabilistico:
CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 5
 CORSO DI STATISTICA (parte 2) - ESERCITAZIONE Dott.ssa Antonella Costanzo a.costanzo@unicas.it Esercizio 1. Approssimazione normale della Poisson (TLC) In un determinato tratto di strada il numero di incidenti
CORSO DI STATISTICA (parte 2) - ESERCITAZIONE Dott.ssa Antonella Costanzo a.costanzo@unicas.it Esercizio 1. Approssimazione normale della Poisson (TLC) In un determinato tratto di strada il numero di incidenti
ELEMENTI DI STATISTICA INFERENZIALE ELEMENTI DI STATISTICA INFERENZIALE
 ELEMENTI DI STATISTICA INFERENZIALE 133. ELEMENTI DI STATISTICA INFERENZIALE In questo paragrafo verranno illustrati alcuni elementi di Statistica che sono essenziali per procedere alla costruzione di
ELEMENTI DI STATISTICA INFERENZIALE 133. ELEMENTI DI STATISTICA INFERENZIALE In questo paragrafo verranno illustrati alcuni elementi di Statistica che sono essenziali per procedere alla costruzione di
Università di Siena. Teoria della Stima. Lucidi del corso di. Identificazione e Analisi dei Dati A.A
 Università di Siena Teoria della Stima Lucidi del corso di A.A. 2002-2003 Università di Siena 1 Indice Approcci al problema della stima Stima parametrica Stima bayesiana Proprietà degli stimatori Stime
Università di Siena Teoria della Stima Lucidi del corso di A.A. 2002-2003 Università di Siena 1 Indice Approcci al problema della stima Stima parametrica Stima bayesiana Proprietà degli stimatori Stime
Stima puntuale di parametri
 Probabilità e Statistica Esercitazioni a.a. 017/018 C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica Stima puntuale di parametri Marco Pietro Longhi Probabilità e Statistica
Probabilità e Statistica Esercitazioni a.a. 017/018 C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica Stima puntuale di parametri Marco Pietro Longhi Probabilità e Statistica
Statistica Metodologica
 Statistica Metodologica Esercizi di Probabilita e Inferenza Silvia Figini e-mail: silvia.figini@unipv.it Problema 1 Sia X una variabile aleatoria Bernoulliana con parametro p = 0.7. 1. Determinare la media
Statistica Metodologica Esercizi di Probabilita e Inferenza Silvia Figini e-mail: silvia.figini@unipv.it Problema 1 Sia X una variabile aleatoria Bernoulliana con parametro p = 0.7. 1. Determinare la media
Università degli Studi Roma Tre Anno Accademico 2017/2018 ST410 Statistica 1
 Università degli Studi Roma Tre Anno Accademico 2017/2018 ST410 Statistica 1 Lezione 1 - Mercoledì 27 Settembre 2017 Introduzione al corso. Richiami di probabilità: spazi di probabilità, variabili aleatorie,
Università degli Studi Roma Tre Anno Accademico 2017/2018 ST410 Statistica 1 Lezione 1 - Mercoledì 27 Settembre 2017 Introduzione al corso. Richiami di probabilità: spazi di probabilità, variabili aleatorie,
P ( X n X > ɛ) = 0. ovvero (se come distanza consideriamo quella euclidea)
 10.4 Convergenze 166 10.4.3. Convergenza in Probabilità. Definizione 10.2. Data una successione X 1, X 2,...,,... di vettori aleatori e un vettore aleatorio X aventi tutti la stessa dimensione k diremo
10.4 Convergenze 166 10.4.3. Convergenza in Probabilità. Definizione 10.2. Data una successione X 1, X 2,...,,... di vettori aleatori e un vettore aleatorio X aventi tutti la stessa dimensione k diremo
Università degli Studi Roma Tre Anno Accademico 2014/2015 ST410 Statistica 1
 Università degli Studi Roma Tre Anno Accademico 2014/2015 ST410 Statistica 1 Lezione 1 - Martedì 23 Settembre 2014 Introduzione al corso. Richiami di probabilità: spazi di probabilità, variabili aleatorie,
Università degli Studi Roma Tre Anno Accademico 2014/2015 ST410 Statistica 1 Lezione 1 - Martedì 23 Settembre 2014 Introduzione al corso. Richiami di probabilità: spazi di probabilità, variabili aleatorie,
UNIVERSITÀ DEGLI STUDI DI PERUGIA
 SIGI, Statistica II, esercitazione n. 3 1 UNIVERSITÀ DEGLI STUDI DI PERUGIA FACOLTÀ DI ECONOMIA CORSO DI LAUREA S.I.G.I. STATISTICA II Esercitazione n. 3 Esercizio 1 Una v.c. X si dice v.c. esponenziale
SIGI, Statistica II, esercitazione n. 3 1 UNIVERSITÀ DEGLI STUDI DI PERUGIA FACOLTÀ DI ECONOMIA CORSO DI LAUREA S.I.G.I. STATISTICA II Esercitazione n. 3 Esercizio 1 Una v.c. X si dice v.c. esponenziale
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica ST410 - Statistica 1 - A.A. 2014/2015 Appello B - 5 Febbraio 2015
 UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica ST410 - Statistica 1 - A.A. 2014/2015 Appello B - 5 Febbraio 2015 1 2 3 4 5 6 7 Tot. Avvertenza: Svolgere ogni esercizio nello spazio assegnato,
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica ST410 - Statistica 1 - A.A. 2014/2015 Appello B - 5 Febbraio 2015 1 2 3 4 5 6 7 Tot. Avvertenza: Svolgere ogni esercizio nello spazio assegnato,
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica ST410 - Statistica 1 - A.A. 2014/2015 II Esonero - 15 Gennaio 2015
 UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica ST410 - Statistica 1 - A.A. 014/015 II Esonero - 15 Gennaio 015 1 3 4 5 6 Tot. Avvertenza: Svolgere ogni esercizio nello spazio assegnato,
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica ST410 - Statistica 1 - A.A. 014/015 II Esonero - 15 Gennaio 015 1 3 4 5 6 Tot. Avvertenza: Svolgere ogni esercizio nello spazio assegnato,
Calcolo delle Probabilità e Statistica Matematica: definizioni prima parte. Cap.1: Probabilità
 Calcolo delle Probabilità e Statistica Matematica: definizioni prima parte Cap.1: Probabilità 1. Esperimento aleatorio (definizione informale): è un esperimento che a priori può avere diversi esiti possibili
Calcolo delle Probabilità e Statistica Matematica: definizioni prima parte Cap.1: Probabilità 1. Esperimento aleatorio (definizione informale): è un esperimento che a priori può avere diversi esiti possibili
Università degli Studi Roma Tre Anno Accademico 2016/2017 ST410 Statistica 1
 Università degli Studi Roma Tre Anno Accademico 2016/2017 ST410 Statistica 1 Lezione 1 - Mercoledì 28 Settembre 2016 Introduzione al corso. Richiami di probabilità: spazi di probabilità, variabili aleatorie,
Università degli Studi Roma Tre Anno Accademico 2016/2017 ST410 Statistica 1 Lezione 1 - Mercoledì 28 Settembre 2016 Introduzione al corso. Richiami di probabilità: spazi di probabilità, variabili aleatorie,
II Esonero - Testo B
 Dip. di Ingegneria, Univ. Roma Tre Prof. E. Scoppola, Dott.M. Quattropani Probabilità e Statistica, 2017-18, I semestre 29 Gennaio 2018 II Esonero - Testo B Cognome Nome Matricola Esercizio 1. (20%) Si
Dip. di Ingegneria, Univ. Roma Tre Prof. E. Scoppola, Dott.M. Quattropani Probabilità e Statistica, 2017-18, I semestre 29 Gennaio 2018 II Esonero - Testo B Cognome Nome Matricola Esercizio 1. (20%) Si
9. Test del χ 2 e test di Smirnov-Kolmogorov. 9.1 Stimatori di massima verosimiglianza per distribuzioni con densità finita
 9. Test del χ 2 e test di Smirnov-Kolmogorov 9. Stimatori di massima verosimiglianza per distribuzioni con densità finita Supponiamo di avere un campione statistico X,..., X n e di sapere che esso è relativo
9. Test del χ 2 e test di Smirnov-Kolmogorov 9. Stimatori di massima verosimiglianza per distribuzioni con densità finita Supponiamo di avere un campione statistico X,..., X n e di sapere che esso è relativo
Tecniche di sondaggio
 SMID a.a. 2005/2006 Corso di Statistica per la Ricerca Sperimentale Tecniche di sondaggio 24/1/2006 Nomenclatura Indicheremo con P una popolazione, con N la sua numerosità, con k la sua etichetta e con
SMID a.a. 2005/2006 Corso di Statistica per la Ricerca Sperimentale Tecniche di sondaggio 24/1/2006 Nomenclatura Indicheremo con P una popolazione, con N la sua numerosità, con k la sua etichetta e con
Università di Siena. Corso di STATISTICA. Parte seconda: Teoria della stima. Andrea Garulli, Antonello Giannitrapani, Simone Paoletti
 Università di Siena Corso di STATISTICA Parte seconda: Teoria della stima Andrea Garulli, Antonello Giannitrapani, Simone Paoletti Master E 2 C Centro per lo Studio dei Sistemi Complessi Università di
Università di Siena Corso di STATISTICA Parte seconda: Teoria della stima Andrea Garulli, Antonello Giannitrapani, Simone Paoletti Master E 2 C Centro per lo Studio dei Sistemi Complessi Università di
4. Si supponga che il tempo impiegato da una lettera spedita dall Italia per arrivare a destinazione segua una distribuzione normale con media
 Esercizi sulle distribuzioni, il teorema limite centrale e la stima puntuale Corso di Probabilità e Inferenza Statistica, anno 007-008, Prof. Mortera 1. Sia X la durata in mesi di una valvola per radio.
Esercizi sulle distribuzioni, il teorema limite centrale e la stima puntuale Corso di Probabilità e Inferenza Statistica, anno 007-008, Prof. Mortera 1. Sia X la durata in mesi di una valvola per radio.
STATISTICA A K (60 ore)
 STATISTICA A K (60 ore) Marco Riani mriani@unipr.it http://www.riani.it STIMA PUNTUALE (p. 55) Il parametro è stimato con un unico valore Esempio: stima della share di un programma TV = % di spettatori
STATISTICA A K (60 ore) Marco Riani mriani@unipr.it http://www.riani.it STIMA PUNTUALE (p. 55) Il parametro è stimato con un unico valore Esempio: stima della share di un programma TV = % di spettatori
Campionamento e stima di parametri
 Sia X una variabile aleatoria associata a un dato esperimento. Ripetiamo l esperimento n volte, ottenendo una famiglia di valori sperimentali della v.a. X : X = (X 1, X 2,..., X n ) ogni X i é una v.a.
Sia X una variabile aleatoria associata a un dato esperimento. Ripetiamo l esperimento n volte, ottenendo una famiglia di valori sperimentali della v.a. X : X = (X 1, X 2,..., X n ) ogni X i é una v.a.
Statistica-UBG Statistica. Prof. Alessandro Fassò. ingegneria.unibg.it/fasso. CdL: Ing.Informatica emeccanica aa 2003/04
 Statistica Prof. Alessandro Fassò ingegneria.unibg.it/fasso CdL: Ing.Informatica emeccanica aa 2003/04 2 a parte Inferenza Statistica Parte 2a -Stima p.1 Inferenza ecampionamento Popolazione: finita/infinita,
Statistica Prof. Alessandro Fassò ingegneria.unibg.it/fasso CdL: Ing.Informatica emeccanica aa 2003/04 2 a parte Inferenza Statistica Parte 2a -Stima p.1 Inferenza ecampionamento Popolazione: finita/infinita,
Statistica Inferenziale
 Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Esercizio 1 (stima puntuale) In un processo di controllo di qualità, siamo interessati al numero mensile di guasti
Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Esercizio 1 (stima puntuale) In un processo di controllo di qualità, siamo interessati al numero mensile di guasti
Metodi statistici per le ricerche di mercato
 Metodi statistici per le ricerche di mercato Prof.ssa Isabella Mingo A.A. 2017-2018 Facoltà di Scienze Politiche, Sociologia, Comunicazione Corso di laurea Magistrale in «Organizzazione e marketing per
Metodi statistici per le ricerche di mercato Prof.ssa Isabella Mingo A.A. 2017-2018 Facoltà di Scienze Politiche, Sociologia, Comunicazione Corso di laurea Magistrale in «Organizzazione e marketing per
E n 1 n. n i. n 2. n 2 ( n
 Lezione n. 7 7.1 Ancora sulle proprietà degli stimatori Esempio 7.1 [continua dall Esempio 6.1] Studiare varianza e MSE dei due stimatori e verificare se T n raggiunge il limite di Cramer- Rao. Soluzione.
Lezione n. 7 7.1 Ancora sulle proprietà degli stimatori Esempio 7.1 [continua dall Esempio 6.1] Studiare varianza e MSE dei due stimatori e verificare se T n raggiunge il limite di Cramer- Rao. Soluzione.
ESERCIZIO 1. Soluzione. X =numero di passeggeri giornaliero
 ESERCIZIO 1 La somma dei numeri di passeggeri di un autoservizio suburbano rilevati in 7 giorni scelti a caso è pari a 385. Si assuma un modello gaussiano per descrivere il numero giornaliero di passeggeri.
ESERCIZIO 1 La somma dei numeri di passeggeri di un autoservizio suburbano rilevati in 7 giorni scelti a caso è pari a 385. Si assuma un modello gaussiano per descrivere il numero giornaliero di passeggeri.
Dispensa di Statistica
 Dispensa di Statistica 1 parziale 2012/2013 Diagrammi... 2 Indici di posizione... 4 Media... 4 Moda... 5 Mediana... 5 Indici di dispersione... 7 Varianza... 7 Scarto Quadratico Medio (SQM)... 7 La disuguaglianza
Dispensa di Statistica 1 parziale 2012/2013 Diagrammi... 2 Indici di posizione... 4 Media... 4 Moda... 5 Mediana... 5 Indici di dispersione... 7 Varianza... 7 Scarto Quadratico Medio (SQM)... 7 La disuguaglianza
Statistica inferenziale, Varese, 18 novembre 2009 Prima parte - Modalità D
 Statistica inferenziale, Varese, 18 novembre 2009 Prima parte - Modalità D Cognome Nome: Part time: Numero di matricola: Diurno: ISTRUZIONI: Il punteggio relativo alla prima parte dell esame viene calcolato
Statistica inferenziale, Varese, 18 novembre 2009 Prima parte - Modalità D Cognome Nome: Part time: Numero di matricola: Diurno: ISTRUZIONI: Il punteggio relativo alla prima parte dell esame viene calcolato
STATISTICA ESERCITAZIONE
 STATISTICA ESERCITAZIONE Dott. Giuseppe Pandolfo 1 Giugno 2015 Esercizio 1 Una fabbrica di scatole di cartone evade il 96% degli ordini entro un mese. Estraendo 300 campioni casuali di 300 consegne, in
STATISTICA ESERCITAZIONE Dott. Giuseppe Pandolfo 1 Giugno 2015 Esercizio 1 Una fabbrica di scatole di cartone evade il 96% degli ordini entro un mese. Estraendo 300 campioni casuali di 300 consegne, in
IL CRITERIO DELLA MASSIMA VEROSIMIGLIANZA
 Metodi per l Analisi dei Dati Sperimentali AA009/010 IL CRITERIO DELLA MASSIMA VEROSIMIGLIANZA Sommario Massima Verosimiglianza Introduzione La Massima Verosimiglianza Esempio 1: una sola misura sperimentale
Metodi per l Analisi dei Dati Sperimentali AA009/010 IL CRITERIO DELLA MASSIMA VEROSIMIGLIANZA Sommario Massima Verosimiglianza Introduzione La Massima Verosimiglianza Esempio 1: una sola misura sperimentale
APPUNTI DI STATISTICA INFERENZIALE. Avalle Fulvia, maggio 2014, ITSOS MARIE CURIE CLASSI 4A BIO e 4B BIO
 APPUNTI DI STATISTICA INFERENZIALE Avalle Fulvia, maggio 2014, ITSOS MARIE CURIE CLASSI 4A BIO e 4B BIO PREREQUISITI VARIABILE ALEATORIA (QUANTITATIVA): è una funzione che associa un numero reale ad ogni
APPUNTI DI STATISTICA INFERENZIALE Avalle Fulvia, maggio 2014, ITSOS MARIE CURIE CLASSI 4A BIO e 4B BIO PREREQUISITI VARIABILE ALEATORIA (QUANTITATIVA): è una funzione che associa un numero reale ad ogni
Richiami di inferenza statistica. Strumenti quantitativi per la gestione. Emanuele Taufer
 Richiami di inferenza statistica Strumenti quantitativi per la gestione Emanuele Taufer Inferenza statistica Inferenza statistica: insieme di tecniche che si utilizzano per ottenere informazioni su una
Richiami di inferenza statistica Strumenti quantitativi per la gestione Emanuele Taufer Inferenza statistica Inferenza statistica: insieme di tecniche che si utilizzano per ottenere informazioni su una
PROVA SCRITTA DI STATISTICA. CLEA/CLEFIN/CLEMIT (cod. 5047/4038/371/377) 3 Novembre 2004 MOD. A
 PROVA SCRITTA DI STATISTICA CLEA/CLEFIN/CLEMIT (cod. 547/438/37/377) 3 Novembre 4 MOD. A Esercizio N. (3 punti). Data la v.s. X avente funzione di densità: / x < 9/4 x < 3 f(x) = / 3 x < 7 / 7 x < 9 altrove
PROVA SCRITTA DI STATISTICA CLEA/CLEFIN/CLEMIT (cod. 547/438/37/377) 3 Novembre 4 MOD. A Esercizio N. (3 punti). Data la v.s. X avente funzione di densità: / x < 9/4 x < 3 f(x) = / 3 x < 7 / 7 x < 9 altrove
Richiami di inferenza statistica Strumenti quantitativi per la gestione
 Richiami di inferenza statistica Strumenti quantitativi per la gestione Emanuele Taufer Inferenza statistica Parametri e statistiche Esempi Tecniche di inferenza Stima Precisione delle stime Intervalli
Richiami di inferenza statistica Strumenti quantitativi per la gestione Emanuele Taufer Inferenza statistica Parametri e statistiche Esempi Tecniche di inferenza Stima Precisione delle stime Intervalli
Statistica ARGOMENTI. Calcolo combinatorio
 Statistica ARGOMENTI Calcolo combinatorio Probabilità Disposizioni semplici Disposizioni con ripetizione Permutazioni semplici Permutazioni con ripetizioni Combinazioni semplici Assiomi di probabilità
Statistica ARGOMENTI Calcolo combinatorio Probabilità Disposizioni semplici Disposizioni con ripetizione Permutazioni semplici Permutazioni con ripetizioni Combinazioni semplici Assiomi di probabilità
Disuguaglianza di Cramér-Rao
 Disuguaglianza di Cramér-Rao (Appunti per gli studenti Silvano Holzer Dipartimento di Scienze Economiche, Aziendali, Matematiche e Statistiche Bruno de Finetti Università degli studi di Trieste Un esperimento
Disuguaglianza di Cramér-Rao (Appunti per gli studenti Silvano Holzer Dipartimento di Scienze Economiche, Aziendali, Matematiche e Statistiche Bruno de Finetti Università degli studi di Trieste Un esperimento
4. Stime & Test. Corso di Simulazione. Anno accademico 2008/09
 Anno accademico 2008/09 Media campionaria X 1, X 2,..., X n v.c. indipendenti con distribuzione F, e: E[X i ] = µ Var[X i ] = σ 2, i = 1,..., n Media campionaria: X n è uno stimatore di µ. È uno stimatore
Anno accademico 2008/09 Media campionaria X 1, X 2,..., X n v.c. indipendenti con distribuzione F, e: E[X i ] = µ Var[X i ] = σ 2, i = 1,..., n Media campionaria: X n è uno stimatore di µ. È uno stimatore
! X (92) X n. P ( X n X ) =0 (94)
 Convergenza in robabilità Definizione 2 Data una successione X 1,X 2,...,X n,... di numeri aleatori e un numero aleatorio X diremo che X n tende in probabilità a X escriveremo X n! X (92) se fissati comunque
Convergenza in robabilità Definizione 2 Data una successione X 1,X 2,...,X n,... di numeri aleatori e un numero aleatorio X diremo che X n tende in probabilità a X escriveremo X n! X (92) se fissati comunque
LE DISTRIBUZIONI CAMPIONARIE
 LE DISTRIBUZIONI CAMPIONARIE Argomenti Principi e metodi dell inferenza statistica Metodi di campionamento Campioni casuali Le distribuzioni campionarie notevoli: La distribuzione della media campionaria
LE DISTRIBUZIONI CAMPIONARIE Argomenti Principi e metodi dell inferenza statistica Metodi di campionamento Campioni casuali Le distribuzioni campionarie notevoli: La distribuzione della media campionaria
lezione n. 6 (a cura di Gaia Montanucci) Verosimiglianza: L = = =. Parte dipendente da β 0 e β 1
 lezione n. 6 (a cura di Gaia Montanucci) METODO MASSIMA VEROSIMIGLIANZA PER STIMARE β 0 E β 1 Distribuzione sui termini di errore ε i ε i ~ N (0, σ 2 ) ne consegue : ogni y i ha ancora distribuzione normale,
lezione n. 6 (a cura di Gaia Montanucci) METODO MASSIMA VEROSIMIGLIANZA PER STIMARE β 0 E β 1 Distribuzione sui termini di errore ε i ε i ~ N (0, σ 2 ) ne consegue : ogni y i ha ancora distribuzione normale,
Elementi di Probabilità e Statistica - 052AA - A.A
 Elementi di Probabilità e Statistica - 05AA - A.A. 014-015 Prima prova di verifica intermedia - 9 aprile 015 Problema 1. Dati due eventi A, B, su uno spazio probabilizzato (Ω, F, P), diciamo che A è in
Elementi di Probabilità e Statistica - 05AA - A.A. 014-015 Prima prova di verifica intermedia - 9 aprile 015 Problema 1. Dati due eventi A, B, su uno spazio probabilizzato (Ω, F, P), diciamo che A è in
Statistica inferenziale, Varese, 18 novembre 2009 Prima parte - Modalità B
 Statistica inferenziale, Varese, 18 novembre 2009 Prima parte - Modalità B Cognome Nome: Part time: Numero di matricola: Diurno: ISTRUZIONI: Il punteggio relativo alla prima parte dell esame viene calcolato
Statistica inferenziale, Varese, 18 novembre 2009 Prima parte - Modalità B Cognome Nome: Part time: Numero di matricola: Diurno: ISTRUZIONI: Il punteggio relativo alla prima parte dell esame viene calcolato
Statistica 2 parte ARGOMENTI
 Statistica 2 parte ARGOMENTI Vettori gaussiani Matrice di covarianza e sua positività Marginali di un vettore normale Trasformazioni affini di vettori normali Indipendenza delle componenti scorrelate di
Statistica 2 parte ARGOMENTI Vettori gaussiani Matrice di covarianza e sua positività Marginali di un vettore normale Trasformazioni affini di vettori normali Indipendenza delle componenti scorrelate di
Statistica Inferenziale
 Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Riepilogo lezione 4 Abbiamo visto: Distribuzioni discrete Modelli probabilistici nel discreto Distribuzione uniforme
Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Riepilogo lezione 4 Abbiamo visto: Distribuzioni discrete Modelli probabilistici nel discreto Distribuzione uniforme
05. Errore campionario e numerosità campionaria
 Statistica per le ricerche di mercato A.A. 01/13 05. Errore campionario e numerosità campionaria Gli schemi di campionamento condividono lo stesso principio di fondo: rappresentare il più fedelmente possibile,
Statistica per le ricerche di mercato A.A. 01/13 05. Errore campionario e numerosità campionaria Gli schemi di campionamento condividono lo stesso principio di fondo: rappresentare il più fedelmente possibile,
Proprietà asintotiche dello stimatore OLS
 Università di Pavia Proprietà asintotiche dello stimatore OLS Eduardo Rossi Sequenze Consideriamo un infinita sequenza di variabili indicizzate con i numeri naturali: X 1, X 2, X 3,...,X N,... = {X N }
Università di Pavia Proprietà asintotiche dello stimatore OLS Eduardo Rossi Sequenze Consideriamo un infinita sequenza di variabili indicizzate con i numeri naturali: X 1, X 2, X 3,...,X N,... = {X N }
Analisi di Regressione Multipla
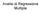 Analisi di Regressione Multipla Stima OLS della relazione Test Score/STR : TestScore! = 698.9.8 STR, R =.05, SER = 18.6 (10.4) (0.5) E una stima credibile dell effetto causale sul rendimento nei test di
Analisi di Regressione Multipla Stima OLS della relazione Test Score/STR : TestScore! = 698.9.8 STR, R =.05, SER = 18.6 (10.4) (0.5) E una stima credibile dell effetto causale sul rendimento nei test di
costruzione di un modello a partire dai dati Quale modello potrebbe essere utilizzato per riprodurre dei dati simili a questi?
 Inferenza statistica costruzione di un modello a partire dai dati segnale analogico in microvolt: 222 190 193 201 187 203 214 199 187 194 218 218 215 190 203 192 197 224 194 207 188 205 191 221 170 231
Inferenza statistica costruzione di un modello a partire dai dati segnale analogico in microvolt: 222 190 193 201 187 203 214 199 187 194 218 218 215 190 203 192 197 224 194 207 188 205 191 221 170 231
assuma valori in un determinato intervallo è data dall integrale della sua densità ( = )=
 VARIABILI ALEATORIE CONTINUE Esistono parecchi fenomeni reali per la cui descrizione le variabili aleatorie discrete non sono adatte. Per esempio è necessaria una variabile aleatoria continua ovvero una
VARIABILI ALEATORIE CONTINUE Esistono parecchi fenomeni reali per la cui descrizione le variabili aleatorie discrete non sono adatte. Per esempio è necessaria una variabile aleatoria continua ovvero una
Gli intervalli di confidenza. Intervallo di confidenza per la media (σ 2 nota) nel caso di popolazione Gaussiana
 Statistica Lez. 1 Gli intervalli di confidenza Intervallo di confidenza per la media (σ nota) nel caso di popolazione Gaussiana Sia X una v.c Gaussiana di media µ e varianza σ. Se X 1, X,..., X n è un
Statistica Lez. 1 Gli intervalli di confidenza Intervallo di confidenza per la media (σ nota) nel caso di popolazione Gaussiana Sia X una v.c Gaussiana di media µ e varianza σ. Se X 1, X,..., X n è un
Correzione terzo compitino, testo A
 Correzione terzo compitino, testo A 24 maggio 2 Parte Esercizio.. Procederemo per esclusione, mostrando come alcune funzioni della lista non possano avere il grafico in figura. La prima cosa che possiamo
Correzione terzo compitino, testo A 24 maggio 2 Parte Esercizio.. Procederemo per esclusione, mostrando come alcune funzioni della lista non possano avere il grafico in figura. La prima cosa che possiamo
Metodi statistici per le ricerche di mercato
 Metodi statistici per le ricerche di mercato Prof.ssa Isabella Mingo A.A. 2016-2017 Facoltà di Scienze Politiche, Sociologia, Comunicazione Corso di laurea Magistrale in «Organizzazione e marketing per
Metodi statistici per le ricerche di mercato Prof.ssa Isabella Mingo A.A. 2016-2017 Facoltà di Scienze Politiche, Sociologia, Comunicazione Corso di laurea Magistrale in «Organizzazione e marketing per
Statistica Inferenziale
 Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Riepilogo lezione 9 Abbiamo visto metodi per la determinazione di uno stimatore puntuale e casi per: Carattere con
Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Riepilogo lezione 9 Abbiamo visto metodi per la determinazione di uno stimatore puntuale e casi per: Carattere con
Esperimentazioni di Fisica 1. Prova in itinere del 12 giugno 2018
 Esperimentazioni di Fisica 1 Prova in itinere del 1 giugno 018 Esp-1 Prova in Itinere n. - - Page of 6 1/06/018 1. (1 Punti) Quesito L incertezza da associare alle misurazioni eseguite con un certo strumento
Esperimentazioni di Fisica 1 Prova in itinere del 1 giugno 018 Esp-1 Prova in Itinere n. - - Page of 6 1/06/018 1. (1 Punti) Quesito L incertezza da associare alle misurazioni eseguite con un certo strumento
Stima dei parametri. La v.c. multipla (X 1, X 2,.., X n ) ha probabilità (o densità): Le f( ) sono uguali per tutte le v.c.
 Stima dei parametri Sia il carattere X rappresentato da una variabile casuale (v.c.) che si distribuisce secondo la funzione di probabilità f(x). Per investigare su tale carattere si estrae un campione
Stima dei parametri Sia il carattere X rappresentato da una variabile casuale (v.c.) che si distribuisce secondo la funzione di probabilità f(x). Per investigare su tale carattere si estrae un campione
Significato probabilistico di σ: su 100 misure, 68.3 hanno probabilità di cadere nell intervallo x σ, x +σ, 95.5 nell intervallo
 Significato probabilistico di σ: su 1 misure, 68.3 hanno probabilità di cadere nell intervallo x σ, x +σ, 95.5 nell intervallo x σ, x + σ e 99.7 nell intervallo x 3 σ, x + 3 Se si considerano campioni
Significato probabilistico di σ: su 1 misure, 68.3 hanno probabilità di cadere nell intervallo x σ, x +σ, 95.5 nell intervallo x σ, x + σ e 99.7 nell intervallo x 3 σ, x + 3 Se si considerano campioni
STATISTICA A K (60 ore)
 STATISTICA A K (60 ore) Marco Riani mriani@unipr.it http://www.riani.it Esercizio: si consideri una generica popolazione X con media µ e varianza σ 2 Siano T 1 =(X 1 +X 2 +X 3 +X 4 )/4 e T 2 =(3X 1 +4X
STATISTICA A K (60 ore) Marco Riani mriani@unipr.it http://www.riani.it Esercizio: si consideri una generica popolazione X con media µ e varianza σ 2 Siano T 1 =(X 1 +X 2 +X 3 +X 4 )/4 e T 2 =(3X 1 +4X
Campionamento. Una grandezza fisica e' distribuita secondo una certa PDF
 Campionamento Una grandezza fisica e' distribuita secondo una certa PDF La pdf e' caratterizzata da determinati parametri Non abbiamo una conoscenza diretta della pdf Possiamo determinare una distribuzione
Campionamento Una grandezza fisica e' distribuita secondo una certa PDF La pdf e' caratterizzata da determinati parametri Non abbiamo una conoscenza diretta della pdf Possiamo determinare una distribuzione
Problema tipico delle applicazioni idrologiche: qual'è la portata con tempo di ritorno T?
 Problema tipico delle applicazioni idrologiche: qual'è la portata con tempo di ritorno T? Il problema dell'inferenza: dato un campione, individuare la distribuzione di probabilità da cui ha avuto origine.
Problema tipico delle applicazioni idrologiche: qual'è la portata con tempo di ritorno T? Il problema dell'inferenza: dato un campione, individuare la distribuzione di probabilità da cui ha avuto origine.
LA MEDIA CAMPIONARIA 14-1
 LA MEDIA CAMPIONARIA Prendiamo un urna e inseriamo 10 palline numerate da 0 a 9 (questa è la nostra popolazione ). La media dei 10 valori è 4.5 (questa è la media vera µ). La varianza dei 10 valori è 8.25
LA MEDIA CAMPIONARIA Prendiamo un urna e inseriamo 10 palline numerate da 0 a 9 (questa è la nostra popolazione ). La media dei 10 valori è 4.5 (questa è la media vera µ). La varianza dei 10 valori è 8.25
Metodi Statistici per il Marketing. #05 Elementi di statistica inferenziale e di teoria dei campioni
 Corso di Metodi Statistici per il Marketing LUISS A.A. 2017-2018 #05 Elementi di statistica inferenziale e di teoria dei campioni 15 Marzo 2018 Alessio Guandalini (Docente: P. D Urso) #05 Elementi di statistica
Corso di Metodi Statistici per il Marketing LUISS A.A. 2017-2018 #05 Elementi di statistica inferenziale e di teoria dei campioni 15 Marzo 2018 Alessio Guandalini (Docente: P. D Urso) #05 Elementi di statistica
Statistica Applicata all edilizia: il modello di regressione
 Statistica Applicata all edilizia: il modello di regressione E-mail: orietta.nicolis@unibg.it 27 aprile 2009 Indice Il modello di Regressione Lineare 1 Il modello di Regressione Lineare Analisi di regressione
Statistica Applicata all edilizia: il modello di regressione E-mail: orietta.nicolis@unibg.it 27 aprile 2009 Indice Il modello di Regressione Lineare 1 Il modello di Regressione Lineare Analisi di regressione
La media e la mediana sono indicatori di centralità, che indicano un centro dei dati.
 La media e la mediana sono indicatori di centralità, che indicano un centro dei dati. Un indicatore che sintetizza in un unico numero tutti i dati, nascondendo quindi la molteplicità dei dati. Per esempio,
La media e la mediana sono indicatori di centralità, che indicano un centro dei dati. Un indicatore che sintetizza in un unico numero tutti i dati, nascondendo quindi la molteplicità dei dati. Per esempio,
CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 3
 CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 3 Dott.ssa Antonella Costanzo a.costanzo@unicas.it Esercizio 1. La v.c. Uniforme Continua Secondo alcuni sondaggi sul sito della Apple (technical support site,
CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 3 Dott.ssa Antonella Costanzo a.costanzo@unicas.it Esercizio 1. La v.c. Uniforme Continua Secondo alcuni sondaggi sul sito della Apple (technical support site,
Nel modello omoschedastico la varianza dell errore non dipende da i ed è quindi pari a σ 0.
 Regressione [] el modello di regressione lineare si assume una relazione di tipo lineare tra il valore medio della variabile dipendente Y e quello della variabile indipendente X per cui Il modello si scrive
Regressione [] el modello di regressione lineare si assume una relazione di tipo lineare tra il valore medio della variabile dipendente Y e quello della variabile indipendente X per cui Il modello si scrive
lezione 4 AA Paolo Brunori
 AA 2016-2017 Paolo Brunori dove eravamo arrivati - abbiamo individuato la regressione lineare semplice (OLS) come modo immediato per sintetizzare una relazione fra una variabile dipendente (Y) e una indipendente
AA 2016-2017 Paolo Brunori dove eravamo arrivati - abbiamo individuato la regressione lineare semplice (OLS) come modo immediato per sintetizzare una relazione fra una variabile dipendente (Y) e una indipendente
Esercitazioni di Statistica Metodologica
 Esercitazioni di Statistica Metodologica June 22, 2009 1 Esercizio La compagnia di telefonia fissa Happy Line ha svolto una indagine sul numero di telefonate effettuate dai suoi clienti la settimana scorsa.
Esercitazioni di Statistica Metodologica June 22, 2009 1 Esercizio La compagnia di telefonia fissa Happy Line ha svolto una indagine sul numero di telefonate effettuate dai suoi clienti la settimana scorsa.
Esercizi di Probabilità e Statistica
 Esercizi di Probabilità e Statistica Samuel Rota Bulò 6 giugno 26 Statistica Esercizio Sia {X n } n una famiglia di v.a. di media µ e varianza σ 2. Verificare che X = n n X i σ 2 = n (X i µ) 2 S 2 = n
Esercizi di Probabilità e Statistica Samuel Rota Bulò 6 giugno 26 Statistica Esercizio Sia {X n } n una famiglia di v.a. di media µ e varianza σ 2. Verificare che X = n n X i σ 2 = n (X i µ) 2 S 2 = n
I appello di calcolo delle probabilità e statistica
 I appello di calcolo delle probabilità e statistica A.Barchielli, L. Ladelli, G. Posta 8 Febbraio 13 Nome: Cognome: Matricola: Docente: I diritti d autore sono riservati. Ogni sfruttamento commerciale
I appello di calcolo delle probabilità e statistica A.Barchielli, L. Ladelli, G. Posta 8 Febbraio 13 Nome: Cognome: Matricola: Docente: I diritti d autore sono riservati. Ogni sfruttamento commerciale
Statistica Inferenziale
 Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Riepilogo lezione 5 Abbiamo visto: Modelli probabilistici nel continuo Distribuzione uniforme continua Distribuzione
Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Riepilogo lezione 5 Abbiamo visto: Modelli probabilistici nel continuo Distribuzione uniforme continua Distribuzione
Costruzione di macchine. Modulo di: Progettazione probabilistica e affidabilità. Marco Beghini. Lezione 7: Basi di statistica
 Costruzione di macchine Modulo di: Progettazione probabilistica e affidabilità Marco Beghini Lezione 7: Basi di statistica Campione e Popolazione Estrazione da una popolazione (virtualmente infinita) di
Costruzione di macchine Modulo di: Progettazione probabilistica e affidabilità Marco Beghini Lezione 7: Basi di statistica Campione e Popolazione Estrazione da una popolazione (virtualmente infinita) di
STATISTICA 1, metodi matematici e statistici Introduzione al linguaggio R Esercitazione 5:
 esercitazione 5 p. 1/14 STATISTICA 1, metodi matematici e statistici Introduzione al linguaggio R Esercitazione 5: 22-04-2005 Luca Monno Università degli studi di Pavia luca.monno@unipv.it http://www.lucamonno.it
esercitazione 5 p. 1/14 STATISTICA 1, metodi matematici e statistici Introduzione al linguaggio R Esercitazione 5: 22-04-2005 Luca Monno Università degli studi di Pavia luca.monno@unipv.it http://www.lucamonno.it
CP210 Introduzione alla Probabilità: Esame 2
 Dipartimento di Matematica, Roma Tre Pietro Caputo 2018-19, II semestre 9 luglio, 2019 CP210 Introduzione alla Probabilità: Esame 2 Cognome Nome Matricola Firma Nota: 1. L unica cosa che si può usare durante
Dipartimento di Matematica, Roma Tre Pietro Caputo 2018-19, II semestre 9 luglio, 2019 CP210 Introduzione alla Probabilità: Esame 2 Cognome Nome Matricola Firma Nota: 1. L unica cosa che si può usare durante
Distribuzione Normale
 Distribuzione Normale istogramma delle frequenze di un insieme di misure relative a una grandezza che può variare con continuità popolazione molto numerosa, costituita da una quantità praticamente illimitata
Distribuzione Normale istogramma delle frequenze di un insieme di misure relative a una grandezza che può variare con continuità popolazione molto numerosa, costituita da una quantità praticamente illimitata
Laboratorio di Chimica Fisica. Analisi Statistica
 Università degli Studi di Bari Dipartimento di Chimica 9 giugno F.Mavelli- Laboratorio Chimica Fisica - a.a. 3-4 F.Mavelli Laboratorio di Chimica Fisica a.a. 3-4 Analisi Statistica dei Dati Analisi Statistica
Università degli Studi di Bari Dipartimento di Chimica 9 giugno F.Mavelli- Laboratorio Chimica Fisica - a.a. 3-4 F.Mavelli Laboratorio di Chimica Fisica a.a. 3-4 Analisi Statistica dei Dati Analisi Statistica
Distribuzione normale
 Distribuzione normale istogramma delle frequenze di un insieme di misure relative a una grandezza che varia con continuità popolazione molto numerosa, costituita da una quantità praticamente illimitata
Distribuzione normale istogramma delle frequenze di un insieme di misure relative a una grandezza che varia con continuità popolazione molto numerosa, costituita da una quantità praticamente illimitata
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2011/12
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 0/ Esercizio Prova scritta del 7/06/0 Siano X e Y due v.a. indipendenti, con distribuzione continua Γ(, ). Si trovino la distribuzione di X Y e di (X Y ). Esercizio
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 0/ Esercizio Prova scritta del 7/06/0 Siano X e Y due v.a. indipendenti, con distribuzione continua Γ(, ). Si trovino la distribuzione di X Y e di (X Y ). Esercizio
Dipartimento di Sociologia e Ricerca Sociale. Corso di Laurea in Sociologia. Insegnamento di Statistica (a.a ) dott.ssa Gaia Bertarelli
 Dipartimento di Sociologia e Ricerca Sociale Corso di Laurea in Sociologia Insegnamento di Statistica (a.a. 2018-2019) dott.ssa Gaia Bertarelli Esercitazione n. 7 1. Utilizzando le tavole della distribuzione
Dipartimento di Sociologia e Ricerca Sociale Corso di Laurea in Sociologia Insegnamento di Statistica (a.a. 2018-2019) dott.ssa Gaia Bertarelli Esercitazione n. 7 1. Utilizzando le tavole della distribuzione
MATEMATICA E STATISTICA CORSO A III COMPITINO 20 Marzo 2009
 MATEMATICA E STATISTICA CORSO A III COMPITINO Marzo 9 SOLUZIONI. () Sia X una variabile aleatoria binomiale con valor medio uguale a 5/; la varianza di X può valere? Giustificare la risposta. Il valor
MATEMATICA E STATISTICA CORSO A III COMPITINO Marzo 9 SOLUZIONI. () Sia X una variabile aleatoria binomiale con valor medio uguale a 5/; la varianza di X può valere? Giustificare la risposta. Il valor
Metodi Statistici per il Management
 Metodi Statistici per il Management Richiami di Inferenza Statistica Simone Borra - Roberto Rocci Indice Probabilità Variabili Casuali Metodologie dell Inferenza Statistica 2 Siano dati i seguenti elementi:
Metodi Statistici per il Management Richiami di Inferenza Statistica Simone Borra - Roberto Rocci Indice Probabilità Variabili Casuali Metodologie dell Inferenza Statistica 2 Siano dati i seguenti elementi:
x ;x Soluzione Gli intervalli di confidenza possono essere ottenuti a partire dalla seguente identità: da cui si ricava: IC x ;x = +
 ESERCIZIO 6.1 Si considerino i 0 campioni di ampiezza n = estratti da una popolazione X di N = 5 elementi distribuiti normalmente, con media µ = 13,6 e σ = 8,33. A partire dalle 0 determinazioni della
ESERCIZIO 6.1 Si considerino i 0 campioni di ampiezza n = estratti da una popolazione X di N = 5 elementi distribuiti normalmente, con media µ = 13,6 e σ = 8,33. A partire dalle 0 determinazioni della
La media e la mediana sono indicatori di centralità, che indicano un centro dei dati.
 La media e la mediana sono indicatori di centralità, che indicano un centro dei dati. Un indicatore che sintetizza in un unico numero tutti i dati, nascondendo quindi la molteplicità dei dati. Per esempio,
La media e la mediana sono indicatori di centralità, che indicano un centro dei dati. Un indicatore che sintetizza in un unico numero tutti i dati, nascondendo quindi la molteplicità dei dati. Per esempio,
ESAME. 9 Gennaio 2017 COMPITO A
 ESAME 9 Gennaio 2017 COMPITO A Cognome Nome Numero di matricola 1) Approssimare tutti i calcoli alla quarta cifra decimale. 2) Ai fini della valutazione si terrà conto solo ed esclusivamente di quanto
ESAME 9 Gennaio 2017 COMPITO A Cognome Nome Numero di matricola 1) Approssimare tutti i calcoli alla quarta cifra decimale. 2) Ai fini della valutazione si terrà conto solo ed esclusivamente di quanto
RICHIAMI DI CALCOLO DELLE PROBABILITÀ
 UNIVERSITA DEL SALENTO INGEGNERIA CIVILE RICHIAMI DI CALCOLO DELLE PROBABILITÀ ing. Marianovella LEONE INTRODUZIONE Per misurare la sicurezza di una struttura, ovvero la sua affidabilità, esistono due
UNIVERSITA DEL SALENTO INGEGNERIA CIVILE RICHIAMI DI CALCOLO DELLE PROBABILITÀ ing. Marianovella LEONE INTRODUZIONE Per misurare la sicurezza di una struttura, ovvero la sua affidabilità, esistono due
