PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2011/12
|
|
|
- Felice Fabriciano Piccolo
- 5 anni fa
- Visualizzazioni
Transcript
1 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 0/ Esercizio Prova scritta del 7/06/0 Siano X e Y due v.a. indipendenti, con distribuzione continua Γ(, ). Si trovino la distribuzione di X Y e di (X Y ). Esercizio In un recipiente sono contenute n palle nere, n palle bianche e n palle rosse, (con n > 3), e si effettuano estrazioni, lasciando fuori ogni volta la palla estratta. Si calcoli la probabilita P (n) che, nelle prime tre estrazioni, siano uscite tre palle dello stesso colore. Si calcoli poi il valore limite di tale probabilita, quando n cresce indefinitamente. Esercizio 3 Una fabbrica produce biglie aventi diametro di lunghezza X (misurata in millimetri). Si supponga che X N(µ, σ = 0.04). Posto di aver misurato un campione casuale di n = 50 biglie e di aver trovato che x = 5 si calcoli l intervallo di confidenza per la media al livello del 5%. Supponendo che il valore di x rimanga invariato determinare il valore minimo di n affinché l ampiezza dell intervallo di confidenza si riduca a 00. Detta Φ la funzione di ripartizione della distribuzione normale N(0, ), utilizzare la seguente tabella: ( Φ(, 8) = 0, 9, Φ(, 645) = 0, 95 Φ(, 96) = 0, 975 Φ(.58) = 0, 995 ) Esercizio Soluzioni compito 7/06/0 Usando il prodotto di convoluzione, non e difficile dedurre che la densita di Z = X Y e data da f Z (z) = 0 0 f X (z + y)f Y (y)dy = z e z y e y dy, dove z = max{0, z}. Un semplice calcolo fornisce allora { f Z (z) = e z e z e z =, z > 0 e z, z 0 = e z,
2 per ogni z reale. Quanto alla distribuzione di Z, intanto si puo osservare che tale variabile e sempre positiva; inoltre, per u > 0 si ha F Z (u) = P ([ Z u]) = P ([ u Z u]) = u 0 f Z (t)dt = e u. Dunque, anche Z ha distribuzione Γ(, ). Per determinare la distribuzione di (X Y ) = Z, basta calcolare la funzione di ripartizione. Per v > 0 si ha infatti P ([Z v]) = P ([ Z v]) = e v, e quindi, derivando f Z (v) = v v e. Esercizio L evento cercato e unione di tre eventi incompatibili, ciascuno relativo al colore della palla estratta. Questi eventi hanno tutti la stessa probabilita, pari a n(n )(n ) = (n )(n ). L evento in questione ha dunque probabilita 3n(3n )(3n ) 3(3n )3n ) P (n) = Un semplice calcolo fornisce il limite: (n )(n ) (3n )(3n ). lim n P (n) = 9. Esercizio 3 Poiché la popolazione di partenza é normale sappiamo che: P ( z α X µ n z α σ ) = α. Quindi con i dati che noi abbiamo risulta α = 0, 05 da cui α/ = 0, 05. Possiamo quindi determinare il valore di z α essere: che dalla tabella sulla funzione normale vediamo z α =, 96. Da cio ricaviamo che l intervallo fiduciario per µ é dato da: e sostituendo con i numeri si ha (5, 96 (X z α σ/ n; X + z α σ/ n) ; 5 +, 96 ) = ( ; ) = (4.9445; )
3 L ampiezza dell intervallo di confidenza e dunque circa 0.. Se si vuole che tale ampiezza si riduca a 0.0, ossia ad del valore trovato per n = 50, bisogna che n venga moltiplicato per il quadrato di, cioe. Pertanto, occorre un campione di 6050 prove, se si vuole che, con la stessa media campionaria, l intervallo di confidenza abbia ampiezza 0.0. (Una stima piu precisa fornisce n = 6047). Prova scritta dell /07/0 Esercizio Sia X una variabile aleatoria con distribuzione continua, di tipo U(0, ). Posto poi, per x [0, ]: f(x) = x, si determini la distribuzione di Y = f(x) e successivamente quella di Z = f(y ). Esercizio Si supponga di lanciare indefinitamente un dado onesto, in condizioni di indipendenza, finche non esca il primo 5. Detta T la variabile aleatoria che rappresenta il numero di lanci occorrenti per la prima uscita del 5, si calcoli la probabilita che il numero intero T abbia 0 come ultima cifra. Esercizio 3 Adoperando le proprieta della funzione Γ, si provi che la funzione f(x; A) = π A 3 x e A x, con x IR, e una densita di probabilita, per qualsiasi parametro reale A 0. Si determini la stima di massima verosimiglianza per A, supponendo noto un campione aleatorio (y,..., y n ) estratto dalla distribuzione che ha f come densita. Soluzioni compito /07/0 Esercizio Un semplice esame della funzione f mostra che si ha { x, x f(x) = x, x. Dunque, chiaramente Y ha valori compresi tra 0 e. Fissato t [0, ], risulta [f(x) t] [x t ] [x t ], e le due alternative (x t e x t sono incompatibili. Dunque P ([Y t]) = P ([X t ]) + P ([X t ]) = t = t. 3
4 Pertanto, la funzione di ripartizione di Y e la stessa di X, e quindi Y U(0, ). A questo punto e ovvio che anche Z ha le stesse caratteristiche, e quindi Z U(0, ). Esercizio Chiaramente, T NB(, ). Poiche T e a valori interi positivi, lo stesso 6 vale per T. Ora, il numero intero T ha come ultima cifra 0 se e solo se e multiplo di 0, e cio accade se e solo se T e multiplo di 0. Dunque, detto E l evento in oggetto, il calcolo della probabilita richiesta si puo svolgere come segue: P (E) = + k= P ([T = 0k]) = + k= 6 (5 6 )0k = + ( )0 ) k = 5 (5 6 )0 ( 5 = k= 6 ) Esercizio 3 Essendo Γ( 3) = π, e poiche la funzione f e pari rispetto a x, si ha f(x; A)dx = 4 π 0 A 3 x e A x dx = π 0 ve v dv = π Γ( 3 ) =, (avendo effettuato la sostituzione v = A x ). Dunque, effettivamente f e una densita per ogni A 0. Ora, la verosimiglianza del campione (y,..., y n ) e data da L(y,..., y n ; A) = ( π ) n A 3n y y...y n e A (y +y +...y n). Eliminando le costanti irrilevanti, bisogna massimizzare, rispetto al parametro A, la funzione L 0 (A) = A 3n e A (y +y +...y n). Derivando, e ponendo S = y + y +...y n, si ottiene L 0(A) = 3nA 3n e SA A 3n e AS AS = A 3n e SA (3n SA ). Si vede ora facilmente che il valore di A che massimizza L 0 (e quindi la verosimiglianza), 3n e A =. S Prova scritta del /09/0 Esercizio Sia X una variabile aleatoria con distribuzione Normale standard. Usando la facile relazione x ax = (x a) a, si calcolino valor medio e varianza di Y = e X. 4
5 Esercizio Si supponga di lanciare un dado onesto 5 volte, e si denoti con S la somma delle 5 facce uscite. Si trovi una relazione tra le quantita P ([S = k]) e P ([S = 05 k]) per k variabile tra 5 e 90 (ossia tutti i valori possibili per S). probabilita che il numero S sia dispari. Se ne deduca la Esercizio 3 Una variabile aleatoria X ha distribuzione normale. Si supponga che σ = 0.9 e che si voglia stimare µ sulla base di osservazioni I.I.D. della X, x,..., x : qual é l ampiezza dell intervallo di confidenza per µ al livello di significativita del 5%? Quante dovrebbero essere le osservazioni, se si vuole che l ampiezza dell intervallo si riduca di un terzo? Detta Φ la funzione di ripartizione della distribuzione normale N(0, ), utilizzare la seguente tabella: ( ) Φ(, 8) = 0, 9, Φ(, 645) = 0, 95 Φ(, 96) = 0, 975 Φ(.58) = 0, 995 Soluzioni compito /09/0 Esercizio Per calcolare E(e X ), basta svolgere l integrale E(e X ) = π Utilizzando la relazione suggerita, avremo Analogamente, avremo E(e X ) = π E(e X ) = π Tramite la relazione suggerita, troveremo e x e x dx = e e (x ) dx = e x e x dx = π e x x dx. e π π = e. π e 4x x dx. E(e X ) = π e e (x ) dx = e. Infine, V (e X ) = E(e X ) E (e X ) = e e. 5
6 Esercizio La relazione richiesta e di uguaglianza: P ([S = k]) = P ([S = 05 k]), per ogni k = 5,..., 90. Per esempio, con k = 5, avremo 05 k = 90: i due eventi corrispondono ad avere tutti oppure tutti 6 rispettivamente; dato che il dado e onesto, i due eventi hanno la stessa probabilita. Dato un valore generico di k, la probabilita che S sia uguale a k viene calcolata come somma di probabilita di eventi del tipo [X = k, X = k,..., X 6 = k 6 ], dove ogni X i denota quante volte esce la faccia i, e le sestuple (k, k,..., k 6 ) sono scelte ogni volta in modo tale che k + k + 3k k 6 = k, (oltre naturalmente alla condizione i k i = 5). Ora, per l onesta del dado, l evento A := [X = k, X = k,..., X 6 = k 6 ] ha la stessa probabilita dell evento simmetrico A := [X = k 6, X = k 5,..., X 6 = k ], che a sua volta e favorevole a S = 05 k, in quanto A comporta che S = k 6 +k k +6k = (7 )k 6 +(7 )k +...+(7 6)k = 7 i k i k = 05 k. In altre parole, comunque si scelga k, e comunque si scelga la sestupla (k,..., k 6 ) in modo favorevole a S = k, la sestupla simmetrica (k 6, k 5,..., k ) e favorevole a S = 05 k, e ha la stessa probabilita di verificarsi. Sommando tali probabilita al variare delle sestuple (k, k,..., k 6 ) in tutti i modi ammissibili, si ottiene la relazione di uguaglianza tra P ([S = k]) e P ([S = 05 k]). Ora, la condizione che S sia dispari equivale a richiedere che S sia uguale a 5, o a 7, ecc. fino a 89: per ciascuno di tali valori (tra loro incompatibili), c e un corrispondente valore pari che ha la stessa probabilita di verificarsi: per 5 c e 90, per 7 c e 88=05-7, ecc. Pertanto, sommando le probabilita di tutti i possibili valori dispari di S si ottiene la stessa probabilita che si otterrebbe sommando tutti i possibili valori pari, e quindi ciascuna di tali somme (P ([S pari] o P ([S dispari])) ha lo stesso valore, cioe. Esercizio 3 Detta x la media aritmetica dei dati x,..., x, l intervallo di confidenza cercato per µ sara [x δ, x + δ], ove δ = σ n z 0.05, ossia δ =
7 L ampiezza dell intervallo é dunque circa.0. Se si vuole ridurre di un terzo tale ampiezza, basta moltiplicare per 9 4 osservazioni, per cui il campione dovra essere costituito da 7 dati. il numero di Prova scritta del 6/09/0 Esercizio Sia X una variabile aleatoria con distribuzione Normale standard. Usando la facile relazione x ax = (x a) a, si calcolino valor medio e varianza di Y = X = e X ln. Esercizio In un recipiente ci sono 4 palline, numerate da a 4. Si supponga di estrarre 5 volte una palla a caso dall urna, rimettendola poi nel recipiente dopo averne annotato il numero. Denotata con S la somma dei numeri annotati, si trovi una relazione tra le quantita P ([S = k]) e P ([S = 5 k]) per k variabile tra 5 e 00 (ossia tutti i valori possibili per S). Se ne deduca la probabilita che il numero S sia pari. Esercizio 3 Una variabile aleatoria X ha distribuzione normale, X N(µ, σ ). Si supponga che σ = 0.5 e che si voglia stimare µ sulla base di 5 osservazioni I.I.D. della X, x,..., x 5 : qual é l ampiezza dell intervallo di confidenza per µ al livello di significativita del 5%? Quante dovrebbero essere le osservazioni, se si vuole che l ampiezza dell intervallo si riduca di un quarto? Detta Φ la funzione di ripartizione della distribuzione normale N(0, ), utilizzare la seguente tabella: ( ) Φ(, 8) = 0, 9, Φ(, 645) = 0, 95 Φ(, 96) = 0, 975 Φ(.58) = 0, 995 Soluzioni compito 6/09/0 Esercizio Si ha πe( X ) = e x ln e x dx = e ln (x ln ) e dx = e ln π, 7
8 per cui E( X ) = e ln.7. Si ha poi, analogamente, πe( X ) = e x ln e x dx = e ln (x ln ) e dx = e ln π, per cui E(4 X ) = e ln.64. In conclusione, V ( X ) = E(4 X ) E ( X ) = e ln e ln Esercizio La relazione richiesta e di uguaglianza: P ([S = k]) = P ([S = 5 k]), per ogni k = 5,..., 00. Per esempio, con k = 5, avremo 5 k = 00: i due eventi corrispondono ad avere tutti oppure tutti 4 rispettivamente; poiche tutte le palline sono equiprobabili, i due eventi hanno la stessa probabilita. Dato un valore generico di k, la probabilita che S sia uguale a k viene calcolata come somma di probabilita di eventi del tipo [X = k, X = k, X 3 = k 3, X 4 = k 4 ], dove ogni X i denota quante volte esce la palla numero i, e le quaterne (k, k, k 3, k 4 ) sono scelte ogni volta in modo tale che k + k + 3k 3 + 4k 4 = k, (oltre naturalmente alla condizione i k i = 5). Ora, per l equiprobabilita, l evento A := [X = k, X = k, X 3 = k 3, X 4 = k 4 ] ha la stessa probabilita dell evento simmetrico A := [X = k 4, X = k 3, X 3 = k, X 4 = k ], che a sua volta e favorevole a S = 5 k, in quanto A comporta che S = k 4 +k 3 +3k +3k +4k = (5 )k +(5 )k +(5 3)k 3 +(5 4)k 4 = 5 i k i k = 5 k. In altre parole, comunque si scelga k, e comunque si scelga la quaterna (k,..., k 4 ) in modo favorevole a S = k, la quaterna simmetrica (k 4,..., k ) e favorevole a S = 5 k, e ha la stessa probabilita di verificarsi. Sommando tali probabilita al variare delle quaterne (k, k, k 3, k 4 ) in tutti i modi ammissibili, si ottiene la relazione di uguaglianza tra P ([S = k]) e P ([S = 5 k]). Ora, la condizione che S sia dispari equivale a richiedere che S sia uguale a 5, o a 7, ecc. fino a 99: per ciascuno di tali valori (tra loro incompatibili), c e un 8
9 corrispondente valore pari che ha la stessa probabilita di verificarsi: per 5 c e 00, per 7 c e 98=5-7, ecc. Pertanto, sommando le probabilita di tutti i possibili valori dispari di S si ottiene la stessa probabilita che si otterrebbe sommando tutti i possibili valori pari, e quindi ciascuna di tali somme (P ([S pari] o P ([S dispari])) ha lo stesso valore, cioe. Esercizio 3 Detta x la media aritmetica dei dati x,..., x 5, l intervallo di confidenza cercato per µ sara [x δ, x + δ], ove δ = σ n z 0.05, ossia δ = L ampiezza dell intervallo é dunque circa Se si vuole ridurre di un quarto tale ampiezza, basta moltiplicare per 6 il numero di 9 osservazioni, per cui il campione dovra essere costituito da dati. 9 Prova scritta del 9/0/0 Esercizio Supponiamo che una variabile aleatoria Y abbia la seguente densita : { hx 3, x > f Y (x) = 0, x, con h opportuna costante positiva. Dopo aver calcolato h, si determini la distribuzione di X =, e si confronti (se possibile) la varianza di X con quella di Y. Y Esercizio Sia (X n ) n una successione I.I.D. di variabili aleatorie di tipo discreto, ciascuna delle quali puo assumere solo i valori 0 e, entrambi con la stessa probabilita. Si ponga poi n S n = X i, i= per n =,,... Dopo aver calcolato valor medio e varianza di S n, si dimostri che, per ogni fissato a, la successione (S n n ) n converge in distribuzione, e se ne determini il limite. Esercizio 3 Sia X una variabile aleatoria la cui funzione di densita e ke θx, x >, f(x; θ) = 0, altrove, 9 n a
10 dove θ > 0. Si chiede di (a) calcolare k ed E(X) in funzione di θ; (b) fornire uno stimatore di θ con il metodo della massima verosimiglianza, sulla base di un campione casuale X,..., X n. Soluzioni compito 9/0/0 Esercizio Essendo x 3 dx =, chiaramente la costante h e uguale a. Per calcolare la distribuzione di X, valutiamo la sua funzione di ripartizione. Intanto, poiche Y assume solo valori maggiori o uguali a, la variabile X = puo assumere solo valori compresi fra 0 e. Ora, se 0 < t < Y si ha P ([X t]) = P ([Y t ]) = x dx = 3 t. Dunque e evidente che la densita f X di X e cosi definita: { 0, t / [0, ] f X (t) = t, t [0, ]. Con facili calcoli si vede poi che E(X) =, 3 E(X ) =, V (X) =, mentre Y 8 non ammette momenti di ordine, in quanto la funzione x non e integrabile in x [, + [. Esercizio Chiaramente, si ha E(X n ) =, E(X n) =, V (X n ) = per ogni n. Pertanto E(S n ) = V (S n ) = n, a causa dell indipendenza. Allora, per il Teorema del Limite Centrale, la successione ( Sn n n / ) n converge in distribuzione alla legge Normale standard. Questo risolve il quesito per quanto riguarda a =. Per a >, la successione ( Sn n n a ) n converge in probabilita (e quindi in distribuzione) a 0. Per dimostrare cio, si fissi ε > 0 e si osservi che esiste in corrispondenza un numero reale M > 0 tale che /t Φ( M) < ε 4 e Φ(M) > ε 4 dove Φ e la funzione di ripartizione della legge Normale standard. Ora, se a >, esiste certamente un intero N tale che n a / < ε M 0
11 per ogni n N. Per la convergenza in distribuzione di (S n) n, esiste poi un intero N > N tale che, per ogni n > N, si abbia P ([ S n n n M]) Φ( M) + ε 4 ε/ e anche P ([ S n n n M]) Φ(M) ε 4 > ε/. Allora, se n > N si ha P ([ S n n n a ] ε]) = P ([ S n n n n a / ε]) P ([ S n n n in quanto n a / ε > M. Ma M]), P ([ S n n n M]) = P ([ S n n n M]) P ([ S n n n < M]) ε, per quanto visto in precedenza. In conclusione, fissato ε > 0, abbiamo trovato un intero N tale che, per ogni intero n > N, risulta P ([ S n n n a ] ε]) ε : questa e esattamente la convergenza in probabilita a 0. Esercizio 3 Essendo e θx dx = θ e θ, il valore di h e θe θ. Allora si ha E(X) = θe θ xe θx dx = + θ. Per quanto riguarda la stima di massima verosimiglianza, assumendo un campione casuale X,..., X n, si ha log(l(θ; x,..., x n )) = n θ + n S n, ove S n = x +... x n. Studiando la derivata rispetto a θ, si ottiene che tale funzione si massimizza quando θ = n, ossia se = x S n n θ n.
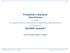
p k q n k = p n (k) = n 12 = 1 = 12 1 12 11 10 9 1 0,1208. q = 1 2 e si ha: p 12 (8) = 12 8 4
 CAPITOLO QUARTO DISTRIBUZIONE BINOMIALE (O DI BERNOULLI) Molti degli esempi che abbiamo presentato nei capitoli precedenti possono essere pensati come casi particolari di uno schema generale di prove ripetute,
CAPITOLO QUARTO DISTRIBUZIONE BINOMIALE (O DI BERNOULLI) Molti degli esempi che abbiamo presentato nei capitoli precedenti possono essere pensati come casi particolari di uno schema generale di prove ripetute,
Statistica Inferenziale
 Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Esercizio 1 (stima puntuale) In un processo di controllo di qualità, siamo interessati al numero mensile di guasti
Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Esercizio 1 (stima puntuale) In un processo di controllo di qualità, siamo interessati al numero mensile di guasti
Corso di Laurea in Ingegneria Informatica e Automatica (A-O) Università di Roma La Sapienza
 Corso di Laurea in Ingegneria Informatica e Automatica (A-O) Università di Roma La Sapienza CALCOLO DELLE PROBABILITÀ E STATISTICA ESAME DEL 28/05/2015 NOME: COGNOME: MATRICOLA: Esercizio 1 Nel gico del
Corso di Laurea in Ingegneria Informatica e Automatica (A-O) Università di Roma La Sapienza CALCOLO DELLE PROBABILITÀ E STATISTICA ESAME DEL 28/05/2015 NOME: COGNOME: MATRICOLA: Esercizio 1 Nel gico del
1) Si consideri un esperimento che consiste nel lancio di 5 dadi. Lo spazio campionario:
 Esempi di domande risposta multipla (Modulo II) 1) Si consideri un esperimento che consiste nel lancio di 5 dadi. Lo spazio campionario: 1) ha un numero di elementi pari a 5; 2) ha un numero di elementi
Esempi di domande risposta multipla (Modulo II) 1) Si consideri un esperimento che consiste nel lancio di 5 dadi. Lo spazio campionario: 1) ha un numero di elementi pari a 5; 2) ha un numero di elementi
Esercitazione # 6. a) Fissato il livello di significatività al 5% si tragga una conclusione circa l opportunità di avviare la campagna comparativa.
 Statistica Matematica A Esercitazione # 6 DUE MEDIE CON VARIANZE NOTE: Esercizio # Le ditte A e B producono sfere luminose. Una volta attivata la reazione chimica che rende luminosa una di queste sfere,
Statistica Matematica A Esercitazione # 6 DUE MEDIE CON VARIANZE NOTE: Esercizio # Le ditte A e B producono sfere luminose. Una volta attivata la reazione chimica che rende luminosa una di queste sfere,
CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 6
 CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 6 Dott.ssa Antonella Costanzo a.costanzo@unicas.it Esercizio 1. Stima puntuale per la proporzione Da un lotto di arance se ne estraggono 400, e di queste 180
CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 6 Dott.ssa Antonella Costanzo a.costanzo@unicas.it Esercizio 1. Stima puntuale per la proporzione Da un lotto di arance se ne estraggono 400, e di queste 180
Elementi di Calcolo delle Probabilità e Statistica per il corso di Analisi Matematica B
 Elementi di Calcolo delle Probabilità e Statistica per il corso di Analisi Matematica B Laurea in Ingegneria Meccatronica A.A. 2010 2011 n-dimensionali Riepilogo. Gli esiti di un esperimento aleatorio
Elementi di Calcolo delle Probabilità e Statistica per il corso di Analisi Matematica B Laurea in Ingegneria Meccatronica A.A. 2010 2011 n-dimensionali Riepilogo. Gli esiti di un esperimento aleatorio
Esercizi del Corso di Statistica. Parte I - Variabili Aleatorie Continue
 Esercizi del Corso di Statistica Parte I - Variabili Aleatorie Continue 1. Costruire la variabile uniforme U sull intervallo [a, b], con a IR e b IR. 2. Sia X una variabile aleatoria tale che: 0 x < 1
Esercizi del Corso di Statistica Parte I - Variabili Aleatorie Continue 1. Costruire la variabile uniforme U sull intervallo [a, b], con a IR e b IR. 2. Sia X una variabile aleatoria tale che: 0 x < 1
Probabilità e Statistica Esercitazioni. a.a. 2006/2007
 Probabilità e Statistica Esercitazioni a.a. 2006/2007 C.d.L.: Ingegneria per l Ambiente ed il Territorio, Ingegneria Civile, Ingegneria Gestionale, Ingegneria dell Informazione C.d.L.S.: Ingegneria Civile
Probabilità e Statistica Esercitazioni a.a. 2006/2007 C.d.L.: Ingegneria per l Ambiente ed il Territorio, Ingegneria Civile, Ingegneria Gestionale, Ingegneria dell Informazione C.d.L.S.: Ingegneria Civile
A = { escono 2 teste e due croci (indipendentemente dall ordine) } B = { al primo tiro esce testa }.
 ESERCIZI ELEMENTARI DI CALCOLO DELLE PROBABILITÀ Teorema della somma 1) Giocando alla roulette, calcolare la probabilità che su una estrazione esca: a) Un numero compreso tra 6 e 12 (compresi) oppure maggiore
ESERCIZI ELEMENTARI DI CALCOLO DELLE PROBABILITÀ Teorema della somma 1) Giocando alla roulette, calcolare la probabilità che su una estrazione esca: a) Un numero compreso tra 6 e 12 (compresi) oppure maggiore
Massimi e minimi vincolati in R 2 - Esercizi svolti
 Massimi e minimi vincolati in R 2 - Esercizi svolti Esercizio 1. Determinare i massimi e minimi assoluti della funzione f(x, y) = 2x + 3y vincolati alla curva di equazione x 4 + y 4 = 1. Esercizio 2. Determinare
Massimi e minimi vincolati in R 2 - Esercizi svolti Esercizio 1. Determinare i massimi e minimi assoluti della funzione f(x, y) = 2x + 3y vincolati alla curva di equazione x 4 + y 4 = 1. Esercizio 2. Determinare
1. Richiami di Statistica. Stefano Di Colli
 1. Richiami di Statistica Metodi Statistici per il Credito e la Finanza Stefano Di Colli Dati: Fonti e Tipi I dati sperimentali sono provenienti da un contesto delimitato, definito per rispettare le caratteristiche
1. Richiami di Statistica Metodi Statistici per il Credito e la Finanza Stefano Di Colli Dati: Fonti e Tipi I dati sperimentali sono provenienti da un contesto delimitato, definito per rispettare le caratteristiche
Carta di credito standard. Carta di credito business. Esercitazione 12 maggio 2016
 Esercitazione 12 maggio 2016 ESERCIZIO 1 Si supponga che in un sondaggio di opinione su un campione di clienti, che utilizzano una carta di credito di tipo standard (Std) o di tipo business (Bsn), si siano
Esercitazione 12 maggio 2016 ESERCIZIO 1 Si supponga che in un sondaggio di opinione su un campione di clienti, che utilizzano una carta di credito di tipo standard (Std) o di tipo business (Bsn), si siano
1. Distribuzioni campionarie
 Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
VARIABILI ALEATORIE CONTINUE
 VARIABILI ALEATORIE CONTINUE Se X è una variabile aleatoria continua, la probabilità che X assuma un certo valore x fissato è in generale zero, quindi non ha senso definire una distribuzione di probabilità
VARIABILI ALEATORIE CONTINUE Se X è una variabile aleatoria continua, la probabilità che X assuma un certo valore x fissato è in generale zero, quindi non ha senso definire una distribuzione di probabilità
Facoltà di Economia Corso di laurea in Economia Aziendale Statistica Esercitazione 1 - Modulo II
 Statistica Esercitazione 1 - Modulo II Esercizio A. Da un mazzo di carte napoletane (composto da 40 carte di cui 28 valori e 12 figure, suddivise in quattro semi di cui due neri e due rossi), vengono estratte
Statistica Esercitazione 1 - Modulo II Esercizio A. Da un mazzo di carte napoletane (composto da 40 carte di cui 28 valori e 12 figure, suddivise in quattro semi di cui due neri e due rossi), vengono estratte
Gli eventi sono stati definiti come i possibili risultati di un esperimento. Ogni evento ha una probabilità
 Probabilità Probabilità Gli eventi sono stati definiti come i possibili risultati di un esperimento. Ogni evento ha una probabilità Se tutti gli eventi fossero ugualmente possibili, la probabilità p(e)
Probabilità Probabilità Gli eventi sono stati definiti come i possibili risultati di un esperimento. Ogni evento ha una probabilità Se tutti gli eventi fossero ugualmente possibili, la probabilità p(e)
Esercizi di Calcolo delle Probabilità e Statistica Matematica
 Esercizi di Calcolo delle Probabilità e Statistica Matematica Lucio Demeio Dipartimento di Ingegneria Industriale e Scienze Matematiche Università Politecnica delle Marche 1. Esercizio (1 marzo 211 n.
Esercizi di Calcolo delle Probabilità e Statistica Matematica Lucio Demeio Dipartimento di Ingegneria Industriale e Scienze Matematiche Università Politecnica delle Marche 1. Esercizio (1 marzo 211 n.
1. Calcolo combinatorio, problemi di conteggio.
 1 1. Calcolo combinatorio, problemi di conteggio. 1. In quanti modi diversi 4 persone possono occupare 8 posti a sedere numerati? (D 8,4. Un allenatore dispone di 18 giocatori per scegliere la formazione
1 1. Calcolo combinatorio, problemi di conteggio. 1. In quanti modi diversi 4 persone possono occupare 8 posti a sedere numerati? (D 8,4. Un allenatore dispone di 18 giocatori per scegliere la formazione
Esercitazioni di statistica
 Esercitazioni di statistica Misure di associazione: Indipendenza assoluta e in media Stefania Spina Universitá di Napoli Federico II stefania.spina@unina.it 22 ottobre 2014 Stefania Spina Esercitazioni
Esercitazioni di statistica Misure di associazione: Indipendenza assoluta e in media Stefania Spina Universitá di Napoli Federico II stefania.spina@unina.it 22 ottobre 2014 Stefania Spina Esercitazioni
Matematica II: Calcolo delle Probabilità e Statistica Matematica
 Matematica II: Calcolo delle Probabilità e Statistica Matematica ELT A-Z Docente: dott. F. Zucca Esercitazione # Esercizi Statistica Descrittiva Esercizio I gruppi sanguigni di persone sono B, B, AB, O,
Matematica II: Calcolo delle Probabilità e Statistica Matematica ELT A-Z Docente: dott. F. Zucca Esercitazione # Esercizi Statistica Descrittiva Esercizio I gruppi sanguigni di persone sono B, B, AB, O,
1a) Calcolare gli estremi dell intervallo di confidenza per µ al 90% in corrispondenza del campione osservato.
 Esercizio 1 Sia X 1,..., X un campione casuale estratto da una variabile aleatoria normale con media pari a µ e varianza pari a 1. Supponiamo che la media campionaria sia x = 2. 1a) Calcolare gli estremi
Esercizio 1 Sia X 1,..., X un campione casuale estratto da una variabile aleatoria normale con media pari a µ e varianza pari a 1. Supponiamo che la media campionaria sia x = 2. 1a) Calcolare gli estremi
a) Osserviamo innanzi tutto che dev essere x > 0. Pertanto il dominio è ]0, + [. b) Poniamo t = log x. Innanzi tutto si ha:
![a) Osserviamo innanzi tutto che dev essere x > 0. Pertanto il dominio è ]0, + [. b) Poniamo t = log x. Innanzi tutto si ha: a) Osserviamo innanzi tutto che dev essere x > 0. Pertanto il dominio è ]0, + [. b) Poniamo t = log x. Innanzi tutto si ha:](/thumbs/28/12902483.jpg) ESERCIZIO - Data la funzione f (x) = (log x) 6 7(log x) 5 + 2(log x) 4, si chiede di: a) calcolare il dominio di f ; ( punto) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire
ESERCIZIO - Data la funzione f (x) = (log x) 6 7(log x) 5 + 2(log x) 4, si chiede di: a) calcolare il dominio di f ; ( punto) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire
Istituzioni di Statistica e Statistica Economica
 Istituzioni di Statistica e Statistica Economica Università degli Studi di Perugia Facoltà di Economia, Assisi, a.a. 2013/14 Esercitazione n. 3 A. Sia una variabile casuale che si distribuisce secondo
Istituzioni di Statistica e Statistica Economica Università degli Studi di Perugia Facoltà di Economia, Assisi, a.a. 2013/14 Esercitazione n. 3 A. Sia una variabile casuale che si distribuisce secondo
E NECESSARIO RICORRERE ALLE VARIABILI CASUALI
 IL CONCETTO DI VARIABILE CASUALE Associare una misura di probabilità al verificarsi di un certo evento (come esito di un esperimento) non sempre è sufficiente a risolvere gran parte dei problemi reali
IL CONCETTO DI VARIABILE CASUALE Associare una misura di probabilità al verificarsi di un certo evento (come esito di un esperimento) non sempre è sufficiente a risolvere gran parte dei problemi reali
MISURA DELLA DISTANZA FOCALE DI UNA LENTE CONVERGENTE
 MISURA DELLA DISTANZA FOCALE DI UNA LENTE CONVERGENTE La distanza focale f di una lente convergente sottile è data dalla formula: da cui 1 f = 1 p + 1 q f = pq p + q dove p e q sono, rispettivamente, le
MISURA DELLA DISTANZA FOCALE DI UNA LENTE CONVERGENTE La distanza focale f di una lente convergente sottile è data dalla formula: da cui 1 f = 1 p + 1 q f = pq p + q dove p e q sono, rispettivamente, le
 Stima per intervalli Nei metodi di stima puntuale è sempre presente un ^ errore θ θ dovuto al fatto che la stima di θ in genere non coincide con il parametro θ. Sorge quindi l esigenza di determinare una
Stima per intervalli Nei metodi di stima puntuale è sempre presente un ^ errore θ θ dovuto al fatto che la stima di θ in genere non coincide con il parametro θ. Sorge quindi l esigenza di determinare una
SESSIONE ORDINARIA 2007 CORSO DI ORDINAMENTO SCUOLE ITALIANE ALL ESTERO - AMERICHE
 SESSIONE ORDINARIA 007 CORSO DI ORDINAMENTO SCUOLE ITALIANE ALL ESTERO - AMERICHE PROBLEMA Si consideri la funzione f definita da f ( x) x, il cui grafico è la parabola.. Si trovi il luogo geometrico dei
SESSIONE ORDINARIA 007 CORSO DI ORDINAMENTO SCUOLE ITALIANE ALL ESTERO - AMERICHE PROBLEMA Si consideri la funzione f definita da f ( x) x, il cui grafico è la parabola.. Si trovi il luogo geometrico dei
CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA. Esercizi su eventi, previsioni e probabilità condizionate
 CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi su eventi, previsioni e probabilità condizionate Nota: Alcuni esercizi sono tradotti, più o meno fedelmente, dal libro A first course in probability
CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi su eventi, previsioni e probabilità condizionate Nota: Alcuni esercizi sono tradotti, più o meno fedelmente, dal libro A first course in probability
Università degli Studi di Milano Bicocca CdS ECOAMM Corso di Metodi Statistici per l Amministrazione delle Imprese CARTE DI CONTROLLO PER VARIABILI
 Università degli Studi di Milano Bicocca CdS ECOAMM Corso di Metodi Statistici per l Amministrazione delle Imprese CARTE DI CONTROLLO PER VARIABILI 1. L azienda Wood produce legno compensato per costruzioni
Università degli Studi di Milano Bicocca CdS ECOAMM Corso di Metodi Statistici per l Amministrazione delle Imprese CARTE DI CONTROLLO PER VARIABILI 1. L azienda Wood produce legno compensato per costruzioni
2. Variabilità mediante il confronto di valori caratteristici della
 2. Variabilità mediante il confronto di valori caratteristici della distribuzione Un approccio alternativo, e spesso utile, alla misura della variabilità è quello basato sul confronto di valori caratteristici
2. Variabilità mediante il confronto di valori caratteristici della distribuzione Un approccio alternativo, e spesso utile, alla misura della variabilità è quello basato sul confronto di valori caratteristici
La variabile casuale Binomiale
 La variabile casuale Binomiale Si costruisce a partire dalla nozione di esperimento casuale Bernoulliano che consiste in un insieme di prove ripetute con le seguenti caratteristiche: i) ad ogni singola
La variabile casuale Binomiale Si costruisce a partire dalla nozione di esperimento casuale Bernoulliano che consiste in un insieme di prove ripetute con le seguenti caratteristiche: i) ad ogni singola
Il prodotto di tre numeri in progressione aritmetica è 16640, il più piccolo è 20. Calcolare i tre numeri.
 Scrivi i primi termini delle seguenti successioni: =1; =; = + Individua la legge che genera ognuna delle seguenti successioni: -1,, -, 4, -5, In una progressione aritmetica la somma del primo, quarto,
Scrivi i primi termini delle seguenti successioni: =1; =; = + Individua la legge che genera ognuna delle seguenti successioni: -1,, -, 4, -5, In una progressione aritmetica la somma del primo, quarto,
Controllo Statistico della Qualità. Qualità come primo obiettivo dell azienda produttrice di beni
 Controllo Statistico della Qualità Qualità come primo obiettivo dell azienda produttrice di beni Qualità come costante aderenza del prodotto alle specifiche tecniche Qualità come controllo e riduzione
Controllo Statistico della Qualità Qualità come primo obiettivo dell azienda produttrice di beni Qualità come costante aderenza del prodotto alle specifiche tecniche Qualità come controllo e riduzione
1 Valore atteso o media
 1 Valore atteso o media Definizione 1.1. Sia X una v.a., si chiama valore atteso (o media o speranza matematica) il numero, che indicheremo con E[X] o con µ X, definito come E[X] = i x i f(x i ) se X è
1 Valore atteso o media Definizione 1.1. Sia X una v.a., si chiama valore atteso (o media o speranza matematica) il numero, che indicheremo con E[X] o con µ X, definito come E[X] = i x i f(x i ) se X è
Ancora sull indipendenza. Se A e B sono indipendenti allora lo sono anche
 Ancora sull indipendenza Se A e B sono indipendenti allora lo sono anche A e B Ā e B Ā e B Sfruttiamo le leggi di De Morgan Leggi di De Morgan A B = Ā B A B = Ā B P (Ā B) = P (A B) = 1 P (A B) = 1 (P (A)
Ancora sull indipendenza Se A e B sono indipendenti allora lo sono anche A e B Ā e B Ā e B Sfruttiamo le leggi di De Morgan Leggi di De Morgan A B = Ā B A B = Ā B P (Ā B) = P (A B) = 1 P (A B) = 1 (P (A)
Integrali doppi - Esercizi svolti
 Integrali doppi - Esercizi svolti Integrali doppi senza cambiamento di variabili Si disegni il dominio e quindi si calcolino gli integrali multipli seguenti:... xy dx dy, con (x, y R x, y x x }; x + y
Integrali doppi - Esercizi svolti Integrali doppi senza cambiamento di variabili Si disegni il dominio e quindi si calcolino gli integrali multipli seguenti:... xy dx dy, con (x, y R x, y x x }; x + y
ESAME DI STATISTICA Nome: Cognome: Matricola:
 ESAME DI STATISTICA Nome: Cognome: Matricola: ISTRUZIONI: Per la prova è consentito esclusivamente l uso di una calcolatrice tascabile, delle tavole della normale e della t di Student. I risultati degli
ESAME DI STATISTICA Nome: Cognome: Matricola: ISTRUZIONI: Per la prova è consentito esclusivamente l uso di una calcolatrice tascabile, delle tavole della normale e della t di Student. I risultati degli
Esercizi di Matematica Finanziaria
 Università degli Studi di Siena Facoltà di Economia Esercizi di Matematica Finanziaria relativi ai capitoli V-X del testo Claudio Pacati a.a. 1998 99 c Claudio Pacati tutti i diritti riservati. Il presente
Università degli Studi di Siena Facoltà di Economia Esercizi di Matematica Finanziaria relativi ai capitoli V-X del testo Claudio Pacati a.a. 1998 99 c Claudio Pacati tutti i diritti riservati. Il presente
Appunti sul corso di Complementi di Matematica- modulo Analisi Prof. B.Bacchelli
 Appunti sul corso di Complementi di Matematica- modulo Analisi Prof. B.Bacchelli 09- Integrale doppio: Riferimenti: R.Adams, Calcolo ifferenziale 2. Capitoli 5.1, 5.2, 5.4. Esercizi 5.3, 5.4 Integrale
Appunti sul corso di Complementi di Matematica- modulo Analisi Prof. B.Bacchelli 09- Integrale doppio: Riferimenti: R.Adams, Calcolo ifferenziale 2. Capitoli 5.1, 5.2, 5.4. Esercizi 5.3, 5.4 Integrale
INDICAZIONI PER LA RICERCA DEGLI ASINTOTI VERTICALI
 2.13 ASINTOTI 44 Un "asintoto", per una funzione y = f( ), è una retta alla quale il grafico della funzione "si avvicina indefinitamente", "si avvicina di tanto quanto noi vogliamo", nel senso precisato
2.13 ASINTOTI 44 Un "asintoto", per una funzione y = f( ), è una retta alla quale il grafico della funzione "si avvicina indefinitamente", "si avvicina di tanto quanto noi vogliamo", nel senso precisato
FUNZIONI CONTINUE - ESERCIZI SVOLTI
 FUNZIONI CONTINUE - ESERCIZI SVOLTI 1) Verificare che x è continua in x 0 per ogni x 0 0 ) Verificare che 1 x 1 x 0 è continua in x 0 per ogni x 0 0 3) Disegnare il grafico e studiare i punti di discontinuità
FUNZIONI CONTINUE - ESERCIZI SVOLTI 1) Verificare che x è continua in x 0 per ogni x 0 0 ) Verificare che 1 x 1 x 0 è continua in x 0 per ogni x 0 0 3) Disegnare il grafico e studiare i punti di discontinuità
Esercizi di Calcolo delle Probabilità con Elementi di Statistica Matematica
 Esercizi di Calcolo delle Probabilità con Elementi di Statistica Matematica Lucio Demeio Dipartimento di Scienze Matematiche Università Politecnica delle Marche 1. Esercizio. Siano X ed Y due variabili
Esercizi di Calcolo delle Probabilità con Elementi di Statistica Matematica Lucio Demeio Dipartimento di Scienze Matematiche Università Politecnica delle Marche 1. Esercizio. Siano X ed Y due variabili
Esercizi di probabilità discreta
 Di seguito, potete trovare i testi (con risposta) degli esercizi svolti (o proposti) nel corso di esercitazioni dell insegnamento di Matematica applicata. 1 Esercizi di probabilità discreta Algebra degli
Di seguito, potete trovare i testi (con risposta) degli esercizi svolti (o proposti) nel corso di esercitazioni dell insegnamento di Matematica applicata. 1 Esercizi di probabilità discreta Algebra degli
MATEMATICA GENERALE Prova d esame del 4 giugno 2013 - FILA A
 MATEMATICA GENERALE Prova d esame del 4 giugno 2013 - FILA A Nome e cognome Matricola I Parte OBBLIGATORIA (quesiti preliminari: 1 punto ciascuno). Riportare le soluzioni su questo foglio, mostrando i
MATEMATICA GENERALE Prova d esame del 4 giugno 2013 - FILA A Nome e cognome Matricola I Parte OBBLIGATORIA (quesiti preliminari: 1 punto ciascuno). Riportare le soluzioni su questo foglio, mostrando i
Studio di funzione. Tutti i diritti sono riservati. E vietata la riproduzione, anche parziale, senza il consenso dell autore. Funzioni elementari 2
 Studio di funzione Copyright c 2009 Pasquale Terrecuso Tutti i diritti sono riservati. E vietata la riproduzione, anche parziale, senza il consenso dell autore. Funzioni elementari 2 Studio di funzione
Studio di funzione Copyright c 2009 Pasquale Terrecuso Tutti i diritti sono riservati. E vietata la riproduzione, anche parziale, senza il consenso dell autore. Funzioni elementari 2 Studio di funzione
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2002 Sessione suppletiva
 ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. Sessione suppletiva Il candidato risolva uno dei due problemi e dei quesiti in cui si articola il questionario. PROBLEMA Nel piano riferito
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. Sessione suppletiva Il candidato risolva uno dei due problemi e dei quesiti in cui si articola il questionario. PROBLEMA Nel piano riferito
Corso di Laurea in Ingegneria Informatica e Automatica (A-O) Università di Roma La Sapienza
 Corso di Laurea in Ingegneria Informatica e Automatica (A-O) Università di Roma La Sapienza CALCOLO DELLE PROBABILITÀ E STATISTICA ESAME DEL 17/2/215 NOME: COGNOME: MATRICOLA: Esercizio 1 Un sistema di
Corso di Laurea in Ingegneria Informatica e Automatica (A-O) Università di Roma La Sapienza CALCOLO DELLE PROBABILITÀ E STATISTICA ESAME DEL 17/2/215 NOME: COGNOME: MATRICOLA: Esercizio 1 Un sistema di
Corso di Laurea in Ingegneria Informatica Anno Accademico 2014/2015 Calcolo delle Probabilità e Statistica Matematica
 Corso di Laurea in Ingegneria Informatica Anno Accademico 2014/2015 Calcolo delle Probabilità e Statistica Matematica Nome N. Matricola Ancona, 14 luglio 2015 1. Tre macchine producono gli stessi pezzi
Corso di Laurea in Ingegneria Informatica Anno Accademico 2014/2015 Calcolo delle Probabilità e Statistica Matematica Nome N. Matricola Ancona, 14 luglio 2015 1. Tre macchine producono gli stessi pezzi
Federico Lastaria. Analisi e Geometria 2. Integrali multipli. Cambi di variabili. 1/21
 Contenuto Integrali doppi. Teorema di Fubini Cambio di variabili: coordinate polari. Cambio di variabili: caso generale. Coordinate sferiche. Federico Lastaria. Analisi e Geometria 2. Integrali multipli.
Contenuto Integrali doppi. Teorema di Fubini Cambio di variabili: coordinate polari. Cambio di variabili: caso generale. Coordinate sferiche. Federico Lastaria. Analisi e Geometria 2. Integrali multipli.
STATISTICA INFERENZIALE
 STATISTICA INFERENZIALE Premessa importante: si ipotizza che il comportamento della popolazione rispetto ad una variabile casuale X viene descritto attraverso una funzione parametrica di probabilità p
STATISTICA INFERENZIALE Premessa importante: si ipotizza che il comportamento della popolazione rispetto ad una variabile casuale X viene descritto attraverso una funzione parametrica di probabilità p
La Funzione Caratteristica di una Variabile Aleatoria
 La Funzione Caratteristica di una Variabile Aleatoria La funzione caratteristica Φ densità di probabilità è f + Φ ω = ω di una v.a., la cui x, è definita come: jωx f x e dx E e j ω Φ ω = 1 La Funzione
La Funzione Caratteristica di una Variabile Aleatoria La funzione caratteristica Φ densità di probabilità è f + Φ ω = ω di una v.a., la cui x, è definita come: jωx f x e dx E e j ω Φ ω = 1 La Funzione
Corso di Analisi Matematica. Successioni e serie numeriche
 a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
Esercitazioni 2013/14
 Esercitazioni 2013/14 Esercizio 1 Due ditte V e W partecipano ad una gara di appalto per la costruzione di un tratto di autostrada che viene assegnato a seconda del prezzo. L offerta fatta dalla ditta
Esercitazioni 2013/14 Esercizio 1 Due ditte V e W partecipano ad una gara di appalto per la costruzione di un tratto di autostrada che viene assegnato a seconda del prezzo. L offerta fatta dalla ditta
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
x log(x) + 3. f(x) =
 Università di Bari, Corso di Laurea in Economia e Commercio Esame di Matematica per l Economia L/Z Dr. G. Taglialatela 03 giugno 05 Traccia dispari Esercizio. Calcolare Esercizio. Calcolare e cos log d
Università di Bari, Corso di Laurea in Economia e Commercio Esame di Matematica per l Economia L/Z Dr. G. Taglialatela 03 giugno 05 Traccia dispari Esercizio. Calcolare Esercizio. Calcolare e cos log d
EQUAZIONI DIFFERENZIALI Esercizi svolti. y = xy. y(2) = 1.
 EQUAZIONI DIFFERENZIALI Esercizi svolti 1. Determinare la soluzione dell equazione differenziale (x 2 + 1)y + y 2 =. y + x tan y = 2. Risolvere il problema di Cauchy y() = 1 2 π. 3. Risolvere il problema
EQUAZIONI DIFFERENZIALI Esercizi svolti 1. Determinare la soluzione dell equazione differenziale (x 2 + 1)y + y 2 =. y + x tan y = 2. Risolvere il problema di Cauchy y() = 1 2 π. 3. Risolvere il problema
Temi di Esame a.a. 2012-2013. Statistica - CLEF
 Temi di Esame a.a. 2012-2013 Statistica - CLEF I Prova Parziale di Statistica (CLEF) 11 aprile 2013 Esercizio 1 Un computer è collegato a due stampanti, A e B. La stampante A è difettosa ed il 25% dei
Temi di Esame a.a. 2012-2013 Statistica - CLEF I Prova Parziale di Statistica (CLEF) 11 aprile 2013 Esercizio 1 Un computer è collegato a due stampanti, A e B. La stampante A è difettosa ed il 25% dei
Politecnico di Milano - Scuola di Ingegneria Industriale. I Prova in Itinere di Statistica per Ingegneria Energetica 9 maggio 2013
 Politecnico di Milano - Scuola di Ineneria Industriale I Prova in Itinere di Statistica per Ineneria Eneretica 9 maio 013 c I diritti d autore sono riservati. Oni sfruttamento commerciale non autorizzato
Politecnico di Milano - Scuola di Ineneria Industriale I Prova in Itinere di Statistica per Ineneria Eneretica 9 maio 013 c I diritti d autore sono riservati. Oni sfruttamento commerciale non autorizzato
La funzione è continua nel suo dominio perchè y = f(x) è composizione di funzioni continue. Il punto x = 0 è un punto isolato per D f.
 FUNZIONI CONTINUE - ALCUNI ESERCIZI SVOLTI SIMONE ALGHISI 1. Continuità di una funzione Dati un insieme D R, una funzione f : D R e x 0 R, si è detto che f è continua in x 0 se sono soddisfatte le seguenti
FUNZIONI CONTINUE - ALCUNI ESERCIZI SVOLTI SIMONE ALGHISI 1. Continuità di una funzione Dati un insieme D R, una funzione f : D R e x 0 R, si è detto che f è continua in x 0 se sono soddisfatte le seguenti
UNIVERSITA DEGLI STUDI DI PADOVA DIPARTIMENTO DI INGEGNERIA IDRAULICA, MARITTIMA E GEOTECNICA
 UNIVERSITA DEGLI STUDI DI PADOVA DIPARTIMENTO DI INGEGNERIA IDRAULICA, MARITTIMA E GEOTECNICA CORSO DI COSTRUZIONI IDRAULICHE A.A. 00-0 PROF. LUIGI DA DEPPO ING. NADIA URSINO ESERCITAZIONE N : Progetto
UNIVERSITA DEGLI STUDI DI PADOVA DIPARTIMENTO DI INGEGNERIA IDRAULICA, MARITTIMA E GEOTECNICA CORSO DI COSTRUZIONI IDRAULICHE A.A. 00-0 PROF. LUIGI DA DEPPO ING. NADIA URSINO ESERCITAZIONE N : Progetto
Il Metodo Scientifico
 Unita Naturali Il Metodo Scientifico La Fisica si occupa di descrivere ed interpretare i fenomeni naturali usando il metodo scientifico. Passi del metodo scientifico: Schematizzazione: modello semplificato
Unita Naturali Il Metodo Scientifico La Fisica si occupa di descrivere ed interpretare i fenomeni naturali usando il metodo scientifico. Passi del metodo scientifico: Schematizzazione: modello semplificato
Appunti: elementi di Probabilità
 Università di Udine, Facoltà di Scienze della Formazione Corso di Laurea in Scienze e Tecnologie Multimediali Corso di Matematica e Statistica (Giorgio T. Bagni) Appunti: elementi di Probabilità. LA PROBABILITÀ..
Università di Udine, Facoltà di Scienze della Formazione Corso di Laurea in Scienze e Tecnologie Multimediali Corso di Matematica e Statistica (Giorgio T. Bagni) Appunti: elementi di Probabilità. LA PROBABILITÀ..
Valori caratteristici di distribuzioni
 Capitolo 3 Valori caratteristici di distribuzioni 3. Valori attesi di variabili e vettori aleatori In molti casi è possibile descrivere adeguatamente una distribuzione di probabilità con pochi valori di
Capitolo 3 Valori caratteristici di distribuzioni 3. Valori attesi di variabili e vettori aleatori In molti casi è possibile descrivere adeguatamente una distribuzione di probabilità con pochi valori di
I appello - 24 Marzo 2006
 Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
Statistica Matematica A - Ing. Meccanica, Aerospaziale I prova in itinere - 19 novembre 2004
 Statistica Matematica A - Ing. Meccanica, Aerospaziale I prova in itinere - 19 novembre 200 Esercizio 1 Tre apparecchiature M 1, M 2 e M 3 in un anno si guastano, in maniera indipendente, con probabilità
Statistica Matematica A - Ing. Meccanica, Aerospaziale I prova in itinere - 19 novembre 200 Esercizio 1 Tre apparecchiature M 1, M 2 e M 3 in un anno si guastano, in maniera indipendente, con probabilità
Corso di Laurea in Ingegneria Informatica e Automatica (A-O) Università di Roma La Sapienza
 Corso di Laurea in Ingegneria Informatica e Automatica (A-O) Università di Roma La Sapienza CALCOLO DELLE PROBABILITÀ E STATISTICA ESAME DEL 17/06/2015 NOME: COGNOME: MATRICOLA: Esercizio 1 Un sistema
Corso di Laurea in Ingegneria Informatica e Automatica (A-O) Università di Roma La Sapienza CALCOLO DELLE PROBABILITÀ E STATISTICA ESAME DEL 17/06/2015 NOME: COGNOME: MATRICOLA: Esercizio 1 Un sistema
PROBABILITÀ - SCHEDA N. 2 LE VARIABILI ALEATORIE
 Matematica e statistica: dai dati ai modelli alle scelte www.dima.unige/pls_statistica Responsabili scientifici M.P. Rogantin e E. Sasso (Dipartimento di Matematica Università di Genova) PROBABILITÀ -
Matematica e statistica: dai dati ai modelli alle scelte www.dima.unige/pls_statistica Responsabili scientifici M.P. Rogantin e E. Sasso (Dipartimento di Matematica Università di Genova) PROBABILITÀ -
Facciamo qualche precisazione
 Abbiamo introdotto alcuni indici statistici (di posizione, di variabilità e di forma) ottenibili da Excel con la funzione Riepilogo Statistiche Facciamo qualche precisazione Al fine della partecipazione
Abbiamo introdotto alcuni indici statistici (di posizione, di variabilità e di forma) ottenibili da Excel con la funzione Riepilogo Statistiche Facciamo qualche precisazione Al fine della partecipazione
Esercitazione #5 di Statistica. Test ed Intervalli di Confidenza (per una popolazione)
 Esercitazione #5 di Statistica Test ed Intervalli di Confidenza (per una popolazione) Dicembre 00 1 Esercizi 1.1 Test su media (con varianza nota) Esercizio n. 1 Il calore (in calorie per grammo) emesso
Esercitazione #5 di Statistica Test ed Intervalli di Confidenza (per una popolazione) Dicembre 00 1 Esercizi 1.1 Test su media (con varianza nota) Esercizio n. 1 Il calore (in calorie per grammo) emesso
DALLA POPOLAZIONE AL CAMPIONE: IL CALCOLO DI PROBABILITÁ
 DALLA POPOLAZIONE AL CAMPIONE: IL CALCOLO DI PROBABILITÁ Andrea Onofri Dipartimento di Scienze Agrarie ed Ambientali Universitá degli Studi di Perugia Versione on-line: http://www.unipg.it/ onofri/rtutorial/index.html
DALLA POPOLAZIONE AL CAMPIONE: IL CALCOLO DI PROBABILITÁ Andrea Onofri Dipartimento di Scienze Agrarie ed Ambientali Universitá degli Studi di Perugia Versione on-line: http://www.unipg.it/ onofri/rtutorial/index.html
Corso di Laurea in Ingegneria Informatica Analisi Numerica
 Corso di Laurea in Ingegneria Informatica Lucio Demeio Dipartimento di Scienze Matematiche 1 2 Analisi degli errori Informazioni generali Libro di testo: J. D. Faires, R. Burden, Numerical Analysis, Brooks/Cole,
Corso di Laurea in Ingegneria Informatica Lucio Demeio Dipartimento di Scienze Matematiche 1 2 Analisi degli errori Informazioni generali Libro di testo: J. D. Faires, R. Burden, Numerical Analysis, Brooks/Cole,
0.1 Esercizi calcolo combinatorio
 0.1 Esercizi calcolo combinatorio Esercizio 1. Sia T l insieme dei primi 100 numeri naturali. Calcolare: 1. Il numero di sottoinsiemi A di T che contengono esattamente 8 pari.. Il numero di coppie (A,
0.1 Esercizi calcolo combinatorio Esercizio 1. Sia T l insieme dei primi 100 numeri naturali. Calcolare: 1. Il numero di sottoinsiemi A di T che contengono esattamente 8 pari.. Il numero di coppie (A,
La distribuzione Gaussiana
 Università del Piemonte Orientale Corso di Laurea in Biotecnologie Corso di Statistica Medica La distribuzione Normale (o di Gauss) Corso di laurea in biotecnologie - Corso di Statistica Medica La distribuzione
Università del Piemonte Orientale Corso di Laurea in Biotecnologie Corso di Statistica Medica La distribuzione Normale (o di Gauss) Corso di laurea in biotecnologie - Corso di Statistica Medica La distribuzione
Esercizi riassuntivi di probabilità
 Esercizi riassuntivi di probabilità Esercizio 1 Una ditta produttrice di fotocopiatrici sa che la durata di una macchina (in migliaia di copie) si distribuisce come una normale con µ = 1600 e 2 = 3600.
Esercizi riassuntivi di probabilità Esercizio 1 Una ditta produttrice di fotocopiatrici sa che la durata di una macchina (in migliaia di copie) si distribuisce come una normale con µ = 1600 e 2 = 3600.
Esercizi di Probabilità e Statistica
 Esercizi di Probabilità e Statistica Samuel Rota Bulò 5 maggio 007 Varabili aleatorie continue, distribuzioni continue e funzione generatrice di momenti. Esercizio Dimostrare la mancanza di memoria della
Esercizi di Probabilità e Statistica Samuel Rota Bulò 5 maggio 007 Varabili aleatorie continue, distribuzioni continue e funzione generatrice di momenti. Esercizio Dimostrare la mancanza di memoria della
Inferenza statistica. Inferenza statistica
 Spesso l informazione a disposizione deriva da un osservazione parziale del fenomeno studiato. In questo caso lo studio di un fenomeno mira solitamente a trarre, sulla base di ciò che si è osservato, considerazioni
Spesso l informazione a disposizione deriva da un osservazione parziale del fenomeno studiato. In questo caso lo studio di un fenomeno mira solitamente a trarre, sulla base di ciò che si è osservato, considerazioni
L indagine statistica
 1 L indagine statistica DEFINIZIONE. La statistica è quella disciplina che si occupa della raccolta di dati quantitativi relativi a diversi fenomeni, della loro elaborazione e del loro utilizzo a fini
1 L indagine statistica DEFINIZIONE. La statistica è quella disciplina che si occupa della raccolta di dati quantitativi relativi a diversi fenomeni, della loro elaborazione e del loro utilizzo a fini
Università di Firenze - Corso di laurea in Statistica Seconda prova intermedia di Statistica. 18 dicembre 2008
 Università di Firenze - Corso di laurea in Statistica Seconda prova intermedia di Statistica 18 dicembre 008 Esame sull intero programma: esercizi da A a D Esame sulla seconda parte del programma: esercizi
Università di Firenze - Corso di laurea in Statistica Seconda prova intermedia di Statistica 18 dicembre 008 Esame sull intero programma: esercizi da A a D Esame sulla seconda parte del programma: esercizi
Esercizi sul calcolo delle probabilità
 Esercizi sul calcolo delle probabilità Svolti e da svolgere (per MAR 13 marzo) Dati due eventi A e B dello spazio campionario Ω. Si sappia che P(A c )=0,3 P(B)=0,4 e P(A B c )=0,5 si determinino le probabilità
Esercizi sul calcolo delle probabilità Svolti e da svolgere (per MAR 13 marzo) Dati due eventi A e B dello spazio campionario Ω. Si sappia che P(A c )=0,3 P(B)=0,4 e P(A B c )=0,5 si determinino le probabilità
MINISTERO DELL'ISTRUZIONE, DELL'UNIVERSITÀ, DELLA RICERCA SCUOLE ITALIANE ALL ESTERO
 Sessione Ordinaria in America 4 MINISTERO DELL'ISTRUZIONE, DELL'UNIVERSITÀ, DELLA RICERCA SCUOLE ITALIANE ALL ESTERO (Americhe) ESAMI DI STATO DI LICEO SCIENTIFICO Sessione Ordinaria 4 SECONDA PROVA SCRITTA
Sessione Ordinaria in America 4 MINISTERO DELL'ISTRUZIONE, DELL'UNIVERSITÀ, DELLA RICERCA SCUOLE ITALIANE ALL ESTERO (Americhe) ESAMI DI STATO DI LICEO SCIENTIFICO Sessione Ordinaria 4 SECONDA PROVA SCRITTA
Esercitazione n o 3 per il corso di Ricerca Operativa
 Esercitazione n o 3 per il corso di Ricerca Operativa Ultimo aggiornamento October 17, 2011 Fornitura acqua Una città deve essere rifornita, ogni giorno, con 500 000 litri di acqua. Si richiede che l acqua
Esercitazione n o 3 per il corso di Ricerca Operativa Ultimo aggiornamento October 17, 2011 Fornitura acqua Una città deve essere rifornita, ogni giorno, con 500 000 litri di acqua. Si richiede che l acqua
Teoria delle scorte. Ricerca operativa Met. e mod. per le decisioni (Informatica Matematica) Pierluigi Amodio
 Teoria delle scorte Ricerca operativa Met. e mod. per le decisioni (Informatica Matematica) Pierluigi Amodio Dipartimento di Matematica Università di Bari Teoria delle scorte p.1/26 definizione del problema
Teoria delle scorte Ricerca operativa Met. e mod. per le decisioni (Informatica Matematica) Pierluigi Amodio Dipartimento di Matematica Università di Bari Teoria delle scorte p.1/26 definizione del problema
NUMERI COMPLESSI. Test di autovalutazione
 NUMERI COMPLESSI Test di autovalutazione 1. Se due numeri complessi z 1 e z 2 sono rappresentati nel piano di Gauss da due punti simmetrici rispetto all origine: (a) sono le radici quadrate di uno stesso
NUMERI COMPLESSI Test di autovalutazione 1. Se due numeri complessi z 1 e z 2 sono rappresentati nel piano di Gauss da due punti simmetrici rispetto all origine: (a) sono le radici quadrate di uno stesso
Soluzione del tema d esame di matematica, A.S. 2005/2006
 Soluzione del tema d esame di matematica, A.S. 2005/2006 Niccolò Desenzani Sun-ra J.N. Mosconi 22 giugno 2006 Problema. Indicando con A e B i lati del rettangolo, il perimetro è 2A + 2B = λ mentre l area
Soluzione del tema d esame di matematica, A.S. 2005/2006 Niccolò Desenzani Sun-ra J.N. Mosconi 22 giugno 2006 Problema. Indicando con A e B i lati del rettangolo, il perimetro è 2A + 2B = λ mentre l area
Dall'analisi dei prospetti informativi diffusi dalla Borsa di Paperopoli Gastone ricava le seguenti informazioni sul rendimento dei tre titoli:
 ESERCIZIO 1 Gastone investe i suoi risparmi in tre titoli (A: Paperone & Co; B: Rockerduck & Co; C: Bassotti & Co) quotati sul mercato di Paperopoli. La composizione percentuale del portafoglio di Gastone
ESERCIZIO 1 Gastone investe i suoi risparmi in tre titoli (A: Paperone & Co; B: Rockerduck & Co; C: Bassotti & Co) quotati sul mercato di Paperopoli. La composizione percentuale del portafoglio di Gastone
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
Tutorato di Probabilità e Statistica
 Università Ca Foscari di Venezia Dipartimento di informatica 20 aprile 2006 Variabili aleatorie... Example Giochiamo alla roulette per tre volte 1 milione sull uscita del numero 29. Qual è la probabilità
Università Ca Foscari di Venezia Dipartimento di informatica 20 aprile 2006 Variabili aleatorie... Example Giochiamo alla roulette per tre volte 1 milione sull uscita del numero 29. Qual è la probabilità
Quantificare la variabilità dei processi ecologici
 Scopo ecologia Quantificare la variabilità dei processi ecologici Comprensione dei meccanismi fondamentale per identificare gli effetti del disturbo antropico e per prevenire alterazioni su scala globale
Scopo ecologia Quantificare la variabilità dei processi ecologici Comprensione dei meccanismi fondamentale per identificare gli effetti del disturbo antropico e per prevenire alterazioni su scala globale
Esercizio 1. Svolgimento
 Esercizio 1 Vengono lanciate contemporaneamente 6 monete. Si calcoli: a) la probabilità che si presentino esattamente 2 testa ; b) la probabilità di ottenere almeno 4 testa ; c) la probabilità che l evento
Esercizio 1 Vengono lanciate contemporaneamente 6 monete. Si calcoli: a) la probabilità che si presentino esattamente 2 testa ; b) la probabilità di ottenere almeno 4 testa ; c) la probabilità che l evento
(concetto classico di probabilità)
 Probabilità matematica (concetto classico di probabilità) Teoria ed esempi Introduzione Il calcolo delle probabilità è la parte della matematica che si occupa di prevedere, sulla base di regole e leggi
Probabilità matematica (concetto classico di probabilità) Teoria ed esempi Introduzione Il calcolo delle probabilità è la parte della matematica che si occupa di prevedere, sulla base di regole e leggi
CRITERI DI CONVERGENZA PER LE SERIE. lim a n = 0. (1) s n+1 = s n + a n+1. (2) CRITERI PER LE SERIE A TERMINI NON NEGATIVI
 Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 1
 CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 1 Dott.ssa Antonella Costanzo a.costanzo@unicas.it Esercizio 1. Distribuzione di probabilità, funzione di ripartizione di una v.c. discreta Il tasso di cambio
CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 1 Dott.ssa Antonella Costanzo a.costanzo@unicas.it Esercizio 1. Distribuzione di probabilità, funzione di ripartizione di una v.c. discreta Il tasso di cambio
ELEMENTI DI CALCOLO DELLE PROBABILITA
 Statistica, CLEA p. 1/55 ELEMENTI DI CALCOLO DELLE PROBABILITA Premessa importante: il comportamento della popolazione rispetto una variabile casuale X viene descritto attraverso una funzione parametrica
Statistica, CLEA p. 1/55 ELEMENTI DI CALCOLO DELLE PROBABILITA Premessa importante: il comportamento della popolazione rispetto una variabile casuale X viene descritto attraverso una funzione parametrica
PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA
 Simulazione 01/15 ANNO SCOLASTICO 01/15 PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Il candidato risolva uno dei due problemi Problema 1 Nella
Simulazione 01/15 ANNO SCOLASTICO 01/15 PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Il candidato risolva uno dei due problemi Problema 1 Nella
Esercizi sui Circuiti RC
 Esercizi sui Circuiti RC Problema 1 Due condensatori di capacità C = 6 µf, due resistenze R = 2.2 kω ed una batteria da 12 V sono collegati in serie come in Figura 1a. I condensatori sono inizialmente
Esercizi sui Circuiti RC Problema 1 Due condensatori di capacità C = 6 µf, due resistenze R = 2.2 kω ed una batteria da 12 V sono collegati in serie come in Figura 1a. I condensatori sono inizialmente
SIMULAZIONE TEST ESAME - 1
 SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
Corso di Calcolo delle Probabilità e Statistica. Esercizi su variabili aleatorie discrete
 Corso di Calcolo delle Probabilità e Statistica Esercizi su variabili aleatorie discrete Es.1 Da un urna con 10 pallina bianche e 15 palline nere, si eseguono estrazioni con reimbussolamento fino all estrazione
Corso di Calcolo delle Probabilità e Statistica Esercizi su variabili aleatorie discrete Es.1 Da un urna con 10 pallina bianche e 15 palline nere, si eseguono estrazioni con reimbussolamento fino all estrazione
Metodi Matematici per l Economia A-K Corso di Laurea in Economia - anno acc. 2012/2013 12 febbraio 2013
 Tempo massimo 2 ore. Consegnare solamente la bella copia. Metodi Matematici per l Economia A-K Corso di Laurea in Economia - anno acc. 212/213 12 febbraio 213 1. Disegnare il grafico della funzione: [1
Tempo massimo 2 ore. Consegnare solamente la bella copia. Metodi Matematici per l Economia A-K Corso di Laurea in Economia - anno acc. 212/213 12 febbraio 213 1. Disegnare il grafico della funzione: [1
Determinare estremo superiore ed estremo inferiore dell insieme ( 1) n A = n + 1 : n IN
 Prima prova di verifica in itinere di ANALISI MATEMATICA Gennaio 00 Determinare estremo superiore ed estremo inferiore dell insieme { } ( ) n A = n + : n IN specificando se si tratta rispettivamente di
Prima prova di verifica in itinere di ANALISI MATEMATICA Gennaio 00 Determinare estremo superiore ed estremo inferiore dell insieme { } ( ) n A = n + : n IN specificando se si tratta rispettivamente di
