ATTIVITA EDUCATIVA 2.
|
|
|
- Giovanna Bartolini
- 10 anni fa
- Visualizzazioni
Transcript
1 ATTIVITA EDUCATIVA 2. Calcolo della latitudine del luogo di osservazione dalle immagini del Sole di mezzanotte. Mr. Miguel Ángel Pío Jiménez. Astronomo Instituto de Astrofísica de Canarias, Tenerife. Dr. Miquel Serra- Ricart. Astronomo Instituto de Astrofísica de Canarias, Tenerife. Mr. Juan Carlos Casado. Astrofotografo tierrayestrellas.com, Barcelona. Dr. Lorraine Hanlon. Astronoma University College Dublin, Irland. Dr. Luciano Nicastro. Astronomo Istituto Nazionale di Astrofisica, IASF Bologna. 1 Obiettivi dell attività. In questa attività impareremo a calcolare la latitudine di un osservatore da immagini digitali e la misura in esse dell'altezza del Sole sull'orizzonte. Gli obiettivi di questa attività sono: - Spiegare il fenomeno del sole di mezzanotte. - Applicare una metodologia per il calcolo di un parametro fisico (Latitudine Geografica) da un osservabili (immagini digitali). - Sostenere l'insegnamento e l'apprendimento della matematica e della fisica, applicando le conoscenze di matematica (algebra e trigonometria) e fisica di base (cinematica) per risolvere un problema pratico. - Comprendere e applicare le tecniche di base di analisi di immagine (scala angolare, misurazione della distanza, ecc.). - Lavorare in modo cooperativo come una squadra, valorizzando i contributi individuali ed esprimendo atteggiamenti democratici. 2 Strumentazione. L attività farà uso di immagini digitali ottenute dal Nord Europa durante il transito di Venere del 6 giugno 2012 (vedi sky-live.tv). 3 Il fenomeno Sole di mezzanotte. Il Sole di mezzanotte è un fenomeno naturale che si verifica nella sua pienezza solo a nord del Circolo Polare Artico e a sud del Circolo Polare Antartico. Dal momento che nel sud del mondo non ci sono insediamenti permanenti sufficientemente vicino al polo (tranne le basi antartiche che sono abitate da alcuni scienziati e personale militare), le regioni abitate che possono godere di questo fenomeno sono tutte nell'emisfero settentrionale: Alaska, Canada, Groenlandia, Norvegia, Svezia, Finlandia, Russia e l'estremità settentrionale dell'islanda. A causa dell inclinazione di circa 23 gradi e 27 minuti dell'asse di rotazione terrestre rispetto all'eclittica, a queste latitudini elevate il Sole non tramonta mai durante l'estate. Midnight Sun 1
2 Figura 1: Mosaico creato per simulare una sequenza di foto del Sole di mezzanotte su 24 ore. Il Sole raggiunge la massima altezza a mezzogiorno, e quella minima a mezzanotte. Crediti: Anda Bereczky. Il Sole di mezzanotte rimane sempre visibile sopra l'orizzonte a queste latitudini (vedi Figura 1). La durata di tempo in cui il sole di mezzanotte rimane visibile dipende dalla latitudine. Ad esempio, al Circolo Polare Artico (latitudine 60 gradi) è visibile solo per 20 ore intorno al solstizio d'estate (tra il 22 e il 24 Giugno), mentre ai poli geografici è visibile per 6 mesi. Ai poli nel corso di un anno, l'alba e il tramonto si osservano una sola volta. Al polo, durante i sei mesi di giorno, il Sole si sposta continuamente vicino all'orizzonte, raggiungendo la sua massima altezza nel cielo al solstizio d'estate. A causa della rifrazione (curvatura della luce solare nell attraversare la nostra atmosfera), il Sole di mezzanotte può essere osservato a latitudini leggermente al di sotto del circolo polare, al massimo fino ad un grado al di sotto (a seconda delle condizioni locali). Ad esempio, il Sole di mezzanotte può essere visto in Islanda, sebbene la maggior parte del paese (l'isola di Grimsey è l eccezione) si trovi a sud del Circolo Polare Artico. Nella più settentrionale delle isole britanniche (e in altri luoghi a latitudini simili) il cielo non diventa completamente buio in questo periodo dell'anno. Come detto, la durata del Sole mezzanotte varia, a seconda della latitudine. Per esempio, nel punto più settentrionale del continente europeo, Capo Nord in Norvegia, il Sole di mezzanotte può essere goduto dal 14 Maggio al 29 Luglio. Tuttavia, un po' più a sud, alla latitudine del Circolo Polare Artico, a Rovaniemi, luogo indicato come riferimento del circolo, è osservabile solo dal 12 Giugno al 1 Luglio. Un quarto del territorio della Finlandia si trova a nord del Circolo Polare Artico e nella parte settentrionale del paese il Sole non tramonta per 73 giorni in estate. Nelle isole Svalbard, in Norvegia, la regione abitata più settentrionale d'europa, non c'è tramonto da 19 Aprile al 23 Agosto circa. Agli estremi sono gli stessi poli, dove il Sole rimane visibile per la metà dell'anno. Trascorso questo tempo, il Sole resta sopra l'orizzonte per parecchie ore ogni giorno, e poi tramonta. Le notti quindi diventano progressivamente più a lunghe, fino al momento opposto dell anno, quando il Sole tramonta per mesi portando alla lunga notte polare. Il momento migliore per osservare questo meraviglioso fenomeno, sarà tra circa le 23:00 e le 01:00 dalla Norvegia. Questo è il momento in cui possiamo vedere come il Sole scende verso l'orizzonte, acquisendo il tipico colore arancio di un tramonto convenzionale, ma poi, invece di nascondersi, raggiungerà un punto in cui comincerà a salire di nuovo, trasformando il tramonto in un'alba. Per il resto del "giorno", il Sole non si vede mai alto come siamo abituati a vederlo da altre latitudini durante l'estate. Pertanto, durante questo periodo, appena al di sopra Midnight Sun 2
3 del Circolo Polare Artico, il Sole non è così intenso come ci si aspetterebbe in questo periodo dell'anno Le notti bianche. Nelle regioni settentrionali della Russia e in altri luoghi che si trovano sopra di 60 gradi di latitudine, ma sono a sud del Circolo Polare Artico (o a nord del Circolo Polare Antartico nell'emisfero meridionale) non si verifica il Sole di mezzanotte, ma si verifica il crepuscolo a mezzanotte. Il Sole tramonta, ma non va più di 6 gradi sotto l'orizzonte (che definisce il crepuscolo), le attività giornaliere, così come la lettura, sono possibili senza luce artificiale, a condizione che il cielo non sia nuvoloso. Questo fenomeno naturale è popolarmente conosciuto con il nome Notti Bianche. Figura 2: Fuochi d artificio all inaugurazione del Festival delle Notti Bianche a San Pietroburgo, Russia. La barca a vela con le vele scarlatte è la fregata Standart (costruita da Pietro I di Russia) La notte polare. La notte polare si verifica durante l'inverno, quando il Sole non sorge per un lungo periodo di tempo e le giornate sono nelle tenebre. In luoghi come le isole Svalbard, la notte polare si estende dal 28 Ottobre fino al 14 Febbraio. Nelle regioni all'interno dei circoli polari (latitudini superiori a 66 gradi a nord o sud), il periodo di tempo in cui il Sole è sotto l'orizzonte varia da 20 ore al Circolo Artico e Antartico, a 179 giorni ai poli nord e sud. Tuttavia, tutto questo tempo non è classificato come notte polare, perché potrebbe esserci della luce del sole dovuta alla rifrazione. E' interessante notare che il Sole resta sopra l'orizzonte per 186 giorni (rispetto ai 179 sotto). La differenza è dovuta solo al fatto che anche se il Sole è solo parzialmente sopra l'orizzonte, è considerato giorno. Midnight Sun 3
4 Figura 3: Notte Polare in Nord Europa. Longyerbyen, Svalbard, Norway. 4 Metodologia 4.1. Movimento apparente del Sole sulla Sfera Celeste. La posizione del Sole sembra cambiare durante il corso dell'anno, così che i punti in cui sorge e tramonta cambiano continuamente. In realtà, ovviamente, sono la posizione e l orientamento della Terra rispetto al Sole che cambiano (Figura 4). Tuttavia, adottiamo qui la convenzione che sia il Sole ad essere in movimento. Il 21 Marzo, equinozio di primavera, il Sole sorge a Est e tramonta ad Ovest. Col passare dei giorni, questi punti si spostano verso nord, prima rapidamente, poi lentamente, fino al 21 Giugno quando, al solstizio d'estate, il Sole raggiunge la massima altezza sopra l'orizzonte per le latitudini settentrionali. Alba e tramonto sono nelle loro posizioni più settentrionali. Midnight Sun 4
5 Figura 4: Rappresentazione del giorno e della notte in funzione del periodo dell anno e dell orbita della Terra attorno al Sole. Dal 21 Giugno, alba e tramonto si muovono lentamente alle loro posizioni di equinozio, da est verso ovest, fino al 22/23 Settembre, equinozio autunnale. Continuano poi a muoversi verso sud fino al 22 Dicembre, solstizio d'inverno. Trascorso tale termine, le posizioni di alba e tramonto iniziano la loro migrazione verso nord ancora una volta, ritornando alla posizione dell equinozio di primavera dopo un anno. L'asse terrestre è inclinato di un angolo di 23 27' rispetto alla linea perpendicolare al piano orbitale (Figura 5). La traiettoria del Sole attraverso il cielo e la sua declinazione quindi cambiano nel corso di un anno (Figura 6) in cui la declinazione del Sole è l'angolo tra i raggi del Sole e il piano dell'equatore terrestre. Figure 5: L asse di rotazione della Terra è inclinato di 23 o 27' rispetto al Polo Nord. Crediti: Wikimedia commons. Midnight Sun 5
6 Figura 6: Declinazione del Sole nel corso di un anno ( Prima che il Sole attraversi l'equatore il 21 Marzo, la sua declinazione è negativa (Figura 6), mentre all'equinozio di primavera il 21 Marzo la sua declinazione è zero. L'altezza massima del Sole sopra l'orizzonte è 90 gradi meno la latitudine del luogo dell'osservatore, φ (cioè 90 φ). La lunghezza del giorno è uguale alla lunghezza della notte all'equinozio. Nei giorni successivi, la declinazione del Sole è positiva, e continua ad aumentare fino a raggiungere 23 27' al solstizio d'estate quando è sopra la testa a mezzogiorno al Tropico del Cancro. Nell'emisfero nord questo è il giorno più lungo e la notte più corta dell'anno e il Sole raggiunge la massima altezza sopra l'orizzonte (= 90 φ = 23 27'). Da allora la declinazione del sole comincia a diminuire fino a 0 o nuovamente il 21 Settembre, momento in cui la lunghezza della giornata uguale nuovamente a quella della notte. La declinazione continua a diminuire, ora con valori negativi, fino al solstizio d'inverno, quando è sopra la testa a mezzogiorno al Tropico del Capricorno (21 Dicembre), raggiungendo il valore minimo di declinazione di 23º 27'. La notte più lunga e il giorno più corto si verificano in questo giorno e l'altezza del Sole sull'orizzonte raggiunge il valore minimo per gli osservatori dell'emisfero settentrionale. La Figura 7 illustra le latitudini a cui si ha la massima altezza del Sole in queste date fondamentali dell anno. Figura 7: Latitudini a cui il Sole è alla sua massima declinazione nel corso di un anno ( Midnight Sun 6
7 4.2. Metodo per calcolare la latitudine. Abbiamo visto nella Sezione 4.1 che la quota massima del Sole dipende non solo dalla latitudine dell'osservatore, ma anche dal periodo dell'anno, dal momento che la declinazione del Sole varia da 23.5 al solstizio d'inverno, a 23.5 al solstizio d'estate, ed è zero agli equinozi. Per calcolare l'altezza del Sole a mezzanotte, in un certo luogo sulla Terra, si usa la seguente espressione: h s = δ s (90 ϕ), dove h s è l altezza del Sole sopra l orizzonte a mezzanotte, φ è la latitudine dell osservatore e δ s è la declinazione del Sole nel giorno considerato. Nel nostro caso, ϕ è la quantità che vogliamo determinare quindi riarrangiando l equazione sopra otteniamo: ϕ = 90 δ s + h s Equazione [1] Teniamo presente che, per semplificare i calcoli, tutti i valori devono essere espressi nelle stesse unità, gradi in questo caso Calcolo dell altezza del Sole sull orizzonte. Misurare l'altezza del Sole è relativamente semplice, e può essere determinata direttamente dalle immagini al momento del passaggio del Sole attraverso il meridiano a mezzanotte. Poiché tale distanza sarà misurata nell'immagine, l unità più semplice da utilizzare per la misura è il numero di pixel. In seguito si applicherà un fattore di scala per convertire la dimensione di un pixel e h s in gradi. 5 Misura del 6 Giugno 2012 da Tromsø, Norvegia Descrizione degli strumenti. Per l'osservazione del fenomeno e la registrazione di immagini in tempo reale, sarà utilizzata una Canon 5D Mark II da 21 M-pixel in combinazione con un filtro idoneo per l'osservazione del Sole Esempi di calcolo per Tromsø. Vogliamo determinare la latitudine da cui l'osservatore sta prendendo le immagini del Sole di mezzanotte. Seguendo il ragionamento teorico sopra abbiamo bisogno di conoscere l'altezza del Sole sopra l'orizzonte al momento e il valore della sua declinazione per il giorno di osservazione, in modo che questi valori possano essere sostituiti nell equazione [1]. Utilizzando un software astronomico che ci permette di sapere, per il 6 giugno 2012, l'altezza a cui il Sole sarà sopra l'orizzonte al momento del Sole di mezzanotte. In questo esempio, per calcolare il fattore di scala di cui abbiamo discusso, usiamo la dimensione del Sole in questa immagine (Figura 8), che è di 42 pixel. La dimensione angolare del Sole è una quantità nota, 0.525º. Quindi applicando il ragionamento della sezione precedente, il valore di scala, ε, è il seguente: Midnight Sun 7
8 Figura 8: Rappresentazione schematica dell altezza hs che si usa nei calcoli.!"#$# ℇ = = !"#$%/!"#$% 42!"# L altezza hs del Sole nell immagine risulta essere 195 pixel, vale a dire che hs = 2 25' 48". Dalle effemeridi, possiamo ottenere il valore della declinazione solare per un dato giorno, che in questo caso è il 6 Giugno Il valore è: δs = 22º 39' 39.42" In fine, sostituendo nell Equazione [1], troviamo che la latitudine dell osservatore è ϕ = 90 δs + hs = 69.77º = 69º 46' 8.58" dove δs, come menzionato è la declinazione del Sole e hs è la suo altezza sull orizzonte misurata in gradi. 6 Suggerimenti Internet. La sfera celeste. Introduzione a sistemi di coordinate astronomici. Trasmissione del transito di Venere in tempo reale su Internet: Spedizioni scientifiche del gruppo Shelios. Sole di mezzanotte visto da Fjellheisen. 360º - Panorama Collezioni di immagini. Midnight Sun 8
Cenni di geografia astronomica. Giorno solare e giorno siderale.
 Cenni di geografia astronomica. Tutte le figure e le immagini (tranne le ultime due) sono state prese dal sito Web: http://www.analemma.com/ Giorno solare e giorno siderale. La durata del giorno solare
Cenni di geografia astronomica. Tutte le figure e le immagini (tranne le ultime due) sono state prese dal sito Web: http://www.analemma.com/ Giorno solare e giorno siderale. La durata del giorno solare
Altezza del sole sull orizzonte nel corso dell anno
 Lucia Corbo e Nicola Scarpel Altezza del sole sull orizzonte nel corso dell anno 2 SD ALTEZZA DEL SOLE E LATITUDINE Per il moto di Rivoluzione che la Terra compie in un anno intorno al Sole, ad un osservatore
Lucia Corbo e Nicola Scarpel Altezza del sole sull orizzonte nel corso dell anno 2 SD ALTEZZA DEL SOLE E LATITUDINE Per il moto di Rivoluzione che la Terra compie in un anno intorno al Sole, ad un osservatore
1.6 Che cosa vede l astronomo
 1.6 Che cosa vede l astronomo Stelle in rotazione Nel corso della notte, la Sfera celeste sembra ruotare attorno a noi. Soltanto un punto detto Polo nord celeste resta fermo; esso si trova vicino a una
1.6 Che cosa vede l astronomo Stelle in rotazione Nel corso della notte, la Sfera celeste sembra ruotare attorno a noi. Soltanto un punto detto Polo nord celeste resta fermo; esso si trova vicino a una
Scegli per ciascuna risposta l'alternativa corretta. Scegli per ciascuna risposta l'alternativa corretta
 ERIICA La Terra e la Luna Cognome Nome Classe Data I/1 ero o also? L eclisse di Sole è dovuta all ombra della Luna che si proietta sulla Terra Durante un eclisse di Sole la Luna può oscurare il Sole anche
ERIICA La Terra e la Luna Cognome Nome Classe Data I/1 ero o also? L eclisse di Sole è dovuta all ombra della Luna che si proietta sulla Terra Durante un eclisse di Sole la Luna può oscurare il Sole anche
I MOTI DELLA TERRA NELLO SPAZIO
 LC23.03.06 I MOTI DELLA TERRA NELLO SPAZIO Prerequisiti: conoscenza del sistema metrico decimale e delle figure geometriche conoscenza del pianeta Terra Obiettivi: studiare i moti che riguardano la Terra
LC23.03.06 I MOTI DELLA TERRA NELLO SPAZIO Prerequisiti: conoscenza del sistema metrico decimale e delle figure geometriche conoscenza del pianeta Terra Obiettivi: studiare i moti che riguardano la Terra
LA FORMA DELLA TERRA
 LA FORMA DELLA TERRA La forma approssimativamente sferica della Terra può essere dimostrata con alcune prove fisiche, valide prima che l Uomo osservasse la Terra dallo Spazio: 1 - Avvicinamento di una
LA FORMA DELLA TERRA La forma approssimativamente sferica della Terra può essere dimostrata con alcune prove fisiche, valide prima che l Uomo osservasse la Terra dallo Spazio: 1 - Avvicinamento di una
Cartografia, topografia e orientamento
 Cartografia, topografia e orientamento Mappa tratta dall archivio dei musei vaticani ANVVFC,, Presidenza Nazionale, febbraio 2008 pag 1 Orbita terrestre e misura del tempo Tutti sappiamo che la terra non
Cartografia, topografia e orientamento Mappa tratta dall archivio dei musei vaticani ANVVFC,, Presidenza Nazionale, febbraio 2008 pag 1 Orbita terrestre e misura del tempo Tutti sappiamo che la terra non
Istituto Comprensivo Statale A. Vespucci
 Istituto Comprensivo Statale A. Vespucci Via Stazione snc, 89811 Vibo Valentia Marina Tel. 0963/572073 telefax 0963/577046 Cod. mecc. VVIC82600R cod. fiscale 96013890791 Distretto Scol. n. 14 [email protected]
Istituto Comprensivo Statale A. Vespucci Via Stazione snc, 89811 Vibo Valentia Marina Tel. 0963/572073 telefax 0963/577046 Cod. mecc. VVIC82600R cod. fiscale 96013890791 Distretto Scol. n. 14 [email protected]
6. Le conseguenze del moto di rivoluzione
 eclittica cerchio massimo sulla sfera celeste percorso apparente del Sole durante l'anno. interseca l'equatore celeste in due punti o nodi : Punto vernale (o punto γ o punto di Ariete) nodo ascendente.
eclittica cerchio massimo sulla sfera celeste percorso apparente del Sole durante l'anno. interseca l'equatore celeste in due punti o nodi : Punto vernale (o punto γ o punto di Ariete) nodo ascendente.
ASTRONOMIA SISTEMI DI RIFERIMENTO
 Sfera celeste ASTRONOMIA Il cielo considerato come l'interno di una sfera cava al fine di descrivere le posizioni e i movimenti degli oggetti astronomici. Ogni particolare osservatore è situato al centro
Sfera celeste ASTRONOMIA Il cielo considerato come l'interno di una sfera cava al fine di descrivere le posizioni e i movimenti degli oggetti astronomici. Ogni particolare osservatore è situato al centro
Orientarsi con un bastone
 Orientarsi con un bastone Pianta in terra un bastone, puntandolo verso il sole in maniera che non faccia ombra sul terreno. Dopo almeno una ventina di minuti apparirà l ombra alla base del bastone, questa
Orientarsi con un bastone Pianta in terra un bastone, puntandolo verso il sole in maniera che non faccia ombra sul terreno. Dopo almeno una ventina di minuti apparirà l ombra alla base del bastone, questa
Misure di base su una carta. Calcoli di distanze
 Misure di base su una carta Calcoli di distanze Per calcolare la distanza tra due punti su una carta disegnata si opera nel modo seguente: 1. Occorre identificare la scala della carta o ricorrendo alle
Misure di base su una carta Calcoli di distanze Per calcolare la distanza tra due punti su una carta disegnata si opera nel modo seguente: 1. Occorre identificare la scala della carta o ricorrendo alle
Sole. Instante 0. Rotazione della Terra
 AP 1 Misura della durata del giorno solare Scuola primaria secondo ciclo - MATERIALE OCCORRENTE Un solarscope Un cronometro o un orologio indicante ore, minuti e secondi Un foglio quadrettato (opzionale)
AP 1 Misura della durata del giorno solare Scuola primaria secondo ciclo - MATERIALE OCCORRENTE Un solarscope Un cronometro o un orologio indicante ore, minuti e secondi Un foglio quadrettato (opzionale)
COM È FATTA UNA MERIDIANA
 COM È FATTA UNA MERIDIANA L orologio solare a cui noi comunemente diamo il nome di meridiana, in realtà dovrebbe essere chiamato quadrante; infatti è così che si definisce il piano su cui si disegnano
COM È FATTA UNA MERIDIANA L orologio solare a cui noi comunemente diamo il nome di meridiana, in realtà dovrebbe essere chiamato quadrante; infatti è così che si definisce il piano su cui si disegnano
L osservatorio è collocato all interno del Parco pineta tra Saronno e Varese. Attorno ad esso troviamo un incredibile distesa di alberi.
 L osservatorio L osservatorio è collocato all interno del Parco pineta tra Saronno e Varese. Attorno ad esso troviamo un incredibile distesa di alberi. All interno troviamo la sala conferenze e i vari
L osservatorio L osservatorio è collocato all interno del Parco pineta tra Saronno e Varese. Attorno ad esso troviamo un incredibile distesa di alberi. All interno troviamo la sala conferenze e i vari
Figura 4. Conclusione
 Forza di Coriolis La forza di Coriolis é una forza che si manifesta su un corpo all interno di un sistema di riferimento (SDR) rotante, quale la terra che ruota su se stessa, quando il corpo stesso si
Forza di Coriolis La forza di Coriolis é una forza che si manifesta su un corpo all interno di un sistema di riferimento (SDR) rotante, quale la terra che ruota su se stessa, quando il corpo stesso si
OROLOGI SOLARI: 26/03/2005 Ing. Mauro Maggioni
 OROLOGI SOLARI: ASTRONOMIA e ARTE 26/03/2005 Ing. Mauro Maggioni IL SOLE e le OMBRE - Durante il corso del giorno il Sole compie un tragitto apparente nel cielo - Ciò significa che è possibile relazionare
OROLOGI SOLARI: ASTRONOMIA e ARTE 26/03/2005 Ing. Mauro Maggioni IL SOLE e le OMBRE - Durante il corso del giorno il Sole compie un tragitto apparente nel cielo - Ciò significa che è possibile relazionare
LA LETTURA DELLA CARTA TOPOGRAFICA Guida all Orientamento G.Corbellini, Ed. Zanichelli 1985
 LA LETTURA DELLA CARTA TOPOGRAFICA Guida all Orientamento G.Corbellini, Ed. Zanichelli 1985 UN PO' DI GEOGRAFIA: I PUNTI CARDINALI Prima di intraprendere la nostra avventura in compagnia della carta e
LA LETTURA DELLA CARTA TOPOGRAFICA Guida all Orientamento G.Corbellini, Ed. Zanichelli 1985 UN PO' DI GEOGRAFIA: I PUNTI CARDINALI Prima di intraprendere la nostra avventura in compagnia della carta e
AERONAUTICA MILITARE CENTRO NAZIONALE METEOROLOGIA E CLIMATOLOGIA AERONAUTICA. Servizio di Climatologia e Documentazione EFFEMERIDI AERONAUTICHE
 AERONAUTICA MILITARE CENTRO NAZIONALE DI METEOROLOGIA E CLIMATOLOGIA AERONAUTICA Servizio di Climatologia e Documentazione EFFEMERIDI AERONAUTICHE 2 0 1 5 AERONAUTICA MILITARE CENTRO NAZIONALE DI METEOROLOGIA
AERONAUTICA MILITARE CENTRO NAZIONALE DI METEOROLOGIA E CLIMATOLOGIA AERONAUTICA Servizio di Climatologia e Documentazione EFFEMERIDI AERONAUTICHE 2 0 1 5 AERONAUTICA MILITARE CENTRO NAZIONALE DI METEOROLOGIA
unità A3. L orientamento e la misura del tempo
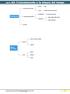 giorno Sole osservazione del cielo notte Stella Polare/Croce del sud longitudine in base all ora locale Orientamento coordinate geografiche latitudine altezza della stella Polare altezza del Sole bussola
giorno Sole osservazione del cielo notte Stella Polare/Croce del sud longitudine in base all ora locale Orientamento coordinate geografiche latitudine altezza della stella Polare altezza del Sole bussola
EFFEMERIDI AERONAUTICHE
 AERONAUTICA MILITARE CENTRO NAZIONALE DI METEOROLOGIA E CLIMATOLOGIA AERONAUTICA Servizio di Climatologia e Documentazione EFFEMERIDI AERONAUTICHE 2014 INDICE Descrizione e modalità d impiego.... III Tavole
AERONAUTICA MILITARE CENTRO NAZIONALE DI METEOROLOGIA E CLIMATOLOGIA AERONAUTICA Servizio di Climatologia e Documentazione EFFEMERIDI AERONAUTICHE 2014 INDICE Descrizione e modalità d impiego.... III Tavole
9. Urti e conservazione della quantità di moto.
 9. Urti e conservazione della quantità di moto. 1 Conservazione dell impulso m1 v1 v2 m2 Prima Consideriamo due punti materiali di massa m 1 e m 2 che si muovono in una dimensione. Supponiamo che i due
9. Urti e conservazione della quantità di moto. 1 Conservazione dell impulso m1 v1 v2 m2 Prima Consideriamo due punti materiali di massa m 1 e m 2 che si muovono in una dimensione. Supponiamo che i due
Domande a scelta multipla 1
 Domande a scelta multipla Domande a scelta multipla 1 Rispondete alle domande seguenti, scegliendo tra le alternative proposte. Cercate di consultare i suggerimenti solo in caso di difficoltà. Dopo l elenco
Domande a scelta multipla Domande a scelta multipla 1 Rispondete alle domande seguenti, scegliendo tra le alternative proposte. Cercate di consultare i suggerimenti solo in caso di difficoltà. Dopo l elenco
6. La Terra. Sì, la terra è la tua casa. Ma che cos è la terra? Vediamo di scoprire qualcosa sul posto dove vivi.
 6. La Terra Dove vivi? Dirai che questa è una domanda facile. Vivo in una casa, in una certa via, di una certa città. O forse dirai: La mia casa è in campagna. Ma dove vivi? Dove sono la tua casa, la tua
6. La Terra Dove vivi? Dirai che questa è una domanda facile. Vivo in una casa, in una certa via, di una certa città. O forse dirai: La mia casa è in campagna. Ma dove vivi? Dove sono la tua casa, la tua
Basi di matematica per il corso di micro
 Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
1 Tempo del Sole e tempo degli orologi
 Lucia Corbo e Nicola Scarpel 3SD TEMPO SOLARE E LONGITUDINE 1 Tempo del Sole e tempo degli orologi La durata del giorno solare, cioè il tempo che intercorre tra due passaggi del Sole in meridiano in una
Lucia Corbo e Nicola Scarpel 3SD TEMPO SOLARE E LONGITUDINE 1 Tempo del Sole e tempo degli orologi La durata del giorno solare, cioè il tempo che intercorre tra due passaggi del Sole in meridiano in una
I punti cardinali EST ORIENTE LEVANTE OVEST OCCIDENTE PONENTE SUD MEZZOGIORNO MERIDIONE NORD MEZZANOTTE SETTENTRIONE
 I punti cardinali Sin dall antichità l uomo ha osservato il movimento apparente del Sole e ha notato che sorge sempre dalla stessa parte, a oriente e tramonta dal lato opposto, a occidente. I termini oriente
I punti cardinali Sin dall antichità l uomo ha osservato il movimento apparente del Sole e ha notato che sorge sempre dalla stessa parte, a oriente e tramonta dal lato opposto, a occidente. I termini oriente
13. Campi vettoriali
 13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
Osservazioni sulla continuità per le funzioni reali di variabile reale
 Corso di Matematica, I modulo, Università di Udine, Osservazioni sulla continuità Osservazioni sulla continuità per le funzioni reali di variabile reale Come è noto una funzione è continua in un punto
Corso di Matematica, I modulo, Università di Udine, Osservazioni sulla continuità Osservazioni sulla continuità per le funzioni reali di variabile reale Come è noto una funzione è continua in un punto
Forze, leggi della dinamica, diagramma del. 28 febbraio 2009 (PIACENTINO - PREITE) Fisica per Scienze Motorie
 Forze, leggi della dinamica, diagramma del corpo libero 1 FORZE Grandezza fisica definibile come l' agente in grado di modificare lo stato di quiete o di moto di un corpo. Ci troviamo di fronte ad una
Forze, leggi della dinamica, diagramma del corpo libero 1 FORZE Grandezza fisica definibile come l' agente in grado di modificare lo stato di quiete o di moto di un corpo. Ci troviamo di fronte ad una
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
L elemento fondamentale è l obiettivo, ovvero la lente o lo specchio che forniscono l immagine dell oggetto.
 Il telescopio, è lo strumento ottico impiegato in astronomia, per osservare e studiare gli oggetti celesti. È generalmente separato in due componenti principali: una parte ottica (costituita dal tubo delle
Il telescopio, è lo strumento ottico impiegato in astronomia, per osservare e studiare gli oggetti celesti. È generalmente separato in due componenti principali: una parte ottica (costituita dal tubo delle
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2004
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
IL MAPPAMONDO PARALLELO
 IL MAPPAMONDO PARALLELO Si libera il globo dal suo supporto Si orienta il globo in modo che il paese dell osservatore sia in cima a esso Si ruota il globo in modo che il suo asse sia nel piano meridiano
IL MAPPAMONDO PARALLELO Si libera il globo dal suo supporto Si orienta il globo in modo che il paese dell osservatore sia in cima a esso Si ruota il globo in modo che il suo asse sia nel piano meridiano
OROLOGIO SOLARE Una meridiana equatoriale
 L Osservatorio di Melquiades Presenta OROLOGIO SOLARE Una meridiana equatoriale Il Sole, le ombre e il tempo Domande guida: 1. E possibile l osservazione diretta del Sole? 2. Come è possibile determinare
L Osservatorio di Melquiades Presenta OROLOGIO SOLARE Una meridiana equatoriale Il Sole, le ombre e il tempo Domande guida: 1. E possibile l osservazione diretta del Sole? 2. Come è possibile determinare
ATTIVITA EDUCATIVA Calcolo dell Attività Solare. Il numero di Wolf.
 ATTIVITA EDUCATIVA Calcolo dell Attività Solare. Il numero di Wolf. Autori: Dr. Miquel Serra-Ricart. Astronomo dell Istituto di Astrofisica, Isole Canarie. Mr. Juan Carlos Casado. Astrofotografo di tierrayestrellas.com,
ATTIVITA EDUCATIVA Calcolo dell Attività Solare. Il numero di Wolf. Autori: Dr. Miquel Serra-Ricart. Astronomo dell Istituto di Astrofisica, Isole Canarie. Mr. Juan Carlos Casado. Astrofotografo di tierrayestrellas.com,
CAPITOLO 1 L ASTRONOMIA DESCRITTIVA
 CAPITOLO 1 L ASTRONOMIA DESCRITTIVA Un famoso scienziato (secondo alcuni fu Bertrand Russell) tenne una volta una conferenza pubblica su un argomento di astronomia. Egli parlò di come la Terra orbiti intorno
CAPITOLO 1 L ASTRONOMIA DESCRITTIVA Un famoso scienziato (secondo alcuni fu Bertrand Russell) tenne una volta una conferenza pubblica su un argomento di astronomia. Egli parlò di come la Terra orbiti intorno
Sole e ombre sul mappamondo da terrestri di Lucia Corbo
 Sole e ombre sul mappamondo da terrestri di Lucia Corbo Mappamondo orientato da extraterrestri Tutti i mappamondi in commercio sono costruiti con l'asse della Terra inclinato di 23 27' rispetto alla verticale;
Sole e ombre sul mappamondo da terrestri di Lucia Corbo Mappamondo orientato da extraterrestri Tutti i mappamondi in commercio sono costruiti con l'asse della Terra inclinato di 23 27' rispetto alla verticale;
ORIENTARSI sulla TERRA
 ORIENTARSI sulla TERRA significato del termine orientarsi : il termine orientarsi indica letteralmente la capacità di individuare l oriente e fa quindi riferimento alla possibilità di localizzare i quattro
ORIENTARSI sulla TERRA significato del termine orientarsi : il termine orientarsi indica letteralmente la capacità di individuare l oriente e fa quindi riferimento alla possibilità di localizzare i quattro
TOPOGRAFI A E ORIENTAMENTO IN MONTAGNA. 04-09-2014 XXIV Corso di Alpinismo A1
 Club Alpino Italiano - Sezione di Bozzolo TOPOGRAFI A E ORIENTAMENTO IN MONTAGNA TOPOGRAFIA E ORIENTAMENTO IN MONTAGNA Cenni di geodesia e topografia Cartografia Lettura ed interpretazione delle carte
Club Alpino Italiano - Sezione di Bozzolo TOPOGRAFI A E ORIENTAMENTO IN MONTAGNA TOPOGRAFIA E ORIENTAMENTO IN MONTAGNA Cenni di geodesia e topografia Cartografia Lettura ed interpretazione delle carte
Esercitazioni Capitolo 3 II Approfondimenti sulla radiazione solare
 Esercitazioni Capitolo 3 II Approfondimenti sulla radiazione solare 1) Si valuti per Genova (λ = 44 24 ) e Palermo (λ = 38 08') la massima altezza angolare β raggiunta sul piano dell orizzonte dal sole
Esercitazioni Capitolo 3 II Approfondimenti sulla radiazione solare 1) Si valuti per Genova (λ = 44 24 ) e Palermo (λ = 38 08') la massima altezza angolare β raggiunta sul piano dell orizzonte dal sole
GLI STRUMENTI DELLA GEOGRAFIA
 VOLUME 1 CAPITOLO 0 MODULO D LE VENTI REGIONI ITALIANE GLI STRUMENTI DELLA GEOGRAFIA 1. Parole per capire A. Conosci già queste parole? Scrivi il loro significato o fai un disegno: Terra... territorio...
VOLUME 1 CAPITOLO 0 MODULO D LE VENTI REGIONI ITALIANE GLI STRUMENTI DELLA GEOGRAFIA 1. Parole per capire A. Conosci già queste parole? Scrivi il loro significato o fai un disegno: Terra... territorio...
Fondamenti osservativi di un Mappamondo Parallelo
 Fondamenti osservativi di un Mappamondo Parallelo Néstor CAMINO Complejo PLAZA DEL CIELO Facultad de Ingeniería (UNPSJB) y ISFD N 804 Esquel, Chubut, Patagonia, ARGENTINA. [email protected] -
Fondamenti osservativi di un Mappamondo Parallelo Néstor CAMINO Complejo PLAZA DEL CIELO Facultad de Ingeniería (UNPSJB) y ISFD N 804 Esquel, Chubut, Patagonia, ARGENTINA. [email protected] -
Analisi e progettazione del software AbcBid studio di caso 6 dicembre 2007 REQUISITI ITERAZIONE 1
 REQUISITI ITERAZIONE 1 abcbid è un sistema per la gestione di vendite all asta. Esso deve gestire gli utenti (che vogliono vendere o acquistare oggetti), gli oggetti venduti all asta, le relative offerte,
REQUISITI ITERAZIONE 1 abcbid è un sistema per la gestione di vendite all asta. Esso deve gestire gli utenti (che vogliono vendere o acquistare oggetti), gli oggetti venduti all asta, le relative offerte,
1 Principali funzioni e loro domini
 Principali funzioni e loro domini Tipo di funzione Rappresentazione Dominio Polinomio intero p() = a n + + a n R p() Polinomio fratto q() 6= q() 2n Radici pari p f() f() 2n+ Radici dispari p f() R Moduli
Principali funzioni e loro domini Tipo di funzione Rappresentazione Dominio Polinomio intero p() = a n + + a n R p() Polinomio fratto q() 6= q() 2n Radici pari p f() f() 2n+ Radici dispari p f() R Moduli
GIROSCOPIO. Scopo dell esperienza: Teoria fisica. Verificare la relazione: ω p = bmg/iω
 GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
4 3 4 = 4 x 10 2 + 3 x 10 1 + 4 x 10 0 aaa 10 2 10 1 10 0
 Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Esperienze di insegnamento dell astronomia tra scuola primaria e secondaria di primo grado
 Esperienze di insegnamento dell astronomia tra scuola primaria e secondaria di primo grado Prof. Cristina Terminiello Complejo Plaza del Cielo Esquel Chubut [email protected] movimenti del sole rispetto
Esperienze di insegnamento dell astronomia tra scuola primaria e secondaria di primo grado Prof. Cristina Terminiello Complejo Plaza del Cielo Esquel Chubut [email protected] movimenti del sole rispetto
La spirale iperbolica: Fu descritta per la prima volta da Pierre Varignon (1654-1722). L equazione, espressa in coordinate polari, è del tipo:
 Esistono delle forme geometriche che sono in grado, per complessi fattori psicologici non del tutto chiariti, di comunicarci un senso d equilibrio, di gradimento e di benessere. Tra queste analizzeremo
Esistono delle forme geometriche che sono in grado, per complessi fattori psicologici non del tutto chiariti, di comunicarci un senso d equilibrio, di gradimento e di benessere. Tra queste analizzeremo
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Una carta geografica diversa la proiezione cartografica di Arno Peters
 Una carta geografica diversa la proiezione cartografica di Arno Peters Nella proiezione di Mercatore la Germania (patria elettiva del geografo) e l Europa si trovano al centro del mondo, sia in senso latitudinale
Una carta geografica diversa la proiezione cartografica di Arno Peters Nella proiezione di Mercatore la Germania (patria elettiva del geografo) e l Europa si trovano al centro del mondo, sia in senso latitudinale
GEOMETRIA DELLE MASSE
 1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
Lunghezza ocale. Donato Di Bello
 F Lunghezza ocale Donato Di Bello Cinepresa, telecamera, macchina fotografica: tre strumenti tecnologici che utilizziamo per registrare la realtà intorno a noi o per trasformare in immagini la nostra fantasia.
F Lunghezza ocale Donato Di Bello Cinepresa, telecamera, macchina fotografica: tre strumenti tecnologici che utilizziamo per registrare la realtà intorno a noi o per trasformare in immagini la nostra fantasia.
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
Capitolo 4. Elasticità. Principi di economia (seconda edizione) Robert H. Frank, Ben S. Bernanke. Copyright 2007 - The McGraw-Hill Companies, srl
 Capitolo 4 Elasticità In questa lezione introdurremo il concetto di elasticità: un indicatore dell entità con cui domanda e offerta reagiscono a variazioni di prezzo, reddito ed altri elementi. Nella lezione
Capitolo 4 Elasticità In questa lezione introdurremo il concetto di elasticità: un indicatore dell entità con cui domanda e offerta reagiscono a variazioni di prezzo, reddito ed altri elementi. Nella lezione
Indica il numero delle ore giornaliere nelle quali un punto (o una superficie) è colpito dalla radiazione solare.
 APPUNTI SUI PERCORSI SOLARI Bibliografia Manuale di architettura bioclimatica - Cristina Benedetti Maggioli Editore SOLEGGIAMENTO. SOLEGGIAMENTO = NUMERO DI ORE Indica il numero delle ore giornaliere nelle
APPUNTI SUI PERCORSI SOLARI Bibliografia Manuale di architettura bioclimatica - Cristina Benedetti Maggioli Editore SOLEGGIAMENTO. SOLEGGIAMENTO = NUMERO DI ORE Indica il numero delle ore giornaliere nelle
f(x) = 1 x. Il dominio di questa funzione è il sottoinsieme proprio di R dato da
 Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
SOLUZIONE DEL PROBLEMA 1 TEMA DI MATEMATICA ESAME DI STATO 2015
 SOLUZIONE DEL PROBLEMA 1 TEMA DI MATEMATICA ESAME DI STATO 015 1. Indicando con i minuti di conversazione effettuati nel mese considerato, la spesa totale mensile in euro è espressa dalla funzione f()
SOLUZIONE DEL PROBLEMA 1 TEMA DI MATEMATICA ESAME DI STATO 015 1. Indicando con i minuti di conversazione effettuati nel mese considerato, la spesa totale mensile in euro è espressa dalla funzione f()
VALUTAZIONE TECNICO ECONOMICA DEL SISTEMA AUTOMATICO DI ORIENTAMENTO CON INSEGUITORE SOLARE DELLA ZILIO S.p.a.
 VALUTAZIONE TECNICO ECONOMICA DEL SISTEMA AUTOMATICO DI ORIENTAMENTO CON INSEGUITORE SOLARE DELLA ZILIO S.p.a. INTRODUZIONE I sistemi solari fotovoltaici per la produzione di energia sfruttano l energia
VALUTAZIONE TECNICO ECONOMICA DEL SISTEMA AUTOMATICO DI ORIENTAMENTO CON INSEGUITORE SOLARE DELLA ZILIO S.p.a. INTRODUZIONE I sistemi solari fotovoltaici per la produzione di energia sfruttano l energia
Il calore del sole e le fasce climatiche della terra
 Il calore del sole e le fasce climatiche della terra 1 Il sole trasmette energia e calore alla terra. Ma, dato che la terra ha una forma simile a quella di una sfera, che ruota su se stessa attorno a un
Il calore del sole e le fasce climatiche della terra 1 Il sole trasmette energia e calore alla terra. Ma, dato che la terra ha una forma simile a quella di una sfera, che ruota su se stessa attorno a un
ESEMPIO 1: eseguire il complemento a 10 di 765
 COMPLEMENTO A 10 DI UN NUMERO DECIMALE Sia dato un numero N 10 in base 10 di n cifre. Il complemento a 10 di tale numero (N ) si ottiene sottraendo il numero stesso a 10 n. ESEMPIO 1: eseguire il complemento
COMPLEMENTO A 10 DI UN NUMERO DECIMALE Sia dato un numero N 10 in base 10 di n cifre. Il complemento a 10 di tale numero (N ) si ottiene sottraendo il numero stesso a 10 n. ESEMPIO 1: eseguire il complemento
Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 2014
 Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 14 Problema 1 Punto a) Osserviamo che g (x) = f(x) e pertanto g () = f() = in quanto Γ è tangente all asse delle ascisse,
Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 14 Problema 1 Punto a) Osserviamo che g (x) = f(x) e pertanto g () = f() = in quanto Γ è tangente all asse delle ascisse,
Istituto Comprensivo di Buddusò - Scuola Primaria - Ins. Dore
 Istituto Comprensivo di Buddusò - Scuola Primaria - Ins. Dore La terra ha la forma di una sfera e per rappresentarla si usa il Mappamondo chiamato anche globo I geografi hanno tracciato sul mappamondo
Istituto Comprensivo di Buddusò - Scuola Primaria - Ins. Dore La terra ha la forma di una sfera e per rappresentarla si usa il Mappamondo chiamato anche globo I geografi hanno tracciato sul mappamondo
Capitolo 13: L offerta dell impresa e il surplus del produttore
 Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
VOLUME 3 CAPITOLO 1 MODULO D LE VENTI REGIONI ITALIANE. Alla fine del capitolo scrivi il significato di queste parole nuove: ... ... ... ... ... ...
 IL SOLE VOLUME 3 CAPITOLO 1 MODULO D LE VENTI REGIONI ITALIANE 1. Paroe per capire Aa fine de capitoo scrivi i significato di queste paroe nuove: Soe... fotosintesi corofiiana. stagioni... pianeti... orbita...
IL SOLE VOLUME 3 CAPITOLO 1 MODULO D LE VENTI REGIONI ITALIANE 1. Paroe per capire Aa fine de capitoo scrivi i significato di queste paroe nuove: Soe... fotosintesi corofiiana. stagioni... pianeti... orbita...
LEZIONE 7. Esercizio 7.1. Quale delle seguenti funzioni è decrescente in ( 3, 0) e ha derivata prima in 3 che vale 0? x 3 3 + x2. 2, x3 +2x +3.
 7 LEZIONE 7 Esercizio 7.1. Quale delle seguenti funzioni è decrescente in ( 3, 0) e ha derivata prima in 3 che vale 0? x 3 3 + x2 2 6x, x3 +2x 2 6x, 3x + x2 2, x3 +2x +3. Le derivate sono rispettivamente,
7 LEZIONE 7 Esercizio 7.1. Quale delle seguenti funzioni è decrescente in ( 3, 0) e ha derivata prima in 3 che vale 0? x 3 3 + x2 2 6x, x3 +2x 2 6x, 3x + x2 2, x3 +2x +3. Le derivate sono rispettivamente,
Lezione 10: Il problema del consumatore: Preferenze e scelta ottimale
 Corso di Scienza Economica (Economia Politica) prof. G. Di Bartolomeo Lezione 10: Il problema del consumatore: Preferenze e scelta ottimale Facoltà di Scienze della Comunicazione Università di Teramo Scelta
Corso di Scienza Economica (Economia Politica) prof. G. Di Bartolomeo Lezione 10: Il problema del consumatore: Preferenze e scelta ottimale Facoltà di Scienze della Comunicazione Università di Teramo Scelta
Web: ParcoAstronomico.it - email: [email protected] - Infotel 349/8470776! 7 Gennaio 2015. Cometa C/2014 Q2 Lovejoy
 SIDEREUS il 1 Parco Astronomico del SALENTO contrada Leopaldi 73050 Salve (LE) Web: ParcoAstronomico.it - email: [email protected] - Infotel 349/8470776 7 Gennaio 2015 Cometa C/2014 Q2 Lovejoy
SIDEREUS il 1 Parco Astronomico del SALENTO contrada Leopaldi 73050 Salve (LE) Web: ParcoAstronomico.it - email: [email protected] - Infotel 349/8470776 7 Gennaio 2015 Cometa C/2014 Q2 Lovejoy
1. Limite finito di una funzione in un punto
 . Limite finito di una funzione in un punto Consideriamo la funzione: f ( ) = il cui dominio risulta essere R {}, e quindi il valore di f ( ) non è calcolabile in =. Quest affermazione tuttavia non esaurisce
. Limite finito di una funzione in un punto Consideriamo la funzione: f ( ) = il cui dominio risulta essere R {}, e quindi il valore di f ( ) non è calcolabile in =. Quest affermazione tuttavia non esaurisce
LEZIONI DEL LABORATORIO DI PROGETTAZIONE TECNICA E STRUTTURALE - A.A. 2013-14 DOCENTE ING. GIUSEPPE DESOGUS IL PERCORSO DEL SOLE
 LEZIONI DEL LABORATORIO DI PROGETTAZIONE TECNICA E STRUTTURALE - A.A. 2013-14 DOCENTE ING. GIUSEPPE DESOGUS IL PERCORSO DEL SOLE LA POSIZIONE DEL SOLE È noto che la terra ruota intorno al sole muovendosi
LEZIONI DEL LABORATORIO DI PROGETTAZIONE TECNICA E STRUTTURALE - A.A. 2013-14 DOCENTE ING. GIUSEPPE DESOGUS IL PERCORSO DEL SOLE LA POSIZIONE DEL SOLE È noto che la terra ruota intorno al sole muovendosi
Il concetto di stop in fotografia
 Il concetto di stop in fotografia Stop. Non vi è conversazione tra fotografi in cui questa parola non sia pronunciata diverse volte. Coloro che non conoscono il gergo fotografico restano piuttosto perplessi
Il concetto di stop in fotografia Stop. Non vi è conversazione tra fotografi in cui questa parola non sia pronunciata diverse volte. Coloro che non conoscono il gergo fotografico restano piuttosto perplessi
La rappresentazione fornita dalle carte geografiche è:
 Le proiezioni geografiche La rappresentazione fornita dalle carte geografiche è: approssimata ridotta simbolica È approssimata perché non è possibile sviluppare su un piano una superficie sferica senza
Le proiezioni geografiche La rappresentazione fornita dalle carte geografiche è: approssimata ridotta simbolica È approssimata perché non è possibile sviluppare su un piano una superficie sferica senza
Consorzio Nettuno - Corso di Matematica 1 Schede di lavoro guidato per le esercitazioni
 Consorzio Nettuno - Corso di Matematica 1 Schede di lavoro guidato per le esercitazioni A cura di Sebastiano Cappuccio SCHEDA N. 6 ARGOMENTO: Grafici di funzioni sottoposte a trasformazioni elementari.
Consorzio Nettuno - Corso di Matematica 1 Schede di lavoro guidato per le esercitazioni A cura di Sebastiano Cappuccio SCHEDA N. 6 ARGOMENTO: Grafici di funzioni sottoposte a trasformazioni elementari.
Grandezze scalari e vettoriali
 Grandezze scalari e vettoriali Esempio vettore spostamento: Esistono due tipi di grandezze fisiche. a) Grandezze scalari specificate da un valore numerico (positivo negativo o nullo) e (nel caso di grandezze
Grandezze scalari e vettoriali Esempio vettore spostamento: Esistono due tipi di grandezze fisiche. a) Grandezze scalari specificate da un valore numerico (positivo negativo o nullo) e (nel caso di grandezze
Anno 4 Grafico di funzione
 Anno 4 Grafico di funzione Introduzione In questa lezione impareremo a disegnare il grafico di una funzione reale. Per fare ciò è necessario studiare alcune caratteristiche salienti della funzione che
Anno 4 Grafico di funzione Introduzione In questa lezione impareremo a disegnare il grafico di una funzione reale. Per fare ciò è necessario studiare alcune caratteristiche salienti della funzione che
Polli e conigli. problemi Piano cartesiano. Numeri e algoritmi Sistemi e loro. geometrica. Relazioni e funzioni Linguaggio naturale e
 Polli e conigli Livello scolare: primo biennio Abilità Interessate Calcolo di base - sistemi Risolvere per via grafica e algebrica problemi che si formalizzano con equazioni. Analizzare semplici testi
Polli e conigli Livello scolare: primo biennio Abilità Interessate Calcolo di base - sistemi Risolvere per via grafica e algebrica problemi che si formalizzano con equazioni. Analizzare semplici testi
Stazionamento di una montatura equatoriale
 Stazionamento di una montatura equatoriale Autore: Focosi Stefano Strumentazione: Celestron SCT C8 su Vixen SP (Super Polaris) Sistema di puntamento: Vixen SkySensor 2000 Sito osservativo: Loc. Molin Nuovo,
Stazionamento di una montatura equatoriale Autore: Focosi Stefano Strumentazione: Celestron SCT C8 su Vixen SP (Super Polaris) Sistema di puntamento: Vixen SkySensor 2000 Sito osservativo: Loc. Molin Nuovo,
DETERMINAZIONE DELL ALTEZZA DI UN ALBERO NEL CORTILE DELLA SCUOLA
 DETERMINAZIONE DELL ALTEZZA DI UN ALERO NEL CORTILE DELLA SCUOLA Attività 1 Si propone alla classe, divisa in gruppi, un problema e si chiede agli studenti di riflettere e di confrontarsi sulle possibili
DETERMINAZIONE DELL ALTEZZA DI UN ALERO NEL CORTILE DELLA SCUOLA Attività 1 Si propone alla classe, divisa in gruppi, un problema e si chiede agli studenti di riflettere e di confrontarsi sulle possibili
La scuola integra culture. Scheda3c
 Scheda3c Gli ELEMENTI DEL CLIMA che caratterizzano le condizioni meteorologiche di una regione sono: la temperatura, la pressione atmosferica, i venti, l umidità e le precipitazioni. La temperatura è data
Scheda3c Gli ELEMENTI DEL CLIMA che caratterizzano le condizioni meteorologiche di una regione sono: la temperatura, la pressione atmosferica, i venti, l umidità e le precipitazioni. La temperatura è data
L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare
 L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare Cap.4 giroscopio, magnetismo e forza di Lorentz teoria del giroscopio Abbiamo finora preso in considerazione le condizionidi equilibrio
L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare Cap.4 giroscopio, magnetismo e forza di Lorentz teoria del giroscopio Abbiamo finora preso in considerazione le condizionidi equilibrio
A.1 Definizione e rappresentazione di un numero complesso
 441 APPENDICE A4 NUMERI COMPLESSI A.1 Definizione e rappresentazione di un numero complesso Si riepilogano i concetti e le operazioni elementari relativi ai numeri complessi. Sia z un numero complesso;
441 APPENDICE A4 NUMERI COMPLESSI A.1 Definizione e rappresentazione di un numero complesso Si riepilogano i concetti e le operazioni elementari relativi ai numeri complessi. Sia z un numero complesso;
Librerie digitali. Video. Gestione di video. Caratteristiche dei video. Video. Metadati associati ai video. Metadati associati ai video
 Video Librerie digitali Gestione di video Ogni filmato è composto da più parti Video Audio Gestito come visto in precedenza Trascrizione del testo, identificazione di informazioni di interesse Testo Utile
Video Librerie digitali Gestione di video Ogni filmato è composto da più parti Video Audio Gestito come visto in precedenza Trascrizione del testo, identificazione di informazioni di interesse Testo Utile
ISTRUZIONI PER LA DETERMINAZIONE DELL OMBREGGIAMENTO DI SUPERFICI TRASPARENTI SU PARETE VERTICALE
 ISTRUZIONI PER LA DETERMINAZIONE DELL OMBREGGIAMENTO DI SUPERFICI TRASPARENTI SU PARETE VERTICALE Per ogni superficie trasparente presente sulle facciate degli edifici è possibile costruire una maschera
ISTRUZIONI PER LA DETERMINAZIONE DELL OMBREGGIAMENTO DI SUPERFICI TRASPARENTI SU PARETE VERTICALE Per ogni superficie trasparente presente sulle facciate degli edifici è possibile costruire una maschera
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
La misura in topografia
 La misura in topografia In questa dispensa di fornisce un cenno agli strumenti e alle tecniche di misura impiegate in topografia. Vengono descritti gli strumenti per misurare le lunghezze, quali il flessometro,
La misura in topografia In questa dispensa di fornisce un cenno agli strumenti e alle tecniche di misura impiegate in topografia. Vengono descritti gli strumenti per misurare le lunghezze, quali il flessometro,
Analisi Matematica di circuiti elettrici
 Analisi Matematica di circuiti elettrici Eserciziario A cura del Prof. Marco Chirizzi 2011/2012 Cap.5 Numeri complessi 5.1 Definizione di numero complesso Si definisce numero complesso un numero scritto
Analisi Matematica di circuiti elettrici Eserciziario A cura del Prof. Marco Chirizzi 2011/2012 Cap.5 Numeri complessi 5.1 Definizione di numero complesso Si definisce numero complesso un numero scritto
INTRODUZIONE I CICLI DI BORSA
 www.previsioniborsa.net 1 lezione METODO CICLICO INTRODUZIONE Questo metodo e praticamente un riassunto in breve di anni di esperienza e di studi sull Analisi Tecnica di borsa con specializzazione in particolare
www.previsioniborsa.net 1 lezione METODO CICLICO INTRODUZIONE Questo metodo e praticamente un riassunto in breve di anni di esperienza e di studi sull Analisi Tecnica di borsa con specializzazione in particolare
MAGAZZINO FISCALE (agg. alla rel. 3.4.1)
 MAGAZZINO FISCALE (agg. alla rel. 3.4.1) Per ottenere valori corretti nell inventario al LIFO o FIFO è necessario andare in Magazzino Fiscale ed elaborare i dati dell anno che ci serve valorizzare. Bisogna
MAGAZZINO FISCALE (agg. alla rel. 3.4.1) Per ottenere valori corretti nell inventario al LIFO o FIFO è necessario andare in Magazzino Fiscale ed elaborare i dati dell anno che ci serve valorizzare. Bisogna
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
LA RETTA. Retta per l'origine, rette orizzontali e verticali
 Retta per l'origine, rette orizzontali e verticali LA RETTA Abbiamo visto che l'equazione generica di una retta è del tipo Y = mx + q, dove m ne rappresenta la pendenza e q il punto in cui la retta incrocia
Retta per l'origine, rette orizzontali e verticali LA RETTA Abbiamo visto che l'equazione generica di una retta è del tipo Y = mx + q, dove m ne rappresenta la pendenza e q il punto in cui la retta incrocia
Logica Numerica Approfondimento 1. Minimo Comune Multiplo e Massimo Comun Divisore. Il concetto di multiplo e di divisore. Il Minimo Comune Multiplo
 Logica Numerica Approfondimento E. Barbuto Minimo Comune Multiplo e Massimo Comun Divisore Il concetto di multiplo e di divisore Considerato un numero intero n, se esso viene moltiplicato per un numero
Logica Numerica Approfondimento E. Barbuto Minimo Comune Multiplo e Massimo Comun Divisore Il concetto di multiplo e di divisore Considerato un numero intero n, se esso viene moltiplicato per un numero
MANUALE di ISTRUZIONI
 1 MANUALE di ISTRUZIONI 2 L ORA NEL MONDO Tutti gli strumenti di misura vengono ideati per eseguire la misura e la lettura di una data grandezza fisica. Per misurare la lunghezza di un oggetto si userà
1 MANUALE di ISTRUZIONI 2 L ORA NEL MONDO Tutti gli strumenti di misura vengono ideati per eseguire la misura e la lettura di una data grandezza fisica. Per misurare la lunghezza di un oggetto si userà
Proiezioni Grafica 3d
 Proiezioni Grafica 3d Giancarlo RINALDO [email protected] Dipartimento di Matematica Università di Messina ProiezioniGrafica 3d p. 1 Introduzione Il processo di visualizzazione in 3D è intrinsecamente
Proiezioni Grafica 3d Giancarlo RINALDO [email protected] Dipartimento di Matematica Università di Messina ProiezioniGrafica 3d p. 1 Introduzione Il processo di visualizzazione in 3D è intrinsecamente
IL CIELO. INAF - Osservatorio Astronomico di Trieste (b) Istituto Comprensivo S. Giovanni Sc. Sec. di primo grado M. Codermatz" - Trieste
 IL CIELO G. Iafrate (a), M. Ramella (a) e V. Bologna (b) (a) INAF - Osservatorio Astronomico di Trieste (b) Istituto Comprensivo S. Giovanni Sc. Sec. di primo grado M. Codermatz" - Trieste Questo modulo
IL CIELO G. Iafrate (a), M. Ramella (a) e V. Bologna (b) (a) INAF - Osservatorio Astronomico di Trieste (b) Istituto Comprensivo S. Giovanni Sc. Sec. di primo grado M. Codermatz" - Trieste Questo modulo
Capitolo V. I mercati dei beni e i mercati finanziari: il modello IS-LM
 Capitolo V. I mercati dei beni e i mercati finanziari: il modello IS-LM 2 OBIETTIVO: Il modello IS-LM Fornire uno schema concettuale per analizzare la determinazione congiunta della produzione e del tasso
Capitolo V. I mercati dei beni e i mercati finanziari: il modello IS-LM 2 OBIETTIVO: Il modello IS-LM Fornire uno schema concettuale per analizzare la determinazione congiunta della produzione e del tasso
1. calcolare l accelerazione del sistema e stabilire se la ruota sale o scende [6 punti];
![1. calcolare l accelerazione del sistema e stabilire se la ruota sale o scende [6 punti]; 1. calcolare l accelerazione del sistema e stabilire se la ruota sale o scende [6 punti];](/thumbs/24/2314490.jpg) 1 Esercizio Una ruota di raggio R = 15 cm e di massa M = 8 Kg può rotolare senza strisciare lungo un piano inclinato di un angolo θ 2 = 30 0, ed è collegato tramite un filo inestensibile ad un blocco di
1 Esercizio Una ruota di raggio R = 15 cm e di massa M = 8 Kg può rotolare senza strisciare lungo un piano inclinato di un angolo θ 2 = 30 0, ed è collegato tramite un filo inestensibile ad un blocco di
I poli magnetici isolati non esistono
 Il campo magnetico Le prime osservazioni dei fenomeni magnetici risalgono all antichità Agli antichi greci era nota la proprietà della magnetite di attirare la limatura di ferro Un ago magnetico libero
Il campo magnetico Le prime osservazioni dei fenomeni magnetici risalgono all antichità Agli antichi greci era nota la proprietà della magnetite di attirare la limatura di ferro Un ago magnetico libero
La propagazione delle onde luminose può essere studiata per mezzo delle equazioni di Maxwell. Tuttavia, nella maggior parte dei casi è possibile
 Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
SOLE TERRA LUNA Percorso didattico A cura di Cosetta Bigalli
 COMUNE DI BOLOGNA CULTURA LABORATORIO PER LA DIDATTICA SOLE TERRA LUNA Percorso didattico A cura di Cosetta Bigalli SOLE TERRA LUNA I moti della Terra e della Luna e le loro conseguenze Giovanna Fortuzzi
COMUNE DI BOLOGNA CULTURA LABORATORIO PER LA DIDATTICA SOLE TERRA LUNA Percorso didattico A cura di Cosetta Bigalli SOLE TERRA LUNA I moti della Terra e della Luna e le loro conseguenze Giovanna Fortuzzi
