Fondamenti osservativi di un Mappamondo Parallelo
|
|
|
- Celia Carbone
- 8 anni fa
- Visualizzazioni
Transcript
1 Fondamenti osservativi di un Mappamondo Parallelo Néstor CAMINO Complejo PLAZA DEL CIELO Facultad de Ingeniería (UNPSJB) y ISFD N 804 Esquel, Chubut, Patagonia, ARGENTINA. nestor.camino@speedy.com.ar -
2 La ricchezza e semplicità del Mappamondo Parallelo Il Mappamondo Parallelo è uno strumento didattico di grande potenzialità e ricchezza di concetti, educativi e culturali, che rende possibile l apprendimento dell Astronomia. Così, è un mezzo che permette di vedere molti concetti essenziali per l Astronomia di Posizione, con precisione e molta semplicità.
3 L apprendimento con il Mappamondo Parallelo Il Mappamondo Parallelo permette una doppia visione : locale e planetaria, per descrivere e spiegare la maggioranza dei fenomeni e concetti dell Astronomia a occhio nudo. Per questo, ci chiediamo quali sono i suoi fondamenti astronomici, per essere coscienti e poter creare gli strumenti didattici adatti ad ogni gruppo di studenti.
4 Quali sono le caratteristiche astronomiche principali di un Mappamondo Parallelo? E necessario che il Mappamondo Parallelo e il pianeta Terra siano omotetici. Questa condizione geometrica tridimensionale si ottiene se: la posizione topocentrica dell osservatore sul Mappamondo Parallelo è allo zenit della sfera; ossia, la verticale astronomica della rappresentazione coincide con la verticale astronomica della realtà. il piano del meridiano astronomico dell osservatore sul Mappamondo Parallelo deve essere contenuto nel meridiano astronomico della realtà.
5 La nascita di un Mappamondo Parallelo Quali sono i passi per trasformare una sfera liscia in un Mappamondo Parallelo rispettando le condizioni geometriche ( omotetia )?
6 La nascita di un Mappamondo Parallelo Lavoriamo con una sfera massiccia, liscia, di cemento bianco, con un diámetro di 48 cm, illuminata dal Sole. Le osservazioni sono state effettuate in vari giorni dell anno, specialmente durante gli equinozi e solstizi, registrando l evoluzione dell illuminazione della sfera.
7 La determinazione della POSIZIONE TOPOCENTRICA di Esquel Il primo passo è determinare qual è il punto della sfera liscia che rappresenterà la posizione topocentrica del punto d osservazione, nel nostro caso di Esquel (Argentina). Per questo è necessario determinare il PIANO DELL ORIZZONTE e la VERTICALE ASTRONOMICA del posto. Lo faremo attraverso la materializzazione di: il piano che forma la superficie dei liquidi in libertà (l ORIZZONTE locale); e la direzione della gravità nel punto di osservazione (la VERTICALE ASTRONOMICA ). Uno gnomone verticale nella posizione topocentrica di Esquel
8 Materializzazione del PIANO DELL ORIZZONTE Il piano che forma la superficie dei liquidi in libertà viene materializzato da una livella a bolla. Materializzaziones del Piano dell Orizzonte (perpendicolare alla direzione della verticale astronomica)
9 Il rapporto tra il PIANO DELL ORIZZONTE e la VERTICALE. La nivelación en dos direcciones perpendiculares materializa el plano del horizonte astronómico. El punto en el que este plano es tangente a la esfera lisa es la posición topocéntrica buscada. Materializzazione della verticale astronomica ( con l uso di una livella a bolla in due direzioni perpendicolari tra loro).
10 Materializzazione del PIANO DELL ORIZZONTE Livellare due direzioni perpendicolari materializza il piano dell orizzonte astronomico. Il punto dove questo piano è tangente alla sfera liscia è la posizione topocentrica ricercata. Materializzazione del Piano dell Orizzonte (perpendicolari alla verticale astronomica)
11 Materializzazione della VERTICALE ASTRONOMICA La direzione di un filo a piombo materializza la direzione della gravità locale. Verticale astronomica di Esquel Questa direzione, unica per ogni posto, si chiama verticale astronomica. Il piano dell orizzonte locale e la verticale astronomica, perpendicolari, definiscono il Sistema Orizzontale Locale delle coordinate astronomiche, indispensabili per lo studio del cielo. Posizione topocentrica di Esquel
12 Materializzazione della VERTICALE ASTRONOMICA Verticale astronomica di Esquel La posizione topocentrica del punto di osservazione si caratterizza per la verticale astronomica. Posizione topocentrica di Esquel
13 L'unicità della verticale astronomica Sia la Terra reale, come nel Mappamondo Parallelo, la verticale astronomica è unica in un certo punto di osservazione. Posizione topocentrica di un altro posto
14 L'unicità della verticale astronomica Per questo cambiando la posizione sull Mappamondo Parallelo la perpendicolare alla sfera no coincide con la direzione del filo a piombo. Verticale astronomica di Esquel Verticale astronomica di un altro posto Verticale astronomica di Esquel Verticale astronomica di un altro posto Posizione topocentrica di un altro posto Posizione topocentrica di un altro posto
15 La determinazione dei POLI GEOGRAFICI Per determinare i poli di rotazione (poli geografici) dell Mappamondo Parallelo è necesario registrare lo stato di illuminazione della sfera liscia durante un equinozio. Durante un equinozio, il terminatore : la linea diffusa che separa la metà del pianeta illuminato direttamente dal Sole (lato diurno) dalla metà all ombra (lato notturno) passa esattamente per i poli di rotazione. Così cercando l intersezione delle linee dei terminatori tra giorno e notte in diversi momenti durante un equinozio è possibile determinare la posizione dei Poli, Nord e Sud.
16 La determinazione dei POLI GEOGRAFICI L attività d osservazione per determinare i poli geografici sulla sfera liscia, futuro Mappamondo Parallelo, deve effettuarsi all equinozio.
17 La determinazione dei POLI GEOGRAFICI Durante un equinozio, le linee limite giorno-notte (i terminatori) contengono i poli geografici e coincidono con i meridiani geografici. Per questa ragione l intersezione dei terminatori (o dei Meridiani) permette di determinare la posizione dei Poli di rotazione Nord e Sud sulla sfera liscia. Evoluzione dei terminatori giorno-notte sulla sfera liscia nel corso di un equinozio Il Polo alto sarà quello che corrisponde all emisfero dell osservatore (Polo Sud per il caso di Esquel), rimanendo l altro nella parte bassa della sfera.
18 La determinazione dei FUSI ORARI Registrano la posizione delle linee limite a intervali di una ora (1 h) è possibile capire il concetto di fuso orario. La distanza angolare tra due linee limite (terminatore) successive separate da un intervallo di 1 ora è di 15. Come conseguenza in un giorno (periodo di rotazione terrestre) si determinano 24 zone di 15 : i fusi orari.
19 La proiezione didattica del lavoro sui Fusi Orari Approfondendo il concetto di fuso orario è possibile lavorare con la Longitudine Geografica, Tempo Solare,Tempo Civile e Tempo Universale. Piccoli orologi solari equatoriali, posizionati sui differente mediani, ma sullo stesso parallelo.
20 La determinazione dell EQUATORE La metà della distanza tra i poli geografici, misurata su diversi meridiani, permette di determinare il circolo massimo dell Equatore. Si può aggiungere che un altra forma per determinare il circolo massimo dell Equatore (piu laboriosa) è a partire dal registro con piccoli gnomoni verticali dei punti sulla sfera liscia durante un equinozio che non fanno sombra al mezzogiorno solare (lo stesso puó essere fatto per determinare i Tropici ai sostizi).
21 La determinazione dei CIRCOLI POLARI Per determinare i circoli polari, Nord e Sud, del Mappamondo Parallelo, è necessario registrare lo stato dell illuminazione della sfera liscia durante un solstizio. Durante un solstizio il terminatore (línea che separa la metà del pianeta illuminata da quella all ombra) si allontana piú che mai dai poli di rotazione. Cosi, registrando il movimento delle linee limite durante un solstizio rimangono definite due regioni circolari, una sempre illuminata (centrata al Polo Sud in dicembre) e l altra sempre all ombra (centrata al Polo Nord in dicembre).
22 La determinazione dei CIRCOLI POLARI L attività d osservazione per determinare i circoli polari sulla sfera liscia, futuro Mappamondo Parallelo, deve effettuarsi a un solstizio.
23 La determinazione dei CIRCOLI POLARI Durante un solstizio, la curva tangente alle linee limite giorno-notte define i Circoli Polari Nord e Sud, e di conseguenza le Calotte Polari. Evoluzione dei terminatori giorno-notte sulla sfera liscia nel corso di un solstizio (viste da Nord) Evoluzione dei terminatori giorno-notte sulla sfera liscia nel corso di un solstizio (viste da Sud)
24 La determinazione dei CIRCOLI POLARI Per ottenere una maggiore precisione nel lavoro didattico, è necessario marcare esattamente i Circoli Polari. Facciamo questo con un compasso, usando come centro il Polo e marcando una circonferenza tangente alle linee limite registrate.
25 La misura indiretta di latitudine Una volta determinata la posizione topocentrica dell posto di osservazione, i poli geografici e i circoli principali (Equatore e Circoli Polari), è possibile effettuare misure indirette della latitudine di alcuni posti importante.
26 La misura indiretta della latitudine di certi luoghi Questo processo di misurazione sarà effettuato attaverso un rapporto di proporzionalità tra la distanza lineare su un meridiano e la distanza angolare corrispondente a due punti sulla sfera. Latitudine sconosciuto Distanza lineare misurata Latitudine data Distanza lineare data
27 La misura indiretta della latitudine dei Circoli Polari Calcoliamo in un primo momento la latitudine del Circolo Polare Sud. I valori di riferimento sono: Distanza angolare Equatore-Polo Sud = 90 Latitudine del Circolo Polare Sud = 66,5 Se è equivalente a I valori misurati sono: poi è equivalente a Distanza lineare Equatore-Polo Sud = 37,5 cm Distanza lineare Equatore-Circolo Polare Sud = 29,0 cm Consideriamo che il risultato è buono (con un errore relativo minore al 10%). La fonte d errore è il fatto che la línea limite (il terminatore) è diffusa e non si può determinare con precisione.
28 La misura indiretta della latitudine dei posto di osservazione (Esquel) Nello stesso modo, calcoliamo la latitudine della nostra città, Esquel. I valori di riferimento sono: Distanza angolare Equatore-Polo Sud = 90 Latitudine de Esquel = 43 I valori misurati sono: Se poi è equivalente a è equivalente a Distanza lineare Equatore-Polo Sud = 37,5 cm Distanza lineare Equatore-Esquel = 18,0 cm É evidente che il risultato è molto più preciso, buono (con un errore relativo minore al 1%). Il processo usato per determinare la posizione topocentrica di Esquel è stato molto più preciso che quello usato per determinare i circoli polari.
29 Il Mappamondo Parallelo e la Educaciòn come mezzo culturale. Il Mappamondo Parallelo è un strumento basato su profondi criteri astronomici, che danno una proiezione senza limiti per la Didattica dell Astronomia. I suoi principi antropologici sono essenziali per una ideologia che considera l Educazione Interculturale come il principale mezzo per la trasformazione delle nostre comunità, in pace, e con rispetto alle diverse identità.
Meridiane sferiche. al XVII Seminario Nazionale di Gnomonica dell Unione Astrofili Italiani
 Meridiane sferiche PP della memoria Dagli orologi solari sferici al mappamondo parallelo uno strumento didattico in pubblicazione negli Atti presentato a Pescia (Pistoia) 15-17 Aprile 2011 al XVII Seminario
Meridiane sferiche PP della memoria Dagli orologi solari sferici al mappamondo parallelo uno strumento didattico in pubblicazione negli Atti presentato a Pescia (Pistoia) 15-17 Aprile 2011 al XVII Seminario
Esperienze di insegnamento dell astronomia tra scuola primaria e secondaria di primo grado
 Esperienze di insegnamento dell astronomia tra scuola primaria e secondaria di primo grado Prof. Cristina Terminiello Complejo Plaza del Cielo Esquel Chubut crister@speedy.com.ar movimenti del sole rispetto
Esperienze di insegnamento dell astronomia tra scuola primaria e secondaria di primo grado Prof. Cristina Terminiello Complejo Plaza del Cielo Esquel Chubut crister@speedy.com.ar movimenti del sole rispetto
TOPOGRAFI A E ORIENTAMENTO IN MONTAGNA. 04-09-2014 XXIV Corso di Alpinismo A1
 Club Alpino Italiano - Sezione di Bozzolo TOPOGRAFI A E ORIENTAMENTO IN MONTAGNA TOPOGRAFIA E ORIENTAMENTO IN MONTAGNA Cenni di geodesia e topografia Cartografia Lettura ed interpretazione delle carte
Club Alpino Italiano - Sezione di Bozzolo TOPOGRAFI A E ORIENTAMENTO IN MONTAGNA TOPOGRAFIA E ORIENTAMENTO IN MONTAGNA Cenni di geodesia e topografia Cartografia Lettura ed interpretazione delle carte
Istituto Comprensivo di Buddusò - Scuola Primaria - Ins. Dore
 Istituto Comprensivo di Buddusò - Scuola Primaria - Ins. Dore La terra ha la forma di una sfera e per rappresentarla si usa il Mappamondo chiamato anche globo I geografi hanno tracciato sul mappamondo
Istituto Comprensivo di Buddusò - Scuola Primaria - Ins. Dore La terra ha la forma di una sfera e per rappresentarla si usa il Mappamondo chiamato anche globo I geografi hanno tracciato sul mappamondo
L IMMAGINE DELLA TERRA
 L IMMAGINE DELLA TERRA 1 Capitolo 1 L orientamento e la misura del tempo Paralleli e meridiani La Terra ha, grossomodo, la forma di una sfera e dunque ha un centro dove si incontrano gli infiniti diametri.
L IMMAGINE DELLA TERRA 1 Capitolo 1 L orientamento e la misura del tempo Paralleli e meridiani La Terra ha, grossomodo, la forma di una sfera e dunque ha un centro dove si incontrano gli infiniti diametri.
Cenni di geografia astronomica. Giorno solare e giorno siderale.
 Cenni di geografia astronomica. Tutte le figure e le immagini (tranne le ultime due) sono state prese dal sito Web: http://www.analemma.com/ Giorno solare e giorno siderale. La durata del giorno solare
Cenni di geografia astronomica. Tutte le figure e le immagini (tranne le ultime due) sono state prese dal sito Web: http://www.analemma.com/ Giorno solare e giorno siderale. La durata del giorno solare
Istituto Comprensivo Statale A. Vespucci
 Istituto Comprensivo Statale A. Vespucci Via Stazione snc, 89811 Vibo Valentia Marina Tel. 0963/572073 telefax 0963/577046 Cod. mecc. VVIC82600R cod. fiscale 96013890791 Distretto Scol. n. 14 vvic82600r@istruzione.it
Istituto Comprensivo Statale A. Vespucci Via Stazione snc, 89811 Vibo Valentia Marina Tel. 0963/572073 telefax 0963/577046 Cod. mecc. VVIC82600R cod. fiscale 96013890791 Distretto Scol. n. 14 vvic82600r@istruzione.it
IL MAPPAMONDO PARALLELO
 IL MAPPAMONDO PARALLELO Si libera il globo dal suo supporto Si orienta il globo in modo che il paese dell osservatore sia in cima a esso Si ruota il globo in modo che il suo asse sia nel piano meridiano
IL MAPPAMONDO PARALLELO Si libera il globo dal suo supporto Si orienta il globo in modo che il paese dell osservatore sia in cima a esso Si ruota il globo in modo che il suo asse sia nel piano meridiano
Scegli per ciascuna risposta l'alternativa corretta. Scegli per ciascuna risposta l'alternativa corretta
 ERIICA La Terra e la Luna Cognome Nome Classe Data I/1 ero o also? L eclisse di Sole è dovuta all ombra della Luna che si proietta sulla Terra Durante un eclisse di Sole la Luna può oscurare il Sole anche
ERIICA La Terra e la Luna Cognome Nome Classe Data I/1 ero o also? L eclisse di Sole è dovuta all ombra della Luna che si proietta sulla Terra Durante un eclisse di Sole la Luna può oscurare il Sole anche
Sistema di riferimento
 Sistema di riferimento Storicamente divisione fra altimetria e planimetria (riferimento fisico riferimento matematico) Oggi dati sempre più integrati Domani? Dato di fatto - L acqua segue leggi fisiche
Sistema di riferimento Storicamente divisione fra altimetria e planimetria (riferimento fisico riferimento matematico) Oggi dati sempre più integrati Domani? Dato di fatto - L acqua segue leggi fisiche
SISTEMI DI RIFERIMENTO E PROIEZIONI
 SISTEMI DI RIFERIMENTO E PROIEZIONI Esistono 3 tipi di dati: 1- Dati tabellari (informativi) 2- Dati geometrici (territoriali) 3- Dati geometrici e tabellari (informativi territoriali) La localizzazione
SISTEMI DI RIFERIMENTO E PROIEZIONI Esistono 3 tipi di dati: 1- Dati tabellari (informativi) 2- Dati geometrici (territoriali) 3- Dati geometrici e tabellari (informativi territoriali) La localizzazione
1.6 Che cosa vede l astronomo
 1.6 Che cosa vede l astronomo Stelle in rotazione Nel corso della notte, la Sfera celeste sembra ruotare attorno a noi. Soltanto un punto detto Polo nord celeste resta fermo; esso si trova vicino a una
1.6 Che cosa vede l astronomo Stelle in rotazione Nel corso della notte, la Sfera celeste sembra ruotare attorno a noi. Soltanto un punto detto Polo nord celeste resta fermo; esso si trova vicino a una
LEZIONI DEL LABORATORIO DI PROGETTAZIONE TECNICA E STRUTTURALE - A.A. 2013-14 DOCENTE ING. GIUSEPPE DESOGUS IL PERCORSO DEL SOLE
 LEZIONI DEL LABORATORIO DI PROGETTAZIONE TECNICA E STRUTTURALE - A.A. 2013-14 DOCENTE ING. GIUSEPPE DESOGUS IL PERCORSO DEL SOLE LA POSIZIONE DEL SOLE È noto che la terra ruota intorno al sole muovendosi
LEZIONI DEL LABORATORIO DI PROGETTAZIONE TECNICA E STRUTTURALE - A.A. 2013-14 DOCENTE ING. GIUSEPPE DESOGUS IL PERCORSO DEL SOLE LA POSIZIONE DEL SOLE È noto che la terra ruota intorno al sole muovendosi
La rappresentazione fornita dalle carte geografiche è:
 Le proiezioni geografiche La rappresentazione fornita dalle carte geografiche è: approssimata ridotta simbolica È approssimata perché non è possibile sviluppare su un piano una superficie sferica senza
Le proiezioni geografiche La rappresentazione fornita dalle carte geografiche è: approssimata ridotta simbolica È approssimata perché non è possibile sviluppare su un piano una superficie sferica senza
Altezza del sole sull orizzonte nel corso dell anno
 Lucia Corbo e Nicola Scarpel Altezza del sole sull orizzonte nel corso dell anno 2 SD ALTEZZA DEL SOLE E LATITUDINE Per il moto di Rivoluzione che la Terra compie in un anno intorno al Sole, ad un osservatore
Lucia Corbo e Nicola Scarpel Altezza del sole sull orizzonte nel corso dell anno 2 SD ALTEZZA DEL SOLE E LATITUDINE Per il moto di Rivoluzione che la Terra compie in un anno intorno al Sole, ad un osservatore
COM È FATTA UNA MERIDIANA
 COM È FATTA UNA MERIDIANA L orologio solare a cui noi comunemente diamo il nome di meridiana, in realtà dovrebbe essere chiamato quadrante; infatti è così che si definisce il piano su cui si disegnano
COM È FATTA UNA MERIDIANA L orologio solare a cui noi comunemente diamo il nome di meridiana, in realtà dovrebbe essere chiamato quadrante; infatti è così che si definisce il piano su cui si disegnano
OROLOGI SOLARI: 26/03/2005 Ing. Mauro Maggioni
 OROLOGI SOLARI: ASTRONOMIA e ARTE 26/03/2005 Ing. Mauro Maggioni IL SOLE e le OMBRE - Durante il corso del giorno il Sole compie un tragitto apparente nel cielo - Ciò significa che è possibile relazionare
OROLOGI SOLARI: ASTRONOMIA e ARTE 26/03/2005 Ing. Mauro Maggioni IL SOLE e le OMBRE - Durante il corso del giorno il Sole compie un tragitto apparente nel cielo - Ciò significa che è possibile relazionare
Cpia di Lecce. Le coordinate geografiche
 Cpia di Lecce Le coordinate geografiche Forma della Terra La Terra è sferica Per la sua rappresentazione si usa il globo o mappamondo Meridiani e paralleli sono linee immaginarie usate dai geografi per
Cpia di Lecce Le coordinate geografiche Forma della Terra La Terra è sferica Per la sua rappresentazione si usa il globo o mappamondo Meridiani e paralleli sono linee immaginarie usate dai geografi per
ASTRONOMIA SISTEMI DI RIFERIMENTO
 Sfera celeste ASTRONOMIA Il cielo considerato come l'interno di una sfera cava al fine di descrivere le posizioni e i movimenti degli oggetti astronomici. Ogni particolare osservatore è situato al centro
Sfera celeste ASTRONOMIA Il cielo considerato come l'interno di una sfera cava al fine di descrivere le posizioni e i movimenti degli oggetti astronomici. Ogni particolare osservatore è situato al centro
VALUTAZIONE TECNICO ECONOMICA DEL SISTEMA AUTOMATICO DI ORIENTAMENTO CON INSEGUITORE SOLARE DELLA ZILIO S.p.a.
 VALUTAZIONE TECNICO ECONOMICA DEL SISTEMA AUTOMATICO DI ORIENTAMENTO CON INSEGUITORE SOLARE DELLA ZILIO S.p.a. INTRODUZIONE I sistemi solari fotovoltaici per la produzione di energia sfruttano l energia
VALUTAZIONE TECNICO ECONOMICA DEL SISTEMA AUTOMATICO DI ORIENTAMENTO CON INSEGUITORE SOLARE DELLA ZILIO S.p.a. INTRODUZIONE I sistemi solari fotovoltaici per la produzione di energia sfruttano l energia
Orientarsi con un bastone
 Orientarsi con un bastone Pianta in terra un bastone, puntandolo verso il sole in maniera che non faccia ombra sul terreno. Dopo almeno una ventina di minuti apparirà l ombra alla base del bastone, questa
Orientarsi con un bastone Pianta in terra un bastone, puntandolo verso il sole in maniera che non faccia ombra sul terreno. Dopo almeno una ventina di minuti apparirà l ombra alla base del bastone, questa
Misure di base su una carta. Calcoli di distanze
 Misure di base su una carta Calcoli di distanze Per calcolare la distanza tra due punti su una carta disegnata si opera nel modo seguente: 1. Occorre identificare la scala della carta o ricorrendo alle
Misure di base su una carta Calcoli di distanze Per calcolare la distanza tra due punti su una carta disegnata si opera nel modo seguente: 1. Occorre identificare la scala della carta o ricorrendo alle
Cartografia, topografia e orientamento
 Cartografia, topografia e orientamento Mappa tratta dall archivio dei musei vaticani ANVVFC,, Presidenza Nazionale, febbraio 2008 pag 1 Orbita terrestre e misura del tempo Tutti sappiamo che la terra non
Cartografia, topografia e orientamento Mappa tratta dall archivio dei musei vaticani ANVVFC,, Presidenza Nazionale, febbraio 2008 pag 1 Orbita terrestre e misura del tempo Tutti sappiamo che la terra non
OROLOGIO SOLARE Una meridiana equatoriale
 L Osservatorio di Melquiades Presenta OROLOGIO SOLARE Una meridiana equatoriale Il Sole, le ombre e il tempo Domande guida: 1. E possibile l osservazione diretta del Sole? 2. Come è possibile determinare
L Osservatorio di Melquiades Presenta OROLOGIO SOLARE Una meridiana equatoriale Il Sole, le ombre e il tempo Domande guida: 1. E possibile l osservazione diretta del Sole? 2. Come è possibile determinare
Gianni Ferrari FORMULE E METODI PER LO STUDIO DEGLI OROLOGI SOLARI PIANI
 Gianni Ferrari FORMULE E METODI PER LO STUDIO DEGLI OROLOGI SOLARI PIANI INDICE ix PARTE I - Definizioni e considerazioni generali Capitolo 1 1 Coordinate equatoriali e azimutali del Sole Relazioni fondamentali
Gianni Ferrari FORMULE E METODI PER LO STUDIO DEGLI OROLOGI SOLARI PIANI INDICE ix PARTE I - Definizioni e considerazioni generali Capitolo 1 1 Coordinate equatoriali e azimutali del Sole Relazioni fondamentali
Sole e ombre sul mappamondo da terrestri di Lucia Corbo
 Sole e ombre sul mappamondo da terrestri di Lucia Corbo Mappamondo orientato da extraterrestri Tutti i mappamondi in commercio sono costruiti con l'asse della Terra inclinato di 23 27' rispetto alla verticale;
Sole e ombre sul mappamondo da terrestri di Lucia Corbo Mappamondo orientato da extraterrestri Tutti i mappamondi in commercio sono costruiti con l'asse della Terra inclinato di 23 27' rispetto alla verticale;
unità A3. L orientamento e la misura del tempo
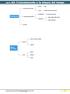 giorno Sole osservazione del cielo notte Stella Polare/Croce del sud longitudine in base all ora locale Orientamento coordinate geografiche latitudine altezza della stella Polare altezza del Sole bussola
giorno Sole osservazione del cielo notte Stella Polare/Croce del sud longitudine in base all ora locale Orientamento coordinate geografiche latitudine altezza della stella Polare altezza del Sole bussola
Usando il pendolo reversibile di Kater
 Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
I MOTI DELLA TERRA NELLO SPAZIO
 LC23.03.06 I MOTI DELLA TERRA NELLO SPAZIO Prerequisiti: conoscenza del sistema metrico decimale e delle figure geometriche conoscenza del pianeta Terra Obiettivi: studiare i moti che riguardano la Terra
LC23.03.06 I MOTI DELLA TERRA NELLO SPAZIO Prerequisiti: conoscenza del sistema metrico decimale e delle figure geometriche conoscenza del pianeta Terra Obiettivi: studiare i moti che riguardano la Terra
Stazionamento di una montatura equatoriale
 Stazionamento di una montatura equatoriale Autore: Focosi Stefano Strumentazione: Celestron SCT C8 su Vixen SP (Super Polaris) Sistema di puntamento: Vixen SkySensor 2000 Sito osservativo: Loc. Molin Nuovo,
Stazionamento di una montatura equatoriale Autore: Focosi Stefano Strumentazione: Celestron SCT C8 su Vixen SP (Super Polaris) Sistema di puntamento: Vixen SkySensor 2000 Sito osservativo: Loc. Molin Nuovo,
CONTROLLO DELLA RADIAZIONE SOLARE
 CAPITL 4 CTRLL DLLA RADIAZI LAR 4.1 Generalità La localizzazione e l orientamento di un edificio per ridurre l esposizione solare estiva e valorizzare quella invernale, sono obiettivi fondamentali per
CAPITL 4 CTRLL DLLA RADIAZI LAR 4.1 Generalità La localizzazione e l orientamento di un edificio per ridurre l esposizione solare estiva e valorizzare quella invernale, sono obiettivi fondamentali per
Processo di rendering
 Processo di rendering Trasformazioni di vista Trasformazioni di vista Il processo di visione in tre dimensioni Le trasformazioni di proiezione 2 Rendering nello spazio 2D Il processo di rendering (visualizzazione)
Processo di rendering Trasformazioni di vista Trasformazioni di vista Il processo di visione in tre dimensioni Le trasformazioni di proiezione 2 Rendering nello spazio 2D Il processo di rendering (visualizzazione)
CAPITOLO 1 L ASTRONOMIA DESCRITTIVA
 CAPITOLO 1 L ASTRONOMIA DESCRITTIVA Un famoso scienziato (secondo alcuni fu Bertrand Russell) tenne una volta una conferenza pubblica su un argomento di astronomia. Egli parlò di come la Terra orbiti intorno
CAPITOLO 1 L ASTRONOMIA DESCRITTIVA Un famoso scienziato (secondo alcuni fu Bertrand Russell) tenne una volta una conferenza pubblica su un argomento di astronomia. Egli parlò di come la Terra orbiti intorno
RETTE, PIANI, SFERE, CIRCONFERENZE
 RETTE, PIANI, SFERE, CIRCONFERENZE 1. Esercizi Esercizio 1. Dati i punti A(1, 0, 1) e B(, 1, 1) trovare (1) la loro distanza; () il punto medio del segmento AB; (3) la retta AB sia in forma parametrica,
RETTE, PIANI, SFERE, CIRCONFERENZE 1. Esercizi Esercizio 1. Dati i punti A(1, 0, 1) e B(, 1, 1) trovare (1) la loro distanza; () il punto medio del segmento AB; (3) la retta AB sia in forma parametrica,
L elemento fondamentale è l obiettivo, ovvero la lente o lo specchio che forniscono l immagine dell oggetto.
 Il telescopio, è lo strumento ottico impiegato in astronomia, per osservare e studiare gli oggetti celesti. È generalmente separato in due componenti principali: una parte ottica (costituita dal tubo delle
Il telescopio, è lo strumento ottico impiegato in astronomia, per osservare e studiare gli oggetti celesti. È generalmente separato in due componenti principali: una parte ottica (costituita dal tubo delle
LA RETTA. Retta per l'origine, rette orizzontali e verticali
 Retta per l'origine, rette orizzontali e verticali LA RETTA Abbiamo visto che l'equazione generica di una retta è del tipo Y = mx + q, dove m ne rappresenta la pendenza e q il punto in cui la retta incrocia
Retta per l'origine, rette orizzontali e verticali LA RETTA Abbiamo visto che l'equazione generica di una retta è del tipo Y = mx + q, dove m ne rappresenta la pendenza e q il punto in cui la retta incrocia
la restituzione prospettica da singolo fotogramma
 la restituzione prospettica da singolo fotogramma arch. francesco guerini francesco.guerini@gmail.com politecnico di Milano, Facoltà di Architettura e Società Laboratorio di Rappresentazione 1 Prof. Andrea
la restituzione prospettica da singolo fotogramma arch. francesco guerini francesco.guerini@gmail.com politecnico di Milano, Facoltà di Architettura e Società Laboratorio di Rappresentazione 1 Prof. Andrea
IL SISTEMA CARTOGRAFICO NAZIONALE
 IL SISTEMA CARTOGRAFICO NAZIONALE La Il paragrafo è intitolato La Carta di Gauss poiché, delle infinite formule che si possono adottare per mettere in corrispondenza i punti dell'ellissoide con quelli
IL SISTEMA CARTOGRAFICO NAZIONALE La Il paragrafo è intitolato La Carta di Gauss poiché, delle infinite formule che si possono adottare per mettere in corrispondenza i punti dell'ellissoide con quelli
LA FORMA DELLA TERRA
 LA FORMA DELLA TERRA La forma approssimativamente sferica della Terra può essere dimostrata con alcune prove fisiche, valide prima che l Uomo osservasse la Terra dallo Spazio: 1 - Avvicinamento di una
LA FORMA DELLA TERRA La forma approssimativamente sferica della Terra può essere dimostrata con alcune prove fisiche, valide prima che l Uomo osservasse la Terra dallo Spazio: 1 - Avvicinamento di una
GEOMETRIA DELLE MASSE
 1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
CONI, CILINDRI, SUPERFICI DI ROTAZIONE
 CONI, CILINDRI, SUPERFICI DI ROTAZIONE. Esercizi x + z = Esercizio. Data la curva x, calcolare l equazione del cilindro avente γ y = 0 come direttrice e con generatrici parallele al vettore v = (, 0, ).
CONI, CILINDRI, SUPERFICI DI ROTAZIONE. Esercizi x + z = Esercizio. Data la curva x, calcolare l equazione del cilindro avente γ y = 0 come direttrice e con generatrici parallele al vettore v = (, 0, ).
B. Vogliamo determinare l equazione della retta
 Risoluzione quesiti ordinamento Quesito N.1 Indicata con α la misura dell angolo CAB, si ha che: 1 Area ( ABC ) = AC AB sinα = 3 sinα π 3 sinα = 3 sinα = 1 α = Il triangolo è quindi retto in A. La misura
Risoluzione quesiti ordinamento Quesito N.1 Indicata con α la misura dell angolo CAB, si ha che: 1 Area ( ABC ) = AC AB sinα = 3 sinα π 3 sinα = 3 sinα = 1 α = Il triangolo è quindi retto in A. La misura
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2004
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
6. Le conseguenze del moto di rivoluzione
 eclittica cerchio massimo sulla sfera celeste percorso apparente del Sole durante l'anno. interseca l'equatore celeste in due punti o nodi : Punto vernale (o punto γ o punto di Ariete) nodo ascendente.
eclittica cerchio massimo sulla sfera celeste percorso apparente del Sole durante l'anno. interseca l'equatore celeste in due punti o nodi : Punto vernale (o punto γ o punto di Ariete) nodo ascendente.
Corso Operatore C.R.I. nel Settore Emergenza Cartografia ed orientamento
 Corso Operatore C.R.I. nel Settore Emergenza Cartografia ed orientamento Contenuti della lezione 1. Definizioni generali 2. Le coordinate geografiche 3. Le carte e le proiezioni 4. Lettura di una carta
Corso Operatore C.R.I. nel Settore Emergenza Cartografia ed orientamento Contenuti della lezione 1. Definizioni generali 2. Le coordinate geografiche 3. Le carte e le proiezioni 4. Lettura di una carta
La distribuzione Normale. La distribuzione Normale
 La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza A.A. 2007/08
 UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza Corso di Disegno Tecnico Industriale per il Corso di Laurea triennale in Ingegneria Meccanica e in Ingegneria Meccatronica Tolleranze
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza Corso di Disegno Tecnico Industriale per il Corso di Laurea triennale in Ingegneria Meccanica e in Ingegneria Meccatronica Tolleranze
Consideriamo due polinomi
 Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
1 Tempo del Sole e tempo degli orologi
 Lucia Corbo e Nicola Scarpel 3SD TEMPO SOLARE E LONGITUDINE 1 Tempo del Sole e tempo degli orologi La durata del giorno solare, cioè il tempo che intercorre tra due passaggi del Sole in meridiano in una
Lucia Corbo e Nicola Scarpel 3SD TEMPO SOLARE E LONGITUDINE 1 Tempo del Sole e tempo degli orologi La durata del giorno solare, cioè il tempo che intercorre tra due passaggi del Sole in meridiano in una
Fig. 2. Proiezioni ortogonali di un parallelepipedo su piani esterni alla figura
 3. LE PROIEZIONI ORTOGONALI Le proiezioni ortogonali sono originate dallo scopo di proiettare su un piano (il foglio della rappresentazione) un oggetto posto nello spazio, che conservi le stesse caratteristiche
3. LE PROIEZIONI ORTOGONALI Le proiezioni ortogonali sono originate dallo scopo di proiettare su un piano (il foglio della rappresentazione) un oggetto posto nello spazio, che conservi le stesse caratteristiche
ORIENTARSI sulla TERRA
 ORIENTARSI sulla TERRA significato del termine orientarsi : il termine orientarsi indica letteralmente la capacità di individuare l oriente e fa quindi riferimento alla possibilità di localizzare i quattro
ORIENTARSI sulla TERRA significato del termine orientarsi : il termine orientarsi indica letteralmente la capacità di individuare l oriente e fa quindi riferimento alla possibilità di localizzare i quattro
PROIEZIONI ORTOGONALI
 PROIEZIONI ORTOGONALI 104 Il metodo della doppia proiezione ortogonale Il metodo attualmente conosciuto come metodo delle proiezioni ortogonali (o proiezioni ortografiche) inizialmente nacque come metodo
PROIEZIONI ORTOGONALI 104 Il metodo della doppia proiezione ortogonale Il metodo attualmente conosciuto come metodo delle proiezioni ortogonali (o proiezioni ortografiche) inizialmente nacque come metodo
GIROSCOPIO. Scopo dell esperienza: Teoria fisica. Verificare la relazione: ω p = bmg/iω
 GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
Proiezioni cartografiche in uso in Italia
 Proiezioni cartografiche in uso in Italia Proiezioni cartografiche in uso in Italia Paolo Zatelli Dipartimento di Ingegneria Civile ed Ambientale Università di Trento Paolo Zatelli Università di Trento
Proiezioni cartografiche in uso in Italia Proiezioni cartografiche in uso in Italia Paolo Zatelli Dipartimento di Ingegneria Civile ed Ambientale Università di Trento Paolo Zatelli Università di Trento
FASCI DI RETTE. scrivere la retta in forma esplicita: 2y = 3x + 4 y = 3 2 x 2. scrivere l equazione del fascio di rette:
 FASCI DI RETTE DEFINIZIONE: Si chiama fascio di rette parallele o fascio improprio [erroneamente data la somiglianza effettiva con un fascio!] un insieme di rette che hanno tutte lo stesso coefficiente
FASCI DI RETTE DEFINIZIONE: Si chiama fascio di rette parallele o fascio improprio [erroneamente data la somiglianza effettiva con un fascio!] un insieme di rette che hanno tutte lo stesso coefficiente
Una carta geografica diversa la proiezione cartografica di Arno Peters
 Una carta geografica diversa la proiezione cartografica di Arno Peters Nella proiezione di Mercatore la Germania (patria elettiva del geografo) e l Europa si trovano al centro del mondo, sia in senso latitudinale
Una carta geografica diversa la proiezione cartografica di Arno Peters Nella proiezione di Mercatore la Germania (patria elettiva del geografo) e l Europa si trovano al centro del mondo, sia in senso latitudinale
CURVE DI LIVELLO. Per avere informazioni sull andamento di una funzione f : D IR n IR può essere utile considerare i suoi insiemi di livello.
 CURVE DI LIVELLO Per avere informazioni sull andamento di una funzione f : D IR n IR può essere utile considerare i suoi insiemi di livello. Definizione. Si chiama insieme di livello k della funzione f
CURVE DI LIVELLO Per avere informazioni sull andamento di una funzione f : D IR n IR può essere utile considerare i suoi insiemi di livello. Definizione. Si chiama insieme di livello k della funzione f
LEZIONI CON I PAD Docente scuola secondaria IC Moglia Carla Casareggio Classi seconde 2014/2015 Proprietà triangoli e quadrilateri con Sketchometry
 LEZIONI CON I PAD Docente scuola secondaria IC Moglia Carla Casareggio Classi seconde 2014/2015 Proprietà triangoli e quadrilateri con Sketchometry La costruzione di figure geometriche al computer con
LEZIONI CON I PAD Docente scuola secondaria IC Moglia Carla Casareggio Classi seconde 2014/2015 Proprietà triangoli e quadrilateri con Sketchometry La costruzione di figure geometriche al computer con
Inserimento di distanze e di angoli nella carta di Gauss
 Inserimento di distanze e di angoli nella carta di Gauss Corso di laurea in Ingegneria per l Ambiente e il Territorio a.a. 2006-2007 Inserimento della distanza reale misurata nella carta di Gauss (passaggio
Inserimento di distanze e di angoli nella carta di Gauss Corso di laurea in Ingegneria per l Ambiente e il Territorio a.a. 2006-2007 Inserimento della distanza reale misurata nella carta di Gauss (passaggio
LA LEGGE DI GRAVITAZIONE UNIVERSALE
 GRAVIMETRIA LA LEGGE DI GRAVITAZIONE UNIVERSALE r La legge di gravitazione universale, formulata da Isaac Newton nel 1666 e pubblicata nel 1684, afferma che l'attrazione gravitazionale tra due corpi è
GRAVIMETRIA LA LEGGE DI GRAVITAZIONE UNIVERSALE r La legge di gravitazione universale, formulata da Isaac Newton nel 1666 e pubblicata nel 1684, afferma che l'attrazione gravitazionale tra due corpi è
DOMINIO E LIMITI. Esercizio 3 Studiare gli insiemi di livello della funzione f, nei seguenti casi: 1) f(x,y) = y2 x 2 + y 2.
 FUNZIONI DI DUE VARIABILI 1 DOMINIO E LIMITI Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia (insiemi aperti, chiusi, limitati, convessi, connessi per archi; punti di
FUNZIONI DI DUE VARIABILI 1 DOMINIO E LIMITI Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia (insiemi aperti, chiusi, limitati, convessi, connessi per archi; punti di
Unità Didattica 3 ESERCITAZIONE IL PLASTICO. Unità Didattica 1 CURVE DI LIVELLO. Unità Didattica 2 PROFILO ALTIMETRICO
 ARGOMENTO INTERDISCIPLINARE: TECNOLOGIA-SCIENZE-GEOGRAFIA Unità Didattica 1 CURVE DI LIVELLO Unità Didattica 2 PROFILO ALTIMETRICO................................. Unità Didattica 3 ESERCITAZIONE IL PLASTICO
ARGOMENTO INTERDISCIPLINARE: TECNOLOGIA-SCIENZE-GEOGRAFIA Unità Didattica 1 CURVE DI LIVELLO Unità Didattica 2 PROFILO ALTIMETRICO................................. Unità Didattica 3 ESERCITAZIONE IL PLASTICO
LIVELLO STUDENT S1. S2. S3. S4. S5. S6.
 LIVELLO STUDENT S1. (5 punti ) La figura mostra due quadrati uguali che hanno in comune esattamente un vertice. È possibile precisare la misura dell'angolo ABC? S2. (7 punti ) Negli usuali fogli (rettangolari)
LIVELLO STUDENT S1. (5 punti ) La figura mostra due quadrati uguali che hanno in comune esattamente un vertice. È possibile precisare la misura dell'angolo ABC? S2. (7 punti ) Negli usuali fogli (rettangolari)
MANUALE di ISTRUZIONI
 1 MANUALE di ISTRUZIONI 2 L ORA NEL MONDO Tutti gli strumenti di misura vengono ideati per eseguire la misura e la lettura di una data grandezza fisica. Per misurare la lunghezza di un oggetto si userà
1 MANUALE di ISTRUZIONI 2 L ORA NEL MONDO Tutti gli strumenti di misura vengono ideati per eseguire la misura e la lettura di una data grandezza fisica. Per misurare la lunghezza di un oggetto si userà
Indici di dispersione
 Indici di dispersione 1 Supponiamo di disporre di un insieme di misure e di cercare un solo valore che, meglio di ciascun altro, sia in grado di catturare le caratteristiche della distribuzione nel suo
Indici di dispersione 1 Supponiamo di disporre di un insieme di misure e di cercare un solo valore che, meglio di ciascun altro, sia in grado di catturare le caratteristiche della distribuzione nel suo
Basi di matematica per il corso di micro
 Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
ENERGIA. Energia e Lavoro Potenza Energia cinetica Energia potenziale Principio di conservazione dell energia meccanica
 1 ENERGIA Energia e Lavoro Potenza Energia cinetica Energia potenziale Principio di conservazione dell energia meccanica 2 Energia L energia è ciò che ci permette all uomo di compiere uno sforzo o meglio
1 ENERGIA Energia e Lavoro Potenza Energia cinetica Energia potenziale Principio di conservazione dell energia meccanica 2 Energia L energia è ciò che ci permette all uomo di compiere uno sforzo o meglio
~ Copyright Ripetizionando - All rights reserved ~ http://ripetizionando.wordpress.com STUDIO DI FUNZIONE
 STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
Lo spessimetro ( a cura di Elena Pizzinini)
 Lo spessimetro ( a cura di Elena Pizzinini) 1) Che cos è? Lo spessivetro è uno strumento (brevettato dalla ditta Saint Gobain) dal funzionamento piuttosto semplice che permette di misurare lo spessore
Lo spessimetro ( a cura di Elena Pizzinini) 1) Che cos è? Lo spessivetro è uno strumento (brevettato dalla ditta Saint Gobain) dal funzionamento piuttosto semplice che permette di misurare lo spessore
Trasformazioni Geometriche 1 Roberto Petroni, 2011
 1 Trasformazioni Geometriche 1 Roberto etroni, 2011 Trasformazioni Geometriche sul piano euclideo 1) Introduzione Def: si dice trasformazione geometrica una corrispondenza biunivoca che associa ad ogni
1 Trasformazioni Geometriche 1 Roberto etroni, 2011 Trasformazioni Geometriche sul piano euclideo 1) Introduzione Def: si dice trasformazione geometrica una corrispondenza biunivoca che associa ad ogni
Sole. Instante 0. Rotazione della Terra
 AP 1 Misura della durata del giorno solare Scuola primaria secondo ciclo - MATERIALE OCCORRENTE Un solarscope Un cronometro o un orologio indicante ore, minuti e secondi Un foglio quadrettato (opzionale)
AP 1 Misura della durata del giorno solare Scuola primaria secondo ciclo - MATERIALE OCCORRENTE Un solarscope Un cronometro o un orologio indicante ore, minuti e secondi Un foglio quadrettato (opzionale)
PROGRAMMAZIONE ANNUALE DELL ATTIVITÀ DIDATTICA
 PROGRAMMAZIONE ANNUALE DELL ATTIVITÀ DIDATTICA EDUCAZIONE ALL AREA ANTROPOLOGICA Classe prima STORIA-GEOGRAFIA-STUDI SOCIALI 1)ORIENTARSI E COLLOCARE NELLO SPAZIO E NEL TEMPO FATTI ED EVENTI 1a) Ordinare
PROGRAMMAZIONE ANNUALE DELL ATTIVITÀ DIDATTICA EDUCAZIONE ALL AREA ANTROPOLOGICA Classe prima STORIA-GEOGRAFIA-STUDI SOCIALI 1)ORIENTARSI E COLLOCARE NELLO SPAZIO E NEL TEMPO FATTI ED EVENTI 1a) Ordinare
Qual è la distanza tra Roma e New York?
 Qual è la distanza tra Roma e New York? Abilità Conoscenze Nuclei coinvolti Utilizzare i vettori e il prodotto Elementi di geometria Spazio e figure scalare nello studio di problemi della sfera: del piano
Qual è la distanza tra Roma e New York? Abilità Conoscenze Nuclei coinvolti Utilizzare i vettori e il prodotto Elementi di geometria Spazio e figure scalare nello studio di problemi della sfera: del piano
Tecniche grafiche per il disegno a mano libera il segno espressivo
 Tecniche grafiche per il disegno a mano libera il segno espressivo Tecnica a tratto o di solo contorno textures e trattamenti di campo chiaroscuro acquerello Alcuni suggerimenti utili.. Una corretta postura
Tecniche grafiche per il disegno a mano libera il segno espressivo Tecnica a tratto o di solo contorno textures e trattamenti di campo chiaroscuro acquerello Alcuni suggerimenti utili.. Una corretta postura
SOLUZIONI D = (-1,+ ).
 SOLUZIONI. Data la funzione f() ( ) ln( ) a) trova il dominio di f b) indica quali sono gli intervalli in cui f() risulta positiva e quelli in cui risulta negativa c) determina le eventuali intersezioni
SOLUZIONI. Data la funzione f() ( ) ln( ) a) trova il dominio di f b) indica quali sono gli intervalli in cui f() risulta positiva e quelli in cui risulta negativa c) determina le eventuali intersezioni
ITIS Mattei Sondrio. Appunti veloci su moodle versione 2.7
 ITIS Mattei Sondrio Appunti veloci su moodle versione 2.7 Generalità Moodle è una piattaforma web per pubblicare corsi, creare test, depositare dispense ecc. Ci sono vari tipi di utenti che usano moodle:
ITIS Mattei Sondrio Appunti veloci su moodle versione 2.7 Generalità Moodle è una piattaforma web per pubblicare corsi, creare test, depositare dispense ecc. Ci sono vari tipi di utenti che usano moodle:
LA GRAFICA E LA GEOMETRIA OPERATIVA
 LA GRAFICA E LA GEOMETRIA OPERATIVA La geometria operativa, contrariamente a quella descrittiva basata sulle regole per la rappresentazione delle forme geometriche, prende in considerazione lo spazio racchiuso
LA GRAFICA E LA GEOMETRIA OPERATIVA La geometria operativa, contrariamente a quella descrittiva basata sulle regole per la rappresentazione delle forme geometriche, prende in considerazione lo spazio racchiuso
Ma cosa si pensava della forma della terra prima delle fotografie?
 Ma cosa si pensava della forma della terra prima delle fotografie? Anassimandro (IV sec. a.c.) Omero (VIII sec. a.c.?) Aristotele (384-322 a.c.) riportava due osservazioni a riprova della sfericità della
Ma cosa si pensava della forma della terra prima delle fotografie? Anassimandro (IV sec. a.c.) Omero (VIII sec. a.c.?) Aristotele (384-322 a.c.) riportava due osservazioni a riprova della sfericità della
La scuola integra culture. Scheda3c
 Scheda3c Gli ELEMENTI DEL CLIMA che caratterizzano le condizioni meteorologiche di una regione sono: la temperatura, la pressione atmosferica, i venti, l umidità e le precipitazioni. La temperatura è data
Scheda3c Gli ELEMENTI DEL CLIMA che caratterizzano le condizioni meteorologiche di una regione sono: la temperatura, la pressione atmosferica, i venti, l umidità e le precipitazioni. La temperatura è data
CONVESSITÀ NELLA GEOMETRIA DEL TAXI DI MINKOWSKI
 CONVESSITÀ NELLA GEOMETRIA DEL TAXI DI MINKOWSKI ELISABETTA AVIZZANO NICOLETTA CAPOTORTO CHIARA CEROCCHI GIORGIO CICCARELLA IVAN COLAVITA EMANUELE DI CARO SERENA NUNZIATA AMANDA PISELLI ANDREA PIEPOLI
CONVESSITÀ NELLA GEOMETRIA DEL TAXI DI MINKOWSKI ELISABETTA AVIZZANO NICOLETTA CAPOTORTO CHIARA CEROCCHI GIORGIO CICCARELLA IVAN COLAVITA EMANUELE DI CARO SERENA NUNZIATA AMANDA PISELLI ANDREA PIEPOLI
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
1 Gli effetti della forza di Coriolis
 LA FORZA DI CORIOLIS di Giulio Mazzolini 2012 1 Gli effetti della forza di Coriolis È un effetto noto che i venti nell emisfero nord deviano sempre verso destra, invece nell emisfero sud deviano sempre
LA FORZA DI CORIOLIS di Giulio Mazzolini 2012 1 Gli effetti della forza di Coriolis È un effetto noto che i venti nell emisfero nord deviano sempre verso destra, invece nell emisfero sud deviano sempre
INTEGRALI DEFINITI. Tale superficie viene detta trapezoide e la misura della sua area si ottiene utilizzando il calcolo di un integrale definito.
 INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
Slide Cerbara parte1 5. Le distribuzioni teoriche
 Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
Progetti SCRUTANDO IL CIELO DEL PARCO
 Progetti SCRUTANDO IL CIELO DEL PARCO Sin dai tempi più remoti il cielo ha avuto grande importanza per l uomo. Il cielo è testimone di miti, di leggende di popoli antichi; narra di terre lontane, di costellazioni
Progetti SCRUTANDO IL CIELO DEL PARCO Sin dai tempi più remoti il cielo ha avuto grande importanza per l uomo. Il cielo è testimone di miti, di leggende di popoli antichi; narra di terre lontane, di costellazioni
Funzioni funzione dominio codominio legge argomento variabile indipendente variabile dipendente
 Funzioni In matematica, una funzione f da X in Y consiste in: 1. un insieme X detto dominio di f 2. un insieme Y detto codominio di f 3. una legge che ad ogni elemento x in X associa uno ed un solo elemento
Funzioni In matematica, una funzione f da X in Y consiste in: 1. un insieme X detto dominio di f 2. un insieme Y detto codominio di f 3. una legge che ad ogni elemento x in X associa uno ed un solo elemento
DISEGNO DI MACCHINE APPUNTI DELLE LEZIONI
 DISEGNO DI MACCHINE APPUNTI DELLE LEZIONI Lezione 3: Proiezioni Ortogonali con il metodo europeo Francesca Campana Le proiezioni ortogonali Le proiezioni ortogonali descrivono bi-dimensionalmente un oggetto
DISEGNO DI MACCHINE APPUNTI DELLE LEZIONI Lezione 3: Proiezioni Ortogonali con il metodo europeo Francesca Campana Le proiezioni ortogonali Le proiezioni ortogonali descrivono bi-dimensionalmente un oggetto
Soluzione di equazioni quadratiche
 Soluzione di equazioni quadratiche Soluzione sulla Retta Algebrica Inseriamo sulla Retta Algebrica le seguenti espressioni polinomiali x e x 3 e cerchiamo di individuare i valori di x per i quali i punti
Soluzione di equazioni quadratiche Soluzione sulla Retta Algebrica Inseriamo sulla Retta Algebrica le seguenti espressioni polinomiali x e x 3 e cerchiamo di individuare i valori di x per i quali i punti
L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare
 L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare Cap.4 giroscopio, magnetismo e forza di Lorentz teoria del giroscopio Abbiamo finora preso in considerazione le condizionidi equilibrio
L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare Cap.4 giroscopio, magnetismo e forza di Lorentz teoria del giroscopio Abbiamo finora preso in considerazione le condizionidi equilibrio
Analisi sensitività. Strumenti per il supporto alle decisioni nel processo di Valutazione d azienda
 Analisi sensitività. Strumenti per il supporto alle decisioni nel processo di Valutazione d azienda Premessa Con l analisi di sensitività il perito valutatore elabora un range di valori invece di un dato
Analisi sensitività. Strumenti per il supporto alle decisioni nel processo di Valutazione d azienda Premessa Con l analisi di sensitività il perito valutatore elabora un range di valori invece di un dato
a) Si descriva, internamente al triangolo, con centro in B e raggio x, l arco di circonferenza di π π
 PROBLEMA Il triangolo rettangolo ABC ha l ipotenusa AB = a e l angolo CAB =. a) Si descriva, internamente al triangolo, con centro in B e raggio, l arco di circonferenza di estremi P e Q rispettivamente
PROBLEMA Il triangolo rettangolo ABC ha l ipotenusa AB = a e l angolo CAB =. a) Si descriva, internamente al triangolo, con centro in B e raggio, l arco di circonferenza di estremi P e Q rispettivamente
G3. Asintoti e continuità
 G3 Asintoti e continuità Un asintoto è una retta a cui la funzione si avvicina sempre di più senza mai toccarla Non è la definizione formale, ma sicuramente serve per capire il concetto di asintoto Nei
G3 Asintoti e continuità Un asintoto è una retta a cui la funzione si avvicina sempre di più senza mai toccarla Non è la definizione formale, ma sicuramente serve per capire il concetto di asintoto Nei
VOLUME 3 CAPITOLO 1 MODULO D LE VENTI REGIONI ITALIANE. Alla fine del capitolo scrivi il significato di queste parole nuove: ... ... ... ... ... ...
 IL SOLE VOLUME 3 CAPITOLO 1 MODULO D LE VENTI REGIONI ITALIANE 1. Paroe per capire Aa fine de capitoo scrivi i significato di queste paroe nuove: Soe... fotosintesi corofiiana. stagioni... pianeti... orbita...
IL SOLE VOLUME 3 CAPITOLO 1 MODULO D LE VENTI REGIONI ITALIANE 1. Paroe per capire Aa fine de capitoo scrivi i significato di queste paroe nuove: Soe... fotosintesi corofiiana. stagioni... pianeti... orbita...
Bartoccini Marco 3 A
 Bartoccini Marco 3 A Le persone e le cose possono stare ferme oppure muoversi,e quando si muovono possono farlo a diverse velocità.il movimento si svolge nello spazio e nel tempo: esso infatti copre una
Bartoccini Marco 3 A Le persone e le cose possono stare ferme oppure muoversi,e quando si muovono possono farlo a diverse velocità.il movimento si svolge nello spazio e nel tempo: esso infatti copre una
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
La spirale iperbolica: Fu descritta per la prima volta da Pierre Varignon (1654-1722). L equazione, espressa in coordinate polari, è del tipo:
 Esistono delle forme geometriche che sono in grado, per complessi fattori psicologici non del tutto chiariti, di comunicarci un senso d equilibrio, di gradimento e di benessere. Tra queste analizzeremo
Esistono delle forme geometriche che sono in grado, per complessi fattori psicologici non del tutto chiariti, di comunicarci un senso d equilibrio, di gradimento e di benessere. Tra queste analizzeremo
INdAM QUESITI A RISPOSTA MULTIPLA
 INdAM Prova scritta per il concorso a 40 borse di studio, 2 borse aggiuntive e a 40 premi per l iscrizione ai Corsi di Laurea in Matematica, anno accademico 2011/2012. Piano Lauree Scientifiche. La prova
INdAM Prova scritta per il concorso a 40 borse di studio, 2 borse aggiuntive e a 40 premi per l iscrizione ai Corsi di Laurea in Matematica, anno accademico 2011/2012. Piano Lauree Scientifiche. La prova
I COLORI DEL CIELO: COME SI FORMANO LE IMMAGINI ASTRONOMICHE
 I COLORI DEL CIELO: COME SI FORMANO LE IMMAGINI ASTRONOMICHE Nell ultima notte di osservazione abbiamo visto bellissime immagini della Galassia, delle sue stelle e delle nubi di gas che la compongono.
I COLORI DEL CIELO: COME SI FORMANO LE IMMAGINI ASTRONOMICHE Nell ultima notte di osservazione abbiamo visto bellissime immagini della Galassia, delle sue stelle e delle nubi di gas che la compongono.
V= R*I. LEGGE DI OHM Dopo aver illustrato le principali grandezze elettriche è necessario analizzare i legami che vi sono tra di loro.
 LEGGE DI OHM Dopo aver illustrato le principali grandezze elettriche è necessario analizzare i legami che vi sono tra di loro. PREMESSA: Anche intuitivamente dovrebbe a questo punto essere ormai chiaro
LEGGE DI OHM Dopo aver illustrato le principali grandezze elettriche è necessario analizzare i legami che vi sono tra di loro. PREMESSA: Anche intuitivamente dovrebbe a questo punto essere ormai chiaro
