1.7 Densità e misure assolutamente continue
|
|
|
- Gennara Rossetti
- 5 anni fa
- Visualizzazioni
Transcript
1 1.7 Densità e misure assolutamente continue Possiamo ora dare la definizione generale di densità. Prendiamo uno spazio misurato (,, µ), dove µ è una misura (non necessariamente di probabilità). Se f : R + è una funzione misurabile tale che f dµ = 1, possiamo definire una misura di probabilità P su (, ) in questo modo: P(A) = f dµ A A La P si chiama probabilità di densità f (rispetto a µ), e si può indicare con le notazioni P = f µ, oppure dp dµ = f Questo concetto è molto usato nel calcolo delle probabilità. sempio 1.46 Una prima applicazione si ha quando è un aperto di R d, = B() e µ è la misura di Lebesgue d-dimensionale. Allora P si dice probabilità (o legge) assolutamente continua (e si sottintende quasi sempre rispetto alla misura di Lebesgue ) di densità f. sempio 1.47 Un altra applicazione, a prima vista meno evidente, si ha con le leggi discrete. Possiamo definire infatti una probabilità discreta definendo sull insieme la cosiddetta misura che conta i punti, definita da µ(a) = Card (A) A Ovviamente questa misura non è una misura di probabilità. Se p : [0,1] è tale che p(x) = 1, possiamo definire x P = p µ, oppure Per questo motivo, p viene detta densità discreta di P. dp dµ = p, sempio 1.48 Sia (Ω, A, P) uno spazio probabilizzato e H un evento non trascurabile di A. Si nota facilmente che la probabilità condizionata P H = P( H) può essere ottenuta da P tramite la densità 1 H /P(H): difatti per ogni A A si ha A 1 H P(H) dp = A H 1 P(H) dp = P(A H) P(H) = P H (A) La conseguenza è quindi che P H ( ) = P( H) è una nuova misura di probabilità su (Ω, A). Diamo ora la seguente definizione. Definizione 1.49 Date due misure µ, ν su (, ), diciamo che ν è assolutamente continua rispetto a µ (e indichiamo questo con ν << µ) se µ(a) = 0 implica ν(a) = 0. Diciamo poi che ν è equivalente a µ (e lo indichiamo con ν µ) se ν << µ e µ << ν. 17
2 Un caso che abbiamo appena visto è quello di misure definite da una densità. Infatti, se ν ha densità f rispetto a µ, allora ν << µ. Per provarlo, se µ(a) = 0 si ha che ν(a) = f dµ = 0 A Questa situazione sembra solo un esempio, ma è in realtà molto significativo. Infatti l esistenza di una densità non è solo una condizione sufficiente, ma anche necessaria per l assoluta continuità, come mostra il seguente teorema, che citiamo omettendo la dimostrazione. Teorema 1.50 (Radon-Nykodim) Se µ e ν sono misure σ-finite su (, ) e ν << µ, allora esiste un unica f L + (,,µ) tale che ν = f µ, o anche f = dν dµ. La funzione f si può chiamare, oltre che densità, anche derivata di Radon-Nykodim di ν rispetto a µ. Una domanda naturale a questo punto è la seguente: che relazione hanno gli integrali calcolati rispetto a una misura ν, che abbia densità f rispetto a un altra misura µ, rispetto agli integrali calcolati rispetto a µ? La risposta è fornita nella seguente Proposizione 1.51 Se g è una funzione misurabile reale su (, ), e µ, ν sono due misure su (, ) tali che ν = f µ, allora g(x) ν(dx) = g(x)f(x) µ(dx) valida ogni volta che uno dei membri abbia senso. Dimostrazione. Si procede come al solito, supponendo all inizio che g sia semplice ed estendendo il risultato prima a funzioni semplici, poi a funzioni positive ed infine a funzioni integrabili. In particolare, supponiamo all inizio che g = n a i1 Ai, con a i R, A i : allora n n n g dν = a i 1 {X Ai } dν = a i ν(a i ) = a i f dµ = A i = n a i 1 Ai f dµ = gf dµ Se g L + ma non è necessariamente semplice, allora esistono (g n ) n L + e semplici tali che g n ր g. Allora, usando due volte il teorema di convergenza monotona, g dν = lim g n dν = lim g n dν = lim g n f dµ = gf dµ n n n Infine, se g L 1, allora scriviamo g = g + g, e si ha g dν = g + dν g dν = g + f dµ g f dµ = gf dµ 18
3 La prima applicazione di questo risultato è il calcolo della speranza di una variabile aleatoria X rispetto ad una probabilità condizionata P H, con H A non trascurabile: abbiamo difatti visto che P H ha densità rispetto a P uguale a 1 H P(H). Allora, se X ha speranza finita, abbiamo PH [X] = X dp H = X 1 [ H P(H) dp = P X 1 ] H = P[X1 H ] P(H) P(H) e resta quindi dimostrata la formula (1.1). Ω 1.8 Legge di una variabile aleatoria Ω Nel paragrafo precedente abbiamo visto che la speranza matematica di una variabile aleatoria non è altro che il suo integrale sullo spazio probabilizzato su cui è definita. Per calcolare concretamente questo valore, tuttavia, questa definizione potrebbe risultare scomoda (ad esempio perchè lo spazio Ω ha una struttura molto complessa), e potrebbero esserci dei modi più semplici. In questo paragrafo vedremo che il calcolo del valore atteso di una variabile aleatoria (o più in generale di una sua funzione misurabile ) può essere ricondotto all integrale su un opportuno spazio misurabile. Il primo risultato è il seguente. Se X è una variabile aleatoria da (Ω, A, P) a valori in (, ), e g è una funzione misurabile reale su (, ), possiamo chiederci quanto vale [g(x)] (se questa quantità è ben definita). Proposizione 1.52 (formula della speranza di una funzione composta) Se X è una variabile aleatoria su (Ω, A, P) a valori in (, ) di legge P X e g è una funzione misurabile reale su (, ), allora [g(x)] = g(x) dp X (x) valida ogni volta che uno dei membri abbia senso. Dimostrazione. Supponiamo all inizio che g = n a i1 Ai, con a i R, A i : allora [ n ] n n [g(x)] = a i 1 {X Ai } = a i P{X A i } = a i P X (A i ) = g(x) dp X (x) Se g L + (,, P X ) ma non è necessariamente semplice, allora esistono (g n ) n L + (,, P X ) e semplici tali che g n ր g. Allora si ha anche che g n (X) ր g(x), e usando due volte il teorema di convergenza monotona (la prima su (Ω, A, P) e la seconda su (,, P X )) si ha [g(x)] = lim [g n(x)] = lim g n (x) dp X (x) = g(x) dp X (x) n n 19
4 Infine, se g L 1 (,, P X ), allora scriviamo g = g + g, e si ha anche che g(x) = g + (X) g (X) L 1 (Ω, A, P); allora [g(x)] = [g + (X)] [g (X)] = g + (x) dp X (x) g (x) dp X (x) = g(x) dp X (x) Una prima applicazione della formula della speranza di una funzione composta nel caso di variabili aleatorie reali è con la funzione g(x) = x. Se X è una variabile aleatoria reale, allora la formula della speranza di una funzione composta ci dà il risultato [X] = x dp X (x) R che permette di ricondurre il calcolo della speranza di una variabile aleatoria definita sullo spazio Ω (che a priori può essere molto complicato) al calcolo di un integrale sulla retta reale. Due applicazioni immediate di questo risultato sono le seguenti. sempio 1.53 (vettori aleatori continui) Un vettore aleatorio n-dimensionale X si dice continuo se la sua legge P X ha densità f rispetto alla misura di Lebesgue λ n. Allora, per quanto appena visto, per ogni funzione g : R tale che una delle due espressioni seguenti abbia senso, vale [g(x)] = g(x) dp X (x) = R n g(x)f(x) dλ n (x) R n sempio 1.54 (vettori aleatori discreti) Se invece X è una variabile aleatoria discreta a valori in un insieme, con densità discreta p X : [0,1], allora abbiamo visto che possiamo considerare p X la densità di P X rispetto alla misura µ che conta i punti. Allora, per ogni funzione g : R tale che una delle espressioni seguenti abbia senso, vale [g(x)] = g(x)p X (x) dµ(x) = g(x)p X (x) x Considerando che la legge di X si può rappresentare come x p X(x)δ x, si può scrivere la formula precedente come [g(x)] = p X (x) g(y) dδ x (y) x Questa è una proprietà generale: se infatti la legge di X è una combinazione lineare (anche infinita) di leggi, allora anche la speranza di funzioni di X si calcola allo stesso modo. Teorema 1.55 Se P X = n=1 p np n, con (p n ) n numeri reali non negativi e di somma unitaria e P n misure di probabilità su (, ), allora [g(x)] = p n g(y) dp n (y) n=1 20
5 Dimostrazione. La dimostrazione è simile a quella della formula della speranza della funzione composta: prima si considerano funzioni della forma g(x) = 1 A, con A. Per linearità, il teorema è vero per ogni g semplice; per monotonia si estende ad ogni g L +, e considerando la decomposizione in parte positiva e parte negativa la relazione è valida per ogni g tale che g(x) è integrabile. 1.9 Misure di Borel sulla retta reale In questa sezione costruiremo misure su (R, B(R)). Queste misure si chiamano misure di Borel su R. Da qui in poi considereremo intervalli aperti a sinistra e chiusi a destra su R, cioé della forma (a, b], oppure (a, + ), oppure, con a b < ; chiamiamo questi intervalli h-intervalli (h sta per half-open). Prendiamo ora una funzione F : R R crescente (nel senso di non decrescente). Diciamo che F é continua a destra se per ogni a R si ha F(a) = lim x a + F(x) Inoltre esistono i limiti F(+ ) = lim x + F(x) e F( ) = lim x F(x) (e possono essere finiti o infiniti). Vogliamo ora definire una misura µ a partire da F in modo che µ((a,b]) = F(b) F(a) Questo è possibile in virtù del seguente risultato. Teorema 1.56 Se F è crescente e c.a d., allora esiste un unica misura µ F su B(R) tale che µ F ((a,b]) = F(b) F(a) per ogni a,b R, a < b. Se G è un altra funzione crescente e c.a d., allora µ F = µ G se e solo se G F è costante. Viceversa, se µ è una misura su B(R) finita su ogni boreliano limitato e definiamo µ((0,x]) se x > 0 F(x) = 0 se x = 0 µ((x,0]) se x < 0 allora F è c.a d. e crescente, e µ = µ F. Infine, µ F si può estendere a una misura completa µ F che è definita su una σ-algebra che in generale contiene B(R). Queste misure vengono comunemente chiamate misure di Lebesgue-Stieltjes. Facciamo ora alcune note. 1. Questo risultato si sarebbe potuto ottenere anche considerando intervalli del tipo [a, b) e funzioni F continue a sinistra. 2. Se µ è una misura di probabilità su (R, B(R)), e poniamo F(x) = µ((, x]), allora µ = µ F. La F si chiama allora funzione di ripartizione cumulativa di µ. 21
6 sempio 1.57 (misura di Lebesgue) Se F(x) = x, allora otteniamo che µ((a, b]) = b a. Questa misura coincide con l usuale misura di Riemann sulle unioni finite di intervalli (ma ricordiamo che ha come dominio B(R)) e si chiama misura di Lebesgue. sempio 1.58 (misure assolutamente continue rispetto a Lebesgue) Consideriamo f : R R + misurabile e tale che R f(x) dx = 1, e definiamo F(x) := x f(t) dt Questa funzione di ripartizione è una funzione assolutamente continua. Allora F definisce una misura di probabilità µ F su (R, B(R)) tale che µ F ([a,b)) = µ F ((a,b)) = µ F ((a,b]) = µ F ([a,b]) := b a f(t) dt µ F ha quindi f come densità rispetto alla misura di Lebesgue. Le misure di questo tipo si dicono misure assolutamente continue (rispetto alla misura di Lebesgue). sempio 1.59 (misure discrete su R) Consideriamo p : R [0,1] tale che x R p(x) = 1, e definiamo F(x) := p(t) Questa funzione di ripartizione è costante a tratti. Allora F definisce una misura di probabilità µ F su (R, P(R)) (e quindi in particolare su (R, B(R)) tale che µ F ((a,b]) = p(t) t x a<t b Facciamo notare che il dominio di µ F in generale contiene B(R). Per vedere questo in un caso semplice, basta considerare la funzione F = 1 {x 0}. Allora µ F = δ 0 è la delta di Dirac nel punto 0 e il completamento é definito su tutta la σ-algebra P(R). Infatti abbiamo che δ 0 (R \ {0}) = 0, quindi è possibile estendere δ 0 ad ogni sottoinsieme di R \ {0} assegnandogli misura nulla. Un altro esempio è dato dalle misure discrete viste sopra. Questi fenomeni possono sembrare patologie tipiche delle misure discrete, ma in realtà riguardano tutte le misure usate comunemente, e in particolare la misura di Lebesgue m (e quindi tutte le misure assolutamente continue!). Infatti anche essa può essere estesa ad una σ-algebra più grande di B(R), che chiameremo L Funzione di ripartizione, pseudoinversa e quantili Analizziamo ora il caso particolare in cui X è una variabile aleatoria reale. In questo caso P X è una misura di probabilità su (R, B(R)), e abbiamo visto che è caratterizzata da F X (t) := P X ((,t]) = P{X t} che prende il nome di funzione cumulativa di distribuzione (o di ripartizione) di X. Abbiamo visto che la corrispondenza tra funzioni crescenti e continue a destra e misure è biunivoca. Si può inoltre dimostrare il seguente risultato. 22
7 Teorema 1.60 Se una funzione F è crescente e continua a destra e tale che lim t F(t) = 0, lim t + F(t) = 1, allora esiste una variabile aleatoria reale X, definita sullo spazio (Ω, A, P) = ((0,1), B((0,1)),λ) (dove λ è la misura di Lebesgue su (0,1)), tale che la sua funzione di ripartizione è F. Dimostrazione. Definiamo, per ogni ω Ω, la funzione Allora abbiamo che X(ω) := min{x R F(x) ω} (1.3) {X > t} = {ω X(ω) > t} = {ω F(t) < ω} = (F(t),1) B((0,1)) = A e quindi X è una variabile aleatoria. Inoltre, se definiamo F X (t) := P{X t}, allora per ogni t R F X (t) = P{X t} = 1 P{X > t} = 1 P(F(t),1) = F(t) = F(t) e quindi abbiamo la tesi. La variabile aleatoria X : (0,1) R definita nell quazione (1.3) prende anche il nome di pseudoinversa della funzione di ripartizione F, e si indica con F 1. Se F è invertibile, allora F 1 è in effetti l inversa di F. In generale, per ogni u > 0 e ogni coppia di numeri reali a < b, abbiamo poi l equivalenza F(a) < u F(b) a < F 1 (u) b (questo si può verificare sia tramite la definizione, sia grazie al precedente teorema). Grazie al teorema, si ha che la legge di F 1, che non è altro che µ F, è l immagine della misura di Lebesgue tramite F 1. Grazie al teorema, si ha che la legge di F 1, che non è altro che µ F, è l immagine della misura di Lebesgue tramite F 1. Per la formula della speranza di una funzione composta, questo significa che per ogni funzione reale g integrabile rispetto a µ F, si ha R g dµ F = [g(x)] = [g(f 1 )] = 1 0 g(f 1 (u)) du quindi, ogni integrale rispetto ad una generica misura µ sulla retta può essere ricondotto ad un integrale rispetto alla misura di Lebesgue. Notiamo poi che la funzione F 1 risolve il seguente problema: data una variabile aleatoria X con funzione di ripartizione F e una soglia di probabilità α (0,1), qual è il minimo numero reale t tale che P{X t} = F(t) α? Tale numero t si chiama quantile di livello α di X, e si indica genericamente con q α. Per come abbiamo costruito F 1, abbiamo semplicemente che q α = F 1 (α). 23
8 1.11 Indipendenza Innanzitutto richiamiamo la nozione di indipendenza tra due eventi. Definizione 1.61 Sia (Ω, A, P) uno spazio probabilizzato e A,B A. Diciamo che A e B sono indipendenti se P(A B) = P(A)P(B) Ovviamente, se almeno uno dei due eventi è trascurabilie, la relazione si riduce a 0 = 0. Vediamo ora come la nozione di indipendenza si può trasferire a variabili aleatorie e a σ-algebre. Definizione 1.62 Sia (Ω, A, P) uno spazio probabilizzato e X : (Ω, A, P) (, ) e Y : (Ω, A, P) (F, F) due variabili aleatorie. Diciamo che X e Y sono indipendenti se, per ogni A e B F, gli eventi {X A} e {Y B} sono indipendenti, cioè se si ha: P{X A}P{Y B} = P{X A,Y B} (1.4) Nota 1.63 Due eventi A,B A sono indipendenti se e solo se 1 A e 1 B lo sono. Dalla definizione, per verificare che X e Y sono indipendenti bisognerebbe effettuare il controllo su ogni possibile coppia di eventi delle loro σ-algebre di arrivo, cosa che a volte può risultare scomoda. Vediamo ora un risultato che permette di limitare questo controllo ad un numero minore di casi. Teorema 1.64 (criterio di indipendenza fondato su due basi) Siano X : (Ω, A, P) (, ) e Y : (Ω, A, P) (F, F) due variabili aleatorie, e siano H una base di e K una base di F. Allora X e Y sono indipendenti se e solo se l quazione (1.4) vale per ogni A H,B K. Dimostrazione. L implicazione solo se è banale. Per dimostrare l implicazione se, procederemo in due passi: nel primo dimostreremo che, se (1.4) vale per ogni A H,B K, allora vale per ogni A H,B F. Fissiamo infatti A H. Se A è trascurabile, allora (1.4) è banalmente verificata, altrimenti (1.4) è equivalente a P{Y B} = P{X A,Y B} P{X A} = P({Y B} {X A}) B K In questa uguaglianza compaiono due misure di probabilità su (F, F): una è la legge di Y, e l altra è la legge di Y condizionata all evento {X A}. Siccome K è una base di F, da questo si deduce che le due leggi coincidono su F. Abbiamo quindi ottenuto che (1.4) vale per ogni A H,B F. Con un ragionamento analogo si riesce a dimostrare che (1.4) vale per ogni A,B F. Presentiamo ora la definizione di indipendenza di σ-algebre. 24
9 Definizione 1.65 Due σ-algebre A e B su Ω si dicono indipendenti se e solo se per ogni A A, B B, gli eventi A e B sono indipendenti. Ovviamente il criterio di indipendenza relativo a due basi si può estendere a questo caso: se due σ-algebre sono generate da due basi, per verificare la loro indipendenza occorre e basta verificare l indipendenza su ogni coppia di eventi delle due basi. Notiamo infine che due variabili aleatorie X e Y sono indipendenti se e solo se le loro σ-algebre generate σ(x) e σ(y ) sono indipendenti. A causa di tutte queste equivalenze, non è difficile interpretare espressioni come indipendenza di variabili aleatorie e/o di eventi da eventi e/o da σ-algebre. Vediamo ora come il concetto di indipendenza si possa estendere ad un insieme di più di due oggetti. Presentiamo la definizione solo per le variabili aleatorie poichè, a causa dell equivalenza appena vista, la cosa si può facilmente estendere al caso di σ-algebre e di eventi. Definizione 1.66 Sia (X i ) i I una famiglia di variabili aleatorie definite sullo stesso spazio probabilizzato (a valori in spazi misurabili eventualmente diversi). Diciamo che le X i sono indipendenti (o che (X i ) i I è una famiglia di variabili aleatorie indipendenti) se, comunque si prendano H,K I disgiunti e non vuoti, si abbia che σ(x i i H) è indipendente da σ(x i i K). Possiamo vedere una famiglia di variabili aleatorie (X i ) i I come un unica variabile aleatoria X a valori nello spazio prodotto ( i I i, i I i ), definita in questo modo: X(ω) := (X i (ω)) i I Con una tale identificazione, la legge della variabile aleatoria X si dice legge congiunta della famiglia (X i ) i I, mentre per ogni indice i I la legge di X i si dice legge marginale i-esima della famiglia (X i ) i I. Inoltre, risulta che (X i ) i I è una famiglia di variabili aleatorie indipendenti se e solo se, comunque si prendano H, K I disgiunti e non vuoti, si abbia che X H := (X h ) h H è indipendente da X K := (X k ) k K. Teorema 1.67 (criterio fondamentale d indipendenza) Sia (X i ) i I una famiglia di variabili aleatorie definite sullo stesso spazio probabilizzato a valori rispettivamente negli spazi ( i, i ). Le due condizioni sono equivalenti: 1. le X i sono indipendenti; 2. la legge congiunta di X = (X i ) i I è uguale alla legge prodotto delle leggi marginali, cioè si ha che { P X } A i = P{X i A i } i I i I per ogni famiglia (A i ) i I con A i i e A i i per i J con J I finito. Dimostrazione. 25
10 1 2) Se J < 2 non c è niente da dimostrare. Se J 2, allora possiamo dividere J = H K, con H e K disgiunti e non vuoti: per definizione di indipendenza si ha allora { P X } A i = P ( j A j } = P {X h A h } i I j J{X ) {X k A k } = h H k K ( ) ( ) = P {X h A h } P {X k A k } h H Ora, H e K hanno cardinalità minore di J, e quindi la tesi si ottiene per induzione sulla cardinalità di J. 2 1) Per ogni H,K I non vuoti e disgiunti, le variabili aleatorie X H := (X h ) h H e X K := (X k ) k K sono indipendenti poichè soddisfano il criterio 1.64, con H e K date rispettivamente da { } H := A h A h h,a h h per un n. finito di h H, K := h H k K { } A k A k k,a k k per un n. finito di k K. k K Difatti per ogni h H A h H, k K A k K si ha { P X H A h,x K } A k = P{X h A h } P{X k A K } = h H k K h H k K { = P X H } { A h P X K } A k h H k K Vediamo infine un utile criterio di calcolo relativo all indipendenza: se (X i ) i I è una famiglia di variabili aleatorie indipendenti a valori rispettivamente in ( i, i ), e g i sono funzioni misurabili definite su ( i, i ), allora anche le variabili aleatorie g i (X i ) sono indipendenti. Inoltre, se le g i sono funzioni misurabili reali, per ogni J I finito si ha che [ ] g i (X i ) = [g i (X i )] i J i J ogniqualvolta uno dei due membri sia definito. Questo risultato è parente stretto del seguente risultato di teoria della misura, che permette di calcolare gli integrali rispetto a una misura prodotto (come quello al primo membro) in termini di integrali delle singole componenti. 26
11 Teorema 1.68 (Fubini - Tonelli) Supponiamo che (,, µ) e (F, F, ν) siano spazi misurati, con µ e ν misure σ-finite. Allora: Fubini: se f L 1 ( F, F,µ ν), allora f(x, ) L 1 (F, F,ν) per q.o. x, f(,y) L 1 (,,µ) per q.o. y F, le funzioni (definite q.o.) F f(x, ) dν e X f(,y) dµ sono rispettivamente in L 1 (,,µ) e in L 1 (F, F,ν) e vale ( ) f(x,y) d(µ ν)(x,y) = f(x, y) dν(y) dµ(x) = (1.5) F F ( ) = f(x, y) dµ(x) dν(y) Tonelli: se f L + ( F, F,µ ν), allora le funzioni F f(x, ) dν e f(,y) dµ sono rispettivamente in L + (,,µ) e in L + (F, F,ν) e vale la (1.5). Per induzione, è possibile calcolare l integrale di una funzione su uno spazio prodotto n-dimensionale iterando gli integrali su ogni componente. Il legame con la formula vista sopra è il seguente: se ad esempio le g i sono limitate, allora (per facilità di notazione, supponiamo che J = {1,..., n}) [ ] g i (X i ) = g 1 (x 1 ) g n (x n ) dp X = i J 1... n n n = g 1 (x 1 ) g n (x n ) d(p X1... P Xn ) = g i dp Xi = [g i (X i )] 1... n i Un altra utile applicazione del teorema di Tonelli è la seguente. Supponiamo che le variabili aleatorie indipendenti X 1,...,X n assumano valori rispettivamente in ( i, i ), i = 1,...,n con leggi µ i aventi densità f i rispetto a misure ν i su ( i, i ). Allora la legge del vettore aleatorio X = (X 1,...,X n ), che per quanto visto sopra è data dalla misura prodotto n µ i, ha densità n f i rispetto alla misura n ν i. Per verificarlo, basta considerare la base della σ-algebra prodotto costituita da I := { n A i A i i }: per ogni n A i I si ha { } n n n n P X A i = P{X i A i } = µ i (A i ) = f i dν i A i e, siccome n f i L + ( 1... n ), per il teorema di Tonelli si ha Q n A i F n f i dν 1... ν n = n A i f i dν i e quindi ( n ) µ 1... µ n = f i ν 1... ν n 27
12 1.12 Vettori aleatori Si chiama vettore aleatorio a valori in R d una variabile aleatoria X = (X 1,...,X d ) a valori nello spazio misurabile (R d, B(R d )). Chiaramente questo significa che ogni componente X i, i = 1,...,d è una variabile aleatoria reale. Dato un vettore aleatorio, la sua legge P X su (R d, B(R d )) si dice legge congiunta di X, mentre la legge P Xi della componente X i si dice i-esima legge marginale per ogni i = 1,...,d. Se X è un vettore aleatorio formato da componenti indipendenti, ovviamente la legge congiunta è il prodotto delle leggi marginali. Più in generale, il legame tra legge congiunta e leggi marginali è il seguente: per ogni i = 1,...,d, A i B(R), abbiamo che d P Xi (A i ) = P X j=1 B j, dove B j := Difatti, con le notazioni appena viste, P Xi (A i ) = P{X i A i } = P X { Ai se j = i, R se j i. sempio 1.69 (vettori aleatori discreti) Supponiamo che X sia un vettore aleatorio discreto, con densità discreta p X. Allora la formula sopra permette di recuperare la nota formula per le densità discrete marginali p Xi (x i ) = p X (x) x 1,...,ˆx i,...,x d Se difatti per ogni x i R tale che P{X i = x i } > 0 poniamo A i := {x i }, con le notazioni sopra abbiamo che d p Xi (x i ) = P{X i A i } = P X = p X (x) = j=1 B j x Q d j=1 B j d j=1 B j x 1,...,ˆx i,...,x d p X (x) sempio 1.70 (vettori aleatori continui) Supponiamo che X sia un vettore aleatorio continuo, con densità f X rispetto alla misura di Lebesgue d-dimensionale λ d. Allora la formula sopra permette di recuperare una analoga della formula per le densità discrete marginali: difatti, per ogni A B(R) e per i = 1,...,d, applicando il teorema di Tonelli si ha P{X i A} = f X dλ d = R... A... R ( ) = f X (x 1,...,x d ) dλ d 1 (x 1,..., ˆx i,...,x d ) dλ 1 (x i ) A R d 1 e quindi X i ammette come densità rispetto alla misura di Lebesgue la funzione f Xi (t) := f X (x 1,...,t,...,x d ) dλ d 1 (x 1,..., ˆx i,...,x d ) R d 1 28
13 La conseguenza del precedente esempio è che, nota la densità congiunta di un vettore aleatorio continuo, è possibile ricavarne le marginali. Il viceversa è però vero solo nel caso di vettori aleatori con componenti indipendenti, in cui la legge congiunta è uguale al prodotto delle leggi marginali e quindi (vedi risultato alla fine della sezione precedente) la densità congiunta è uguale al prodotto delle densità marginali. Nel caso in cui un vettore aleatorio non abbia componenti indipendenti non è nemmeno detto che, anche se le componenti ammettono una densità marginale, il vettore aleatorio ammetta una densità congiunta. sempio 1.71 Consideriamo Y U(0,1) e definiamo il vettore aleatorio X = (X 1,X 2 ) := (Y,Y ). Allora entrambe le componenti di X ammettono come densità 1 (0,1) rispetto alla misura di Lebesgue, tuttavia X non ammette densità congiunta. Difatti, se per assurdo ammettesse una densità congiunta f X, si avrebbe che, definito ad esempio A := {(x,x) x (0,1)} B(R 2 ), si avrebbe P{X A} = f X dλ 2 = 0 poichè λ 2 (A) = 0; ma si avrebbe anche, per come è definito X, e si arriverebbe ad un assurdo. P{X A} = P{(Y,Y ) A} = 1 Nel caso di vettori aleatori continui, è possibile calcolare gli integrali di Lebesgue che appaiono nel calcolo di speranze, probabilità, ecc., usando tutte le tecniche dell integrazione multipla. Tra le varie tecniche, citiamo qui per completezza il caso di cambiamento di variabili. Proposizione 1.72 (composizione di un vettore aleatorio con diffeomorfismi) Sia X vettore aleatorio continuo di densità f X a valori in un aperto B R d, e Y := ϕ(x), con ϕ : B R d diffeomorfismo di classe C 1 (quindi con immagine ϕ(b) R d. Allora anche Y è continuo, e ha densità data da f Y (y) := f X (ϕ 1 (y)) det Jϕ 1 (y) Dimostrazione. Per ogni A B(ϕ(B)) si ha P{Y A} = P{ϕ(X) A} = P{X ϕ 1 (A)} = A ϕ 1 (A) f X (x) dλ d (x) Facendo il cambio di variabili y := ϕ(x), l integrale diventa P{Y A} = f X (ϕ 1 (y)) det Jϕ 1 (y) dλ d (y) e si ha la tesi. A 29
1. Si scelga a caso un punto X dell intervallo [0, 2], con distribuzione uniforme di densità. f X (x) = [0,2](x)
![1. Si scelga a caso un punto X dell intervallo [0, 2], con distribuzione uniforme di densità. f X (x) = [0,2](x) 1. Si scelga a caso un punto X dell intervallo [0, 2], con distribuzione uniforme di densità. f X (x) = [0,2](x)](/thumbs/97/134407840.jpg) Esercizi di Calcolo delle Probabilità della 3 a settimana (Corso di Laurea in Matematica, Università degli Studi di Padova). Esercizio.. Sia (X, Y ) un vettore aleatorio bidimensionale con densità uniforme
Esercizi di Calcolo delle Probabilità della 3 a settimana (Corso di Laurea in Matematica, Università degli Studi di Padova). Esercizio.. Sia (X, Y ) un vettore aleatorio bidimensionale con densità uniforme
Si noti che questa definizione dice esattamente che
 DISUGUAGLIANZA INTEGRALE DI JENSEN IN DIMENSIONE FINITA LIBOR VESELY integrazione. Prima disuguaglianza integrale di Jensen.. Motivazione. Siano un insieme convesso in uno spazio vettoriale, f : (, + ]
DISUGUAGLIANZA INTEGRALE DI JENSEN IN DIMENSIONE FINITA LIBOR VESELY integrazione. Prima disuguaglianza integrale di Jensen.. Motivazione. Siano un insieme convesso in uno spazio vettoriale, f : (, + ]
20. Prodotto di spazi di misura. I teoremi di Tonelli e di Fubini.
 20. Prodotto di spazi di misura. I teoremi di Tonelli e di Fubini. 20.1. Prodotto di σ-algebre. Definizione 20.1.1. (σ-algebra prodotto. Dati n spazi misurabili (Ω 1, A 1,..., (Ω n, A n, si chiama σ-algebra
20. Prodotto di spazi di misura. I teoremi di Tonelli e di Fubini. 20.1. Prodotto di σ-algebre. Definizione 20.1.1. (σ-algebra prodotto. Dati n spazi misurabili (Ω 1, A 1,..., (Ω n, A n, si chiama σ-algebra
Matematica con elementi di Informatica
 Variabili aleatorie Matematica con elementi di Informatica Tiziano Vargiolu Dipartimento di Matematica vargiolu@math.unipd.it Corso di Laurea Magistrale in Chimica e Tecnologie Farmaceutiche Anno Accademico
Variabili aleatorie Matematica con elementi di Informatica Tiziano Vargiolu Dipartimento di Matematica vargiolu@math.unipd.it Corso di Laurea Magistrale in Chimica e Tecnologie Farmaceutiche Anno Accademico
Misure e loro proprietà (appunti per il corso di Complementi di Analisi Matematica per Fisici, a.a )
 Misure e loro proprietà (appunti per il corso di Complementi di Analisi Matematica per Fisici, a.a. 2006-07 Sia Ω un insieme non vuoto e sia A una σ-algebra in Ω. Definizione 1. (Misura. Si chiama misura
Misure e loro proprietà (appunti per il corso di Complementi di Analisi Matematica per Fisici, a.a. 2006-07 Sia Ω un insieme non vuoto e sia A una σ-algebra in Ω. Definizione 1. (Misura. Si chiama misura
ANALISI MATEMATICA 4. Prova scritta del 24 gennaio 2013
 Prova scritta del 24 gennaio 2013 Esercizio 1. Sia Ω R 3 un insieme misurabile secondo Lebesgue e di misura finita. Sia {f n } n N una successione di funzioni f n : Ω R misurabili e tali che 1) f n (x)
Prova scritta del 24 gennaio 2013 Esercizio 1. Sia Ω R 3 un insieme misurabile secondo Lebesgue e di misura finita. Sia {f n } n N una successione di funzioni f n : Ω R misurabili e tali che 1) f n (x)
(2) se A A, allora A c A; (3) se {A n } A, allora +
 1. Spazi di misura In questo paragrafo accenneremo alla nozione di spazio di misura. Definizione 1. Sia X un insieme non vuoto. Una famiglia A di sottoinsiemi di X è una σ-algebra se : (1) A; (2) se A
1. Spazi di misura In questo paragrafo accenneremo alla nozione di spazio di misura. Definizione 1. Sia X un insieme non vuoto. Una famiglia A di sottoinsiemi di X è una σ-algebra se : (1) A; (2) se A
8. Completamento di uno spazio di misura.
 8. Completamento di uno spazio di misura. 8.1. Spazi di misura. Spazi di misura completi. Definizione 8.1.1. (Spazio misurabile). Si chiama spazio misurabile ogni coppia ordinata (Ω, A), dove Ω è un insieme
8. Completamento di uno spazio di misura. 8.1. Spazi di misura. Spazi di misura completi. Definizione 8.1.1. (Spazio misurabile). Si chiama spazio misurabile ogni coppia ordinata (Ω, A), dove Ω è un insieme
Esame di Calcolo delle Probabilità del 11 dicembre 2007 (Corso di Laurea Triennale in Matematica, Università degli Studi di Padova).
 Esame di Calcolo delle Probabilità del dicembre 27 (Corso di Laurea Triennale in Matematica, Università degli Studi di Padova). Cognome Nome Matricola Es. Es. 2 Es. Es. 4 Somma Voto finale Attenzione:
Esame di Calcolo delle Probabilità del dicembre 27 (Corso di Laurea Triennale in Matematica, Università degli Studi di Padova). Cognome Nome Matricola Es. Es. 2 Es. Es. 4 Somma Voto finale Attenzione:
11. Misure con segno.
 11. Misure con segno. 11.1. Misure con segno. Sia Ω un insieme non vuoto e sia A una σ-algebra in Ω. Definizione 11.1.1. (Misura con segno). Si chiama misura con segno su A ogni funzione ϕ : A R verificante
11. Misure con segno. 11.1. Misure con segno. Sia Ω un insieme non vuoto e sia A una σ-algebra in Ω. Definizione 11.1.1. (Misura con segno). Si chiama misura con segno su A ogni funzione ϕ : A R verificante
Teoria della misura. Tiziano Vargiolu Dipartimento di Matematica Pura ed Applicata via Belzoni, Padova
 Teoria della misura Tiziano Vargiolu Dipartimento di Matematica Pura ed Applicata via Belzoni, 7-35131 Padova email: vargiolu@galileo.math.unipd.it 8 ottobre 23 Indice Introduzione iii 1 Teoria della misura
Teoria della misura Tiziano Vargiolu Dipartimento di Matematica Pura ed Applicata via Belzoni, 7-35131 Padova email: vargiolu@galileo.math.unipd.it 8 ottobre 23 Indice Introduzione iii 1 Teoria della misura
Integrali Curvilinei
 Integrali Curvilinei Gianluca Gorni 11 gennaio 2006 1 Lunghezza di una curva Definizione 1.1. Una curva N-dimensionale è una funzione definita su un intervallo (compatto, se non specificato altrimenti)
Integrali Curvilinei Gianluca Gorni 11 gennaio 2006 1 Lunghezza di una curva Definizione 1.1. Una curva N-dimensionale è una funzione definita su un intervallo (compatto, se non specificato altrimenti)
Calcolo delle probabilità. Tiziano Vargiolu Dipartimento di Matematica Pura ed Applicata via Trieste, Padova
 Calcolo delle probabilità Tiziano Vargiolu Dipartimento di Matematica Pura ed pplicata via Trieste, 63-35121 Padova email: vargiolu@math.unipd.it nno ccademico 2011/2012 Indice Introduzione ii 1 Probabilità
Calcolo delle probabilità Tiziano Vargiolu Dipartimento di Matematica Pura ed pplicata via Trieste, 63-35121 Padova email: vargiolu@math.unipd.it nno ccademico 2011/2012 Indice Introduzione ii 1 Probabilità
Variabili aleatorie binomiali e di Poisson
 Variabili aleatorie binomiali e di Poisson Tiziano Vargiolu Dipartimento di Matematica Pura ed Applicata via Trieste, 63-35121 Padova email: vargiolu@math.unipd.it 9 gennaio 2007 Indice 1 Variabili aleatorie
Variabili aleatorie binomiali e di Poisson Tiziano Vargiolu Dipartimento di Matematica Pura ed Applicata via Trieste, 63-35121 Padova email: vargiolu@math.unipd.it 9 gennaio 2007 Indice 1 Variabili aleatorie
I teoremi della funzione inversa e della funzione implicita
 I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
COMPATTEZZA. i) X è compatto, cioè ogni ricoprimento aperto ammette un sottoricoprimento finito.
 1 COMPATTEZZA Sia X un sottoinsieme di R. Una famiglia A di sottoinsiemi aperti di R si dice ricoprimento aperto di X se X A, cioè se X è contenuto nell unione degli elementi di A. Una sottofamiglia di
1 COMPATTEZZA Sia X un sottoinsieme di R. Una famiglia A di sottoinsiemi aperti di R si dice ricoprimento aperto di X se X A, cioè se X è contenuto nell unione degli elementi di A. Una sottofamiglia di
Matematica per l Economia, a.a Integrazione al libro di testo
 Matematica per l Economia, a.a. 2016 2017 Integrazione al libro di testo Gianluca Amato 20 dicembre 2016 1 Note ed errata corrige Sezione 2.3, definizione di dominio. La definizione di dominio data dal
Matematica per l Economia, a.a. 2016 2017 Integrazione al libro di testo Gianluca Amato 20 dicembre 2016 1 Note ed errata corrige Sezione 2.3, definizione di dominio. La definizione di dominio data dal
Prima prova in itenere di Istituzioni di Probabilità
 Prima prova in itenere di Istituzioni di Probabilità 14 novembre 2012 Esercizio 1. Un processo di Ornstein-Uhlenbec modificato (OUM) è un processo reale, con R come insieme dei tempi, con traiettorie continue,
Prima prova in itenere di Istituzioni di Probabilità 14 novembre 2012 Esercizio 1. Un processo di Ornstein-Uhlenbec modificato (OUM) è un processo reale, con R come insieme dei tempi, con traiettorie continue,
Esercizi 8 12 gennaio 2009
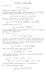 Sia α > e Esercizi 8 2 gennaio 29 f(x, y = ( + x 2 + y 2 α. Dimostrare che f appartiene a L p ( 2, con α p >. Osserviamo innanzitutto che, essendo f continua, l integrale di f p su 2 è uguale all integrale
Sia α > e Esercizi 8 2 gennaio 29 f(x, y = ( + x 2 + y 2 α. Dimostrare che f appartiene a L p ( 2, con α p >. Osserviamo innanzitutto che, essendo f continua, l integrale di f p su 2 è uguale all integrale
Analisi a più variabili: Misura di Peano - Jordan ed Integrale di Riemann
 Analisi a più variabili: Misura di Peano - Jordan ed Integrale di Riemann 1 Definizione (Algebra): T P Ω è un'algebra se: A, B T A B T, Ω T A T A C T Se A i T A i T si dice σ-algebra Definizione (Misura):
Analisi a più variabili: Misura di Peano - Jordan ed Integrale di Riemann 1 Definizione (Algebra): T P Ω è un'algebra se: A, B T A B T, Ω T A T A C T Se A i T A i T si dice σ-algebra Definizione (Misura):
14. Confronto tra l integrale di Lebesgue e l integrale di Riemann.
 4. Confronto tra l integrale di Lebesgue e l integrale di Riemann. Lo scopo di questo capitolo è quello di mettere a confronto i vari tipi di integrale (di Riemann, generalizzato e improprio) di funzioni
4. Confronto tra l integrale di Lebesgue e l integrale di Riemann. Lo scopo di questo capitolo è quello di mettere a confronto i vari tipi di integrale (di Riemann, generalizzato e improprio) di funzioni
5.3 Alcune classi di funzioni integrabili
 3. Si verifichi che per ogni f, g : [a, b] R si ha f g = g + (f g) 0, f g = f + g f g; dedurne che se f, g R(a, b) allora f g, f g R(a, b). [Traccia: si osservi che basta verificare che f 0 R(a, b), e
3. Si verifichi che per ogni f, g : [a, b] R si ha f g = g + (f g) 0, f g = f + g f g; dedurne che se f, g R(a, b) allora f g, f g R(a, b). [Traccia: si osservi che basta verificare che f 0 R(a, b), e
Le derivate parziali
 Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
GEOMETRIA 1 seconda parte
 GEOMETRIA 1 seconda parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 40 index Spazi vettoriali 1 Spazi vettoriali 2 Sottospazi 3 Sistemi
GEOMETRIA 1 seconda parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 40 index Spazi vettoriali 1 Spazi vettoriali 2 Sottospazi 3 Sistemi
IL TEOREMA DEGLI ZERI Una dimostrazione di Ezio Fornero
 IL TEOREMA DEGLI ZERI Una dimostrazione di Ezio Fornero Il teorema degli zeri è fondamentale per determinare se una funzione continua in un intervallo chiuso [ a ; b ] si annulla in almeno un punto interno
IL TEOREMA DEGLI ZERI Una dimostrazione di Ezio Fornero Il teorema degli zeri è fondamentale per determinare se una funzione continua in un intervallo chiuso [ a ; b ] si annulla in almeno un punto interno
Analisi Reale. Anno Accademico Roberto Monti. Versione del 13 Ottobre 2014
 Analisi Reale Anno Accademico 2014-2015 Roberto Monti Versione del 13 Ottobre 2014 1 Contents Chapter 1. Introduzione alla teoria della misura 5 1. Misure esterne e misure su σ-algebre. Criterio di Carathéodory
Analisi Reale Anno Accademico 2014-2015 Roberto Monti Versione del 13 Ottobre 2014 1 Contents Chapter 1. Introduzione alla teoria della misura 5 1. Misure esterne e misure su σ-algebre. Criterio di Carathéodory
Analisi II, a.a Soluzioni 1. j j + 1 ; ( 1)j
 Analisi II, a.a. 7-8 Soluzioni Calcolare le seguenti distanze e norme: (i d (x, y dove x = {x j } e y = {y j } sono le successioni di l definite da x j = ( j, y j = j/(j + ; (ii d (f, g dove f, g sono
Analisi II, a.a. 7-8 Soluzioni Calcolare le seguenti distanze e norme: (i d (x, y dove x = {x j } e y = {y j } sono le successioni di l definite da x j = ( j, y j = j/(j + ; (ii d (f, g dove f, g sono
Elementi di Teoria degli Insiemi
 Elementi di Teoria degli Insiemi 2016/17 Esercizi di Giacomo Bertolucci (matr. 519430) Lezioni 7-10 Lezione 7 Esercizio 1. Dimostrare che, se A R con A ℵ 0, allora R A è denso in R. Se così non fosse,
Elementi di Teoria degli Insiemi 2016/17 Esercizi di Giacomo Bertolucci (matr. 519430) Lezioni 7-10 Lezione 7 Esercizio 1. Dimostrare che, se A R con A ℵ 0, allora R A è denso in R. Se così non fosse,
Elementi di analisi matematica e complementi di calcolo delle probabilita T
 Elementi di analisi matematica e complementi di calcolo delle probabilita T Presentiamo una raccolta di quesiti per la preparazione alla prova orale di Elementi di analisi matematica e complementi di calcolo
Elementi di analisi matematica e complementi di calcolo delle probabilita T Presentiamo una raccolta di quesiti per la preparazione alla prova orale di Elementi di analisi matematica e complementi di calcolo
Dimostrazione. Indichiamo con α e β (finiti o infiniti) gli estremi dell intervallo I. Poniamo
 C.6 Funzioni continue Pag. 114 Dimostrazione del Corollario 4.25 Corollario 4.25 Sia f continua in un intervallo I. Supponiamo che f ammetta, per x tendente a ciascuno degli estremi dell intervallo, iti
C.6 Funzioni continue Pag. 114 Dimostrazione del Corollario 4.25 Corollario 4.25 Sia f continua in un intervallo I. Supponiamo che f ammetta, per x tendente a ciascuno degli estremi dell intervallo, iti
Note di Teoria della Probabilità.
 Note di Teoria della Probabilità. In queste brevi note, si richiameranno alcuni risultati di Teoria della Probabilità, riguardanti le conseguenze elementari delle definizioni di probabilità e σ-algebra.
Note di Teoria della Probabilità. In queste brevi note, si richiameranno alcuni risultati di Teoria della Probabilità, riguardanti le conseguenze elementari delle definizioni di probabilità e σ-algebra.
Alcuni complementi sulla misura di Lebesgue in R N
 Alcuni complementi sulla misura di Lebesgue in R N Notazioni m Misura di Lebesgue in R N m e Misura esterna di Lebesgue in R N ; m e (E) = inf m(v ) V aperti V E m i Misura interna di Lebesgue in R N ;
Alcuni complementi sulla misura di Lebesgue in R N Notazioni m Misura di Lebesgue in R N m e Misura esterna di Lebesgue in R N ; m e (E) = inf m(v ) V aperti V E m i Misura interna di Lebesgue in R N ;
4 Funzioni continue. Geometria I 27. Cfr: Sernesi vol II, cap I, 4 [1].
![4 Funzioni continue. Geometria I 27. Cfr: Sernesi vol II, cap I, 4 [1]. 4 Funzioni continue. Geometria I 27. Cfr: Sernesi vol II, cap I, 4 [1].](/thumbs/96/128120172.jpg) Geometria I 27 4 Funzioni continue Cfr: Sernesi vol II, cap I, 4 [1]. Le funzioni continue tra spazi topologici si dicono anche mappe. Si può dimostrare, esattamente come in (2.10) e in (1.10), che vale
Geometria I 27 4 Funzioni continue Cfr: Sernesi vol II, cap I, 4 [1]. Le funzioni continue tra spazi topologici si dicono anche mappe. Si può dimostrare, esattamente come in (2.10) e in (1.10), che vale
Esercitazione del 28/10/2011 Calcolo delle probabilità
 Esercitazione del 28/0/20 Calcolo delle probabilità Distribuzione di una funzione di una variabile aleatoria discreta. Sia X una variabile aletoria discreta, sia f una funzione da in, se Y := f(x) allora
Esercitazione del 28/0/20 Calcolo delle probabilità Distribuzione di una funzione di una variabile aleatoria discreta. Sia X una variabile aletoria discreta, sia f una funzione da in, se Y := f(x) allora
AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE
 AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE Sia g C 1 R 2 ), c R. L insieme γ = γ c := {x, y) R 2 : gx, y) = c} si chiama insieme
AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE Sia g C 1 R 2 ), c R. L insieme γ = γ c := {x, y) R 2 : gx, y) = c} si chiama insieme
1 Successioni di funzioni
 Analisi Matematica 2 Successioni di funzioni CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 6 SERIE DI POTENZE Supponiamo di associare ad ogni n N (rispettivamente ad ogni n p, per qualche
Analisi Matematica 2 Successioni di funzioni CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 6 SERIE DI POTENZE Supponiamo di associare ad ogni n N (rispettivamente ad ogni n p, per qualche
Esame di Calcolo delle Probabilità del 12 dicembre 2005 (Corso di Laurea Triennale in Matematica, Università degli Studi di Padova).
 Esame di Calcolo delle Probabilità del 2 dicembre 2005 (Corso di Laurea Triennale in Matematica, Università degli Studi di Padova). Cognome Nome Matricola Es. Es. 2 Es. 3 Es. 4 Somma Voto parziale Prima
Esame di Calcolo delle Probabilità del 2 dicembre 2005 (Corso di Laurea Triennale in Matematica, Università degli Studi di Padova). Cognome Nome Matricola Es. Es. 2 Es. 3 Es. 4 Somma Voto parziale Prima
Elementi di analisi matematica e complementi di calcolo delle probabilita T
 Elementi di analisi matematica e complementi di calcolo delle probabilita T Presentiamo una raccolta di quesiti per la preparazione alla prova orale di Elementi di analisi matematica e complementi di calcolo
Elementi di analisi matematica e complementi di calcolo delle probabilita T Presentiamo una raccolta di quesiti per la preparazione alla prova orale di Elementi di analisi matematica e complementi di calcolo
Esercitazione del 16/04/2019 Istituzioni di Calcolo delle Probabilità
 Esercitazione del 6/04/09 Istituzioni di Calcolo delle Probabilità David Barbato Nozioni di riepilogo con esercizi Distribuzione di una funzione di una variabile aleatoria discreta. Sia X una variabile
Esercitazione del 6/04/09 Istituzioni di Calcolo delle Probabilità David Barbato Nozioni di riepilogo con esercizi Distribuzione di una funzione di una variabile aleatoria discreta. Sia X una variabile
Serie trigonometriche e di Fourier Ci occuperemo di serie le cui ridotte N-esime sono polinomi trigonometrici di grado (o ordine) N:
 Serie trigonometriche e di Fourier Ci occuperemo di serie le cui ridotte N-esime sono polinomi trigonometrici di grado (o ordine) N: S N (x) = N n=0 (a n cos (nx) + b n sin (nx)), a n, b n R (periodiche
Serie trigonometriche e di Fourier Ci occuperemo di serie le cui ridotte N-esime sono polinomi trigonometrici di grado (o ordine) N: S N (x) = N n=0 (a n cos (nx) + b n sin (nx)), a n, b n R (periodiche
Limiti e continuità. Hynek Kovarik. Analisi A. Università di Brescia. Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi A 1 / 68
 Limiti e continuità Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi A 1 / 68 Cenni di topologia La nozione di intorno Sia x 0 R e r > 0.
Limiti e continuità Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi A 1 / 68 Cenni di topologia La nozione di intorno Sia x 0 R e r > 0.
Il teorema di Vitali-Lebesgue
 Il teorema di Vitali-Lebesgue Gianluca Gorni Università di Udine gennaio 0 Nel 90 Giuseppe Vitali e Henri Lebesgue, indipendentemente uno dall altro, trovarono che si possono caratterizzare in modo elegante
Il teorema di Vitali-Lebesgue Gianluca Gorni Università di Udine gennaio 0 Nel 90 Giuseppe Vitali e Henri Lebesgue, indipendentemente uno dall altro, trovarono che si possono caratterizzare in modo elegante
COPPIE DI VARIABILI ALEATORIE
 COPPIE DI VAIABILI ALEATOIE E DI NADO 1 Funzioni di ripartizione congiunte e marginali Definizione 11 Siano X, Y va definite su uno stesso spazio di probabilità (Ω, F, P La coppia (X, Y viene detta va
COPPIE DI VAIABILI ALEATOIE E DI NADO 1 Funzioni di ripartizione congiunte e marginali Definizione 11 Siano X, Y va definite su uno stesso spazio di probabilità (Ω, F, P La coppia (X, Y viene detta va
23 INVERTIBILITÀ E CONTINUITÀ
 23 INVERTIBILITÀ E CONTINUITÀ Ricordiamo che se A, B sono insiemi e f : A B è una funzione iniettiva, ovvero a 1 a 2 = fa 1 ) fa 2 ), allora la relazione gb) = a fa) = b definisce una funzione g : Im f
23 INVERTIBILITÀ E CONTINUITÀ Ricordiamo che se A, B sono insiemi e f : A B è una funzione iniettiva, ovvero a 1 a 2 = fa 1 ) fa 2 ), allora la relazione gb) = a fa) = b definisce una funzione g : Im f
0.1 Spazi Euclidei in generale
 0.1. SPAZI EUCLIDEI IN GENERALE 1 0.1 Spazi Euclidei in generale Sia V uno spazio vettoriale definito su R. Diremo, estendendo una definizione data in precedenza, che V è uno spazio vettoriale euclideo
0.1. SPAZI EUCLIDEI IN GENERALE 1 0.1 Spazi Euclidei in generale Sia V uno spazio vettoriale definito su R. Diremo, estendendo una definizione data in precedenza, che V è uno spazio vettoriale euclideo
Sequenze (Sistemi) di Variabili Aleatorie Se consideriamo un numero di variabili aleatorie, generalmente dipendenti si parla equivalentemente di:
 Teoria dei Fenomeni Aleatori AA 01/13 Sequenze (Sistemi) di Variabili Aleatorie Se consideriamo un numero di variabili aleatorie, generalmente dipendenti si parla equivalentemente di: N-pla o Sequenza
Teoria dei Fenomeni Aleatori AA 01/13 Sequenze (Sistemi) di Variabili Aleatorie Se consideriamo un numero di variabili aleatorie, generalmente dipendenti si parla equivalentemente di: N-pla o Sequenza
NOTE SULLE FUNZIONI CONVESSE DI UNA VARIABILE REALE
 NOTE SULLE FUNZIONI CONVESSE DI UNA VARIABILE REALE ROBERTO GIAMBÒ 1. DEFINIZIONI E PRIME PROPRIETÀ In queste note saranno presentate alcune proprietà principali delle funzioni convesse di una variabile
NOTE SULLE FUNZIONI CONVESSE DI UNA VARIABILE REALE ROBERTO GIAMBÒ 1. DEFINIZIONI E PRIME PROPRIETÀ In queste note saranno presentate alcune proprietà principali delle funzioni convesse di una variabile
COMPLETAMENTO DI SPAZI METRICI
 COMPLETAMENTO DI SPAZI METRICI 1. Successioni di Cauchy e spazi metrici completi Definizione 1.1. Una successione x n n N a valori in uno spazio metrico X, d si dice di Cauchy se, per ogni ε > 0 esiste
COMPLETAMENTO DI SPAZI METRICI 1. Successioni di Cauchy e spazi metrici completi Definizione 1.1. Una successione x n n N a valori in uno spazio metrico X, d si dice di Cauchy se, per ogni ε > 0 esiste
SPAZI COMPATTI. Proposizione 2 Sia (X, d) uno spazio metrico. Se esso è sequenzialmente compatto allora è completo.
 SPAZI COMPATTI D ora in poi tutti gli spazi topologici sono di Hausdorff. Definizione 1 Uno spazio topologico (X, τ) si dice sequenzialmente compatto, o compatto per successioni, se ogni successione di
SPAZI COMPATTI D ora in poi tutti gli spazi topologici sono di Hausdorff. Definizione 1 Uno spazio topologico (X, τ) si dice sequenzialmente compatto, o compatto per successioni, se ogni successione di
ANALISI MATEMATICA 4. Prova scritta del 24 gennaio 2013
 Prova scritta del 24 gennaio 2013 Esercizio 1. Sia Ω R 3 un insieme misurabile secondo Lebesgue e di misura finita. Sia {f n } n N una successione di funzioni f n : Ω R misurabili e tali che 1) f n (x)
Prova scritta del 24 gennaio 2013 Esercizio 1. Sia Ω R 3 un insieme misurabile secondo Lebesgue e di misura finita. Sia {f n } n N una successione di funzioni f n : Ω R misurabili e tali che 1) f n (x)
1 Funzioni reali di una variabile reale
 1 Funzioni reali di una variabile reale Qualche definizione e qualche esempio che risulteranno utili più avanti Durante tutto questo corso studieremo funzioni reali di una variabile reale, cioè Si ha f
1 Funzioni reali di una variabile reale Qualche definizione e qualche esempio che risulteranno utili più avanti Durante tutto questo corso studieremo funzioni reali di una variabile reale, cioè Si ha f
Complementi di Analisi Matematica Ia. Carlo Bardaro
 Complementi di Analisi Matematica Ia Carlo Bardaro Capitolo 1 Elementi di topologia della retta reale 1.1 Intorni, punti di accumulazione e insiemi chiusi Sia x 0 IR un fissato punto di IR. Chiameremo
Complementi di Analisi Matematica Ia Carlo Bardaro Capitolo 1 Elementi di topologia della retta reale 1.1 Intorni, punti di accumulazione e insiemi chiusi Sia x 0 IR un fissato punto di IR. Chiameremo
P ( X n X > ɛ) = 0. ovvero (se come distanza consideriamo quella euclidea)
 10.4 Convergenze 166 10.4.3. Convergenza in Probabilità. Definizione 10.2. Data una successione X 1, X 2,...,,... di vettori aleatori e un vettore aleatorio X aventi tutti la stessa dimensione k diremo
10.4 Convergenze 166 10.4.3. Convergenza in Probabilità. Definizione 10.2. Data una successione X 1, X 2,...,,... di vettori aleatori e un vettore aleatorio X aventi tutti la stessa dimensione k diremo
0 se y c 1 (y)) se c < y < d. 1 se y d
 Capitolo. Parte IX Exercise.. Sia X una variabile aleatoria reale assolutamente continua e sia (a,b) un intervallo aperto (limitato o illimitato) di R, tale che P(X (a,b)) =. Sia ϕ : (a,b) R una funzione
Capitolo. Parte IX Exercise.. Sia X una variabile aleatoria reale assolutamente continua e sia (a,b) un intervallo aperto (limitato o illimitato) di R, tale che P(X (a,b)) =. Sia ϕ : (a,b) R una funzione
SPAZI TOPOLOGICI. La nozione di spazio topologico è più generale di quella di spazio metrizzabile.
 SPAZI TOPOLOGICI La nozione di spazio topologico è più generale di quella di spazio metrizzabile. Definizione 1 Uno spazio topologico (X, τ) è una coppia costituita da un insieme X e da una famiglia τ
SPAZI TOPOLOGICI La nozione di spazio topologico è più generale di quella di spazio metrizzabile. Definizione 1 Uno spazio topologico (X, τ) è una coppia costituita da un insieme X e da una famiglia τ
Corso di Analisi Matematica
 Corso di Laurea in Ingegneria Edile Corso di DERIVATE Lucio Demeio Dipartimento di Ingegneria Industriale e delle Scienze Matematiche Secanti e tangenti Sia f : D R, sia I = [a, b] oppure I = (a, b),
Corso di Laurea in Ingegneria Edile Corso di DERIVATE Lucio Demeio Dipartimento di Ingegneria Industriale e delle Scienze Matematiche Secanti e tangenti Sia f : D R, sia I = [a, b] oppure I = (a, b),
Esercizi di Calcolo delle Probabilità
 Esercizi di Calcolo delle Probabilità M. Pratelli e M. Romito Gli esercizi che seguono sono stati proposti nel corso Probabilità dell Università di Pisa negli a.a. 2012-13 e 2013-14 (M. Romito) e 2014-15
Esercizi di Calcolo delle Probabilità M. Pratelli e M. Romito Gli esercizi che seguono sono stati proposti nel corso Probabilità dell Università di Pisa negli a.a. 2012-13 e 2013-14 (M. Romito) e 2014-15
Esercizi per il corso di Analisi 6.
 Esercizi per il corso di Analisi 6. 1. Si verifichi che uno spazio normato (X, ) è uno spazio vettoriale topologico con la topologia indotta dalla norma. Si verifichi poi che la norma è una funzione continua
Esercizi per il corso di Analisi 6. 1. Si verifichi che uno spazio normato (X, ) è uno spazio vettoriale topologico con la topologia indotta dalla norma. Si verifichi poi che la norma è una funzione continua
Sviluppi e derivate delle funzioni elementari
 Sviluppi e derivate delle funzioni elementari In queste pagine dimostriamo gli sviluppi del prim ordine e le formule di derivazioni delle principali funzioni elementari. Utilizzeremo le uguaglianze lim
Sviluppi e derivate delle funzioni elementari In queste pagine dimostriamo gli sviluppi del prim ordine e le formule di derivazioni delle principali funzioni elementari. Utilizzeremo le uguaglianze lim
ALGEBRE DI BOOLE. (d) x, y X x y oppure y x.
 ALGEBRE DI BOOLE Un insieme parzialmente ordinato è una coppia ordinata (X, ) dove X è un insieme non vuoto e " " è una relazione binaria definita su X tale che (a) x X x x (riflessività) (b) x, y, X se
ALGEBRE DI BOOLE Un insieme parzialmente ordinato è una coppia ordinata (X, ) dove X è un insieme non vuoto e " " è una relazione binaria definita su X tale che (a) x X x x (riflessività) (b) x, y, X se
Esercizi di Elementi di Teoria degli Insiemi, Parte 1 Fabrizio Anelli
 Esercizi di Elementi di Teoria degli Insiemi, Parte 1 Fabrizio Anelli Lezione 1, Esercizio 1 Dimostrare che per le coppie di Kuratowski vale che (a, b) = (a, b ) a = a b = b. Perché i due insiemi {{a},
Esercizi di Elementi di Teoria degli Insiemi, Parte 1 Fabrizio Anelli Lezione 1, Esercizio 1 Dimostrare che per le coppie di Kuratowski vale che (a, b) = (a, b ) a = a b = b. Perché i due insiemi {{a},
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Primi elementi di combinatoria Federico Lastaria, Analisi e Geometria 1
 Politecnico di Milano. Scuola di Ingegneria Industriale e dell Informazione Analisi e Geometria 1 Federico Lastaria Primi elementi di combinatoria 11 Ottobre 2016 Indice 1 Elementi di combinatoria 2 1.1
Politecnico di Milano. Scuola di Ingegneria Industriale e dell Informazione Analisi e Geometria 1 Federico Lastaria Primi elementi di combinatoria 11 Ottobre 2016 Indice 1 Elementi di combinatoria 2 1.1
Corso di Metodi Matematici per l Ingegneria A.A. 2016/2017 Esercizi svolti su misura e integrale di Lebesgue, spazi L p, operatori lineari continui
 Corso di Metodi Matematici per l Ingegneria A.A. 26/27 Esercizi svolti su misura e integrale di Lebesgue, spazi L p, operatori lineari continui Marco Bramanti Politecnico di Milano December 4, 26 Esercizi
Corso di Metodi Matematici per l Ingegneria A.A. 26/27 Esercizi svolti su misura e integrale di Lebesgue, spazi L p, operatori lineari continui Marco Bramanti Politecnico di Milano December 4, 26 Esercizi
non solo otteniamo il valore cercato per la validità della (1.4), ma anche che tale valore non dipende da
 NOTE INTEGRATIVE PER IL CORSO DI ANALISI MATEMATICA 2 ANNO ACCADEMICO 2012/13 NOTE SULLA CONTINUITÀ UNIFORME D.BARTOLUCCI, D.GUIDO Sia f(x) = x 3, x [ 1, 1]. Si ha 1. La continuità uniforme x 3 y 3 = x
NOTE INTEGRATIVE PER IL CORSO DI ANALISI MATEMATICA 2 ANNO ACCADEMICO 2012/13 NOTE SULLA CONTINUITÀ UNIFORME D.BARTOLUCCI, D.GUIDO Sia f(x) = x 3, x [ 1, 1]. Si ha 1. La continuità uniforme x 3 y 3 = x
Disuguaglianza di Cramér-Rao
 Disuguaglianza di Cramér-Rao (Appunti per gli studenti Silvano Holzer Dipartimento di Scienze Economiche, Aziendali, Matematiche e Statistiche Bruno de Finetti Università degli studi di Trieste Un esperimento
Disuguaglianza di Cramér-Rao (Appunti per gli studenti Silvano Holzer Dipartimento di Scienze Economiche, Aziendali, Matematiche e Statistiche Bruno de Finetti Università degli studi di Trieste Un esperimento
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
DIFFERENZIAZIONE. Sia f una funzione reale di variabile reale con dominio un intervallo. Se f è derivabile in un punto x 0, allora: f(x) f(x 0 ) lim
 DIFFERENZIAZIONE 1 Regola della catena Sia f una funzione reale di variabile reale con dominio un intervallo. Se f è derivabile in un punto x 0, allora: f(x) f(x 0 ) lim = f (x 0 ). x x 0 x x 0 Questa
DIFFERENZIAZIONE 1 Regola della catena Sia f una funzione reale di variabile reale con dominio un intervallo. Se f è derivabile in un punto x 0, allora: f(x) f(x 0 ) lim = f (x 0 ). x x 0 x x 0 Questa
Appunti del Corso Analisi 1
 Appunti del Corso Analisi 1 Anno Accademico 2011-2012 Roberto Monti Versione del 5 Ottobre 2011 1 Contents Chapter 1. Cardinalità 5 1. Insiemi e funzioni. Introduzione informale 5 2. Cardinalità 7 3.
Appunti del Corso Analisi 1 Anno Accademico 2011-2012 Roberto Monti Versione del 5 Ottobre 2011 1 Contents Chapter 1. Cardinalità 5 1. Insiemi e funzioni. Introduzione informale 5 2. Cardinalità 7 3.
VETTORI DI VARIABILI ALEATORIE
 VETTOI DI VAIABILI ALEATOIE E. DI NADO 1. Funzioni di ripartizione congiunte e marginali Definizione 1.1. Siano X 1, X 2,..., X n v.a. definite su uno stesso spazio di probabilità (Ω, F, P ). La n-pla
VETTOI DI VAIABILI ALEATOIE E. DI NADO 1. Funzioni di ripartizione congiunte e marginali Definizione 1.1. Siano X 1, X 2,..., X n v.a. definite su uno stesso spazio di probabilità (Ω, F, P ). La n-pla
Geometria e Topologia I (U1-4) 2006-mag-10 61
 Geometria e Topologia I (U1-4) 2006-mag-10 61 (15.9) Teorema. Consideriamo il piano affine. Se A A 2 (K) è un punto e r una retta che non passa per A, allora esiste unica la retta per A che non interseca
Geometria e Topologia I (U1-4) 2006-mag-10 61 (15.9) Teorema. Consideriamo il piano affine. Se A A 2 (K) è un punto e r una retta che non passa per A, allora esiste unica la retta per A che non interseca
Esercizi di Elementi di Teoria degli Insiemi
 Esercizi di Elementi di Teoria degli Insiemi Gemma di Petrillo 531909 3 aprile 2018 1 Esercizi sulla prima parte Esercizio 1.1. I seguenti fatti sono equivalenti: 1. Se < A i i I > è una sequenza di insiemi
Esercizi di Elementi di Teoria degli Insiemi Gemma di Petrillo 531909 3 aprile 2018 1 Esercizi sulla prima parte Esercizio 1.1. I seguenti fatti sono equivalenti: 1. Se < A i i I > è una sequenza di insiemi
Esercizi di Analisi Reale
 sercizi di Analisi Reale Corso di Laurea in Matematica Terminologia. Sia R n un insieme misurabile. Una funzione positiva misurabile f su, cioè una funzione f : [, ] misurabile, ammette sempre integrale
sercizi di Analisi Reale Corso di Laurea in Matematica Terminologia. Sia R n un insieme misurabile. Una funzione positiva misurabile f su, cioè una funzione f : [, ] misurabile, ammette sempre integrale
Alcuni complementi di teoria dell integrazione.
 Alcuni complementi di teoria dell integrazione. In ciò che segue si suppone di avere uno spazio di misura (,, µ) 1 Sia f una funzione misurabile su un insieme di misura positiva tale che f 0. Se fdµ =
Alcuni complementi di teoria dell integrazione. In ciò che segue si suppone di avere uno spazio di misura (,, µ) 1 Sia f una funzione misurabile su un insieme di misura positiva tale che f 0. Se fdµ =
TOPOLOGIA - APPUNTI SETTIMANA 2/12/2013-5/11/2013
 TOPOLOGIA - APPUNTI SETTIMANA 2/12/2013-5/11/2013 KIERAN G. O GRADY - 9 DICEMBRE 2013 1. Connessione Se X è uno spazio topologico connesso per archi vale il Teorema dei valori intermedi : dati una f :
TOPOLOGIA - APPUNTI SETTIMANA 2/12/2013-5/11/2013 KIERAN G. O GRADY - 9 DICEMBRE 2013 1. Connessione Se X è uno spazio topologico connesso per archi vale il Teorema dei valori intermedi : dati una f :
Funzioni di n variabili a valori vettoriali
 Funzioni di n variabili a valori vettoriali Ultimo aggiornamento: 22 maggio 2018 1 Differenziale per funzioni da R n in R k Una funzione F : A R n R k può essere vista come una k-upla di funzioni scalari
Funzioni di n variabili a valori vettoriali Ultimo aggiornamento: 22 maggio 2018 1 Differenziale per funzioni da R n in R k Una funzione F : A R n R k può essere vista come una k-upla di funzioni scalari
Diario Complementi di Probabilità a.a. 2017/2018
 Diario Complementi di Probabilità a.a. 2017/2018 Testi di riferimento: [W] Probability with martingales, D.Williams [Bi] Probability and measure, P.Billingsley [Ba] Appunti del corso di Calcolo delle Probabilità
Diario Complementi di Probabilità a.a. 2017/2018 Testi di riferimento: [W] Probability with martingales, D.Williams [Bi] Probability and measure, P.Billingsley [Ba] Appunti del corso di Calcolo delle Probabilità
Sequenze (Sistemi) di Variabili Aleatorie Se consideriamo un numero di variabili aleatorie, generalmente dipendenti si parla equivalentemente di:
 Teoria dei Fenomeni Aleatori AA 01/13 Sequenze (Sistemi) di Variabili Aleatorie Se consideriamo un numero di variabili aleatorie, generalmente dipendenti si parla equivalentemente di: N-pla o Sequenza
Teoria dei Fenomeni Aleatori AA 01/13 Sequenze (Sistemi) di Variabili Aleatorie Se consideriamo un numero di variabili aleatorie, generalmente dipendenti si parla equivalentemente di: N-pla o Sequenza
i) la somma e il prodotto godano delle proprietà associativa, commutativa e distributiva;
 1 Spazi vettoriali 11 Definizioni ed assiomi Definizione 11 Un campo è un insieme K dotato di una operazione somma K K K, (x, y) x + y e di una operazione prodotto K K K, (x, y) xy tali che i) la somma
1 Spazi vettoriali 11 Definizioni ed assiomi Definizione 11 Un campo è un insieme K dotato di una operazione somma K K K, (x, y) x + y e di una operazione prodotto K K K, (x, y) xy tali che i) la somma
Proposizione 2 Il polinomio minimo di t corrisponde all annullatore minimale di M V.
 Fogli NON riletti. Grazie per ogni segnalazione di errori. L esempio qui sviluppato vuole mostrare in concreto il significato dei risultati trattati a lezione e qui velocemente riassunti. Si assume che
Fogli NON riletti. Grazie per ogni segnalazione di errori. L esempio qui sviluppato vuole mostrare in concreto il significato dei risultati trattati a lezione e qui velocemente riassunti. Si assume che
Teorema delle Funzioni Implicite
 Teorema delle Funzioni Implicite Sia F una funzione di due variabili definita in un opportuno dominio D di R 2. Consideriamo l equazione F (x, y) = 0, questa avrà come soluzioni coppie di valori (x, y)
Teorema delle Funzioni Implicite Sia F una funzione di due variabili definita in un opportuno dominio D di R 2. Consideriamo l equazione F (x, y) = 0, questa avrà come soluzioni coppie di valori (x, y)
Eventi numerici e variabili aleatorie
 Capitolo Eventi numerici e variabili aleatorie. Probabilità di eventi numerici Nel capitolo precedente si sono considerate le nozioni di esperimento, risultato, evento. Un evento è individuato dai risultati
Capitolo Eventi numerici e variabili aleatorie. Probabilità di eventi numerici Nel capitolo precedente si sono considerate le nozioni di esperimento, risultato, evento. Un evento è individuato dai risultati
APPUNTI DI TEORIA DEGLI INSIEMI. L assioma della scelta e il lemma di Zorn Sia {A i } i I
 APPUNTI DI TEORIA DEGLI INSIEMI MAURIZIO CORNALBA L assioma della scelta e il lemma di Zorn Sia {A i } i I un insieme di insiemi. Il prodotto i I A i è l insieme di tutte le applicazioni α : I i I A i
APPUNTI DI TEORIA DEGLI INSIEMI MAURIZIO CORNALBA L assioma della scelta e il lemma di Zorn Sia {A i } i I un insieme di insiemi. Il prodotto i I A i è l insieme di tutte le applicazioni α : I i I A i
Alcuni spazi funzionali con ordine di derivazione reale
 Alcuni spazi funzionali con ordine di derivazione reale Nel seguito Ω denota un di IR n. Per garantire l effettiva validità dei risultati e l equivalenza delle definizioni che diamo a quelle originali
Alcuni spazi funzionali con ordine di derivazione reale Nel seguito Ω denota un di IR n. Per garantire l effettiva validità dei risultati e l equivalenza delle definizioni che diamo a quelle originali
UNIVERSITÀ DI ROMA TOR VERGATA. Analisi Matematica II per Ingegneria Prof. C. Sinestrari
 UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Risposte (sintetiche) ai quesiti degli esercizi del 12.X.2018 1. (a) Ω è aperto, Ω = {0, 1, 2}, Ω = Ω, Ω = [0, 1]
UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Risposte (sintetiche) ai quesiti degli esercizi del 12.X.2018 1. (a) Ω è aperto, Ω = {0, 1, 2}, Ω = Ω, Ω = [0, 1]
Esistenza ed unicità per equazioni differenziali
 Esistenza ed unicità per equazioni differenziali Per concludere queste lezioni sulle equazioni differenziali vogliamo dimostrare il teorema esistenza ed unicità per il problema di Cauchy. Faremo la dimostrazione
Esistenza ed unicità per equazioni differenziali Per concludere queste lezioni sulle equazioni differenziali vogliamo dimostrare il teorema esistenza ed unicità per il problema di Cauchy. Faremo la dimostrazione
Capitolo IV SPAZI VETTORIALI EUCLIDEI
 Capitolo IV SPAZI VETTORIALI EUCLIDEI È ben noto che in VO 3 si possono considerare strutture più ricche di quella di spazio vettoriale; si pensi in particolare all operazioni di prodotto scalare di vettori.
Capitolo IV SPAZI VETTORIALI EUCLIDEI È ben noto che in VO 3 si possono considerare strutture più ricche di quella di spazio vettoriale; si pensi in particolare all operazioni di prodotto scalare di vettori.
Variabili aleatorie parte 2. 1 Definizione di funzione di ripartizione o funzione cumulativa (CDF)
 Statistica e analisi dei dati Data: 11 aprile 2016 Variabili aleatorie parte 2 Docente: Prof. Giuseppe Boccignone Scriba: Alessandra Birlini 1 Definizione di funzione di ripartizione o funzione cumulativa
Statistica e analisi dei dati Data: 11 aprile 2016 Variabili aleatorie parte 2 Docente: Prof. Giuseppe Boccignone Scriba: Alessandra Birlini 1 Definizione di funzione di ripartizione o funzione cumulativa
Corso di Analisi Matematica. Calcolo differenziale
 a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Calcolo differenziale Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Calcolo differenziale Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
Topologia, continuità, limiti in R n
 Topologia, continuità, limiti in R n Ultimo aggiornamento: 18 febbraio 2017 1. Preliminari Prima di iniziare lo studio delle funzioni di più variabili, in generale funzioni di k variabili e a valori in
Topologia, continuità, limiti in R n Ultimo aggiornamento: 18 febbraio 2017 1. Preliminari Prima di iniziare lo studio delle funzioni di più variabili, in generale funzioni di k variabili e a valori in
Funzioni condizionatamente definite positive
 Funzioni condizionatamente definite positive Nelle lezioni precedenti abbiamo visto come il problema di interpolazione ci abbia portato all uso di funzioni definite positive. Tuttavia, ci sono funzioni
Funzioni condizionatamente definite positive Nelle lezioni precedenti abbiamo visto come il problema di interpolazione ci abbia portato all uso di funzioni definite positive. Tuttavia, ci sono funzioni
NOTE DI ALGEBRA LINEARE v = a 1 v a n v n, w = b 1 v b n v n
 NOTE DI ALGEBRA LINEARE 2- MM 9 NOVEMBRE 2 Combinazioni lineari e generatori Sia K un campo e V uno spazio vettoriale su K Siano v,, v n vettori in V Definizione Un vettore v V si dice combinazione lineare
NOTE DI ALGEBRA LINEARE 2- MM 9 NOVEMBRE 2 Combinazioni lineari e generatori Sia K un campo e V uno spazio vettoriale su K Siano v,, v n vettori in V Definizione Un vettore v V si dice combinazione lineare
ESERCITAZIONE 7 : FUNZIONI
 ESERCITAZIONE 7 : FUNZIONI e-mail: tommei@dm.unipi.it web: www.dm.unipi.it/ tommei Ricevimento: Martedi 16-18 Dipartimento di Matematica, piano terra, studio 126 20 Novembre 2012 Corso di recupero Docente:
ESERCITAZIONE 7 : FUNZIONI e-mail: tommei@dm.unipi.it web: www.dm.unipi.it/ tommei Ricevimento: Martedi 16-18 Dipartimento di Matematica, piano terra, studio 126 20 Novembre 2012 Corso di recupero Docente:
AL210 - Appunti integrativi - 3
 AL210 - Appunti integrativi - 3 Prof. Stefania Gabelli - a.a. 2016-2017 Nello studio delle strutture algebriche, sono interessanti le relazioni che sono compatibili con le operazioni. Vogliamo dimostrare
AL210 - Appunti integrativi - 3 Prof. Stefania Gabelli - a.a. 2016-2017 Nello studio delle strutture algebriche, sono interessanti le relazioni che sono compatibili con le operazioni. Vogliamo dimostrare
Calcolo differenziale per funzioni di più variabili
 Calcolo differenziale per funzioni di più variabili Riccarda Rossi Università di Brescia Analisi Matematica B Derivate direzionali e parziali Consideriamo un insieme aperto Ω R n e un campo scalare f :
Calcolo differenziale per funzioni di più variabili Riccarda Rossi Università di Brescia Analisi Matematica B Derivate direzionali e parziali Consideriamo un insieme aperto Ω R n e un campo scalare f :
X (o equivalentemente rispetto a X n ) è la
 Esercizi di Calcolo delle Probabilità della 5 a settimana (Corso di Laurea in Matematica, Università degli Studi di Padova). Esercizio 1. Siano (X n ) n i.i.d. di Bernoulli di parametro p e definiamo per
Esercizi di Calcolo delle Probabilità della 5 a settimana (Corso di Laurea in Matematica, Università degli Studi di Padova). Esercizio 1. Siano (X n ) n i.i.d. di Bernoulli di parametro p e definiamo per
Introduzione alla Matematica per le Scienze Sociali - parte II
 Introduzione alla Matematica per le Scienze Sociali - parte II Lucrezia Fanti Istituto Nazionale per l Analisi delle Politiche Pubbliche (INAPP) lucrezia.fanti@uniroma1.it Lucrezia Fanti Intro Matematica
Introduzione alla Matematica per le Scienze Sociali - parte II Lucrezia Fanti Istituto Nazionale per l Analisi delle Politiche Pubbliche (INAPP) lucrezia.fanti@uniroma1.it Lucrezia Fanti Intro Matematica
Soluzione dei problemi assegnati
 ANALISI MATEMATICA 3 Soluzione dei problemi assegnati anno accademico 2018/19 prof. Antonio Greco http://people.unica.it/antoniogreco Dipartimento di Matematica e Informatica Università di Cagliari 23-5-2019
ANALISI MATEMATICA 3 Soluzione dei problemi assegnati anno accademico 2018/19 prof. Antonio Greco http://people.unica.it/antoniogreco Dipartimento di Matematica e Informatica Università di Cagliari 23-5-2019
