LE COORDINATE CELESTI
|
|
|
- Evangelina Moretti
- 9 anni fa
- Просмотров:
Транскрипт
1 LE COORDINATE CELESTI La sfera celeste Una prima osservazione del cielo, diurno o notturno che sia, rivela che esso appare come una superficie continua, sulla quale sembrano fissate le stelle e vediamo invece muoversi il Sole, la Luna e i Pianeti. Questa superficie appare rotonda, giustificando quindi il nome che le si dà: Sfera Celeste. Questo nome compete dunque a quella superficie continua che sembra avvolgere tutto il nostro globo; il fatto di assimilarla ad una sfera ha una giustificazione geometrica: l'osservazione ad occhio nudo non è in grado di rivelare che le stelle sono a diverse distanze dalla Terra, esse appaiono tutte come fossero egualmente distanti da noi. La superficie che gode della proprietà che tutti i suoi punti sono egualmente distanti dal centro è appunto la sfera. Un'osservazione più accurata rivela che tutta la volta celeste sembra ruotare durante la giornata in modo uniforme intorno a due punti fissi, opposti tra loro, che prendono il nome di Poli Celesti. Congiungendo i due Poli tra loro con una retta otteniamo l'asse del Mondo. Figura 1 - Coordinate di un astro S visto da un punto O: x,y,z, sono le sue coordinate rettilinee rispetto al sistema di assi OXYZ; le ampiezze degli archi XS e S S, corrispondenti alla posizione sferica S di S, sono le coordinate sferiche dell astro. Il fatto che il cielo sembri ruotare intorno all'asse del Mondo ci dice subito che la Terra ruota intorno a quest'asse. Il moto apparente del cielo non è altro che il riflesso del moto reale della Terra intorno al suo asse. Figura 2 - La rotazione della sfera celeste A) L osservatore si trova al polo nord: tutte le stelle descrivono cerchi paralleli all orizzonte; nessuna stella sorge e nessuna tramonta. B) L osservatore si trova all equatore: tutte le stelle descrivono cerchi attorno alla linea orizzontale nord-sud (linea meridiana) e tutte le stelle sorgono e tramontano. C) L osservatore si trova ad una latitudine intermedia settentrionale: tutte le stelle descrivono archi obliqui rispetto all orizzonte; le stelle che distano dal polo nord celeste (PN) di un arco minore della latitudine del luogo non tramontano mai, quelle che distano dal polo sud celeste di un arco minore di tale latitudine non si vedono mai, le altre sorgono e tramontano. 1
2 Figura 3 - L'asse del mondo e l'asse della Terra sono coincidenti e di conseguenza i Poli celesti e i poli terrestri sono allineati Figura 4 Equatore Terrestre ed Equatore Celeste L'asse del mondo e l'asse della Terra sono coincidenti e di conseguenza i Poli celesti e i poli terrestri sono allineati (figura 3). Possiamo dire che i Poli celesti sono la proiezione sulla volta celeste dei Poli terrestri e prendono gli stessi nomi. Quindi la proiezione del polo Nord Terrestre si chiama Polo Nord Celeste ed analogamente per il Polo Sud. Definiti i Poli, è immediato comprendere cosa si intenda per Centro della Terra: è il punto medio del segmento che ha per estremi i Poli terrestri. Occorre tenere presente che, al momento, considereremo la Terra come sferica e, di massima, in tutto il procedere di questo testo, non sarà necessario fare altrimenti; pertanto potremo ritenere che il baricentro della Terra ed il suo centro geometrico coincidano, salvo precisare quando sarà necessario. Una delle proprietà della sfera è che tutti i piani passanti per il centro determinano sulla superficie dei Cerchi Massimi. I cerchi determinati invece da piani non passanti per il centro prendono il nome di Cerchi Minori. Consideriamo allora il piano passante per il centro e perpendicolare all'asse del mondo: questo piano determina un cerchio massimo che prende il nome di Equatore Terrestre, e, per esteso all'infinito, interseca la sfera celeste prendendo il nome di Equatore Celeste (figura 4). Le coordinate geografiche Si consideri la sfera terrestre. Siano N e S i poli Nord e Sud rispettivamente; l'equatore è indicato in tutte lettere (figura 5). Definiamo Paralleli tutti e soli i cerchi formati da piani paralleli all'equatore e Meridiani tutti i semicerchi passanti per i Poli. Parleremo di Paralleli Nord parlando dei cerchi minori contenuti nella semisfera compresa tra l'equatore ed il polo Nord, analogamente faremo per i Paralleli Sud. I paralleli Nord vengono anche indicati premettendo il segno +, con il segno - verranno indicati i paralleli Sud. I meridiani non hanno segno, ma vengono indicati con un numero a partire da un meridiano scelto come meridiano Figura 5 Coordinate terrestri 2
3 zero. Come conseguenza di tutto questo, per determinare la posizione di un punto sulla Terra basterà indicare quali sono il parallelo ed il meridiano passanti per quel punto. Nella figura prendiamo come fondamentale il meridiano indicato con NGQ sia PP' il meridiano per il punto P, del quale vogliamo determinare la posizione. L'angolo OCP', indicato con λ, tra il meridiano fondamentale e il meridiano per P misurato in gradi lungo l'equatore con verso da ovest ad est, ossia antiorario, prende il nome di Longitudine del punto P. L'angolo φ tra l'equatore ed il parallelo per P prende il nome di Latitudine del punto e, come già detto, è positivo nell'emisfero Nord e negativo nell'emisfero Sud. Come meridiano fondamentale o Meridiano Origine si assume il meridiano passante per l'osservatorio di Greenwich, esattamente quello che passa per il centro dell'antico strumento dei passaggi di Flamsteed. Questo meridiano prende il numero zero e viene comunemente detto Meridiano Zero. Quindi, per definire la posizione di un punto sulla Terra, basta dare la coppia di coordinate λ, φ di questo punto. Si deduce immediatamente dall'esame della figura che le latitudini vanno da +90 a -90, mentre le longitudini vanno da 0 a 360. Chiaramente, tutti i punti dell'equatore hanno latitudine 0. Talvolta le longitudini vengono riferite ad un meridiano diverso da quello di Greenwich: in tal caso, questo dev'essere chiaramente indicato. Sistemi di coordinate astronomiche. Per individuare univocamente la posizione di un punto sulla sfera celeste è necessario definire un sistema di riferimento. Per far questo è necessario premettere alcune nozioni sulla geometria della sfera. Si definisce asse della sfera una qualunque retta passante per il suo centro. Poli sono i due punti diametralmente opposti in cui l'asse interseca la superficie sferica. Piano fondamentale è il piano passante per il centro della sfera e perpendicolare all'asse. Cerchio base si chiama il cerchio intersezione del piano fondamentale con la superficie della sfera. Cerchi ausiliari sono i cerchi intersezione di piani perpendicolari al piano fondamentale e passanti per il centro. I Figura 6 Coordinate celesti cerchi ausiliari sono perpendicolari, per costruzione, al cerchio base e passano tutti per i poli. (vedi figura 6) Cerchio base e cerchi ausiliari sono esempi di cerchi massimi, cioè di quella famiglia di cerchi che nascono dall'intersezione della superficie sferica con piani passanti per il centro della sfera e che sono chiamati così perché sono quelli di lunghezza massima. Infatti, qualunque altro cerchio tracciato sulla superficie della sfera può sempre considerarsi generato dall'intersezione con un piano non passante per il centro: questi cerchi sono detti minori. Ne sono esempi sulla superficie terrestre i paralleli di latitudine. Per determinare un sistema di riferimento sulla sfera si procede quindi così (vedi figura 6): 1. Si sceglie un asse; questa scelta determina i poli, il piano fondamentale, il cerchio base e i cerchi ausiliari. 2. Sul cerchio base di sceglie un punto O come origine e un verso di percorrenza lungo il cerchio. 3
4 3. Dato un punto S qualsiasi sulla superficie sferica si traccia il cerchio ausiliario passante per esso: viene determinato così il punto P intersezione del cerchio ausiliario col cerchio base. 4. A partire dall'origine, sul cerchio base, ci si muove nel verso prescelto verso il punto P: l'ampiezza angolare dell'arco così descritto rappresenta la prima coordinata sferica del punto S che si chiama ascissa sferica. 5. Dal punto P, lungo il cerchio ausiliario ci si muove verso S descrivendo un arco la cui ampiezza angolare è la seconda coordinata di S detta ordinata sferica. A seconda che il punto S si trovi in uno o nell'altro dei due emisferi in cui il cerchio base divide la superficie sferica, ci si muoverà lungo il cerchio ausiliario verso l'uno o l'altro dei poli: si sceglie una volta per tutte uno dei due versi come positivo e il valore dell'ordinata sferica sarà di conseguenza positivo o negativa a seconda che si percorra il cerchio ausiliario in verso concorde o meno con quello prescelto. Di conseguenza tutti i punti di un emisfero avranno ordinate sferiche positive e tutti quelli dell'altro negative. L'ascissa sferica potrà assumere un valore qualsiasi compreso tra 0 e 360, ovvero, misurando gli archi in ore, minuti e secondi, tra 0h e 24h; l'ordinata sferica, a meno del segno, potrà assumere qualsiasi valore tra 0 e 90. I vari sistemi di coordinate astronomiche differiscono tra loro semplicemente per la scelta dell'asse. Sistema altazimutale. In questo sistema l'asse è scelto coincidente con la direzione della verticale alla superficie terrestre passante per la posizione dell'osservatore. I poli sono quindi i due punti della sfera celeste: uno direttamente sopra la testa, detto zenit, e l altro sotto i piedi dell'osservatore, detto nadir (figura 7). Il cerchio base è la linea dell'orizzonte razionale approssimato bene dall'orizzonte visibile solo in mare aperto e al livello del mare. L'origine è il punto cardinale Nord sull'orizzonte e il verso di percorrenza quello concorde col moto delle lancette dell'orologio (verso orario), ovvero nel senso da Nord verso Est[ 1 ]. I cerchi ausiliari si chiamano Cerchi d'altezza o Verticali (nella figura 7 il Figura 7 Sistema altazimutale cerchio che passa per lo Zenit, il punto S che contraddistingue l astro e il Nadir). L'ascissa sferica, misurata lungo l'orizzonte, prende il nome di Azimut e si indica generalmente con la lettera A. L'ordinata sferica si chiama Altezza e si indica con h. Un valore negativo dell'altezza corrisponde ovviamente ad un astro sotto l'orizzonte e quindi non visibile. L'arco complementare di h sul cerchio d'altezza, cioè l'arco dallo zenit verso il punto S si chiama distanza zenitale e si indica con z. Si ha perciò: z = 90 - h Tutti i punti di uno stesso cerchio d'altezza avranno il medesimo valore dell'azimut. Tutti i punti con la [ 1 ] In alcuni testi l origine è il Sud il verso sempre quello orario (cioè da Sud verso Ovest che ha azimut A = 90 ) 4
5 stessa altezza giaceranno invece su un circolo minore detto proprio cerchio di uguale altezza o, con termine arabo, almucantarat. Il verticale passante per i punti cardinali Nord e Sud si chiama meridiano locale o semplicemente meridiano. Il nome trae origine dal fatto che esso è attraversato dal Sole ad ogni mezzogiorno. Il sistema altazimutale, molto usato in geodesia, lo è invece poco in astronomia essenzialmente per due motivi: L'apparente rotazione diurna della sfera celeste fa sì che entrambe le coordinate di un astro (azimut ed altezza) varino durante la giornata in modo non uniforme: si pensi che al momento del sorgere e del tramontare gli astri hanno altezza zero, mentre hanno altezza massima al momento del transito al meridiano locale, cioè all'istante della cosiddetta culminazione superiore. L'altezza pertanto cresce prima della culminazione e decresce dopo. Un astro che sorge ad Est ha azimut uguale a 90, al tramonto, a Ovest, ha azimut uguale a 270, passando per tutti i valori intermedi. Poiché l'asse del sistema coincide con la direzione della verticale passante per l'osservatore, il sistema altazimutale è un sistema locale in quanto, variando la posizione dell'osservatore sulla Terra varia la verticale e quindi il valore delle coordinate altazimutali. Per questi motivi il sistema di riferimento più usato in astronomia è quello equatoriale. Il sistema equatoriale. Figura 8 Sistema equatoriale Figura 9 Coordinate equatoriali ed eclittica L'asse di questo sistema è scelto coincidente con quello di rotazione della Terra: ciò elimina immediatamente uno dei difetti del sistema altazimutale, poiché l'equatoriale è unico per tutti gli osservatori in quanto l'asse è lo stesso per tutti. Ovviamente i poli saranno il Polo Celeste Nord e quello Sud. Il piano fondamentale è il piano dell'equatore e il cerchio base è l Equatore Celeste. L'origine è un punto particolare di questo chiamato Primo Punto d'ariete o Punto Vernale o ancora Punto Gamma dal simbolo greco con cui comunemente lo si indica, γ. Esso è il punto dell'equatore celeste in cui il Sole si trova il giorno dell'equinozio di Primavera. Quindi il Punto Gamma è uno dei due punti in cui l'equatore celeste è intersecato dal cerchio massimo su cui vediamo proiettato il cammino del Sole durante l'anno 5
6 (riflesso del moto reale di rivoluzione della Terra intorno al Sole), detto Eclittica (vedi figure 8 e 9). Precisamente il Punto Gamma è il punto in cui il Sole transita passando dall'emisfero celeste sud (emisfero australe) a quello nord (emisfero boreale). Il verso di percorrenza scelto è quello antiorario. I cerchi ausiliari prendono il nome di cerchi orari. L'ascissa sferica si chiama Ascensione Retta e si indica con la lettera greca α; essa si misura, per motivi che chiariremo in seguito, in ore, minuti e secondi. L'ordinata, positiva nell'emisfero boreale, si chiama Declinazione e si indica con δ. I cerchi minori di uguale declinazione si chiamano Paralleli celesti. Poiché l'intero sistema di riferimento, cerchio base, cerchi orari, punto γ, partecipa della rotazione diurna che si svolge proprio intorno all'asse del sistema, è evidente che i valori di α e di δ risulteranno costanti e viene eliminato così anche l'altro difetto del sistema altazimutale. Tuttavia, mentre in quest'ultimo l'origine (il punto cardinale Nord) non varia la sua posizione durante il giorno, nel sistema equatoriale il punto γ in istanti differenti si troverà in differenti parti del cielo e quindi la sola conoscenza dei valori di α e di δ di un astro non basta ad individuarne la posizione ad un istante determinato. Per far questo dobbiamo introdurre qualche altro concetto. Angolo orario e Tempo Siderale Locale Il verticale che, nel sistema altazimutale, avevamo definito meridiano locale è anche un cerchio orario, in quanto passa per i poli celesti. La sua intersezione con l'equatore celeste si chiama Mezzocielo (M), questo nome deriva dal fatto che alle nostre latitudini si trova all'incirca a metà distanza angolare tra l'orizzonte e lo zenit. Ricordiamo infatti che l'altezza del Polo Celeste Nord sul punto cardinale Nord è uguale alla latitudine del luogo, quindi l altezza dell equatore celeste sul punto cardinale Sud è pari al complemento a 90 della latitudine del luogo di osservazione. Per Macerata, essendo la latitudine di 43 18, si ha che il Polo Nord Celeste è alto sul punto cardinale Nord 43 18, mentre l equatore celeste è alto (= ) sul punto cardinale Sud. Figura 10 L angolo orario Figura 11 Tempo Siderale Locale L'arco, misurato percorrendo in verso orario l'equatore celeste dal mezzocielo all'intersezione (P) del cerchio orario passante per l'astro S con l'equatore si chiama angolo orario H dell'astro (vedi figura 10). Al momento del transito dell'astro al meridiano, il suo angolo orario è uguale a zero. Un'ora dopo, la volta celeste avrà ruotato di un arco pari a 15 (essendo infatti 360 /24 ore = 15 ad ora), misurando 6
7 gli archi in ore, minuti e secondi, il suo angolo orario sarà allora esattamente 1 h. Anche il punto γ avrà, istante per istante, un determinato valore del suo angolo orario che prende il nome di Tempo Siderale Locale (TSL). Il Tempo Siderale Locale è quindi la distanza del punto γ dal mezzocielo ed pari alla somma, in valore assoluto, degli archi γp, cioè dell'ascensione retta α dell'astro e dell'arco PM, ossia del suo angolo orario H. Abbiamo così ricavato la relazione: TSL = H + α L'angolo orario è ovviamente comodo misurano in ore, minuti e secondi e l'uso frequentissimo della relazione precedente spiega perché anche le ascensioni rette utilizzino la stessa unità. L'angolo orario ed il tempo siderale sono legati alla posizione del meridiano e quindi dell'osservatore; infatti nel definirli si è aggiunto l'aggettivo locale proprio per sottolineare questo fatto. Il meridiano locale di ciascun osservatore può essere sempre considerato la proiezione sulla sfera celeste del meridiano geografico passante per l'osservatore. Poiché sulla Terra la differenza tra due meridiani si misura con la differenza tra le longitudini geografiche, anche i meridiani celesti locali dei due osservatori saranno separati tra loro da un numero di gradi pari alla differenza suddetta. Sulla Terra, come già detto, le longitudini prendono come riferimento il meridiano di Greenwich; conoscendo il valore dell'angolo orario di un astro a Greenwich, indicato con H g, per trovare l'angolo orario H λ alla longitudine λ, basterà quindi effettuare la sottrazione: H g = H λ - λ. Il segno meno nasce dalla convenzione di considerare negative le longitudine ad Est di Greenwich, cioè le longitudini crescono in senso antiorario, mentre gli angoli orari vengono (lo dice il nome stesso!) contati in senso orario. Nella pratica dei conti bisogna ricordare di esprime le longitudini in ore e non in gradi: la conversione è semplice se si ricorda che 15 corrispondono ad 1h. La formula che dà il TSL fornisce anche un mezzo immediato per calcolarlo senza troppi conti: quando l'astro transita in meridiano, per definizione il suo angolo orario è nullo. Quindi la sua ascensione retta α è uguale al valore del TSL. Basterà quindi, per una stella di α nota, attendere che essa transiti in meridiano, per conoscere il TSL. Esempio il 21 gennaio 2008 Betelgeuse (α Orionis) passa al meridiano di Macerata alle ore 21h 59m 24s essendo quindi per definizione H = 0 e conoscendo l ascensione retta (α = 5h 55m 37s) si ricava che il Tempo Siderale Locale per Macerata è 5h 55m 37s. C è da notare che a causa della precessione degli equinozi (il lento movimento della direzione dell asse di rotazione terrestre) le coordinate equatoriali non rimangono le stesse, ma variano lentamente. 7
La sfera celeste. Coordinate locali altazimutali Coordinate universali equatoriali
 La sfera celeste Coordinate locali altazimutali Coordinate universali equatoriali Volta celeste Volta parte della sfera visibile al di sopra dell orizzonte celeste (intersezione del piano tangente all
La sfera celeste Coordinate locali altazimutali Coordinate universali equatoriali Volta celeste Volta parte della sfera visibile al di sopra dell orizzonte celeste (intersezione del piano tangente all
PREREQUISITI ASPETTI TEORICI
 .- 1 - PREREQUISITI ASPETTI TEORICI LA SFERA CELESTE ED I SUOI ELEMENTI VOLTA E SFERA CELESTE LE PRINCIPALI COORDINATE ASTRONOMICHE COORDINATE ORIZZONTALI E COORDINATE EQUATORIALI pag. 2 pag. 3 CORRISPONDENZA
.- 1 - PREREQUISITI ASPETTI TEORICI LA SFERA CELESTE ED I SUOI ELEMENTI VOLTA E SFERA CELESTE LE PRINCIPALI COORDINATE ASTRONOMICHE COORDINATE ORIZZONTALI E COORDINATE EQUATORIALI pag. 2 pag. 3 CORRISPONDENZA
Le Coordinate Astronomiche
 Le Stelle vanno a scuola Le Coordinate Astronomiche Valentina Alberti Novembre 2003 1 2 INDICE Indice 1 Coordinate astronomiche 3 1.1 Sistema dell orizzonte o sistema altazimutale.......... 3 1.2 Sistema
Le Stelle vanno a scuola Le Coordinate Astronomiche Valentina Alberti Novembre 2003 1 2 INDICE Indice 1 Coordinate astronomiche 3 1.1 Sistema dell orizzonte o sistema altazimutale.......... 3 1.2 Sistema
sfera celeste e coordinate astronomiche
 sfera celeste e coordinate astronomiche sfera celeste La sfera celeste appare come una grande sfera che ruota su se stessa, al cui centro sta la Terra immobile, e sulla cui superficie stanno le stelle
sfera celeste e coordinate astronomiche sfera celeste La sfera celeste appare come una grande sfera che ruota su se stessa, al cui centro sta la Terra immobile, e sulla cui superficie stanno le stelle
NAVIGAZIONE ASTRONOMICA. Circolo Astrofili di Mestre Guido Ruggieri
 3 Novembre 2008, ore 21:00 Introduzione. Orientamento sulla Terra. Coordinate orizzontali degli astri, azimuth e altezza. Coordinate equatoriali degli astri, Ascensione Retta e Declinazione. 17 Novembre
3 Novembre 2008, ore 21:00 Introduzione. Orientamento sulla Terra. Coordinate orizzontali degli astri, azimuth e altezza. Coordinate equatoriali degli astri, Ascensione Retta e Declinazione. 17 Novembre
Elementi di Astronomia di posizione. Sabina Sabatini INAF Istituto di Astrofisica e Planetologia Spaziale
 Elementi di Astronomia di posizione Sabina Sabatini INAF Istituto di Astrofisica e Planetologia Spaziale [email protected] 5 Febbraio 2016 Le coordinate astronomiche Definiscono le posizioni
Elementi di Astronomia di posizione Sabina Sabatini INAF Istituto di Astrofisica e Planetologia Spaziale [email protected] 5 Febbraio 2016 Le coordinate astronomiche Definiscono le posizioni
3. Le coordinate geografiche: latitudine e longitudine
 Introduzione 3. Le coordinate geografiche: latitudine e longitudine Ogni volta che vogliamo individuare un punto sulla superficie terrestre gli associamo due numeri, le coordinate geografiche: la latitudine
Introduzione 3. Le coordinate geografiche: latitudine e longitudine Ogni volta che vogliamo individuare un punto sulla superficie terrestre gli associamo due numeri, le coordinate geografiche: la latitudine
1. LA SFERA CELESTE I SUOI PUNTI E LINEE FONDAMENTALI.
 1. LA SFERA CELESTE I SUOI PUNTI E LINEE FONDAMENTALI. In una notte: di cielo sereno, se alziamo gli occhi in alto vediamo il cielo trapuntato di astri lucenti. Essi ci appaiano tutti alla stessa distanza,
1. LA SFERA CELESTE I SUOI PUNTI E LINEE FONDAMENTALI. In una notte: di cielo sereno, se alziamo gli occhi in alto vediamo il cielo trapuntato di astri lucenti. Essi ci appaiano tutti alla stessa distanza,
Elementi di Astronomia di posizione, sistemi di coordinate, costellazioni
 Elementi di Astronomia di posizione, sistemi di coordinate, costellazioni Olimpiadi di Astronomia 2019 INAF-IAPS Istituto di Astrofisica e Planetologia Spaziale Preparazione selezione Interregionale Lazio
Elementi di Astronomia di posizione, sistemi di coordinate, costellazioni Olimpiadi di Astronomia 2019 INAF-IAPS Istituto di Astrofisica e Planetologia Spaziale Preparazione selezione Interregionale Lazio
SISTEMI DI COORDINATE SULLA SUPERFICIE SFERICA (di mortola carlo)
 SISTEMI DI COORDINATE SULLA SUPERFICIE SFERICA (di mortola carlo) Per individuare univocamente un punto di una superficie sferica si possono utilizzare due sistemi di coordinate sferiche, e precisamente:
SISTEMI DI COORDINATE SULLA SUPERFICIE SFERICA (di mortola carlo) Per individuare univocamente un punto di una superficie sferica si possono utilizzare due sistemi di coordinate sferiche, e precisamente:
29/10/2017. luminescenza.
 Orientarsi significa determinare la propria posizione rispetto a dei punti di riferimento. In passato il riferimento era il punto da cui sorge il sole (dal latino oriri, sorgere). Per orientarsi la prima
Orientarsi significa determinare la propria posizione rispetto a dei punti di riferimento. In passato il riferimento era il punto da cui sorge il sole (dal latino oriri, sorgere). Per orientarsi la prima
La Sfera Celeste ed il sistema Sole-Terra-Luna
 La Sfera Celeste ed il sistema Sole-Terra-Luna Lezione 2 http://www.arcetri.astro.it/~marconi/astro07/ Sommario La Sfera Celeste. Sistemi di riferimento. Misura del tempo. I moti di rotazione e rivoluzione
La Sfera Celeste ed il sistema Sole-Terra-Luna Lezione 2 http://www.arcetri.astro.it/~marconi/astro07/ Sommario La Sfera Celeste. Sistemi di riferimento. Misura del tempo. I moti di rotazione e rivoluzione
Moti della Terra. Rotazione Rivoluzione Precessione e nutazioni Moti millenari
 Moti della Terra Rotazione Rivoluzione Precessione e nutazioni Moti millenari Asse terrestre 23 27 asse equatore Piano eclittica L asse terrestre -passante per il centro, emergente ai Poli, punti della
Moti della Terra Rotazione Rivoluzione Precessione e nutazioni Moti millenari Asse terrestre 23 27 asse equatore Piano eclittica L asse terrestre -passante per il centro, emergente ai Poli, punti della
LATITUDINE E LONGITUDINE
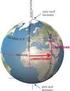 LATITUDINE E LONGITUDINE La posizione di un punto sul globo terrestre si misura per mezzo dei meridiani e dei paralleli. I meridiani, linee idealmente tracciate intorno alla Terra passando per i poli,
LATITUDINE E LONGITUDINE La posizione di un punto sul globo terrestre si misura per mezzo dei meridiani e dei paralleli. I meridiani, linee idealmente tracciate intorno alla Terra passando per i poli,
LA TERRA. La Terra studiata come copro celeste, risulta essere un PIANETA un copro celeste di forma sferica che ruota attorno ad una stella il SOLE
 IL PIANETA TERRA LA TERRA La Terra studiata come copro celeste, risulta essere un PIANETA un copro celeste di forma sferica che ruota attorno ad una stella il SOLE FORMA E DIMENSIONI DELLA TERRA Agli
IL PIANETA TERRA LA TERRA La Terra studiata come copro celeste, risulta essere un PIANETA un copro celeste di forma sferica che ruota attorno ad una stella il SOLE FORMA E DIMENSIONI DELLA TERRA Agli
LA TERRA. La TERRA ha la forma di una grande sfera un po schiacciata alle estremità, chiamate POLI.
 LA TERRA La TERRA ha la forma di una grande sfera un po schiacciata alle estremità, chiamate POLI. Per poterla studiare possiamo rappresentare la TERRA per mezzo di un mappamondo (globo). Su di esso possiamo
LA TERRA La TERRA ha la forma di una grande sfera un po schiacciata alle estremità, chiamate POLI. Per poterla studiare possiamo rappresentare la TERRA per mezzo di un mappamondo (globo). Su di esso possiamo
Problema 10. Un osservatore nota che tutte le stelle con la stessa ascensione retta tramontano nello stesso istante. Dove si trova l osservatore?
 Olimpiadi Italiane di Astronomia 2018 Corso di preparazione alla Gara Interregionale Categoria Senior e Junior 2 30 gennaio 2018 Problema 1. Un osservatore misura per il Polo Nord Celeste un altezza di
Olimpiadi Italiane di Astronomia 2018 Corso di preparazione alla Gara Interregionale Categoria Senior e Junior 2 30 gennaio 2018 Problema 1. Un osservatore misura per il Polo Nord Celeste un altezza di
Anno Accademico 2007/2008. Astronomia. Corso di Laurea in Scienze Naturali. Alessandro Marconi
 Anno Accademico 2007/2008 Astronomia Corso di Laurea in Scienze Naturali Alessandro Marconi Dipartimento di Astronomia e Scienza dello Spazio, Università di Firenze Bibliografia Il testo su cui sono basate
Anno Accademico 2007/2008 Astronomia Corso di Laurea in Scienze Naturali Alessandro Marconi Dipartimento di Astronomia e Scienza dello Spazio, Università di Firenze Bibliografia Il testo su cui sono basate
OLIMPIADI ITALIANE DI ASTRONOMIA. Angoli e Coordinate
 Corso di preparazione alle Olimpiadi INAF Osservatorio Astronomico di Teramo Scuola Secondaria di I Grado «F. Savini» Teramo OLIMPIADI ITALIANE DI ASTRONOMIA Angoli e Coordinate Mauro Dolci INAF - Osservatorio
Corso di preparazione alle Olimpiadi INAF Osservatorio Astronomico di Teramo Scuola Secondaria di I Grado «F. Savini» Teramo OLIMPIADI ITALIANE DI ASTRONOMIA Angoli e Coordinate Mauro Dolci INAF - Osservatorio
Il sistema Terra. Un sistema è un insieme di elementi che interagiscono tra loro
 Il sistema Terra Un sistema è un insieme di elementi che interagiscono tra loro Esistono tre tipi di sistemi: 1. i sistemi aperti: scambiano materia ed energia con l ambiente 2. i sistemi chiusi: scambiano
Il sistema Terra Un sistema è un insieme di elementi che interagiscono tra loro Esistono tre tipi di sistemi: 1. i sistemi aperti: scambiano materia ed energia con l ambiente 2. i sistemi chiusi: scambiano
Sfera Celeste e Coordinate Astronomiche. A. Stabile Dipartimento di Ingegneria Università degli Studi del Sannio Benevento Atripalda, 9 Maggio 2011
 Astronomiche A. Stabile Dipartimento di Ingegneria Università degli Studi del Sannio Benevento Atripalda, 9 Maggio 2011 Unità di lunghezza e distanze tipiche 1. Sistema Solare: 1 UA = 149,5 milioni di
Astronomiche A. Stabile Dipartimento di Ingegneria Università degli Studi del Sannio Benevento Atripalda, 9 Maggio 2011 Unità di lunghezza e distanze tipiche 1. Sistema Solare: 1 UA = 149,5 milioni di
Elementi di Astronomia di posizione, sistemi di coordinate, costellazioni
 Elementi di Astronomia di posizione, sistemi di coordinate, costellazioni Olimpiadi di Astronomia 2019 INAF-IAPS Istituto di Astrofisica e Planetologia Spaziale Preparazione selezione Interregionale Lazio
Elementi di Astronomia di posizione, sistemi di coordinate, costellazioni Olimpiadi di Astronomia 2019 INAF-IAPS Istituto di Astrofisica e Planetologia Spaziale Preparazione selezione Interregionale Lazio
Latitudine e longitudine
 La volta celeste Fin dall antichità gli uomini si orientavano osservando le stelle e, a tale scopo, hanno conesse costruito dei sistemi di riferimento: le costellazioni. Le stelle vengono tradizionalmente
La volta celeste Fin dall antichità gli uomini si orientavano osservando le stelle e, a tale scopo, hanno conesse costruito dei sistemi di riferimento: le costellazioni. Le stelle vengono tradizionalmente
IL MOTO di ROTAZIONE. CONSEGUENZE del MOTO di ROTAZIONE
 IL MOTO di ROTAZIONE moto di rotazione: il moto di rotazione è il movimento che la Terra compie attorno al proprio asse, da ovest verso est, in senso antiorario per un osservatore posto al polo nord celeste;
IL MOTO di ROTAZIONE moto di rotazione: il moto di rotazione è il movimento che la Terra compie attorno al proprio asse, da ovest verso est, in senso antiorario per un osservatore posto al polo nord celeste;
UNITÀ DIDATTICA 11 LE COORDINATE GEOGRAFICHE
 UNITÀ DIDATTICA 11 LE COORDINATE GEOGRAFICHE 11.1 Il reticolato geografico La forma della Terra si discosta poco da quella di una sfera. Sulla superficie terrestre, considerata come sferica, è possibile
UNITÀ DIDATTICA 11 LE COORDINATE GEOGRAFICHE 11.1 Il reticolato geografico La forma della Terra si discosta poco da quella di una sfera. Sulla superficie terrestre, considerata come sferica, è possibile
I moti della Terra & la misura del Tempo (Junior 1, Junior2 e Senior)
 Olimpiadi Italiane di Astronomia 2019 I moti della Terra & la misura del Tempo (Junior 1, Junior2 e Senior) Olimpiadi di Astronomia 2019 Selezione Interregionale Lazio [email protected]
Olimpiadi Italiane di Astronomia 2019 I moti della Terra & la misura del Tempo (Junior 1, Junior2 e Senior) Olimpiadi di Astronomia 2019 Selezione Interregionale Lazio [email protected]
Società alpina delle Giulie Sezione di Trieste del Club Alpino Italiano. Topografia e orientamento
 Società alpina delle Giulie Sezione di Trieste del Club Alpino Italiano Topografia e orientamento Introduzione Per un alpinista sapersi orientare in montagna è altrettanto importante che saper arrampicare
Società alpina delle Giulie Sezione di Trieste del Club Alpino Italiano Topografia e orientamento Introduzione Per un alpinista sapersi orientare in montagna è altrettanto importante che saper arrampicare
ASTRONOMIA SISTEMI DI RIFERIMENTO
 Sfera celeste ASTRONOMIA Il cielo considerato come l'interno di una sfera cava al fine di descrivere le posizioni e i movimenti degli oggetti astronomici. Ogni particolare osservatore è situato al centro
Sfera celeste ASTRONOMIA Il cielo considerato come l'interno di una sfera cava al fine di descrivere le posizioni e i movimenti degli oggetti astronomici. Ogni particolare osservatore è situato al centro
Nocchiero. Appunti di Scienze della navigazione a cura del Prof. Natalino Usai LE CARTE NAUTICHE
 Nocchiero Appunti di Scienze della navigazione a cura del Prof. Natalino Usai LE CARTE NAUTICHE Le carte Nautiche Un modello in scala della sfera terrestre mal si adatterebbe per il normale impiego della
Nocchiero Appunti di Scienze della navigazione a cura del Prof. Natalino Usai LE CARTE NAUTICHE Le carte Nautiche Un modello in scala della sfera terrestre mal si adatterebbe per il normale impiego della
L Astrolabio. di Alberto Nicelli. GAE Gruppo Astrofili Eporediesi
 L Astrolabio di Alberto Nicelli GAE Gruppo Astrofili Eporediesi L Astrolabio (vedi kit allegato) è così costituito: Il Piatto, che riproduce in proiezione stereografica: o l Orizzonte Locale, relativo
L Astrolabio di Alberto Nicelli GAE Gruppo Astrofili Eporediesi L Astrolabio (vedi kit allegato) è così costituito: Il Piatto, che riproduce in proiezione stereografica: o l Orizzonte Locale, relativo
1.1 Trasformazioni DI COORDINATE.
 1.1 Trasformazioni DI COORDINATE. Facendo passare per l'astro A il rispettivo verticale e il circolo orario otteniamo un triangolo sferico, detto triangolo di posizione. Detto triangolo ha per vertici
1.1 Trasformazioni DI COORDINATE. Facendo passare per l'astro A il rispettivo verticale e il circolo orario otteniamo un triangolo sferico, detto triangolo di posizione. Detto triangolo ha per vertici
LA LATITUDINE E LA LONGITUDINE
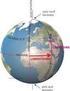 LC.06.02.06 LA LATITUDINE E LA LONGITUDINE Prerequisiti: nozioni scientifiche e matematiche acquisite durante la scuola secondaria di primo grado Obiettivi: studio della latitudine e della longitudine
LC.06.02.06 LA LATITUDINE E LA LONGITUDINE Prerequisiti: nozioni scientifiche e matematiche acquisite durante la scuola secondaria di primo grado Obiettivi: studio della latitudine e della longitudine
Le coordinate geografiche
 Le coordinate geografiche La Terra non ha la forma di una sfera perfetta: per descriverla e rappresentarla la si approssima a una forma ellissoidale leggermente schiacciata ai poli, detta geoide. Per identificare
Le coordinate geografiche La Terra non ha la forma di una sfera perfetta: per descriverla e rappresentarla la si approssima a una forma ellissoidale leggermente schiacciata ai poli, detta geoide. Per identificare
L alternanza delle stagioni
 L alternanza delle stagioni Le cause Si potrebbe pensare che l alternarsi delle stagioni sia dovuto al fatto che la Terra si trovi in estate più vicino e in inverno più lontano dal Sole. Purtroppo le cose
L alternanza delle stagioni Le cause Si potrebbe pensare che l alternarsi delle stagioni sia dovuto al fatto che la Terra si trovi in estate più vicino e in inverno più lontano dal Sole. Purtroppo le cose
In prima approssimazione, guardandoci intorno. Note su Nord-Sud-Est-Ovest Enrica Giordano e Nicoletta Lanciano febbraio 2008
 Note su Nord-Sud-Est-Ovest Enrica Giordano e Nicoletta Lanciano febbraio 2008 Le cose devono essere apprese solo per essere nuovamente disimparate, oppure, cosa più probabile, per essere corrette R. Feynman
Note su Nord-Sud-Est-Ovest Enrica Giordano e Nicoletta Lanciano febbraio 2008 Le cose devono essere apprese solo per essere nuovamente disimparate, oppure, cosa più probabile, per essere corrette R. Feynman
Est Greenwich 5
 La terra La Terra, per gli scopi pratici della navigazione, può essere considerata, senza apprezzabili errori, come perfettamente sferica, costituita da una superficie liscia ed omogenea. La terra ruota
La terra La Terra, per gli scopi pratici della navigazione, può essere considerata, senza apprezzabili errori, come perfettamente sferica, costituita da una superficie liscia ed omogenea. La terra ruota
La forma della Terra
 La forma della Terra Sfericità della Terra (nave che si allontana scompare all orizzonte linea apparente che separa terra e cielo a causa della curvatura della superficie terrestre, prima vedo lo scafo
La forma della Terra Sfericità della Terra (nave che si allontana scompare all orizzonte linea apparente che separa terra e cielo a causa della curvatura della superficie terrestre, prima vedo lo scafo
I principali movimenti della Terra sono: il moto di rotazione (intorno al proprio asse) il moto di rivoluzione (intorno al Sole)
 I MOTI DELLA TERRA I principali movimenti della Terra sono: il moto di rotazione (intorno al proprio asse) il moto di rivoluzione (intorno al Sole) La Terra compie anche movimenti minori detti moti millenari,
I MOTI DELLA TERRA I principali movimenti della Terra sono: il moto di rotazione (intorno al proprio asse) il moto di rivoluzione (intorno al Sole) La Terra compie anche movimenti minori detti moti millenari,
1. Il pianeta blu 2. La longitudine e la latitudine 3. I moti della Terra nello spazio 4. Luce e buio sulla Terra 5. La Luna, il nostro satellite 6.
 1. Il pianeta blu 2. La longitudine e la latitudine 3. I moti della Terra nello spazio 4. Luce e buio sulla Terra 5. La Luna, il nostro satellite 6. Le eclissi 7. Le maree Il pianeta blu Ecco come appare
1. Il pianeta blu 2. La longitudine e la latitudine 3. I moti della Terra nello spazio 4. Luce e buio sulla Terra 5. La Luna, il nostro satellite 6. Le eclissi 7. Le maree Il pianeta blu Ecco come appare
Il tempo. Appunti di Geografia a cura di A. Pulvirenti
 Il tempo Appunti di Geografia a cura di A. Pulvirenti Le immagini presenti in questo file sono state reperite in rete o modificate da testi cartacei e vengono utilizzate solo per l elevato contenuto didattico.
Il tempo Appunti di Geografia a cura di A. Pulvirenti Le immagini presenti in questo file sono state reperite in rete o modificate da testi cartacei e vengono utilizzate solo per l elevato contenuto didattico.
GEOMETRIA ANALITICA. Il Piano cartesiano
 GEOMETRIA ANALITICA La geometria analitica consente di studiare e rappresentare per via algebrica informazioni di tipo geometrico. Lo studio favorisce una più immediata visualizzazione di informazioni,
GEOMETRIA ANALITICA La geometria analitica consente di studiare e rappresentare per via algebrica informazioni di tipo geometrico. Lo studio favorisce una più immediata visualizzazione di informazioni,
Unità 4 Paragrafo 1 La forma e le dimensioni della Terra
 Unità 4 Paragrafo 1 La forma e le dimensioni della Terra forma ellissoide di rotazione più precisamente geoide sfera schiacciata ai poli solido più gonio dove ci sono i continenti e un po depresso nelle
Unità 4 Paragrafo 1 La forma e le dimensioni della Terra forma ellissoide di rotazione più precisamente geoide sfera schiacciata ai poli solido più gonio dove ci sono i continenti e un po depresso nelle
La Misura del Mondo (Fondamenti di Astronomia)
 La Misura del Mondo (Fondamenti di Astronomia) 1 Moti e coordinate Dipartimento di Astronomia Università di Bologna L intero cielo appare ruotare in modo regolare attorno a un asse, detto asse del mondo
La Misura del Mondo (Fondamenti di Astronomia) 1 Moti e coordinate Dipartimento di Astronomia Università di Bologna L intero cielo appare ruotare in modo regolare attorno a un asse, detto asse del mondo
Moti della Terra: Rotazione, Rivoluzione, Moti millenari
 Moti della Terra: Rotazione, Rivoluzione, Moti millenari moto di rotazione giorno sidereo: 23h 56m 4s velocità di rotazione moto di rotazione: conseguenze Alternarsi del dì e della notte Moto apparente
Moti della Terra: Rotazione, Rivoluzione, Moti millenari moto di rotazione giorno sidereo: 23h 56m 4s velocità di rotazione moto di rotazione: conseguenze Alternarsi del dì e della notte Moto apparente
Il reticolato geografico. Meridiani e paralleli.
 Il reticolato geografico. Meridiani e paralleli. Per localizzare un punto qualsiasi sulla superficie terrestre, cioè per individuarne la posizione esatta, i geografi hanno tracciato sul globo terrestre
Il reticolato geografico. Meridiani e paralleli. Per localizzare un punto qualsiasi sulla superficie terrestre, cioè per individuarne la posizione esatta, i geografi hanno tracciato sul globo terrestre
unità 5. L orientamento e la misura del tempo
 giorno Sole osservazione del cielo notte Stella Polare/Croce del sud longitudine in base all ora locale Orientamento coordinate geografiche latitudine altezza della stella Polare altezza del Sole bussola
giorno Sole osservazione del cielo notte Stella Polare/Croce del sud longitudine in base all ora locale Orientamento coordinate geografiche latitudine altezza della stella Polare altezza del Sole bussola
GLI STRUMENTI DELLA GEOGRAFIA
 GLI STRUMENTI DELLA GEOGRAFIA Che cos è la geografia La geografia (dal greco géo, Terra, e graphìa, scrittura, disegno) è la disciplina che studia e descrive la Terra e il rapporto che esiste fra l uomo
GLI STRUMENTI DELLA GEOGRAFIA Che cos è la geografia La geografia (dal greco géo, Terra, e graphìa, scrittura, disegno) è la disciplina che studia e descrive la Terra e il rapporto che esiste fra l uomo
Il moto di rotazione della Terra
 Il moto di rotazione della Terra La Terra compie un movimento di rotazione intorno all asse terrestre da Ovest verso Est in verso antiorario. La velocità angolare di rotazione è uguale per tutti i punti
Il moto di rotazione della Terra La Terra compie un movimento di rotazione intorno all asse terrestre da Ovest verso Est in verso antiorario. La velocità angolare di rotazione è uguale per tutti i punti
Elementi di Astronomia di posizione
 Elementi di Astronomia di posizione Giuseppe Cutispoto INAF Osservatorio Astrofisico di Catania [email protected] Versione 27 Gennaio 2014 La Sfera Celeste Quando osserviamo il cielo notturno abbiamo
Elementi di Astronomia di posizione Giuseppe Cutispoto INAF Osservatorio Astrofisico di Catania [email protected] Versione 27 Gennaio 2014 La Sfera Celeste Quando osserviamo il cielo notturno abbiamo
pianeta Terra caratteristiche generali
 pianeta Terra caratteristiche generali Eratostene 275 195 ac http://www.youtube.com/watch?v=-o99ih9kbpw pianeta Terra alcune delle caratteristiche principali Massa: 5,9 x 10 24 kg Raggio medio: 6.371
pianeta Terra caratteristiche generali Eratostene 275 195 ac http://www.youtube.com/watch?v=-o99ih9kbpw pianeta Terra alcune delle caratteristiche principali Massa: 5,9 x 10 24 kg Raggio medio: 6.371
Punti nel piano cartesiano
 Punti nel piano cartesiano In un piano consideriamo due rette perpendicolari che chiamiamo x e. Solitamente, disegniamo la retta x (ascisse) orizzontalmente e orientata da sinistra a destra, la retta e
Punti nel piano cartesiano In un piano consideriamo due rette perpendicolari che chiamiamo x e. Solitamente, disegniamo la retta x (ascisse) orizzontalmente e orientata da sinistra a destra, la retta e
C I R C O N F E R E N Z A...
 C I R C O N F E R E N Z A... ESERCITAZIONI SVOLTE 3 Equazione della circonferenza di noto centro C e raggio r... 3 Equazione della circonferenza di centro C passante per un punto A... 3 Equazione della
C I R C O N F E R E N Z A... ESERCITAZIONI SVOLTE 3 Equazione della circonferenza di noto centro C e raggio r... 3 Equazione della circonferenza di centro C passante per un punto A... 3 Equazione della
MISURE DI ERATOSTENE E PROVE DEL MOTO DI ROTAZIONE TERRESTRE. Presentazione di Emma Donisi, Elena Perego, Camilla Antonietti, Alessandro D'Archi
 MISURE DI ERATOSTENE E PROVE DEL MOTO DI ROTAZIONE TERRESTRE Presentazione di Emma Donisi, Elena Perego, Camilla Antonietti, Alessandro D'Archi Mappa Eratostene Prima di lui Teoria Pratica Dopo di lui
MISURE DI ERATOSTENE E PROVE DEL MOTO DI ROTAZIONE TERRESTRE Presentazione di Emma Donisi, Elena Perego, Camilla Antonietti, Alessandro D'Archi Mappa Eratostene Prima di lui Teoria Pratica Dopo di lui
MOVIMENTI DELLA TERRA MOTO UNICO E COMPLESSO
 MOVIMENTI DELLA TERRA MOTO UNICO E COMPLESSO MOTI MILLENARI MOVIMENTI DELLA TERRA Sono contemporanei ROTAZIONE RIVOLUZIONE MOTI PRINCIPALI ROTAZIONE Definiz.: è il movimento che la Terra compie intorno
MOVIMENTI DELLA TERRA MOTO UNICO E COMPLESSO MOTI MILLENARI MOVIMENTI DELLA TERRA Sono contemporanei ROTAZIONE RIVOLUZIONE MOTI PRINCIPALI ROTAZIONE Definiz.: è il movimento che la Terra compie intorno
Topografia e orientamento
 CAI - ALPINISMO GIOVANILE Secondo Corso Di Avvicinamento Alla Montagna 2012 Topografia e orientamento C A I B o r g o m a n e r o A l p i n i s m o G i o v a n i l e 2 0 1 2 Pagina 1 Introduzione Per un
CAI - ALPINISMO GIOVANILE Secondo Corso Di Avvicinamento Alla Montagna 2012 Topografia e orientamento C A I B o r g o m a n e r o A l p i n i s m o G i o v a n i l e 2 0 1 2 Pagina 1 Introduzione Per un
Progetto Laboratori Lauree Scientifiche
 Progetto Laboratori Lauree Scientifiche Laboratorio sulle funzioni trigonometriche Le ore di insolazione giornaliera in funzione della latitudine Bozza di progetto Nel seguito verrà presentata la descrizione
Progetto Laboratori Lauree Scientifiche Laboratorio sulle funzioni trigonometriche Le ore di insolazione giornaliera in funzione della latitudine Bozza di progetto Nel seguito verrà presentata la descrizione
Gli indizi a favore di questa ipotesi erano molteplici:
 La forma della Terra Nell antichità la forma della Terra è stata oggetto di numerose ipotesi. Nonostante la limitatezza degli strumenti di osservazione di allora, già gli antichi svilupparono l idea che
La forma della Terra Nell antichità la forma della Terra è stata oggetto di numerose ipotesi. Nonostante la limitatezza degli strumenti di osservazione di allora, già gli antichi svilupparono l idea che
STRUMENTI DELLA GEOGRAFIA L ORIENTAMENTO
 STRUMENTI DELLA GEOGRAFIA L ORIENTAMENTO M ERIDIANI E PARALLELI LE CARTE G EOGRAFICHE LE FOTOGRAFIE LA STATISTICA CHE COS È LA GEOGRAFIA? Parola che deriva dal greco: Gea= terra + grafein = scrivere descrizione
STRUMENTI DELLA GEOGRAFIA L ORIENTAMENTO M ERIDIANI E PARALLELI LE CARTE G EOGRAFICHE LE FOTOGRAFIE LA STATISTICA CHE COS È LA GEOGRAFIA? Parola che deriva dal greco: Gea= terra + grafein = scrivere descrizione
Scuola Primaria Classi 4 A e 4 B Is5tuto Comprensivo Castelverde Roma
 Scuola Primaria Classi 4 A e 4 B Is5tuto Comprensivo Castelverde Roma Orientamento topologico Ø cerchiamo punti di riferimento Ø chiediamo indicazioni Ø consultiamo la cartina Cerchiamo dei pun5 di riferimento.
Scuola Primaria Classi 4 A e 4 B Is5tuto Comprensivo Castelverde Roma Orientamento topologico Ø cerchiamo punti di riferimento Ø chiediamo indicazioni Ø consultiamo la cartina Cerchiamo dei pun5 di riferimento.
Dall astronomia alla geografia astronomica. La Terra vista dallo spazio. (NASA)
 3. Il pianeta Terra Isola di Sakhalin (Unione Sovietica), 1 settembre 1983. Un volo di linea della Korean Air Lines, con a bordo 289 persone tra passeggeri e membri dell equipaggio, entra, per errore,
3. Il pianeta Terra Isola di Sakhalin (Unione Sovietica), 1 settembre 1983. Un volo di linea della Korean Air Lines, con a bordo 289 persone tra passeggeri e membri dell equipaggio, entra, per errore,
MOTO DI ROTAZIONE da ovest verso est asse terrestre
 I moti della Terra La Terra compie numerosi movimenti poiché gira: intorno a se stessa a 0,4 Km/s; attorno al Sole a 30 Km/s; insieme a tutto il sistema solare a 220 Km/s quindi è come se si muovesse
I moti della Terra La Terra compie numerosi movimenti poiché gira: intorno a se stessa a 0,4 Km/s; attorno al Sole a 30 Km/s; insieme a tutto il sistema solare a 220 Km/s quindi è come se si muovesse
OLIMPIADI ITALIANE DI ASTRONOMIA GARA INTERREGIONALE - Categoria Senior. Problemi con soluzioni
 OLIMPIADI ITALIANE DI ASTRONOMIA 2012 GARA INTERREGIONALE - Categoria Senior Problemi con soluzioni Problema 1. Un sistema binario visuale si trova ad una distanza D=42 anni-luce dalla Terra. Le due stelle
OLIMPIADI ITALIANE DI ASTRONOMIA 2012 GARA INTERREGIONALE - Categoria Senior Problemi con soluzioni Problema 1. Un sistema binario visuale si trova ad una distanza D=42 anni-luce dalla Terra. Le due stelle
Jay Phelan, Maria Cristina Pignocchino. Scopriamo le scienze della Terra
 Jay Phelan, Maria Cristina Pignocchino Scopriamo le scienze della Terra Capitolo 3 I moti della Terra e il sistema Terra-Luna 3 1. Il moto di rotazione della Terra /1 La rotazione terrestre si compie da
Jay Phelan, Maria Cristina Pignocchino Scopriamo le scienze della Terra Capitolo 3 I moti della Terra e il sistema Terra-Luna 3 1. Il moto di rotazione della Terra /1 La rotazione terrestre si compie da
CONOSCENZE 1. gli enti fondamentali e le loro. 2. la posizione reciproca di punto, retta, piano 3. gli angoli e le loro proprietaá
 GEOMETRIA PREREQUISITI l conoscere le caratteristiche del sistema decimale l conoscere le proprietaá delle quattro operazioni e operare con esse l operare con le misure angolari CONOSCENZE 1. gli enti
GEOMETRIA PREREQUISITI l conoscere le caratteristiche del sistema decimale l conoscere le proprietaá delle quattro operazioni e operare con esse l operare con le misure angolari CONOSCENZE 1. gli enti
Lezione 6 Richiami di Geometria Analitica
 1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
descrivere le caratteristiche della sfera utilizzare le formule inerenti. Introduzione
 Anno 4 Sfera 1 Introduzione In questa lezione parleremo di un importante solido di rotazione detto sfera. Ne daremo la definizione, ne studieremo le caratteristiche e le formule a essa inerenti. Al termine
Anno 4 Sfera 1 Introduzione In questa lezione parleremo di un importante solido di rotazione detto sfera. Ne daremo la definizione, ne studieremo le caratteristiche e le formule a essa inerenti. Al termine
Quadro riassuntivo di geometria analitica
 Quadro riassuntivo di geometria analitica IL PIANO CARTESIANO (detta ascissa o coordinata x) e y quella dall'asse x (detta ordinata o coordinata y). Le coordinate di un punto P sono: entrambe positive
Quadro riassuntivo di geometria analitica IL PIANO CARTESIANO (detta ascissa o coordinata x) e y quella dall'asse x (detta ordinata o coordinata y). Le coordinate di un punto P sono: entrambe positive
Moti della Terra: Rotazione, Rivoluzione, Moti millenari
 Moti della Terra: Rotazione, Rivoluzione, Moti millenari moto di rotazione giorno sidereo: 23h 56m 4s velocità di rotazione moto di rotazione: conseguenze Alternarsi del dì e della notte Moto apparente
Moti della Terra: Rotazione, Rivoluzione, Moti millenari moto di rotazione giorno sidereo: 23h 56m 4s velocità di rotazione moto di rotazione: conseguenze Alternarsi del dì e della notte Moto apparente
LE COORDINATE CARTESIANE
 CORSO ZERO DI MATEMATICA per Ing. Chimica e Ing. delle Telecomunicazioni GEOMETRIA ANALITICA Prof. Erasmo Modica [email protected] LE COORDINATE CARTESIANE Quando si vuole fissare un sistema di coordinate
CORSO ZERO DI MATEMATICA per Ing. Chimica e Ing. delle Telecomunicazioni GEOMETRIA ANALITICA Prof. Erasmo Modica [email protected] LE COORDINATE CARTESIANE Quando si vuole fissare un sistema di coordinate
Andamento e periodo delle funzioni goniometriche
 Andamento e periodo delle funzioni goniometriche In questa dispensa ricaviamo gli andamenti delle funzioni goniometriche seno, coseno, tangente e cotangente tra 0 e 360, detti, rispettivamente, sinusoide,
Andamento e periodo delle funzioni goniometriche In questa dispensa ricaviamo gli andamenti delle funzioni goniometriche seno, coseno, tangente e cotangente tra 0 e 360, detti, rispettivamente, sinusoide,
OLIMPIADI ITALIANE DI ASTRONOMIA 2014 FINALE NAZIONALE Prova Teorica - Categoria Junior
 OLIMPIADI ITALIANE DI ASTRONOMIA 2014 FINALE NAZIONALE Prova Teorica - Categoria Junior 1. Le quattro stagioni Si scrivano gli intervalli entro cui variano l ascensione retta ( ) e la declinazione ( )
OLIMPIADI ITALIANE DI ASTRONOMIA 2014 FINALE NAZIONALE Prova Teorica - Categoria Junior 1. Le quattro stagioni Si scrivano gli intervalli entro cui variano l ascensione retta ( ) e la declinazione ( )
162. Determinazione approssimata delle coordinate geografiche terrestri Michele T. Mazzucato
 162. Determinazione approssimata delle coordinate geografiche terrestri Michele T. Mazzucato cercherò stanotte di precisare la nostra latitudine e domani a mezzogiorno la nostra longitudine. Cyrus Smith
162. Determinazione approssimata delle coordinate geografiche terrestri Michele T. Mazzucato cercherò stanotte di precisare la nostra latitudine e domani a mezzogiorno la nostra longitudine. Cyrus Smith
La prospettiva e i suoi strumenti teorici e tecnici
 Dispense del Corso di Disegno, tenuto da Riccardo Migliari nella Facoltà di Architettura Ludovico Quaroni della Sapienza Università di Roma nell Anno Accademico 2009 2010 La prospettiva e i suoi strumenti
Dispense del Corso di Disegno, tenuto da Riccardo Migliari nella Facoltà di Architettura Ludovico Quaroni della Sapienza Università di Roma nell Anno Accademico 2009 2010 La prospettiva e i suoi strumenti
GEOMETRIA ANALITICA
 GEOMETRIA ANALITICA [email protected] LE COORDINATE CARTESIANE Quando si vuole fissare un sistema di coordinate cartesiane su una retta r, è necessario considerare: un punto O detto origine; un
GEOMETRIA ANALITICA [email protected] LE COORDINATE CARTESIANE Quando si vuole fissare un sistema di coordinate cartesiane su una retta r, è necessario considerare: un punto O detto origine; un
Impiego luoghi di posizione isolati rilevamento di sicurezza
 PAS A056 C180 LEZIONE 4 Impiego luoghi di posizione isolati rilevamento di sicurezza Impiego luoghi di posizione isolati rlv / allineam. guida dist. sicurezza Punto con rilevamenti successivi stesso oggetto
PAS A056 C180 LEZIONE 4 Impiego luoghi di posizione isolati rilevamento di sicurezza Impiego luoghi di posizione isolati rlv / allineam. guida dist. sicurezza Punto con rilevamenti successivi stesso oggetto
Condizione di allineamento di tre punti
 LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
GEOMETRIA ANALITICA NELLO SPAZIO (3D Geometry)
 GEOMETRIA ANALITICA NELLO SPAZIO (3D Geometry) SISTEMA DI RIFERIMENTO NELLO SPAZIO La geometria analitica dello spazio è molto simile alla geometria analitica del piano. Per questo motivo le formule sono
GEOMETRIA ANALITICA NELLO SPAZIO (3D Geometry) SISTEMA DI RIFERIMENTO NELLO SPAZIO La geometria analitica dello spazio è molto simile alla geometria analitica del piano. Per questo motivo le formule sono
