AUTOMI A STATI FINITI. G. Ciaschetti
|
|
|
- Simona Baroni
- 8 anni fa
- Visualizzazioni
Transcript
1 AUTOMI A STATI FINITI G. Ciaschetti
2 CONTENUTI Definizione di sistema Classificazione dei sistemi Definizione di modello Algebra degli schemi a blocchi Sistemi sequenziali Automi a stati finiti Macchina di Turing
3 Definizione di sistema Un sistema è un insieme di elementi che interagiscono tra loro per svolgere una particolare funzione o raggiungere un determinato obiettivo. ESEMPI - il sistema nervoso - il sistema politico - un sistema di equazioni - un sistema di irrigazione - il sistema di elaborazione - un robot NON ESEMPI - una classe - i numeri naturali - le istruzioni del linguaggio C - i voti di uno studente OBIETTIVO?
4 Definizione di sistema La teoria dei sistemi, ossia lo studio quantitativo dei sistemi, nasce dalla necessità di analizzare un sistema per capire quali sono i suoi elementi e quali relazioni intercorrono tra di essi, per - comprenderne meglio il funzionamento - spiegare il verificarsi di fenomeni naturali - intervenire per modificare la risposta del sistema - predire la risposta del sistema in futuro Lo stato di un sistema è l insieme dei valori che assumono tutti i diversi parametri del sistema, cioè le grandezze fisiche o matematiche che descrivono in che situazione esso si trova. Queste prendono il nome di variabili di stato.
5 Definizione di sistema ESEMPIO: Il computer o sistema di elaborazione Obiettivo: archiviare ed elaborare informazioni (giocare, comunicare, ecc ) Elementi - CPU - memoria RAM - Hard Disk - Tastiera - Monitor - Bus - Mouse - Relazione tra gli elementi - la scheda madre, che con i suoi circuiti mette in collegamento le varie parti del sistema - la logica di funzionamento (algebra di Boole, circuiti sommatori, CU, ciclo fetch/decode/execute, ) Parametri del sistema Stati del sistema - Velocità CPU - Spento - Occupazione HD - Acceso, in attesa - - Acceso, in esecuzione
6 Definizione di sistema Un sistema aperto può essere visto come un dispositivo che trasforma gli ingressi del sistema (le cause) nelle uscite del sistema (gli effetti). i Sistema (trasformazione) u ESEMPI: - un computer con stampante trasforma le azioni dell utente, la corrente elettrica e un foglio bianco in una pagina di un libro; - una macchinetta del caffè trasforma il caffè in polvere, l acqua, l energia elettrica, i soldi e l azione di premere un tasto in un prelibato caffè caldo; - un motore trasforma benzina in energia meccanica.
7 Definizione di sistema ESEMPI O: sistema lampada/interruttore Elementi: interruttore, lampada Obiettivo: illuminare (una stanza) Stati: acceso, spento Ingressi: int. chiuso, int. aperto Uscite: luce, buio Tabella di transizione di stato INTERRUTTORE STATO aperto chiuso lampada accesa lampada spenta lampada accesa lampada spenta lampada spenta lampada accesa Tabella di trasformazione INTERRUTTORE STATO aperto chiuso lampada accesa buio luce lampada spenta buio luce
8 Definizione di sistema ESEMPI O: sistema lampada/interruttore Diagramma degli stati aperto, buio chiuso, luce chiuso, luce Tabella di transizione di stato INTERRUTTORE STATO aperto chiuso lampada accesa lampada spenta lampada accesa lampada spenta lampada spenta lampada accesa spenta aperto, buio accesa Tabella di trasformazione INTERRUTTORE STATO aperto chiuso lampada accesa buio luce lampada spenta buio luce
9 Definizione di sistema Un sistema non è necessariamente un entità fisica: esistono sistemi astratti che servono a spiegare fenomeni naturali cercando di identificarne il rapporto causa/effetto. In questa accezione, un sistema può essere visto come un modo, cioè l insieme di regole e/o relazioni tra elementi astratti che trasformano le cause in effetti. ESEMPI - un sistema al totocalcio: come combinare più giocate tra loro - il sistema per fare soldi: le azioni da intraprendere per ottenere un vantaggio economico - il sistema di scaricare la mia donna: senza commento ( )
10 Classificazione dei sistemi naturali vs. artificiali: se presenti in natura o costruiti dall uomo (es. sistema solare, computer) statici vs. dinamici: se cambiano il loro stato nel tempo oppure no (es. sistema dei continenti, pendolo) chiusi vs. aperti: se interagiscono o no con l esterno (es. sistema di telecamere di un museo, sistema digerente) deterministici vs. stocastici: se è possibile prevedere o meno la risposta del sistema (es. computer, sistema atmosferico) combinatori vs. sequenziali: se sono dotati di memoria o meno (es. circuito elettrico, ascensore) stazionari (o invarianti): se la risposta del sistema non dipende dal particolare istante di tempo (es. pipeline) continui: se l evoluzione del sistema dipende dall istante in cui si trova (es. sistema di lluminazione cittadino) discreti: se l evoluzione del sistema avviene a scatti (es. orologio digitale)
11 Classificazione dei sistemi Si noti che la classificazione di un sistema in un modo oppure in un altro dipende dall osservatore, dal livello di dettaglio e dai fini dell analisi che si vuole effettuare. ESEMPI - frigorifero (chiuso per chi deve trasportarlo, aperto per la massaia) - quadro (statico per il visitatore, dinamico per il restauratore) - sistema stellare (statico per un romantico, dinamico per un astrofisico) - ascensore (discreto per l utilizzatore, continuo per il progettista)
12 Definizione di modello Un modello è una rappresentazione di un sistema, e permette di studiare un sistema tralasciandone gli aspetti non essenziali ai fini della sua analisi. ESEMPI ESEMPIO SISTEMA - sistema stradale - ponte sullo stretto - sistema preda/predatore - problema da risolvere - sistema informativo aziendale MODELLO - mappa - plastico/disegno 3D - equazione differenziale - algoritmo - database Un modello può essere matematico, fisico, grafico, logico,
13 Definizione di modello Un modello è in generale un astrazione del sistema che esso rappresenta, cioè risulta semplificato rispetto al sistema stesso. Modelli troppo semplici, però, possono essere poco rappresentativi, mentre modelli troppo complessi possono risultare inutilizzabili. Occorre allora, in fase di modellazione del sistema, trovare un giusto compromesso tra l operatività del modello, cioè la sua fruibilità, e la sua aderenza, cioè quanto precisamente esso rappresenta il sistema. Inoltre, modelli più semplici sono in generale più robusti, ossia tendono a rimanere validi anche a seguito di cambiamenti del sistema e del contesto, mentre modelli troppo complessi possono risultare presto inutilizzabili (es. virus, dinosauri)
14 Algebra degli schemi a blocchi Un semplice modello per rappresentare e studiare i sistemi quello degli schemi a blocchi. Il sistema è visto come un insieme di sottosistemi interconnessi tra loro, ognuno dei quali è rappresentato mediante un blocco o blackbox (scatola nera): si specifica, per ogni blocco, quali sono i suoi ingressi e le sue uscite, e non cosa c è al suo interno. Gli elementi utilizzati in questo modello sono: u 1 i f u i 2 i 1 i 1 +i 2 + i u 2 u 3 blocco di trasferimento u = f(i) nodo sommatore i = i 1 + i 2 diramazione i = u 1 = u 2 = u 3
15 Algebra degli schemi a blocchi ESEMPIO: controllo automatico della temperatura temperatura + cella frigorifera temperatura regola temperatura controllo temperatura
16 Sistemi combinatori Un sistema combinatorio è un sistema che non ha memoria, cioè la risposta del sistema dipende soltanto dall ingresso che ad esso si applica, e non dal suo stato. ESEMPIO: un tubo idraulico (un semplice sistema costituito da un solo elemento, un tubo, che ha lo scopo di far arrivare ad una estremità il flusso d acqua che entra nell altra estremità) è un sistema combinatorio, in quanto la grandezza quantità di flusso in uscita dipende solo dalla grandezza quantità di flusso in entrata. ESEMPIO: un circuito combinatorio formato da porte logiche è un sistema combinatorio che ottiene una uscita booleana che dipende solo dal valore delle variabili booleane in ingresso.
17 Sistemi combinatori flusso in ingresso flusso in uscita x y z ( x y) z
18 Sistemi sequenziali Un sistema sequenziale è un sistema che ha memoria, cioè la risposta del sistema dipende dall ingresso che ad esso si applica, e dal suo stato. ESEMPIO: una vasca da bagno è un sistema sequenziale, in quanto la grandezza quantità di flusso in uscita dipende dalla grandezza quantità di flusso in entrata, e dallo stato della vasca, cioè dal livello dell acqua presente. Maggiore è l acqua presente nella vasca, maggiore è la pressione, e dunque maggiore sarà il flusso in uscita, a parità di flusso in ingresso. ESEMPIO: un ascensore è un sistema sequenziale la cui uscita (il movimento che fa l ascensore), dipende dall ingresso (il tasto premuto) e dallo stato (la posizione dell ascensore).
19 Sistemi sequenziali i stato livello = 0 u = f(i, s) i stato livello = 5 u = f(i, s)
20 Sistemi sequenziali input tasto 3 output sali 2 piani stato piano 1 input tasto 3 output scendi 1 piano stato piano 4
21 Automi a stati finiti Un automa a stati finiti è un sistema dinamico, sequenziale, invariante e discreto. Significa che l azione che l automa intraprende (uscita) dipende solo da uno o più segnali d ingresso e dallo stato dell automa. C è un numero finito di possibili stati. i u = f(i, s) sistema sequenziale continuo i u = f(i, s) sistema sequenziale discreto AUTOMA
22 Automi a stati finiti ESEMPIO: Ascensore start pulsante 0 2 quale pulsante? quale piano? 1 quale piano? quale piano? fermo scendi scendi sali fermo scendi sali sali fermo
23 Automi a stati finiti ESEMPIO: Semaforo start no c è segnale? si timer colore? rosso verde giallo/verde spegni rosso accendi verde accendi giallo spegni verde spegni giallo accendi rosso
24 Automi a stati finiti Un automa a stati finiti è una quintupla A = {I, U, S,, } definito da: - Un insieme finito di valori degli ingressi I - Un insieme finito di valori delle uscite U - Un insieme finito degli stati S - Un insieme di regole di transizione di stato,, che specifica lo stato futuro del sistema noti lo stato attuale e l ingresso : S x I S - Un insieme di regole di trasformazione delle uscite,, che fornisce l uscita noti lo stato attuale e l ingresso : S x I U
25 Automa di Mealy Se l uscita di un automa dipende direttamente dall ingresso, si parla in questo caso di automa improprio o automa di Mealy. Graficamente, può essere rappresentato come segue: I S n S n+1 U S n S n+1 = elemento di ritardo
26 Automa di Moore Se l uscita di un automa non dipende direttamente dall ingresso, si parla in questo caso di automa proprio o automa di Moore. Graficamente, può essere rappresentato come segue: I S n S n+1 U S n S n+1 = elemento di ritardo
27 Diagrama degli stati Le regole di transizione di stato : S x I S e le regole di trasformazione delle uscite : S x I U di un automa possono essere rappresentate in un diagramma degli stati, un grafo orientato in cui i nodi corrispondono agli stati, e gli archi corrispondono alle transizioni da uno stato all altro del sistema. ESEMPI O: sistema lampada/interruttore diagramma degli stati aperto, buio chiuso, luce chiuso, luce spenta accesa aperto, buio
28 Grafo di Mealy Se l automa è l automa di Mealy, il corrispondente diagramma degli stati è detto grafo di Mealy. I nodi del grafo corrispondono agli stati, e le funzioni e sono riportate sugli archi. i 1, u 2 i 2, u 2 s 0 s 1 i 1, u 2 i 1, u 1 s 2 i 2, u 2 i 2, u 2
29 Grafo di Moore Se l automa è l automa di Moore, il corrispondente diagramma degli stati è detto grafo di Moore. Nei nodi del grafo sono indicati gli stati e le uscite (ricordiamo, infatti, che in questo automa le uscite sono direttamente collegate agli stati)e la funzione è riportata sugli archi. i 1 i 2 s 0 /u 0 s 1 /u 1 i 1 i 1 s 2 /u 2 i 2 i 2
30 Diagrama degli stati ESEMPI O: sistema lampada/interruttore Questo sistema può essere rappresentato con entrambi i tipi di automi, in quanto l uscita (buio/luce) dipende direttamente dallo stato della lampada (accesa/spenta) Grafo di Mealy Grafo di Moore aperto, buio chiuso, luce chiuso, luce aperto chiuso chiuso spenta accesa spenta /buio accesa /luce aperto, buio aperto
31 Costruiamo un automa ESEMPI O: vogliamo costruire un automa che riconosca la parla ORO in una stringa. Supponiamo che la seconda O riconosciuta sia da considerare come la fine della sequenza, e non anche l inizio di una nuova sequenza. Ad esempio, se la stringa in ingresso è ORORO verrà riconosciuta una sola parola e non due. Insieme degli ingressi: I = {O, R} Insieme delle uscite: U = {si, no} Insieme degli stati: S = {s 0, s 1, s 2 } dove: s 0 s 1 s 2 : è lo stato di partenza: non è stato ancora riconosciuto nessun carattere della sequenza; : è lo stato in cui è stato riconosciuto il primo carattere della sequenza; : è lo stato in cui è stato riconosciuto il secondo carattere della sequenza.
32 Costruiamo un automa Rappresentiamo ora le funzioni e con il diagramma di Mealy s 0 stato iniziale Nello stato s 0, se l automa riceve in ingresso la lettera R, resta nello stesso stato, se invece riceve in ingresso la lettera O, passa nello stato s 1. R, no s 0 O, no s transizione dallo stato 1 iniziale s 0 allo stato s 1
33 Costruiamo un automa Nello stato s 1, quando cioè l automa ha già riconosciuto il primo carattere, se l automa riceve in ingresso la lettera R passa allo stato s 2, se invece riceve in ingresso la lettera O, resta nello stesso stato. R, no O, no s 0 O, no s transizione dallo stato 1 iniziale s 1 allo stato s 2 R, no s 2
34 Costruiamo un automa Nello stato s 2, quando cioè l automa ha già riconosciuto il primo e il secondo carattere, se esso riceve in ingresso la lettera O torna allo stato s 0 con uscita SI. Se invece riceve in ingresso la lettera R, torna allo stato s 0 ma con uscita NO. R, no O, no s 0 O, no s transizione dallo stato 1 iniziale s 2 allo stato s 0 R, no O, si s 2 R, no ESERCIZIO: qual è l uscita dell automa con la sequenza in ingresso OOORRRORRORO?
35 Costruiamo un automa Ci chiediamo se è possibile costruire un automa di Moore per lo stesso riconoscitore di stringhe. La risposta è affermativa, ma occorre in questo caso aggiungere un ulteriore stato: lo stato finale corrispondente all uscita SI. R O s 0, no O s 1, no R O R R s 3, si O s 2, no ESERCIZIO: costruire un automa che riconosce la sequenza 1111 in una stringa di bit
36 Il modello matematico/logico Se vogliamo effettivamente realizzare un automa, dobbiamo passare dalla sua rappresentazione grafica (il grafo del diagramma degli stati) a una sua rappresentazione matematico/logica, che ci permetterà di costruire i circuiti. Facendo riferimento all esempio precedente, il riconoscitore di sequenze ORO in una stringa, possiamo costruire il seguente modello: ingressi x O 0 R 1 uscite z no 0 si 1 stati s 0 s 1 s 2 -- y 1 y
37 Il modello matematico/logico ingressi x O 0 R 1 uscite z no 0 si 1 R, no s 0 R, no stati s 0 s 1 s 2 -- O, no y 1 y s 1 O, no TABELLA DI HUFFMAN variabili di stato y 1 y variabili di ingresso x=0 x=1 01,0 01,0 00,1 --,- 00,0 11,0 00,0 --,- R, no O, si s 2
38 Il modello matematico/logico SINTESI DI CIRCUITI: Mappe di Karnaugh x 0 1 variabile di stato y 1 y 1 y i 1 i n 1 n n y1 x y1 y2 variabili di stato y 1 y variabili di ingresso x=0 x=1 01,0 01,0 00,1 --,- 00,0 11,0 00,0 --,- variabile di stato y 2 variabile di uscita z x 0 1 y 1 y i 1 i y n 1 n n 2 y1 y2 x y2 x 0 1 y 1 y i i n z x y1
39 Il circuito logico x z y 1 n y 1 n+1 y 2 n y 2 n+1 y 2 n y 1 n y 2 n+1 y 1 n+1 ESERCIZIO: costruire il modello matematico e il circuito per l automa che riconosce la sequenza 1111
40 La macchina di Turing Alla base del concetto di sistema automatico di calcolo, usato da tutti i moderni computer, c è un modello di macchina astratta proposto nel 1936 dal matematico inglese Alan Turing. Si tratta di un automa a stati finiti, che fa riferimento alla normale attività dell uomo quando deve eseguire dei calcoli: il lavoro è controllato dalla mente umana, mentre un foglio di carta e una penna sono usati per segnare i dati e le operazioni, cioè vengono usati come supporto di memoria per l input (dati) e l output (risultati). La macchina di Turing (MdT) può essere definita, intuitivamente, come un dispositivo in grado di operare su un numero finito di simboli, mediante una successione finita di passi e secondo determinate regole (programma), non considerando (astrazione) i tempi di calcolo e i possibili limiti di spazio di memoria.
41 La macchina di Turing La MdT è un dispositivo costituito da: - Un nastro che rappresenta il supporto di memoria, costituito da un numero infinito di caselle, ognuna delle quali può contenere un solo simbolo di un dato alfabeto; - Una testina di lettura/scrittura (TLS) che accede a una singola casella, leggendone il simbolo contenuto o scrivendoci su un nuovo simbolo; - Un meccanismo di controllo (automa) che, in base al proprio stato, alle regole e al simbolo letto, decide di eseguire una delle seguenti operazioni elementari: 1) comandare alla TLS di scrivere un nuovo simbolo 2) spostare a sinistra la TLS di una casella 3) spostare a destra la TLS di una casella 4) fermare la macchina
42 La macchina di Turing Formalmente, la macchina di Turing è definita da una quintupla dove: MdT = {S, IU,,, } S IU : S x IU S insieme degli stati, tra cui lo stato iniziale s 0 e lo stato finale s F insieme dei simboli di input/output funzione di transizione di stato: dato uno stato e un simbolo in input, pone la macchina in un nuovo stato : S x IU IU funzione di trasformazione delle uscite: dato uno stato e un simbolo di input, determina un simbolo di output : S x IU {sx, dx, =} funzione di movimento della TLS (sposta a sinistra di una casella, sposta a destra di una casella, non muovere)
43 La macchina di Turing La parte di controllo della MdT può essere rappresentata mediante un diagramma degli stati, utilizzando il grafo di Mealy, riportando sugli archi del grafo anche gli spostamenti della TLS, oltre agli ingressi e le uscite. Tra i simboli dell insieme IU, c è un simbolo particolare denotato con # che rappresenta il simbolo nullo: è il simbolo che si trova in tutte le caselle del nastro all inizio. Successivamente, su alcune delle caselle del nastro verranno scritti (dall esterno) i simboli di input che la macchina di Turing dovrà leggere. Una volta dato l input, la MdT può cominciare il suo lavoro partendo dallo stato s 0. Il risultato finale dell elaborazione è contenuto nelle caselle del nastro, quando la MdT si trova nello stato finale s F.
44 La macchina di Turing ESEMPIO: progettare una MdT checalcola il successivo di un numero binario # # # # # # # # # # # Definiamo la nostra MdT: IU {0, 1, #} Spostamenti della TLS {=, <} S {s 0, s 1, s 2, s F } dove s 0 = stato iniziale: la testina si trova sul bit meno significativo del numero binario s 1 = assenza di riporto: la MdT dovrà copiare i restanti bit muovendosi verso sinistra s 2 = presenza di riporto: la MdT cancella il simbolo 1 e scrive 0, oppure cancella il simbolo 0 e scrive 1, e si muove a sinistra s F = stato finale: la macchina ha finito il suo compito e si ferma
45 La macchina di Turing Per definire le funzioni,,, costruiamo il diagramma degli stati (di Mealy) All inizio, cioè nello stato s 0, se la MdT legge in ingresso il carattere #, passa nello stato finale s F senza scrivere nulla: significa che non è stato dato nessun numero in input. Se invece legge il simbolo 0, passa nello stato s 1 (assenza di riporto), scrive 1 e si muove a sinistra. Se, infine, legge il simbolo 1, passa nello stato s 2 (presenza di riporto), scrive 0 e si muove a sinistra. s 0 s 1 s 0 0,1,< s # # 1 1 # # 1,0,< s 0 s 2 s 2 s F 0 1 # # 0 0 # #
46 La macchina di Turing Quando la MdT si trova nello stato s 1, se legge in ingresso il carattere #, passa nello stato finale s F senza scrivere nulla: significa che ha terminato il proprio lavoro. Se invece legge il simbolo 0 o il simbolo 1, resta nello stato s 1 (assenza di riporto: deve solo ricopiare i restanti simboli), riscrive il simbolo letto e si muove a sinistra. 0,0,< 1,1,< s 1 s 1 s 0 0,1,< s # # 1,0,< #,#,= s 1 s 1 s 2 s F # #
47 La macchina di Turing Quando la MdT si trova nello stato s 2, se legge in ingresso il simbolo #, passa nello stato s 1, scrive 1 e si sposta a sinistra. Se invece legge il simbolo 0, passa nello stato s 1, scrive 1 e si sposta a sinistra. Se invece legge il simbolo 1, resta nello stato s 2, scrive 0 e si sposta a sinistra s 0 0,1,< s 1 0,0,< 1,1,< s 2 # # 1 0 s 1 # ,0,< 1,0,< #,#,= s 2 s F s # s # s 2 s # #
48 La macchina di Turing A titolo di esempio, riportiamo il comportamento della macchina sull input 1011 s 0 # # # # # # # # s 2 # # # # # # # # s 2 # # # # # # # # s 1 # # # # # # # # s 1 # # # # # # # # s F # # # # # # # #
49 ALGORITMI E MACCHINA DI TURING La macchina di Turing Ricordando la definizione e le proprietà di un algoritmo (vedi dispense Le basi della programmazione della classe III), notiamo che esiste una stretta analogia tra un algoritmo e la MdT: ALGORITMO 1) usa un dispositivo di calcolo 2) procede in modo discreto 3) deve essere finito 4) deve essere deterministico 5) non deve essere ambiguo 6) deve essere generale 7) deve essere completo MdT 1) è un dispositivo di calcolo 2) passa da uno stato all altro in modo discreto 3) ha un numero finito di stati e di transizioni di stato, e uno stato finale 4) è deterministica 5) ogni passo è specificato con esattezza 6) è generale 7) se opportunamente progettata, è completa Un algoritmo è una MdT in grado di risolvere una data classe di problemi
50 TESI DI CHURCH-TURING La macchina di Turing L insieme delle funzioni computabili, ossia dei problemi risolvibili con un sistema di calcolo automatico, coincide con l insieme delle funzioni Turing-computabili, ossia l insieme dei problemi per cui è possibile costruire una MdT che li risolve. La tesi di Church-Turing non è dimostrabile: occorrerebbe prendere tutti i possibili problemi per cui è possibile sviluppare un algoritmo che li risolve, e costruire la relativa MdT, il che è impossibile. La tesi di Church-Turing tuttavia è confutabile, ma nessuno finora è riuscito a farlo: è sempre stato possibile costruire una MdT per la risoluzione di un problema computabile. THE END
Appunti di Sistemi Elettronici
 Prof.ssa Maria Rosa Malizia 1 LA PROGRAMMAZIONE La programmazione costituisce una parte fondamentale dell informatica. Infatti solo attraverso di essa si apprende la logica che ci permette di comunicare
Prof.ssa Maria Rosa Malizia 1 LA PROGRAMMAZIONE La programmazione costituisce una parte fondamentale dell informatica. Infatti solo attraverso di essa si apprende la logica che ci permette di comunicare
Le Macchine di Turing
 Le Macchine di Turing Come è fatta una MdT? Una MdT è definita da: un nastro una testina uno stato interno un programma uno stato iniziale Il nastro Il nastro è infinito suddiviso in celle In una cella
Le Macchine di Turing Come è fatta una MdT? Una MdT è definita da: un nastro una testina uno stato interno un programma uno stato iniziale Il nastro Il nastro è infinito suddiviso in celle In una cella
Automi. Sono così esempi di automi una lavatrice, un distributore automatico di bibite, un interruttore, una calcolatrice tascabile,...
 Automi Con il termine automa 1 s intende un qualunque dispositivo o un suo modello, un qualunque oggetto, che esegue da se stesso un particolare compito, sulla base degli stimoli od ordini ricevuti detti
Automi Con il termine automa 1 s intende un qualunque dispositivo o un suo modello, un qualunque oggetto, che esegue da se stesso un particolare compito, sulla base degli stimoli od ordini ricevuti detti
Automazione Industriale (scheduling+mms) scheduling+mms. adacher@dia.uniroma3.it
 Automazione Industriale (scheduling+mms) scheduling+mms adacher@dia.uniroma3.it Introduzione Sistemi e Modelli Lo studio e l analisi di sistemi tramite una rappresentazione astratta o una sua formalizzazione
Automazione Industriale (scheduling+mms) scheduling+mms adacher@dia.uniroma3.it Introduzione Sistemi e Modelli Lo studio e l analisi di sistemi tramite una rappresentazione astratta o una sua formalizzazione
Laurea Specialistica in Informatica
 Corso di Laurea in FISICA Laurea Specialistica in Informatica Fisica dell informazione 1 Elementi di Architettura degli elaboratori Prof. Luca Gammaitoni Informazioni sul corso: www.fisica.unipg unipg.it/gammaitoni/fisinfoit/gammaitoni/fisinfo
Corso di Laurea in FISICA Laurea Specialistica in Informatica Fisica dell informazione 1 Elementi di Architettura degli elaboratori Prof. Luca Gammaitoni Informazioni sul corso: www.fisica.unipg unipg.it/gammaitoni/fisinfoit/gammaitoni/fisinfo
Reti sequenziali sincrone
 Reti sequenziali sincrone Un approccio strutturato (7.1-7.3, 7.5-7.6) Modelli di reti sincrone Analisi di reti sincrone Descrizioni e sintesi di reti sequenziali sincrone Sintesi con flip-flop D, DE, T
Reti sequenziali sincrone Un approccio strutturato (7.1-7.3, 7.5-7.6) Modelli di reti sincrone Analisi di reti sincrone Descrizioni e sintesi di reti sequenziali sincrone Sintesi con flip-flop D, DE, T
Macchine a stati finiti G. MARSELLA UNIVERSITÀ DEL SALENTO
 Macchine a stati finiti 1 G. MARSELLA UNIVERSITÀ DEL SALENTO Introduzione Al più alto livello di astrazione il progetto logico impiega un modello, la cosiddetta macchina a stati finiti, per descrivere
Macchine a stati finiti 1 G. MARSELLA UNIVERSITÀ DEL SALENTO Introduzione Al più alto livello di astrazione il progetto logico impiega un modello, la cosiddetta macchina a stati finiti, per descrivere
Macchine a stati finiti. Sommario. Sommario. M. Favalli. 5th June 2007
 Sommario Macchine a stati finiti M. Favalli 5th June 27 4 Sommario () 5th June 27 / 35 () 5th June 27 2 / 35 4 Le macchine a stati si utilizzano per modellare di sistemi fisici caratterizzabili mediante:
Sommario Macchine a stati finiti M. Favalli 5th June 27 4 Sommario () 5th June 27 / 35 () 5th June 27 2 / 35 4 Le macchine a stati si utilizzano per modellare di sistemi fisici caratterizzabili mediante:
Appunti sulla Macchina di Turing. Macchina di Turing
 Macchina di Turing Una macchina di Turing è costituita dai seguenti elementi (vedi fig. 1): a) una unità di memoria, detta memoria esterna, consistente in un nastro illimitato in entrambi i sensi e suddiviso
Macchina di Turing Una macchina di Turing è costituita dai seguenti elementi (vedi fig. 1): a) una unità di memoria, detta memoria esterna, consistente in un nastro illimitato in entrambi i sensi e suddiviso
Macchine a stati finiti. Sommario. Sommario. M. Favalli. Le macchine a stati si utilizzano per modellare di sistemi fisici caratterizzabili mediante:
 Sommario Macchine a stati finiti M. Favalli Engineering Department in Ferrara 4 Sommario (ENDIF) Analisiesintesideicircuitidigitali / 35 (ENDIF) Analisiesintesideicircuitidigitali 2 / 35 4 Le macchine
Sommario Macchine a stati finiti M. Favalli Engineering Department in Ferrara 4 Sommario (ENDIF) Analisiesintesideicircuitidigitali / 35 (ENDIF) Analisiesintesideicircuitidigitali 2 / 35 4 Le macchine
Elementi di Informatica e Programmazione
 Elementi di Informatica e Programmazione Il concetto di Algoritmo e di Calcolatore Corsi di Laurea in: Ingegneria Civile Ingegneria per l Ambiente e il Territorio Università degli Studi di Brescia Cos
Elementi di Informatica e Programmazione Il concetto di Algoritmo e di Calcolatore Corsi di Laurea in: Ingegneria Civile Ingegneria per l Ambiente e il Territorio Università degli Studi di Brescia Cos
Informazione analogica e digitale
 L informazione L informazione si può: rappresentare elaborare gestire trasmettere reperire L informatica offre la possibilità di effettuare queste operazioni in modo automatico. Informazione analogica
L informazione L informazione si può: rappresentare elaborare gestire trasmettere reperire L informatica offre la possibilità di effettuare queste operazioni in modo automatico. Informazione analogica
Fasi di creazione di un programma
 Fasi di creazione di un programma 1. Studio Preliminare 2. Analisi del Sistema 6. Manutenzione e Test 3. Progettazione 5. Implementazione 4. Sviluppo 41 Sviluppo di programmi Per la costruzione di un programma
Fasi di creazione di un programma 1. Studio Preliminare 2. Analisi del Sistema 6. Manutenzione e Test 3. Progettazione 5. Implementazione 4. Sviluppo 41 Sviluppo di programmi Per la costruzione di un programma
Macchine sequenziali
 Corso di Calcolatori Elettronici I A.A. 2010-2011 Macchine sequenziali Lezione 14 Università degli Studi di Napoli Federico II Facoltà di Ingegneria Automa a Stati Finiti (ASF) E una prima astrazione di
Corso di Calcolatori Elettronici I A.A. 2010-2011 Macchine sequenziali Lezione 14 Università degli Studi di Napoli Federico II Facoltà di Ingegneria Automa a Stati Finiti (ASF) E una prima astrazione di
Strutturazione logica dei dati: i file
 Strutturazione logica dei dati: i file Informazioni più complesse possono essere composte a partire da informazioni elementari Esempio di una banca: supponiamo di voler mantenere all'interno di un computer
Strutturazione logica dei dati: i file Informazioni più complesse possono essere composte a partire da informazioni elementari Esempio di una banca: supponiamo di voler mantenere all'interno di un computer
ALGEBRA DELLE PROPOSIZIONI
 Università di Salerno Fondamenti di Informatica Corso di Laurea Ingegneria Corso B Docente: Ing. Giovanni Secondulfo Anno Accademico 2010-2011 ALGEBRA DELLE PROPOSIZIONI Fondamenti di Informatica Algebra
Università di Salerno Fondamenti di Informatica Corso di Laurea Ingegneria Corso B Docente: Ing. Giovanni Secondulfo Anno Accademico 2010-2011 ALGEBRA DELLE PROPOSIZIONI Fondamenti di Informatica Algebra
E possibile modificare la lingua dei testi dell interfaccia utente, se in inglese o in italiano, dal menu [Tools
 Una breve introduzione operativa a STGraph Luca Mari, versione 5.3.11 STGraph è un sistema software per creare, modificare ed eseguire modelli di sistemi dinamici descritti secondo l approccio agli stati
Una breve introduzione operativa a STGraph Luca Mari, versione 5.3.11 STGraph è un sistema software per creare, modificare ed eseguire modelli di sistemi dinamici descritti secondo l approccio agli stati
Esame di INFORMATICA
 Università di L Aquila Facoltà di Biotecnologie Esame di INFORMATICA Lezione 4 MACCHINA DI VON NEUMANN Anni 40 i dati e i programmi che descrivono come elaborare i dati possono essere codificati nello
Università di L Aquila Facoltà di Biotecnologie Esame di INFORMATICA Lezione 4 MACCHINA DI VON NEUMANN Anni 40 i dati e i programmi che descrivono come elaborare i dati possono essere codificati nello
INTRODUZIONE AGLI ALGORITMI INTRODUZIONE AGLI ALGORITMI INTRODUZIONE AGLI ALGORITMI INTRODUZIONE AGLI ALGORITMI
 INTRODUZIONE AGLI ALGORITMI Prima di riuscire a scrivere un programma, abbiamo bisogno di conoscere un metodo risolutivo, cioè un metodo che a partire dai dati di ingresso fornisce i risultati attesi.
INTRODUZIONE AGLI ALGORITMI Prima di riuscire a scrivere un programma, abbiamo bisogno di conoscere un metodo risolutivo, cioè un metodo che a partire dai dati di ingresso fornisce i risultati attesi.
Le macchine di Turing
 Le macchine di Turing Alan Turing (1912-1954) 1954) Il problema della decisione i L Entscheidungsproblem [il problema della decisione] è risolto se si conosce una procedura che permette di decidere la
Le macchine di Turing Alan Turing (1912-1954) 1954) Il problema della decisione i L Entscheidungsproblem [il problema della decisione] è risolto se si conosce una procedura che permette di decidere la
Algebra Di Boole. Definiamo ora che esiste un segnale avente valore opposto di quello assunto dalla variabile X.
 Algebra Di Boole L algebra di Boole è un ramo della matematica basato sul calcolo logico a due valori di verità (vero, falso). Con alcune leggi particolari consente di operare su proposizioni allo stesso
Algebra Di Boole L algebra di Boole è un ramo della matematica basato sul calcolo logico a due valori di verità (vero, falso). Con alcune leggi particolari consente di operare su proposizioni allo stesso
Architettura di un computer
 Architettura di un computer Modulo di Informatica Dott.sa Sara Zuppiroli A.A. 2012-2013 Modulo di Informatica () Architettura A.A. 2012-2013 1 / 36 La tecnologia Cerchiamo di capire alcuni concetti su
Architettura di un computer Modulo di Informatica Dott.sa Sara Zuppiroli A.A. 2012-2013 Modulo di Informatica () Architettura A.A. 2012-2013 1 / 36 La tecnologia Cerchiamo di capire alcuni concetti su
Calcolatori Elettronici A a.a. 2008/2009. RETI SEQUENZIALI: ESERCIZI Massimiliano Giacomin
 Calcolatori Elettronici A a.a. 2008/2009 RETI SEQUENZIALI: ESERCIZI Massimiliano Giacomin 1 Esercizio 1: implementazione di contatori Un contatore è un dispositivo sequenziale che aggiorna periodicamente
Calcolatori Elettronici A a.a. 2008/2009 RETI SEQUENZIALI: ESERCIZI Massimiliano Giacomin 1 Esercizio 1: implementazione di contatori Un contatore è un dispositivo sequenziale che aggiorna periodicamente
Sommario. Definizione di informatica. Definizione di un calcolatore come esecutore. Gli algoritmi.
 Algoritmi 1 Sommario Definizione di informatica. Definizione di un calcolatore come esecutore. Gli algoritmi. 2 Informatica Nome Informatica=informazione+automatica. Definizione Scienza che si occupa dell
Algoritmi 1 Sommario Definizione di informatica. Definizione di un calcolatore come esecutore. Gli algoritmi. 2 Informatica Nome Informatica=informazione+automatica. Definizione Scienza che si occupa dell
Scopo della lezione. Informatica. Informatica - def. 1. Informatica
 Scopo della lezione Informatica per le lauree triennali LEZIONE 1 - Che cos è l informatica Introdurre i concetti base della materia Definire le differenze tra hardware e software Individuare le applicazioni
Scopo della lezione Informatica per le lauree triennali LEZIONE 1 - Che cos è l informatica Introdurre i concetti base della materia Definire le differenze tra hardware e software Individuare le applicazioni
All interno del computer si possono individuare 5 componenti principali: SCHEDA MADRE. MICROPROCESSORE che contiene la CPU MEMORIA RAM MEMORIA ROM
 Il computer è un apparecchio elettronico che riceve dati di ingresso (input), li memorizza e gli elabora e fornisce in uscita i risultati (output). Il computer è quindi un sistema per elaborare informazioni
Il computer è un apparecchio elettronico che riceve dati di ingresso (input), li memorizza e gli elabora e fornisce in uscita i risultati (output). Il computer è quindi un sistema per elaborare informazioni
Il sapere tende oggi a caratterizzarsi non più come un insieme di contenuti ma come un insieme di metodi e di strategie per risolvere problemi.
 E. Calabrese: Fondamenti di Informatica Problemi-1 Il sapere tende oggi a caratterizzarsi non più come un insieme di contenuti ma come un insieme di metodi e di strategie per risolvere problemi. L'informatica
E. Calabrese: Fondamenti di Informatica Problemi-1 Il sapere tende oggi a caratterizzarsi non più come un insieme di contenuti ma come un insieme di metodi e di strategie per risolvere problemi. L'informatica
Chapter 1. Circuiti sequenziali: macchine a stati
 Chapter 1 Circuiti sequenziali: macchine a stati Nella prima parte del corso ci siamo occupati dei circuiti combinatori. In un circuito combinatorio con un ouput Z funzione degli input X 1 ; : : : X n,
Chapter 1 Circuiti sequenziali: macchine a stati Nella prima parte del corso ci siamo occupati dei circuiti combinatori. In un circuito combinatorio con un ouput Z funzione degli input X 1 ; : : : X n,
I componenti di un Sistema di elaborazione. Memoria centrale. È costituita da una serie di CHIP disposti su una scheda elettronica
 I componenti di un Sistema di elaborazione. Memoria centrale Memorizza : istruzioni dati In forma BINARIA : 10001010101000110101... È costituita da una serie di CHIP disposti su una scheda elettronica
I componenti di un Sistema di elaborazione. Memoria centrale Memorizza : istruzioni dati In forma BINARIA : 10001010101000110101... È costituita da una serie di CHIP disposti su una scheda elettronica
1.4b: Hardware. (Memoria Centrale)
 1.4b: Hardware (Memoria Centrale) Bibliografia Curtin, Foley, Sen, Morin Informatica di base, Mc Graw Hill Ediz. Fino alla III : cap. 3.11, 3.13 IV ediz.: cap. 2.8, 2.9 Questi lucidi Memoria Centrale Un
1.4b: Hardware (Memoria Centrale) Bibliografia Curtin, Foley, Sen, Morin Informatica di base, Mc Graw Hill Ediz. Fino alla III : cap. 3.11, 3.13 IV ediz.: cap. 2.8, 2.9 Questi lucidi Memoria Centrale Un
Macchine a Stati finiti
 Macchine a Stati finiti Prof. Alberto Borghese Dipartimento di Scienze dell nformazione borghese@di.unimi.it Università degli Studi di Milano Riferimento al Patterson: Sezione B.0 /3 Sommario Macchine
Macchine a Stati finiti Prof. Alberto Borghese Dipartimento di Scienze dell nformazione borghese@di.unimi.it Università degli Studi di Milano Riferimento al Patterson: Sezione B.0 /3 Sommario Macchine
ESEMPIO 1: eseguire il complemento a 10 di 765
 COMPLEMENTO A 10 DI UN NUMERO DECIMALE Sia dato un numero N 10 in base 10 di n cifre. Il complemento a 10 di tale numero (N ) si ottiene sottraendo il numero stesso a 10 n. ESEMPIO 1: eseguire il complemento
COMPLEMENTO A 10 DI UN NUMERO DECIMALE Sia dato un numero N 10 in base 10 di n cifre. Il complemento a 10 di tale numero (N ) si ottiene sottraendo il numero stesso a 10 n. ESEMPIO 1: eseguire il complemento
Nozione di algoritmo. Gabriella Trucco
 Nozione di algoritmo Gabriella Trucco Programmazione Attività con cui si predispone l'elaboratore ad eseguire un particolare insieme di azioni su particolari informazioni (dati), allo scopo di risolvere
Nozione di algoritmo Gabriella Trucco Programmazione Attività con cui si predispone l'elaboratore ad eseguire un particolare insieme di azioni su particolari informazioni (dati), allo scopo di risolvere
Intelligenza Artificiale
 Intelligenza Artificiale Esercizi e Domande di Esame Tecniche di Ricerca e Pianificazione Esercizi Griglia Si consideri un ambiente costituito da una griglia n n in cui si muove un agente che può spostarsi
Intelligenza Artificiale Esercizi e Domande di Esame Tecniche di Ricerca e Pianificazione Esercizi Griglia Si consideri un ambiente costituito da una griglia n n in cui si muove un agente che può spostarsi
Origini e caratteristiche dei calcolatori elettronici
 Origini e caratteristiche dei calcolatori elettronici Lunedì, 09 ottobre 2006 Supercomputer, mainframe 1 Server, workstation, desktop, notebook, palmare Un po di storia 1642 Biagio Pascal 1671 Leibniz
Origini e caratteristiche dei calcolatori elettronici Lunedì, 09 ottobre 2006 Supercomputer, mainframe 1 Server, workstation, desktop, notebook, palmare Un po di storia 1642 Biagio Pascal 1671 Leibniz
Cenni su algoritmi, diagrammi di flusso, strutture di controllo
 Cenni su algoritmi, diagrammi di flusso, strutture di controllo Algoritmo Spesso, nel nostro vivere quotidiano, ci troviamo nella necessità di risolvere problemi. La descrizione della successione di operazioni
Cenni su algoritmi, diagrammi di flusso, strutture di controllo Algoritmo Spesso, nel nostro vivere quotidiano, ci troviamo nella necessità di risolvere problemi. La descrizione della successione di operazioni
Sintesi di Reti Sequenziali Sincrone
 Sintesi di Reti Sequenziali Sincrone Maurizio Palesi Maurizio Palesi 1 Macchina Sequenziale Una macchina sequenziale è definita dalla quintupla (I,U,S,δ,λ) dove: I è l insieme finito dei simboli d ingresso
Sintesi di Reti Sequenziali Sincrone Maurizio Palesi Maurizio Palesi 1 Macchina Sequenziale Una macchina sequenziale è definita dalla quintupla (I,U,S,δ,λ) dove: I è l insieme finito dei simboli d ingresso
Esercizio su MT. Svolgimento
 Esercizio su MT Definire una macchina di Turing deterministica M a nastro singolo e i concetti di configurazione e di transizione. Sintetizzare una macchina di Turing trasduttore che trasformi un numero
Esercizio su MT Definire una macchina di Turing deterministica M a nastro singolo e i concetti di configurazione e di transizione. Sintetizzare una macchina di Turing trasduttore che trasformi un numero
Architettura di un calcolatore
 2009-2010 Ingegneria Aerospaziale Prof. A. Palomba - Elementi di Informatica (E-Z) 7 Architettura di un calcolatore Lez. 7 1 Modello di Von Neumann Il termine modello di Von Neumann (o macchina di Von
2009-2010 Ingegneria Aerospaziale Prof. A. Palomba - Elementi di Informatica (E-Z) 7 Architettura di un calcolatore Lez. 7 1 Modello di Von Neumann Il termine modello di Von Neumann (o macchina di Von
CPU. Maurizio Palesi
 CPU Central Processing Unit 1 Organizzazione Tipica CPU Dispositivi di I/O Unità di controllo Unità aritmetico logica (ALU) Terminale Stampante Registri CPU Memoria centrale Unità disco Bus 2 L'Esecutore
CPU Central Processing Unit 1 Organizzazione Tipica CPU Dispositivi di I/O Unità di controllo Unità aritmetico logica (ALU) Terminale Stampante Registri CPU Memoria centrale Unità disco Bus 2 L'Esecutore
Sistema operativo. Sommario. Sistema operativo...1 Browser...1. Convenzioni adottate
 MODULO BASE Quanto segue deve essere rispettato se si vuole che le immagini presentate nei vari moduli corrispondano, con buona probabilità, a quanto apparirà nello schermo del proprio computer nel momento
MODULO BASE Quanto segue deve essere rispettato se si vuole che le immagini presentate nei vari moduli corrispondano, con buona probabilità, a quanto apparirà nello schermo del proprio computer nel momento
Risolvere un problema significa individuare un procedimento che permetta di arrivare al risultato partendo dai dati
 Algoritmi Algoritmi Risolvere un problema significa individuare un procedimento che permetta di arrivare al risultato partendo dai dati Il procedimento (chiamato algoritmo) è composto da passi elementari
Algoritmi Algoritmi Risolvere un problema significa individuare un procedimento che permetta di arrivare al risultato partendo dai dati Il procedimento (chiamato algoritmo) è composto da passi elementari
Dispensa di Informatica I.1
 IL COMPUTER: CONCETTI GENERALI Il Computer (o elaboratore) è un insieme di dispositivi di diversa natura in grado di acquisire dall'esterno dati e algoritmi e produrre in uscita i risultati dell'elaborazione.
IL COMPUTER: CONCETTI GENERALI Il Computer (o elaboratore) è un insieme di dispositivi di diversa natura in grado di acquisire dall'esterno dati e algoritmi e produrre in uscita i risultati dell'elaborazione.
4 3 4 = 4 x 10 2 + 3 x 10 1 + 4 x 10 0 aaa 10 2 10 1 10 0
 Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
SISTEMI DI ELABORAZIONE DELLE INFORMAZIONI
 SISTEMI DI ELABORAZIONE DELLE INFORMAZIONI Prof. Andrea Borghesan venus.unive.it/borg borg@unive.it Ricevimento: martedì, 12.00-13.00. Dip. Di Matematica Modalità esame: scritto + tesina facoltativa 1
SISTEMI DI ELABORAZIONE DELLE INFORMAZIONI Prof. Andrea Borghesan venus.unive.it/borg borg@unive.it Ricevimento: martedì, 12.00-13.00. Dip. Di Matematica Modalità esame: scritto + tesina facoltativa 1
Lezione 8. La macchina universale
 Lezione 8 Algoritmi La macchina universale Un elaboratore o computer è una macchina digitale, elettronica, automatica capace di effettuare trasformazioni o elaborazioni su i dati digitale= l informazione
Lezione 8 Algoritmi La macchina universale Un elaboratore o computer è una macchina digitale, elettronica, automatica capace di effettuare trasformazioni o elaborazioni su i dati digitale= l informazione
un nastro di carta prolungabile a piacere e suddiviso in celle vuote o contenenti al più un unico carattere;
 Algoritmi 3 3.5 Capacità di calcolo Il matematico inglese Alan Turing (1912-1954) descrisse nel 1936 un tipo di automi, oggi detti macchine di Turing, e fornì una della prime definizioni rigorose di esecuzione
Algoritmi 3 3.5 Capacità di calcolo Il matematico inglese Alan Turing (1912-1954) descrisse nel 1936 un tipo di automi, oggi detti macchine di Turing, e fornì una della prime definizioni rigorose di esecuzione
LABORATORIO DI SISTEMI
 ALUNNO: Fratto Claudio CLASSE: IV B Informatico ESERCITAZIONE N : 1 LABORATORIO DI SISTEMI OGGETTO: Progettare e collaudare un circuito digitale capace di copiare le informazioni di una memoria PROM in
ALUNNO: Fratto Claudio CLASSE: IV B Informatico ESERCITAZIONE N : 1 LABORATORIO DI SISTEMI OGGETTO: Progettare e collaudare un circuito digitale capace di copiare le informazioni di una memoria PROM in
Lezione 2 OPERAZIONI ARITMETICHE E LOGICHE ARCHITETTURA DI UN ELABORATORE. Lez2 Informatica Sc. Giuridiche Op. aritmetiche/logiche arch.
 Lezione 2 OPERAZIONI ARITMETICHE E LOGICHE ARCHITETTURA DI UN ELABORATORE Comunicazione importante dalla prossima settimana, la lezione del venerdì si terrà: dalle 15:00 alle 17.15 in aula 311 l orario
Lezione 2 OPERAZIONI ARITMETICHE E LOGICHE ARCHITETTURA DI UN ELABORATORE Comunicazione importante dalla prossima settimana, la lezione del venerdì si terrà: dalle 15:00 alle 17.15 in aula 311 l orario
Indice generale. OOA Analisi Orientata agli Oggetti. Introduzione. Analisi
 Indice generale OOA Analisi Orientata agli Oggetti Introduzione Analisi Metodi d' analisi Analisi funzionale Analisi del flusso dei dati Analisi delle informazioni Analisi Orientata agli Oggetti (OOA)
Indice generale OOA Analisi Orientata agli Oggetti Introduzione Analisi Metodi d' analisi Analisi funzionale Analisi del flusso dei dati Analisi delle informazioni Analisi Orientata agli Oggetti (OOA)
Hardware, software e periferiche. Facoltà di Lettere e Filosofia anno accademico 2008/2009 secondo semestre
 Hardware, software e periferiche Facoltà di Lettere e Filosofia anno accademico 2008/2009 secondo semestre Riepilogo - Concetti di base dell informatica L'informatica è quel settore scientifico disciplinare
Hardware, software e periferiche Facoltà di Lettere e Filosofia anno accademico 2008/2009 secondo semestre Riepilogo - Concetti di base dell informatica L'informatica è quel settore scientifico disciplinare
23/02/2014. Dalla scorsa lezione. La Macchina di Von Neumann. Uomo come esecutore di algoritmi
 Dalla scorsa lezione LABORATORIO DI PROGRAMMAZIONE Corso di laurea in matematica LA MACCHINA DI VON NEUMANN Marco Lapegna Dipartimento di Matematica e Applicazioni Universita degli Studi di Napoli Federico
Dalla scorsa lezione LABORATORIO DI PROGRAMMAZIONE Corso di laurea in matematica LA MACCHINA DI VON NEUMANN Marco Lapegna Dipartimento di Matematica e Applicazioni Universita degli Studi di Napoli Federico
Fondamenti di Informatica. Allievi Automatici A.A. 2014-15 Nozioni di Base
 Fondamenti di Informatica Allievi Automatici A.A. 2014-15 Nozioni di Base Perché studiare informatica? Perché l informatica è uno dei maggiori settori industriali, e ha importanza strategica Perché, oltre
Fondamenti di Informatica Allievi Automatici A.A. 2014-15 Nozioni di Base Perché studiare informatica? Perché l informatica è uno dei maggiori settori industriali, e ha importanza strategica Perché, oltre
IL SISTEMA OPERATIVO IL SISTEMA OPERATIVO INTERFACCE TESTUALI INTERFACCE TESTUALI FUNZIONI DEL SISTEMA OPERATIVO INTERFACCE GRAFICHE
 IL SISTEMA OPERATIVO Insieme di programmi che opera al di sopra della macchina fisica, mascherandone le caratteristiche e fornendo agli utenti funzionalità di alto livello. PROGRAMMI UTENTE INTERPRETE
IL SISTEMA OPERATIVO Insieme di programmi che opera al di sopra della macchina fisica, mascherandone le caratteristiche e fornendo agli utenti funzionalità di alto livello. PROGRAMMI UTENTE INTERPRETE
Architettura del calcolatore
 Architettura del calcolatore La prima decomposizione di un calcolatore è relativa a due macro-componenti: Hardware Software Architettura del calcolatore L architettura dell hardware di un calcolatore reale
Architettura del calcolatore La prima decomposizione di un calcolatore è relativa a due macro-componenti: Hardware Software Architettura del calcolatore L architettura dell hardware di un calcolatore reale
lo 2 2-1 - PERSONALIZZARE LA FINESTRA DI WORD 2000
 Capittol lo 2 Visualizzazione 2-1 - PERSONALIZZARE LA FINESTRA DI WORD 2000 Nel primo capitolo sono state analizzate le diverse componenti della finestra di Word 2000: barra del titolo, barra dei menu,
Capittol lo 2 Visualizzazione 2-1 - PERSONALIZZARE LA FINESTRA DI WORD 2000 Nel primo capitolo sono state analizzate le diverse componenti della finestra di Word 2000: barra del titolo, barra dei menu,
Architettura hardware
 Ricapitolando Architettura hardware la parte che si può prendere a calci Il funzionamento di un elaboratore dipende da due fattori principali 1) dalla capacità di memorizzare i programmi e i dati 2) dalla
Ricapitolando Architettura hardware la parte che si può prendere a calci Il funzionamento di un elaboratore dipende da due fattori principali 1) dalla capacità di memorizzare i programmi e i dati 2) dalla
Flip-flop, registri, la macchina a stati finiti
 Architettura degli Elaboratori e delle Reti Lezione 9 Flip-flop, registri, la macchina a stati finiti Proff. A. Borghese, F. Pedersini Dipartimento di Scienze dell nformazione Università degli Studi di
Architettura degli Elaboratori e delle Reti Lezione 9 Flip-flop, registri, la macchina a stati finiti Proff. A. Borghese, F. Pedersini Dipartimento di Scienze dell nformazione Università degli Studi di
ALGORITMI e PROGRAMMI Programmazione: Lavoro che si fa per costruire sequenze di istruzioni (operazioni) adatte a svolgere un dato calcolo
 ALGORITMI e PROGRAMMI Programmazione: Lavoro che si fa per costruire sequenze di istruzioni (operazioni) adatte a svolgere un dato calcolo INPUT: dati iniziali INPUT: x,y,z AZIONI esempio: Somma x ed y
ALGORITMI e PROGRAMMI Programmazione: Lavoro che si fa per costruire sequenze di istruzioni (operazioni) adatte a svolgere un dato calcolo INPUT: dati iniziali INPUT: x,y,z AZIONI esempio: Somma x ed y
Sistemi Web! per il turismo! - lezione 3 -
 Sistemi Web per il turismo - lezione 3 - I computer sono in grado di eseguire molte operazioni, e di risolvere un gran numero di problemi. E arrivato il momento di delineare esplicitamente il campo di
Sistemi Web per il turismo - lezione 3 - I computer sono in grado di eseguire molte operazioni, e di risolvere un gran numero di problemi. E arrivato il momento di delineare esplicitamente il campo di
NOZIONI ELEMENTARI DI HARDWARE E SOFTWARE
 CORSO INTRODUTTIVO DI INFORMATICA NOZIONI ELEMENTARI DI HARDWARE E SOFTWARE Dott. Paolo Righetto 1 CORSO INTRODUTTIVO DI INFORMATICA Percorso dell incontro: 1) Alcuni elementi della configurazione hardware
CORSO INTRODUTTIVO DI INFORMATICA NOZIONI ELEMENTARI DI HARDWARE E SOFTWARE Dott. Paolo Righetto 1 CORSO INTRODUTTIVO DI INFORMATICA Percorso dell incontro: 1) Alcuni elementi della configurazione hardware
Elementi di informatica
 Elementi di informatica L elaboratore elettronico (ovvero, il computer ) Monitor Unità centrale Casse acustiche Mouse Tastiera PREMESSA Insegnare con l'ausilio dei multimedia è una tecnica che giunge agli
Elementi di informatica L elaboratore elettronico (ovvero, il computer ) Monitor Unità centrale Casse acustiche Mouse Tastiera PREMESSA Insegnare con l'ausilio dei multimedia è una tecnica che giunge agli
Laboratorio di Informatica
 per chimica industriale e chimica applicata e ambientale LEZIONE 4 La CPU e l esecuzione dei programmi 1 Nelle lezioni precedenti abbiamo detto che Un computer è costituito da 3 principali componenti:
per chimica industriale e chimica applicata e ambientale LEZIONE 4 La CPU e l esecuzione dei programmi 1 Nelle lezioni precedenti abbiamo detto che Un computer è costituito da 3 principali componenti:
Introduzione alla programmazione in C
 Introduzione alla programmazione in C Testi Consigliati: A. Kelley & I. Pohl C didattica e programmazione B.W. Kernighan & D. M. Ritchie Linguaggio C P. Tosoratti Introduzione all informatica Materiale
Introduzione alla programmazione in C Testi Consigliati: A. Kelley & I. Pohl C didattica e programmazione B.W. Kernighan & D. M. Ritchie Linguaggio C P. Tosoratti Introduzione all informatica Materiale
Informatica per le discipline umanistiche 2 lezione 14
 Informatica per le discipline umanistiche 2 lezione 14 Torniamo ai concetti base dellʼinformatica. Abbiamo sinora affrontato diversi problemi: avere unʼidentità online, cercare pagine Web, commentare il
Informatica per le discipline umanistiche 2 lezione 14 Torniamo ai concetti base dellʼinformatica. Abbiamo sinora affrontato diversi problemi: avere unʼidentità online, cercare pagine Web, commentare il
Dropbox di classe. É un servizio internet fornito gratuitamente (funzioni base).
 Dropbox di classe Lo scopo del servizio Dropbox di classe è quello di far conoscere ai docenti del nostro istituto il funzionamento di un sistema di Cloud Storage, pronto e facile da usare, per esplorare
Dropbox di classe Lo scopo del servizio Dropbox di classe è quello di far conoscere ai docenti del nostro istituto il funzionamento di un sistema di Cloud Storage, pronto e facile da usare, per esplorare
Calcolatori: Algebra Booleana e Reti Logiche
 Calcolatori: Algebra Booleana e Reti Logiche 1 Algebra Booleana e Variabili Logiche I fondamenti dell Algebra Booleana (o Algebra di Boole) furono delineati dal matematico George Boole, in un lavoro pubblicato
Calcolatori: Algebra Booleana e Reti Logiche 1 Algebra Booleana e Variabili Logiche I fondamenti dell Algebra Booleana (o Algebra di Boole) furono delineati dal matematico George Boole, in un lavoro pubblicato
Laboratorio di Architettura degli Elaboratori A.A. 2015/16 Circuiti Logici
 Laboratorio di Architettura degli Elaboratori A.A. 2015/16 Circuiti Logici Per ogni lezione, sintetizzare i circuiti combinatori o sequenziali che soddisfino le specifiche date e quindi implementarli e
Laboratorio di Architettura degli Elaboratori A.A. 2015/16 Circuiti Logici Per ogni lezione, sintetizzare i circuiti combinatori o sequenziali che soddisfino le specifiche date e quindi implementarli e
Architettura hardware
 Architettura dell elaboratore Architettura hardware la parte che si può prendere a calci Sistema composto da un numero elevato di componenti, in cui ogni componente svolge una sua funzione elaborazione
Architettura dell elaboratore Architettura hardware la parte che si può prendere a calci Sistema composto da un numero elevato di componenti, in cui ogni componente svolge una sua funzione elaborazione
La specifica del problema
 2.9 (Caso di studio facoltativo) Pensare a oggetti: esame del problema Iniziamo ora a esaminare il nostro caso di studio di progettazione e implementazione orientate agli oggetti. Le sezioni Pensare a
2.9 (Caso di studio facoltativo) Pensare a oggetti: esame del problema Iniziamo ora a esaminare il nostro caso di studio di progettazione e implementazione orientate agli oggetti. Le sezioni Pensare a
TECNICHE DI SIMULAZIONE
 TECNICHE DI SIMULAZIONE INTRODUZIONE Francesca Mazzia Dipartimento di Matematica Università di Bari a.a. 2004/2005 TECNICHE DI SIMULAZIONE p. 1 Introduzione alla simulazione Una simulazione è l imitazione
TECNICHE DI SIMULAZIONE INTRODUZIONE Francesca Mazzia Dipartimento di Matematica Università di Bari a.a. 2004/2005 TECNICHE DI SIMULAZIONE p. 1 Introduzione alla simulazione Una simulazione è l imitazione
Architettura dei computer
 Architettura dei computer In un computer possiamo distinguere quattro unità funzionali: il processore (CPU) la memoria principale (RAM) la memoria secondaria i dispositivi di input/output Il processore
Architettura dei computer In un computer possiamo distinguere quattro unità funzionali: il processore (CPU) la memoria principale (RAM) la memoria secondaria i dispositivi di input/output Il processore
SISTEMI DI NUMERAZIONE E CODICI
 SISTEMI DI NUMERAZIONE E CODICI Il Sistema di Numerazione Decimale Il sistema decimale o sistema di numerazione a base dieci usa dieci cifre, dette cifre decimali, da O a 9. Il sistema decimale è un sistema
SISTEMI DI NUMERAZIONE E CODICI Il Sistema di Numerazione Decimale Il sistema decimale o sistema di numerazione a base dieci usa dieci cifre, dette cifre decimali, da O a 9. Il sistema decimale è un sistema
GHPPEditor è un software realizzato per produrre in modo rapido e guidato un part program per controlli numerici Heidenhain.
 *+33(GLWRU GHPPEditor è un software realizzato per produrre in modo rapido e guidato un part program per controlli numerici Heidenhain. Il programma si basa su un architettura di tasti funzionali presenti
*+33(GLWRU GHPPEditor è un software realizzato per produrre in modo rapido e guidato un part program per controlli numerici Heidenhain. Il programma si basa su un architettura di tasti funzionali presenti
Funzionalità di un Algoritmo
 ALGORITMI Cosa è un algoritmo Un algoritmo è una sequenza di azioni che consente di pervenire alla soluzione di un problema mediante una sequenza finita di operazioni, completamente e univocamente determinate.
ALGORITMI Cosa è un algoritmo Un algoritmo è una sequenza di azioni che consente di pervenire alla soluzione di un problema mediante una sequenza finita di operazioni, completamente e univocamente determinate.
Introduzione all'architettura dei Calcolatori
 Introduzione all'architettura dei Calcolatori Introduzione Che cos è un calcolatore? Come funziona un calcolatore? è possibile rispondere a queste domande in molti modi, ciascuno relativo a un diverso
Introduzione all'architettura dei Calcolatori Introduzione Che cos è un calcolatore? Come funziona un calcolatore? è possibile rispondere a queste domande in molti modi, ciascuno relativo a un diverso
FSM: Macchine a Stati Finiti
 FSM: Macchine a Stati Finiti Sommario Introduzione Automi di Mealy Automi di Moore Esempi Introduzione Metodo per descrivere macchine di tipo sequenziale Molto utile per la descrizione di Unità di controllo
FSM: Macchine a Stati Finiti Sommario Introduzione Automi di Mealy Automi di Moore Esempi Introduzione Metodo per descrivere macchine di tipo sequenziale Molto utile per la descrizione di Unità di controllo
C. P. U. MEMORIA CENTRALE
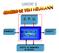 C. P. U. INGRESSO MEMORIA CENTRALE USCITA UNITA DI MEMORIA DI MASSA La macchina di Von Neumann Negli anni 40 lo scienziato ungherese Von Neumann realizzò il primo calcolatore digitale con programma memorizzato
C. P. U. INGRESSO MEMORIA CENTRALE USCITA UNITA DI MEMORIA DI MASSA La macchina di Von Neumann Negli anni 40 lo scienziato ungherese Von Neumann realizzò il primo calcolatore digitale con programma memorizzato
Corso di Informatica
 Corso di Informatica Modulo T2 1 Sistema software 1 Prerequisiti Utilizzo elementare di un computer Significato elementare di programma e dati Sistema operativo 2 1 Introduzione In questa Unità studiamo
Corso di Informatica Modulo T2 1 Sistema software 1 Prerequisiti Utilizzo elementare di un computer Significato elementare di programma e dati Sistema operativo 2 1 Introduzione In questa Unità studiamo
Tipologie di macchine di Turing
 Tipologie di macchine di Turing - Macchina di Turing standard - Macchina di Turing con un nastro illimitato in una sola direzione - Macchina di Turing multinastro - Macchina di Turing non deterministica
Tipologie di macchine di Turing - Macchina di Turing standard - Macchina di Turing con un nastro illimitato in una sola direzione - Macchina di Turing multinastro - Macchina di Turing non deterministica
Gestione della memoria centrale
 Gestione della memoria centrale Un programma per essere eseguito deve risiedere in memoria principale e lo stesso vale per i dati su cui esso opera In un sistema multitasking molti processi vengono eseguiti
Gestione della memoria centrale Un programma per essere eseguito deve risiedere in memoria principale e lo stesso vale per i dati su cui esso opera In un sistema multitasking molti processi vengono eseguiti
I Problemi e la loro Soluzione. Il Concetto Intuitivo di Calcolatore. Risoluzione di un Problema. Esempio
 Il Concetto Intuitivo di Calcolatore Fondamenti di Informatica A Ingegneria Gestionale Università degli Studi di Brescia Docente: Prof. Alfonso Gerevini I Problemi e la loro Soluzione Problema: classe
Il Concetto Intuitivo di Calcolatore Fondamenti di Informatica A Ingegneria Gestionale Università degli Studi di Brescia Docente: Prof. Alfonso Gerevini I Problemi e la loro Soluzione Problema: classe
Excel. A cura di Luigi Labonia. e-mail: luigi.lab@libero.it
 Excel A cura di Luigi Labonia e-mail: luigi.lab@libero.it Introduzione Un foglio elettronico è un applicazione comunemente usata per bilanci, previsioni ed altri compiti tipici del campo amministrativo
Excel A cura di Luigi Labonia e-mail: luigi.lab@libero.it Introduzione Un foglio elettronico è un applicazione comunemente usata per bilanci, previsioni ed altri compiti tipici del campo amministrativo
Esercizi per il recupero del debito formativo:
 ANNO SCOLASTICO 2005/2006 CLASSE 3 ISC Esercizi per il recupero del debito formativo: Disegnare il diagramma e scrivere la matrice delle transizioni di stato degli automi a stati finiti che rappresentano
ANNO SCOLASTICO 2005/2006 CLASSE 3 ISC Esercizi per il recupero del debito formativo: Disegnare il diagramma e scrivere la matrice delle transizioni di stato degli automi a stati finiti che rappresentano
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
MATERIA : SISTEMI ELETTRICI AUTOMATICI INS. TEORICO: PROF. CIVITAREALE ALBERTO
 PIANO DI LAVORO CLASSE 4 ES A.S. 2014-2015 MATERIA : SISTEMI ELETTRICI AUTOMATICI INS. TEORICO: PROF. CIVITAREALE ALBERTO INS. TECNICO-PRATICO: PROF. BARONI MAURIZIO MODULO 1: SISTEMI E MODELLI (30 ore)
PIANO DI LAVORO CLASSE 4 ES A.S. 2014-2015 MATERIA : SISTEMI ELETTRICI AUTOMATICI INS. TEORICO: PROF. CIVITAREALE ALBERTO INS. TECNICO-PRATICO: PROF. BARONI MAURIZIO MODULO 1: SISTEMI E MODELLI (30 ore)
Algoritmo. I dati su cui opera un'istruzione sono forniti all'algoritmo dall'esterno oppure sono il risultato di istruzioni eseguite precedentemente.
 Algoritmo Formalmente, per algoritmo si intende una successione finita di passi o istruzioni che definiscono le operazioni da eseguire su dei dati (=istanza del problema): in generale un algoritmo è definito
Algoritmo Formalmente, per algoritmo si intende una successione finita di passi o istruzioni che definiscono le operazioni da eseguire su dei dati (=istanza del problema): in generale un algoritmo è definito
INFORMATICA GENERALE. Prof Alberto Postiglione Dipartim. Scienze della Comunicazione Univ. Salerno. Università degli Studi di Salerno
 INFORMATICA GENERALE Prof. Alberto Postiglione Dipartimento Scienze della Comunicazione Università degli Studi di Salerno : Introduzione alla Programmazione Bibliografia 14 apr 2010 Dia 2 Curtin, (vecchie
INFORMATICA GENERALE Prof. Alberto Postiglione Dipartimento Scienze della Comunicazione Università degli Studi di Salerno : Introduzione alla Programmazione Bibliografia 14 apr 2010 Dia 2 Curtin, (vecchie
Appunti del corso di Informatica 1 (IN110 Fondamenti) 2 Algoritmi e diagrammi di flusso
 Università Roma Tre Facoltà di Scienze M.F.N. Corso di Laurea in Matematica Appunti del corso di Informatica 1 (IN110 Fondamenti) 2 Algoritmi e diagrammi di flusso Marco Liverani (liverani@mat.uniroma3.it)
Università Roma Tre Facoltà di Scienze M.F.N. Corso di Laurea in Matematica Appunti del corso di Informatica 1 (IN110 Fondamenti) 2 Algoritmi e diagrammi di flusso Marco Liverani (liverani@mat.uniroma3.it)
Database 1 biblioteca universitaria. Testo del quesito
 Database 1 biblioteca universitaria Testo del quesito Una biblioteca universitaria acquista testi didattici su indicazione dei professori e cura il prestito dei testi agli studenti. La biblioteca vuole
Database 1 biblioteca universitaria Testo del quesito Una biblioteca universitaria acquista testi didattici su indicazione dei professori e cura il prestito dei testi agli studenti. La biblioteca vuole
Matematica Computazionale Lezione 4: Algebra di Commutazione e Reti Logiche
 Matematica Computazionale Lezione 4: Algebra di Commutazione e Reti Logiche Docente: Michele Nappi mnappi@unisa.it www.dmi.unisa.it/people/nappi 089-963334 ALGEBRA DI COMMUTAZIONE Lo scopo di questa algebra
Matematica Computazionale Lezione 4: Algebra di Commutazione e Reti Logiche Docente: Michele Nappi mnappi@unisa.it www.dmi.unisa.it/people/nappi 089-963334 ALGEBRA DI COMMUTAZIONE Lo scopo di questa algebra
DI D AGRA R MM M I M A BLOCC C H C I TEORI R A E D D E SERC R I C ZI 1 1
 DIAGRAMMI A BLOCCHI TEORIA ED ESERCIZI 1 1 Il linguaggio dei diagrammi a blocchi è un possibile formalismo per la descrizione di algoritmi Il diagramma a blocchi, o flowchart, è una rappresentazione grafica
DIAGRAMMI A BLOCCHI TEORIA ED ESERCIZI 1 1 Il linguaggio dei diagrammi a blocchi è un possibile formalismo per la descrizione di algoritmi Il diagramma a blocchi, o flowchart, è una rappresentazione grafica
Funzioni funzione dominio codominio legge argomento variabile indipendente variabile dipendente
 Funzioni In matematica, una funzione f da X in Y consiste in: 1. un insieme X detto dominio di f 2. un insieme Y detto codominio di f 3. una legge che ad ogni elemento x in X associa uno ed un solo elemento
Funzioni In matematica, una funzione f da X in Y consiste in: 1. un insieme X detto dominio di f 2. un insieme Y detto codominio di f 3. una legge che ad ogni elemento x in X associa uno ed un solo elemento
Algoritmi e strutture dati. Codici di Huffman
 Algoritmi e strutture dati Codici di Huffman Memorizzazione dei dati Quando un file viene memorizzato, esso va memorizzato in qualche formato binario Modo più semplice: memorizzare il codice ASCII per
Algoritmi e strutture dati Codici di Huffman Memorizzazione dei dati Quando un file viene memorizzato, esso va memorizzato in qualche formato binario Modo più semplice: memorizzare il codice ASCII per
Dispense di Informatica per l ITG Valadier
 La notazione binaria Dispense di Informatica per l ITG Valadier Le informazioni dentro il computer All interno di un calcolatore tutte le informazioni sono memorizzate sottoforma di lunghe sequenze di
La notazione binaria Dispense di Informatica per l ITG Valadier Le informazioni dentro il computer All interno di un calcolatore tutte le informazioni sono memorizzate sottoforma di lunghe sequenze di
Algebra booleana. Si dice enunciato una proposizione che può essere soltanto vera o falsa.
 Algebra booleana Nel lavoro di programmazione capita spesso di dover ricorrere ai principi della logica degli enunciati e occorre conoscere i concetti di base dell algebra delle proposizioni. L algebra
Algebra booleana Nel lavoro di programmazione capita spesso di dover ricorrere ai principi della logica degli enunciati e occorre conoscere i concetti di base dell algebra delle proposizioni. L algebra
connessioni tra i singoli elementi Hanno caratteristiche diverse e sono presentati con modalità diverse Tali relazioni vengono rappresentate QUINDI
 Documenti su Internet LINGUAGGI DI MARKUP Internet permette (tra l altro) di accedere a documenti remoti In generale, i documenti acceduti via Internet sono multimediali, cioè che possono essere riprodotti
Documenti su Internet LINGUAGGI DI MARKUP Internet permette (tra l altro) di accedere a documenti remoti In generale, i documenti acceduti via Internet sono multimediali, cioè che possono essere riprodotti
Esercizio data base "Biblioteca"
 Rocco Sergi Esercizio data base "Biblioteca" Database 2: Biblioteca Testo dell esercizio Si vuole realizzare una base dati per la gestione di una biblioteca. La base dati conterrà tutte le informazioni
Rocco Sergi Esercizio data base "Biblioteca" Database 2: Biblioteca Testo dell esercizio Si vuole realizzare una base dati per la gestione di una biblioteca. La base dati conterrà tutte le informazioni
ARCHITETTURE MICROPROGRAMMATE. 1. Necessità di un architettura microprogrammata 1. Cos è un architettura microprogrammata? 4
 ARCHITETTURE MICROPROGRAMMATE. 1 Necessità di un architettura microprogrammata 1 Cos è un architettura microprogrammata? 4 Struttura di una microistruzione. 5 Esempi di microprogrammi 9 Esempio 1 9 Esempio
ARCHITETTURE MICROPROGRAMMATE. 1 Necessità di un architettura microprogrammata 1 Cos è un architettura microprogrammata? 4 Struttura di una microistruzione. 5 Esempi di microprogrammi 9 Esempio 1 9 Esempio
Elementi di Architettura e Sistemi Operativi. problema punti massimi i tuoi punti problema 1 6 problema 2 7 problema 3 7 problema 4 10 totale 30
 Elementi di Architettura e Sistemi Operativi Bioinformatica - Tiziano Villa 22 Giugno 2012 Nome e Cognome: Matricola: Posta elettronica: problema punti massimi i tuoi punti problema 1 6 problema 2 7 problema
Elementi di Architettura e Sistemi Operativi Bioinformatica - Tiziano Villa 22 Giugno 2012 Nome e Cognome: Matricola: Posta elettronica: problema punti massimi i tuoi punti problema 1 6 problema 2 7 problema
