Bioinformatica e Biostatistica /12 Modulo di Biostatistica
|
|
|
- Aldo Spada
- 5 anni fa
- Visualizzazioni
Transcript
1 Bioinformatica e Biostatistica /12 Modulo di Biostatistica Alessandra Micheletti Dipartimento di Matematica, Università degli Studi di Milano alessandra.micheletti@unimi.it
2 Introduzione Il Calcolo delle Probabilità è la base su cui poggiano tutti i metodi statistici. ESEMPIO: immaginate di aver messo a punto un metodo che dovrebbe permettere di predeterminare il sesso del nascituro, facendo aumentare le probabilità di generare una femmina. Se, messo alla prova su un campione di 100 coppie, il vostro sistema porta ad avere a) 98 femmine e 2 maschi b) 60 femmine e 40 maschi potete affermare che il metodo funziona nel caso a)? E nel caso b)?
3 Caso a): sebbene sia possibile avere 98 femmine su 100 nascite anche senza interventi esterni, si tratta di una situazione talmente improbabile da essere scartata (la sua prob. è dell ordine di ), quindi concluderemo che il metodo è efficace evento raro o estremo (vedremo che sarà bassa la probabilità di commettere un errore nel trarre questa conclusione)
4 Caso b): se assumiamo che, in assenza di trattamenti la prob. di nascita di un maschio sia 1 2, la probabilità di osservare fino a 40 maschi su 100 nuovi nati in assenza di trattamenti è = 2.8% (vedremo come si calcola più avanti). Questa probabilità è abbastanza bassa da poter dire che il trattamento è efficace? Con che probabilità commetto un errore nell assumere che il trattamento sia efficace in questo caso? È quindi evidente che per effettuare inferenza statistica sui dati occorre prima imparare gli elementi alla base del Calcolo delle Probabilità.
5 Un esperimento aleatorio è caratterizzato dall insieme Ω di tutti i suoi possibili esiti (risultati). Ω = spazio dei campioni ogni elemento ω Ω è detto evento elementare. ESEMPI? (Provateci voi...)
6 Esempi
7 Lo spazio dei campioni può essere finito (es.: lancio di un dado: Ω = {1, 2, 3, 4, 5, 6}) infinito numerabile (es.: numero di telefonate che arrivano a un centralino in un mese: Ω = N = {numeri naturali}) infinito non numerabile (es.: durata del funzionamento di una lampadina: Ω = R + = numeri reali positivi)
8 Lo spazio dei campioni può essere finito (es.: lancio di un dado: Ω = {1, 2, 3, 4, 5, 6}) infinito numerabile (es.: numero di telefonate che arrivano a un centralino in un mese: Ω = N = {numeri naturali}) infinito non numerabile (es.: durata del funzionamento di una lampadina: Ω = R + = numeri reali positivi)
9 Lo spazio dei campioni può essere finito (es.: lancio di un dado: Ω = {1, 2, 3, 4, 5, 6}) infinito numerabile (es.: numero di telefonate che arrivano a un centralino in un mese: Ω = N = {numeri naturali}) infinito non numerabile (es.: durata del funzionamento di una lampadina: Ω = R + = numeri reali positivi)
10 Sia P(Ω) = {sottoinsiemi di Ω}. Vorremo definire una probabilità come una funzione definita su P(Ω) a valori in [0, 1] che ad ogni A sottoinsieme di Ω associ un numero compreso fra 0 e 1. Di quali sottoinsiemi di Ω (detti eventi) vorremo calcolare la probabilità?
11 Esempio: Consideriamo il lancio di un dado. Possibili eventi sono: A =il risultato del lancio è 1 = {1} B =il risultato del lancio è un numero pari = {2} {4} {6} = {2, 4, 6} C =il risultato del lancio è maggiore di 2 = {3} {4} {5} {6} = {3, 4, 5, 6} D =il risultato del lancio è maggiore di 2 ed è pari = B C = {4, 6} E =il risultato del lancio è minore o uguale a 2= C C...
12 L evento A è semplice, mentre gli eventi B, C, D sono composti e si possono vedere come unione o intersezione di altri eventi, elementari e non. Dunque eventi di nostro interesse saranno dati da unioni, intersezioni, complementari di altri eventi. Dato uno spazio dei campioni Ω, diremo che un insieme F di sottoinsiemi di Ω è una famiglia di eventi aleatori se essa è una.
13 Definizione. Una famiglia F di sottoinsiemi di Ω è una se soddisfa le seguenti condizioni: A1. Ω F; A2. se {A n } n N, con A n elementi di F, allora n N A n F; A3. se A F allora A C F. Proprietà derivanti dalla definizione: 1) Anche l insieme vuoto è un elemento di F
14 Definizione. Una famiglia F di sottoinsiemi di Ω è una se soddisfa le seguenti condizioni: A1. Ω F; A2. se {A n } n N, con A n elementi di F, allora n N A n F; A3. se A F allora A C F. Proprietà derivanti dalla definizione: 1) Anche l insieme vuoto è un elemento di F
15 2) Le unioni finite di elementi di F appartengono a F 3) Le intersezioni di elementi di F appartengono a F 4) se A, B F allora A B F
16 2) Le unioni finite di elementi di F appartengono a F 3) Le intersezioni di elementi di F appartengono a F 4) se A, B F allora A B F
17 2) Le unioni finite di elementi di F appartengono a F 3) Le intersezioni di elementi di F appartengono a F 4) se A, B F allora A B F
18 La coppia (Ω, F) viene detta spazio probabilizzabile. Su di essa si può definire correttamente una misura di probabilità. Ci sono vari modi per definirla.
19 Definizione. Dato uno spazio probabilizzabile (Ω, F), si definisice misura di probabilità o semplicemente probabilità P ogni funzione P : F [0, 1] che soddisfi le seguenti proprietà: P1. P(Ω) = 1 P2. sia {A n } n N una famiglia di eventi disgiunti, ossia tali che A i A j = per i j; allora ( k ) P A i = i=1 k P(A i ) (se la famiglia è finita) i=1 ( ) P A i = P(A i ). (se la famiglia è infinita) i=1 i=1 P2. si chiama ADDITIVITÀ e ci dice che la probabilità di unioni DISGIUNTE di eventi è uguale alla somma delle probabilità dei singoli eventi
20 Definizione. Dato uno spazio probabilizzabile (Ω, F), si definisice misura di probabilità o semplicemente probabilità P ogni funzione P : F [0, 1] che soddisfi le seguenti proprietà: P1. P(Ω) = 1 P2. sia {A n } n N una famiglia di eventi disgiunti, ossia tali che A i A j = per i j; allora ( k ) P A i = i=1 k P(A i ) (se la famiglia è finita) i=1 ( ) P A i = P(A i ). (se la famiglia è infinita) i=1 i=1 P2. si chiama ADDITIVITÀ e ci dice che la probabilità di unioni DISGIUNTE di eventi è uguale alla somma delle probabilità dei singoli eventi
21 Consideriamo ancora l esempio del lancio di un dado EQUILIBRATO. Sappiamo che Ω = {1, 2, 3, 4, 5, 6}. Per assegnare le probabilità P({i}), i = 1,..., 6 dobbiamo chiederci quanto siamo disposti a scommettere su ciascun numero (=evento elementare). Intuitivamente, se ci fidiamo del fatto che il dado sia equilibrato, assegneremo a ogni evento elementare probabilità 1 numero di elementi in Ω = 1 6.
22 Consideriamo ancora l esempio del lancio di un dado EQUILIBRATO. Sappiamo che Ω = {1, 2, 3, 4, 5, 6}. Per assegnare le probabilità P({i}), i = 1,..., 6 dobbiamo chiederci quanto siamo disposti a scommettere su ciascun numero (=evento elementare). Intuitivamente, se ci fidiamo del fatto che il dado sia equilibrato, assegneremo a ogni evento elementare probabilità 1 numero di elementi in Ω = 1 6.
23 Definizione. Lo spazio di probabilità (Ω, F, P) costituisce un modello equiprobabile o uniforme se M1. Ω è finito; M2. F è l insieme di tutti i sottoinsiemi di Ω M3. per ogni ω Ω, P({ω}) = costante.
24 Definizione. Lo spazio di probabilità (Ω, F, P) costituisce un modello equiprobabile o uniforme se M1. Ω è finito; M2. F è l insieme di tutti i sottoinsiemi di Ω M3. per ogni ω Ω, P({ω}) = costante.
25 Definizione. Lo spazio di probabilità (Ω, F, P) costituisce un modello equiprobabile o uniforme se M1. Ω è finito; M2. F è l insieme di tutti i sottoinsiemi di Ω M3. per ogni ω Ω, P({ω}) = costante.
26 Per il modello uniforme valgono le seguenti proprietà P1. per ogni ω Ω si ha P({ω}) = 1 numero di elementi di Ω P2. per ogni evento A sottoinsieme di Ω si ha P(A) = numero di elementi di A numero di elementi di Ω o anche casi favorevoli P(A) = definizione classica della probabilità di casi possibili un evento: poco operativa, soprattutto se Ω ha infiniti elementi! Esempi?
27 Per il modello uniforme valgono le seguenti proprietà P1. per ogni ω Ω si ha P({ω}) = 1 numero di elementi di Ω P2. per ogni evento A sottoinsieme di Ω si ha P(A) = numero di elementi di A numero di elementi di Ω o anche casi favorevoli P(A) = definizione classica della probabilità di casi possibili un evento: poco operativa, soprattutto se Ω ha infiniti elementi! Esempi?
28 E se non mi fido sul fatto che il dado sia equilibrato? Posso lanciare il dado molte volte e calcolare la frequenza relativa all evento {esce il numero i} rispetto al numero totale di lanci: f (i) = e posso approssimare P({i}) con f (i). numero di volte in cui è uscito i numero totale di lanci Cosa accade però al variare del numero di lanci?
29 Quelli sopra sono istogrammi che riportano le frequenze relative del lancio di un dado equilibrato. Notiamo che le frequenze si stabilizzano attorno a 1/6 solo per un alto numero di lanci.
30 Ciò può indurre a identificare la frequenza relativa di un evento con la sua probabilità, quando il numero degli esperimenti sia sufficientemente grande (tenda a ). Ciò corrisponde alla definizione frequentista della probabilità anch essa poco operativa, talvolta, poichè non è sempre possibile effettuare molti esperimenti Esempio: supponete di voler calcolare la probabilità di morire ingerendo 1 mg di mercurio...
31 Ciò può indurre a identificare la frequenza relativa di un evento con la sua probabilità, quando il numero degli esperimenti sia sufficientemente grande (tenda a ). Ciò corrisponde alla definizione frequentista della probabilità anch essa poco operativa, talvolta, poichè non è sempre possibile effettuare molti esperimenti Esempio: supponete di voler calcolare la probabilità di morire ingerendo 1 mg di mercurio...
32 Ciò può indurre a identificare la frequenza relativa di un evento con la sua probabilità, quando il numero degli esperimenti sia sufficientemente grande (tenda a ). Ciò corrisponde alla definizione frequentista della probabilità anch essa poco operativa, talvolta, poichè non è sempre possibile effettuare molti esperimenti Esempio: supponete di voler calcolare la probabilità di morire ingerendo 1 mg di mercurio...
33 Proprietà derivanti dalla definizione alla Kolmogorov 1. P(A C ) = 1 P(A) per ogni evento A F. 2. P( ) = 0
34 Eventi che hanno probabilità 1 si dicono certi, eventi che hanno probabilità 0 si dicono impossibili. Esempio. L evento {il giorno di Pasqua cade di domenica} è un evento certo. L evento {il giorno di Pasqua cade di mercoledi} è un evento impossibile.
35 3. se A, B F e B è contenuto in A, allora P(A) = P(B) + P(A B) Infatti A è unione disgiunta di B e di A B applico additività. 4. se A, B F e B è contenuto in A, allora P(B) P(A)
36 Esempi: Nel lancio di un dado equilibrato, siano A = {esce un numero pari}, A B = {esce 2 o 4}
37 5. se A, B F qualsiasi, P(A B) = P(A) + P(B) P(A B)
38 Esempio. Nel lancio di un dado equilibrato, consideriamo A = {esce un numero compreso fra 2 e 4} = {2, 3, 4} P(A) = 3 6 B = {esce un numero 3} = {3, 4, 5, 6} P(B) = 4 6 A B = {esce un numero compreso fra 2 e 4 e 3} = {3, 4} P(A B) = 2 6 A B = {esce un numero compreso fra 2 e 4 o 3} = {2, 3, 4, 5, 6} P(A B) = 5 6 =
39 Esempio. Nel lancio di un dado equilibrato, consideriamo A = {esce un numero compreso fra 2 e 4} = {2, 3, 4} P(A) = 3 6 B = {esce un numero 3} = {3, 4, 5, 6} P(B) = 4 6 A B = {esce un numero compreso fra 2 e 4 e 3} = {3, 4} P(A B) = 2 6 A B = {esce un numero compreso fra 2 e 4 o 3} = {2, 3, 4, 5, 6} P(A B) = 5 6 =
40 Esempio. Nel lancio di un dado equilibrato, consideriamo A = {esce un numero compreso fra 2 e 4} = {2, 3, 4} P(A) = 3 6 B = {esce un numero 3} = {3, 4, 5, 6} P(B) = 4 6 A B = {esce un numero compreso fra 2 e 4 e 3} = {3, 4} P(A B) = 2 6 A B = {esce un numero compreso fra 2 e 4 o 3} = {2, 3, 4, 5, 6} P(A B) = 5 6 =
41 6. Principio di inclusione-esclusione: siano A 1,..., A n F, allora P( n i=1 A i) = n i=1 P(A i) i<j P(A i A j ) + i<j<k P(A i A j A k ) + + ( 1) n+1 P(A 1 A n )
42 Distribuzioni NON equiprobabili La distribuzione equiprobabile o uniforme è solo un esempio dei tanti tipi diversi di distribuzione che incontreremo. Esempio. Si consideri il lancio di 2 dadi e si sommino i puntini delle due facce superiori. Lo spazio dei campioni del lancio dei due dadi é Ω = {(1, 1), (1, 2), (2, 1), (1, 3), (3, 1),..., (6, 6)} mentre lo spazio dei campioni della variabile somma delle due facce è: Ω 1 = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}. Notiamo che gli elementi di Ω sono equiprobabili (supponendo che i dadi siano entrambi equilibrati e i dadi non si influenzino a vicenda nei lanci), mentre gli elementi di Ω 1 non lo sono.
43 Lavoriamo su Ω per calcolare le probabilità degli elementi (eventi elementari) di Ω 1 : P({i}) = casi favorevoli casi possibili = numero di coppie con cui ottengo i numero totale di coppie in Ω
44 P(somma facce sia 2) = P(somma facce sia 3) = P(somma facce sia 4) = numero di coppie che danno somma 2 numero totale di coppie in Ω numero di coppie che danno somma 3 numero totale di coppie in Ω numero di coppie che danno somma 4 numero totale di coppie in Ω... = 1 36 = 2 36 = 3 36
45 Quindi l istogramma delle probabilità degli elementi di Ω 1 è
46 Se aumentiamo il numero di dadi che lanciamo e approssimiamo la distribuzione della somma delle facce con l approccio frequentista (simulo lanci e disegno l istogramma delle frequenze relative) otteniamo:
47 Questo esempio ci mostra che esistono vari tipi di aleatorietà ; le diverse aleatorietà si rappresentano attraverso diverse misure di probabilità. Esse sono legate a diverse distribuzioni delle variabili in gioco; per calcolare tali distribuzioni spesso si può far ricorso a spazi dei campioni ausiliari, i cui elementi sono equiprobabili, in modo da ricorrere a un conteggio degli elementi degli insiemi considerati, per calcolare opportuni rapporti di { casi favorevoli}/{ casi possibili } Per calcolare tali rapporti in casi più complessi di quelli visti finora faremo ricorso al calcolo combinatorio.
48 Questo esempio ci mostra che esistono vari tipi di aleatorietà ; le diverse aleatorietà si rappresentano attraverso diverse misure di probabilità. Esse sono legate a diverse distribuzioni delle variabili in gioco; per calcolare tali distribuzioni spesso si può far ricorso a spazi dei campioni ausiliari, i cui elementi sono equiprobabili, in modo da ricorrere a un conteggio degli elementi degli insiemi considerati, per calcolare opportuni rapporti di { casi favorevoli}/{ casi possibili } Per calcolare tali rapporti in casi più complessi di quelli visti finora faremo ricorso al calcolo combinatorio.
49 Questo esempio ci mostra che esistono vari tipi di aleatorietà ; le diverse aleatorietà si rappresentano attraverso diverse misure di probabilità. Esse sono legate a diverse distribuzioni delle variabili in gioco; per calcolare tali distribuzioni spesso si può far ricorso a spazi dei campioni ausiliari, i cui elementi sono equiprobabili, in modo da ricorrere a un conteggio degli elementi degli insiemi considerati, per calcolare opportuni rapporti di { casi favorevoli}/{ casi possibili } Per calcolare tali rapporti in casi più complessi di quelli visti finora faremo ricorso al calcolo combinatorio.
50 Questo esempio ci mostra che esistono vari tipi di aleatorietà ; le diverse aleatorietà si rappresentano attraverso diverse misure di probabilità. Esse sono legate a diverse distribuzioni delle variabili in gioco; per calcolare tali distribuzioni spesso si può far ricorso a spazi dei campioni ausiliari, i cui elementi sono equiprobabili, in modo da ricorrere a un conteggio degli elementi degli insiemi considerati, per calcolare opportuni rapporti di { casi favorevoli}/{ casi possibili } Per calcolare tali rapporti in casi più complessi di quelli visti finora faremo ricorso al calcolo combinatorio.
51 Permutazioni Disposizioni Combinazioni Permutazioni Assegnati n oggetti distinti si dice che essi sono ordinati in un allineamento se sono collocati in posizioni numerate da 1 a n. Esempio. T,G,C,A G,C,A,T A,C,T,G... sono allineamenti delle 4 basi che compongono i nucleotidi del DNA. Domanda: quante sequenze ordinate diverse posso formare con le 4 basi A,C,G,T?
52 Permutazioni Disposizioni Combinazioni Posizioni: La posizione 1 la posso riempire in 4 modi diversi; per ogni scelta sulla prima posizione posso riempire la posizione 2 in 3 modi diversi; per ogni scelta sulle prime due posizioni, posso riempire la posizione 3 in 2 modi diversi; per ogni scelta sulle prime tre posizioni, posso riempire la posizione 4 in 1 solo modo. Il numero di sequenze cercato è , ossia il prodotto dei primi 4 interi.
53 Permutazioni Disposizioni Combinazioni Posizioni: La posizione 1 la posso riempire in 4 modi diversi; per ogni scelta sulla prima posizione posso riempire la posizione 2 in 3 modi diversi; per ogni scelta sulle prime due posizioni, posso riempire la posizione 3 in 2 modi diversi; per ogni scelta sulle prime tre posizioni, posso riempire la posizione 4 in 1 solo modo. Il numero di sequenze cercato è , ossia il prodotto dei primi 4 interi.
54 Permutazioni Disposizioni Combinazioni Posizioni: La posizione 1 la posso riempire in 4 modi diversi; per ogni scelta sulla prima posizione posso riempire la posizione 2 in 3 modi diversi; per ogni scelta sulle prime due posizioni, posso riempire la posizione 3 in 2 modi diversi; per ogni scelta sulle prime tre posizioni, posso riempire la posizione 4 in 1 solo modo. Il numero di sequenze cercato è , ossia il prodotto dei primi 4 interi.
55 Permutazioni Disposizioni Combinazioni Posizioni: La posizione 1 la posso riempire in 4 modi diversi; per ogni scelta sulla prima posizione posso riempire la posizione 2 in 3 modi diversi; per ogni scelta sulle prime due posizioni, posso riempire la posizione 3 in 2 modi diversi; per ogni scelta sulle prime tre posizioni, posso riempire la posizione 4 in 1 solo modo. Il numero di sequenze cercato è , ossia il prodotto dei primi 4 interi.
56 Permutazioni Disposizioni Combinazioni Posizioni: La posizione 1 la posso riempire in 4 modi diversi; per ogni scelta sulla prima posizione posso riempire la posizione 2 in 3 modi diversi; per ogni scelta sulle prime due posizioni, posso riempire la posizione 3 in 2 modi diversi; per ogni scelta sulle prime tre posizioni, posso riempire la posizione 4 in 1 solo modo. Il numero di sequenze cercato è , ossia il prodotto dei primi 4 interi.
57 Permutazioni Disposizioni Combinazioni Posizioni: La posizione 1 la posso riempire in 4 modi diversi; per ogni scelta sulla prima posizione posso riempire la posizione 2 in 3 modi diversi; per ogni scelta sulle prime due posizioni, posso riempire la posizione 3 in 2 modi diversi; per ogni scelta sulle prime tre posizioni, posso riempire la posizione 4 in 1 solo modo. Il numero di sequenze cercato è , ossia il prodotto dei primi 4 interi.
58 Permutazioni Disposizioni Combinazioni Supponiamo ora di avere n elementi diversi (ad esempio n lettere diverse, n palline di colori tutti diversi, n bambini da disporre in una fila,...) e ci chiediamo quante sequenze ordinate diverse, P n, degli n elementi possiamo formare? Procedendo come prima troviamo che P n = n (n 1) (n 2) (n 3) 1 = n! e P n si dicono permutazioni di n elementi
59 Permutazioni Disposizioni Combinazioni Disposizioni semplici Definizione. Si dice disposizione semplice di n oggetti di classe k ogni allineamento di k oggetti diversi scelti fra gli n (notazione: D n,k. ATTENZIONE: k < n) Esempio. Oggetti: A,C,G,T (n = 4) Quante triplette (sequenze di k = 3 oggetti) formate da basi tutte diverse fra loro possiamo formare? Cerco D 4,3. Posso elencarle: ATG, GCA, GAC,...
60 Permutazioni Disposizioni Combinazioni Oppure: come prima, considero le posizioni da riempire La posizione 1 la posso riempire in 4 modi diversi; per ogni scelta sulla prima posizione posso riempire la posizione 2 in 3 modi diversi; per ogni scelta sulle prime due posizioni, posso riempire la posizione 3 in 2 modi diversi; Quindi D 4,3 = 4 3 2
61 Permutazioni Disposizioni Combinazioni Oppure: come prima, considero le posizioni da riempire La posizione 1 la posso riempire in 4 modi diversi; per ogni scelta sulla prima posizione posso riempire la posizione 2 in 3 modi diversi; per ogni scelta sulle prime due posizioni, posso riempire la posizione 3 in 2 modi diversi; Quindi D 4,3 = 4 3 2
62 Permutazioni Disposizioni Combinazioni Oppure: come prima, considero le posizioni da riempire La posizione 1 la posso riempire in 4 modi diversi; per ogni scelta sulla prima posizione posso riempire la posizione 2 in 3 modi diversi; per ogni scelta sulle prime due posizioni, posso riempire la posizione 3 in 2 modi diversi; Quindi D 4,3 = 4 3 2
63 Permutazioni Disposizioni Combinazioni Oppure: come prima, considero le posizioni da riempire La posizione 1 la posso riempire in 4 modi diversi; per ogni scelta sulla prima posizione posso riempire la posizione 2 in 3 modi diversi; per ogni scelta sulle prime due posizioni, posso riempire la posizione 3 in 2 modi diversi; Quindi D 4,3 = 4 3 2
64 Permutazioni Disposizioni Combinazioni Oppure: come prima, considero le posizioni da riempire La posizione 1 la posso riempire in 4 modi diversi; per ogni scelta sulla prima posizione posso riempire la posizione 2 in 3 modi diversi; per ogni scelta sulle prime due posizioni, posso riempire la posizione 3 in 2 modi diversi; Quindi D 4,3 = 4 3 2
65 Permutazioni Disposizioni Combinazioni In generale: D n,k = n (n 1) (n 2) (n k + 1) = n (n 1) (n k + 1) (n k) (n k 1) 1 (n k) (n k 1) 1 = n! (n k)!
66 Permutazioni Disposizioni Combinazioni Disposizioni con ripetizione Definizione. Si dice disposizione con ripetizione di n oggetti di classe k ogni allineamento di k oggetti scelti fra gli n, dove gli oggetti possono essere anche ripetuti più volte (notazione: Dn,k R. ATTENZIONE: qui può essere k < n, k = n, k > n) Esempio. Oggetti: A,C,G,T (n = 4) Quante triplette (sequenze di k = 3 oggetti) possiamo formare, ripetendo anche le basi? (Esempi: TTG, ACT,CTC,...) Dunque D R 4,3 = 43
67 Permutazioni Disposizioni Combinazioni In generale: Dunque D R n,k = nk Esercizio: in quanti modi diversi posso riempire una colonna di una schedina del totocalcio?
68 Permutazioni Disposizioni Combinazioni In generale: Dunque D R n,k = nk Esercizio: in quanti modi diversi posso riempire una colonna di una schedina del totocalcio?
69 Permutazioni Disposizioni Combinazioni In generale: Dunque D R n,k = nk Esercizio: in quanti modi diversi posso riempire una colonna di una schedina del totocalcio?
70 Permutazioni Disposizioni Combinazioni Combinazioni Definizione. Si dice combinazione di k oggetti scelti fra n ogni raggruppamento, comunque ordinato, di k degli n oggetti, diversi fra loro. Quindi due combinazioni differiscono solo per gli elementi che contengono e non per l ordine con cui appaiono: CGT e GTC sono la stessa combinazione! Contiamo le combinazioni di n elementi di classe k (denotiamole con C n,k ):
71 Permutazioni Disposizioni Combinazioni C n,k = D n,k /{n. di sequenze di k oggetti che differiscono solo per l ordine degli elementi} = D n,k = = P k n(n 1)(n 2)... (n k + 1) k! ( ) n! n k!(n k)! =: k ( n ) k è detto coefficiente binomiale
72 Regola della Probabilità totale Probabilità condizionata Definizione 1. Siano A 1, A 2 due eventi in F con P(A 1 ) > 0. Si dice probabilità condizionata di A 2 dato che si è realizzato A 1 la quantità P(A 2 A 1 ) = P(A 1 A 2 ). P(A 1 ) Esempio. Supponiamo di lanciare un dado due volte in sequenza. Sia A 2 = {la somma dei due lanci dà 2} Se i lanci non si influenzano, lanciare due volte un dado o una volta due dadi, e poi sommarne le facce, è la stessa cosa. Quindi abbiamo già visto che P(A 2 ) = 1 36
73 Regola della Probabilità totale Supponiamo ora di sapere che si è verificato A 1 = {il primo lancio dà 1} adesso P(A 2 A 1 ) =
74 Regola della Probabilità totale Eventi indipendenti Definizione. Due eventi A 1, A 2 in F sono indipendenti se P(A 2 A 1 ) = P(A 2 ) o, equivalentemente, se P(A 1 A 2 ) = P(A 1 )P(A 2 ). Dunque la probabilità dell intersezione di due eventi indipendenti è il prodotto delle probabilità dei singoli eventi.
75 Regola della Probabilità totale Esempio. Nell esempio precedente di due lanci di un dado, consideriamo A 1 = {il primo lancio dà 1} A 2 = {il secondo lancio dà 3}
76 Regola della Probabilità totale Regola della Probabilità totale Notiamo che dalla definizione di probabilità condizionata abbiamo che per ogni coppia di eventi A e B P(A B) = P(A B)P(B)
77 Regola della Probabilità totale Supponiamo ora che gli eventi B 1, B 2,..., B k formino una partizione di Ω ossia B i B j = per ogni i j k i=1 B i = Ω Allora A = (A B 1 ) (A B 2 ) (A B k ) e le unioni sono disgiunte
78 Regola della Probabilità totale Applicando quindi la additività otteniamo P(A) = P(A B 1 ) + P(A B 2 ) + + P(A B k ) ossia P(A) = P(A B 1 )P(B 1 ) + P(A B 2 )P(B 2 ) + + P(A B k )P(B k ) Questa è detta regola della probabilità totale.
Bioinformatica e Biostatistica /13 Modulo di Biostatistica
 Bioinformatica e Biostatistica - 2012/13 Modulo di Biostatistica Alessandra Micheletti Dipartimento di Matematica, Università degli Studi di Milano via Saldini 50, Milano alessandra.micheletti@unimi.it
Bioinformatica e Biostatistica - 2012/13 Modulo di Biostatistica Alessandra Micheletti Dipartimento di Matematica, Università degli Studi di Milano via Saldini 50, Milano alessandra.micheletti@unimi.it
Statistica Inferenziale
 Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Riepilogo lezione 1 Abbiamo visto: Definizioni di statistica, statistica inferenziale, probabilità (interpretazione
Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Riepilogo lezione 1 Abbiamo visto: Definizioni di statistica, statistica inferenziale, probabilità (interpretazione
Calcolo delle Probabilità
 Calcolo delle Probabilità Il calcolo delle probabilità studia i modelli matematici delle cosiddette situazioni di incertezza. Molte situazioni concrete sono caratterizzate a priori da incertezza su quello
Calcolo delle Probabilità Il calcolo delle probabilità studia i modelli matematici delle cosiddette situazioni di incertezza. Molte situazioni concrete sono caratterizzate a priori da incertezza su quello
PROBABILITA. DEFINIZIONE: Ogni singolo risultato di un esperimento casuale si chiama evento elementare
 PROBABILITA La teoria della probabilità si applica ad esperimenti aleatori o casuali: ossia, esperimenti il cui risultato non è prevedibile a priori. Ad esempio, lancio di un dado, lancio di una moneta,
PROBABILITA La teoria della probabilità si applica ad esperimenti aleatori o casuali: ossia, esperimenti il cui risultato non è prevedibile a priori. Ad esempio, lancio di un dado, lancio di una moneta,
NOZIONI DI CALCOLO DELLE PROBABILITÀ
 NOZIONI DI CALCOLO DELLE PROBABILITÀ ESPERIMENTO CASUALE: un esperimento si dice casuale quando gli esiti (manifestazioni o eventi) non possono essere previsti con certezza. PROVA: le ripetizioni, o occasioni
NOZIONI DI CALCOLO DELLE PROBABILITÀ ESPERIMENTO CASUALE: un esperimento si dice casuale quando gli esiti (manifestazioni o eventi) non possono essere previsti con certezza. PROVA: le ripetizioni, o occasioni
Definizione formale di probabilitá
 Definizione formale di probabilitá 10 marzo 2017 Si introducono la definizione assiomatica di probabilitá e alcune proprietá elementari che ne derivano 1 Eventi e insiemi Poiché un evento é definito come
Definizione formale di probabilitá 10 marzo 2017 Si introducono la definizione assiomatica di probabilitá e alcune proprietá elementari che ne derivano 1 Eventi e insiemi Poiché un evento é definito come
6.2 La probabilità e gli assiomi della probabilità
 6.2 La probabilità e gli assiomi della probabilità L introduzione alla teoria della probabilità può essere vista come un applicazione della teoria degli insiemi. Essa si occupa degli esperimenti il cui
6.2 La probabilità e gli assiomi della probabilità L introduzione alla teoria della probabilità può essere vista come un applicazione della teoria degli insiemi. Essa si occupa degli esperimenti il cui
Introduzione al Calcolo delle Probabilità
 Introduzione al Calcolo delle Probabilità In tutti quei casi in cui le manifestazioni di un fenomeno (EVENTI) non possono essere determinate a priori in modo univoco, e i risultati possono essere oggetto
Introduzione al Calcolo delle Probabilità In tutti quei casi in cui le manifestazioni di un fenomeno (EVENTI) non possono essere determinate a priori in modo univoco, e i risultati possono essere oggetto
ELEMENTI DI PROBABILITA (parte 2) 1 / 27
 ELEMENTI DI PROBABILITA (parte 2) 1 / 27 Combinazioni 2 / 27 Supponiamo di non essere interessati all ordine in cui sono disposti gli oggetti, per cui la parola abc sia indistinguibile dalla parola bca.
ELEMENTI DI PROBABILITA (parte 2) 1 / 27 Combinazioni 2 / 27 Supponiamo di non essere interessati all ordine in cui sono disposti gli oggetti, per cui la parola abc sia indistinguibile dalla parola bca.
Equidistribuzione su un insieme finito
 su un insieme finito È la distribuzione che abbiamo già visto per il lancio del dado. Se {x 1, x 2,..., x n } sono gli n diversi valori che una variabile aleatoria X può assumere e tali valori sono equiprobabili,
su un insieme finito È la distribuzione che abbiamo già visto per il lancio del dado. Se {x 1, x 2,..., x n } sono gli n diversi valori che una variabile aleatoria X può assumere e tali valori sono equiprobabili,
Per capire qual è l altezza media degli italiani è stato intervistato un campione di 1523 cittadini. La media campionaria dell altezza risulta essere:
 PROBABILITÀ E STATISTICA Per capire qual è l altezza media degli italiani è stato intervistato un campione di 1523 cittadini. La media campionaria dell altezza risulta essere: x = 172, 3 cm Possiamo affermare
PROBABILITÀ E STATISTICA Per capire qual è l altezza media degli italiani è stato intervistato un campione di 1523 cittadini. La media campionaria dell altezza risulta essere: x = 172, 3 cm Possiamo affermare
1 Ingredienti base del CDP. 2 Denizioni classica e frequentista. 3 Denizione assiomatica. 4 La σ-algebra F. 5 Esiti equiprobabili
 1 Ingredienti base del CDP 2 Denizioni classica e frequentista 3 Denizione assiomatica 4 La σ-algebra F 5 Esiti equiprobabili 6 Esperimento casuale 7 Probabilità condizionata Ingredienti base del CDP eventi
1 Ingredienti base del CDP 2 Denizioni classica e frequentista 3 Denizione assiomatica 4 La σ-algebra F 5 Esiti equiprobabili 6 Esperimento casuale 7 Probabilità condizionata Ingredienti base del CDP eventi
FRAME 0.3. E possibile partecipare a tre appelli su 5 (esclusi i compitini). Farà fede l iscrizione alle liste elettroniche.
 FRAME 0.1. S.M. Ross, Calcolo delle Probabilità, Apogeo 2004. C. Mariconda, A. Tonolo, Matematica Discreta, a.a. 2005-2006, Libreria Progetto, 2005 (costo 6 euro. Compitini FRAME 0.2. 13 maggio, ore 9.30
FRAME 0.1. S.M. Ross, Calcolo delle Probabilità, Apogeo 2004. C. Mariconda, A. Tonolo, Matematica Discreta, a.a. 2005-2006, Libreria Progetto, 2005 (costo 6 euro. Compitini FRAME 0.2. 13 maggio, ore 9.30
Matematica e Statistica per Scienze Ambientali
 per Scienze Ambientali Insiemi e Combinatoria - Appunti 1 1 Dipartimento di Matematica Sapienza, Università di Roma Roma, 23 - Ottobre 2012 Il concetto di insieme Non tratterò la teoria assiomatica degli
per Scienze Ambientali Insiemi e Combinatoria - Appunti 1 1 Dipartimento di Matematica Sapienza, Università di Roma Roma, 23 - Ottobre 2012 Il concetto di insieme Non tratterò la teoria assiomatica degli
ES.2.2. Consideriamo un esperimento statistico definito da un insieme Ω di risultati possibili. Una partizione finita di Ω è una sequenza di K eventi
 ES22 1 Variabili aleatorie discrete Consideriamo un esperimento statistico definito da un insieme Ω di risultati possibili Una partizione finita di Ω è una sequenza di K eventi A 1, A 2 A k A K necessari
ES22 1 Variabili aleatorie discrete Consideriamo un esperimento statistico definito da un insieme Ω di risultati possibili Una partizione finita di Ω è una sequenza di K eventi A 1, A 2 A k A K necessari
Statistica e analisi dei dati Data: 29 Febbraio Lezione 3
 Statistica e analisi dei dati Data: 29 Febbraio 2016 Lezione 3 Docente: Prof. Giuseppe Boccignone Scriba: Sara Fasano 1 Definizione formale di Probabilitá Sia dato lo spazio probabilizzabile (S, F). Definizione
Statistica e analisi dei dati Data: 29 Febbraio 2016 Lezione 3 Docente: Prof. Giuseppe Boccignone Scriba: Sara Fasano 1 Definizione formale di Probabilitá Sia dato lo spazio probabilizzabile (S, F). Definizione
Calcolo delle Probabilità
 Calcolo delle Probabilità Il calcolo delle probabilità studia i modelli matematici delle cosidette situazioni di incertezza. Molte situazioni concrete sono caratterizzate a priori da incertezza su quello
Calcolo delle Probabilità Il calcolo delle probabilità studia i modelli matematici delle cosidette situazioni di incertezza. Molte situazioni concrete sono caratterizzate a priori da incertezza su quello
Lezione 1. 1 Probabilità e statistica. 2 Definizioni di probabilità. Statistica e analisi dei dati Data: 22 Febbraio 2016
 Statistica e analisi dei dati Data: 22 Febbraio 2016 Lezione 1 Docente: Prof. Giuseppe Boccignone Scriba: Nicolò Pisaroni 1 Probabilità e statistica Probabilità: Un modello probabilistico é una descrizione
Statistica e analisi dei dati Data: 22 Febbraio 2016 Lezione 1 Docente: Prof. Giuseppe Boccignone Scriba: Nicolò Pisaroni 1 Probabilità e statistica Probabilità: Un modello probabilistico é una descrizione
Calcolo combinatorio
 Calcolo combinatorio Fattoriale: n! = n( n 1)( n 2)...1 1 1 n n = 0 Fattoriale discendente: n( n 1)...( n k + 1) n! (n) k = = ( n k)! 1 1 k n k = 0 Coefficiente binomiale (k n) : n (n) = k n! = k k! k!(
Calcolo combinatorio Fattoriale: n! = n( n 1)( n 2)...1 1 1 n n = 0 Fattoriale discendente: n( n 1)...( n k + 1) n! (n) k = = ( n k)! 1 1 k n k = 0 Coefficiente binomiale (k n) : n (n) = k n! = k k! k!(
Test di preparazione all esame. Attenzione a non confonedere il coefficiente. n(n 1) (n m + 1) m(m 1) 2 1
 Test di preparazione all esame. Attenzione a non confonedere il coefficiente binomiale ( ) n m con la frazione n m. I coefficiente binomiale si può calcolare come ( ) n m = n(n 1) (n m + 1). m(m 1) 2 1
Test di preparazione all esame. Attenzione a non confonedere il coefficiente binomiale ( ) n m con la frazione n m. I coefficiente binomiale si può calcolare come ( ) n m = n(n 1) (n m + 1). m(m 1) 2 1
Note introduttive alla probabilitá e alla statistica
 Note introduttive alla probabilitá e alla statistica 1 marzo 2017 Presentiamo sinteticamente alcuni concetti introduttivi alla probabilitá e statistica 1 Probabilità e statistica Probabilità: Un modello
Note introduttive alla probabilitá e alla statistica 1 marzo 2017 Presentiamo sinteticamente alcuni concetti introduttivi alla probabilitá e statistica 1 Probabilità e statistica Probabilità: Un modello
Probabilità. Spazi di probabilità
 Probabilità Paolo Montanari Appunti di Matematica Probabilità 1 Spazi di probabilità Un esperimento si dice casuale quando esso può essere ripetuto quante volte si vuole, ed il risultato di ogni esecuzione
Probabilità Paolo Montanari Appunti di Matematica Probabilità 1 Spazi di probabilità Un esperimento si dice casuale quando esso può essere ripetuto quante volte si vuole, ed il risultato di ogni esecuzione
INCERTEZZA e PROBABILITA
 Incertezza e Probabilità INCERTEZZA e PROBABILITA Esempi: Qual è la probabilità che la pallina si posi su un numero dispari? Qual è la probabilità che uno studente di Monza passi l esame di Statistica
Incertezza e Probabilità INCERTEZZA e PROBABILITA Esempi: Qual è la probabilità che la pallina si posi su un numero dispari? Qual è la probabilità che uno studente di Monza passi l esame di Statistica
Probabilità. Qual è la probabilità di ottenere il numero 5?
 Lancio un dado Probabilità Qual è la probabilità di ottenere il numero 5? Ho una prova ossia un esperimento = lancio dado Ho il risultato di tale prova = faccia contrassegnata dal numero 5 Il risultato
Lancio un dado Probabilità Qual è la probabilità di ottenere il numero 5? Ho una prova ossia un esperimento = lancio dado Ho il risultato di tale prova = faccia contrassegnata dal numero 5 Il risultato
PROBABILITA. Sono esempi di fenomeni la cui realizzazione non è certa a priori e vengono per questo detti eventi aleatori (dal latino alea, dado)
 L esito della prossima estrazione del lotto L esito del lancio di una moneta o di un dado Il sesso di un nascituro, così come il suo peso alla nascita o la sua altezza.. Il tempo di attesa ad uno sportello
L esito della prossima estrazione del lotto L esito del lancio di una moneta o di un dado Il sesso di un nascituro, così come il suo peso alla nascita o la sua altezza.. Il tempo di attesa ad uno sportello
Probabilità. Introduzione. Esperimento casuale (o aleatorio): Può venir riproposto infinite volte.
 Matematica Capitolo 4 Ivan Zivko Introduzione Esperimento casuale (o aleatorio): uò venir riproposto infinite volte. Il risultato (o esito) varia all interno di un certo numero (anche infinito) di casi
Matematica Capitolo 4 Ivan Zivko Introduzione Esperimento casuale (o aleatorio): uò venir riproposto infinite volte. Il risultato (o esito) varia all interno di un certo numero (anche infinito) di casi
MATEMATICA. a.a. 2014/15
 MATEMATICA a.a. 2014/15 5. Introduzione alla probabilità: Definizioni di probabilità. Evento, prova, esperimento. Eventi indipendenti e incompatibili. Probabilità condizionata. Teorema di Bayes CONCETTI
MATEMATICA a.a. 2014/15 5. Introduzione alla probabilità: Definizioni di probabilità. Evento, prova, esperimento. Eventi indipendenti e incompatibili. Probabilità condizionata. Teorema di Bayes CONCETTI
Appunti di Calcolo delle Probabilità per il corso di Modelli Matematici per le Scienze Sociali
 1 Calcolo combinatorio Appunti di Calcolo delle Probabilità per il corso di Modelli Matematici per le Scienze Sociali Si dice disposizione semplice di n oggetti di classe K (con k n) ogni allineamento
1 Calcolo combinatorio Appunti di Calcolo delle Probabilità per il corso di Modelli Matematici per le Scienze Sociali Si dice disposizione semplice di n oggetti di classe K (con k n) ogni allineamento
Probabilita' mediante l'analisi combinatoria D n,k =Disposizioni di n oggetti a k a k (o di classe k)
 Probabilita' mediante l'analisi combinatoria D n,k =Disposizioni di n oggetti a k a k (o di classe k) Nel calcolo del numero di modalita' con cui si presenta un evento e' utile talvolta utilizzare le definizioni
Probabilita' mediante l'analisi combinatoria D n,k =Disposizioni di n oggetti a k a k (o di classe k) Nel calcolo del numero di modalita' con cui si presenta un evento e' utile talvolta utilizzare le definizioni
Calcolo delle Probabilità Soluzioni 1. Spazio campionario ed eventi
 ISTITUZIONI DI STATISTICA A. A. 2007/2008 Marco Minozzo e Annamaria Guolo Laurea in Economia del Commercio Internazionale Laurea in Economia e Amministrazione delle Imprese Università degli Studi di Verona
ISTITUZIONI DI STATISTICA A. A. 2007/2008 Marco Minozzo e Annamaria Guolo Laurea in Economia del Commercio Internazionale Laurea in Economia e Amministrazione delle Imprese Università degli Studi di Verona
Calcolo della probabilità
 Calcolo della probabilità GLI EVENTI Un evento è un fatto che può accadere o non accadere. Se esso avviene con certezza si dice evento certo, mentre se non può mai accadere si dice evento impossibile.
Calcolo della probabilità GLI EVENTI Un evento è un fatto che può accadere o non accadere. Se esso avviene con certezza si dice evento certo, mentre se non può mai accadere si dice evento impossibile.
IL CALCOLO DELLE PROBABILITA
 IL CALCOLO DELLE PROBABILITA INTRODUZIONE Già 3000 anni fa gli Egizi praticavano un antenato del gioco dei dadi, che si svolgeva lanciando una pietra. Il gioco dei dadi era diffuso anche nell antica Roma,
IL CALCOLO DELLE PROBABILITA INTRODUZIONE Già 3000 anni fa gli Egizi praticavano un antenato del gioco dei dadi, che si svolgeva lanciando una pietra. Il gioco dei dadi era diffuso anche nell antica Roma,
Salto in alto oltre le formule
 Corso PON Competenze per lo sviluppo Liceo Scientifico "Bonaventura Rescigno Ing. Ivano Coccorullo Prof.ssa Laura Falcone Teoria della Probabilità Legge empirica del caso: in un grande numero di prove,
Corso PON Competenze per lo sviluppo Liceo Scientifico "Bonaventura Rescigno Ing. Ivano Coccorullo Prof.ssa Laura Falcone Teoria della Probabilità Legge empirica del caso: in un grande numero di prove,
Modelli descrittivi, statistica e simulazione
 Modelli descrittivi, statistica e simulazione Master per Smart Logistics specialist Roberto Cordone (roberto.cordone@unimi.it) Teoria della probabilità Cernusco S.N., mercoledì 8 marzo 2017 1 / 23 Teoria
Modelli descrittivi, statistica e simulazione Master per Smart Logistics specialist Roberto Cordone (roberto.cordone@unimi.it) Teoria della probabilità Cernusco S.N., mercoledì 8 marzo 2017 1 / 23 Teoria
Cosa dobbiamo già conoscere?
 Cosa dobbiamo già conoscere? Come opera la matematica: dagli ai teoremi. Che cosa è una funzione, il suo dominio e il suo codominio. Che cosa significa n j=1 A j dove A j sono insiemi. Che cosa significa
Cosa dobbiamo già conoscere? Come opera la matematica: dagli ai teoremi. Che cosa è una funzione, il suo dominio e il suo codominio. Che cosa significa n j=1 A j dove A j sono insiemi. Che cosa significa
NOZIONI DI CALCOLO DELLE PROBABILITÀ ALCUNE DEFINIZIONI
 NOZIONI DI CALCOLO DELLE PROBABILITÀ ALCUNE DEFINIZIONI ESPERIMENTO CASUALE: un esperimento si dice casuale quando gli esiti (manifestazioni o eventi) non possono essere previsti con certezza. PROVA: le
NOZIONI DI CALCOLO DELLE PROBABILITÀ ALCUNE DEFINIZIONI ESPERIMENTO CASUALE: un esperimento si dice casuale quando gli esiti (manifestazioni o eventi) non possono essere previsti con certezza. PROVA: le
Progetto Lauree Scientifiche Liceo Classico L.Ariosto, Ferrara Dipartimento di Matematica Università di Ferrara 24 Gennaio 2012
 Progetto Lauree Scientifiche Liceo Classico L.Ariosto, Ferrara Dipartimento di Matematica Università di Ferrara 24 Gennaio 2012 Concetti importanti da (ri)vedere funzione vettore matrice cenni di calcolo
Progetto Lauree Scientifiche Liceo Classico L.Ariosto, Ferrara Dipartimento di Matematica Università di Ferrara 24 Gennaio 2012 Concetti importanti da (ri)vedere funzione vettore matrice cenni di calcolo
2. Introduzione alla probabilità
 . Introduzione alla probabilità Carla Seatzu, 8 Marzo 008 Definizioni preliminari: Prova: è un esperimento il cui esito è aleatorio Spazio degli eventi elementari: è l insieme Ω di tutti i possibili esiti
. Introduzione alla probabilità Carla Seatzu, 8 Marzo 008 Definizioni preliminari: Prova: è un esperimento il cui esito è aleatorio Spazio degli eventi elementari: è l insieme Ω di tutti i possibili esiti
Introduzione al calcolo delle probabilità
 Introduzione al calcolo delle probabilità L. Boni Approccio empirico OSSERVAZIONE IPOTESI TEORIA DOMINANTE ESPERIMENTO L esperimento Un esperimento (dal latino ex, da, e perire, tentare, passare attraverso
Introduzione al calcolo delle probabilità L. Boni Approccio empirico OSSERVAZIONE IPOTESI TEORIA DOMINANTE ESPERIMENTO L esperimento Un esperimento (dal latino ex, da, e perire, tentare, passare attraverso
Modelli probabilistici variabili casuali
 Modelli probabilistici variabili casuali Le variabili casuali costituiscono il legame tra il calcolo della probabilità e gli strumenti di statistica descrittiva visti fino ad ora. Idea: pensiamo al ripetersi
Modelli probabilistici variabili casuali Le variabili casuali costituiscono il legame tra il calcolo della probabilità e gli strumenti di statistica descrittiva visti fino ad ora. Idea: pensiamo al ripetersi
Statistica ARGOMENTI. Calcolo combinatorio
 Statistica ARGOMENTI Calcolo combinatorio Probabilità Disposizioni semplici Disposizioni con ripetizione Permutazioni semplici Permutazioni con ripetizioni Combinazioni semplici Assiomi di probabilità
Statistica ARGOMENTI Calcolo combinatorio Probabilità Disposizioni semplici Disposizioni con ripetizione Permutazioni semplici Permutazioni con ripetizioni Combinazioni semplici Assiomi di probabilità
FRAME giugno ore 9.30, 6 luglio ore settembre ore 9.30, 19 settembre ore 14.30
 FRAME 0.1. S.M. Ross, Calcolo delle Probabilità, Apogeo 2004. C. Mariconda, A. Tonolo, Mat D, I parte e II parte, dispense ROSSE, Libreria Progetto, 2005. Dispensina su integrali multipli, copisteria di
FRAME 0.1. S.M. Ross, Calcolo delle Probabilità, Apogeo 2004. C. Mariconda, A. Tonolo, Mat D, I parte e II parte, dispense ROSSE, Libreria Progetto, 2005. Dispensina su integrali multipli, copisteria di
Combinatoria. Lezione del 12/02/2014. Stage di Parma Progetto Olimpiadi
 Combinatoria Lezione del 12/02/2014 Stage di Parma Progetto Olimpiadi Fattoriali e Binomiali Fattoriale: n!=n*(n-1)*(n-2)* 2*1 0!=1 Binomiale (n,k)= n!/(k!(n-k)!) I binomiali formano il triangolo di tartaglia
Combinatoria Lezione del 12/02/2014 Stage di Parma Progetto Olimpiadi Fattoriali e Binomiali Fattoriale: n!=n*(n-1)*(n-2)* 2*1 0!=1 Binomiale (n,k)= n!/(k!(n-k)!) I binomiali formano il triangolo di tartaglia
3.1 La probabilità: eventi e variabili casuali
 Capitolo 3 Elementi di teoria della probabilità Abbiamo già notato come, per la ineliminabile presenza degli errori di misura, quello che otteniamo come risultato della stima del valore di una grandezza
Capitolo 3 Elementi di teoria della probabilità Abbiamo già notato come, per la ineliminabile presenza degli errori di misura, quello che otteniamo come risultato della stima del valore di una grandezza
La PROBABILITA è un numero che si associa ad un evento E ed esprime il grado di aspettativa circa il suo verificarsi.
 La maggior parte dei fenomeni, ai quali assistiamo quotidianamente, può manifestarsi in vari modi, ma è quasi sempre impossibile stabilire a priori quale di essi si presenterà ogni volta. La PROBABILITA
La maggior parte dei fenomeni, ai quali assistiamo quotidianamente, può manifestarsi in vari modi, ma è quasi sempre impossibile stabilire a priori quale di essi si presenterà ogni volta. La PROBABILITA
Probabilità. Fulvio Bisi-Anna Torre
 Probabilità Fulvio Bisi-Anna Torre FRATELLI E SORELLE Per la ricorrenza della festa della mamma, la sig.ra Luisa organizza una cena a casa sua, con le sue amiche che hanno almeno una figlia femmina. La
Probabilità Fulvio Bisi-Anna Torre FRATELLI E SORELLE Per la ricorrenza della festa della mamma, la sig.ra Luisa organizza una cena a casa sua, con le sue amiche che hanno almeno una figlia femmina. La
Matematica con elementi di Informatica
 Probabilità discreta Matematica con elementi di Informatica Tiziano Vargiolu Dipartimento di Matematica vargiolu@math.unipd.it Corso di Laurea Magistrale in Chimica e Tecnologie Farmaceutiche Anno Accademico
Probabilità discreta Matematica con elementi di Informatica Tiziano Vargiolu Dipartimento di Matematica vargiolu@math.unipd.it Corso di Laurea Magistrale in Chimica e Tecnologie Farmaceutiche Anno Accademico
Psicometria II: Laura Picconi.
 Psicometria II: Laura Picconi http://www.psicometria.unich.it/ http://www.psicometria.unich.it/ Sezione avvisi E necessario leggere con attenzioni gli avvisi e le comunicazioni che sono pubblicati sul
Psicometria II: Laura Picconi http://www.psicometria.unich.it/ http://www.psicometria.unich.it/ Sezione avvisi E necessario leggere con attenzioni gli avvisi e le comunicazioni che sono pubblicati sul
Richiami sul calcolo delle probabilità
 robabilità Richiami sul calcolo delle probabilità TEORIA DEI SEGNALI LAUREA IN INGEGNERIA DELL INFORMAZIONE Modello matematico Sommario Assiomi del calcolo delle probabilità robabilità di un evento robabilità
robabilità Richiami sul calcolo delle probabilità TEORIA DEI SEGNALI LAUREA IN INGEGNERIA DELL INFORMAZIONE Modello matematico Sommario Assiomi del calcolo delle probabilità robabilità di un evento robabilità
Introduzione alla probabilità
 Introduzione alla probabilità Osservazione e studio dei fenomeni naturali: a. Caso deterministico: l osservazione fornisce sempre lo stesso risultato. b. Caso stocastico o aleatorio: l osservazione fornisce
Introduzione alla probabilità Osservazione e studio dei fenomeni naturali: a. Caso deterministico: l osservazione fornisce sempre lo stesso risultato. b. Caso stocastico o aleatorio: l osservazione fornisce
Figura 7: Ruota della Fortuna. Quanti sono i casi possibili? G. Sanfilippo - CdP - STAD - Lezione 2 del 12 Aprile pag. 15
 Figura 7: Ruota della Fortuna. Quanti sono i casi possibili? G. Sanfilippo - CdP - STAD - Lezione 2 del 12 Aprile 2012- pag. 15 Casi Possibili B= La lancetta indica il Blu V= La lancetta indica il Verde
Figura 7: Ruota della Fortuna. Quanti sono i casi possibili? G. Sanfilippo - CdP - STAD - Lezione 2 del 12 Aprile 2012- pag. 15 Casi Possibili B= La lancetta indica il Blu V= La lancetta indica il Verde
SOMMARIO 1 Introduzione al calcolo delle probabilità 2. 2 Cenni di calcolo combinatorio 4
 SOMMARIO 1 Introduzione al calcolo delle probabilità 2 1.1 La probabilità 2 1.1.1 Legge empirica del caso: legge dei grandi numeri 2 1.1.2 Proprietà additiva della probabilità 2 1.1.3 Probabilità condizionata
SOMMARIO 1 Introduzione al calcolo delle probabilità 2 1.1 La probabilità 2 1.1.1 Legge empirica del caso: legge dei grandi numeri 2 1.1.2 Proprietà additiva della probabilità 2 1.1.3 Probabilità condizionata
1. Descrivere gli spazi campionari dei seguenti esperimenti casuali: 1. lancio di un dado 2. lancio di due dadi 3.
 Corso di Laurea INTERFACOLTÀ - Esercitazione di Statistica n 6 ESERCIZIO 1: 1. Descrivere gli spazi campionari dei seguenti esperimenti casuali: 1. lancio di un dado 2. lancio di due dadi 3. lancio di
Corso di Laurea INTERFACOLTÀ - Esercitazione di Statistica n 6 ESERCIZIO 1: 1. Descrivere gli spazi campionari dei seguenti esperimenti casuali: 1. lancio di un dado 2. lancio di due dadi 3. lancio di
Combinatoria. Lezione del 04/01/2010. Stage di Terni Progetto Olimpiadi
 Combinatoria Lezione del 04/01/2010 Stage di Terni Progetto Olimpiadi Fattoriali e Binomiali Fattoriale: n!=n*(n-1)*(n-2)* 2*1 0!=1 Binomiale (n,k)= n!/(k!(n-k)!) I binomiali formano il triangolo di tartaglia
Combinatoria Lezione del 04/01/2010 Stage di Terni Progetto Olimpiadi Fattoriali e Binomiali Fattoriale: n!=n*(n-1)*(n-2)* 2*1 0!=1 Binomiale (n,k)= n!/(k!(n-k)!) I binomiali formano il triangolo di tartaglia
Foglio di esercizi 1-7 Marzo 2019 Probabilità e statistica Ingegneria Meccanica Alessandro Ciallella
 Foglio di esercizi 1-7 Marzo 2019 Probabilità e statistica Ingegneria Meccanica Alessandro Ciallella Esercizio 1. Una serratura si apre con un codice decimale di quattro cifre. Trovare i numeri N 1 ed
Foglio di esercizi 1-7 Marzo 2019 Probabilità e statistica Ingegneria Meccanica Alessandro Ciallella Esercizio 1. Una serratura si apre con un codice decimale di quattro cifre. Trovare i numeri N 1 ed
Teoria della probabilità
 Introduzione alla teoria della probabilità Teoria della probabilità Primi sviluppi nel XVII secolo (Pascal( Pascal, Fermat, Bernoulli); Nasce nell ambito dei giochi d azzardo; d La prima formalizzazione
Introduzione alla teoria della probabilità Teoria della probabilità Primi sviluppi nel XVII secolo (Pascal( Pascal, Fermat, Bernoulli); Nasce nell ambito dei giochi d azzardo; d La prima formalizzazione
STATISTICA 1 ESERCITAZIONE 8
 STATISTICA 1 ESERCITAZIONE 8 Dott. Giuseppe Pandolfo 18 Novembre 2013 CALCOLO DELLE PROBABILITA Elementi del calcolo delle probabilità: 1) Esperimento: fenomeno caratterizzato da incertezza 2) Evento:
STATISTICA 1 ESERCITAZIONE 8 Dott. Giuseppe Pandolfo 18 Novembre 2013 CALCOLO DELLE PROBABILITA Elementi del calcolo delle probabilità: 1) Esperimento: fenomeno caratterizzato da incertezza 2) Evento:
Probabilità: l alfabeto Statistica: il minimo indispensabile. Dati: statistica descrittiva Inferenza statistica
 ... trasformazioni logaritmiche e semilogaritmiche leggi di crescita e decrescita funzioni composte, domini limiti elementari crescenza e decrescenza di funzioni convessità e concavità di funzioni massimi
... trasformazioni logaritmiche e semilogaritmiche leggi di crescita e decrescita funzioni composte, domini limiti elementari crescenza e decrescenza di funzioni convessità e concavità di funzioni massimi
UNIVERSITÀ di ROMA TOR VERGATA
 UNIVERSITÀ di ROMA TOR VERGATA Corso di Laurea Magistrale in Scienze della Nutrizione Umana Corso di Statistica Medica, anno 05-6 P.Baldi Lista di esercizi, 8 gennaio 06. Esercizio Si sa che in una schedina
UNIVERSITÀ di ROMA TOR VERGATA Corso di Laurea Magistrale in Scienze della Nutrizione Umana Corso di Statistica Medica, anno 05-6 P.Baldi Lista di esercizi, 8 gennaio 06. Esercizio Si sa che in una schedina
Qualche Esempio di Processo Markoviano
 Qualche Esempio di Processo Markoviano Giugno 2002 O.Caligaris Alcuni problemi con caratteristiche comuni La Rovina del Giocatore Un Giocatore gioca contro il banco Ad ogni puntata può vincere 1 gettone
Qualche Esempio di Processo Markoviano Giugno 2002 O.Caligaris Alcuni problemi con caratteristiche comuni La Rovina del Giocatore Un Giocatore gioca contro il banco Ad ogni puntata può vincere 1 gettone
Statistica Sociale e Criminale (12 CFU) A.A. 2015/2016
 Statistica Sociale e Criminale (12 CFU) A.A. 2015/2016 CdL Sociologia e Criminologia Simone Di Zio Dove siamo MODULO 3. L Inferenza statistica 3.1 Probabilità e variabili casuali 3.2 Le tecniche di campionamento
Statistica Sociale e Criminale (12 CFU) A.A. 2015/2016 CdL Sociologia e Criminologia Simone Di Zio Dove siamo MODULO 3. L Inferenza statistica 3.1 Probabilità e variabili casuali 3.2 Le tecniche di campionamento
Le variabili casuali o aleatorie
 Le variabili casuali o aleatorie Intuitivamente un numero casuale o aleatorio è un numero sul cui valore non siamo certi per carenza di informazioni - ad esempio la durata di un macchinario, il valore
Le variabili casuali o aleatorie Intuitivamente un numero casuale o aleatorio è un numero sul cui valore non siamo certi per carenza di informazioni - ad esempio la durata di un macchinario, il valore
6. PROBABILITÀ. Definizione Due eventi A e B si dicono incompatibili se il verificarsi di uno esclude il verificarsi dell altro,
 6. PROBABILITÀ L introduzione alla teoria della probabilità può essere vista come un applicazione della teoria degli insiemi. Essa si occupa degli esperimenti il cui esito è incerto. Ebbe origine a metà
6. PROBABILITÀ L introduzione alla teoria della probabilità può essere vista come un applicazione della teoria degli insiemi. Essa si occupa degli esperimenti il cui esito è incerto. Ebbe origine a metà
Probabilità. Ing. Ivano Coccorullo
 Ing. Ivano Coccorullo PROBABILITA Teoria della Eventi certi, impossibili e casuali Nella scienza e nella tecnologia è fondamentale il principio secondo il quale ogni volta che si realizza un insieme di
Ing. Ivano Coccorullo PROBABILITA Teoria della Eventi certi, impossibili e casuali Nella scienza e nella tecnologia è fondamentale il principio secondo il quale ogni volta che si realizza un insieme di
Probabilità mediante l'analisi combinatoria D n,k = Disposizioni di n oggetti a k a k (o di classe k)
 Probabilità mediante l'analisi combinatoria D n,k = Disposizioni di n oggetti a k a k (o di classe k) Nel calcolo del numero di modalità con cui si presenta un evento e' utile talvolta utilizzare le definizioni
Probabilità mediante l'analisi combinatoria D n,k = Disposizioni di n oggetti a k a k (o di classe k) Nel calcolo del numero di modalità con cui si presenta un evento e' utile talvolta utilizzare le definizioni
Lezione 2. La probabilità oggettiva : definizione classica e frequentistica e loro problemi
 Lezione 2 La probabilità oggettiva : definizione classica e frequentistica e loro problemi La definizione classica Definizione classica: La probabilità di un evento E è il rapporto tra il numero dei casi
Lezione 2 La probabilità oggettiva : definizione classica e frequentistica e loro problemi La definizione classica Definizione classica: La probabilità di un evento E è il rapporto tra il numero dei casi
Il Corso di Fisica per Scienze Biologiche
 Il Corso di Fisica per Scienze Biologiche Ø Prof. Attilio Santocchia Ø Ufficio presso il Dipartimento di Fisica (Quinto Piano) Tel. 75-585 278 Ø E-mail: attilio.santocchia@pg.infn.it Ø Web: http://www.fisica.unipg.it/~attilio.santocchia/
Il Corso di Fisica per Scienze Biologiche Ø Prof. Attilio Santocchia Ø Ufficio presso il Dipartimento di Fisica (Quinto Piano) Tel. 75-585 278 Ø E-mail: attilio.santocchia@pg.infn.it Ø Web: http://www.fisica.unipg.it/~attilio.santocchia/
Probabilità e Statistica
 Corso PON Competenze per lo sviluppo Liceo Scientifico "Bonaventura Rescigno Ing. Ivano Coccorullo Prof.ssa Angela D Ambrosio Calcolo Combinatorio Calcolo Combinatorio ü Molti dei problemi classici
Corso PON Competenze per lo sviluppo Liceo Scientifico "Bonaventura Rescigno Ing. Ivano Coccorullo Prof.ssa Angela D Ambrosio Calcolo Combinatorio Calcolo Combinatorio ü Molti dei problemi classici
Salto in alto oltre le formule
 Corso PON Competenze per lo sviluppo Liceo Scientifico "Bonaventura Rescigno Ing. Ivano Coccorullo Prof.ssa Elisa Salvati Calcolo Combinatorio Calcolo Combinatorio ü Molti dei problemi classici di calcolo
Corso PON Competenze per lo sviluppo Liceo Scientifico "Bonaventura Rescigno Ing. Ivano Coccorullo Prof.ssa Elisa Salvati Calcolo Combinatorio Calcolo Combinatorio ü Molti dei problemi classici di calcolo
Informazione, Entropia e Probabilità
 Informazione, Entropia e Probabilità Alessandro Lenci Università di Pisa, Dipartimento di Linguistica Via Santa Maria, 36, 56100 Pisa, Italy alessandro.lenci@ilc.cnr.it Linguaggio e comunicazione - LO042
Informazione, Entropia e Probabilità Alessandro Lenci Università di Pisa, Dipartimento di Linguistica Via Santa Maria, 36, 56100 Pisa, Italy alessandro.lenci@ilc.cnr.it Linguaggio e comunicazione - LO042
Appunti di statistica
 Appunti di statistica. Concetti generali La probabilità è una quantificazione del grado di aspettativa nei confronti di un evento. Considereremo la probabilità un concetto elementare. La quantificazione
Appunti di statistica. Concetti generali La probabilità è una quantificazione del grado di aspettativa nei confronti di un evento. Considereremo la probabilità un concetto elementare. La quantificazione
Introduzione al calcolo delle probabilità
 Introduzione al calcolo delle probabilità venti certi, impossibili, aleatori Supponiamo di lanciare un dado e consideriamo i seguenti eventi : ={ esce un numero compreso tra e 6 (estremi inclusi) } 2 ={
Introduzione al calcolo delle probabilità venti certi, impossibili, aleatori Supponiamo di lanciare un dado e consideriamo i seguenti eventi : ={ esce un numero compreso tra e 6 (estremi inclusi) } 2 ={
Sperimentazioni di Fisica I mod. A Statistica - Lezione 3
 Sperimentazioni di Fisica I mod. A Statistica - Lezione 3 A Garfagnini, M Mazzocco, C Sada Dipartimento di Fisica G. Galilei, Università di Padova AA 2014/2015 Elementi di Teoria della Probabilità L ineliminabile
Sperimentazioni di Fisica I mod. A Statistica - Lezione 3 A Garfagnini, M Mazzocco, C Sada Dipartimento di Fisica G. Galilei, Università di Padova AA 2014/2015 Elementi di Teoria della Probabilità L ineliminabile
Esercizi su variabili aleatorie discrete
 Esercizi su variabili aleatorie discrete Esercizio 1. Data la variabile aleatoria discreta X, caratterizzata dalla seguente rappresentazione nello spazio degli stati: 1 0,25 X = { 0 0,50 1 0,25 calcolare
Esercizi su variabili aleatorie discrete Esercizio 1. Data la variabile aleatoria discreta X, caratterizzata dalla seguente rappresentazione nello spazio degli stati: 1 0,25 X = { 0 0,50 1 0,25 calcolare
Tutorato I Probabilità e Statistica a.a. 2015/2016
 Tutorato I Probabilità e Statistica a.a. 2015/2016 Argomenti: probabilità uniforme; probabilità condizionata; formula di Bayes; formula delle probabilità totali; indipendenza. Esercizio 1. Siano A, B,
Tutorato I Probabilità e Statistica a.a. 2015/2016 Argomenti: probabilità uniforme; probabilità condizionata; formula di Bayes; formula delle probabilità totali; indipendenza. Esercizio 1. Siano A, B,
Problema Posto s = n 2 a) calcolare la somma s per n=30 b) determinare il più piccolo intero n tale che s>30000
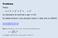 Problema Posto s = 1 2 + 2 2 + 3 2 + + n 2 a) calcolare la somma s per n=30 b) determinare il più piccolo intero n tale che s>30000 Somma quadrati (for next).xlsm Somma quadrati (do loop).xlsm Nota La
Problema Posto s = 1 2 + 2 2 + 3 2 + + n 2 a) calcolare la somma s per n=30 b) determinare il più piccolo intero n tale che s>30000 Somma quadrati (for next).xlsm Somma quadrati (do loop).xlsm Nota La
PROBABILITÁ e CALCOLO COMBINATORIO
 PROBABILITÁ e CALCOLO COMBINATORIO Prof. Enrico Terrone A. S: 2008/09 Probabilità e calcolo combinatorio Abbiamo visto la definizione classica di probabilità: probabilità dell evento = (casi favorevoli)
PROBABILITÁ e CALCOLO COMBINATORIO Prof. Enrico Terrone A. S: 2008/09 Probabilità e calcolo combinatorio Abbiamo visto la definizione classica di probabilità: probabilità dell evento = (casi favorevoli)
Ψ PSICOMETRIA. Corso di laurea triennale (classe 34) STATISTICA INFERENZIALE
 Ψ PSICOMETRIA Corso di laurea triennale (classe 34) STATISTICA INFERENZIALE STATISTICA INFERENZIALE CAMPIONE caratteristiche conosciute POPOLAZIONE caratteristiche sconosciute STATISTICA INFERENZIALE STIMA
Ψ PSICOMETRIA Corso di laurea triennale (classe 34) STATISTICA INFERENZIALE STATISTICA INFERENZIALE CAMPIONE caratteristiche conosciute POPOLAZIONE caratteristiche sconosciute STATISTICA INFERENZIALE STIMA
Statistica. Lezioni : 13 (b) e 14. Probabilità 1
 Corsi di Laurea: a.a. 2018-19 Diritto per le Imprese e le istituzioni Scienze Internazionali dello Sviluppo e della Cooperazione Statistica Probabilità 1 Lezioni : 13 (b) e 14 1 Contenuti 1. Esperimenti
Corsi di Laurea: a.a. 2018-19 Diritto per le Imprese e le istituzioni Scienze Internazionali dello Sviluppo e della Cooperazione Statistica Probabilità 1 Lezioni : 13 (b) e 14 1 Contenuti 1. Esperimenti
Lanciando un dado, il tuo compagno esclama: uscirà 1, 2, 3, 4, 5 o 6 oppure: uscirà il numero 4. uscirà il numero 9
 Lanciando un dado, il tuo compagno esclama: uscirà 1, 2, 3, 4, 5 o 6 oppure: uscirà il numero 4 o ancora: uscirà il numero 9 Possiamo dire che le previsione del tuo compagno sono la prima certa, la seconda
Lanciando un dado, il tuo compagno esclama: uscirà 1, 2, 3, 4, 5 o 6 oppure: uscirà il numero 4 o ancora: uscirà il numero 9 Possiamo dire che le previsione del tuo compagno sono la prima certa, la seconda
Note di Teoria della Probabilità.
 Note di Teoria della Probabilità. In queste brevi note, si richiameranno alcuni risultati di Teoria della Probabilità, riguardanti le conseguenze elementari delle definizioni di probabilità e σ-algebra.
Note di Teoria della Probabilità. In queste brevi note, si richiameranno alcuni risultati di Teoria della Probabilità, riguardanti le conseguenze elementari delle definizioni di probabilità e σ-algebra.
Probabilità Condizionale - 1
 Probabilità Condizionale - 1 Come varia la probabilità al variare della conoscenza, ovvero delle informazioni in possesso di chi la calcola? ESEMPIO - Calcolare la probabilità che in una estrazione della
Probabilità Condizionale - 1 Come varia la probabilità al variare della conoscenza, ovvero delle informazioni in possesso di chi la calcola? ESEMPIO - Calcolare la probabilità che in una estrazione della
«l arte di contare senza contare»
 «l arte di contare senza contare» Numero di oggetti disponibili Numero di oggetti che costituiscono una sola estrazione Regole per costruire le estrazioni: se si possono utilizzare tutti gli oggetti o
«l arte di contare senza contare» Numero di oggetti disponibili Numero di oggetti che costituiscono una sola estrazione Regole per costruire le estrazioni: se si possono utilizzare tutti gli oggetti o
STATISTICA A K (63 ore) Marco Riani
 STATISTICA A K (63 ore) Marco Riani mriani@unipr.it http://www.riani.it Esempio totocalcio Gioco la schedina mettendo a caso i segni 1 X 2 Qual è la prob. di fare 14? Esempio Gioco la schedina mettendo
STATISTICA A K (63 ore) Marco Riani mriani@unipr.it http://www.riani.it Esempio totocalcio Gioco la schedina mettendo a caso i segni 1 X 2 Qual è la prob. di fare 14? Esempio Gioco la schedina mettendo
Variabili aleatorie. Variabili aleatorie e variabili statistiche
 Variabili aleatorie Variabili aleatorie e variabili statistiche Nelle prime lezioni, abbiamo visto il concetto di variabile statistica : Un oggetto o evento del mondo reale veniva associato a una certa
Variabili aleatorie Variabili aleatorie e variabili statistiche Nelle prime lezioni, abbiamo visto il concetto di variabile statistica : Un oggetto o evento del mondo reale veniva associato a una certa
P (A) = P (B) = P (A ^ B) = P (A _ B) = P (A _ A c B)= P ([A _ B] ^ [A c _ B c ]) =
![P (A) = P (B) = P (A ^ B) = P (A _ B) = P (A _ A c B)= P ([A _ B] ^ [A c _ B c ]) = P (A) = P (B) = P (A ^ B) = P (A _ B) = P (A _ A c B)= P ([A _ B] ^ [A c _ B c ]) =](/thumbs/60/44901085.jpg) Esercizio 7 2 Un esperimento consiste nel lanciare una moneta e nell estrarre una pallina da un urna contenente 4 palline numerate da 1 a 4. Consideriamo gli eventi: A = Esce Testa, B = Si estrae la pallina
Esercizio 7 2 Un esperimento consiste nel lanciare una moneta e nell estrarre una pallina da un urna contenente 4 palline numerate da 1 a 4. Consideriamo gli eventi: A = Esce Testa, B = Si estrae la pallina
Elementi di Analisi Combinatoria
 Elementi di Analisi Combinatoria Angelica Malaspina Dipartimento di Matematica, Informatica ed Economia Università degli Studi della Basilicata, Italy angelica.malaspina@unibas.it Lo studio dei vari raggruppamenti
Elementi di Analisi Combinatoria Angelica Malaspina Dipartimento di Matematica, Informatica ed Economia Università degli Studi della Basilicata, Italy angelica.malaspina@unibas.it Lo studio dei vari raggruppamenti
ESERCITAZIONE 5: PROBABILITÀ DISCRETA
 ESERCITAZIONE 5: PROBABILITÀ DISCRETA e-mail: tommei@dm.unipi.it web: www.dm.unipi.it/ tommei Ricevimento: Martedi 16-18 Dipartimento di Matematica, piano terra, studio 126 6 Novembre 2012 Esercizi 1-2
ESERCITAZIONE 5: PROBABILITÀ DISCRETA e-mail: tommei@dm.unipi.it web: www.dm.unipi.it/ tommei Ricevimento: Martedi 16-18 Dipartimento di Matematica, piano terra, studio 126 6 Novembre 2012 Esercizi 1-2
incompatibili compatibili complementari eventi composti probabilità composta
 Un evento si dice casuale, o aleatorio, se il suo verificarsi dipende esclusivamente dal caso. La probabilità matematica p di un evento aleatorio è il rapporto fra il numero dei casi favorevoli f e il
Un evento si dice casuale, o aleatorio, se il suo verificarsi dipende esclusivamente dal caso. La probabilità matematica p di un evento aleatorio è il rapporto fra il numero dei casi favorevoli f e il
È l insieme di tutti i possibili esiti di un esperimento aleatorio; si indica generalmente con il simbolo.
 A Ripasso Terminologia DOMADE Spazio campionario Evento Evento certo Evento elementare Evento impossibile Evento unione Evento intersezione Eventi incompatibili Evento contrario RISPOSTE È l insieme di
A Ripasso Terminologia DOMADE Spazio campionario Evento Evento certo Evento elementare Evento impossibile Evento unione Evento intersezione Eventi incompatibili Evento contrario RISPOSTE È l insieme di
Elementi di Teoria della Probabilità
 Elementi di Teoria della Probabilità Alcune definizioni iniziali: Fenomeno casuale: fenomeno ripetibile (almeno in teoria) infinite volte che può manifestarsi in diverse modalità, imprevedibili singolarmente,
Elementi di Teoria della Probabilità Alcune definizioni iniziali: Fenomeno casuale: fenomeno ripetibile (almeno in teoria) infinite volte che può manifestarsi in diverse modalità, imprevedibili singolarmente,
Statistica. Lezione : 17. Variabili casuali
 Corsi di Laurea: a.a. 2018-19 Diritto per le Imprese e le istituzioni Scienze Internazionali dello Sviluppo e della Cooperazione Statistica Variabili casuali Lezione : 17 Docente: Alessandra Durio 1 Contenuti
Corsi di Laurea: a.a. 2018-19 Diritto per le Imprese e le istituzioni Scienze Internazionali dello Sviluppo e della Cooperazione Statistica Variabili casuali Lezione : 17 Docente: Alessandra Durio 1 Contenuti
Scopo del Corso: Lezione 1. La Probabilità. Organizzazione del Corso e argomenti trattati: Prerequisiti:
 Lezione 1 La Probabilità Scopo del Corso: Introduzione alla probabilità e alle procedure di inferenza statistica Introduzione ad alcune importanti tecniche di analisi multivariata dei dati Organizzazione
Lezione 1 La Probabilità Scopo del Corso: Introduzione alla probabilità e alle procedure di inferenza statistica Introduzione ad alcune importanti tecniche di analisi multivariata dei dati Organizzazione
Probabilità e Statistica Esercitazioni. a.a. 2009/2010. C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica
 Probabilità e Statistica Esercitazioni a.a. 2009/2010 C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica Estrazioni II Ines Campa Probabilità e Statistica - Esercitazioni
Probabilità e Statistica Esercitazioni a.a. 2009/2010 C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica Estrazioni II Ines Campa Probabilità e Statistica - Esercitazioni
Alcune nozioni preliminari di teoria elementare di insiemi e funzioni
 Alcune nozioni preliminari di teoria elementare di insiemi e funzioni Alberto Pinto Corso Propedeutico - METS A.A. 2013/2014 1 Insiemi 1.1 Generalità Diamo la definizione di insieme secondo Georg Cantor,
Alcune nozioni preliminari di teoria elementare di insiemi e funzioni Alberto Pinto Corso Propedeutico - METS A.A. 2013/2014 1 Insiemi 1.1 Generalità Diamo la definizione di insieme secondo Georg Cantor,
