Sistemi lineari a coe costanti in IR 2
|
|
|
- Faustino Bello
- 4 anni fa
- Visualizzazioni
Transcript
1 Capitolo 4 Sistemi lineari a coe costanti in IR 2 cienti I sistemi lineari omogenei a coe cienti costanti Ẋ = AX, A 2 IR N IR N, (4.1) possono essere risolti esplicitamente. Indicando con e A l esponenziale della matrice A, la soluzione del problema di Cauchy Ẋ = AX X(t 0 )=X 0, (4.2) è la funzione X(t, t 0,X 0 )=e A(t t 0) X 0. Anche se conosciamo (almeno in linea di principio) le soluzioni del sistema, è utile rappresentarle graficamente, in modo da avere un quadro sintetico del comportamento complessivo del sistema. D ora in poi, trattando di sistemi autonomi, anziché considerare la soluzione generale X(t, t 0,X 0 ) del problema di Cauchy consideriamo solo la soluzione X(t, 0,X 0 ), indicandola semplicemente come X(t, X 0 ). Tutte le altre si ottengono per traslazione rispetto a t. I sistemi lineari sono la più semplice famiglia di sistemi omogenei, ovvero di sistemi definiti da campi vettoriali le cui componenti sono funzioni positivamente omogenee delle variabili: Ẋ = P (X), P( X) = d P (X), > 0. (4.3) 57
2 58 CAPITOLO 4. SISTEMI LINEARI IN IR 2 La principale proprietà di tali sistemi è l invarianza per omotetie della famiglia delle orbite. Se X(t) è una soluzione, posto Y (t) = X( d 1 t), con 2 IR, >0, abbiamo: Ẏ =( X ) = d 1 Ẋ = d P (X) = d P Y = d P (Y )=P(Y), d quindi anche Y è una soluzione di (4.3). La soluzione Y (t) è ottenuta dalla X(t) mediante un omotetia di coe ciente ed un riscalamento del tempo di un fattore d 1. In altre parole, l orbita di Y (t) si ottiene da quella di X(t) mediante una dilatazione. La possibilità di trasformare una matrice ponendola in forma canonica di Jordan permette di ridurre lo studio della famiglia dei sistemi di erenziali lineari a coe cienti costanti a quello di un numero finito di sistemi lineari. Il passo principale consiste nell e ettuare un cambio di variabili lineare, come in (3.10), che trasforma il sistema di erenziale in un sistema dalla stuttura ablocchi. In questo paragrafo presentiamo la classificazione dei sistemi in dimensione 2. Inizialmente assumiamo che A sia non-degenere, ovvero che det A 6= 0, quindi che (3.9) abbia un unico punto critico. Indichiamo con 1, 2 idue autovalori di A. Sono entrambi diversi da 0, perché 1 2 =deta 6= < 1 < 2 oppure 2 < 1 < 0 Il sistema ridotto alla forma canonica ha la forma ẋ = 1 x ẏ = 2 y, In questo caso, la famiglia delle soluzioni del sistema è x(t, x0, )=e 1t x 0 y(t, x 0, )=e 2t. (4.4) Indicando con x(t) ey(t) le funzioni x(t, x 0, )ey(t, x 0, ), per x 0 6=0e 6= 0 possiamo scrivere x(t) x 0 = e 1t, y(t) = e 2t.
3 < 1 < 2 OPPURE 2 < 1 < 0 59 Gli esponenziali sono positivi, per cui i rapporti a sinistra dei segni = sono a loro volta positivi, quindi possiamo considerare qualsiasi loro potenza ad esponente reale, in particolare x(t) 2 y(t) 1 = e 1 2t =. Da qui abbiamo x 0 x(t) 2 y(t) 1 = x Questa relazione mostra che il rapporto x(t) 2 è costante rispetto a t, così y(t) 1 come ogni funzione di tale rapporto. Questo è vero in particolare per la funzione I a (x, y) = arg( x 2, y 1 ), definita anche sugli assi, ma non nell origine. Ogni asse contiene tre orbite distinte, una delle quali è il punto di equilibrio. Le altre si ricavano dalle relazioni in (4.4) ponendo x 0 =0o = 0. La funzione I a (x, y) è l integrale primo usualmente associato a questa classe di sistemi lineari. I a (x, y) non ha un estensione continua all origine. Infatti, se tale estensione esistesse, per continuità dovrebbe assumere in O lo stesso valore che ha sulle soluzioni che tendono ad O, pert! 1(autovalori positivi) o per per t! +1 (autovalori negativi). Poiché ogni soluzione tende ad O per t! 1oper per t! +1, I a (x, y) sarebbe costante, contraddizione. Nel caso degli autovalori positivi, tutte le orbite tranne quelle contenute nell asse y sono tangenti all asse x, perché l esponenziale e 2t è u n i n fi n i t e - simo di ordine superiore rispetto a e 1t,pert! 1. Osservazione analoga vale per autovalori di segno negativo. L origine viene detta punto critico di tipo nodo. Nodo stabile, sele soluzioni tendono asintoticamente ad O per t! +1 (autovalori negativi), nodo instabile, se le soluzioni tendono asintoticamente ad O per t! 1 (autovalori positivi). I semiassi sono separatrici, in quanto separano il piano in settori aperti, i quadranti, in cui le orbite hanno comportamenti analoghi. Nel primo quadrante le componenti x(t) ey(t) di ogni soluzione sono positive e convergono ad O tangenzialmente all asse x, nel secondo abbiamo x(t) < 0, y(t) > 0 e e convergenza ad O tangenzialmente all asse x, e similmente negli altri settori/quadranti.
4 60 CAPITOLO 4. SISTEMI LINEARI IN IR 2 Figura 4.1: alcune soluzioni di ẋ = x, ẏ = 2y = 2 = 6= 0, matrice diagonalizzabile Il sistema in forma canonica ha la forma ẋ = x ẏ = y, La famiglia delle soluzioni del sistema è x(t, x0, )=e t x 0 y(t, x 0, )=e t Le orbite sono semirette aperte con origine in O. Se gli autovalori sono positivi le soluzioni divergono, se sono negativi tendono all origine, come in figura (4.2). L origine viene detta nodo stellato. Stabile, se le soluzioni tendono asintoticamente ad O per t! +1, instabile, se le soluzioni tendono asintoticamente ad O per t! 1. La funzione I(x, y) = arg(x, y)
5 = 2 = 6= 0, MATRICE NON DIAGONALIZZABILE 61 definita nel piano privato dell origine, è un integrale primo del sistema. Anche questo integrale non ha un estensione continua ad O. Questo tipo di sistema non ha separatrici. Figura 4.2: alcune soluzioni di ẋ = x, ẏ = y = 2 = 6= 0, matrice non diagonalizzabile Il sistema ridotto alla forma canonica ha la forma ẋ = x + y ẏ = y, Integrando la seconda equazione otteniamo y(t) = e t. Sostituendo questa espressione nella prima equazione otteniamo un equazione lineare non omogenea, ẋ = x + e t, la cui soluzione è e t (x 0 + t). Quindi la famiglia delle soluzioni del sistema è x(t, x0, )=e t (x 0 + t) y(t, x 0, )=e t. Per ricavare un integrale primo, eliminiamo t dal sistema di cui sopra. Se 6= 0, allora y(t, x 0, ) 6= 0 per ogni t 2 IR, quindi possiamo scrivere e t = y(t), t = 1 y(t) log,
6 62 CAPITOLO 4. SISTEMI LINEARI IN IR 2 il che ci permette di scrivere, a partire dalla prima uguaglianza, x(t) =x 0 e t + te t = x 0 y(t) apple x0 + ty(t) =y(t) + 1 y(t) log. Per y(t) 6= 0 possiamo dividere per y(t), ottenendo x(t) y(t) = x y(t) log = x log y(t) 1 log y0. e portiamo a primo membro solo i termini che dipen- Moltiplichiamo per dono da t, x(t) y(t) Questo dimostra che la funzione log y(t) = x 0 log. I(x, y) = x y log y è costante lungo le soluzioni, ovvero è un integrale primo definito per y 6= 0. ogni funzione di I(x, y) è a sua volta un integrale primo, come, ad esempio, e I(x,y) = e x y y. Questo integrale non è definito per y = 0, e non ha un estensione continua all asse x. Anche questo sistema non ha integrali primi continui non costanti definiti su tutto il piano, perché ogni integrale primo continuo anche in O avrebbe lo stesso valore in ogni punto del piano, poiché tutte le soluzioni tendono ad O per t! +1 opert! 1. Nella figura 4.3 rappresentiamo alcune soluzioni. Se <0, le soluzioni tendono asintoticamente ad O per t! +1. Se > 0, le soluzioni tendono asintoticamente ad O per t! 1. Anche in questo caso l origine viene detta punto critico di tipo nodo. Nodo stabile, se le soluzioni tendono asintoticamente ad O per t! +1, nodo instabile, se le soluzioni tendono asintoticamente ad O per t! 1. Questo sistema ha due sole separatrici, i due semiassi aperti dell asse x.
7 < 0 < 2 63 Figura 4.3: alcune soluzioni di ẋ = x + y, ẏ = y < 0 < 2 La famiglia delle soluzioni del sistema ha la stessa forma che per il nodo, ma il fatto che i due autovalori hanno segni opposti cambia la struttura della famiglia delle orbite. x(t, x0, )=e 1t x 0 y(t, x 0, )=e 2t Da un punto di vista algebrico non c è di erenza tra questo sistema e quello della sezione 4.1, di cui riportiamo un integrale primo, I(x, y) = x 2 y 1 = x 2 y 1. A di erenza che nella sezione 4.1, gli esponenti 1 e 2 sono entrambi positivi. Otteniamo un esempio semplice per 1 = 1, 2 = 1, a cui corrisponde l integrale primo I 21 (x, y) =xy.
8 64 CAPITOLO 4. SISTEMI LINEARI IN IR 2 In questo caso le orbite sono dei rami di iperbole. I semiassi aperti sono separatrici. Le soluzioni con orbita contenuta in un asse tendono all origine per t che va a +1, quelle con orbita contenuta nell altro asse tendono all origine per t che va a 1. Il punto critico viene detto sella. Un tipico ritratto di fase di sistema lineare con una sella è riportato nella figura 4.4. Figura 4.4: alcune soluzioni di ẋ = x, ẏ = 2y 4.5 1,2 = ± i Il sistema ridotto alla forma canonica ha la forma ẋ = y ẏ = x. In coordinate polari, abbiamo ṙ =0 =.
9 4.6. 1,2 = ± I, µ 6= 0 65 Le soluzioni del sistema in forma polare sono r(t, r0, 0 )=r 0 (t, r 0, 0 )= 0 t. Passando a coordinate rettangolari, otteniamo le soluzioni del problema di Cauchy per il sistema originale. x(t, x0, )=x 0 cos( t)+ sen ( t) y(t, x 0, )= x 0 sen ( t)+ cos( t). Essendo ṙ = 0, la funzione I(x, y) =x 2 + y 2 è un integrale primo. Le orbite sono circonferenze centrate in O. Inquesto caso l origine viene detta punto critico di tipo centro. Tutte le orbite tranne il punto critico hanno lo stesso comportamento qualitativo, quindi questo sistema non ha separatrici. Nella figura 4.5 rappresentiamo alcune soluzioni. Se > 0, le curve vengono percorse in senso orario, se <0, le curve vengono percorse in senso antiorario ,2 = ± i, µ 6= 0 Il sistema in forma canonica ha la forma ẋ = x + y ẏ = x + y. In coordinate polari, abbiamo ṙ = r =. In coordinate polari il sistema è disaccoppiato, e possiamo risolvere separatamente le due equazioni: r(t, r0, 0 )=r 0 e t (t, r 0, 0 )= 0 t. Per trovare un integrale primo procediamo come nei casi precedenti: t = 1 r(t) log, t = 0 (t). r 0
10 66 CAPITOLO 4. SISTEMI LINEARI IN IR 2 Figura 4.5: alcune soluzioni di ẋ = y, ẏ = x Imponendo l uguaglianza dei secondi membri e moltiplicando per, abbiamo r(t) log = ( 0 (t)), r 0 da cui, portando a primo membro i termini dipendenti da t ed a secondo membro quelli costanti: log r(t)+ (t) = log r 0 + 0, così mostrando che la funzione J(r, ) = log r + è costante lungo le soluzioni. Le soluzioni del sistema orignale si ottengono mediante il passaggio a coordinate rettangolari: 8 q < x(t, x 0, )= x y2 0 e t cos(arg(x 0, ) t) q : y(t, x 0, )= x y2 0 e t sen (arg(x 0, ) t). L integrale primo assume la forma q I(x, y) = log x 2 + y 2 + arg(x, y).
11 4.7. A 6= 0, DET A = 0 67 Le orbite sono delle spirali logaritmiche. Se <0, le soluzioni tendono asintoticamente a O per t! +1. Se > 0, le soluzioni tendono asintoticamente ad O per t! 1. L origine viene detta punto critico di tipo fuoco. Fuoco stabile, sele soluzioni tendono asintoticamente a O per t! +1, fuoco instabile, sele soluzioni tendono asintoticamente ad O per t! 1. Figura 4.6: alcune soluzioni di ẋ = 4y x, ẏ = 4x y 4.7 A 6= 0, det A =0 Consideriamo una matrice A con determinante nullo. Se A è la matrice zero, tutti i punti del sistema sono punti critici, e tutte le soluzioni sono costanti. Assumiamo che il rango di A sia 1. A ha almeno un elemento non nullo, e le sue righe sono proporzionali. Assumiamo che il sistema possa essere
12 68 CAPITOLO 4. SISTEMI LINEARI IN IR 2 scritto come segue, eventualmente scambiando la ẋ con la ẏ, ẋ = ax + by ẏ = ax + by. Tutti i punti della retta ax + by = 0 sono punti critici. Inoltre, su ogni retta di equazione ax + by = L il campo vettoriale è costante, (L, L). Il sistema ha l integrale primo I(x, y) = x y, i cui insiemi di livello sono rette. Le orbite non costanti sono semirette con origine sulla retta ax + by = 0. Le orbite vengono percorse verso la retta critica se l unico autovalore non nullo è negativo, nel verso opposto se è positivo. Figura 4.7: alcune soluzioni di ẋ = x y, ẏ = 2x 2y
Operazioni elementari sui sistemi di erenziali
 Capitolo 3 Operazioni elementari sui sistemi di erenziali 3.1 Derivate lungo le soluzioni Uno strumento fondamentale nello studio delle proprietà di un sistema differenziale è la derivata di opportune
Capitolo 3 Operazioni elementari sui sistemi di erenziali 3.1 Derivate lungo le soluzioni Uno strumento fondamentale nello studio delle proprietà di un sistema differenziale è la derivata di opportune
FM1 - Equazioni differenziali e meccanica
 Corso di laurea in Matematica - Anno Accademico 2006/2007 FM1 - Equazioni differenziali e meccanica Prima prova d esonero (03-04-2006) CORREZIONE Esercizio 1. Lo spettro Σ(A) della matrice A si trova risolvendo
Corso di laurea in Matematica - Anno Accademico 2006/2007 FM1 - Equazioni differenziali e meccanica Prima prova d esonero (03-04-2006) CORREZIONE Esercizio 1. Lo spettro Σ(A) della matrice A si trova risolvendo
UNIVERSITÀ DEGLI STUDI DI SALERNO Prova scritta di Matematica II 06 Luglio 2011
 UNIVERSITÀ DEGLI STUDI DI SALERNO Prova scritta di Matematica II 6 Luglio Gli studenti che devono sostenere l esame da 9 CFU risolvano i quesiti numero 3-4-5-6-7-8-9 Gli studenti che devono sostenere l
UNIVERSITÀ DEGLI STUDI DI SALERNO Prova scritta di Matematica II 6 Luglio Gli studenti che devono sostenere l esame da 9 CFU risolvano i quesiti numero 3-4-5-6-7-8-9 Gli studenti che devono sostenere l
Sistemi differenziali 2 2: esercizi svolti. 1 Sistemi lineari Stabilità nei sistemi lineari
 Sistemi differenziali : esercizi svolti 1 Sistemi lineari Stabilità nei sistemi lineari 14 1 Sistemi differenziali : esercizi svolti 1 Sistemi lineari Gli esercizi contrassegnati con il simbolo * presentano
Sistemi differenziali : esercizi svolti 1 Sistemi lineari Stabilità nei sistemi lineari 14 1 Sistemi differenziali : esercizi svolti 1 Sistemi lineari Gli esercizi contrassegnati con il simbolo * presentano
Esercizi sulle coniche (prof.ssa C. Carrara)
 Esercizi sulle coniche prof.ssa C. Carrara Alcune parti di un esercizio possono ritrovarsi in un altro esercizio, insieme a parti diverse. È un occasione per affrontarle da un altra angolazione.. Determinare
Esercizi sulle coniche prof.ssa C. Carrara Alcune parti di un esercizio possono ritrovarsi in un altro esercizio, insieme a parti diverse. È un occasione per affrontarle da un altra angolazione.. Determinare
Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u.
 Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u. Definizione Una conica è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro coordinate omogenee (x,
Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u. Definizione Una conica è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro coordinate omogenee (x,
Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u.
 Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u. Definizione Una conica è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro coordinate omogenee (x,
Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u. Definizione Una conica è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro coordinate omogenee (x,
Parte 12b. Riduzione a forma canonica
 Parte 2b. Riduzione a forma canonica A. Savo Appunti del Corso di Geometria 202-3 Indice delle sezioni. Coniche, 2. Esempio di riduzione, 4 3. Teoremi fondamentali, 6 4. Come determinare l equazione canonica,
Parte 2b. Riduzione a forma canonica A. Savo Appunti del Corso di Geometria 202-3 Indice delle sezioni. Coniche, 2. Esempio di riduzione, 4 3. Teoremi fondamentali, 6 4. Come determinare l equazione canonica,
Funzioni di Dulac e fattori integranti
 Capitolo 9 Funzioni di Dulac e fattori integranti Consideriamo un sistema di erenziale di classe C 1 definito in una regione R 2, ẋ = P (x, y) (9.1) ẏ = Q(x, y). Indichiamo con div(p, Q) la divergenza
Capitolo 9 Funzioni di Dulac e fattori integranti Consideriamo un sistema di erenziale di classe C 1 definito in una regione R 2, ẋ = P (x, y) (9.1) ẏ = Q(x, y). Indichiamo con div(p, Q) la divergenza
Esercizi sulle coniche (prof.ssa C. Carrara)
 Esercizi sulle coniche prof.ssa C. Carrara Alcune parti di un esercizio possono ritrovarsi in un altro esercizio, insieme a parti diverse. È un occasione per affrontarle più volte.. Stabilire il tipo di
Esercizi sulle coniche prof.ssa C. Carrara Alcune parti di un esercizio possono ritrovarsi in un altro esercizio, insieme a parti diverse. È un occasione per affrontarle più volte.. Stabilire il tipo di
Traiettorie nello spazio degli stati
 . Traiettorie nello spazio degli stati Per mostrare i tipici andamenti delle traiettorie nello spazio degli stati in funzione della posizione dei poli del sistema si farà riferimento ad un esempio: un
. Traiettorie nello spazio degli stati Per mostrare i tipici andamenti delle traiettorie nello spazio degli stati in funzione della posizione dei poli del sistema si farà riferimento ad un esempio: un
Coniche R. Notari 15 Aprile
 Coniche R. Notari 15 Aprile 2006 1 1. Notazioni. Proposizione 1 Ogni conica si rappresenta tramita un equazione algebrica di secondo grado della forma a 11 x 2 +2a 12 xy + a 22 y 2 + +2a 13 x + 2a 23 y
Coniche R. Notari 15 Aprile 2006 1 1. Notazioni. Proposizione 1 Ogni conica si rappresenta tramita un equazione algebrica di secondo grado della forma a 11 x 2 +2a 12 xy + a 22 y 2 + +2a 13 x + 2a 23 y
SISTEMI DI EQUAZIONI DIFFERENZIALI- ESERCIZI SVOLTI
 SISTEMI DI EQUAZIONI DIFFERENZIALI- ESERCIZI SVOLTI Generalità sui sistemi Sia xt, yt la soluzione del problema di Cauchy Posto vt = e xtyt, calcolare v x = 3x x = y = x y = 0 Sia x = 3x y y = x + y Scrivere
SISTEMI DI EQUAZIONI DIFFERENZIALI- ESERCIZI SVOLTI Generalità sui sistemi Sia xt, yt la soluzione del problema di Cauchy Posto vt = e xtyt, calcolare v x = 3x x = y = x y = 0 Sia x = 3x y y = x + y Scrivere
19 Marzo Equazioni differenziali.
 19 Marzo 2019 Equazioni differenziali. Definizione 1. Si chiama equazione differenziale una relazione che coinvolge una o più derivate di una funzione incognita y(x), la funzione stessa, funzioni di x
19 Marzo 2019 Equazioni differenziali. Definizione 1. Si chiama equazione differenziale una relazione che coinvolge una o più derivate di una funzione incognita y(x), la funzione stessa, funzioni di x
Sistemi di Equazioni Differenziali
 Sistemi di Equazioni Differenziali Nota introduttiva: Lo scopo di queste dispense non è trattare la teoria riguardo ai sistemi di equazioni differenziali, ma solo dare un metodo risolutivo pratico utilizzabile
Sistemi di Equazioni Differenziali Nota introduttiva: Lo scopo di queste dispense non è trattare la teoria riguardo ai sistemi di equazioni differenziali, ma solo dare un metodo risolutivo pratico utilizzabile
H precedente. Procedendo come sopra, si costruisce la matrice del cambiamento di base
 Geometria analitica e algebra lineare, anno accademico 9/1 Commenti ad alcuni esercizi 17 Diagonalizzazione di matrici simmetriche Coniche Commenti ad alcuni degli esercizi proposti 17 Diagonalizzazione
Geometria analitica e algebra lineare, anno accademico 9/1 Commenti ad alcuni esercizi 17 Diagonalizzazione di matrici simmetriche Coniche Commenti ad alcuni degli esercizi proposti 17 Diagonalizzazione
Corso di Laurea in Scienza dei Materiali PROVA SCRITTA DI GEOMETRIA DEL 12/07/2016 SOLUZIONE DEGLI ESERCIZI PROPOSTI
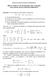 Corso di Laurea in Scienza dei Materiali PROVA SCRITTA DI GEOMETRIA DEL 12/07/2016 SOLUZIONE DEGLI ESERCIZI PROPOSTI Esercizio 1 Si consideri la conica affine d equazione 9x 2 + 6y 2 4xy 6x + 8y = 1 (1)
Corso di Laurea in Scienza dei Materiali PROVA SCRITTA DI GEOMETRIA DEL 12/07/2016 SOLUZIONE DEGLI ESERCIZI PROPOSTI Esercizio 1 Si consideri la conica affine d equazione 9x 2 + 6y 2 4xy 6x + 8y = 1 (1)
CLASSIFICAZIONE DELLE CONICHE AFFINI
 CLASSIFICAZIONE DELLE CONICHE AFFINI Pre-requisiti necessari. Elementi di geometria analitica punti e rette nel piano cartesiano, conoscenza delle coniche in forma canonica). Risoluzione di equazioni e
CLASSIFICAZIONE DELLE CONICHE AFFINI Pre-requisiti necessari. Elementi di geometria analitica punti e rette nel piano cartesiano, conoscenza delle coniche in forma canonica). Risoluzione di equazioni e
Simmetrie e reversibilità
 Capitolo 9 Simmetrie e reversibilità Come nello studio del grafico di una funzione, una simmetria elementare (funzione pari, dispari o periodica) permette di ridurre l analisi ad una opportuna porzione
Capitolo 9 Simmetrie e reversibilità Come nello studio del grafico di una funzione, una simmetria elementare (funzione pari, dispari o periodica) permette di ridurre l analisi ad una opportuna porzione
GEOMETRIA svolgimento di uno scritto del 11 Gennaio 2012
 GEOMETRIA svolgimento di uno scritto del Gennaio ) Trovare una base per lo spazio delle soluzioni del seguente sistema omogeneo: x + y 5z = 3x y + z = x y + 8z =. Il sistema può essere scritto in forma
GEOMETRIA svolgimento di uno scritto del Gennaio ) Trovare una base per lo spazio delle soluzioni del seguente sistema omogeneo: x + y 5z = 3x y + z = x y + 8z =. Il sistema può essere scritto in forma
2.1 Osservazioni sull esercitazione del
 ¾ ½¾º¼ º¾¼½ Queste note (attualmente, e probabilmente per un bel po ) sono altamente provvisorie e (molto probabilmente) non prive di errori. 2.1 Osservazioni sull esercitazione del 5.3.214 2.1.1 Equazione
¾ ½¾º¼ º¾¼½ Queste note (attualmente, e probabilmente per un bel po ) sono altamente provvisorie e (molto probabilmente) non prive di errori. 2.1 Osservazioni sull esercitazione del 5.3.214 2.1.1 Equazione
Coniche in forma generale
 LE CONICHE Fissiamo nel piano un sistema di riferimento cartesiano ortogonaleo, x, y, u. Coniche in forma generale Una conica è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro
LE CONICHE Fissiamo nel piano un sistema di riferimento cartesiano ortogonaleo, x, y, u. Coniche in forma generale Una conica è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro
X = x + 1. X = x + 1
 CONICHE. Esercizi Esercizio. Classificare, ridurre a forma canonica (completando i quadrati), e disegnare le seguenti coniche: γ : x y + x = 0; γ : x + 4x y + = 0; γ 3 : x + y + y + 0 = 0; γ 4 : x + y
CONICHE. Esercizi Esercizio. Classificare, ridurre a forma canonica (completando i quadrati), e disegnare le seguenti coniche: γ : x y + x = 0; γ : x + 4x y + = 0; γ 3 : x + y + y + 0 = 0; γ 4 : x + y
LEZIONE 23. ax 2 + bxy + cy 2 + dx + ey + f
 LEZIONE 23 23.1. Riduzione delle coniche a forma canonica. Fissiamo nel piano un sistema di riferimento Oxy e consideriamo un polinomio di grado 2 in x, y a meno di costanti moltiplicative non nulle, diciamo
LEZIONE 23 23.1. Riduzione delle coniche a forma canonica. Fissiamo nel piano un sistema di riferimento Oxy e consideriamo un polinomio di grado 2 in x, y a meno di costanti moltiplicative non nulle, diciamo
Equazioni del 2. ordine omogenee a coeff. costanti
 Equazioni del. ordine omogenee a coeff. costanti Hanno la forma Ricordiamo che la soluzione dell equazione e Pertanto cerchiamo le soluzioni sempre sotto forma di esponenziali. y"" + ay" + by = 0 Try y
Equazioni del. ordine omogenee a coeff. costanti Hanno la forma Ricordiamo che la soluzione dell equazione e Pertanto cerchiamo le soluzioni sempre sotto forma di esponenziali. y"" + ay" + by = 0 Try y
Geometria BAER Canale I Esercizi 12
 Geometria BAER Canale I Esercizi Alcuni di questi esercizi forse sono un po difficili visto che abbiamo fatto questa parte un po in fretta, ma si può sempre provare. Esercizio. Si scrivano le equazioni
Geometria BAER Canale I Esercizi Alcuni di questi esercizi forse sono un po difficili visto che abbiamo fatto questa parte un po in fretta, ma si può sempre provare. Esercizio. Si scrivano le equazioni
24.1 Coniche e loro riduzione a forma canonica
 Lezione 24 24. Coniche e loro riduzione a forma canonica Fissiamo nel piano un sistema di riferimento Oxy e consideriamo un polinomio di grado 2 in x, y amenodicostantimoltiplicativenonnulle,diciamo ax
Lezione 24 24. Coniche e loro riduzione a forma canonica Fissiamo nel piano un sistema di riferimento Oxy e consideriamo un polinomio di grado 2 in x, y amenodicostantimoltiplicativenonnulle,diciamo ax
Esercizio 1, 6 punti [ ] Sapendo che una grandezza P(t) è caratterizzata dalle seguenti proprietà:
![Esercizio 1, 6 punti [ ] Sapendo che una grandezza P(t) è caratterizzata dalle seguenti proprietà: Esercizio 1, 6 punti [ ] Sapendo che una grandezza P(t) è caratterizzata dalle seguenti proprietà:](/thumbs/103/158017970.jpg) Modellistica Ambientale/Modelli Matematici Ambientali - A.A. 2014/2015 Quinta prova scritta, Appello estivo 23 Settembre 2015 Parte comune a Modellistica Ambientale e Modelli Matematici Ambientali Schema
Modellistica Ambientale/Modelli Matematici Ambientali - A.A. 2014/2015 Quinta prova scritta, Appello estivo 23 Settembre 2015 Parte comune a Modellistica Ambientale e Modelli Matematici Ambientali Schema
Geometria analitica: curve e superfici
 Geometria analitica: curve e superfici geometriche algebriche e matrici e isometrie Riduzione Invarianti Studio di coniche Intersezione con rette e tangenti in forma parametrica 006 Politecnico di Torino
Geometria analitica: curve e superfici geometriche algebriche e matrici e isometrie Riduzione Invarianti Studio di coniche Intersezione con rette e tangenti in forma parametrica 006 Politecnico di Torino
ẋ 1 = 2x 1 + (sen 2 (x 1 ) + 1)x 2 + 2u (1) y = x 1
 Alcuni esercizi risolti su: - calcolo dell equilibrio di un sistema lineare e valutazione delle proprietà di stabilità dell equilibrio attraverso linearizzazione - calcolo del movimento dello stato e dell
Alcuni esercizi risolti su: - calcolo dell equilibrio di un sistema lineare e valutazione delle proprietà di stabilità dell equilibrio attraverso linearizzazione - calcolo del movimento dello stato e dell
2 2 2 A = Il Det(A) = 2 quindi la conica è non degenere, di rango 3.
 Studio delle coniche Ellisse Studiare la conica di equazione 2x 2 + 4xy + y 2 4x 2y + 2 = 0. Per prima cosa dobbiamo classificarla. La matrice associata alla conica è: 2 2 2 A = 2 2 2 Il DetA = 2 quindi
Studio delle coniche Ellisse Studiare la conica di equazione 2x 2 + 4xy + y 2 4x 2y + 2 = 0. Per prima cosa dobbiamo classificarla. La matrice associata alla conica è: 2 2 2 A = 2 2 2 Il DetA = 2 quindi
Algebra lineare Geometria 1 15 luglio 2009
 Algebra lineare Geometria 1 15 luglio 2009 Esercizio 1. Nello spazio vettoriale reale R 3 [x] si considerino l insieme A k = {1 + x, k + (1 k)x 2, 1 + (k 1)x 2 + x 3 }, il vettore v k = k + kx x 3 e la
Algebra lineare Geometria 1 15 luglio 2009 Esercizio 1. Nello spazio vettoriale reale R 3 [x] si considerino l insieme A k = {1 + x, k + (1 k)x 2, 1 + (k 1)x 2 + x 3 }, il vettore v k = k + kx x 3 e la
II Università degli Studi di Roma
 Versione preliminare gennaio TOR VERGATA II Università degli Studi di Roma Dispense di Geometria. Capitolo 3. 7. Coniche in R. Nel Capitolo I abbiamo visto che gli insiemi di punti P lineare di primo grado
Versione preliminare gennaio TOR VERGATA II Università degli Studi di Roma Dispense di Geometria. Capitolo 3. 7. Coniche in R. Nel Capitolo I abbiamo visto che gli insiemi di punti P lineare di primo grado
GEOMETRIA PIANA. 1) sia verificata l uguaglianza di segmenti AC = CB (ossia C è punto medio del segmento AB);
 VETTORI E GEOMETRIA ANALITICA 1 GEOMETRIA PIANA Segmenti e distanza tra punti. Rette in forma cartesiana e parametrica. Posizioni reciproche di due rette, parallelismo e perpendicolarità. Angoli e distanze.
VETTORI E GEOMETRIA ANALITICA 1 GEOMETRIA PIANA Segmenti e distanza tra punti. Rette in forma cartesiana e parametrica. Posizioni reciproche di due rette, parallelismo e perpendicolarità. Angoli e distanze.
Coniche - risposte 1.9
 Coniche - risposte. CAMBI DI COORDINATE ) ) cosπ/) sinπ/). a. Rotazione di π/, la matrice di rotazione è = sinπ/) cosπ/) ) ) ) X = Y X = Quindi le formule sono: cioè: Y = X e inversamente Y = = Y X = b.
Coniche - risposte. CAMBI DI COORDINATE ) ) cosπ/) sinπ/). a. Rotazione di π/, la matrice di rotazione è = sinπ/) cosπ/) ) ) ) X = Y X = Quindi le formule sono: cioè: Y = X e inversamente Y = = Y X = b.
che può anche essere scritta omettendo la variabile indipendente,
 Capitolo 1 Esempi elementari Iniziamo lo studio delle equazioni di erenziali descrivendo l insieme S delle soluzioni di alcune equazioni elementari. Denotiamo con ẋ(t) la derivata di x(t) rispetto alla
Capitolo 1 Esempi elementari Iniziamo lo studio delle equazioni di erenziali descrivendo l insieme S delle soluzioni di alcune equazioni elementari. Denotiamo con ẋ(t) la derivata di x(t) rispetto alla
FM210 - Fisica Matematica I
 FM21 - Fisica Matematica I Seconda Prova Scritta [16-2-212] Soluzioni Problema 1 1. Chiamiamo A la matrice del sistema e cerchiamo anzitutto gli autovalori della matrice: l equazione secolare è (λ + 2β)λ
FM21 - Fisica Matematica I Seconda Prova Scritta [16-2-212] Soluzioni Problema 1 1. Chiamiamo A la matrice del sistema e cerchiamo anzitutto gli autovalori della matrice: l equazione secolare è (λ + 2β)λ
Alcuni esercizi sulle equazioni di erenziali
 Alcuni esercizi sulle equazioni di erenziali Calcolo dell integrale generale Per ciascuna delle seguenti equazioni di erenziali calcolare l insieme di tutte le possibili soluzioni. SUGGERIMENTO: Ricordatevi
Alcuni esercizi sulle equazioni di erenziali Calcolo dell integrale generale Per ciascuna delle seguenti equazioni di erenziali calcolare l insieme di tutte le possibili soluzioni. SUGGERIMENTO: Ricordatevi
CAPITOLO 14. Quadriche. Alcuni esercizi di questo capitolo sono ripetuti in quanto risolti in maniera differente.
 CAPITOLO 4 Quadriche Alcuni esercizi di questo capitolo sono ripetuti in quanto risolti in maniera differente. Esercizio 4.. Stabilire il tipo di quadrica corrispondente alle seguenti equazioni. Se si
CAPITOLO 4 Quadriche Alcuni esercizi di questo capitolo sono ripetuti in quanto risolti in maniera differente. Esercizio 4.. Stabilire il tipo di quadrica corrispondente alle seguenti equazioni. Se si
Un fascio di coniche è determinato da una qualsiasi coppia di sue coniche distinte.
 Piano proiettivo Conica: curva algebrica reale del II ordine. a 11 x 2 1 + 2a 12 x 1 x 2 + a 22 x 2 2 + 2a 13 x 1 x 3 + 2a 23 x 2 x 3 + a 33 x 2 3 = 0 x T A x = 0 Classificazione proiettiva delle coniche:
Piano proiettivo Conica: curva algebrica reale del II ordine. a 11 x 2 1 + 2a 12 x 1 x 2 + a 22 x 2 2 + 2a 13 x 1 x 3 + 2a 23 x 2 x 3 + a 33 x 2 3 = 0 x T A x = 0 Classificazione proiettiva delle coniche:
COMPITO IN CLASSE DI MATEMATICA Funzioni di due variabili Classe 5ª D. Fila A
 Esercizio 1 Determinare il dominio della seguente funzione: COMPITO IN CLASSE DI MATEMATICA Funzioni di due variabili Classe 5ª D Fila A (a) f (, ln( + 4 Esercizio Calcolare le derivate parziali delle
Esercizio 1 Determinare il dominio della seguente funzione: COMPITO IN CLASSE DI MATEMATICA Funzioni di due variabili Classe 5ª D Fila A (a) f (, ln( + 4 Esercizio Calcolare le derivate parziali delle
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Coniche
 Analisi Matematica 1 e Matematica 1 Geometria Analitica: Coniche Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Contenuti Coniche
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Coniche Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Contenuti Coniche
Traccia dello svolgimento di alcuni esercizi del compito del 15/04/08
 Traccia dello svolgimento di alcuni esercizi del comito del //8 Esercizio.. L esercizio richiede di risolvere in generale il seguente sistema lineare @ A = b a. Il sistema ^A = b ammette soluzioni se Rg(
Traccia dello svolgimento di alcuni esercizi del comito del //8 Esercizio.. L esercizio richiede di risolvere in generale il seguente sistema lineare @ A = b a. Il sistema ^A = b ammette soluzioni se Rg(
Corso di Geometria Meccanica, Elettrotecnica Esercizi 11: soluzioni
 Corso di Geometria 0- Meccanica Elettrotecnica Esercizi : soluzioni Esercizio Scrivere la matrice canonica di ciascuna delle seguenti trasformazioni lineari del piano: a) Rotazione di angolo π b) Rotazione
Corso di Geometria 0- Meccanica Elettrotecnica Esercizi : soluzioni Esercizio Scrivere la matrice canonica di ciascuna delle seguenti trasformazioni lineari del piano: a) Rotazione di angolo π b) Rotazione
Analisi Matematica I per Ingegneria Gestionale, a.a Secondo compitino e primo appello, 12 gennaio 2017 Testi 1
 Secondo compitino e primo appello, gennaio 7 Testi Prima parte, gruppo.. Determinare l insieme di definizione della funzione arcsin(e ).. Determinare lo sviluppo di Taylor di ordine 4 (in ) della funzione
Secondo compitino e primo appello, gennaio 7 Testi Prima parte, gruppo.. Determinare l insieme di definizione della funzione arcsin(e ).. Determinare lo sviluppo di Taylor di ordine 4 (in ) della funzione
1 Ampliamento del piano e coordinate omogenee
 1 Ampliamento del piano e coordinate omogenee Vogliamo dare una idea, senza molte pretese, dei concetti che stanno alla base di alcuni calcoli svolti nella classificazione delle coniche. Supponiamo di
1 Ampliamento del piano e coordinate omogenee Vogliamo dare una idea, senza molte pretese, dei concetti che stanno alla base di alcuni calcoli svolti nella classificazione delle coniche. Supponiamo di
3.1 Esempio 1. Queste note (attualmente, e probabilmente per un bel po ) sono altamente provvisorie e (molto probabilmente) non prive di errori.
 ½ º¼ º¾¼½ Queste note (attualmente e probabilmente per un bel po sono altamente provvisorie e (molto probabilmente non prive di errori 31 Esempio 1 Consideriamo il sistema ẋ = 1 3 (x y(1 x y = f 1(xy ẏ
½ º¼ º¾¼½ Queste note (attualmente e probabilmente per un bel po sono altamente provvisorie e (molto probabilmente non prive di errori 31 Esempio 1 Consideriamo il sistema ẋ = 1 3 (x y(1 x y = f 1(xy ẏ
CORSO DI LAUREA IN INGEGNERIA MECCANICA A.A PROVA SCRITTA DI GEOMETRIA DEL Corsi dei Proff. M. BORDONI, A.
 CORSO DI LAUREA IN INGEGNERIA MECCANICA A.A. - PROVA SCRITTA DI GEOMETRIA DEL -- Corsi dei Proff. M. BORDONI, A. FOSCHI Esercizio. E data l applicazione lineare L : R 4 R 3 definita dalla matrice A = 3
CORSO DI LAUREA IN INGEGNERIA MECCANICA A.A. - PROVA SCRITTA DI GEOMETRIA DEL -- Corsi dei Proff. M. BORDONI, A. FOSCHI Esercizio. E data l applicazione lineare L : R 4 R 3 definita dalla matrice A = 3
Esercizi per Geometria II Geometria euclidea e proiettiva
 Esercizi per Geometria II Geometria euclidea e proiettiva Filippo F. Favale 8 aprile 014 Esercizio 1 Si consideri E dotato di un riferimento cartesiano ortonormale di coordinate (x, y) e origine O. Si
Esercizi per Geometria II Geometria euclidea e proiettiva Filippo F. Favale 8 aprile 014 Esercizio 1 Si consideri E dotato di un riferimento cartesiano ortonormale di coordinate (x, y) e origine O. Si
ESERCIZI DEL TUTORATO DI FISICA MATEMATICA. 1. Prima parte Esercizio 1.1 (G. Stefani). Sia X il campo vettoriale lineare associato alla matrice A =.
 ESERCIZI DEL TUTORATO DI FISICA MATEMATICA GIORGIO STEFANI Sommario. I seguenti esercizi sono stati svolti durante il tutorato per il corso di Fisica Matematica dell a.a. 0-03, tenuto dal Prof. A. Lovison.
ESERCIZI DEL TUTORATO DI FISICA MATEMATICA GIORGIO STEFANI Sommario. I seguenti esercizi sono stati svolti durante il tutorato per il corso di Fisica Matematica dell a.a. 0-03, tenuto dal Prof. A. Lovison.
Corso di Geometria Ing. Informatica e Automatica Test 1: soluzioni
 Corso di Geometria Ing. Informatica e Automatica Test : soluzioni k Esercizio Data la matrice A = k dipendente dal parametro k, si consideri il k sistema lineare omogeneo AX =, con X = x x. Determinare
Corso di Geometria Ing. Informatica e Automatica Test : soluzioni k Esercizio Data la matrice A = k dipendente dal parametro k, si consideri il k sistema lineare omogeneo AX =, con X = x x. Determinare
gfurnari CERCHIO ED IPERBOLI
 CERCHIO ED IPERBOLI La funzione complessa cerchio, come viene confermato dall equivalente (al solo fine degli zeri, ma comunque anche come campo di esistenza) funzione ovoidale, esiste per tutti i punti
CERCHIO ED IPERBOLI La funzione complessa cerchio, come viene confermato dall equivalente (al solo fine degli zeri, ma comunque anche come campo di esistenza) funzione ovoidale, esiste per tutti i punti
Equazioni Differenziali Ordinarie
 Equazioni Differenziali Ordinarie Modello di Malthus per la crescita delle popolazioni Ṅ t N t = con coeff di natalità coeff di mortalità Si indica più semplicemente come Primo esempio di equazione differenziale
Equazioni Differenziali Ordinarie Modello di Malthus per la crescita delle popolazioni Ṅ t N t = con coeff di natalità coeff di mortalità Si indica più semplicemente come Primo esempio di equazione differenziale
Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) CONICHE DI
 Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) CONICHE DI R. Docente: Prof. F. Flamini Esercizi Riepilogativi Svolti Esercizio
Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) CONICHE DI R. Docente: Prof. F. Flamini Esercizi Riepilogativi Svolti Esercizio
Teorema 14 Un insieme compatto e invariante M 6= ; è stabile se e solo se ogni sua componente connessa è stabile.
 Capitolo 8 Stabilità In questo capitolo diamo le definizioni fondamentali di stabilità per insiemi compatti. Definizione 20 Un insieme compatto M, M 6= ;, si dice stabile se ogni intorno U M di M contiene
Capitolo 8 Stabilità In questo capitolo diamo le definizioni fondamentali di stabilità per insiemi compatti. Definizione 20 Un insieme compatto M, M 6= ;, si dice stabile se ogni intorno U M di M contiene
Sistemi Dinamici Corso di Laurea in Matematica Prova parziale del ẋ = y y 2 + 2x
 Sistemi Dinamici Corso di Laurea in Matematica Prova parziale del --08 Esercizio. 0 punti Studiare al variare del parametro µ R con µ, la stabilità dell origine per il sistema ẋ = µy + y x 3 x 5 ẏ = x
Sistemi Dinamici Corso di Laurea in Matematica Prova parziale del --08 Esercizio. 0 punti Studiare al variare del parametro µ R con µ, la stabilità dell origine per il sistema ẋ = µy + y x 3 x 5 ẏ = x
Fasci di Coniche. Salvino Giuffrida. 2. Determinare e studiare il fascio Φ delle coniche che passano per A (1, 0) con tangente
 1 Fasci di Coniche Salvino Giuffrida 1. Determinare e studiare il fascio Φ delle coniche che passano per O = (0, 0), con tangente l asse y, e per i punti (1, 0), (1, ). Determinare vertice e asse della
1 Fasci di Coniche Salvino Giuffrida 1. Determinare e studiare il fascio Φ delle coniche che passano per O = (0, 0), con tangente l asse y, e per i punti (1, 0), (1, ). Determinare vertice e asse della
Equazioni differenziali lineari
 Sito Personale di Ettore Limoli Lezioni di Matematica Prof. Ettore Limoli Sommario Lezioni di Matematica... Equazioni differenziali lineari... Generalità... Equazione differenziale lineare omogenea del
Sito Personale di Ettore Limoli Lezioni di Matematica Prof. Ettore Limoli Sommario Lezioni di Matematica... Equazioni differenziali lineari... Generalità... Equazione differenziale lineare omogenea del
Appunti ed esercizi sulle coniche
 1 LA CIRCONFERENZA 1 Appunti ed esercizi sulle coniche Versione del 1 Marzo 011 1 La circonferenza Nel piano R, fissati un punto O = (a, b) e un numero r > 0, la circonferenza (o cerchio) C di centro O
1 LA CIRCONFERENZA 1 Appunti ed esercizi sulle coniche Versione del 1 Marzo 011 1 La circonferenza Nel piano R, fissati un punto O = (a, b) e un numero r > 0, la circonferenza (o cerchio) C di centro O
FM210 - Fisica Matematica I
 FM21 - Fisica Matematica I Prima Prova Scritta [26-1-212] Soluzioni Problema 1 1. Riscriviamo il sistema come e risolviamo la prima equazione: xt) = x e 3t + 2 ẋ = 3x + 2, ẏ = y + z 3, ż = 2x + z, Inserendo
FM21 - Fisica Matematica I Prima Prova Scritta [26-1-212] Soluzioni Problema 1 1. Riscriviamo il sistema come e risolviamo la prima equazione: xt) = x e 3t + 2 ẋ = 3x + 2, ẏ = y + z 3, ż = 2x + z, Inserendo
1 Sistemi Dinamici Esercizio del Parziale del 29/11/2010
 1 Sistemi Dinamici Esercizio del Parziale del 29/11/2010 Si consideri il sistema dinamico con { ẋ = y ẏ = d U(x) U(x) = 2 ( x 2 3 x + 4 ) e x/2. (2) 1. Tracciare qualitativamente le curve di fase del sistema
1 Sistemi Dinamici Esercizio del Parziale del 29/11/2010 Si consideri il sistema dinamico con { ẋ = y ẏ = d U(x) U(x) = 2 ( x 2 3 x + 4 ) e x/2. (2) 1. Tracciare qualitativamente le curve di fase del sistema
Corso di Laurea in Scienza dei Materiali PROVA SCRITTA DI GEOMETRIA DEL 27/09/2016 SOLUZIONE DEGLI ESERCIZI PROPOSTI
 Corso di Laurea in Scienza dei Materiali PROVA SCRITTA DI GEOMETRIA DEL 7/9/6 SOLUZIONE DEGLI ESERCIZI PROPOSTI Esercizio. Si consideri la quadrica affine C d equazione cartesiana xy + yz z + 4x =. ()
Corso di Laurea in Scienza dei Materiali PROVA SCRITTA DI GEOMETRIA DEL 7/9/6 SOLUZIONE DEGLI ESERCIZI PROPOSTI Esercizio. Si consideri la quadrica affine C d equazione cartesiana xy + yz z + 4x =. ()
Lezione 24 - Esercitazioni di Algebra e Geometria - Anno accademico
 CONICHE in A ~ (C) Punti propri (x P,y P ) hanno coordinate omogenee [(x P,y P, )], Punti impropri hanno coordinate omogenee [(l,m, )]. L equazione di una conica in coordinate non omogenee (x,y) C: a,
CONICHE in A ~ (C) Punti propri (x P,y P ) hanno coordinate omogenee [(x P,y P, )], Punti impropri hanno coordinate omogenee [(l,m, )]. L equazione di una conica in coordinate non omogenee (x,y) C: a,
Università di Pisa. Corso di Laurea in Ingegneria Meccanica Geometria e Algebra Lineare
 Università di Pisa Corso di Laurea in Ingegneria Meccanica Geometria e Algebra Lineare Cognome e Nome: Corso di studi: Anno di iscrizione: Numero di matricola: Scritto n. 1 del 16 Esercizio 1. Si studi
Università di Pisa Corso di Laurea in Ingegneria Meccanica Geometria e Algebra Lineare Cognome e Nome: Corso di studi: Anno di iscrizione: Numero di matricola: Scritto n. 1 del 16 Esercizio 1. Si studi
L algebra lineare nello studio delle coniche
 L algebra lineare nello studio delle coniche È possibile utilizzare le tecniche dell algebra lineare per studiare e classificare le coniche. Data l equazione generale di una conica, si considera la sua
L algebra lineare nello studio delle coniche È possibile utilizzare le tecniche dell algebra lineare per studiare e classificare le coniche. Data l equazione generale di una conica, si considera la sua
[ ], classe. ( ) = 0 di grado n. [ ] di terne non nulle di. [ ] = x 1 x LE CONICHE DEL PIANO REALE
![[ ], classe. ( ) = 0 di grado n. [ ] di terne non nulle di. [ ] = x 1 x LE CONICHE DEL PIANO REALE [ ], classe. ( ) = 0 di grado n. [ ] di terne non nulle di. [ ] = x 1 x LE CONICHE DEL PIANO REALE](/thumbs/84/89684391.jpg) LE CONICHE DEL PIANO REALE 1. - IL PIANO PROIETTIVO REALE A) Coordinate omogenee Ad ogni punto P= x,y del piano R associamo una terna ordinata ( x 0, x 1, x ) non nulla in modo che: x = x 1 x 0 y = x x
LE CONICHE DEL PIANO REALE 1. - IL PIANO PROIETTIVO REALE A) Coordinate omogenee Ad ogni punto P= x,y del piano R associamo una terna ordinata ( x 0, x 1, x ) non nulla in modo che: x = x 1 x 0 y = x x
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette
 Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Contenuti Nel Piano
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Contenuti Nel Piano
Università di Pisa. Corso di Laurea in Ingegneria Meccanica Geometria e Algebra Lineare
 Università di Pisa Corso di Laurea in Ingegneria Meccanica Geometria e Algebra Lineare Cognome e Nome: Corso di studi: Anno di iscrizione: Numero di matricola: Scritto n. 1 del 016 Esercizio 1. Si studi
Università di Pisa Corso di Laurea in Ingegneria Meccanica Geometria e Algebra Lineare Cognome e Nome: Corso di studi: Anno di iscrizione: Numero di matricola: Scritto n. 1 del 016 Esercizio 1. Si studi
Le equazioni funzionali sono equazioni in cui l incognita è una funzione.
 EQUAZIONI DIF F ERENZIALII Le equazioni funzionali sono equazioni in cui l incognita è una funzione. ESEMPIO. Trovare una funzione f : R! R tale che f(x) = f (x) per ogni x R. Come subito si vede, ogni
EQUAZIONI DIF F ERENZIALII Le equazioni funzionali sono equazioni in cui l incognita è una funzione. ESEMPIO. Trovare una funzione f : R! R tale che f(x) = f (x) per ogni x R. Come subito si vede, ogni
RIPASSO E APPROFONDIMENTO DI ARGOMENTI DEL TERZO ANNO
 RIPASSO E APPROFONDIMENTO DI ARGOMENTI DEL TERZO ANNO 1 La circonferenza. 2 La parabola. 3 L ellisse. L iperbole. 5 Le coniche. 6 Equazione generale di una conica. 7 Calcolo delle principali caratteristiche
RIPASSO E APPROFONDIMENTO DI ARGOMENTI DEL TERZO ANNO 1 La circonferenza. 2 La parabola. 3 L ellisse. L iperbole. 5 Le coniche. 6 Equazione generale di una conica. 7 Calcolo delle principali caratteristiche
Prova scritta di Geometria 30/01/2017 Ing. Meccanica a.a. 2016/17
 Prova scritta di Geometria 30/0/207 Ing. Meccanica a.a. 206/7 Cognome...................................... Nome...................................... L esame consiste di sei esercizi, e ha la durata di
Prova scritta di Geometria 30/0/207 Ing. Meccanica a.a. 206/7 Cognome...................................... Nome...................................... L esame consiste di sei esercizi, e ha la durata di
Geometria affine e proiettiva
 Geometria affine e proiettiva Laura Facchini 7 aprile 20 Esercizio. Sia E 4 il 4-spazio euclideo numerico dotato del riferimento cartesiano standard di coordinate (x, y, z, w. Siano P (0, 0,,, P (, 2,,,
Geometria affine e proiettiva Laura Facchini 7 aprile 20 Esercizio. Sia E 4 il 4-spazio euclideo numerico dotato del riferimento cartesiano standard di coordinate (x, y, z, w. Siano P (0, 0,,, P (, 2,,,
Soluzione del Compitino di Sistemi Dinamici del 16 novembre 2016
 Soluzione del Compitino di Sistemi Dinamici del 6 novembre 6 Esercizio Sia data la seguente matrice 3 3 a coecienti reali 4 A = 3. / 9/ Si consideri il seguente sistema dinamico continuo lineare: Ẋ = AX
Soluzione del Compitino di Sistemi Dinamici del 6 novembre 6 Esercizio Sia data la seguente matrice 3 3 a coecienti reali 4 A = 3. / 9/ Si consideri il seguente sistema dinamico continuo lineare: Ẋ = AX
Sistemi di erenziali in IR N
 Capitolo 2 Sistemi di erenziali in IR N 2.1 Il problema di Cauchy Consideriamo una regione, ovvero un aperto connesso IR N+1 ed un applicazione F 2 C 0 (, IR N ). Indichiamo con X(t) una funzione di classe
Capitolo 2 Sistemi di erenziali in IR N 2.1 Il problema di Cauchy Consideriamo una regione, ovvero un aperto connesso IR N+1 ed un applicazione F 2 C 0 (, IR N ). Indichiamo con X(t) una funzione di classe
NOME COGNOME MATRICOLA CANALE
 NOME COGNOME MATRICOLA CANALE Fondamenti di Algebra Lineare e Geometria Proff. R. Sanchez - T. Traetta - C. Zanella Ingegneria Gestionale, Meccanica e Meccatronica, dell Innovazione del Prodotto, Meccatronica
NOME COGNOME MATRICOLA CANALE Fondamenti di Algebra Lineare e Geometria Proff. R. Sanchez - T. Traetta - C. Zanella Ingegneria Gestionale, Meccanica e Meccatronica, dell Innovazione del Prodotto, Meccatronica
Esercizi per Geometria II Geometria euclidea e proiettiva
 Esercizi per Geometria II Geometria euclidea e proiettiva Filippo F. Favale 10 aprile 01 Esercizio 1 Sia E 3 lo spazio euclideo tridimensionale dotato di un riferimento cartesiano ortonormale di coordinate
Esercizi per Geometria II Geometria euclidea e proiettiva Filippo F. Favale 10 aprile 01 Esercizio 1 Sia E 3 lo spazio euclideo tridimensionale dotato di un riferimento cartesiano ortonormale di coordinate
0 0 c. d 1. det (D) = d 1 d n ;
 Registro Lezione di Algebra lineare del 23 novembre 216 1 Matrici diagonali 2 Autovettori e autovalori 3 Ricerca degli autovalori, polinomio caratteristico 4 Ricerca degli autovettori, autospazi 5 Matrici
Registro Lezione di Algebra lineare del 23 novembre 216 1 Matrici diagonali 2 Autovettori e autovalori 3 Ricerca degli autovalori, polinomio caratteristico 4 Ricerca degli autovettori, autospazi 5 Matrici
II Università degli Studi di Roma
 Versione preliminare dicembre 200 TOR VERGATA II Università degli Studi di Roma Dispense di Geometria. Capitolo 3. 8. Quadriche in R 3. In questo paragrafo studiamo le quadriche in R 3. Definizione. Una
Versione preliminare dicembre 200 TOR VERGATA II Università degli Studi di Roma Dispense di Geometria. Capitolo 3. 8. Quadriche in R 3. In questo paragrafo studiamo le quadriche in R 3. Definizione. Una
Geometria A. Università degli Studi di Trento Corso di laurea in Matematica A.A. 2017/ Maggio 2018 Prova Intermedia
 Geometria A Università degli Studi di Trento Corso di laurea in Matematica A.A. 7/8 Maggio 8 Prova Intermedia Il tempo per la prova è di ore. Durante la prova non è permesso l uso di appunti e libri. Esercizio
Geometria A Università degli Studi di Trento Corso di laurea in Matematica A.A. 7/8 Maggio 8 Prova Intermedia Il tempo per la prova è di ore. Durante la prova non è permesso l uso di appunti e libri. Esercizio
2x 2 + 4x 2y + 1 = 2(x 2 + 2x + 1 1) 2y + 1 = 2(x + 1) 2 2(y ) = 0.
 CONICHE E QUADRICHE. Esercizi Esercizio. Classificare, ridurre a forma canonica (completando i quadrati), e disegnare le seguenti coniche: γ : x y + x = 0; γ : x + 4x y + = 0; γ : x + y + y + 0 = 0; γ
CONICHE E QUADRICHE. Esercizi Esercizio. Classificare, ridurre a forma canonica (completando i quadrati), e disegnare le seguenti coniche: γ : x y + x = 0; γ : x + 4x y + = 0; γ : x + y + y + 0 = 0; γ
Traiettorie nello spazio degli stati
 Capitolo. INTRODUZIONE. Traiettorie nello spazio degli stati Per mostrare i tipici andamenti delle traiettorie nello spazio degli stati in funzione della posizione dei poli del sistema si farà riferimento
Capitolo. INTRODUZIONE. Traiettorie nello spazio degli stati Per mostrare i tipici andamenti delle traiettorie nello spazio degli stati in funzione della posizione dei poli del sistema si farà riferimento
Matematica e Statistica
 Matematica e Statistica Prova d Esame (0/09/200) Università di Verona - Laurea in Biotecnologie - A.A. 2009/0 Matematica e Statistica Prova d Esame di MATEMATICA (0/09/200) Università di Verona - Laurea
Matematica e Statistica Prova d Esame (0/09/200) Università di Verona - Laurea in Biotecnologie - A.A. 2009/0 Matematica e Statistica Prova d Esame di MATEMATICA (0/09/200) Università di Verona - Laurea
Corso di Laurea in Ingegneria Gestionale - Sede di Fermo Anno Accademico 2009/2010 Matematica 2 Esercizi d esame
 Corso di Laurea in Ingegneria Gestionale - ede di Fermo Anno Accademico 2009/2010 Matematica 2 Esercizi d esame Nome... N. Matricola... Fermo, gg/mm/aaaa 1. tabilire l ordine di ciascuna delle seguenti
Corso di Laurea in Ingegneria Gestionale - ede di Fermo Anno Accademico 2009/2010 Matematica 2 Esercizi d esame Nome... N. Matricola... Fermo, gg/mm/aaaa 1. tabilire l ordine di ciascuna delle seguenti
Equazioni di erenziali Ordinarie
 Equazioni di erenziali Ordinarie Carmelo Pierpaolo Parello Sapienza Università di oma Questa bozza: marzo 01 Contents 1 Concetto e de nizione EDO lineari del primo ordine 3.1 Soluzione delle equazioni
Equazioni di erenziali Ordinarie Carmelo Pierpaolo Parello Sapienza Università di oma Questa bozza: marzo 01 Contents 1 Concetto e de nizione EDO lineari del primo ordine 3.1 Soluzione delle equazioni
Sistemi lineari omogenei di equazioni differenziali
 Sistemi lineari omogenei di equazioni differenziali E. Paolini 5 dicembre 2014 esponenziale di matrici Sia A una matrice quadrata n n. Definiamo la norma (norma operatoriale) di A come segue: dove v =
Sistemi lineari omogenei di equazioni differenziali E. Paolini 5 dicembre 2014 esponenziale di matrici Sia A una matrice quadrata n n. Definiamo la norma (norma operatoriale) di A come segue: dove v =
Geometria e algebra lineare 20/6/2017 Corso di laurea in Ing. Elett. Tel., Ing. Inf. Org. e Informatica Correzione. x 2y = 0
 Geometria e algebra lineare 20/6/2017 Corso di laurea in Ing. Elett. Tel., Ing. Inf. Org. e Informatica Correzione A Esercizio 1A Siano r la retta di equazioni { x + y 2z = 1 e P il punto di coordinate
Geometria e algebra lineare 20/6/2017 Corso di laurea in Ing. Elett. Tel., Ing. Inf. Org. e Informatica Correzione A Esercizio 1A Siano r la retta di equazioni { x + y 2z = 1 e P il punto di coordinate
AUTOVALORI, AUTOVETTORI, AUTOSPAZI
 AUTOVALORI, AUTOVETTORI, AUTOSPAZI. Esercizi Esercizio. Sia f : R 3 R 3 l endomorfismo definito da f(x, y, z) = (x+y, y +z, x+z). Calcolare gli autovalori ed una base per ogni autospazio di f. Dire se
AUTOVALORI, AUTOVETTORI, AUTOSPAZI. Esercizi Esercizio. Sia f : R 3 R 3 l endomorfismo definito da f(x, y, z) = (x+y, y +z, x+z). Calcolare gli autovalori ed una base per ogni autospazio di f. Dire se
Didattica della Matematica per il triennio Geometria sintetica e geometria analitica
 Didattica della Matematica per il triennio Geometria sintetica e geometria analitica anno acc. 2012/2013 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Didattica della Matematica
Didattica della Matematica per il triennio Geometria sintetica e geometria analitica anno acc. 2012/2013 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Didattica della Matematica
Autovalori ed autovettori di un endomorfismo
 Autovalori ed autovettori di un endomorfismo Endomorfismo = applicazione (funzione) lineare da un spazio vettoriale V in sé stesso 1. Data una funzione lineare, scriverne la matrice associata dei coefficienti:
Autovalori ed autovettori di un endomorfismo Endomorfismo = applicazione (funzione) lineare da un spazio vettoriale V in sé stesso 1. Data una funzione lineare, scriverne la matrice associata dei coefficienti:
Università Carlo Cattaneo Ingegneria gestionale Analisi matematica a.a. 2016/2017 EQUAZIONI DIFFERENZIALI 2
 Università Carlo Cattaneo Ingegneria gestionale Analisi matematica a.a. 2016/2017 EQUAZIONI DIFFERENZIALI 2 ESERCIZI CON SOLUZIONE 1. Risolvere il seguente problema di Cauchy: 1 2 1 2 L equazione differenziale
Università Carlo Cattaneo Ingegneria gestionale Analisi matematica a.a. 2016/2017 EQUAZIONI DIFFERENZIALI 2 ESERCIZI CON SOLUZIONE 1. Risolvere il seguente problema di Cauchy: 1 2 1 2 L equazione differenziale
Geometria e Topologia I 22 Giugno 2005 (U1-10, 9:00 11:00) [PROVA PARZIALE]1/8
![Geometria e Topologia I 22 Giugno 2005 (U1-10, 9:00 11:00) [PROVA PARZIALE]1/8 Geometria e Topologia I 22 Giugno 2005 (U1-10, 9:00 11:00) [PROVA PARZIALE]1/8](/thumbs/103/157085746.jpg) Geometria e Topologia I 22 Giugno 2005 (U-0, 9:00 :00) [PROVA PARZIALE]/8 Correzione 0 () In A 3 (R) siano dati i tre punti A =, B = 0, C =. 0 (a) A B e C sono allineati? Dipendenti? (b) Dimostrare che
Geometria e Topologia I 22 Giugno 2005 (U-0, 9:00 :00) [PROVA PARZIALE]/8 Correzione 0 () In A 3 (R) siano dati i tre punti A =, B = 0, C =. 0 (a) A B e C sono allineati? Dipendenti? (b) Dimostrare che
Fissiamo nello spazio un sistema di riferimento cartesiano ortogonale O, x, y, z, u.
 Fissiamo nello spazio un sistema di riferimento cartesiano ortogonale O, x, y, z, u. Definizione Una quadriche è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro coordinate omogenee
Fissiamo nello spazio un sistema di riferimento cartesiano ortogonale O, x, y, z, u. Definizione Una quadriche è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro coordinate omogenee
24 giugno Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a COGNOME... NOME... N. MATRICOLA...
 4 giugno 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore.
4 giugno 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore.
Unità Didattica N 08 I sistemi di primo grado a due incognite 1. U.D. N 08 I sistemi di primo grado a due incognite
 Unità Didattica N 08 I sistemi di primo grado a due incognite 1 U.D. N 08 I sistemi di primo grado a due incognite 01) Coordinate cartesiane 0) I sistemi di primo grado a due incognite 03) Metodo di sostituzione
Unità Didattica N 08 I sistemi di primo grado a due incognite 1 U.D. N 08 I sistemi di primo grado a due incognite 01) Coordinate cartesiane 0) I sistemi di primo grado a due incognite 03) Metodo di sostituzione
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 2 Secondo Appello 7 Settembre 2016
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo Appello 7 Settembre 6 Cognome: Nome: Matricola: Es.: punti Es.: 7 punti Es.3: 7 punti Es.4: 7 punti Totale. Sia f : R 3 R 3 l applicazione
Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo Appello 7 Settembre 6 Cognome: Nome: Matricola: Es.: punti Es.: 7 punti Es.3: 7 punti Es.4: 7 punti Totale. Sia f : R 3 R 3 l applicazione
Geometria analitica del piano pag 32 Adolfo Scimone
 Geometria analitica del piano pag 32 Adolfo Scimone CAMBIAMENTI DI SISTEMA DI RIFERIMENTO Consideriamo il piano cartesiano R 2 con un sistema di riferimento (O,U). Se introduciamo in R 2 un secondo sistema
Geometria analitica del piano pag 32 Adolfo Scimone CAMBIAMENTI DI SISTEMA DI RIFERIMENTO Consideriamo il piano cartesiano R 2 con un sistema di riferimento (O,U). Se introduciamo in R 2 un secondo sistema
TEMI D ESAME DI ANALISI MATEMATICA I
 TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria - CCS Edile ed Edile/Architettura
 Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria - CCS Edile ed Edile/Architettura IV Appello del corso di Geometria Docente F. Flamini, Roma, /9/ NORME SVOLGIMENTO Scrivere negli appositi
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria - CCS Edile ed Edile/Architettura IV Appello del corso di Geometria Docente F. Flamini, Roma, /9/ NORME SVOLGIMENTO Scrivere negli appositi
