LINGUAGGI PER LA RAPPRESENTAZIONE DELLA CONOSCENZA
|
|
|
- Niccoletta Angeli
- 4 anni fa
- Visualizzazioni
Transcript
1 LINGUAGGI PER LA RAPPRESENTAZIONE DELLA CONOSCENZA Linguaggio formale: SINTASSI SEMANTICA + Sistema di inferenza Sintassi: insieme delle espressioni ben formate (linguaggio) Semantica: interpretazione M del linguaggio Logiche Logica proposizionale: proposizioni + connettivi Logica del primo ordine (o Logica dei predicati): termini + predicati + connettivi + quantificatori Logica epistemica: operatori l agente sa che..., l agente crede che... Logica temporale: operatori: sarà sempre vero che..., in qualche momento futuro sarà vero che..., A è vero fino a che è vero B 1
2 LOGICA Si occupa della formalizzazione del ragionamento FORMA DI UN RAGIONAMENTO: 1. SE c è il sole, ALLORA fa caldo 2. c è il sole QUINDI: fa caldo 1. SE il compito è sufficiente, ALLORA sei esonerato dallo scritto 2. il compito è sufficiente QUINDI: sei esonerato dallo scritto Forma comune: 1. SE A, ALLORA B 2. A QUINDI: B 1. A B 2. A B LOGICA SIMBOLICA : formalizzazione mediante simboli LOGICA MATEMATICA : studio della forma del ragionamento matematico Studio della forma: Astrazione dal contenuto ASTRARRE SIGNIFICA SEMPLIFICARE: sbarazzandosi dei dettagli, si guardano oggetti diversi da uno stesso punto di vista, e gli si può dare un trattamento uniforme 2
3 Logica e Informatica 1. Ruolo esterno e teorico: logica come meta-informatica Esempi: nozione di calcolabilità risultati di indecidibilità classificazione dei problemi secondo la loro complessità 2. Ruolo interno e pratico: Esempi: Fondamento di paradigmi di programmazione programmazione logica (basata su metodi di dimostrazione automatica): il programmatore specifica CHE COSA si deve calcolare, senza occuparsi di COME programmazione funzionale (basata sul lambda-calcolo) Semantica di linguaggi di programmazione Linguaggi di specifica formale Specifica algebrica di tipi astratti di dati Verifica di proprietà di programmi (correttezza, terminazione,...), verifica dell affidabilità di sistemi hardware e software Linguaggio di rappresentazione e ragionamento in IA 3
4 Logica classica (proposizionale e dei predicati) Rappresentazione di conoscenza dichiarativa e studio delle forme di ragionamento su questo tipo di conoscenza 1. SE c è il sole, ALLORA fa caldo 2. c è il sole QUINDI: fa caldo 1. SE il compito è sufficiente, ALLORA sei esonerato dallo scritto 2. il compito è sufficiente QUINDI: sei esonerato dallo scritto Forma comune: 1. SE A, ALLORA B 2. A QUINDI: B A B B A 1. Tutti i triangoli sono poligoni 2. ABC è un triangolo QUINDI: ABC è un poligono 1. Tutti i pinguini sono mammiferi 2. Alberto è un pinguino QUINDI: Alberto è un mammifero Forma comune: 1. Tutti gli A sono B 2. l oggetto c è un A QUINDI: c è un B x(a(x) B(x)) B(c) A(c) 4
5 Quando un ragionamento è corretto? 1. Tutti i ladri sono ricchi 2. B è ricco QUINDI: B è un ladro 1. SE i controllori di volo scioperano, ALLORA prenderò il treno 2. O scioperano i controllori, oppure scioperano i piloti QUINDI: prenderò il treno 1. SE i controllori di volo scioperano, ALLORA prenderò il treno 2. SE i piloti scioperano, ALLORA prenderò il treno 3. O scioperano i controllori, oppure scioperano i piloti QUINDI: prenderò il treno 1. SE ABC è un triangolo equilatero, allora è un poligono regolare 2. SE ABC è un triangolo isoscele, allora è un poligono regolare 3. ABC è un triangolo equilatero oppure isoscele QUINDI: ABC è un poligono regolare 1. Non esiste nessun numero naturale minore di zero QUINDI: tutti i numeri naturali minori di zero sono dispari 5
6 Logica Classica Elementi di base: proposizioni (o enunciati), che possono essere VERE o FALSE Logica proposizionale: ogni enunciato è un atomo non ulteriormente analizzabile Caino è fratello di Abele è rappresentato da un atomo p A ogni paziente piace qualche dottore è rappresentato da un atomo q Gli enunciati semplici (atomi o variabili proposizionali) possono essere composti per formare enunciati complessi (formule proposizionali), mediante operatori logici (connettivi proposizionali: NOT, AND, OR, IF/THEN, IFF) Caino è fratello di Abele OPPURE a ogni paziente piace qualche dottore p q Caino NON è fratello di Abele p Caino è fratello di Abele E a ogni paziente piace qualche dottore p q SE Caino è fratello di Abele, ALLORA a ogni paziente piace qualche dottore p q Caino è fratello di Abele SE E SOLO SE a ogni paziente piace qualche dottore p q Ricorsivamente: SE Caino NON è fratello di Abele, ALLORA Caino è fratello di Abele OPPURE a ogni paziente piace qualche dottore p (p q) 6
7 Logica Proposizionale Classica La logica proposizionale studia il significato dei connettivi e le forme di ragionamento corretto rappresentabili mediante formule proposizionali SINTASSI La sintassi di un linguaggio determina quali sono le espressioni corrette del linguaggio. Espressioni della logica proposizionale: formule Un linguaggio proposizionale è costruito sulla base di un determinato insieme P di variabili proposizionali P = {p, q, r} P = {p 0, p 1, p 2,...} P = {caino fratello di abele, pazienti dottori,...} 7
8 Definizione induttiva dell insieme delle formule proposizionali di un linguaggio basato su P Dato un insieme P di variabili proposizionali, l insieme delle formule proposizionali costruite sulla base di P, P rop[p ], è definito induttivamente: 1. ogni variabile proposizionale è una formula 2. e sono formule 3. se A è una formula, allora anche A è una formula 4. se A e B sono formule, allora anche (A B), (A B), (A B), (A B) sono formule 5. nient altro è una formula 1. P P rop[p ] 2. P rop[p ] e P rop[p ] 3. se A P rop[p ], allora A P rop[p ] 4. se A P rop[p ] e B P rop[p ], allora (A B) P rop[p ], (A B) P rop[p ], (A B) P rop[p ] e (A B) P rop[p ] 5. nient altro è in P rop[p ] 8
9 Esempio Se P = {p, q, r, s}, sono in P rop[p ]: p, q, r, s,,, p, q, r, s,,, (p q), (p q), (q r), (r s),... (p q), ((p q) (q r)), ((q r) s),... ( (p q) ((p q) (q r))), ((q r) s) ),... 9
10 Convenzioni sull uso delle parentesi si possono omettere le parentesi esterne: (p q) si può scrivere p q associatività: da sinistra a destra (se non indicato altrimenti dall uso di parentesi) ((p q) r) si può scrivere p q r ((p q) r) si può scrivere p q r (p (q r)) NON si può scrivere p q r precedenza dei connettivi:,,,, (se non indicato altrimenti dall uso di parentesi) (p (q r)) si può scrivere p q r (p (q r)) si può scrivere (p q r) (p (q r)) NON si può scrivere p q r (p (q r)) NON si può scrivere p q r Quindi: s p q r abbrevia (s ((p q) r)) p (p r q) abbrevia (p (p (r q))) p q r s abbrevia ((p q) (r s)) p q r è diverso da p (q r) 10
11 Semantica Linguaggio = Dominio Prop[P] = Bool = {T, F } Correttezza dei ragionamenti Un ragionamento è corretto se ogni volta che le premesse sono vere, è vera anche la conclusione La semantica della logica proposizionale stabilisce il significato dei connettivi logici. Il significato delle variabili proposizionali può variare (possono essere interpretate in modi diversi). Qual è il significato di p q? Dipende dal significato di p e q: se p è vero e q è vero, allora p q è vero, altrimenti è falso. Interpretazione di un linguaggio: determina come interpretare le variabili proposizionali 11
12 Interpretazione di P M: assegnazione di un booleano (valore di verità) a ogni variabile in P M : P Bool. Esempio: se P = {p, q, r}, ci sono 8 possibili interpretazioni di P : p q r M 1 T T T M 2 T T F M 3 T F T T F F M 4 p q r M 5 F T T M 6 F T F M 7 F F T F F F M 8 Interpretazione di una formula F : interpretazione del linguaggio di F (l insieme delle variabili proposizionali che occorrono in F ). 12
13 Semantica dei connettivi logici {,,,, } = Funzioni booleane T F NOT F T AND OR IMP IF F T T T T T T T F F T F F F T F T T F F F F F T T = N OT = AN D = OR = IM P = IF F 13
14 Definizione induttiva del significato delle formule in una interpretazione M = A: A è vera in M Se M : P Bool, definiamo M = A per induzione su A: 1. M = p sse M(p) = T, se p P ; 2. M = e M = ; 3. M = A sse M = A 4. M = A B sse M = A e M = B 5. M = A B sse M = A oppure M = B 6. M = A B sse M = A oppure M = B 7. M = A B sse M = A e M = B, oppure M = A e M = B 14
15 Valore di verità di una formula in una interpretazione M(A) = T sse M = A: A B A A B A B A B A B T T F T T T T T F F T F F F T T F T T F F F F F T T Calcolo di M(A): esempio p q r p p q ( p q) r T T F F T F Tavola di verità di una formula: calcolo del suo valore in ogni interpretazione p q r p p q ( p q) r T T T F T T F T T T T T T F T F F T F F T T T T T T F F T F F T F T T F T F F F F T F F F T T F 15
16 Vedere anche il programma truthtable, accessibile dalla pagina del corso cialdea/ocaml/logica/truthtable/ > truthtable -help Uso: truthtable [-o <output-file>] <input-file> -o nome del file di output -help Display this list of options Il file formula contiene il testo p -> q & r. > truthtable formula p q r (p->(q&r)) T T T T T T F F T F T F T F F F F T T T F T F T F F T T F F F T CNF: ((-pvq)&(-pvr)) DNF: (-pv(q&r)) 16
17 Logica e linguaggio naturale La negazione inverte il valore di verità del suo argomento Una congiunzione ( ) è vera se e solo se entrambi gli argomenti sono veri Una doppia implicazione ( ) è vera se e solo se i due argomenti hanno lo stesso valore di verità: IFF è l uguaglianza sui booleani sarai promosso (p) se e solo se avrai scritto almeno 125 programmi corretti (c) : p c condizione necessaria e sufficiente per passare l esame (p) è studiare (s) e avere fortuna (f) : p (s f) La disgiunzione ( ) è l OR inclusivo p q p q p q p q (p q) T T T F T F T F T T F T F T T T F T F F F F T F Andrò al cinema (c) o al teatro (t): (c t) xs=[] (p) oppure ys=[] (q) : p q 17
18 Implicazione L implicazione ( ) è l implicazione materiale: Se A è falsa: A B è vera se B è vera: A B è vera A B è falsa se e solo se A è vera e B è falsa Se x è una potenza di 2 maggiore di 1, allora x è pari è vero sempre (per ogni x): anche se x = 10 anche se x = 7 Antonio dice se piove, vengo a prenderti alla stazione 1. Piove, e A. va alla stazione: ha detto la verità? 2. Piove, e A. non va alla stazione: ha detto la verità? 3. Non piove, e Antonio va lo stesso: ha detto la verità? 4. Non piove, e A. non va alla stazione: ha detto la verità? 18
19 Modelli, contromodelli, formule soddisfacibili Una interpretazione M è un modello di F (o soddisfa F ) sse M = F. Esempio: A = (p q) q. Se M(p) = F e M(q) = F, allora M è un modello di A. Una interpretazione M è un contromodello di F sse M = F. Esempio: se M (p) = T e M (q) = F, M è un contromodello di A. F è soddisfacibile sse esiste un modello di F. Esempio: poiché esiste un modello di A (M tale che M(p) = F e M(q) = F ), A è soddisfacibile. 19
20 Formule logicamente valide F è logicamente valida o è una tautologia ( = F ) se e solo se per ogni interpretazione M di F, M = F ; cioè se non esistono contromodelli di F Esempi: A = (p q) q è soddisfacibile, ma non è valida: esiste anche un contromodello di A. p (p q) è una tautologia: p q p q p (p q) T T T T T F T T F T T T F F F T 20
21 Alcune tautologie (dimostrarle per esercizio) 1. A A (identità) 2. A (B A) (affermazione del conseguente) 3. A (A B) (negazione dell antecedente) 4. B (ex falso quodlibet) 5. A A (terzo escluso) 6. (A A) (non contraddizione) 7. (A B) ((A B) A) (riduzione all assurdo) 8. ((A B) A) A (legge di Pierce) 21
22 Esempio: per dimostrare che la legge di Pierce è una tautologia, possiamo costruirne la tavola di verità e verificare che è vera in ogni interpretazione: > truthtable pierce B A (((A->B)->A)->A) T T T T F T F T T F F T CNF: T DNF: T Oppure possiamo ragionare come segue: Sia M una qualsiasi interpretazione: dimostriamo che se M = (A B) A allora M = A. Supponiamo dunque M = (A B) A: si hanno due possibilità: M = A B, quindi in particolare M = A. M = A. In entrambi i casi M = A. 22
23 Formule contraddittorie F è una contraddizione (o è insoddisfacibile) se e solo se per ogni interpretazione M di F, M = F ; cioè se non esistono modelli di F Esempio: (p (p q)) A è una tautologia se e solo se A è una contraddizione A è una contraddizione se e solo se A è una tautologia A è una contraddizione se e solo se A non è soddisfacibile 23
24 Alcune equivalenze logiche importanti: 1. A A Equivalenza logica A e B sono logicamente equivalenti (A B) sse 2. Commutatività e associatività di e : 3. Leggi distributive: = A B cioè se per ogni interpretazione M di A e B: M = A sse M = B A B B A, A B B A, A (B C) (A B) C, A (B C) (A B) C (A (B C)) ((A B) (A C)) (A (B C)) ((A B) (A C)) 24
25 4. Leggi di De Morgan: 5. Doppia negazione: A A 6. Leggi di assorbimento: 7. Definibilità di : (A B) ( A B) (A B) ( A B) A (A B) A A (A B) A A B (A B) (B A) 8. Interdefinibilità dei connettivi logici,, : 9. Contrapposizione: A B A B (A B) (A B) ( A B) A B A B ( A B) (A B) A B ( A B) A B (A B) ( B A) Esercizio: dimostrare le equivalenze logiche precedenti 25
26 Forme Normali Congiuntive (FNC) e Disgiuntive (FND) LETTERALE: atomo (p) o negazione di un atomo ( p) Una formula è in FNC sse ha la forma D 1... D k dove ogni D i è una disgiunzione di letterali Ogni formula è logicamente equivalente a una formula in FNC Una formula è in FND sse ha la forma C 1... C k dove ogni C i è una congiunzione di letterali Ogni formula è logicamente equivalente a una formula in FND Esempio: trasformazione in FNC di ( (p q) (q (r (s p)))) (p q) (q (r ( s p))) (p q) (q (r ( s p))) ( p q) (q (r ( s p))) ( p q) (q (r ( s p))) ( p q) ((q r) (q ( s p))) p q (q r) (q s p) 26
27 Esercizio: Trovare forme normali congiuntive e disgiuntive logicamente equivalenti a 1. (A B) ( A C) 2. A (B A) Vedere anche il programma truthtable, accessibile dalla pagina del corso 27
28 Trasformazione di formule in forma normale congiuntiva 1. Eliminare le implicazioni e le doppie implicazioni A B A B (A B) A B A B ( A B) ( B A) (A B) (A B) ( A B) 2. Portare le negazioni sugli atomi (A B) A B (A B) A B A A 3. Distribuire su (A B) C (A C) (B C) C (A B) (C A) (C B) 28
29 Algoritmo per la trasformazione in CNF 1. Eliminare le implicazioni e le doppie implicazioni e portare le negazioni sugli atomi (trasformare A in forma normale negativa NNF) 2. Ricorsivamente: se A ha la forma B C: distribuire l or più esterno su tutte le congiunzioni nella formula CN F (B) CN F (C) se A ha la forma B C: il risultato è CNF (B) CNF (C) altrimenti (A è un letterale) il risultato è A 3. Eventualmente, semplificare la formula ottenuta 29
30 Esercizi Per ciascuno dei seguenti enunciati: a) determinare un linguaggio per esprimerlo, b) scrivere una formula proposizionale che lo rappresenti, c) determinare un modello e un contromodello. 1. Condizione necessaria per passare l esame è studiare o avere fortuna. 2. Condizione sufficiente perché faccia caldo è che sia estate e non piova 3. Se nevica, diventa più freddo 4. Solo se colpisci il vetro con un martello lo romperai 5. Condizione necessaria e sufficiente perché ABC sia un triangolo isoscele è che abbia esattamente tre lati e che abbia almeno due angoli uguali. 6. È falso che la lista xs è vuota oppure il valore di found è true 7. La lista xs non è vuota e il valore di found è false 8. Prendo il libro e arrivo 9. Arrivo e prendo il libro 10. Puoi andare al cinema o alla festa, ma non puoi fare tutte e due le cose 11. Per dare l esame, devi studiare 12. Tutti i corvi sono neri 13. Qualcuno è colpevole 30
31 Formule e funzioni booleane I connettivi che abbiamo introdotto sono sufficienti a esprimere tutte le possibili funzioni booleane? Ogni formula A determina una funzione booleana f A Sia A[p 1,...p k ] una formula con k lettere proposizionali. A corrisponde a una funzione booleana a k argomenti: per ogni possibile assegnazione M: f A (M(p 1 ),..., M(p k )) = M(A) Esempio: A = p q f A è tale che: f A (T, T ) = T f A (F, T ) = F f A (T, F ) = T f A (F, F ) = T Se = A B, allora f A = f B Ogni funzione booleana è determinata da qualche formula Ogni funzione booleana a k argomenti corrisponde a una formula proposizionale (o a una classe di equivalenza di fbf): Per ogni funzione booleana f esiste una formula A tale che f A = f 31
32 Se f : Bool k Bool, Adeguatezza dei connettivi allora esiste A f P rop[p 1,..., p k ] tale che per ogni assegnazione M : {p 1,..., p k } Bool: M(A f ) = f(m(p 1 ),..., M(p k )) A f si può costruire utilizzando soltanto,, : Esempio di costruzione di A f : {,, } è un insieme adeguato di connettivi x 1 x 2 f(x 1, x 2 ) A[p 1, p 2 ] T T F T F T = (p 1 p 2 ) F T T = ( p 1 p 2 ) F F T = ( p 1 p 2 ) (forma normale disgiuntiva) Esercizio: Definire una qualsiasi funzione booleana a 3 argomenti, descrivendone i valori in forma di tabella, e determinare una formula con tre lettere proposizionali che la rappresenta. 32
33 Due connettivi particolari Esistono connettivi che da soli sono sufficienti ad esprimere tutte le funzioni booleane: Il tratto di Sheffer (o negazione alternativa) è il connettivo con la seguente tavola di verità: A B A B T T F T F T F T T F F T { } è un insieme adeguato di connettivi. Infatti A A A A B ((A A) (B B)) (verificarlo per esercizio) La negazione congiunta, la cui tavola di verità è: A B A B T T F T F F F T F F F T costituisce un insieme adeguato di connettivi. Infatti A A A A B ((A A) (B B)) (verificarlo per esercizio) 33
34 Conseguenza logica M è un modello di un insieme di formule S sse è un modello di ciascuna formula in S A è una conseguenza logica di un insieme di formule S S = A sse ogni modello di S è un modello di A p q, p r, q r = r Infatti: sia M una qualsiasi interpretazione tale che: 1. M = p q 2. M = p r 3. M = q r Per 1, M(p) = T oppure M(q) = T. Nel primo caso, M(r) = T (per 2) Nel secondo caso M(r) = T (per 3) Quindi, in ogni caso, M(r) = T. p, q p = q Infatti, se M(p) = T e M(q) = F : M = p, M = q p, ma M = q. 34
35 Ragionamenti corretti Un ragionamento che dalle ipotesi S conclude A è corretto sse S = A. Per verificare se A 1,..., A n = B si può: Fare la tavola di verità per A 1... A n B e controllare se è una tautologia Cercare un contromodello per A 1... A n B: se la ricerca (sistematica) fallisce, allora A 1,..., A n = B Dimostrare B a partire da A 1,..., A n, utilizzando un insieme di regole di ragionamento corrette Implementare un metodo di dimostrazione automatica ed eseguire il programma sul problema A 1,..., A n = B Per dimostrare che A 1,..., A n = B c è un unico metodo: trovare un interpretazione M tale che M = {A 1,..., A n } e M = B. 35
36 Uso delle tavole di verità. Cavalieri e furfanti A dice: Io sono un furfante oppure B è un cavaliere. Cosa sono A e B? Descrizione del problema: 1. A ( A B) 2. A ( A B) A = A è un cavaliere B = B è un cavaliere Con le tavole di verità possiamo determinare quali sono le interpretazioni di A e B in cui le due formule 1 e 2 sono entrambe vere, e rispondere dunque alla domanda cosa sono A e B? : A B A ( A B) A ( A B) T T T T T F F T F T T F F F T F Quindi l unica interpetazione in cui 1 e 2 sono entrambe vere è quella in cui A e B sono entrambe vere: A e B sono entrambi cavalieri. In altri termini: A ( A B), A ( A B) = A A ( A B), A ( A B) = B 36
37 Ragionamento per assurdo: ricerca di un contromodello A dice: Io sono un furfante oppure B è un cavaliere. Cosa sono A e B? 1. A ( A B) 2. A ( A B) Il problema è quello di determinare se A oppure A è una conseguenza logica di 1 e 2, e se B oppure B è una conseguenza logica di 1 e 2. Per determinare se A è una conseguenza logica di 1 e 2: tutti i modelli di 1 e 2 sono modelli di A. Sia M una qualunque interpretazione che rende vere 1 e 2 e supponiamo (per assurdo) che M = A. M = A def. di M = ( A B) 2 e def. di M = A B M = A def. di M = A contraddizione Quindi M = A è assurdo e deve essere M = A. Esercizio. Determinare con lo stesso metodo che B è una conseguenza logica di 1 e 2. 37
38 Ragionamento per assurdo È stato compiuto un furto. I ladri sono fuggiti con un furgone. Sono implicati tre uomini: A, B, C. Si sa che C non lavora mai senza la complicità di A e B non sa guidare. A è colpevole? Linguaggio: A (A è colpevole), B, C Ipotesi: S = {A B C, C A, B (A C)} Tesi: A Controllare se A B C, C A, B (A C) = A Per assurdo: Assumiamo che esista M tale che: 1. M = A B C 2. M = C A 3. M = B (A C) 4. M = A, cioè M(A) = F Quindi: M = C, altrimenti 2 sarebbe falso M = A C M = B, altrimenti 3 sarebbe falso Ma allora anche 1 è falso: assurdo 38
39 Ragionamento diretto Per ogni interpretazione M, se M = S, allora M = A Ragionamento per casi A B C, C A, B (A C) = A Sia M qualsiasi interpretazione tale che M = S: poiché M = A B C, o M = A, oppure M = B, oppure M = C. Mostriamo che in tutti e tre i casi M = A: a) se M = A, allora M = A b) se M = B, allora M = A C (da 3): b1) se M = A, allora M = A b2) se M = C allora M = A, per 2 quindi nel caso b) M = A c) se M = C, allora M = A, per 2 39
40 Una logica Λ è definita da: Sintassi Alfabeto A (insieme non vuoto di simboli) Linguaggio L A (formule ben formate: fbf) Spesso definito induttivamente principio di induzione strutturale sulle fbf ricorsione sulle fbf Semantica Apparato deduttivo (sistema di inferenza) Assiomi Ax L Regole di inferenza R = {R 1, R 2,...}, con R i L n i (relazioni su fbf) A 1,..., A ni 1 A n Se Ax e R sono decidibili: teoria assiomatica 40
41 Linguaggio proposizionale con e Assiomi: A1. A (B A) A2. (A (B C)) ((A B) (A C)) A3. ( B A) (( B A) B) Regola di inferenza: A Sistema di inferenza hilbertiano per la logica proposizionale A B B (MP P ) Se A 1,..., A n A è una regola di inferenza R, allora A deriva da A 1,..., A n mediante R. 41
42 Derivazioni e dimostrazioni Derivazione di A da S: sequenza A 1,..., A n di formule tale che A n = A e per ogni i: A i è un assioma, oppure A i S, oppure A i deriva da formule precedenti mediante una regola di inferenza Se esiste una derivazione di A da S allora A è derivabile da S: S A Una derivazione di A da Ø è una dimostrazione di A. Se esiste una dimostrazione di A: A allora A è dimostrabile (o è un teorema) Esempio: H p p 1. (p ((p p) p)) ((p (p p)) (p p)) Assioma A2 2. p ((p p) p) Assioma A1 3. (p (p p)) (p p) MP P (1, 2) 4. p (p p) Assioma A1 5. p p MP P (3, 4) Sostituibilità nelle derivazioni: Se S A allora S[B/p] A[B/p] 42
43 Semantica di una logica Λ 1. Interpretazione del linguaggio M Dominio di interpretazione D Funzione di interpretazione L D 2. Nozione di verità in una interpretazione M = A Validità = A : per ogni M, M = A Soddisfacibilità: esiste M, tale che M = A Conseguenza logica S = A : per ogni M, se M = G per ogni G in S, allora M = A Corrispondenza tra apparato deduttivo e semantica S = A sse S A = A sse A (debole) Il sistema Hilbertiano è corretto e completo rispetto alla semantica della logica proposizionale: Se S A allora S = A: correttezza Se S = A allora S A: completezza 43
44 Proprietà della derivabilità Se S S e S A, allora S A (monotonicità) S A sse esiste un sottoinsieme finito S di S tale che S A (compattezza) Se S A e per ogni B S, S B, allora S A (taglio) Una teoria assiomatica è semidecidibile Possibili proprietà di S = A Se S S e S = A, allora S = A (monotonicità) S = A sse esiste un sottoinsieme finito S di S tale che S = A (compattezza) se S = A e per ogni B S, S = B, allora S = A (taglio) L insieme delle formule valide è ricorsivo (decidibilità) L insieme delle formule valide è ricorsivamente enumerabile (semidecidibilità) Chiusura deduttiva di S: T (S) = {A S A} T (S) è anche chiamata la teoria di S e le formule di S sono gli assiomi della teoria 44
45 Esistono Limiti di un sistema deduttivo logiche non monotone elef ante(pippo) = grigio(pippo) elef ante(pippo), albino(pippo) = grigio(pippo) logiche non compatte P A teoria dell aritmetica del secondo ordine: P A = A sse A è vera nell interpretazione standard su IN P A, q(0), q(1), q(2),... = xq(x) ma xq(x) non è conseguenza logica di alcun sottoinsieme finito di P A {q(0), q(1), q(2),...} logiche in cui non vale il taglio logiche non decidibili (logica dei predicati) logiche non semidecidibili 45
LOGICA FORMALE. Logiche
 LOGICA FORMALE Linguaggio formale (sintassi + semantica) + Sistema di inferenza Sintassi: insieme delle espressioni ben formate (linguaggio) Semantica: interpretazione M del linguaggio Logica classica:
LOGICA FORMALE Linguaggio formale (sintassi + semantica) + Sistema di inferenza Sintassi: insieme delle espressioni ben formate (linguaggio) Semantica: interpretazione M del linguaggio Logica classica:
Logica: materiale didattico
 Logica: materiale didattico M. Cialdea Mayer. Logica (dispense): http://cialdea.dia.uniroma3.it/teaching/logica/materiale/dispense-logica.pdf Logica dei Predicati (Logica per l Informatica) 01: Logica
Logica: materiale didattico M. Cialdea Mayer. Logica (dispense): http://cialdea.dia.uniroma3.it/teaching/logica/materiale/dispense-logica.pdf Logica dei Predicati (Logica per l Informatica) 01: Logica
Fondamenti di Informatica 2
 Fondamenti di Informatica 2 Linguaggi e Complessità : Lezione 1 Corso Fondamenti di Informatica 2 Marco Schaerf, 2009-2010 Linguaggi e Complessità : Lezione 1 1 Logica proposizionale Linguaggio matematico
Fondamenti di Informatica 2 Linguaggi e Complessità : Lezione 1 Corso Fondamenti di Informatica 2 Marco Schaerf, 2009-2010 Linguaggi e Complessità : Lezione 1 1 Logica proposizionale Linguaggio matematico
Logica. Dispense per il corso di Logica per L Informatica a.a. 2013/2014
 Logica Dispense per il corso di Logica per L Informatica a.a. 2013/2014 (estratte dal libro: M. Cialdea Mayer. Logica. Linguaggio, ragionamento, calcolo. Esculapio, 2002, con alcune integrazioni e correzioni)
Logica Dispense per il corso di Logica per L Informatica a.a. 2013/2014 (estratte dal libro: M. Cialdea Mayer. Logica. Linguaggio, ragionamento, calcolo. Esculapio, 2002, con alcune integrazioni e correzioni)
Logica proposizionale
 Logica proposizionale Proposizione: frase compiuta che è sempre o vera o falsa. Connettivi Posti in ordine di precedenza: not, and, or, implica, doppia implicazione Sintassi Le proposizioni sono costituite
Logica proposizionale Proposizione: frase compiuta che è sempre o vera o falsa. Connettivi Posti in ordine di precedenza: not, and, or, implica, doppia implicazione Sintassi Le proposizioni sono costituite
Introduzione alla logica matematica
 Introduzione alla logica matematica, Paolo Bison, A.A. 2004-05, 2004-10-26 p.1/29 Introduzione alla logica matematica Silvana Badaloni Paolo Bison Fondamenti di Informatica 1 A.A. 2004/05 Università di
Introduzione alla logica matematica, Paolo Bison, A.A. 2004-05, 2004-10-26 p.1/29 Introduzione alla logica matematica Silvana Badaloni Paolo Bison Fondamenti di Informatica 1 A.A. 2004/05 Università di
Problemi decidibili, semidecidibili, indecidibili
 Problemi decidibili, semidecidibili, indecidibili (Paragrafo 3.5 delle dispense) Il problema di determinare se una formula A della logica proposizionale sia valida o no può essere risolto mediante un procedimento
Problemi decidibili, semidecidibili, indecidibili (Paragrafo 3.5 delle dispense) Il problema di determinare se una formula A della logica proposizionale sia valida o no può essere risolto mediante un procedimento
Introduzione alla logica matematica. Logica matematica. Paolo Bison
 Introduzione alla logica matematica Paolo Bison Fondamenti di Informatica Ingegneria Meccanica Università di Padova A.A. 2008/09 Logica matematica formalizzazione dei meccanismi di ragionamento la logica
Introduzione alla logica matematica Paolo Bison Fondamenti di Informatica Ingegneria Meccanica Università di Padova A.A. 2008/09 Logica matematica formalizzazione dei meccanismi di ragionamento la logica
Logica proposizionale
 Fondamenti di Informatica per la Sicurezza a.a. 2008/09 Logica proposizionale Stefano Ferrari UNIVERSITÀ DEGLI STUDI DI MILANO DIPARTIMENTO DI TECNOLOGIE DELL INFORMAZIONE Stefano Ferrari Università degli
Fondamenti di Informatica per la Sicurezza a.a. 2008/09 Logica proposizionale Stefano Ferrari UNIVERSITÀ DEGLI STUDI DI MILANO DIPARTIMENTO DI TECNOLOGIE DELL INFORMAZIONE Stefano Ferrari Università degli
Ragionamento Automatico Richiami di tableaux proposizionali
 Richiami di logica e deduzione proposizionale Ragionamento Automatico Richiami di tableaux proposizionali (L. Carlucci Aiello & F. Pirri: SLL, Cap. 5) La logica proposizionale I tableau proposizionali
Richiami di logica e deduzione proposizionale Ragionamento Automatico Richiami di tableaux proposizionali (L. Carlucci Aiello & F. Pirri: SLL, Cap. 5) La logica proposizionale I tableau proposizionali
Sistemi di inferenza Consentono di derivare formule da altre formule: formalizzazione del ragionamento. Un sistema di inferenza è costituito da: un
 Sistemi di inferenza Consentono di derivare formule da altre formule: formalizzazione del ragionamento. Un sistema di inferenza è costituito da: un insieme di assiomi un insieme di regole di inferenza,
Sistemi di inferenza Consentono di derivare formule da altre formule: formalizzazione del ragionamento. Un sistema di inferenza è costituito da: un insieme di assiomi un insieme di regole di inferenza,
Logica per la Programmazione
 Logica del Primo Ordine: Motivazioni, Sintassi e Interpretazioni Logica per la Programmazione Lezione 1 Calcolo Proposizionale: sintassi e semantica Tautologie Esempi di Formalizzazione di Enunciati pag.
Logica del Primo Ordine: Motivazioni, Sintassi e Interpretazioni Logica per la Programmazione Lezione 1 Calcolo Proposizionale: sintassi e semantica Tautologie Esempi di Formalizzazione di Enunciati pag.
CALCOLO PROPOSIZIONALE: CENNI
 CALCOLO PROPOSIZIONALE: CENNI Francesca Levi Dipartimento di Informatica February 26, 2016 F.Levi Dip.to Informatica Informatica per le Scienze Umane a.a. 15/16 pag. 1 La Logica La logica è la disciplina
CALCOLO PROPOSIZIONALE: CENNI Francesca Levi Dipartimento di Informatica February 26, 2016 F.Levi Dip.to Informatica Informatica per le Scienze Umane a.a. 15/16 pag. 1 La Logica La logica è la disciplina
si vuole verificare: P5: pioverà
 Logica matematica ntroduzione alla logica matematica ilvana adaloni Paolo ison Fondamenti di nformatica AA 20004 niversità di Padova formalizzazione dei meccanismi di ragionamento la logica studia proposizioni
Logica matematica ntroduzione alla logica matematica ilvana adaloni Paolo ison Fondamenti di nformatica AA 20004 niversità di Padova formalizzazione dei meccanismi di ragionamento la logica studia proposizioni
Sistemi Deduttivi. Marco Piastra. Intelligenza Artificiale I. Intelligenza Artificiale I - A.A Sistemi Deduttivi[1]
![Sistemi Deduttivi. Marco Piastra. Intelligenza Artificiale I. Intelligenza Artificiale I - A.A Sistemi Deduttivi[1] Sistemi Deduttivi. Marco Piastra. Intelligenza Artificiale I. Intelligenza Artificiale I - A.A Sistemi Deduttivi[1]](/thumbs/88/115134024.jpg) Intelligenza Artificiale I Sistemi Deduttivi Marco Piastra Intelligenza Artificiale I - A.A. 2010- Sistemi Deduttivi[1] Calcolo simbolico? Una fbf è conseguenza logica di un insieme di fbf sse qualsiasi
Intelligenza Artificiale I Sistemi Deduttivi Marco Piastra Intelligenza Artificiale I - A.A. 2010- Sistemi Deduttivi[1] Calcolo simbolico? Una fbf è conseguenza logica di un insieme di fbf sse qualsiasi
NOZIONI DI LOGICA PROPOSIZIONI.
 NOZIONI DI LOGICA PROPOSIZIONI. Una proposizione è un affermazione che è vera o falsa, ma non può essere contemporaneamente vera e falsa. ESEMPI Sono proposizioni : 7 è maggiore di 2 Londra è la capitale
NOZIONI DI LOGICA PROPOSIZIONI. Una proposizione è un affermazione che è vera o falsa, ma non può essere contemporaneamente vera e falsa. ESEMPI Sono proposizioni : 7 è maggiore di 2 Londra è la capitale
Intelligenza Artificiale. Logica proposizionale: calcolo simbolico
 Intelligenza Artificiale Logica proposizionale: calcolo simbolico Marco Piastra Logica formale (Parte 2) - 1 Parte 2 Calcolo logico Assiomi Derivazioni Derivazioni e conseguenza logica Completezza Logica
Intelligenza Artificiale Logica proposizionale: calcolo simbolico Marco Piastra Logica formale (Parte 2) - 1 Parte 2 Calcolo logico Assiomi Derivazioni Derivazioni e conseguenza logica Completezza Logica
Introduzione alla logica
 Corso di Intelligenza Artificiale 2011/12 Introduzione alla logica iola Schiaffonati Dipartimento di Elettronica e Informazione Sommario 2 Logica proposizionale (logica di Boole) Logica del primo ordine
Corso di Intelligenza Artificiale 2011/12 Introduzione alla logica iola Schiaffonati Dipartimento di Elettronica e Informazione Sommario 2 Logica proposizionale (logica di Boole) Logica del primo ordine
LOGICA MATEMATICA PER INFORMATICA (A.A. 12/13)
 LOGICA MATEMATICA PER INFORMATICA (A.A. 12/13) DISPENSA N. 4 Sommario. Dimostriamo il Teorema di Completezza per il Calcolo dei Predicati del I ordine. 1. Teorema di Completezza Dimostriamo il Teorema
LOGICA MATEMATICA PER INFORMATICA (A.A. 12/13) DISPENSA N. 4 Sommario. Dimostriamo il Teorema di Completezza per il Calcolo dei Predicati del I ordine. 1. Teorema di Completezza Dimostriamo il Teorema
Logica: nozioni di base
 Fondamenti di Informatica Sistemi di Elaborazione delle Informazioni Informatica Applicata Logica: nozioni di base Antonella Poggi Anno Accademico 2012-2013 DIPARTIMENTO DI SCIENZE DOCUMENTARIE LINGUISTICO
Fondamenti di Informatica Sistemi di Elaborazione delle Informazioni Informatica Applicata Logica: nozioni di base Antonella Poggi Anno Accademico 2012-2013 DIPARTIMENTO DI SCIENZE DOCUMENTARIE LINGUISTICO
Ragionamento formalei. Ragionamento formale
 Ragionamento formale La necessità e l importanza di comprendere le basi del ragionamento formale, utilizzato in matematica per dimostrare teoremi all interno di teorie, è in generale un argomento piuttosto
Ragionamento formale La necessità e l importanza di comprendere le basi del ragionamento formale, utilizzato in matematica per dimostrare teoremi all interno di teorie, è in generale un argomento piuttosto
Esercitazioni per il corso di Logica Matematica
 Esercitazioni per il corso di Logica Matematica Luca Motto Ros 02 marzo 2005 Nota importante. Queste pagine contengono appunti personali dell esercitatore e sono messe a disposizione nel caso possano risultare
Esercitazioni per il corso di Logica Matematica Luca Motto Ros 02 marzo 2005 Nota importante. Queste pagine contengono appunti personali dell esercitatore e sono messe a disposizione nel caso possano risultare
Semantica proposizionale. Unit 2, Lez 3 e 4 Corso di Logica
 Semantica proposizionale Unit 2, Lez 3 e 4 Corso di Logica Sommario Semantica dei connettivi Costruzione delle tavole di verità Tautologie, contraddizioni e contingenze Semantica delle forme argomentative
Semantica proposizionale Unit 2, Lez 3 e 4 Corso di Logica Sommario Semantica dei connettivi Costruzione delle tavole di verità Tautologie, contraddizioni e contingenze Semantica delle forme argomentative
Esercizi sul Calcolo Proposizionale
 Esercizi sul Calcolo Proposizionale Francesco Sborgia Matricola: 459245 December 7, 2015 1 Esercizio 1 Per ogni formula A dimostrare che ρ(a) = min{n A F n } Definizione 1. Ricordiamo che, dato un linguaggio
Esercizi sul Calcolo Proposizionale Francesco Sborgia Matricola: 459245 December 7, 2015 1 Esercizio 1 Per ogni formula A dimostrare che ρ(a) = min{n A F n } Definizione 1. Ricordiamo che, dato un linguaggio
API. Ripasso di logica. Davide Martinenghi. Politecnico di Milano. API Davide Martinenghi (1/30)
 API Ripasso di logica Davide Martinenghi Politecnico di Milano API Davide Martinenghi (1/30) Logica proposizionale - sintassi L è un linguaggio della logica proposizionale L alfabeto di L è composto da
API Ripasso di logica Davide Martinenghi Politecnico di Milano API Davide Martinenghi (1/30) Logica proposizionale - sintassi L è un linguaggio della logica proposizionale L alfabeto di L è composto da
CALCOLO PROPOSIZIONALE. Corso di Logica per la Programmazione Andrea Corradini
 CALCOLO PROPOSIZIONALE Corso di Logica per la Programmazione Andrea Corradini andrea@di.unipi.it UN PROBLEMA DI DEDUZIONE LOGICA (da un test d ingresso) Tre amici, Antonio, Bruno e Corrado, sono incerti
CALCOLO PROPOSIZIONALE Corso di Logica per la Programmazione Andrea Corradini andrea@di.unipi.it UN PROBLEMA DI DEDUZIONE LOGICA (da un test d ingresso) Tre amici, Antonio, Bruno e Corrado, sono incerti
Ragionamenti e metodi di dimostrazione. Liceo Scientifico Statale S. Cannizzaro Prof.re E. Modica
 Ragionamenti e metodi di dimostrazione Liceo Scientifico Statale S. Cannizzaro Prof.re E. Modica Proposizioni Si definisce proposizione una frase alla quale è possibile attribuire uno e un solo valore
Ragionamenti e metodi di dimostrazione Liceo Scientifico Statale S. Cannizzaro Prof.re E. Modica Proposizioni Si definisce proposizione una frase alla quale è possibile attribuire uno e un solo valore
Fondamenti teorici e programmazione
 Fondamenti teorici e programmazione FTP(A) - modb Lezione 8 F.Bonchi Dip.to Informatica Fondamenti teorici e programmazione (A) - modb a.a. 2018/19 pag. 1 Ragionamento formale Comprendere le basi del ragionamento
Fondamenti teorici e programmazione FTP(A) - modb Lezione 8 F.Bonchi Dip.to Informatica Fondamenti teorici e programmazione (A) - modb a.a. 2018/19 pag. 1 Ragionamento formale Comprendere le basi del ragionamento
Fondamenti di Informatica 2, Linguaggi e Complessità : Logica I Parte Lucidi di M.Schaerf e A.Marchetti Spaccamela
 Fondamenti di Informatica 2 Linguaggi e Complessità :LogicaIParte Lucidi di M.Schaerf e A.Marchetti Spaccamela Fondamenti di Informatica 2: Logica } Indice degli argomenti Introduzione: Motivazioni, Prove,
Fondamenti di Informatica 2 Linguaggi e Complessità :LogicaIParte Lucidi di M.Schaerf e A.Marchetti Spaccamela Fondamenti di Informatica 2: Logica } Indice degli argomenti Introduzione: Motivazioni, Prove,
DIMOSTRAZIONI DI EQUIVALENZE, SUI CONNETTIVI E SULL'AMBIGUITA' DELLA SINTASSI. Corso di Logica per la Programmazione
 DIMOSTRAZIONI DI EQUIVALENZE, SUI CONNETTIVI E SULL'AMBIGUITA' DELLA SINTASSI Corso di Logica per la Programmazione SULLE LEGGI DEL CALCOLO PROPOSIZIONALE Abbiamo visto le leggi per l'equivalenza ( ),
DIMOSTRAZIONI DI EQUIVALENZE, SUI CONNETTIVI E SULL'AMBIGUITA' DELLA SINTASSI Corso di Logica per la Programmazione SULLE LEGGI DEL CALCOLO PROPOSIZIONALE Abbiamo visto le leggi per l'equivalenza ( ),
Logica Proposizionale
 Intelligenza rtificiale I Logica Proposizionale Introduzione Marco Piastra Intelligenza rtificiale I -.. 28-29 29 Introduzione al corso ] lgebre di Boole Definizione Una collezione di oggetti X su cui
Intelligenza rtificiale I Logica Proposizionale Introduzione Marco Piastra Intelligenza rtificiale I -.. 28-29 29 Introduzione al corso ] lgebre di Boole Definizione Una collezione di oggetti X su cui
Luca Costabile Esercizi di Logica Matematica Dispensa Calcolo Proposizionale 1
 Luca Costabile Esercizi di Logica Matematica Dispensa Calcolo Proposizionale 1 Esercizio 1.12 Per dimostrare che per ogni funzione esiste una formula in cui compaiono le variabili tale che la corrispondente
Luca Costabile Esercizi di Logica Matematica Dispensa Calcolo Proposizionale 1 Esercizio 1.12 Per dimostrare che per ogni funzione esiste una formula in cui compaiono le variabili tale che la corrispondente
CALCOLO PROPOSIZIONALE
 CALCOLO PROPOSIZIONALE UN PROBLEMA DI DEDUZIONE LOGICA (da un test d ingresso) Tre amici, Antonio, Bruno e Corrado, sono incerti se andare al cinema. Si sa che: Se Corrado va al cinema, allora ci va anche
CALCOLO PROPOSIZIONALE UN PROBLEMA DI DEDUZIONE LOGICA (da un test d ingresso) Tre amici, Antonio, Bruno e Corrado, sono incerti se andare al cinema. Si sa che: Se Corrado va al cinema, allora ci va anche
NOZIONI DI LOGICA. Premessa
 NOZIONI DI LOGICA Premessa Il compito principale della logica è quello di studiare il nesso di conseguenza logica tra proposizioni, predisponendo delle tecniche per determinare quando la verità di una
NOZIONI DI LOGICA Premessa Il compito principale della logica è quello di studiare il nesso di conseguenza logica tra proposizioni, predisponendo delle tecniche per determinare quando la verità di una
METODI MATEMATICI PER L INFORMATICA
 METODI MATEMATICI PER L INFORMATICA Tutorato Lezione 2 17/03/2016 Corso per matricole congrue a 1 Docente: Margherita Napoli Tutor: Amedeo Leo Applicazioni della logica proposizionale La logica ha una
METODI MATEMATICI PER L INFORMATICA Tutorato Lezione 2 17/03/2016 Corso per matricole congrue a 1 Docente: Margherita Napoli Tutor: Amedeo Leo Applicazioni della logica proposizionale La logica ha una
DIMOSTRAZIONI DI EQUIVALENZE, SUI CONNETTIVI E SULL'AMBIGUITA' DELLA SINTASSI. Corso di Logica per la Programmazione A.A. 2013/14 Andrea Corradini
 DIMOSTRAZIONI DI EQUIVALENZE, SUI CONNETTIVI E SULL'AMBIGUITA' DELLA SINTASSI Corso di Logica per la Programmazione A.A. 2013/14 Andrea Corradini SULLE LEGGI DEL CALCOLO PROPOSIZIONALE Abbiamo visto le
DIMOSTRAZIONI DI EQUIVALENZE, SUI CONNETTIVI E SULL'AMBIGUITA' DELLA SINTASSI Corso di Logica per la Programmazione A.A. 2013/14 Andrea Corradini SULLE LEGGI DEL CALCOLO PROPOSIZIONALE Abbiamo visto le
Intelligenza Artificiale. Breve introduzione alla logica classica (Parte 2)
 Intelligenza Artificiale Breve introduzione alla logica classica (Parte 2) Marco Piastra Logica formale (Parte 2) - Introduzione alla logica formale Parte. Preambolo: algebra di Boole, proposizioni, conseguenza
Intelligenza Artificiale Breve introduzione alla logica classica (Parte 2) Marco Piastra Logica formale (Parte 2) - Introduzione alla logica formale Parte. Preambolo: algebra di Boole, proposizioni, conseguenza
Logica per la Programmazione
 Logica per la Programmazione Lezione 2 Dimostrazione di tautologie Proof System pag. 1 Un Problema di Deduzione Logica [da un test di ingresso] Tre amici, Antonio, Bruno e Corrado, sono incerti se andare
Logica per la Programmazione Lezione 2 Dimostrazione di tautologie Proof System pag. 1 Un Problema di Deduzione Logica [da un test di ingresso] Tre amici, Antonio, Bruno e Corrado, sono incerti se andare
Logica Proposizionale
 Logica Proposizionale Dispense del corso di Fondamenti di Informatica I tratte da M. Cialdea (U. di Roma Tre) Introduzione alla logica proposizionale A.A. 2013/2014 Indice 1 Introduzione 1 2 Il linguaggio
Logica Proposizionale Dispense del corso di Fondamenti di Informatica I tratte da M. Cialdea (U. di Roma Tre) Introduzione alla logica proposizionale A.A. 2013/2014 Indice 1 Introduzione 1 2 Il linguaggio
Logica dei Predicati (o Logica del Primo Ordine)
 Logica dei Predicati (o Logica del Primo Ordine) Il mondo è analizzato in termini di OGGETTI, PROPRIETÀ, RELAZIONI. I numeri primi maggiori di due sono dispari oggetti: due; relazioni e proprietà: essere
Logica dei Predicati (o Logica del Primo Ordine) Il mondo è analizzato in termini di OGGETTI, PROPRIETÀ, RELAZIONI. I numeri primi maggiori di due sono dispari oggetti: due; relazioni e proprietà: essere
Intelligenza Artificiale. Logica proposizionale: calcolo automatico
 Intelligenza Artificiale Logica proposizionale: calcolo automatico Marco Piastra Logica formale (Parte 3) - Parte 3 Calcolo automatico Forme normali ed a clausole Risoluzione e refutazione Forward chaining
Intelligenza Artificiale Logica proposizionale: calcolo automatico Marco Piastra Logica formale (Parte 3) - Parte 3 Calcolo automatico Forme normali ed a clausole Risoluzione e refutazione Forward chaining
UNIVERSITÀ DEGLI STUDI LA SAPIENZA CORSO DI STUDI IN INFORMATICA ESERCITAZIONI AL CORSO DI LOGICA MATEMATICA LOGICA PROPOSIZIONALE
 UNIVERSITÀ DEGLI STUDI LA SAPIENZA CORSO DI STUDI IN INFORMATICA ESERCITAZIONI AL CORSO DI LOGICA MATEMATICA LOGICA PROPOSIZIONALE TAVOLE DI VERITÀ, COLETEZZA VERO-FUNZIONALE Esercizio 1. Calcola le tavole
UNIVERSITÀ DEGLI STUDI LA SAPIENZA CORSO DI STUDI IN INFORMATICA ESERCITAZIONI AL CORSO DI LOGICA MATEMATICA LOGICA PROPOSIZIONALE TAVOLE DI VERITÀ, COLETEZZA VERO-FUNZIONALE Esercizio 1. Calcola le tavole
Esercizi di Logica Matematica
 Esercizi di Logica Matematica Francesco Bottacin 1 Logica Proposizionale Esercizio 1.1. Eliminare le parentesi non necessarie nelle seguenti formule: 1. ((A B) ( C)) 2. (A (B ( C))) 3. ((A B) (C D)) 4.
Esercizi di Logica Matematica Francesco Bottacin 1 Logica Proposizionale Esercizio 1.1. Eliminare le parentesi non necessarie nelle seguenti formule: 1. ((A B) ( C)) 2. (A (B ( C))) 3. ((A B) (C D)) 4.
Logica proposizionale classica. Studia il comportamento dei connettivi proposizionali quali ( And ) e ( Or )
 Logica proposizionale classica Studia il comportamento dei connettivi proposizionali quali ( And ) e ( Or ) Parte da una famiglia di enunciati atomici di cui non analizziamo la struttura interna, che rappresentiamo
Logica proposizionale classica Studia il comportamento dei connettivi proposizionali quali ( And ) e ( Or ) Parte da una famiglia di enunciati atomici di cui non analizziamo la struttura interna, che rappresentiamo
Prerequisiti Matematici
 Prerequisiti Matematici Richiami di teoria degli insiemi Relazioni d ordine, d equivalenza Richiami di logica Logica proposizionale, tabelle di verità, calcolo dei predicati Importante: Principio di Induzione
Prerequisiti Matematici Richiami di teoria degli insiemi Relazioni d ordine, d equivalenza Richiami di logica Logica proposizionale, tabelle di verità, calcolo dei predicati Importante: Principio di Induzione
Intelligenza Artificiale. Logica proposizionale classica (Parte 2)
 Intelligenza Artificiale Logica proposizionale classica (Parte 2) Marco Piastra Logica formale (Parte 2) - Introduzione alla logica formale Parte. Preambolo: algebra di Boole, proposizioni, conseguenza
Intelligenza Artificiale Logica proposizionale classica (Parte 2) Marco Piastra Logica formale (Parte 2) - Introduzione alla logica formale Parte. Preambolo: algebra di Boole, proposizioni, conseguenza
Fondamenti di Informatica 2, Linguaggi e Complessità : Logica I Parte Lucidi di M.Schaerf e A.Marchetti Spaccamela
 Fondamenti di Informatica 2 Linguaggi e Complessità : Logica I Parte Lucidi di M.Schaerf e A.Marchetti Spaccamela Fondamenti di Informatica 2: Logica Indice degli argomenti Introduzione: Motivazioni, Prove,
Fondamenti di Informatica 2 Linguaggi e Complessità : Logica I Parte Lucidi di M.Schaerf e A.Marchetti Spaccamela Fondamenti di Informatica 2: Logica Indice degli argomenti Introduzione: Motivazioni, Prove,
FOL: Linguaggio, Semantica e Calcolo
 FOL: Linguaggio, Semantica e Calcolo Integrazione materiale Brachman&Levesque Matteo Palmonari Dipartimento di Informatica, Sistemistica e Comunicazione Università di Milano-Bicocca Composizionalità del
FOL: Linguaggio, Semantica e Calcolo Integrazione materiale Brachman&Levesque Matteo Palmonari Dipartimento di Informatica, Sistemistica e Comunicazione Università di Milano-Bicocca Composizionalità del
Introduzione alla Logica Proposizionale
 Introduzione alla Logica Proposizionale Marta Cialdea Mayer a.a. 2010/2011 Indice 1 Logica e informatica 2 2 La logica proposizionale 4 2.1 Il linguaggio della logica proposizionale............... 4 2.2
Introduzione alla Logica Proposizionale Marta Cialdea Mayer a.a. 2010/2011 Indice 1 Logica e informatica 2 2 La logica proposizionale 4 2.1 Il linguaggio della logica proposizionale............... 4 2.2
14. Nozione di modello e verità di un predicato
 14. Nozione di modello e verità di un predicato Per definire la validità di un predicato facciamo uso della nozione di modello. Intuitivamente un modello definisce in modo primitivo l interpretazione delle
14. Nozione di modello e verità di un predicato Per definire la validità di un predicato facciamo uso della nozione di modello. Intuitivamente un modello definisce in modo primitivo l interpretazione delle
ESERCIZI DI LOGICA MATEMATICA A.A Alessandro Combi
 ESERCIZI DI LOGICA MATEMATICA A.A. 2015-16 Alessandro Combi Esercizio 1.7 Per ogni formula A, dimostrare che ρ(a) = min{n A F n } Soluzione: Chiamo rank(a) = min{n A F n }. Bisogna provare che rank segue
ESERCIZI DI LOGICA MATEMATICA A.A. 2015-16 Alessandro Combi Esercizio 1.7 Per ogni formula A, dimostrare che ρ(a) = min{n A F n } Soluzione: Chiamo rank(a) = min{n A F n }. Bisogna provare che rank segue
NOZIONI DI LOGICA. Premessa
 NOZIONI DI LOGICA Premessa Il compito principale della logica è quello di studiare il nesso di conseguenza logica tra proposizioni, predisponendo delle tecniche per determinare quando la verità di una
NOZIONI DI LOGICA Premessa Il compito principale della logica è quello di studiare il nesso di conseguenza logica tra proposizioni, predisponendo delle tecniche per determinare quando la verità di una
Logica per la Programmazione Corso di Laurea in INFORMATICA a.a. 2016/17
 Logica per la Programmazione Corso di Laurea in INFORMATICA a.a. 2016/17 Andrea Corradini e Francesca Levi Dipartimento di Informatica E-mail: andrea@di.unipi.it, francesca.levi@unipi.it A. Corradini e
Logica per la Programmazione Corso di Laurea in INFORMATICA a.a. 2016/17 Andrea Corradini e Francesca Levi Dipartimento di Informatica E-mail: andrea@di.unipi.it, francesca.levi@unipi.it A. Corradini e
Ragionamento Automatico Richiami di calcolo dei predicati
 Richiami di logica del primo ordine Ragionamento Automatico Richiami di calcolo dei predicati (SLL: Capitolo 7) Sintassi Semantica Lezione 2 Ragionamento Automatico Carlucci Aiello, 2004/05Lezione 2 0
Richiami di logica del primo ordine Ragionamento Automatico Richiami di calcolo dei predicati (SLL: Capitolo 7) Sintassi Semantica Lezione 2 Ragionamento Automatico Carlucci Aiello, 2004/05Lezione 2 0
ISTITUTO TECNICO STATALE COMMERCIALE E PER GEOMETRI A. MARTINI Castelfranco Veneto (TV) Elementi di Logica
 settembre 008 Elementi di Logica 1. Nozioni preliminari La logica studia come funziona il pensiero e il ragionamento espresso attraverso degli enunciati Il ragionamento è un sistema di enunciati che permette
settembre 008 Elementi di Logica 1. Nozioni preliminari La logica studia come funziona il pensiero e il ragionamento espresso attraverso degli enunciati Il ragionamento è un sistema di enunciati che permette
Logica per la Programmazione Corso di Laurea in INFORMATICA a.a. 2015/16
 Logica per la Programmazione Corso di Laurea in INFORMATICA a.a. 2015/16 Andrea Corradini e Francesca Levi Dipartimento di Informatica E-mail: andrea@di.unipi.it, francesca.levi@unipi.it A. Corradini e
Logica per la Programmazione Corso di Laurea in INFORMATICA a.a. 2015/16 Andrea Corradini e Francesca Levi Dipartimento di Informatica E-mail: andrea@di.unipi.it, francesca.levi@unipi.it A. Corradini e
LOGICA FUZZY, I LOGICA PROPOSIZIONALE CLASSICA VINCENZO MARRA
 LOGICA FUZZY, I LOGICA PROPOSIZIONALE CLASSICA VINCENZO MARRA 1. Sintassi L insieme dei numeri naturali è N = 1, 2,...}. Si consideri l alfabeto A = (, ), X,, $,,,,, }, e sia A l insieme delle stringhe
LOGICA FUZZY, I LOGICA PROPOSIZIONALE CLASSICA VINCENZO MARRA 1. Sintassi L insieme dei numeri naturali è N = 1, 2,...}. Si consideri l alfabeto A = (, ), X,, $,,,,, }, e sia A l insieme delle stringhe
C1: L C1 C2: L C2 C: C1 C2
 Abbiamo visto Gli agenti logici applicano inferenze a una base di conoscenza per derivare nuove informazioni. Concetti base della logica: sintassi: struttura formale delle sentenze semantica: verita` di
Abbiamo visto Gli agenti logici applicano inferenze a una base di conoscenza per derivare nuove informazioni. Concetti base della logica: sintassi: struttura formale delle sentenze semantica: verita` di
Logica per la Programmazione
 Logica per la Programmazione Lezione 2 Dimostrazione di Tautologie Tabelle di Verità Dimostrazioni per sostituzione Leggi del Calcolo Proposizionale A. Corradini e F.Levi Dip.to Informatica Logica per
Logica per la Programmazione Lezione 2 Dimostrazione di Tautologie Tabelle di Verità Dimostrazioni per sostituzione Leggi del Calcolo Proposizionale A. Corradini e F.Levi Dip.to Informatica Logica per
15. Nozione di modello e verità di un predicato
 15. Nozione di modello e verità di un predicato Def. 0.1 (modello di un linguaggio predicativo) Dato linguaggio predicativo L con costanti c j e predicati atomici P k (x 1,..., x n ) un modello per L è
15. Nozione di modello e verità di un predicato Def. 0.1 (modello di un linguaggio predicativo) Dato linguaggio predicativo L con costanti c j e predicati atomici P k (x 1,..., x n ) un modello per L è
LOGICA a.a Esempio di domande 2 prof.ssa Giovanna Corsi
 LOGICA a.a. 2014-2015 Esempio di domande 2 prof.ssa Giovanna Corsi January 4, 2015 1. (a) Cosa dice il cosiddetto Assioma di Aristotele? (b) Qual è la contraria di Tutti gli uomini sono mortali? (c) Qual
LOGICA a.a. 2014-2015 Esempio di domande 2 prof.ssa Giovanna Corsi January 4, 2015 1. (a) Cosa dice il cosiddetto Assioma di Aristotele? (b) Qual è la contraria di Tutti gli uomini sono mortali? (c) Qual
13. Nozione di modello e verità di un predicato
 13. Nozione di modello e verità di un predicato Def. 0.1 (modello di un linguaggio predicativo) Dato linguaggio predicativo L con costanti c j e predicati atomici P k (x 1,..., x n ) un modello per L è
13. Nozione di modello e verità di un predicato Def. 0.1 (modello di un linguaggio predicativo) Dato linguaggio predicativo L con costanti c j e predicati atomici P k (x 1,..., x n ) un modello per L è
INSIEMI. DEF. Un INSIEME è una qualsiasi collezione di oggetti.
 INSIEMI DEF. Un INSIEME è una qualsiasi collezione di oggetti. Esso è ben definito quando è chiaro se un oggetto appartiene o non appartiene all insieme stesso. Esempio. E possibile definire l insieme
INSIEMI DEF. Un INSIEME è una qualsiasi collezione di oggetti. Esso è ben definito quando è chiaro se un oggetto appartiene o non appartiene all insieme stesso. Esempio. E possibile definire l insieme
Elementi di Algebra e Logica Determinare la tavola della verità di ciascuna delle seguenti forme proposizionali:
 Elementi di Algebra e Logica 2008. 8. Logica. 1. Determinare la tavola della verità di ciascuna delle seguenti forme proposizionali: (a) p ( q r); (b) p (q r); (c) (p q) ( p r); (d) (p q) ( p r); (e) (p
Elementi di Algebra e Logica 2008. 8. Logica. 1. Determinare la tavola della verità di ciascuna delle seguenti forme proposizionali: (a) p ( q r); (b) p (q r); (c) (p q) ( p r); (d) (p q) ( p r); (e) (p
Specifica formale. Verifica formale (Prima parte) 03: Logica temporale lineare 1 / 26
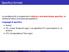 Specifica formale La correttezza di un programma è relativa a una determinata specifica: la verifica formale è connessa alle specifiche Linguaggi di specifica Automi LTL (Linear Temporal Logic): una specifica
Specifica formale La correttezza di un programma è relativa a una determinata specifica: la verifica formale è connessa alle specifiche Linguaggi di specifica Automi LTL (Linear Temporal Logic): una specifica
Logica per la Programmazione
 Logica per la Programmazione Lezione 4 Dimostrazione di Implicazioni Tautologiche Principio di sostituzione per l implicazione Occorrenze positive e negative Altre tecniche di dimostrazione Forme Normali
Logica per la Programmazione Lezione 4 Dimostrazione di Implicazioni Tautologiche Principio di sostituzione per l implicazione Occorrenze positive e negative Altre tecniche di dimostrazione Forme Normali
Logica per la Programmazione
 Logica del Primo Ordine: Motivazioni, Sintassi e Interpretazioni Logica per la Programmazione Lezione 8 Modelli, Formule Valide, Conseguenza Logica Proof Systems Regole di inferenza per Calcolo Proposizionale
Logica del Primo Ordine: Motivazioni, Sintassi e Interpretazioni Logica per la Programmazione Lezione 8 Modelli, Formule Valide, Conseguenza Logica Proof Systems Regole di inferenza per Calcolo Proposizionale
Linguaggi. Claudio Sacerdoti Coen 04/03/ : Forme normali. Universitá di Bologna. Forme normali e canoniche
 Linguaggi 9: Forme normali Universitá di Bologna 04/03/2011 Outline 1 Wikipedia: In matematica la forma canonica di un oggetto à una maniera uniforme utilizzata per descriverlo in
Linguaggi 9: Forme normali Universitá di Bologna 04/03/2011 Outline 1 Wikipedia: In matematica la forma canonica di un oggetto à una maniera uniforme utilizzata per descriverlo in
Sintassi. Linguaggi. 4: Sintassi. Claudio Sacerdoti Coen. Universitá di Bologna 24/02/2011. Claudio Sacerdoti Coen
 Linguaggi 4: Universitá di Bologna 24/02/2011 Outline 1 Wikipedia: La sintassi è la branca della linguistica che studia i diversi modi in cui le parole si uniscono tra loro per formare
Linguaggi 4: Universitá di Bologna 24/02/2011 Outline 1 Wikipedia: La sintassi è la branca della linguistica che studia i diversi modi in cui le parole si uniscono tra loro per formare
15. Nozione di modello e verità di un predicato
 15. Nozione di modello e verità di un predicato Def. (modello di un linguaggio predicativo) Dato linguaggio predicativo L con costanti c j e predicati atomici P k (x 1,..., x n ) un modello per L è dato
15. Nozione di modello e verità di un predicato Def. (modello di un linguaggio predicativo) Dato linguaggio predicativo L con costanti c j e predicati atomici P k (x 1,..., x n ) un modello per L è dato
Logica booleana. Bogdan Maris ( )
 Logica booleana 1 Algebra di Boole Opera con i soli valori di verità 0 o 1 (variabili booleane o logiche) La struttura algebrica studiata dall'algebra booleana è finalizzata all'elaborazione di espressioni
Logica booleana 1 Algebra di Boole Opera con i soli valori di verità 0 o 1 (variabili booleane o logiche) La struttura algebrica studiata dall'algebra booleana è finalizzata all'elaborazione di espressioni
Nome: Corso di laurea: Matricola:
 Nome: Corso di laurea: Matricola: Università degli studi di Trieste Corso di Laurea in Informatica Esame di Fondamenti Logici dell Informatica 24 Aprile 2006, versione A Vero/Falso Dire se le seguenti
Nome: Corso di laurea: Matricola: Università degli studi di Trieste Corso di Laurea in Informatica Esame di Fondamenti Logici dell Informatica 24 Aprile 2006, versione A Vero/Falso Dire se le seguenti
Un po di logica. Christian Ferrari. Laboratorio di matematica
 Un po di logica Christian Ferrari Laboratorio di matematica 1 Introduzione La logica è la disciplina che studia le condizioni di correttezza del ragionamento. Il suo scopo è quindi quello di elaborare
Un po di logica Christian Ferrari Laboratorio di matematica 1 Introduzione La logica è la disciplina che studia le condizioni di correttezza del ragionamento. Il suo scopo è quindi quello di elaborare
Cenni di logica e calcolo proposizionale
 Cenni di logica e calcolo proposizionale Corso di Laurea in Informatica Università degli Studi di Bari (sede Brindisi) Analisi Matematica S.Milella (sabina.milella@uniba.it) Cenni di logica 1 / 10 Proposizioni
Cenni di logica e calcolo proposizionale Corso di Laurea in Informatica Università degli Studi di Bari (sede Brindisi) Analisi Matematica S.Milella (sabina.milella@uniba.it) Cenni di logica 1 / 10 Proposizioni
Logica per la Programmazione
 Logica del Primo Ordine: Motivazioni, Sintassi e Interpretazioni Logica per la Programmazione Lezione 7 Formule Valide, Conseguenza Logica Proof System per la Logica del Primo Ordine Leggi per i Quantificatori
Logica del Primo Ordine: Motivazioni, Sintassi e Interpretazioni Logica per la Programmazione Lezione 7 Formule Valide, Conseguenza Logica Proof System per la Logica del Primo Ordine Leggi per i Quantificatori
Logica per la Programmazione
 Logica per la Programmazione Lezione 12 Linguaggio di Programmazione Imperativo: Sintassi e Semantica Concetto di Tripla di Hoare Soddisfatta pag. 1 Introduzione Dall inizio del corso ad ora abbiamo introdotto,
Logica per la Programmazione Lezione 12 Linguaggio di Programmazione Imperativo: Sintassi e Semantica Concetto di Tripla di Hoare Soddisfatta pag. 1 Introduzione Dall inizio del corso ad ora abbiamo introdotto,
Errata corrige del libro Introduzione alla logica e al linguaggio matematico
 Errata corrige del libro Introduzione alla logica e al linguaggio matematico 28 gennaio 2009 Capitolo 1 Pag. 7, Definizione 6. Il complemento di un sottoinsieme A di I è il sottoinsieme A = {x I : x /
Errata corrige del libro Introduzione alla logica e al linguaggio matematico 28 gennaio 2009 Capitolo 1 Pag. 7, Definizione 6. Il complemento di un sottoinsieme A di I è il sottoinsieme A = {x I : x /
Introduzione alla logica proposizionale
 Introduzione alla logica proposizionale Mauro Bianco Questa frase è falsa Contents 1 Proposizioni 1 2 Altri operatori 4 Nota : Le parti delimitate da *** sono da considerarsi facoltative. 1 Proposizioni
Introduzione alla logica proposizionale Mauro Bianco Questa frase è falsa Contents 1 Proposizioni 1 2 Altri operatori 4 Nota : Le parti delimitate da *** sono da considerarsi facoltative. 1 Proposizioni
Richiami teorici ed esercizi di Logica
 Facoltà di ingegneria Università della Calabria Corsi di Potenziamento Matematica e Logica A. A. 2008-2009 Richiami teorici ed esercizi di Logica Proposizioni logiche: Ogni espressione matematica alla
Facoltà di ingegneria Università della Calabria Corsi di Potenziamento Matematica e Logica A. A. 2008-2009 Richiami teorici ed esercizi di Logica Proposizioni logiche: Ogni espressione matematica alla
T1: Logica, discorso e conoscenza. Logica classica
 T1: Logica, discorso e conoscenza Primo modulo: Logica classica ovvero Deduzione formale vs verità: un introduzione ai teoremi limitativi Simone Martini Dipartimento di Scienze dell Informazione Alma mater
T1: Logica, discorso e conoscenza Primo modulo: Logica classica ovvero Deduzione formale vs verità: un introduzione ai teoremi limitativi Simone Martini Dipartimento di Scienze dell Informazione Alma mater
RISOLUZIONE IN LOGICA PROPOSIZIONALE. Giovanna D Agostino Dipartimento di Matemaica e Informatica, Università di Udine
 RISOLUZIONE IN LOGICA PROPOSIZIONALE Giovanna D Agostino Dipartimento di Matemaica e Informatica, Università di Udine 1. Risoluzione Definitione 1.1. Un letterale l è una variabile proposizionale (letterale
RISOLUZIONE IN LOGICA PROPOSIZIONALE Giovanna D Agostino Dipartimento di Matemaica e Informatica, Università di Udine 1. Risoluzione Definitione 1.1. Un letterale l è una variabile proposizionale (letterale
Intelligenza Artificiale I
 Intelligenza rtificiale I Logica formale Primi elementi Marco Piastra Logica formale - Primi elementi - Sottoinsiemi e operatori Sottoinsiemi U Insieme di riferimento (insieme sostegno) {,, C, } Collezione
Intelligenza rtificiale I Logica formale Primi elementi Marco Piastra Logica formale - Primi elementi - Sottoinsiemi e operatori Sottoinsiemi U Insieme di riferimento (insieme sostegno) {,, C, } Collezione
LOGICA DEL PRIMO ORDINE: PROOF SYSTEM. Corso di Logica per la Programmazione A.A. 2013/14 Andrea Corradini
 LOGICA DEL PRIMO ORDINE: PROOF SYSTEM Corso di Logica per la Programmazione A.A. 2013/14 Andrea Corradini LOGICA DEL PRIMO ORDINE: RIASSUNTO Sintassi: grammatica libera da contesto (BNF), parametrica rispetto
LOGICA DEL PRIMO ORDINE: PROOF SYSTEM Corso di Logica per la Programmazione A.A. 2013/14 Andrea Corradini LOGICA DEL PRIMO ORDINE: RIASSUNTO Sintassi: grammatica libera da contesto (BNF), parametrica rispetto
Logica per la Programmazione
 Logica per la Programmazione Lezione 11 Linguaggio di Programmazione Imperativo: Sintassi e Semantica Concetto di Tripla di Hoare Soddisfatta pag. 1 Introduzione Dall inizio del corso ad ora abbiamo introdotto,
Logica per la Programmazione Lezione 11 Linguaggio di Programmazione Imperativo: Sintassi e Semantica Concetto di Tripla di Hoare Soddisfatta pag. 1 Introduzione Dall inizio del corso ad ora abbiamo introdotto,
Sesto modulo: Logica Obiettivi 1. individuare dei "calcoli logici" che consentano di meccanizzare l attività deduttiva
 Sesto modulo: Logica Obiettivi 1. individuare dei "calcoli logici" che consentano di meccanizzare l attività deduttiva 2. stabilire quali ragionamenti sono corretti e quali no 3. distinguere tra condizione
Sesto modulo: Logica Obiettivi 1. individuare dei "calcoli logici" che consentano di meccanizzare l attività deduttiva 2. stabilire quali ragionamenti sono corretti e quali no 3. distinguere tra condizione
9 Calcolo dei sequenti LC p
 9 Calcolo dei sequenti LC p In questa sezione mostriamo un metodo più elegante, semplice e soprattutto AUTOMATICO per mostrare se una proposizione è valida o meno e soddisfacibile o meno. Tale metodo è
9 Calcolo dei sequenti LC p In questa sezione mostriamo un metodo più elegante, semplice e soprattutto AUTOMATICO per mostrare se una proposizione è valida o meno e soddisfacibile o meno. Tale metodo è
Intelligenza Artificiale. Logica Prime definizioni
 Intelligenza rtificiale Logica Prime definizioni Marco Piastra Logica formale (Parte ) - Parte Sottoinsiemi lgebra di oole Linguaggio proposizionale Soddisfacibilità Conseguenza logica Logica formale (Parte
Intelligenza rtificiale Logica Prime definizioni Marco Piastra Logica formale (Parte ) - Parte Sottoinsiemi lgebra di oole Linguaggio proposizionale Soddisfacibilità Conseguenza logica Logica formale (Parte
Logica degli enunciati; Operazioni con le proposizioni; Proprietà delle operazioni logiche; Tautologie; Regole di deduzione; Logica dei predicati;
 Logica degli enunciati; Operazioni con le proposizioni; Proprietà delle operazioni logiche; Tautologie; Regole di deduzione; Logica dei predicati; Implicazione logica. Equivalenza logica; Condizione necessaria,
Logica degli enunciati; Operazioni con le proposizioni; Proprietà delle operazioni logiche; Tautologie; Regole di deduzione; Logica dei predicati; Implicazione logica. Equivalenza logica; Condizione necessaria,
Intelligenza Artificiale. Breve introduzione alla logica classica (Parte 1)
 Intelligenza Artificiale Breve introduzione alla logica classica (Parte ) Marco Piastra Logica formale (Parte ) - Introduzione alla logica formale Parte. Preambolo: algebra di Boole, proposizioni, conseguenza
Intelligenza Artificiale Breve introduzione alla logica classica (Parte ) Marco Piastra Logica formale (Parte ) - Introduzione alla logica formale Parte. Preambolo: algebra di Boole, proposizioni, conseguenza
Logica proposizionale
 Università di Bergamo Facoltà di Ingegneria Intelligenza Artificiale Paolo Salvaneschi A7_2 V1.1 Logica proposizionale Il contenuto del documento è liberamente utilizzabile dagli studenti, per studio personale
Università di Bergamo Facoltà di Ingegneria Intelligenza Artificiale Paolo Salvaneschi A7_2 V1.1 Logica proposizionale Il contenuto del documento è liberamente utilizzabile dagli studenti, per studio personale
Sintassi e semantica della logica proposizionale
 Sintassi e semantica della logica proposizionale 1 Il linguaggio proposizionale L 0 Definizione 1.1 (lfabeto di L 0 ). L alfabeto di L 0 si compone dei seguenti insiemi di simboli SIMOLI LOGICI : i connettivi,,,,.
Sintassi e semantica della logica proposizionale 1 Il linguaggio proposizionale L 0 Definizione 1.1 (lfabeto di L 0 ). L alfabeto di L 0 si compone dei seguenti insiemi di simboli SIMOLI LOGICI : i connettivi,,,,.
Maiuscole e minuscole
 Maiuscole e minuscole Abilità interessate Distinguere tra processi induttivi e processi deduttivi. Comprendere il ruolo e le caratteristiche di un sistema assiomatico. Riconoscere aspetti sintattici e
Maiuscole e minuscole Abilità interessate Distinguere tra processi induttivi e processi deduttivi. Comprendere il ruolo e le caratteristiche di un sistema assiomatico. Riconoscere aspetti sintattici e
Intelligenza Artificiale. Logica proposizionale classica (Parte 1)
 Intelligenza Artificiale Logica proposizionale classica (Parte ) Marco Piastra Logica formale (Parte ) - Introduzione alla logica formale Parte. Preambolo: algebra di Boole, proposizioni, conseguenza logica
Intelligenza Artificiale Logica proposizionale classica (Parte ) Marco Piastra Logica formale (Parte ) - Introduzione alla logica formale Parte. Preambolo: algebra di Boole, proposizioni, conseguenza logica
Esercitazioni per il corso di Logica Matematica
 Esercitazioni per il corso di Logica Matematica Luca Motto Ros 27 febbraio 2005 Nota importante. Queste pagine contengono appunti personali dell esercitatore e sono messe a disposizione nel caso possano
Esercitazioni per il corso di Logica Matematica Luca Motto Ros 27 febbraio 2005 Nota importante. Queste pagine contengono appunti personali dell esercitatore e sono messe a disposizione nel caso possano
Introduzione alla logica proposizionale
 Introduzione alla logica proposizionale Francesco Paoli Dispense per gli studenti March 6, 2013 1 Linguaggi proposizionali Nel presente modulo studieremo la logica proposizionale classica. In generale,
Introduzione alla logica proposizionale Francesco Paoli Dispense per gli studenti March 6, 2013 1 Linguaggi proposizionali Nel presente modulo studieremo la logica proposizionale classica. In generale,
Logica per la Programmazione
 Logica per la Programmazione Lezione 12 Linguaggio di Programmazione Imperativo: Sintassi e Semantica Tripla di Hoare soddisfatta A. Corradini e F.Levi Dip.to Informatica Logica per la Programmazione a.a.
Logica per la Programmazione Lezione 12 Linguaggio di Programmazione Imperativo: Sintassi e Semantica Tripla di Hoare soddisfatta A. Corradini e F.Levi Dip.to Informatica Logica per la Programmazione a.a.
Intelligenza Artificiale I
 Intelligenza Artificiale I - AA 27/28 Intelligenza Artificiale I Logica formale Introduzione Marco Piastra Logica formale - Introduzione - Intelligenza Artificiale I - AA 27/28 Sistematicità del linguaggio
Intelligenza Artificiale I - AA 27/28 Intelligenza Artificiale I Logica formale Introduzione Marco Piastra Logica formale - Introduzione - Intelligenza Artificiale I - AA 27/28 Sistematicità del linguaggio
