Logica dei Predicati (o Logica del Primo Ordine)
|
|
|
- Norma Pace
- 5 anni fa
- Visualizzazioni
Transcript
1 Logica dei Predicati (o Logica del Primo Ordine) Il mondo è analizzato in termini di OGGETTI, PROPRIETÀ, RELAZIONI. I numeri primi maggiori di due sono dispari oggetti: due; relazioni e proprietà: essere un numero primo, essere dispari (proprietà), essere maggiore di (relazione a due argomenti); Per ogni oggetto x, se x è un numero primo e x è maggiore di due, allora x è dispari: x(primo(x) maggiore(x, 2) dispari(x)) x: variabile 2: costante primo, dispari, maggiore: simboli di predicato : quantificatore universale connettivi proposizionali Atomi: relazioni tra oggetti Quantificatori: per ogni ( ), esiste ( ) Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 1 / 41
2 Logica dei predicati: sintassi (linguaggi del primo ordine) Alfabeto : 1 Simboli logici (comuni a tutti i linguaggi del primo ordine): Variabili: x, y, z, x 1, x 2,... (insieme infinito); Connettivi proposizionali e costanti, ; Quantificatori:, ; Simboli separatori (parentesi e virgola); eventualmente, se si tratta di un linguaggio con uguaglianza, il simbolo di predicato =. 2 Simboli non logici (specifici del singolo linguaggio): simboli di predicato, con associata arità : {p n, q m, r k,...}; l insieme dei simboli di predicato non logici può essere vuoto solo se si tratta di un linguaggio con uguaglianza (che ha comunque il simbolo = ); altrimenti è un insieme non vuoto. Costanti: a, b, c, a 1, a 2,...; Simboli funzionali, con associata arità : f n 1 1, f n 2 2,... Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 2 / 41
3 Termini Una formula atomica rappresenta il fatto che una data relazione vale tra alcuni oggetti. maggiore(2, 0) Per definire le formule si deve prima definire una classe di espressioni con le quali si possano denotare gli oggetti: i termini del linguaggio. Definizione induttiva dell insieme dei termini: Ogni variabile è un termine Ogni costante è un termine Se t 1,.., t n sono termini e f n è un simbolo funzionale, allora f (t 1,..., t n ) è un termine Termini chiusi: senza variabili Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 3 / 41
4 Termini Una formula atomica rappresenta il fatto che una data relazione vale tra alcuni oggetti. maggiore(2, 0) Per definire le formule si deve prima definire una classe di espressioni con le quali si possano denotare gli oggetti: i termini del linguaggio. Definizione induttiva dell insieme dei termini: Ogni variabile è un termine Ogni costante è un termine Se t 1,.., t n sono termini e f n è un simbolo funzionale, allora f (t 1,..., t n ) è un termine Termini chiusi: senza variabili Definizione ricorsiva dell insieme vars(t) delle variabili che occorrono in un termine t se t è una variabile x, allora vars(t) = {x} se t è una costante, allora vars(t) = se t = f (t 1,..., t n ), allora vars(t) = vars(t 1 )... vars(t n ) Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 3 / 41
5 Formule 1 Se p è un simbolo di predicato a n argomenti, e t 1,..., t n sono termini, allora p(t 1,..., t n ) è una formula (formula atomica) 2 e sono formule (atomiche) 3 se A è una formula, allora anche A è una formula 4 se A e B sono formule, allora anche (A B), (A B), (A B), (A B) sono formule 5 Se A è una formula e x una variabile, allora xa e xa sono formule 6 Nient altro è una formula Esempi fratello(caino, abele) fratello(giovanni, robin_hood) fratello(x, abele) assassino(x) x(fratello(x, abele) assassino(x)) x(fratello(x, abele) assassino(x)) x(fratello(x, y) fratello(y, x)) x(padre(x, abele) padre(x, caino)) x y(fratello(x, y) z(padre(z, x) padre(z, y))) Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 4 / 41
6 Variabili libere e vincolate Scopo o campo d azione di un quantificatore: di x in xa: A di x in xa: A scopo di x scopo di x {}}{{}}{ p(c) x (q(x, c) y (p(y) r(x, y, z)) ) x y q(x, y) }{{}}{{} scopo di y scopo di y Occorrenza vincolata di una variabile: x è la variabile di un quantificatore oppure occorre nello scopo di un quantificatore x o x Occorrenza libera di x: occorrenza non vincolata p( x ) x (q( x, y ) q(c, x )) x è libera in A sse ha almeno un occorrenza libera in A (variabili libere variabili globali variabili vincolate variabili locali) Formula chiusa : senza variabili libere Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 5 / 41
7 Definizione ricorsiva dell insieme delle variabili libere in una formula se A = p(t 1,..., t n ) allora free_vars(a) = vars(t 1 )... vars(t n ) se A = o A = allora free_vars(a) = se A = A 1 allora free_vars(a) = free_vars(a 1 ) se A = A 1 A 2 dove è un connettivo binario, allora free_vars(a) = free_vars(a 1 ) free_vars(a 2 ) se A = Qx A 1 dove Q è un quantificatore, allora free_vars(a) = free_vars(a 1 ) {x} Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 6 / 41
8 Sostituzione di variabili con termini Se A è una formula, x una variabile e t un termine: A[t/x] denota la formula che si ottiene da A sostituendo ogni occorrenza livera della variabile x con il termine t Sostituzione simultanea: Esempio: A[t 1 /x 1,..., t n /x n ] p(x, y)[f (y)/x, f (x)/y] = p(f (y), f (x)) p(x, y)[f (y)/x][f (x)/y] = p(f (y), y)[f (x)/y] = p(f (f (x)), f (x)) p(x, y)[f (x)/y][f (y)/x] = p(x, f (x))[f (y)/x] = p(f (y), f (f (y))) N.B. Solo le occorrenze libere vengono sostituite: p( x, c) x(q(x, y ) y r(y))[t 1 /x, t 2 /y] = p(t 1, c) x(q(x, t 2 ) y r(y)) Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 7 / 41
9 Significato delle formule x p(x) y q(y) z (p(z) q(z)) è vera o falsa? Dove? Nel dominio D = {1, 2} Come sono interpretati p e q? p(x) = x è pari q(x) = x è maggiore o uguale a 1 Estensione di p: {2} Estensione di q: {1, 2} x p(x) è vero se esiste d {1, 2} tale che d {2} x q(x) è vero se esiste d {1, 2} tale che d {1, 2} z (p(z) q(z)) è vero se esiste d {1, 2} tale che d {2} e d {1, 2} Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 8 / 41
10 Significato delle formule x p(x) y q(y) z (p(z) q(z)) è vera o falsa? Dove? Nel dominio D = {1, 2} Come sono interpretati p e q? p(x) = x è pari q(x) = x è maggiore o uguale a 1 Estensione di p: {2} Estensione di q: {1, 2} x p(x) è vero se esiste d {1, 2} tale che d {2} x q(x) è vero se esiste d {1, 2} tale che d {1, 2} z (p(z) q(z)) è vero se esiste d {1, 2} tale che d {2} e d {1, 2} Consideriamo ora il dominio D = {1, 2} p(x) = x è pari; estensione: {2} q(x) = x è dispari; estensione: {1} xp(x) è vero se esiste d {1, 2} tale che d {2} xq(x) è vero se esiste d {1, 2} tale che d {1} z(p(z) q(z)) è vero se esiste d {1, 2} tale che d {2} e d {1} Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 8 / 41
11 Semantica: interpretazione di un linguaggio Sia L un linguaggio, con costanti C, simboli funzionali F e simboli di predicato P Interpretazione di L: 1 Insieme non vuoto D (dominio o universo dell interpretazione) 2 Funzione di interpretazione che associa: a ogni c C un elemento M(c) D a ogni f n F una funzione M(f ) : D n D a ogni p n P una relazione n-aria su D: M(p) D n Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 9 / 41
12 Semantica: interpretazione di un linguaggio Sia L un linguaggio, con costanti C, simboli funzionali F e simboli di predicato P Interpretazione di L: 1 Insieme non vuoto D (dominio o universo dell interpretazione) 2 Funzione di interpretazione che associa: a ogni c C un elemento M(c) D a ogni f n F una funzione M(f ) : D n D a ogni p n P una relazione n-aria su D: M(p) D n Per linguaggi con eguaglianza: = è un simbolo logico e l interpretazione di = è sempre l identità: M(=) = {< d, d > d D} Interpretazione di una formula A: interpetazione di qualsiasi linguaggio che contenga tutti i simboli non logici di A Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 9 / 41
13 Esempio Sono interpretazioni di x p(a, x), e del linguaggio con C = {a}, F =, P = {p}: M 1 con dominio IN, M(a) = 0, e M(p) = { n, m IN 2 n m}. Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 10 / 41
14 Esempio Sono interpretazioni di x p(a, x), e del linguaggio con C = {a}, F =, P = {p}: M 1 con dominio IN, M(a) = 0, e M(p) = { n, m IN 2 n m}. M 2 con dominio IN, M(a) = 1, e M(p) = { n, m IN 2 n m}. Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 10 / 41
15 Esempio Sono interpretazioni di x p(a, x), e del linguaggio con C = {a}, F =, P = {p}: M 1 con dominio IN, M(a) = 0, e M(p) = { n, m IN 2 n m}. M 2 con dominio IN, M(a) = 1, e M(p) = { n, m IN 2 n m}. M 3 con dominio Z, M(a) = 0, e M(p) = { x, y Z 2 x y}. Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 10 / 41
16 Esempio Sono interpretazioni di x p(a, x), e del linguaggio con C = {a}, F =, P = {p}: M 1 con dominio IN, M(a) = 0, e M(p) = { n, m IN 2 n m}. M 2 con dominio IN, M(a) = 1, e M(p) = { n, m IN 2 n m}. M 3 con dominio Z, M(a) = 0, e M(p) = { x, y Z 2 x y}. M 4 con dominio S uguale all insieme di tutte le sequenze finite di caratteri alfanumerici, M(a) = ɛ (la sequenza vuota), e M(p) = { s 1, s 2 S 2 s 1 è una sottosequenza di s 2 }. Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 10 / 41
17 Esempio Sono interpretazioni di x p(a, x), e del linguaggio con C = {a}, F =, P = {p}: M 1 con dominio IN, M(a) = 0, e M(p) = { n, m IN 2 n m}. M 2 con dominio IN, M(a) = 1, e M(p) = { n, m IN 2 n m}. M 3 con dominio Z, M(a) = 0, e M(p) = { x, y Z 2 x y}. M 4 con dominio S uguale all insieme di tutte le sequenze finite di caratteri alfanumerici, M(a) = ɛ (la sequenza vuota), e M(p) = { s 1, s 2 S 2 s 1 è una sottosequenza di s 2 }. M 5 con dominio D = {0, 1, 2}, M(a) = 1 e M(p) = { 0, 1, 0, 2, 1, 0, 2, 1 } Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 10 / 41
18 Interpretazione dei termini chiusi 1 se c è una costante in L, l interpretazione di c è M(c); 2 se f (t 1,..., t n ) è un termine chiuso, la sua interpretazione è M(f (t 1,..., t n )) = M(f )(M(t 1 ),..., M(t n )) Esempio: se C = {zero}, F = {succ, sum, times} e M = IN, {0}, {λx.x + 1, +, } : M(times(succ(succ(zero)), sum(succ(zero), zero))) = M(times)(M(succ(succ(zero))), M(sum(succ(zero), zero))) = M(succ(succ(zero)) M(sum(succ(zero), zero)) = M(succ)(M(succ(zero))) M(sum)(M(succ(zero)), M(zero)) = (M(succ(zero)) + 1) (M(succ(zero)) + M(zero)) = (M(succ)(M(zero)) + 1) (M(succ)(M(zero)) + 0) = ((M(zero) + 1) + 1) ((M(zero) + 1) + 0) = ((0 + 1) + 1) ((0 + 1) + 0) = 2 1 = 2 Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 11 / 41
19 Interpretazione di termini con variabili Come interpretiamo le variabili? Assegnazione: s : X D Interpretazione di un termine t secondo l assegnazione s: s(t) 1 se x X è una variabile, allora s(x) = s(x); 2 se c è una costante in L, allora s(c) = M(c); 3 se f (t 1,..., t n ) è un termine, allora s(t) = M(f )(s(t 1 ),..., s(t n )). Esempio: M su IN, con M(f ) = λn.2 n e s tale che s(x) = 3: s(f (x)) = M(f )(s(x)) = (λn.2 n)(s(x)) = (λn.2 n)3 = 2 3 = 6 Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 12 / 41
20 Interpretazione delle formule: assegnazioni Dipende dall interpretazione delle variabili libere che occorrono nella formula. Sia M su IN, M(f ) = λn.2 n, M(p) = { n, m n 2 m}, e s tale che s(x) = 3 e s(y) = 5; s tale che s (x) = 4 e s (y) = 5 La formula p(x, f (y)) è vera in M secondo l assegnazione s, (è vero che ) Ma è falsa in M secondo l assegnazione s (è falso che ) Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 13 / 41
21 Varianti di un assegnazione x-varianti s è una x-variante di s sse per ogni variabile y diversa da x: s (y) = s(y). Esempio: le due assegnazioni qui sotto, s e s, sono x 4 -varianti l una dell altra. x 1 1 x 1 1 x 2 2 x 2 2 x 3 3 x 3 3 x 4 4 x 4 44 x 5 5 x s = s[44/x 4 ] e s = s [4/x 4 ] Notazione: s[d/x] è la x-variante di s che assegna d a x N.B. Per ogni assegnazione s e variabile x, s è una x-variante di se stessa: s = s[s(x)/x] Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 14 / 41
22 Semantica di una formula in un interpretazione, secondo un assegnazione data A è vera in M secondo l assegnazione s (o s soddisfa A in M) (M, s) = A 1 (M, s) = p(t 1,..., t n ) sse s(t 1 ),..., s(t n ) M(p) 2 (M, s) = e (M, s) = ; 3 (M, s) = A sse (M, s) = A; 4 (M, s) = A B sse (M, s) = A e (M, s) = B; 5 (M, s) = A B sse (M, s) = A oppure (M, s) = B; 6 (M, s) = A B sse (M, s) = A oppure (M, s) = B; 7 (M, s) = A B sse (M, s) = A e (M, s) = B, oppure (M, s) = A e (M, s) = B 8 (M, s) = xa sse per ogni d D: (M, s[d/x]) = A 9 (M, s) = xa sse esiste d D, tale che: (M, s[d/x]) = A Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 15 / 41
23 Esempio Sia M con D = {1, 2}, M(p) = {2} e M(q) = {1, 2}, e sia s qualsiasi assegnazione su D (M, s) = y(p(y) q(y)) se e solo se esiste d {1, 2} tale che (M, s[d/y]) = p(y) q(y). Poiché ci sono solo due oggetti nel dominio, questo vale se e solo se si verifica uno di questi due casi: 1 (M, s[1/y]) = p(y) q(y): perché ciò sia vero si devono verificare entrambi i casi seguenti: a. (M, s[1/y]) = p(y): ciò vale se e solo se s[1/y](y) M(p), cioè 1 {2}, ma questo è falso. b. (M, s[1/y]) = q(y). Poiché (a) è falso, è falso anche il caso 1. 2 (M, s[2/y]) = p(y) q(y): perché ciò sia vero si devono verificare entrambi i casi seguenti: a. (M, s[2/y]) = p(y): ciò vale se e solo se s[2/y](y) M(p), cioè 2 {2}, e questo è vero. b. (M, s[2/y]) = q(y): ciò vale se e solo se s[2/y](y) M(q), cioè 2 {1, 2}, e anche questo è vero. Quindi il caso 2 è vero. Logica Perciò dei Predicati è vero (Logicache per l Informatica) per ogni assegnazione 02: First Order Logic s, (M, s) = y(p(y) q(y)). 16 / 41
24 Esercizi Siano: M con dominio D = {1, 2}, M(p) = {2} e M(q) = {1, 2} M uguale a M tranne che M(q) = {1}. M uguale a M tranne che M (p) =. Sia inoltre s qualsiasi assegnazione su D. 1 Verificare se (M, s) = y(p(y) q(y)). 2 Verificare se (M, s) = x(p(x) q(x)). 3 Verificare se (M, s) = x(p(x) q(x)). 4 Verificare se (M, s) = x(p(x) q(x)). 5 Verificare se (M, s) = x(p(x) q(x)). 6 Verificare se (M, s) = x p(x) x q(x). 7 Verificare se (M, s) = x p(x) x q(x). 8 Verificare se (M, s) = x(p(x) q(x)) 9 Verificare se (M, s) = x(p(x) q(x)) 10 Verificare se (M, s) = x(p(x) q(x)) Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 17 / 41
25 Quando un assegnazione non soddisfa una formula? 1 (M, s) = p(t 1,..., t n ) sse (M, s) = A Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 18 / 41
26 Quando un assegnazione non soddisfa una formula? (M, s) = A 1 (M, s) = p(t 1,..., t n ) sse s(t 1 ),..., s(t n ) M(p) 2 (M, s) = è sempre falso e (M, s) = è sempre vero; 3 (M, s) = A sse Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 18 / 41
27 Quando un assegnazione non soddisfa una formula? (M, s) = A 1 (M, s) = p(t 1,..., t n ) sse s(t 1 ),..., s(t n ) M(p) 2 (M, s) = è sempre falso e (M, s) = è sempre vero; 3 (M, s) = A sse (M, s) = A; 4 (M, s) = A B sse Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 18 / 41
28 Quando un assegnazione non soddisfa una formula? (M, s) = A 1 (M, s) = p(t 1,..., t n ) sse s(t 1 ),..., s(t n ) M(p) 2 (M, s) = è sempre falso e (M, s) = è sempre vero; 3 (M, s) = A sse (M, s) = A; 4 (M, s) = A B sse (M, s) = A oppure (M, s) = B; 5 (M, s) = A B sse Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 18 / 41
29 Quando un assegnazione non soddisfa una formula? (M, s) = A 1 (M, s) = p(t 1,..., t n ) sse s(t 1 ),..., s(t n ) M(p) 2 (M, s) = è sempre falso e (M, s) = è sempre vero; 3 (M, s) = A sse (M, s) = A; 4 (M, s) = A B sse (M, s) = A oppure (M, s) = B; 5 (M, s) = A B sse (M, s) = A e (M, s) = B; 6 (M, s) = A B sse Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 18 / 41
30 Quando un assegnazione non soddisfa una formula? (M, s) = A 1 (M, s) = p(t 1,..., t n ) sse s(t 1 ),..., s(t n ) M(p) 2 (M, s) = è sempre falso e (M, s) = è sempre vero; 3 (M, s) = A sse (M, s) = A; 4 (M, s) = A B sse (M, s) = A oppure (M, s) = B; 5 (M, s) = A B sse (M, s) = A e (M, s) = B; 6 (M, s) = A B sse (M, s) = A e (M, s) = B; 7 (M, s) = A B sse Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 18 / 41
31 Quando un assegnazione non soddisfa una formula? (M, s) = A 1 (M, s) = p(t 1,..., t n ) sse s(t 1 ),..., s(t n ) M(p) 2 (M, s) = è sempre falso e (M, s) = è sempre vero; 3 (M, s) = A sse (M, s) = A; 4 (M, s) = A B sse (M, s) = A oppure (M, s) = B; 5 (M, s) = A B sse (M, s) = A e (M, s) = B; 6 (M, s) = A B sse (M, s) = A e (M, s) = B; 7 (M, s) = A B sse (M, s) = A e (M, s) = B, oppure (M, s) = A e (M, s) = B 8 (M, s) = xa sse Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 18 / 41
32 Quando un assegnazione non soddisfa una formula? (M, s) = A 1 (M, s) = p(t 1,..., t n ) sse s(t 1 ),..., s(t n ) M(p) 2 (M, s) = è sempre falso e (M, s) = è sempre vero; 3 (M, s) = A sse (M, s) = A; 4 (M, s) = A B sse (M, s) = A oppure (M, s) = B; 5 (M, s) = A B sse (M, s) = A e (M, s) = B; 6 (M, s) = A B sse (M, s) = A e (M, s) = B; 7 (M, s) = A B sse (M, s) = A e (M, s) = B, oppure (M, s) = A e (M, s) = B 8 (M, s) = xa sse esiste d D, tale che: (M, s[d/x]) = A 9 (M, s) = xa sse Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 18 / 41
33 Quando un assegnazione non soddisfa una formula? (M, s) = A 1 (M, s) = p(t 1,..., t n ) sse s(t 1 ),..., s(t n ) M(p) 2 (M, s) = è sempre falso e (M, s) = è sempre vero; 3 (M, s) = A sse (M, s) = A; 4 (M, s) = A B sse (M, s) = A oppure (M, s) = B; 5 (M, s) = A B sse (M, s) = A e (M, s) = B; 6 (M, s) = A B sse (M, s) = A e (M, s) = B; 7 (M, s) = A B sse (M, s) = A e (M, s) = B, oppure (M, s) = A e (M, s) = B 8 (M, s) = xa sse esiste d D, tale che: (M, s[d/x]) = A 9 (M, s) = xa sse per ogni d D: (M, s[d/x]) = A Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 18 / 41
34 Verità e falsità di una formula in una interpretazione A è vera in M(M = A) sse per ogni assegnazione s su M: (M, s) = A. A è falsa in una interpretazione M sse Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 19 / 41
35 Verità e falsità di una formula in una interpretazione A è vera in M(M = A) sse per ogni assegnazione s su M: (M, s) = A. A è falsa in una interpretazione M sse nessuna assegnazione la soddisfa: per ogni assegnazione s su M: (M, s) = A Una formula può non essere né vera né falsa in una interpretazione M Proprietà della verità/falsità 1 A è falsa in M sse M = A; M = A sse A è falsa in M. Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 19 / 41
36 Verità e falsità di una formula in una interpretazione A è vera in M(M = A) sse per ogni assegnazione s su M: (M, s) = A. A è falsa in una interpretazione M sse nessuna assegnazione la soddisfa: per ogni assegnazione s su M: (M, s) = A Una formula può non essere né vera né falsa in una interpretazione M Proprietà della verità/falsità 1 A è falsa in M sse M = A; M = A sse A è falsa in M. 2 Nessuna formula può essere contemporaneamente vera e falsa in una interpretazione. Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 19 / 41
37 Verità e falsità di una formula in una interpretazione A è vera in M(M = A) sse per ogni assegnazione s su M: (M, s) = A. A è falsa in una interpretazione M sse nessuna assegnazione la soddisfa: per ogni assegnazione s su M: (M, s) = A Una formula può non essere né vera né falsa in una interpretazione M Proprietà della verità/falsità 1 A è falsa in M sse M = A; M = A sse A è falsa in M. 2 Nessuna formula può essere contemporaneamente vera e falsa in una interpretazione. 3 M = A sse M = xa. Quindi M = A sse M = x 1... x n A (chiusura universale di A). Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 19 / 41
38 Verità e falsità di una formula in una interpretazione A è vera in M(M = A) sse per ogni assegnazione s su M: (M, s) = A. A è falsa in una interpretazione M sse nessuna assegnazione la soddisfa: per ogni assegnazione s su M: (M, s) = A Una formula può non essere né vera né falsa in una interpretazione M Proprietà della verità/falsità 1 A è falsa in M sse M = A; M = A sse A è falsa in M. 2 Nessuna formula può essere contemporaneamente vera e falsa in una interpretazione. 3 M = A sse M = xa. Quindi M = A sse M = x 1... x n A (chiusura universale di A). 4 Se s(x) = s (x) per ogni variabile x che occorre libera in A, allora (M, s) = A sse (M, s ) = A (Lemma di coincidenza). Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 19 / 41
39 Verità e falsità di una formula in una interpretazione A è vera in M(M = A) sse per ogni assegnazione s su M: (M, s) = A. A è falsa in una interpretazione M sse nessuna assegnazione la soddisfa: per ogni assegnazione s su M: (M, s) = A Una formula può non essere né vera né falsa in una interpretazione M Proprietà della verità/falsità 1 A è falsa in M sse M = A; M = A sse A è falsa in M. 2 Nessuna formula può essere contemporaneamente vera e falsa in una interpretazione. 3 M = A sse M = xa. Quindi M = A sse M = x 1... x n A (chiusura universale di A). 4 Se s(x) = s (x) per ogni variabile x che occorre libera in A, allora (M, s) = A sse (M, s ) = A (Lemma di coincidenza). 5 Se A è chiusa, allora per ogni M o M = A oppure M = A (o tutte le assegnazioni soddisfano A, oppure nessuna la soddisfa). Se A è chiusa, M = A sse esiste s tale che (M, s) = A. Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 19 / 41
40 Esempio: dimostrare che M = A o M = A Sia A = x p(a, x) e: M 1 con dominio IN, M 1 (a) = 0, e M 1 (p) = { n, m IN 2 n m}. M 1 = A sse per ogni s: (M 1, s) = A sse per ogni n IN, (M 1, s[n/x]) = p(a, x) sse per ogni n IN, s[n/x](a), s[n/x](x) M 1 (p) sse per ogni n IN, 0, n M 1 (p) sse per ogni n IN, 0 n: vero Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 20 / 41
41 Esempio C = {felix, silvestro, giovanni, riccardo} F = {padre 1 } P = {gatto 1, fratello 2, =} Sia M con: D = {0, 1, 2, 3} M(felix) = 0, M(silvestro) = 1, M(giovanni) = 2, M(riccardo) = 2 M(padre) = {< 0, 0 >, < 1, 0 >, < 2, 3 >, < 3, 2 >} M(padre) = F tale che F(0) = 0, F(1) = 0, F(2) = 3, F(3) = 2 M(gatto) = {0, 1}, M(fratello) = {< 0, 1 >, < 1, 0 >} A = gatto(padre(padre(silvestro))) M = A sse per ogni assegnazione s: (M, s) = A sse s(padre(padre(silvestro))) M(gatto) sse F(s(padre(silvestro))) {0, 1} sse F(F(s(silvestro))) {0, 1} sse F (F(1)) {0, 1} sse F (0) {0, 1} sse 0 {0, 1}: vero Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 21 / 41
42 Esempio (segue) A = x (padre(silvestro) = x gatto(x)) M = x(padre(silvestro) = x gatto(x)) sse Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 22 / 41
43 Esempio (segue) A = x (padre(silvestro) = x gatto(x)) M = x(padre(silvestro) = x gatto(x)) sse per ogni assegnazione s: (M, s) = A sse Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 22 / 41
44 Esempio (segue) A = x (padre(silvestro) = x gatto(x)) M = x(padre(silvestro) = x gatto(x)) sse per ogni assegnazione s: (M, s) = A sse esiste d D tale che (M, s[d/x]) = padre(silvestro) = x gatto(x) sse esiste d D tale che Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 22 / 41
45 Esempio (segue) A = x (padre(silvestro) = x gatto(x)) M = x(padre(silvestro) = x gatto(x)) sse per ogni assegnazione s: (M, s) = A sse esiste d D tale che (M, s[d/x]) = padre(silvestro) = x gatto(x) sse esiste d D tale che (M, s[d/x]) = padre(silvestro) = x e (M, s[d/x]) = gatto(x) sse esiste d D tale che Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 22 / 41
46 Esempio (segue) A = x (padre(silvestro) = x gatto(x)) M = x(padre(silvestro) = x gatto(x)) sse per ogni assegnazione s: (M, s) = A sse esiste d D tale che (M, s[d/x]) = padre(silvestro) = x gatto(x) sse esiste d D tale che (M, s[d/x]) = padre(silvestro) = x e (M, s[d/x]) = gatto(x) sse esiste d D tale che s[d/x](padre(silvestro)), s[d/x](x) M(=) e Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 22 / 41
47 Esempio (segue) A = x (padre(silvestro) = x gatto(x)) M = x(padre(silvestro) = x gatto(x)) sse per ogni assegnazione s: (M, s) = A sse esiste d D tale che (M, s[d/x]) = padre(silvestro) = x gatto(x) sse esiste d D tale che (M, s[d/x]) = padre(silvestro) = x e (M, s[d/x]) = gatto(x) sse esiste d D tale che s[d/x](padre(silvestro)), s[d/x](x) M(=) e s[d/x](x) M(gatto) sse esiste d D tale che Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 22 / 41
48 Esempio (segue) A = x (padre(silvestro) = x gatto(x)) M = x(padre(silvestro) = x gatto(x)) sse per ogni assegnazione s: (M, s) = A sse esiste d D tale che (M, s[d/x]) = padre(silvestro) = x gatto(x) sse esiste d D tale che (M, s[d/x]) = padre(silvestro) = x e (M, s[d/x]) = gatto(x) sse esiste d D tale che s[d/x](padre(silvestro)), s[d/x](x) M(=) e s[d/x](x) M(gatto) sse esiste d D tale che M(padre)(M(silvestro)), d M(=) e Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 22 / 41
49 Esempio (segue) A = x (padre(silvestro) = x gatto(x)) M = x(padre(silvestro) = x gatto(x)) sse per ogni assegnazione s: (M, s) = A sse esiste d D tale che (M, s[d/x]) = padre(silvestro) = x gatto(x) sse esiste d D tale che (M, s[d/x]) = padre(silvestro) = x e (M, s[d/x]) = gatto(x) sse esiste d D tale che s[d/x](padre(silvestro)), s[d/x](x) M(=) e s[d/x](x) M(gatto) sse esiste d D tale che M(padre)(M(silvestro)), d M(=) e d M(gatto) sse esiste d D tale che F(1) = d e d M(gatto) sse esiste d D tale che 0 = d e d M(gatto) sse 0 {0, 1}: VERO Esercizi: determinare l interpretazione delle formule x(padre(silvestro) = x y(padre(x) = y gatto(y))) x( padre(x) = felix padre(x) = padre(giovanni)) Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 22 / 41
50 Soddisfacibilità, validità, equivalenza logica A è soddisfacibile: esiste un interpretazione M di A e un assegnazione s su M tale che (M, s) = A. Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 23 / 41
51 Soddisfacibilità, validità, equivalenza logica A è soddisfacibile: esiste un interpretazione M di A e un assegnazione s su M tale che (M, s) = A. A è valida ( = A) sse è vera in ogni sua interpretazione: per ogni M e per ogni s: (M, s) = A. A è valida sse A non è soddisfacibile. Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 23 / 41
52 Soddisfacibilità, validità, equivalenza logica A è soddisfacibile: esiste un interpretazione M di A e un assegnazione s su M tale che (M, s) = A. A è valida ( = A) sse è vera in ogni sua interpretazione: per ogni M e per ogni s: (M, s) = A. A è valida sse A non è soddisfacibile. A è contraddittoria (o insoddisfacibile) sse essa è falsa in ogni interpretazione: non esistono M e s tali che (M, s) = A. Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 23 / 41
53 Soddisfacibilità, validità, equivalenza logica A è soddisfacibile: esiste un interpretazione M di A e un assegnazione s su M tale che (M, s) = A. A è valida ( = A) sse è vera in ogni sua interpretazione: per ogni M e per ogni s: (M, s) = A. A è valida sse A non è soddisfacibile. A è contraddittoria (o insoddisfacibile) sse essa è falsa in ogni interpretazione: A implica logicamente B non esistono M e s tali che (M, s) = A. per ogni M e s, se (M, s) = A, allora (M, s) = B. Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 23 / 41
54 Soddisfacibilità, validità, equivalenza logica A è soddisfacibile: esiste un interpretazione M di A e un assegnazione s su M tale che (M, s) = A. A è valida ( = A) sse è vera in ogni sua interpretazione: per ogni M e per ogni s: (M, s) = A. A è valida sse A non è soddisfacibile. A è contraddittoria (o insoddisfacibile) sse essa è falsa in ogni interpretazione: A implica logicamente B non esistono M e s tali che (M, s) = A. per ogni M e s, se (M, s) = A, allora (M, s) = B. A e B sono logicamente equivalenti (A B) per ogni M e s: (M, s) = A sse (M, s) = B. Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 23 / 41
55 Soddisfacibilità, validità, equivalenza logica A è soddisfacibile: esiste un interpretazione M di A e un assegnazione s su M tale che (M, s) = A. A è valida ( = A) sse è vera in ogni sua interpretazione: per ogni M e per ogni s: (M, s) = A. A è valida sse A non è soddisfacibile. A è contraddittoria (o insoddisfacibile) sse essa è falsa in ogni interpretazione: A implica logicamente B non esistono M e s tali che (M, s) = A. per ogni M e s, se (M, s) = A, allora (M, s) = B. A e B sono logicamente equivalenti (A B) per ogni M e s: (M, s) = A sse (M, s) = B. Sia S un insieme di formule: (M, s) = S sse per ogni formula C in S, (M, s) = C. Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 23 / 41
56 Conseguenza logica A è una conseguenza logica di S (S = A) per ogni M e per ogni s, se (M, s) = S, allora anche (M, s) = A. S = A è più forte della relazione A è vera in tutte le interpretazioni in cui sono vere tutte le formule in S. S = A per ogni M, s : [(M, s) = S (M, s) = A] A è vera in tutte le interpretazioni in cui sono vere tutte le formule in S per ogni M: M = S M = A per ogni M [per ogni s : (M, s) = S per ogni s : (M, s) = A] Infatti, per la proprietà 3 della slide 19: per ogni M, se M = p(x) allora M = x p(x). Ma p(x) = x p(x): Sia M con dominio D = {0, 1} e M(p) = {0}, e s tale che s(x) = 0. Allora (M, s) = p(x), ma (M, s) = x p(x). Quindi non per ogni M e s, se (M, s) = p(x) allora (M, s) = x p(x). Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 24 / 41
57 Logica dei predicati e linguaggio naturale: quantificatore esistenziale Esiste un corvo nero: x(corvo(x) nero(x)) L intersezione tra l insieme dei corvi e quello degli oggetti neri non è vuota Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 25 / 41
58 Logica dei predicati e linguaggio naturale: quantificatore esistenziale Esiste un corvo nero: x(corvo(x) nero(x)) L intersezione tra l insieme dei corvi e quello degli oggetti neri non è vuota x(corvo(x) nero(x)) è vero in ogni interpretazione in cui esista un oggetto d che non è un corvo (oppure esiste almeno un oggetto nero d ): Se d M(corvo) (d non è un corvo) oppure se d M(nero) (d è nero) allora per ogni s: (M, s[d /x]) = corvo(x) oppure (M, s[d /x]) = nero(x). Questo vale sse (M, s[d /x]) = corvo(x) nero(x), che implica esiste d D tale che (M, s[d/x]) = corvo(x) nero(x), cioè (M, s) = x(corvo(x) nero(x)) x(corvo(x) nero(x)) x( corvo(x) nero(x)) Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 25 / 41
59 Logica dei predicati e linguaggio naturale: quantificatore universale Tutti i corvi sono neri: x(corvo(x) nero(x)) L insieme dei corvi è incluso nell insieme degli oggetti neri Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 26 / 41
60 Logica dei predicati e linguaggio naturale: quantificatore universale Tutti i corvi sono neri: x(corvo(x) nero(x)) L insieme dei corvi è incluso nell insieme degli oggetti neri x(corvo(x) nero(x)) : tutti sono corvi e sono neri x(corvo(x) nero(x)) x corvo(x) x nero(x) Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 26 / 41
61 Affermazioni vere a vuoto (I) x(corvo(x) nero(x)) è vera in ogni interpretazione in cui non esistano corvi: Per ogni d D, d M(corvo) (non ci sono corvi) vale sse: per ogni s e per ogni d D, (M, s[d/x]) = corvo(x). Ciò implica che: per ogni s e per ogni d D, (M, s[d/x]) = corvo(x) oppure (M, s[d/x]) = nero(x), che equivale a: per ogni s e per ogni d D, (M, s[d/x]) = corvo(x) nero(x), cioè: per ogni s, (M, s) = x(corvo(x) nero(x)). x(corvo(x) nero(x)) x( corvo(x) nero(x)) Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 27 / 41
62 Affermazioni vere a vuoto (I) x(corvo(x) nero(x)) è vera in ogni interpretazione in cui non esistano corvi: Per ogni d D, d M(corvo) (non ci sono corvi) vale sse: per ogni s e per ogni d D, (M, s[d/x]) = corvo(x). Ciò implica che: per ogni s e per ogni d D, (M, s[d/x]) = corvo(x) oppure (M, s[d/x]) = nero(x), che equivale a: per ogni s e per ogni d D, (M, s[d/x]) = corvo(x) nero(x), cioè: per ogni s, (M, s) = x(corvo(x) nero(x)). x(corvo(x) nero(x)) x( corvo(x) nero(x)) x(corvo(x) nero(x)) è falsa sse esiste un oggetto d tale che (M, s[d/x]) = corvo(x) nero(x), cioè tale che: (M, s[d/x]) = corvo(x) e (M, s[d/x]) = nero(x) (esiste un corvo che non è nero: un controesempio) In particolare, esiste un corvo. Dunque, se non esistono corvi, x(corvo(x) nero(x)) non può essere falsa, quindi è vera. Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 27 / 41
63 Affermazioni vere a vuoto (II) È vero o falso che: Ogni numero in {1, 3, 5, 7} è dispari Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 28 / 41
64 Affermazioni vere a vuoto (II) È vero o falso che: Ogni numero in {1, 3, 5, 7} è dispari Ogni numero in {1, 3, 4, 5, 7} è dispari. Perché? Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 28 / 41
65 Affermazioni vere a vuoto (II) È vero o falso che: Ogni numero in {1, 3, 5, 7} è dispari Ogni numero in {1, 3, 4, 5, 7} è dispari. Perché? Ogni numero dispari compreso tra 2 e 8 è primo Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 28 / 41
66 Affermazioni vere a vuoto (II) È vero o falso che: Ogni numero in {1, 3, 5, 7} è dispari Ogni numero in {1, 3, 4, 5, 7} è dispari. Perché? Ogni numero dispari compreso tra 2 e 8 è primo Ogni numero dispari compreso tra 2 e 10 è primo. Perché? Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 28 / 41
67 Affermazioni vere a vuoto (II) È vero o falso che: Ogni numero in {1, 3, 5, 7} è dispari Ogni numero in {1, 3, 4, 5, 7} è dispari. Perché? Ogni numero dispari compreso tra 2 e 8 è primo Ogni numero dispari compreso tra 2 e 10 è primo. Perché? È vero o falso che: Ogni numero appartenente all insieme vuoto è dispari Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 28 / 41
68 Affermazioni vere a vuoto (II) È vero o falso che: Ogni numero in {1, 3, 5, 7} è dispari Ogni numero in {1, 3, 4, 5, 7} è dispari. Perché? Ogni numero dispari compreso tra 2 e 8 è primo Ogni numero dispari compreso tra 2 e 10 è primo. Perché? È vero o falso che: Ogni numero appartenente all insieme vuoto è dispari Ogni numero maggiore di 10 e minore di 3 è primo Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 28 / 41
69 Affermazioni vere a vuoto (II) È vero o falso che: Ogni numero in {1, 3, 5, 7} è dispari Ogni numero in {1, 3, 4, 5, 7} è dispari. Perché? Ogni numero dispari compreso tra 2 e 8 è primo Ogni numero dispari compreso tra 2 e 10 è primo. Perché? È vero o falso che: Ogni numero appartenente all insieme vuoto è dispari Ogni numero maggiore di 10 e minore di 3 è primo qualsiasi sia P: per ogni numero naturale k < 0 vale P(k) Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 28 / 41
70 Affermazioni vere a vuoto (II) È vero o falso che: Ogni numero in {1, 3, 5, 7} è dispari Ogni numero in {1, 3, 4, 5, 7} è dispari. Perché? Ogni numero dispari compreso tra 2 e 8 è primo Ogni numero dispari compreso tra 2 e 10 è primo. Perché? È vero o falso che: Ogni numero appartenente all insieme vuoto è dispari Ogni numero maggiore di 10 e minore di 3 è primo qualsiasi sia P: per ogni numero naturale k < 0 vale P(k) Per ogni proprietà P, per ogni k vale P(k) Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 28 / 41
71 Affermazioni vere a vuoto (II) È vero o falso che: Ogni numero in {1, 3, 5, 7} è dispari Ogni numero in {1, 3, 4, 5, 7} è dispari. Perché? Ogni numero dispari compreso tra 2 e 8 è primo Ogni numero dispari compreso tra 2 e 10 è primo. Perché? È vero o falso che: Ogni numero appartenente all insieme vuoto è dispari Ogni numero maggiore di 10 e minore di 3 è primo qualsiasi sia P: per ogni numero naturale k < 0 vale P(k) Per ogni proprietà P, per ogni k vale P(k) Esercizi del paragrafo 3.6 delle dispense, pag. 65 e seguenti (in particolare, quelli dei gruppi F, G e N). Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 28 / 41
72 Alcune formule valide (dimostrarne la validità per esercizio) x p(x) p(t) Assumiamo che la formula non sia valida: esiste una sua interpretazione M e un assegnazione s su M tali che (M, s) = x p(x) p(t); cioè: (M, s) = x p(x) per ogni d D, (M, s[d/x]) = p(x), per ogni d D: s[d/x](x) M(p); per ogni d D: d M(p). (M, s) = p(t). Dunque, se s(t) = d, d M(p). Contraddizione Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 29 / 41
73 Alcune formule valide (dimostrarne la validità per esercizio) x p(x) p(t) Assumiamo che la formula non sia valida: esiste una sua interpretazione M e un assegnazione s su M tali che (M, s) = x p(x) p(t); cioè: (M, s) = x p(x) per ogni d D, (M, s[d/x]) = p(x), per ogni d D: s[d/x](x) M(p); per ogni d D: d M(p). (M, s) = p(t). Dunque, se s(t) = d, d M(p). Contraddizione x A x A x A x A Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 29 / 41
74 Alcune formule valide (dimostrarne la validità per esercizio) x p(x) p(t) Assumiamo che la formula non sia valida: esiste una sua interpretazione M e un assegnazione s su M tali che (M, s) = x p(x) p(t); cioè: (M, s) = x p(x) per ogni d D, (M, s[d/x]) = p(x), per ogni d D: s[d/x](x) M(p); per ogni d D: d M(p). (M, s) = p(t). Dunque, se s(t) = d, d M(p). Contraddizione x A x A x A x A x A x A x A x A Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 29 / 41
75 Alcune formule valide (dimostrarne la validità per esercizio) x p(x) p(t) Assumiamo che la formula non sia valida: esiste una sua interpretazione M e un assegnazione s su M tali che (M, s) = x p(x) p(t); cioè: (M, s) = x p(x) per ogni d D, (M, s[d/x]) = p(x), per ogni d D: s[d/x](x) M(p); per ogni d D: d M(p). (M, s) = p(t). Dunque, se s(t) = d, d M(p). Contraddizione x A x A x A x A x(a B) xa xb x A x A x A x A x(a B) xa B Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 29 / 41
76 Alcune formule valide (dimostrarne la validità per esercizio) x p(x) p(t) Assumiamo che la formula non sia valida: esiste una sua interpretazione M e un assegnazione s su M tali che (M, s) = x p(x) p(t); cioè: (M, s) = x p(x) per ogni d D, (M, s[d/x]) = p(x), per ogni d D: s[d/x](x) M(p); per ogni d D: d M(p). (M, s) = p(t). Dunque, se s(t) = d, d M(p). Contraddizione x A x A x A x A x(a B) xa xb xa xb x(a B) x A x A x A x A x(a B) xa B x(a B) xa xb Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 29 / 41
77 Alcune formule valide (dimostrarne la validità per esercizio) x p(x) p(t) Assumiamo che la formula non sia valida: esiste una sua interpretazione M e un assegnazione s su M tali che (M, s) = x p(x) p(t); cioè: (M, s) = x p(x) per ogni d D, (M, s[d/x]) = p(x), per ogni d D: s[d/x](x) M(p); per ogni d D: d M(p). (M, s) = p(t). Dunque, se s(t) = d, d M(p). Contraddizione x A x A x A x A x(a B) xa xb xa xb x(a B) x A x A x A x A x(a B) xa B x(a B) xa xb y xa x ya Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 29 / 41
78 Alcune formule non valide 1 ( xp(x) xq(x)) x(p(x) q(x)) xp(x) xq(x) è vera quando xp(x) è falsa (non tutti gli oggetti del dominio sono in M(p)). Ma non è detto che, in questo caso, ogni oggetto in M(p) sia anche in M(q). Contromodello: D = {0, 1}, M(p) = {0}, M(q) =. 2 x(p(x) q(x)) xp(x) xq(x) Pensare alle interpretazioni di p e q: essere pari e essere dispari 3 xp(x) xq(x) x(p(x) q(x)) Come al punto precedente 4 x yp(x, y) y xp(x, y) Pensare alla differenza tra continuità (per ogni x 0 I esiste δ > 0... : δ dipende da x 0 ) e continuità uniforme (esiste δ > 0 tale che per ogni x 0 I... : δ è lo stesso per ogni punto) Esercizio: completare le dimostrazioni della non validità di tali formule Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 30 / 41
79 Come fare per... Dimostrare che: la formula A è valida: per assurdo; si assume che esista un contromodello (M, s) di A e si giunge ad un assurdo; la formula A non è valida: si costruisce un contromodello: (M, s) = A Dimostrare che: S = A: per assurdo: si assume che esistano un interpretazione M e un assegnazione s, tali che (M, s) = S e (M, s) = A, e si giunge ad un assurdo; dimostrazione diretta: si assume che M e s siano qualsiasi interpretazione e assegnazione tali che (M, s) = S, e si dimostra che (M, s) = A S = A: si costruisce un contromodello, cioè un interpretazione M e un assegnazione s, tali che (M, s) = S e (M, s) = A. Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 31 / 41
80 Forme normali prenesse Una formula è in forma normale prenessa se ha la forma: Q 1 x 1 Q 2 x 2...Q n x }{{ n } }{{} A prefisso matrice dove la matrice è senza quantificatori Ogni formula è logicamente equivalente a una formula in forma normale prenessa. Equivalenze logiche utili per trasformare una formula in forma prenessa: Ridenominazione di variabili vincolate: Se x non occorre in B, allora: xa ya[y/x] xa ya[y/x] } y nuova xa B x(a B) xa B x(a B) xa B x(a B) xa B x(a B) xa B x(a B) xa B x(a B) B xa x(b A) B xa x(b A) xa x A xa x A Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 32 / 41
81 Trasformazione di formule in forma prenessa: Esempio ( x y p(x, y) ( x p( x, c) y q( y ))) Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 33 / 41
82 Trasformazione di formule in forma prenessa: Esempio ( x y p(x, y) ( x p( x, c) y q( y ))) ( x y p(x, y) ( x 1 p( x 1, c) y 1 q( y 1 ))) Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 33 / 41
83 Trasformazione di formule in forma prenessa: Esempio ( x y p(x, y) ( x p( x, c) y q( y ))) ( x y p(x, y) ( x 1 p( x 1, c) y 1 q( y 1 ))) x ( y p(x, y) x 1 (p(x 1, c) y 1 q(y 1 ))) Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 33 / 41
84 Trasformazione di formule in forma prenessa: Esempio ( x y p(x, y) ( x p( x, c) y q( y ))) ( x y p(x, y) ( x 1 p( x 1, c) y 1 q( y 1 ))) x ( y p(x, y) x 1 (p(x 1, c) y 1 q(y 1 ))) x y (p(x, y) x 1 y 1 (p(x 1, c) q(y 1 ))) Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 33 / 41
85 Trasformazione di formule in forma prenessa: Esempio ( x y p(x, y) ( x p( x, c) y q( y ))) ( x y p(x, y) ( x 1 p( x 1, c) y 1 q( y 1 ))) x ( y p(x, y) x 1 (p(x 1, c) y 1 q(y 1 ))) x y (p(x, y) x 1 y 1 (p(x 1, c) q(y 1 ))) x y x 1 y 1 (p(x, y) (p(x 1, c) q(y 1 ))) Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 33 / 41
86 Trasformazione di formule in forma prenessa: Esempio ( x y p(x, y) ( x p( x, c) y q( y ))) ( x y p(x, y) ( x 1 p( x 1, c) y 1 q( y 1 ))) x ( y p(x, y) x 1 (p(x 1, c) y 1 q(y 1 ))) x y (p(x, y) x 1 y 1 (p(x 1, c) q(y 1 ))) x y x 1 y 1 (p(x, y) (p(x 1, c) q(y 1 ))) x y x 1 y 1 (p(x, y) (p(x 1, c) q(y 1 ))) Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 33 / 41
87 Trasformazione di formule in forma prenessa: Esempio ( x y p(x, y) ( x p( x, c) y q( y ))) ( x y p(x, y) ( x 1 p( x 1, c) y 1 q( y 1 ))) x ( y p(x, y) x 1 (p(x 1, c) y 1 q(y 1 ))) x y (p(x, y) x 1 y 1 (p(x 1, c) q(y 1 ))) x y x 1 y 1 (p(x, y) (p(x 1, c) q(y 1 ))) x y x 1 y 1 (p(x, y) (p(x 1, c) q(y 1 ))) x y x 1 y 1 (p(x, y) (p(x 1, c) q(y 1 ))) Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 33 / 41
88 Sostituzione di variabili con termini Abbiamo visto che = x p(x) p(t) Ma è sempre vero che = xa A[t/x]? Esempio: x y (x < y) è vero nell interpretazione standard su IN Quindi anche y (0 < y), y (1 < y),..., y (2 + 1 < y) Consideriamo t = y + 1 e y (x < y)[t/x]: è vero che y (y + 1 < y)? Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 34 / 41
89 Sostituzione di variabili con termini Abbiamo visto che = x p(x) p(t) Ma è sempre vero che = xa A[t/x]? Esempio: x y (x < y) è vero nell interpretazione standard su IN Quindi anche y (0 < y), y (1 < y),..., y (2 + 1 < y) Consideriamo t = y + 1 e y (x < y)[t/x]: è vero che y (y + 1 < y)? Non per ogni termine t : = x y (x < y) y (t < y) A[t/x] non dice sempre di t quello che A dice di x: y (x < y) dice che esiste un numero maggiore di x, ma y (y + 1 < y) non dice che esiste un numero maggiore di y + 1. Ci si deve assicurare che nessuna variabile in t venga catturata da un quantificatore in A Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 34 / 41
90 Termini sostituibili per una variabile in una formula t è sostituibile per x in A sse nessuna occorrenza libera di x in A si trova nel campo d azione di un quantificatore y o y, dove y occorre in t (nessuna variabile di t verrebbe catturata da un quantificatore in A, se x venisse sostituita da t) f (y) è sostituibile per x in zp(z, x), è sostituibile per x in xp(z, x), non è sostituibile per x in yp(y, x), non è sostituibile per x in yp(y, x) Se t è sostituibile per x in A, allora = xa A[t/x] = A[t/x] xa Se t è un termine chiuso, o se t = x, allora t è sostituibile per x in A, quindi = xa A[t/x] Quando scriviamo A[t/x], intendiamo sempre che t è sostituibile per x in A Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 35 / 41
91 Sistema di inferenza hilbertiano Linguaggio del primo ordine con, e Assiomi: 1 A (B A) 2 (A (B C)) ((A B) (A C)) 3 ( B A) (( B A) B) 4 xa A[t/x] se t è sostituibile per x in A 5 x(a B) (A xb) se A non contiene x libera Regole di inferenza: 1 MPP: A A B B 2 Generalizzazione A xa Gli altri connettivi e sono simboli definiti Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 36 / 41
92 Teorie del primo ordine Linguaggio del primo ordine Sistema di inferenza : assiomi logici regole di inferenza assiomi propri (o non logici), che descrivono il dominio di interesse Il sistema costituito dai soli assiomi logici e regole di inferenza è il Calcolo dei Predicati del Primo Ordine Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 37 / 41
93 Esempi di teorie (I) Teoria dei grafi non orientati P = {R 2 }, F = C = Assioma proprio: x y(r(x, y) R(y, x)) Teoria degli ordini parziali P = {<}, F = C = Assiomi propri: x (x < x) x y z(x < y y < z x < z) Teorie con uguaglianza, dove i simboli di predicato includono = Assiomi propri: x(x = x) (riflessivita ) x y(x = y (A A )) dove A si ottiene da A sostituendo alcune (non necessariamente tutte) occorrenze libere di x con y Sono derivabili: x y(x = y y = x) x y z(x = y y = z x = z) Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 38 / 41
94 Esempi di teorie (II) Teoria dei numeri P = {=}, F = {succ, +, }, C = {0} Assiomi propri: assiomi per l uguaglianza + x (0 = succ(x)) x y(succ(x) = succ(y) x = y) x(x + 0 = x) x y(x + succ(y) = succ(x + y)) x(x 0 = 0) x y(x succ(y) = x + (x y)) A[0/x] x(a A[succ(x)/x]) xa (schema d assiomi: principio di induzione matematica) Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 39 / 41
95 Proprietà della logica dei predicati Semidecidibilità Se I è un sistema di inferenza, in cui la proprietà di essere un assioma di I e la relazione di derivabilità mediante ciascuna regola di inferenza di I sono nozioni decidibili, e se il linguaggio è numerabile, allora la nozione di derivabilità in I è semidecidibile: S I A è semidecidibile (l insieme delle formule valide è ricorsivamente enumerabile) Indecidibilità Il calcolo dei predicati è indecidibile: Se L è un linguaggio con almeno una costante e un simbolo di predicato binario, allora l insieme delle formule valide di L non è ricorsivo Casi di decidibilità: calcolo monadico (i predicati sono tutti a un solo argomento) formule puramente esistenziali: x 1... x n A, dove A è senza quantificatori né simboli funzionali formule puramente universali: x 1... x n A, dove A è senza quantificatori né simboli funzionali Logica dei Predicati (Logica per l Informatica) 02: First Order Logic 40 / 41
I numeri primi maggiori di due sono dispari
 Logica dei Predicati o Logica del Primo Ordine Il mondo è analizzato in termini di OGGETTI, PROPRIETÀ, RELAZIONI. oggetti: due; I numeri primi maggiori di due sono dispari relazioni e proprietà: essere
Logica dei Predicati o Logica del Primo Ordine Il mondo è analizzato in termini di OGGETTI, PROPRIETÀ, RELAZIONI. oggetti: due; I numeri primi maggiori di due sono dispari relazioni e proprietà: essere
Ragionamento Automatico Richiami di calcolo dei predicati
 Richiami di logica del primo ordine Ragionamento Automatico Richiami di calcolo dei predicati (SLL: Capitolo 7) Sintassi Semantica Lezione 2 Ragionamento Automatico Carlucci Aiello, 2004/05Lezione 2 0
Richiami di logica del primo ordine Ragionamento Automatico Richiami di calcolo dei predicati (SLL: Capitolo 7) Sintassi Semantica Lezione 2 Ragionamento Automatico Carlucci Aiello, 2004/05Lezione 2 0
Logica: materiale didattico
 Logica: materiale didattico M. Cialdea Mayer. Logica (dispense): http://cialdea.dia.uniroma3.it/teaching/logica/materiale/dispense-logica.pdf Logica dei Predicati (Logica per l Informatica) 01: Logica
Logica: materiale didattico M. Cialdea Mayer. Logica (dispense): http://cialdea.dia.uniroma3.it/teaching/logica/materiale/dispense-logica.pdf Logica dei Predicati (Logica per l Informatica) 01: Logica
Sistemi di dimostrazione
 Sistemi di dimostrazione Un sistema di deduzione (o dimostrazione) consiste di un insieme di assiomi (a volte vuoto) un insieme di regole di inferenza Una deduzione (o derivazione) di una formula A da
Sistemi di dimostrazione Un sistema di deduzione (o dimostrazione) consiste di un insieme di assiomi (a volte vuoto) un insieme di regole di inferenza Una deduzione (o derivazione) di una formula A da
Logica proposizionale
 Logica proposizionale Proposizione: frase compiuta che è sempre o vera o falsa. Connettivi Posti in ordine di precedenza: not, and, or, implica, doppia implicazione Sintassi Le proposizioni sono costituite
Logica proposizionale Proposizione: frase compiuta che è sempre o vera o falsa. Connettivi Posti in ordine di precedenza: not, and, or, implica, doppia implicazione Sintassi Le proposizioni sono costituite
LOGICA MATEMATICA PER INFORMATICA (A.A. 12/13)
 LOGICA MATEMATICA PER INFORMATICA (A.A. 12/13) DISPENSA N. 4 Sommario. Dimostriamo il Teorema di Completezza per il Calcolo dei Predicati del I ordine. 1. Teorema di Completezza Dimostriamo il Teorema
LOGICA MATEMATICA PER INFORMATICA (A.A. 12/13) DISPENSA N. 4 Sommario. Dimostriamo il Teorema di Completezza per il Calcolo dei Predicati del I ordine. 1. Teorema di Completezza Dimostriamo il Teorema
Problemi decidibili, semidecidibili, indecidibili
 Problemi decidibili, semidecidibili, indecidibili (Paragrafo 3.5 delle dispense) Il problema di determinare se una formula A della logica proposizionale sia valida o no può essere risolto mediante un procedimento
Problemi decidibili, semidecidibili, indecidibili (Paragrafo 3.5 delle dispense) Il problema di determinare se una formula A della logica proposizionale sia valida o no può essere risolto mediante un procedimento
LOGICA MATEMATICA PER INFORMATICA
 LOGICA MATEMATICA PER INFORMATICA A.A. 10/11, DISPENSA N. 2 Sommario. Assiomi dell identità, modelli normali. Forma normale negativa, forma normale prenessa, forma normale di Skolem. 1. L identità Esistono
LOGICA MATEMATICA PER INFORMATICA A.A. 10/11, DISPENSA N. 2 Sommario. Assiomi dell identità, modelli normali. Forma normale negativa, forma normale prenessa, forma normale di Skolem. 1. L identità Esistono
Teorema 1.1. (Teorema di Compattezza) Sia Γ un insieme di formule di un linguaggio proposizionale.
 versione 12 ottobre 2011 1.1. Logica Proposizionale. 1. Teorema di Compattezza e risultati limitativi Teorema 1.1. (Teorema di Compattezza) Sia Γ un insieme di formule di un linguaggio proposizionale.
versione 12 ottobre 2011 1.1. Logica Proposizionale. 1. Teorema di Compattezza e risultati limitativi Teorema 1.1. (Teorema di Compattezza) Sia Γ un insieme di formule di un linguaggio proposizionale.
Alberi di sequenti per un linguaggio predicativo L 1.
 Alberi di sequenti per un linguaggio predicativo L 1. Si estenda il linguaggio L 1 con un insieme C infinito numerabile di costanti individuali. Un multinsieme è un insieme con ripetizioni. Un sequente
Alberi di sequenti per un linguaggio predicativo L 1. Si estenda il linguaggio L 1 con un insieme C infinito numerabile di costanti individuali. Un multinsieme è un insieme con ripetizioni. Un sequente
Linguaggi. Claudio Sacerdoti Coen 03/12/ : Logica del prim ordine. Universitá di Bologna. Logica del prim ordine
 Linguaggi 17: Logica del prim ordine Universitá di Bologna 03/12/2014 Outline Logica del prim ordine 1 Logica del prim ordine Quantificatori Logica del prim ordine Wikipedia: Nella
Linguaggi 17: Logica del prim ordine Universitá di Bologna 03/12/2014 Outline Logica del prim ordine 1 Logica del prim ordine Quantificatori Logica del prim ordine Wikipedia: Nella
Fondamenti di Informatica 2
 Fondamenti di Informatica 2 Linguaggi e Complessità : Lezione 1 Corso Fondamenti di Informatica 2 Marco Schaerf, 2009-2010 Linguaggi e Complessità : Lezione 1 1 Logica proposizionale Linguaggio matematico
Fondamenti di Informatica 2 Linguaggi e Complessità : Lezione 1 Corso Fondamenti di Informatica 2 Marco Schaerf, 2009-2010 Linguaggi e Complessità : Lezione 1 1 Logica proposizionale Linguaggio matematico
METODI MATEMATICI PER L INFORMATICA
 METODI MATEMATICI PER L INFORMATICA ANNO ACCADEMICO 2011/2012 Sommario. Sintassi e semantica della Logica dei predicati. Proprietà fondamentali dei quantificatori. Strutture, soddisfacibilità e verità
METODI MATEMATICI PER L INFORMATICA ANNO ACCADEMICO 2011/2012 Sommario. Sintassi e semantica della Logica dei predicati. Proprietà fondamentali dei quantificatori. Strutture, soddisfacibilità e verità
Logica per la Programmazione
 Logica del Primo Ordine: Motivazioni, Sintassi e Interpretazioni Logica per la Programmazione Lezione 7 Formule Valide, Conseguenza Logica Proof System per la Logica del Primo Ordine Leggi per i Quantificatori
Logica del Primo Ordine: Motivazioni, Sintassi e Interpretazioni Logica per la Programmazione Lezione 7 Formule Valide, Conseguenza Logica Proof System per la Logica del Primo Ordine Leggi per i Quantificatori
Logica per la Programmazione
 Logica del Primo Ordine: Motivazioni, Sintassi e Interpretazioni Logica per la Programmazione Lezione 8 Modelli, Formule Valide, Conseguenza Logica Proof Systems Regole di inferenza per Calcolo Proposizionale
Logica del Primo Ordine: Motivazioni, Sintassi e Interpretazioni Logica per la Programmazione Lezione 8 Modelli, Formule Valide, Conseguenza Logica Proof Systems Regole di inferenza per Calcolo Proposizionale
LOGICA MATEMATICA PER INFORMATICA
 LOGICA MATEMATICA PER INFORMATICA A.A. 10/11, SETTIMANA N. 1 Sommario. Introduciamo il linguaggio e la sintassi e la semantica della Logica del I Ordine. Introduciamo i concetti di teoria, teoria completa,
LOGICA MATEMATICA PER INFORMATICA A.A. 10/11, SETTIMANA N. 1 Sommario. Introduciamo il linguaggio e la sintassi e la semantica della Logica del I Ordine. Introduciamo i concetti di teoria, teoria completa,
LOGICA FORMALE. Logiche
 LOGICA FORMALE Linguaggio formale (sintassi + semantica) + Sistema di inferenza Sintassi: insieme delle espressioni ben formate (linguaggio) Semantica: interpretazione M del linguaggio Logica classica:
LOGICA FORMALE Linguaggio formale (sintassi + semantica) + Sistema di inferenza Sintassi: insieme delle espressioni ben formate (linguaggio) Semantica: interpretazione M del linguaggio Logica classica:
Prerequisiti Matematici
 Prerequisiti Matematici Richiami di teoria degli insiemi Relazioni d ordine, d equivalenza Richiami di logica Logica proposizionale, tabelle di verità, calcolo dei predicati Importante: Principio di Induzione
Prerequisiti Matematici Richiami di teoria degli insiemi Relazioni d ordine, d equivalenza Richiami di logica Logica proposizionale, tabelle di verità, calcolo dei predicati Importante: Principio di Induzione
API. Ripasso di logica. Davide Martinenghi. Politecnico di Milano. API Davide Martinenghi (1/30)
 API Ripasso di logica Davide Martinenghi Politecnico di Milano API Davide Martinenghi (1/30) Logica proposizionale - sintassi L è un linguaggio della logica proposizionale L alfabeto di L è composto da
API Ripasso di logica Davide Martinenghi Politecnico di Milano API Davide Martinenghi (1/30) Logica proposizionale - sintassi L è un linguaggio della logica proposizionale L alfabeto di L è composto da
LOGICA DEL PRIMO ORDINE: PROOF SYSTEM. Corso di Logica per la Programmazione A.A. 2013/14 Andrea Corradini
 LOGICA DEL PRIMO ORDINE: PROOF SYSTEM Corso di Logica per la Programmazione A.A. 2013/14 Andrea Corradini LOGICA DEL PRIMO ORDINE: RIASSUNTO Sintassi: grammatica libera da contesto (BNF), parametrica rispetto
LOGICA DEL PRIMO ORDINE: PROOF SYSTEM Corso di Logica per la Programmazione A.A. 2013/14 Andrea Corradini LOGICA DEL PRIMO ORDINE: RIASSUNTO Sintassi: grammatica libera da contesto (BNF), parametrica rispetto
NOZIONI DI LOGICA PROPOSIZIONI.
 NOZIONI DI LOGICA PROPOSIZIONI. Una proposizione è un affermazione che è vera o falsa, ma non può essere contemporaneamente vera e falsa. ESEMPI Sono proposizioni : 7 è maggiore di 2 Londra è la capitale
NOZIONI DI LOGICA PROPOSIZIONI. Una proposizione è un affermazione che è vera o falsa, ma non può essere contemporaneamente vera e falsa. ESEMPI Sono proposizioni : 7 è maggiore di 2 Londra è la capitale
LINGUAGGI PER LA RAPPRESENTAZIONE DELLA CONOSCENZA
 LINGUAGGI PER LA RAPPRESENTAZIONE DELLA CONOSCENZA Linguaggio formale: SINTASSI SEMANTICA + Sistema di inferenza Sintassi: insieme delle espressioni ben formate (linguaggio) Semantica: interpretazione
LINGUAGGI PER LA RAPPRESENTAZIONE DELLA CONOSCENZA Linguaggio formale: SINTASSI SEMANTICA + Sistema di inferenza Sintassi: insieme delle espressioni ben formate (linguaggio) Semantica: interpretazione
Luca Costabile Esercizi di Logica Matematica Dispensa Calcolo Proposizionale 1
 Luca Costabile Esercizi di Logica Matematica Dispensa Calcolo Proposizionale 1 Esercizio 1.12 Per dimostrare che per ogni funzione esiste una formula in cui compaiono le variabili tale che la corrispondente
Luca Costabile Esercizi di Logica Matematica Dispensa Calcolo Proposizionale 1 Esercizio 1.12 Per dimostrare che per ogni funzione esiste una formula in cui compaiono le variabili tale che la corrispondente
NOZIONI DI LOGICA. Premessa
 NOZIONI DI LOGICA Premessa Il compito principale della logica è quello di studiare il nesso di conseguenza logica tra proposizioni, predisponendo delle tecniche per determinare quando la verità di una
NOZIONI DI LOGICA Premessa Il compito principale della logica è quello di studiare il nesso di conseguenza logica tra proposizioni, predisponendo delle tecniche per determinare quando la verità di una
Riassunto delle puntate precedenti:
 Riassunto delle puntate precedenti: Definizioni (informali) di enunciato e argomento Definizione (informale) di argomento corretto Definizione (formale) del linguaggio della logica enunciativa. Definizione
Riassunto delle puntate precedenti: Definizioni (informali) di enunciato e argomento Definizione (informale) di argomento corretto Definizione (formale) del linguaggio della logica enunciativa. Definizione
RELAZIONI TRA SINTASSI E SEMANTICA
 RELAZIONI TRA SINTASSI E SEMANTICA INTERPRETAZIONI E MODELLI Sia Γ un insieme di enunciati dichiarativi (asserzioni che hanno valore T o F) Una intepretazione assegna un significato ad ogni componente
RELAZIONI TRA SINTASSI E SEMANTICA INTERPRETAZIONI E MODELLI Sia Γ un insieme di enunciati dichiarativi (asserzioni che hanno valore T o F) Una intepretazione assegna un significato ad ogni componente
Logica per la Programmazione
 Logica per la Programmazione Lezione 6 Logica del Primo Ordine Motivazioni Sintassi Interpretazioni Formalizzazione pag. 1 Limiti del Calcolo Proposizionale Nella formalizzazione di enunciati dichiarativi,
Logica per la Programmazione Lezione 6 Logica del Primo Ordine Motivazioni Sintassi Interpretazioni Formalizzazione pag. 1 Limiti del Calcolo Proposizionale Nella formalizzazione di enunciati dichiarativi,
LOGICA MATEMATICA PER INFORMATICA (A.A. 12/13)
 LOGICA MATEMATICA PER INFORMATICA (A.A. 12/13) DISPENSA N. 3 Sommario. Introduciamo il Calcolo dei Predicati del I ordine e ne dimostriamo le proprietà fondamentali. Discutiamo il trattamento dell identità
LOGICA MATEMATICA PER INFORMATICA (A.A. 12/13) DISPENSA N. 3 Sommario. Introduciamo il Calcolo dei Predicati del I ordine e ne dimostriamo le proprietà fondamentali. Discutiamo il trattamento dell identità
Intelligenza Artificiale. Logica proposizionale: calcolo simbolico
 Intelligenza Artificiale Logica proposizionale: calcolo simbolico Marco Piastra Logica formale (Parte 2) - 1 Parte 2 Calcolo logico Assiomi Derivazioni Derivazioni e conseguenza logica Completezza Logica
Intelligenza Artificiale Logica proposizionale: calcolo simbolico Marco Piastra Logica formale (Parte 2) - 1 Parte 2 Calcolo logico Assiomi Derivazioni Derivazioni e conseguenza logica Completezza Logica
Il calcolo di deduzione naturale NK per la logica dei predicati. xa A[t/x] (E )
![Il calcolo di deduzione naturale NK per la logica dei predicati. xa A[t/x] (E ) Il calcolo di deduzione naturale NK per la logica dei predicati. xa A[t/x] (E )](/thumbs/95/123975111.jpg) Il calcolo di deduzione naturale NK per la logica dei predicati A xa (I ) se A non dipende da ipotesi contenenti x libera xa A[t/x] (E ) se t è sostituibile per x in A A[t/x] xa (I ) se t è sostituibile
Il calcolo di deduzione naturale NK per la logica dei predicati A xa (I ) se A non dipende da ipotesi contenenti x libera xa A[t/x] (E ) se t è sostituibile per x in A A[t/x] xa (I ) se t è sostituibile
NOZIONI DI LOGICA. Premessa
 NOZIONI DI LOGICA Premessa Il compito principale della logica è quello di studiare il nesso di conseguenza logica tra proposizioni, predisponendo delle tecniche per determinare quando la verità di una
NOZIONI DI LOGICA Premessa Il compito principale della logica è quello di studiare il nesso di conseguenza logica tra proposizioni, predisponendo delle tecniche per determinare quando la verità di una
Sistemi Deduttivi. Marco Piastra. Intelligenza Artificiale I. Intelligenza Artificiale I - A.A Sistemi Deduttivi[1]
![Sistemi Deduttivi. Marco Piastra. Intelligenza Artificiale I. Intelligenza Artificiale I - A.A Sistemi Deduttivi[1] Sistemi Deduttivi. Marco Piastra. Intelligenza Artificiale I. Intelligenza Artificiale I - A.A Sistemi Deduttivi[1]](/thumbs/88/115134024.jpg) Intelligenza Artificiale I Sistemi Deduttivi Marco Piastra Intelligenza Artificiale I - A.A. 2010- Sistemi Deduttivi[1] Calcolo simbolico? Una fbf è conseguenza logica di un insieme di fbf sse qualsiasi
Intelligenza Artificiale I Sistemi Deduttivi Marco Piastra Intelligenza Artificiale I - A.A. 2010- Sistemi Deduttivi[1] Calcolo simbolico? Una fbf è conseguenza logica di un insieme di fbf sse qualsiasi
Ragionamento Automatico Richiami di tableaux proposizionali
 Richiami di logica e deduzione proposizionale Ragionamento Automatico Richiami di tableaux proposizionali (L. Carlucci Aiello & F. Pirri: SLL, Cap. 5) La logica proposizionale I tableau proposizionali
Richiami di logica e deduzione proposizionale Ragionamento Automatico Richiami di tableaux proposizionali (L. Carlucci Aiello & F. Pirri: SLL, Cap. 5) La logica proposizionale I tableau proposizionali
LOGICA DEL PRIMO ORDINE: MOTIVAZIONI, SINTASSI E INTERPRETAZIONI. Corso di Logica per la Programmazione A.A Andrea Corradini
 LOGICA DEL PRIMO ORDINE: MOTIVAZIONI, SINTASSI E INTERPRETAZIONI Corso di Logica per la Programmazione A.A. 2013 Andrea Corradini LIMITI DEL CALCOLO PROPOSIZIONALE Nella formalizzazione di enunciati dichiarativi,
LOGICA DEL PRIMO ORDINE: MOTIVAZIONI, SINTASSI E INTERPRETAZIONI Corso di Logica per la Programmazione A.A. 2013 Andrea Corradini LIMITI DEL CALCOLO PROPOSIZIONALE Nella formalizzazione di enunciati dichiarativi,
Specifica formale. Verifica formale (Prima parte) 03: Logica temporale lineare 1 / 26
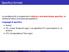 Specifica formale La correttezza di un programma è relativa a una determinata specifica: la verifica formale è connessa alle specifiche Linguaggi di specifica Automi LTL (Linear Temporal Logic): una specifica
Specifica formale La correttezza di un programma è relativa a una determinata specifica: la verifica formale è connessa alle specifiche Linguaggi di specifica Automi LTL (Linear Temporal Logic): una specifica
Elementi di logica. SCOPO: introdurre nozioni di logica & vocabolario per una corretta interpretazione delle dimostrazioni.
 Elementi di logica SCOPO: introdurre nozioni di logica & vocabolario per una corretta interpretazione delle dimostrazioni. Quantificatori: elementi fondamentali del linguaggio matematico. quantificatore
Elementi di logica SCOPO: introdurre nozioni di logica & vocabolario per una corretta interpretazione delle dimostrazioni. Quantificatori: elementi fondamentali del linguaggio matematico. quantificatore
ESERCIZI DI LOGICA MATEMATICA A.A Alessandro Combi
 ESERCIZI DI LOGICA MATEMATICA A.A. 2015-16 Alessandro Combi Esercizio 1.7 Per ogni formula A, dimostrare che ρ(a) = min{n A F n } Soluzione: Chiamo rank(a) = min{n A F n }. Bisogna provare che rank segue
ESERCIZI DI LOGICA MATEMATICA A.A. 2015-16 Alessandro Combi Esercizio 1.7 Per ogni formula A, dimostrare che ρ(a) = min{n A F n } Soluzione: Chiamo rank(a) = min{n A F n }. Bisogna provare che rank segue
1 Calcolo dei predicati del I ordine. Semantica
 1 Calcolo dei predicati del I ordine. Semantica Ricordiamo la sintassi del calcolo dei predicati. 1.1 Sintassi. Sintassi. Un linguaggio del calcolo dei predicati L = (Pred, Fun, Const) consiste di (1)
1 Calcolo dei predicati del I ordine. Semantica Ricordiamo la sintassi del calcolo dei predicati. 1.1 Sintassi. Sintassi. Un linguaggio del calcolo dei predicati L = (Pred, Fun, Const) consiste di (1)
Esercizi di Logica Matematica (parte 2)
 Luca Costabile Esercizio 317 Esercizi di Logica Matematica (parte 2) Dimostro per induzione sulla costruzione del termine : - Supponiamo che sia una variabile :, - Supponiamo che sia una variabile diversa
Luca Costabile Esercizio 317 Esercizi di Logica Matematica (parte 2) Dimostro per induzione sulla costruzione del termine : - Supponiamo che sia una variabile :, - Supponiamo che sia una variabile diversa
Logica Predicativa. 1 Linguaggi predicativi
 Logica Predicativa 1 Linguaggi predicativi I linguaggi predicativi differiscono da quello proposizionale per una più fine analisi della struttura delle affermazioni atomiche e per un nuovo tipo di connessione
Logica Predicativa 1 Linguaggi predicativi I linguaggi predicativi differiscono da quello proposizionale per una più fine analisi della struttura delle affermazioni atomiche e per un nuovo tipo di connessione
Logica per la Programmazione
 Logica per la Programmazione Lezione 7 Semantica della Logica del Primo Ordine Interpretazioni (richiamo) Un esempio informale di semantica Semantica dei termini Semantica delle formule Esempi A. Corradini
Logica per la Programmazione Lezione 7 Semantica della Logica del Primo Ordine Interpretazioni (richiamo) Un esempio informale di semantica Semantica dei termini Semantica delle formule Esempi A. Corradini
Logica per la Programmazione
 Logica per la Programmazione Lezione 6 Logica del Primo Ordine Motivazioni Sintassi Interpretazioni Formalizzazione A. Corradini e F.Levi Dip.to Informatica Logica per la Programmazione a.a. 2015/16 pag.
Logica per la Programmazione Lezione 6 Logica del Primo Ordine Motivazioni Sintassi Interpretazioni Formalizzazione A. Corradini e F.Levi Dip.to Informatica Logica per la Programmazione a.a. 2015/16 pag.
Introduzione alla logica
 Corso di Intelligenza Artificiale 2011/12 Introduzione alla logica iola Schiaffonati Dipartimento di Elettronica e Informazione Sommario 2 Logica proposizionale (logica di Boole) Logica del primo ordine
Corso di Intelligenza Artificiale 2011/12 Introduzione alla logica iola Schiaffonati Dipartimento di Elettronica e Informazione Sommario 2 Logica proposizionale (logica di Boole) Logica del primo ordine
Cenni di logica. Hynek Kovarik. Università di Brescia. Analisi Matematica A
 Cenni di logica Hynek Kovarik Università di Brescia Analisi Matematica A Hynek Kovarik (Università di Brescia) Cenni di logica Analisi Matematica A 1 / 21 Scopo: introdurre nozioni di logica & terminologia
Cenni di logica Hynek Kovarik Università di Brescia Analisi Matematica A Hynek Kovarik (Università di Brescia) Cenni di logica Analisi Matematica A 1 / 21 Scopo: introdurre nozioni di logica & terminologia
Logica per la Programmazione
 Logica del Primo Ordine: Motivazioni, Sintassi e Interpretazioni Logica per la Programmazione Lezione 7 Semantica della Logica del Primo Ordine pag. 1 Esempio di Semantica: Alfabeto e Interpretazioni Consideriamo
Logica del Primo Ordine: Motivazioni, Sintassi e Interpretazioni Logica per la Programmazione Lezione 7 Semantica della Logica del Primo Ordine pag. 1 Esempio di Semantica: Alfabeto e Interpretazioni Consideriamo
T1: Logica, discorso e conoscenza. Logica classica
 T1: Logica, discorso e conoscenza Primo modulo: Logica classica ovvero Deduzione formale vs verità: un introduzione ai teoremi limitativi Simone Martini Dipartimento di Scienze dell Informazione Alma mater
T1: Logica, discorso e conoscenza Primo modulo: Logica classica ovvero Deduzione formale vs verità: un introduzione ai teoremi limitativi Simone Martini Dipartimento di Scienze dell Informazione Alma mater
METODI MATEMATICI PER L INFORMATICA
 P METODI MATEMATICI PER L INFORMATICA Tutorato Lezione 3 31/03/2016 Corso per matricole congrue a 1 Docente: Margherita Napoli Tutor: Amedeo Leo Predicati e quantificatori Esercizio 9 pagina 53 P(x): x
P METODI MATEMATICI PER L INFORMATICA Tutorato Lezione 3 31/03/2016 Corso per matricole congrue a 1 Docente: Margherita Napoli Tutor: Amedeo Leo Predicati e quantificatori Esercizio 9 pagina 53 P(x): x
Linguaggi. Claudio Sacerdoti Coen 08/04/ : Logica del prim ordine. Universitá di Bologna. Logica del prim ordine
 Linguaggi 17: Logica del prim ordine Universitá di Bologna 08/04/2011 Outline Logica del prim ordine 1 Logica del prim ordine Quantificatori Logica del prim ordine Wikipedia: Nella
Linguaggi 17: Logica del prim ordine Universitá di Bologna 08/04/2011 Outline Logica del prim ordine 1 Logica del prim ordine Quantificatori Logica del prim ordine Wikipedia: Nella
Logica. 7: Conseguenza ed equivalenza logica in logica classica proposizionale. Claudio Sacerdoti Coen. Universitá di Bologna
 Logica 7: Conseguenza ed equivalenza logica in logica classica proposizionale Universitá di Bologna 30/11/2016 Outline Conseguenza logica per la logica proposizionale Wikipedia:
Logica 7: Conseguenza ed equivalenza logica in logica classica proposizionale Universitá di Bologna 30/11/2016 Outline Conseguenza logica per la logica proposizionale Wikipedia:
Logica. Claudio Sacerdoti Coen 07/10/ : Connotazione, denotazione, invarianza per sostituzione. Universitá di Bologna
 Logica 3: Connotazione, denotazione, invarianza per sostituzione Universitá di Bologna 07/10/2015 Outline 1 Connotazione, denotazione, invarianza per sostituzione Connotazione vs
Logica 3: Connotazione, denotazione, invarianza per sostituzione Universitá di Bologna 07/10/2015 Outline 1 Connotazione, denotazione, invarianza per sostituzione Connotazione vs
15. Nozione di modello e verità di un predicato
 15. Nozione di modello e verità di un predicato Def. 0.1 (modello di un linguaggio predicativo) Dato linguaggio predicativo L con costanti c j e predicati atomici P k (x 1,..., x n ) un modello per L è
15. Nozione di modello e verità di un predicato Def. 0.1 (modello di un linguaggio predicativo) Dato linguaggio predicativo L con costanti c j e predicati atomici P k (x 1,..., x n ) un modello per L è
Logica per la Programmazione
 Logica per la Programmazione Lezione 7 Semantica della Logica del Primo Ordine Interpretazioni Formalizzazione Un esempio informale di semantica Semantica dei termini Semantica delle formule Esempi A.
Logica per la Programmazione Lezione 7 Semantica della Logica del Primo Ordine Interpretazioni Formalizzazione Un esempio informale di semantica Semantica dei termini Semantica delle formule Esempi A.
15. Nozione di modello e verità di un predicato
 15. Nozione di modello e verità di un predicato Def. (modello di un linguaggio predicativo) Dato linguaggio predicativo L con costanti c j e predicati atomici P k (x 1,..., x n ) un modello per L è dato
15. Nozione di modello e verità di un predicato Def. (modello di un linguaggio predicativo) Dato linguaggio predicativo L con costanti c j e predicati atomici P k (x 1,..., x n ) un modello per L è dato
LOGICA a.a Esempio di domande 2 prof.ssa Giovanna Corsi
 LOGICA a.a. 2014-2015 Esempio di domande 2 prof.ssa Giovanna Corsi January 4, 2015 1. (a) Cosa dice il cosiddetto Assioma di Aristotele? (b) Qual è la contraria di Tutti gli uomini sono mortali? (c) Qual
LOGICA a.a. 2014-2015 Esempio di domande 2 prof.ssa Giovanna Corsi January 4, 2015 1. (a) Cosa dice il cosiddetto Assioma di Aristotele? (b) Qual è la contraria di Tutti gli uomini sono mortali? (c) Qual
COMPITO di LOGICA PER INFORMATICA (fila 1) 21 settembre 2005
 COMPITO di LOGICA PER INFORMATICA (fila 1) 21 settembre 2005 Nome: Matricola: Esercizio 1.1 Si consideri la seguente scrittura ( ((x) ((y) P (x)(y))))( ((y) ((x) P (y)(x)))) Supponendo fissate le arietà
COMPITO di LOGICA PER INFORMATICA (fila 1) 21 settembre 2005 Nome: Matricola: Esercizio 1.1 Si consideri la seguente scrittura ( ((x) ((y) P (x)(y))))( ((y) ((x) P (y)(x)))) Supponendo fissate le arietà
Logica per la Programmazione
 Logica per la Programmazione Lezione 6 Logica del Primo Ordine Motivazioni Sintassi di Termini e Formule Formule aperte e chiuse A. Corradini e F.Levi Dip.to Informatica Logica per la Programmazione a.a.
Logica per la Programmazione Lezione 6 Logica del Primo Ordine Motivazioni Sintassi di Termini e Formule Formule aperte e chiuse A. Corradini e F.Levi Dip.to Informatica Logica per la Programmazione a.a.
Linguaggi. Claudio Sacerdoti Coen 11/12/ : Logica del prim ordine. Universitá di Bologna. Logica del prim ordine
 Linguaggi 17: Universitá di Bologna 11/12/2017 Outline 1 Quantificatori Wikipedia: Nella logica i quantificatori sono espressioni come qualcosa (quantificatore esistenziale) e ogni
Linguaggi 17: Universitá di Bologna 11/12/2017 Outline 1 Quantificatori Wikipedia: Nella logica i quantificatori sono espressioni come qualcosa (quantificatore esistenziale) e ogni
Linguaggi. Claudio Sacerdoti Coen 13/12/ : Semantica della logica del prim ordine. Universitá di Bologna
 Linguaggi 18: Universitá di Bologna 13/12/2017 Outline 1 Semantica classica della logica del prim ordine Al fine di definire la semantica classica di un linguaggio del prim ordine
Linguaggi 18: Universitá di Bologna 13/12/2017 Outline 1 Semantica classica della logica del prim ordine Al fine di definire la semantica classica di un linguaggio del prim ordine
LOGICA DEL PRIMO ORDINE: MOTIVAZIONI, SINTASSI E INTERPRETAZIONI
 LOGICA DEL PRIMO ORDINE: MOTIVAZIONI, SINTASSI E INTERPRETAZIONI LIMITI DEL CALCOLO PROPOSIZIONALE Nella formalizzazione di enunciati dichiarativi, gli enunciati atomici non hanno struttura (sono rappresentati
LOGICA DEL PRIMO ORDINE: MOTIVAZIONI, SINTASSI E INTERPRETAZIONI LIMITI DEL CALCOLO PROPOSIZIONALE Nella formalizzazione di enunciati dichiarativi, gli enunciati atomici non hanno struttura (sono rappresentati
Logica proposizionale
 Fondamenti di Informatica per la Sicurezza a.a. 2008/09 Logica proposizionale Stefano Ferrari UNIVERSITÀ DEGLI STUDI DI MILANO DIPARTIMENTO DI TECNOLOGIE DELL INFORMAZIONE Stefano Ferrari Università degli
Fondamenti di Informatica per la Sicurezza a.a. 2008/09 Logica proposizionale Stefano Ferrari UNIVERSITÀ DEGLI STUDI DI MILANO DIPARTIMENTO DI TECNOLOGIE DELL INFORMAZIONE Stefano Ferrari Università degli
Intelligenza Artificiale. Logica del primo ordine (introduzione)
 Intelligenza Artificiale Logica del primo ordine (introduzione) Marco Piastra Logica formale (Parte 4) - 1 Parte 4 Linguaggio del primo ordine Soddisfacibilità Modelli Conseguenza logica Logica formale
Intelligenza Artificiale Logica del primo ordine (introduzione) Marco Piastra Logica formale (Parte 4) - 1 Parte 4 Linguaggio del primo ordine Soddisfacibilità Modelli Conseguenza logica Logica formale
Cenni di logica e calcolo proposizionale
 Cenni di logica e calcolo proposizionale Corso di Laurea in Informatica Università degli Studi di Bari (sede Brindisi) Analisi Matematica S.Milella (sabina.milella@uniba.it) Cenni di logica 1 / 10 Proposizioni
Cenni di logica e calcolo proposizionale Corso di Laurea in Informatica Università degli Studi di Bari (sede Brindisi) Analisi Matematica S.Milella (sabina.milella@uniba.it) Cenni di logica 1 / 10 Proposizioni
14. Nozione di modello e verità di un predicato
 14. Nozione di modello e verità di un predicato Per definire la validità di un predicato facciamo uso della nozione di modello. Intuitivamente un modello definisce in modo primitivo l interpretazione delle
14. Nozione di modello e verità di un predicato Per definire la validità di un predicato facciamo uso della nozione di modello. Intuitivamente un modello definisce in modo primitivo l interpretazione delle
Nome: Corso di laurea: Matricola:
 Nome: Corso di laurea: Matricola: Università degli studi di Trieste Corso di Laurea in Informatica Esame di Fondamenti Logici dell Informatica 24 Aprile 2006, versione A Vero/Falso Dire se le seguenti
Nome: Corso di laurea: Matricola: Università degli studi di Trieste Corso di Laurea in Informatica Esame di Fondamenti Logici dell Informatica 24 Aprile 2006, versione A Vero/Falso Dire se le seguenti
Logica per la Programmazione
 Logica per la Programmazione Lezione 9 Logica del Primo Ordine con Insiemi ed Intervalli Formalizzazione di Enunciati: Array e Sequenze pag. 1 Rappresentazioni Intensionali ed Estensionali di Insiemi Assumiamo
Logica per la Programmazione Lezione 9 Logica del Primo Ordine con Insiemi ed Intervalli Formalizzazione di Enunciati: Array e Sequenze pag. 1 Rappresentazioni Intensionali ed Estensionali di Insiemi Assumiamo
Complementi alle Dispense di Logica Matematica corso A e B
 Complementi alle Dispense di Logica Matematica corso A e B Alessandro Andretta alessandro.andretta@unito.it Matteo Viale matteo.viale@unito.it 1 Deduzione naturale Una derivazione di B da A 1,..., A n,
Complementi alle Dispense di Logica Matematica corso A e B Alessandro Andretta alessandro.andretta@unito.it Matteo Viale matteo.viale@unito.it 1 Deduzione naturale Una derivazione di B da A 1,..., A n,
LOGICA MATEMATICA. Sonia L Innocente. Corso di Laurea. Informatica e Tecnologie/Informatica Industriale
 LOGICA MATEMATICA Corso di Laurea Informatica e Tecnologie/Informatica Industriale Argomento 1. Logica dei Predicati del Primo Ordine a.a. 2013-2014 (Camerino) 1 / 57 Outline Introduzione 1 Introduzione
LOGICA MATEMATICA Corso di Laurea Informatica e Tecnologie/Informatica Industriale Argomento 1. Logica dei Predicati del Primo Ordine a.a. 2013-2014 (Camerino) 1 / 57 Outline Introduzione 1 Introduzione
Semantica proposizionale. Unit 2, Lez 3 e 4 Corso di Logica
 Semantica proposizionale Unit 2, Lez 3 e 4 Corso di Logica Sommario Semantica dei connettivi Costruzione delle tavole di verità Tautologie, contraddizioni e contingenze Semantica delle forme argomentative
Semantica proposizionale Unit 2, Lez 3 e 4 Corso di Logica Sommario Semantica dei connettivi Costruzione delle tavole di verità Tautologie, contraddizioni e contingenze Semantica delle forme argomentative
RELAZIONI TRA SINTASSI E SEMANTICA
 RELAZIONI TRA SINTASSI E SEMANTICA INTERPRETAZIONI E MODELLI Sia un insieme di enunciati dichiarativi (asserzioni che hanno valore T o F) Una intepretazione assegna un significato ad ogni componente degli
RELAZIONI TRA SINTASSI E SEMANTICA INTERPRETAZIONI E MODELLI Sia un insieme di enunciati dichiarativi (asserzioni che hanno valore T o F) Una intepretazione assegna un significato ad ogni componente degli
Forme normali, clausole e Calcolo con regola di Risoluzione
 Forme normali, clausole e Calcolo con regola di Risoluzione Esempi di equivalenze valide α β (α β ) (α β ) α ( β γ ) ( xα ) ( xα ) α α α α β α β α β (α β ) (α γ ) x α x α V α α F α 1 Forma normale congiuntiva
Forme normali, clausole e Calcolo con regola di Risoluzione Esempi di equivalenze valide α β (α β ) (α β ) α ( β γ ) ( xα ) ( xα ) α α α α β α β α β (α β ) (α γ ) x α x α V α α F α 1 Forma normale congiuntiva
1 Richiami di logica matematica
 Geometria e Topologia I 7 marzo 2005 1 1 Richiami di logica matematica Definire cos è un enunciato, una proposizione (elemento primitivo della logica delle proposizioni). La definizione è data in termini
Geometria e Topologia I 7 marzo 2005 1 1 Richiami di logica matematica Definire cos è un enunciato, una proposizione (elemento primitivo della logica delle proposizioni). La definizione è data in termini
FOL: Linguaggio, Semantica e Calcolo
 FOL: Linguaggio, Semantica e Calcolo Integrazione materiale Brachman&Levesque Matteo Palmonari Dipartimento di Informatica, Sistemistica e Comunicazione Università di Milano-Bicocca Composizionalità del
FOL: Linguaggio, Semantica e Calcolo Integrazione materiale Brachman&Levesque Matteo Palmonari Dipartimento di Informatica, Sistemistica e Comunicazione Università di Milano-Bicocca Composizionalità del
Lo studioso di logica si chiede se la conclusione segue correttamente dalla premesse fornite e se premesse sono buone per accettare la conclusione.
 Logica binaria La logica è la scienza del corretto ragionamento e consiste nello studio dei principi e dei metodi che consentono di individuare il corretto ragionamento. Lo studioso di logica si chiede
Logica binaria La logica è la scienza del corretto ragionamento e consiste nello studio dei principi e dei metodi che consentono di individuare il corretto ragionamento. Lo studioso di logica si chiede
LOGICA DEL PRIMO ORDINE CON INSIEMI E INTERVALLI. Corso di Logica per la Programmazione
 LOGICA DEL PRIMO ORDINE CON INSIEMI E INTERVALLI Corso di Logica per la Programmazione RAPPRESENTAZIONI INTENSIONALI ED ESTENSIONALI DI INSIEMI Assumiamo come universo i naturali e i sottoinsiemi di naturali
LOGICA DEL PRIMO ORDINE CON INSIEMI E INTERVALLI Corso di Logica per la Programmazione RAPPRESENTAZIONI INTENSIONALI ED ESTENSIONALI DI INSIEMI Assumiamo come universo i naturali e i sottoinsiemi di naturali
Logica: nozioni di base
 Fondamenti di Informatica Sistemi di Elaborazione delle Informazioni Informatica Applicata Logica: nozioni di base Antonella Poggi Anno Accademico 2012-2013 DIPARTIMENTO DI SCIENZE DOCUMENTARIE LINGUISTICO
Fondamenti di Informatica Sistemi di Elaborazione delle Informazioni Informatica Applicata Logica: nozioni di base Antonella Poggi Anno Accademico 2012-2013 DIPARTIMENTO DI SCIENZE DOCUMENTARIE LINGUISTICO
Ragionamenti e metodi di dimostrazione. Liceo Scientifico Statale S. Cannizzaro Prof.re E. Modica
 Ragionamenti e metodi di dimostrazione Liceo Scientifico Statale S. Cannizzaro Prof.re E. Modica Proposizioni Si definisce proposizione una frase alla quale è possibile attribuire uno e un solo valore
Ragionamenti e metodi di dimostrazione Liceo Scientifico Statale S. Cannizzaro Prof.re E. Modica Proposizioni Si definisce proposizione una frase alla quale è possibile attribuire uno e un solo valore
Logica per la Programmazione
 Logica del Primo Ordine: Motivazioni, Sintassi e Interpretazioni Logica per la Programmazione Lezione 9 Proof System per la Logica del Primo Ordine Leggi per i Quantificatori Regole di inferenza: Generalizzazione
Logica del Primo Ordine: Motivazioni, Sintassi e Interpretazioni Logica per la Programmazione Lezione 9 Proof System per la Logica del Primo Ordine Leggi per i Quantificatori Regole di inferenza: Generalizzazione
Intelligenza Artificiale I
 Intelligenza Artificiale I Logica del primo ordine: predicati e relazioni Marco Piastra Predicati e relazioni [1] Strutture semantiche proposizionali (già viste) Mondi possibili descritti tramite affermazioni
Intelligenza Artificiale I Logica del primo ordine: predicati e relazioni Marco Piastra Predicati e relazioni [1] Strutture semantiche proposizionali (già viste) Mondi possibili descritti tramite affermazioni
INSIEMI. DEF. Un INSIEME è una qualsiasi collezione di oggetti.
 INSIEMI DEF. Un INSIEME è una qualsiasi collezione di oggetti. Esso è ben definito quando è chiaro se un oggetto appartiene o non appartiene all insieme stesso. Esempio. E possibile definire l insieme
INSIEMI DEF. Un INSIEME è una qualsiasi collezione di oggetti. Esso è ben definito quando è chiaro se un oggetto appartiene o non appartiene all insieme stesso. Esempio. E possibile definire l insieme
T1: Logica, discorso e conoscenza. Logica classica
 T1: Logica, discorso e conoscenza Primo modulo: Logica classica ovvero Deduzione formale vs verità: un introduzione ai teoremi limitativi Simone Martini Dipartimento di Scienze dell Informazione Alma mater
T1: Logica, discorso e conoscenza Primo modulo: Logica classica ovvero Deduzione formale vs verità: un introduzione ai teoremi limitativi Simone Martini Dipartimento di Scienze dell Informazione Alma mater
Istituzioni di Logica Matematica
 Istituzioni di Logica Matematica Sezione 11 del Capitolo 3 Alessandro Andretta Dipartimento di Matematica Università di Torino A. Andretta (Torino) Istituzioni di Logica Matematica AA 2013 2014 1 / 19
Istituzioni di Logica Matematica Sezione 11 del Capitolo 3 Alessandro Andretta Dipartimento di Matematica Università di Torino A. Andretta (Torino) Istituzioni di Logica Matematica AA 2013 2014 1 / 19
Logica per la Programmazione
 Logica per la Programmazione Lezione 10 Logica del Primo Ordine con Insiemi ed Intervalli Formalizzazione di Enunciati: Array e Sequenze A. Corradini e F.Levi Dip.to Informatica Logica per la Programmazione
Logica per la Programmazione Lezione 10 Logica del Primo Ordine con Insiemi ed Intervalli Formalizzazione di Enunciati: Array e Sequenze A. Corradini e F.Levi Dip.to Informatica Logica per la Programmazione
Logica Matematica: tipiche domande da esame
 Logica Matematica: tipiche domande da esame A. Berarducci Versione del 7 Gen. 2018 1. Si dimostri che ogni formula proposizionale può essere messa in forma normale disgiuntiva e in forma normale disgiuntiva.
Logica Matematica: tipiche domande da esame A. Berarducci Versione del 7 Gen. 2018 1. Si dimostri che ogni formula proposizionale può essere messa in forma normale disgiuntiva e in forma normale disgiuntiva.
Intelligenza Artificiale II. Logica del Primo Ordine Parte Teoria
 Intelligenza Artificiale II Logica del Primo Ordine Parte 1.2 - Teoria Marco Piastra Logica del primo ordine (2) - 1 2 Linguaggio e semantica Logica del primo ordine (2) - 2 Linguaggio del primo ordine
Intelligenza Artificiale II Logica del Primo Ordine Parte 1.2 - Teoria Marco Piastra Logica del primo ordine (2) - 1 2 Linguaggio e semantica Logica del primo ordine (2) - 2 Linguaggio del primo ordine
Logica del primo ordine: predicati e relazioni
 Intelligenza Artificiale I Logica del primo ordine: predicati e relazioni Marco Piastra Predicati e relazioni 1] Esempio preliminare Soluzione di un equazione algebrica x 2 + ax + b = 0 x 2 + 2(a/2)x +
Intelligenza Artificiale I Logica del primo ordine: predicati e relazioni Marco Piastra Predicati e relazioni 1] Esempio preliminare Soluzione di un equazione algebrica x 2 + ax + b = 0 x 2 + 2(a/2)x +
LOGICA DEL PRIMO ORDINE: SEMANTICA. Corso di Logica per la Programmazione A.A. 2010/11 Andrea Corradini, Paolo Mancarella
 LOGICA DEL PRIMO ORDINE: SEMANTICA Corso di Logica per la Programmazione A.A. 2010/11 Andrea Corradini, Paolo Mancarella LA SEMANTICA DELLA LOGICA DEL PRIMO ORDINE Sia fissato un linguaggio L del primo
LOGICA DEL PRIMO ORDINE: SEMANTICA Corso di Logica per la Programmazione A.A. 2010/11 Andrea Corradini, Paolo Mancarella LA SEMANTICA DELLA LOGICA DEL PRIMO ORDINE Sia fissato un linguaggio L del primo
Aniello Murano Decidibilità delle teorie logiche
 Aniello Murano Decidibilità delle teorie logiche 11 Lezione n. Parole chiave: Teorie logiche Corso di Laurea: Informatica Codice: Email Docente: murano@ na.infn.it A.A. 2008-2009 Prefazione Nelle lezioni
Aniello Murano Decidibilità delle teorie logiche 11 Lezione n. Parole chiave: Teorie logiche Corso di Laurea: Informatica Codice: Email Docente: murano@ na.infn.it A.A. 2008-2009 Prefazione Nelle lezioni
1 Richiami di logica matematica
 Geometria e Topologia I 2006-mar-05 1 1 Richiami di logica matematica Definire cos è un enunciato, una proposizione (elemento primitivo della logica delle proposizioni). La definizione è data in termini
Geometria e Topologia I 2006-mar-05 1 1 Richiami di logica matematica Definire cos è un enunciato, una proposizione (elemento primitivo della logica delle proposizioni). La definizione è data in termini
LEZIONI 30/09/09-2/10/09
 LEZIONI 30/09/09-2/10/09 1. Introduzione La Logica viene usata in Informatica in tutte quelle situazioni in cui un sistema informatico viene modellato da un oggetto matematico e si vuole ragionare in modo
LEZIONI 30/09/09-2/10/09 1. Introduzione La Logica viene usata in Informatica in tutte quelle situazioni in cui un sistema informatico viene modellato da un oggetto matematico e si vuole ragionare in modo
METODI MATEMATICI PER L INFORMATICA
 METODI MATEMATICI PER L INFORMATICA Tutorato Lezione 5 05/05/2016 Corso per matricole congrue a 1 Docente: Margherita Napoli Tutor: Amedeo Leo Dimostrazioni e prove Esercizio 7 pagina 91 Utilizzare una
METODI MATEMATICI PER L INFORMATICA Tutorato Lezione 5 05/05/2016 Corso per matricole congrue a 1 Docente: Margherita Napoli Tutor: Amedeo Leo Dimostrazioni e prove Esercizio 7 pagina 91 Utilizzare una
Esercizi di Logica Matematica
 Esercizi di Logica Matematica Francesco Bottacin 1 Logica Proposizionale Esercizio 1.1. Eliminare le parentesi non necessarie nelle seguenti formule: 1. ((A B) ( C)) 2. (A (B ( C))) 3. ((A B) (C D)) 4.
Esercizi di Logica Matematica Francesco Bottacin 1 Logica Proposizionale Esercizio 1.1. Eliminare le parentesi non necessarie nelle seguenti formule: 1. ((A B) ( C)) 2. (A (B ( C))) 3. ((A B) (C D)) 4.
Introduzione ad alcuni sistemi di logica modale
 Introduzione ad alcuni sistemi di logica modale Laura Porro 16 maggio 2008 1 Il calcolo proposizionale Prendiamo come primitivi i simboli del Calcolo Proposizionale (PC) tradizionale a due valori 1 : un
Introduzione ad alcuni sistemi di logica modale Laura Porro 16 maggio 2008 1 Il calcolo proposizionale Prendiamo come primitivi i simboli del Calcolo Proposizionale (PC) tradizionale a due valori 1 : un
13. Nozione di modello e verità di un predicato
 13. Nozione di modello e verità di un predicato Def. 0.1 (modello di un linguaggio predicativo) Dato linguaggio predicativo L con costanti c j e predicati atomici P k (x 1,..., x n ) un modello per L è
13. Nozione di modello e verità di un predicato Def. 0.1 (modello di un linguaggio predicativo) Dato linguaggio predicativo L con costanti c j e predicati atomici P k (x 1,..., x n ) un modello per L è
