Geometria Differenziale
|
|
|
- Giacinto Salvatori
- 4 anni fa
- Visualizzazioni
Transcript
1 Geometria Differenziale Foglio 4 - Superfici Esercizio 1. Si considerino la curva α : R R 3 definita ponendo α(t) = (cos(t), sin(t), t) e la superficie elementare P : R (0, + ) R 3 di equazioni parametriche P(u, v) = (u cos v, u sin v, 1 + v u). 1. Verificare che il sostegno di α è contenuto nel sostegno di P. 2. Calcolare la curvatura normale e la curvatura geodetica di α e stabilire se α è una geodetica. Esercizio 2. Si consideri la superficie elementare P : R 2 R 3 definita ponendo P(u, v) = (2v u, v 2u, 2u 2 + 5uv 2v 2 ). 2. Si determinino le direzioni asintotiche nel punto Q = P(0, 0). 3. Sia C la curva intersezione della superficie con il piano x + y = 0; si determinino curvatura e torsione di C. 4. Si dimostri che la direzione tangente a C in Q è una delle direzioni principali e si determini l altra. Esercizio 3. Sia γ : ( ε, ε) R 3 una curva di fortemente regolare e C parametrizzata mediante il parametro lunghezza d arco s. 1. Si consideri la superficie formata dal tubo che avvolge γ, parametrizzata da: P(s, ϑ) = γ(s) + cos ϑ n(s) + sin ϑ b(s), dove s ( ε, ε), θ (0, 2π), n indica il versore normale e b il versore binormale lungo γ. Calcolare il versore normale e la prima forma fondamentale in funzione di ϑ, della curvatura e della torsione di γ. 2. Dimostrare che, per ogni s 0 ( ε, ε) la curva α data da s = s 0 è una geodetica. 1
2 2 Esercizio 4. Si consideri la superficie elementare P : R + ( π, π) R 3 definita ponendo P(u, v) = (ln(u) cos(v), ln(u) sin(v), v). Determinare la natura dei punti della superficie. Trovare le direzioni principali e le direzioni asintotiche nel punto P(1, 0). La curva γ(t) = P(e t, 0) è una geodetica? Esercizio 5. Sia P : R 2 R 3 la superficie elementare definita dalle equazioni P(u, v) = (u, u 3 + v 3 + 2uv, v). 2. Si determinino le coniche di Dupin della superficie nel punto P(0, 0). 3. La curva γ(t) = P(t, t) è una linea asintotica? 4. Si calcoli la torsione di γ. Esercizio 6. Sia P : R 2 R 3 la superficie elementare definita dalle equazioni P(u, v) = (u v, 3uv, u + v) 1. Si trovi la natura dei punti della superficie al variare di u e v. 2. Si trovino le curvature principali e le direzioni principali nel punto Q = (0, 0, 0). 3. Si trovino le coniche di Dupin e le direzioni asintotiche nel punto Q = (0, 0, 0). 4. Si stabilisca se le linee coordinate sono linee asintotiche e/o geodetiche. 5. Si mostri che la superficie è rigata e si stabilisca se è sviluppabile. Esercizio 7. Sia P : R + (0, 2π) R 3 la superficie elementare definita dalle equazioni P(u, v) = (sinh(u) cos(v), sinh(u) sin(v), v) 2. Si determinino le curvature e le direzioni principali della superficie nel punto P(0, π). 3. La curva γ(t) = (sinh(t) cos(t), sinh(t) sin(t), t) è una linea di curvatura? 4. E una geodetica?
3 3 Esercizio 8. Si consideri la superficie elementare: P : ( π, π) (0, 2) R 3 definita ponendo P(u, v) = (sin u + v cos u, u + v, cos u v sin u). 1. Si determini la natura dei punti di S. 2. Si verifichi che per ogni punto di S esiste una sola direzione asintotica e la si determini. 3. Si provi che S è una superficie rigata e si dica se è sviluppabile. Esercizio 9. Sia P : ( π 2, 3π ) 2 R + R 3 la superficie elementare definita dalle equazioni P(u, v) = (v cos(u), v sin(u), 2 sin(u)) 1. Si trovi la natura dei punti di S = P (( π 2, 3π ) 2 R + ) al variare dei parametri u e v. 2. Si stabilisca se le curve P(u 0, v) sono linee di curvatura, linee asintotiche, geodetiche. 3. Si mostri che la superficie è rigata e si stabilisca se è sviluppabile. Esercizio 10. Sia P : (0, 2π) (0, 2π) R 3 la superficie elementare definita dalle equazioni P(u, v) = (sin u + 2) cos v, (sin u + 2) sin v, u) 1. Si trovi la natura dei punti di S = P((0, 2π) (0, 2π)) al variare dei parametri u e v. 2. Si trovino le direzioni asintotiche e le curvature principali nel punto P(π/2, π). 3. Le curve di equazioni u = π/2 e u = π sono geodetiche? 4. Si calcolino i simboli di Christoffel Γ 1 11 e Γ2 11 di P. Esercizio 11. Sia γ una curva fortemente parametrizzata con parametro arco su una superficie S, Si mostri che, se γ è una linea asintotica ed una geodetica, allora γ è una linea retta. Esercizio 12. Sia γ una curva fortemente regolare parametrizzata con parametro arco su una superficie S. Si mostri che se γ è sia una linea di curvatura che una geodetica allora γ è piana. Inoltre si fornisca un esempio di una linea di curvatura che è una curva piana e non è una geodetica.
4 4 Esercizio 13. Sia γ : J R 3 una curva fortemente regolare, semplice e liscia, parametrizzata rispetto alla lunghezza d arco. Sia P : J ( ε, ε) R 3 definita ponendo P(u, v) = γ(u) + vb(u), ove b indica il versore binormale a γ. Sapendo che, per ε sufficientemente piccolo P è iniettiva, si mostri che P è una superficie elementare e che γ è una geodetica. Esercizio 14. Sia P : Ω R 3 una superficie elementare di supporto P(Ω) = S, priva di punti umbilici. Sia γ : J Ω S una curva su S, parametrizzata con il parametro naturale, e sia p un punto del supporto di γ. In T p S sia {e 1, e 2 } la base ortonormale delle direzioni principali, e siano k 1 e k 2 le curvature principali. Sia n g il versore in T p S che forma una base ortonormale positivamente orientata con il versore tangente a γ in p, denotato con t. Si definisca la torsione geodetica di γ come τ g := L(t) n g. 1. Si provi che τ g = (k 2 k 1 ) cos ϑ sin ϑ, ove ϑ è l angolo tra e 1 e t. 2. Si provi che τ g è identicamente nulla se e solo se γ è una linea di curvatura. Esercizio 15. Sia S R 3 una superficie e p S un suo punto. Sia γ : J S una geodetica, parametrizzata con parametro naturale, tale che γ(0) = p. 1. Si provi che, se la curvatura κ di γ in p non è nulla e γ è una curva piana, allora il versore tangente a γ in p, t γ (0) è un autovettore dell operatore di Weingarten. 2. Se ne deduca che se ogni geodetica di S è una curva piana allora S è contenuta in un piano o in una sfera. Esercizio 16. Sia S R 3 una superficie i cui punti sono tutti iperbolici. Si provi che su S non possono esistere due geodetiche che sono il bordo di una regione semplice R come in figura. /2 1 R 2 /2
5 5 Esercizio 17. Sia S R 3 una superficie differenziabile compatta che ha solo punti ellittici. Si provi che S è omeomorfa alla sfera. Esercizio 18. Sia S R 3 una superficie differenziabile compatta, e sia P S il punto la cui distanza dall origine è massima. Si provi che il versore P/ P è normale ad S in P. Si provi inoltre che P è un punto ellittico. (Suggerimento: si mostri che le curvature normali in P sono in modulo maggiori o uguali a 1/ P ). Esercizio 19. Si provi che non esiste una superficie differenziabile compatta S R 3 con curvatura media identicamente nulla. Esercizio 20. Sia S R 3 una superficie differenziabile compatta omeomorfa alla sfera, tale che in ogni punto la sua curvatura di Gauss è maggiore di una costante positiva K 0. Qual è la massima area che può avere S?
Esercizi tratti da temi d esame
 Gianluca Occhetta Esercizi tratti da temi d esame Geometria IV e V unità didattica 00 11 0 1 0 1111111111 Università di Trento Dipartimento di Matematica Via Sommarive 14 38050 - ovo (TN) 1 Topologia
Gianluca Occhetta Esercizi tratti da temi d esame Geometria IV e V unità didattica 00 11 0 1 0 1111111111 Università di Trento Dipartimento di Matematica Via Sommarive 14 38050 - ovo (TN) 1 Topologia
GEOMETRIA DIFFERENZIALE - GENNAIO 2012
 GEOMETRIA DIFFERENZIALE - GENNAIO 0 N.B.: Gli esercizi e bis sono ALTERNATIVI l uno all altro Esercizio. (9 punti) Sia P :(0, /)! R la curva piana definita dalle equazioni parametriche P(t) = 4 ( cos(t)
GEOMETRIA DIFFERENZIALE - GENNAIO 0 N.B.: Gli esercizi e bis sono ALTERNATIVI l uno all altro Esercizio. (9 punti) Sia P :(0, /)! R la curva piana definita dalle equazioni parametriche P(t) = 4 ( cos(t)
Geometria 3 A.A Esercizi. Irriducibilità di polinomi di più variabili. Discriminante.
 Geometria 3 A.A. 2015 2016 Esercizi Irriducibilità di polinomi di più variabili. Discriminante. Risultante. Si dimostri che il polinomio di Fermat f(x 1,..., x n ) = x d 1 + + x d n è irriducibile in C[x
Geometria 3 A.A. 2015 2016 Esercizi Irriducibilità di polinomi di più variabili. Discriminante. Risultante. Si dimostri che il polinomio di Fermat f(x 1,..., x n ) = x d 1 + + x d n è irriducibile in C[x
Geometria 3 A.A Esercizi. Irriducibilità di polinomi di più variabili. Discriminante.
 Geometria 3 A.A. 2017 2018 Esercizi Irriducibilità di polinomi di più variabili. Discriminante. Risultante. Sia K un campo. Si dimostri che un polinomio f(x) K[x] di grado d, dove 2 d 3, è riducibile se
Geometria 3 A.A. 2017 2018 Esercizi Irriducibilità di polinomi di più variabili. Discriminante. Risultante. Sia K un campo. Si dimostri che un polinomio f(x) K[x] di grado d, dove 2 d 3, è riducibile se
Geometria 3 A.A Esercizi. Irriducibilità di polinomi di più variabili. Discriminante.
 Geometria 3 A.A. 2016 2017 Esercizi Irriducibilità di polinomi di più variabili. Discriminante. Risultante. Si dimostri che il polinomio f(x, y) = x 2 y +x 5 +1 è irriducibile in C[x, y]. Sia K un campo.
Geometria 3 A.A. 2016 2017 Esercizi Irriducibilità di polinomi di più variabili. Discriminante. Risultante. Si dimostri che il polinomio f(x, y) = x 2 y +x 5 +1 è irriducibile in C[x, y]. Sia K un campo.
Esercizi per il corso di Geometria 2
 Esercizi per il corso di Geometria 2 Davide Astesiano 2 giugno 209 Martedì 4/05/209 Exercise -: Si prenda una curva piana e si dimostri che la definizione di curvatura nella forma k(s) = σ, è equivalente
Esercizi per il corso di Geometria 2 Davide Astesiano 2 giugno 209 Martedì 4/05/209 Exercise -: Si prenda una curva piana e si dimostri che la definizione di curvatura nella forma k(s) = σ, è equivalente
Esercizi su curvatura e torsione.
 Esercizi su curvatura e torsione. e-mail: maurosaita@tiscalinet.it Versione provvisoria, gennaio 016. 1 Indice 1 Curvatura e torsione 1.1 Curve parametrizzate alla lunghezza d arco................... 1.
Esercizi su curvatura e torsione. e-mail: maurosaita@tiscalinet.it Versione provvisoria, gennaio 016. 1 Indice 1 Curvatura e torsione 1.1 Curve parametrizzate alla lunghezza d arco................... 1.
Geometria 3 A.A Esercizi
 Geometria 3 A.A. 2014 2015 Esercizi Equivalenza omo- Omotopia di applicazioni contiue. topica. Si dimostri che lo spazio X = {x R 2 : x 1} è connesso. Si dimostri che lo spazio topologico è connesso. X
Geometria 3 A.A. 2014 2015 Esercizi Equivalenza omo- Omotopia di applicazioni contiue. topica. Si dimostri che lo spazio X = {x R 2 : x 1} è connesso. Si dimostri che lo spazio topologico è connesso. X
1 Rette e piani nello spazio
 1 Rette e piani nello spazio Esercizio 1.1 È assegnato un riferimento cartesiano 0xyz. Sono assegnati la retta x = t, r : y = t, z = t, il piano π : x + y + z = 0 ed il punto P = (1, 1, 1). Scrivere le
1 Rette e piani nello spazio Esercizio 1.1 È assegnato un riferimento cartesiano 0xyz. Sono assegnati la retta x = t, r : y = t, z = t, il piano π : x + y + z = 0 ed il punto P = (1, 1, 1). Scrivere le
Geometria 3 A.A Esercizi
 Geometria 3 A.A. 2012 2013 Esercizi Omotopia di applicazioni contiue. Si dimostri che lo spazio X = {x R 2 : x 1} è connesso. Siano x, y punti di uno spazio topologico X. Si dimostri che le applicazioni
Geometria 3 A.A. 2012 2013 Esercizi Omotopia di applicazioni contiue. Si dimostri che lo spazio X = {x R 2 : x 1} è connesso. Siano x, y punti di uno spazio topologico X. Si dimostri che le applicazioni
Esercizi 2: Curve dello spazio Soluzioni
 Esercizi 2: Curve dello spazio Soluzioni. Esercizio Si consideri la curva (elica circolare): a α(t) = a sin t, t R, bt dove a >. a) Calcolare curvatura e torsione di α nel generico punto t. b) Determinare
Esercizi 2: Curve dello spazio Soluzioni. Esercizio Si consideri la curva (elica circolare): a α(t) = a sin t, t R, bt dove a >. a) Calcolare curvatura e torsione di α nel generico punto t. b) Determinare
Geometria Differenziale: soluzioni test
 Geometria Differenziale: soluzioni test Esercizio. Sia α : I R 3 una curva biregolare dello spazio, parametrizzata dall ascissa curvilinea. a) Definire curvatura, torsione e riferimento di Frenet di α.
Geometria Differenziale: soluzioni test Esercizio. Sia α : I R 3 una curva biregolare dello spazio, parametrizzata dall ascissa curvilinea. a) Definire curvatura, torsione e riferimento di Frenet di α.
Esame scritto di Geometria 2
 Esame scritto di Geometria Appello del primo luglio 016 Esercizio 1 Si consideri la curva dipendente dal parametro h R: α h : R R 3, α h (s) = ( 1 cos s, sin s + hs, sin s hs). 4 4 1. Si determini il valore
Esame scritto di Geometria Appello del primo luglio 016 Esercizio 1 Si consideri la curva dipendente dal parametro h R: α h : R R 3, α h (s) = ( 1 cos s, sin s + hs, sin s hs). 4 4 1. Si determini il valore
Vi prego di segnalare ogni inesattezza o errore tipografico a
 ESERCIZI DI GEOMETRIA 4 Vi prego di segnalare ogni inesattezza o errore tipografico a mll@unife.it Geometria proiettiva Esercizio 1. Dire quali tra le seguenti coordinate omogenee dei punti in P 2 rappresentano
ESERCIZI DI GEOMETRIA 4 Vi prego di segnalare ogni inesattezza o errore tipografico a mll@unife.it Geometria proiettiva Esercizio 1. Dire quali tra le seguenti coordinate omogenee dei punti in P 2 rappresentano
Curve parametrizzate. Esercizi. 1 Curve parametrizzate con parametri arbitrari. Curvatura. Torsione
 Curve parametrizzate. Esercizi Mauro Saita e-mail: maurosaita@tiscalinet.it Versione provvisoria, gennaio 014. 1 1 Curve parametrizzate con parametri arbitrari. Curvatura. Torsione Qui di seguito si riporta
Curve parametrizzate. Esercizi Mauro Saita e-mail: maurosaita@tiscalinet.it Versione provvisoria, gennaio 014. 1 1 Curve parametrizzate con parametri arbitrari. Curvatura. Torsione Qui di seguito si riporta
GEOMETRIA B Esercizi
 GEOMETRIA B 2016-17 BARBARA NELLI A.A. 2016-17 Alcuni degli esercizi sono presi dal libro DC [1]. 1. Esercizi Esercizio 1.1. Sia α : I R 3 una curva parametrizzata e sia v R 3 un vettore fissato. Assumiamo
GEOMETRIA B 2016-17 BARBARA NELLI A.A. 2016-17 Alcuni degli esercizi sono presi dal libro DC [1]. 1. Esercizi Esercizio 1.1. Sia α : I R 3 una curva parametrizzata e sia v R 3 un vettore fissato. Assumiamo
Geometria Differenziale 2017/18 Esercizi 3
 Geometria Differenziale 217/18 Esercizi 3 1 Superfici I 1.1 Esercizio a) Verificare che l ellissoide Σ : x2 a 2 + y2 b 2 + z2 c 2 = 1 è una superficie regolare in tutti i suoi punti. b) Dare una parametrizzazione
Geometria Differenziale 217/18 Esercizi 3 1 Superfici I 1.1 Esercizio a) Verificare che l ellissoide Σ : x2 a 2 + y2 b 2 + z2 c 2 = 1 è una superficie regolare in tutti i suoi punti. b) Dare una parametrizzazione
Anno Accademico 2017/2018
 Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2017/2018 Scuola di Scienze Matematiche, Fisiche e Naturali Corsi di Laurea o di Diploma Laurea in Matematica Insegnamento Geometria
Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2017/2018 Scuola di Scienze Matematiche, Fisiche e Naturali Corsi di Laurea o di Diploma Laurea in Matematica Insegnamento Geometria
Esercizi 5 soluzioni
 Esercizi 5 soluzioni Alessandro Savo, Geometria Differenziale 27-8 Esercizi su geodetiche e curve su superfici. Esercizio Determinare l area della regione del paraboloide z = x 2 + y 2 compresa tra i piani
Esercizi 5 soluzioni Alessandro Savo, Geometria Differenziale 27-8 Esercizi su geodetiche e curve su superfici. Esercizio Determinare l area della regione del paraboloide z = x 2 + y 2 compresa tra i piani
Geometria Differenziale 2017/18 Esercizi I
 Geometria Differenziale 17/18 Esercizi I 1 Esercizi sulle curve piane 1.1 Esercizio Si consideri la curva parametrizzata sin t, t [, π]. cos(t) a) Stabilire per quali valori di t la parametrizzazione è
Geometria Differenziale 17/18 Esercizi I 1 Esercizi sulle curve piane 1.1 Esercizio Si consideri la curva parametrizzata sin t, t [, π]. cos(t) a) Stabilire per quali valori di t la parametrizzazione è
Gennaio 17. January 24, 2017
 Gennaio 7 January 24, 207 Prova scritta di Geometria Differenziale 7.0.207 Ingegneria Meccanica, a.a. 206-207 Cognome...................................... Nome...................................... L
Gennaio 7 January 24, 207 Prova scritta di Geometria Differenziale 7.0.207 Ingegneria Meccanica, a.a. 206-207 Cognome...................................... Nome...................................... L
ARGOMENTI MATEMATICA PER L INGEGNERIA
 ARGOMENTI DI MATEMATICA PER L INGEGNERIA VOLUME 2 Esercizi proposti Quando non diversamente precisato, nel seguito si intenderà( sempre che nel piano sia stato introdotto un sistema cartesiano ortogonale
ARGOMENTI DI MATEMATICA PER L INGEGNERIA VOLUME 2 Esercizi proposti Quando non diversamente precisato, nel seguito si intenderà( sempre che nel piano sia stato introdotto un sistema cartesiano ortogonale
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1 Secondo Appello 9 Luglio 2014
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo Appello 9 Luglio Cognome: Nome: Matricola: Compito A Es: punti Es: 6 punti Es: 8 punti Es: 8 punti Totale Data la funzione f : D
Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo Appello 9 Luglio Cognome: Nome: Matricola: Compito A Es: punti Es: 6 punti Es: 8 punti Es: 8 punti Totale Data la funzione f : D
Geometria Differenziale
 Geometria Differenziale Prova scritta di Geometria Differenziale 18.03.2016 Ingegneria Meccanica, a.a. 2015-2016 Cognome...................................... Nome......................................
Geometria Differenziale Prova scritta di Geometria Differenziale 18.03.2016 Ingegneria Meccanica, a.a. 2015-2016 Cognome...................................... Nome......................................
sen n x( tan xn n n=1
 8 Gennaio 2016 Nome (in stampatello): 1) (8 punti) Discutere la convergenza della serie di funzioni al variare di x in [ 1, 1]. n x( tan xn n ) xn sen n 2) (7 punti) Provare che la forma differenziale
8 Gennaio 2016 Nome (in stampatello): 1) (8 punti) Discutere la convergenza della serie di funzioni al variare di x in [ 1, 1]. n x( tan xn n ) xn sen n 2) (7 punti) Provare che la forma differenziale
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1 Secondo Appello 5 Settembre 2016
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo Appello Settembre 6 Cognome: Nome: Matricola: Compito A Es. : 6 punti Es. : 9 punti Es. : 6 punti Es. : punti Totale. a) Disegnare
Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo Appello Settembre 6 Cognome: Nome: Matricola: Compito A Es. : 6 punti Es. : 9 punti Es. : 6 punti Es. : punti Totale. a) Disegnare
Curve e integrali curvilinei
 6 Curve e integrali curvilinei 6.1. Esempi ed esercizi svolti e/o proposti Esempio 6.1.1. Si consideri la curva parametrica ϕ: t [0,2π] ϕ(t) = (acos(t),asin(t),bt) R 3 dove a e b sono due costanti positive.
6 Curve e integrali curvilinei 6.1. Esempi ed esercizi svolti e/o proposti Esempio 6.1.1. Si consideri la curva parametrica ϕ: t [0,2π] ϕ(t) = (acos(t),asin(t),bt) R 3 dove a e b sono due costanti positive.
Geometria 4 (nuovo ordinamento) Esame scritto del 1/4/2004
 Esame scritto del /4/2004 Le risposte non giustificate o illeggibili non saranno corrette. A fianco di ogni domanda è indicato il punteggio. Si è ammessi all orale con un punteggio minimo di 2/33. Esercizio.
Esame scritto del /4/2004 Le risposte non giustificate o illeggibili non saranno corrette. A fianco di ogni domanda è indicato il punteggio. Si è ammessi all orale con un punteggio minimo di 2/33. Esercizio.
Università di Trieste Facoltà d Ingegneria. Esercizi sulle curve, le superfici, i campi vettoriali. Dott. Franco Obersnel
 Università di Trieste Facoltà d Ingegneria. Esercizi sulle curve, le superfici, i campi vettoriali. Dott. Franco Obersnel Esercizio 1 Sia f : [a, b] IR 2 una funzione di classe C 1 su [a, b]. consideri
Università di Trieste Facoltà d Ingegneria. Esercizi sulle curve, le superfici, i campi vettoriali. Dott. Franco Obersnel Esercizio 1 Sia f : [a, b] IR 2 una funzione di classe C 1 su [a, b]. consideri
1 Limiti e continuità
 Calcolo infinitesimale e differenziale Gli esercizi indicati con l asterisco (*) sono più impegnativi. Limiti e continuità Si ricorda che per una funzione di più variabili, la definizione di continuità
Calcolo infinitesimale e differenziale Gli esercizi indicati con l asterisco (*) sono più impegnativi. Limiti e continuità Si ricorda che per una funzione di più variabili, la definizione di continuità
Università di Verona Facoltà di Scienze Matematiche, Fisiche e Naturali. Corso di Laurea Triennale in Matematica Applicata
 Università di Verona Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea Triennale in Matematica Applicata Soluzioni degli appelli di Analisi Matematica Antonio Marigonda Anni 9-7 ii Soluzioni
Università di Verona Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea Triennale in Matematica Applicata Soluzioni degli appelli di Analisi Matematica Antonio Marigonda Anni 9-7 ii Soluzioni
Esercizi di riepilogo sulle curve. 1. Si fornisca una parametrizzazione per le seguenti curve:
 Esercizi di riepilogo sulle curve. Si fornisca una parametrizzazione per le seguenti curve: (a) l ellisse = {(x, y) R x + y = } α(t) = (3 cost, sin t), t [, π]. (b) = {(x, y) R x + y =, x } α(t) = (3 cost,
Esercizi di riepilogo sulle curve. Si fornisca una parametrizzazione per le seguenti curve: (a) l ellisse = {(x, y) R x + y = } α(t) = (3 cost, sin t), t [, π]. (b) = {(x, y) R x + y =, x } α(t) = (3 cost,
Prova scritta di Geometria - B
 Prova scritta di Geometria - B Tempo: 2h+20m. Fisica) + 20 m. Matematica).) 0 punti) Si consideri la funzione d : R 2 R 2 R 0 se x = y dx; y) = d E x; y) + 4 se x y dove d E è la distanza euclidea su R
Prova scritta di Geometria - B Tempo: 2h+20m. Fisica) + 20 m. Matematica).) 0 punti) Si consideri la funzione d : R 2 R 2 R 0 se x = y dx; y) = d E x; y) + 4 se x y dove d E è la distanza euclidea su R
Esempi di superfici.
 Esempi di superfici.. Grafici di funzioni. Sia Ω IR un dominio in IR e sia f: Ω IR una funzione C. Il suo grafico è una supeficie parametrizzata in IR 3 della forma u v f(u, v) La superficie S è regolare
Esempi di superfici.. Grafici di funzioni. Sia Ω IR un dominio in IR e sia f: Ω IR una funzione C. Il suo grafico è una supeficie parametrizzata in IR 3 della forma u v f(u, v) La superficie S è regolare
Prova scritta di Geometria - A
 Prova scritta di Geometria - A Tempo: h+0m. Fisica) + 0 m. Matematica).) 0 punti) Si consideri la funzione d : R R R 0 se x = y dx; y) = d E x; y) + se x y dove d E è la distanza euclidea su R. a.) Scrivere
Prova scritta di Geometria - A Tempo: h+0m. Fisica) + 0 m. Matematica).) 0 punti) Si consideri la funzione d : R R R 0 se x = y dx; y) = d E x; y) + se x y dove d E è la distanza euclidea su R. a.) Scrivere
Prova scritta di Geometria differenziale - 27/2/2012
 Prova scritta di Geometria differenziale - 27/2/2012 Tempo disponibile: 3 ore Non sono ammesse calcolatrici, appunti o libri di testo. Una copia degli appunti è disponibile per libera consultazione alla
Prova scritta di Geometria differenziale - 27/2/2012 Tempo disponibile: 3 ore Non sono ammesse calcolatrici, appunti o libri di testo. Una copia degli appunti è disponibile per libera consultazione alla
Esercizi su curve e integrali di linea. 1. Si forniscano almeno due parametrizzazioni per la semicirconferenza
 Esercizi su curve e integrali di linea 1. Si forniscano almeno due parametrizzazioni per la semicirconferenza : {(x, y) R, x + y 4, y } Soluzione: possibili parametrizzazioni per la curva sono: α 1 (t)
Esercizi su curve e integrali di linea 1. Si forniscano almeno due parametrizzazioni per la semicirconferenza : {(x, y) R, x + y 4, y } Soluzione: possibili parametrizzazioni per la curva sono: α 1 (t)
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016
 Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Foglio 3 Esercizi su forme differenziali lineari ed integrali di seconda specie (alcuni con cenno di soluzione).
 Università degli Studi di Padova Facoltà di Ingegneria Laurea in Ingegneria Gestionale e MeccanicaMeccatronica, V. Casarino P. Mannucci (-) Foglio 3 Esercizi su forme differenziali lineari ed integrali
Università degli Studi di Padova Facoltà di Ingegneria Laurea in Ingegneria Gestionale e MeccanicaMeccatronica, V. Casarino P. Mannucci (-) Foglio 3 Esercizi su forme differenziali lineari ed integrali
Provadiprova 1 - aggiornamento del 23 Ottobre 2013
 Università di Trento - Corso di Laurea in Ingegneria Civile e Ambientale Analisi matematica - a.a. 03-4 - Prof. Gabriele Anzellotti Provadiprova - aggiornamento del 3 Ottobre 03 a) Curve: rappresentazione
Università di Trento - Corso di Laurea in Ingegneria Civile e Ambientale Analisi matematica - a.a. 03-4 - Prof. Gabriele Anzellotti Provadiprova - aggiornamento del 3 Ottobre 03 a) Curve: rappresentazione
Corso di Matematica B - Ingegneria Informatica Testi di Esercizi. A1. Siano u, v, w vettori. Quali tra le seguenti operazioni hanno senso?
 A. Languasco - Esercizi Matematica B - 4. Geometria 1 A: Vettori geometrici Corso di Matematica B - Ingegneria Informatica Testi di Esercizi A1. Siano u, v, w vettori. Quali tra le seguenti operazioni
A. Languasco - Esercizi Matematica B - 4. Geometria 1 A: Vettori geometrici Corso di Matematica B - Ingegneria Informatica Testi di Esercizi A1. Siano u, v, w vettori. Quali tra le seguenti operazioni
Esercizi su curve e funzioni reali di più variabili reali 1Febbraio 2010
 Esercizi su curve e funzioni reali di più variabili reali 1Febbraio 1 1.Si calcoli la lunghezza della curva di equazione g y = 1 x 1 log x x [1, e].. Sia f(x, y, ) = x + y e sia il sostegno della curva
Esercizi su curve e funzioni reali di più variabili reali 1Febbraio 1 1.Si calcoli la lunghezza della curva di equazione g y = 1 x 1 log x x [1, e].. Sia f(x, y, ) = x + y e sia il sostegno della curva
Esercizi I : curve piane
 Esercizi I : curve piane. Esercizio Si consideri la curva parametrizzata sin t, t [, 2π]. cos(2t) a) Stabilire per quali valori di t la parametrizzazione è regolare. b) Sia Γ la traccia di α. Descrivere
Esercizi I : curve piane. Esercizio Si consideri la curva parametrizzata sin t, t [, 2π]. cos(2t) a) Stabilire per quali valori di t la parametrizzazione è regolare. b) Sia Γ la traccia di α. Descrivere
Analisi Matematica 2
 Esercizio 1 Analisi Matematica 2 12 gennaio 2017 Si consideri la curva piana γ di parametrizzazione α(t) = (sin(t), sin(2t)), t [0, π]. 1. Si disegni (approssimativamente) il suo sostegno, specificando
Esercizio 1 Analisi Matematica 2 12 gennaio 2017 Si consideri la curva piana γ di parametrizzazione α(t) = (sin(t), sin(2t)), t [0, π]. 1. Si disegni (approssimativamente) il suo sostegno, specificando
Istituzioni di Matematica II 5 Luglio 2010
 Istituzioni di Matematica II 5 Luglio 010 1. Classificare, al variare del parametro α R, la forma quadratica (1 + α )x + 4xy + αy.. i) Si determinino tutti i punti critici della seguente funzione f(x,
Istituzioni di Matematica II 5 Luglio 010 1. Classificare, al variare del parametro α R, la forma quadratica (1 + α )x + 4xy + αy.. i) Si determinino tutti i punti critici della seguente funzione f(x,
Cognome: Nome: Matricola: Prima parte Scrivere le risposte ai due seguenti quesiti A e B su questa facciata e sul retro di questo foglio.
 Analisi e Geometria Terzo appello 4 settembre 207 Compito F Docente: Numero di iscrizione all appello: Cognome: Nome: Matricola: Prima parte Scrivere le risposte ai due seguenti quesiti A e B su questa
Analisi e Geometria Terzo appello 4 settembre 207 Compito F Docente: Numero di iscrizione all appello: Cognome: Nome: Matricola: Prima parte Scrivere le risposte ai due seguenti quesiti A e B su questa
Argomento 6: Derivate Esercizi. I Parte - Derivate
 6: Derivate Esercizi I Parte - Derivate E. 6.1 Calcolare le derivate delle seguenti funzioni: 1) log 5 3 + cos ) + 3 + 4 + 3 3) 5 tan 4) ( + 3e ) sin 5) arctan( + 1) 6) log 7) 10) + + 3 8) 3 3 1 + 16 11)
6: Derivate Esercizi I Parte - Derivate E. 6.1 Calcolare le derivate delle seguenti funzioni: 1) log 5 3 + cos ) + 3 + 4 + 3 3) 5 tan 4) ( + 3e ) sin 5) arctan( + 1) 6) log 7) 10) + + 3 8) 3 3 1 + 16 11)
1. Disegnare nel piano di Gauss i seguenti insiemi di numeri complessi:
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1 Test di autovalutazione 1. Disegnare nel piano di Gauss i seguenti insiemi di numeri complessi: (a) A = {z C : z, 0 arg z /} (b) B = {w
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1 Test di autovalutazione 1. Disegnare nel piano di Gauss i seguenti insiemi di numeri complessi: (a) A = {z C : z, 0 arg z /} (b) B = {w
Analisi e Geometria 1 - Seconda Prova - 2 Febbraio 2016 Terza parte (Compito A)
 Politecnico di Milano, Scuola di Ingegneria Industriale e dell Informazione Analisi e Geometria 1 - Seconda Prova - 2 Febbraio 216 Terza parte (Compito A) Sia data, per ogni valore del parametro reale
Politecnico di Milano, Scuola di Ingegneria Industriale e dell Informazione Analisi e Geometria 1 - Seconda Prova - 2 Febbraio 216 Terza parte (Compito A) Sia data, per ogni valore del parametro reale
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1 Terzo Appello 8 Settembre 2014
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria Terzo Appello 8 Settembre 24 Cognome: Nome: Matricola: Compito A Es.: 9 punti Es.2: 8 punti Es.3: 8 punti Es.4: 8 punti Totale. Sia F la
Politecnico di Milano Ingegneria Industriale Analisi e Geometria Terzo Appello 8 Settembre 24 Cognome: Nome: Matricola: Compito A Es.: 9 punti Es.2: 8 punti Es.3: 8 punti Es.4: 8 punti Totale. Sia F la
Complementi ed Esercizi di Geometria Differenziale - A. Sambusetti 1
 Complementi ed Esercizi di Geometria Differenziale - A. Sambusetti 1 7 Campi vettoriali. Siano S, S d-sottovarietà differenziabili di R n : un applicazione f : S R è detta una funzione su S; un applicazione
Complementi ed Esercizi di Geometria Differenziale - A. Sambusetti 1 7 Campi vettoriali. Siano S, S d-sottovarietà differenziabili di R n : un applicazione f : S R è detta una funzione su S; un applicazione
Geometria BAER Canale I Esercizi 12
 Geometria BAER Canale I Esercizi Esercizio. x = 0 x = Date le rette r : y = t e s : y = t, si verifichi che sono sghembe e si scrivano le equazioni z = t z = t parametriche di una retta r ortogonale ed
Geometria BAER Canale I Esercizi Esercizio. x = 0 x = Date le rette r : y = t e s : y = t, si verifichi che sono sghembe e si scrivano le equazioni z = t z = t parametriche di una retta r ortogonale ed
Prima prova di verifica in itinere di ANALISI MATEMATICA II. 12 Marzo 2008 Compito A. 1 (punti 3)
 anno accademico 007-008 Prima prova di verifica in itinere di ANALISI MATEMATICA II Marzo 008 Compito A (punti ) y = x + xy + y x. (punti 4) y + y x = ln x x y. (punti ) y = y + y ln y. 4 (punti 6) Determinare
anno accademico 007-008 Prima prova di verifica in itinere di ANALISI MATEMATICA II Marzo 008 Compito A (punti ) y = x + xy + y x. (punti 4) y + y x = ln x x y. (punti ) y = y + y ln y. 4 (punti 6) Determinare
Analisi Matematica 2 per Matematica Esempi di compito, secondo semestre 2012/2013
 Analisi Matematica 2 per Matematica Esempi di compito, secondo semestre 2012/2013 Primo compito. Si consideri la regione stokiana E di R 3 definita dalle disuguaglianze: { + y 2 a 2 0 z tan α)x b) dove
Analisi Matematica 2 per Matematica Esempi di compito, secondo semestre 2012/2013 Primo compito. Si consideri la regione stokiana E di R 3 definita dalle disuguaglianze: { + y 2 a 2 0 z tan α)x b) dove
DEFINIZIONE. u (u; v); α 3. v (u; v); α 3. ha rango 2 in ogni punto della parametrizzazione. DEFINIZIONE
 DEFINIZIONE Una superficie in R 3 è un applicazione α : U R 3, di classe almeno C. In realtà, tratteremo solamente superfici di classe C. Inoltre, U R deve essere un aperto, e α deve essere iniettiva.
DEFINIZIONE Una superficie in R 3 è un applicazione α : U R 3, di classe almeno C. In realtà, tratteremo solamente superfici di classe C. Inoltre, U R deve essere un aperto, e α deve essere iniettiva.
Università degli Studi di Roma Tre Corso di Laurea in Ingegneria civile a.a. 2015/2016 Complementi di Matematica (A-K) Secondo Appello 5 Luglio 2016.
 Università degli Studi di Roma Tre Corso di Laurea in Ingegneria civile a.a. 5/6 Complementi di Matematica (A-K) Secondo Appello 5 Luglio 6. Cognome e nome Matricola Specificare quale esame si deve sostenere:
Università degli Studi di Roma Tre Corso di Laurea in Ingegneria civile a.a. 5/6 Complementi di Matematica (A-K) Secondo Appello 5 Luglio 6. Cognome e nome Matricola Specificare quale esame si deve sostenere:
Es. 1 Es. 2 Es. 3 Es. 4 Totale Teoria. Punteggi degli esercizi: Es.1: 8 punti; Es.2: 8 punti; Es.3: 8 punti; Es.4: 8 punti.
 Es. 1 Es. 2 Es. 3 Es. 4 Totale Teoria Analisi e Geometria 1 Seconda prova in itinere 1 Febbraio 21 Compito A Docente: Politecnico di Milano Ingegneria Industriale Cognome: Nome: Matricola: Punteggi degli
Es. 1 Es. 2 Es. 3 Es. 4 Totale Teoria Analisi e Geometria 1 Seconda prova in itinere 1 Febbraio 21 Compito A Docente: Politecnico di Milano Ingegneria Industriale Cognome: Nome: Matricola: Punteggi degli
Geometria 4, Matematica, I appello, 17 giugno Svolgimento.
 Geometria 4, Matematica, I appello, 7 giugno 03. Svolgimento. Esercizio. Sia C la curva rappresentata dalla funzione x(t) = ( cos t + t sin t, sin t t cos t, sin t t cos t + ) (t > 0). Dire quali delle
Geometria 4, Matematica, I appello, 7 giugno 03. Svolgimento. Esercizio. Sia C la curva rappresentata dalla funzione x(t) = ( cos t + t sin t, sin t t cos t, sin t t cos t + ) (t > 0). Dire quali delle
a. Si enunci e dimostri il teorema della media integrale per funzioni continue. (5 punti)
 COMPITO A a. Si enunci e dimostri il teorema della media integrale per funzioni continue. 5 punti b. Si scriva l equazione di un piano generico, specificando qual la direzione normale ad esso, e si scriva
COMPITO A a. Si enunci e dimostri il teorema della media integrale per funzioni continue. 5 punti b. Si scriva l equazione di un piano generico, specificando qual la direzione normale ad esso, e si scriva
Es. 1 Es. 2 Es. 3 Es. 4 Totale Teoria. Punteggi degli esercizi: Es.1: 8 punti; Es.2: 8 punti; Es.3: 8 punti; Es.4: 6 punti.
 Es. 1 Es. 2 Es. 3 Es. Totale Teoria Analisi e Geometria 1 Seconda prova in itinere 0 Febbraio 2013 Compito A Docente: Politecnico di Milano Ingegneria Industriale Cognome: Nome: Matricola: Punteggi degli
Es. 1 Es. 2 Es. 3 Es. Totale Teoria Analisi e Geometria 1 Seconda prova in itinere 0 Febbraio 2013 Compito A Docente: Politecnico di Milano Ingegneria Industriale Cognome: Nome: Matricola: Punteggi degli
ESERCIZI SULLE CURVE
 ESERCIZI SULLE CURVE VALENTINA CASARINO Esercizi per il corso di Fondamenti di Analisi Matematica, (Ingegneria Gestionale, dell Innovazione del Prodotto, Meccanica e Meccatronica, Università degli studi
ESERCIZI SULLE CURVE VALENTINA CASARINO Esercizi per il corso di Fondamenti di Analisi Matematica, (Ingegneria Gestionale, dell Innovazione del Prodotto, Meccanica e Meccatronica, Università degli studi
Geometria iperbolica - Primo foglio Andrea Petracci
 Geometria iperbolica - Primo foglio Andrea Petracci Esercizio 1. Teorema (Hopf-Rinow). Se M è una varietà riemanniana connessa, allora le seguenti affermazioni sono equivalenti: (1) M è completa con la
Geometria iperbolica - Primo foglio Andrea Petracci Esercizio 1. Teorema (Hopf-Rinow). Se M è una varietà riemanniana connessa, allora le seguenti affermazioni sono equivalenti: (1) M è completa con la
Analisi 2 Fisica e Astronomia
 Analisi Fisica e Astronomia Appello scritto del 8 Luglio 0. Soluzione Esercizio 7 pti Sia α > 0 un parametro e consideriamo la curva piana γ : [0, ] R γt = t cos, t sin, se t 0, ], e γ0 = 0, 0. t α t α
Analisi Fisica e Astronomia Appello scritto del 8 Luglio 0. Soluzione Esercizio 7 pti Sia α > 0 un parametro e consideriamo la curva piana γ : [0, ] R γt = t cos, t sin, se t 0, ], e γ0 = 0, 0. t α t α
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006. Matematica 2 (Analisi)
 Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Analisi Matematica 3
 Testi delle prove d esame del corso di Analisi Matematica 3 presso la Facoltà di Ingegneria Bruno Rubino L Aquila, 2006 Indice 1 Curve 3 2 Superfici 4 3 Teorema di Gauss-Green e formula dell area 4 4 Campi
Testi delle prove d esame del corso di Analisi Matematica 3 presso la Facoltà di Ingegneria Bruno Rubino L Aquila, 2006 Indice 1 Curve 3 2 Superfici 4 3 Teorema di Gauss-Green e formula dell area 4 4 Campi
0.1 Arco di curva regolare
 .1. ARCO DI CURVA REGOLARE 1.1 Arco di curva regolare Se RC(O, i, j, k ) è un riferimento cartesiano fissato per lo spazio euclideo E, e se v (t) = x(t) i + y(t) j + z(t) k è una funzione a valori vettoriali
.1. ARCO DI CURVA REGOLARE 1.1 Arco di curva regolare Se RC(O, i, j, k ) è un riferimento cartesiano fissato per lo spazio euclideo E, e se v (t) = x(t) i + y(t) j + z(t) k è una funzione a valori vettoriali
Scritto Generale del Corso di Analisi Matematica Calcolare la soluzione generale dell equazione differenziale. y (7) + y (6) + y + y = 0.
 del Corso di Analisi Matematica 4 1 y (7) + y (6) + y + y = 0.. Discutere la convergenza puntuale e uniforme della serie di Fourier della funzione f(x) = x ( T < x T ) di periodo T. In particolare, calcolare
del Corso di Analisi Matematica 4 1 y (7) + y (6) + y + y = 0.. Discutere la convergenza puntuale e uniforme della serie di Fourier della funzione f(x) = x ( T < x T ) di periodo T. In particolare, calcolare
Prova scritta di Geometria differenziale - 27/9/2012
 Prova scritta di Geometria differenziale - 27/9/2012 Tempo disponibile: 3 ore Non sono ammesse calcolatrici, appunti o libri di testo. Una copia degli appunti è disponibile per libera consultazione alla
Prova scritta di Geometria differenziale - 27/9/2012 Tempo disponibile: 3 ore Non sono ammesse calcolatrici, appunti o libri di testo. Una copia degli appunti è disponibile per libera consultazione alla
Analisi Matematica II Corso di Ingegneria Gestionale Compito del (x y) log
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del -6-4 Esercizio. punti Data la funzione { x y log +, fx, y = x +y 4 x, y,, x, y =, i dire in quali punti del dominio è continua; ii dire
Analisi Matematica II Corso di Ingegneria Gestionale Compito del -6-4 Esercizio. punti Data la funzione { x y log +, fx, y = x +y 4 x, y,, x, y =, i dire in quali punti del dominio è continua; ii dire
Esercizi. f(x, y, z) = exp(xz) + zy sin(xyz) + cos(xy 3 )
 Esercizi 1. Determinare le derivate parziali di f(x, y, z) = exp(xz) + zy sin(xyz) + cos(xy 3 ) 2. Scrivere l equazione del piano tangente e della retta normale al grafico ln(xy) + cos(x + y) nel punto
Esercizi 1. Determinare le derivate parziali di f(x, y, z) = exp(xz) + zy sin(xyz) + cos(xy 3 ) 2. Scrivere l equazione del piano tangente e della retta normale al grafico ln(xy) + cos(x + y) nel punto
Le soluzioni del foglio 3
 Le soluzioni del foglio 3 1. Esercizio Consideriamo la famiglia di elicoidi, vedi Figura 1, x = u cos(v), y = u sin(v), z = kv, u 1, v π Quella proposta nell esercizio corrisponde alla scelta k = 1 Matrice
Le soluzioni del foglio 3 1. Esercizio Consideriamo la famiglia di elicoidi, vedi Figura 1, x = u cos(v), y = u sin(v), z = kv, u 1, v π Quella proposta nell esercizio corrisponde alla scelta k = 1 Matrice
Esercizi sulle funzioni f : R 2 R. Soluzioni
 Esercizi sulle funzioni f : R R Soluzioni. Disegnare il grafico della funzione f : R R, nei casi: (a) f(, ) =. La funzione dipende solo dalla coordinata. In questo caso il grafico rappresenta un piano
Esercizi sulle funzioni f : R R Soluzioni. Disegnare il grafico della funzione f : R R, nei casi: (a) f(, ) =. La funzione dipende solo dalla coordinata. In questo caso il grafico rappresenta un piano
Es. 1 Es. 2 Es. 3 Es. 4 Totale Teoria. Punteggi degli esercizi: Es.1: 8 punti; Es.2: 8 punti; Es.3: 8 punti; Es.4: 8 punti.
 Es. Es. Es. 3 Es. 4 Totale Teoria Analisi e Geometria Terzo appello 8 Settembre 4 Compito B Docente: Politecnico di Milano Ingegneria Industriale Cognome: Nome: Matricola: Punteggi degli esercizi: Es.:
Es. Es. Es. 3 Es. 4 Totale Teoria Analisi e Geometria Terzo appello 8 Settembre 4 Compito B Docente: Politecnico di Milano Ingegneria Industriale Cognome: Nome: Matricola: Punteggi degli esercizi: Es.:
Cognome: Nome: Matricola: a. Si enunci e dimostri il teorema della media integrale per funzioni continue. (5 punti)
 Analisi e Geometria Seconda Prova 3 gennaio 207 Docente: Politecnico di Milano Scuola di Ingegneria Industriale e dell Informazione Cognome: Nome: Matricola: a. Si enunci e dimostri il teorema della media
Analisi e Geometria Seconda Prova 3 gennaio 207 Docente: Politecnico di Milano Scuola di Ingegneria Industriale e dell Informazione Cognome: Nome: Matricola: a. Si enunci e dimostri il teorema della media
Geometria BAER Canale I Esercizi 11
 Geometria BAER Canale I Esercizi Esercizio. Scrivere la matrice delle seguenti trasformazioni ortogonali del piano (a Proiezione ortogonale sulla retta x + y = 0 (b Rotazione di π/4 seguita da riflessione
Geometria BAER Canale I Esercizi Esercizio. Scrivere la matrice delle seguenti trasformazioni ortogonali del piano (a Proiezione ortogonale sulla retta x + y = 0 (b Rotazione di π/4 seguita da riflessione
Geometria BAER Canale A-K Esercizi 11
 Geometria BAER 6-7 Canale A-K Esercizi Esercizio. Scrivere la matrice delle seguenti trasformazioni ortogonali del piano (a Proiezione ortogonale sulla retta x + y = (b Rotazione di π/4 seguita da riflessione
Geometria BAER 6-7 Canale A-K Esercizi Esercizio. Scrivere la matrice delle seguenti trasformazioni ortogonali del piano (a Proiezione ortogonale sulla retta x + y = (b Rotazione di π/4 seguita da riflessione
GEOMETRIA 28 Giugno minuti
 GEOMETRIA 28 Giugno 2017 90 minuti A Istruzioni: Scrivere cognome, nome, matricola in STAMPATELLO negli appositi spazi. Per ogni quiz nella prima parte, indicare l affermazione giudicata corretta nella
GEOMETRIA 28 Giugno 2017 90 minuti A Istruzioni: Scrivere cognome, nome, matricola in STAMPATELLO negli appositi spazi. Per ogni quiz nella prima parte, indicare l affermazione giudicata corretta nella
Cognome:... Nome:... Matricola:
 Cognome:... Nome:... Matricola: Università di Milano - Bicocca Corso di laurea di primo livello in Scienze statistiche ed economiche Corso di laurea di primo livello in Statistica e gestione delle informazioni
Cognome:... Nome:... Matricola: Università di Milano - Bicocca Corso di laurea di primo livello in Scienze statistiche ed economiche Corso di laurea di primo livello in Statistica e gestione delle informazioni
Analisi Matematica II, Anno Accademico Ingegneria Cvile Ambientale Edile
 Analisi Matematica II, Anno Accademico 2015-2016 Ingegneria Cvile Ambientale Edile FOGLIO DI ESERCIZI 6, dall 11 Novembre al 20 Novembre 2015 Calcolo Differenziale 1 Altri esercizi ed esempi sull argomento
Analisi Matematica II, Anno Accademico 2015-2016 Ingegneria Cvile Ambientale Edile FOGLIO DI ESERCIZI 6, dall 11 Novembre al 20 Novembre 2015 Calcolo Differenziale 1 Altri esercizi ed esempi sull argomento
Analisi Matematica 2. Superfici e integrali superficiali. Superfici e integrali superficiali 1 / 27
 Analisi Matematica 2 Superfici e integrali superficiali Superfici e integrali superficiali 1 / 27 Superficie Sia D un dominio connesso di R 2 (per def. un dominio connesso é la chiusura di un aperto connesso).
Analisi Matematica 2 Superfici e integrali superficiali Superfici e integrali superficiali 1 / 27 Superficie Sia D un dominio connesso di R 2 (per def. un dominio connesso é la chiusura di un aperto connesso).
Preparazione al primo foglio di esercizi di Analisi 2
 Preparazione al primo foglio di esercizi di Analisi 2 Verona, 2 ottobre 2017 Esercizio 1. Si tracci il graco delle seguenti regioni del piano cartesiano: (1.1 D 1 := {(x, y R 2 : x 2 + y 2 1, x + 3y 2
Preparazione al primo foglio di esercizi di Analisi 2 Verona, 2 ottobre 2017 Esercizio 1. Si tracci il graco delle seguenti regioni del piano cartesiano: (1.1 D 1 := {(x, y R 2 : x 2 + y 2 1, x + 3y 2
Corso di Matematica 3 o A.A. 2016/2017 Argomenti delle lezioni
 Corso di Matematica 3 o A.A. 2016/2017 Argomenti delle lezioni 1 lezione. Martedí 27 settembre. 2 ore. Richiami sulle applicazioni lineari tra spazi vettoriali di dimensione finita. Il teorema di rappresentazione.
Corso di Matematica 3 o A.A. 2016/2017 Argomenti delle lezioni 1 lezione. Martedí 27 settembre. 2 ore. Richiami sulle applicazioni lineari tra spazi vettoriali di dimensione finita. Il teorema di rappresentazione.
Cenni di geometria differenziale delle superfici.
 Cenni di geometria differenziale delle superfici. 1. Superfici parametrizzate nello spazio. Definizione. Una superficie parametrizzata in IR 3 è un applicazione S: Ω IR 3, (u, S 1(u, S 2 (u,, S 3 (u, doe
Cenni di geometria differenziale delle superfici. 1. Superfici parametrizzate nello spazio. Definizione. Una superficie parametrizzata in IR 3 è un applicazione S: Ω IR 3, (u, S 1(u, S 2 (u,, S 3 (u, doe
(a) Dire quale/i fra i seguenti vettori assegnati sono autovettori di A, precisando il relativo autovalore:
 CORSO DI GEOMETRIA E ALGEBRA Cognome e Nome: Corso di Laurea: 6 gennaio 27 Matricola: Anno di corso: (8 pt Si consideri la matrice A = 4 4 4 4 4 4 (a Dire quale/i fra i seguenti vettori assegnati sono
CORSO DI GEOMETRIA E ALGEBRA Cognome e Nome: Corso di Laurea: 6 gennaio 27 Matricola: Anno di corso: (8 pt Si consideri la matrice A = 4 4 4 4 4 4 (a Dire quale/i fra i seguenti vettori assegnati sono
Dom. 1 Dom 2 Es. 1 Es. 2 Es. 3 Es. 4 Totale. Cognome: Nome: Matricola:
 Dom. Dom Es. Es. Es. Es. 4 Totale Analisi e Geometria Terzo appello 05 settembre 06 Compito A Docente: Numero nell elenco degli iscritti: Cognome: Nome: Matricola: Prima parte. Nel campo complesso C, l
Dom. Dom Es. Es. Es. Es. 4 Totale Analisi e Geometria Terzo appello 05 settembre 06 Compito A Docente: Numero nell elenco degli iscritti: Cognome: Nome: Matricola: Prima parte. Nel campo complesso C, l
d (x; y) = 0 se e solo se d 1 (x; y) = d 2 (x; y) = 0, dato che entrambe le distanze hanno valori positivi. Ma questo è possibile solo se x = y.
 Distanze. a) d (x; y) = se e solo se d (x; y) = d (x; y) =, dato che entrambe le distanze hanno valori positivi. Ma questo è possibile solo se x = y. d (y; x) = d (y; x) + d (y; x) = d (x; y) + d (x; y)
Distanze. a) d (x; y) = se e solo se d (x; y) = d (x; y) =, dato che entrambe le distanze hanno valori positivi. Ma questo è possibile solo se x = y. d (y; x) = d (y; x) + d (y; x) = d (x; y) + d (x; y)
Prova scritta di Geometria.
 Prova scritta di Geometria TEMPO: h+0m (FISICA) + 30 m (MATEMATICA) PROBLEMA ) (5 punti) Sia data la forma bilineare g : R 3 R 3 R, espressa, rispetto alla base standard di R 3, da: g ((x ; x ; x 3 ) ;
Prova scritta di Geometria TEMPO: h+0m (FISICA) + 30 m (MATEMATICA) PROBLEMA ) (5 punti) Sia data la forma bilineare g : R 3 R 3 R, espressa, rispetto alla base standard di R 3, da: g ((x ; x ; x 3 ) ;
Analisi Matematica II Politecnico di Milano Ingegneria Industriale
 Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #8. Sia f : R 2 R la funzione definita da 2 y 2 per (, y) (, ) f(, y) 2 + y 2 per (, y) (, ). (a) Stabilire se f è continua
Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #8. Sia f : R 2 R la funzione definita da 2 y 2 per (, y) (, ) f(, y) 2 + y 2 per (, y) (, ). (a) Stabilire se f è continua
ANALISI VETTORIALE ESERCIZI SULLE SUPERFICI
 ANALII VETTORIALE EERCIZI ULLE UPERFICI Esercizio Calcolare l area della superficie dove Σ {(x, y, z) (x, y) E, z 2 + x 2 + y 2 } E {(x, y) x 2 + y 2 4}. Essendo la superficie Σ data come grafico di una
ANALII VETTORIALE EERCIZI ULLE UPERFICI Esercizio Calcolare l area della superficie dove Σ {(x, y, z) (x, y) E, z 2 + x 2 + y 2 } E {(x, y) x 2 + y 2 4}. Essendo la superficie Σ data come grafico di una
Analisi Matematica 1 per Matematica Esempi di compiti, secondo trimestre 2010/2011
 Analisi Matematica per Matematica Esempi di compiti, secondo trimestre 200/20 Primo compito. Esercizio. Studiare la funzione y = f() = log( + e 3 ) 2 e disegnarne il grafico. È vero che la funzione ha
Analisi Matematica per Matematica Esempi di compiti, secondo trimestre 200/20 Primo compito. Esercizio. Studiare la funzione y = f() = log( + e 3 ) 2 e disegnarne il grafico. È vero che la funzione ha
Università degli Studi di Bergamo Corso integrato di Analisi 1 (Geometria e Algebra Lineare) 3 settembre 2009 Tema A
 Università degli Studi di Bergamo Corso integrato di Analisi (Geometria e Algebra Lineare) settembre 009 Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
Università degli Studi di Bergamo Corso integrato di Analisi (Geometria e Algebra Lineare) settembre 009 Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
LEZIONE 37. x 2 a 2 + y2. b 2 = 2z, x 2. a 2 y2. b 2 = 2z. Esempio Sia S il cilindro luogo dei punti P = (x, y, z) soddisfacenti l equazione
 LEZIONE 37 37.1. Altri esempi di superfici. In questo paragrafo daremo altri esempi di superfici. Esempio 37.1.1. Sia D R 2 un aperto. Allora il grafico Γ ϕ di una funzione ϕ: D R 3 di classe C 1 è una
LEZIONE 37 37.1. Altri esempi di superfici. In questo paragrafo daremo altri esempi di superfici. Esempio 37.1.1. Sia D R 2 un aperto. Allora il grafico Γ ϕ di una funzione ϕ: D R 3 di classe C 1 è una
Corso di Metodi Matematici per l Ingegneria A.A. 2016/2017 Esercizi svolti sulle funzioni di variabile complessa (1)
 Corso di Metodi Matematici per l Ingegneria A.A. 2016/2017 Esercizi svolti sulle funzioni di variabile complessa 1) Marco Bramanti Politecnico di Milano November 7, 2016 1 Funzioni olomorfe e campi di
Corso di Metodi Matematici per l Ingegneria A.A. 2016/2017 Esercizi svolti sulle funzioni di variabile complessa 1) Marco Bramanti Politecnico di Milano November 7, 2016 1 Funzioni olomorfe e campi di
Le curve differenziabili. (Appunti per il corso di geometria III) Vincenzo Ancona Una curva differenziabile regolare e un applicazione
 Le curve differenziabili (Appunti per il corso di geometria III) Vincenzo Ancona 1. Curve differenziabili. Definizione 1.1. Una curva differenziabile regolare e un applicazione α(t) = (α 1 (t), α 2 (t),
Le curve differenziabili (Appunti per il corso di geometria III) Vincenzo Ancona 1. Curve differenziabili. Definizione 1.1. Una curva differenziabile regolare e un applicazione α(t) = (α 1 (t), α 2 (t),
1) Studiare la natura dei seguenti integrali impropri: 2x2 1. x dx (c) e x + 1. log x. n n + 1 n (a) n=1. (b) n + log n n 2n 2 1.
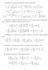 ) Studiare la natura dei seguenti integrali impropri: 0 x 3 dx (b) + 2x2 2 x 2 + 2 dx (c) e x + 0 e x dx (g) (d) + 0 + 0 x( + x) dx x sin x x 2 dx (h) (e) 0 + log x x 2 dx (f) 2 log x dx x + log( + x 2
) Studiare la natura dei seguenti integrali impropri: 0 x 3 dx (b) + 2x2 2 x 2 + 2 dx (c) e x + 0 e x dx (g) (d) + 0 + 0 x( + x) dx x sin x x 2 dx (h) (e) 0 + log x x 2 dx (f) 2 log x dx x + log( + x 2
PROVA SCRITTA DI GEOMETRIA 2 14 Febbraio 2017
 PROVA SCRITTA DI GEOMETRIA 2 14 Febbraio 2017 La prova orale deve essere sostenuta entro il 28 Febbraio 2017 A Fissato un sistema di riferimento cartesiano nello spazio si consideri la quadriche Q di equazione
PROVA SCRITTA DI GEOMETRIA 2 14 Febbraio 2017 La prova orale deve essere sostenuta entro il 28 Febbraio 2017 A Fissato un sistema di riferimento cartesiano nello spazio si consideri la quadriche Q di equazione
Corso di Analisi Matematica 2. Corso di Laurea in Ingegneria Biomedica Prof. A. Iannizzotto Prove d esame 2014/2015
 Corso di Analisi Matematica 2 in Ingegneria Biomedica Prof. A. Iannizzotto Prove d esame 2014/2015 Appello del 21 novembre 2014 Tempo: 150 minuti 1. Enunciare la definizione di forma differenziale esatta
Corso di Analisi Matematica 2 in Ingegneria Biomedica Prof. A. Iannizzotto Prove d esame 2014/2015 Appello del 21 novembre 2014 Tempo: 150 minuti 1. Enunciare la definizione di forma differenziale esatta
Prova Scritta di di Meccanica Analitica. 10 Febbraio 2017
 Prova Scritta di di Meccanica Analitica 10 Febbraio 017 Problema 1 Si consideri un punto materiale di massa m soggetto alla forza peso e vincolato ad una curva in un piano verticale y x x Schematizzare
Prova Scritta di di Meccanica Analitica 10 Febbraio 017 Problema 1 Si consideri un punto materiale di massa m soggetto alla forza peso e vincolato ad una curva in un piano verticale y x x Schematizzare
