Analisi Matematica 3
|
|
|
- Costanzo Randazzo
- 5 anni fa
- Visualizzazioni
Transcript
1 Testi delle prove d esame del corso di Analisi Matematica 3 presso la Facoltà di Ingegneria Bruno Rubino L Aquila, 2006
2 Indice 1 Curve 3 2 Superfici 4 3 Teorema di Gauss-Green e formula dell area 4 4 Campi vettoriali 5 5 Teorema di Stokes 8 6 Teorema di Gauss 10 7 Equazioni del prim ordine 12 8 Equazioni di tipo ellittico 13 9 Equazioni di tipo parabolico Equazioni di tipo iperbolico Serie di Fourier Funzioni di una variabile complessa Trasformata di Laplace Trasformata di Fourier Ulteriori esercizi 27 2
3 1 Curve Esercizio 1.1 (10 gennaio 2005) Calcolare la lunghezza della curva γ parametrizzata da x = 3t 2 t [0, 1] y = 4t 2. Esercizio 1.2 (4 aprile 2005) Calcolare la lunghezza di curva cartesiana γ il cui supporto è grafico della funzione ( ) x 1 x + 1 sin per 0 < x 1 x y = 0 per x = 0. Esercizio 1.3 (5 settembre 2005) Sia data la curva γ : [0, 1] Γ R 2 definita da: γ(t) = { x(t) = t 2 y(t) = t Dimostrare (giustificando opportunamente la risposta) che la curva è rettificabile e successivamente calcolarne la lunghezza. 2. Dato il campo vettoriale F : R 2 R 2 definito da F (x, y) = (2xy, x 2 + y), calcolare il suo lavoro lungo la curva Γ. 3. Dimostrare (giustificando opportunamente la risposta) che il campo vettoriale F è conservativo nel suo dominio di definizione e successivamente calcolare un suo potenziale e verificare infine il risultato del punto 2. Esercizio 1.4 (7 aprile 2006) Calcolare la lunghezza della curva γ : [ 1, 1] R definita da γ(t) = (t, 3t 2, 6t 3 ). 3
4 2 Superfici Esercizio 2.1 (22 luglio 2005) Calcolare l area della superficie piana delimitata dalla curva γ = { (x, y, ) R 2 : y x 2 0, x 2 + y 2 4 }. Esercizio 2.2 (5 settembre 2005) Calcolare l area della superficie del paraboloide Π = { (x, y, z) R : z = x 2 + 3y 2, z 1 }. Esercizio 2.3 (24 luglio 2006) Calcolare l area della superficie sferica Γ di centro l origine e raggio 5 staccata dal cono di equazione x = 2 y 2 + z 2. 3 Teorema di Gauss-Green e formula dell area Esercizio 3.1 (6 dicembre 2004) Facendo uso della formula dell area, calcolare l area della superficie piana { } 2 S = (x, y) R 2 : x 2, x2 + y 2 1. Esercizio 3.2 (2 dicembre 2005) Facendo uso della formula dell area, calcolare l area della superficie piana S = { (x, y) R 2 : y x 2, x 2 + y 2 2 }. Esercizio 3.3 (4 luglio 2006) Facendo uso della formula dell area, calcolare l area dell insieme T la cui frontiera è sostegno della curva parametrizzata da x = 2(1 + cos t) cos t ϕ : y = 2(1 + cost) sin t. π t π 4
5 Esercizio 3.4 (22 settembre 2006) Mediante la formula dell area, calcolare l area della superficie del dominio D = { (x, y) R 2 : 2 x y 4 x } 2. Esercizio 3.5 (24 marzo 2006) Verificare il teorema di Gauss Green per il campo vettoriale F (x, y) = (x 2 4y 2, x 2 + 4y 2 ) e la regione D = { (x, y) R 2 : 1 x 2 + y 2 4 }. 4 Campi vettoriali Esercizio 4.1 (10 gennaio 2005) Sia dato il campo vettoriale ( ) y 2 x 2 F (x, y) = (x 2 + y 2 ) 2, 2xy (x 2 + y 2 ) 2. a) Determinare il dominio di R 2 in cui F è definito e C 1. b) Verificare che F è irrotazionale. c) Stabilire a priori se F è conservativo e, in caso affermativo, determinare un suo potenziale. Esercizio 4.2 (21 marzo 2005) Sia dato il campo vettoriale ( 2x + 2x 3 + 2xy 2 F (x, y) =, 2y ) 2x2 y 2y 3. x 2 + y 2 x 2 + y 2 Determinare il dominio di R 2 in cui F è definito e C 1. Verificare che F è irrotazionale. Stabilire a priori se F è conservativo e, in caso affermativo, determinare un suo potenziale. 5
6 Esercizio 4.3 (4 aprile 2005) Sia dato il campo vettoriale ( y + x 2 + y 2 F (x, y) =, x + ) x2 + y 2. x 2 + y 2 x 2 + y 2 Determinare il dominio di R 2 in cui F è definito e C 1. Verificare se F è irrotazionale. Stabilire a priori se F è conservativo e, in caso affermativo, determinare un suo potenziale. Esercizio 4.4 (4 luglio 2005) Sia dato il campo vettoriale ( F (x, y) = 3x 2 + 2xy x 2 + y, log ( x 2 + y 2) ) + 2y2. 2 x 2 + y 2 Determinare il dominio di R 2 in cui F è definito e C 1. Verificare che F è irrotazionale. Stabilire a priori se F è conservativo e, in caso affermativo, determinare un suo potenziale. Calcolare poi il lavoro per andare da A = (0, 1) a B = (1, 0). Esercizio 4.5 (19 settembre 2005) Nel dominio Ω = { (x, y, z) R 3 : x 2 + y 2 2, z π/4 } si consideri il campo vettoriale irrotazionale ( x tan 2 (z) y tan(z) + 2x F (x, y, z) = (y x tan(z)) 2 + (2x 2 + y 2 1), x tan(z) + 2y (y x tan(z)) 2 + (2x 2 + y 2 1), ) + x2 tan 3 (z) xy tan 2 (z) + x 2 tan(z) xy. (y x tan(z)) 2 + (2x 2 + y 2 1) Stabilire a priori se è conservativo e, in caso affermativo, calcolarne un potenziale. 6
7 Esercizio 4.6 (5 novembre 2005) Sia dato il campo vettoriale ( ) x F (x, y) = x 2 + y x 1 2 (x 1) 2 + y, y 2 x 2 + y y 2 (x 1) 2 + y 2 Determinare il dominio di R 2 in cui F è definito e di classe C 1. Verificare se F è irrotazionale. Stabilire a priori se F è conservativo e, in caso affermativo, determinare il suo potenziale P tale che P (2, 0) = 0. Esercizio 4.7 (13 gennaio 2006) Sia dato il campo vettoriale ( 4xz F (x, y, z) = 4x2 + y 2 1, yz 4x2 + y 2 1, ) 4x 2 + y 2 1. Determinare il dominio di R 3 in cui F è definito e C 1. Verificare che F è irrotazionale. Stabilire a priori se F è conservativo e, in caso affermativo, determinare un suo potenziale. Esercizio 4.8 (24 marzo 2006) Sia dato il campo vettoriale ( ) x y F (x, y) = x 2 + y, x + y 2 x 2 + y 2 Determinare il dominio di R 2 in cui F è definito e C 1. Verificare che F è irrotazionale. Stabilire a priori se F è conservativo e, in caso affermativo, determinare un suo potenziale. 7
8 Esercizio 4.9 (4 luglio 2006) Sia dato il campo vettoriale F (x, y) = (1 + ye xy, xe xy + cos y). Dire se F è conservativo e, in caso affermativo, calcolarne un potenziale. Esercizio 4.10 (22 settembre 2006) Dato il campo vettoriale su R 2 ( ) 8x 8 F (x, y) = 4(x 1) 2 + y, 2y, 2 4(x 1) 2 + y 2 (a) Determinare il dominio di F, (b) Stabilire se F è conservativo sul suo dominio, (c) In caso di risposta affermativa alla domanda (b), determinare un potenziale per F. 5 Teorema di Stokes Esercizio 5.1 (6 dicembre 2004) Verificare il teorema di Stokes per il campo vettoriale F (x, y, z) = e la superficie ( 2xz x 2 + y 2, 2yz x 2 + y, z + log ( x 2 + y 2) ). 2 S = { (x, y, z) R 3 : z = 0, 1 x 2 + y 2 4 } orientata con versore normale n = (0, 0, 1). Esercizio 5.2 (21 marzo 2005) Verificare il teorema di Stokes in R 3 per il campo vettoriale F (x, y, z) = (x, y, z) 8
9 e la superficie C = { (x, y, z) R 3 : z 2 = x 2 + y 2, 1 z 4 }. Esercizio 5.3 (4 aprile 2005) Verificare il teorema di Stokes in R 3 per il campo vettoriale F (x, y, z) = (x, y, z) e la superficie Q = { (x, y, z) R 3 : z = 0, x 1, y 1 }. Esercizio 5.4 (19 settembre 2005) Verificare l uguaglianza stabilita dal Teorema di Stokes in R 3 per il campo vettoriale F = (2x, 3y, z) e la superficie S frontiera della regione R = { (x, y, z) R 3 : x 2 + y 2 = 1, 0 z x + 2 }. Esercizio 5.5 (2 dicembre 2005) Verificare il teorema di Stokes per il campo vettoriale F (x, y, z) = ( yz, xz, xy + z 2) e la superficie S = { (x, y, z) R 3 : z = x 2 + y 2, 1 z 4 } orientata in modo tale che la terza componente del versore normale sia negativa. Esercizio 5.6 (7 aprile 2006) Facendo uso del teorema di Stokes calcolare la circuitazione del campo vettoriale F (x, y, z) = (cos(πy), sin(πx), 0) attorno al rettangolo di vertici A = (0, 1, 0), B = (0, 0, 1), C = (1, 0, 1), D = (1, 1, 0) percorso in senso antiorario per una persona in piedi che guarda dall orgine. 9
10 6 Teorema di Gauss Esercizio 6.1 (20 dicembre 2004) Verificare il teorema di Gauss per il campo vettoriale F (x, y, z) = (y, z, 0). e il dominio D = { (x, y, z) R 3 : 0 z 1, x 2 + y 2 4 }. Esercizio 6.2 (10 gennaio 2005) Verificare il teorema di Gauss in R 2 per il campo vettoriale F (x, y) = (x, xy). e la regione D = { (x, y) R 2 : x 2, 0 y 4 + cos x }. Esercizio 6.3 (22 luglio 2005) Verificare il teorema della divergenza per il campo vettoriale F (x, y, z) = (sin x, cos y, 0) e il dominio D = { (x, y, z) R 3 : z 0, x 2 + y 2 + z 2 1 }. Esercizio 6.4 (5 novembre 2005) Verificare il teorema di Gauss in R 3 per il campo vettoriale F (x, y, z) = (3x, y, z) e il dominio S = { (x, y, z) R 3 : x 2 + y 2 + z 2 81 }. 10
11 Esercizio 6.5 (16 dicembre 2005) Verificare il teorema di Gauss per il campo vettoriale F (x, y, z) = ( (x 1) 2, 2xy, 2z ) e l insieme Ω = { (x, y, z) R 3 : y 2 + z 2 x 2, 0 x 1 }. Esercizio 6.6 (13 gennaio 2006) Verificare il teorema di Gauss per il campo vettoriale F (x, y, z) = (x, y, z) e il dominio D = { (x, y, z) R 3 : z x 2 + y 2 1, z x 2 y }. Esercizio 6.7 (24 luglio 2006) Verificare il teorema di Gauss per il campo vettoriale F (x, y, z) = (x + y + z, y 2, z 2 ) e il dominio D = { (x, y, z) R 3 : x 0, y 0, z 0, x 2 + y 2 + z 2 1 } Esercizio 6.8 (5 settembre 2006) Si consideri il parallelepipedo D = { (x, y, z) R 3 : 0 x 3, 0 y 2, 0 z 1 }. Verificare il teorema di Gauss per il dominio D e il campo vettoriale F (x, y, z) = (0, 0, xyz). 11
12 7 Equazioni del prim ordine Esercizio 7.1 (6 dicembre 2004) Determinare la soluzione del problema di Cauchy u t + tu x = u + t u(x, 0) = sin x. Esercizio 7.2 (20 dicembre 2004) Determinare la soluzione del problema di Cauchy u t sin(t) u x = x + t u(x, 0) = x 1. Esercizio 7.3 (21 marzo 2005) Determinare la soluzione del problema di Cauchy { xu x + yu y = u + 1 u(1, y) = y Esercizio 7.4 (4 luglio 2005) Utilizzando il metodo delle curve caratteristiche, determinare la soluzione del problema di Cauchy (xt x)u t + u x = 1 u(x, 0) = x. Esercizio 7.5 (22 luglio 2005) Utilizzando il metodo delle curve caratteristiche, determinare la soluzione del problema di Cauchy u t + u x = x + u u(x, 0) = sin x + cos x. 12
13 Esercizio 7.6 (5 settembre 2005) Utilizzando il metodo delle curve caratteristiche, determinare la soluzione del problema di Cauchy 2u t + log(t)u x = tu u(x, 1) = 2x. Esercizio 7.7 (19 settembre 2005) Utilizzando il metodo delle curve caratteristiche, determinare la soluzione del problema di Cauchy 2yu x xu y = u in x > 0, y < 0 u(x, 0) = x per x > 0. Esercizio 7.8 (16 dicembre 2005) Facendo uso del metodo delle caratteristiche, risolvere il seguente problema di Cauchy: { u t + x cos(t)u x = x cos(t) u(x, 0) = 2x 3. 8 Equazioni di tipo ellittico Esercizio 8.1 (20 dicembre 2004) Mediante l uso della separazione delle variabili, risolvere il seguente problema: u xx + 9 u yy = 0 0 < x < π, 0 < y < π u (x, 0) = cos(3x) 0 < x < π u (x, π) = cos(5x) 0 < x < π u x (0, y) = u x (π, y) = 0 0 < y < π. Esercizio 8.2 (21 marzo 2005) Mediante l uso della separazione delle variabili, risolvere il seguente problema: { u = 0 per ρ < 1 u = sin(ϑ) + 3 cos(ϑ) per ρ = 1, dove u = u(ρ, ϑ), u = u ρρ + 1 ρ u ρ + 1 ρ 2 u ϑϑ. 13
14 Esercizio 8.3 (4 aprile 2005) Mediante l uso della separazione delle variabili, risolvere il seguente problema: u xx + u yy = 0 0 < x < π, 0 < y < 1 u (x, 0) = sin(3x) + sin(7x) 0 < x < π u (x, 1) = 2 sin(7x) 0 < x < π u (0, y) = u (π, y) = 0 0 < y < 1. Esercizio 8.4 (22 luglio 2005) Mediante l uso della separazione delle variabili, risolvere il seguente problema: u xx + u yy = 0, 0 < x < π, 0 < y < π, u(x, 0) = u(x, π) = 0, 0 < x < π, u x (0, y) = u x (π, y) = sin(4y), 0 < y < π. Esercizio 8.5 (4 luglio 2006) Mediante l uso della separazione delle variabili, risolvere il seguente problema u xx + u yy = 0 0 < x < π, 0 < y < π, u(x, 0) = 0 0 < x < π, u(x, π) = sin(5x) 0 < x < π, u(0, y) = u(π, y) = 0 0 < y < π. Esercizio 8.6 (24 luglio 2006) Mediante l uso della separazione delle variabili, risolvere il seguente problema u xx + 4u yy = 0 0 < x < π, 0 < y < π, u(x, 0) = sin x 0 < x < π, u(x, π) = sin(3x) 0 < x < π, u(0, y) = u(π, y) = 0 0 < y < π. 14
15 9 Equazioni di tipo parabolico Esercizio 9.1 (6 dicembre 2004) Mediante l uso della separazione delle variabili, risolvere il seguente problema: u t 9u xx = 0 0 < x < π, t > 0 u (x, 0) = sin(3x) 3 sin(5x) 0 < x < π u (0, t) = u (π, t) = 0 t > 0. Esercizio 9.2 (10 gennaio 2005) Mediante l uso della separazione delle variabili, risolvere il seguente problema: u t u xx = 0 0 < x < π, t > 0, u x (0, t) = u x (π, t) = 0 t > 0, u (x, 0) = 1 + cos x + 3 cos(10x) 0 < x < π. Esercizio 9.3 (4 luglio 2005) Mediante l uso della separazione delle variabili, risolvere il seguente problema: u t 9u xx = 0, 0 < x < π, t > 0, u(x, 0) = 1 + sin x, 0 < x < π, u x (0, t) = u x (π, t) = 0, t > 0. Esercizio 9.4 (19 settembre 2005) Mediante il metodo di separazione di variabili, risolvere il seguente problema: u t 3u xx = 0 0 < x < π, t > 0, u(x, 0) = 1 cos(2x) 0 < x < π, 2 u x (0, t) = u x (π, t) = 0 t > 0. 15
16 Esercizio 9.5 (13 gennaio 2006) Mediante l uso della separazione delle variabili, risolvere il seguente problema: u t 2u xx = 0 0 < x < 3, t > 0 u(x, 0) = 7 cos ( 5π 3 x) 5 cos ( 7π x) 0 < x < 3 3 u x (0, t) = u x (3, t) = 0 t > 0. Esercizio 9.6 (5 settembre 2006) Mediante l uso della separazione delle variabili, risolvere il seguente problema u t 2u xx = 0 0 < x < 1, t > 0, u(x, 0) = 3 cos(πx) 5 cos(2πx) < x < 1, u x (0, t) = u x (1, t) = 0 t > Equazioni di tipo iperbolico Esercizio 10.1 (5 settembre 2005) Mediante l uso della separazione delle variabili, risolvere il seguente problema: u tt 2u xx = 0, 0 < x < π, t > 0, u(x, 0) = 3 + cos(2x), 0 < x < π, u t (x, 0) = 5, 0 < x < π, u x (0, t) = u x (π, t) = 0, t > 0. Esercizio 10.2 (2 dicembre 2005) Mediante l uso della separazione delle variabili, risolvere il seguente problema: u tt 16u xx = 0 0 < x < π, t > 0 u(x, 0) = cos(6x) 0 < x < π u t (x, 0) = cos(3x) 0 < x < π u x (0, t) = u x (π, t) = 0 t > 0. 16
17 Esercizio 10.3 (24 marzo 2006) Mediante l uso della separazione delle variabili, risolvere il seguente problema: u tt 2u xx = 0 0 < x < 6, u(x, 0) = f(x) 0 < x < 6 u t (x, 0) = 0 0 < x < 6 u (0, t) = u (6, t) = 0 t R, dove f(x) = { 2x se 0 x 3, 12 2x se 3 < x 6. Esercizio 10.4 (22 settembre 2006) Mediante l uso della separazione delle variabili, risolvere il seguente problema u tt 4u xx = 0 0 < x < π, t > 0, u(x, 0) = 5 sin 2x 0 < x < π, u t (x, 0) = sin 4x, u(0, t) = u(π, t) = 0 t > Serie di Fourier Esercizio 11.1 (6 dicembre 2004) Sia data la funzione 2π periodica dispari definita in [0, π] da f(x) = 1 cos x. Dopo averla disegnata, determinarne la relativa serie di Fourier. Studiare le proprietà di convergenza puntuale ed uniforme di tale serie. Esercizio 11.2 (20 dicembre 2004) Sia data la funzione f : R R 17
18 a) pari, b) 2π-periodica, c) tale che, nell intervallo [0, π], è definita da f(x) = sin x sin(3x). 6.1) Dopo averla disegnata, determinarne la relativa serie di Fourier. 6.2) Studiare le proprietà di convergenza puntuale ed uniforme di tale serie. Esercizio 11.3 (10 gennaio 2005) Sia data la funzione che nell intervallo [0, π] è espressa da f(x) = sin x cos x. a) Disegnare f in [0, π]. b) Estendere f nell intervallo [ π, π] pari e in particolare disegnarla. c) Estendere f 2π-periodica a tutta la retta reale e in particolare disegnarla. d) Determinare i coefficienti di Fourier di tale funzione f : R R. e) Studiare le proprietà di convergenza puntuale ed uniforme di tale serie. Esercizio 11.4 (21 marzo 2005) Sia data la funzione 2π periodica definita da f(x) = a) Disegnare la funzione. { cos(2x) per π x 0, 1 + sin x per 0 < x < π. b) Determinare i coefficienti di Fourier di tale funzione. 18
19 c) Studiare le proprietà di convergenza puntuale ed uniforme della serie di Fourier associata. Esercizio 11.5 (4 aprile 2005) Sia data la funzione 2π periodica definita in [ π, π) come f(x) = sin ( x 2 ). a) Disegnare la funzione. b) Determinare i coefficienti di Fourier di tale funzione. c) Studiare le proprietà di convergenza puntuale ed uniforme della serie di Fourier associata. Esercizio 11.6 (4 luglio 2005) Sia data la funzione 2π periodica definita in ( π, π] come 1 per π < x < π, π < x π, 2 2 f(x) = 0 per π x π. 2 2 a) Disegnare la funzione. b) Determinare i coefficienti di Fourier di tale funzione. c) Studiare le proprietà di convergenza puntuale ed uniforme della serie di Fourier associata. Esercizio 11.7 (22 luglio 2005) Sia data la funzione 2π periodica definita in ( π, π] come 1 per π < x < π, π < x π, 2 2 f(x) = x per π x < 0, 2 x per 0 x π. 2 19
20 a) Disegnare la funzione. b) Determinare i coefficienti di Fourier di tale funzione. c) Studiare le proprietà di convergenza puntuale ed uniforme della serie di Fourier associata. Esercizio 11.8 (5 settembre 2005) Sia data la funzione pari e 2π periodica definita in [0, π] come 1 per π < x π, 2 f(x) = 2 π x per 0 x π. 2 a) Disegnare la funzione in [ 2π, 2π]. b) Determinare i coefficienti di Fourier di tale funzione. c) Studiare le proprietà di convergenza puntuale ed uniforme della serie di Fourier associata. Esercizio 11.9 (19 settembre 2005) Calcolare lo sviluppo in serie di Fourier delle funzioni 1-periodiche che nell intervallo ( 1, 1 2 2) valgono u(t) = sin t, v(t) = cos t. Esercizio (16 dicembre 2005) Sia f(x) la funzione definita da: { 2x 0 x π 2 f(x) =, π π x π, 2 estesa dispari nell intervallo [ π, 0] e periodica di periodo 2π. Disegnare il grafico di f(x). 20
21 Determinare la serie di Fourier associata ad f(x). Studiare la convergenza puntuale e uniforme di tale serie, giustificando opportunamente le affermazioni. Esercizio (16 dicembre 2005) Sia f(x) la funzione definita da: { 2x 0 x π 2 f(x) =, π π x π, 2 estesa dispari nell intervallo [ π, 0] e periodica di periodo 2π. Disegnare il grafico di f(x). Determinare la serie di Fourier associata ad f(x). Studiare la convergenza puntuale e uniforme di tale serie, giustificando opportunamente le affermazioni. Esercizio (7 aprile 2006) Dopo averla disegnata, sviluppare in serie di Fourier la funzione f : [0, 2π] R definita da f(x) = max{π x, 0}, dove con max{a, b} si indica il massimo tra a e b. 12 Funzioni di una variabile complessa Esercizio 12.1 (5 novembre 2005) Sia data la funzione di variabile complessa f(z) = (z + 1) 2 e 1 z 2 Scrivere tutti i possibili sviluppi di Laurent di f centrati in z 0 = 2. Classificare il punto z 0 e determinare il residuo della f in quel punto. 21
22 Esercizio 12.2 (2 dicembre 2005) Sia data la funzione f(z) = sin2 (z) z(z 2 + 1) Studiarne i punti singolari isolati, classificarli e calcolarne i residui. Esercizio 12.3 (16 dicembre 2005) Sia data la funzione u : R 2 definita da: R u(x, y) = 1 2 x cos(x) ( e y + e y) y sin(x) ( e y e y) + x 2 y 2. Verificare che u è armonica su R 2. Determinare la famiglia delle armoniche coniugate di u. Determinare la famiglia di funzioni olomorfe di cui u è la parte reale. Esercizio 12.4 (16 dicembre 2005) Data la funzione f(z) = z2 + 4z 4 (z 1) 2 (z 2), determinarne i punti singolari isolati, classificarli e calcolare i residui in tali punti. Sviluppare quindi f(z) in serie di Laurent centrata in z 0 = 1 e convergente in i. Esercizio 12.5 (13 gennaio 2006) Utilizzando il teorema dei residui, calcolare il seguente integrale: 2π 0 2 cos x 3 4 sin 2 x + cos 2 x dx. Esercizio 12.6 (13 gennaio 2006) Determinare lo sviluppo in serie di Laurent della funzione f(z) = z nell insieme D = {z C : z i < 2}. z
23 Esercizio 12.7 (24 marzo 2006) Determinare lo sviluppo in serie di Laurent centrato in z 0 = 5 per la funzione f(z) = (z + 3)3 (z + 5) 3 Classificare poi z 0 e determinare il residuo di f in tale punto. Esercizio 12.8 (7 aprile 2006) Data la funzione u(x, y) = e 3x sin(3y), a) verificare che u è una funzione armonica; b) trovare tutte le funzioni olomorfe f di cui u è parte reale. Esercizio 12.9 (7 aprile 2006) Mediante il metodo dei residui calcolare l integrale 2π 0 dϑ cos ϑ Esercizio (4 luglio 2006) Si calcoli l integrale improprio + 0 dx 1 + x 6 Esercizio (24 luglio 2006) Facendo uso dei metodi di analisi complessa, si calcoli il seguente integrale + xe 2ix (1 + x 2 ) (4 + x 2 ) dx Esercizio (24 luglio 2006) Dopo aver verificato che la funzione u(x, y) = x 2 y 2 è armonica nel piano (x, y), scrivere le armoniche coniugate. 23
24 Esercizio (5 settembre 2006) Facendo uso dei metodi di analisi complessa, si calcoli il seguente integrale di variabile reale + 0 sin x x(1 + x 2 ) dx Esercizio (22 settembre 2006) Data la funzione di variabile complessa f(z) = 1 (z + 1)(z 3), (a) Determinare e classificare i punti di singolarità di f, (b) Scrivere lo sviluppo di Laurent di f centrato in z = 0 e convergente in 2i. 13 Trasformata di Laplace Esercizio 13.1 (2 dicembre 2005) Facendo uso della trasformata di Laplace, risolvere il seguente problema di Cauchy { y 3y + 3y y = sin t y(0) = y (0) = y (0) = α al variare del parametro reale α. Esercizio 13.2 (16 dicembre 2005) Facendo uso della trasformata di Laplace, risolvere il seguente problema di Cauchy: y 3y + 2y = e t y(0) = 1 y (0) = 8. 24
25 Esercizio 13.3 (13 gennaio 2006) Facendo uso della trasformata di Laplace, risolvere il seguente problema di Cauchy ẋ = y 1 ẏ = 2x + y x(0) = 3, y(0) = 5. Esercizio 13.4 (24 marzo 2006) Facendo uso della trasformata di Laplace, risolvere il seguente problema di Cauchy y (t) + y(t) = (H(t π) H(t)) cos t y(0) = y (0) = 0, dove H è la funzione di Heaviside. Esercizio 13.5 (7 aprile 2006) Facendo uso della trasformata di Laplace, risolvere il seguente problema di Cauchy u = v v = 5u 2v u(0) = 0, v(0) = 1. Esercizio 13.6 (4 luglio 2006) Mediante la trasformata di Laplace, risolvere il seguente problema di Cauchy: y (t) + 2y (t) + 2y(t) = H(t π) y(0) = 0, y (0) = 1 dove H(τ) indica la funzione di Heaviside. Esercizio 13.7 (24 luglio 2006) Mediante la trasformata di Laplace, risolvere il seguente problema di Cauchy: y (t) 3y (t) = 4e t H(t) y(0) = 0, y (0) = 1 dove H(τ) indica la funzione di Heaviside. 25
26 Esercizio 13.8 (5 settembre 2006) Mediante la trasformata di Laplace, risolvere la seguente equazione: y(t) 2 t 0 [(t τ) sin(t τ)]y(τ)dτ = 2 th(t), dove H(τ) indica la funzione di Heaviside. Esercizio 13.9 (22 settembre 2006) Risolvere il seguente problema mediante l uso della Trasformata di Laplace y 2y + y = H(t)e t y(0) = 1 y (0) = 0 y (0) = 1, dove H(t) è la funzione di Heaviside. 14 Trasformata di Fourier Esercizio 14.1 (24 marzo 2006) Sia u(x) = 1 x 2 + 4x + 5 ( e (x 1) H(x 1) ), x R, dove indica la convoluzione. Calcolare la trasformata di Fourier di u. Esercizio 14.2 (4 luglio 2006) Applicando la trasformata di Fourier (rispetto ad x), esprimere come prodotto di convoluzione la soluzione del seguente problema di Cauchy: u t 2 u x 2 u 2 x = 0 per (x, t) R2 u(x, 0) = e x per x R. 26
27 Esercizio 14.3 (5 settembre 2006) Si calcoli la trasformata di Fourier di f(t) = 1 4 e 5t Esercizio 14.4 (22 settembre 2006) Facendo uso dei metodi di analisi complessa, si calcoli la trasformata di Fourier della funzione f(x) = 1 x 2 2x Ulteriori esercizi Esercizio 15.1 (10 gennaio 2005) Classificare l equazione alle derivate parziali del second ordine nelle variabili (x, y) u xx + u xy + u yy + u x + u y + u = x + y. Esercizio 15.2 (4 luglio 2005) Calcolare il flusso del campo vettoriale F (x, y, z) = (x, y, z) attraverso la superficie Ω = { (x, y, z) R 3 : x = 0, y 2 + z 2 1 }. Esercizio 15.3 (5 settembre 2006) Si calcoli (a meno del segno) il flusso del campo vettoriale F (x, y, z) = (0, 0, xyz) attraverso il rettangolo di vertici A = (0, 0, 0), B = (3, 0, 0), C = (0, 2, 1), D = (3, 2, 1). 27
Corso di Analisi Matematica 2
 Corso di Analisi Matematica 2 in Ingegneria Biomedica Prof. A. Iannizzotto Prove d esame 2016 Versione del 27 ottobre 2016 Appello del 15 gennaio 2016 Tempo: 150 minuti 1. Enunciare le definizioni di campo
Corso di Analisi Matematica 2 in Ingegneria Biomedica Prof. A. Iannizzotto Prove d esame 2016 Versione del 27 ottobre 2016 Appello del 15 gennaio 2016 Tempo: 150 minuti 1. Enunciare le definizioni di campo
Corso di Analisi Matematica 2. Corso di Laurea in Ingegneria Biomedica Prof. A. Iannizzotto Prove d esame 2014/2015
 Corso di Analisi Matematica 2 in Ingegneria Biomedica Prof. A. Iannizzotto Prove d esame 2014/2015 Appello del 21 novembre 2014 Tempo: 150 minuti 1. Enunciare la definizione di forma differenziale esatta
Corso di Analisi Matematica 2 in Ingegneria Biomedica Prof. A. Iannizzotto Prove d esame 2014/2015 Appello del 21 novembre 2014 Tempo: 150 minuti 1. Enunciare la definizione di forma differenziale esatta
Analisi Matematica 2. Michele Campiti. Prove scritte di. Ingegneria Industriale a.a
 Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005
 Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Clinica Canale PZ A.A. 2017/2018 Codocente: Dott. Salvatore Fragapane
 DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Clinica Canale PZ A.A. 07/08 Codocente: Dott. Salvatore Fragapane Lezione - 09/03/08, dalle 6.00 alle 8.00 in aula 6 Es. Studiare
DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Clinica Canale PZ A.A. 07/08 Codocente: Dott. Salvatore Fragapane Lezione - 09/03/08, dalle 6.00 alle 8.00 in aula 6 Es. Studiare
Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione
![Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione](/thumbs/88/116749009.jpg) Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione [E.2] Disegnare nel piano cartesiano il dominio della funzione ( 4 x 2 y 2) ) (1 x 2 y2 y + x 2. 4 1 y ex y y x
Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione [E.2] Disegnare nel piano cartesiano il dominio della funzione ( 4 x 2 y 2) ) (1 x 2 y2 y + x 2. 4 1 y ex y y x
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica II del c.1.
 Prova scritta di Analisi Matematica II del 14-07-1999 - c.1 1) Sia (d n ) una successione di numeri reali tali che inf d n > 0. Studiare il carattere della serie + n=1 al variare del parametro reale positivo
Prova scritta di Analisi Matematica II del 14-07-1999 - c.1 1) Sia (d n ) una successione di numeri reali tali che inf d n > 0. Studiare il carattere della serie + n=1 al variare del parametro reale positivo
es.1 es.2 es.3 es.4 es.5 somma Analisi Matematica 2: Secondo Parziale, , Versione A Cognome e nome:...matricola:...
 es.1 es. es.3 es. es.5 somma 6 6 6 6 6 3 Analisi Matematica : Secondo Parziale, 3.5.16, Versione A Cognome e nome:....................................matricola:......... 1. Dimostrare che la forma differenziale
es.1 es. es.3 es. es.5 somma 6 6 6 6 6 3 Analisi Matematica : Secondo Parziale, 3.5.16, Versione A Cognome e nome:....................................matricola:......... 1. Dimostrare che la forma differenziale
Corso di Analisi Matematica 2
 Corso di Analisi Matematica 2 in Ingegneria Biomedica Prof A Iannizzotto Prove d esame 2017 Versione del 17 settembre 2017 Appello del 9 gennaio 2017 Tempo: 150 minuti 1 Determinare gli estremi globali
Corso di Analisi Matematica 2 in Ingegneria Biomedica Prof A Iannizzotto Prove d esame 2017 Versione del 17 settembre 2017 Appello del 9 gennaio 2017 Tempo: 150 minuti 1 Determinare gli estremi globali
Esercizi di Analisi Matematica 3. Prima parte
 Esercizi di Analisi Matematica 3 per le Facoltà di Ingegneria Prima parte Corrado Lattanzio e Bruno Rubino Versione preliminare L Aquila, ottobre 5 Indice 1 Curve, superfici e campi vettoriali 3 1.1 Curve
Esercizi di Analisi Matematica 3 per le Facoltà di Ingegneria Prima parte Corrado Lattanzio e Bruno Rubino Versione preliminare L Aquila, ottobre 5 Indice 1 Curve, superfici e campi vettoriali 3 1.1 Curve
Corso di Laurea in Ingegneria Gestionale - Sede di Fermo Anno Accademico 2009/2010 Matematica 2 Esercizi d esame
 Corso di Laurea in Ingegneria Gestionale - ede di Fermo Anno Accademico 2009/2010 Matematica 2 Esercizi d esame Nome... N. Matricola... Fermo, gg/mm/aaaa 1. tabilire l ordine di ciascuna delle seguenti
Corso di Laurea in Ingegneria Gestionale - ede di Fermo Anno Accademico 2009/2010 Matematica 2 Esercizi d esame Nome... N. Matricola... Fermo, gg/mm/aaaa 1. tabilire l ordine di ciascuna delle seguenti
Esercizio III Calcolare la trasformata di Fourier della funzione. Esercizio IV Sviluppare la funzione. Tema d esame. Giugno 2004
 Tema d esame. Giugno 24 Esercizio I Calcolare il seguente integrale col metodo dei residui 2π dφ < a < () + a 2 2a cos φ Esercizio II Trovare la soluzione dell equazione di Laplace nella regione del piano
Tema d esame. Giugno 24 Esercizio I Calcolare il seguente integrale col metodo dei residui 2π dφ < a < () + a 2 2a cos φ Esercizio II Trovare la soluzione dell equazione di Laplace nella regione del piano
Compiti di Analisi Matematica 2
 UNIVERSITÀ DEGLI STUDI DEL SALENTO FACOLTÀ DI INGEGNERIA Compiti di Analisi Matematica 2 per il C.d.L. in Ingegneria dell Informazione Angela Albanese Informazioni legali: Questi appunti sono prodotti
UNIVERSITÀ DEGLI STUDI DEL SALENTO FACOLTÀ DI INGEGNERIA Compiti di Analisi Matematica 2 per il C.d.L. in Ingegneria dell Informazione Angela Albanese Informazioni legali: Questi appunti sono prodotti
ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009)
 ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009) 1. Sia S = { } (x, y, z) : x 2 + y 2 = 4, 0 z 3 + x. Scrivere le equazioni parametriche di una superficie regolare che abbia S come sostegno. 2. Enunciare
ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009) 1. Sia S = { } (x, y, z) : x 2 + y 2 = 4, 0 z 3 + x. Scrivere le equazioni parametriche di una superficie regolare che abbia S come sostegno. 2. Enunciare
Istituzioni di Matematica II 5 Luglio 2010
 Istituzioni di Matematica II 5 Luglio 010 1. Classificare, al variare del parametro α R, la forma quadratica (1 + α )x + 4xy + αy.. i) Si determinino tutti i punti critici della seguente funzione f(x,
Istituzioni di Matematica II 5 Luglio 010 1. Classificare, al variare del parametro α R, la forma quadratica (1 + α )x + 4xy + αy.. i) Si determinino tutti i punti critici della seguente funzione f(x,
1) Studiare la natura dei seguenti integrali impropri: 2x2 1. x dx (c) e x + 1. log x. n n + 1 n (a) n=1. (b) n + log n n 2n 2 1.
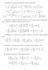 ) Studiare la natura dei seguenti integrali impropri: 0 x 3 dx (b) + 2x2 2 x 2 + 2 dx (c) e x + 0 e x dx (g) (d) + 0 + 0 x( + x) dx x sin x x 2 dx (h) (e) 0 + log x x 2 dx (f) 2 log x dx x + log( + x 2
) Studiare la natura dei seguenti integrali impropri: 0 x 3 dx (b) + 2x2 2 x 2 + 2 dx (c) e x + 0 e x dx (g) (d) + 0 + 0 x( + x) dx x sin x x 2 dx (h) (e) 0 + log x x 2 dx (f) 2 log x dx x + log( + x 2
Esercizi di Analisi Matematica II assegnati nell A.A. 2011/12. Corsi di laurea in Ingegneria Elettronica ed Informatica
 Esercizi di Analisi Matematica II assegnati nell A.A. 2011/12 Corsi di laurea in Ingegneria Elettronica ed Informatica 1) Rappresentare nel piano xy i campi di esistenza delle seguenti funzioni: a) xy
Esercizi di Analisi Matematica II assegnati nell A.A. 2011/12 Corsi di laurea in Ingegneria Elettronica ed Informatica 1) Rappresentare nel piano xy i campi di esistenza delle seguenti funzioni: a) xy
UNIVERSITÀ DI ROMA TOR VERGATA. Analisi Matematica II per Ingegneria Prof. C. Sinestrari
 UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Esercizi 17.XI.2017 1. Verificare che le curve definite dalle seguenti parametrizzazioni sono regolari, o regolari
UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Esercizi 17.XI.2017 1. Verificare che le curve definite dalle seguenti parametrizzazioni sono regolari, o regolari
Prova scritta di Analisi Matematica T-B, Ingegneria Meccanica, 17/06/2014
 Prova scritta di Analisi Matematica T-B, Ingegneria Meccanica, 17/06/2014 MATRICOLA:...NOME e COGNOME:............................................. Desidero sostenere la prova orale al prossimo appello
Prova scritta di Analisi Matematica T-B, Ingegneria Meccanica, 17/06/2014 MATRICOLA:...NOME e COGNOME:............................................. Desidero sostenere la prova orale al prossimo appello
Università di Trieste Facoltà d Ingegneria. Esercizi sulle curve, le superfici, i campi vettoriali. Dott. Franco Obersnel
 Università di Trieste Facoltà d Ingegneria. Esercizi sulle curve, le superfici, i campi vettoriali. Dott. Franco Obersnel Esercizio 1 Sia f : [a, b] IR 2 una funzione di classe C 1 su [a, b]. consideri
Università di Trieste Facoltà d Ingegneria. Esercizi sulle curve, le superfici, i campi vettoriali. Dott. Franco Obersnel Esercizio 1 Sia f : [a, b] IR 2 una funzione di classe C 1 su [a, b]. consideri
Recupero 1 compitino di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2017/2018. Prof. M. Bramanti.
 Recupero compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 7/8. Prof. M. Bramanti Tema n 3 4 5 6 Tot. Cognome e nome in stampatello codice persona o n di matricola
Recupero compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 7/8. Prof. M. Bramanti Tema n 3 4 5 6 Tot. Cognome e nome in stampatello codice persona o n di matricola
1 x 2 y 2 dxdy D. 3 (1 ρ2 ) 3/2 = 1 3. = π 12.
 INGEGNERIA CIVILE - AMBIENTE E TERRITORIO ANALISI MATEMATICA II SOLUZIONI DELLA PROVA SCRITTA DEL 19-6-15 ESERCIZIO 1 Calcolare 1 x y dxdy D dove D è il dominio piano delimitato dalla curva x + y x e dalle
INGEGNERIA CIVILE - AMBIENTE E TERRITORIO ANALISI MATEMATICA II SOLUZIONI DELLA PROVA SCRITTA DEL 19-6-15 ESERCIZIO 1 Calcolare 1 x y dxdy D dove D è il dominio piano delimitato dalla curva x + y x e dalle
Prima prova di verifica in itinere di ANALISI MATEMATICA II. 12 Marzo 2008 Compito A. 1 (punti 3)
 anno accademico 007-008 Prima prova di verifica in itinere di ANALISI MATEMATICA II Marzo 008 Compito A (punti ) y = x + xy + y x. (punti 4) y + y x = ln x x y. (punti ) y = y + y ln y. 4 (punti 6) Determinare
anno accademico 007-008 Prima prova di verifica in itinere di ANALISI MATEMATICA II Marzo 008 Compito A (punti ) y = x + xy + y x. (punti 4) y + y x = ln x x y. (punti ) y = y + y ln y. 4 (punti 6) Determinare
3) Enunciare e dimostrare le regole di trasformazione algebriche e analitiche della trasformata di Fourier.
 Lecce, 16/4/2008 1) Calcolare il valor principale del seguente integrale: x + 1 (x 2 + 4)x dx Y (t) 3Y (t) + 2Y (t) = H(t 1) e t t > 0, Y (0) = 0, Y (0) = 1, 3) Enunciare e dimostrare le regole di trasformazione
Lecce, 16/4/2008 1) Calcolare il valor principale del seguente integrale: x + 1 (x 2 + 4)x dx Y (t) 3Y (t) + 2Y (t) = H(t 1) e t t > 0, Y (0) = 0, Y (0) = 1, 3) Enunciare e dimostrare le regole di trasformazione
1 x 2 y 2 dxdy D. 3 (1 ρ2 ) 3/2 = 1 3. = π 12.
 INGEGNERIA CIVILE - AMBIENTE E TERRITORIO ANALISI MATEMATICA II SOLUZIONI DELLA PROVA SCRITTA DEL 19-6-15 ESERCIZIO 1 Calcolare 1 x y dxdy D dove D è il dominio piano delimitato dalla curva x + y = x e
INGEGNERIA CIVILE - AMBIENTE E TERRITORIO ANALISI MATEMATICA II SOLUZIONI DELLA PROVA SCRITTA DEL 19-6-15 ESERCIZIO 1 Calcolare 1 x y dxdy D dove D è il dominio piano delimitato dalla curva x + y = x e
Corso di Laurea in Ingegneria Informatica Anno Accademico 2012/2013 Analisi Matematica 1
 Corso di Laurea in Ingegneria Informatica Anno Accademico 2012/2013 Analisi Matematica 1 Nome... N. Matricola... Ancona, 12 gennaio 2013 1. Sono dati i numeri complessi z 1 = 1 + i; z 2 = 2 3 i; z 3 =
Corso di Laurea in Ingegneria Informatica Anno Accademico 2012/2013 Analisi Matematica 1 Nome... N. Matricola... Ancona, 12 gennaio 2013 1. Sono dati i numeri complessi z 1 = 1 + i; z 2 = 2 3 i; z 3 =
Ingegneria Elettronica Prova scritta di Analisi Matematica II del giorno ( 3) n x n n + 1
 Prova scritta di Analisi Matematica II del giorno 31-01-2007 1) Studiare la serie di potenze ( 3) n x n n + 1 2) Determinare i punti di estremo relativo ed assoluto della funzione seguente f(x, y) = x
Prova scritta di Analisi Matematica II del giorno 31-01-2007 1) Studiare la serie di potenze ( 3) n x n n + 1 2) Determinare i punti di estremo relativo ed assoluto della funzione seguente f(x, y) = x
Analisi 4 - SOLUZIONI (15/07/2015)
 Corso di Laurea in Matematica Analisi 4 - SOLUZIONI (5/7/5) Docente: Claudia Anedda ) Calcolare l area della superficie totale della regione di spazio limitata, interna al paraboloide di equazione x +y
Corso di Laurea in Matematica Analisi 4 - SOLUZIONI (5/7/5) Docente: Claudia Anedda ) Calcolare l area della superficie totale della regione di spazio limitata, interna al paraboloide di equazione x +y
9/11/2010 (I prova in itinere): solo test a risposta multipla
 9/11/2010 (I prova in itinere): solo test a risposta multipla 23/12/2010 (II prova in itinere, II parte) Esercizio 1. Posto Σ = {(x, y, z) R 3 x 2 + y 2 + z 2 = 4, z 1}, si chiede di calcolare il flusso
9/11/2010 (I prova in itinere): solo test a risposta multipla 23/12/2010 (II prova in itinere, II parte) Esercizio 1. Posto Σ = {(x, y, z) R 3 x 2 + y 2 + z 2 = 4, z 1}, si chiede di calcolare il flusso
Prima prova parziale di Analisi Matematica 2 Ing. Informatica e dell Automazione A.A. 2013/14 scheda 1
 Prima prova parziale di Analisi Matematica 2 Ing. Informatica e dell Automazione A.A. 203/4 scheda ) Calcolare l integrale doppio ZZ dove A = {(x, y) : x + y apple}. xy dx dy, A 2) Sia la curva nello spazio
Prima prova parziale di Analisi Matematica 2 Ing. Informatica e dell Automazione A.A. 203/4 scheda ) Calcolare l integrale doppio ZZ dove A = {(x, y) : x + y apple}. xy dx dy, A 2) Sia la curva nello spazio
Curve e integrali curvilinei
 6 Curve e integrali curvilinei 6.1. Esempi ed esercizi svolti e/o proposti Esempio 6.1.1. Si consideri la curva parametrica ϕ: t [0,2π] ϕ(t) = (acos(t),asin(t),bt) R 3 dove a e b sono due costanti positive.
6 Curve e integrali curvilinei 6.1. Esempi ed esercizi svolti e/o proposti Esempio 6.1.1. Si consideri la curva parametrica ϕ: t [0,2π] ϕ(t) = (acos(t),asin(t),bt) R 3 dove a e b sono due costanti positive.
Campi vettoriali. 1. Sia F (x, y) = ye x i + (e x cos y) j un campo vettoriale. Determinare un potenziale per F, se esiste.
 Campi vettoriali. Sia F (x, y = ye x i + (e x cos y j un campo vettoriale. Determinare un potenziale per F, se esiste.. Sia F (x, y = xy i + x j un campo vettoriale. Determinare un potenziale per F, se
Campi vettoriali. Sia F (x, y = ye x i + (e x cos y j un campo vettoriale. Determinare un potenziale per F, se esiste.. Sia F (x, y = xy i + x j un campo vettoriale. Determinare un potenziale per F, se
Ingegneria Tessile, Biella Analisi II
 Ingegneria Tessile, Biella Analisi II Esercizi svolti In questo file sono contenute le soluzioni degli esercizi sui campi vettoriali (cf foglio 5 di esercizi) Attenzione: in alcuni esercizi il calcolo
Ingegneria Tessile, Biella Analisi II Esercizi svolti In questo file sono contenute le soluzioni degli esercizi sui campi vettoriali (cf foglio 5 di esercizi) Attenzione: in alcuni esercizi il calcolo
Esercizi. f(x, y, z) = exp(xz) + zy sin(xyz) + cos(xy 3 )
 Esercizi 1. Determinare le derivate parziali di f(x, y, z) = exp(xz) + zy sin(xyz) + cos(xy 3 ) 2. Scrivere l equazione del piano tangente e della retta normale al grafico ln(xy) + cos(x + y) nel punto
Esercizi 1. Determinare le derivate parziali di f(x, y, z) = exp(xz) + zy sin(xyz) + cos(xy 3 ) 2. Scrivere l equazione del piano tangente e della retta normale al grafico ln(xy) + cos(x + y) nel punto
Corso di Analisi Matematica 2
 Corso di Analisi Matematica 2 in Ingegneria Biomedica Prof. A. Iannizzotto Prove d esame 2017 Versione del 3 luglio 2017 Appello del 9 gennaio 2017 Tempo: 150 minuti 1. Determinare gli estremi globali
Corso di Analisi Matematica 2 in Ingegneria Biomedica Prof. A. Iannizzotto Prove d esame 2017 Versione del 3 luglio 2017 Appello del 9 gennaio 2017 Tempo: 150 minuti 1. Determinare gli estremi globali
Prima Prova Scritta 18/03/1997
 Prima Prova Scritta 18/03/1997 1 + x y6 f(x, y) = x 6 + y 6, (x, y) (0, 0) k, (x, y) = (0, 0) A 2 Determinare, per k R, l insieme di continuità di f. B 2 Determinare, per k R, l insieme di differenziabilità
Prima Prova Scritta 18/03/1997 1 + x y6 f(x, y) = x 6 + y 6, (x, y) (0, 0) k, (x, y) = (0, 0) A 2 Determinare, per k R, l insieme di continuità di f. B 2 Determinare, per k R, l insieme di differenziabilità
Quesito 1. f(x, y) = xy log (x 2 + y 2 ) Quesito 2. Quesito 3. y = 2y3 +x 3. xy 2 y(1) = 1. Quesito 4
 Corso di laurea in Ing. Meccanica, a.a. 2002/2003 Prova scritta di Analisi Matematica 2 del 7 gennaio 2003 Determinare gli eventuali estremi relativi della funzione f(x, y) = xy log (x 2 + y 2 ) Calcolare
Corso di laurea in Ing. Meccanica, a.a. 2002/2003 Prova scritta di Analisi Matematica 2 del 7 gennaio 2003 Determinare gli eventuali estremi relativi della funzione f(x, y) = xy log (x 2 + y 2 ) Calcolare
Analisi Matematica 2. Michele Campiti. Prove scritte di. Ingegneria Industriale a.a
 Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 2014 2015 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi
Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 2014 2015 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi
Corso di Analisi Matematica 2
 Corso di Analisi Matematica 2 in Ingegneria Biomedica Prof. A. Iannizzotto Prove d esame 2017 Versione del 22 giugno 2017 Appello del 9 gennaio 2017 Tempo: 150 minuti 1. Determinare gli estremi globali
Corso di Analisi Matematica 2 in Ingegneria Biomedica Prof. A. Iannizzotto Prove d esame 2017 Versione del 22 giugno 2017 Appello del 9 gennaio 2017 Tempo: 150 minuti 1. Determinare gli estremi globali
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica II del
 Prova scritta di nalisi Matematica II del 12-06-2001. C1 1) Studiare la convergenza semplice, uniforme e totale della serie di funzioni seguente ( 1) [ n 2 ] n x 1 + n 2 x. n=0 2) Data la funzione (x 2
Prova scritta di nalisi Matematica II del 12-06-2001. C1 1) Studiare la convergenza semplice, uniforme e totale della serie di funzioni seguente ( 1) [ n 2 ] n x 1 + n 2 x. n=0 2) Data la funzione (x 2
Recupero 1 compitino di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2016/2017. Prof. M. Bramanti.
 Recupero 1 compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 16/17. Prof. M. Bramanti 1 Tema n 1 3 4 6 Tot. Cognome e nome in stampatello codice persona o n di
Recupero 1 compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 16/17. Prof. M. Bramanti 1 Tema n 1 3 4 6 Tot. Cognome e nome in stampatello codice persona o n di
Scritto Generale del Corso di Analisi Matematica Calcolare la soluzione generale dell equazione differenziale. y (7) + y (6) + y + y = 0.
 del Corso di Analisi Matematica 4 1 y (7) + y (6) + y + y = 0.. Discutere la convergenza puntuale e uniforme della serie di Fourier della funzione f(x) = x ( T < x T ) di periodo T. In particolare, calcolare
del Corso di Analisi Matematica 4 1 y (7) + y (6) + y + y = 0.. Discutere la convergenza puntuale e uniforme della serie di Fourier della funzione f(x) = x ( T < x T ) di periodo T. In particolare, calcolare
Analisi Matematica 2 per Matematica Esempi di compito, secondo semestre 2012/2013
 Analisi Matematica 2 per Matematica Esempi di compito, secondo semestre 2012/2013 Primo compito. Si consideri la regione stokiana E di R 3 definita dalle disuguaglianze: { + y 2 a 2 0 z tan α)x b) dove
Analisi Matematica 2 per Matematica Esempi di compito, secondo semestre 2012/2013 Primo compito. Si consideri la regione stokiana E di R 3 definita dalle disuguaglianze: { + y 2 a 2 0 z tan α)x b) dove
Università di Verona Facoltà di Scienze Matematiche, Fisiche e Naturali. Corso di Laurea Triennale in Matematica Applicata
 Università di Verona Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea Triennale in Matematica Applicata Soluzioni degli appelli di Analisi Matematica Antonio Marigonda Anni 9-7 ii Soluzioni
Università di Verona Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea Triennale in Matematica Applicata Soluzioni degli appelli di Analisi Matematica Antonio Marigonda Anni 9-7 ii Soluzioni
Analisi Matematica 2: Secondo Parziale, , Versione A. Cognome e nome:...matricola:...
 Analisi Matematica : Secondo Parziale, 6.6.7, Versione A Cognome e nome:....................................matricola:......... es. es. es.3 es.4 es.5 es.6 es.7 somma 5cr. 6 6 6 6 6 - - 3 9cr. 5 5 5 5
Analisi Matematica : Secondo Parziale, 6.6.7, Versione A Cognome e nome:....................................matricola:......... es. es. es.3 es.4 es.5 es.6 es.7 somma 5cr. 6 6 6 6 6 - - 3 9cr. 5 5 5 5
CORSO DI LAUREA IN INGEGNERIA ELETTRONICA Prof. A. Avantaggiati (prova scritta del I MODULO di ANALISI MATEMATICA II - 14 gennaio 2000) Compito A
 CORSO DI LAUREA IN INGEGNERIA ELETTRONICA Prof. A. Avantaggiati (prova scritta del I MODULO di ANALISI MATEMATICA II - 14 gennaio 000) Compito A COGNOME... NOME... Data l equazione differenziale y 3 cos
CORSO DI LAUREA IN INGEGNERIA ELETTRONICA Prof. A. Avantaggiati (prova scritta del I MODULO di ANALISI MATEMATICA II - 14 gennaio 000) Compito A COGNOME... NOME... Data l equazione differenziale y 3 cos
Analisi Matematica II. Prove Parziali A.A. 1992/2017
 Complementi di Analisi Polo di Savona Analisi Matematica II Complementi di Analisi Matematica Prove Parziali A.A. 1992/2017 1- PrPzCa.TEX [] Complementi di Analisi Polo di Savona Prima Prova Parziale 92/93
Complementi di Analisi Polo di Savona Analisi Matematica II Complementi di Analisi Matematica Prove Parziali A.A. 1992/2017 1- PrPzCa.TEX [] Complementi di Analisi Polo di Savona Prima Prova Parziale 92/93
Registro dell insegnamento. Emanuele Paolini
 UNIVERSITÀ DEGLI STUDI DI FIRENZE Registro dell insegnamento Anno Accademico 2009/2010 Facoltà: Insegnamento: Ingegneria (Università di Pisa) Analisi Matematica II e Complementi di Analisi Matematica Settore:..........................
UNIVERSITÀ DEGLI STUDI DI FIRENZE Registro dell insegnamento Anno Accademico 2009/2010 Facoltà: Insegnamento: Ingegneria (Università di Pisa) Analisi Matematica II e Complementi di Analisi Matematica Settore:..........................
x = t y = t z = t 3 1 A = B = 1 2
 11/1/05 Teoria: Enunciare e discutere il teorema di Lagrange. Esercizio 1. Determinare l equazione cartesiana del piano passante per P 0 = (1,, 1) e contenente i vettori u = (,, ) e v = (1, 5, 4). Risposta
11/1/05 Teoria: Enunciare e discutere il teorema di Lagrange. Esercizio 1. Determinare l equazione cartesiana del piano passante per P 0 = (1,, 1) e contenente i vettori u = (,, ) e v = (1, 5, 4). Risposta
Esercizi sull integrazione II
 ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) - COMPL. DI ANALISI MATEMATICA (A-K) (C.d.L. Ing. Civile) A.A.28-29 - Prof. G.Cupini Esercizi sull integrazione II (Grazie agli studenti
ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) - COMPL. DI ANALISI MATEMATICA (A-K) (C.d.L. Ing. Civile) A.A.28-29 - Prof. G.Cupini Esercizi sull integrazione II (Grazie agli studenti
Analisi Matematica II Politecnico di Milano Ingegneria Industriale
 Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #. Sia P l insieme di tutti i parallelepipedi che giacciono nel primo ottante con tre facce sui piani coordinati e un
Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #. Sia P l insieme di tutti i parallelepipedi che giacciono nel primo ottante con tre facce sui piani coordinati e un
Analisi Vettoriale A.A Soluzioni del Foglio 4
 Analisi Vettoriale A.A. 26-27 - Soluzioni del Foglio 4 Esercizio 4.1. Sia Σ la superficie cartesiana z = 1 x y, (x, y) = {x 2 + y 2 1}, determinare in ogni punto di Σ il versore normale diretto nel verso
Analisi Vettoriale A.A. 26-27 - Soluzioni del Foglio 4 Esercizio 4.1. Sia Σ la superficie cartesiana z = 1 x y, (x, y) = {x 2 + y 2 1}, determinare in ogni punto di Σ il versore normale diretto nel verso
sen n x( tan xn n n=1
 8 Gennaio 2016 Nome (in stampatello): 1) (8 punti) Discutere la convergenza della serie di funzioni al variare di x in [ 1, 1]. n x( tan xn n ) xn sen n 2) (7 punti) Provare che la forma differenziale
8 Gennaio 2016 Nome (in stampatello): 1) (8 punti) Discutere la convergenza della serie di funzioni al variare di x in [ 1, 1]. n x( tan xn n ) xn sen n 2) (7 punti) Provare che la forma differenziale
Analisi Matematica 2: Secondo Parziale, , Versione A. Cognome e nome:...matricola:...
 Analisi Matematica : Secondo Parziale, 1.6.17, Versione A Cognome e nome:....................................matricola:......... es.1 es. es.3 es. es.5 es.6 es.7 somma 5cr. 6 6 6 6 6 - - 3 9cr. 5 5 5 5
Analisi Matematica : Secondo Parziale, 1.6.17, Versione A Cognome e nome:....................................matricola:......... es.1 es. es.3 es. es.5 es.6 es.7 somma 5cr. 6 6 6 6 6 - - 3 9cr. 5 5 5 5
calcolare il lavoro di E lungo il segmento da A = ( 1, 1, 1) a B = (1, 1, 1), calcolare rot ( E ), determinare un potenziale U(x, y, z) per E.
 ANALISI VETTORIALE Soluzione esonero.1. Esercizio. Assegnato il campo E (x, y, z) = x(y + z ), y(x + z ), z(x + y ) } 1111 calcolare il lavoro di E lungo il segmento da A = ( 1, 1, 1) a B = (1, 1, 1),
ANALISI VETTORIALE Soluzione esonero.1. Esercizio. Assegnato il campo E (x, y, z) = x(y + z ), y(x + z ), z(x + y ) } 1111 calcolare il lavoro di E lungo il segmento da A = ( 1, 1, 1) a B = (1, 1, 1),
Foglio 3 Esercizi su forme differenziali lineari ed integrali di seconda specie (alcuni con cenno di soluzione).
 Università degli Studi di Padova Facoltà di Ingegneria Laurea in Ingegneria Gestionale e MeccanicaMeccatronica, V. Casarino P. Mannucci (-) Foglio 3 Esercizi su forme differenziali lineari ed integrali
Università degli Studi di Padova Facoltà di Ingegneria Laurea in Ingegneria Gestionale e MeccanicaMeccatronica, V. Casarino P. Mannucci (-) Foglio 3 Esercizi su forme differenziali lineari ed integrali
Prima prova in itinere di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2017/2018. Prof. M. Bramanti.
 Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 07/08. Prof. M. Bramanti Tema n 4 5 6 Tot. Cognome e nome (in stampatello) codice persona (o n
Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 07/08. Prof. M. Bramanti Tema n 4 5 6 Tot. Cognome e nome (in stampatello) codice persona (o n
Analisi Matematica 1
 Michele Campiti Prove scritte di Analisi Matematica Ingegneria Industriale aa 28 29 y f g x La funzione seno e la funzione esponenziale Raccolta delle tracce di Analisi Matematica per Ingegneria Industriale,
Michele Campiti Prove scritte di Analisi Matematica Ingegneria Industriale aa 28 29 y f g x La funzione seno e la funzione esponenziale Raccolta delle tracce di Analisi Matematica per Ingegneria Industriale,
Raccolta esami di Analisi II
 Esame del 18 gennaio 2011 Raccolta esami di Analisi II Corsi di laurea in Ing. Edile-Architettura e Civile-Ambientale V = x,, z : x 2 + 2 4, x 2 + 2 z x 2 + 2 } a disegnare l intersezione di V con il piano
Esame del 18 gennaio 2011 Raccolta esami di Analisi II Corsi di laurea in Ing. Edile-Architettura e Civile-Ambientale V = x,, z : x 2 + 2 4, x 2 + 2 z x 2 + 2 } a disegnare l intersezione di V con il piano
Secondo appello di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 2017/2018. Prof. M. Bramanti. Tema n 1.
 Secondo appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 17/18. Prof. M. Bramanti 1 Tema n 1 5 6 7 Tot. Cognome e nome in stampatello) codice persona o n di matricola)
Secondo appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 17/18. Prof. M. Bramanti 1 Tema n 1 5 6 7 Tot. Cognome e nome in stampatello) codice persona o n di matricola)
Scritto d esame di Analisi Matematica II
 Capitolo 2: Scritti d esame 145 Pisa, 1 Gennaio 2005 e gli insiemi f(x, y) = x 2 x 2 y + y, A = {(x, y) R 2 : x 2 + y 2 6, x 0, y 0}, B = {(x, y) R 2 : x 0, y 0}. (a) massimo e minimo di f(x, y) in A,
Capitolo 2: Scritti d esame 145 Pisa, 1 Gennaio 2005 e gli insiemi f(x, y) = x 2 x 2 y + y, A = {(x, y) R 2 : x 2 + y 2 6, x 0, y 0}, B = {(x, y) R 2 : x 0, y 0}. (a) massimo e minimo di f(x, y) in A,
Analisi Matematica 2 Quaderno degli esercizi settimanali. Roberto Monti. Fisica e Astronomia Anno Accademico
 Analisi Matematica 2 Quaderno degli esercizi settimanali Roberto Monti Fisica e Astronomia Anno Accademico 2018-19 Indice Introduzione 5 Settimana 1. Serie numeriche I 7 Settimana 2. Serie numeriche II
Analisi Matematica 2 Quaderno degli esercizi settimanali Roberto Monti Fisica e Astronomia Anno Accademico 2018-19 Indice Introduzione 5 Settimana 1. Serie numeriche I 7 Settimana 2. Serie numeriche II
Facoltà di Ingegneria Prova scritta di Analisi Matematica II. Lecce, y y x = x3 y 4. y(1) = 1.
 Lecce, 10.4.2003 1. Risolvere il seguente problema di Cauchy: y y x = x3 y 4 y(1) = 1. 2. Determinare gli estremi della funzione f(x, y) = x 2 y 2 nell insieme } E = {(x, y) R 2 : (x 1) 2 + y2 4 1, y 0.
Lecce, 10.4.2003 1. Risolvere il seguente problema di Cauchy: y y x = x3 y 4 y(1) = 1. 2. Determinare gli estremi della funzione f(x, y) = x 2 y 2 nell insieme } E = {(x, y) R 2 : (x 1) 2 + y2 4 1, y 0.
Prima prova in itinere di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2016/2017. Prof. M. Bramanti.
 Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 016/017. Prof. M. Bramanti 1 Tema n 1 4 5 6 Tot. Cognome e nome in stampatello) codice persona
Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 016/017. Prof. M. Bramanti 1 Tema n 1 4 5 6 Tot. Cognome e nome in stampatello) codice persona
Esonero di Analisi Matematica (A)
 Esonero di Analisi Matematica (A) Ingegneria Civile, 26 novembre 2001 () 1. Studiare il seguente limite: lim x x + ( e 1/x cos 1 ). x 2. Studiare gli eventuali massimi e minimi relativi ed assoluti della
Esonero di Analisi Matematica (A) Ingegneria Civile, 26 novembre 2001 () 1. Studiare il seguente limite: lim x x + ( e 1/x cos 1 ). x 2. Studiare gli eventuali massimi e minimi relativi ed assoluti della
Esame di Analisi Matematica 2 25/2/2013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 2012/2013
 Esame di Analisi Matematica 2 25/2/203 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 202/203 A Esercizio 0. Riportare esclusivamente la risposta a ciascuno dei questi a-d di sotto. Gli elaborati
Esame di Analisi Matematica 2 25/2/203 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 202/203 A Esercizio 0. Riportare esclusivamente la risposta a ciascuno dei questi a-d di sotto. Gli elaborati
CODICE= Compiti di Analisi Matematica II per il Corso di Laurea in Ingegneria Edile A.A , Appelli 1, 2, 3 e 4
 Compiti di Analisi Matematica II per il Corso di Laurea in Ingegneria Edile A.A. 00-0, Appelli,, 3 e 4 Cognome: Nome: Matricola: CODICE = 33877 A B C D E 3 4 5 6 7 8 9 CODICE=33877 PARTE A. Lo sviluppo
Compiti di Analisi Matematica II per il Corso di Laurea in Ingegneria Edile A.A. 00-0, Appelli,, 3 e 4 Cognome: Nome: Matricola: CODICE = 33877 A B C D E 3 4 5 6 7 8 9 CODICE=33877 PARTE A. Lo sviluppo
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016
 Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
COMPLEMENTI DI ANALISI MATEMATICA A.A Primo appello del 5/5/2010
 COMPLEMENTI DI ANALISI MATEMATICA A.A. 29- Primo appello del 5/5/2 Qui trovate le tracce delle soluzioni degli esercizi del compito. Ho tralasciato i calcoli da Analisi (che comunque sono parte della risoluzione),
COMPLEMENTI DI ANALISI MATEMATICA A.A. 29- Primo appello del 5/5/2 Qui trovate le tracce delle soluzioni degli esercizi del compito. Ho tralasciato i calcoli da Analisi (che comunque sono parte della risoluzione),
1 Limiti e continuità
 Calcolo infinitesimale e differenziale Gli esercizi indicati con l asterisco (*) sono più impegnativi. Limiti e continuità Si ricorda che per una funzione di più variabili, la definizione di continuità
Calcolo infinitesimale e differenziale Gli esercizi indicati con l asterisco (*) sono più impegnativi. Limiti e continuità Si ricorda che per una funzione di più variabili, la definizione di continuità
Contents. 1. Funzioni di più variabili.
 RACCOLTA DI ESERCIZI PER IL CORSO DI ANALISI MATEMATICA II A.A. 03/04 CORSI DI LAUREA IN INGEGNERIA DELL EDILIZIA, INGEGNERIA EDILE-ARCHITETTURA PROF. D. BARTOLUCCI Contents. Funzioni di più variabili..
RACCOLTA DI ESERCIZI PER IL CORSO DI ANALISI MATEMATICA II A.A. 03/04 CORSI DI LAUREA IN INGEGNERIA DELL EDILIZIA, INGEGNERIA EDILE-ARCHITETTURA PROF. D. BARTOLUCCI Contents. Funzioni di più variabili..
(4 5) n. n +7 n +2 (1 3 )n, 8 n 6 n, X 1. (n!) 2. ln n. (15) n 3 n3, 4 n!. n 2 (1 + 1 n )n,
 CORSO di LAUREA IN INGEGNERIA BIOMEDICA, ELETTRICA ELETTRONICA, ENERGETICA ed INFORMATICA ESERCIZI DI ANALISI MATEMATICA B - FOGLIO ) Discutere il carattere della serie al variare di 2 R. (4 5) n 2) Determinare
CORSO di LAUREA IN INGEGNERIA BIOMEDICA, ELETTRICA ELETTRONICA, ENERGETICA ed INFORMATICA ESERCIZI DI ANALISI MATEMATICA B - FOGLIO ) Discutere il carattere della serie al variare di 2 R. (4 5) n 2) Determinare
Analisi Matematica 2 5 febbraio Risposte. (Giusta = 3, non data = 0, sbagliata = 1) Versione Es. 1 Es. 2 Es. 3 Es. 4 Es. 5 Es. 6 Es.
 Analisi Matematica 2 5 febbraio 2013 Nome, Cognome, Matricola: Cognome del Docente: Risposte. (Giusta = 3, non data = 0, sbagliata = 1) Versione Es. 1 Es. 2 Es. 3 Es. 4 Es. 5 Es. 6 Es. 7 1 Esercizio 1.
Analisi Matematica 2 5 febbraio 2013 Nome, Cognome, Matricola: Cognome del Docente: Risposte. (Giusta = 3, non data = 0, sbagliata = 1) Versione Es. 1 Es. 2 Es. 3 Es. 4 Es. 5 Es. 6 Es. 7 1 Esercizio 1.
Terzo esonero. 21 marzo Esercizio
 Terzo esonero 2 marzo 27. Esercizio Disegnare l insieme D : x, y) : x y 2 x, 2x 2 y 2x} e calcolarne l area. Determinare una trasformazione lineare che mandi D in un rettangolo. Calcolare l integale doppio
Terzo esonero 2 marzo 27. Esercizio Disegnare l insieme D : x, y) : x y 2 x, 2x 2 y 2x} e calcolarne l area. Determinare una trasformazione lineare che mandi D in un rettangolo. Calcolare l integale doppio
Prima prova parziale di Analisi Matematica 2 Ing. Informatica e dell Automazione A.A. 2013/14 17/05/2014
 Prima prova parziale di Analisi Matematica 2 Ing. Informatica e dell Automazione A.A. 203/4 7/05/204 ) Calcolare l integrale doppio ZZ ( x + y ) dx dy, A A è il quadrato di vertici (, 0), (, 2), (, 2),
Prima prova parziale di Analisi Matematica 2 Ing. Informatica e dell Automazione A.A. 203/4 7/05/204 ) Calcolare l integrale doppio ZZ ( x + y ) dx dy, A A è il quadrato di vertici (, 0), (, 2), (, 2),
Es. 1 Es. 2 Es. 3 Es. 4 Totale
 Es. Es. Es. Es. 4 Totale Analisi e Geometria Seconda prova in itinere Docente: luglio Cognome: Nome: Matricola: Ogni risposta dev essere giustificata. Gli esercizi vanno svolti su questi fogli, nello spazio
Es. Es. Es. Es. 4 Totale Analisi e Geometria Seconda prova in itinere Docente: luglio Cognome: Nome: Matricola: Ogni risposta dev essere giustificata. Gli esercizi vanno svolti su questi fogli, nello spazio
COMPLEMENTI DI ANALISI MATEMATICA II. Prova scritta del 20 gennaio 2014
 Prova scritta del 20 gennaio 2014 Studiare la convergenza puntuale e uniforme della serie di potenze n x 2n 2n + e n. Valutare poi la misurabilità e l integrabilità secondo Lebesgue della funzione somma
Prova scritta del 20 gennaio 2014 Studiare la convergenza puntuale e uniforme della serie di potenze n x 2n 2n + e n. Valutare poi la misurabilità e l integrabilità secondo Lebesgue della funzione somma
ESERCIZI DI ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 2006/2007
 ESERCIZI I ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 006/007 1 FUNZIONI IN UE VARIABILI (I parte) Insiemi di definizione eterminare gli insiemi di definizione delle seguenti funzioni in due
ESERCIZI I ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 006/007 1 FUNZIONI IN UE VARIABILI (I parte) Insiemi di definizione eterminare gli insiemi di definizione delle seguenti funzioni in due
Analisi Matematica 2 3 febbraio Risposte. (Giusta = 3, non data = 0, sbagliata = 1) Versione Es. 1 Es. 2 Es. 3 Es. 4 Es. 5 Es. 6 Es.
 Analisi Matematica 2 3 febbraio 204 Nome, Cognome, Matricola: Cognome del Docente: Risposte. (Giusta = 3, non data = 0, sbagliata = ) Esercizio. Se il raggio di convergenza della serie di potenze a n (x
Analisi Matematica 2 3 febbraio 204 Nome, Cognome, Matricola: Cognome del Docente: Risposte. (Giusta = 3, non data = 0, sbagliata = ) Esercizio. Se il raggio di convergenza della serie di potenze a n (x
Quarto appello di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano A.A. 2017/2018. Prof. M. Bramanti. y = 1+y2
 Quarto appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano A.A. 7/8. Prof. M. Bramanti Es. 3 5 6 7 Tot. Punti Cognome e nome in stampatello) codice persona o n di matricola) n d
Quarto appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano A.A. 7/8. Prof. M. Bramanti Es. 3 5 6 7 Tot. Punti Cognome e nome in stampatello) codice persona o n di matricola) n d
b) Dimostrare che se f(x) è differenziabile in x 0, allora è continua in x 0.
 Analisi Matematica II - Calcolo in più variabili Nome, Cognome, Matricola: Corso di Laurea: Versione A Avvertenza: La prova d esame si compone di due esercizi e di due quesiti. La risposta ai quesiti va
Analisi Matematica II - Calcolo in più variabili Nome, Cognome, Matricola: Corso di Laurea: Versione A Avvertenza: La prova d esame si compone di due esercizi e di due quesiti. La risposta ai quesiti va
ARGOMENTI MATEMATICA PER L INGEGNERIA
 ARGOMENTI DI MATEMATICA PER L INGEGNERIA VOLUME 2 Esercizi proposti Quando non diversamente precisato, nel seguito si intenderà( sempre che nel piano sia stato introdotto un sistema cartesiano ortogonale
ARGOMENTI DI MATEMATICA PER L INGEGNERIA VOLUME 2 Esercizi proposti Quando non diversamente precisato, nel seguito si intenderà( sempre che nel piano sia stato introdotto un sistema cartesiano ortogonale
Analisi Matematica III
 Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 7 gennaio 00 (Cognome) (Nome) (Numero di matricola) Esercizio Si consideri la successione
Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 7 gennaio 00 (Cognome) (Nome) (Numero di matricola) Esercizio Si consideri la successione
Esercizi su curve e funzioni reali di più variabili reali 1Febbraio 2010
 Esercizi su curve e funzioni reali di più variabili reali 1Febbraio 1 1.Si calcoli la lunghezza della curva di equazione g y = 1 x 1 log x x [1, e].. Sia f(x, y, ) = x + y e sia il sostegno della curva
Esercizi su curve e funzioni reali di più variabili reali 1Febbraio 1 1.Si calcoli la lunghezza della curva di equazione g y = 1 x 1 log x x [1, e].. Sia f(x, y, ) = x + y e sia il sostegno della curva
Analisi Matematica III
 Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 1 giugno 4 (Cognome (Nome (Numero di matricola Esercizio 1 Si consideri la successione
Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 1 giugno 4 (Cognome (Nome (Numero di matricola Esercizio 1 Si consideri la successione
Risposta La curva r è regolare a tratti per via di quanto succede della sua rappresentazione parametrica nel punto t = 1: pur riuscendo
 ANALISI VETTORIALE OMPITO PER LE VAANZE DI FINE D ANNO Esercizio Sia r(t) la curva regolare a tratti x = t, y = t, t [, ] e x = t, y = t, t [, ]. alcolare la lunghezza di r, calcolare, dove esistono, i
ANALISI VETTORIALE OMPITO PER LE VAANZE DI FINE D ANNO Esercizio Sia r(t) la curva regolare a tratti x = t, y = t, t [, ] e x = t, y = t, t [, ]. alcolare la lunghezza di r, calcolare, dove esistono, i
si ha La lunghezza L si calcola per ciascun tratto L = (2t)2 + (3t 2 ) dt+ 2 (3t2 ) 2 + (2t) 2 dt = 4t2 + 9t 4 dt = t
 ANALISI VETTORIALE Soluzione esercizi 1 gennaio 211 6.1. Esercizio. Sia Γ la curva regolare a tratti di rappresentazione parametrica x = t 2, y = t, t [, 1] e x = t, y = t 2, t [1, 2] calcolare la lunghezza,
ANALISI VETTORIALE Soluzione esercizi 1 gennaio 211 6.1. Esercizio. Sia Γ la curva regolare a tratti di rappresentazione parametrica x = t 2, y = t, t [, 1] e x = t, y = t 2, t [1, 2] calcolare la lunghezza,
Scritto d esame di Matematica I
 Capitolo 2: Scritti d esame 139 Pisa, 19 Gennaio 2005 x 1 + (x + 1) log x (x 1)(2x 2). 2. Studiare la convergenza dei seguenti integrali impropri 1 dx e 2x 1, 0 dx e 2x 1, e, nel caso in cui convergano,
Capitolo 2: Scritti d esame 139 Pisa, 19 Gennaio 2005 x 1 + (x + 1) log x (x 1)(2x 2). 2. Studiare la convergenza dei seguenti integrali impropri 1 dx e 2x 1, 0 dx e 2x 1, e, nel caso in cui convergano,
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006. Matematica 2 (Analisi)
 Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
ELIO CABIB. Esami di Analisi 2
 ELIO CABIB Esami di Analisi ELIO CABIB cabib@uniud.it professore di Analisi Matematica Università di Udine Esami di Analisi Indice Appelli 997-98 3//998..................................... 6//998.....................................
ELIO CABIB Esami di Analisi ELIO CABIB cabib@uniud.it professore di Analisi Matematica Università di Udine Esami di Analisi Indice Appelli 997-98 3//998..................................... 6//998.....................................
Esercizi sulla convoluzione e la trasformata di Laplace di distribuzioni raccolti dai temi d esame
 Esercizi sulla convoluzione e la trasformata di Laplace di distribuzioni raccolti dai temi d esame Esercizio 1 Sia U(p) la funzione, definita in un sottoinsieme di C, U(p) := log p2 + a 2 p 2, dove si
Esercizi sulla convoluzione e la trasformata di Laplace di distribuzioni raccolti dai temi d esame Esercizio 1 Sia U(p) la funzione, definita in un sottoinsieme di C, U(p) := log p2 + a 2 p 2, dove si
Esempi di esercizi d esame A.A. 2006/07 Analisi Matematica 2 Ingegneria Elettronica Proff. G. Vergara Caffarelli e L. Giacomelli
 Esempi di esercizi d esame A.A. 6/7 Analisi Matematica Ingegneria Elettronica Proff. G. Vergara Caffarelli e L. Giacomelli versione preliminare, si prega di segnalare eventuali errori *) Determinare e
Esempi di esercizi d esame A.A. 6/7 Analisi Matematica Ingegneria Elettronica Proff. G. Vergara Caffarelli e L. Giacomelli versione preliminare, si prega di segnalare eventuali errori *) Determinare e
Raccolta di esercizi per il corso Analisi matematica IV unità didattica (compatta) a.a. 07/08. Silvano Delladio
 Raccolta di esercizi per il corso Analisi matematica IV unità didattica (compatta) a.a. 07/08 Silvano Delladio September 9, 2008 Chapter 1 Integrali multipli 1.1 Sia B R 3 la palla di raggio 2 centrata
Raccolta di esercizi per il corso Analisi matematica IV unità didattica (compatta) a.a. 07/08 Silvano Delladio September 9, 2008 Chapter 1 Integrali multipli 1.1 Sia B R 3 la palla di raggio 2 centrata
Raccolta di esercizi di ANALISI MATEMATICA III per il Corso di Laurea in Fisica a.a. 09/10. Silvano Delladio
 Raccolta di esercizi di ANALISI MATEMATICA III per il Corso di Laurea in Fisica a.a. 09/10 Silvano Delladio September 13, 2010 Chapter 1 Integrali multipli 1.1 Sia B R 3 la palla di raggio 2 centrata nell
Raccolta di esercizi di ANALISI MATEMATICA III per il Corso di Laurea in Fisica a.a. 09/10 Silvano Delladio September 13, 2010 Chapter 1 Integrali multipli 1.1 Sia B R 3 la palla di raggio 2 centrata nell
Quarto appello di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 2016/2017. Prof. M. Bramanti.
 Quarto appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 6/. Prof. M. Bramanti Tema n 6 Tot. Cognome e nome in stampatello codice persona o n di matricola n d ordine
Quarto appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 6/. Prof. M. Bramanti Tema n 6 Tot. Cognome e nome in stampatello codice persona o n di matricola n d ordine
Versione preliminare si prega di segnalare eventuali errori
 Analisi matematica (I mod) Ing. Elettronica PROFF. GIACOMELLI e VERGARA CAFFARELLI ESEMPI DI ESERCIZI D ESAME A.A.8/9 Versione preliminare si prega di segnalare eventuali errori *) Determinare (purché
Analisi matematica (I mod) Ing. Elettronica PROFF. GIACOMELLI e VERGARA CAFFARELLI ESEMPI DI ESERCIZI D ESAME A.A.8/9 Versione preliminare si prega di segnalare eventuali errori *) Determinare (purché
COMPLEMENTI DI ANALISI MATEMATICA II. Prova scritta del 20 gennaio 2014
 Prova scritta del 2 gennaio 214 Studiare la convergenza puntuale e uniforme della serie di potenze n=1 n x 2n 2n + e n. Valutare poi la misurabilità e l integrabilità secondo Lebesgue della funzione somma
Prova scritta del 2 gennaio 214 Studiare la convergenza puntuale e uniforme della serie di potenze n=1 n x 2n 2n + e n. Valutare poi la misurabilità e l integrabilità secondo Lebesgue della funzione somma
Funzioni di due variabili: Limiti, Continuità, Differenziabilità
 Funzioni di due variabili: Limiti, Continuità, Differenziabilità 1 arctan( x y), (x, y) (0, 0) f(x, y) = x2 + y2 0, (x, y) = (0, 0) A 3 Stabilire se f è continua e differenziabile in (0, 0) B 2 Stabilire
Funzioni di due variabili: Limiti, Continuità, Differenziabilità 1 arctan( x y), (x, y) (0, 0) f(x, y) = x2 + y2 0, (x, y) = (0, 0) A 3 Stabilire se f è continua e differenziabile in (0, 0) B 2 Stabilire
