Esercizi sulla convoluzione e la trasformata di Laplace di distribuzioni raccolti dai temi d esame
|
|
|
- Fausta Corso
- 5 anni fa
- Visualizzazioni
Transcript
1 Esercizi sulla convoluzione e la trasformata di Laplace di distribuzioni raccolti dai temi d esame Esercizio 1 Sia U(p) la funzione, definita in un sottoinsieme di C, U(p) := log p2 + a 2 p 2, dove si è scelta la branca naturale per la funzione logaritmo definita in C \ z R, z }. 1. Determinare il dominio di U e verificare a priori che U è la trasformata di Laplace di qualche distribuzione U D +(R). 2. Derivando U determinare U a meno di una distribuzione dipendente da una costante; 3. Tenendo conto del comportamento asintotico di U, determinare la costante. Esercizio 2 Scrivere la seguente equazione integro-differenziale in (, + ) nell incognita u C 1 (R) tu (t) + u(t) = 2 u(s) sin(t s) ds, t > sotto forma di equazione di convoluzione per la distribuzione U := H(t)u(t) D +(R). Determinare poi tutte le soluzioni distribuzionali di tale equazione e, tra queste, individuare le soluzioni che sono associate ad una funzione u regolare. Esercizio 3 Calcolare le distribuzioni A 1, B 1, inverse rispetto al prodotto di convoluzione in D +(R), delle seguenti A(t) := δ (t) + H(t), B(t) := δ(t) + 2ωH(t) cos(ωt). Esercizio 4 Si consideri la distribuzione A = δ + H D +(R); date una funzione f C (R), mostrare che l equazione di convoluzione nella incognita u C 1 (R) A ( H u ) = δ + H f. equivale al problema di Cauchy in avanti per un equazione integro-differenziale. Trovare la soluzione corrispondente a f. Calcolare infine la soluzione U D +(R) di A U = δ 3. Esercizio 5 Siano X, Y D +(R) due distribuzioni a valori reali e Laplace-trasformabili, che risolvono il sistema X X Y Y =H(t)t cos t 2X Y =H(t)t sin t Posto Z := X + iy, calcolare Z Z e determinare di conseguenza Z, X, Y. -1
2 Esercizio 6 Determinare l unica soluzione u D +(R) dell equazione differenziale d 3 u dt u 3 2d2 dt + d u 2 dt 2u = 2δ Esercizio 7 Si considerino le successioni di distribuzioni Calcolare i limiti in D (R) T n := δ 1/n, S n := n(t n T 2n ). T := lim n T n, S := lim n S n. Sia ora U n D +(R) l unica soluzione dell equazione differenziale U n U n = S n. Dopo aver scritto tale equazione come equazione di convoluzione in D +(R), determinare A D +(R) in modo che U n si possa rappresentare nella forma U n = A S n. Finalmente, calcolare esplicitamente U n e il limite U := lim n U n in D (R). Esercizio 8 Al variare del parametro λ R, determinare la distribuzione U λ D +(R) la cui trasformata di Laplace è p U λ (p) := (p + 1) 2 + λ. È vero che lim λ U λ = U nel senso di L 1 (R)? Esercizio 9 Calcolare la distribuzione T := δ e t. Determinare poi A D +(R) in modo che A T = δ. Esercizio 1 Sia f ε (t) := ε 1 1 (,ε) (t) e u ε la funzione regolare che risolve l equazione u ε(t) + 4u ε (t) 5 Posto U ε (t) := H(t)u ε (t), si determini il limite u ε (s) ds = f ε (t), u ε () =. U (t) = lim ε U ε (t) nel senso delle distribuzioni. Verificare infine che U ε = U f ε. -2
3 Esercizio 11 Sia g una distribuzione a supporto compatto; dimostrare le seguenti affermazioni: 1. Se f è una distribuzione T -periodica, allora f g è T -periodica. 2. Se f risolve l equazione omogenea in D (R) d n dt f + a d n 1 n n 1 dt f + a d n 2 n 1 n 2 dt f a d n 2 1 dt f + a f = allora anche f g la risolve. 3. In particolare, se f è un polinomio, anche f g è un polinomio. Esercizio 12 Sia f ε (t) := ε 1 1 (,ε) (t) e u ε la funzione regolare che risolve l equazione u ε(t) + 2u ε (t) 8 Posto U ε (t) := H(t)u ε (t), si determini il limite u ε (s) ds = f ε (t), u ε () =. U (t) = lim ε U ε (t) nel senso delle distribuzioni. Verificare infine che U ε = U f ε. Esercizio 13 Sia T la trasformazione lineare (filtro) definita in D +(R) che ad ogni segnale causale d ingresso f associa la distribuzione u = T (f) D +(R) soluzione dell equazione u + H(t)e t u = f. 1. Calcolare E := T (δ ) e la sua trasformata di Laplace E = L (E). 2. Mostrare che E(p) < 1 se Re p > 1/2. 3. Si consideri poi la successione di segnali f n costruiti nel modo seguente: si parte da un segnale in ingresso f D +(R) e si chiama f 1 l uscita T (f ); si riprende f 1 come nuovo ingresso e si chiama f 2 l uscita T (f 1 ). Iterando il procedimento si ottiene una successione di segnali f n che soddisfano la relazione ricorrente f n+1 = T (f n ). Si esprima f n come convoluzione a partire da f. 4. Dopo aver calcolato F n := L (f n ), si trovi il limite puntuale di F n (p) e il limite lim n + f n in D +(R). -3
4 Esercizio 14 Per n N sia 1 n la funzione caratteristica dell intervallo ]2nπ, 2(n + 1)π[ e sia sin t se 2nπ < t < 2(n + 1)π, f n (t) := 1 n (t) sin t = altrimenti. 1. Si calcoli g n := f n + f n. 2. Si calcoli la trasformata di Laplace F n (p) di f n. 3. Si calcolino le serie f(t) := n= f n (t), t R, F(p) := n= F n (p), p C, precisando l insieme di convergenza puntuale e indicando se vi è convergenza anche rispetto ad altre nozioni conosciute (ad es. uniforme, distribuzionale, in L 1 (R), etc.). Esercizio 15 Sia T la trasformazione definita in D +(R) che associa ad ogni distribuzione f l unica soluzione u := T (f) D +(R) dell equazione differenziale u 4u = f. Sia S la trasformazione definita in D +(R) che associa ad ogni distribuzione g l unica soluzione v := S(g) D +(R) dell equazione differenziale v + v = g. Calcolare E := T (δ), F := S(δ) e G := T (S(δ)). Verificare che G (iv) 3G 4G = δ. Calcolare finalmente la soluzione del problema di Cauchy in avanti (t > ) w (iv) (t) 3w (t) 4w(t) =, w() =, w () = 1, w () = w () =. Esercizio 16 Determinare quali delle seguenti funzioni della variabile complessa p = x+iy sono trasformate di Laplace di distribuzioni, giustificando accuratamente la risposta: ( ) 1 cos p, e p2, tan p, log(sin p), 1 cosh p, x iy x 2 + y 2. Di tali funzioni antitrasformabili si calcoli poi l integrale complesso lungo la circonferenza Γ di centro l origine e raggio 2π, orientata in senso antiorario. -4
5 Esercizio 17 Per n N chiamiamo 1 n la funzione caratteristica dell intervallo (2 n, 2 n+1 ), definita da 1 se 1 < t < 1, 2 1 n (t) := n 2 n 1 altrimenti. Si considerino le funzioni reali v a (t) := n= a n 1 n (t) dipendenti dal parametro a >. Dire per quali valori di a la funzione v a è trasformabile secondo Laplace, determinare il dominio della sua trasformata di Laplace V a e calcolare V a (). Calcolare infine V a (p) a 2 V a(p/2). (Per quest ultimo calcolo può essere d aiuto ricordare la formula L [u] = U L [u(λt)](p) = 1 U(p/λ), per λ >.) λ Esercizio Per α, β > calcolare la convoluzione ( δ + αδ) ( δ + βδ). 2. Calcolare la soluzione u α S (R) dell equazione differenziale 3. Scrivere l equazione differenziale u α + αu α = δ in R. u (iv) 3u + 2u = δ in R, in forma di equazione di convoluzione e esprimerne la soluzione in termini delle funzioni u α precedentemente calcolate. Esercizio 19 Discutere se le seguenti funzioni della variabile complessa s sono trasformate di Laplace di distribuzioni e, in caso affermativo, calcolarne l antitrasformata: s 4 (s 1)(s + 2), + 2 n= e n + (s n), n= e p/n (s + n), Re s 2 Im s, log s s 2. -5
6 Esercizio 2 In funzione di u R calcolare la soluzione del problema di Cauchy u (t) + 6u (t) + 11u (t) + 6u(t) = sin t, t > ; u() = u, u () =, u () =. Determinare poi l unica funzione periodica v tale che lim u(t) v(t) =, indipendentemente dal valore di u. t + Esercizio 21 Per α R sia T α il filtro che ad una funzione causale v associa la soluzione u α = T α [v] dell equazione integro-differenziale d u dt α(t) + u α (t) + αe t e x u α (x) dx = v(t) per t > ; u(t) per t. Si esprima T α [v] come convoluzione di v con una distribuzione causale e si calcoli quest ultima in funzione del parametro α. Si calcoli T 1 [H(t 3)]. Per quali valori di α il filtro è stabile nella norma di L (R)? Esercizio 22 Calcolare le antitrasformate di Laplace di U(s) := (s 1) 4, V(s) := d ds (e 4s s 2 s 2 2s + 2 Esercizio 23 Sia T il filtro lineare causale che sulle funzioni causali u è definito da T [u] := 2u(t) + Trovare le distribuzioni u 1, u 2 D +(R) tali che T [u 1 ] = δ(t), T [u 2 ] = v(t) = e x/2 u(t x) dx, t > ; n= ). ( 1) n 1 (n,n+1) (t). Si consiglia di disegnare accuratamente v e H v, ricordando che 1 se n t n + 1; 1 (n,n+1) (t) = altrimenti. Esercizio 24 Calcolare i prodotti di convoluzione u := sinc(t α) sinc(t + β), α, β R; v := δ (t) e t rect(t). -6
7 Esercizio 25 Determinare le soluzioni causali e Laplace trasformabili u dell equazione di convoluzione u (t) u(t 1) = H(t 2)(t 2). Esercizio 26 Determinare a priori se i segnali causali u e v, le cui trasformate di Laplace sono rispettivamente s 2 log s U(s) :=, V(s) := (s 1) 2 s, 2 sono funzioni o distribuzioni. Calcolare poi u e v. Esercizio 27 Determinare le soluzioni causali e Laplace trasformabili u dell equazione di convoluzione (attenzione: precisione nei calcoli!) ( δ (t) δ(t π) ) ( δ(t) H(t π) ) u = δ(t) + 2H(t π) cos(t) 1 (,2π) (t) sin t. Esercizio 28 Determinare quali condizioni devono soddisfare û e α R perchè l equazione di convoluzione u sin(πt) = sin(απt) abbia una soluzione u L 1 (R). Esercizio 29 Calcolare il prodotto di convoluzione u(t) := ( δ(t 1) δ(t + 1) ) ( δ(t 2) δ(t + 2) ) ( δ(t 3) δ(t + 3) ). Esercizio 3 Calcolare il prodotto di convoluzione e it t 2. Esercizio 31 Calcolare i prodotti di convoluzione u(t) := δ (t) ( t 2 + t + 2 ), v(t) := H(t)e 2t H(t)e 2t H(t)e 2t H(t)e 2t H(t)e 2t. Esercizio 32 Scrivere il problema di Cauchy in avanti u (t) 2u (t) + u (t) 2u(t) = t >, u() = u () =, u () = 1 come equazione di convoluzione e calcolarne la soluzione u; esprimere poi tramite un opportuno integrale la soluzione dell equazione v (t) 2v (t) + v (t) 2v(t) = f(t) t >, v() = v () = v () = dipendente da una generica funzione continua f. -7
Esercizi sulla trasformata di Fourier di distribuzioni raccolti dai temi d esame
 Esercizi sulla trasformata di Fourier di distribuzioni raccolti dai temi d esame Esercizio Sia T > 0 e f : R R la funzione reale T -periodica la cui restrizione all intervallo [0, T ] vale f(t) := t(t
Esercizi sulla trasformata di Fourier di distribuzioni raccolti dai temi d esame Esercizio Sia T > 0 e f : R R la funzione reale T -periodica la cui restrizione all intervallo [0, T ] vale f(t) := t(t
Analisi Matematica 3
 Testi delle prove d esame del corso di Analisi Matematica 3 presso la Facoltà di Ingegneria Bruno Rubino L Aquila, 2006 Indice 1 Curve 3 2 Superfici 4 3 Teorema di Gauss-Green e formula dell area 4 4 Campi
Testi delle prove d esame del corso di Analisi Matematica 3 presso la Facoltà di Ingegneria Bruno Rubino L Aquila, 2006 Indice 1 Curve 3 2 Superfici 4 3 Teorema di Gauss-Green e formula dell area 4 4 Campi
COGNOME... NOME... Matricola... Corso Prof... Esame di ANALISI MATEMATICA II - 27 Gennaio cos x
 COGNOME... NOME... Matricola... Corso Prof.... Esame di ANALISI MATEMATICA II - 27 Gennaio 25 A ESERCIZIO. 4 punti) Verificare che la serie 7 2 cos x ) n è convergente per ogni x R, e calcolarne la somma.
COGNOME... NOME... Matricola... Corso Prof.... Esame di ANALISI MATEMATICA II - 27 Gennaio 25 A ESERCIZIO. 4 punti) Verificare che la serie 7 2 cos x ) n è convergente per ogni x R, e calcolarne la somma.
NUMERI COMPLESSI. = 2 + 5i A3) Calcolare in forma trigonometrica le soluzioni complesse dell equazione iz 4 9 = 0
 NUMERI COMPLESSI A) Calcolare in forma cartesiana ( + i) 3 = A) ( + 5i) (3 + 4i) Calcolare in forma cartesiana = + 5i A3) Calcolare in forma trigonometrica le soluzioni complesse dell equazione iz 4 9
NUMERI COMPLESSI A) Calcolare in forma cartesiana ( + i) 3 = A) ( + 5i) (3 + 4i) Calcolare in forma cartesiana = + 5i A3) Calcolare in forma trigonometrica le soluzioni complesse dell equazione iz 4 9
Compito di Analisi Matematica III. Compito A
 c.d.l. Ingegneria elettronica e c.d.l. Ingegneria Informatica (M Z) 7 gennaio 2008. Determinare i residui nei punti singolari e nel punto all infinito della funzione z 2 sen z + 2. Determinare la trasformata
c.d.l. Ingegneria elettronica e c.d.l. Ingegneria Informatica (M Z) 7 gennaio 2008. Determinare i residui nei punti singolari e nel punto all infinito della funzione z 2 sen z + 2. Determinare la trasformata
n=1 c n <. Data la seguente serie di trigonometrica + sin cn 1 cos 2 c2 n sin 2nx, n 2a + 3
 Facoltà di Scienze MM. FF. e NN. A.A. 013/014 I Esercitazione 30 Aprile 014 Esercizio 1. Dato il problema di Cauchy x = 3 + cos 3 x, x(0) = 0, studiare esistenza e unicità locale e globale. Provare che
Facoltà di Scienze MM. FF. e NN. A.A. 013/014 I Esercitazione 30 Aprile 014 Esercizio 1. Dato il problema di Cauchy x = 3 + cos 3 x, x(0) = 0, studiare esistenza e unicità locale e globale. Provare che
La trasformata di Laplace
 La trasformata di Laplace (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi DIMS Universitá di Trento anno accademico 2005/2006 La trasformata di Laplace 1 / 34 Outline 1 La trasformata di
La trasformata di Laplace (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi DIMS Universitá di Trento anno accademico 2005/2006 La trasformata di Laplace 1 / 34 Outline 1 La trasformata di
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica II del
 Prova scritta di nalisi Matematica II del 12-06-2001. C1 1) Studiare la convergenza semplice, uniforme e totale della serie di funzioni seguente ( 1) [ n 2 ] n x 1 + n 2 x. n=0 2) Data la funzione (x 2
Prova scritta di nalisi Matematica II del 12-06-2001. C1 1) Studiare la convergenza semplice, uniforme e totale della serie di funzioni seguente ( 1) [ n 2 ] n x 1 + n 2 x. n=0 2) Data la funzione (x 2
TEMI D ESAME DI ANALISI MATEMATICA 1. x 1 + x y
 TEMI D ESAME DI ANALISI MATEMATICA GRAZIANO CRASTA E LUIGI ORSINA, A.A. 203/4. SPAZI METRICI, TOPOLOGIA, COMPLETEZZA Esercizio.. Dimostrare che la funzione d(, y) := + y + y, y R, è una distanza su R.
TEMI D ESAME DI ANALISI MATEMATICA GRAZIANO CRASTA E LUIGI ORSINA, A.A. 203/4. SPAZI METRICI, TOPOLOGIA, COMPLETEZZA Esercizio.. Dimostrare che la funzione d(, y) := + y + y, y R, è una distanza su R.
Esercizi sulle equazioni differenziali
 Esercizi sulle equazioni differenziali Equazioni differenziali lineari del primo ordine. () u (t) = t [t + u(t)]; () u(t) sin t + u (t) = cos t u (t) sin t; (3) u(t) = + t u (t) + ; Risolvere i seguenti
Esercizi sulle equazioni differenziali Equazioni differenziali lineari del primo ordine. () u (t) = t [t + u(t)]; () u(t) sin t + u (t) = cos t u (t) sin t; (3) u(t) = + t u (t) + ; Risolvere i seguenti
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006. Matematica 2 (Analisi)
 Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
, α N, quando f è una delle seguenti
 . Determinare lim 0 + α f, α R, e lim 0 α f funzioni: f = ln 8 cos4+, f = ln f = sin sine., α N, quando f è una delle seguenti, f = ln ln, sin sin. Calcolare la derivata della funzione f definita da f
. Determinare lim 0 + α f, α R, e lim 0 α f funzioni: f = ln 8 cos4+, f = ln f = sin sine., α N, quando f è una delle seguenti, f = ln ln, sin sin. Calcolare la derivata della funzione f definita da f
x = t y = t z = t 3 1 A = B = 1 2
 11/1/05 Teoria: Enunciare e discutere il teorema di Lagrange. Esercizio 1. Determinare l equazione cartesiana del piano passante per P 0 = (1,, 1) e contenente i vettori u = (,, ) e v = (1, 5, 4). Risposta
11/1/05 Teoria: Enunciare e discutere il teorema di Lagrange. Esercizio 1. Determinare l equazione cartesiana del piano passante per P 0 = (1,, 1) e contenente i vettori u = (,, ) e v = (1, 5, 4). Risposta
5.7 Esercizi (V Settimana)
 5.7 Esercizi (V Settimana) 7 5.7 Esercizi (V Settimana) 5.7. Sia data f :(R 3 ) (R 3 ) da f(a,b,c) =(a + b, b, a + b + c). Si scriva la f sotto forma del prodotto di un vettore riga per una matrice A;.
5.7 Esercizi (V Settimana) 7 5.7 Esercizi (V Settimana) 5.7. Sia data f :(R 3 ) (R 3 ) da f(a,b,c) =(a + b, b, a + b + c). Si scriva la f sotto forma del prodotto di un vettore riga per una matrice A;.
UNIVERSITÀ DEGLI STUDI DI PERUGIA Corso di Analisi Matematica III - 9 CFU C.d.S. Triennale in Matematica A.A. 2016/2017 I Esercitazione 12 Aprile 2017
 C.d.S. Triennale in Matematica A.A. 2016/2017 I Esercitazione 12 Aprile 2017 Esercizio 1. Data la successione di funzioni f n t = en1+t4 + e nt2 n 3 + e, t R, n1+t2 a determinare l insieme di convergenza
C.d.S. Triennale in Matematica A.A. 2016/2017 I Esercitazione 12 Aprile 2017 Esercizio 1. Data la successione di funzioni f n t = en1+t4 + e nt2 n 3 + e, t R, n1+t2 a determinare l insieme di convergenza
Compito di Analisi Matematica, Seconda parte, COGNOME: NOME: MATR.:
 Compito di Analisi Matematica, Seconda parte, gennaio 9 Tema X COGNOME: NOME: MATR.: Esercizio. ( Determinare al variare di β R la soluzione di y (x + y (x + y(x = e x + x tale che y( = β = y (. ( Al variare
Compito di Analisi Matematica, Seconda parte, gennaio 9 Tema X COGNOME: NOME: MATR.: Esercizio. ( Determinare al variare di β R la soluzione di y (x + y (x + y(x = e x + x tale che y( = β = y (. ( Al variare
TEMI D ESAME DI ANALISI MATEMATICA I
 TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
SEGNALI E SISTEMI Proff. L. Finesso, M. Pavon e S. Pinzoni (a.a ) Homework assignment #2 Testo e Soluzione
 SEGNALI E SISTEMI Proff. L. Finesso, M. Pavon e S. Pinzoni (a.a. 00-005) Homework assignment # Testo e Soluzione Esercizio Si consideri l equazione differenziale ordinaria, lineare a coefficienti costanti
SEGNALI E SISTEMI Proff. L. Finesso, M. Pavon e S. Pinzoni (a.a. 00-005) Homework assignment # Testo e Soluzione Esercizio Si consideri l equazione differenziale ordinaria, lineare a coefficienti costanti
Analisi Matematica 2. Michele Campiti. Prove scritte di. Ingegneria Industriale a.a
 Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
x + 1 2x], g(x) = x x + 2, h(x) = ln(x 1 2x 2 4x).
![x + 1 2x], g(x) = x x + 2, h(x) = ln(x 1 2x 2 4x). x + 1 2x], g(x) = x x + 2, h(x) = ln(x 1 2x 2 4x).](/thumbs/102/153351382.jpg) Funzioni Esercizio Siano f, g due funzioni definite da fx) = x x 2, gx) = ln x Trovare l insieme di definizione di f e g 2 Determinare le funzioni composte f g e g f, precisandone insieme di definizione
Funzioni Esercizio Siano f, g due funzioni definite da fx) = x x 2, gx) = ln x Trovare l insieme di definizione di f e g 2 Determinare le funzioni composte f g e g f, precisandone insieme di definizione
Esercizi su: insiemi, intervalli, intorni. 4. Per ognuna delle successive coppie A e B di sottoinsiemi di Z determinare A B, A B, a) A C d) C (A B)
 Esercizi su: insiemi, intervalli, intorni. Per ognuna delle successive coppie A e B di sottoinsiemi di N determinare A B, A B, A c e B c. a) A = { N + = 0}, B = { N = 6}, b) A = { N < 5}, B = { N < },
Esercizi su: insiemi, intervalli, intorni. Per ognuna delle successive coppie A e B di sottoinsiemi di N determinare A B, A B, A c e B c. a) A = { N + = 0}, B = { N = 6}, b) A = { N < 5}, B = { N < },
La trasformata di Laplace
 La trasformata di Laplace (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi DIMS Università di Trento anno accademico 2008/2009 (aggiornata al 21/09/2008) La trasformata di Laplace 1 / 31
La trasformata di Laplace (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi DIMS Università di Trento anno accademico 2008/2009 (aggiornata al 21/09/2008) La trasformata di Laplace 1 / 31
CORSO DI LAUREA in Fisica, aa 2017/18 (canale Pb-Z)
 CORSO DI LAUREA in Fisica, aa 2017/18 (canale Pb-Z) Equazioni lineari del II ordine a coefficienti costanti: questo è un richiamo dei risultati con altri esempi svolti. Il testo di riferimento è Bramanti
CORSO DI LAUREA in Fisica, aa 2017/18 (canale Pb-Z) Equazioni lineari del II ordine a coefficienti costanti: questo è un richiamo dei risultati con altri esempi svolti. Il testo di riferimento è Bramanti
Prove d esame a.a , ,
 Prove d esame aa 4 5, 5 6, 6 7 Andrea Corli 6 gennaio 8 Sono qui raccolti i testi delle prove d esame assegnati negli aa 4 5, 5 6, 6 7, relativi al Corso di Analisi Matematica I (semestrale, crediti),
Prove d esame aa 4 5, 5 6, 6 7 Andrea Corli 6 gennaio 8 Sono qui raccolti i testi delle prove d esame assegnati negli aa 4 5, 5 6, 6 7, relativi al Corso di Analisi Matematica I (semestrale, crediti),
Ingegneria Elettronica Prova scritta di Analisi Matematica II del giorno ( 3) n x n n + 1
 Prova scritta di Analisi Matematica II del giorno 31-01-2007 1) Studiare la serie di potenze ( 3) n x n n + 1 2) Determinare i punti di estremo relativo ed assoluto della funzione seguente f(x, y) = x
Prova scritta di Analisi Matematica II del giorno 31-01-2007 1) Studiare la serie di potenze ( 3) n x n n + 1 2) Determinare i punti di estremo relativo ed assoluto della funzione seguente f(x, y) = x
ANALISI MATEMATICA 3. esercizi assegnati per la prova scritta del 31 gennaio 2011
 esercizi assegnati per la prova scritta del 31 gennaio 2011 Esercizio 1. Per x > 0 e n N si ponga f n (x) = ln ( n 5 x ) a) Provare l integrabilità delle funzioni f n in (0, + ). 3 + n 4 x 2. b) Studiare
esercizi assegnati per la prova scritta del 31 gennaio 2011 Esercizio 1. Per x > 0 e n N si ponga f n (x) = ln ( n 5 x ) a) Provare l integrabilità delle funzioni f n in (0, + ). 3 + n 4 x 2. b) Studiare
Matematica II - ING ELT Appello del 27/7/2009. Nome e cognome:... Recupero I parte Recupero II parte Scritto completo. { x log y. se y > 0 f(x, y) :=
 Matematica II - ING ELT Appello del 27/7/2009 Nome e cognome:...... Scegliere una delle opzioni sottostanti Matricola:... Recupero I parte Recupero II parte Scritto completo Esercizio 1 Si consideri la
Matematica II - ING ELT Appello del 27/7/2009 Nome e cognome:...... Scegliere una delle opzioni sottostanti Matricola:... Recupero I parte Recupero II parte Scritto completo Esercizio 1 Si consideri la
1 Limiti e continuità
 Calcolo infinitesimale e differenziale Gli esercizi indicati con l asterisco (*) sono più impegnativi. Limiti e continuità Si ricorda che per una funzione di più variabili, la definizione di continuità
Calcolo infinitesimale e differenziale Gli esercizi indicati con l asterisco (*) sono più impegnativi. Limiti e continuità Si ricorda che per una funzione di più variabili, la definizione di continuità
Scritto d esame di Analisi Matematica I
 Capitolo 2: Scritti d esame 07 Pisa, 8 Gennaio 999. Studiare il comportamento della serie al variare del parametro α > /2. ( ) n n sin α n 2α 2. Sia ( ) f(x) = log + sin3 x. 2 (a) Determinare la derivata
Capitolo 2: Scritti d esame 07 Pisa, 8 Gennaio 999. Studiare il comportamento della serie al variare del parametro α > /2. ( ) n n sin α n 2α 2. Sia ( ) f(x) = log + sin3 x. 2 (a) Determinare la derivata
11.1. Esercizio. Dato il numero complesso z = 2 + i 2, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8.
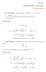 ANALISI Soluzione esercizi gennaio 0.. Esercizio. Dato il numero complesso z = + i, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8. z = i ( ) + ( ) =, π z = arg(z) = 4
ANALISI Soluzione esercizi gennaio 0.. Esercizio. Dato il numero complesso z = + i, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8. z = i ( ) + ( ) =, π z = arg(z) = 4
EQUAZIONI DIFFERENZIALI
 EQUAZIONI DIFFERENZIALI 1 Primo ordine - variabili separabili Sia dato il problema di Cauchy seguente: { y = a(x)b(y) Si proceda come segue y(x 0 ) = y 0 (1) Si calcolino le radici dell equazione b(y)
EQUAZIONI DIFFERENZIALI 1 Primo ordine - variabili separabili Sia dato il problema di Cauchy seguente: { y = a(x)b(y) Si proceda come segue y(x 0 ) = y 0 (1) Si calcolino le radici dell equazione b(y)
Modelli e Metodi Matematici della Fisica. S1/AC
 Modelli e Metodi Matematici della Fisica. S1/AC Cesi A.A. 9 1 Nome Cognome 6 CFU (AA 9-1) 8 CFU 4 CFU (solo analisi complessa) 4 + 6 CFU altro: problema voto 1 4 6 7 8 9 Test totale coeff. voto in trentesimi
Modelli e Metodi Matematici della Fisica. S1/AC Cesi A.A. 9 1 Nome Cognome 6 CFU (AA 9-1) 8 CFU 4 CFU (solo analisi complessa) 4 + 6 CFU altro: problema voto 1 4 6 7 8 9 Test totale coeff. voto in trentesimi
COMPLEMENTI DI ANALISI MATEMATICA DI BASE. Prova scritta del 26 gennaio 2005
 Prova scritta del 26 gennaio 2005 Esercizio 1. Posto B = x R 2 : x 2 2}, sia f n } una successione di funzioni (misurabili e) integrabili in B tali che f n f q.o. in B e, per ogni n N, f n (x) 2 x 3 per
Prova scritta del 26 gennaio 2005 Esercizio 1. Posto B = x R 2 : x 2 2}, sia f n } una successione di funzioni (misurabili e) integrabili in B tali che f n f q.o. in B e, per ogni n N, f n (x) 2 x 3 per
Scritto d esame di Matematica I
 Capitolo 2: Scritti d esame 139 Pisa, 19 Gennaio 2005 x 1 + (x + 1) log x (x 1)(2x 2). 2. Studiare la convergenza dei seguenti integrali impropri 1 dx e 2x 1, 0 dx e 2x 1, e, nel caso in cui convergano,
Capitolo 2: Scritti d esame 139 Pisa, 19 Gennaio 2005 x 1 + (x + 1) log x (x 1)(2x 2). 2. Studiare la convergenza dei seguenti integrali impropri 1 dx e 2x 1, 0 dx e 2x 1, e, nel caso in cui convergano,
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica II del c.1.
 Prova scritta di Analisi Matematica II del 14-07-1999 - c.1 1) Sia (d n ) una successione di numeri reali tali che inf d n > 0. Studiare il carattere della serie + n=1 al variare del parametro reale positivo
Prova scritta di Analisi Matematica II del 14-07-1999 - c.1 1) Sia (d n ) una successione di numeri reali tali che inf d n > 0. Studiare il carattere della serie + n=1 al variare del parametro reale positivo
Prova scritta di Analisi Matematica III
 18 luglio 2016 f n (x) = 1 n e (x n)2 (x R, n N ). 2. Si scriva la disuguaglianza di Bessel per la funzione f, periodica di periodo 2π, tale che 0 x [ π, 0) f (x) = 2 x x [0, π). 3. Si consideri l equazione
18 luglio 2016 f n (x) = 1 n e (x n)2 (x R, n N ). 2. Si scriva la disuguaglianza di Bessel per la funzione f, periodica di periodo 2π, tale che 0 x [ π, 0) f (x) = 2 x x [0, π). 3. Si consideri l equazione
ESERCIZI DI ANALISI MATEMATICA II. sin(tv) v. f(v) dv = (1 + t) (e 1/t + 1)
 ESERCIZI DI ANALISI MATEMATICA II Equazioni differenziali ED 1 Stabilire se l equazione integrale f(t) 1/2 0 sin(tv) v f(v) dv = (1 + t) (e 1/t + 1) ammette una soluzione nello spazio C([0, 1/2]). (Suggerimento:
ESERCIZI DI ANALISI MATEMATICA II Equazioni differenziali ED 1 Stabilire se l equazione integrale f(t) 1/2 0 sin(tv) v f(v) dv = (1 + t) (e 1/t + 1) ammette una soluzione nello spazio C([0, 1/2]). (Suggerimento:
A Analisi Matematica 1 (Corso di Laurea in Informatica e Bioinformatica) Simulazione compito d esame
 COGNOME NOME Matr. A Analisi Matematica (Corso di Laurea in Informatica e Bioinformatica) Firma dello studente Tempo: 3 ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
COGNOME NOME Matr. A Analisi Matematica (Corso di Laurea in Informatica e Bioinformatica) Firma dello studente Tempo: 3 ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
Analisi Matematica I
 Versione: 4 novembre 7 Università di Pisa Corso di laurea in Ingegneria Gestionale Testi e soluzioni degli scritti d esame di Analisi Matematica I a.a. 6-7 Giovanni Alberti Giovanni Alberti Dipartimento
Versione: 4 novembre 7 Università di Pisa Corso di laurea in Ingegneria Gestionale Testi e soluzioni degli scritti d esame di Analisi Matematica I a.a. 6-7 Giovanni Alberti Giovanni Alberti Dipartimento
9/11/2010 (I prova in itinere): solo test a risposta multipla
 9/11/2010 (I prova in itinere): solo test a risposta multipla 23/12/2010 (II prova in itinere, II parte) Esercizio 1. Posto Σ = {(x, y, z) R 3 x 2 + y 2 + z 2 = 4, z 1}, si chiede di calcolare il flusso
9/11/2010 (I prova in itinere): solo test a risposta multipla 23/12/2010 (II prova in itinere, II parte) Esercizio 1. Posto Σ = {(x, y, z) R 3 x 2 + y 2 + z 2 = 4, z 1}, si chiede di calcolare il flusso
ANALISI MATEMATICA I, Compito scritto del 5/07/2016 Corso di Laurea in Matematica. COGNOME e NOME... MATR T
 ANALISI MATEMATICA I, Compito scritto del 5/7/6 Corso di Laurea in Matematica COGNOME e NOME... MATR... 3 4 T Nelle risposte devono essere riportati anche i conti principali e le motivazioni principali.
ANALISI MATEMATICA I, Compito scritto del 5/7/6 Corso di Laurea in Matematica COGNOME e NOME... MATR... 3 4 T Nelle risposte devono essere riportati anche i conti principali e le motivazioni principali.
Matematica - Prova d esame (09/09/2004)
 Matematica - Prova d esame (9/9/) Università di Verona - Laurea in Biotecnologie AI - A.A. /. Disegnare sul piano di Gauss i numeri z = i, w = i e z iw. Scrivere la forma trigonometrica di w e calcolare
Matematica - Prova d esame (9/9/) Università di Verona - Laurea in Biotecnologie AI - A.A. /. Disegnare sul piano di Gauss i numeri z = i, w = i e z iw. Scrivere la forma trigonometrica di w e calcolare
METODI MATEMATICI. SECONDA PROVA IN ITINERE del 27 gennaio 2003
 METODI MATEMATICI SECONDA PROVA IN ITINERE del 27 gennaio 23 COGNOME e NOME NUMERO di MATRICOLA ) Si consideri la funzione f : R R definita da (t + 3) 2 χ [ 3, ] + χ ],[ + (t 3) 2 χ [,3]. Studiare a priori
METODI MATEMATICI SECONDA PROVA IN ITINERE del 27 gennaio 23 COGNOME e NOME NUMERO di MATRICOLA ) Si consideri la funzione f : R R definita da (t + 3) 2 χ [ 3, ] + χ ],[ + (t 3) 2 χ [,3]. Studiare a priori
Temi d esame di Analisi Matematica 1
 Temi d esame di Analisi Matematica 1 Area di Ingegneria dell Informazione - a cura di M. Bardi 31.1.95 f(x) = xe arctan 1 x (insieme di definizione, segno, iti ed asintoti, continuità e derivabilità, crescenza
Temi d esame di Analisi Matematica 1 Area di Ingegneria dell Informazione - a cura di M. Bardi 31.1.95 f(x) = xe arctan 1 x (insieme di definizione, segno, iti ed asintoti, continuità e derivabilità, crescenza
Analisi Matematica I per Ingegneria Gestionale, a.a Scritto del secondo appello, 5 febbraio 2018 Testi 1
 Analisi Matematica I per Ingegneria Gestionale, a.a. 7-8 Scritto del secondo appello, 5 febbraio 8 Testi Prima parte, gruppo.. Trovare r > e α [ π, π] per cui vale l identità 3 sin 3 cos = r sin( + α)..
Analisi Matematica I per Ingegneria Gestionale, a.a. 7-8 Scritto del secondo appello, 5 febbraio 8 Testi Prima parte, gruppo.. Trovare r > e α [ π, π] per cui vale l identità 3 sin 3 cos = r sin( + α)..
Metodi Matematici per la Fisica
 Metodi Matematici per la Fisica Prova scritta - 6 ottobre 0 Esercizio (6 punti Si usi il metodo dei residui per calcolare l integrale J (z + sin 3 (/z, z con il cammino d integrazione percorso in senso
Metodi Matematici per la Fisica Prova scritta - 6 ottobre 0 Esercizio (6 punti Si usi il metodo dei residui per calcolare l integrale J (z + sin 3 (/z, z con il cammino d integrazione percorso in senso
PROVE SCRITTE DI ANALISI MATEMATICA II (V.O.), ANNO 2002
 PROVE SCRITTE DI ANALISI MATEMATICA II (V.O.), ANNO 22 Prova scritta del 1/1/22 Si esamini la serie di funzioni: 1 log x (e n + n), definita per x IR. Si determini l insieme S in cui tale serie converge,
PROVE SCRITTE DI ANALISI MATEMATICA II (V.O.), ANNO 22 Prova scritta del 1/1/22 Si esamini la serie di funzioni: 1 log x (e n + n), definita per x IR. Si determini l insieme S in cui tale serie converge,
Scritto d esame di Analisi Matematica II
 Capitolo 2: Scritti d esame 145 Pisa, 1 Gennaio 2005 e gli insiemi f(x, y) = x 2 x 2 y + y, A = {(x, y) R 2 : x 2 + y 2 6, x 0, y 0}, B = {(x, y) R 2 : x 0, y 0}. (a) massimo e minimo di f(x, y) in A,
Capitolo 2: Scritti d esame 145 Pisa, 1 Gennaio 2005 e gli insiemi f(x, y) = x 2 x 2 y + y, A = {(x, y) R 2 : x 2 + y 2 6, x 0, y 0}, B = {(x, y) R 2 : x 0, y 0}. (a) massimo e minimo di f(x, y) in A,
Matematica con esercitazioni, Modulo 2. Analisi matematica. Diario delle lezioni.
 Matematica con esercitazioni, Modulo. Analisi matematica. Diario delle lezioni. Laurea triennale Chimica e tecnologie per l ambiente e per i materiali. Rimini Avvertenza per gli studenti: il libro di testo
Matematica con esercitazioni, Modulo. Analisi matematica. Diario delle lezioni. Laurea triennale Chimica e tecnologie per l ambiente e per i materiali. Rimini Avvertenza per gli studenti: il libro di testo
1) D0MINIO. x x 4x + 3 Determinare il dominio della funzione f (x) = x Deve essere
 ) DMINIO + 3 Determinare il dominio della funzione f ) + 3 Deve essere Ovviamente, inoltre: se > + 3 ) 3) quindi < o 3 se < + 3, + 3 quindi 7 Determinare il dominio della funzione f ) + 5 Deve essere +
) DMINIO + 3 Determinare il dominio della funzione f ) + 3 Deve essere Ovviamente, inoltre: se > + 3 ) 3) quindi < o 3 se < + 3, + 3 quindi 7 Determinare il dominio della funzione f ) + 5 Deve essere +
Analisi Matematica I per Ingegneria Gestionale, a.a Scritto del secondo appello, 1 febbraio 2017 Testi 1
 Analisi Matematica I per Ingegneria Gestionale, a.a. 206-7 Scritto del secondo appello, febbraio 207 Testi Prima parte, gruppo.. Trovare le [0, π] che risolvono la disequazione sin(2) 2. 2. Dire se esistono
Analisi Matematica I per Ingegneria Gestionale, a.a. 206-7 Scritto del secondo appello, febbraio 207 Testi Prima parte, gruppo.. Trovare le [0, π] che risolvono la disequazione sin(2) 2. 2. Dire se esistono
Tutorato di Complementi di Analisi Matematica e Statistica Parte di Analisi 6 e 10 aprile 2017
 Tutorato di Complementi di Analisi Matematica e Statistica Parte di Analisi 6 e 10 aprile 2017 Esercizi: serie di potenze e serie di Taylor 1 Date le serie di potenze a.) n=2 ln(n) n 3 (x 5)n b.) n=2 ln(n)
Tutorato di Complementi di Analisi Matematica e Statistica Parte di Analisi 6 e 10 aprile 2017 Esercizi: serie di potenze e serie di Taylor 1 Date le serie di potenze a.) n=2 ln(n) n 3 (x 5)n b.) n=2 ln(n)
UNIVERSITÀ DEGLI STUDI DI PERUGIA Facoltà di Scienze MM. FF. e NN.
 A.A. 213/214 2 Novembre 213 I esercitazione Esercizio 1. Dato il problema di Cauchy ( e y 2 2 1 ) arctan 3y 5 y = 2 sin (1) 2 x 2, 1 + x 2 y() = 1, (b) provare che la soluzione y di (3) è definita in tutto
A.A. 213/214 2 Novembre 213 I esercitazione Esercizio 1. Dato il problema di Cauchy ( e y 2 2 1 ) arctan 3y 5 y = 2 sin (1) 2 x 2, 1 + x 2 y() = 1, (b) provare che la soluzione y di (3) è definita in tutto
Analisi Matematica I per Ingegneria Gestionale, a.a Scritto del quarto appello, 12 giugno 2017 Testi 1. n a + n 2a n 4 log(1 + 1/n 2 )
 Scritto del quarto appello, giugno 07 Testi Prima parte, gruppo. cartesiane: a) (, ); b) (0, ); c) (, 3). + sin(e ); b) lim log(); c) lim 0 + + sin(/ ). 3. Scrivere lo sviluppo di Talor di ordine 6 (in
Scritto del quarto appello, giugno 07 Testi Prima parte, gruppo. cartesiane: a) (, ); b) (0, ); c) (, 3). + sin(e ); b) lim log(); c) lim 0 + + sin(/ ). 3. Scrivere lo sviluppo di Talor di ordine 6 (in
Calcolo I - Corso di Laurea in Fisica - 18 Giugno 2018 Soluzioni Scritto. f(x) = ( ln 1 + x + 1 ) =
 Calcolo I - Corso di Laurea in Fisica - 8 Giugno 08 Soluzioni Scritto ) Data la funzione fx) = ln + x + ) a) Calcolare il dominio, asintoti ed eventuali punti di non derivabilità; b) Calcolare, se esistono,
Calcolo I - Corso di Laurea in Fisica - 8 Giugno 08 Soluzioni Scritto ) Data la funzione fx) = ln + x + ) a) Calcolare il dominio, asintoti ed eventuali punti di non derivabilità; b) Calcolare, se esistono,
ARGOMENTI MATEMATICA PER L INGEGNERIA
 ARGOMENTI DI MATEMATICA PER L INGEGNERIA VOLUME 2 Esercizi proposti Quando non diversamente precisato, nel seguito si intenderà( sempre che nel piano sia stato introdotto un sistema cartesiano ortogonale
ARGOMENTI DI MATEMATICA PER L INGEGNERIA VOLUME 2 Esercizi proposti Quando non diversamente precisato, nel seguito si intenderà( sempre che nel piano sia stato introdotto un sistema cartesiano ortogonale
COMPLEMENTI DI ANALISI MATEMATICA II. Prova scritta del 20 gennaio 2014
 Prova scritta del 2 gennaio 214 Studiare la convergenza puntuale e uniforme della serie di potenze n=1 n x 2n 2n + e n. Valutare poi la misurabilità e l integrabilità secondo Lebesgue della funzione somma
Prova scritta del 2 gennaio 214 Studiare la convergenza puntuale e uniforme della serie di potenze n=1 n x 2n 2n + e n. Valutare poi la misurabilità e l integrabilità secondo Lebesgue della funzione somma
1 Analisi mat. I - Esercizi del 13/10/99
 Analisi mat. I - Esercizi del //99 ES. Delle seguenti funzioni determinare: il dominio l immagine gli eventuali asintoti l insieme dove sono continue e quali siano estendibili per continuita. Determinare
Analisi mat. I - Esercizi del //99 ES. Delle seguenti funzioni determinare: il dominio l immagine gli eventuali asintoti l insieme dove sono continue e quali siano estendibili per continuita. Determinare
ISTITUZIONI DI ANALISI SUPERIORE B Prova scritta del 17/3/2003
 ISTITUZIONI DI ANALISI SUPEIOE B Prova scritta del 7/3/3 Sia f : C la funzione così definita: { se t
ISTITUZIONI DI ANALISI SUPEIOE B Prova scritta del 7/3/3 Sia f : C la funzione così definita: { se t
APPLICAZIONI di MATEMATICA ESERCIZI parte 8
 APPLICAZIONI di MATEMATICA ESERCIZI parte 8 Esercizi teorici Es. 1.1 - Sia F razionale, reale positiva e F (0) = 0. Stabilire se è RP la funzione G(s) = F (s 24) Es. 1.2 - Sia F reale, razionale e sia
APPLICAZIONI di MATEMATICA ESERCIZI parte 8 Esercizi teorici Es. 1.1 - Sia F razionale, reale positiva e F (0) = 0. Stabilire se è RP la funzione G(s) = F (s 24) Es. 1.2 - Sia F reale, razionale e sia
Equazioni differenziali
 Equazioni differenziali In un equazione differenziale l incognita da trovare è una funzione, di cui è data, dall equazione, una relazione con le sue derivate (fino ad un certo ordine) e la variabile libera:
Equazioni differenziali In un equazione differenziale l incognita da trovare è una funzione, di cui è data, dall equazione, una relazione con le sue derivate (fino ad un certo ordine) e la variabile libera:
Esame di Analisi Funzionale e Trasformate Seconda prova in itinere. Giugno 2019 A.A. 2018/2019. Prof. M. Bramanti Tema A
 Esame di Analisi Funzionale e Trasformate Seconda prova in itinere. Giugno 9 A.A. 8/9. Prof. M. Bramanti Tema A Cognome: Nome N matr. o cod. persona: Dom Dom Dom Es Es Es Tot. Punti Domande di teoria rispondere
Esame di Analisi Funzionale e Trasformate Seconda prova in itinere. Giugno 9 A.A. 8/9. Prof. M. Bramanti Tema A Cognome: Nome N matr. o cod. persona: Dom Dom Dom Es Es Es Tot. Punti Domande di teoria rispondere
La trasformata di Laplace
 La trasformata di Laplace (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi DIMS Università di Trento anno accademico 2006/2007 La trasformata di Laplace 1 / 50 Outline 1 La trasformata di
La trasformata di Laplace (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi DIMS Università di Trento anno accademico 2006/2007 La trasformata di Laplace 1 / 50 Outline 1 La trasformata di
Esame di Metodi Matematici per l Ingegneria
 Esame di Metodi Matematici per l Ingegneria Prof. M. Bramanti Politecnico di Milano, A.A. 05/6 Prima prova in itinere. Novembre 05 Tema A Cognome: Nome N matr. o cod. persona: Domande di teoria (rispondere
Esame di Metodi Matematici per l Ingegneria Prof. M. Bramanti Politecnico di Milano, A.A. 05/6 Prima prova in itinere. Novembre 05 Tema A Cognome: Nome N matr. o cod. persona: Domande di teoria (rispondere
Università degli Studi di Bergamo Facoltà di Ingegneria Matematica I Appello del 5 Febbraio 2007 Tema A
 Università degli Studi di Bergamo Facoltà di Ingegneria Matematica I Appello del 5 Febbraio 7 Tema A Cognome e Nome Matr... Disegnare un grafico approssimativo della funzione f() log( ). Indicare sul grafico
Università degli Studi di Bergamo Facoltà di Ingegneria Matematica I Appello del 5 Febbraio 7 Tema A Cognome e Nome Matr... Disegnare un grafico approssimativo della funzione f() log( ). Indicare sul grafico
determinare una soluzione y(t) dell equazione completa e, quindi dedurne tutte le y(t) soluzioni dell equazione.
 ANALISI VETTORIALE Soluzione esercizi 4 febbraio 2011 10.1. Esercizio. Assegnata l equazione lineare omogenea di primo ordine y + a y = 0 determinare le soluzioni di tale equazione in corrispondenza ai
ANALISI VETTORIALE Soluzione esercizi 4 febbraio 2011 10.1. Esercizio. Assegnata l equazione lineare omogenea di primo ordine y + a y = 0 determinare le soluzioni di tale equazione in corrispondenza ai
Analisi Matematica I per Ingegneria Gestionale, a.a Scritto del terzo appello, 19 febbraio 2018 Testi 1
 Scritto del terzo appello, 9 febbraio 208 Testi Prima parte, gruppo.. Per ciascuno dei seguenti punti dare le coordinate (polari o cartesiane) che mancano: a) = 0, = ; r = α = b) = 3, = 3; r = α = c) r
Scritto del terzo appello, 9 febbraio 208 Testi Prima parte, gruppo.. Per ciascuno dei seguenti punti dare le coordinate (polari o cartesiane) che mancano: a) = 0, = ; r = α = b) = 3, = 3; r = α = c) r
Equazioni lineari secondo ordine a coefficienti continui. (Soluzione generale omogenea associata) + (Soluzione particolare).
 Equazioni differenziali Equazioni lineari secondo ordine a coefficienti continui Si tratta di equazioni del tipo y + a(ty + b(ty = f(t, t I. La soluzione generale è della forma (Soluzione generale omogenea
Equazioni differenziali Equazioni lineari secondo ordine a coefficienti continui Si tratta di equazioni del tipo y + a(ty + b(ty = f(t, t I. La soluzione generale è della forma (Soluzione generale omogenea
Compiti d Esame A.A. 2005/2006
 Compiti d Esame A.A. 25/26 UNIVERSITÀ DEGLI STUDI DI PERUGIA A.A. 25/26 I Esercitazione 21 Aprile 26 { y = xy ln(xy) si chiede di dimostrare che: y(1) = 1, (a) ammette un unica soluzione massimale y =
Compiti d Esame A.A. 25/26 UNIVERSITÀ DEGLI STUDI DI PERUGIA A.A. 25/26 I Esercitazione 21 Aprile 26 { y = xy ln(xy) si chiede di dimostrare che: y(1) = 1, (a) ammette un unica soluzione massimale y =
Esercitazione sulle serie di Fourier
 Esercitazione sulle serie di Fourier 3 novembre. Calcolo dei coefficienti di Fourier e di somme di serie speciali Esercizio. Si consideri il segnale u : R R, -periodico, definito nell intervallo, π, da
Esercitazione sulle serie di Fourier 3 novembre. Calcolo dei coefficienti di Fourier e di somme di serie speciali Esercizio. Si consideri il segnale u : R R, -periodico, definito nell intervallo, π, da
Analisi Matematica I per Ingegneria Gestionale, a.a Secondo compitino e primo appello, 12 gennaio 2017 Testi 1
 Secondo compitino e primo appello, gennaio 7 Testi Prima parte, gruppo.. Determinare l insieme di definizione della funzione arcsin(e ).. Determinare lo sviluppo di Taylor di ordine 4 (in ) della funzione
Secondo compitino e primo appello, gennaio 7 Testi Prima parte, gruppo.. Determinare l insieme di definizione della funzione arcsin(e ).. Determinare lo sviluppo di Taylor di ordine 4 (in ) della funzione
Prove scritte di Analisi I - Informatica
 Prove scritte di Analisi I - Informatica Prova scritta del 3 gennaio Esercizio Stabilire il comportamento delle seguenti serie: n= n + 3 sin n, n= ( ) n n + 3 sin n, n= (n)! (n!), n= n + n 9 n + n. Esercizio
Prove scritte di Analisi I - Informatica Prova scritta del 3 gennaio Esercizio Stabilire il comportamento delle seguenti serie: n= n + 3 sin n, n= ( ) n n + 3 sin n, n= (n)! (n!), n= n + n 9 n + n. Esercizio
Analisi I Ingegneria Chimica e Aerospaziale 1 o compitino
 1 o compitino 1 febbraio 215 1 Si consideri la funzione f : R R definita da { f) = 2 log se se = a) Si dimostri che f è continua e derivabile su tutto R b) Si dica se f ammette derivata seconda in ogni
1 o compitino 1 febbraio 215 1 Si consideri la funzione f : R R definita da { f) = 2 log se se = a) Si dimostri che f è continua e derivabile su tutto R b) Si dica se f ammette derivata seconda in ogni
Analisi Matematica 3, a.a Scritto del quinto appello, 11 settembre 2019 Testi 1
 Scritto del quinto appello, 11 settembre 019 Testi 1 1. a) Dato u L 1 R), sia vx) := u x); esprimere ˆv in termini di û. b) Caratterizzare le funzioni u L 1 R) tali che û è una funzione dispari a valori
Scritto del quinto appello, 11 settembre 019 Testi 1 1. a) Dato u L 1 R), sia vx) := u x); esprimere ˆv in termini di û. b) Caratterizzare le funzioni u L 1 R) tali che û è una funzione dispari a valori
c.l. Fisica Analisi 2 prof. Molteni/Vignati 20 Giugno 2017 II prova intermedia versione A cos x sin x. Soluzione del P.C.: α = 2, β = 1.
 Cognome Nome Matr. c.l. Fisica Analisi 2 prof. Molteni/Vignati 20 Giugno 2017 II prova intermedia versione A 1A](6 p.ti) Determinare la soluzione generale di y 4y + 3y = 3x 1 + 5 cos x. y 4y + 3y = 3x
Cognome Nome Matr. c.l. Fisica Analisi 2 prof. Molteni/Vignati 20 Giugno 2017 II prova intermedia versione A 1A](6 p.ti) Determinare la soluzione generale di y 4y + 3y = 3x 1 + 5 cos x. y 4y + 3y = 3x
2) Scrivere la soluzione generale del seguente sistema di equazioni differenziali lineari del primo ordine. y 1 = 2y 1 5y 3 y 2
 Corso di Laurea in Matematica Analisi Matematica 3/Analisi 4 - SOLUZIONI (8/6/5) Docente: Claudia Anedda ) Trovare il limite puntuale della successione di funzioni f k (t) = cos(kt), t R. Stabilire se
Corso di Laurea in Matematica Analisi Matematica 3/Analisi 4 - SOLUZIONI (8/6/5) Docente: Claudia Anedda ) Trovare il limite puntuale della successione di funzioni f k (t) = cos(kt), t R. Stabilire se
ANALISI MATEMATICA II 8 Febbraio 2010 ore 11:00 Versione A. Analisi II 7,5 cr. Analisi D Analisi II V.O. es. 1,2,3 es. 2,4,5 es 2,4,5.
 ANALISI MAEMAICA II 8 Feraio ore : Versione A Nome, Cognome: Docente: Corso di Laurea: Matricola Analisi II 7,5 cr. Analisi D Analisi II V.O. es.,,3 es.,4,5 es,4,5 Codice corso 9ACI ESERCIZIO Dato il sistema
ANALISI MAEMAICA II 8 Feraio ore : Versione A Nome, Cognome: Docente: Corso di Laurea: Matricola Analisi II 7,5 cr. Analisi D Analisi II V.O. es.,,3 es.,4,5 es,4,5 Codice corso 9ACI ESERCIZIO Dato il sistema
Corso di laurea in Scienze Biologiche Compito di Istituzioni di Matematiche assegnato il 16 giugno 1999
 assegnato il 16 giugno 1999 16 2 x+7 x 2 + 3x 4 + (2x + 1)2 2 Scrivere l equazione della circonferenza passante per i punti A = (0, 2), B = (0, 10) e tangente alla retta r di equazione x 8 = 0 3 Sia f
assegnato il 16 giugno 1999 16 2 x+7 x 2 + 3x 4 + (2x + 1)2 2 Scrivere l equazione della circonferenza passante per i punti A = (0, 2), B = (0, 10) e tangente alla retta r di equazione x 8 = 0 3 Sia f
ANALISI MATEMATICA II Sapienza Università di Roma - Laurea in Ingegneria Informatica Esame del 10 giugno Soluzioni compito 1
 ANALISI MATEMATICA II Sapienza Università di Roma - Laurea in Ingegneria Informatica Esame del 0 giugno 06 - Soluzioni compito E Si trovi l insieme di definizione I, di convergenza puntuale A e la funzione
ANALISI MATEMATICA II Sapienza Università di Roma - Laurea in Ingegneria Informatica Esame del 0 giugno 06 - Soluzioni compito E Si trovi l insieme di definizione I, di convergenza puntuale A e la funzione
Analisi Matematica III
 Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 1 giugno 4 (Cognome (Nome (Numero di matricola Esercizio 1 Si consideri la successione
Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 1 giugno 4 (Cognome (Nome (Numero di matricola Esercizio 1 Si consideri la successione
Test scritto di Matematica I Pisa, 18 Gennaio 2002
 Capitolo 1: Test d esame 57 Pisa, 18 Gennaio 2002 sinh( + 2) = sinh(2 + 1) = = 1 cosh(sin ) è una funzione periodica L equazione 2 log(2 + 20 ) = 0 non ha soluzioni reali L insieme (, y) R 2 : 3, y 2 2y
Capitolo 1: Test d esame 57 Pisa, 18 Gennaio 2002 sinh( + 2) = sinh(2 + 1) = = 1 cosh(sin ) è una funzione periodica L equazione 2 log(2 + 20 ) = 0 non ha soluzioni reali L insieme (, y) R 2 : 3, y 2 2y
Equazioni differenziali lineari di ordine n
 Equazioni differenziali lineari di ordine n Si tratta di equazioni del tipo u (n) (t) + a 1 (t)u (n 1) (t) +... + a n 1 (t)u (t) + a n (t)u(t) = f(t), t I, (1) con n intero 2 ed I R intervallo reale, in
Equazioni differenziali lineari di ordine n Si tratta di equazioni del tipo u (n) (t) + a 1 (t)u (n 1) (t) +... + a n 1 (t)u (t) + a n (t)u(t) = f(t), t I, (1) con n intero 2 ed I R intervallo reale, in
Analisi Matematica I
 Università degli Studi di Genova Facoltà di Ingegneria - Polo di Savona via Cadorna 7-7 Savona Tel. +39 9 264555 - Fax +39 9 264558 Analisi Matematica I Testi d esame e Prove parziali Analisi Matematica
Università degli Studi di Genova Facoltà di Ingegneria - Polo di Savona via Cadorna 7-7 Savona Tel. +39 9 264555 - Fax +39 9 264558 Analisi Matematica I Testi d esame e Prove parziali Analisi Matematica
Esame di Metodi Matematici per l Ingegneria Primo appello. Febbraio 2017 A.A. 2016/2017. Prof. M. Bramanti Tema A
 Esame di Metodi Matematici per l Ingegneria Primo appello. Febbraio 7 A.A. /7. Prof. M. Bramanti Tema A Cognome: Nome N matr. o cod. persona: Dom Dom Dom 3 Es Es Es 3 Tot. Punti Domande di teoria rispondere
Esame di Metodi Matematici per l Ingegneria Primo appello. Febbraio 7 A.A. /7. Prof. M. Bramanti Tema A Cognome: Nome N matr. o cod. persona: Dom Dom Dom 3 Es Es Es 3 Tot. Punti Domande di teoria rispondere
Analisi Matematica 3/Analisi 4 - SOLUZIONI (20/01/2016)
 Corso di Laurea in Matematica Docente: Claudia Anedda Analisi Matematica 3/Analisi 4 - SOLUZIONI (//6) ) i) Dopo averla classificata, risolvere l equazione differenziale tẋ x = t cos(t), t >. ii) Scrivere
Corso di Laurea in Matematica Docente: Claudia Anedda Analisi Matematica 3/Analisi 4 - SOLUZIONI (//6) ) i) Dopo averla classificata, risolvere l equazione differenziale tẋ x = t cos(t), t >. ii) Scrivere
Prima prova in itinere di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2017/2018. Prof. M. Bramanti.
 Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 07/08. Prof. M. Bramanti Tema n 4 5 6 Tot. Cognome e nome (in stampatello) codice persona (o n
Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 07/08. Prof. M. Bramanti Tema n 4 5 6 Tot. Cognome e nome (in stampatello) codice persona (o n
Outline. 1 La trasformata di Laplace. 2 Proprietá della Trasformata. 3 Calcolo di alcune trasformate. 4 Altre proprietá della trasformata di Laplace
 Outline 1 La trasformata di Laplace La trasformata di Laplace (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi DIMS Universitá di rento anno accademico 25/26 2 Proprietá della rasformata
Outline 1 La trasformata di Laplace La trasformata di Laplace (Metodi Matematici e Calcolo per Ingegneria) Enrico Bertolazzi DIMS Universitá di rento anno accademico 25/26 2 Proprietá della rasformata
Matematica - Prova d esame (25/06/2004)
 Matematica - Prova d esame (/6/4) Università di Verona - Laurea in Biotecnologie AI - A.A. /4. (a) Disegnare sul piano di Gauss i numeri z = i e w = i, e scriverne la forma trigonometrica. Calcolare z
Matematica - Prova d esame (/6/4) Università di Verona - Laurea in Biotecnologie AI - A.A. /4. (a) Disegnare sul piano di Gauss i numeri z = i e w = i, e scriverne la forma trigonometrica. Calcolare z
Appello Straordinario AC
 Appello Straordinario AC 2016-2017 Esercizio I Si consideri la seguente funzione f(z) f(z) = 1 (e z 1) sin(z). 1. Si determini la natura della singolarità di f in z = 0. 2. Nel caso si tratti di una singolarità
Appello Straordinario AC 2016-2017 Esercizio I Si consideri la seguente funzione f(z) f(z) = 1 (e z 1) sin(z). 1. Si determini la natura della singolarità di f in z = 0. 2. Nel caso si tratti di una singolarità
Analisi Matematica I
 Versione: 7 settembre 23 Università di Pisa Corso di laurea in Ingegneria Gestionale Testi e soluzioni degli scritti d esame di Analisi Matematica I a.a. 22-3 Giovanni Alberti e Vincenzo M. Tortorelli
Versione: 7 settembre 23 Università di Pisa Corso di laurea in Ingegneria Gestionale Testi e soluzioni degli scritti d esame di Analisi Matematica I a.a. 22-3 Giovanni Alberti e Vincenzo M. Tortorelli
ANALISI MATEMATICA II 6 luglio 2010 Versione A
 ANALISI MATEMATICA II 6 luglio 2 Versione A Nome Cognome: Matricola Codice corso Docente: Corso di Laurea: Analisi II 75 cr. Analisi D Analisi II V.O. Analisi C es. 23 es. 245 es 24 es. es. 3 pinti b c
ANALISI MATEMATICA II 6 luglio 2 Versione A Nome Cognome: Matricola Codice corso Docente: Corso di Laurea: Analisi II 75 cr. Analisi D Analisi II V.O. Analisi C es. 23 es. 245 es 24 es. es. 3 pinti b c
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005
 Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
COMPLEMENTI DI ANALISI MATEMATICA A.A Primo appello del 5/5/2010
 COMPLEMENTI DI ANALISI MATEMATICA A.A. 29- Primo appello del 5/5/2 Qui trovate le tracce delle soluzioni degli esercizi del compito. Ho tralasciato i calcoli da Analisi (che comunque sono parte della risoluzione),
COMPLEMENTI DI ANALISI MATEMATICA A.A. 29- Primo appello del 5/5/2 Qui trovate le tracce delle soluzioni degli esercizi del compito. Ho tralasciato i calcoli da Analisi (che comunque sono parte della risoluzione),
Esercizi. Misti iniziali. Più variabili. 1. Data la funzione. F (x) = x3 3 + x e t2 dt. se ne studino massimi, minimi, flessi, limiti a ±.
 Esercizi Misti iniziali. Data la funzione se ne studino massimi, minimi, flessi, iti a ±. 2. Provare che Più variabili F x) = 3. Calcolare, se esistono, i seguenti iti a) b) c) d) x,y),) x 2 + y 2 2 x,y),)
Esercizi Misti iniziali. Data la funzione se ne studino massimi, minimi, flessi, iti a ±. 2. Provare che Più variabili F x) = 3. Calcolare, se esistono, i seguenti iti a) b) c) d) x,y),) x 2 + y 2 2 x,y),)
Esercizi Analisi 1. Foglio 1-19/09/2018. n(n + 1)(2n + 1) 6. (3k(k 1) + 1) = n 3. a n = 1 + a k
 Esercizi Analisi Foglio - 9/09/208 Dimostrare che per ogni a, b e per ogni n N si ha: n a n b n = (a b) a n j b j j= Dimostrare che per ogni n N si ha: n j 2 = j= n(n + )(2n + ) 6 Dimostrare che per ogni
Esercizi Analisi Foglio - 9/09/208 Dimostrare che per ogni a, b e per ogni n N si ha: n a n b n = (a b) a n j b j j= Dimostrare che per ogni n N si ha: n j 2 = j= n(n + )(2n + ) 6 Dimostrare che per ogni
EQUAZIONI DIFFERENZIALI Esercizi con soluzione
 EQUAZIONI DIFFERENZIALI Esercizi con soluzione 1. Calcolare l integrale generale delle seguenti equazioni differenziali lineari del primo ordine: (a) y 2y = 1 (b) y + y = e x (c) y 2y = x 2 + x (d) 3y
EQUAZIONI DIFFERENZIALI Esercizi con soluzione 1. Calcolare l integrale generale delle seguenti equazioni differenziali lineari del primo ordine: (a) y 2y = 1 (b) y + y = e x (c) y 2y = x 2 + x (d) 3y
Test scritto di Matematica I Pisa, 15 Gennaio 2003
 Capitolo 1: Test d esame 69 Pisa, 15 Gennaio 2003 sin(2) = 2 cos sin per ogni R La funzione 3 + e è monotona su tutto R La funzione sin(cosh ) è periodica La funzione f(, y) = 2 2 + y 2 + 7 non ha punti
Capitolo 1: Test d esame 69 Pisa, 15 Gennaio 2003 sin(2) = 2 cos sin per ogni R La funzione 3 + e è monotona su tutto R La funzione sin(cosh ) è periodica La funzione f(, y) = 2 2 + y 2 + 7 non ha punti
Prima Prova Scritta 18/03/1997
 Prima Prova Scritta 18/03/1997 1 + x y6 f(x, y) = x 6 + y 6, (x, y) (0, 0) k, (x, y) = (0, 0) A 2 Determinare, per k R, l insieme di continuità di f. B 2 Determinare, per k R, l insieme di differenziabilità
Prima Prova Scritta 18/03/1997 1 + x y6 f(x, y) = x 6 + y 6, (x, y) (0, 0) k, (x, y) = (0, 0) A 2 Determinare, per k R, l insieme di continuità di f. B 2 Determinare, per k R, l insieme di differenziabilità
Prove d'esame a.a
 Prove d'esame a.a. 010011 Andrea Corli 7 dicembre 011 Sono qui raccolti i testi delle prove d'esame assegnati nell'a.a. 01011, relativi al Corso di Complementi di Analisi Matematica, Laurea Magistrale
Prove d'esame a.a. 010011 Andrea Corli 7 dicembre 011 Sono qui raccolti i testi delle prove d'esame assegnati nell'a.a. 01011, relativi al Corso di Complementi di Analisi Matematica, Laurea Magistrale
