Recupero 1 compitino di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2016/2017. Prof. M. Bramanti.
|
|
|
- Daniella Garofalo
- 4 anni fa
- Visualizzazioni
Transcript
1 Recupero 1 compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 16/17. Prof. M. Bramanti 1 Tema n Tot. Cognome e nome in stampatello codice persona o n di matricola n d ordine v. elenco Equazioni differenziali 1. a. Scrivere l integrale generale dell equazione y + 3y + y =. b. Scrivere l integrale generale dell equazione y + 3y + y = 4e x cos x. [Nell applicare il metodo di somiglianza, si raccomanda di utilizzare il metodo degli esponenziali complessi]. 1
2 . Risolvere il problema di Cauchy { y + y x log x = 3x y e = e precisando qual è il più ampio intervallo su cui la soluzione del problema di Cauchy è definita. Curve e integrali di linea 3. Si consideri l arco di curva piana γ di equazione polare [ ρ = 1 + cos θ, per θ, π ]. Calcolare l integrale di linea γ yds.
3 Calcolo differenziale per funzioni di più variabili 4. Sia E R l insieme di definizione della funzione f x, y = arcsin log x + y x + y 3 Dopo aver determinato analiticamente l insieme E e averlo disegnato, dire se: E è aperto Sì No E è chiuso Sì No E è limitato Sì No E è connesso Sì No. Si consideri la funzione: { x y log1+x +y 4 f x, y = x +y per x, y, per x, y =,. a. Stabilire se f è continua in,. b. Stabilire se f è derivabile in,, calcolando in caso affermativo f,. c. Stabilire se f è differenziabile in,, giustificando la risposta. 3
4 6. Dopo aver determinato tutti i punti stazionari della seguente funzione, studiarne la natura cioè decidere se sono punti di minimo, massimo, o sella. f x, y = x y 1 + x + y. 4
5 Recupero compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 16/17. Prof. M. Bramanti 1 Tema n Tot. Cognome e nome in stampatello codice persona o n di matricola n d ordine v. elenco 1. Dimostrare che l equazione f x, y = log 1 + x 3 y + sin πy definisce implicitamente una e una sola funzione x = h y in un intorno di y = 1, e calcolare h 1.
6 . Calcolare l integrale doppio T xe y dxdy dove T è il trapezio di vertici,, 1, 3, 4, 3, 7,. Per impostare l integrale si richiede di fare una figura e scrivere la rappresentazione analitica di T come dominio x-semplice. 3. Calcolare il volume e il centroide di un solido omogeneo rappresentato da: } z Ω = {x, y, z : z h, x + y R 1 h con R, h > parametri fissati. Prestare cura nell impostazione dell esercizio: visualizzare l insieme, per osservare e sfruttarne le simmetrie, e riportare l impostazione del calcolo del centroide a partire dalla definizione. 6
7 4. Calcolare il lavoro del campo vettoriale x F = x + y, y x + y, z x + y lungo l arco di curva γ di equazioni parametriche: x = t cos t y = t sin t t [, π]. z = t. Scrivere le equazioni parametriche della superficie Σgenerata dalla rotazione attorno all asse zdella curva γdel piano xz { x = R cos 3 φ [ z = R sin 3 φ φ π, π ] e calcolarne l elemento d area, semplificando l espressione ottenuta. Quindi determinarne l area e il momento d inerzia rispetto all asse z, supponendo si tratti di una superficie materiale omogenea di massa m. Suggerimento: applicare la formula che consente di calcolare l elemento d area di Σ a partire dalle equazioni parametriche di γ. 7
8 6. Si consideri la funzione π-periodica definita in [ π, π] da { sin x se x π f x = se π x. a. Dopo aver tracciato il grafico di f sul periodo [ π, π]: in base alla teoria, cosa è possibile dire sulla rapidità di convergenza a zero dei coeffi cienti di Fourier, per questa funzione? Cosa è possibile dire circa la convergenza puntuale della serie di Fourier? Rispondere motivando le affermazioni fatte. b. Calcolare esplicitamente i coeffi cienti di Fourier di f, semplificare opportunamente l espressione ottenuta per i coeffi cienti di Fourier e scrivere la serie di Fourier. Prestare attenzione alle eccezioni che nascono per k = 1. 8
9 Recupero 1 compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano A.A. 16/17. Prof. M. Bramanti Svolgimento Tema n 1 Equazioni differenziali 1. a. Scrivere l integrale generale dell equazione y + 3y + y =. b. Scrivere l integrale generale dell equazione y + 3y + y = 4e x cos x. Es Tot. Punti [Nell applicare il metodo di somiglianza, si raccomanda di utilizzare il metodo degli esponenziali complessi]. a. b. Poiché α + 3α + = α + 1 α + =, α = 1, α = y x = c 1 e x + c e x. 4e x cos x = Re 4e x 1+i, cerco prima una soluzione particolare dell equazione nel campo complesso Cerco w + 3w + w = 4e x 1+i. w x = Ae x 1+i w x = A 1 + i e x 1+i w x = A 1 + i e x 1+i, quindi { } Ae x 1+i 1 + i i + = 4e x 1+i A { 3 4i 3 + 6i + } = i A = = = 4 + i 4 + i w x = 4 + i e x cos x + i sin x 9
10 perciò una soluzione particolare dell equazione completa di partenza è y x = Re 4 + i e x cos x + i sin x = e x 4 cos x + sin x e l integrale generale dell equazione completa è y x = c 1 e x + c e x + e x cos x + sin x.. Risolvere il problema di Cauchy { y + y x log x = 3x y e = e precisando qual è il più ampio intervallo su cui la soluzione del problema di Cauchy è definita. Equazione del prim ordine lineare, a x = 1 x log x ; A x = dx = log log x x log x } y x = e {c log log x + e log log x 3xdx = 1 { } c + 3 x log x dx. log x Poiché la condizione di Cauchy è assegnata in x = e e log e = 1 >, possiamo supporre log x > in un intorno del punto in cui si assegna la condizione, per cui porremo log x = log x. x log xdx = x x log x 1 x x dx = log x x 4 perciò l integrale generale è per x > 1 y x = 1 { } x x c + 3 log x log x 4 Imponiamo la condizione iniziale e e = y e = c + 3 e = c e c = e 4 1
11 e la soluzione è y x = 1 { } e x log x x log x, 4 definita sull intervallo massimale 1, +. Curve e integrali di linea 3. Si consideri l arco di curva piana γ di equazione polare [ ρ = 1 + cos θ, per θ, π ]. Calcolare l integrale di linea γ yds. Si ha: ds = ρ + ρ dθ = = + 4 cos θdθ 1 + cos θ + sin θ dθ mentre perciò 1 γ yds = y = ρ sin θ = 1 + cos θ sin θ 1 + cos θ sin θ + 4 cos θdθ cos θ = u; sin θdθ = du; u [1, ] = u + 4udu + 4u = t; + 4u = t ; 4du = tdt; du = 1 tdt; t [, 3 ] ; u = t 1 + u 3 + 4udu = 1 + t t 1 tdt = 1 3 t t 3 dt 4 = 1 [ ] t 3 4 t3 = 1 3 [ ] 1 = 1 [ 7 4 ] =
12 Calcolo differenziale per funzioni di più variabili 4. Sia E R l insieme di definizione della funzione f x, y = arcsin log x + y x + y 3 Dopo aver determinato analiticamente l insieme E e averlo disegnato, dire se: E è aperto Sì No E è chiuso Sì No E è limitato Sì No E è connesso Sì No x + y > 1 log x + y 1, e 1 x + y e x + y 3 >, y > x /3 Quindi E = {x, y : e 1 x + y e, y > x /3} E è aperto Sì No E è chiuso Sì No E è limitato Sì No E è connesso Sì No. Si consideri la funzione: { x y log1+x +y 4 f x, y = x +y per x, y, per x, y =,. a. Stabilire se f è continua in,. b. Stabilire se f è derivabile in,, calcolando in caso affermativo f,. c. Stabilire se f è differenziabile in,, giustificando la risposta. perciò a. Per x, y in un intorno dell origine è: log 1 + x + y 4 log 1 + x + y f x, y x y log 1 + x + y x + y. Poiché log1+x +y x +y è una funzione radiale e log1+ρ ρ 1 per ρ, per x, y, si ha log 1 + x + y x + y 1, x y 1
13 e f x, y, perciò f è continua in,. b. f x, = x log 1 + x x = log 1 + x x per x, perciò f, =. x f, y = y log 1 + y 4 y y 3 perciò f, =, y in particolare f è derivabile in,. c. La differenziabilità di f in, equivale alla condizione Ma: g x, x = g x, y x x log 1 + x + x 4 x 3/ f x, y per x, y,. x + y x x x 3/ 3 = sgn 1 x 3/ per x 3/ ±. In particolare g x, y non tende a zero per x, y,, e f non è differenziabile in,. 6. Dopo aver determinato tutti i punti stazionari della seguente funzione, studiarne la natura cioè decidere se sono punti di minimo, massimo, o sella. f x, y = x y 1 + x + y. f x = 1+x +y xx y 1+x +y f y = 1+x +y yx y 1+x +y { 1 x + y + xy = 1 x + y xy = = 1 x +y +xy 1+x +y = = 1 x +y xy 1+x +y = sottraendo membro a membro { + 4xy = 1 x + y + xy = { y = 1 x x + 1 4x = { x 4 = 1 4, x = ± 1 y = 1 13
14 e i punti stazionari sono: 1, 1, 1 1,. Calcoliamo la matrice hessiana. f xx = x + y 1 + x + y 1 + x + y x 1 x + y + xy 1 + x + y 4 = y x 1 + x + y 4x 1 x + y + xy 1 + x + y 3 f xy = y + x 1 + x + y 4y 1 x + y + xy 1 + x + y 3 f yy = y x 1 + x + y 4y 1 x + y xy 1 + x + y 3 Studiamo ora la natura dei punti stazionari: sfruttando le relazioni x + y = e xy = 1 che valgono in entrambi i punti stazionari, e semplificano le scritture. 1 f xx, 1 = 3 = 1 1 f yy, 1 = 3 = 1 1 f xy, 1 = Hf 1, 1 [ ] 1 = 1 definita negativa, 1, 1 è punto di massimo relativo. Poiché le funzioni f xx, f yy, f xy sono tutte funzioni dispari come si osserva dall espressione analitica, senza rifare i calcoli possiamo concludere che Hf 1 [ ] 1 1, = definita positiva, 1 1 1, è punto di minimo relativo. 14
15 1
16 Recupero compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano A.A. 16/17. Prof. M. Bramanti Svolgimento Tema n 1 1. Dimostrare che l equazione f x, y = log 1 + x 3 y + sin πy Es Tot. Punti definisce implicitamente una e una sola funzione x = h y in un intorno di y = 1, e calcolare h 1. Si ha: f x, 1 = log x 3 1 = x 3 1 = 1 x = 3. f x x, y = 3x 1 + x 3 y f 3, 1 = 3 3 4, x e per il teorema di Dini, essendo f C 1, f 3, 1 =, f 3 x, 1, l equazione f x, y = definisce implicitamente una e una sola funzione x = h y in un intorno di y = 1; risulta h 1 = 3 e f 3 h y, 1 1 = 3., 1 Calcoliamo perciò f y f x f 4y x, y = y 3, 1 = 4 π f 3 h y, 1 1 = 1 + x 3 + π cos πy y f x 3, 1 = 4 π = 4 + π Calcolare l integrale doppio T xe y dxdy 16
17 dove T è il trapezio di vertici,, 1, 3, 4, 3, 7,. Per impostare l integrale si richiede di fare una figura e scrivere la rappresentazione analitica di T come dominio x-semplice. e I lati obliqui del trapezio stanno sulle rette y = x, y = x + 7. Quindi T xe y dxdy = = T = {x, y : y 3, y 7 x y} 3 y y 7 3 e y 3 xe y dx dy = 3 e y [ x [ y y 7 ] dy = 3 ] y dy y 7 3 e y = ye y dy 4 e y dy { [ ye y = ] 3 } 3 + e y dy 4 3 e y dy = 1e [ e y ] 3 = 1e 3 + = [1y 4] dy 4 1 e 3 e 3 = 3 + e 3 = e Calcolare il volume e il centroide di un solido omogeneo rappresentato da: } z Ω = {x, y, z : z h, x + y R 1 h con R, h > parametri fissati. Prestare cura nell impostazione dell esercizio: visualizzare l insieme, per osservare e sfruttarne le simmetrie, e riportare l impostazione del calcolo del centroide a partire dalla definizione. Si tratta di un solido di rotazione: 17
18 quindi sarà per simmetria x c = y c =. h Ω = dxdydz = Ω x +y R z 1 h dxdy dz h z h = πr 1 dz = πr 1 + z z h h dz h [ ] z = πr {h h + [ ] } h h h 3 z3/ = πr {h + h 43 } h = 1 6 πr h. z c = 1 zdxdydz = 1 h z Ω Ω Ω = 6 h z πr zπr 1 dz = 6 h h h [ z = 6 h [ 1 = z3 3h 4 h x +y R 1 z ] h h z/ = 6 [ h h + h 3 4 h ] [ ] h = 6 h = 1 h. 4. Calcolare il lavoro del campo vettoriale x F = x + y, y x + y, z x + y lungo l arco di curva γ di equazioni parametriche: x = t cos t y = t sin t t [, π]. z = t 3 z h dxdy 1 + z z h dz h ] dz r t = cos t t sin t, sin t + t cos t, t F r t = cos t, sin t, t L = = = = F r t r t dt cos t t sin t, sin t + t cos t, t cos t, sin t, t dt cos t t sin t cos t + sin t + t sin t cos t + t dt 1 + t dt = π + 3 π3 = π π3 18
19 . Scrivere le equazioni parametriche della superficie Σ generata dalla rotazione attorno all asse z della curva γ del piano xz { x = R cos 3 φ [ z = R sin 3 φ φ π, π ] e calcolarne l elemento d area, semplificando l espressione ottenuta. Quindi determinarne l area e il momento d inerzia rispetto all asse z, supponendo si tratti di una superficie materiale omogenea di massa m. Suggerimento: applicare la formula che consente di calcolare l elemento d area di Σ a partire dalle equazioni parametriche di γ. x = R cos 3 φ cos θ Σ : y = R cos 3 φ sin θ z = R sin 3 φ ds = a φ φ a φ + b φ dφdθ con a φ = R cos 3 φ, b φ = R sin 3 φ a φ = 3R cos φ sin φ; b φ = 3R sin φ cos φ; a φ + b φ = 9R cos φ sin φ [ π, π ], θ [, π]. ds = R cos 3 φ3r cos φ sin φ dφdθ = 3R cos 4 φ sin φ dφdθ Σ = ds = π 3R cos 4 φ sin φ dφ Σ = 6πR π cos 4 φ sin φdφ = 1πR [ cos φ ] π/ = 1 πr. I = m x + y ds = m Σ Σ 1πR π R cos 6 φ 3R cos 4 φ sin φ dφ π = mr cos 1 φ sin φdφ = mr [ cos11 φ 11 ] π/ = 11 mr. 19
20 6. Si consideri la funzione π-periodica definita in [ π, π] da { sin x se x π f x = se π x. a. Dopo aver tracciato il grafico di f sul periodo [ π, π]: in base alla teoria, cosa è possibile dire sulla rapidità di convergenza a zero dei coeffi cienti di Fourier, per questa funzione? Cosa è possibile dire circa la convergenza puntuale della serie di Fourier? Rispondere motivando le affermazioni fatte. b. Calcolare esplicitamente i coeffi cienti di Fourier di f, semplificare opportunamente l espressione ottenuta per i coeffi cienti di Fourier e scrivere la serie di Fourier. Prestare attenzione alle eccezioni che nascono per k = 1. a. La funzione periodizzata è continua su R e regolare a tratti. Perciò la serie di Fourier di f converge puntualmente a f ovunque e i coeffi cienti di Fourier tendono a zero come o 1/k. b. La funzione non è né pari né dispari, occorre calcolare tutti i coeffi cienti. Utilizzando le identità sin α cos β = 1 {sin α + β + sin α β} sin α sin β = 1 {cos α β cos α + β}
21 si ha, per k = 1,, 3... a k = 1 π = 1 π per k 1 = 1 π mentre mentre = 1 π = 1 π = 1 π π f x cos kx dx = 1 π [ [sin k + 1 x + sin 1 k x] dx cos k + 1 x k + 1 [ cos k + 1 π k + 1 [ 1 k + + sin x cos kx dx ] π cos k 1 x k 1 cos k 1 π + 1 k 1 ] k + 1 1k k k k 1 1 k + 1 a 1 = 1 π a = 1 π k 1 b k = 1 π = 1 π per k 1 = 1 π e la serie di Fourier di f è sin x cos xdx = 1 π sin xdx = π. π f x sin kx dx = 1 π k ] k 1 = 1 π sin xdx = sin x sin kx dx [cos k 1 x cos k + 1 x] dx [ ] π sin k 1 x sin k + 1 x = k 1 k + 1 b 1 = 1 π f x = 1 π + 1 sin x 1 π = 1 π + 1 sin x π sin xdx = 1. k= k=1 1 k + 1 k 1 cos kx 1 4k cos kx 1 1 k + 1 k 1 1
22 Grafico di f x insieme alla sua somma parziale di Fourier fino a n = 6:
23 Primo appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 16/17. Prof. M. Bramanti 1 Tema n Tot. Cognome e nome in stampatello codice persona o n di matricola n d ordine v. elenco 1. a. Scrivere l integrale generale dell equazione y + 3y + y =. b. Scrivere l integrale generale dell equazione y + 3y + y = 4e x cos x. Nell applicare il metodo di somiglianza, si raccomanda di utilizzare il metodo degli esponenziali complessi.. Si consideri la funzione: { x y log1+x +y 4 f x, y = x +y per x, y, per x, y =,. a. Stabilire se f è continua in,. b. Stabilire se f è derivabile in,, calcolando in caso affermativo f,. c. Stabilire se f è differenziabile in,, giustificando la risposta. 3. Dopo aver determinato tutti i punti stazionari della seguente funzione, studiarne la natura cioè decidere se sono punti di minimo, massimo, o sella. f x, y = 4. Calcolare l integrale doppio T x y 1 + x + y. xe y dxdy dove T è il trapezio di vertici,, 1, 3, 4, 3, 7,. Per impostare l integrale si richiede di fare una figura e scrivere la rappresentazione analitica di T come dominio x-semplice. 3
24 . Calcolare il volume e il centroide di un solido omogeneo rappresentato da: } z Ω = {x, y, z : z h, x + y R 1 h con R, h > parametri fissati. Prestare cura nell impostazione dell esercizio: visualizzare l insieme, per osservare e sfruttarne le simmetrie, e riportare l impostazione del calcolo del centroide a partire dalla definizione. 6. Calcolare il lavoro del campo vettoriale x F = x + y, y x + y, z x + y lungo l arco di curva γ di equazioni parametriche: x = t cos t y = t sin t t [, π]. z = t 7. Si consideri la funzione π-periodica definita in [ π, π] da { sin x se x π f x = se π x. a. Dopo aver tracciato il grafico di fsul periodo [ π, π]: in base alla teoria, cosa è possibile dire sulla rapidità di convergenza a zero dei coeffi cienti di Fourier, per questa funzione? Cosa è possibile dire circa la convergenza puntuale della serie di Fourier? Rispondere motivando le affermazioni fatte. b. Calcolare esplicitamente i coeffi cienti di Fourier di f, semplificare opportunamente l espressione ottenuta per i coeffi cienti di Fourier e scrivere la serie di Fourier. Prestare attenzione alle eccezioni che nascono per k = 1. 4
25 Primo appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 16/17. Prof. M. Bramanti 1 Tema n Tot. Cognome e nome in stampatello codice persona o n di matricola n d ordine v. elenco 1. Risolvere il problema di Cauchy { y + y x log x = 3x y e = e precisando qual è il più ampio intervallo su cui la soluzione del problema di Cauchy è definita.. Si consideri l arco di curva piana γ di equazione polare [ ρ = 1 + cos θ, per θ, π ]. Calcolare l integrale di linea γ yds. 3. Dopo aver determinato tutti i punti stazionari della seguente funzione, studiarne la natura cioè decidere se sono punti di minimo, massimo, o sella. f x, y = x x + y Dimostrare che l equazione f x, y = log 1 + x 3 y + sin πy definisce implicitamente una e una sola funzione x = h y in un intorno di y = 1, e calcolare h 1.
26 . Si consideri la regione piana Σ descritta in coordinate polari da Σ = { ρ, θ : θ [, π], ρ Re θ} con R > parametro fissato. Calcolare, mediante opportuni integrali doppi, l area di Σ e la coordinata x del centroide. 6. Scrivere le equazioni parametriche della superficie Σ generata dalla rotazione attorno all asse z della curva γ del piano xz { x = R cos 3 φ [ z = R sin 3 φ φ π, π ] e calcolarne l elemento d area, semplificando l espressione ottenuta. Quindi determinarne l area e il momento d inerzia rispetto all asse z, supponendo si tratti di una superficie materiale omogenea di massa m. Suggerimento: applicare la formula che consente di calcolare l elemento d area di Σ a partire dalle equazioni parametriche di γ. 7. Si consideri la funzione π-periodica definita in [ π, π] da { cos x se x π f x = se π x. a. Dopo aver tracciato il grafico di fsul periodo [ π, π]: in base alla teoria, cosa è possibile dire sulla rapidità di convergenza a zero dei coeffi cienti di Fourier, per questa funzione? Cosa è possibile dire circa la convergenza puntuale della serie di Fourier? Rispondere motivando le affermazioni fatte. b. Calcolare esplicitamente i coeffi cienti di Fourier di f, semplificare opportunamente l espressione ottenuta per i coeffi cienti di Fourier e scrivere la serie di Fourier. Prestare attenzione alle eccezioni che nascono per k = 1. 6
27 Primo appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano A.A. 16/17. Prof. M. Bramanti Svolgimento Tema n 1 Es Tot. Punti 1. a. Scrivere l integrale generale dell equazione y + 3y + y =. b. Scrivere l integrale generale dell equazione y + 3y + y = 4e x cos x. Nell applicare il metodo di somiglianza, si raccomanda di utilizzare il metodo degli esponenziali complessi. a. b. Poiché α + 3α + = α + 1 α + =, α = 1, α = y x = c 1 e x + c e x. 4e x cos x = Re 4e x 1+i, cerco prima una soluzione particolare dell equazione nel campo complesso Cerco w + 3w + w = 4e x 1+i. w x = Ae x 1+i w x = A 1 + i e x 1+i w x = A 1 + i e x 1+i, quindi { } Ae x 1+i 1 + i i + = 4e x 1+i A { 3 4i 3 + 6i + } = i A = = = 4 + i 4 + i w x = 4 + i e x cos x + i sin x 7
28 perciò una soluzione particolare dell equazione completa di partenza è y x = Re 4 + i e x cos x + i sin x = e x 4 cos x + sin x e l integrale generale dell equazione completa è y x = c 1 e x + c e x + e x cos x + sin x.. Si consideri la funzione: { x y log1+x +y 4 f x, y = x +y per x, y, per x, y =,. a. Stabilire se f è continua in,. b. Stabilire se f è derivabile in,, calcolando in caso affermativo f,. c. Stabilire se f è differenziabile in,, giustificando la risposta. perciò a. Per x, y in un intorno dell origine è: log 1 + x + y 4 log 1 + x + y f x, y x y log 1 + x + y x + y. Poiché log1+x +y x +y è una funzione radiale e log1+ρ ρ 1 per ρ, per x, y, si ha log 1 + x + y x + y 1, x y e f x, y, perciò f è continua in,. b. f x, = x log 1 + x x = log 1 + x x per x, perciò f, =. x f, y = y log 1 + y 4 y y 3 perciò in particolare f è derivabile in,. f, =, y 8
29 Ma: c. La differenziabilità di f in, equivale alla condizione g x, x = g x, y x x log 1 + x + x 4 x 3/ f x, y per x, y,. x + y x x x 3/ 3 = sgn 1 x 3/ per x 3/ ±. In particolare g x, y non tende a zero per x, y,, e f non è differenziabile in,. 3. Dopo aver determinato tutti i punti stazionari della seguente funzione, studiarne la natura cioè decidere se sono punti di minimo, massimo, o sella. f x, y = x y 1 + x + y. f x = 1+x +y xx y 1+x +y f y = 1+x +y yx y 1+x +y { 1 x + y + xy = 1 x + y xy = = 1 x +y +xy 1+x +y = = 1 x +y xy 1+x +y = sottraendo membro a membro { + 4xy = 1 x + y + xy = { y = 1 x x + 1 4x = { x 4 = 1 4, x = ± 1 y = 1 e i punti stazionari sono: 1, 1, 1 1,. Calcoliamo la matrice hessiana. f xx = x + y 1 + x + y 1 + x + y x 1 x + y + xy 1 + x + y 4 = y x 1 + x + y 4x 1 x + y + xy 1 + x + y 3 f xy = y + x 1 + x + y 4y 1 x + y + xy 1 + x + y 3 f yy = y x 1 + x + y 4y 1 x + y xy 1 + x + y 3 9
30 Studiamo ora la natura dei punti stazionari: sfruttando le relazioni x + y = e xy = 1 che valgono in entrambi i punti stazionari, e semplificano le scritture. 1 f xx, 1 = 3 = 1 1 f yy, 1 = 3 = 1 1 f xy, 1 = Hf 1, 1 [ ] 1 = 1 definita negativa, 1, 1 è punto di massimo relativo. Poiché le funzioni f xx, f yy, f xy sono tutte funzioni dispari come si osserva dall espressione analitica, senza rifare i calcoli possiamo concludere che Hf 1 [ ] 1 1, = definita positiva, 1 1 1, è punto di minimo relativo. 3
31 4. Calcolare l integrale doppio T xe y dxdy dove T è il trapezio di vertici,, 1, 3, 4, 3, 7,. Per impostare l integrale si richiede di fare una figura e scrivere la rappresentazione analitica di T come dominio x-semplice. e I lati obliqui del trapezio stanno sulle rette y = x, y = x + 7. Quindi T xe y dxdy = = T = {x, y : y 3, y 7 x y} 3 y y 7 3 e y 3 xe y dx dy = 3 e y [ x [ y y 7 ] dy = 3 ] y dy y 7 3 e y = ye y dy 4 e y dy { [ ye y = ] 3 } 3 + e y dy 4 3 e y dy = 1e [ e y ] 3 = 1e 3 + = [1y 4] dy 4 1 e 3 e 3 = 3 + e 3 = e Calcolare il volume e il centroide di un solido omogeneo rappresentato da: } z Ω = {x, y, z : z h, x + y R 1 h con R, h > parametri fissati. Prestare cura nell impostazione dell esercizio: visualizzare l insieme, per osservare e sfruttarne le simmetrie, e riportare l impostazione del calcolo del centroide a partire dalla definizione. 31
32 Si tratta di un solido di rotazione: quindi sarà per simmetria x c = y c =. h Ω = dxdydz = Ω x +y R z 1 h dxdy dz h z h = πr 1 dz = πr 1 + z z h h dz h [ ] z = πr {h h + [ ] } h h h 3 z3/ = πr {h + h 43 } h = 1 6 πr h. z c = 1 zdxdydz = 1 h z Ω Ω Ω = 6 h z πr zπr 1 dz = 6 h h h [ z = 6 h [ 1 = z3 3h 4 h x +y R 1 z ] h h z/ = 6 [ h h + h 3 4 h ] [ ] h = 6 h = 1 h. 6. Calcolare il lavoro del campo vettoriale x F = x + y, y x + y, z x + y lungo l arco di curva γ di equazioni parametriche: x = t cos t y = t sin t t [, π]. z = t 3 z h dxdy 1 + z z h dz h ] dz 3
33 r t = cos t t sin t, sin t + t cos t, t F r t = cos t, sin t, t L = = = = F r t r t dt cos t t sin t, sin t + t cos t, t cos t, sin t, t dt cos t t sin t cos t + sin t + t sin t cos t + t dt 1 + t dt = π + 3 π3 = π π3 7. Si consideri la funzione π-periodica definita in [ π, π] da { sin x se x π f x = se π x. a. Dopo aver tracciato il grafico di fsul periodo [ π, π]: in base alla teoria, cosa è possibile dire sulla rapidità di convergenza a zero dei coeffi cienti di Fourier, per questa funzione? Cosa è possibile dire circa la convergenza puntuale della serie di Fourier? Rispondere motivando le affermazioni fatte. b. Calcolare esplicitamente i coeffi cienti di Fourier di f, semplificare opportunamente l espressione ottenuta per i coeffi cienti di Fourier e scrivere la serie di Fourier. Prestare attenzione alle eccezioni che nascono per k = 1. a. La funzione periodizzata è continua su R e regolare a tratti. Perciò la serie di Fourier di f converge puntualmente a f ovunque e i coeffi cienti di Fourier tendono a zero come o 1/k. b. La funzione non è né pari né dispari, occorre calcolare tutti i coeffi cienti. Utilizzando le identità sin α cos β = 1 {sin α + β + sin α β} sin α sin β = 1 {cos α β cos α + β} 33
34 si ha, per k = 1,, 3... a k = 1 π = 1 π per k 1 = 1 π mentre mentre = 1 π = 1 π = 1 π π f x cos kx dx = 1 π [ [sin k + 1 x + sin 1 k x] dx cos k + 1 x k + 1 [ cos k + 1 π k + 1 [ 1 k + + sin x cos kx dx ] π cos k 1 x k 1 cos k 1 π + 1 k 1 ] k + 1 1k k k k 1 1 k + 1 a 1 = 1 π a = 1 π k 1 b k = 1 π = 1 π per k 1 = 1 π e la serie di Fourier di f è sin x cos xdx = 1 π sin xdx = π. π f x sin kx dx = 1 π k ] k 1 = 1 π sin xdx = sin x sin kx dx [cos k 1 x cos k + 1 x] dx [ ] π sin k 1 x sin k + 1 x = k 1 k + 1 b 1 = 1 π f x = 1 π + 1 sin x 1 π = 1 π + 1 sin x π sin xdx = 1. k= k=1 1 k + 1 k 1 cos kx 1 4k cos kx 1 1 k + 1 k 1 34
35 Grafico di f x insieme alla sua somma parziale di Fourier fino a n = 6: 3
36 Primo appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano A.A. 16/17. Prof. M. Bramanti Svolgimento Tema n Es Tot. Punti 1. Risolvere il problema di Cauchy { y + y x log x = 3x y e = e precisando qual è il più ampio intervallo su cui la soluzione del problema di Cauchy è definita. Equazione del prim ordine lineare, a x = 1 x log x ; A x = dx = log log x x log x } y x = e {c log log x + e log log x 3xdx = 1 { } c + 3 x log x dx. log x Poiché la condizione di Cauchy è assegnata in x = e e log e = 1 >, possiamo supporre log x > in un intorno del punto in cui si assegna la condizione, per cui porremo log x = log x. x log xdx = x x log x 1 x x dx = log x x 4 perciò l integrale generale è per x > 1 y x = 1 { } x x c + 3 log x log x 4 Imponiamo la condizione iniziale e e = y e = c + 3 e = c e c = e 4 36
37 e la soluzione è y x = 1 { } e x log x x log x, 4 definita sull intervallo massimale 1, +.. Si consideri l arco di curva piana γ di equazione polare [ ρ = 1 + cos θ, per θ, π ]. Calcolare l integrale di linea γ yds. Si ha: ds = ρ + ρ dθ = = + 4 cos θdθ 1 + cos θ + sin θ dθ mentre perciò 1 γ yds = y = ρ sin θ = 1 + cos θ sin θ 1 + cos θ sin θ + 4 cos θdθ cos θ = u; sin θdθ = du; u [1, ] = u + 4udu + 4u = t; + 4u = t ; 4du = tdt; du = 1 tdt; t [, 3 ] ; u = t 1 + u 3 + 4udu = 1 + t t 1 tdt = 1 3 t t 3 dt 4 = 1 [ ] t 3 4 t3 = 1 3 [ ] 1 = 1 [ 7 4 ] = Dopo aver determinato tutti i punti stazionari della seguente funzione, studiarne la natura cioè decidere se sono punti di minimo, massimo, o sella. f x, y = x x + y 1. 37
38 { fx = x + y 1 + x x + y 1 x = x + y 1 x + y 1 = f y = 4xy x + y 1 = x + y 1 = è una circonferenza di punti critici. Se x + y 1, { x + y 1 = 4xy = x = = y 1 =, y = ±1 y = = x 1 =, x = ± 1 e i punti stazionari sono:, ±1, ± 1,, e la circonferenza x + y 1 =. In realtà i punti, ±1 sono già compresi sulla circonferenza. Calcoliamo la matrice hessiana. f xx = x x + y 1 + 1x x + y 1 = x x + y 1 + x + y = x 1x + 6y 6 f xy = 4y x + y 1 + 8x y = 4y 9x + y 1 f yy = 4x x + y 1 + 8xy = 4x x + 3y 1 Hf x, y = [ x 1x + 6y 6 4y 9x + y 1 ] 4y 9x + y 1 4x x + 3y 1 [ ] Hf, ±1 = caso dubbio Hf ± 1 [ ] ± 6, = ± definita negativa, positiva rispettivamente. 1, punto di massimo relativo 1, punto di minimo relativo Studiamo sia il caso dubbio che la circonferenza di punti stazionari mediante il metodo del segno. La funzione si annulla sulla circonferenza e sulla retta x =, fuori da questi insiemi è positiva se e solo se x >. Si ottiene quindi v. grafico: 38
39 -i punti sulla circonferenza x + y = 1 per cui x > sono punti di minimo; -i punti sulla circonferenza x + y = 1 per cui x < sono punti di massimo; -i punti, ±1 sono di sella. 4. Dimostrare che l equazione f x, y = log 1 + x 3 y + sin πy definisce implicitamente una e una sola funzione x = h y in un intorno di y = 1, e calcolare h 1. Si ha: f x, 1 = log x 3 1 = x 3 1 = 1 x = 3. f x x, y = 3x 1 + x 3 y f 3, 1 = 3 3 4, x e per il teorema di Dini, essendo f C 1, f 3, 1 =, f 3 x, 1, l equazione f x, y = definisce implicitamente una e una sola funzione x = h y in un intorno di y = 1; risulta h 1 = 3 e f h y 1 = f x 3, 1 3, 1. 39
40 Calcoliamo perciò f y f 4y x, y = y 3, 1 = 4 π f 3 h y, 1 1 = 1 + x 3 + π cos πy y f x 3, 1 = 4 π = 4 + π Si consideri la regione piana Σ descritta in coordinate polari da Σ = { ρ, θ : θ [, π], ρ Re θ} con R > parametro fissato. Calcolare, mediante opportuni integrali doppi, l area di Σ e la coordinata x del centroide. Ora: da cui e Σ = = R Σ dxdy = [ e θ ] π = R 4 Re θ x c = 1 4 xdxdy = Σ Σ R e 4π 1 = 4 R e 4π 1 I = e 3θ = e6π 1 3 = e6π 1 3 [ ρ 3 cos θ 3 ρdρ e 4π 1. ] Re θ Re θ dθ = [ e 3θ cos θ dθ = f g 3 cos θ [ ] e 3θ π + 9 sin θ 1 9 I, ] π dθ = ρ cos θρdρ 4R 3 e 4π 1 R e θ dθ dθ e 3θ + sin θdθ 3 e 3θ 9 I = 9 e 6π 1 = 3 e 6π R 3 x c = 3 e 4π 1 1 cos θdθ e 6π 1 = e 6π 1 e 4π 1 R. 4 e 3θ cos θdθ.
41 6. Scrivere le equazioni parametriche della superficie Σ generata dalla rotazione attorno all asse z della curva γ del piano xz { x = R cos 3 φ [ z = R sin 3 φ φ π, π ] e calcolarne l elemento d area, semplificando l espressione ottenuta. Quindi determinarne l area e il momento d inerzia rispetto all asse z, supponendo si tratti di una superficie materiale omogenea di massa m. Suggerimento: applicare la formula che consente di calcolare l elemento d area di Σ a partire dalle equazioni parametriche di γ. x = R cos 3 φ cos θ Σ : y = R cos 3 φ sin θ z = R sin 3 φ ds = a φ φ a φ + b φ dφdθ con a φ = R cos 3 φ, b φ = R sin 3 φ a φ = 3R cos φ sin φ; b φ = 3R sin φ cos φ; a φ + b φ = 9R cos φ sin φ [ π, π ], θ [, π]. ds = R cos 3 φ3r cos φ sin φ dφdθ = 3R cos 4 φ sin φ dφdθ Σ = ds = π 3R cos 4 φ sin φ dφ Σ = 6πR π cos 4 φ sin φdφ = 1πR [ cos φ ] π/ = 1 πr. I = m x + y ds = m Σ Σ 1πR π R cos 6 φ 3R cos 4 φ sin φ dφ π = mr cos 1 φ sin φdφ = mr [ cos11 φ 11 ] π/ = 11 mr. 41
42 7. Si consideri la funzione π-periodica definita in [ π, π] da { cos x se x π f x = se π x. a. Dopo aver tracciato il grafico di fsul periodo [ π, π]: in base alla teoria, cosa è possibile dire sulla rapidità di convergenza a zero dei coeffi cienti di Fourier, per questa funzione? Cosa è possibile dire circa la convergenza puntuale della serie di Fourier? Rispondere motivando le affermazioni fatte. b. Calcolare esplicitamente i coeffi cienti di Fourier di f, semplificare opportunamente l espressione ottenuta per i coeffi cienti di Fourier e scrivere la serie di Fourier. Prestare attenzione alle eccezioni che nascono per k = 1. a. La funzione periodizzata è regolare a tratti ma discontinua. Perciò la serie di Fourier di f, in [ π, π], converge puntualmente a f ovunque tranne in ±π, dove converge a 1/, e in, dove converge a 1/. I coeffi cienti di Fourier saranno o 1 ma non o 1/k. b. La funzione non è né pari né dispari, occorre calcolare tutti i coeffi cienti. Utilizzando le identità cos α cos β = 1 {cos α + β + cos α β} sin α cos β = 1 {sin α + β + sin α β} 4
43 si ha, per k = 1,, 3... mentre a k = 1 π = 1 π per k 1 = 1 π π f x cos kx dx = 1 π cos x cos kx dx [cos k + 1 x + cos k 1 x] dx [ ] π sin k + 1 x sin k 1 x + = k + 1 k 1 b k = 1 π = 1 π per k 1 = 1 π mentre = 1 π = 1 π = k π a 1 = 1 π a = 1 π π f x sin kx dx = 1 π [ cos xdx = 1 cos xdx =. [sin k + 1 x + sin k 1 x] dx cos k + 1 x k + 1 [ cos k + 1 π k + 1 [ 1 k sin kx cos xdx ] π cos k 1 x k 1 cos k 1 π + 1 k 1 ] k k k k k 1 1 k + 1 b 1 = 1 π k 1 e la serie di Fourier di f è f x = 1 cos x + 1 π sin x cos xdx = 1 π = 1 cos x + 4 π k= k=1 1 k + 1 k k 1 k ] k 1 = 1 k π sin xdx = k 4k sin kx 1 sin kx 1 k + 1 k 1 43
44 Grafico di f x insieme alla sua somma parziale di Fourier fino a n = 1: 44
Recupero 1 compitino di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2017/2018. Prof. M. Bramanti.
 Recupero compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 7/8. Prof. M. Bramanti Tema n 3 4 5 6 Tot. Cognome e nome in stampatello codice persona o n di matricola
Recupero compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 7/8. Prof. M. Bramanti Tema n 3 4 5 6 Tot. Cognome e nome in stampatello codice persona o n di matricola
Secondo appello di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 2017/2018. Prof. M. Bramanti. Tema n 1.
 Secondo appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 17/18. Prof. M. Bramanti 1 Tema n 1 5 6 7 Tot. Cognome e nome in stampatello) codice persona o n di matricola)
Secondo appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 17/18. Prof. M. Bramanti 1 Tema n 1 5 6 7 Tot. Cognome e nome in stampatello) codice persona o n di matricola)
Quarto appello di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano A.A. 2017/2018. Prof. M. Bramanti. y = 1+y2
 Quarto appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano A.A. 7/8. Prof. M. Bramanti Es. 3 5 6 7 Tot. Punti Cognome e nome in stampatello) codice persona o n di matricola) n d
Quarto appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano A.A. 7/8. Prof. M. Bramanti Es. 3 5 6 7 Tot. Punti Cognome e nome in stampatello) codice persona o n di matricola) n d
Terzo appello di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano A.A. 2018/2019. Prof. M. Bramanti. { y + y. 2 1 x 2 y (0) = 1.
 Terzo appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano A.A. 8/9. Prof. M. Bramanti Es. 5 6 7 Tot. Punti Cognome e nome in stampatello codice persona o n di matricola n d ordine
Terzo appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano A.A. 8/9. Prof. M. Bramanti Es. 5 6 7 Tot. Punti Cognome e nome in stampatello codice persona o n di matricola n d ordine
Terzo appello di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 2016/2017. Prof. M. Bramanti.
 Terzo appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 6/7. Prof. M. Bramanti Tema n 5 6 7 Tot. Cognome e nome in stampatello codice persona o n di matricola n
Terzo appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 6/7. Prof. M. Bramanti Tema n 5 6 7 Tot. Cognome e nome in stampatello codice persona o n di matricola n
Seconda prova in itinere di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2016/2017. Prof. M. Bramanti.
 Seconda prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 16/17. Prof. M. Bramanti 1 Tema n 1 5 6 Tot. Cognome e nome in stampatello codice persona o n
Seconda prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 16/17. Prof. M. Bramanti 1 Tema n 1 5 6 Tot. Cognome e nome in stampatello codice persona o n
Quarto appello di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 2016/2017. Prof. M. Bramanti.
 Quarto appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 6/. Prof. M. Bramanti Tema n 6 Tot. Cognome e nome in stampatello codice persona o n di matricola n d ordine
Quarto appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 6/. Prof. M. Bramanti Tema n 6 Tot. Cognome e nome in stampatello codice persona o n di matricola n d ordine
Secondo appello di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano A.A. 2018/2019. Prof. M. Bramanti
 Secondo appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano A.A. 8/9. Prof. M. Bramanti Es. 6 7 Tot. Punti Cognome e nome in stampatello codice persona o n di matricola n d ordine
Secondo appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano A.A. 8/9. Prof. M. Bramanti Es. 6 7 Tot. Punti Cognome e nome in stampatello codice persona o n di matricola n d ordine
Prima prova in itinere di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2017/2018. Prof. M. Bramanti.
 Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 07/08. Prof. M. Bramanti Tema n 4 5 6 Tot. Cognome e nome (in stampatello) codice persona (o n
Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 07/08. Prof. M. Bramanti Tema n 4 5 6 Tot. Cognome e nome (in stampatello) codice persona (o n
Prima prova in itinere di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2016/2017. Prof. M. Bramanti.
 Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 016/017. Prof. M. Bramanti 1 Tema n 1 4 5 6 Tot. Cognome e nome in stampatello) codice persona
Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 016/017. Prof. M. Bramanti 1 Tema n 1 4 5 6 Tot. Cognome e nome in stampatello) codice persona
Seconda prova in itinere di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2018/2019. Prof. M. Bramanti.
 Seconda prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 8/9. Prof. M. Bramanti Tema n 4 5 6 Tot. Cognome e nome in stampatello codice persona o n di
Seconda prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 8/9. Prof. M. Bramanti Tema n 4 5 6 Tot. Cognome e nome in stampatello codice persona o n di
Seconda prova in itinere di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2017/2018. Prof. M. Bramanti.
 Seconda prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 7/8. Prof. M. Bramanti Tema n 3 4 5 6 Tot. Cognome e nome in stampatello codice persona o n di
Seconda prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 7/8. Prof. M. Bramanti Tema n 3 4 5 6 Tot. Cognome e nome in stampatello codice persona o n di
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica II del c.1.
 Prova scritta di Analisi Matematica II del 14-07-1999 - c.1 1) Sia (d n ) una successione di numeri reali tali che inf d n > 0. Studiare il carattere della serie + n=1 al variare del parametro reale positivo
Prova scritta di Analisi Matematica II del 14-07-1999 - c.1 1) Sia (d n ) una successione di numeri reali tali che inf d n > 0. Studiare il carattere della serie + n=1 al variare del parametro reale positivo
Analisi Matematica 2. Michele Campiti. Prove scritte di. Ingegneria Industriale a.a
 Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica II del
 Prova scritta di nalisi Matematica II del 12-06-2001. C1 1) Studiare la convergenza semplice, uniforme e totale della serie di funzioni seguente ( 1) [ n 2 ] n x 1 + n 2 x. n=0 2) Data la funzione (x 2
Prova scritta di nalisi Matematica II del 12-06-2001. C1 1) Studiare la convergenza semplice, uniforme e totale della serie di funzioni seguente ( 1) [ n 2 ] n x 1 + n 2 x. n=0 2) Data la funzione (x 2
Esonero di Analisi Matematica II (A)
 Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005
 Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
Recupero 1 compitino di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2018/2019. Prof. M. Bramanti
 Recupero 1 compiino di Analisi Maemaica Ingegneria Eleronica. Poliecnico di Milano Es. Puni A.A. 18/19. Prof. M. Bramani 1 Tema n 1 3 4 5 6 To. Cognome e nome in sampaello codice persona o n di maricola
Recupero 1 compiino di Analisi Maemaica Ingegneria Eleronica. Poliecnico di Milano Es. Puni A.A. 18/19. Prof. M. Bramani 1 Tema n 1 3 4 5 6 To. Cognome e nome in sampaello codice persona o n di maricola
Alcuni esercizi risolti da esami di anni passati
 Alcuni esercizi risolti da esami di anni passati Andrea Braides ( x. Calcolare, se esiste, il limite lim (x,y (, x + y log + y + x 3 y. x + y Dato che log( + s = s + o(s per s, abbiamo lim (x,y (, ( x
Alcuni esercizi risolti da esami di anni passati Andrea Braides ( x. Calcolare, se esiste, il limite lim (x,y (, x + y log + y + x 3 y. x + y Dato che log( + s = s + o(s per s, abbiamo lim (x,y (, ( x
Esercizi di Analisi Matematica II assegnati nell A.A. 2011/12. Corsi di laurea in Ingegneria Elettronica ed Informatica
 Esercizi di Analisi Matematica II assegnati nell A.A. 2011/12 Corsi di laurea in Ingegneria Elettronica ed Informatica 1) Rappresentare nel piano xy i campi di esistenza delle seguenti funzioni: a) xy
Esercizi di Analisi Matematica II assegnati nell A.A. 2011/12 Corsi di laurea in Ingegneria Elettronica ed Informatica 1) Rappresentare nel piano xy i campi di esistenza delle seguenti funzioni: a) xy
Seconda prova in itinere di Analisi Matematica 1 Ingegneria Elettronica. Politecnico di Milano. A.A. 2015/2016. Prof. M. Bramanti.
 Seconda prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 5/6. Prof. M. Bramanti Tema n 3 5 6 Tot. Cognome e nome (in stampatello) codice persona (o n
Seconda prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 5/6. Prof. M. Bramanti Tema n 3 5 6 Tot. Cognome e nome (in stampatello) codice persona (o n
ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009)
 ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009) 1. Sia S = { } (x, y, z) : x 2 + y 2 = 4, 0 z 3 + x. Scrivere le equazioni parametriche di una superficie regolare che abbia S come sostegno. 2. Enunciare
ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009) 1. Sia S = { } (x, y, z) : x 2 + y 2 = 4, 0 z 3 + x. Scrivere le equazioni parametriche di una superficie regolare che abbia S come sostegno. 2. Enunciare
Analisi Matematica 3
 Testi delle prove d esame del corso di Analisi Matematica 3 presso la Facoltà di Ingegneria Bruno Rubino L Aquila, 2006 Indice 1 Curve 3 2 Superfici 4 3 Teorema di Gauss-Green e formula dell area 4 4 Campi
Testi delle prove d esame del corso di Analisi Matematica 3 presso la Facoltà di Ingegneria Bruno Rubino L Aquila, 2006 Indice 1 Curve 3 2 Superfici 4 3 Teorema di Gauss-Green e formula dell area 4 4 Campi
DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Clinica Canale PZ A.A. 2017/2018 Codocente: Dott. Salvatore Fragapane
 DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Clinica Canale PZ A.A. 07/08 Codocente: Dott. Salvatore Fragapane Lezione - 09/03/08, dalle 6.00 alle 8.00 in aula 6 Es. Studiare
DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Clinica Canale PZ A.A. 07/08 Codocente: Dott. Salvatore Fragapane Lezione - 09/03/08, dalle 6.00 alle 8.00 in aula 6 Es. Studiare
Analisi Matematica II Politecnico di Milano Ingegneria Industriale
 Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #. Sia P l insieme di tutti i parallelepipedi che giacciono nel primo ottante con tre facce sui piani coordinati e un
Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #. Sia P l insieme di tutti i parallelepipedi che giacciono nel primo ottante con tre facce sui piani coordinati e un
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica 2 del 29 settembre 2012
 Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9 settembre A) Data la funzione f(x, y) = { xy x se (x, y) (, ) se (x, y) = (, ), i) stabilire se risulta continua
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9 settembre A) Data la funzione f(x, y) = { xy x se (x, y) (, ) se (x, y) = (, ), i) stabilire se risulta continua
(1) Determinare l integrale generale dell equazione
 FONDAMENTI DI ANALISI MATEMATICA (9 cfu Commissione F. Albertini, V. Casarino, M. Motta Ingegneria Gestionale, Meccanica e Meccatronica, Vicenza Vicenza, 3 settembre 8 Quarto appello Avvertenza: Nella
FONDAMENTI DI ANALISI MATEMATICA (9 cfu Commissione F. Albertini, V. Casarino, M. Motta Ingegneria Gestionale, Meccanica e Meccatronica, Vicenza Vicenza, 3 settembre 8 Quarto appello Avvertenza: Nella
Analisi Matematica II 20062/23033 Ing. Edile/Meccanica Prova scritta completa 27/01/2015
 Analisi Matematica II 20062/23033 Ing. Edile/Meccanica Prova scritta completa 27/0/205 (9 crediti) Esercizio. Si verifichi se nel punto (0, 0) la funzione 3 ye y 2 /x 4 se x 0 f (x, y) = 0 se x = 0, è
Analisi Matematica II 20062/23033 Ing. Edile/Meccanica Prova scritta completa 27/0/205 (9 crediti) Esercizio. Si verifichi se nel punto (0, 0) la funzione 3 ye y 2 /x 4 se x 0 f (x, y) = 0 se x = 0, è
ESERCIZI DI ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 2006/2007
 ESERCIZI I ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 006/007 1 FUNZIONI IN UE VARIABILI (I parte) Insiemi di definizione eterminare gli insiemi di definizione delle seguenti funzioni in due
ESERCIZI I ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 006/007 1 FUNZIONI IN UE VARIABILI (I parte) Insiemi di definizione eterminare gli insiemi di definizione delle seguenti funzioni in due
sen n x( tan xn n n=1
 8 Gennaio 2016 Nome (in stampatello): 1) (8 punti) Discutere la convergenza della serie di funzioni al variare di x in [ 1, 1]. n x( tan xn n ) xn sen n 2) (7 punti) Provare che la forma differenziale
8 Gennaio 2016 Nome (in stampatello): 1) (8 punti) Discutere la convergenza della serie di funzioni al variare di x in [ 1, 1]. n x( tan xn n ) xn sen n 2) (7 punti) Provare che la forma differenziale
Analisi Matematica II Politecnico di Milano Ingegneria Industriale
 Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #7. Sia f : R R la funzione definita da a) Determinare i massimi e minimi di f. b) Mostrare che f è limitata. fx, y) xy
Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #7. Sia f : R R la funzione definita da a) Determinare i massimi e minimi di f. b) Mostrare che f è limitata. fx, y) xy
Terzo Appello di Analisi Matematica 2 Ing. Elettronica Politecnico di Milano A.A. 2012/2013. Prof. M. Bramanti Tema n 1
 Es. 3 4 6 7 8 Tot. Punti Terzo Appello di Analisi Matematica Ing. Elettronica Politecnico di Milano A.A. 0/03. Prof. M. Bramanti Tema n Cognome e nome (in stampatello) codice persona n d'ordine (v. elenco)
Es. 3 4 6 7 8 Tot. Punti Terzo Appello di Analisi Matematica Ing. Elettronica Politecnico di Milano A.A. 0/03. Prof. M. Bramanti Tema n Cognome e nome (in stampatello) codice persona n d'ordine (v. elenco)
1 x 2 y 2 dxdy D. 3 (1 ρ2 ) 3/2 = 1 3. = π 12.
 INGEGNERIA CIVILE - AMBIENTE E TERRITORIO ANALISI MATEMATICA II SOLUZIONI DELLA PROVA SCRITTA DEL 19-6-15 ESERCIZIO 1 Calcolare 1 x y dxdy D dove D è il dominio piano delimitato dalla curva x + y x e dalle
INGEGNERIA CIVILE - AMBIENTE E TERRITORIO ANALISI MATEMATICA II SOLUZIONI DELLA PROVA SCRITTA DEL 19-6-15 ESERCIZIO 1 Calcolare 1 x y dxdy D dove D è il dominio piano delimitato dalla curva x + y x e dalle
1 x 2 y 2 dxdy D. 3 (1 ρ2 ) 3/2 = 1 3. = π 12.
 INGEGNERIA CIVILE - AMBIENTE E TERRITORIO ANALISI MATEMATICA II SOLUZIONI DELLA PROVA SCRITTA DEL 19-6-15 ESERCIZIO 1 Calcolare 1 x y dxdy D dove D è il dominio piano delimitato dalla curva x + y = x e
INGEGNERIA CIVILE - AMBIENTE E TERRITORIO ANALISI MATEMATICA II SOLUZIONI DELLA PROVA SCRITTA DEL 19-6-15 ESERCIZIO 1 Calcolare 1 x y dxdy D dove D è il dominio piano delimitato dalla curva x + y = x e
Facoltà di Ingegneria Prova scritta di Analisi Matematica II. Lecce, y y x = x3 y 4. y(1) = 1.
 Lecce, 10.4.2003 1. Risolvere il seguente problema di Cauchy: y y x = x3 y 4 y(1) = 1. 2. Determinare gli estremi della funzione f(x, y) = x 2 y 2 nell insieme } E = {(x, y) R 2 : (x 1) 2 + y2 4 1, y 0.
Lecce, 10.4.2003 1. Risolvere il seguente problema di Cauchy: y y x = x3 y 4 y(1) = 1. 2. Determinare gli estremi della funzione f(x, y) = x 2 y 2 nell insieme } E = {(x, y) R 2 : (x 1) 2 + y2 4 1, y 0.
1) Studiare la natura dei seguenti integrali impropri: 2x2 1. x dx (c) e x + 1. log x. n n + 1 n (a) n=1. (b) n + log n n 2n 2 1.
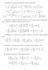 ) Studiare la natura dei seguenti integrali impropri: 0 x 3 dx (b) + 2x2 2 x 2 + 2 dx (c) e x + 0 e x dx (g) (d) + 0 + 0 x( + x) dx x sin x x 2 dx (h) (e) 0 + log x x 2 dx (f) 2 log x dx x + log( + x 2
) Studiare la natura dei seguenti integrali impropri: 0 x 3 dx (b) + 2x2 2 x 2 + 2 dx (c) e x + 0 e x dx (g) (d) + 0 + 0 x( + x) dx x sin x x 2 dx (h) (e) 0 + log x x 2 dx (f) 2 log x dx x + log( + x 2
Prima Prova Scritta 18/03/1997
 Prima Prova Scritta 18/03/1997 1 + x y6 f(x, y) = x 6 + y 6, (x, y) (0, 0) k, (x, y) = (0, 0) A 2 Determinare, per k R, l insieme di continuità di f. B 2 Determinare, per k R, l insieme di differenziabilità
Prima Prova Scritta 18/03/1997 1 + x y6 f(x, y) = x 6 + y 6, (x, y) (0, 0) k, (x, y) = (0, 0) A 2 Determinare, per k R, l insieme di continuità di f. B 2 Determinare, per k R, l insieme di differenziabilità
Prove scritte dell esame di Analisi Matematica II a.a. 2015/2016
 Prove scritte dell esame di Analisi Matematica II a.a. 5/6 C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 6 giugno 6. Determinare massimi e minimi
Prove scritte dell esame di Analisi Matematica II a.a. 5/6 C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 6 giugno 6. Determinare massimi e minimi
Analisi 4 - SOLUZIONI (15/07/2015)
 Corso di Laurea in Matematica Analisi 4 - SOLUZIONI (5/7/5) Docente: Claudia Anedda ) Calcolare l area della superficie totale della regione di spazio limitata, interna al paraboloide di equazione x +y
Corso di Laurea in Matematica Analisi 4 - SOLUZIONI (5/7/5) Docente: Claudia Anedda ) Calcolare l area della superficie totale della regione di spazio limitata, interna al paraboloide di equazione x +y
Matematica e Statistica
 Matematica e Statistica Prova d esame (26/06/203) Università di Verona - Laurea in Biotecnologie - A.A. 202/3 Matematica e Statistica Prova di MATEMATICA (26/06/203) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (26/06/203) Università di Verona - Laurea in Biotecnologie - A.A. 202/3 Matematica e Statistica Prova di MATEMATICA (26/06/203) Università di Verona - Laurea in Biotecnologie
Prove scritte dell esame di Analisi Matematica II a.a. 2016/2017
 Prove scritte dell esame di Analisi Matematica II a.a. 6/7 C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 5 giugno 7. Assegnati ( l insieme E {(x,
Prove scritte dell esame di Analisi Matematica II a.a. 6/7 C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 5 giugno 7. Assegnati ( l insieme E {(x,
Analisi Matematica III
 Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 1 giugno 4 (Cognome (Nome (Numero di matricola Esercizio 1 Si consideri la successione
Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 1 giugno 4 (Cognome (Nome (Numero di matricola Esercizio 1 Si consideri la successione
Analisi 4 - SOLUZIONI (17/01/2013)
 Corso di Laurea in Matematica Analisi 4 - SOLUZIONI 7//23 Docente: Claudia Anedda Utilizzando uno sviluppo in serie noto, scrivere lo sviluppo in serie di MacLaurin della funzione fx = 32 + x, specificando
Corso di Laurea in Matematica Analisi 4 - SOLUZIONI 7//23 Docente: Claudia Anedda Utilizzando uno sviluppo in serie noto, scrivere lo sviluppo in serie di MacLaurin della funzione fx = 32 + x, specificando
Analisi Matematica II 14 Giugno 2019
 Analisi Matematica II 14 Giugno 2019 Cognome: Nome: Matricola: 1. (10 punti) Si determinino i sottoinsiemi del piano in cui valgano, rispettivamente, continuità, derivabilità e differenziabilità della
Analisi Matematica II 14 Giugno 2019 Cognome: Nome: Matricola: 1. (10 punti) Si determinino i sottoinsiemi del piano in cui valgano, rispettivamente, continuità, derivabilità e differenziabilità della
PROVE SCRITTE DI ANALISI MATEMATICA II (V.O.), ANNO 2002
 PROVE SCRITTE DI ANALISI MATEMATICA II (V.O.), ANNO 22 Prova scritta del 1/1/22 Si esamini la serie di funzioni: 1 log x (e n + n), definita per x IR. Si determini l insieme S in cui tale serie converge,
PROVE SCRITTE DI ANALISI MATEMATICA II (V.O.), ANNO 22 Prova scritta del 1/1/22 Si esamini la serie di funzioni: 1 log x (e n + n), definita per x IR. Si determini l insieme S in cui tale serie converge,
TEMI D ESAME DI ANALISI MATEMATICA I
 TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
D : 0 E : arctan 2 1 F : 2 arctan 1. 3y + 3y y = 0 y(0) = 3 y (0) = 0.
 Analisi Matematica B 31 marzo 003 Compito 1 1. L integrale 1 x arctan( 1 x ) dx vale Risp.: A : arctan 1 1 B : C : arctan 1 3 D : 0 E : arctan 1 F : arctan 1 + arctan 1. Sia ỹ(x) la soluzione del problema
Analisi Matematica B 31 marzo 003 Compito 1 1. L integrale 1 x arctan( 1 x ) dx vale Risp.: A : arctan 1 1 B : C : arctan 1 3 D : 0 E : arctan 1 F : arctan 1 + arctan 1. Sia ỹ(x) la soluzione del problema
Analisi Matematica 3 (Fisica), , M. Peloso e L. Vesely Prova scritta del 14 luglio 2009 Breve svolgimento (con alcuni conti omessi)
 Analisi Matematica 3 Fisica, 8-9, M. Peloso e L. Vesely Prova scritta del 4 luglio 9 Breve svolgimento con alcuni conti omessi. a Dimostrare che l insieme G = { x, y R : x + x + log y = ye x} coincide
Analisi Matematica 3 Fisica, 8-9, M. Peloso e L. Vesely Prova scritta del 4 luglio 9 Breve svolgimento con alcuni conti omessi. a Dimostrare che l insieme G = { x, y R : x + x + log y = ye x} coincide
PROVA SCRITTA DI ANALISI MATEMATICA 2 Corso di laurea in Matematica 4 Luglio Risoluzione a cura di N. Fusco & G. Floridia
 PROVA SCRITTA DI ANALISI MATEMATICA Corso di laurea in Matematica 4 Luglio 6 Risoluzione a cura di N Fusco & G Floridia Discutere la convergenza puntuale, assoluta, uniforme e totale della serie di funzioni
PROVA SCRITTA DI ANALISI MATEMATICA Corso di laurea in Matematica 4 Luglio 6 Risoluzione a cura di N Fusco & G Floridia Discutere la convergenza puntuale, assoluta, uniforme e totale della serie di funzioni
ANALISI B alcuni esercizi proposti
 ANALISI B alcuni esercizi proposti G.P. Leonardi Parte II 1 Limiti e continuità per funzioni di 2 variabili Esercizio 1.1 Calcolare xy log(1 + x ) lim (x,y) (0,0) 2x 2 + 5y 2 Esercizio 1.2 Studiare la
ANALISI B alcuni esercizi proposti G.P. Leonardi Parte II 1 Limiti e continuità per funzioni di 2 variabili Esercizio 1.1 Calcolare xy log(1 + x ) lim (x,y) (0,0) 2x 2 + 5y 2 Esercizio 1.2 Studiare la
Prima prova di verifica in itinere di ANALISI MATEMATICA II. 12 Marzo 2008 Compito A. 1 (punti 3)
 anno accademico 007-008 Prima prova di verifica in itinere di ANALISI MATEMATICA II Marzo 008 Compito A (punti ) y = x + xy + y x. (punti 4) y + y x = ln x x y. (punti ) y = y + y ln y. 4 (punti 6) Determinare
anno accademico 007-008 Prima prova di verifica in itinere di ANALISI MATEMATICA II Marzo 008 Compito A (punti ) y = x + xy + y x. (punti 4) y + y x = ln x x y. (punti ) y = y + y ln y. 4 (punti 6) Determinare
Prove d Esame A.A. 2012/2013
 Complementi di Analisi Polo di Savona Complementi di Analisi Matematica Prove d Esame A.A. 2012/2013 1- PrCam.TEX [] Complementi di Analisi Polo di Savona Prima Prova parziale 23/11/2011 Prima Prova parziale
Complementi di Analisi Polo di Savona Complementi di Analisi Matematica Prove d Esame A.A. 2012/2013 1- PrCam.TEX [] Complementi di Analisi Polo di Savona Prima Prova parziale 23/11/2011 Prima Prova parziale
Terzo appello di Analisi Matematica 1 Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 2015/2016. Prof. M. Bramanti.
 Terzo appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 5/6. Prof. M. Bramanti Tema n 5 6 7 Tot. Cognome e nome in stampatello codice persona o n di matricola n
Terzo appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 5/6. Prof. M. Bramanti Tema n 5 6 7 Tot. Cognome e nome in stampatello codice persona o n di matricola n
Analisi Matematica 3 (Fisica) Prova scritta del 27 gennaio 2012 Uno svolgimento
 Analisi Matematica 3 (Fisica) Prova scritta del 27 gennaio 22 Uno svolgimento Prima di tutto, eccovi alcuni commenti che potrebbero aiutarvi a svolgere meglio le prove scritte. Ad ogni domanda del testo
Analisi Matematica 3 (Fisica) Prova scritta del 27 gennaio 22 Uno svolgimento Prima di tutto, eccovi alcuni commenti che potrebbero aiutarvi a svolgere meglio le prove scritte. Ad ogni domanda del testo
Matematica e Statistica (A-E, F-O, P-Z)
 Matematica e Statistica (A-E, F-O, P-Z) Prova d esame (08/07/20) Università di Verona - Laurea in Biotecnologie - A.A. 200/ Matematica e Statistica (A-E, F-O, P-Z) Prova di MATEMATICA (A-E, F-O, P-Z) (08/07/20)
Matematica e Statistica (A-E, F-O, P-Z) Prova d esame (08/07/20) Università di Verona - Laurea in Biotecnologie - A.A. 200/ Matematica e Statistica (A-E, F-O, P-Z) Prova di MATEMATICA (A-E, F-O, P-Z) (08/07/20)
Terzo Appello di Analisi Matematica 2 Ing. Elettronica Politecnico di Milano A.A. 2014/2015. Prof. M. Bramanti Tema n 1
 Es. 3 4 5 6 7 8 Tot. Punti Terzo Appello di Analisi Matematica Ing. Elettronica Politecnico di Milano A.A. 04/05. Prof. M. ramanti Tema n ognome e nome (in stampatello) codice persona n d'ordine (v. elenco)
Es. 3 4 5 6 7 8 Tot. Punti Terzo Appello di Analisi Matematica Ing. Elettronica Politecnico di Milano A.A. 04/05. Prof. M. ramanti Tema n ognome e nome (in stampatello) codice persona n d'ordine (v. elenco)
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016
 Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Esame di Analisi Matematica 2 24/7/2013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 2012/2013
 Esame di Analisi Matematica 4/7/013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 01/013 A Cognome (in STAMPATELLO):... Nome (in STAMPATELLO):... CFU:... Esercizio 1. Sia f : R R una funzione
Esame di Analisi Matematica 4/7/013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 01/013 A Cognome (in STAMPATELLO):... Nome (in STAMPATELLO):... CFU:... Esercizio 1. Sia f : R R una funzione
Prove scritte dell esame di Analisi Matematica II a.a. 2011/2012
 Prove scritte dell esame di Analisi Matematica II a.a. / C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 7 giugno. ( punti) Disegnare l insieme E (x,
Prove scritte dell esame di Analisi Matematica II a.a. / C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 7 giugno. ( punti) Disegnare l insieme E (x,
TRACCIA DELLE SOLUZIONI DEI PROBLEMI DELL ESAME DEL 2/9/2011
 TRACCIA DELLE SOLUZIONI DEI PROBLEMI DELL ESAME DEL /9/11 Esercizio 1 a. Dopo aver scritto l equazione parametrica C(t) della curva di equazione cartesiana y = x x, si calcolino i vettori T(t), N(t) e
TRACCIA DELLE SOLUZIONI DEI PROBLEMI DELL ESAME DEL /9/11 Esercizio 1 a. Dopo aver scritto l equazione parametrica C(t) della curva di equazione cartesiana y = x x, si calcolino i vettori T(t), N(t) e
Analisi Matematica II Corso di Ingegneria Gestionale Compito del f(x, y) = (x 2 2y 2 ) e x y
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8--5 - È obbligatorio consegnare tutti i fogli anche la brutta e il testo - Le risposte senza giustificazione sono considerate nulle Esercizio
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8--5 - È obbligatorio consegnare tutti i fogli anche la brutta e il testo - Le risposte senza giustificazione sono considerate nulle Esercizio
Secondo Appello di Analisi Matematica 2 Ing. Elettronica Politecnico di Milano A.A. 2014/2015. Prof. M. Bramanti Tema n 1
 Es. 2 3 4 5 6 7 8 Tot. Punti Secondo Appello di Analisi Matematica 2 Ing. Elettronica Politecnico di Milano A.A. 204/205. Prof. M. ramanti Tema n Cognome e nome (in stampatello) codice persona n d'ordine
Es. 2 3 4 5 6 7 8 Tot. Punti Secondo Appello di Analisi Matematica 2 Ing. Elettronica Politecnico di Milano A.A. 204/205. Prof. M. ramanti Tema n Cognome e nome (in stampatello) codice persona n d'ordine
exp(x 2 ) 1 (1 + x 2 ) 2/5 1
 Esame di Matematica II Corso di Laurea Triennale in Scienza dei Materiali Esame di Complementi di Matematica Corso di Laurea Triennale in Scienze e Tecnologie Chimiche 18 Luglio 6 Motivare le soluzioni.
Esame di Matematica II Corso di Laurea Triennale in Scienza dei Materiali Esame di Complementi di Matematica Corso di Laurea Triennale in Scienze e Tecnologie Chimiche 18 Luglio 6 Motivare le soluzioni.
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica 2 del 19/06/2010 A
 Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9/6/ A ) ata la funzione f(x, y) x y log( + x + y ), a) stabilire dove risulta derivabile parzialmente nel suo
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9/6/ A ) ata la funzione f(x, y) x y log( + x + y ), a) stabilire dove risulta derivabile parzialmente nel suo
Prove scritte dell esame di Analisi Matematica II a.a. 2013/2014
 Prove scritte dell esame di Analisi Matematica II a.a. 3/4 C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 9 giugno 4. (8 punti) Risolvere il problema
Prove scritte dell esame di Analisi Matematica II a.a. 3/4 C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 9 giugno 4. (8 punti) Risolvere il problema
Analisi Matematica 2 (Corso di Laurea in Informatica)
 COGNOME NOME Matr. Firma dello studente A Tempo: 3 ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
COGNOME NOME Matr. Firma dello studente A Tempo: 3 ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
Esercizi sull integrazione II
 ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) - COMPL. DI ANALISI MATEMATICA (A-K) (C.d.L. Ing. Civile) A.A.28-29 - Prof. G.Cupini Esercizi sull integrazione II (Grazie agli studenti
ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) - COMPL. DI ANALISI MATEMATICA (A-K) (C.d.L. Ing. Civile) A.A.28-29 - Prof. G.Cupini Esercizi sull integrazione II (Grazie agli studenti
COMPLEMENTI DI ANALISI MATEMATICA A.A Primo appello del 5/5/2010
 COMPLEMENTI DI ANALISI MATEMATICA A.A. 29- Primo appello del 5/5/2 Qui trovate le tracce delle soluzioni degli esercizi del compito. Ho tralasciato i calcoli da Analisi (che comunque sono parte della risoluzione),
COMPLEMENTI DI ANALISI MATEMATICA A.A. 29- Primo appello del 5/5/2 Qui trovate le tracce delle soluzioni degli esercizi del compito. Ho tralasciato i calcoli da Analisi (che comunque sono parte della risoluzione),
Matematica e Statistica
 Matematica e Statistica Prova d Esame (26/07/2010) Università di Verona - Laurea in Biotecnologie - A.A. 2009/10 1 Matematica e Statistica Prova d Esame di MATEMATICA (26/07/2010) Università di Verona
Matematica e Statistica Prova d Esame (26/07/2010) Università di Verona - Laurea in Biotecnologie - A.A. 2009/10 1 Matematica e Statistica Prova d Esame di MATEMATICA (26/07/2010) Università di Verona
INGEGNERIA MECCANICA - CANALE L-Z ANALISI MATEMATICA II SOLUZIONI DELLA PROVA SCRITTA DEL COMPITO A. ( 1) k 2k + 1 e(2k+1)(x+y),
 1 INGEGNERIA MECCANICA - CANALE L-Z ANALISI MATEMATICA II SOLUZIONI DELLA PROVA SCRITTA DEL 1-6-16 - COMPITO A ESERCIZIO 1 Studiare la convergenza assoluta, puntuale e totale della serie k + 1 e(k+1)(x+y),
1 INGEGNERIA MECCANICA - CANALE L-Z ANALISI MATEMATICA II SOLUZIONI DELLA PROVA SCRITTA DEL 1-6-16 - COMPITO A ESERCIZIO 1 Studiare la convergenza assoluta, puntuale e totale della serie k + 1 e(k+1)(x+y),
CORSO DI LAUREA IN INFORMATICA ANALISI MATEMATICA I MODULO, I E II MODULO, II MODULO II PROVA SCRITTA DI GENNAIO 2006: SOLUZIONI
 CORSO DI LAUREA IN INFORMATICA ANALISI MATEMATICA I MODULO, I E II MODULO, II MODULO II PROVA SCRITTA DI GENNAIO 2006: SOLUZIONI Notiamo che lo studio delle funzioni assegnate f,..., f 4 si riduce a considerare
CORSO DI LAUREA IN INFORMATICA ANALISI MATEMATICA I MODULO, I E II MODULO, II MODULO II PROVA SCRITTA DI GENNAIO 2006: SOLUZIONI Notiamo che lo studio delle funzioni assegnate f,..., f 4 si riduce a considerare
Istituzioni di Matematica II 5 Luglio 2010
 Istituzioni di Matematica II 5 Luglio 010 1. Classificare, al variare del parametro α R, la forma quadratica (1 + α )x + 4xy + αy.. i) Si determinino tutti i punti critici della seguente funzione f(x,
Istituzioni di Matematica II 5 Luglio 010 1. Classificare, al variare del parametro α R, la forma quadratica (1 + α )x + 4xy + αy.. i) Si determinino tutti i punti critici della seguente funzione f(x,
Primo appello di Analisi Matematica 1 Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 2015/2016. Prof. M. Bramanti.
 Primo appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 5/6. Prof. M. Bramanti Tema n 5 6 7 Tot. Cognome e nome in stampatello codice persona o n di matricola n
Primo appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 5/6. Prof. M. Bramanti Tema n 5 6 7 Tot. Cognome e nome in stampatello codice persona o n di matricola n
Cognome Nome Matricola Codice ESEMPIO 1
 Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di derivata di una funzione in un punto. Sia A R N ; sia a A; sia f : A R M ; sia f differenziabile in a; allora la derivata di f in a è...
Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di derivata di una funzione in un punto. Sia A R N ; sia a A; sia f : A R M ; sia f differenziabile in a; allora la derivata di f in a è...
PRIMI ESERCIZI SU INTEGRALI DOPPI E TRIPLI. x x 2 + y 2 dxdy, tan(x + y) x + y. (x y) log (x + y) dxdy,
 PRIMI ESERCIZI SU INTEGRALI DOPPI E TRIPLI VALENTINA CASARINO Esercizi per il corso di Analisi Matematica, (Ingegneria Gestionale, dell Innovazione del Prodotto, Meccanica e Meccatronica, Università degli
PRIMI ESERCIZI SU INTEGRALI DOPPI E TRIPLI VALENTINA CASARINO Esercizi per il corso di Analisi Matematica, (Ingegneria Gestionale, dell Innovazione del Prodotto, Meccanica e Meccatronica, Università degli
Analisi Matematica II Corso di Ingegneria Gestionale Compito A del , se (x, y) = (0, 0) ( x e. + y x e (y2 )
 Analisi Matematica II Corso di Ingegneria Gestionale Compito A del -6-9 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito A del -6-9 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Biomedica Compito del
 Analisi Matematica II Corso di Ingegneria Biomedica Compito del 7-- Esercizio. punti Data la funzione fx, y = log x + y x + y + x y i trovare tutti i punti critici; ii trovare massimo e minimo assoluti
Analisi Matematica II Corso di Ingegneria Biomedica Compito del 7-- Esercizio. punti Data la funzione fx, y = log x + y x + y + x y i trovare tutti i punti critici; ii trovare massimo e minimo assoluti
Esame di Metodi Matematici per l Ingegneria
 Esame di Metodi Matematici per l Ingegneria Prof. M. Bramanti Politecnico di Milano, A.A. 014/15 Seconda prova in itinere. Giugno 015 Cognome: Nome N matr. o cod. persona: Domande a risposta aperta (rispondere
Esame di Metodi Matematici per l Ingegneria Prof. M. Bramanti Politecnico di Milano, A.A. 014/15 Seconda prova in itinere. Giugno 015 Cognome: Nome N matr. o cod. persona: Domande a risposta aperta (rispondere
ANALISI MATEMATICA 2 - INGEGNERIA MECCANICA ED ENERGETICA A.A PROVA SCRITTA DEL 28/1/19
 ANALISI MATEMATICA - INGEGNERIA MECCANICA E ENERGETICA A.A. 8-9 PROVA SCRITTA EL 8//9 Scrivere nome cognome e numero di matricola in stampatello su tutti i fogli da consegnare. Consegnare solo la bella
ANALISI MATEMATICA - INGEGNERIA MECCANICA E ENERGETICA A.A. 8-9 PROVA SCRITTA EL 8//9 Scrivere nome cognome e numero di matricola in stampatello su tutti i fogli da consegnare. Consegnare solo la bella
Contents. 1. Funzioni di più variabili.
 RACCOLTA DI ESERCIZI PER IL CORSO DI ANALISI MATEMATICA II A.A. 03/04 CORSI DI LAUREA IN INGEGNERIA DELL EDILIZIA, INGEGNERIA EDILE-ARCHITETTURA PROF. D. BARTOLUCCI Contents. Funzioni di più variabili..
RACCOLTA DI ESERCIZI PER IL CORSO DI ANALISI MATEMATICA II A.A. 03/04 CORSI DI LAUREA IN INGEGNERIA DELL EDILIZIA, INGEGNERIA EDILE-ARCHITETTURA PROF. D. BARTOLUCCI Contents. Funzioni di più variabili..
Compiti d Esame A.A. 2005/2006
 Compiti d Esame A.A. 25/26 UNIVERSITÀ DEGLI STUDI DI PERUGIA A.A. 25/26 I Esercitazione 21 Aprile 26 { y = xy ln(xy) si chiede di dimostrare che: y(1) = 1, (a) ammette un unica soluzione massimale y =
Compiti d Esame A.A. 25/26 UNIVERSITÀ DEGLI STUDI DI PERUGIA A.A. 25/26 I Esercitazione 21 Aprile 26 { y = xy ln(xy) si chiede di dimostrare che: y(1) = 1, (a) ammette un unica soluzione massimale y =
ANALISI MATEMATICA 3
 ANALISI MATEMATICA 3 Corso di laurea triennale in Fisica, F480 Prova scritta del 8//003 prof. Marco Vignati ] Sia dato il problema di Cauchy xy + y = 0 i) Determinarne la soluzione locale. y () = 3 ii)
ANALISI MATEMATICA 3 Corso di laurea triennale in Fisica, F480 Prova scritta del 8//003 prof. Marco Vignati ] Sia dato il problema di Cauchy xy + y = 0 i) Determinarne la soluzione locale. y () = 3 ii)
Analisi Matematica 2. Michele Campiti. Prove scritte di. Ingegneria Industriale a.a
 Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 2009 2010 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi
Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 2009 2010 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica I del c.
 Prova scritta di Analisi Matematica I del 22-5-2 - c. ) Provare che 3 3è irrazionale. 2) Provare che il grafico di f(x) =(x ) + 2 sin[(x ) ]:R \{} R ammette la retta di equazione x = come asintoto verticale.
Prova scritta di Analisi Matematica I del 22-5-2 - c. ) Provare che 3 3è irrazionale. 2) Provare che il grafico di f(x) =(x ) + 2 sin[(x ) ]:R \{} R ammette la retta di equazione x = come asintoto verticale.
CORSO DI LAUREA IN INGEGNERIA ELETTRONICA Prof. A. Avantaggiati (prova scritta del I MODULO di ANALISI MATEMATICA II - 14 gennaio 2000) Compito A
 CORSO DI LAUREA IN INGEGNERIA ELETTRONICA Prof. A. Avantaggiati (prova scritta del I MODULO di ANALISI MATEMATICA II - 14 gennaio 000) Compito A COGNOME... NOME... Data l equazione differenziale y 3 cos
CORSO DI LAUREA IN INGEGNERIA ELETTRONICA Prof. A. Avantaggiati (prova scritta del I MODULO di ANALISI MATEMATICA II - 14 gennaio 000) Compito A COGNOME... NOME... Data l equazione differenziale y 3 cos
Matematica e Statistica
 Matematica e Statistica Prova d Esame (0/09/200) Università di Verona - Laurea in Biotecnologie - A.A. 2009/0 Matematica e Statistica Prova d Esame di MATEMATICA (0/09/200) Università di Verona - Laurea
Matematica e Statistica Prova d Esame (0/09/200) Università di Verona - Laurea in Biotecnologie - A.A. 2009/0 Matematica e Statistica Prova d Esame di MATEMATICA (0/09/200) Università di Verona - Laurea
Scritto di Analisi Vettoriale ( ) proff. F. De Marchis, F. Lanzara, E. Montefusco
 COGNOM, NOM e MATRICOLA: Scritto di Analisi Vettoriale 8..18) proff. F. De Marchis, F. Lanzara,. Montefusco DOCNT: De Marchis Lanzara Montefusco Se ammesso, sosterrò la prova orale: questo appello in un
COGNOM, NOM e MATRICOLA: Scritto di Analisi Vettoriale 8..18) proff. F. De Marchis, F. Lanzara,. Montefusco DOCNT: De Marchis Lanzara Montefusco Se ammesso, sosterrò la prova orale: questo appello in un
b) Dimostrare che se f(x) è differenziabile in x 0, allora è continua in x 0.
 Analisi Matematica II - Calcolo in più variabili Nome, Cognome, Matricola: Corso di Laurea: Versione A Avvertenza: La prova d esame si compone di due esercizi e di due quesiti. La risposta ai quesiti va
Analisi Matematica II - Calcolo in più variabili Nome, Cognome, Matricola: Corso di Laurea: Versione A Avvertenza: La prova d esame si compone di due esercizi e di due quesiti. La risposta ai quesiti va
Cognome Nome Matricola Codice ESEMPIO 1
 Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di sistema fondamentale di soluzioni di un equazione differenziale lineare d ordine n omogenea. Sia I un intervallo non banale di R; siano
Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di sistema fondamentale di soluzioni di un equazione differenziale lineare d ordine n omogenea. Sia I un intervallo non banale di R; siano
Secondo appello di Analisi Matematica 1 Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 2015/2016. Prof. M. Bramanti.
 Secondo appello di Analisi Matematica 1 Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 01/01. Prof. M. Bramanti 1 Tema n 1 4 7 Tot. Cognome e nome in stampatello) codice persona o n di matricola)
Secondo appello di Analisi Matematica 1 Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 01/01. Prof. M. Bramanti 1 Tema n 1 4 7 Tot. Cognome e nome in stampatello) codice persona o n di matricola)
Analisi Matematica II - Ingegneria Meccanica/Energetica - 29 Gennaio 2018
 nalisi Matematica II - Ingegneria Meccanica/Energetica - 29 Gennaio 218 1) ia data la funzione f(x, y, z) = (x 2 + y 2 1) 2 + 8 a) tudiare l esistenza di massimi e minimi assoluti della funzione f nella
nalisi Matematica II - Ingegneria Meccanica/Energetica - 29 Gennaio 218 1) ia data la funzione f(x, y, z) = (x 2 + y 2 1) 2 + 8 a) tudiare l esistenza di massimi e minimi assoluti della funzione f nella
calcolare il lavoro di E lungo il segmento da A = ( 1, 1, 1) a B = (1, 1, 1), calcolare rot ( E ), determinare un potenziale U(x, y, z) per E.
 ANALISI VETTORIALE Soluzione esonero.1. Esercizio. Assegnato il campo E (x, y, z) = x(y + z ), y(x + z ), z(x + y ) } 1111 calcolare il lavoro di E lungo il segmento da A = ( 1, 1, 1) a B = (1, 1, 1),
ANALISI VETTORIALE Soluzione esonero.1. Esercizio. Assegnato il campo E (x, y, z) = x(y + z ), y(x + z ), z(x + y ) } 1111 calcolare il lavoro di E lungo il segmento da A = ( 1, 1, 1) a B = (1, 1, 1),
Analisi Matematica II Corso di Ingegneria Gestionale Compito del A
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del -7-5 - A Esercizio ( punti Data la funzione f(x, y = x + y + 4xy 8x 4y + 4 i trovare tutti i punti critici e, se possibile, caratterizzarli
Analisi Matematica II Corso di Ingegneria Gestionale Compito del -7-5 - A Esercizio ( punti Data la funzione f(x, y = x + y + 4xy 8x 4y + 4 i trovare tutti i punti critici e, se possibile, caratterizzarli
Cognome Nome Matricola Codice ESEMPIO 1
 Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di forma differenziale chiusa. Sia A R N ; sia A aperto; sia ω = N i=1 ω i dx i una forma differenziale su A; sia ω di classe C 1 ; si dice
Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di forma differenziale chiusa. Sia A R N ; sia A aperto; sia ω = N i=1 ω i dx i una forma differenziale su A; sia ω di classe C 1 ; si dice
ESAMI E ESERCITAZIONI A.A. 2010/11. Calcolare la lunghezza del grafico di f. Suggerimento: ricordare che, se h(u) è una funzione continua e.
 ESAMI E ESERCITAZIONI AA 2010/11 ANDREA RATTO Sommario In questo file presentiamo esercitazioni ed esami relativi al Corso Integrato di Matematica per Scienze dell Architettura 1 Esercitazione del 2 Maggio
ESAMI E ESERCITAZIONI AA 2010/11 ANDREA RATTO Sommario In questo file presentiamo esercitazioni ed esami relativi al Corso Integrato di Matematica per Scienze dell Architettura 1 Esercitazione del 2 Maggio
Recupero sul 1 compitino di Analisi Matematica 2 Ing. Elettronica Politecnico di Milano A.A. 2014/2015. Prof. M. Bramanti Tema n 1
 Es. 4 5 6 Tot. Punti Recupero sul compitino di Analisi Matematica Ing. Elettronica Politecnico di Milano A.A. 04/05. Prof. M. ramanti Tema n Cognome e nome (in stampatello) codice persona n d'ordine (v.
Es. 4 5 6 Tot. Punti Recupero sul compitino di Analisi Matematica Ing. Elettronica Politecnico di Milano A.A. 04/05. Prof. M. ramanti Tema n Cognome e nome (in stampatello) codice persona n d'ordine (v.
Matematica e Statistica
 Matematica e Statistica Prova d esame (0/0/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/0/03) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (0/0/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/0/03) Università di Verona - Laurea in Biotecnologie
Ingegneria Elettronica Prova scritta di Analisi Matematica II del giorno ( 3) n x n n + 1
 Prova scritta di Analisi Matematica II del giorno 31-01-2007 1) Studiare la serie di potenze ( 3) n x n n + 1 2) Determinare i punti di estremo relativo ed assoluto della funzione seguente f(x, y) = x
Prova scritta di Analisi Matematica II del giorno 31-01-2007 1) Studiare la serie di potenze ( 3) n x n n + 1 2) Determinare i punti di estremo relativo ed assoluto della funzione seguente f(x, y) = x
a) Il denominatore dev essere diverso da zero. Studiamo il trinomio x 2 5x + 6. Si ha: x 1,2 = 5 ± se x ], 2[ ]3, + [;
![a) Il denominatore dev essere diverso da zero. Studiamo il trinomio x 2 5x + 6. Si ha: x 1,2 = 5 ± se x ], 2[ ]3, + [; a) Il denominatore dev essere diverso da zero. Studiamo il trinomio x 2 5x + 6. Si ha: x 1,2 = 5 ± se x ], 2[ ]3, + [;](/thumbs/69/60588320.jpg) ESERCIZIO - Data la funzione f (x) + x2 2x x 2 5x + 6, si chiede di: a) calcolare il dominio di f ; (2 punti) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire se f ha asintoti
ESERCIZIO - Data la funzione f (x) + x2 2x x 2 5x + 6, si chiede di: a) calcolare il dominio di f ; (2 punti) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire se f ha asintoti
Soluzioni dello scritto di Analisi Matematica II - 10/07/09. C.L. in Matematica e Matematica per le Applicazioni
 Soluzioni dello scritto di Analisi Matematica II - /7/9 C.L. in Matematica e Matematica per le Applicazioni Proff. K. Payne, C. Tarsi, M. Calanchi Esercizio. a La funzione f è limitata e essendo lim fx
Soluzioni dello scritto di Analisi Matematica II - /7/9 C.L. in Matematica e Matematica per le Applicazioni Proff. K. Payne, C. Tarsi, M. Calanchi Esercizio. a La funzione f è limitata e essendo lim fx
