D : 0 E : arctan 2 1 F : 2 arctan 1. 3y + 3y y = 0 y(0) = 3 y (0) = 0.
|
|
|
- Carla Gatto
- 4 anni fa
- Visualizzazioni
Transcript
1 Analisi Matematica B 31 marzo 003 Compito 1 1. L integrale 1 x arctan( 1 x ) dx vale Risp.: A : arctan 1 1 B : C : arctan 1 3 D : 0 E : arctan 1 F : arctan 1 + arctan 1. Sia ỹ(x) la soluzione del problema di Cauchy Allora ỹ(1) vale y 3y + 3y y = 0 y(0) = 3 y (0) = 0 y (0) = 0. Risp.: A : 0 B : 3 e C : 3e D : 3 E : F : e 3 3. Sia f : R R la funzione definita da f(x, y) = x e 7y e sia v = (v 1, v ) un versore di R. Allora risulta (1, 1) = 0 se e soltanto se f v Risp.: A : v 1 = 8v B : v 1 = 1, v = 0 C : v 1 = 7v D : v 1 = 0, v = 1 E : v 1 = 1, v = 1 F : v 1 = 1, v = 4. Sia f : R R la funzione definita da f(x, y) = x 4 + y 4 4xy. Allora i punti P 1 = (0, 0) e P = (1, 1) sono per f Risp.: A : P 1 di sella, P di sella B : P 1 non è stazionario, P di minimo C : P 1 di massimo e P non è stazionario D : P 1 di sella, P di massimo, E : P 1 di sella, P di minimo F : P 1 di massimo, P di minimo 5. Si consideri la funzione g(x, y) = x cos πy nel dominio A = [0, 1] [0, 1]. Definendo M = max g(x, y), (x,y) A m = min g(x, y), si ha che (x,y) A Risp.: A : m = 1, M = 1 B : m = 0, M = C : m = 0, M = 1 D : m =, M = E : m = 1, M = F : m = 1, M = 0 6. Data la curva Γ di rappresentazione parametrica r (t) = 3(cos t + sin t) i 1 + 3(sin t cos t) i, 0 t π, il versore tangente a Γ nel punto (x 0, y 0 ) = (3, 3) corrispondente a t 0 = π è Risp.: A : ( 1 1, ) B : (1, 0) C : ( 3, 1 ) D : (, 1) E : (0, 1) F : (1, ) 7. Calcolare l integrale curvilineo 3xds, dove Γ è la curva di equazioni parametriche x = (cos t), y = (sin t) con 0 t π. Risp.: A : B : 3 C : D : 3 E : 3 F : 1 4 e3 8. Calcolare l integrale curvilineo Γ Γ e x +y (xdx + ydy), nel primo quadrante e percorso in senso antiorario. dove Γ è l arco di ellisse di equazione x + y 3 = 1 contenuto Risp.: A : e B : (e 3 + e ) C : e D : 1 (e3 e ) E : 3 F : 1 4 (e3 1)
2 9. Sia F = (F 1, F ) : A R R un campo vettoriale di classe C su A aperto connesso. Sia B A semplicemente connesso; se F 1 y (x, y) = F (x, y) x (x, y) A, allora delle seguenti affermazioni (a) F è un gradiente in A (b) F è un gradiente in B (c) Γ 1 F dγ1 = 0 per ogni curva chiusa Γ 1 a valori in A (d) Γ F dγ è indipendente dalla traiettoria per ogni curva Γ a valori in B (e) F1 e F sono differenziabili in A le uniche corrette sono Risp.: A : a c e B : a b c C : a c d D : b c e E : a b d F : b d e 10. L integrale doppio 7 T x 3 y x + y dxdy Risp.: A : B : 5 C : 3 D : 3 4 E : 1 64 F :, dove T = {(x, y) R : 1 x + y, 0 y x} vale
3 Cognome e nome Firma Corso di Laurea: per l ambiente e il territorio ; dell automazione industriale; civile; gestionale; dell informazione; dei materiali; meccanica. Analisi Matematica B 31 marzo 003 Compito 1 Istruzioni. 1. COMPILARE la parte soprastante la prima riga continua. In particolare, scrivere cognome e nome in stampatello e la firma sopra la riga punteggiata e segnare il corso di laurea.. SEGNARE nelle due tabelle riportate in questa pagina, in modo incontrovertibile, la lettera corrispondente alla risposta scelta per ognuna delle domande riportate nel foglio allegato; in caso di correzione, apporre un SI vicino alla risposta scelta. 3. PUNTEGGI: risposta esatta = +3; risposta sbagliata = 0.5; risposta non data = PROIBITO usare libri, quaderni, calcolatori. 5. CONSEGNARE solo questo foglio. 6. TEMPO a disposizione: 150 min. Risposte relative ai fogli allegati
4 31 marzo 003 ANALISI MATEMATICA B RISULTATI Es.1 Es. Es.3 Es.4 Es.5 Compito 1 F B C E E Compito C F E A B Compito 3 B C A D C Compito 4 F B D F E Compito 5 D F F B B Compito 6 B C B C C Es.6 Es.7 Es.8 Es.9 Es.10 Compito 1 A D D F A Compito D B B C E Compito 3 F F E B C Compito 4 B D D E B Compito 5 C B A D E Compito 6 E F F A C
5 Analisi Matematica B 14 aprile 003 Compito 1 1. L integrale 7 log e x ex 1 dx vale Risp.: A : 3 (e7 1) 3/ + (e 7 1) 1/ 8 3 B : 3 (e7 1) 3/ C : (e 7 1) 1/ D : (e 7 1) 1/ + (e 7 5) 1/ E : 8 3 F : 0. Sia ỹ(x) la soluzione del problema di Cauchy { y = x y + x Allora lim x ỹ vale y(0) = 1. Risp.: A : 3 B : 0 C : 1 D : + E : 3 F : e 3 3. Sia f la funzione definita da f(x, y) = y x + log(3x) + 7. Allora il dominio di f è dato da 1 x y Risp.: A : un semicerchio B : un quarto di cerchio C : un semipiano D : un ottavo di cerchio E : una corona circolare F : la parte di piano esterna a un cerchio 4. Sia f : R R la funzione definita da f(x, y) = 1 6 y3 + 1 x + xy + 1x. Allora essa ammette Risp.: A : un punto di massimo relativo e un punto di sella B : due punti di massimo relativo C : due punti di minimo relativo D : due punti di sella E : nessun punto stazionario F : un punto di minimo relativo e un punto di sella 5. Si consideri la funzione g(x, y) = x + y 1 nel dominio A = {(x, y) R : x + y }. Definendo M = g(x, y), si ha che max (x,y) A Risp.: A : M = 1 B : M = 3 C : M = D : M = 4 E : M = 0 F : M = 5 6. Data la curva Γ di rappresentazione parametrica r (t) = 3(t cos t + sin t) i 1 + 3(t sin t cos t) i, 0 t π, il versore tangente a Γ nel punto (x 0, y 0 ) = (0, 3) corrispondente a t 0 = 0 è Risp.: A : (1, 0) B : (3, 0) C : ( 3, 1 ) D : ( 1, 1 ) E : ( 1, 1 ) F : (1, 1) 7. Calcolare l integrale curvilineo percorsa in senso antiorario. Γ 1 x dx + xdy, Risp.: A : π B : 3 π C : π D : 3π E : π F : 1 3 dove Γ è l arco di ellisse di equazione x + y 4 8. Sia F : R + R R definito da ( ) ) yx α i F (x, y) = 1 + x + arctan y 1 + (log(1 + x ) + xα i 1 + y, con α R. Allora F ha integrale curvilineo indipendente dalla traiettoria se e solo se Risp.: A : α = B : α = 1 C : α = 1 D : α = E : α = 3 F : α = 0 = 1, x 0, 9. Sia f : A R n R una funzione differenziabile in A. Sia x 0 A un punto di massimo assoluto interno ad A per f. Allora delle seguenti affermazioni (a) x 0 è un punto di massimo relativo per f (b) esiste almeno un punto x 1 A di minimo assoluto per f (c) esiste almeno un punto x A di minimo relativo per f (d) x 0 è un punto stazionario per f (e) f è continua in A le uniche corrette sono Risp.: A : a c e B : a b c C : a c d D : a d e E : b c e F : a b d 10. L integrale doppio T 3x x y + 1 dxdy, dove T = {(x, y) R : 0 x 1, y x y + 1} vale Risp.: A : log 4 B : log 3 C : log D : 3 log 3 E : 0 F :
6 Cognome e nome Firma Corso di Laurea: per l ambiente e il territorio ; dell automazione industriale; civile; gestionale; dell informazione; dei materiali; meccanica. Analisi Matematica B 14 aprile 003 Compito 1 Istruzioni. 1. COMPILARE la parte soprastante la prima riga continua. In particolare, scrivere cognome e nome in stampatello e la firma sopra la riga punteggiata e segnare il corso di laurea.. SEGNARE nelle due tabelle riportate in questa pagina, in modo incontrovertibile, la lettera corrispondente alla risposta scelta per ognuna delle domande riportate nel foglio allegato; in caso di correzione, apporre un SI vicino alla risposta scelta. 3. PUNTEGGI: risposta esatta = +3; risposta sbagliata = 0.5; risposta non data = PROIBITO usare libri, quaderni, calcolatori. 5. CONSEGNARE solo questo foglio. 6. TEMPO a disposizione: 150 min. Risposte relative ai fogli allegati
7 14 aprile 003 ANALISI MATEMATICA B RISULTATI Es.1 Es. Es.3 Es.4 Es.5 Compito 1 A C D F B Compito B A E C D Compito 3 C F B D E Compito 4 A D E F C Compito 5 C B E F E Compito 6 D F B E A Es.6 Es.7 Es.8 Es.9 Es.10 Compito 1 A E B D C Compito F E C B B Compito 3 C B A F E Compito 4 A F A E C Compito 5 B D C C A Compito 6 C E A F E
8 Analisi Matematica B settembre 003 Compito 1 1. L integrale e 1 1 x 1 log x dx vale Risp.: A : 3 B : e 3 C : π D : 3 E : 3π F : log. Sia ỹ(x) la soluzione del problema di Cauchy Allora ỹ(1) vale y + y = 3x y(0) = 0 y (0) = 6. Risp.: A : 4 B : 1 C : 0 D : 5 E : 1 4 F : 1 3. Sia f : A R R definita da f(x, y) = y arcsin x + π 3xy. Allora f( 1 9, ) vale Risp.: A : (, π 36 + π 3) F : (3 π, π 41 + π 3 ) B : ( 3 π, π 36 + π 3) C : ( 3 π, π 3) D : ( π 3, π 36 + π 18 3) E : ( π 3, π 36 ) 4. Sia f : R R la funzione definita da f(x, y) = (x y) cos(πx) + 7. Quanti punti stazionari ammette la funzione f nell insieme A = {(x, y) R : x <, y < }? Risp.: A : B : 1 C : 3 D : 6 E : 0 F : 4 5. Si consideri la funzione g(x, y) = x + y x y nel quadrato A = {(x, y) R : 0 x, 0 y }. Definendo M = max g(x, y), m = min g(x, y), si ha che (x,y) A (x,y) A Risp.: A : m =, M = B : m =, M = 0 C : m = 1, M = 1 D : m = 0, M = 1 E : m = 1, M = 4 F : m = 3, M = 3 6. Data la curva Γ di rappresentazione parametrica r (t) = (cos t) i1 + (sin t) i, 0 t π, la lunghezza della curva è Risp.: A : 3π B : π C : D : 3 E : 4 F : 4 7. Calcolare l integrale curvilineo 1, x 0, y 0} percorsa in senso antiorario. Γ xe x +y ds, dove Γ è la frontiera del settore circolare {(x, y) R : x +y Risp.: A : 4π B : eπ C : (e + 1) D : (e + 1) E : 3π F : 3(e + ) 1 8. Calcolare l integrale curvilineo Γ 1 + x dx + 1 dy, dove Γ è l arco di circonferenza di centro l origine e raggio + y 1, che unisce i punti A(1, 0) e B(0, 1) percorso in senso antiorario. Risp.: A : 0 B : log 3 π 4 C : log 3 π 3 D : log 3 π 4 E : log 4 3 π 3 F : log 9. Sia f : A R n R con A aperto. Sia f C 1 (A) con f x j affermazioni C 0 (A), per ogni j = 1,, n. Allora delle seguenti (a) f è differenziabile in A (b) f è continua in A (c) f ammette tutte le derivate direzionali in ogni x 0 A (d) f ammette massimo assoluto in A (e) f ammette minimo assoluto in A (f) i, j = 1,, n con i j, f x i x j = f x j x i in A le uniche corrette sono Risp.: A : a b c B : a c d C : a b e D : a c d f E : a d e f F : b c d e ( ) y 10. L integrale doppio xy exp T x + y dxdy, dove T = {(x, y) R : x 0, y 0, 1 x + y 4} vale Risp.: A : e 3 B : 15 8 (e 3) C : 15 8 (e 1) D : 1 8 (e 1) E : 15 8 e F : 15 8 (e + )
9 Cognome e nome Firma Corso di Laurea: per l ambiente e il territorio ; dell automazione industriale; civile; gestionale; dell informazione; dei materiali; meccanica. Analisi Matematica B settembre 003 Compito 1 Istruzioni. 1. COMPILARE la parte soprastante la prima riga continua. In particolare, scrivere cognome e nome in stampatello e la firma sopra la riga punteggiata e segnare il corso di laurea.. SEGNARE nelle due tabelle riportate in questa pagina, in modo incontrovertibile, la lettera corrispondente alla risposta scelta per ognuna delle domande riportate nel foglio allegato; in caso di correzione, apporre un SI vicino alla risposta scelta. 3. PUNTEGGI: risposta esatta = +3; risposta sbagliata = 0.5; risposta non data = PROIBITO usare libri, quaderni, calcolatori. 5. CONSEGNARE solo questo foglio. 6. TEMPO a disposizione: 150 min. Risposte relative ai fogli allegati
10 settembre 003 ANALISI MATEMATICA B RISULTATI Es.1 Es. Es.3 Es.4 Es.5 Compito 1 C A D F B Compito A D B C E Compito 3 B E A F C Compito 4 B C D E C Compito 5 A F C C F Compito 6 C E A D B Es.6 Es.7 Es.8 Es.9 Es.10 Compito 1 E C B A C Compito D A F B D Compito 3 A D C E F Compito 4 F C D F A Compito 5 D B E B D Compito 6 A D F C F
11 Analisi Matematica B 16 settembre 003 Compito 1 1. Sia F(t) la primitiva di f(t) = 4t (1+t ) tale che lim F(t) = 3. Allora F(0) vale t + Risp.: A : B : 4 C : 7π D : 0 E : 3π + 1 F : 1. Sia ỹ(x) la soluzione del problema di Cauchy Allora lim ỹ(x) vale x { y y(1 + e x ) = e x y(0) =. Risp.: A : B : 1 C : 4 log D : log E : 0 F : + 3. Sia f la funzione definita da f(x, y) = 1 (cos(πx)) 3xy + 3 log(x y) + 7. Allora il dominio di f è dato da: Risp.: A : metà del primo quadrante e metà del quarto quadrante B : metà del terzo quadrante e metà del secondo quadrante C : il primo quadrante D : metà del primo quadrante e metà del terzo quadrante E : il secondo quadrante F : il primo e il secondo quadrante 4. Sia f : R R la funzione definita da f(x, y) = x 3 y 7xy. Allora essa ammette Risp.: A : tre punti di sella B : due punti di sella e uno di minimo C : due punti di massimo e uno di sella D : tre punti di massimo E : tre punti di minimo F : un punto di sella, un punto di minimo e uno di massimo 5. Si consideri la funzione g(x, y) = x y xy + xy nel dominio A = {(x, y) R : x 0, y 0, x y 1}. Definendo M = max g(x, y), m = min g(x, y), si ha che (x,y) A (x,y) A Risp.: A : m = 0, M = 3 B : m = 1 7, M = 0 C : m = 1, M = 1 D : m = 1 3, M = 0 E : m = 1, M = 4 F : m =, M = 3 6. Data la curva Γ di rappresentazione parametrica r (t) = 4(cos t) i1 + (cos t + sin t) i, 0 t π, la lunghezza della curva è Risp.: A : 9π B : 4π C : π D : π 4 E : F : 4π 7. Calcolare l integrale curvilineo y(t) = sin log t con 1 t e. Γ xyds, dove Γ è la curva di equazioni parametriche x(t) = cos log t, Risp.: A : 3 B : 1 4 e3 C : 1 4 (1 cos 4) D : 1 cos 4 E : 1 4 F : 1 4 log ( ) xy 8. Calcolare l integrale curvilineo dx + 3y x Γ y x y x + 1 dy, dove Γ è la poligonale di vertici A = (0, 1), B = ( 1, ), C(1, ) percorsa da A verso C. Risp.: A : 3 B : 0 C : 4 D : E : 1 F : 3 9. Sia f : A R 3 R; sia x 0 R 3 un punto stazionario per f tale che esista un suo intorno I per cui f C (I). Sia H la matrice hessiana di f in x 0 e λ 1, λ, λ 3 i relativi autovalori. Allora delle seguenti implicazioni (a) λ 1 = λ = λ 3 = 1 x 0 è un punto di minimo relativo per f (b) λ 1 = λ = 1 e λ 3 = 0 x 0 è un punto di minimo relativo per f (c) λ 1 = λ = 1 e λ 3 = 0 è un caso dubbio (d) λ 1 = 1, λ = 1 e λ 3 = 0 è un caso dubbio (e)λ 1 = λ = 1 e λ 3 = 1 x 0 è un punto di sella per f (f) λ 1 = λ = λ 3 = 1 x 0 è un punto di sella per f le uniche corrette sono Risp.: A : a c e B : a b d C : a c d D : a b f E : b d e f F : b e f
12 10. L integrale doppio T (x y) 1 + (x y) dxdy, dove T = {(x, y) R : 0 x, 0 x y } vale Risp.: A : arctan B : 3 C : arctan D : 3 ( arctan ) E : F : ( arctan )
13 Cognome e nome Firma Corso di Laurea: per l ambiente e il territorio ; dell automazione industriale; civile; gestionale; dell informazione; dei materiali; meccanica. Analisi Matematica B 16 settembre 003 Compito 1 Istruzioni. 1. COMPILARE la parte soprastante la prima riga continua. In particolare, scrivere cognome e nome in stampatello e la firma sopra la riga punteggiata e segnare il corso di laurea.. SEGNARE nelle due tabelle riportate in questa pagina, in modo incontrovertibile, la lettera corrispondente alla risposta scelta per ognuna delle domande riportate nel foglio allegato; in caso di correzione, apporre un SI vicino alla risposta scelta. 3. PUNTEGGI: risposta esatta = +3; risposta sbagliata = 0.5; risposta non data = PROIBITO usare libri, quaderni, calcolatori. 5. CONSEGNARE solo questo foglio. 6. TEMPO a disposizione: 150 min. Risposte relative ai fogli allegati
14 16 settembre 003 ANALISI MATEMATICA B RISULTATI Es.1 Es. Es.3 Es.4 Es.5 Compito 1 F C D A B Compito A E F D C Compito 3 C B A E E Compito 4 F C C B B Compito 5 A E E C D Compito 6 C B B E E Es.6 Es.7 Es.8 Es.9 Es.10 Compito 1 B C C A F Compito C B E D A Compito 3 F F A F D Compito 4 B D C B E Compito 5 C B F C A Compito 6 F E A E D
15 Analisi Matematica B 18 dicembre 003 Compito 1 1. L integrale π π/ 1 + cos x dx vale Risp.: A : 4( 1) B : C : D : ( 1) E : 0 F :. La soluzione y(x) dell equazione x y = y(x 1) tale che lim x + y(x) x = è Risp.: A : y(x) = xe 1 x B : y(x) = xe x C : y(x) = xe 1 x D : y(x) = x E : y(x) = x +3x+3 x F : y(x) = x + e x 3. Sia f la funzione definita da f(x, y) = 4x y + + y log (7x). Allora il dominio di f è dato da Risp.: A : un semipiano B : un triangolo rettangolo con i cateti sugli assi coordinati C : un triangolo isoscele con i lati uguali sugli assi coordinati D : un trapezio rettangolo E : la parte di piano esterna a un triangolo F : l unione di due triangoli 4. Sia f(x, y) = xy (7x + 7y 1) e siano A + = {(x, y) R : x > 0, y > 0}, A = {(x, y) R : x > 0, y < 0}. Allora la funzione f ha Risp.: A : solamente un massimo locale in A + B : solamente un minimo locale in A C : solamente un massimo locale in A D : solamente un minimo locale in A + E : un minimo locale in A + e un massimo locale in F : un massimo locale in A + e un minimo locale in A A 5. Si consideri la funzione g(x, y) = x y nel dominio A = {(x, y) R : x 0, y 0, x + y 1}. Allora Risp.: A : ha infiniti punti di minimo assoluto e un massimo assoluto in ( 3, 1 3 ) B : non ha massimi e minimi assoluti C : ha infiniti punti di minimo assoluto e un massimo assoluto in ( 1 3, 3 ) D : ha minimo assoluto in (0, 0) e massimo assoluto in ( 1, 1 ) E : ha infiniti punti di massimo assoluto F : ha punti di massimo assoluto 6. Data la curva piana Γ di rappresentazione parametrica r (t) = 3 sin t cos t i 1 +3 sin 3 t i, 0 < t < π, la velocità scalare v (t), dove v (t) è il vettore velocità nel punto t = π 4 vale Risp.: A : 3 B : 5 C : 3 5 D : E : 3 F : Calcolare l integrale curvilineo Γ x ds, dove Γ è l arco di curva y(x) = log x, con 1 x. Risp.: A : 5 3/ 3/ B : 1 3 (53/ 3/ ) C : / D : 3 3/ 3/ E : 3 F : 3 /3 8. Calcolare l integrale curvilineo Γ xy dx + (x y + 4x)dy, dove Γ = Γ 1 Γ con Γ 1 circonferenza di rappresentazione parametrica r (t) = cos t i 1 + sin t i, 0 t 3 π e Γ è il segmento di estremi A = (0, ) e B = (, 0) percorso da A verso B. Risp.: A : (3π + ) B : 4(3π + 1) C : 3 D : 4(3π + ) E : 4(π + ) F : 3π 9. Sia F = (F 1, F ) : R R. Sia A R aperto connesso, F 1, F C 1 (A), F è un gradiente in A. Allora delle seguenti affermazioni (a) F è un gradiente in R (b) F è un gradiente in B A, B aperto connesso (c) F 1 y = F x in B A, B aperto connesso (d) Γ F dγ = 0 per ogni curva chiusa Γ con sostegno in R (e) F C (A) le uniche corrette sono Risp.: A : a c e B : b c C : a b D : c d E : d e F : b e
16 10. L integrale doppio T f(x, y) dxdy, dove T = {(x, y) R : 0 x 1, 0 y } e f(x, y) = { x + y se x + y 1 0 x y se x + y 1 < 0 vale Risp.: A : 35/6 B : 15/7 C : 1/6 D : 7/1 E : 5/6 F : 35/1
17 Cognome e nome Firma Corso di Laurea: per l ambiente e il territorio ; dell automazione industriale; civile; gestionale; dell informazione; dei materiali; meccanica. Analisi Matematica B 18 dicembre 003 Compito 1 Istruzioni. 1. COMPILARE la parte soprastante la prima riga continua. In particolare, scrivere cognome e nome in stampatello e la firma sopra la riga punteggiata e segnare il corso di laurea.. SEGNARE nelle due tabelle riportate in questa pagina, in modo incontrovertibile, la lettera corrispondente alla risposta scelta per ognuna delle domande riportate nel foglio allegato; in caso di correzione, apporre un SI vicino alla risposta scelta. 3. PUNTEGGI: risposta esatta = +3; risposta sbagliata = 0.5; risposta non data = PROIBITO usare libri, quaderni, calcolatori. 5. CONSEGNARE solo questo foglio. 6. TEMPO a disposizione: 150 min. Risposte relative ai fogli allegati
18
19 Analisi Matematica B 6 marzo 004 Compito 1 1. L area della regione limitata di piano individuata dalle funzioni f(x) = 1 4 x3 + e g(x) = x x + vale Risp.: A : 1 4 B : C : 1 D : 0 E : 1 F : 1 3. Sia ỹ(x) la soluzione del problema di Cauchy y y x = 3 x x +1 y(1) = 3 π 4. Allora ỹ( 3) vale Risp.: A : 3 π B 3 : 3 C 3 : 3 log 1 π 3 D : tan E 3 : 3 F : 3 3 π 3. Sia f la funzione definita da f(x, y) = sin x + 4y. Il piano tangente al grafico di f nel punto (π, 0, f(π, 0)) ha equazione Risp.: A : (z+x)+3y π = 0 B : π(z x)+3y+π = 0 C : π(z+x)+y π = 0 D : π (z+x)+y 3π = 0 E : z + x + 4y π = 0 F : z + x + πy π = 0 4. Sia f la funzione definita da f(x, y) = x y + y x. Allora per essa i punti P 1 (7, 7) e P (0, 1) sono 7 Risp.: A : P 1 di massimo e P non stazionario B : P 1 e P di massimo C : P 1 non stazionario e P di sella D : P 1 e P di sella E : P 1 di sella e P non stazionario F : P 1 di minimo e P di massimo 5. Si consideri la funzione g(x, y) = x + y x + nel dominio A = {(x, y) R : x + y 4}. Allora, definendo M = g(x, y) e m = min g(x, y), si ha max (x,y) A (x,y) A Risp.: A : M = 9 e m = B : M = 9 e m = 1 C : M = 10 e m = D : M = 10 e m = 1 E : M = 9 e m = 1 F : M = 10 e m = 6. Calcolare la lunghezza L della curva di rappresentazione parametrica r (t) = e t i 1 + e t i + t i 3, t [0, 1]. Risp.: A : L = e + B : L = e 3 C : L = e D : L = e E : L = e 3 + F : L = e Calcolare l integrale curvilineo Γ 1 z ds, dove Γ è la curva di rappresentazione parametrica r (t) = t cos t i 1 + t sin t i + t i 3, t [0, 1]. Risp.: A : 7(3 3/ 3/ ) B : 1(3 3/ 3/ ) C : 6(5 3/ 3 3/ ) D : (5 3/ 3/ ) E : 7(3 3/ 3/ ) 3 F : (3 3/ 3/ ) 3 8. Calcolare l integrale curvilineo (t sin t) i 1 + (1 cos t) i, 0 t π. Γ (4 y)dx + xdy, dove Γ è la curva di rappresentazione parametrica r (t) = Risp.: A : (3π + ) B : 8π C : 4(3π + 1) D : 8π E : 4(π + ) F : 3π 9. Sia Γ una curva piana rettificabile congiungente i punti (0, 0) e (14, 7) avente rappresentazione parametrica r (t), t [a, b]. Allora delle seguenti affermazioni (a) r C 1 ([a, b]) (b) detta L la lunghezza di Γ, vale L 7 5 (c) esiste almeno una poligonale inscritta in Γ avente lunghezza infinita (d) l estremo superiore delle lunghezze delle poligonali inscritte in Γ è finito (e) il vettore tangente ha lunghezza costante le uniche corrette sono Risp.: A : a b B : a c C : a d D : b d e E : c e F : b d 10. L integrale doppio 15 y dxdy 11 T Risp.: A : π B : 1 3 C : π 3 D : 3 E : 1 F :, dove T = {(x, y) R : x 0, x + y, x y} vale
20 Cognome e nome Firma Corso di Laurea: per l ambiente e il territorio ; dell automazione industriale; civile; gestionale; dell informazione; dei materiali; meccanica. Analisi Matematica B 6 marzo 004 Compito 1 Istruzioni. 1. COMPILARE la parte soprastante la prima riga continua. In particolare, scrivere cognome e nome in stampatello e la firma sopra la riga punteggiata e segnare il corso di laurea.. SEGNARE nelle due tabelle riportate in questa pagina, in modo incontrovertibile, la lettera corrispondente alla risposta scelta per ognuna delle domande riportate nel foglio allegato; in caso di correzione, apporre un SI vicino alla risposta scelta. 3. PUNTEGGI: risposta esatta = +3; risposta sbagliata = 0.5; risposta non data = PROIBITO usare libri, quaderni, calcolatori. 5. CONSEGNARE solo questo foglio. 6. TEMPO a disposizione: 150 min. Risposte relative ai fogli allegati
21 Prova scritta del 6 marzo 004 ANALISI MATEMATICA B RISULTATI Es.1 Es. Es.3 Es.4 Es.5 Compito 1 F A C E D Compito A B A F C Compito 3 C A C B D Compito 4 B B A E C Compito 5 F F C D D Compito 6 C E D B A Es.6 Es.7 Es.8 Es.9 Es.10 Compito 1 C A B F E Compito E D C A D Compito 3 F A B E F Compito 4 E F C D D Compito 5 A B E F C Compito 6 F C B E A
22 Analisi Matematica B 6 aprile 004 Compito 1 1. L integrale π/ 0 sin x + cos x 1 + sin x dx vale Risp.: A : log 3 π/4 B : log 3+π/4 C : log π/4 D : 3 log +π/ E : log +π/4 F : 3 log π/. Sia ỹ(x) la soluzione del problema di Cauchy y + y + y = 1, Allora lim ỹ(x) vale x + Risp.: A : 1 B : 1 C : D : 0 E : 3 F : 3 y(0) = 1, y (0) = Siano f la funzione definita da f(x, y) = log(3x + y) 3 x e v = ( 1, 1 ). Trovare il punto P = (x0, y 0 ) sulla bisettrice del primo e terzo quadrante, con ascissa positiva, tale che f v (x 0, y 0 ) = 0. Risp.: A : ( 3, ) 3 B : (, ) C : (1, 1) D : (, ) E : ( 1, ) 1 F : ( 1 3, ) Sia f la funzione definita da f(x, y) = log(x y) + log(y + 4). Allora f ammette Risp.: A : un unico punto di massimo B : un unico punto di minimo C : due punti di sella D : un unico punto di sella E : un punto di sella e uno di minimo F : un punto di sella e uno di massimo 5. Si consideri la funzione f(x, y) = x + y definita sull ellisse E di equazione g(x, y) := x xy + y 4 = 0. Posto M = f(x, y) e m = min f(x, y), si ha max (x,y) E (x,y) E Risp.: A : M = 3 e m = 3 B : M = 4 e m = 0 C : M = 0 e m = 4 D : M = 4 e m = 3 E : M = 3 e m = 4 F : M = 4 e m = 4 6. Sia L la lunghezza della curva di rappresentazione parametrica r(t) = e t cos t i 1 + e t sin t i, t [0, π]. Allora Risp.: A : L = + B : L = (1 e π ) C : L = (1 e π ) D : L = E : L = (1 e π ) F : L = 0 7. Calcolare l integrale curvilineo 8 x y dx + xy dy Γ esteso all arco di circonferenza Γ di rappresentazione parametrica r(t) = ( cos t, sin t ), Risp.: A : π B : π C : D : 4π E : 3 F : 4 t [0, π/]. 8. Dato il campo vettoriale F (x, y, z) = x(y z) i + x j + ( x + 3z ) k, sia ϕ il potenziale che vale nel punto (0, 0, 0). Si calcoli ϕ(7, 1, 1). Risp.: A : 1 B : 3 C : D : 1 E : 0 F : 9. Siano f : B R R con B insieme chiuso e limitato, A l insieme dei punti interni di B. Supponiamo che f sia continua in B e che f x e f y esistano e siano continue in A. Allora delle seguenti affermazioni (a) f differenziabile in A (b) f x y = f y x in A (c) f limitata in B (d) esistono tutte le derivate direzionali in ogni punto di A (e) f C (A) (f) f C 0 (A) le uniche corrette sono Risp.: A : (a) (b) B : (a) (d) (f) C : (c) (d) (e) D : (a) (c) (d) (f) E : (b) (c) (d) F : (a) (e) (f) 10. L integrale doppio Q y log(7xy + 1) (7xy + 1) log (y + 1) dxdy, Risp.: A : 1 14 B : 1 7 C : 0 D : 1 E : e F : 1 7 dove Q = [0, 1/7] [1, ] vale
23 Cognome e nome Firma Corso di Laurea: per l ambiente e il territorio ; dell automazione industriale; civile; gestionale; dell informazione; dei materiali; meccanica. Analisi Matematica B 6 aprile 004 Compito 1 Istruzioni. 1. COMPILARE la parte soprastante la prima riga continua. In particolare, scrivere cognome e nome in stampatello e la firma sopra la riga punteggiata e segnare il corso di laurea.. SEGNARE nelle due tabelle riportate in questa pagina, in modo incontrovertibile, la lettera corrispondente alla risposta scelta per ognuna delle domande riportate nel foglio allegato; in caso di correzione, apporre un SI vicino alla risposta scelta. 3. PUNTEGGI: risposta esatta = +3; risposta sbagliata = 0.5; risposta non data = PROIBITO usare libri, quaderni, calcolatori. 5. CONSEGNARE solo questo foglio. 6. TEMPO a disposizione: 150 min. Risposte relative ai fogli allegati
24 Prova scritta del 6 aprile 004 ANALISI MATEMATICA B RISULTATI Es.1 Es. Es.3 Es.4 Es.5 Compito 1 E A A D F Compito B D C B D Compito 3 C B E A E Compito 4 C C D E E Compito 5 F D A E A Compito 6 F A A C B Es.6 Es.7 Es.8 Es.9 Es.10 Compito 1 E B B D A Compito C F F B C Compito 3 E C C D A Compito 4 B E F D D Compito 5 D D D A E Compito 6 D D A B B
25 Analisi Matematica B 8 luglio 004 Compito 1 1. Sia F la primitiva della funzione f(x) = sin x + cos x tan x tale che lim F (x) = 1. Allora F ( x π/ 3π) vale Risp.: A : log B : log C : log D : log E : 3 + log 3+1 F : log 3. Sia ỹ(x) la soluzione del problema di Cauchy y y = 3e x y(0) = 3 y (0) = 1 y (0) = 1. Allora lim ỹ(x) vale x + Risp.: A : 4 B : 3 3 C : 3 log 3 D : 3 E : F : 3 3. Sia A R il dominio della funzione f definita da f(x, y) = 7y x + arcsin y. Allora l area di A vale Risp.: A : B : C : 7 D : 7 E 5 : 0 F : + 4. Sia f la funzione definita da f(x, y) = x 4 + y 3 4x 3y. Allora per essa i punti P 1 (0, 0), P (0, ), P 3 (, 3) sono Risp.: A : P 1 di massimo, P e P 3 non stazionari B : P 1 di massimo, P di sella e P 3 non stazionario C : P 1 e P di massimo, P 3 di sella D : P 1 non stazionario, P e P 3 di minimo E : P 1 e P di sella, P 3 non stazionario F : P 1 di minimo, P di sella e P 3 non stazionario 5. Si consideri la funzione g(x, y) = 3(x + y ) definita sull ellisse E di equazione ( ) x 1 + y = 1. Allora, definendo M = g(x, y) e m = min g(x, y), si ha max (x,y) E (x,y) E Risp.: A : M = 7 e m = 3 B : M = 3 e m = 1 C : M = 5 e m = 3 D : M = 5 e m = E : M = 3 e m = 1 F : M = 7 e m = 6. Sia data la curva piana di rappresentazione parametrica r (t) = 3(t sin t + cos t) i 1 + 3(t cos t sin t) i, t [0, π]. Il suo versore tangente T (t) calcolato nel punto t = π vale Risp.: A : T (π) = (1, 0) B : T (π) = (0, 1) C : T (π) = (0, 1) D : T (π) = ( 1, 1 ) E : T (π) = ( 1, 0) F : T (π) = ( 1, 1 ) 7. Calcolare l integrale curvilineo Γ 3 x ds, dove Γ è la curva di rappresentazione parametrica r (t) = sin t i 1 + cos t i, Risp.: A : 4 B : 3 3 C : 3 D : E : 5 F : 4 t [0, π]. 8. Calcolare l integrale curvilineo (xy + x 4)dx + (x + y)dy, dove Γ è il quarto di ellisse di equazione ) Γ + y = 1 contenuto nel primo quadrante, percorso in senso antiorario. ( x Risp.: A : (3π + ) B : 5 C : 4(3π + 1) D : 4 E : 4(π + ) F : 3π
26 9. Sia Q = [a, b] [c, d]. Sia f : Q R di classe C 0 (Q). Delle seguenti affermazioni (a) f è integrabile su Q (b) f C 1 (Q) (c) f è differenziabile in Q (d) f ammette almeno un punto di massimo assoluto in Q (e) f ammette almeno un punto di minimo assoluto in Q (f) esiste x 0 Q tale che f( x 0 ) = 0 le uniche corrette sono Risp.: A : a b B : d e C : a c e D : a d e E : d f F : a d e f 10. L integrale doppio T log(x 1) log y dxdy, dove T = {(x, y) R : x 3, 1 y } vale Risp.: A : (log +1) B : (log ) C : ( log 1) D : log + E : 4(log +1) F : 4(log log )
27 Cognome e nome Firma Corso di Laurea: per l ambiente e il territorio ; dell automazione industriale; civile; gestionale; dell informazione; dei materiali; meccanica. Analisi Matematica B 8 luglio 004 Compito 1 Istruzioni. 1. COMPILARE la parte soprastante la prima riga continua. In particolare, scrivere cognome e nome in stampatello e la firma sopra la riga punteggiata e segnare il corso di laurea.. SEGNARE nelle due tabelle riportate in questa pagina, in modo incontrovertibile, la lettera corrispondente alla risposta scelta per ognuna delle domande riportate nel foglio allegato; in caso di correzione, apporre un SI vicino alla risposta scelta. 3. PUNTEGGI: risposta esatta = +3; risposta sbagliata = 0.5; risposta non data = PROIBITO usare libri, quaderni, calcolatori. 5. CONSEGNARE solo questo foglio. 6. TEMPO a disposizione: 150 min. Risposte relative ai fogli allegati
28 8 luglio 004 ANALISI MATEMATICA B RISULTATI Es.1 Es. Es.3 Es.4 Es.5 Compito 1 C A A B F Compito F F D C E Compito 3 A C F E B Compito 4 B C A D F Compito 5 F B D C E Compito 6 A D F E B Es.6 Es.7 Es.8 Es.9 Es.10 Compito 1 E A B D C Compito A E B A D Compito 3 D A D E F Compito 4 C E B A B Compito 5 B A D F C Compito 6 C B F E A
29 Analisi Matematica B 8 aprile 005 Compito 1 1. L integrale π/ sin dx vale x + cos x Risp.: A : π B : π C : 3 π D : E : 3π F : 3 3π. Sia ỹ(x) la soluzione del problema di Cauchy x y (x) + 3y(x) = 1 x y(1) = 5. Allora ỹ() vale Risp.: A : 3 4 B : 3 C : 3 D : 5 4 E : 3 F : 5 3. Sia f : R R la funzione definita da f(x, y) = Calcolare f v (0, 0), dove v = ( 1, 1 ). { x + (y x) se xy 0 x + y + y 3 se xy < 0. Risp.: A : 1 B : 1 C : D : E : 3 F : 3 4. Sia f : R R la funzione definita da f(x, y) = 4x 3 +3y 1xy. Allora per essa i punti P 1 = (0, ) e P = (, 4) sono Risp.: A : P 1 di massimo relativo e P non stazionario B : P 1 e P di minimo relativo C : P 1 non stazionario e P di massimo relativo D : P 1 e P di sella E : P 1 non stazionario e P di minimo relativo F : P 1 di minimo relativo e P di sella 5. Si consideri la funzione g(x, y) = x y 3 definita su Q = [ 1, 1] [0, ]. Allora, posti M = g(x, y) e m = min g(x, y), si ha max (x,y) Q (x,y) Q Risp.: A : M = e m = 0 B : M = 3 3 e m = 1 C : M = 1 e m = 0 D : M = 1 e m = 1/ E : M = 3 3 e m = 1 F : M = 3 3 e m = 0 6. Sia data la curva piana di rappresentazione parametrica r (t) = cos t i 1 + cos t sin t i, t [0, π]. Il suo versore tangente T (t) calcolato nel punto t = π 4 vale Risp.: A : T ( π 4 ) = ( 1, 0) B : T ( π 4 ) = (1, 0) C : T ( π 4 ) = (0, 1) D : T ( π 4 ) = (0, 1) E : T ( π 4 ) = ( 1, 1 ) F : T ( π 4 ) = ( 1, 1 ) 7. Calcolare l integrale curvilineo Risp.: A : Γ B : 10 C : (y/3) ds, dove Γ è il segmento di estremi (0, 0) e (1/, 3/). 1 x 3 D : 7 5 E : F : 6 7 ( 1 y + 8. Si considerino il campo vettoriale y x x F (x, y) definito da F (x, y) = i 1 + y x y x e l integrale curvilineo I = F d r, dove Γ è il segmento di estremi A = (0, 1) e B = (, 5), percorso da A verso B. Allora Γ ) i Risp.: A : F non è conservativo e I = log 5 B : F è conservativo e I = + log 5 C : F è conservativo e I = 3 log 10 D : F non è conservativo e I = 3 + log E : F è conservativo e I = log 5 F : F non è conservativo e I = log 10
30 Analisi Matematica B 8 aprile 005 Compito 1 9. Sia F (x, y) = F 1 (x, y) i 1 + F (x, y) i un campo vettoriale definito in A aperto connesso di R. Sia F C 0 (A) e F abbia integrale curvilineo indipendente dalla traiettoria. Allora delle seguenti affermazioni (a) F è un gradiente in A (b) esistono F 1 y, F x in A e F 1 y = F x in A (c) F dγ = 0 per ogni curva chiusa Γ Γ regolare con sostegno in A (d) F ammette potenziale ϕ C (A) (e) per ogni P, Q A esiste ϕ 1 : A R, ϕ 1 C 1 (A) tale che F dγ1 = ϕ 1 (Q) ϕ 1 (P ), per ogni curva Γ 1 regolare con sostegno in A e di estremi P e Q Γ 1 (f) F 1 e F sono differenziabili in A le uniche corrette sono Risp.: A : a c B : b d e C : a b c f D : a c e E : d f F : a d e 10. L integrale doppio Risp.: A : T ( ) 5x y + 6 dxdy, dove T = {(x, y) R : x + y 1, y 0, y x} vale π B : C 4 : π D : E 3 4 : π F : π
31 Cognome e nome Firma Corso di Laurea: per l ambiente e il territorio ; dell automazione industriale; civile; gestionale; dell informazione; dei materiali; meccanica. Analisi Matematica B 8 aprile 005 Compito 1 Istruzioni. 1. COMPILARE la parte soprastante la prima riga continua. In particolare, scrivere cognome e nome in stampatello e la firma sopra la riga punteggiata e segnare il corso di laurea.. SEGNARE nelle due tabelle riportate in questa pagina, in modo incontrovertibile, la lettera corrispondente alla risposta scelta per ognuna delle domande riportate nel foglio allegato; in caso di correzione, apporre un SI vicino alla risposta scelta. 3. PUNTEGGI: risposta esatta = +3; risposta sbagliata = 0.5; risposta non data = PROIBITO usare libri, quaderni, calcolatori. 5. CONSEGNARE questo foglio e i fogli su cui sono stati svolti gli esercizi. 6. TEMPO a disposizione: 150 min. Risposte relative ai fogli allegati
32 8 APRILE 005 ANALISI MATEMATICA B SECONDO APPELLO RISULTATI Es.1 Es. Es.3 Es.4 Es.5 Compito 1 B A D E F Compito A B F A C Compito 3 C F A B D Compito 4 A A D F C Compito 5 C B F A D Compito 6 D F A E B Es.6 Es.7 Es.8 Es.9 Es.10 Compito 1 A C B D F Compito B E F E D Compito 3 E A C A C Compito 4 B C B E F Compito 5 E E F A B Compito 6 D A C F C
33 Analisi Matematica B 30 giugno 005 Compito 1 1. L integrale 3 0 3x (1 + x dx vale ) Risp.: A : arctan B : 3 (arctan ) C : 3 arctan 3 D : 9 10 E : arctan F : 3 y (x) = e x y. Sia ỹ(x) la soluzione del problema di Cauchy Allora lim ỹ(x) vale x y(0) = 3. Risp.: A : log(e 3 1) B : 3 C : log(e 3 + 1) D : log(e 3 1) E : 3 F : e Siano f, g le funzioni definite da f(x, y) = 1 7(x + y ) (x + y ) e g(x, y) = log(1 7(x + y )) + xy. Siano D f e D g i domini di f e g rispettivamente. Allora Risp.: A : D f Dg = B : D f Dg = R C : D f \ D g è una circonferenza D : D g è limitato e D f è illimitato E : D f è limitato e D g è illimitato F : D f D g 4. Sia f la funzione definita da f(x, y) = x y + 48 x + 8 y per (x, y) R \ {x = 0 y = 0}. Allora per essa i punti P 1 = (, ), P = (, ) e P 3 = (, ) sono Risp.: A : P 1 di massimo relativo e P non stazionario e P 3 di sella B : P 1 e P di minimo relativo e P 3 di sella C : P 1 non stazionario, P di minimo relativo e P 3 di sella D : P 1 non stazionario e P e P 3 di minimo relativo E : P 1 e P di sella e P 3 di minimo relativo F : P 1 non stazionario P e P 3 di sella 5. Si consideri la funzione f(x, y) = sin(y αx) con α R e l insieme A = {(x, y) R : x < 0, 0 y 1 x ex }. Allora Risp.: A : f ammette massimo ma non minimo su A per ogni α R B : f ammette minimo ma non massimo su A per ogni α R C : f non ammette massimo e minimo su A per ogni α R D : f ammette massimo ma non minimo su A per α > 0 E : f ammette minimo ma non massimo su A per α > 0 F : f ammette massimo e minimo su A per ogni α R 6. Sia data la curva di rappresentazione parametrica r (t) = 7e t cos t i 1 + 7e t sin t i + 7e t i 3, t [ 1, ]. Allora l ascissa curvilinea s(t), calcolata a partire da t = 0, vale Risp.: A : 7(e t 1) B : 3(e t 1) C : 7 3e t D : 7 3(e t 1) E : 7 3(e t 5) F : 7 3(e t 3) 7. Calcolare l integrale curvilineo Γ y 3/ ds, r (t) = (t sin t) i 1 + (1 cos t) i, t [0, π] dove Γ è la curva di rappresentazione parametrica Risp.: A : 6 B : 6π C : 6π 3 D : π E : 6π F : 8. Si consideri il campo vettoriale F (x, y) = e x+y8( (arctan x x ) i 1 + 8y 7 arctan x ) i. Sia φ(x, y) il suo potenziale tale che φ(0, ) = 7. Allora φ(1, 1) vale Risp.: A : πe B : πe + 7 C : πe + 7 D : e E : πe 4 7 F : πe
34 Analisi Matematica B 30 giugno 005 Compito 1 9. Sia f : [a, b] R, f C 1 ([a, b]). Allora delle seguenti affermazioni (a) F : [a, b] R tale che F (x) = x 1 b f(t)dt è derivabile in ]a, b[ (b) c [a, b] tale che f(c) = a b a a f(t)dt c [a, b] tale che f (c) = 0 (d) c [a, b] tale che f(c) = 0 (e) b a f (t)dt = f(b) f(a) (f) la curva Γ avente rappresentazione parametrica r (t) = t i 1 + f(t) i, t [a, b] è rettificabile le uniche corrette sono Risp.: A : a b c f B : a b e f C : a c e f D : b c e f E : a d e f F : a d e 10. L integrale doppio vale T ( y log(y + 3) ) dxdy (x + 1) (x + y + 3) Risp.: A : log 5 B : 1 4 log 5 C : 1 3 log 5 D : 1 4 log 5 E : 1 4 log 5 F : 1 3 log3 5 (c), dove T = {(x, y) R : 0 x y }
35 Cognome e nome Firma Corso di Laurea: per l ambiente e il territorio ; dell automazione industriale; civile; gestionale; dell informazione; dei materiali; meccanica. Analisi Matematica B 30 giugno 005 Compito 1 Istruzioni. 1. COMPILARE la parte soprastante la prima riga continua. In particolare, scrivere cognome e nome in stampatello e la firma sopra la riga punteggiata e segnare il corso di laurea.. SEGNARE nelle due tabelle riportate in questa pagina, in modo incontrovertibile, la lettera corrispondente alla risposta scelta per ognuna delle domande riportate nel foglio allegato; in caso di correzione, apporre un SI vicino alla risposta scelta. 3. PUNTEGGI: risposta esatta = +3; risposta sbagliata = 0.5; risposta non data = PROIBITO usare libri, quaderni, calcolatori. 5. CONSEGNARE questo foglio e i fogli su cui sono stati svolti gli esercizi. 6. TEMPO a disposizione: 150 min. Risposte relative ai fogli allegati
36 30 giugno 005 ANALISI MATEMATICA B TERZO APPELLO RISULTATI Es.1 Es. Es.3 Es.4 Es.5 Compito 1 B A C C F Compito D F A E B Compito 3 E B E D A Compito 4 B D C A F Compito 5 A F D E D Compito 6 E B E F B Es.6 Es.7 Es.8 Es.9 Es.10 Compito 1 D E A B D Compito C C E E A Compito 3 F F C D E Compito 4 D E E C D Compito 5 B C F D B Compito 6 F A C E A
37 Analisi Matematica B 19 settembre 005 Compito 1 1. L integrale Risp.: arctan e x cosh x dx vale A : arctan e π 16 B : 3 arctan e C : 3(arctan e π 16 ) D : 3 16 π E : 3(arctan e + π 16 ) F : 3(arctan e + π 16 ). Sia y(x) la soluzione del problema di Cauchy Allora y (0) vale y (x) + y(x) = e 3x y(0) = 3. Risp.: A : 3 B : C : 5 D : 1 E : 5 F : 4 3. Siano f : R R e g : R R le funzioni definite da g(x, y) = x 7y + 1. Allora posto h = g f si ha che h(0, 0) vale f (x, y) = (x y, x + y + 1) e Risp.: A : ( 14, 14) B : (14, 14) C : ( 14, 14) D : ( 7, 7) E : (7, 7) F : ( 7, 7) 4. Sia f la funzione definita da f(x, y) = 1 log(x + y ) x + y + 3 per (x, y) R \ (0, 0). Allora per essa i punti P 1 = ( 5, 1 5 ), P = ( 1 5, 5 ) sono Risp.: A : P 1 di minimo relativo e P non stazionario B : P 1 di sella e P non stazionario C : P 1 di massimo relativo e P non stazionario D : P 1 non stazionario e P di sella E : P 1 non stazionario e P di minimo relativo F : P 1 non stazionario e P di massimo relativo 5. Si consideri la funzione f(x, y) = (x + y) y + x e il triangolo chiuso A di vertici (0, 0), (1, 0) e (0, 1). Allora posti M = max (x,y) A f(x, y) e m = min (x,y) A f(x, y) si ha Risp.: A : M = 1, m = 0 B : M = 3, m = 0 C : M =, m = 0 D : M = 4, m = 0 E : M =, m = 1 F : M = 3, m = 1 6. Sia data la curva di rappresentazione parametrica r (t) = cos t i 1 + sin t i + αt i 3, t [0, π], α R +. Allora r (t) = 3 se e solo se Risp.: A : α = 3 B : α = 5 C : α = 5 D : α = E : α = 4 F : α = 1 7. Calcolare l integrale curvilineo r (t) = cosh t i 1 + sinh t i, t [0, log ]. Γ 5y x x + y ds, dove Γ è la curva di rappresentazione parametrica Risp.: A : 1 B : 1 C : D : E : 5 F 3 : 3 8. Sia α R. Si consideri il campo vettoriale [ (log x + 1)(e F (x, y) = x x y + 1) i e y 1 + sinh(7αy) ] i. Allora F è conservativo se e solo se Risp.: A : α = 7 B : α = 1 7 C : α D : α = E : α = 3 7 F : α = 1 7
38 Analisi Matematica B 19 settembre 005 Compito 1 9. Sia A aperto di R 3, f : A R, f C (A), (x 0, y 0, z 0 ) A tale che f(x 0, y 0, z 0 ) = 0 e deth f (x 0, y 0, z 0 ) < 0. Allora delle seguenti affermazioni (a) (x 0, y 0, z 0 ) è un punto di sella per f (b) (x 0, y 0, z 0 ) è un punto stazionario per f (c) f è differenziabile in A (d) f x (x 0, y 0, z 0 ) = f y (x 0, y 0, z 0 ) (e) f y z = f z y in A (f) (x 0, y 0, z 0 ) è un punto di massimo relativo per f le uniche corrette sono Risp.: A : a b c f B : a c e f C : b c e D : b c d e E : a d e f F : a b d 10. L integrale doppio T x + 5y (x + y ) 3/4 dxdy, dove T = {(x, y) R : x 0, y 3x, x + y 9} vale Risp.: A : 6 3 B : 6 C : 6+ 3 D : E : F : 3
39 Cognome e nome Firma Corso di Laurea: per l ambiente e il territorio ; dell automazione industriale; civile; gestionale; dell informazione; dei materiali; meccanica. Analisi Matematica B 19 settembre 005 Compito 1 Istruzioni. 1. COMPILARE la parte soprastante la prima riga continua. In particolare, scrivere cognome e nome in stampatello e la firma sopra la riga punteggiata e segnare il corso di laurea.. SEGNARE nelle due tabelle riportate in questa pagina, in modo incontrovertibile, la lettera corrispondente alla risposta scelta per ognuna delle domande riportate nel foglio allegato; in caso di correzione, apporre un SI vicino alla risposta scelta. 3. PUNTEGGI: risposta esatta = +3; risposta sbagliata = 0.5; risposta non data = PROIBITO usare libri, quaderni, calcolatori. 5. CONSEGNARE questo foglio e i fogli su cui sono stati svolti gli esercizi. 6. TEMPO a disposizione: 150 min. Risposte relative ai fogli allegati
40 19 settempre 005 ANALISI MATEMATICA B QUARTO APPELLO RISULTATI Es.1 Es. Es.3 Es.4 Es.5 Compito 1 C E A B C Compito D A F D B Compito 3 F C E E E Compito 4 A E B B D Compito 5 B B F F C Compito 6 E C E D E Es.6 Es.7 Es.8 Es.9 Es.10 Compito 1 C B F D E Compito E C E C A Compito 3 A D B E B Compito 4 C E F B E Compito 5 E C A E D Compito 6 A A B B F
41 Analisi Matematica B 14 dicembre 005 Compito 1 3 log x 1. L integrale 1 x ( 9 log ) dx vale x ( ) ( Risp.: A : 1 log 9 B : 1 9 log 3 ( ) log F : log 3 9 log log 3 ) ( C : log 9 9 log 3 ) ( D : log 9 9 log 3 ) E : 1 log ( 3 9 log 3 ). Sia y(x) la soluzione del problema di Cauchy ( 1 + e 7x ) yy = e 7x y(0) = 1. Allora 1 (y (x) 1) vale ( Risp.: A : 1 7 log 1+e 7x ) F : 1 7 log ( 1 + e 7x) ( B : log ) 1+e 7x C : 1 7 log ( ) 1+e 7x ( D : log ) 1+e 7x E : 1 7 log ( 1 + e 7x) 3. Siano α > 0, E α = {(x, y) R : 0 y < αx} e sia v = (11, 7). Allora la funzione x se (x, y) Eα f(x, y) = x xy se (x, y) E α è derivabile in (0, 0) nella direzione individuata da v se e solo se Risp.: A : 0 < α 7 11 B : α > 7 11 C : 0 < α 11 7 D : α > 11 7 E : α 11 F : α 7 4. Sia f : R R la funzione definita da f(x, y) = x 3 y + 7xy 3. Allora Risp.: A : f non ammette punti stazionari B : f ammette un punto di sella e un punto di minimo C : f ammette solo un punto di minimo D : f ammette solo un punto di sella E : f ammette solo un punto di massimo F : f ammette un punto di minimo e un punto di massimo 5. Sia Q = [ 1, 1] [ 1, 1] e sia f(x, y) = 3y x + y. Allora detti m e M il minimo e il massimo di f su Q si ha Risp.: A : m = 0 e M = 6 B : m = 6 e M = 0 C : m = 6 e M = 3 4 D : m = 3 4 e M = 6 E : m = 0 e M = 3 4 F : m = 6 e M = 6 6. Sia data la curva piana di rappresentazione parametrica r (t) = (t sin t + cos t) i 1 + ( t cos t + sin t) i, t [ π, π]. Allora la sua lunghezza è Risp.: A : π B : π C : 4π D : π E : π F : 0 7. Calcolare l integrale curvilineo Γ xe x +y ds, {(x, y) R : x + y, x 0, y 0} Risp.: dove Γ è la frontiera del settore circolare A : ( +1)e 1 B : e C : e D : 3e 1 E : 5e 1 F : 5 e 8. Dato il campo vettoriale F : R R definito da F (x, y) = 3 y arctan x ( ) 1 + x i 1 + log 3 arctan x i, sia ϕ il suo potenziale che vale 0 nel punto (0, 7). Allora ϕ(1, 1) vale Risp.: A : 3 16 π B : 3 16 π C : 9 16 π D : 3 4 π E : 9 4 π F : 3 4 π
42 9. Siano A aperto di R, B A aperto semplicemente connesso, e sia F = (F 1, F ) : A R R tale che F C 1 (A) e rot F = 0 su A. Delle seguenti affermazioni (a) F è un gradiente in A (b) F è un gradiente in B (c) F1 y in A (e) F1 x le uniche corrette sono = F y in A (f) F ha integrale curvilineo indipendente dalla traiettoria in B Risp.: A : a b c f B : c d C : b c f D : b f E : a b e f F : c d f = F x in A (d) se F C (A) allora F è un gradiente 10. L integrale doppio T 8 y 3 (x + y ) 3 dxdy dove T = {(x, y) R : 1 x + y 4, 3x y 3x} vale Risp.: A : 5 B : 0 C : 10 3 D : 0 3 E : 5 F : 3
43 14 dicembre 005 ANALISI MATEMATICA B QUINTO APPELLO RISULTATI Es.1 Es. Es.3 Es.4 Es.5 Compito 1 B C A D F Compito A D F B A Compito 3 F E C C B Compito 4 D A F B D Compito 5 C C E D B Compito 6 E F D E C Es.6 Es.7 Es.8 Es.9 Es.10 Compito 1 A E B C A Compito E B A D F Compito 3 D A F A E Compito 4 B F E E B Compito 5 F D D A C Compito 6 C B B F D
Cognome e nome... Firma... Matricola...
 Analisi Matematica B 0 gennaio 2017 COMPITO 1 Cognome e nome................................ Firma................ Matricola................ Corso di Laurea: AMBL; CIVL; GESL. Istruzioni 1. COMPILARE la
Analisi Matematica B 0 gennaio 2017 COMPITO 1 Cognome e nome................................ Firma................ Matricola................ Corso di Laurea: AMBL; CIVL; GESL. Istruzioni 1. COMPILARE la
x + 2x(e 1 x 1) 4 lim x sinh 1 x E : 0 F :
 ANALISI MATEMATICA 1 - PARTE II 11 gennaio 2010 Compito 1 1. Il limite vale sin 1 lim x sinh 1 x x + 2x(e 1 x 1) 4 Risp.: A : 1 B : e 6 C : e D : 1 6 E : 0 F : 2. Sia y(x) la soluzione del problema di
ANALISI MATEMATICA 1 - PARTE II 11 gennaio 2010 Compito 1 1. Il limite vale sin 1 lim x sinh 1 x x + 2x(e 1 x 1) 4 Risp.: A : 1 B : e 6 C : e D : 1 6 E : 0 F : 2. Sia y(x) la soluzione del problema di
Cognome e nome... Matricola... Firma...
 Analisi Matematica I 7 Settembre 06 Compito Cognome e nome................................ Matricola................ Firma................ Corso di Laurea: edile-architettura Istruzioni. COMPILARE la parte
Analisi Matematica I 7 Settembre 06 Compito Cognome e nome................................ Matricola................ Firma................ Corso di Laurea: edile-architettura Istruzioni. COMPILARE la parte
x + 2x(e 1 x 1) 4 lim x sinh 1 x E : 0 F : Re(z + 3) e iπ/2 z 2 z z 5(z + z)i Im i 3 R n! (n + 1) n sin lim E : α 0 F : α > 1 3 D : α < 1 3
 ANALISI MATEMATICA 1 11 gennaio 2010 Compito 1 1. Il limite sin 1 lim x sinh 1 x x + 2x(e 1 x 1) 4 Risp.: A : 1 B : 1 6 C : e 6 D : e E : 0 F : 2. Sia y(x) la soluzione del problema di Cauchy y 4 sin x
ANALISI MATEMATICA 1 11 gennaio 2010 Compito 1 1. Il limite sin 1 lim x sinh 1 x x + 2x(e 1 x 1) 4 Risp.: A : 1 B : 1 6 C : e 6 D : e E : 0 F : 2. Sia y(x) la soluzione del problema di Cauchy y 4 sin x
y 6y + 5y = e 5x y(0) = 0 y (0) = 5 4.
 ANALISI MATEMATICA febbraio 25 Compito. Il numero complesso ( ) 6 3+i +i Risp.: A : 8i B : i C : i D : 8i E : 4i F : 4i 2. Il limite della successione lim n + (log(7 + 2en ) n) Risp.: A : B : e 2 C : +
ANALISI MATEMATICA febbraio 25 Compito. Il numero complesso ( ) 6 3+i +i Risp.: A : 8i B : i C : i D : 8i E : 4i F : 4i 2. Il limite della successione lim n + (log(7 + 2en ) n) Risp.: A : B : e 2 C : +
arctan y Stabilire se esistono (ed in caso affermativo calcolarle) f (0, 0) non esistono, mentre g(x, y) = (x y + 1) log(x y + 1)
 Analisi Matematica II FACSIMILE 1 FOGLIO A Cognome e nome................................ Firma................ Matricola................ Corso di Laurea: MECLT MATLT AUTLT EDIQQ Istruzioni 1. COMPILARE
Analisi Matematica II FACSIMILE 1 FOGLIO A Cognome e nome................................ Firma................ Matricola................ Corso di Laurea: MECLT MATLT AUTLT EDIQQ Istruzioni 1. COMPILARE
CODICE= Compiti di Analisi Matematica II per il Corso di Laurea in Ingegneria Edile A.A , Appelli 1, 2, 3 e 4
 Compiti di Analisi Matematica II per il Corso di Laurea in Ingegneria Edile A.A. 00-0, Appelli,, 3 e 4 Cognome: Nome: Matricola: CODICE = 33877 A B C D E 3 4 5 6 7 8 9 CODICE=33877 PARTE A. Lo sviluppo
Compiti di Analisi Matematica II per il Corso di Laurea in Ingegneria Edile A.A. 00-0, Appelli,, 3 e 4 Cognome: Nome: Matricola: CODICE = 33877 A B C D E 3 4 5 6 7 8 9 CODICE=33877 PARTE A. Lo sviluppo
Ingegneria Elettronica Prova scritta di Analisi Matematica II del giorno ( 3) n x n n + 1
 Prova scritta di Analisi Matematica II del giorno 31-01-2007 1) Studiare la serie di potenze ( 3) n x n n + 1 2) Determinare i punti di estremo relativo ed assoluto della funzione seguente f(x, y) = x
Prova scritta di Analisi Matematica II del giorno 31-01-2007 1) Studiare la serie di potenze ( 3) n x n n + 1 2) Determinare i punti di estremo relativo ed assoluto della funzione seguente f(x, y) = x
Analisi Matematica 2 (Corso di Laurea in Informatica)
 COGNOME NOME Matr. Firma dello studente A Tempo: 3 ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
COGNOME NOME Matr. Firma dello studente A Tempo: 3 ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
Prima prova in itinere di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2017/2018. Prof. M. Bramanti.
 Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 07/08. Prof. M. Bramanti Tema n 4 5 6 Tot. Cognome e nome (in stampatello) codice persona (o n
Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 07/08. Prof. M. Bramanti Tema n 4 5 6 Tot. Cognome e nome (in stampatello) codice persona (o n
ESERCIZI DI ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 2006/2007
 ESERCIZI I ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 006/007 1 FUNZIONI IN UE VARIABILI (I parte) Insiemi di definizione eterminare gli insiemi di definizione delle seguenti funzioni in due
ESERCIZI I ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 006/007 1 FUNZIONI IN UE VARIABILI (I parte) Insiemi di definizione eterminare gli insiemi di definizione delle seguenti funzioni in due
1. Riconoscere la natura delle coniche rappresentate dalle seguenti equazioni e disegnarle:
 Università degli Studi della Basilicata Corsi di Laurea in Chimica / Scienze Geologiche Matematica II A. A. 204-205 (dott.ssa Vita Leonessa) Esercizi proposti n. 3: Funzioni a due variabili. Riconoscere
Università degli Studi della Basilicata Corsi di Laurea in Chimica / Scienze Geologiche Matematica II A. A. 204-205 (dott.ssa Vita Leonessa) Esercizi proposti n. 3: Funzioni a due variabili. Riconoscere
Politecnico di Bari - A.A. 2012/2013 Corso di Laurea in Ingegneria Elettrica Esame di ANALISI MATEMATICA - 3 Luglio 2013.
 Esame di ANALISI MATEMATICA - 3 Luglio 2013 (1) Studiare il carattere della serie numerica n 1( 1) n F 0 (n), dove F (x) = Z x 0 log(1 + e t2 ) dt (x 1). (6 punti) log(1 + e t2 ) (2) ata la funzione f(x,
Esame di ANALISI MATEMATICA - 3 Luglio 2013 (1) Studiare il carattere della serie numerica n 1( 1) n F 0 (n), dove F (x) = Z x 0 log(1 + e t2 ) dt (x 1). (6 punti) log(1 + e t2 ) (2) ata la funzione f(x,
Esercizi di Analisi Matematica II assegnati nell A.A. 2011/12. Corsi di laurea in Ingegneria Elettronica ed Informatica
 Esercizi di Analisi Matematica II assegnati nell A.A. 2011/12 Corsi di laurea in Ingegneria Elettronica ed Informatica 1) Rappresentare nel piano xy i campi di esistenza delle seguenti funzioni: a) xy
Esercizi di Analisi Matematica II assegnati nell A.A. 2011/12 Corsi di laurea in Ingegneria Elettronica ed Informatica 1) Rappresentare nel piano xy i campi di esistenza delle seguenti funzioni: a) xy
6. Integrali curvilinei
 6. Integrali curvilinei Davide Catania davide.catania@unibs.it Esercitazioni di Analisi Matematica 2 A.A. 2016/17 Integrali curvilinei di campi scalari Integrali curvilinei di campi vettoriali Campi vettoriali
6. Integrali curvilinei Davide Catania davide.catania@unibs.it Esercitazioni di Analisi Matematica 2 A.A. 2016/17 Integrali curvilinei di campi scalari Integrali curvilinei di campi vettoriali Campi vettoriali
ANALISI MATEMATICA 2 - INGEGNERIA MECCANICA ED ENERGETICA A.A PROVA SCRITTA DEL 28/1/19
 ANALISI MATEMATICA - INGEGNERIA MECCANICA E ENERGETICA A.A. 8-9 PROVA SCRITTA EL 8//9 Scrivere nome cognome e numero di matricola in stampatello su tutti i fogli da consegnare. Consegnare solo la bella
ANALISI MATEMATICA - INGEGNERIA MECCANICA E ENERGETICA A.A. 8-9 PROVA SCRITTA EL 8//9 Scrivere nome cognome e numero di matricola in stampatello su tutti i fogli da consegnare. Consegnare solo la bella
si ha La lunghezza L si calcola per ciascun tratto L = (2t)2 + (3t 2 ) dt+ 2 (3t2 ) 2 + (2t) 2 dt = 4t2 + 9t 4 dt = t
 ANALISI VETTORIALE Soluzione esercizi 1 gennaio 211 6.1. Esercizio. Sia Γ la curva regolare a tratti di rappresentazione parametrica x = t 2, y = t, t [, 1] e x = t, y = t 2, t [1, 2] calcolare la lunghezza,
ANALISI VETTORIALE Soluzione esercizi 1 gennaio 211 6.1. Esercizio. Sia Γ la curva regolare a tratti di rappresentazione parametrica x = t 2, y = t, t [, 1] e x = t, y = t 2, t [1, 2] calcolare la lunghezza,
Corso di Laurea in Ingegneria Gestionale - Sede di Fermo Anno Accademico 2009/2010 Matematica 2 Esercizi d esame
 Corso di Laurea in Ingegneria Gestionale - ede di Fermo Anno Accademico 2009/2010 Matematica 2 Esercizi d esame Nome... N. Matricola... Fermo, gg/mm/aaaa 1. tabilire l ordine di ciascuna delle seguenti
Corso di Laurea in Ingegneria Gestionale - ede di Fermo Anno Accademico 2009/2010 Matematica 2 Esercizi d esame Nome... N. Matricola... Fermo, gg/mm/aaaa 1. tabilire l ordine di ciascuna delle seguenti
Esercizi. f(x, y, z) = exp(xz) + zy sin(xyz) + cos(xy 3 )
 Esercizi 1. Determinare le derivate parziali di f(x, y, z) = exp(xz) + zy sin(xyz) + cos(xy 3 ) 2. Scrivere l equazione del piano tangente e della retta normale al grafico ln(xy) + cos(x + y) nel punto
Esercizi 1. Determinare le derivate parziali di f(x, y, z) = exp(xz) + zy sin(xyz) + cos(xy 3 ) 2. Scrivere l equazione del piano tangente e della retta normale al grafico ln(xy) + cos(x + y) nel punto
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005
 Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
Università degli Studi di Salerno - Facoltà di Ingegneria Matematica II - Prova Scritta - 09/06/2006
 Matematica II - Prova Scritta - 09/06/2006 f(x, y) = (y x)e x2 y 2, 2. Risolvere le seguenti equazioni differenziali: y 2 = 1 1 (2x y) 2, y 2y + y 2y = e x (x 1). 3. Calcolare il seguente integrale curvilineo
Matematica II - Prova Scritta - 09/06/2006 f(x, y) = (y x)e x2 y 2, 2. Risolvere le seguenti equazioni differenziali: y 2 = 1 1 (2x y) 2, y 2y + y 2y = e x (x 1). 3. Calcolare il seguente integrale curvilineo
Massimi e minimi vincolati
 Massimi e minimi vincolati Sia f una funzione differenziabile, definita su un aperto A di R N. Se K è un sottoinsieme chiuso e limitato di A, per il teorema di Weierstrass f assume massimo e minimo su
Massimi e minimi vincolati Sia f una funzione differenziabile, definita su un aperto A di R N. Se K è un sottoinsieme chiuso e limitato di A, per il teorema di Weierstrass f assume massimo e minimo su
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica II del c.1.
 Prova scritta di Analisi Matematica II del 14-07-1999 - c.1 1) Sia (d n ) una successione di numeri reali tali che inf d n > 0. Studiare il carattere della serie + n=1 al variare del parametro reale positivo
Prova scritta di Analisi Matematica II del 14-07-1999 - c.1 1) Sia (d n ) una successione di numeri reali tali che inf d n > 0. Studiare il carattere della serie + n=1 al variare del parametro reale positivo
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica II del
 Prova scritta di nalisi Matematica II del 12-06-2001. C1 1) Studiare la convergenza semplice, uniforme e totale della serie di funzioni seguente ( 1) [ n 2 ] n x 1 + n 2 x. n=0 2) Data la funzione (x 2
Prova scritta di nalisi Matematica II del 12-06-2001. C1 1) Studiare la convergenza semplice, uniforme e totale della serie di funzioni seguente ( 1) [ n 2 ] n x 1 + n 2 x. n=0 2) Data la funzione (x 2
ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009)
 ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009) 1. Sia S = { } (x, y, z) : x 2 + y 2 = 4, 0 z 3 + x. Scrivere le equazioni parametriche di una superficie regolare che abbia S come sostegno. 2. Enunciare
ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009) 1. Sia S = { } (x, y, z) : x 2 + y 2 = 4, 0 z 3 + x. Scrivere le equazioni parametriche di una superficie regolare che abbia S come sostegno. 2. Enunciare
Istituzioni di Matematica II 5 Luglio 2010
 Istituzioni di Matematica II 5 Luglio 010 1. Classificare, al variare del parametro α R, la forma quadratica (1 + α )x + 4xy + αy.. i) Si determinino tutti i punti critici della seguente funzione f(x,
Istituzioni di Matematica II 5 Luglio 010 1. Classificare, al variare del parametro α R, la forma quadratica (1 + α )x + 4xy + αy.. i) Si determinino tutti i punti critici della seguente funzione f(x,
Prove d Esame A.A. 2012/2013
 Complementi di Analisi Polo di Savona Complementi di Analisi Matematica Prove d Esame A.A. 2012/2013 1- PrCam.TEX [] Complementi di Analisi Polo di Savona Prima Prova parziale 23/11/2011 Prima Prova parziale
Complementi di Analisi Polo di Savona Complementi di Analisi Matematica Prove d Esame A.A. 2012/2013 1- PrCam.TEX [] Complementi di Analisi Polo di Savona Prima Prova parziale 23/11/2011 Prima Prova parziale
Figura 1. F = {y 2, x 2 }
 ANALISI VETTORIALE Soluzione esercizi 14 gennaio 211 7.1. Esercizio. Assegnato il campo vettoriale F = y 2, x 2 calcolare la circuitazione τ ds ovvero ( y 2 dx + x 2 dy ) essendo Ω il quadrato di vertici
ANALISI VETTORIALE Soluzione esercizi 14 gennaio 211 7.1. Esercizio. Assegnato il campo vettoriale F = y 2, x 2 calcolare la circuitazione τ ds ovvero ( y 2 dx + x 2 dy ) essendo Ω il quadrato di vertici
Quesito 1. f(x, y) = xy log (x 2 + y 2 ) Quesito 2. Quesito 3. y = 2y3 +x 3. xy 2 y(1) = 1. Quesito 4
 Corso di laurea in Ing. Meccanica, a.a. 2002/2003 Prova scritta di Analisi Matematica 2 del 7 gennaio 2003 Determinare gli eventuali estremi relativi della funzione f(x, y) = xy log (x 2 + y 2 ) Calcolare
Corso di laurea in Ing. Meccanica, a.a. 2002/2003 Prova scritta di Analisi Matematica 2 del 7 gennaio 2003 Determinare gli eventuali estremi relativi della funzione f(x, y) = xy log (x 2 + y 2 ) Calcolare
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006. Matematica 2 (Analisi)
 Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
TRACCIA DELLE SOLUZIONI DEI PROBLEMI DELL ESAME DEL 2/9/2011
 TRACCIA DELLE SOLUZIONI DEI PROBLEMI DELL ESAME DEL /9/11 Esercizio 1 a. Dopo aver scritto l equazione parametrica C(t) della curva di equazione cartesiana y = x x, si calcolino i vettori T(t), N(t) e
TRACCIA DELLE SOLUZIONI DEI PROBLEMI DELL ESAME DEL /9/11 Esercizio 1 a. Dopo aver scritto l equazione parametrica C(t) della curva di equazione cartesiana y = x x, si calcolino i vettori T(t), N(t) e
I PROVA SCRITTA DI ANALISI MATEMATICA A Ing. [Informatica, Telecomunicazioni](L-Z)
 I PROVA SCRITTA DI ANALISI MATEMATICA A Ing. [Informatica, Telecomunicazioni](L-Z)](/thumbs/75/72088693.jpg) I PROVA SCRITTA DI ANALISI MATEMATICA A Ing. [Informatica, Telecomunicazioni](L-Z) (Alberto PARMEGGIANI) A.A. 1999/2000: 22 Ottobre 1999 (1) COGNOME e NOME (Stampatello): MATRICOLA: N.B. Ogni risposta
I PROVA SCRITTA DI ANALISI MATEMATICA A Ing. [Informatica, Telecomunicazioni](L-Z) (Alberto PARMEGGIANI) A.A. 1999/2000: 22 Ottobre 1999 (1) COGNOME e NOME (Stampatello): MATRICOLA: N.B. Ogni risposta
Risposta La curva r è regolare a tratti per via di quanto succede della sua rappresentazione parametrica nel punto t = 1: pur riuscendo
 ANALISI VETTORIALE OMPITO PER LE VAANZE DI FINE D ANNO Esercizio Sia r(t) la curva regolare a tratti x = t, y = t, t [, ] e x = t, y = t, t [, ]. alcolare la lunghezza di r, calcolare, dove esistono, i
ANALISI VETTORIALE OMPITO PER LE VAANZE DI FINE D ANNO Esercizio Sia r(t) la curva regolare a tratti x = t, y = t, t [, ] e x = t, y = t, t [, ]. alcolare la lunghezza di r, calcolare, dove esistono, i
UNIVERSITÀ DI ROMA TOR VERGATA. Analisi Matematica II per Ingegneria Prof. C. Sinestrari
 UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Esercizi 17.XI.2017 1. Verificare che le curve definite dalle seguenti parametrizzazioni sono regolari, o regolari
UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Esercizi 17.XI.2017 1. Verificare che le curve definite dalle seguenti parametrizzazioni sono regolari, o regolari
Forme differenziali lineari
 Forme differenziali lineari Sia Ω R un insieme aperto e siano A, B, C: Ω R funzioni continue in Ω. Si definisce forma differenziale ω in Ω l espressione ω = A(x, y, z)dx + B(x, y, z)dy + C(x, y, z)dz Data
Forme differenziali lineari Sia Ω R un insieme aperto e siano A, B, C: Ω R funzioni continue in Ω. Si definisce forma differenziale ω in Ω l espressione ω = A(x, y, z)dx + B(x, y, z)dy + C(x, y, z)dz Data
Fondamenti di Analisi Matematica II per IPIM-IEN, 14/02/13. Tema 1 (parte di esercizi)
 Fondamenti di Analisi Matematica II per IPIM-IEN, 14/02/13 Nota bene: è obbligatorio scrivere le sole risposte richieste su questo foglio senza giustificazione. I passaggi principali dei calcoli e le loro
Fondamenti di Analisi Matematica II per IPIM-IEN, 14/02/13 Nota bene: è obbligatorio scrivere le sole risposte richieste su questo foglio senza giustificazione. I passaggi principali dei calcoli e le loro
(a) Le derivate parziali f x. f y = x2 + 2xy + 3 si annullano contemporaneamente in (1, 2) e ( 1, 2). Le derivate seconde di f valgono.
 Esercizio 1 Si consideri la funzione f(x, y) = x 2 y + xy 2 + y (a) Determinare i punti di massimo e minimo relativo e di sella del grafico di f. (b) Determinare i punti di massimo e minimo assoluto di
Esercizio 1 Si consideri la funzione f(x, y) = x 2 y + xy 2 + y (a) Determinare i punti di massimo e minimo relativo e di sella del grafico di f. (b) Determinare i punti di massimo e minimo assoluto di
Esercizi su curve e funzioni reali di più variabili reali 1Febbraio 2010
 Esercizi su curve e funzioni reali di più variabili reali 1Febbraio 1 1.Si calcoli la lunghezza della curva di equazione g y = 1 x 1 log x x [1, e].. Sia f(x, y, ) = x + y e sia il sostegno della curva
Esercizi su curve e funzioni reali di più variabili reali 1Febbraio 1 1.Si calcoli la lunghezza della curva di equazione g y = 1 x 1 log x x [1, e].. Sia f(x, y, ) = x + y e sia il sostegno della curva
Analisi Matematica III
 Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 1 giugno 4 (Cognome (Nome (Numero di matricola Esercizio 1 Si consideri la successione
Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 1 giugno 4 (Cognome (Nome (Numero di matricola Esercizio 1 Si consideri la successione
1) Studiare la natura dei seguenti integrali impropri: 2x2 1. x dx (c) e x + 1. log x. n n + 1 n (a) n=1. (b) n + log n n 2n 2 1.
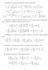 ) Studiare la natura dei seguenti integrali impropri: 0 x 3 dx (b) + 2x2 2 x 2 + 2 dx (c) e x + 0 e x dx (g) (d) + 0 + 0 x( + x) dx x sin x x 2 dx (h) (e) 0 + log x x 2 dx (f) 2 log x dx x + log( + x 2
) Studiare la natura dei seguenti integrali impropri: 0 x 3 dx (b) + 2x2 2 x 2 + 2 dx (c) e x + 0 e x dx (g) (d) + 0 + 0 x( + x) dx x sin x x 2 dx (h) (e) 0 + log x x 2 dx (f) 2 log x dx x + log( + x 2
Il punto (0, 0) è per f : (a) di massimo locale (b) di minimo locale (c) di sella (d) nessuno di questi.
 Corso di Algebra Lineare e Analisi Matematica II Anno Accademico 2013-2014 PRIMA PROVA SCRITTA DI ANALISI MATEMATICA II Pisa, 07.06.14 Nome e cognome Matricola 1. Sia γ : IR IR 3 una curva di classe C
Corso di Algebra Lineare e Analisi Matematica II Anno Accademico 2013-2014 PRIMA PROVA SCRITTA DI ANALISI MATEMATICA II Pisa, 07.06.14 Nome e cognome Matricola 1. Sia γ : IR IR 3 una curva di classe C
ARGOMENTI MATEMATICA PER L INGEGNERIA
 ARGOMENTI DI MATEMATICA PER L INGEGNERIA VOLUME 2 Esercizi proposti Quando non diversamente precisato, nel seguito si intenderà( sempre che nel piano sia stato introdotto un sistema cartesiano ortogonale
ARGOMENTI DI MATEMATICA PER L INGEGNERIA VOLUME 2 Esercizi proposti Quando non diversamente precisato, nel seguito si intenderà( sempre che nel piano sia stato introdotto un sistema cartesiano ortogonale
Recupero 1 compitino di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2016/2017. Prof. M. Bramanti.
 Recupero 1 compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 16/17. Prof. M. Bramanti 1 Tema n 1 3 4 6 Tot. Cognome e nome in stampatello codice persona o n di
Recupero 1 compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 16/17. Prof. M. Bramanti 1 Tema n 1 3 4 6 Tot. Cognome e nome in stampatello codice persona o n di
Campi vettoriali. 1. Sia F (x, y) = ye x i + (e x cos y) j un campo vettoriale. Determinare un potenziale per F, se esiste.
 Campi vettoriali. Sia F (x, y = ye x i + (e x cos y j un campo vettoriale. Determinare un potenziale per F, se esiste.. Sia F (x, y = xy i + x j un campo vettoriale. Determinare un potenziale per F, se
Campi vettoriali. Sia F (x, y = ye x i + (e x cos y j un campo vettoriale. Determinare un potenziale per F, se esiste.. Sia F (x, y = xy i + x j un campo vettoriale. Determinare un potenziale per F, se
Prima Prova Scritta 18/03/1997
 Prima Prova Scritta 18/03/1997 1 + x y6 f(x, y) = x 6 + y 6, (x, y) (0, 0) k, (x, y) = (0, 0) A 2 Determinare, per k R, l insieme di continuità di f. B 2 Determinare, per k R, l insieme di differenziabilità
Prima Prova Scritta 18/03/1997 1 + x y6 f(x, y) = x 6 + y 6, (x, y) (0, 0) k, (x, y) = (0, 0) A 2 Determinare, per k R, l insieme di continuità di f. B 2 Determinare, per k R, l insieme di differenziabilità
Alcuni esercizi risolti da esami di anni passati
 Alcuni esercizi risolti da esami di anni passati Andrea Braides ( x. Calcolare, se esiste, il limite lim (x,y (, x + y log + y + x 3 y. x + y Dato che log( + s = s + o(s per s, abbiamo lim (x,y (, ( x
Alcuni esercizi risolti da esami di anni passati Andrea Braides ( x. Calcolare, se esiste, il limite lim (x,y (, x + y log + y + x 3 y. x + y Dato che log( + s = s + o(s per s, abbiamo lim (x,y (, ( x
Esonero di Analisi Matematica II (A)
 Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
A Analisi Matematica 2 (Corso di Laurea in Informatica) Simulazione compito d esame
 COGNOME NOME Matr. Firma dello studente A Analisi Matematica (Corso di Laurea in Informatica) Simulazione compito Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
COGNOME NOME Matr. Firma dello studente A Analisi Matematica (Corso di Laurea in Informatica) Simulazione compito Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
Estremi. 5. Determinare le dimensioni di una scatola rettangolare di volume v assegnato, che abbia la superficie minima.
 Estremi 1. Determinare gli estremi relativi di f(x, y) = e x (x 1)(y 1) + (y 1).. Determinare gli estremi relativi di f(x, y) = y (y + 1) cos x. 3. Determinare gli estremi relativi di f(x, y) = xye x +y..
Estremi 1. Determinare gli estremi relativi di f(x, y) = e x (x 1)(y 1) + (y 1).. Determinare gli estremi relativi di f(x, y) = y (y + 1) cos x. 3. Determinare gli estremi relativi di f(x, y) = xye x +y..
Politecnico di Torino II Facoltà di Architettura Esame di Istituzioni di Matematiche II
 Politecnico di Torino II Facoltà di Architettura Esame di Istituzioni di Matematiche II 5 Gennaio 008 Teoria: Scrivere l espressione della lunghezza dell arco di curva grafico della funzione f(x) = x +
Politecnico di Torino II Facoltà di Architettura Esame di Istituzioni di Matematiche II 5 Gennaio 008 Teoria: Scrivere l espressione della lunghezza dell arco di curva grafico della funzione f(x) = x +
Analisi Matematica II - INGEGNERIA Gestionale - B 20 luglio 2017 Cognome: Nome: Matricola:
 Analisi Matematica II - INGEGNERIA Gestionale - B luglio 7 Cognome: Nome: Matricola: IMPORTANTE: Giustificare tutte le affermazioni e riportare i calcoli essenziali Esercizio [8 punti] Data la matrice
Analisi Matematica II - INGEGNERIA Gestionale - B luglio 7 Cognome: Nome: Matricola: IMPORTANTE: Giustificare tutte le affermazioni e riportare i calcoli essenziali Esercizio [8 punti] Data la matrice
sen n x( tan xn n n=1
 8 Gennaio 2016 Nome (in stampatello): 1) (8 punti) Discutere la convergenza della serie di funzioni al variare di x in [ 1, 1]. n x( tan xn n ) xn sen n 2) (7 punti) Provare che la forma differenziale
8 Gennaio 2016 Nome (in stampatello): 1) (8 punti) Discutere la convergenza della serie di funzioni al variare di x in [ 1, 1]. n x( tan xn n ) xn sen n 2) (7 punti) Provare che la forma differenziale
Foglio 3 Esercizi su forme differenziali lineari ed integrali di seconda specie (alcuni con cenno di soluzione).
 Università degli Studi di Padova Facoltà di Ingegneria Laurea in Ingegneria Gestionale e MeccanicaMeccatronica, V. Casarino P. Mannucci (-) Foglio 3 Esercizi su forme differenziali lineari ed integrali
Università degli Studi di Padova Facoltà di Ingegneria Laurea in Ingegneria Gestionale e MeccanicaMeccatronica, V. Casarino P. Mannucci (-) Foglio 3 Esercizi su forme differenziali lineari ed integrali
Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione
![Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione](/thumbs/88/116749009.jpg) Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione [E.2] Disegnare nel piano cartesiano il dominio della funzione ( 4 x 2 y 2) ) (1 x 2 y2 y + x 2. 4 1 y ex y y x
Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione [E.2] Disegnare nel piano cartesiano il dominio della funzione ( 4 x 2 y 2) ) (1 x 2 y2 y + x 2. 4 1 y ex y y x
b) Dimostrare che se f(x) è differenziabile in x 0, allora è continua in x 0.
 Analisi Matematica II - Calcolo in più variabili Nome, Cognome, Matricola: Corso di Laurea: Versione A Avvertenza: La prova d esame si compone di due esercizi e di due quesiti. La risposta ai quesiti va
Analisi Matematica II - Calcolo in più variabili Nome, Cognome, Matricola: Corso di Laurea: Versione A Avvertenza: La prova d esame si compone di due esercizi e di due quesiti. La risposta ai quesiti va
Esercizio 2 SI NO Determinare l equazione cartesiana del piano passante per il punto P 0 = (2, 3, 1) e contenente
 GENNAIO 2014 A Calcolare gli autovalori della matrice ( 2 ) 2 1 3 Determinare l equazione cartesiana del piano passante per il punto P 0 = (2, 3, 1) e contenente i due vettori u = (1, 2, 2) e v = (5, 3,
GENNAIO 2014 A Calcolare gli autovalori della matrice ( 2 ) 2 1 3 Determinare l equazione cartesiana del piano passante per il punto P 0 = (2, 3, 1) e contenente i due vettori u = (1, 2, 2) e v = (5, 3,
DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Clinica Canale PZ A.A. 2017/2018 Codocente: Dott. Salvatore Fragapane
 DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Clinica Canale PZ A.A. 07/08 Codocente: Dott. Salvatore Fragapane Lezione - 09/03/08, dalle 6.00 alle 8.00 in aula 6 Es. Studiare
DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Clinica Canale PZ A.A. 07/08 Codocente: Dott. Salvatore Fragapane Lezione - 09/03/08, dalle 6.00 alle 8.00 in aula 6 Es. Studiare
ISTITUZIONI DI MATEMATICHE II
 ISTITUZIONI DI MATEMATIHE II SEONDO ESONERO Esercizio 1. Data la funzione f(x, y) = (x + y )(1 y) i) se ne studi il segno. ii) Si trovino i punti critici di f e se ne studi le natura. iii) Sia D = {(x,
ISTITUZIONI DI MATEMATIHE II SEONDO ESONERO Esercizio 1. Data la funzione f(x, y) = (x + y )(1 y) i) se ne studi il segno. ii) Si trovino i punti critici di f e se ne studi le natura. iii) Sia D = {(x,
Compiti d Esame A.A. 2005/2006
 Compiti d Esame A.A. 25/26 UNIVERSITÀ DEGLI STUDI DI PERUGIA A.A. 25/26 I Esercitazione 21 Aprile 26 { y = xy ln(xy) si chiede di dimostrare che: y(1) = 1, (a) ammette un unica soluzione massimale y =
Compiti d Esame A.A. 25/26 UNIVERSITÀ DEGLI STUDI DI PERUGIA A.A. 25/26 I Esercitazione 21 Aprile 26 { y = xy ln(xy) si chiede di dimostrare che: y(1) = 1, (a) ammette un unica soluzione massimale y =
Prove scritte dell esame di Analisi Matematica II a.a. 2016/2017
 Prove scritte dell esame di Analisi Matematica II a.a. 6/7 C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 5 giugno 7. Assegnati ( l insieme E {(x,
Prove scritte dell esame di Analisi Matematica II a.a. 6/7 C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 5 giugno 7. Assegnati ( l insieme E {(x,
Cognome Nome Matricola Codice ESEMPIO 1
 Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di forma differenziale chiusa. Sia A R N ; sia A aperto; sia ω = N i=1 ω i dx i una forma differenziale su A; sia ω di classe C 1 ; si dice
Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di forma differenziale chiusa. Sia A R N ; sia A aperto; sia ω = N i=1 ω i dx i una forma differenziale su A; sia ω di classe C 1 ; si dice
Prima prova in itinere di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2016/2017. Prof. M. Bramanti.
 Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 016/017. Prof. M. Bramanti 1 Tema n 1 4 5 6 Tot. Cognome e nome in stampatello) codice persona
Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 016/017. Prof. M. Bramanti 1 Tema n 1 4 5 6 Tot. Cognome e nome in stampatello) codice persona
Cognome Nome Matricola Codice ESEMPIO 1
 Cognome Nome Matricola Codice ESEMPIO 1 [1] (E) Trovare i punti critici e i punti di massimo e di minimo relativo della seguente funzione: f : R 3 R, (x, y, z) x 2 xy + z 2 + 1 [2] (E) Calcolare il seguente
Cognome Nome Matricola Codice ESEMPIO 1 [1] (E) Trovare i punti critici e i punti di massimo e di minimo relativo della seguente funzione: f : R 3 R, (x, y, z) x 2 xy + z 2 + 1 [2] (E) Calcolare il seguente
Analisi Matematica 2 (Corso di Laurea in Informatica)
 COGNOME NOME Matr. Firma dello studente Analisi Matematica 2 (Corso di Laurea in Informatica) 2.02.2012 B Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta.
COGNOME NOME Matr. Firma dello studente Analisi Matematica 2 (Corso di Laurea in Informatica) 2.02.2012 B Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta.
PROVA SCRITTA DI ISTITUZIONI DI MATEMATICA II - 21 GIUGNO 2018
 1 PROVA SCRITTA DI ISTITUZIONI DI MATEMATICA II - 1 GIUGNO 018 Cognome e nome Matr. REGOLE D ESAME 1) Non è ammesso l uso di libri appunti calcolatrici cellulari etc. Soltanto carta e penna! ) Il compito
1 PROVA SCRITTA DI ISTITUZIONI DI MATEMATICA II - 1 GIUGNO 018 Cognome e nome Matr. REGOLE D ESAME 1) Non è ammesso l uso di libri appunti calcolatrici cellulari etc. Soltanto carta e penna! ) Il compito
Facoltà di Ingegneria Prova scritta di Analisi Matematica II. Lecce, y y x = x3 y 4. y(1) = 1.
 Lecce, 10.4.2003 1. Risolvere il seguente problema di Cauchy: y y x = x3 y 4 y(1) = 1. 2. Determinare gli estremi della funzione f(x, y) = x 2 y 2 nell insieme } E = {(x, y) R 2 : (x 1) 2 + y2 4 1, y 0.
Lecce, 10.4.2003 1. Risolvere il seguente problema di Cauchy: y y x = x3 y 4 y(1) = 1. 2. Determinare gli estremi della funzione f(x, y) = x 2 y 2 nell insieme } E = {(x, y) R 2 : (x 1) 2 + y2 4 1, y 0.
Cognome Nome Matricola Codice ESEMPIO 1
 Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di derivata di una funzione in un punto. Sia A R N ; sia a A; sia f : A R M ; sia f differenziabile in a; allora la derivata di f in a è...
Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di derivata di una funzione in un punto. Sia A R N ; sia a A; sia f : A R M ; sia f differenziabile in a; allora la derivata di f in a è...
a) 1 n b) n cos(nx) n 2 + x 2, c) nx n2 x nx 2 (su IR), 1 + nx x x 2 e) n + x 2, f) nx (come sopra), n sin x g) 2n2 x 2 1 n 2 x + n,
 1. Determinare, ove esista, il limite puntuale delle seguenti successioni di funzioni, e stabilire se esse convergono uniformemente sugli insiemi indicati alla fine della riga. 1 n 1 + n2 x 2, b) n cos(nx)
1. Determinare, ove esista, il limite puntuale delle seguenti successioni di funzioni, e stabilire se esse convergono uniformemente sugli insiemi indicati alla fine della riga. 1 n 1 + n2 x 2, b) n cos(nx)
Analisi Matematica 2. Michele Campiti. Prove scritte di. Ingegneria Industriale a.a
 Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Es. 1 Es. 2 Es. 3 Es. 4 Totale Teoria. Punteggi degli esercizi: Es.1: 8 punti; Es.2: 8 punti; Es.3: 8 punti; Es.4: 8 punti.
 Es. 1 Es. 2 Es. 3 Es. 4 Totale Teoria Analisi e Geometria 1 Seconda prova in itinere 1 Febbraio 21 Compito A Docente: Politecnico di Milano Ingegneria Industriale Cognome: Nome: Matricola: Punteggi degli
Es. 1 Es. 2 Es. 3 Es. 4 Totale Teoria Analisi e Geometria 1 Seconda prova in itinere 1 Febbraio 21 Compito A Docente: Politecnico di Milano Ingegneria Industriale Cognome: Nome: Matricola: Punteggi degli
Analisi 4 - SOLUZIONI (compito del 29/09/2011)
 Corso di laurea in Matematica Analisi 4 - SOLUZIONI compito del 9/09/0 Docente: Claudia Anedda Calcolare, tramite uno sviluppo in serie noto, la radice quinta di e la radice cubica di 9 Utilizzando la
Corso di laurea in Matematica Analisi 4 - SOLUZIONI compito del 9/09/0 Docente: Claudia Anedda Calcolare, tramite uno sviluppo in serie noto, la radice quinta di e la radice cubica di 9 Utilizzando la
Esercizi. Misti iniziali. Più variabili. 1. Data la funzione. F (x) = x3 3 + x e t2 dt. se ne studino massimi, minimi, flessi, limiti a ±.
 Esercizi Misti iniziali. Data la funzione se ne studino massimi, minimi, flessi, iti a ±. 2. Provare che Più variabili F x) = 3. Calcolare, se esistono, i seguenti iti a) b) c) d) x,y),) x 2 + y 2 2 x,y),)
Esercizi Misti iniziali. Data la funzione se ne studino massimi, minimi, flessi, iti a ±. 2. Provare che Più variabili F x) = 3. Calcolare, se esistono, i seguenti iti a) b) c) d) x,y),) x 2 + y 2 2 x,y),)
ANALISI B alcuni esercizi proposti
 ANALISI B alcuni esercizi proposti G.P. Leonardi Parte II 1 Limiti e continuità per funzioni di 2 variabili Esercizio 1.1 Calcolare xy log(1 + x ) lim (x,y) (0,0) 2x 2 + 5y 2 Esercizio 1.2 Studiare la
ANALISI B alcuni esercizi proposti G.P. Leonardi Parte II 1 Limiti e continuità per funzioni di 2 variabili Esercizio 1.1 Calcolare xy log(1 + x ) lim (x,y) (0,0) 2x 2 + 5y 2 Esercizio 1.2 Studiare la
Prova in itinere di Matematica Pisa, 26 novembre 2005
 Università di Pisa - Corso di Laurea in Ingegneria Informatica Prova in itinere di Matematica Pisa, 26 novembre 25 Numero compito: 256 Tempo ora. Non si possono usare calcolatrici. Segnare le risposte
Università di Pisa - Corso di Laurea in Ingegneria Informatica Prova in itinere di Matematica Pisa, 26 novembre 25 Numero compito: 256 Tempo ora. Non si possono usare calcolatrici. Segnare le risposte
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 18 febbraio 2010 Tema A
 Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 18 febbraio 21 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 18 febbraio 21 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio
Cognome Nome Matricola Codice ESEMPIO 1
 Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Teorema sulla condizione affinchè φ(t) = e λt sia una soluzione di un equazione differenziale lineare d ordine n a coefficienti costanti. Siano a 1, a
Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Teorema sulla condizione affinchè φ(t) = e λt sia una soluzione di un equazione differenziale lineare d ordine n a coefficienti costanti. Siano a 1, a
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016
 Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Università degli Studi di Roma Tre Corso di Laurea in Ingegneria civile a.a. 2015/2016 Complementi di Matematica (A-K) Secondo Appello 5 Luglio 2016.
 Università degli Studi di Roma Tre Corso di Laurea in Ingegneria civile a.a. 5/6 Complementi di Matematica (A-K) Secondo Appello 5 Luglio 6. Cognome e nome Matricola Specificare quale esame si deve sostenere:
Università degli Studi di Roma Tre Corso di Laurea in Ingegneria civile a.a. 5/6 Complementi di Matematica (A-K) Secondo Appello 5 Luglio 6. Cognome e nome Matricola Specificare quale esame si deve sostenere:
Es. 1 Es. 2 Es. 3 Es. 4 Totale Teoria
 Es. Es. Es. 3 Es. 4 Totale Teoria Analisi e Geometria Docente: Politecnico di Milano Ingegneria Industriale 5 Settembre Compito A Cognome: Nome: Matricola: Punteggi degli esercizi: Es.: 6 punti; Es.: punti;
Es. Es. Es. 3 Es. 4 Totale Teoria Analisi e Geometria Docente: Politecnico di Milano Ingegneria Industriale 5 Settembre Compito A Cognome: Nome: Matricola: Punteggi degli esercizi: Es.: 6 punti; Es.: punti;
APPELLO DI ISTITUZIONI DI MATEMATICA II - SETTEMBRE 2017
 1 APPELLO DI ISTITUZIONI DI MATEMATICA II - SETTEMBRE 2017 Cognome e nome Matr. REGOLE D ESAME 1) Non è ammesso l uso di libri, appunti, calcolatrici, cellulari, etc. Soltanto carta e penna! 2) Il compito
1 APPELLO DI ISTITUZIONI DI MATEMATICA II - SETTEMBRE 2017 Cognome e nome Matr. REGOLE D ESAME 1) Non è ammesso l uso di libri, appunti, calcolatrici, cellulari, etc. Soltanto carta e penna! 2) Il compito
Ingegneria Tessile, Biella Analisi II
 Ingegneria Tessile, Biella Analisi II Esercizi svolti In questo file sono contenute le soluzioni degli esercizi sui campi vettoriali (cf foglio 5 di esercizi) Attenzione: in alcuni esercizi il calcolo
Ingegneria Tessile, Biella Analisi II Esercizi svolti In questo file sono contenute le soluzioni degli esercizi sui campi vettoriali (cf foglio 5 di esercizi) Attenzione: in alcuni esercizi il calcolo
COMPLEMENTI DI ANALISI MATEMATICA A.A Primo appello del 5/5/2010
 COMPLEMENTI DI ANALISI MATEMATICA A.A. 29- Primo appello del 5/5/2 Qui trovate le tracce delle soluzioni degli esercizi del compito. Ho tralasciato i calcoli da Analisi (che comunque sono parte della risoluzione),
COMPLEMENTI DI ANALISI MATEMATICA A.A. 29- Primo appello del 5/5/2 Qui trovate le tracce delle soluzioni degli esercizi del compito. Ho tralasciato i calcoli da Analisi (che comunque sono parte della risoluzione),
Integrali doppi. Hynek Kovarik. Analisi Matematica 2. Università di Brescia
 Integrali doppi Hynek Kovarik Università di Brescia nalisi Matematica 2 Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 1 / 47 Motivazione: calcolo di volume Hynek Kovarik
Integrali doppi Hynek Kovarik Università di Brescia nalisi Matematica 2 Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 1 / 47 Motivazione: calcolo di volume Hynek Kovarik
Prova in itinere di Matematica Pisa, 26 novembre 2005
 Università di Pisa - Corso di Laurea in Ingegneria Informatica Prova in itinere di Matematica Pisa, 26 novembre 25 Numero compito: 256 Tempo ora. Non si possono usare calcolatrici. Segnare le risposte
Università di Pisa - Corso di Laurea in Ingegneria Informatica Prova in itinere di Matematica Pisa, 26 novembre 25 Numero compito: 256 Tempo ora. Non si possono usare calcolatrici. Segnare le risposte
Corso di laurea: Ingegneria aerospaziale e meccanica Programma di Fondamenti di Analisi Matematica II a.a. 2012/13 Docente: Fabio Paronetto
 Corso di laurea: Ingegneria aerospaziale e meccanica Programma di Fondamenti di Analisi Matematica II a.a. 2012/13 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo
Corso di laurea: Ingegneria aerospaziale e meccanica Programma di Fondamenti di Analisi Matematica II a.a. 2012/13 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo
Corso di Matematica 3 o A.A. 2016/2017 Argomenti delle lezioni
 Corso di Matematica 3 o A.A. 2016/2017 Argomenti delle lezioni 1 lezione. Martedí 27 settembre. 2 ore. Richiami sulle applicazioni lineari tra spazi vettoriali di dimensione finita. Il teorema di rappresentazione.
Corso di Matematica 3 o A.A. 2016/2017 Argomenti delle lezioni 1 lezione. Martedí 27 settembre. 2 ore. Richiami sulle applicazioni lineari tra spazi vettoriali di dimensione finita. Il teorema di rappresentazione.
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 3 settembre 2009 Tema A
 Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 3 settembre 29 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 3 settembre 29 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio
COGNOME: NOME: MATR.: 1. Si consideri la serie di Fourier data da n 2
 COGNOME: NOME: MATR.: Ingegneria Aerospaziale. Analisi Matematica 2. Compito del 16 febbraio 2019 - PARTE A 1. Si consideri la serie di Fourier data da n 2 sin(2nt). Diamo per buono che esiste il limite
COGNOME: NOME: MATR.: Ingegneria Aerospaziale. Analisi Matematica 2. Compito del 16 febbraio 2019 - PARTE A 1. Si consideri la serie di Fourier data da n 2 sin(2nt). Diamo per buono che esiste il limite
ESERCIZI SULLE CURVE
 ESERCIZI SULLE CURVE VALENTINA CASARINO Esercizi per il corso di Fondamenti di Analisi Matematica, (Ingegneria Gestionale, dell Innovazione del Prodotto, Meccanica e Meccatronica, Università degli studi
ESERCIZI SULLE CURVE VALENTINA CASARINO Esercizi per il corso di Fondamenti di Analisi Matematica, (Ingegneria Gestionale, dell Innovazione del Prodotto, Meccanica e Meccatronica, Università degli studi
Analisi Matematica II - Ingegneria Meccanica/Energetica - 29 Gennaio 2018
 nalisi Matematica II - Ingegneria Meccanica/Energetica - 29 Gennaio 218 1) ia data la funzione f(x, y, z) = (x 2 + y 2 1) 2 + 8 a) tudiare l esistenza di massimi e minimi assoluti della funzione f nella
nalisi Matematica II - Ingegneria Meccanica/Energetica - 29 Gennaio 218 1) ia data la funzione f(x, y, z) = (x 2 + y 2 1) 2 + 8 a) tudiare l esistenza di massimi e minimi assoluti della funzione f nella
Cognome Nome matr. Corso di laurea in Tecniche dell edilizia Istituzioni di Analisi Matematica a.a. 2008/09 compito finale 31/08/09 (fila A)
 Cognome Nome matr. Corso di laurea in Tecniche dell edilizia Istituzioni di Analisi Matematica a.a. 2008/09 compito finale 31/08/09 (fila A) Compilare immediatamente con i propri dati l intestazione. Rispondere
Cognome Nome matr. Corso di laurea in Tecniche dell edilizia Istituzioni di Analisi Matematica a.a. 2008/09 compito finale 31/08/09 (fila A) Compilare immediatamente con i propri dati l intestazione. Rispondere
calcolare il lavoro di E lungo il segmento da A = ( 1, 1, 1) a B = (1, 1, 1), calcolare rot ( E ), determinare un potenziale U(x, y, z) per E.
 ANALISI VETTORIALE Soluzione esonero.1. Esercizio. Assegnato il campo E (x, y, z) = x(y + z ), y(x + z ), z(x + y ) } 1111 calcolare il lavoro di E lungo il segmento da A = ( 1, 1, 1) a B = (1, 1, 1),
ANALISI VETTORIALE Soluzione esonero.1. Esercizio. Assegnato il campo E (x, y, z) = x(y + z ), y(x + z ), z(x + y ) } 1111 calcolare il lavoro di E lungo il segmento da A = ( 1, 1, 1) a B = (1, 1, 1),
Analisi Matematica II 14 Giugno 2019
 Analisi Matematica II 14 Giugno 2019 Cognome: Nome: Matricola: 1. (10 punti) Si determinino i sottoinsiemi del piano in cui valgano, rispettivamente, continuità, derivabilità e differenziabilità della
Analisi Matematica II 14 Giugno 2019 Cognome: Nome: Matricola: 1. (10 punti) Si determinino i sottoinsiemi del piano in cui valgano, rispettivamente, continuità, derivabilità e differenziabilità della
Prova Finale di Tipo B e Prova di Accesso alla Laura Special. Dip. Matematica - Università Roma Tre. 2 febbraio 2005
 Prova Finale di Tipo B e Prova di Accesso alla Laura Special Dip. Matematica - Università Roma Tre 2 febbraio 2005 Istruzioni. a) La sufficienza viene raggiunta con un punteggio di almeno 20 punti in ciascuno
Prova Finale di Tipo B e Prova di Accesso alla Laura Special Dip. Matematica - Università Roma Tre 2 febbraio 2005 Istruzioni. a) La sufficienza viene raggiunta con un punteggio di almeno 20 punti in ciascuno
Analisi Matematica 2 Quaderno degli esercizi settimanali. Roberto Monti. Fisica e Astronomia Anno Accademico
 Analisi Matematica 2 Quaderno degli esercizi settimanali Roberto Monti Fisica e Astronomia Anno Accademico 2018-19 Indice Introduzione 5 Settimana 1. Serie numeriche I 7 Settimana 2. Serie numeriche II
Analisi Matematica 2 Quaderno degli esercizi settimanali Roberto Monti Fisica e Astronomia Anno Accademico 2018-19 Indice Introduzione 5 Settimana 1. Serie numeriche I 7 Settimana 2. Serie numeriche II
Analisi Matematica 2 5 febbraio Risposte. (Giusta = 3, non data = 0, sbagliata = 1) Versione Es. 1 Es. 2 Es. 3 Es. 4 Es. 5 Es. 6 Es.
 Analisi Matematica 2 5 febbraio 2013 Nome, Cognome, Matricola: Cognome del Docente: Risposte. (Giusta = 3, non data = 0, sbagliata = 1) Versione Es. 1 Es. 2 Es. 3 Es. 4 Es. 5 Es. 6 Es. 7 1 Esercizio 1.
Analisi Matematica 2 5 febbraio 2013 Nome, Cognome, Matricola: Cognome del Docente: Risposte. (Giusta = 3, non data = 0, sbagliata = 1) Versione Es. 1 Es. 2 Es. 3 Es. 4 Es. 5 Es. 6 Es. 7 1 Esercizio 1.
Analisi Matematica 2. Michele Campiti. Prove scritte di. Ingegneria Industriale a.a
 Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 2014 2015 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi
Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 2014 2015 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi
Prima prova di verifica in itinere di ANALISI MATEMATICA II. 12 Marzo 2008 Compito A. 1 (punti 3)
 anno accademico 007-008 Prima prova di verifica in itinere di ANALISI MATEMATICA II Marzo 008 Compito A (punti ) y = x + xy + y x. (punti 4) y + y x = ln x x y. (punti ) y = y + y ln y. 4 (punti 6) Determinare
anno accademico 007-008 Prima prova di verifica in itinere di ANALISI MATEMATICA II Marzo 008 Compito A (punti ) y = x + xy + y x. (punti 4) y + y x = ln x x y. (punti ) y = y + y ln y. 4 (punti 6) Determinare
0.1 Arco di curva regolare
 .1. ARCO DI CURVA REGOLARE 1.1 Arco di curva regolare Se RC(O, i, j, k ) è un riferimento cartesiano fissato per lo spazio euclideo E, e se v (t) = x(t) i + y(t) j + z(t) k è una funzione a valori vettoriali
.1. ARCO DI CURVA REGOLARE 1.1 Arco di curva regolare Se RC(O, i, j, k ) è un riferimento cartesiano fissato per lo spazio euclideo E, e se v (t) = x(t) i + y(t) j + z(t) k è una funzione a valori vettoriali
