Integrali doppi. Hynek Kovarik. Analisi Matematica 2. Università di Brescia
|
|
|
- Valentina Fumagalli
- 4 anni fa
- Visualizzazioni
Transcript
1 Integrali doppi Hynek Kovarik Università di Brescia nalisi Matematica 2 Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 1 / 47
2 Motivazione: calcolo di volume Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 2 / 47
3 Definizione di integrale doppio Sia R = [a, b] [c, d] e sia f : R R una funzione limitata. Date due suddivisioni D 1 = {a = x < x 1 < < x n = b} e D 2 = {c = y < y 1 < < y m = d} di [a, b] e [c, d], chiamiamo somma inferiore e somma superiore di f rispetto alla griglia D 1 D 2 le quantità s(f, D 1 D 2 ) = ( ) inf f (x i x i 1 )(y j y j 1 ) [x i 1,x i ] [y j 1,y j ] i,j e S(f, D 1 D 2 ) = i,j ( sup f [x i 1,x i ] [y j 1,y j ] ) (x i x i 1 )(y j y j 1 ) Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 3 / 47
4 Chiamo inoltre i valori e I(f ) = sup D 1,D 2 s(f, D 1 D 2 ) J(f ) = inf D 1,D 2 S(f, D 1 D 2 ) l integrale inferiore e l integrale superiore di f. Dalla definizione segue che I(f ) J(f ). Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 4 / 47
5 Definizione (Funzioni integrabili e integrale doppio) Sia R = [a, b] [c, d] e sia f : R R una funzione limitata. Diciamo che f è integrabile secondo Riemann se I(f ) = J(f ). Tale valore si indica con f (x, y) dx dy, e si dice integrale doppio di f su R. R Per f = 1 si ha R dx dy = area(r). Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 5 / 47
6 Teorema (Le funzioni continue sono integrabili) Sia R = [a, b] [c, d] e sia f : R R una funzione continua. llora f è integrabile secondo Riemann. Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 6 / 47
7 Teorema (Proprietà dell integrale doppio) Sia R = [a, b] [c, d] e siano f, g : R R due funzioni integrabili. llora valgono le seguenti proprietà: 1 Linearità: per ogni α, β R risulta (α f (x, y) + β g(x, y)) dx dy = α f (x, y) dx dy R R + β g(x, y) dx dy. 2 Confronto: se f (x, y) g(x, y) per ogni (x, y) R, si ha f (x, y) dx dy g(x, y) dx dy R 3 Confronto con il modulo: f (x, y) dx dy R R R R f (x, y) dx dy. Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 7 / 47
8 Teorema (Formule di riduzione per rettangoli) Sia R = [a, b] [c, d] e sia f : R R una funzione integrabile. Supponiamo che per ogni x [a, b] l applicazione y f (x, y) sia integrabile su [c, d]. llora si ha ( b ) d f (x, y) dx dy = f (x, y) dy dx. (1) R a nalogamente, se per ogni y [c, d] l applicazione x f (x, y) è integrabile su [a, b], allora si ha ( d ) b f (x, y) dx dy = f (x, y) dx dy. (2) R c c a Interpretazione geometrica... Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 8 / 47
9 Esempio Se R = [, 1] [, 2] e f (x, y) = x 2 y, allora si ha ( 1 ) 2 f dx dy = x 2 y dy dx = R 1 [ ] y x dx 2 = 1 2x 2 dx = 2 3. oppure R f dx dy = 2 ( ) 1 x 2 y dx dy = 2 [ x 3 y 3 ] 1 dy = y dx = 2 3. Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 9 / 47
10 Integrali doppi su insiemi generali Definizione (Funzione caratteristica) Sia R 2. La funzione 1 : R 2 R definita da { 1 se (x, y), 1 (x, y) = se (x, y) si dice funzione caratteristica di. Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 1 / 47
11 Definizione (Integrale doppio su insiemi generali) Sia R = [a, b] [c, d] e sia R. Diciamo che è un insieme di Jordan, se la funzione 1 è integrabile secondo Riemann. In tal caso, data una funzione integrabile f : R R, poniamo f dx dy := 1 f dx dy R Per f = 1 si ha dx dy = area(). Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 11 / 47
12 Proprietà elementari Sia R = [a, b] [c, d] e siano 1, 2 R insiemi di Jordan. Siano inoltre f, g : R R funzioni integrabili. Valgono queste proprietà : 1 dditività : se 1 2 =, allora f dx dy = 1 2 f dx dy + 1 f dx dy 2 2 Confronto: se f (x, y) g(x, y) per ogni (x, y) R, allora j f dx dy j g dx dy j = 1, 2. 3 Confronto con il modulo: si ha f dx dy j f dx dy j = 1, 2. j Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 12 / 47
13 Casi particolari: simmetrie 1. Sia R 2 un insieme di Jordan. Supponiamo che sia simmetrico rispetto all asse delle y, cioè per ogni (x, y) R 2 vale (x, y) ( x, y). Sia f : R integrabile. Valgono le seguenti affermazioni: 1 Se f è dispari in x, cioè f ( x, y) = f (x, y), allora f dx dy =. 2 Se f è pari in x, cioè f ( x, y) = f (x, y), allora f dx dy = 2 f dx dy x dove x = {(x, y) : x }. Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 13 / 47
14 Esempio L insieme = {(x, y) R 2 : 1 x 1, y 1 + x 2 } è simmetrico rispetto all asse delle y. La funzione f (x, y) = sin(x 3 ) e x arctan(1 + y 3 ) è dispari in x. Dunque f dx dy =. Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 14 / 47
15 Casi particolari: simmetrie 2. Sia R 2 un insieme di Jordan. Supponiamo che sia simmetrico rispetto all asse delle x, cioè per ogni (x, y) R 2 vale (x, y) (x, y). Sia f : R integrabile. Valgono le seguenti affermazioni: 1 Se f è dispari in y, cioè f (x, y) = f (x, y), allora f dx dy =. 2 Se f è pari in y, cioè f (x, y) = f (x, y), allora f dx dy = 2 f dx dy y dove y = {(x, y) : y }. Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 15 / 47
16 Esempio L insieme = {(x, y) R 2 : 1 y 1, x y 2 } è simmetrico rispetto all asse delle x. La funzione f (x, y) = log(1 + x 2 + y 2 ) arctan(sin y) è dispari in y. Dunque f dx dy =. Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 16 / 47
17 Casi particolari: insiemi normali Definizione (Insiemi normali rispetto all asse x) Siano α, β : [a, b] R due funzioni tali che α(x) β(x) x [a, b] L insieme = { (x, y) R 2 : a x b, α(x) y β(x) } è detto insieme normale rispetto all asse delle x. Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 17 / 47
18 Casi particolari: insiemi normali Definizione (Insiemi normali rispetto all asse y) Siano γ, δ : [c, d] R due funzioni tali che γ(y) δ(y) y [c, d] L insieme = { (x, y) R 2 : c y d, γ(y) x δ(y) } è detto insieme normale rispetto all asse delle y. Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 18 / 47
19 Gli insiemi normali determinati da due funzioni integrabili α, β : [a, b] R o γ, δ : [c, d] R sono insiemi di Jordan. Esistono insiemi normali sia rispetto all asse delle x sia rispetto all asse delle y: rettangoli, triangoli, etc. Dall altra parte, esistono insiemi che non sono normali rispetto a nessuno degli assi: corona circolare,... Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 19 / 47
20 Teorema (Formule di riduzione per insiemi normali) Sia R 2 e sia R un rettangolo tale che R. Sia inoltre f : R una funzione integrabile. Valgono le seguenti affermazioni: 1 Se è normale rispetto all asse delle x e determinato dalle funzioni integrabili α, β : [a, b] [c, d], allora ( b ) β(x) f (x, y) dx dy = f (x, y) dy dx. (3) a α(x) 2 Se è normale rispetto all asse delle y e determinato dalle funzioni integrabili γ, δ : [c, d] [a, b], allora ( d ) δ(y) f (x, y) dx dy = f (x, y) dx dy. (4) c γ(y) Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 2 / 47
21 Dimostrazione: Per definizione si ha f (x, y) dx dy = f (x, y) 1 (x, y) dx dy. Supponiamo per esempio che sia normale rispetto all asse delle x: = { (x, y) R 2 : a x b, α(x) y β(x) } R Sia R = [a, b] [c, d]. pplicando la formula di riduzione per rettangoli alla funzione f 1 si ottiene ( b ) d f (x, y) 1 (x, y) dx dy = f (x, y) 1 (x, y) dy dx R da cui la tesi = a b a c ( ) β(x) f (x, y) dy dx, α(x) Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 21 / 47
22 Esempio 1 : Sia f : R 2 R data da f (x, y) = y e sia = {(x, y) R 2 : x 1, x 2 y x} Siccome è normale rispetto all asse delle x e determinato dalle funzioni α(x) = x 2 e β(x) = x, posso applicare la formula di riduzione (3) con a = e b = 1: y dx dy = = = ( ) x y dy dx = x 2 ( x 2 x 4 ) dx = ( ) = [ y 2 2 ] x x 2 dx (x x 4 ) dx Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 22 / 47
23 Osserviamo che è normale anche rispetto all asse delle y, e determinato dalle funzioni γ(y) = y 2 e δ(y) = y : = {(x, y) R 2 : y 1, y 2 x y} Quindi dalla formula di riduzione (4) con c = e d = 1 si ottiene ( 1 ) y ( 1 ) y y dx dy = y dx dy = y dx dy y 2 y 2 = 1 y( y y 2 ) dy = 1 (y 3/2 y 3 ) dy = [ ] y 5/2 [ y 4 4 ] 1 = = 3 2 Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 23 / 47
24 Esempio 2 : Sia f : R 2 R data da f (x, y) = sin(y 2 ) e sia { = (x, y) R 2 : x 2 π, x 2 y } π Quindi è normale rispetto all asse x. pplico la formula di riduzione (3): ( 2 π ) π sin(y 2 ) dx dy = sin(y 2 ) dy dx... x 2... non concludo nulla! Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 24 / 47
25 Rappresento come insieme normale rispetto all asse y: { = (x, y) R 2 : y } π, x 2y Dalla formula di riduzione (4) ottengo ( sin(y 2 π ) 2y ) dx dy = sin(y 2 ) dx dy... = π 2y sin(y 2 ) dy = = [ cos t ] π = 2 π sin t dt ltro esempio: si veda il tema d esame del Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 25 / 47
26 Cambiamento di variabili Definizione (Cambiamento di variabili) Siano U, V R 2 due aperti. Diciamo che G : V U è un cambiamento di variabili di classe C 1 tra U e V se G C 1 (V ), G è invertibile con G 1 : U V di classe C 1. Interpretazione: passiamo dalle coordinate (x, y) U alle nuove coordinate (u, v) V definite da x = G 1 (u, v), y = G 2 (u, v). Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 26 / 47
27 Jacobiano Definizione (Jacobiano di un cambio di variabili) Siano U, V R 2 due aperti e sia G : V U è un cambiamento di variabili di classe C 1. Chiamiamo jacobiano di G l applicazione J G : V R definita da u G 1 (u, v) v G 1 (u, v) J G (u, v) = det (5) u G 2 (u, v) v G 2 (u, v) Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 27 / 47
28 Teorema (Cambiamento di variabili) Siano U, V R 2 due aperti e sia G : V U un cambiamento di variabili di classe C 1. Sia f : U R una funzione integrabile e sia U un insieme di Jordan. llora G 1 () è di Jordan e vale f (x, y) dx dy = f (G 1 (u, v), G 2 (u, v)) J G (u, v) du dv (6) G 1 () L insieme G 1 () è la controimmagine di tramite l appicazione G : G 1 () = {(u, v) V : G(u, v) }. Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 28 / 47
29 Coordinate polari Sono le coordinate (r, θ) [, ) [, 2π] definite dal cambio di variabili x = r cos θ, y = r sin θ. Quindi u = r, v = θ, G 1 (r, θ) = r cos θ e G 2 (r, θ) = r sin θ. Dalla formula (5) calcoliamo il jacobiano: cos θ r sin θ J G (r, θ) = det = r cos 2 θ + r sin 2 θ = r sin θ r cos θ Dunque dall equazione (6) si ottiene f (x, y) dx dy = G 1 () f (r cos θ, r sin θ) r dr dθ Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 29 / 47
30 Esempio 1: Consideriamo l integrale doppio x 2 dx dy, + y 2 dove = {(x, y) R 2 : x 2 + y 2 1}. Con il passaggio alle coordinate polari si ottiene G 1 () = {(r, θ) : r 1, θ 2π} = [, 1] [, 2π] Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 3 / 47
31 Quindi x 2 dx dy = + y 2 1 2π 1 r dr dθ 1 + r 2 = 1 ( ) 2π dθ r 1 + r 2 dr = 1 2πr 1 + r 2 dr [ ] 1 = π log(1 + r 2 ) = π log 2. Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 31 / 47
32 Esempio 2: Consideriamo l integrale doppio y dx dy, x 2 + y 2 dove = {(x, y) R 2 : x 2 + y 2 4, y}. Con il passaggio alle coordinate polari si ottiene G 1 () = {(r, θ) : r 2, θ π} = [, 2] [, π] Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 32 / 47
33 Quindi y 2 x 2 + y dx dy = 2 π r sin θ r r dr dθ = 2 ( π ) sin θ dθ r dr = 2 [ cos θ ] π r dr = 2 2r dr = [ r 2] 2 = 4. Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 33 / 47
34 Coordinate polari generalizzate Sono le coordinate (r, θ) [, ) [, 2π] definite dal cambio di variabili x = a r cos θ, y = b r sin θ, a, b >. Quindi u = r, v = θ, G 1 (r, θ) = ar cos θ e G 2 (r, θ) = br sin θ. Dalla formula (5) calcoliamo lo jacobiano: a cos θ ar sin θ J G (r, θ) = det b sin θ br cos θ = a b r cos 2 θ + a b r sin 2 θ = a b r Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 34 / 47
35 Dunque dall equazione (6) si ottiene f (x, y) dx dy = ab f (a r cos θ, b r sin θ) r dr dθ G 1 () Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 35 / 47
36 Esempio: Calcoliamo l area dell insime = {(x, y) R 2 : x 2 a 2 + y 2 } b 2 1. Con il passaggio alle coordinate polari generalizzate x = a r cos θ, y = b r sin θ si ottiene r 2 1. Quindi G 1 () = {(r, θ) : r 1, θ 2π} = [, 1] [, 2π] da cui area() = dx dy = ab r dr dθ G 1 () = ab 1 ( ) 2π dθ r dr = a b π. Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 36 / 47
37 Teorema di Green Teorema (Green) Sia Γ una curva chiusa e regolare a tratti a valori in R 2 percorsa in senso antiorario. Sia la regione di piano interna alla curva Γ. Sia Ω un aperto di R 2 contenente e la sua frontiera (la curva Γ). Sia F : Ω R 2, F(x, y) = (F 1 (x, y), F 2 (x, y)) di classe C 1 (Ω). llora ( F2 x F ) 1 dx dy = F dγ y Γ Il Teorema di Green vale anche quando Ω non è semplicemente connesso. Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 37 / 47
38 Dimostrazione: Ci limitiamo al caso di insiemi normali rispetto a entrambi gli assi. Siano G, H : R 2 dati da G(x, y) = (F 1 (x, y), ), H(x, y) = (, F2 (x, y)) llora F = G + H e vale F dγ = Γ Γ G dγ + H dγ (7) Γ Siccome è normale rispetto all asse x, esiste un intervallo [a, b] e due funzioni α, β : [a, b] R, di classe C 1 a tratti, tali che = { (x, y) R 2 : a x b, α(x) y β(x) } Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 38 / 47
39 Quindi Γ = Γ 1 Γ 2 Γ 3 Γ 4, dove Γ 1,..., Γ 4 sono le curve con le rappresentazioni parametriche r 1 (x) = (x, α(x)), x [a, b], r 2 (y) = (b, y), y [α(b), β(b)] r 3 (x) = (b + a x, β(b + a x)), x [a, b], r 4 (y) = (a, β(a) + α(a) y), y [α(a), β(a)] Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 39 / 47
40 Dunque G dγ = Γ G dγ1 + Γ 1 G dγ3 Γ 3 = = = b + a b a b a b a (F 1 (x, α(x)), ) (1, α (x)) dx (F 1 (b + a x), β(b + a x), ) ( 1, β (x)) dx (F 1 (x, α(x)) b ( F 1 (x, α(x)) F 1 (x, β(x)) a (F 1 (b + a x, β(b + a x))dx ) dx, (8) dove abbiamo usato la sostituzione t = b + a x nel secondo integrale. Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 4 / 47
41 D altra parte, usando la formula di riduzione per insiemi normali rispetto all asse x si ottiene ( F b ) β(x) 1 F 1 (x, y) dx dy = (x, y) dy dx y a α(x) y = b a (F 1 (x, α(x)) F 1 (x, β(x))) dx Quindi il confronto con l equazione (8) implica che F 1 (x, y) dx dy = G dγ y Γ Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 41 / 47
42 Nello stesso modo, usando il fatto che è normale anche rispetto all asse delle y, si mostra che F 2 (x, y) dx dy = H dγ (esercizio) x Dunque ( F2 x F ) 1 dx dy = y Γ Γ G dγ + H dγ = F dγ Γ Γ Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 42 / 47
43 Una conseguenza del Teorema di Green Teorema Sia R 2 semplicemente connesso e sia F : R 2 un campo di classe C 1 ( ). Se F è irrotazionale, allora F è conservativo in. Dimostrazione: Sia Γ una curva chiusa regolare a tratti a valori in. Sia B la regione delimitata da Γ. llora B = Γ e siccome è semplicemente connesso si ha B. Quindi per il Teorema di Green ( F2 F dγ = Γ B x F ) 1 dxdy =. y }{{} Questo vale per ogni curva chiusa regolare a tratti a valori in. Quindi F è conservativo. = Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 43 / 47
44 lcune applicazioni del Teorema di Green Esempio ( ) Sia Γ il bordo, percorso in senso antiorario, della semi-corona circolare delimitata dalle circonferenze x 2 + y 2 = 1 e x 2 + y 2 = 4 e contenuta nel semispazio {(x, y) R 2 : y }. Calcolare F dγ, dove Γ ( 2y 2 F(x, y) = 7 esin x, xy 7 + ) y Sia la regione delimitata dalla curva Γ. Per il Teorema di Green si ha ( F2 F dγ = x F ) 1 dxdy = 3 y dxdy y 7 Γ Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 44 / 47
45 Con il passaggio alle coordinate polari x = r cos θ, y = r sin θ si ottiene Quindi G 1 () = {(r, θ) : 1 r 2, θ π} = [1, 2] [, π]. 3 7 y dxdy = ( π = = 2 ) r sin θdθ r dr = r 2 dr Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 45 / 47
46 lcune applicazioni del Teorema di Green Calcolo dell area: Sia R 2. Se F : R 2 R 2 è tale che ( F2 x F ) 1 (x, y) = 1 (x, y), (9) y allora per il Teorema di Green vale area() = 1 dxdy = Possibili scelte di F che soddifanno (9): F(x, y) = (, x) F(x, y) = ( y, ), F(x, y) = 1 ( y, x). 2 F dγ, Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 46 / 47
47 Esempio Ricalcoliamo l area dell insime = {(x, y) R 2 : x 2 a 2 + y 2 } b 2 1. { } Sia Γ = (x, y) R 2 : x 2 + y 2 = 1 il bordo di percorso in senso a 2 b 2 antiorario. Rappresentazione parametrica di Γ: r(t) = (a cos t, b sin t), t [, 2π]. llora scegliendo F(x, y) = (, x) si ha area() = F dγ = 2π (, a cos t) ( a sin t, b cos t) dt = 2π ab cos 2 t dt = ab π Hynek Kovarik (Università di Brescia) Integrali curvilinei nalisi Matematica 2 47 / 47
Integrali doppi. Riccarda Rossi. Università di Brescia. Analisi Matematica B
 Integrali doppi Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Integrali doppi Analisi Matematica B 1 / 92 Motivazione per l integrale di Riemann: calcolo
Integrali doppi Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Integrali doppi Analisi Matematica B 1 / 92 Motivazione per l integrale di Riemann: calcolo
Analisi Matematica 2. Integrali doppi. Integrali doppi 1 / 24
 Analisi Matematica 2 Integrali doppi Integrali doppi 1 / 24 Integrali doppi su domini rettangolari. Sia f (x, y) una funzione limitata nel rettangolo Q = [a, b] [c, d] e sia D 1 = {x 0 = a, x 1,, x m =
Analisi Matematica 2 Integrali doppi Integrali doppi 1 / 24 Integrali doppi su domini rettangolari. Sia f (x, y) una funzione limitata nel rettangolo Q = [a, b] [c, d] e sia D 1 = {x 0 = a, x 1,, x m =
Integrali di superficie
 Integrali di superficie Hynek Kovarik Università di Brescia Analisi Matematica 2 Hynek Kovarik (Università di Brescia) Integrali curvilinei Analisi Matematica 2 1 / 27 Superfici in forma parametrica Procediamo
Integrali di superficie Hynek Kovarik Università di Brescia Analisi Matematica 2 Hynek Kovarik (Università di Brescia) Integrali curvilinei Analisi Matematica 2 1 / 27 Superfici in forma parametrica Procediamo
quando il limite delle somme di Riemann esiste. In tal caso diciamo che la funzione è integrabile sul rettangolo.
 Integrali multipli Consideriamo, inizialmente il caso degli integrali doppi. Il concetto di integrale doppio è l estensione della definizione di integrale per una funzione reale di una variabile reale
Integrali multipli Consideriamo, inizialmente il caso degli integrali doppi. Il concetto di integrale doppio è l estensione della definizione di integrale per una funzione reale di una variabile reale
Risposta La curva r è regolare a tratti per via di quanto succede della sua rappresentazione parametrica nel punto t = 1: pur riuscendo
 ANALISI VETTORIALE OMPITO PER LE VAANZE DI FINE D ANNO Esercizio Sia r(t) la curva regolare a tratti x = t, y = t, t [, ] e x = t, y = t, t [, ]. alcolare la lunghezza di r, calcolare, dove esistono, i
ANALISI VETTORIALE OMPITO PER LE VAANZE DI FINE D ANNO Esercizio Sia r(t) la curva regolare a tratti x = t, y = t, t [, ] e x = t, y = t, t [, ]. alcolare la lunghezza di r, calcolare, dove esistono, i
Analisi Matematica II Corso di Ingegneria Gestionale Compito del A
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del -7-5 - A Esercizio ( punti Data la funzione f(x, y = x + y + 4xy 8x 4y + 4 i trovare tutti i punti critici e, se possibile, caratterizzarli
Analisi Matematica II Corso di Ingegneria Gestionale Compito del -7-5 - A Esercizio ( punti Data la funzione f(x, y = x + y + 4xy 8x 4y + 4 i trovare tutti i punti critici e, se possibile, caratterizzarli
Derivate. Hynek Kovarik. Analisi A. Università di Brescia. Hynek Kovarik (Università di Brescia) Derivate Analisi A 1 / 33
 Derivate Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Derivate Analisi A 1 / 33 Definizione: rapporto incrementale Sia f : domf R R. Dati x 1, x 2 domf con x 1 x
Derivate Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Derivate Analisi A 1 / 33 Definizione: rapporto incrementale Sia f : domf R R. Dati x 1, x 2 domf con x 1 x
Foglio 3 Esercizi su forme differenziali lineari ed integrali di seconda specie (alcuni con cenno di soluzione).
 Università degli Studi di Padova Facoltà di Ingegneria Laurea in Ingegneria Gestionale e MeccanicaMeccatronica, V. Casarino P. Mannucci (-) Foglio 3 Esercizi su forme differenziali lineari ed integrali
Università degli Studi di Padova Facoltà di Ingegneria Laurea in Ingegneria Gestionale e MeccanicaMeccatronica, V. Casarino P. Mannucci (-) Foglio 3 Esercizi su forme differenziali lineari ed integrali
D : 0 E : arctan 2 1 F : 2 arctan 1. 3y + 3y y = 0 y(0) = 3 y (0) = 0.
 Analisi Matematica B 31 marzo 003 Compito 1 1. L integrale 1 x arctan( 1 x ) dx vale Risp.: A : arctan 1 1 B : C : arctan 1 3 D : 0 E : arctan 1 F : arctan 1 + arctan 1. Sia ỹ(x) la soluzione del problema
Analisi Matematica B 31 marzo 003 Compito 1 1. L integrale 1 x arctan( 1 x ) dx vale Risp.: A : arctan 1 1 B : C : arctan 1 3 D : 0 E : arctan 1 F : arctan 1 + arctan 1. Sia ỹ(x) la soluzione del problema
Forme differenziali e campi vettoriali: esercizi svolti
 Forme differenziali e campi vettoriali: esercizi svolti 1 Esercizi sul Teorema di Green......................... 2 2 Esercizi sul Teorema di Stokes......................... 4 3 Esercizi sul Teorema di
Forme differenziali e campi vettoriali: esercizi svolti 1 Esercizi sul Teorema di Green......................... 2 2 Esercizi sul Teorema di Stokes......................... 4 3 Esercizi sul Teorema di
PRIMI ESERCIZI SU INTEGRALI DOPPI E TRIPLI. x x 2 + y 2 dxdy, tan(x + y) x + y. (x y) log (x + y) dxdy,
 PRIMI ESERCIZI SU INTEGRALI DOPPI E TRIPLI VALENTINA CASARINO Esercizi per il corso di Analisi Matematica, (Ingegneria Gestionale, dell Innovazione del Prodotto, Meccanica e Meccatronica, Università degli
PRIMI ESERCIZI SU INTEGRALI DOPPI E TRIPLI VALENTINA CASARINO Esercizi per il corso di Analisi Matematica, (Ingegneria Gestionale, dell Innovazione del Prodotto, Meccanica e Meccatronica, Università degli
Calcolo differenziale II
 Calcolo differenziale II Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Derivate (II) Analisi Matematica 1 1 / 36 Massimi e minimi Definizione Sia A R, f
Calcolo differenziale II Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Derivate (II) Analisi Matematica 1 1 / 36 Massimi e minimi Definizione Sia A R, f
Prove scritte dell esame di Analisi Matematica II a.a. 2013/2014
 Prove scritte dell esame di Analisi Matematica II a.a. 3/4 C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 9 giugno 4. (8 punti) Risolvere il problema
Prove scritte dell esame di Analisi Matematica II a.a. 3/4 C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 9 giugno 4. (8 punti) Risolvere il problema
Calcolo differenziale I
 Calcolo differenziale I Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Derivate Analisi Matematica 1 1 / 25 Definizione: rapporto incrementale Sia f : A
Calcolo differenziale I Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Derivate Analisi Matematica 1 1 / 25 Definizione: rapporto incrementale Sia f : A
si ha La lunghezza L si calcola per ciascun tratto L = (2t)2 + (3t 2 ) dt+ 2 (3t2 ) 2 + (2t) 2 dt = 4t2 + 9t 4 dt = t
 ANALISI VETTORIALE Soluzione esercizi 1 gennaio 211 6.1. Esercizio. Sia Γ la curva regolare a tratti di rappresentazione parametrica x = t 2, y = t, t [, 1] e x = t, y = t 2, t [1, 2] calcolare la lunghezza,
ANALISI VETTORIALE Soluzione esercizi 1 gennaio 211 6.1. Esercizio. Sia Γ la curva regolare a tratti di rappresentazione parametrica x = t 2, y = t, t [, 1] e x = t, y = t 2, t [1, 2] calcolare la lunghezza,
Analisi Matematica II 14 Giugno 2019
 Analisi Matematica II 14 Giugno 2019 Cognome: Nome: Matricola: 1. (10 punti) Si determinino i sottoinsiemi del piano in cui valgano, rispettivamente, continuità, derivabilità e differenziabilità della
Analisi Matematica II 14 Giugno 2019 Cognome: Nome: Matricola: 1. (10 punti) Si determinino i sottoinsiemi del piano in cui valgano, rispettivamente, continuità, derivabilità e differenziabilità della
Soluzione della Prova Parziale di Analisi Matematica III - 17/02/04. C.L. in Matematica e Matematica per le Applicazioni. Prof. Kevin R.
 Soluzione della Prova Parziale di Analisi Matematica III - 7//4 C.L. in Matematica e Matematica per le Applicazioni Prof. Kevin R. Payne Esercizio. a. Ricordiamo inanzitutto la seguente: efinizione: Si
Soluzione della Prova Parziale di Analisi Matematica III - 7//4 C.L. in Matematica e Matematica per le Applicazioni Prof. Kevin R. Payne Esercizio. a. Ricordiamo inanzitutto la seguente: efinizione: Si
Analisi Matematica II (Prof. Paolo Marcellini) 1 Esercizi tratti da temi d esame di anni precedenti
 Analisi Matematica II (Prof. Paolo Marcellini) Università degli Studi di Firenze Corso di laurea in Matematica Esercitazione del 8// Michela Eleuteri eleuteri@math.unifi.it web.math.unifi.it/users/eleuteri
Analisi Matematica II (Prof. Paolo Marcellini) Università degli Studi di Firenze Corso di laurea in Matematica Esercitazione del 8// Michela Eleuteri eleuteri@math.unifi.it web.math.unifi.it/users/eleuteri
Analisi Matematica 2. Trasformazioni integrali. Trasformazioni integrali 1 / 29
 Analisi Matematica 2 Trasformazioni integrali Trasformazioni integrali 1 / 29 Trasformazioni integrali. 1) Formule di Gauss-Green: nel piano: trasformano un integrale doppio in un integrale curvilineo,
Analisi Matematica 2 Trasformazioni integrali Trasformazioni integrali 1 / 29 Trasformazioni integrali. 1) Formule di Gauss-Green: nel piano: trasformano un integrale doppio in un integrale curvilineo,
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica II del
 Prova scritta di nalisi Matematica II del 12-06-2001. C1 1) Studiare la convergenza semplice, uniforme e totale della serie di funzioni seguente ( 1) [ n 2 ] n x 1 + n 2 x. n=0 2) Data la funzione (x 2
Prova scritta di nalisi Matematica II del 12-06-2001. C1 1) Studiare la convergenza semplice, uniforme e totale della serie di funzioni seguente ( 1) [ n 2 ] n x 1 + n 2 x. n=0 2) Data la funzione (x 2
Lezione 13 (7 dicembre) Polinomio di Taylor Integrale definito: significato geometrico Primitiva di una funzione
 Lezione 13 (7 dicembre) Polinomio di Taylor Integrale definito: significato geometrico Primitiva di una funzione Polinomio di Taylor e approssimazioni Approssimazione di una funzione nell intorno di un
Lezione 13 (7 dicembre) Polinomio di Taylor Integrale definito: significato geometrico Primitiva di una funzione Polinomio di Taylor e approssimazioni Approssimazione di una funzione nell intorno di un
COMPLEMENTI DI ANALISI MATEMATICA A.A Primo appello del 5/5/2010
 COMPLEMENTI DI ANALISI MATEMATICA A.A. 29- Primo appello del 5/5/2 Qui trovate le tracce delle soluzioni degli esercizi del compito. Ho tralasciato i calcoli da Analisi (che comunque sono parte della risoluzione),
COMPLEMENTI DI ANALISI MATEMATICA A.A. 29- Primo appello del 5/5/2 Qui trovate le tracce delle soluzioni degli esercizi del compito. Ho tralasciato i calcoli da Analisi (che comunque sono parte della risoluzione),
Analisi Matematica II Politecnico di Milano Ingegneria Industriale
 Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #7. Sia f : R R la funzione definita da a) Determinare i massimi e minimi di f. b) Mostrare che f è limitata. fx, y) xy
Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #7. Sia f : R R la funzione definita da a) Determinare i massimi e minimi di f. b) Mostrare che f è limitata. fx, y) xy
Analisi Matematica II Corso di Ingegneria Gestionale Compito del f(x, y) = sin( x 2 + 2y 2 )
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 9--9 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo - Le risposte senza giustificazione sono considerate nulle Esercizio
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 9--9 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo - Le risposte senza giustificazione sono considerate nulle Esercizio
PROVE SCRITTE DI ANALISI MATEMATICA II (V.O.), ANNO 2002
 PROVE SCRITTE DI ANALISI MATEMATICA II (V.O.), ANNO 22 Prova scritta del 1/1/22 Si esamini la serie di funzioni: 1 log x (e n + n), definita per x IR. Si determini l insieme S in cui tale serie converge,
PROVE SCRITTE DI ANALISI MATEMATICA II (V.O.), ANNO 22 Prova scritta del 1/1/22 Si esamini la serie di funzioni: 1 log x (e n + n), definita per x IR. Si determini l insieme S in cui tale serie converge,
es.1 es.2 es.3 es.4 es.5 somma Analisi Matematica 2: Secondo Parziale, , Versione A Cognome e nome:...matricola:...
 es.1 es. es.3 es. es.5 somma 6 6 6 6 6 3 Analisi Matematica : Secondo Parziale, 3.5.16, Versione A Cognome e nome:....................................matricola:......... 1. Dimostrare che la forma differenziale
es.1 es. es.3 es. es.5 somma 6 6 6 6 6 3 Analisi Matematica : Secondo Parziale, 3.5.16, Versione A Cognome e nome:....................................matricola:......... 1. Dimostrare che la forma differenziale
ESERCITAZIONE 9: INTEGRALI DEFINITI. CALCOLO DELLE AREE E ALTRE APPLICAZIONI
 ESERCITAZIONE 9: INTEGRALI DEFINITI. CALCOLO DELLE AREE E ALTRE APPLICAZIONI Tiziana Raparelli 5/5/9 CONOSCENZE PRELIMINARI Vogliamo calcolare f ( x, ax + bx + c ) dx. Se a =, allora basta porre bx + c
ESERCITAZIONE 9: INTEGRALI DEFINITI. CALCOLO DELLE AREE E ALTRE APPLICAZIONI Tiziana Raparelli 5/5/9 CONOSCENZE PRELIMINARI Vogliamo calcolare f ( x, ax + bx + c ) dx. Se a =, allora basta porre bx + c
Prove scritte dell esame di Analisi Matematica II a.a. 2015/2016
 Prove scritte dell esame di Analisi Matematica II a.a. 5/6 C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 6 giugno 6. Determinare massimi e minimi
Prove scritte dell esame di Analisi Matematica II a.a. 5/6 C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 6 giugno 6. Determinare massimi e minimi
Soluzione della Prova Scritta di Analisi Matematica III - 28/02/02. C.L. in Matematica e Matematica per le Applicazioni. Prof. Kevin R.
 Soluzione della Prova Scritta di Analisi Matematica III - 28/2/2 C.L. in Matematica e Matematica per le Applicazioni Prof. Kevin R. Payne Esercizio 1. 1a. Teorema: (di ini) Sia Φ : A R n R R dove A è aperto.
Soluzione della Prova Scritta di Analisi Matematica III - 28/2/2 C.L. in Matematica e Matematica per le Applicazioni Prof. Kevin R. Payne Esercizio 1. 1a. Teorema: (di ini) Sia Φ : A R n R R dove A è aperto.
Analisi Matematica 2. Trasformazioni integrali. Trasformazioni integrali 1 / 15
 Analisi Matematica 2 Trasformazioni integrali Trasformazioni integrali 1 / 15 Trasformazioni integrali. 1) Formule di Gauss-Green: nel piano: trasformano un integrale doppio in un integrale curvilineo,
Analisi Matematica 2 Trasformazioni integrali Trasformazioni integrali 1 / 15 Trasformazioni integrali. 1) Formule di Gauss-Green: nel piano: trasformano un integrale doppio in un integrale curvilineo,
Analisi Matematica II Corso di Ingegneria Gestionale Compito A del , se (x, y) = (0, 0) ( x e. + y x e (y2 )
 Analisi Matematica II Corso di Ingegneria Gestionale Compito A del -6-9 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito A del -6-9 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Calcolo 2B - Analisi III dicembre 2004
 Calcolo 2B - Analisi III dicembre 2. Verificare esplicitamente il teorema di Stokes in R 2 : dω = ω per la -forma: nella regione piana data da: ω = x 2 + y 2 dx = x, y x 2 + y 2 ª x, y y 2x 2ª 2. Considerato
Calcolo 2B - Analisi III dicembre 2. Verificare esplicitamente il teorema di Stokes in R 2 : dω = ω per la -forma: nella regione piana data da: ω = x 2 + y 2 dx = x, y x 2 + y 2 ª x, y y 2x 2ª 2. Considerato
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 2 Secondo compito in itinere 30 Giugno 2016
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo compito in itinere Giugno 6 Cognome: Nome: Matricola: Es.: 9 punti Es.: 9 punti Es.: 6 punti Es.4: 9 punti Totale. Si consideri
Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo compito in itinere Giugno 6 Cognome: Nome: Matricola: Es.: 9 punti Es.: 9 punti Es.: 6 punti Es.4: 9 punti Totale. Si consideri
Istituzioni di Matematica II 3 luglio 2014
 Istituzioni di Matematica II 3 luglio 14 1. i Si dica se la matrice é diagonalizzabile. A = 1 1 1 ii Si studi il carattere della forma quadratica q(, y, z = + y + z Soluzioni. i La matrice é simmetrica
Istituzioni di Matematica II 3 luglio 14 1. i Si dica se la matrice é diagonalizzabile. A = 1 1 1 ii Si studi il carattere della forma quadratica q(, y, z = + y + z Soluzioni. i La matrice é simmetrica
(a) è chiuso; (b) il punto (1, 1/e) è punto di accumulazione di A; (c) è convesso.
 Cognome Nome Matricola Laurea Civ Amb Gest Inf Eln Tlc Mec Non scrivere qui 1 3 4 5 6 Università degli Studi di Parma Dipartimento di Ingegneria e Architettura Esame di Analisi Matematica Soluzioni AA
Cognome Nome Matricola Laurea Civ Amb Gest Inf Eln Tlc Mec Non scrivere qui 1 3 4 5 6 Università degli Studi di Parma Dipartimento di Ingegneria e Architettura Esame di Analisi Matematica Soluzioni AA
ANALISI MATEMATICA L-B, INTEGRALI MULTIPLI
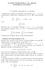 NLISI MTEMTIC L-, 25-6. INTEGRLI MULTIPLI. Funzioni sommabili di n variabili Studieremo l integrale di Riemann per funzioni f(x,..., x n ) di n variabili reali a valori reali. L integrale di f su R n verrà
NLISI MTEMTIC L-, 25-6. INTEGRLI MULTIPLI. Funzioni sommabili di n variabili Studieremo l integrale di Riemann per funzioni f(x,..., x n ) di n variabili reali a valori reali. L integrale di f su R n verrà
Integrali (M.S. Bernabei & H. Thaler)
 Integrali (M.S. Bernabei & H. Thaler) Integrali. Motivazione Che cos é un integrale? Sia f 0 e limitata b a f ( x) dx area f ( x, y) dxdy volume Definizione di integrale: b a dove f ( x) dx lim n n k b
Integrali (M.S. Bernabei & H. Thaler) Integrali. Motivazione Che cos é un integrale? Sia f 0 e limitata b a f ( x) dx area f ( x, y) dxdy volume Definizione di integrale: b a dove f ( x) dx lim n n k b
Politecnico di Torino II Facoltà di Architettura Esame di Istituzioni di Matematiche II
 Politecnico di Torino II Facoltà di Architettura Esame di Istituzioni di Matematiche II 5 Gennaio 008 Teoria: Scrivere l espressione della lunghezza dell arco di curva grafico della funzione f(x) = x +
Politecnico di Torino II Facoltà di Architettura Esame di Istituzioni di Matematiche II 5 Gennaio 008 Teoria: Scrivere l espressione della lunghezza dell arco di curva grafico della funzione f(x) = x +
Analisi Matematica III
 Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 7 gennaio 00 (Cognome) (Nome) (Numero di matricola) Esercizio Si consideri la successione
Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 7 gennaio 00 (Cognome) (Nome) (Numero di matricola) Esercizio Si consideri la successione
Esempi di esercizi d esame A.A. 2006/07 Analisi Matematica 2 Ingegneria Elettronica Proff. G. Vergara Caffarelli e L. Giacomelli
 Esempi di esercizi d esame A.A. 6/7 Analisi Matematica Ingegneria Elettronica Proff. G. Vergara Caffarelli e L. Giacomelli versione preliminare, si prega di segnalare eventuali errori *) Determinare e
Esempi di esercizi d esame A.A. 6/7 Analisi Matematica Ingegneria Elettronica Proff. G. Vergara Caffarelli e L. Giacomelli versione preliminare, si prega di segnalare eventuali errori *) Determinare e
Polinomi di Taylor. Hynek Kovarik. Università di Brescia. Analisi Matematica 1
 Polinomi di Taylor Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Polinomi di Taylor Analisi Matematica 1 1 / 18 Introduzione Sia f : I R e sia x 0 I. Problemi:
Polinomi di Taylor Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Polinomi di Taylor Analisi Matematica 1 1 / 18 Introduzione Sia f : I R e sia x 0 I. Problemi:
Recupero 1 compitino di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2016/2017. Prof. M. Bramanti.
 Recupero 1 compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 16/17. Prof. M. Bramanti 1 Tema n 1 3 4 6 Tot. Cognome e nome in stampatello codice persona o n di
Recupero 1 compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 16/17. Prof. M. Bramanti 1 Tema n 1 3 4 6 Tot. Cognome e nome in stampatello codice persona o n di
ANALISI MATEMATICA 2 - INGEGNERIA MECCANICA ED ENERGETICA A.A PROVA SCRITTA DEL 28/1/19
 ANALISI MATEMATICA - INGEGNERIA MECCANICA E ENERGETICA A.A. 8-9 PROVA SCRITTA EL 8//9 Scrivere nome cognome e numero di matricola in stampatello su tutti i fogli da consegnare. Consegnare solo la bella
ANALISI MATEMATICA - INGEGNERIA MECCANICA E ENERGETICA A.A. 8-9 PROVA SCRITTA EL 8//9 Scrivere nome cognome e numero di matricola in stampatello su tutti i fogli da consegnare. Consegnare solo la bella
1. Cambiamenti di coordinate affini Esempio 1.1. Si debba calcolare l integrale doppio. (x + y) dx dy =
 . Cambiamenti di coordinate affini Esempio.. Si debba calcolare l integrale doppio (x + y) dx dy essendo il parallelogramma di vertici (, ), (, ), (3, 3), (, 3) nel quale é possibile riconoscere, vedi
. Cambiamenti di coordinate affini Esempio.. Si debba calcolare l integrale doppio (x + y) dx dy essendo il parallelogramma di vertici (, ), (, ), (3, 3), (, 3) nel quale é possibile riconoscere, vedi
Analisi Matematica II Corso di Ingegneria Gestionale Compito del f(x, y) = x 2 + y 3 4y. 4 1, y 2 2(1 + }
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8-09-07 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8-09-07 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del f(x, y) = (x 2 2y 2 ) e x y
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8--5 - È obbligatorio consegnare tutti i fogli anche la brutta e il testo - Le risposte senza giustificazione sono considerate nulle Esercizio
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8--5 - È obbligatorio consegnare tutti i fogli anche la brutta e il testo - Le risposte senza giustificazione sono considerate nulle Esercizio
Analisi 2 Fisica e Astronomia
 Analisi Fisica e Astronomia Appello scritto del 8 Luglio 0. Soluzione Esercizio 7 pti Sia α > 0 un parametro e consideriamo la curva piana γ : [0, ] R γt = t cos, t sin, se t 0, ], e γ0 = 0, 0. t α t α
Analisi Fisica e Astronomia Appello scritto del 8 Luglio 0. Soluzione Esercizio 7 pti Sia α > 0 un parametro e consideriamo la curva piana γ : [0, ] R γt = t cos, t sin, se t 0, ], e γ0 = 0, 0. t α t α
ISTITUZIONI DI MATEMATICHE II
 ISTITUZIONI DI MATEMATIHE II SEONDO ESONERO Esercizio 1. Data la funzione f(x, y) = (x + y )(1 y) i) se ne studi il segno. ii) Si trovino i punti critici di f e se ne studi le natura. iii) Sia D = {(x,
ISTITUZIONI DI MATEMATIHE II SEONDO ESONERO Esercizio 1. Data la funzione f(x, y) = (x + y )(1 y) i) se ne studi il segno. ii) Si trovino i punti critici di f e se ne studi le natura. iii) Sia D = {(x,
Politecnico di Bari - A.A. 2012/2013 Corso di Laurea in Ingegneria Elettrica Esame di ANALISI MATEMATICA - 3 Luglio 2013.
 Esame di ANALISI MATEMATICA - 3 Luglio 2013 (1) Studiare il carattere della serie numerica n 1( 1) n F 0 (n), dove F (x) = Z x 0 log(1 + e t2 ) dt (x 1). (6 punti) log(1 + e t2 ) (2) ata la funzione f(x,
Esame di ANALISI MATEMATICA - 3 Luglio 2013 (1) Studiare il carattere della serie numerica n 1( 1) n F 0 (n), dove F (x) = Z x 0 log(1 + e t2 ) dt (x 1). (6 punti) log(1 + e t2 ) (2) ata la funzione f(x,
Analisi 4 - SOLUZIONI (15/07/2015)
 Corso di Laurea in Matematica Analisi 4 - SOLUZIONI (5/7/5) Docente: Claudia Anedda ) Calcolare l area della superficie totale della regione di spazio limitata, interna al paraboloide di equazione x +y
Corso di Laurea in Matematica Analisi 4 - SOLUZIONI (5/7/5) Docente: Claudia Anedda ) Calcolare l area della superficie totale della regione di spazio limitata, interna al paraboloide di equazione x +y
Analisi Matematica II Politecnico di Milano Ingegneria Industriale
 Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #8. Sia f : R 2 R la funzione definita da 2 y 2 per (, y) (, ) f(, y) 2 + y 2 per (, y) (, ). (a) Stabilire se f è continua
Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #8. Sia f : R 2 R la funzione definita da 2 y 2 per (, y) (, ) f(, y) 2 + y 2 per (, y) (, ). (a) Stabilire se f è continua
Integrali superficiali e teorema della divergenza
 Integrali superficiali e teorema della divergenza Data una superficie regolare = ϕ(k), con ϕ : K R R 3, e una funzione continua f : R, definiamo integrale di ϕ su f dσ := (f ϕ) ϕ u ϕ v dudv = f(ϕ(u, v))
Integrali superficiali e teorema della divergenza Data una superficie regolare = ϕ(k), con ϕ : K R R 3, e una funzione continua f : R, definiamo integrale di ϕ su f dσ := (f ϕ) ϕ u ϕ v dudv = f(ϕ(u, v))
Analisi Matematica 3 (Fisica), , M. Peloso e L. Vesely Prova scritta del 14 luglio 2009 Breve svolgimento (con alcuni conti omessi)
 Analisi Matematica 3 Fisica, 8-9, M. Peloso e L. Vesely Prova scritta del 4 luglio 9 Breve svolgimento con alcuni conti omessi. a Dimostrare che l insieme G = { x, y R : x + x + log y = ye x} coincide
Analisi Matematica 3 Fisica, 8-9, M. Peloso e L. Vesely Prova scritta del 4 luglio 9 Breve svolgimento con alcuni conti omessi. a Dimostrare che l insieme G = { x, y R : x + x + log y = ye x} coincide
Serie di Fourier. Hynek Kovarik. Analisi Matematica 2. Università di Brescia
 Serie di Fourier Hynek Kovarik Università di Brescia Analisi Matematica 2 Hynek Kovarik (Università di Brescia) Serie di Fourier Analisi Matematica 2 1 / 37 Polinomi trigonometrici Definizione Si dice
Serie di Fourier Hynek Kovarik Università di Brescia Analisi Matematica 2 Hynek Kovarik (Università di Brescia) Serie di Fourier Analisi Matematica 2 1 / 37 Polinomi trigonometrici Definizione Si dice
Campi vettoriali. 1. Sia F (x, y) = ye x i + (e x cos y) j un campo vettoriale. Determinare un potenziale per F, se esiste.
 Campi vettoriali. Sia F (x, y = ye x i + (e x cos y j un campo vettoriale. Determinare un potenziale per F, se esiste.. Sia F (x, y = xy i + x j un campo vettoriale. Determinare un potenziale per F, se
Campi vettoriali. Sia F (x, y = ye x i + (e x cos y j un campo vettoriale. Determinare un potenziale per F, se esiste.. Sia F (x, y = xy i + x j un campo vettoriale. Determinare un potenziale per F, se
Funzioni continue. Hynek Kovarik. Università di Brescia. Analisi Matematica 1
 Funzioni continue Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 1 / 44 Funzioni continue Definizione Siano f : A
Funzioni continue Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 1 / 44 Funzioni continue Definizione Siano f : A
Recupero 1 compitino di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2017/2018. Prof. M. Bramanti.
 Recupero compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 7/8. Prof. M. Bramanti Tema n 3 4 5 6 Tot. Cognome e nome in stampatello codice persona o n di matricola
Recupero compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 7/8. Prof. M. Bramanti Tema n 3 4 5 6 Tot. Cognome e nome in stampatello codice persona o n di matricola
ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009)
 ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009) 1. Sia S = { } (x, y, z) : x 2 + y 2 = 4, 0 z 3 + x. Scrivere le equazioni parametriche di una superficie regolare che abbia S come sostegno. 2. Enunciare
ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009) 1. Sia S = { } (x, y, z) : x 2 + y 2 = 4, 0 z 3 + x. Scrivere le equazioni parametriche di una superficie regolare che abbia S come sostegno. 2. Enunciare
Analisi Matematica 2. Superfici e integrali superficiali. Superfici e integrali superficiali 1 / 27
 Analisi Matematica 2 Superfici e integrali superficiali Superfici e integrali superficiali 1 / 27 Superficie Sia D un dominio connesso di R 2 (per def. un dominio connesso é la chiusura di un aperto connesso).
Analisi Matematica 2 Superfici e integrali superficiali Superfici e integrali superficiali 1 / 27 Superficie Sia D un dominio connesso di R 2 (per def. un dominio connesso é la chiusura di un aperto connesso).
Quarto appello di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano A.A. 2017/2018. Prof. M. Bramanti. y = 1+y2
 Quarto appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano A.A. 7/8. Prof. M. Bramanti Es. 3 5 6 7 Tot. Punti Cognome e nome in stampatello) codice persona o n di matricola) n d
Quarto appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano A.A. 7/8. Prof. M. Bramanti Es. 3 5 6 7 Tot. Punti Cognome e nome in stampatello) codice persona o n di matricola) n d
ESERCIZI DI ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 2006/2007
 ESERCIZI I ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 006/007 1 FUNZIONI IN UE VARIABILI (I parte) Insiemi di definizione eterminare gli insiemi di definizione delle seguenti funzioni in due
ESERCIZI I ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 006/007 1 FUNZIONI IN UE VARIABILI (I parte) Insiemi di definizione eterminare gli insiemi di definizione delle seguenti funzioni in due
Analisi Matematica 3 (Fisica) Prova scritta del 17 febbraio 2012 Un breve svolgimento delle versioni A
 Analisi Matematica 3 (Fisica) Prova scritta del 7 febbraio Un breve svolgimento delle versioni A Vi sarò grato per la segnalazione di eventuali errori. Esercizio. (a) Dimostrare che l equazione () (3 +
Analisi Matematica 3 (Fisica) Prova scritta del 7 febbraio Un breve svolgimento delle versioni A Vi sarò grato per la segnalazione di eventuali errori. Esercizio. (a) Dimostrare che l equazione () (3 +
Integrale curvilinei (o di densità) 19 Novembre 2018
 Integrale curvilinei (o di densità) 19 Novembre 2018 Indice: urve parametrizzate nello spazio. Lunghezza di una curva. Integrali curvilinei. Applicazioni geometriche e fisiche. Federico Lastaria. Analisi
Integrale curvilinei (o di densità) 19 Novembre 2018 Indice: urve parametrizzate nello spazio. Lunghezza di una curva. Integrali curvilinei. Applicazioni geometriche e fisiche. Federico Lastaria. Analisi
Funzioni di più variabli: dominio, limiti, continuità
 Funzioni di più variabli: dominio, limiti, continuità Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Funzioni di più variabli Analisi Matematica B 1 /
Funzioni di più variabli: dominio, limiti, continuità Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Funzioni di più variabli Analisi Matematica B 1 /
ANALISI VETTORIALE ESERCIZI SULLE SUPERFICI
 ANALII VETTORIALE EERCIZI ULLE UPERFICI Esercizio Calcolare l area della superficie dove Σ {(x, y, z) (x, y) E, z 2 + x 2 + y 2 } E {(x, y) x 2 + y 2 4}. Essendo la superficie Σ data come grafico di una
ANALII VETTORIALE EERCIZI ULLE UPERFICI Esercizio Calcolare l area della superficie dove Σ {(x, y, z) (x, y) E, z 2 + x 2 + y 2 } E {(x, y) x 2 + y 2 4}. Essendo la superficie Σ data come grafico di una
Analisi Matematica 2: Secondo Parziale, , Versione A. Cognome e nome:...matricola:...
 Analisi Matematica : Secondo Parziale, 1.6.17, Versione A Cognome e nome:....................................matricola:......... es.1 es. es.3 es. es.5 es.6 es.7 somma 5cr. 6 6 6 6 6 - - 3 9cr. 5 5 5 5
Analisi Matematica : Secondo Parziale, 1.6.17, Versione A Cognome e nome:....................................matricola:......... es.1 es. es.3 es. es.5 es.6 es.7 somma 5cr. 6 6 6 6 6 - - 3 9cr. 5 5 5 5
Funzioni di più variabli: dominio, limiti, continuità
 Funzioni di più variabli: dominio, limiti, continuità Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Funzioni di più variabli Analisi Matematica B 1 /
Funzioni di più variabli: dominio, limiti, continuità Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Funzioni di più variabli Analisi Matematica B 1 /
R. Capone Analisi Matematica Integrali multipli
 Integrali multipli Consideriamo, inizialmente il caso degli integrali doppi. Il concetto di integrale doppio è l estensione della definizione di integrale per una funzione reale di una variabile reale
Integrali multipli Consideriamo, inizialmente il caso degli integrali doppi. Il concetto di integrale doppio è l estensione della definizione di integrale per una funzione reale di una variabile reale
Esercizi su curve e funzioni reali di più variabili reali 1Febbraio 2010
 Esercizi su curve e funzioni reali di più variabili reali 1Febbraio 1 1.Si calcoli la lunghezza della curva di equazione g y = 1 x 1 log x x [1, e].. Sia f(x, y, ) = x + y e sia il sostegno della curva
Esercizi su curve e funzioni reali di più variabili reali 1Febbraio 1 1.Si calcoli la lunghezza della curva di equazione g y = 1 x 1 log x x [1, e].. Sia f(x, y, ) = x + y e sia il sostegno della curva
7. Integrazione delle funzioni di più variabili (II)
 7. Integraione delle funioni di più variabili (II) http://eulero.ing.unibo.it/~baroi/scam/scam-tr.7b.pdf 7.5 Area del parallelogramma costruito su due vettori. Volume del parallelepipedo costruito su tre
7. Integraione delle funioni di più variabili (II) http://eulero.ing.unibo.it/~baroi/scam/scam-tr.7b.pdf 7.5 Area del parallelogramma costruito su due vettori. Volume del parallelepipedo costruito su tre
Cognome Nome Matricola Codice ESEMPIO 1
 Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di derivata di una funzione in un punto. Sia A R N ; sia a A; sia f : A R M ; sia f differenziabile in a; allora la derivata di f in a è...
Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di derivata di una funzione in un punto. Sia A R N ; sia a A; sia f : A R M ; sia f differenziabile in a; allora la derivata di f in a è...
Corso di Laurea in Informatica Applicata Esame di Analisi Matematica Prova scritta del 10 gennaio 2007
 Corso di Laurea in Informatica Applicata Esame di Analisi Matematica Prova scritta del 0 gennaio 007 Primo esercizio. È assegnato il numero complesso z = + i. (a) Posto z = + i, determinare la forma trigonometrica
Corso di Laurea in Informatica Applicata Esame di Analisi Matematica Prova scritta del 0 gennaio 007 Primo esercizio. È assegnato il numero complesso z = + i. (a) Posto z = + i, determinare la forma trigonometrica
Prima prova in itinere di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2017/2018. Prof. M. Bramanti.
 Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 07/08. Prof. M. Bramanti Tema n 4 5 6 Tot. Cognome e nome (in stampatello) codice persona (o n
Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 07/08. Prof. M. Bramanti Tema n 4 5 6 Tot. Cognome e nome (in stampatello) codice persona (o n
Analisi Matematica 2 per Matematica Esempi di compito, secondo semestre 2012/2013
 Analisi Matematica 2 per Matematica Esempi di compito, secondo semestre 2012/2013 Primo compito. Si consideri la regione stokiana E di R 3 definita dalle disuguaglianze: { + y 2 a 2 0 z tan α)x b) dove
Analisi Matematica 2 per Matematica Esempi di compito, secondo semestre 2012/2013 Primo compito. Si consideri la regione stokiana E di R 3 definita dalle disuguaglianze: { + y 2 a 2 0 z tan α)x b) dove
Analisi Matematica 2: Scritto Generale, Cognome e nome:...matricola:...
 Analisi Matematica 2: Scritto Generale, 21.02.2017 Cognome e nome:....................................matricola:......... es.1 es.2 es.3 es.4 es.5 es.6 es.7 somma 5cr. 6 6 6 6 6 - - 30 6/9cr. 5 5 5 5 5
Analisi Matematica 2: Scritto Generale, 21.02.2017 Cognome e nome:....................................matricola:......... es.1 es.2 es.3 es.4 es.5 es.6 es.7 somma 5cr. 6 6 6 6 6 - - 30 6/9cr. 5 5 5 5 5
Analisi Matematica 2. Michele Campiti. Prove scritte di. Ingegneria Industriale a.a
 Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Il Principio di Piero della Francesca e il volume della volta a padiglione
 Il Principio di Piero della Francesca e il volume della volta a padiglione Flaviano Battelli Dipartimento di Scienze Matematiche Università Politecnica delle Marche Ancona La volta a padiglione è la regione
Il Principio di Piero della Francesca e il volume della volta a padiglione Flaviano Battelli Dipartimento di Scienze Matematiche Università Politecnica delle Marche Ancona La volta a padiglione è la regione
Prima prova in itinere di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2016/2017. Prof. M. Bramanti.
 Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 016/017. Prof. M. Bramanti 1 Tema n 1 4 5 6 Tot. Cognome e nome in stampatello) codice persona
Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 016/017. Prof. M. Bramanti 1 Tema n 1 4 5 6 Tot. Cognome e nome in stampatello) codice persona
PROVE SCRITTE DI ANALISI MATEMATICA II (V.O.), ANNO 2005
 PROVE SRITTE DI ANALISI MATEMATIA II (V.O.), ANNO 25 Prova scritta del 6/4/25 Si consideri la serie di potenze n=1 2n 2n 1 (2n + 1)!. Dopo aver determinato il suo insieme E di convergenza, si trovi una
PROVE SRITTE DI ANALISI MATEMATIA II (V.O.), ANNO 25 Prova scritta del 6/4/25 Si consideri la serie di potenze n=1 2n 2n 1 (2n + 1)!. Dopo aver determinato il suo insieme E di convergenza, si trovi una
UNIVERSITÀ DI ROMA TOR VERGATA. Analisi Matematica II per Ingegneria Prof. C. Sinestrari
 UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Esercizi 17.XI.2017 1. Verificare che le curve definite dalle seguenti parametrizzazioni sono regolari, o regolari
UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Esercizi 17.XI.2017 1. Verificare che le curve definite dalle seguenti parametrizzazioni sono regolari, o regolari
Ω : 0 z x 2 y 2 + 5, x 2 + y 2 1. Soluzione: Tenuto conto che. 1 + f 2 x + f 2 y dx dy. riesce, servendosi delle coordinate polari,
 ANALISI VETTORIALE Soluzione scritto 19 settembre 11 4.1. Esercizio. Assegnata la superficie cartesiana S : z = x y + 5, x + y 1 calcolare l area di S calcolare il volume di Tenuto conto che Ω : z x y
ANALISI VETTORIALE Soluzione scritto 19 settembre 11 4.1. Esercizio. Assegnata la superficie cartesiana S : z = x y + 5, x + y 1 calcolare l area di S calcolare il volume di Tenuto conto che Ω : z x y
CORSO DI ANALISI MATEMATICA 2 SOLUZIONI ESERCIZI PROPOSTI 15/04/2013
 CORSO DI ANALISI MATEMATICA SOLUZIONI ESERCIZI PROPOSTI 5/04/03 D.BARTOLUCCI, D.GUIDO. Integrali Impropri Esercizio. (CRITERIO DEL CONFRONTO). Dimostrare che se f : (a, b] R e g(x) : (a, b] R sono integrabili
CORSO DI ANALISI MATEMATICA SOLUZIONI ESERCIZI PROPOSTI 5/04/03 D.BARTOLUCCI, D.GUIDO. Integrali Impropri Esercizio. (CRITERIO DEL CONFRONTO). Dimostrare che se f : (a, b] R e g(x) : (a, b] R sono integrabili
1) i) Determinare il valore massimo e il valore minimo assunti dalla funzione. f (x, y) = x e x2 y 2
 1 X Cognome:... Nome:... Matricola: Università di Milano - Bicocca Corso di laurea di primo livello in Sciene statistiche ed economiche Corso di laurea di primo livello in Statistica e gestione delle informaioni
1 X Cognome:... Nome:... Matricola: Università di Milano - Bicocca Corso di laurea di primo livello in Sciene statistiche ed economiche Corso di laurea di primo livello in Statistica e gestione delle informaioni
es.1 es.2 es.3 es.4 es.5 somma Analisi Matematica 2: Primo Parziale, , Versione A Cognome e nome:...matricola:...
 es. es. es. es.4 es.5 somma 5 4 8 8 5 Analisi Matematica : Primo Parziale,.4.7, Versione A Cognome e nome:....................................matricola:.......... Calcolare la lunghezza della curva di
es. es. es. es.4 es.5 somma 5 4 8 8 5 Analisi Matematica : Primo Parziale,.4.7, Versione A Cognome e nome:....................................matricola:.......... Calcolare la lunghezza della curva di
Seconda prova in itinere di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2016/2017. Prof. M. Bramanti.
 Seconda prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 16/17. Prof. M. Bramanti 1 Tema n 1 5 6 Tot. Cognome e nome in stampatello codice persona o n
Seconda prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 16/17. Prof. M. Bramanti 1 Tema n 1 5 6 Tot. Cognome e nome in stampatello codice persona o n
Corso di laurea in Ingegneria civile - ambientale - edile Esame di Analisi matematica II Prova scritta del 29 giugno 2018
 Corso di laurea in Ingegneria civile - ambientale - edile Esame di Analisi matematica II Prova scritta del 29 giugno 28 Esercizio Si consideri la successione di funzioni {f n } n N + definita da f n (x)
Corso di laurea in Ingegneria civile - ambientale - edile Esame di Analisi matematica II Prova scritta del 29 giugno 28 Esercizio Si consideri la successione di funzioni {f n } n N + definita da f n (x)
Quarto appello di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 2016/2017. Prof. M. Bramanti.
 Quarto appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 6/. Prof. M. Bramanti Tema n 6 Tot. Cognome e nome in stampatello codice persona o n di matricola n d ordine
Quarto appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 6/. Prof. M. Bramanti Tema n 6 Tot. Cognome e nome in stampatello codice persona o n di matricola n d ordine
Esercizi sull integrazione
 ANALII MAMAICA -B (L-Z) (C.d.L. Ing. Gestionale) Università di Bologna - A.A.8-9 - Prof. G.Cupini sercizi sull integrazione (Grazie agli studenti del corso che comunicheranno eventuali errori) sercizio.
ANALII MAMAICA -B (L-Z) (C.d.L. Ing. Gestionale) Università di Bologna - A.A.8-9 - Prof. G.Cupini sercizi sull integrazione (Grazie agli studenti del corso che comunicheranno eventuali errori) sercizio.
Analisi Matematica II - Ingegneria Meccanica/Energetica - 29 Gennaio 2018
 nalisi Matematica II - Ingegneria Meccanica/Energetica - 29 Gennaio 218 1) ia data la funzione f(x, y, z) = (x 2 + y 2 1) 2 + 8 a) tudiare l esistenza di massimi e minimi assoluti della funzione f nella
nalisi Matematica II - Ingegneria Meccanica/Energetica - 29 Gennaio 218 1) ia data la funzione f(x, y, z) = (x 2 + y 2 1) 2 + 8 a) tudiare l esistenza di massimi e minimi assoluti della funzione f nella
Il sostegno di una curva C è l immagine Im C della funzione C, cioè l insieme di tutti i punti C(t), al variare di t in [a, b]: R 2
![Il sostegno di una curva C è l immagine Im C della funzione C, cioè l insieme di tutti i punti C(t), al variare di t in [a, b]: R 2 Il sostegno di una curva C è l immagine Im C della funzione C, cioè l insieme di tutti i punti C(t), al variare di t in [a, b]: R 2](/thumbs/99/141851732.jpg) urve parametrizzate Definizione Una curva parametrizzata nello spazio R 3 è una funzione [a, b] R 3 t (t) = (x(t), (t), z(t)) t [a, b] Il sostegno di una curva è l immagine Im della funzione, cioè l insieme
urve parametrizzate Definizione Una curva parametrizzata nello spazio R 3 è una funzione [a, b] R 3 t (t) = (x(t), (t), z(t)) t [a, b] Il sostegno di una curva è l immagine Im della funzione, cioè l insieme
Curve. Hynek Kovarik. Analisi Matematica 2. Università di Brescia. Hynek Kovarik (Università di Brescia) Curve Analisi Matematica 2 1 / 28
 Curve Hynek Kovarik Università di Brescia Analisi Matematica 2 Hynek Kovarik (Università di Brescia) Curve Analisi Matematica 2 1 / 28 Curve Definizione (Curva in R n ) Chiamiamo curva a valori in R n
Curve Hynek Kovarik Università di Brescia Analisi Matematica 2 Hynek Kovarik (Università di Brescia) Curve Analisi Matematica 2 1 / 28 Curve Definizione (Curva in R n ) Chiamiamo curva a valori in R n
Esprimendo il vettore (u, v) in coordinate polari (u = r cos θ, v = r sin θ), si ha. = u2 v 0 0 u 0 v
 Università di Milano - Bicocca Corso di laurea di primo livello in Scienze statistiche ed economiche Corso di laurea di primo livello in Statistica e gestione delle informazioni Matematica II rova scritta
Università di Milano - Bicocca Corso di laurea di primo livello in Scienze statistiche ed economiche Corso di laurea di primo livello in Statistica e gestione delle informazioni Matematica II rova scritta
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016
 Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Analisi Matematica II Politecnico di Milano Ingegneria Industriale
 Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #5. Sia f : R R la funzione definita da f(x, y) x + x + y + x + y (x, y) R. (a) Determinare il segno di f. (b) Calcolare
Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #5. Sia f : R R la funzione definita da f(x, y) x + x + y + x + y (x, y) R. (a) Determinare il segno di f. (b) Calcolare
ANALISI VETTORIALE COMPITO PER CASA DEL 6/12/ y x 2 + y 2 dxdy =
 ANALII VTTORIAL COMPITO PR CAA DL 6// sercizio Calcolare l integrale y x + y dxdy dove è l intersezione del cerchio del piano di centro l origine e raggio con il semipiano dato da y x. Risposta In questo
ANALII VTTORIAL COMPITO PR CAA DL 6// sercizio Calcolare l integrale y x + y dxdy dove è l intersezione del cerchio del piano di centro l origine e raggio con il semipiano dato da y x. Risposta In questo
Analisi Matematica II Corso di Ingegneria Gestionale Compito del f(x, y) = 3x 2 x 2 y + y + 1
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del --5 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo - Le risposte senza giustificazione sono considerate nulle Esercizio
Analisi Matematica II Corso di Ingegneria Gestionale Compito del --5 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo - Le risposte senza giustificazione sono considerate nulle Esercizio
Analisi Matematica 2. Curve e integrali curvilinei. Curve e integrali curvilinei 1 / 29
 Analisi Matematica 2 Curve e integrali curvilinei Curve e integrali curvilinei 1 / 29 Curve in R 2 e R 3 Intuitivamente: una curva é un insieme di punti nello spazio in cui una particella puó muoversi
Analisi Matematica 2 Curve e integrali curvilinei Curve e integrali curvilinei 1 / 29 Curve in R 2 e R 3 Intuitivamente: una curva é un insieme di punti nello spazio in cui una particella puó muoversi
Campi conservativi. Riccarda Rossi. Università di Brescia. Analisi Matematica B
 Campi conservativi Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Campi conservativi Analisi Matematica B 1 / 99 Premessa Riccarda Rossi (Università di
Campi conservativi Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Campi conservativi Analisi Matematica B 1 / 99 Premessa Riccarda Rossi (Università di
1) i) Rappresentare sia attraverso disequazioni, sia attraverso un disegno, il dominio della funzione
 Università di Milano - Bicocca Corso di laurea di primo livello in Scienze statistiche ed economiche Corso di laurea di primo livello in Statistica e gestione delle informazioni Matematica II.7.8 SOLUZIONE
Università di Milano - Bicocca Corso di laurea di primo livello in Scienze statistiche ed economiche Corso di laurea di primo livello in Statistica e gestione delle informazioni Matematica II.7.8 SOLUZIONE
I = 1 2. dtdx. (x 2 + t) 7/2 t=x 2 = 1 2 = 27/2 1. x 7 dx = 27/ b) Il segmento OP in figura. t=0. x=0
 X Università di Milano - Bicocca Corso di laurea di primo livello in Scienze statistiche ed economiche Corso di laurea di primo livello in Statistica e gestione delle informazioni Analisi Matematica II
X Università di Milano - Bicocca Corso di laurea di primo livello in Scienze statistiche ed economiche Corso di laurea di primo livello in Statistica e gestione delle informazioni Analisi Matematica II
